船舶结构力学复习题
- 格式:doc
- 大小:2.37 MB
- 文档页数:20

目录第1章绪论 (2)第2章单跨梁的弯曲理论 (2)第3章杆件的扭转理论 (16)第4章力法 (18)第5章位移法 (29)第6章能量法 (42)第7章矩阵法 (57)第9章矩形板的弯曲理论 (70)第10章杆和板的稳定性 (76)第1章绪论1.1题1)承受总纵弯曲构件:连续上甲板,船底板,甲板及船底纵骨,连续纵桁,龙骨等远离中和轴的纵向连续构件(舷侧列板等)2)承受横弯曲构件:甲板强横梁,船底肋板,肋骨3)承受局部弯曲构件:甲板板,平台甲板,船底板,纵骨等4)承受局部弯曲和总纵弯曲构件:甲板,船底板,纵骨,递纵桁,龙骨等1.2题甲板板:纵横力(总纵弯曲应力沿纵向,横向货物或上浪水压力,横向作用)舷侧外板:横向水压力等骨架限制力沿中面内底板:主要承受横向力货物重量,骨架限制力沿中面为纵向力舱壁板:主要为横向力如水,货压力也有中面力第2章单跨梁的弯曲理论2.1题设坐标原点在左跨时与在跨中时的挠曲线分别为v(x)与v(1x)1)图2.1333 2334243()()()424 ()26666l l ll l lp x p x p x M x N xv xEI EI EI EI EI---=++++原点在跨中:3230111104()4()266llp xM x N xv x vEI EI EI-=+++,'11'11()0()022(0)0(0)2l lv vpv N⎧==⎪⎨⎪==⎩2)3323()3 2.2()266llp xN xMxv x xEI EI EIθ-=+++图3)333002()2 2.3()666xx x llp xN x qx dxv x xEI EI EIθ-=++-⎰图2.2题a)33111311131(3)(2)616444641624 pp ppl plv v vEI EI⎡⎤⎡⎤=+=⨯⨯-+⨯-⨯⎢⎥⎢⎥⎣⎦⎣⎦=3512plEI333321911()61929641624pl pl plV EI EI EI⎡⎤⎛⎫=-++=⎪⎢⎥⎝⎭⎣⎦b)2'292(0)(1)3366Ml Ml PlvEI EI EI-=+++=2220.157316206327Pl Pl PlEIEI EI-+=⨯2291()(1)3366Ml Ml PllEI EI EIθ-=+-+=2220.1410716206327Pl Pl PlEIEI EI---=⨯()()()2222133311121333363l lp llv m mEIl EI⎛⎫⎛⎫⎪ ⎪⎛⎫⎝⎭⎝⎭⎡⎤=----+⎪⎣⎦⎝⎭=2372430plEIc) ()44475321927682304qlql qllvEI EI EI=-=()23233 '11116(0)962416683612l q lql pl ql ql v EIEI EI EI EI⎡⎤=--=--=⎢⎥⎣⎦d)2.1 图、2.2 图和2.3 图的弯矩图与剪力图如图2.1、图2.2和图2.3图2.1图2.2图2.3 2.3题1)()32212120624452313120Ml ql l l Mlq q EI EI EI EI q l M θ⎡⎤=---+=⎢⎥⎣⎦∴=右2)32101732418026q l Ml l l Mllq EI EI EIEIθ⎡⎤=-++-⎢⎥⎣⎦ =3311117131824360612080q l q l EI EI ⎛⎫-++-=-⎪⨯⎝⎭ 2.4 题2.5图 3000()6N x v x v x EIθ=++,()00v A p N =-300()6x v x Ap x A N EI θ⎛⎫∴=++- ⎪⎝⎭如图2.4, ()()0v l v l '==由得300200200060263l Ap l A N EI l N EI pl Ap l EI pN θθθ⎫⎛⎫++-=⎪⎪⎪⎝⎭⎬⎪+=⎪⎭⎧-==-⎪⎨⎪=⎩解出3333()1922pl x x v x EI l l ⎛⎫∴=-+ ⎪⎝⎭图2.42.6图()()()()()()()2300122300012120001221223121212260,42026622M x N x v x x EI EIv l v l M l N l EI EI M l l l EI EIEI M l N l N l EI EI x x v x x l l θθθθθθθθθθθθθθ=++'==⎫⎧=--++=⎪⎪⎪⎪⎬⎨⎪⎪=+++=⎪⎪⎩⎭++∴=++由得解得2.5题2.5图:(剪力弯矩图如2.5)()132023330222002332396522161848144069186pl Mp pR p ll p pl v AR EI EI v l Mlpl pl pl v EI EI EI EI v Ml pl pl pl v l EI EI EI EIθ-∴==-===⋅=⎛⎫=-=-= ⎪⎝⎭-'==--=-=-()16A pa b b M A l K l ⎡⎤=++⎢⎥⎣⎦, 图2.5 111,0,6632A l a l b A K ====+=将代入得:()16312pl pl M ==2.7图:(剪力弯矩图如2.6)341113422244440.052405021005112384240100572933844009600l ql ql v A R EI EI l ql ql v A R EI EIl ql ql v EI EI ql ql EI EI==⋅===⋅=⎛⎫⎛⎫=++ ⎪ ⎪⎝⎭⎝⎭⎛⎫=+=⎪⎝⎭ 图2.6()()3331233312111202424401007511117242440100300v v ql ql qlEI l EI EIv v ql ql qll EI l EI EIθθ-⎛⎫=-=-+=⎪⎝⎭--⎛⎫=--=--+= ⎪⎝⎭2.8图(剪力弯矩图如2.7)()2221401112124,,0,11,82411118243212121248243,82864AA Qa b M A K l Q qa a l b A K ql ql M ql qlql R ql v AR EIα⎡⎤⎛⎫=⋅++⎢⎥⎪⎝⎭⎢⎥⎣⎦======++==⨯⨯⨯+==-===由,代入得图2.7442433032355238412816384111(0)246246448192()6488l qlql Ml ql v EI EI EI EI v ql Ml ql EI l EI EI ql EIl ql ql l M EI EI θθα⎛⎫∴=+-=⎪⎝⎭⎛⎫=--=-- ⎪⎝⎭=-=-=-⋅=2.6题. []1max 2max 2113212132142.()()62()()62()()242(0)sN EIv s sss s N dv dx dx dx GGA N EI v dx v C GA GA EI ax bx v v v f x cx d f x ax b C GA EI EIax bx f x f x c a x d GA GA qx qx f x f x EI EIv v τγ'''====-''=−−−→-+⎡⎤''∴=+=++++-+++⎢⎥⎣⎦⎛⎫''=-+++-+ ⎪⎝⎭''==''=⎰式中由于11142323432342(0)00()()00242602,224()241222425()23848s s s s s d b v l v l ql EI ql al EI c a l EI GA EIGA qlal EIql ql c EI EIqx qlx qx qx ql v x xEI EI GA EI GA l ql ql v EI GA ===''==⎧⎛⎫-++-=⎪⎪⎪⎝⎭⎨⎪+=⎪⎩=⎛⎫∴=--++ ⎪⎝⎭∴=+可得出由得方程组:解出:a=2.7.题先推广到两端有位移,,,i i j j θθ∆∆情形:212,i j s EI GA l β⎛⎫∆=∆-∆=⎪⎝⎭令 321011322162(0)(0)()62()2sii i i j i i j s jjEIaxbxv cx d ax GA v d v v c al bl EIv l l al GA al v l bl θθθθθ=+++-=∆∴==∆⎫⎪⎬'=∴=⎪⎭⎫=∆∴+++∆-=∆⎪⎪⎬⎪'=∴+=⎪⎭而由由由()()()2213121i j j i i j a l l b l l l θθθβθθθθβ⎧∆⎡⎤=+-⎪⎣⎦+⎪⎨-⎪∆=-+-⎪+⎩解出()()()()()()()()()()()()1121(0)(0)62416642162(0)(0)1()(0)()()4261j i i j i j i j j i j iEI M EIv EIb l l EI l l l EI N EIv EIa l l N l N EI M l EIv l EI b al l l βθβθββθβθβθθββθβθβ∆⎡⎤''∴===+--+⎢⎥+⎣⎦⎡⎤=-∆-∆+++-+⎢⎥+⎣⎦⎧⎡⎤''===+-∆-∆⎪⎢⎥+⎣⎦⎪⎪=⎨⎪∆⎡⎤⎪''==+=++--⎢⎥+⎪⎣⎦⎩令上述结0i j ∆=∆=∆果中,即同书中特例 2.8题 已知:20375225, 1.8,751050kgl cm t cm s cm cm σ=⨯====1025100.7576.875kg q hs cmγ==⨯⨯=形心至球心表面1240.9 5.0419.862t y h e cm =+-=+-=形心至最外板纤维321186105.94433.5219.86t I y e cm w cm y =+=∴===()322186101449.45.940.3660.988,()0.980Iw cm y u x u u ϕ======== ()()()222212012020176.8752250.988320424.1212176.8752250.980158915)242415891510501416433.53204241050127114503204241050378433.5ql M x u kg cm ql M u kgcm M kg cm w M kg cm w M kg w ϕσσσσσσ==⨯⨯==-=-⨯⨯⨯=-=+=+==+=+==+=+=中中球头中板固端球头端(2max 21416kg cm cm σ⎫⎪⎪⎪⎪∴=⎬⎪⎪⎪⎪⎭若不计轴向力影响,则令u=0重复上述计算:222max 0176.875225241050142424433.5142414160.56%1424ql kg w cm σσσ⨯==+=+=⨯-=球头中相对误差:结论:轴向力对弯曲应力的影响可忽略不及计。

实际结构的理想化图形或计算图形:船体结构是由板和骨架等构件组成的空间复杂结构,在进行结构计算之前需要对实际的船体结构加以简化,简化后的结构图形称为实际结构的理想化图形或计算图形2.刚架:由于杆系中各杆互相刚性连接,并受到杆系平面内的载荷作用,故称这种杆系为刚架或肋股框架3.板架:在垂直于杆系平面的载荷作用下发生弯曲,这种杆系称为交叉梁系或称板架 4.梁的弯曲要素:梁的弯矩M、剪力N、横截面转角、扰度r5.梁的复杂弯曲:如果梁的抗弯刚度EI不大或轴向力很大,那么轴向力所引起的弯曲要素就不能忽略,同时考虑横向和轴向这两种载荷作用的弯曲,就称为梁的复杂弯曲6.叠加原理:复杂弯曲梁的弯曲要素可以用叠加原理求的,其叠加原理为:当梁上同时受到几个不同的横向荷重及一定的轴向力作用时,分别求出在该轴向力作用下的各个横向荷重单独作用于梁时的弯曲要素,然后进行叠加,即得到在该轴向力作用下几个不同的横向荷重同时作用于梁时的弯曲要素7.静定结构:几何不变而又没有多余联系的体系,其反力和内力只需根据静力平衡方程即可求得,所谓几何不变体系是指如果不考虑材料应变所产生的变形,体系在受到任何载荷作用后能够保持其固有的几何形状和位置的体系8.超静定结构:几何不变但却存在多余联系的体系9.超静定次数:通常将多余的联系或多余约束力的数目称为结构的超静定次数10.力法:把多余约束力作为基本未知量的计算方法称为力法11.位移法:以杆系结构节点处的位移作为基本未知量的方法12.矩阵位移法:把位移法分析杆系结构的全过程以矩阵形式来表示13.杆元:基本结构中的每一根超静定单跨梁称之为位移法的计算单元或杆元14.平面刚架杆元要考虑同时发生弯曲变形和拉压变形。
平面板架杆元要考虑其同时发生弯曲变形和扭转变形。
15、船体结构中的板架,为双向正交梁系。
并且双向梁的数目一般是不相等的。
其中数目较多的一组梁叫做主向梁,与其正交的数目较少的梁叫做交叉构件。
16、简单板架:为主向梁于交叉构件都是等截面的板架。

船舶结构⼒学复习题2014.4船舶结构⼒学复习题1、⽤初参数法求图中所⽰受均布载荷作⽤的单跨梁挠曲线⽅程,其中柔性系数为3A l48EI=。
x2、如图所⽰单跨梁的抗弯刚度为EI,跨长为l,跨中受集中⼒P的作⽤,右端弹性固定端EI l3/=α,请⽤初参数法求解图⽰单跨梁的挠曲线⽅程。
3、⽤⼒法求解图中所⽰结构在⽀座0处的转⾓和⽀座1处的⽀反⼒,已知,lll==1201,各杆的抗弯刚度均为EI,集中弯矩M2ql=,弹性⽀座的柔性系数为/3A l24EI=。
(15分)q1A2M4、采⽤位移法求图⽰结构节点2和4的转⾓。
各杆的长度及断⾯惯性矩均为l及I,已知2/2ql=M。
5、如图中所⽰结构,列出求解梁0-1-2的位移法⽅程式组。
已知,lll==1201,断⾯惯性矩均为I。
26、如图所⽰双跨梁,在3处受到⼀弯矩m ,⽤⼒法求2处弯矩2M 。
37、如图所⽰的结构,杆1-2长为l ,刚度为EI ,在右端受有集中⼒P 的作⽤。
试⽤应⼒能原理求右端在集中⼒P 作⽤下的挠度。
P8、设图⽰梁的挠曲线⽅程)(x l ax v -=,⽤李兹法求解此梁的挠曲线。
qx9、⽤矩阵法求解图中的结构,单元和节点编号如图所⽰,采⽤平⾯弯曲杆单元,试解答下列问题:(1)计算各单元的刚度矩阵;(2)写出结构总刚度矩阵;(3)写出以矩阵形式表⽰的节点平衡⽅程式;(4)对节点平衡⽅程式进⾏约束处理,写出约束处理后的⽅程式。
已知:平⾯弯曲杆单元刚度矩阵公式为[]=4 6/- 12/ 2 6/- 4 6/ 12/- 6/ 12222 对称 l l l l l l l EI K eq123,EI l,EI l10、⽤矩阵法求解图中的结构,单元和节点编号如图所⽰,采⽤平⾯弯曲杆单元,试解答下列问题:(1)计算各单元的刚度矩阵;(2)写出结构总刚度矩阵;(3)写出以矩阵形式表⽰的节点平衡⽅程式;(4)对节点平衡⽅程式进⾏约束处理,写出约束处理后的⽅程式。


船体结构力学试题答案一、选择题1. 船体结构中,最常见的骨架类型是()。
A. 纵向骨架B. 横向骨架C. 混合骨架D. 桁架结构答案:B2. 船体钢板的厚度选择主要取决于()。
A. 船体尺寸B. 船只用途C. 载荷大小D. 所有上述因素答案:D3. 船体结构设计中,以下哪项不是考虑的因素?()。
A. 船体的稳定性B. 船体的强度C. 船体的美观性D. 船体的耐腐蚀性答案:C4. 在船体结构力学中,剪力和弯矩的计算是为了确保()。
A. 船体的刚性B. 船体的强度C. 船体的稳定性D. 船体的安全性答案:B5. 船体结构中,横梁的主要作用是()。
A. 连接船首和船尾B. 支撑船体的横向结构C. 增加船体的纵向强度D. 减少船体的重量答案:B二、填空题1. 船体结构设计的基本目标是确保船体具有足够的________和________,以适应各种海洋环境和操作条件。
答案:强度、稳定性2. 在船体结构中,船底板的主要功能是提供________和________。
答案:刚性、防水性3. 船体结构的强度计算需要考虑船体在________、________和________状态下的应力分布。
答案:静水、波浪、风载4. 船体结构设计中,通常采用________方法来优化船体的重量和性能。
答案:有限元分析5. 船体结构的耐腐蚀性设计中,常用的方法是应用________和________技术。
答案:防腐涂层、阳极保护三、简答题1. 简述船体结构中的纵向骨架和横向骨架的作用。
答:纵向骨架是船体结构的主体,它沿船长方向布置,主要作用是承受船体的纵向弯曲和扭曲载荷,保持船体的形状和刚性。
横向骨架则沿船宽方向布置,包括横梁、隔板等,其主要作用是支撑船体的横向载荷,增强船体的横向强度和整体稳定性。
2. 阐述船体结构设计中载荷的分类及其影响。
答:船体结构设计中考虑的载荷通常分为静态载荷和动态载荷。
静态载荷包括船体自重、固定设备的重量、货物重量等,它们对船体结构产生持续的、稳定的应力。
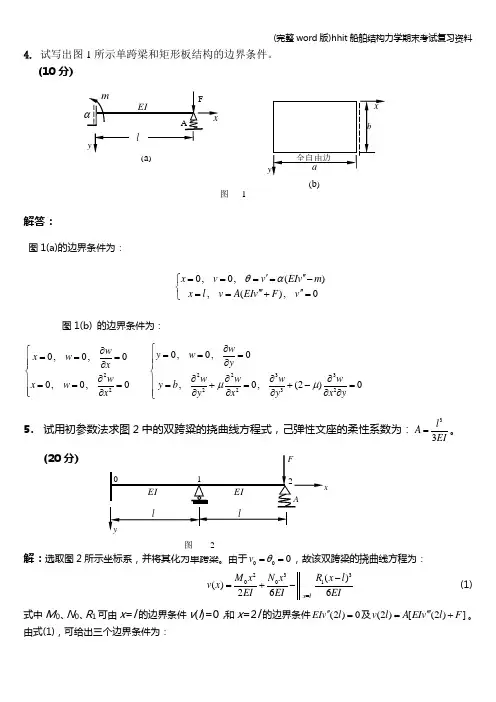
4. 试写出图1所示单跨梁和矩形板结构的边界条件。
(10分)解答:图1(a)的边界条件为:0,0,(),(),0x v v EIv m x l v A EIv F v θα'''====-⎧⎨'''''==+=⎩图1(b) 的边界条件为:22233222320,0,00,0,00,0,0,0,(2)0w w y w x w y x w w w w w x w y b x y x y x y μμ∂⎧∂⎧======⎪⎪∂⎪⎪∂⎨⎨∂∂∂∂∂⎪⎪====+=+-=⎪⎪∂∂∂∂∂∂⎩⎩5. 试用初参数法求图2中的双跨粱的挠曲线方程式,己弹性文座的柔性系数为:33l A EI =。
(20分)解:选取图200233001()()266x lM x N x R x l v x EI EIEI=-=+-(1)式中M 0、N 0、R 1可由x =l 的边界条件v (l )=0,和x =2l 的边界条件(2)0EIv l ''=及(2)[(2)]v l A EIv l F '''=+。
由式(1),可给出三个边界条件为:0000110010262042()363M N lM N l R l R l l M Nl N R F ⎫+=⎪⎪+-=⎬⎪⎪+-=-+⎭(2) 解方程组式(2),得0012610,,111111M Fl N F R F =-==将以上初参数及支反力代入式(1),得挠曲线方程式为:2335()()111133x lFl F Fv x x x x l EI EIEI==-+-- 一. (15分)用初参数法求图示梁的挠曲线方程,已知3l EI α=,36lA EI=,q 均布。
αAqEI ,L解:梁的挠曲线方程为:处的边界条件为: ;处的边界条件:故有:及有二式可解得:;于是梁的挠曲线方程为:三、(20分)用能量法求解如图所示梁的静不定性。

hhit-船舶结构力学-期末考试复习资料处的边界条件:故有:及有二式可解得:;于是梁的挠曲线方程为:三、(20分)用能量法求解如图所示梁的静不定性。
已知图中E 为常数,柔性系数,端部受集中弯矩m 作用,悬臂端的惯性矩是其余部分的2倍。
解:取挠曲线函数为 ,满足梁两端的位移边界条件,即x=0时,3/(12)A l EI LLmx=3L/2时,说明此挠曲线函数满足李兹法的要求,下面进行计算。
(1) 计算应变能。
此梁的应变能包括两部分,一是梁本身的弯曲应变能,二是弹性支座的应变能。
注意到梁是变断面的,故有总的应变能为(2)计算力函数。
此梁的力函数为(3) 计算总位能故梁的挠曲线方程为弹性支座处的挠度为四、(20)用位移法求解下图连续梁的静不定问题。
已知:, , , ,画出弯矩图。
解:设节点1、2、3的转角为,由题意可知。
根据平衡条件有节点1:节点2:其中:将其代入整理,联立求解得:P ql =1223l l l ==1223I I I ==/(6)l EI α=;故:;;;弯矩图:四、(20分)用力法求解下图连续梁的静不定问题。
已知:其中杆件EI为常数,分布力q2P/L,集中弯矩m=PL,画出弯矩图。
解: 本例的刚架为一次静不定结构,现将支座1处切开,加上未知弯矩M1,原来作用于节点1上的外力矩m可考虑在杆0-1上亦可考虑在杆1-2上,今考虑在杆1-2上。
于是得到两根单跨梁如上图所示。
变形连续条件为节点1转角连续,利用单跨梁的弯曲要素表,这个条件给出:解得:弯矩图:6、用位移法计算下面刚架结构的杆端弯矩为了书写方便,将钢架的各节点分别命名为0、1、2和3,如上面右图所示。
解:1、确定未知转角的数目本题0、1、2三个节点都可能发生转动,故有三个未知转角 。
解题时将以上三个节点作刚性固定。
2、计算各杆的固端弯矩M 01 = -qL212M 10 =qL212M 12 =M 13 =M 21 =M 31 =003、计算因转角引起的杆端弯矩M 01 =′4EI 01L θ0+2EI 01Lθ1M 10 =′4EI 01L θ1+2EI 01L θ0M 12 =′4EI 12L θ1+2EI 12L θ2M 21 =′4EI 12L θ2+2EI 12Lθ1θ0θ1θ2、、M 13 =′4EI 13Lθ1M 31 =′2EI 13θ14、对节点0、1、2列出弯矩平衡方程式对“0”节点:M 01M 01′+= -qL24EI 01θ0+2EI 01θ1+= 0= -qL28E L θ0+4E Lθ1+= 0对“1”节点:M 10M 10′+12M 12′+13M 13′+++=qL24EI 01θ1+2EI 01θ0+4EI 12L θ1+2EI 12L θ2+4EI 13L θ1+= 0=0=qL2124Eθ0++32E θ1+6E θ2= 021M21′+对“2”节点:4EI21θ2+2EI21θ1=12Eθ2+6Eθ1== 0 = 0即: -qL28Eθ0+4Eθ1+= 0qL2 124Eθ0++32ELθ1+6ELθ2= 012E L θ2+6ELθ1= 0θ1θ2θ0===11qL3864EqL3216EqL3432E-解得未知转角:5、计算各杆的杆端弯矩M01 = M10 =M01 +M01′M10M10 =′+= -qL24EI01θ0+2EI01θ1 += -qL28ELθ0+4ELθ1 += -qL28EL+4EL+11qL3864EqL3216E-( )=-0.083+0.102-0.0185=0qL2 124EI01θ1+2EI01θ0+=qL2 8Eθ1+4Eθ0 +=qL2 8E+4E+11qL3864EqL3216E-( )=0.083+0.051-0.037 =0.097qL2LM 13 =M 21M 3113M 13 =′ +M 21M 21′+4EI 21L θ2+2EI 21L θ1=12E L +6E ==M 31 =′2EI 13θ1 =M 12 =12M 12 =′ +12E + 6E qL3216E -( )qL3432E= -0.056+0.0139= - 0.042qL2qL3432E qL3216E -( )= 0qL3216E -( )= - 0.056qL2 = 6E qL3216E -( )= - 0.028qL2二、(16分)图1所示结构,已知作用在杆中点的弯矩M , 和EI ,l 用初参数法求单跨梁的挠曲线方程。
![船舶结构力学习题集答案[1]](https://uimg.taocdn.com/f9413970aaea998fcc220eea.webp)
目录第1章绪论 (2)第2章单跨梁的弯曲理论 (2)第3章杆件的扭转理论 (15)第4章力法 (17)第5章位移法 (28)第6章能量法 (41)第7章矩阵法 (56)第9章矩形板的弯曲理论 (69)第10章杆和板的稳定性 (75)第1章绪论1.1题1)承受总纵弯曲构件:连续上甲板,船底板,甲板及船底纵骨,连续纵桁,龙骨等远离中和轴的纵向连续构件(舷侧列板等)2)承受横弯曲构件:甲板强横梁,船底肋板,肋骨3)承受局部弯曲构件:甲板板,平台甲板,船底板,纵骨等4)承受局部弯曲和总纵弯曲构件:甲板,船底板,纵骨,递纵桁,龙骨等1.2题甲板板:纵横力(总纵弯曲应力沿纵向,横向货物或上浪水压力,横向作用)舷侧外板:横向水压力等骨架限制力沿中面内底板:主要承受横向力货物重量,骨架限制力沿中面为纵向力舱壁板:主要为横向力如水,货压力也有中面力第2章单跨梁的弯曲理论2.1题设坐标原点在左跨时与在跨中时的挠曲线分别为v(x)与v(1x)1)图2.1o333 2334243()()()424 ()26666l l ll l lp x p x p x M x N xv xEI EI EI EI EI---=++++o原点在跨中:3230111104()4()266llp xM x N xv x vEI EI EI-=+++o,'11'11()0()022(0)0(0)2l lv vpv N⎧==⎪⎨⎪==⎩2)3323()3 2.2()266llp xN xMxv x xEI EI EIθ-=+++o o图3)333002()2 2.3()666xx x llp xN x qx dxv x xEI EI EIθ-=++-⎰o o图2.2题a)33111311131(3)(2)616444641624 pp ppl plv v vEI EI⎡⎤⎡⎤=+=⨯⨯-+⨯-⨯⎢⎥⎢⎥⎣⎦⎣⎦=3512plEI333321911()61929641624pl pl pl V EI EI EI⎡⎤⎛⎫=-++=⎪⎢⎥⎝⎭⎣⎦b)2'292 (0)(1)3366Ml Ml PlvEI EI EI-=+++=2220.157316206327Pl Pl PlEIEI EI-+=⨯2291()(1)3366Ml Ml PllEI EI EIθ-=+-+=2220.1410716206327Pl Pl PlEIEI EI---=⨯()()()2222133311121333363l lp llv m mEIl EI⎛⎫⎛⎫⎪ ⎪⎛⎫⎝⎭⎝⎭⎡⎤=----+⎪⎣⎦⎝⎭=2372430plEIc) ()44475321927682304qlql qllvEI EI EI=-=()23233 '11116(0)962416683612l q lql pl ql ql v EI EI EI EI EI⎡⎤=--=--=⎢⎥⎣⎦d)2.1o图、2.2o图和2.3o图的弯矩图与剪力图如图2.1、图2.2和图2.3图2.1图2.2图2.32.3题1)()32212120624452313120Ml ql l l Mlq q EI EI EI EI q l M θ⎡⎤=---+=⎢⎥⎣⎦∴=Q 右2)32101732418026q l Ml l l Ml lq EI EI EIEI θ⎡⎤=-++-⎢⎥⎣⎦=3311117131824360612080q l q l EI EI⎛⎫-++-=-⎪⨯⎝⎭ 2.4 题2.5o图 3000()6N x v x v x EIθ=++Q ,()00v A p N =-300()6x v x Ap x A N EI θ⎛⎫∴=++- ⎪⎝⎭如图2.4, ()()0v l v l '==由得300200200060263l Ap l A N EI l N EI pl Ap l EI pN θθθ⎫⎛⎫++-=⎪⎪⎪⎝⎭⎬⎪+=⎪⎭⎧-==-⎪⎨⎪=⎩解出 3333()1922pl x x v x EI l l ⎛⎫∴=-+ ⎪⎝⎭图2.42.6o图()()()()()()()2300122300012120001221223121212260,42026622M x N x v x x EI EIv l v l M l N l EI EI M l l l EI EIEI M l N l N l EI EI x x v x x l l θθθθθθθθθθθθθθ=++'==⎫⎧=--++=⎪⎪⎪⎪⎬⎨⎪⎪=+++=⎪⎪⎩⎭++∴=++由得解得 2.5题2.5o图:(剪力弯矩图如2.5)()132023330222002332396522161848144069186pl Mp pR p ll p pl v AR EI EI v l Mlpl pl pl v EI EI EI EI v Ml pl pl pl v l EI EI EI EIθ-∴==-===⋅=⎛⎫=-=-=⎪⎝⎭-'==--=-=-()16A pa b b M A l K l ⎡⎤=++⎢⎥⎣⎦, 图2.5 111,0,6632A l a l b A K ====+=将代入得:()16312pl pl M ==2.7o图:(剪力弯矩图如2.6)341113422244440.052405021005112384240100572933844009600l ql ql v A R EI EI l ql ql v A R EI EIl qlql v EI EI ql ql EI EI==⋅===⋅=⎛⎫⎛⎫=++ ⎪ ⎪⎝⎭⎝⎭⎛⎫=+=⎪⎝⎭ 图2.6()()3331233312111202424401007511117242440100300v v ql ql ql EI l EI EIv v ql ql qll EI l EI EIθθ-⎛⎫=-=-+=⎪⎝⎭--⎛⎫=--=--+=⎪⎝⎭2.8o图(剪力弯矩图如2.7)()2221401112124,,0,11,82411118243212121248243,82864AA Qa b M A K l Q qa a l b A K ql ql M ql qlql R ql v AR EIα⎡⎤⎛⎫=⋅++⎢⎥⎪⎝⎭⎢⎥⎣⎦======++==⨯⨯⨯+==-===由,代入得图2.7442433032355238412816384111(0)246246448192()6488l qlql Ml ql v EI EI EI EI v ql Ml ql EI l EI EI ql EIl ql ql l M EI EI θθα⎛⎫∴=+-=⎪⎝⎭⎛⎫=--=-- ⎪⎝⎭=-=-=-⋅=2.6题. []1max 2max 2113212132142.()()62()()62()()242(0)sN EIv s sss s N dv dx dx dx GGA N EI v dx v C GA GA EI ax bx v v v f x cx d f x ax b C GA EI EIax bx f x f x c a x d GA GA qx qx f x f x EI EIv v τγ'''====-''=−−−→-+⎡⎤''∴=+=++++-+++⎢⎥⎣⎦⎛⎫''=-+++-+ ⎪⎝⎭''==''=⎰式中由于11142323432342(0)00()()00242602,224()241222425()23848s s s ssd b v l v l ql EI ql al EI c a l EI GA EIGA qlal EIql ql c EI EIqx qlx qx qx qlv x x EI EI GA EI GA l ql ql v EI GA ===''==⎧⎛⎫-++-=⎪⎪⎪⎝⎭⎨⎪+=⎪⎩=⎛⎫∴=--++⎪⎝⎭∴=+可得出由得方程组:解出:a=2.7.题先推广到两端有位移,,,i i j j θθ∆∆情形:212,i j s EI GA l β⎛⎫∆=∆-∆=⎪⎝⎭令 321011322162(0)(0)()62()2sii i i j i i j s jjEIax bx v cx d ax GA v d v v c al bl EIv l l al GA al v l bl θθθθθ=+++-=∆∴==∆⎫⎪⎬'=∴=⎪⎭⎫=∆∴+++∆-=∆⎪⎪⎬⎪'=∴+=⎪⎭Q 而由由由()()()2213121i j j i i j a l l b l l l θθθβθθθθβ⎧∆⎡⎤=+-⎪⎣⎦+⎪⎨-⎪∆=-+-⎪+⎩解出 ()()()()()()()()()()()()1121(0)(0)62416642162(0)(0)1()(0)()()4261j i i j i j i j j i j i EI M EIv EIb l l EI l l l EI N EIv EIa l l N l N EI M l EIv l EI b al l l βθβθββθβθβθθββθβθβ∆⎡⎤''∴===+--+⎢⎥+⎣⎦⎡⎤=-∆-∆+++-+⎢⎥+⎣⎦⎧⎡⎤''===+-∆-∆⎪⎢⎥+⎣⎦⎪⎪=⎨⎪∆⎡⎤⎪''==+=++--⎢⎥+⎪⎣⎦⎩令上述结0i j ∆=∆=∆果中,即同书中特例2.8题 已知:20375225, 1.8,751050kgl cm t cm s cm cm σ=⨯====1025100.7576.875kgq hs cm γ==⨯⨯=面积2cm 距参考轴cm面积距3cm惯性矩4cm自惯性矩4cm外板1.845⨯ 81 0 0 0 (21.87)略 球扁钢O N 24a38.75 9430.2 2232 ∑119.8 15.6 604.5 9430.22253.9ABC=11662224604.55.04116628610119.8BBe cm I C cm AA===-=-=275 1.838.75174min ,4555A cm l lI be s cm=⨯+=⎧⎫===⎨⎬⎩⎭计算外力时面积计算时,带板形心至球心表面1240.9 5.0419.862t y h e cm =+-=+-=形心至最外板纤维321186105.94433.5219.86t I y e cm w cm y =+=∴===()32206186101449.45.9422510501740.3662221086100.988,()0.980Iw cm y A l u EI x u u σϕ===⨯===⨯⨯== ()()()222212012020176.8752250.988320424.1212176.8752250.980158915)242415891510501416433.53204241050127114503204241050378433.5ql M x u kg cm ql M u kgcm M kg cm w M kg cm w M kg w ϕσσσσσσ==⨯⨯==-=-⨯⨯⨯=-=+=+==+=+==+=+=中中球头中板固端球头端(2max 21416kg cm cm σ⎫⎪⎪⎪⎪∴=⎬⎪⎪⎪⎪⎭若不计轴向力影响,则令u=0重复上述计算:222max 0176.875225241050142424433.5142414160.56%1424ql kg w cm σσσ⨯==+=+=⨯-=球头中相对误差:结论:轴向力对弯曲应力的影响可忽略不及计。

xy 船舶海洋结构力学复习1、请用初参数法确定图示单跨梁0-1的挠曲线方程,其中单跨梁的刚度为EI ,跨长为l ,均布载荷q 如图所示。
左端刚性固定,右端弹性支座的柔性系数EIl A 4831=。
2、请用初参数法确定图示单跨梁0-1的挠曲线方程,其中单跨梁的刚度为EI ,跨长为l ,均布载荷q 如图所示。
左右端均为刚性固定。
3、用力法计算图示结构1点的弯矩1M ,已知杆1-2及杆2-3的刚度均为EI ,l l l ==2312。
4、用力法计算图示结构2点的弯矩2M ,已知杆1-2及杆2-3的刚度均为EI ,l l l ==2312,ql P =,且P 作用于杆1-2的跨中。
qx5、请用位移法解如图所示结构,只写出正则方程即可,不必求解。
各杆的长度及刚度均为l 及EI 。
6、请用位移法解如图所示结构,只写出正则方程即可,不必求解。
各杆的长度及刚度均为l 及EI ,P 分别作用于杆1-2及2-3的跨中。
7、如图所示的结构,杆1-2长为l ,刚度为EI ,在右端受有集中力P 的作用。
试用应力能原理求右端在集中力P 作用下的挠度。
8、请用应力能原理计算图示简单钢架的端点1在外力 P 作用下的垂向位移。
已知112l l =,223l l =,各杆的刚度均为EI 。
9、设有一纵骨架式船,船底肋板间距为1.2m,纵骨间距为0.7m ,如要保证船底板的临界应力达到2/240mm N cr =σ,求所需板厚为多少?10、设有一纵骨架式船,船底纵桁为T 型材,断面尺寸为:翼板100⨯102m m ,腹板180⨯82m m 。
请分别计算纵桁翼板和腹板的临界应力cr σ。
11、四周自由支持的矩形板长边cm a 400=, 短边cm b 100=,板受垂直于板面的均布载荷2/05.0mm N q =作用,板厚cm t 8.0=,材料弹性模量为25101.2mm N E ⨯=。
(1)请写出板筒形弯曲的条件。
(2)按筒形弯曲画出本题矩形板的计算模型,并计算板中心的挠度及弯矩。

武汉理工大学船舶结构力学试卷第一部分:选择题(共10题,每题2分,共20分)1.下列哪个是船舶结构力学研究的基本内容? A. 船体质量计算 B. 船体刚度分析 C. 船体强度计算 D. 以上都是2.船舶结构的稳定性主要指的是船舶在运行过程中的稳定性。
A. 对 B.错3.船舶结构设计中,根据规范要求的材料强度进行计算的过程称为什么?A. 结构分析B. 材料选择C. 强度校核D. 强度设计4.船舶结构中的绞杆是指由多个拉杆组成的结构元件。
A. 对 B. 错5.船舶结构设计中,常用的梁模型可以分为几种? A. 2种 B. 3种 C. 4种 D. 5种6.下列哪个是船舶结构强度计算中常用的理论方法? A. 有限元法 B. 欧拉-伯努利梁理论 C. 弹性力学理论 D. 塑性力学理论7.船舶结构设计中,常用的板模型可以分为几种? A. 2种 B. 3种 C. 4种 D. 5种8.结构载荷是指作用在船舶结构上的力、力矩和温度等外部力的总和。
A. 对B. 错9.船舶结构设计中,常用的组合模型可以分为几种? A. 2种 B. 3种 C.4种 D. 5种10.船舶结构强度计算中,常用的破坏准则有哪几种? A. 链接失效准则B. 屈曲失效准则C. 疲劳失效准则D. 以上都是第二部分:简答题(共5题,每题10分,共50分)1.简述船舶结构力学的基本概念和研究对象。
船舶结构力学是研究船舶结构在受力和变形条件下的力学行为的科学。
它主要研究船舶结构的力学特性、稳定性和强度计算。
船舶结构的力学行为包括结构的刚度、稳定性和强度等方面的问题。
研究对象主要包括船体、船舱、船舱顶、甲板等船舶结构的各个部分及其相互关系。
2.简述船舶结构设计的基本流程。
船舶结构设计的基本流程包括需求分析、基础设计、安全设计、结构细节设计和校核等步骤。
首先根据客户的需求分析确定船舶的基本性能要求,然后进行基础设计,包括船体的主要尺寸和形状设计。
接下来进行安全设计,确定材料的选择和结构的强度计算。
船舶结构⼒学习题册第⼀章绪论计算⾻架断⾯惯性矩时的表格算法断⾯形式构件名称构件⾯积a (cm 2)构件形⼼距参考轴距离(cm ) ay ay 2构件对其形⼼的惯性矩i (cm 4)带板腹板⾯板 … … … … … … … … … … … … / … /ABC⽔平构件对其形⼼的惯性矩可以不计。
断⾯中和轴离参考轴距离ε=B/A(cm)断⾯对中和轴的惯性矩 I=C-εB(cm 4)最⼩断⾯模数 W min =I/y*max (cm 3)第⼆章单跨梁的弯曲理论⼀.初参数法1.⽤初参数法求两端⾃由⽀持在刚性⽀座上,受均布载荷的梁的挠曲线。
2.⽤初参数法图2所⽰受集中⼒作⽤的单跨梁的挠曲线⽅程式。
梁的左端为弹性固定,柔性系数为α=l/(3EI)。
梁的右端为弹性⽀座,柔性系数为A=l3/(48EI)。
3.两端刚性固定的梁,不受外荷重,当其右⽀座发⽣位移△时,求其挠曲线与断⾯弯矩与剪⼒。
4⽤初参数法求图中单跨梁的挠曲线⽅程式。
5. 图中的双跨梁,试⽤初参数法解之,求出挠曲线⽅程式,设弹性⽀座的柔性系数为A=l3/(3EI)。
6.考虑剪切影响,试导出图中梁的挠曲线⽅程式及两端的弯矩及剪⼒,并将结果推⼴到梁左端与右端分别有位移△i,θi及△j,θj 时的情况。
梁的长度为l,断⾯惯性矩为I,有效抗剪⾯积为A s。
7. 如图所⽰变断⾯梁,⽤初参数法解之。
图中P=q l,求出挠曲线⽅程式及P⼒作⽤点处的挠度和转⾓。
8.⽤初参数法求图所⽰单跨梁的挠曲线⽅程式,转⾓⽅程式,弯矩⽅程式,剪⼒⽅程式。
推导中可令a=αEI/l (1)求出当α→∞时梁两瑞的转⾓,进⾏分析讨论。
(2)求出当α→0时梁左端的转⾓、弯矩及梁右端的转⾓,进⾏分析讨论。
a⼆.利⽤弯曲要素表进⾏计算1.利⽤弯曲要素表进⾏计算(1)计算图a中两端刚性固定梁的弯曲要素/(3EI)(2)求图b所⽰悬臂梁⾃由端点的挠度和转⾓。
α=l(3)求图c所⽰梁的左端弯矩和右端⽀反⼒。
船舶结构力学习题及答案船舶结构力学习题及答案船舶结构力学是船舶工程中的重要学科,它研究船舶结构在不同载荷作用下的力学特性。
在船舶设计和维修中,船舶结构力学的知识是必不可少的。
下面将介绍几个船舶结构力学的学习题及答案,帮助读者更好地理解和掌握这一学科。
1. 问题:什么是船舶结构的静力学特性?答案:船舶结构的静力学特性是指结构在静力平衡状态下的性能,包括刚度、强度和稳定性等。
刚度是指结构对外力的抵抗能力,强度是指结构承受外力时不发生破坏的能力,稳定性是指结构在受到外力作用时不发生失稳的能力。
2. 问题:船舶结构的刚度和强度有何区别?答案:船舶结构的刚度和强度是两个不同的概念。
刚度是指结构在受到外力作用时变形的抵抗能力,通常用刚度系数来表示。
强度是指结构在受到外力作用时不发生破坏的能力,通常用强度参数来表示。
刚度和强度是船舶结构力学中两个重要的性能指标,设计和维修船舶结构时需要考虑它们的平衡。
3. 问题:什么是船舶结构的疲劳强度?答案:船舶结构的疲劳强度是指结构在长期循环载荷作用下不发生破坏的能力。
船舶在航行中会受到多种载荷的作用,如波浪载荷、船舶自重和货物重量等。
这些载荷的反复作用会导致结构的疲劳破坏,因此需要对船舶结构进行疲劳强度分析和设计。
4. 问题:船舶结构的稳定性有哪些因素影响?答案:船舶结构的稳定性受到多种因素的影响。
其中最重要的因素是船舶的重心和浮心位置。
当船舶的重心和浮心位置不在同一垂直线上时,会产生偏倾力矩,导致船舶发生倾覆。
此外,船舶的形状、船体的稳定性曲线和外部环境等因素也会对船舶结构的稳定性产生影响。
5. 问题:如何计算船舶结构的荷载?答案:计算船舶结构的荷载需要考虑多个因素,包括船舶自重、货物重量、燃油重量、波浪载荷等。
其中,船舶自重可以通过船舶的设计参数和结构重量来计算;货物重量可以通过货物的数量和单位重量来计算;燃油重量可以通过燃油的密度和船舶的燃油消耗量来计算;波浪载荷可以通过波浪的特性和船舶的运行状态来计算。
1、海工遇见的环境条件。
(1)波浪(包括引起砰击和变化的浮力效应)(2)风(特别是作用在细长杆的湍风流)(3)海流(对波浪产生的力,或诱导的湍流有作用时)(4)以及由作业的机械设备引起的机械振动等。
2、疲劳破坏阶段及每个阶段特点材料发生疲劳破坏要经历三个阶段,即裂纹起始或萌生、裂纹稳定扩展和裂纹失稳扩展(断裂)。
裂纹起始或萌生:(1)在交变载荷下,金属零件表面产生不均匀滑移、金属内的非金属夹杂物和应力集中等均可能是产生疲劳裂纹核心的策源地。
(2)滑移带随着疲劳的进行逐步加宽加深,在表面出现挤出带和挤入槽,这种挤入槽就是疲劳裂纹策源地。
(3)另外金属的晶界及非金属夹杂物等处以及零件应力集中的部位(台阶、尖角、键槽等)均会产生不均匀滑移,最后也形成疲劳裂纹核心。
疲劳裂纹的扩展:(1)在交变应力的作用下,裂纹从金属材料的表面上的滑移带、挤入槽或非金属夹杂物等处开始,沿着最大切应力方向(和主应力方向成45°角)的晶面向内扩展。
扩展速度慢,如没有应力集中,直接进入第二阶段。
(2)改变方向,沿着与正应力相垂直的方向扩展,扩展途径穿晶并速度很快3、疲劳破坏断面特征和疲劳破坏的特征疲劳断口的宏观特征:(1)有裂纹源、疲劳裂纹扩展区和最后断裂区三个部分;(2)裂纹扩展区断面较光滑、平整,通常可见“海滩条带”,有腐蚀痕迹;(3)裂纹源通常在高应力区或材料缺陷处;(4)与静载荷相比,即使是延性材料,也没有明显的塑性变形;(5)工程实际上的表面裂纹,一般呈半椭圆形。
疲劳断口的微观特征:利用高倍电子显微镜可以观察到三种不同的疲劳裂纹扩展微观破坏形式,即微解理型、条纹型和微孔聚合型。
疲劳条纹的形成与载荷循环有关,由条纹间距可以估计裂纹扩展速率。
微解理型对应于比较低的裂纹扩展速率(10-5-10-7mm/c);条纹型对应的裂纹扩展速率(10-6-10-3mm/c);微孔聚合型对应于较高的裂纹扩展速率(10-4-10-1mm/c)。
武汉理工大学考试试题纸( A 卷)课程名称: 船舶结构力学 专业班级:一、(30分)简答题1. 船体结构中分别列出承受总纵弯曲、横向和局部弯曲、既受总纵弯曲又受横向弯曲构件的名称(5)答:1)承受总纵弯曲构件:连续上甲板,船底板,甲板及船底纵骨,连续纵桁,龙骨等远离中和轴的纵向连续构件(舷侧列板等)。
2)承受横向弯曲构件:甲板强横梁,船底肋板,肋骨。
3)承受局部弯曲构件:甲板板,平台甲板,船底板,纵骨等。
4)承受横向弯曲和总纵弯曲构件:甲板,船底板等。
2. 给出单跨梁弯曲时,弯曲要素M 、N 、v 之间的关系式,刚性固定在刚性支座 上和弹性支座的边界条件表达式。
(5)答:(1) , ,(2)a 、刚性固定在刚性支座:梁在刚性固定端处挠度与转角均为零而弯矩、剪力不等于零,其边界条件为:b 、弹性支座:式中: A —弹性支座的柔性系数,K —刚性系数。
左端断面:右端断面:自由支持: 刚性固定:3. 哪些因数对单跨杆稳定性有影响,是怎样影响的?柱子曲线有什么用途?简单估算一等截面双跨梁的欧拉力,两跨的长度分别为1L ,2L 。
(10)答: (1) 单跨杆的欧拉力一般表达式:影响因素:杆的长度L,长度越长,杆越不稳定,反之亦然;杆的截面惯性矩I,截面惯性矩越大杆越稳定,反之亦然;材料的弹性模数E,杆的弹性模数越大越稳定;杆的相当长度系数,杆的长度与断面均相同的条件下,两端固定程度越大,欧拉力越大,杆越稳定。
(2) 柱子曲线用途:柱子曲线的用途:当杆件的柔度λ已知时,通过查不同材料的柱子曲线图可得其失稳应力,从而解决压杆的非弹性稳定性问题。
(3) 等截面双跨梁的欧拉力求解:支座1断面的转角连续方程式写作:由于M≠0,故又因为故得:其中最小的一个根所对应的轴向力就是所需的欧拉力,用图解法求解。
若则有 ,得此双跨压杆的欧拉力为:若 ,同样用图解法可得的最小一个根为:得等跨度压杆的欧拉力为:当时,欧拉力在以下范围之内:4.简述薄板筒形弯曲的条件和求解方法。
船舶结构力学复习题船舶结构力学复习习题第一章绪论思考题:1.什么叫做船体总纵弯曲?船体的总纵强度与局部强度有什么区别与联系?2.一个完整的船体结构计算图形应包含哪些具体内容?为什么对同一船体结构其计算图形不是固定的、一成不变的3.船舶在航行时为什么会发生扭转现象?船体结构中还有哪些构件在受载后会发生扭转。
4.连续梁、桁架、刚架、板架的区别与联系。
第二章单跨梁的弯曲理论主要内容及解题要点1.本章叙述等断面单跨粱(包括普通梁、复杂弯曲梁及弹性基础梁)的弯曲理论,要求在己知梁的尺度、材料、荷重及边界条件下能够求出梁的弯曲要好——梁的挠度、转角、弯矩及剪力,从而可计算出梁的应力与变形。
求解单跨梁弯曲的基本方法是弯曲微分方程式的积分法,即初参数法,实用方法是利用己知的梁的弯曲要素表和叠加法。
1.粱弯曲微分方程式是根据什么基本假定导出的,有什么物理意义,适用范围怎样。
2.单跨梁初参数法中的四个参数指什么参数?它们与坐标系统的选择有没有关系?3.为什么当单跨梁两端为自由支持与单跨梁两路为弹性支座支持时,在同样外荷重作用下两梁断面的弯矩和剪力都相等;而当梁两端是刚性因定与梁两端为弹性固定时,在同样外荷重作用下两梁断面的弯矩和剪力都不同?4.梁的边界条件与梁本身的计算长度、剖面几何要素、跨间荷重有没有关系?为什么?5.叠加法的适用条件。
5.当梁的边界点上作用有集中外力P或集中外弯矩M时,一种处理是把该外力放在梁端,写进边界条件中去。
另一种处理是把该项外力放在梁上,不写进边界条件。
在求解梁的弯曲要素时,两种处理方法的具体过程有哪些不同?最后结果有没有差别?6.粱的弹性支座与弹性固定端各有什么特点?它们与梁本身所受的外荷重(包括大小、方向及分布范围)有没有关系?有哪些分类?第三章力法主要内容及解题要点:1.本章叙述用力法分析杆系结构的原理及其在舱体结构中的应用。
研究的对象为船体结构中的连续梁、不可动节点简单刚架及板架。
此外还着重讨论了船体结构中弹性支座与弹性固定端的形成及其柔性系数的计算问题。
2.本章所述的力法以单跨梁建立的弯曲要素表和叠加原理为基础,通过以结构中某些特殊节点(如支座处、断面变化处、相交节点处)的节点力(或力矩)为基本未知量,以这些节点处的变形连续条件建立方程式,解出未知力,从而将复杂的杆系结构化为一根根在节点处相联系的单跨梁。
因此力法在具体计算时对象仍为单跨粱。
3。
对于在刚性支座上的连续梁及不可动节点简单刚架可以将结构在支座或节点处拆为一段段两端自由支持的单跨梁加上未知弯矩,然后用转角连续条件求解。
因此有几个未知弯矩必有几个相应的转角连续方程式即三弯矩方程式。
对于在弹性文座上的连续粱,还需在每一个弹性支座处列补充方程式,最后所得的转角连续方程式即为五弯矩方程式。
4.在板架(交叉梁系)计算中,将主向梁与交叉构件在节点处分开代以节点力,再用主向梁与交叉构件相交节点挠度相等的条件求解。
对于船体板架,一般认为外荷重全部由主向粱承受。
一根交叉构件与许多根同样主向梁组成的板架的解法是综合力法与弹性支座概念而形成的计算方法。
计算时交叉构件化为弹性基础梁,弹性基础梁的荷重及弹性基础刚度与主向梁上的荷重形式、主向梁边界情况有关。
求解弹性基础梁,即可通过其挠度(板架的节点挠度)求出节点力。
5,在连续粱与平面刚架结构中,如果与所研究的受载杆件有不受外载荷的杆或杆系与之相连,则总可以将不受载的杆及杆系化为受载杆的弹性固定端。
方法是,(1)将受载杆与其相连的不受载杆或杆系在连接支座处分开,加上弯矩M,此弯矩亦可令其为l。
(2)计算不受栽扦在M作用断面处的转角a,a必然与M同方向,a与M的比值就是所需的受载杆弹性固定端的柔性系数。
在板架或一般的交叉粱系结构中,原则上说不受载杆对受载杆的支持可化为弹性支座,只要对不受载杆能写出在与受载杆相交节点处节点力R与挠度v之间的正比关系。
弹性支座的柔性系数立=R/v,计算方法与步骤与上述弹性固定端的计算相同。
思考题:1.力法的概念,如何建立力法方程式。
2.什么是力法的基本结构和基本未知量;基本结构与原结构有什么异同;力法正则方程式的物理意义是什么。
3.刚架与板架的受力特征和变形特征有何区别?4.力法可否用来计算不可动节点的复杂刚架?如可以,应如何做?5.用力法计算某些支座有一定已知位移的连续梁或平面刚架时应注意什么问题?6.在杆系结构中,可以把其中的一些杆件化为其他杆件的弹性文座或弹性固定端,其简化的条件怎样?步骤加怀在简化时经常会用到哪几种类型公式?第四章矩阵位移法一、位移法主要内容及解题要点1.本章讲述用位移法分析杆系结构的原理及在船体结构中的应用。
研究的主要对象为船体结构中的不可动节点复杂刚架,可动节点简单刚架及简单板架等,最后还介绍了弯矩分配法的原理及计算步骡。
【注意】由于位移法中所采用的杆端弯曲要素的符号法则与第二章单跨梁及第四章力法中不完全相同,因此首先要明确位移法中新的符号规定,杆件两端的弯短与转角一律以顿时针方向为正;杆端的剪力与挠度要根据杆件的局部坐标来定,故两个端点处的剪力与挠度的正向相同。
2.位移法解杆系问题时是将各组成杆件视为两端刚性固定的单跨梁,然后强迫可以发生位移的支座或节点断面产生协调一致的变形,并要满足支座或节点处力的平衡条件。
因此位移法的几何协调条件自行满足,联系位移与力的关系的物理条件是刚度系数,建立方程式组的条件是力的平衡条件,基本未知数是位移。
本章的位移法还是第七章矩阵法的基础。
3.用位移法求解不可动节点复杂刚架是角变形法。
计算时首先分析结构中有几个文座或节点可以发生转角,并把这些转角作为基本未知数,再在这些文座或节点处列出汇交杆件的弯矩平衡方程式。
这样,—有几个未知转角就有几个相应的弯矩平衡方程式,即可联立求出转角。
最后通过转角计算杆端的弯矩及势力。
在进行上述计算比要注意到,1)法中之杆端弯矩为固端弯短与杆端发生转角的弯矩之和,2)固端弯矩可从两端刚性固定的单跨梁的弯曲要素表查到,但注意表中弯矩的符号规定与位移法不同。
3)在建立支座或节点的弯矩平衡方程式时,果该节点上有外加弯矩(即点集中力),方程中应予计入。
4.用位移法解可动节点简单刚架及板架时,先分析结构中有几个节点或支座将发生转角及线位移(挠度),并把它们作为未知量。
然后对每一个发生转角的节点或支座处列弯矩平衡方程式,对每一个发生线位移的节点或支座处列剪力平衡方程式,因此未知数的数日与方程式的数目相同,问题可以解决。
在建立节点或支座的弯矩及剪力平衡方程亦需计入该处的外加弯矩与集中力。
如果节点或支座还有弹性支座(柔性系数为人)及弹性固定端(柔性系数为。
l),则在建立剪力及弯矩平衡方程时亦应分别计入。
思考题1.与力法相比,位移法有何优点与缺点?二、矩阵位移法主要内容及解题要点1.矩阵法又称矩阵位移法或直接刚度法。
它的原理与符号规定均与第五章位移法相同,只是表达形式更规格化以便编制程序在计算机上实施运算。
矩阵法可用来求解一切杆系结构,本章讨论的对象为招架、连接梁、刚架及板架等。
2.用矩阵法分析杆系结构的步骤为,(1)将结构离散为杆元及节点,建立杆元坐标系与结构整体坐标系;(2)建立杆元坐标系中之杆元刚度矩阵[Kle;(3)坐标转换得结构坐标系中杆元刚度矩阵[K],并将它写成分割子矩阵的形式;(4)用对号入座的方法建立结构在结构坐标系中的总刚度矩;(5)计算节点的外载荷矩阵[P],并建立整个结构全部节点的平衡方程式;(6)将平衡方程式进行约束处理后求解,得节点位移;(7)将节点位移转换到局部坐标系中,再利用刚度矩阵[k]计算各杆元的杆瑞力并进一步求出杆元的内力及变形。
3.矩阵法的关键是建立各类杆元的刚度矩阵。
根据结构形式及杆元的节点位移(自由度数),平面衍架、刚架及板架的刚度矩阵。
思考题:1. 和位移法相比矩阵法在解题过程中有什么特点?2.何渭节点自由度、杆元的杆端力及节点外裁荷?3 何谓单元刚度矩阵?它们的阶数是由什么决定的?4.由单元刚度矩阵组成结构刚度矩阵的物理意义是什么?当组集总刚度矩眸时可遵循的规律是什么?5.矩阵法中为什么要进行约束处理?6.根据什么原则划分杆系结构中的节点、杆单元及确定节点编号?7.如何理解“固端力之负值即为等效节点力”这句话?如何对总刚写出相应的外力列阵。
为什么用矩阵法算出的杆端力还耍迭加上固端力?为什么在画弯矩图时还耍迭加上杆间外荷重产生的弯矩?8.怎样理解“节点位移和端点力一一对应”?为什么矩阵法中节点位移和端点力的排列次序一经确定就不要改变了?为什么要建立结构坐标系和杆元局部坐标系两套坐标系统?9.总刚度方程是什么性质的方程?在求出节点位移后,如何求未知的支座反力?10.矩阵法中对“结构对称,载荷对称”的结构如何处理?对位于对称面上的结构件及弹性支座应如何处理?对计算结果又应如何处理7第五章能量原理思考题1.一粱上同时受到两个集中力时应变能可否分别计算每一力作用时的应变能再相加,为什么?2一杆系结构承受拉(压)、弯曲、剪切与扭转四种载荷时,应变能可否分别计算每一种裁荷作用时的应变能再相加,为什么?3.什么是体系总位能、力函数。
4.试说明虚位移原理与虚力原理两者的区别。
5.‘虚位移医理代表了结构体系的静力边界条件和内部协调条件”此论断正确吗? 、6.“虚力原理代表了结构体系的位移边界条件及内部协调条件”此论断正确吗?7.什么是应变能?何谓余能,有何区别?第七章薄板的弯曲理论I 主要内容及解题要点1.本章研究船体结构中矩形薄平板的弯曲问题。
要求在结定板的尺度、材料、边界条件及外荷至时能求出板的应力与变形。
所用的方法有微分方程式的积分法、能量法及有限元法。
作用于船体平板的荷重有两类,一是垂直于板平而的荷重(横荷重),二是作用于板中面的荷重(中面荷重)。
由于薄板的弯曲刚度很小所以当板弯曲时因四周支座的约束作用也会产生中面拉力,这一特点应予以注意。
如果板上只受横荷重而无中面荷重或中面荷重很小面可以不计,则此种板称为刚性板。
如果板上有横荷重又有中面荷重(外加的或因板弯曲引起的中面拉力),则板处于复杂弯曲状况此种板称为柔性板。
2。
筒形弯曲是矩形板弯曲的一个特例。
板发生筒形弯曲的条件是:板的边长比大于2.5,板的的荷重沿长边不变化,此时可在板的中部沿短边取出单位宽度的板条梁来研究,因此板的简形弯曲问题实质上是梁的弯曲问题。
在具体计算时,用板的筒形刚度代替普通梁的弯曲刚度,则梁的弯曲微分方程式及弯曲要素表的结果均可用于筒形弯曲中的板条梁。
据此:。
(1)对于刚性板的横弯曲,可直接利用梁的弯曲要素表计算;(2)对于柔性板的复杂弯曲,即板上有横荷重及外加中面力可直接利用梁复杂弯曲的弯曲要索表计算; (3)当板有横荷重并且挠度较大而产生有中面拉力,先用附录附图3—a、3—b根据参数U求出中面力的大小,再用梁复杂弯曲要素表求解。