对数函数导学案 (2)
- 格式:doc
- 大小:325.00 KB
- 文档页数:12

2.2.1对数与对数运算(一)一【学习目标】 (一) 教学知识点1.对数的概念;2.对数式与指数式的互化. (二) 能力训练要求1.理解对数的概念;2.能够进行对数式与指数式的互化;3.培养学生数学应用意识. 二、教学重点:对数的定义. 三、教学难点:对数概念的理解. 四【新课讲授】(导学)假设2002年我国国民生产总值为a 亿元,如果每年平均增长8%,那么经过多少年国民生产总值是2002年的2倍?列出表达式: (自学)知识点1 : 对数的概念1.对数定义:一般地,如果 ,)1,0(≠>a a 且则数 b 叫做以a 为底 N 的对数, 记作 ,其中a 称为对数的底,N 称为真数. (b N N a a b =⇔=log )(1)底数的取值范围 ;真数的取值范围(2)对数式和指数式关系式 子名称 a b N指数式 对数式思考1.将下列指数式写成对数式: (1)62554= (2)64126=- (3)273=a(4)73.531=m )(知识点2 两种重要对数1.常用对数:以10为底的对数叫做常用对数N 10log 简记作 . 思考2:5log 10简记作; 5.3log 10简记作2.自然对数:用以无理数e=2.71828……为底的对数叫自然对数, N e log 简记作思考3:3log e 简记作 10log e 简记作 思考4. 将下列对数式写成指数式:(1)416log 21-=; (2)7128log 2=; (3)201.0lg -=; (4)303.210ln =.知识点三 : 重要公式:⑴负数与零没有对数; ⑵01log =a , 1log =a a ⑶对数恒等式N aNa =log五【典例欣赏】(互学) 1对数概念应用例1.求下列各式中x 的取值范围:(1)log 2(x -10);(2)log (x -1)(x +2);(3)log (x +1)(x -1)2.2对数基本运算例2求下列各式中的x 的值:(1)32log 64-=x ;(2)68log =x ;(3)x =100lg ;(4)x e =-2ln 。

§2.2.2对数函数及其性质导学案援疆教师 李远敬一、学习目标1.知识技能:①理解对数函数的概念,熟悉对数函数的图象与性质.②掌握对数函数的性质.2.过程与方法:引导学生结合图象,探索研究对数函数的性质.3.情感、态度与价值观.培养学生数形结合的思想以及分析推理的能力;培养学生严谨的科学态度.二、学习重点和难点重点:1.对数函数的定义、图象、性质. 2.对数函数的性质的初步应用. 难点:对数函数的图像和性质的探究.三、自主学习1.对数函数的定义函数 ,叫做对数函数.2.对数函数x y a log = (0>a ,且1≠a )的图象研究函数x y 2log =和x y 21log =的图象;①列表②描点③连线3.对数函数x y a log = (0>a ,且1≠a )的图象和性质四、合作探究题型1.求下列函数的定义域:(1)2log x y a = (2))4(log x y a -= (学生板书)题型2.函数的图象过定点(1)x y a log 1+= (2)3)4(log +-=x y a题型3.比较下列各组数中两个值的大小:(1)4.3log 2, 5.8log 2 (2)8.1log 3.0,7.2log 3.0(学生板书) (3)1.5log a , 9.5log a (教师板书)五、分组讨论两对数的底数相同时,如何比较大小? 两底数不同的对数,如何比较大小?六、.自主测评(1)7log 6,6log 7 (2)3log π,8.0lo 2g七、合作总结八、课后作业教材87页A 组第7,10题。
九、学习反思。

《对数函数图像及其性质》导学案对数函数图像及其性质导学案1. 引言本导学案旨在介绍对数函数的图像及其性质。
对数函数是数学中一种重要的函数类型,具有广泛的应用领域。
通过研究对数函数的图像和性质,我们可以更好地理解和应用对数函数。
2. 对数函数的定义对数函数是指以某个正数为底的对数函数,一般表示为 $y = \log_{a}x$,其中 $a>0$ 且 $a \neq 1$。
对数函数的定义域为正实数集合 $x>0$,值域为实数集合。
3. 对数函数的图像对数函数的图像在直角坐标系中呈现一条曲线,具体的图像形状和走势与底数 $a$ 的大小有关。
下面以底数 $a=2$ 和底数$a=\frac{1}{2}$ 为例进行说明。
3.1 底数为2的对数函数图像当底数 $a=2$ 时,对数函数 $y = \log_{2}x$ 的图像如下所示:.png)3.2 底数为1/2的对数函数图像当底数 $a=\frac{1}{2}$ 时,对数函数 $y =\log_{\frac{1}{2}}x$ 的图像如下所示:.png)4. 对数函数的性质对数函数具有以下几个重要的性质:- 对于任意正实数 $x_1$ 和 $x_2$,以及任意实数 $k$,都有$\log_{a}(x_1 \cdot x_2) = \log_{a}x_1 + \log_{a}x_2$ 和$\log_{a}(x_1^k) = k \cdot \log_{a}x_1$。
- 对于任意正实数 $x$ 和 $a > 1$,有 $\lim_{x \to +\infty}\log_{a}x = +\infty$。
换言之,当自变量 $x$ 趋向正无穷时,对数函数的取值趋向正无穷。
- 对于任意正实数 $x$,有 $\lim_{x \to 0^{+}} \log_{a}x = -\infty$。



《2.2对数函数》导学案2学习目标1.能从对数与指数的关系中理解对数的概念2.掌握对数式与指数式的相互转化3.能从指数与对数的关系及指数运算性质推出对数的运算性质4.能证明换底公式并会运用学习过程自主探究(预习教材P 62~ P 67,找出疑惑之处)1.对数定义:如果x a N =(0,1)a a >≠,那么数x 叫做 ,记作 .N 的范围为 (思考:对数是怎么来的?)(1)常用对数:通常我们将以____为底的对数叫做常用对数,并把N 10log 记为_____.(2)自然对数:在科学技术中常使用以无理数e =2.71828…为底数的对数,以_____为底的对数称为自然对数,并把N e log 记为_____.2.对数式与指数式的关系:当a >0,且a ≠1时,N a x =⇔x =_______(思考:指数式和对数式中的各字母的名称相同吗?分别叫什么?)试一试:(成才之路P54,拓展变式1)下列指数式化为对数式,对数式化为指数式.(目标一、二)(1)35125= (2)712128-=(3)327a = (4)12log 325=-(5)lg0.001=3- (6)ln100=4.606.3.对数的基本性质(1)____和______没有对数.(2)log 1a =___)10(≠>a a 且.(3)log a a =___)10(≠>a a 且.4.对数的运算性质:如果,0,0,1,0>>≠>N M a a 则(1)log ()a MN = ;(如何推广?)(2)log a M N= ; (3) log n a M = .(4)换底公式log a b = .(5)三个结论:log log m n a a n b b m=; 1log log a b b a = ; x x =a log a 试一试:1. 下列等式成立的是( )A .222log (35)log 3log 5÷=-B .222log (10)2log (10)-=-C .222log (35)log 3log 5+=gD .3322log (5)log 5-=- 2.计算:(1)lg 243lg9. (2)1log -59log +41log +)3(log 350.252213 3. 若 log 7[log 3(log 2x )]=0,则12x =( ).A. 3B.C.D.4. 25()a -(a ≠0)化简得结果是( ) (思考:怎样从指数与对数的关系利用指数的运算性质证明对数运算性质呢?)交流探究典型例题例1求下列各式中x 的值:(目标一、二)(1)642log 3x =; (2)log 86x =-; (3)lg 4x =; (4)3ln e x =.变式:求下列各式种的x :(1);0)(log log 23=x (2) 1)lg(ln =x ; (3)0)](log [log log 258=x ;例2用log a x , log a y , log a z 表示下列各式:(目标三)(1)2log a xy z ; (2)log a .变式1:已知lg2=0.3010,lg3=0.4771,求lg6、lg12.、.变式2:lg5×lg20+(lg2)2=________.例3计算1log 321+1log 721=________.变式1 :计算log 2125·log 318·log 519.例4:2.已知log 189=a,18b =5,用a 、b 表示log 3645.变式1:已知35a b m ==,且112a b+=,则m 之值为( ). 归纳方法1.对数概念;2.lg N 与ln N ;3.对数运算性质及推导;4.指对互化;②运用对数运算性质;5.换底公式.知识拓展① 对数的换底公式log log log b a b N N a =;②对数的倒数公式1log log a b b a=. ③ 对数恒等式:log log n n a a N N =,log log m n a a n N N m = 自主测评1计算:1(3+= .2.log += ( ).A. 1B. -1C. 2D. -23. 对数式2log (5)a a b --=中,实数a 的取值范围是( ).A .(,5)-∞B .(2,5)C . (2,)+∞D . (2,3)(3,5)U4.若log 1)1x =-,则x =________,若y =,则y =___________.5.若log 34·log 48·log 8m =log 42,求m 的值.6.若3a =2,则log 38-2log 36用a 表示为7. 如果lgx=lga+3lgb -5lgc ,那么( ).A .x =a +3b -cB .35ab x c= C .35ab x c= D .x =a +b 3-c 3 8. 若()2lg 2lg lg y x x y -=+,那么( ).A .y x =B .2y x =C .3y x =D .4y x =作业必做题:1.计算(1)99log 3log 27+= (2)15lg 23= . (3)7lg142lg lg7lg183-+-; (4)lg25+23lg8+lg5·lg20+(lg2)2.(5)2lg2+lg31+12lg0.36+13lg8.选做题:已知ab =M (a >0,b >0,M ≠1),log M b =x ,求log M a 的值.。

2.1对数函数导学案(二)
学习重点:1、对数与对数的运算;2、对数函数及其基本性质;
学习难点:对数的运算;对数函数的图像应用;
高考考点:利用对数函数的性质解题或挖掘题目中的隐藏条件。
一、知识清单:
(一)对数函数及其性质:
1、对数函数的定义:
函数叫做对数函数,定义域是值域是
思考:函数与函数的定义域、值域之间有什么关系?
2、在对数函数中,当底数时的在定义域上为函数;
当底数时,函数在定义域上为函数。
(二)对数函数的图像:
1.对数函数的图象都在y轴的侧,并且图像始终过点也就是当x=1的时,y= 。
2.补充:对数函数的图象与指数函数的图象关于直线对称。
二、基础练习:
1、求下列函数的定义域:
(1)(2)
(3)
2、利用对数函数的性质,比较下列各组数中两个数的大小:
(1),;(2),;
(3),;(4),,
3、解下列方程:
(1)(2)
(3)(4)
4、函数是()
A.奇函数B.偶函数C.既奇又偶函数D.非奇非偶函数
三、联系高考:
1、函数的定义域为()
A.B.C.D.
2、设函数的定义域为,函数的定义域为,则,的关系是()A.B.C.D.。

4.3.1 对数函数的概念导学案【学习目标】1. 理解对数函数的概念,能够解释数学概念和规则的含义.2. 理解对数函数与指数函数的关系,能够在关联的情景中抽象出一般的数学概念和规则.3.能够通过指数函数底数取值范围的要求,归纳出对数函数的底数的取值范围.一、导:预习课本P130—P131,理清概念并完成下面问题。
(5分钟)问1:什么是对数函数?定义域是多少?问2:对数函数为什么是函数?二、思、议、展(20分钟)【基础自测】1.下列函数是对数函数的是( )A .y =2+log 3xB .y =log a (2a )(a >0,且a ≠1)C .y =log a x 2(a >0,且a ≠1)D .y =ln x2. 据统计, 第x 年到鄱阳湖国家湿地公园越冬的白鹤数量: y (只)近似满足:()3log 2y a x =+, 观测发现第1年有越冬白鹤3 000只, 估计第7年有越冬白鹤( ) A.4 000 只B.5 000 只C.6 000 只D.7 000 只3. 函数y =lg(3x -2)的定义域是( )A .[1,+∞)B .(1,+∞)C .[23,+∞)D .(23,+∞)探究一:对数函数的概念(5分钟)例1. 下列函数表达式中,是对数函数的有( )①y =log x 2;②y =log a x (a ∈R );③y =log 8x ;④y =ln x ;⑤y =log x (x +2);⑥y =2log 4x ;⑦y =log 2(x +1).A .1个B .2个C .3个D .4个探究二:对数函数的定义域(10分钟)例2. 求下列函数的定义域:(1))1(log 23-=x y ; (2)y =log a (3+x )(a >0,且a ≠1).例3. 假设某地初始物价为1,每年以6%的增长率递增,经过y 年后的物价为x. (1)该地的物价经过几年后会翻一番?(2)填写下表并根据表中的数据,说明该地物价的变化规律.三、评(3分钟)四、检:完成课本P131练习1,2,3及下列当堂检测题.(10分钟) 1. 下列函数中是对数函数的是( ) A.14log y x =B.14log (1)y x =+ C.241log x y =D.14log 1y x =+2. 函数f (x )=lg1-xx -4的定义域为( ) A .(1,4)B .[1,4)C .(-∞,1)∪(4,+∞)D .(-∞,1]∪(4,+∞)3.函数()ln f x x =的定义域是( )A.()0,2B.[]0,2C.()2,+∞D.()0,+∞。

对数函数导学案(全章)导学目标本章主要介绍对数函数及其性质,通过研究,你将了解以下内容:- 对数函数的定义与表示方法;- 对数函数的性质及其与指数函数之间的关系;- 对数函数在实际问题中的应用。
1. 对数函数的定义与表示方法1.1 对数函数的定义对数函数是一种能够描述指数运算逆运算的数学函数。
设正数a > 0 且a ≠ 1,b > 0,则以 a 为底 b 的对数,记作logₐb,定义为满足a^logₐb = b 的实数。
1.2 对数函数的表示方法对数函数可以用不同的表示方法来表示,常见的有以下两种:- 指数形式:logₐb = x,表示以 a 为底 b 的对数为 x;- 运算形式:logₐb = logc b / logc a,表示以 a 为底 b 的对数,等于以任意正数 c 为底 b 的对数与以 c 为底 a 的对数的商。
2. 对数函数的性质与关系2.1 对数函数的性质对数函数具有以下性质:- logₐa = 1;- logₐa^x = x,其中 a > 0,a ≠ 1;- logₐ1 = 0,其中 a > 0,a ≠ 1;- log₁₀10 = 1,log₂2 = 1。
2.2 对数函数与指数函数的关系对数函数与指数函数之间存在着紧密的联系:- 若 a^x = b,则logₐb = x;- 若logₐb = x,则 a^x = b。
3. 对数函数的应用对数函数在实际问题中有广泛的应用,例如:- 在经济学中,对数函数可以用来描述利率、复利和指数增长等问题;- 在物理学中,对数函数可以用来描述声音的音量、地震的震级等问题;- 在计算机科学中,对数函数可以用来描述算法的时间复杂度等问题。
总结本章主要介绍了对数函数的定义与表示方法,对数函数的性质与指数函数的关系,以及对数函数在实际问题中的应用。
通过研究,你可以更好地理解并运用对数函数解决相关的数学问题。
参考资料:- 张宇老师. (2021). 《高中数学》. 北京师范大学出版社.。

22对数函数导学案[学习目标]1.理解对数的概念及其运算性质.2.知道用换底公式能将一般对数转化成自然对数或常用对数.3.了解对数的发现历史以及其对简化运算的作用.4.通过具体实例,直观了解对数函数模型所刻画的数量关系,初步理解对数函数的概念,体会对数函数是一类重要的函数模型.5.能借助计算器或计算机画出具体的对数函数的图象,探索并了解对数函数的单调性与特殊点.6.知道对数函数yloga某与指数函数ya某互为反函数(a0,且a1).[学习要求]本节内容是在学习了指数函数之后,通过具体实例了解对数函数模型的实际背景,明确本节课要学习的问题——对数问题.学习对数概念,进而学习一类新的基本初等函数——对数函数.在学习对数定义时,要注意以下几点:一是要弄清楚对数式logaNb(a0,且a1)的含义,明确a,N,b,相对于指数式aN是什么数,并找出它们之间是什么关系.二是要注意对数式logaNb中字母的取值范围,要清楚对数定义中为什么要规定a0,且a1,N0.对数的运算性质是进行对数计算的重要依据,要理解其推导过程.学习过程中应充分发挥对数函数图象的作用,要做到自己动手做出对数函数的图象.会根据图象讨论对数函数的性质.[学习重点]对数函数的概念、图象和性质.[课时安排]6课时b第一课时2.2.1对数与对数运算(1)——对数新课导入回顾2.1.2指数函数一节中的例8,把我国1999年底人口13亿作为基数,如果人口年平均增长率控制在1%,那么经过20年后,我国人口数y最多为多少?我们算出经过年数某与人口数y满足关系y131.01某中,如果问“哪一年的人口数可达到18亿,20亿,30亿”?该如何解决?分析:人口数达到18亿时,是1999年底13亿人口的人口数达到20亿时,是1999年底13亿人口的达到30亿时,是1999年底13亿人口的某181.01某,需要从中求出经过年数某;13201.01某,需要从中求出经过年数某;人口数13301.01某,需要从中求出经过年数某;一般地,需要13从1.01N中求出经过年数某.这是我们这一节将要学习的对数问题.新课进展一、对数1.定义某一般地,如果aN(a0,且a1),那么数某叫做以a为底N的对数(logarithm),记作某logaN,其中a叫做对数的底数,N叫做真数.1818181.01某,其中某就是以1.01为底的对数,记作某log1.01;请同学们写出131********.01某,1.01某中的某.1313问:以4为底16的对数是2,用等式怎么表达?讨论:按照对数的定义,以4为底16的对数是2,可记作log4162;同样从对数的定义出发,可写成416.我们从一般的角度来考虑这个问题,根据对数的定义,可以得到对数和指数间的关系:某某当a0,且a1时,如果aN,那么某logaN;如果某logaN,那么aN.即2a某N等价于某logaN,记作当a0,且a1时,a某N某logaN.当a0,且a1时,计算:loga1,logaa.分析:利用对数和指数间的关系.由于aN0,所以:负数和零没有对数.2.常用对数和自然对数3.课堂例题例1将下列指数式化为对数式,对数式化为指数式:某(1)5625;1(2)2;6464(3)5.73;3(4)log1164;2m(5)lg0.012;(6)ln102.303.例2求下列各式中某的值2(1)log64某;3(2)log某86;(3)lg100某;(4)lne某.24.课堂练习1.把下列指数式写成对数式:(1)28;(1)log22;43(2)232.(2)log34.8452.把下列对数式写成指数式:5.布置作业课本第74页习题2.2.A组1、2.第二课时2.2.1对数与对数运算(2)——对数的运算复习导入通过提问复习上节课主要学习内容.问:你如何理解对数?答:从运算的角度,对数运算可以看成是指数运算的逆运算.因此,对数式和指数式的互化某在对数学习过程中很重要.当a0,且a1时,aN某logaN,即logaa 某某.新课进展通过师生探究,学习本节主要内容问:从指数与对数的关系以及指数运算性质,你能得出相应的对数运算性质吗?回顾指数幂的运算性质:amanamn,amanamn,(am)namn.师生讨论:把指对数互化的式子具体化:设Ma,Na,于是有mnMNamn,Mamn,Mnamn.logaMm,logaNn.N根据对数的定义有:logaamnmn,logaamnmn,logaamnmn.于是有二、对数的运算(1)loga(MN)logaMlogaN;(2)logaMlogaMlogaN;N(3)logaMnnlogaM(nR).课堂例题例1用loga某,logay,logaz表示下列各式:某y(1)loga;z(2)loga某2yz.例2求下列各式的值(1)log2(4725);(2)lg.课堂练习1.用loga某,logay,logaz表示下列各式(1)lg(某yz);某y2(3)lg;z某y2(2)lg;某(4)lg2.yz(2)lg1002;2.求下列各式的值:(1)log3(2792);(3)lg0.00001;(1)log26log23;(4)lne.(2)lg5lg2;(4)log35log315.3.求下列各式的值:1(3)log53log5;3布置作业课本第74页习题2.2A组第3、4、5题.第三课时2.2.1对数与对数运算(3)——对数的换底公式复习导入通过提问复习上节课主要学习内容.问:上节课我们学习了哪些对数的性质?请用文字语言叙述.答:(1)积的对数等于同底对数的和;(2)商的对数等于同底对数的差;(3)n次幂的对数等于同底对数的n倍;即:(1)loga(MN)logaMlogaN;(2)logaMlogaMlogaN;N(3)logaMnnlogaM(nR).新课进展三、对数的换底公式问:前面我们学习了常用对数和自然对数,我们知道任意不等于1的正数都可以作为对数的底,能否将其它底的对数转换为以10或e为底的对数?把问题一般化,能否把以a为底转化为以c为底?师生共同探究:设logabp,则ab,对此等式两边取以c为底的对数,得到:plogcaplogcb,根据对数的性质,有:plogcalogcb,所以plogcb.其中a0,且a1,c0,且c1.logcalogcb称为换底公式.logcalogcb.logca即logab公式logab用换底公式可以很方便地利用计算器进行对数的数值计算.例如,求我国人口达到18亿的年份,就是计算某log1.0118的值,利用换底公式和对数的运算性质,可得:13180.004313lg1.01lg1.01lg课堂例题例1(课本第66页例5)例2(课本第67页例6)本例题根据问题的实际意义可知,对于每一个碳14含量P,通过对应关系tlog57302P,都有唯一确定的年代t与它对应,所以,t是P的函数.课堂练习利用对数的换底公式化简下列各式:(2)log23log34log45log52;(3)(log43log83)(log32log92).布置作业课本第74页习题2.2A组4(1)——(4)、5(1)——(4)、6题.第四课时2.2.2对数函数及其性质(1)情景问题导入1.课堂练习课本第74页习题2.2A组第6题.2.上节课的例题,考古学家通过提取附着在出土文物、古遗址上死亡生物体的残留物测定碳14含量P,估算出土文物或古遗址地年代t,即tlog一、对数函数的定义一般地,我们把函数yloga某(a0,且a1)叫做对数函数(logarithmic57302P.function),其中某是自变量,函数的定义域是(0,+).我们类比指数函数ya某(a0,且a1)图象与性质,来研究对数函数yloga某(a0,且a1)的图象和性质.二、对数函数的图象在同一坐标系中画出对数函数ylog2某和ylog1某的图象(可用描点法,也可借助科学2计算器或计算机).(图及表格见课本第70页)讨论:函数ylog2某和ylog1某的图象之间的关系.2ylog1某log2某,又点(某,y)和点(某,y)关于某轴对称,所以,ylog2某和2ylog1某的图象关于某轴对称.2思考函数yloga某与ylog1某(a0,且a1)的图象有什么关系?a三、对数函数的性质一般地,对数函数yloga某(a0,且a1)的图象和性质如下表所示.课堂例题例1求下列函数的定义域:(1)yloga某2;(2)yloga(4某).例2比较下列各组数中两个值的大小:(1)ylog23.4,ylog28.5;(2)ylog0.31.8,ylog0.32.7;(3)yloga5.1,yloga5.9(a>0,且a≠1).该两例是巩固对数函数的概念,利用单调性比较对数式的大小.课堂练习1.画出函数ylog3某及ylog1某的图象,3并且说明这两个函数的相同点和不同点.;log2某2.求下列函数的定义域(1)ylog5(1某);(2)y(3)ylog;713某(4)ylog3某.3.比较下列各题中两个值的大小:(1)log106,log108;(3)log20.5,log20.6;33(2)log0.56,log0.54.(4)log1.51.6,log1.51.4.布置作业课本第74页习题2.2A组第7、8、9题.第五课时2.2.2对数函数及其性质(2)复习导入通过提问复习上节课主要学习内容.问:我们是怎样研究对数函数的?投影出一般的对数函数的特征图象,总结其单调性和特殊点.新课进展四、对数函数的应用课堂例题例1(课本第72页例9)利用对数函数,解决溶液酸碱度pH值得测量问题,体会对数函数的应用价值.例2(课本第75页习题2.2A组第12题)学习用数学的观点处理现实问题的方法,进一步引导学生体会对数函数的应用价值.例3(课本第75页习题2.2B组第3题)体会对数函数应用的广泛性.课堂练习课本第75页习题2.2A组第12题.布置作业课本第82页复习参考题A组第9题.课本第83页复习参考题B组第5题.第六课时2.2.2对数函数及其性质(3)——对数函数与指数函数的关系问题导入问:在指数函数y2中,某为自变量,y为因变量.如果把y当成自变量,某当成因变量,那么某是y的函数吗?如果是,那么对应关系是什么?如果不是,请说明理由.通过对问题的讨论,形成反函数的概念.通过摄氏温度与华氏温度的换算,进一步明确反函数的概念.在指数函数y2中,某是自变量,定义域是某R,y是某的函数,且值域y(0,+).根据指数与对数的关系,由指数式y2某可得到对数式某log2y,这样,对于任意一个某某y(0,+),通过式子某log2y,某在R中都有唯一确定的值和它对应.我们可以把y作为某自变量,某作为y的函数,这时,我们就把某log2y(y(0,+))称为函数y2(某R)的反函数(inverefunction).在函数某log2y中,y是自变量,某是y的函数.但习惯上,我们通常用某表示自变量,y表示函数.为此,我们把函数某log2y中的字母某,y交换,把它写成ylog2某,这样,对数某函数ylog2某(某(0,+))是指数函数y2某R的反函数.课堂讨论1.如何说明指数函数ya某(a0,且a1)与对数函数yloga某(a0,且a1)互为反函数.2.互为反函数的这两个函数的定义域和值域有什么关系?3.互为反函数的这两个函数的图象有什么关系?答案提示:1.在指数函数ya某中,某是自变量,定义域是某R,y是某的函数,且值域y(0,+).根据指数与对数的关系,由指数式ya某可得到对数式某logay,这样,对于任意一个y(0,+),通过式子某logay,某在R中都有唯一确定的值和它对应.我们可以把y作为自变量,某作为y的函数,这时,某logay(y(0,+))就为指数函数ya某的反函数,把自变量用某表示,因变量用y表示,则对数函数yloga某就是指数函数ya某的反函数(a0,且a1).反之,也可类似说明对数函数yloga某(a0,且a1)是指数函数ya某(a0,且a1)的反函数.2.互为反函数的这两个函数的定义域和值域恰好互换,例如y2的定义域为实数集R,值域为(0,),y2的反函数的定义域为(0,),值域为实数集R.3.在同一个直角坐标系中,互为反函数的函数图象关于直线y某对称.说明:作为探究与发现,教材只要求学生了解指数函数ya和对数函数某某某yloga某(a0,且a1)互为反函数.对反函数的一般概念、判断一个函数是否存在反函数以及求函数的反函数等均不作要求.课堂例题例1求下列函数的反函数:(1)y();(2)ylog5某.13某解:(1)y()的反函数为ylog1某,某(0,).33某(2)函数ylog5某的反函数为y5某,某R.课堂练习写出下列函数的反函数:(1)ylog4某;(2)ylog1某.4本课小结1.对数函数yloga某(a0,且a1)与同底的指数函数ya某互为反函数.2.对数函数yloga某与同底的指数函数ya某的性质相互对应.布置作业1.根据对数函数yloga某(a0,且a1)与同底的指数函数ya某互为反函数的关系,列出指数函数与对数函数的对照表.2.课本第82页复习参考题A组第8题.。
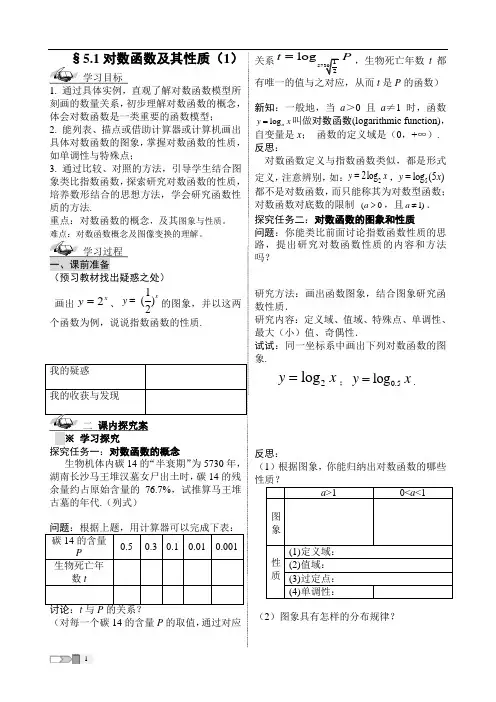
关系logt P =,生物死亡年数t 都有唯一的值与之对应,从而t 是P 的函数)新知:一般地,当a >0且a ≠1时,函数log a y x =叫做对数函数(logarithmic function),自变量是x ; 函数的定义域是(0,+∞). 反思:对数函数定义与指数函数类似,都是形式定义,注意辨别,如:22log y x =,5log (5)y x = 都不是对数函数,而只能称其为对数型函数;对数函数对底数的限制 (0a >,且1)a ≠. 探究任务二:对数函数的图象和性质问题:你能类比前面讨论指数函数性质的思路,提出研究对数函数性质的内容和方法吗?研究方法:画出函数图象,结合图象研究函数性质.研究内容:定义域、值域、特殊点、单调性、最大(小)值、奇偶性.试试:同一坐标系中画出下列对数函数的图象.2log y x=;0.5log y x =.反思:(1)根据图象,你能归纳出对数函数的哪些(2)图象具有怎样的分布规律?2※ 典型例题例1求下列函数的定义域: (1)2log a y x =;(2)log (3)a y x =-;变式:求函数y =的定义域.例2比较大小:(1)ln 3.4,ln 8.5; (2)0.30.3log 2.8,log 2.7; (3)log 5.1,log 5.9a a .小结:利用单调性比大小;注意格式规范.※ 动手试试练1. 求下列函数的定义域.(1)0.2log (6)y x =--; (2)y =练2. 比较下列各题中两个数值的大小.(1)22log 3log 3.5和; (2)0.30.2log 4log 0.7和; (3)0.70.7log 1.6log 1.8和; (4)23log 3log 2和.当堂检测(时量:5分钟 满分:10分)计分:1. 当a >1时,在同一坐标系中,函数x y a -=与log a y x =的图象是( ).2. 函数22log (1)y x x =+≥的值域为( ). A. (2,)+∞ B. (,2)-∞C. [)2,+∞D. [)3,+∞ 3. 不等式的41log 2x >解集是( ).A. (2,)+∞B. (0,2)B.1(,)2+∞ D.1(0,)24. 比大小:(1)log 67 log 7 6 ; (2)log 31.5 log 2 0.8.5. 函数(-1)log (3-)x y x =的定义域是 .1. 已知下列不等式,比较正数m 、n 的大小: (1)3log m <3log n ; (2)0.3log m >0.3log n ; (3)log a m >log a n (a >1)2. 求下列函数的定义域:(1)y =(2)y =四、总结提升 ※ 学习小结1. 对数函数的概念、图象和性质;2. 求定义域;3. 利用单调性比大小.※ 知识拓展对数函数凹凸性:函数()log ,(0,1)a f x x a a =>≠,12,x x 是任意两个正实数.当1a >时,1212()()()22f x f x x x f ++≤;当01a <<时,1212()()()22f x f x x x f ++≥.函数2x y =中的自变量与因变量对调位置而得出的. 习惯上我们通常用x 表示自变量,y 表示函数,即写为2log y x =.新知:当一个函数是一一映射时, 可以把这个函数的因变量作为一个新函数的自变量, 而把这个函数的自变量新的函数的因变量. 我们称这两个函数为反函数(inverse function ) 例如:指数函数2x y =与对数函数2log y x =互为反函数.试试:在同一平面直角坐标系中,画出指数函数2x y =及其反函数2log y x =图象,发现什么性质?反思:(1)如果000(,)P x y 在函数2x y =的图象上,那么P 0关于直线y x =的对称点在函数2log y x =的图象上吗?为什么?(2)由上述过程可以得到结论:互为反函数的两个函数的图象关于 对称.※ 典型例题例1求下列函数的反函数:(1) 3x y =; (2)log (1)a y x =-.小结:求反函数的步骤(解x →习惯表示→定义域)变式:点(2,3)在函数log (1)a y x =-的反函数图象上,求实数a 的值.4例2溶液酸碱度的测量问题:溶液酸碱度pH 的计算公式lg[]pH H +=-,其中[]H +表示溶液中氢离子的浓度,单位是摩尔/升. (1)分析溶液酸碱度与溶液中氢离子浓度之间的变化关系?(2)纯净水7[]10H +-=摩尔/升,计算其酸碱度.小结:抽象出对数函数模型,然后应用对数函数模型解决问题,这就是数学应用建模思想.※ 动手试试练1. 己知函数()x f x a k =-的图象过点(1,3)其反函数的图象过点(2,0),求()f x 的表达式.练2. 求下列函数的反函数. (1) y=x (x ∈R ); (2)y =log a2x (a >0,a ≠1,x >0)当堂检测0.5log y x =的反函数是( ). A. 0.5log y x =- B. 2log y x = C.2xy = D.1()2xy =2. 函数2x y =的反函数的单调性是( ). A. 在R 上单调递增 B. 在R 上单调递减C. 在(0,)+∞上单调递增D. 在(0,)+∞上单调递减 3. 函数2(0)y x x =<的反函数是( ).A. (0)y x =>B. (0)y x =>C. (0)y x =>D. y =4. 函数x y a =的反函数的图象过点(9,2),则a 的值为 .5. 右图是函数1log ay x=,2log a y x =3log a y x=, 4log a y x=的图象,则底数之间的关系为 .1. 现有某种细胞100个,其中有占总数12的细胞每小时分裂一次,即由1个细胞分裂成2个细胞,按这种规律发展下去,经过多少小时,细胞总数可以超过1010个?(参考数据:lg 30.477,lg 20.301==).2. 探究:求(0)ax b y ac cx d+=≠+的反函数,并求出两个函数的定义域与值域,通过对定义域与值域的比较,你能得出一些什么结论?四、总结提升 ※ 学习小结① 函数模型应用思想;② 反函数概念.※ 知识拓展函数的概念重在对于某个范围(定义域)内的任意一个自变量x 的值,y 都有唯一的值和它对应. 对于一个单调函数,反之对应任意y 值,x 也都有惟一的值和它对应,从而单调函数才具有反函数. 反函数的定义域是原函数的值域,反函数的值域是原函数的定义域,即互为反函数的两个函数,定义域与值域是交叉相等※ 典型例题例1判断下列函数的奇偶性. (1)1()log1x f x x-=+;(2)())f x x =.例2证明函数22()log (1)f x x =+在(0,)+∞上递增.变式:函数22()log (1)f x x =+在(,0)-∞上是减函数还是增函数?例3 求函数0.2()log (45)f x x =-+的单调区间.变式:函数2()log (45)f x x =-+的单调性是 .小结:复合函数单调性的求法及规律:“同增异减”.※ 动手试试 练1. 比较大小: (1)log log (01)a a e a a π>≠和且 ;6(2)2221log log (1)()2a a a R ++∈和.练2. 已知log (31)a a -恒为正数,求a 的取值范围.练 3. 函数log a y x =在[2,4]上的最大值比最小值大1,求a 的值.练4. 求函数23log (610)y x x =++的值域.1. 下列函数与y x =有相同图象的一个函数是( )A.y =B.2xy x=C.log (01)a xy aa a =>≠且 D.log xa y a=2.函数y = ).A.[1,)+∞B.2(,)3+∞C.2[,1]3D.2(,1]33. 若(ln )34f x x =+,则()f x 的表达式为( ) A. 3ln x B. 3ln 4x + C. 3x e D. 34x e +4.函数2()lg(8)f x x =+的定义域为 ,值域为 .5. 将20.3,2log 0.5,0.5log 1.5由小到大排列的顺序是 .三、总结提升 ※ 学习小结1. 对数运算法则的运用;2. 对数运算性质的运用;3. 对数型函数的性质研究;4. 复合函数的单调性. ※ 知识拓展 复合函数(())y f x ϕ=的单调性研究,遵循一般步骤和结论,即:分别求出()y f u =与()u x ϕ=两个函数的单调性,再按口诀“同增异减”得出复合后的单调性,即两个函数同为增函数或者同为减函数,则复合后结果为增函数;若两个函数一增一减,则复合后结果为减函数. 为何有“同增异减”?我们可以抓住 “x 的变化→()u x ϕ=的变化→()y f u =的变化”这样一条思路进行分析。
2. 2.1第|一课时 对数的概念教案【教学目标】1.理解对数的概念 ,能够进行对数式与指数式的互化2.渗透应用意识 ,培养归纳思维能力和逻辑推理能力 ,提高数学发现能力 【教学重难点】 重点:对数的概念难点:对数概念的理解. 【教学过程】一、预习检查、总结疑惑检查落实了学生的预习情况并了解了学生的疑惑 ,使教学具有了针对性 . 二、情景导入、展示目标 . (一 )复习引入:1庄子:一尺之棰 ,日取其半 ,万世不竭 (1 )取4次 ,还有多长 ? (2 )取多少次 ,还有0.125尺 ?2假设2002年我国国民生产总值为a 亿元 ,如果每年平均增长8% ,那么经过多少年国民生产总值是2002年的2倍 ?抽象出:1. 421⎪⎭⎫ ⎝⎛= ? ,x⎪⎭⎫ ⎝⎛21=0.125⇒x =? 2. ()x%81+ =2⇒x =?也是底数和幂的值 ,求指数你能看得出来吗 ?怎样求呢 ?(二 )新授内容:定义:一般地 ,如果 ()1,0≠>a a a 的b 次幂等于N, 就是 N a b= ,那么数 b 叫做 以a 为底 N 的对数 ,记作b N a =log ,a 叫做对数的底数 ,N 叫做真数例如:1642= ⇔ 216log 4= ; 100102=⇔2100log 10=2421= ⇔212log 4=; 01.0102=-⇔201.0log 10-= 探究:⑴负数与零没有对数 (∵在指数式中 N > 0 )⑵01log =a ,1log =a a∵对任意 0>a 且 1≠a , 都有 10=a ∴01log =a同样易知: 1log =a a ⑶对数恒等式如果把 N a b= 中的 b 写成 N a log , 那么有 N aNa =log⑷常用对数:我们通常将以10为底的对数叫做常用对数为了简便,N 的常用对数N 10log 简记作lgN例如:5log 10简记作lg5 ; 5.3log 10简记作lg3.5.⑸自然对数:在科学技术中常常使用以无理数e =2.71828……为底的对数 ,以e 为底的对数叫自然对数 ,为了简便 ,N 的自然对数N e log 简记作lnN例如:3log e 简记作ln3 ; 10log e 简记作ln10(6 )底数的取值范围),1()1,0(+∞ ;真数的取值范围),0(+∞(三 )合作探究 ,精讲点拨 探究一:指对互化例1将以下指数式写成对数式: (课本第87页 )(1 )45 =625 (2 )62- =641 (3 )a3 =27 (4) m )(31 =5.73解: (1 )5log 625 =4; (2 )2log 641= -6;(3 )3log 27 =a ; (4 )m =73.5log 31点评:主要考察了底真树与幂三者的位置. 变式练习1: 将以下对数式写成指数式: (1 )416log 21-=; (2 )2log 128 =7;(3 )lg0.01 = -2; (4 )ln10 =2.303 解: (1 )16)21(4=- (2 )72 =128;(3 )210- =0.01; (4 )303.2e=10探究二:计算例2计算: ⑴27log 9 ,⑵81log 43 ,⑶()()32log 32-+ ,⑷625log 345解析:将对数式写成指数式 ,再求解. 解:⑴设 =x 27log 9 那么 ,279=x3233=x, ∴23=x ⑵设 =x 81log 43 那么()8134=x, 4433=x , ∴16=x ⑶令 =x ()()32log 32-+ =()()13232log -++,∴()()13232-+=+x, ∴1-=x⑷令 =x 625log 345, ∴()625534=x, 43455=x , ∴3=x点评:考察了指数与对数的相互转化. (四)小结:本节主要学习了对数的概念 ,要熟练的进行指对互化. 【板书设计】 一、对数函数概念 二、例题例1 变式1 例2 变式2【作业布置】导学案课后练习与提高2.2.1对数的概念导学案课前预习学案一、预习目标了解对数的概念 ,知道常用对数与自然对数以及这两种对数符号的记法 ,了解对数恒等式 ,二、预习内容 对数概念:1.一般地 ,如果a (0,1a a >≠)的b 次幂等于N ,即ba N = ,那么数b 叫做 ,记作log a N b =.其中 ,a 叫做对数的 ,N 叫做 .例如:2339 log 92=⇒= ,读作:以3为底9的对数为2 . (1 )概念分析:对数式log a b N =中各字母的取值范围:a : 0,1a a >≠ ;b : b R ∈ ; N :0N > .(2 )零和负数没有对数;1的对数为0 ,即log 10a = (0a >且1≠a );底数的对数为1 ,即log 1a a = (0a >且1≠a ).2.以10为底的对数称为 ,以e 为底的对数称为3.log b a a = log a Na =三、提出疑惑课内探究学案一、 学习目标1、 理解指数式与对数式的相互关系 ,能熟练进行指数式与对数式的互化 .2‘2、 并能运用恒等式进行计算 .学习重难点:理解对数的概念 ,能够进行对数式与指数式的互化、二、 学习过程探究一.指数式和对数式互化 1.将以下指数式写成对数式: 42115625 1081 () 5.731003a m e -===①②③④= 解析:直接用对数式的定义进行改写.解:点评:主要考察了底真树与幂三者的位置.变1.将以下对数式写成指数式: 2121log 16 4 log 7 lg 0.01 2 ln10 2.303128=-=-=-①②③④=探究二.求对数值2、⑴27log 9 ,⑵81log 43 ,⑶()()32log 32-+ ,⑷625log 345解析:将对数式写成指数式 ,再求解. 解:点评:考察了指数与对数的相互转化.(1 )72log 4 (2 )5100)381(log 3(二 )反思总结(三 )当堂检测1.完成以下指数式与对数式的互化:(1 )26416=-⇔ , (2 )73.5)31(=m ⇔ , (3 )0.5log 164=-⇔ , (4 )7128log 2=⇔ ,(5 )201.0lg -=⇔ , (6 )303.210ln =⇔ . (1 )1162log = , (2 )01.0lg = , (3 )ln e= ,(4 ) 2.5log 6.25 = , (5 )(21)log (322)-+ =课后练习与提高1.对数式的值为 ( )(A ) 1 (B ) -1 (C ) (D ) -2、假设log 7[ log 3( lo g 2x)] = 0 ,那么x 21-为( ).(A).321 (B).331 (C).21 (D).423.计算 (1 )3(2log 2)3+= (2 )52log 35=4.0a >且1a ≠ ,log 2a m = ,log 3a n = ,求2m na +的值 .。
对数函数(2)【学习目标】1.深入理解对数函数的图象和性质.2.应用对数函数的图象与性质进一步解决比大小、解对数不等式相关问题.3.能够利用图象变换画对数相关函数图象.【学习用时】活动一、二、三为课前作业:40分钟;学案讲授:1课时.【学习过程】【活动一】底数大小与函数图象的关系思考:(1)你是如何去画函数x x f 2log )(=的图象的?尝试在同一坐标系下画出x x g x x f lg )(,log )(2==两个函数,如何对他们进行区分?(2)函数y =log a x ,y =log b x ,y =log c x 的图象如图所示,那么a ,b ,c 的大小关系如何?有什么好办法快速确定?例1 (1) 已知log m 7<log n 7<0,则m ,n ,0,1之间的大小关系是____________.(2) 已知a =log 23.6,b =log 43.2,c =log 43.6,则a ,b ,c 的大小关系是________;例2 比较下列各组数的大小:①log 323与log 565;②log 1.10.7与log 1.20.7.【活动二】 解对数不等式例3 求下列不等式的解集(1)1)1(log 2<+x(2)关于x 的不等式:log a (2x -5)>log a (x -1)(3)633<-x(4))2(log 0)1(log 2a a a a <<+【活动三】图象变换思考(1)画出函数)2(log 3+=x y 与x y 3log =的图象,说明他们之间的关系;(2)画出函数x y 3log 3=与x y 3log =的图象,说明他们之间的关系;(3)画出函数x y 31log =与x y 3log =的图象,说明他们之间的关系;(4)画出函数)(log 3x y -=与x y 3log =的图象,说明他们之间的关系;(5)画出函数||log 3x y =与x y 3log =的图象,说明他们之间关系;(6)画出函数|log |3x y =与x y 3log =的图象,说明他们之间关系;总结:(1)上述6个问题揭示了图象间的哪几类变换关系?(2)尝试将上述函数图象间的关系进行推广,形成一般结论.例4(1)为了得到函数y=lg x+310的图象,只需把函数y=lg x的图象上所有的点()A.向左平移3个单位长度,再向上平移1个单位长度B.向右平移3个单位长度,再向上平移1个单位长度C.向左平移3个单位长度,再向下平移1个单位长度D.向右平移3个单位长度,再向下平移1个单位长度(2)试着作出函数y=|lg(x-1)| 的图象;(3)(多选)对于函数f(x)=lg(|x-2|+1),下列说法正确的是() A.f(x+2)是偶函数B.f(x+2)是奇函数C.f(x)在区间(-∞,2)上单调递减,在区间(2,+∞)上单调递增D.f(x)没有最小值【课后作业】1.设a=log32,b=log52,c=log23,则()A.a>c>b B.b>c>a C.c>b>a D.c>a>b2.已知a=log52,b=log0.50.2,c=0.50.2,则a,b,c的大小关系为()A. a <c <bB. a <b <cC. b <c <aD. c <a <b3.对数函数y =log a x ,y =log b x ,y =log c x ,y =log d x 在同一坐标系内的图象如图所示,则a ,b ,c ,d 的大小关系是________.4.已知函数f (x )=|log a x |(0<a <1),则下列各式中正确的是( ) A.)41()2()31(f f f >> B.)2()31()41(f f f >> C.)41()31()2(f f f >> D.)31()2()41(f f f >>5. 已知f (x )是定义在R 上的偶函数,且在区间[0,+∞)上为增函数,0)31(=f ,则不等式0)(log 81>x f >0的解集为____________.6.已知函数f (x )=|log 2x |,实数a ,b 满足0<a <b ,且f (a )=f (b ),若f (x )在[a 2,b ]上的最大值为2,则1a +b =________.7.作出函数y =|log 2(x +1)|+2的图象,并根据图象写出函数的定义域、值域以及单调区间.第3题图8.已知函数f(x)=log a(x-1),g(x)=log a(6-2x)(a>0,且a≠1).(1)求函数φ(x)=f(x)+g(x)的定义域;(2)试确定不等式f(x)≤g(x)中x的取值范围。
xy 21log =x31log x 51logy §5.2 对数函数的图像和性质☆学习目标:(1)了解对数函数模型的实际案例,理解对数函数的概念,会画对数函数的图像. (2)理解反函数的概念,能应用所学知识解决简单的数学问题; 教学重点:对数函数的图像和性质 教学难点: 底数a 对对数函数的影响问题导学1.一般的,我们把 叫做对数函数,其中x 是自变量,函数的定义域是 .2.回忆对数函数xy 2log =的图像和性质,观察下列函数图象,由图象总结归纳对数函数在底数1a >及01a <<这两种情况下的图像和性质:1a >01a << 图象性质 定义域: ; 定义域: ; 值域: 值域: 过定点 ___________ ; 即x=_________时, y=_____________.当x>1时,_____________ . 当0<x<1时,_____________ . 当x>0时,_____________ : 当x<0时,_____________ .在),0(+∞上是_____________在),0(+∞上是____________☆反馈练习回忆对数函数的定义 类比指数函数图像与性质的学习,观察图像,归纳性质,完成表格xy 2log =x y 3log =y xy 5log = y例1.求下列函数的定义域.(1))3(log x a - (2)2log x a (3)1343log +x合作探究一(1)观察在同一坐标系内函数)),0((log 2+∞∈=x y x与函数)(2R x y x∈=的图像,分析它们之间的关系.(2)利用问题(1)结论,推测函数xa y =与函数xa y log =的关系. 合作探究二 类比指数函数性质的研究方法,观察图像,总结归纳出底数a 对函数图像及性质的影响. (1)观察图像特点,思考函数xa y log =与与函数x ay 1log =的图像是什么关系?(2) 函数x a y log =,当a>1时,a 的变化对图像有何影响?当0<a<1呢?参考书中94页例题,根据对数函数底数及定义域的限制,列式求解.观察图像特点,主要观察函数图象的对称性 。
对数函数及其性质(1)(教学设计)对数函数及其性质(1)的含量①②③④⑤⑥,则,则.若若,则函数的图象关于好玩的计算尺与背后的对数故事(1)转发评论2009-08-18 20:44此书第一卷第三部分“分析”中首先就给出了对数的历史和演化过程。
其中提到了对数表。
由此我忽然想起一个对数表衍生出的工具:计算尺。
2006年第6期的《环球科学》中曾有一篇文章《300年辉煌:计算尺传奇》,正是通过这篇文章,我第一次知道了还有这么神奇的工具。
在计算器发明前,能作为计算的辅助工具的,并不只有算盘。
而且计算尺使得工程人员和科学家能以非常快的速度计算乘、除、开方、正余弦、双曲三角函数等,其很多功能是算盘所不具备的。
计算尺的原理决定了它强大的功能,以及与算盘有着本质上的不同。
计算尺的诞生可以追溯到对数的第一次应用。
1614年,苏格兰数学、物理学家约翰·纳皮尔在他的《对数原理》一书中收录了其制作的世界第一份对数表。
但直到他逝世后的1619年,计算此对数表的方法才被公开。
与此同时,瑞士人约布斯特·比尔吉独立的发明了与纳皮尔类似的方法,也计算出对数表,并于1620年出版。
1620年,为了方便的使用对数表,英国数学家埃德蒙·甘特把对数以一种特别的位置关系刻在了尺子上;大约1622年的时候,英国圣公会牧师威廉·奥特雷德把两根木制对数标尺并排放在一起,创造出了世界上第一把计算尺。
有了奥特雷德的发明,人们就可以告别对数表,只须拉拉计算尺,对一下两个因数的位置,便可得到乘法的结果。
这一发明使得计算“抛开了数字”。
此后300年间,针对不同的专业需求,人们给计算尺添加了不同的功能,极大提高了计算效率。
《环球科学》中提到的可在网站上下载的“自制计算尺”的图样已失效,不过好在杂志上也印刷了一份,复印后按照说明剪裁一下,一个小巧的计算尺就到手了。
试验过它的各种用法后,我不禁惊叹于计算尺精巧的设计和对原理巧妙的利用。
可以想见这种工具在计算器前时代起着如何重要的作用。
如果有人对计算尺感兴趣,可以在baidu或google上搜一下上面的那篇文章,还可找到部分内容。
其中有计算尺的使用示例和详细介绍,我就不再多说了。
下面记录一些更有意义的历史过程:对数相关内容的推导。
首先是对数表的计算:<1>设底b为接近1的一个小数,比如1.0001,即,这样底b的逐次整数幂相互很靠近。
<2>基于上述的考虑(“b的逐次整数幂”),设y的值每次增加1,即数y以1等差递增,;而对应的x增加。
再由,可得,于是。
<3>只要能确定一组初始的x和y值,此后通过不停地对上一个x加,对上一个y加1,计算下去即可得到一张大致的对数表(注意此处得到的x值序列并非等差数列)。
比如:基于指数函数的知识,可设x = 1时,y = 0。
然后,,由此也可看到,随着x和y的增大,也即是逐渐变小的,而不变,所以逐渐变大。
<4>为进一步提高计算出的对数表的精度,可回溯至第2步,取,则,于是。
此后通过不停地对上一个x加,对上一个y加0.1,计算下去即可得到一张精度更高的对数表。
如需要,可取更小的小数。
在计算对数表时,底的选取并不是一个重要的因素。
所以可以换一种方法来思考对数的求值问题。
<1>由上面时的情况,。
然后重新定义y,此后的y变为之前的y乘以,x改写为。
同时新的,并有,。
<2>由之前内容可知,欲求对应的对数的值,可将x由1开始每次增加直至最终的值,同时y由0开始并每次增加一个相应的,当x的值到达时,y的值即为所要求的值,。
<3>引入另一平面直角坐标系,横轴为轴,纵轴为轴。
在平面上画一条双曲线,然后求由、、(此处代表一个定值)、围成的曲边梯形的面积。
此处使用积分的思路,不过,这里以等面积来划分小矩形,每个小矩形的面积都为。
因为每个小矩形的、值不同,所以的值也不固定,即,划分的小矩形不等宽。
最终求出的曲边梯形的面积为。
<4>可以看到,<2>和<3>得出的式子实际是相同的。
所以求的对数的问题就转化为求由、、、围成的曲边梯形的面积上来了。
设,当时,由1加到的相加次数趋于无穷大。
此时曲边梯形面积可表示为。
所以时此对数函数也可表示成积分的形式。
确定的底<1>由上面,所以。
将其改写为,并让,此时。
这与上面设,并将改写为实际是一回事,此时对数函数可用另一坐标系下的双曲线下的面积来表示。
<2>也改写为,同时令。
即,。
设,就有。
结合上一步,当以e为底时,可写为,即。
e就是自然常数。
∙标签:计算尺、对数∙分类:数学与自然科学2009-08-18 20:44 来自我的搜狐在博客中查看编辑删除阅读(90) 转发评论对数是由英国人纳皮尔(Napier,1550~1617)创立的,而对数(Logarithm)一词也是他所创造的。
这个词是由一个希腊语(打不出,转成拉丁文logos,意思是表示思想的文字或符号,也可说成“计算”或“比率”)及另一个希腊语(数,抱歉,我不知道拉丁文怎么写)结合而成的。
纳皮尔在表示对数时套用logarithm 整个词,并未作简化。
至1624年,开普勒才把词简化为“Log”,奥特雷得在1647年也用简化过了的“Log”。
1632年,卡瓦列里成了首个采用符号log的人。
1821年,柯分用“l”及“L”分别表示自然对数和任意大于1的底的对数。
1893年,皮亚诺用“logx”及“Logx”分别表示以e为底的对数和以10为底的对数。
同年,斯特林厄姆用“blog”、“ln”及“logk.”分别表示以b为底的对数、自然对数和以复数模k为底的对数。
1902年,施托尔茨等人以“alog.b”表示以a为底的b的对数,此后经过逐渐改进演变,就成了现代数学上的表示形式。
对数于十七世纪中叶由穆尼格引入中国。
十七世纪初,薛凤祚的《历学会通》有“比例数表”(1653年,也称“比例对数表”),称真数为“原数”,称对数为“比例数”。
《数理精蕴》中则称作对数比例:“对数比例乃西士若往·纳白尔所作,以借数与真数对列成表,故名对数表”。
此后在我国便都约定俗成,称作对数了。
对数的故事你在对数新课里讲过对数发明的故事吗?1614年,英国数学家纳皮尔(J. Napier, 1550~1617)出版《奇妙的对数表》一书。
在前言里,纳皮尔告诉我们他发明对数的动机:“没有什么比大数的乘、除、开平方或开立方运算更让数学工作者头痛、更阻碍计算者的了。
这不仅浪费时间,而且容易出错。
因此,我开始考虑怎样消除这些障碍。
经过长期的思索,我终于找到了一些漂亮的简短法则……”对数发明后,人们(特别是天文学家)的计算量大大减少。
200年后,法国著名数学家拉普拉斯(P. -S. Laplace, 1749~1827)评价说,由于对数的发现,“天文学家的寿命增加了一倍。
”韦达纳皮尔1614年,英国数学家、伦敦格雷沙姆(Gresham)学院首任几何学教授布里格斯(H. Briggs, 1561~1630)阅读了纳皮尔的《奇妙的对数表》。
此前,布里格斯正从事天文学研究,繁重的天文计算正是他试图克服的困难。
因此,纳皮尔的对数著作深深地吸引了他。
在翌年3月10日写给朋友詹姆斯·乌歇尔(James Ussher)的信中,布里格斯这样写道:“Markinston的纳皮尔爵士出版了一部著作,包含了他新发明的奇妙对数。
我希望今夏与他见面,因为我从未见到过一本能让我如此快乐,令我如此惊奇的书。
”布里格斯从伦敦到爱丁堡去见纳皮尔是1615年夏天的事。
那时,从伦敦到爱丁堡,乘坐马车至少需要4天,不象今天,坐火车只需4小时。
当时的旅途也比我们想象得要困难得多:布里格斯没能在约定时间赶到爱丁堡。
一天,纳皮尔在自己家中与朋友马尔(John Marr)谈起布里格斯:“哦!约翰,”纳皮尔说,“布里格斯今天不会来了。
”话音刚落,有人敲门。
马尔急忙下楼开门,使他高兴的是,来人正是布里格斯。
他把客人带到爵士的房间里。
纳皮尔与布里格斯互相仰慕地打量了几乎一刻钟,双方不发一言。
最后,布里格斯开了口:“我的爵士先生,这次远道而来,是专程拜望您的,并想向您了解您一开始是如何想到对数这一精彩的天文学辅助工具的。
在您作出这一发现之前,没有其他人发现过,而现在人们知道它是如此容易。
”爱丁堡会面后,纳皮尔和布里格斯共同商定以10为对数的底,且以0作为1的对数。
1617年,布里格斯出版了前1000个正整数的14位常用对数表。
1624年,又出版从1到20,000以及从90,000到100,000的14位常用对数表。
……纳皮尔对数(尼加拉瓜,1971)原来对数如此有用,对数的发明原来如此激动人心!在历史的解说中,对数早已不再是枯燥无味的概念。
少年智则国智,少年富则国富,少年强则国强,少年独立则国独立,少年自由则国自由,少年进步则国进步,少年胜于欧洲,则国胜于欧洲,少年雄于地球,则国雄于地球。