时间测量中随机误差的分布规律
- 格式:doc
- 大小:240.50 KB
- 文档页数:4


第2章1.传递函数是指零初始条件下输出量的拉普拉斯变换与输入量的拉普拉斯变换之比。
(√)2.传递函数既描述了系统的动态性能,也说明了系统的物理结构。
(×)3.幅频特性和相频特性共同表达了测量系统的频率响应特性。
4.测量系统的动态特性一般可以从时(间)域和频(率)域两方面进行分析。
5.用试验测定动态参数的方法有频率响应法、阶跃响应法、随机信号法。
6.测量系统的输出量与输入量之间关系可采用传递函数表示,试说明串联环节、并联环节及反馈联接的传递函数的表示方法。
答:串联环节:并联环节:正反馈环节:负反馈环节:7.试述测量系统的动态响应的含意、研究方法及评价指标。
答:含义:在瞬态参数动态测量中,在瞬态参数动态测量中,要求通过系统所获得的输出信号能准确地重现输入信号要求通过系统所获得的输出信号能准确地重现输入信号的全部信息,而测量系统的动态响应正是用来评价系统正确传递和显示输入信号的重要指标。
研究方法:研究方法:对测量系统施加某些已知的典型输入信号,包括阶跃信号、对测量系统施加某些已知的典型输入信号,包括阶跃信号、对测量系统施加某些已知的典型输入信号,包括阶跃信号、正弦信号、正弦信号、正弦信号、脉冲脉冲信号、斜升信号,通常是采用阶跃信号和正弦信号作为输入量来研究系统对典型信号的响应,以了解测量系统的动态特性,以此评价测量系统。
评价指标:稳定时间t s 、最大过冲量A d 。
8. 8. 某一力传感器拟定为二阶系统,其固有频率为某一力传感器拟定为二阶系统,其固有频率为800Hz 800Hz,阻尼比为,阻尼比为0.140.14。
问使用该传感器。
问使用该传感器)()()()()()()()()(21s H s H s Z s X s Y s Z s X s T s H ===)()()()()()()()(2121s H s H s X s Y s Y s X s Y s H +=+==)()(1)()()()(s H s H s H s X s Y s H B A A -==)()(1)()()()(s H s H s H s X s Y s H B A A +==作频率为400Hz 正弦变化的外力测试时,其振幅和相位角各为多少?正弦变化的外力测试时,其振幅和相位角各为多少?解:解:(())2222411⎪⎪⎭⎫ ⎝⎛+⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-=n n A ωωξωωω()222280040014.0480040011⎪⎭⎫ ⎝⎛⨯+⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-=31.1≈ ()212⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-=n n arctg ωωωωξωϕ2800400180040014.02⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛⨯⨯-=arctg 610-≈9. 9. 用一阶系统对用一阶系统对100Hz 的正弦信号进行测量时,如果要求振幅误差为10%10%以内,时间常数以内,时间常数应为多少?如果用该系统对50Hz 的正弦信号进行测试,其幅值误差和相位误差为多少?的正弦信号进行测试,其幅值误差和相位误差为多少? 解:(1)%10)2100(111)(111)(1)(22≤⨯+-=+-=-=∆πτωτωωA A 则 s 41071.7-⨯≤τ(2)%81.2)1071.7250(111)(111)(1)(242≤⨯⨯⨯+-=+-=-=∆-πωτωωA A τ取7.717.71××10-4时,时, ︒-=⨯⨯⨯-=-=-62.13)1071.7250()(24πωτωϕarctg arctg相位误差小于等于13.6213.62°°10. 10. 用传递函数为用传递函数为1/(0.0025s +1)+1)的一阶系统进行周期信号测量。

实验名称:时间测量中随机误差的分布规律实验目的:用常规仪器(如电子秒表,频率计等)测量时间间隔,通过对时间和频率测量的随机误差分布,学习用统计方法研究物理现象的过程和研究随机误差的分布规律。
实验器材及规格:秒表0.01s实验原理:1常用时间测量仪器的简要原理:机械节拍器:由齿轮带动摆做周期性运动,摆动周期可以通过改变摆锤的位置来连续调节。
电子节拍器:由石英晶体震荡器,计数器,译码器,电源,分档控制及显示部分组成。
按一定频率发出有规律的声音和闪光。
电子秒表:机心由CMOS集成电路组成,石英晶体震荡器做时标,一般用6位液晶数字显示。
连续累积时间59min,59.99s,分辨频率为0.01s。
V AFN多用数字测试仪:由PMOS集成元件和100kHs石英晶体震荡器构成。
可测量记数,震动,累计,速度,加速度,碰撞,频率,转速,角速,脉宽等。
时标由DC10集成电路和100kHs石英晶体震荡器构成。
2在不考虑系统误差的前提下,用时间测量仪器,测量同一时间N次,统计时间分布规律,并且分析误差。
当N趋于无穷时,各测量值出现的概率密度可用正态分布的概率密度函数表示:221()/21()niiX Xf x eσ=⎡⎤--⎢⎥⎢⎥⎣⎦∑=平均值计算公式:1/niiX X n==∑标准差计算公式:Xσ=(1)统计直方图方法在一组等精度测量的N个结果中,找出最大最小值,再有此得到极差max minR X X=-。
将极差分为K 个部分。
每个区间长度x ∆MAX MINX X R x K K-∆== 将落在每个区间的次数称为频数,i n N 称为频率。
最后以X 为横轴i nN为纵轴做图。
(2)密度分布曲线利用直方图中得到的概率密度值,以概率密度值为纵坐标,x 为横坐标可的密度分布曲线,数据处理:最小值min 1.76X s=最大值m a x 2.15X s=平均值 1.96X s =标准差0.072sσ=0.0051s Ua σ==因为人反应时间约为0.2s,秒表仪器误差约为0.01s,所以取 B 类不确定度B ∆0.95t =1.96 , 0.95k =1.96.误差合成:0.13s U ==P ≥0.95测量结果 ()1.960.13T s =± P ≥0.95图表统计如下:取区间数K=15,区间长0.028s 。

实验报告:时间测量中随机误差的分布规律张贺PB07210001一、实验题目:时间测量中随机误差的分布规律二、实验目的:用常规仪器(如电子秒表、频率计等)测量时间间隔,通过对时间和频率测量的随机误差分布,学习用统计方法研究物理现象的过程和研究随机误差分布的规律。
三、实验仪器:电子秒表、机械节拍器四、实验原理:1.常用时间测量仪表的简要原理:(1)机械节拍器:由齿轮带动摆做周期性运动,摆动周期可以通过改变摆锤的位置连续调节。
(2)电子节拍器:由石英晶体振荡器、计数器、译码器、电源和分档控制及显示部分组成。
电子节拍器按一定的频率发出有规律的声响和闪光,声、光节拍范围为 1.5~0.28846s,分为39挡,各挡发生和闪光的持续时间约为0.18s。
(3)电子秒表:兼有数种测时功能(秒、分、时、日、月和星期),便于携带和测量的常用电子计时器。
电子秒表机芯由CMOS 集成电路组成,用石英晶体振荡器作时标,一般用六位液晶数字显示,其连续积累时间数为59min59.99s 。
分辨率为0.01s ,平均日差0.5s 。
(4) V AFN 多用数字测试仪:由PMOS 集成元件和100kHz 石英晶体振荡器构成。
可测量计数、振动、累计、速度、加速度、碰撞、频率、转速、角速、脉宽。
时标:由DC10集成电路和100kHz 石英晶体振荡器组成。
电路可直接输出0.01ms ,0.1ms ,1ms ,10ms ,0.1s ,1s 六挡方波脉冲作为时标信号和闸门时间。
石英晶体振荡器的稳定度为1.2×105-s/d ;频率测量范围1Hz~100kHz ;电信号输入幅度为300mV 。
2. 统计分布规律的研究:假设在近似消除了系统误差(或系统误差很小,可忽略不计,或系统误差为一恒定值)的条件下,对某物理量x 进行N 次等精度测量,当测量次数N 趋向无穷大时,各测量值出现的概率密度分布可用正态分布(又称高斯分布)的概率密度函数表示,]2)(exp[21)(22--=σπσx x x f (1)式中x 为测量的算术平均值,σ为测量列的标准差,nxx ni i∑==1(2)1)(12--=∑=n x x ni i σ (3)⎰-=aadx x f a P )()( (4)式中a=σ,2σ,3σ. (1) 统计直方图方法统计直方图是用实验研究某一物理现象统计分布规律的一种直观的方法。

第1章绪论一、填空题1.几何参数互换性功能互换性2.完全互换不完全互换不完全互换3.误差检测4.基础标准产品标准方法标准安全和环境保护标准5.R5 R10 R20 R40 先疏后密R80 参数分级很细或基本系列中的优先数不能适应实际情况二、选择题1.ABCD 2.A B 3.B三、判断题1.×2.×3.√4.√四、问答题1.什么是互换性?互换性在机械设计与制造中的意义如何?答:互换性是指在同一规格的一批零件或部件中,任取其一,不需任何挑选、调整或修配(如钳工修理)就能装在机器上,达到规定的性能要求。
互换性给产品的设计、制造、使用和维修都带来了很大的方便。
(1)设计方面从设计方面看,由于采用按互换性原则设计和生产的标准零件和部件,可以简少绘图、计算等设计工作量,缩短设计周期,提高设计的可靠性,有利于产品的多样化和计算机辅助设计。
(2)制造方面从制造方面看,互换性有利于组织大规模专业化生产,有利于采用先进的工艺和高效的专用设备,有利于实现加工和装配过程的机械化、自动化。
互换性与测量技术(3)使用和维修方面从使用和维修方面看,具有互换性的零部件在磨损或损坏后可以及时更换,因而减少了机器的维修时间和费用,可保证机器工作的连续性和持久性,提高了机器的使用价值。
因此,互换性对保证产品质量、提高生产率、降低产品成本、降低劳动强度等方面均具有重要意义,它已成为现代机械制造业中一个普遍遵循的原则。
2.完全互换和不完全互换有何区别?答:完全互换是指在零部件装配或更换时,不需要选择、调整或修配,就可以达到预定的装配精度要求。
例如,常见的螺栓、螺母等标准件的互换性就属于完全互换。
不完全互换是指在装配前需要将零部件预先分组或在装配时需要进行少量修配调整才能达到装配精度的要求。
例如,拖拉机、汽车的活塞销和活塞销孔装配时的分组法装配、减速机轴承盖装配时的垫片厚度调整法装配等都属于不完全互换。
3.按级别分,标准可分为哪几类?答:按级别分,我国的标准可分为国家标准、行业标准、地方标准和企业标准四级。

实验报告05级 少年班 陈晨 Pb05000827实验题目:单摆的设计和研究实验目的:利用经典的单摆公式,给出的器材和对重力加速度g 的测量精度的要求,进行简单的设计性实验基本方法的训练学会应用误差均分原则选用适当的仪器和测量方法,学习积累放大法的原理及应用。
实验仪器:实验室提供以下器材(及参数):游标卡尺、米尺、千分尺、电子秒表、支架、细线(尼龙线)、钢球、摆幅测量标尺(提供硬白纸板自制)、天平(公用)。
假设摆长l ≈70.00cm ;摆球直径D ≈2.00cm ;摆动周期T ≈1.700s ;米尺精度Δ米≈0.05cm ;卡尺精度Δ卡≈0.002cm ;千分尺精度Δ千≈0.001cm ;秒表精度Δ秒≈0.01s ;根据统计分析,实验人员开、停秒表总的反映时间近似为Δ人≈0.2s 。
实验原理:单摆结构如图,当摆角充分小(一般θ<5○)摆球直径充分短(相对于摆线)时,单摆的一级近似周期公式为 glT π2= 因此通过测量摆动周期T ,摆长L 可得224T Lg π=实验内容:1、 用误差均分原理设计一单摆装置,测量重力加速度g ,设计要求:(1) 根据误差均分原理,自行设计实验方案,合理选择测量仪器和方法。
(2) 写出详细的推导过程,实验步骤。
(3) 用自制的单摆装置测量重力加速度g ,测量精度要求%1<∆gg。
2、对重力加速度g 的测量结果进行误差分析和数据处理,检验实验结果是否达到设计要求。
实验设计:以下利用误差均分原理设计一套单摆装置,测量重力加速度g ,测量精度要求%1<∆gg。
由于glT π2=,所以224T L g π=取对数 T L g ln 2ln 4ln ln 2-+=π 求微分TdTL dL g dg 2-= 按最大不确定度公式估算,有TTL L g g ∆+∆=∆2 应用均分原理%5.0≤∆L L ,%5.02≤∆TT将摆长L 和摆球直径D 的粗测值cm l 00.70≈,cm D 00.2≈代入,有 cm l 35.0≤∆和cm D 01.0≤∆结合器材精度参数考虑,选用精度足够的米尺测摆线长,游标卡尺测小球直径。

实验报告实验名称 时间测量中随机误差的分布规律实验目的 用常规仪器(如电子秒表、频率计等)测量时间间隔,通过对时间和频率测量的随机误差分布,学习用统计方法研究物理现象的过程和研究随机误差分布的规律。
实验仪器 机械节拍器,电子秒表。
实验原理 1.常用时间测量仪表的简要原理(1)机械节拍器(2)电子节拍器 (3)电子秒表(4)VAFN 多用数字测试仪用电子秒表测量机械节拍器发声的时间间隔,机械节拍器按一定的频率发出有规律的声响,电子秒表用石英晶体振荡器作时标,一般用六位液晶数字显示,其连续积累时间为59min59.99s,分辨率为0.01s,平均日差0.5s 。
2.统计分布规律的研究假设在近似消除了系统误差(或系统误差很小,可忽略不计,或系统误差为一恒定值)的条件下,对某物理量x 进行N 次等精度测量,当测量次数N 趋向无穷时,各测量值出现的概率密度分布可用正态分布(有成高斯分布)的概率密度函数表示,]2)x -(x ex p[-21)(22σπσ=x f (1) 其中 nxx n1i i∑==(2)1-n )x -(xn1i 2i∑==σ (3)⎰=aa-f(x)dx P(a) (4)式中a=σ,2σ,3σ分别对应不同的置信概率。
(1)统计直方图方法用统计直方图表示被研究对象的规律简便易行,直观清晰。
在一组等精度测量所得的N 个结果x 1,x 2,…,x N 中,找出它的最大值x max 与最小值x min ,并求出级差R=x max - x min ,由级差分为K 个小区间,每个小区域的间隔(△x )的大小就等于Kx -x K R minmax =。
统计测量结果出现在某个小区域内的次数n i 称为频数,Nni 为频率,Nni∑为累计频率,称为频率密度。
以测量值x 值为横坐标,以xN n i∆⋅为纵坐标,便可得到统计直方图。
(2)概率密度分布曲线利用式(1)求出各小区域中点的正态分布的概率密度值f (x ),以f (x )为纵坐标,x 为横坐标,可得概率密度分布曲线。

时间测量中随机误差的分布规律PB06210273 张成实验名称:时间测量中随机误差的分布规律实验目的:用常规仪器(如电子秒表、频率计等)测量时间间隔,通过对时间和频率的测量的随机误差分布,学习用统计法研究物理现象的过程和研究随机误差的分布规律。
实验原理:1、 常用时间测量仪器的简要原理:① 机械节拍器由齿轮带动摆动作周期性运动。
② 电子节拍器按一定的频率发出有规律的声响和闪光。
③ 电子秒表机芯有CMOS 集成电路组成,用石英晶体振荡器作时标。
④ VAFN 多用数字测试仪由PMOS 集成元件和100KHz 石英晶体振荡器构成,可测量计数、振动、累计、速度、加速度、碰撞、频率、转速、角速脉宽等物理量。
2、 统计分布规律的研究正态分布概率密度函数:()]2exp[21)(22σπσxx x f --=nxx ni i∑==1,()112--=∑=n x x ni iσ , ⎰-=aadx x f a P )()(① 统计直方图法:计算试验数据的极差min max x x R -=,每小区域的间隔:Kx x K R x minmax -==∆ 频数i n ,相对频数%/)/(N n i ,累计频数%/)/(∑N n i ,频率密度xN n i∆⋅ ② 概率密度分布曲线:以)(x f 为纵坐标,x 为横坐标,可得概率密度分布曲线。
实验内容:用电子秒表测量电子节拍器的周期,共测量150次,每次测量3个周期的时长。
数据处理:s nxx ni i213.415091.6311===∑= s n x xni i0.0981)(12=--=∑=σ 测量结果的不确定度:A 类不确定度(95.0=p )s nu a 008.0==σ95.0=p ,96.1=t ,s u t a p 016.0008.096.1=⨯=B 类不确定度:s s s B 2.001.02.0=,,=,=估仪估仪估∆=∆∴∆>>∆∆∆12.03=∆=BB u 测量值的合成标准不确定度:s u u U B A 12.022=+=数据中93.3min =x ,44.4max =x ,所以级差51.0min max =-=x x R 。

测量技术基础机械加工车间工作的机械加工工人必须掌握的多种测量技术,量具、量仪以游标卡尺、千分尺、和百分表为主。
对于某一测量对象,一般有多种测量技术可供选择,而某一种测量技术又往往可用于不同的测量对象。
用于同一测量对象,不同测量技术的效果可能大致相同,也可能大不相同。
按照测量的进行方式,测量技术可分为以下两种。
①直接比较测量技术:在测量中,将被测量与已和其值的同一种量相比较。
其测量不确定度主要取决于标准量值的不确定度和比较器的灵敏度和分辨力,它可克服由于测量装置的动态范围不够和频率响应不好所引入的非线性误差。
替代法、换位法等属于这一类。
②非直接比较测量技术:不是将被测量的全值与标准量值相比较的比较测量。
微差法、符合法、补偿法、谐振法、衡消法等属于这一类。
在建立计量标准的测量中,经常采用基本测量技术,即绝对测量技术。
这是通过对有关的基本量的测量来确定被测量值。
其测量不确定度一般是通过实验、分析和计算得出,精度高,但所需装置复杂。
第一讲概述课题:1. 测量技术的概念2. 长度基准与尺寸传递3.量块的基本知识4.形位公差值及有关规定课堂类型:讲授教学目的:1.了解测量技术的基本概念及尺寸传递2.重点掌握量块的使用方法。
教学重点:量块的使用方法。
教具:量块教学方法:例举习题讲解量块的使用,使学生掌握其主要内容教学过程:一、引入新课题由提问学生长度单位的意义引入新课.二、教学内容4.1 概述4.1.1测量技术的概念1.测量是指为确定被测量值而进行的一组操作过程。
其实质是将被测的量L与具有计量单位的标准量E进行比较,从而确定比值q的过程,即q= L/E测量过程包括以下四个要素:(1)测量对象主要指几何量,包括长度、角度、表面形状和位置误差、表面粗糙度以及螺纹、齿轮的各种参数等。
(2)计量单位长度单位为米(m),在机械制造中常用单位为毫米(mm)、微米(μm);角度单位是弧度(rad),实用中常以度(°)、分(′)、秒(″)为单位。

核科学技术学院 2010 级 学号 PB10214023 姓名 张浩然 日期 2011-3-24时间测量中的随机误差分布规律PB10214023 张浩然一、实验题目:时间测量中的随机误差分布规律二、实验目的:同常规仪器测量时间间隔,通过对时间和频率测量的随机误差分布,学习用统计方法研究物理现象的过程和研究随机误差分布的规律。
三、实验仪器:电子秒表、机械节拍器四、实验原理:1、仪器原理机械节拍器能按一定频率发出有规律的声响,前者利用齿轮带动摆作周期运动,后者利用石英晶体的振荡完成周期运动;电子秒表用石英晶体振荡器作时标测时,精度可达0.01s ; 2、统计分布规律原理在近似消除了系统误差的前提下,对时间t 进行N 次等精度测量,当N 趋于无穷大时,各测量值出现的概率密度分布可用正态分布的概率密度函数表示:222)(21)(σπσx x ex f --=其中n x x ni i∑==1,为测量的算术平均值,1)(12--=∑n x xniσ,为测量列的标准差,有 ⎰-=aa dxx f a P )()(,σσσ3,2,=a利用统计直方图表示测量列的分布规律,简便易行、直观明了。
在本实验中利用f(x)得到概率密度分布曲线,并将其与统计直方图进行比较,在一定误差范围内认为是拟合的,可认为概率密度分布基本符合正态分布,其中的误差是由于环境、仪器、人的判断误差、N 的非无穷大等所决定的。
五、实验步骤:1、检查实验仪器是否能正常工作,秒表归零;2、将机械节拍器上好发条使其摆动,用秒表测量节拍器四个周期所用时间,在核科学技术学院2010 级学号PB10214023 姓名张浩然日期2011-3-24等精度条件下重复测量约200次(本实验中实际测量224次),记录每次的测量结果;3、对数据进行处理(计算平均值、标准差、作出相应图表、误差分析等);六、数据处理:1.实验数据如下:(单位:s)初步分析得2.由公式(2)(3)计算得: (单位:s)x=平均值 2.415σ=标准差0.1198473.机械节拍器的频数和频率密度分布:令K=16核科学技术学院 2010 级 学号 PB10214023 姓名 张浩然 日期 2011-3-24有 0max min ()/0.04625x x x K ∆=-= (单位:s ) 取max min ()/0.05x x x K ∆=-=(单位:s )有测量数据的频数和频率密度分布表如下: 小区域/s 小区域中点值/s 频数i n /s 相对频数(/)/%i n N累计频数(/)/%i n N ∑1.95-2.20 1.975 1 0.446428571 0.446428571 2.20-2.05 2.025 1 0.446428571 0.892857143 2.05-2.10 2.075 1 0.446428571 1.339285714 2.10-2.15 2.125 3 1.339285714 2.678571429 2.15-2.20 2.175 2 0.8928571433.571428571 2.20-2.25 2.225 7 3.1256.696428571 2.25-2.30 2.275 177.589285714 14.28571429 2.30-2.35 2.325 31 13.83928571 28.125 2.35-2.40 2.375 28 12.540.6252.40-2.45 2.425 44 19.64285714 60.26785714 2.45-2.50 2.475 26 11.60714286 71.875 2.50-2.55 2.525 35 15.625 87.5 2.55-2.60 2.575 14 6.2593.752.60-2.65 2.625 10 4.464285714 98.21428571 2.65-2.70 2.675 3 1.339285714 99.55357143 2.70-2.752.72510.4464285711004.统计直方图和概率密度分布曲线图像:核科学技术学院 2010 级 学号 PB10214023 姓名 张浩然 日期 2011-3-245.不确定度分析:0.950.015694973s A U t n==对于电子秒表,人的反应时间为0.2s ,远大于0.01s ,则取B ∆=∆估;对于秒表,取C=3。
随机误差1定义随机误差(又称偶然误差)是指测量结果与同一待测量的大量重复测量的平均结果之差。
“同一待测量的大量重复测量的平均结果”指在重复条件下得到待测量的期望值或所有可能测得值的平均值。
它的特点:大小和方向都不固定,也无法测量或校正。
随机误差的性质是:随着测定次数的增加,正负误差可以相互抵偿,误差的平均值将逐渐趋向于零。
2特征即使测试系统的灵敏度足够高,在相同的测量条件下,对同一量值进行多次等精度测量时,仍会有各种偶然的,无法预测的不确定因素干扰而产生测量误差,其绝对值和符号均不可预知。
虽然单次测量的随机误差没有规律,但多次测量的总体却服从统计规律,通过对测量数据的统计处理,能在理论上估计起对测量结果的影响。
随机误差不能用修正或采取某种技术措施的办法来消除。
3产生因素其产生因素十分复杂,如电磁场的微变,零件的摩擦、间隙,热起伏,空气扰动,气压及湿度的变化,测量人员的感觉器官的生理变化等,以及它们的综合影响都可以成为产生随机误差的因素。
统计学概念4抽样误差在随机误差中,最重要的是抽样误差。
我们从同一总体中随机抽取若干个大小相同的样本,各样本平均数(或平均率)之间会有所不同。
这些样本间的差异,同时反映了样本与总体间的差异。
它是由于从总体中抽取样本才出现的误差,统计上称为抽样误差(或抽样波动)。
例如,抽样误差在医学生物实验中最主要的来源是个体的变异。
所以这是一种难以控制的、不可避免的误差。
但抽样误差是有一定规律的。
研究和运用抽样误差的规律,是根据样本估计总体时所必须领会的基本概念之一,也是医学统计学的重要内容之一。
5实验误差随机误差中还包括重复误差。
它是由于对同一受试对象或检样采用同一方法重复测定时所出现的误差。
如用天平称同一个烧杯的重量,重复测定多次,其结果会有某些波动。
控制重复误差的手段主要是改进测定方法,提高操作者的熟练程度。
重复是摸清实验误差大小的手段,以便分析和减少实验误差。
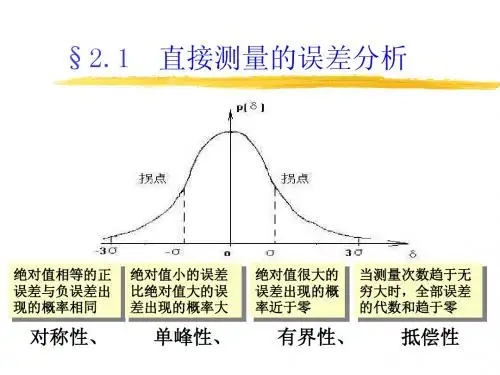
6统计规律测量值的随机误差分布规律有正态分布、t分布、三角分布和均匀分布等,但测量值大多数都服从正态分布,在此主要以正态分布为主进行介绍。
1: 电子计数器的测频误差包括____误差和____误差。
±1量化、标准频率2: 频率计除测频、测周外,扩展功能有测频率比、测时间间隔、测相位差、自检3: 在测量周期时的主要误差有:____ 和____ 。
通用计数器采用较小的____可以减小±1误差的影响。
量化误差、标准频率误差、频标4: 在测量周期时,为减少被测信号受到干扰造成的转换误差,电子计数器应采用多周期测量法。
5: 采用电子计数器测频时,当被计数频率一定时,____可以减小±1误差对测频误差的影响;当闸门时间一定时,____,则由±1误差产生的测频误差越大。
增大闸门时间、被计数频率越低6: 在进行频率比测量时,应将____的信号加在B通道,取出____(周期倍乘为1)作为计数的闸门信号,将____ 的信号加在A通道,作为被计数的脉冲。
频率较低、一个周期、频率较高;7: 一个信号源频率实际值和其标准值的相对偏差定义为____ , 而把信号源频率变化的不确定性定义为频率准确度、频率稳定度8: 在测量阿仑方差时,其采样方法与标准的偏差不同,它的两次相邻测量之间是连续的。
二、判断题:1: 一个频率源的频率稳定度愈高,则频率准确度也愈高。
(错)2: 当被测频率大于中界频率时,宜选用测周的方法;当被测频率小于中界频率时,宜选用测频的方法。
(错)3: 当计数器进行自校时,从理论上来说不存在±1个字的量化误差。
(对)4: 在测量低信噪比信号的周期时,计数器通常采用周期倍乘,这主要是为了克服±1误差的影响。
( 错) 5: 用计数器直接测周的误差主要有三项:即量化误差、触发误差以及标准频率误差。
(对)6: 使用模拟内插法和游标法不能从根本上来消除±1个字的量化误差。
(对)7: 标准频率的相对不确定度应该比±1误差引起的测频误差小一个量级。
(对)三、选择题:1、在通用计数器测量低频信号的频率时,采用倒数计数器是为了( D)A.测量低频周期B.克服转换误差C.测量低频失真D.减小测频时的量化误差影响2、用于电子计数器中的高精度晶体振荡器,通常采取了____措施。
随机误差项
随机误差项是指在实验或调查中,由于不可避免的偶然因素导致的测量误差。
这些误差可能来自于仪器的精度、实验操作的不稳定性、被测量对象的不确定性等因素。
由于随机误差的存在,同一实验在不同时间或不同人员进行时,测量结果可能存在一定程度的差异。
随机误差通常是在大量重复实验中出现的,它们的分布是随机的,符合正态分布或类似正态分布的分布。
在统计学中,我们通常采用均值和标准差来描述随机误差的规律性。
当均值接近0时,说明随机误差的平均值为0,而标准差越小,说明随机误差越小,即实验结果越稳定。
为了减小随机误差的影响,我们可以采取多种方法,如增加数据量、提高实验设备的精度、改善实验操作等。
当然,我们也可以通过数据分析的方法来探究随机误差的影响,比如采用方差分析等方法,以便更好地理解实验结果的可靠性和精度。
- 1 -。
实验报告
实验题目:时间测量中随机误差的分布规律
实验目的:用常规仪器(如电子秒表、频率计等)测量时间间隔,通过对时间和频率测量的
随机误差分布,学习用统计方法研究物理现象的过程和研究随机误差分布的规律。
实验原理:1. 常用时间测量仪表的简要原理
(1) 机械节拍器 (2) 电子节拍器 (3) 电子秒表
(4) V AFN 多用数字测试仪的性能
2. 统计分布规律的研究
在近似消除了系统误差的条件下,对某物理量进行等精度测量,当次数趋向无穷时,各测量值出现的概率密度分布可用正交分布函数表示: 正态分布概率密度函数
]2)x -(x ex p[-21
)(2
2
σπ
σ=x f (1) 其中 n
x
x n
1
i i
∑== (2)
1
-n )x -(x
n
1
i 2
i
∑==
σ (3) ⎰
=a
a
-f(x)dx P(a) (4) 式中a=σ,2σ,3σ
(1) 统计直方图法
在一组等精度测量所得的N 个结果x 1,x 2,…,x N 中,找出其最大值与最小值,并求出级差R=x max -x min ,由级差分为K 个小区间,每个小区域的间隔
(△x )的大小就等于
K
x -x K R min
max =。
结果出现在某个小区域内的次数n i 称为频数,则
N
n i 为频率,
N n i ∑为累计频率,x N n i ∆⋅称为频率密度。
(2) 利用式(1)求出各小区域中点的正态分布的概率密度值f (x ),以f (x )为
纵坐标,x 为横坐标,可得概率密度分布曲线。
实验内容:1. 时间间隔测量:用电子秒表测量机械节拍器的摆动周期或电子节拍器的周期。
2. 统计概率研究:时间测量均要求在相同条件下,重复测量200次以上。
(1)计算结果的x 和σ
(2)计算各区中点的f (x )
(3)合理划分小区间数K ,并确定其间隔,计算各区间的频率、相对频率、相
对频率密度和累计频率,以频率密度为纵坐标,测量值x 为横坐标,作统计
直方图,并将f(x)—x中曲线绘在统计直方图中,检验测量值分布是否符
合正态分布。
(4)计算测量列误差出现在±σ,±2σ,±3σ范围内的概率。
(5)计算测量平均值的标准差,并正确写出测量结果完整的表达式。
x max=4.02 x min=3.60 R=0.42 K=15 △x=0.03
节拍器的频数和频率密度分布
小区域/s 小区域中点
值/s
频数n i
相对频数
(n i /N)/%
累计频数
(∑n i/N)/%
频率密度
n i/(N*△x)
3.59 3.62 3.60510.50.50.16667 3.62 3.65 3.6353 1.520.5 3.65 3.68 3.6655 2.5
4.50.83333 3.68 3.71 3.6959 4.59 1.5
3.71 3.74 3.725 8 4 13 1.33333 3.74 3.77 3.755 20 10 23 3.33333 3.77 3.8 3.785 25 12.5 35.5
4.16667 3.8 3.83 3.815 27 13.5 49 4.5 3.83 3.86 3.845 31 1
5.5 64.5 5.16667 3.86 3.89 3.875 24 12 7
6.5 4 3.89 3.92 3.905 24 12 88.5 4 3.92 3.95 3.935 11 5.5 94 1.83333 3.95 3.98 3.965 5 2.5 96.5 0.83333 3.98 4.01 3.995 4 2 98.5 0.66667 4.01 4.04 4.025 3 1.5 100 0.5
=0.08149,x σ=u =0.00576。
05
10
15
20
25
30
n /N (%)
t (s)
统计直方图
试验结果分析:
根据公式得:
(1) A 类不确定度为:
s
n
u 00568.0==
σ
0.00576
(2) 测量列误差出现在],[σσ-、]2,2[σσ-、]3,3[σσ-范围内的概率分别为:
⎰=σ
σ
σ-f(x)dx )P(=0.683 )P(2σ=0.955 )P(3σ=0.997
(3) 对200组时间数据的处理
考虑置信概率P=0.95的情况, 电子秒表误差分布为正态分布,可取
95.0t =1.96 仪∆=0.01s c=3 s
n
u 00568.0==
σ
0.00576 B 类不确定度在0.95的置信概率下置信因子为k=1.96
由不确定度合成公式得
2
2
95095.0())
(仪。
c
k u t U At
∆+==0.008375 所以,
X=3.826t )0188.06147.4(±=0.008375 P=0.95
同样可求得
X=3.826t )0188.06147.4(±=0.004187 P=0.68 X=3.826t )0188.06147.4(±=0.01265 P=0.99
误差分析:
1、机械仪表的精确度不高,为系统误差
2、外界影响因素较多,会影响实验者的测量,难以保证完全等精度,造成人为实验误差
3、实验只进行200次,未达到无穷次,结果必定会偏离正态分布
思考题:
1、 若测量结果偏离正态分布,试分析产生偏离的主要因素。
a) 机械仪表的精确度不高,为系统误差
b) 外界影响因素较多,会影响实验者的测量,难以保证完全等精度,造成人为实
验误差
c) 实验只进行200次,未达到无穷次,结果必定会偏离正态分布
2、 在不考虑系统误差的条件下,对某一物理量进行多次等精度测量时随机误差的分布
有哪些特征?
中间多,两头少,中间对称
07物理系 PB07203143
王一飞 2008-4-3。