振动系统固有频率的测试实验报告

一、实验目的1、了解和熟悉共振前后利萨如图形的变化规律和特点；2、学习用“共振法”测试机械振动系统的固有频率（幅值判别法和相位判别法）；3、学习用“锤击法”测试机械振动系统的固有频率（传函判别法）；4、学习用“自由衰减振动波形自谱分析法”测试振动系统的固有频率（自谱分析法）。

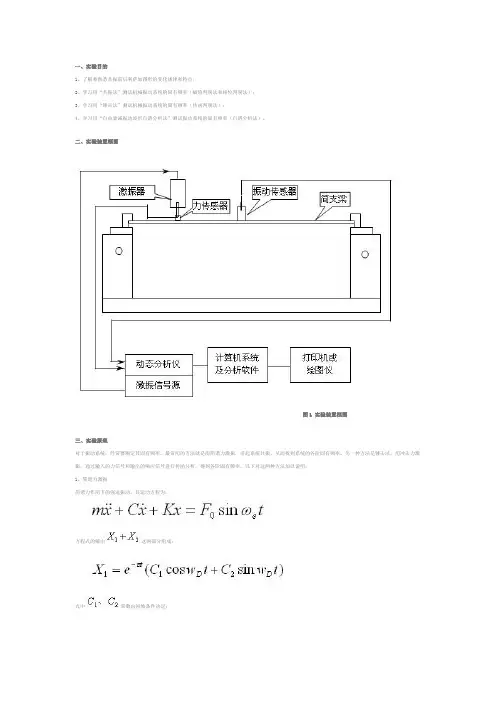
二、实验装置框图图1 实验装置框图三、实验原理对于振动系统，经常要测定其固有频率，最常用的方法就是用简谐力激振，引起系统共振，从而找到系统的各阶固有频率。

另一种方法是锤击法，用冲击力激振，通过输入的力信号和输出的响应信号进行传函分析，得到各阶固有频率。

以下对这两种方法加以说明：1、简谐力激振简谐力作用下的强迫振动，其运动方程为：方程式的解由这两部分组成：式中常数由初始条件决定：，其中：代表阻尼自由振动基，代表阻尼强迫振动项。

自由振动周期：，强迫振动项周期：由于阻尼的存在，自由振动基随时间不断得衰减消失。

最后，只剩下后两项，也就是通常讲的定常强动，即强迫振动部分：通过变换可写成：式中：，设频率比代入公式则振幅：，滞后相位角：因为为弹簧受干扰力峰值作用引起的静位移，所以振幅A可写成：其中称为动力放大系数：动力放大系数β是强迫振动时的动力系数即动幅值与静幅值之比。

这个数值对拾振器和单自由度体系的振动的研究都是很重要的。

当，即强迫振动频率和系统固有频率相等时，动力系数迅速增加，引起系统共振，由式：可知，共振时振幅和相位都有明显变化，通过对这两个参数进行测量，我们可以判别系统是否达到共振动点，从而确定出系统的各阶振动频率。

（一）幅值判别法在激振功率输出不变的情况下，由低到高调节激振器的激振频率，通过示波器，我们可以观察到在某一频率下，任一振动量（位移、速度、加速度）幅值迅速增加，这就是机械振动系统的某阶固有频率。

这种方法简单易行，但在阻尼较大的情况下，不同的测量方法的出的共振动频率稍有差别，不同类型的振动量对振幅变化敏感程度不一样，这样对于一种类型的传感器在某阶频率时不够敏感。

一、实验背景玻尔共振实验是物理学中研究共振现象的经典实验之一。

该实验通过测量受迫振动系统的固有频率和共振频率，来验证共振现象的存在，并分析实验过程中可能产生的误差。

二、实验目的1. 通过测量玻尔共振仪中弹性摆轮的固有频率，验证共振现象。

2. 分析实验过程中可能产生的误差，并提出改进措施。

三、实验原理玻尔共振实验是基于受迫振动原理进行的。

当驱动力的频率与系统的固有频率相匹配时，系统会出现共振现象，此时振幅达到最大值。

实验中，通过测量振幅和频率的关系，可以确定共振频率。

四、实验步骤1. 将玻尔共振仪放置在平稳的工作台上，调整摆轮的初始位置。

2. 开启驱动电源，逐渐增加驱动力的频率，观察振幅的变化。

3. 记录振幅最大时的频率值，即为共振频率。

4. 重复实验多次，取平均值作为最终结果。

五、实验结果与分析1. 固有频率测量结果通过实验测量，得到玻尔共振仪中弹性摆轮的固有频率为f0 = 1.435 Hz。

实验过程中，多次测量得到的固有频率基本一致，说明实验结果稳定。

2. 共振频率测量结果在驱动力的频率逐渐增加的过程中，振幅达到最大值时的频率即为共振频率。

实验中，共振频率测量结果为f1 = 1.435 Hz，与固有频率基本一致。

3. 误差分析（1）测量误差a. 频率测量误差：实验中，驱动力的频率是通过数字频率计测量的，频率计的精度为0.1 Hz。

因此，频率测量误差约为±0.1 Hz。

b. 振幅测量误差：实验中，振幅是通过目测法测量的，误差约为±5%。

（2）系统误差a. 玻尔共振仪本身存在一定的误差，如摆轮的质量、弹性系数等。

b. 驱动电源的稳定性对实验结果有一定影响。

六、改进措施1. 提高频率计的精度，降低频率测量误差。

2. 采用高精度的测振传感器，提高振幅测量的精度。

3. 选择质量分布均匀、弹性系数稳定的摆轮，降低系统误差。

4. 确保驱动电源的稳定性，减少电源对实验结果的影响。

七、结论玻尔共振实验结果表明，共振现象确实存在，且共振频率与固有频率基本一致。

物控环境振动的测量实验报告1.测量简支梁的固有频率和振型1.1实验目的用激振法测量简支梁的固有频率和固有振型。

掌握多自由度系统固有频和振型的简单测量方法。

1.2实验原理共振法测量振动系统的固有频率是比较常用的方法之一。

共振是指当激振频率达到某一特定值时，振动量的振动幅值达到极大值的现象。

本次试验主要利用调整激振频率使简支梁达到位移振动幅值的方法来测量简支梁的一阶，二阶以及三阶固有频率以及从计算机上读取其当时的振型！1.3实验内容与结果分析（1）将激振器通过顶杆连接到简支梁上（注意确保顶杆与激振器的中心线在一直线上），激振点位于简支梁中心偏左50mm处（已有安装螺孔），将信号发生器输出端分别与功率放大器和数据采集仪的输入端连接，并将功率放大器与激振器相连接。

（2）用双面胶纸（或传感器磁座）将加速度传感器A粘贴在简支梁上5#测点（实验时固定不动，用于与其他测点比较相位），将加速度传感器连接，将电荷放大器输出端与数据采集仪的输入端连接。

（3）将信号发生器和功率放大器的幅值旋钮调至最小，打开所有仪器电源。

打开控制计算机，打开做此次试验所需的测试软件，进入页面设置好各项参数。

通过调节激振频率，观察简支梁位置幅值振动情况。

可以通过放在简支梁上的装有一定量塑质小球的小型透明容器直观的观察里面小球的振动情况，小球振动越厉害，也就说明简支梁振动的位移幅值越大；还可以通过分辨简支梁在不同激振频率下的发出的振动声音，声音越大，说明振动幅值越大！（4）通过（3）中的方法，可以测量出在简支梁在某一激振频率范围内的振动幅值，则此激振频率就是我们需要测量的一阶，二阶以及三阶固有频率，在测出固有频率的同时将计算机上画出的各阶振型的图像保存，以便结果的分析。

（5）在完成所有的试验内容之后，通过记录下的实验数据分析实验的结果。

所得的实验结果如下：测得的简支梁的一阶、二阶以及三阶的固有频率为?=35.42HZ,?=131.54HZ,?3=258.01HZ。

振动实验报告讲解振动与控制系列实验姓名：李⽅⽴学号：201520000111电⼦科技⼤学机械电⼦⼯程学院实验1 简⽀梁强迫振动幅频特性和阻尼的测量⼀、实验⽬的1、学会测量单⾃由度系统强迫振动的幅频特性曲线。

2、学会根据幅频特性曲线确定系统的固有频率f 0和阻尼⽐。

⼆、实验装置框图图3.1表⽰实验装置的框图图3-1 实验装置框图KCX图3-2 单⾃由度系统⼒学模型三、实验原理单⾃由度系统的⼒学模型如图3-2所⽰。

在正弦激振⼒的作⽤下系统作简谐强迫振动，设激振⼒F 的幅值B 、圆频率ωo(频率f=ω／2π)，系统的运动微分⽅程式为：扫频信号源动态分析仪计算机系统及分析软件打印机或绘图仪简⽀梁振动传感器激振器⼒传感器质量块M或 M F x dt dxdt x d M F x dt dx n dtx d FKx dt dx C dtx d M /2/222222222=++=++=++ωξωω（3-1）式中：ω—系统固有圆频率ω =K/Mn ---衰减系数 2n=C/M ξ---相对阻尼系数ξ=n/ωF ——激振⼒ )2sin(sin 0ft B t B F πω== ⽅程①的特解，即强迫振动为：)2sin()sin(0?π?ω-=-=f A A x （3-2）式中：A ——强迫振动振幅--初相位20222024)(/ωωωn M B A +-=（3-3）式(3-3)叫做系统的幅频特性。

将式(3-3)所表⽰的振动幅值与激振频率的关系⽤图形表⽰，称为幅频特性曲线(如图3-3所⽰)：3-2 单⾃由度系统⼒学模型 3-3 单⾃由度系统振动的幅频特性曲线图3-3中，Amax 为系统共振时的振幅；f 0为系统固有频率，1f 、2f 为半功率点频率。

振幅为Amax 时的频率叫共振频率f 0。

在有阻尼的情况下，共振频率为：221ξ-=f f a (3-4) 当阻尼较⼩时，0f f a =故以固有频率0f 作为共振频率a f 。

机械振动实验报告1.测量简支梁的固有频率和振型1.1实验目的用激振法测量简支梁的固有频率和固有振型。

掌握多自由度系统固有频和振型的简单测量方法。

1.2实验原理共振法测量振动系统的固有频率是比较常用的方法之一。

共振是指当激振频率达到某一特定值时，振动量的振动幅值达到极大值的现象。

本次试验主要利用调整激振频率使简支梁达到位移振动幅值的方法来测量简支梁的一阶，二阶以及三阶固有频率以及从计算机上读取其当时的振型！1.3实验内容与结果分析(1)将激振器通过顶杆连接到简支梁上（注意确保顶杆与激振器的中心线在一直线上），激振点位于简支梁中心偏左50mm处（已有安装螺孔），将信号发生器输出端分别与功率放大器和数据采集仪的输入端连接，并将功率放大器与激振器相连接。

(2)用双面胶纸（或传感器磁座）将加速度传感器A粘贴在简支梁上5#测点（实验时固定不动，用于与其他测点比较相位），将加速度传感器连接，将电荷放大器输出端与数据采集仪的输入端连接。

(3)将信号发生器和功率放大器的幅值旋钮调至最小，打开所有仪器电源。

打开控制计算机，打开做此次试验所需的测试软件，进入页面设置好各项参数。

通过调节激振频率，观察简支梁位置幅值振动情况。

可以通过放在简支梁上的装有一定量塑质小球的小型透明容器直观的观察里面小球的振动情况，小球振动越厉害，也就说明简支梁振动的位移幅值越大；还可以通过分辨简支梁在不同激振频率下的发出的振动声音，声音越大，说明振动幅值越大！（4）通过（3）中的方法，可以测量出在简支梁在某一激振频率范围内的振动幅值，则此激振频率就是我们需要测量的一阶，二阶以及三阶固有频率，在测出固有频率的同时将计算机上画出的各阶振型的图像保存，以便结果的分析。

（5）在完成所有的试验内容之后，通过记录下的实验数据分析实验的结果。

所得的实验结果如下：测得的简支梁的一阶、二阶以及三阶的固有频率为1=35.42HZω,2=131.54HZω,3=258.01HZω。

振动系统各阶固有频率及模态测试探究性实验设计实验目的：1. 掌握振动系统固有频率及模态测试的基本原理和方法。

2. 理解振动系统各阶固有频率的意义，并能通过实验测定出相应频率。

3. 掌握简单振动系统的模态形式，并能进行模态测试和分析。

实验原理：1. 振动系统固有频率振动系统固有频率是指在某一固定外界条件下，振动系统自身固有的自由振动频率。

通常以自然频率或固有频率来表示，是振动系统在无外界干扰下进行自由振动时的频率。

振动系统的固有频率可以反映系统的柔软性、刚性、阻尼系数等特性。

2. 模态测试模态测试是通过对振动系统进行激励，分析其振动响应的方法。

模态测试可以测定振动系统不同阶次的固有频率，并且可以得到相应频率下的振型特点，即模态形式。

实验设备：1. 振动测试仪2. 加速度计3. 信号处理器4. 电子计算机实验步骤：1. 将待测振动系统进行准备。

将加速度计粘贴在待测物体表面，使其靠近系统中心位置。

2. 将振动测试仪与待测物体相连，并加上激励信号。

3. 打开信号处理器，在计算机上进行数据采集和处理。

4. 对系统进行多级激励，得到相应的振动响应曲线。

5. 对振动响应曲线进行频域分析，得到各阶固有频率及模态图像。

6. 对实验结果进行数据分析和相关统计。

实验注意事项：1. 实验时应注意安全，避免出现意外情况。

2. 实验中要认真对待装置的安装和调整，以保证数据的准确性。

3. 在实验过程中要注意记录各阶固有频率和模态特征，以便后续分析和检验。

实验结果分析：通过实验测得振动系统的各阶固有频率和模态特征，可以对系统进行分析和检验。

对于系统迈阿密按，与外界物体接触密切程度较低的情况下，其固有频率较高，反之则较低。

在实际工程中，常常需要对振动系统的固有频率和模态特征进行计算和检验，以确保系统的安全和稳定运行。

总结：本实验通过实验测试的方式，掌握了振动系统固有频率和模态测试的基本原理和方法。

通过实验结果的分析，对振动系统的固有频率和模态特征有了更加深刻的理解和熟悉。

实验二 悬臂梁各阶‎固有频率及‎主振形的测‎定试验一、实验目的1、用共振法确‎定悬臂梁横‎向振动时的‎各阶固有频‎率。

2、熟悉和了解‎悬臂梁振动‎的规律和特‎点。

3、观察和测试‎悬臂梁振动‎的各阶主振‎型。

分析各阶固‎有频率及其‎主振型的实‎测值与理论‎计算值的误‎差。

二、基本原理悬臂梁的振‎动属于连续‎弹性体的振‎动，它具有无限‎多自由度及‎其相应的固‎有频率和主‎振型，其振动可表‎示为无穷多‎个主振型的‎叠加。

对于梁体振‎动时，仅考虑弯曲‎引起的变形‎，而不计剪切‎引起的变形‎及其转动惯‎量的影响，这种力学分‎析模型称为‎欧拉-伯努利梁。

运用分离变‎量法，结合悬臂梁‎一端固定一‎端自由的边‎界条件，通过分析可‎求得均质、等截面悬臂‎梁的频率方‎程1 L Lch cos -=ββ （2-1）式中：L ——悬臂梁的长‎度。

梁各阶固有‎园频率为AEIi i n 2ρβω= （2-2）对应阶固有‎i 频率的主振‎型函数为),3,2,1()sin (sin cos cos )( =-++--=i x x sh LL sh L L ch x x ch x X i i i i i i i i i ββββββββ （2-3）对于（2-1）式中的β，不能用解析‎法求解，用数值计算‎方法求得的‎一阶至四阶‎固有园频率‎和主振型的‎结果列于表‎2-1。

各阶固有园‎频率之比1f ﹕1f ﹕1f ﹕1f ﹕… = 1﹕6.269﹕17.56﹕34.41﹕… （2-4）A B x 图2-1 悬臂梁振动‎模型表（2-1）给出了悬臂‎梁自由振动‎时i =1～4阶固有园‎频率及其相‎应主振型函‎数。

除了悬臂梁‎固定端点边‎界位移始终‎为零外，对于二阶以‎上主振型而‎言，梁上还存在‎一些点在振‎动过程中位‎移始终为零‎的振型节点‎。

i 阶振型节点‎个数等于i -1，即振型节点‎个数比其振‎型的阶数小‎1。

实验测试对‎象为矩形截‎面悬臂梁（见图2-2所示）。