5-3 电偶极辐射
- 格式:ppt
- 大小:1.08 MB
- 文档页数:20

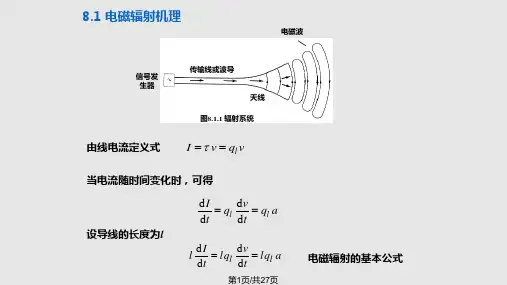
偶极子辐射
偶极子辐射是指由一个偶极子在电磁场中发出的辐射。
一个偶极子是由正电荷和负电荷之间存在一个短距离的分离,形成一个电偶极矩。
当偶极子受到电磁场的作用时,它会受到力的影响,从而开始振荡,并在周围产生辐射。
偶极子辐射的强度与偶极子的振荡频率有关,与电偶极矩的大小成正比。
当偶极子的频率与电磁场的频率相同,并且偶极子的长度远小于辐射的波长时,辐射的效果最大化。
偶极子辐射的特点是辐射强度随着距离的平方反比,辐射场的方向性强,辐射的频率与振荡频率相同,并且辐射的波长远大于偶极子的尺寸。
由于偶极子辐射的特性,它在天线设计和微波辐射等领域中得到广泛应用。




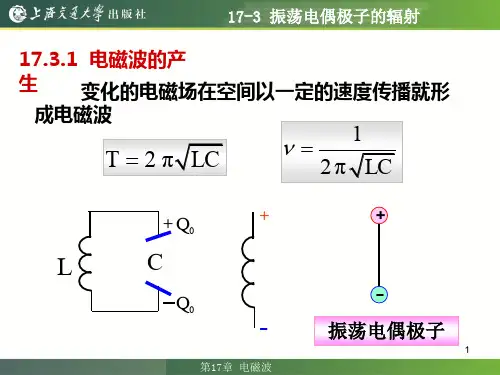
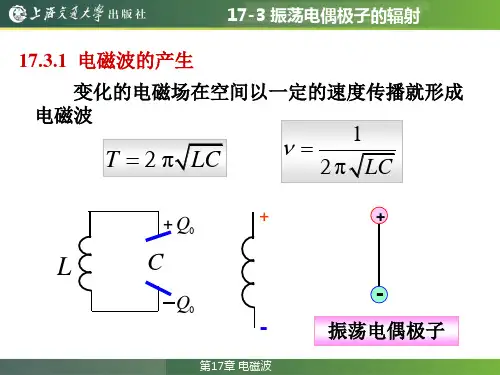
电偶极子辐射场公式的推导
电偶极子辐射场是物理学、电磁学和天文学的重要现象。
它描述的是一个小的
点源(作为辐射源),其双极性会在空间中传播,给出了“电偶极子辐射场”的公式。
因此,对于推导出这一公式而言,对其理论基础的理解及其运用就显得极为重要。
首先,要想推导出“电偶极子辐射场”的公式,必须具有对基础知识的充分理解,并运用物理学的基本知识,进行相关逻辑推理以及关于“电偶”技术的理论认知。
其次,如果要推导出“电偶极子辐射场”的公式,必须熟悉及掌握一些相关的数学知识,其中包括:高等数学、泛函分析以及多元函数运动等,同时,还要牢记一些基本几何知识,如和平面几何,三角几何以及曲面几何等,当然,推导中还要运用一定的数学和电磁场理论。
基于以上考虑,“电偶极子辐射场”的公式推导需要运用激进方法,即先从物
理因素出发,推导出电磁场的飞行力学方程;然后,将所有的数学、物理及电磁学知识进行融会贯通,推导出所要求的“电偶极子辐射场”的公式,并以此为基础来considering相关实际问题。
总而言之,推导“电偶极子辐射场”的公式,是非常重要的物理、电磁学和天
文学理论,但是,其过程并不容易,其前提是具备扎实的基本理论知识,并且要能把各个学科知识有机地融会贯通,以获得场定量的表达,从而能有效解决实际问题。


电偶极子天线的辐射电阻作者:赵海军来源:《现代电子技术》2009年第21期摘要:在部分有关电磁场理论的教材中,编者讨论短天线的辐射功率时,由于作了某些近似处理而所得天线的辐射电阻值偏差较大。
从天线辐射的电磁场理论和平均能流密度出发,使物理概念和数学工具相结合,运用矢量运算推导出精确的结果,即电偶极子(短)天线的实际辐射电阻要比文献中的近似结果小数十倍,因而为准确把握天线的辐射能力提供了依据。
关键词:电偶极子;电磁场;天线;辐射电阻中图分类号:TN82 文献标识码:A文章编号:1004-373X(2009)21-074-02Radiation Resistance of Electric Dipole AntennaZHAO Haijun(College of Technology and Engineering,Lanzhou University ofTechnology,Lanzhou,730050,China)Abstract:Deviation of the antenna radiation resistance seems larger in some textbooks about the electromagnetic theory for the editors have made some similar treatment when discussing the radiation power of short bining the concept of physical with mathematical tools and the precise results are gained,that is the real radiation resistance of electric dipole (short) antenna is about ten times smaller than that of the approximate results in the actual literature by researching the electromagnetic field theory and average energy density.This offers evidence to grasp the radiated ability accurately.Keywords:electric dipole;EMF;antenna;radiation resistance0 引言交变运动中按特殊方式分布的电荷电流系统产生电磁波辐射。