下载文档原格式
平面多边形内外点判断1 引言多边形在计算机图形学中有广泛应用，他们一般要求具有一下性质：（1）封闭：任何一条边有且只有两个端点，每个端点都是两条边的交点。
（2）不自交：任何两条边只有在相邻的情况下才相交，并且交点就是边的端点。
（3）有向：任何一条边都有方向，并且边的方向是一致的。
下面介绍一下多边形的一些基本概念。
（1）多边形：多边形是一个首尾相连的多边线，它可以用点序列P0 P1P2….P n表示，P0 P1，P1P2，…….P n-1P n称为多边形的边，P0 P1P2….P n 称为多边形的顶点。
（2）简单多边形：如果一个多边形所有的顶点均不相同,任何一个顶点都属于一条边，任何两条不相邻的边不相交，则这个多边形是简单多边形。
在计算机图形学中应用的多边形一般都是简单多边形，并且规定多边形沿逆时针方向时方向为正，沿顺时针方向时方向为负。
点在多边形内外关系的判断是关于多边形的一种基本算法，在计算机图形学中应用广泛，在石油地质制图系统中也有应用。
点在多边形内外关系的判断的经典方法主要有射线法和标号法两种，这两种方法实现起来比较复杂，而且在临界情况下可靠性不好。
有些资料中提出的利用多边形有向面积判断多边形方向可靠性很好，但是计算量相对较大，提出的判断点在多边形内外的方法是将多边形分解成一系列三角形，根据点与三角形的关系判断点与三角形的关系，但是没有讨论三角形退化为直线等情况的处理方法，而这些退化情况将导致算法不稳定。
2、多边形方向的判断方法给定多边形P=P0 P1P2……P n如图形1所示。
多边形方向的判断方法如下（1）遍历多边形P，找到P沿X，Y方向的最大值、最小值点分别为P i,P j,P k,P l；（2）定义矢量Z＝（0，0，1）。
将P i，P j，P k，P l的下标从小到大排序得到j，k，l，i，下标相同的点，不计重复只保留一个。
如果只剩下两点，转步骤4，如果只剩下三点，转步骤5；（3）连接P j，P k，P l，Pi，P j，得到一个四边形P’=PjP k P l P i，其中P’0=P j，P’1=P k，P’2=P l，P’3=Pi，转步骤6；（4）设剩下的两点为P i，P j，则如果（P i-1P i*P i P i+1）.Z>0，则P的方向为正；如果（P i-1 P i*P i P i+1）.Z<0，则P的方向为负，结束。
点在凸多边形内外的判定点在凸多边形内外的判定1. 引言点在凸多边形内外的判定是几何学中的一项基础知识。
它在计算机图形学、地理信息系统以及其他领域中都有很广泛的应用。
判断一个点是否在凸多边形内部可能会涉及到一些数学算法和几何概念，但只要我们理解了其原理，就能够轻松地进行点的位置判断。
2. 原理解析2.1 凸多边形的定义凸多边形是指没有凹陷部分的多边形。
它的内角都小于180度，并且多边形中的任意两点之间的线段都在多边形内部。
这个定义非常关键，因为只有凸多边形才能使用简单的算法进行点的位置判断。
2.2 射线法射线法是一种常见且简单有效的点在凸多边形内外判定方法。
其基本思想是从点向多边形外部发射一条射线，判断射线与多边形的交点数量。
如果交点数量为奇数，则点在多边形内部，否则在外部。
射线法可以通过以下步骤进行：2.2.1 选取一条水平线，使得它能够穿过待判断的点。
2.2.2 从待判断的点沿着水平线方向发射一条射线。
2.2.3 分别计算射线与多边形的各个边的交点。
2.2.4 统计交点的数量。
2.2.5 如果交点数量为奇数，则点在多边形内部；如果交点数量为偶数，则点在多边形外部。
3. 实例分析为了更好地理解点在凸多边形内外判定的过程，我们来看一个简单的例子。
假设有一个凸多边形，顶点分别为A、B、C、D，点P是我们待判断的点。
3.1 射线的选取我们选取一条水平线，穿过待判断的点P。
3.2 射线的发射与交点计算从点P沿着水平线方向发射射线。
射线与多边形的各个边的交点如下：- 射线与边AB的交点为R1；- 射线与边BC的交点为R2；- 射线与边CD的交点为R3；- 射线与边DA的交点为R4。
3.3 交点数量统计统计交点的数量，我们可以得到以下结果：- 交点数量为奇数，点P在多边形内部。
4. 个人观点与总结对于凸多边形内外判定，射线法是一种简单而有效的方法。
射线法的思路清晰，易于理解和实现。
它在实际应用中具有一定的优势，特别是在计算机图形学中。
提丢斯-波得定则提丢斯-波得定则（Thiessen-Polygon）是一种GIS（地理信息系统）中常用的算法，它用来将地图上的点根据离它们最近的地理要素分组，形成多边形区域。
这些多边形区域称为泰森多边形或提丢斯多边形。
提丢斯-波得定则可以用来确定最佳的分配区域，以便更好地了解地理数据并做出准确的决策。
提丢斯-波得定则算法是由Patton H. Thiessen于1911年在美国农业部门的出版物上首次描述的。
在地图制作和区域分区方面，提丢斯算法被广泛应用，它的主要思想是将一个平面区域划分成多个互不重叠的区域，并将每个点从中心吸引到最近的边界。
提丢斯-波得定则算法可以通过以下步骤简单地实现：第一步是定义要素集。
该要素集可以包括任意地理要素，例如建筑物、水体、树林或其他地理特征。
在提丢斯-波得定则的应用中，要素经常是点要素，这些点要素直接使用GPS或其他定位系统获取。
第二步是在要素集中找到区域的边界。
这些区域的边界应该是所有要素点的最近邻边界，这意味着每个区域应该由其内部点组成而不被其他区域穿过。
通过找到各个区域的边界，可以形成相应的多边形区域。
第三步是构建泰森多边形。
以每个要素点为中心，画出一个围绕在该点最近邻要素上的圆，然后在这些圆之间构建连线，这样就可以形成多边形区域。
这些区域的边界通常是由相邻多边形之间的中垂线确定的。
使用提丢斯-波得定则算法可以实现多种操作，例如：1.确定分散区域和邻近区域：通过对多边形区域进行分组，可以确定哪些区域是最接近的，以便更好地了解地理数据的分布情况和在不同区域之间做出更准确的决策。
2.确定缓冲区域：使用提丢斯-波得定则算法可以很容易地识别地图上的缓冲区域，这些区域可以用于限制建筑物或其他地理要素的发展，并保护生态环境。
3.确定交通覆盖区域：对于交通规划和交通分析，提丢斯-波得算法可以确定交通覆盖范围，帮助交通规划者更好地了解城市空间发展，更好地优化城市交通。
提丢斯-波得定则算法虽然简单，但在GIS栅格分析中具有很高的实用价值，广泛应用于地图制作、资源管理、城市规划、农业和自然环境保护等领域。
平⾯多边形内外点判断平⾯多边形内外点判断1 引⾔多边形在计算机图形学中有⼴泛应⽤，他们⼀般要求具有⼀下性质：（1）封闭：任何⼀条边有且只有两个端点，每个端点都是两条边的交点。
（2）不⾃交：任何两条边只有在相邻的情况下才相交，并且交点就是边的端点。
（3）有向：任何⼀条边都有⽅向，并且边的⽅向是⼀致的。
下⾯介绍⼀下多边形的⼀些基本概念。
（1）多边形：多边形是⼀个⾸尾相连的多边线，它可以⽤点序列P0 P1P2….P n表⽰，P0 P1，P1P2，…….P n-1P n称为多边形的边，P0 P1P2….P n 称为多边形的顶点。
（2）简单多边形：如果⼀个多边形所有的顶点均不相同,任何⼀个顶点都属于⼀条边，任何两条不相邻的边不相交，则这个多边形是简单多边形。
在计算机图形学中应⽤的多边形⼀般都是简单多边形，并且规定多边形沿逆时针⽅向时⽅向为正，沿顺时针⽅向时⽅向为负。
点在多边形内外关系的判断是关于多边形的⼀种基本算法，在计算机图形学中应⽤⼴泛，在⽯油地质制图系统中也有应⽤。
点在多边形内外关系的判断的经典⽅法主要有射线法和标号法两种，这两种⽅法实现起来⽐较复杂，⽽且在临界情况下可靠性不好。
有些资料中提出的利⽤多边形有向⾯积判断多边形⽅向可靠性很好，但是计算量相对较⼤，提出的判断点在多边形内外的⽅法是将多边形分解成⼀系列三⾓形，根据点与三⾓形的关系判断点与三⾓形的关系，但是没有讨论三⾓形退化为直线等情况的处理⽅法，⽽这些退化情况将导致算法不稳定。
2、多边形⽅向的判断⽅法给定多边形P=P0 P1P2……P n如图形1所⽰。
多边形⽅向的判断⽅法如下（1）遍历多边形P，找到P沿X，Y⽅向的最⼤值、最⼩值点分别为P i,P j,P k,P l；（2）定义⽮量Z＝（0，0，1）。
将P i，P j，P k，P l的下标从⼩到⼤排序得到j，k，l，i，下标相同的点，不计重复只保留⼀个。
如果只剩下两点，转步骤4，如果只剩下三点，转步骤5；（3）连接P j，P k，P l，Pi，P j，得到⼀个四边形P’=PjP k P l P i，其中P’0=P j，P’1=P k，P’2=P l，P’3=Pi，转步骤6；（4）设剩下的两点为P i，P j，则如果（P i-1P i*P i P i+1）.Z>0，则P的⽅向为正；如果（P i-1 P i*P i P i+1）.Z<0，则P的⽅向为负，结束。
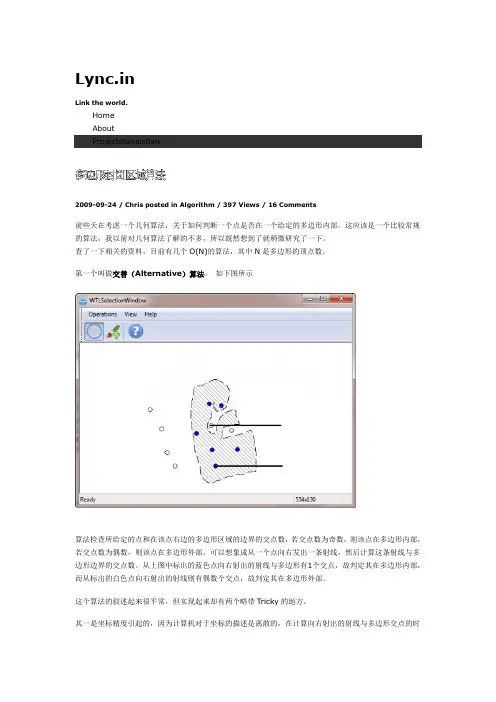
一、概述多边形（polygon）是几何学中的一个重要概念，指的是一个由连续的直线段所组成的闭合图形。
计算多边形内部的点到多边形边框的最近距离是一个经典的几何学问题，其在计算机图形学、地理信息系统等领域有着重要的应用。
本文将对这一问题进行深入探讨，并给出相应的算法和实现方法。
二、问题描述多边形内部的点到多边形边框的最近距离，是指对于给定的一个多边形和一个点，要求计算该点到多边形边框的最近距离。
这个问题的解决不仅需要考虑几何学的原理，还需要结合计算机算法的设计和实现。
因为多边形的形状和尺寸多种多样，所以对于不同的多边形，需要采用不同的算法来计算其内部点到边框的最近距离。
三、问题分析1. 几何学角度：从几何学的角度来看，对于任意一个多边形和一个点，可以使用点到线段的距离公式来计算点到多边形边框的最近距离。
这涉及到点、直线、线段等几何学概念的运用。
2. 算法设计：基于几何学的原理，需要设计相应的算法来实现点到多边形边框最近距离的计算。
不同的多边形可能需要不同的算法来处理，如凸多边形和凹多边形可能要采用不同的算法。
3. 实现方法：在计算机程序中，需要将设计好的算法转化为具体的代码实现。
这涉及到数据结构、算法复杂度等计算机科学的知识。
四、相关工作在计算多边形内部点到边框的最近距离方面，已经有不少学者做出了相关的研究工作。
他们提出了一些经典的算法和方法，如距离场法、边界扩展法、分段线性逼近法等。
这些方法在一定范围内都能解决多边形内部点到边框的最近距离问题，并且在某些场景下有着较好的效果。
五、解决方案1. 距离场法：这种方法利用距离场的概念，将多边形边框上的点扩展成一组网格，然后利用距离场的计算方式，可以轻松得到多边形边框上的点到多边形内部任意一点的最近距离。
2. 边界扩展法：该方法通过对多边形边框进行扩展，将多边形的内部和外部划分为不同的区域，然后通过对每个区域进行扫描，可以得到多边形内部点到边框的最近距离。
判断⼀个坐标点是否在不规则多边形内部的算法在GIS（地理信息管理系统）中，判断⼀个坐标是否在多边形内部是个经常要遇到的问题。
乍听起来还挺复杂。
根据W. Randolph Franklin 提出的PNPoly算法，只需区区⼏⾏代码就解决了这个问题。
假设多边形的坐标存放在⼀个数组⾥，⾸先我们需要取得该数组在横坐标和纵坐标的最⼤值和最⼩值，根据这四个点算出⼀个四边型，⾸先判断⽬标坐标点是否在这个四边型之内，如果在这个四边型之外，那可以跳过后⾯较为复杂的计算，直接返回false。
if (p.x < minX || p.x > maxX || p.y < minY || p.y > maxY) {// 这个测试都过不了。
直接返回false；}接下来是核⼼算法部分：int pnpoly(int nvert, float *vertx, float *verty, float testx, float testy){int i, j, c = 0;for (i = 0, j = nvert-1; i < nvert; j = i++) {if ( ((verty[i]>testy) != (verty[j]>testy)) &&(testx < (vertx[j]-vertx[i]) * (testy-verty[i]) / (verty[j]-verty[i]) + vertx[i]) )c = !c;}return c;}Argument Meaningnvert Number of vertices in the polygon. Whether to repeat the first vertex at the end is discussed below.vertx, verty Arrays containing the x- and y-coordinates of the polygon's vertices.testx, testy X- and y-coordinate of the test point.额，代码就这么简单，但到底啥意思呢：⾸先，参数nvert 代表多边形有⼏个点。
任意多边形中心点算法英文回答：To find the center point of an arbitrary polygon, one common algorithm is the centroid method. The centroid, also known as the geometric center or barycenter, is the average of all the points in the polygon. It can be calculated by finding the average of the x-coordinates and y-coordinates of all the vertices.Here's how the algorithm works:1. Calculate the sum of the x-coordinates and y-coordinates of all the vertices.2. Divide the sum of x-coordinates by the number of vertices to get the average x-coordinate.3. Divide the sum of y-coordinates by the number of vertices to get the average y-coordinate.4. The center point of the polygon is the point with the average x-coordinate and average y-coordinate.For example, let's consider a triangle with vertices at (1,1), (4,5), and (7,2).1. Sum of x-coordinates = 1 + 4 + 7 = 12。
python泰森多边形
Python是一种高级编程语言，广泛应用于Web开发、数据分析、人工智能等领域。
而泰森多边形是一种计算几何学上的经典算法，用
于将一组点连接成一个凸多边形。
首先，我们需要了解什么是凸多边形。
一个凸多边形是指内部没
有凹陷的多边形，也就是任意两个点之间的线段都在多边形内部。
而
泰森多边形是指在一组点中找到一个点集，使得这个点集中的点可以
围成一个凸多边形，并且这个点集中各个点到原始点集中的点的距离
最短。
使用Python实现泰森多边形可以使用scipy库中的spatial模块。
通过调用spatial模块的Delaunay类，我们可以创建一个Delaunay三角剖分对象。
接着，我们遍历这个三角剖分对象中所有的
三角形，找到与原始点集中的点最近的顶点，并将这些顶点与原始点
集合并，最终就可以得到泰森多边形了。
当然，使用Python实现泰森多边形还有其他的方法和工具，比
如使用matplotlib库来可视化结果、使用numpy库来进行向量和矩阵
计算等等。
不过，无论使用何种方法和工具，泰森多边形这个算法都
是一项非常重要的计算几何学问题，在计算机图形学、CAD等领域都有广泛的应用。
有兴趣的读者可以尝试自己使用Python实现泰森多边形，以此来深入理解计算几何学的基础知识。
再经典不过的算法了：
// 功能：判断点是否在多边形内
// 方法：求解通过该点的水平线与多边形各边的交点
// 结论：单边交点为奇数，成立!
//参数：
// POINT p 指定的某个点
// LPPOINT ptPolygon 多边形的各个顶点坐标（首末点可以不一致）
// int nCount 多边形定点的个数
BOOL PtInPolygon (POINT p, LPPOINT ptPolygon, int nCount)
{
int nCross = 0;
for (int i = 0; i < nCount; i++)
{
POINT p1 = ptPolygon[i];
POINT p2 = ptPolygon[(i + 1) % nCount];
// 求解y=p.y 与p1p2 的交点
if ( p1.y == p2.y ) // p1p2 与y=p0.y平行
continue;
if ( p.y < min(p1.y, p2.y) ) // 交点在p1p2延长线上
continue;
if ( p.y >= max(p1.y, p2.y) ) // 交点在p1p2延长线上
continue;
// 求交点的X 坐标--------------------------------------------------------------
double x = (double)(p.y - p1.y) * (double)(p2.x - p1.x) / (double)(p2.y - p1.y) + p1.x;
if ( x > p.x )
nCross++; // 只统计单边交点
}
// 单边交点为偶数，点在多边形之外---
return (nCross % 2 == 1);
}
1. 叉乘判别法（只适用于凸多边形）
想象一个凸多边形，其每一个边都将整个2D屏幕划分成为左右两边，连接每一边的第一个端点和要测试的点得到一个矢量v，将两个2维矢量扩展成3维的，然后将该边与v叉乘，判断结果3维矢量中Z分量的符号是否发生变化，进而推导出点是否处于凸多边形内外。
这里要注意的是，多边形顶点究竟是左手序还是右手序，这对具体判断方式有影响。
2. 面积判别法（只适用于凸多边形）
第四点分别与三角形的两个点组成的面积分别设为S1,S2,S3，只要S1+S2+S3>原来的三角形面积就不在三角形范围中.可以使用海伦公式。
推广一下是否可以得到面向凸多边形的算法？（不确定）
3. 角度和判别法（适用于任意多边形）
double angle = 0;
realPointList::iterator iter1 = points.begin();
for (realPointList::iterator iter2 = (iter1 + 1); iter2 < points.end(); ++iter1, ++iter2)
{
double x1 = (*iter1).x - p.x;
double y1 = (*iter1).y - p.y;
double x2 = (*iter2).x - p.x;
double y2 = (*iter2).y - p.y;
angle += angle2D(x1, y1, x2, y2);
}
if (fabs(angle - span::PI2) < 0.01) return true;
else return false;
另外，可以使用bounding box来加速。
if (p.x < (*iter)->boundingBox.left ||
p.x > (*iter)->boundingBox.right ||
p.y < (*iter)->boundingBox.bottom ||
p.y > (*iter)->boundingBox.top) 。
对于多边形来说，计算bounding box非常的简单。
只需要把水平和垂直方向上的最大最小值找出来就可以了。
对于三角形：第四点分别与三角形的两个点的交线组成的角度分别设为j1,j2,j3，只要j1+j2+j3>360就不在三角形范围中。
4. 水平/垂直交叉点数判别法（适用于任意多边形）
注意到如果从P作水平向左的射线的话，如果P在多边形内部，那么这条射线与多边形的
交点必为奇数，如果P在多边形外部，则交点个数必为偶数（0也在内）。
所以，我们可以顺序考虑多边形的每条边，求出交点的总个数。
还有一些特殊情况要考虑。
假如考虑边(P1,P2)，
1)如果射线正好穿过P1或者P2,那么这个交点会被算作2次，处理办法是如果P的从坐标与P1,P2中较小的纵坐标相同，则直接忽略这种情况
2)如果射线水平，则射线要么与其无交点，要么有无数个，这种情况也直接忽略。
3)如果射线竖直，而P0的横坐标小于P1,P2的横坐标，则必然相交。
4)再判断相交之前，先判断P是否在边(P1,P2)的上面，如果在，则直接得出结论：P再多边形内部。
射线算法
1. 已知点point(x,y)和多边形Polygon（x1,y1;x2,y2;….xn,yn;）；
2. 以point为起点，以无穷远为终点作平行于X轴的直线line(x,y; -∞,y)；
3. 循环取得(for(i=0;i<n;i++))多边形的每一条边side(xi,yi;xi+1,yi+1)，且判断是否平行于X轴，如果平行continue，否则，i++；
4. 同时判断point(x,y)是否在side上，如果是，则返回1(点在多边形
上)，否则继续下面的判断；
5. 判断线side与line是否有交点，如果有则count++，否则，i++。
6. 判断交点的总数，如果为奇数则返回0（点在多边形内），偶数则返回2（点在多边形外）。
