下载文档原格式
机械原理直击考点重点第一部分机构的结构分析本章主要知识点有：机构的组成；机构运动简图及绘制；机构的自由度的计算；平面机构的组成原理和结构分析，以上知识点必须掌握，其中自由度的计算是重中之重。
基础阶段，复习时间是从5月份至8月份，以上基础知识点必须理解掌握。
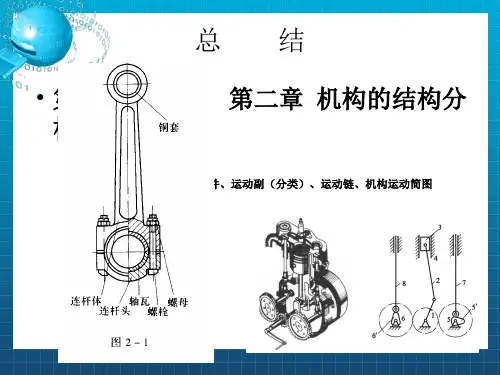
【例题】计算下面机构的自由度F，指出机构中存在的复合铰链、局部自由度、虚约束。
指出机构具有确定运动应具备的条件。
分析：此题目是第1章机构的结构分析在2009年考过的一道题目，本章主要介绍机构的组成，平面机构运动简图，及机构自由度的计算。
★重点内容：平面机构运动简图及机构自由度的计算▲难点内容：平面机构运动简图该题目即是整本书的重点也是历年的必考点，它重要是因为历年真题都把考核机构的自由度计算作为重中之重，这是必考的知识点。
该题目涉及到的知识点是机构运动简图的识别、机构自由度的计算公式、复合铰链、局部自由度、虚约束的准确识别，机构有确定运动的条件。
这是同学分析题目的第一步，要知道它考的是什么考点（基础复习），第二步要明确命题规律（强化复习），第三步是要站在命题人的角度思考问题（冲刺复习），“如果我是命题组人，为什么出这道题，想考察同学哪方面的能力”。
解题：设运动链中共有PL个低副和PH个高副，平面机构的自由度F=3n —2PL—PH，图中有活动构件n=9，低副PL=13，高副PH=0，其中铰链A处是复合铰链，没有局部自由度和虚约束。
自由度F=3 x 9—2 x 13—0=1，机构具有确定运动的条件是只有一个原动件。
注：解题时头脑中必须概念清晰，掌握扎实的基本知识。
以本题为例，细致分析题目要求，必须清楚复合铰链、局部自由度、虚约束的定义以及机构具有确定运动的条件。
第二部分平面机构的运动分析本章主要知识点有：速度瞬心法；矢量方程图解法，分两种情形：1 统一构件上两点间的速度和加速度的关系，2 两构件上重合点间的速度和加速度的关系；速度多边形及速度影像；加速度多边形及加速度影像；图解法对平面机构进行运动分析；解析法做平面机构的运动分析，其中速度瞬心法和矢量方程图解法是重中之重。
哈工大（威海）《机械原理》知识点整理整理人：131310405郭勇辰第一章1.机械是机器与机构的总称。
2.机器是一种人为实物组合的具有确定机械运动的装置，用来完成有用功、转换能量或处理信息，以代替或减轻人类的劳动。
3.现代化机器具有四个组成部分：原动机、传动机、执行机构和控制系统。
4.一部机器通常包含一个或若干个机构。
机构是一个具有相对机械运动的构件系统，或称它是用来传递与变换运动和动力的可动装置。
第二章1.构件与零件的区别在于：构件是运动的单元，而零件是制造的单元。
一个构件既可以是一个零件，也可以是由若干零件装配而成的刚性体。
2.运动副：两构件间的直接接触又能产生一定相对运动的活动连接成为运动副。
3.一个运动副引入的约束数目最多只能是5个，最少是1个。
4.运动链：若干构件通过运动副连接而成的构件系统称为运动链。
运动链中各构件首位封闭，则称为闭式链，否则为开式链。
5.机构：如果将运动链中的一个构件固定作为参考坐标系，则这种运动链称为机构。
6.运动副的分类：把引入1个约束的运动副称为Ⅰ级副，以此类推；以面接触的运动副称为低副，以点或线接触的运动副称为高副；如果两运动副元素间只能相互做平面平行运动，则称之为平面运动副，否则为空间运动副；7.不按比例绘制的运动简图成为机构示意图。
8.机构运动简图的单位为m/mm（图纸上1mm所代表的真实长度）。
9.自由度：确定一个构件或机构的运动（或位置）所需的独立参数的数目。
10.机构具有确定运动的条件是：机构的自由度大于零，且机构的原动件数目等于机构的自由度数。
11.计算自由度时注意三种情况：复合铰链、局部自由度、虚约束。
12.复合铰链：由两个以上构件在同一处构成的重合转动副。
13.局部自由度：不影响整个机构运动的自由度。
14. 虚约束：起重复限制作用的约束。
（虚约束的几种情况在P17）15. 三维空间中，一个活动构件具有6个自由度。
16. 任何机构都包含机架、原动件和从动件系统三个部分。
《机械原理》辅导资料十三一、课程课件的学习重点研究对象：机械系统—由原动机、传动系统、执行机构组成。
研究内容：1、建立机械系统的等效动力学模型；2、机械运转速度波动的调节。
作用在机械系统上的力：驱动力和工作阻力。
其余外力，如重力、惯性力、摩擦力等，在一般情况下与驱动力和工作阻力相比要小很多，故在研究稳定运转的动力学问题时常忽略不计。
原动机：电动机、液压马达、气压泵、内燃机…机械特性：原动机输出的驱动力与某些运动参数的函数关联。
工作阻力的变化规律主要取决于工作机的类型及工艺特点。
机械系统的等效动力学模型主要内容：1、机械运动方程式；2、等效动力学模型；3、机械运动方程建立。
机械运动方程式：建立作用在机械上的力和力矩、构件上的质量、转动惯量和运动参数之间的函数关系式。
等效动力学模型：目的：将单自由度机械系统，简化为等效构件（一个构件）运动；通过等效构件建立最简单的等效动力学模型，简化研究机械真实运动问题。
等效原则：动能相等，功率相等。
等效构件：常取绕定轴转动或作直线运动构件。
三、重要知识点补充1、机器的运转过程机器的运转过程分起动阶段、稳定运转阶段和停车阶段。
在起动阶段，原动件的速度从零上升到它的正常工作速度，驱动力作的功（驱动功）大于阻力作的功（阻抗功），机器动能增加，机器的运转速度逐渐增加；在稳定运转阶段，原动件的平均角速度保持稳定，因每个瞬间的驱动功与阻抗功不相等，机器运转速度会发生波动，但就一个周期而言，机器的总驱动功与总阻抗功是相等的，一个周期的始末，机器的速度也是相等的；在停车阶段，撤去驱动力，原动件的速度从正常工作速度下降到零，驱动功小于阻抗功，机器运转速度逐渐减小，直至停止。
2、机器等效动力学模型机器运转的真实运动规律取决于作用在它所有构件上各力所作的功和它的所有运动构件的动能变化。
根据动能定理，某一瞬间机器总动能的增量dE应等于该瞬间机器上各外力所作的元功之和dW，该机器的运动方程式为：dE=dW。
基本概念：机器、机构、机械、零件、构件、机架、原动件和从动件。
机构运动简图的绘制、运动链成为机构的条件和机构的组成原理是本章学习的重点。
1. 机构运动简图的绘制为保证机构运动简图与实际机械有完全相同的结构和运动特性，对绘制好的简图需进一步检查与核对(运动副的性质和数目来检查)。
2. 运动链成为机构的条件运动链成为机构的条件是：原动件数目等于运动链的自由度数目。
机构自由度的计算错误会导致对机构运动的可能性和确定性的错误判断，从而影响机械设计工作的正常进行。
准确识别复合铰链、局部自由度和虚约束，并做出正确处理。
(1) 复合铰链复合铰链是指两个以上的构件在同一处以转动副相联接时组成的运动副。
k 个在同一处形成复合铰链的构件，其转动副的数目应为 (k-1) 个。
(2) 局部自由度局部自由度是机构中某些构件所具有的并不影响其他构件的运动的自由度。
局部自由度常发生在为减小高副磨损而增加的滚子处。
从机构自由度计算公式中将局部自由度减去，也可以将滚子及与滚子相连的构件固结为一体，预先将滚子除去不计，然后再利用公式计算自由度。
(3) 虚约束虚约束是机构中所存在的不产生实际约束效果的重复约束。
计算自由度时，首先将引入虚约束的构件及其运动副除去不计，然后用自由度公式进行计算。
虚约束都是在一定的几何条件下出现的，这些几何条件有些是暗含的，有些则是明确给定的。
对于暗含的几何条件，需通过直观判断来识别虚约束；对于明确给定的几何条件，则需通过严格的几何证明才能识别。
3. 机构的组成原理与结构分析机构的组成过程和机构的结构分析过程正好相反，前者是研究如何将若干个自由度为零的基本杆组依次联接到原动件和机架上，以组成新的机构，它为设计者进行机构创新设计提供了一条途径；后者是研究如何将现有机构依次拆成基本杆组、原动件及机架，以便对机构进行结构分类。
1 ．基本概念：速度瞬心、绝对速度瞬心和相对速度瞬心(数目、位置的确定) ，以及“三心定理”。
第一章绪论基本概念：机器、机构、机械、零件、构件、机架、原动件和从动件。
第二章平面机构的结构分析机构运动简图的绘制、运动链成为机构的条件和机构的组成原理是本章学习的重点。
1. 机构运动简图的绘制机构运动简图的绘制是本章的重点，也是一个难点。
为保证机构运动简图与实际机械有完全相同的结构和运动特性，对绘制好的简图需进一步检查与核对（运动副的性质和数目来检查）。
2. 运动链成为机构的条件判断所设计的运动链能否成为机构，是本章的重点。
运动链成为机构的条件是：原动件数目等于运动链的自由度数目。
机构自由度的计算错误会导致对机构运动的可能性和确定性的错误判断，从而影响机械设计工作的正常进行。
机构自由度计算是本章学习的重点。
准确识别复合铰链、局部自由度和虚约束，并做出正确处理。
(1) 复合铰链复合铰链是指两个以上的构件在同一处以转动副相联接时组成的运动副。
正确处理方法：k个在同一处形成复合铰链的构件，其转动副的数目应为(k-1)个。
(2) 局部自由度局部自由度是机构中某些构件所具有的并不影响其他构件的运动的自由度。
局部自由度常发生在为减小高副磨损而增加的滚子处。
正确处理方法：从机构自由度计算公式中将局部自由度减去，也可以将滚子及与滚子相连的构件固结为一体，预先将滚子除去不计，然后再利用公式计算自由度。
(3) 虚约束虚约束是机构中所存在的不产生实际约束效果的重复约束。
正确处理方法：计算自由度时，首先将引入虚约束的构件及其运动副除去不计，然后用自由度公式进行计算。
虚约束都是在一定的几何条件下出现的，这些几何条件有些是暗含的，有些则是明确给定的。
对于暗含的几何条件，需通过直观判断来识别虚约束；对于明确给定的几何条件，则需通过严格的几何证明才能识别。
3. 机构的组成原理与结构分析机构的组成过程和机构的结构分析过程正好相反，前者是研究如何将若干个自由度为零的基本杆组依次联接到原动件和机架上，以组成新的机构，它为设计者进行机构创新设计提供了一条途径；后者是研究如何将现有机构依次拆成基本杆组、原动件及机架，以便对机构进行结构分类。
