定积分与不等式的证明

探讨定积分不等式的证明方法定积分是微积分中重要的概念之一，它在数学和其他学科中有着广泛的应用。

定积分不等式是对定积分的一种推广和扩展，它可以用来证明数学中的很多重要不等式。

定积分不等式的证明方法有很多种。

下面将介绍其中的几种常见证明方法。

1.利用积分的定义定积分的定义是通过极限来定义的，可以用积分和极限的性质来证明定积分不等式。

一般的证明步骤如下：（1）通过积分的定义，将定积分转化为极限的形式。

（3）利用极限的性质，对被积函数和不等式进行变换和处理，最终得到待证不等式。

2.利用积分的性质和中值定理（1）利用中值定理，将定积分表示为导数的形式。

（3）利用中值定理和被积函数的性质，对待证不等式进行变换和处理，最终得到待证不等式。

3.利用积分的性质和数学归纳法数学归纳法是数学中常用的证明方法之一，可以用来证明定积分不等式。

具体的证明方法如下：（1）利用积分的性质，将待证不等式转化为一系列具有相似性质的子不等式。

（2）对待证不等式的子不等式进行归纳证明，即先证明基本情况，然后假设第n个不等式成立，再通过已知的前n个不等式得到第n+1个不等式。

（3）通过数学归纳法的证明，得到待证不等式。

这种证明方法的优点是简单直接，能够通过归纳证明得到待证不等式，但需要对数学归纳法的性质和待证不等式的子不等式非常熟悉。

除了以上的方法，还可以利用几何意义、特殊函数的性质、不等式的基本性质等进行证明。

不同的证明方法适用于不同的场合和问题，需要根据具体情况选择合适的方法。

综上所述，定积分不等式的证明方法有很多种，可以利用积分的定义、性质和中值定理，数学归纳法等进行证明。

不同的证明方法有不同的优点和适用范围，需要根据具体情况选择合适的方法。

对于定积分不等式的证明方法的深入理解和熟练应用，对于深化对定积分的理解和掌握具有重要意义。

热点追踪Җ㊀广东㊀李文东㊀㊀不等式的证明是高考的重要内容,证明的方法多㊁难度大,特别是一些数列和型的不等式．这类不等式常见于高中数学竞赛题和高考压轴题中,由于证明难度较大,往往令人望而生畏．其中有些不等式若利用定积分的几何意义证明,则可达到以简驭繁㊁以形助数的解题效果．１㊀利用定积分证明数列和型不等式数列和型不等式的一般模式为ðni ＝１a i ＜g (n )(或ðni ＝１a i ＞g (n )),g (n )可以为常数．不失一般性,设数列a n ＝f (n )＞０,此类问题可以考虑如下的定积分证明模式．(１)若f (x )单调递减．因为f (i )＜ʏii －１f (x )d x ,从而ðni ＝１a i ＝ðn i ＝１f (i )＜ðni ＝１ʏii－１f (x )d x ＝ʏn０f (x )d x ．㊀㊀又因为ʏi i －１f (x )d x ＜f (i －１),从而ʏn ＋１１f (x )d x ＝ðn ＋１i ＝２ʏi i－１f (x )d x ＜ðn ＋１i ＝２f (i －１)＝ðni ＝１a i．㊀㊀(２)若f (x )单调递增．因为f (i )＞ʏi i －１f (x )d x ,从而ðni ＝１a i＝ðni ＝１f (i )＞ðni ＝１ʏii－１f (x )d x ＝ʏn０f (x )d x ．㊀㊀又因为ʏii －１f (x )d x ＞f (i －１),从而ʏn ＋１１f (x )d x ＝ðn ＋１i ＝２ʏii－１f (x )d x ＞ðn ＋１i ＝２f (i －１)＝ðni ＝１a i ．例１㊀(２０１３年广东卷理１９,节选)证明:１＋１２２＋１３２＋ ＋１n２＜７４(n ɪN ∗)．分析㊀本题证法大多采用裂项放缩来证明,为了得到更一般的结论,我们这里采用定积分来证明．证明㊀因为函数y ＝１xα(α＞０且αʂ１)在(０,＋ɕ)上单调递减,故ʏii －１１x αd x ＞１iα(i ȡ３),从而当αʂ１时,ðni ＝１１i α＜１＋１２α＋ðni ＝３ʏii －１１x αd x ＝１＋１２α＋ʏn２１x αd x ＝１＋１２α－１(α－１)x α－１n ２＝１＋１２α＋１(α－１)２α－１－１(α－１)nα－１．㊀㊀利用这个不等式可以得到一些常见的不等式．若α＝１２,则ðn i ＝１１i＜１－３２＋２n ＝２n －１＋(２－３２)＜２n －１．㊀㊀当α＞１时,ðni ＝１１iα＜１＋１２α＋１(α－１)２α－１＝１＋α＋１α－１ １２α．特别地,若α＝２,则ðni ＝１１i ２＜１＋２＋１２－１ １２２＝７４;若α＝３,则ðni ＝１１i３＜１＋３＋１３－１ １２３＝５４;若α＝３２,则ðni ＝１１ii＜１＋３２＋１３２－１ １２３２＝１＋５２４＜３;若α＝１,则１n＜ʏnn －１１x d x ＝l n x nn －１＝l n n －l n (n －１),从而可以得到１２＋１３＋ ＋１n ＋１＜ʏn ＋１１１xd x ＝l n (n ＋１),１n ＋１＋１n ＋２＋ ＋１２n＜ʏ２nn１xd x ＝l n２．㊀㊀另一方面,１n －１＞ʏnn －１１xd x ＝l n x n n －１＝l n n －l n (n －１),则１＋１２＋１３＋ ＋１n －１＞ʏn１１x d x ＝l n n ．㊀㊀当α＝１时,借助定积分的几何意义上述不等式４２热点追踪还可以进一步加强．图１是函数y ＝１x的部分图象,显然S 曲边梯形A B C F ＜S 梯形A B C F ,于是ʏn ＋１n１x d x ＜１２(１n ＋１n ＋１),得l n (１＋１n )＜１２(１n ＋１n ＋１),令n ＝１,２, ,n ,并采用累加法可得１＋１２＋１３＋ ＋１n＞l n (n ＋１)＋n２(n＋１)(n ȡ１)．图１例２㊀证明:l n ４２n ＋１＜ðni ＝１i４i ２－１(n ɪN ∗)．分析㊀由于i ４i ２－１＝１４(１２i －１＋１２i ＋１),l n ４２n ＋１＝１４l n (２n ＋１),故证明l n (２n ＋１)＜ðni ＝１(１２i －１＋１２i ＋１)．构造函数f (x )＝１２x ＋１,显然f (x )单调递减,考虑到ðni ＝１(１２i －１＋１２i ＋１)的结构,对函数f (x )采用类似图１中的梯形面积放缩．证明㊀由分析得ʏii －１１２x ＋１d x ＜１２(１２i －１＋１２i ＋１),故１２l n (２n ＋１)＝ʏn０１２x ＋１d x ＝ðni ＝１ʏii －１１２x ＋１d x ＜１２ðni ＝１(１２i －１＋１２i ＋１),不等式两边除以１２即为所证．例３㊀证明１３＋１５＋１７＋ ＋１２n ＋１＜１２l n (n ＋１)(n ɪN ∗)．分析㊀若考虑函数y ＝１２x ＋１,则有１２i ＋１＜ʏii －１１２x ＋１d x ,则ðni ＝１１２i ＋１＜ðni ＝１ʏii －１１２x ＋１d x ＝ʏn０１２x ＋１d x ＝１２l n (２x ＋１)n０＝１２l n (２n ＋１),达不到所证的精度,必须改变定积分放缩的精度．证明㊀结合不等式的右边,考虑函数f (x )＝１x．如图２所示,在区间[i ,i ＋１]上,取区间的中点i ＋１２,并以１i ＋１２为高作矩形A E F B ,则S 矩形A E F B ＜ʏi ＋１i １x d x ．于是有２２i ＋１＝１i ＋１２＜ʏi ＋１i１xd x ,则ðni ＝１２２i ＋１＜ðni ＝１ʏi ＋１i１xd x ＝ʏn ＋１１１xd x ＝l n (n ＋１),即ðn i ＝１１２i ＋１＜１２ln (n ＋１)．图２例４㊀设n 是正整数,r 为正有理数．(１)求函数f (x )＝(１＋x )r ＋１－(r ＋１)x －１(x ＞－１)的最小值;(２)证明:n r ＋１－(n －１)r ＋１r ＋１＜n r＜(n ＋１)r ＋１－nr ＋１r ＋１;(３)设x ɪR ,记[x ]为不小于x 的最小整数,例如[２]＝２,[π]＝４,[－３２]＝－１．令S ＝３８１＋３８２＋３８３＋ ＋３１２５,求[S ]的值．(参考数据:８０４３ʈ３４４ ７,８１４３ʈ３５０ ５,１２５４３ʈ６２５ ０,１２６４３ʈ６３１ ７．)分析㊀出题者的本意是利用第(１)问中的伯努利不等式来证明后两问,但这里我们利用积分来证明．证明㊀(１)f m i n (x )＝０(求解过程略)．(２)因为r 为正有理数,函数y ＝x r 在(０,＋ɕ)上单调递增,故ʏnn －１x r d x ＜nr,而５２热点追踪ʏnn －１x rd x ＝x r ＋１r ＋１n n －１＝n r ＋１－(n －１)r ＋１r ＋１,故n r ＋１－(n －１)r ＋１r ＋１＜n r．同理可得n r＜ʏn ＋１n x rd x ＝x r ＋１r ＋１n ＋１n ＝(n ＋１)r ＋１－n r ＋１r ＋１,从而n r ＋１－(n －１)r ＋１r ＋１＜n r＜(n ＋１)r ＋１－n r ＋１r ＋１．(３)由于i １３＜ʏi ＋１i x １３d x ＜(i ＋１)１３,故S ＝ð１２５i ＝８１i１３＜ð１２５i ＝８１ʏi ＋１ix １３dx ＝ʏ１２６８１x １３dx ＝３４x ４３１２６８１＝３４(１２６４３－８１４３),３４(１２５４３－８０４３)＝３４x ４３１２５８０＝ʏ１２５８０x １３d x ＝ð１２４i ＝８０ʏi ＋１ix １３d x ＜ð１２４i ＝８０(i ＋１)１３＝S ．３４(１２５４３－８０４３)＜S ＜３４(１２６４３－８０４３)．代入数据,可得３４(１２５４３－８０４３)ʈ２１０．２,３４(１２６４３－８１４３)ʈ２１０．９．由[S ]的定义,得[S ]＝２１１．２㊀利用积分证明函数不等式我们知道ʏx ２x １fᶄ(x )d x ＝f (x ２)－f (x １),因此,对于与f (x ２)－f (x １)有关的问题,可以从定积分的角度去思考．若f (x )的导数f ᶄ(x )在区间(a ,b )上单㊀图３调递减且f ᶄ(x )为凹函数,如图３所示．设A C 的中点为B ,过点B 作B G ʅx 轴与f (x )交于点G ,过点G 作f (x )的切线与直线AH 和C D 分别交于点F 和I ．设A (x １,０),C (x ２,０),则f (x ２)－f (x １)＝ʏx ２x １fᶄ(x )d x ＝S 曲边梯形A C J H ,S 矩形A C D E ＝f ᶄ(x ２＋x １２)(x ２－x １)．因为S 曲边三角形E G H ＞S әE F G ＝S әD I G ＞S 曲边三角形J D G ,S 曲边梯形A C J H －S 矩形A C D E ＝S 曲边三角形E G H －S 曲边三角形J D G ＞０,于是有f (x ２)－f (x １)x ２－x １＞f ᶄ(x ２＋x １２)．借助上述几何意义,一般地我们有如下结论．(１)若函数f (x )的导数f ᶄ(x )在区间(a ,b )上为凹函数,则对于任意的a ＜x １＜x ２＜b ,有f (x ２)－f (x １)x ２－x １＞f ᶄ(x ２＋x １２);(２)若函数f (x )的导数f ᶄ(x )在区间(a ,b )上为凸函数,则对于任意的a ＜x １＜x ２＜b ,有f (x ２)－f (x １)x ２－x １＜f ᶄ(x ２＋x１２)．例５㊀(１)函数f (x )＝l n x ,因为f ᶄ(x )＝１x在(０,＋ɕ)上为凹函数,则对任意０＜x １＜x ２,有l n x ２－l n x １x ２－x １＞１x ２＋x １２,即x ２－x １l n x ２－l n x １＜x １＋x ２２,此为对数均值不等式．(２)函数f (x )＝x l n x ,因为f ᶄ(x )＝１＋l n x 在(０,＋ɕ)上为凸函数,则对任意０＜x １＜x ２,有x ２l n x ２－x １l n x １x ２－x １＜１＋l n x ２＋x １２．许多考题都是以此为背景命题,比如,如下高三模拟考试的压轴题．例６㊀已知函数f (x )＝l n x －a x ２２＋(a －１)x －３２a(a ＞０),在函数f (x )的图象上是否存在不同两点A (x １,y １),B (x ２,y ２),线段A B 中点的横坐标为x ０,直线A B 的斜率为k ,使得k ＞f ᶄ(x ０)．简证㊀由于f ᶄ(x )＝１x－a x ＋a －１(a ＞０)在(０,＋ɕ)上为凹函数,可见结论成立!例７㊀设函数f (x )＝xex ,若x １ʂx ２,且f (x １)＝f (x ２),证明:x １＋x ２＞２．分析㊀本题的本质是极值点偏移问题,常见证法是利用对称性构造函数,这里采用定积分来证明．证明㊀不妨设x １＜x ２,由f ᶄ(x )＝１－x ex ,可知f (x )在(－ɕ,１]上单调递增,在[１,＋ɕ)上单调递减,且f (０)＝０．当x ＞０时,f (x )＞０,可知０＜x １＜１＜x ２．设x １e x １＝x ２e x ２＝t ,则x １＋x ２＝t (e x １＋e x ２),x ２－x １＝t (e x ２－e x １),考虑函数y ＝e x ,则根据定积分的梯形面积放缩有e x ２－e x １＝ʏx ２x １e xd x ＜(e x １＋e x２)(x ２－x １)２,则x ２－x １t ＜１２ x ２＋x １t(x ２－x １),故x １＋x ２＞２．(作者单位:广东省中山市中山纪念中学)６２。

定积分的计算和积分不等式摘要：本文首先介绍了定积分的几种计算方法：牛顿—莱布尼兹公式，分部积分法，换元积分法，积分值的估计。

其次再介绍了积分不等式的几种证明：用微分学的方法证明积分不等式，利用被积函数的不等式证明积分不等式，在不等式两端取变限积分证明新的不等式，利用积分性质证明不等式，利用积分中值定理证明不等式。

关键字：定积分；牛顿—莱布尼兹公式；分部积分法；换元积分法The Definite Integral Compute and Integral InequalityAbstract: In this paper, firstly, mainly introduced a few kinds computational method of definite integral: Newton-Leibniz, definite integration by parts, integration by substitution, definite integral by estimate value. Secondly, this paper also introduced a few kinds of integral invariant: using the method of differential calculus to prove integral invariant; making use of integrand invariant to prove integral invariant; using transfinite integrate to prove integral invariant; using integral characteristic to prove integral invariant; making use of integral mean value theorem to prove integral invariant.Key word:Definite integral; Newton-Leibniz; definite integration by parts; integration by substitution.引言数学分析是数学专业中一门重要的基础课，定积分的计算和积分不等式无疑是数学分析中一个重要的方面。

《积分不等式_（全文）》第1章积分不等式1.1 定积分不等式的证明定理1.1 方法1：柯西-施瓦茨不等式设f(x),g(x)在[a,b]上连续,则有∫b a f2(x)dx∫bag2(x)dx≥(∫baf(x)g(x)dx)2等号成立的必要条件是存在常数k使得 f(x)=kg(x). 习题1.1: 设f(x)在区间[0,1]上连续,且1≤f(x)≤3,证明:1≤∫10f(x)dx∫11f(x)dx≤43证明:由Cauchy-Schwarz不等式:∫1 0f(x)dx∫11f(x)dx≥(∫1√f(x)√1f(x)dx)2=1又由基本不等式得：∫1 0f(x)dx∫13f(x)dx≤14(∫1f(x)dx+∫13f(x)dx)2再由条件1≤f(x)≤3,有((f(x)-1)(f(x)-3)≤0,则f(x)+3f(x)≤4⇒∫1(f(x)+3f(x))dx≤4即可得1≤∫10f(x)dx∫k1f(x)dx≤43□定理1.2 方法2：琴声不等式连续的凸函数，则有：g(1b−a ∫baf(x)dx)≤1b−a∫bag(f(x))dx若g(x)是[m，M]上的连续凹函数时，上式中的不等号相反。

习题1.2: 证明:对于连续函数f(x)>0, 有ln∫10f(x)dx≥∫1lnf(x)dx证明:令g(x)=lnx,则. g′′(x)=1x ,g′′(x)=−1x2<0,所以g(x)为凹函数，可由上式琴声不等式定理，可得ln∫10f(x)dx≥∫1lnf(x)dx或利用定积分定义，将[0，1]分』等分，可取x=1n,由“算术平均数≥几何平均数“得：1 n ∑k=1n f(kn)≥√f(1n)⋯f(nn)n=e1n∑k=1n lnf(k n)⇒∫10f(x)dx≥e lim n→∞1n∑k=1n lnf(kn)=e∫10lnf(x)dx然后两边取对数即证.∫b a tf(t)dt≤2b−a6[(2b+a)f(b)+(2a+b)f(a)]事业证明：利用琴声不等式，对于任意R∈[0，1]，则有：Rf(x₁)+(1﹣R)f(x₂)≥f(Rx₁+(1﹣R)x₂) 所以再令t=xb+(1-x)a有:∫b a lf(t)dt=(b−a)∫1[xb+(1−x)a]f(xb+(1−x)a)≤(b−a)∫1[xb+(1−x)a][xf(b)+(1−x)f(a)]dx≤2b−n6[(2b+a)f(b)+(2a+b)f(a)]证明：对任意x∈[0,π2],有1-cosx ≤ sinx, 即得到∫x 0sintdt≤∫xcostdt,显然有∫π2sinxdx=∫π2cosxdx=1,且函数11+x2在[0,π2]上单调递减，所以可以利用斯蒂文森不等式,若f(x)在[a,b]上单调递减,则∫b a f(x)g1(t)dt≤∫baf(x)g2(t)dt,即有：∫n2sinx1+x2dx≤∫n2cosx1+x2dx习题1.4: 证明:∫π20sinx1+x2dx≤∫π2cosx1+x2dx习题1.5: 设a>0, f(x)在[0,a]上连续可导,证明:|f (0)|≤1a ∫a|f (x )|dx +∫a|f ′(x )|dx证明：由积分第一中值定理，有1a∫a 0|f (x )|dx =|f (ξ)|,ξ∈[0,a ] ∫z|f ′(x )|dx ≥∫z|f ′(x )|dx ≥|∫ḡf ′(ξ)dx|=|f (ξ)−f (0)|≥|f (0)|−|f (ξ)|习题1.6: 设 f(x)在[0,1]上连续可导,证明:|f (12)|≤∫10|f (x )|dx +12∫1|f ′′(x )|dx证明：由积分第一中值定理，有 [0,12],f (ξ)|dx =12|f (ξ)|,ξ∈[0,12]. 再由N-L 公式, f (12)=f (ξ)+∫12ξf ′(x )dx,04所以有：|f (12)|≤|f (ξ)|+∫120|f ′(x )|dx ≤2∫ℎ|f (x )|dx ∫1|f ′(x )|dx′(1)即1a ∫a|f (x )|dx +∫a|f ′(x )|dx ≥|f (ξ)|+|f (0)|−|f (ξ)|=f (0)|f (12)|≤|f (ξ)|+∫112|f ′(x )|dx ≤2∫112|f (x )|dx ∫112|f ′(x )|dx (2)用(1)与(2)式相加即证.习题1.7: 设f(x)在[a,b]上有一阶连续导数,f(a)=f(b)=0,求证:∫b a|f (x )|dx ≤(b−a )24M其中M 为|f'(x)|在[a,b]上的最大值。

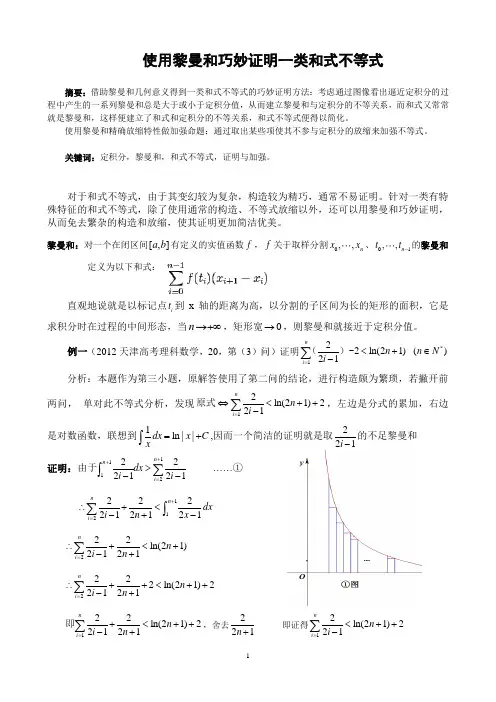
使用黎曼和巧妙证明一类和式不等式摘要：借助黎曼和几何意义得到一类和式不等式的巧妙证明方法：考虑通过图像看出逼近定积分的过程中产生的一系列黎曼和总是大于或小于定积分值，从而建立黎曼和与定积分的不等关系，而和式又常常就是黎曼和，这样便建立了和式和定积分的不等关系，和式不等式便得以简化。

使用黎曼和精确放缩特性做加强命题：通过取出某些项使其不参与定积分的放缩来加强不等式。

关键词：定积分，黎曼和，和式不等式，证明与加强。

对于和式不等式，由于其变幻较为复杂，构造较为精巧，通常不易证明。

针对一类有特殊特征的和式不等式，除了使用通常的构造、不等式放缩以外，还可以用黎曼和巧妙证明，从而免去繁杂的构造和放缩，使其证明更加简洁优美。

黎曼和：对一个在闭区间[,]a b 有定义的实值函数f ，f 关于取样分割0,,n x x 、01,,n t t -的黎曼和定义为以下和式：直观地说就是以标记点i t 到x 轴的距离为高，以分割的子区间为长的矩形的面积，它是求积分时在过程的中间形态，当n →+∞，矩形宽0→，则黎曼和就接近于定积分值。

例一（2012天津高考理科数学，20，第（3）问）证明122ln(21)21ni n i =<+-∑（）- *()n N ∈ 分析：本题作为第三小题，原解答使用了第二问的结论，进行构造颇为繁琐，若撇开前两问， 单对此不等式分析，发现12ln(21)221ni n i =⇔<++-∑原式，左边是分式的累加，右边是对数函数，联想到1ln ||dx x C x =+⎰,因而一个简洁的证明就是取221i -的不足黎曼和证明：1112222121n n i dx i i ++=>--∑⎰由于 ……① 112222212121nn i dx i n x +=∴+<-+-∑⎰222ln(21)2121ni n i n =∴+<+-+∑222ln(21)22121ni n i n =∴++2<++-+∑122ln(21)22121ni n i n =+<++-+∑即，舍去221n + 即证得12ln(21)221ni n i =<++-∑这样，通过不足近似值逼近时的黎曼和小于相应定积分值，即可轻松证得该和式不等式。

定积分不等式及其最佳常数的两种证明方法定积分不等式是指对于$f(x)$在$[a,b]$上连续，$g(x)$在$[a,b]$上单调递增和非负，有以下不等式成立：$$\int_a^bf(x)g(x)dx\le\frac{b-a}{2}\left(\int_a^bf^2(x)dx+\frac{1}{g^2(a)}\int_a^bg^2(x)dx\ right)$$其中等号成立当且仅当$f(x)=k\cdot g(x)$，其中$k$是一个常数。

这个不等式也被称为“加权平均值-平方根平均值不等式”，可以用两种不同的证明方法：一种是基于几何意义的证明，另一种是基于分部积分的证明。

方法一：首先考虑一个几何上的问题：对于函数$f(x)$，我们可以将其图像在区间$[a,b]$上折叠，形成一个平行四边形，可以证明该平行四边形的面积等于$\int_a^bf(x)dx$。

现在我们假设将平行四边形“割”成两半，所得的两个“三角形”的底分别为$\frac{b-a}{2}$和$\frac{b-a}{2}g(a)$。

则根据三角形面积公式，这两个“三角形”的面积分别为$\frac{1}{2}\int_a^bf^2(x)dx$和$\frac{1}{2g^2(a)}\int_a^bg^2(x)dx$。

由于$g(x)$是单调递增且非负的，所以可以想象这两个“三角形”肯定包含在一条斜率为$k$（其中$k$为常数）的直线下方。

因此，我们可以将这个直线逆时针旋转一定角度，得到一个新的平行四边形，其底仍为$\frac{b-a}{2}$和$\frac{b-a}{2}g(a)$，高为$\frac{1}{2}(k+\frac{1}{g(a)})$（即平行四边形的两个高之和的一半）。

根据面积公式，这个新的平行四边形的面积为$\frac{b-a}{2}(k+\frac{1}{g(a)})\cdot\int_a^bf(x)g(x)dx$。

由于这个新平行四边形的面积应不小于原平行四边形的面积，因此我们可以得到不等式：$$\int_a^bf(x)g(x)dx\le\frac{b-a}{2}\left(\int_a^bf^2(x)dx+\frac{1}{g^2(a)}\int_a^bg^2(x)dx\ right)$$并且等号成立当且仅当$f(x)=k\cdot g(x)$。

定积分不等式证明方法要证明一个定积分的不等式，通常可以使用下面的方法：1.使用函数的性质：a.利用函数的递增性或递减性：如果能够证明被积函数在积分区间上是递增函数或递减函数，那么可以利用这个性质来证明不等式。

b.利用函数的凸性或凹性：如果被积函数在积分区间上是凸函数或凹函数，那么可以利用这个性质来证明不等式。

c.利用函数的导数性质：如果能够证明被积函数的导数在积分区间上具有一些特定的性质，比如非负或非正，那么可以利用这个性质来证明不等式。

2.使用定积分的性质：a.利用定积分的线性性质：如果能够将被积函数表示为两个或多个可积函数的线性组合，那么可以利用定积分的线性性质来证明不等式。

b.利用定积分与函数极限的关系：如果被积函数是一个收敛函数序列的极限函数，那么可以利用定积分与函数极限的关系来证明不等式。

c.利用平均值定理：如果能够找到一个介于被积函数在积分区间上的最大值和最小值之间的常数函数，那么可以利用平均值定理来证明不等式。

3.使用面积比较法：a.利用图形的几何性质：将被积函数与一个已知函数或图形进行比较，通过比较图形的面积大小来证明不等式。

b.利用图形的对称性：如果能够将积分区间对称分割，或者利用函数的对称性，那么可以利用对称性来证明不等式。

4.使用特殊技巧：a.利用变量替换：通过对积分变量进行适当的代换，可以将原来的不等式转化为更加简单的形式，从而更容易证明。

b.利用积分的可加性：如果被积函数具有可加性的性质，即可以将积分区间分成多个子区间进行求积分，那么可以利用这个性质来证明不等式。

以上是一些常用的定积分不等式证明方法，但并不是穷尽的。

在实际问题中，根据具体的情况可能需要结合多种方法来证明不等式。

最后，需要强调的是，在证明中需要合理运用数学工具和定义、定理，推导过程要严密，逻辑要清晰，以确保证明的正确性和严谨性。

积分不等式的证明方法及其应用一、积分不等式的证明方法：1.使用定积分定义证明：对于一个函数f(x)，如果在[a,b]上f(x)≥0，那么可以使用定积分的定义进行证明。

将[a,b]分成n个小区间，每个小区间长度为Δx=(b-a)/n，那么对于每个小区间，存在一个ξi ∈ [x_{i-1}, x_i]，使得f(ξi)Δx_i≤∫_{x_{i-1}}^{x_i} f(x)dx。

对于所有小区间，将不等式相加并取极限即可得到定积分不等式。

2.使用导数的性质证明：对于一个函数f(x)，如果能够表示出它的导数f'(x)，那么可以使用导数的性质进行证明。

首先计算f'(x)，然后判断f'(x)的正负性，再根据函数在[a,b]上的取值情况，可以得到相应的不等式。

例如，如果f'(x)≥0，那么f(x)在[a,b]上是单调递增的，可以得到∫_a^bf(x)dx≥∫_a^b f(a)dx=f(a)(b-a)。

3.使用恒等式和变量替换证明：对于一个复杂的积分不等式，有时可以通过引入合适的恒等式或进行变量替换来简化证明过程。

例如，对于形如∫_a^b f(x)g(x)dx≥0的不等式，可以通过将f(x)g(x)拆分为两个函数的平方和，然后应用恒等式a^2+b^2≥0进行证明。

或者，可以通过进行变量替换将不等式转化为更简单的形式，然后再进行证明。

二、积分不等式的应用：1.极值问题：2.凸函数与切线问题：3.平均值不等式：平均值不等式是积分不等式的一种特殊情况，它可以用于证明平均值与极值之间的关系。

例如，对于一个连续函数f(x)，可以通过证明(1/(b-a))∫_a^b f(x)dx≥ƒ(ξ)来得到平均值与极值之间的关系。

4.泛函分析问题：总结起来，积分不等式的证明方法包括定积分定义证明、导数性质证明、恒等式和变量替换证明等等。

而积分不等式的应用包括解决极值问题、研究凸函数的性质、平均值不等式以及泛函分析问题等。

第三章一元积分学第三节定积分值的估计及不等式定积分值的估计及不等式证明是一个较难的问题，方法多样，用到的知识（微分学的知识，积分学的知识等）也很多。

总的说来：（1）主要用积分学的知识，除了定积分的性质、积分中值定理、计算方法外，以下几个简单的不等式也是有用的：b b(i)若f(x) <g(x)(x 引a,b])，则J f (x)dx < J g(x)dx .a ab b(ii) I f f(x)dx| 兰f l f (x) |dx.ad b(iii )若f(X)>0(X 引a,b]), a<c<d<b,则f f (x)dx < f f (x)dx.9 £(iv)(柯西不等式)[f f (x)g(x)dxr < a f 2(x)dx a g2(x)dx（2）主要用微分学的知识，包括前面己讲过的利用微分学知识证明不等式的一切方法.（3）利用二重积分、级数等.值得注意的是：题目的解法往往有多种，同一题目其解答过程中往往要用到各种知识和方法.、■莎 2例1.判断积分[sin x dx的符号分析：这个积分值是求不出来的.如果被积函数在积分区间上有确切的符号，那么积分值的符号很容易判断.如果被积函数在积分区间上有正、有负，那么应根据被积函数的正、负情况将积分区间分成部分区间，然后利用积分学等方面的知识比较在这些部分区间上的积分值（实际上是比较积分值的绝对值）.本题中被积函数si nx2在积分区间上有正、有负，先作，一2*烦2 1 ^sin t换兀：t =x ,把积分变为（sinx dx=5t -^dt后，问题更清晰，因而想到/莎 2 1 2；rs int 1 F兀sin t ,^si ntsinxdx=?0 ;r dt=2d寅dx+J兀至此积分的符号凭直觉已经能判断了. 但严格说明还需做一些工作，上式右端两个积分的积分区间不一样，为了方便比较，应将两个积分放在同一积分区间上进行比较. 有了这些分析和思路后，解答就容易了.解：令t =x2，则0 sin/dx^L 于dt—2(0 于dx+J兀于dt)2兀sin t 兀一sin u 兀sin t对上式右端后一积分换元，u*得d r 右du—0右dt从而广sinx2dx—丄(f字dx-f严dt) 0 2 0JT看V u +兀1兀1 1=-f (k -- )sintdt >02 J t+J注：本题的解答过程不复杂，但其过程中有两个技巧很有用(1)将积分区间分成部分区间 (尤其是等分区间，特别是二等分) (2)如要比较两个在不同积分区间上的积分的大小，可通过换元变成相同积分区间上的积分，然后比较.迟. 3例 2 .设a A 0，证明：(xa sinx dx『a ■sinx dx > 亍分析：：从形式上看很象柯西不等式，但两个积分的积分区间不一样，前面的积分可用教材上介绍的一个等式0，f(sinx)dx = jr 02 f(sinx)dx变为［0,亍］上的积分,再用柯西不等式便可得结论。

定积分不等式及其最佳常数的两种证明方法定积分不等式指的是如下形式的不等式：$\left(\int_{a}^{b} f(x)g(x) dx\right)^2 \leq \int_{a}^{b} f(x)^2 dx \int_{a}^{b} g(x)^2 dx$其中，$f(x)$ 和$g(x)$ 是$[a,b]$ 区间上的可积函数。

这个不等式在数学分析、物理学、经济学等领域都有广泛的应用。

下面介绍两种证明方法：方法一：使用柯西-施瓦茨不等式定积分不等式可以通过柯西-施瓦茨不等式来证明。

具体地，考虑如下积分：$\int_{a}^{b} \left[f(x) - \frac{\int_{a}^{b} f(x)g(x) dx}{\int_{a}^{b} g(x)^2 dx} g(x)\right]^2 dx$其中，$f(x)$ 和$g(x)$ 是$[a,b]$ 区间上的可积函数。

这个积分可以表示为：$\int_{a}^{b} \left[f(x)^2 -2f(x) \frac{\int_{a}^{b} f(x)g(x) dx}{\int_{a}^{b} g(x)^2 dx}g(x) + \left(\frac{\int_{a}^{b} f(x)g(x) dx}{\int_{a}^{b} g(x)^2 dx}\right)^2 g(x)^2 \right] dx$对于第二项，由于柯西-施瓦茨不等式，有：$\int_{a}^{b} 2f(x) \frac{\int_{a}^{b} f(x)g(x) dx}{\int_{a}^{b} g(x)^2 dx}g(x) dx \leq 2\sqrt{\int_{a}^{b} f(x)^2 dx \int_{a}^{b} g(x)^2 dx}$对于第三项，由于$\int_{a}^{b} g(x)^2 dx > 0$，所以它是非负的。

因此，将这三个积分的结果加起来，得到：$\int_{a}^{b} \left[f(x) - \frac{\int_{a}^{b} f(x)g(x) dx}{\int_{a}^{b} g(x)^2 dx}\right]^2 dx \geq 0$展开后即可得到定积分不等式。

定积分不等式的证明1. 引入定积分的定义: 首先回顾定积分的定义，对于函数f(x)在区间[a,b]上的定积分记为∫[a,b]f(x)dx。

在区间[a,b]上划分任意n个子区间，每个子区间的长度为Δx，选取任意的代表点ξ_i，那么定积分可以近似表示为∑[i=1->n]f(ξ_i)Δx。

2. 引入上和下和: 上和S_n表示将子区间的长度无限逼近为0时，以ξ_i为代表点的定积分的极限值。

即S_n = lim[n->∞](∑[i=1->n]f(ξ_i)Δx)。

同理，我们可以引入下和I_n = lim[n->∞](∑[i=1->n]f(η_i)Δx)，其中η_i为每个子区间内的最小值。

3.证明下和的单调性:为了证明定积分的不等式，我们首先证明了下和的单调性。

假设f(x)在区间[a,b]上是单调增加的函数，那么我们可以得到下面的不等式：a<x_1<η_1<f(x_1)(1)x_2<η_2<f(x_2)(2).....x_n<η_n<f(x_n)(n)根据定义我们知道，η_i是每个子区间内的最小值，那么对于上面的不等式，我们可以将其累加得到：a<x_1<η_1<f(x_1)a+x_1<x_1+η_1<η_1+f(x_1)a+x_1+x_2<x_1+x_2+η_2<η_1+η_2+f(x_2).....a+x_1+x_2+...+x_n<x_1+x_2+...+x_n+η_n<η_1+η_2+...+η_n+f( x_n)上面的不等式可以简化为：a+b_n<S_n<I_n+b_n其中b_n=f(x_1)+f(x_2)+...+f(x_n)。

根据定积分的性质，极限的运算可以通过分别求逐项求极限来进行。

那么我们可以得到：lim[n->∞](a + b_n) < lim[n->∞]S_n < lim[n->∞](I_n + b_n)。

借助定积分证明不等式作者：赵曜来源：《中学数学杂志(高中版)》2015年第06期定积分及微积分基本定理由于各地高考考纲中对考生的要求较低，其在高考中的相关题目大多为基础题型.然而这并不意味着这方面的知识不需要多加练习并熟练运用，因为在高考题尤其是压轴题的不等式证明中，联系定积分及其几何意义往往会有出奇制胜的神奇效果.先来看一道例题.例1 证明：12+13+ (1)分析1 本题要证的结论是一个十分优美的不等式，而且此不等式在近年高考中以不同形式多次出现并要求考生证明.例如，2014年高考陕西卷理科数学压轴题、2015年高考广东卷理科数学压轴题的证题核心都是上述不等式.传统的证明方法是将不等式右边裂项，并与左边一一对应寻找关系构造函数求解.证明1 设函数f（x）=x+ln（1-x），x∈（0，1）时，f′（x）=1-11-x=-x1-x取x=1n∈（0，1），n∈N+，则有1n分析2 仔细观察原不等式，不难发现左边的和式中每一项都是函数f（x）=1x的函数值，而右侧则是函数g（x）=lnx的函数值，从而考虑将其看作原函数与导函数，这样一来右侧的原函数便可以看作对导函数的一个积分，再设法将左边与面积相联系，得到如下解法.证明2 作f（x）=1x的图像（图1），设点（n-1，0），（n-1，1n），（n，0），（n，1n），（n∈N+且n≥2）围成的n个矩形的面积之和（即图中阴影部分）为S1，曲线y=1x，x∈[1，n]与x轴围成的曲边梯形面积为S2，根据图像显然有S2>S1.又由于S1=1×12+1×13+…+1×1n=∑ni=21i，S2=∫n11xdx=lnn所以原不等式得证.图1从上面的证明中，相信大家已经领略到了积分法证明不等式的优美之处.虽然比较之下函数构造法的复杂度不高、计算量也不大，但在分析问题的过程中，通过一目了然的函数图像，积分法的思路显得远比函数法简洁且易于捕捉.在上题中，定积分的主要作用在于赋予不等式中某一项或几项几何意义，然后再通过面积的比较直截了当地证明原不等式.下面的这道例题也使用了这种方法，不过在面积的比较上使用了一些技巧.例2 设函数f（x）=ln（x+1），若-1f（x）-f（x2）x-x2是否恒成立？证明你的结论.分析与证明看到此题要证明的不等式结构，很容易联想到曲线割线的斜率.如果作出f （x）=lnx的图像，不难看出结论是显然成立的，但若要利用割线斜率来证明此题需要使用到拉格朗日中值定理，而中值定理却并不属于高考涉及的知识.因此重新观察原不等式.注意到函数f（x）结构十分简单，因而如果熟练掌握利用定积分证明不等式的思想，不难想到将原函数函数值之差转化为导函数f′（x）=1x+1的定积分.如此一来，原不等式化为如下形式：∫xx1f′（x）dxx-x1>∫x2xf′（x）dxx2-x.（*）转化之后，下一步便是同上题一样作出f′（x）图像，联系上式积分式的几何意义，尝试寻找与面积相关的关系.如图2所示，取点A，B，C，D，E，F，则∫xx1f′（x）dx即为曲边体形AEFD的面积，设为S1；同理设S2=SEBCF=∫x2xf′（x）dx.同时又有DF=x-x1，FC=x2-x.于是（*）式又进一步化为S1DF>S2CF.图2由于不易直接判断两边分式的大小，考虑借助中间量EF.过E作MN平行于x轴交直线AD、CB于M，N，注意到S1DF>SMEFDDF=EF=SENCFCF>S2CF，所以原不等式得证.此题为湖南长沙高考模拟的一道理科数学压轴题，原题答案给出的证明方法是通过构造函数分别比较不等式两边与1x+1的大小.事实上，在上述证明中，中间量线段EF的长对应的值即为f′（x）=1x+1.尽管这两种方法看上去异曲同工，但在实际解题过程中，中间量的寻找难度却相差很大.定积分把抽象的代数式转化为了具体的几何图形及其面积，大大降低了寻找中间量的难度，从而有效地保证了解题思路的流畅连贯，不至使思路受阻而无法解出此题.这两道例题的方法相似，都是通过面积的比较直接证明不等式.可以用这类方法解决的题目，其所求证的不等式大多具有较为明显的结构特点：如例题一，原函数与导函数同时出现在不等式中；或如例题二，不等式或变形后的不等式中涉及函数值之差.在这类问题的解决过程中积分法一旦能够有用武之地，它的优势通常都是十分显著的.这是因为此类题目在出题时制定的标准答案多为导数方法，题目的难点和易错点也大都存在于函数的构造、导数的计算等过程中，因而使用定积分常常能够巧妙的避开这些困难之处另辟蹊径，更加有效地逼近答案.但定积分在不等式证明中的作用绝不仅限于此.我们知道，放缩是不等式证明中最重要最有效的方法之一，实际上利用定积分也可以实现对不等式的“放缩”.常见的放缩是通过添加、删除或改变常数、代数式等来实现，而接下来要介绍的方法则是对整个命题进行强化，其实质都是通过证明原命题的充分不必要条件来达到证明原命题的目的.例3 已知函数f（x）=xex，求证：对任意x∈（0，1），f（1-x）分析1 先化简原命题，代入自变量得1-xe1-x证明1 要证1-xe1-x证明2 要证原命题，即证f（1）-f（1-x）>-[f（1+x）-f（1）]，即∫11-xf′（t）dt>∫1+x1[-f′（t）]dt，强化命题，只需证对任意x∈（0，1），f′（1-x）>-f′（1+x）即证1-（1-x）e1-x>-1-（1+x）e1+x，即xe1-x>xe1+x显然成立，所以原不等式得证.证明2中对命题的一次强化正确性是比较显然的.由于不等号两边积分式的积分区间长度相同，如果保证了左段函数值总是“对应地”（关于直线x=1对称地）大于右段函数值，那么函数左段的定积分自然也大于右段的定积分.或者更为直观地说：设两曲边梯形A和B等底，使A和B的底边重合，若A的上轮廓总是高于B的上轮廓，A的面积当然要大于B的面积.这其实类似于立体几何中的祖暅定理.基于这个结论，我们把对原函数函数值的比较转化为了对导函数函数值的比较，从而极大地降低了证明的难度，得到了一个甚至直接观察就可以证明的不等式.相比之下，第一种方法首先需要进行多次变形的尝试以找到一个易于构造函数、构造出的函数易于分析的不等式结构，然后又需要计算二阶导数来分析函数单调性并利用单调性证明原不等式，显得十分的复杂、繁琐.以上的三道例题充分证明了定积分在不等式证明中是一个化繁为简、出奇制胜的有力工具，而不仅仅是一个在高考中只能用来解答基础题的知识.利用定积分证明不等式不仅能降低证明的难度，更能使证明过程更加简洁、优美，在解题实践中若能做到多用、巧用和活用，必能获得事半功倍的效果.。

证明一类定积分不等式的有效方法证明一类定积分不等式的有效引言定积分是高等数学中重要的概念之一，它在数学理论和实际问题的求解中都起着重要作用。

在证明定积分的性质和定理时，我们常常需要使用一类定积分不等式。

本文将详细介绍多种有效的方法，来证明这类不等式。

方法一：函数性质法•步骤一：首先，我们需要分析被积函数的性质。

•步骤二：利用被积函数的单调性或凸凹性等特点，将定积分不等式转化为某个已知不等式的形式。

•步骤三：根据这个已知不等式的结论，推导出原定积分不等式的结论。

方法二：积分中值定理法•步骤一：使用积分中值定理，将被积函数表示为一个中值的形式。

•步骤二：根据中值的性质，将定积分不等式转化为某个已知不等式的形式。

•步骤三：根据这个已知不等式的结论，推导出原定积分不等式的结论。

方法三：换元法•步骤一：通过适当的换元变量，将定积分不等式的被积函数转化为一个更加简单的形式。

•步骤二：利用换元后的简单形式，推导出原定积分不等式的结论。

方法四：样本函数法•步骤一：我们可以构造一个样本函数，使得定积分不等式在这个样本函数上成立。

•步骤二：通过对样本函数进行适当的变换，将原定积分不等式推广到更一般的情况。

方法五：数学归纳法•步骤一：首先，我们需要证明定积分不等式在某个特殊情况下成立。

•步骤二：假设定积分不等式在某个特殊情况下成立。

•步骤三：通过数学归纳法，将定积分不等式推广到更一般的情况。

方法六：微积分定理法•步骤一：使用微积分中的主要定理，如泰勒展开定理、拉格朗日中值定理等。

•步骤二：利用这些定理，将定积分不等式转化为已知定理或性质的形式。

•步骤三：根据这些已知定理的结论，推导出原定积分不等式的结论。

方法七：数值方法•步骤一：通过数值近似计算，获取定积分不等式的近似结果。

•步骤二：通过不断改进数值计算方法，逐渐提高定积分不等式的精确度。

•步骤三：通过比较数值结果与理论结果的差距，验证定积分不等式的有效性。

以上是一些常用的方法，用于证明一类定积分不等式的有效性。

探讨定积分不等式的证明方法定积分不等式是数学中的一种重要的不等式，它在数学分析、微积分和概率论等领域中具有广泛的应用。

证明定积分不等式的方法也非常多样，下面将介绍几种常用的证明方法。

对于给定的定积分不等式，我们可以通过研究被积函数的性质来进行证明。

常用的方法有以下几种。

1.利用导数和极值的性质对于被积函数f(x)，我们可以通过研究f'(x)的符号和f(x)的极值来判断f(x)在给定区间上的大小关系。

通过推导f'(x)的性质和计算f(x)的极值点，可以得到定积分不等式的证明。

2.利用函数的凸性或凹性凸函数具有性质：对于给定的区间上任意两个点，函数在这两个点之间的值不大于这两个点处的函数值的线性插值。

而凹函数则相反，函数在这两个点之间的值不小于这两个点处的函数值的线性插值。

通过研究函数的凸性或凹性，我们可以得到定积分不等式的证明。

3.利用函数的连续性和单调性如果被积函数f(x)在给定区间上是连续的，且在该区间上单调递增或单调递减，则可以利用这些性质来进行证明。

通过推导f(x)的导数或利用中值定理，可以得到定积分不等式的证明。

定积分不等式的证明通常需要对积分区间进行适当的分割，以便研究被积函数的性质。

常用的方法有以下几种。

1.利用分段函数的性质进行分割被积函数f(x)在给定区间上可能是分段定义的，在不同的区间段上具有不同的性质。

通过将给定区间分成几个子区间，并对每个子区间上的被积函数进行分析，可以得到定积分不等式的证明。

2.利用辅助函数进行分割如果被积函数f(x)难以分割或分析，我们可以引入辅助函数g(x)来研究定积分不等式。

通过将f(x)与g(x)进行比较，可以将定积分不等式转化为对辅助函数g(x)的定积分的不等式来进行证明。

积分中值定理是微积分中的基本定理之一，它为定积分不等式的证明提供了有力的工具。

常用的方法有以下几种。

1.利用平均值定理平均值定理是积分中值定理的一种特殊形式，它将定积分转化为函数的平均值与函数在给定区间上的其中一点处的函数值的乘积。