中国全要素生产率的变化
- 格式:doc
- 大小:160.00 KB
- 文档页数:8

市场经济的全要素生产率中国的技术创新与效率提升市场经济的全要素生产率——中国的技术创新与效率提升市场经济的全要素生产率是衡量一个国家或地区经济发展水平的重要指标。
全要素生产率包括资本、劳动和技术的综合运用效率,是经济增长的关键要素。
而在中国,技术创新和效率提升成为实现市场经济全要素生产率增长的关键。
一、中国市场经济的全要素生产率现状中国市场经济的全要素生产率在过去几十年一直保持着较高的增长势头。
通过技术进步、人力资源优化配置和资本积累等因素的综合作用,中国的经济增长迅猛,但与发达国家相比,全要素生产率仍然存在一定差距。
这主要是由于技术创新水平相对较低以及资源配置效率有待进一步提高等原因。
二、技术创新是中国市场经济全要素生产率提升的关键技术创新是提高市场经济全要素生产率的重要途径。
在中国,技术创新体现在以科技研发为核心的创新模式上。
通过加大科技投入、加强科技创新能力培养等,中国的技术创新水平逐渐提升,为市场经济的全要素生产率增长提供了强有力的支撑。
三、效率提升是中国市场经济全要素生产率提升的保障在技术创新基础上,提高效率是中国市场经济全要素生产率增长的重要保障。
通过优化各项资源配置、加强管理创新等,中国的市场经济效率逐渐提升,为全要素生产率的提高创造良好的环境。
例如,推动企业制度改革、优化市场环境、提高生产力等都是提升市场经济效率的有效手段。
四、技术创新与效率提升相互促进形成正向循环技术创新和效率提升在中国市场经济中相互促进,形成了良性的正向循环。
技术创新的推动可以提升企业的生产力和竞争力,从而促进效率的提升;而效率的提升又为技术创新提供了更广阔的市场和更好的环境。
两者相互促进,形成了良性循环。
五、未来中国市场经济全要素生产率提升的挑战与发展方向未来中国市场经济全要素生产率的提升面临着一些挑战。
首先,技术创新水平仍然相对较低,需要进一步加大科技投入、推动科技成果转化等。
其次,资源配置与生产要素效率仍然有待进一步提高,需要深化改革、优化市场环境等。
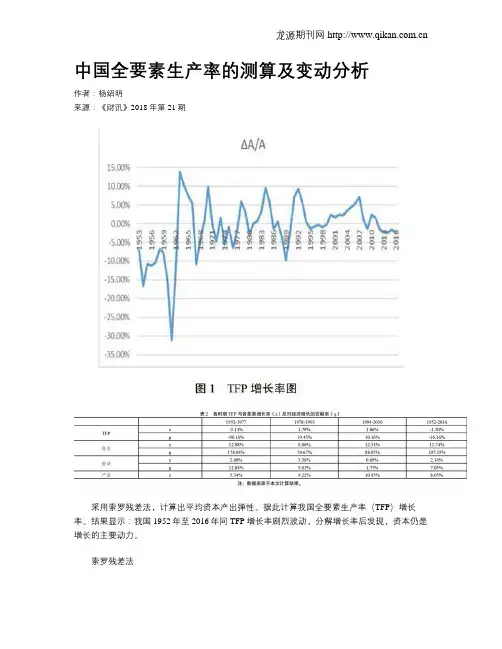
中国全要素生产率的测算及变动分析作者:杨绍明来源:《财讯》2018年第21期采用索罗残差法,计算出平均资本产出弹性。
据此计算我国全要素生产率(TFP)增长率。
结果显示:我国1952年至2016年间TFP增长率剧烈波动,分解增长率后发现,资本仍是增长的主要动力。
索罗残差法资本产出弹性全要素生产率问题提出全要素生产率(Total FactorProductivity,TFP)是长期支撑经济体增长的重要因素,对其的测度具有较强的理论与现实意义。
易纲等(2003)对证明我国经济增长中存在效率提升。
郭庆旺和贾俊雪(2005)采用三种模型计算了我国TFP增长率,结果都表明经济的波动与TFP 增长率密切相关。
牛龙(2013)认为这近三十年间,我国经济增长的8.7%来源于劳动增加,49.4%来源于资本增加,41.8%来源于技术进步。
罗良文和梁圣蓉(2016)发现我国经济增长主要来源于资本投入,技术进步的贡献只占到百分之十几。
已有文献的结论并不一致。
理论准备以Cobb-Douglas生产函数为基础的模型推导过程,主要分为两步:(1)计算资本与劳动的产出弹性。
Yt=AtKtaLt(1-a)(2.1)Yt、Al、Kt、Lt为第t年产出、资本存量、劳动力数量;a为资本产出弹性整理并化简公式(2.1):数据处理本文以1952年至2016年为研究区间。
总产出 Yt为GDP,用CPI换算成以1952年价格;劳动Lt为全国就业人员;资本Kt为我国的资本存量,但此数据需要进行测算。
采用永续盘存法(Kt=(1-8)Kt-1+lt/Pt,It、Pt为第t年固定资产投资、固定资产价格指数;δ为固定资产折旧率)测算资本存量。
It采用固定资本形成总额数据。
Pt采用借鉴张军(2004)介绍的方法构的造固定资本形成总额指数。
基期资本存量Ko采用单豪杰(2008)测算的结果342亿元(1952年价)。
δ采用陈昌兵(2014)计算的结果5.65%。

中国全要素生产率估算与分析根据最新的统计数据,中国的全要素生产率一直处于较快增长的状态。
在过去几十年里,中国经济实现了快速增长,并且不断提高了生产率水平。
这主要得益于中国不断推进经济改革,加大对技术创新的投入,改善了生产要素的配置和利用效率。
通过对中国全要素生产率的估算与分析,我们可以发现一些特点和趋势。
首先,在产业结构升级和技术创新的推动下,中国的全要素生产率持续提升。
在传统产业向现代产业转型的过程中,劳动力的素质和技能不断提高,技术水平逐步提升,资本投入和利用效率逐渐改善,这些都对全要素生产率的增长起到了支撑作用。
其次,中国的全要素生产率在不同地区和行业之间存在较大的差异。
东部沿海地区的全要素生产率水平相对较高,而中西部地区的全要素生产率则相对较低。
在行业方面,高科技产业和服务业的全要素生产率明显高于传统制造业和农业。
这表明中国地区之间和行业之间的发展不平衡问题依然存在,需要进一步加强政策引导和扶持。
综上所述,中国的全要素生产率在不断增长,但仍面临着不平衡的地区和行业发展状况。
未来,中国需要加大对技术创新的投入,促进产业结构升级和转型升级,加强对全要素生产率的测算和分析,以实现经济高质量发展和可持续增长。
中国全要素生产率(TFP)的估算与分析是我们了解中国经济的发展与竞争力的重要途径。
全要素生产率是衡量经济效率和创新能力的一个关键指标,它是指在市场运作的条件下,多种生产要素共同参与生产,经济体系产出的增长除了由劳动力和资本进步外,还包括了一种由全要素生产率技术变动所引起的增长。
简而言之,全要素生产率代表了除了劳动力和资本外,其他要素(如技术、管理等)对经济增长的贡献。
中国经济的快速发展在过去几十年里取得了巨大成功,同时也在全要素生产率上取得了显著成绩。
按照最新的统计数据,中国的全要素生产率一直在持续增长。
这种增长主要是由于中国政府在长期经济改革方面的成功举措,以及在技术创新和知识产权保护方面的努力。

中国经济全要素生产率的分析与提升策略近年来,中国的经济总体呈现出逐步稳定和增长的态势。
尽管如此,中国经济的增长却由过去的大量投资驱动,向现在的消费驱动转变。
但是,中国的经济仍存在一些问题,其中最重要的是全要素生产率(TFP)。
全要素生产率是指一种衡量技术进步、组织、管理和改进的能力的指标。
它是衡量生产力的最佳指标之一,因为它为产品和服务提供了更好的质量和更高的效率。
因此,全要素生产率的提高对经济增长至关重要。
首先,让我们深入了解全要素生产率和其对经济增长的贡献。
一、什么是全要素生产率全要素生产率(TFP)是以不同生产要素(包括劳动力、资本等),对产品和服务生产所需的过程进行评估产出的效率。
TFP是一个综合因素,它可以深入了解生产力的最终结果。
它的计算方法是将实际产出除以生产要素的投入量,这使得我们可以很好地了解技术进步、组织和管理的影响。
全要素生产率和劳动生产率的区别在于,劳动生产率只衡量人们手动操作的效率,而全要素生产率则更全面地衡量所有可以影响生产力的元素。
因此,通过提高全要素生产率,可以提高企业和行业的效率,提高产品和服务的质量和数量,从而产生更大的经济效益。
全要素生产率的提高在经济发展中至关重要。
经济学家们一直在寻找各种方法来提高全要素生产率,因为全要素生产率是一个重要的影响国家经济增长的因素。
二、中国的全要素生产率现状尽管中国的经济已经取得了巨大的进展,但中国的全要素生产率并未得到很大的提高。
这主要是由于以下几个原因:1.资源依赖中国的经济发展在长时间内依赖于资源能源密集型产业,导致了资本、补贴和资源的短缺问题,这限制了中国的生产力和竞争力的提升。
2.科技创新水平低中国的科技创新水平并不高,导致中国在世界舞台上的地位大幅下降。
尽管中国靠低成本的劳动力和产品在制造业方面取得了重大成功,但成功是建立在简单、重复的工作基础上的。
如果没有在技术研发方面大举投资,将很难继续提高经济全要素生产率。

中国的全要素生产率与国际比较研究全要素生产率是衡量经济增长的重要指标之一。
在全要素生产率的计算中,不仅仅考虑了劳动力和资本的贡献,还考虑了其他因素,例如技术进步、科学创新、管理水平和资源利用效率等等。
因此,全要素生产率能够更全面地反映一个国家经济增长的质量和效率。
近年来,中国的全要素生产率一直是国内外学者关注的热点。
在国际上,中国的全要素生产率与其它国家相比还有一定的差距。
但是,在过去几十年的时间里,中国的全要素生产率发生了非常大的变化,逐渐走向了国际化水平。
首先,我们来看看中国全要素生产率的发展历程。
20世纪80年代初期,中国的全要素生产率基本处于低水平。
中国经济的主要特点是产业结构单一、技术水平落后、生产效率低下和资源利用效率不高等等问题。
由于缺乏技术、资金和市场等方面的支持,中国的全要素生产率难以得到提高。
但是,在改革开放的大背景下,中国经济逐渐得到了改善和发展。
经过20多年的发展和积累,中国的全要素生产率逐渐提高,发展速度也逐渐加快。
2010年,中国的全要素生产率超过了世界平均水平。
然而,在与其它经济体的比较中,中国的全要素生产率仍然有所差距。
特别是与发达国家的比较,差距更加明显。
这主要是因为一些制约全要素生产率提高的因素仍然存在,例如产业结构过于单一、劳动力市场不灵活、科技创新水平有所不足等等。
为提高全要素生产率,中国政府提出了一系列的政策和措施。
例如调整经济结构、提高科技创新能力、加大对中小企业的支持等等。
此外,中国政府还积极扩大对外开放,采取了一系列措施促进产业升级和创新发展,通过与国际上其他国家和地区的合作促进全要素生产率的提高。
然而,在未来,中国的全要素生产率面临着一些困难和挑战。
例如经济增长速度放缓、人口老龄化、资源环保压力等等。
在此背景下,中国需要继续采取一系列政策和措施,着力解决上述问题,为全要素生产率的提高提供更加坚实的基础和保障。
最后,在进行全要素生产率比较时,我们还需要注意到不同国家和地区的差异性。

中国全要素生产率为何明显下降首先,中国经济正处于由投资驱动向创新驱动转型的关键时期。
在过去几十年的高速经济增长中,中国通过大规模的基础设施建设和高投资来推动经济增长。
然而,这种模式使得资源配置效率低下,导致投资回报递减。
同时,高额的投资还未能有效地转化为技术创新和机构变革,无法提高全要素生产率。
其次,中国产业结构的问题也是导致全要素生产率下降的原因之一、在中国经济快速发展的过程中,重工业和制造业一直是主导产业,而服务业和高技术产业相对较弱。
重工业和制造业的劳动密集型和资源密集型特点使得中国经济在生产率方面存在局限。
与此同时,服务业和高技术产业的发展相对滞后,缺乏创新能力和技术引领作用,进一步影响了全要素生产率的提高。
第三,劳动力素质和教育水平对全要素生产率的影响也不可忽视。
尽管中国人口数量庞大,但劳动力素质整体上还不够高。
教育水平和技能培训的不足使得劳动力无法有效地运用现代管理技术和高新技术,限制了全要素生产率的提高。
此外,中国人口老龄化问题也对全要素生产率产生了负面影响。
老年人口增加导致劳动力供给减少,劳动力市场紧张,也给企业的招聘和人力成本带来了压力。
这些问题可能会导致企业生产效率下降,从而影响全要素生产率的改善。
最后,环境污染和资源短缺也是中国全要素生产率下降的原因。
过去几十年的高速增长给环境带来了巨大的负面影响,降低了自然资源使用的效率,并造成了严重的环境污染问题。
环境问题对经济生产和劳动力健康产生了负面影响,进一步限制了全要素生产率的提高。
为了应对这些挑战和问题,中国政府已经采取了一系列的政策措施。
例如,推动供给侧结构性,促进经济结构调整,加大对创新和高技术产业的投资,提高教育质量和培训力度,加强环境保护等。
这些政策的逐步实施将有助于提高全要素生产率,推动中国经济实现可持续发展。

基于DEA—Malmquist指数法中国小麦主产区全要素生产率变化特征分析摘要:本文利用数据包络分析(DEA)和Malmquist生产率指数方法,对中国小麦主产区的全要素生产率进行分析。
通过对2000-2019年的数据进行分析,发现了中国小麦主产区全要素生产率的变化特征,并对其产生的影响因素进行了分析和讨论。
研究结果显示,小麦主产区的生产率总体呈现出较好的增长趋势,但存在着一些地区生产率增长较快,而有些地区却呈现出生产率下降的情况。
影响生产率变化的因素包括技术水平、管理水平、资源配置等,需要进一步研究和优化。
一、引言小麦是中国的主要粮食作物之一,对于国家的粮食安全和农业经济发展具有重要意义。
随着农业生产技术的不断进步和中国农业结构的不断调整,小麦的全要素生产率也在不断变化。
对中国小麦主产区的全要素生产率进行分析和研究,对于指导农业生产、提高农业效益具有积极的意义。
二、DEA—Malmquist指数法简介数据包络分析(DEA)是由Charnes, Cooper和Rhodes于1978年提出的一种评价农业生产效率的方法,它主要用于衡量农业生产中各种资源的利用效率。
而Malmquist生产率指数方法则是由Malmquist在1953年提出的,主要用于分析产出和投入之间的变化趋势,从而得出总体生产率的变化趋势。
DEA—Malmquist指数法是将DEA和Malmquist生产率指数结合在一起,通过计算各个农业生产单元的效率得分和生产率指数,从而得出某一时间段内各个农业生产单元的全要素生产率的变化情况。
三、中国小麦主产区全要素生产率变化特征分析1. 数据来源和选取本文选取了2000-2019年中国小麦主产区的各个生产单元的生产数据,包括小麦种植面积、产量、投入资源等,共计20年的数据。
通过对这些数据进行处理和整理,得出了每个生产单元在不同年份的生产效率得分和生产率指数。
利用DEA方法对各个小麦主产区的生产效率进行计算,得出各个生产单元在不同年份的生产效率得分。

全国及区域全要素生产率变动分析全国及区域全要素生产率变动分析摘要:一直以来,C-D生产函数模型及在此基础上产生的索洛残差法在估算TFP及其增长率时得到广泛应用,笔者从模型的设定、数据的获取、参数估计等方面对该方法进行了系统分析、探讨和修正,在此基础上估算了全国及31个省1978年~2010年间的TFP及其增长率。
结果表明:中国的TFP增长率总体上处于较高水平。
分阶段看,2001年~2010年和1978年~1984年的TFP增长率明显较高。
分区域看,东部的TFP及其增长率都明显高于中部和西部。
各省区的TFP 与经济发展水平、TFP增长率与经济增长速度都有很强的正相关性。
关键词:全要素生产率;增长率;生产函数;弹性作者简介:叶宗裕(1962-),男,浙江江山人,浙江师范大学经济与管理学院教授,应用数学硕士,主要从事经济统计,计量经济模型及应用研究。
中图分类号:F061.5文献标识码:A文章编号:1006-1096(2014)01-0014-06收稿日期:2012-11-14一、问题的提出最近10多年来,许多学者研究了全要素生产率(TFP)及其相关问题。
包括全国或省际TFP及其增长率的测算、TFP的收敛检验、技术进步对经济增长的贡献分析、分析TFP与省区收入差距的关系等。
对TFP相关问题的研究,必需建立在对TFP的准确估算基础上。
虽然对全国或省际TFP的测算已有大量的研究成果发表,但许多研究在估算方法、资料的来源和处理等方面存在许多问题,估算结果的准确性不能令人满意。
关于TFP,学者们已经有了基本一致的观点:包括资本和劳动等投入要素之外的所有影响产出的因素。
虽然估算TFP的方法多种多样,但由于C-D生产函数模型中各变量和参数的含义明确、直观,结果易于理解,在估算TFP及其增长率时得到广泛应用。
本文从模型的设定、数据的获取、参数估计等方面对该方法进行了系统分析、探讨和修正,在此基础上估算了全国及31个省份1978年~2010年间的TFP及其增长率,并对结果进行了分析。

中国区域经济增长的全要素生产率变化研究中国区域经济增长的全要素生产率变化研究随着中国经济的快速增长,区域经济发展的不平衡问题日益引起人们的关注。
了解和研究中国区域经济增长的全要素生产率变化,对于推动经济发展、实现可持续发展具有重要意义。
本文旨在探讨中国区域经济增长的全要素生产率变化,分析其影响因素,并提出相应的政策建议。
全要素生产率(TFP)是衡量一个经济体整体效益的重要指标。
它反映了一个经济体在给定的产出和输入条件下的有效使用程度。
中国作为一个广大的国家,各个地区的经济发展水平不尽相同,因此区域经济增长的全要素生产率也存在差异。
首先,中国区域经济增长的全要素生产率变化与经济结构调整密切相关。
在中国经济转型升级的过程中,不同地区的经济结构调整程度不同,进而影响到全要素生产率的变化。
一方面,随着中国经济的转型,很多传统产业逐渐萎缩,新兴产业逐渐崛起。
一些经济发达地区在转型过程中更加注重技术创新和创新能力的提高,从而促进了全要素生产率的增长。
另一方面,一些地区的转型速度较慢,仍依赖于传统产业,导致全要素生产率增长缓慢。
因此,要推动中国区域经济增长的全要素生产率变化,需要加快经济结构调整,提升产业升级水平。
其次,人力资本投资是影响中国区域经济增长的全要素生产率变化的关键因素之一。
人力资本是经济发展的重要驱动力,也是全要素生产率的重要组成部分。
一些研究表明,教育程度和技能水平越高的地区,其全要素生产率增长越快。
因此,中国政府应该加大对人力资本的投资,提高教育质量,促进技能培训,以提高全要素生产率。
再次,科技创新能力是中国区域经济增长的全要素生产率变化的重要因素。
科技创新是推动经济发展的重要动力,也是提高全要素生产率的重要途径。
一些研究发现,在中国,科技创新能力较强的地区,其全要素生产率增长较快。
因此,中国政府应该加强对科技创新的支持和引导,提高科技企业的研发能力,推动科技创新与经济发展的深度融合,以提高全要素生产率。

我国全要素生产率的分解及变动趋势内容摘要:本文利用数据包络方法,对2002-2010年以来我国不同区域的全要素生产率进行了测算,采用了Malmquist指数的方法对我国经济的TFP进行了进一步的分解,以此探讨我国经济增长的动力。
实证结果显示,我国全国总体及东部、中部、西部分地区在此阶段TFP增长有限,对GDP贡献不够;Malmquist 指数的结果也显示了我国各地区的TFP增长中由技术进步指数带动的和由效率改进带动的效应程度大体相同,我国经济要想实现可持续发展还必须进一步提升技术进步的作用。
关键词:TFP增长率Malmquist指数DEA方法区域差异Solow在研究美国的经济增长时发现,在人均收入增长中由要素投入量增加带来的是很少的,而真正能够推动经济长期持续增长的因素应该是全要素生产率(TFP)。
全要素生产率即综合反映经济发展过程中投入产出效果的指标。
因此,我国经济增长中TFP所占的比重或者发挥的贡献成为学者们研究与关注的重点。
文献回顾目前关于TFP的研究成果比较丰富,主要集中在以下几个层面:第一方面是运用线性回归的方式,根据索洛理论,采取物资资本、劳动力投入、人力资本等指标作为解释变量,来试图分析各个投入变量及TFP的贡献。
该方法必须事先设定生产函数形式,而且要求满足苛刻的假设前提。
Nehru和Dhare Shwar、Collins和Bosworth分别使用了包含很多国家的样本资料进行了测度。
第二方面是放在了全要素生产率的增长率的分解中,试图分析我国TFP增长中技术进步效率和生产效率变化的情况,采用的方法较前有很大区别。
其主要思路是将估计的前沿生产函数的变化来度量技术进步的变化;用测度到的观察点到前沿面的距离来度量生产效率的改进。
采用此方法的关键是前沿生产面的估计。
目前主要有SFA方法和DEA方法。
SFA方法同样需要设定生产函数的具体形式,而且处理误差时还需要一定的分别假设;而DEA方法时通过线性规划来得到前沿函数,不需要对生产函数的具体形式进行假设,对误差的处理是将其作为无效率的结果。

中国全要素生产率增长率的变化及提升途径——基于产业视角摘要:本文从产业的角度出发,对中国全要素生产率的变化情况进行分析,探讨了目前存在的问题以及提升全要素生产率的途径和建议。
总体来说,提高技术创新水平、加强产业结构优化、深入推进供给侧结构性改革,注重企业自主创新和人才培养等措施是提升中国全要素生产率的重要途径。
关键词:全要素生产率、技术创新、产业结构优化、供给侧结构性改革、企业自主创新、人才培养一、背景介绍全要素生产率是指生产所需的所有生产要素如资本、劳动和技术等的利用效率,是衡量一个国家经济发展水平的重要指标。
在中国的经济发展过程中,全要素生产率的提升对推动经济增长和提高人民生活水平具有重要作用。
然而,随着国家经济的快速发展,中国的全要素生产率增速已经出现了明显的下降态势,因此需要进一步探究如何提升全要素生产率。
二、中国全要素生产率的变化自20 世纪80 年代开始,中国的全要素生产率呈逐年提高的趋势,但是在2012 年后开始下降,尤其是2015 年之后下降幅度更为明显。
具体而言,从2012 年到2016 年,中国全要素生产率的年均增长率仅为2.3%,远低于2002 年到2011 年的年均增长率(5.4%)。
这表明中国目前面临着全要素生产率增长缓慢的问题,如果不及时采取措施,将会对中国的经济增长和发展带来负面影响。
三、中国全要素生产率下降的原因1.技术创新水平不高在中国的经济发展中,缺乏自主创新是一个重要的制约因素。
虽然近年来科技投入有所增加,但是整体上来看,中国在科技研发和创新方面的投入仍然较低,技术能力和水平相对较弱。
这导致中国的创新能力不足,无法迅速引进和吸收国际先进技术。
因此,技术创新水平不高是当前中国全要素生产率下降的重要原因之一。
2.产业结构不合理当前中国的产业结构仍然不够优化,以重工业和基础设施建设为主导的传统产业占据了比较大的比重,而高科技、高附加值产业的发展相对较缓慢。
这导致中国产业结构不够灵活和多元化,无法满足不断变化的市场需求。
中国全要素生产率和估算和分析中国的全要素生产率在近几十年来一直呈现出持续增长的趋势。
根据国家统计局发布的数据,中国的全要素生产率在过去30年中年均增长率超过了3%,这说明中国的生产效率不断提高,对经济增长的贡献也在不断增加。
这一趋势的背后,主要原因是中国政府的改革开放政策带来了技术进步和资源配置的优化,以及不断推进的产业升级和创新发展。
然而,中国的全要素生产率增长也面临一些挑战。
首先是劳动力成本的上升和人口结构的变化,这使得中国的劳动力资源优势有所减弱。
其次是产业结构的调整和转型,一些传统行业的生产效率相对低下,而新兴产业和高科技行业的充分发展需要更多的技术投入和创新。
同时,环境污染和资源约束也给中国的生产效率带来了一定的压力。
为了更好地提高全要素生产率,中国政府和企业可以从以下几个方面着手:加大对科技创新的投入和支持,鼓励企业加强技术改进和创新;推动产业升级和结构转型,鼓励发展新兴产业和高附加值产业;优化资源配置和提升劳动力素质,提高生产要素的利用效率;加强环境保护和资源节约,建立可持续发展的生产方式和产业链。
总之,中国的全要素生产率估算和分析对于经济发展和战略规划都具有重要意义。
通过不断推动科技创新和产业升级,优化资源配置和提升劳动力素质,中国可以更好地提高生产效率,实现经济可持续增长和高质量发展。
中国的全要素生产率(TFP)是一个富有启发性的经济指标,它可以帮助我们更好地理解中国经济的发展现状和未来趋势。
随着经济社会的不断发展,中国全要素生产率估算和分析成为了经济研究和政策制定的重要内容。
本文将继续从人力资本、资本投资、科技创新等方面对中国全要素生产率进行更深入的讨论。
首先,人力资本作为生产要素之一,对全要素生产率的影响非常显著。
中国拥有庞大且不断增长的劳动力资源,然而,随着人口结构的变化和城乡发展不平衡,人力资源的质量和配置也面临一些挑战。
为了提高人力资本的质量和利用效率,中国需要进一步加强教育和技能培训,提升劳动者的素质和技能水平。
改革开放以来中国全要素生产率变动的估算内容摘要:本文采取了索洛余值法对我国改革开放以来全要素生产率(TFP)增长率进行估计,并对我国全要素生产率增长和经济增长渊源做了简要分析。
关键词:全要素生产率索洛余值法经济增长众学者对全要素生产率的估计存在较多分歧。
归根结底,主要还是数据和方法的选择不同。
因此,本文试图选取较为精确的指标,选择1979-2009年较为有代表性的时间区间,采取较广泛的索洛余值法来分析我国全要素生产率的变动。
要素投入指标的选择与数据处理(一)资本投入数据1.资本投入的流量指标。
资本形成总额和全社会固定资产投资总额这两个数据序列都是资本投入流量的重要指标。
全社会固定资产投资总额是从货币投入角度反映各年度全社会的投资需求,资本形成总额是从最终使用角度反映各年度全社会的投资需求,显然资本形成总额更能准确反映资本投入的实际效果。
资本形成总额包括固定资本形成总额和存货增加两部分。
20世纪90年代中期,我国由短缺经济转变为局部过剩,造成了存货的大量增加,然而这些存货的增加并不能形成真正的生产力,因此,笔者将存货增加从资本形成总额中剔除,只保留固定资产投资形成总额,并将其作为资本投入的流量指标。
2.资本投入的存量指标。
估算资本存量的基本思想来自于“永续盘存法”。
(1)式为“永续盘存法”的基本公式,其中,K1表示第t年的资本存量,Kt-1表示第t-1年的资本存量,It表示第t年的固定资本形成总额,δ为固定资本折旧率。
由(1)式可知,各年的资本存量数据可由基期全社会资本存量加上可比价固定资本形成总额,逐年汇总得到。
具体而言:第一,以1978年为基期,1978年的资本存量为8663.6亿元(1978年不变价)。
这个数据是张军、章元2003年估算出来的,他们指出1978年底我国固定资本存量为12361.96亿元(1952年不变价),根据以1952年为基年的固定资产价格指数1978年为0.700827,可以估算出以1978为基期的资本存量为8663.6亿元(12361.96×0.700827)。
中国区域经济增长的全要素生产率变化研究的开题报告一、研究背景与意义随着中国经济的快速发展,区域经济增长已经成为人们关注的热点问题之一。
然而,当前中国各地区经济增长发展水平的差异仍然比较大,这不仅会影响国家的整体经济发展水平,还会导致地区间的经济差距进一步拉大。
因此,研究中国区域经济增长的全要素生产率变化,对于促进地区间经济发展的均衡和可持续发展具有重要的意义。
二、研究内容和目标本研究旨在通过对中国各地区的经济发展和全要素生产率变化进行研究,揭示区域经济增长的全要素生产率变化规律和影响因素。
具体研究内容包括以下几个方面:1. 探究全要素生产率的概念、计算方法和评价指标体系;2. 分析中国各地区经济增长的现状和特征;3. 基于面板数据模型,研究全要素生产率变化对区域经济增长的贡献;4. 分析影响全要素生产率变化的主要因素,并制定相应的政策建议。
三、研究方法和技术路线本研究主要采用面板数据模型进行分析,所使用的数据主要来自于国家统计局和各地方统计局公布的年度统计数据以及相关研究机构发布的统计数据报告。
步骤如下:1. 清洗并整理所需数据,并进行描述性统计分析;2. 构建全要素生产率计算模型,并计算各地区的全要素生产率水平;3. 构建经济增长模型,并分析全要素生产率变化对区域经济增长的影响;4. 运用计量经济学方法进行数据分析,并得出相关结论和政策建议。
四、研究预期结果和影响通过本研究,预计可以得出以下结果:1. 揭示中国区域经济增长的全要素生产率变化规律和影响因素;2. 分析不同地区全要素生产率水平的差异,为促进区域间经济发展均衡提供参考;3. 指导制定区域经济发展政策,以提高全要素生产率水平。
本研究的成果对于促进中国区域经济增长的均衡和可持续发展具有一定的理论和实践意义,同时也对相关学科领域的研究和应用具有一定的参考价值。
中国制造业企业全要素生产率研究中国制造业企业全要素生产率研究一、引言全要素生产率(Total Factor Productivity,TFP)是衡量企业生产效率的重要指标,也是评估一个国家或地区的经济发展水平的重要指标之一。
中国制造业作为全球最大的制造业国家,其企业的全要素生产率一直备受关注。
本文将探讨中国制造业企业全要素生产率的研究现状以及未来的发展趋势。
二、研究现状1. 从总体上看,中国制造业企业的全要素生产率呈现逐年提高的趋势。
随着改革开放的深入推进和技术进步的加速,中国制造业企业的生产效率得到了显著的提升。
尤其是在过去几十年中,中国制造业企业通过引进国外先进技术和管理经验,以及自主创新和自主研发,不断提高了企业的生产效率。
2. 从行业的角度来看,不同行业的全要素生产率差异较大。
一些传统行业,如纺织、服装等,由于劳动密集型特点以及缺乏技术创新,其全要素生产率相对较低。
而一些高科技行业,如电子、机械等,由于技术密集型特点和较高的研发投入,其全要素生产率相对较高。
此外,国内市场需求的变化和国际市场竞争的加剧也对不同行业的全要素生产率产生了影响。
3. 在研究方法上,过去主要使用计算TFP的传统方法,但由于这些方法忽视了企业之间异质性的影响,导致了对全要素生产率的估计结果偏低。
近年来,一些学者开始使用面板数据模型和非参数方法等新颖的研究方法,以更准确地估计企业的全要素生产率。
三、未来发展趋势1. 技术创新的推动。
中国制造业企业在技术创新方面还存在较大的差距。
政府和企业需要加大对技术创新的投入,加强知识产权保护,促进科技与产业的融合,推动制造业由劳动密集型向技术密集型转型,提升全要素生产率。
2. 产业结构的调整。
当前,中国制造业正面临诸多挑战,如高成本、低附加值、环境污染等。
未来,需要通过产业结构调整和优化,加快发展高技术产业,提高全要素生产率。
3. 人力资源的培养与投入。
人力资源是企业全要素生产率的重要驱动力量。
中国全要素生产率的变化:2000-2008江春1吴磊2滕芸 3内容摘要:本文使用序列DEA和当期DEA方法测算了中国2000至2008年的Malmquist生产率指数,并在规模报酬固定的假设下将其分解为技术效率变化指数和技术变化指数。
结果显示自2000年以来全国及各省份的全要素生产率均发生下降,近年来中国的经济增长几乎完全依赖于要素投入的增加。
全要素生产率持续降低是同期资本产出比率迅速上升造成的,这反映出中国经济增长过于依赖投资、收入分配不合理,同时也反映出金融体系的不健全。
关键词:全要素生产率;DEA;资本产出比一、引言改革开放三十多年来,中国的经济增长迅猛,取得了世所瞩目的成就。
但与此同时,资源消耗巨大、要素配置效率差、产品附加值低、产业结构不合理等诸多问题始终让人们疑虑中国经济增长的持续性。
中国经济增长的质量究竟如何,经济增长到底是来源于要素的投入还是来源于效率的提高?全要素生产率(TFP),作为衡量经济增长质量的重要指标,越来越受到经济学者的广泛重视,提高全要素生产率也被视为中国未来经济增长的决定因素(胡鞍钢,2003)[1]。
Chow(1993)[2]开启了对中国经济增长来源的研究,他认为中国在改革开放前TFP基本稳定,经济增长的主要动力是资本积累,而改革开放后TFP以每年2.7%的速度增长。
颜鹏飞和王兵(2004)[3]将中国改革开放以来的经济发展划分为两个阶段,测算得到第一个阶段——1978-1991年间,中国TFP年均增长为-0.17%;第二阶段1992-2001年间则为0.79%。
Y oung(2003)[4]采用自行调整后的数据测算1978年至1998年间中国的TFP增长率为1.4%等等。
但是目前这类研究对中国TFP增长率的估计存在较大分歧,即便针对同一时期的研究,不同学者作者简介:江春(1960—),男,武汉大学经济与管理学院金融系(武汉,430072),教授。
研究方向:宏观金融理论与金融发展理论。
矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。
如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。
㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。
(2 列出开发利用方案编制所依据的主要基础性资料的名称。
如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。
对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。
二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。
2、国内近、远期的需求量及主要销向预测。
㈡产品价格分析
1、国内矿产品价格现状。
2、矿产品价格稳定性及变化趋势。
三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。
2、矿区矿产资源概况。
3、该设计与矿区总体开发的关系。
㈡该设计项目的资源概况
1、矿床地质及构造特征。
2、矿床开采技术条件及水文地质条件。