单相正弦交流电
- 格式:ppt
- 大小:1.34 MB
- 文档页数:66


单相交流电路之正弦交流电一、正弦交流电的三要素正弦交流电是指其数值大小、方向都按正弦的规律周而复始循环变化的电势电压与电流。
要完全掌握正弦交流电,必须掌握交流电的三要素,数值、频率和角频率,相位关系,正弦交流电的三要素是极大值(或有效值)、频率(或角频率)及相位(或初相位)。
L正弦交流电的数值1)瞬时值正弦交流电在变化过程中,任意确定时刻t的数值,称为正弦交流电的瞬时值,如图2- 15中的e1 o瞬时值用小写符号表示,如i、e、U 等。
2)最大值正弦交流电的最大值又称极大值,振幅值也可称为极值,是指在变化过程中,正弦交流电出现的最大瞬时值,用符号ED (图2- 15)、I口、U□表示。
图2-1,正弦交潦电的波形图3)有效值正弦交流电的有效值是衡量它发热做功的一个基本量。
就是说,交流电流和直流电流分别通过同一电阻,如果经过相同时间产生同样热量,则交流电流的有效值等于直流电流的大小。
因此,定义正弦交流电的有效值是从发热做功方面与直流等效的值称为交流电的有效值,从数学角度,它又可以称为方均根值。
有效值用大写符号表示,如E、I、U o正弦交流电的瞬时值,可以用数学解析式表达,即u=U□sin(ωt+φ)正弦交流电的有效值与极大值的关系为或"=同,Z w= √2Λ Ejli= √25,实际上,交流电路的分析与计算过程中,主要用交流电的有效值,例如,电器铭牌上标定的电压、电流,仪表(电流表、电压表)测量的指示值以及计算电路的电压、电流等都是有效值。
2.频率和角频率1)频率和周期(1)频率:是指正弦交流电单位时间(S)内循环变化的次数,用符号f表示,单位为赫兹(HZ).-般50Hz.、60HZ称为工频交流电。
(2)周期:是指正弦交流电每循环一次所经历的时间(s),即正弦交流电从0值到极大值再到0值再变化到负的最大值然后回到0值的过程所经历的时间称,用符号T表示,单位为秒(s)。
频率与周期的关系为f=l∕T2)角频率角频率是指正弦交流电每秒循环变化所经历的弧度(这里指角度),用符号co表示,单位是弧度/秒(red/s)。



单相正弦交流电公式
单相正弦交流电的公式为:e=Emsin(ωt+φ),其中:
e 代表电动势的瞬时值,单位为伏特(V)。
Em 代表电动势的最大值,单位为伏特(V)。
ω 代表角频率,单位为弧度/秒(rad/s)。
t 代表时间,单位为秒(s)。
φ 代表初相角,单位为弧度(rad)或度(°)。
另外,正弦交流电的电压瞬时值、电流瞬时值、电动势瞬时值等都可以用相应的公式表示。
例如,单相正弦交流电的电压瞬时值公式为:
u=Umsin(ωt+φu),其中:
u 代表电压的瞬时值,单位为伏特(V)。
Um 代表电压的最大值,单位为伏特(V)。
φu 代表初相角,单位为弧度(rad)或度(°)。

单相正弦交流电路之基本物理量与表示方法一、 知识要求1、 掌握正弦交流电的瞬时值,最大值、有效值、平均值、周期、频率、角频率、初相位及相位差的含义、符号、数学式、单位及计算。
2、 掌握正弦交流电的四种表示方法,会作相量图,会用相量法分析、计算正弦交流电路。
二、 复习提要:1、 交流电的产生与概念: (1)、交流电:大小和方向随时间变化的电压、电流或电动势。
周期性交流电:大小和方向随时间作周期性变化的交流电。
周期性交流电分为正弦交流电和非正弦交流电。
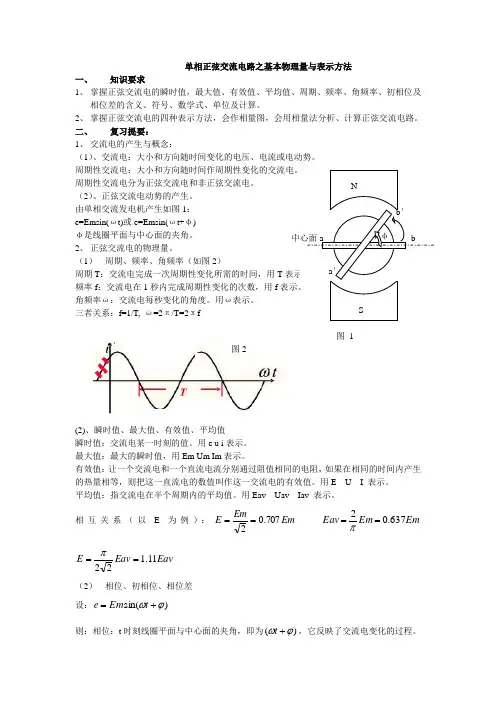
(2)、正弦交流电动势的产生。
由单相交流发电机产生如图1: e=Emsin(ωt)或e=Emsin(ωt+φ) φ是线圈平面与中心面的夹角。
2、 正弦交流电的物理量。
(1) 周期、频率、角频率(如图2)周期T :交流电完成一次周期性变化所需的时间,用T 表示。
频率f :交流电在1秒内完成周期性变化的次数,用f 表示。
角频率ω:交流电每秒变化的角度。
用ω表示。
三者关系:f=1/T, ω=2π/T=2πf(2)、瞬时值、最大值、有效值、平均值瞬时值:交流电某一时刻的值。
用e u i 表示。
最大值:最大的瞬时值,用Em Um Im 表示。
有效值:让一个交流电和一个直流电流分别通过阻值相同的电阻,如果在相同的时间内产生的热量相等,则把这一直流电的数值叫作这一交流电的有效值。
用E U I 表示。
平均值:指交流电在半个周期内的平均值。
用Eav Uav Iav 表示。
相互关系(以E 为例):Em Em E 707.02==Em Em Eav 637.02==πEav Eav E 11.122==π(2) 相位、初相位、相位差 设:)sin(ϕω+=t Em e则:相位:t 时刻线圈平面与中心面的夹角,即为)(ϕω+t ,它反映了交流电变化的过程。
φ 中心面a b a ′ b ′ N S 图 1图2初相位:t=0时的相位,即ϕ,它反映了交流电变化的起点,可正可负也可为零。


单相正弦交流电路公开课教案第一章:引言1.1 课程背景本课程旨在帮助学生掌握单相正弦交流电路的基本概念、原理和分析方法。
通过学习本课程,学生将能够了解单相正弦交流电路在日常生活和工程应用中的重要性,并能够运用所学知识分析和解决相关问题。
1.2 教学目标了解单相正弦交流电路的基本概念和特点掌握正弦交流电的产生和描述方法学会使用复数表示法分析交流电路能够运用欧姆定律、功率公式等分析交流电路的性能第二章:正弦交流电的基本概念2.1 正弦交流电的定义正弦交流电是一种随时间变化的电压或电流,其波形呈正弦曲线。
正弦交流电的幅值、频率和初相位是描述其特性的重要参数。
2.2 正弦交流电的产生正弦交流电可以通过交流发电机或变压器产生。
交流发电机利用电磁感应原理,通过旋转磁场和线圈的相对运动产生正弦交流电。
变压器则通过电磁感应原理,改变电压和电流的幅度和频率。
2.3 正弦交流电的表示方法正弦交流电可以用解析表达式、波形图和相位图等方式表示。
解析表达式通常采用正弦函数的形式,包括幅值、频率和初相位等参数。
波形图可以直观地展示正弦交流电随时间变化的波形。
相位图则可以表示正弦交流电的相位关系。
第三章:复数表示法3.1 复数的概念复数是由实部和虚部组成的数学表达式,可以用来表示交流电路中的电压和电流。
复数的几何表示法可以直观地展示电压和电流的相位关系。
3.2 复数的运算复数之间可以进行加法、减法、乘法和除法等运算。
这些运算可以通过复数的代数表示法或几何表示法进行。
3.3 复数在交流电路中的应用在交流电路中,电压和电流可以表示为复数。
通过复数的运算,可以分析电路中的相位关系、幅值变化等问题。
第四章:欧姆定律和功率公式4.1 欧姆定律欧姆定律是分析交流电路的基础,它描述了电压、电流和电阻之间的关系。
在正弦交流电路中,欧姆定律可以表示为电压和电流的复数形式的乘积等于电阻的复数形式。
4.2 功率公式功率是交流电路中重要的性能指标,可以表示为电压和电流的乘积的瞬时值或平均值。

单相正弦交流电路本章主要介绍了正弦交流电的基本概念、正弦交流电路的分析方法和正弦交流电路功率因数问题。
本章要求:1、 掌握正弦交流电基本概念,特别是有效值,初相位和相位差2、 掌握正弦量表示方法,特别是相量表示方法。
3、 熟悉单一参数电路的电压、电流关系及能量转换关系4、 了解电路基本定律的相量形式5、 能够对一般正弦交流电路进行分析和计算,掌握交流电路的功率及其计算。
6、 了解功率因数提高的意义及方法 引言:电路的物理量(电压、电流等),按其波形类型,大致可分为正弦交流电路:若电路中的电源(电动势)及由此产生的电压、电流均为正弦交流量,则这样的电路称为正弦交流电路。
若电源是单相的,就是单相正弦交流电路(举几个实例如日光灯电路、电风扇电路等),三相电源供电的则是三相正弦交流电路。
交流电应用很广,举例说明。
周期量交流量(大小、方向均做周期性变)非周期量(如电容充电电压)脉动量(大小做周期性变化,而方向不变)如:i 非正弦交流量,如:i正弦交流量i§3-1正弦交流电的基本概念概念:大小、方向均随时间作正弦规律变化的饿电流、电压、电动势等物理量均称为正弦交流电,简称交流电或正弦量 正弦量的波形图如下:三角函数表示:u=U m sin(wt+ϕu ) i=I m sin(wt+ϕi ) u 、i 为电流、电压的瞬时值周期、频率、角频率周波:变化一个循环称为一个周波周期T :正弦量变化一个周波所需的时间单位S频率f :每秒钟变化的周波数,单位:Hz, f=1/T,工作频率f=50Hz,周期T=0.02S 角频率w :每秒钟变化的弧度数,单位:弧度/秒(rad/s ),w=2πf=Tπ2f=50Hz 时,w=314rad/s一、幅值:最大的瞬时值,用大写字母加下标m 表示,如U m 、I m 二、初相:u=U m sin(wt+ϕu )正弦量三要素U m 、I m —最大值(最值),表示正弦量大小w —角频率,反映正弦量变化快慢 ϕu 、ϕi —初相位,反映t=0时刻正弦量的瞬时值大小,即正弦量初始值大小。