最新文档
-
画一幅色彩和谐的画_1页数:20
-
超市员工培训内容页数:14
-
保卫萝卜3公园爬梯2关攻略页数:7
-
云南省股权投资基金备案管理试行办法页数:2
-
让爱走进孩子的心灵(改)页数:2
-
仓储合同(样式七)页数:5
-
《运动的描述》ppt初中人教版1页数:15
-
建立迷人的个性页数:11

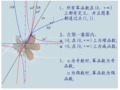



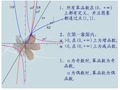
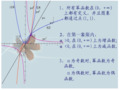









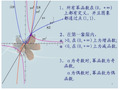

![指数函数对数函数比较大小题型总结[精品文档]](https://img.taocdn.com/s1/s/e476df2d6c175f0e7dd13732.jpg)
