2018届初三数学中考复习 几何证明与计算 专题复习训练题 含答案

2018-2019届数学中考复习《图形与证明》专项练习试卷（50道选择题）1、如图，已知点 D是∠ABC的平分线上一点，点 P在 BD上，PA⊥AB，PC⊥BC，垂足分别为 A，C．下列结论错误的是（）A. ∠ADB=∠CDB．B. △ABP≌△CBPC. △ABD ≌△CBDD. AD=CP来源：黑龙江省哈尔滨市松北区 2017—2018 学年度下学期七年级期末调研测试数学试卷2、某多边形的内角和是其外角和的3倍，则此多边形的边数是（）A．8B．7C．6D．5来源：四川大学附属中学西区学校2017—2018学年度下期八年级6月学月测试卷（含答案）3、“人之初性本善”这六个字分别写在某个正方体纸盒的六个面上，将这个正方体展开成如图所示的平面图，那么在原正方体中，和“善”相对的字是（）A．人B．性C．之D．初来源：【全国校级联考】盐城市阜宁县第二次2018届九年级模拟（二模）试卷4、如图, ∠1与∠2的关系是（）A．对顶角B．同位角C．内错角D．同旁内角来源：浙江省余姚市兰江中学2017-2018学年七年级下学期期中考试数学试题5、下列说法中正确的个数是（）①射线AB与射线BA是同一条射线；②两点确定一条直线；③两条射线组成的图形叫做角；④两点之间直线最短；⑤若AB=BC，则点B是AC的中点．A．1个B．2个C．3个D．4个来源：【北师大版】初一数学第一学期4.3角同步练习6、如图，在中，AD⊥BC于 D， AB=3，DB=2，DC=1，则AC等于（）A．6B．C．D．4来源：【全国区级联考】湖北省襄阳市襄城区2017-2018学年八年级下学期期末测试数学试题7、如图，在ABCD 中，DE平分∠ADC，AD=8，BE=3，则ABCD 的周长是（）A．14B．16C．24D．26来源：【全国区级联考】湖北省襄阳市襄城区2017-2018学年八年级下学期期末测试数学试题8、如果△ABC的两边长分别为3和5，那么连接△ABC三边中点D，E，F，所得的△DEF的周长可能是( )A．3B．4C．5D．6来源：2017-2018学年八年级数学下册（湘教版）期末单元测试卷第2章四边形9、如图是一个能折成长方体的模型，那么由它折成的长方体是下列图形中的( )A．B．C．D．来源：人教版七年级数学上册同步练习：4.4课题学习设计制作长方体形状的包装纸盒10、已知线段AB＝6cm,在直线AB上画线段AC＝2，则BC的长为（）A．4cm B．8cm C．4cm或8cm D．不能确定来源：黑龙江省鸡东县平阳中学2016-2017学年七年级下学期期末考试数学试题11、如果从A看B的方向为北偏东，那么从B看A的方向为（）A．南偏东65°B．南偏西65°C．南偏东25°D．南偏西25°来源：黑龙江省鸡东县平阳中学2016-2017学年七年级下学期期末考试数学试题12、如图，用尺规作出∠AOB的角平分线OE，在作角平分线过程中，用到的三角形全等的判定方法是（）A．ASA；B．SSS；C．SAS；D．AAS；来源：2017-2018学年第二学期八年级数学《全等三角形》单元测试题【苏科版】13、如图，AB是⊙O的弦，CD与⊙O相切于点B，若∠ABC＝140°，则∠OAB的度数为( )A．40°B．45°C．50°D．55°来源：【全国区级联考】广西贵港市覃塘区2018届九年级第二次模拟考试数学试题14、不能判定四边形ABCD为平行四边形的条件是A．，B．，C．，D．，来源：【全国市级联考】浙江省衢州市2017-2018学年下期八年级期中考试数学试题15、将一副三角板如图放置，使点A在DE上，BC∥DE，则∠ACE的度数为（）A．B．C．D．来源：【全国校级联考】山东省淄博市高青县2018届九年级第一次模拟考试数学试题16、如图，把等腰直角三角尺的直角顶点放在直尺的一边上，则∠1＋∠2的度数为（）A．60°B．90°C．120°D．135°来源：江苏省无锡市滨湖区2018届九年级下学期调研考试数学试题17、在△ABC中，∠C＝90°，，那么∠B的度数为（）A．60°B．45°C．30°D．30°或60°来源：【全国校级联考】盐城市阜宁县第二次2018届九年级模拟（二模）试卷18、将一副三角尺按如图的方式摆放，其中l1∥l2，则∠α的度数是（）A．30°B．45°C．60°D．70°来源：2018年北京市朝阳区中考数学模拟试卷19、如图是某个几何体的展开图，该几何体是（）A．正方体B．圆锥C．圆柱D．三棱柱来源：2018年北京市朝阳区中考数学模拟试卷20、如图，在□ ABCD中，AD=4，点E，F分别是BD，CD的中点，则EF等于（）A．2B．3C．4D．5来源：湖南省张家界市永定区2018届九年级第一次模拟考试数学试题21、如图,把长方形ABCD沿EF对折,若∠1=50°,则∠AEF的度数为（）A．100°B．120°C．115°D．130°来源：浙江省余姚市兰江中学2017-2018学年七年级下学期期中考试数学试题22、如图,下列判断正确的是( )A．若∠1=∠2,则AB∥CD B．若∠1=∠2,则AD∥BCC．若∠A=∠3,则AD∥BC D．若∠A+∠ADC=180°,则AD∥BC来源：浙江省余姚市兰江中学2017-2018学年七年级下学期期中考试数学试题23、将一把直尺与一块三角板如图放置，若，则为（）A．B．C．D．来源：广东省汕头市濠江区2018届九年级中考模拟考试数学试题24、如图，已知△ABC为直角三角形，∠C=90°，若沿图中虚线剪去∠C，则∠1+∠2等于（）A．135°B．150°C．270°D．90°来源：【全国校级联考】湖北省恩施州利川市谋道镇苏马荡教育集团2018届春季九年级下学期中考适应性考试数学试题25、如图，，=120º，平分，则等于（）A．60ºB．50ºC．30ºD．35º来源：广东省深圳市耀华实验学校2017-2018学年七年级下学期期中考试数学试题26、下列真命题中，逆命题是假命题的是（）A．等腰三角形的两底角相等B．全等三角形的三组对应边分别相等C．若a=b，则a2=b2D．若a2>b2，则|a|>|b|来源：四川大学附属中学西区学校2017—2018学年度下期八年级6月学月测试卷（含答案）27、若一个多边形的内角和为 540°，那么这个多边形对角线的条数为（）A．5B．6C．7D．8来源：黑龙江省哈尔滨市松北区 2017—2018 学年度下学期七年级期末调研测试数学试卷28、以下列各组线段为边，能构成三角形的是（）A．2，3，6B．3，4，5C．2，7，9D．，3，来源：黑龙江省哈尔滨市松北区 2017—2018 学年度下学期七年级期末调研测试数学试卷29、如图，正方形ABCD中，点 E、F 分别在边 BC、CD 上，且 BE=CF.连接 AE、BF.下列结论错误的是（）A. AE=BFB. AE⊥BFC. ∠DAE=∠BFCD. ∠AEB+∠BFC=1200来源：【全国区级联考】湖北省襄阳市襄城区2017-2018学年八年级下学期期末测试数学试题30、下列关于四边形的说法，正确的是（）A．四个角相等的菱形是正方形B．对角线互相垂直的四边形是菱形C．有两边相等的平行四边形是菱形D．两条对角线相等的四边形是菱形来源：宁夏银川市第十八中学2017-2018学年下期八年级数学期末测试题31、如图，P为正方形ABCD的对角线AC上任意一点，PE⊥AB于E，PF⊥BC于F，若AC＝，则四边形PEBF的周长为( )A．B．2C．2D．1来源：2017-2018学年八年级数学下册（湘教版）期末单元测试卷第2章四边形32、如图，一个梯子AB斜靠在一竖直的墙AO上，测得AO＝2 m．若梯子的顶端沿墙下滑0.5米，这时梯子的底端也恰好外移0.5米，则梯子的长度AB为（）A．2.5 m B．3 m C．1.5 m D．3.5 m来源：湖北省武汉市硚口区2016~2017学年八年级下学期期末考试数学试题33、如图，若四边形ABCD是菱形,则下列结论不成立的是（）A．AC=BD B．AO⊥BO C．∠BAD＝∠BCD D．AB=AD来源：湖北省武汉市硚口区2016~2017学年八年级下学期期末考试数学试题34、如图所示的正方体的展开图是( )A．B．C．D．来源：人教版七年级数学上册同步练习：4.4课题学习设计制作长方体形状的包装纸盒35、如图，AB∥CD，CE∥BF，A. E、F、D在一直线上，BC与AD交于点O，且OE=OF，则图中有全等三角形的对数为（）A． 2B. 3C. 4D. 5来源：2017-2018学年第二学期八年级数学《全等三角形》单元测试题【苏科版】36、如图，AC与BD相交于O，∠1=∠4，∠2=∠3，△ABC的周长为25cm，△AOD的周长为17cm，则AB=（）A．4cm ；B．8cm；C．12cm；D．无法确定；来源：2017-2018学年第二学期八年级数学《全等三角形》单元测试题【苏科版】37、如图，已知△ABC为等边三角形，点D、E分别在边BC、AC上，且AE=CD，AD与BE相交于点F．则∠BFD的度数为（）A. 45°B. 90°C. 60°D. 30°来源：2017-2018学年第二学期八年级数学《全等三角形》单元测试题【苏科版】38、如图，在△ABC中，∠C=90°，DE⊥AB于D，BC=BD，已知AC=3㎝，那么AE+DE 等于（）A．2㎝；B．3㎝；C．4㎝；D．5㎝；来源：2017-2018学年第二学期八年级数学《全等三角形》单元测试题【苏科版】39、如图，在△ABC中，动点P在∠ABC的平分线BD上，动点M在BC边上，若BC=3，∠ABC=45°，则PM+PC的最小值是( )D．3A．2B．C．来源：【全国区级联考】广西贵港市覃塘区2018届九年级第二次模拟考试数学试题40、对于下列命题：①是最简二次根式；②a2b与-ab是同类项；③分式方程无解；④对角线互相垂直的平行四边形是菱形，其中真命题有( )A．1个B．2个C．3个D．4个来源：【全国区级联考】广西贵港市覃塘区2018届九年级第二次模拟考试数学试题41、如图，在菱形ABCD中，对角线AC与BD相交于点O，若AB=2，∠ABC=60°，则BD 的长为（）A．2B．3C．D．2来源：2017-2018学年八年级数学下册（湘教版）期末单元测试卷第2章四边形42、如图，∠BAC内有一点P，过点P作直线l∥AB，交AC于E点．今欲在∠BAC的两边上各找一点Q、R，使得P为QR的中点，以下是甲、乙两人的作法：甲：①过P作直线l1∥AC，交直线AB于F点，并连接EF；②过P作直线l2∥EF，分别交两直线AB、AC于Q、R两点，则Q、R即为所求．乙：①在直线AC上另取一点R，使得AE=ER；②作直线PR，交直线AB于Q点，则Q、R即为所求．下列判断正确的是（）A. 两人皆正确B. 两人皆错误C. 甲正确，乙错误D. 甲错误，乙正确来源：2018年河北省唐山市路南区中考数学一模试卷43、如图，在中，，将绕顶点逆时针旋转得到Rt△DEC,点M 是BC的中点，点P是DE的中点，连接PM，若BC =2,∠BAC=30°，则线段PM的最大值是（）A．4B．3C．2D．1来源：【全国市级联考】福建省福州市屏东中学、泉州七中2018届九年级5月适应性联考数学试题44、如图，在△ABC中，∠C=90°，AC=4，BC=2，点A、C分别在x轴、y轴上，当点A 在x轴上运动时，点C随之在y轴上运动.在运动过程中，点B到原点的最大距离是( )A. 6B. 2C. 2D. 2＋2来源：天津市河西区梅江中学 2018年八年级数学下册期末模拟测试卷（含答案）45、如图，正方形ABCD中，点E、F分别在BC、CD上，△AEF是等边三角形，连接AC交EF于G，下列结论：①BE=DF；②∠DAF=15°，③AC垂直平分EF，④BE+DF=EF，⑤S△AEC=S△ABC，其中正确结论有（）个．A. 5B. 4C. 3D. 2来源：宁夏银川市第十八中学2017-2018学年下期八年级数学期末测试题46、如图，在▱ABCD中，对角线AC与BD相交于点O，过点O作EF⊥AC交BC于点E，交AD于点F，连接AE、CF．则四边形AECF是（）A．梯形B．矩形C．菱形D．正方形来源：宁夏银川市第十八中学2017-2018学年下期八年级数学期末测试题47、如图，在四边形ABCD中，∠ABC=90°，∠BAD=60°，AC=AD，AC平分∠BAD，M，N分别为AC，CD的中点，BM的延长线交AD于点E，连接MN，BN．对于下列四个结论：①MN∥AD；② BM=MN；③△BAE≌△ACB；④AD=BN，其中正确结论的序号是( )A．①②③④B．①②③C．①②④D．①②来源：【全国区级联考】广西贵港市覃塘区2018届九年级第二次模拟考试数学试题48、如图，在平面直角坐标系中，A（0，2），动点B、C从原点O同时出发，分别以每秒1个单位和每秒2个单位长度的速度沿x轴正方向运动，以点A为圆心，OB的长为半径画圆；以BC为一边，在x轴上方作等边△BCD.设运动的时间为t秒，当⊙A与△BCD 的边BD所在直线相切时，t的值为（）C．4＋6D．4－6A．B．来源：江苏省无锡市滨湖区2018届九年级下学期调研考试数学试题49、如图，在中，是的中点，将沿翻折得到，连接，则线段的长等于( )A．2B．C．D．来源：【全国市级联考】江苏省苏州市2018届九年级中考数学模拟试题50、如图，在梯形中，，中位线与对角线交于两点，若cm, cm，则的长等于( )A．10 cm B．13 cm C．20 cm D．26 cm来源：【全国市级联考】江苏省苏州市2018届九年级中考数学模拟试题参考答案1、D2、A3、B4、B5、A6、B7、D8、D9、D10、C11、D12、B13、C14、A15、B16、D17、C18、C19、B20、A21、C22、A23、C24、C25、C26、C27、A28、B29、D30、A31、C32、A33、A34、D35、B36、B37、C38、B39、B40、B41、D42、A43、B44、D45、C46、C47、C48、C49、D50、D【解析】1、分析: 根据角平分线的性质得出距离相等，结合其它条件证三角形全等，得出结论与各选项进行比对，答案可得.详解: ∵点D是∠ABC的平分线上一点，点P在BD上，PA⊥AB，PC⊥BC，∴△ABP≌△CBP∴AB=BC，点D是∠ABC的平分线上一点，∴△ABD≌△CBD，∴AD=CD，故D不对．故选：D.点睛: 本题主要考查了角平分线的性质；得出两对三角形全等是正确解决本题的关键.2、【分析】抓住多边形的内角和是其外角和的3倍，可得(n-2)×180°=360°×3，解方程即可. 【详解】设多边形的边数是n,因为，多边形的外角和都是360°.多边形的内角和是(n-2)×180°所以，(n-2)×180°=360°×3所以n=8故正确选项为A.【点睛】本题考核知识点：多边形的内角和公式和多边形外角和.解题关键：熟记内角和公式和多边形外角和是360°.3、分析：根据正方体相对的面在展开图中“隔一相对”的规律解答即可.详解：由正方体展开图的特点知，“人”与“初”相对，“之”与“本”相对，“性”与“善”相对.故选B.点睛：本题考查了正方体展开图中相对面的识别，也考查了学生的空间想象能力，解答本题的关键是熟练掌握正方体相对面上的文字在展开图中的特征.4、分析：根据同位角的概念：两条直线被第三条直线所截形成的角中，若两个角分别在截线的同侧，且在两条被截直线的同旁，具有这样位置关系的一对角叫做同位角。

初三几何证明练习题和答案几何证明是初中数学中的重要内容，通过练习不同类型的几何证明题，可以帮助学生理解并掌握几何证明的基本方法与技巧。

本文将为大家提供一些初三几何证明的练习题和答案，希望对同学们的学习有所帮助。

1. 题目：已知ABCD是平行四边形，证明∠ABC + ∠ADC = 180°。

证明：解：连接AC，根据平行四边形的性质可知∠ADC = ∠ACB，所以要证明∠ABC + ∠ADC = 180°，只需证明∠ABC + ∠ACB = 180°。

由角的内外（对顶、同旁）定理可知∠ACB + ∠ABC = 180°，即∠ABC + ∠ACB = 180°。

所以，∠ABC + ∠ADC = 180°得证。

2. 题目：已知直角三角形ABC中，∠ACB = 90°，AC = 5cm，BC= 12cm，证明AB = 13cm。

证明：解：根据勾股定理可得AB² = AC² + BC²。

代入已知条件，即可得AB² = 5² + 12² = 25 + 144 = 169。

开方可得AB = 13cm。

所以，AB = 13cm得证。

3. 题目：已知直角三角形ABC中，∠ACB = 90°，AC = BC，证明∠ABC = 45°。

证明：解：连接AB，根据等腰直角三角形的性质可知∠ACB = ∠CAB。

所以，∠ABC = 180° - ∠ACB - ∠CAB = 180° - ∠ACB - ∠ACB = 180° - 2∠ACB。

由于∠ACB = 90°，代入得∠ABC = 180° - 2 × 90° = 0°。

所以，∠ABC = 0°，即∠ABC = 45°得证。

4. 题目：已知ABCD是一个平行四边形，E为AD的中点，证明BE平分∠CBD。

初中几何证明题经典题（一）1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ． 求证：CD ＝GF ．（初二）.如下图做GH ⊥AB,连接EO 。

由于GOFE 四点共圆，所以∠GFH ＝∠OEG , 即△GHF ∽△OGE,可得EO GF =GO GH =COCD,又CO=EO ，所以CD=GF 得证。

2、已知：如图，P 是正方形ABCD 内点，∠PAD ＝∠PDA ＝150． 求证：△PBC 是正三角形．（初二）.3、如图，已知四边形ABCD 、A 1B 1C 1D 1都是正方形，A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．（初二）APCDB D 2C 2 B 2 A 2D 1C 1B 1C B DA A 1 AFGCEBOD4、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．经典题（二）1、已知：△ABC 中，H 为垂心（各边高线的交点），O（1）求证：AH ＝2OM ； （2）若∠BAC ＝600，求证：AH ＝AO ．（初二）2、设MN 是圆O 外一直线，过O 作OA ⊥MN 于A ，自A 及D 、E ，直线EB及CD 分别交MN 于P 、Q ． 求证：AP ＝AQ ．（初二）3、如果上题把直线MN 由圆外平移至圆内，则由此可得以下命题：设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN 于P 、Q ． 求证：AP ＝AQ ．（初二）4、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ，点P 是EF 的中点．BF求证：点P 到边AB 的距离等于AB 的一半．经典题（三）1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．（初二）2、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证：AE ＝AF ．（初二）3、设P 是正方形ABCD 一边求证：PA ＝PF ．（初二）4、如图，PC 切圆O 于C ，AC 为圆的直径，PEFB 、D ．求证：AB ＝DC ，BC ＝AD ．（初三）经典题（四）1、已知：△ABC 是正三角形，P 是三角形内一点，PA ＝3，PB ＝4，PC ＝5． 求：∠APB 的度数．（初二）2、设P 是平行四边形ABCD 内部的一点，且∠PBA ＝∠PDA ． 求证：∠PAB ＝∠PCB ．（初二）3、设ABCD 为圆内接凸四边形，求证：AB ·CD ＋AD ·BC ＝AC ·BD ．（初三）4、平行四边形ABCD 中，设E 、F 分别是BC 、AB 上的一点，AE 与CF 相交于P ，且 AE ＝CF ．求证：∠DPA ＝∠DPC ．（初二）经典难题（五）1、 设P 是边长为1的正△ABC 内任一点，L ＝PA ＋PB ＋PC ，求证：≤L ＜2．2、已知：P 是边长为1的正方形ABCD 内的一点，求PA ＋PB ＋PC 的最小值． A P CB P A D CB C B D A F PD E CB A APCB3、P为正方形ABCD内的一点，并且PA＝a，PB＝2a，PC＝3a，求正方形的边长．4、如图，△ABC中，∠ABC＝∠ACB＝800，D、E分别是AB、AC上的点，∠DCA＝300，∠EBA＝200，求∠BED的度数．经典题（一）1.如下图做GH⊥AB,连接EO。

初中几何证明题经典题（一）1、已知：如图，0是半圆的圆心，C、E是圆上的两点，CD丄AB , EF丄AB , EG丄CO. 求证：CD = GF .（初二）.如下图做GH丄AB,连接EO。

由于GOFE四点共圆，所以/ GFH =Z OEG, 即厶GHFOGE,可得EO = GO = CO，又CO=EO，所以CD=GF 得证。

GF GH CD2、已知：如图，P是正方形ABCD内点，/ PAD =Z PDA = 15°. 求证：△ PBC是正三角形.（初二）3、如图，已知四边形ABCD、A i B i C i D i都是正方形，A2、B2、C2、D2分别是AA i、BB i、CC i、DD i的中点.及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证：AP = AQ .（初二）3、如果上题把直线 MN 由圆外平移至圆内，则由此可得以下命题:设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN P 、Q .4、 1、求证：四边形 A 2B 2C 2D 2是正方形.（初二）已知: 求证: 如图，在四边形 的延长线交 / DEN = Z△ ABC 中, MN F .ABCD 中，AD = BC , M 、N 分别是 AB 、CD 的中点，AD 、BC 于E 、F .经典题（二）已知： (1) 求证：AH = 20M ;(2) 若/ BAC = 60°,求证:H 为垂心 （各边高线的交点），0为外心，且 0M 丄BC 于M . AH = A0 .(初二)2、设MN 是圆O 外一直线，过O 作OA 丄MN 于A ，自A 引圆的两条直线，交圆于DCGN求证：AP = AQ .（初二）ECAM NP4、如图，分别以厶 ABC 的AC 和BC 为一边，在△ ABC 的外侧作正方形 ACDE 和正方形 CBFG ，点P 是EF 的中点.求证：点P 到边AB 的距离等于 AB 的一半.（初二）经典题（二）1、如图，四边形 ABCD 为正方形, 求证：CE = CF .（初二）2、如图，四边形 ABCD 为正方形，DE // AC ,且CE = CA ，直线EC 交DA 延长线于F . 求证：AE = AF .（初二）DE // AC , AE = AC , AE 与 CD 相交于 F .FEAD1、设P 是边长为1的正△ ABC 内任一点,4、如图，PC 切圆0于C , AC 为圆的直径，PEF 为圆的割线，AE 、AF 与直线PO 相交于3、设ABCD 为圆内接凸四边形，求证： AB • CD + AD • BC = AC • BD .（初三）B 、D .求证: AB = DC , BC = AD .（初三）1、已知：△ ABC 是正三角形，P 是三角形内一点 求：/ APB 的度数.（初二）2、设P 是平行四边形 ABCD 内部的一点，且/求证：/ PAB = Z PCB .（初二）4、平行四边形 ABCD 中，设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且AE = CF .求证：/ DPA =Z DPC .（初二）AO DB EFC求证:4、如图，△ ABC 中，/ ABC =Z ACB = 80°, D、E 分别是AB、AC 上的点，/ DCA = 30°, / EBA = 20°，求/ BED 的度数. LiB C经典题（一）1•如下图做GH丄AB,连接E0。

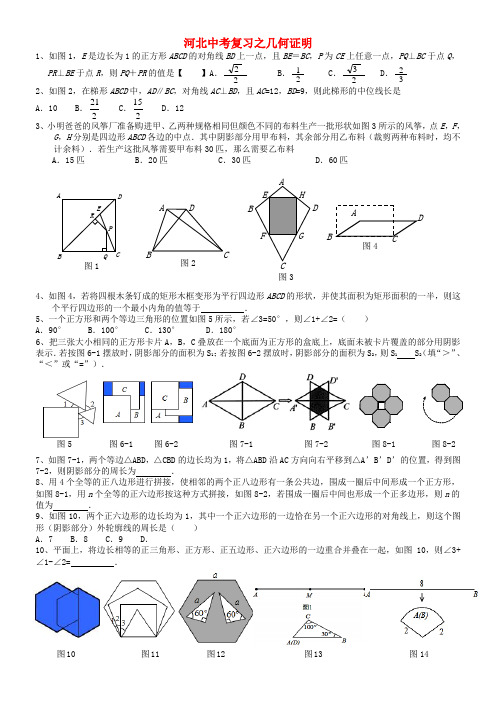
河北中考复习之几何证明1、如图1，E是边长为1的正方形ABCD的对角线BD上一点，且BE＝BC，P为CE上任意一点，PQ⊥BC于点Q，PR⊥BE于点R，则PQ＋PR的值是【】A．22B．21 C．23 D．322、如图2，在梯形ABCD中，AD∥BC，对角线AC⊥BD，且AC=12，BD=9，则此梯形的中位线长是A．10 B．212C．152D．123、小明爸爸的风筝厂准备购进甲、乙两种规格相同但颜色不同的布料生产一批形状如图3所示的风筝，点E，F，G，H分别是四边形ABCD各边的中点．其中阴影部分用甲布料，其余部分用乙布料（裁剪两种布料时，均不计余料）．若生产这批风筝需要甲布料30匹，那么需要乙布料A．15匹B．20匹C．30匹D．60匹4、如图4，若将四根木条钉成的矩形木框变形为平行四边形ABCD的形状，并使其面积为矩形面积的一半，则这个平行四边形的一个最小内角的值等于．5、一个正方形和两个等边三角形的位置如图5所示，若∠3=50°，则∠1+∠2=（）A．90° B．100° C．130° D．180°6、把三张大小相同的正方形卡片A，B，C叠放在一个底面为正方形的盒底上，底面未被卡片覆盖的部分用阴影表示．若按图6-1摆放时，阴影部分的面积为S1；若按图6-2摆放时，阴影部分的面积为S2，则S1 S2（填“＞”、“＜”或“=”）．7、如图7-1，两个等边△ABD，△CBD的边长均为1，将△ABD沿AC方向向右平移到△A’B’D’的位置，得到图7-2，则阴影部分的周长为．8、用4个全等的正八边形进行拼接，使相邻的两个正八边形有一条公共边，围成一圈后中间形成一个正方形，如图8-1，用n个全等的正六边形按这种方式拼接，如图8-2，若围成一圈后中间也形成一个正多边形，则n的值为．9、如图10，两个正六边形的边长均为1，其中一个正六边形的一边恰在另一个正六边形的对角线上，则这个图形（阴影部分）外轮廓线的周长是（）A．7 B．8 C．9 D．10、平面上，将边长相等的正三角形、正方形、正五边形、正六边形的一边重合并叠在一起，如图10，则∠3+∠1-∠2= ．BCDEF GHA图3AB CD图4图2AB CDABDCERPQ图1图5 图6-1 图7-1 图8-2图6-2 图7-2 图8-1图14 图10 图11 图12 图1312、如图12，边长为a 的正六边形内有两个三角形（数据如图），则空白阴影s s A ． 3 B．4 C ．5 D ． 613、如图13，M 是铁丝AD 的中点，将该铁丝首尾相接折成△ABC ，且∠B=30°，∠C=100°，如图13．则下列说法正确的是（ ）A ．点M 在AB 上 B ．点M 在BC 的中点处 C ．点M 在BC 上，且距点B 较近，距点C 较远D ．点M 在BC 上，且距点C 较近，距点B 较远14、如图14，将长为8cm 的铁丝首尾相接围成半径为2cm 的扇形．则扇形s =15、小宇同学在一次手工制作活动中，先把一张矩形纸片按图9—1的方式进行折叠，使折痕的左侧部分比右侧部分短1cm ；展开后按图9—2的方式再折叠一次，使第二次折痕的左侧部分比右侧部分长1cm ，再展开后，在纸上形成的两条折痕之间的距离是A ．0.5cmB ．1cmC ．1.5cmD ．2cm16、如图15，等边△ABC 的边长为1cm ，D 、E 分别是AB 、AC 上的点，将△ADE 沿直线DE 折叠，点A 落在点A ′处，且点A ′在△ABC 外部，则阴影部分图形的周长为 cm ．17、如图16，△ABC 中，D ，E 分别是边AB ，AC 的中点．若DE=2，则BC=（ ）A ．2 B ．3 C ．4 D ．5 18、如图17，将长为2、宽为1的矩形纸片分割成n 个三角形后，拼成面积为2的正方形，则n ≠（ ） A ．2 B ．3 C ．4 D ．519、如图1是边长为1的六个小正方形组成的图形，它可以围成图2的正方体，则图1中小正方形顶点A ，B 围成的正方体上的距离是（ ）A ．0 B ．1 C ．2 D ． 320、如图14，已知△ABC （AC ＜BC ），用尺规在BC 上确定一点P ，使PA+PC=BC ，则符合要求的作图痕迹是（ ）A ．B ．C ．D ．20、嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的，她先用尺规作出了如图1的四边形ABCD ，并写出了如下不完整的已知和求证． 已知：如图1，在四边形ABCD 中，BC=AD ，AB= 求证：四边形ABCD 是 四边形． （1）在方框中填空，以补全已知和求证； （2）按嘉淇的想法写出证明；（3）用文字叙述所证命题的逆命题为 ． 21、如图，△ABC 中，AB=AC ，∠BAC=40°，将△ABC 绕点A 按逆时针方向旋转100°．得到△ADE ，连接BD ，CE 交于点F ．左 右左 右 第二次折叠 第一次折叠 图9－1 图9－2 图15 图16 图17 图14（1）求证：△ABD≌△ACE；（2）求∠ACE的度数；（3）求证：四边形ABFE是菱形．22、如图，在四边形ABCD中，AB=AD，CB=CD，E是CD上一点，BE交AC于F，连接DF．（1）证明：∠BAC=∠DAC，∠AFD=∠CFE．（2）若AB∥CD，试证明四边形ABCD是菱形；（3）在（2）的条件下，又知∠EFD=∠BCD，请问你能推出什么结论？（直接写出一个结论，要求结论中含有字母E）23、如图，在▱ABCD中，点E，F分别在AB，DC上，且ED⊥DB，FB⊥BD．（1）求证：△AED≌△CFB；（2）若∠A=30°，∠DEB=45°，求证：DA=DF．22．在▱ABCD中，过点D作DE⊥AB于点E，点F 在边CD上，DF=BE，连接AF，BF．（1）求证：四边形BFDE是矩形；（2）若CF=3，BF=4，DF=5，求证：AF平分∠DAB．23、在一平直河岸l同侧有A，B两个村庄，A，B到l的距离分别是3 km和2 km，AB= a km（a＞1）．现计划在河岸l上建一抽水站P，用输水管向两个村庄供水．方案设计某班数学兴趣小组设计了两种铺设管道方案：图13-1是方案一的示意图，设该方案中 管道长度为d 1，且d 1=PB+BA （km ）（其中BP ⊥ l 于点P ）；图13-2是方案二的示意图，设该方案中管道长度为d 2 ，且d 2=PA +PB （km ）（其中点A '与点A 关于l 对称，A 'B 与l 交于点P ）．观察计算（1）在方案一中，d 1= km （用含a的式子表示）；（2）在方案二中，组长小宇为了计算d 2的长，作了如图13-3所示的辅助线，请你按小宇同学的思路计算，d 2=km （用含a 的式子表示）． 探索归纳（1）①当a = 4时，比较大小： d 1 d 2（填“＞”、“=”或“＜”）；②当a = 6时，比较大小： d 1 d 2（填“＞”、“=”或“＜”）；（2）请你参考右边方框中的方法指导，就a （当a ＞1时）的所有取值情况进行分析，要使铺设的管道长度较短，应选择方案一还是方案二？24、在正方形ABCD 中，点E 是AD 上一动点，MN ⊥AB 分别交AB ，CD 于M ，N ，连接BE 交MN 于点O ，过O 作OP ⊥BE 分别交AB ，CD 于P ，Q ．探究：（1）如图①，当点E 在边AD 上时，请你动手测量三条线段AE ，MP ，NQ 的长度，猜测AE 与MP+NQ 之间的数量关系，并证明你所猜测的结论；探究：（2）如图②，若点E 在DA 的延长线上时，AE ，MP ，NQ 之间的数量关系又是怎样请直接写出结论； 再探究：（3）如图③，连接并延长BN 交AD 的延长线DG 于H ，若点E 分别在线段DH 和射线HG 上时，请在图③中完成符合题意的图形，并判断AE ，MP ，NQ 之间的数量关系又分别怎样？请直接写出结论．25、在图14-1至图14-3中，点B 是线段AC 的中点，点D 是线段CE 的中点．四边形BCGF 和CDHN 都是正方形．AE 的中点是M ．（1）如图14-1，点E 在AC 的延长线上，点N 与点G 重合时，点M 与点C 重合，求证：FM = MH ，FM ⊥MH ；∵22()()m n m n m n -=+-，m +n ＞0， ∴（22m n -）与（m n -）的符号相同． 当22m n -＞0时，m n -＞0，即m ＞n ； 当22m n -= 0时， m n -= 0，即m =n 当22m n -＜0时，m n -＜0，即m ＜n ． 方法指导 当不易直接比较两个正数m 与n 的 大小时，可以对它们的平方进行比较：A l 图13 -1 A B l A ' 图13 -2 A B P C 图13 -3 K l A ' BPC（2）将图14-1中的CE 绕点C 顺时针旋转一个锐角，得到图14-2，求证：△FMH 是等腰直角三角形； （3）将图14-2中的CE 缩短到图14-3的情况，△FMH 还是等腰直角三角形吗？（不必说明理由）26、操作示例 对于边长均为a 的两个正方形ABCD 和EFGH ，按图11—1所示的方式摆放，再沿虚线BD ，EG 剪开后，可以按图中所示的移动方式拼接为图11—1中的四边形BNED ．从拼接的过程容易得到结论：①四边形BNED 是正方形； ②S 正方形ABCD +S 正方形EFGH =S 正方形BNED ．实践与探究（1）对于边长分别为a ，b （a ＞b ）的两个正方形ABCD 和EFGH ，按图11—2所示的方式摆放，连结DE ，过点D 作DM ⊥DE ，交AB 于点M ，过点M 作MN ⊥DM ，过点E 作EN ⊥DE ，MN 与EN 相交于点N ．①证明四边形MNED 是正方形，并用含a ，b 的代数式表 示正方形MNED 的面积；②在图11—2中，将正方形ABCD 和正方形EFGH 沿虚线剪开后，能够拼接为正方形MNED ．请简略说明你的拼接方法（类比图11—1，用数字表示对应的图形）．（2）对于n （n 是大于2的自然数）个任意的正方形，能否通过若干次拼接，将其拼接为一个正方形？请简要说明你的理由．27、如图14—1，14—2，四边形ABCD 是正方形，M 是AB 延长线上一点．直角三角尺的一条直角边经过点D ，且直角顶点E 在AB 边上滑动（点E 不与点A ，B 重合），另一条直角边与∠CBM 的平分线BF 相交于点F ．（1）如图14—1，当点E 在AB 边的中点位置时： ①通过测量DE ，EF 的长度，猜想DE 与EF 满足的数量关系是 ；②连接点E 与AD 边的中点N ，猜想NE 与BF 满足的数量关系是 ；③请证明你的上述两个猜想．（2）如图14—2，当点E 在AB 边上的任意位置时，请你在AD 边上找到一点N ，使得NE =BF ，进而猜想此时DE 与EF 有怎样的数量关系．28、如图13－1，一等腰直角三角尺GEF 的两条直角边与正方形ABCD 的两条边分别重合在一起．现正方形ABCD 保持不动，将三角尺GEF 绕斜边EF 的中点O （点O 也是BD 中点）按顺时针方向旋转． （1）如图13－2，当EF 与AB 相交于点M ，GF 与BD 相交于点N 时，通过观察或测量BM ，FN 的长度，猜想BM ，FN 满足的数量关系，并证明你的猜想；A B C D E F GM图11—2（H ） A CDF图14—1 N A B C D E M F 图14—2 43 2 1 A B C D E F （H ） 图11—1 （G ） 5 6图14（2）若三角尺GEF 旋转到如图13－3所示的位置时，线段FE 的延长线与AB 的延长线相交于点M ，线段BD 的延长线与GF 的延长线相交于点N ，此时，（1）中的猜想还成立吗？若成立，请证明；若不成立，请说明理由．29、在图14-1—14-5中，正方形ABCD 的边长为a ，等腰直角三角形FAE 的斜边AE ＝2b ，且边AD 和AE 在同一直线上．操作示例 当2b ＜a 时，如图14-1，在BA 上选取点G ，使BG ＝b ，连结FG 和CG ，裁掉△FAG 和△CGB 并分别拼接到△FEH 和△CHD 的位置构成四边形FGCH ．思考发现小明在操作后发现：该剪拼方法就是先将△FAG 绕点F 逆时针旋转90°到△FEH 的位置，易知EH 与AD 在同一直线上．连结CH ，由剪拼方法可得DH =BG ，故△CHD ≌△CGB ，从而又可将△CGB 绕点C 顺时针旋转90°到△CHD 的位置．这样，对于剪拼得到的四边形FGCH （如图14-1），过点F 作FM ⊥AE 于点M （图略），利用SAS 公理可判断△HFM ≌△CHD ，易得FH =HC =GC =FG ，∠FHC =90°．进而根据正方形的判定方法，可以判断出四边形FGCH 是正方形．实践探究（1）正方形FGCH 的面积是 ；（用含a ，b 的式子表示）（2）类比图14-1的剪拼方法，请你就图14-2—图14-4的三种情形分别画出剪拼成一个新正方形的示意图．联想拓展小明通过探究后发现：当b ≤a 时，此类图形都能剪拼成正方形，且所选取的点G 的位置在BA 方向上随着b 的增大不断上移．当b ＞a 时，如图14-5的图形能否剪拼成一个正方形？若能，请你在图中画出剪拼的示意图；若不能，简要说明理由．图E 图图（2b ＝a ） （a ＜2b ＜2a ） （b图14-1 （2b ＜a ）图（b ＞a ） 图13－2 G图13－3图13－1 A ( E )D。

2018年数学中考代数几何综合问题（1）专项练习1. 如图⑴，在平面直角坐标系中，O 为坐标原点，抛物线2+8+16+6y ax ax a =经过点B （0，4）。

⑴求抛物线的解析式；⑵设抛物线的顶点为D ，过点D 、B 作直线交x 轴于点A ，点C 在抛物线的对称轴上，且C 点的纵坐标为4-，连接BC 、AC 。

求证：△ABC 是等腰直角三角形；⑶在⑵的条件下，将直线DB 沿y 轴向下平移，平移后的直线记为l ，直线l 与x 轴、y 轴分别交于点A ′、B ′，是否存在直线l ，使△A ′B ′C 是直角三角形，若存在，求出直线l 的解析式，若不存在，请说明理由。

2. 二次函数2y ax bx c =++的图象的一部分如图所示。

已知它的顶点M 在第二象限，且经过点A （1，0）和点B （0，1）。

（1）试求a ，b 所满足的关系式；所满足的关系式；（2）设此二次函数的图象与x 轴的另一个交点为C ，当△AMC 的面积为△ABC 面积的54倍时，求a 的值； （3）是否存在实数a ，使得△ABC 为直角三角形。

若存在，请求出a 的值；若不存在，请说明理由。

请说明理由。

3. 如图，在平面直角坐标系中，二次函数26y ax x c =++的图象经过点A （4，0）、B （-1，0），与y 轴交于点C ，点D 在线段OC 上，OD =t ，点E 在第二象限，∠ADE =90°，12tan DAE Ð=，EF ⊥OD ，垂足为F 。

（1）求这个二次函数的解析式；）求这个二次函数的解析式；（2）求线段EF 、OF 的长（用含t 的代数式表示）；的值。

（3）当△ECA为直角三角形时，求t的值。

代数几何综合问题（1）专项练习参考答案1. （1）解：由题意知：16a+6=4解得：a=81-故抛物线的解析式为：4812+--=x x y 。

⑵证明：由抛物线的解析式知：顶点D 坐标为（－4，6）∵点C 的纵坐标为－4，且在抛物线的对称轴上，∴C 点坐标为（－4，－4） 设直线BD 解析式为：()40y kx k =+¹，有：644k =-+，∴12k =-∴直线BD 解析式为142y x =-+ ∴直线BD 与x 轴的交点A 的坐标为（8，0） 过点C 作CE ⊥y 轴于点E ，则CE =4，BE =8 又∵OB =4，OA =8，∴CE =OB ，BE =OA ，∠CEB =∠BOA =90° ∴△CEB ≌△BOA （SAS ） ∴CB =AB ，∠CBE =∠BAO∵∠BAO +∠ABO =90°，∴∠CBE +∠ABO =90° 即∠ABC =90° ∴△ABC 是等腰直角三角形。

平面几何初步一、选择题1. （ 福建福州，3，3分）如图，直线a ，b 被直线c 所截，∠1和∠2的位置关系是A ．同位角B ．内错角C ．同旁内角D ．对顶角【答案】B【逐步提示】本题考查了同位角、内错角、同位角和对顶角的识别，解题的关键是认识三线八角，根据内错角的定义可得答案．【详细解答】解：直线a ，b 被直线c 所截，∠1与∠2是内错角，故选择B .【解后反思】三线八角中的某两个角是不是同位角、内错角或同旁内角，完全由那两个角在图形中的相对位置决定．在复杂的图形中判别三类角时，应从角的两边入手，具有上述关系的角必有两边在同一直线上，此直线即为截线，而另外不在同一直线上的两边，它们所在的直线即为被截的线． 【关键词】内错角；同位角；同旁内角；对顶角2. （ 甘肃省武威市、白银市、定西市、平凉市、酒泉市、临夏州、张掖市等9市，6，3分）如图，AB ∥CD ，DE ⊥CE ，∠1=34º，则∠DCE 的度数为（ ）A ． 34º B．54º C． 66º D ． 56º1BE第6题图【答案】D 【逐步提示】本题考查了平行线的性质，解题的关键是将线的位置关系转化为角的数量关系，应用平行线的性质：两直线平行线内错角相等得出∠EDC 的度数，再利用直角三角形两锐角互余得出∠DCE 的度数． 【详细解答】解：∵AB ∥CD ，∴ ∠EDC ＝∠1＝34°．∵DE ⊥CE ∴ ∠DEC ＝90°，∴∠EDC ＋∠DCE ＝90°．∴∠DCE ＝90°－34°=56º，故选择D ．【解后反思】本题考查了平行线的性质即两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补.【关键词】平行线的性质；垂直的定义；直角三角形的性质； 3. （ 甘肃省天水市，5，4分）如图，直线AB ∥CD ，OG 是∠EOB 的平分线，∠EFD ＝70°，则∠BOG 的度数是（ ） A ．70° B ．20° C ．35° D ．40°【答案】C【逐步提示】本题考查了平行线的性质和角平分线的定义，解题关键是注意两直线平行，相关的同位角相等、内错角相等及同旁内角互补．要求∠BOG 的度数，关键是先求∠EOB 的度数，这可根据∠EFD ＝70°，联想到两直线CO A B D E FG平行，同位角相等解决．【详细解答】解：∵AB∥CD，∴∠EOB＝∠EFD＝70°．又∵OG平分∠EOB，∴∠BOG＝12∠EOB＝12×70°＝35°．故选择C．【解后反思】平行线间的角离不开同位角、同旁内角，及内错角等知识，另外还要和三角形的内角和定理，及外角等于与它不相邻的两内角和知识相联系，只要从这些方面思考，就不难得到解决．【关键词】平行线的性质；角的平分线．4.（广东茂名，5，3分）如图，直线a、b被直线c所截，若a∥b，∠1=60°，那么∠2的度数为（）A．120°B．90°C．60°D．30°【答案】C【逐步提示】本题考查了平行线的性质，解题的关键是识别出图中的∠1、∠2是两条平行直线a、b被第三条直线c截出的一组相等的同位角．直接利用“两直线平行，同位角相等”解题即可.【详细解答】解：∵a∥b，∴∠1=∠2. ∵∠1=60°，∴∠2=60°.故选择C .【解后反思】“两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补”这是由直线的位置关系得出角的数量关系，“同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行；”这是由角的数量关系得出直线的位置关系，这里体现了数形结合的思想．【关键词】同位角；平行线的性质5.（贵州省毕节市，8，3分）如图，直线a//b，∠1＝85°，∠2＝35°，则∠3＝（）（第8题图）A. 85°B. 60°C. 50°D. 35°【答案】C【逐步提示】本题考查平行线的性质，三角形外角和定理，解题的关键是能从图中发现∠3与∠1、∠2的联系．【详细解答】解：如图，∵a//b，∴∠4＝∠3．又∵∠1＝∠2＋∠4，∴∠4＝∠1－∠2＝85°－35°＝50°，∴∠3＝50°，故选择C.【解后反思】此类问题容易出错的地方是找不到图形中角与角之间的数量关系．【关键词】平行线的性质；三角形外角和定理6.（河北省，13，2分）如图，将□ABCD沿对角线AC折叠，使点B落在点B’处.若∠1=∠2=44°，则∠B为（）A．66°B．104°C．114°D．124°【答案】C【逐步提示】根据平行线的性质和折叠的性质得到∠BAC=12∠B’AB=12∠1=22°，再在△ABC中根据三角形内角和定理求得∠B的度数.【详细解答】解：∵四边形ABCD是平行四边形，∴AB∥CD，∴∠B’AB=∠1=44°.根据折叠的性质可知∠BAC=12∠B’AB=12×44°=22°.又∵∠2=44°，∴∠B=180°－22°-44°=114°，故答案为选项C.【解后反思】折叠问题是属于轴对称变换，折叠后图形的形状和大小不变，三角形折叠后得到的三角形与原三角形全等，对应边和对应角相等.【关键词】平行四边形的性质；平行线的性质；折叠；三角形内角和定理7.（湖北省黄冈市，3，3分）如图，直线a∥b,∠1=550，则∠2= （）A.350B.450C. 550D.650【答案】C【逐步提示】本题考查了平行线的性质“两直线平行，同位角相等”及对顶角的性质“对顶角相等”，解题的关键是能观察出∠1与∠2之间的联系而不走弯路．由图易发现，∠1的对顶角与∠2是同位角，a∥b是沟通∠1与∠2的桥梁．【详细解答】解：如图，∵a∥b，∴∠3＝∠2．∵∠3＝∠1，∴∠2＝∠1＝55°，故选择C.【解后反思】此类题主要考查形式为选择或填空，解决此类题型常用的方法是根据平行线的性质：两直线平行同位角相等、两直线平行内错角相等，两直线平行同旁内角互补，结合对顶角相等或邻补角和为180°，直接求出正确答案后做出选择．【关键词】平行线的性质；对顶角。

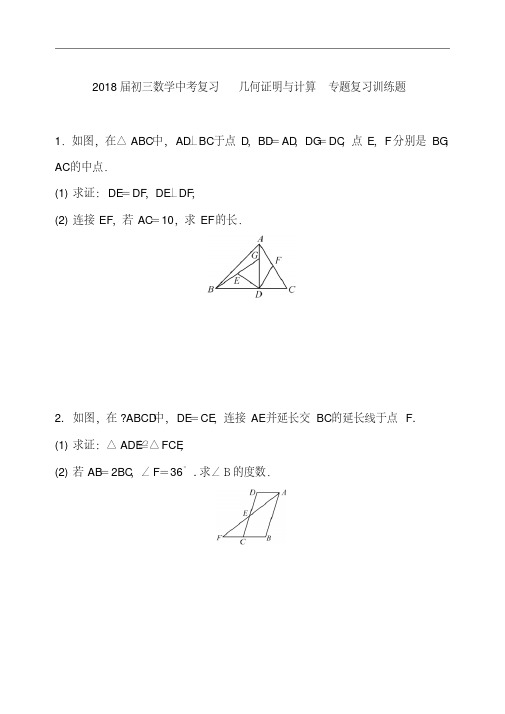
3.2几何证明及通过几何计算进行说理问题例1 2017年杭州市中考第22题如图1,在厶ABC中，BC> AC,/ ACB = 90°,点D在AB边上，DE丄AC于点E.(1)若AD =- , AE = 2,求EC 的长；DB 3(2)设点F在线段EC上，点G在射线CB上，以F、C、G为顶点的三角形与△ EDC 有一个锐角相等，FG交CD于点P •问：线段CP可能是△ CFG的高还是中线？或两者都有可能？请说明理由.例2 2017年安徽省中考第23题如图1,正六边形ABCDEF的边长为a, P是BC边上的一动点，过P作PM//AB交AF 于M，作PN//CD交DE于N.(1)①/ MPN =②求PM + PN = 3a;(2)如图2，点O是AD的中点，联结OM、ON.求证：0M = ON.(3)如图3,点O是AD的中点,四边形，并说明理由.OG平分/ MON，判断四边形OMGN是否为特殊的图1 图3例3 2018 年上海市黄浦区中考模拟第24题已知二次函数y=—x2+ bx+ c的图像经过点P(0, 1)与Q(2, —3).( 1 )求此二次函数的解析式；(2)若点A是第一象限内该二次函数图像上一点，过点A作x轴的平行线交二次函数图像于点B，分别过点B、A作x轴的垂线，垂足分别为C、D，且所得四边形ABCD恰为正方形．①求正方形的ABCD 的面积；②联结PA、PD, PD交AB于点E，求证：△ PADPEA.3.2几何证明及通过几何计算进行说理问题答案例1 2017年杭州市中考第22题如图1,在厶ABC中，BC> AC,/ ACB = 90°,点D在AB边上，DE丄AC于点E.(1)若AD =- , AE = 2,求EC 的长；DB 3(2)设点F在线段EC上，点G在射线CB上，以F、C、G为顶点的三角形与△ EDC 有一个锐角相等，FG交CD于点P •问：线段CP可能是△ CFG的高还是中线？或两者都有可能？请说明理由.动感体验请打开几何画板文件名“ 15杭州22”，拖动点D在AB上运动，可以体验到，CP既可以是△ CFG的高，也可以是△ CFG的中线.思路点拨CFG与厶EDC都是直角三角形，有一个锐角相等，分两种情况.2. 高和中线是直角三角形的两条典型线，各自联系着典型的定理，一个是直角三角形的两锐角互余，一个是直角三角形斜边上的中线等于斜边的一半.3. 根据等角的余角相等，把图形中相等的角都标记出来.满分解答(1)由/ ACB = 90°, DE丄AC,得DE//BC .所以些=AD =1 •所以_L =!•解得EC= 6.EC DB 3 EC 3(2)^ CFG与厶EDC都是直角三角形，有一个锐角相等，分两种情况：①如图2，当/ 1 = / 2时，由于/ 2与/ 3互余，所以/ 2与/ 3也互余.因此/ CPF = 90°.所以CP是厶CFG的高.②如图3，当/ 1 = / 3时，PF = PC.又因为/ 1与/ 4互余，/ 3与/ 2互余，所以/ 4=/ 2.所以PC= PG .所以PF = PC = PG .所以CP是厶CFG的中线.综合①、②，当CD是/ ACB的平分线时，CP既是△ CFG的高，也是中线(如图4).图2 图3 图4考点伸展这道条件变换的题目，不由得勾起了我们的记忆：如图5,在厶ABC中，点D是AB边上的一个动点，DE//BC交AC于E, DF//AC交BC于F，那么四边形CEDF是平行四边形.如图6,当CD平分/ ACB时，四边形CEDF是菱形.如图7,当/ACB=90°，四边形CEDF是矩形.如图8,当/ ACB= 90° , CD平分/ ACB时，四边形CEDF是正方形.图6图7 图8例2 2017年安徽省中考第23题如图1,正六边形ABCDEF的边长为a, P是BC边上的一动点，过P作PM//AB交AF于M，作PN//CD交DE于N.(1)①/ MPN =②求PM + PN = 3a;（2）如图2，点O是AD的中点，联结OM、ON.求证：0M = ON.（3）如图3,点O是AD的中点,四边形，并说明理由.动感体验请打开几何画板文件名“ 14安徽23”，拖动点P运动，可以体验到，PM + PN等于正六边形的3条边长.△ AOM ◎△ BOP , △ COP^A DON ,所以OM = OP = ON.还可以体验到，△ MOG与厶NOG是两个全等的等边三角形，四边形OMGN是菱形.思路点拨1. 第（1）题的思路是，把PM + PN转化到同一条直线上.2•第（2）题的思路是，以O为圆心，OM为半径画圆，这个圆经过点N、P •于是想到联结OP，这样就出现了两对全等三角形.3.第（3）题直觉告诉我们，四边形OMGN是菱形.如果你直觉△ MOG与厶NOG是等边三角形，那么矛盾就是如何证明/ MON = 120 ° .满分解答(1)①/ MPN = 60°②如图4，延长FA、ED交直线BC与M'、N ；那么△ ABM'、△ MPM '、△ DCN'、△ EPN都是等边三角形.所以PM + PN= M N = M B + BC+ CN = 3a.(2)如图5，联结OP .由(1)知，AM = BP, DN = CP.由AM = BP,/ OAM = Z OBP = 60°, OA = OB, 得厶AOM ◎△ BOP .所以OM = OP .同理△ COP也厶DON，得ON = OP .所以OM = ON .（3）四边形OMGN是菱形.说理如下：由（2）知，/ AOM =Z BOP,/ DON =Z COP （如图5）.OG平分/ MON，判断四边形OMGN是否为特殊的图4 图5图1 图3图6所以/ AOM + / DON = / BOP+Z COP= 60° .所以/ MON = 120° . 如图6,当OG 平分Z MON 时，Z MOG =/ NOG = 60° .又因为Z AOF = Z FOE = Z EOD = 60°,于是可得Z AOM = Z FOG = Z EON . 于是可得厶AOM ◎△ FOG ◎△ EON .所以OM = OG = ON.所以△ MOG与厶NOG是两个全等的等边三角形.所以四边形OMGN的四条边都相等，四边形OMGN是菱形.考点伸展在本题情景下，菱形OMGN的面积的最大值和最小值各是多少？因为△ MOG与厶NOG是全等的等边三角形，所以OG最大时菱形的面积最大，OG最小时菱形的面积最小.OG的最大值等于OA,此时正三角形的边长为a，菱形的最大面积为-^a2.2OG与EF垂直时最小，此时正三角形的边长为3a ,菱形的最小面积为色』a2.2 8例3 2018年上海市黄浦区中考模拟第24题已知二次函数y=—x2+ bx+ c的图像经过点P(0, 1)与Q(2, —3).(1)求此二次函数的解析式；(2)若点A是第一象限内该二次函数图像上一点，过点A作x轴的平行线交二次函数图像于点B，分别过点B、A作x轴的垂线，垂足分别为C、D，且所得四边形ABCD恰为正方形.①求正方形的ABCD的面积；②联结PA、PD, PD交AB于点E，求证：△ PADPEA.动感体验请打开几何画板文件名“ 13黄浦24”，拖动点A在第一象限内的抛物线上运动，可以体验到，/ PAE与/ PDA总保持相等，△ PAD与厶PEA保持相似.请打开超级画板文件名“ 13黄浦24”，拖动点A在第一象限内的抛物线上运动，可以体验到，/ PAE与/ PDA总保持相等，△ PAD与厶PEA保持相似.思路点拨1•数形结合，用抛物线的解析式表示点A的坐标，用点A的坐标表示AD、AB的长，当四边形ABCD是正方形时，AD = AB.2. 通过计算/ PAE与/ DPO的正切值，得到/ PAE = Z DPO =Z PDA ,从而证明厶PADPEA.满分解答(1)将点c =1,P(0, 1)、Q(2, —3)分别代入y=—x2+ bx+ c,得解得b=0,以2b 1 二-3. C=1.所以该二次函数的解析式为y= —x2+ 1.(2)①如图1,设点A的坐标为(x, —x2+ 1),当四边形ABCD恰为正方形时，AD = AB.此时y A= 2x A.解方程—x2+ 1 = 2x,得x - -1 _ 2 .所以点A的横坐标为••.2-1.因此正方形ABCD的面积等于[2( 2 -1)]2 =12 _8 2 .②设OP 与AB 交于点F，那么PF =OP -OF =1 - 2( & -1) =3-= ( "2 - 1)2.所以tan N PAE = 〔)=近_1 .AF 血―1又因为tan • PDA 二tan • DPO = = 2 -1 ,OP所以/ PAE=Z PDA.考点伸展事实上，对于矩形ABCD，总有结论△ PAD s\ PEA•证明如下：如图2,设点A 的坐标为(x, —x2+ 1)，那么PF = OP —OF = 1 —( —x2+ 1) = x2.2所以tan ZPA^PF =- x .AF x又因为tan . PDA =tan. DPO =x , OP所以/ PAE=Z PDA .因此△ PADPEA .。

2018重庆中考数学25题⼏何证明2０17年12⽉04⽇⽉之恒的初中数学组卷⼀.解答题（共23⼩题）１.（201７?贵港)已知:△ABC是等腰直⾓三⾓形,动点P在斜边AＢ所在的直线上,以PＣ为直⾓边作等腰直⾓三⾓形PCQ，其中∠PCQ=９０°，探究并解决下列问题:(1）如图①,若点Ｐ在线段AB上,且AC=1+,PA=,则:①线段PＢ= ,PC= ；②猜想:PA2，PB2,ＰQ２三者之间的数量关系为;（2）如图②,若点Ｐ在ＡB的延长线上,在(1)中所猜想的结论仍然成⽴,请你利⽤图②给出证明过程;(3)若动点P满⾜=，求的值.（提⽰：请利⽤备⽤图进⾏探求）2．（20１7?保亭县模拟)如图1,在△ABC和△EＤＣ中，AＣ＝ＣE＝CＢ=CD,∠ＡCB＝∠ＥCD=9０°,AB与ＣＥ交于F,ＥD与AB、ＢＣ分别交于Ｍ、H.（1)试说明CＦ=CＨ;（2）如图2,△ＡＢC不动,将△EDＣ从△ABＣ的位置绕点C顺时针旋转,当旋转⾓∠ＢＣD 为多少度时，四边形AＣＤM是平⾏四边形,请说明理由;（3）当ＡC＝时,在(2)的条件下,求四边形ACＤM的⾯积．3．(20１７春?嘉兴期末）如图,菱形ＡBCD中,∠ABC＝6０°,有⼀度数为60°的∠MＡＮ绕点A旋转．（1）如图①,若∠ＭＡN的两边AM，AN分别交ＢC，CD于点Ｅ，F，则线段ＣE,ＤＦ的⼤⼩关系如何?请证明你的结论；(2)如图②,若∠ＭAN的两边AM,ＡＮ分别交ＢＣ,CD的延长线于点E，F,则线段CE,ＤＦ还有（1)中的结论吗？请说明你的理由.４．(201７?营⼝)【问题探究】（１）如图1,锐⾓△ＡBC中分别以AB、AC为边向外作等腰△ABE和等腰△ＡCＤ，使AE=ＡB,AＤ=AC,∠BAE=∠CAD，连接B Ｄ,CE，试猜想ＢD与CE的⼤⼩关系，并说明理由．【深⼊探究】（2）如图2，四边形AＢCD中，ＡB=7cm,ＢC=３ｃm,∠ABC=∠ACD＝∠ADC=45°,求BD 的长．(３)如图3，在(2）的条件下，当△ＡCD在线段AC的左侧时，求BD的长.5.（2０17?菏泽)如图,已知∠ＡＢC=90°，Ｄ是直线AB上的点，AD＝BC．(１)如图1，过点A作AF⊥ＡB，并截取ＡF=BD，连接ＤC、DF、ＣＦ，判断△ＣDF的形状并证明；(2）如图2，E是直线ＢC上⼀点,且CE=BD，直线AＥ、CD相交于点P,∠APD的度数是⼀个固定的值吗?若是,请求出它的度数;若不是，请说明理由．6.（20１7春?重庆校级期末）如图1，△AＢC中,BE⊥AＣ于点Ｅ,AD⊥BC于点D,连接DE.(1)若AB=BＣ，DＥ＝１,ＢE=3,求△ＡBＣ的周长;（2）如图2，若ＡB＝BC,AD=BD,∠ADＢ的⾓平分线DF交ＢE于点F，求证:ＢF=DＥ;(3)如图3,若ＡB≠BC,AD=ＢD，将△AＤC沿着ＡC翻折得到△ＡGＣ,连接DG、EＧ,请猜想线段AＥ、BＥ、DG之间的数量关系,并证明你的结论.7．（20１7?于洪区⼀模）如图1,在△ABC中，∠ＡCB为锐⾓，点D为射线BC上⼀点,连接ＡD,以AD为⼀边且在AD的右侧作正⽅形ADEF.(1)如果ＡB＝AC，∠BＡC＝９0°,①当点D在线段BＣ上时(与点B不重合),如图2,线段CF、BD所在直线的位置关系为,线段CＦ、BＤ的数量关系为；②当点D在线段BC的延长线上时,如图3,①中的结论是否仍然成⽴,并说明理由;(2）如果AB≠ＡＣ，∠BAC是锐⾓,点D在线段ＢC上,当∠AＣＢ满⾜什么条件时,ＣF⊥BC(点C、F不重合），并说明理由．8．（20１7?绍兴)（1)如图1,正⽅形ABＣD中，点E，F分别在边ＢC,CＤ上,∠ＥAF=45°,延长CD到点Ｇ,使ＤＧ=BE，连结EF，AG．求证：ＥＦ=FG.（2）如图，等腰直⾓三⾓形ABC中，∠BAC=9０°,AB＝AC,点M,N在边BC上,且∠ＭＡN ＝45°,若BM=1，ＣN=3,求ＭN的长．9.（2０17?东营）（1)如图(１）,已知:在△ABC中,∠BAC=9０°,AB=AＣ,直线ｍ经过点A，BD⊥直线m，CE⊥直线m，垂⾜分别为点D、Ｅ.证明：DE=BD+CE.（2)如图(2）,将(1)中的条件改为:在△ABＣ中，AB=AC，Ｄ、A、Ｅ三点都在直线m上，并且有∠BＤA=∠AEC=∠ＢＡC=α,其中α为任意锐⾓或钝⾓.请问结论DE=BD+CE是否成⽴?如成⽴，请你给出证明；若不成⽴，请说明理由.(３）拓展与应⽤：如图（３)，D、E是Ｄ、A、Ｅ三点所在直线m上的两动点（D、A、E 三点互不重合)，点F为∠ＢAC平分线上的⼀点，且△ＡBF和△ACF均为等边三⾓形,连接ＢD、CE,若∠ＢDA＝∠ＡEC=∠BAC,试判断△DEＦ的形状．10.(2017?昭通）已知△ABC为等边三⾓形,点D为直线BＣ上的⼀动点（点D不与Ｂ、Ｃ重合），以AD为边作菱形ADEＦ(A、D、Ｅ、F按逆时针排列),使∠DＡＦ=6０°，连接CＦ.(1)如图１，当点D在边BC上时,求证：①BＤ＝CＦ；②AC=ＣF+ＣＤ;(２）如图2,当点D在边ＢＣ的延长线上且其他条件不变时,结论AＣ=ＣF+CＤ是否成⽴?若不成⽴,请写出ＡC、CＦ、ＣD之间存在的数量关系，并说明理由；（3)如图3,当点D在边ＣB的延长线上且其他条件不变时，补全图形,并直接写出AC、CF、CD之间存在的数量关系.11.（2０１7?常德）已知两个共⼀个顶点的等腰Rt△ABＣ，Rt△CEF,∠ＡBC=∠ＣEＦ=９0°,连接AF,M是ＡＦ的中点,连接ＭB、ME．（1)如图1,当CＢ与CＥ在同⼀直线上时，求证：ＭB∥CＦ；(２)如图１,若CB＝a,CE＝2a，求BＭ,ME的长;(3)如图2，当∠BＣE=４5°时,求证：BM=ME.１２．(２017?庐阳区校级模拟)如图，将两个全等的直⾓三⾓形△AＢD、△ACE拼在⼀起（图1)．△AＢＤ不动，（１）若将△ACＥ绕点A逆时针旋转，连接ＤE，M是DE的中点，连接MB、MC(图2）,证明:MB＝MC.（2)若将图1中的CE向上平移,∠CAE不变,连接ＤＥ,M是ＤE的中点,连接MB、MC（图３），判断并直接写出MＢ、MC的数量关系．(３)在（2)中,若∠CＡE的⼤⼩改变(图4），其他条件不变，则（2）中的MB、MＣ的数量关系还成⽴吗？说明理由. 13．(2017?武汉模拟)已知△ＡBC中，ＡＢ＝ＡＣ.（1)如图1，在△AＤE中,若AD=AE,且∠DAＥ=∠BAC，求证：CD=BE；（2)如图2,在△ADＥ中,若∠DＡE=∠BAC=60°,且CＤ垂直平分AＥ,AD=３，CＤ＝4,求BD 的长；（３)如图3，在△ＡDＥ中，当BD垂直平分AＥ于H，且∠ＢAＣ=2∠AＤＢ时，试探究CD２，ＢD2,AH2之间的数量关系,并证明．１4．(２017?长春)感知:如图①，点Ｅ在正⽅形ABＣD的边BＣ上,ＢＦ⊥AE于点Ｆ，DG⊥AE于点G，可知△AＤG≌△ＢAF.（不要求证明)拓展:如图②,点B、Ｃ分别在∠ＭAN的边ＡM、AN上,点E、F在∠MＡＮ内部的射线AD 上,∠1、∠2分别是△ABＥ、△ＣＡF的外⾓．已知AB=AC,∠１=∠2＝∠BAC,求证：△ＡＢＥ≌△CAF．应⽤:如图③,在等腰三⾓形ABC中，AB=ＡC,ＡB＞BＣ.点D在边BＣ上,CD=２BD,点Ｅ、F在线段AＤ上，∠1=∠2=∠BＡC.若△ABC的⾯积为9,则△ABE与△ＣDF的⾯积之和为.15．（20１7?昌平区模拟）（１）如图，在四边形ABCD中,AB=AＤ,∠B=∠D＝90°，E、F分别是边BC、CD上的点,且∠EAＦ=∠BＡD.求证：EF=BE＋ＦD;(2)如图，在四边形ABCD中,AB=AD，∠B＋∠D=１80°,E、F分别是边BC、CD上的点,且∠EＡF＝∠BAD,(1）中的结论是否仍然成⽴？(3)如图,在四边形ABCD中，ＡB＝ＡD，∠B+∠ＡDＣ=180°,E、Ｆ分别是边ＢC、CD延长线上的点，且∠ＥAF=∠BAＤ,(１)中的结论是否仍然成⽴?若成⽴，请证明;若不成⽴，请写出它们之间的数量关系,并证明.1６.(201７?哈尔滨模拟)已知△ABC是等腰三⾓形,AB=AC,Ｄ为边BC上任意⼀点,DE⊥AB 于E,DF⊥AC于Ｆ,且E,Ｆ分别在边ＡB,AＣ上．(1）如图a，当△AＢC是等边三⾓形时,证明:AＥ+AF=BC．(2）如图b,若△ＡBＣ中,∠ＢAＣ=120°,探究线段AＥ,ＡF,AB之间的数量关系,并对你的猜想加以证明.(3)如图c，若△ABＣ中,AB=１0，ＢＣ＝16,EＦ=6,利⽤你对（1），（２）两题的解题思路计算出线段CD（BD＞CD)的长．17.（2０17?绍兴）数学课上，李⽼师出⽰了如下框中的题⽬.⼩敏与同桌⼩聪讨论后,进⾏了如下解答:（1)特殊情况?探索结论当点E为AB的中点时，如图１,确定线段AE与的DB⼤⼩关系．请你直接写出结论：AE ＤB(填“＞"，“＜"或“=”）.（2)特例启发,解答题⽬解:题⽬中，AE与DB的⼤⼩关系是：ＡE DB（填“＞”,“<”或“=”).理由如下：如图2，过点E作ＥF∥ＢC，交AC于点F，（请你完成以下解答过程)(3)拓展结论，设计新题在等边三⾓形ABC中,点E在直线AB上,点D在直线BC上,且ＥD=EC.若△ＡBC的边长为1，AE＝２，求CＤ的长（请你直接写出结果).18．(２017?沈阳)已知,△AＢC为等边三⾓形，点D为直线BC上⼀动点(点D不与B、C重合）.以AD为边作菱形ＡDEF,使∠DＡＦ=6０°,连接ＣＦ.(1)如图1,当点D在边ＢＣ上时，①求证：∠ADB=∠AFC；②请直接判断结论∠AFＣ=∠ＡCB+∠DAC是否成⽴；(2）如图2,当点D在边BC的延长线上时,其他条件不变,结论∠ＡＦC=∠ACB+∠ＤAC是否成⽴?请写出∠ＡFＣ、∠ＡＣB、∠DAC之间存在的数量关系,并写出证明过程;（3)如图3，当点D在边CB的延长线上时，且点A、F分别在直线BC的异侧,其他条件不变,请补全图形，并直接写出∠AFＣ、∠ACB、∠DAC之间存在的等量关系．19.（20１７?梅州)如图1,已知线段ＡB的长为2a，点P是AB上的动点(P不与Ａ,B重合),分别以AP、PB为边向线段AB的同⼀侧作正△APC和正△PBD.（1)当△ＡPＣ与△PBＤ的⾯积之和取最⼩值时,AP= ;(直接写结果)（2）连接AＤ、ＢC，相交于点Q,设∠ＡQＣ=α,那么α的⼤⼩是否会随点P的移动⾯变化?请说明理由;（3）如图2,若点P固定,将△PBD绕点Ｐ按顺时针⽅向旋转(旋转⾓⼩于180°),此时α的⼤⼩是否发⽣变化?(只需直接写出你的猜想,不必证明)2０．（20１７?抚顺）如图1,在△ABC中，∠ABC=90°,AB=BＣ，BD为斜边ＡC上的中线，将△ABD绕点D顺时针旋转α(0°<α＜18０°）,得到△EFD，点A的对应点为点E，点B的对应点为点F，连接BE、CＦ．（１)判断BE与ＣF的位置、数量关系，并说明理由;(2)若连接BF、CE,请直接写出在旋转过程中四边形BCＥF能形成哪些特殊四边形；（3）如图2,将△AＢＣ中AB=BC改成AＢ≠ＢC时，其他条件不变,直接写出α为多少度时(1）中的两个结论同时成⽴.２１.（2017?安徽模拟）如图，在△AＢC中,AB=AＣ＝a，ＢC＝b,且2a>ｂ,BG⊥AC于G，DE⊥AB于E,DF⊥ＡC于F.（1）在图(1）中，D是BC边上的中点,计算ＤE+DF和BG的长(⽤a,b表⽰),并判断DＥ＋DF与ＢG的关系.(2)在图(2)中，D是线段BC上的任意⼀点,ＤE+ＤＦ与ＢＧ的关系是否仍然成⽴?如果成⽴,证明你的结论;如果不成⽴,请说明理由．（３）在图(3）中,D是线段BC延长线上的点，探究DE、ＤF与ＢG的关系．（不要求证明)2２．(２01７?丹东）如图,已知等边三⾓形AＢC中,点D，Ｅ，Ｆ分别为边AB,AC，BC的中点,M为直线BC上⼀动点,△DMN为等边三⾓形(点Ｍ的位置改变时,△DMＮ也随之整体移动）．(1)如图1,当点M在点B左侧时,请你判断EN与MＦ有怎样的数量关系？点F是否在直线N Ｅ上?都请直接写出结论，不必证明或说明理由;(2）如图2,当点M在BC上时,其它条件不变，（1）的结论中EN与MF的数量关系是否仍然成⽴?若成⽴，请利⽤图２证明;若不成⽴,请说明理由；(３）若点M在点Ｃ右侧时,请你在图３中画出相应的图形,并判断（１）的结论中EN与MF 的数量关系是否仍然成⽴？若成⽴，请直接写出结论,不必证明或说明理由．23．(２0１7?铁岭）△ABＣ是等边三⾓形,点Ｄ是射线BC上的⼀个动点（点D不与点B、C重合)，△AＤE是以AD为边的等边三⾓形，过点E作ＢC的平⾏线，分别交射线ＡB、ＡC于点F、G,连接BＥ.（1）如图(ａ）所⽰,当点Ｄ在线段ＢC上时．①求证:△AＥB≌△ADC;②探究四边形BＣGE是怎样特殊的四边形？并说明理由；(2)如图(b)所⽰，当点Ｄ在ＢC的延长线上时，直接写出（１)中的两个结论是否成⽴；(3)在(２)的情况下,当点D运动到什么位置时,四边形BCGＥ是菱形？并说明理由．。

2018年中考数学几何证明综合题热点聚焦(1)专项练习1. 已知：在△AOB 与△COD 中，OA ＝OB ，OC ＝OD ，︒=∠=∠90COD AOB 。

（1）如图1，点C 、D 分别在边OA 、OB 上，连接AD 、BC ，点M 为线段BC 的中点，连接OM ，则线段AD 与OM 之间的数量关系是__________，位置关系是__________。

（2）如图2，将图1中的△COD 绕点O 逆时针旋转，旋转角为α（︒<<︒900α）。

连接AD 、BC ，点M 为线段BC 的中点，连接OM 。

请你判断（1）中的两个结论是否仍然成立。

若成立，请证明；若不成立，请说明理由。

（3）如图3，将图1中的△COD 绕点O 逆时针旋转到使△COD 的一边OD 恰好与△AOB 的边OA 在同一条直线上时，点C 落在OB 上，点M 为线段BC 的中点。

请你判断（1）中线段AD 与OM 之间的数量关系是否发生变化，写出你的猜想，并加以证明。

2. 在Rt △ABC 中，AB=BC ，∠B=90°，将一块等腰直角三角板的直角顶点O 放在斜边AC 上，将三角板绕点O 旋转。

（1）当点O 为AC 中点时，①如图1，三角板的两直角边分别交AB ，BC 于E 、F 两点，连接EF ，猜想线段AE 、CF 与EF 之间存在的等量关系（无需证明）；②如图2，三角板的两直角边分别交AB ，BC 延长线于E 、F 两点，连接EF ，判断①中的猜想是否成立。

若成立，请证明；若不成立，请说明理由；（2）当点O 不是AC 中点时，如图3，三角板的两直角边分别交AB ，BC 于E 、F 两点，若14 AO AC =，求OE OF的值。

3. 在矩形ABCD 中，点F 在AD 延长线上，且DF =DC ，M 为AB 边上一点，N 为MD 的中点，点E 在直线CF 上（点E 、C 不重合）。

（1）如图1，若AB =BC ，点M 、A 重合，E 为CF 的中点，试探究BN 与NE 的位置关系及BMCE 的值，并证明你的结论；（2）如图2，且若AB =BC ，点M 、A 不重合，BN =NE ，你在（1）中得到的两个结论是否成立，若成立，加以证明；若不成立，请说明理由；（3）如图3，若点M、A不重合，BN=NE，你在（1）中得到的两个结论是否成立，若不成立，请直接写出你的结论。

专题复习3 几何的证明与计算◆考点链接几何的证明与计算是中考的必考题型，几何的证明题常以全等和相似为载体，与圆的有关知识相结合；几何计算题则是把几何知识与代数知识有机结合起来，渗透数形结合思想，重在考查分析问题的能力、逻辑思维和推理能力． ◆典例精析【例题1】（天津）已知Rt △ABC 中，∠ACB=90°，AC=6，BC=8． （1）如图①，若半径为r 1的⊙O 1是Rt △ABC 的内切圆，求r 1；（2）如图②，若半径为r 2的两个等圆⊙O 1、⊙O 2外切，且⊙O 1与AC 、AB 相切，⊙O 2与BC 、AB 相切，求r 2；（3）如图③，当n 是大于2的正整数时，若半径为r n 的n 个等圆⊙O 1、⊙O 2、…、⊙O n 依次外切，且⊙O 1与AC 、AB 相切，⊙O n 与BC 、AB 相切，⊙O 2、⊙O 3、…、⊙O n－1均与AB 边相切，求r n ．解：（1）∵在Rt △ABC 中，∠ACB=90°，AC=6，BC=8，∴．如图，设⊙O 1与Rt △ABC 的边AB 、BC 、CA 分别切于点D 、E 、F ，连接O 1D 、O 1E 、O 1F 、AO 1、BO 1、CO 1．于是，O 1D ⊥AB ，O 1E ⊥BC ，O 1F ⊥AC ，S △AO1C =12AC·O 1F=12AC·r 1=3r 1， S △BO1C =12BC·O 1E=12BC·r 1=4r 1，S △AO1B =12AB·O 1D=12AB·r 1=5r 1， S △ABC =12AC·BC=24．又∵S △ABC =S △AO1C +S △BO1C +S △AO1B ， ∴24=3r 1+4r 1+5r 1， ∴r 1=2．（2）如图，连接AO 1、BO 2、CO 1、CO 2、O 1O 2，则S △AO1C =12AC·r 2=3r 2， S △BO2C =12BC·r 2=4r 2，∵等圆⊙O 1、⊙O 2外切， ∴O 1O 2=2r 2，且O 1O 2∥AB ．过点C 作CM ⊥AB 于点M ，交O 1O 2于点N ，则CM=AC BC AB =245， CN=CM －r 2=245－r 2，∴S △CO1O2 =12O 1O 2·CN=（245－r 2）r 2，∴S 梯形AO1O2B =12（2r 2+10）r 2=（r 2+5）r 2．∵S △ABC =S △AO1C +S △BO2C +S △CO1O2 +S 梯形AO1O2B ， ∴24=3r 2+4r 2+（245－r 2）r 2+（r 2+5）r 2． 解得r 2=107． （3）如图，连接AO 1、BO n 、CO 1、CO n 、O 1O n ，则S △AO1C =12AC·r n =3r n ， S △BOnC =12BC·r n =4r n ，∵等圆⊙O 1、⊙O 2、…、⊙O n 依次外切，且均与AB 边相切，∴O 1、O 2、…、O n 均在直线O 1O n 上，且O 1O n ∥AB ， ∴O 1O n =（n －2）2r n +2r n =2（n －1）r n ．过点C 作CH ⊥AB 于点H ，交O 1O n 于点K ，则CH=245，CK=245－r n ． ∴S △CO1On =12O 1O n ·CK=（n －1）（245－r n ）r n ．S 梯形AO1OnB =12[2（n －1）r n +10]r n =[（n －1）r n +5]r n ．∵S △ABC =S △AO1C +S △BOnC +S △CO1On +S 梯形AO1OnB ， ∴24=3r n +4r n +（n －1）（245－r n ）r n +[（n －1）r n +5]r n ， 解得r n =1023n +． 评析：通过面积关系，建立所求半径的等量关系式，也是解决几何计算题一种重要的途径．【例题2】如图，AB 是⊙O 的直径，AE 平分∠BAF 交⊙O 于E 点，过点E 作直线与AF 垂直交AF 的延长线于D 点，交AB 延长线于C 点． （1）求证：CD 与⊙O 相切于点E ；（2）若CE·DE=154，AD=3，求⊙O 的直径及∠AED 的正切值． 解题思路：（1）连OE ，证OE ⊥CD ；（2）利用三角形相似线段成比例求半径．解：（1）连OE ，易证∠OEA=∠OAE=∠EAD ，∠OED=90°，得 OE ⊥CD ，CD 与⊙O 相切．（2）连BE 有BE=OE ，易证Rt △ABE ∽Rt △AED ，△CBE ∽△CEA ，得5,4DE BE CB CO OEBC AD AE CE AC AD====又，设⊙O •半径为R ， 则CO=R+54，CA=54+2R ，∴45853R R R +=+，解得R=158或R=－1（舍），∴⊙O 直径为154，由CE 2=CB·CA=254，∴CE=52，DE=32，tan∠AED=2．评析：本题第（2）小题是几何计算，不少考生怕这种题型，•因它与证明题不同，证明题的结论是确定的，有目标可寻，而计算题则需要根据题设条件和学过的知识去分析和探索，包括一定的运算能力，这就要求考生平时多练习，多思考，增强信心，才能攻克这样的难关．◆探究实践【问题】（重庆）已知四边形ABCD中，P是对角线BD上的一点，过P作MN∥AD，EF•∥CD，分别交AB、CD、AD、BC于M、N、E、F，设a=PM·PE，b=PN·PF，解答下列问题：（1）当四边形ABCD是矩形时，见图①，请判断a与b的大小关系，•并说明理由；（2）当四边形ABCD是平行四边形，且∠A为锐角时，见图②，（1）•中的结论是否成立？请说明理由；（3）在（2）的条件下，设BPPD=k，是否存在这样的实数k，使得49PEAMABCSS∆=？若存在，请求出满足条件的所有k的值；若不存在，请说明理由．解题思路：（1）利用面积关系可证a=b；（2）可证S PEAM=PM·PE．sin∠MPE，S PNCF=PN·PF，•sin∠FPN．由S PEAM=S PNCF，可得a=b；（3）利用等高三角形面积比等于底边之比可求k值．（1）解：a=S矩形PEAM=S△BDA－S△PMB－S△PDE，b=S矩形PNCF=S△DBC－S△BFP－S△DPN，可证得a=b．（2）解：成立．仿（1）有S PEAM=S PNCF，作EH⊥MN，可证S PEAM=EH·PM=PM·PE．sin∠MPE．同理S PNCF=PN·PF．sin∠FPN．由sin ∠MPE=sin ∠FPN ，可得PM·PE=PN·PF ．即a=b ．（3）解法一：存在．连结AP ，设△PMB 、△PMA 、△PEA 、△PED 的面积分别为S 1、S 2、S 3、S 4，即．1221431342423423231234424,..,4,924,(21)9PEAM ABD s ks s k s S S BM BP AE BP s ks S AM PD S DE PD s s ks s s S S S S S S S S kS k k S ∆=⎧⎧=⎪=====∴⎨⎨==⎩⎪=⎩+∴==+++=++即即∴2k 2－5k+2=0，∴k 1=2，k 2=12． 解法二：由（2）可知SPEAM =AE·AM ．sinA=29AD·ABsinA ． 22222sin 2,sin 1,,,111,,11142,2520,119PEAM PEAM PEAMABD ABD ABCDS S S S S S AE AM A AE AMAD AB A AD AB BP BP k PD k PD BD k BD k AE BP k AM PD AD BD k AB BD k k k k k k ∆∆∴=======++====++∴⨯⨯=-+=++又即而即∴k=2或12．评析：巧用面积法解题，可化难为易，应引起注意．◆中考演练一、填空题1．（黄冈）如图1，在ABCD中，EF∥AB，DE：EA=2：3，EF=4，则CD=_______．(1) (2) (3) (4)2．（四川）如图2，AB、AC是互相垂直的两条弦，AB=8cm，AC=6cm，•则⊙O•半径OA长为_______cm．二、选择题1．（福州）如图3，EF过矩形ABCD对角线交于点O，且分别交AB、CD于E、F，•那么阴影部分的面积是矩形ABCD面积的（）．A．15B．14C．13D．3102．（黄冈）如图4，△ABC中，AB=AC，D为BC中点，E为AD上任意一点，过C 作CF∥AB交BE的延长线于F，交AC于G，连结CE，下列结论中不正确的是（）．A．AD平分∠BAC B．BE=CFC．BE=CE D．若BE=5，GE=4，则GF=9 4三、解答题1．（长春）如图，在等腰梯形ABCD中，AD∥BC，∠C=60°，AD=CD．E、F分别在AD、CD上，DE=CF，AF、BE交于点P，请你量一量∠BPF的度数，并证明你的结论．2．（青岛）已知：如图，AB是⊙O的直径，C为⊙O上一点，且∠BCE=∠CAB，•CE 交AB的延长线于点E，AD⊥AB，交EC的延长线于点D．（1）求证：DE是⊙O的切线．（2）若CE=3，BE=2，求CD的长．◆实战模拟一、填空题1．（四川）如图5，在半径为3的⊙O中，B是劣弧AC的中点，连结AB并延长到D，使BD=AB，连结AC、BC、CD．如果AB=2，那么CD=________．(5) (6) (7)2．（杭州）如图6，在等腰Rt△ABC中，AC=BC，以斜边AB为一边作等边△ABD，•使点C、D在AB的同侧；再以CD为一边作等边△CDE，使点C、E在AD的异侧．若AE=1，•则CD的长为________．3．（沈阳）如图7，已知在⊙O中，直径MN=10，正方形ABCD•的四个顶点分别在半径OM、OP以及⊙O上，并且∠POM=45°，则AB的长为________．二、选择题1．（宁波）如图8，在四边形ABCD中，E是AB上一点，EC∥AD，DE∥BC．若S△BEC=1，S△BEC=3，则S△CDE等于（）．A ．2B ．32C D(8) (9) (10)2．（河南）如图9，半径为4的两等圆相外切，•它们的一条外公切线与两圆围成的阴影部分中，存在的最大圆的半径等于（ ）． A ．12 B ．23 C ．34D ．1 3．（深圳）如图10，AB 是⊙O 直径，点D 、E 是半圆的三等分点，AE 、BD 延长线交于点C ．若CE=2，则图中阴影部分的面积是（ ）．A ．43π B ．23π C ．23π D ．13π三、解答题1．（宁夏）如图，在Rt △ABC 中，∠C=90°，AC=3，BC=4，点E 在直角边AC 上（点E 与A 、C 两点均不重合），点F 在斜边AB 上（点F 与A 、B 两点均不重合）． （1）若EF 平分Rt △ABC 的周长，设AE 的长为x ，试用含x 的代数式表示△AEF 的面积；（2）是否存在线段EF 将Rt △ABC 的周长和面积同时平分？若存在，求出此时AE 的长；若不存在，说明理由．2．（烟台）如图，从⊙O外一点A作⊙O的切线AC、AC，切点分别为B、C，且⊙O 直径BD=6，连结CD、AO．（1）求证：CD∥AO；（2）设CD=x，AO=y，求y与x之间的函数关系式，并写出自变量x的取值范围；（3）若AO+CD=11，求AB的长．答案:中考演练一、1．10 2．5二、1．B 2．B三、1．证△ABE≌△DAF，∠BPF=120°2．（1）连结OC，证∠OCE=90°（2）CD=15 8实战模拟一、1．4323二、1．C 2．D 3．A三、1．（1）作FD⊥AC，由Rt△ADF∽Rt△ACB，得FD=45（6－x），S△AEF=－25x2+125x（0<x<3）（2）由－25x+125x=3，得x12x=（舍）2．（1）提示：证明AO⊥BC （2）△BDC∽△AOB，18BD DCyAO OB x=∴=，0<x<6（3）12122911()1892x xx yAB xy y y==+=⎧⎧⎧∴==⎨⎨⎨===⎩⎩⎩解得舍去。

初三证明几何练习题和答案在初三的数学学习中，证明几何是一个重要的内容。

通过证明几何的练习，不仅可以提高学生的逻辑思维和推理能力，还能加深对几何概念的理解。

本文将提供一些初三常见的证明几何练习题和答案，以供学生参考。

1. 设AO和BO是直线段垂直平分线，点C在直线AB上。

证明：∠ACO = ∠BCO。

解答：首先，根据直线段垂直平分线的定义，AO和BO互相垂直且平分直线段AB。

设∠ACO的度数为x，∠BCO的度数为y。

则根据垂直平分线的性质可知∠COA = ∠COB = 90°。

再根据直线上的角平分线性质可知∠COA = ∠AOC = x/2，∠COB= ∠BOC = y/2。

又由于∠COA = 90°，则x/2 + y/2 = 90°，即x + y = 180°。

因此，根据等量关系可得∠ACO = ∠BCO，证明完成。

2. 在△ABC中，垂直平分线BD交边AC于点E，证明：AE = EC。

解答：根据垂直平分线的定义，BD是边AC的垂直平分线，即BD垂直于AC且平分边AC。

设AE的长度为x，EC的长度为y。

根据垂直平分线的性质可知∠BDE = ∠BDE = 90°，∠BED =∠CED。

由于△BDE和△BEC中∠BDE = ∠BEC = 90°，则两个三角形中的另外两个角也相等，即∠BDE = ∠BEC。

又由于∠BDE = ∠BEC，三角形内角和为180°，则∠BED + ∠BDE + ∠BEC = 180°。

代入角度的数值可得∠BED + 90° + ∠BED = 180°，即∠BED = 45°。

进一步，根据角平分线的性质可知∠AEB = ∠BEC，即∠AEB = 45°。

因为∠AEB为三角形△AEB的内角，所以△AEB的另外两个角之和也为180°。

因此，180° = 45° + x + 45°，化简得180° = x + 90°，即x = 90°，即AE的长度为90°。

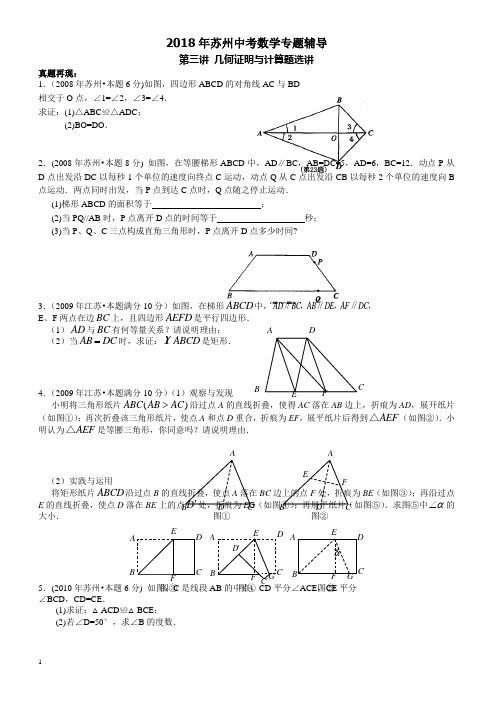
2018年苏州中考数学专题辅导第三讲 几何证明与计算题选讲真题再现： 1．（2008年苏州•本题6分)如图，四边形ABCD 的对角线AC 与BD 相交于O 点，∠1=∠2，∠3=∠4． 求证：(1)△ABC ≌△ADC ；(2)BO=DO ．2．(2008年苏州•本题8分) 如图，在等腰梯形ABCD 中，AD ∥BC ，AB=DC=5，AD=6，BC=12．动点P 从D 点出发沿DC 以每秒1个单位的速度向终点C 运动，动点Q 从C 点出发沿CB 以每秒2个单位的速度向B 点运动．两点同时出发，当P 点到达C 点时，Q 点随之停止运动． (1)梯形ABCD 的面积等于 ；(2)当PQ//AB 时，P 点离开D 点的时间等于 秒； (3)当P 、Q 、C 三点构成直角三角形时，P 点离开D 点多少时间?3．（2009年江苏•本题满分10分）如图，在梯形ABCD 中，AD BC AB DE AF DC ∥，∥，∥， E 、F 两点在边BC 上，且四边形AEFD 是平行四边形．（1）AD 与BC 有何等量关系？请说明理由； （2）当AB DC =时，求证：ABCD 是矩形．4．（2009年江苏•本题满分10分）（1）观察与发现 小明将三角形纸片()ABC AB AC >沿过点A 的直线折叠，使得AC 落在AB 边上，折痕为AD ，展开纸片（如图①）；再次折叠该三角形纸片，使点A 和点D 重合，折痕为EF ，展平纸片后得到AEF △（如图②）．小明认为AEF △是等腰三角形，你同意吗？请说明理由． （2）实践与运用 将矩形纸片ABCD 沿过点B 的直线折叠，使点A 落在BC 边上的点F 处，折痕为BE （如图③）；再沿过点E 的直线折叠，使点D 落在BE 上的点D '处，折痕为E G （如图④）；再展平纸片（如图⑤）．求图⑤中α∠的大小． 5．(2010年苏州•本题6分) 如图，C 是线段AB 的中点，CD 平分∠ACE ，CE 平分∠BCD ，CD=CE ．(1)求证：△ACD ≌△BCE ；(2)若∠D=50°，求∠B 的度数．AD C F EB ACD B 图① A CD B 图②FE E D D C B A图③ E D C A B F G C ' D 'A D E CB F G α 图④ 图⑤6．(2010年苏州•本题8分) 如图，在△ABC中，∠C=90°，AC=8，BC=6．P是AB边上的一个动点(异于A、B两点)，过点P分别作AC、BC边的垂线，垂足为M、N．设AP=x．(1)在△ABC中，AB= ；(2)当x= 时，矩形PMCN的周长是14；(3)是否存在x的值，使得△PAM的面积、△PBN的面积与矩形PMCN的面积同时相等?请说出你的判断，并加以说明．7．（2011年苏州•本题6分）如图，已知四边形ABCD是梯形，AD∥BC，∠A＝90°，BC＝BD，CE⊥BD，垂足为E．(1)求证：△ABD≌△ECB；(2)若∠DBC＝50°，求∠DCE的度数．8．（2011年苏州•本题8分）如图，小明在大楼30米高（即PH＝30米）的窗口P处进行观测，测得山坡上A 处的俯角为15°，山脚B处的俯角为60°，已知该山坡的坡度i（即tan∠ABC）为1：3，点P、H、B、C、A在同一个平面上．点H、B、C在同一条直线上，且PH⊥HC．(1)山坡坡角（即∠ABC）的度数等于▲度；(2)求A、B两点间的距离（结果精确到0.1米，参考数据：3≈1.732）．9．(2012年苏州•本题6分)如图，在梯形ABCD中，已知AD∥BC，AB＝CD，延长线段CB到E，使BE ＝AD，连接AE、AC．(1)求证：△ABE≌CDA；(2)若∠DAC＝40°，求∠EAC的度数．10．(2012年苏州•本题8分）如图，已知斜坡AB长60米，坡角（即∠BAC)为30°，BC⊥AC．现计划在斜坡中点D处挖去部分坡体（用阴影表示）修建一个平行于水平线CA的平台DE和一条新的斜坡BE．（请将下面2小题的结果都精确到0.1米，参考数据：3≈1. 732)．(1)若修建的斜坡BE的坡角（即∠BEF）不大于45°，则平台DE的长最多为米；(2)—座建筑物GH距离坡脚A点27米远（即AG＝27米），小明在D点测得建筑物顶部H的仰角（即∠HDM）为30°．点B 、C 、A 、G 、H 在同一个平面上，点C 、A 、G 在同一条直线上，且HG 丄CG,问建筑物GH 高为多少米？11．（7分）（2013•苏州）如图，在一笔直的海岸线l 上有A ，B 两个观测站，A 在B 的正东方向，AB ＝2（单位：km ）．有一艘小船在点P 处，从A 测得小船在北偏西60°的方向，从B 测得小船在北偏东45°的方向． (1)求点P 到海岸线l 的距离；(2)小船从点P 处沿射线AP 的方向航行一段时间后，到达点C 处．此时，从B 测得小船在北偏西15°的方向．求点C 与点B 之间的距离．（上述2小题的结果都保留根号）12．（8分）（2013•苏州）如图，点P 是菱形ABCD 对角线AC 上的一点，连接DP 并延长DP 交边AB 于点E ，连接BP 并延长BP 交边AD 于点F ，交CD 的延长线于点G ．(1)求证：△APB ≌△APD ；(2)已知DF ：FA ＝1：2，设线段DP 的长为x ，线段PF 的长为y ． ①求y 与x 的函数关系式；②当x ＝6时，求线段FG 的长． 13．（6分）（2014年•苏州）如图，在Rt △ABC 中，∠ACB ＝90°，点D 、F 分别在AB ，AC 上，CF ＝CB ．连接CD ，将线段CD 绕点C 按顺时针方向旋转90°后得CE ，连接EF ． (1)求证：△BCD ≌△FCE ；(2)若EF ∥CD ．求∠BDC 的度数．14．（8分）（2015年•苏州）如图，在△ABC 中，AB =AC ．分别以B 、C 为圆心，BC 长为半径在BC 下方画弧，设两弧交于点D ，与AB 、AC 的延长线分别交于点E 、F ，连接AD 、BD 、CD ． （1）求证：AD 平分∠BAC ；（2）若BC =6，∠BAC ＝50︒，求DE 、DF 的长度之和（结果保留π）．CBA15．（2016年苏州•8分）如图，在菱形ABCD 中，对角线AC 、BD 相交于点O,过点D 作对角线BD 的垂线交BA 的延长线于点E ．(1)证明：四边形ACDE 是平行四边形； (2)若AC=8，BD=6，求△ADE 的周长．16. （2017年苏州•本题8分）如图，∠A =∠B ，AE =BE ，点D 在C A 边上，12∠=∠，AE 和D B 相交于点O ．（1）求证：C ∆AE ≌D ∆BE ； （2）若142∠=，求D ∠B E 的度数．模拟训练：1．(2017年常熟市•本题满分8分) 如图，在Rt ABC ∆中，90C ∠=︒，斜边AB 的垂直平分线MN 分别交BC 、AB 于点D 、E ，过点A 作//AF BC ，交MN 于点F . (1)求证:四边形ADBF 是菱形;(2)若4,8AC BC ==，求菱形ADBF 的周长。

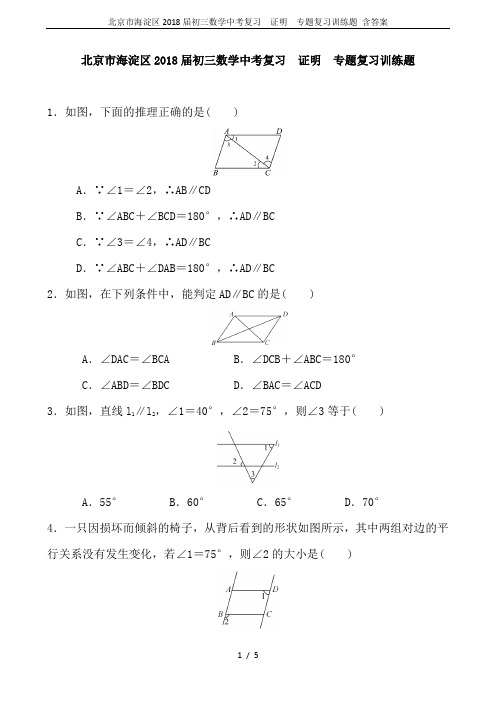
北京市海淀区2018届初三数学中考复习证明专题复习训练题1．如图，下面的推理正确的是( )A．∵∠1＝∠2，∴AB∥CDB．∵∠ABC＋∠BCD＝180°，∴AD∥BCC．∵∠3＝∠4，∴AD∥BCD．∵∠ABC＋∠DAB＝180°，∴AD∥BC2．如图，在下列条件中，能判定AD∥BC的是( )A．∠DAC＝∠BCA B．∠DCB＋∠ABC＝180°C．∠ABD＝∠BDC D．∠BAC＝∠ACD3．如图，直线l1∥l2，∠1＝40°，∠2＝75°，则∠3等于( )A．55° B．60° C．65° D．70°4．一只因损坏而倾斜的椅子，从背后看到的形状如图所示，其中两组对边的平行关系没有发生变化，若∠1＝75°，则∠2的大小是( )A．75° B．115° C．65° D．105°5. 如图，在△ABC中，∠ACB＝90°，CD∥AB，∠ACD＝40°，则∠B的度数为( )A．40° B．50° C．60° D．70°6．如图，AE平分∠BAC，CE平分∠ACD，不能判定AB∥CD的条件是( )A．∠1＝∠2 B．∠1＋∠2＝90°C．∠3＋∠4＝90° D．∠2＋∠3＝90°7. 如图，AB∥CD∥EF，AC∥DF.若∠BAC＝120°，则∠CDF等于( )A．60° B．120° C．150° D．180°8. 如图，有一条直的宽纸带按图示的方式折叠，则∠α的度数是( )A．50° B．60° C．75° D．85°9. 如图，在△ABC中，∠A＝63°，直线MN∥BC，且分别与AB，AC相交于点D，E，若∠AEN＝133°，则∠B的度数为_______．10. 如图，直线a，b被直线c所截，若a∥b，∠1＝40°，∠2＝70°，则∠3＝_______度．11. 完成下面的证明过程．已知：如图所示，∠1和∠D互余，∠C和∠D互余．求证：AB∥CD.证明：∵∠1和∠D互余(已知)，∴∠1＋∠D＝90°(________________)．∵∠C和∠D互余(已知)，∴∠C＋∠D＝90°(________________)．∴∠1＝∠C(__________)．∴AB∥CD(__________________________)．12. 如图，AB∥DE，∠1＝∠2，试判断AE与DC的位置关系，并说明理由．13. 命题“若a是自然数，则代数式(5a＋2)(5a＋1)＋3的值是5的倍数”是真命题还是假命题？如果认为是假命题，请说明理由；如果认为是真命题，请给出证明．14. 如图，AB，CD相交于点O，且∠C＝∠1，试问：当∠2与∠D的大小关系为何时，有AC∥BD？请证明你的结论．答案：1—8 DACDB AAC9. 70°10. 11011. 互余的定义互余的定义等量关系内错角相等，两直线平行12. 解：AE∥DC.理由：∵AB∥DE，∴∠1＝∠AED.∵∠1＝∠2，∴∠AED＝∠2.∴AE∥DC.13. 解：是真命题．证明如下：原式＝5(5a2＋3a＋1)．∵a是自然数，则代数式5a2＋3a＋1是自然数．∴代数式(5a＋2)(5a＋1)＋3的值是5的倍数．14. 解：当∠2＝∠D时，AC∥BD.证明：∵∠1＝∠2，∠C＝∠1，∴∠2＝∠C，当∠D＝∠2时，有∠C＝∠D，∴AC∥BD.。