高等代数教学大纲(12学分)
- 格式:doc
- 大小:1.03 MB
- 文档页数:20
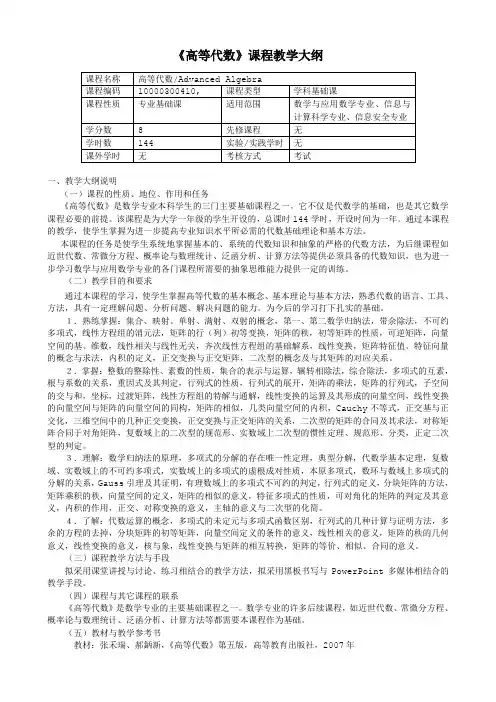
《高等代数》课程教学大纲一、教学大纲说明(一)课程的性质、地位、作用和任务《高等代数》是数学专业本科学生的三门主要基础课程之一。
它不仅是代数学的基础,也是其它数学课程必要的前提。
该课程是为大学一年级的学生开设的,总课时144学时,开设时间为一年。
通过本课程的教学,使学生掌握为进一步提高专业知识水平所必需的代数基础理论和基本方法。
本课程的任务是使学生系统地掌握基本的、系统的代数知识和抽象的严格的代数方法,为后继课程如近世代数、常微分方程、概率论与数理统计、泛函分析、计算方法等提供必须具备的代数知识,也为进一步学习数学与应用数学专业的各门课程所需要的抽象思维能力提供一定的训练。
(二)教学目的和要求通过本课程的学习,使学生掌握高等代数的基本概念、基本理论与基本方法,熟悉代数的语言、工具、方法,具有一定理解问题、分析问题、解决问题的能力。
为今后的学习打下扎实的基础。
1.熟练掌握:集合、映射、单射、满射、双射的概念,第一、第二数学归纳法,带余除法,不可约多项式,线性方程组的消元法,矩阵的行(列)初等变换,矩阵的秩,初等矩阵的性质,可逆矩阵,向量空间的基、维数,线性相关与线性无关,齐次线性方程组的基础解系,线性变换,矩阵特征值、特征向量的概念与求法,内积的定义,正交变换与正交矩阵,二次型的概念及与其矩阵的对应关系。
2.掌握:整数的整除性、素数的性质,集合的表示与运算,辗转相除法,综合除法,多项式的互素,根与系数的关系,重因式及其判定,行列式的性质,行列式的展开,矩阵的乘法,矩阵的行列式,子空间的交与和,坐标,过渡矩阵,线性方程组的特解与通解,线性变换的运算及其形成的向量空间,线性变换的向量空间与矩阵的向量空间的同构,矩阵的相似,几类向量空间的内积,Cauchy不等式,正交基与正交化,三维空间中的几种正交变换,正交变换与正交矩阵的关系,二次型的矩阵的合同及其求法,对称矩阵合同于对角矩阵,复数域上的二次型的规范形、实数域上二次型的惯性定理、规范形、分类,正定二次型的判定。

《高等代数》课程教学大纲Advanced Algebra执笔人:颜昌元编写日期:2012.7一、课程基本信息1.课程编号: 07010112,070101132.课程性质/类别:专业基础课/ 必修课3.学时/学分:160 学时/ 10 学分4.适用专业:数学与应用数学、信息与计算科学、统计学二、课程教学目标及学生应达到的能力《高等代数》是大学数学专业三门重要基础课程之一。
因其内容的抽象性和理论的结构化及应用之广泛,既是数学在其它学科应用的必需基础课程,又是数学修养的核心课程。
该课程的教学目标是使学生掌握代数基本知识和理论,逐步培养学生的抽象思维能力和逻辑推理能力,使学生获得较熟练的演算技能与初步的应用能力,为后续专业课程的学习打下基础,适当了解代数的一些历史与背景。
该课程应突出传授数学思想和数学方法,突出高等代数中等价分类、结构分解、同构对应的思想,揭示课程内部本质的有机联系。
在教学过程中根据具体教学内容,帮助学生体会人类认识客观世界的一般规律:从具体个例提升到抽象本质再应用到一般情形,及本课程中体现的唯物主义辩证法;帮助学生体会本课程统一性、简单性、对称性、整齐性、不变性、奇异性等数学的内在美。
三、课程教学内容与基本要求本课程开课时间:第一学年(共两学期),共160 学时;其中,第一学期,每周5学时,共80学时;第二学期,每周5学时,共 80学时。
(一)多项式 (20 学时)1.主要内容:(1)数域(2)一元多项式(3)整除的概念(4)最大公因式(5)因式分解定理(6)重因式(7)多项式函数(8)复系数与实系数多项式的因式分解(9)有理系数多项式2.基本要求:(1)熟练掌握和应用带余除法定理。
(2)熟练掌握最大公因式和互素的判别方法和性质。
(3)熟练掌握和应用因式分解定理。
(4)掌握不可约多项式的基本性质。
(5)掌握重因式和重根的联系。
(6)掌握复系数和实系数多项式的标准分解式;(7)掌握有理系数多项式的Gauss 引理,Eisenstein 判别法。

《高等代数》课程教学大纲适用专业数学与应用数学(师范)、数学与应用数学总学时 168学分 10一、编写说明(一)本课程的性质、地位和作用高等代数是数学与应用数学专业(师范)、数学与应用数学专业的一门重要的专业基础课,其主要内容有多项式理论与线性代数两部分。
本课程的教学目的是使学生初步掌握基本的、系统的代数知识和抽象的严格的代数方法,为后继课程如近世代数、常微分方程、概率论与数理统计、泛函分析、计算方法等提供必须具备的代数知识,也为进一步学习数学与应用数学专业的各门课程所需要的抽象思维能力提供一定的训练。
高等代数课程是中学代数的继续和提高。
通过本课程的教学,要使学生加深对中学代数的理解。
本课程在教学中要求学生确切理解高等代数中的基本概念,不仅要正确掌握这些概念的内涵,还要了解这些概念的实际背景。
对于一些基本的重要概念,还要求了解它们产生与发展的过程及概念推广的原则;与中学代数有直接联系或者平行的概念,要求学生能与中学数学中相应概念加以比较,以确立较高的观点。
对于高等代数中的基本理论,要求学生掌握基本理论的结果,对于典型定理还要求掌握论证方法或思想,同时要求学生能了解严谨的理论体系,体会建立这种体系的抽象的代数方法。
通过本课程的教学,要求学生能显著地提高应用基本概念、基本理论作抽象论证的能力;较好地掌握基本的论证方法与基本的计算方法,特别要掌握基本的线性代数计算法。
(二)本大纲制订的依据根据本专业人才的培养目标所需要的基本理论和基本技能的要求,根据本课程的教学性质、条件和教学实践而制定。
(三)大纲内容选编原则与要求1.本大纲所列各单元讲授顺序与北京大学数学系几何与代数教研室代数小组编《高等代数》(高等教育出版社第二版)所列基本相同,讲授时可根据具体情况作适当调整。
2.为了避免教学上的难点过于集中,有些定理的掌握可以侧重于定理的结果和证明定理的方法,以达到掌握基本的代数方法的目的。
3.每一章的重点内容要重点讲解,在讲清概念的基础上,通过适当的练习(习题课、作业、问题探讨)以达到掌握高等代数中常用的计算方法、基本运算中的技能和技巧以及提高综合计算和解决问题的能力的目的。
《高等代数》课程教学大纲一.课程教学目的与任务本课程是我院数学系数学教育专业的一门重要基础课程。
其主要任务是使学生获得数学的基本思想方法和多项式理论、行列式、线性方程组、矩阵论、向量空间、线性变换、欧氏空间、二次型等方面的系统知识。
它一方面为后继课程(如近世代数、数论、离散数学、计算方法、微分方程、泛函分析)提供一些所需的基础理论和知识;另一方面还对提高学生的抽象思维、辑推理及运算能力,开发学生智能,加强“三基”(基础知识、基本理论、基本理论)和培养学生创造性能力等起到重要作用。
二.与各课程的联系本课程是数学专业的后继课程:如近世代数、数论、离散数学、计算方法、微分方程、泛函分析等的先导课程和基础课程。
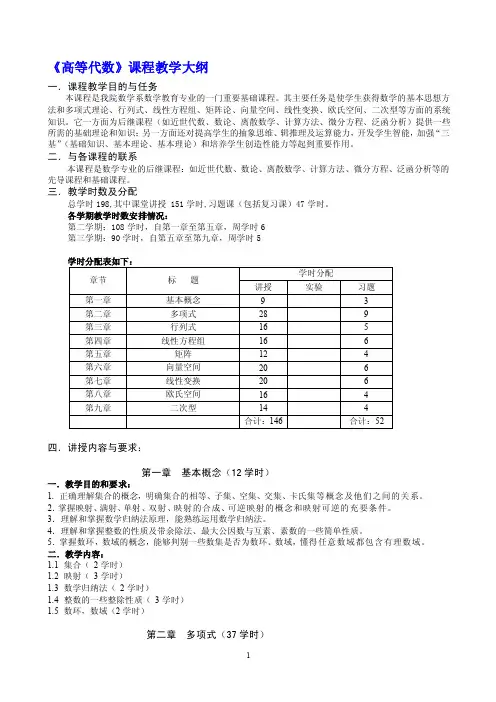
三.教学时数及分配总学时198,其中课堂讲授 151学时,习题课(包括复习课)47学时。
各学期教学时数安排情况:第二学期:108学时,自第一章至第五章,周学时6第三学期:90学时,自第五章至第九章,周学时5四.讲授内容与要求:第一章基本概念(12学时)一.教学目的和要求:1. 正确理解集合的概念,明确集合的相等、子集、空集、交集、卡氏集等概念及他们之间的关系。
2.掌握映射、满射、单射、双射、映射的合成、可逆映射的概念和映射可逆的充要条件。
3.理解和掌握数学归纳法原理,能熟练运用数学归纳法。
4.理解和掌握整数的性质及带余除法、最大公因数与互素、素数的一些简单性质。
5.掌握数环,数域的概念,能够判别一些数集是否为数环、数域,懂得任意数域都包含有理数域。
二.教学内容:1.1 集合(2学时)1.2 映射(3学时)1.3 数学归纳法(2学时)1.4 整数的一些整除性质(3学时)1.5 数环,数域(2学时)第二章多项式(37学时)一.教学目的和要求:1.掌握数域上一元多项式的概念、运算以及多项式的和与积的次数。
2.正确理解多项式的整除概念和性质。
理解和掌握带余除法。
3.掌握最大公因式的概念、性质、求法以及多项式互素的概念和性质4.理解不可约多项式的概念,掌握多项式唯一因式分解定理。

高等代数课程教学大纲一、课程说明1、课程性质:高等代数是高等院校数学系数学与应用数学专业的一门重要基础课。
对学生数学思想的形成有着重要意义,是进一步学习近世代数、常微分方程等后继课的基础,也为深入理解中学数学打下必要的基础。
高等代数是现代数学的基础知识,是学习其它数学学科和现代科学知识的必备基础和重要工具,尤其在本世纪,计算机技术、通讯信息技术和现代生物工程技术已成为最热门的学科领域,这些学科的发展均需要代数学的知识与支持。
高等代数也是师范院校数学与应用数学专业的一门重要基础课程,既是中学代数的继续和提高,对于中学数学教学工作具有重要的理论指导作用,又是输送更高层次优秀人才的专业知识保证。
2、课程教学目的要求(1)使学生掌握多项式理论、线性代数理论的基础知识和基本理论,着重培养学生解决问题的基本技能。
(2) 使学生熟悉和掌握本课程所涉及的现代数学中的重要思想方法,提高其抽象思维、逻辑推理和代数运算的能力。
(3) 使学生进一步掌握具体与抽象、特殊与一般、有限与无限等辩证关系,培养其辩证唯物主义观点。
(4) 逐步培养学生的对真理知识的发现和创新的能力,训练其对特殊实例的观察、分析、归纳、综合、抽象概括和探索性推理的能力。
(5) 使学生对中学数学有关内容从理论上有更深刻的认识,以便能够居高临下地掌握和处理高级中学数学教材,进一步提高中学数学教学质量。
(6) 根据教学的实际内容的需要,对大纲所列各章内容,分别提出了具体的目的要求,教学时必须着重抓住重点内容进行教学。
本课程分以一元多项式为主体的多项式理论和线性代数两部分。
线性代数部分涉及行列式、矩阵、线性方程组、二次型、线性空间、线性变换、λ-矩阵、欧几里得空间等。
本课程教学重点应放在多项式理论与线性代数理论。
多项式理论以一元多项式的因式分解唯一性定理为主体介绍了有关多项式的一些必要的知识,为后继课提供准备;线性代数部分则较为系统地介绍了线性方程组,线性空间与线性变换理论。

高等代数教学大纲代数教研室[本大纲以北大数学系编《高等代数》第四版为依据拟定,共需约216学时 (讲授144学时+习题课72学时)][本大纲以北大数学系编《高等代数》第四版为依据拟定,共需约216学时 (讲授144学时+习题课72学时)]课程总体目标1.理解和掌握高等代数中的一些基本概念和基础知识,如数域、多项式、n阶行列式、线性方程组、矩阵、二次型、向量空间、线性变换、 矩阵、欧氏空间、以及双线性函数与辛空间等抽象代数基本概念。
2.具备逻辑推理、抽象思维与综合分析的能力,能运用高等代数中的基础知识、基本理论进行推理和证明。
3.熟练掌握高等代数中常用的方法。
4.了解近世代数研究的对象和基本方法.第一章多项式(26学时)(一)教学目的和要求1)熟练掌握一元多项式的基本概念及其运算。
2)熟练掌握一元多项式的整除,最大公因子,互素的概念,性质及有关的证明。
3)熟练掌握不可约多项式的概念,性质,理解因式分解定理的意义,掌握复数域,实数域上的多项式的标准分解式及复数域,实数域上不可约多项式4)会直接利用艾森斯坦因判别法,会求Q[x]中的多项式的有理根。
(二)教学内容1)多项式的概念及其运算:多项式的定义,多项式相等,零多项式,多项式次数。
2)多项式和与积的定义;带余除法,用带余除法求商和余式,商与余存在及唯一性定理;多项式的值与多项式的根的定义,余数定理,综合除法,用综合除法求多项式的值;多项式的次数与根的个数的关系,多项式相等的定义。
3)多项式整除的定义,性质;最大公因式的定义;用辗转相除法求最大公因式,最大公因式的存在与唯一性定理;最大公因式的性质;互素的定义及等价条件;不可约多项式的定义及等价条件;不可约多项式的性质;因式分解定理及标准分解式。
4)重因式:重因式的定义,系数与重因式的关系;无重因式的充要条件,去掉重因式的方法;重根的定义,重根与系数的关系。
5)复数域和实数域上的多项式的因式分解:代数学基本定理,C[x]上的不可约多项式,多项式的标准分解式,C上的n次多项式有n个根;R上的不可约多项式,多项式的标准分解式。

高等代数教学大纲一、课程简介本课程主要介绍高等代数的基本概念、定义和定理,包括线性空间、线性变换、矩阵、行列式、特征值、特征向量等内容。
通过本课程的学习,学生应该能够掌握高等代数的基本理论和方法,进一步培养其分析问题的能力和解决问题的能力。
二、教学目标1.掌握高等代数的基本概念、定义和定理。
2.熟练掌握线性空间、线性变换、矩阵、行列式、特征值、特征向量等内容。
3.培养学生分析问题、解决问题的能力。
4.培养学生数学建模的能力。
三、教学内容和教学方法1. 教学内容1.线性空间的定义与基本性质。
2.线性变换的定义与基本性质。
3.矩阵的基本运算和性质。
4.行列式的概念和性质。
5.特征值、特征向量和对角化。
6.线性方程组和矩阵消元算法。
7.正定矩阵、二次型和极值问题。
8.线性代数应用:最小二乘法、主成分分析、特征值应用等。
2. 教学方法1.讲授理论,强调概念的起源和本质。
2.给出典型例题,讲解例题的解法和思路,以帮助学生理解和掌握知识。
3.组织学生进行课上小组讨论和课后思考题目,促使学生主动思考问题、独立思考问题。
4.给学生提供大量题目,帮助学生掌握基本概念和技能。
5.激发学生兴趣,带领学生开展独立或团队研究性学习,鼓励学生探索和创新。
四、教学进度和考核方式1. 教学进度本课程可设置为2个学期,共36周,每周2-3次课程。
章节教学内容学时数第1章线性空间4周第2章线性变换4周第3章矩阵与行列式5周第4章特征值与特征向量3周第5章线性方程组与消元法4周章节教学内容学时数第6章正定矩阵与二次型3周第7章应用3周综合总复习2周2. 考核方式1.平时表现:包括出勤、作业、小测、小论文等,占总成绩的30%。
2.期中考试:占总成绩的30%。
3.期末考试:占总成绩的40%。
五、参考资料1.《线性代数及其应用》(美)Gilbert Strang 著,机械工业出版社。
2.《线性代数基础教程》(美)Bernard Kolman 著,高等教育出版社。

《高等代数》课程教学大纲一、课程基本信息1、课程代码:MA1092、课程名称(中文):高等代数课程名称(英文):Higher Algebra3、学时/学分:72学时+ 18学时(习题课)/4学分4、先修课程:解析几何5、面向对象:联读班。
6、开课院(系)、教研室:理学院数学系,代数和组合数学教研室7、推荐教学参考书:《大学代数》,陆少华、沈灏编著,上海交大出版社,2002。
《高等代数》,北京大学数学力学系。
二、课程的性质和任务高等代数是一门重要的数学基础课。
代数的理论、方法和思想已渗透到数学与科学的各个领域。
随着通信与计算机科学的迅速发展,高等代数作为描述离散对象的各学科的重要基础,其地位与作用越来越重要。
同时,代数课程还承担着提高学生数学素养,训练与培养思维能力、计算能力与建立数学模型能力的任务。
通过《高等代数》课程的学习,应使学生能较好地熟悉与掌握多项式理论及线性代数的基本概念、理论与方法,并能运用到所学专业中去。
三、教学内容和要求《高等代数》高等代数的教学内容分为八部分,对不同的内容提出不同的教学要求。
(数字表示供参考的相应的学时数)第一章数与多项式(10)1数环与数域(2)2一元多项式、最大公因式(2)3 多项式的因式分解理论(4)4 习题课(2)要求:熟悉数环与数域的基本概念与运算法则;理解因子分解唯一性定理;熟练掌握求最大公因式的辗转相除法。
第二章行列式(10)1 行列式的定义与基本性质(4)2 行列式的按行展开,Laplace定理(2)3 行列式的计算(2)4 习题课(2)要求:熟悉行列式的基本性质、掌握行列式的常用计算方法。
第三章矩阵(12)1 矩阵的概念与矩阵运算(2)2 矩阵的初等变换与相抵标准形、矩阵的秩(4)3 习题课(2)4 逆矩阵与矩阵的求逆(2)5 分块矩阵,例(2)要求:熟练掌握矩阵的加、乘与求逆运算;熟练掌握求矩阵相抵标准形的初等变换方法。
第四章线性方程组(12)1 解线性方程组的矩阵消元法(2)2 Cramer法则,例(2)3 n维向量组的线性关系、向量组的等价与向量组的秩(4)4 线性方程组的矩阵形式、向量形式;线性方程组解的结构(2)5 习题课(2)要求:掌握线性方程组的求解理论与解线性方程组的矩阵消元法;理解线性方程组解的几何意义。

《高等代数》教学大纲一、课程基本信息1、课程名称:高等代数2、课程类别:数学类基础课程3、课程学分:_____学分4、课程总学时:_____学时5、授课对象:_____专业学生二、课程目标1、知识目标使学生掌握多项式理论、行列式、线性方程组、矩阵、向量空间、线性变换、欧氏空间和二次型等高等代数的基本概念、基本理论和基本方法。
2、能力目标培养学生的抽象思维能力、逻辑推理能力、运算能力和空间想象能力,能够运用所学知识解决实际问题。
3、素质目标通过课程学习,培养学生严谨的治学态度和创新精神,提高学生的数学素养和综合素质。
三、课程内容1、多项式(1)多项式的概念和运算理解多项式的定义、次数、系数等概念,掌握多项式的加法、乘法和除法运算。
(2)多项式的整除性掌握多项式整除的概念和性质,了解带余除法和余数定理。
(3)最大公因式理解最大公因式的概念,掌握辗转相除法求最大公因式。
(4)因式分解定理掌握多项式的因式分解定理,了解不可约多项式的概念和性质。
2、行列式(1)行列式的定义和性质理解行列式的定义,掌握行列式的性质和计算方法。
(2)行列式的展开定理掌握行列式按行(列)展开定理,能够利用展开定理计算行列式。
(3)克莱姆法则了解克莱姆法则,能够用克莱姆法则解线性方程组。
3、线性方程组(1)线性方程组的解的判定掌握线性方程组有解的判定定理,能够判断线性方程组是否有解。
(2)线性方程组的解的结构理解线性方程组解的结构,掌握齐次线性方程组基础解系的求法。
4、矩阵(1)矩阵的概念和运算理解矩阵的定义,掌握矩阵的加法、乘法、数乘和转置运算。
(2)矩阵的逆掌握矩阵可逆的条件和求逆矩阵的方法。
(3)矩阵的秩理解矩阵秩的概念,掌握矩阵秩的求法。
5、向量空间(1)向量空间的定义和性质理解向量空间的定义和基本性质,掌握向量空间的基和维数的概念。
(2)子空间了解子空间的概念和判定方法,掌握子空间的交与和的运算。
6、线性变换(1)线性变换的定义和性质理解线性变换的定义,掌握线性变换的性质和运算。

教学大纲一.课程的教学目的和要求通过这门课的学习,使学生掌握高等代数的基本知识,基本方法,基本思路,为进一步学习专业课打下良好的基础,适当地了解代数的一些历史,一些背景。
要突出传授数学思想和数学方法,让学生尽早地更多地掌握数学的思想和方法。
突出高等代数中等价分类的思想,分解结构的思想,同构对应的思想,揭示课程内部的本质的有机联系。
通过活泼互动的课堂教学,刺激学生的学习兴趣;通过探索讨论课,调动学生的学习主动性;通过写专题读书报告,训练学生的查阅资料和归纳总结的能力;通过难题攻关,享受理解和应用数学思想和方法的乐趣,提高创新能力。
二.课程的主要内容:《高等代数》分为两个部分主要内容。
一块是基本工具性质的,包括多项式,行列式,矩阵初步,二次型。
既然是工具性质的,因而除了多项式内容外,也是数学专业以外的理科、工科、经管类《线性代数》的内容。
另外一块是研究线性空间的结构,这是研究代数结构的起点和模型。
从元素的角度看,研究向量间的线性表示,线性相关性,基向量;从子集角度看,研究子空间和直和分解;从空间之间的关系来研究空间结构,就是线性映射,线性变换,线性映射的核与值域,Jordan标准形对应的空间分解。
而欧氏空间则是具体的研究空间的例子。
三.教学重点与难点:在讲解内容的同时,要尽早地更多讲授高等代数中的数学的思想和方法,重点是传授代数学的基本思想,如等价分类的思想,分解结构的思想,特别是同构对应的思想。
所选教材以线性空间为纲的做法,即把高等代数的主要内容放在线性空间的框架下展开,同时将必要的代数方法做了尽可能详细的介绍。
所以讲课的难点在于把握几何直观和代数方法的对应关系和互动关系,使学生即能从几何的观点更好地理解内容,又可把握简洁和直接的代数方法。
四.课程教材和参考书:教材:姚慕生编著,高等代数,复旦大学出版社,第一版(2003年)参考书:1. 姚慕生编著,高等代数(指导丛书),复旦大学出版社(2003)2. 北京大学数学系编,高等代数,高等教育出版社,北京(1987)3. 张禾瑞、郝炳新,高等代数,高等教育出版社,北京(1999)4. 樊恽、郑延履、刘合国,线性代数学习指导,科学出版社,北京(2003)5. 林亚南编:高等代数方法选讲,2002年,见厦门大学精品课程“高等代数”网站,五.课程内容及学时分配本课程开课时间:第一学年(共三学期),共180学时;其中,第一学期,72课时,期中考1次;第二学期,78课时,期中考1次;第三学期,30课时;以上不包括复习考试周。

《高等代数》课程教学大纲课程编号:090085、090022总学时:162学分:8适用专业:数学与应用数学、信息与计算科学课程类型:专业必修课开课单位:一、课程的性质、目的与任务通过本课程的教学,使学生对高等代数乃至代数学的思想和方法有较深刻的认识, 提高他们的抽象思维、逻辑推理和运算的能力;使学生初步地掌握基本的、系统的代数知识和抽象的、严格的代数方法,进而加深对中学代数的理解;使学生能应用代数思想和方法去理解与处理有关的问题, 培养与提高代数的理论分析问题与解决问题的能力;使学生学习数学学科后续课程(如近世代数、离散数学、计算方法、偏微分方程、泛函分析等)提供一些所需要的基础理论和知识;使学生在智能开发、创新能力培养等方面获得重要的平台。
《高等代数》是数学与应用数学、信息与计算科学本科专业最重要的基础课程之一,是数学各专业报考研究生的必考课程之一,也是理论性、应用性很强的一门数学基础课。
讲授本课程的目的主要在于培养学生的代数基础理论和思想素质,基本掌握代数中的论证方法, 获得较熟练的演算技能和初步应用的技巧, 提高分析问题、解决问题的能力,为进一步学习其它数学知识打下坚实的基础。
本课程的主要任务是通过教学的主要环节(课堂讲授与讨论、习题课、作业、辅导答疑等),使学生学习和掌握多项式理论、线性代数的代数理论(行列式、线性方程组、矩阵、λ矩阵)及线性代数的几何理论(线性空间、线性变换、欧氏空间)。
二次型、-二、课程教学内容和基础要求(1)理解多项式的定义,掌握最大公因式,互素,不可约多项式, 因式分解等有关的一系列性质。
(2)理解行列式的定义, 掌握行列式的基本运算性质和行列式的行(列)展开性质;理解向量组的线性相关性,掌握线性方程组的通解求法;理解矩阵的概念和运算,掌握矩阵的可逆、矩阵的分块、矩阵的等价关系的性质及应用;理解二次型的定义,掌握二次型的标准形的求法及正定二次型的一系列性质。
(3)理解线性空间的定义,掌握交空间、和空间及直和的判定及性质;理解线性变换的定义及简单性质,掌握线性变换在不同基下的矩阵的性质、线性变换的值域与核的应用问题;会求矩阵的若当标准形;理解欧氏空间及对称变换的定义,掌握对称变换与实对称矩阵之间的关系的有关性质。
高等代数课程教学大纲《高等代数》课程教学大纲课程编号:总学时数:160(理论160)总学分数:10课程性质:学科基础课程适用于专业:数学与应用领域数学、信息与排序科学一、课程的任务和基本要求:本课程就是本科院校数学与应用领域数学、信息与排序科学专业的一门必修课程的关键基础课。
课程的主要任务就是系统了解多项式理论、行列式、线性方程组和矩阵、二次型和双线性函数、线性空间和线性变换,λ-矩阵和欧氏空间等内容,通过课程自学,建议学生系统地掌控这些内容的基本概念和基本理论以及代数学研究问题的基本方法,培育学生的抽象思维、逻辑推理和运算能力,为学生后继课程的自学奠定稳固的基础。
二、基本内容和要求:(一)多项式1、数域及一元多项式的概念和运算2、多项式的整除性、带余除法、最大公因式3、多项式的因式分解、轻因式、多项式函数及多项式的木4、复数域,实数域和有理数域上多项式的因式分解5、多元多项式及等距多项式要求:理解一元多项式的有关概念,掌握多项式的运算,最大公因式和有理根的求法,互素,有无重因式的判别方法,能够熟练运用一元多项式的基本概念、基本理论和基本方法证明多项式中的一些问题。
了解多元多项式。
(二)行列式1、n阶行列式的定义和性质2、行列式按行(列于)进行的公式3、拉普拉斯定理4、克兰姆法则建议:认知行列式的概念,行列式的性质,掌控行列式的计算方法,克兰姆法则的运用。
(三)线性方程组1、线性方程组的消元法2、n佩向量的概念、运算、性质3、向量组的线性相关性4、矩阵的秩,线性方程组有解的判别法5、线性方程组的解结构建议:能够娴熟运用窭元法求解线性方程组,掌控矩阵的秩、向量组的秩及很大线性毫无关系组的带发修行,掌控向量组的线性相关性的基本概念和结论,矩阵秩的有关概念和方法。
能娴熟利用向量组的有关科学知识分析探讨关于线性方程组的一些问题并能够恰当采用存有求解辨别法。
(四)矩阵1、矩阵的运算、性质2、可逆矩阵的概念、性质,逆矩阵的求法3、矩阵的分块运算、应用4、初等矩阵与初等变换的关系,用初等变换arise矩阵的方法要求:能熟练地进行矩阵的运算,熟悉矩阵乘积的行列式及秩的定理,掌握可逆矩阵的概念、性质、初等变换和初等矩阵的关系。
高等代数(1)课程教学大纲第一部分前言一、课程基本信息1.课程类别:专业基础课2.开课单位:数学与财经系3.适用专业:数学与应用数学专业4.备选教材:《高等代数(第三版)》,北京大学数学系几何与代数教研室前代数组编.高等教育出版社,2003.二、课程性质和目标高等代数是数学与应用数学专业的一门重要基础课程。
本课程的主要内容是多项式理论和线性代数理论。
通过本课程的教学,使学生掌握代数基本理论和基本方法,培养学生代数方面的科学的思维、抽象的思维,逻辑推理、提高运算以及解决实际应用的能力,为进一步学习专业后续课程奠定坚实的代数基础。
本课程的教学目的是使学生获得一元多项式,行列式,线性方程组,矩阵等方面的系统知识,为进一步学习近世代数,复变函数、等后续课程打下坚实的基础,也为深入理解初等数学、指导中学数学教学提供了高等的专业知识与重要的方法论。
通过本门课程系统的学习与严格的训练,全面掌握高等代数的基本理论知识;培养抽象的逻辑思维能力与推理论证能力;具备熟练的运算能力与技巧;提高建立数学模型,并应用代数学的理论知识解决实际应用问题的能力。
三、课程学时与学分教学时数:96学时,其中理论教学81学时,实践教学15学时学分数: 6 学分教学时数具体分配:第二部分教学内容及其要求第一章多项式1.教学目标:要求学生理解数域的概念;掌握一元多项式的概念、运算及基本性质;掌握带余除法与整除性的关系,会进行相关运算;会求多项式的最大公因式;理解不可约多项式的概念,掌握求重因式的方法;理解多项式在不同的数域的因式分解形式;掌握Eisenstein判别法,会求有理系数多项式的根。
2.教学重点:整除概念,带余除法及整除的性质,最大公因式、互素、辗转相除法、不可约多项式概念、性质,k重因式与k重根的关系。
3.教学难点:因式分解及唯一性定理,多项式根的理论,复(实)系数多项式分解定理,本原多项式,Eisenstein判别法。
4.教学时数5.教学内容纲要:第一节数域一、代数研究的基本问题。
高等代数教学大纲(Higher Algebra)前言教学大纲是一门课程的指导性文件.教学大纲的科学化、规范化,对建设良好的教学秩序,提高教学质量,搞好教学管理等方面都有很重要的意义.为此,我们根据学校有关文件,编写了《高等代数》这门课程的教学大纲.《高等代数》这门课程是数学系各专业的必修专业基础课程之一,可为后继课程的学习打下必要的基础.它是数学系各专业硕士研究生入学考试的必考课程.它除培养学生掌握必要的基础知识之外,同时着重训练学生掌握数学结构的观念、公理化的方法、纯形式化的思维,从而在知识结构、综合素质、创新能力等方面对学生加以全面培养和整体提高.本课程的基本内容有: 包括:多项式,行列式,线性方程组, 矩阵,二次型,线性空间, 线λ矩阵,欧几里得内积空间,双线性函数和辛空间.重点是下列几章:多项式,行性变换, -列式,线性方程组, 矩阵,二次型,线性空间, 线性变换,欧几里得内积空间.通过本课程的学习,学生能正确理解矩阵、行列式、线性空间、线性变换、欧几里得空间等有关概念, 能理解并掌握线性方程组理论和多项式的理论,并能熟练地应用它们,为后续课程的学习打下坚实的基础.本课程作为基础课,对其它课程依赖不大,当然,如果在学完《空间解析几何》之后开设效果会更好.本课程作为基础课,应在大学低年级学生中开设,建议对本科一年级学生开设.本课程为一学年课程.教材: 《高等代数学》(第三版)北京大学数学系几何与代数教研室前代数小组, 高等教育出版社,2003年。
参考书:《线性代数》吴赣昌主编,中国人民大学出版社,2006年《高等代数学》姚慕生编, 复旦大学出版社,1999《高等代数新方法》王品超主编,山东教育出版社,1989年《高等代数学》(第二版)张贤科主编,清华大学出版社,2002年《Linear Algebra》S.K.Jain, A.D.Gunawardena,机械工业出版社,2003年建议学时分配课程内容第一章多项式[教学目的与要求]通过本章学习,实现如下目的:(1)理解整除、最大公因式、互素、多项式的不可约性、重因式、本原多项式等概念;(2)熟练掌握整除的性质;(3)熟练掌握最大公因式的求法;(4)熟练掌握有无重因式的判别方法;(5)熟练掌握整系数多项式的有理根的求法;(6)熟练掌握整系数多项式在有理数域上不可约的艾森斯坦判别法;(7)掌握复系数多项式因式分解定理、实系数多项式因式分解定理、有理系数多项式的因式分解定理的应用;(8)掌握韦达定理和多元多项式的基本性质.[教学重点]整除的性质、最大公因式的求法、有无重因式的判别方法、整系数多项式的有理根的求法、整系数多项式不可约的艾森斯坦判别法;复系数多项式因式分解定理、实系数多项式因式分解定理、有理系数多项式的因式分解定理的应用.[教学难点]整系数多项式的有理根的求法、整系数多项式不可约的艾森斯坦判别法.[教学内容]§1.1. 数域数域的定义和例子§1.2. 一元多项式一、一元多项式的定义二、一元多项式的运算和运算律§1.3. 整除的概念一、带余除法二、整除的定义和几个常用的性质§1.4. 最大公因式一、最大公因式的定义和求法二、互素§1.5. 因式分解定理一、不可约多项式的定义和简单性质二、因式分解唯一性定理§1.6. 重因式重因式的定义和性质§1.7. 多项式函数一、余数定理二、多项式的根或零点§1.8. 复系数与实系数多项式的因式分解一、复系数多项式的因式分解定理 二、实系数多项式的因式分解定理§1.9. 有理系数多项式一、本原多项式的定义和高斯引理 二、整系数多项式的有理根的求法 三、爱森斯坦判别法§1.10. 多元多项式多元多项式的定义及其次数§1.11. 对称多项式一、初等对称多项式二、对称多项式基本定理思考题1. 证明:多项式)(x f 整除任意多项式的充要条件是)(x f 是零次多项式.2. 设b a ,为两个不相等的常数.证明:多项式)(x f 被))((b x a x --除所得的余式为ba b bf a af x b a b f a f --+--)()()()(3. 证明:1|1--n d x x 当且仅当n d |.4. 设k 为正整数.证明:)(|x f x k 当且仅当)(|x f x .5. 已知242)(234---+=x x x x x f ,22)(234---+=x x x x x g ,求)(),(x v x u 使))(),(()()()()(x g x f x g x v x f x u =+. 6. 证明:如果)(|)(x f x d ,)(|)(x g x d ,且)()()()()(x g x v x f x u x d +=,则)(x d 是)(x f 与)(x g 的最大公因式.7. 证明:如果1))(),((=x g x f ,1))(),((=x h x f ,则1))()(),((=x h x g x f . 8. 证明:如果1))(),((=x g x f ,则1))(),((=mmx g x f . 9. 若1))(),((21=x f x f ,则对任意的)(x g ,))(),(())(),(())(),()((2121x g x f x g x f x g x f x f =.10.判断下列多项式在有理数域上是否有重因式,若有,则求出重因式,并确定重数(1)1)(24++=x x x f(2)277251815)(2346+-++-=x x x x x x f11.设)(x p 是)(x f '的k 重因式,能否说)(x p 是)(x f 的1+k 重因式,为什么?12.设n 为正整数,证明:如果)(|)(x g x f nn ,则)(|)(x g x f .13.设)(x p 为数域P 上的不可约多项式,)(x f 与)(x g 为数域P 上的多项式.证明:如果)()(|)(x g x f x p +,且)()(|)(x g x f x p ,则)(|)(x f x p ,且)(|)(x g x p .14.设)(x f 为数域P 上的n 次多项式,证明:如果)(|)(x f x f ',则nb x a x f )()(-=,其中P b a ∈,.15.求多项式92)(24++=x x x f 与944)(234-+-=x x x x g 的公共根.16.求多项式61510)(25-+-=x x x x f 的所有根,并确定重数.第二章 行列式[教学目的与要求] 通过本章学习,实现如下目的: (1) 理解行列式的概念;(2) 能熟练应用行列式的性质和展开定理计算行列式; (3) 会用Cramer 法则求解线性方程组. [教学重点]行列式的计算、Cramer 法则. [教学难点] 行列式的定义 [教学内容]§2.1. 引言二阶、三阶行列式与线性方程组的解§2.2. 排列一、排列及排列逆序数的定义 二、奇偶排列§2.3. n 阶行列式 n 阶行列式的定义§2.4. n 阶行列式的性质 n 阶行列式的性质及其推论§2.5. 行列式的计算n 阶行列式的计算§2.6. 行列式按一行一列展开一、n 阶行列式按一行一列展开定理 二、范德蒙(Vandermonde )行列式§2.7. 克拉默(Cramer )法则 克拉默(Cramer )法则§2.8. 拉普拉斯(Laplace )定理 行列式的乘法规则一、拉普拉斯(Laplace )定理 二、行列式的乘法规则思考题1. 求下列排列的逆序数:(1))2(24)12(13n n -; (2)21)1( -n n . 2. 写出四阶行列式中含有因子4123a a 的项,并指出应带的符号. 3.用行列式的定义计算下列行列式:(1)00001002001000nn -; (2)000000053524342353433323125242322211312a a a a a a a a a a a a a a a a . 4.用行列式的性质及行列式的展开定理计算下列行列式:(1)xa a a a x a a a a x a a a a xn nn321212121; (2)na a a +++11111111121,其中021≠n a a a(3)12125431432321-n n n; (4)221222212121211nn n n n na x a a a a a a a x a a a a a a a x +++其中021≠n x x x .(5)x a a a a a x x x n n n +-----122110000010001;(6)nnn n n nn n nna a a a a a a a a a a a21222212222121111---5. 已知4阶行列式D 中的第1行上的元素分别为4,0,2,1-,其余子式分别为1,5,2,1--;第3行上元素的余子式分别为x ,7,1,6-;求行列式D 的值,及x 的值.6.设4阶行列式1234302186427531中第4行元素的余子式分别为44434241,,,M M M M ,代数余子式分别为44434241,,,A A A A ,求44434241432A A A A +++,44434241432M M M M +++.7. 设4阶行列式2211765144334321中第4行元素的代数余子式分别为44434241,,,A A A A ,求4241A A +与4443A A +.8. 设行列式nn0010301002112531-中第1行元素的代数余子式分别为n A A A 11211,,, ,求n A A A 11211+++ .第三章 线性方程组[教学目的与要求] 通过本章学习,实现如下目的:(1) 掌握向量的线性表示、线性相关性的判别法; (2) 掌握极大无关组的求法; (3) 掌握矩阵秩的求法;(4) 掌握线性方程组解情况的判定方法; (5) 掌握齐次线性方程组的基础解系的求法; (6) 掌握非齐次线性方程组解结构定理[教学重点] 向量的线性表示、线性相关性、极大无关组、向量组的秩、矩阵的秩、齐次线性方程组的基础解系.[教学难点] 极大无关组、矩阵的秩.[教学内容]§3.1. 消元法消元法§3.2. n 维向量空间n 维向量及其运算§3.3. 线性相关性一、线性表示二、向量组的线性相关性 三、向量组的极大无关组、秩§3.4. 矩阵的秩矩阵的行秩、列秩、秩§3.5. 线性方程组有解判定定理线性方程组有解判定定理§3.6. 线性方程组解的结构一、齐次线性方程组的解结构 二、非齐次线性方程组的解结构§3.7. 二元高次方程组二元高次方程组可作为选学内容.思考题1.设)1,1,1(1λα+=,)1,1,1(2λα+=,)1,1,1(3λα+=,),,0(2λλβ=.问当λ为何值时(1)β不能由321,,ααα线性表出?(2)β可由321,,ααα线性表出,并且表示法唯一?(3)β可由321,,ααα线性表出,并且表示法不唯一? 2.设)1,2,(1a =α,)0,,2(2a =α,)1,1,1(3-=α,问a 为何值时321,,ααα线性相关?3. 求下列向量组的一个极大无关组,并将其余向量表为该极大无关组的线性组合.(1))5,2,1(1-=α,)1,2,3(2-=α,)17,10,3(3-=α;(2))4,0,1,1(1-=α,)6,5,1,2(2=α,)0,2,1,1(3--=α,)14,7,0,3(4=α. 4.已知21,ββ是非齐次线性方程组b Ax =的两个解,21,αα是其导出组0=Ax 的基础解系,21,k k 是任意常数,则b Ax =的通解是( ).(A)2)(2121211ββααα-+++k k ; (B)2)(2121211ββααα++-+k k ;(C)2)(2121211ββββα-+-+k k ; (D)2)(2121211ββββα++-+k k .5.设A 为秩为3的45⨯矩阵,321,,ααα是非齐次线性方程组b Ax =的三个不同的解,若)0,0,0,2(2321=++ααα,)8,6,4,2(321=+αα,求方程组b Ax =的通解. 6.设b Ax =为4元线性方程组,其系数矩阵A 的秩为3,又321,,ααα是b Ax =的三个解,且)0,2,0,2(1=α,)0,2,2,0(32=+αα,求方程组b Ax =的通解.7.已知β是非齐次线性方程组b Ax =的解,s ααα,,,21 是其导出组0=Ax 的基础解系,证明s αβαβαββ+++,,,,21 是b Ax =解向量组的极大无关组.8.线性方程组⎪⎪⎩⎪⎪⎨⎧=+--=+--=+++=+++243214312143214321121053153363132k x x x x x x k x x x x x x x x x x ,当21,k k 取何值时,无解?有唯一解?有无穷多解?在方程组有无穷多解时,用导出组的基础解系表示其全部解.第四章 矩阵[教学目的与要求] 通过本章学习,实现如下目的:(1) 能熟练地进行矩阵的各种运算(加、减、数乘、乘、转置、求逆等); (2) 能熟练掌握矩阵的初等变换,理解初等变换和初等矩阵的关系; (3) 能掌握各种求逆矩阵的方法; (4) 会应用分块乘法的初等变换. [教学重点]矩阵的各种运算(加、减、数乘、乘、转置、求逆等);矩阵的初等变换; 初等变换求逆法;分块乘法的初等变换.[教学难点] 分块乘法的初等变换 [教学内容]§2.1. 矩阵的概念的一些背景矩阵的概念§2.2. 矩阵的运算一、矩阵的加法、减法 二、矩阵的乘法三、数与矩阵的乘法 四、矩阵的转置§2.3. 矩阵乘积的行列式与秩一、矩阵乘积的行列式 二、矩阵乘积的秩§2.4. 矩阵的逆一、矩阵可逆的定义 二、伴随矩阵求逆法§2.5. 矩阵的分块一、分块矩阵的概念 二、分块矩阵的运算三、几种分块矩阵的逆矩阵§2.6. 初等矩阵一、初等矩阵及其性质 二、初等变换求逆法§2.7. 分块乘法的初等变换及应用举例一、分块乘法的初等变换二、分块乘法的初等变换应用举例思考题1. 举例说明下列命题是错误的:(1) 若02=A ,则0=A ;(2) 若A A =2,则0=A 或E A =;(3) 若E A =2,则E A =或E A -=; (4) 若AY AX =,且0≠A ,则Y X =. 2. 证明(1)2222)(B AB A B A +±=±成立当且仅当BA AB =; (2)22))((B A B A B A -=-+成立当且仅当BA AB =. 3.已知n n ij a A ⨯=)(为n 阶方阵,写出:(1)2A 的k 行l 列元素; (2)TAA 的k 行l 列元素; (3)A A T的k 行l 列元素. 4. 已知)3,2,1(=α,)31,21,1(=β.设矩阵βαT A =,求n A . 5. 证明:对任意的n m ⨯矩阵A ,T AA 和A A T都是对称矩阵.6. 设A 是n 阶方阵,且E AA T=,1||=A ,求||n E A -.7.已知A 为三阶方阵,且21||=A ,求|2)3(|*1A A --.8.已知⎪⎪⎪⎭⎫ ⎝⎛--=100021201A ,求1*])[(-T A .9.(1)已知⎪⎪⎪⎭⎫ ⎝⎛=300130113A ,矩阵B 满足B A AB 2+=,求B ;(2)已知⎪⎪⎪⎭⎫ ⎝⎛=101020101A ,矩阵B 满足B A E AB +=+2,求B ;(3)已知)1,2,1(-=diag A ,矩阵B 满足E BA BA A 82*-=,求B . 10.已知⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛987654321100010101100001010A ,求A .11.(1)证明)()()(B r A r B A r +≤+;(2)若n 阶矩阵B A ,满足0=AB ,证明n B r A r ≤+)()(;(3)若n 阶矩阵A 满足A A =2,证明n E A r A r =-+)()(;(4)若n 阶矩阵A 满足E A =2,证明n E A r E A r =-++)()(. 12.(1)B A ,为两个n 阶方阵,证明||||B A B A AB BA -⋅+=; (2)B A ,分别为m n ⨯和n m ⨯矩阵,证明||||BA E AB E E AB E m n nm -=-=.第五章 二次型[教学目的与要求] 通过本章学习,实现如下目的:(1)掌握用非退化线性替换把二次型化成标准形和规范形的方法; (2)会判断二次型的正定性.[教学重点] 二次型化标准形和规范形的方法;惯性定理;二次型的正定性. [教学难点] 惯性定理 [教学内容]§5.1. 二次型及其矩阵表示一、二次型及其矩阵表示 二、矩阵的合同§5.2. 标准形化二次型为标准形的配方法§5.3. 唯一性一、复二次型的规范形二、实二次型的规范形、惯性定理§5.4. 正定二次型一、正定二次型的概念和判定方法二、半正定二次型简介思考题1.写出下列二次型AX X '的矩阵,其中 (1)⎪⎪⎪⎭⎫⎝⎛---=205213111A ; (2)⎪⎪⎪⎪⎪⎭⎫⎝⎛=nn n n n n a a a a a a a a a A 212222111211 2. 设二次型32212221442x x x x x x f --+=,分别作下列可逆线性变换,求新二次型的矩阵,(1)Y X ⎪⎪⎪⎭⎫⎝⎛--=100210211; (2)Y X ⎪⎪⎪⎪⎪⎭⎫⎝⎛--=2101101121.3.分别用配方法和初等变换法化下列二次型为标准形,并写出所作的非退化线性替换(1)2332223121214322x x x x x x x x x f +++++=; (2)323121622x x x x x x f -+=.4. 分别在实数域和复数域上将3题中的两个二次型进一步化成规范型,并写出所作的非退化线性替换.5. 证明:秩等于r的对称矩阵可以表示成r个秩等于1的对称矩阵之和. 6. 证明:一个实二次型可以分解成两个实系数的一次齐次多项式的乘积的充分必要条件是,它的秩等于2和符号差等于0,或者秩等于1. 7. t 取什么值时,下列二次型是正定的:(1)3231212222214223x x x x x tx x x x f +-+++=; (2)32312123222161024x x x x x tx x x x f +++++=.8. 证明:如果A 正定,则1-A 和*A 也都正定.9.已知m 阶实对称矩阵A 正定,B 是n m ⨯矩阵,证明:AB B T正定的充要条件是n B r =)(.10. 已知A 为实矩阵,证明:)()(A r A A r ='.第六章 线性空间[教学目的与要求] 通过本章学习,实现如下目的:(1)能熟练地判断所给非空集合在指定的运算下能否构成线性空间; (2)会判断所给非空子集能否构成子空间; (3)会判断子空间之间的和是否为直和; (4)会判断两个线性空间的同构;(5)能熟练掌握线性空间基和维数的求法;(6)能熟练求向量在基下的坐标、基到基的过渡矩阵; (7)能熟练地求和空间的维数;(7)能熟练地应用维数公式求交空间的基与维数.[教学重点] 线性空间的定义、子空间的直和、维数公式、线性空间的同构. [教学难点] 线性空间的定义 [教学内容]§6.1. 集合 映射一、集合的概念和运算二、映射的概念、映射的乘法、逆映射§6.2. 线性空间的定义与简单性质一、线性空间的定义 二、线性空间的简单性质§6.3. 维数 基与坐标一、线性表示、线性相关和线性无关、向量组的等价 二、线性空间的基、维数,向量的坐标§6.4. 基变换与坐标变换一、基到基的过渡矩阵 二、坐标变换公式§6.5. 线性子空间一、线性子空间的定义二、线性子空间的维数和基§6.6. 子空间的交与和一、子空间的交 二、子空间的和§6.7. 子空间的直和一、两个子空间的直和 二、多个子空间的直和§6.8. 线性空间的同构一、线性空间同构的定义 二、同构映射的性质思考题1.检验下列集合对于所规定的运算是否构成给定数域上的线性空间:(1) 数域P 上的对角线元素的和为零的所有n 阶方阵所成的集合,对于矩阵的加法和数量乘法;(2) 设},|2{Q b a b a V ∈+=,Q 为有理数域,对于通常数的加法和乘法; (3) 设},|),{(R b a b a V ∈=,R 为实数域,定义加法和数乘如下:),(),(),(21212211b b a a b a b a +=+, ),(),(kb ka b a k = )(R k ∈.(4) 按照通常的数的运算,实数域R 是否构成实数域R 上的线性空间?是否构成复数域C 上的线性空间?(5) 按照通常的数的运算,复数域C 是否构成实数域R 上的线性空间?是否构成复数域C 上的线性空间? (6) +R 是全体正实数组成的集合,定义加法和数乘如下:ab b a =⊕, k a a k =⋅,这里+∈R b a ,,R k ∈.2.证明:在数域P 上的线性空间V 中,成立以下运算律:(1)βαβαk k k -=-)(;(2)αααl k l k -=-)(.这里P l k ∈,,V ∈βα,.3.实数域R 按照通常的乘法构成实数域R 上的线性空间.全体正实数集合+R 对1(6)题中定义的加法和数乘也构成实数域R 上的线性空间,能否据此说明+R 是线性空间R 的一个子空间?+R 是线性空间R 的子空间吗?4. 设)1,2,1(1-=α,)3,1,0(2-=α,)0,1,1(3-=α;)5,1,2(1=β,)1,3,2(2-=β,)2,3,1(3=β,(1) 证明:321,,ααα和321,,βββ都是3R 的基; (2) 求321,,ααα到321,,βββ的过渡矩阵; (3) 求向量)1,4,1(=α在两组基下的坐标.5. 在线性空间nR 中,判断下列哪些子集是子空间,(1)},|),0,,0,{(11R a a a a n n ∈ ;(2)}0|),,,{(121=∑=ni in aa a a ;(3)}1|),,,{(121=∑=ni in aa a a ;(4)},,2,1,|),,,{(21n i Z a a a a i n =∈.6. 举例说明线性空间的两个子空间的并一般不是子空间.两个子空间的并仍是子空间的充要条件是什么?7. 设线性空间V 含有非零向量,21,V V 是V 的任意两个真子空间,证明:V V V ≠⋃21. 8.在线性空间3][x P 中,求向量组21-=x α,x 22=α,x -=13α,24x =α 的一个极大无关组.9. 判断正误,并说明理由.(1)V 是n 维向量空间,V r ∈αα,,1 ,则r αα,,1 是子空间),,(1r L αα 的一组基;(2)n 个向量n αα,,1 是n 维向量空间V 的一组生成元,则n αα,,1 一定是V 的一组基;(3)向量空间V 的维数等于V 的任一生成组所含向量的个数; (4)任一向量空间都有基; (5)若向量空间V 的每一个向量都可以由n αα,,1 唯一的线性表示,则n αα,,1 是V 的一组基;(6)若s αα,,1 与t ββ,,1 的极大无关组分别是r i i αα,,1 与p j j ββ,,1 ,则),,(),,(11t s L L ββαα +的一组基为r i i αα,,1 p j j ββ,,1 .10. 下列向量组是否为3][x P 的基:(1)}22,,1,1{2322++++++x x x x x x x ; (2)},22,1,1{322x x x x x -+--. 11.求下列子空间的维数:(1)3))4,2,5(),2,4,1(),1,3,2((R L ⊆--; (2)][),1,1(22x P x x x x L ⊆---;(3)],[),,(32b a C e e e L x xx⊆,],[b a C 表示区间],[b a 上的全体连续函数空间.12.设⎪⎪⎪⎭⎫ ⎝⎛=000100010A ,求33⨯P 中所有与A 可交换的矩阵组成的子空间的维数和一组基.13.令},|{1A A P A A V n n ='∈=⨯,},|{2A A P A A V n n -='∈=⨯,证明21V V P n n ⊕=⨯. 14.设n αα,,1 是P 上n 维线性空间V 的一组基,A 是P 上的一个s n ⨯矩阵,令A n s ),,(),,(11ααββ =,证明:)(),,(dim 1A r L s =ββ . 15.证明:线性空间][x P 可以和它的真子空间同构.第七章 线性变换[教学目的与要求] 通过本章学习,实现如下目的: (1) 能熟练掌握线性变换的运算; (2) 能理解线性变换与矩阵的关系;(3) 能熟练地求线性变换的特征值与特征向量;(4) 理解哈密尔顿—凯莱(Hamilton-Caylay )定理; (5) 能熟练地将矩阵对角化;(6) 能熟练地求出线性变换的值域与核; (7) 了解若尔当标准形理论.[教学重点] 线性变换与矩阵的关系;线性变换的特征值与特征向量;线性变换的值域与核;矩阵对角化.[教学难点] 矩阵的对角化 [教学内容]§7.1. 线性变换的定义一、线性变换的定义 二、线性变换的简单性质§7.2. 线性变换的运算一、线性变换的乘法 二、线性变换的加法三、线性变换的数量乘法 四、线性变换的逆§7.3. 线性变换的矩阵一、线性变换的矩阵 二、矩阵的相似§7.4. 特征值与特征向量一、线性变换特征值与特征向量的概念 二、线性变换特征值与特征向量的求法 三、哈密顿-凯莱定理§7.5. 对角矩阵一、特征向量的性质二、线性变换的矩阵可以是对角矩阵的条件§7.6. 线性变换的值域与核一、线性变换的值域 二、线性变换的核§7.7. 不变子空间一、不变子空间二、不变子空间与线性变换矩阵的化简§7.8. 若尔当(Jordan )标准形介绍若尔当标准形介绍§7.9. 最小多项式最小多项式概念和性质思考题1.线性空间V 到V 的同构映射称为线性空间V 的自同构.线性空间V 的线性变换和它的自同构有什么异同?2.A 是线性空间V 的线性变换,s αα,,1 是V 中一组线性无关的向量,问)(,),(1s ααA A 是否仍线性无关?试举例说明. 3.设A 是n 维线性空间V 的线性变换,证明:(1)A 是线性空间V 的自同构当且仅当A 把线性无关的向量组变成线性无关的向量组;(2)A 把线性空间V 中某一组线性无关的向量变成一组线性相关的向量的充要条件是A 把V 中某个非零向量变成零向量,即}0{)0(1≠-A ;(3)A 是线性空间V 的自同构当且仅当}0{)0(1=-A .4.已知⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----=7931181332111511A ,定义4P 的变换为:ξξA =A ,4P∈ξ,证明A 为4P 的线性变换,并求A 的核和象空间以及它们的维数.5.为什么线性变换的问题可以转化为相应的矩阵的问题去研究?)(V L 与nn P ⨯有什么关系?求出线性空间)(V L 的维数.6.设⎪⎪⎭⎫ ⎝⎛=4321A ,求22⨯P 的如下线性变换A 在基⎪⎪⎭⎫ ⎝⎛=00011ε,⎪⎪⎭⎫⎝⎛=00102ε,⎪⎪⎭⎫ ⎝⎛=01003ε,⎪⎪⎭⎫⎝⎛=10004ε下的矩阵. (1)AX X =)(A ; (2)XA X =)(A .7.在3R 中,试求关于基)0,0,1(1=ε,)0,1,1(2=ε,)1,1,1(3=ε的矩阵为⎪⎪⎪⎭⎫ ⎝⎛---=221101211A 的线性变换.8.设三维线性空间线性变换A 在基321,,ααα下的矩阵为⎪⎪⎪⎭⎫⎝⎛---=6788152051115A ,求A 在基321,,βββ下的矩阵,其中321132αααβ++=,321243αααβ++=,321322αααβ++=.若3212αααξ-+=,求)(ξA 在基321,,βββ下的坐标.9.设三维线性空间线性变换A 在基321,,ααα下的矩阵为⎪⎪⎪⎭⎫⎝⎛=333231232221131211a a a a a a a a a A , 求(1)A 在基123,,ααα下的矩阵;(2)A 在基321,,αααk 下的矩阵;)0(≠k (3)A 在基3221,,αααα+下的矩阵.10.四维线性空间V 的线性变换A 在基4321,,,αααα下的矩阵为⎪⎪⎪⎪⎪⎭⎫⎝⎛----=3707011311013412A ,求:(1)A 的值域; (2)A 的核;(3)在A 的值域中选一组基,把它扩充成线性空间V 的基; (4)在A 的核中选一组基,把它扩充成线性空间V 的基.11.若矩阵A 与B 相似,证明:(1) 若A 与B 可逆,则1-A 与1-B 相似; (2) 对任意的常数k ,kA 与kB 相似;(3) 对任意的正整数m ,mA 与mB 相似;(4) 对于任意多项式)(x f ,)(A f 与)(B f 相似.12.若矩阵A 与B 相似,C 与D 相似,证明:⎪⎪⎭⎫⎝⎛C A 00与⎪⎪⎭⎫⎝⎛D B 00相似. 13.取定矩阵n n P A ⨯∈.对于任意的nn P X ⨯∈,定义变换A 为XA AX X -=)(A ,(1) 证明A 为线性空间nn P ⨯的线性变换;(2) 若⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=n A λλλ00000021,求线性变换A 在基},1|{n j i E ij ≤≤下的矩阵. 14.在线性空间3P 中,定义线性变换A 为),,(),,(312321x x x x x x =A .令}2,1,|)0,,{(21=∈=i P x x x S i ,则S 是3P 的一个子空间,试问S 是否为线性变换A 的不变子空间.15.V 为数域P 上的一个线性空间,A 为V 的一个线性变换,][)(x P x f ∈,如果S 为线性变换A 的不变子空间,则S 线性变换)(A f 的不变子空间.16.若S 为线性空间V 的线性变换A 和B 的不变子空间,则S 也是B A +和AB 的不变子空间.17.若21,S S 为线性空间V 的线性变换A 的不变子空间,则21S S ⋂,21S S +也是A 的不变子空间. 18.若S 为线性空间V 的线性变换A 的不变子空间,当线性变换A 可逆时,则S 也是1-A的不变子空间. 19.若A 是线性空间V 的线性变换,且满足A A=2,证明:(1)}|)({)0(1V ∈-=-ξξξA A; (2))Im()0(1A A ⊕=-V .20.n 阶矩阵A 和B 相似时,它们有相同的特征多项式.反过来对吗?即n 阶矩阵A 和B 有相同的特征多项式时,哪它们相似吗?试举例说明.21.A 是线性空间V 的线性变换,证明A 可逆的充分必要条件是A 的特征值都非零. 22.证明线性变换A 的一个特征向量不能同时属于两个不同的特征值.23.证明:对角形矩阵⎪⎪⎪⎪⎪⎭⎫ ⎝⎛n a a a 0021和⎪⎪⎪⎪⎪⎭⎫ ⎝⎛n b b b 0021 相似的充分必要条件是n b b b ,,,21 是n a a a ,,,21 的一个排列.24.设A 是复数域C 上的一个n 阶矩阵,n λλλ,,,21 是A 的全部特征值(按重数计算),证明:(1)如果][)(x C x f ∈是次数大于0的多项式,则)(,),(),(21n f f f λλλ 是)(A f 的全部特征值;(2)如果A 可逆,则n λλλ,,,21 全部不等于零; (3)如果A 可逆,则nλλλ1,,1,121 为1-A 的全部特征值.25.设三维线性空间V 的线性变换A 在基321,,ααα下的矩阵为⎪⎪⎪⎭⎫ ⎝⎛----=533242111A , 求:(1)A 的特征值和特征向量;(2)是否存在V 的基321,,βββ使得线性变换A 在其下的矩阵为对角形.若这样的基321,,βββ存在,试写出由基321,,ααα到321,,βββ的过渡矩阵T .以及A 在321,,βββ下的矩阵;(3)计算AT T 1-.第八章 -λ矩阵[教学目的与要求] 通过本章学习,实现如下目的: (1)会求-λ矩阵的标准形 (2)会求-λ矩阵的行列式因子(3)会求矩阵A 的初等因子,并能写出A 若尔当标准形 (4)会求矩阵A 的有理标准形[教学重点] 矩阵A 的初等因子,矩阵的A 若尔当标准形 [教学难点] 矩阵相似的条件 [教学内容]§8.1. -λ矩阵一、-λ矩阵的秩 二、-λ矩阵的可逆§8.2. -λ矩阵在初等变换下的标准形一、-λ矩阵的初等变换 二、-λ矩阵的标准形§8.3. 不变因子一、-λ矩阵的行列式因子 二、-λ矩阵的不变因子§8.4. 相似矩阵的条件两个矩阵相似的充要条件§8.5. 初等因子一、初等因子的概念 二、初等因子的求法§8.6. 若尔当(Jordan )标准形理论推导一、若尔当矩阵的概念二、矩阵的若尔当标准形的求法§8.7. 矩阵的有理标准形一、有理形矩阵的概念 二、有理标准形的求法思考题1.求下列矩阵的初等因子、不变因子、行列式因子,并写出若当标准形.(1)⎪⎪⎪⎭⎫ ⎝⎛-----222333111, (2)⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----0167121700140013, (3)⎪⎪⎪⎪⎪⎭⎫ ⎝⎛10021*********1. 2. 已知nn P A ⨯∈,证明A 与A '相似.3. 设复矩阵⎪⎪⎪⎭⎫ ⎝⎛-=102002c b a A ,(1)求出A 的一切可能的若当标准形;(2)给出A 可对角化的条件.第九章 欧几里得空间[教学目的与要求] 通过本章学习,实现如下目的:(1) 掌握求标准正交基的施密特(Schmidt )正交化方法;(2) 会判断两个欧氏空间的同构; (3) 理解正交变换与正交矩阵的关系; (4) 会求欧氏空间子空间的正交补;(5) 能熟练地把实对称矩阵正交相似于对角矩阵; (6) 能掌握最小二乘法.[教学重点] 求标准正交基的施密特(Schmidt )正交化方法;欧氏空间的同构;正交变换;对乘变换;实对称矩阵正交相似于对角矩阵的方法.[教学难点] 最小二乘法[教学内容] §9.1. 定义与基本性质一、内积与欧氏空间的定义 二、向量的长度 三、向量的正交四、欧氏空间基的度量矩阵§9.2. 标准正交基一、标准正交基的概念 二、标准正交基的求法§9.3. 同构一、欧氏空间同构的概念 二、欧氏空间同构的充要条件§9.4. 正交变换一、正交变换的定义 二、正交变换的性质§9.5. 子空间一、欧氏空间中子空间的正交 二、欧氏空间子空间的正交补§9.6. 实对称矩阵的标准形一、对称变换二、实对称矩阵的特征值特征向量的性质 三、实对称矩阵的对角化四、二次型化标准形的正交变换法§9.7. 向量到子空间的距离 最小二乘法一、向量到子空间的距离 二、最小二乘法§9.8. 酉空间介绍一、酉空间的概念二、酉空间中的一些重要结论思考题1.下列线性空间对给定的二元函数),(βα是否构成欧氏空间(1)在线性空间nR 中,对任意向量),,(1n a a =α,),,(1n b b =β,定义二元函数∑==ni i i b a 1||),(βα(2)在线性空间nn R ⨯中,对任意向量nn RB A ⨯∈,,定义二元函数)(),(A B tr B A '=2. 在欧氏空间4R 中求出两个单位向量使它们同时与下面三个向量正交.)0,4,1,2(1-=α,)2,2,1,1(2--=α,)4,5,2,3(3=α3. 称||),(βαβα-=d 为向量α和β间的距离.证明:),(),(),(βγγαβαd d d +≤. 4.设α,β是欧氏空间中任意两个非零向量,证明:(1))0(>=k k βα的充分必要条件是α和β间的夹角为零; (2))0(<=k k βα的充分必要条件是α和β间的夹角为π. 5. 已知)0,1,2,0(1=α,)0,0,1,1(2-=α,)1,0,2,1(3-=α,)1,0,0,1(4=α是4R 的一个基,对这个基正交化,求出4R 的一个标准正交基.6. 在欧氏空间]1,1[-C 里,对基32,,,1x x x 正交化,求出]1,1[-C 的一个标准正交基. 7. 已知))0,2,0(),0,0,1((L W =是3R 的一个子空间,求⊥W . 8.设21,,W W W 为欧氏空间V 的子空间,则(1)W W =⊥⊥)(;(2)如果21W W ⊂,则⊥⊥⊂12W W ; (3)⊥⊥⊥⋂=+2121)(W W W W . 9.求正交矩阵T 使得AT T '成对角形.其中A 为(1)⎪⎪⎪⎭⎫ ⎝⎛--510810228211; (2)⎪⎪⎪⎭⎫ ⎝⎛----114441784817. 10.用正交的线性替换化下列二次型为标准形(1)322322214332x x x x x f +++=;(2)43324121242322212222x x x x x x x x x x x x f +--++++=; (3)434232413121222222x x x x x x x x x x x x f ++--+=.第十章 双线性函数与辛空间 *[教学目的与要求] 通过本章学习,实现如下目的:(1)理解线性函数的定义,熟悉线性函数的简单性质 (2)理解线性空间与其对偶空间的同构关系(3)理解双线性度量空间、正交空间、准欧氏空间、辛空间等概念 [教学重点] 对偶空间和对偶基、双线性函数、双线性度量空间、正交空间、准欧氏空间、辛空间等概念。