子波基本理论与提取方法
- 格式:doc
- 大小:127.00 KB
- 文档页数:5

地震子波提取方法综述
地震子波是指地震波在地下介质中传播时所经历的各种反射、折射和散射等作用后形成的波形。
地震子波是地震勘探中重要的信息来源,能够提供地下介质的物理特征,如密度、速度、厚度等信息。
因此,地震子波的提取是地震勘探数据处理的重要步骤。
目前,针对地震子波的提取方法主要可以分为时域方法和频域方法。
时域方法主要包括叠加法、全波形反演法、小波变换法等。
叠加法是一种经典的地震子波提取方法,它通过多次叠加同一接收器上的不同地震记录得到地震子波。
全波形反演法则是一种利用弹性波方程直接求解地震子波的方法,它能够提高地震子波的分辨率和准确度。
小波变换法则是一种将地震记录分解成不同尺度和频率的方法,它能够提取地震信号中不同频率的成分,从而得到更加详细的地下介质信息。
频域方法主要包括卷积模拟法、稀疏表示法、奇异值分解法等。
卷积模拟法通过将地震记录与已知的地下介质模型进行卷积,得到地震子波。
稀疏表示法则是一种通过求解稀疏线性方程组来提取地震子波的方法,它能够提高地震子波的信噪比和分辨率。
奇异值分解法则是一种将地震记录矩阵分解成奇异值矩阵和特征向量矩阵的方法,从而得到地震信号中的主要成分。
综上所述,地震子波的提取是地震勘探数据处理中的一个重要环节,不同的提取方法各有优劣,应根据实际情况进行选择和应用。
未来,随着地震勘探技术的不断发展,地震子波提取方法也将不断地进
行改进和创新。

地震子波提取方法综述
地震子波提取方法综述
地震勘探是一种通过使用反射波测量地下岩层和地质结构的方法,以
便了解地下情况的技术。
能够提取地震信号中的子波,是地震勘探中
非常重要的技术。
下面将综述几种常用地震子波提取方法:
1.匹配滤波
匹配滤波是一种常用的地震子波提取方法,其基本思想是用一个已知
的波形去匹配地震记录中的波形。
匹配滤波的主要作用就是对地震信
号进行滤波增强,提高信噪比。
该方法在提取精细地震子波方面的效
果比较好。
2.小波变换
小波变换是一种将时间和频率相互联结的数学工具。
对于地震子波提
取来说,小波变换能够使原始信号中的各个频率分量得到充分的展开,并且可以将高频噪声和低频信号有效分离,从而提高地震信号的信噪比。
3.奇异值分解
奇异值分解是一种用于分解矩阵的数学技术。
在地震子波提取中,通
过将地震记录矩阵分解成多个低能量层和高能量层,可以得到最佳的
地震子波提取结果。
该方法对于提取高频率的子波有着很好的效果。
4.模拟退火
模拟退火是一种常用的优化算法,用于解决函数优化问题。
在地震子波提取中,使用模拟退火算法可以搜索地震信号的最优解,并提取出更加精细和准确的地震子波。
该方法在提取特定类型的井测距数据中效果比较好。
以上是几种常用地震子波提取方法的综述。
不同的提取方法各有优缺点,需要根据具体情况选择合适的方法进行使用。
在实际应用中,也可以将不同的提取方法进行组合,以达到更好的效果。


地震子波提取方法论文摘要:在信噪比较高的情况下最小相位和混合子波相位均适应性良好。
在信噪比降低后,混合相位提取子波受影响较大。
通过对实际模型的处理,表明了该方法的有效性和实用性。
1 子波基本理论子波包括最小相位子波、最大相位子波、混合相位子波。
子波的Z变换是一个多项式。
若此多项式的全部零点均在单位圆外,则为最小相位子波;在单位圆内为最大相位子波,零点在单位圆的内外都有,则为混合相位子波。
2 复赛谱域提取子波法复赛谱域提取子波法研究的是一种非线性系统,或者说是一种线性滤波的推广。
对于一个线性系统,它可以满足以下迭加原理:T[ax1+bx2]=aT[x1]+bT[x2](1)式中a、b为常数,T为表示函数。
一个信号是由多个信号相加合成的,利用线性滤波的方法,就能有效地把它们分开。
如果一个信号不是由多个信号相加,而是由多个信号中褶积合成的,那么,用这种线性滤波的方法就不能将其分开。
对于这种信号的处理,我们仍可利用(2)式的基本思想,把它推广到褶积合成的信号。
为此我们需要一个称为同态系统的变换系统D,它具有把一个褶积关系转变为相加关系的特征系统。
从(2)式可见,线性系统特别适用于分开相加合成的信号;也就是说,一个系统可以这样处理:D[(a)x1*(b)x2]=aD[x1]+bD[x2](2)上式中(a)表示标量乘,(a)x1表示x1与自身褶积a次,(b)也是如此。
系统L是一个一般的线性系统,满足:L[ax1+bx2]=aL[x1]+bL[x2] L[x·?啄(t±?子)]=L[x]?啄(t±?子)(3)系统D-1为D的逆变换特征系统,是把经过处理的相加关系转化为褶积关系输出,即:D-1[ax1+bx2]=(a)D-1[x1]*(b)D[x2](4)系统定义为这种D→L→D-1的标准格式,其突出的优点是,只要确定了特征系统D之后,它在整个反褶积过程中保持不变,并将一个非线性过程转化为线性运算。

常用地震子波提取方法简介[摘要]子波在地震处理和解释中都是一个极其重要的概念,提取制作一个适合地震工区的子波,在作合成地震记录标定及反演工作时都具有极其重要的意义。
[关键词]子波振幅谱相位谱统计子波中图分类号:p315 文献标识码:a 文章编号:1009-914x(2013)09-0161-02子波在地震处理和解释中都是一个极其重要的概念,地震子波是地震记录褶积模型的一个分量,通常指由2至3个或多个相位组成的地震脉冲,确切地说,地震子波就是地震能量由震源通过复杂的地下路径传播到接收器所记录下来的质点运动速度(陆上检波器)或压力(海上检波器)的远场时间域响应。
一个子波可以由它的振幅谱和相位谱来定义,相位谱的类型可以是零相位、常数相位、最小相位、混合相位等;对零相位和常数相位子波而言,可简单将其看作是一系列不同振幅和频率的正弦波的集合,所有的正弦波都是零相位或常数相位的;在频率域中,子波提取问题由两部分组成:确定振幅谱和相位谱,确定相位谱更加困难,并且是反演中误差的主要来源。
通常子波提取方法分为三个主要类型:①、完全确定法:直接应用地表检波器或其它仪器直接测量子波。
②、纯统计法:只根据地震数据确定子波,这种方法很难测定可靠性的相位谱。
通常是为了回避确定子波的困难,使用自相关统计原理,从地震数据中提取地震道的振幅谱来作为子波的振幅谱。
对子波的相位谱则做最小相位或零相位的假设。
③、使用测井曲线法:使用测井曲线提取常相位子波,子波的振幅谱由地震数据自相关获得。
其相位谱假定为一常数,由解一个任意度的最小平方整形滤波器得到平均相位。
使用测井曲线提取全子波,由测井声阻抗计算的反射系数与地震道用最小平方拟合的方法求取子波的振幅谱和相位谱。
此方法的优点在于能够计算一个精确的子波。
但它对井和地震道之间的匹配关系非常敏感。
即使用测井曲线与地震数据结合,理论上这种方法能够提取井点位置精确的相位信息,但问题是该方法要求测井和地震间必须要有良好的对应关系,而将深度域样点转换为双程旅行时的深时转换可能产生不恰当的对应关系,而这种不恰当的对应关系必将影响子波提取的结果。
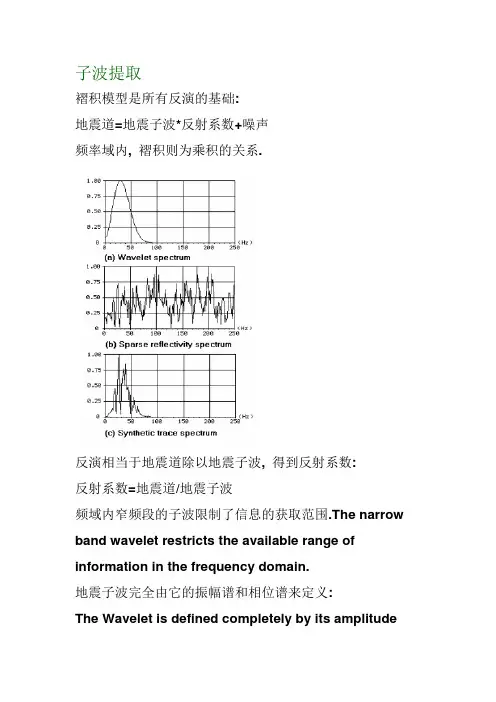
子波提取褶积模型是所有反演的基础:地震道=地震子波*反射系数+噪声频率域内, 褶积则为乘积的关系.反演相当于地震道除以地震子波, 得到反射系数:反射系数=地震道/地震子波频域内窄频段的子波限制了信息的获取范围.The narrow band wavelet restricts the available range of information in the frequency domain.地震子波完全由它的振幅谱和相位谱来定义:The Wavelet is defined completely by its amplitudespectrum and its phase spectrum:在有限频率范围内, 相位谱通常可近似为一条直线. 直线的截距是子波的常数相位旋转, 它是子波的最佳表征. 直线的斜率标示着子波的时移.The intercept of the line is the constant phase rotation which best characterizes this wavelet.The slope of the line measures the time-shift of the wavelet.极性的约定:极性约定是一个特殊的子波相位问题. 默认的约定便是: 声阻抗的增加在零相位的地震数据上代表一个波峰.A special wavelet phase issue is the Polarity convention.The default convention is that an increase in acoustic impedance is represented as a peak on zero-phase seismic data:另一个默认的约定便是: 声阻抗的增加在零相位的地震数据上代表一个波谷.The alternate convention is that an increase in acoustic impedance is represented as a trough on zero-phase seismic data:使用ì极性约定菜单î可以设置极性约定:The polarity convention is set using the SyntheticPolarity Convention menu:地震子波在时间和空间上都存在着变化, 即具有时变性和空变性, 这是基于以下几个原因:Wavelets in the earth vary both laterally (spatially) and temporally for a variety of reasons:近地表效应(空变)Near surface effects (space variant)频率吸收(时变和空变)Frequency-dependent absorption (space and time variant)层间多次波(时变和空变)Inter-bed multiples (space and time variant)NMO 拉伸处理过程中的人为因素Processing artifactsSTRATA 假定子波是常数, 不随时间和空间变化: 时间不变性: 这意味着反演就是在有限的时窗内求最优化的波阻抗Time invariant: This means that the inversion is optimized for a limited time window.空间不变性: 这意味着去除子波的空变后被最优化处理. 通常, 许多方法有可以用来提取子波. STRATA中用了以下几种:In general, a variety of methods can be used for wavelet extraction. Some are available in STRATA. (1) 仅用地震数据估计地震子波的振幅谱. 假设相位谱已经从别的渠道得知.子相关autocorrelation最大熵谱分析maximum entropy spectral analysis交互谱分析cross spectral analysisSTRATA中统计子波的提取用自相关: Statistical wavelet extraction uses the autocorrelation(2) 单独使用地震数据估算振幅谱和相位谱Estimate both amplitude and phase spectra from the seismic data alone.最小熵子波估计高阶力矩法higher order momentsSTRATA 不用这种方法, 因为STRATA认为该方法不可靠.(3) 使用给定的测量数据估计振幅谱和相位谱Estimate both amplitude and phase spectra using deterministic measurements.海洋信号marine signaturesVSP 分析STRATA中, 以ASCII文件形式读入外部子波(4) 用地震和测井资料估算振幅谱和相位谱Estimate both amplitude and phase spectra using both seismic and well log measurements.STRATA中用测井资料提取全子波.(5) 用地震资料和测井资料估算振幅谱和常数相位谱STRATA中用测井资料提取常数相位子波.STRATA中提取子波的方法:第一步, 是否用测井资料来估算子波的相位. 关键是看测井资料与地震资料的相关性是否好. 通常情况下, 必须首先进行手动校正测井曲线. The critical issue for this decision is how well the logs tie the seismic data. Usually, manual correlation must be done to align the logs first.1 提取统计子波(不用井资料):这个过程只是通对地震道进行自相关计算子波的振幅谱, 并假设已知子波的相位.主要参数:ï道范围(通常设置为较大值以增加统计所用的道数) Trace range (usually set this large to increase statistics)ï时窗(至少应该为子波长度的两倍)ï子波长度(取决于层厚和分辨率, 层厚一般取200ms, 薄层取50~100ms).2 用测井资料提取子波:用测井资料提取子波:此方法用测井资料估算子波的振幅谱和相位谱. 效果取决于测井曲线和地震道的相关程度.主要参数:选择要用的井(只用标定效果好的井)道范围(距井的距离)时窗子波长度3 用测井资料计算单一常数相位值该方法使用地震道的自相关计算子波的振幅谱, 与统计子波提取方法中一样, 用测井资料计算子波的相位谱, 并且相位谱被近似为一个单一的常数谱.This procedure calculates the amplitude spectrum of the wavelet using the autocorrelation of the seismic traces,exactly as in the statistical procedure.The phase spectrum is approximated as a single constant value, using the well logs.这种方法比较稳定, 特别是测井资料与地震数据的相关性较差时.This procedure is more robust than the full phase spectrum calculation, especially when the tie between logs and seismic is poor.计算相位的步骤:(1) 用统计子波提取方法计算子波(不用井资料).(2) 对所提取的子波进行一系列的常相位旋转(3) 用每一次旋转后的子波计算合成道, 并且与地震道进行相关.(4) 选出与地震道产生最大相关值的相位旋转子波提取中的问题:用井提取子波时, 必须首先求出测井曲线之间的最优化相关To extract a wavelet using logs, an optimum correlation must be done first.正确地相关必须以子波已知为前提To perform correlation properly, the wavelet must already be known.实际子波提取的流程:(1) 用统计子波提取来确定一个初步的子波, 假设子波的近似相位已知.(2) 拉伸或压缩测井曲线来标定地震道.(3) 使用新的测井曲线来提取新的子波.(4) 重复第(2)、(3)步,直到提取的子波达到要求为止.。


物质波知识点总结1. 物质波的提出与基本原理物质波理论最早由德布罗意提出,他认为微观粒子具有波动特性。
这一理论的提出是基于早先的光子理论,即光是一种波动,所以粒子也可以表现出波动的性质。
德布罗意通过一系列推导和实验观察得出了与波动性质相关的基本公式,即德布罗意波长公式:\[ \lambda = \frac{h}{p} \]其中,λ为德布罗意波长,h为普朗克常数,p为粒子的动量。
这一公式表明了粒子的波长与动量成反比,即动量越大,波长越短,波动性越显著。
物质波的提出与普朗克量子论以及光的波粒二象性有着密切的联系。
普朗克提出了能量量子化的概念,即能量不是连续的,而是离散的。
而光的波粒二象性也表明了光既可以表现为波动,也可以表现为粒子。
物质波的提出,进一步强化了微观粒子的波动性质,为后来的量子力学的建立奠定了基础。
2. 物质波的性质和实验观察物质波具有一系列独特的性质和行为,这些性质在实验观察中得到了验证,也为量子力学的建立提供了有力的证据。
首先,物质波的波长与动量成反比的关系在实验中得到了验证。
例如,电子的衍射实验表明了电子具有波动性质,其波长与动量成反比,与德布罗意波长公式吻合。
这一实验结果进一步验证了物质波的存在以及波动性质。
其次,物质波的干涉现象也得到了实验观察的证实。
类似于光的干涉实验,电子的干涉实验也表明了电子具有波动性质。
在双缝干涉实验中,电子的波动性质表现出明显的干涉条纹,这一实验结果再次证实了物质波的存在。
除此之外,物质波还具有量子力学中的波函数和波包的性质。
波函数描述了微观粒子的波动性质,而波包则描述了粒子的局域性。
这些物质波的性质在量子力学中发挥着重要的作用,为我们理解微观世界提供了重要的信息。
3. 物质波的应用物质波的存在和性质对于微观世界的研究以及现代技术的发展具有重要的意义。
物质波在量子力学和量子力学相关技术中有着广泛的应用。
首先,物质波在微观粒子的研究中发挥着重要的作用。
例如,通过电子衍射实验和双缝干涉实验,我们可以了解微观粒子的波动特性和行为规律。
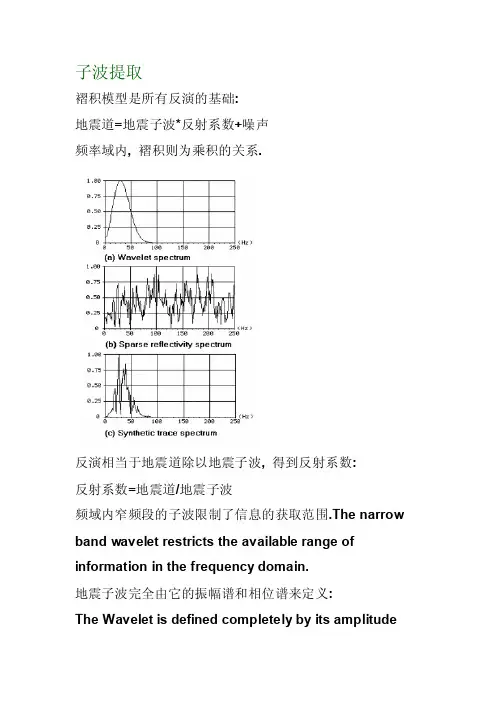
子波提取褶积模型是所有反演的基础:地震道=地震子波*反射系数+噪声频率域内, 褶积则为乘积的关系.反演相当于地震道除以地震子波, 得到反射系数:反射系数=地震道/地震子波频域内窄频段的子波限制了信息的获取范围.The narrow band wavelet restricts the available range of information in the frequency domain.地震子波完全由它的振幅谱和相位谱来定义:The Wavelet is defined completely by its amplitudespectrum and its phase spectrum:在有限频率范围内, 相位谱通常可近似为一条直线. 直线的截距是子波的常数相位旋转, 它是子波的最佳表征. 直线的斜率标示着子波的时移.The intercept of the line is the constant phase rotation which best characterizes this wavelet.The slope of the line measures the time-shift of the wavelet.极性的约定:极性约定是一个特殊的子波相位问题. 默认的约定便是: 声阻抗的增加在零相位的地震数据上代表一个波峰.A special wavelet phase issue is the Polarity convention.The default convention is that an increase in acoustic impedance is represented as a peak on zero-phase seismic data:另一个默认的约定便是: 声阻抗的增加在零相位的地震数据上代表一个波谷.The alternate convention is that an increase in acoustic impedance is represented as a trough on zero-phase seismic data:使用ì极性约定菜单î可以设置极性约定:The polarity convention is set using the SyntheticPolarity Convention menu:地震子波在时间和空间上都存在着变化, 即具有时变性和空变性, 这是基于以下几个原因:Wavelets in the earth vary both laterally (spatially) and temporally for a variety of reasons:近地表效应(空变)Near surface effects (space variant)频率吸收(时变和空变)Frequency-dependent absorption (space and time variant)层间多次波(时变和空变)Inter-bed multiples (space and time variant)NMO 拉伸处理过程中的人为因素Processing artifactsSTRATA 假定子波是常数, 不随时间和空间变化: 时间不变性: 这意味着反演就是在有限的时窗内求最优化的波阻抗Time invariant: This means that the inversion is optimized for a limited time window.空间不变性: 这意味着去除子波的空变后被最优化处理. 通常, 许多方法有可以用来提取子波. STRATA中用了以下几种:In general, a variety of methods can be used for wavelet extraction. Some are available in STRATA. (1) 仅用地震数据估计地震子波的振幅谱. 假设相位谱已经从别的渠道得知.子相关autocorrelation最大熵谱分析maximum entropy spectral analysis交互谱分析cross spectral analysisSTRATA中统计子波的提取用自相关: Statistical wavelet extraction uses the autocorrelation(2) 单独使用地震数据估算振幅谱和相位谱Estimate both amplitude and phase spectra from the seismic data alone.最小熵子波估计高阶力矩法higher order momentsSTRATA 不用这种方法, 因为STRATA认为该方法不可靠.(3) 使用给定的测量数据估计振幅谱和相位谱Estimate both amplitude and phase spectra using deterministic measurements.海洋信号marine signaturesVSP 分析STRATA中, 以ASCII文件形式读入外部子波(4) 用地震和测井资料估算振幅谱和相位谱Estimate both amplitude and phase spectra using both seismic and well log measurements.STRATA中用测井资料提取全子波.(5) 用地震资料和测井资料估算振幅谱和常数相位谱STRATA中用测井资料提取常数相位子波.STRATA中提取子波的方法:第一步, 是否用测井资料来估算子波的相位. 关键是看测井资料与地震资料的相关性是否好. 通常情况下, 必须首先进行手动校正测井曲线. The critical issue for this decision is how well the logs tie the seismic data. Usually, manual correlation must be done to align the logs first.1 提取统计子波(不用井资料):这个过程只是通对地震道进行自相关计算子波的振幅谱, 并假设已知子波的相位.主要参数:ï道范围(通常设置为较大值以增加统计所用的道数) Trace range (usually set this large to increase statistics)ï时窗(至少应该为子波长度的两倍)ï子波长度(取决于层厚和分辨率, 层厚一般取200ms, 薄层取50~100ms).2 用测井资料提取子波:用测井资料提取子波:此方法用测井资料估算子波的振幅谱和相位谱. 效果取决于测井曲线和地震道的相关程度.主要参数:选择要用的井(只用标定效果好的井)道范围(距井的距离)时窗子波长度3 用测井资料计算单一常数相位值该方法使用地震道的自相关计算子波的振幅谱, 与统计子波提取方法中一样, 用测井资料计算子波的相位谱, 并且相位谱被近似为一个单一的常数谱.This procedure calculates the amplitude spectrum of the wavelet using the autocorrelation of the seismic traces,exactly as in the statistical procedure.The phase spectrum is approximated as a single constant value, using the well logs.这种方法比较稳定, 特别是测井资料与地震数据的相关性较差时.This procedure is more robust than the full phase spectrum calculation, especially when the tie between logs and seismic is poor.计算相位的步骤:(1) 用统计子波提取方法计算子波(不用井资料).(2) 对所提取的子波进行一系列的常相位旋转(3) 用每一次旋转后的子波计算合成道, 并且与地震道进行相关.(4) 选出与地震道产生最大相关值的相位旋转子波提取中的问题:用井提取子波时, 必须首先求出测井曲线之间的最优化相关To extract a wavelet using logs, an optimum correlation must be done first.正确地相关必须以子波已知为前提To perform correlation properly, the wavelet must already be known.实际子波提取的流程:(1) 用统计子波提取来确定一个初步的子波, 假设子波的近似相位已知.(2) 拉伸或压缩测井曲线来标定地震道.(3) 使用新的测井曲线来提取新的子波.(4) 重复第(2)、(3)步,直到提取的子波达到要求为止.。

地震子波的再认识一、地震子波概念:地震子波是地震记录褶积模型的一个分量,通常指由2至3个或多个相位组成的地震脉冲,确切地说,地震子波就是地震能量由震源通过复杂的地下路径传播到接收器所记录下来的质点运动速度(陆上检波器)或压力(海上检波器)的远场时间域响应。
一个子波可以由它的振幅谱和相位谱来定义,相位谱的类型可以是零相位、常数相位、最小相位、混合相位等;对零相位和常数相位子波而言,可简单将其看作是一系列不同振幅和频率的正弦波的集合,所有的正弦波都是零相位或常数相位的(如90°);在频率域中,子波提取问题由两部分组成:确定振幅谱和相位谱,确定相位谱更加困难,并且是反演中误差的主要来源。
二、子波提取方法:子波提取方法分为三个主要类型:1)、纯确定法:即用地表检波器或其它仪器直接测量子波;2)、纯统计法:即只根据地震数据测定子波,这种方法很难测定可靠性的相位谱;3)、使用测井曲线法:即使用测井曲线与地震数据结合,理论上这种方法能够提取井点位置精确的相位信息,但问题是该方法要求测井和地震间必须要有良好的对应关系,而将深度域样点转换为双程旅行时的深时转换可能产生不恰当的对应关系,而这种不恰当的对应关系必将影响子波提取的结果。
子波在各地震道之间是变化的,而且是旅行时间函数,即子波是时变和空变的,也就是说,对每个地震剖面而言,都应该能提取大量的子波,但在实际应用中提取可变子波可能会引起更多的不确定性,比较实用的做法是对整个剖面或某个目的层只提取单一的平均子波。
三、零相位子波和常数相位子波:零相位子波和常数相位子波(Zero Phase and Constant Phase Wavelets.) 首先,让我们来考虑雷克子波(Ricker Wavelet),雷克子波由一个波峰和两波谷,或叫两个旁瓣组成, 雷克子波依赖它的主频,也就是说,它的振幅谱的峰值频率,或主周期在时间域的反函数(主周期可以通过测量波谷到波谷的时间来获得)。

第32卷 第2期物探化探计算技术2010年3月基金项目:国家重点基础研究发展规划(2007CB209400);国家自然基金(40874054)收稿日期:2009-07-29 改回日期:2009-12-31文章编号:1001)1749(2010)02)0120)06地震反演系统中的子波提取方法孙学凯1,冯世民2(1.中国矿业大学煤层气探测理论与方法教育部重点实验室,江苏徐州 221008;2.河北煤田地质局物测地质队,河北邢台 540000)摘 要:在地震反演过程中,子波质量至关重要,它将直接影响着最终的反演结果。
这里详细地讨论了S trata 地震反演系统中提取子波的几种常用方法,并对它们的特点做了简要分析。
最后,提出了一种新的提取子波方法,利用反演误差对子波进行相位校正,使误差图上的相关能量尽可能达到最小,用校正后的最佳子波进行地震反演,在淮南张集煤矿西三采区地震反演中,获得了满意的地质效果。
关键词:地震反演;子波提取;误差图中图分类号:P 63114 文献标识码:A0 前言地震反演就是利用观测数据恢复地下地质结构和岩石性质的方法,狭义地说,反演就是从有限频带宽度的地震数据中恢复出宽带波阻抗,因此地震反演通常特指波阻抗反演。
波阻抗反演技术是岩性地震勘探的重要手段之一,它可以把具有高纵向分辨率的测井资料,与连续好的地震资料联系起来,实现优势互补,从而大大提高了三维地震资料的纵向、横向分辨率和对地下地质情况的勘探研究程度[1~3]。
当前,Strata 地震反演系统是煤田地震反演中应用最广泛的地震反演系统[4~9]。
在地震反演过程中,子波提取是最复杂的问题之一。
Strata 地震反演系统中提供了以下三种提取子波的方法:(1)利用地震资料提取子波。
(2)利用测井资料提取子波。
(3)利用地震资料与测井资料联合提取子波[10、11]。
但在大多情况下,这三种方法提取的子波很少能真正符合或接近正确的地震子波,因而会造成不小的计算误差。
子波基本理论与提取方法
1地震子波基本原理
由震源激发、经地下传播并被人们在地面或井中接收到的地震波通常是一个短的脉冲振动,称该振动为振动子波。
它可以理解为有确定起始时间和有限能量,在很短时间内衰减的一个信号。
地震子波其振动的一个根本属性是振动的非周期性。
因此,它的动力学参数应有别于描述周期振动的振幅、频率、相位等参数,而用振幅谱、相位谱等概念来描述。
子波一般是物理可实现的,特别是地震子波,作为一个物理滤波器的响应函数,自然是物理可实现的,所有必定为非零相子波,但不同子波相位延迟不同。
子波包括最小相位子波、最大相位子波、混合相位子波。
子波的Z 变换是一个多项式:
n n z b z b z b b z B ++++=...)(221
若此多项式的全部零点均在单位圆外,则为最小相位子波;在单位圆内,为最大相位子波;零点在单位圆的内外都有,则为混合相位子波。
2地震子波的数学模型
实际中的地震子波是一个很复杂的问题,因为地震子波与地层岩石性质有关,地层岩石性质本身就是一个复杂体。
为了研究方便,仍需要对地震子波进行模拟,目前普遍认为雷克提出的地震子波数学模型具有广泛的代表性,即称雷克子波。
最小相位的地震子波的数学模型为:
ft e t b at π2sin )(2-=
式中:f 为子波的主频;)ln(22M f =α为子波衰减系数;|/|21m m M =为最
大波峰值1m 和最大波谷值2m 之对比。
其波形大致如图所示:
3地震子波提取的基本方法
地震子波的提取方法有两大类:第一类是确定性子波提取方法;第二类是统计性子波提取方法。
确定性子波提取方法指的是利用测井资料首先计算出反射系
数序列,然后结合井旁地震道由褶积理论求出地震子波,它的优点是不需要对反射系数序列的分布作任何假设,能得到较为准确的子波,而统计性方法的优点是不需要测井信息也可以得到子波的估计,但缺点是需对所用的地震资料和地下的反射系数序列的分布进行某种假设,所得子波理论上的精度不是高很。
正是由于这个原因,所以本文将分别最这两种方法进行C 语言的编程实现,来对统计性子波提取方法和确定性子波进行地震信号反褶积的效果作一下对比和演示。
4统计性子波提取方法原理
虽然子波一般是未知的,但地震记录中包含有子波,因此,可以从地震记录中求取子波。
虽然目前求取地震子波的方法也很多,但下面还是介绍一下统计求取子波方法。
若将子波作为一般信号对待,则子波也可用)(t s 表示,假设反射系数是随机的白噪序列,则有地震记录)(t x 的自相关和子波)(t s 的自相关相等,于是有记录的振幅谱|)(|ωX 和子波的振幅谱|)(|ωS 相等
|)(||)(|ωωX S =
及其对数也相等
|)(|ln |)(|ln ωωX S =
理论已证明,当子波为最小相位时,其对数谱序列(或称复赛谱))(n S ∧
是因果序列
ωωππωππ
d e S n S j ⎰-∧=|)(|ln 1)( 由于|)(|ln ωS 为实偶函数,因此)(n S ∧是实的因果序列。
任何实序列都可写成奇部和偶部序列之和,故)(n S ∧可写成:
)()()(n e S n o S n S ∧∧∧+= 即子波对数谱序列)(n S ∧的奇部)(n o S ∧和偶部)(n e S ∧
有下述两个性质:
第一,由于)(n S ∧
的因果性,起奇部和偶部有如下关系
)()()(n e S n sign n o S ∧∧=
)()()()()(n n o S n o S n sign n e S δ∧∧∧+= 式中,
1 0>n
=)(n sign 0 0=n
-1 0<n
第二,)(n S ∧
的偶部和奇部的傅里叶变换为其傅里叶变换的实部和虚部。
设)(n S ∧的傅里叶变换为)(Re )(f i S f r S ∧∧=,)(Im )(f S f i S ∧∧=,)(f S ∧为子波的对数谱,则
)()()(f i S i f r S f S ∧
∧∧+= 由傅里叶变换性质有
)()(f e S n e S F ∧∧=⎥⎦
⎤⎢⎣⎡ )()(f o S i n o S F ∧∧=⎥⎦
⎤⎢⎣⎡ 故有
)()()(f i S i f r S f S ∧
∧∧+= )()(f o S i f e S ∧
∧+=
即
)()(f r S f e S ∧∧=
)()(f i S f o S ∧∧= 于是求子波的方法可归结为:
1)用多道统计的方法获得可靠的子波对数谱的实部。
由子波谱
πωωωj e S S |)(|)(=
则有
|)(|ln )(ωωS S =∧
)(|)(|ln ωϕωi S +=
由若干道振幅谱的几何平均(或多道记录的相关函数平均)确定子波振幅谱的对数谱|)(|ln ωS 。
2)由子波振幅谱对数求子波相位谱)(|ωϕ。
计算公式为
)(|)(|ln n e S S IFT ∧
→ω
)()()(n e S n sign n o S ∧∧=
)()(ωϕFT n o S →∧ 3)计算子波)(t S 。
由)(ωS 及)(ωϕ得
)(|)(|)(t S e S S FT
j →=πωωω
由于干扰的影响和反射系数序列不完全相关性,故需对子波的振幅谱和相位谱进行整形处理,另外,这种方法理论上仅适应最小相位的情况,为适应混合相位记录,可以先采用指数滤波的方法使地震记录最小相位化,再对求取的子波进行反向指数加权。