主动土压力计算表格
- 格式:xls
- 大小:18.00 KB
- 文档页数:2

标题:深度探讨主动土压力和被动土压力的计算方法在土木工程和建筑领域,土压力是一个重要且复杂的问题。
主动土压力和被动土压力作为其中的重要概念,对土壤力学和结构设计有着重要的影响。
本文将深入探讨主动土压力和被动土压力的计算方法,并结合实际案例和Excel计算进行详细的分析和阐述。
一、主动土压力的计算1. 主动土压力的定义主动土压力是指土壤对于支撑结构施加的压力,通常是指土壤对于墙体的侧向压力。
在土木工程中,主动土压力是结构设计中必须考虑的重要参数之一。
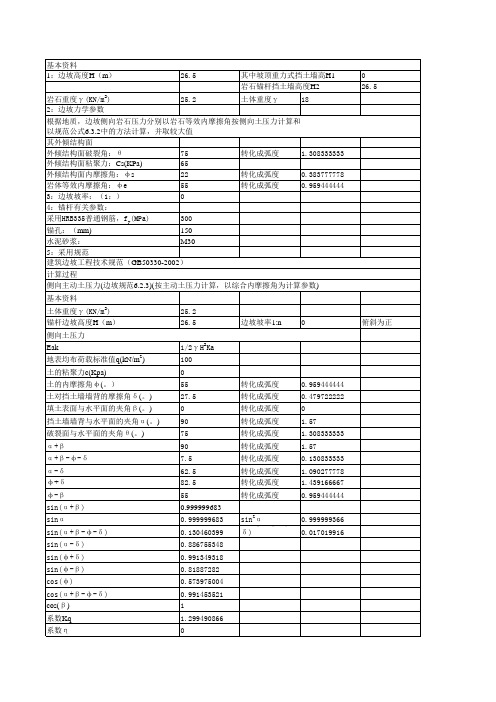
2. 主动土压力的计算公式根据土力学的理论,主动土压力可以通过柯尔蒂斯公式来计算,公式如下:KaγH^2/2其中,Ka是土压力系数,γ是土的单位重,H是土壤高度。
通过这一公式,我们可以简单快速地计算出主动土压力的大小。
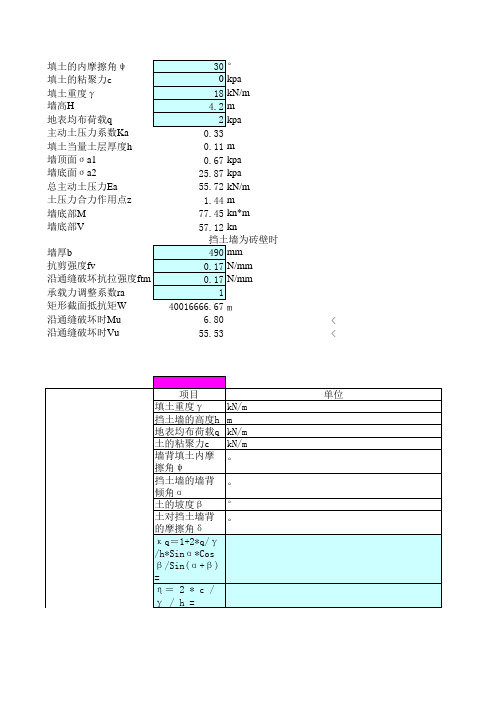
3. 实际案例分析举例来说,我们可以考虑一个简单的挡土墙结构,墙高5米,土的单位重为18kN/m³,土压力系数为0.35。
通过柯尔蒂斯公式的计算,我们可以得出挡土墙所受的主动土压力大小为315kN。
这个例子展示了主动土压力的计算方法以及其在实际工程中的应用。
二、被动土压力的计算1. 被动土压力的定义被动土压力是指支撑结构对土壤施加的反向压力,通常是指土壤对于桩基或承台的侧向压力。
在基础工程中,被动土压力是一个关键的设计参数。
2. 被动土压力的计算公式根据土力学的理论,被动土压力可以通过阿基米德原理来计算,公式如下:KpγH^2/2同样,其中Kp是土压力系数,γ是土的单位重,H是土壤高度。
通过这一公式,我们可以准确地计算出被动土压力的大小。
3. 实际案例分析假设我们有一个桩基基础工程,桩的长度为15米,土的单位重为20kN/m³,土压力系数为0.4。
通过阿基米德原理的计算,我们可以得出桩基所受的被动土压力大小为900kN。
这个例子展示了被动土压力的计算方法以及其在实际工程中的应用。
三、个人观点和总结回顾通过本文的深入探讨,我们了解了主动土压力和被动土压力的计算方法,并且结合实际案例进行了详细的分析。

主动土压力和被动土压力计算公式(一)主动土压力和被动土压力计算公式1. 主动土压力计算公式•主动土压力表示土体对结构物外表面施加的压力,一般为土体的推力。
•主动土压力计算公式通常根据不同的土体力学模型选择不同的计算方法。
Coulomb法则•Coulomb法则是主动土压力计算的一种常用方法,适用于强砂土和礁岩土质。
•Coulomb法则的计算公式为:P a=K a⋅γ⋅H⋅(1+sinδ)(1−sinδ)–P a表示主动土压力–K a表示活动土压力系数–γ表示土体的体积重度–H表示土体高度–δ表示土体的内摩擦角示例•假设一段高度为10米的砂土墙,砂土的重度为18kN/m³,内摩擦角为30°,求主动土压力。
•已知数据:–H=10m–γ=18kN/m³–δ=30°将•根据Coulomb法则的计算公式可得:P a=K a⋅γ⋅H⋅(1+sinδ)(1−sinδ)已知数据代入计算可得:P a=K a⋅18kN/m³⋅10m⋅(1+sin30°)(1−sin30°)偏应力曲线法•偏应力曲线法也是常用的主动土压力计算方法,适用于软黏土和弱砂土质。
•偏应力曲线法的计算公式为:P a=K a⋅γ⋅H⋅c⋅tan(ϕ′+ϕ)–P a表示主动土压力–K a表示活动土压力系数–γ表示土体的体积重度–H表示土体高度–c表示土体的凝聚力–ϕ′表示土体的内摩擦角–ϕ表示土体的地下水位倾角示例•假设一段高度为8米的软黏土墙,土体的重度为19kN/m³,凝聚力为35kPa,内摩擦角为20°,地下水位倾角为5°,求主动土压力。
•已知数据:–H=8m–γ=19kN/m³–c=35kPa–ϕ′=20°–ϕ=5°•根据偏应力曲线法的计算公式可得:P a=K a⋅γ⋅H⋅c⋅tan(ϕ′+ϕ)将已知数据代入计算可得:P a=K a⋅19kN/m³⋅8m⋅35kPa⋅tan(20°+5°)2. 被动土压力计算公式•被动土压力表示土体对结构物内表面施加的压力,一般为土体的抗力。


[ 指南] 土体主动、主动土压力概念及计算公式主动土压力挡土墙向前移离填土,随着墙的位移量的逐渐增大,土体作用于墙上的土压力逐渐减小,当墙后土体达到主动极限平衡状态并出现滑动面时,这时作用于墙上的土压力减至最小,称为主动土压力P。
a被动土压力挡土墙在外力作用下移向填土,随着墙位移量的逐渐增大,土体作用于墙上的土压力逐渐增大,当墙后土体达到被动极限平衡状态并出现滑动面时,这时作用于墙上的土压力增至最大,称为被动土压力P。
上述三种土压力的移动情况和它们在相同条件下的数值比较,p可用图6-2 来表示。
由图可知P,P,P。
poa朗肯基本理论朗肯土压力理论是英国学者朗肯(Rankin)1857 年根据均质的半无限土体的应力状态和土处于极限平衡状态的应力条件提出的。
在其理论推导中, 首先作出以下基本假定。
(1) 挡土墙是刚性的墙背垂直;(2) 挡土墙的墙后填土表面水平;(3) 挡土墙的墙背光滑,不考虑墙背与填土之间的摩擦力。
把土体当作半无限空间的弹性体,而墙背可假想为半无限土体内部的铅直平面,根据土体处于极限平衡状态的条件,求出挡土墙上的土压力。
如果挡土墙向填土方向移动压缩土体,Z仍保持不变,但Z将不断增大并超过Z值,ZXZ当土墙挤压土体使z增大到使土体达到被动极限平衡状态时,如图6-4的应力园O, Z x3z变为小主应力,Z变为大主应力,即为朗肯被动土压力(p) 。
土体中产生的两组破裂面与xp,45:, 水平面的夹角为。
2 朗肯主动土压力的计算根据土的极限平衡条件方程式,,2 Z =Z tg(45?+)+2c?tg(45?+) 1322,,2 Z =Z tg(45?-)-2c?tg(45?-) 3122土体处于主动极限平衡状态时,Z = Z =Y z, Z = Z =p,代入上式得1z3xa1) 填土为粘性土时填土为粘性土时的朗肯主动土压力计算公式为,,2,ap= 丫ztg(45?-)-2c?tg(45?-)= 丫zK-2c (6-3) aa22由公式(6-3) ,可知,主动土压力p 沿深度Z 呈直线分布,如图6-5 所示。

主动土压力挡土墙向前移离填土,随着墙的位移量的逐渐增大,土体作用于墙上的土压力逐渐减小,当墙后土体达到主动极限平衡状态并出现滑动面时,这时作用于墙上的土压力减至最小,称为主动土压力P a 。
被动土压力挡土墙在外力作用下移向填土,随着墙位移量的逐渐增大,土体作用于墙上的土压力逐渐增大,当墙后土体达到被动极限平衡状态并出现滑动面时,这时作用于墙上的土压力增至最大,称为被动土压力P p 。
上述三种土压力的移动情况和它们在相同条件下的数值比较,可用图6-2来表示。
由图可知P p >P o >P a 。
朗肯基本理论朗肯土压力理论是英国学者朗肯(Rankin )1857年根据均质的半无限土体的应力状态和土处于极限平衡状态的应力条件提出的。
在其理论推导中,首先作出以下基本假定。
(1)挡土墙是刚性的墙背垂直; (2)挡土墙的墙后填土表面水平;(3)挡土墙的墙背光滑,不考虑墙背与填土之间的摩擦力。
把土体当作半无限空间的弹性体,而墙背可假想为半无限土体内部的铅直平面,根据土体处于极限平衡状态的条件,求出挡土墙上的土压力。
如果挡土墙向填土方向移动压缩土体,σz 仍保持不变,但σx 将不断增大并超过σz 值,当土墙挤压土体使σx 增大到使土体达到被动极限平衡状态时,如图6-4的应力园O 3,σz 变为小主应力,σx 变为大主应力,即为朗肯被动土压力(p p )。
土体中产生的两组破裂面与水平面的夹角为245ϕ-︒。
朗肯主动土压力的计算根据土的极限平衡条件方程式σ1=σ3tg 2(45°+2ϕ)+2c ·tg(45°+2ϕ) σ3=σ1tg 2(45°-ϕ)-2c ·tg(45°-ϕ)当z=H 时p a =γHK a -2cK a在图中,压力为零的深度z 0,可由p a =0的条件代入式(6-3)求得a0K c 2z γ=(6-4)在z 0深度范围内p a 为负值,但土与墙之间不可能产生拉应力,说明在z 0深度范围内,填土对挡土墙不产生土压力。

土体主动、主动土压力概念及计算公式[ 指南] 土体主动、主动土压力概念及计算公式主动土压力挡土墙向前移离填土,随着墙的位移量的逐渐增大,土体作用于墙上的土压力逐渐减小,当墙后土体达到主动极限平衡状态并出现滑动面时,这时作用于墙上的土压力减至最小,称为主动土压力P。
a 被动土压力挡土墙在外力作用下移向填土,随着墙位移量的逐渐增大,土体作用于墙上的土压力逐渐增大,当墙后土体达到被动极限平衡状态并出现滑动面时,这时作用于墙上的土压力增至最大,称为被动土压力P。
上述三种土压力的移动情况和它们在相同条件下的数值比较,p 可用图6-2 来表示。
由图可知P,P,P。
poa朗肯基本理论朗肯土压力理论是英国学者朗肯(Rankin)1857 年根据均质的半无限土体的应力状态和土处于极限平衡状态的应力条件提出的。
在其理论推导中, 首先作出以下基本假定。
(1) 挡土墙是刚性的墙背垂直;(2) 挡土墙的墙后填土表面水平;(3) 挡土墙的墙背光滑,不考虑墙背与填土之间的摩擦力。
把土体当作半无限空间的弹性体,而墙背可假想为半无限土体内部的铅直平面,根据土体处于极限平衡状态的条件,求出挡土墙上的土压力。
如果挡土墙向填土方向移动压缩土体,Z仍保持不变,但Z将不断增大并超过Z值,ZXZ当土墙挤压土体使z增大到使土体达到被动极限平衡状态时,如图6-4的应力园O, Z x3z变为小主应力,Z变为大主应力,即为朗肯被动土压力(p) 。
土体中产生的两组破裂面与xp,45:, 水平面的夹角为。
2 朗肯主动土压力的计算根据土的极限平衡条件方程式,,2 Z =Z tg(45?+)+2c?tg(45?+) 1322,,2 Z =Z tg(45?-)-2c?tg(45?-) 3122土体处于主动极限平衡状态时,Z = Z =Y z, Z = Z =p,代入上式得1z3xa1) 填土为粘性土时填土为粘性土时的朗肯主动土压力计算公式为,,2,ap= 丫ztg(45?-)-2c?tg(45?-)= 丫zK-2c (6-3) aa22由公式(6-3) ,可知,主动土压力p 沿深度Z 呈直线分布,如图6-5 所示。

[指南]土体主动、主动土压力概念及计算公式主动土压力挡土墙向前移离填土,随着墙的位移量的逐渐增大,土体作用于墙上的土压力逐渐减小,当墙后土体达到主动极限平衡状态并出现滑动面时,这时作用于墙上的土压力减至最小,称为主动土压力P。
a被动土压力挡土墙在外力作用下移向填土,随着墙位移量的逐渐增大,土体作用于墙上的土压力逐渐增大,当墙后土体达到被动极限平衡状态并出现滑动面时,这时作用于墙上的土压力增至最大,称为被动土压力P。
上述三种土压力的移动情况和它们在相同条件下的数值比较,p可用图6-2来表示。
由图可知P,P,P。
poa朗肯基本理论朗肯土压力理论是英国学者朗肯(Rankin)1857年根据均质的半无限土体的应力状态和土处于极限平衡状态的应力条件提出的。
在其理论推导中,首先作出以下基本假定。
(1)挡土墙是刚性的墙背垂直;(2)挡土墙的墙后填土表面水平;(3)挡土墙的墙背光滑,不考虑墙背与填土之间的摩擦力。
把土体当作半无限空间的弹性体,而墙背可假想为半无限土体内部的铅直平面,根据土体处于极限平衡状态的条件,求出挡土墙上的土压力。
如果挡土墙向填土方向移动压缩土体,ζ仍保持不变,但ζ将不断增大并超过ζ值,zxz当土墙挤压土体使ζ增大到使土体达到被动极限平衡状态时,如图6-4的应力园O,ζx3z变为小主应力,ζ变为大主应力,即为朗肯被动土压力(p)。
土体中产生的两组破裂面与xp,45:,水平面的夹角为。
2朗肯主动土压力的计算根据土的极限平衡条件方程式,,2ζ=ζtg(45?+)+2c?tg(45?+) 1322,,2ζ=ζtg(45?-)-2c?tg(45?-) 3122土体处于主动极限平衡状态时,ζ=ζ=γz,ζ=ζ=p,代入上式得 1z3xa1)填土为粘性土时填土为粘性土时的朗肯主动土压力计算公式为,,2,ap=γztg(45?-)-2c?tg(45?-)=γzK-2c (6-3) aa22由公式(6-3),可知,主动土压力p沿深度Z呈直线分布,如图6-5所示。

主动土压力挡土墙向前移离填土,随着墙的位移量的逐渐增大,土体作用于墙上的土压力逐渐减小,当墙后土体达到主动极限平衡状态并出现滑动面时,这时作用于墙上的土压力减至最小,称为主动土压力P a 。
被动土压力挡土墙在外力作用下移向填土,随着墙位移量的逐渐增大,土体作用于墙上的土压力逐渐增大,当墙后土体达到被动极限平衡状态并出现滑动面时,这时作用于墙上的土压力增至最大,称为被动土压力P p 。
上述三种土压力的移动情况和它们在相同条件下的数值比较,可用图6-2来表示。
由图可知P p >P o >P a 。
朗肯基本理论朗肯土压力理论是英国学者朗肯(Rankin )1857年根据均质的半无限土体的应力状态和土处于极限平衡状态的应力条件提出的。
在其理论推导中,首先作出以下基本假定。
(1)挡土墙是刚性的墙背垂直; (2)挡土墙的墙后填土表面水平;(3)挡土墙的墙背光滑,不考虑墙背与填土之间的摩擦力。
把土体当作半无限空间的弹性体,而墙背可假想为半无限土体内部的铅直平面,根据土体处于极限平衡状态的条件,求出挡土墙上的土压力。
如果挡土墙向填土方向移动压缩土体,σz 仍保持不变,但σx 将不断增大并超过σz 值,当土墙挤压土体使σx 增大到使土体达到被动极限平衡状态时,如图6-4的应力园O 3,σz 变为小主应力,σx 变为大主应力,即为朗肯被动土压力(p p )。
土体中产生的两组破裂面与水平面的夹角为245ϕ-︒。
朗肯主动土压力的计算根据土的极限平衡条件方程式当z=H 时p a =γHK a -2cK a在图中,压力为零的深度z 0,可由p a =0的条件代入式(6-3)求得a0K c 2z γ=(6-4)在z 0深度范围内p a 为负值,但土与墙之间不可能产生拉应力,说明在z 0深度范围内,填土对挡土墙不产生土压力。
墙背所受总主动土压力为P a ,其值为土压力分布图中的阴影部分面积,即γ+-γ=--γ=22c 2K cH 2K H 21)z H )(K c 2HK (21P a a 0a a a (6-5)2)填土为无粘性土(砂土)时根据极限平衡条件关系方程式,主动土压力为a a zK )245(ztg p 2γ=ϕ-︒γ= (6-6)上式说明主动土压力P a 沿墙高呈直线分布,即土压力为三角形分布,如图6-6所示。

土体主动、主动土压力概念及计算公式[指南]土体主动、主动土压力概念及计算公式主动土压力挡土墙向前移离填土,随着墙的位移量的逐渐增大,土体作用于墙上的土压力逐渐减小,当墙后土体达到主动极限平衡状态并出现滑动面时,这时作用于墙上的土压力减至最小,称为主动土压力P。
a 被动土压力挡土墙在外力作用下移向填土,随着墙位移量的逐渐增大,土体作用于墙上的土压力逐渐增大,当墙后土体达到被动极限平衡状态并出现滑动面时,这时作用于墙上的土压力增至最大,称为被动土压力P。
上述三种土压力的移动情况和它们在相同条件下的数值比较,p 可用图6-2来表示。
由图可知P,P,P。
poa朗肯基本理论朗肯土压力理论是英国学者朗肯(Rankin)1857年根据均质的半无限土体的应力状态和土处于极限平衡状态的应力条件提出的。
在其理论推导中,首先作出以下基本假定。
(1)挡土墙是刚性的墙背垂直;(2)挡土墙的墙后填土表面水平;(3)挡土墙的墙背光滑,不考虑墙背与填土之间的摩擦力。
把土体当作半无限空间的弹性体,而墙背可假想为半无限土体内部的铅直平面,根据土体处于极限平衡状态的条件,求出挡土墙上的土压力。
如果挡土墙向填土方向移动压缩土体,ζ仍保持不变,但ζ将不断增大并超过ζ值,zxz当土墙挤压土体使ζ增大到使土体达到被动极限平衡状态时,如图6-4的应力园O,ζx3z变为小主应力,ζ变为大主应力,即为朗肯被动土压力(p)。
土体中产生的两组破裂面与xp,45:,水平面的夹角为。
2朗肯主动土压力的计算根据土的极限平衡条件方程式,,2ζ=ζtg(45?+)+2c?tg(45?+) 1322,,2ζ=ζtg(45?-)-2c?tg(45?-) 3122土体处于主动极限平衡状态时,ζ=ζ=γz,ζ=ζ=p,代入上式得1z3xa1)填土为粘性土时填土为粘性土时的朗肯主动土压力计算公式为,,2,ap=γztg(45?-)-2c?tg(45?-)=γzK-2c (6-3) aa22由公式(6-3),可知,主动土压力p沿深度Z呈直线分布,如图6-5所示。

[指南]土体主动、主动土压力概念及计算公式主动土压力挡土墙向前移离填土,随着墙的位移量的逐渐增大,土体作用于墙上的土压力逐渐减小,当墙后土体达到主动极限平衡状态并出现滑动面时,这时作用于墙上的土压力减至最小,称为主动土压力P。
a被动土压力挡土墙在外力作用下移向填土,随着墙位移量的逐渐增大,土体作用于墙上的土压力逐渐增大,当墙后土体达到被动极限平衡状态并出现滑动面时,这时作用于墙上的土压力增至最大,称为被动土压力P。
上述三种土压力的移动情况和它们在相同条件下的数值比较,p可用图6-2来表示。
由图可知P,P,P。
poa朗肯基本理论朗肯土压力理论是英国学者朗肯(Rankin)1857年根据均质的半无限土体的应力状态和土处于极限平衡状态的应力条件提出的。
在其理论推导中,首先作出以下基本假定。
(1)挡土墙是刚性的墙背垂直;(2)挡土墙的墙后填土表面水平;(3)挡土墙的墙背光滑,不考虑墙背与填土之间的摩擦力。
把土体当作半无限空间的弹性体,而墙背可假想为半无限土体内部的铅直平面,根据土体处于极限平衡状态的条件,求出挡土墙上的土压力。
如果挡土墙向填土方向移动压缩土体,ζ仍保持不变,但ζ将不断增大并超过ζ值,zxz当土墙挤压土体使ζ增大到使土体达到被动极限平衡状态时,如图6-4的应力园O,ζx3z变为小主应力,ζ变为大主应力,即为朗肯被动土压力(p)。
土体中产生的两组破裂面与xp,45:,水平面的夹角为。
2朗肯主动土压力的计算根据土的极限平衡条件方程式,,2ζ=ζtg(45?+)+2c?tg(45?+) 1322,,2ζ=ζtg(45?-)-2c?tg(45?-) 3122土体处于主动极限平衡状态时,ζ=ζ=γz,ζ=ζ=p,代入上式得 1z3xa1)填土为粘性土时填土为粘性土时的朗肯主动土压力计算公式为,,2,ap=γztg(45?-)-2c?tg(45?-)=γzK-2c (6-3) aa22由公式(6-3),可知,主动土压力p沿深度Z呈直线分布,如图6-5所示。