小学奥数之环形跑道专题

小升初奥数行程问题-环形跑道经典例题
小升初奥数行程问题-环形跑道经典例题
经典例题
例1、运动场的跑道一圈长400m，甲骑自行车每分钟490m；乙
跑步平均每分钟跑250m。

两人从同一地点同时同向出发，至少经过
多少分钟两人又同时到达起点？
例2、甲乙两车同时从同一点A出发，沿周长6千米的圆形跑道
以相反的方向行驶。

甲车每小时行驶65千米，乙车每小时行驶55
千米。

一旦两车迎面相遇，则乙车立刻调头；一旦甲车从后面追上
乙车，则甲车立刻调头，那么两车出发后第11次相遇的地点距离A
点有多少米？(每一次甲车追上乙车也看作一次相遇)
例4、一个圆的周长为90厘米，三个点把这个圆圈分成三等分，3只甲虫A、B、C按顺时针方向分别在这三个点上，它们同时按顺
时针方向沿着圆爬行，A的速度为每秒10厘米，B的速度为每秒5
厘米，C的速度为每秒3厘米。

问3只甲虫爬出多少时间后第一次
到达同一位置？
例5、如图在400米的跑道上有A、B两点相距170米，甲乙同
时分别从A、B两点出发，顺时针方向跑步。

每秒钟甲跑5米，乙跑
4米，两人每跑100米，都要休息10秒。

甲需多少秒才能追上乙？。

1、 掌握如下两个关系：（1）环形跑道问题同一地点出发，如果是相向而行，则每合走一圈相遇一次（2）环形跑道问题同一地点出发，如果是同向而行，则每追上一圈相遇一次2、遇见多人多次相遇、追及能够借助线段图进行分析3、用比例解、数论等知识解环形跑道问题本讲中的行程问题是特殊场地行程问题之一。

是多人（一般至少两人）多次相遇或追及的过程解决多人多次相遇与追击问题的关键是看我们是否能够准确的对题目中所描述的每一个行程状态作出正确合理的线段图进行分析。

一、在做出线段图后，反复的在每一段路程上利用：路程和=相遇时间×速度和路程差=追及时间×速度差二、解环形跑道问题的一般方法：环形跑道问题，从同一地点出发，如果是相向而行，则每合走一圈相遇一次；如果是同向而行，则每追上一圈相遇一次．这个等量关系往往成为我们解决问题的关键。

环线型同一出发点直径两端 同向：路程差nS nS + 相对(反向)：路程和nS模块一、常规的环形跑道问题【例 1】 一个圆形操场跑道的周长是500米，两个学生同时同地背向而行．黄莺每分钟走66米，麻雀每分钟走59米．经过几分钟才能相遇【考点】行程问题之环形跑道 【难度】2星 【题型】解答【解析】 黄莺和麻雀每分钟共行6659125+=（千米），那么周长跑道里有几个125米，就需要几分钟，即500(6659)5001254÷+=÷=（分钟）．【答案】4分钟【巩固】 周老师和王老师沿着学校的环形林荫道散步，王老师每分钟走55米，周老师每分钟走65米。

已知林荫道周长是480米，他们从同一地点同时背向而行。

在他们第10次相遇后，王老师再走 米就回到出发点。

【考点】行程问题之环形跑道 【难度】2星 【题型】填空【关键词】希望杯,4年级,1试【解析】 几分钟相遇一次：480÷（55＋65）=4（分钟）知识精讲 教学目标环形跑道问题10次相遇共用：4×10=40（分钟）王老师40分钟行了：55×40=2200（米）2200÷480=4（圈）……280（米）所以正好走了4圈还多280米，480－280=200（米）答：再走200米回到出发点。

2019年小学奥数应用题专题——环形跑道问题1．一个圆形操场跑道的周长是500米，两个学生同时同地背向而行．黄莺每分钟走66米，麻雀每分钟走59米．经过几分钟才能相遇?2．小张和小王各以一定速度，在周长为500米的环形跑道上跑步．小王的速度是200米/分．⑴小张和小王同时从同一地点出发，反向跑步，1分钟后两人第一次相遇，小张的速度是多少米/分？⑵小张和小王同时从同一点出发，同一方向跑步，小张跑多少圈后才能第一次追上小王？3．(2019年第八届“春蕾杯”小学数学邀请赛决赛)上海小学有一长300米长的环形跑道，小亚和小胖同时从起跑线起跑，小亚每秒钟跑6米，小胖每秒钟跑4米，(1)小亚第一次追上小胖时两人各跑了多少米？(2)小亚第二次追上小胖两人各跑了多少圈？4．一条环形跑道长400米，甲骑自行车每分钟骑450米，乙跑步每分钟250米，两人同时从同地同向出发，经过多少分钟两人相遇？5．小新和正南在操场上比赛跑步，小新每分钟跑250米，正南每分钟跑210米，一圈跑道长800米，他们同时从起跑点出发，那么小新第三次超过正南需要多少分钟？6．幸福村小学有一条200米长的环形跑道，冬冬和晶晶同时从起跑线起跑，冬冬每秒钟跑6米，晶晶每秒钟跑4米，问冬冬第一次追上晶晶时两人各跑了多少米，第2次追上晶晶时两人各跑了多少圈？第1页/共25页7．在300米的环形跑道上，田奇和王强同学同时同地起跑，如果同向而跑2分30秒相遇，如果背向而跑则半分钟相遇，求两人的速度各是多少？8．在400米的环形跑道上，甲、乙两人同时同地起跑，如果同向而行3分20秒相遇，如果背向而行40秒相遇，已知甲比乙快，求甲、乙的速度各是多少？9．两名运动员在湖的周围环形道上练习长跑．甲每分钟跑250米，乙每分钟跑200米，两人同时同地同向出发，经过45分钟甲追上乙；如果两人同时同地反向出发，经过多少分钟两人相遇？10．(第4届希望杯培训题)在环形跑道上，两人在一处背靠背站好，然后开始跑，每隔4分钟相遇一次；如果两人从同处同向同时跑，每隔20分钟相遇一次，已知环形跑道的长度是1600米，那么两人的速度分别是多少？11．两人在环形跑道上跑步，两人从同一地点出发，小明每秒跑3米，小雅每秒跑4米，反向而行，45秒后两人相遇。

小学奥数环形跑道典型试题1.甲和乙两人分别从一圆形场地的直径两端点同时开始以匀速按相反的方向绕此圆形路线运动，当乙走了100米以后，他们第一次相遇，在甲走完一周前60米处又第二次相遇.求此圆形场地的周长．2．在一圆形跑道上，甲从 A 点、乙从 B 点同时出发反向而行，6 分后两人相遇，再过4 分甲到达 B 点，又过 8 分两人再次相遇.甲、乙环行一周各需要多少分？3．如下图所示的三条圆形跑道，每条跑道的长都是0.5千米，A、B、C三位运动员同时从交点O出发，分别沿三条跑道跑步，他们的速度分别是每小时4千米，每小时8千米，每小时6千米。

问：从出发到三人第一次相遇，他们共跑了多少千米？CB AO4．甲、乙二人在同一条椭圆形跑道上作特殊训练：他们同时从同一地点出发，沿相反方向跑，每人跑完第一圈到达出发点后立即回头加速跑第二圈，跑第一圈时，乙的速度是甲速度的2/3.甲跑第二圈时速度比第一圈提高了1/3；乙跑第二圈时速度提高了1/5．已知沿跑道看从甲、乙两人第二次相遇点到第一次相遇点的最短路程是190米，那么这条椭圆形跑道长多少米?5.在一个周长为90CM的园上，三只小虫分别从三等分园的ABC三点同时同向出发沿圆周爬行，已知A点小虫速度为10CM/秒，B点小虫速度为5CM/秒，C点小虫速度为3CM/秒，求3只小虫出发后多久第一次到达同一位置？6．丁丁和乐乐各拿了一辆玩具甲虫在400米跑道上进行比赛，丁丁的玩具甲虫每分钟跑30米，乐乐的玩具甲虫每分钟跑20米，但乐乐带了一个神秘遥控器，按第一次会使丁丁的玩具甲虫以原来速度的10%倒退1分钟，按第二次会使丁丁的玩具甲虫以原来速度的20%倒退1分钟，以此类推，按第N次，使丁丁的玩具甲虫以原来的速度的10%N倒退1分钟，然后再按原来的速度继续前进，如果乐乐在比赛中最后获胜，他最少按几次遥控器7.甲，乙两人沿400米环形跑道练习跑步，两人同时从跑道的同一地点向相反方向跑去。

第13讲第一天1.高高、途途两人在300米长的环形跑道上跑步，若同时同地背向出发，高高的速度是每秒2米，途途的速度是每秒3米，那么出发后（ ）秒，两人第10次相遇。

A.300B.540C.600D.700 【答案】C【解析】300÷（2＋3）×10＝600（秒）。

2.乐乐、快快两人在400米长的环形跑道上跑步，若同时同地背向出发，乐乐的速度是每秒5米，快快的速度是每秒3米，那么出发后（ ）秒，两人第12次相遇。

A.500B.600C.550D.650【答案】B【解析】400÷（5＋3）×12＝600（秒）。

第二天1.黑猫、白猫在400米的环形跑道上跑步，从相距100米的地方，同时出发，背向而行。

黑猫每秒跑6米，白猫每秒跑4米，出发后（ ）秒，两只猫第二次相遇。

A.60B.50C.40D.70【答案】D【解析】（400－100）÷（6＋4）＋400÷（6＋4）＝70（秒）。

100米白猫2.小山羊、小绵羊在640米的环形跑道上跑步，从相距160米的地方，同时出发，背向而行。

小山羊每秒跑5米，小绵羊每秒跑3米。

那么，出发后（）秒，小山羊第三次和小绵羊相遇。

A.220B.240C.260D.280【答案】A【解析】（640－160）÷（5＋3）＋640÷（5＋3）×2＝220（秒）。

第三天：1.OK博士和懒懒狮两人在240米长的环形跑道上跑步，同时同地同向出发。

OK 博士的速度是每分钟跑300米，懒懒狮的速度是每分钟180米，那么出发后（）秒，OK博士第5次追上懒懒狮。

A.400B.200C.600D.500【答案】C【解析】240÷（300－180）×5×60＝600（秒）。

2.高高、OK博士两人在300米长的环形跑道上跑步，同时同地同向出发。

高高的速度是每秒2米，OK博士的速度是每秒5米，那么出发后（）秒，OK博士第10次追上高高。

小学奥数：环形跑道问题环形跑道:同相向而行的等量关系:乙程-甲程=跑道长,背向而行的等量关系:乙程+甲程=跑道长。

一个周长为400米的正方形ABCD跑道,甲在B点，乙在A点，甲的速度是每秒25米，乙的速度是是每秒5米，问多长时间后甲乙第一次相遇？分析：因为是环形跑道，所以方向为逆时针，还是顺时针，不知道，所以需要分类讨论.（对于不确定的事情，又合理的问题需要分类讨论）逆时针时：可以转化为一般形成问题中的相遇问题。

把BC、CD、AD拉直，问题转化为一般的行程问题：转化为甲乙相向而行的相遇过程，其中相距的路程是300米.等量关系：甲的路程+乙的路程=相距路顺时针时：分析：因为甲的速度快，乙的速度慢，乙是追不上甲的，要想相遇，必须是甲追上乙，转化行程问题的追及问题：依上图，问题可以转化为：甲在A点，乙在B点，同时向右跑的追及问题，开始甲乙相距300米.等量关系：甲的路程-乙行的路程=相距路程转化为一般的行程问题后，问题可以迎刃而解。

这里体现了一个数学思想---转化思想，把未知的知识转化为已知的知识，把复杂的问题，转化为简单的问题，是获得新知的一个很重要的手段。

1.甲、乙两人从400米的环形跑道上一点A背向同时出发，8分钟后两人第五次相遇，已知每秒钟甲比乙多走0.1米，那么两人第五次相遇的地点与点A沿跑道上的最短路程是多少米；2.二人沿一周长400米的环形跑道均速前进，甲行一圈4分钟，乙行一圈7分钟，他们同时同地同向出发，甲走10圈，改反向出发，每次甲追上乙或迎面相遇时二人都要击掌。

问第十五次击掌时，甲走多长时间乙走多少路程？3.林玲在450米长的环形跑道上跑一圈，已知他前一半时间每秒跑5米，后一半时间每秒跑4米，那么他后一半路程跑了多少秒？4.某人在360米的环形跑道上跑了一圈，已知他前一半时间每秒跑5米，后一半时间每秒跑4米，则他后一半路程跑了多少秒？5.一条环形跑道长400米，小青每分钟跑260米，小兰每分钟跑210米，两人同时出发，经过多少分钟两人相遇（不用解方程）6.两人在环形跑道上跑步，两人从同一地点出发，小明每秒跑3米，小雅每秒跑4米，反向而行，45秒后两人相遇。

【导语】海阔凭你跃，天⾼任你飞。

愿你信⼼满满，尽展聪明才智;妙笔⽣花，谱下锦绣第⼏篇。

学习的敌⼈是⾃⼰的知⾜，要使⾃⼰学⼀点东西，必需从不⾃满开始。

以下是为⼤家整理的《⼩学奥数环形跑道练习及答案【三篇】》供您查阅。

【第⼀篇】在⼀个圆形跑道上，甲从A点、⼄从B点同时出发反向⽽⾏，8分钟后两⼈相遇，再过6分钟甲到B点，⼜过10分钟两⼈再次相遇，则甲环⾏⼀周需要()？ A.24分钟 B.26分钟 C.28分钟 D.30分钟 解析：选择C。

甲、⼄两⼈从第⼀次相遇到第⼆次相遇，⽤了6+10=16分钟。

也就是说，两⼈16分钟⾛⼀圈。

从出发到两⼈第⼀次相遇⽤了8分钟，所以两⼈共⾛半圈，即从A到B是半圈，甲从A到B⽤了8+6=14分钟，故甲环⾏⼀周需要14×2=28分钟。

也是⼀个倍数关系。

【第⼆篇】甲、⼄两⼈环绕周长400⽶的跑道跑步，如果两⼈从同⼀地点出发背向⽽⾏，那么经过2分钟相遇，如果两⼈从同⼀地点出发同向⽽⾏，那么经过20分钟两⼈相遇，已知甲的速度⽐⼄快，求甲、⼄两⼈跑步的速度各是多少？ 分析： ①由两⼈从同⼀地点出发背向⽽⾏，经过2分钟相遇知两⼈每分钟共⾏：400÷2=200(⽶)； ②由两⼈从同⼀地点出发同向⽽⾏，经过20分钟相遇知甲每分钟⽐⼄多⾛：400÷20=20(⽶)； 根据和差问题的解法可知：200⽶再加上20⽶即甲的速度的2倍，或200减去20⽶即是⼄速度的2倍，由此列式解答即可. 解答：解：(400÷2+400÷20)÷2， =220÷2， =110(⽶)； 400÷2-110=90(⽶)； 答：甲每分钟跑110⽶，⼄每分钟跑90⽶. 点评：此题属于追及应⽤题，做此题的关键是结合题意，根据路程、速度和时间的关系，进⾏列式解答即可得出结论.【第三篇】例题：在⼀个圆形跑道上，甲从A点、⼄从B点同时出发反向⽽⾏，8分钟后两⼈相遇，再过6分钟甲到B点，⼜过10分钟两⼈再次相遇，则甲环⾏⼀周需要()？ A.24分钟 B.26分钟 C.28分钟 D.30分钟 解析：选择C。

行程问题——环形跑道环形跑道问题就是封闭路线上的追及问题,关键是要掌握从并行到下次追及的路程差恰好是一圈的长度。

1、相遇问题：题型特点:甲、乙两人同时从同地反向出发。

解题规律：两人相遇时一起走一圈（跑道周长）。

之后每见面一次，就一起走1圈；见面n次,两人一起走n个周长。

2、追及问题:题型特点：甲、乙两人同时从同地同向出发。

解题规律:开始出发时由于速度不同两人之间的距离会越来越远，之后快的会追上慢的，此时快的人比慢的人多走1圈(路程差为跑道周长）。

之后每追上一次，就多走1圈；追上n次，快的就比慢的多走n个周长。

3、需要处理的问题：a、环形跑道中速度、时间、路程之间的关系处理。

b、多次追及问题的处理。

c、不同地点出发的追及问题.1、一个圆形荷花池的周长为400米，甲、乙两人绕荷花池顺时针跑步。

甲每分钟跑250米，乙每分钟跑200米，现在甲在乙后面50米，甲第二次追上乙需要多少分钟？2、一条环形跑道长400米，小青每分钟跑260米，小兰每分钟跑140米，两人同时反向出发，经过几分钟两人相遇？3、上海小学有一长300米长的环形跑道,小亚和小胖同时从起跑线起跑，小亚每秒钟跑6米,小胖每秒钟跑4米，小亚第一次追上小胖时,小胖跑了多少米？4、幸福村小学有一条200米长的环形跑道,冬冬和晶晶同时从起跑线起跑,冬冬每秒钟跑6米，晶晶每秒钟跑4米,问冬冬第2次追上晶晶时，冬冬跑了多少圈？5、甲、乙二人骑自行车从环形公路上的同一地点出发，背向而行.现在已知甲走一圈的时间为75分钟，如果在出发后第50分钟甲、乙两人相遇，那么乙走一圈的时间是多少分钟？6、甲、乙二人骑自行车从环形公路上同一地点同时出发，背向而行.现在已知甲走一圈的时间是70 分钟，如果在出发后45分钟甲、乙二人相遇，那么乙走一圈的时间是多少分钟?7、两名运动员在湖的周围环形道上练习长跑．甲每分钟跑250米,乙每分钟跑200米,两人同时同地同向出发，经过45分钟甲追上乙；如果两人同时同地反向出发，经过几分钟两人相遇?8、在400米的环形跑道上,甲、乙两人同时同地起跑，如果同向而行3分20秒相遇，如果背向而行40秒相遇,已知甲比乙快，求甲的速度是多少米/秒？9、环形跑道的周长是800米，甲乙两名运动员同时顺时针自起点出发，甲的速度是每分钟400米，乙的速度是每分钟375米。

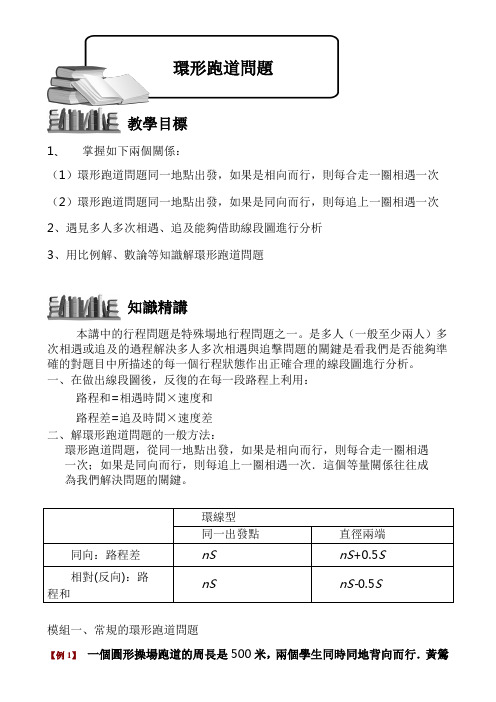
1、 掌握如下兩個關係： （1）環形跑道問題同一地點出發，如果是相向而行，則每合走一圈相遇一次（2）環形跑道問題同一地點出發，如果是同向而行，則每追上一圈相遇一次2、遇見多人多次相遇、追及能夠借助線段圖進行分析3、用比例解、數論等知識解環形跑道問題本講中的行程問題是特殊場地行程問題之一。

是多人（一般至少兩人）多次相遇或追及的過程解決多人多次相遇與追擊問題的關鍵是看我們是否能夠準確的對題目中所描述的每一個行程狀態作出正確合理的線段圖進行分析。

一、在做出線段圖後，反復的在每一段路程上利用：路程和=相遇時間×速度和路程差=追及時間×速度差二、解環形跑道問題的一般方法：環形跑道問題，從同一地點出發，如果是相向而行，則每合走一圈相遇一次；如果是同向而行，則每追上一圈相遇一次．這個等量關係往往成為我們解決問題的關鍵。

環線型 同一出發點 直徑兩端 同向：路程差nS nS +0.5S 相對(反向)：路程和 nS nS-0.5S模組一、常規的環形跑道問題【例 1】 一個圓形操場跑道的周長是500米，兩個學生同時同地背向而行．黃鶯知識精講 教學目標環形跑道問題每分鐘走66米，麻雀每分鐘走59米．經過幾分鐘才能相遇?【巩固】周老師和王老師沿著學校的環形林蔭道散步，王老師每分鐘走55米，周老師每分鐘走65米。

已知林蔭道周長是480米，他們從同一地點同時背向而行。

在他們第10次相遇後，王老師再走米就回到出發點。

【例 2】上海小學有一長300米長的環形跑道，小亞和小胖同時從起跑線起跑，小亞每秒鐘跑6米，小胖每秒鐘跑4米，(1)小亞第一次追上小胖時兩人各跑了多少米？(2)小亞第二次追上小胖兩人各跑了多少圈？【巩固】小張和小王各以一定速度，在周長為500米的環形跑道上跑步．小王的速度是200米/分．⑴小張和小王同時從同一地點出發，反向跑步，1分鐘後兩人第一次相遇，小張的速度是多少米/分？⑵小張和小王同時從同一點出發，同一方向跑步，小張跑多少圈後才能第一次追上小王？【巩固】一條環形跑道長400米，甲騎自行車每分鐘騎450米，乙跑步每分鐘250米，兩人同時從同地同向出發，經過多少分鐘兩人相遇？【巩固】小新和正南在操場上比賽跑步，小新每分鐘跑250米，正南每分鐘跑210米，一圈跑道長800米，他們同時從起跑點出發，那麼小新第三次超過正南需要多少分鐘？【巩固】幸福村小學有一條200米長的環形跑道，冬冬和晶晶同時從起跑線起跑，冬冬每秒鐘跑6米，晶晶每秒鐘跑4米，問冬冬第一次追上晶晶時兩人各跑了多少米，第2次追上晶晶時兩人各跑了多少圈？【巩固】小明和小剛清晨來到學校操場練習跑步，學校操場是400米的環形跑道，小剛對小明說：“咱們比比看誰跑的快”，於是兩人同時同向起跑，結果10分鐘後小明第一次從背後追上小剛，同學們一定知道誰跑得快了，小明的速度是每分鐘跑140米，那麼如果小明第3次從背後追上小剛時，小剛一共跑了米．【巩固】如圖1，有一條長方形跑道，甲從A點出發，乙從C點同時出發，都按順時針方向奔跑，甲每秒跑5米，乙每秒跑4.5米。

小学奥数系列3-2-4环形跑道问题（二）一、环形跑道问题1. A、B是圆的直径的两端，甲在A点，乙在B点同时出发反向而行，两人在C点第一次相遇，在D点第二次相遇．已知C离A有75米，D离B有55米，求这个圆的周长是多少米？2. 两辆电动小汽车在周长为360米的圆形道上不断行驶，甲车每分行驶20米．甲、乙两车同时分别从相距90米的A，B 两点相背而行，相遇后乙车立即返回，甲车不改变方向，当乙车到达B点时，甲车过B点后恰好又回到A点．此时甲车立即返回（乙车过B点继续行驶），再过多少分与乙车相遇？3. 周长为400米的圆形跑道上，有相距100米的A、B两点．甲、乙两人分别从A，B两点同时相背而跑，两人相遇后，乙即转身与甲同向而跑，当甲跑到A时，乙恰好跑到B．如果以后甲、乙跑的速度和方向都不变，那么甲追上乙时，甲从出发开始，共跑了多少米?4. 在一圆形跑道上，甲从 A 点、乙从 B 点同时出发反向而行，6 分后两人相遇，再过4 分甲到达 B 点，又过 8 分两人再次相遇.甲、乙环行一周各需要多少分？5. 甲、乙两车同时从同一点出发，沿周长6千米的圆形跑道以相反的方向行驶．甲车每小时行驶65千米，乙车每小时行驶55千米．一旦两车迎面相遇，则乙车立刻调头；一旦甲车从后面追上一车，则甲车立刻调头，那么两车出发后第11次相遇的地点距离有多少米？6. 甲、乙二人沿一周长400米的环形跑道均速前进，甲行一圈4分钟，乙行一圈7分钟，他们同时同地同向出发，甲走1 0圈，改反向出发，每次甲追上乙或迎面相遇时二人都要击掌。

问第十五次击掌时，甲走多长时间、乙走多少路程？7. 如图所示，某单位沿着围墙外面的小路形成一个边长300米的正方形．甲、乙两人分别从两个对角处沿逆时针方向同时出发．如果甲每分走90米，乙每分走70米，那么经过多少时间甲才能看到乙？8. 如图，一个长方形的房屋长13米，宽8米．甲、乙两人分别从房屋的两个墙角出发，甲每秒钟行3米，乙每秒钟行2米.问：经过多长时间甲第一次看见乙?9. 如图，在400米的环形跑道上，A，B两点相距100米。

小学奥数之环形跑道问题练习题及答案1.在400米的环形跑道上，A、B两点相距100米，。

甲、乙两人分别从A、B两点同时出发，按照逆时针方向跑步，甲每秒跑5米，乙每秒跑4米，每人每跑100米，都要停10秒钟。

那么，甲追上乙需要的时间是多少秒?答案：假设没有休息那么100/(5—4)=100秒钟在100/5=20秒100/20-1=4(次)100+4*10=140秒2.小明在360米的环形跑道上跑一圈，已知他前半时间每秒跑5米，后半时间每秒跑4米，为他后半路程用了多少时间?答案：x÷4=(360-x)÷5×=160(360÷2-160)÷5+160÷4=44分3.林琳在450吗长的环形跑道上跑一圈，已知她前一半时间每秒跑5米，后一半时间每秒跑4米，那么她的后一半路程跑了多少秒答案：设总时间为X，则前一半的时间为X/2，后一半时间同样为X/2X/2*5+X/2*4=360X=80总共跑了80秒前40秒每秒跑5米，40秒后跑了200米后40秒每秒跑4米，40秒后跑了160米后一半的路程为360/2=180米后一半的路程用的时间为(200-180)/5+40=44秒【篇二】小君在360米长的环形跑道上跑一圈。

已知他前一半时间每秒跑5米，后一半时间每秒跑4米。

那么小君后一半路程用了多少秒?答案：设时间X秒5X=360-4X9X=360X=40后一半时间的路程=40*4=160米后一半路程=360/2=180米后一半路程用每秒跑5米路程=180-160=20米后一半路程用每秒跑5米时间=20/5=4秒后一半路程时间=4+40=44秒答：后一半路程用了44秒小明在420米长的环形跑道上跑了一圈，已知他前一半时间每秒跑8米，后一半时间每秒跑6米.求他后一半路程用了多少时间?答案：设总用时X秒。

前一半时间和后一半时间都是X/2。

然后前一半跑8*(X/2)米，后一半跑6*(X/2)米，总共加起来等于420米。

六年级奥数题及答案-跑道
导语：六年级既是我们学习的冲刺阶段，又是我们为升学打基础的关键时期，所以同学们一定要抓住每一次练习的机会，给自己增强实力。

环形跑道周长是500米，甲、乙两人从起点按顺时针方向同时出发.甲每分跑120米，乙每分跑100米，两人都是每跑200米停下休息1分.甲第一次追上乙需多少分?
答案与解析：
甲比乙多跑500米，应比乙多休息2次，即2分.在甲多休息的2分内，乙又跑了200米，所以在与甲跑步的相同时间里，甲比乙多跑500+200=700(米)，甲跑步的时间为700÷(120-100)=35(分).共跑了120×35=4200(米)，中间休息了4200÷200-1=20(次)，即20分.所以甲第一次追上乙需35+20=55(分).。

小学奥数应用题专题--环形跑道问题（六年级）竞赛测试姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题评卷人得分（每空xx 分，共xx分）【题文】一个圆形操场跑道的周长是500米，两个学生同时同地背向而行．黄莺每分钟走66米，麻雀每分钟走59米．经过几分钟才能相遇?【答案】4【解析】黄莺和麻雀每分钟共行（千米），那么周长跑道里有几个米，就需要几分钟，即（分钟）．【题文】小张和小王各以一定速度，在周长为米的环形跑道上跑步．小王的速度是米/分．⑴小张和小王同时从同一地点出发，反向跑步，分钟后两人第一次相遇，小张的速度是多少米/分？⑵小张和小王同时从同一点出发，同一方向跑步，小张跑多少圈后才能第一次追上小王？【答案】300 3【解析】⑴两人相遇，也就是合起来跑了一个周长的行程．小张的速度是（米/分）．⑵在环形的跑道上，小张要追上小王，就是小张比小王多跑一圈（一个周长），因此需要的时间是：（分）．（圈）．【题文】 (2008年第八届“春蕾杯”小学数学邀请赛决赛)上海小学有一长米长的环形跑道，小亚和小胖同时从起跑线起跑，小亚每秒钟跑米，小胖每秒钟跑米，小亚第一次追上小胖时两人各跑了多少米？小亚第二次追上小胖两人各跑了多少圈？【答案】900 600,4 6【解析】第一次追上时，小亚多跑了一圈，所以需要秒，小亚跑了（米）。

小胖跑了（米）；第一次追上时，小胖跑了圈，小亚跑了圈，所以第二次追上时，小胖跑圈，小亚跑圈。

【题文】一条环形跑道长400米，甲骑自行车每分钟骑450米，乙跑步每分钟250米，两人同时从同地同向出发，经过多少分钟两人相遇？【答案】2【解析】(分钟)．【题文】小新和正南在操场上比赛跑步，小新每分钟跑250米，正南每分钟跑210米，一圈跑道长800米，他们同时从起跑点出发，那么小新第三次超过正南需要多少分钟？【答案】60【解析】小新第一次超过正南是比正南多跑了一圈，根据，可知小新第一次超过正南需要：(分钟)，第三次超过正南是比正南多跑了三圈，需要(分钟)．【题文】幸福村小学有一条200米长的环形跑道，冬冬和晶晶同时从起跑线起跑，冬冬每秒钟跑6米，晶晶每秒钟跑4米，问冬冬第一次追上晶晶时两人各跑了多少米，第2次追上晶晶时两人各跑了多少圈？【答案】600 400,6 4【解析】这是一道封闭路线上的追及问题，冬冬与晶晶两人同时同地起跑，方向一致．因此，当冬冬第一次追上晶晶时，他比晶晶多跑的路程恰是环形跑道的一个周长(200米)，又知道了冬冬和晶晶的速度，于是，根据追及问题的基本关系就可求出追及时间以及他们各自所走的路程．①冬冬第一次追上晶晶所需要的时间：(秒)②冬冬第一次追上晶晶时他所跑的路程应为：(米)③晶晶第一次被追上时所跑的路程：(米)④冬冬第二次追上晶晶时所跑的圈数：(圈)⑤晶晶第2次被追上时所跑的圈数：(圈)【题文】在300米的环形跑道上，田奇和王强同学同时同地起跑，如果同向而跑2分30秒相遇，如果背向而跑则半分钟相遇，求两人的速度各是多少？【答案】4 6【解析】同向而跑，这实质是快追慢．起跑后，由于两人速度的差异，造成两人路程上的差异，随着时间的增长，两人间的距离不断拉大，到两人相距环形跑道的半圈时，相距最大．接着，两人的距离又逐渐缩小，直到快的追上慢的，此时快的比慢的多跑了一圈．背向而跑即所谓的相遇问题，数量关系为：路程和速度和相遇时间．同向而行2分30秒相遇，2分30秒＝150秒，两个人的速度和为：（米/秒），背向而跑则半分钟即30秒相遇，所以两个人的速度差为：（米/秒）.两人的速度分别为：(米/秒)，(米/秒)【题文】在400米的环形跑道上，甲、乙两l【解析】在封闭的环形道上同向运动属追及问题，反向运动属相遇问题．同地出发，其实追及路程或相隔距离就是环形道一周的长．这道题的解题关键就是先求出环形道一周的长度．环形道一周的长度可根据两人同向出发，45分钟后甲追上乙，由追及问题，两人速度差为：(米/分)，所以路程差为：(米)，即环形道一圈的长度为2250米．所以反向出发的相遇时间为：(分钟)．【题文】 (第4届希望杯培训题)在环形跑道上，两人在一处背靠背站好，然后开始跑，每隔4分钟相遇一次；如果两人从同处同向同时跑，每隔20分钟相遇一次，已知环形跑道的长度是1600米，那么两人的速度分别是多少？【答案】240 160【解析】两人反向沿环形跑道跑步时，每隔4分钟相遇一次，即两人4分钟共跑完一圈；当两人同向跑步时，每20分钟相遇一次，即其中的一人比另一人多跑一圈需要20分钟．两人速度和为：(米/分)，两人速度差为：(米/分)，所以两人速度分别为：(米/分)，(米/分)【题文】两人在环形跑道上跑步，两人从同一地点出发，小明每秒跑3米，小雅每秒跑4米，反向而行，45秒后两人相遇。

环形跑道问题教学目标1、掌握如下两个关系：（1）环形跑道问题同一地点出发，如果是相向而行，则每合走一圈相遇一次（2）环形跑道问题同一地点出发，如果是同向而行，则每追上一圈相遇一次2、遇见多人多次相遇、追及能够借助线段图进行分析3、用比例解、数论等知识解环形跑道问题知识精讲本讲中的行程问题是特殊场地行程问题之一.是多人（一般至少两人）多次相遇或追及的过程解决多人多次相遇与追击问题的关键是看我们是否能够准确的对题目中所描述的每一个行程状态作出正确合理的线段图进行分析.一、在做出线段图后，反复的在每一段路程上利用：路程和=相遇时间×速度和路程差=追及时间×速度差二、解环形跑道问题的一般方法：环形跑道问题，从同一地点出发，如果是相向而行，则每合走一圈相遇一次；如果是同向而行，则每追上一圈相遇一次．这个等量关系往往成为我们解决问题的关键.环线型同一出发点直径两端同向：路程差nS nS+0.5S 相对(反向)：路程和nS nS-0.5S模块一、常规的环形跑道问题【例 1】一个圆形操场跑道的周长是500米，两个学生同时同地背向而行．黄莺每分钟走66米，麻雀每分钟走59米．经过几分钟才能相遇?【巩固】周老师和王老师沿着学校的环形林荫道散步，王老师每分钟走55米，周老师每分钟走65米.已知林荫道周长是480米，他们从同一地点同时背向而行.在他们第10次相遇后，王老师再走米就回到出发点.【例 2】上海小学有一长300米长的环形跑道，小亚和小胖同时从起跑线起跑，小亚每秒钟跑6米，小胖每秒钟跑4米，(1)小亚第一次追上小胖时两人各跑了多少米？(2)小亚第二次追上小胖两人各跑了多少圈？【巩固】小张和小王各以一定速度，在周长为500米的环形跑道上跑步．小王的速度是200米/分．⑴小张和小王同时从同一地点出发，反向跑步，1分钟后两人第一次相遇，小张的速度是多少米/分？⑵小张和小王同时从同一点出发，同一方向跑步，小张跑多少圈后才能第一次追上小王？【巩固】一条环形跑道长400米，甲骑自行车每分钟骑450米，乙跑步每分钟250米，两人同时从同地同向出发，经过多少分钟两人相遇？【巩固】小新和正南在操场上比赛跑步，小新每分钟跑250米，正南每分钟跑210米，一圈跑道长800米，他们同时从起跑点出发，那么小新第三次超过正南需要多少分钟？【巩固】幸福村小学有一条200米长的环形跑道，冬冬和晶晶同时从起跑线起跑，冬冬每秒钟跑6米，晶晶每秒钟跑4米，问冬冬第一次追上晶晶时两人各跑了多少米，第2次追上晶晶时两人各跑了多少圈？【巩固】小明和小刚清晨来到学校操场练习跑步，学校操场是400米的环形跑道，小刚对小明说：“咱们比比看谁跑的快”，于是两人同时同向起跑，结果10分钟后小明第一次从背后追上小刚，同学们一定知道谁跑得快了，小明的速度是每分钟跑140米，那么如果小明第3次从背后追上小刚时，小刚一共跑了米．【巩固】如图1，有一条长方形跑道，甲从A点出发，乙从C点同时出发，都按顺时针方向奔跑，甲每秒跑5米，乙每秒跑4.5米.当甲第一次追上乙时，甲跑了圈.【例 3】两名运动员在湖的周围环形道上练习长跑．甲每分钟跑250米，乙每分钟跑200米，两人同时同地同向出发，经过45分钟甲追上乙；如果两人同时同地反向出发，经过多少分钟两人相遇？【巩固】两人在环形跑道上跑步，两人从同一地点出发，小明每秒跑3米，小雅每秒跑4米，反向而行，45秒后两人相遇.如果同向而行，几秒后两人再次相遇【巩固】一条环形跑道长400米，小青每分钟跑260米，小兰每分钟跑210米，两人同时出发，经过多少分钟两人相遇【巩固】甲、乙两人从400米的环形跑道上一点A背向同时出发，8分钟后两人第五次相遇，已知每秒钟甲比乙多走0.1米，那么两人第五次相遇的地点与点A沿跑道上的最短路程是多少米?【例 4】在300米的环形跑道上，田奇和王强同学同时同地起跑，如果同向而跑2分30秒相遇，如果背向而跑则半分钟相遇，求两人的速度各是多少？【巩固】在400米的环形跑道上，甲、乙两人同时同地起跑，如果同向而行3分20秒相遇，如果背向而行40秒相遇，已知甲比乙快，求甲、乙的速度各是多少？【例 5】周老师和王老师沿着学校的环形林荫道散步，王老师每分钟走55米，周老师每分钟走65米.已知林荫道周长是480米，他们从同一地点同时背向而行.在他们第10次相遇后，王老师再走米就回到出发点.【巩固】在周长为200米的圆形跑道—条直径的两端，甲、乙两人分别以6米/秒，5米/秒的骑车速度同时同向出发，沿跑道行驶.问：16分钟内，甲追上乙多少次?3【巩固】在环形跑道上，两人在一处背靠背站好，然后开始跑，每隔4分钟相遇一次；如果两人从同处同向同时跑，每隔20分钟相遇一次，已知环形跑道的长度是1600米，那么两人的速度分别是多少？【例 6】甲、乙二人在操场的400米跑道上练习竞走，两人同时出发，出发时甲在乙后面，出发后6分甲第一次超过乙，22分时甲第二次超过乙.假设两人的速度保持不变，问：出发时甲在乙后面多少米？【例 7】在400 米的环行跑道上，A，B 两点相距100 米.甲、乙两人分别从A，B 两点同时出发，按逆时针方向跑步.甲甲每秒跑 5 米，乙每秒跑 4 米，每人每跑100 米，都要停10 秒钟.那么甲追上乙需要时间是多少秒？【例 8】在环形跑道上，两人都按顺时针方向跑时，每12分钟相遇一次，如果两人速度不变，其中一人改成按逆时针方向跑，每隔4分钟相遇一次，问两人跑一圈各需要几分钟？【例 9】有甲、乙、丙3人，甲每分钟行走120米，乙每分钟行走100米，丙每分钟行走70米.如果3个人同时同向，从同地出发，沿周长是300米的圆形跑道行走，那么多少分钟之后，3人又可以相聚在跑道上同一处?【例 10】甲、乙二人骑自行车从环形公路上同一地点同时出发，背向而行.现在已知甲走一圈的时间是70分钟，如果在出发后45分钟甲、乙二人相遇，那么乙走一圈的时间是多少分钟?【例 11】林琳在450米长的环形跑道上跑一圈，已知她前一半时间每秒跑5米，后一半时间每秒跑4米，那么她的后一半路程跑了多少秒？【巩固】某人在360米的环形跑道上跑了一圈，已知他前一半时间每秒跑5米，后一半时间每秒跑4米，则他后一半路程跑了多少秒？【例 12】 甲、乙、丙在湖边散步，三人同时从同一点出发，绕湖行走，甲速度是每小时5.4千米， 乙速度是每小时4.2千米，她们二人同方向行走，丙与她们反方向行走，半个小时后甲和丙相遇，在过5分钟，乙与丙相遇.那么绕湖一周的行程是多少？【例 13】 甲和乙两人分别从圆形场地的直径两端点同时开始以匀速按相反的方向绕此圆形路线运动，当乙走了100米以后，他们第一次相遇，在甲走完一周前60米处又第二次相遇.求此圆形场地的周长？【巩固】 如图，A 、B 是圆的直径的两端，小张在A 点，小王在B 点同时出发反向行走，他们在C 点第一次相遇，C 离A 点80米；在D 点第二次相遇，D 点离B 点6O 米.求这个圆的周长.【巩固】 如图，有一个圆，两只小虫分别从直径的两端A 与C 同时出发，绕圆周相 向而行．它们第一次相遇在离A 点8厘米处的B 点，第二次相遇在离C 点处6厘米的D 点，问，这个圆周的长是多少?第一次相遇第二次相遇DC BA【巩固】 A 、B 是圆的直径的两端，甲在A 点，乙在B 点同时出发反向而行，两人在C 点第一次相遇，在D 点第二次相遇．已知C 离A 有75米，D 离B 有55米，求这个圆的周长是多少米？【例 14】两辆电动小汽车在周长为360米的圆形道上不断行驶，甲车每分行驶20米．甲、乙两车同时分别从相距90米的A，B两点相背而行，相遇后乙车立即返回，甲车不改变方向，当乙车到达B点时，甲车过B点后恰好又回到A点．此时甲车立即返回（乙车过B点继续行驶），再过多少分与乙车相遇？【巩固】周长为400米的圆形跑道上，有相距100米的A，B两点．甲、乙两人分别从A，B两点同时相背而跑，两人相遇后，乙即转身与甲同向而跑，当甲跑到A时，乙恰好跑到B ．如果以后甲、乙跑的速度和方向都不变，那么甲追上乙时，甲从出发开始，共跑了多少米?【巩固】在一圆形跑道上，甲从A 点、乙从B 点同时出发反向而行，6 分后两人相遇，再过4 分甲到达 B 点，又过8 分两人再次相遇.甲、乙环行一周各需要多少分？【例 15】如下图所示的三条圆形跑道，每条跑道的长都是0.5千米，A、B、C三位运动员同时从交点O 出发，分别沿三条跑道跑步，他们的速度分别是每小时4千米，每小时8千米，每小时6千米.问：从出发到三人第一次相遇，他们共跑了多少千米？CB AO【例 16】甲、乙两车同时从同一点A出发，沿周长6千米的圆形跑道以相反的方向行驶．甲车每小时行驶65千米，乙车每小时行驶55千米．一旦两车迎面相遇，则乙车立刻调头；一旦甲车从后面追上一车，则甲车立刻调头，那么两车出发后第11次相遇的地点距离有多少米？【巩固】二人沿一周长400米的环形跑道均速前进，甲行一圈4分钟，乙行一圈7分钟，他们同时同地同向出发，甲走10圈，改反向出发，每次甲追上乙或迎面相遇时二人都要击掌.问第十五次击掌时，甲走多长时间乙走多少路程？【例 17】下如右图所示，某单位沿着围墙外面的小路形成一个边长300米的正方形．甲、乙两人分别从两个对角处沿逆时针方向同时出发．如果甲每分走90米，乙每分走70米，那么经过多少时间甲才能看到乙？【巩固】如图，一个长方形的房屋长13米，宽8米．甲、乙两人分别从房屋的两个墙角出发，甲每秒钟行3米，乙每秒钟行2米.问:经过多长时间甲第一次看见乙?【例 18】下图是一个边长90米的正方形，甲、乙两人同时从A点出发，甲逆时针每分行75米，乙顺时针每分行45米．两人第一次在CD边（不包括C，D两点）上相遇，是出发以后的第几次相遇？【例 19】如图，8时10分，有甲、乙两人以相同的速度分别从相距60米的A，B两地顺时针方向沿长方形ABCD的边走向D点.甲8时20分到D点后，丙、丁两人立即以相同速度从D点出发.丙由D向A走去，8时24分与乙在E点相遇；丁由D向C走去，8时30分在F点被乙追上.问三角形BEF的面积为多少平方米?【例 20】甲、乙两人从周长为1600米的正方形水池ABCD相对的两个顶点A，C同时出发绕池边沿A→B→C→D→A的方向行走.甲每分行50米，乙每分行46米，甲、乙第一次在同一边上行走，是发生在出发后的第多少分？第一次在同一边上行走了多少分？【例 21】如图，长方形ABCD中AB∶BC=5∶4.位于A点的第一只蚂蚁按A→B→C→D→A的方向，位于C点的第二只蚂蚁按C→B→A→D→C的方向同时出发，分别沿着长方形的边爬行.如果两只蚂蚁第一次在B点相遇，则两只蚂蚁第二次相遇在()边上.(A)AB(B)BC(C)CD【例 22】在一个周长90厘米的圆上，有三个点将圆周三等分.A，B，C三个爬虫分别在这三点上，它们每秒依次爬行10厘米、5厘米、3厘米.如果它们同时出发按顺时针方向沿圆周爬行，那么它们第一次到达同一位置需多长时间？模块二、环形跑道——变道问题【例 23】如图2，一个边长为50米的正方形围墙，甲、乙两人分别从A、C两点同时出发，沿闹墙按顺时针方向运动，已知甲每秒走5米，乙每秒走3米，则至少经过秒甲、乙走到正方形的同一条边上.【例 24】如图是一个跑道的示意图，沿ACBEA走一圈是400米，沿ACBDA走一圈是275米，其中A到B 的直线距离是75米．甲、乙二人同时从A点出发练习长跑，甲沿ACBDA的小圈跑，每100米用24秒，乙沿ACBEA的大圈跑，每100米用21秒，问：⑴乙跑第几圈时第一次与甲相遇？⑵发多长时间甲、乙再次在A相遇？ADB【例 25】如图所示，大圈是400米跑道，由A到B的跑道长是200米，直线距离是50米.父子俩同时从A 点出发逆时针方向沿跑道进行长跑锻炼，儿子跑大圈，父亲每跑到B点便沿直线跑.父亲每100米用20秒，儿子每100米用19秒.如果他们按这样的速度跑，儿子在跑第几圈时，第一次与父亲相遇？A【例 26】 如图，学校操场的400米跑道中套着300米小跑道，大跑道与小跑道有200米路程相重．甲以每秒6米的速度沿大跑道逆时针方向跑，乙以每秒4米的速度沿小跑道顺时针方向跑，两人同时从两跑道的交点A 处出发，当他们第二次在跑道上相遇时，甲共跑了多少米?甲甲【例 27】 有一种机器人玩具装置，配备长、短不同的两条跑道，其中长跑道长400厘米，短跑道长300厘米，且有200厘米的公用跑道(如下图).机器人甲按逆时针方向以每秒6厘米的速度在长跑道上跑动，机器人乙按顺时针方向以每秒4厘米的速度在短跑道上跑动.如果甲、乙两个机器人同时从A 点出发，那么当两个机器人在跑道上第3次迎面相遇时，机器人甲距离出发点A 点多少厘米?200200【例 28】 下图是一个玩具火车轨道，A 点有个变轨开关，可以连接B 或者C . 小圈轨道的周长是1.5 米，大圈轨道的周长是3 米. 开始时，A 连接C ，火车从A 点出发，按照顺时针方向在轨道上移动，同时变轨开关每隔1 分钟变换一次轨道连接. 若火车的速度是每分钟10 米，则火车第10 次回到A 点时用了 秒钟.CB A【例 29】下图中有两个圆只有一个公共点A，大圆直径48厘米，小圆直径30厘米.两只甲虫同时从A点出发，按箭头所指的方向以相同速度分别沿两个圆爬行.问：当小圆上甲虫爬了几圈时，两只甲虫首次相距最远？【例 30】三个环行跑道如图排列，每个环行跑道周长为210厘米；甲、乙两只爬虫分别从A、B两地按箭头所示方向出发，甲爬虫绕1、2号环行跑道作“8”字形循环运动，乙爬虫绕3、2号环行跑道作“8”字形循环运动，已知甲、乙两只爬虫的速度分别为每分钟20厘米和每分钟l5厘米，甲、乙两爬虫第二次相遇时，甲爬虫爬了多少厘米?A231B【巩固】一个圆周长90厘米，3个点把这个圆周分成三等分，3只爬虫A，B，C分别在这3个点上．它们同时出发，按顺时针方向沿着圆周爬行．A的速度是10厘米/秒，B的速度是5厘米/秒，C的速度是3厘米/秒，3只爬虫出发后多少时间第一次到达同一位置？【例 31】如图所示，甲沿长为400米大圆的跑道顺时针跑步，乙则沿两个小圆八字形跑步(图中给出跑动路线的次序：12341-----）.如果甲、乙两人同时从A点出发，且甲、乙二人的速度分别是每秒3米和5米，问两人第三次相遇的时间是出发后秒.A4132B【例 32】如图，两个圆环形跑道，大圆环的周长为600米，小圆环的周长为400米.甲的速度为每秒6米，乙的速度为每秒4米.甲、乙二人同时由A点起跑，方向如图所示，甲沿大圆环跑一圈，就跑上小圆环，方向不变，沿小圆环跑一圈，又跑上大圆环，方向也不变；而乙只沿小圆环跑.问：甲、乙可能相遇的位置距离A点的路程是多少？(路程按甲跑的计算)甲模块三、环形跑道——变速问题【例 33】甲、乙两人沿400 米环形跑道练习跑步，两人同时从跑道的同一地点向相反方向跑去.相遇后甲比原来速度增加2 米／秒，乙比原来速度减少 2 米／秒，结果都用24 秒同时回到原地.求甲原来的速度.【例 34】环形跑道周长是500米，甲、乙两人从起点按顺时针方向同时出发.甲每分跑120米，乙每分跑100米，两人都是每跑200米停下休息1分.甲第一次追上乙需多少分？【例 35】甲、乙两人同时同地同向出发，沿环形跑道匀速跑步．如果出发时乙的速度是甲的2.5倍，当乙第一次追上甲时，甲的速度立即提高25%，而乙的速度立即减少20%，并且乙第一次追上甲的地点与第二次追上甲的地点相距100米，那么这条环形跑道的周长是米．【例 36】如图所示，甲、乙两人从长为400米的圆形跑道的A点背向出发跑步.跑道右半部分(粗线部分）道路比较泥泞，所以两人的速度都将减慢，在正常的跑道上甲、乙速度均为每秒8米，而在泥泞道路上两人的速度均为每秒4米.两人一直跑下去，问：他们第99次迎面相遇的地方距A点还有米.A【例 37】甲、乙二人在同一条椭圆形跑道上作特殊训练：他们同时从同一地点出发，沿相反方向跑，每人跑完第一圈到达出发点后立即回头加速跑第二圈，跑第一圈时，乙的速度是甲速度的2/3.甲跑第二圈时速度比第一圈提高了1/3；乙跑第二圈时速度提高了1/5．已知沿跑道看从甲、乙两人第二次相遇点到第一次相遇点的最短路程是190米，那么这条椭圆形跑道长多少米?【例 38】如图3-5，正方形ABCD是一条环形公路．已知汽车在AB上时速是90千米，在BC上的时速是120千米，在CD上的时速是60千米，在DA上的时速是80千米．从CD上一点P，同时反向各发出一辆汽车，它们将在AB中点相遇．如果从PC的中点M，同时反向各发出一辆汽车，它们将在AB上一点N相遇．问A至N的距离除以N至B的距离所得到的商是多少?【例 39】一条环形道路，周长为2千米．甲、乙、丙3人从同一点同时出发，每人环行2周．现有自行车2辆，乙和丙骑自行车出发，甲步行出发，中途乙和丙下车步行，把自行车留给其他人骑．已知甲步行的速度是每小时5千米，乙和丙步行的速度是每小时4千米，3人骑车的速度都是每小时20千米．请你设计一种走法，使3个人2辆车同时到达终点．那么环行2周最少要用多少分钟?。

环形跑道问题练习题（附答案和详解）1.在400M的环形跑道上，A、B两点相距100M，。

甲、乙两人分别从A、B两点同时出发，按照逆时针方向跑步，甲每秒跑5M，乙每秒跑4M，每人每跑100M，都要停10秒钟。

那么，甲追上乙需要的时间是多少秒？2.小明在360M的环形跑道上跑一圈，已知他前半时间每秒跑5M，后半时间每秒跑4M，为他后半路程用了多少时间？3.林琳在450吗长的环形跑道上跑一圈，已知她前一半时间每秒跑5M，后一半时间每秒跑4M，那么她的后一半路程跑了多少秒4.小君在360M长的环形跑道上跑一圈。

已知他前一半时间每秒跑5M，后一半时间每秒跑4M。

那么小君后一半路程用了多少秒？5.小明在420M长的环形跑道上跑了一圈，已知他前一半时间每秒跑8M，后一半时间每秒跑6M.求他后一半路程用了多少时间？6.二人沿一周长400M的环形跑道均速前进，甲行一圈4分钟，乙行一圈7分钟，他们同时同地同向出发，甲走10圈，改反向出发，每次甲追上乙或迎面相遇时二人都要击掌。

问第十五次击掌时，甲走多长时间乙走多少路程？7、乙两车同时从同一点出发，沿周长6千M的圆形跑道以相反的方向行驶．甲车每小时行驶65千M，乙车每小时行驶55千M．一旦两车迎面相遇，则乙车立刻调头；一旦甲车从后面追上乙车，则甲车立刻调头，那么两车出发后第11次相遇的地点距离点有多少M？(每一次甲车追上乙车也看作一次相遇)答案：1、答案：假设没有休息那么100/（5—4）=100秒钟在秒（次）100+4*10=140秒2、答案：x÷4=（360-x）÷5×=160（360÷2-160）÷5＋160÷4＝44分3、答案：设总时间为X，则前一半的时间为X/2，后一半时间同样为X/2X/2*5+X/2*4=360X=80总共跑了80秒前40秒每秒跑5M，40秒后跑了200M后40秒每秒跑4M，40秒后跑了160M后一半的路程为后一半的路程用的时间为（200-180）/5+40=44秒4、答案：设时间X秒5X=360-4X 9X=360 X=40后一半时间的路程=40*4=160M后一半路程用每秒跑5M路程=180-160=20M后一半路程用每秒跑5M时间=20/5=4秒后一半路程时间=4+40=44秒答：后一半路程用了44秒5、答案：设总用时X秒。

小学数学奥数竞赛环形跑道问题专项练习试卷及答案解析（20道）1、如图，8时10分,有甲、乙两人以相同的速度分别从相距60米的A，B两地顺时针方向沿长方形ABCD的边走向D点.甲8时20分到D点后,丙、丁两人立即以相同速度从D点出发.丙由D向A走去,8时24分与乙在E点相遇；丁由D向C走去，8时30分在F点被乙追上.问三角形BEF的面积为多少平方米?2、两辆电动小汽车在周长为360米的圆形道上不断行驶，甲车每分行驶20米．甲、乙两车同时分别从相距90米的A，B两点相背而行，相遇后乙车立即返回，甲车不改变方向，当乙车到达B点时，甲车过B点后恰好又回到A点．此时甲车立即返回（乙车过B点继续行驶），再过多少分与乙车相遇？3、在300米的环形跑道上，田奇和王强同学同时同地起跑，如果同向而跑2分30秒相遇，如果背向而跑则半分钟相遇，求两人的速度各是多少？4、两名运动员在湖的周围环形道上练习长跑．甲每分钟跑250米，乙每分钟跑200米，两人同时同地同向出发，经过45分钟甲追上乙；如果两人同时同地反向出发，经过多少分钟两人相遇？5、小张和小王各以一定速度，在周长为米的环形跑道上跑步．小王的速度是米/分．⑴小张和小王同时从同一地点出发，反向跑步，分钟后两人第一次相遇，小张的速度是多少米/分？⑵小张和小王同时从同一点出发，同一方向跑步，小张跑多少圈后才能第一次追上小王？6、甲和乙两人分别从圆形场地的直径两端点同时开始以匀速按相反的方向绕此圆形路线运动，当乙走了100米以后，他们第一次相遇，在甲走完一周前60米处又第二次相遇。

求此圆形场地的周长？7、林琳在450米长的环形跑道上跑一圈，已知她前一半时间每秒跑5米，后一半时间每秒跑4米，那么她的后一半路程跑了多少秒？8、甲、乙二人骑自行车从环形公路上同一地点同时出发，背向而行.现在已知甲走一圈的时间是70分钟，如果在出发后45分钟甲、乙二人相遇，那么乙走一圈的时间是多少分钟?9、甲、乙、丙在湖边散步，三人同时从同一点出发，绕湖行走，甲速度是每小时5.4千米，乙速度是每小时4.2千米，她们二人同方向行走，丙与她们反方向行走，半个小时后甲和丙相遇，在过5分钟，乙与丙相遇。