小学奥数：几何中的重叠问题.专项练习及答案解析

教学目标1. 了解容斥原理二量重叠和三量重叠的内容；2. 掌握容斥原理的在组合计数等各个方面的应用．知识要点一、两量重叠问题在一些计数问题中，经常遇到有关集合元素个数的计算．求两个集合并集的元素的个数，不能简单地把两个集合的元素个数相加，而要从两个集合个数之和中减去重复计算的元素个数，即减去交集的元素个数，用式子可表示成： A B A B A B （其中符号“ ”读作“并”，相当于中文“和”或者“或”的意思；符号“ 读作“交”，相当于中文“且”的意思．）则称这一公式为包含与排除原理，简称容斥原理．图示如下:A表示小圆部分，B表示大圆部分，C表示大圆与小圆的公共部分，记为： A B ，即阴影面积．图示如下: A表示小圆部分，B表示大圆部分，C表示大圆与小圆的公共部分，记为： A B ，即阴影面积．第一步：分别计算集合A、B的元素个数，然后加起来，即先1求A B （意思A是B把A、B 的一切元素都“包含”进来，加在一起）；第二步：从上面的和中减去交集的元素个数，即减去 C A B （意思是“排除”了重复计算的元素个数）．、三量重叠问题A类、B 类与C 类元素个数的总和A类元素的个数B类元素个数C 类元素个数既是A类又是B类的元素个数既是B类又是C类的元素个数既是A类又是C类的元素个数同时是A类、B类、C类的元素个数．用符号表示为：A B C A B C A B B C A C A B C ．图示如下：ABAB 包含与排除原理告诉我们，要计算两个集合A、B的并集 A B 的元素的个数，可分以下两步进行：ABC3ABC在解答有关包含排除问题时，我们常常利用圆圈图 （韦恩图 ）来帮助分析思考．例题精讲模块一、三量重叠问题例 1】 一栋居民楼里的住户每户都订了 2 份不同的报纸。

如果该居民楼的住户只订了甲、乙、丙三种报 纸，其中甲报 30 份，乙报 34 份，丙报 40份，那么既订乙报又订丙报的有 __________________ 户。

1. 瞭解容斥原理二量重疊和三量重疊的內容；2. 掌握容斥原理的在組合計數等各個方面的應用．一、兩量重疊問題 在一些計數問題中，經常遇到有關集合元素個數的計算．求兩個集合並集的元素的個數，不能簡單地把兩個集合的元素個數相加，而要從兩個集合個數之和中減去重複計算的元素個數，即減去交集的元素個數，用式子可表示成：A B A B A B =+-(其中符號“”讀作“並”，相當於中文“和”或者“或”的意思；符號“”讀作“交”，相當於中文“且”的意思．)則稱這一公式為包含與排除原理，簡稱容斥原理．圖示如下:A 表示小圓部分，B 表示大圓部分，C 表示大圓與小圓的公共部分，記為：A B ，即陰影面積．圖示如下:A 表示小圓部分，B 表示大圓部分，C 表示大圓與小圓的公共部分，記為：A B ，即陰影面積．包含與排除原理告訴我們，要計算兩個集合A B 、的並集AB 的元素的個數，可分以下兩步進行：第一步：分別計算集合A B 、的元素個數，然後加起來，即先求A B +(意思是把A B 、的一切元素都“包含”進來，加在一起)；第二步：從上面的和中減去交集的元素個數，即減去C AB =(意思是“排除”了重複計算的元素個數)． 二、三量重疊問題A 類、B 類與C 類元素個數的總和A =類元素的個數B +類元素個數C +類元素個數-既是A 類又是B 類的元素個數-既是B 類又是C 類的元素個數-既是A 類又是C 類的元素個數+同時是A 類、B 類、C 類的元素個數．用符號表示為：A B C A B C A B B C A C A B C =++---+．圖示如下：教學目標知識要點7-7-3.幾何中的重疊問題1．先包含——A B +重疊部分A B 計算了2次，多加了1次；2．再排除——A B A B +-把多加了1次的重疊部分A B 減去．在解答有關包含排除問題時，我們常常利用圓圈圖(韋恩圖)來幫助分析思考．【例 1】 把長38釐米和53釐米的兩根鐵條焊接成一根鐵條．已知焊接部分長4釐米，焊接後這根鐵條有多長？【考點】幾何中的重疊問題 【難度】1星 【題型】解答【解析】 因為焊接部分為兩根鐵條的重合部分，所以，由包含排除法知，焊接後這根鐵條長3853487+-=(釐米)．【答案】87釐米【巩固】 把長23釐米和37釐米的兩根鐵條焊接成一根鐵條．已知焊接部分長3釐米，焊接後這根鐵條有多長？【考點】幾何中的重疊問題 【難度】1星 【題型】解答【解析】 焊接部分為兩根鐵條的重合部分，由包含排除法知，焊接後這根鐵條長：2337357+-=(釐米)．【答案】57釐米【例 2】 兩張長4釐米，寬2釐米的長方形紙擺放成如圖所示形狀．把它放在桌面上，覆蓋面積有多少平方釐米？【考點】幾何中的重疊問題 【難度】1星 【題型】解答例題精講圖中小圓表示A 的元素的個數，中圓表示B 的元素的個數，大圓表示C 的元素的個數．1．先包含：A B C ++ 重疊部分A B 、B C 、C A 重疊了2次，多加了1次． 2．再排除：A B C A B B C A C ++--- 重疊部分A B C 重疊了3次，但是在進行A B C ++- A B B C A C --計算時都被減掉了． 3．再包含：A B C A B B C A C A B C ++---+．图32厘米4厘米【解析】 兩個長方形如圖擺放時出現了重疊(見圖中的陰影部分)，重疊部分恰好是邊長為2釐米的正方形，如果利用兩個42⨯的長方形面積之和來計算被覆蓋桌面的面積，那麼重疊部分在兩個長方形面積中各被計算了一次，而實際上這部分只需計算一次就可以了．所以，被覆蓋面積=長方形面積之和-重疊部分．於是，被覆蓋面積4222212=⨯⨯-⨯=(平方釐米)．【答案】12釐米【巩固】 如圖3，一張長8釐米，寬6釐米，另一個正方形邊長為6釐米，它們中間重疊的部分是一個邊長為4釐米的正方形，求這個組合圖形的面積．【考點】幾何中的重疊問題 【難度】1星 【題型】解答图3【解析】 兩個圖形如圖擺放時出現了重疊(見圖中的陰影部分)，重疊部分恰好是邊長為4釐米的正方形，如果利用長方形和正方形面積之和來計算被覆蓋桌面的面積，那麼重疊部分在長方形和正方形面積中各被計算了一次，而實際上這部分只需計算一次就可以了．所以，組合圖形的面積=長方形面積+正方形面積-重疊部分．於是，組合圖形的面積：86664468⨯+⨯-⨯=(平方釐米)．【答案】68平方釐米【巩固】 一個長方形長12釐米，寬8釐米，另一個長方形長10釐米，寬6釐米，它們中間重疊的部分是一個邊長4釐米的正方形，求這個組合圖形的面積．【考點】幾何中的重疊問題 【難度】1星 【題型】解答【解析】 兩個長方形如圖擺放時出現了重疊(見圖中的陰影部分)，重疊部分恰好是邊長為4釐米的正方形，如果利用兩個長方形面積之和來計算被覆蓋桌面的面積，那麼重疊部分在兩個長方形面積中各被計算了一次，而實際上這部分只需計算一次就可以了．所以，組合圖形的面積=長方形面積之和-重疊部分．於是，組合圖形的面積12810644140=⨯+⨯-⨯=(平方釐米)．【答案】140平方釐米【例 3】三個面積均為50平方釐米的圓紙片放在桌面上(如圖)，三個紙片共同重疊的面積是10平方釐米．三個紙片蓋住桌面的總面積是100釐米．問：圖中陰影部分面積之和是多少？【考點】幾何中的重疊問題【難度】2星【題型】解答C BA10【解析】將圖中的三個圓標上A、B、C．根據包含排除法，三個紙片蓋住桌面的總面積=(A圓面積B+圓面積C+圓面積-）（A與B重合部分面積A+與C重合部分面積B+與C重合部分面積+）三個紙片共同重疊的面積，得：100505050A=++-（）（與B重合部分面積A+與C重合部分面積B+與C重合部分面積10+），得到A、B、C三個圓兩兩重合面積之和為：16010060-=平方釐米，而這個面積對應於圓上的那三個紙片共同重疊的面積的三倍與陰影部分面積的和，即：60103=⨯+陰影部分面積，則陰影部分面積為：603030-=(平方釐米)．【答案】30平方釐米【巩固】如圖，已知甲、乙、丙3個圓的面積均為30，甲與乙、乙與丙、甲與丙重合部分的面積分別為6，8，5，而3個圓覆蓋的總面積為73．求陰影部分的面積．【考點】幾何中的重疊問題【難度】2星【題型】解答【解析】設甲圓組成集合A，乙圓組成集合B，丙圓組成集合C．A B C===30，A B=6，B C=8，A C=5，A B C=73，而A B C=A B C+--A B B C A C A B C--+.有73=30×3-6-8-5+A B C，即A B C=2，即甲、乙、丙三者的公共面積(⑧部分面積)為2．那麼只是甲與乙(④)，乙與丙(⑥)，甲與丙(⑤)的公共的面積依次為6-2=4，8-2=6，5-2=3，所以有陰影部分(①、②、③部分之和)的面積為73-4-6-3-2=58．【答案】58【例 4】如圖，三角形紙板、正方形紙板、圓形紙板的面積相等，都等於60平方釐米．陰影部分的面積總和是40平方釐米，3張板蓋住的總面積是100平方釐米，3張紙板重疊部分的面積是多少平方釐米？【考點】幾何中的重疊問題【難度】3星【題型】解答【解析】了三次．所以三張紙重疊部分的面積60310040220（）(平方釐米)．=⨯--÷=【答案】20平方釐米【巩固】如圖所示，A、B、C分別是面積為12、28、16的三張不同形狀的紙片，它們重疊在一起，露在外面的總面積為38．若A與B、B與C的公共部分的面積分別為8、7，A、B、C這三張紙片的公共部分為3．求A與C公共部分的面積是多少？【考點】幾何中的重疊問題【難度】3星【題型】解答【解析】設A與C公共部分的面積為x，由包含與排除原理可得：⑴先“包含”：把圖形A、B、C的面積相加：12281656++=，那麼每兩個圖形的公共部分的面積都重複計算了1次，因此要排除掉．⑵再“排除”：5687x---，這樣一來，三個圖形的公共部分被全部減掉，因此還要再補回．⑶再“包含”：56873x---+，這就是三張紙片覆蓋的面積．根據上面的分析得：5687338x=．x---+=，解得：6【答案】6。

1. 了解容斥原理二量重叠和三量重叠的内容；2. 掌握容斥原理的在组合计数等各个方面的应用．一、两量重叠问题在一些计数问题中，经常遇到有关集合元素个数的计算．求两个集合并集的元素的个数，不能简单地把两个集合的元素个数相加，而要从两个集合个数之和中减去重复计算的元素个数，即减去交集的元素个数，用式子可表示成：A B A B A B =+-U I (其中符号“U ”读作“并”，相当于中文“和”或者“或”的意思；符号“I ”读作“交”，相当于中文“且”的意思．)则称这一公式为包含与排除原理，简称容斥原理．图示如下:A 表示小圆部分，B 表示大圆部分，C 表示大圆与小圆的公共部分，记为：A B I ，即阴影面积．图示如下:A 表示小圆部分，B 表示大圆部分，C 表示大圆与小圆的公共部分，记为：A B I ，即阴影面积．包含与排除原理告诉我们，要计算两个集合A B 、的并集A B U 的元素的个数，可分以下两步进行：第一步：分别计算集合A B 、的元素个数，然后加起来，即先求A B +(意思是把A B 、的一切元素都“包含”进来，加在一起)；第二步：从上面的和中减去交集的元素个数，即减去C A B =I (意思是“排除”了重复计算的元素个数)．二、三量重叠问题A 类、B 类与C 类元素个数的总和A =类元素的个数B +类元素个数C +类元素个数-既是A 类又是B 类的元素个数-既是B 类又是C 类的元素个数-既是A 类又是C 类的元素个数+同时是A 类、B 类、C 类的元素个数．用符号表示为：A B C A B C A B B C A C A B C =++---+U U I I I I I ．图示如下：在解答有关包含排除问题时，我们常常利用圆圈图(韦恩图)来帮助分析思考．教学目标知识要点7-7-3.几何中的重叠问题1．先包含——A B +重叠部分A B I 计算了2次，多加了1次； 2．再排除——A B A B +-I把多加了1次的重叠部分A B I 减去．图中小圆表示A 的元素的个数，中圆表示B 的元素的个数，大圆表示C 的元素的个数．1．先包含：A B C ++重叠部分A B I 、B C I 、C A I 重叠了2次，多加了1次． 2．再排除：A B C A B B C A C ++---I I I重叠部分A B C I I 重叠了3次，但是在进行A B C ++- A B B C A C --I I I 计算时都被减掉了． 3．再包含：A B C A B B C A C A B C ++---+I I I I I ．【例 1】 把长38厘米和53厘米的两根铁条焊接成一根铁条．已知焊接部分长4厘米，焊接后这根铁条有多长？【考点】几何中的重叠问题 【难度】1星 【题型】解答 【解析】 因为焊接部分为两根铁条的重合部分，所以，由包含排除法知，焊接后这根铁条长3853487+-=(厘米)．【答案】87厘米【巩固】 把长23厘米和37厘米的两根铁条焊接成一根铁条．已知焊接部分长3厘米，焊接后这根铁条有多长？【考点】几何中的重叠问题 【难度】1星 【题型】解答 【解析】 焊接部分为两根铁条的重合部分，由包含排除法知，焊接后这根铁条长：2337357+-=(厘米)． 【答案】57厘米【例 2】 两张长4厘米，宽2厘米的长方形纸摆放成如图所示形状．把它放在桌面上，覆盖面积有多少平方厘米？【考点】几何中的重叠问题 【难度】1星 【题型】解答图32厘米4厘米【解析】 两个长方形如图摆放时出现了重叠(见图中的阴影部分)，重叠部分恰好是边长为2厘米的正方形，如果利用两个42⨯的长方形面积之和来计算被覆盖桌面的面积，那么重叠部分在两个长方形面积中各被计算了一次，而实际上这部分只需计算一次就可以了．所以，被覆盖面积=长方形面积之和-重叠部分．于是，被覆盖面积4222212=⨯⨯-⨯=(平方厘米)．【答案】12厘米【巩固】 如图3，一张长8厘米，宽6厘米，另一个正方形边长为6厘米，它们中间重叠的部分是一个边长为4厘米的正方形，求这个组合图形的面积．【考点】几何中的重叠问题 【难度】1星 【题型】解答图3468【解析】 两个图形如图摆放时出现了重叠(见图中的阴影部分)，重叠部分恰好是边长为4厘米的正方形，如果利用长方形和正方形面积之和来计算被覆盖桌面的面积，那么重叠部分在长方形和正方形面积中各被计算了一次，而实际上这部分只需计算一次就可以了．所以，组合图形的面积=长方形面积+正方形面积-重叠部分．于是，组合图形的面积：86664468⨯+⨯-⨯=(平方厘米)．【答案】68平方厘米【巩固】 一个长方形长12厘米，宽8厘米，另一个长方形长10厘米，宽6厘米，它们中间重叠的部分是一个边长4厘米的正方形，求这个组合图形的面积．【考点】几何中的重叠问题 【难度】1星 【题型】解答6412例题精讲【解析】两个长方形如图摆放时出现了重叠(见图中的阴影部分)，重叠部分恰好是边长为4厘米的正方形，如果利用两个长方形面积之和来计算被覆盖桌面的面积，那么重叠部分在两个长方形面积中各被计算了一次，而实际上这部分只需计算一次就可以了．所以，组合图形的面积=长方形面积之和-重叠部分．于是，组合图形的面积12810644140=⨯+⨯-⨯=(平方厘米)．【答案】140平方厘米【例 3】三个面积均为50平方厘米的圆纸片放在桌面上(如图)，三个纸片共同重叠的面积是10平方厘米．三个纸片盖住桌面的总面积是100厘米．问：图中阴影部分面积之和是多少？【考点】几何中的重叠问题【难度】2星【题型】解答CBA10【解析】将图中的三个圆标上A、B、C．根据包含排除法，三个纸片盖住桌面的总面积=(A圆面积B+圆面积C+圆面积-）（A与B重合部分面积A+与C重合部分面积B+与C重合部分面积+）三个纸片共同重叠的面积，得：100505050A=++-（）（与B重合部分面积A+与C重合部分面积B+与C重合部分面积10+），得到A、B、C三个圆两两重合面积之和为：16010060-=平方厘米，而这个面积对应于圆上的那三个纸片共同重叠的面积的三倍与阴影部分面积的和，即：60103=⨯+阴影部分面积，则阴影部分面积为：603030-=(平方厘米)．【答案】30平方厘米【巩固】如图，已知甲、乙、丙3个圆的面积均为30，甲与乙、乙与丙、甲与丙重合部分的面积分别为6，8，5，而3个圆覆盖的总面积为73．求阴影部分的面积．【考点】几何中的重叠问题【难度】2星【题型】解答【解析】设甲圆组成集合A，乙圆组成集合B，丙圆组成集合C．A B C===30，A BI=6，B CI=8，A CI=5，A B CU U=73，而A B CU U=A B C+--A B B C A C A B C--+I I I I I.有73=30×3-6-8-5+A B CI I，即A B CI I=2，即甲、乙、丙三者的公共面积(⑧部分面积)为2．那么只是甲与乙(④)，乙与丙(⑥)，甲与丙(⑤)的公共的面积依次为6-2=4，8-2=6，5-2=3，所以有阴影部分(①、②、③部分之和)的面积为73-4-6-3-2=58．【答案】58【例 4】如图，三角形纸板、正方形纸板、圆形纸板的面积相等，都等于60平方厘米．阴影部分的面积总和是40平方厘米，3张板盖住的总面积是100平方厘米，3张纸板重叠部分的面积是多少平方厘米？【考点】几何中的重叠问题【难度】3星【题型】解答部分的面积60310040220（）(平方厘米)．=⨯--÷=【答案】20平方厘米【巩固】如图所示，A、B、C分别是面积为12、28、16的三张不同形状的纸片，它们重叠在一起，露在外面的总面积为38．若A与B、B与C的公共部分的面积分别为8、7，A、B、C这三张纸片的公共部分为3．求A与C公共部分的面积是多少？【考点】几何中的重叠问题【难度】3星【题型】解答【解析】设A与C公共部分的面积为x，由包含与排除原理可得：⑴先“包含”：把图形A、B、C的面积相加：12281656++=，那么每两个图形的公共部分的面积都重复计算了1次，因此要排除掉．⑵再“排除”：5687x---，这样一来，三个图形的公共部分被全部减掉，因此还要再补回．⑶再“包含”：56873---+，这就是三张纸片覆盖的面积．x根据上面的分析得：5687338x=．---+=，解得：6x【答案】6。

几何中的重叠问题1. 了解容斥原理二量重叠和三量重叠的内容；2. 掌握容斥原理的在组合计数等各个方面的应用．一、两量重叠问题在一些计数问题中，经常遇到有关集合元素个数的计算．求两个集合并集的元素的个数，不能简单地把两个集合的元素个数相加，而要从两个集合个数之和中减去重复计算的元素个数，即减去交集的元素个数，用式子可表示成：A B A B A B =+-(其中符号“”读作“并”，相当于中文“和”或者“或”的意思；符号“”读作“交”，相当于中文“且”的意思．)则称这一公式为包含与排除原理，简称容斥原理．图示如下:A 表示小圆部分，B 表示大圆部分，C 表示大圆与小圆的公共部分，记为：A B ，即阴影面积．图示如下:A 表示小圆部分，B 表示大圆部分，C 表示大圆与小圆的公共部分，记为：A B ，即阴影面积．包含与排除原理告诉我们，要计算两个集合A B 、的并集A B 的元素的个数，可分以下两步进行： 第一步：分别计算集合A B 、的元素个数，然后加起来，即先求A B +(意思是把A B 、的一切元素都“包含”进来，加在一起)；第二步：从上面的和中减去交集的元素个数，即减去C A B =(意思是“排除”了重复计算的元素个数)． 二、三量重叠问题A 类、B 类与C 类元素个数的总和A =类元素的个数B +类元素个数C +类元素个数-既是A 类又是B 类的元素个数-既是B 类又是C 类的元素个数-既是A 类又是C 类的元素个数+同时是A 类、B 类、C 类的元素个数．用符号表示为：A B C A B C A B B C A C A B C =++---+．图示如下：在解答有关包含排除问题时，我们常常利用圆圈图(韦恩图)来帮助分析思考．教学目标 知识要点 1．先包含——A B + 重叠部分A B 计算了2次，多加了1次； 2．再排除——A B A B +- 把多加了1次的重叠部分A B 减去．图中小圆表示A 的元素的个数，中圆表示B 的元素的个数，大圆表示C 的元素的个数．1．先包含：A B C ++ 重叠部分A B 、B C 、C A 重叠了2次，多加了1次． 2．再排除：A B C A B B C A C ++--- 重叠部分A B C 重叠了3次，但是在进行A B C ++- A B B C A C --计算时都被减掉了． 3．再包含：A B C A B B C A C A B C ++---+．【例 1】 把长38厘米和53厘米的两根铁条焊接成一根铁条．已知焊接部分长4厘米，焊接后这根铁条有多长？【考点】几何中的重叠问题 【难度】1星 【题型】解答【解析】 因为焊接部分为两根铁条的重合部分，所以，由包含排除法知，焊接后这根铁条长3853487+-=(厘米)．【答案】87厘米【巩固】 把长23厘米和37厘米的两根铁条焊接成一根铁条．已知焊接部分长3厘米，焊接后这根铁条有多长？【考点】几何中的重叠问题 【难度】1星 【题型】解答【解析】 焊接部分为两根铁条的重合部分，由包含排除法知，焊接后这根铁条长：2337357+-=(厘米)．【答案】57厘米【例 2】 两张长4厘米，宽2厘米的长方形纸摆放成如图所示形状．把它放在桌面上，覆盖面积有多少平方厘米？【考点】几何中的重叠问题 【难度】1星 【题型】解答图32厘米4厘米【解析】 两个长方形如图摆放时出现了重叠(见图中的阴影部分)，重叠部分恰好是边长为2厘米的正方形，如果利用两个42⨯的长方形面积之和来计算被覆盖桌面的面积，那么重叠部分在两个长方形面积中各被计算了一次，而实际上这部分只需计算一次就可以了．所以，被覆盖面积=长方形面积之和-重叠部分．于是，被覆盖面积4222212=⨯⨯-⨯=(平方厘米)．【答案】12厘米【巩固】 如图3，一张长8厘米，宽6厘米，另一个正方形边长为6厘米，它们中间重叠的部分是一个边长为4厘米的正方形，求这个组合图形的面积．【考点】几何中的重叠问题 【难度】1星 【题型】解答图3 【解析】 两个图形如图摆放时出现了重叠(见图中的阴影部分)，重叠部分恰好是边长为4厘米的正方形，如果利用长方形和正方形面积之和来计算被覆盖桌面的面积，那么重叠部分在长方形和正方形面积中各被计算了一次，而实际上这部分只需计算一次就可以了．所以，组合图形的面积=长方形面积+正方形面积-重叠部分．于是，组合图形的面积：86664468⨯+⨯-⨯=(平方厘米)．【答案】68平方厘米【巩固】 一个长方形长12厘米，宽8厘米，另一个长方形长10厘米，宽6厘米，它们中间重叠的部分是一个边长4厘米的正方形，求这个组合图形的面积．【考点】几何中的重叠问题 【难度】1星 【题型】解答例题精讲12【解析】 两个长方形如图摆放时出现了重叠(见图中的阴影部分)，重叠部分恰好是边长为4厘米的正方形，如果利用两个长方形面积之和来计算被覆盖桌面的面积，那么重叠部分在两个长方形面积中各被计算了一次，而实际上这部分只需计算一次就可以了．所以，组合图形的面积=长方形面积之和-重叠部分．于是，组合图形的面积12810644140=⨯+⨯-⨯=(平方厘米)．【答案】140平方厘米【例 3】 三个面积均为50平方厘米的圆纸片放在桌面上(如图)，三个纸片共同重叠的面积是10平方厘米．三个纸片盖住桌面的总面积是100厘米．问：图中阴影部分面积之和是多少？【考点】几何中的重叠问题 【难度】2星 【题型】解答CBA10 【解析】 将图中的三个圆标上A 、B 、C ．根据包含排除法，三个纸片盖住桌面的总面积=(A 圆面积B +圆面积C +圆面积-）（A 与B 重合部分面积A +与C 重合部分面积B +与C 重合部分面积+）三个纸片共同重叠的面积，得：100505050A =++-（）（与B 重合部分面积A +与C 重合部分面积B +与C 重合部分面积10+），得到A 、B 、C 三个圆两两重合面积之和为：16010060-=平方厘米，而这个面积对应于圆上的那三个纸片共同重叠的面积的三倍与阴影部分面积的和，即：60103=⨯+阴影部分面积，则阴影部分面积为：603030-=(平方厘米)．【答案】30平方厘米【巩固】 如图，已知甲、乙、丙3个圆的面积均为30，甲与乙、乙与丙、甲与丙重合部分的面积分别为6，8，5，而3个圆覆盖的总面积为73．求阴影部分的面积．【考点】几何中的重叠问题 【难度】2星 【题型】解答【解析】 设甲圆组成集合A ，乙圆组成集合B ，丙圆组成集合C ． A B C ===30，A B =6，B C =8，A C =5，A B C =73，而A B C =A B C +--A B B C A C A B C --+.有73=30×3-6-8-5+AB C ，即A B C =2，即甲、乙、丙三者的公共面积(⑧部分面积)为2．那么只是甲与乙(④)，乙与丙(⑥)，甲与丙(⑤)的公共的面积依次为6-2=4，8-2=6，5-2=3，所以有阴影部分(①、②、③部分之和)的面积为73-4-6-3-2=58．【答案】58【例 4】 如图，三角形纸板、正方形纸板、圆形纸板的面积相等，都等于60平方厘米．阴影部分的面积总和是40平方厘米，3张板盖住的总面积是100平方厘米，3张纸板重叠部分的面积是多少平方厘米？【考点】几何中的重叠问题 【难度】3星【题型】解答【解析】 阴部分的面积60310040220=⨯--÷=（）(平方厘米)．【答案】20平方厘米【巩固】如图所示，A、B、C分别是面积为12、28、16的三张不同形状的纸片，它们重叠在一起，露在外面的总面积为38．若A与B、B与C的公共部分的面积分别为8、7，A、B、C这三张纸片的公共部分为3．求A与C公共部分的面积是多少？【考点】几何中的重叠问题【难度】3星【题型】解答【解析】设A与C公共部分的面积为x，由包含与排除原理可得：⑴先“包含”：把图形A、B、C的面积相加：12281656++=，那么每两个图形的公共部分的面积都重复计算了1次，因此要排除掉．⑵再“排除”：5687x---，这样一来，三个图形的公共部分被全部减掉，因此还要再补回．⑶再“包含”：56873---+，这就是三张纸片覆盖的面积．x根据上面的分析得：5687338x=．x---+=，解得：6【答案】6。

数学竞赛小学奥数几何中的重叠问题1. 了解容斥原理二量重叠和三量重叠的内容；2. 掌握容斥原理的在组合计数等各个方面的应用．一、两量重叠问题在一些计数问题中，经常遇到有关集合元素个数的计算．求两个集合并集的元素的个数，不能简单地把两个集合的元素个数相加，而要从两个集合个数之和中减去重复计算的元素个数，即减去交集的元素个数，用式子可表示成：A B A B A B =+-(其中符号“”读作“并”，相当于中文“和”或者“或”的意思；符号“”读作“交”，相当于中文“且”的意思．)则称这一公式为包含与排除原理，简称容斥原理．图示如下:A表示小圆部分，B 表示大圆部分，C 表示大圆与小圆的公共部分，记为：AB ，即阴影面积．图示如下:A 表示小圆部分，B 表示大圆部分，C 表示大圆与小圆的公共部分，记为：A B ，即阴影面积．包含与排除原理告诉我们，要计算两个集合A B 、的并集AB 的元素的个数，可分以下两步进行：第一步：分别计算集合A B 、的元素个数，然后加起来，即先求A B +(意思是把A B 、的一切元素都“包含”进来，加在一起)；第二步：从上面的和中减去交集的元素个数，即减去C A B =(意思是“排除”了重复计算的元素个数)．二、三量重叠问题A 类、B 类与C 类元素个数的总和A =类元素的个数B +类元素个数C +类元素个数-既是A 类又是B类的元素个数-既是B 类又是C 类的元素个数-既是A 类又是C 类的元素个数+同时是A 类、B 类、C 类的元素个数．用符号表示为：A B C A B C A B B C A C A B C =++---+．图示如下：7-7-3.几何中的重叠问题教学目标知识要点1．先包含——A B + 重叠部分AB 计算了2次，多加了1次；在解答有关包含排除问题时，我们常常利用圆圈图(韦恩图)来帮助分析思考．【例 1】 把长38厘米和53厘米的两根铁条焊接成一根铁条．已知焊接部分长4厘米，焊接后这根铁条有多长？ 【考点】几何中的重叠问题 【难度】1星 【题型】解答【解析】 因为焊接部分为两根铁条的重合部分，所以，由包含排除法知，焊接后这根铁条长3853487+-=(厘米)．【答案】87厘米【巩固】 把长23厘米和37厘米的两根铁条焊接成一根铁条．已知焊接部分长3厘米，焊接后这根铁条有多长？ 【考点】几何中的重叠问题 【难度】1星 【题型】解答【解析】 焊接部分为两根铁条的重合部分，由包含排除法知，焊接后这根铁条长：2337357+-=(厘米)． 【答案】57厘米【例 2】 两张长4厘米，宽2厘米的长方形纸摆放成如图所示形状．把它放在桌面上，覆盖面积有多少平方厘米？ 【考点】几何中的重叠问题 【难度】1星 【题型】解答【解析】 两个长方形如图摆放时出现了重叠(见图中的阴影部分)，重叠部分恰好是边长为2厘米的正方形，如果利用两个42⨯的长方形面积之和来计算被覆盖桌面的面积，那么重叠部分在两个长方形面积中各被计算了一次，而实际上这部分只需计算一次就可以了．所以，被覆盖面积=长方形面积之和-重叠部分．于是，被覆盖面积4222212=⨯⨯-⨯=(平方厘米)．【答案】12厘米 图32厘米4厘米例题精讲图中小圆表示A 的元素的个数，中圆表示B 的元素的个数，大圆1．先包含：A B C ++ 重叠部分AB 、BC 、C A 重叠了2次，多加了1次．2．再排除：A B C A B B C A C ++---【巩固】 如图3，一张长8厘米，宽6厘米，另一个正方形边长为6厘米，它们中间重叠的部分是一个边长为4厘米的正方形，求这个组合图形的面积． 【考点】几何中的重叠问题 【难度】1星 【题型】解答【解析】 两个图形如图摆放时出现了重叠(见图中的阴影部分)，重叠部分恰好是边长为4厘米的正方形，如果利用长方形和正方形面积之和来计算被覆盖桌面的面积，那么重叠部分在长方形和正方形面积中各被计算了一次，而实际上这部分只需计算一次就可以了．所以，组合图形的面积=长方形面积+正方形面积-重叠部分．于是，组合图形的面积：86664468⨯+⨯-⨯=(平方厘米)．【答案】68平方厘米【巩固】 一个长方形长12厘米，宽8厘米，另一个长方形长10厘米，宽6厘米，它们中间重叠的部分是一个边长4厘米的正方形，求这个组合图形的面积． 【考点】几何中的重叠问题 【难度】1星 【题型】解答【解析】 两个长方形如图摆放时出现了重叠(见图中的阴影部分)，重叠部分恰好是边长为4厘米的正方形，如果利用两个长方形面积之和来计算被覆盖桌面的面积，那么重叠部分在两个长方形面积中各被计算了一次，而实际上这部分只需计算一次就可以了．所以，组合图形的面积=长方形面积之和-重叠部分．于是，组合图形的面积12810644140=⨯+⨯-⨯=(平方厘米)．【答案】140平方厘米【例 3】 三个面积均为50平方厘米的圆纸片放在桌面上(如图)，三个纸片共同重叠的面积是10平方厘米．三个纸片盖住桌面的总面积是100厘米．问：图中阴影部分面积之和是多少？ 【考点】几何中的重叠问题 【难度】2星 【题型】解答【解析】 将图中的三个圆标上A 、B 、C ．根据包含排除法，三个纸片盖住桌面的总面积=(A 圆面积B+圆面积C +圆面积-）（A 与B 重合部分面积A +与C 重合部分面积B +与C 重合部分面积+）三个纸片共同重叠的面积，得：100505050A =++-（）（与B 重合部分面积A +与C 重合部分面积B +与C 重合部分面积10+），得到A 、B 、C 三个圆两两重合面积之和为：16010060-=平方厘米，而这个面积对应于圆上的那三个纸片共同重叠的面积的三倍与阴影部分面积的和，即：60103=⨯+阴影部分面积，则阴影部分面积为：603030-=(平方厘米)．【答案】30平方厘米 图3468106412CBA10【巩固】 如图，已知甲、乙、丙3个圆的面积均为30，甲与乙、乙与丙、甲与丙重合部分的面积分别为6，8，5，而3个圆覆盖的总面积为73．求阴影部分的面积． 【考点】几何中的重叠问题 【难度】2星 【题型】解答 【解析】 设甲圆组成集合A ，乙圆组成集合B ，丙圆组成集合C ．=30，=6，=8，=5，=73，而=.有73=30×3-6-8-5+，即=2，即甲、乙、丙三者的公共面积(⑧部分面积)为2．那么只是甲与乙(⑧)，乙与丙(⑧)，甲与丙(⑧)的公共的面积依次为6-2=4，8-2=6，5-2=3，所以有阴影部分(⑧、⑧、⑧部分之和)的面积为73-4-6-3-2=58．【答案】58【例 4】 如图，三角形纸板、正方形纸板、圆形纸板的面积相等，都等于60平方厘米．阴影部分的面积总和是40平方厘米，3张板盖住的总面积是100平方厘米，3张纸板重叠部分的面积是多少平方厘米？ 【考点】几何中的重叠问题 【难度】3星 【题型】解答【解析】 阴叠部分的面积60310040220=⨯--÷=（）(平方厘米)．【答案】20平方厘米【巩固】 如图所示，A 、B 、C 分别是面积为12、28、16的三张不同形状的纸片，它们重叠在一起，露在外面的总面积为38．若A 与B 、B 与C 的公共部分的面积分别为8、7，A 、B 、C 这三张纸片的公共部分为3．求A 与C 公共部分的面积是多少？ 【考点】几何中的重叠问题 【难度】3星 【题型】解答【解析】 设A 与C 公共部分的面积为x ，由包含与排除原理可得：⑧ 先“包含”：把图形A 、B 、C 的面积相加：12281656++=，那么每两个图形的公共部分的面积都重复计算了1次，因此要排除掉．⑧ 再“排除”：5687x ---，这样一来，三个图形的公共部分被全部减掉，因此还要再补回． ⑧ 再“包含”：56873x ---+，这就是三张纸片覆盖的面积． 根据上面的分析得：5687338x ---+=，解得：6x =．【答案】6A B C ==AB BC A C A B C AB C A B C +--A B B C A C A B C --+AB C A B C。

奥数素养思维强化练习——重叠问题班级：姓名：学号：一、知识点：1. 含义重叠问题是数学上非常常见的一类数学问题，它要用到数学中的一个非常重要的原理：容斥原理，即当两个(或多个)计数部分有重复包含时，为了不重复计数，应从他们的和中排除重复部分。

2. 解题思路和方法解决重叠问题时，必须从条件入手进行认真的分析，有时还要画图，借助图形进行思考，找出哪些是重叠的和重叠的次数，明确求的是哪一部分，从而找出解答方法。

当两个计数部分重叠时，可从它们的单项和中减去重叠的部分，得出总数。

二、精讲练习★1.二（1）班同学人人参加课外活动，有20人参加英语班，有26人参加电脑班，每人至少参加一项。

其中4人两个班都参加。

二（1）班一共有多少人？★2.成了一块木板。

如果这块钉在起的木板长120厘米，中把两块一样长的木板像如图一样钉在一起，中间重叠部分是16厘米，这两块木板各长多少厘米？★3.101个同学带着矿泉水和水果去春游，其中矿泉水的78人，带水果的有71人，只带矿泉水和只带水果的各有多少人？★★4.冬天来了，一群大雁排成一队飞向南方，有一只穿花衣服的大雁非常漂亮。

从前面数，它排第6,；从后面数它排第3。

一共有多少只大雁？★★5.芳草地小学四年级的64人都会钢琴或画画中的一种，其中有58人学钢琴，43人学画画，问只学钢琴和只学画画的分别各有多少人？★★6.世博澳门馆100万名旅客中，若每人至少懂中文和英语两种语种之一，其中懂中文的有58万人，懂英语的有50万人。

只懂中文和只懂英语的各有多少人？★★7.某校对五年级100名同学进行学习兴趣调查，结果有58人喜欢语文，有38人喜欢数学，有52人喜欢外语。

而且喜欢语文和数学(但不喜欢外语)的有6人，喜欢数学和外语(但不喜欢语文)的有4人，三科都喜欢的有12人，而且每人至少喜欢一科。

问有多少同学只喜欢语文？★★★8.学校乐器队招收了42名新学员，其中会拉小提琴的有25名，会弹电子琴的有22名，两项都不会的有3名。

7-7-3.几何中的重叠问题目t雌瞬鯛「五年级奥数几何中的重叠问题教师版2.掌握容斥原理的在组合计数等各个方面的应用.—、两量重叠I可题在一些计数问题中，经常遇到有关集合元素个数的计算.求两个集合并集的元素的个数, 不能简单地把两个集合的元素个数相加，而要从两个集合个数之和中减去莹复计算的元素个数•即减去交集的元素个数，用式子可表示成：AUB = A+B-ADB（其中符号“ir读作“并二相当于中文“和"或者“或"的意思;符号“rr读作"交相当于中文“且"的意思.）则称这一公式为包含与排除原理，简称容斥原理.图示如下:A表示小圆部分.3表示大圆部分,C表示大圆与小圆的公共部分，记为：APIB,即阴影面积.图示如下:A表示小圆部分,3表示大圆部分,C表示大圆与小圆的公共部分，记为：即阴影面枳.先包含•重叠部分AHB计算了2次，多加了1次;X2.再扌非除——A +把多加了1次的电叠部分人“3减去.包含与排除原理告诉我们，要计算两个集合A、B的并集AIJB的元素的个数，可分以下两步进行：第一步：分别计算集合A 3的元素个数，然后加起来，即先求A + B（意思是把A、B的一切元素都“包含''进来，加在一起）：第二步：从上面的和中减去交集的元素个数,即减去C = Ap\B（t思是"排除"了重复计算的元素个数）.二、三量重叠问题A类、B类与C类元素个数的总和=A类元素的个数+B类元素个数+C类元素个数- 既是A类又是B类的元素个数-既是B类又是C类的元素个数-既是A类又是C类的元素个数+同时是A类.B 类、C类的元素个数.用符号表示为：A\JB\JC = A + B + C-Ar\B-Br\C-AC\C + Ar\Br\C ・图示攻口下：图中小圆表示A的元素的个数，中圆表示3的元素的个数，大圆表示C的元素的个数.1・先包含：A + B + C A重亞部分ADB、BCIC、CDA重亞了2次，多加了1次.2・再排除：A + B + C-AnB-BnC — AAC重叠部分ADBCIC电叠了3次，但是在进行A + B + C- AnB — BDC — AClC计算时都被减掉了.再包含：A + B + C-AnB-BAC-AAC + AABnC^^y 在解答有关包含排除问题时，我们常常利用圆圈图（韦恩图）来帮助分析思考.【例11把长38厘米和53厘米的两根铁条焊接成一根铁条.已知焊接部分长4厘米，焊接后这根铁条有多长？【考点】几何中的磴叠问題【难度】1星【题型】解答【解析】因为焊接部分为两根铁条的重合部分，所以•由包含排除法知，焊接后这根铁条长38 + 53-4 = 87（厘米）. 【答案】87厘米【巩固】把长23厘米和37厘米的两根铁条焊接成一根铁条.已知焊接部分长3厘米，焊接后这根铁条有多长？【考点】几何中的重叠问題【难度】1星【题型】解答【解析】焊接部分为两根铁条的重合部分，由包含排除法知，焊接后这根铁条长：23 + 37-3 = 57（厘米）.【答案】57厘米【例2］两张长4厘米，宽2厘米的长方形纸摆放成如图所示形状•把它放在桌面上,覆盖面积有多少平方厘米？【考点】几何中的重叠问題【难度】1星【题型】解答【解析】两个长方形如图摆放时出现了重叠（见图中的阴影部分），重叠部分恰好是边长为2 厘米的正方形，如果利用两个4x2的长方形面枳之和来计算被覆盖桌面的面积，那么重査部分在两个长方形面积中各被计算了一次，而实际上这部分只需计算一次就可以了.所以，被覆盖面积=长方形面积之和■重査部分.于是，被覆盖面积= 4x2x2-2x2 = 12 （平方厘米）.【答案】12厘米【巩固】如图3,—张长8厘米，宽6厘米,另一个正方形边长为6厘米,它们中间重叠的部分是一个边长为4厘米的正方形，求这个组合图形的面积.【考点】几何中的重叠问題 【难度】1星 【题型】解答【解析】两个图形如图摆放时出现了重叠（见图中的阴影部分），重叠部分恰好是边长为4厘 米的正方形，如果利用长方形和正方形面积之和来计算被覆盖桌面的面积，那么重叠 部分在长方形和正方形面积中各被计算了 一次,而实际上这部分只需计算一次就可 以了.所以，组合图形的面积=长方形面积+正方形面积-重査部分.于是,组合图 形的面积：8x6 + 6x6-4x4 =68（平方厘米）.【答案】68平方厘米【巩固】一个长方形长12厘米，宽8厘米，另一个长方形长10厘米，宽6厘米，它们中间重叠的 部分是一个边长4厘米的正方形，求这个组合图形的面积.【考点】几何中的重叠问題 【难度】1星 【题型】解答12 84610【解析】两个长方形如图摆放时出现了重叠（见图中的阴影部分）座叠部分恰好是边长为4 厘米的正方形，如果利用两个长方形面积之和来计算被覆盖桌面的面积，那么重査部 分在两个长方形面积中各被计算了一次，而实际上这部分只需计算一次就可以 了.所以，组合图形的面积=长方形面积之和-重叠部分.于是，纽合图形的面积 = 12x8 + 10x6-4x4 = 140（平方厘米）.【答案】140平方厘米三个面积均为50平方厘米的圆纸片放在桌面上（如图），三个纸片共同重叠的面积 是10平方厘米.三个纸片盖住桌面的总面积是100厘米•问：图中阴影部分面积 之和是多少？【解析】将图中的三个圆标上A 、3、C •根扌居包含排除法，三个纸片盖住桌面的总面积=（A 國面积+3圆面积+C 圆面积）-（A 与3重合部分面积+A 与C 重合部分面积+3 与C 重合部分面积）+三个纸片共同重叠的面积，得：100 =（50 + 50 + 50）-（A 与B 重合部分面积+A 与C 重合部分面枳+3与C 重合部分面积）+ 10,得到A 、B 、C 三 个圆两两重合面积之和为：160-100 = 60平方厘米，而这个面积对应于圆上的那三 个纸片共同重査的面积的三倍与阴影部分面积的和，即：60 = 10x3+阴影部分面积, 則阴影部分面积为：60 - 30 = 30（平方厘米）.【答案】30平方厘米【巩固】如图，已知甲、乙、丙3个圆的面积均为30,甲与乙、乙与丙.甲与丙重合部分的面 积分别为6,8（,而3个圆覆盖的总面积为73.求阴影部分的面积.【考点】几何中的匿叠问題 【难度】2星 【题型】解答【例3】 几何中的重叠问题【解析】设甲圆组成集合A.乙圆组成集合B,丙圆组成集合C.|A| = |B| = \C\ =30, | A fl B| =6, D C| =&\AQC\ =5, | A U B U C| =73,而|AUBUC|=|A| + |B|-|C|-|An5|-|BnC|-|AnC|+|AnBnC|.有73=30x3-6-8-5+1A A B Q C| | A Q B A C| =2^P甲.乙、丙三者的公共面积（⑧部分面积）为2・那么只是甲与乙（④），乙与丙（⑥），甲与丙（⑤）的公共的面积依次为6-2=4,8-2=6,5-2=3.所以有阴影部分（①.②、③部分之和）的面积为73-4-6-3-2=58.【答案】58【例4】如图,三角形纸板、正方形纸板.圆形纸板的面积相等，都等于60平方厘米.阴影部分的面积总和是40平方厘米,3张板盖住的总面积是100平方厘米,3张纸板重叠部分的面积是多少平方厘米？【考点】几何中的重叠问題【难度】3星【题型】解答【解析】阴影部分是有两块重叠的部分，被计算两次，而三张纸莹叠部分是被计算了三次.所以三张纸重叠部分的面积=（60 x 3-100 - 40）十2 = 20（平方厘米）・【答案】20平方厘米【巩固】如图所示泌.3、C分别是面积为12. 28. 16的三张不同形状的纸片，它们亟叠在一起，露在外面的总面积为38.若A与〃、3与C的公共部分的面积分别为8. 7M. B. C这三张纸片的公共部分为3.求A与C公共部分的面积是多少？【考点】几何中的匿叠问題【难度】3星【题型】解答【解析】设A与C公共部分的面积为■由包含与排除原理可得：⑴先'电含"：把图形A、B、C的面积相加：12 + 28 + 16 = 56,那么每两个图形的公共部分的面积都重复计算了1次，因此要排除掉.（2）再“排除‘‘：56-8-7-兀,这样一来，三个图形的公共部分被全部减掉，因此还要再补回.（3）再“包含56-8-7-X + 3,这就是三张纸片覆盖的面积.根据上面的分析得：56-8-7-人+3 = 38.解得：x = 6・【答案】6。

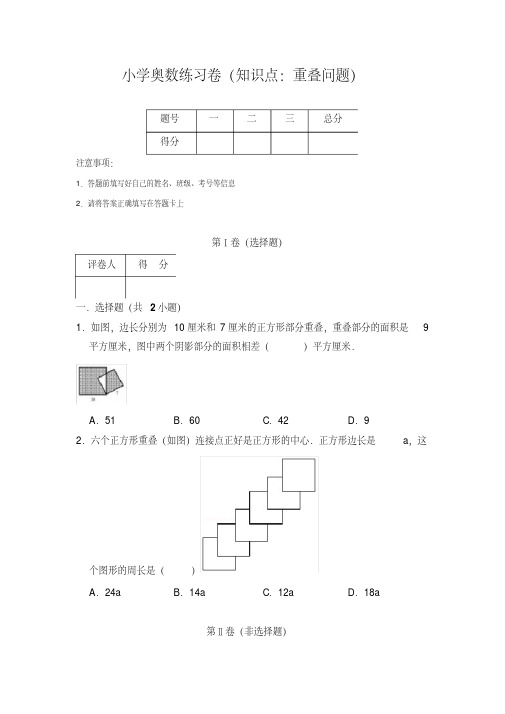
小学奥数练习卷（知识点：重叠问题）注意事项：1．答题前填写好自己的姓名、班级、考号等信息2．请将答案正确填写在答题卡上第Ⅰ卷（选择题）一．选择题（共2小题）1．如图，边长分别为10厘米和7厘米的正方形部分重叠，重叠部分的面积是9平方厘米，图中两个阴影部分的面积相差（）平方厘米．A．51B．60C．42D．92．六个正方形重叠（如图）连接点正好是正方形的中心．正方形边长是a，这个图形的周长是（）A．24a B．14a C．12a D．18a第Ⅱ卷（非选择题）二．填空题（共29小题）3．如图的三张正方形的纸，铺在桌面上一共遮盖的面积是平方厘米．（单位：厘米）4．有红、黄、绿三块大小一样的正方形纸片，放在一个正方形盒内，它们之间互相叠合，如图所示，已知露在外的部分中，红色面积是20，黄色面积是14，绿色面积是10，那么正方形盒子的面积是．5．将4个边长为2的正方形如图放置在桌面上，则它们在桌面上所能覆盖的面积是．6．如图，将正方形纸片ABCD折叠，使点A、B重合于点O，则∠EFO=度．7．用10张同样长度的纸条粘接成一条长41厘米的纸带，如果每个接头处都重叠1厘米，那么原来的每张纸条都长厘米．8．如图，把三个面积同是S平方厘米的圆放置在桌面上，桌面被圆覆盖的面积是2S+10平方厘米，图中两圆重叠的两块（有阴影部分）的面积相等，有一直线L过A、B两圆的圆心．直线L下方被覆盖的面积是25平方厘米，那么，S=平方厘米．9．两幅图表示两个箭头画在不同的4厘米×4厘米方格内的情况．现在将这两个箭头画在同一副4厘米×4厘米的方格内，则这两个箭头的重叠部分的面积为平方厘米．10．如图，在一个长、宽分别为19厘米和11厘米的大长方形内放了四个正方形，那么没有被正方形覆盖的小长方形（图中阴影部分）的面积是平方厘米．11．如图，正方形ABCD的面积为196平方厘米，它包含了两个有部分重叠的小正方形．其中，较大的那个小正方形面积是较小的那个小正方形面积的4倍，而且两个正方形的重叠部分面积为1平方厘米．那么，阴影部分面积为平方厘米．12．有一根绳子第一次把它按下左图方式对折，在对折处标记①；第二次我们将它按下中图方式对折，在对折处分别标记②、③；第三次我们将它按下右图方式对折，如果下右图中①号点和③号点之间的距离为30厘米，那么这根绳子的总长度是厘米．（绳子之间无缝隙，绳粗以及转弯处损耗都忽略不计）．13．有一根绳子，第一次把它按左图方式对折，在对折处标记①，第二次我们将它按中图方式对折，在对折处在对折处分别标记②、③；第三次我们将它按下右图方式对折，如果右图中②号点和③号点之间的距离为20厘米，那么这根绳子的总长度是厘米（绳子之间无缝隙，绳粗以及转弯处损耗都忽略不计）14．如图，已知正方形ABCD面积为2520；E、F、G、H为边上的靠近正方形顶点的四等分点，连AG、EC、HB、DF．那么图中“X”部分的面积是．15．一个长方形的相框长为40厘米，宽为32厘米，放入一张长为32厘米宽为28厘米的相片，则相框中没有被照片覆盖的部分的面积是平方厘米．16．有六根木条，各长50厘米．现要将它们依次首尾相接钉在一起，每两根木条中间钉在一起的部分长10厘米．钉好后木条总长厘米．17．如图，三角形纸板、正方形纸板、圆形纸板的面积相等，都等于60平方厘米．阴影部分的面积总和是40平方厘米，3张板盖住的总面积是100平方厘米，3张纸板重叠部分的面积是平方厘米．18．小芳和小红共重72千克，小敏和小芳共重69千克，小敏和小红共重65千克．小芳体重是千克，小红体重是千克，小敏体重是千克．19．两个长方形如图叠放，图上已标出一些线段的长．EF=．20．图中，三张大小一样的等边三角形透明玻璃纸，各被分为49个大小相同的小等边三角形，每张玻璃纸上都各有16个小等边三角形涂上了阴影，如果把这三张玻璃纸重叠在一起，看到的阴影小等边三角形共有个．21．如图所示，两个形状和大小都相同的直角△ACB和△EDF的面积都是10cm2，每个直角的直角顶点都恰好落在另一个直角三角形斜边上，这两个直角三角形的重叠部分是一个长方形．那么四边形ABEF的面积是cm2．22．如图，有6个边长是1的小正方形，一个压着一个，上面的正方形的一个顶点恰好是下一个正方形的中心，上面正方形的中心的下面恰好是下面正方形的一个顶点，那么这个图形最后所形成的多边形的周长是；如果一共有20个边长是1的正方形按上述方法叠在一起，那么最后形成的多边形的周长是．23．如图，两个正方形的边长分别为10厘米和7厘米，甲、乙两块空白区域的面积之和为87平方厘米，那么阴影部分的面积是平方厘米．24．5个相同正方形纸片按相同的方向叠放在一起（如图），相邻两个正方形的一个角都与另一个正方形的中心点重合，如果所构成图形的周长是120厘米，那么这个图形覆盖的面积是平方厘米．25．今天是12月19日，我们将由边长为1的阴影小正方形组成的数字1、2、1、9放在8×5的大长方形中，将大长方形旋转180°，就变成了“6121”，如果将这两个8×5的大长方形重叠放置．那么重叠的阴影格子共有个．26．今天是12月19日，我们将电子数字1、2、1、9放在如图中8×5的长方形中，每个阴影小格子都是边长为1的正方形，将它旋转180°，就变成了“6121”，如果将这两个8×5的长方形重叠放置，那么重叠的1×1的阴影格子共有个．27．3个相同的正方形纸片按相同的方向叠放在一起（如图），顶点A和B分别与正方形中心点重合，如果所构成图形的周长是48厘米，那么这个图形覆盖的面积是平方厘米．28．将边长为10厘米的五张正方形纸片如图那样放置，每张小正方形纸片被盖住的部分是一个较小的正方形，它的边长是原正方形边长的一半，则图3中的图形外轮廓（图中粗线条）的周长为厘米．29．如图，五个圆相交后被分成了九个区域，现在两个区域里已分别填上数字15、16，请在另外七个区域里分别填进2，3，4，5，7，8，9这七个数字，使每个圆内的数字和是20．30．如图所示，一个正方形和一个长方形有一部分重叠，阴影部分甲比阴影部分乙的面积大6平方厘米，正方形的面积是10平方厘米，长方形的长为8厘米，则长方形的宽是厘米．31．如图是同一个等腰三角形的螺旋．这个等腰三角形中的最大角是100°．灰色三角形的编号是0，余下的三角形编号分别1、2、3、4、…，后一个三角形分别与前一个三角形有一条边重合，如图所示．从图中可以看出3号三角形只是部分地覆盖了0号三角形．请问第一个完全覆盖0号三角形的是号三角形．三．解答题（共19小题）32．某校四年级四个班总共有176名学生，其中一班和二班共有87名，一班和三班共有82名，二班和三班共有85名，那么，四班有多少名学生？33．两个相同的正方形重合在一起，将上层的正方形向右移动3厘米，再向下移动5厘米，得到如图所示的图形，已知阴影部分的面积是57平方厘米，求正方形的边长．34．小丽把两根长1米的纸条粘在一起，成为一根长170厘米的纸条，中间粘贴起来的纸条长度是厘米．35．如图1，从边长是6厘米的正方形纸片的正中间挖去一个正方形，得到一个宽为1厘米的方框，将四个这样的方框如图6所示依次垂直交叉放在桌面上，求桌面被这些方框盖住的面积（图2中阴影部分的面积）．36．两个相同的长方形纸片，每块面积为48平方厘米．如图所示叠放在一起盖住的面积为72平方厘米．已知重叠部分的四边形ABCD的一条对角线BD为6厘米，则每张长方形纸片的长是多少厘米？37．如图，三个一样大小的正方形放在一个长方形的盒内，A和B是两个正方形重叠部分，C，D，E是空出的部分，这些部分都是长方形，它们的面积比是A：B：C：D：E=1：2：3：4：5．那么这个长方形的长与宽之比是多少？38．三条边长分别为5厘米、12厘米、13厘米的直角三角形，如图1，将它的短直角边对折到斜边上去与斜边重合，如图2．那么图2中阴影部分（即未被盖住部分）的面积是多少平方米？39．（如图）五环图由内径为4分米，外径为5分米的5个圆环组成，其中相交的小曲边四边形的面积都相等，已知5个圆环盖住的总面积是122.5平方分米．每个小曲边四边形的面积是．40．如图，小正方形的被阴影部分覆盖，大正方形的被阴影覆盖，那么，小正方形的阴影部分与大正方形阴影部分面积之比是．41．桌子上放有甲、乙、丙三个正方形，甲、丙有部分重叠，乙、丙有部分重叠．甲、丙重叠部分占甲正方形面积的；乙、丙重叠部分占乙正方形面积的．丙正方形与甲、乙正方形重叠部分占丙正方形面积的．甲正方形和乙正方形面积的和是丙正方形面积的求：甲正方形面积与乙正方形面积的比．（要求化为最简整数比）42．桌面上放有四张大小不同的正方形纸片边长分别为2，3，4，5，若分别取走边长为2，3，4，5的正方形纸片中的一个，则剩下的三张纸片覆盖的面积分别减少2，3，4，5，那么四张纸片覆盖的面积是多少？43．城中小学四年级有四个班．已知四（1）班、四（2）班共81人，四（2）班、四（3）班共83人，四（3）班、四（4）班共86人，四（1）班比四（4）班多2人，问四个班各有多少人？（只写答案，不列式）44．将同样大小的长方形纸像如图那样重叠在一起，每个长方形的长是12厘米，每个重叠部分是2厘米．那么，10张这样的纸连接起来的长度是多少厘米？45．将等边三角形纸片按图1所示步骤折叠3次（图1中的虚线是三边的中点的连线），然后沿两边的重点的边减去一角（如图2）．将剩下的纸片展开、平铺，得到的图形是46．长度为L的一条木棍，分别用红、蓝、黑线将它等分为8，12和18段，在各划分线处将木棍锯开，问一共可以得到多少段？其中最短的一段的长是多少？47．如图，两个正方形边长分别是5厘米和4厘米，图中阴影部分为重叠部分．则两个正方形的空白部分的面积相差多少平方厘米？48．五个大球与三个小球共重42克，五个小球与三个大球共重38克，则大球与小球各重多少克？49．阿明在喝茶的时候做了一个小实验．他把一根筷子笔直的插到杯底，他量了一下被水浸湿部分的长度是10厘米．他把筷子掉个头，将另一端笔直的插到杯底，这时候他发现，筷子干的部分比湿的部分短10厘米．那麽这根筷子长多少厘米？50．两块大小不同的等腰直角三角板，直角边分别是10厘米和6厘米，如图那样重合，求重合部分（阴影部分）的面积．参考答案与试题解析一．选择题（共2小题）1．如图，边长分别为10厘米和7厘米的正方形部分重叠，重叠部分的面积是9平方厘米，图中两个阴影部分的面积相差（）平方厘米．A．51B．60C．42D．9【分析】大正方形的面积是10×10=100平方厘米，它的阴影部分的面积是100﹣9=91平方厘米；同理，小正方形的面积是7×7=49平方厘米，它的阴影部分的面积是49﹣9=50平方厘米；然后求两个阴影部分的面积差即可．【解答】解：（10×10﹣9）﹣（7×7﹣9）=91﹣40=51（平方厘米）答：图中两个阴影部分的面积相差51平方厘米．故选：A．【点评】本题考查了重叠问题，本题还可以这样解答：因为重叠部分的面积是9平方厘米，所以两个阴影部分的面积差，就等于两个正方形的面积差，即10×10﹣7×7=51平方厘米．2．六个正方形重叠（如图）连接点正好是正方形的中心．正方形边长是a，这个图形的周长是（）A．24a B．14a C．12a D．18a【分析】这六个正方形重叠在一起，第一个和最后一个正方形的长度为3a+3a，中间4个正方形的长度是2a×4=8a，把这些长度加起来就是这个图形的周长．【解答】解：3a+3a+2a×4=14a，答：这个图形的周长是14a；故选：B．【点评】此题考查了学生空间想象力以及分析图形的能力，同时考查了图形周长的计算方法．二．填空题（共29小题）3．如图的三张正方形的纸，铺在桌面上一共遮盖的面积是14.25平方厘米．（单位：厘米）【分析】要求一共遮盖的面积，把正个图行补全为一个长1.5+2+1=4.5厘米、宽为3+1=4厘米的大长方形的面积，减去左上角、右上角、右下角的长方形的面积，长和宽的数据已经算出标在图上，然后求出面积差即可．【解答】解：1.5+2+1=4.5（厘米）3+1=4（厘米）4×4.5﹣1.5×1﹣1.5×1﹣0.5×1.5=18﹣3﹣0.75=14.25（平方厘米）故答案为：14.25．【点评】此题属于重叠问题，重点搞清重叠的是哪一部分，是解决本题的关键．4．有红、黄、绿三块大小一样的正方形纸片，放在一个正方形盒内，它们之间互相叠合，如图所示，已知露在外的部分中，红色面积是20，黄色面积是14，绿色面积是10，那么正方形盒子的面积是51.2．【分析】先作辅助线，在黄色纸片中截出面积为a的部分，又因为红色部分是正方形，所以可得等量关系式：黄色面积﹣a=绿色面积+a，由此列方程求出a 的面积；再由红黄绿的比例关系列出比例式解答即可．【解答】解：作辅助线，在黄色纸片中截出面积为a的部分，如图所示．所以14﹣a=10+a解得：a=2设空白部分面积为x，将上图转化为，14﹣2=1210+2=12所以，=解得：x=7.2正方形盒子的面积为：12+20+12+7.2=51.2答：正方形盒子的面积是51.2．故答案为：51.2．【点评】本题考查了比较复杂的重叠问题，关键是求出中间黄与绿的重叠部分．5．将4个边长为2的正方形如图放置在桌面上，则它们在桌面上所能覆盖的面积是13．【分析】重叠部分是一个边长是1小正方形，用4个大正方形的面积和减去3个小正方形的面积，就是被盖住桌面的面积．【解答】解：2×2×4﹣1×1×3=16﹣3=13答：它们在桌面上所能覆盖的面积是13．故答案为：13．【点评】本题的重点是求出每张纸覆盖的面积，再求覆盖的总面积．6．如图，将正方形纸片ABCD折叠，使点A、B重合于点O，则∠EFO=30度．【分析】根据轴对称的性质，折叠前后图形的形状和大小不变，得出△OCD是等边三角形，折叠前后角相等以及三角形的内角和定理，求出∠BFC的度数，再根据平角是180度求得∠EFO的度数．【解答】解：沿DE折叠，所以AD=OD，同理可得BC=OC，则：OD=DC=OC，△OCD是等边三角形，所以∠DCO=60°，∠OCB=90°﹣60°=30°；由于是对折，所以CF平分∠OCB，∠BCF=30°÷2=15°∠BFC=180°﹣90°﹣15°=75°所以∠EFO=180°﹣75°×2=30°．故答案为：30．【点评】本题考查图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称．7．用10张同样长度的纸条粘接成一条长41厘米的纸带，如果每个接头处都重叠1厘米，那么原来的每张纸条都长5厘米．【分析】由于最后一张的末尾没有粘接，所以10张纸条粘接在一起共有9处重叠，所以用现在的总长度41厘米，加上9个1厘米求出没重叠前的总长度和，然后再除以10即可解决问题．【解答】解：（41+1×9）÷10=50÷10=5（厘米）答：原来的每张纸条都长5厘米；故答案为：5．【点评】明确10张纸条粘接在一起共有9处重叠，是解答此题的关键．8．如图，把三个面积同是S平方厘米的圆放置在桌面上，桌面被圆覆盖的面积是2S+10平方厘米，图中两圆重叠的两块（有阴影部分）的面积相等，有一直线L过A、B两圆的圆心．直线L下方被覆盖的面积是25平方厘米，那么，S=14平方厘米．【分析】由题意，3S﹣2S阴影=2S+10，2S﹣1.5S阴影=25，解方程可得S．【解答】解：由题意，3S﹣2S阴影=2S+10，2S﹣1.5S阴影=25，解得S=14．故答案为14．【点评】本题考查重叠问题，考查方程思想，正确建立方程是关键．9．两幅图表示两个箭头画在不同的4厘米×4厘米方格内的情况．现在将这两个箭头画在同一副4厘米×4厘米的方格内，则这两个箭头的重叠部分的面积为6平方厘米．【分析】将两个图形重合，可得重叠部分，即可求出重叠部分的面积．【解答】解：重叠部分如图所示，重叠部分的面积为6平方厘米．故答案为6．【点评】本题考查重叠问题，考查数形结合的数学思想，正确作出重叠部分是关键．10．如图，在一个长、宽分别为19厘米和11厘米的大长方形内放了四个正方形，那么没有被正方形覆盖的小长方形（图中阴影部分）的面积是6平方厘米．【分析】最大的正方形的边长是长方形的宽，也就是11厘米，次大的正方形的边长是19﹣11=8厘米，再小一点的正方形的边长是11﹣8=3厘米，最后剩余小长方形的长是3厘米，宽是8﹣3﹣3=2厘米，再根据长方形的面积公式求解即可．【解答】解：最大正方形的边长是11厘米，次大正方形的边长：19﹣11=8（厘米）最小正方形的边长是：11﹣8=3（厘米）阴影长方形的长是3厘米，宽是8﹣3﹣3=2（厘米）3×2=6（平方厘米）答：没有被正方形覆盖的小长方形（图中阴影部分）的面积是6平方厘米．故答案为：6．【点评】首先根据最大的正方形的边长是长方形的宽确定出最大正方形的边长，再依次找出其它正方形的边长，最后得出阴影部分的长和宽，再根据长方形的面积=长×宽求解．11．如图，正方形ABCD的面积为196平方厘米，它包含了两个有部分重叠的小正方形．其中，较大的那个小正方形面积是较小的那个小正方形面积的4倍，而且两个正方形的重叠部分面积为1平方厘米．那么，阴影部分面积为72平方厘米．【分析】求出大正方形的边长是小正方形边长的2倍，并且大正方形和小正方形的边长之和是14+1=15厘米，可得小正方形的边长为15÷3=5厘米，大正方形的边长为5×2=10厘米．进而小长方形的面积为（5﹣1 ）×（10﹣1）=36（cm2），即可求出两个小长方形的面积．【解答】解：正方形的面积为196平方厘米，所以边长为14厘米．重叠面积为1平方厘米，所以边长为1厘米；较大正方形是较小正方形面积的4倍，因此大正方形的边长是小正方形边长的2倍，并且大正方形和小正方形的边长之和是14+1=15厘米所以小正方形的边长为15÷3=5厘米，大正方形的边长为5×2=10厘米．小长方形的面积为（5﹣1 ）×（10﹣1）=36（cm2），所以两个小长方形的面积为36×2=72（cm2）故答案为72．【点评】本题考查面积的计算，考查重叠问题，考查学生分析解决问题的能力，求出大正方形的边长是小正方形边长的2倍，并且大正方形和小正方形的边长之和是14+1=15厘米是关键．12．有一根绳子第一次把它按下左图方式对折，在对折处标记①；第二次我们将它按下中图方式对折，在对折处分别标记②、③；第三次我们将它按下右图方式对折，如果下右图中①号点和③号点之间的距离为30厘米，那么这根绳子的总长度是360厘米．（绳子之间无缝隙，绳粗以及转弯处损耗都忽略不计）．【分析】由第二幅图可知：①到②、①到③、②到端点，③到端点的距离全相等；由第三幅图可知，②到端点的绳子被平均分成3份，由于①到②，③到端点的距离相等，所以每一份的距离是30厘米，则②到端点的绳长是30×3=90厘米，绳子的全长是90×4=360厘米．【解答】解：由第二幅图可知：①到②、①到③、②到端点，③到端点的距离全相等；由第三幅图可知，②到端点的绳子被平均分成3份，由于：①到②、③到端点的距离相等，所以每一份的距离是30厘米，则②到端点的绳长是30×3=90（厘米），绳子的全长是90×4=360（厘米）．答：这根绳子的总长度是360厘米．故答案为：360．【点评】解决本题注意观察图，找清楚各部分长度之间的关系是解决本题的关键．13．有一根绳子，第一次把它按左图方式对折，在对折处标记①，第二次我们将它按中图方式对折，在对折处在对折处分别标记②、③；第三次我们将它按下右图方式对折，如果右图中②号点和③号点之间的距离为20厘米，那么这根绳子的总长度是120厘米（绳子之间无缝隙，绳粗以及转弯处损耗都忽略不计）【分析】由第二幅图可知：①到②、①到③、②到端点，③到端点的距离全相等；由第三幅图可知，②到端点的绳子被平均分成3份，设每一份为x，则③到绳子末端的距离=20+x，那么3x=20+x，进而可求出x，从而求得绳子的全长．【解答】解：由第二幅图可知：①到②、①到③、②到端点，③到端点的距离全相等；由第三幅图可知，②到端点的绳子被平均分成3份设每一份为x，则③到绳子末端的距离=20+x，那么3x=20+x，x=10（厘米），则③到绳子末端的距离为30厘米，绳子的全长是30×4=120（厘米）．故答案为：120．【点评】解决本题注意观察图，找清楚各部分长度之间的关系是解决本题的关键．14．如图，已知正方形ABCD面积为2520；E、F、G、H为边上的靠近正方形顶点的四等分点，连AG、EC、HB、DF．那么图中“X”部分的面积是1155．【分析】将阴影部分看成两个平行四边形重叠在一起，重叠部分是一个菱形，菱形的两条对角线长度分别是AE和，所以重叠面积是正方形面积的，两个平行四边形的面积都是正方形面积的，所以一共是正方形面积的，再根据分数乘法的意义求出阴影部分的面积．【解答】解：如图：中间菱形的两条对角线长度分别是AE和，AE=AD×÷2=所以重叠面积是正方形面积的，两个平行四边形的面积都是正方形面积的，+﹣=2520×=1155答：图中“X”部分的面积是1155．故答案为：1155．【点评】解决本题关键是得出重叠的菱形部分的面积与正方形面积的关系，从而得出阴影部分是正方形面积的几分之几，再根据分数乘法的意义求解．15．一个长方形的相框长为40厘米，宽为32厘米，放入一张长为32厘米宽为28厘米的相片，则相框中没有被照片覆盖的部分的面积是384平方厘米．【分析】放入一张长为32厘米宽为28厘米的相片，则被照片覆盖的部分的面积是这张相片的面积，分别求出相框和相片的面积，然后用相框的面积减去相片的面积即可．【解答】解：40×32﹣32×28=32×（40﹣28）=32×12=384（平方厘米）答：相框中没有被照片覆盖的部分的面积是384平方厘米．故答案为：384．【点评】此题考查了长方形面积公式的灵活运用．16．有六根木条，各长50厘米．现要将它们依次首尾相接钉在一起，每两根木条中间钉在一起的部分长10厘米．钉好后木条总长250厘米．【分析】六根木条依次首尾相接钉在一起，重叠部分有6﹣1=5（次）；要减少10×5=50（厘米）；所以钉好后木条总长是：50×6﹣50=250（厘米）；据此解答．【解答】解：根据分析可得，50×6﹣10×5，=300﹣50，=250（厘米）；答：钉好后木条总长250厘米．故答案为：250．【点评】本题可以按植树问题解答，先求出间隔数也就是重叠的次数，知识点：重叠的次数=段数﹣1．17．如图，三角形纸板、正方形纸板、圆形纸板的面积相等，都等于60平方厘米．阴影部分的面积总和是40平方厘米，3张板盖住的总面积是100平方厘米，3张纸板重叠部分的面积是20平方厘米．【分析】60×3=180，此时未重叠面积计算了一次，阴影部分面积计算了两次，3张纸板重叠部分的面积计算了三次，180﹣100=80，此时减去了3张板盖住的总面积，则阴影部分面积计算了一次，3张纸板重叠部分的面积计算了两次；80﹣40，此时减去了阴影面积，则3张纸板重叠部分的面积计算了两次；所以，三张纸板重叠部分的面积为40÷2=20平方厘米；由此解答即可．【解答】解：（60×3﹣100﹣40）÷2=40÷2=20（平方厘米）；答：3张纸板重叠部分的面积是20平方厘米．故答案为：20．【点评】此题属于重叠问题，比较复杂，应认真分析题意，看清要求的是什么，必须求出什么，重叠的部分是多少，进而解答得出结论．18．小芳和小红共重72千克，小敏和小芳共重69千克，小敏和小红共重65千克．小芳体重是38千克，小红体重是34千克，小敏体重是31千克．【分析】把小芳和小红共重72千克，小敏和小芳共重69千克，小敏和小红共重65千克，这三部分体重和相加，就是这个三个小朋友体重的2倍，再除以2，求出3个小朋友的体重，然后减去72千克，就是小敏的体重，同理求出其它小朋友的体重．【解答】解：三人的体重和；（72+69+65）÷2=206÷2=103（千克）小敏：103﹣72=31（千克）小红：103﹣69=34（千克）小芳：103﹣65=38（千克）答：小芳体重是38千克，小红体重是34千克，小敏体重是31千克．故答案为：38，34，31．【点评】解决本题关键是求出这三个人体重和的2倍．19．两个长方形如图叠放，图上已标出一些线段的长．EF=32．【分析】连接ED，三角形AED的面积是：（15+25）×20÷2=400，又因为三角形AED的面积是长方形AEDG的面积的一半，所以长方形AEDG的面积是：400×2=800，所以，EF的长：800÷25=32，据此解答．。

1. 了解容斥原理二量重叠和三量重叠的内容；2. 掌握容斥原理的在组合计数等各个方面的应用．一、两量重叠问题在一些计数问题中，经常遇到有关集合元素个数的计算．求两个集合并集的元素的个数，不能简单地把两个集合的元素个数相加，而要从两个集合个数之和中减去重复计算的元素个数，即减去交集的元素个数，用式子可表示成：A B A B A B =+-(其中符号“”读作“并”，相当于中文“和”或者“或”的意思；符号“”读作“交”，相当于中文“且”的意思．)则称这一公式为包含与排除原理，简称容斥原理．图示如下:A 表示小圆部分，B 表示大圆部分，C 表示大圆与小圆的公共部分，记为：A B ，即阴影面积．图示如下:A 表示小圆部分，B 表示大圆部分，C 表示大圆与小圆的公共部分，记为：AB ，即阴影面积．包含与排除原理告诉我们，要计算两个集合A B 、的并集A B 的元素的个数，可分以下两步进行：第一步：分别计算集合A B 、的元素个数，然后加起来，即先求A B +(意思是把A B 、的一切元素都“包含”进来，加在一起)；第二步：从上面的和中减去交集的元素个数，即减去C A B =(意思是“排除”了重复计算的元素个数)．二、三量重叠问题A 类、B 类与C 类元素个数的总和A =类元素的个数B +类元素个数C +类元素个数-既是A 类又是B 类的元素个数-既是B 类又是C 类的元素个数-既是A 类又是C 类的元素个数+同时是A 类、B 类、C 类的元素个数．用符号表示为：A B C A B C A B B C A C A B C =++---+．图示如下：在解答有关包含排除问题时，我们常常利用圆圈图(韦恩图)来帮助分析思考．教学目标知识要点7-7-3.几何中的重叠问题1．先包含——A B +重叠部分A B 计算了2次，多加了1次； 2．再排除——A B A B +-把多加了1次的重叠部分A B 减去．图中小圆表示A 的元素的个数，中圆表示B 的元素的个数，大圆表示C 的元素的个数．1．先包含：A B C ++重叠部分A B 、B C 、C A 重叠了2次，多加了1次． 2．再排除：A B C A B B C A C ++---重叠部分A B C 重叠了3次，但是在进行A B C ++- A B B C A C --计算时都被减掉了． 3．再包含：A B C A B B C A C A B C ++---+．【例 1】 把长38厘米和53厘米的两根铁条焊接成一根铁条．已知焊接部分长4厘米，焊接后这根铁条有多长？【考点】几何中的重叠问题 【难度】1星 【题型】解答 【解析】 因为焊接部分为两根铁条的重合部分，所以，由包含排除法知，焊接后这根铁条长3853487+-=(厘米)．【答案】87厘米【巩固】 把长23厘米和37厘米的两根铁条焊接成一根铁条．已知焊接部分长3厘米，焊接后这根铁条有多长？【考点】几何中的重叠问题 【难度】1星 【题型】解答 【解析】 焊接部分为两根铁条的重合部分，由包含排除法知，焊接后这根铁条长：2337357+-=(厘米)． 【答案】57厘米【例 2】 两张长4厘米，宽2厘米的长方形纸摆放成如图所示形状．把它放在桌面上，覆盖面积有多少平方厘米？【考点】几何中的重叠问题 【难度】1星 【题型】解答图32厘米4厘米【解析】 两个长方形如图摆放时出现了重叠(见图中的阴影部分)，重叠部分恰好是边长为2厘米的正方形，如果利用两个42⨯的长方形面积之和来计算被覆盖桌面的面积，那么重叠部分在两个长方形面积中各被计算了一次，而实际上这部分只需计算一次就可以了．所以，被覆盖面积=长方形面积之和-重叠部分．于是，被覆盖面积4222212=⨯⨯-⨯=(平方厘米)．【答案】12厘米【巩固】 如图3，一张长8厘米，宽6厘米，另一个正方形边长为6厘米，它们中间重叠的部分是一个边长为4厘米的正方形，求这个组合图形的面积．【考点】几何中的重叠问题 【难度】1星 【题型】解答图3468【解析】 两个图形如图摆放时出现了重叠(见图中的阴影部分)，重叠部分恰好是边长为4厘米的正方形，如果利用长方形和正方形面积之和来计算被覆盖桌面的面积，那么重叠部分在长方形和正方形面积中各被计算了一次，而实际上这部分只需计算一次就可以了．所以，组合图形的面积=长方形面积+正方形面积-重叠部分．于是，组合图形的面积：86664468⨯+⨯-⨯=(平方厘米)．【答案】68平方厘米【巩固】 一个长方形长12厘米，宽8厘米，另一个长方形长10厘米，宽6厘米，它们中间重叠的部分是一个边长4厘米的正方形，求这个组合图形的面积．【考点】几何中的重叠问题 【难度】1星 【题型】解答例题精讲12【解析】 两个长方形如图摆放时出现了重叠(见图中的阴影部分)，重叠部分恰好是边长为4厘米的正方形，如果利用两个长方形面积之和来计算被覆盖桌面的面积，那么重叠部分在两个长方形面积中各被计算了一次，而实际上这部分只需计算一次就可以了．所以，组合图形的面积=长方形面积之和-重叠部分．于是，组合图形的面积12810644140=⨯+⨯-⨯=(平方厘米)．【答案】140平方厘米【例 3】 三个面积均为50平方厘米的圆纸片放在桌面上(如图)，三个纸片共同重叠的面积是10平方厘米．三个纸片盖住桌面的总面积是100厘米．问：图中阴影部分面积之和是多少？【考点】几何中的重叠问题 【难度】2星 【题型】解答CBA10【解析】 将图中的三个圆标上A 、B 、C ．根据包含排除法，三个纸片盖住桌面的总面积=(A 圆面积B +圆面积C +圆面积-）（A 与B 重合部分面积A +与C 重合部分面积B +与C 重合部分面积+）三个纸片共同重叠的面积，得：100505050A =++-（）（与B 重合部分面积A +与C 重合部分面积B +与C 重合部分面积10+），得到A 、B 、C 三个圆两两重合面积之和为：16010060-=平方厘米，而这个面积对应于圆上的那三个纸片共同重叠的面积的三倍与阴影部分面积的和，即：60103=⨯+阴影部分面积，则阴影部分面积为：603030-=(平方厘米)．【答案】30平方厘米【巩固】 如图，已知甲、乙、丙3个圆的面积均为30，甲与乙、乙与丙、甲与丙重合部分的面积分别为6，8，5，而3个圆覆盖的总面积为73．求阴影部分的面积．【考点】几何中的重叠问题 【难度】2星 【题型】解答 【解析】 设甲圆组成集合A ，乙圆组成集合B ，丙圆组成集合C ．A B C ===30，A B =6，B C =8，A C =5，A B C =73，而AB C =A B C +--A B B C A C A B C --+.有73=30×3-6-8-5+AB C ，即A B C =2，即甲、乙、丙三者的公共面积(⑧部分面积)为2．那么只是甲与乙(④)，乙与丙(⑥)，甲与丙(⑤)的公共的面积依次为6-2=4，8-2=6，5-2=3，所以有阴影部分(①、②、③部分之和)的面积为73-4-6-3-2=58．【答案】58【例 4】 如图，三角形纸板、正方形纸板、圆形纸板的面积相等，都等于60平方厘米．阴影部分的面积总和是40平方厘米，3张板盖住的总面积是100平方厘米，3张纸板重叠部分的面积是多少平方厘米？【考点】几何中的重叠问题 【难度】3星【题型】解答【解析】 阴部分的面积60310040220=⨯--÷=（）(平方厘米)．【答案】20平方厘米【巩固】如图所示，A、B、C分别是面积为12、28、16的三张不同形状的纸片，它们重叠在一起，露在外面的总面积为38．若A与B、B与C的公共部分的面积分别为8、7，A、B、C这三张纸片的公共部分为3．求A与C公共部分的面积是多少？【考点】几何中的重叠问题【难度】3星【题型】解答【解析】设A与C公共部分的面积为x，由包含与排除原理可得：⑴先“包含”：把图形A、B、C的面积相加：12281656++=，那么每两个图形的公共部分的面积都重复计算了1次，因此要排除掉．⑵再“排除”：5687x---，这样一来，三个图形的公共部分被全部减掉，因此还要再补回．⑶再“包含”：56873---+，这就是三张纸片覆盖的面积．x根据上面的分析得：5687338x=．---+=，解得：6x【答案】6一年级（上）一.准备课1.数一数2.比多少二.位置1.上、下、前、后2.左、右三.1—5的认识和加减法1.1—5的认识2.比多少3.第几4.分和合5.加法6.减法7.0四.认识图形（一）认识图形五.6—10的认识和加减法1.6和72.8和93.104.连加、连减、加减混合六.11—20各数的认识1.11—20各数的认识2.10加几、十几加几和相应的减法七.认识钟表认识钟表八.20以内的进位加法2.8、7、9加几3.5、4、3、2加几4.解决问题一年级（下）一.认识图形（二）认识图形二.20以内的退位减法1.十几减92.十几减8、7、63.十几减5、4、3、24.解决问题三.分类与整理分类与整理四.100以内数的认识1.数数、数的组成2.数的顺序、比较大小3.解决问题4.整十数加一位数及相应的减法五.认识人民币1.认识人民币2.简单的计算六.100以内的加法和减法(一)1.整十数加、减整十数2.两位数加一位数、整十数3.两位数减一位数、整十数4.解决问题七.找规律1.找规律（一）2.找规律（二）二年级（上）一.长度单位1.厘米和米2.线段二.100以内的加法和减法(二)1.加法3.连加、连减和加减混合三.角的初步认识1.认识角2.认识直角3.认识钝角和锐角四.表内乘法（一）1.乘法的初步认识2.5的乘法口诀3.2、3、4的乘法口诀4.6的乘法口诀五.观察物体（一）观察物体（一）六.表内乘法（二）7、8、9的乘法口诀七.认识时间认识时间八.数学广角—搭配（一）数学广角—搭配（一）二年级（下）一.数据收集整理数据收集整理二.表内除法（一）1.除法的初步认识2.用2-6的乘法口诀求商3.解决问题三.图形的运动（一）1.轴对称图形2.平移和旋转四.表内除法（二）1.用7、8、9的乘法口诀求商2.解决问题五.混合运算混合运算六.有余数的除法1.有余数的除法的意义和计算2.解决问题七.万以内数的认识1.1000以内数的识2 .10000以内数的认识3 .整百、整千数加减法八.克和千克克和千克九.数学广角—推理生活中的推理三年级（上）一.时、分、秒1.秒的认识2.时间的计算二.万以内的加法和减法（一）1.口算两位数加减两位数2.几百几十加减几百几十3.三位数加减三位数的估算三.测量1.毫米、分米的认识2.千米的认识3.吨的认识四.万以内的加法和减法（二）1.加法2.减法五.倍的认识倍的认识六.多位数乘一位数1.口算乘法2.笔算乘法3.含0的乘法4.估算与解决问题七.长方形和正方形1.四边形2.周长、长方形和正方形周长八.分数的初步认识1.分数的初步认识（一）2.分数的初步认识（二）3.分数的简单计算4.分数的简单应用九.数学广角——集合集合思想三年级（下）一位置与方向（一）1 认识东、南、西、北四个方向2 认识东北、东南、西北、西南四个方向二除数是一位数的除法1 口算除法2 一位数出两、三位数的笔算除法3 商的中间或末尾有0的笔算除法4 用估算解决问题三复式统计表复式统计表四两位数乘两位数1 口算乘法2 笔算乘法五面积1 面积和面积单位2 长方形、正方形面积的计算3 面积单位间的进率六.年、月、日1 年、月、日2 24时计时法七小数的初步认识1 认识小数2 简单的小数加、减法八数学广角——搭配（二）数学广角——搭配（二）四年级（上）一大数的认识1 亿以内数的认识（一）2 亿以内数的认识（二）3 数的产生、十进制计数法和亿以上数的认识4 计算工具的认识、算盘和计算器5 1亿有多大二公顷和平方千米2 认识平方千米三角的度量1 线段、直线、射线和角2 角的度量3 角的分类4 画角四三位数乘两位数1 笔算乘法（一）2 笔算乘法（二）五平行四边形和梯形1 平行与垂直2平行四边形和梯形六除数是两位数的除法1 口算除法2 笔算除法（一）3 笔算除法（二）4 笔算除法（三）5 笔算除法（四）6 商的变化规律七条形统计图条形统计图八数学广角——优化数学广角——优化四年级（下）一四则运算1 加减法的意义和各部分间的关系2 乘除法的意义和各部分间的关系3 括号二观察物体（二）观察物体（二）三运算定律1 加法运算定律2 乘法运算定律四小数的意义和性质1 小数的意义和读写法2 小数的性质和大小比较3 小数点移动引起小数大小的变化4 小数与单位换算5 小数的近似数五三角形1 三角形的特性2 三角形的分类3 三角形的内角和六小数的加法和减法2 小数加减混合运算3 整数加法运算定律推广到小数七图形的运动（二）1 轴对称2 平移八平均数与条形统计图1 平均数2 复式条形统计图九数学广角——鸡兔同笼数学广角——鸡兔同笼五年级（上）一小数乘法1 小数乘整数2 小数乘小数3 积的近似数4 整数乘法二位置位置三小数除法1 除数是整数的小数除法2 一个数除以小数3 商的近似数4 循环小数5 用计算器探索规律6 解决问题四可能性事件发生的可能性五简易方程1 用字母表示数2 方程的意义及等式的性质3 解方程4 实际问题与方法六多边形的面积1 平行四边形的面积2 三角形的面积3 梯形的面积4 组合图形的面积七数学广角——植树问题数学广角——植树问题五年级（下）一观察物体（三）观察物体（三）二因数与倍数1 因数和倍数2 2、5、3的倍数的特征3 质数和合数三长方体和正方体1 长方体和正方体的认识2 长方体和正方体的表面积3 长方体和正方体的体积4 体积单位间的进率5 容积和容积单位四分数的意义和性质1 分数的意义2 真分数和假分数3 分数的基本性质4 约分5 通分6 分数和小数的互化五图形的运动（三）图形的运动（三）六分数的加法和减法1 同分母分数加减法2 异分母分数加减法3 分数加减混合运算七折线统计图折线统计图八数学广角——找次品数学广角——找次品六年级（上）一分数乘法1 分数乘法2 小数乘分数与分数混合运算3 解决问题二位置与方向（二）位置与方向三分数除法1 倒数的认识2 分数除法3 分数四则混合运算4 分数应用题四比1 比的意义2 比的基本性质3 比的应用五圆1 圆的认识2 圆的周长3 圆的面积4 扇形六百分数（一）1 百分数的意义和写法2 百分数与小数、分数的互化3 用百分数解决问题七扇形统计图扇形统计图八数学广角——数与形六年级（下）一负数负数二百分数(二)1 折扣2 成数3 税率4 利率三圆柱与圆锥1 圆柱2 圆锥四比例1 比例的意义和基本性质2 正比例和反比例的意义3 比例的应用五数学广角——鸽巢问题数学广角——鸽巢问题小学五年级数学上册复习教学知识点归纳总结第一单元小数乘法1、小数乘整数：@意义——求几个相同加数的和的简便运算。

小学奥数专题-重叠问题(精华版) XXX奥数重叠问题专题日常生活或数学问题中，在把一些数据按照某个标准分类时，常常出现其中的一部分数据同时属于两种或两种以上不同的类别，这样在计算总数时就会出现重复计算的情况，这类问题就叫做重叠问题。

重叠问题中涉及到的容斥原理是奥数的四大原理之一，是奥数重要知识点。

学生研究奥数，一定要掌握容斥原理。

下面小编给大家分享解决重叠的方法。

1.解答重叠问题要用到数学中一个重要原理——包含与排除原理，即当两个计数部分有重复包含时，为了不重复计数，应从它们的和中排除重复部分。

2.解答重叠问题的应用题，必须从条件入手进行认真的分析，有时还要画出图示，借助图形进行思考，找出哪些是重复的，重复了几次。

明确需要要求的是哪一部分，从而找出解答方法。

3.在数学中，我们经常用平面上封闭曲线的内部代表集合和集合之间的关系。

这种图称为XXX（也叫文氏图）。

4.解答重叠问题的常用方法是：先不考虑重叠的情况，把有重复包含的几个计数部分加起来，再从它们的和中排除重复部分元素的个数，使得计算的结果既无遗漏又不重复。

这个原理叫做包含与排斥原理，也叫容斥原理。

5.容斥道理1：如果被计数的对象，被分为A、B两大类，则：被计数对象的总个数=A类元素的个数+B类元素的个数-同时属于A类和B类的元素个数。

容斥道理2：如果被计数的对象，被分为A、B、C三大类，则：被计数对象的总个数=A类元素的个数+B类元素的个数+C类元素的个数-同时属于A类和B类元素的个数-同时属于A类和C类元素个数-同时属于B类和C类元素个数+同时属于A类、B类、C类元素个数。

一、重叠问题之长度：（1）拼接（对接）（2）搭接（3）打结题目1：（搭接正问题：求总长度）把两段同样是20厘米长的纸条粘合在一起，形成一段更长的纸条。

中间堆叠的局部是6厘米，粘好的纸条长几何厘米？题目2：（搭接反问题一：等长搭接，求原来长度）把两段一样长的纸条粘合在一起，形成一段更长的纸条。

1. 了解容斥原理二量重叠和三量重叠的内容；2. 掌握容斥原理的在组合计数等各个方面的应用．一、两量重叠问题 在一些计数问题中，经常遇到有关集合元素个数的计算．求两个集合并集的元素的个数，不能简单地把两个集合的元素个数相加，而要从两个集合个数之和中减去重复计算的元素个数，即减去交集的元素个数，用式子可表示成：A B A B A B =+-U I (其中符号“U ”读作“并”，相当于中文“和”或者“或”的意思；符号“I ”读作“交”，相当于中文“且”的意思．)则称这一公式为包含与排除原理，简称容斥原理．图示如下:A 表示小圆部分，B 表示大圆部分，C 表示大圆与小圆的公共部分，记为：A B I ，即阴影面积．图示如下:A 表示小圆部分，B 表示大圆部分，C 表示大圆与小圆的公共部分，记为：A B I ，即阴影面积．包含与排除原理告诉我们，要计算两个集合A B 、的并集A B U 的元素的个数，可分以下两步进行：第一步：分别计算集合A B 、的元素个数，然后加起来，即先求A B +(意思是把A B 、的一切元素都“包含”进来，加在一起)；第二步：从上面的和中减去交集的元素个数，即减去C A B =I (意思是“排除”了重复计算的元素个数)．二、三量重叠问题A 类、B 类与C 类元素个数的总和A =类元素的个数B +类元素个数C +类元素个数-既是A 类又是B 类的元素个数-既是B 类又是C 类的元素个数-既是A 类又是C 类的元素个数+同时是A 类、B 类、C 类的元素个数．用符号表示为：A B C A B C A B B C A C A B C =++---+U U I I I I I ．图示如下：教学目标知识要点7-7-3.几何中的重叠问题1．先包含——A B +重叠部分A B I 计算了2次，多加了1次；2．再排除——A B A B +-I把多加了1次的重叠部分A B I 减去．在解答有关包含排除问题时，我们常常利用圆圈图(韦恩图)来帮助分析思考．【例 1】 把长38厘米和53厘米的两根铁条焊接成一根铁条．已知焊接部分长4厘米，焊接后这根铁条有多长？【考点】几何中的重叠问题 【难度】1星 【题型】解答【解析】 因为焊接部分为两根铁条的重合部分，所以，由包含排除法知，焊接后这根铁条长3853487+-=(厘米)．【答案】87厘米【巩固】 把长23厘米和37厘米的两根铁条焊接成一根铁条．已知焊接部分长3厘米，焊接后这根铁条有多长？【考点】几何中的重叠问题 【难度】1星 【题型】解答【解析】 焊接部分为两根铁条的重合部分，由包含排除法知，焊接后这根铁条长：2337357+-=(厘米)．【答案】57厘米【例 2】 两张长4厘米，宽2厘米的长方形纸摆放成如图所示形状．把它放在桌面上，覆盖面积有多少平方厘米？【考点】几何中的重叠问题 【难度】1星 【题型】解答图32厘米4厘米【解析】 两个长方形如图摆放时出现了重叠(见图中的阴影部分)，重叠部分恰好是边长为2厘米的正方形，如果利用两个42⨯的长方形面积之和来计算被覆盖桌面的面积，那么重叠部分在两个长方形面积中各被计算了一次，而实际上这部分只需计算一次就可以了．所以，被覆盖面积=长方形面积之和-重叠部分．于是，被覆盖面积4222212=⨯⨯-⨯=(平方厘米)．【答案】12厘米例题精讲图中小圆表示A 的元素的个数，中圆表示B 的元素的个数，大圆表示C 的元素的个数．1．先包含：A B C ++ 重叠部分A B I 、B C I 、C A I 重叠了2次，多加了1次． 2．再排除：A B C A B B C A C ++---I I I 重叠部分A B C I I 重叠了3次，但是在进行A B C ++- A B B C A C --I I I 计算时都被减掉了． 3．再包含：A B C A B B C A C A B C ++---+I I I I I ．【巩固】 如图3，一张长8厘米，宽6厘米，另一个正方形边长为6厘米，它们中间重叠的部分是一个边长为4厘米的正方形，求这个组合图形的面积．【考点】几何中的重叠问题 【难度】1星 【题型】解答图3 【解析】 两个图形如图摆放时出现了重叠(见图中的阴影部分)，重叠部分恰好是边长为4厘米的正方形，如果利用长方形和正方形面积之和来计算被覆盖桌面的面积，那么重叠部分在长方形和正方形面积中各被计算了一次，而实际上这部分只需计算一次就可以了．所以，组合图形的面积=长方形面积+正方形面积-重叠部分．于是，组合图形的面积：86664468⨯+⨯-⨯=(平方厘米)．【答案】68平方厘米【巩固】 一个长方形长12厘米，宽8厘米，另一个长方形长10厘米，宽6厘米，它们中间重叠的部分是一个边长4厘米的正方形，求这个组合图形的面积．【考点】几何中的重叠问题 【难度】1星 【题型】解答【解析】 两个长方形如图摆放时出现了重叠(见图中的阴影部分)，重叠部分恰好是边长为4厘米的正方形，如果利用两个长方形面积之和来计算被覆盖桌面的面积，那么重叠部分在两个长方形面积中各被计算了一次，而实际上这部分只需计算一次就可以了．所以，组合图形的面积=长方形面积之和-重叠部分．于是，组合图形的面积12810644140=⨯+⨯-⨯=(平方厘米)．【答案】140平方厘米【例 3】 三个面积均为50平方厘米的圆纸片放在桌面上(如图)，三个纸片共同重叠的面积是10平方厘米．三个纸片盖住桌面的总面积是100厘米．问：图中阴影部分面积之和是多少？【考点】几何中的重叠问题 【难度】2星 【题型】解答CBA10【解析】 将图中的三个圆标上A 、B 、C ．根据包含排除法，三个纸片盖住桌面的总面积=(A 圆面积B +圆面积C +圆面积-）（A 与B 重合部分面积A +与C 重合部分面积B +与C 重合部分面积+）三个纸片共同重叠的面积，得：100505050A =++-（）（与B 重合部分面积A +与C 重合部分面积B +与C 重合部分面积10+），得到A 、B 、C 三个圆两两重合面积之和为：16010060-=平方厘米，而这个面积对应于圆上的那三个纸片共同重叠的面积的三倍与阴影部分面积的和，即：60103=⨯+阴影部分面积，则阴影部分面积为：603030-=(平方厘米)．【答案】30平方厘米【巩固】 如图，已知甲、乙、丙3个圆的面积均为30，甲与乙、乙与丙、甲与丙重合部分的面积分别为6，8，5，而3个圆覆盖的总面积为73．求阴影部分的面积．【考点】几何中的重叠问题 【难度】2星 【题型】解答【解析】 设甲圆组成集合A ，乙圆组成集合B ，丙圆组成集合C ．A B C ===30，A B I =6，B C I =8，A C I =5，A B C U U =73，而A B C U U =A B C +--A B B C A C A B C --+I I I I I .有73=30×3-6-8-5+A B C I I ，即A B C I I =2，即甲、乙、丙三者的公共面积(⑧部分面积)为2．那么只是甲与乙(④)，乙与丙(⑥)，甲与丙(⑤)的公共的面积依次为6-2=4，8-2=6，5-2=3，所以有阴影部分(①、②、③部分之和)的面积为73-4-6-3-2=58．【答案】58【例 4】 如图，三角形纸板、正方形纸板、圆形纸板的面积相等，都等于60平方厘米．阴影部分的面积总和是40平方厘米，3张板盖住的总面积是100平方厘米，3张纸板重叠部分的面积是多少平方厘米？【考点】几何中的重叠问题 【难度】3星 【题型】解答【解析】 阴而三张纸重叠部分是被计算了三次．所以三张纸重叠部分的面积60310040220=⨯--÷=（）(平方厘米)．【答案】20平方厘米【巩固】 如图所示，A 、B 、C 分别是面积为12、28、16的三张不同形状的纸片，它们重叠在一起，露在外面的总面积为38．若A 与B 、B 与C 的公共部分的面积分别为8、7，A 、B 、C 这三张纸片的公共部分为3．求A 与C 公共部分的面积是多少？【考点】几何中的重叠问题 【难度】3星 【题型】解答【解析】 设A 与C 公共部分的面积为x ，由包含与排除原理可得：⑴ 先“包含”：把图形A 、B 、C 的面积相加：12281656++=，那么每两个图形的公共部分的面积都重复计算了1次，因此要排除掉．⑵ 再“排除”：5687x ---，这样一来，三个图形的公共部分被全部减掉，因此还要再补回．⑶ 再“包含”：56873x ---+，这就是三张纸片覆盖的面积．根据上面的分析得：5687338x ---+=，解得：6x =．【答案】6。

1. 了解容斥原理二量重叠和三量重叠的内容；2. 掌握容斥原理的在组合计数等各个方面的应用．一、两量重叠问题 在一些计数问题中，经常遇到有关集合元素个数的计算．求两个集合并集的元素的个数，不能简单地把两个集合的元素个数相加，而要从两个集合个数之和中减去重复计算的元素个数，即减去交集的元素个数，用式子可表示成：A B A B A B =+-(其中符号“”读作“并”，相当于中文“和”或者“或”的意思；符号“”读作“交”，相当于中文“且”的意思．)则称这一公式为包含与排除原理，简称容斥原理．图示如下:A 表示小圆部分，B 表示大圆部分，C 表示大圆与小圆的公共部分，记为：A B ，即阴影面积．图示如下:A 表示小圆部分，B 表示大圆部分，C 表示大圆与小圆的公共部分，记为：A B ，即阴影面积．包含与排除原理告诉我们，要计算两个集合A B 、的并集A B 的元素的个数，可分以下两步进行：第一步：分别计算集合A B 、的元素个数，然后加起来，即先求A B +(意思是把A B 、的一切元素都“包含”进来，加在一起)；第二步：从上面的和中减去交集的元素个数，即减去C A B =(意思是“排除”了重复计算的元素个数)．二、三量重叠问题A 类、B 类与C 类元素个数的总和A =类元素的个数B +类元素个数C +类元素个数-既是A 类又是B 类的元素个数-既是B 类又是C 类的元素个数-既是A 类又是C 类的元素个数+同时是A 类、B 类、C 类的元素个数．用符号表示为：A B C A B C A B B C A C A B C =++---+．图示如下：教学目标知识要点7-7-1.容斥原理之重叠问题（一）1．先包含——A B + 重叠部分A B 计算了2次，多加了1次； 2．再排除——A B A B +- 把多加了1次的重叠部分A B 减去．在解答有关包含排除问题时，我们常常利用圆圈图(韦恩图)来帮助分析思考．两量重叠问题【例 1】 小明喜欢：踢足球、上网、游泳、音乐、语文、数学；小英喜欢：数学、英语、音乐、陶艺、跳绳。

重叠问题练习题答案重叠问题通常指的是在数学或逻辑问题中，两个或多个集合或事件有共同的部分。

下面是一些重叠问题练习题的答案：1. 练习题：一个班级有50名学生，其中30人参加了数学俱乐部，20人参加了科学俱乐部。

如果两个俱乐部共有的学生数为10人，那么没有参加任何俱乐部的学生有多少人？答案：首先，我们计算两个俱乐部的学生总数：30（数学俱乐部）+ 20（科学俱乐部）- 10（两个俱乐部共有的学生）= 40人。

班级总人数为50人，所以没有参加任何俱乐部的学生数为50 - 40 = 10人。

2. 练习题：在一个社区中，有200户家庭，其中100户有宠物，80户有花园。

如果同时拥有宠物和花园的家庭有40户，那么没有宠物也没有花园的家庭有多少户？答案：首先，我们计算有宠物和花园的家庭总数：100（有宠物）+ 80（有花园）- 40（同时拥有宠物和花园）= 140户。

社区总家庭数为200户，所以没有宠物也没有花园的家庭数为200 - 140 = 60户。

3. 练习题：一个图书馆有1000本书，其中300本是科幻小说，200本是历史书籍。

如果同时属于科幻和历史类别的书籍有50本，那么既不是科幻也不是历史的书籍有多少本？答案：首先，我们计算科幻和历史书籍的总数：300（科幻小说）+ 200（历史书籍）- 50（同时属于科幻和历史的书籍）= 450本。

图书馆总书籍数为1000本，所以既不是科幻也不是历史的书籍数为1000 - 450 = 550本。

4. 练习题：一个学校有500名学生，其中200名学生参加了体育队，150名学生参加了合唱团。

如果同时参加体育队和合唱团的学生有50人，那么没有参加任何团队的学生有多少人？答案：首先，我们计算参加体育队和合唱团的学生总数：200（体育队）+ 150（合唱团）- 50（同时参加两个团队的学生）= 300人。

学校总学生数为500人，所以没有参加任何团队的学生数为500 - 300 = 200人。

重叠问题知识集锦在很多计数问题中，常常要把所要计数的对象分为若干个不重复又不遗漏的类型，使得每类便于计数。

但是实际的问题却往往较为复杂，而且容易混为一团，难以区分，而要准确无误的计算事物的个数就得运用容斥原理，这类问题往往被称为重叠问题，也叫包含于排除问题。

例题集合例1 一个班有学生42人，参加体育代表队的有30人，参加文艺代表队的有25人，并且每个人至少参加了一个队，这个班两队都参加的有几个人？练习1 三年级有200名学生全部都参加了小组活动。

报名参加体育小组的有180人，参加文娱小组的有160人。

问体育和文娱两个小组都参加的有多少人？例2 四年级某个班的同学都参加兴趣小组的活动，已知有28人参加歌唱小组，26人参加美术小组，两个小组都参加的有9人。

该班共有多少人？练习2 某班56人，参加语文竞赛的有28人，参加数学竞赛的有27人，如果两科都没参加的有25人，那么同时参加语文、数学竞赛的有多少人？例3 有100位旅客，其中10人既不懂英语，又不懂俄语，有75人懂英语，有83人懂俄语。

那么这100位旅客中既懂英语又懂俄语的有多少人？练习3 有40名运动员，其中有25人会摔跤，有20人会击剑，有10人摔跤、击剑都不会。

问既会摔跤又会击剑的运动员有多少名？例4 某公司除6人没有参加业余培训学习外，其余员工都参加了学习。

参加计算机学习的有27人，参加外语学习的有32人，两种科目都参加的有11人。

该公司共有多少名员工？练习4 学校文艺组的成员每人至少会演奏一种乐器。

已知会拉风琴的有24人，会弹电子琴的有17人，其中两种乐器都会演奏的有8人。

这个文艺组一共有多少人？例5 燕燕要制作一架飞机模型，只差下图所示的a的边长，一时求不出来，被难住了。

已知正方形与三角形一部分重叠着，乙三角形面积比甲三角形面积大5平方厘米。

请你帮她算一下（单位：厘米）。

练习5 桌面上放有一张长12厘米、宽8厘米的长方形纸片和一张边长为7厘米的正方形纸片（如图所示）。

小学奥数重叠问题例题分析小学奥数重叠问题例题分析知识要点：前面已学过排队问题，从前面数，从后面数，丽丽都排第6，这一排共有几个人？这里丽丽被重复数了两次，有时我们也把这类问题叫重叠问题。

[ 例1 ]洗好的8块手帕夹在绳子上晾干，同一个夹子夹住相邻的两块手帕的两边，这样一共要多少个夹子？分析：由图知道，两块手帕有一边重叠，用3个夹子。

三块手帕有两边重叠，用4个夹子，我们发现夹子数总比手帕数多1，因此8块手帕就要用9个夹子。

[ 例2 ]把图画每两张重叠在一起钉在墙上，现在有5张画要多少个图钉呢？分析：每排两张画要6个图钉，每排三张画要8个图钉，每排四张画要10个图钉。

可以看出，图画每增加一张，图钉就要增加2颗，那么5张画要12个图钉。

[ 例3 ]有两块一样长的木板，钉在一起，如果每块木板长25厘米，中间钉在一起的长5厘米，现在长木板有多长？分析：把两块木板钉起来，钉在一起的地方的.长度就是重叠的部分。

现在的总长就是原来两个总长的和减去重叠的部分。

算式：25+25-5=45（厘米）所以现在木板长45厘米。

[ 例4 ]张老师出了两道题，做对第一题的有13人，做对第二题的有22人，两道题都做对的有8人，这个班一共有多少人？分析：做对第一题的13个人里，有8个人也做对第二题，那么做对第二题的22个人里这8个人就又重复数了一次，因此把做对第一题的人数和做对第二题的人数和起来，再减去重复数的这8个人。

算式：13+22-8=27（人）所以这个班一共有27人。

[ 例5 ]四根长都是8厘米的绳子，把它们打结连在一起，成为一根长绳，打结处每根绳用去1厘米，绳结长度不计，现在这根长绳长多少厘米？分析：两根绳有一个结，三根绳有两个结，那么四根绳有三个结。

一个结用去1+1=2厘米，那么三个结用去2+2+2=6厘米，绳子总长8+8+8+8=32厘米，减去打结的6厘米，32-6=26，现在这根长绳是26厘米。

五年级奥数题：重叠问题1．甲、乙两队合修一条水渠，甲队每天修14.5米，乙队3天修46.5米，照这样计算，两队合修6天，共修水渠多少米？2．用绳子测一口井的深度．绳子两折时，多余60厘米；绳子三折时，还差40厘米．求绳长和井深．3．甲、乙两筐苹果，如果从甲筐中拿出18个放进乙筐，两筐的苹果就同样多，如果从乙筐拿出13个放进甲筐，甲筐里的苹果就是乙筐的3倍．甲、乙两筐原来各有苹果多少个？4．一个水池，单开进水管，6分钟可将空水池注满，单开出水管8分钟可将满池水放完，若同时打开进、出水管，多少分钟可将水池注满？5．甲、乙两人修路队共有76人，甲队增加本队人数的4倍，乙队增加本队人数的6倍后，两队共增加了384人，求甲、乙两队原有各有多少人？6．一个食堂买来面粉是大米的2倍，每天吃30千克大米，40千克面粉，几天后大米全部吃完，面粉还剩余160千克，这个食堂买来大米和面粉各多少千克？7．甲的存款是乙的5倍，如果甲取出60元，乙存入60元，那么乙的存款是甲的2倍．甲、乙原有存款各有多少元？8．10年前母亲的年龄是女儿的7倍，10年后母亲的年龄是女儿的2倍．现在母亲的年龄是多少岁？9．甲、乙两车同时从A、B两地相向而行，第一次两车在距B地64千米外相遇，相遇后两车仍以原速度继续行驶，并在到达对方车站后立即沿原路返回，途中两车在距A地48千米处第二次相遇，两次相遇后之间相距多少千米？10．某列车通过250米长的隧道用25秒，通过210米长的隧道用23秒，若该列车与另一列车长150米，时速为72千米的列车相遇，错车而过需要_________秒钟？11．买来5角、2角、1角5分三种邮票，共20张，总值5元5角，其中5角和1角5分的邮票张数相等，问三种邮票各购几张？．12．客车从甲地开往开乙地，货车从乙地开往甲地，每小时客车比货车多得12千米，经过4小时相遇．相遇后，两车继续按原方向前进，又经过3小时客车到达乙地，这时货车离乙地多少米？13．仓库里原有化肥若干吨，第一天取出全部的一半多30吨，第二次取出余下的一半少100吨，第三次取出150吨，最后还剩下70吨，这批化肥原有多少吨？14．三个植树队共植树1800棵，甲队植树的棵数是乙队的2倍，乙队植树的棵数比丙队少200棵，三队各植树多少棵？15．如果买3盒水彩笔和5个书包，需要259元，如果买2盒水彩笔和3个书包，需要161元，2个书包和2盒水彩笔共要多少元？16．一个两位数，十位数字与个位数字之和是10，数字之差是4，且个位数字小于十位数字，这个两数是多少？17．一群公猴、母猴、小猴共38只，每天摘桃266个．已知1只公猴每天摘桃10个，1只母猴每天摘桃8个，1只小猴每天摘桃5个．又知公猴比母猴少4只，那么这群猴子中，小猴有多少只？18．有鸡蛋16箩，每只大箩可容180个，每只小箩可容120个，共值570元．若将每个鸡蛋便宜5分出售，则可得款456元，大箩、小箩各多少只？五年级奥数题：重叠问题参考答案与试题解析1．甲、乙两队合修一条水渠，甲队每天修14.5米，乙队3天修46.5米，照这样计算，两队合修6天，共修水渠多少米？2．用绳子测一口井的深度．绳子两折时，多余60厘米；绳子三折时，还差40厘米．求绳长和井深．，折三折时，每段就是全长的，全长的（）就÷，，本题的关键是绳长一定，折二折每段是全长的，折三折每段是全长的3．甲、乙两筐苹果，如果从甲筐中拿出18个放进乙筐，两筐的苹果就同样多，如果从乙筐拿出13个放进甲筐，甲筐里的苹果就是乙筐的3倍．甲、乙两筐原来各有苹果多少个？4．一个水池，单开进水管，6分钟可将空水池注满，单开出水管8分钟可将满池水放完，若同时打开进、出水管，多少分钟可将水池注满？；单开出分钟可将满池水放完，每分钟，同时打开进、出水管，每分钟进水﹣﹣（﹣÷，5．甲、乙两人修路队共有76人，甲队增加本队人数的4倍，乙队增加本队人数的6倍后，两队共增加了384人，求甲、乙两队原有各有多少人？6．一个食堂买来面粉是大米的2倍，每天吃30千克大米，40千克面粉，几天后大米全部吃完，面粉还剩余160千克，这个食堂买来大米和面粉各多少千克？x﹣）÷，7．甲的存款是乙的5倍，如果甲取出60元，乙存入60元，那么乙的存款是甲的2倍．甲、乙原有存款各有多少元？8．10年前母亲的年龄是女儿的7倍，10年后母亲的年龄是女儿的2倍．现在母亲的年龄是多少岁？x+10=9．甲、乙两车同时从A、B两地相向而行，第一次两车在距B地64千米外相遇，相遇后两车仍以原速度继续行驶，并在到达对方车站后立即沿原路返回，途中两车在距A地48千米处第二次相遇，两次相遇后之间相距多少千米？10．某列车通过250米长的隧道用25秒，通过210米长的隧道用23秒，若该列车与另一列车长150米，时速为72千米的列车相遇，错车而过需要10秒钟？11．买来5角、2角、1角5分三种邮票，共20张，总值5元5角，其中5角和1角5分的邮票张数相等，问三种邮票各购几张？．12．客车从甲地开往开乙地，货车从乙地开往甲地，每小时客车比货车多得12千米，经过4小时相遇．相遇后，两车继续按原方向前进，又经过3小时客车到达乙地，这时货车离乙地多少米？13．仓库里原有化肥若干吨，第一天取出全部的一半多30吨，第二次取出余下的一半少100吨，第三次取出150吨，最后还剩下70吨，这批化肥原有多少吨？14．三个植树队共植树1800棵，甲队植树的棵数是乙队的2倍，乙队植树的棵数比丙队少200棵，三队各植树多少棵？15．如果买3盒水彩笔和5个书包，需要259元，如果买2盒水彩笔和3个书包，需要161元，2个书包和2盒水彩笔共要多少元？16．一个两位数，十位数字与个位数字之和是10，数字之差是4，且个位数字小于十位数字，这个两数是多少？17．一群公猴、母猴、小猴共38只，每天摘桃266个．已知1只公猴每天摘桃10个，1只母猴每天摘桃8个，1只小猴每天摘桃5个．又知公猴比母猴少4只，那么这群猴子中，小猴有多少只？18．有鸡蛋16箩，每只大箩可容180个，每只小箩可容120个，共值570元．若将每个鸡蛋便宜5分出售，则可得款456元，大箩、小箩各多少只？。