专题13 两边夹-2021年高考数学一轮复习优拔尖必刷压轴题(新高考地区专用)

2021届高考数学金榜押题卷（二）（新高考版）【满分：150分】一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.若集合{}234,{1,0,1,2,3}A xx x B =+<=-∣，则A B =( )A.{}1,0-B.{}1,1-C.{}1,0,1-D.{}0,1,2,32.已知i 是虚数单位，设复数2ii 2ia b -+=+，其中,a b ∈R ，则a b +的值为( ) A.75B.75-C.15D.15-3.《九章算术》第三章“哀分”中有如下问题：“今有甲持钱四百八十，乙持钱三百，丙持钱二百二十，凡三人俱出关，关税百钱，欲以钱数多少衰出之，问乙出几何？”其意为：“今有甲带了480钱，乙带了300钱，丙带了220钱，三人一起出关，共需要交关税100钱，依照钱的多少按比例出钱”，则乙应出( ) A.50B.32C.31D.304.已知0.3 1.132, 2.3,log 6a b c ===，则a ，b ，c 的大小关系为( ) A.c a b <<B.c b a <<C.a c b <<D.b c a <<5.已知首项为2的等比数列{}n a 的前n 项和为n S ，若360a a +=，则20202021S S +=( ) A.0B.1C.2D.36.已知直线y ax b =+与曲线()1e x f x x =--相切，则b a -的最小值是( ) A.12e-B.21e -C.2e-D.2e7.如图，正方体1111ABCD A B C D -中，,E F 分别为棱1111,C D A D 的中点，则异面直线DE 与AF 所成角的余弦值是( )A.45B.35310108.已知函数πsin (0)6y x ωω⎛⎫=+> ⎪⎝⎭在区间(0,π)上恰有3个零点，则ω的取值范围是( )A.717,66⎛⎤ ⎥⎝⎦B.230,6⎛⎤ ⎥⎝⎦C.1723,66⎡⎫⎪⎢⎣⎭D.1723,66⎛⎤ ⎥⎝⎦二、多项选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得3分，有选错的得0分. 9.已知||1,|3=-=∣a a b ,a b 所成的角为60︒，则( ) A.||2=bB.()⊥-a b aC.//a bD.1⋅=a b10.十六世纪中叶，英国数学家雷科德在《砺智石》一书中首先把“=”作为等号使用，后来英国数学家哈利奥特首次使用“<”和“>”符号，并逐渐被数学界接受，不等号的引入对不等式的发展影响深远.若实数a b >，则下列不等式不一定成立的是( ) A.1a b> B.222a b ab +<C.2b a a b+ D.11a b< 11.在平面直角坐标系xOy 中，点(4,4)M 在抛物线22(0)y px p =>上，抛物线的焦点为F ，延长MF 与抛物线相交于点N ，则下列结论正确的是( ) A.抛物线的准线方程为1x =- B.17||4MN =C.OMN 的面积为72D.||||||||MF NF MF NF +=12.已知函数()sin ,f x x x x =∈R ，则下列说法正确的有( ) A.()f x 是偶函数 B.()f x 是周期函数C.在区间π,π2⎛⎫⎪⎝⎭上，()f x 有且只有一个极值点D.过点(0,0)作曲线()y f x =的切线，有且仅有3条 三、填空题：本题共4小题，每小题5分，共20分.13.已知ππ,22α⎛⎫∈- ⎪⎝⎭，若9cos 26cos 50αα++=，则sin α=_________.14.83412x x ⎛- ⎪⎝⎭的展开式中7x -的系数为_____________. 15.已知三棱锥A BCD -中，点A 在平面BCD 上的射影与点D 重合，4AD CD ==.若135CBD ∠=︒，则三棱锥A BCD -的外接球的体积为____________.16.已知双曲线2222:1(0,0)x y C a b a b-=>>的右焦点为F ，左顶点为A ，过点F 作C 的一条渐近线的垂线，垂足为M .若1tan 2MAF ∠=，则C 的离心率为_______________.四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.17.（10分）在①23sin sin sin sin 3b B c C b C a A ⎛⎫+=+ ⎪ ⎪⎭；②222cos sin sin sin cos C B C B A +=+；③22cos b a C c =+这三个条件中任选一个，补充在下面的问题中并作答.在ABC 中，角A ，B ，C 所对的边分别是a ，b ，c ，_______________. （1）求角A ；（2）若10,a ABC =的面积为83，求ABC 的周长. 注：如果选择多个条件分别解答，按第一个解答计分.18.（12分）已知数列{}n a 的前n 项和n S ，满足()21n n S a =-，数列{}n b 满足221log log n n n b a a +=+.（1）求数列{}{}n n a b 、的通项公式；（2）若数列{}n c 满足：n n n c a b =⋅，且n T 为数列{}n c 的前n 项和，求n T . 19.（12分）如图所示，在四棱锥P ABCD -中，底面ABCD 是直角梯形，,90,,AD BC BCD E F ∠=︒分别是棱BC ，PC 的中点，且122AD CD BC ===.（1）求证：平面PAB 平面FED ；（2）若点P 在平面ABCD 内的射影H 恰为AB 的中点，设1PH =，求二面角C EF D --的余弦值.20.（12分）随着手机游戏的发展，在给社会带来经济利益的同时，也使许多人深陷其中，从而产生一些负面的影响.A ，B 两所学校为了解学生每天玩游戏的时间，各自抽取了100名学生进行调查，得到的数据如表所示： A 学校B 学校（1）以样本估计总体，计算A 学校学生日游戏时间的平均数以及B 学校学生日游戏时间的中位数.（2）为了调查家长对孩子玩游戏的态度，学校相关领导随机抽取了200名男性家长和200名女性家长进行调查，并将所得结果统计如表所示，判断是否有99.9%的把握认为家长对孩子玩游戏的态度与家长性别有关？附：()()()()()22n ad bc K a b c d a c b d -=++++，其中n a b c d =+++.21.（12分）已知椭圆2222:1(0)x y C a b a b +=>>的离心率e =原点到过点(,0),(0,)A aB b -. （1）求椭圆C 的方程；（2）如果直线1(0)y kx k =+≠交椭圆C 于不同的两点E ，F ，且E ，F 都在以B 为圆心的圆上，求实数k 的值.22.（12分）已知函数()(ln 1)()f x x k x k =--∈R .（1）若曲线()y f x =在(1,(1))f 处的切线与直线20x y -=平行，求实数k 的值； （2）若对于任意12,(0,3]x x ∈，且()()12122122,x x f x f x x x <+<+恒成立，求实数k 的取值范围.答案以及解析一、单项选择题 1.答案：A解析：234x x +<，即(4)(1)0x x +-<，解得41x -<<，所以(4,1)A =-，所以{}1,0A B =-，故选A. 2.答案：D解析：因为22i (2i)34i i 2i (2i)(2i)55a b --+===-++-，所以34,55a b ==-，所以15a b +=-.故选D. 3.答案：D解析：根据分层抽样原理，抽样比例为300348030022010=++，所以乙应交关税为100⨯33010=钱.故选D. 4.答案：C解析：0.30.5 1.13322 1.414, 2.3 2.3,2log 6log 1.5a b c =<==>>=>=，所以a ，b ，c 的大小关系为a c b <<，故选C. 5.答案：C解析：设等比数列{}n a 的公比为(0)q q ≠.因为1362,0a a a =+=，所以()23210q q +=，解得1q =-，所以202020212020202121(1)21(1)21111S S ⎡⎤⎡⎤⨯--⨯--⎣⎦⎣⎦+=+=++.故选C.6.答案：A解析：由()1e x f x x =--得()1e x f x '=--，则()0,()f x f x '<单调递减，故直线y ax b =+与曲线()f x 只有一个切点，设切点为(),1e t P t t --，则曲线()f x 在点P 处的切线方程为()1e 1e ()t t y t x t -++=---，即()1e (1)e 1t t y x t =-++-+，所以()1e ,(1)e 1t t a b t =-+=-+，则t (1)e 11e e 2t t b a t t -=-+++=+，设()e 2t g t t =+，则()(1)e t g t t '=+，易知()g t 在(,1)-∞-上单调递减，在(1,)-+∞上单调递增，所以当1t =-时，()g t 取得最小值，为12e -，即b a -的最小值为12e-.7.答案：A解析：如图，取11A B 的中点N ，连接EN ，FN ，AN ，由E ，N 分别为11C D ，11A B 的中点，则11//EN A D 且11EN A D =，在正方体中11//AD A D 且11AD A D =，所以//EN AD 且EN AD =，所以四边形ANED 为平行四边形，所以//AN DE ，则FAN ∠(或其补角)为异面直线DE 与AF 所成角.设正方体的棱长为2，则在ANF 中，1112,2NF D B AN ===415AF =+=，所以222cos 2AF AN FN FAN AF AN+-∠=⋅5524.5255+-==⨯⨯故选A.8.答案：D解析：由(0,π)x ∈，可得πππ,π666x ωω⎛⎫+∈+ ⎪⎝⎭，函数πsin (0)6y x ωω⎛⎫=+> ⎪⎝⎭在区间(0,π)上恰有3个零点，等价于函数sin y x =在区间ππ,π66ω⎛⎫+ ⎪⎝⎭上恰有3个零点，故π3ππ4π6ω<+，解得172366ω<.故选D. 二、多项选择题 9.答案：ABD解析：因为,a b 所成的角为60︒，故选项C 错误；由题意得2222||()23-=-=-⋅+=a b a b a a b b ，所以||2=b ，故选项A 正确；2||||cos601,()0︒⋅==⋅-=⋅-=a b a b a b a a b a ，故选项B ，D 正确.故选ABD.10.答案：ACD解析：对于选项A ：当1,2a b =-=-时，满足a b >，此时112a b =<，故A 不一定成立；对于选项B ：因为2222()0a b ab a b +-=->，所以222a b ab +>，即222a b ab +<，所以222a b ab +<一定成立，故B 一定成立；对于选项C ：当1,1a b ==-时，满足a b >，此时1122b aa b+=--=-<，故C 不一定成立；对于选项D ：当1,1a b==-时，满足a b >，此时1111a b=>=-，故D 不一定成立.故选ACD. 11.答案：AD 解析：点(4,4)M 在抛物线20)2(y px p =>上，224242,4p p y x ∴=⋅⇒=∴=，焦点为(1,0)，准线为1x =-，A 正确，因为(4,4)M ，故404413MF k -==-，故直线MF 为：4(1)3y x =-， 联立22416(1)449(1)3y xx x x y x ⎧=⎪⇒-=⇒=⎨=-⎪⎩14或14,,1,||44x N MF ⎛⎫=∴-∴=+ ⎪⎝⎭155,||,||52424p p NF MN ==+=∴=+52544=，B 错误；||||||MF NF MN +==25||||4MF NF =⋅，D 正确； OMN 的面积为()11||22M N OF y y ⋅-=⨯5152⨯=，故C 错误.故选AD.12.答案：ACD解析：对于选项A ：因为函数()f x 的定义域为R ，显然()()f x f x =-，所以函数()f x 是偶函数，故A 正确.对于选项B ：若()f x 是周期函数，则存在非零常数T ，使得()()f x T f x +=，令0x =，则(0)()sin 0f f T T T ===，因为0T ≠，所以sin 0T =，则π,T k k =∈Z 且0k ≠.则(π)(π)sin(π)sin (),f k x k x k x x x f x k +=++≠=∈Z 且0k ≠，故不存在非零常数T ，使得()()f x T f x +=，故B 错误.对于选项C ：()sin ,,()sin cos 'f x x x x f x x x x =∈=+R ，令()sin cos g x x x x =+，则()2co si 's n g x x x x =-.当π,π2x ⎛⎫∈ ⎪⎝⎭时，()2cos in 's 0g x x x x =-<，故)'(f x 单调递减.又π10,(π)π02''f f ⎛⎫=>=-< ⎪⎝⎭，故'()0f x =在π,π2⎛⎫⎪⎝⎭上有且仅有一个解，故()f x 有且只有一个极值点，故C 正确.对于选项D ：设切点的坐标为(,sin )t t t ，则切线方程为sin (sin cos )()y t t t t t x t -=+-，将(0,0)代入，得2cos 0t t =，解得0t =或ππ,2t k k =+∈Z .若0t =，则切线方程为0y =；若ππ,2t k k =+∈Z ，则切线方程为y x =±，故D 正确. 故选ACD. 三、填空题13.答案：. 解析：由题可知()292cos -1+6cos 5=0αα+，即29cos +3cos 20,(3cos 1)(3cos 2)0.αααα-=∴-+=ππ1,,cos ,sin 223ααα⎛⎫∈-∴=∴== ⎪⎝⎭.14.答案：112解析：8⎛- ⎝的展开式的通项8411148362188C 2(1)C (1)2rr r r rr r rr T x xx----+⎛⎫=⋅⋅-⋅=⋅-⋅⋅ ⎪⎝⎭，令11476r -=-，解得6r =，故所求系数为6628C (1)2284112⨯-⨯=⨯=.15.答案：解析：如图，设BCD 的外接圆圆心为1O ，半径为r ，三棱锥A BCD -的外接球球心为O ，半径为R ，则1OO ⊥平面BCD ，故122ADOO ==.在BCD 中，由正弦定理得2sin CDr CBD==∠r =，则R ==.故球O 的体积3344ππ33V R ==⨯=.16.答案：5 3解析：如图所示，双曲线2222:1(0,0)x yCa ba b-=>>的右焦点(,0)F c，左顶点(,0)A a-.由双曲线的对称性不妨取渐近线方程为by xa=-，则过点(,0)F c且与直线by xa=-垂直的直线FM的方程为()ay x cb=-.联立(),,ay x cbby xa⎧=-⎪⎪⎨⎪=-⎪⎩解得2,a abx yc c==-，即2,a abMc c⎛⎫-⎪⎝⎭.作MN AF⊥于点N，在AMN中，由1tan2MAF∠=，可得2||1||2()abMN cAN aac-==--，整理得2a c b+=，所以()2222()44a cbc a+==-，整理得223250c ac a--=，即23250e e--=，解得53e=或1e=-（舍去），故双曲线C的离心率为53.四、解答题17.答案：（1）选择①：因为sin sin sin sin b B c C C a A ⎫+=+⎪⎪⎭，所以由正弦定理可得22sin b c C a a ⎫+=+⎪⎪⎭，即222sin b c a C +-=，则由余弦定理可得2cos sin bc A C =，所以sin cos sin C A A C =.因为sin 0C ≠，所以cos A A =，即tan A =. 因为(0,π)A ∈，所以π3A =. 选择②：由222cos sin sin sin cos C B C B A +=+， 得2221sin sin sin sin 1sin C B C B A -+=+-， 即222sin sin sin sin sin B C A B C +-=， 由正弦定理得222b c a bc +-=.由余弦定理得2221cos 22b c a A bc +-==. 因为(0,π)A ∈，所以π3A =.选择③：由22cos b a C c =+，结合正弦定理得 2sin 2sin cos sin B A C C =+.因为πA B C ++=，所以sin sin()B A C =+，则2sin()2(sin cos cos sin )2sin cos sin A C A C A C A C C +=+=+， 所以2cos sin sin A C C =.因为(0,π)C ∈，所以sin 0C ≠，故1cos 2A =. 因为(0,π)A ∈，所以π3A =. （2）由（1）知π3A =.因为11πsin sin 223ABCSbc A bc ===，所以32bc =. 由余弦定理得，22222cos ()3a b c bc A b c bc =+-=+-，即22()3100332196b c a bc +=+=+⨯=，所以14b c +=， 所以ABC 的周长为24a b c ++=. 18.答案：(1)21n n S a =-，①当1n =时，1121S a =-，解得11a =； 当2n 时1121n n S a --=-，② ①-②，得122n n n a a a -=-，即12(2)nn a n a -=， ∴数列{}n a 是首项为1，公比为2的等比数列，从而12n n a -=.221log log 121n n n b a a n n n +=+=-+=-.(2)由（1）得1(21)2n n c n -=-⋅，2213252(23)2n n T n -∴=+⨯+⨯++-⨯1(21)2,n n -+-⨯① 232123252(23)n T n =⨯+⨯+⨯++-⨯12(21)2n n n -+-⨯，②①-②，得()12112222n n T --=+⨯++-(21)2n n -⨯122212(21)212n n n --⨯=+⨯--⨯-(23)23n n =-⋅+. (23)23n n T n ∴=-⋅+.19.答案：（1）E 是BC 的中点，12BE BC ∴=. 1,,,2ADBC AD BC AD BE AD BE =∴=，∴四边形ABED 是平行四边形，ED AB ∴.又ED ⊄平面,PAB AB ⊂平面,PAB ED∴平面PAB .,E F 分别是棱BC ，PC 的中点，EFBP ∴.又EF ⊂/平面,PAB BP ⊂平面,PAB EF∴平面PAB .,ED EF 是平面FED 内两条相交直线，∴平面PAB平面FED .（2）连接HE，AE，AC.点P在平面ABCD内的射影H恰为AB的中点，PH∴⊥平面ABCD，,PH AB PH HE∴⊥⊥.由12,2AD CD BC E===是BC的中点，90BCD∠=°，得22222,2,1AB AE BE AC AD CD HE BH=+==+===，222HE BH BE∴+=，则HE AB⊥.故以H为坐标原点，HB，HE，HP所在直线分别为x，y，z轴建立如图所示的空间直角坐标系H xyz-，则11(0,0,0),(0,1,0),(1,0,0),(1,2,0),(0,0,1),,1,22H E A C P F⎛⎫---⎪⎝⎭.设平面CEF的法向量(,,)x y z=n，11,0,,(1,1,0)22EF EC⎛⎫=-=-⎪⎝⎭，0,0,EFEC⎧⋅=⎪∴⎨⋅=⎪⎩nn即110,220,x zx y⎧-+=⎪⎨⎪-+=⎩令1z=，得(1,1,1)=n.平面PAB平面,FED∴平面EFD的一个法向量为(0,1,0)=m.由图可知二面角C EF D--的平面角为锐角，∴设二面角C EF D--的平面角为π2θθ⎛⎫<<⎪⎝⎭，则||13cos||||33θ⋅===n mn m，∴二面角C EF D--的余弦值为33.20.答案：（1）A学校学生日游戏时间的平均数为350.1450.14550.16650.2750.18850.13950.0964.7⨯+⨯+⨯+⨯+⨯+⨯+⨯=（min）.B学校学生日游戏时间的中位数为5037102070107425----+⨯=（min）.（2）由已知可得2×2列联表：则()2240013639161648.17210.828200200297103K⨯⨯-⨯=≈<⨯⨯⨯，所以没有99.9%的把握认为家长对孩子玩游戏的态度与家长性别有关.21.答案：（1）因为222ca b ca=-=，所以2a b=.原点到直线:1x yABa b-=的距离d==解得4,2a b==.故椭圆C的方程为221164x y+=.（2）由题意联立221,1,164y kxx y=+⎧⎪⎨+=⎪⎩消去y整理得()22148120k x kx++-=，可知0∆>.设()()1122,,,,E x yF x y EF的中点(),M MM x y，则122241,121414M M Mx x kx y kxk k+-===+=++.因为E，F都在以B为圆心的圆上，且(0,2)B-，所以21MMykx+⋅=-，所以20M Mx ky k++=，即224201414k kkk k-++=++，即2(81)0k k-=. 又因为0k≠，所以218k=，解得k=.经检验，k =满足题意. 22.答案：（1）由题意得()'ln f x x k =-，又曲线()y f x =在(1,(1))f 处的切线与直线20x y -=平行， 所以1'(1)ln12f k =-=，解得12k =-. （2）因为()()122122f x f x x x +<+，所以()()121222f x f x x x -<-. 记2()()h x f x x=-， 因为12,(0,3]x x ∈，且()()1212,x x h x h x <<， 所以2()()h x f x x =-在(0,3]上单调递增. 所以22()ln 0'h x x k x =-+在(0,3]上恒成立且等号不恒成立，即22ln k x x +在(0,3]上恒成立且等号不恒成立. 记22()ln u x x x =+，则23314'4()x u x x x x -=-=.令234()0'x u x x -==，解得2,2x x ==-（舍去） 当02x <<时，()0,'()u x u x <单调递减， 当23x <<时，()0,'()u x u x >单调递增， 所以在(0,3]上，当2x =时，()u x 取得最小值， 221(2)ln 2ln 222u =+=+， 所以1ln 22k +，故实数k 的取值范围为1,ln 22⎛⎤-∞+ ⎥⎝⎦.。

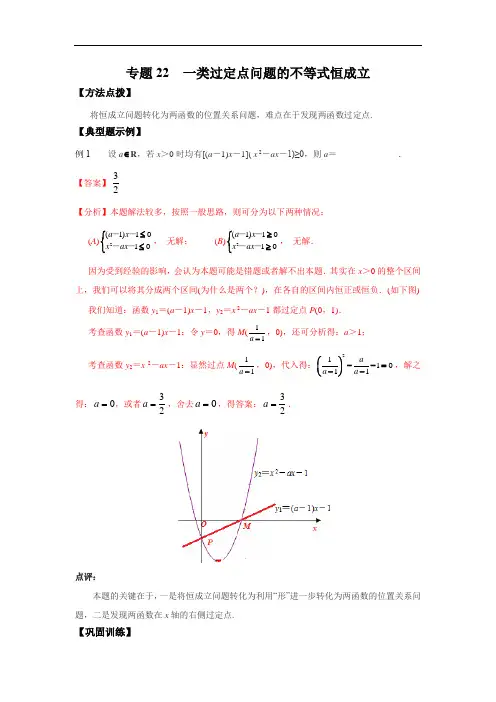
专题22 一类过定点问题的不等式恒成立【方法点拨】将恒成立问题转化为两函数的位置关系问题，难点在于发现两函数过定点.【典型题示例】例1 设a R ，若x ＞0时均有[(a －1)x －1]( x 2－ax －1)≥0，则a ＝______________．【答案】 【分析】本题解法较多，按照一般思路，则可分为以下两种情况：(A )， 无解； (B )， 无解． 因为受到经验的影响，会认为本题可能是错题或者解不出本题．其实在x ＞0的整个区间上，我们可以将其分成两个区间(为什么是两个？)，在各自的区间内恒正或恒负．(如下图)我们知道：函数y 1＝(a －1)x －1，y 2＝x 2－ax －1都过定点P (0，1)．考查函数y 1＝(a －1)x －1：令y ＝0，得M (，0)，还可分析得：a ＞1； 考查函数y 2＝x 2－ax －1：显然过点M (，0)，代入得：，解之得：，或者，舍去，得答案：．点评：本题的关键在于，一是将恒成立问题转化为利用“形”进一步转化为两函数的位置关系问题，二是发现两函数在x 轴的右侧过定点.【巩固训练】 ∈23=a 2(1)1010a x x ax ≤⎧⎨≤⎩－－－－2(1)1010a x x ax ≥⎧⎨≥⎩－－－－11a -11a -211011a a a ⎛⎫--= ⎪--⎝⎭3a 0==或者a 23=a 0=a 23=a1. 对任意的(0,)x ∈+∞，不等式22(2)ln 0ax a x x +-≥恒成立，则实数a 的取值的集合是 ．2.对任意的(0,)x ∈+∞，不等式2(ln )(210)0x x a x ax a-+-++≤恒成立，则实数a 的取值范围是 ．3.已知不等式2(3)()0ax x b +-≤对于任意的(0,)x ∈+∞恒成立，其中,a b 是整数，则a b +的取值集合为__________.【答案或提示】 1.【答案】{}1【解析】设22()2f x ax a x =+-，()ln g x x = 因为()ln g x x =恒过点（1,0），所以必有2(1)200f a a a ⎧=+-=⎨>⎩，解之得1a =. 2.【答案】【分析】考虑从“形”出发. 设()lnx f x x a a =-+，2()210g x x ax =-++又0a>，所以a =．∴31a =-⎧⎪=，或13a =-⎧⎪= 解之得：31ab =-⎧⎨=⎩，或19a b =-⎧⎨=⎩ 所以28a b +=-或，故a b +的取值集合为}8,2{-.。

2024年高考压轴卷【新高考卷】数学·全解全析一、单选题1．已知集合105x A x x ⎧⎫+=≥⎨⎬-⎩⎭，(){}22log 16B x y x ==-，则()R A B ⋂=ð（）A ．()1,4-B ．[]1,4-C ．(]1,5-D ．()4,52．宋代是中国瓷器的黄金时代，涌现出了五大名窑：汝窑、官窑、哥窑、钧窑、定窑．其中汝窑被认为是五大名窑之首．如图1，这是汝窑双耳罐，该汝窑双耳罐可近似看成由两个圆台拼接而成，其直观图如图2所示．已知该汝窑双耳罐下底面圆的直径是12厘米，中间圆的直径是20厘米，上底面圆的直径是8厘米，高是14厘米，且上、下两圆台的高之比是3:4，则该汝窑双耳罐的体积是（）A ．1784π3B ．1884π3C ．2304π3D ．2504π33．如图，左车道有2辆汽车，右车道有3辆汽车等待合流，则合流结束时汽车通过顺序共有（）种.A ．10B ．20C ．60D ．120【答案】A【分析】合流结束时5辆车需要5个位置，第一步从5个位置选2个位置安排左边的2辆汽车，第二步剩下3个位置安排右边的3辆汽车，从而由分步乘法计数原理可得结果.【详解】设左车辆汽车依次为12,A A ，右车辆汽车依次为123,,B B B ，则通过顺序的种数等价于将12,A A 安排在5个顺序中的某两个位置（保持12,A A 前后顺序不变），123,,B B B 安排在其余3个位置（保持123,,B B B 前后顺序不变），123,,B B B ，所以，合流结束时汽车通过顺序共有2353C C 10=.故选：A.4．已知等比数列{}n a 的各项均为负数，记其前n 项和为n S ，若6467813,8S S a a a -=-=-，则2a =（）A ．－8B ．－16C ．－32D ．－485．已知圆C ：22()1x y m +-=，直线l ：()1210m x y m ++++=，则直线l 与圆C 有公共点的必要不充分条件是（）A ．11m -≤≤B ．112m -≤≤C ．10m -≤≤D ．102m ≤≤6．已知函数2()log f x x =，则对任意实数,a b ，“0a b +≤”是“()()0f a f b +≤”的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件故选：C.7．已知0.50.2a =，cos2b =，lg15c =，则（）A ．a b c <<B ．c a b <<C ．b c a <<D ．b a c<<8．从椭圆22:1(0)x y C a b a b+=>>外一点()00,P x y 向椭圆引两条切线，切点分别为,A B ，则直线AB 称作点P关于椭圆C 的极线，其方程为00221x x y ya b+=.现有如图所示的两个椭圆12,C C ，离心率分别为12,e e ，2C 内含于1C ，椭圆1C 上的任意一点M 关于2C 的极线为l ，若原点O 到直线l 的距离为1，则2212e e -的最大值为（）A ．12B ．13C ．15D ．14二、多选题9．已知非零复数1z ，2z 在复平面内对应的点分别为1Z ，2Z ，O 为坐标原点，则下列说法正确的是（）A ．若1211z z -=-，则12=z z B ．若1212z z z z +=-，则120OZ OZ ⋅=C ．若1212z z z z +=-，则120z z ⋅=D ．若1212z z z z +=+，则存在实数t ，使得21z tz =10．已知四面体ABCD的一个平面展开图如图所示，其中四边形AEFD是边长为B，C分别为AE，FD的中点，BD=）⊥A．BE CDB．BE与平面DCE所成角的余弦值为15C．四面体ABCD的内切球半径为30D．四面体ABCD的外接球表面积为8π【点睛】11．对于数列{}n a （N n a +∈），定义k b 为1a ，2a ，…，k a 中最大值（1,2,,k n =⋅⋅⋅）（N n +∈），把数列{}n b 称为数列{}n a 的“M 值数列”.如数列2，2，3，7，6的“M 值数列”为2，2，3，7，7，则（）A ．若数列{}n a 是递减数列，则{}n b 为常数列B ．若数列{}n a 是递增数列，则有n na b =C ．满足{}n b 为2，3，3，5，5的所有数列{}n a 的个数为8D ．若()1()2N n n a n -+=-∈，记n S 为{}n b 的前n 项和，则1001002(21)3S =-三、填空题12．已知向量()1,1,4a b == ，且b 在a 上的投影向量的坐标为()2,2--，则a 与b的夹角为.13．已知公比q 大于1的等比数列{}n a 满足135a a +=，22a =.设22log 7n n b a =-，则当5n ≥时，数列{}n b 的前n 项和n S =.14．已知椭圆2222:1(0)x y C a b a b+=>>的左、右焦点分别为12,F F ，过点2F 且斜率为34-的直线与C 交于,A B两点．若112AF F F ⊥，则C 的离心率为；线段AB 的垂直平分线与x 轴交于点D ，则22BF DF =．5.【点睛】方法点睛：椭圆求离心率或者范围关键是找到关于,a c 的齐次式求得.四、解答题15．如图，在平面四边形ABCD ，已知1BC =，3cos 5BCD ∠=-.（1）若AC 平分BCD ∠，且2AB =，求AC 的长；（2）若45CBD ∠=︒，求CD 的长.16．如图，在三棱柱111ABC A B C -中，ABC △是边长为2的正三角形，侧面11BB C C 是矩形，11AA A B =．(1)求证：三棱锥1A ABC -是正三棱锥；(2)若三棱柱111ABC A B C -的体积为221AC 与平面11AA B B 所成角的正弦值．【答案】(1)证明见解析(2)23【分析】（1）根据线面垂直的判定定理及性质定理，证明1A O ⊥平面ABC 即可；（2）建立空间直角坐标系，利用向量法求线面角正弦即可.【详解】（1）分别取AB ，BC 中点D ，E ，连接CD ，AE 交于点O ，则点O 为正三角形ABC 的中心．因为11AA A B CA CB ==，得1CD AB AD AB ⊥⊥，，又11,,A D CD D A D CD =⊂ 平面1A CD ，所以AB ⊥平面1A CD ，又1A O ⊂平面1A CD ，则1AB A O ⊥；取11B C 中点1E ，连接111A E E E ，，则四边形11AA E E 是平行四边形，因为侧面11BB C C 是矩形，所以1BC EE ⊥，又BC AE ⊥，又11,,EE AE E EE AE =⊂ 平面11AA E E ，所以BC ⊥平面11AA E E ，又1A O ⊂平面11AA E E ，则1BC A O ⊥；又AB BC B ⋂=，,AB BC ⊂平面ABC ，所以1A O ⊥平面ABC ，所以三棱锥1A ABC -是正三棱锥．17．某学校为了解本学期学生参加公益劳动的情况，从学校内随机抽取了500名高中学生进行在线调查，收集了他们参加公益劳动时间（单位:小时）分配情况等数据，并将样本数据分成[0,2],(2,4]，(4,6],(6,8],(8,10],(10,12],(12,14],(14,16]，(16,18]九组，绘制成如图所示的频率分布直方图.(1)为进一步了解这500名学生参加公益劳动时间的分配情况，从参加公益劳动时间在(12,14],(14,16],(16,18]三组内的学生中，采用分层抽样的方法抽取了10人，现从这10人中随机抽取3人.记参加公益劳动时间在(14,16]内的学生人数为X ，求X 的分布列和期望；(2)以调查结果的频率估计概率，从该学校所有高中学生中随机抽取20名学生，用“20()P k ”表示这20名学生中恰有k 名学生参加公益劳动时间在(10,12]（单位:小时）内的概率，其中0,1,2,,20k = .当20()P k 最大时，写出k 的值.18．已知双曲线(22:10,0x y C a b a b-=>>）的左右焦点分别为12,F F ，C 的右顶点到直线2:a l x c =的距离为1，双曲线右支上的点到1F 的最短距离为3(1)求双曲线C 的方程；(2)过2F 的直线与C 交于M 、N 两点，连接1MF 交l 于点Q ，证明：直线QN 过x 轴上一定点.【点睛】方法点睛：求解直线过定点问题常用方法如下：（1）“特殊探路，一般证明（2）“一般推理，特殊求解”：即设出定点坐标，根据题设条件选择参数，建立一个直线系或曲线的方程，再根据参数的任意性得到一个关于定点坐标的方程组，以这个方程组的解为坐标的点即为所求点；（3）求证直线过定点()00,x y ，常利用直线的点斜式方程()00y y k x x -=-或截距式y kx b =+来证明.19．函数()e xf x a x=-图像与x 轴的两交点为()()()1221,0,0A x B x x x >，(1)令()()ln h x f x x x =-+，若()h x 有两个零点，求实数a 的取值范围；(2)证明：121x x <；(3)证明：当5a ≥时，以AB 为直径的圆与直线)1y x =+恒有公共点．（参考数据：0.25 2.5e 1.3e 12.2≈≈，）。

（新高考）2021年最新高考冲刺压轴卷数 学注意事项：1、本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

答题前，考生务必将自己的姓名、考生号填写在答题卡上。

2、回答第Ⅰ卷时，选出每小题的答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号。

写在试卷上无效。

3、回答第Ⅱ卷时，将答案填写在答题卡上，写在试卷上无效。

4、考试结束，将本试卷和答题卡一并交回。

第Ⅰ卷一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．命题“()0,x ∀∈+∞，2log 1x >”的否定是（ ） A ．()0,x ∀∈+∞，2log 1x ≤ B ．()00,x ∃∈+∞，20log 1x ≤ C ．()0,x ∀∉+∞，2log 1x ≤ D ．()00,x ∃∈+∞，20log 1x >【答案】B【解析】根据全称命题的否定是特称命题可知，命题“()0,x ∀∈+∞，2log 1x >”的否定为“()00,x ∃∈+∞，20log 1x ≤”． 故选B ．2．已知集合{}*28xM x =∈<N ，{}N x x a =<．若MN 有且仅有1个元素，则实数a 的取值范围是（ ）A ．(]0,1 B ．[]0,1C ．(]1,2D ．[]1,2【答案】C【解析】因为{}{}{}**2831,2x M x x x =∈<=∈<=N N ，{}N x x a =<，结合M N 有且仅有1个元素知{}1MN =，所以12a <≤，故选C ．3．已知圆O 的半径为1，A ，B 是圆O 上两个动点，2OA OB OA OB +=-⋅，则OA ，OB 的夹角为（ ） A ．π3B ．2π3C ．3π4D ．5π6【答案】B 【解析】22222cos ,OA OB OA OB OA OB OA OB +=++⋅=+〈〉，22cos ,OA OB OA OB -⋅=-〈〉2cos ,OA OB =-〈〉，解得cos ,1OA OB 〈〉=或1cos ,2OA OB 〈〉=-， 由题意得cos ,0OA OB 〈〉≤，故2π,3OA OB 〈〉=，故OA ，OB 的夹角为2π3．故选B ．4．已知数列{}n a ，1()n a f n =，其中()f n 若{}n a 的前m 项和为20， 则m =（ ） A ．15 B ．30C ．60D ．110【答案】D【解析】由题意知，函数()f n又由()11f =，()21f =，()32f =，()42f =，()52f =，()62f =，()73f =，()83f =，()93f =，()103f =，()113f =，()123f =，，由此可得()f n 2个1，4个2，6个3，8个4，，又由数列{}n a 满足1()n a f n =， 可得1234567812111,,,23a a a a a a a a a ==========， 则122a a +=，34562a a a a +++=，78122a a a +++=，，因为{}n a 的前m 项和为20，即10220m S =⨯=，可得数列{}m 构成首项为2，公差为2的对称数列的前10项和， 所以10910221102m ⨯=⨯+⨯=，故选D ． 5．关于直线m 、n 与平面α、β，有以下四个命题： ①若//m α，βn//且//αβ，则//m n ； ②若m α⊥，n β⊥且αβ⊥，则m n ⊥； ③若m α⊥，βn//且//αβ，则m n ⊥； ④若//m α，n β⊥且αβ⊥，则//m n ． 其中真命题的序号是（ ） A ．①② B ．③④C ．①④D ．②③【答案】D【解析】对于①，若//m α，βn//且//αβ，则m 与n 平行、相交或异面，①错误； 对于②，如下图所示：设a αβ=，因为αβ⊥，在平面β内作直线l a ⊥，由面面垂直的性质定理可知l α⊥，m α⊥，//m l ∴，n β⊥，l β⊂，n l ∴⊥，因此，m n ⊥，②正确；对于③，若m α⊥，//αβ，则m β⊥， 因为βn//，过直线n 作平面γ使得a βγ=，由线面平行的性质定理可得//n a ，m β⊥，a β⊂，则m a ⊥，因此m n ⊥，③正确；对于④，若//m α，n β⊥且αβ⊥，则m 与n 平行、相交或异面，④错误， 故选D ．6．已知函数()222,0log 0x x x f x x x ⎧--≤⎪=⎨>⎪⎩，，若1234x x x x <<<，且()()()()1234f x f x f x f x ===，给出下列结论：①121x x +=-，②341x x =，③1234102x x x x <+++<，④123401x x x x <<，其中所有正确命题的编号是（ ） A ．①② B ．②③C ．②④D ．②③④【答案】D【解析】函数()2202,0log x x x f x x x ⎧≤--⎪=⎨>⎪⎩，的图象如下图所示，函数22y x x =--的图象关于直线1x =-对称，则122x x +=-，故①错误； 由()()34f x f x =得2324log log x x =，∴2324log log x x -=， 则()234log 0x x =，∴341x x =，故②正确； 设()()()()1234f x f x f x f x k ====， 由221y x x =--≤，所以01k <<， 由2log 1x =-，得12x =，则3112x <<，∵12343433122x x x x x x x x +++=-++=+-， ∴1234331120,2x x x x x x ⎛⎫+++=+-∈ ⎪⎝⎭，故③正确； 由22y x x =--的对称轴方程为1x =-，由图可知()12,1x ∈--， 又()2123412111122x x x x x x x x x x ==--=--，∴()212341120,1x x x x x x =--∈，故④正确，故选D ．7．已知ABC △中，D 、E 分别是线段BC 、AC 的中点，AD 与BE 交于点O ，且90BOC ∠=︒，若2BC =，则ABC △周长的最大值为（ ）A．2+B．2C．2+D．2+【答案】A【解析】在ABC △中，D 、E 分别是线段BC 、AC 的中点，AD 与BE 交于点O ， 则O 为ABC △的重心， 因为90BOC ∠=°，故112OD BC ==，则33AD OD ==． ()()111222AD AB BD AB BC AB AC AB AB AC =+=+=+-=+，2AD AB AC ∴=+，所以()222242AD AB AC AB AC AB AC =+=++⋅，即2222222242cos 22AB AC BC AD AB AC AB AC BAC AB AC AB AC AB AC+-=++⋅⋅∠=++⋅⋅⋅2222222224AB AC BC AB AC =+-=+-，所以，()()22222222240222AB AC AB AC AB AC AB AC AB AC AB AC =+=+++≥++⋅=+，AB AC ∴+≤AB AC ==因此，ABC △周长的最大值为2，故选A ．8．如图，水平桌面上放置一个棱长为4的正方体水槽，水面高度恰为正方体棱长的一半，在该正方体侧面11CDD C 上有一个小孔E ，E 点到CD 的距离为3，若该正方体水槽绕CD 倾斜（CD 始终在桌面上），则当水恰好流出时，侧面11CDD C 与桌面所成角的正切值为（ ）A B ．12C D ．2【答案】D【解析】由题意知，水的体积为44232⨯⨯=，如图所示，设正方体水槽绕CD 倾斜后，水面分别与棱1111,,,AA BB CC DD 交于,,,M N P Q ， 由题意知3PC =，水的体积为32BCPN S CD ⋅=，322BN PC BC CD +∴⋅⋅=，即344322BN +⨯⨯=，1BN ∴=， 在平面11BCC B 内，过点1C 作1C H NP ∥交1BB 于H ， 则四边形1NPC H 是平行四边形，且11NHPC ==，又侧面11CDD C 与桌面所成的角即侧面11CDD C 与水面MNPQ 所成的角， 即侧面11CDD C 与平面11HC D 所成的角，其平面角为111HC C B HC ∠=∠， 在直角三角形11B HC 中，111114tan 22B C B HC B H ===，故选D ．二、多项选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分． 9．已知i 为虚数单位，以下四个说法中正确的是（ ） A ．234i i i i 0+++= B ．复数3i z =-的虚部为i -C ．若2(1)i 2z =+，则复平面内z 对应的点位于第二象限D ．已知复数z 满足11z z -=+，则z 在复平面内对应的点的轨迹为直线 【答案】AD【解析】A 选项，234i i i i i 1i 10+++=--+=，故A 选项正确； B 选项，z 的虚部为1-，故B 选项错误；C 选项，214i 4i 34i z =++=-+，34i z =--，对应坐标为()3,4--在第三象限， 故C 选项错误；D 选项，()111z z z -=+=--表示z 到1,0A 和()1,0B -两点的距离相等， 故z 的轨迹是线段AB 的垂直平分线，故D 选项正确， 故选AD ．10．下列四个函数，同时满足：①直线()12b y x b =+∈R 能作为函数的图象的切线；②函数()()4y f x f x =+的最小值为4的是（ ） A ．()1f x x=B ．()sin f x x =C ．()xf x e =D ．()2f x x =【答案】CD【解析】对于A ：()21f x x '=-，对于任意0x ≠，2112x -=无解， 所以直线12y x b =+不能作为切线； 对于B ：()1cos 2f x x '==，有解，但()()44f x f x +≥，当且仅当()2f x =时取等号， 又sin 1x ≤，所以不符合题意；对于C ：()12xf x e '==，有解，()()444x x f x e f x e +=+≥=， 当且仅当2x e =时，等号成立，故C 正确；对于D ：()122f x x '==，14x =，又2244x x +≥=，当且仅当x =D 正确， 故选CD ．11．已知函数()()πcos 10,2f x A x A ϕϕ⎛⎫=++>< ⎪⎝⎭，若函数()y f x =的部分图象如图所示，则下列说法正确的是（ ）A ．函数()f x 的图象关于直线π6x =对称 B ．函数()f x 的图象关于点5π,16⎛⎫-⎪⎝⎭对称 C ．将函数2sin 1y x =+的图象向左平移5π6个单位可得函数()f x 的图象D ．函数()f x 在区间π,02⎡⎤-⎢⎥⎣⎦上的值域为1,3⎤⎦ 【答案】BC【解析】结合函数()y f x =的图象易知，函数()f x 的最大值3，最小值为1-， 则2A =，()()2cos 1f x x ϕ=++， 代入点()0,2，则2cos 12ϕ+=，1cos 2ϕ=， 因为π2ϕ<，所以π3ϕ=，()π2cos 13f x x ⎛⎫=++ ⎪⎝⎭，()ππ3x k k +=∈Z ，即()ππ3x k k =-+∈Z ，函数()f x 关于()ππ3x k k =-+∈Z 对称， A 错误；πππ32xk k Z ，即()ππ6x k k =+∈Z ，函数()f x 关于点()ππ,16k k ⎛⎫+∈ ⎪⎝⎭Z 对称， B 正确；函数2sin 1y x =+的图象向左平移5π6个单位，得出()5ππππ2sin 12sin 12cos 16323f x x x x ⎛⎫⎛⎫⎛⎫=++=+++=++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，C 正确； 当,02πx ⎡⎤∈-⎢⎥⎣⎦时，π,ππ363x ⎡⎤+∈-⎢⎥⎣⎦，1cos ,132πx ⎛⎫⎡⎤+∈ ⎪⎢⎥⎝⎭⎣⎦，()[]2,3f x ∈，D 错误，故选BC ．12．过双曲线2222:1x y C a b-=（0a >，0b >）的右焦点F 引C 的一条渐近线的垂线，垂足为A ，交另一条渐近线于点B ．若FB AF λ=，23λ≤≤，则C 的离心率可以是（ ）A．2B．3C．2D ．2【答案】BC【解析】右焦点(c,0)F ，设一渐近线OA 的方程为by x a=， 则另一渐近线OB 的方程为by x a=-， 由FA 与OA 垂直可得FA 的方程为()ay x c b=--， 联立方程2222()b y x a c a ax a a b c y x c b ⎧=⎪⎪⇒==⎨+⎪=--⎪⎩， 可得A 的横坐标为2a c；联立方程()2222222b y x a c ca ax a a b a c y x c b ⎧=-⎪⎪⇒==⎨--⎪=--⎪⎩， 可得B 的横坐标为2222ca a c-． 因为FB AF λ=，所以()2222222222()22c c a ca a c a c c a c c a c cλλ---=-⇒=⨯--，可得2222222c e a c e λ==--， 因为23λ≤≤，所以22322e e≤-≤，即22222340432324602e e e e e e ⎧-≥⎪⎪-⇒≤≤⇒≤≤⎨-⎪≤⎪-⎩， BC 满足题意，AD 不合题意， 故选BC ．第Ⅱ卷三、填空题：本大题共4小题，每小题5分．13．写出一个符合“对12,x x ∀∈R ，当12x x ≠时，()()()12120f x x x x --<⎡⎤⎣⎦”的函数()f x =____________．【答案】x -（答案不唯一）【解析】设12,x x ∀∈R ，12x x <，则()()12f x f x >， 由单调性的定义可知，函数()f x 是定义域为R 的减函数， 所以函数()f x x =-满足题意． 故答案为x -．14．100(1的展开式中有理项的个数为________．【答案】34 【解析】131100C (2)r r r T x +=，所以0,3,6,,99r =⋯时为有理项，共34个，故答案为34．15．高三年级毕业成人礼活动中，要求A ，B ，C 三个班级各出三人，组成33⨯小方阵，则来自同一班级的同学既不在同一行，也不在同一列的概率为______．【答案】1140【解析】根据题意，A ，B ，C 三个班级各出三人，组成33⨯小方阵，有99A 种安排方法， 若来自同一班级的同学既不在同一行，也不在同一列，则第一行队伍的排法有33A 6=种；第二行队伍的排法有2种；第三行队伍的排法有1种； 第一行的每个位置的人员安排方法有33327⨯⨯=种，第二行的每个位置的人员安排有2228⨯⨯=种，第三行的每个位置的人员安排有1111⨯⨯=种，则自同一班级的同学既不在同一行，也不在同一列的概率9962278110A 4P ⨯⨯⨯==，故答案为1140． 16．已知实数0a >且1a ≠，()xaf x a x =-为定义在()0,∞+上的函数，则()f x 至多有______个零点；若()f x 仅有1个零点，则实数a 的取值范围为_________． 【答案】2，(){}0,1e【解析】令()0f x =（0x >，0a >且1a ≠），可得x a a x =， 等式x a a x =两边取自然对数得ln ln x a a x =，即ln ln x ax a=， 构造函数()ln x g x x =，其中0x >，则()21ln xg x x-'=． 当0x e <<时，()0g x '>，此时函数()g x 单调递增； 当x e >时，()0g x '<，此时函数()g x 单调递减．所以，()()max 1g x g e e ==，且当1x >时，()ln 0xg x x=>，如下图所示：由图象可知，直线ln a y a=与函数()ln xg x x =的图象至多有两个交点，所以，函数()f x 至多有2个零点． 若函数()f x 只有一个零点，则ln 1a a e =或ln 0a a<，解得01a <<或a e =． 故答案为2，(){}0,1e ．四、解答题：本大题共6个大题，共70分，解答应写出文字说明、证明过程或演算步骤．17．（10分）如图，在四边形ABCD 中，//AB CD ，90ADC ∠=︒，ABC △为锐角三角形，且3AB =，AC =，60ABC ∠=︒．（1）求sin BAC ∠的值； （2）求BCD △的面积．【答案】（1；（2【解析】（1）在锐角ABC △中，3AB =，AC =，60ABC ∠=︒，由正弦定理得sin sin AB ABC ACB AC ⋅∠∠==，又因为ABC △为锐角三角形，cos ACB ∴∠=．sin sin πππsin 33BAC ACB ACB ⎡⎤⎛⎫⎛⎫∠=-+∠=+∠ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦，π1sin sin cos cos sin 331427πBAC ACB ACB ∴∠=∠⋅+∠⋅=+=． （2）//AB CD ，∴∠=∠ACD BAC ，sin sin ACD BAC ∴∠=∠=． 在ADC Rt △中，sin AD AC ACD =⨯∠==，2CD ∴==，BCD ACD S S =△△，又12ACD S AD CD =⨯=△BCD S ∴=△ 18．（12分）给出以下两个条件：①数列{}n a 的首项11a =，23a =，且14n n a a n ++=，②数列{}n a 的首项11a =，且()2121n n n S S n ++=．从上面①②两个条件中任选一个解答下面的问题．（1）求数列{}n a 的通项公式； （2）设数列{}n b 满足122n a nb n +=⨯，求数列{}n b 的前n 项和n T ．注：如果选择多个条件分别解答，按第一个解答计分． 【答案】（1）21n a n =-；（2）()1122n n T n +=-⨯+．【解析】若选条件①：（1）由条件14n n a a n ++=，得()2141n n a a n +++=+，两式相减得24n n a a +-=，∴数列{}21k a -，{}2()k a k ∈Z 均为公差为4的等差数列．∵11a =，()2114143k a k k -=+-=-， ∴当n 为奇数时，21n a n =-；∵23a =，∴()234141k a k k =+-=-， 当n 为偶数时，21n a n =-， 综上，21n a n =-． （2）由（1）得1222n a n n b n n +=⨯=⨯，则其前n 项和为212222n n T n =⨯+⨯++⨯①，∴231212222n n T n +=⨯+⨯++⨯②，①-②得()2131211212111222222n n n n n n T n ++-=⨯+⨯-=-⨯+⨯++-⨯-⨯()1122n n +=-⨯-，∴()1122n nT n +=-⨯+．若选条件②：（1）∵()2121n n n S S n ++=，∴222121S S =，232232S S =，242343S S =，…，()2211n n S n S n -=-， 上面1n -个式子相乘得2211n S n S =（2n ≥），∴2n ≥时，2221121n n S S n a n ===， 而1n =时，111n S S a ===，也满足上面等式，∴2n S n =， ∴2n ≥时，()221121n n n a S S n n n -=-=--=-，而1n =时，11n a a ==，也满足上面等式， ∴21n a n =-．（2）由（1）得1222n a n n b n n +=⨯=⨯，则其前n 项和为212222n n T n =⨯+⨯++⨯①，∴231212222n n T n +=⨯+⨯++⨯②，①-②得()213121*********2222n n nn n n T n ++-=⨯+⨯-=-⨯+⨯++-⨯-⨯()1122n n +=-⨯-，∴()1122n nT n +=-⨯+．19．（12分）如图，在直四棱柱1111ABCD A BC D -中，底面ABCD 是边长为2的菱形，且13AA =，E ，F 分别为1CC ，1BD 的中点．（1）证明：EF ⊥平面11BB D D ；（2）若60DAB ∠=︒，求二面角11A BE D --的余弦值．【答案】（1）证明见解析；（2． 【解析】（1）如图所示：连接AC 交BD 于O 点，连接OF ，F 为1BD 的中点， 所以1//OF DD ，112OF DD =， 又E 为1CC 的中点﹐11//CC DD ，所以1//CE DD ，112CE DD =，所以//OF CE ，OF CE =，所以四边形OFEC 为平行四边形，//OC FE ．直四棱柱1111ABCD A BC D -中，1DD ⊥平面ABCD ，OC ⊂平面ABCD ， 所以1DD OC ⊥．又因为底面ABCD 是菱形，所以OC BD ⊥， 又1DD BD D =，1DD ⊂平面11BB D D ，BD ⊂平面11BB D D ，所以OC ⊥平面11BB D D ，所以EF ⊥平面11BB D D ． （2）建立如图空间直角坐标系O xyz -，由60DAB ∠=︒，知2BD AB BC ===， 又13AA =，则()1,0,0B，32E ⎛⎫⎪⎝⎭，()10,A ，()11,0,3D -， 设(),,x y z =n 为平面1A BE 的一个法向量，由100A B BE ⎧⋅=⎪⎨⋅=⎪⎩n n，得30302x z x z ⎧-=⎪⎨-+=⎪⎩，令y =()=n ；设()111,,x y z =m 为平面1D BE 的一个法向量，由100BD BE ⎧⋅=⎪⎨⋅=⎪⎩m m，即11111230302x z x z -+=⎧⎪⎨-+=⎪⎩，令13x =，可得()3,0,2=m ，cos ,⋅===⋅m nn m m n， 如图可知二面角11A BE D --为锐角，所以二面角11A BE D --． 20．（12分）某商城玩具柜台元旦期间促销，购买甲、乙系列的盲盒，并且集齐所有的产品就可以赠送元旦礼品．而每个甲系列盲盒可以开出玩偶1A ，2A ，3A 中的一个，每个乙系列盲盒可以开出玩偶1B ，2B 中的一个．（1）记事件n E ：一次性购买n 个甲系列盲盒后集齐1A ，2A ，3A 玩偶；事件n F ：一次性购买n 个乙系列盲盒后集齐1B ，2B 玩偶；求概率()6P E 及()5P F ；（2）礼品店限量出售甲、乙两个系列的盲盒，每个消费者每天只有一次购买机会，且购买时，只能选择其中一个系列的一个盲盒．通过统计发现：第一次购买盲盒的消费者购买甲系列的概率为15，购买乙系列的概率为45；而前一次购买甲系列的消费者下一次购买甲系列的概率为14，购买乙系列的概率为34；前一次购买乙系列的消费者下一次购买甲系列的概率为12，购买乙系列的概率为12；如此往复，记某人第n 次购买甲系列的概率为n Q ． ①n Q ；②若每天购买盲盒的人数约为100，且这100人都已购买过很多次这两个系列的盲盒，试估计该礼品店每天应准备甲、乙两个系列的盲盒各多少个．【答案】（1）()62027P E =，()51516P F =；（2）①1151245n n Q -⎛⎫=--+ ⎪⎝⎭；②应准备甲系列盲盒40个，乙系列盲盒60个．【解析】（1）由题意基本事件共有：63种情况， 其中集齐1A ，2A ，3A玩偶的个数可以分三类情况， 1A ，2A ，3A 玩偶中，每个均有出现两次，共222642C C C 种；1A ，2A ，3A 玩偶中，一个出现一次，一个出现两次，一个出现三次，共32136313C C C A 种； 1A ，2A ，3A 玩偶中，两个出现一次，另一个出现四次，共142362C A C 种， 故()22232134264263136266C C C C C C A 3A C 20327P E ++==． 根据题意，先考虑一次性购买n 个乙系列盲盒没有集齐1B ，2B 玩偶的概率，即5112P +=， 所以()5511151216P F +=-=． （2）①由题意可知：115Q =，当2n ≥时，()1111124n n n Q Q Q --=-+， ∴1221545n n Q Q -⎛⎫-=-- ⎪⎝⎭， 所以25n Q ⎧⎫-⎨⎬⎩⎭是以15-为首项，14-为公比的等比数列， ∴1151245n n Q -⎛⎫=--+ ⎪⎝⎭， ②因为每天购买盲盒的100人都已购买过很多次，所以，对于每一个人来说，某天来购买盲盒时，可以看作n 趋向无穷大， 所以购买甲系列的概率近似于25，假设用ξ表示一天中购买甲系列盲盒的人数，则2100,5B ξ⎛⎫ ⎪⎝⎭，所以()2100405E ξ=⨯=，即购买甲系列的人数的期望为40， 所以礼品店应准备甲系列盲盒40个，乙系列盲盒60个．21．（12分）已知椭圆()222210x y a ba b +=>>的离心率为2，右焦点为F ，上顶点为A ，左顶点为B ，且 ||||10FA FB ⋅=+ （1）求椭圆的方程；（2）已知()4,0C -，()4,0D ，点P 在椭圆上，直线PC ，PD 分别与椭圆交于另一点M ，N ，若CP CM λ=，DP DN μ=，求证：λμ+为定值．【答案】（1）221105x y +=；（2）证明见解析． 【解析】（1）设(),0F c ，由题意得||FA a =，||FB a c =+，2c a =，222a b c =+， ()||||10FA FB a a c ∴⋅=+=+210a =，25b =，∴椭圆的方程为221105x y +=．（2）设()00,P x y ，()11,M x y ，()22,N x y ， 由CP CM λ=，DP DN μ=，得()()00114,4,x y x y λ+=+，()()00224,4,x y x y μ-=-，()010141x x y y λλλ⎧-=-∴⎨=⎩，()020241x x y y μμμ⎧-=-⎨=⎩，()1284x x λμλμ∴-=-+，①又点P ，M ，N 均在椭圆上，由220022222111105105x y x y λλλ⎧+=⎪⎪⎨⎪+=⎪⎩且01y y λ=，得()()01012110x x x x λλλ-+=-，()01512x x λλ∴+=-+．② 同理，由220022222221105105x y x y μμμ⎧+=⎪⎪⎨⎪+=⎪⎩且02y y μ=，得()()22002110x x x x μμμ-+=-，()02512x x μμ∴+=+．③ 联立②③得()12552x x λμλμ-=-+-．④联立①④得263λμ+=，λμ∴+为定值263． 22．（12分）已知函数2()1()x f x ax a e=++∈R ． （1）若函数()f x 在区间(1,)+∞上单调递增，求实数a 的取值范围；（2）当0a ≠时，讨论函数()()3g x f x a =--的零点个数，并给予证明．【答案】（1）2,e ⎡⎫+∞⎪⎢⎣⎭；（2）当0a <时，函数()g x 有且只有一个零点；当0a >时，函数()g x 有两个零点，证明见解析．【解析】（1）2()xf x a e '=-， 由题意得()0f x '≥，即2x a e ≥在区间(1,)+∞上恒成立． 当(1,)x ∈+∞时，220,x e e ⎛⎫∈ ⎪⎝⎭，所以2a e≥， 故实数a 的取值范围为2,e ⎡⎫+∞⎪⎢⎣⎭．（2）由已知得2()2x g x ax a e =+--，则22()x x x ae g x a e e-'=-=． 当0a <时，()0g x '<，函数()g x 单调递减，又(0)0g a =->，2(1)20eg =-<，故函数()g x 有且只有一个零点． 当0a >时，令()0g x '<，得2ln x a<，函数()g x 单调递减； 令()0g x '>，得2ln x a >，函数()g x 单调递增， 而222ln ln 0g a a a a ⎛⎫⎛⎫=-< ⎪ ⎪⎝⎭⎝⎭，2220a aa g a e ++⎛⎫=> ⎪⎝⎭， （ln x x <在(0,)+∞上恒成立）由于ln x x >，所以222ln a a a a +>>，所以()g x 在22ln ,a a a +⎛⎫ ⎪⎝⎭上存在一个零点．又2222ln ln 22a a g a a a a ⎛⎫++⎛⎫=- ⎪ ⎪++⎝⎭⎝⎭，且222ln ln 2a a a <++， 设22()ln 2a a h a a ++=-，则222211()1022a a a h a a a a a +-+'=-=>++++在(0,)+∞上恒成立， 故()h a 在(0,)+∞上单调递增．而(0)0h =，所以()0>h a 在(0,)+∞上恒成立，所以22ln 02g a a ⎛⎫> ⎪++⎝⎭， 所以()g x 在222ln ,ln 2a a a ⎛⎫ ⎪++⎝⎭上存在一个零点． 综上所述，当0a <时，函数()g x 有且只有一个零点；当0a >时，函数()g x 有两个零点．坚持希望一天，一个瞎子和一个瘸子结伴去寻找那种仙果，他们一直走呀走，途中他们翻山越岭。

专题13 结构不良题（三角函数与解三角形）结构不良题型是新课改地区新增加的题型，所谓结构不良题型就是给出一些条件，另外的条件题目中给出三个，学生可以从中选择1个或者2个作为条件，进行解题。

一、题型选讲题型一 、研究三角形是否存在的问题例1、【2020年新高考全国Ⅰ卷】在①ac =sin 3c A =，③c =这三个条件中任选一个，补充在下面问题中，若问题中的三角形存在，求c 的值；若问题中的三角形不存在，说明理由．问题：是否存在ABC △，它的内角,,A B C 的对边分别为,,a b c ，且sin A B =，6C π=，________? 注：如果选择多个条件分别解答，按第一个解答计分． 【解析】方案一：选条件①．由6C π=和余弦定理得2222a b c ab +-=．由sin A B =及正弦定理得a ．222=b c =．由①ac =1a b c ==．因此，选条件①时问题中的三角形存在，此时1c =． 方案二：选条件②．由6C π=和余弦定理得2222a b c ab +-=．由sin A B =及正弦定理得a ．222=b c =，6B C π==，23A π=．由②sin 3c A =，所以6c b a ===．因此，选条件②时问题中的三角形存在，此时c = 方案三：选条件③．由6C π=和余弦定理得2222a b c ab +-=．由sin A B =及正弦定理得a ．222=b c =．由③c =，与b c =矛盾．因此，选条件③时问题中的三角形不存在．例2、（2021年徐州联考）在①cos cos 2c B b C +=，②πcos()cos 2b Cc B -=，③sin cos B B +条件中任选一个，补充在下面问题中，若问题中的三角形存在，求ABC △的面积；若问题中的三角形不存在，说明理由．问题：是否存在ABC △，它的内角A ，B ，C 的对边分别为a ，b ，c ，且π6A =，______________，4b =？注：如果选择多个条件分别解答，按第一个解答计分． 【解析】选择①：由余弦定理可知，222222cos cos 222a c b a b c c B b B c b a ac ab+-+-+=⋅+⋅==，……4分由正弦定理得，sin sin 1b A B a ==，又(0,π)B ∈，所以π2B =，…………………6分所以ABC △是直角三角形，则c =ABC △的面积12S ac ==…10分 选择②：由正弦定理得，πsin cos()sin cos 2B C C B -=，即sin sin sin cos B C C B =， 又(0,π)C ∈，所以sin 0C ≠，所以sin cos B B =，即tan 1B =， 又(0,π)B ∈，所以π4B =．……………………………………………………………4分由正弦定理得，sin sin b Aa B==，…………………………………………………6分所以ABC △的面积1ππsin )sin()2246S ab C A B ==+=+=+.…10分 选择③：因为πsin cos )4B B B ++=πsin()14B +=， 又(0,π)B ∈，所以ππ5π(,)444B +∈，所以ππ42B +=，即π4B =．…………………4分由正弦定理得，sin sin b Aa B==，…………………………………………………6分所以ABC △的面积1ππsin )sin()2246S ab C A B ==+=+=+.…10分 题型二、运用正余弦定理研究边、角及面积例3、【2020年高考北京】在ABC 中，11a b +=，再从条件①、条件②这两个条件中选择一个作为己知，求： （Ⅰ）a 的值：（Ⅱ）sin C 和ABC 的面积．条件①：17,cos 7c A ==-； 条件②：19cos ,cos 816A B ==．注：如果选择条件①和条件②分别解答，按第一个解答计分． 【解析】选择条件①（Ⅰ）17,cos 7c A ==-，11a b +=22222212cos (11)72(11)7()7a b c bc A a a a =+-∴=-+--⋅⋅-8a ∴=（Ⅱ）1cos (0,)sin 77A A A π=-∈∴==，由正弦定理得：7sin sin sin sin 7a c C A C C ==∴=11sin (118)8222S ba C ==-⨯⨯=选择条件②（Ⅰ）19cos ,cos ,(0,)816A B A B π==∈，sin 816A B ∴====由正弦定理得：6sin sin a b a A B === （Ⅱ）91sin sin()sin cos sin cos 8161684C A B A B B A =+=+=+⨯=11sin (116)622S ba C ==-⨯=例4、（2020届山东省日照市高三上期末联考）在①ABC ∆面积2ABC S ∆=，②6ADC π∠=这两个条件中任选一个，补充在下面问题中，求AC . 如图，在平面四边形ABCD 中，34ABC π∠=，BAC DAC ∠=∠，______，24CD AB ==，求AC .【解析】 选择①：113sin 2sin 2224ABC S AB BC ABC BC π∆=⋅⋅⋅∠=⋅⋅⋅=所以BC = 由余弦定理可得2222cos AC AB BC AB BC ABC =+-⋅⋅∠482220⎛=+-⨯⨯= ⎝⎭所以AC ==选择②设BAC CAD θ∠=∠=，则04πθ<<，4BCA πθ∠=-，在ABC ∆中sin sin AC ABABC BCA =∠∠，即23sin sin 44AC ππθ=⎛⎫- ⎪⎝⎭所以sin 4AC πθ=⎛⎫- ⎪⎝⎭在ACD ∆中，sin sin AC CD ADC CAD=∠∠，即4sin sin 6AC πθ=所以2sin AC θ=.所以2sin sin 4πθθ=⎛⎫- ⎪⎝⎭，解得2sin cos θθ=， 又04πθ<<，所以sin 5θ=，所以2sin AC θ==例5、（湖北黄冈高三联考）在①，②，③这三个条件中任选一个，补充在下面的横线上，并加以解答.已知的内角，，所对的边分别是，，，若______.（1）求角；（2）若，求周长的最小值，并求出此时的面积.【解析】（1）选①，由正弦定理得，∵，即，∵，∴，∴，∴. ··········································5分选②，∵，，由正弦定理可得，∵，∴，∵，∴. ·················································5分 选③，∵，由已知结合正弦定理可得， ∴，∴，∵，∴. ·················································5分 （2）∵，即，∴，解得，当且仅当时取等号，b a =2sin tan b A a B =()()sin sin sin ac A c A B b B -++=ABC A B C a b c B 4a c +=ABC ABC sin sin B A =sin 0A ≠cos 1B B -=π1sin 62B ⎛⎫-= ⎪⎝⎭0πB <<ππ5π666B -<-<ππ66B -=π3B =2sin tan b A a B =sin 2sin cos a Bb A B =sin 2sin sin sin cos BB A A B=⋅sin 0A ≠1cos 2B =()0,πB ∈π3B =()()sin sin πsin A BC C +=-=()22a c a cb -+=222a cb ac +-=2221cos 222a cb ac B ac ac +-===()0,πB ∈π3B =()22222cos 3163ba c ac B a c ac ac =+-=+-=-2316acb =-221632a c b +⎛⎫-≤ ⎪⎝⎭2b ≥2a c ==∴，周长的最小值为6，此时的面积. ··········10分 例6、（2021年南京金陵中学联考）现给出两个条件：①2c －3b ＝2a cos B ，②(2b －3c )cos A ＝3a cos C ，从中选出一个条件补充在下面的问题中，并以此为依据求解问题．在△ABC 中，a ，b ，c 分别为内角A ，B ，C 所对的边，________． (1)求A ；(2)若a ＝3－1，求△ABC 周长的最大值．【解析】若选择条件①2c －3b ＝2a cos B ．(1)由余弦定理可得2c －3b ＝2a cos B ＝2a ·a 2＋c 2－b 22ac ，整理得c 2＋b 2－a 2＝3bc ，………2分可得cos A ＝b 2＋c 2－a 22bc ＝3bc 2bc ＝32．…………………………………………………3分 因为A ∈(0，π)，所以A ＝π6． …………………………………………………………5分 (2)由余弦定理a 2＝b 2＋c 2－2bc cos A ，得(3－1)2＝b 2＋c 2－2bc ·32，………6分即4－23＝b 2＋c 2－3bc ＝(b ＋c )2－(2＋3)bc ，亦即(2＋3)bc ＝(b ＋c )2－(4－23)， 因为bc ≤(b ＋c )24，当且仅当b ＝c 时取等号， 所以(b ＋c )2－(4－23)≤(2＋3)×(b ＋c )24，解得b ＋c ≤22，…………………………………………………………8分 当且仅当b ＝c ＝2时取等号． 所以a ＋b ＋c ≤22＋3－1，即△ABC周长的最大值为22＋3－1．…………………………………………………10分 若选择条件②(2b －3c )cos A ＝3a cos C ． (1)由条件得2b cos A ＝3a cos C ＋3c cos A ，由正弦定理得2sin B cos A ＝3(sin A cos C ＋sin C cos A )＝3sin(A ＋C )＝3sin B ．………2分 因为sin B ≠0，所以cos A ＝32，…………………………………………………3分 因为A ∈(0，π)，所以A ＝π6． (2)同上例7、（2020·全国高三专题练习（文））在ABC 中，a ，b ，c 分别为内角A ，B ，C 的对边，且满()(sin sin )sin )b a B A c B C -+=-.（1）求A 的大小； （2）再在①2a =，②4B π=，③=c 这三个条件中，选出两个使ABC 唯一确定的条件补充在下面的问题中，并解答问题.若________，________，求ABC 的面积.min 2b =ABCABC 1sin 2S ac B ==【答案】（1）6A π=；（2）见解析【解析】（1）因为()(sin sin )sin )b a B A c B C -+=-， 又由正弦定理sin sin sin a b cA B C==，得()())b a b a c c -+=-，即222b c a +-=，所以222cos 222b c A bc bc a +===-， 因为0A π<<， 所以6A π=.（2）方案一：选条件①和②.由正弦定理sin sin a b A B=，得sin sin ab B A ==由余弦定理2222cos b a c ac B =+-，得222222cos4c c π=+-⨯，解得c =所以ABC 的面积11sin 2122S ac B ==⨯⨯=. 方案二：选条件①和③.由余弦定理2222cos a b c bc A =+-，得222433b b b =+-，则24b =，所以2b =.所以c =，所以ABC 的面积111sin 2222S bc A ==⨯⨯=题型三、考查三角函数的图像与性质例8、（2020届山东省泰安市高三上期末）在①函数()()1sin 20,22f x x πωϕωϕ⎛⎫=+>< ⎪⎝⎭的图象向右平移12π个单位长度得到()g x 的图象，()g x 图象关于原点对称；②向量()3sin ,cos 2m x x ωω=，()11cos ,,0,24n x f x m n ωω⎛⎫=>=⋅ ⎪⎝⎭；③函数()1cos sin 64f x x x πωω⎛⎫=+- ⎪⎝⎭()0ω>这三个条件中任选一个，补充在下面问题中，并解答．已知_________，函数()f x 的图象相邻两条对称轴之间的距离为2π．（1）若02πθ<<，且sin 2θ=，求()f θ的值； （2）求函数()f x 在[]0,2π上的单调递减区间． 【解析】解：方案一：选条件① 由题意可知，22T ππω==，1ω∴= ()()1sin 22f x x ϕ∴=+，()1sin 226g x x πϕ⎛⎫∴=+- ⎪⎝⎭，又函数()g x 图象关于原点对称，,6k k Z πϕπ∴=+∈，2πϕ<，6πϕ∴=，()1sin 226f x x π⎛⎫∴=+ ⎪⎝⎭，（1）0,sin 2πθθ<<=，4πθ∴=，()4f f πθ⎛⎫∴= ⎪⎝⎭12sin 23π=4=； （2）由3222,262k x k k Z πππππ+≤+≤+∈，得2,63k x k k Z ππππ+≤≤+∈，令0k =，得263x ππ≤≤，令1k =，得7563x ππ≤≤，∴函数()f x 在[]0,2π上的单调递减区间为275,,,6363ππππ⎡⎤⎡⎤⎢⎥⎢⎥⎣⎦⎣⎦．方案二：选条件②()113sin ,cos 2,cos ,24m x x n x ωωω⎛⎫== ⎪⎝⎭，()f x m n ∴=⋅1cos cos 24x x x ωωω=+112cos 222x x ωω⎫=+⎪⎪⎝⎭1sin 226x πω⎛⎫=+ ⎪⎝⎭， 又22T ππω==，1ω∴=，()1sin 226f x x π⎛⎫∴=+ ⎪⎝⎭，（1）0,sin 2πθθ<<=，4πθ∴=，()4f f πθ⎛⎫∴= ⎪⎝⎭12sin 23π=4=； （2）由3222,262k x k k Z πππππ+≤+≤+∈，得2,63k x k k Z ππππ+≤≤+∈，令0k =，得263x ππ≤≤，令1k =，得7563x ππ≤≤，∴函数()f x 在[]0,2π上的单调递减区间为275,,,6363ππππ⎡⎤⎡⎤⎢⎥⎢⎥⎣⎦⎣⎦．方案三：选条件③()1cos sin 64f x x x πωω⎛⎫=+- ⎪⎝⎭1cos sin cos cos sin 664x x x ππωωω⎛⎫=+- ⎪⎝⎭211cos cos 24x x x ωω=+-12cos 24x x ωω=+112cos 2222x x ωω⎛⎫=+ ⎪ ⎪⎝⎭1sin 226x πω⎛⎫=+ ⎪⎝⎭， 又22T ππω==，1ω∴=，()1sin 226f x x π⎛⎫∴=+ ⎪⎝⎭，（1）0,sin 22πθθ<<=，4πθ∴=，()4f f πθ⎛⎫∴= ⎪⎝⎭12sin 23π==； （2）由3222,262k x k k Z πππππ+≤+≤+∈，得2,63k x k k Z ππππ+≤≤+∈，令0k =，得263x ππ≤≤，令1k =，得7563x ππ≤≤.∴函数()f x 在[]0,2π上的单调递减区间为275,,,6363ππππ⎡⎤⎡⎤⎢⎥⎢⎥⎣⎦⎣⎦．二、达标训练1、（2021年江苏连云港联考）已知有条件①(2)cos cos b c A a C -=, 条件②45cos 2cos 2=+⎪⎭⎫⎝⎛+A A π;请在上述两个条件中任选一个，补充在下面题目中，然后解答补充完整的题目．在锐角△ABC 中，内角 A , B , C 所对的边分别为a , b,c , a =7, b +c =5, 且满足．(1) 求角A 的大小； (2) 求△ABC 的面积．（注：如果选择多个条件分别解答，按第一个解答计分．）【解析】（1）选择条件①()2cos cos b c A a C -=,…………………………………1分 法1：由正弦定理得()2sin sin cos sin cos B C A A C -=, ………2分所以()2sin cos sin sin B A A C B =+=,………………………3分 因为sin 0B ≠, 所以1cos 2A =………………………………4分 又π0,2A ⎛⎫∈ ⎪⎝⎭,…………………5分 所以3A π=. ………………………………………………………6分法2：由余弦定理得()222222222b c a a b c b c abc ab+-+--=，……2分 化简得222b c a bc +-=………………………………………3分则2221cos 22b c a A bc +-==， ………………………………4分又π0,2A ⎛⎫∈ ⎪⎝⎭,……………………5分 所以3A π=. ………………………………………………6分（1）选择条件②25cos cos 24A A π⎛⎫++= ⎪⎝⎭………………………………………1分 法3：因为cos sin 2A A π⎛⎫+=-⎪⎝⎭，所以25sin cos 4A A += ……………2分因为22sin cos 1A A +=，所以251cos cos 4A A -+=…………3分化简得21cos 02A ⎛⎫-= ⎪⎝⎭，解得1cos 2A =, ………………………4分 又()0,A π∈,………………………5分 所以3A π=. ……………………………………………………6分 （2）由余弦定理2222cos3a b c bc π=+-, ……………………………7分 得()273b c bc =+-，…………………………………………………8分所以()2763b c bc bc +-=⇒=， ……………………………10分于是ABC ∆的面积11sin 62222S bc A ==⨯⨯=．………12分 2、（2021年泰州高三期中）在①a=√2,②S=C 2 cosB ， ③C=π3这三个条件中任选-一个，补充在下面问题中，并对其进行求解.问题:在∆A BC 中，内角A, B,C 的对边分别为a,b,c,面积为S ，√3bcosA=acosC+ccosA ，b=1,____________，求 c 的值.注:如果选择多个条件分别解答，按第一个解答计分。

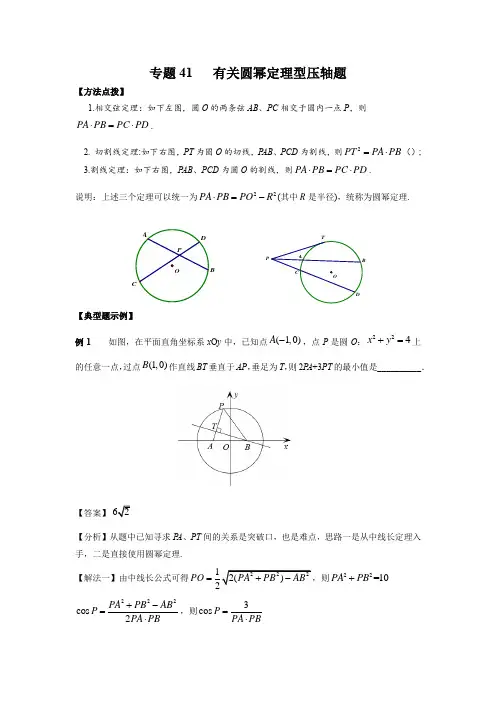
专题41 有关圆幂定理型压轴题【方法点拨】1.相交弦定理：如下左图，圆O 的两条弦AB 、PC 相交于圆内一点P ，则PA PB PC PD ⋅=⋅.2. 切割线定理:如下右图，PT 为圆O 的切线，P AB 、PCD 为割线，则2PT PA PB =⋅（）; 3.割线定理：如下右图，P AB 、PCD 为圆O 的割线，则PA PB PC PD ⋅=⋅.说明：上述三个定理可以统一为22PA PB PO R ⋅=-(其中R 是半径)，统称为圆幂定理.【典型题示例】例1 如图，在平面直角坐标系x O y 中，已知点(1,0)A -，点P 是圆O ：224x y +=上的任意一点，过点(1,0)B 作直线BT 垂直于AP ，垂足为T ，则2P A +3PT 的最小值是__________．【答案】 【分析】从题中已知寻求P A 、PT 间的关系是突破口，也是难点，思路一是从中线长定理入手，二是直接使用圆幂定理. 【解法一】由中线长公式可得22212()2PO PA PB AB =+-，则22=10PA PB + 222cos 2PA PB AB P PA PB+-=⋅，则3cos P PA PB =⋅93221862PT PA PA+=+≥=CAODPBTPOACD在Rt PBT ∆中，cos PT PB P =，即3PT PA=所以9232PA PT PA PA +=+≥2PA =时取等） 【解法二】∵BT ∵ AP ，∵点T 的轨迹是圆，其方程是：x 2+y 2=1，过点P 作该圆的切线PC ，C 为切点，则PC23PC PA PT =⋅=所以9232PA PT PA PA +=+≥2PA =时取等）. 点评：解法二中，先运用定直线张直角，得到隐圆，然后运用切割线定理得出定值，最后再使用基本不等式予以解决，思路简洁、解法明快.在有关解析几何的题目中，首先考虑相关的几何性质是解决这类问题的首选方向.在∵AOM 中，由正弦定理得：OMsinA =√5，而OA ＝OM =2， 所以sinA =√5，所以tan A =2.故直线AB 的斜率为2．例3 在平面直角坐标系xOy 中，过点(1,0)M 的直线l 与圆225x y +=交于,A B 两点，其中A 点在第一象限，且2BM MA =，则直线l 的方程为 ．【答案】y ＝x －1【分析】本题思路有下列几种：①利用向量坐标设点转化，点参法；②设直线方程的在x轴上的截距式，联立方程组；③垂径定理后二次解三角形；④相交弦定理；⑤利用”爪”型结构,得2133OM OA OB =+,两边平方求得AOB ∠的余弦值. 【解法一】：易知直线l 的斜率必存在，设直线l 的方程为y ＝k (x －1)．由BM →＝2MA →，设BM ＝2t ，MA ＝t .如图，过原点O 作OH ∵l 于点H ，则BH ＝3t2.设OH ＝d ，在Rt∵OBH 中，d 2＋⎝⎛⎭⎫3t 22＝r 2＝5. 在Rt∵OMH 中，d 2＋⎝⎛⎭⎫t 22＝OM 2＝1，解得d 2＝12， 则d 2＝k 2k 2＋1＝12，解得k ＝1或k ＝－1. 因为点A 在第一象限， BM →＝2MA →，由图知k ＝1， 所以所求的直线l 的方程为y ＝x －1.2BM MA =，设BM ＝2t ，MA ＝t【解法二】由又过点M 的直径被M 分成两段长为51-、51+由相交弦定理得()()225151t =-+，解之得2t =过原点O 作OH ∵l 于点H ，在Rt∵OBH 中，d 2＋⎝⎛⎭⎫3t 22＝r 2＝5，解得d 2＝12，（下同解法一，略）. 【解法三】设A (x 1，y 1)，B (x 2，y 2)，则BM →＝(1－x 2，－y 2)，MA →＝(x 1－1，y 1)．因为BM →＝2MA →，所以⎩⎪⎨⎪⎧1－x 2＝2(x 1－1)，－y 2＝2y 1.当直线AB 的斜率不存在时，BM →＝MA →，不符合题意．当直线AB 的斜率存在时，设直线AB 的方程为y ＝k (x －1)，联立⎩⎪⎨⎪⎧ y ＝k (x －1)，x 2＋y 2＝5，得(1＋k 2)y 2＋2ky －4k 2＝0，则⎩⎪⎨⎪⎧y 1＋y 2＝－2k1＋k 2，y 1·y 2＝－4k 21＋k2，－y 2＝2y 1，解得⎩⎪⎨⎪⎧y 1＝2k1＋k 2，y 2＝－4k1＋k 2，所以y 1·y 2＝－8k 2(1＋k 2)2＝－4k 21＋k 2，即k 2＝1.又点A 在第一象限，所以k ＝1，即直线AB 的方程为y ＝x －1.【解法四】设A (x 1，y 1)，B (x 2，y 2)，则BM →＝(1－x 2，－y 2)，MA →＝(x 1－1，y 1)．因为BM →＝2MA →，所以⎩⎪⎨⎪⎧ 1－x 2＝2(x 1－1)，－y 2＝2y 1，即⎩⎪⎨⎪⎧－x 2＝2x 1－3，－y 2＝2y 1. 又⎩⎪⎨⎪⎧ x 21＋y 21＝5，x 22＋y 22＝5，代入可得⎩⎪⎨⎪⎧x 21＋y 21＝5，(2x 1－3)2＋4y 21＝5，解得x 1＝2，代入可得y 1＝±1.又点A 在第一象限，故A (2,1)，由点A 和点M 的坐标可得直线AB 的方程为y ＝x －1. 点评：上述各种解法中，以解法一、解法二最简、最优.【巩固训练】1. 在平面直角坐标系xoy 中，M 是直线3x =上的动点，以M 为圆心的圆M ，若圆M 截x 轴所得的弦长恒为4，过点O 作圆M 的一条切线，切点为P ，则点P 到直线2100x y +-=距离的最大值为 .2.在平面直角坐标系xOy 中，圆C ：222()x m y r -+=(m ＞0)．已知过原点O 且相互垂直的两条直线l 1和l 2，其中l 1与圆C 相交于A ，B 两点，l 2与圆C 相切于点D ．若AB ＝OD ，则直线l 1的斜率为 ．3. 在平面直角坐标系xOy 中，设直线2y x =-+与圆222x y r +=(0)r >交于A B 、两点，O 为坐标原点，若圆上一点C 满足5344OC OA OB =+，则r = ．4.在平面直角坐标系xOy 中，已知点()0,1P 在圆C ：22222410++-+-+=x y mx y m m 内，若存在过点P 的直线交圆C 于A 、B 两点，且∵PBC 的面积是∵PAC 的面积的2倍，则实数m 的取值范围为 ．5.在平面直角坐标系xOy 中，圆22:(2)()3C x y m ++-=．若圆C 存在以G 为中点的弦AB ，且2AB GO =，则实数m 的取值范围是 ．6.已知直线3y ax =+与圆22280x y x ++-=相交于,A B 两点，点()00,P x y 在直线2y x =上且PA PB =，则0x 的取值范围为 .【答案与提示】1.【答案】 2.【答案】 【解析一】作CE ∵AB 于点E ，则 ，由OECD 是矩形，知CE 2＝OD 2，∵，化简得， 即cos∵OCD ＝＝tan∵COB ＝tan∵OCD∵直线l 1的斜率为．设OD ＝t (又∵直线l 13.244164416OC ⎝⎭即222225159cos 16816r r r AOB r =+∠+，整理化简得3cos 5AOB ∠=-. 22222221144CE BC BE BC AB BC OD =-=-=-2222215()44r m r m r -=--=222254r mm r -=-3r m =CD OC r m =22m t =Rt COE ∆过点O 作AB 的垂线交AB 于D ，则23cos 2cos 15AOB AOD ∠=∠-=-，得21cos 5AOD ∠=.又圆心到直线的距离OD ==222212cos 5OD AOD r r ∠===，r = 【解法二】注意到线性表示时的系数和为2，联想“三点共线”. 由5344OC OA OB =+，即153288OC OA OB =+ 得A B D 、、三点共线（其中D 是AB 的中点），且:3:5AD BD =， 设，5BD x =思路一：垂径定理后二次解三角形，()222224r x r x ⎧⎛⎫=⎪ ⎪⎝⎭⎨⎪=⎩，解之得r =.思路二：相交弦定理，()22335224r r x x r x ⎧⋅=⋅⎪⎨⎪=+⎩，解之得r4.【答案】4,49⎡⎫⎪⎢⎣⎭5.【答案】[【提示】易知OA OB ⊥，考察临界状态，只需过原点作圆的切线，切点弦的张角大于等于直角即可.6. 【答案】 (1,0)(0,2)-⋃专题42 抛物线过焦点的弦【方法点拨】设AB 是过抛物线y 2＝2px (p ＞0)焦点F 的弦，若A (x 1，y 1)，B (x 2，y 2)，α为弦AB 的倾斜角．则 (1)x 1x 2＝p 24，y 1y 2＝－p 2.(2)|AF |＝p 1－cos α，|BF |＝p1＋cos α (其中点A 在x 轴上侧，点B 在x 轴下侧) .(3)弦长|AB |＝x 1＋x 2＋p ＝2psin 2α.3AD x =(4)1|AF |＋1|BF |＝2p. (5)以弦AB 为直径的圆与准线相切．【典型题示例】例 1 已知抛物线()02:2>=p px y C 的焦点F 到其准线的距离为4，圆()12:22=+-y x M ，过F 的直线l 与抛物线C 和圆M 从上到下依次交于A ，P ，Q ，B四点，则BQ AP 4+的最小值为 . 【答案】13【分析】易知4p =，圆心(2,0)M 即为焦点F ，故445AP BQ AF BF +=+-，再利用抛物线的定义，进一步转化为445A B AP BQ x x +=++，利用4A B x x =、基本不等式即可. 【解析】易知4p =，圆心(2,0)M 即为焦点F所以()()414145AP BQ AF BF AF BF +=-+-=+- 根据抛物线的定义22A A p AF x x =+=+，22B B pBF x x =+=+ 所以()()4242545A B A B AP BQ x x x x +=+++-=++又244A B p x x ==所以445513A B AP BQ x x +=++≥=，当且仅当4A B x x =，即41A B x x =⎧⎨=⎩时等号成立，此时直线l的方程是y =-所以BQ AP 4+的最小值为13.例2 已知斜率为k 的直线l 过抛物线C ：y 2＝2px （p ＞0）的焦点，且与抛物线C 交于A ，B 两点，抛物线C 的准线上一点M （－1，－1）满足MA ·MB ＝0，则｜AB ｜＝ （ ） A． B． C ．5 D ．6 【答案】C【分析】将MA ·MB ＝0直接代入坐标形式，列出关于A ，B 中点坐标的方程，再利用斜率布列一方程，得到关于A ，B 中点坐标的方程组即可.这里需要说明的是，MA ·MB ＝0转化的方法较多，如利用斜边中线等于斜边一半等，但均不如上法简单.【解析】易知p =2设A （x 1，y 1），B （x 2，y 2），则x 1x 2=1，y 1y 2=－4，11(1,1)MA x y =++，22(1,1)MB x y =++ ∵MA ·MB ＝0∵1212(1)(1)(1)(1)0x x y y +++++=，化简得12121x x y y +++= 设A 、B 中点坐标为（x 0，y 0），则0012x y += ∵ 又由直线的斜率公式得12122212121204244AB y y y y k k y y x x y y y --=====-+-，001y k x =- ∵00021y y x =-，即2002(1)y x =- ∵ 由∵、∵解得032x =∵12025AB x x p x p =++=+=，答案选C. 点评：本题的命题的原点是阿基米德三角形，即从圆锥曲线准线上一点向圆锥曲线引切线，则两个切点与该点所构成的三角形是以该点为直角顶点的直角三角形.以此为切入点解决此题，方法则更简洁.例3 过抛物线y 2＝4x 的焦点F 的直线l 与抛物线交于A ，B 两点，若|AF |＝2|BF |，则|AB |等于( ) A.4 B.92C.5D.6【答案】B【解析】 由对称性不妨设点A 在x 轴的上方，如图设A ，B 在准线上的射影分别为D ，C ，作BE ∵AD 于E ，设|BF |＝m ，直线l 的倾斜角为θ，则|AB |＝3m ， 由抛物线的定义知|AD |＝|AF |＝2m ，|BC |＝|BF |＝m ， 所以cos θ＝|AE ||AB |＝13，∵sin2θ＝8 9.又y2＝4x，知2p＝4，故利用弦长公式|AB|＝2psin2θ＝92.【巩固训练】1.设F 为抛物线C ：y 2＝3x 的焦点，过F 且倾斜角为30°的直线交C 于A ，B 两点，O 为坐标原点，则∵OAB 的面积为( ) A.334B.938C.6332D.942.已知抛物线C ：y 2＝2px (p >0)的焦点F 到准线的距离为2，过点F 的直线与抛物线交于P ，Q 两点，M 为线段PQ 的中点，O 为坐标原点，则下列结论正确的是( ) A.抛物线C 的准线方程为y ＝－1 B.线段PQ 的长度最小为4 C.点M 的坐标可能为(3，2) D.OP →·OQ →＝－3恒成立3.已知抛物线C ：y 2＝4x 的焦点为F ，过F 的直线l 交C 于A ，B 两点，分别过A ，B 作准线l 的垂线，垂足分别为P ，Q .若|AF |＝3|BF |，则|PQ |＝________.4.已知抛物线C 的焦点为F ，过F 的直线与抛物线C 交于A ，B 两点，若112AF BF+=，则符合条件的抛物线C 的一个方程为__________．5.过抛物线22y x =的焦点F 作直线交抛物线于,A B 两点，若25,,12AB AF BF =<则AF = .6.过抛物线24y x =的焦点F 的直线交该抛物线于,A B 两点，若||3AF =，则||BF=______.【答案与提示】1.【答案】D【解析一】 由已知得焦点坐标为F ⎝⎛⎭⎫34，0，因此直线AB 的方程为y ＝33⎝⎛⎭⎫x －34，即4x －43y －3＝0.与抛物线方程联立，化简得4y 2－123y －9＝0， 故|y A －y B |＝（y A ＋y B ）2－4y A y B ＝6. 因此S ∵OAB ＝12|OF ||y A －y B |＝12×34×6＝94.【解析二】 由2p ＝3，及|AB |＝2p sin 2α得|AB |＝2p sin 2α＝3sin 230°＝12. 原点到直线AB 的距离d ＝|OF |·sin 30°＝38，故S ∵AOB ＝12|AB |·d ＝12×12×38＝94.2.【答案】 BCD【解析】因为焦点F 到准线的距离为2，所以抛物线C 的焦点为F (1，0)，准线方程为x ＝－1，A 错误.当线段PQ 垂直于x 轴时长度最小，此时|PQ |＝4，B 正确.设P (x 1，y 1)，Q (x 2，y 2)，直线PQ 的方程为x ＝my ＋1.联立得方程组⎩⎪⎨⎪⎧y 2＝4x ，x ＝my ＋1.消去x 并整理，得y 2－4my －4＝0，Δ＝16m 2＋16>0，则y 1＋y 2＝4m ，所以x 1＋x 2＝m (y 1＋y 2)＋2＝4m 2＋2，所以M (2m 2＋1，2m ).当m ＝1时，可得M (3，2)，C 正确.可得y 1y 2＝－4，x 1x 2＝(my 1＋1)(my 2＋1)＝m 2y 1y 2＋m (y 1＋y 2)＋1＝1，所以OP →·OQ →＝x 1x 2＋y 1y 2＝－3，D 正确.故选BCD.3.【答案】 833【解析】F (1，0)，不妨设A 在第一象限，A (x 1，y 1)，B (x 2，y 2)，由|AF |＝3|BF |得y 1＝－3y 2∵设l AB ：y ＝k (x －1)与抛物线方程联立得 ky 2－4y －4k ＝0，y 1＋y 2＝4k ，y 1·y 2＝－4，∵结合∵∵解得y 2＝－233，|PQ |＝|y 1－y 2|＝|－3y 2－y 2|＝－4y 2＝833.4.【答案】满足焦准距为1即可，如22y x =. 【解析】由公式112AF BF p +=得22p=，解得1p =，满足焦准距为1即可，如22y x =等. 5.【答案】65 【解析一】设AF =m ，BF =n ，则有25121121mnm n Pp ，解得65=m 或45m =(舍).【解析二】抛物线22y x =的焦点坐标为)0,21(，准线方程为21-=x 设A ，B 的坐标分别为),(),,(2211y x y x ，则414221==p x x 设n BF m AF ==,，则21,2121-=-=n x m x 所以有⎪⎪⎩⎪⎪⎨⎧=+=--122541)21)(21(n m n m ，解得65=m 或45=n ，所以65=AF . 6.【答案】32【解析】直接由112n m p+=立得（其中m ，n 是焦点弦被焦点所分得的两线段长，p 就是焦准距）.专题43 椭圆、双曲线的焦点弦被焦点分成定比【方法点拨】1. 设椭圆2222:1(0)x y C a b a b+=＞＞的右焦点为F ，过F 的直线l 与椭圆相交于A B、两点，直线l 的倾斜角为θ，且=()AF FB λλ＞0，则e θλ、、间满足1cos 1e λθλ-=+. 2.长短弦公式:如下图,长弦=1cos ep AF e θ-,短弦=1cos epBF e θ+（其中p 是焦参数，即焦点到对应准线的距离，θ是直线l 与x 轴的夹角，而非倾斜角）. 说明：（1）公式1的推导使用椭圆的第二定义，不必记忆，要有“遇过将焦半径转化为到准线距离”的意识即可.（2）双曲线也有类似结论.【典型题示例】例1 已知椭圆方程为2214x y +=，AB 为椭圆过右焦点F 的弦，则的最小值为 ．||2||AF FB ∴+FxAB O【解析】由，得，，则椭圆的离心率为，右准线方程为如图，过作于，则，∵ 设的倾斜角为， 则，∵联立∵∵，可得，同理可得，．令，，，． ．当且仅当，即时上式取等号．．． 2214x y +=2a =c e =:l x =A AM l ⊥M ||||AF AM =AB θ||||||cos ||cos ||cos AM CF AF AF AF θθθ=-==||AF =||BF =||2||AF BF ∴+===cos t θ=[1t ∈-1]1||2||32(612AF FB ∴+==-322(6)1263t=-+++326363t +=+t =||2||AF FB ∴+例2 （2021·江苏南京盐城二调·7）已知双曲线()2222100x y C a b a b-=>>：，的左、右焦点分别为F 1，F 2，过点F 2作倾斜角为θ的直线l 交双曲线C 的右支于A ，B 两点，其中点A 在第一象限，且cos θ＝14.若|AB |＝|AF 1|，则双曲线C 的离心率为A ．4B ．15C ．32 D ．2【答案】D【解析】22cos b AF a c θ=-，22cos b BF a c θ=+，2222122122230124b AB AF BF AF a AF BF a a e e ac =+==+⇒=⇒=⇒--=⇒+2e =．例3 已知椭圆C ：x 2a 2＋y 2b 2＝1(a>b>0)的离心率为32，与过右焦点F 且斜率为k (k >0)的直线相交于A ，B 两点．若AF →＝3FB →，则k ＝________.【答案】2 【解析】如右图，设l 为椭圆的右准线，过A 、BxDFB BAyO B / A /分别向l 作垂线AA /、BB /，A /、B /分别是垂足，过B 作AA /垂线BD ，D 是垂足 设BF =t ，AF =3t则t BB e '=，3t AA e'= Rt ABD 中，2,4tAD AB t e==故1cos2AD AB e θ===又k >0，所以tan k θ==.【巩固训练】1. 设F 1，F 2分别是椭圆E ：x 2a 2＋y 2b 2＝1(a >b >0)的左、右焦点，过点F 1的直线交椭圆E 于A ，B 两点．若|AF 1|＝3|F 1B |，AF 2∵x 轴，则椭圆E 的离心率为________．2.已知F 是椭圆C 的一个焦点，B 是短轴的一个端点，线段BF 的延长线交C 于点D ，且BF ＝2FD ，则C 的离心率为________．3. 已知F 是抛物线24C y x =：的焦点，过F 且斜率为1的直线交C 于A B ，两点．设FA FB >，则FA 与FB 的比值等于 ．4.已知1F ，2F 是椭圆2222:1(0)x y E a b a b+=>>的左右焦点，若E 上存在不同两点A ，B ，使得123F A F B =，则该椭圆的离心率的取值范围为( )A ．1，1)B ．1)C ．(21)D ．(0,2【答案与提示】1.【解析】如右图，设直线AB 的倾斜角为θ则12Rt AF F ，21212,b F F c AF a==所以cos θ=由|AF 1|＝3|F 1B |、长短弦公式得：31cos 1cos ep epe e θθ=-+，化简得：2cos 1e θ=1=，即4e ===解之得：213e （负值已舍），所以33e . 2.【答案】333.【答案】3+4.【答案】C【解析】延长1AF 交椭圆于1A ，根据椭圆的对称性，则211F B A F =，1113F A A F =， 由12F A F B λ=，且1||1cos ep F A e θ=-，11||1cos epA F e θ=+，由112A F F B =，所以1cos 1cos ep epe e λθθ=-+，整理得1cos 1e λθλ-=+，其中[0θ∈，2)π， 由A ，B 不重合，所以0θ≠，cos e e θ=<，解得2e >，所以，椭圆的离心率的取值范围(21)．专题44 数列的性质【方法点拨】1.数列是定义在正整数集或其有限子集上的函数，数列的函数性主要涉及数列的单调性（判断数列的增减性和确定数列中最大（小）项，求数列最值等）等；2.数列中的恒成立问题较函数中恒成立问题更难，但方法是想通的，一般都要分离参数，一般都要转化为研究单调性，但由于数列定义域是离散型变量,不连续，这给研究数列的单调性带来了难度,其一般解决方法是作差或作商.【典型题示例】例1 若不等式1n ＋1＋1n ＋2＋…＋13n ＋1>a －7对一切正整数n 都成立，则正整数a 的最大值为________． 【答案】8【分析】要求正整数a 的最大值，应先求a 的取值范围，关键是求出代数式1n ＋1＋1n ＋2＋…＋13n ＋1的最小值，可将其视为关于n 的函数，通过单调性求解． 【解析】令f (n )＝1n ＋1＋1n ＋2＋…＋13n ＋1(n ∵N *)，对任意的n ∵N *，f (n ＋1)－f (n )＝13n ＋2＋13n ＋3＋13n ＋4－1n ＋1＝23(n ＋1)(3n ＋2)(3n ＋4)>0，所以f (n )在N *上是增函数．又f (1)＝1312，对一切正整数n ，f (n )>a －7都成立的充要条件是1312>a －7，所以a <9712，故所求正整数a 的最大值是8.点评：本题是构造函数法解题的很好的例证．如果对数列求和，那就会误入歧途．本题构造函数f (n )，通过单调性求其最小值解决了不等式恒成立的问题．利用函数思想解题必须从不等式或等式中构造出函数关系并研究其性质，才能使解题思路灵活变通.例 2 已知常数0λ≥，设各项均为正数的数列{}n a 的前n 项和为n S ,满足：11a =，()11131n n n n n n a S S a a λ+++=+⋅+（*n ∈N ）．若112n n a a +<对一切*n ∈N 恒成立，则实数λ的取值范围是 ． 【答案】13λ>【分析】已知条件()11131n n n n n na S S a a λ+++=+⋅+中含“项、和”，需抓住特征，实施消和. 【解析】∵()11131n n n n n na S S a a λ+++=+⋅+ 0n a > ， ∴1131n n nn nS S a a λ++-=⋅+ 则212131S S a a λ-=⋅+，2323231S S a a λ-=⋅+，11131n n n n n S S a a λ----=⋅+()2n ≥ 相加，得()2113331n nnS n a λ--=+++-则()3322n n n S n a n λ⎛⎫-=+⋅≥ ⎪⎝⎭上式对1n =也成立，∴()*332n n n S n a n N λ⎛⎫-=+⋅≥ ⎪⎝⎭． ③∴()1*13312n n n S n a n N λ++⎛⎫-=++⋅≥ ⎪⎝⎭． ④④－③，得1113333122n n n n n a n a n a λλ+++⎛⎫⎛⎫--=++⋅-+⋅ ⎪ ⎪⎝⎭⎝⎭即11333322n n n n n a n a λλ++⎛⎫⎛⎫--+⋅=+⋅ ⎪ ⎪⎝⎭⎝⎭∵0λ≥，∴133330,022n n n n λλ+--+>+> . ∵112n n a a +<对一切*n ∈N 恒成立，∴332n n λ-+1133()22n n λ+-<+对一切*n ∈N 恒成立． 即233n nλ>+对一切*n ∈N 恒成立． 记233n n n b =+,则()()()111423622233333333n n n n n n n n n n b b +++-⋅-+-=-=++++ 当1n =时，10n n b b +-=； 当2n ≥时，10n n b b +->∴ 1213b b ==是{}n b 中的最大项． 综上所述，λ的取值范围是13λ>.【巩固训练】1.已知数列中，则在数列则数列的前50项中最小项为第 项，最大项为第____项.2.等比数列的首项，公比，设，则中第______项最大.3.已知，则在数列的最大项为第______项.4. 若不等式1n ＋1＋1n ＋2＋…＋13n ＋1>a －7对一切正整数n 都成立，则正整数a 的最大值为________．5.数列若对任意恒成立，则正整数m 的最小值为 .6．已知数列{a n }的前n 项和S n ＝3n (λ－n )－6，若数列{a n }单调递减，则λ的取值范围是 A ．(－∞，2)B ．(－∞，3)C ．(－∞，4)D ．(－∞，5)7．已知数列{}n a 的前n 项和n S 满足21n n S a =-.若对任意正整数n 都有10n n S S λ+-<恒成立，则实数λ的取值范围为（ ） A ．(),1-∞B ．12⎛⎫-∞ ⎪⎝⎭，C ．13⎛⎫-∞ ⎪⎝⎭，D ．14⎛⎫-∞ ⎪⎝⎭，8．已知数列{}n a 的通项公式为1133144--⎡⎤⎛⎫⎛⎫=-⎢⎥ ⎪⎪⎝⎭⎝⎭⎢⎥⎣⎦n n n a ，则数列{}n a 中的最小项为（ ）. A ．1aB ．2aC ．3aD ．4a9．已知数列{}n a 满足：1a a =，()1581n n n a a n N a *+-=∈-，若对任意的正整数n ，都有3n a >，则实数a 的取值范围（ ） A ．()0,3B ．()3,+∞C ．[)3,4D ．[)4,+∞ 10．已知数列{}n a 满足13a =，()()*131nn n a a n N n++=∈，若*n N ∃∈，使得{}na )n a n N *=∈{}n a {}n a 11000a =12q =123()n n p a a a a n N *=⋅⋅⋅⋅⋅⋅⋅∈123,,,,,()nP P P P n N *⋅⋅⋅⋅⋅⋅∈2()20n na n N n *=∈+{}n a ,,141,1}{22221211n n nn n a a a S a a a a +++==+=+ 记满足3012m S S n n ≤-+*N n ∈340n n a k -⋅>成立，则实数k 的取值范围是（ ）A ．1,4⎛⎫-∞ ⎪⎝⎭B ．(],0-∞C ．3,8⎛⎫-∞ ⎪⎝⎭D ．27,64⎛⎫-∞ ⎪⎝⎭【答案与提示】1.【答案】8、9 【提示】79807918080n n a n n --==+--，类比一次分式函数性质.2.【答案】10【提示】1110002n n a -⎛⎫=⨯ ⎪⎝⎭，11110002n n n n p a p --⎛⎫==⨯ ⎪⎝⎭，令111100012n n n p p --⎛⎫=⨯≥ ⎪⎝⎭解得11n ≥. 3.【答案】 4、5 【提示】212020n n a n n n==++，利用对勾函数性质. 4.【答案】8【分析】 要求正整数a 的最大值，应先求a 的取值范围，关键是求出代数式1n ＋1＋1n ＋2＋…＋13n ＋1的最小值，可将其视为关于n 的函数，通过单调性求解． 【解析】令f (n )＝1n ＋1＋1n ＋2＋…＋13n ＋1(n ∵N *)，对任意的n ∵N *，f (n ＋1)－f (n )＝13n ＋2＋13n ＋3＋13n ＋4－1n ＋1 ＝23n ＋13n ＋23n ＋4>0，所以f (n )在N *上是增函数．又f (1)＝1312，对一切正整数n ，f (n )>a －7都成立的充要条件是1312>a －7，所以a <9712，故所求正整数a 的最大值是8.5.【答案】10 【提示】2141n na a ++=得221114n n a a +-=，2143n n a =-，2143n a n =-，222211221111414581n n n n n S S a a a n n n ++++-=++⋅⋅⋅+=++⋅⋅⋅++++，仿上题求最大值. 6.【答案】A【解析】()113221,2n n n n a S S n n λ--=-=--≥，139a λ=-，因为{}n a 单调递减，所以()10,2n n a a n --<≥，所以()213410,3n n n a a n n λ---=⋅--<≥，且21360a a λ-=-<，所以只需10n λ--<，3n ≥，且2λ<， 所以2λ<，故选A ． 7.【答案】C【解析】当1n =时，1121S a =-，即1121a a =-，得11a =；当2n ≥时，由21n n S a =-，得1121n n S a --=-，两式相减得122n n n a a a -=-，得12n n a a -=，12nn a a -∴=，所以，数列{}n a 为等比数列，且首项为1，公比为2，11122n n n a --∴=⨯=.12122121n n n n S a -∴=-=⨯-=-，由10n n S S λ+-<，得()()11111112121112221212221n nnn n n n S S λ+++++---<===----， 所以，数列1n n S S +⎧⎫⎨⎬⎩⎭单调递增，其最小项为122211213S S -==-，所以，13λ<， 因此，实数λ的取值范围是1,3⎛⎫-∞ ⎪⎝⎭，故选C ． 8.【答案】C【解析】因为11331044n n n a --⎡⎤⎛⎫⎛⎫=-≤⎢⎥ ⎪⎪⎝⎭⎝⎭⎢⎥⎣⎦,()n N +∈ 所以11331044n n n a --⎡⎤⎛⎫⎛⎫-=-≥⎢⎥ ⎪⎪⎝⎭⎝⎭⎢⎥⎣⎦, 所以112+12344314n n n a --⎡⎤⎛⎫⎛⎫-⎢⎥ ⎛⎫ ⎪⎪≤= ⎪ ⎪ ⎪⎝⎭⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦-,当且仅当1314331441log 12n n n --⎛⎫⎛⎫- ⎪⎪⎝⎭⎝==⎭⇒+取“=”. 又因为3413log 142<+<.当3n =时,2233363144256a ⎡⎤⎛⎫⎛⎫=-=-⎢⎥ ⎪⎪⎝⎭⎝⎭⎢⎥⎣⎦. 当4n =时,334339991444096a ⎡⎤⎛⎫⎛⎫=-=-⎢⎥ ⎪⎪⎝⎭⎝⎭⎢⎥⎣⎦. 所以数列{}n a 中的最小项为3a .故选：C. 9.【答案】B 【解析】1585(1)335(3)111n n n n n n n a a a a a a a +---===->---， 又351y x =--在区间(3,)+∞上单调递增， 113n n a a a a +∴>>⋯>=>，∴实数a 的取值范围(3,)+∞，故选：B ．10.【答案】D 【解析】∵()()*131n n n a a n N n++=∈,∵131n n a a n n +=+, 记nn a b n=,则{}n b 是以13b =,3q =的等比数列, ∵3n n b =,∵3n n a n =⋅, ∵*n N ∃∈,340n n a k -⋅>,等价于*n N ∃∈，334n k n ⎛⎫< ⎪⎝⎭，即max334n n k ⎛⎫< ⎪ ⎪⎝⎭⎛⎫ ⎪⎝⎭令34n n c n ⎛⎫ ⎪⎝⎭=,则()11333314444n n nn n n n n c c ++-⎛⎫⎛⎫⎛⎫+⋅⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭-=-=∵3n <时,1n n c c +>;4n ≥时,1n n c c +<. ∵123456c c c c c c <<=>>,∵34max381464n n c c ⎛⎫ ⎪⎛⎫=== ⎪⎭ ⎪⎝⎝⎭. ∵2764k <,∵实数k 的取值范围为27,64⎛⎫-∞ ⎪⎝⎭,故选：D.专题45 数列通项结构的应用【方法点拨】1.数列{a n }是等差数列∵a n ＝pn ＋q (p ，q 为常数).2. 数列{a n }是等差数列∵S n ＝An 2＋Bn (A ，B 为常数).3. 已知S n 是等差数列{a n }的前n 项和，则⎩⎨⎧⎭⎬⎫S n n 也是等差数列，且其首项为a 1，公差为{a n }公差的12.4.两个等差数列{a n }、{b n }的前n 项和S n 、T n 之间的关系为1212--=n n n n T S b a . 5.两个等差数列{a n }、{b n }的前n 项和分别为S n 、T n ，若DCn B An T S n n ++=，则Dm C B n A b a m n +-+-=)12()12(. 【典型题示例】例1 n S 是公差为2的等差数列{}n a 的前n 项和，若数列也是等差数列，则1a =________.【答案】1-或3【分析】用特殊值法，也可直接抓住等差数列的结构特征解题. 【解析一】（特殊值法）由题意211(1)2(1)2n n n S na n a n -=+⨯=+-，∵数列是等差数列∵=，=解得11a =-或13a =，11a =-1n =-，13a =1n ==+，均为n 的一次函数，数列是等差数列， 故1a 的值为－1或3.【解析一】（特殊值法）由题意211(1)2(1)2n n n S na n a n -=+⨯=+-，∵数列是等差数列=n 的一次式，即21(1)+1n a n +-是完全平方式∵21(1)40a --=解之得11a =-或13a =（下同解法一）．例2 已知{}n a 是首项为2，公比为()1q q >的等比数列，且{}n a 的前n 项和为n S，若q = ．【答案】2【解析】因为{}n a 是首项为2，公比为()1q q >的等比数列．所以()1122221111n n n n a q q q S qq q q---===+----． 222112n n q q S q=++-+--{}2n S +也为等比数列．所以2201q+=-，即2q ．点评：等比数列通项的结构特征是：(0)nn a Aq Aq =≠、. 例3 已知两个等差数列{}n a 和{}n b 的前n 项和分别为A n 和n B ，且7453n n A n B n +=+，则使得nna b 为整数的正整数n 的个数是 . 【答案】5【解析】根据等差数列前n 项和的公式不难得到：2121(21)7(21)45719(21)(21)31n n n n n n a n a A n n b n b B n n ----++====--++ （﹡） （﹡）式是一个关于n 的一次齐次分式，遇到此类问题的最基本的求解策略是“部分分式”——即将该分式逆用通分，将它转化为分子为常数，只有分母中含有变量n 因为7197(1)12127111n n n n n +++==++++ 所以，要求使得nna b 为整数的正整数n ，只需1n +为12的不小于2的正约数 所以12,3,4,6,12n +=例4 已知S n 是等差数列{a n }的前n 项和，若a 1＝－2 014，S 2 0142 014－S 2 0082 008＝6，则S 2 020等于________.【答案】2 020【解析】由等差数列的性质可得⎩⎨⎧⎭⎬⎫S n n 也为等差数列，设其公差为d ， 则S 2 0142 014－S 2 0082 008＝6d ＝6，∵d ＝1，且首项为S 11＝－2 014. 故S 2 0162 016＝S 11＋2 015d ＝－2 014＋2 015＝1，∵S 2 020＝1×2 020＝2 020.【巩固训练】1.记等差数列{a n }的前n 项和为n S ，已知12a，且数列也为等差数列，则13a= .2. 已知公差大于零的等差数列{a n }的前n 项和为S n ，且满足a 3·a 4＝117，a 2＋a 5＝22，数列{b n }满足b n ＝S nn ＋c（其中c ≠0），若{b n }为等差数列，则c 的值等于________.3. 设等比数列{a n }，{b n }的前n 项和分别为S n ，T n ，若对任意自然数n 都有314n n n S T +=，则33a b 的值为________. 4. 设n S ，n T 分别是等差数列{}n a ，{}n b 的前n 项和，已知2142n n S n T n +=-，*n N ∈，则1011318615a ab b b b +=++ ．5.已知n S 是等差数列{}n a 的前n 项和，若77S =，1575S =，则数列n S n ⎧⎫⎨⎬⎩⎭的前20项和为 ．6. 已知数列的{a n }的前n 项和S n ，若{a n }和都是等差数列，则10n nS a +的最小值是 .【答案与提示】1.【答案】50【解析】设该等差数列的公差为d ，则由等差数列求和公式得2(1)2(2)222n n n d dS n d n n -=+=+-.又因为数列为等差数列，202d-=，故4d .所以1311250a a d.2.【答案】－12【解析】 设等差数列{a n }的公差为d ，且d ＞0，由等差数列的性质，得a 2＋a 5＝a 3＋a 4＝22，所以a 3，a 4是关于x 的方程x 2－22x ＋117＝0的解，所以a 3＝9，a 4＝13，易知a 1＝1，d ＝4，故通项为a n ＝1＋(n －1)×4＝4n －3. 所以b n ＝S nn ＋c ＝2n 2－n n ＋c.法一 （特殊值法）所以b 1＝11＋c ，b 2＝62＋c ，b 3＝153＋c (c ≠0).令2b 2＝b 1＋b 3，解得c ＝－12.当c ＝－12时，b n ＝2n 2－n n －12＝2n ，当n ≥2时，b n －b n －1＝2.故当c ＝－12时，数列{b n }为等差数列.法二 由b n ＝S nn ＋c ＝n （1＋4n －3）2n ＋c ＝2n ⎝⎛⎭⎫n －12n ＋c ，∵c ≠0，∵可令c ＝－12，得到b n ＝2n .∵b n ＋1－b n ＝2(n ＋1)－2n ＝2(n ∵N *)， ∵数列{b n }是公差为2的等差数列.即存在一个非零常数c ＝－12，使数列{b n }也为等差数列.3.【答案】9【解析】联想等比数列的前n 项和的结构特征，可知：1(19)19n n a S -=-，1(13)13n n b T -=-，且11a b = 所以2339()93a b ==. 4.【答案】4178【提示】因为318615b b b b +=+，所以10101110112011318615615101120a a a a a S ab b b b b b b b T +++===++++.5.【答案】55【解析】由等差数列的性质得⎩⎨⎧⎭⎬⎫S n n 也是等差数列，设nnS b n=，其公差为d 且7717S b ==，1515515S b ==，所以12d =，12b =-所以n S n ⎧⎫⎨⎬⎩⎭的前20项和即为{}n b 的前20项和，故为2019120(2)5522⨯⨯-+⨯=.6.【答案】21【解析】设该等差数列的公差为d ，则由等差数列求和公式得211(1)()222n n n d dS na d n a n -=+=+-.又因为数列为等差数列，102da -=，故12d a .所以221011(10)12121[(21)]21(21)4212n n S n a n a n a n ++==-++≥--，当且仅当10n =时，“=”成立.所以10n nS a +的最小值是21.专题46 数列奇偶项问题【方法点拨】定义 在数列n a 中，若任意nN ，存在t N 且2t，都有ntna a d （d为常数），则称数列n a 是“隔项成等差”数列.类型1 1nnnta a a An B ：由111n nn t nnnt a a a An B a a a AnAB，两式相减得1(2)nt na a A n，这就得到“隔项成等差”数列n a ，特别的，当0A时，数列n a 为周期数列.类型2 21nnntS S S An Bn C ：由21211(1)(1)n nn t nnnt S S S An BnC S S S A n B n C，两式相减得12(2)n nnta a a An A B n ，这样，类型2就转化为类型1了，所不同的是不包含首项1a .类型3 1(1)n nna a AnB ：对n 赋值，有2122212221222nn nnnna a An B a a An A B a a AnAB，通过加减可得212122242n n nna a A a a AnAB，从而222432n n a a An A B ，所以2224n na a A ，这就得到“隔项成等差”数列.【典型题示例】例1 数列{}n a 满足111(1)n n n a a n ++=-+-，且601a <<．记数列{}n a 的前n 项和为n S ，则当n S 取最大值时n 为( ) A ．11 B ．12 C ．11或13 D ．12或13【答案】C【解析】设1a t =，由111(1)n n n a a n ++=-+-，可得29a t =-，31a t =+，46a t =-，52a t =+，63a t =-，73a t =+，8a t =-，⋯， 601a <<可得031t <-<，可得23t <<，则数列{}n a 的奇数项为首项为t ，公差为1的等差数列；偶数项为首项为9t -，公差为3-的等差数列，且每隔两项的和为9，7，5，3，1，1-，⋯，为递减，可得1095753125S ==++++=，11112530S a t=+=+，1225124S =-=，131********S a t t =+=++=+，1424321S =-=，⋯，则当n S 取最大值时11n =或13．例2 设数列{}n a 的前n 项和为n S ，已知()2*427n n S a n n n N =-+∈，则11a =_______．【答案】－2【解析】由()2*427n n S a n n n N =-+∈得，21142(1)7(1)(2)n n S a n n n --=--+-≥两式相减得，221144272(1)7(1)(2)n n n n S S a n n a n n n ---=-+-+---≥ 即14(2)n n a a n n -+=-+≥，所以125(3)n n a a n n --+=-+≥ 两式相减得，21(3)n n a a n --=-≥又将1n =代入()2*427n n S a n n n N =-+∈得，13a =所以1115(1)2a a =+⨯-=-.例3 数列{}n a 满足2(1)31nn n a a n ++-=-，前16项和为540，则1a = ______________.【答案】7【分析】对n 为奇偶数分类讨论，分别得出奇数项、偶数项的递推关系，由奇数项递推公式将奇数项用1a 表示，由偶数项递推公式得出偶数项的和，建立1a 方程，求解即可得出结论. 【解析】2(1)31nn n a a n ++-=-，当n 为奇数时，231n n a a n +=+-；当n 为偶数时，231n n a a n ++=-. 设数列{}n a 前n 项和为n S ，16123416S a a a a a =+++++13515241416()()a a a a a a a a =+++++++111111(2)(10)(24)(44)(70)a a a a a a =++++++++++ 11(102)(140)(5172941)a a ++++++++ 118392928484540a a =++=+=，17a∴=.点评：本题综合考查数列的递推公式的应用、数列的并项求和、分类讨论思想和数学计算能力.【巩固训练】1.数列{}n a 满足1(1)21n n n a a n ++-=-，则其前60项和为________.2.已知数列{}n a 的前n 项和为n S ，()112nn n n S a =--，*n N ∈，则123100+S S S S +++⋅⋅⋅= .3. 设n S 为数列{}n a 的前n 项和，1(1),,2nn n n S a n N *=--∈则 （1）3a =_____； （2）12100S S S ++⋅⋅⋅+= ． 4.已知数列{}n a 的前n 项和为n S ，对任意N n +∈，1(1)32n n n nS a n =-++-且 1()()0n n t a t a +--<恒成立，则实数t 的取值范围是 ．5.各项均为正数的数列{}n a 的前n 项和为n S ，且13n n n S a a +=，则21nkk a==∑ ．6.设数列满足，数列前n 项和是，对任意的，，若，当n 是偶数时，的表达式是___________．7. 若数列n a 满足1236nnna a a n ，且数列n a 的前n 项的和n S 总满足2nS An Bn C （其中A B C 、、为常数），则数列n a 的通项公式是na .8. 若数列n a 满足1236n nna a a n ，且2112a a ，若数列n a 单调递增，则1a 的取值范围为 .{}n a 123411,1,4,4a a a a ===={}n a n S *n N ∈()()242122cos x n n n n n n n a af x x a a a x e a a +++++=++--()00f '=n S【答案与提示】1.【答案】1830【解析】由1(1)21n n n a a n ++-=-，可得211a a -=，323a a +=，435a a -=，547a a +=， 657a a -=，7611a a -=，···，10099199a a -=所以312a a +=，428a a +=，752a a +=，8624a a +=，9112a a +=，121040a a +=，···，所以从第一项起，每四项的和构成以10为首项，16为公差的等差数列 所以{}n a 前60项和为1514151016=18302⨯⨯+⨯. 2.【答案】10011(1)32- 【提示】奇偶项分别成等差数列.3.【答案】116-；10011(1)32- 【解法一】∵1(1)2n n n n S a =-- ∵当2n ≥时，11111(1)2n n n n S a ----=--两式相减得111111(1)(1)22n n n n n n n n S S a a -----=----+，即111(1)(1)2n n n n n n a a a --=---+当n 是偶数时，112n n n n a a a -=++，所以112n n a -=-，即n 是奇数时，112n n a +=-；当n 是奇数时，1122n n n a a -=-+，1111222n n n n a a --=-+=，即当n 是偶数时，12nna =. ∵12100121002100111()()()222S S S a a a ++⋅⋅⋅+=--+-+⋅⋅⋅+-2410013992100111()()()222a a a a a a =++⋅⋅⋅+-++⋅⋅⋅+-++⋅⋅⋅+2410035992100111111111()()()222222222=++⋅⋅⋅++++⋅⋅⋅+-++⋅⋅⋅+24100210010011111111()()(1)22222232=++⋅⋅⋅+-++⋅⋅⋅+=-. 【解法二】∵1(1)2nn n n S a =--∵11(1)()2nn n n nS S S -=---当n 是偶数时，112n n n n S S S -=--，112n n S -=-，即当n 是奇数时，112nn S +=-； 当n 是奇数时，112n n n n S S S -=-+-，11202n nnS S -=+=，即当n 是偶数时，0n S =； 210212100241001002111111122()(1)12223212S S S -++⋅⋅⋅+=-++⋅⋅⋅+=-=--. 4.【答案】31144t【解析】当1n时，134a 当2n时，11111(1)42n n n n S a n ----=-++-，所以11(1)(1)12nnn n n na a a -=-+--+ 当n 为偶数时，1112n n a -=-； 当n 为奇数时，11212n n n a a -=--+，即1112122n n n a --=--+，1232n na -=-. 所以113,211,2nn n n a n +⎧-⎪⎪=⎨⎪-⎪⎩为偶数为奇数.当n 为偶数时，1113,324n n a ⎡⎫=-∈⎪⎢⎣⎭，当n 为奇数时，11311,24n n a +⎛⎤=-∈-- ⎥⎝⎦ 又因为1()()0n n t a t a +--<恒成立，1n n a t a +<<，所以31144t. 5.【答案】3(1)2n n + 【解析】∵13n n n S a a += ∵-1-13n n n S a a =（2n ≥）两式相减得-11-13()()n n n n n S S a a a +-=-，即1-13()n n n n a a a a +=- 又因为{}n a 的各项均为正数，所以1-13n n a a +-=（2n ≥） 当1n =时，由13n n n S a a +=得111233S a a a ==，所以23a = 故2468,,,,a a a a ⋅⋅⋅是以23a =为首项，公差为3的等差数列 ∵21(1)3(1)3322nk k n n n n a n =⨯-+=⨯+⨯=∑. 6.【答案】241332n n-+⨯【解析】：， 因为，所以，即，所以数列中所有的奇数项成等比数列，所有的偶数项成等比数列，所以当n 是偶数时，的表达式是． 7.【答案】3n a n8.【答案】1123(,)52a 专题47 利用拆凑法求不等式的最值【方法点拨】1. 已知的一边是二次齐次可分解，另一边是常数，可考虑换元法；2. 例2、例3中使用了拆凑用以“凑形”，其目的在于一次使用基本不等式，能实现约分或倍数关系.【典型题示例】例1 （2021·江苏省泰州中学九月测·16）若实数x ，y 满足2221x xy y +-=，则222522x yx xy y--+的最大值为______． 【答案】4【解析】因为()()2222x xy y x y x y +-=-+，()()22x y x y x y -=--+，()()22225222x xy y x y x y -+=-++，设2x y u -=，x y v +=，故原问题可转化为“已知1u v ⋅=，求22u vu v-+的最大值”． 又因为()()2221242u v u v u v u v uv u v u v--==≤=+-+-+- ()()242122sin x n n n n n n n a af x a a a x e a a +++++'=-+--()00f '=2420n n n n a a a a +++-=242n n n n a aa a +++={}n a n S 22111114424111433214nn nn⎡⎤⎛⎫⎛⎫⎢⎥⋅- ⎪⋅- ⎪⎢⎥⎝⎭⎝⎭⎣⎦+=-+-⨯-所以222522x yx xy y --+，当且仅当u v -=故答案为：4． 例2 已知,,x y z R +∈，则222xy yzx y zμ+=++的最大值是________【分析】本题变量个数较多且不易消元，考虑利用均值不等式进行化简，要求得最值则需要分子与分母能够将变量消掉，观察分子为,xy yz 均含y ，故考虑将分母中的2y 拆分与22,x z 搭配，即22222221122xy yz xy yzx y z x y y z μ++==++⎛⎫⎛⎫+++ ⎪ ⎪⎝⎭⎝⎭，而222211,22x y z y +≥=+≥，所以μ≤=. 点评：本题在拆分2y 时还有一个细节，因为分子,xy yz 的系数相同，所以要想分子分母消去变量，则分母中,xy yz 也要相同，从而在拆分2y 的时候要平均地进行拆分（因为22,x z 系数也相同）．所以利用均值不等式消元要善于调整系数，使之达到消去变量的目的． 例3 若实数x ，y 满足x 2＋2xy －1＝0，则x 2＋y 2的最小值是________．【分析】思路1：注意到条件与所求均含有两个变量，从简化问题的角度来思考，消去一个变量，转化为只含有一个变量的函数，从而求它的最小值．本题中可直接由已知解得y ，代人所求消去y ；也可将直接使用“1”的代换，将所求转化为关于x ，y 的二次齐次分式.思路2：由所求的结论为x 2＋y 2，想到将条件应用基本不等式构造出x 2＋y 2，然后将x 2＋y 2求解出来即可．【解析一】从结论出发，注意到已知中不含“y 2”项，故拆“x 2”项的系数 设x 2＋y 2=tx 2 +(1－t )x 2＋y 2=tx 2 +[(1－t )x 2＋y 2]≥tx 2 +2√1−t xy (0<t<1) ∵ 则t :2√1−t =1:2，解之得：t =−1+√52。

专题13 两边夹【方法点拨】1．重要不等式：(1)对数形式：x ≥1＋ln x (x >0)，当且仅当x ＝1时，等号成立．(2)指数形式：e x ≥x ＋1(x ∈R )，当且仅当x ＝0时，等号成立．进一步可得到一组不等式链：e x >x ＋1>x >1＋ln x (x >0，且x ≠1)．2．树立一个转化的意识，即“等”与“不等”间的互化.【典型题示例】例1若实数,a b 满足()22ln ln 2422a ab b +≥+-，则（ ）A. 14a b +=B. 124a b -=C. 23a b +> D. 241a b -< 【答案】A【分析】思路一：据果变形，直接使用重要不等式)0(ln 1>≥-x x x ，两边夹逼将不等式转化为等式.思路二：一边一个变量，构造两个函数，分别求出其最值，夹逼将不等式转化为等式.【解析一】∵()()()222ln ln 2ln ln 2ln ln 42a ab a b b +=+=+ ∴()22ln ln 44222a ab b +≥+- 易知)0(ln 1>≥-x x x ，当且仅当x =1时，“=”成立∴221ln 22a a -≥，()41ln 4b b -≥当且仅当a =14b =时，“=”成立 根据不等式性质有()2242ln ln 422a a b b +-≥+ 所以()22ln ln 44222a ab b +=+-此时必有a =14b =（下略）. 【解析二】∵()22ln ln 2422a ab b +≥+-∴()22ln 4ln 222a ab b -+≥-- 令2()2ln 2a f a a =-，()()4ln 22gb b b =--利用导数知识易求得max ()ln 21f a f ==-，min ()()ln 21g b g b ==-所以()()f a g b ≤，即()22ln ln 2422a ab b +≤+- 故()22ln ln 2422a a b b +=+-，此时a =14b =（下略）. 例2 （2020·赣榆中学第二学期期初模拟检测·14）已知都是正数，，，则的最大值是 ． 【答案】 【分析】由()(ln ln )ln cde c d cd cd e+≥⇔≥，换元令(0)cd t t =>，则ln t t e ≥，考虑“形”， ln tt e≤恒成立，夹逼得cd e =，同理处置，最后使用基本不等式求解.【解析】()(ln ln )ln cde c d cd cd e+≥⇔≥，令(0)cd t t =>，则ln t t e ≥事实上ln tt≤（当且仅当t e =时，“=”成立），故cd e =； d c b a ,,,cd d c e ≥+)ln (ln )(42b a eb a +≤-+dc cdab ++22e +)(42b a e b a +≤-+成立） 故的最大值是．【巩固训练】1.已知正实数,x y 满足22ln ln 2xy x y +-=+，则y x = ． 2.（2019·江苏苏州·最后一卷）己知实数a ，b ，c 满足e a+c +e 2b−c−1≤a +2b +1（e 为自然对数的底数），则a 2+b 2的最小值是 . 3.若对于任意正实数,x y ，不等式2242x y x y ax e e +---≤++恒成立，则实数a 的最大值是 ．4. 己知实数a ，b 满足2lna −e 2b ≥a 2−2b −2（e 为自然对数的底数），则a +2b = .dc cdab ++22e +【答案或提示】1.2.【答案】【分析】将已知变形为e a+c +e 2b−c−1≤[(a +c ）+1]+[(2b −c −1)+1]，联系重要不等式e x ≥x +1，夹逼得. 【解析】∵ ∴， 所以又∵ ∴当且仅当时成立 ∴，所以. 3.【答案】124.【答案】115=021=0a c b c +-+，e 1x x ≥+e a c a c +≥+21e 21b c b c -+≥-+()()21e+e +21=21a cb c a c b c a b +-+≥+-+++21e +e 21a c b c a b +-+≤++21e +e =21a c b c a b +-+++=021=0a c b c +-+，()22222151=2424c c a b c c -⎛⎫+=-+-+ ⎪⎝⎭22min 15a b ⎡⎤+=⎣⎦。

专题20利用拆凑法求多元不等式的最值【方法点拨】1. 已知的一边是二次齐次可分解，另一边是常数，可考虑换元法：2. 例2、例3中使用了拆凑用以“凑形"，其目的在于一次使用基本不等式，能实现约分或 倍数关系.【典型题示例】例1（2021江苏省泰州中学九月测∙16）若实数I y 满足2x 2+xy^y 2=l ,则【答案】—4【解析】因为2x 2 + Λ>,-y 2= (2X-y)(x +y), x-2y = (2x-y)-(x÷y), 5X 2-2xy + 2y 2=(2x-y)~+(x + y)2,设Ix-y = ιι, χ+y = y 9 故原问题可转化为-V = E 求善二的最大值：ιr + ∖^又因为斗=…=— ≤ /1=邑li '+v~ 0γ-v )+2zγv(z∕-v)÷- 2」D 丄4M-V ψ f；/-V所叫二2X2严最大值为字当且仅*十皿取等号• 故答案为：E例2已知兀”ZWRj 则P =：''+严「的最大值是 __________________++君【答案】—2【分析】本题变量个数较多且不易消元，考虑利用均值不等式进行化简，要求得最值则需要 分子与分母能够将变莹消掉■观菸分子为Λy,W 均含y,故考虑将分母中的于拆分与X2,Z 2X-Iy5x 2-2xy + 2y 2的最大值为 ________搭配，即P=严严,—— ---- Xf+z所以AT+>7 =T2X√2Λ7÷√2>7 2 •点评：本题在拆分F时还有一个细节，因为分子_yy,yz的系数相同，所以要想分子分母消去变量，则分母中Jtyyz也要相同，从而在拆分F的时候要平均地进行拆分(因为X2,Z2系数也相同).所以利用均值不等式消元要基于调整系数，使之达到消去变量的目的.例3 若实数X, y满足√÷⅛-l=0,则x2+y2的最小值是____________________________ .【分析】思路1：注意到条件与所求均含有两个变量，从简化问题的角度来思考，消去一个变量，转化为只含有一个变量的函数，从而求它的最小值.本题中可直接由已知解得>，,代人所求消去y;也可将直接使用“1“的代换，将所求转化为关于X, y的二次齐次分式.思路2：由所求的结论为W+尸，想到将条件应用基本不等式构造出W+护，然后将χ2 +护求解出来即可.【解析一】从结论出发，注意到已知中不含‘护”项，故拆项的系数设X2÷K=Zx2—t x2+y2=tt2—t X2+ v f2]≥Zx2√1 - t Xy(O<∕vl)则『：√1→,解之得：匸三逻代人※得：X2÷y2≥~1^τ (x2xj,> 1；' 5.：工+尸的最小值是【解析二】从已知出发，注意到结论中不含“罚“项，故拆‘为，“项的系数设√+2Ay=λ-2+2(rγ)(i y)<χ-2+[(A∙)2+(; λ∙)2]= (l+∕2)√+ 討⅛⅛=1:IcF 略).W lJ(I÷【巩固训练】/ 2 + b? + 2 )■ + 51 •已知d",*(0,÷∞),则W [ +「 +、的最小值为________________IbC + Cic2•已知正实数x, y满足√≈+τv-2尸=1,则5x-2y的最小值为TS。

2021年高考考前押题密卷（新高考卷）数学·全解全析13．0.77 14．320- 15．43 16．12 π31．C【详解】{}Z 33A x x x =∈≤-≥或，{}1B x x =≥，332,1,0,1,2UA x Z x所以UA B 1,22．B【详解】将“∃”改为“∀”，同时否定“>”即可，p ⌝为“20,lg(1)0x x x ∀>-+≤”，故选：B ． 3．B 【详解】设参赛选手共有n 位，则总比赛场次为2n C ，即(1)2n n -场，且n N +∈，2n ≥， 由题意知：任意一场比赛结束，选手的总得分为2分，故所有选手总得分为(1)n n -分且为偶数， ∴当(1)132n n -=，得12n =；当(1)134n n -=，n 无整数解； ∴12n =(位). 4．D 【详解】去掉最高分93和最低分79，剩余数据从小到大排序为84,84,84,86,87，则中位数为84，平均值为85. 故选：D. 5．A 【详解】由题知()31()31x x e f x x x e -=-⋅+的定义域为(),-∞+∞．因为()()()333111()333()111x x x x xx e e e f x x x x x x x f x e e e ------=-+⋅=--⋅=-⋅=+++， 所以()f x 是偶函数，函数图象关于y 轴对称，排除选项B ；又221(2)201e f e -=⨯>+，故排除选项C ，D.6．C 【详解】解：因为4AB =，2AD =，4AB AD ⋅=， 所以cos 42cos 4AB AD A A =⨯=，所以1cos 2A =， 因为(0,)A π∈，所以3A π=，因为DE AB ⊥，所以6ADE π∠=，所以112AE AD ==，DE == 所以413=-=-=BE AB AE ，所以在Rt EBD 中，BD ===所以1cos 2DE EDB BD ∠===，因为F 是DE 中点，所以12DF DE ==，13cos 222DF DB DF DB EDB ⋅=∠==， 故选：C7．B 【详解】由已知得∴ABD ，∴CBD 均为等边三角形.如图所示，设球心为O ，∴BCD 的中心为O '，取BD 的中点F ，连接AF ，CF ，OO '，OB ，O B '，AO ， 则AF BD ⊥，CF BD ⊥，得BD ⊥平面AFC ，且可求得AF CF ==， 而15cm AC =，所以120AFC ∠=︒.在平面AFC 中过点A 作CF 的垂线，与CF 的延长线交于点E ， 由BD ⊥平面AFC ，得BD AE ⊥，故AE ⊥平面BCD ，过点O 作OG AE ⊥于点G ， 则四边形O EGO '是矩形.则()2sin 60cm 33O B BC '=︒⨯=，)1cm 23O F O B ''==，()15sin 60cm 2AE AF =︒=，)sin 30cm 3EF AF =︒=. 设球的半径为R ，cm OO x '=，则由222OO O B OB ''+=，222OA AG GO =+，得221003x R +=，22215232x R ⎛⎛⎫++-= ⎪ ⎝⎭⎝⎭，解得5cm x =，R =. 故三棱锥A BCD -外接球的表面积()227004cm 3S R ππ==. 8．A 【详解】根据题意，若要求“友情点对”，可把0x <时的函数图像关于原点对称， 研究对称过去的图像和0x ≥时的图像有两交点即可，2(0)y ax x =<关于原点对称的解析式为2(0)y ax x =->，考查3x x y e=的图像和2(0)y ax x =->的交点，可得32x x ax e =-，x x a e =-，令()x x g x e =-1()0x x g x e-'==， 所以(0,1)x ∈，()0g x '<，()g x 为减函数，(1,)x ∈+∞，()0g x '>，()g x 为增函数，1(1)g e=-，其图象为，故若要x x a e =-有两解，只要10a e-<<即可， 故选：A 9．BD 【详解】由1z ii z -=+，可得()()()2121111i i i z i i i i ⋅+===-+--+， 所以1z i =--，所以A 不正确；由z ==B 正确；由z 在复平面内对应点为()1,1-，位于第二象限，所以C 不正确； 由()2212z i i =-+=-，则2z 为纯虚数，所以D 正确． 10．AB 【详解】由诱导公式()()()cos cos k x k x k ππ-=+∈Z ，()cos cos 22k x k x k ππππ⎛⎫⎛⎫++=-+-∈ ⎪ ⎪⎝⎭⎝⎭Z ， 所以()()()f k x f k x k ππ-=+∈Z ，()22f k x f k x k ππππ⎛⎫⎛⎫++=-+-∈ ⎪ ⎪⎝⎭⎝⎭Z ，即()y f x =的图象关于直线()x k k π=∈Z 对称，()y f x =的图象关于点(),02k k ππ⎛⎫+∈ ⎪⎝⎭Z 对称，所以A 选项、B 选项正确；()2sin sin sin sin 0cos 2f x x x x x x x ππ⎛⎫='-+>-+=<< ⎪⎝⎭，则()y f x =在,2ππ⎛⎫ ⎪⎝⎭上单调递增，C 选项错误；当,2x ππ⎛⎫∈ ⎪⎝⎭趋近2π时，()f x 趋于负无穷大，所以()y f x =没有最小值，则D 选项错误.11．BD 【详解】由题意可得24a =，所以2a =，由点)P在椭圆内部可得：22114b+<，可得224b <<，即2244c <-< ，所以0c <<，对A ，c e a =，所以0e <<，故A 错误； 对B，当4e =时，2c =，2(2F ,1222242QF QP a QF QP a PF +=-+≤+=+，故B 正确； 对C ，由A知02e <<，当2e =时，当Q 在短轴端点时，12FQF ∠最大，此时2212224cos 1102a c FQF a-∠==-=，此时1290FQF ∠=，由0e <<12FQF ∠在椭圆在最扁时的最大值都小于90， 所以不存在点Q 使得120QF QF ⋅=，即C 错误； 对D ，122121212121144414()2QF QF QF QF QF QF QF QF QF QF ++==≥==+⋅⋅，故D 正确； 12．BCD 【详解】()f x 的定义域为()0,∞+，且()21ln xf x x-'=，当()0f x '>，即0e x <<时，()f x 单调递增；当()0f x '<，即x e >时，()f x 单调递减，所以()f x 的单调递增区间为()0,e ，单调递减区间为(),e +∞.由于1x =时，()0f x =，且当x e >时，()0f x >，故()f x 只有一个零点，所以A 选项不正确； 由于()f x 的单调性，可得()()max 11,0f x f e m e e==∴<<，所以B 选项正确； 由()f x 的单调区间，可画出函数()f x 的简图.由1204x x <<<，()()12f x f x m ==，可知10x e <<，24e x <<.因为()f x 在(),e +∞上单调递减，可知()()()2ln 4ln 24242f x f f >===，故有()()12f x f >.因为()f x 在()0,e 上单调递增，所以12x >.综上，有12x e <<，所以C 选项正确；因为3e π<<，由指数函数单调性可知，3e e π>，e 33π>，3e ππ>；由幂函数单调性可知，3e e π>，33e π>，3e ππ>，即有33e e ππ<<，33e e ππ<<，故这6个数的最大数在3π与3π之中，最小数在3e 与e 3之中.由3e π<<及()f x 的单调性，有()()()3f f f e π<<，即ln ln3ln 3e e ππ<<.由ln ln 33ππ<，可得3ln ln3ππ<，即3ln ln 3ππ<，所以33ππ<；同理可得e 33e <.综上可得，6个数中最大数是3π，最小数是3e ，所以D 选项正确， 故选：BCD.13．0.77 【详解】由题意，随机变量X 服从正态分布()210,N σ，可得对称轴10x =，则812102+=，因为()80.23P X <=，根据正态分布曲线的对称性，可得()()12180.77P X P X <=-<=. 14．320- 【详解】令1x =，可得612a x x x ⎛⎫⎛⎫+- ⎪⎪⎝⎭⎝⎭的展开式中各项系数的和为6(1)(12)3a +⋅-=，2a ∴=．6612122a x x x x x x =⎛⎫⎛⎫⎛⎫⎛⎫+-+- ⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭6224461111(2)(126016024016064)x x x x x x x=+-+-+⋅-+故该展开式中常数项为()2160320⨯-=-，15．43【详解】设圆1O 与12MF F △的三边的切点分别为A ，B ，C ，如图令MA MC m ==，11AF BF n ==，22BF CF t ==，根据双曲线的定义可得()()2,2,m n m t a n t c ⎧+-+=⎨+=⎩可得n a c =+，由此可知，在12F F M △中，1O B x ⊥轴于B ，同理2O B x ⊥轴于B ， ∴12O O x ⊥轴.过圆心2O 作1CO 的垂线，垂足为D . 易知直线l 的倾斜角θ与21O O D ∠大小相等. 不妨设14R =，21R =，则215O O =，13O D =， 所以根据勾股定理，24O D =，所以4tan 3θ=.16．12 π3【详解】（1）由平面//ABCD 平面//EFGH 平面MNPQ ，可将MZ 平移至平面ABCD 内，记为AZ '，且Z CD '∈（如左图），此时有//MZ AZ '．在正方形ABCD 中，:2:1BK KC =，根据平面几何知识可算得:1:2DZ Z C ''=，从而12QZ DZ ZP Z C '=='．（2）根据正四棱台EFGH MNPQ -的对称性，只需考虑该几何体的截面FNQH 在圆上．如右图，设球心为O ，半径为OH OQ OF r ===，由题意知4FH =，2NQ =，在Rt NSF △中有NF =，1FS =，从而1NS TR ==，故Rt ORH △中有OR =Rt OTQ △中有OT =，所以由1OT OR -==，解得r =．几何体EFGH MNPQ -外接球的体积为34π3V =π3=．故答案为：12π．17．【详解】解：（∴）由()()11110212a a a =++，得2112520a a -+=，解得12a =或112a =． 由于11a >，所以12a =．因为()()10212n n n S a a =++，所以210252n n n S a a =++．故221111101010252252n n n n n n n a S S a a a a ++++=-=++---，整理，得()()2211250n n n n a a a a ++--+=，即()()11250n n n n a a a a +++--=⎡⎤⎣⎦．因为数列{}n a 满足1n n a a +>，所以{}n a 是单调递增数列，且12a =，故10n n a a ++≠，因此152n n a a +-=， 则数列{}n a 是以2为首项，52为公差的等差数列， 所以()()51215122n a n n =+-=-． （∴）若选∴：满足条件的正整数m ，n ，k 存在，如1m =，2n =，3k =．假设存在m ，n ，*k N ∈，且m n k <<，使得()3n m k S S S -=．因为25344n S n n =+，则2225353533444444n n m m k k ⎡⎤⎛⎫+-+=+ ⎪⎢⎥⎝⎭⎣⎦，整理，得()()22235353n mn m kk ⎡⎤-+-=+⎣⎦，所以不妨设()()2223,3,n m k n m k ⎧-=⎪⎨-=⎪⎩，所以13m k =，23n k =．所以取3k =，则1m =，2n =．若选∴：满足条件的正整数m ，n ，k 不存在． 理由如下：假设存在m ，n ，*k N ∈，且m n k <<，使得()2m n k a a a +=， 则()15151512m n k -+-=-，整理，得3225m n k +-=，()* 显然，左边为整数，所以()*式不成立．故满足条件的正整数m ，n ，k 不存在． 18．【详解】解：（1）依题意11sin 22ABC S ab C c ===△4c =， 因为3C π=，所以8ab =．由余弦定理得222a b ab c +-=，因此22()340a b c ab +=+=，即a b +=． 故ABC的周长为4． （2）由（1）及正弦定理可得，21222b a b a a b ab c +++===22sin sin A Aπ⎫⎛-+ ⎪==（其中θ为锐角，且tan 2θ=） 由题意可知203A π<<，因此，当2A πθ+=时，21a b +取得最大值3．19．【详解】（1）如图，连接CE ，因为几何体是由等高的半个圆柱和14个圆柱拼接而成， 所以45ECD DCG ∠=∠=，90ECG ∠=，CE CG ⊥， 因为//BC EF ，BC EF =，所以四边形BCEF 为平行四边形，//BF EC ，BF CG ⊥， 因为BC ⊥平面ABF ，BF ⊂平面ABF ，所以BC BF ⊥， 因为BC CG C ⋂=，所以BF ⊥平面BCG ，因为因为BF ⊂平面BFD ，所以平面BFD ⊥平面BCG .（2）如图，以A 为坐标原点建立空间直角坐标系，设2AF =，AD t =，则()0,0,0A 、()0,2,0B 、()2,0,0F 、0,0,D t 、1,1,Gt ，()0,2,0AB =，()1,1,AG t =-，()2,2,0FB =-，()2,0,FD t =-，设平面BDF 的一个法向量为(),,n x y z =， 则00n FB n FD ⎧⋅=⎨⋅=⎩，整理得22020x y x tz -+=⎧⎨-+=⎩，令2z =，则,,2nt t ，设平面ABG 的一个法向量为(),,m x y z '''=，则00m AB m AG ⎧⋅=⎨⋅=⎩，整理得00y x y tz ''''=⎧⎨-++=⎩，令1z '=，则,0,1mt ，22cos ,2m n m n m nt⋅==⋅因为平面BDF 与平面ABG所成锐二面角的余弦值为5， 25=，解得2t =，即2AD =， 因为DA ⊥平面ABF ，所以DFA ∠即直线DF 与平面ABF 所成的角， 在ADF 中，因为90DAF ∠=，2AD AF ==，所以45DFA ∠=， 故直线DF 与平面ABF 所成的角为45. 20．【详解】（1）由题意，当点M 在椭圆的左顶点时，M 到1F 的距离最短，则1a c -=，当点M 在椭圆的上顶点（或下顶点）时，12MF F △的面积最大，此时12MF F △为等边三角形，则2a c =，联立22212a c a c a b c ⎧-=⎪=⎨⎪=+⎩，解得2,1,a c b ===故椭圆C 的方程为22143x y +=.（2）2||PF AB 为定值. 证明：由题意可知，动直线l 的斜率存在，设其方程为(1)y k x =-，联立22143(1)x y y k x ⎧+=⎪⎨⎪=-⎩，得()()2222348430k x k x k +-+-=. 设()11,A x y ，()22,B x y ，则2122834kx x k +=+，()21224334k x x k-=+， 设AB 的中点为()00,Q x y ，则212024234x x k x k +==+，()0023134k y k x k -=-=+. 当0k ≠时，线段AB 的垂直平分线的方程为2223143434k k y x k k k ⎛⎫--=-- ⎪++⎝⎭，令0y =，得2234k x k =+，即22,034k P k ⎛⎫ ⎪+⎝⎭， 所以()222223113434k k PF k k+=-=++.AB ==()2212134k k +=+. 所以()()2222231134||412134k PF k AB k k ++==++. 当0k =时，l 的方程为0y =， 此时，24AB a ==，21PF c ==，21||4PF AB =. 综上，2||PF AB 为定值. 21．【详解】（1）由表格数据知：1234535x ++++==，90951051001101005y ++++==，5152215ˆ5i ii ii x y xy bxx==-∴=-∑∑()()222222190295310541005110531001234553⨯+⨯+⨯+⨯+⨯-⨯⨯=++++-⨯459102==，由回归直线经过样本点的中心(),x y 可知：9ˆ10032a =⨯+，173ˆ2a ∴=，则回归直线方程为：9173ˆ22yx =+． 预测2020年12月份该企业所获得的利润为：917312140.522⨯+=（万元）． （2）根据题意知ξ所有可能取值为：0，50，100，150，200，250，300，350，()313302432P ξ⎛⎫∴==⨯= ⎪⎝⎭；()3111502432P ξ⎛⎫==⨯= ⎪⎝⎭；()223113910022432P C ξ⎛⎫==⨯⨯=⎪⎝⎭；()223111315022432P C ξ⎛⎫==⨯⨯= ⎪⎝⎭；()213113920022432P C ξ⎛⎫==⨯⨯= ⎪⎝⎭；()213111325022432P C ξ⎛⎫==⨯⨯= ⎪⎝⎭；()31333002432P ξ⎛⎫==⨯= ⎪⎝⎭；()31113502432P ξ⎛⎫==⨯= ⎪⎝⎭；ξ∴的分布列为：()319393305010015020025030032323232323232E ξ∴=⨯+⨯+⨯+⨯+⨯+⨯+⨯+135032⨯3252=， 即每件产品需要修复的平均费用为3252元. 22．【详解】解：（1）因为()2e 1x f x x =-，所以2()(2)e x f x x x '=+．所以(0)1f =-，(0)0f '=．所以曲线()y f x =在点(0,(0))f 处的切线方程为10y +=． （2）因为()xg x e ax =-，定义域为R ， 所以()xg x e a '=-．∴当0a ≤时，()0g x '>． 所以()g x 在R 上单调递增．∴当0a >时，令()0g x '=，得ln x a =，所以当0a >时，()g x 与()g x '在(,)-∞+∞上的变化情况如下：所以()g x 在(),ln a -∞内单调递减，在()ln ,a +∞内单调递增． 由∴∴可知，当0a ≤时，()g x 在R 上单调递增．当0a >时，()g x 在(),ln a -∞内单调递减，在[ln ,)a +∞内单调递增 （3）因为()()()F x f x g x =-， 所以2()(1)e 1x F x x ax =-+-， 所以2()(21)e x F x x x a '=+-+．令()()h x F x '=，所以2()(41)0xh x x x e '=++>．所以()h x 在区间[0,)+∞上单调递增，即()F x '在区间[0,)+∞上单调递增． 所以()(0)1F x F a ''=-+≥． 因为1a ≥，所以()0F x '≥．所以()F x 在区间[0,)+∞上单调递增． 所以()(0)2F x F =-≥．所以当1a ≥时，()F x 在区间[0,)+∞上的最小值是2-.。

2021年新高考数学名校地市选填压轴题好题汇编（十八）一．选择题（共35小题）1．（2021•临汾模拟）已知1F ，2F 分别为双曲线22221(0,0)x y a b a b-=>>的左，右焦点，过右焦点2F 倾斜角为30︒的直线与双曲线的两支分别相交于A ，B 两点，且点A 在右支上，1AB BF ⊥，则此双曲线的离心率(e = )A 1B C D ．2【解答】解：设双曲线的半焦距为c ，则12||2F F c =， 由过右焦点2F 倾斜角为30︒的直线，可得1230F F B ∠=︒，在直角三角形12F F B 中，可得1||2sin30BF c c =︒=，2||2cos30BF c =︒=，由双曲线的定义可得21||||2BF BF c a --=，即(1c a =，所以1ce a==． 故选：A ．2．（2021•临汾模拟）已知圆22:(2)(3)2C x y -+-=．若直线:0l x y m ++=上存在点P ，过点P 作圆O 的两条切线，切点为A ，B ，使得60APB ∠=︒，则m 的取值范围是( ) A ．(,9)-∞-B ．(-∞，9][1-，)+∞C ．(1,)-+∞D ．[9-，1]-【解答】解：根据题意，圆22:(2)(3)2C x y -+-=的圆心为(2,3)，半径r = 过点P 作圆O 的两条切线，切点为A ，B ，连接PC ， 若60APB ∠=︒，则30APC ∠=︒，又由CA PA ⊥，则||2||2PC CA r ===若直线:0l x y m ++=上存在点P ，满足60APB ∠=︒， 则有C 到直线l 的距离22d =，解可得：91m --，即m 的取值范围为[9-．1]-， 故选：D ．3．（2021•临汾模拟）点A ，B ，C ，D 在同一个球的球面上，1AB BC ==，120ABC ∠=︒，若四面体ABCD，则这个球的表面积为( ) A ．50081πB ．4πC ．259πD ．1009π【解答】解：根据题意知，A 、B 、C 三点均在球心O 的表面上， 且||||1AB AC ==，120ABC ∠=︒，BC ∴=，ABC ∴∆外接圆半径22r =，即1r =，111sin1202ABC S ∆∴=⨯⨯⨯︒=小圆的圆心为Q ，若四面体ABCD 的体积的最大值，由于底面积ABC S ∆不变，高最大时体积最大，所以，DQ 与面ABC 垂直时体积最大，最大值为13ABC S DQ ∆⨯=3DQ ∴=，设球的半径为R ，则在直角AQO ∆中，222OA AQ OQ =+，即2221(3)R R =+-，53R ∴=，∴球的表面积为25100499ππ=， 故选：D ．4．（2021•山西一模）函数()|log |1(0,1)x a f x a x a a =->≠有两个零点，则a 的取值范围为( ) A ．(1,)+∞B ．1(1,)e e -⎧⎫+∞⎨⎬⎩⎭C ．{}(1,)e e -+∞D ．1(1,)e ⎧⎫+∞⎨⎬⎩⎭【解答】解：由()|log |10x a f x a x =-=，得1|log |a xx a =，即11||()x alog x a =， 由题意，函数1||ay log x =与1()x y a =的图象有两个交点，当1a >时，两函数的图象有两个交点；当01a <<时，函数1||a y log x =与1()x y a =的图象有两个交点时，注意到1a y log x =与1()x y a =互为反函数，图象关于y x =对称，可知函数1()x y a =的图象与y x =相切，设切点的横坐标为0x ，则0001()11()1x x x a ln aa ⎧=⎪⎪⎨⎪=⎪⎩，解得01e x e a e -=⎧⎪⎨⎪=⎩． a ∴的取值范围为1(1,)e e -⎧⎫+∞⎨⎬⎩⎭．故选：B ．5．（2021•山西一模）已知数列{}n a 中，11a =，237a =，对于3n >，且n N ∈，有21212n n n n n a a a a a ----⋅=-，若2021(p a p q =，*q N ∈，且p ，q 互质），则p q +等于( ) A ．8089 B ．8088C ．8087D ．8086【解答】解：由21212n n n n n a a a a a ----⋅=-两边取倒数可得：2121122121n n n n n n n a a a a a a a -------==-⋅， 即1121111n n n n a a a a ----=-，故数列1{}na 为等差数列， 其首项为111a =，公差为211143a a -=， 故14411(1)33n n n a -=+-⨯=，*n N ∈， 所以202138083a =，因为p ，q 互质，且为正整数， 所以3p =，8083q =， 所以8086p q +=， 故选：D ．6．（2021•山西一模）一个圆锥的底面圆周和顶点都在一个球面上，已知圆锥的底面面积与球面面积比值为29，则这个圆锥体积与球体积的比值为( ) A ．881B ．827C ．481或881D ．427或827【解答】解：不妨设球的表面积为24R π， 由圆锥底面面积是这个球面面积的29， 可得圆锥的底面积为289R π，则圆锥的底面半径为r ， 由几何体的特征知球心到圆锥底面的距离，球的半径以及圆锥底面的半径三者可以构成一个直角三角形，13R ，则圆锥体积较小者的高为：1233R R R -=；可得圆锥体积较大者的高为：1433R R R +=．故圆锥体积与球体积的比为：231243334273R R ππ⋅⋅=⋅或231483334273RR ππ⋅⋅=⋅， 故选：D ．7．（2021•河南模拟）已知1F ，2F 是双曲线2222:1(0,0)x y C a b a b-=>>的左、右焦点，过点1F的直线交y 轴于点N ，交双曲线右支于点M ，若2||||MN F N =，则双曲线C 的离心率为( ) ABC ．2D【解答】解：因为N 在y 轴上，所以12||||||NF F N MN ==，所以△12MF F 为直角三角形， 即212MF F F ⊥且N 是1MF 的中点，所以22||b MF a =，又121212||||2,||MF MF F F c k F F ===，所以有22ac，222)ac c a =-，解得ce a== 故选：B ．8．（2021•河南模拟）若存在实数x ，y 满足3y y lnx x e e --++，则(x y += ) A ．1-B ．0C ．1D ．e【解答】解：令()3f x lnx x =-+，则11()1xf x x x-'=-=， 所以()f x 在(0,1)上单调递增，在(1,)+∞上单调递减， 所以()max f x f =（1）1132ln =-+=，令()y y g y e e -=+，则2y y e e -+，当且仅当0y =时取等号， 又3y y lnx x e e --++，所以32y y lnx x e e --+=+=，所以1x =，0y =，1x y +=， 故选：C ．9．（2021•宝鸡二模）已知双曲线2222:1(0,0)x y C a b a b-=>>的左、右焦点分别为1F ，2F ，O 为坐标原点，P为双曲线在第一象限上的点，直线PO ，2PF 分别交双曲线C 的左，右支于另一点M ，N ，若12||3||PF PF =，且260MF N ∠=︒，则双曲线的离心率为( )A B ．3 C ．2 D 【解答】解：由双曲线的定义可得12||||2PF PF a -=， 由12||3||PF PF =，可得2||PF a =，1||3PF a =， 结合双曲线性质可以得到||||PO MO =， 而12||||FO F O =， 结合四边形对角线平分，可得四边形12PF MF 为平行四边形， 结合260MF N ∠=︒，故1260F MF ∠=︒， 对三角形12F MF ，用余弦定理，得到22212121212||||||2||||cos MF MF F F MF MF F PF +-=⋅⋅∠， 结合12||3||PF PF =，可得1||MF a =， 2||3MF a =，12||2F F c =，代入上式子中，得到2222943a a c a +-=，即2274a c =，结合离心率满足ce a=，即可得出e =，故选：D ．10．（2021•宝鸡二模）如图是一个底面半径和高都是1的圆锥形容器，匀速给容器注水，则容器中水的体积V 是水面高度x 的函数()V f x =，若正数a ，b 满足1a b +=，则f （a ）f +（b ）的最小值为( )A ．12πB ．6π C ．4π D ．3π 【解答】解：圆锥形容器的底面半径与高均为1，又水面高度为x ，∴容器中水的体积31()3V f x x π==，1a b +=，1(01)b a a ∴=-<<，则f （a ）f +（b ）3311(1)33a a ππ=+-3232111(133)333a a a a a a πππππ=+-+-=-+， 其对称轴方程为12a =， ∴当12a =时，111[()()]42312min f a f b ππππ+=-+=． 故选：A ．11．（2020•定远县模拟）已知函数()||f x lnx =，20,01,()|4|2,1x g x x x <⎧=⎨-->⎩若关于x 的方程()()f x m g x +=恰有三个不相等的实数解，则m 的取值范围是( ) A ．[0，2]lnB ．(22,0)ln --C ．(22ln --，0]D ．[0，22)ln +【解答】解：设()()h x f x m =+， 作出函数()f x 和()g x 的图象如图则()h x 是()f x 的图象沿着1x =上下平移得到，由图象知B 点的纵坐标为h （1）f =（1）1m ln m m +=+=，A 点的纵坐标为g （2）2=-，当2x =时，h （2）2ln m =+，g （1）0=， 要使方程()()f x m g x +=恰有三个不相等的实数解， 则等价为()h x 与()g x 的图象有三个不同的交点， 则满足(1)(1)(2)(2)h g h g ⎧⎨>⎩，即022m m ln ⎧⎨+>-⎩得022m m ln ⎧⎨>--⎩，即220ln m --<，即实数m 的取值范围是(22ln --，0]， 故选：C ．12．（2020•黑龙江二模）已知双曲线22221(0,0)x y a b a b-=>>与函数0)y x =的图象交于点P ，若函数y =的图象与点P 处的切线过双曲线左焦点(4,0)F -，则双曲线的离心率是( )A B C D【解答】解：设P 的坐标为(m ，左焦点(4,0)F -，函数的导数()f x '，则在P 处的切线斜率()k f m ='=， 即42m m +=，得4m =， 则(4,2)P ，设右焦点为(4,0)A ，则2||||1)a PF PA =-==，即1a =， 4c =，∴双曲线的离心率c e a ==故选：D ．13．（2021•咸阳二模）四面体ABCD 中，ABD ∆和CBD ∆均为正三角形，且它们所在平面互相垂直，已知2AB =，则四面体ABCD 外接球的表面积为( ) A ．12πB ．163πC ．203πD ．16π【解答】解：设三角形BCD 外接圆半径r ，圆心F ，球的半径R ，球心O ， 取BD 中点M ，由ABD ∆和CBD ∆均为正三角形，且它们所在平面互相垂直可得AM BD ⊥，CM BD ⊥，AM ⊥平面BCD ， 过F 作平面BCD 的垂线，过A 作MF 的平行线，两直线交于E ，则四边形AMCE 为矩形，O 在EF 上，EF PM =由正弦定理得22sin 60r =︒，即r =，故MF =， 设OF d =，则所以22222)R d d =+=+-，解得d ，253R =， 则四面体ABCD 外接球的表面积22043S R ππ==． 故选：C ．14．（2021•咸阳二模）已知函数()cos22sin f x x x a =++，函数12()log g x x =．若任意1[6x π∈-，]π，都有21[2x ∈，4]，使得12()()f x g x =成立，则实数a 的取值范围为( )A ．3[2-，1]2-B ．1[2-，1]C ．1[2，5]2D ．[0，1]2【解答】解：设()f x 在[6π-，]π的值域为A ，()g x 在1[2，4]的值域为B ，由题意可得A B ⊆，又2()cos 22sin 2sin 2sin 1f x x x a x x a =++=-+++， 令sin t x =，由[6x π∈-，]π，可得1[2t ∈-，1]， 则2221y t t a =-+++在12t =时，y 取得最大值32a +，在12t =-时，y 取得最小值12a -，即1[2A a =-，3]2a +， 又12()log g x x =在1[2，4]递减，可得[2B =-，1]，所以122312a a ⎧--⎪⎪⎨⎪+⎪⎩，解得3122a --，故选：A ．15．（2021•未央区校级模拟）如图所示，在直角梯形BCEF 中，90CBF BCE ∠=∠=︒，A 、D 分别是BF 、CE 上的点，//AD BC ，且22AB DE BC AF ===（如图1)．将四边形ADEF 沿AD 折起，连结BE 、BF 、CE （如图2)．在折起的过程中，下列说法中错误的个数是( )①//AC 平面BEF ；②B 、C 、E 、F 四点不可能共面； ③若EF CF ⊥，则平面ADEF ⊥平面ABCD ； ④平面BCE 与平面BEF 可能垂直． A ．0B ．1C ．2D ．3【解答】解：对于①，在图2中记AC 与BD 的交点（中点）为O ，取BE 的中点为M ，连结MO ，易证得四边形AOMF 为平行四边形，即//AC FM ，//AC ∴平面BEF ，故①正确；对于②，如果四点共面，则由//BC 平面////ADEF BC EF AD AD EF ⇒⇒=，与已知矛盾，故②不正确； 对于③，在梯形ADEF 中，易得EF FD ⊥，又EF CF ⊥，EF ∴⊥平面CDF ，即有CD EF ⊥，CD ∴⊥平面ADEF ，则平面ADEF ⊥平面ABCD ，故③正确；对于④，延长AF 至G 使得AF FG =，连结BG 、EG ，易得平面BCE ⊥平面ABF ，过F 作FN BG ⊥于N ，则FN ⊥平面BCE ．若平面BCE ⊥平面BEF ，则过F 作直线与平面BCE 垂直，其垂足在BE 上，矛盾，故④错误． 故选：C ．16．（2021•未央区校级模拟）已知实数0a >，1a ≠，函数2,1()4,1x a x f x x alnx x x ⎧<⎪=⎨++⎪⎩在R 上单调递增，则实数a 的取值范围是( ) A ．25aB ．5a <C ．35a <<D ．12a <【解答】解：函数()f x 在R 上单调递增，∴当1x <时，有1a >；当1x 时，322424()20a x axf x x x x x-+'=-+=恒成立， 令3()24g x x ax =+-，[1x ∈，)+∞，则2()6g x x a '=+，0a >，()0g x '∴>，即()g x 在[1，)+∞上单调递增，()g x g ∴（1）242a a =+-=-，要使当1x 时，()0f x '恒成立，则20a -，解得2a ． 函数()f x 在R 上单调递增，∴还需要满足14111a aln ++，即5a ， 综上，a 的取值范围是25a ． 故选：A ．17．（2019•株洲二模）如图，已知正方体1111ABCD A B C D -的棱长为2，E 为棱1CC 的中点，F 为棱1AA 上的点，且满足1:1:2A F FA =，点F ，B ，E ，G ，H 为过B ，E ，F 三点的面BMN 与正方体1111ABCD A B C D -的棱的交点，则下列说法错误的是( )A ．//HF BEB ．三棱锥的体积14B BMN V -=C ．直线MN 与面11A B BA 的夹角是45︒D ．11:1:3D G GC =【解答】解：A 项：因为面1//AD 面1BC ，且面1AD 与面MBN 的交线为FH ， 面1BC 与面MBN 的交线为BE ，所以//HF BE ，A 正确；B 项：1:1:2A F FA =，1:1:2MA AB =，11MA =，同理可得12C N BC ==，14B N =，11111112344332B BMN N MBB BMB V V S B N --∆==⋅=⋅⋅⋅⋅=，B 正确；C 项：1B N ⊥面11A B BA ，所以1NMB ∠即为所求线面角， 14tan 13NMB ∠=≠，即14NMB π∠≠，C 错；D 项：111112C G NC MB NB ==，13MB =，132C G ∴=， 112D G ∴=，11:1:3D G GC=，D 对． 故选：C ．18．（2019•淄博一模）已知()(sin )x f x θ=，(0,)2πθ∈，设21(log 2a f =，4(log 3)b f =，16(log 5)c f =，则a ，b ，c 的大小关系是( ) A ．c a b >>B ．a c b >>C ．b a c >>D ．c b a >>【解答】解：根据题意，()(sin )x f x θ=，(0,)2πθ∈，则0sin 1θ<<，则函数()(sin )x f x θ=为减函数，又由24161log log log 72=，416log 3log 9=，则有16241log 5log log 32<<，则c a b >>， 故选：A ．19．（2021•临渭区二模）已知定义在R 上的奇函数，满足(2)()0f x f x -+=，当(0x ∈，1]时，2()log f x x =-，若函数()()sin F x f x x π=-，在区间[1-，]m 上有10个零点，则m 的取值范围是( ) A ．[3.5，4)B ．(3.5，4]C ．(3，4]D ．[3，4)【解答】解：由()f x 为奇函数，则()()f x f x =--， 又(2)()0f x f x -+=，得：(2)()f x f x -=-，即函数()f x 是其图象关于点(1,0)对称，且周期为2的奇函数， 又sin y x π=的图象关于(,0)k 对称， 其图象如图所示：在区间[1-，]m 上有10个零点，则实数m 的取值范围为：[3.5，4)， 故选：A ．20．（2021•临渭区二模）已知抛物线2:8C y x =的焦点为F ，直线l 过焦点F 与抛物线C 分别交于A ，B 两点，且直线l 不与x 轴垂直，线段AB 的垂直平分线与x 轴交于点(10,0)P ，则AOB ∆的面积为( )A ．B ．C ．D ．【解答】解：设直线:2l x ty =+，1(A x ，1)y ，2(B x ，2)y ， 则由282y x x ty ⎧=⎨=+⎩，可以得到28160y ty --=，所以AB 的中点2(42M t +，4)t ，线段AB 的垂直平分线与x 轴交于点(10,0)P ，故0t ≠． 所以AB 的中垂线的方程为：2112(42)48y x t t x t t t t=---+=-++，令0y =可得282x t =+，解方程21082t =+，得1t =±．此时2212|||116AB y y t =-=+=，O 到AB 的距离为d ==1162OAB S ∆=⨯ 故选：C ．21．（2021•西安模拟）“4a <-”是“函数2()2x af x x +=-在区间(2,)+∞上单调递增”的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．不充分也不必要条件【解答】解：2(2)4(2)44()(2)422x x a af x x x x -+-+++==-++--，当40a +<时，即4a <-时，函数()f x 在(2,)+∞为增函数，即充分性成立，当40a +>时， 44ay x x+=++在)+∞上为增函数，()f x ∴在2，)+∞上为增函数，若()f x 在区间(2,)+∞上单调递增，220a ，得4a =-，此时4a <-不成立，即必要性不成立，即“4a <-”是“函数2()2x af x x +=-在区间(2,)+∞上单调递增”的充分不必要条件，故选：A ．22．（2021•凉山州模拟）已知函数31()()12f x x =-+，则1220192020()()()()2021202120212021f f f f ++⋯⋯++的值为( ) A ．1B ．2C ．2020D ．2021【解答】解：函数31()()12f x x =-+，设1m n +=，则有11()22m n -=--，所以3311()()()1()2222f m f n m n +=-+--+=，所以当1m n +=时，()()2f m f n +=， 令1220192020()()()()2021202120212021S f f f f =++⋯⋯++， 所以12020202012[()()][()()]220202021202120212021S f f f f =++⋯++=⨯， 故1220192020()()()()20202021202120212021S f f f f =++⋯⋯++=． 故选：C ．23．（2021•凉山州模拟）集合{1A =，2，3，4}，()y f x =是A 到A 的函数，方程()(())f x f f x =恰好有两个不同的根，且f （1）+（2）f +（3）f +（4）10=，则函数()y f x x =-的零点个数为( ) A ．1B ．2C ．1或2D ．4【解答】解：函数()y f x =是A 到A 的函数，意思为1x =，2x =，3x =，4x =分别与1y =，2y =，3y =，4y =中的某一个对应，又f （1）f +（2）f +（3）f +（4）10=，①当是123410+++=或223310+++=或114410+++=这三种情况， 比如1对2，2对2，3对3，4对3，即f （1）(f f =（1）)2=，f （3）(f f =（3）)3=，有f （2）2=，f （3）3=两个零点，②当是333110+++=或222410+++=这两种情况，比如1对4，2对2，3对2，4对2，则f （3）(f f =（3）)2=，f （4）(f f =（4）)2=， 此时只有f （2）2=一个零点， 故选：C ．24．（2021•凉山州模拟）1F 、2F 分别为双曲线22221(0,0)x y a b a b-=>>的焦点，以12F F 为直径的圆依次与双曲线的渐近线交于A 、B 、C 、D 四点，1233AM AB AD =+，若直线MA ，MC 的斜率之积为12，则双曲线的离心率(e = ) AB1CD【解答】解：如图，如图，CM MA CA +=，()CD CB CA AB AD +==-+，1233AM AB AD =+，12213333CM CA AM AB AD AB AD AB AD =+=--++=--，联立圆222x y c +=与双曲线的渐近线方程， 可得(,)A a b -，(,)B a b ，(,)C a b -，(,)D a b --，(2,0)AB a =，(0,2)AD b =-，24(,)33AM a b =-，42(,)33CM a b =-，∴4323AMb k a -=，2343CM b k a =-， 由题意，4213324233b ba a -⋅=-，即222ab =，c e a ∴==．故选：C ．25．（2021•凉山州模拟）在ABC ∆中，22sin 30A A --=，若B C <，0m >，0n >，且222(1)tan 2tan 10m B B m --+-=，sin21C += 2n ，则有( )A ．m n <B ．m n >C ．1mn <D ．2mn >【解答】解：因为22sin 30A A --=，所以22(1cos )30A A ---=，整理得21)0A +=，即cos A =， 由A 为三角形内角得34A π=，4B C π+=， 因为B C <， 所以84B C ππ<<<，04C B π<-<，又22222(1)tan 2tan 1(1)(1tan )2tan 0m B B m m B B --+-=-+-=，所以222212sin 1sin 20cos m B m Bcos B B cos B----==，所以21sin 2sin 45m B -=<︒=， 所以221sin 2(sin cos )m B B B =+=+，因为22sin 21(sin cos )n C C C =+=+，0m >，0n >，所以sin cos )4m B B B π=+=+，sin cos )4n C C C π=+=+，则m n <，A 正确，B 错误；(sin cos )(sin cos )sin sin sin cos sin cos cos cos sin()cos()2mn B B C C B C B C C B B C B C B C =++=+++=++-<，D 错误；又cos()cos4B C π->，所以sin()cos()B C B C ++->=C 错误． 故选：A ．26．（2021•凉山州模拟）1F ，2F 分别为双曲线22221(0,0)x y a b a b-=>>的焦点，以12F F 为直径的圆依次与双曲线的渐近线交于A 、B 、C 、D 四点，M 为直线BD 上一点，若直线MA ，MC 的斜率之积为12，则双曲线的离心率(e = ) AB1CD【解答】解：可设1(,0)F c -，2(,0)F c ， 以12F F 为直径的圆的方程为222x y c +=， 双曲线的渐近线方程为by x a=±，联立222x y c by x a ⎧+=⎪⎨=±⎪⎩，解得四个交点(,)a b ，(,)a b -，(,)a b --，(,)m a b -， 可设(,)A a b -，(,)B a b ，(,)C a b -，(,)D a b --， 设0(M x ，0)y ，因为M 在BD 上，可得00by x a=， 即0(M x ，0)bx a，则0000()()MAb x b b x a a k x a a x a --==++，0000()()MC b x bb x a a k x a a x a ++==--， 所以2212MA MCb k k a ⋅==，则c e a ===，故选：C ．27．（2021•凉山州模拟）在ABC ∆中，34A π=，若B C <，0m >，0n >，且222(1)tan 2tan 10m B B m --+-=，2sin 21C n +=，则有( )A ．m n <B ．m n >C ．1mn <D ．2mn >【解答】解：因为34A π=，B C <， 所以4B B π<-，即8B π<，因为22222(1)tan 2tan 1(1)(1tan )2tan m B B m m B B --+-=-+-，222212sin 1sin 20cos m B m B cos B B cos B---=-==，所以21sin 2m B -=<所以221sin 2(sin cos )m B B B =+=+， 又0m >，所以sin cos m B B =+， 因为2sin 21C n +=，0n >， 所以sin cos n C C =+，所以12(1)2m n <+<，A 正确，B 错误；因为(sin cos )(sin cos )sin sin sin cos sin cos cos cos cos()sin()2mn B B C C B C B C C B B C B C B C =++=+++=-++<， 又cos()cos45B C ->︒，2mn <<，即122mn <<，C ，D 错误． 故选：A ．28．（2021•宜宾模拟）已知函数3(91)()1x log f x x+=-，下列说法正确的是( )A ．()f x 既不是奇函数也不是偶函数B ．()f x 的图象与sin y x =有无数个交点C ．()f x 在(0,)+∞上为减函数D ．()f x 的图象与2y =有两个交点【解答】解：根据题意，依次分析选项：对于A ，函数3(91)()1x log f x x+=-，其定义域为{|0}x x ≠，则333391()(91)(91)(91)9()()1120()x x x x x log log log log f x f x x x x x -++++-+=-+-=--=-，则()f x 为奇函数，A 错误；对于B ，函数3331[9(1)](91)119()111log (1)9x xx x log log f x xxx⋅++=-=-=++⋅，当0x >时，10x >，1119x +>，311log (1)09x x+⋅>，()1sin f x x >>， 又由()f x 为奇函数，则当0x <时，()1f x <-， 则()f x 的图象与sin y x =没有交点，B 错误； 对于C ，当0x >时，1x ，119x +都是单调递减，31log (1)9x +单调递减，故()f x 单调递减，C 正确；对于D ，若()2f x =，则有3(91)12x log x +-=，即3log (91)3x x +=，变形可得9127x x +=，即11()()1327x x +=， 设11()()()327x x g x =+，则()g x 为减函数且在其值域为(0,)+∞，则()1g x =有且只有1解，即()f x 的图象与2y =只有一个交点，D 错误， 故选：C ．29．（2021•宜宾模拟）已知A ，B 是以F 为焦点的抛物线24y x =上的两点，点A 在第一象限且3AF FB =，以AB 为直径的圆与准线的公共点为C ，则点C 的纵坐标为( ) A ．1B ．43CD【解答】解：如图，根据抛物线的定义，可得AA AF '=，BB BF '=，2AA BB AD BF ∴'-'==，4AF BF BF ∴+=，60DAB ∴∠=︒，即直线AB 的倾斜角为60︒，:1)AB y x ∴=-，21)(34y x A y x⎧=-⎪⇒⎨=⎪⎩，，1(3B，，设(1,)C m -，因为C 为圆上的点，故AC BC ⊥，(4,AC m =--，4(3CB =，)m -，∴22164040033AC BC m m m ⋅=⇒---++=⇒+=⇒． 故选：D ．30．（2021•宜宾模拟）已知以F 为焦点的抛物线24y x =上的两点A ，B 满足3AF FB =，则点A 的横坐标为( ) A ．1B ．43C ．2D ．3【解答】解：设直线AB 的斜率为k ，则直线AB 的方程为：(1)y k x =-， 联立方程组2(1)4y k x y x=-⎧⎨=⎩，消元得：2222(24)0k x k x k -++=，设1(A x ，1)y ，2(B x ，2)y ，则121x x =．3AF FB =，(1,0)F ， 1213(1)x x ∴-=-，解方程组1212113(1)x x x x =⎧⎨-=-⎩，可得13x =，213x =，故选：D ．31．（2021•宜宾模拟）已知函数3(91)()1x log f x x+=-，下列说法正确的是( )A ．()f x 既不是奇函数也不是偶函数B ．()f x 的图象与sin y x =有无数个交点C ．()f x 的图象与2y =只有一个交点D ．(2)(1)f f -<-【解答】解：根据题意，依次分析选项：对于A ，函数3(91)()1x log f x x+=-，其定义域为{|0}x x ≠，则333391()(91)(91)(91)9()()1120()x x x x x log log log log f x f x x x x x -++++-+=-+-=--=-，则()f x 为奇函数，A 错误；对于B ，函数3(91)()1x log f x x+=-，当0x >时，有39()1211xlog f x x >-=-=， 又由()f x 为奇函数，则当0x <时，()1f x <-，即()f x 在R 上值域为(-∞，1)(1-⋃，)+∞，则()f x 的图象与sin y x =没有交点，B 错误，对于C ，若()2f x =，则有3(91)12x log x +-=，即3log (91)3x x +=，变形可得9127x x +=，即11()()1327x x +=， 设11()()()327x x g x =+，则()g x 为减函数且其值域为(0,)+∞，则()1g x =有且只有1解，即()f x 的图象与2y =只有一个交点，C 正确，对于D，233333182(1)2(91)1828181(2)11()log log 2229log log log f x-+++-=-=--=-=-⨯=- 33311010(1)log (1)1(log 1)log 993f -=-+-=-+=-，则有(2)(1)f f ->-，D 错误， 故选：C ．32．（2021•四川模拟）已知1F ，2F 是双曲线2222:1(0,0)x y C a b a b-=>>的左，右焦点，过点1F 且倾斜角为30︒的直线与双曲线的左，右两支分别交于点A ，B ．若22||||AF BF =，则双曲线C 的离心率为( ) ABC ．2D【解答】解：如图，取AB 中点M ，连结2F M ，22||||AF BF =，2F M AB ∴⊥，设22||||AF BF x ==，21||||2AF AF a -=，1||2AF x a ∴=-， 又12||||2BF BF a -=，1||2BF x a ∴=+， 11||||||4AB BF AF a ∴=-=，||||2AM BM a ∴==， 11||||||F M BF BM x ∴=-=，2||MF c =，在△12F MF 中可得2224c x c +=， 在2AMF ∆中，222(2)a c x +=， 消去x 化简得222c a =，∴离心率ce a==． 故选：A ．33．（2021•四川模拟）若(1)(0x e a x lnax a -+>，0)x >，则a 的最大值为( ) A ．4eB ．2e C ．e D ．2e【解答】解：因为(1)x e a x lnax -+，0x >，0a >， 所以x e x ax lnax ++，即x lnax e x e lnax ++， 令()(0)x f x e x x =+>，则()10x f x e '=+>，所以()f x 在(0,)+∞上单调递增， 由()()f x f lnax ，可得x lnax ，x lnx lna +， 则lna x lnx -恒成立，所以()min lna x lnx -， 令()g x x lnx =-，1()1g x x'=-，令()0g x '=，得1x =， 当(0,1)x ∈，()0g x '<，()g x 单调递减，在(1,)x ∈+∞，()0g x '>，()g x 单调递增， 所以()min g x g =（1）1=， 所以1lna ，解得0a e <， 所以a 的最大值为e ． 故选：C ．34．（2021•武侯区校级模拟）已知函数()x f x ax e =-与函数()1g x xlnx =+的图像上恰有两对关于x 轴对称的点，则实数a 的取值范围为( )A ．(1,)e -+∞B ．1(,)2e -+∞ C ．1[,)2e -+∞ D ．(,1)e -∞-【解答】解：由已知可得，方程()()f x g x =-在(0,)+∞上有两解，即1x e a lnx x x =--在(0,)+∞上有解．设1()x e h x lnx x x =--，则222(1)11(1)(1)()x x e x x e h x x x x x ---'=-+=， 令()0h x '=，得1x =，∴当01x <<时，()0f x '<，当1x >时，()0f x '>，()h x ∴在(0,1)上单调递减，在(1,)+∞上单调递增．∴当1x =时，()h x 取得最小值h （1）1e =-，0x →时，()h x →+∞，x →+∞时，()h x →+∞，∴实数a 的取值范围是(1,)e -+∞．故选：A ．35．（2021•武侯区校级模拟）在正方体1111ABCD A B C D -中，点P 在正方形11ADD A 内，且不在棱上，则下列结论正确的个数为( )①在正方形11DCC D 内一定存在一点Q ，使得//PQ AC ； ②在正方形11DCC D 内一定存在一点Q ，使得PQ AC ⊥；③在正方形11DCC D 内一定存在一点Q ，使得平面1//PQC 平面ABC ； ④在正方形11DCC D 内一定存在一点Q ，使得AC ⊥平面1PQC ．A ．1B ．2C ．3D ．4【解答】解：A 、作平面11ACC A 的无数个平行平面，与平面11ADD A 、11DCC D 都有交线，∴在正方形11DCC D 内一定存在一点Q ，使得//PQ AC ，故A 正确；B 、作平面11ACC A 的无数个垂直平面，与平面11ADD A 、11DCC D 不一定都有交线，∴在正方形11DCC D 内不一定存在一点Q ，使得PQ AC ⊥，故B 错误；C 、作平面ABC 的无数个平行平面，点1C 都不在平面内，∴在正方形11DCC D 内不一定存在一点Q ，使得平面1//PQC 平面ABC ，故C 错误；D 、作平面11ACC A 的无数个平面，点1C 都不在平面内，∴在正方形11DCC D 内不一定存在一点Q ，使得AC ⊥平面1PQC ，故D 错误．故选：A ．二．填空题（共15小题）36．（2021•临汾模拟）已知函数12()935x x f x m m +=-⋅+-．若存在0x R ∈，使得00()()f x f x -=-，则m 的取值范围是 [1-，)+∞ ．【解答】解：函数12()935x x f x m m +=-⋅+-，若存在0x R ∈，使得00()()f x f x -=-，则00()()0f x f x -+=， 即000011229359350x x x x m m m m --++-⋅+-+-⋅+-=， 设0033x x t -=+，则2t ，方程可化为2232120t mt m -+-=，2t ，即关于t 的方程2232120t mt m -+-=在[2，)+∞上有解， 令22()3212g x t mt m =-+-，由题意得，则△2298480m m =-+，f （2）22680m m =--，34m 或g （2）0， ∴4143m m m -⎧⎪⎨⎪⎩或或14m -， 解得4m 或14m -， 即1m -，故答案为：[1-，)+∞．37．（2021•山西一模）已知抛物线22(0)y px p =>的焦点为F ，点(2pM -，0)，点F 的直线与此抛物线交于A ，B ，两点，若||24AB =且tan AMB ∠=p = 6 ． 【解答】解：设直线:2pAB x my =+，设1(A x ，2)y ，2(B x ，2)y ，联立222p x my y px⎧=+⎪⎨⎪=⎩，整理可得：2220y mpy p --=，可得122y y mp +=，212y y p =-，21212122112121212121212()()2()2()(2)0()()()()()()22AM BMy y y y y my p y my p my y p y y m p p mp k k p p my p my p my p my P my p my p my p my p x x +++++⋅-+⋅+=+=+====++++++++++， 所以可得AMF BMF ∠=∠，22tan tan 1AMFAMB tan AMF∠∠==-∠，又AMF ∠为锐角，解得tan AMF ∠ 设AF BF >，如图作AH x ⊥轴交于H ， 由题意可得M 在抛物线的准线上，作准线l ， 作AA l '⊥，垂足为A '，则tan sin AH AH AH AMF AFH MH AA AF ∠====∠=' 所以4AFH π∠=，所以1m =，所以12|||424AB y y p -=， 所以6p =． 故答案为：6．38．（2021•山西一模）在平面四边形ABCD 中，BC CD ⊥，135B ∠=︒，D ∠为锐角，3BC =，AD =AC =sin ACB ∠=，CD = ． 【解答】解：如图：135ABC ∠=︒，||3BC =，||AC =||AD =设BAC α∠=，BCA β∠=，ACD θ∠=，||CD m =则，在三角形ABC ∆中，由正弦定理得sin135sin AC BCα=︒，解得sin α=，则cos α=sin sin(45)sin )ACB ααα∠=︒-=-，BC CD ⊥cos sin ACD ACB ∴∠=∠=， 在三角形ACD ∆中，由余弦定理得2222cos AD AC CD AC CD θ=+-⨯⨯，即2222m =+-⨯， 1m ∴=或5，当1m =时222140450CD AD AC +-=+-<，此时D ∠为钝角，舍去，，5． 39．（2021•河南模拟）如图所示，在平面四边形ABCD 中，AB BD ⊥，AB BD =，BC CD =，2AD =，在ABC ∆中，角A ，B ，C 的对应边分别为a ，b ，c ，若22cos c ab C =，则ACD ∆的面积为．【解答】解：AB BD =，AB BD ⊥，∴在等腰直角ABD ∆中AD =，在ABC ∆中，由余弦定理得2222cos a b ab C c +-=， 又已知22cos c ab C =， 2222a b c ∴+=，又,,a BC CD b AC AD ====，222AC CD AD ∴+=， AC CD ∴⊥，作CF BD ⊥分别交BD ，AD 于点F ，E ， BC CD =，E ，F 分别为线段AD ，BD 的中点， 45CED ∴∠=︒，1CE ED ==，∴122sin 452ACD ECD S S EC ED ∆∆==⨯⨯⨯⨯︒=．．40．（2021径为2；内切球的体积为 ．【解答】解：由题意可得，该多面体为正四面体，棱长为 如图，设底面三角形的中心为E ，则2BE =，则AE ==∴正四面体的体积13BCD V S ∆=⨯r ，则11433BCD BCD S r S ∆∆⨯⨯=⨯2r =．内切球的体积为343π⨯．．41．（2020•东莞市一模）已知三棱锥P ABC -中，1PA =，PB AB =CA CB =面PBA ⊥面ABC ，则此三棱锥的外接球的表面积为253π． 【解答】解：取AB 的中点D ，连接PD ，CD ，1PA =，PB =，AB =222AB PA PB ∴=+，得90APB ∠=︒，则12AD AB =又CA CB =，CD AB ∴⊥，且CD =又面PAB ⊥面ABC ，面PAB ⋂面ABC AB =，CD ⊂平面ABC ， CD ∴⊥平面PAB ，∴外接球的球心在直线CD 上，设球心为O ，连接OA ，则OA 为外接球的半径，设为R ，则222()R AD CD R =+-，即323R =+，解得R =， ∴外接球的表面积22543S R ππ==， 故答案为：253π．42．（2021•未央区校级模拟）已知20,01(),()|||9|3,1x f x g x lnx x x <⎧==⎨-->⎩，若函数()()(0)y f x g x m x =+->恰有两个不相等的零点，则实数m 的取值范围为 (33,0)[5ln -，)+∞ ．【解答】解：由()()0y f x g x m =+-=得()()g x m f x -=-， 设220,01()()6,1312,3x h x f x x x x x <⎧⎪=-=-<⎨⎪->⎩，设()()||m x g x m lnx m =-=-， 作出()h x 和()m x 的图象如图：m （1）m =-，当0m -=时，即0m =时，m （3）3ln =，此时h （3）3m =>（3），即此时两个函数有3个交点，不满足条件．当0m ->时，即0m <时，要使两个函数有两个交点，则此时只需要满足m （3）3ln m h =-<（3）3=，即33m ln >-， 此时330ln m -<<，当0m -<时，即0m >时，此时当01x <时，两个函数一定有一个交点， 则此时只要在1x >时有一个交点即可， 此时当1x →，f （1）5→-，m （1）m =- 此时只要满足m （1）5m =--，即5m 即可， 综上实数m 的取值范围是5m 或330ln m -<<， 故答案为：(33,0)[5ln -，)+∞，43．（2019•汕尾一模）已知数列{}n a 的首项1111,,,31nn n n n n n a a a b a a S a ++===+为数列{}n b 的前n 项和．若n S t <恒成立，则t 的最小值为13． 【解答】解：数列{}n a 的首项111,31nn n a a a a +==+， 则：1113n na a +-=（常数） 故数列1{}na 是以111a =为首项，3为公差的等差数列．则：132n a n =-（首项符合通项）． 故：132n a n =-， 11111()(32)(31)33231n n n b a a n n n n +===--+-+，111111111(1)(1)344732313313n S n n n =-+-+⋯+-=-<-++，由于数列{}n b 的前n 项和n S t <恒成立， 故：13t， 则：t 的最小值为13，故答案为：13．44．（2021•临渭区二模）已知1F 、2F 分别是双曲线22:12x C y -=的左、右焦点，过点1F 且垂直于x 轴的直线与双曲线C 相交于A ，B 两点，则2ABF ∆的内切圆的半径为． 【解答】解：由双曲线的方程可得22a =，21b =，所以可得左焦点1(F 0)，右焦点2F 0)， 因为过点1F 且垂直于x 轴的直线与双曲线C 相交于A ，B ，所以A B x x ==2A B b y y a =-==即(A，(B，所以211||22ABF S AB =⋅=，22||||AF BF ===，设内切圆的半径为r ，则2221(||||||)2ABF AB AF BF r S++⋅=，可得122r +⋅=r =． 45．（2021•西安模拟）已知函数2()f x x ax b =++有两个零点1x 、2x ，且12102x x -<<<<，则直线(2)30a x by -+-=的斜率的取值范围是 3[2，)+∞ ．【解答】解：二次函数2()f x x ax b =++有两个零点1x ，2x ， 且12102x x -<<<<，则1x ，2x 是函数()f x 的两个零点， ∴(1)10(0)0(2)240f a b f b f a b -=-++>⎧⎪=<⎨⎪=++>⎩，画出可行域如图，由图可知，(1,0)A ，(2,0)B -， 联立24010a b a b ++=⎧⎨-++=⎩，解得(1,2)C --．直线(2)30a x by -+-=的斜率为212a b ba -=-， 其几何意义为可行域内动点(,)ab 与定点(2,0)连线斜率的倒数， 由图可知，0PA k =，202123PC k --==--， ∴直线(2)30a x by -+-=的斜率的取值范围是3[2，)+∞．故答案为：3[2，)+∞．46．（2021•凉山州模拟）已知三棱柱111ABC A B C -，1AA ⊥面ABC ，P 为△111A B C 内的一点（含边界），且ABC ∆为边长为2的等边三角形，12AA =，M 、N 分别为AC 、BC 的中点，下列命题正确的有 ①② ． ①若P 为11A C 的中点时，则过A 、P 、B 三点的平面截三棱柱表面的图形为等腰梯形； ②若P 为11A C 的中点时，三棱锥1P C MN -的体积V =； ③若P 为11A C 的中点时，1//NP A B ；④若AP 与平面ABC 所成的角与P BC A --的二面角相等，则满足条件的P 的轨迹是椭圆的一部分．【解答】解：对于①，取11B C 的中点Q ，连结PQ ，AP ，BP ，如图（1）所示， 则PQ 为△111C A B 的中位线，所以11//PQ A B ， 因为11//A B AB ，所以//PQ AB ，故梯形ABOP 即为过A ，P ，B 三点的截面，在Rt △1AA P 中，AP在Rt △1BB Q 中，BQ ，所以AP BQ =，故梯形ABQP 为等腰梯形，故选项①正确； 对于②，过点N 作ND AC ⊥，垂足为D ，如图（1）所示， 因为1AA ⊥平面ABC ，ND ⊂平面ABC ，所以1AA ND ⊥， 又1ACAA A =，所以ND ⊥平面11AA C C ，所以N 到平面1PMC 的距离即为12ND BM =， 所以11112PMC SPM PC =⋅⋅=，则11113P C MN N PMC PMC V V SND --==⋅⋅=②正确； 对于③，设1BC 的中点为E ，如图（2）所示， 则PE 为△11C A B 的中位线，所以1//PE A B ， 因为PNPE P =，PN ⊂/平面11C A B ，则PN 与1A B 不平行，故选项③错误；对于④，过点P 作PS ⊥平面ABC ，垂足为S ，连结AS ， 过S 作SR BC ⊥与点R ，连结PR ， 过点P 作11PT B C ⊥于点T ，连结1A P ， 因为四边形1AA PS 为矩形，所以1AS A P =， 四边形PSRT 为矩形，所以SR PT =， 因为PS BC ⊥，SR BC ⊥，且PSSR S =，所以BC ⊥平面PSR ，又PR ⊂平面PSR ，所以BC PR ⊥，所以PRS ∠即为二面角P BC A --的平面角，因为PS ⊥平面ABC ，所以PAS ∠即为PA 与平面ABC 所成的角， 所以PAS PRS ∠=∠，因为,tan tan PS PSAS SR PAS PRS==∠∠，所以AS SR =，则有1A P PT =，所以点P 到定点1A 的距离等于点P 到定直线11B C 的距离，所以点P 的轨迹为抛物线1(A 为焦点，11B C 为准线），故选项④错误． 故正确的是①②． 故答案为：①②．47．（2021•宜宾模拟）在三棱锥D ABC -中，ABC ∆是边长为的等边三角形且平面ABC ⊥平面ABD ，若三棱锥D ABC -的四个顶点都在同一个球面上，且该球的表面积为20π，则三棱维D ABC -体积的最大值为【解答】解：取AB 的中点E ，连结CE ，设O '为ABC ∆的中心，则O '在直线CE 上，因为平面ABC ⊥平面ABD ，平面ABC ⋂平面ABD AB =，CE ⊂平面ABC ，所以CE ⊥平面ABD ， 设ABD ∆所在的截面圆的圆心为1O ，过1O 作CE 的平行线，过O '作1O E 的平行线，两平行线交于点O ，则O 为外接球的球心，连结OC ，设外接球的半径为R ，则有2420R ππ=，故R OC在等边ABC ∆中，3CE ==，所以223CO CE '==，在Rt △CO O '中，1OO '=，故11O E =，在Rt △1EO E 中，12O B ， 所以ABD ∆所在的截面圆的半径为2r =，故点D 到直线AB 距离的最大值为1123O E r +=+=，所以三棱维D ABC -体积的最大值为2113333ABC V S ∆=⋅⋅=⨯=故答案为：48．（2021•宜宾模拟）在三棱锥D ABC -中，平面ABC ⊥平面ABD ，AB AD ⊥，4AB AD ==，6ACB π∠=，若三棱锥D ABC -的四个顶点都在同一个球面上，则该球的表面积为 80π． ． 【解答】解：设ABC ∆的外心为1O ，半径r ，三棱锥D ABC -的外接球球心O ，半径R ， 过1O 作AD 的平行线，过D 作1AO 的平行线，两条直线交于E ， 因为平面ABC ⊥平面ABD ，平面ABC ⋂平面ABD AB =，AB AD ⊥，所以AD ⊥平面ABC ， 因为1OO ⊥平面ABC ， 所以1//OO AD ， 则四边形1ADEO 为矩形，易得O 为1EO 中点，ABC ∆中，由正弦定理得，428sin sin 6AB r ACB π===∠，所以4r =，2222116420R AO r OO ==+=+=， 故2480S R ππ==． 故答案为：80π．49．（2021•四川模拟）设球的半径为34，该球的内接圆锥（顶点在球面上，底面为某平面与球的截面）的体积为V ，则V 的最大值为6π． 【解答】解：如图，设圆锥的高底面半径r ，高h ，OO x '=，则34h x =+，则r =， 2232933927()()()33164341664V r h x x x x x πππ==-+=--++， 令323927()41664f x x x x =--++，则239()3216f x x x '=--+，易得当104x <<时，()0f x '>，函数单调递增，当14x >时，()0f x '<，函数单调递减， 故当14x =时，函数()f x 取得最大值16，此时V 取得最大值6π． 故答案为：6π．50．（2021•武侯区校级模拟）如图，椭圆2222:1(0)x y a b a bΓ+=>>的离心率为e ，F 是Γ的右焦点，点P 是Γ上第一象限内任意一点．且sin cos POF POF ∠<∠，(0).0OQ OP FQ OP λλ=>⋅=，若e λ>，则离心率e 的取值范围是 ，1) ．【解答】解：设||OF c =，(0)2POF πθθ∠=<<，因为0FQ OP ⋅=，所以OQ FQ ⊥，所以点Q 的坐标为2(cos c θ，sin cos )c θθ，又因为(0)OQ OP λλ=>，所以点P 的坐标为2sin cos (,)ccos c θθθλλ，代入椭圆方程可得：2422222221c cos c sin cos a b θθθλλ+=，化简可得：24222222222c cos c sin cos c e a b aθθθλ=+>=，又因为222a b c =+，则化简可得：22221b cos a cos θθ<+恒成立，因为sin cos POF POF ∠<∠，所以04πθ<<，所以cos θ∈，所以代入cos θ，可得2213b a，所以解得c e a ==，故答案为：．。

2021年新高考数学名校地市选填压轴题好题汇编一．选择题（共19小题）1．（2021•天心区校级一模）如图所示，直线l 为双曲线C ：x 2a −y 2b =1（a ＞0，b ＞0）的一条渐近线，F 1，F 2是双曲线C 的左、右焦点，F 1关于直线l 的对称点为F 1′，且F 1′是以F 2为圆心，以半焦距c 为半径的圆上的一点，则双曲线C 的离心率为（ ）A ．√2B ．√3C ．2D ．3【解析】解：直线l 为双曲线C ：x 2a 2−y 2b 2=1（a ＞0，b ＞0）的一条渐近线，则直线l为y =bax ，∵F 1，F 2是双曲线C 的左、右焦点， ∴F 1（﹣c ，0），F 2（c ，0），∵F 1关于直线l 的对称点为F 1′，设F 1′为（x ，y ）， ∴y x+c=−a b，y+02=b a•x−c2，解得x =b 2−a 2c ，y =−2ab c，∴F 1′（b 2−a 2c，−2abc ），∵F 1′是以F 2为圆心，以半焦距c 为半径的圆上的一点， ∴（b 2−a 2c−c ）2+（−2abc−0）2＝c 2， 整理可得4a 2＝c 2， 即2a ＝c ， ∴e =ca =2，故选：C ．2．（2020秋•海门市校级月考）已知函数f(x)=sin(ωx +π6)+cosωx(ω＞0)在[0，π]内有且仅有3个零点，则ω的取值范围是（ ） A ．[83，113) B ．(83，113] C ．(103，133] D ．[103，133) 【解析】解：f(x)=sin(ωx +π6)+cosωx =sinωxcos π6+cosωxsin π6+cosωx =√32sinωx +32cosωx =√3sin(ωx +π3)． ∵当x ∈[0，π]时，ωx +π3∈[π3，πω+π3]， ∵f （x ）在[0，π]有且仅有3个零点， ∴3π≤πω+π3＜4π， 综上：83≤ω＜113．故选：A ．3．（2020秋•海曙区校级期中）已知|a →|＝|b →|＝1，a →⋅b →=12，c →=(m ，1−m)，d →=(n ，1−n)（m ，n ∈R ）．存在a →，b →，对于任意实数m ，n ，不等式|a →−c →|+|b →−d →|≥T 恒成立，则实数T 的取值范围为（ ）A ．(−∞，√3+√2]B ．[√3+√2，+∞)C ．(−∞，√3−√2]D ．[√3−√2，+∞) 【解析】解：设a →=OA →，b →=OB →，c →=OC →，d →=OD →， 由c →=(m ，1−m)，d →=(n ，1−n)（m ，n ∈R ）可知，C ，D 两点在直线y ＝﹣x +1上运动，A ，B 两点在单位圆上运动， 因为cos ＜a →，b →＞=a →⋅b→|a →||b →|=121×1=12，所以∠AOB =π3，又|a →−c →|+|b →−d →|=AC +BD ，先固定A ，B 两点， 如图，当AC ⊥CD ，BD ⊥CD 时，AC +BD 有最小值d ，取AB的中点M，过M作直线的垂线MN，AC+BD有最小值d＝2MN，当点A，B运动时，MN≤OM+OE=√32+√22，所以d max=(2MN)max=√3+√2，即T≤√3+√2．故选：A．4．（2020秋•海曙区校级期中）设a∈R，则函数f（x）＝||x2﹣3x+2|﹣a|的零点个数最多有（）A．4个B．6个C．8个D．12个【解析】解：函数f（x）＝||x2﹣3x+2|﹣a|的零点等价于方程f（x）＝||x2﹣3x+2|﹣a|＝0的根，即求|x2﹣3x+2|＝a根的个数，即求函数y＝|x2﹣3x+2|与y＝a的图象交点的个数，作出函数y＝|x2﹣3x+2|与y＝a的图象如图所示，由图象可知，函数y＝|x2﹣3x+2|与y＝a的图象交点最多有4个，故函数f（x）＝||x2﹣3x+2|﹣a|的零点个数最多有4个．故选：A．5．（2021春•沈阳期末）设f （x ）是定义在R 上的函数，f （0）＝2，对任意x ∈R ，f （x ）+f ′（x ）＞1，则不等式e x f （x ）＞e x +1的解集为（ ） A ．（0，+∞）B ．（﹣∞，0）C ．（﹣∞，﹣1）∪（1，+∞）D ．（﹣∞，﹣1）∪（0，1）【解析】解：令g （x ）＝e x f （x ）﹣e x ， 则g ′（x ）＝e x f （x ）+e x f ′（x ）﹣e x ， ∵对任意x ∈R ，f （x ）+f ′（x ）＞1， ∴g ′（x ）＝e x [f （x ）+f ′（x ）﹣1]＞0， ∴函数y ＝g （x ）在R 上单调递增． ∵f （0）＝2， ∴g （0）＝1．∴当x ＜0时，g （x ）＜1； 当x ＞0时，g （x ）＞1． ∵e x f （x ）＞e x +1， ∴e x f （x ）﹣e x ＞1， 即g （x ）＞1， ∴x ＞0． 故选：A ．6．（2021春•芗城区校级月考）若函数f （x ）＝e x ﹣e ﹣x +sin x ﹣x ，则满足f （a ﹣2ln （|x |+1））+f （x 22）≥0恒成立的实数a 的取值范围为（ ）A ．[2ln2−12，+∞) B ．(ln2−14，+∞) C ．[74，+∞)D ．(32，+∞)【解析】解：函数f （x ）＝e x ﹣e ﹣x +sin x ﹣x ，故函数f （x ）的定义域是R ，关于原点对称，且f （﹣x ）＝e ﹣x ﹣e x +sin （﹣x ）+x ＝﹣（e x ﹣e ﹣x +sin x ﹣x ）＝﹣f （x ），故函数f （x ）是定义在R 上的奇函数， 且满足f （a ﹣2ln （|x |+1））+f （x 22）≥0恒成立，故f （a ﹣2ln （|x |+1））≥﹣f （x 22）＝f （−x 22）， 由cos x ∈[﹣1，1]，f ′（x ）＝e x +e ﹣x +cos x ﹣1≥2√e x ⋅e −x +cos x ﹣1＝cos x +1≥0（当且仅当x ＝0时“＝”成立）， 故函数f （x ）在R 单调递增，由f （a ﹣2ln （|x |+1））≥f （−x 22），故a ﹣2ln （|x |+1）≥−x 22，即a ≥2ln （|x |+1）−x 22，令g （x ）＝2ln （|x |+1）−x 22，欲使a ≥2ln （|x |+1）−x 22恒成立，则a ≥g （x ）max 恒成立，g （﹣x ）＝2ln （|﹣x |+1）−(−x)22=2ln （|x |+1）−x 22=g （x ），且函数g （x ）的定义域是R ，关于原点对称， 故函数g （x ）是定义在R 上的偶函数，故要求解g （x ）在R 上的最大值，只需要求解函数g （x ）在[0，+∞）上的最大值即可， 当x ∈[0，+∞）时，g （x ）＝2ln （x +1）−x 22， 故g ′（x ）=2x+1−x =−(x+2)(x−1)x+1， 故当x ∈[0，1]时，x ﹣1≤0，则g ′（x ）≥0，g （x ）在[0，1]上递增， 当x ∈（1，+∞）时，x ﹣1＞0，则g ′（x ）＜0，g （x ）在（1，+∞）递减， 故g （x ）max ＝g （1）＝2ln 2−12，故a ≥2ln 2−12，故a 的取值范围是[2ln 2−12，+∞）， 故选：A ．7．（2021春•泰安期末）四边形ABCD 中，AB ＝BC ，AD ⊥DC ，AC ＝2，∠ACD ＝θ，若DB →⋅AC →=13，则cos2θ等于（ ）A ．23B ．13C ．12D ．16【解析】解：如图所示，取AC 的中点O ，连接OD ，OB ， ∵AB ＝BC ，OA ＝OC ， ∴OB ⊥AC ， ∴OB →•AC →=0；又∵DB →⋅AC →=13，DB →=DO →+OB →，DO →=12（DA →+DC →），∴（DO →+OB →）•AC →=DO →•AC →+OB →•AC →=12（DA →+DC →）•AC → =12（DA →+DC →）•（DC −DA →） =−12DA →2+12DC →2=13①，又AD ⊥DC ，∴DA →2+DC →2=AC →2=4②， 由①②解得DC →2=73， ∴|DC →|=√73，∴cos θ=|DC →||AC →|=√732； ∴cos2θ＝2cos 2θ﹣1＝2×712−1=16． 故选：D ．8．（2021•郑州一模）已知函数f(x)={e x −a ，x ≤02x −a ，x ＞0(a ∈R)，若函数f （x ）在R 上有两个零点，则实数a 的取值范围是（ ） A ．（0，1]B ．[1，+∞）C ．（0，1）D ．（﹣∞，1]【解析】解：当x ≤0时，f （x ）单调递增，∴f （x ）≤f （0）＝1﹣a ， 当x ＞0时，f （x ）单调递增，且f （x ）＞﹣a ． ∵f （x ）在R 上有两个零点， ∴{1−a ≥0−a ＜0，解得0＜a ≤1． 故选：A ．9．（2021春•河南月考）已知三棱柱ABC ﹣DEF ，DA ，DE ，DF 两两互相垂直，且DA ＝DE ＝DF ，M ，N 分别是BE ，AB 边的中点，P 是线段CA 上任意一点，过三点P ，M ，N 的平面与三棱柱ABC ﹣DEF 的截面有以下几种可能：①三角形；②四边形；③五边形；④六边形．其中所有可能的编号是（ ）A ．①②B ．③④C ．①②③D ．②③④【解析】解：以点D 为原点，DA 为x 轴，DE 为y 轴，DF 为z 轴，延长MN 分别交x 轴，y 轴于点N '，M '．连接N 'P 交z 轴于点P '，则过P ，M ，N 三点的平面与过点N '，M '，P '的平面相同， 当点P 与点A 重合时，截面为四边形； 当0＜P A ＜12AC 时，截面为五边形；当12AC ≤P A ＜AC 时，截面为四边形；当点P 与点C 重合时，截面为三角形；而该三棱柱只有五个面，截面与每个面相交最多产生五条交线，故截面形状最多为五边形，即不可能为六边形． 故选：C ．10．（2020秋•沙坪坝区校级期末）已知函数f(x)={|log 2x|0＜x ＜2sin(π4x)2≤x ≤10，若存在实数x 1，x 2，x 3，x 4使得f （x 1）＝f （x 2）＝f （x 3）＝f （x 4）且x 1＜x 2＜x 3＜x 4，则(x 3−1)(x 4−1)x 1x 2+2x 4−5x 3的取值范围是（ ） A ．（14，17）B ．（14，19）C ．（17，19）D ．(17，774]【解析】解：作出函数f （x ）的图象如图所示：因为存在实数x 1，x 2，x 3，x 4，满足x 1＜x 2＜x 3＜x 4， 且f （x 1）＝f （x 2）＝f （x 3）＝f （x 4）， ∴12＜x 1＜1，1＜x 2＜2，2＜x 3＜4，8＜x 4＜10，∵﹣log 2x 1＝log 2x 2，∴log 21x 1=log 2x 2，∴x 1x 2＝1，∵y ＝sinπx 4关于直线x ＝6对称，∴x 3+x 4＝12，∴(x 3−1)(x 4−1)x 1x 2+2x 4−5x 3=（x 3﹣1）（x 4﹣1）+2x 4﹣5x 3＝x 3x 4﹣6x 3+x 4+1＝﹣x 32+5x 3+13＝﹣（x 3−52）2+774， 令g （x 3）＝﹣（x 3−52）2+774，则g （x 3）在（2，52）是增函数，在（52，4）递减， ∵g （2）＝19，g （4）＝17，g （52）=774，∴17＜g （x 3）≤774． 故选：D ．11．（2020秋•渝中区校级月考）直线l 1：3x ﹣4y +13＝0，l 2：3x ﹣4y +23＝0，圆M ：（x ﹣a ）2+（y ﹣b ）2＝r 2与直线l 1和l 2都相切，AB 是圆M 的一条直径，N （﹣1，0），则NA →⋅NB →的最小值为（ ） A ．6B ．7C ．8D ．9【解析】解：直线l 1：3x ﹣4y +13＝0，l 2：3x ﹣4y +23＝0，则l 1和l 2平行， 又圆M ：（x ﹣a ）2+（y ﹣b ）2＝r 2与直线l 1和l 2都相切， ∴圆心在直线l ：3x ﹣4y +18＝0上，点N （﹣1，0）到直线l 的距离d min ＝3，且AB 是圆M 的一条直径， 则NA →⋅NB →=(NM →+MA →)⋅(NM →+MB →)=(NM →−12AB →)⋅(NM →+12AB →)=|NM →|2−14|AB →|2，∵直线l 1和l 2的距离为22=2，∴|AB →|=2，∴NA →⋅NB →=|NM →|2−1， 又|NM →|min =|−3+18|5=3， ∴NA →⋅NB →的最小值为8， 故选：C ．12．（2020秋•河南月考）已知函数f （x ）为定义在R 上且图像连续的偶函数，满足xf '（x ）＞0（或xf '（x ）＜0）在（﹣∞，0）∪（0，+∞）恒成立．若把函数y ＝f （x ）向右平移4个单位可得函数y ＝g （x ），则方程g(x)=g(2−1x+1)的所有根之和为（ ） A ．4B ．6C ．10D ．12【解析】解：函数f （x ）为定义在R 上且图像连续的偶函数，满足xf '（x ）＞0（或xf '（x ）＜0）在（﹣∞，0）∪（0，+∞）恒成立， 可得f （x ）在（﹣∞，0）、（0，+∞）都单调，由题意可得g （x ）的图像关于直线x ＝4对称，且在（﹣∞，4），（0，+∞）内都单调， 若g(x)=g(2−1x+1)，可得x ＝2−1x+1或8﹣x ＝2−1x+1， 由x ＝2−1x+1即x 2﹣x ﹣1＝0，有两个实根，其和为1； 由8﹣x ＝2−1x+1即x 2﹣5x ﹣7＝0，有两个实根，其和为5． 所以方程g(x)=g(2−1x+1)的所有根之和为1+5＝6． 故选：B ．13．（2020秋•河南月考）已知函数f （x ）=3x−13x +1+x |x |+2，且f （﹣a ）+f （2a ﹣3）＞4，则实数a 的取值范围是（ ） A ．（1，+∞）B ．（32，+∞）C ．（3，+∞）D ．（4，+∞）【解析】解：因为f （x ）=3x−1x +x |x |+2＝3−2x +x |x |，所以f （﹣x ）+f （x ）＝3−23−x+1−x |﹣x |+3−23x +1+x |x |， ＝6−2⋅3x1+3x −23x+1＝6﹣2＝4，因为f （﹣a ）+f （2a ﹣3）＞4＝f （a ）+f （﹣a ）， 所以f （2a ﹣3）＞f （a ），又f （x ）=3x−13x +1+x |x |+2＝3−23x +1+x |x |在R 上单调递增，所以2a ﹣3＞a ， 解得a ＞3． 故选：C ．14．（2020•新课标Ⅱ）设函数f （x ）的定义域为R ，满足f （x +1）＝2f （x ），且当x ∈（0，1]时，f （x ）＝x （x ﹣1）．若对任意x ∈（﹣∞，m ]，都有f （x ）≥−89，则m 的取值范围是（ ） A ．（﹣∞，94]B ．（﹣∞，73]C ．（﹣∞，52]D ．（﹣∞，83]【解析】解：因为f （x +1）＝2f （x ），∴f （x ）＝2f （x ﹣1），∵x ∈（0，1]时，f （x ）＝x （x ﹣1）∈[−14，0]，∴x ∈（1，2]时，x ﹣1∈（0，1]，f （x ）＝2f （x ﹣1）＝2（x ﹣1）（x ﹣2）∈[−12，0]； ∴x ∈（2，3]时，x ﹣1∈（1，2]，f （x ）＝2f （x ﹣1）＝4（x ﹣2）（x ﹣3）∈[﹣1，0]， 当x ∈（2，3]时，由4（x ﹣2）（x ﹣3）=−89解得x =73或x =83， 若对任意x ∈（﹣∞，m ]，都有f （x ）≥−89，则m ≤73．故选：B ．15．（2020秋•吴忠月考）已知圆O ：x 2+y 2＝r 2（r ＞0）与x 轴的交点为A 、B ，以A 、B 为左、右焦点的双曲线C ：x 2a 2−y 2b 2=1（a ＞0，b ＞0）的右支与圆O 交于P ，Q 两点，若直线PQ 与x 轴的交点恰为线段AB 的一个四等分点，则双曲线的离心率等于（ ） A ．√3+1B ．2√3−1C ．√3+12D ．2√3−12【解析】解：由题意可知PQ 为OB 的中垂线， 因为点A ，B 坐标为（﹣r ，0），（r ，0）， 所以PQ 方程为x =r 2，与x 2+y 2＝r 2联立， 可取P(r2，√3r2)，Q(r 2，−√3r2)，所以双曲线的焦距2c ＝2r ，即c ＝r ，因为|PA|=(r 2+r)2+(3r2)2=√3r ，|PB|=(r 2−r)2+(3r2)2=r ，由双曲线定义可得2a =|PA|−|PB|=(√3−1)r ，a =(√3−1)r2， 所以双曲线的离心率e =c a =√3−12r=√3+1． 故选：A ．16．（2020秋•吉林月考）已知双曲线C ：x 29−y 27=1的左焦点为F ，过原点的直线l 与双曲线C 的左、右两支分别交于A ，B 两点，则1|FA|−4|FB|的取值范围是（ ）A ．[−16，37)B ．[−16，37]C ．[−16，0)D ．[−16，+∞)【解析】解：设|AF |＝m ，|BF |＝n ，由双曲线的右焦点为F ′，连接BF ′，AF ′， 由对称性可得四边形AFBF ′为平行是变形， 则|BF ′|＝|AF |＝m ， 所以n ﹣m ＝2a ＝6，所以n ＝m +6，且m ≥c ﹣a ＝1， 则1|FA|−4|FB|=1m −4m+6，设f （m ）=1m −4m+6，m ≥1， 所以f ′（m ）=−1m 2+4(m+6)2=3m 2−12m−36m 2(m+6)2=3(m+2)(m−6)m 2(m+6)2，所以当1＜m ＜6时，f ′（m ）＜0，f （m ）单调递减， 当m ＞6时，f ′（m ）＞0，f （m ）单调递增， 当m →+∞时，f （m ）→0， 所以f （m ）min ＝f （6）=16−46+6=−16， f （1）＝1−47=37， 所以f （m ）∈[−16，37]，故选：B ．17．（2020秋•安徽月考）函数f （x ）={x 2−2ax +a 2，x ＜3ax −1116，x ≥3，数列{a n }满足a n ＝f （n ），n ∈N *，且为递增数列．则实数a 的取值范围是（ ） A ．（0，1）B ．（34，32）C ．[34，1）D ．[54，32）【解析】解：x ＜3时，f （x ）＝x 2﹣2ax +a 2，数列{a n }满足a n ＝f （n ），n ∈N *，且为递增数列．所以a 1＝1﹣2a +a 2＜a 2＝4﹣4a +a 2，解得a ＜32，可得：{0＜a ＜3222−2a ⋅2+a 2＜3a −1116，解得34＜a ＜32．故选：B ．18．（2020秋•安徽月考）已知函数f （x ）＝e 2x +（a ﹣2）e x ﹣x 有两个零点，则实数a 取值范围是（ ） A ．（0，1）B ．（1，+∞）C ．（﹣∞，1）D ．（﹣∞，﹣1）【解析】解：令f （x ）＝0，则a ＝﹣e x +xe ﹣x +2，令g （x ）＝﹣e x +xe ﹣x +2，则g ′(x)=−e x +(1−x)e −x =1−x−e 2xe x， 令h （x ）＝1﹣x ﹣e 2x ，易知函数h （x ）单调递减，又h （0）＝0，故当x ∈（﹣∞，0）时，h （x ）＞0，则g ′（x ）＞0，g （x ）单调递增， 当x ∈（0，+∞）时，h （x ）＜0，则g ′（x ）＜0，g （x ）单调递减， ∴g （x ）max ＝g （0）＝1，又当x →﹣∞时，g （x ）→﹣∞，当x →+∞时，g （x ）→﹣∞， ∴a ＜1． 故选：C ．19．（2020秋•北碚区校级月考）已知函数f （x ）＝lnx ﹣ax ，若不等式f （x +1）＞x ﹣ae x 在x ∈（0，+∞）上恒成立，则实数a 的取值范围为（ ） A ．（﹣∞，1]B ．[1，+∞）C ．（﹣∞，0]D ．[0，1]【解析】解：f （e x ）＝x ﹣ae x ，所以f （x +1）≥x ﹣ae x 在（0，+∞）上恒成立， 等价于f （x +1）≥f （e x ）在（0，+∞）上恒成立， 令g （x ）＝x +1﹣e x ，x ＞0，g ′（x ）＝1﹣e x ，当x ＞0时，g ′（x ）＜0，所以g （x ）单调递减， 所以g （x ）＜g （0）＝0，所以1＜x +1＜e x ， 所以只需f （x ）在（1，+∞）上单调递减， 即x ＞1，f ′（x ）≤0恒成立， 即x ＞1时，1x −a ≤0恒成立，即a ≥1x，因为(1x)max =1，所以a ≥1，即实数a 的取值范围是[1，+∞）． 故选：B ．二．多选题（共13小题）20．（2020秋•临沂期末）如图，一个结晶体的形状为平行六面体ABCD ﹣A 1B 1C 1D 1，其中，以顶点A 为端点的三条棱长都相等，且它们彼此的夹角都是60°，下列说法中正确的是（ ）A ．(AA 1→+AB →+AD →)2=2(AC →)2B ．AC 1→⋅(AB →−AD →)=0 C ．向量B 1C →与AA 1→的夹角是60° D ．BD 1与AC 所成角的余弦值为√63【解析】解：因为以A 为端点的三条棱长都相等，且彼此的夹角为60°，不妨设棱长为a ，对于A ，（AA 1→+AB →+AD →）2=AC 1→2＝3a 2+3×2a 2×12=6a 2， 因为AC →2＝（AB →+AD →）2＝2a 2+2a 2×12=3a 2，则2（AC →）2＝6a 2，所以（AA 1→+AB →+AD →）2＝2AC 1→2，故A 正确；对于B ，因为AC 1→⋅(AB →−AD →)=（AA 1→+AB →+AD →）（AB →−AD →）=AA 1→⋅AB →−AA 1→⋅AD →+AB →2−AB →⋅AD →+AD →⋅AB →−AD →2＝0，故B 正确；对于C ，因为B 1C →=A 1D →，显然△AA 1D 为等边三角形，则∠AA 1D ＝60°， 所以向量A 1D →与AA 1→的夹角为120°，向量B 1C →与AA 1→的夹角为120°，故C 不正确； 对于D ，因为BD 1→=AD →+AA 1→−AB →，AC →=AB →+AD →，则|BD 1→|=√(AD →+AA 1→−AB →)2=√2a ，|AC →|=√(AB →+AD →)2=√3a ， 所以BD 1→⋅AC →=（AD →+AA 1→−AB →）（AB →+AD →）＝a 2， 所以cos ＜BD 1→，AC →＞=BD 1→⋅AC →|BD 1→||AC →|=a 22a×3a=√66，故D 不正确．故选：AB ．21．（2021春•扬中市校级月考）已知函数y ＝f （x ）在R 上可导且f （0）＝1，其导函数f ′（x ）满足（x +1）[f ′（x ）﹣f （x ）]＞0，对于函数g （x ）=f(x)e x ，下列结论正确的是（ ） A ．函数g （x ） 在（﹣∞，﹣1）上为增函数 B ．x ＝﹣1是函数g （x ）的极小值点 C ．函数 g （x ）必有2 个零点D ．e 2f （e ）＞e e f （2） 【解析】解：g ′（x ）=f′(x)−f(x)e x，∵（x +1）[f ′（x ）﹣f （x ）]＞0，∴当x ＜﹣1时，f ′（x ）﹣f （x ）＜0，当x ＞﹣1时，f ′（x ）﹣f （x ）＞0， ∴当x ＜﹣1时，g ′（x ）＜0，当x ＞﹣1时，g ′（x ）＞0，∴g （x ）在（﹣∞，﹣1）上单调递减，在（1，+∞）上单调递增，故A 错误； x ＝﹣1是g （x ）的极小值点，故B 正确；g （x ）的极小值为g （﹣1）＝ef （﹣1），故当g （﹣1）＞0时，g （x ）没有零点，故C 错误；由g （x ）在（﹣1，+∞）上单调递增可得g （2）＜g （e ），即f(2)e ＜f(e)e ，∴e e f （2）＜e 2f （e ），故D 正确． 故选：BD ．22．（2020秋•城厢区校级期中）已知抛物线x 2＝4y 的焦点为F ，A （x 1，y 1），B （x 2，y 2）是抛物线上两点，则下列结论正确的是（ ） A ．点F 的坐标为（1，0）B ．若A ，F ，B 三点共线，则OA →⋅OB →=−3C ．若直线OA 与OB 的斜率之积为−14，则直线AB 过点FD ．若|AB |＝6，则AB 的中点到x 轴距离的最小值为2【解析】解：抛物线x 2＝4y 中的p ＝2，则焦点F 坐标为（0，1），故A 错误， 设直线AB 的方程为y ＝kx +1，联立方程可得{x 2=4y y =kx +1，消y 可得x 2﹣4kx ﹣4＝0，∴x 1+x 2＝4k ，x 1x 2＝﹣4， ∴y 1y 2＝k 2x 1x 2+k （x 1+x 2）+1＝1，∴OA →•OB →=x 1x 2+y 1y 2＝﹣4+1＝﹣3，故B 正确， 设直线AB 的方程为y ＝kx +m ，联立方程可得{x 2=4yy =kx +m ，消y 可得x 2﹣4kx ﹣4m ＝0，∴x 1+x 2＝4k ，x 1x 2＝﹣4m ，∴y 1y 2＝k 2x 1x 2+k （x 1+x 2）+m 2＝﹣4k 2m +4mk 2+m 2＝m 2， ∵直线OA 与OB 的斜率之积为−14，∴y1x1•y2x2=−14，即m2−4m =−14，解得m＝1，∴直线AB的方程为y＝kx+1，即直线过点F；故C正确，∵|AB|=√1+k2•√(x1+x2)2−4x1x2=√1+k2•√16k2+16m=6，∴4（1+k2）（k2+m）＝9，∴m=94(1+k2)−k2，∵y1+y2＝k（x1+x2）+2m＝4k2+2m，∴AB的中点到x轴距离d＝2k2+m＝2k2+94(1+k2)−k2＝k2+94(1+k2)=k2+1+94(1+k2)−1≥2√(k2+1)⋅94(1+k2)−1＝3﹣1＝2，当且仅当k2=12时取等号，故AB的中点到x轴距离的最小值为2，故D正确．综上所述：结论正确的是BCD．故选：BCD．23．（2020秋•潍坊月考）已知函数f(x)=|x|e|x|+1，g(x)={f(x)，x≤0x2−2x+a，x＞0，且g（1）＝0，则关于x的方程g（g（x）﹣t）﹣1＝0实根个数的判断正确的是（）A．当t＜﹣2时，方程g（g（x）﹣t）﹣1＝0没有相异实根B．当−1+1e＜t＜0或t＝﹣2时，方程g（g（x）﹣t）﹣1＝0有1个相异实根C．当1＜t＜1+1e时，方程g（g（x）﹣t）﹣1＝0有2个相异实根D．当﹣1＜t＜−1+1e或0＜t≤1或t=1+1e时，方程g（g（x）﹣t）﹣1＝0有4个相异实根【解析】解：当x≤0时，f(x)=|x|e|x|+1=−xe−x+1=−xe x+1，因为g（1）＝0，所以1﹣2+a＝0，所以a＝1，所以g(x)={−xe x +1，x ≤0x 2−2x +1，x ＞0，图象如图所示：当x ≤0时，﹣x ≥0，e x ＞0，则﹣xe x +1≥1，当且仅当x ＝0时等号成立，g （x ）在（﹣∞，﹣1）上是增加的，在（﹣1，0）上是减少的； 当x ＞0时，f （x ）在（0，1）上是减少的，在（1，+∞）上是增加的， 故g （x ）≥g （﹣1）＝0恒成立．故g （x ）在（﹣∞，﹣1）上是增加的，在（﹣1，1）上是减少的，在（1，+∞）上是增加的．令m ＝g （x ）﹣t ，则g （m ）﹣1＝0， 解得：m ＝0或m ＝2， 当m ＝0即g （x ）﹣t ＝0时， g （x ）＝t ，当t ＜﹣2时，g （x ）＜﹣2，无解， 当m ＝2即g （x ）﹣t ＝2时， g （x ）＝2+t ，当t ＜﹣2时，g （x ）＜0，无解，故方程g （g （x ）﹣t ）﹣1＝0没有相异实根， 故A 正确；当t ＝﹣2时，由A 可知：g （x ）＝0，解得x ＝1， 当−1+1e ＜t ＜0时，2+t ∈(1+1e ，2)，由上可知f （x ）在x ＝﹣1时取得极大值为g （﹣1）=1+1e ， 结合图象可知，此时y ＝2+t 与g （x ）有且仅有一个交点， 故B 正确；当1＜t ＜1+1e 时，g （x ）＝t 或g （x ）＝2+t ， 若g （x ）＝t ，结合图象可知g （x ）与y ＝t 有三个不同的交点，若g（x）＝2+t，2+t∈(3，3+1e )，此时g（x）与y＝t有一个交点，故方程g（g（x）﹣t）﹣1＝0有4个相异实根，故C错误；当﹣1＜t＜−1+1e时，g（x）＝2+t∈(1，1+1e)，由C可知此时有三个不等实根，当0＜t≤1时，g（x）＝t或g（x）＝2+t，当g（x）＝t时，由图可知有两个不等实根，当g（x）＝2+t时，由图可知有一个实根，当t=1+1e时，g（x）＝t或g（x）＝2+t，当g（x）＝t时，由图可知有两个不等实根，当g（x）＝2+t时，由图可知有一个实根，故此时方程g（g（x）﹣t）﹣1＝0共有9个不等实根，故D错误．故选：AB．24．（2021•2月份模拟）如图，正方体ABCD﹣A1B1C1D1的棱长为a，线段B1D1上有两个动点E，F，且EF=√22a，以下结论正确的有（）A．AC⊥BEB．点A到△BEF的距离为定值C．三棱锥A﹣BEF的体积是正方体ABCD﹣A1B1C1D1体积的112D．异面直线AE，BF所成的角为定值【解析】解：对于A，根据题意，AC⊥BD，AC⊥DD1，AC⊥平面BDD1B1，所以AC⊥BE，所以A正确；对于B，A到平面BDD1B1的距离是定值，所以点A到△BEF的距离为定值，则B正确；对于C，三棱锥A﹣BEF的体积为V三棱锥A﹣BEF=13•12EF•AB•BB1•sin45°=13×12×√22a×a×√22a=112a3，三棱锥A﹣BEF的体积是正方体ABCD﹣A1B1C1D1体积的112，正确；对于D，异面直线AE，BF所成的角为定值，命题D错误；故选：ABC．25．（2021春•芗城区校级月考）已知函数f（x）＝sin（3x﹣φ）（−π2＜φ＜π2）的图象关于直线x =π4对称，则（ ） A ．函数y ＝f （x ）的图象向左平移π12个单位长度得到的图象关于原点对称B ．函数y ＝f （x ）在[0，π4]上单调递增C ．函数y ＝f （x ）在[0，2π]有且仅有3个极大值点D ．若|f （x 1）﹣f （x 2）|＝2，则|x 1﹣x 2|的最小值为2π3【解析】解：∵函数f （x ）＝sin （3x ﹣φ）（−π2＜φ＜π2）的图象关于直线x =π4对称， 则3×π4−φ＝k π+π2，k ∈Z ，∴φ=π4，函数f （x ）＝sin （3x −π4）． 函数y ＝f （x ）的图象向左平移π12个单位长度，得到y ＝sin （3x +3π12−π4）＝sin3x 的图象，显然所得图象关于原点对称，故A 正确；当x ∈[0，π4]，3x −π4∈[−π4，π2]，故函数y ＝f （x ）在[0，π4]上单调递增，故B 正确；当x ∈[0，2π]，3x −π4∈[−π4，23π4]，故当3x −π4=π2，5π2，9π2时，函数f （x ）取得最大值，故C 正确；若|f （x 1）﹣f （x 2）|＝2，则|x 1﹣x 2|的最小值为f （x ）的半个周期，即12×2π3=π3，故D错误， 故选：ABC ．26．（2020•威海一模）设函数f （x ）＝2cos2x ﹣2﹣cos2x，则（ ）A ．f （x ）在(0，π2)单调递增 B ．f （x ）的值域为[−32，32] C ．f （x ）的一个周期为πD ．f(x +π4)的图象关于点(π4，0)对称【解析】解：令t ＝cos2x ，t ∈[﹣1，1]，函数化为：f （x ）=2t −12t ，由复合函数的单调性可知，f （x ）在(0，π2)单调递减，不正确；函数的最大值为：2−12=32，最小值为：12−2=−32，所以f （x ）的值域为[−32，32]，正确；t ＝cos2x 的周期为：π，所以f （x ）的一个周期为π，正确；x =π4时，t ＝0，函数f （x ）＝0，所以函数f （x ）的图象关于点(π4，0)对称，不是f(x +π4)的图象关于点(π4，0)对称，所以D 不正确； 故选：BC ．27．（2020秋•顺德区月考）数学中有许多形状优美、寓意独特的几何体，“等腰四面体”就是其中之一，所谓等腰四面体，就是指三组对棱分别相等的四面体．关于“等腰四面体”，以下结论正确的是（ ）A ．“等腰四面体”每个顶点出发的三条棱一定可以构成三角形B ．“等腰四面体”的四个面均为全等的锐角三角形C ．三组对棱长度分别为5，6，7的“等腰四面体“的体积为2√95D ．三组对棱长度分别为a ，b ，c 的“等腰四面体“的外接球直径为√a 2+b 2+c 2 【解析】解：如图，将“等腰四面体”补成一个长方体，设此“等腰四面体”的对棱棱长分别为a ，b ，c ，与之对应的长方体的长宽高分别为x ，y ，z ，则{x 2+y 2=a 2y 2+z 2=b 2x 2+z 2=c 2，得x 2=a 2+c 2−b 22，y 2=a 2+b 2−c 22，z 2=b 2+c 2−a 22， 结合图形，容易判断出选项AB 都是正确的；对于C ，由a ＝5，b ＝6，c ＝7，得x =√19，y =√6，z =√30，因为“等腰四面体”的体积是对应长方体的体积减去四个小三棱锥的体积，所以“等腰四面体”的体积为xyz −4×13×12xyz =13xyz =2√95，故选项C 正确；对于D ，三组对棱长度分别为a ，b ，c 的“等腰四面体”的外接球直径为2R =√x 2+y 2+z 2≠√a 2+b 2+c 2，故选项D 错误． 故选：ABC ．28．（2020秋•湛江期中）已知a ＝log 3π，b ＝log π3，c =log π13，则（ ） A ．ab ＜a +b ＜b +cB ．ac ＜b +c ＜bcC ．ac ＜bc ＜b +cD ．b +c ＜ab ＜a +b【解析】解：∵0＜logπ3＜1＜log3π，∴0＜b＜1＜a，且c=logπ13＜0，∴ac＜bc＜0，b+c=logπ3+logπ13=0，∴ac＜bc＜b+c，即C正确，B错误；∵ab＝log3π•logπ3＝1，a+b＝log3π+logπ3＞1，∴b+c＜ab＜a+b，即D正确，A错误．故选：CD．29．（2020秋•琼山区校级期末）已知函数f（x）＝e x，g(x)=ln x2+12的图象与直线y＝m分别交于A、B两点，则（）A．|AB|的最小值为2+ln2B．∃m使得曲线f（x）在A处的切线平行于曲线g（x）在B处的切线C．函数f（x）﹣g（x）+m至少存在一个零点D．∃m使得曲线f（x）在点A处的切线也是曲线g（x）的切线【解析】解：令f（x）＝e x＝m，得x＝lnm，令g(x)=ln x2+12=m，得x=2e m−12，则点A（lnm，m）、B(2e m−12，m)，如下图所示：由图象可知，|AB|=2e m−12−lnm，其中m＞0，令ℎ(m)=2e m−12−lnm，则ℎ′(m)=2e m−12−1m，则函数y＝h'（m）单调递增，且ℎ′(12)=0，当0＜m＜12时，h'（m）＜0，当m＞12时，h'（m）＞0．∴函数ℎ(m)=2e m−12−lnm在(0，12)上单调递减，在(12，+∞)上单调递增，∴|AB|min=ℎ(12)=2−ln12=2+ln2，A选项正确；∵f（x）＝e x，g(x)=ln x2+12，则f'（x）＝e x，g′(x)=1x，曲线y＝f（x）在点A处的切线斜率为f'（lnm）＝m，曲线y＝g（x）在点B处的切线斜率为g′(2e m−12)=12e m−12，令f′(lnm)=g′(2e m−12)，即m=12e m−12，即2me m−12=1，则m=12满足方程2mem−12=1，∴∃m使得曲线y＝f（x）在A处的切线平行于曲线y＝g（x）在B处的切线，B选项正确；构造函数F(x)=f(x)−g(x)+m=e x−ln x2+m−12，可得F′(x)=e x−1x，函数F′(x)=e x−1x在（0，+∞）上为增函数，由于F′(1e)=√e−2＜0，F'（1）＝e﹣1＞0，则存在t∈(12，1)，使得F′(t)=et−1t=0，可得t＝﹣lnt，当0＜x＜t时，F'（x）＜0；当x＞t时，F'（x）＞0．∴F(x)min=F(t)=e t−ln t2+m−12=e t−lnt+m+ln2−12=1t+t+m+ln2−12＞2√t⋅1t+m+ln2−12=32+ln2+m＞0，∴函数F（x）＝f（x）﹣g（x）+m没有零点，C选项错误；设曲线y＝f（x）在点A处的切线与曲线y＝g（x）相切于点C（n，g（n）），则曲线y＝f（x）在点A处的切线方程为y﹣m＝e lnm（x﹣lnm），即y＝mx+m（1﹣lnm），同理可得曲线y＝g（x）在点C处的切线方程为y=1nx+ln n2−12，∴{m=1nm(1−lnm)=ln n2−12，消去n得m−(m−1)lnm+ln2+12=0，令G(x)=x−(x−1)lnx+ln2+12，则G′(x)=1−x−1x−lnx=1x−lnx，函数y＝G'（x）在（0，+∞）上为减函数，∵G'（1）＝1＞0，G′(2)=12−ln2＜0，则存在s∈（1，2），使得G′(s)=1s−lns=0，且s=e1s．当0＜x＜s时，G′（x）＞0，当x＞s时，G′（x）＜0．∴函数y＝G（x）在（2，+∞）上为减函数，∵G(2)=52＞0，G(8)=172−20ln2＜0，由零点存定理知，函数y＝G（x）在（2，+∞）上有零点，即方程m −(m −1)lnm +ln2+12=0有解． ∴∃m 使得曲线y ＝f （x ）在点A 处的切线也是曲线y ＝g （x ）的切线． 故选：ABD ．30．（2020秋•渝中区校级月考）在三棱锥A ﹣BCD 中，△ABC ，△BCD 都是边长为2√3的正三角形，AD ＝a （0＜a ＜6），M 是棱AC 的中点，则在a 的变化过程中，下列说法正确的是（ ）A ．直线AD 与直线BC 所成的角都为π2B ．当a =2√3时，三棱锥A ﹣BCD 的体积取得最大值C ．当a =3√3时，三棱锥A ﹣BCD 的外接球的表面积为28π D ．存在某个实数a ，使得∠MBD ＝90°【解析】解：对于A ：取BC 的中点E ，如图1所示：图（1）则AE ⊥BC ，DE ⊥BC ，则BC ⊥平面ADE ，故AD ⊥BC ， 故选项A 正确；对于B ：因为棱长为2√3，则AE ＝DE ＝3，故当AE ⊥平面BCD 时，三棱锥的A ﹣BCD 的体积取得最大值，则a =3√2，故B 错误； 对于C ：当a =3√3时，∠AED ＝120°，分别取平面ABC 和平面BCD 的外心O 1，O 2， 如图2所示：图（2），可求得|O 1E |＝|O 2E |＝1，|O 2B |＝|O 2C |＝|O 2D |＝2，过|O 2D|2+|OO 2|2=7分别作平面ABC 和平面BCD 的垂线交点为O ，则平面图如图2， 因为∠AED ＝120°，则∠O 1EO 2＝120°，则∠OEO 2＝60°，则|OO2|=√3，则外接球半径R2=|O2D|2+|OO2|2=7，故球的表面积为4πR2＝28π，故C正确；对于D：如图3所示：图（3），当A∈平面BCD时，A与G点重合，故A在平面BCD的投影为GD，因为M是棱AC的中点，故M在平面BCD的投影为M1M2，其中M1，M2分别是GC，CD的中点，因为∠MBD＝90°，则∠M'BD＝90°，其中M'在M1M2上，则M'与M1重合，此时a＝6，故不成立，则D错误；综上所述，故选：AC．31．（2020秋•渝中区校级月考）函数f（x）＝lnx+1，g（x）＝e x﹣1，下列说法正确的是（）（参考数据：e2≈7.39，e3≈20.09，ln2≈0.69，ln3≈1.10）A．存在实数m，使得直线y＝x+m与y＝f（x）相切也与y＝g（x）相切B．存在实数k，使得直线y＝kx﹣1与y＝f（x）相切也与y＝g（x）相切C．函数g（x）﹣f（x）在区间(23，+∞)上不单调D．当x∈（0，1）时，g(x)−f(x)＞16恒成立【解析】解：对于选项A，B是考查公切线问题，设直线l分别与y＝f（x）与y＝g（x）分别相切于点P（x1，y1），Q（x2，y2），则y1=f(x1)=lnx1+1，y2=g(x2)=e x2−1，且f′(x)=1x，g′(x)=ex，故1x1=e x2，且lnx1+1−e x2+1x1−x2=e x2，−x2−e x2+21e x2−x2=e x2，化简得(e x2−1)(x2−1)=0，故x2＝0或x2＝1，故公切线y＝kx+b的斜率为k＝1或ℎ′(23)＞0，对应的截距分别是b＝0或b＝﹣1，故公切线为y＝x或y＝ex﹣1，故选项A，B都正确；对于选项C，D：是考查g（x）﹣f（x）的问题，令h（x）＝g（x）﹣f（x）＝e x﹣lnx﹣2，则ℎ′(x)=e x−1x，ℎ″(x)=ex+1x2，故x＞0时，ℎ″(x)=e x+12＞0，ℎ′(x)=e x−1x在（0，+∞）上单调递增，又ℎ′(23)=e23−32，e2−278=7.39−278＞0，则ℎ′(23)＞0，故x∈(23，+∞)时，h'（x）＞0，故函数g（x）﹣f（x）在区间(23，+∞)上单调递增，故选项C错误；又ℎ′(12)=√e−2＜0，ℎ′(23)＞0，故存在x0∈(12，23)，使得h'（x0）＝0，即e x0−1x=0，lnx0＝﹣x0，且x∈(12，x0)时，h'（x）＜0，x∈（x0，1）时，h'（x）＞0，故h（x）在x∈(12，x0)上单调递减，在x∈(x0，23)上单调递增，则h（x）≥h（x0），ℎ(x0)=e x0−lnx0−2=1x0+x0−2＞32+23−2=16，故选项D正确．故选：ABD．32．（2020秋•霞山区校级月考）已知定义在R上的奇函数f（x）满足以下条件：①f（2﹣x）＝f（2+x），②f（x）在区间（0，2]内单调递增，③f（1）＝0，则以下判断正确的是（）A．f（x）是周期函数，最小正周期是8B．f（x）的图象关于直线x＝2对称C．f（x）在区间（﹣5，5）上有9个零点D．当x∈（﹣3，﹣1）时，f（x）＞0【解析】解：由f（2﹣x）＝f（2+x）得函数关于x＝2对称，故B正确，∵f（x）是奇函数，∴f（2﹣x）＝f（2+x）＝﹣f（x﹣2），即f（x+4）＝﹣f（x），则f（x+8）＝﹣f（x+4）＝f（x），即函数是周期函数，最小正周期为8，故A正确，∵f（x）在区间（0，2]内单调递增，∴f（x）在区间[﹣2，0）内单调递增，∵f（1）＝0，∴f（﹣1）＝﹣f（1）＝0，f（3）＝f（1）＝0，f（﹣3）＝f（3）＝0，f （4）＝f（0）＝0，f（﹣4）＝0，即f（x）在区间（﹣5，5）上有7个零点，故C正确，当x∈（﹣3，﹣1）时，f（x）＜0，故D错误，故选：AB．三．填空题（共18小题）33．（2021•天津）设a+b＝2，b＞0，则当a＝﹣2时，12|a|+|a|b取得最小值．【解析】解：法一：∵a+b＝2，b＞0，∴12|a|+|a|b=12|a|+|a|2−a，（a＜2）设f（a）=12|a|+|a|2−a，（a＜2），画出此函数的图象，如图所示．利用导数研究其单调性得，当a＜0时，f（a）=−12a+a a−2，f′（a）=12−2(a−2)2=−(3a−2)(a+2)2a2(a−2)2，当a＜﹣2时，f′（a）＜0，当﹣2＜a＜0时，f′（a）＞0，故函数在（﹣∞，﹣2）上是减函数，在（﹣2，0）上是增函数，∴当a＝﹣2时，12|a|+|a|b取得最小值34．同样地，当0＜a＜2时，得到当a=23时，12|a|+|a|b取得最小值54．综合，则当a＝﹣2时，12|a|+|a|b取得最小值．法二：因为a+b＝2，b＞0，要取得最小值，则a＜0，则12|a|+|a|b=a+b4|a|+|a|b=a4|a|+b4|a|+|a|b，≥a4|a|+2√b4|a|⋅|a|b=a4|a|+1=−14+1=34，当且仅当b4|a|=|a|b，a＜0时取等号，此时b＝﹣2a，因为a+b＝2，所以a＝﹣2，b＝4，故答案为：﹣2．34．（2021春•扬中市校级月考）红外线自动测温门能有效避免测温者与被测温者的近距离接触，降低潜在的病毒感染风险，为防控新冠肺炎，某厂生产的红外线自动测温门，其测量体温误差服从正态分布N（0.1，0.32），从已经生产出的测温门中随机取出一件，则其测量体温误差在区间（0.4，0.7）内的概率为13.59%．（附：若随机变量ξ服从正态分布N（μ，σ2），则P（μ﹣σ＜ξ＜μ+σ）＝68.27%，P（μ﹣2σ＜ξ＜μ+2σ）＝95.45%）【解析】解：由红外线自动测温门测量体温误差服从正态分布N（0.1，0.32），得μ＝0.1，σ＝0.3．∴测量体温误差在区间（0.4，0.7）内的概率为：P（0.4＜ξ＜0.7）＝P（μ+σ＜ξ＜μ+2σ）=12[P（μ﹣2σ＜ξ＜μ+2σ）﹣P（μ﹣σ＜ξ＜μ+σ）]＝13.59%．故答案为：13.59%．35．（2020秋•下城区校级月考）若存在两个正实数x ，y 使等式x +m （y ﹣x ）（lny ﹣lnx ）＝0成立，（其中e ＝2.71828…），则实数m 的取值范围是 （﹣∞，0） ． 【解析】解：方程变形为m =x(x−y)(lny−lnx)，所以1m=(x−y)(lny−lnx)x=(1−y x)⋅ln y x，设t =yx＞0 且t ≠1，设g （t ）＝（1﹣t ）lnt ， 那么g ′(t)=−lnt +(1−t)⋅1t =−lnt +1t −1， g ″(t)=−1t−1t 2=−t+1t 2＜0 恒成立， 所以g '（t ）是单调递减函数， 当t ＝1时，g '（1）＝0，当t ∈（0，1）时，g '（t ）＞0，函数单调递增， 当t ∈（1，+∞），g '（t ）＜0，函数单调递减， 所以g （t ）在t ＝1时，取得最大值，g （1）＝0， 即1m＜0，解得：m ＜0，故答案为：（﹣∞，0）．36．（2020秋•海曙区校级期中）在△OAB 中，已知|OB →|=√2，|AB →|=1，∠AOB ＝45°，点P 满足OP →=λOA →+μOB →，其中2λ+μ＝3，|OP →|的最小值为 3√55． ．【解析】解：∵|OB →|=√2，|AB →|=1，∠AOB ＝45°， ∴AB sin45°=OB sinA，即√22=√2sinA，则sin A ＝1，即A ＝90°， 即△OAB 为等腰直角三角形，则OA ⊥AB ， 则OB →=OA →+AB →，∵OP →=λOA →+μOB →，2λ+μ＝3，∴OP →=λOA →+μOB →=（λ+μ）OA →+μAB →=（λ+3﹣2λ）OA →+（3﹣2λ）AB →=（3﹣λ）OA →+（3﹣2λ）AB →．则|OP →|2＝（3﹣λ）2OA →2+（3﹣2λ）2AB →2＝（3﹣λ）2+（3﹣2λ）2＝5λ2﹣18λ+18＝5（λ−95）2+95，即当=95时，取得最小值95，此时|OP →|的最小值为√95=3√55，故答案为：3√55．37．（2020•拉萨二模）设函数f （x ）＝e x （2x ﹣1）﹣ax +a ，其中a ＜1，若存在唯一的整数x 0，使得f （x 0）＜0，则a 的取值范围是 [32e，1） ．【解析】解：函数f （x ）＝e x （2x ﹣1）﹣ax +a ，其中a ＜1， 设g （x ）＝e x （2x ﹣1），y ＝ax ﹣a ， ∵存在唯一的整数x 0，使得f （x 0）＜0，∴存在唯一的整数x 0，使得g （x 0）在直线y ＝ax ﹣a 的下方， ∵g ′（x ）＝e x （2x +1）， ∴当x ＜−12时，g ′（x ）＜0，∴当x =−12时，[g （x ）]min ＝g （−12）=−2e −12．当x ＝0时，g （0）＝﹣1，g （1）＝e ＞0，直线y ＝ax ﹣a 恒过（1，0），斜率为a ，故﹣a ＞g （0）＝﹣1， 且g （﹣1）＝﹣3e ﹣1≥﹣a ﹣a ，解得32e≤a ＜1．∴a 的取值范围是[32e，1）．故答案为：[32e，1）．38．（2020秋•福州期中）设S n是数列{a n}的前n项和，满足a n2+1＝2a n S n，且a n＞0，则S64＝8．【解析】解：由a n2+1＝2a n S n，可得（S n﹣S n﹣1）2+1＝2（S n﹣S n﹣1）S n（n≥2），整理可得，S n2﹣S n﹣12＝1，又当n＝1时，a12+1＝2a1S1，解得S12＝1，所以数列{S n2}是首项为1，公差为1的等差数列，则S n2＝n，由a n＞0，可得S n＞0，故S n=√n，所以S64=√64=8．故答案为：8．39．（2020秋•厦门期末）2020年是苏颂诞辰1000周年．苏颂发明的水运仪象台被誉为世界上最早的天文钟．水运仪象台的原动轮叫枢轮，是一个直径约3.4米的水轮，它转一圈需要30分钟．如图，当点P从枢轮最高处随枢轮开始转动时，退水壶内水面位于枢轮中心下方1.19米处．此时打开退水壶出水口，壶内水位以每分钟0.017米的速度下降，将枢轮转动视为匀速圆周运动，则点P至少经过12分钟（结果取整数）进入水中．（参考数据：cos π15≈0.98，cos2π15≈0.91，cosπ5≈0.81）【解析】解：设x分钟后P点转至A点，和水面重合，OP＝OA＝r＝1.7m，如图所示：，则x分钟后，OB＝1.19+0.017x，∴cos∠AOB=OBOA=1.19+0.017x1.7=0.7+0.01x，∵转一圈需要30分钟，∴每分钟转12°，当∠AOB＝24°时，x＝13，代入得：0.91≠0.7+0.01×13（舍去），当∠AOB＝36°时，x＝12，代入得：0.81≈0.7+0.01×12，可取，∴点P至少经过12分钟进入水中．故答案为：12．40．（2020•房山区二模）已知函数f（x）＝x|2x﹣a|﹣1．①当a＝0时，不等式f（x）+1＞0的解集为（0，+∞）；②若函数f（x）有三个不同的零点，则实数a的取值范围是（2√2，+∞）．【解析】解：①当a＝0时，不等式f（x）+1＞0⇔x|2x|﹣1+1＞0，即2x|x|＞0，若x＜0，得﹣2x2＞0，不合题意；若x＝0，得0＞0，不合题意；若x＞0，得2x2＞0，则x＞0．综上，当a＝0时，不等式f（x）+1＞0的解集为（0，+∞）；②若函数f（x）有三个不同的零点，即方程x|2x﹣a|﹣1＝0有3个不同根．即|2x﹣a|=1x有三个解，令y ＝|2x ﹣a |，则y =1x {2x −a ，x ≥a2a −2x ，x ＜a2，画出两个函数的图象，如图：x ＜a 2，y =1x ，由y ′=−1x 2=−2，解得x =√22，x =−√22（舍去）， 此时切点坐标（√22，√2），代入y ＝a ﹣2x ，可得a ＝2×√22+√2=2√2， 函数f （x ）＝x |2x ﹣a |﹣1有三个零点， 则实数a 的取值范围为（2√2，+∞）． 故答案为：（0，+∞）；（2√2，+∞）．41．（2020•和平区校级一模）已知平行四边形ABCD 的面积为9√3，∠BAD =2π3，|AD →|＝6，E 为线段BC 的中点，若F 为线段DE 上的一点，且AF →=λAB →+56AD →，则λ＝ 13；AF →⋅AE→的值为 9 ．【解析】解：根据题意，作出如下所示图形，∵E 为线段BC 的中点，∴AB →=AE →+EB →=AE →−12BC →=AE →−12AD →．∵AF →=λAB →+56AD →，且D 、E 、F 三点共线，∴AF →=λ（AE →−12AD →）+56AD →=λAE →+（56−λ2）AD →，∴λ+56−λ2=1，解得λ=13．∵平行四边形ABCD 的面积为9√3，∠BAD =2π3，|AD →|＝6，∴9√3=2×12|AB |•|AD |sin ∠BAD ＝|AB |×6sin2π3，解得|AB |＝3．∴AF →⋅AE →=（13AB →+56AD →）•（AB →+12AD →）=13AB →2+AB →⋅AD →+512AD →2=13×9+3×6×cos 2π3+512×36=9．故答案为：13；9．42．（2020秋•顺德区月考）已知直线l ：2x +y ﹣2＝0过抛物线C ：y 2＝mx 的焦点F ，且与y 轴交于点P ，M 是抛物线C 上一点，O 为坐标原点，FM 的中点Q 满足PQ →=λ（PM→|PM →|+PO→|PO →|），则∠PMF ＝ 90° ，点M 的坐标为 （1，2） ．【解析】解：令直线中y ＝0，可得x ＝1，由题意可得抛物线的焦点为（1，0），P （0，2）， 所以m 4=1，所以m ＝4，即抛物线的方程为：y 2＝4x ， 因为PQ →=λ（PM→|PM →|+PO →|PO →|），所以PQ 平分∠OPM ，作QN ⊥y 轴于N ，作MM 1⊥y 轴于M 1，交抛物线的准线于M 2， 则2|QN |＝|MM 1|+|OF |＝|MM 2|＝|MF |， 所以|QN |=12|MF |＝|QM |， 由PQ 平分∠OPM ，所以QM ⊥PM ，可得∠PMF ＝90°， 则M 在以线段PF 为直径的圆上，设M （x 0，y 0），则（x 0﹣1）2+（y 0﹣1）2=54，将x 0=y 024，代入 y 0（y 03+12y 0﹣32）＝0，且y 0≠0，所以y 03+12y 0﹣32＝0⇒（y 0﹣2）（y 02+2y 0+16）＝0， 解得：y 0＝2，可得x 0＝1， 所以M 的坐标（1，2）， 故答案为90°，（1，2）．。

⎨【方法点拨】专题 10 平凡恒等式 平凡恒等式 a + b = max {a + b , a - b }. 说明：1. 平凡恒等式即三角不等式 a - b ≤ a ± b ≤ a + b 的延拓，其证明只需对 a 、b的符号分类讨论即可.2. 遇到“双绝对值”问题使用平凡恒等式可实现“秒杀”.【典型题示例】例 1 函数 f (x ) = cos x + cos 2x 的最小值是 .【答案】 2思路一：换元+奇偶性+去绝对值f (x ) = cos x + cos 2x = cos x + 2 cos 2 x -1是偶函数设cos x = t (-1 ≤ t ≤ 1)⎧-2t 2 + t +1, 0 ≤ t < 则 y = t + 2t 2 -1 = ⎪ ⎪2t 2 - t -1, ⎩ 22 ≤ t ≤ 12（下略）.思路二：周期性+奇偶性+去绝对值f (x ) = cos x + cos 2x 是偶函数，且其最小正周期是π⎧2 cos 2 x + cos x -1, x ∈ ⎡ π⎤f (x ) = cos x + cos 2x ⎪ ⎣⎢0,4⎦⎥= ⎨ ⎛ π π⎤ （下略）.⎪-2 cos 2 x + cos x +1, x ∈ , ⎥ ⎪⎩ ⎝ 4 2 ⎦思路三：平凡恒等式y = max {cos x + cos 2x , cos x - cos 2x }设cos x = t (-1 ≤ t ≤ 1)则 y = max {2t 2 + t -1 , 2t 2 - t -1 }， t ∈[-1,1]由 2t 2 + t -1 = 2t 2 - t -1 得t = 2，此时取得最小值2 22⎪2 6 6 yy min= 2 .1【答案】22 2 【解析】| (a + b ) ⋅ e |≤| a ⋅ e | + | b ⋅ e |≤ ⇒| a + b |≤ ⇒| a | 最大值为 1 .2+ | b | +2a ⋅ b ≤ 6 ⇒ a ⋅ b ≤ ，即2【巩固训练】1. 函数 f (x ) = sin x + sin 3x 的最大值是 .2.在平面直角坐标系中，定义 d (P , Q ) = x 1 - x 2 + y 1 - y 2 为 P (x 1, y 1 ) ， Q (x 2 , y 2 ) 两点之间的“折线距离”，则椭圆上 x 2+ 22 = 1的一点 P 和直线 4x + 3y -12 = 0上的一点 Q 的“折 线距离”的最小值是 .16 61.【答案】 22.【答案】3 -4 3.【答案】 - 1 2 【答案或提示】【解析】| (a + b ) ⋅ e |≤| a ⋅ e | + | b ⋅ e |≤ ⇒| a + b |≤ ⇒| a |2 最大值为 1 .2+ | b |2 +2a ⋅ b ≤ 6 ⇒ a ⋅ b ≤ 1 ，即 2 41。

压轴题目冲破练——平面解析几何A 组 专项基础训练 (时刻：40分钟)一、选择题1.已知两条直线l 1：y ＝x ，l 2：ax －y ＝0，其中a 为实数，当这两条直线的夹角在⎝ ⎛⎭⎪⎫0，π12内变更时，a 的取值范围是( )A.(0,1)B.⎝ ⎛⎭⎪⎪⎫33，3 C.⎝ ⎛⎭⎪⎪⎫33，1∪(1，3)D.(1，3)答案 C解析 直线l 1的倾斜角为π4，依题意l 2的倾斜角的取值范围为⎝ ⎛⎭⎪⎫π4－π12，π4∪⎝ ⎛⎭⎪⎫π4，π4＋π12，即⎝ ⎛⎭⎪⎫π6，π4∪⎝ ⎛⎭⎪⎫π4，π3，从而l 2的斜率a 的取值范围为⎝ ⎛⎭⎪⎪⎫33，1∪(1，3). 2.假设圆(x －3)2＋(y ＋5)2＝r 2上有且只有两个点到直线4x －3y －2＝0的距离等于1，那么半径r 的取值范围是( )A.(4,6)B.[4,6)C.(4,6]D.[4,6]答案 A解析 因为圆心(3，－5)到直线4x －3y －2＝0的距离为|4×3－3×－5－2|42＋32＝5，因此当半径r ＝4时，圆上有1个点到直线4x －3y －2＝0的距离等于1，当半径r ＝6时，圆上有3个点到直线4x －3y －2＝0的距离等于1，因此圆上有且只有两个点到直线4x －3y －2＝0的距离等于1时，4<r <6. 3.已知双曲线x 2a 2－y 2b 2＝1 (a >0，b >0)与抛物线y 2＝8x 有一个公共的核心F ，且两曲线的一个交点为P ，假设|PF |＝5，那么双曲线的渐近线方程为( )A.y ＝±3xB.y ＝±33x C.y ＝±2x D.y ＝±22x答案 A解析 设点P (x 0，y 0).依题意得，核心F (2,0)，⎩⎪⎨⎪⎧x 0＋2＝5，y 20＝8x 0，于是有x 0＝3，y 20＝24； ⎩⎪⎨⎪⎧a 2＋b 2＝4，9a 2－24b2＝1，由此解得a 2＝1，b 2＝3，因此该双曲线的渐近线方程是y ＝±bax ＝±3x .4.已知抛物线y 2＝8x的核心F 到双曲线C ：y 2a2－x 2b2＝1(a >0，b >0)渐近线的距离为455，点P 是抛物线y 2＝8x上的一动点，P 到双曲线C 的上核心F 1(0，c )的距离与到直线x ＝－2的距离之和的最小值为3，那么该双曲线的方程为( )A.y 22－x 23＝1B.y 2－x 24＝1C.y 24－x 2＝1D.y 23－x 22＝1 答案 C解析 由题意得，抛物线y 2＝8x 的核心F (2,0)， 双曲线C ：y 2a2－x 2b 2＝1(a >0，b >0)的一条渐近线的方程为ax －by ＝0，∵抛物线y 2＝8x的核心F 到双曲线C ：y 2a2－x 2b 2＝1(a >0，b >0)渐近线的距离为455，∴2aa 2＋b 2＝455，∴a＝2b .∵P 到双曲线C 的上核心F 1(0，c )的距离与到直线x ＝－2的距离之和的最小值为3， ∴|FF 1|＝3，∴c 2＋4＝9，∴c ＝5，∵c 2＝a 2＋b 2，a ＝2b ，∴a ＝2，b ＝1. ∴双曲线的方程为y 24－x 2＝1，应选C.5.已知椭圆E 的左、右核心别离为F 1、F 2，过F 1且斜率为2的直线交椭圆E 于P 、Q 两点，假设△PF 1F 2为直角三角形，那么椭圆E 的离心率为( )A.53B.23C.23D.13答案 A解析 由题意可知，∠F 1PF 2是直角，且tan∠PF 1F 2＝2，∴|PF 2||PF 1|＝2，又|PF 1|＋|PF 2|＝2a ，∴|PF 1|＝2a 3，|PF 2|＝4a3.依照勾股定理得⎝ ⎛⎭⎪⎫2a 32＋⎝ ⎛⎭⎪⎫4a 32＝(2c )2，因此离心率e ＝ca ＝53.二、填空题 6.若是x 2k －2＋y 21－k＝－1表示核心在y 轴上的双曲线，那么它的半焦距c 的取值范围是________.答案 (1，＋∞)解析 将原方程化成标准方程为y 2k －1－x 2k －2＝1.由题意知k －1>0且k －2>0，解得k >2.又a 2＝k －1，b 2＝k －2，因此c 2＝a 2＋b 2＝2k －3>1， 因此c >1，故半焦距c 的取值范围是(1，＋∞).7.假设点(3,1)是抛物线y 2＝2px 一条弦的中点，且这条弦所在直线的斜率为2，那么p ＝________. 答案 2解析 设弦两头点为P 1(x 1，y 1)，P 2(x 2，y 2)，则⎩⎪⎨⎪⎧y 21＝2px 1y 22＝2px 2，两式相减得，y 1－y 2x 1－x 2＝2p y 1＋y 2＝2.又∵y 1＋y 2＝2，∴p ＝2.8.已知抛物线x 2＝4y 的核心为F ，通过F 的直线与抛物线相交于A ，B 两点，那么以AB 为直径的圆在x 轴上所截得的弦长的最小值是________. 答案 23解析 由抛物线概念得以AB 为直径的圆与抛物线的准线相切，利用直角三角形中勾股定理取得弦长的解析式，再求弦长的最小值.设以AB 为直径的圆的半径为r ，那么|AB |＝2r ≥4，r ≥2，且圆心到x 轴的距离是r －1，因此在x 轴上所截得的弦长为2r 2－r －12＝22r －1≥23，即弦长的最小值是2 3.三、解答题9.已知椭圆C 的中心为坐标原点O ，一个长轴极点为(0,2)，它的两个短轴极点和核心所组成的四边形为正方形，直线l 与y 轴交于点P (0，m )，与椭圆C 交于异于椭圆极点的两点A ，B ，且AP →＝2PB →. (1)求椭圆的方程； (2)求m 的取值范围.解 (1)由题意，知椭圆的核心在y 轴上， 设椭圆方程为y 2a2＋x 2b 2＝1(a >b >0)，由题意，知a ＝2，b ＝c ，又a 2＝b 2＋c 2，那么b ＝2，因此椭圆方程为y 24＋x 22＝1.(2)设A (x 1，y 1)，B (x 2，y 2)，由题意，知直线l 的斜率存在， 设其方程为y ＝kx ＋m ，与椭圆方程联立，即⎩⎪⎨⎪⎧y 2＋2x 2＝4，y ＝kx ＋m ，消去y ，得(2＋k 2)x 2＋2mkx ＋m 2－4＝0，Δ＝(2mk )2－4(2＋k 2)(m 2－4)>0，由根与系数的关系，知⎩⎪⎨⎪⎧x 1＋x 2＝－2mk2＋k 2，x 1·x 2＝m 2－42＋k 2，又AP →＝2PB →，即有(－x 1，m －y 1)＝2(x 2，y 2－m )， 因此－x 1＝2x 2.则⎩⎪⎨⎪⎧x 1＋x 2＝－x 2，x 1x 2＝－2x 22，因此m 2－42＋k 2＝－2⎝ ⎛⎭⎪⎫2mk 2＋k 22. 整理，得(9m 2－4)k 2＝8－2m 2，又9m 2－4＝0时等式不成立，因此k 2＝8－2m 29m 2－4>0，得49<m 2<4，现在Δ>0. 因此m 的取值范围为⎝ ⎛⎭⎪⎫－2，－23∪⎝ ⎛⎭⎪⎫23，2.10.已知中心在原点的椭圆C ：x 2a 2＋y 2b 2＝1的一个核心为F 1(0,3)，M (x,4)(x >0)为椭圆C 上一点，△MOF 1的面积为32. (1)求椭圆C 的方程；(2)是不是存在平行于OM 的直线l ，使得直线l 与椭圆C 相交于A ，B 两点，且以线段AB 为直径的圆恰好通过原点？假设存在，求出直线l 的方程；假设不存在，说明理由. 解 (1)因为椭圆C 的一个核心为F 1(0,3)， 因此c ＝3，b 2＝a 2＋9，那么椭圆C 的方程为x 2a 2＋y 2a 2＋9＝1，因为x >0，因此1OMF S ∆＝12×3×x ＝32，解得x ＝1.故点M 的坐标为(1,4).因为点M (1,4)在椭圆上，因此1a 2＋16a 2＋9＝1，得a 4－8a 2－9＝0，解得a 2＝9或a 2＝－1(不合题意，舍去)，则b 2＝9＋9＝18，因此椭圆C 的方程为x 29＋y 218＝1.(2)假设存在符合题意的直线l 与椭圆C 相交于A (x 1，y 1)，B (x 2，y 2)两点，其方程为y ＝4x ＋m (因为直线OM 的斜率k ＝4)，由⎩⎪⎨⎪⎧y ＝4x ＋m ，x 29＋y218＝1，消去y 化简，得18x 2＋8mx ＋m 2－18＝0.进而取得x 1＋x 2＝－8m 18，x 1·x 2＝m 2－1818.因为直线l 与椭圆C 相交于A ，B 两点， 因此Δ＝(8m )2－4×18×(m 2－18)>0， 化简得m 2<162，解得－92<m <92.因为以线段AB 为直径的圆恰好通过原点， 因此OA →·OB →＝0，因此x 1x 2＋y 1y 2＝0.又y 1y 2＝(4x 1＋m )(4x 2＋m )＝16x 1x 2＋4m (x 1＋x 2)＋m 2，x 1x 2＋y 1y 2＝17x 1x 2＋4m (x 1＋x 2)＋m 2＝17m 2－1818－32m 218＋m 2＝0.解得m ＝±102.由于±102∈(－92，92)，因此符合题意的直线l 存在，且所求的直线l 的方程为y ＝4x ＋102或y ＝4x －102.B 组 专项能力提升 (时刻：25分钟)1.由直线y ＝x ＋1上的一点向圆(x －3)2＋y 2＝1引切线，那么切线长的最小值为( ) A.1B.22C.7D.3答案 C 解析 如下图， 设直线上一点P ，切点为Q ，圆心为M ，那么|PQ |即为切线长，MQ 为圆M 的半径，长度为1，|PQ |＝|PM |2－|MQ |2＝|PM |2－1，要使|PQ |最小，即求|PM |的最小值，此题转化为求直线y ＝x ＋1上的点到圆心M 的最小距离， 设圆心到直线y ＝x ＋1的距离为d ，则d ＝|3－0＋1|12＋－12＝2 2.因此|PM |的最小值为2 2.因此|PQ |＝|PM |2－1≥222－1＝7.2.在抛物线y ＝x 2＋ax －5(a ≠0)上取横坐标为x 1＝－4，x 2＝2的两点，过这两点引一条割线，有平行于该割线的一条直线同时与抛物线和圆5x 2＋5y 2＝36相切，那么抛物线极点的坐标为 ( )A.(－2，－9)B.(0，－5)C.(2，－9)D.(1，－6)答案 A解析 当x 1＝－4时，y 1＝11－4a ；当x 2＝2时，y 2＝2a －1，因此割线的斜率k ＝11－4a －2a ＋1－4－2＝a －2.设直线与抛物线的切点横坐标为x 0，由y ′＝2x ＋a 得切线斜率为2x 0＋a ，∴2x 0＋a ＝a －2，∴x 0＝－1. ∴直线与抛物线的切点坐标为(－1，－a －4)，切线方程为y ＋a ＋4＝(a －2)(x ＋1)，即(a －2)x －y －6＝0. 圆5x 2＋5y 2＝36的圆心到切线的距离d ＝6a －22＋1.由题意得6a －22＋1＝65，即(a －2)2＋1＝5.又a ≠0，∴a ＝4，现在，y ＝x 2＋4x －5＝(x ＋2)2－9， 极点坐标为(－2，－9). 3.过椭圆x 2a 2＋y 2b 2＝1(a >b >0)的左极点A 且斜率为1的直线与椭圆的另一个交点为M ，与y 轴的交点为B ，假设|AM |＝|MB |，那么该椭圆的离心率为________. 答案63解析 由题意知A 点的坐标为(－a,0)， 设直线的方程为y ＝x ＋a ，∴B 点的坐标为(0，a )，故M 点的坐标为⎝ ⎛⎭⎪⎫－a 2，a 2，代入椭圆方程得a 2＝3b 2，∴2a 2＝3c 2，∴e ＝63.4.设抛物线y 2＝2x 的核心为F ，过F 的直线交该抛物线于A ，B 两点，那么|AF |＋4|BF |的最小值为________. 答案92解析 设A (x 1，y 1)，B (x 2，y 2)，那么由抛物线概念可得|AF |＋4|BF |＝x 1＋p2＋4⎝ ⎛⎭⎪⎫x 2＋p 2＝x 1＋12＋4⎝⎛⎭⎪⎫x 2＋12＝x 1＋4x 2＋52，设直线AB 的方程为ky ＝x －12，联立抛物线方程得方程组⎩⎪⎨⎪⎧ky ＝x －12，y 2＝2x消元整理得y 2－2ky－1＝0，由根与系数的关系可得y 1y 2＝－1，又A ，B 在抛物线上，代入方程得y 21y 22＝2x 1·2x 2＝4x 1x 2＝1，即x 1x 2＝14，因此依照大体不等式|AF |＋4|BF |＝x 1＋4x 2＋52≥2x 1×4x 2＋52＝2＋52＝92，当且仅当x 1＝4x 2时取得最小值92.5.已知抛物线Ω的极点是坐标原点O ，核心F 在y 轴正半轴上，过点F 的直线l 与抛物线交于M ，N 两点，且知足OM →·ON →＝－3. (1)求抛物线Ω的方程；(2)假设直线y ＝x 与抛物线Ω交于A ，B 两点，在抛物线Ω上是不是存在异于A ，B 的点C ，使得通过A ，B ，C 三点的圆和抛物线Ω在点C 处有相同的切线？假设存在，求出点C 的坐标；假设不存在，请说明理由.解 (1)依题意，设抛物线Ω的方程为x 2＝2py (p >0)， 则F (0，p2)，由直线l 的斜率存在，设为k ， 得l 的方程为y ＝kx ＋p2，联立方程⎩⎪⎨⎪⎧x 2＝2py ，y ＝kx ＋p2，消去y 并整理，得x 2－2pkx －p 2＝0.设M (x 1，y 1)，N (x 2，y 2)，那么x 1＋x 2＝2pk ，x 1x 2＝－p 2， 又y 1y 2＝(kx 1＋p 2)(kx 2＋p2)＝k 2x 1x 2＋12kp (x 1＋x 2)＋p 24＝k 2·(－p 2)＋12kp ·2kp ＋p 24＝p 24.因此OM →·ON →＝x 1x 2＋y 1y 2＝－p 2＋p 24＝－3，因为p >0，解得p ＝2，故所求抛物线Ω的方程为x 2＝4y .(2)联立方程⎩⎪⎨⎪⎧x 2＝4y ，y ＝x ，可求得A (0,0)，B (4,4)，假设抛物线Ω上存在异于A ，B 的点C ，且设C 的坐标为(t ，t 24)(t ≠0，t ≠4)，使得通过A ，B ，C 三点的圆和抛物线Ω在点C 处有相同的切线，令圆心为E (a ，b )，那么由⎩⎪⎨⎪⎧|EA |＝|EB |，|EA |＝|EC |，得⎩⎪⎨⎪⎧a 2＋b 2＝a －42＋b －42，a 2＋b 2＝a －t2＋b －t 242，即⎩⎪⎨⎪⎧a ＋b ＝4，4a ＋tb ＝2t ＋t 38，解得⎩⎪⎨⎪⎧a ＝－t 2＋4t8，b ＝t 2＋4t ＋328. ①因为抛物线Ω在点C 处的切线斜率k ′＝y ′|x ＝t ＝t2(t ≠0，t ≠4)，又该切线与EC 垂直，因此b －t 24a －t ·t 2＝－1， 即2a ＋bt －2t －t 34＝0. ② 将①代入②得，2(－t 2＋4t 8)＋t ·t 2＋4t ＋328－2t －t 34＝0， 即t 3－2t 2－8t ＝0，因为t ≠0，t ≠4，解得t ＝－2. 故存在点C 且坐标为(－2,1).。

2 2 2 2 a + a 1 + a a a 2 2专题 13 两边夹【方法点拨】1．重要不等式：(1)对数形式：x ≥1＋ln x (x >0)，当且仅当 x ＝1 时，等号成立． (2)指数形式：e x ≥x ＋1(x ∈R )，当且仅当 x ＝0 时，等号成立．进一步可得到一组不等式链： e x >x ＋1>x >1＋ln x (x >0，且 x ≠1)．2．树立一个转化的意识，即“等”与“不等”间的互化.【典型题示例】2例 1若实数 a , b 满足 2 l n a + ln (2b ) ≥ + 4b - 2 ，则（）2A. a + b = + 1 4C. a 2+ b > 3 B. a - 2b = - 1 4D. a 2- 4b < 1【答案】A【分析】思路一：据果变形，直接使用重要不等式 x - 1 ≥ ln x (x > 0) ，两边夹逼将不等式转化为等式.思路二：一边一个变量，构造两个函数，分别求出其最值，夹逼将不等式转化为等式.【解析一】∵ 2 l n a + ln (2b ) = ln a 2+ ln (2b ) = ln a 2+ ln (4b ) ∴ ln a2 ln (4b ) ≥ + 4b - 22 2易知 x - 1 ≥ ln x (x > 0) ，当且仅当 x =1 时，“=”成立∴a -1 ≥ ln a ， 4b -1 ≥ ln (4b )当且仅当 a = ，b = 时，“=”成立 2 2a 2根据不等式性质有+ 4b - 2 ≥ ln a4+ ln (4b )所以ln a 2 22 ln (4b ) = + 4b - 22 2此时必有 a = ， b = 1（下略）.42【解析二】∵ 2 l n a + ln (2b ) ≥ + 4b - 222∴ 2 ln a - + ≥ 4b - ln (2b )- 22222 22ab cd a a = = 2令 f (a ) = 2 ln a - ， g (b ) = 4b - ln (2b )- 22利用导数知识易求得 f (a )max = f ( 2) = ln 2 -1， g (b )min = g (b ) = ln 2 -1 2所以 f (a ) ≤ g (b ) ，即 2 ln a + ln (2b ) ≤ + 4b - 22a 21 故2 l n a + ln (2b ) = + 4b - 2 ，此时a = ， b = （下略）.2 4例 2 （2020·赣榆中学第二学期期初模拟检测·14）已知 a , b , c , d 都是正数，e (ln c + ln d ) ≥ cd ，4e 【答案】 2 + a +b -2≤ (a + b ) ，则 + cd c+ d 的最大值是．2【分析】由 e (ln c + ln d ) ≥ cd ⇔ ln (cd ) ≥cd，换元令 cd = t (t > 0) ，则 ln t ≥ t，考虑e“形”， ln t ≤ t恒成立，夹逼得cd = e ，同理处置4e eea +b -2≤ (a + b ) ，最后使用基本不等式求解.【解析】e (ln c + ln d ) ≥ cd ⇔ ln (cd ) ≥cd ，令cd = t (t > 0) ，则ln t ≥ teet事实上ln t ≤ （当且仅当t = e 时，“=”成立），故cd = e ；ea + - + - a +b u -2u 2 4e b 2 ≤ (a + b ) ⇔ e a b 2≤ ，令 4 = u (u > 0) ， 则e ≤ 4事实上eu -2u 2（当且仅当u = 2 时，“=”成立），故 4= 2 ；a +b 所以 ≤ = 2 ， cd ≤ cd （当且仅当a = b ，c =d 时，“=”2 c + d 2 cd 2 2成立）ab ea +b a + b e ≥e cd故 c + d的最大值是2 + ．2【巩固训练】1.已知正实数 x , y 满足 x+ 2 y - 2 = ln x + ln y ，则 x y=．22.（2019·江苏苏州·最后一卷）己知实数 a ，b ，c 满足e a u l u e 2b —l —1 ≤ a u 2b u 1（e 为自然对数的底数），则a 2u b 2的最小值是 .3.若对于任意正实数 x , y ，不等式 4ax ≤ e x + y -2+ e x - y -2 + 2 恒成立，则实数 a 的最大值是．4. 己知实数 a ，b 满足 2ln a — e 2b ≤ a 2 — 2b — 2（e 为自然对数的底数），则 a +2b =.ab +【答案或提示】1.【答案】2.【答案】15【分析】将已知变形为e a u l u e2b—l—1≤[(a u l）u1]u[2b—l—1u 1]，联系重要不等式e x≤x u1，夹逼得a +c=0，2b -c +1=0 .【解析】∵ e x ≥x +1 ∴e a+c ≥a +c ，e2b-c+1 ≥ 2b -c +1所以e a+c +e2b-c+1 ≥(a +c)+ (2b -c +1)=a + 2b +1又∵e a +c+e2b -c +1 ≤a + 2b +1 ∴e a+c +e2b-c+1 =a + 2b +1当且仅当a +c=0，2b -c +1=0 时成立∴a2+b2=(-c)2⎛c -1 ⎫2+ ⎪ = 5c2 -c+1，所以⎡⎣a2+b2⎤⎦ =1.⎝2 ⎭ 4 2 4 min 5 13.【答案】24.【答案】12。