当前位置：文档之家 › 第2章 逻辑代数基础 习题解答

第2章 逻辑代数基础 习题解答

  • 格式：doc
  • 大小：711.00 KB
  • 文档页数：10

下载文档原格式

  / 10

合集下载

人邮社数字电路逻辑设计习题答案

人邮社数字电路逻辑设计习题答案

习题参考解答第1章基本知识1．什么是数字信号？什么是模拟信号？（注：所有蓝色标题最后均去掉！）答案：数字信号：指信号的变化在时间上和数值上都是断续的，或者说是离散的，这类信号有时又称为离散信号。

例如，在数字系统中的脉冲信号、开关状态等。

模拟信号：指在时间上和数值上均作连续变化的信号。

例如，温度、交流电压等信号。

2．数字系统中为什么要采用二进制？答案：二进制具有运算简单、物理实现容易、存储和传送方便、可靠等优点。

3．机器数中引入反码和补码的主要目的是什么？答案：将减法运算转化为加法运算，统一加、减运算，使运算更方便。

4．BCD码与二进制数的区别是什么?答案：二进制数是一种具有独立进位制的数，而BCD码是用二进制编码表示的十进制数。

5．采用余3码进行加法运算时，应如何对运算结果进行修正？为什么？答案：两个余3码表示的十进制数相加时，对运算结果修正的方法是：如果有进位，则结果加3；如果无进位，则结果减3。

为了解决四位二进制运算高位产生的进位与一位十进制运算产生的进位之间的差值。

6．奇偶检验码有哪些优点和不足？答案：奇偶检验码的优点是编码简单，相应的编码电路和检测电路也简单。

缺点是只有检错能力，没有纠错能力，其次只能发现单错，不能发现双错。

7．按二进制运算法则计算下列各式。

答案：（1）110001 （2）110.11 （3）10000111 （4）1018．将下列二进制数转换成十进制数、八进制数和十六进制数。

答案：（1）（117）10 ，（165）8 ，（75）16（2）（0.8281）10 ，（0.65）8 ，（0.D4）16（3）（23.25）10 ，（27.2）8 ，（17. 4）169．将下列十进制数转换成二进制数、八进制数和十六进制数（精确到二进制小数点后4位）。

答案：（1）（1000001）2 ，（101）8 ，（41）16（2）（0.0100）2 ，（0.20）8 ，（0.40）16（3）（100001.0101）2 ，（41.24）8 ，（21.50）1610．写出下列各数的原码、反码和补码。

课后习题第2章逻辑代数及其化简

课后习题第2章逻辑代数及其化简

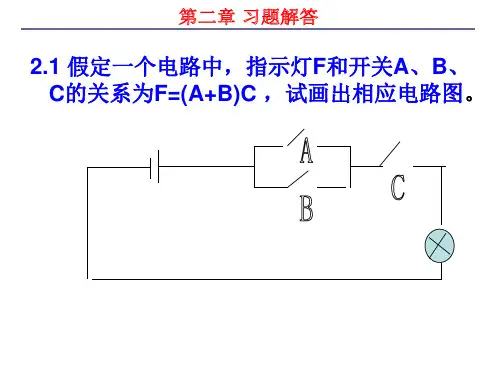
第 2 章代数及其化2-1 分将十制数，和成二制数。

解答：10=(1,210=(111,,1100,⋯)210=(1,0111,,1100, ⋯ ) 22-2 分将二制数101101. 和成十制数。

解答：(101101.) 2 =(45.)102=102-3 分将二制数和成十六制数。

解答：2 =(0010,,1100)2=(26.9C) 162=(1,0101,,1110)2=162-4 分将十六制数和成二制数。

解答：16=(11,1010,,1110,1011)2(6C2B.4A7) 16=(110,1100,0010,,1010,0111)22-5 用真表法明以下等式：(1)AB+ AC+ BC= AB+ C(2)AB+ AB+ BC = AB+ AB+ AC(3)AB+ BC+ CA= AB+ BC+ CA(4)AB+ AB+ BC+ AC= A+ BC(5)AB+ BC + CD + DA= ABCD + ABCD(6)AB+ AB+ ABC= A+ B明：(1)ABACBCABC真值表以下所示：A B C AB AC BC AB C0000000111010000111110000101111101111111由真值表可知，逻辑等式建立。

(2) AB AB BC AB AB AC真值表以下所示：A B C AB AB BC AB AB AC0000000100010110111110011101111100011111由真值表可知，逻辑等式建立。

(3) AB BC CA AB BC CA真值表以下所示：A B C AB BC CA AB BC CA0000000111010110111110011101111101111100由真值表可知，逻辑等式建立。

(4)AB AB BC AC A BC真值表以下所示：A B C AB AB BC AC A BC0001100111010110111110000101001100011111由真值表可知，逻辑等式建立。

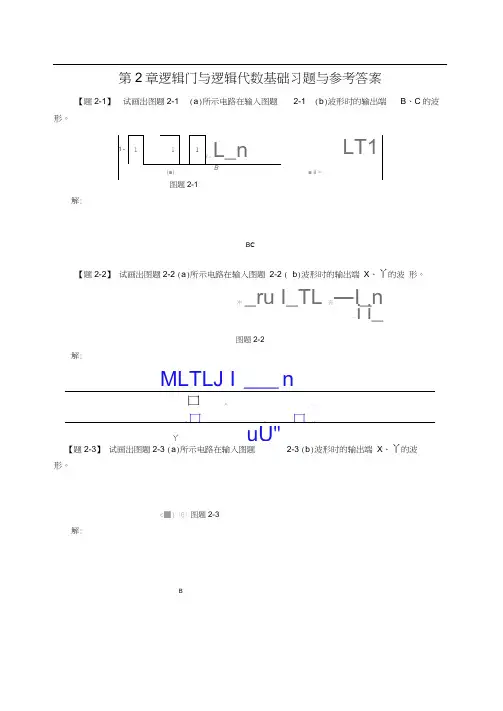
第2章-逻辑门与逻辑代数基础-习题与参考答案3-12

第2章-逻辑门与逻辑代数基础-习题与参考答案3-12

第2章逻辑门与逻辑代数基础习题与参考答案【题2-1】试画岀图题2-1 (a)所示电路在输入图题2-1 (b)波形时的输岀端B、C的波形。

解:B C【题2-2】试画岀图题2-2 (a)所示电路在输入图题2-2 ( b)波形时的输岀端X、丫的波形。

冲_ru I_TL 丧―I_n 一i i_图题2-2解:MLTLJ I ___ n口_n_ i_..x 口n 口n丫uU"【题2-3】试画岀图题2-3 (a)所示电路在输入图题2-3 (b)波形时的输岀端X、丫的波形。

<■) ⑹ 图题2-3解:B【题2-9】 如果如下乘积项的值为 1,试写岀该乘积项中每个逻辑变量的取值。

【题2-4】 试画岀图题2-4 (a )所示电路在输入图题 2-4 ( b )波形时的输岀端 X 、丫的波 形。

解:A J ~I _n ___ rvLB X.丫【题2-5】 试设计一逻辑电路，其信号 A 可以控制信号 B ，使输岀丫根据需要为 Y=B 或Y= B 。

解：可采用异或门实现，Y AB AB ，逻辑电路如下：【题2-6】某温度与压力检测装置在压力信号 A 或温度信号B 中有一个岀现高电平时， 输岀低电平的报警信号，试用门电路实现该检测装置。

解：压力信号、温度信号与报警信号之间的关系为： Y 「B ，有如下逻辑图。

【题2-7】某印刷裁纸机，只有操作工人的左右手同时按下开关 A 与B 时，才能进行裁纸操作，试用逻辑门实现该控制。

解：开关A 、B 与裁纸操作之间的关系为 丫 A B ，逻辑图如下：【题2-8】 某生产设备上有水压信号 A 与重量信号B ，当两信号同时为低电平时，检测电 路输出高电平信号报警，试用逻辑门实现该报警装置。

解：水压信号A 、重量信号B 与报警信号之间的关系为 Y 厂B ，逻辑图如下：A 「＞ 1(1) AB ; (2) ABC ; (3) ABC ; (4) ABC解：(1) A=1 , B=1(2)A=1、B=1、C=0(3)A=0, B=1, C=0(4)A=1, B=0 或C=1【题2-10】如果如下和项的值为0,试写岀该和项中每个逻辑变量的取值。

数电习题解答_杨志忠_第二章练习题_部分

数电习题解答_杨志忠_第二章练习题_部分

教材：数字电子技术基础（“十五”国家级规划教材） 杨志忠 卫桦林 郭顺华 编著高等教育出版社2009年7月第2版； 2010年1月 北京 第2次印刷；第二章 逻辑代数基础练习题P58【题2.2】用逻辑函数的基本公式和定律将下列逻辑函数式化简为最简与或表达式。

解题思路：要求熟练理解、运用逻辑代数的定理和公式。

（3）、(1)()Y A ABC ABC BC BC A BC BC C B B A C =++++=++++=+；（4）、()Y AB BD DCE AD AB D A B DCE AB D AB DCE AB D =+++=+++=++=+； （8）、()()()(())()Y A B C D E A B C DE A B C DE A B C DE DE =++++++=++++++=i i ； （9）、()()()Y A C BD A BD B C DE BC ABCD ABD BC BDE BC B =+++++=++++=； 【2.3】、证明下列恒等式（证明方法不限）。

解题思路：熟练使用逻辑函数公式和相关定理、真值表、卡诺图完成证明。

（9）、()A ABC ACD C D E A CD E ++++=++；证明：()A ABC ACD C D E A ACD CDE A CD CDE A CD E ++++=++=++=++； （10）、()()BC D D B C AD B B D ++++=+；证明：()()()())BC D D B C AD B BC D B C AD B BC D BC AD B BC D AD B B D++++=++++=+++=+++=+；【2.4】、根据对偶规则求出下列逻辑函数的对偶式。

解题思路：对任何表达式，将“·”和“+”互换，所有1、0互换，原变量和非变量保持不变、而且原运算顺序不变；可得到一个新的表达式，此式是原式的对偶式。

（1）、()()Y A B C A B C =+++；解：'()()Y A B C A BC =++i i（4）、()()()()Y A C A B C B C A B C =++++++；解：'Y AC ABC BC ABC =+++； 【2.5】、根据反演规则求下列逻辑函数的反函数；解题思路：对任何一个表达式，将“·”和“+” 、原变量和反变量互换，所有1、0互换，而且原运算顺序不变；所得表达式是原式的反。

数字逻辑第四版华科出版1~7全答案

数字逻辑第四版华科出版1~7全答案
1.7 将下列十进制数转换成二进制数、八进制数和十六进制 数(精确到小数点后4位)。
（1） 29 （2） 0.27 （3） 33.33
解答： （1） 29 = (11101)2＝(65)8＝(1D)16 （2） 0.27 = (0.0100)2＝(0.21)8＝(0.4 )16
（3）33.33 = (100001.0101)2 = (41.24)8= (41.2508)8= (41.2507)8 = (21.5)16 = (21.547B)16=(21.547A)16
ABCD
AB CD 00 01 11 10
00
1 11
01
1 11
11 1 1 1 1
所以，F（A,B,C,D） =m(3-15)
10
1 11
=M(0-2)
精选ppt
22
习题课
2.8 用卡诺图化简法求出下列逻辑函数的最简“与－或”表 达式和最简“或－与”表达式。
（1） F (A ,B ,C ,D ) A B A C D A C B C （2） F (A ,B ,C ,D ) B D C D (B C )A ( B D ) （3） F ( A ,B , C ,D ) M ( 2 , 4 , 6 , 1 , 1 , 1 0 , 1 1 , 1 2 , 1 3 ) 4 5 解答： （1） F (A ,B ,C ,D ) A B A C D A C B C
yzxyyzxz精选ppt191926用逻辑代数的公理定理和规则将下列逻辑函数化简为最简与或表达式精选ppt2020精选ppt212127将下列逻辑函数表示成最小项之和及最大项之积形式00011110abcd00011110所以m471215m03811精选ppt222200011110abcd00011110所以m315m02精选ppt232328用卡诺图化简法求出下列逻辑函数的最简与或表达式和最简或与表达式

第二章习题答案

第二章习题答案

2-1举出现实生活中的一些相互对立的、处于矛盾状态的事物。

试着给这些对立的事物赋予逻辑“0”和逻辑“1”。

2-2为什么称布尔代数为“开关代数”？2-3基本逻辑运算有哪些？写出它们的真值表。

答：与、或、非。

2-4什么是逻辑函数？它与普通代数中的函数在概念上有什么异同？2-5如何判定两个逻辑函数的相等？2-6逻辑函数与逻辑电路的关系是什么？ 答：逻辑电路是能完成某一逻辑运算的电子线路，而逻辑函数可以描述该电路的逻辑功能。

2-7什么是逻辑代数公理？逻辑代数公理与逻辑代数基本定律或定理的关系是什么？2-8用真值表证明表2.3.2中的“0-1律”，“自等律”，“互补律”，“重叠律”和“还原律”。

2-9分别用真值表和逻辑代数基本定律或定理证明下列公式。

1.)C A )(B A (BC A ++=+ 证明：右边=A+AB+AC+BC=A+BC=左边2.B A B A A +=+证明：左边=AB+AB+AB=AB+AB+AB+AB=A+B=右边 3.A AB A =+证明：左边=A(1+B)=A=右边 4.C A B A C A AB +=+证明：左边=(A+B)(A+C)=0+AB+AC+BC=AB+AC=右边 5.AC B A BCD C A AB +=++A B F 0 0 0 0 1 0 1 0 0 1 11与A B F 0 0 0 0 1 1 1 0 1 1 11或A F 0 1 1 0非证明：左边=AB+AC+ABCD+ABCD=AB+AC=右边6.)(+BA+)(+++C=AB)()(CAA(CB)证明：两边取对偶，得AB+AC+BC=AB+AC，得证。

7.)(+B+)(++A=AB)(CAA()C证明：左边右边=AB+AC+BC=AB+AC得证。

8.AA(=B++))(BA证明：设F=(A+B)(A+B)则F’=AB+AB=AF=(F’)’=A得证。

9.A(A=+AB)证明：左边=A+AB=A=右边，得证。

第二章 逻辑代数基础习题解答

第二章 逻辑代数基础习题解答

（2）F ( A B)(A C)(C DE ) E F [ A B AC C(D E)] E
F [ AB AC C(D E)] E
（3）F [ AB (C D) AC]
F AB (C D) AC [( A B )(C D AC )] F [( A B)(CD A C )]
2.8 用卡诺图化简法求出下列逻辑函数的最简 “与-或” 表达式和最简“或-与”表达式。 （1）F ( A, B, C, D) A B A CD AC BC （2）F ( A, B, C, D) BC D D(B C)(AD B)
， （3）F ( A, B, C, D) M (2,4,6,10,1112,13,14,15)
G( A, B, C, D) ( AB BC AC)( A B C) ABC
解： （1）F ( A, B, C, D) B D A D C D ACD G ( A, B, C, D) BD CD A CD ABD
卡诺图如下：
由卡诺图知： F D
b．求必要质蕴涵项（右上角加“*”标记） c．找出函数的最小覆盖
∴ F ( A, B, C, D) P1 P2 P4 BD CD B D 或 F ( A, B, C, D) P1 P3 P4 BD BC B D
（2）F ( A, B, C, D) m(3,5,8,9,10,12) d ( 0,1,2,13)
( A B AC BC)(A C) ABC A B C
2.3
用真值表验证下列表达式。
（1）AB AB ( A B)(A B) （2） ( A B)( A B) ( AB A B) 解：等式（1）、（2）的真值表如表T2.3所示。

数字逻辑 第二章习题答案

数字逻辑 第二章习题答案
D E )G ] F A B[(C D ) E G ] F ' A B[(C D ) E G ]
2.6用代数化简法求下列逻辑函数的最简与或表达式。 （1）F=AB+ ABC BC AB ( AB B )C AB ( A B )C AB AC BC AB AC (2) F AB B BCD AB B A B (3) F ( A B C )( A B )( A B C ) ( A B )( A B ) B
(2) AB AB AB AB 1 证明：AB AB AB AB A( B B ) A( B B ) A A 1
(3) AABC ABC ABC ABC 证明：AABC A( A B C ) AB AC AB (C C ) AC ( B B ) ABC ABC ABC ABC ABC ABC ABC
• (2)
• 2.8用卡诺图化简法求出下列逻辑函数的最简“与-或”表达式和最简 “或-与”表达式。
(4) F BC D D( B C )( AC B) BC D ( B C )( AC B) BC D BC ( AC B ) BC D AC B B D AC
• 7． 将下列逻辑函数表示成“最小项之和” 形式及“最大项之积”的简写形式。
(4) ABC ABC AB BC AC 证明： BC AC AB ( A B)( B C )( A C ) ( AB AC BC )( A C ) ABC ABC ABC
2.4求反函数和对偶函数 （2）F=(A+B)( A+C)(C+DE)+ E F [ AB AC C ( D E )]E F ' [ AB AC C ( D E )]E (3) F ( A B )(C D AC ) F AB C ( D A C ) F ' AB C ( D A C )

人邮社数字电路逻辑设计习题答案

人邮社数字电路逻辑设计习题答案
9．将下列十进制数转换成二进制数、八进制数和十六进制数（精确
到二进制小数点后4位）。 答案：（1）（1000001）2
（2）（0.0100）2，
（3）（100001.0101）2 10．写出下列各数的原码、 答案：（1）原码=反码=补码=0.1011
（2）原码=1.1100， 反码=1.0011，补码=1.0100（3）原码=110110，反码=101001，补码=101010
7．按二进制运算法则计算下列各式。
答案：（1）110001（2）110.11（3）10000111（4）101 8．将下列二进制数转换成十进制数、八进制（2）（0.8281）10， （0.65）8，
（3）（23.25）10， （27.2）8，
5．采用余3码进行加法运算时，应如何对运算结果进行修正？为什
么？
答案：两个余3码表示的十进制数相加时，对运算结果修正的方 法是：如果有进位，则结果加3；如果无进位，则结果减3。为了解 决四位二进制运算高位产生的进位与一位十进制运算产生的进位之 间的差值。
6．奇偶检验码有哪些优点和不足？ 答案：奇偶检验码的优点是编码简单，相应的编码电路和检测电 路也简单。缺点是只有检错能力，没有纠错能力，其次只能发现单错， 不能发现双错。
理和规则十分熟练时化简比较方便；缺点是没有固定的规律和步骤， 技巧性强，且通常难以判断化简结果是否达到了最简单。9．用卡诺图化简逻辑函数时，应如何画卡诺圈才能求得一个函数的 最简与—或表达式？
答案：注意两点： 第一，在覆盖所有1方格的前提下，卡诺圈的 个数应达到最少；第二，在满足合并规律的前提下，每个卡诺圈的大 小应达到最大。
11.已知［N］补=1.0110，求［N］原，［N］反和N。
答案：［N］原码=1.1010,［N］反码=1.0101,N= -0.1010

逻辑代数基础习题解答

逻辑代数基础习题解答
组合逻辑电路中的竞争与冒险
分析电路中可能出现的竞争与冒险现象，采取相应措施进行消除或 抑制。
时序逻辑电路分析与设计
分析时序逻辑电路
了解时序逻辑电路的基本概念和组成，包括触发器、寄存器、计数器等。根据给定的电路图，分 析电路的工作原理和功能。
设计时序逻辑电路
根据实际需求，确定输入与输出之间的逻辑关系以及电路的状态转换关系。选择合适的触发器类 型，设计状态转换表和状态转换图，并进行电路连接。
备考策略指导
明确考试要求
了解考试形式和评分标准，明确备考方向和重 点。
制定复习计划
根据考试要求和自身情况，制定合理的复习计 划，并按照计划有序进行复习。
多做模拟试题
通过做模拟试题来检验自己的学习成果，找出自己的不足之处，有针对性地进 行弥补。
考试技巧点拨
仔细审题
在考试时，认真阅读题目，理解题意和要求 ，避免因为误解题意而导致失分。
题目1：逻辑代数中，基本的逻辑运算包括哪些？
02
A. 与、或、非
03
B. 与、或、异或
选择题解析
C. 与、非、同或 D. 或、非、异或 答案：A. 与、或、非
选择题解析
• 题目2：在逻辑代数中，下列哪个公式是正 确的？
选择题解析
C. A + A'B = A + B
B. A(A + B) = AB
表示方法
逻辑函数可以用多种方法表示，如真值表、逻辑表达式、卡诺图等。其中，真值表是列出所有输入组合及对应输 出的表格；逻辑表达式是用逻辑运算符和逻辑变量表示的式子；卡诺图是一种图形化表示方法，用于简化逻辑函 数。
02 逻辑代数化简方法
公式化简法
利用基本公式进行化简

第2章逻辑代数基础习题部分解

第2章逻辑代数基础习题部分解

并 项3
吸收2
吸2
BCD BCD BC BD
并 项4
BC BC BD
2.11 用公式法化简下列各式。 (1) F ABC ACD AC (2) F AC D BC BD AB AC B C
(3) F ( A B)( A B C )( A C )(B C D)
按最简式构成的逻辑电路，所用的门电路 最少，连线最少。
2.6什么叫约束、约束项和约束条件?在化简具有 约束的逻辑函数时，充分利用约束条件有什么好 处?
输入变量中不允许出现或不会出现的取值组 合叫约束，约束所代表的最小项称为约束项 （或称任意项、无关项），全体约束项的和 为0是函数的约束条件 。
正确利用约束项有时可以使函数化简结果更简 单。
卡诺图将n个变量分成两组排列在行和列上， 在行上和列上都按循环码顺序排列。
2.4什么叫最小项?最小项有什么性质?
最小项
最小项的性质： ① ② ③
2.5什么叫最简与或表达式?化简逻辑函数表达式 的意义是什么?
一个与或表达式中包含的乘积项数最少， 而且每个乘积项里的因子也最少时，则 称此逻辑函数为最简与或式。
(1)子
提取公因子后消因子
AB A CD AC 提取公因子后消因子 提取公因子后消因子
AB CD AC
消项
消项
(3) F (A B)(A BC)( A C )(B C D)
(1) 左 AB AC (BC)D
用消项公式配项
反演定理
AB AC BCBCD
消因子
AB AC D
(2)左 A C A B ACD BC

第二章逻辑代数基础-习题

第二章逻辑代数基础-习题

= ( AC + AD+ B)( A + C)
= AC + A B + BC + ACD = AC + AB
2011年6月15日星期三
11
2.12 用卡诺图法把下列函数 化简为最简与或式。 化简为最简与或式。 (1) F ( A, B, C ) = ∑ m(0,1,2,4,5,7)
(3) F ( A, B, C , D) = ∑ m(0,1,4,7,9,10,13) + ∑φ (2,5,8,12,15)
2011年6月15日星期三
7
2.10试写出下列各函数表达式 的F和F′的最小项 试写出下列各函数表达式F的 和 的最小项 试写出下列各函数表达式 表达式。 表达式。
(1) F = ABCD + ACD + BC D
2011年6月15日星期三
8
解： ) F ( A, B, C , D) = ABCD + ACD + BC D (1
(1) F = A + ABC + ABC + BC + B ( 2) F = ( A + B )( A + B + C )( A + C )( B + C + D)
解： ) F = A + ABC + ABC + BC + B (1
= A + A( BC + BC ) + B = A+ B ( 2) F = ( A + B )( A + B + C )( A + C )( B + C + D) F ′ = AB + ABC + A C + BCD = AB + A C + BCD = AB + A C

数电课件第二章逻辑代数基础小结和习题

数电课件第二章逻辑代数基础小结和习题
吸收定理的应用场景包括简化复杂的逻辑电路和逻辑表达式，提高电路的性能和可读性。在电路设计中，吸收定理可以帮助 设计师减少不必要的元件和连线，降低成本和功耗。
分配定理
分配定理是逻辑代数中的另一个基本定理，它表明对于任何逻 辑变量A、B和C，有(A AND B) OR (A AND C) = A AND (B OR C)。这个定理表明，在逻辑表达式中，括号可以被分配到 不同的位置，而不会改变表达式的值。
要点二
详细描述
输入选择法化简是通过分析输入变量的取值组合，选择合 适的变量组合，使得逻辑函数表达式达到最简的过程。这 种方法需要仔细分析输入变量的取值情况，通过选择合适 的变量组合，消除多余的因子和项，最终得到最简的逻辑 函数表达式。输入选择法化简在处理具有多个输入变量的 复杂逻辑函数时特别有效，能够显著降低表达式的复杂度 。
习题三解析与解答
总结词
真值表构建
详细描述
这道题要求根据给定的逻辑表达式构建真值 表，主要考察了学生对逻辑函数和真值表的 理解。通过构建真值表，可以深入理解逻辑 函数的逻辑关系和输出结果，进一步加深对
逻辑代数原理的理解和应用。
06 总结与展望
本章总结
逻辑代数概念
介绍了逻辑代数的基本概念， 包括逻辑变量、基本逻辑运算
VS
详细描述
卡诺图法化简是将逻辑函数表达式转换为 卡诺图形式，然后通过观察和合并相邻的 1或0值区域，简化逻辑函数表达式的过 程。这种方法直观易懂，易于掌握，特别 适合于多变量的逻辑函数表达式的化简。 通过卡诺图法化简，可以有效地减少变量 的个数，简化逻辑函数的复杂度。
输入选择法化简
要点一
总结词
通过选择不同的输入变量组合，使得逻辑函数表达式达到 最简的方法。

逻辑代数基础习题资料

逻辑代数基础习题资料

逻辑代数基础习题第二章 逻辑代数基础[题2.1] 选择题以下表达式中符合逻辑运算法则的是 。

A.C ·C =C 2B.1+1=10C.0<1D.A+1=12. 逻辑变量的取值１和０可以表示： 。

A.开关的闭合、断开B.电位的高、低C.真与假D.电流的有、无3. 当逻辑函数有n 个变量时，共有 个变量取值组合。

A. nB. 2nC. n 2D. 2n4. 逻辑函数的表示方法中具有唯一性的是 。

A .真值表 B.表达式 C.逻辑图 D.卡诺图5. 在 输入情况下，“与非”运算的结果是逻辑0。

A ．全部输入是0 B.任一输入是0 C.仅一输入是0 D.全部输入是16．在 输入情况下，“或非”运算的结果是逻辑0。

A ．全部输入是0 B.全部输入是1C.任一输入为0，其他输入为1D.任一输入为17． 求一个逻辑函数F 的对偶式，可将F 中的 。

A .“·”换成“+”，“+”换成“·”B.原变量换成反变量，反变量换成原变量C.变量不变D.常数中“0”换成“1”，“1”换成“0”E.常数不变8. 在同一逻辑函数式中，下标号相同的最小项和最大项是关系。

A ．互补 B.相等 C.没有关系9. F=A +BD+CDE+ D= 。

A. AB. A+DC. DD. A+BD10．A+BC= 。

A .A+B B.A+C C.（A+B ）（A+C ） D.B+C11.逻辑函数F=)(B A A ⊕⊕= 。

A.BB.AC.B A ⊕D. B A ⊕[题2.2]判断题（正确打√，错误的打×）1． 逻辑变量的取值，1比0大。

（ ）2． 异或函数与同或函数在逻辑上互为反函数。

（ ）3．若两个函数具有相同的真值表，则两个逻辑函数必然相等。

（）4．因为逻辑表达式A+B+AB=A+B成立，所以AB=0成立。

（）5．若两个函数具有不同的真值表，则两个逻辑函数必然不相等。

（）6．若两个函数具有不同的逻辑函数式，则两个逻辑函数必然不相等。

阎石《数字电子技术基础》(第5版)(课后习题 逻辑代数基础)【圣才出品】

阎石《数字电子技术基础》(第5版)(课后习题 逻辑代数基础)【圣才出品】

第2章　逻辑代数基础2.1 试用列真值表的方法证明下列异或运算公式。

（1）A⊕0＝A（2）A⊕1＝A ＇（3）A⊕A＝0（4）A⊕A＇＝1（5）（A⊕B）⊕C＝A⊕（B⊕C）（6）A（B⊕C）＝AB⊕AC （7）A⊕B＇＝（A⊕B）＇＝A⊕B⊕1证明：左式和右式的真值表若相同，则表达式得证。

真值表如表2-1所示。

表2-12.2 证明下列逻辑恒等式（方法不限）（1）AB ＇＋B ＋A ＇B ＝A ＋B（2）（A ＋C ＇）（B ＋D ）（B ＋D ＇）＝AB ＋BC ＇（3）（（A ＋B ＋C ＇）＇C ＇D ）＇＋（B ＋C ＇）（AB ＇D ＋B ＇C ＇）＝1（4）A ＇B ＇C ＇＋A （B ＋C ）＋BC ＝（AB ＇C ＇＋A ＇B ＇C ＋A ＇BC ＇）＇证明:（1）左边＝AB'＋B ＋A'B ＝AB'＋（B ＋A'B ）＝AB'＋B ＝A ＋B ＝右边（2）左边＝（A ＋C'）（B ＋D ）（B ＋D'）（A ＋C'）（B ＋BD ＋BD'）＝B （A ＋C'）＝AB ＋BC'＝右边（3）()()()()()'''''''''''''''A B C C D B C AB D B C A B C C D AB C D B C +++++=+++++''''A B C C D B C =+++++=1即左边＝右边（4）左右两式的真值表如表2-2所示。

表2-2由表2-9可知，等式成立。

2.3 已知逻辑函数Y 1和Y 2的真值表如表2-3（a ）、（b ）所示，试写出Y 1和Y 2的逻辑函数式。

表2-3（a ）表2-3（b）解：由表2-3（a）可得，Y1的逻辑函数式为：Y1＝A'B'C'＋A'B'C＋AB'C'＋AB'C＋ABC由表2-3（b）可得，Y2的逻辑函数式为：Y2＝A'B'C'D＋A'B'CD'＋A'BC'D'＋A'BCD＋AB'C'D'＋AB'CD＋ABC'D＋ABCD'2.4 已知逻辑函数的真值表如表2-4（a）、（b）所示，试写出对应的逻辑函数式。

第2章逻辑代数基础

第2章逻辑代数基础

第二章 逻辑代数基础2.1 基本要求1. 掌握逻辑代数三种基本运算的表示方法—真值表、表达式、图形符号。

2. 掌握逻辑代数的基本公式和常用公式，熟练运用公式进行化简。

3. 熟练掌握逻辑代数的三个基本定理，会运用定理进行等式的证明以及求表达式和函数式的反，会求一个表达式的对偶式。

4．熟练掌握逻辑函数式的各种表示方法—表达式、逻辑图形、卡诺图、真值表，并能进行各种表达形式的转换。

5．掌握逻辑函数的最小项和最大项的表示方法。

6．掌握逻辑函数的卡诺图化简法（包括含无关项的逻辑函数的化简），熟练的进行逻辑式之间不同表示形式的转换。

（与或式—与非式，与或式—与或非式）2.2自测题一、填空题1. 逻辑代数又称为 代数。

最基本的逻辑关系有 、 、 三种。

2. 逻辑函数的常用表示方法有 、 、 、 。

3．逻辑函数B A AB Y +=的对偶式为 ，反函数为 。

4．函数 BCF C A AB Y ++=的最简与或式为 。

二、选择题1．异或逻辑的与或表达式是（ ）。

A. B A AB +B. B A B A +C. ABD. B A2. 当逻辑函数有n 个变量时，共有 个变量取值组合？A. nB. 2nC. n 2D. 2n3．A+BC=（ ）。

A .A+B B.A+C C.（A+B ）（A+C ） D.B+C4. 以下表达式中符合逻辑运算法则的是 ( )。

A. A+A=2AB.1+1=1C.A+1=AD.A+1=15．在（ ）输入情况下，“或非”运算的结果是逻辑0。

A ．全部输入是0 B.任一输入是0 C.仅一输入是1 D.全部输入是1三、判断题（正确打√，错误的打×）1． 逻辑变量的取值，１比０大。

（ ）。

2． 异或函数与同或函数在逻辑上互为反函数，互为对偶式。

（ ）。

3．若两个函数具有相同的真值表，则两个逻辑函数必然相等。

（ ）。

4．若两个函数具有不同的逻辑函数式，则两个逻辑函数必然不相等。

（ ）5．逻辑函数两次求反则还原，逻辑函数的对偶式再作对偶变换也还原为它本身。

逻辑代数基础习题

逻辑代数基础习题

第二章 逻辑代数基础[题2.1] 选择题以下表达式中符合逻辑运算法则的是 。

A.C ·C=C 2B.1+1=10C.0<1D.A+1=12. 逻辑变量的取值１和０可以表示： 。

A.开关的闭合、断开B.电位的高、低C.真与假D.电流的有、无3. 当逻辑函数有n 个变量时，共有 个变量取值组合。

A. nB. 2nC. n 2D. 2n4. 逻辑函数的表示方法中具有唯一性的是 。

A .真值表 B.表达式 C.逻辑图 D.卡诺图5. 在 输入情况下，“与非”运算的结果是逻辑0。

A ．全部输入是0 B.任一输入是0 C.仅一输入是0 D.全部输入是16．在 输入情况下，“或非”运算的结果是逻辑0。

A ．全部输入是0 B.全部输入是1C.任一输入为0，其他输入为1D.任一输入为17． 求一个逻辑函数F 的对偶式，可将F 中的 。

A .“·”换成“+”，“+”换成“·”B.原变量换成反变量，反变量换成原变量C.变量不变D.常数中“0”换成“1”，“1”换成“0”E.常数不变8. 在同一逻辑函数式中，下标号相同的最小项和最大项是关系。

A ．互补 B.相等 C.没有关系9. F=A +BD+CDE+ D= 。

A. AB. A+DC. DD. A+BD10．A+BC= 。

A .A+B B.A+C C.（A+B ）（A+C ） D.B+C11.逻辑函数F=)(B A A ⊕⊕= 。

A.BB.AC.B A ⊕D. B A ⊕[题2.2]判断题（正确打√，错误的打×）1． 逻辑变量的取值，1比0大。

（ ）2． 异或函数与同或函数在逻辑上互为反函数。

（ ）3．若两个函数具有相同的真值表，则两个逻辑函数必然相等。

（ ）4．因为逻辑表达式A+B+AB=A+B 成立，所以AB=0成立。

（ ）5．若两个函数具有不同的真值表，则两个逻辑函数必然不相等。

（ ）6．若两个函数具有不同的逻辑函数式，则两个逻辑函数必然不相等。

第2章 逻辑代数基础 习题解答

第2章 逻辑代数基础 习题解答

第2章 逻辑代数基础2.1 明下列异或运算公式。

（7）1A B A B A B ⊕=⊕=⊕⊕2.2 用逻辑代数的基本公式和定律将下列逻辑函数式化简为最简与－或表达式。

(4)Y AB BD DCE AD =+++＝D(A+B)+AB+DCE =DAB+AB+DCE =D+AB+DCE =D+AB(6)()()Y A B CD A CD AC A D =++++()CD A B A ACD CD ACDCDC D+++=+==+＝ (9)()()()Y A C BD A BD B C DE BC =+++++()()A BD AC B C C DE ABD B B=++++=+=(10)()Y AC BC BD A B C ABCD ABDE =++++++()(1)A C B C BDE BC BD A C A BC BD ++++++++＝ ＝2.3 证明下列恒等式（证明方法不限）。

()()()A B C A B CA B C A BC A B C A B C A BC A B C A BCABC ⊕⊕=⊕⊕⊕+⊕+⊕+=（6）解：左式＝ ＝ ＝ ＝ ＝右式结果与等式右边相恒等，证毕。

(10)()()BC D D B C AD B B D ++++=+()()BC D D BC AD B BC D AD B B D=++⋅+=+++=+ 2.4 根据对偶规则求出下列逻辑函数的对偶式。

(2)()()Y A B C AB C D ABC D =+++++解：'()[()]()Y A BC A B CD A B C D =+++++ (3)Y AB BC CA =++解：'()()()Y A B B C C A =+++2.5 根据反演规则，求出下列逻辑函数的反函数。

(2)[()]Y A BC CD E F =++解：[()()]Y A B C C D E F =++++(3)Y A B CD C D AB =+++++解：()()YAB C D CD A B =++2.6 将下列逻辑函数变换为最小项之和的表达式： (4)()Y A B C A B C =+++++()Y A B C A B C =+++++∑解： ＝(A+B+C)+(A+B)C =A+B+C+AC+BC=A+B+C=A(B+B)(C+C)+B(A+A)(C+C)+C(A+A)(B+B)=ABC+ABC+ABC+ABC+ABC+ABC+ABC =m(1,2,3,4,5,6,7)2.7 用卡诺图化简下列逻辑函数为最简与－或表达式。

逻辑代数与逻辑函数

逻辑代数与逻辑函数

第二章 逻辑代数与逻辑函数 习题答案2.2 什么是逻辑函数?它和普通代数中的函数有何不同？解：逻辑代数中，任何一个对于几个逻辑变量，用算子“·”、“+”、“-”进行有限次逻辑运算及括号、符号等构成的逻辑表达式。

称为n 个变量的“逻辑函数”。

它和普通代数中的函数不同在于普通代数中的变量取值可以是任意值。

所以其函数取值也可以是任意值；而逻辑变量的取值只有“0”、“1”两种因而由逻辑变量构成的逻辑函数的取值也只有“0”和“1”两种。

2.4 什么是最小项?什么是最大项?它们具有什么性质?解： 最小项：对于几个变量的逻辑函数来说，它的“与项”是由几个变量相与（包含几个文字）而成的，即每个变量以原变量或反变量形式在与项中出现一次且仅出现一次，那这个“与项”就称为该逻辑函数的最小项。

最大项：对于几个变量的逻辑函数来说，它的“或项”是由几个变量相或（包含几个文字）而成的，即每个变量以原变量或反变量形式在或项中出现一次且仅出现一次，那这个“或项”就称为该逻辑函数的最大项。

最大项与最小项的性质：（1）关于最小项和最大项本身的性质：若mi 和mj 是逻辑函数F 的两个不同的最小项，Mi 和Mj 是逻辑函数F 的两个不同的最大项，即i ≠j ，则有： m i ·m j =0; M i +M j =1(2) 关于最小项和最大项关系的性质：逻辑函数的同一下标的最小项和最大项是互补的，即：i i M m = im Mi =(3) 关于最小项和最大项表示逻辑函数时的性质：a 、函数的全部最小项的“逻辑和”等于“恒等于1”，即：1mi 1n 20i =∑-=b 、同一个逻辑函数用最不项和最大项表达式分别表示时，表达式中所包含的最小项和最大项下标互补。

2.6 用逻辑定理证明下列等式：（1）D A D C C B B A D C B A ABCD +++=+ 证明：右边=D A *D C *C B *B A (反演法) =)D A (*)D C (*)C B (*)B A (++++)(ABCD D C BC BC C A CAD A C CA A D C C A AD B A D C B A C A B A 分配律++++++++=)10,(D C B A A B C D 律互补律-+==左边所以原等式成立（2）CA CB B AC A C B B A ++=++证明：C)A C B B A ()'(++=左边)C A (*)C B (*)B A (+++= C B A ABC +=；故左边)'C B A ABC (+= )'C A C B B A (=+=)C A (*)C B (*)B A ()'(+++=右边;C B A A B C+= 故右边)'C B A ABC (+= ∴左边=右边注：上述是基于逻辑规则，而不是基于逻辑定理！ （3）C *)B A (C B A AB ⊕=++ 证明：左边)(C *B A *AB 反演律=)(C *)B A (*)B A (反演律二次求反律++= )(C *)B B B A B A A A (分配律+++= )10,(C *)B A B A (律互补律-+= C *)B A (⊕==右边所以原等式成立。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第2章 逻辑代数基础2.1 明下列异或运算公式。

（7）1A B A B A B ⊕=⊕=⊕⊕2.2 用逻辑代数的基本公式和定律将下列逻辑函数式化简为最简与－或表达式。

(4)Y AB BD DCE AD =+++＝D(A+B)+AB+DCE =DAB+AB+DCE =D+AB+DCE =D+AB(6)()()Y A B CD A CD AC A D =++++()CD A B A ACD CD ACDCDC D+++=+==+ ＝ (9)()()()Y A C BD A BD B C DE BC =+++++()()A BD AC B C C DE ABD B B=++++=+=(10)()Y AC BC BD A B C ABCD ABDE =++++++()(1)A C B C BDE BC BD A C A BC BD ++++++++＝ ＝2.3 证明下列恒等式（证明方法不限）。

()()()A B C A B C A B C A BC A B C A B C A BC A B C A BC A B C ⊕⊕=⊕⊕⊕+⊕+⊕+= （6）解：左式＝ ＝ ＝ ＝ ＝右式结果与等式右边相恒等，证毕。

(10)()()BC D D B C AD B B D ++++=+()()BC D D BC AD B BC D AD B B D=++⋅+=+++=+ 2.4 根据对偶规则求出下列逻辑函数的对偶式。

(2)()()Y A B C AB C D ABC D =+++++解：'()[()]()Y A BC A B CD A B C D =+++++ (3)Y AB BC CA =++解：'()()()Y A B B C C A =+++2.5 根据反演规则，求出下列逻辑函数的反函数。

(2)[()]Y A BC CD E F =++解：[()()]Y A B C C D E F =++++(3)Y A B CD C D AB =+++++解：()()YAB C D CD A B =++2.6 将下列逻辑函数变换为最小项之和的表达式： (4)()Y A B C A B C =+++++()Y A B C A B C =+++++∑解： ＝(A+B+C)+(A+B)C =A+B+C+AC+BC=A+B+C=A(B+B)(C+C)+B(A+A)(C+C)+C(A+A)(B+B)=ABC+ABC+ABC+ABC+ABC+ABC+ABC =m(1,2,3,4,5,6,7)2.7 用卡诺图化简下列逻辑函数为最简与－或表达式。

(4)Y ACD BCD BD AB BCD =++++由逻辑函数式作卡诺图，得最简与－或表达式 Y A B AC D=++ (6)()()Y ABC BD A C B D AC =++++解：先将逻辑函数中非号下面的表达式()()ABC BD A C B D AC ++++变换为与－或表达式，即：()()ABC BD A C B D AC ABC ABD BCD ACD++++=+++然后作出四变量卡诺图，并在卡诺图对应位置填0，其余位置填1，即为原逻辑函数的卡诺图，如图所示：由卡诺图得最简与－或表达式：Y AC AB AD BD =+++2.8 用卡诺图化简下列逻辑函数为最简与－或表达式。

(4)(,,,)(0,1,2,3,4,6,8,9,10,11,12,14)Y A B C D m =∑B(,,,)Y A B C D B D =+这一题，也可以用圈0的方法进行求解。

(6)(,,,)(1,3,8,9,10,11,14,15)Y A B C D m =∑(,,,)Y A B C D AB AC BD =++2.9 用卡诺图化简下列具有无关项的逻辑函数为最简与－或表达式。

(4)(,,,)(3,6,8,9,11,12)(0,1,2,13,14,15)Y A B C D m d =+∑∑(,,,)Y A B C D AC BD BCD =++或者：(,,,)Y A B C D AC BD ACD =++(6)(,,,)(1,3,5,8,9,13)(7,10,11,14,15)Y A B C D m d =+∑∑D(,,,)Y A B C D D AB =+2.10 写出下列逻辑函数的最大项表达式。

(6) Y ACD ABD BCD BCD =+++解：()()()()(2,5,9,10,11,13,14)(0,1,3,4,6,7,8,12,15)ACD B B ABD C C BCD A A BCD A A ABCD ABCD ABCD ABCD ABCD ABCD ABCD m M =+++++++=++++++==∑∏(7) (,,,)(1,4,7,8,10,12,14,15)Y A B C D m =∑解：(,,,)(1,4,7,8,10,12,14,15)Y A B C D m =∑∏ ＝M(0,2,3,5,6,9,11,13)2.11用卡诺图化简下式为最简或－与表达式。

(2)()()()()()Y A B D A B D A B D A C D B C D =++++++++++()()()Y B D B D A B C =++++(6)(,,,)(1,3,9,10,15)(6,8,12,13,14)Y A B C D M d =∏∏()()()()Y A B D A C A B A D =+++++2.12 列出以下各题的真值表，并写出输出逻辑函数表达式。

(2) X 为输入变量，Y 为输出函数。

X 输入为8421BCD 码，Y 为4位二进制数。

当05X ≤≤ 时，Y=X+1；当69X ≤≤时，Y=X-1。

解：根据题意，列出真值表:XYA B C D E F G H 000000010001001000100011001101000100010101010110011001010111011010000111111题2.11（2）由真值表写出输出逻辑函数E ABCDF ABCD ABCD ABCD ABCD ABCD ABCD YG ABCD ABCD ABCD ABCD ABCDH ABCD ABCD ABCD ABCD ABCD⎧=⎪=+++++⎪⎨=++++⎪⎪=++++⎩ 2.13 将下列逻辑函数化简为最简与－或表达式，并用与非门实现。

(2) Y AB A C BC CD =+++解：由逻辑函数作卡诺图，得最简与－或表达式，再变换为与－非形式。

C题2.12（2）Y A B D C A B D C A B D C=++=++=ABCDY题2.12(2) 图(3) Y AB BC ABC ABCD=+++解：(1)(1) AB C BC AD AB BC AB BC AC ABC BC ABC BBC ABC BBC=+++=+=++=+=+=⋅A BC YABC解二：题2.13(3) 图2.14用卡诺图判别逻辑函数Y 和Z之间的关系。

(3) Y AB ACD AD D Z AB D=+++=+解：由逻辑函数作卡诺图，如图所示：D2.13Z由卡诺图知逻辑函数Y 和Z恒等。

2.15 已知下列逻辑函数，试用卡诺图分别求出121212,Y Y Y Y Y Y+⊕和12(,,)(0,1,3)(1)(,,)(0,4,5,7)Y A B CmY A B C m⎧=⎪⎨=⎪⎩∑∑解：由逻辑函数作出卡诺图，如图所示，并化简得：题2.14(1)YY11Y 1得:121212Y Y B CY Y ABCY Y AB C⎧+=+⎪⎪=⎨⎪⊕=+⎪⎩补充例子：用公式法化简下列逻辑函数为最简与—或式：1()F A B AB AB AB BAB AB AB BAB AB B B AB B A=⊕++⋅=++=++=+=+2()()()()()()()()()F A B C A B C ABC BD BC DCE A BC A B C A B C BD B C A AB AC ABC BC A B C BD BC A BC A B C BD BC A AB AC ABC BC BD BC A BC BD BC A B BD A B D=++++++=+++++++=++++++++=+++++=++++++=+++=++=++3()()()()F AC BD BCD ABC A C BC B D CD A C B B C D AC AB BD BC AB BD BC=+++=+++=+++=+++=++41F ABCD BC AB AC BC BCD ABC ABD B AB AC BCD ABC ABD A B A C BCD ABC ABD A B BCD A BC BD B CD A C D B CD A B C D C D =+++++=+++++=+++++=++++=++++=++++=+++++=用卡诺图化简下列逻辑函数为最简与 — 或式：1F AC BD BCD ABC =+++解：1F AB BD BC =++2F ACD BCD BD BCD =+++解：2F AC D =+3(,,,)(3,6,8,9,11,12,13)F A B C D m ABC ABD ABC ⎧=⎪⎨++=⎪⎩∑约束条件 解：3F AC BD BCD =++4(,,,)(0,1,2,3,4,6,8)F A B C D m AB AC ⎧=⎪⎨+=⎪⎩∑约束条件 解：4F D AB =+。