数字逻辑电路(A)》复习题逻辑代数基础
- 格式:doc
- 大小:99.00 KB
- 文档页数:3

《数字逻辑电路》试题一一、填空题1.()10=()2=()8=()16。
2.()2=()10。
3.()10=( ) 8421-BCD。
4.A⊕0= 。
5.大体门电路包括、、。
6.A⊙B= 。
7.N各逻辑变量组成某个逻辑函数,那么其完整的真值表应有种不同的组合。
8.数字逻辑电路包括两类,别离是电路和电路。
9.JK触发器的特性方程是。
10.任何时刻,电路的输出,不仅与该时刻电路的输入有关,而且还与电途经去的输入有关的电路,称为电路。
11.F(A,B,C,D)=CD,它包括了个最小项。
12.A(A+B)= 。
13.F=AB+AC,这种形式的逻辑函数表达式称为。
14.F=A·B·A·C这种形式的逻辑函数表达式称为。
15.有18个信息需用二进制代码来表示它们,那么最少需要位二进制。
16.与将JK触发器作成T’(翻转)触发器,应使其J= , K= 。
17.设计一个25进制计数器,最少需要个触发器。
二、选择题1.已知字符T的ASCII码值的十进制数表示为84,若是将最高位设置为奇校验位,那么字符T的ASCⅡ码值设置奇校验位后,它的二进制表示为( )A 01001101B 11001101C 01101011 D2. 以下个数中最大的是()A (.0101) 2B 16C 10 C 83. 在一个逻辑电路中,有两个输入信号X、Y和一个输出信号V。
当且仅当X=一、Y=0时,V=0,那么V的逻辑表达式为()A X+YB X·YC X·YD X+Y4. A·A·B·B·C=( )A ABC C 1D 05. A+BC+AB+A=( )A AB AC 1D 06. F(A,B,C)=ABC+ABC+ABC=( )A ∑m(0,2,4)B ∑m(3,5,7)C ∑m(1,3,5)D ∑m(4,5,7)7. A⊕B=( )A AB+ AB B AB + ABC A BD A B8. 对正逻辑而言,某电路是与门,那么对负逻辑而言是()A 与门B 与非门C 或非门D 或门触发器在同步工作时,假设现态Q n=0,要求抵达次态Q n+1=1,那么应使JK=( )A 00B 01C 1XD X110.图(1)中要求输出F=B,那么A应为( )A 0B 1 A =1 FC B BD B 图(1)三、化简以下函数表达式一、代数化简:Y=(AB+A B+A B)(A+B+D+A B D)二、Y=AB+A B+A B3、卡诺图化简:F=(A,B,C,D)=∑m(0,1,2,3,4,6,8,9,10,11,12,14)四、芯片的应用1.别离用74138和74153实现逻辑函数表达式F=AB+BC+AC2.用1.用与非门设计一个组合电路,用来检测并行输入的四位二进制数B4B3B2B1当其值大于或等于5时,输出F=1,反之F=0。

一、填空题(共15空,每空2分,共30分)1.二进制数(1110.0111)2对应的等值十六进制数为____E.7_______。
2. 十进制数 -13的8位二进制补码为____11110011________。
3.与普通二进制代码相比,格雷码最大优点是相邻两个代码之间有___1_____位发生变化。
4. 逻辑表达式''=++()Y AB C D 的反演式为(())Y A B C D '''''=+。
5. 若使JK 触发器的J=K ,构成的新触发器称为____T_____触发器。
6. 基本RS 触发器的约束条件是_____RS=0____。
7. 写出两个逻辑变量A 、B 的全部最小项,,,AB A B AB A B ''''。
8. 三态门逻辑符号如下图,写出输出Y 与输入A 和EN '之间的关系01A E N Y EN ''=⎧=⎨'=⎩高阻态。
9. 下图所示由T 触发器构成的电路中,初始状态为Q=0,写出在连续4个时钟信号作用下,Q 的4个输出结果依次为___1 0 1 0____。
8题图 9题图10.如下面真值表所示,写出Y 与A 、B 逻辑表达式的最简与或形式:Y(A,B)=+A B ''。
11.8线-3线优先编码器输入为I 0-I 7,当优先级别最高的I 7有效时,输出210Y Y Y '''=__000__。
12.一个四输入端或非门,使其输出为1的输入变量取值组合有__15___种。
13.四位左移寄存器预置1011,其串行输入端固定接0,在2个移位脉冲作用下,得新的四位数据为__1100__。
14. A/D 转换过程中,量化级越多,电路越复杂,转换精度越__高___。
15. 若10位D/A 转换器的V REF =-10V ,输入数字量最高位为1,其它位均为0,求输出模拟电压值___5V___。



逻辑代数基础复习题本页仅作为文档封面,使用时可以删除This page is only the cover as a document 2021year一. 填空题1.最基本的逻辑门有____门、_____门和_____门。
2.对于二值逻辑问题,若输入变量为n 个,则完整的真值表有_____种不同输入组合。
3.实现下列数制的转换:[14]10= [ ]2,[10110]2 = [ ]10,[2E]16=[ ]10。
4.A+A=________,A + 1=_______,A + (A + B)=________。
5.“或非”门用作“非门”时,不用的输入端可_______,“与非”门用作“非门”时,不用的输入端可_______。
(填“接地”或“接高电平”)用 表示高电平,用 表示低电平的赋值方法叫负逻辑。
A A + = 、A A ⊕= 。
逻辑代数的吸收律有:A + AB = ;A += 。
B A 一个逻辑门,当只有全部输入都是高电平时,输出才是低电平,该逻辑门是 ;当只有全部输入都是低电平时,输出才是高电平,该逻辑门是 。
逻辑函数Z AB AB =+中,当A =0,B =0时,Z =____________;当A =1,B =1时,Z =________________。
第1小题逻辑代数的三种基本运算是_____________、____________和___________。
第 2小题设A和B为两个二进制数,并且A=1,B=1,则A+B=_______。
若A和B是两个逻辑变量,并且A=1,B=1,则A+B=_________。
第 3小题设A为逻辑变量,则=•A A ______,A A +=_______,=⊕A A ______, =⊕A A ______。
根据逻辑代数的吸收律:(A+B )(A+B+C+D )= 。
C B C AB C A ++的最简表达式为 。
设A和B为两个二进制数,并且A=1,B=1,则A+B=_______。

一. 单项选择题1、要使JK 触发器在时钟作用下的次态与现态相反,J\K 端取值应为( )。
A. J=K=0B. J=0,K=1C. J=1,K=0D. J=K=1 2、已知74LS138译码器的输入三个使能端均有效时,地址码(A2为高位,A0为低位)A2A1A0=111,则输出Y0-Y7是( )。
A . 10111111 B .11011111 C .11101111 D .11111110 3、下列触发器中,克服了空翻现象的有( )。
A.边沿D 触发器B.钟控RS 触发器C.基本RS 触发器D.钟控JK 触发器 4、电平异步时序逻辑电路,不允许两个或两个以上输入信号( )。
A.同时为1 B. 同时为0 C. 同时改变 D.同时出现 5、边沿D 触发器是时钟脉冲CP 的( )触发的。
A .下降沿B .上升沿C .高电平D .低电平6、某计数器的状态转换图如下,其计数的容量为( )A .5 B. 6 C .7 D. 87、组合电路通常由( )组成。
A .逻辑门电路B .触发器C .计数器 8、在何种输入情况下,“与非”运算的结果式逻辑“0”( ) A .全部输入是“0” B .任意输入是“0” C .仅一输入是“0”D .全部输入是“1” 9、最大项和最小项的关系是( )A .i i m M =B .=i i m MC .1i i m M ⋅=D .无关系 10、在四变量卡诺图中,逻辑上不相邻的一组最小项为( )。
A. m1与m3B.m4与m6C. m5与m13D. m2与m8 11、下列集成电路芯片中,( )属于时序逻辑电路。
A .译码器B .寄存器C .编码器D .选择器 12、设计一个9进制同步计数器,至少需要( )个触发器。
A .4B .5C .6D .1813、若4位异步二进制减法计数器当前的状态是1110,下一个输入时钟脉冲后,其内容变为( )。
A .1100B .1101C .1110D .111114、函数F(A,B,C)=AB+BC+AC 的最小项表达式为( )。

数字逻辑电路复习题1、数制与编码(-21)10 =( )10补(78.8)16=( )10(0.375)10=( )2(65634.21)8=( )16(121.02)16=( )4(49)10 =( )2=( )16(-1011)2 =( )反码=( )补码四位二进制数1111的典型二进制格林码为( )2、化简逻辑函数F (A 、B 、C 、D )=∏M (0、2、5、7、8、10、13、15)。
3、说明同步时序逻辑电路的分析步骤。
4、说明什么是组合逻辑电路。
5、说明什么是Moore 型时序逻辑电路。
6、完成下列代码之间的转换:(1)(0101 1011 1101 0111.0111)8421BCD =( )10;(2)(359.25)10=( )余3;(3)(1010001110010101)余3=( )8421BCD 。
7、试写出下列二进制数的典型Gray 码:101010,10111011。
8、用逻辑代数公理和定理证明:①C B A ⊕⊕=A ⊙B ⊙C②)B A (⊕⊙B A AB = ③C AB C B A C B A ABC A ++=⋅ ④C A C B B A C A C B B A ++=++ ⑤1B A B A B A AB =+++9、将下列函数转化成为最小项表达式和最大项表达式①F (A 、B 、C 、D )=)D C )(C B A )(B A )(C B A (++++++②F (A 、B 、C )=C A C B A BC A C AB +++③F (A 、B 、C 、D )=)B AC )(C B (D D BC ++++④F (A 、B 、C 、D )=ABCD D C B A D B A B C +++10、利用卡诺图化简逻辑函数F (A 、B 、C 、D )=4m (10,11,12,13,14,15)∑ 11、将下列函数简化,并用“与非”门和“或非”门实现该电路并判断有无竞争冒险现象,并予以消除。


第1章 逻辑代数基础一、选择题(多选题)1.以下代码中为无权码的为 。
A. 8421BCD 码B. 5421BCD 码C. 余三码D. 格雷码2.一位十六进制数可以用 位二进制数来表示。
A. 1B. 2C. 4D. 163.十进制数25用8421BCD 码表示为 。
A.10 101B.0010 0101C.100101D.101014.与十进制数(53.5)10等值的数或代码为 。
A.(0101 0011.0101)8421BCDB.(35.8)16C.(110101.1)2D.(65.4)85.与八进制数(47.3)8等值的数为:A. (100111.011)2B.(27.6)16C.(27.3 )16D. (100111.11)26.常用的B C D 码有 。
A.奇偶校验码B.格雷码C.8421码D.余三码7.与模拟电路相比,数字电路主要的优点有 。
A.容易设计B.通用性强C.保密性好D.抗干扰能力强8. 逻辑变量的取值1和0可以表示: 。
A.开关的闭合、断开B.电位的高、低C.真与假D.电流的有、无9.求一个逻辑函数F 的对偶式,可将F 中的 。
A .“·”换成“+”,“+”换成“·”B.原变量换成反变量,反变量换成原变量C.变量不变D.常数中“0”换成“1”,“1”换成“0”E.常数不变10. A+BC= 。
A .A +B B.A +C C.(A +B )(A +C ) D.B +C11.在何种输入情况下,“与非”运算的结果是逻辑0。
A .全部输入是0 B.任一输入是0 C.仅一输入是0 D.全部输入是112.在何种输入情况下,“或非”运算的结果是逻辑0。
A .全部输入是0 B.全部输入是1 C.任一输入为0,其他输入为1 D.任一输入为113.以下表达式中符合逻辑运算法则的是 。
A. C ·C =C 2B.1+1=10C.0<1D.A +1=114. 当逻辑函数有n 个变量时,共有 个变量取值组合?A. nB. 2nC. n 2D. 2n15. 逻辑函数的表示方法中具有唯一性的是 。

逻辑代数基础试题及答案1. 逻辑代数中,与运算的符号是什么?答案:与运算的符号是“∧”。
2. 逻辑代数中,或运算的符号是什么?答案:或运算的符号是“∨”。
3. 逻辑代数中,非运算的符号是什么?答案:非运算的符号是“¬”。
4. 逻辑代数中,异或运算的符号是什么?答案:异或运算的符号是“⊕”。
5. 逻辑代数中,同或运算的符号是什么?答案:同或运算的符号是“≡”。
6. 逻辑代数中,如何表示变量A和变量B的与运算?答案:变量A和变量B的与运算表示为“A∧B”。
7. 逻辑代数中,如何表示变量A和变量B的或运算?答案:变量A和变量B的或运算表示为“A∨B”。
8. 逻辑代数中,如何表示变量A的非运算?答案:变量A的非运算表示为“¬A”。
9. 逻辑代数中,如何表示变量A和变量B的异或运算?答案:变量A和变量B的异或运算表示为“A⊕B”。
10. 逻辑代数中,如何表示变量A和变量B的同或运算?答案:变量A和变量B的同或运算表示为“A≡B”。
11. 在逻辑代数中,德摩根定律是什么?答案:德摩根定律包括两个部分,即(¬A)∨(¬B) = ¬(A∧B)和 (¬A)∧(¬B) = ¬(A∨B)。
12. 逻辑代数中,如何证明A∧(A∨B) = A?答案:根据分配律,A∧(A∨B) = (A∧A)∨(A∧B)。
由于A∧A = A,所以表达式简化为A∨(A∧B)。
由于A∨A = A,最终表达式简化为A。
13. 逻辑代数中,如何证明A∨(¬A∧B) = A∨B?答案:根据分配律,A∨(¬A∧B) = (A∨¬A)∧(A∨B)。
由于A∨¬ A = 1(真),表达式简化为1∧(A∨B)。
由于任何变量与1的与运算结果都是该变量本身,最终表达式简化为A∨B。
14. 逻辑代数中,如何证明A∧(¬A∨B) = ¬A∨B?答案:根据分配律,A∧(¬A∨B) = (A∧¬A)∨(A∧B)。

一、选择填空题1、下列四个数中与十六进制数(63)16相等的是( B)A. (100)10B. (01100011)2C. (01100011)8421BCDD. (100100011)82、十进制数118对应的2进制数为( D)A. (1010110)2B. (1111000)2C. (1110111)2D. (1110110)23、下列等式不成立的是( C )A. A+A B=A+BB. A+AB=AC. AB+A C+BC=AB+BCD. A B+BA+AB+A B=14、以下说法中,______是正确的。
( A)A. 一个逻辑函数全部最小项之和恒等于1B. 一个逻辑函数全部最小项之和恒等于0C. 一个逻辑函数全部最小项之积恒等于1D. 一个逻辑函数中任意两个不同的最小项之积恒等于15、下列电路中,不属于组合逻辑电路的是( C)A.编码器B.全加器C.寄存器D.译码器6、由或非门构成的同步RS触发器,输入S、R的约束条件是( D)A.SR=0B.SR=1C.S+R=0D.S+R=17、T触发器,在T=1时,加上时钟脉冲,则触发器( D)A.保持原态B.置0C.置1D.翻转8、F=A(A+B)+B(B+C+D)=( A)A.BB.A+BC.1D.C9、一个8选一数据选择器的数据输入端有_______个。
( C)A.1B.2C.8D.410、同步时序电路和异步时序电路比较,其差异在于后者( B )A.没有触发器B.没有统一的时钟脉冲控制C.没有稳定状态D.输出只与内部状态有关11、欲使D触发器按Q n+1=Q工作,应使输入D=( D )nA.0B.1C.QD.Q12、[10101]2转换为十进制数是(C)A.11B.15C.21D.2513、不是最小项ABCD 逻辑相邻的最小项是( C ) A.A BCD B.A B CD C.A B C D D.AB C D14、.用8-3线编码器扩展成16-4线需要的数量是( B )A.1片B.2片C.3片D.4片15、全加器的输入全为“1”时,和数输出端输出是( B )A. 0B. 1C. 10D. 1116、要使D 触发器输出保持“0”可以设定( A )A.D=0B.D=1C.D=QD.D=Q17、对于触发器和组合逻辑电路,以下(D )的说法是正确的。


数字逻辑复习题 *红色表示知识点说明文字01数制码制和逻辑代数533多选题341.下列BCD码中有权码有( )。
A.8421BCD B.余3BCDC.5211BCD D.格雷(循环)码\\AC2.下列BCD码中无权码有( )。
A.8421BCD B.余3BCDC.5211BCD D.格雷(循环)码\\BD3.下列二进制数中是奇数的有( )。
A.0001 B.0000C.1 D.101\\ACD4.下列8421BCD码中是偶数的有( )。
A.0 B.0C.0 D.0001\\BC5.下列十六进制数中是奇数的有( )。
A.37F B.2B8C.34E D.FF7\\AD6.下列十六进制数中是偶数的有( )。
A.37F B.2B8C.34D D.F3E\\BD7.比十进制数大的数是( )。
A.二进制数 B.8421BCD码C.八进制数 D.十六进制数\\AC8.比十进制数10D小的数是( )。
A.十六进制数10H B.二进制数10BC.8421BCD码00010000 D.八进制数10Q\\BD9.5211BCD码的特点是( )。
A.具有逻辑相邻性 B.具有奇偶校验特性C.是一种有权码 D.按二进制数进行计数时自动解决了进位问题\\CD10.余3BCD码的特点是( )。
A.当作二进制码看比等值的8421BCD码多3 B.是一种有权码C.按二进制进行加法时自动解决了进位问题 D.具有逻辑相邻性\\AC11.格雷(循环)码的特点是( )。
A.逻辑相邻 B.折叠性C.是一种有权码 D.反射性\\ABD12.下列二进制数中能被4整除的有( )。
A.000 B.0000C. D.101\\AC13.下列十六进制数中能被4整除的有( )。
A.37C B.2B8\\AB14.下列八进制数中能被4整除的有( )。
A.3732 B.3614C.5216 D.6710\\BD15.下列十六进制数中能被8整除的有( )。
A.37C0 B.2B7C.348 D.F3E\\AC16.下列代码中那些属于BCD码( )。

数字逻辑概论与逻辑代数一、选择题:1、是8421BCD 码的是( )A. 0101B. 1010C. 1100D. 11112、=++++B A A C B A ( )A. 1B. AC. AD. A+B+C3、欲对全班53个学生以二进制代码表示,至少需要二进制码的位数是( ) A. 6 B. 5 C. 10 D. 534、在数字电路中,晶体管的工作状态为:( )A.饱和或截止;B.放大;C.饱和或放大;D. 饱和; 5、以下式子中不正确的是( )A .B A B A +=+ B . A A A +=C . 1A A •=D . 11A += 6、在数字电路中,稳态时三极管一般工作在( )状态。
在图示电路中,若0i u <,则三极管T ( ),此时uo =( )A .开关,截止,3.7VB .放大,截止,5VC .开关,饱和,0.3VD .开关,截止,5V7、N 个变量可以构成( )个最小项。
A . 2NB . 2NC 、ND 、 2N -1 8、数字电路中的工作信号为( )。
A . 脉冲信号 B . 随时间连续变化的电信号 C .直流信号 D .模拟信号 9、下列等式不成立的是( )A. AB+AC+BC=AB+BCB. (A+B)(A+C)=A+BCC. A+AB=AD. 1=+++B A AB B A B A 10、和二进制数(1100110111)2等值的十六进制数是( )。
A. (337)16B. (637)16C. (1467)16D. (C37)16 11、逻辑函数F=A ⊕(A ⊕B)=( )A.BB.AC.A ⊕BD.A ⊙B12、下面描述逻辑功能的方法中,具有唯一性的是( ) A. 真值表 B. 逻辑函数表达式 C.波形图 D.逻辑图13、最小项D C AB 逻辑相邻项是( )A.ABCDB.D BC AC.D C B AD.CD B A14、若逻辑表达式F A B =+,则下列表达式中与F 相同的是( )A.F AB =B.F AB =C. F A B =+D.不确定15、以下代码中为无权码的为( )。

逻辑代数基础一、选择题 ( 多项选择 )1. 以下表达式中符合逻辑运算法则的是。
2+1 = 10 C. 0 < 1+ 1 = 1· C= C2.逻辑变量的取值1和0可以表示:。
A. 开关的闭合、断开B.电位的高、低C. 真与假D.电流的有、无3.当逻辑函数有n 个变量时,共有个变量取值组合?A. nB.2nC.n 2D. 2 n4.逻辑函数的表示方法中具有唯一性的是。
A . 真值表 B.表达式 C.逻辑图 D.卡诺图=A B +BD+CDE+A D=。
(加一个盈余项AD)A. AB DB.( A B) DC.( A D)( B D )D. (A D )(B D)6. 逻辑函数 F= A( A B)=。
C. A BD.A B7.求一个逻辑函数 F 的对偶式,可将 F 中的。
A . “·”换成“ +”,“ +”换成“·”B. 原变量换成反变量,反变量换成原变量C. 变量不变D. 常数中“ 0 ”换成“ 1 ”,“ 1 ”换成“ 0 ”E. 常数不变8. A+BC=。
A . A+ B+C C.( A+ B)( A+ C)+ C9 .在何种输入情况下,“ 与非”运算的结果是逻辑 0 。
DA .全部输入是 0 B.任一输入是 0 C.仅一输入是 0 D.全部输入是 11 0 .在何种输入情况下,“ 或非”运算的结果是逻辑 0。
A .全部输入是 0 B.全部输入是 1 C. 任一输入为0,其他输入为 1 D. 任一输入为 1二、判断题(正确打√,错误的打×)1.逻辑变量的取值,1比0大。
(× )。
2.异或函数与同或函数在逻辑上互为反函数。
(√ )。
3.若两个函数具有相同的真值表,则两个逻辑函数必然相等。
(× )。
4.因为逻辑表达式A+B+AB=A+B成立,所以AB=0成立。
(×)5.若两个函数具有不同的真值表,则两个逻辑函数必然不相等。
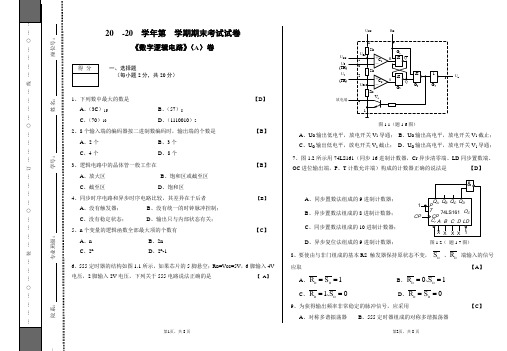
第1页,共8页第2页,共8页院系: 专业班级: 学号: 姓名: 座位号:20 -20 学年第 学期期末考试试卷《数字逻辑电路》(A )卷一、选择题(每小题2分,共20分)1、下列数中最大的数是 【D 】 A 、(3C )16 B 、(57)8C 、(70)10D 、(1110010)22、8个输入端的编码器按二进制数编码时,输出端的个数是 【B 】 A 、2个 B 、3个C 、4个D 、8个3、逻辑电路中的晶体管一般工作在【B 】A 、放大区B 、饱和区或截至区C 、截至区D 、饱和区4、同步时序电路和异步时序电路比较,其差异在于后者 【B 】 A 、没有触发器; B 、没有统一的时钟脉冲控制; C 、没有稳定状态; D 、输出只与内部状态有关;5、n 个变量的逻辑函数全部最大项的个数有 【C 】 A 、n B 、2n C 、2nD 、2n -16、555定时器的结构如图1.1所示,如果芯片的5脚悬空;RD =V CC =5V ,6脚输入4V 电压,2脚输入2V 电压,下列关于555电路说法正确的是 【 A 】U CC U CO U 6(TH)(TR)U oR D U 2放电端图1.1(题1.6图)A 、U O 输出低电平,放电开关V 1导通;B 、U O 输出高电平,放电开关V 1截止;C 、U O 输出低电平,放电开关V 1截止;D 、U O 输出高电平,放电开关V 1导通; 7、图1.2所示用74LS161(同步16进制计数器,Cr 异步清零端、LD 同步置数端、OC 进位输出端,P 、T 计数允许端)构成的计数器正确的说法是 【D 】A 、同步置数法组成的9进制计数器;B 、异步置数法组成的8进制计数器;C 、同步置数法组成的10进制计数器;D 、异步复位法组成的9进制计数器; 图1.2( 题1.7图) 8、要使由与非门组成的基本RS 触发器保持原状态不变,D S 、D R 端输入的信号应取 【A 】 A 、1==D D S RB 、10==D D S R 、C 、01==D DS R 、 D 、0==D D S R9、为获得输出频率非常稳定的脉冲信号,应采用 【C 】A 、对称多谐振荡器B 、555定时器组成的对称多谐振荡器第3页,共8页第4页,共8页装订线内不许答题 C 、石英晶体振荡器 D 、单稳态触发器 10、下列关于TTL 与非门闲置输入端的处理不正确的是 【D 】 A 、直接接电源电压VccB 、与有用输入端并联使用C 、外界干扰小时,可以剪断或悬空D 、直接接地1、二进制数-110011的补码是 1001101 。


数字逻辑电路试题及答案一、填空题(每空1分,共10分)1.数字电路分为两大类,分别是组合逻辑电路和时序逻辑电路。
2.2006个1连续异或的结果是__0___;而2007个1连续同或的结果是__1__.3.已知某函数F的反函数为,则其原函数F= ;而F的对偶函数则为F*= 。
4.试将函数,写成标准的积之和形式,即(0,1,2,4,5,6,8,9,10 ).5.逻辑代数中的三种基本逻辑运算是与、或、非。
6.1个触发器可以存放 1 位二进制数,它具有记忆功能。
二、选择题(每小题2分,共10分)1.已知某电路的输入A、B和输出Y的波形如下图所示,该电路实现的函数表达式为 D 。
(A)A⊙B (B)A?B(C) (D)2.用0,1两个符号对100个信息进行编码,则至少需要 B 。
(A)8位(B) 7位(C) 9位(D) 6位3.下列电路中属于组合电路的是 D 。
(A)集成触发器(B)多谐振荡器(C)二进制计数器(D)3—8译码器4.下列电路中只有一个稳定状态的是 C 。
(A)集成触发器(B) 施密特触发器(C)单稳态触发器(D) 多谐振荡器5.为产生周期性矩形波,应当选用 C 。
(A) 施密特触发器(B) 单稳态触发器(C) 多谐振荡器 (D) 译码器三、逻辑函数化简(共10分)用卡诺图法化简下列逻辑函数,结果为最简与或式。
(每题5分,共10分) .解:四、分析题(共45分)1.(本题10分)写出下图的逻辑表达式和真值表,并化简为最简与或表达式。
⒉列真值表:(2分)2. (本题10分)试对已给器件,在所示输入波形CP、D、及作用下,画其输出波形Q及.假设电路初态Q(0)=1,且不计传输延迟解:3.(本题10分) 试分析图示时序电路,列出状态转换表及全状态转换图,说明电路功能,并分析能否自启动,设初始状态为00。
解:⑴写激励方程(2分) J1=Q0n,,K1=K0=1,⑵写状态方程(2分) ,)⑶列全状态转换表(2分) ⑷画全状态转换图(2分⑸功能(2分):该电路为一个三进制同步计数器,并且具有自启动功能。
逻辑代数基础
一、选择题(多项选择)
1. 以下表达式中符合逻辑运算法则的是 。
·C =C 2 +1=10 C.0<1 +1=1
2. 逻辑变量的取值1和0可以表示: 。
A.开关的闭合、断开
B.电位的高、低
C.真与假
D.电流的有、无
3. 当逻辑函数有n 个变量时,共有 个变量取值组合
A. n
B. 2n
C. n 2
D. 2n
4. 逻辑函数的表示方法中具有唯一性的是 。
A .真值表 B.表达式 C.逻辑图 D.卡诺图 =A
B +BD+CDE+A D= 。
(加一个盈余项AD ) A.D B A + B.D B A )(+ C.))((D B D A ++ D.))((D B D A ++
6.逻辑函数F=)(B A A ⊕⊕ = 。
C.B A ⊕
D. B A ⊕
7.求一个逻辑函数F 的对偶式,可将F 中的 。
A .“·”换成“+”,“+”换成“·”
B.原变量换成反变量,反变量换成原变量
C.变量不变
D.常数中“0”换成“1”,“1”换成“0”
E.常数不变
8.A+BC= 。
A .A +
B +
C C.(A +B )(A +C ) +C
9.在何种输入情况下,“与非”运算的结果是逻辑0。
D
A .全部输入是0 B.任一输入是0 C.仅一输入是0 D.全部输入是1
10.在何种输入情况下,“或非”运算的结果是逻辑0。
A .全部输入是0 B.全部输入是1 C.任一输入为0,其他输入为1 D.任一输入为1
二、判断题(正确打√,错误的打×)
1. 逻辑变量的取值,1比0大。
( × )。
2. 异或函数与同或函数在逻辑上互为反函数。
( √ )。
3.若两个函数具有相同的真值表,则两个逻辑函数必然相等。
( × )。
4.因为逻辑表达式A+B+AB=A+B 成立,所以AB=0成立。
( × )
5.若两个函数具有不同的真值表,则两个逻辑函数必然不相等。
( √ )
6.若两个函数具有不同的逻辑函数式,则两个逻辑函数必然不相等。
( × )
7.逻辑函数两次求反则还原,逻辑函数的对偶式再作对偶变换也还原为它本身。
( √ )
8. 因为逻辑表达式A B +A B +AB=A+B+AB 成立,所以A B +A B= A+B 成立。
( × )
三、填空题
1. 逻辑代数又称为 代数。
最基本的逻辑关系有 、 、 三种。
常用的几种复合逻辑运算为 、 、 、 、 。
2. 逻辑函数的常用表示方法有 、 、 。
3. 逻辑代数中与普通代数相似的定律有 、 、 。
摩根定律又称为 。
4. 逻辑代数的三个重要规则是 、 、 。
5.逻辑函数F=A +B+C D 的反函数F = A B (C+D ) 。
6.逻辑函数F=A (B+C )·1的对偶函数是 A+BC+0 。
7.添加项公式AB+A C+BC=AB+A C 的对偶式为 。
8.逻辑函数F=A B C D +A+B+C+D= 。
9.逻辑函数F=AB B A B A B A +++= 。
10.已知函数的对偶式为B A +BC D C +,则它的原函数为 。
四、思考题
1. 逻辑代数与普通代数有何异同
2. 逻辑函数的三种表示方法如何相互转换
3. 为什么说逻辑等式都可以用真值表证明
4. 对偶规则有什么用处
第二章答案
一、选择题
1. D
2. ABCD
3. D
4. AD
5. AC
6. A
7. ACD
8.C
9.D
10.BCD
二、判断题
1.×
2.√
3.√
4.×
5.√
6.×
7.√
8.×
三、填空题
1.布尔与或非与非或非与或非同或异或
2.逻辑表达式真值表逻辑图
3.交换律分配律结合律反演定律
4.代入规则对偶规则反演规则
5.A B(C+D)
6.A+BC+0
7.(A+B)(A+C)(B+C)=(A+B)(A+C)
8.1
9.0
10.)
•
+
A+
B
+
•
(
)
(C
B
D
C
四、思考题
1.都有输入、输出变量,都有运算符号,且有形式上相似的某些定理,但逻辑代数的取值只能有0和1两种,而普通代数不限,且仅有逻辑含义,无数值大小,运算符号所代表的意义也不同。
2.通常从真值表容易写出标准最小项表达式,从逻辑图易于逐级推导得逻辑表达式,从与或表达式或最小项表达式易于列出真值表。
3.因为真值表具有唯一性。
4.可使公式的推导和记忆减少一半,有时可利于将或与表达式化简。