江苏省靖江市新港城初级中学九年级数学双休日作业(11.2811.29)(无答案) 苏科版

九年级数学家庭作业（11.23）班级 姓名1.△ABC 中，a 、b 、c 分别是∠A、∠B、∠C 的对边，如果a 2+b 2=c 2，那么下列结论正确的是（ ） A ．bcosB=cB ．csinA=aC ．a tanA=bD ．2.在Rt△ABC 中，∠C=90°，sinA=，则cosB 等于（ ） A ． B ．C ．D ．3.如果∠A 为锐角，且sinA=0.6，那么（ ）A ．0°＜A≤30°B ．30°＜A ＜45°C ．45°＜A ＜60°D ．60°＜A≤90°4. 已知直角三角形ABC 中，斜边AB 的长为m ，40B ∠=，则直角边BC 的长是（ ）A ．sin 40mB ．cos 40mC ．tan 40mD ．tan 40m5.在Rt △ABC 中，∠C=90°，AC=5，BC=12，则sinA=_______，tanB=_______.6.如图，正方形ABCD 的边长为4，点M 在边DC 上，M 、N 两点关于对角线AC 对称，若DM =1，则tan ∠ADN = ．7.在同一时刻两根木竿在太阳光下的影子如图所示，其中木竿AB=2m ，它的影子BC=1.6m ，木竿PQ 的影子有一部分落在了墙上，PM=1.2m ，MN=0.8m ，则木竿PQ 的长度为________m ．（6） （7） （8） 8.如图，在△ABC 中，AB=AC=5，BC=8．若∠BPC=∠BAC ，则tan ∠BPC= ． 9.如图，已知△ABC 是面积为的等边三角形，△ABC∽△ADE，AB=2AD ，∠BAD=45°，AC 与DE 相交于点F ，则△AEF 的面积等于________（结果保留根号）．10.（1）22160cos 2)12015(-⎪⎭⎫ ⎝⎛-+-（2）已知23)10sin(=︒-α，求α。

九年级数学双休日作业（2015.10.17-10.18）一、选择题：1、方程322-=x x 的根的情况是 ( ) A ．有一个实数根 B ．有两个相等的实数根 C ．有两个不相等的实数根 D ．没有实数根2、若⊙O 的直径为6cm ，OA=5 cm ，那么点A 与⊙O 的位置关系是 ( ) A ．点A 在圆外 B. 点A 在圆上 C.点A 在圆内 D.不能确定3、下列四个命题：①直径是弦；②经过三个点一定可以作圆；③三角形的外心到三角形各顶点的距离都相等；④半径相等的两个半圆是等弧。

其中正确的有 ( ) A ．4个 B ．3个 C ．2个 D ．1个4、如图，⊙O 是△ABC 的外接圆，连结OA 、OB ，且点C 、O 在弦AB 的同侧，若∠ABO=50°， 则∠ACB 的度数为 ( ) A ．50° B ．45° C ．30° D ．40°5、已知Rt △ABC 中，∠C=90°，AC=3，BC=4，以C 为圆心，r 为半径的圆与边AB 有两个交点，则r 的取值范围是 ( ) A ．512=r B ．512>r C ．3＜r ＜4 D ．3512≤<r 6、如图，∠BAC=∠DAF=90°，AB=AC ，AD=AF ，点D 、E 为BC 边上的两点，且∠DAE=45°，连接EF 、BF ，则下列结论：①△AED ≌△AEF ；②△ABE ∽△AC D ；③BE+DC ＞DE ；④BE2+DC2=DE2，其中正确的有（ ）个．A. 1B.2C.3D.4第4题 第6题 二、填空题7、已知一元二次方程0342=--xx的两根分别为1x,2x，则12x x+=．8、一元二次方程x2=2x的解是9、方程x2﹣9x+18=0的两个根是等腰三角形的底和腰，则这个等腰三角形的周长为10、如图，四边形ABCD是⊙O的内接四边形，若∠BOD=80°，则∠BCD的度数是__ ___11、如图，在Rt△ABC内有边长分别为a，b，c的三个正方形，则a，b，c满足的关系式为12、如图，在△ABC中，60BAC∠=︒，90ABC∠=︒，直线1l//2l//3l，1l与2l之间距离是1，2l与3l 之间距离是2．且1l，2l，3l分别经过点A， B，C，则边AC的长为．第10题第11题第12题13、点M,N是线段AB的黄金分割点，若AB=10cm，则MN等于cm．14、如图，一条排水管的截面如图所示，已知排水管的半径1OA m=，水面宽 1.2AB m=，某天下雨后，水管水面上升了0.2m，则此时排水管水面宽CD等于m.15、如图，AB是⊙O的直径，AB=16，点M在⊙O上，∠MAB=30°,N是弧MB的中点,P是直径AB上的一动点，若MN=2，则△PMN周长的最小值为 _____16、如图，AB为⊙O的直径，AC交⊙O于E点，BC交⊙O于D点，CD=BD，∠C=70°．现给出以下四个结论：①∠A=45°；②AC=AB；③AE=BE；④CE•AB=2BD2．其中正确结论的序号是__________．第14题 第15题 第16题 三、解答题 17.解方程：（1）4x 2－2x －1=0 （2）22)25(96x x x -=+-18、先化简，再求值：11)213(2+÷-+-x x x ，其中x 满足x 2-2x -4=019、如图，BD 为平行四边形ABCD 的对角线，O 为BD 的中点，EF⊥BD 于点O ，与AD 、BC 分别交于点E 、F ．求证：DE=DF ．20、商场某种商品平均每天可销售30件，每件盈利50元，为了尽快减少库存，商场决定采取适当的降价措施，经调查发现，每件商品每降价1元，商场每天可多售出2件，设每件商品降低x 元据此规律，请回答：（1）商场日销售量增加__________件，每件商品盈利__________元（用含x 的代数式表示） （2）在上述条件不变，销售正常的情况下，每件商品降价多少元时，商场日盈利可达到2100元？N M ABOC 21、已知：△ABC 的两边AB 、AC 的长是关于x 的一元二次方程x 2﹣（2k+3）x+k 2+3k+2=0的两个实数根，第三边BC 的长为5．（1）k 为何值时，△ABC 是以BC 为斜边的直角三角形？ （2）k 为何值时，△ABC 是等腰三角形？并求△ABC 的周长．22、四边形ABCD 内接于⊙O ，并且AD 是⊙O 的直径，C 是弧BD 的中点，AB 和DC 的延长线交于⊙O 外一点E .求证：BC =EC .23、如图，在半径为5的⊙O 中，∠AOB ＝900，点C 是弧AB 上的一个动点（不与点A 、B 重合），OM ⊥BC ，ON ⊥AC ，垂足分别为M 、N ． （1）当BC ＝6时，求线段OM 的长；（2）当点C 在弧AB 上运动时，△MON 中是否存在长度保持不变的边？如果存在，请指出并求其长度；如果不存在，请说明理由．24、如图，已知AB是⊙O的弦，OB=2，∠B=30°，C是弦AB上的任意一点（不与点A、B重合），连接CO并延长CO交⊙O于点D，连接AD．（1）弦长AB等于__________（结果保留根号）；（2）当∠D=20°时，求∠BOD的度数；（3）当AC的长度为多少时，以A、C、D为顶点的三角形与以B、C、0为顶点的三角形相似？请写出解答过程．25、如图，A、B、C、D为矩形的4个顶点，AB=16cm，BC=6cm，动点P、Q分别以3cm/s、2cm/s的速度从点A、C同时出发，点Q从点C向点D移动．（1）若点P从点A移动到点B停止，点P、Q分别从点A、C同时出发，问经过2s时P、Q两点之间的距离是多少cm？（2）若点P从点A移动到点B停止，点Q随点P的停止而停止移动，点P、Q分别从点A、C同时出发，问经过多长时间P、Q两点之间的距离是10cm？（3）若点P沿着AB→BC→CD移动，点P、Q分别从点A、C同时出发，点Q从点C移动到点D停止时，点P随点Q的停止而停止移动，试探求经过多长时间△PBQ的面积为12cm2？。

D九年级数学周末作业一、选择题1.下列方程:①x 2=0,②21x-2=0,③2x 2+3x=(1+2x)(2+x),④32x =0,⑤8x 2-2y+ 1=0中,一元二次方程的个数是 ( ) A ．1个 B ．2个 C ．3个 D ．4个2.如果两条弦相等，那么 ( ) A ．这两条弦所对的弧相等 B ．这两条弦所对的圆心角相等 C ．这两条弦所对的圆周角相等 D ．以上答案都不对3．下列说法中，正确的是 ( ) A ．两个半圆是等弧 B ．同圆中优弧与半圆的差必是劣弧 C ．长度相等的弧是等弧 D ．同圆中优弧与劣弧的差必是优弧4.利用配方法将x 2＋2x ＋3=0化为a(x －h)2＋k=0 (a ≠0)的形式为 ( )A ．(x －1)2－2=0 B ．(x －1)2＋2=0 C ．(x ＋1)2＋2=0 D ．(x ＋1)2－2=05.如图，⊙O 中，点A 、O 、D 以及点B 、O 、C 分别在一条直线上，图中弦有( )A ．2条B ．3条C ．4条D ．5条6.⊙O 的半径为R ，圆心到点A 的距离为d ，且R 、d 分别是方程x 2－6x ＋8＝0的两根，则点A 与⊙O 的位置关系是 （ ） A ．点A 在⊙O 内部 B ．点A 在⊙O 上 C ．点A 在⊙O 外部 D ．不能确定 二、填空题7.一公园占地面积约为8000002m ，若按比例尺1∶2000缩小后，其面积约为 2m ． 8.与是同类二次根式，则x = .9.已知方程2x 2﹣mx ﹣10=0的一根是﹣5，求方程的另一根为 ，m 的值为 10．如图，在平行四边形ABCD 中，E 在DC 上，若DE ：EC=1：2，EF=2，则BF= ．11．庆“五一”，市工会组织篮球比赛，赛制为单循环形式（每两队之间都赛一场），共进行了45场比赛，这次有 队参加比赛．12.关于x 的方程0122=+-x kx 有实数根，则k 的取值范围是13．若x 1，x 2是方程x 2﹣2x ﹣4=0的两个不相等的实数根，则代数式2x 12﹣2x 1+x 22+2015的值是 14.某小区2013年绿化面积为2000平方米，计划2015年绿化面积要达到2880平方米．如果每年绿化面积的增长率相同，那么这个增长率是15．如图，△ABC 中，AB=18，AC=16，D 在AB 上，AD=9，在AC 上取一点P ，问AP = 时，以A 、P 、D 为顶点的三角形与△ABC 相似．16.如图为△ABC 与△DEC 重迭的情形，其中E 在BC 上，AC 交DE 于F 点，且AB∥DE．若△ABC 与△DEC 的面积相等，且EF=9，AB=12，则DF=(15) (16) 三、解答题17. 解方程：（1） 2(3)4(3)0x x x -+-= （2） （20+x ）（300-x ）=817618.先化简，再求值：，其中a 满足方程a 2+4a +1=0。

江苏省靖江市新港城初级中学2016届九年级数学双休日作业（11.28-11.29）（无答案）苏科版编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（江苏省靖江市新港城初级中学2016届九年级数学双休日作业（11.28-11.29）（无答案）苏科版）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为江苏省靖江市新港城初级中学2016届九年级数学双休日作业（11.28-11.29）（无答案）苏科版的全部内容。

（第5题）（第3题） （第4题）九年级数学双休日作业（11。

28—11。

29）一、选择题1．一元二次方程x 2－x －2＝0的解是（ ）．A ．x 1＝1，x 2＝2B ．x 1＝1,x 2＝－2C ．x 1＝－1，x 2＝－2D ．x 1＝－1，x 2＝2 2．已知1是关于x 的一元二次方程（m ﹣1)x 2+x+1=0的一个根,则m 的值是( ) A ． 1 B ． ﹣1 C ．0 D ． 无法确定3．如图,一艘海轮位于灯塔P 的北偏东30°方向，距离灯塔60海里的A 处，它沿正南方向航行一段时间后，到达位于灯塔P 的南偏东45°方向上的B 处，这时,海轮所在的B 处与灯塔P 的距离为（ ）．A ．302海里 B．303海里 C ．60海里 D ．306海里 4．如图，A ，B 两地被池塘隔开,小明通过下列方法测出了A 、B 间的距离：先在AB 外选一点C ，然后测出AC ，BC 的中点M ，N ，并测量出MN 的长为6m ,由此他就知道了A 、B 间的距离．有关他这次探究活动的描述错误的是 （ ）．A ．AB ＝12m B ．MN ∥ABC ．△CMN ∽△CABD ．CM ∶MA ＝1∶2 5. 如图，已知∠POx=120°，OP=4，则点P 的坐标是（ ）A ． （2,4）B ． （﹣2，4)C ． (﹣2,2）D ． (﹣2，2)6.如图，⊙O 的半径为1，△ABC 是⊙O 的内接等边三角形，点D 、E 在圆上,四边形BCDE 为矩形，这个矩形的面积是( ）．A ．2B ． 错误!C ． 错误!D ． 错误!二、填空题7．已知:5:2x y =，那么():x y y +=8．如图，已知⊙O 的半径为5，⊙O 的一条弦AB 长为8,那么以4为半径的同心圆与弦AB 位置关系是（第6题）（第14题）（第15题）C9．如图，在△ABC 中，DE ∥BC ,DE 与边AB 相交于点D ,与边AC 相交于点E ． 如果3AD =,4BD =，2AE =，那么AC = ．10．如图，圆锥的表面展开图由一扇形和一个圆组成，已知圆的面积为100π，扇形的圆心角为120°，这个扇形的面积为 ．11．如图，添加一个条件： ，使△ADE ∽△ACB ．12．已知y 是关于x 的函数，函数图象如图所示，则当y ＞0时，自变量x 的取值范围是 ．13．如图，一块直角三角板ABC 的斜边AB 与量角器的直径恰好重合，点D 对应的刻度是58°,则∠ACD 的度数为（第13题)14。

九年级数学双休日作业（11.21-11.22）一、选择题1．下列关于x 的方程是一元二次方程的是（ ）A ．01=+xB ．0332=-+x xC ．01333=++x xD ．0132=-+xx x 2. 如图，⊙O 中，弦AB 、CD 相交于P ，∠A =40°，则∠D =（ ）A ．15°B ．40°C ．35° D．75°3. Rt △ABC ，∠C ＝900，AB ＝6，cosB ＝23，则BC 的长为（ ）A.4B.2 5C.18 1313D.121313（第4题）4.如图，在网格中，小正方形的边长均为1，点A ，B ，C 都在格点上，则∠ABC 的正切值是( )A ．2B ．C ．D ． 5.为实数，其中设a a N a a M ,73,145222-=-=则M 与N 的大小关系是( )A ．M ＜N B.M ＞N C.M≥N D．不能确定6. 已知:两点A （5，6）、B （7，2），先将线段AB 向左平移一个单位，再以原点O 为位似中心，在第一象限内将其缩小为原来的21得到线段CD ，则点A 的对应点C 的坐标为（ ） A ．（2，3） B ．（3，1） C ．（2，1） D ．（3，3） 二、填空题7. 已知y x 32=，则x ：y 等于 ．8．已知△ABC ∽△DEF ，如果∠A ＝75°，∠B ＝25°，则∠F ＝ ．9. 已知点A 在半径为R 的⊙O 内，点A 与点O 的距离为6，则R 的取值范围是 ． 10. 已知α、β均为锐角，且满足()01tan |21sin |2=-+-βα，则________=+βα．11．如图，AB 是⊙O 的直径，CD 是⊙O 的弦，∠ACD=25°，则∠BAD 的度数为 ．（第2题）12．如图，某水库堤坝横断面迎水坡AB 的坡比是3:1，堤坝高BC =60m ，则应水坡面AB 的长度是=m ．13. 如图，在△ABC 中，D 是AB 上一点，F 是BC 上一点，DE ∥BC ,交AC 于点E ，若 △ADE 与△ABC 的面积的比为1：9，则△ADE 与△DEF 的面积的比为 ． 14．已知实数m 是关于x 的方程01322=--x x 的一根，则代数式2232--m m 值为 ． 15．若等腰△ABC 中，AB=AC=10 cm, ∠A=120°, ⊙O 恰好将等腰△ABC 完全覆盖，则 ⊙O 的半径为 cm ．16．如图，AB 为⊙O 的直径，点C 是⊙O 上的一点，AB=8 cm ，∠A=30°，点D 是弦AC 上的一点，动点P 从点C 沿CA 以2cm/s 的速度向点D 运动，再沿DO 以1cm /s 的速度向 点O 运动，设点P 在整个运动过程中的时间为t ，则t 的最小值是 s ． 三、解答题17．计算 sin 245°＋cos 230°－tan 45°18．解下列方程：⑴04542=--x x ⑵()623+=+x x x19.已知关于x 的一元二次方程x 2－(2k ＋1)x ＋k 2＋k ＝0． (1)求证：方程有两个不相等的实数根；(2)若周长为16的等腰△ABC 的两边AB ，AC 的长是方程的两个实数根，求k 的值BAEDCBA 第11题图第12题图第13题图20.在国家的宏观调控下，某市的商品房成交价由今年3月份的14000 2/m 元下降到5月份的126002/m 元，⑴问4、50.95 ）⑵如果房价继续回落，按此降价的百分率，你预测到7月份该市的商品房成交均价是否会跌破100002/m 元？请说明理由。

1九年级数学家庭作业（11.23）班级 姓名1.△ABC 中，a 、b 、c 分别是∠A、∠B、∠C 的对边，如果a 2+b 2=c 2，那么下列结论正确的是（ ） A ．bcosB=cB ．csinA=aC ．a tanA=bD ．2.在Rt△ABC 中，∠C=90°，sinA=，则cosB 等于（ ） A ． B ．C ．D ．3.如果∠A 为锐角，且sinA=0.6，那么（ ）A ．0°＜A≤30°B ．30°＜A ＜45°C ．45°＜A ＜60°D ．60°＜A≤90°4. 已知直角三角形ABC 中，斜边AB 的长为m ，40B ∠=，则直角边BC 的长是（ ）A ．sin 40mB ．cos 40mC ．tan 40mD ．tan 40m5.在Rt △ABC 中，∠C=90°，AC=5，BC=12，则sinA=_______，tanB=_______.6.如图，正方形ABCD 的边长为4，点M 在边DC 上，M 、N 两点关于对角线AC 对称，若DM =1，则tan ∠ADN = ．7.在同一时刻两根木竿在太阳光下的影子如图所示，其中木竿AB=2m ，它的影子BC=1.6m ，木竿PQ 的影子有一部分落在了墙上，PM=1.2m ，MN=0.8m ，则木竿PQ 的长度为________m ．（6） （7） （8） 8.如图，在△ABC 中，AB=AC=5，BC=8．若∠BPC=∠BAC ，则tan ∠BPC= ． 9.如图，已知△ABC 是面积为的等边三角形，△ABC∽△ADE，AB=2AD ，∠BAD=45°，AC 与DE 相交于点F ，则△AEF 的面积等于________（结果保留根号）．10.（1）22160cos 2)12015(-⎪⎭⎫ ⎝⎛-+-（2）已知23)10sin(=︒-α，求α。

DA新港城中学九年级数学双休日作业（11.7-11.8）一、选择题1．已知：4.0=a ，3=b ，9=c ，2.1=d ，下列各式中，正确的是（ ）A.a b =c d B. a c =d b C.a b =d c D.d c =b a2．若关于x 的方程0142=--x ax 是一元二次方程，则a 满足的条件是（ ） A ．a ＞0 B ．0≠a C ．0<a D ．4≠a3．如图D 、E 分别是ABC ∆的AB 、 AC 边上点，,DE BC //S △ADE ∶S 四边形DECB =1∶8那么AE∶AC 等于（ ） A ．1∶9 B．1∶3 C ．1∶8 D ．1∶24．如图，在△ABC 中，点D 是AC 边上的一点，且AB 是AD 与AC 的比例中项，则下列结论中，错误的是 （ ）A ．∠C=∠ABDB ．∠ABC=∠ADBC ．AC AD BC BD = D ．ABADBC BD =5.如图，在矩形ABCD 中，AB =4，AD =5，AD 、AB 、BC 分别与⊙O 相切于E 、F 、G 三点，过点D 作⊙O 的切线交BC 于点M ，则DM 的长为( ) A. 133 B. 923(3) (4) (5) 6．根据关于x 的一元二次方程12=++q px x ，可列表如下：则方程2+px x 的正数解满足 （ ）A ．0.5＜x ＜1B ．1＜x ＜1.1C ．1.1＜x ＜1.2D ．1.2＜x ＜1.3 二、填空题7.圆心角为60°，半径为4cm 的扇形的弧长为 cm8.如图，321////l l l ，AM ＝2，MB ＝3，CN ＝1.8，则CD ＝_________．9.在比例尺为1：5000的地图上，测得一个多边形地块的面积为362cm ，则这个多边形地 块的实际面积是____________2m (结果用科学记数法表示)．10．若关于x 的方程kx 2+2x －1=0有两个不等的实数根，则k 的取值范围是______________． 11.若正三角形的半径为2，则此正三角形的边长为____________．12．若圆锥圆锥的母线长为4cm ，底面半径为2cm ，则圆锥的侧面积为 ． 13．如图，小明把手臂水平向前伸直，手持小尺竖直，瞄准小尺的两端E 、F ，不断调整站 立的位置，使在点D 处恰好能看到铁塔的顶部B 和底部A ，设小明的手臂长l=45cm,，小 尺长a=15cm,，点D 到铁塔底部的距离AD=42m ，则铁塔的高度是__________m ． 14．如图，在△ABC 中，点G 是△ABC 的重心，BG 和CG 延长线分别交AC 和AB 于 点D 和E ，则CEGC的值为_____________．第9题 第12题 第13题 第15题 15．某工厂两年内产值翻了两番，则该工厂产值年平均增长率是_____________． 16．如图，在正方形ABCD 中，E 是AD 的中点，DF⊥EC 于点F ，连结AF ，则下列四个结论：①△EDF∽△ECD；②AF 平分∠EAC；③AF：AB=2：5； ④AEF AFC S S ∆∆=4； 其中，正确的是 (请将正确结论的序号填在横线上)．17.如图，一个半径为r 的圆形纸片在边长为a （a ≥）的等边三角形内任意运动，则在该等边三角形内，这个圆形纸片“不能接触到的部分”的面积是 三、解答题17．解下列方程：(1)5232+=+x x ）（ (2)x x 6132=-(用配方法)18．先化简，再求值：)1(111222+-÷-+m m m m ）（，其中m 是方程03222=--x x 的根．19．如图，某小区有一块长为24米，宽为8米的矩形空地，计划在其中修建两块相同的矩形绿地，它们的面积之和为72米2，两块绿地之间及周边留有宽度相等的人行通道．求人行道的宽度20．若关于x 的一元二次方程1)(2=-+m x x ）（． (1)求证：无论m 取何实数，原方程总有两个不相等的实数根； (2)若原方程有一个根为1-，求m 的值和此方程的另一个根．21．在平面直角坐标系中，△ABC 的三个顶点坐标分别为A(2，﹣4)，B(3，﹣2)，C(6，﹣3)．MDCBE (1)画出△ABC 关于x 轴对称的△A 1B 1C 1；(2)以M 点为位似中心，在网格中画出△A 1B 1C 1的位似图形 △A 2B 2C 2，使△A 2B 2C 2与△A 1B 1C 1的相似比为2∶1． (3)请写出(2)中放大后的△A 2B 2C 2中A 2B 2边的中点P 的坐标．22．己知：如图，在菱形ABCD 中，点M 、N 分别在边AD 、AB ，∠DCM =∠BCN ，CN 与BD 交于点E ． (1)求证：DM=BN ；(2)当四边形MNBE 是平行四边形时，求证：DMDCMA DM ．23．如图，四边形OABC 是平行四边形，以O 为圆心，OA 为半径的圆交AB 于D ，延长AO 交⊙O 于E ，连接CD ，CE ，若CE 是⊙O 的切线，（1）求证：CD 是⊙O 的切线；（2）若BC=3，AB=5，求平行四边形OABC 的面积．NMG E DCB A 备用图图2图1ABCDQP ABCDPQ D CBA24.某兴趣小组开展课外活动．如图，小明从点M 出发以1.5米／秒的速度，沿射线MN 方向匀速前进，2秒后到达点B ，此时他(AB)在某一灯光下的影长为MB ，继续按原速行走2秒到达点D ，此时他(CD)在同一灯光下的影子GD 仍落在其身后，并测得这个影长GD 为1.2米，然后他将速度提高到原来的1.5倍，再行走2秒到达点F ，此时点A ，C ，E 三点共线．(1)请在图中画出光源O 点的位置，并画出小明位于点F 时在这个灯光下的影长FH(不写画法)； (2)求小明到达点F 时的影长FH 的长．25．如图，矩形ABCD 中，AB=6，BC=10，点P 在边BC 上，点Q 在边CD 上， (1)如图1，将△ADQ 沿AQ 折叠，点D 恰好与点P 重合，求CQ 的长； (2)如图2，若CQ=2，且△ABP 与△PCQ 相似，求BP 的长；(3)若点Q 是CD 边上的一点，且BC 上不存在．．．满足AP⊥PQ 的点P ，请探究：此时CQ 的长必须满足什么条件？。

九年级数学双休日作业（9.19-9.20）一、选择题：1.下列方程是关于x 的一元二次方程的是（ ）A ．02=++c bx ax B.2112=+x xC.1222-=+x x x D.)1(2)1(32+=+x x 2.用配方法解方程01822=+-x x 时,应先把它变形为（ ）A.15)4(22=-xB.15)4(2=-x C.7)2(2=-x D.27)2(2=-x 3.若5200k +<，则关于x 的一元二次方程240x x k +-=的根的情况是（ ） A. 没有实数根 B. 有两个相等的实数根 C. 有两个不相等的实数根 D. 无法判断4.如图，在ABC ∆中，BC DE //，若cm AD cm AC cm AB 3,5,7===，则=DE （ ）A.cm 415 B.cm 320C.cm 715 D.cm 7205.已知0)2m 2()x 1(m x 2=----两根之和等于两根之积，则m 的值为（ ） A.1 B.—1 C.2 D.—26.下列论断：①顺次连接三角形各边的中点，所得的三角形与原三角形相似；②两边长分是 3、4的Rt △ABC 与两边长分别是6、8的Rt △DEF 相似；③若两个三角形的边长分别是4、 6、8和6、8、10，则这两个三角形相似；④一个三角形的三边长分别为6 cm 、9 cm 、7.5 cm ， 另一个三角形的三边长分别为8 cm 、12 cm 、10 cm ，则这两个三角形相似，其中正确的有 ( )A ．1个B ．2个C ．3个D ．4个 二、填空题7.若关于y 的方程5)2(2=+-m y 有实数根，则m 的取值范围是 ．8.若1x =是关于x 的一元二次方程230x mx n ++=的解，则62m n += .9.如图，在△ABC 中，两条中线BE ，CD 相交于点O ，则S △DOE ：S △DCE = 。

EABCD第4题10.关于x 的方程01x 2ax 2=++的两个实数根同号，则a 的取值范围是__________. 如图，在△ABC 中，CD ⊥AB ，垂足为D ．下列条件：①∠A ＋∠B ＝90°；②AB 2＝AC 2＋BC 2；③AC CD AB BD=；④CD 2＝AD ·BD ，其中能证明△ABC 是直角三角形的有_______． 11.若关于x 的一元二次方程22(1)10kx k x k +++-=有两个实数根，则k 的取值范围是 .12.已知α，β是方程x 2+2006x+1=0的两个根，则（1+2008α+α2）（1+2008β+β2）的值为 。

九年级数学双休日作业(12.19-12.20)一、选择题1．在函数y ＝x －3中，自变量x 的取值范围是 （ ）A ．x ＞3B ．x ≥3C ．x ≥－3D ．x ≤32．关于x 的一元二次方程2210x a ++-=（a-1）x 一个根是0，a 的值为（ ）A ． 1B ．-1C ．1或-1D ．03．菱形具有而矩形不一定具有的性质是 ( )A ．对角线互相垂直B ．对角线相等C ．对角线互相平分D ．对角互补4．已知圆锥的底面半径为2cm ，母线长为5cm ，则圆锥的侧面积是 （ ）A ．220cmB ．220cm πC ．210cm πD ．25cm π5．已知二次函数2y ax bx c =++的图像如图所示，则下列结论正确的是（ ）A ．0a >B ．02=+b aC ．240b ac -<D ．0a b c -+>6．如图，平面直角坐标系中，⊙A 的圆心在x 轴上，半径为1，直线l 为22y x =-， 若⊙A 沿x 轴向右运动，当⊙A 与l 有公共点时，点A 移动的最大距离是（ ）B.3C.二、填空题7．方程x 2－5x ＝0的根是 ．8.a 的值为 .9．若12x x ，是一元二次方程2560x x -+=的两个根，则12x x = .10．如图，量角器放在∠BAC 的上面，则∠BAC ＝ °.(第5题)第10题 第15题A B C DE F 第12题图11．已知抛物线322--=x x y ，若点P （2-，5）与点Q 关于该抛物线的对称轴对称，则点Q 的坐标是 ．12．如图，有一块边长为4的正方形塑料模板ABCD ，将一块足够大的直角三角板的直角顶点落在A 点，两条直角边分别与CD 交于点F ，与CB 延长线交于点E ．则四边形AECF 的面积是 ．13．如图，是二次函数y=ax 2+bx+c 图象的一部分，其对称轴为直线x=1，若其与x 轴一交点为A （3，0），则由图象可知，不等式ax 2+bx+c ＜0的解集是 _________ ．14.抛物线y=x 2﹣2x+1与坐标轴交点个数为 .15．如图，△ABC 内接于⊙0，∠B=∠OAC, OA = 4cm ，则AC= cm.1645︒的扇形AOB 内部作一个矩形CDEF ，使点C 在OA 上，点D 、E 在OB 上，点F 在AB 弧上，并且2EF DE =，则EF = .三、解答题17．计算或化简：（1）0(π2009)|2|-+ （2）)622554(83--⨯BC D18．解方程2560x x--=⑴x2-4x+1=0 ⑵19. 如图，每个小方格都是边长为1个单位的小正方形，B，C，D三点都是格点（每个小方格的顶点叫格点）．（1）找出格点A，连接AB，AD使得四边形ABCD为菱形；（2）画出菱形ABCD绕点A逆时针旋转90°后的菱形AB1C1D1，并求点C旋转到点C1所经过的路线长．20．如图，抛物线y=﹣x2+2x+c与x轴交于A，B两点，它的对称轴与x轴交于点N，过顶点M作ME⊥y轴于点E，连结BE交MN于点F，已知点A的坐标为（﹣1，0）．（1）求该抛物线的解析式及顶点M的坐标．（2）求△EMF与△BNF的面积之比．21．如图，用两段等长的铁丝恰好可以分别围成一个正五边形和一个正六边形，其中正五边形的边长为（217x +）cm ，正六边形的边长为（22x x +）cm(其中x>0).求这两段铁丝的总长.22．在北京2008年第29届奥运会前夕，某超市在销售中发现：奥运会吉祥物“福娃”平均每天可售出20套，每件盈利40元。

九年级数学双休日作业（12.5-12.6）一．选择题1．关于x 的方程ax 2﹣3x+1=0是一元二次方程，则（ ）A ．a ＞0 B.a ≥0 C ．a ≠0 D.a=12．在Rt △ABC 中，∠C=90°，AC=12，BC=5，则sinA 的值是（ ）A ． B. C. D ．3．某商店购进一种商品，单价为30元．试销中发现这种商品每天的销售量P （件）与每件的销售价x （元）满足关系：P=100﹣2x ．若商店在试销期间每天销售这种商品获得200元的利润，根据题意，下面所列方程正确的是（ ）A ．（x ﹣30）（100﹣2x ）=200B ．x （100﹣2x ）=200C ．（30﹣x ）（100﹣2x ）=200D ．（x ﹣30）（2x ﹣100）=2004．如图，AB 是⊙O 的直径，⊙O 交BC 的中点于D ，DE ⊥AC 于E ，连接AD ，则下列结论：①AD ⊥BC ；②∠EDA=∠B ；③OA=AC ；④DE 是⊙O 的切线，正确的个数是（ ）A ．1 个B ．2个C ．3 个D ．4个5．若点M （﹣2，y 1），N （﹣1，y 2），P （8，y 3）在抛物线2132y x =-+上，则下列结论正确的是（ ） A ． y 1＜y 2＜y 3 B ． y 2＜y 1＜y 3 C ． y 3＜y 1＜y 2 D ． y 1＜y 3＜y 26．如图，在平面直角坐标系xOy 中，直线AB 过点A （﹣3，0），B （0，3），⊙O 的半径为1（O 为坐标原点），点P 在直线AB 上，过点P 作⊙O 的一条切线PQ ，Q 为切点，则切线长PQ 的最小值为（ ）A ．B ． 2C ． 3D ．二、填空题7．已知x=﹣1是方程x 2+mx ﹣5=0的一个根，则方程的另一根为 ．8．在Rt △ABC 中，∠C=90°，AB=6，cosB=，则AC 的长为 ．9．已知圆锥的底面半径为3，侧面积为π15，则这个圆锥的侧面展开图的圆心角的度数是 ．10．若锐角α满足2sin(α－15°)－1＝0，则tan α＝ ．11.若实数a 、b 、c 满足9a ﹣3b+c=0，则方程ax 2+bx+c=0必有一个根是 ．12.如图，A 、B 、C 是⊙上的三个点，∠ABC=130°，则∠AOC 的度数是 ．13．如图，在▱ABCD 中，E 在AB 上，CE 、BD 交于F ，若AE ：BE=4：3，且BF=2，则DF= ..14．已知等边三角形ABC 的高为4，在这个三角形内有一点P ，若点P 到AB 的距离是1，点P 到A C 的距离是2，则点P 到BC 的距离是 ．15.把二次函数y =错误！未找到引用源。

江苏省靖江市新港城初级中学2016届九年级数学双休日作业（9.12-13）（无答案）苏科版编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（江苏省靖江市新港城初级中学2016届九年级数学双休日作业（9.12-13）（无答案）苏科版）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为江苏省靖江市新港城初级中学2016届九年级数学双休日作业（9.12-13）（无答案）苏科版的全部内容。

九年级数学双休日作业班级： 姓名： 一、选择题：1、在下列各式中：①x 2+3=y ②2 x 2- 3x=2x(x — 1) – 1 ③3 x 2- 4x = 5④x 2=—x1+2是一元二次方程的共有（ )A 。

0个B 。

1个C 。

2个D 。

3个 2、一元二次方程x 2﹣2x ﹣1=0的解是（ ） A. x 1=x 2=1 B 。

x 1=1+,x 2=﹣1﹣C 。

x 1=1+, x 2=1﹣ D. x 1=﹣1+, x 2=﹣1﹣为3、若x=﹣2是关于x 的一元二次方程x 2﹣ax+a 2=0的一个根，则a 的值（ ） A 。

1或4B.﹣1或﹣4C ．﹣1或4D ．1或﹣44、如图，△ABC 中，AE 交BC 于点D ，∠C =∠E ，AD ：DE =3：5，AE =8，BD =4，则DC 的长等于( ） A ．B ．C ．D ．根，5、若关于x 的一元二次方程2(1)220k x x -+-=有两个不相等的实数则k 的取值范围是（ ） 1 A.12k >B 。

12k ≥ C.12k >且k ≠1 D 。

12k ≥且k ≠6、如图，在矩形AOBC 中，点A 的坐标是(﹣2,1），点C 的纵坐标是4,则B 、C 两点的坐标分别是（ ）A ．（，3)、（﹣，4）B 。

九年级数学家庭作业（11.11）1.如图，AB 是⊙O 的直径，AC 是⊙O 的切线，连接OC 交⊙O 于点D ，连接BD ，∠C=40°．则∠ABD 的度数是（ ）A ．30°B ．25°C ．20°D ．15°（1） （2） （3）2.如图，在ABC ∆中，如果BC DE //，AC DF //，则下列比例式中不正确的是（ ）A.FB CF EC AE =B.AC DF BC BF =C.AC AB AE AC =D.BCAB FC AD = 3.如图，用一张半径为24cm 的扇形纸板制作一顶圆锥形帽子（接缝忽略不计），如果圆锥形帽子的底面半径为10cm ，那么这张扇形纸板的面积是（ ）A. 240πcm 2 B ．480πcm 2 C. 1200πcm 2 D ．2400πc m 24.如图，AD 是正五边形ABCDE 的一条对角线，则∠BAD= 度．（4） （9） （11）5.若关于x 的方程052=++k x x 有实数根，则k 的取值范围是 ．6.一元二次方程03x x 2=--两根的倒数和等于__________.7.圆心角为120，弧长为12π的扇形半径为 ．8.如果－1是关于x 的方程0422=-+bx x 的一个根，则b 是 ．9.如图，在⊙O 的内接四边形ABCD 中，AB ＝3，AD ＝5，∠BAD ＝60°，点C 为弧BD 的中点，则AC 的长是______________．10.若矩形的长和宽是方程2x 2﹣16x+m=0（0＜m≤32）的两根，则矩形的周长为 ．11.如图，半径为5的半圆的初始状态是直径平行于桌面上的直线b ，然后把半圆沿直线b 进行无滑动滚动，使半圆的直径与直线b 重合为止，则圆心O 运动路径的长度等于 ．12.解下列方程：（1）01432=--x x （配方法） （2）（x ﹣1）2+2x （x ﹣1）=013.先化简再求值： 232(1)121x x x x x ---÷--+，其中x 是方程22x x =的根．14.如图，AB 为⊙O 的直径，AC 、DC 为弦，∠ACD=60°，P 为AB 延长线上的点，∠APD=30°．（1）求证：DP 是⊙O 的切线；（2）若⊙O 的半径为3cm ，求图中阴影部分的面积．15.在图的方格纸中，△OAB 的顶点坐标分别为O （0，0）、A （-2，-1）、B （-1，-3），△O 1A 1B 1与△OAB 是关于点P为位似中心的位似图形．（1）在图中标出位似中心P 的位置，并写出点P 及点B的对应点B 1的坐标；（2）以原点O 为位似中心，在位似中心的同侧画出△OAB的一个位似△OA 2B 2，使它与△OAB 的相似比为2：1．并写出点B 的对应点B 2的坐标；（3）△OAB 内部一点M 的坐标为（a ，b ），写出M 在△OA 2B 2中的对应点M 2的坐标；16.如图，在Rt△ABC中，AC=6，BC=8，点D为边CB上的一个动点（点D不与点B重合），过D作DO⊥AB，垂足为O，点B′在边AB上，且与点B关于直线DO对称，连接DB′，AD．（1）求证：△DOB∽△ACB；（2）若AD平分∠CAB，求线段BD的长；（3）当△AB′D为等腰三角形时，求线段BD的长．。

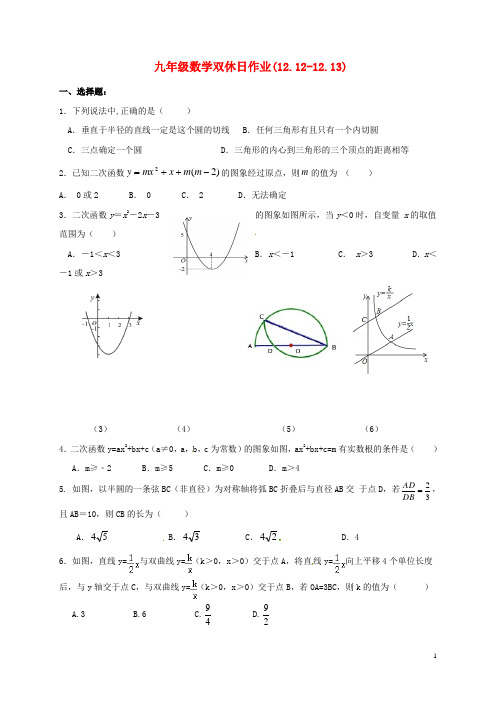
九年级数学双休日作业(12.12-12.13)一、选择题：1．下列说法中,正确的是（）A．垂直于半径的直线一定是这个圆的切线 B．任何三角形有且只有一个内切圆C．三点确定一个圆 D．三角形的内心到三角形的三个顶点的距离相等2．已知二次函数)2(2-++=mmxmxy的图象经过原点，则m的值为（）A． 0或2 B． 0 C． 2 D．无法确定3．二次函数y＝x2－2x－3的图象如图所示，当y＜0时，自变量 x的取值范围为（）A．－1＜x＜3 B．x＜－1 C． x＞3 D．x＜－1或x＞3（3）（4）（5）（6）4．二次函数y=ax2+bx+c（a≠0，a，b，c为常数）的图象如图，ax2+bx+c=m有实数根的条件是（） A．m≥﹣2 B．m≥5 C．m≥0D．m＞45. 如图，以半圆的一条弦BC（非直径）为对称轴将弧BC折叠后与直径AB交于点D ，若32=DBAD，且AB＝10，则CB的长为（）A．54 B．34 C．24 D．46．如图，直线y=与双曲线y=（k＞0，x＞0）交于点A，将直线y=向上平移4个单位长度后，与y轴交于点C，与双曲线y=（k＞0，x＞0）交于点B，若OA=3BC，则k的值为（）A.3B.6C.94D.92二．填空题7.已知α、β均为锐角，且满足21sin (tan 1)02αβ-+-=，则α+β= 8. 在△ABC 中，∠C ＝90°，∠A ＝45°，则BC ：AC ：AB ＝__ _． 9. 已知圆锥的底面的半径为3cm ，高为4cm ，则它的侧面积为 。

10．若抛物线y ＝x 2－bx ＋9的顶点在y 轴上，则b 的值为______。

11．（1）将抛物线y=x 2﹣2x+3向上平移2个单位长度，再向右平移3个单位长度后，得到的抛物线的解析式为 。

物线21(2)43y x =++关于x 轴对称的抛物线的解析式为______ （2）抛_。

12．（1）已知抛物线y=ax 2+bx+c 与x 轴的公共点是（﹣4，0），（2，0），则这条抛物线的对称轴是直线 _________ ．（2）关于x 的函数y=（m 2﹣1）x 2﹣（2m+2）x+2的图象与x 轴只有一个公共点，则m 的值是 .13.r R ,分别为等边三角形的外接圆和内切圆半径，则=r R : ．14．在Rt△ABC 中，∠C = 90°，AC = 6，BC = 8，⊙O 为△ABC 的内切圆，则⊙O 的半径等于 15．如图，矩形ABCD 的长AB=6cm ，宽AD=3cm ．O 是AB 的中点，OP⊥AB，两半圆的直径分别为AO 与OB ．抛物线y=ax 2经过C 、D 两点，则图中阴影部分的面积是 _____ cm 2．（15） （16）16.如图，矩形纸片ABDC 中，AB=5，AC=3，将纸片折叠，使点B 落在边CD 上的B′处，折 痕为AE ．在折痕AE 上存在一点P 到边CD 的距离与到点B 的距离相等，则此相等距离为 __________. 三、解答题： 17．计算和解方程：(1) ()013311260sin 2π--⎪⎭⎫ ⎝⎛-+︒- （2）05222=--x x （3）32121---=-x x x18．先化简，再求值1212312+-+-÷⎪⎭⎫ ⎝⎛+-x x x x x x ，其中x 满足022=-+x x19.（1）已知二次函数的图象以A （－1，4）为顶点，且过点B （2，－5） ①求该函数的关系式；②求该函数图象与坐标轴的交点坐标；（2）抛物线过（－1，0），（3，0），（1，－5）三点，求二次函数的解析式；20.已知二次函数y ＝（m 2－2）x 2－4mx ＋n 的图象的对称轴是x ＝2，且最高点在直线y ＝21x ＋1上，求这个二次函数的解析式。

九年级数学双休日作业（10.31-11.1）一、选择题：1.下列说法中，正确的是( )A．同一条弦所对的两条弧一定是等弧 B．长度相等的两条弧是等弧C．两条直线被一组平行线所截，所得的对应线段成比例D．三角形的外心到三角形各边的距离相等2．用配方法解方程x2﹣2x﹣5=0时，变形正确的是( )A．（x﹣2）2=9 B．（x﹣1）2=6 C．（x+2）2=9 D．（x+1）2=63．⊙A半径为5，圆心A的坐标为（1，0），点P的坐标为（﹣2，4），则点P与⊙A的位置关系是( ) A．点P在⊙A上B．点P在⊙A内C．点P在⊙A外D．点P在⊙A上或外4．一元二次方程x2﹣2x﹣1=0的根的情况为( )A．有两个相等的实数根B．有两个不相等的实数根C．只有一个实数根D．没有实数根5．已知一元二次方程x2﹣3x+1=0的两个根分别是x1、x2，则x12x2+x1x22的值为( )A．﹣3 B．3 C．﹣6 D．66.如图，AB是⊙O的直径，弦CD⊥AB，垂足为M，下列结论不成立的是( )A．CM=DM B．=C．∠ACD=∠ADC D．OM=MD二、填空题：7.方程（x﹣1）2=4的解为__________．8.关于x的一元二次方程（a﹣1）x2+x+（a2﹣1）=0的一个根是0，则a的值是__________．9.顶角为36°的等腰三角形称为黄金三角形．如图，△ABC、△BDC、△DEC都是黄金三角形，已知AB=1，则D E=__________．（9）（13）（14）10.某种衬衣的价格经过连续两次降价后，由每件150元降至96元，平均每次降价的百分率是__________．11．直径为10cm的⊙O中，弦AB=5cm，则弦A B所对的圆周角是__________．12．一个三角形的两边长分别为4cm和7cm，第三边长是一元二次方程x2﹣10x+21=0的实数根，则三角形的周长是__________cm．13.如图，⊙O的半径是2，直线l与⊙O相交于A、B两点，M、N是⊙O上的两个动点，且在直线l 的异侧，若∠AMB=45°，则四边形MANB面积的最大值是__________．14.如图，△ABC中，∠BAC=60°，∠ABC=45°，AB=，D是线段BC上的一个动点，以AD为直径画⊙O分别交AB、AC于E、F，连接EF，则线段EF长度的最小值为__________．15.如图，AB是⊙O的直径，弦BC＝2cm，F是弦BC的中点，∠ABC＝60°，若动点E以2cm/s的速度从点A出发沿着A→B→A的方向运动，设运动时间为t(s)(0≤t<3)，连接EF，则当t为_____ __s时，△BEF是直角三角形．三、解答题：16.解下列方程：（1）3x2+5x+1=0．（2）（3x+1）2=4（x﹣2）2．17．先化简，再求值：（﹣）÷，其中，a 是方程x 2+3x+1=0的根．18．如图，AD 为⊙O 的直径，BA 、BC 、CD 分别切⊙O 的于点A 、E 、D 。

九年级数学家庭作业（11.9）1.下列说法中，结论错误的是（ ）A ．直径相等的两个圆是等圆 B. 三角形的外心是这个三角形三条角平分线的交点C. 圆中最长的弦是直径D. 一条弦把圆分成两条弧，这两条弧可能是等弧2.已知线段a =4，b =9，线段x 是a ，b 的比例中项，则x 等于（ ）A ．6 B. 6或－6 C. －6 D. 363.如图，△ABC 的三个顶点都在⊙O 上，∠BAC 的平分线交BC 于点D ，交⊙O 于点E ，则与△ABD 相似的三角形有（ ）A.3个B.2个C.1个D.0个4.已知△ABC ，AB=5，AC=4，BC=6，AB 上有一动点D （不与A 、B 点重合），过点D 作直线截△ABC ，使截得的三角形与△ABC 相似，满足这样条件的直线可作有 条．( )A ．2条B ．3条C ．4条D ．3条或4条5. 在Rt△ABC 中，∠C=90°，AC=12，BC=5，将△AB C 绕边AC 所在直线旋转一周得到圆锥， 则该圆锥的侧面积是 .6.一元二次方程012)1(2=---x x k 有两个不相等的实数根，则k 的取值范围是7.若一元二次方程ax 2=b （ab ＞0）的两个根分别是m+1与2m ﹣4，则m=8.圆锥的底面圆的周长是4π cm ，母线长是6 cm ，则该圆锥的侧面展开图的圆心角的度数 是9.在Rt △ABC 中，∠C = 90°，AC = 3，BC = 4，点O 、点G 分别是Rt △ABC 的外心和重心，连结OG ，则OG =10.如图，已知梯形ABCD 中，AB∥CD，△COD 与△AOB 的周长比为1：2，则CD ：AB= ，S △COB ：S △COD = .11.如图，长为4 cm ，宽为3 cm 的长方形木板，在桌面上做无滑动的翻滚（顺时针方向），木板上点A 位置变化为A →A 1→A 2，其中第二次翻滚被桌面上一小木块挡住，使木板与桌面成30°角，则点A 翻滚到A 2位置时共走过的路径长为 .12.解方程： （1）36)12(4=-+x x x （2）22310x x --= （用配方法）13.先化简,再求值:)225(4232---÷--x x x x x ，其中x 是一元二次方程04622=-+x x 的根。

九年级数学双休日作业（2015.10.24-10.25）一、选择题1.下列方程中是关于x 的一元二次方程的是（ ） A.2210x x+= B. ax 2+bx+c=0 C.（x ﹣1）（x+2）=1 D. 3x 2﹣2xy ﹣5y 2=0 2.已知⊙O 的半径为5，圆心O 到直线l 的距离为3，则反映直线l 与⊙O 的位置关系的图形是( )3.下列命题中，假命题的个数是 （ ）①垂直于半径的直线一定是这个圆的切线； ②圆有且只有一个外切三角形；③三角形有且只有一个内切圆； ④三角形的内心到三角形的三个顶点的距离相等．A ．1B ．2C ．3D ．44.一元二次方程x 2﹣8x ﹣1=0配方后可变形为（ ） 175.如图，⊙O 的半径为5，若OP=3，则经过点P 的弦长可能是 （ ）A ．3B ．6C ．9D ．126.如图，⊙O 的半径OD ⊥弦AB 于点C ，连结AO 并延长交⊙O 于点E ，连结EC ．若AB=8，CD=2，则EC 的长为（ ）A ．2B ．8C ．2D ．2 二、填空题7.方程x 2+x=0的解是8.两条直角边是6和8的直角三角形，其内切圆的半径是 ． 9.222)2(4___p x p x -=+- 10.已知0654≠==a b c ，则a c b +的值为 ． 11.半径为2的圆中，弦AB 、AC 的长分别2和2，则∠BAC 的度数是 。

12.如图，点I 为△ABC 的内心，点O 为△ABC 的外心，若∠BOC=140°，则∠BIC= ° 13.如图，直线126l ,l ,,l ⋅⋅⋅ 是一组等距离的平行线，过直线1l 上的点A 作两条射线，分别与直线3l ，6l 相交于点B ，E ，C ，F . 若BC =2，则EF 的长是 。

14.已知m ，n 是方程0522=-+x x 的两个实数根，则=+22n mn m — ．15. 如图，Rt△ABC 的内切圆⊙O 与两直角边AB ，BC 分别相切于点D ，E ，过劣弧DE （不包括端点D ，E ）上任一点P 作⊙O 的切线MN 与AB ，BC 分别交于点M ，N ，若⊙O 的半径为r ，则Rt△MBN 的周长为 。