惯性矩总结(含常用惯性矩公式)==

极惯性矩常用计算公式：Ip=∫Aρ^2dA矩形对于中线(垂直于h边的中轴线)的惯性矩：b*h^3/12三角形：b*h^3/36圆形对于圆心的惯性矩：π*d^4/64环形对于圆心的惯性矩：π*D^4*（1-α^4)/64;α=d/D§16-1 静矩和形心平面图形的几何性质一般与杆件横截面的几何形状和尺寸有关，下面介绍的几何性质表征量在杆件应力与变形的分析与计算中占有举足轻重的作用。

静矩：平面图形面积对某坐标轴的一次矩，如图Ⅰ-1所示。

定义式：，(Ⅰ-1）量纲为长度的三次方。

由此可得薄板重心的坐标为同理有所以形心坐标，（Ⅰ-2）或，由式（Ⅰ-2）得知，若某坐标轴通过形心，则图形对该轴的静矩等于零，即，；，则；反之，若图形对某一轴的静矩等于零，则该轴必然通过图形的形心。

静矩与所选坐标轴有关，其值可能为正，负或零。

如一个平面图形是由几个简单平面图形组成，称为组合平面图形。

设第i块分图形的面积为，形心坐标为，则其静矩和形心坐标分别为，（Ⅰ-3），（Ⅰ-4）【例I-1】求图Ⅰ-2所示半圆形的及形心位置。

【解】由对称性，，。

现取平行于轴的狭长条作为微面积所以读者自己也可用极坐标求解。

【例I-2】确定形心位置，如图Ⅰ-3所示。

【解】将图形看作由两个矩形Ⅰ和Ⅱ组成，在图示坐标下每个矩形的面积及形心位置分别为矩形Ⅰ：mm2mm，mm矩形Ⅱ：mm2mm，mm整个图形形心的坐标为§16-2 惯性矩和惯性半径惯性矩：平面图形对某坐标轴的二次矩，如图Ⅰ-4所示。

，(Ⅰ-5)量纲为长度的四次方，恒为正。

相应定义，(Ⅰ-6)为图形对轴和对轴的惯性半径。

组合图形的惯性矩设，(Ⅰ-7)若以表示微面积到坐标原点的距离,则定义图形对坐标原点的极惯性矩（Ⅰ-8）因为所以极惯性矩与（轴）惯性矩有关系（Ⅰ-9）式（Ⅰ-9）表明，图形对任意两个互相垂直轴的（轴）惯性矩之和，等于它对该两轴交点的极惯性矩。

下式（Ⅰ-10）定义为图形对一对正交轴、轴的惯性积。

极惯性矩常用计算公式：Ip=∫Aρ^2dA矩形对于中线(垂直于h边的中轴线)的惯性矩：b*h^3/12三角形：b*h^3/36圆形对于圆心的惯性矩：π*d^4/64环形对于圆心的惯性矩：π*D^4*（1-α^4)/64;α=d/D§16-1 静矩和形心平面图形的几何性质一般与杆件横截面的几何形状和尺寸有关，下面介绍的几何性质表征量在杆件应力与变形的分析与计算中占有举足轻重的作用。

静矩：平面图形面积对某坐标轴的一次矩，如图Ⅰ-1所示。

定义式：，(Ⅰ-1）量纲为长度的三次方。

由此可得薄板重心的坐标为同理有所以形心坐标，（Ⅰ-2）或，由式（Ⅰ-2）得知，若某坐标轴通过形心，则图形对该轴的静矩等于零，即，；，则；反之，若图形对某一轴的静矩等于零，则该轴必然通过图形的形心。

静矩与所选坐标轴有关，其值可能为正，负或零。

如一个平面图形是由几个简单平面图形组成，称为组合平面图形。

设第i块分图形的面积为，形心坐标为，则其静矩和形心坐标分别为，（Ⅰ-3），（Ⅰ-4）【例I-1】求图Ⅰ-2所示半圆形的及形心位置。

【解】由对称性，，。

现取平行于轴的狭长条作为微面积所以读者自己也可用极坐标求解。

【例I-2】确定形心位置，如图Ⅰ-3所示。

【解】将图形看作由两个矩形Ⅰ和Ⅱ组成，在图示坐标下每个矩形的面积及形心位置分别为矩形Ⅰ：mm2mm，mm矩形Ⅱ：mm2mm，mm整个图形形心的坐标为§16-2 惯性矩和惯性半径惯性矩：平面图形对某坐标轴的二次矩，如图Ⅰ-4所示。

，(Ⅰ-5)量纲为长度的四次方，恒为正。

相应定义，(Ⅰ-6)为图形对轴和对轴的惯性半径。

组合图形的惯性矩设，(Ⅰ-7)若以表示微面积到坐标原点的距离,则定义图形对坐标原点的极惯性矩（Ⅰ-8）因为所以极惯性矩与（轴）惯性矩有关系（Ⅰ-9）式（Ⅰ-9）表明，图形对任意两个互相垂直轴的（轴）惯性矩之和，等于它对该两轴交点的极惯性矩。

下式（Ⅰ-10）定义为图形对一对正交轴、轴的惯性积。

矩形对于中线(垂直于h边的中轴线)的惯性矩：b*h^3/12三角形：b*h^3/36圆形对于圆心的惯性矩：π*d^4/64环形对于圆心的惯性矩：π*D^4*（1-α^4)/64;α=d/D§16-1 静矩和形心平面图形的几何性质一般与杆件横截面的几何形状和尺寸有关，下面介绍的几何性质表征量在杆件应力与变形的分析与计算中占有举足轻重的作用。

静矩：平面图形面积对某坐标轴的一次矩，如图Ⅰ-1所示。

定义式：，(Ⅰ-1）量纲为长度的三次方。

由于均质薄板的重心与平面图形的形心有相同的坐标和。

则由此可得薄板重心的坐标为同理有所以形心坐标，（Ⅰ-2）或，由式（Ⅰ-2）得知，若某坐标轴通过形心，则图形对该轴的静矩等于零，即，；，则；反之，若图形对某一轴的静矩等于零，则该轴必然通过图形的形心。

静矩与所选坐标轴有关，其值可能为正，负或零。

如一个平面图形是由几个简单平面图形组成，称为组合平面图形。

设第i块分图形的面积为，形心坐标为，则其静矩和形心坐标分别为，（Ⅰ-3），（Ⅰ-4）【例I-1】求图Ⅰ-2所示半圆形的及形心位置。

【解】由对称性，，。

现取平行于轴的狭长条作为微面积所以读者自己也可用极坐标求解。

【例I-2】确定形心位置，如图Ⅰ-3所示。

【解】将图形看作由两个矩形Ⅰ和Ⅱ组成，在图示坐标下每个矩形的面积及形心位置分别为矩形Ⅰ：mm2mm，mm矩形Ⅱ：mm2mm，mm整个图形形心的坐标为§16-2 惯性矩和惯性半径惯性矩：平面图形对某坐标轴的二次矩，如图Ⅰ-4所示。

，(Ⅰ-5)量纲为长度的四次方，恒为正。

相应定义，(Ⅰ-6)为图形对轴和对轴的惯性半径。

组合图形的惯性矩设为分图形的惯性矩，则总图形对同-轴惯性矩为，(Ⅰ-7)若以表示微面积到坐标原点的距离,则定义图形对坐标原点的极惯性矩（Ⅰ-8）因为所以极惯性矩与（轴）惯性矩有关系（Ⅰ-9）式（Ⅰ-9）表明，图形对任意两个互相垂直轴的（轴）惯性矩之和，等于它对该两轴交点的极惯性矩。

极惯性矩常用计算公式：Ip=∫Aρ^2dA矩形对于中线(垂直于h边的中轴线)的惯性矩：b*h^3/12三角形：b*h^3/36圆形对于圆心的惯性矩：π*d^4/64环形对于圆心的惯性矩：π*D^4*（1-α^4)/64;α=d/D§16-1 静矩和形心平面图形的几何性质一般与杆件横截面的几何形状和尺寸有关，下面介绍的几何性质表征量在杆件应力与变形的分析与计算中占有举足轻重的作用。

静矩：平面图形面积对某坐标轴的一次矩，如图Ⅰ-1所示。

定义式：，(Ⅰ-1）量纲为长度的三次方。

由于均质薄板的重心与平面图形的形心有相同的坐标和。

则由此可得薄板重心的坐标为同理有所以形心坐标，（Ⅰ-2）或，由式（Ⅰ-2）得知，若某坐标轴通过形心，则图形对该轴的静矩等于零，即，；，则；反之，若图形对某一轴的静矩等于零，则该轴必然通过图形的形心。

静矩与所选坐标轴有关，其值可能为正，负或零。

如一个平面图形是由几个简单平面图形组成，称为组合平面图形。

设第i块分图形的面积为，形心坐标为，则其静矩和形心坐标分别为，（Ⅰ-3），（Ⅰ-4）【例I-1】求图Ⅰ-2所示半圆形的及形心位置。

【解】由对称性，，。

现取平行于轴的狭长条作为微面积所以读者自己也可用极坐标求解。

【例I-2】确定形心位置，如图Ⅰ-3所示。

【解】将图形看作由两个矩形Ⅰ和Ⅱ组成，在图示坐标下每个矩形的面积及形心位置分别为矩形Ⅰ：mm2mm，mm矩形Ⅱ：mm2mm，mm整个图形形心的坐标为§16-2 惯性矩和惯性半径惯性矩：平面图形对某坐标轴的二次矩，如图Ⅰ-4所示。

，(Ⅰ-5)量纲为长度的四次方，恒为正。

相应定义，(Ⅰ-6)为图形对轴和对轴的惯性半径。

组合图形的惯性矩设为分图形的惯性矩，则总图形对同-轴惯性矩为，(Ⅰ-7)若以表示微面积到坐标原点的距离,则定义图形对坐标原点的极惯性矩（Ⅰ-8）因为所以极惯性矩与（轴）惯性矩有关系（Ⅰ-9）式（Ⅰ-9）表明，图形对任意两个互相垂直轴的（轴）惯性矩之和，等于它对该两轴交点的极惯性矩。

极惯性矩常用计算公式[精华]极惯性矩常用计算公式:Ip=?Aρ^2dA矩形对于中线(垂直于h边的中轴线)的惯性矩:b*h^3/12三角形:b*h^3/36圆形对于圆心的惯性矩:π*d^4/64环形对于圆心的惯性矩:π*D^4*(1-α^4)/64;α=d/D?16-1 静矩和形心平面图形的几何性质一般与杆件横截面的几何形状和尺寸有关，下面介绍的几何性质表征量在杆件应力与变形的分析与计算中占有举足轻重的作用。

静矩:平面图形面积对某坐标轴的一次矩，如图?-1所示。

定义式:， (?-1)量纲为长度的三次方。

由于均质薄板的重心与平面图形的形心有相同的坐标和。

则由此可得薄板重心的坐标为同理有所以形心坐标， (?-2) 或，由式(?-2)得知，若某坐标轴通过形心，则图形对该轴的静矩等于零，即，;，则;反之，若图形对某一轴的静矩等于零，则该轴必然通过图形的形心。

静矩与所选坐标轴有关，其值可能为正，负或零。

如一个平面图形是由几个简单平面图形组成，称为组合平面图形。

设第i块分图形的面积为，形心坐标为，则其静矩和形心坐标分别为， (?-3)， (?-4)【例I-1】求图?-2所示半圆形的及形心位置。

【解】由对称性，，。

现取平行于轴的狭长条作为微面积所以读者自己也可用极坐标求解。

【例I-2】确定形心位置，如图?-3所示。

【解】将图形看作由两个矩形?和?组成，在图示坐标下每个矩形的面积及形心位置分别为矩形?:mm2mm，mm矩形?:mm2mm，mm 整个图形形心的坐标为?16-2 惯性矩和惯性半径惯性矩:平面图形对某坐标轴的二次矩，如图?-4所示。

， (?-5)量纲为长度的四次方，恒为正。

相应定义， (?-6)为图形对轴和对轴的惯性半径。

组合图形的惯性矩设为分图形的惯性矩，则总图形对同-轴惯性矩为， (?-7)若以表示微面积到坐标原点的距离,则定义图形对坐标原点的极惯性矩(?-8) 因为所以极惯性矩与(轴)惯性矩有关系(?-9) 式(?-9)表明，图形对任意两个互相垂直轴的(轴)惯性矩之和，等于它对该两轴交点的极惯性矩。

前引360知识：惯性矩是一个物理量，通常被用作描述一个物体抵抗弯曲的能力。

惯性矩的国际单位为(m^4)。

百度知识：惯性矩(moment of inertia of an area)是一个几何量，通常被用作描述截面抵抗弯曲的性质。

惯性矩的国际单位为(m4)。

即面积二次矩，也称面积惯性矩，而这个概念与质量惯性矩（即转动惯量）是不同概念。

截面惯性矩（I=截面面积X截面轴向长度的二次方）结构构件惯性矩I x结构设计和计算过程中，构件惯性矩I x为截面各微元面积与各微元至与X轴线平行或重合的中和轴距离二次方乘积的积分。

主要用来计算弯矩作用下绕X轴的截面抗弯刚度。

结构构件惯性矩I y结构设计和计算过程中，构件惯性矩I y为截面各微元面积与各微元至与Y轴线平行或重合的中和轴距离二次方乘积的积分。

主要用来计算弯矩作用下绕Y轴的截面抗弯刚度。

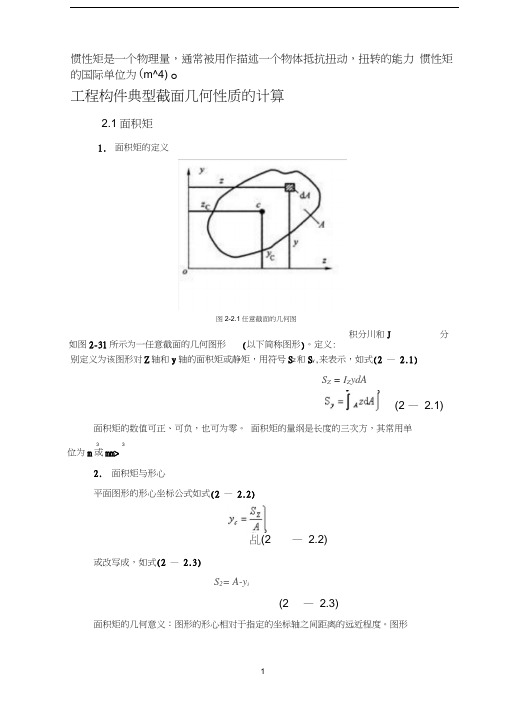
工程构件典型截面几何性质的计算2.1面积矩1．面积矩的定义图2-2.1任意截面的几何图形如图2-2.1所示为一任意截面的几何图形(以下简称图形)。

定义：积分和分别定义为该图形对z轴和y轴的面积矩或静矩，用符号S z和S y，来表示，如式(2—2.1)(2—2.1)面积矩的数值可正、可负，也可为零。

面积矩的量纲是长度的三次方，其常用单位为m3或mm3。

2．面积矩与形心平面图形的形心坐标公式如式(2—2.2)(2—2.2)或改写成，如式(2—2.3)(2—2.3)面积矩的几何意义：图形的形心相对于指定的坐标轴之间距离的远近程度。

图形形心相对于某一坐标距离愈远，对该轴的静距（面积矩）绝对值愈大。

图形对通过其形心的轴的静距（面积矩）等于零；反之，图形对某一轴的面积矩等于零，该轴一定通过图形形心。

形心确定的规律：（a）图形有对称轴时，形心必在此对称轴上。

（b）图形有两个对称轴时，形心必在此两对称轴的交点处。

3．组合截面面积矩和形心的计算组合截面对某一轴的面积矩等于其各简单图形对该轴面积矩的代数和。

LOGO惯性矩的计算方法及常用截面惯性矩计算公式在此输入你的公司名称惯性矩的计算方法及常用截面惯性矩计算公式截面图形的几何性质一.重点及难点:（一）.截面静矩和形心1•静矩的定义式如图1所示任意有限平面图形，取其单元如面积dA，定义它对任意轴的一次矩为它对该轴的静矩，即dS y 二xdAdSx = ydA整个图形对y、z轴的静矩分别为S y = A xdA(1-Sx= A ydA1)2.形心与静矩关系图1-1设平面图形形心C的坐标为y C,z C则0-S y x =A (1-2)推论1如果y轴通过形心（即x = 0），则静矩Sy=0 ；同理，如果x轴通过形心（即y = 0），则静矩Sx=o；反之也成立。

推论2如果x、y轴均为图形的对称轴，则其交点即为图形形心；如果y轴为图形对称轴，贝昭形形心必在此轴上。

3.组合图形的静矩和形心设截面图形由几个面积分别为A,A2,A3……A n的简单图形组成，且一直各族图形的形心坐标分别为x1,y1; x2,y2; x3,y3，则图形对y轴和x轴的静矩分别为n nS y = * S yi i A i Xii -1 i-1 nnS x 八 S xi 八 A i y ii 4i 4截面图形的形心坐标为A i4.静矩的特征（1）界面图形的静矩是对某一坐标轴所定义的，故静矩与坐标轴有关。

（2）静矩有的单位为m 3（3）静矩的数值可正可负，也可为零。

图形对任意形心轴的静矩必定 为零，反之，若图形对某一轴的静矩为零，则该轴必通过图形的形心。

⑷ 若已知图形的形心坐标。

则可由式（I-1）求图形对坐标轴的静矩。

若已知图形对坐标轴的静矩，则可由式（1-2）求图形的形心坐标。

组 合图形的形心位置，通常是先由式（I-3）求出图形对某一坐标系的静 矩，然后由式（I-4）求出其形心坐标。

（二）■惯性矩惯性积惯性半径1. 惯性矩定义 设任意形状的截面图形的面积为 A （图I-3），则图形对0点的极 惯性矩定义为 I p = A （2dA（1-5）图形对y 轴和x 轴的光性矩分别定义为 I y 二 A X 2dA ， I x 「A y 2dA （I-6）惯性矩的特征（1）界面图形的极惯性矩是对某一极点定义的； 轴惯性矩是对某一坐标轴定义的。

惯性矩是一个物理量，通常被用作描述一个物体抵抗扭动，扭转的能力惯性矩的国际单位为(m^4) O工程构件典型截面几何性质的计算2.1面积矩1.面积矩的定义别定义为该图形对Z轴和y轴的面积矩或静矩，用符号S Z和S y,来表示，如式(2 —2.1)面积矩的数值可正、可负，也可为零。

面积矩的量纲是长度的三次方，其常用单3 3位为m或mm>2.面积矩与形心平面图形的形心坐标公式如式(2 —2.2)乩(2 — 2.2)或改写成，如式(2 —2.3)S2= A-y i(2 —2.3)面积矩的几何意义：图形的形心相对于指定的坐标轴之间距离的远近程度。

图形如图2-31所示为一任意截面的几何图形(以下简称图形)。

定义:积分川和J 分(2 —2.1)图2-2.1任意截面的几何图形S Z= I Z ydA形心相对于某一坐标距离愈远，对该轴的面积矩绝对值愈大。

图形对通过其形心的轴的面积矩等于零；反之，图形对某一轴的面积矩等于零, 该轴一定通过图形形心。

3 •组合截面面积矩和形心的计算组合截面对某一轴的面积矩等于其各简单图形对该轴面积矩的代数和。

如式 (2 — 2.4)Σ¾ =Σj ⅛z J (2 — 2.4)式中，A 和y i 、Z i 分别代表各简单图形的面积和形心坐标。

组合平面图形的形心位 置由式(2 — 2.5)确定2.2极惯性矩、惯性矩和惯性积1 •极惯性矩任意平面图形如图2-31所示，其面积为A 。

定义：积分丨「’川称为图形对O 点的 极惯性矩，用符号I P ，表示，如式(2 — 2.6)'[ 」(2 — 2.6)极惯性矩是相对于指定的点而言的，即同一图形对不同的点的极惯性矩一般是不同的。

极惯性矩恒为正，其量纲是长度的4次方，常用单位为m 4或mr ⅛(1)圆截面对其圆心的极惯性矩，如式(2 — 7)IP- 32 (2 — 2.7)(2)对于外径为D 内径为d 的空心圆截面对圆心的极惯性矩，如式(2 — 2.8)_(1 —況)P 32(2 — 2.8)式中，：二d/D 为空心圆截面内、外径的比值。

惯性矩总结(含常用惯性矩公式)惯性矩总结（含常用惯性矩公式）惯性矩是描述物体对旋转运动惯性性质的物理量。

它们在工程、物理学和机械设计等领域中起着非常重要的作用。

本文将对惯性矩进行总结，并介绍一些常用的惯性矩公式。

一、惯性矩的定义惯性矩又称为转动惯量或转动惯性矩，用符号I表示。

惯性矩描述了物体对于绕特定轴线旋转的难易程度。

它与物体的质量分布和轴线的位置有关。

对于一个质量分布均匀的物体，其惯性矩可以通过对质量元素的微小体积进行积分来计算。

二、常用惯性矩公式1. 刚体绕轴线旋转的惯性矩对于一个刚体绕轴线旋转，其惯性矩可以表示为：I = ∫r^2dm其中，r是质量元素到轴线的距离，dm是质量元素的微小质量。

2. 常见几何形状的惯性矩公式常见几何形状的惯性矩公式如下：- 环状物体绕其对称轴的惯性矩公式：I = (mR^2)/2其中，m是环状物体的质量，R是环的半径。

- 圆盘绕其对称轴的惯性矩公式：I = (mR^2)/4其中，m是圆盘的质量，R是圆盘的半径。

- 长棒绕其一端垂直轴的惯性矩公式：I = (mL^2)/3其中，m是长棒的质量，L是长棒的长度。

- 长方体绕通过其质心轴的惯性矩公式：I = (m(a^2 + b^2))/12其中，m是长方体的质量，a和b分别是长方体的两个相邻边的长度。

3. 复杂形状的惯性矩公式对于一些复杂的形状，可以利用积分来计算其惯性矩。

例如，对于一个半径为R的圆柱体，其绕通过其质心轴的惯性矩可以表示为：I = (mR^2)/2 + ∫(r^2 - R^2)dm其中，r是圆柱体内任意一点到轴线的距离。

三、应用举例惯性矩广泛应用于工程和物理学中的各种问题。

例如，在机械设计中，惯性矩用于计算旋转部件的稳定性和旋转惯量。

在物理学中，惯性矩用于描述刚体的转动运动和角动量。

以机械工程为例，当设计一个旋转的零件时，需要计算其惯性矩，以确定所需要的力矩和加速度。

同时，惯性矩也可以用来评估旋转零件的稳定性。

惯性矩(moment of inertia of an area)是一个几何量，通常被用作描述截面抵抗弯曲的性质。

惯性矩的国际单位为(m4)。

即面积二次矩，也称面积惯性矩，而这个概念与质量惯性矩（即转动惯量）是不同概念。

面积元素dA与其至z轴或y轴距离平方的乘积y2dA或z2dA的积分，分别称为该面积元素对于z轴或y轴的惯性矩或截面二次轴矩。

惯性矩的数值恒大于零对Z轴的惯性矩：对Y轴的惯性矩：截面对任意一对互相垂直轴的惯性矩之和，等于截面对该二轴交点的极惯性矩。

极惯性矩常用计算公式：矩形对于中线(垂直于h边的中轴线)的惯性矩：三角形：圆形对于坐标轴的惯性矩：圆形对于圆心的惯性矩：环形对于圆心的惯性矩：，需要明确因为坐标系不同计算公式也不尽相同。

结构构件惯性矩Ix结构设计和计算过程中，构件惯性矩Ix为截面各微元面积与各微元至与X 轴线平行或重合的中和轴距离二次方乘积的积分。

主要用来计算弯矩作用下绕X 轴的截面抗弯刚度。

结构构件惯性矩Iy结构设计和计算过程中，构件惯性矩Iy为截面各微元面积与各微元至与Y 轴线平行或重合的中和轴距离二次方乘积的积分。

主要用来计算弯矩作用下绕Y 轴的截面抗弯刚度。

静矩静矩（面积X面内轴一次）把微元面积与各微元至截面上指定轴线距离乘积的积分称为截面的对指定轴的静矩Sx=∫ydA。

静矩就是面积矩，是构件的一个重要的截面特性，是截面或截面上某一部分的面积乘以此面积的形心到整个截面的型心轴之间的距离得来的，是用来计算应力的。

注意：惯性矩是乘以距离的二次方,静矩是乘以距离的一次方，惯性矩和面积矩（静矩）是有区别的。

分类截面惯性矩截面惯性矩（I=截面面积X截面轴向长度的二次方）截面惯性矩：the area moment of inertiacharacterized an object's ability to resist bending and is required to calculate displacement.截面各微元面积与各微元至截面某一指定轴线距离二次方乘积的积分Ix= y^2dF.截面极惯性矩截面极惯性矩（Ip=面积X垂直轴二次）。

惯性矩计算公式推导惯性矩是力学中的一个重要组成部分，它可以说是受到外力作用时产生的物体的重要特征。

它表示了一个物体的运动状态，可以从物体的形状，大小，重量和分布中计算出来。

惯性矩的计算方法有很多种，常用的有惯性矩计算公式法、积分法和向量法。

惯性矩计算公式法是一个基本的计算方法，它定义了一系列计算惯性矩的公式，根据物体的形状，大小，重量等信息，可以用这些公式来计算惯性矩。

概括来说，惯性矩计算公式法的公式可以分为三类，即角惯性矩公式，矩惯性矩公式和面惯性矩公式。

我们可以根据物体的几何形状来选择相应的计算方法，也可以综合使用多种计算方法。

（1）角惯性矩公式：角惯性矩可以用一种简洁的公式来计算，即I=mr其中，I代表惯性矩，m代表质量，r代表半径。

根据这个公式，我们可以计算出圆柱形物体的惯性矩，只需将该物体的质量和半径代入公式即可。

例如，当物体的质量为m，半径为r时，惯性矩计算结果为I=mr2.（2）矩惯性矩公式：矩惯性矩的计算公式有多种，其中一种是：I =mri其中，I代表惯性矩，m表示质量，r表示距离，i表示不同质点。

根据这个公式，我们可以计算出物体中不同质点的惯性矩，只需将该物体的质量和距离代入公式即可。

例如，当物体的质量为m1、m2、m3和距离为r1、r2、r3时，惯性矩计算结果可以表示为I=m1r1+m2r2+m3r3。

（3）面惯性矩公式：面惯性矩的计算公式为：I=mgA其中，I代表惯性矩，m表示质量，g表示重力加速度，A表示物体的表面积。

根据这个公式，我们可以计算出物体的惯性矩，只需将该物体的质量、重力加速度和表面积代入公式即可。

例如，当物体的质量为m，重力加速度为g，表面积为A时，惯性矩计算结果为I=mgA。

以上就是惯性矩计算公式的推导，掌握这些公式之后，我们就可以根据物体的几何形状、大小、质量和分布来计算物体的惯性矩，从而更好地分析和研究物体在外力作用下的运动状态。

惯性矩总结(含常用惯性矩公式) 惯性矩，这是一个听起来有点高深莫测的词汇，但是它其实跟我们的生活息息相关。

今天，我就来给大家讲讲惯性矩这个家伙，看看它到底是个什么玩意儿，以及它在我们日常生活中有哪些应用。

咱们来简单了解一下惯性矩的概念。

惯性矩，就是一个物体在受到外力作用时，能够保持静止或者匀速运动的性质。

换句话说，惯性矩就是一个物体的“稳定系数”。

有了惯性矩，我们就可以更好地了解一个物体在受到外力作用时的稳定性了。

那么，惯性矩又是如何计算出来的呢？这里就涉及到了一些常用的惯性矩公式。

咱们先来看看第一个公式：1.1 绕轴旋转的惯性矩公式假设有一个物体，它绕着一个轴旋转。

那么，这个物体的绕轴旋转惯性矩就是它的质心到轴的距离的平方乘以密度。

用数学公式表示就是：Ix = 0.5 * m * r^2 * ρ其中，Ix表示绕轴旋转的惯性矩，m表示物体的质量，r表示物体的半径，ρ表示物体的密度。

这个公式告诉我们，一个物体绕着一个轴旋转时的惯性矩，与其质量、半径和密度有关。

这个公式只适用于绕轴旋转的情况。

如果物体是其他方式运动的，我们还需要考虑其他因素。

接下来，我们来看看另一个常用的惯性矩公式：2.1 平行于面的惯性矩公式假设有一个物体，它在一个平面上滑动。

那么，这个物体在这个平面上的平行滑动惯性矩就是它的宽度乘以高度乘以密度。

用数学公式表示就是：Iy = w * h * ρ其中，Iy表示平行于面的惯性矩，w表示物体的宽度，h表示物体的高度，ρ表示物体的密度。

这个公式告诉我们，一个物体在一个平面上滑动时的惯性矩，与其宽度、高度和密度有关。

这个公式只适用于平行于面的情况。

如果物体是其他方式运动的，我们还需要考虑其他因素。

我们来看看第三个常用的惯性矩公式：3.1 沿着轴线的惯性矩公式假设有一个物体，它沿着一个轴线方向受到力的作用。

那么，这个物体沿着轴线的惯性矩就是它的质量乘以长度的平方除以2。

用数学公式表示就是：Iz = m * L^2 / 2其中，Iz表示沿着轴线的惯性矩，m表示物体的质量，L表示物体的长度。

极惯性矩常⽤计算公式极惯性矩常⽤计算公式：Ip=∫Aρ^2dA矩形对于中线(垂直于h边的中轴线)的惯性矩：b*h^3/12三⾓形：b*h^3/36圆形对于圆⼼的惯性矩：π*d^4/64环形对于圆⼼的惯性矩：π*D^4*（1-α^4)/64;α=d/D§16-1 静矩和形⼼平⾯图形的⼏何性质⼀般与杆件横截⾯的⼏何形状和尺⼨有关，下⾯介绍的⼏何性质表征量在杆件应⼒与变形的分析与计算中占有举⾜轻重的作⽤。

静矩：平⾯图形⾯积对某坐标轴的⼀次矩，如图Ⅰ-1所⽰。

定义式：，(Ⅰ-1）量纲为长度的三次⽅。

由此可得薄板重⼼的坐标为同理有所以形⼼坐标，（Ⅰ-2）或，由式（Ⅰ-2）得知，若某坐标轴通过形⼼，则图形对该轴的静矩等于零，即，；，则；反之，若图形对某⼀轴的静矩等于零，则该轴必然通过图形的形⼼。

静矩与所选坐标轴有关，其值可能为正，负或零。

如⼀个平⾯图形是由⼏个简单平⾯图形组成，称为组合平⾯图形。

设第i块分图形的⾯积为，形⼼坐标为，则其静矩和形⼼坐标分别为，（Ⅰ-3），（Ⅰ-4）【例I-1】求图Ⅰ-2所⽰半圆形的及形⼼位置。

【解】由对称性，，。

现取平⾏于轴的狭长条作为微⾯积所以读者⾃⼰也可⽤极坐标求解。

【例I-2】确定形⼼位置，如图Ⅰ-3所⽰。

【解】将图形看作由两个矩形Ⅰ和Ⅱ组成，在图⽰坐标下每个矩形的⾯积及形⼼位置分别为矩形Ⅰ：mm2mm，mm矩形Ⅱ：mm2mm，mm整个图形形⼼的坐标为§16-2 惯性矩和惯性半径惯性矩：平⾯图形对某坐标轴的⼆次矩，如图Ⅰ-4所⽰。

，(Ⅰ-5)量纲为长度的四次⽅，恒为正。

相应定义，(Ⅰ-6)为图形对轴和对轴的惯性半径。

组合图形的惯性矩设，(Ⅰ-7)若以表⽰微⾯积到坐标原点的距离,则定义图形对坐标原点的极惯性矩（Ⅰ-8）所以极惯性矩与（轴）惯性矩有关系（Ⅰ-9）式（Ⅰ-9）表明，图形对任意两个互相垂直轴的（轴）惯性矩之和，等于它对该两轴交点的极惯性矩。

下式（Ⅰ-10）定义为图形对⼀对正交轴、轴的惯性积。