高三数学-2016届高三12月联合调研测试数学(文理)试题

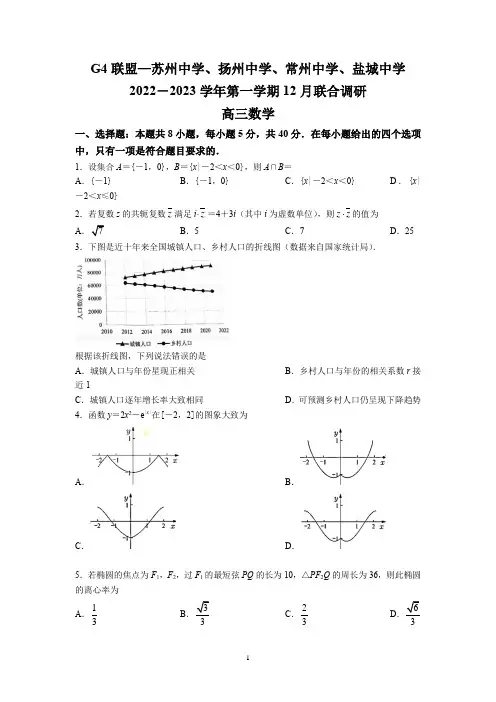
G4联盟—苏州中学、扬州中学、常州中学、盐城中学2022－2023学年第一学期12月联合调研高三数学一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．设集合A＝{－1，0}，B＝{x|－2＜x＜0}，则A∩B＝A．{－1} B．{－1，0} C．{x|－2＜x＜0} D．{x|－2＜x≤0}2．若复数z的共轭复数z满足i⋅z＝4＋3i（其中i为虚数单位），则z z⋅的值为A7B．5C．7D．25 3．下图是近十年来全国城镇人口、乡村人口的折线图（数据来自国家统计局）．根据该折线图，下列说法错误的是A．城镇人口与年份星现正相关B．乡村人口与年份的相关系数r接近1C．城镇人口逐年增长率大致相同D．可预测乡村人口仍呈现下降趋势4．函数y＝2x2－e|x|在[－2，2]的图象大致为A．B．C．D．5．若椭圆的焦点为F1，F2，过F1的最短弦PQ的长为10，△PF2Q的周长为36，则此椭圆的离心率为A．13B．33C．23D636．南宋时期，秦九韶就创立了精密测算雨量、雨雪的方法，他在《数学九章》载有“天池盆测雨”题，使用一个圆台形的天池盆接雨水．观察发现体积一半时的水深大于盆高的一半，体积一半时的水面面积大于盆高一半时的水面面积，若盆口半径为a ，盆地半径为b （0＜b ＜a ），根据如上事实，可以抽象出的不等关系为A 33322a ba b+<B 22a ba b+< C ．22222a b a b ++⎛⎫< ⎪⎝⎭D ．33322a b a b ++⎛⎫<⎪⎝⎭7．在数列{a n }中，()()111sin sin 10n n n n a a a a ++-⋅+=，则该数列项数的最大值为 A ．9B ．10C ．11D ．128．在△ABC 中，AB ＝4，BC ＝3，CA ＝2，点P 在该三角形的内切圆上运动，若AP mAB nAC =+（m ，n 为实数），则m ＋n 的最小值为A ．518B ．13C ．718D ．49二、选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．9．已知a ＞0，b ＞0，a ＋b ＝1，则 A ．114a b+≤B ．2222a b+≥C ．log 2a ＋log 2b ≤－2D ．1sin sin 2sin2a b +≤ 10．已知函数()x a a x f x e e --=+，()x a a x g x e e --=-，则 A ．函数y ＝g （x ）有且仅有一个零点B ．f ′（x ）＝g （x ）且g ′（x ）＝f （x ）C ．函数y ＝f （x ）g （x ）的图象是轴对称图形D ．函数()()g x y f x =在R 上单调递增11．乒乓球（tabletennis ），被称为中国的“国球”，是一种世界流行的球类体育项目，是推动外交的体育项目，被誉为“小球推动大球”．某次比赛采用五局三胜制，当参赛甲、乙两位中有一位赢得三局比赛时，就由该选手晋级而比赛结束．每局比赛皆须分出胜负，且每局比赛的胜负不受之前已赛结果影响．假设甲在任一局赢球的概率为p （0≤p ≤1），实际比赛局数的期望值记为f （p ），下列说法正确的是 A ．三局就结束比赛的概率为p 3＋（1－p ）3B ．f （p ）的常数项为3C ．1435f f ⎛⎫⎛⎫< ⎪⎪⎝⎭⎝⎭D ．13328f ⎛⎫=⎪⎝⎭ 12．在四棱锥P －ABCD 中，底面ABCD 为正方形，P A ⊥底面ABCD ，P A ＝AB ＝1．G 为PC的中点，M 为平面PBD 上一点下列说法正确的是 A ．MG 的最小值为36B ．若MA ＋MG ＝1，则点M 的轨迹是椭圆C ．若156MA =M 的轨迹围成图形的面积为12π D ．存在点M ，使得直线BM 与CD 所成角为30°三、填空题：本题共4小题，每小题5分，共20分．13．在6x x ⎛- ⎝的展开式中，常数项为 ．14．如图，将绘有函数()sin 2f x M πϕ⎛⎫=+⎪⎝⎭（M ＞0，0＜φ＜π）部分图象的纸片沿x 轴折成直二面角，此时A ，B 10φ＝ ．15．我们利用“错位相减”的方法可求等比数列的前n 项和，进而可利用该法求数列{（2n －1）⋅3n }的前n 项和S n ，其操作步骤如下： 由于S n ＝1×31＋3×32＋…＋（2n －1）⋅3n ，()23131333213n n S n +=⨯+⨯++-⋅，从而()()21232323213n n n S n +=--⨯++⨯+-⋅，所以()1133n n S n +=-⋅+，始比如上方法可求数列{n 2⋅3n }的前n 项和T n ，则2T n ＋3＝ ．16．已知函数f （x ）是定义在R 上的偶函数，且当x ≥0时，f （x ）＝2x ．若对任意x ∈[1，3]，不等式f （x ＋a ）≤f 2（x ）恒成立，则实数a 的取值范围是 ．四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．17．（本小题满分10分）在数列{a n }中，a ＝1，其前n 项和S n 满足2S n ＝（n ＋1）a n ，n ∈N *． （1）求数列{a n }的通项公式a n ； （2）若m 为正整数，记集合22n nn a a m a ⎧⎫⎪⎪+⎨⎬⎪⎪⎩⎭≤的元素个数为b m ，求数列{b m }的前20项和．18．（本小题满分12分）在轴截面为正方形ABCD 的圆柱中，M ，N 分别为弧AD ，弧BC 的中点，且在平面ABCD 的两侧．（1）求证：四边形ANCM 是矩形； （2）求二面角B －MN －C 的余弦值．19．（本小题满分12分）文化月活动中，某班级在宣传栏贴出标语“学好数学好”，可以不同断句产生不同意思，“学/好数学/好”指要学好的数学，“学好/数学/好”强调数学学习的重要性，假设一段时间后，随机有N 个字脱落．（1）若N ＝3，用随机变量X 表示脱落的字中“学”的个数，求随机变量X 的分布列及期望；（2）若N ＝2，假设某同学检起后随机贴回，求标语恢复原样的概率． 20．（本小题满分12分）记△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知b ＝1，c ＝2． （1）若2CD DB =，2AD CB ⋅=，求A ； （2）若23C B π-=，求△ABC 的面积． 21．（本小题满分12分）在平面直角坐标系xOy 中，已知点P 在抛物线C 1：y 2＝4x 上，圆C 2：（x －2）2＋y 2＝r 2（0＜r ＜2）．（1）若r ＝1，Q 为圆C 2上的动点，求线段PQ 长度的最小值；（2）若点P 的纵坐标为4，过P 的直线m ，n 与圆C 2相切，分别交抛物线C 1于A ，B （异于点P ），求证：直线AB 过定点． 22．（本小题满分12分）若对实数x 0，函数f （x ），g （x ）满足f （x 0）＝g （x 0）且f ′（x 0）＝g ′（x 0），则称()()()00,,f x x x F x g x x x <⎧⎪=⎨⎪⎩≥为“平滑函数”，x 0为该函数的“平滑点”．已知()323122x f x ax x x =-+，g （x ）＝bx ln x ． （1）若1是平滑函数F （x ）的“平滑点”， （ⅰ）求实数a ，b 的值；（ⅱ）若过点P （2，t ）可作三条不同的直线与函数y ＝F （x ）的图象相切，求实数t的取值范围；（2）对任意b ＞0，判断是否存在a ≥1，使得函数F （x ）存在正的“平滑点”，并说明理由．G4联盟—苏州中学、扬州中学、常州中学、盐城中学2022-2023学年第一学期12月联合调研高三数学答案及其解析一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．【答案】A 2．【答案】D【解析】4334i z i z i ⋅=+⇒=-，所以25z z ⋅= 3．【答案】B【解析】因为乡村人口与年份望负线性相关关系，所以r 接近－1，故选B 4．【答案】D 5．【答案】C【解析】由题意得22245109436b b a a a ⎧⎧==⎪⇒⎨⎨=⎩⎪=⎩，所以226c a b =-=，故椭圆离心率为23c e a == 6．【答案】D 7．【答案】C 【解析】()()()()()()11112111cos cos sin sin sin 2n n n n n n n n n n n n n a a a a a a a a a a a a a +++++++--+--++⎡⎤⎡⎤⎣⎦⎣⎦-⋅+==-21sin 10n a =，所以{}2sin n a 为等差数列，公差为110，所以()2211sin sin 1110n a a n =+-⨯≤，所以110n -211sin 111a n -⇒≤≤≤，故选C 8．【答案】B【解析】()m n AP mAB nAC m n AB AC m n m n ⎛⎫=+=++⎪++⎝⎭，由P 在内切圆上，故APm n m n AB AC m n m n +=⎛⎫+ ⎪++⎝⎭，则11cos 16A =，所以BC 边上高为15h =圆半径15r =，故由平行线等比关系，可得213h r m n h -+=≥，故选B 二、选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．9．【答案】BCD 【解析】选项A ，应该是114a b+≥，B ：22221a ba b+++≥，B 正确；C ：222log log 2log 22a ba b ++=-≤，C 正确；D ：1sin sin 2sincos 2sin 222a b a b a b +-+=⋅≤，D 正确；答案为BCD 10．【答案】ABD【解析】AB 正确，因为()f x 关于x a =轴对称，()g x 关于(),0a 中心对称，故()()f xg x 为中心对称图形，C 错误：而()()()()()220'g x f x q x f x B x ⎡⎤-=>⎢⎥∠⎣⎦或根据一般得分离常数变形可知D 正确；答案为：ABD 11．【答案】ABD 【解析】 显然A 正确；()()()()()323131223343141151f p p p C p p C p p C p p ⎡⎤⎡⎤=+-+-+-+⨯-⎣⎦⎣⎦()03f =，13328f B ⎛⎫=⇒ ⎪⎝⎭，D 正确； 求导或根据()f p 关于12对称，且p 越极端，越可能快结束，有11412352--≤，得1435f f ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭， 故答案为：ABD 12．【答案】ABC 【解析】A 选项判断：应用等体积法，可()()min min 11223MG AG =≥，A 正确； B 选项：因为面PBD 不与AG 垂直，也不平行，故轨迹不可能时圆，即为椭圆，B 正确； C 选项判断：设MH ⊥面PBD ，H ∈面PBD ，2151612MA HM =⇒=，故C 正确；D 选项判断：由于CD 与面PBD 夹角θ满足1sin 23θ=>，故[],6πθπθ∉-，D 错误； 综上所述，答案为ABC三、填空题：本题共4小题，每小题5分，共20分．13．【答案】15【解析】展开式的通项为()()36621661rr rr Tr C x C x x --+⎛==- ⎝，当31602r -=，4r =时，为常数项15 14．【答案】56π【解析】如图，因为()f x 的周期为242T ππ==，所以22T CD ==，22TCD ==，所以22AB AC BC +22410M =+=解得3M =所以()32f x x πϕ⎛⎫=+ ⎪⎝⎭，所以()3032f ϕ==，1sin 2ϕ=，因为0ϕπ<<，所以6πϕ=或56π，又因为函数()f x 在y 轴右侧单调递减，所以56πϕ=． 15．【答案】()2113n n n +-+⋅【解析】2122213233n n T n =⨯+⨯+⋯+⋅① 222321313233n n T n +=⨯+⨯+⨯+⋅②②－①()()()222222322123123233133n n n T n n n +⎡⎤=-+-⋅+-⋅++--⋅+⋅⎣⎦()()3321333532133n n n n +=--⋅+⋅++-⋅+⋅()()212112333313n n n n n S n S n n n +++=---+⋅=-+⋅=-+⋅所以()212313n n T n n ++=-+⋅16．【答案】[]3,1-． 【解析】()()()()[]2221,3f x a fx f x f x x +==⇒∀∈≤，[]23,1x a a +⇒∈-≤四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．17．（本小题满分10分） 解析：（1）()()()()()111212221212nn n n n n n n n n a S n a a S S n a na n n a na n n---=+⇒=-=+-⇒-=⇒=≥≥11111n n a a a n n -===⇒=- （2）2214222n n a n m m n m a n n ⎛⎫+⇒+⇒-+ ⎪⎝⎭≤≤≤， 因为1422n n ⎛⎫+ ⎪⎝⎭≥，当且仅当2n =时成立， 所以10b =，21b =，当3n ≥，35b =，47b =，59b =，611b =，…，2339b = 所以{}m b 的前20项和为()135739378+++++=．18．（本小题满分12分） 【解析】（1）设轴截面正方形ABCD 边长为2a ，取弧BC 另一侧的中点Q ， 则BC 与NQ 垂直平分，且2BC NQ a ==， 所以四边形BNCQ 为正方形，2BQ NC a ==，因为M 为弧AD 中点，所以MQ AB ∥，四边形ABQM 为矩形， 所以AM BQ ∥，所以AM CN ∥，所以四边形AMCN 为平行四边形， 因为226AN AB BN a =+，2222MN MQ QN a =+=，所以22228AM AN MN a +==，所以AM ⊥AN ，所以四边形ANCM 为矩形； （2）由（1）知，226MB MC MQ QB a ==+=，2BN CN a ==，22MN a =，所以2MNB MNC π∠=∠=所以MNB MNC ∆∆≌，Rt △MBN 斜边MN 上的高626222a a h a==， 作BP ⊥MN ，则CP ⊥MN ，∠BPC 即为二面角B -MN -C 的平面角，6BP CP ==，2BC a =， 在△BPC 中，由余弦定理得222222341cos 233BP CP BC a a BPC BP CP a +--∠===-⨯， 二面角B -MN -C 的余弦值为13- 19．（本小题满分12分） 【解析】（1）随机变量X 的可能取值为0，1，2，12C()33351010C P X C ===，()1223356110C C P X C ===，()2123353210C C P X C ===，随机变量X 的分布列如下表：X 012P110 610 310随机变量X 的期望为()012 1.2101010E X =⨯+⨯+⨯= 法二：随机变量X 服从超几何分布X ～H （3，2，5），所以()26355E X =⨯= （2）设脱落一个“学”为事件A ，脱落一个“好”为事件B ，脱落一个“数”为事件C ，事件M 为脱落两个字M AA BB AB AC BC =++++，()2225110C P AA C ==，()2225110C P BB C ==，()112225410C C P AB C ⋅==，()112125210C C P AC C ⋅==，()112125210C C P BC C ⋅==， 所以某同学捡起后随机贴回，标语恢复原样的概率为()()()()()()()11413125525P P AA P BB P AB P AC P BC =+⨯+++⨯=+⨯=，法二：掉下的两个字不同的概率为1020.810p -==， 所以标语恢复原样的概率为()110.62p p -+=． 20．（本小题满分12分） 解：（1）()112123333CD DB AD AB BD AB BC AB AC AB AB AC =⇒=+=+=+-=+ 所以()22212118112cos 233333333AD CB AB AC AB AC AB AC AB AC A ⎛⎫⋅=+-=--⋅=--⨯⨯=⇒⎪⎝⎭1cos 2A =，因为()0,A π∈，所以3A π=（2）法一：因为23C B π-=，所以562A C π=-，62AB π=-， 因为2c b =，sin 2sinC B =，则5sin 2sin 6262A A ππ⎛⎫⎛⎫-=-⎪ ⎪⎝⎭⎝⎭化简整理得3tan 29A =， 所以22tan332sin 141tan 2AA A ==+ 故面积为133sin 2S bc A == 法二：因为2sin 2sin c b C B =⇒=， 因为23C B π-=， 所以23sin 2sin sin 3B B B B π⎛⎫+=⇒=⎪⎝⎭①， 联立22sin cos 1B B +=②解得3sin 27cos 27B B ⎧=⎪⎪⎨⎪=⎪⎩， 所以3sin 2sin 7C B ==232C B ππ=+> 所以cos 0C <，则2cos 1sin 7C C =-=所以()33sin sin sin cos cos sin 14A B C B C B C =+=+=所以△ABC 的面积为133sin 214ABC S bc A ∆==． 21．（本小题满分12分）【解析】 （1）设()2,2P t t ，则()222212411PQ PC t t --+-≥，当()0,0P ，Q 为2PC 线段与圆2C 的交点时，min 1PQ = （2）题意可知()4,4P ，过P 点直线()44y k x -=-与圆2C 相切， 2241k r k -=+，即()222416160r k k r --+-=，① 设直线AB 为：()()441m x n y -+-=，则与抛物线C 的交点方程可化为： ()()()()()()24844444(4)4y y m x n y x m x n y -+--+-=--+-⎡⎤⎡⎤⎣⎦⎣⎦， 令44y z x -=-，则：()()2188440n z m n z m ++--=，② 题意有，①②方程同解，故有()()()[]()2233164164818444y r r m n m n -⎡⎤⎣=---+⨯=--+-⎦-， 即：2111m n -=，故：直线AB 恒过()6,7-．22．（本小题满分12分）【解析】 （1）（ⅰ）()21'332f x ax a =-+，()[]'1lng x b x =+， 由题意可知10a -=，且532a b -=， 故解得：1a =，12b =， （ⅱ）进一步()323,122ln ,12x x x x F x x x ⎧-+<⎪⎪=⎨⎪⎪⎩≥，过点()2,P t 作()F x 的切线，切点()(),x F x 满足方程：()()()2F x t F x x -=-，故题意等价于方程：()()()'2t F x F x x =--有3个不同根，()()()()'2p x F x F x x =--，()()()''2p x F x x =--，代入得1,2x ⎛⎫∈-∞ ⎪⎝⎭时，()p x 单调递减，1,22x ⎡⎫∈⎪⎢⎣⎭时，()p x 单调递增，[)2,x ∈+∞时，()p x 单调递减， 故()13,2,ln 228t p x x ⎧⎫⎛⎫⎛⎫∈∈=-⎨⎬ ⎪ ⎪⎝⎭⎝⎭⎩⎭ （2）题意等价于：0b ∀>，是否1a ∃≥，使得[]3223ln 221331ln 2x ax x bx x ax x b x ⎧-+=⎪⎪⎨⎪-+=+⎪⎩有解 消a 有：()313212ln 122ln 1x x b x b x ---=-⇒=-，其中由0b >，可得23x e ⎛∈ ⎝， 故题意进一步化简23x e ⎛∀∈ ⎝，是否1a ∃≥，使得()3ln 3122ln 1x x x a x x -+=-成立， 23x e ⎛⇔∀∈ ⎝，()23ln 3122ln 1x x x x x -+-≤是否恒成立 设()()2243ln 231q x x x x x x =--+-，()()'83ln q x x x =-， 故2,13x ⎛⎫∈ ⎪⎝⎭时，单调递减，(x e ∈，()q x 单调递增，故：()()10q x q =≥得证，即0b ∀>，31a ≥，使得()F x 存在的“平滑点”．。

2024年重庆市高考数学三诊试卷一、单选题：本题共8小题，每小题5分，共40分.在每小题给出的选项中，只有一项是符合题目要求的.1.已知集合2{|10}A x x =-=，集合{}1,1,3B a a =+-，若A B ⊆，则=a （）A.1-B.0C.1D.2【答案】B 【解析】【分析】利用子集的概念求解.【详解】集合{}2{|10}1,1A x x =-==-，集合{}1,1,3B a a =+-，若A B ⊆，又11a a +>-，所以1111a a +=⎧⎨-=-⎩，解得0.a =故选：B2.设复数z 满足2i 1z z -=，则z 的虚部为（）A.13B.13-C.3D.3-【答案】A 【解析】【分析】设复数i(,R)z a b a b =+∈，根据题意，列出方程，结合复数相等，求得b 的值，即可求解.【详解】设复数i(,R)z a b a b =+∈，因为复数z 满足2i 1z z -=，可得()22i i i 1a b a b +--=，即()22i 1a b b a -+-=，则21a b -=，20b a -=，解得13b =，所以复数z 的虚部为13.故选：A.3.已知一种服装的销售量(y 单位：百件)与第x 周的一组相关数据统计如表所示，若两变量x ，y 的经验回归方程为ˆ 1.37.9yx =-+，则=a （）x 12345y66a31A.2B.3C.4D.5【答案】C 【解析】【分析】根据统计图表中的数据，求得样本中心，代入回归直线方程，即可求解.【详解】解：由统计图表中的数据，可得()11234535x =⨯++++=，()116663155a y a +=⨯++++=，即样本中心为16(3,5a +，因为两变量,x y 的经验回归方程为ˆ 1.37.9yx =-+，则161.337.95a+-⨯+=，解得 4.a =故选：C.4.若圆锥的母线长为2，且母线与底面所成角为π4，则该圆锥的侧面积为（）A.B.2πC. D.4π【答案】C 【解析】【分析】根据题意，求得圆锥底面圆的半径，结合圆锥的侧面积公式，即可求解.【详解】圆锥的母线长为2，母线与底面所成角为π4，所以底面圆的半径为2sin π4r ==，所以该圆锥的侧面积为π2S ==侧.故选：C5.重庆某高校去年招收学生来自成渝地区2400人，除成渝外的西部地区2000人，中部地区1400人，东部地区1800人，港澳台地区400人.学校为了解学生的饮食习惯，拟选取40人作样本调研，为保证调研结果的代表性，则从该校去年招收的成渝地区学生中不同的抽样结果种数为（）A.402400C B.242400C C.122400C D.102400C 【答案】C 【解析】【分析】根据分层抽样的性质计算即可。

广东省七校联合体2016届高三第二次联考试卷 数学理 第Ⅰ卷一、选择题：01．设复数z 满足33z i zi -=+，则z =( ) A ．3 B ．-3 C ．3iD ．-3i02．求值cos20cos351sin 20=-( )A ．22B ．-22C ．2D ．-203．“a≤-3”是“f(x)=-|x+a|在内的一个数来表示，该数越接近10表示满意度越高．为了解某地幸福感指数 [0，2) [2，4) [4，6) [6，8) 男居民人数 10 20 220 125 125 女居民人数1010180175125根据表格，解答下面的问题：(Ⅰ)在右图中绘出频率分布直方图，并估算该地区居民幸福感指数的平均值；(Ⅱ)如果居民幸福感指数不小于6，则认为其幸福．为了进一步了解居民的幸福满意度，调查组又在该地区随机抽取4对夫妻进行调查，用X 表示他们之中幸福夫妻(夫妻二人都感到幸福)的对数，求X 的分布列及期望(以样本的频率作为总体的概率)． 19．(本小题满分12分)如图是某直四棱柱被平面α所截得的部分， 底面ABCD 是矩形，侧棱GC 、ED 、FB 都垂 直于底面ABCD ，GC=3，AB=22，BC=5， 四边形AEFG 为菱形，经过C 且垂直于AG 的 平面与EG 、AG 、FG 分别交于点M 、H 、N ； ⑴求证：CN ⊥BH ；⑵求面AFGE 与底面ABCD 所成二面角的余弦值。

20．(本小题满分12分)椭圆2222 :1(0)y x C a b a b +=>>的上顶点为A ，4(,)33b P 是C 上的一点,以AP 为直径的圆经过椭圆C 的右焦点F ．⑴求椭圆C 的方程；⑵设过点M (2,0)的动直线l 与椭圆C 相交于D 、E 两点，求ODE △面积的最大值 21．(本小题满分12分)已知函数()(2)2ln 2f x a x x a =--+-，1()xg x xe -=⑴若函数()f x 在区间1(0,)2无零点，求实数a 的最小值；⑵若对任意给定的0(0,]x e ∈，方程0()()f x g x =在(0,]e 上总存在两个不等的实根，求实数a 的取值范围．请考生在第(22)、(23)、(24)三题中任选一题做答。

2023-2024学年第二学期期初联合调研试题
高三数学2024.2
一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．
=1+i2023，则复数z对应点位于第（）象限
1. 复数z满足z
2+3i
米8. 斜率为的直线l 经过双曲线22
221(0,0)x y
a b a b -
=>>的左焦点，与双曲线左，右两支
分别交于A ，B 两点，以双曲线右焦点2F 为圆心的圆经过A ，B ，则该双曲线的离心率为
（ ）二、多项选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分．12
1F
三、填空题：本题共3小题，每小题5分，共15分．
________
四、解答题：本题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤．
F
(2)若PD ⊥平面ABCD ，E 为AB 的中点，2PD AD CD ===，
60BAD ∠=︒，求二面角P CE F --的正切值.
2023-2024学年第二学期期初联合调研试题
高三数学答案2024.2 1-8. ACABCADD 9.AD 10.ABD 11.BCD
12.2±13. 5 14.2e
AFG，
………………………………………………………………7分
BAD=︒时，
60
因为PD⊥平面ABCD，EC⊂
⊥，
所以PD EC
因为PD，DM是平面PDM 所以EC⊥平面PDM，
因为PM⊂平面PDM，FM⊂
分6。

2015-2016 第一学期高三数学12 月（文）学生学业能力调研试卷考生注意：1.本试卷第Ⅰ卷基础题（ 123 分）第Ⅱ卷提升题（27 分）两部分，共150 分。

2.试卷书写规范工整，卷面整齐清楚，酌情减3-5分，并计入总分。

知识与技术学习能力习惯养成总分内容会合函数分析导数立体数列数形联合卷面整齐分数56330141919443-5150第 I 卷基础题（共123 分）一、选择题（每题 5 分，共 35 分）1．已知a,b R ， i 为虚数单位,若a 1 bi2i, 则实数a b（）1iA．2B． 3C． 4D． 52.设首项为 1，公比为2a n的前 n 项和为S n，则()的等比数列3A．Sn2a n1B．Sn 3a n 2 C． Sn 4 3a n D．Sn 3 2a n3.已知过点 P(2,2) 的直线与圆( x1) 2y2 5 相切，且与直线ax y 10 垂直，则a等于 ()A．－1． 1C． 21B D.224.已知函数的图象如下图，则其导函数的图象可能是（）5. 定义在R 上的偶函数知足：对随意的，都有. 则以下结论正确的选项是()A．f (0.32) f ( 20.3 ) f (log 2 5)B．f (log25) f (20.3 ) f (0.32 )C．f (log25) f (0.32 )f(20.3 )D．f (0.32) f (log 25 ) f (20 .3 )6.已知函数f (x)x 22x x0，若 f ( x)ax ，则 a 的取值范围是()ln( x1)x0A． ( －∞， 0]B．( －∞，0)C．[ －2,1]D．[ － 2,0]7.已知点G是ABC重心,AG AB AC(,R) ,A120 , AB AC2,则 AG 的最小值是() A.3B.2C. 322D.334二、填空题：（每题 5 分，共35 分）8.已知会合 A x | y lg(2 x x2 ) ， B y | y2x , x 0，则A B9．ABC 中，AB AC2, BC23，点D在BC边上，ADC 45 ，则AD 的长度等于．10.右图为某几何体的三视图，则该几何体的体积为 _______11. 设函数y ax2bx k (k 0) 在x0处获得极值，且曲线y f (x)以点(1, f (1))处的切线垂直于直线x 2y 1 0 ，则a b 的值为．12. 椭圆ax2by2 1 与直线y 1 x 交于 A, B 两点，过原点和线段AB 中点的直线的斜率为3，则b2a的值为 __________ ．13.函数 f ( x)是定义在R上的偶函数，且知足f ( x 2) f ( x) ．当 x[0 ， 1] 时，f ( x) 2x .若在区间 [ 2 ， 3 ] 上方程 ax+2 a f (x)0 恰有四个不相等的实数根，则实数 a 的取值范围是________．14. 已知a0,b 0 若 a b 2 ，则14的最小为．1a1b三、解答题：（共53 分）15.(10分)已知函数f ( x) 2 3 sin( x) cos( x) sin(2x) ．44（1）求f ( x)的最小正周期和单一递减区间；（2）若将f (x)的图像向右平移个单位，获取函数g ( x) 的图像，求函数g(x) 在区间40,上的最大值和最小值．216. (10分)咖啡馆配制两种饮料, 甲种饮料每杯含奶粉9 克、咖啡 4克、糖 3 克 , 乙种饮料每杯含奶粉 4 克、咖啡 5 克、糖 10 克 . 已知每日原料的使用限额为奶粉3600 克、咖啡 2000克、糖 3000 克 , 甲种饮料每杯能获收益 0.7元 , 乙种饮料每杯能获收益 1.2 元, 每日应配制两种饮料各多少杯能赢利最大?17. (10分 ) 如图，四边形ABCD 为菱形，ACFE 为平行四边形，且平面ACFE平面ABCD ，设 BD 与 AC 订交于点 G ， H 为 FG 的中点．（1）证明：BD CH ；（2）若AB BD 2, AE3,CH3；2①求三棱锥 F BDC 的体积．②求二面角B DF C 的余弦值.18.（ 11分）已知椭圆C :x2y2 1 a b0的左、右焦点分别为 F1，F2，离心率为 1 ，a2b22 M 为椭圆上随意一点且△MF1 F2的周长等于6．（1）求椭圆C的方程；（2）以M为圆心，MF1为半径作圆M ，当圆 M 与直线 l : x 4 有公共点时，求MF1 F2面积的最大值．19. （ 12 分）（ 1）已知函数f (x)x 22x m，若对全部 x(1,) 都有 f ( x)m 成x 立，求 m 的取值范围.（ 2）已知函数 f ( x)22 ( a0). 若关于都有a ln xx (0,) f (x) 2(a 1) x建立，试求a的取值范围；（3）设 a 0, a 1 ，f (x)x2a x，对 x (1,1) ，均有 f (x)1，求a的范围2第Ⅱ卷提升题（共27 分）20. （ 12 分）（ 1）判断函数f ( x)ln x2的零点个数；x（2）函数g ( x)2ln x x2b(b R) .在区间[ e1, e]上有两个零点，务实数 b 的取x值范围；（3）达成填空用方程表述用函数零点表述若函数 y f (x) 和y g( x) 的图像在(a, b) 内有交点21.（15分）数列a n的前 n 项和为 S n2a n 2 ，数列 b n是首项为 a1，公差不为零的等差数列 , 且b1,b3, b11成等比数列 .（1）求数列a n与 b n的通项公式；（2）关于n N 不等式b1b2b3b nm 恒建立，求m 取值范围；a1a2a3a n（3）令c n( 1)n 1 6n1，求数列c n的前n项和 T n.b n bn 12015-2016 第一学期高三数学12 月（文）学生学业能力调研试卷知识与技术学习能力习惯养成总分得分框第Ⅰ卷基础题（共123 分）一、选择题（每题 5 分，共 35分）题号1234567答案二、填空题（每题 5 分，共 35分）8.9._________ 10._________11. __________12._______13.________14. __________三、解答题（本大题共 4 题，共53 分）15.（10 分）16.（10 分）17.（10 分）18.（11 分）.19.（12 分）第Ⅱ卷提升题（共27 分）20.（12 分）（1）（2）（3）达成填空用方程表述用函数零点表述若 函 数 y f (x) 和y g (x) 的 图 像 在 ( a,b)内有交点21. （15 分）（1）（ 2）（ 3）答案一、选择题（每题5 分，共 35 分）题号 1 2 3 4 5 6 7 答案BDCAADC二、填空题（每题5 分，共 35 分）8. （ 1，2） 9.__ 10.____ _ 11. ____1______12.__________ 13._____(2, 2) _____ 14. __________5 3三、解答题15.15. （ 1），（ 2）最大值为2，最小值为－ 1.解（1）.（2）由已知得，，，故当即时，；故当即时，，故函数 g（x）在区间上的最大值为2，最小值为－ 1.16、解 : 设每日配制甲种饮料x 杯、乙种饮料y 杯能够获取最大收益, 收益总数为z 元.由条件知 :z=0.7x+1.2y,变量x、y知足作出不等式组所表示的可行域如下图.作直 l:0.7x+1.2y=0,把直 l 向右上方平移至A点的地点 ,z=0.7x+1.2y 取最大 .由方程得 A 点坐 (200,240).即每日配制甲种料200 杯, 乙种料240 杯方可利最大.17、（ 1）明：四形ABCD菱形BD AC ，⋯⋯⋯⋯又面 ACFE面ABCD=ACBD 平面 ABCD ⋯⋯⋯⋯面 ABCD 面 ACFE C⋯⋯⋯BD 面 ACFE CH面 ACFE ,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯BD CH⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯（2）在FCG 中， CG CF3,CH3 , CH GF2因此GCF 120 ,⋯⋯⋯⋯GF 3 ⋯⋯⋯⋯BD面 ACFE ， GF面 ACFEBD GF ,⋯⋯⋯⋯⋯SBDF 1BD GF1 2 3 3 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯22又 CH BD,CH GF ,BD GF G,BD, GF平面BDFCH平面BDF...........................................VF BDC VC BDF1S BDF CH1333⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3322注：另两种求体方法18.19解 : （1）m 2 3 4（2）02 a（3）1ea 2, a 1 220.（1）1 个（2）1b ≤2 e 1e21. a n2n , b n3n1。

一、选择题：本大题共8小题，每小题5分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1. 已知全集R U =，{}22≤≤-=x x M ，{}1<=x x N ，那么M N ⋂=（ ）A ．{}12<≤-x xB ．{}12<<-x xC ．{}2-<x xD ．{}2≤x x2.在ABC ∆中，“3A π>”是“sin A >”的（ ） A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件3.已知,m n 是两条不同．．的直线，,,αβγ是三个不同．．的平面，则下列命题中正确的是（ ）A. 若,,//αγαβγβ⊥⊥则B. 若//,,,//m n m n αβαβ⊂⊂则C. 若//,,,//m n m n αβαβ⊥⊥则D. 若//,//,//m n m n αα则5.已知正实数b a ,满足321=+ba ，则()()21++b a 的最小值是 （ ） A. 163 B. 950 C. 499 D. 66．等差数列}{n a 的前n 项和为n S ，其中*N n ∈，则下列命题错误的是（ ） A ．若0>n a ，则n S 0> B ．若n S 0>，则0>n aC ．若0>n a ，则}{n S 是单调递增数列D ．若}{n S 是单调递增数列，则0>n a7.若x ，y 满足⎩⎨⎧x ＋y －2≥0，kx －y ＋2≥0，y ≥0，且z ＝y －x 的最小值为－4，则k 的值为( )A ．－2B ．12-C ．12D ．28．知函数⎩⎨⎧>+-≤+=0,1)1(0,2)(2x x f x x x x f ，当]10,0[∈x 时，关于x 的方程51)(-=x x f 的所有解的和为（ ） A ．55 B ．100 C ．110 D ．120非选择题部分二、填空题：本题共有7小题，第9、10、11、12题每空4分，第13、14、15题每空5分，共47分.9．计算：2log 2= ，24log 3log 32+= ．10．函数()22cos )2sin cos f x x x x x =-+的最小正周期为 ，单调递增区间为 。

2015年12月份高三数学试题资源包括：河南省八市重点高中2015-2016学年高二12月联考数学（理）试题河南省八市重点高中2015-2016学年高二12月联考数学（文）试题广东省汕尾市2016届高三12月调研考试数学文试题（扫描版）江苏省江阴市青阳中学2016届高三12月联合调研测试数学（文理）试题广东省汕尾市2016届高三12月调研考试数学理试题（扫描版）四川省成都市高2016届高三第一次诊断考试数学理试题（WORD版）四川省成都市2016届高三第一次诊断性检测数学文试卷启慧·全国大联考2016届高三12月联考试题数学（文）Word版含解析启慧·全国大联考2016届高三12月联考试题数学（理）Word版含解析福建省漳州八校2016届高三12月联考理科数学试卷福建省漳州八校2016届高三12月联考文科数学试卷山东省平度市2016届高三统一抽考数学（理）试题山东省平度市2016届高三统一抽考数学（文）试题黑龙江省哈尔滨市第六中学2016届高三12月月考文数试题解析黑龙江省哈尔滨市第六中学2016届高三12月月考理数试题解析江西省新余市第一中学2016届高三上学期第四次模拟考试文数试题解析江西省新余市第一中学2016届高三上学期第四次模拟考试理数试题解析湖北省武汉市华中师范大学第一附属中学、黄石二中、孝感高中、荆州中学等八校2016届高三上学期第一次联考理数试题解析湖北省武汉市华中师范大学第一附属中学、黄石二中、孝感高中、荆州中学等八校2016届高三上学期第一次联考理数试题解析江门市2015年普通高中高三调研测试数学（理科）试题江门市2015年普通高中高三调研测试数学（文科）试题2016届江西省南昌二中高三上学期第四次考试（数学文卷）2016届江西省南昌二中高三上学期第四次考试（数学理卷）2016届山西省康杰中学、临汾一中、忻州一中、长治二中高三上学期第二次联考（数学文）2016届山西省康杰中学、临汾一中、忻州一中、长治二中高三上学期第二次联考（数学理）2016届河北省邯郸市第一中学高三一轮收官考试（数学文）2016届河北省邯郸市第一中学高三一轮收官考试（数学理）数学文卷·2016届四川省成都七中高三上学期一诊模拟考试数学理卷·2016届四川省成都七中高三上学期一诊模拟考试数学理卷·2016届江西省师大附中、临川一中高三上学期第一次联考试题数学文卷·2017届湖北省荆州中学高二上学期第二次月考数学文卷·2016届内蒙古赤峰二中高三上学期第三次（12月）月考数学理卷·2016届内蒙古赤峰二中高三上学期第三次（12月）月考数学文卷·2016届浙江省嘉兴一中、杭州高级中学、宁波效实中学等五校高三上学期第一次联考数学理卷·2016届浙江省嘉兴一中、杭州高级中学、宁波效实中学等五校高三上学期第一次联考数学理卷·2016届山东省枣庄三中高三12月质量检测数学文卷·2016届山东省枣庄三中高三12月质量检测数学（文）卷·2016届吉林省东北师大附中高三上学期第二次模拟考试数学理卷·2016届河南省信阳高级中学高三上学期第八次大考数学理卷·2016届云南省玉溪一中高三第四次月考数学（文）卷·2017届江西省丰城中学高二上学期第三次月考试题数学（理）卷·2016届安徽省马鞍山二中、安师大附中、淮北一中、铜陵一中高三第三次联考数学（文）卷·2016届安徽省马鞍山二中、安师大附中、淮北一中、铜陵一中高三第三次联考数学文卷·2016届广西桂林中学高三12月月考数学理卷·2016届广西桂林中学高三12月月考数学文卷·2016届湖北省宜昌一中高三上学期12月月考数学理卷·2016届湖北省宜昌一中高三上学期12月月考数学文卷·2016届辽宁省沈阳二中高三上学期12月月考数学理卷·2016届辽宁省沈阳二中高三上学期12月月考数学文卷·2016届辽宁省抚顺市第一中学高三上学期12月月考（2015.12）word 版数学理卷·2016届辽宁省抚顺市第一中学高三上学期12月月考（2015.12）word 版数学理卷·2016届吉林省实验中学高三上学期第四次模拟考试数学文卷·2016届吉林省实验中学高三上学期第四次模拟考试数学理卷·2016届河南省郑州一中高三联考数学文卷·2016届河南省郑州一中高三联考数学文（普通班）卷·2016届甘肃省天水一中高三上学期第三次考试数学文（辅导班）卷·2016届甘肃省天水一中高三上学期第三次考试数学理（普通班）卷·2016届甘肃省天水一中高三上学期第三次考试数学理（辅导班）卷·2016届甘肃省天水一中高三上学期第三次考试数学理卷·2016届河南省开封市高三第一次质量检测模拟考试数学文卷·2016届河南省开封市高三第一次质量检测模拟考试数学文卷·2016届湖北省鄂豫晋冀陕五省高三12月联考数学理卷·2016届湖北省鄂豫晋冀陕五省高三12月联考数学卷·2016届福建省闽粤联合体高三第三次联考数学文卷·2016届重庆市南开中学高三12月月考试题数学理卷·2016届重庆市南开中学高三12月月考试题数学理卷·2016届吉林省长春市十一中高三上学期12月月考数学文卷·2016届吉林省长春市十一中高三上学期12月月考数学理卷·2016届吉林省长春外国语学校高三上学期第二次质量检测数学文卷·2016届吉林省长春外国语学校高三上学期第二次质量检测数学文卷·2016届重庆市巴蜀中学高三上学期第三次月考数学理卷·2016届重庆市巴蜀中学高三上学期第三次月考海南省海南中学2016届高三第四次月考数学（文）试题海南省海南中学2016届高三第四次月考数学（理）试题天津市2016届高三“五校”联考数学（文）试题天津市2016届高三“五校”联考数学（理）试题江西省于都实验中学2016届高三上学期第三次大考数学（文）试题江西省于都实验中学2016届高三上学期第三次大考数学（理）试题广东省汕尾市2016届高三12月调研考试数学理试题福建省四地六校2016届高三第三次联考数学（文）试题福建省四地六校2016届高三第三次联考数学（理）试题上海市崇明县2016届高三第一次高考模拟考试数学试卷（WORD版）2016届广东云浮、揭阳、清远、阳江等八市联考数学理（含解析和分析）上海市崇明县2016届高三第一次高考模拟考试数学试卷（pdf版）上海市普陀区2016届高三12月教学质量调研数学理试题上海市普陀区2016届高三12月教学质量调研数学文试题山东省淄博市2016届高三12月摸底考试数学（理）试题山东省淄博市2016届高三12月摸底考试数学（文）试题[dl href=""]2015年12月份高三数学试题[/dl]提取码：u979。

2015-2016学年广东省广州市六校联考高三（上）12月调研数学试卷（理科）一．选择题：本大题共12小题，每小题5分．在每个小题给出的四个选项中，只有一项是符合题目要求的．1．已知全集为R，集合A={x|2x≥1}，B={x|x2﹣3x+2≤0}，则A∩∁R B=（）A．{x|x≤0}B．{x|1≤x≤2}C．{x|0≤x＜1或x＞2}D．{x|0≤x＜1或x≥2}2．若复数z=（a∈R，i是虚数单位）是纯虚数，则|a+2i|等于（）A．2 B．2C．4 D．83．下列函数中，在其定义域内既是增函数又是奇函数的是（）A．B．y=﹣log2x C．y=3x D．y=x3+x4．在公差不为零的等差数列{a n}中，2a3﹣a72+2a11=0，数列{b n}是等比数列，且b7=a7，则log2（b6b8）的值为（）A．2 B．4 C．8 D．15．若a=2x，b=，c=lo，则“a＞b＞c”是“x＞1”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分又不必要条件6．执行如图所示的程序框图，则输出的结果是（）A．14 B．15 C．16 D．177．双曲线tx2﹣y2﹣1=0的一条渐近线与直线x﹣2y+1=0平行，则双曲线的离心率为（）A．B．C．D．8．已知△ABC的三个角A，B，C所对的边分别是a，b，c，且3bcosA﹣3acosB=c，则下列结论正确的是（）A．tanB=2tanA B．tanA=2tanB C．tanBtanA=2 D．tanA+tanB=2 9．一个几何体的三视图如图所示，则这个几何体的体积为（）A．B．C．D．10．有7张卡片分别写有数字1，1，1，2，2，3，4，从中任取4张，可排出的四位数有（）个．A．78 B．102 C．114 D．12011．已知三棱锥P﹣ABC的四个顶点都在球O的球面上，若PA=AB=2，AC=1，∠BAC=120°，且PA⊥平面ABC，则球O的表面积为（）A．B．C．12πD．15π12．已知函数f（x）=ln，若f（）+f（）+…+f（）=503（a+b），则a2+b2的最小值为（）A．6 B．8 C．9 D．12二．填空题：本大题共4小题，每小题5分．13．已知直线AB：x+y﹣6=0与抛物线y=x2及x轴正半轴围成的阴影部分如图所示，若从Rt△AOB区域内任取一点M（x，y），则点M取自阴影部分的概率为．14．△ABC的内角A，B，C所对的边分别为a，b，c，且a，b，c成等比数列，若sinB=，cosB=，则a+c的值为．15．设x、y满足约束条件，若目标函数z=ax+by（a＞0，b＞0）的最大值为2，当+的最小值为m时，则y=sin（mx+）的图象向右平移后的表达式为．16．设△A n B n C n的三边长分别为a n，b n，c n，n=1，2，3…，若b1＞c1，b1+c1=2a1，a n+1=a n，b n+1=，c n+1=，则∠A n的最大值是．三．解答题：解答应写出文字说明，证明过程或演算步骤．（共5大题，每题12分）17．已知函数f（x）=2sinxcosx﹣3sin2x﹣cos2x+3．（1）当x∈[0，]时，求f（x）的值域；（2）若△ABC的内角A，B，C的对边分别为a，b，c，且满足=，=2+2cos （A+C），求f（B）的值．18．如图，在四棱锥P﹣ABCD中，底面ABCD为直角梯形，AD∥BC，∠ADC=90°，平面PAD⊥底面ABCD，Q为AD的中点，M是棱PC上的点，PA=PD=2，BC=AD=1，CD=．（1）求证：平面PQB⊥平面PAD；（2）若二面角M﹣BQ﹣C为30°，设PM=tMC，试确定t的值．19．某电视台推出一档游戏类综艺节目，选手面对1﹣5号五扇大门，依次按响门上的门铃，门铃会播放一段音乐，选手需正确回答这首歌的名字，回答正确，大门打开，并获得相应的家庭梦想基金，回答每一扇门后，选手可自由选择带着目前的奖金离开，还是继续挑战后面的门以获得更多的梦想基金，但是一旦回答错误，游戏结束并将之前获得的所有梦想基金清零；整个游戏过程中，选手有一次求助机会，选手可以询问亲友团成员以获得正确答案．1﹣5号门对应的家庭梦想基金依次为3000元、6000元、8000元、12000元、24000元（以上基金金额为打开大门后的累积金额，如第三扇大门打开，选手可获基金总金额为8000元）；设某选手正确回答每一扇门的歌曲名字的概率为p i（i=1，2，…，5），且p i=（i=1，2，…，5），亲友团正确回答每一扇门的歌曲名字的概率均为，该选手正确回答每一扇门的歌名后选择继续挑战后面的门的概率均为；（1）求选手在第三扇门使用求助且最终获得12000元家庭梦想基金的概率；（2）若选手在整个游戏过程中不使用求助，且获得的家庭梦想基金数额为X（元），求X 的分布列和数学期望．20．已知椭圆的焦点坐标为F1（﹣1，0），F2（1，0），过F2垂直于长轴的直线交椭圆于P、Q两点，且|PQ|=3．（1）求椭圆的方程；（2）过F2的直线l与椭圆交于不同的两点M、N，则△F1MN的内切圆的面积是否存在最大值？若存在求出这个最大值及此时的直线方程；若不存在，请说明理由．21．已知函数f（x）=a x+x2﹣xlna（a＞0，a≠1）．（1）求函数f（x）在点（0，f（0））处的切线方程；（2）求函数f（x）单调增区间；（3）若存在x1，x2∈[﹣1，1]，使得|f（x1）﹣f（x2）|≥e﹣1（e是自然对数的底数），求实数a的取值范围．请考生在（22）、（23）、（24）三题中任选一题作答．注意：只能做所选定的题目．如果多做，则按所做第一个题目计分，作答时，请用2B铅笔在答题卡上将所选题号后的方框涂黑．【选修4-1：几何证明选讲】22．如图，⊙O的半径为6，线段AB与⊙相交于点C、D，AC=4，∠BOD=∠A，OB与⊙O相交于点E．（1）求BD长；（2）当CE⊥OD时，求证：AO=AD．【选修4-4：坐标系与参数方程】23．在平面直角坐标系xoy中，以O为极点，x轴的正半轴为极轴的极坐标系中，直线l的极坐标方程为θ=，曲线C的参数方程为．（1）写出直线l与曲线C的直角坐标方程；（2）过点M平行于直线l1的直线与曲线C交于A、B两点，若|MA||MB|=，求点M轨迹的直角坐标方程．【选修4-5：不等式选讲】24．设函数f（x）=|2x+1|﹣|x﹣4|．（1）解不等式f（x）＞0；（2）若f（x）+3|x﹣4|≥m对一切实数x均成立，求m的取值范围．2015-2016学年广东省广州市六校联考高三（上）12月调研数学试卷（理科）参考答案与试题解析一．选择题：本大题共12小题，每小题5分．在每个小题给出的四个选项中，只有一项是符合题目要求的．1．已知全集为R，集合A={x|2x≥1}，B={x|x2﹣3x+2≤0}，则A∩∁R B=（）A．{x|x≤0}B．{x|1≤x≤2}C．{x|0≤x＜1或x＞2}D．{x|0≤x＜1或x≥2}【考点】交、并、补集的混合运算．【分析】先求出集合AB，再求出B的补集，根据交集的定义即可求出．【解答】解：∵全集为R，集合A={x|2x≥1}={x|x≥0}，B={x|x2﹣3x+2≤0}={x|1≤x≤2}，∴∁R B={x|x＜1或x＞2}，∴A∩∁R B={x|0≤x＜1或x＞2}故选：C【点评】本题考查了交、并、补集的混合运算，熟练掌握各自的定义是解本题的关键．2．若复数z=（a∈R，i是虚数单位）是纯虚数，则|a+2i|等于（）A．2 B．2C．4 D．8【考点】复数求模；复数的基本概念；复数代数形式的乘除运算．【分析】先将z计算化简成代数形式，根据纯虚数的概念求出a，再代入|a+2i|计算即可．【解答】解：z==．根据纯虚数的概念得出∴a=2．∴|a+2i|=|2+2i|==2故选B．【点评】本题考查了复数代数形式的混合运算，纯虚数的概念、复数的模．考查的均为复数中基本的运算与概念．3．下列函数中，在其定义域内既是增函数又是奇函数的是（）A．B．y=﹣log2x C．y=3x D．y=x3+x【考点】奇偶性与单调性的综合．【分析】A：y=﹣在（0，+∞），（﹣∞，0）上单调递增，但是在整个定义域内不是单调递增函数；B：y=﹣log2x的定义域（0，+∞）关于原点不对称，不是奇函数；C：y=3x不是奇函数；D：y=x3+x，f（﹣x）=（﹣x）3+（﹣x）=﹣x3﹣x=﹣f（x）是奇函数，且由幂函数的性质可知函数在R上单调递增【解答】解：A：y=﹣在（0，+∞），（﹣∞，0）上单调递增，但是在整个定义域内不是单调递增函数，故A错误B：y=﹣log2x的定义域（0，+∞）关于原点不对称，不是奇函数，故B错误C：y=3x不是奇函数，故C错误D：y=x3+x，f（﹣x）=（﹣x）3+（﹣x）=﹣x3﹣x=﹣f（x）是奇函数，且由幂函数的性质可知函数在R上单调递增，故D正确故选D【点评】本题主要考查了函数的奇偶性及函数的单调性的判断，尤其y=﹣的单调区间的求解是解答中容易出现错误的地方，要注意掌握．4．在公差不为零的等差数列{a n}中，2a3﹣a72+2a11=0，数列{b n}是等比数列，且b7=a7，则log2（b6b8）的值为（）A．2 B．4 C．8 D．1【考点】等差数列的性质．【分析】根据数列{a n}为等差数列可知2a7=a3+a11，代入2a3﹣a72+2a11=0中可求得a7，再根据{b n}是等比数列可知b6b8=b72=a72代入log2（b6b8）即可得到答案．【解答】解：∵数列{a n}为等差数列，∴2a7=a3+a11，∵2a3﹣a72+2a11=0，∴4a7﹣a72=0∵a7≠0∴a7=4∵数列{b n}是等比数列，∴b6b8=b72=a72=16∴log2（b6b8）=log216=4故选：B【点评】本题主要考查了等比中项和等差中项的性质．属基础题．5．若a=2x，b=，c=lo，则“a＞b＞c”是“x＞1”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分又不必要条件【考点】必要条件、充分条件与充要条件的判断．【分析】根据函数的图象和性质，结合充分条件和必要条件的定义即可得到结论．【解答】解：如右图可知，“x＞1”⇒“a＞b＞c”，但“a＞b＞c”⇏“x＞1”，即“a＞b＞c”是“x＞1”的必要不充分条件．故选B．【点评】本题考查指对幂三种基本初等函数的图象和充要条件的概念等基础知识，利用数形结合是解决本题的关键．6．执行如图所示的程序框图，则输出的结果是（）A．14 B．15 C．16 D．17【考点】程序框图．【分析】通过分析循环，推出循环规律，利用循环的次数，求出输出结果．【解答】解：第一次循环：，n=2；第二次循环：，n=3；第三次循环：，n=4；…第n次循环：=，n=n+1令解得n＞15∴输出的结果是n+1=16故选：C．【点评】本题考查程序框图的应用，数列的应用，考查分析问题解决问题的能力．7．双曲线tx2﹣y2﹣1=0的一条渐近线与直线x﹣2y+1=0平行，则双曲线的离心率为（）A．B．C．D．【考点】双曲线的简单性质．【分析】根据题意，将双曲线化成标准形式求出渐近线为y=x，从而y=x与直线x ﹣2y+1=0平行算出t=4．由此得到双曲线的方程，进而算出它的离心率．【解答】解：∵双曲线tx2﹣y2﹣1=0，即tx2﹣y2=1，∴双曲线的渐近线为y=x，∵一条渐近线与直线x﹣2y+1=0平行，∴渐近线的斜率为，即=，得t=双曲线的方程为，得a=2，b=1，c==∴此双曲线的离心率为e=故选：B【点评】本题给出含有字母的双曲线，在其渐近线与已知直线平行的情况下求双曲线的离心率．着重考查了直线的位置关系、双曲线的简单几何性质等知识，属于中档题．8．已知△ABC的三个角A，B，C所对的边分别是a，b，c，且3bcosA﹣3acosB=c，则下列结论正确的是（）A．tanB=2tanA B．tanA=2tanB C．tanBtanA=2 D．tanA+tanB=2【考点】正弦定理．【分析】由题意和正弦定理可得3sinBcosA﹣3sinAcosB=sinC=sin（A+B），由三角函数的和差角公式及弦化切的思想可得．【解答】解：∵△ABC的三个角A，B，C所对的边分别是a，b，c，且3bcosA﹣3acosB=c，∴由正弦定理可得3sinBcosA﹣3sinAcosB=sinC，∴3sinBcosA﹣3sinAcosB=sin（A+B），∴3sinBcosA﹣3sinAcosB=sinBcosA+sinAcosB，即2sinBcosA=4sinAcosB，两边同除以cosAcosB可得2tanB=4tanA，即tanB=2tanA，故选：A．【点评】本题考查正弦定理，涉及三角函数公式和弦化切的思想，属基础题．9．一个几何体的三视图如图所示，则这个几何体的体积为（）A．B．C．D．【考点】由三视图求面积、体积．【分析】这个几何体由半个圆锥与一个四棱锥组合而成，从而求两个体积之和即可．【解答】解：这个几何体由半个圆锥与一个四棱锥组合而成，半个圆锥的体积为××π×1×=；四棱锥的体积为×2×2×=；故这个几何体的体积V=；故选D．【点评】本题考查了学生的空间想象力与计算能力，属于基础题．10．有7张卡片分别写有数字1，1，1，2，2，3，4，从中任取4张，可排出的四位数有（）个．A．78 B．102 C．114 D．120【考点】排列、组合的实际应用．【分析】根据题意，分四种情况讨论：①、取出的4张卡片种没有重复数字，即取出的4张卡片中的数字为1、2、3、4，②、取出的4张卡片种有2个重复数字，则2个重复的数字为1或2，③若取出的4张卡片为2张1和2张2，④、取出的4张卡片种有3个重复数字，则重复的数字为1，分别求出每种情况下可以排出四位数的个数，由分类计数原理计算可得答案．【解答】解：根据题意，分四种情况讨论：①、取出的4张卡片种没有重复数字，即取出的4张卡片中的数字为1、2、3、4，此时有A44=24种顺序，可以排出24个四位数；②、取出的4张卡片种有2个重复数字，则2个重复的数字为1或2，若重复的数字为1，在2、3、4中取出2个，有C32=3种取法，安排在四个位置中，有A42=12种情况，剩余位置安排数字1，可以排出3×12=36个四位数，同理，若重复的数字为2，也可以排出36个重复数字；③、若取出的4张卡片为2张1和2张2，在4个位置安排两个1，有C42=6种情况，剩余位置安排两个2，则可以排出6×1=6个四位数；④、取出的4张卡片种有3个重复数字，则重复的数字为1，在2、3、4中取出1个卡片，有C31=3种取法，安排在四个位置中，有C41=4种情况，剩余位置安排1，可以排出3×4=12个四位数；则一共有24+36+36+6+12=114个四位数；故选C．【点评】本题考查排列组合的运用，解题时注意其中重复的数字，要结合题意，进行分类讨论．11．已知三棱锥P﹣ABC的四个顶点都在球O的球面上，若PA=AB=2，AC=1，∠BAC=120°，且PA⊥平面ABC，则球O的表面积为（）A．B．C．12πD．15π【考点】球的体积和表面积；球内接多面体．【分析】求出BC，可得△ABC外接圆的半径，从而可求该三棱锥的外接球的半径，即可求出三棱锥的外接球表面积．【解答】解：∵AB=2，AC=1，∠BAC=120°，∴BC==，∴三角形ABC的外接圆直径2r===，∴r=，∵PA⊥面ABC，PA=2，由于三角形OPA为等腰三角形，则有该三棱锥的外接球的半径R==，∴该三棱锥的外接球的表面积为S=4πR2=4π×（）2=．故选：A．【点评】本题考查三棱锥的外接球表面积，考查直线和平面的位置关系，确定三棱锥的外接球的半径是关键．12．已知函数f（x）=ln，若f（）+f（）+…+f（）=503（a+b），则a2+b2的最小值为（）A．6 B．8 C．9 D．12【考点】对数的运算性质．【分析】利用f（x）+f（e﹣x）==lne2=2，可得a+b=4，再利用基本不等式的性质即可得出．【解答】解：∵f（x）+f（e﹣x）==lne2=2，∴503（a+b）=f（）+f（）+…+f（）=++…+==2012，∴a+b=4，∴a2+b2≥==8，当且仅当a=b=2时取等号．故选：B．【点评】本题考查了对数的运算性质、基本不等式的性质，考查了推理能力与计算能力，属于难题．二．填空题：本大题共4小题，每小题5分．13．已知直线AB：x+y﹣6=0与抛物线y=x2及x轴正半轴围成的阴影部分如图所示，若从Rt△AOB区域内任取一点M（x，y），则点M取自阴影部分的概率为．【考点】几何概型；定积分在求面积中的应用．【分析】欲求所投的点落在阴影内部的概率，利用几何概型解决，只须利用定积分求出阴影图的面积，最后利用它们的面积比求得即可概率．【解答】解：由定积分可求得阴影部分的面积为S=∫02x2dx+∫26（6﹣x）dx==，又Rt△AOB的面积为：所以p==．故答案为：．【点评】本题考查了利用定积分求面积以及几何摡型知识，考查运算求解能力，考查数形结合思想、化归与转化思想．属于基础题．14．△ABC的内角A，B，C所对的边分别为a，b，c，且a，b，c成等比数列，若sinB=，cosB=，则a+c的值为3．【考点】余弦定理．【分析】由a，b，c成等比数列，可得b2=ac，由sinB=，cosB=，可解得ac=13，再由余弦定理求得a2+c2=37，从而求得（a+c）2的值，即可得解．【解答】解：∵a，b，c成等比数列，∴b2=ac，∵sinB=，cosB=，∴可得=1﹣，解得：ac=13，∵由余弦定理：b2=a2+c2﹣2accosB=ac=a2+c2﹣ac×，解得：a2+c2=37．∴（a+c）2=a2+c2+2ac=37+2×13=63，故解得a+c=3．故答案为：3．【点评】本题主要考查正弦定理和余弦定理的应用，以及同角三角函数的基本关系、诱导公式的应用，属于中档题．15．设x、y满足约束条件，若目标函数z=ax+by（a＞0，b＞0）的最大值为2，当+的最小值为m时，则y=sin（mx+）的图象向右平移后的表达式为y=sin2x．【考点】函数y=Asin（ωx+φ）的图象变换；简单线性规划．【分析】首先根据线性规划问题和基本不等式求出函数的最值，再利用正弦型函数的图象变换问题，求出结果．【解答】解：设x、y的线性约束条件解得A（1，1）目标函数z=ax+by（a＞0，b＞0）的最大值为2即：a+b=2所以：则：则y=sin（2x+）的图象向右平移后的表达式为：y=sin2x故答案为：y=sin2x【点评】本题考查的知识要点：线性规划问题，基本不等式的应用，正弦型函数的图象变换问题，属于基础题型．16．设△A n B n C n 的三边长分别为a n ，b n ，c n ，n=1，2，3…，若b 1＞c 1，b 1+c 1=2a 1，a n +1=a n ，b n +1=，c n +1=，则∠A n 的最大值是．【考点】基本不等式在最值问题中的应用；正弦定理；余弦定理的应用．【分析】根据数列的递推关系得到b n +c n =2a 1为常数，然后利用余弦定理以及基本不等式即可得到结论．【解答】解：∵a n +1=a n ，∴a n =a 1，∵b n +1=，c n +1=，∴b n +1+c n +1=a n +=a 1+，∴b n +1+c n +1﹣2a 1=（b n +c n ﹣2a 1），又b 1+c 1=2a 1，∴当n=1时，b 2+c 2﹣2a 1=（b 1+c 1+﹣2a 1）=0，当n=2时，b 3+c 3﹣2a 1=（b 2+c 2+﹣2a 1）=0，…∴b n +c n ﹣2a 1=0，即b n +c n =2a 1为常数，∵b n ﹣c n =（﹣）n ﹣1（b 1﹣c 1）， ∴当n →+∞时，b n ﹣c n →0，即b n →c n ，则由基本不等式可得b n +c n =2a 1≥2，∴b n c n，由余弦定理可得=（b n +c n ）2﹣2b n c n ﹣2b n c n cosA n ，即（a 1）2=（2a 1）2﹣2b n c n （1+cosA n ），即2b n c n （1+cosA n ）=3（a 1）2≤2（a 1）2（1+cosA n ），即3≤2（1+cosA n ）， 解得cosA n，∴0＜A n，即∠A n的最大值是，故答案为：【点评】本题考查数列以及余弦定理的应用，利用基本不等式是解决本题的关键，综合性较强，运算量较大，难度较大．三．解答题：解答应写出文字说明，证明过程或演算步骤．（共5大题，每题12分）17．已知函数f（x）=2sinxcosx﹣3sin2x﹣cos2x+3．（1）当x∈[0，]时，求f（x）的值域；（2）若△ABC的内角A，B，C的对边分别为a，b，c，且满足=，=2+2cos （A+C），求f（B）的值．【考点】正弦定理；三角函数中的恒等变换应用．【分析】（1）由三角函数公式化简可得f（x）=2sin（2x+）+1，由x的范围结合三角函数的运算可得；（2）由三角函数公式和已知数据可得c=2a，b=a，代入余弦定理可得cosA=，可得A=30°，进而可得C=90°，B=60°，代入可得其值．【解答】解：（1）∵f（x）=2sinxcosx﹣3sin2x﹣cos2x+3=sin2x﹣3﹣+3=sin2x﹣cos2x+1=2sin（2x+）+1，∵x∈[0，]，∴2x+∈[，]，∴sin（2x+）∈[，1]，∴f（x）=2sin（2x+）+1∈[0，3]；（2）∵=2+2cos（A+C），∴sin（2A+C）=2sinA+2sinAcos（A+C），∴sinAcos（A+C）+cosAsin（A+C）=2sinA+2sinAcos（A+C），∴﹣sinAcos（A+C）+cosAsin（A+C）=2sinA，即sinC=2sinA，由正弦定理可得c=2a，又由=可得b=a，由余弦定理可得cosA===，∴A=30°，由正弦定理可得sinC=2sinA=1，C=90°，由三角形的内角和可得B=60°，∴f（B）=f（60°）=2【点评】本题考查三角形的正余弦定理，涉及三角函数的公式，属中档题．18．如图，在四棱锥P﹣ABCD中，底面ABCD为直角梯形，AD∥BC，∠ADC=90°，平面PAD⊥底面ABCD，Q为AD的中点，M是棱PC上的点，PA=PD=2，BC=AD=1，CD=．（1）求证：平面PQB⊥平面PAD；（2）若二面角M﹣BQ﹣C为30°，设PM=tMC，试确定t的值．【考点】用空间向量求平面间的夹角；平面与平面垂直的判定；与二面角有关的立体几何综合题．【分析】（Ⅰ）法一：由AD∥BC，BC=AD，Q为AD的中点，知四边形BCDQ为平行四边形，故CD∥BQ．由∠ADC=90°，知QB⊥AD．由平面PAD⊥平面ABCD，知BQ⊥平面PAD．由此能够证明平面PQB⊥平面PAD．法二：由AD∥BC，BC=AD，Q为AD的中点，知四边形BCDQ为平行四边形，故CD ∥BQ．由∠ADC=90°，知∠AQB=90°．由PA=PD，知PQ⊥AD，故AD⊥平面PBQ．由此证明平面PQB⊥平面PAD．（Ⅱ）由PA=PD，Q为AD的中点，知PQ⊥AD．由平面PAD⊥平面ABCD，且平面PAD∩平面ABCD=AD，知PQ⊥平面ABCD．以Q为原点建立空间直角坐标系，利用向量法能够求出t=3．【解答】解：（Ⅰ）证法一：∵AD∥BC，BC=AD，Q为AD的中点，∴四边形BCDQ为平行四边形，∴CD∥BQ．∵∠ADC=90°∴∠AQB=90°，即QB⊥AD．又∵平面PAD⊥平面ABCD，且平面PAD∩平面ABCD=AD，∴BQ⊥平面PAD．∵BQ⊂平面PQB，∴平面PQB⊥平面PAD．…证法二：AD∥BC，BC=AD，Q为AD的中点，∴四边形BCDQ为平行四边形，∴CD∥BQ．∵∠ADC=90°∴∠AQB=90°．∵PA=PD，∴PQ⊥AD．∵PQ∩BQ=Q，∴AD⊥平面PBQ．∵AD⊂平面PAD，∴平面PQB⊥平面PAD．…（Ⅱ）∵PA=PD，Q为AD的中点，∴PQ⊥AD．∵平面PAD⊥平面ABCD，且平面PAD∩平面ABCD=AD，∴PQ⊥平面ABCD．如图，以Q为原点建立空间直角坐标系．则平面BQC的法向量为；Q（0，0，0），，，．设M（x，y，z），则，，∵，∴，∴…在平面MBQ中，，，∴平面MBQ法向量为．…∵二面角M﹣BQ﹣C为30°，∴，∴t=3．…【点评】本题考查平面与平面垂直的证明，求实数的取值．综合性强，难度大，是高考的重点．解题时要认真审题，仔细解答，注意合理地进行等价转化，合理地运用向量法进行解题．19．某电视台推出一档游戏类综艺节目，选手面对1﹣5号五扇大门，依次按响门上的门铃，门铃会播放一段音乐，选手需正确回答这首歌的名字，回答正确，大门打开，并获得相应的家庭梦想基金，回答每一扇门后，选手可自由选择带着目前的奖金离开，还是继续挑战后面的门以获得更多的梦想基金，但是一旦回答错误，游戏结束并将之前获得的所有梦想基金清零；整个游戏过程中，选手有一次求助机会，选手可以询问亲友团成员以获得正确答案．1﹣5号门对应的家庭梦想基金依次为3000元、6000元、8000元、12000元、24000元（以上基金金额为打开大门后的累积金额，如第三扇大门打开，选手可获基金总金额为8000元）；设某选手正确回答每一扇门的歌曲名字的概率为p i（i=1，2，…，5），且p i=（i=1，2，…，5），亲友团正确回答每一扇门的歌曲名字的概率均为，该选手正确回答每一扇门的歌名后选择继续挑战后面的门的概率均为；（1）求选手在第三扇门使用求助且最终获得12000元家庭梦想基金的概率；（2）若选手在整个游戏过程中不使用求助，且获得的家庭梦想基金数额为X（元），求X 的分布列和数学期望．【考点】离散型随机变量的期望与方差；离散型随机变量及其分布列．【分析】（1）记事件“选手正确回答第i扇门歌曲”为Ai记事件“亲友团正确回答歌曲名字”为B，记事件“回答正确后选择继续挑战”为C，第三扇门选手答不出才求助，由此能求出选手在第三扇门使用求助且最终获得12000元家庭梦想基金的概率．（2）X可能的取值有：0，3000，6000，8000，12000，24000，分别求出相应的概率，由此能求出X的分布列和数学期望．【解答】解：设事件“该选手回答正确第i扇门的歌曲名称”为事件A i，“使用求助回答正确歌曲名称”为事件B，事件“每一扇门回答正确后选择继续挑战下一扇门”为事件C；则，，，，，P（B）=，P（C）=…（1）设事件“选手在第三扇门使用求助且最终获得12000元家庭梦想基金”为事件A，则：A=A1CA2C BCA4=×=…∴选手在第三扇门使用求助且最终获得12000元家庭梦想基金的概率为；…（2）X的所有可能取值为：0，3000，6000，8000，12000，24000；…P（X=3000）=P（A1）==；P（X=6000）=P（A1 CA2）==；P（X=8000）=P（A1 CA2 CA3）==；P（X=12000）=P（A1 CA2 CA3 CA4）==；P（X=24000）=P（A1 CA2 CA3 CA4 CA5）==；…P（X=0）=P（）+P（A1C）+P（A1CA2C）+P（A1CA2CA3C）+P（A1CA2CA3CA4C）==；…∴X的分布列为：∴EX=0×+3000×+6000×+8000×+12000×+24000×=1250+1000+500+250+250=3250（元）∴选手获得的家庭梦想基金数额为X的数学期望为3250（元）…．【点评】本题考查概率的求法，考查离散型随机变量的分布列和数学期望的求法，是中档题，解题时要认真审题，注意对立事件概率计算公式的合理运用．20．已知椭圆的焦点坐标为F1（﹣1，0），F2（1，0），过F2垂直于长轴的直线交椭圆于P、Q两点，且|PQ|=3．（1）求椭圆的方程；（2）过F2的直线l与椭圆交于不同的两点M、N，则△F1MN的内切圆的面积是否存在最大值？若存在求出这个最大值及此时的直线方程；若不存在，请说明理由．【考点】直线与圆锥曲线的综合问题；椭圆的标准方程．【分析】（1）设椭圆方程，由焦点坐标可得c=1，由|PQ|=3，可得=3，又a2﹣b2=1，由此可求椭圆方程；（2）设M（x1，y1），N（x2，y2），不妨y1＞0，y2＜0，设△F1MN的内切圆的径R，则△F1MN的周长=4a=8，（|MN|+|F1M|+|F1N|）R=4R，因此最大，R就最大．设直线l的方程为x=my+1，与椭圆方程联立，从而可表示△F1MN的面积，利用换元法，借助于导数，即可求得结论．【解答】解：（1）设椭圆方程为=1（a＞b＞0），由焦点坐标可得c=1…由|PQ|=3，可得=3，…又a2﹣b2=1，解得a=2，b=，…故椭圆方程为=1…（2）设M（x1，y1），N（x2，y2），不妨y1＞0，y2＜0，设△F1MN的内切圆的径R，则△F1MN的周长=4a=8，（|MN|+|F1M|+|F1N|）R=4R因此最大，R就最大，…由题知，直线l的斜率不为零，可设直线l的方程为x=my+1，由得（3m2+4）y2+6my﹣9=0，…得，，则=，…令t=，则t≥1，则，…令f（t）=3t+，则f′（t）=3﹣，≤3，当t≥1时，f′（t）≥0，f（t）在[1，+∞）上单调递增，有f（t）≥f（1）=4，S△F1MN≤3，即当t=1，m=0时，S△F1MN=4R，∴R max=，这时所求内切圆面积的最大值为π．S△F1MN故直线l：x=1，△F1MN内切圆面积的最大值为π…【点评】本题考查椭圆的标准方程，考查直线与椭圆的位置关系，考查三角形面积的计算，考查学生分析解决问题的能力，分析得出最大，R就最大是关键．21．已知函数f（x）=a x+x2﹣xlna（a＞0，a≠1）．（1）求函数f（x）在点（0，f（0））处的切线方程；（2）求函数f（x）单调增区间；（3）若存在x1，x2∈[﹣1，1]，使得|f（x1）﹣f（x2）|≥e﹣1（e是自然对数的底数），求实数a的取值范围．【考点】利用导数研究曲线上某点切线方程；利用导数研究函数的单调性；利用导数求闭区间上函数的最值．【分析】（1）先求函数的导函数f′（x），再求所求切线的斜率即f′（0），由于切点为（0，0），故由点斜式即可得所求切线的方程；（2）先求原函数的导数得：f'（x）=a x lna+2x﹣lna=2x+（a x﹣1）lna，再对a进行讨论，得到f'（x）＞0，从而函数f（x）在（0，+∞）上单调递增．（3）f（x）的最大值减去f（x）的最小值大于或等于e﹣1，由单调性知，f（x）的最大值是f（1）或f（﹣1），最小值f（0）=1，由f（1）﹣f（﹣1）的单调性，判断f（1）与f （﹣1）的大小关系，再由f（x）的最大值减去最小值f（0）大于或等于e﹣1求出a的取值范围．【解答】解：（1）∵f（x）=a x+x2﹣xlna，∴f′（x）=a x lna+2x﹣lna，∴f′（0）=0，f（0）=1即函数f（x）图象在点（0，1）处的切线斜率为0，∴图象在点（0，f（0））处的切线方程为y=1；（2）由于f'（x）=a x lna+2x﹣lna=2x+（a x﹣1）lna＞0①当a＞1，y=2x单调递增，lna＞0，所以y=（a x﹣1）lna单调递增，故y=2x+（a x﹣1）lna 单调递增，∴2x+（a x﹣1）lna＞2×0+（a0﹣1）lna=0，即f'（x）＞f'（0），所以x＞0故函数f（x）在（0，+∞）上单调递增；②当0＜a＜1，y=2x单调递增，lna＜0，所以y=（a x﹣1）lna单调递增，故y=2x+（a x﹣1）lna单调递增，∴2x+（a x﹣1）lna＞2×0+（a0﹣1）lna=0，即f'（x）＞f'（0），所以x＞0故函数f（x）在（0，+∞）上单调递增；综上，函数f（x）单调增区间（0，+∞）；（3）因为存在x1，x2∈[﹣1，1]，使得|f（x1）﹣f（x2）|≥e﹣1，所以当x∈[﹣1，1]时，|（f（x））max﹣（f（x））min|=（f（x））max﹣（f（x））min≥e﹣1，由（2）知，f（x）在[﹣1，0]上递减，在[0，1]上递增，所以当x∈[﹣1，1]时，（f（x））min=f（0）=1，（f（x））max=max{f（﹣1），f（1）}，而f（1）﹣f（﹣1）=（a+1﹣lna）﹣（+1+lna）=a﹣﹣2lna，记g（t）=t﹣﹣2lnt（t＞0），因为g′（t）=1+﹣=（﹣1）2≥0（当t=1时取等号），所以g（t）=t﹣﹣2lnt在t∈（0，+∞）上单调递增，而g（1）=0，所以当t＞1时，g（t）＞0；当0＜t＜1时，g（t）＜0，也就是当a＞1时，f（1）＞f（﹣1）；当0＜a＜1时，f（1）＜f（﹣1）①当a＞1时，由f（1）﹣f（0）≥e﹣1⇒a﹣lna≥e﹣1⇒a≥e，②当0＜a＜1时，由f（﹣1）﹣f（0）≥e﹣1⇒+lna≥e﹣1⇒0＜a≤，综上知，所求a的取值范围为a∈（0，]∪[e，+∞）．【点评】本题考查了基本函数导数公式，导数的几何意义，利用导数研究函数的单调性及利用导数求闭区间上函数的最值．属于中档题．请考生在（22）、（23）、（24）三题中任选一题作答．注意：只能做所选定的题目．如果多做，则按所做第一个题目计分，作答时，请用2B铅笔在答题卡上将所选题号后的方框涂黑．【选修4-1：几何证明选讲】22．如图，⊙O的半径为6，线段AB与⊙相交于点C、D，AC=4，∠BOD=∠A，OB与⊙O相交于点E．（1）求BD长；（2）当CE⊥OD时，求证：AO=AD．【考点】相似三角形的判定．【分析】（1）证明△OBD∽△AOC，通过比例关系求出BD即可．（2）通过三角形的两角和，求解角即可．【解答】解：（1）∵OC=OD，∴∠OCD=∠ODC，∴∠OAC=∠ODB．∵∠BOD=∠A，∴△OBD∽△AOC．∴，∵OC=OD=6，AC=4，∴，∴BD=9．…（2）证明：∵OC=OE，CE⊥OD．∴∠COD=∠BOD=∠A．∴∠AOD=180°﹣∠A﹣∠ODC=180°﹣∠COD﹣∠OCD=∠ADO．∴AD=AO …【点评】本题考查三角形相似，角的求法，考查推理与证明，距离的求法．【选修4-4：坐标系与参数方程】23．（2016大庆校级模拟）在平面直角坐标系xoy中，以O为极点，x轴的正半轴为极轴的极坐标系中，直线l的极坐标方程为θ=，曲线C的参数方程为．（1）写出直线l与曲线C的直角坐标方程；（2）过点M平行于直线l1的直线与曲线C交于A、B两点，若|MA||MB|=，求点M轨迹的直角坐标方程．【考点】直线与圆锥曲线的综合问题；简单曲线的极坐标方程；参数方程化成普通方程．【分析】（1）利用极坐标与直角坐标方程的互化，直接写出直线l的普通方程，消去参数可得曲线C的直角坐标方程；（2）设点M（x0，y0）以及平行于直线l1的直线参数方程，直线l1与曲线C联立方程组，通过|MA||MB|=，即可求点M轨迹的直角坐标方程．通过两个交点推出轨迹方程的范围，【解答】解：（1）直线l的极坐标方程为θ=，所以直线斜率为1，直线l：y=x；曲线C的参数方程为．消去参数θ，可得曲线…（2）设点M（x0，y0）及过点M的直线为由直线l1与曲线C相交可得：，即：，x2+2y2=6表示一椭圆…取y=x+m代入得：3x2+4mx+2m2﹣2=0由△≥0得故点M的轨迹是椭圆x2+2y2=6夹在平行直线之间的两段弧…【点评】本题以直线与椭圆的参数方程为载体，考查直线与椭圆的综合应用，轨迹方程的求法，注意轨迹的范围的求解，是易错点．【选修4-5：不等式选讲】24．（2016南安市校级模拟）设函数f（x）=|2x+1|﹣|x﹣4|．（1）解不等式f（x）＞0；（2）若f（x）+3|x﹣4|≥m对一切实数x均成立，求m的取值范围．【考点】绝对值不等式的解法．【分析】（1）对x讨论，分当x≥4时，当﹣≤x＜4时，当x＜﹣时，分别解一次不等式，再求并集即可；。

2023-2024学年高二年级12月三校联合调研测试数学试卷一、选择题（本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1. 已知等比数列{}n a 中，11a =，48a=−，则公比q =（ ）A. 2B. 4−C. 4D. 2−【答案】D 【解析】【分析】根据等比数列的知识求得正确答案.【详解】依题意33418,2a a q q q ===−=−. 故选：D2. 已知过(,2),(,1)A m B m m −−两点的直线的倾斜角是45 ，则,A B 两点间的距离为（ ）A. 2B.C. D. 【答案】C 【解析】【分析】利用倾斜角求出1m =，然后利用两点间距离公式即可得出答案. 【详解】由题知，12tan 451m m m−−=°=−−， 解得1m =，故(1,2),(1,0)A B −，则,A B 故选：C3. 直线320x my m +−=平分圆C ：22220x x y y ++−=，则m =（ ）A.32B. 1C. -1D. -3【答案】D 【解析】【分析】求出圆心，结合圆心在直线上，代入求值即可.【详解】22220x x y y ++−=变形为()()22112x y ++−=，故圆心为()1,1−，由题意得圆心()1,1−在320x my m +−=上，故320m m −+−=，解得3m =−.故选：D4. 设双曲线()222210,0x y a b a b−=>>的虚轴长为2，焦距为 ）A. y =B. 2y x =±C. y x =±D. 12y x =±【答案】C 【解析】【分析】根据题意得到1b =，c =a =.【详解】由题意得22b =，2c =1b =，c =故a故双曲线渐近线方程为b y x x a=±. 故选：C5. 椭圆22192x y +=中以点()21M ，为中点的弦所在直线斜率为（ ） A. 49−B.12C.D. −【答案】A 【解析】【分析】先设出弦的两端点的坐标，分别代入椭圆方程，两式相减后整理即可求得弦所在的直线的斜率． 【详解】设弦的两端点为()11A x y ，，()22B x y ，，代入椭圆得22112222192192x y x y += += ， 两式相减得()()()()12121212092x x x x y y y y −+−++=，即()()()()1212121292x x x x y y y y −+−+=−，即()()1212121229x x y y y y x x +−−=+−， 即12122492y y x x −×−=×−， 即121249y y x x −=−−，∴弦所在的直线的斜率为49−， 故选:A ．6. 已知()1,0F c −，()2,0F c 是椭圆()2222:10x yC a b a b+=>>的左、右焦点，若椭圆C 上存在一点P 使得212PF PF c ⋅=，则椭圆C 的离心率e 的取值范围是（ ）A.B.C.D.【答案】B 【解析】 【分析】设点P .【详解】设()00,P x y ，则()22002210x ya b a b +=>>，∴2220021x y b a=−， 由212PF PF c ⋅=，∴()()20000,,c x y c x y c −−−⋅−−=， 化为2222x c y c −+=，∴22220212x x b c a+−=， 整理得()2222023a x c a c=−， ∵220x a ≤≤，∴()2222203a c a a c≤−≤，e ≤≤，故选：B7. 过动点(),P a b （0a ≠）作圆C：(223x y +−=的两条切线，切点分别为A ，B ，且60APB ∠=°，则ba的取值范围是（ ）A.B.C. , −∞+∞D.(),−∞∪+∞【答案】D 【解析】【分析】求出PC =，确定动点(),P a b 的轨迹方程，从而结合ba表示圆(2212x y +−=上的点与坐标原点连线的斜率，利用距离公式列出不等式，即可求得答案. 【详解】由题意知圆C：(223x y +−=因为A ，B 分别为两条切线PA ，PB 的切点，且60APB ∠=°，则30APC BPC ∠=∠=°，所以2PC AC ==，所以动点(),P a b在圆(2212x y +−=上且0a ≠，b a表示圆(2212x y +−=上的点与坐标原点连线的斜率， 设bk a=，则直线y kx =与圆(2212x y +−=有公共点，≤，解得k ≤k ≥，即ba的取值范围是(),−∞∪+∞， 故选：D8. 已知数列{}n a 满足()2123111N 23n a a a n n na n +++++=+∈ ，设数列{}nb 满足：121n n n n b a a ++=，数列{}n b 的前n 项和为n T ，若()N 1n nT n n λ+<∈+恒成立，则实数λ的取值范围为（ ） A. 1,4+∞B. 1,4+∞C. 3,8∞+D. 38 +∞,【答案】D 【解析】【分析】首先利用递推关系式求出数列的通项公式，进一步利用裂项相消法求数列的和，最后利用函数的单调性求出结果.【详解】数列{}n a 满足212311123n a a a a n n n++++=+ ，① 当2n ≥时，()2123111111231n n a a a a n n −++++−−=+− ，②①−②得，12n a n n=，故22n a n =， 则()()2222121211114411n n n n n b a a n n n n +++===− ++， 则()()22222211111111114223411n T n n n=−+−++−=− ++，由于()N 1n nT n n λ+<∈+恒成立，故()2111411nn n λ −< ++， 整理得：()21144441n n n λ+>=+++，因()11441n ++随n 的增加而减小， 所以当1n =时，()11441n ++最大，且38， 即38λ>. 故选：D二、选择题（本大题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求全部选对的得5分，部分选对的得2分，有选错的得0分．）为9. 下列说法正确的是（ ）A. 直线20x y −−=与两坐标轴围成的三角形的面积是2 B. 点()0,2关于直线1y x =+的对称点为()1,1 C. 过()()1122,,,x y x y 两点的直线方程为112121y y x x y y x x −−=−− D. 已知点()1,2P，向量()m =，过点P 作以向量m为方向向量的直线为l ，则点()3,1A 到直线l的距离为1【答案】ABD 【解析】【分析】由直线方程，求得在坐标轴上的截距，利用面积公式，可判定A 正确；根据点关于直线的对称的求法，求得对称点的坐标，可判定B 正确；根据直线的两点式方程的条件，可判定C 错误；根据题意，求得直线l 的方程，结合点到直线的距离公式，可判定D 正确.【详解】对于A 中，令0x =，可得=2y −，令0y =，可得2x =，则直线20x y −−=与两坐标轴围成三角形的面积12222S =××=，所以A 正确； 对于B 中，设()0,2关于直线1y x =+对称点坐标为(),m n ，则212122n mn m − =−+ =+ ，解得1,1m n ==，所以B 正确； 对于C 中，直线的两点式使用的前提是1212,x x y y ≠≠，所以C 错误；对于D中，以向量()m =为方向向量的直线l的斜率k =，则过点P 的直线l的方程为)12y x −+，即10x +−−=， 则点()3,1A 到直线l的距离1d −，所以D 正确． 故选：ABD ．的10. 已知椭圆221259x y +=上一点P ，椭圆的左､右焦点分别为12,F F ，则（ ）A. 若点P 的横坐标为2，则1325PF = B. 1PF 的最大值为9C. 若12F PF ∠为直角，则12PF F △的面积为9D. 若12F PF ∠为钝角，则点P的横坐标的取值范围为 【答案】BCD 【解析】【分析】对A ，可直接解出点P 坐标，求两点距离； 对B ，1PF 最大值为a c +对C ，设1PF x =，则210PF x =-，列勾股定理等式，可求面积；对D ，所求点P 在以原点为圆心，4c =为半径的圆内，求出椭圆与该圆的交点横坐标即可判断.【详解】椭圆的长半轴为5a=，半焦距为4=c ，∴()()124,0,4,0F F −对A ，2x =时，代入椭圆方程得，=，1175PF ==，A 错； 对B ，1PF 的最大值为9a c +=，B 对；对C ，12F PF ∠为直角，设1PF x =，则210PF x =-，则有()222210810180x x x x +-=⇒-+=，则12PF F △的面积为()11810922x x −==，C 对； 对D ，以原点为圆心，4c =为半径作圆，则12F F 为圆的直径，则点P 在圆内时，12F PF ∠为钝角，联立2222125916x y x y += +=，消y得x =，故点P的横坐标的取值范围为 ，D 对. 故选：BCD11. 已知数列{}n a 满足12a =，12,2,n n na n a a n ++ = 为奇数，为偶数，设2n n b a =，记数列{}n a 的前2n 项和为2n S ，数列{}n b 的前n 项和为n T ，则（ ）A. 520a =B. 32nn b =×C. 12632n n T n +=−−+×D. 2261232n n S n +=−−+×【答案】ACD 【解析】【分析】分析1n a +与n a 的递推关系，根据数列{}n a 的奇数项、偶数项以及分组求和法求得2,n n T S .【详解】依题意，2132435424,28,210,220a a a a a a a a =+====+===，A 选项正确. 112432b a ==≠×，所以B 选项错误.当n 为偶数时，2111222n n n n a a a a ++++==+=+，所以()2222n n a a ++=+，而226a +=，所以1122262,622nn nn a a −−+=×=×−，所以12242662622nn nT a a a n − ++++×++×−()16122263212n n n n +−=−=−−+×−，所以C 选项正确.当n 为奇数时，()211122224n n n n n a a a a a ++++++，所以()2424n n a a ++=+，而146a =，所以11122462,624n n nn a a +−−+=×=×−，所以1213521662624n n a a a a n −−+++++×++×−()16124463212n n n n +−=−=−−+×−，所以()()11224632263261232n n n n S n n n +++=−−+×+−−+×=−−+×，所以D 选项正确.故选：ACD【点睛】求解形如()11n n a pa q p +=+≠的递推关系式求通项公式的问题，可考虑利用配凑法，即配凑为()1n n a p a λλ++=+的形式，再结合等比数列的知识来求得n a .求关于奇数、偶数有关的数列求和问题，可考虑利用分组求和法来进行求解.12. 画法几何的创始人——法国数学家蒙日发现：在椭圆()2222:10x y C a b a b+=>>中，任意两条互相垂直的切线的交点都在同一个圆上，它的圆心是椭圆的中心，半径等于长、短半轴平方和的算术平方根，这个圆就称为椭圆C 的蒙日圆，其圆方程为2222x y a b +=+．已知椭圆C，点A ，B 均在椭圆C 上，直线:40l bx ay +−=，则下列描述正确的为（ ） A. 点A 与椭圆C 的蒙日圆上任意一点的距离最小值为bB. 若l 上恰有一点P 满足：过P 作椭圆C 的两条切线互相垂直，则椭圆C 的方程为2213x y +=C. 若l 上任意一点Q 都满足0QA QB ⋅>，则01b <<D. 若1b =，椭圆C 的蒙日圆上存在点M 满足MA MB ⊥，则AOB【答案】BCD 【解析】【分析】根据椭圆上点到原点最大距离为a ，蒙日圆上的点到椭圆上点的距离最小值为半径减去a 可判断A ，利用相切列出方程即可求得椭圆的方程，可判断B ，分析可得点Q 应在蒙日圆外，解不等式从而判断C ，依据题意表示出面积表达式并利用基本不等式即可求出面积最大值，可判断D.【详解】由离心率c e a ==，且222a b c =+可得223a b ， 所以蒙日圆方程2224x y b +=； 对于A ，由于原点O 到蒙日圆上任意一点的距离为2b ，原点O到椭圆上任意一点的距离最大值为a ，所以椭圆C 上的点A 与椭圆C的蒙日圆上任意一点的距离最小值为(2b −，即A 错误；对于B ，由蒙日圆定义可知：直线:40l bx ay +−=与蒙日圆2224x y b +=相切， 则圆心到直线l422b b=，解得1b =； 所以椭圆C 的方程为2213x y +=，即B 正确；对于C ，根据蒙日圆定义可知：蒙日圆上的点与椭圆上任意两点之间的夹角范围为π0,2，若若l 上任意一点Q 都满足0QA QB ⋅>，可知点Q 应在蒙日圆外，所以此时直线l 与蒙日圆2224x y b +=422b b >，解得11b −<<， 又0a b >>，所以可得01b <<，即C 正确.对于D ，易知椭圆C 的方程为2213x y +=，即2233x y +=，蒙日圆方程为224x y +=， 不妨设()0,Mx y ，因为其在蒙日圆上，所以22004xy +=，设()()1122,,,A x y B x y ，又MA MB ⊥，所以可知,MA MB 与椭圆相切，此时可得直线MA 的方程为1133x x y y +=，同理直线MB 的方程为2233x x y y +=； 将()00,M x y 代入,MA MB 直线方程中可得101020203333x x y y x x y x +=+= ，所以直线AB 的方程即为0033x x y y +=， 联立00223333x x y y x y +=+=，消去y 整理可得()2222000036990x y x x x y +−+−=； 由韦达定理可得200121222220000699,33x y x x x x x y x y −+==++, 所以()20202122y AB y +=+， 原点O 到直线AB的距离为d，因此AOB 的面积()2020********AOBy S AB d y +=⋅=×=+333222==≤=；，即201y =时等号成立， 因此AOBD 正确； 故选：BCD的【点睛】方法点睛：在求解椭圆中三角形面积最值问题时，经常利用弦长公式和点到直线距离公式表示出三角形面积的表达式，再利用基本不等式或函数单调性即可求得结果.三、填空题（本大题共4小圆，每小题5分，共20分）13. 在等差数列{}n a 中，n S 为前n 项和，7825a a =+，则11S =_________. 【答案】55 【解析】【分析】根据下标和性质求出6a ，再根据等差数列前n 项和公式及下标和性质计算可得.【详解】在等差数列{}n a 中7825a a =+，又7862a a a =+，所以65a =， 所以()111611611112115522a a a S a +×====. 故答案为：5514. 已知点P 为椭圆C ：22195x y +=上一点，点1F ，2F 分别为椭圆C 的左、右焦点，若122PF PF =，则12PF F △的内切圆半径为_____【解析】【分析】首先求12,PF PF 的值，再求12PF F △的面积，再利用三角形内切圆的半径表示面积，即可求解．【详解】因为12||||26PF PF a +==，12||2||PF PF =，所以12||4,||2PF PF ==， 212954,||24c F F c −====，则121||||4F F PF ==，等腰12PF F △边2PF 上的高h =，所以12122PF F S =×= ，设22PF F 的内切圆半径为r ，则121211(||||||)1022PF PF F F r r ++×=××=所以r =15. 已知圆M经过((()2,,1,0,A C B −．若点()3,2P ，点Q 是圆M 上的一个动点，则MQ PQ ⋅的最小值为__________．【答案】4−【解析】【分析】先利用待定系数法求出圆的方程，再利用数量积的运算律转化结合数量积的定义求出. 【详解】设圆M 的一般方程为220x y Dx Ey F ++++=，由于圆经过(2,A，(B ，()1,0C −，所以有72072010D F D F D F ++=++=−+=，解得203D E F =− = =− ， 所以圆M 的一般方程为22230x y x +−−=，即标准方程为()2214x y −+=. 则圆M 的圆心()1,0M ，半径2==r MQ ，且=MP，因为()2424 ⋅=⋅−=−⋅≥−×=−MQ PQ MQ MQ MP MQ MQ MP ，当且仅当MQ 与MP同向时，等号成立，所以MQ PQ ⋅的最小值为4−.故答案为：4−.16. 已知双曲线C ：()222210,0x y a b a b−=>>的左、右焦点分别为1F ，2F ，过点1F 作倾斜角为30 的直线l 与C 的左、右两支分别交于点P ，Q ，若()2222220F P F Q F P F Q F P F Q+⋅−=，则C 的离心率为______．【解析】【分析】由()2222220F P F Q F P F Q F P F Q+⋅−=，2PF Q ∠的平分线与直线PQ 垂直，结合图像，根据双曲线的定义，找出各边的关系，列出等式，求解.【详解】依题意，由()2222220F P F Q F P F Q F P F Q+⋅−=， 得22220F P F Q QP F P F Q+⋅=，即2PF Q ∠的平分线与直线PQ 垂直， 如图，设2PF Q ∠的平分线2F D 与直线PQ 交于点D ，则22PF D QF D ∠=∠，2290F DP F DQ ∠=∠= ，又22DF DF =， 所以22PDF QDF ≌△△2QF ．由题得()1,0F c −，()2,0F c ，设2DF h =，2QF s =，1PF t =，在12Rt DF F △中，1290F DF ∠=，1230DF F ∠=，则h c =，1DF =，由双曲线的性质可得122122QF QF PQ t s a PF PF s t a −=+−=−=−= ，解得4PQ a =，则2PDQD a ==，所以在2Rt QDF△中，s=又12t DF PD a =−=−，2s t a −=)22a a −−=，，整理得222ac =，所以cea==四、解答题（本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤．） 17. 已知数列{}n a 满足：122,4a a ==，数列{}n a n −为等比数列． （1）求数列{}n a 的通项公式；（2）求和：12nn S a a a =++⋅⋅⋅+． 【答案】（1）12n n −+ （2）2112122n n n ++− 【解析】【分析】（1）首先求出11a −，22a −，即可求出等比数列{}n a n −的通项公式，从而求出{}n a 的通项公式；（2）利用分组求和法计算可得. 【小问1详解】因为12a =，24a =，数列{}n a n −为等比数列，所以111a −=，222a −=2=，即{}n a n −是以1为首项，2为公比等比数列， 所以12n n a n −−=，则12n n a n −=+. 【小问2详解】12n n S a a a =++⋅⋅⋅+01211222322n n −=++++++++()()01211232222n n −=+++++++++()2112112121222n n n n n n +−=+=++−−. 18. 已知圆()()22:121M x y ++−=，直线l 过原点()0,0O ． （1）若直线l 与圆M 相切，求直线l 的方程；（2）若直线l 与圆M 交于P ，Q 两点，当MPQ 的面积最大时，求直线l 的方程．的【答案】（1）0x =或34y x =− （2）y x =−或7y x =−．【解析】【分析】（1）根据直线l 的斜率是否存在进行分类讨论，结合圆心到直线的距离等于半径来求得直线l 的方程.（2）设出直线l 的方程，由点到直线的距离公式、弦长公式求得三角形PQM 面积的表达式，结合二次函数的性质求得MPQ 的面积最大时直线l 的方程. 【小问1详解】①当直线l 的斜率不存在时，直线l 为0x =，显然符合直线与圆相切， ②当斜率存在时，设直线为y kx =，圆M 的圆心坐标()1,2-，圆心到直线的距离d由题意得：直线l 与圆M1，解得：34k =−，所以直线l 的方程为：34y x =−， 综上所述，直线l 的方程为：0x =或34y x =− 【小问2详解】直线l 的斜率不存在时，直线l 为0x =与圆相切，不符合题意，故直线l 斜率必存在， 设直线l 的方程为：y mx =， 圆心到直线的距离d，弦长PQ ==，所以12PQM S PQ d =⋅⋅=△当212d =时，面积S 最大，12=，整理得2870m m ++=，解得7m =−，或1m =−，所以直线l 的方程：y x =−或7y x =−．19.如图，已知A ，(0,0)B ，(12,0)C，直线:(20l k x y k −−=．（1）证明直线l 经过某一定点，并求此定点坐标； （2）若直线l 等分ABC 的面积，求直线l 的一般式方程；（3）若P ，李老师站在点P 用激光笔照出一束光线，依次由BC （反射点为K ）、AC （反射点为I ）反射后，光斑落在P 点，求入射光线PK 的直线方程． 【答案】（1）证明见解析，定点坐标为(2,； （2170y +−=； （3）2100x −=． 【解析】【分析】（1）整理得到(2))0k x y −+−=，从而得到方程组，求出定点坐标； （2）求出定点P 在直线AB 上，且||8AM =，由12AMD ABC S S =得到3||||94AD AC ==，设出00(,)D x y ，由向量比例关系得到D 点坐标，得到直线方程；（3）作出辅助线，确定P 关于BC 和AC 的对称点1,P 2P ，得到12P P k =由对称性得PK k =写成直线方程. 【小问1详解】直线:(20l k x y k +−−=可化为(2))0k x y −+−=，令200x y −= −=，解得2x y = = l经过的定点坐标为(2,；【小问2详解】因为A ，(0,0)B ，(12,0)C ，所以||||||12ABAC BC ===， 由题意得直线AB方程为y =，故直线l经过的定点M 在直线AB 上，所以||8AM ==，设直线l 与AC 交于点D ，所以12AMD ABC S S =，即111||||sin ||||sin 222AM AD A AB AC A =××，所以3||||94AD AC ==， 设00(,)D x y ，所以34AD AC = ，即003(6,(6,4x y −−=−，所以0212x =，0y =D ，将D 点坐标代入直线l的方程，解得k =， 所以直线l 170y+−=； 【小问3详解】设P 关于BC 的对称点1(2,P −，关于AC 的对称点2(,)P m n ， 直线AC12612x −=−，即)12y x −，直线AC的方程为12)y x −，所以(12122m =−+ =− ，解得14,m n ==2P ， 由题意得12,,,P K I P四点共线，12P P k =PK k =， 所以入射光线PK的直线方程为2)y x −−，即2100x +−=．20.已知两定点()()12,2,0F F ，满足条件212PF PF −=的点P 的轨迹是曲线E ，直线1y kx =−与曲线E 交于A ，B （1）求曲线E 的方程； （2）求实数k 的取值范围；（3）若||AB =AB 的方程． 【答案】20. ()2210x y x −=<21. ()1−22.10x y ++= 【解析】【分析】（1）由双曲线的定义得其方程为()2210x y x −=<；（2）由于直线和双曲线相交于左支，且有两个交点，故联立直线的方程和双曲线的方程，消去y 后得到关于x 的一元二次方程的判别式大于零，且韦达定理两根的和小于零，两根的积大于零，由此列不等式组，求解k 的取值范围； （3）由AB =，利用弦长公式，结合韦达定理列出关于k 的方程，解方程即可得结果. 【小问1详解】由双曲线定义可知，曲线E是以()1F，)2F为焦点的双曲线的左支，且c =由2122PF PF a −==，所以1a =，1b ，所以曲线E 的方程为()2210x y x −=<.故曲线E 的方程为：()2210x y x −=<.【小问2详解】设()11,A x y ，()22,B x y ，由题意联立方程组2211x y y kx −= =− ，消去y 得()221220k x kx −+−=， 又因为直线与双曲线左支交于两点，有()()222122122102810201201k k k k x x k x x k −≠ ∆=+−> − +=< −− => −，解得1k <<−. 故k的取值范围为()1−. 【小问3详解】因为2AB x =−====，整理化简得422855250k k −+=，解得257k =或254k =， 因为1k<<−，所以k =AB 10x y ++=. 故直线AB 10x y ++=. 的【点睛】关键点睛：（2）（3）中根据直线与曲线联立后利用韦达定理，再结合弦长公式从而求解. 21. 设数列{}n a 的前n 项和为n S ，且122n n n S a +=−，数列{}n b 满足2log 1nn a b n =+，其中*N n ∈. （1）证明2n n a为等差数列，求数列{}n a 的通项公式；（2）求数列21n a n+的前n 项和为n T ；（3）求使不等式1321111111n m b b b −+⋅+⋅⋅⋅⋅⋅+≥n 都成立的最大实数m 的值.【答案】（1）证明见解析；(1)2nn a n =+⋅ （2）188(4)4339n n T n =+⋅− （3【解析】【分析】（1）根据数列递推式可得122nn n a a −−=，整理变形结合等差数列定义即可证明结论，并求得数列的通项公式；（2）利用错位相减法即可求得答案； （3）将原不等式化为()111111321n+++≥ −调性，将不等式恒成立问题转化为函数最值问题，即可求得答案. 【小问1详解】当1n =时，11124a S a ==−，则14a =， 当2n ≥时，11,22nn n n n n a S S a a −−∴=−−=，即11122n n n n a a −−−=，即2n n a 是以122a =为首项，公差为1的等差数列， 故(1,22)1n n n n a n a n =++⋅∴= 【小问2详解】由（1）可得2(1)41n n a n n =+⋅+， 故22434(1)4n n T n =×+×+++⋅ ，故231424344(1)4n n n T n n +=×+×++⋅++⋅ ，则231324444(1)4n n n T n +−=×++++−+⋅14(14)884(1)4(4)41433n n n n n +−=+−+⋅=−+⋅−， 故188(4)4339n n T n =+⋅−； 【小问3详解】22log log 21n n n a b n n ===+，则1321111111n m b b b − +⋅+⋅⋅⋅⋅⋅+≥即()111111321n+++≥ −即11321n m −≤对任意正整数n 都成立，令()11111?·1321n f n +++−=则()111111?·11321211n n f n  ++++−++故()()11f n f n +=>， 即(),N f n n +∈随着n 的增大而增大，故()()1f n f ≥m ≤， 即实数m【点睛】关键点睛：第三问根据数列不等式恒成立问题求解参数的最值问题时，要利用分离参数法推得111111321n m +++−≤ 对任意正整数n 都成立，之后的关键就在于构造函数，并判断该函数的单调性，从而利用最值求得答案.22. 已知椭圆C 的中心在坐标原点，两焦点12,F F 在x 轴上，离心率为12，点P 在C 上，且12PF F △的周长为6．（1）求椭圆C 的标准方程；（2）过点()4,0M 的动直线l 与C 相交于A ，B 两点，点B 关于x 轴的对称点为D ，直线AD 与x 轴的交点为E ，求ABE 的面积的最大值． 【答案】（1）22143x y += （2【解析】【分析】（1）根据题意得到22212226c a a c a b c = +==+，再解方程组即可. （2）首先设出直线l 的方程，联立直线与椭圆方程，根据韦达定理、点,B D 关于x 轴对称、,,A E D 三点共线得到()1,0E ，从而得到ABES = ，再利用换元法求解最值即可. 【小问1详解】由题知：2221222261c a a a c b a b c c == +=⇒ =+=， 所以椭圆22:143x y C += 【小问2详解】如图所示：设直线():40l x ty t =+≠，()()1122,,,A x y B x y . ()222243424360143x ty t y ty x y =+ ⇒+++= += . ()()2224434360t t ∆−+×>，解得24t >.1222434t y y t −+=+，1223634y y t =+. 因为点,B D 关于x 轴对称，所以()22,D x y −. 设()0,0E x ，因为,,A E D 三点共线，所以AE DE k k =. 即121020y y x x x x −=−−，即()()120210y x x y x x −=−−. 解得()()()12211212122101212124424y ty y ty ty y y y y x y x x y y y y y y ++++++===+++ 2364124t t×=−+=. 所以点()1,0E 为定点，3EM =.1212ABE AME BME S S S EM y y =−=⋅−=令0m =>，则()22181818163163443ABE m m S m m m m===≤++++△ 当且仅当163m m =，即m =时取等号. 所以ABE。

河北省邯郸市2025届高三第一次调研考试数学试题一、单选题：本题共8小题，每小题5分，共40分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.已知a =(x,−1)，b =(2,1)，若(a−2b )//b ，则x = ( )A. −2B. −1C. 1D. 22.若z +1z−1=2i ，则z = ( )A. 45−35iB. 35−45iC. 35+45iD. 45+35i3.已知S n 为等差数列{a n }的前n 项和，且S 13S 9=269，则a 7a 5= ( )A. 3B. 2C. 43D. 234.已知正三棱台ABC−A′B′C′的体积为1423，若AB =2，A′B′=4，则该正三棱台的高为( )A. 263B. 14615 C. 14627D. 4335.已知sin (α−β)=13，tan α=3tan β，则sin (α+β)= ( )A. 16B. 13C. 12D. 236.在第33届夏季奥运会期间，中国中央电视台体育频道在某比赛日安排甲、乙、丙、丁4个人参加当天A ，B ，C 三个比赛场地的现场报道，且每个场地至少安排一人，甲不在A 场地的不同安排方法数为( )A. 32B. 24C. 18D. 127.已知函数f(x)=(x−1)2−sin x x 2+1，g(x)=ax +1(a ≠0)，若y =f(x)和y =g(x)图象存在3个交点(x 1,y 1)，(x 2,y 2)，(x 3,y 3)，则y 1+y 2+y 3= ( )A. 1B. 2C. 3D. 48.设双曲线C:x 2a 2−y 2b 2=1(a >0,b >0)的左、右焦点分别为F 1，F 2，点P 在双曲线C 上，过点P 作两条渐近线的垂线，垂足分别为D ，E ，若PF 1⋅PF 2=0，且3|PD||PE|=S △PF 1F 2，则双曲线C 的离心率为( )A. 233B.2 C.3 D. 2二、多选题：本题共3小题，共18分。

2015-2016学年江苏省南京市六校联考高三（上）12月调研数学试卷一、填空题（共14小题每小题5分共计70分．将正确答案填入答题纸的相应横线上）1．设集合M={2，0，x}，集合N={0，1}，若N⊆M，则x= ．2．已知复数z满足（3+4i）z=1（i为虚数单位），则z的模为．3．已知m为实数，直线l1：mx+y+3=0，l2：（3m﹣2）x+my+2=0，则“m=1”是“l1∥l2”的条件（请在“充要、充分不必要、必要不充分、既不充分也不必要”中选择一个填空）．4．根据如图所示的伪代码，最后输出的S的值为．5．现有5道试题，其中甲类试题2道，乙类试题3道，现从中随机取2道试题，则至少有1道试题是乙类试题的概率为．6．若实数x，y满足约束条件，则目标函数z=2x+y的最小值为．7．已知等比数列{a n}的前n项和为S n，若a2a8=2a3a6，S5=﹣62，则a1的值是．8．已知||=1，||=2，与的夹角为120°，，则与的夹角为．9．已知，则cos（30°﹣2α）的值为．10．设椭圆的左、右焦点分别为F1、F2，左准线为l，若在椭圆上存在点P，使得当PQ⊥l于点Q时，四边形PQF1F2为平行四边形，则此椭圆的离心率e的取值范围是．11．若x．y均为正实数，且x+2y=4，则+的最小值是．12．在△ABC中，已知BC=2， =1，则△ABC面积的最大值是．13．已知圆O：x2+y2=4，直线l：x+y﹣4=0，A为直线l上一点，若圆O上存在两点B、C，使得∠BAC=60°，则点A的横坐标的取值范围是．14．若函数f（x）=恰有2个零点，则实数a的取值范围是．二、解答题（本大题共6小题，共90分．请在答题纸指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．）15．已知向量=（sinx，），=（cosx，﹣1）．（1）当∥时，求tan（x﹣）的值；（2）设函数f（x）=2（+）•，当x∈[0，]时，求f（x）的值域．16．如图，在多面体ABCDEF中，四边形ABCD是菱形，AC，BD相交于点O，EF∥AB，AB=2EF，平面BCF⊥平面ABCD，BF=CF，点G为BC的中点．（1）求证：直线OG∥平面EFCD；（2）求证：直线AC⊥平面ODE．17．如图，椭圆C： +=1（a＞b＞0）的离心率e=，椭圆C的右焦点到右准线的距离为，椭圆C的下顶点为D．（1）求椭圆C的方程；（2）若过D点作两条互相垂直的直线分别与椭圆C相交于点P、M．求证：直线PM经过一定点．18．如图，某广场中间有一块边长为2百米的菱形状绿化区ABCD，其中BMN是半径为1百米的扇形，∠ABC=，管理部门欲在该地从M到D修建小路；在上选一点P（异于M、N两点），过点P修建与BC平行的小路PQ．（1）设∠PBC=θ，试用θ表示修建的小路与线段PQ及线段QD的总长度l；（2）求l的最小值．19．已知数列{a n}的前n项和为S n，且对一切正整数n都有．（I）求证：a n+1+a n=4n+2；（II）求数列{a n}的通项公式；（III）是否存在实数a，使不等式对一切正整数n都成立？若存在，求出a的取值范围；若不存在，请说明理由．20．已知函数f（x）=e x﹣ax2﹣bx﹣1，其中a，b∈R，e为自然对数的底数．（1）若函数f（x）在点（1，f（1））处的切线方程是y=（e﹣1）x﹣1，求实数a及b的值；（2）设g（x）是函数f（x）的导函数，求函数g（x）在区间[0，1]上的最小值；（3）若f（1）=0，函数f（x）在区间（0，1）内有零点，求a的取值范围．【选做题】本题包括、、、四小题，请选定其中两题，并在答题卡指定区域内作答，若多做，则按作答的前两题评分.解答题应写出文字说明、证明过程或演算步骤.（选修4-1：几何证明选讲）21．选修4﹣1：几何证明选讲如图，AB是⊙O的一条切线，切点为B，直线ADE，CFD，CGE都是⊙O的割线，已知AC=AB．求证：FG∥AC．（选修4-2：矩阵与变换）22．（2012•盐城一模）已知矩阵，若矩阵AB对应的变换把直线l：x+y﹣2=0变为直线l′，求直线l′的方程．选修4-4：坐标系与参数方程23．选修4﹣4：坐标系与参数方程在平面直角坐标系xOy中，圆C的参数方程为（θ为参数，r＞0）．以O为极点，x轴正半轴为极轴建立极坐标系，直线l的极坐标方程为．若圆C上的点到直线l的最大距离为3，求r的值．选修4-5：不等式选讲24．已知实数x，y，z满足x+y+z=2，求2x2+3y2+z2的最小值．【必做题】第22题、第23题，每题10分，共计20分，请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤.25．袋中装有围棋黑色和白色棋子共7枚，从中任取2枚棋子都是白色的概率为．现有甲、乙两人从袋中轮流摸取一枚棋子．甲先摸，乙后取，然后甲再取，…，取后均不放回，直到有一人取到白棋即终止．每枚棋子在每一次被摸出的机会都是等可能的．用X表示取棋子终止时所需的取棋子的次数．（1）求随机变量X的概率分布列和数学期望E（X）；（2）求甲取到白球的概率．26．设f（x）是定义在R上的函数，已知n∈N*，且g（x）=C f（）x0（1﹣x）n+C f（）x1（1﹣x）n﹣1+C f（）x2（1﹣x）n﹣2+…+C f（）x n（1﹣x）n．（1）若f（x）=1，求g（x）；（2）若f（x），求g（x）．2015-2016学年江苏省南京市六校联考高三（上）12月调研数学试卷参考答案与试题解析一、填空题（共14小题每小题5分共计70分．将正确答案填入答题纸的相应横线上）1．设集合M={2，0，x}，集合N={0，1}，若N⊆M，则x= 1 ．【考点】集合的包含关系判断及应用．【专题】集合．【分析】根据条件N⊆M，确定元素关系，进行求解即可，从而得到x的值．【解答】解：∵集合M={2，0，x}，N={0，1}，∴若N⊆M，则集合N中元素均在集合M中，∴x=1．故答案为：1．【点评】本题主要考查集合的包含关系的应用，利用N⊆M，确定元素关系．一般集合中问题，如果含有参数，求解之后要注意对集合进行验证．属于基础题．2．已知复数z满足（3+4i）z=1（i为虚数单位），则z的模为．【考点】复数求模．【专题】数系的扩充和复数．【分析】复数方程两边求模推出结果即可．【解答】解：复数z满足（3+4i）z=1（i为虚数单位），可得：|（3+4i）z|=1，即|3+4i||z|=1，可得5|z|=1．∴z的模为：．故答案为：．【点评】本题考查复数的模的求法，基本知识的考查．3．已知m为实数，直线l1：mx+y+3=0，l2：（3m﹣2）x+my+2=0，则“m=1”是“l1∥l2”的充分不必要条件（请在“充要、充分不必要、必要不充分、既不充分也不必要”中选择一个填空）．【考点】直线的一般式方程与直线的平行关系．【专题】计算题．【分析】把m=1代入可判l1∥l2”成立，而“l1∥l2”成立可推出m=1，或m=2，由充要条件的定义可得答案．【解答】解：当m=1时，方程可化为l1：x+y+3=0，l2：x+y+2=0，显然有“l1∥l2”成立；而若满足“l1∥l2”成立，则必有，解得m=1，或m=2，不能推出m=1，故“m=1”是“l1∥l2”的充分不必要条件．故答案为：充分不必要【点评】本题考查直线的一般式方程与直线的平行关系，属基础题．4．根据如图所示的伪代码，最后输出的S的值为55 ．【考点】伪代码．【专题】计算题；转化思想；试验法；算法和程序框图．【分析】分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是累加并输出S=1+2+3+4+5+…+10的值，利用等差数列的求和公式计算即可得解．【解答】解：分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是累加并输出满足条件S=1+2+3+4+5+…+10值．由于：S=1+2+3+4+5+…+10=55，故输出的S值为55．故答案为：55；【点评】本题考查的知识点是伪代码，其中根据已知分析出循环的循环变量的初值，终值及步长，是解答的关键，属于基础题．5．现有5道试题，其中甲类试题2道，乙类试题3道，现从中随机取2道试题，则至少有1道试题是乙类试题的概率为．【考点】计数原理的应用．【专题】应用题；排列组合．【分析】利用组合的方法求出甲类试题2道，乙类试题3道，从中随机取2道试题的方法，全是甲类试题，有1种方法，利用对立事件的概率公式求出至少有1道试题是乙类试题的概率．【解答】解：甲类试题2道，乙类试题3道，从中随机取2道试题，共有=10种方法，全是甲类试题，有1种方法，∴至少有1道试题是乙类试题的概率为1﹣=．故答案为：．【点评】此题考查概率的求法：如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=．6．若实数x，y满足约束条件，则目标函数z=2x+y的最小值为 1 ．【考点】简单线性规划．【专题】不等式的解法及应用．【分析】作出不等式组对应的平面区域，利用z的几何意义，即可得到结论．【解答】解：作出不等式组对应的平面区域如图：由z=2x+y得y=﹣2x+z，平移直线y=﹣2x+z，由图象可知当直线y=﹣2x+z经过点A时，直线的截距最小，此时z最小，由，解得，即A（0，1），此时z=0×2+1=1，故答案为：1【点评】本题主要考查线性规划的应用，利用数形结合是解决本题的关键．7．已知等比数列{a n}的前n项和为S n，若a2a8=2a3a6，S5=﹣62，则a1的值是﹣2 ．【考点】等比数列的通项公式．【专题】计算题；等差数列与等比数列．【分析】由题意可知，q≠1，结合等比数列的通项公式及求和公式可得，解方程可求【解答】解：∵a2a8=2a3a6，S5=﹣62∴q≠1∴解方程可得，q=2，a1=﹣2故答案为：﹣2【点评】本题主要考查了等比数列的通项公式及求和公式的简单应用，属于基础试题8．已知||=1，||=2，与的夹角为120°，，则与的夹角为90°．【考点】平面向量数量积的坐标表示、模、夹角．【专题】平面向量及应用．【分析】利用向量的数量积运算和向量垂直与数量积的关系即可得出．【解答】解：∵||=1，||=2，与的夹角为120°，∴===﹣1．∵，∴，∴=，∴﹣（﹣1）=，∴=0．∴．∴与的夹角为90°．【点评】本题考查了向量的数量积运算和向量垂直与数量积的关系，属于基础题．9．已知，则cos（30°﹣2α）的值为．【考点】二倍角的余弦；两角和与差的余弦函数．【专题】三角函数的求值．【分析】利用诱导公式求得sin（15°﹣α）=，再利用二倍角的余弦公式可得cos（30°﹣2α）=1﹣2sin2（15°﹣α），运算求得结果．【解答】解：∵已知，∴sin（15°﹣α）=，则cos（30°﹣2α）=1﹣2sin2（15°﹣α）=，故答案为．【点评】本题主要考查诱导公式，二倍角的余弦公式的应用，属于中档题．10．设椭圆的左、右焦点分别为F1、F2，左准线为l，若在椭圆上存在点P，使得当PQ⊥l于点Q时，四边形PQF1F2为平行四边形，则此椭圆的离心率e的取值范围是（，1）．【考点】椭圆的简单性质．【专题】计算题．【分析】PQF1F2为平行四边形对边相等．推出PQ=F1F2=2C．设P（x1，y1）． P在X负半轴，利用P的横坐标的范围，得到关系式，即可得到椭圆离心率的范围．【解答】解：因为PQF1F2为平行四边形，对边相等．所以，PQ=F1F2，所以PQ=2C．设P（x1，y1）． P在X负半轴，﹣x1=﹣2c＜a，所以2c2+ac﹣a2＞0，即2e2+e﹣1＞0，解得e，因为椭圆e取值范围是（0，1），所以此题答案为（，1）．故答案为：（，1）．【点评】本题是中档题，考查椭圆的基本性质，找出P的横坐标与椭圆长半轴的关系是解题的关键，考查计算能力，转化思想．11．若x．y均为正实数，且x+2y=4，则+的最小值是 2 ．【考点】基本不等式．【专题】整体思想；换元法；不等式的解法及应用．【分析】令x+2=m，y+1=n，整体换元由基本不等式可得．【解答】解：令x+2=m，y+1=n，则x=m﹣2，y=n﹣1，∵x，y均为正实数，且x+2y=4，∴m＞2且n＞1，且m﹣2+2（n﹣1）=4即m+2n=8，换元可得+=+=+=m+﹣4+2n+﹣4=+==，由8=m+2n≥2可得mn≤8，∴≥2，当且仅当=即m=2n时取等号，结合m+2n=8可解得m=4且n=2，即x=2且y=1．故答案为：2．【点评】本题考查基本不等式求最值，整体换元是解决问题的关键，属中档题．12．在△ABC中，已知BC=2， =1，则△ABC面积的最大值是．【考点】向量在几何中的应用．【专题】计算题；综合题．【分析】根据=1，及向量的数量积的定义式得到cosA=1，两边平方得到1=AB2AC2cos2A，根据三角形的面积公式S=|AB||AC|sinA，两边平方，两式相加，得到1+4S2=AB2AC2，根据余弦定理和基本不等式即可求得三角形面积的最大值．【解答】解：∵ =1，∴ cosA=1∴1=AB2AC2cos2A（1）又∵S=|AB||AC|sinA∴4S2=AB2AC2sin2A（2）（1）+（2）得：1+4S2=AB2AC2（cos2A+sin2A）即1+4S2=AB2AC2由题知： =﹣，∴BC2=AC2﹣2+AB2=AC2+AB2﹣2∵BC=2，∴AC2+AB2=6由不等式：AC2+AB2≥2AC•AB 当且仅当，AC=AB时，取等号∴6≥2AC•AB即AC•AB≤3∴1+4S2=AB2AC2《9∴4S2≤8，即：S2≤2∴S≤，所以△ABC面积的最大值是：．故答案为．【点评】此题是个中档题．考查向量在几何中的应用和向量的数量积的定义式，以及余弦定理、三角形的面积公式和基本不等式求最值等基础知识和基本方法，综合性强，考查了学生灵活应用知识分析、解决问题的能力．13．已知圆O：x2+y2=4，直线l：x+y﹣4=0，A为直线l上一点，若圆O上存在两点B、C，使得∠BAC=60°，则点A的横坐标的取值范围是[0，4] ．【考点】直线与圆的位置关系．【专题】计算题；转化思想；综合法；直线与圆．【分析】先确定从直线上的点向圆上的点连线成角，当且仅当两条线均为切线时才是最大的角，进而求出OA的长度为4，故可转化为在直线上找到一点，使它到点O的距离为4．【解答】解：由题意，从直线上的点向圆上的点连线成角，当且仅当两条线均为切线时才是最大的角，不妨设切线为AP，AQ，则∠PAQ为60°时，∠POQ为120°，所以OA的长度为4，故问题转化为在直线上找到一点，使它到点O的距离为4．设A（x0，4﹣x0），则∵O（0，0），∴x02+（4﹣x0）2=16∴x0=0或4∴满足条件的点A横坐标的取值范围是[0，4]．故答案为：[0，4]．【点评】本题考查直线与圆的方程的应用，考查学生分析解决问题的能力，解题的关键是明确从直线上的点向圆上的点连线成角，当且仅当两条线均为切线时才是最大的角．14．若函数f（x）=恰有2个零点，则实数a的取值范围是[，1）∪[3，+∞）．【考点】函数零点的判定定理．【专题】计算题；分类讨论；函数的性质及应用．【分析】①当a≤0时，f（x）＞0恒成立，②当a＞0时，由3x﹣a=0讨论，再由x2﹣3ax+2a2=（x﹣a）（x﹣2a）讨论，从而确定方程的根的个数．【解答】解：①当a≤0时，f（x）＞0恒成立，故函数f（x）没有零点；②当a＞0时，3x﹣a=0，解得，x=log3a，又∵x＜1；∴当a∈（0，3）时，log3a＜1，故3x﹣a=0有解x=log3a；当a∈[3，+∞）时，log3a≥1，故3x﹣a=0在（﹣∞，1）上无解；∵x2﹣3ax+2a2=（x﹣a）（x﹣2a），∴当a∈（0，）时，方程x2﹣3ax+2a2=0在[1，+∞）上无解；当a∈[，1）时，方程x2﹣3ax+2a2=0在[1，+∞）上有且仅有一个解；当a∈[1，+∞）时，方程x2﹣3ax+2a2=0在[1，+∞）上有且仅有两个解；综上所述，当a∈[，1）或a∈[3，+∞）时，函数f（x）=恰有2个零点，故答案为：[，1）∪[3，+∞）．【点评】本题考查了分段函数的性质的应用及分类讨论的思想应用．二、解答题（本大题共6小题，共90分．请在答题纸指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．）15．已知向量=（sinx，），=（cosx，﹣1）．（1）当∥时，求tan（x﹣）的值；（2）设函数f（x）=2（+）•，当x∈[0，]时，求f（x）的值域．【考点】平面向量数量积的运算；平面向量共线（平行）的坐标表示．【专题】计算题；三角函数的求值；三角函数的图像与性质；平面向量及应用．【分析】（1）运用向量的关系的坐标表示和同角的商数关系及两角差的正切公式，计算即可得到；（2）运用向量的数量积的坐标表示和二倍角公式及两角和的正弦公式，化简f（x），再由正弦函数的图象和性质，即可得到f（x）的值域．【解答】解：（1）∥即有cosx+sinx=0，即tanx=﹣，tan（x﹣）===﹣7；（2）f（x）=2（+）•=2cosx（sinx+cosx）+=sin2x+cos2x+=sin（2x+）+，当x∈[0，]时，2x+∈[，]，即，则f（x）≤+，则f（x）的值域为[+]．【点评】本题考查平面向量的共线和数量积的坐标表示，考查三角函数的化简和求值，考查正弦函数的图象和性质，考查运算能力，属于中档题．16．如图，在多面体ABCDEF中，四边形ABCD是菱形，AC，BD相交于点O，EF∥AB，AB=2EF，平面BCF⊥平面ABCD，BF=CF，点G为BC的中点．（1）求证：直线OG∥平面EFCD；（2）求证：直线AC⊥平面ODE．【考点】直线与平面平行的判定；直线与平面垂直的判定．【专题】空间位置关系与距离．【分析】（1）根据线线平行推出线面平行；（2）根据线面垂直的判定定理进行证明即可．【解答】证明（1）∵四边形ABCD是菱形，AC∩BD=O，∴点O是BD的中点，∵点G为BC的中点∴OG∥CD，…又∵OG⊄平面EFCD，CD⊂平面EFCD，∴直线OG∥平面EFCD．…（2）∵BF=CF，点G为BC的中点，∴FG⊥BC，∵平面BCF⊥平面ABCD，平面BCF∩平面ABCD=BC，FG⊂平面BCF，FG⊥BC∴FG⊥平面ABCD，…∵AC⊂平面ABCD∴FG⊥AC，∵，，∴OG∥EF，OG=EF，∴四边形EFGO为平行四边形，∴FG∥EO，…∵FG⊥AC，FG∥EO，∴AC⊥EO，∵四边形ABCD是菱形，∴AC⊥DO，∵AC⊥EO，AC⊥DO，EO∩DO=O，EO、DO在平面ODE内，∴AC⊥平面ODE．…【点评】本题考查了线面平行，线面垂直的判定定理，本题属于中档题．17．如图，椭圆C： +=1（a＞b＞0）的离心率e=，椭圆C的右焦点到右准线的距离为，椭圆C的下顶点为D．（1）求椭圆C的方程；（2）若过D点作两条互相垂直的直线分别与椭圆C相交于点P、M．求证：直线PM经过一定点．【考点】直线与圆锥曲线的关系；椭圆的标准方程．【专题】计算题；数形结合；转化思想；综合法；圆锥曲线的定义、性质与方程．【分析】（1）由题意可得c2=a2，又﹣c=，且a2=b2+c2，解得b=1，则a=3，即可得解椭圆C的方程；（2）设直线PD的斜率为k，由得P（，），M（，），作直线l关于y轴的对称直线l′，可知定点在y轴上，当k=1时，P（，），M（﹣，），可求此时直线PM经过y轴上的点T（0，），证明k PT=k MT，即可得解P，M，T三点共线，即直线PM经过点T．【解答】解：（1）依题意知 e=，则c2=a2，…又﹣c=，且a2=b2+c2，∴b=1，则a=3，∴方程为+y2=1．…（2）由题意知直线PD，MD的斜率存在且不为0，设直线PD的斜率为k，则PD：y=kx﹣1，由得P（，），…用﹣去代k，得M（，），…作直线l关于y轴的对称直线l′，此时得到的点P′、M′关于y轴对称，则PM与P′M′相交于y轴，可知定点在y轴上，当k=1时，P（，），M（﹣，），此时直线PM经过y轴上的点T（0，），…∵k PT=，…k MT==…∴k PT=k MT，∴P，M，T三点共线，即直线PM经过点T，故直线PM经过定点T（0，）．…【点评】本题考查椭圆方程的求法，考查直线是否过定点的判断与求法，解题时要认真审题，注意函数与方程思想的合理运用，属于中档题．18．如图，某广场中间有一块边长为2百米的菱形状绿化区ABCD，其中BMN是半径为1百米的扇形，∠ABC=，管理部门欲在该地从M到D修建小路；在上选一点P（异于M、N两点），过点P修建与BC平行的小路PQ．（1）设∠PBC=θ，试用θ表示修建的小路与线段PQ及线段QD的总长度l；（2）求l的最小值．【考点】在实际问题中建立三角函数模型．【专题】综合题；转化思想；综合法；解三角形．【分析】（1）由题意，QP ，交AB 于E 利用正弦定理，求出EP ，EB ，即可用θ表示修建的小路与线段PQ 及线段QD 的总长度l ；（2）求导数，确定函数的单调性，即可求l 的最小值．【解答】解：（1）由题意，延长QP ，交AB 于E ，则=（﹣θ）， △BPE 中，∠EPB=θ，∠EBP=﹣θ，∠BEP=，∴EP=sin （﹣θ），EB=sin θ，∴PQ=2﹣sin （﹣θ），QD=2﹣sin θ，∴l=﹣θ+2﹣sin （﹣θ）+2﹣sin θ=4﹣sin （﹣θ）﹣sin θ+﹣θ=4﹣2sin （θ+）+﹣θ（0＜θ＜）；（2）l′=﹣2cos （θ+）﹣1，∴0＜θ＜时，l′＜0，＜θ＜，时，l′＞0，∴θ=时，l 取得最小值，最小值为（4﹣+）百米．【点评】本题考查三角函数中的恒等变换应用，考查正弦定理与两角差与两角和的正弦，考查导数知识的运用，考查运算求解能力，属于中档题．19．已知数列{a n }的前n 项和为S n ，且对一切正整数n 都有．（I ）求证：a n+1+a n =4n+2；（II ）求数列{a n }的通项公式；（III）是否存在实数a，使不等式对一切正整数n都成立？若存在，求出a的取值范围；若不存在，请说明理由．【考点】数列与不等式的综合；等差数列的通项公式；等差关系的确定．【专题】综合题．【分析】（I）由，知，由此能够导出．（II）在中，令n=1，得a1=2，代入（I）得a2=4．由a n+1+a n=4n+2，知a n+2+a n+1=4n+6，故a n+2﹣a n=4，由此能导出数列{a n}的通项公式是a n=2n．（III）＜等价于，令f（n）=，则f（n）＞0，由此能够导出存在实数a，符合题意，并能求出其取值范围．【解答】解：（I）∵，∴=，∴，即．（II）在中，令n=1，得a1=2，代入（I）得a2=4．∵a n+1+a n=4n+2，∴a n+2+a n+1=4n+6，两式相减，得：a n+2﹣a n=4，∴数列{a n}的偶数项a2，a4，a6，…，a26，…依次构成一个等差数列，且公差为d=4，∴当n为偶数时， =，当n为奇数时，n+1为偶数，由上式及（I）知：a n=4n+2﹣a n+1=4n+2﹣2（n+1）=2n，∴数列{a n}的通项公式是a n=2n．（III）＜，等价于，令f（n）=，则由（II）知f（n）＞0，∴═===．∴f（n+1）＜f（n），即f（n）的值随n的增大而减小，∴n∈N*时，f（n）的最大值为，若存在实数a，符合题意，则必有：，即，它等价于，解得，或，因此，存在实数a，符合题意，其取值范围为．【点评】本题考查数列和不等式的综合应用，考查运算求解能力，推理论证能力；考查化归与转化思想．对数学思维的要求比较高，有一定的探索性．综合性强，难度大，是高考的重点．解题时要认真审题，仔细解答．20．已知函数f（x）=e x﹣ax2﹣bx﹣1，其中a，b∈R，e为自然对数的底数．（1）若函数f（x）在点（1，f（1））处的切线方程是y=（e﹣1）x﹣1，求实数a及b的值；（2）设g（x）是函数f（x）的导函数，求函数g（x）在区间[0，1]上的最小值；（3）若f（1）=0，函数f（x）在区间（0，1）内有零点，求a的取值范围．【考点】利用导数研究曲线上某点切线方程；函数的零点；导数在最大值、最小值问题中的应用．【专题】分类讨论；方程思想；分析法；导数的综合应用．【分析】（1）求出函数的导数，求得切线的斜率和切点，由切线的方程，解得a，b；（2）求得g（x）及导数，对a讨论，当2a≤0即a≤0时，当ln（2a）≤0即0＜a≤时，当0＜ln（2a）＜1即＜a＜时，当ln（2a）≥1即a≥时，求出单调区间可得最小值；（3）求出导数，f（1）=0，即有e﹣a﹣b﹣1=0，可得b=e﹣a﹣1，结合（1），（2）运用函数零点存在定理，结合函数的单调性，即可得到所求范围．【解答】解：（1）由f（x）=e x﹣ax2﹣bx﹣1，得f′（x）=e x﹣2ax﹣b，∴f（1）=e﹣a﹣b﹣1，f′（1）=e﹣2a﹣b，∵函数f（x）在点（1，f（1））处的切线方程是y﹣（e﹣a﹣b﹣1）=（e﹣2a﹣b）（x﹣1），由切线的方程y=（e﹣1）x﹣1，可得e﹣a﹣b﹣1=e﹣1﹣1，e﹣2a﹣b=e﹣1，解得a=0，b=1；（2）由f（x）=e x﹣ax2﹣bx﹣1得f′（x）=e x﹣2ax﹣b，∴g（x）=f′（x）=e x﹣2ax﹣b，∴g′（x ）=e x﹣2a ．当2a≤0即a≤0时，e x ﹣2a ＞0对一切x ∈[0，1]恒成立， ∴g（x ）在[0，1]内单调递增，∴g（x ）在[0，1]上的最小值是g （0）=1﹣b ； 当2a ＞0即a ＞0时，令g′（x ）=0，得x=ln （2a ）， 从而有①当ln （2a ）≤0即0＜a≤时，列表如下：依表格知g （x ）在[0，1]上的最小值是g （0）=1﹣b ； ②当0＜ln （2a ）＜1即＜a ＜时，列表如下：依表格知g （x ）在[0，1]上的最小值是g （ln （2a ））=2a ﹣2aln （2a ）﹣b ； ③当ln （2a ）≥1即a≥时，列表如下：依表格知g （x ）在[0，1]上的最小值是g （1）=e ﹣2a ﹣b ． 综上所述：当a≤时，g （x ）在[0，1]上的最小值是1﹣b ；当＜a ＜时，g （x ）在[0，1]上的最小值是2a ﹣2aln （2a ）﹣b ； 当a≥时，g （x ）在[0，1]上的最小值是e ﹣2a ﹣b ． （3）f （x ）=e x ﹣ax 2﹣bx ﹣1，g （x ）=f′（x ）=e x ﹣2ax ﹣b ， 由f （1）=0，即有e ﹣a ﹣b ﹣1=0，可得b=e ﹣a ﹣1，∴g（x）=e x﹣2ax﹣e+a+1，又f（0）=0．若函数f（x）在区间（0，1）内有零点，设x0为f（x）在区间（0，1）内的一个零点，则由f（0）=f（x0）=0可知，f（x）在区间（0，x0）内不可能单调递增，也不可能单调递减．则g（x）在区间（0，x0）内不可能恒为正，也不可能恒为负．故g（x）在区间（0，x0）内存在零点x1．同理g（x）在区间（x0，1）内存在零点x2．故函数f（x）在区间（0，1）内至少有三个单调区间，g（x）在区间（0，1）内至少有两个零点．由（2）知当a≤或a≥时，函数g（x）即f′（x）在区间[0，1]内单调，不可能满足“函数f（x）在区间（0，1）内至少有三个单调区间”这一要求．若＜a＜，此时g（x）在区间（0，ln（2a））内单调递减，在区间（ln（2a），1）内单调递增．因此x1∈（0，ln（2a）），x2∈（ln（2a），1），又g（x）min=g（ln（2a））=2a﹣2aln（2a）﹣e+a+1=3a﹣2aln（2a）﹣e+1，令h（x）=3x﹣2xln（2x）﹣e+1（＜x＜），则h′（x）=3﹣2ln（2x）﹣2x••2=1﹣2ln（2x），令h′（x）=0得x=，列表如下：，），）﹣依表格知：当＜x＜时，h（x）min=﹣e+1＜0，∴g（x）min=3a﹣2aln（2a）﹣e+1＜0恒成立，于是，函数f（x）在区间（0，1）内至少有三个单调区间⇔⇔⇔e﹣2＜a＜1．综上所述：a的取值范围为（e﹣2，1）．【点评】本题考查导数的运用：求切线的方程和单调区间、极值和最值，考查分类讨论的思想方法，考查函数方程的转化思想的运用，属于难题．【选做题】本题包括、、、四小题，请选定其中两题，并在答题卡指定区域内作答，若多做，则按作答的前两题评分.解答题应写出文字说明、证明过程或演算步骤.（选修4-1：几何证明选讲）21．选修4﹣1：几何证明选讲如图，AB是⊙O的一条切线，切点为B，直线ADE，CFD，CGE都是⊙O的割线，已知AC=AB．求证：FG∥AC．【考点】相似三角形的判定；与圆有关的比例线段．【专题】选作题．【分析】利用切割线定理可得AB2=AD•AE．由AC=AB，得到AC2=AD•AE，而∠CAE公用，由相似三角形的判定定理可得△ACE∽△ADC．于是∠AEC=∠ACD，由圆的内接四边形的性质可得∠CFG=∠AEC．进而可得FG∥AC．【解答】证明：∵AB是⊙O的一条切线，∴AB2=AD•AE．∵AC=AB，∴AC2=AD•AE，即．又∵∠CAE公用，∴△ACE∽△ADC．∴∠AEC=∠ACD．由四边形DEGF是⊙O的内接四边形，∴∠CFG=∠AEC．∴∠ACD=∠CFG，∴FG∥AC．【点评】熟练掌握切割线定理、相似三角形的判定定理和性质定理、圆的内接四边形的性质、平行线的判定定理是解题的关键．（选修4-2：矩阵与变换）22．（2012•盐城一模）已知矩阵，若矩阵AB对应的变换把直线l：x+y﹣2=0变为直线l′，求直线l′的方程．【考点】逆矩阵与投影变换；矩阵与矩阵的乘法的意义．【专题】计算题．【分析】先计算矩阵AB对应的变换，再求出在变换下点的坐标之间的对应关系，从而可求直线l'的方程．【解答】解：∵，∴=…，在直线l上任取一点P（x′，y′），经矩阵AB变换为点Q（x，y），则，∴，即…代入x′+y′﹣2=0中得，∴直线l′的方程为4x+y﹣8=0…【点评】本题重点考查矩阵变换，考查矩阵变换的运用，解题的关键是求出矩阵AB对应的变换选修4-4：坐标系与参数方程23．选修4﹣4：坐标系与参数方程在平面直角坐标系xOy中，圆C的参数方程为（θ为参数，r＞0）．以O为极点，x轴正半轴为极轴建立极坐标系，直线l的极坐标方程为．若圆C上的点到直线l的最大距离为3，求r的值．【考点】点的极坐标和直角坐标的互化；直线与圆的位置关系；参数方程化成普通方程．【专题】直线与圆．【分析】将直线和圆的方程化为直角坐标方程，利用直线和圆的位置关系求解．【解答】解：圆的直角坐标方程为（x+）2+（y+）2=r2，圆心的直角坐标（﹣，﹣）直线l的极坐标方程为即为x+y﹣=0，圆心O（﹣，﹣）到直线的距离d==2．圆O上的点到直线的最大距离为 2+r=3，解得r=1．【点评】本题考查极坐标、参数方程与普通方程互化的基础知识，考查点到直线距离公式等．选修4-5：不等式选讲24．已知实数x，y，z满足x+y+z=2，求2x2+3y2+z2的最小值．【考点】柯西不等式在函数极值中的应用．【专题】计算题；压轴题．【分析】利用题中条件：“x+y+z=2”构造柯西不等式：这个条件进行计算即可．【解答】解：由柯西不等式可知：故，当且仅当，即： 2x2+3y2+z2取得最小值为．【点评】本题考查用综合法证明不等式，关键是利用解题．【必做题】第22题、第23题，每题10分，共计20分，请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤.25．袋中装有围棋黑色和白色棋子共7枚，从中任取2枚棋子都是白色的概率为．现有甲、乙两人从袋中轮流摸取一枚棋子．甲先摸，乙后取，然后甲再取，…，取后均不放回，直到有一人取到白棋即终止．每枚棋子在每一次被摸出的机会都是等可能的．用X表示取棋子终止时所需的取棋子的次数．（1）求随机变量X的概率分布列和数学期望E（X）；（2）求甲取到白球的概率．【考点】离散型随机变量及其分布列；古典概型及其概率计算公式；离散型随机变量的期望与方差．【专题】计算题；转化思想；概率与统计．【分析】（1）由已知先出白子个数，进而可得随机变量X的概率分布列和数学期望E（X）；（2）记事件A=“甲取到白球”，则事件A包括以下三个互斥事件：A1=“甲第1次取球时取出白球”；A2=“甲第2次取球时取出白球”；A3=“甲第3次取球时取出白球”．利用互斥事件概率加法公式，可得：甲取到白球的概率．【解答】解：设袋中白球共有x个，则依题意知： =，即=，即 x2﹣x﹣6=0，解之得x=3，（x=﹣2舍去）．…（1）袋中的7枚棋子3白4黑，随机变量X的所有可能取值是1，2，3，4，5．P（x=1）==，P（x=2）==，P（x=3）==，P（x=4）==，P（x=5）==，…（注：此段的分配是每错1个扣，错到4个即不得分．）随机变量X的概率分布列为：所以E（X）=1×+2×+3×+4×+5×=2．…（2）记事件A=“甲取到白球”，则事件A包括以下三个互斥事件：A1=“甲第1次取球时取出白球”；A2=“甲第2次取球时取出白球”；A3=“甲第3次取球时取出白球”．依题意知：P（A1）==，P（A2）==，P（A3）==，…（注：此段的分配是每错1个扣，错到3个即不得分．）所以，甲取到白球的概率为P（A）=P（A1）+P（A2）+P（A3）=…【点评】本题考查的知识点是古典概型的概率计算公式，随机变量的分布列和数学期望，互斥事件概率加法公式，难度中档．26．设f（x）是定义在R上的函数，已知n∈N*，且g（x）=C f（）x0（1﹣x）n+C f（）x1（1﹣x）n﹣1+C f（）x2（1﹣x）n﹣2+…+C f（）x n（1﹣x）n．（1）若f（x）=1，求g（x）；（2）若f（x），求g（x）．。

2016届高三12月联合调研测试
数 学
参考公式：样本数据123,,,,n x x x x 的方差2
211()n i i S x x n ==-∑，其中11n i i x x n ==∑. 一、填空题：本大题共14小题，每小题5分，共70分．请把答案填写在答题卡相应的．．．．．．位置上．．．
. 1、 已知集合{13,}A x x x Z =≤≤∈，{}m B ,4,2=，若{}3,2=⋂B A ，则实数m =▲_.
【考点】集合的运算 【试题解析】，因为，所以 【答案】3
2、 已知复数,43,221i z i x z +=+=2
1z z 若
为纯虚数，则实数x 的值为▲ . 【考点】复数综合运算
【试题解析】
，因为为纯虚数，所以 解得
【答案】
3、 三张卡片上分别写有数字1、2、3，将它们排成一行，恰好排成顺序为“321”的概率为
▲ ．
【考点】古典概型
【试题解析】
数学1，2，3任意排列共有种，所以概率为 【答案】 4、 某产品在连续7天检验中，不合格品的个数分别为3，2，1，0，0，0，1，则这组数据
的方差为▲．
【考点】样本的数据特征。

数学试卷（理工类）考生注意：1.答卷前，考生务必在答题纸大将姓名、座位号、准考据号等填写清楚。

2.本试卷共有 23 道试题，满分 150 分，考试时间 120 分钟。

一. 填空题 (本大题满分 56 分）本大题共有14 题，只需求直接填写结果，每题填对得4分，不然一律得零分 .1．函数f ( x) x( x) 的反函数是 f(x)_____________ .2、已知a, b, a 和 b 的夹角为，则 a b___________.3、幂函数y f ( x)的图象过点 (, ) ，则 f ( )_________ .4、方程log ( x)log(x) 的解为_______________.5、若直线l的一个法向量n( , ) ，若直线 l 的一个方向向量 d( ,) ，则 l 与 l的夹角 =.(用反三角函数表示 ).6、直线l : x y交圆 x y于 A、 B两点，则AB _______.7、已知,, 且tan()，则 cos.8、无量等比数列a n的前 n 项和为S n，若 S, S，则 lim S n_______ .n9、已知f ( x) kx x 有两个不一样的零点，则实数k 的取值范围是.10、已知a、b、c是ABC 中A、B、 C 的对边，若 a, A，ABC 的面积为，则ABC 的周长为.11 、奇函数f (x)的定义域为 R ，若f ( x)为偶函数，且 f ( )，则f () f () _______.___12、已知等比数列a n的前 n 项和为S n，若S , S , S成等差数列，且a a a，若 S n，则 n 的取值范围为.13、设m R, 过定点A的动直线 x my和过定点 B 的动直线mx y m交于点P，则PA PB 的最大值是.14、设x表示不超出x的最大整数，如,.. 给出以下命题：①对随意的实数x ，都有 x x x ；②对随意的实数x, y ，都有x y x y ；③ lglg lg lg lg；④若函数 f ( x)x x，当 x, n (n N * ) 时，令 f (x)的值域为A，记会合A中元素个数为 a n，则a n的最小值为. 此中全部真命题的序号为.n二．选择题( 本大题满分20个结论是正确的，选对得15、数列a n的前n项和为分）本大题共有 4 题，每题都给出四个结论，此中有且只有一5 分，不然一律得零分.S n n ，则 a 的值为（）A 、B、C、D、 6416、a是直线ax y a和x(a) y a平行且不重合的（）A、充足非必需条件B、必需非充足条件C、充要条件D、既不充足又不用要条件17 、将f ( x)si n x 的图象右移 () 个单位后得到 g( x) 的图象.若满足f (x )g(x )的x , x，有x x 的最小值为，则的值为（）A、B、C、D、18、已知函数e x mx 、 x 、x R ，总有 f ( x )、f ( x2 )、f ( x3 ) 为f ( x)，若对随意e x某一个三角形的边长，则实数m 的取值范围是（）A、,B、 ,C、 ,D、,三．解答题 (本大题满分74 分 ) 本大题共有 5 题，解答以下各题一定写出必需的步骤. 19．（此题共 2 小题，满分12 分。

2015-2016学年广东省江门市高三(上）12月调研数学试卷(理科）一、选择题：本大题共12小题，每小题5分，满分60分．在每小题给出的四个选项中,只有一项是符合题目要求的．1．设集合A={x|x2﹣3x+2＜0}，B=｛x｜2＜2x＜8}，则(）A．A=B B．A⊆B C．A⊇B D．A∩B=∅2．已知i为虚数单位,则复数z=在复平面内对应的点位于（）A．第一象限 B．第二象限 C．第三象限 D．第四象限3．sin20°cos110°+cos160°sin70°=(）A．﹣1 B．0 C．1 D．以上均不正确4．点P从点O出发，按逆时针方向沿周长为l的图形运动一周，O，P两点连线的距离y与点P走过的路程x的函数关系如右图所示,那么点P所走的图形是（）A．B． C．D．5．若“∀x∈R，x2+mx+2m﹣3≥0”为假命题，则m的取值范围是（）A．（﹣∞，2］∪[6，+∞）B．(﹣∞，2)∪（6,+∞）C．［2，6]D．（2,6）6．已知实数1，m，9构成一个等比数列，则圆锥曲线+y2=1的焦距为（）A．4 B．2C．或2 D．2或47．已知函数f(x）=sin（ωx+φ）（ω＞0，|φ｜＜）的最小正周期是π，若将其图象向右平移个单位后得到的图象关于原点对称，则函数f（x）的图象（）A．关于直线x=对称B．关于直线x=对称C．关于点（，0）对称 D．关于点（，0)对称8．点O是△ABC所在平面内的一点（O不在直线BC上)，若=3+，则△ABC与△OBC的面积之比为()A．B．C．D．49．在平面直角坐标系中，A，B分别是x轴和y轴上的动点，若以AB为直径的圆C与直线2x+y﹣4=0相切，则圆C面积的最小值为（）A．πB．πC．（6﹣2）πD．π10．一个几何体的三视图如图所示，则此几何体的体积是(）A．112 B．80 C．72 D．642=2S n+n+4，11．已知正项数列｛a n}，a2﹣1、a3、a7成等比数列，{a n｝前n项和S n满足a n+1则(n﹣6）S n的最小值为（)A．﹣26 B．﹣27 C．﹣28 D．﹣3012．已知函数f（x）=，若函数f（x）的图象在点A、B处的切线重合,则a的取值范围是（）A．（﹣1,+∞）B．（﹣ln2,+∞) C．(﹣2,﹣1）D．（1，2）二、填空题：本大题共4小题，每小题5分，满分20分．13．若奇函数f（x）满足对任意x∈R都有f（2+x）+f（2﹣x）=0，且f(1）=9，则f+f已知抛物线y=x2与双曲线﹣x2=1（a＞0）有共同的焦点F，则双曲线的渐近线方程为______．15．若实数x,y满足，则的最小值为______．16．如图，正方体ABCD﹣A1B1C1D1的棱长为1,P对角线BD1的三等分点，P到直线CC1的距离为______三、解答题：解答应写出文字说明、证明过程或演算步骤．17．已知｛a n}是一个等差数列,｛a n｝的前n项和记为S n，a1=4，S3=21（1）求数列｛a n｝的通项公式;（2）设数列{b n｝满足b1=，b n﹣b n=2，求数列{b n}的通项公式．+118．在△ABC中，角A、B、C的对边分别为a、b、c，3（b2+c2)=3a2+2bc．(1）若sinB=cosC，求tanC；（2）若△ABC的面积S=5，求边长a的最小值．19．如图4，已知正三棱柱ABC﹣A1B1C1，延长BC至D，使C为BD的中点．（1）求证：平面AC1D⊥平面AA1B；（2）若AC=2，AA1=4，求二面角C1﹣AD﹣B的余弦值．20．已知椭圆C： +=1（a＞b＞0）的离心率为，且a+b=3．（1）求椭圆C的方程；(2）直线x+y﹣m=0（m是正常数）与椭圆C交于P、Q两点，当•=时，求直线PQ 的方程．21．已知函数f（x）=（m+）lnx+﹣x,其中常数m＞0．（1)当m=2时，求f（x）的极大值;（2)已知m≥4,设A（x1，f(x1）)、B（x2,f(x2））是曲线y=f（x）上的相异两点，l1、l2是曲线y=f（x)在A、B两点处的切线，若l1∥l2，求x1+x2的取值范围．【选做题】（共1小题，满分10分）22．已知平面向量、、满足条件++=，｜｜=||=｜｜=1．（1）求证：△P1P2P3是正三角形；（2）试判断直线OP1与直线P2P3的位置关系，并证明你的判断．【选做题】（共1小题，满分0分）23．已知α、β、γ是三个平面，α∩β=a,α∩γ=b，β∩γ=c（1)若a∩b=O，求证：a、b、c三线共点；（2）若a∥b,试判断直线a与直线c的位置关系,并证明你的判断．【选做题】（(共1小题，满分0分）24．已知圆C：x2+y2﹣x+2y=0和直线l：x﹣y+1=0(1）试判断直线l与圆C之间的位置关系，并证明你的判断；（2）求与圆C关于直线l对称的圆的方程．2015—2016学年广东省江门市高三（上）12月调研数学试卷（理科）参考答案与试题解析一、选择题:本大题共12小题,每小题5分，满分60分．在每小题给出的四个选项中,只有一项是符合题目要求的．1．设集合A={x|x2﹣3x+2＜0},B=｛x|2＜2x＜8}，则（）A．A=B B．A⊆B C．A⊇B D．A∩B=∅【考点】集合的包含关系判断及应用．【分析】解二次不等式和指数不等式求出集合A,B，进而可判断出集合A,B的包含关系．【解答】解：∵集合A={x|x2﹣3x+2＜0｝=（1，2)，B=｛x|2＜2x＜8}=(1，3)，∴A⊆B，故选：B2．已知i为虚数单位，则复数z=在复平面内对应的点位于（）A．第一象限 B．第二象限 C．第三象限 D．第四象限【考点】复数的代数表示法及其几何意义．【分析】利用复数代数形式的乘除运算化简,求出复数z所对应点的坐标得答案．【解答】解：∵z==,∴复数z=在复平面内对应的点的坐标为（2，﹣1）,位于第四象限．故选：D．3．sin20°cos110°+cos160°sin70°=（）A．﹣1 B．0 C．1 D．以上均不正确【考点】两角和与差的正弦函数．【分析】利用诱导公式化简，然后利用两角和与差的三角函数化简求解即可．【解答】解：sin20°cos110°+cos160°sin70°=﹣sin20°sin20°﹣cos20°cos20°=﹣cos0°=﹣1．故选：A．4．点P从点O出发，按逆时针方向沿周长为l的图形运动一周，O，P两点连线的距离y与点P走过的路程x的函数关系如右图所示，那么点P所走的图形是（）A．B． C．D．【考点】函数的图象与图象变化．【分析】本题考查的是函数的图象与图象变化的问题．在解答时首先要充分考查所给四个图形的特点，包括对称性、圆滑性等,再结合所给O，P两点连线的距离y与点P走过的路程x 的函数图象即可直观的获得解答．【解答】解：由题意可知：对于A、B，当p位于A,B图形时，函数变化有部分为直线关系,不可能全部是曲线，由此即可排除A、B，对于C，其图象变化不会是对称的，由此排除C，故选D．5．若“∀x∈R,x2+mx+2m﹣3≥0”为假命题，则m的取值范围是（）A．（﹣∞，2]∪［6，+∞) B．（﹣∞,2）∪（6，+∞) C．［2，6]D．（2,6）【考点】全称命题．【分析】根据全称命题的定义和性质转化为一元二次函数进行求解即可．【解答】解：若“∀x∈R，x2+mx+2m﹣3≥0”为假命题，即“∃x∈R，x2+mx+2m﹣3＜0"为真命题，则判别式△=m2﹣4(2m﹣3）＞0,即m2﹣8m+12＞0．解得m＞6或m＜2，故选:B．6．已知实数1,m,9构成一个等比数列，则圆锥曲线+y2=1的焦距为（）A．4 B．2C．或2 D．2或4【考点】椭圆的简单性质；双曲线的简单性质．【分析】利用等比数列的等比中项求出m,然后求解一的焦距即可．【解答】解：实数1，m，9构成一个等比数列，则m=±3，当m=3时，圆锥曲线+y2=1是椭圆，c==，焦距为2．当m=﹣3时，圆锥曲线+y2=1是双曲线，c==2,焦距为：4．故选：D．7．已知函数f(x）=sin（ωx+φ）（ω＞0，｜φ｜＜）的最小正周期是π，若将其图象向右平移个单位后得到的图象关于原点对称,则函数f（x）的图象（）A．关于直线x=对称B．关于直线x=对称C．关于点（，0）对称 D．关于点（,0）对称【考点】函数y=Asin（ωx+φ)的图象变换．【分析】根据三角函数的性质求出函数的解析式进行求解即可．【解答】解：∵函数f（x）=sin（ωx+φ）（ω＞0，|φ｜＜）的最小正周期是π，∴T==π,解得ω=2，即f（x）=sin(2x+φ）,将其图象向右平移个单位后得到y=sin[2（x﹣）+φ］=sin(2x+φ﹣），若此时函数关于原点对称，则φ﹣=kπ，即φ=+kπ，k∈Z，∵|φ｜＜,∴当k=﹣1时，φ=．即f（x）=sin(2x）．由2x=，解得x=+,k∈Z，故当k=0时，函数的对称轴为x=，故选：B8．点O是△ABC所在平面内的一点（O不在直线BC上），若=3+，则△ABC与△OBC的面积之比为（）A．B．C．D．4【考点】向量在几何中的应用．【分析】连接OA，交BC于P，根据三点共线设=x，=xt+t（1﹣x），利用平面向量的基本定理列方程组解得t即可得出AP，OP的数量关系，从而得出三角形的面积比．【解答】解：连接OA,交BC于P，∵B，P，C三点共线，不妨设=x，又A，P,O三点共线,设=xt+t（1﹣x），∵=3+，∴，解得t=．∴O在AP的延长线上．∴AP=OP．∴=．故选：C．9．在平面直角坐标系中，A，B分别是x轴和y轴上的动点，若以AB为直径的圆C与直线2x+y﹣4=0相切，则圆C面积的最小值为（）A．πB．πC．（6﹣2）πD．π【考点】直线与圆的位置关系．【分析】如图,设AB的中点为C，坐标原点为O,圆半径为r,由已知得｜OC｜=｜CE｜=r，过点O作直线2x+y﹣4=0的垂直线段OF，交AB于D，交直线2x+y﹣4=0于F，则当D恰为AB中点时,圆C的半径最小，即面积最小．【解答】解：如图，设AB的中点为C，坐标原点为O，圆半径为r，由已知得|OC｜=｜CE|=r，过点O作直线2x+y﹣4=0的垂直线段OF,交AB于D，交直线2x+y﹣4=0于F,则当D恰为OF中点时，圆C的半径最小,即面积最小此时圆的直径为O（0,0）到直线2x+y﹣4=0的距离为:d==，此时r=∴圆C的面积的最小值为：S min=π×(）2=．故选：A．10．一个几何体的三视图如图所示，则此几何体的体积是（)A．112 B．80 C．72 D．64【考点】由三视图求面积、体积．【分析】由三视图可知此几何体是由一个棱柱和一个棱锥构成的组合体,代入数据分别求棱柱与棱锥的体积即可．【解答】解：由三视图可知，此几何体是由一个棱柱和一个棱锥构成的组合体，棱柱的体积为4×4×4=64；棱锥的体积为×4×4×3=16；则此几何体的体积为80;故选B．2=2S n+n+4，则11．已知正项数列{a n}，a2﹣1、a3、a7成等比数列，｛a n｝前n项和S n满足a n+1(n﹣6）S n的最小值为（）A．﹣26 B．﹣27 C．﹣28 D．﹣30【考点】数列递推式．【分析】由数列递推式可得数列{a n}为等差数列，并求得公差,结合a2﹣1、a3、a7成等比数列求出首项，得到{a n}前n项和S n，代入(n﹣6)S n，利用导数求得最值．2=2S n+n+4 ①，得【解答】解:由a n+1a n2=2S n+n﹣1+4（n≥2）②，﹣1两式作差得：．∴,∵a n＞0,=a n+1．∴a n+1﹣a n=1．即a n+1则数列｛a n}为等差数列，∴a3=a2+d,a7=a2+5d，由a2﹣1、a3、a7成等比数列，得，即d2=3a2d﹣a2﹣5d，∴=．则．∴（n﹣6）S n=（n﹣6）=．令f（n）=n3﹣3n2﹣18n,则f′(n)=3n2﹣6n﹣18．由f′（n）=0,解得：n=1+．∵n∈N，∴取n=4．∴当n=4时，f（n）有最小值为﹣56,∴（n﹣6）S n的最小值为﹣28．故选；C．12．已知函数f（x）=,若函数f（x）的图象在点A、B处的切线重合，则a的取值范围是（)A．（﹣1，+∞）B．（﹣ln2，+∞） C．(﹣2，﹣1）D．(1,2)【考点】利用导数研究曲线上某点切线方程；分段函数的应用．【分析】先根据导数的几何意义写出函数f（x)在点A、B处的切线方程，再利用两直线重合的充要条件列出关系式，从而得出a=lnx2+（﹣）2﹣1，最后利用导数研究它的单调性和最值，即可得出a的取值范围．【解答】解：设A（x1，y1)，B(x2，y2），当x1＜x2＜0，或0＜x1＜x2时，f′(x1）≠f′(x2)，故x1＜0＜x2,当x1＜0时，函数f（x）在点A（x1，f（x1）)处的切线方程为：y﹣(x12+x1+a）=（2x1+1)（x﹣x1）；当x2＞0时,函数f（x）在点B（x2，f（x2））处的切线方程为y﹣lnx2=（x﹣x2)；两直线重合的充要条件是=2x1+1①，lnx2﹣1=﹣x12+a②，由①及x1＜0＜x2得0＜＜1，由①②得a=lnx2+（﹣）2﹣1=﹣ln+（﹣1）2﹣1,令t=，则0＜t＜1，且a=（t﹣1）2﹣1﹣lnt，设h（t)=（t﹣1）2﹣1﹣lnt，（0＜t＜1），则h′（t)=（t﹣1）﹣=＜0，∴h（t）在（0，1）为减函数，则h（t）＞h（1)=﹣ln1﹣1,∴a＞﹣1，∴若函数f（x）的图象在点A，B处的切线重合，a的取值范围(﹣1，+∞)．故选：A．二、填空题：本大题共4小题，每小题5分，满分20分．13．若奇函数f（x)满足对任意x∈R都有f（2+x）+f（2﹣x)=0，且f（1）=9，则f+f满足对任意x∈R都有f（2+x)+f（2﹣x)=0，可得：f（x+2）=f（x﹣2）,∴函数的周期T=4，f（1）=9，且对任意x都有f（﹣x）=﹣f（x），取x=0可得f（0）=﹣f（0），解得f（0）=0，x=0时，f(2）=0∴f+f+f（﹣1)+f（0）=﹣f（1)+0=﹣9故答案为：﹣9．14．已知抛物线y=x2与双曲线﹣x2=1（a＞0）有共同的焦点F，则双曲线的渐近线方程为y=．【考点】抛物线的简单性质;双曲线的简单性质．【分析】求出抛物线的焦点坐标，然后求出双曲线的a,即可求解双曲线的渐近线方程．【解答】解：∵抛物线方程为x2=8y，∴2p=8，=2,可得抛物线的焦点为F(0，2）．∵抛物线y=x2与双曲线﹣x2=1（a＞0）有共同的焦点F，∴双曲线的上焦点为（0,2），可得c==2，解得a2=3，可得a=且b=1，∴双曲线﹣x2=1（a＞0）的渐近线方程为y=x．故答案为：y=15．若实数x,y满足，则的最小值为1．【考点】简单线性规划．【分析】作出可行域,目标函数z=表示可行域内的点与原点连线的斜率，数形结合可得．【解答】解：作出所对应的可行域(如图阴影），目标函数z=表示可行域内的点与原点连线的斜率，∴当直线经过点A（1，1）时z取最小值1故答案为：1．16．如图，正方体ABCD﹣A1B1C1D1的棱长为1，P对角线BD1的三等分点，P到直线CC1的距离为【考点】点、线、面间的距离计算．【分析】如图所示，连接B1D1，作MP∥B1B，连接C1M，则C1M等于P到直线CC1的距离,利用余弦定理，求出C1M即可．【解答】解：如图所示，连接B1D1，作MP∥B1B，连接C1M,则C1M等于P到直线CC1的距离．∵P对角线BD1的三等分点，∴B1M=，∴C1M==，∴P到直线CC1的距离等于．故答案为:．三、解答题：解答应写出文字说明、证明过程或演算步骤．17．已知｛a n}是一个等差数列，{a n}的前n项和记为S n，a1=4,S3=21（1)求数列｛a n｝的通项公式;﹣b n=2，求数列{b n}的通项公式．（2）设数列｛b n｝满足b1=，b n+1【考点】数列递推式；数列的求和．【分析】(1）设数列{a n｝的公差为d，由已知得3×4+•d=21，由此能求出数列｛a n}的通项公式．（2）由b n﹣b n=2=23n+1，由此利用叠加法能求出数列{b n｝的通项公式．+1【解答】解：（1）设数列{a n}的公差为d，由已知得3×4+•d=21…解得d=3…，{a n }的通项公式为a n =3n +1… (2）由（1）得b n +1﹣b n =2=23n +1…当n ≥2时，b n =（b n ﹣b n ﹣1)+（b n ﹣1﹣b n ﹣2）+...+（b 2﹣b 1）+b 1，... ∴b n =23n ﹣2+23n ﹣5+ (24)=+=×23n +1（n ≥2）…∵b 1=满足b n =×23n +1，∴b n =×23n +1,n ∈N +…18．在△ABC 中，角A 、B 、C 的对边分别为a 、b 、c ，3（b 2+c 2）=3a 2+2bc ． （1）若sinB=cosC ，求tanC ；（2）若△ABC 的面积S=5,求边长a 的最小值． 【考点】余弦定理；正弦定理． 【分析】（1）利用余弦定理表示出cosA ，将已知等式变形后代入求出cosA 的值，进而确定出sinA 的值，根据sinB=cosC,B=π﹣(A +C ）,求出tanC 的值即可； （2)利用三角形面积公式表示出三角形ABC 面积，将已知面积与sinA 的值代入求出bc 的值，已知等式变形，利用基本不等式求出a 的最小值即可． 【解答】解：（1）∵3（b 2+c 2）=3a 2+2bc ，即b 2+c 2﹣a 2=bc ，∴cosA==，又A 为三角形内角， ∴sinA==,∵sinB=cosC ，∴sin （A +C ）=cosC ，∴cosC +sinC=cosC ，即sinC=cosC ，∴tanC=；（2）∵S=5，∴bcsinA=5,∵sinA=,∴bc=15，∵b 2+c 2≥2bc ，b 2+c 2=a 2+bc ， ∴a 2≥2bc ﹣bc=bc=20,∴a ≥2，则a 的最小值为2．19．如图4，已知正三棱柱ABC ﹣A 1B 1C 1，延长BC 至D ，使C 为BD 的中点．（1）求证:平面AC1D⊥平面AA1B；（2）若AC=2,AA1=4，求二面角C1﹣AD﹣B的余弦值．【考点】二面角的平面角及求法；平面与平面垂直的判定．【分析】(1)推导出AB⊥AD，AA1⊥AD，从而AD⊥平面AA1B，由此能证明平面AC1D⊥平面AA1B．（2）以A为原点，AD为x轴，AB为y轴，AA1为z轴，建立空间直角坐标系，利用向量法能求出二面角C1﹣AD﹣B的余弦值．【解答】解：(1）证明:由已知△ABC是正三角形，∠BAC=∠BCA=60°，又∵AC=BC=CD,∴∠CAD=∠CDA=30°，…∴∠BAD=30°+60°=90°，AB⊥AD，…又∵AA1⊥底面ABD,∴AA1⊥AD，…∵AB∩AA1=A，∴AD⊥平面AA1B，…又∵AD⊂平面AC1D，∴平面AC1D⊥平面AA1B．…解：（2）∵AA1⊥底面ABD，AB⊥AD，∴如图，以A为原点，AD为x轴，AB为y轴,AA1为z轴，建立空间直角坐标系…A（0,0，0），D（2，0，0），C1（，1，4），…=（2，0，0)，=(）,…设平面ADC1的法向量=（x,y,z），则,取z=1，则=（0,﹣4，1）,…取平面ADB的法向量为=（0,0，1），则cos＜＞===，由图知二面角C1﹣AD﹣B为锐角，∴二面角C1﹣AD﹣B的余弦值为．…20．已知椭圆C: +=1（a＞b＞0）的离心率为，且a+b=3．(1)求椭圆C的方程;（2）直线x+y﹣m=0(m是正常数)与椭圆C交于P、Q两点，当•=时,求直线PQ的方程．【考点】椭圆的简单性质;直线与圆锥曲线的关系．【分析】（1）由已知=，c+a=3，a2=b2+c2，联立解出即可得出．(2）设P（x1，y1）,Q（x2，y2），直线方程与椭圆方程联立化为5x2﹣8mx+4m2﹣4=0，利用△＞0，根与系数的关系及其数量积运算性质•=，解出即可得出．【解答】解：（1）由已知=，c+a=3，a2=b2+c2，解得a=2，b=1．∴椭圆C的标准方程为+y2=1．（2)设P（x1，y1）,Q(x2，y2)，联立,化为5x2﹣8mx+4m2﹣4=0，由△＞0,得64m2﹣20(4m2﹣4）＞0，即m2＜5，∵m＞0，∴．∴x1+x2=,x1x2=．∵•=，∴x1x2+y1y2=,又y1y2=（﹣x1+m）(﹣x2+m）=x1x2﹣m(x1+x2）+m2，∴2x1x2﹣m（x1+x2)+m2=，﹣+m2=，解得m2=4,又．∴m=2,∴PQ的方程为x+y﹣2=0．21．已知函数f（x)=(m+)lnx+﹣x，其中常数m＞0．(1）当m=2时,求f（x）的极大值；（2）已知m≥4，设A（x1，f（x1)）、B(x2，f（x2））是曲线y=f(x）上的相异两点，l1、l2是曲线y=f(x）在A、B两点处的切线，若l1∥l2，求x1+x2的取值范围．【考点】利用导数研究函数的极值；利用导数研究曲线上某点切线方程．【分析】（1）求函数的导数，得到函数的单调区间，从而求出函数的极大值即可；（2)求函数的导数，根据导数的几何意义，结合基本不等式的性质即可得到结论．【解答】解:（1）当m=2时,f(x）=lnx+﹣x，f′（x）=﹣﹣1，(x＞0），∴f′(x）=﹣，（x＞0）,由f′（x)＞0,得：＜x＜2；由f′（x）＜0，得:0＜x＜或x＞2，∴f（x）在（，2）上单调递增,在（0，）和（2,+∞）上单调递减，=f（2）=ln2﹣；∴f(x)极大值（2）f′（x）=﹣﹣1，(x＞0），由已知f′（x1)=f′（x2），（x1，x2＞0且x1≠x2)得：∴﹣=﹣，即x1+x2=（m+）x1x2，∵x1≠x2，∴由不等式性质可得x1•x2＜恒成立，又∵x1,x2＞0，m＞0，∴x1+x2＜（m+）,∴x1+x2＞对m≥4恒成立，令g（m）=m+，（m≥4)，则g′（m）=1﹣,∵m≥4，∴g′（m）＞0，∴g（m)在[4，+∞)递增，∴g（m）≥g（4）=，记h（x）=f′（x）=﹣（x﹣m)(x﹣),h′（x）=﹣（m+）（x﹣），h（x）=f′（x）的符号与单调性为：x （0,）（,) （，m）m (m，+∞）f′(x）的符号﹣0 +++0 ﹣f′（x）的单调性↗↗最大值↘↘若f′（x1）=f′（x2）=0,则x1=,x2=m（以下均假设x1＜x2），l1在l2的下方，l1∥l2;若f′（x1）=f′（x2）＜0，则x1∈(0，)，x2∈（m，+∞），l1、l2在点（m，f（m））的两侧，l1∥l2；若f′（x1）=f′（x2）＞0，则x1∈（，)，x2∈（,m），l1、l2在点（，f（）)的两侧,l1∥l2；综上所述,l1∥l2时，x1+x2＞=，x1+x2的取值范围是(，+∞)．【选做题】（共1小题，满分10分）22．已知平面向量、、满足条件++=,｜|=｜｜=｜｜=1．(1）求证：△P1P2P3是正三角形;(2)试判断直线OP1与直线P2P3的位置关系，并证明你的判断．【考点】两点间的距离公式；向量的模．【分析】（1）（法一）根据向量的运算法则计算出|｜=|｜=||，从而判断三角形的形状；（法二)设出坐标，根据坐标运算得到P1P2=P1P3=P2P3，判断三角形的形状；(2）根据向量乘积是0，得到向量垂直即可．【解答】证明：（1）（法一)∵++=，∴+=﹣,∴=，∴+2•+=，∵||=|｜=｜|=1，∴===1，∴•=﹣,=|﹣｜2=﹣2•+=3, ∴｜|=，同理|｜=｜|=，∴△P1P2P3是正三角形；（方法二）设P1（x1,y1）,P2（x2,y2）,P3（x3，y3），∵|｜=|｜=||=1,∴，∵++=，∴，∴，∴+=+，∴2x1 x2+2y1 y2=﹣1,∴p1p2==，P1P3=P2P3=，∴P1P2=P1P3=P2P3,∴△P1P2P3是正三角形；（2）OP1⊥P2P3，证明：∵++=，∴=﹣﹣, ∴•=（﹣）=（﹣﹣)（﹣）=﹣，∵|｜=｜｜=|｜=1，=，∴•=0，OP1⊥P2P3．【选做题】（共1小题，满分0分）23．已知α、β、γ是三个平面,α∩β=a,α∩γ=b，β∩γ=c(1）若a∩b=O，求证：a、b、c三线共点;（2)若a∥b，试判断直线a与直线c的位置关系，并证明你的判断．【考点】空间中直线与直线之间的位置关系；平面的基本性质及推论．【分析】（1）由已知O∈a，O∈b，O∈β,O∈γ，由β∩γ=c，得O∈c，由此能证明a、b、c三线共点．（2）由已知a⊄γ，b⊂γ，a∥γ,从而得到a∥c．【解答】证明：（1）∵a∩b=O，∴O∈a，O∈b，∵α∩β=a，a∩γ=b，∴α⊂β，b⊂γ，∴O∈β，O∈γ，又∵β∩γ=c，∴O∈c,即O∈a,O∈b，O∈c，∴a、b、c三线共点．解：（2）a∥c．证明如下：∵α∩β=a，α∩γ=b,a∥b，∴a⊄γ，b⊂γ,又∵a∥b,∴a∥γ，又∵a⊂β，β∩γ=c，∴a∥c．【选做题】(（共1小题，满分0分)24．已知圆C：x2+y2﹣x+2y=0和直线l：x﹣y+1=0(1）试判断直线l与圆C之间的位置关系，并证明你的判断;（2)求与圆C关于直线l对称的圆的方程．【考点】直线与圆的位置关系．【分析】（1)求出圆心与直线的距离与半径比较，即可得出结论；（2）求出圆心C关于直线l的对称点，即可求与圆C关于直线l对称的圆的方程．【解答】解：(1）直线l与圆C的位置关系是相离…由x2+y2﹣x+2y=0即（x﹣）2+（y+1)2=得,圆心C（，﹣1)，半径r=…圆心到直线l：x﹣y+1=0的距离d==＞r…即直线l与圆C相离…（2)设圆心C关于直线l的对称点为C′（x，y）则C,C′的中点(,）在直线l上，且CC′⊥l…∴…,解得x=﹣2,y=，即对称圆的圆心为C′（﹣2,）…对称圆的半径r=，方程为（x+2）2+(y﹣）2=…2016年9月29日。

2015-2016学年上海市普陀区高三（上）12月调研数学试卷(理科）一、填空题(本大题56分）本大题共有14小题，要求直接将结果填写在答题纸对应的空格中，每小空格填对得4分,填错或不正确的位置一律得零分)1．若全集U=R,集合M=｛x｜x(x﹣2）≤0｝，N=｛1，2,3，4｝，则N∩∁U M= ．2．若函数,，则f（x）+g（x）= ．3．在（2x﹣1）7的二项展开式中，第四项的系数为．4．在，则函数y=tanx的值域为．5．在数列｛a n}中，a1=1,，则数列的各项和为．6．若函数f(x）=(x≥0)的反函数是f﹣1(x），则不等式f﹣1（x）＞f(x）的解集为．7．设O为坐标原点，若直线与曲线相交于A、B点,则扇形AOB的面积为．8．若正六棱柱的底面边长为10，侧面积为180,则这个棱柱的体积为．9．若在北纬45°的纬度圈上有A、B两地，经度差为90°，则A、B两地的球面距离与地球半径的比值为．10．方程的解x= ．11．设P是双曲线上的动点，若P到两条渐近线的距离分别为d1,d2，则d1•d2= ．12．如图,已知正方体ABCD﹣A1B1C1D,若在其12条棱中随机地取3条，则这三条棱两两是异面直线的概率是（结果用最简分数表示）13．若F是抛物线y2=4x的焦点,点P i（i=1，2，3，…，10）在抛物线上，且,则= ．14．若函数最大值记为g（t），则函数g（t）的最小值为．二、选择题（本大题20分，共4小题，每小题5分)15．下列命题中的假命题是（）A．若a＜b＜0，则 B．若，则0＜a＜1 C．若a＞b＞0，则a4＞b4D．若a＜1，则16．若集合，则“x ∈A”是“x∈B”成立的( ）A．充分非必要条件B．必要非充分条件C．充要条件 D．既不充分也不必要条件17．如图,在四面体ABCD,AB=CD，M，N分别是BC，AD的中点，若AB与CD所成的角的大小为60°,则MN和CD所成的角的大小为（）A．30°B．60°C．30°或60° D．15°或60°18．若函数,关于x的方程f2(x）﹣（a+1）f（x)+a=0,给出下列结论：①存在这样的实数a，使得方程由3个不同的实根；②不存在这样的实数a，使得方程由4个不同的实根；③存在这样的实数a，使得方程由5个不同的实数根；④不存在这样的实数a，使得方程由6个不同的实数根．其中正确的个数是( ）A．1个B．2个 C．3个 D．4个三、解答题：（本大题满分74分）本大题共有5题，解答下列各题必须在答题纸规定的方框内写出必要的步骤.19．如图，椭圆+=1的左、右两个焦点分别为F1、F2，A为椭圆的右顶点，点P在椭圆上且∠PF1F2=arccos（1）计算|PF1｜的值x（2)求△PF1A的面积．20．某种“笼具”由内，外两层组成，无下底面，内层和外层分别是一个圆锥和圆柱,其中圆柱与圆锥的底面周长相等,圆柱有上底面，制作时需要将圆锥的顶端剪去,剪去部分和接头忽略不计，已知圆柱的底面周长为24πcm,高为30cm，圆锥的母线长为20cm．（1)求这种“笼具”的体积（结果精确到0.1cm3）；（2)现要使用一种纱网材料制作50个“笼具”，该材料的造价为每平方米8元，共需多少元？21．已知函数f（x)=2sin2x+sin2x﹣1．(1）求函数f(x)的单调递增区间；（2）设，其中0＜x0＜π，求tanx0的值．22．已知n∈N*，数列{a n}的前n项和为S n,且2a n﹣S n=1．（1）求证：数列{a n}是等比数列，并求出通项公式；(2）对于任意a i、a j∈{a1，a2，…，a n}（其中1≤i≤n，1≤j≤n，i、j均为正整数）,若a i和a j的所有乘积a i•a j 的和记为T n，试求的值；（3)设，若数列{c n｝的前n 项和为C n，是否存在这样的实数t，使得对于所有的n 都有成立,若存在，求出t的取值范围；若不存在，请说明理由．23．已知集合M是满足下列性质的函数f（x）的全体,存在实数a、k（k≠0），对于定义域内的任意x均有f（a+x）=kf（a﹣x）成立,称数对（a，k）为函数f（x）的“伴随数对”（1)判断f（x）=x2是否属于集合M，并说明理由；(2）若函数f（x）=sinx∈M，求满足条件的函数f（x）的所有“伴随数对”;（3）若（1,1）,（2，﹣1)都是函数f（x）的“伴随数对”,当1≤x＜2时，；当x=2时,f（x）=0．求当2014≤x≤2016时，函数y=f（x）的零点．2015—2016学年上海市普陀区高三(上）12月调研数学试卷（理科)参考答案与试题解析一、填空题（本大题56分）本大题共有14小题，要求直接将结果填写在答题纸对应的空格中，每小空格填对得4分,填错或不正确的位置一律得零分）1．若全集U=R,集合M=｛x|x（x﹣2）≤0},N=｛1，2，3，4｝，则N∩∁U M= {3，4｝．【考点】交、并、补集的混合运算．【分析】求解一元二次不等式化简M，求出其补集，再由交集运算得答案．【解答】解：∵M={x|x（x﹣2）≤0｝={x｜0≤x≤2}，∴∁U M={x｜x＜0或x＞2｝，又N=｛1，2，3，4｝，∴N∩∁U M=｛3，4｝．故答案为：{3,4｝．2．若函数,，则f（x）+g（x）= 1（0≤x≤1)．【考点】函数解析式的求解及常用方法．【分析】容易求出f（x），g（x）的定义域，求交集便可得出f（x）+g(x)的定义域，并可求得f（x）+g（x）=．【解答】解：；解得,0≤x≤1;∴（0≤x≤1）．故答案为:．3．在(2x﹣1)7的二项展开式中，第四项的系数为﹣560 ．【考点】二项式系数的性质．【分析】直接利用二项式定理写出结果即可即可．【解答】解:在（2x﹣1）7的二项展开式中，第四项的系数为:=﹣560．故答案为：﹣560．4．在，则函数y=tanx的值域为[﹣1，1] ．【考点】正切函数的图象．【分析】根据正切函数的图象与性质，求出x∈［﹣，]时函数y=tanx的值域即可．【解答】解：∵，∴﹣1≤tanx≤1，∴函数y=tanx的值域为［﹣1，1]．故答案为：[﹣1，1]．5．在数列{a n}中,a1=1，,则数列的各项和为2n﹣1 ．【考点】数列的求和．【分析】由，变形a n+1+1=2（a n+1)，利用等比数列的通项公式即可得出．【解答】解：∵,∴a n+1+1=2(a n+1）,∴数列{a n+1｝是等比数列,首项为2，公比为2．∴a n+1=2n，∴a n=2n﹣1．故答案为：2n﹣1．6．若函数f（x)=（x≥0）的反函数是f﹣1（x），则不等式f﹣1（x）＞f（x)的解集为｛x|x＞1｝．【考点】反函数．【分析】由y=f(x）=（x≥0)，求出f﹣1（x)=x3，x ≥0,由此能求出不等式f﹣1(x）＞f（x）的解集．【解答】解：设y=f（x）=(x≥0），则x=y3，x,y互换，得f﹣1（x)=x3，x≥0,∵f﹣1（x）＞f（x),∴，∴x9＞x，∴x8＞1，解得x＞1．∴不等式f﹣1(x）＞f（x）的解集为｛x｜x＞1}．故答案为:｛x|x＞1}．7．设O为坐标原点，若直线与曲线相交于A、B点,则扇形AOB的面积为．【考点】直线与圆的位置关系；扇形面积公式．【分析】通过曲线方程确定曲线表示单位圆在x轴上方的部分（含于x轴的交点),y=时，∠AOB=π，即可求出扇形AOB的面积．【解答】解：由曲线，得x2+y2=1（y≥0)∴曲线表示単位圆在x轴上方的部分（含于x轴的交点)y=时，∠AOB=π,扇形AOB的面积为=．故答案为：．8．若正六棱柱的底面边长为10，侧面积为180，则这个棱柱的体积为450．【考点】棱柱、棱锥、棱台的体积．【分析】根据侧面积公式求出棱柱的高，根据底面边长求出底面积,代入体积公式得出体积．【解答】解：设棱柱的底面边长为a，高为h，则S侧=6ah=60h=180，解得h=3．S 底==150．∴正六棱柱的体积V=S 底h=450．故答案为:450．9．若在北纬45°的纬度圈上有A、B两地，经度差为90°，则A、B两地的球面距离与地球半径的比值为．【考点】球面距离及相关计算．【分析】求出球心角，然后A、B两点的距离，求出两点间的球面距离，即可求出A、B两地的球面距离与地球半径的比值．【解答】解:地球的半径为R，在北纬45°，而AB=R，所以A、B的球心角为：,所以两点间的球面距离是：，所以A、B两地的球面距离与地球半径的比值为；故答案为：．10．方程的解x= log 23 ．【考点】对数的运算性质．【分析】化简可得4x﹣5=4（2x﹣2)，从而可得(2x)2﹣4•2x+3=0，从而解得．【解答】解：∵，∴4x﹣5=4(2x﹣2)，即（2x）2﹣4•2x+3=0，∴2x=1（舍去)或2x=3;∴x=log23，故答案为：log23．11．设P是双曲线上的动点，若P到两条渐近线的距离分别为d1，d2，则d1•d2= ．【考点】双曲线的简单性质．【分析】先确定两条渐近线方程,设双曲线C上的点P （x，y）,求出点P到两条渐近线的距离，结合P在双曲线C上，即可求d1•d2的值．【解答】解：由条件可知：两条渐近线分别为x±y=0设双曲线C上的点P(x，y)，则点P到两条渐近线的距离分别为d1=，d2=所以d1•d2=•==．故答案为：．12．如图,已知正方体ABCD﹣A1B1C1D,若在其12条棱中随机地取3条,则这三条棱两两是异面直线的概率是（结果用最简分数表示)【考点】列举法计算基本事件数及事件发生的概率；空间中直线与直线之间的位置关系．【分析】正方体ABCD﹣A1B1C1D，在其12条棱中随机地取3条，先求出基本事件总数，再求出这三条棱两两是异面直线包含的基本事件个数,由此能求出这三条棱两两是异面直线的概率．【解答】解：正方体ABCD﹣A1B1C1D，在其12条棱中随机地取3条，基本事件总数n==220,这三条棱两两是异面直线包含的基本事件个数m=8,∴这三条棱两两是异面直线的概率是p===．故答案为：．13．若F是抛物线y2=4x的焦点，点P i（i=1，2，3，…，10)在抛物线上,且,则= 200 ．【考点】抛物线的简单性质．【分析】根据抛物线的定义得抛物线上的点到焦点的距离等于该点到准线的距离，因此求出抛物线的准线方程，结合题中数据加以计算，即可得到本题答案．【解答】解：∵抛物线y2=4x的焦点为F（1，0),准线为x=﹣1，∴根据抛物线的定义，P i（i=1，2，3，…,2015)到焦点的距离等于P i到准线的距离，即|P i F|=x i+1，,可得1﹣x 1+1﹣x2+…+1﹣x100=0，∴x1+x2+…+x100=100∴｜P1F|+|P2F|+…|P100F｜=（x1+1)+（x2+1）+…+（x100+1）=(x1+x2+…+x100）+100=100+100=200．故答案为:200．14．若函数最大值记为g（t)，则函数g（t)的最小值为．【考点】函数的最值及其几何意义．【分析】化简sinx+=sinx+3+﹣3，从而可得0≤sinx+3+﹣3≤，从而求得g（t）=f max（x）=，从而求值．【解答】解：∵sinx+=sinx+3+﹣3,∵﹣1≤sinx≤1，∴2≤sinx+3≤4,∴3≤sinx+3+≤，∴0≤sinx+3+﹣3≤,∴g(t)=f max（x）=,∴当t=时，函数g（t）有最小值为；故答案为；．二、选择题（本大题20分，共4小题，每小题5分) 15．下列命题中的假命题是( )A．若a＜b＜0,则B．若，则0＜a＜1 C．若a＞b＞0，则a4＞b4D．若a＜1，则【考点】命题的真假判断与应用．【分析】正确选项进行证明，不正确选项，举出反例即可．【解答】解：对于A,a＜b＜0,则•a＜•b，∴，正确对于B,，则＞0，∴0＜a＜1，正确对于C，a＞b＞0，a4＞b4，正确;对于D，a=，=2＞1，不正确,故选:D．16．若集合，则“x ∈A”是“x∈B”成立的（）A．充分非必要条件B．必要非充分条件C．充要条件 D．既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断．【分析】先分别求出集合A，B，然后根据必要条件、充分条件和充要条件的定义进行判断．【解答】解：∵≥0，∴0≤x＜3，∴A=（0，3]，∵lg｜2x﹣3｜＜0=lg1，∴|2x﹣3｜＜1，且2x﹣3≠0，∴1＜x＜2，且x≠∴B=(1，）∪（，2)，∴“x∈A”是“x∈B”成立的必要非充分条件，故选:B．17．如图，在四面体ABCD，AB=CD，M，N分别是BC，AD的中点，若AB与CD所成的角的大小为60°，则MN和CD所成的角的大小为（）A．30°B．60°C．30°或60° D．15°或60°【考点】异面直线及其所成的角．【分析】取BD中点O，连结MO、NO,由已知得∠ONM是MN和CD所成的角（或补角），且∠MON=60°，OM=ON，由此能求出MN和CD所成的角的大小．【解答】解:取BD中点O，连结MO、NO，∵在四面体ABCD，AB=CD，M，N分别是BC，AD 的中点，AB与CD所成的角的大小为60°，∴MO，NO，∴∠ONM是MN和CD所成的角（或所成角的补角），且∠MON=60°,OM=ON,∴∠ONM=60°，或∠ONM=30°，∴MN和CD所成的角为60°或30°．故选:C．18．若函数,关于x的方程f2(x）﹣（a+1）f（x)+a=0，给出下列结论：①存在这样的实数a，使得方程由3个不同的实根；②不存在这样的实数a，使得方程由4个不同的实根;③存在这样的实数a,使得方程由5个不同的实数根；④不存在这样的实数a，使得方程由6个不同的实数根．其中正确的个数是（）A．1个B．2个 C．3个 D．4个【考点】根的存在性及根的个数判断．【分析】由f2（x）﹣（a+1）f(x）+a=0可解得f（x）=1或f（x）=a，作函数的图象，从而讨论求解．【解答】解：∵f2（x）﹣(a+1)f（x)+a=0,∴f（x)=1或f（x）=a，作函数的图象如下，，当a=1时,方程有3个不同的实根,故①正确；当a＞1或a≤﹣1时,方程有6个不同的实根，故④不正确；当﹣1＜a＜1时,方程有5个不同的实根，故③正确;综上可知，不存在这样的实数a,使得方程由4个不同的实根；故②正确；故选：C．三、解答题：（本大题满分74分）本大题共有5题,解答下列各题必须在答题纸规定的方框内写出必要的步骤。

2015-2016学年江苏省南京市六校联考高三（上）12月调研数学试卷一、填空题（共14小题每小题5分共计70分．将正确答案填入答题纸的相应横线上）1．设集合M={2，0，x}，集合N={0，1}，若N⊆M，则x= ．2．已知复数z满足（3+4i）z=1（i为虚数单位），则z的模为．3．已知m为实数，直线l1：mx+y+3=0，l2：（3m﹣2）x+my+2=0，则“m=1”是“l1∥l2”的条件（请在“充要、充分不必要、必要不充分、既不充分也不必要”中选择一个填空）．4．根据如图所示的伪代码，最后输出的S的值为．5．现有5道试题，其中甲类试题2道，乙类试题3道，现从中随机取2道试题，则至少有1道试题是乙类试题的概率为．6．若实数x，y满足约束条件，则目标函数z=2x+y的最小值为．7．已知等比数列{a n}的前n项和为S n，若a2a8=2a3a6，S5=﹣62，则a1的值是．8．已知||=1，||=2，与的夹角为120°，，则与的夹角为．9．已知，则cos（30°﹣2α）的值为．10．设椭圆的左、右焦点分别为F1、F2，左准线为l，若在椭圆上存在点P，使得当PQ⊥l于点Q时，四边形PQF1F2为平行四边形，则此椭圆的离心率e的取值范围是．11．若x．y均为正实数，且x+2y=4，则+的最小值是．12．在△ABC中，已知BC=2， =1，则△ABC面积的最大值是．13．已知圆O：x2+y2=4，直线l：x+y﹣4=0，A为直线l上一点，若圆O上存在两点B、C，使得∠BAC=60°，则点A的横坐标的取值范围是．14．若函数f（x）=恰有2个零点，则实数a的取值范围是．二、解答题（本大题共6小题，共90分．请在答题纸指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．）15．已知向量=（sinx，），=（cosx，﹣1）．（1）当∥时，求tan（x﹣）的值；（2）设函数f（x）=2（+）•，当x∈[0，]时，求f（x）的值域．16．如图，在多面体ABCDEF中，四边形ABCD是菱形，AC，BD相交于点O，EF∥AB，AB=2EF，平面BCF⊥平面ABCD，BF=CF，点G为BC的中点．（1）求证：直线OG∥平面EFCD；（2）求证：直线AC⊥平面ODE．17．如图，椭圆C： +=1（a＞b＞0）的离心率e=，椭圆C的右焦点到右准线的距离为，椭圆C的下顶点为D．（1）求椭圆C的方程；（2）若过D点作两条互相垂直的直线分别与椭圆C相交于点P、M．求证：直线PM经过一定点．18．如图，某广场中间有一块边长为2百米的菱形状绿化区ABCD，其中BMN是半径为1百米的扇形，∠ABC=，管理部门欲在该地从M到D修建小路；在上选一点P（异于M、N两点），过点P修建与BC平行的小路PQ．（1）设∠PBC=θ，试用θ表示修建的小路与线段PQ及线段QD的总长度l；（2）求l的最小值．19．已知数列{a n}的前n项和为S n，且对一切正整数n都有．（I）求证：a n+1+a n=4n+2；（II）求数列{a n}的通项公式；（III）是否存在实数a，使不等式对一切正整数n都成立？若存在，求出a的取值范围；若不存在，请说明理由．20．已知函数f（x）=e x﹣ax2﹣bx﹣1，其中a，b∈R，e为自然对数的底数．（1）若函数f（x）在点（1，f（1））处的切线方程是y=（e﹣1）x﹣1，求实数a及b的值；（2）设g（x）是函数f（x）的导函数，求函数g（x）在区间[0，1]上的最小值；（3）若f（1）=0，函数f（x）在区间（0，1）内有零点，求a的取值范围．【选做题】本题包括、、、四小题，请选定其中两题，并在答题卡指定区域内作答，若多做，则按作答的前两题评分.解答题应写出文字说明、证明过程或演算步骤.（选修4-1：几何证明选讲）21．选修4﹣1：几何证明选讲如图，AB是⊙O的一条切线，切点为B，直线ADE，CFD，CGE都是⊙O的割线，已知AC=AB．求证：FG∥AC．（选修4-2：矩阵与变换）22．（2012•盐城一模）已知矩阵，若矩阵AB对应的变换把直线l：x+y﹣2=0变为直线l′，求直线l′的方程．选修4-4：坐标系与参数方程23．选修4﹣4：坐标系与参数方程在平面直角坐标系xOy中，圆C的参数方程为（θ为参数，r＞0）．以O为极点，x轴正半轴为极轴建立极坐标系，直线l的极坐标方程为．若圆C上的点到直线l的最大距离为3，求r的值．选修4-5：不等式选讲24．已知实数x，y，z满足x+y+z=2，求2x2+3y2+z2的最小值．【必做题】第22题、第23题，每题10分，共计20分，请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤.25．袋中装有围棋黑色和白色棋子共7枚，从中任取2枚棋子都是白色的概率为．现有甲、乙两人从袋中轮流摸取一枚棋子．甲先摸，乙后取，然后甲再取，…，取后均不放回，直到有一人取到白棋即终止．每枚棋子在每一次被摸出的机会都是等可能的．用X表示取棋子终止时所需的取棋子的次数．（1）求随机变量X的概率分布列和数学期望E（X）；（2）求甲取到白球的概率．26．设f（x）是定义在R上的函数，已知n∈N*，且g（x）=C f（）x0（1﹣x）n+C f（）x1（1﹣x）n﹣1+C f（）x2（1﹣x）n﹣2+…+C f（）x n（1﹣x）n．（1）若f（x）=1，求g（x）；（2）若f（x），求g（x）．2015-2016学年江苏省南京市六校联考高三（上）12月调研数学试卷参考答案与试题解析一、填空题（共14小题每小题5分共计70分．将正确答案填入答题纸的相应横线上）1．设集合M={2，0，x}，集合N={0，1}，若N⊆M，则x= 1 ．【考点】集合的包含关系判断及应用．【专题】集合．【分析】根据条件N⊆M，确定元素关系，进行求解即可，从而得到x的值．【解答】解：∵集合M={2，0，x}，N={0，1}，∴若N⊆M，则集合N中元素均在集合M中，∴x=1．故答案为：1．【点评】本题主要考查集合的包含关系的应用，利用N⊆M，确定元素关系．一般集合中问题，如果含有参数，求解之后要注意对集合进行验证．属于基础题．2．已知复数z满足（3+4i）z=1（i为虚数单位），则z的模为．【考点】复数求模．【专题】数系的扩充和复数．【分析】复数方程两边求模推出结果即可．【解答】解：复数z满足（3+4i）z=1（i为虚数单位），可得：|（3+4i）z|=1，即|3+4i||z|=1，可得5|z|=1．∴z的模为：．故答案为：．【点评】本题考查复数的模的求法，基本知识的考查．3．已知m为实数，直线l1：mx+y+3=0，l2：（3m﹣2）x+my+2=0，则“m=1”是“l1∥l2”的充分不必要条件（请在“充要、充分不必要、必要不充分、既不充分也不必要”中选择一个填空）．【考点】直线的一般式方程与直线的平行关系．【专题】计算题．【分析】把m=1代入可判l1∥l2”成立，而“l1∥l2”成立可推出m=1，或m=2，由充要条件的定义可得答案．【解答】解：当m=1时，方程可化为l1：x+y+3=0，l2：x+y+2=0，显然有“l1∥l2”成立；而若满足“l1∥l2”成立，则必有，解得m=1，或m=2，不能推出m=1，故“m=1”是“l1∥l2”的充分不必要条件．故答案为：充分不必要【点评】本题考查直线的一般式方程与直线的平行关系，属基础题．4．根据如图所示的伪代码，最后输出的S的值为55 ．【考点】伪代码．【专题】计算题；转化思想；试验法；算法和程序框图．【分析】分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是累加并输出S=1+2+3+4+5+…+10的值，利用等差数列的求和公式计算即可得解．【解答】解：分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是累加并输出满足条件S=1+2+3+4+5+…+10值．由于：S=1+2+3+4+5+…+10=55，故输出的S值为55．故答案为：55；【点评】本题考查的知识点是伪代码，其中根据已知分析出循环的循环变量的初值，终值及步长，是解答的关键，属于基础题．5．现有5道试题，其中甲类试题2道，乙类试题3道，现从中随机取2道试题，则至少有1道试题是乙类试题的概率为．【考点】计数原理的应用．【专题】应用题；排列组合．【分析】利用组合的方法求出甲类试题2道，乙类试题3道，从中随机取2道试题的方法，全是甲类试题，有1种方法，利用对立事件的概率公式求出至少有1道试题是乙类试题的概率．【解答】解：甲类试题2道，乙类试题3道，从中随机取2道试题，共有=10种方法，全是甲类试题，有1种方法，∴至少有1道试题是乙类试题的概率为1﹣=．故答案为：．【点评】此题考查概率的求法：如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=．6．若实数x，y满足约束条件，则目标函数z=2x+y的最小值为 1 ．【考点】简单线性规划．【专题】不等式的解法及应用．【分析】作出不等式组对应的平面区域，利用z的几何意义，即可得到结论．【解答】解：作出不等式组对应的平面区域如图：由z=2x+y得y=﹣2x+z，平移直线y=﹣2x+z，由图象可知当直线y=﹣2x+z经过点A时，直线的截距最小，此时z最小，由，解得，即A（0，1），此时z=0×2+1=1，故答案为：1【点评】本题主要考查线性规划的应用，利用数形结合是解决本题的关键．7．已知等比数列{a n}的前n项和为S n，若a2a8=2a3a6，S5=﹣62，则a1的值是﹣2 ．【考点】等比数列的通项公式．【专题】计算题；等差数列与等比数列．【分析】由题意可知，q≠1，结合等比数列的通项公式及求和公式可得，解方程可求【解答】解：∵a2a8=2a3a6，S5=﹣62∴q≠1∴解方程可得，q=2，a1=﹣2故答案为：﹣2【点评】本题主要考查了等比数列的通项公式及求和公式的简单应用，属于基础试题8．已知||=1，||=2，与的夹角为120°，，则与的夹角为90°．【考点】平面向量数量积的坐标表示、模、夹角．【专题】平面向量及应用．【分析】利用向量的数量积运算和向量垂直与数量积的关系即可得出．【解答】解：∵||=1，||=2，与的夹角为120°，∴===﹣1．∵，∴，∴=，∴﹣（﹣1）=，∴=0．∴．∴与的夹角为90°．【点评】本题考查了向量的数量积运算和向量垂直与数量积的关系，属于基础题．9．已知，则cos（30°﹣2α）的值为．【考点】二倍角的余弦；两角和与差的余弦函数．【专题】三角函数的求值．【分析】利用诱导公式求得sin（15°﹣α）=，再利用二倍角的余弦公式可得cos（30°﹣2α）=1﹣2sin2（15°﹣α），运算求得结果．【解答】解：∵已知，∴sin（15°﹣α）=，则cos（30°﹣2α）=1﹣2sin2（15°﹣α）=，故答案为．【点评】本题主要考查诱导公式，二倍角的余弦公式的应用，属于中档题．10．设椭圆的左、右焦点分别为F1、F2，左准线为l，若在椭圆上存在点P，使得当PQ⊥l于点Q时，四边形PQF1F2为平行四边形，则此椭圆的离心率e的取值范围是（，1）．【考点】椭圆的简单性质．【专题】计算题．【分析】PQF1F2为平行四边形对边相等．推出PQ=F1F2=2C．设P（x1，y1）． P在X负半轴，利用P的横坐标的范围，得到关系式，即可得到椭圆离心率的范围．【解答】解：因为PQF1F2为平行四边形，对边相等．所以，PQ=F1F2，所以PQ=2C．设P（x1，y1）． P在X负半轴，﹣x1=﹣2c＜a，所以2c2+ac﹣a2＞0，即2e2+e﹣1＞0，解得e，因为椭圆e取值范围是（0，1），所以此题答案为（，1）．故答案为：（，1）．【点评】本题是中档题，考查椭圆的基本性质，找出P的横坐标与椭圆长半轴的关系是解题的关键，考查计算能力，转化思想．11．若x．y均为正实数，且x+2y=4，则+的最小值是 2 ．【考点】基本不等式．【专题】整体思想；换元法；不等式的解法及应用．【分析】令x+2=m，y+1=n，整体换元由基本不等式可得．【解答】解：令x+2=m，y+1=n，则x=m﹣2，y=n﹣1，∵x，y均为正实数，且x+2y=4，∴m＞2且n＞1，且m﹣2+2（n﹣1）=4即m+2n=8，换元可得+=+=+=m+﹣4+2n+﹣4=+==，由8=m+2n≥2可得mn≤8，∴≥2，当且仅当=即m=2n时取等号，结合m+2n=8可解得m=4且n=2，即x=2且y=1．故答案为：2．【点评】本题考查基本不等式求最值，整体换元是解决问题的关键，属中档题．12．在△ABC中，已知BC=2， =1，则△ABC面积的最大值是．【考点】向量在几何中的应用．【专题】计算题；综合题．【分析】根据=1，及向量的数量积的定义式得到cosA=1，两边平方得到1=AB2AC2cos2A，根据三角形的面积公式S=|AB||AC|sinA，两边平方，两式相加，得到1+4S2=AB2AC2，根据余弦定理和基本不等式即可求得三角形面积的最大值．【解答】解：∵ =1，∴ cosA=1∴1=AB2AC2cos2A（1）又∵S=|AB||AC|sinA∴4S2=AB2AC2sin2A（2）（1）+（2）得：1+4S2=AB2AC2（cos2A+sin2A）即1+4S2=AB2AC2由题知： =﹣，∴BC2=AC2﹣2+AB2=AC2+AB2﹣2∵BC=2，∴AC2+AB2=6由不等式：AC2+AB2≥2AC•AB 当且仅当，AC=AB时，取等号∴6≥2AC•AB即AC•AB≤3∴1+4S2=AB2AC2《9∴4S2≤8，即：S2≤2∴S≤，所以△ABC面积的最大值是：．故答案为．【点评】此题是个中档题．考查向量在几何中的应用和向量的数量积的定义式，以及余弦定理、三角形的面积公式和基本不等式求最值等基础知识和基本方法，综合性强，考查了学生灵活应用知识分析、解决问题的能力．13．已知圆O：x2+y2=4，直线l：x+y﹣4=0，A为直线l上一点，若圆O上存在两点B、C，使得∠BAC=60°，则点A的横坐标的取值范围是[0，4] ．【考点】直线与圆的位置关系．【专题】计算题；转化思想；综合法；直线与圆．【分析】先确定从直线上的点向圆上的点连线成角，当且仅当两条线均为切线时才是最大的角，进而求出OA的长度为4，故可转化为在直线上找到一点，使它到点O的距离为4．【解答】解：由题意，从直线上的点向圆上的点连线成角，当且仅当两条线均为切线时才是最大的角，不妨设切线为AP，AQ，则∠PAQ为60°时，∠POQ为120°，所以OA的长度为4，故问题转化为在直线上找到一点，使它到点O的距离为4．设A（x0，4﹣x0），则∵O（0，0），∴x02+（4﹣x0）2=16∴x0=0或4∴满足条件的点A横坐标的取值范围是[0，4]．故答案为：[0，4]．【点评】本题考查直线与圆的方程的应用，考查学生分析解决问题的能力，解题的关键是明确从直线上的点向圆上的点连线成角，当且仅当两条线均为切线时才是最大的角．14．若函数f（x）=恰有2个零点，则实数a的取值范围是[，1）∪[3，+∞）．【考点】函数零点的判定定理．【专题】计算题；分类讨论；函数的性质及应用．【分析】①当a≤0时，f（x）＞0恒成立，②当a＞0时，由3x﹣a=0讨论，再由x2﹣3ax+2a2=（x﹣a）（x﹣2a）讨论，从而确定方程的根的个数．【解答】解：①当a≤0时，f（x）＞0恒成立，故函数f（x）没有零点；②当a＞0时，3x﹣a=0，解得，x=log3a，又∵x＜1；∴当a∈（0，3）时，log3a＜1，故3x﹣a=0有解x=log3a；当a∈[3，+∞）时，log3a≥1，故3x﹣a=0在（﹣∞，1）上无解；∵x2﹣3ax+2a2=（x﹣a）（x﹣2a），∴当a∈（0，）时，方程x2﹣3ax+2a2=0在[1，+∞）上无解；当a∈[，1）时，方程x2﹣3ax+2a2=0在[1，+∞）上有且仅有一个解；当a∈[1，+∞）时，方程x2﹣3ax+2a2=0在[1，+∞）上有且仅有两个解；综上所述，当a∈[，1）或a∈[3，+∞）时，函数f（x）=恰有2个零点，故答案为：[，1）∪[3，+∞）．【点评】本题考查了分段函数的性质的应用及分类讨论的思想应用．二、解答题（本大题共6小题，共90分．请在答题纸指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．）15．已知向量=（sinx，），=（cosx，﹣1）．（1）当∥时，求tan（x﹣）的值；（2）设函数f（x）=2（+）•，当x∈[0，]时，求f（x）的值域．【考点】平面向量数量积的运算；平面向量共线（平行）的坐标表示．【专题】计算题；三角函数的求值；三角函数的图像与性质；平面向量及应用．【分析】（1）运用向量的关系的坐标表示和同角的商数关系及两角差的正切公式，计算即可得到；（2）运用向量的数量积的坐标表示和二倍角公式及两角和的正弦公式，化简f（x），再由正弦函数的图象和性质，即可得到f（x）的值域．【解答】解：（1）∥即有cosx+sinx=0，即tanx=﹣，tan（x﹣）===﹣7；（2）f（x）=2（+）•=2cosx（sinx+cosx）+=sin2x+cos2x+=sin（2x+）+，当x∈[0，]时，2x+∈[，]，即，则f（x）≤+，则f（x）的值域为[+]．【点评】本题考查平面向量的共线和数量积的坐标表示，考查三角函数的化简和求值，考查正弦函数的图象和性质，考查运算能力，属于中档题．16．如图，在多面体ABCDEF中，四边形ABCD是菱形，AC，BD相交于点O，EF∥AB，AB=2EF，平面BCF⊥平面ABCD，BF=CF，点G为BC的中点．（1）求证：直线OG∥平面EFCD；（2）求证：直线AC⊥平面ODE．【考点】直线与平面平行的判定；直线与平面垂直的判定．【专题】空间位置关系与距离．【分析】（1）根据线线平行推出线面平行；（2）根据线面垂直的判定定理进行证明即可．【解答】证明（1）∵四边形ABCD是菱形，AC∩BD=O，∴点O是BD的中点，∵点G为BC的中点∴OG∥CD，…又∵OG⊄平面EFCD，CD⊂平面EFCD，∴直线OG∥平面EFCD．…（2）∵BF=CF，点G为BC的中点，∴FG⊥BC，∵平面BCF⊥平面ABCD，平面BCF∩平面ABCD=BC，FG⊂平面BCF，FG⊥BC∴FG⊥平面ABCD，…∵AC⊂平面ABCD∴FG⊥AC，∵，，∴OG∥EF，OG=EF，∴四边形EFGO为平行四边形，∴FG∥EO，…∵FG⊥AC，FG∥EO，∴AC⊥EO，∵四边形ABCD是菱形，∴AC⊥DO，∵AC⊥EO，AC⊥DO，EO∩DO=O，EO、DO在平面ODE内，∴AC⊥平面ODE．…【点评】本题考查了线面平行，线面垂直的判定定理，本题属于中档题．17．如图，椭圆C： +=1（a＞b＞0）的离心率e=，椭圆C的右焦点到右准线的距离为，椭圆C的下顶点为D．（1）求椭圆C的方程；（2）若过D点作两条互相垂直的直线分别与椭圆C相交于点P、M．求证：直线PM经过一定点．【考点】直线与圆锥曲线的关系；椭圆的标准方程．【专题】计算题；数形结合；转化思想；综合法；圆锥曲线的定义、性质与方程．【分析】（1）由题意可得c2=a2，又﹣c=，且a2=b2+c2，解得b=1，则a=3，即可得解椭圆C的方程；（2）设直线PD的斜率为k，由得P（，），M（，），作直线l关于y轴的对称直线l′，可知定点在y轴上，当k=1时，P（，），M（﹣，），可求此时直线PM经过y轴上的点T（0，），证明k PT=k MT，即可得解P，M，T三点共线，即直线PM经过点T．【解答】解：（1）依题意知 e=，则c2=a2，…又﹣c=，且a2=b2+c2，∴b=1，则a=3，∴方程为+y2=1．…（2）由题意知直线PD，MD的斜率存在且不为0，设直线PD的斜率为k，则PD：y=kx﹣1，由得P（，），…用﹣去代k，得M（，），…作直线l关于y轴的对称直线l′，此时得到的点P′、M′关于y轴对称，则PM与P′M′相交于y轴，可知定点在y轴上，当k=1时，P（，），M（﹣，），此时直线PM经过y轴上的点T（0，），…∵k PT=，…k MT==…∴k PT=k MT，∴P，M，T三点共线，即直线PM经过点T，故直线PM经过定点T（0，）．…【点评】本题考查椭圆方程的求法，考查直线是否过定点的判断与求法，解题时要认真审题，注意函数与方程思想的合理运用，属于中档题．18．如图，某广场中间有一块边长为2百米的菱形状绿化区ABCD，其中BMN是半径为1百米的扇形，∠ABC=，管理部门欲在该地从M到D修建小路；在上选一点P（异于M、N两点），过点P修建与BC平行的小路PQ．（1）设∠PBC=θ，试用θ表示修建的小路与线段PQ及线段QD的总长度l；（2）求l的最小值．【考点】在实际问题中建立三角函数模型．【专题】综合题；转化思想；综合法；解三角形．【分析】（1）由题意，QP，交AB于E利用正弦定理，求出EP，EB，即可用θ表示修建的小路与线段PQ及线段QD的总长度l；（2）求导数，确定函数的单调性，即可求l的最小值．【解答】解：（1）由题意，延长QP，交AB于E，则=（﹣θ），△BPE中，∠EPB=θ，∠EBP=﹣θ，∠BEP=，∴EP=sin（﹣θ），EB=sinθ，∴PQ=2﹣sin（﹣θ），QD=2﹣sinθ，∴l=﹣θ+2﹣sin（﹣θ）+2﹣sinθ=4﹣sin（﹣θ）﹣sinθ+﹣θ=4﹣2sin（θ+）+﹣θ（0＜θ＜）；（2）l′=﹣2cos（θ+）﹣1，∴0＜θ＜时，l′＜0，＜θ＜，时，l′＞0，∴θ=时，l取得最小值，最小值为（4﹣+）百米．【点评】本题考查三角函数中的恒等变换应用，考查正弦定理与两角差与两角和的正弦，考查导数知识的运用，考查运算求解能力，属于中档题．19．已知数列{a n}的前n项和为S n，且对一切正整数n都有．（I）求证：a n+1+a n=4n+2；（II）求数列{a n}的通项公式；（III）是否存在实数a，使不等式对一切正整数n都成立？若存在，求出a的取值范围；若不存在，请说明理由．【考点】数列与不等式的综合；等差数列的通项公式；等差关系的确定．【专题】综合题．【分析】（I）由，知，由此能够导出．（II）在中，令n=1，得a1=2，代入（I）得a2=4．由a n+1+a n=4n+2，知a n+2+a n+1=4n+6，故a n+2﹣a n=4，由此能导出数列{a n}的通项公式是a n=2n．（III）＜等价于，令f（n）=，则f（n）＞0，由此能够导出存在实数a，符合题意，并能求出其取值范围．【解答】解：（I）∵，∴=，∴，即．（II）在中，令n=1，得a1=2，代入（I）得a2=4．∵a n+1+a n=4n+2，∴a n+2+a n+1=4n+6，两式相减，得：a n+2﹣a n=4，∴数列{a n}的偶数项a2，a4，a6，…，a26，…依次构成一个等差数列，且公差为d=4，∴当n为偶数时， =，当n为奇数时，n+1为偶数，由上式及（I）知：a n=4n+2﹣a n+1=4n+2﹣2（n+1）=2n，∴数列{a n}的通项公式是a n=2n．（III）＜，等价于，令f（n）=，则由（II）知f（n）＞0，∴═===．∴f（n+1）＜f（n），即f（n）的值随n的增大而减小，∴n∈N*时，f（n）的最大值为，若存在实数a，符合题意，则必有：，即，它等价于，解得，或，因此，存在实数a，符合题意，其取值范围为．【点评】本题考查数列和不等式的综合应用，考查运算求解能力，推理论证能力；考查化归与转化思想．对数学思维的要求比较高，有一定的探索性．综合性强，难度大，是高考的重点．解题时要认真审题，仔细解答．20．已知函数f（x）=e x﹣ax2﹣bx﹣1，其中a，b∈R，e为自然对数的底数．（1）若函数f（x）在点（1，f（1））处的切线方程是y=（e﹣1）x﹣1，求实数a及b的值；（2）设g（x）是函数f（x）的导函数，求函数g（x）在区间[0，1]上的最小值；（3）若f（1）=0，函数f（x）在区间（0，1）内有零点，求a的取值范围．【考点】利用导数研究曲线上某点切线方程；函数的零点；导数在最大值、最小值问题中的应用．【专题】分类讨论；方程思想；分析法；导数的综合应用．【分析】（1）求出函数的导数，求得切线的斜率和切点，由切线的方程，解得a，b；（2）求得g（x）及导数，对a讨论，当2a≤0即a≤0时，当ln（2a）≤0即0＜a≤时，当0＜ln（2a）＜1即＜a＜时，当ln（2a）≥1即a≥时，求出单调区间可得最小值；（3）求出导数，f（1）=0，即有e﹣a﹣b﹣1=0，可得b=e﹣a﹣1，结合（1），（2）运用函数零点存在定理，结合函数的单调性，即可得到所求范围．【解答】解：（1）由f（x）=e x﹣ax2﹣bx﹣1，得f′（x）=e x﹣2ax﹣b，∴f（1）=e﹣a﹣b﹣1，f′（1）=e﹣2a﹣b，∵函数f（x）在点（1，f（1））处的切线方程是y﹣（e﹣a﹣b﹣1）=（e﹣2a﹣b）（x﹣1），由切线的方程y=（e﹣1）x﹣1，可得e﹣a﹣b﹣1=e﹣1﹣1，e﹣2a﹣b=e﹣1，解得a=0，b=1；（2）由f（x）=e x﹣ax2﹣bx﹣1得f′（x）=e x﹣2ax﹣b，∴g（x）=f′（x）=e x﹣2ax﹣b，∴g′（x ）=e x﹣2a ．当2a≤0即a≤0时，e x ﹣2a ＞0对一切x ∈[0，1]恒成立， ∴g（x ）在[0，1]内单调递增，∴g（x ）在[0，1]上的最小值是g （0）=1﹣b ； 当2a ＞0即a ＞0时，令g′（x ）=0，得x=ln （2a ）， 从而有①当ln （2a ）≤0即0＜a≤时，列表如下：依表格知g （x ）在[0，1]上的最小值是g （0）=1﹣b ； ②当0＜ln （2a ）＜1即＜a ＜时，列表如下：依表格知g （x ）在[0，1]上的最小值是g （ln （2a ））=2a ﹣2aln （2a ）﹣b ；③当ln （2a）≥1即a≥时，列表如下：依表格知g （x ）在[0，1]上的最小值是g （1）=e ﹣2a ﹣b ． 综上所述：当a≤时，g （x ）在[0，1]上的最小值是1﹣b ；当＜a ＜时，g （x ）在[0，1]上的最小值是2a ﹣2aln （2a ）﹣b ； 当a≥时，g （x ）在[0，1]上的最小值是e ﹣2a ﹣b ． （3）f （x ）=e x ﹣ax 2﹣bx ﹣1，g （x ）=f′（x ）=e x ﹣2ax ﹣b ， 由f （1）=0，即有e ﹣a ﹣b ﹣1=0，可得b=e ﹣a ﹣1，∴g（x ）=e x﹣2ax ﹣e+a+1，又f （0）=0． 若函数f （x ）在区间（0，1）内有零点， 设x 0为f （x ）在区间（0，1）内的一个零点， 则由f （0）=f （x 0）=0可知，f （x ）在区间（0，x 0）内不可能单调递增，也不可能单调递减． 则g （x ）在区间（0，x 0）内不可能恒为正，也不可能恒为负．故g （x ）在区间（0，x 0）内存在零点x 1．同理g （x ）在区间（x 0，1）内存在零点x 2． 故函数f （x ）在区间（0，1）内至少有三个单调区间， g （x ）在区间（0，1）内至少有两个零点．由（2）知当a≤或a≥时，函数g （x ）即f′（x ）在区间[0，1]内单调， 不可能满足“函数f （x ）在区间（0，1）内至少有三个单调区间”这一要求．若＜a ＜，此时g （x ）在区间（0，ln （2a ））内单调递减，在区间（ln （2a ），1）内单调递增．因此x 1∈（0，ln （2a ）），x 2∈（ln （2a ），1），又g （x ）min =g （ln （2a ））=2a ﹣2aln （2a ）﹣e+a+1=3a ﹣2aln （2a ）﹣e+1，令h （x ）=3x ﹣2xln （2x ）﹣e+1（＜x ＜），则h′（x ）=3﹣2ln （2x ）﹣2x••2=1﹣2ln （2x ），令h′（x ）=0得x=，列表如下：） （，﹣e+1减依表格知：当＜x ＜时，h （x ）min =﹣e+1＜0， ∴g（x ）min =3a ﹣2aln （2a ）﹣e+1＜0恒成立，于是，函数f （x ）在区间（0，1）内至少有三个单调区间⇔⇔⇔e ﹣2＜a ＜1．综上所述：a的取值范围为（e﹣2，1）．【点评】本题考查导数的运用：求切线的方程和单调区间、极值和最值，考查分类讨论的思想方法，考查函数方程的转化思想的运用，属于难题．【选做题】本题包括、、、四小题，请选定其中两题，并在答题卡指定区域内作答，若多做，则按作答的前两题评分.解答题应写出文字说明、证明过程或演算步骤.（选修4-1：几何证明选讲）21．选修4﹣1：几何证明选讲如图，AB是⊙O的一条切线，切点为B，直线ADE，CFD，CGE都是⊙O的割线，已知AC=AB．求证：FG∥AC．【考点】相似三角形的判定；与圆有关的比例线段．【专题】选作题．【分析】利用切割线定理可得AB2=AD•AE．由AC=AB，得到AC2=AD•AE，而∠CAE公用，由相似三角形的判定定理可得△ACE∽△ADC．于是∠AEC=∠ACD，由圆的内接四边形的性质可得∠CFG=∠AEC．进而可得FG∥AC．【解答】证明：∵AB是⊙O的一条切线，∴AB2=AD•AE．∵AC=AB，∴AC2=AD•AE，即．又∵∠CAE公用，∴△ACE∽△ADC．∴∠AEC=∠ACD．由四边形DEGF是⊙O的内接四边形，∴∠CFG=∠AEC．∴∠ACD=∠CFG，∴FG∥AC．【点评】熟练掌握切割线定理、相似三角形的判定定理和性质定理、圆的内接四边形的性质、平行线的判定定理是解题的关键．（选修4-2：矩阵与变换）22．（2012•盐城一模）已知矩阵，若矩阵AB对应的变换把直线l：x+y﹣2=0变为直线l′，求直线l′的方程．【考点】逆矩阵与投影变换；矩阵与矩阵的乘法的意义．【专题】计算题．【分析】先计算矩阵AB对应的变换，再求出在变换下点的坐标之间的对应关系，从而可求直线l'的方程．【解答】解：∵，∴=…，在直线l上任取一点P（x′，y′），经矩阵AB变换为点Q（x，y），则，∴，即…代入x′+y′﹣2=0中得，∴直线l′的方程为4x+y﹣8=0…【点评】本题重点考查矩阵变换，考查矩阵变换的运用，解题的关键是求出矩阵AB对应的变换选修4-4：坐标系与参数方程23．选修4﹣4：坐标系与参数方程在平面直角坐标系xOy中，圆C的参数方程为（θ为参数，r＞0）．以O为极点，x轴正半轴为极轴建立极坐标系，直线l的极坐标方程为．若圆C上的点到直线l的最大距离为3，求r的值．【考点】点的极坐标和直角坐标的互化；直线与圆的位置关系；参数方程化成普通方程．【专题】直线与圆．【分析】将直线和圆的方程化为直角坐标方程，利用直线和圆的位置关系求解．【解答】解：圆的直角坐标方程为（x+）2+（y+）2=r2，圆心的直角坐标（﹣，﹣）直线l的极坐标方程为即为x+y﹣=0，圆心O（﹣，﹣）到直线的距离d==2．圆O上的点到直线的最大距离为 2+r=3，解得r=1．【点评】本题考查极坐标、参数方程与普通方程互化的基础知识，考查点到直线距离公式等．选修4-5：不等式选讲24．已知实数x，y，z满足x+y+z=2，求2x2+3y2+z2的最小值．【考点】柯西不等式在函数极值中的应用．【专题】计算题；压轴题．【分析】利用题中条件：“x+y+z=2”构造柯西不等式：这个条件进行计算即可．【解答】解：由柯西不等式可知：故，当且仅当，即： 2x2+3y2+z2取得最小值为．【点评】本题考查用综合法证明不等式，关键是利用解题．【必做题】第22题、第23题，每题10分，共计20分，请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤.25．袋中装有围棋黑色和白色棋子共7枚，从中任取2枚棋子都是白色的概率为．现有甲、乙两人从袋中轮流摸取一枚棋子．甲先摸，乙后取，然后甲再取，…，取后均不放回，直到有一人取到白棋即终止．每枚棋子在每一次被摸出的机会都是等可能的．用X表示取棋子终止时所需的取棋子的次数．（1）求随机变量X的概率分布列和数学期望E（X）；（2）求甲取到白球的概率．【考点】离散型随机变量及其分布列；古典概型及其概率计算公式；离散型随机变量的期望与方差．【专题】计算题；转化思想；概率与统计．【分析】（1）由已知先出白子个数，进而可得随机变量X的概率分布列和数学期望E（X）；（2）记事件A=“甲取到白球”，则事件A包括以下三个互斥事件：A1=“甲第1次取球时取出白球”；A2=“甲第2次取球时取出白球”；A3=“甲第3次取球时取出白球”．利用互斥事件概率加法公式，可得：甲取到白球的概率．【解答】解：设袋中白球共有x个，则依题意知： =，即=，即 x2﹣x﹣6=0，解之得x=3，（x=﹣2舍去）．…（1）袋中的7枚棋子3白4黑，随机变量X的所有可能取值是1，2，3，4，5．P（x=1）==，P（x=2）==，P（x=3）==，P（x=4）==，P（x=5）==，…（注：此段的分配是每错1个扣，错到4个即不得分．）随机变量X的概率分布列为：所以E（X）=1×+2×+3×+4×+5×=2．…（2）记事件A=“甲取到白球”，则事件A包括以下三个互斥事件：A1=“甲第1次取球时取出白球”；A2=“甲第2次取球时取出白球”；A3=“甲第3次取球时取出白球”．依题意知：P（A1）==，P（A2）==，P（A3）==，…（注：此段的分配是每错1个扣，错到3个即不得分．）所以，甲取到白球的概率为P（A）=P（A1）+P（A2）+P（A3）=…【点评】本题考查的知识点是古典概型的概率计算公式，随机变量的分布列和数学期望，互斥事件概率加法公式，难度中档．26．设f（x）是定义在R上的函数，已知n∈N*，且g（x）=C f（）x0（1﹣x）n+C f（）x1（1﹣x）n﹣1+C f（）x2（1﹣x）n﹣2+…+C f（）x n（1﹣x）n．（1）若f（x）=1，求g（x）；（2）若f（x），求g（x）．。

辽宁省教研教改联合体2025届高三第一次调研考试数学试题试卷满分：150分考试时间：120分钟一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合{2,1,0,1,2}A =--，{}2|1B x x =>，则()R A B =I ð（）A.{}2,1,0,1-- B.{}1,0,1- C.{}2,2- D.{}1,1-2.已知复数13i1iz +=-的实部为()2,i 2i a z =+的虚部为b ，则()1i z a b =++在复平面内对应的点位于（）A .第一象限B.第二象限C.第三象限D.第四象限3.设a ，b 是向量，则“()()·0a b a b +-=”是“a b =- 或a b = ”的（）．A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件4.下列结论正确的是（）A.已知一组样本数据1x ，2x ，…，n x (12n x x x <<⋯<)，现有一组新的数据122x x +，232x x +，…，12n nx x -+，12n x x +，则与原样本数据相比，新的数据平均数不变，方差变大B.已知具有线性相关关系的变量x ，y ，其线性回归方程为ˆ0.3yx m =-，若样本点的中心为(),2.8m ，则实数m 的值是4C.50名学生在一模考试中的数学成绩()2~120,X N σ，已知(140)0.2P X >=，则[]100,140X ∈的人数为20人D.已知随机变量1~,3X B n ⎛⎫ ⎪⎝⎭，若()316E X +=，则5n =5.已知双曲线22:1,3y C x O -=为坐标原点，若直线2y x =+与双曲线C 的两条渐近线分别交于点,A B ，则OAB 内切圆的半径等于（）A.1- B.2 C.2 D.1-6.已知函数()ln e x xf x =的极值点为0x ，则010e ln x x =（）A.2e B.2 C.1eD.17.在菱形ABCD 中，2AB =，AC =ABC 沿对角线AC 折起，使点B 到达B '的位置，且二面角B AC D '--为直二面角，则三棱锥B ACD '-的外接球的表面积为（）A .5πB.16πC.20πD.100π8.设a 、b 、()0,1c ∈满足sin a b =，cos b c =，tan c a =，则（）A.2a c b +<，2ac b <B.2a c b +<，2ac b >C.2a c b +>，2ac b < D.2a c b +>，2ac b >二、选择题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分.9.已知函数()22sin cos f x x x x =-，则下列说法正确的是（）A.()f x 的值域为22⎡--⎣B.()f x 的对称中心为ππ,062k ⎛⎫+⎪⎝，Z k ∈C.()f x 在π0,2⎛⎫⎪⎝⎭上的单减区间为ππ,62⎛⎫ ⎪⎝⎭D.()f x 在50,π6⎛⎫⎪⎝⎭上的极值点个数为110.已知抛物线22(0)x py p =>的焦点为F ，过点F 的直线l 与抛物线交于A 、B 两点（点A 在第一象限），1||FA 与1||FB 的等差中项为12．抛物线在点A 、B 处的切线交于点M ，过点M 且垂直于y 轴的直线与y 轴交于点N ，O 为坐标原点，P 为抛物线上一点，则下列说法正确的是（）A.1p = B.tan AOB ∠的最大值为43-C.||||PN PF D.22MA MB +的最小值为1611.已知函数()e ln xf x a a x =--，则下列说法正确的有（）A.若a<0，则()f x 的值域为RB.若1a =，则过原点有且仅有一条直线与曲线()y f x =相切C.存在0a >，使得()f x 有三个零点D.若()0f x ≥，则a 的取值范围为[]0,e 三、填空题：本题共3小题，每小题5分，共15分.12.在数列{}n a 中，已知112a =，()12n n n a na ++=，则数列{}n a 的前2024项和2024S =__________．13.已知π0,2α⎛⎫∈ ⎪⎝⎭，若()0,2πβ∃∈，使()()2sin cos (αβαβα+++--成立，则β=__________．14.设严格递增的整数数列1a ，2a ，…，20a 满足11a =，2040a =.设f 为12a a +，23a a +，…，1920a a +这19个数中被3整除的项的个数，则f 的最大值为________，使得f 取到最大值的数列{}n a 的个数为________.四、解答题：本题共5小题，共77分.解答应写出文字说明、证明过程或演算步骤.15.已知,,a b c 分别为ABC 三个内角,,A B C 的对边，且cos sin b A A a c =+（1）求B ；（2）若2,b ABC =△的D 为AC 边上一点，满足2CD AD =，求BD 的长．16.已知函数2)()(e x f x x ax =-.（1）若曲线()y f x =在=1x -处的切线与y 轴垂直，求()y f x =的极值.（2）若()f x 在(0,)+∞只有一个零点，求a .17.如图，在四棱锥P ABCD -中，底面ABCD 是直角梯形，AB CD ，90ABC ∠=︒，且PA PD AD ==，PC PB =.（1）若O 为AD 的中点，证明：平面POC ⊥平面ABCD ；（2）若60CDA ∠=︒，112AB CD ==，线段PD 上的点M 满足DM DP λ= ，且平面PCB 与平面ACM夹角的余弦值为7，求实数λ的值.18.测试发现，某位惯用脚为右脚的足球球员甲在罚点球时，踢向球门左侧、中间和右侧的概率分别为0.5，0.1和0.4，并且，踢向左侧、中间和右侧时分别有0.1，0.2和0.2的概率踢飞或踢偏（没有射正）.守门员在扑点球一般会提前猜测方向.测试发现，某位守门员乙在扑点球时猜右侧（即足球运动员甲在罚点球时，踢向球门左侧）、中间和左侧（即足球运动员甲在罚点球时，踢向球门右侧）的概率分别为0.6，0.1和0.3.当他猜中方向为左侧或者右侧来时扑出点球的概率均为0.5，当他猜中方向为中间时，扑出点球的的概率为0.8.（1）求球员甲面对守门员乙时，第1次罚点球罚丢的概率；（2）若球员甲在上一轮罚丢点球，则下一轮面对球员甲罚点球时，守门员乙的信心将会激增，在猜中方向的前提下，所有方向扑出点球概率都会在原来的基础上增加0.1；若球员甲在上一轮罚进点球，守门员乙将会变得着急，会有0.2的概率提前移动，在守门员乙提前移动的情况下，若球员甲罚丢点球，则可获得重罚机会.已知守门员乙提前移动时扑出三个方向点球的概率均会增加0.1.假定因为守门员乙提前移动球员甲重罚点球仍属于第二轮，且重罚时守门员乙不再提前移动.（i ）求球员甲第二轮罚进点球的概率；（ii ）设()P k 为球员甲在第k 轮罚进点球的概率，若ξ满足对于{}1,2,3,4,5k ∀∈，()1()P P k ξ≥，直接写出符合题意的ξ.（注：最终结果均保留两位小数.）19.设A ，B 为椭圆C ：22143x y +=的短轴端点，P 为椭圆上异于A ，B 的任意一点，D 在直线4x =上．（1）求直线PA ，PB 的斜率的乘积；（2）证明：5π12APB ∠>；（3）过右焦点F 作x 轴的垂线l ，E 为l 上异于F 的任意一点，直线DF 交C 于M ，N 两点，记直线ED ，EM，EN的斜率分别为1k，2k，3k，是否存在1k，2k，3k的某个排列，使得这三个数成等差数列？若存在，加以证明；若不存在，请说明理由．。