《精品》2009年中考二次函数试题

中招专题训一一二次函数及其应用一、填空题：（每题 3分，共36分）21、 抛物线 y =— x + 1的开口向 __________ .2、 抛物线 y = 2x 2的对称轴是 __________ .3、 函数y = 2 （x — 1）2图象的顶点坐标为 ______ .4、 将抛物线 y = 2x 2向下平移2个单位，所得的抛物线的解析式为 ___________________5、 函数y = x 2+ bx + 3的图象经过点（一1, 0），贝U b= ________6、 二次函数 y = （x — 1）2+ 2,当x= _______ 时，y 有最小值.1（ 6分）如图，矩形的长是 4cm , 长和宽都增加 x cm ,那么面积增加 ycm ,① 求y 与x 之间的函数关系式•② 求当边长增加多少时，面积增加 8cm 2 7、 9、10、 11、 12函数 y = 2 （x — 1）2+ 3，当 x 8、将 y = x 2— 2x + 3 化成 y = a （x — h ）2+ k 的形式，则 y =_ 若点 A （ 2, m ）在函数y = x 2— 1的图像上，贝U A 点的坐标是. 抛物线y = 2x 2+ 3x — 4与y 轴的交点坐标是 _______________ . 请写出一个二次函数以（2, 3）为顶点，且开口向上• ____________已知二次函数 时，函数值 y 随x 的增大而增大.次函数的解析式是 二、选择题：（每题 1、在圆的面积公式 A 、一次函数关系2、已知函数 A 、土 2y = ax 2 + bx + c 的图像如图所示：则这个二y = _____ .3分，共18分）S = n r 2中，s 与r 的关系是 B 、正比例函数关系 y = （m + 2） x |m|是二次函数，贝U ） C 、反比例函数关系 m 等于（ ）5、 抛物线A 、开口向 6、 抛物线 A 、0 三、解答题： 2 y =—x 不具有的性质是 B 、对称轴是y 轴y = x 2 — 4x + c 的顶点在 B 、4（共 46 分） x 轴, ）C 、与y 轴不相交 贝U c 的值是（C 、一 4 最咼点是原点宽是 .2 3cm ，如果将xx2（8分）已知抛物线的顶点坐标是（一2, 1），且过点（1,—2），求抛物线的解析式3 （8分）用6m长的铝合金型材做一个形状如图所示的矩形窗框，应做成长、宽各为多少时，才能使做成的窗框的透光面积最大？最大透光面积是多少？4（6分）某农场种植一种蔬菜，销售员张平根据往年的销售情况，对今年种蔬菜的销售价格进行了预测，预测情况如图，图中的抛物线表示这种蔬菜销售价与月份之间的关系•观察图像，你能得到关于这种蔬菜销售情况的哪些信息？（至少写出四条）6（10分）有一个抛物线形的拱形桥洞，桥洞离水面的最大高度为所示，把它的图形放在直角坐标系中•①求这条抛物线所对应的函数关系式•②如图，在对称轴右边1m处，桥洞离水面的高是多少？*千克销售价（元）和投掷的最大高度4m，。

二次函数1．（2009，广东湛江）下列说法中：①4的算术平方根是±2;②2与8-是同类二次根式；③点(23)P -，关于原点对称的点的坐标是(23)--，；④抛物线21(3)12y x =--+的顶点坐标是(31)，． 其中正确的是（ ）A ．①②④B ．①③C ．②④D ．②③④1.（2009，广东清远）已知二次函数2y ax bx c =++中的x y ，满足下表：x … 2-1-0 1 2 … y…42- 2-…求这个二次函数关系式．19.（2009佛山市）（1）请在坐标系中画出二次函数的大致图象；（2）在同一个坐标系中画出的图象向上平移两个单位后的图象；（3）直接写出平移后的图象的解析式. 注：图中小正方形网格的边长为1.24．（2009佛山市）阅读材料：把形如2ax bx c ++的二次三项式(或其一部分)配成完全平方式的方法叫做配方法. 配方法的基本形式是完全平方公式的逆写，即2222()a ab b a b ±+=±．例如：22(1)3(2)2x x x -+-+、、2213224x x ⎛⎫-+ ⎪⎝⎭是224x x -+的三种不同形式的配方（即“余项”分别是常数项、一次项、二次项——见横线上的部分）．请根据阅读材料解决下列问题：（1）比照上面的例子，写出242x x -+三种不同形式的配方； （2）将22a ab b ++配方(至少两种形式)；（3）已知2223240a b c ab b c ++---+=，求a b c ++的值． 解：（1）242x x -+的配方（略）．（2）2222213()24a ab b a b ab a b b ⎛⎫++=+-=++ ⎪⎝⎭．（3）222324a b c ab b c ++---+=22213(2)(1)024a b b c ⎛⎫-+-+-= ⎪⎝⎭．从而1020102a b b c -=-=-=，，．即1a =，2b =，1c =．所以4a b c ++=． 24.（2009，广东茂名）如图2，在Rt ABC △中，906024BAC C BC ∠=∠==°，°，，点P 是BC 边上的动点（点P 与点B C 、不重合），过动点P 作PD BA ∥交AC 于点D ． （1）若ABC △与DAP △相似，则APD ∠是多少度？（2）试问：当PC 等于多少时，APD △的面积最大？最大面积是多少？24、解：（1）当△ABC 与△DAP 相似时，∠APD 的度数是60°或30°． （2）设PC x =，∵PD BA ∥，90BAC ∠=°，∴90PDC ∠=°， 又∵60C ∠=°，∴24cos6012AC == °，1cos602CD x x == °，∴1122AD x =-，而3sin 602PD x x == °，∴1131122222APD S PD AD x x ⎛⎫==-⎪⎝⎭ △ 2233(24)(12)18388x x x =--=--+． ∴PC 等于12时，APD △的面积最大，最大面积是183．1.（2009，山东聊城）徒骇河大桥是我市第一座特大型桥梁，大桥桥体造型新颖，气势恢宏，两条拱肋如长虹卧波，极具时代气息(如图①)．大桥为中承式悬索拱桥，大桥的主拱肋ACB 是抛物线的一部分(如图②)，跨径AB 为100m ，拱高OC 为25m ，抛物线顶点C 到桥面的距离为17m ．(1)请建立适当的坐标系，求该抛物线所对应的函数关系式；(2)七月份汛期来临，河水水位上涨，假设水位比AB 所在直线高出1.96m ，这时位于水面上的拱肋的跨径是多少？在不计桥面厚度的情况，一条高出水面4.6m 的游船是否能够顺利通过大桥？60A D CB 图2P。

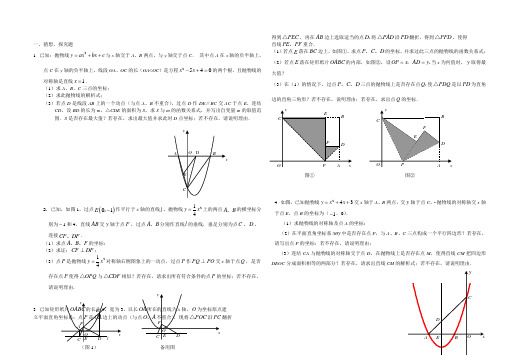
一、猜想、探究题1. 已知：抛物线2y ax bx c =++与x 轴交于A 、B 两点，与y 轴交于点C ． 其中点A 在x 轴的负半轴上，点C 在y 轴的负半轴上，线段OA 、OC 的长（OA <OC ）是方程2540x x -+=的两个根，且抛物线的对称轴是直线1x =．（1）求A 、B 、C 三点的坐标； （2）求此抛物线的解析式；（3）若点D 是线段AB 上的一个动点（与点A 、B 不重合），过点D 作DE ∥BC 交AC 于点E ，连结CD ，设BD 的长为m ，△CDE 的面积为S ，求S 与m 的函数关系式，并写出自变量m 的取值范围．S 是否存在最大值？若存在，求出最大值并求此时D 点坐标；若不存在，请说明理由．2. 已知，如图1，过点()01E -，作平行于x 轴的直线l ，抛物线214y x =上的两点A B 、的横坐标分别为-1和4，直线AB 交y 轴于点F ，过点A B 、分别作直线l 的垂线，垂足分别为点C 、D ，连接CF DF 、．（1）求点A B F 、、的坐标； （2）求证：CF DF ⊥； （3）点P 是抛物线214y x =对称轴右侧图象上的一动点，过点P 作PQ PO ⊥交x 轴于点Q ，是否存在点P 使得OPQ △与CDF △相似？若存在，请求出所有符合条件的点P 的坐标；若不存在，请说明理由．3.，以长翻折得到PEC △，再在AB 边上选取适当的点D ，将PAD △沿PD 翻折，得到PFD △，使得 直线PE PF 、重合．（1）若点E 落在BC 边上，如图①，求点P C D 、、的坐标，并求过此三点的抛物线的函数关系式； （2）若点E 落在矩形纸片OABC 的内部，如图②，设OP x AD y ==，，当x 为何值时，y 取得最大值？（3）在（1）的情况下，过点P C D 、、三点的抛物线上是否存在点Q ，使PDQ △是以PD 为直角边的直角三角形？若不存在，说明理由；若存在，求出点Q 的坐标．4. 如图，已知抛物线243y x x =++交x 于点E ，点B 的坐标为（1-，0）． （1）求抛物线的对称轴及点A （2）在平面直角坐标系xoy 请写出点P （3）连结CA 与抛物线的对称轴交于点DEOC（图1） 备用图图①5. 如图①， 已知抛物线32++=bx ax y （a ≠0）与x 轴交于点A （1，0）和点B （－3，0），与y 轴交于点C ．（1）求抛物线的解析式；（2）设抛物线的对称轴与x 轴交于点M ，问在对称轴上是否存在点P ，使△CMP 为等腰三角形？若存在，请直接写出所有符合条件的点P 的坐标；若不存在，请说明理由．（3）如图②，若点E 为第二象限抛物线上一动点，连接BE 、CE ，求四边形BOCE 面积的最大值，并求此时E 点的坐标．二、动态几何 6. 如图，在梯形ABCD 中，906DC AB A AD ∠==∥，°，厘米，4DC =厘米，BC 的坡度34i =∶，动点P 从A 出发以2厘米/秒的速度沿AB 方向向点B 运动，动点Q 从点B 出发以3厘米/秒的速度沿B C D →→方向向点D 运动，两个动点同时出发，当其中一个动点到达终点时，另一个动点也随之停止．设动点运动的时间为t 秒． （1）求边BC 的长；（2）当t 为何值时，PC 与BQ 相互平分；（3）连结PQ ，设PBQ △的面积为y ，探求y 与t 的函数关系式，求t 为何值时，y 有最大值？最大值是多少？7. 已知：直线112y x =+与y 轴交于A ，与x 轴交于D ，抛物线212y x bx c =++与直线交于A 、E 两点，与x 轴交于B 、C 两点，且B 点坐标为 （1，0）．（1）求抛物线的解析式；（2）动点P 在x 轴上移动，当△P AE 是直角三角形时，求点P 的坐标．（3）在抛物线的对称轴上找一点M ，使||AM MC -的值最大，求出点M 的坐标．8. 已知：抛物线()20y ax bx c a =++≠的对称轴为1x =-，与x 轴交于A B ，两点，与y 轴交于点C ，其中()30A -，、()02C -，．（1）求这条抛物线的函数表达式．（2）已知在对称轴上存在一点P ，使得PBC △的周长最小．请求出点P 的坐标． （3）若点D 是线段OC 上的一个动点（不与点O 、点C 重合）．过点D 作DE PC ∥交x 轴于点E ．连接PD 、PE ．设CD 的长为m ，PDE △的面积为S ．求S 与m 之间的函数关系式．试说明S 是否存在最大值，若存在，请求出最大值；若不存在，请说明理由．9. 如图1，已知抛物线经过坐标原点O 和x 轴上另一点E ，的图① 图②顶点A 与点O 重合，AD AB 、分别在x 轴、y 轴上，且2AD =，3AB =．（1）求该抛物线所对应的函数关系式；（2）将矩形ABCD 以每秒1个单位长度的速度从图1所示的位置沿x 轴的正方向匀速平行移动，同时一动点P 也以相同的速度．．．．．从点A 出发向B 匀速移动．设它们运动的时间为t 秒（03t ≤≤），直线AB 与该抛物线的交点为N （如图2所示）．①当52t =时，判断点P 是否在直线ME 上，并说明理由； ②设以P N C D 、、、为顶点的多边形面积为S ，试问S 是否存在最大值？若存在，求出这个最大值；若不存在，请说明理由．10. 已知抛物线：x x y 22121+-=． （1）求抛物线1y 的顶点坐标．（2）将抛物线1y 向右平移2个单位，再向上平移1个单位，得到抛物线2y ，求抛物线2y 的解析式． （3）如下图，抛物线2y 的顶点为P ，x 轴上有一动点M ，在1y 、2y 这两条抛物线上是否存在点N ，使O （原点）、P 、M 、N 四点构成以OP 为一边的平行四边形，若存在，求出N 点的坐标；若不存在，请说明理由．【提示：抛物线c bx ax y ++=2（0a ≠）的对称轴是，a bx 2-=顶点坐标是2424b ac b aa ⎛⎫-- ⎪⎝⎭，】11. 如图，已知抛物线C 1：()522-+=x a y 的顶点为P ，与x 轴相交于A 、B 两点（点A 在点B的左边），点B 的横坐标是1．（1）求P 点坐标及a 的值；（4分）（2）如图（1），抛物线C 2与抛物线C 1关于x 轴对称，将抛物线C 2向右平移，平移后的抛物线记为C 3，C 3的顶点为M ，当点P 、M 关于点B 成中心对称时，求C 3的解析式；（4分）（3）如图（2），点Q 是x 轴正半轴上一点，将抛物线C 1绕点Q 旋转180°后得到抛物线C 4．抛物线C 4的顶点为N ，与x 轴相交于E 、F 两点（点E 在点F 的左边），当以点P 、N 、F 为顶点的三角形是直角三角形时，求点Q 的坐标．（5分）12.8)，．抛物线y =（1（2B 向终点D E ．①过点E 作EF AD ⊥于点F ，交抛物线于点G ．当t 为何值时，线段EG 最长？ ②连接EQ ．在点P Q 、运动的过程中，判断有几个时刻使得CEQ △是等腰三角形？ 请直接写出相应的t 值．图2图1 图1 图213. 如图1，已知正比例函数和反比例函数的图像都经过点M （－2，1-），且P （1-，－2）为双曲线上的一点，Q 为坐标平面上一动点，P A 垂直于x 轴，QB 垂直于y 轴，垂足分别是A 、B ． （1）写出正比例函数和反比例函数的关系式；（2）当点Q 在直线MO 上运动时，直线MO 上是否存在这样的点Q ，使得△OBQ 与△OAP 面积相等？如果存在，请求出点的坐标，如果不存在，请说明理由；（3）如图2，当点Q 在第一象限中的双曲线上运动时，作以OP 、OQ 为邻边的平行四边形OPCQ ，求平行四边形OPCQ 周长的最小值．14. 如图，矩形ABCD 中，AB = 6cm ，AD = 3cm ，点E 在边DC 上，且DE = 4cm ．动点P 从点A 开始沿着A →B →C →E 的路线以2cm/s 的速度移动，动点Q 从点A 开始沿着AE 以1cm/s 的速度移动，当点Q 移动到点E 时，点P 停止移动．若点P 、Q 从点A 同时出发，设点Q 移动时间为t （s ），P 、Q 两点运动路线与线段PQ 围成的图形面积为S （cm 2），求S 与t 的函数关系式．15. 如图，已知二次函数22)(m k m x y -++=的图象与x 轴相交于两个不同的点1(0)A x ，、2(0)B x ，，与y 轴的交点为C ．设ABC △的外接圆的圆心为点P ．（1）求P ⊙与y 轴的另一个交点D 的坐标；（2）如果AB 恰好为P ⊙的直径，且ABC △的面积等于5，求m 和k 的值．16. 如图，点A B 、坐标分别为（4，0）、（0，8），点C 是线段OB 上一动点，点E 在x 轴正半轴上，四边形OEDC 是矩形，且2OE OC =．设(0)OE t t =>，矩形OEDC 与AOB △重合部分的面积为S ．根据上述条件，回答下列问题：（1）当矩形OEDC 的顶点D 在直线AB 上时，求t 的值； （2）当4t =时，求S 的值；图1 xy B ()A OMQP图2xy()B CAOMPQD E P AC Q（3）直接写出S 与t 的函数关系式；（不必写出解题过程） （4）若12S =，则t = ．17. 直线364y x =-+与坐标轴分别交于A B 、两点，动点P Q 、同时从O 点出发，同时到达A 点，运动停止．点Q 沿线段OA 运动，速度为每秒1个单位长度，点P 沿路线O →B →A 运动． （1）直接写出A B 、两点的坐标；（2）设点Q 的运动时间为t 秒，OPQ △的面积为S ，求出S 与t 之间的函数关系式； （3）当485S =时，求出点P 的坐标，并直接写出以点O P Q 、、为顶点的平行四边形的第四个顶点M 的坐标．18. 如图1，过△ABC 的三个顶点分别作出与水平线垂直的三条直线，外侧两条直线之间的距离叫△ABC 的“水平宽”（a ），中间的这条直线在△ABC 内部的线段的长度叫△ABC 的“铅垂高”（h ）．我们可得出一种计算三角形面积的新方法：ah S ABC 21=∆，即三角形面积等于水平宽与铅垂高乘积的一半．解答下列问题：如图2，抛物线顶点坐标为点C （1，4），交x 轴于点A （3，0），交y 轴于点B ． （1）求抛物线和直线AB 的解析式； （2） 求△CAB 的铅垂高CD 及CAB S △；（3） 设点P 是抛物线（在第一象限内）上的一个动点，是否存在一点P ，使S △P AB =89S △CAB ，若存在，求出P 点的坐标；若不存在，请说明理由．19. 如图，在平面直角坐标系中，点A C 、的坐标分别为(10)(03)--，、，，点B 在x 轴上．已知某二次函数的图象经过A 、B 、C 三点，且它的对称轴为直线1x =，点P 为直线BC 下方的二次函数图象上的一个动点（点P 与B 、C 不重合），过点P 作y 轴的平行线交BC 于点F ． （1）求该二次函数的解析式；（2）若设点P 的横坐标为m ，用含m 的代数式表示线段PF 的长． （3）求PBC △面积的最大值，并求此时点P 的坐标．xAO QPBy A BC铅垂高水平宽 ha图1图2 x CO y AB D 1 1 x yB F O A CPx =120. 如图所示，菱形ABCD 的边长为6厘米，60B ∠=°．从初始时刻开始，点P 、Q 同时从A 点出发，点P 以1厘米/秒的速度沿A C B →→的方向运动，点Q 以2厘米/秒的速度沿A B C D →→→的方向运动，当点Q 运动到D 点时，P 、Q 两点同时停止运动，设P 、Q 运动的时间为x 秒时，APQ △与ABC △重叠部分．．．．的面积为y 平方厘米（这里规定：点和线段是面积为O 的三角形），解答下列问题： （1）点P 、Q 从出发到相遇所用时间是 秒；（2）点P 、Q 从开始运动到停止的过程中，当APQ △是等边三角形时x 的值是 秒； （3）求y 与x 之间的函数关系式．21. 定义一种变换：平移抛物线1F 得到抛物线2F ，使2F 经过1F 的顶点A ．设2F 的对称轴分别交12F F ，于点D B ，，点C 是点A 关于直线BD 的对称点．（1）如图1，若1F ：2y x =，经过变换后，得到2F ：2y x bx =+，点C 的坐标为(20)，，则①b 的值等于______________；②四边形ABCD 为（ ）A ．平行四边形B ．矩形C ．菱形D ．正方形（2）如图2，若1F ：2y ax c =+，经过变换后，点B 的坐标为(21)c -，，求ABD △的面积； （3）如图3，若1F ：2127333y x x =-+，经过变换后，AC =P 是直线AC 上的动点，求点P 到点D 的距离和到直线AD 的距离之和的最小值． 22. 如图，已知直线112y x =-+交坐标轴于B A ，两点，以线段AB 为边向上作正方形ABCD ，过点C D ，A ，的抛物线与直线另一个交点为E ．（1）请直接写出点D C ,的坐标； （2）求抛物线的解析式；（3）若正方形以每秒5个单位长度的速度沿射线AB 下滑，直至顶点D 落在x 轴上时停止．设正方形落在x 轴下方部分的面积为S ，求S 关于滑行时间t 的函数关系式，并写出相应自变量t 的取值范围；（4）在（3）的条件下，抛物线与正方形一起平移，同时停止，求抛物线上E C , 两点间的抛物线弧所扫过的面积．23. 如图，点A B 、坐标分别为（4，0）、（0，8），点C 是线段OB 上一动点，点E 在x 轴正半轴上，四边形OEDC 是矩形，且2OE OC =．设(0)OE t t =>，矩形OEDC 与AOB △重合部分的面积为S ．根据上述条件，回答下列问题：（1）当矩形OEDC 的顶点D 在直线AB 上时，求t 的值； （2）当4t =时，求S 的值；（3）直接写出S 与t 的函数关系式；（不必写出解题过程） （4）若12S =，则t = ．24. 如图所示，某校计划将一块形状为锐角三角形ABCABC 的边BC 长120米，高AD 长80米．学校计划将它分割成AHG △、EFGH 四部分（如图）．其中矩形EFGH 的一边EF 在边BC 上，其余两个顶点H 、G 分别在边AB 、AC（图1）（图2）（图3）备用图112x -+上．现计划在AHG △上种草，每平米投资6元；在BHE △、FCG △上都种花，每平方米投资10元；在矩形EFGH 上兴建爱心鱼池，每平方米投资4元．（1）当FG 长为多少米时，种草的面积与种花的面积相等？（2）当矩形EFGH 的边FG 为多少米时，ABC △空地改造总投资最小？最小值为多少？25. 已知：12t t ，是方程22240t t +-=的两个实数根，且12t t <，抛物线223y x bx c =++的图象经过点12(0)(0)A t B t ，，，．（1）求这个抛物线的解析式；（2）设点()P x y ，是抛物线上一动点，且位于第三象限，四边形OPAQ 是以OA 为对角线的平行四边形，求OPAQ Y 的面积S 与x 之间的函数关系式，并写出自变量x 的取值范围；（3）在（2）的条件下，当OPAQ Y 的面积为24时，是否存在这样的点P ，使OPAQ Y 为正方形？若存在，求出P 点坐标；若不存在，说明理由．三、说理题26. 如图，抛物线经过(40)(10)(02)A B C -，，，，，三点．（1）求出抛物线的解析式；（2）P 是抛物线上一动点，过P 作PM x ⊥轴，垂足为M ，是否存在P 点，使得以A ，P ，M 为顶点的三角形与OAC △相似？若存在，请求出符合条件的点P 的坐标；若不存在，请说明理由； （3）在直线AC 上方的抛物线上有一点D ，使得DCA △的面积最大，求出点D 的坐标．27. 如图，在平面直角坐标系xOy 中，半径为1的圆的圆心O 在坐标原点，且与两坐标轴分别交于A B C D 、、、四点．抛物线2y ax bx c =++与y 轴交于点D ，与直线y x =交于点M N 、，且MA NC 、分别与圆O 相切于点A 和点C ．（1）求抛物线的解析式；（2）抛物线的对称轴交x 轴于点E ，连结DE ，并延长DE 交圆O 于F ，求EF 的长．（3）过点B 作圆O 的切线交DC 的延长线于点P ，判断点P 是否在抛物线上，说明理由．28. 如图1，已知：抛物线212y x bx c =++与x 轴交于A B 、两点，与y 轴交于点C ，经过B C 、两点的直线是122y x =-，连结AC ． （1）B C 、两点坐标分别为B （_____，_____）、C （_____，_____），抛物线的函数关系式为______________；（2）判断ABC △的形状，并说明理由；（3）若ABC △内部能否截出面积最大的矩形DEFC （顶点D E F 、、、G 在ABC △各边上）？A GH K B E D F C若能，求出在AB 边上的矩形顶点的坐标；若不能，请说明理由．[抛物线2y ax bx c =++的顶点坐标是24,24b ac b a a ⎛⎫-- ⎪⎝⎭]29. 已知：如图，在平面直角坐标系xOy 中，矩形OABC 的边OA 在y 轴的正半轴上，OC 在x 轴的正半轴上，OA =2，OC =3．过原点O 作∠AOC 的平分线交AB 于点D ，连接DC ，过点D 作DE ⊥DC ，交OA 于点E ．（1）求过点E 、D 、C 的抛物线的解析式；（2）将∠EDC 绕点D 按顺时针方向旋转后，角的一边与y 轴的正半轴交于点F ，另一边与线段OC 交于点G ．如果DF 与（1）中的抛物线交于另一点M ，点M 的横坐标为65，那么EF =2GO 是否成立？若成立，请给予证明；若不成立，请说明理由；（3）对于（2）中的点G ，在位于第一象限内的该抛物线上是否存在点Q ，使得直线GQ 与AB 的交点P 与点C 、G 构成的△PCG 是等腰三角形？若存在，请求出点Q 的坐标；若不存在，请说明理由．30. 如图所示，将矩形OABC 沿AE 折叠，使点O 恰好落在BC 上F 处，以CF 为边作正方形CFGH ，延长BC 至M ，使CM CE EO =-，再以CM 、CO 为边作矩形CMNO ． （1）试比较EO 、EC 的大小，并说明理由． （2）令CFGHCMNOS m S =四边形四边形，请问m 是否为定值？若是，请求出m 的值；若不是，请说明理由．（3）在（2）的条件下，若113CO CE Q ==，，为AE 上一点且23QF =，抛物线2y mx bx c =++经过C 、Q 两点，请求出此抛物线的解析式．（4）在（3）的条件下，若抛物线2y mx bx c =++与线段AB 交于点P ，试问在直线BC 上是否存在点K ，使得以P 、B 、K 为顶点的三角形与AEF △相似？若存在，请求直线KP 与y 轴的交点T 的坐标；若不存在，请说明理由．图1 图2(备用)x。

1. (2009杭州) 已知点P （x ，y ）在函数x x y -+=21的图象上，那么点P 应在平面直角坐标系中的A.第一象限B. 第二象限C. 第三象限D. 第四象限 2. （2009南州）抛物线的图象如图1所示，根据图象可知，抛物线的解析式可能．．是（ ） A 、y=x 2-x-2 B 、y=121212++-x C 、y=121212+--x x D 、y=22++-x x 3. （2009莆田）二次函数2241y x x =-++的图象如何平移就褥到22y x =-的图像( )A ．向左平移1个单位，再向上平移3个单位．B ．向右平移1个单位，再向上平移3个单位．C ．向左平移1个单位，再向下平移3个单位．D ．向右平移1个单位，再向下平移3个单位。

4. （2009丽水）已知二次函数y ＝ax 2＋bx ＋c(a ≠0)的图象如图所示，给出以下结论： ①a ＞0.②该函数的图象关于直线1x =对称. ③当13x x =-=或时，函数y 的值都等于0. 其中正确结论的个数是 A ．3 B ．2 C ．1 D ．05. （2009嘉兴）已知0≠a ，在同一直角坐标系中，函数ax y =与2ax y =的图象有可能是（ ▲ ）6. （2009广州）二次函数2)1(2+-=x y 的最小值是（ ） （A ）2 （B ）1 （C ）-1 （D ）-27. （2009烟台）二次函数2y ax bx c =++的图象如图所示，则一次函数24y bx b ac=+-与反比例函数a b cy x++=在同一坐标系内的图象大致为（ ）图1(第7题) OACD xxxx8. （2009黄石）已知二次函数y=ax 2+bx+c （a ≠0）的图象如图3所示， 下列结论：①abc ＞0 ②2a+b ＜0 ③4a －2b+c ＜0 ④a+c ＞0， 其中正确结论的个数为（ ）A 、4个B 、3个C 、2个D 、1个9. （2009湖州）已知抛物线2y ax bx c =++（a ＞0）的对称轴为直线1x =，且经过点()()212y y -1，，，，试比较1y 和2y 的大小：1y _2y （填“>”，“<”或“=”） 10. (2009重庆)某电视机生产厂家去年销往农村的某品牌电视机每台的售价y （元）与月份x 之间满足函数关系260050+-=x y ，去年的月销售量p （万台）与月份x 之间成（1（2）由于受国际金融危机的影响，今年1、2月份该品牌电视机销往农村的售价都比去年12月份下降了%m ，且每月的销售量都比去年12月份下降了%5.1m 。

专题训练——二次函数一、选择题1.把抛物线2x y =向右平移2个单位得到的抛物线是( )A 、2x y 2+=B 、2x y 2-=C 、2)2x (y +=D 、2)2x (y -= 2．抛物线2(1)3y x =-+的对称轴是（ ） A ．直线1x =B ．直线3x =C ．直线1x =-D ．直线3x =-3、若A （1,413y -），B （2,45y -），C （3,41y ）为二次函数245y x x =+-的图象上的三点，则1,y 2,y 3y 的大小关系是（ ）A ．123y y y <<B ．213y y y <<C ．312y y y <<D ．132y y y <<4、已知：二次函数()220y ax bx a b a =+++≠的图像为下列图像之一，则a 的值为( )A .－1B ． 1C . －3D . －45、已知二次函数c bx ax y ++=2的图象过点A （1，2），B （3，2），C （5，7）．若点M （-2，y 1），N （-1，y 2），K （8，y 3）也在二次函数c bx ax y ++=2的图象上，则下列结论正确的是A ．y 1＜y 2＜y 3B ．y 2＜y 1＜y 3C ．y 3＜y 1＜y 2D ．y 1＜y 3＜y 26、若A （-4，y 1），B （-3，y 2），C （1，y 3）为二次函数y=x 2+4x-5的图象上的三点，则y 1，y 2，y 3的大小关系是（ ）A 、y 1＜y 2＜y 3B 、y 2＜y 1＜y 3C 、y 3＜y 1＜y 2D 、y 1＜y 3＜y 27.若一次函数(1)y m x m =++的图像过第一、三、四象限,则函数2y mx mx =-（ ） A.有最大值4m B..有最大值4m -C.有最小值4m D.有最小值8、如图，记抛物线21y x =-+的图象与x 正半轴的交点为A ，将线段OA 分成n 等份．设分点分别为1P ，2P ，…，1n P -，过每个分点作x 轴的垂线，分别与抛物线交于点1Q ，2Q ，…，1n Q -，再记直角三角形11OPQ ，122PPQ ，…的面积分别为1S ，2S ，…，这样就有21312n S n -=，22342n S n -=，…；记121n W S S S -=+++…，当n 越来越大时，你猜想W 最接近的常数是（ ） A ．23B ．12C ．13D ．149.二次函数22(1)3y x =-+的图象的顶点坐标是（ ）A ．(13)，B ．(13)-，C ．(13)-，D ．(13)--， 10．二次函数2(0)y ax bx c a =++≠的图象如图4所示，则下列说法不正确的是（ ）A ． 240b ac ->B ．0a >C ．0c >D ．02ba-<11.二次函数2y ax bx c =++的图像如图所示，则点c Q a b ⎛⎫ ⎪⎝⎭，在（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限12．二次函数y = ax 2+ bx + c 的部分对应值如下表：利用二次函数的图象可知，当函数值y ＜0时，x 的取值范围是（ ）． A ．x ＜0或x ＞2 B ．0＜x ＜2 C ．x ＜－1或x ＞3 D ．－1＜x ＜3（第8题） x13.已知二次函数2y ax bx c =++（其中000a b c >><，，），关于这个二次函数的图象有如下说法：①图象的开口一定向上；②图象的顶点一定在第四象限；③图象与x 轴的交点至少有一个在y 轴的右侧．以上说法正确的个数为（ ） A ．0B ．1C ．2D ．314.二次函数362+-=x kx y 的图象与x 轴有交点，则k 的取值范围是【 】A ．3<kB ．03≠<k k 且C ．3≤kD ．03≠≤k k 且15.已知反比例函数xky =的图象如下右图所示，则二次函数222k x kx y +-=的图象大致为【 】16．一个函数的图象如图，给出以下结论： ①当0x =时，函数值最大；②当02x <<时，函数y 随x 的增大而减小；③存在001x <<，当0x x =时，函数值为0． 其中正确的结论是（ ）A ．①②B ．①③C ．②③D ．①②③17.如图，正方形ABCD 的边长为10，四个全等的小正方形的对称中心分别在正方形ABCD 的顶点上，且它们的各边与正方形ABCD 各边平行或垂直．若小正方形的边长为x ，且010x <≤，阴影部分的面积为y ，则能反映y 与x 之间函数关系的大致图象是（ ）A ．B ．xC ．D ．A ．B ．C ．D ．18.二次函数c bx ax y ++=2的图象如图所示，则下列关系式不正确的是（ ）A 、a ＜0B 、abc ＞0C 、c b a ++＞0D 、ac b 42-＞019. 在同一直角坐标系中，函数y mx m =+和222y mx x =-++（m 是常数，且0m ≠）的图象可能．．是（ ）20. 在平面直角坐标系中，如果抛物线y ＝2x 2不动，而把x 轴、y 轴分别向上、向右平移2个单位，那么在新坐标系下抛物线的解析式是 ( )A ．y ＝2(x －2)2 + 2B ．y ＝2(x + 2)2－2C ．y ＝2(x －2)2－2D ．y ＝2(x + 2)2 + 2 21.已知二次函数2(0)y ax bx c a =++≠的图象如图所示， 当0y <时，x 的取值范围是（ ） A ．13x -<<B ．3x >C ．1x <-D ．3x >或1x <-22．二次函数342++=x x y 的图像可以由二次函数2x y =的图像 平移而得到，下列平移正确的是A ．先向左平移2个单位，再向上平移1个单位B ．先向左平移2个单位，再向下平移1个单位C ．先向右平移2个单位，再向上平移1个单位D ．先向右平移2个单位，再向下平移1个单位23．抛物线5422---=x x y 经过平移得到22x y -=，平移方法是（ ）A ．向左平移1个单位，再向下平移3个单位B ．向左平移1个单位，再向上平移3个单位C ．向右平移1个单位，再向下平移3个单位Ａ．Ｂ．Ｃ． Ｄ．D ．向右平移1个单位，再向上平移3个单位 24.下列命题：①若0a b c ++=，则240b ac -≥；②若b a c >+，则一元二次方程20ax bx c ++=有两个不相等的实数根； ③若23b a c =+，则一元二次方程20ax bx c ++=有两个不相等的实数根； ④若240b ac ->，则二次函数的图像与坐标轴的公共点的个数是2或3.其中正确的是（ ）．Ａ.只有①②③ Ｂ．只有①③④ Ｃ．只有①④ Ｄ． 只有②③④． 25．函数1y x x=+的图象如图所示，下列对该函数性质的论断不可能正确．．．．．的是（ ） A ．该函数的图象是中心对称图形B ．当0x >时，该函数在1x =时取得最小值2C ．在每个象限内，y 的值随x 值的增大而减小D ．y 的值不可能为1二、填空题1.将抛物线2(0)y ax bx c a =++≠向下平移3个单位，再向左平移4个单位得到抛物线2245y x x =--+，则原抛物线的顶点坐标是 。

全国免费客户服务电话：400-715-6688地址：西安经济技术开发区凤城一路8号御道华城A 座10层2009年中考试题专题之14-二次函数与一元二次方程试题及答案一、选择题 1、（2009年台湾）下列哪一个函数，其图形与x 轴有两个交点？(A) y =17(x +83)2+2274 (B) y =17(x -83)2+2274 (C) y = -17(x -83)2-2274 (D) y = -17(x +83)2+2274。

2、（2009年台州市）已知二次函数c bx ax y ++=2的y 与x 的部分对应值如下表：x… 1- 0 1 3 … y…3-131…A ．抛物线开口向上B ．抛物线与y 轴交于负半轴C ．当x ＝4时，y ＞0D ．方程02=++c bx ax 的正根在3与4之间二、填空题1、（2009年内蒙古包头）将一条长为20cm 的铁丝剪成两段，并以每一段铁丝的长度为周长各做成一个正方形，则这两个正方形面积之和的最小值是cm 2．2、（2009年甘肃白银）抛物线2y x bx c =-++的部分图象如图8所示，请写出与其关系式、图象相关的2个正确结论：，．（对称轴方程，图象与x 正半轴、y 轴交点坐标例外）3、（2009年甘肃庆阳）从地面垂直向上抛出一小球，小球的高度h （米）与小球运动时间t （秒）的函数关系式是29.8 4.9h t t =-，那么小球运动中的最大高度为米．4、（2009年包头）将一条长为20cm 的铁丝剪成两段，并以每一段铁丝的长度为周长各做成一个正方形，则这两个正方形面积之和的最小值 是cm 2．5、（2009年包头）已知二次函数2y ax bx c =++的图象与x 轴交于点(20)-，、1(0)x ，，且112x <<，与y 轴的正半轴的交点在(02)，的下方．下列结论：①420a b c -+=；②0a b <<；③20a c +>；④210a b -+>．其中正确结论的个数是个．三、解答题1、（2009年北京市）已知关于x 的一元二次方程22410x x k ++-=有实数根，k 为正整数.（1）求k 的值；（2）当此方程有两个非零的整数根时，将关于x 的二次函数2241y x x k =++-的图象向下平移8个单位，求平移后的图象的解析式；（3）在（2）的条件下，将平移后的二次函数的图象在x 轴下方的部分沿x 轴翻折，图象的其余部分保持不变，得到一个新的图象.请你结合这个新的图象回答：当直线()12y x b b k =+<与此图象有两个公共点时，b 的取值范围. 2、（2009 安徽）已知某种水果的批发单价与批发量的函数关系如图（1）所示． （1）请说明图中①、②两段函数图象的实际意义． 【解】（2）写出批发该种水果的资金金额w （元）与批发量m （kg ）之间的函数关系式；在下图的坐标系中画出该函数图象；指出金额在什 么范围内，以同样的资金可以批发到较多数量的该种水果． （3）经调查，某经销商销售该种水果的日最高销量与零售价之间的函数关系如图（2）所示，该经销商拟每日售出60kg 以上该种水果， 且当日零售价不变，请你帮助该经销商设计进货和销售的方案， 使得当日获得的利润最大．3、（2009年常德市）已知二次函数过点A （0，2-），B （1-，0），C （5948，）． （1）求此二次函数的解析式； （2）判断点M （1，12）是否在直线AC 上？ （3）过点M （1，12）作一条直线l 与二次函数的图象交于E 、F 两点（不同于A ，B ，C 三点），请自已给出E 点的坐标，并证明△BEF 是直角三角形．4、（2009年湖南长沙）为了扶持大学生自主创业，市政府提供了80万元无息贷款，用于某大学生开办公司生产并销售自主研发的一种电子产品，并约定用该公司经营的利润逐步偿还无息贷款．已知该产品的生产成本为每件40元，员工每人每月的工资为2500元，公司每月需支付其它费用15万元．该产品每月销售量y （万件）与销售单价x （元）之间的函数关系如图所示．（1）求月销售量y （万件）与销售单价x （元）之间的函数关系式；（2）当销售单价定为50元时，为保证公司月利润达到5万元（利润＝销售额－生产成本－员工工资－其它费用），该公司可安排员工多少人？（3）若该公司有80名员工，则该公司最早可在几个月后还清无息贷款？5、（2009年内蒙古包头）某商场试销一种成本为每件60元的服装，规定试销期间销售单价不低于成本单价，且获利不得高于45%，经试销发现，销售量y （件）与销售单价x（元）图8符合一次函数y kx b =+，且65x =时，55y =；75x =时，45y =． （1）求一次函数y kx b =+的表达式；（2）若该商场获得利润为W 元，试写出利润W 与销售单价x 之间的关系式；销售单价定为多少元时，商场可获得最大利润，最大利润是多少元？（3）若该商场获得利润不低于500元，试确定销售单价x 的范围．6、（2009年杭州市）已知平行于x 轴的直线)0(≠=a a y 与函数x y =和函数xy 1=的图象分别交于点A 和点B ，又有定点P （2，0）． （1）若0>a ，且tan ∠POB =91，求线段AB 的长； （2）在过A ，B 两点且顶点在直线x y =上的抛物线中，已知线段AB =38，且在它的对称轴左边时，y 随着x 的增大而增大，试求出满足条件的抛物线的解析式；（3）已知经过A ，B ，P 三点的抛物线，平移后能得到259x y =的图象，求点P 到直线AB 的距离． 7、（2009年娄底）已知关于x 的二次函数y =x 2-（2m -1）x +m 2+3m +4.（1）探究m 满足什么条件时，二次函数y 的图象与x 轴的交点的个数.（2）设二次函数y 的图象与x 轴的交点为A （x 1，0），B （x 2，0），且21x +22x =5，与y轴的交点为C ，它的顶点为M ，求直线CM 的解析式.9、（2009烟台市）某商场将进价为2000元的冰箱以2400元售出，平均每天能售出8台，为了配合国家“家电下乡”政策的实施，商场决定采取适当的降价措施.调查表明：这种冰箱的售价每降低50元，平均每天就能多售出4台．（1）假设每台冰箱降价x 元，商场每天销售这种冰箱的利润是y 元，请写出y 与x 之间的函数表达式；（不要求写自变量的取值范围）（2）商场要想在这种冰箱销售中每天盈利4800元，同时又要使百姓得到实惠，每台冰箱应降价多少元？（3）每台冰箱降价多少元时，商场每天销售这种冰箱的利润最高？最高利润是多少？O 1 1y x =1y x =P (2，0)xy（第24题）10、（2009年孝感）已知抛物线2234y x kx k =+-（k 为常数，且k ＞0）．（1）证明：此抛物线与x 轴总有两个交点；（2）设抛物线与x 轴交于M 、N 两点，若这两点到原点的距离分别为OM 、ON ，且1123ON OM -=，求k 的值．11、（2009年新疆）（1）用配方法把二次函数243y x x =-+变成2()y x h k =-+的形成． （2）在直角坐标系中画出243y x x =-+的图象．（3）若1122()()A x y B x y ，，，是函数243y x x =-+图象上的两点，且121x x <<，请比较12y y ，的大小关系．（直接写结果）（4）把方程2432x x -+=的根在函数243y x x =-+的图象上表示出来． 【12、（2009年天津市）已知函数212y x y x bx c αβ==++，，，为方程120y y -=的两个根，点()1M T ，在函数2y 的图象上． （Ⅰ）若1132αβ==，，求函数2y 的解析式； （Ⅱ）在（Ⅰ）的条件下，若函数1y 与2y 的图象的两个交点为A B ，，当ABM △的面积为112时，求t 的值； （Ⅲ）若01αβ<<<，当01t <<时，试确定T αβ，，三者之间的大小关系，并说明理由．12、（2009年广西梧州）如图（9）-1，抛物线23y ax ax b =-+经过A （1-，0），C （3，2-）两点，与y 轴交于点D ，与x 轴交于另一点B ． （1）求此抛物线的解析式；（2）若直线)0(1≠+=k kx y 将四边形ABCD 面积二等分，求k 的值；（3）如图（9）-2，过点E （1，1）作EF ⊥x 轴于点F ，将△AEF 绕平面内某点旋转180°得△MNQ （点M 、N 、Q 分别与点A 、E 、F 对应），使点M 、N 在抛物线上，作MG ⊥x 轴于点G ，若线段MG ︰AG ＝1︰2，求点M ，N 的坐标．13、2009年包头）某商场试销一种成本为每件60元的服装，规定试销期间销售单价不低于成本单价，且获利不得高于45%，经试销发现，销售量y （件）与销售单价x （元）符合一次函数y kx b =+，且65x =时，55y =；75x =时，45y =． （1）求一次函数y kx b =+的表达式；（2）若该商场获得利润为W 元，试写出利润W 与销售单价x 之间的关系式；销售单价定为多少元时，商场可获得最大利润，最大利润是多少元？（3）若该商场获得利润不低于500元，试确定销售单价x 的范围．14、（2009年北京市）已知关于x 的一元二次方程22410x x k ++-=有实数根，k 为正整数. （1）求k 的值；（2）当此方程有两个非零的整数根时，将关于x 的二次函数2241y x x k =++-的图象向下平移8个单位，求平移后的图象的解析式； （3）在（2）的条件下，将平移后的二次函数的图象在x 轴下方的部分沿x轴翻折，图象的其余部分保持不变，得到一个新的图象.请你结合这个新的图象回答：当直线()12y x b b k =+<与此图象有两个公共点时，b 的取值范围.15、（09湖南怀化）如图11，已知二次函数22)(m k m x y -++=的图象与x 轴相交于两个不同的点1(0)A x ，、2(0)B x ，，与y 轴的交点为C ．设ABC △的外接圆的圆心为点P ．（1）求P ⊙与y 轴的另一个交点D 的坐标；y=kx +1图（9）-1图（9）-2（2）如果AB 恰好为P ⊙的直径，且ABC △的面积等于5，求m 和k 的值．16、(2009年达州)如图11，抛物线)1)(3(-+=x x a y 与x 轴相交于A 、B 两点（点A 在点B 右侧），过点A 的直线交抛物线于另一点C ，点C 的坐标为（-2，6）.(1)求a 的值及直线AC 的函数关系式；(2)P 是线段AC 上一动点，过点P 作y 轴的平行线，交抛物线于点M ，交x 轴于点N. ①求线段PM 长度的最大值；②在抛物线上是否存在这样的点M ，使得△CMP 与△APN 相似？如果存在，请直接写出所有满足条件的点M 的坐标（不必写解答过程）；如果不存在，请说明理由. 17、（2009年邵阳市）如图（十二）直线l 的解析式为y ＝－x+4, 它与x 轴、y 轴分相交于A 、B 两点，平行于直线l 的直线m 从原点O 出发，沿x 轴的正方向以每秒1个单位长度的速度运动，它与x 轴、y 轴分别相交于M 、N 两点，运动时间为t 秒（0<t ≤4）． （1）求A 、B 两点的坐标；（2）用含t 的代数式表示△MON 的面积S 1；（3）以MN 为对角线作矩形OMPN,记 △MPN 和△OAB 重合部分的面积为S 2 ； ①当2<t ≤4时，试探究S 2 与之间的函数关系；②在直线m 的运动过程中，当t 为何值时，S 2 为△OAB 的面积的165？18、(2009年肇庆市)已知一元二次方程210x px q +++=的一根为 2． （1）求q 关于p 的关系式；（2）求证：抛物线2y x px q =++与x 轴有两个交点；（3）设抛物线2y x px q =++的顶点为 M ，且与 x 轴相交于A （1x ，0）、B （2x ，0）两点，求使△AMB 面积最小时的抛物线的解析式．。

二次函数：考点：二次函数的概念、图像及性质1．（2009）抛物线（是常数）的顶点坐标是（ ）A ．B ．C ．D ．2．（2009）将抛物线向上平移一个单位后，得以新的抛物线，那么新的抛物线的表达式是 ． 3．（2010）将直线 y = 2 x ─ 4 向上平移5个单位后，所得直线的表达式是__________.（2011）抛物线y ＝－(x ＋2)2－3的顶点坐标是（ ）． A ．（2，－3） B ．（－2，3） C ．（2，3） D ．（－2，－3） （2012）将抛物线2y x x =+向下平移2个单位，所得新抛物线的表达式是 ． （2013）如果将抛物线向下平移1个单位，那么所得新抛物线的表达式是（ ）A ．B ．C ．D ．（2014）如果将抛物线y ＝x 2向右平移1个单位，那么所得的抛物线的表达式是（ ） (A ) 21y x =-； (B ) 21y x =+； (C ) 2(1)y x =-； (D ) 2(1)y x =+． （2015）如果将抛物线y ＝x 2＋2x －1向上平移，使它经过点A (0，3)，那么所得新抛物线的表达式是_______________．（2016）如果将抛物线22y x =+向下平移1个单位，那么所得新抛物线的表达式是（ ） A. 2(1)2y x =-+ B. 2(1)2y x =++ C. 21y x =+ D.23y x =+（2017）已知一个二次函数的图像开口向上，顶点坐标为（0，-1），那么一个二次函数的解析式可以是 。

（只需写一个）考点：以二次函数为母体的综合题（2009）填空选择各考了一道二次函数题，第24以一次函数为母体 （2010）如图，已知平面直角坐标系xOy ，抛物线y ＝－x 2＋bx ＋c 过点A(4,0)、B(1,3) ．（1）求该抛物线的表达式，并写出该抛物线的对称轴和顶点坐标；（2）记该抛物线的对称轴为直线l ，设抛物线上的点P(m,n)在第四象限，点P 关于直线l 的对称点为E ，点E 关于y 轴的对称点为F ，若四边形OAPF 的面积为20，求m 、n 的值．22()y x m n =++m n ，()m n ，()m n -，()m n -，()m n --，22y x =-22y x =+2(1)2y x =-+2(1)2y x =++21y x =+23y x =+（2011）已知平面直角坐标系xOy （如图1），一次函数334y x =+的图像与y 轴交于点A ，点M 在正比例函数32y x =的图像上，且MO ＝MA ．二次函数y ＝x 2＋bx ＋c 的图像经过点A 、M ．（1）求线段AM 的长；（2）求这个二次函数的解析式；（3）如果点B 在y 轴上，且位于点A 下方，点C 在上述二次函数的图像上，点D 在一次函数334y x =+的图像上，且四边形ABCD 是菱形，求点C 的坐标．（2012）如图7，在平面直角坐标系中，二次函数26y ax x c =++的图像经过()()4,0,1,0A B -与y轴交于C ，点D 在线段OC 上，OD t =，点E 在第二象限内，90ADE ∠=︒，1tan ,2DAE EF OD ∠=⊥，垂足为F ．（1）求这个二次函数的解析式； （2）求线段,EF OF 的长（用含t 的代数式表示）；（3）当ECA CAO ∠=∠时，求t 的值．（2013）如图9，在平面直角坐标系中，顶点为xoy Mxy11OMAB Oy图9图9的抛物线经过点和轴正半轴上的点，= 2，．（1）求这条抛物线的表达式；（2）联结，求的大小；（3）如果点在轴上，且△与△相似，求点的坐标．（2014）在平面直角坐标系中(如图9)，已知抛物线223y x bx c =++与x 轴交于点A (－1，0)和点B ，与y 轴交于点C (0，－2)．(1)求该抛物线的表达式，并写出其对称轴； (2)点E 为该抛物线的对称轴与x 轴的交点，点F 在对称轴上，四边形ACEF 为梯形，求点F 的坐标；(3)点D 为该抛物线的顶点，设点P (t ，0)，且t ﹥3，如果△BDP 和△CDP 的面积相等，求t 的值．（2015）已知在平面直角坐标系xOy 中(如图)，抛物线y ＝ax 2－4与x 轴的负半轴相交于点A ，与y 轴相交2(0y ax bx a =+>）A x B AO OB =0120AOB ∠=OM AOM ∠C x ABC AOM C于点B ，AB ＝25．点P 在抛物线上，线段AP 与y 轴的正半轴交于点C ，线段BP 与x 轴 相交于点D ．设点P 的横坐标为m ． (1)求这条抛物线的表达式；(2)用含m 的代数式表示线段CO 的长； (3)当tan ∠ODC ＝23时，求∠P AD 的正弦值．（2016）如图，抛物线25y ax bx =+-（0a ≠）经过点(4,5)A -，与x 轴的负半轴交于点B ，与y 轴交于点C ，且5OC OB =，抛物线的顶点为D ；（1）求这条抛物线的表达式；（2）联结AB 、BC 、CD 、DA ，求四边形ABCD 的面积；（3）如果点E 在y 轴的正半轴上，且BEO ABC ∠=∠， 求点E 的坐标；（2017）已知在平面直角坐标系xOy 中（如图），已知抛物线y=-x 2+bx+c 经过点A （2,2），对称轴是直线x=1，顶点为B 。

LYR(2010-10-03)中考真题 2009 一元二次方程部分填空题1.（重庆綦江）一元二次方程x 2=16的解是 ．2.（2009威海）若关于x 的一元二次方程2(3)0x k x k +++=的一个根是2-，则另一个根是______．3．（2009山西省太原市）某种品牌的手机经过四、五月份连续两次降价，每部售价由3200元降到了2500元．设平均每月降价的百分率为x ，根据题意列出的方程是 ．4.（2009年江苏省）某县2008年农民人均年收入为7 800元，计划到2010年，农民人均年收入达到9 100元．设人均年收入的平均增长率为x ，则可列方程 ．5．（2009年甘肃庆阳）若关于x 的方程2210x x k ++-=的一个根是0，则k = ．6.某果农2006年的年收入为5万元，由于党的惠农政策的落实，2008年年收入增加到7.2万元，则平均每年的增长率是__________.7.（2009年包头）将一条长为20cm 的铁丝剪成两段，并以每一段铁丝的长度为周长各做成一个正方形，则这两个正方形面积之和的最小值是 cm 2．8.（2009年莆田）已知1O ⊙和2O ⊙的半径分别是一元二次方程()()120x x --=的两根，且122OO =，则1O ⊙和2O ⊙的位置关系是 ．9.（2009年莆田）出售某种文具盒，若每个获利x 元，一天可售出()6x -个，则当x = 元时，一天出售该种文具盒的总利润y10.(2009年本溪)11．由于甲型H1N1流感（起初叫猪流感）的影响，在一个月内猪肉价格两次大幅下降．由原来每斤16元下调到每斤9元，求平均每次下调的百分率是多少？设平均每次下调的百分率为x ，则根据题意可列方程为 ．B图②11．(2009年温州)方程(x-1)2=4的解是12．（2009临沂）某制药厂两年前生产1吨某种药品的成本是100万元，随着生产技术的进步，现在生产1吨这种药品的成本为81万元，．则这种药品的成本的年平均下降率为______________．13．（2009年哈尔滨）如果2是一元二次方程x 2＋bx ＋2＝0的一个根，那么常数b 的值为 ．14、（2009年兰州）阅读材料：设一元二次方程ax 2+bx +c ＝0(a ≠0)的两根为x 1，x 2，则两根与方程系数之间有如下关系：x 1+x 2＝－b a ，x 1·x 2＝ca .根据该材料填空：已知x 1、x 2是方程x 2+6x +3＝0的两实数根，则21x x +12xx 的值为 ．15．(2009年宁德市)方程042=-x x 的解是______________．16．（2009年赤峰市）已知关于x 的方程x 2-3x+2k=0的一个根是1，则k=17、（2009年崇左）分解因式：2242x x -+= ．18．（2009年崇左）一元二次方程230x mx ++=的一个根为1-，则另一个根为 ．19．（2009年湖北十堰市）方程(x ＋2)(x －1)=0的解为 ．20．（2009年山东青岛市）某公司2006年的产值为500万元，2008年的产值为720万元，则该公司产值的年平均增长率为 ．21．（2009年山西省）请你写出一个有一根为1的一元二次方程： ．22．（2009年山西省）请你写出一个有一根为1的一元二次方程： ． 选择题23．（2009年黄石市）三角形两边的长是3和4，第三边的长是方程212350x x -+=的根，则该三角形的周长为（ ）A ．14B ．12C ．12或14D ．以上都不对24．（2009年铁岭市）为了美化环境，某市加大对绿化的投资．2007年用于绿化投资20万元，2009年用于绿化投资25万元，求这两年绿化投资的年平均增长率．设这两年绿化投资的年平均增长率为x ，根据题意所列方程为（ ）A ．22025x =B ．20(1)25x +=C ．220(1)25x +=D ．220(1)20(1)25x x +++=25．（2009年安徽）某市2008年国内生产总值（GDP ）比2007年增长了12%，由于受到国际金融危机的影响，预计今年比2008年增长7%，若这两年GDP 年平均增长率为x %，则x %满足的关系是…………………………【 】A ．12%7%%x +=B ．(112%)(17%)2(1%)x ++=+C ．12%7%2%x +=D ．2(112%)(17%)(1%)x ++=+26．(2009武汉)5．已知2x =是一元二次方程220x mx ++=的一个解，则m 的值是（ ）A ．3-B ．3C ．0D ．0或327.(2009成都)若关于x 的一元二次方程2210kx x --=有两个不相等的实数根，则k 的取值范围是（ ）(A)1k >- (B) 1k >-且0k ≠ (c)1k < (D) 1k <且0k ≠28．（2009年湖南长沙）已知关于x 的方程260x kx --=的一个根为3x =，则实数k 的值为（ ）A ．1B ．1-C ．2D ．2-29.（2009山西省太原市）用配方法解方程2250x x --=时，原方程应变形为（ ） A ．()216x += B ．()216x -=C ．()229x +=D ．()229x -=30. （2009襄樊市）为了改善居民住房条件，我市计划用未来两年的时间，将城镇居民的住房面积由现在的人均约为210m 提高到212.1m ，若每年的年增长率相同，则年增长率为（ ）A ．9%B ．10%C ．11%D ．12%31（2009呼和浩特）用配方法解方程23610x x -+=，则方程可变形为（ ）A ．21(3)3x -=B ．213(1)3x -=C ．2(31)1x -=D ．22(1)3x -=32（2009青海）方程29180x x -+=的两个根是等腰三角形的底和腰，则这个三角形的周长为（ ） A ．12 B ．12或15 C ．15 D ．不能确定33（2009青海）在一幅长为80cm ，宽为50cm 的矩形风景画的四周镶一条相同宽度的金色纸边，制成一幅矩形挂图，如图5所示，如果要使整个挂图的面积是5400cm 2，设金色纸边的宽为x cm ，那么x 满足的方程是（ ）A ．213014000x x +-=B ．2653500x x +-=C ．213014000x x --=D ．2653500x x --=34. （2009襄樊市）如图5，在ABCD 中，AE BC ⊥于E ，AE EB EC a ===，且a 是一元二次方程2230x x +-=的根，则ABCD 的周长为（ ）A．4+ B．12+ C．2+ D．212+35.（2009年台州市）用配方法解一元二次方程542=-x x 的过程中，配方正确的是（ ）A ．（1)22=+xB ．1)2(2=-xC ．9)2(2=+xD ．9)2(2=-x36．（2009年甘肃庆阳）如图3，在宽为20米、长为30米的矩形地面上修建两条同样宽的道路，余下部分作为耕地．若耕地面积需要551米2，则修建的路宽应为（ ）A ．1米B ．1.5米C ．2米D ．2.5米37．（2009年甘肃庆阳）方程240x -=的根是（ ）A ．2x =B ．2x =-C ．1222x x ==-，D ．4x =ADCEB图538.（2009年河南）方程2x =x 的解是 【 】（A ）x =1 （B ）x =0 (C) x 1=1 x 2=0 (D) x 1=﹣1 x 2=039.(2009年鄂州)10、某农机厂四月份生产零件50万个，第二季度共生产零件182万个.设该厂五、六月份平均每月的增长率为x ，那么x 满足的方程是（ ） A 、182)1(502=+x B ．182)1(50)1(50502=++++x x C 、50(1+2x)＝182 D ．182)21(50)1(5050=++++x x40.（2009江西）为了让江西的山更绿、水更清，2008年省委、省政府提出了确保到2010年实现全省森林覆盖率达到63%的目标，已知2008年我省森林覆盖率为60.05%，设从2008年起我省森林覆盖率的年平均增长率为x ，则可列方程（ ）A ．()60.051263%x +=B ．()60.051263x +=C ．()260.05163%x +=D ．()260.05163x +=41. （2009年烟台市）设a b ，是方程220090x x +-=的两个实数根，则22a a b ++的值为（ ） A ．2006 B ．2007 C ．2008 D ．200942.（2009年清远）方程216x =的解是（ ）A ．4x =±B ．4x =C ．4x =-D ．16x =43.（2009年衡阳市）两圆的圆心距为3，两圆的半径分别是方程0342=+-x x 的两个根，则两圆的位置关系是 （ ） A ．相交 B ．外离 C ．内含 D ．外切44．（2009年日照）若n （0n ≠）是关于x 的方程220x mx n ++=的根，则m +n 的值为A.1B.2C.-1D.-245.（2009年长沙）已知关于x 的方程260x kx --=的一个根为，则实数k 的值为（ ）A ．1B ．1-C ．2D ．2-46.（2009年包头）关于x 的一元二次方程2210x mx m -+-=的两个实数根分别是12x x 、，且22127x x +=，则212()x x -的值是（ ）A ．1B ．12C ．13D ．2547.(2009宁夏)2．某旅游景点三月份共接待游客25万人次，五月份共接待游客64万人次，设每月的平均增长率为x ，则可列方程为（ ）AA ．225(1)64x +=B ．225(1)64x -=C ．264(1)25x +=D ．264(1)25x -=48．（2009眉山）若方程2310x x --=的两根为1x 、2x ，则1211x x +的值为( )A ．3B ．－3C ．13D ．13-49．（2009东营）若n （0n ≠）是关于x 的方程220x mx n ++=的根，则m +n 的值为（ ）（A ）1 （B ）2（C ）-1 （D ）-250．(2009年南充)方程(3)(1)3x x x -+=-的解是（ ）A ．0x =B ．3x =C ．3x =或1x =-D ．3x =或0x =51.（2009年兰州）2008年爆发的世界金融危机，是自上世纪三十年代以来世界最严重的一场金融危机。

25．(12分)已知抛物线b ax ax y ++-=22与x 轴的一个交点为A (-1,0)，与y 轴的正半轴交于点C ．⑴直接写出抛物线的对称轴，及抛物线与x 轴的另一个交点B 的坐标； ⑵当点C 在以AB 为直径的⊙P 上时，求抛物线的解析式；⑶坐标平面内是否存在点M ，使得以点M 和⑵中抛物线上的三点A 、B 、C 为顶点的四边形是平行四边形？若存在，请求出点M 的坐标；若不存在，请说明理由．25．解：⑴对称轴是直线：1=x ，点B 的坐标是(3,0)． ……2分说明：每写对1个给1分，“直线”两字没写不扣分．⑵如图，连接PC ，∵点A 、B 的坐标分别是A (-1,0)、B (3,0)，∴AB ＝4．∴．AB PC 242121=⨯==在Rt △POC 中，∵O P ＝PA －OA ＝2－1＝1， ∴．PO PC OC 3122222=-=-=∴b ＝．3 ………………………………3分 当01=-=，y x 时，，a a 032=+--∴．a 33=………………………………4分 ∴．x x y 3332332++-= ………………5分 ⑶存在．……………………………6分理由：如图，连接AC 、BC ．设点M 的坐标为),(y x M ．①当以AC 或BC 为对角线时，点M 在x 轴上方，此时CM ∥AB ，且CM ＝AB ． 由⑵知，AB ＝4，∴|x |＝4，3==OC y ．∴x ＝±4．∴点M 的坐标为)3,4()3,4(-或M ．…9分说明：少求一个点的坐标扣1分．②当以AB 为对角线时，点M 在x 轴下方．过M 作MN ⊥AB 于N ，则∠MNB ＝∠AOC ＝90°．∵四边形AMBC 是平行四边形，∴AC ＝MB ，且AC ∥MB ．∴∠CAO ＝∠MBN ．∴△AOC ≌△BNM ．∴BN ＝AO ＝1，MN ＝CO ＝3． ∵OB ＝3，∴0N ＝3－1＝2．∴点M 的坐标为(2,3)M -． ……………………………12分说明：求点M 的坐标时，用解直角三角形的方法或用先求直线解析式，然后求交点M 的坐标的方法均可，请参照给分．综上所述，坐标平面内存在点M ，使得以点A 、B 、C 、M 为顶点的四边形是平行四边形．其坐标为123(4,3),(4,3),(2,3)M M M --．说明：①综上所述不写不扣分；②如果开头“存在”二字没写，但最后解答全部正确，不扣分。

中考试题专题之13-二次函数试题及答案一、选择题 1、（2009年台湾）向上发射一枚炮弹，经x 秒后的高度为y 公尺，且时间与高度关系为y =ax 2+bx 。

若此炮弹在第7秒与第14秒时的高度相等，则再下列哪一个时间的高度是最高的？(A) 第8秒 (B) 第10秒 (C) 第12秒 (D) 第15秒 。

2、（2009年泸州）在平面直角坐标系中，将二次函数22x y =的图象向上平移2个单位，所得图象的解析式为A ．222-=x yB ．222+=x y C ．2)2(2-=x y D ．2)2(2+=x y3、 (2009年四川省内江市)抛物线3)2(2+-=x y 的顶点坐标是（ ） A ．（2，3） B ．（－2，3） C ．（2，－3） D ．（－2，－3） 5、（2009年桂林市、百色市）二次函数2(1)2y x =++的最小值是（ ）． A ．2 B ．1 C ．－3 D ．236、(2009年上海市)抛物线22()y x m n =++（m n ，是常数）的顶点坐标是（ ）A ．()m n ，B ．()m n -，C ．()m n -，D ．()m n --，7、(2009年陕西省)根据下表中的二次函数c bx ax y ++=2的自变量x 与函数y 的对应值，可判断二次函数的图像与x 轴【 】x … －112…y … －1 47-－2 47- … A ．只有一个交点B ．有两个交点，且它们分别在y 轴两侧C ．有两个交点，且它们均在y 轴同侧D ．无交点8、（2009威海）二次函数2365y x x =--+的图象的顶点坐标是（ ） A ．(18)-， B ．(18)，C ．(12)-，D ．(14)-，9、（2009湖北省荆门市）函数y =ax ＋1与y =ax 2＋bx ＋1（a ≠0）的图象可能是（ ）解析：本题考查函数图象与性质，当0a >时，直线从左向右是上升的，抛物线开口向上，D 是错的，函数y =ax ＋1与y =ax 2＋bx ＋1（a ≠0）的图象必过（0，1），所以C 是正确的，故选C ． 10、（2009年贵州黔东南州）抛物线的图象如图所示，根据图象可知，抛物线的解析式可能．．是（ ）A 、y=x 2-x-2 B 、y=121212++-x C 、y=121212+--x x D 、y=22++-x x11、（2009年齐齐哈尔市）已知二次函数2(0)y ax bx c a =++≠的图象如图所示，则下列结论：0ac >①；②方程2ax bx c ++=的两根之和大于0；y ③随x 的增大而增大；④0a b c -+<，其中正确的个数（） A ．4个B ．3个C ．2个D ．1个12、（2009年深圳市）二次函数c bx ax y ++=2的图象如图2所示，若点A （1，y 1）、B （2，y 2）是它图象上的两点，则y 1与y 2的大小关系是（ ） A ．21y y < B ．21y y = C ．21y y >D ．不能确定12、（2009桂林百色）二次函数2(1)2y x =++的最小值是（ ）．B ．C ．D ．A ．2B ．1C ．－3D ．2313、（2009丽水市）已知二次函数y ＝ax 2＋bx ＋c(a ≠0)的图象如图所示，给出以下结论： ①a ＞0.②该函数的图象关于直线1x =对称. ③当13x x =-=或时，函数y 的值都等于0. 其中正确结论的个数是（ ） A ．3 B ．2 C ．1 D ．014、（2009烟台市）二次函数2y ax bx c =++的图象如图所示，则一次函数24y bx b ac =+-与反比例函数a b cy x++=在同一坐标系内的图象大致为（ ）15、（2009年甘肃庆阳）图6（1）是一个横断面为抛物线形状的拱桥，当水面在l 时，拱顶（拱桥洞的最高点）离水面2m ，水面宽4m ．如图6（2）建立平面直角坐标系，则抛物线的关系式是（ ）A ．22y x =- B ．22y x = C ．212y x=-D ．212y x =16、（2009年甘肃庆阳）将抛物线22y x =向下平移1个单位，得到的抛物线是（ ） A ．22(1)y x =+B ．22(1)y x =-C ．221y x =+D ．221y x =-17、（2009年广西南宁）已知二次函数2y ax bx c =++（0a ≠）的图象如图4所示，有下列四个结论：20040b c b ac <>->①②③④0a b c -+<，其中正确的个数有（ ） A ．1个B ．2个C ．3个D ．4个图6（1） 图6（2）xxxxO18、(2009年鄂州)已知=次函数y＝ax2+bx+c的图象如图．则下列5个代数式：ac，a+b+c，4a－2b+c，2a+b，2a－b中，其值大于0的个数为（）A．2 B 3 C、4 D、519、（2009年孝感）将函数2y x x=+的图象向右平移a(0)a>个单位，得到函数232y x x=-+的图象，则a的值为A．1 B．2 C．3 D．420、（2009泰安）抛物线1822-+-=xxy的顶点坐标为（A）（-2，7）（B）（-2，-25）（C）（2，7）（D）（2，-9）21、（2009年烟台市）二次函数2y a x b x c=++的图象如图所示，则一次函数24y b x b a c=+-与反比例函数a b cyx++=在同一坐标系内的图象大致为（）22、（2009年嘉兴市）已知0≠a，在同一直角坐标系中，函数axy=与2axy=的图象有可能是（▲）图4x x xx x23、（2009年新疆）如图，直角坐标系中，两条抛物线有相同的对称轴，下列关系不正确．．．的是（ ） A ．h m =B ．k n =C ．k n >D ．00h k >>，24、（2009年天津市）在平面直角坐标系中，先将抛物线22y x x =+-关于x 轴作轴对称变换，再将所得的抛物线关于y 轴作轴对称变换，那么经两次变换后所得的新抛物线的解析式为（ ）A ．22y x x =--+ B ．22y x x =-+- C ．22y x x =-++D ．22y x x =++25、（2009年南宁市）已知二次函数2y ax bx c =++（0a ≠）的图象如图所示，有下列四个结论：20040b c b ac <>->①②③④0a b c -+<，其中正确的个数有（ ） A ．1个B ．2个C ．3个D ．4个26、（2009年衢州）二次函数2(1)2y x =--的图象上最低点的坐标是A ．(-1，-2)B ．(1，-2)C ．(-1，2)D ．(1，2) 27、（2009年舟山）二次函数2(1)2y x =--的图象上最低点的坐标是A ．(-1，-2)B ．(1，-2)C ．(-1，2)D ．(1，2) 28、（2009年广州市）二次函数2)1(2+-=x y 的最小值是（ ）A.2 （B ）1 （C ）-1 （D ）-229、（2009年济宁市）小强从如图所示的二次函数2y ax bx c =++的图象中，观察得出了下面五条信息：（1）0a <；（2） 1c >；（3）0b >；（4） 0a b c ++>； （5）0a b c -+>. 你认为其中正确信息的个数有A ．2个B ．3个C ．4个D ．5个30、（2009年广西钦州）将抛物线y ＝2x 2向上平移3个单位得到的抛物线的解析式是（ ） A ．y ＝2x 2＋3B ．y ＝2x 2－3C ．y ＝2（x ＋3）2D ．y ＝2（x －3）231、(2009宁夏)二次函数2(0)y ax bx c a =++≠的图象如图所示，对称轴是直线1x =，则下列四个结论错误．．的是（ ）D A ．0c > B ．20a b += C ．240b ac -> D ．0a b c -+>32、(2009年南充)抛物线(1)(3)(0)y a x x a =+-≠的对称轴是直线（ ）A ．1x =B ．1x =-C ．3x =-D ．3x =33、(2009年湖州)已知图中的每个小方格都是边长为1的小正方形，每个小正方形的顶点称为格点，请你在图中任意画一条抛物线，问所画的抛物线最多能经过81个格点中的多少个？（ ） A ．6 B ．7 C ．8 D ．9 34、（2009年兰州）在同一直角坐标系中，函数y mx m =+和函数222y mx x =-++（m 是常数，且0m ≠）的图象可能．．是（8题图）（第12题）35、（2009年兰州）把抛物线2y x =-向左平移1个单位，然后向上平移3个单位，则平移后抛物线的解析式为 A ．2(1)3y x =--- B ．2(1)3y x =-+- C ．2(1)3y x =--+D ．2(1)3y x =-++36、（2009年兰州）二次函数c bx ax y ++=2的图象如图6所示，则下列关系式不正确的是A ．a ＜0 B.abc ＞0C.c b a ++＞0D.ac b 42-＞037、（2009年遂宁）把二次函数3412+--=x x y 用配方法化成()k h x a y +-=2的形式A.()22412+--=x yB. ()42412+-=x yC.()42412++-=x yD. 321212+⎪⎭⎫ ⎝⎛-=x y 39、（2009年广州市）二次函数2)1(2+-=x y 的最小值是（ ）A.2 （B ）1 （C ）-1 （D ）-2【关键词】二次函数41、（2009年台湾）向上发射一枚炮弹，经x 秒后的高度为y 公尺，且时间与高度关系为y =ax 2+bx 。

09年二次函数典型试题一、选择题1、（09年台湾）向上发射一枚炮弹，经x 秒后的高度为y 公尺，且时间与高度关系为y =ax 2+bx 。

若此炮弹在第7秒与第14秒时的高度相等，则再下列哪一个时间的高度是最高的?( ) (A) 第8秒 (B) 第10秒 (C) 第12秒 (D) 第15秒 。

2、(09年上海市)抛物线22()y x m n =++（m n ，是常数）的顶点坐标是（ ）A ．()m n ，B ．()m n -，C ．()m n -，D ．()m n --，3、(09年陕西省)根据下表中的二次函数c bx ax y ++=2的自变量x 与函数y 的对应值，可判断二次函数的图像与x 轴A ．只有一个交点B ．有两个交点，且它们分别在y 轴两侧C ．有两个交点，且它们均在y 轴同侧D ．无交点4、（09威海）二次函数2365y x x =--+的图象的顶点坐标是（ ）A ．(18)-，B ．(18)，C ．(12)-，D ．(14)-，5、（09湖北省荆门市）函数y =ax ＋1与y =ax 2＋bx ＋1（a ≠0）的图象可能是（ ）6、（09年贵州黔东）抛物线的图象如图所示，根据图象可知，抛物线的解析式可能．．是（ ）A 、y=x 2-x-2 B 、y=121212++-x C 、y=121212+--x x D 、y=22++-x x7、（09年齐齐哈尔市）已知二次函数2(0)y ax bx c a =++≠的图象如图所示，则下列结论：0ac >①；②方程20ax bx c ++=的两根之和大于0；y ③随x 的增大而增大；④0a b c -+<，其中正确的个数（ ）A ．4个B ．3个C ．2个D ．1个8、（09烟台市）二次函数2y ax bxc =++的图象如图所示，则一次函数24y bx b ac =+-与反比例函数a b cy x++=在同一坐标系内的图象大致为（ ） A ． B ． C ． D ．（15题图）图49、（09年南宁）已知二次函数2y ax bx c =++（0a ≠）的图象如图4所示，有下列四个结论：20040b c b ac <>->①②③④0a b c -+<，其中正确的个数有（ A ．1个 B ．2个 C ．3个 D ．4个10、（09年孝感）将函数2y x x =+的图象向右平移a (0)a >数232y x x =-+的图象，则a 的值为（ ） A ．1 B ．2 C ．3 D ．411、（09泰安）抛物线1822-+-=x x y 的顶点坐标为（A ）（-2，7） （B ）（-2，-25） （C ）（2，7） （D ）（2，-9）12、（09年新疆）如图，直角坐标系中，两条抛物线有相同的对称轴，下列关系 不正．．确．的是（ ） A ．h m =B ．k n =C ．k n >D ．00h k >>，13、（09年天津市）在平面直角坐标系中，先将抛物线22y x x =+-关于x 轴作轴对称变换，再将所得的抛物线关于y 轴作轴对称变换，那么经两次变换后所得的新抛物线的解析式为（ ） A ．22y x x =--+ B ．22y x x =-+-C ．22y x x =-++D ．22y x x =++14、（09年济宁市）小强从如图所示的二次函数2y ax bx c =++的图象中，观察得出了下面五条信息：（1）0a <；（2） 1c >；（3）0b >；（4） 0a b c ++>； （5中正确信息的个数有A ．2个B ．3个C ．4个D ．5个15、(09宁夏)二次函数2(0)y ax bx c a =++≠线1x =，则下列四个结论错误．．的是（ ）D A ．0c > B ．20a b +=C ．240b ac -> D ．0a b c -+>16、(09年南充)抛物线(1)(3)(0)y a x x a =+-≠的对称轴是直线（ ） A ．1x = B ．1x =- C ．3x =- D ．3x =17、（09年兰州）在同一直角坐标系中，函数y mx m =+和函数222y mx x =-++（m 是常数，且0m ≠）的图象可能．．是xxxx图618、（09年黄石市）已知二次函数2y ax bx c =++的图象如图所示，有以下结论：①0a b c ++<；②1a b c -+>；③0abc >；④420a b c -+<；⑤1c a ->其中所有正确结论的序号是（ ）A ．①②B ． ①③④C ．①②③⑤D ．①②③④⑤二、填空题1、（09年安徽）已知二次函数的图象经过原点及点（12-x 轴的另一交点到原点的距离为12、（09襄樊市）抛物线2y x bx c =-++的图象如图6为 ．3、（09湖北省荆门市）函数(2)(3)y x x =--4、5、（09年贵州省黔东南州）二次函数322--=x x y 的图象的解析式是_________________。

中考试题专题之13-二次函数试题及答案一、选择题 1、〔2009年台湾〕向上发射一枚炮弹，经x 秒后的高度为y 公尺，且时间与高度关系为y =ax 2+bx 。

假设此炮弹在第7秒与第14秒时的高度相等，则再以下哪一个时间的高度是最高的？(A) 第8秒 (B) 第10秒 (C) 第12秒 (D) 第15秒 。

2、〔2009年泸州〕在平面直角坐标系中，将二次函数22x y =的图象向上平移2个单位，所得图象的解析式为A ．222-=x yB ．222+=x yC ．2)2(2-=x yD ．2)2(2+=x y3、 (2009年四川省内江市)抛物线3)2(2+-=x y 的顶点坐标是〔 〕 A ．〔2，3〕 B ．〔－2，3〕 C ．〔2，－3〕 D ．〔－2，－3〕 5、〔2009年桂林市、百色市〕二次函数2(1)2y x =++的最小值是〔 〕． A ．2 B ．1 C ．－3 D ．236、(2009年上海市)抛物线22()y x m n =++〔m n ，是常数〕的顶点坐标是〔 〕A ．()m n ，B ．()m n -，C ．()m n -，D ．()m n --，7、(2009年陕西省)根据下表中的二次函数c bx ax y ++=2的自变量x 与函数y 的对应值，可判断二次函数的图像与x 轴【 】x … －1 012 …y … －1 47-－2 47- … A ．只有一个交点 B ．有两个交点，且它们分别在y 轴两侧 C ．有两个交点，且它们均在y 轴同侧 D ．无交点8、〔2009威海〕二次函数2365y x x =--+的图象的顶点坐标是〔 〕A ．(18)-，B ．(18)，C ．(12)-，D ．(14)-，9、〔2009湖北省荆门市〕函数y =ax ＋1与y =ax 2＋bx ＋1〔a ≠0〕的图象可能是〔 〕解析：此题考查函数图象与性质，当0a >时，直线从左向右是上升的，抛物线开口向上，D 是错的，函数y =ax ＋1与y =ax 2＋bx ＋1〔a ≠0〕的图象必过〔0，1〕，所以C 是正确的，故选C ． 10、〔2009年贵州黔东南州〕抛物线的图象如下图，根据图象可知，抛物线的解析式可能．．是〔 〕A 、y=x 2-x-2 B 、y=121212++-x C 、y=121212+--x x D 、y=22++-x x11、〔2009年齐齐哈尔市〕已知二次函数2(0)y ax bx c a =++≠的图象如下图，则以下结论：0ac >①；②方程20ax bx c ++=的两根之和大于0；y ③随x 的增大而增大；④0a b c -+<，其中正确的个数〔〕 A ．4个B ．3个C ．2个D ．1个12、〔2009年深圳市〕二次函数c bx ax y ++=2的图象如图2所示，假设点A 〔1，y 1〕、B 〔2，y 2〕是它图象上的两点，则y 1与y 2的大小关系是〔 〕A ．21y y <B ．21y y =C ．21y y >D ．不能确定12、〔2009桂林百色〕二次函数2(1)2y x =++的最小值是〔 〕．xyO 1 A ． B ． C ． D ．1111xo yyo x yo xxoyA ．2B ．1C ．－3D ．2313、〔2009丽水市〕已知二次函数y ＝ax 2＋bx ＋c(a ≠0)的图象如下图，给出以下结论： ①a ＞0.②该函数的图象关于直线1x =对称. ③当13x x =-=或时，函数y 的值都等于0. 其中正确结论的个数是〔 〕 A ．3 B ．2 C ．1 D ．014、〔2009烟台市〕二次函数2y ax bx c =++的图象如下图，则一次函数24y bx b ac =+-与反比例函数a b cy x++=在同一坐标系内的图象大致为〔 〕15、〔2009年甘肃庆阳〕图6〔1〕是一个横断面为抛物线形状的拱桥，当水面在l 时，拱顶〔拱桥洞的最高点〕离水面2m ，水面宽4m ．如图6〔2〕建立平面直角坐标系，则抛物线的关系式是〔 〕A ．22y x =-B ．22y x =C ．212y x =-D ．212y x =16、〔2009年甘肃庆阳〕将抛物线22y x =向下平移1个单位，得到的抛物线是〔 〕 A ．22(1)y x =+B ．22(1)y x =-C ．221y x =+D ．221y x =-17、〔2009年广西南宁〕已知二次函数2y ax bx c =++〔0a ≠〕的图象如图4所示，有以下四个结论：20040b c b ac <>->①②③④0a b c -+<，其中正确的个数有〔 〕 A ．1个B ．2个C ．3个D ．4个图6〔1〕 图6〔2〕1-1O xyy xO y xO B ．C ．yxO A ．y xO D ．O18、(2009年鄂州)已知=次函数y ＝ax 2+bx+c 的图象如图．则以下5个代数式：ac ，a+b+c ，4a －2b+c ，2a+b ，2a －b 中，其值大于0的个数为〔 〕 A ．2 B 3 C 、4D 、519、〔2009年孝感〕将函数2y x x =+的图象向右平移a (0)a >个单位，得到函数232y x x =-+的图象，则a 的值为A ．1B ．2C ．3D ．420、〔2009泰安〕抛物线1822-+-=x x y 的顶点坐标为 〔A 〕〔-2，7〕 〔B 〕〔-2，-25〕 〔C 〕〔2，7〕 〔D 〕〔2，-9〕21、〔2009年烟台市〕二次函数2y ax bx c =++的图象如下图，则一次函数24y bx b ac =+-与反比例函数a b cy x++=在同一坐标系内的图象大致为〔 〕22、〔2009年嘉兴市〕已知0≠a ，在同一直角坐标系中，函数ax y =与2ax y =的图象有可能是〔 ▲ 〕1图4O y31- 1 O xy yxO y xO B ．yxO A ．y xO Oy x1-1xyO 1-1xyO1-1xyO1-123、〔2009年新疆〕如图，直角坐标系中，两条抛物线有相同的对称轴，以下关系不正确的．．．．选项是．．．〔 〕 A ．h m = B ．k n =C ．k n >D ．00h k >>，24、〔2009年天津市〕在平面直角坐标系中，先将抛物线22y x x =+-关于x 轴作轴对称变换，再将所得的抛物线关于y 轴作轴对称变换，那么经两次变换后所得的新抛物线的解析式为〔 〕A ．22y x x =--+B ．22y x x =-+-C ．22y x x =-++D ．22y x x =++25、〔2009年南宁市〕已知二次函数2y ax bx c =++〔0a ≠〕的图象如下图，有以下四个结论：20040b c b ac <>->①②③④0a b c -+<，其中正确的个数有〔 〕 A ．1个B ．2个C ．3个D ．4个26、〔2009年衢州〕二次函数2(1)2y x =--的图象上最低点的坐标是A ．(-1，-2)B ．(1，-2)C ．(-1，2)D ．(1，2) 27、〔2009年舟山〕二次函数2(1)2y x =--的图象上最低点的坐标是A ．(-1，-2)B ．(1，-2)C ．(-1，2)D ．(1，2) 28、〔2009年广州市〕二次函数2)1(2+-=x y 的最小值是〔 〕A.2 〔B 〕1 〔C 〕-1 〔D 〕-229、〔2009年济宁市〕小强从如下图的二次函数2y ax bx c =++的图象中，观察得出了下面五条信息：〔1〕0a <；〔2〕 1c >；〔3〕0b >；〔4〕 0a b c ++>； 〔5〕0a b c -+>. 你认为其中正确信息的个数有A ．2个B ．3个C ．4个D ．5个30、〔2009年广西钦州〕将抛物线y ＝2x 2向上平移3个单位得到的抛物线的解析式是〔 〕 A ．y ＝2x 2＋3B ．y ＝2x 2－3C ．y ＝2〔x ＋3〕2D ．y ＝2〔x －3〕231、(2009宁夏)二次函数2(0)y ax bx c a =++≠的图象如下图，对称轴是直线1x =，则以下四个结论错误的选项是．．．．．．〔 〕D A ．0c > B ．20a b += C ．240b ac -> D ．0a b c -+>32、(2009年南充)抛物线(1)(3)(0)y a x x a =+-≠的对称轴是直线〔 〕A ．1x =B ．1x =-C ．3x =-D ．3x =33、(2009年湖州)已知图中的每个小方格都是边长为1的小正方形，每个小正方形的顶点称为格点，请你在图中任意画一条抛物线，问所画的抛物线最多能经过81个格点中的多少个？〔 〕 A ．6 B ．7 C ．8 D ．9 34、〔2009年兰州〕在同一直角坐标系中，函数y mx m =+和函数222y mx x =-++〔m 是常数，且0m ≠〕的图象可能．．是111-O x y〔8题图〕1211O1xy 〔第12题〕35、〔2009年兰州〕把抛物线2y x =-向左平移1个单位，然后向上平移3个单位，则平移后抛物线的解析式为 A ．2(1)3y x =--- B ．2(1)3y x =-+- C ．2(1)3y x =--+D ．2(1)3y x =-++36、〔2009年兰州〕二次函数c bx ax y ++=2的图象如图6所示，则以下关系式不正确的选项是A ．a ＜0 B.abc ＞0C.c b a ++＞0D.ac b 42-＞037、〔2009年遂宁〕把二次函数3412+--=x x y 用配方法化成()k h x a y +-=2的形式A.()22412+--=x yB. ()42412+-=x yC.()42412++-=x yD. 321212+⎪⎭⎫ ⎝⎛-=x y 39、〔2009年广州市〕二次函数2)1(2+-=x y 的最小值是〔 〕A.2 〔B 〕1 〔C 〕-1 〔D 〕-2【关键词】二次函数41、〔2009年台湾〕向上发射一枚炮弹，经x 秒后的高度为y 公尺，且时间与高度关系为y =ax 2+bx 。