第六讲排列组合的综合应用练习

五春第6讲 排列组合公式一、知识要点 排列：一般地，从n 个不同的元素中任取出m 个（m ≤n ）元素，按照一定的顺序排成一列．叫做从n 个不同元素中取出m 个元素的一个排列，记作mp n 。

组合：一般地，从n 个不同元素中取出m 个（m ≤n ）元素组成一组，不计较组内各元素的次序，叫做从n 个不同元素中取出m 个元素的一个组合，记作mC n 。

二、例题精选【例1】 计算下列各式的结果：（1）3839-p p （2）！！99100÷ （3）3839C -C【巩固1】计算下列各式的结果： （1）4737p p + （2）！！5-6 （3）4737C C +【例2】 某班要在10名同学中选出3名同学去参加夏令营，问共有多少种选法？如果在10这人中选3人分别担任队长、副队长、生活委员，问有多少种选法？【巩固2】有4个同学一起去郊游，照相时，必须有一名同学给其他3人拍照，共可能有多少种拍照情况？（照相时3人站成一排）【例3】 在厦门与上海间通行的某列高铁共途径10个车站（包括起始点），问：①共需要准备多少种车票？ ②共有多少中不同的票价？（距离相同则票价相同）【巩固3】某班毕业生中有10名同学相见，他们互相都握了一次手，问这次聚会大家一共握了多少次手？如果大家互相都对彼此说了“再见”，那大家总共会说多少句“再见”？【例4】5个人并排站成一排，其中甲必须站在中间有多少种不同的站法？甲乙必须站在两边共有多少种不同站法？【巩固4】10个人围成一圈，从中选出两个不相邻的人，共有多少种不同选法？【例5】一种电子表在6时25分31秒时的显示为6:25:31，那么从9时到10时这段时间里，此表的5个数字都不相同的时刻一共有多少个?【巩固5】有一些四位数的4个数字分别是2个不同的奇数和2个不同的偶数，而且不含有数字0。

这样的四位数有几个？【例6】*平面内100条直线两两相交，最多可以出现多少个交点？三、回家作业 【作业1】计算：【作业2】计算：【作业3】某校举行排球单循环赛，有12个队参加，每两队要进行一场比赛。

6.2.3 排列组合的综合运用（精练）【题组一全排列】1．（2020·中山大学附属中学高二期中）一个市禁毒宣传讲座要到4个学校开讲，一个学校讲一次，不同的次序种数为( )A．4 B．44C．24 D．48【答案】C【解析】一个市禁毒宣传讲座要到4个学校开讲，一个学校讲一次，不同的次序种数为44=432124A⨯⨯⨯=. 故选：C2．（2020·全国高二单元测试）3名学生报名参加篮球、足球、排球、计算机课外兴趣小组，每人选报一门，则不同的报名方案有________种.【答案】64【解析】由题意参加篮球、足球、排球、计算机课外兴趣小组，每个学生有4种选择，则3名同学共有34=64种报名方案.故答案为：64.3．（2020·上海高二专题练习）若把英文单词“hello”的字母的顺序写错了，则可能出现的错误共有_________种．【答案】59【解析】由题意知本题是一个排列组合及简单的计数问题五个字母进行全排列共有55120A=种结果，字母中包含2个l，∴五个字母进行全排列的结果要除以2，共有60种结果，在这60种结果里有一个是正确的，∴可能出现的错误的种数是60159-=，故答案为：59．4．（2021·浙江衢州市）将9个相同的球放到3个不同的盒子中，每个盒子至少放一个球，且每个盒子中球的个数互不相同，则不同的分配方法共有________种.【答案】18【解析】将9个相同的球分成个数不同的3份，有（1,2,6），（1,3,5），（2,3,4）三种情况，再将这3份个数不同的球放到3个不同的盒子中，有336A=种情况，所以不同的分配方法共有1863=⨯种.故答案为：185．（2020·天津河西区·高二期中）学校要安排一场文艺晚会的11个节目的演出顺序，除第1个节目和最后1个节目已确定外，4个音乐节目要求排在第2，5，7，10的位置，3个舞蹈节目要求排在第3，6，9的位置，2个曲艺节目要求排在第4，8的位置，则不同的排法有_____种.（用数字作答）【答案】288【解析】4个音乐节目要求排在第2，5，7，10的位置，有44A=24种排法；3个舞蹈节目要求排在第3，6，9的位置，有336A=种排法；2个曲艺节目要求排在第4，8的位置，有222A=种排法.故共有24×6×2＝288种排法.故答案为：288.6．（2020·河南）2020年新型冠状病毒肆虐全球，目前我国疫情已经得到缓解，为了彰显我中华民族的大爱精神，我国决定派遣具有丰富抗击疫情经验的四支不同的医疗队A、B、C、D，前往四个国家E、F、G、H进行抗疫技术指导，每支医疗队到一个国家，那么总共有______（请用数字作答）种的不同的派遣方法.如果已知A医疗队被派遣到H国家，那么此时B医疗队被派遣到E国的概率是______.【答案】241 3【解析】由题意可知，每支医疗队到一个国家的派遣方法数为4424A=，由于A医疗队被派遣到H国家，则B医疗队可派遣到其它3个国家，因此，B医疗队被派遣到E国的概率是13.故答案为：24；13.【题组二相邻问题】1．（2020·沙坪坝区·重庆八中）小涛、小江、小玉与本校的另外2名同学一同参加《中国诗词大会》的决赛，5人坐成一排，若小涛与小江、小玉都相邻，则不同坐法的总数为（）A．6 B．12 C．18 D．24【答案】B【解析】解：将小涛与小江、小玉捆绑在一起，与其他两个人全排列，其中小涛位于小江、小玉之间，按照分步乘法计算原理可得323212A A⋅=故选：B2．（2020·宁夏吴忠市·吴忠中学高二期末）将A，B，C，D，E，F这6个字母随机排成一排组成一个信息码，则所得信息码恰好满足A，B，C三个字母连在一起，且B在A与C之间的概率为（）A．112B．15C．115D．215【答案】C【解析】由捆绑法可得所求概率为242466A A 1A 15P ==.故答案为C 3．（2020·陕西彬州市·高二月考）5个男生，2个女生排成一排，若女生不能排在两端，但又必须相邻，则不同的排法种数为 A ．480B ．720C ．960D ．1440【答案】C【解析】两个女生必须相邻，捆绑222A =，女生不能排两端，则从5个男生中任选两人排两端，2520A =，剩余3个男生与捆绑在一起的2个女生看成4个元素，排在其余位置，4424A =，所以不同的排法种数为：22425422024960A A A ⋅⋅=⨯⨯=．4．（2020·广东广州市）2020年初，全国各大医院抽调精兵强将前往武汉参加新型冠状病毒肺炎阻击战，各地医护人员分别乘坐6架我国自主生产的“运20”大型运输机，编号为1，2，3，4，5，6号，要求到达武汉天河飞机场时，每五分钟降落一架，其中1号与6号相邻降落，则不同的安排方法有（ ） A ．60 B ．120 C ．144 D ．240【答案】D【解析】由题意，因为1号与6号相邻降落，可1号与6号排列后看作一个，同其它飞机进行全排， 将则不同的安排方法有2525240A A =种.故选：D.5．（2020·莒县教育局教学研究室高二期中）3名男生､3名女生排成一排，男生必须相邻，女生也必须相邻的排法种数为（ ） A ．2 B ．9C ．72D ．36【答案】C【解析】根据题意男生一起有336A =排法，女生一起有336A =排法，一共有3333272A A =种排法，故选：C .．6．（2020·江苏宿迁市·宿迁中学高二期中）三位女歌手和她们各自的指导老师合影，要求每位歌手与她们的老师站一起，这六人排成一排，则不同的排法数为（ ） A ．24 B ．48C ．60D ．96【答案】B【解析】先将三位女歌手和她们各自的指导老师捆绑在一起，记为三个不同元素进行全排，再将各自女歌手和她的指导老师进行全排，则不同的排法数3222322248N A A A A ==，故选：B.【题组三 不相邻问题】1．（2020·全国）六个人排队，甲乙不能排一起，丙必须排在前两位的概率为（ ） A ．760B ．16C ．1360D ．14【答案】C【解析】丙排第一，除甲乙外还有3人，共33A 种排法，此时共有4个空，插入甲乙可得24A ，此时共有3234=612=72A A ⋅⨯种可能；丙排第二，甲或乙排在第一位，此时有1424C A 排法，甲和乙不排在第一位， 则剩下3人有1人排在第一位，则有122323C A A 种排法， 此时故共有1412224323+=84C A C A A 种排法. 故概率6672841360P A +==. 故选：C.2．（2020·全国）将编号为1、2、3、4、5的5个小球全部放入A 、B 、C 三个盒子内，若每个盒子不空，且放在同一个盒子内的小球编号不相连，则不同的方法总数有（ ） A ．42 B ．36 C ．48 D ．60【答案】A【解析】将编号为1、2、3、4、5的5个小球，根据小球的个数可分为1、1、3或1、2、2两组. ①当三个盒子中的小球个数分别为1、1、3时，由于放在同一个盒子里的小球编号互不相连， 故3个小球的编号只能是1、3、5的在一个盒子里，故只有一种分组方法，再分配到三个盒子，此时共有336A =种分配方法；②当三个盒子中的小球个数分别为1、2、2时，由于放在同一个盒子里的小球编号互不相连，此时放2个小球的盒子中小球的编号分别为()1,3、()2,4或()1,3、()2,5或()1,4、()2,5或()1,4、()3,5或()1,5、()2,4或()2,4、()3,5，共6种，再分配到三个盒子中，此时，共有33636A =种.综上所述，不同的放法种数为64362+=种.故选：A.3．（2020·全国）某节目组决定把《将进酒》《山居秋暝》《望岳》《送杜少府之任蜀州》和另外确定的两首诗词排在后六场做节目开场诗词，并要求《将进酒》与《望岳》相邻，且《将进酒》排在《望岳》的前面，《山居秋暝》与《送杜少府之任蜀州》不相邻，且均不排在最后，则后六场开场诗词的排法有（）A．72种B．48种C．36种D．24种【答案】C【解析】首先可将《将进酒》与《望岳》捆绑在一起和另外确定的两首诗词进行全排列，共有336A=种排法，再将《山居秋暝》与《送杜少府之任蜀州》插排在3个空里(最后一个空不排)，共有236A=种排法，则后六场开场诗词的排法有6636⨯=种，故选：C.4．（2020·防城港市防城中学高二期中）5个人排成一排，其中甲与乙不相邻，而丙与丁必须相邻，则不同的排法种数为（）A．72B．48C．24D．60【答案】C【解析】先将丙与丁捆绑，形成一个“大元素”与戊进行排列，然后再将甲、乙插空，由分步乘法计数原理可知，不同的排法种数为22222324A A A=种.故选：C.5.．（2020·北京丰台区·高二期末）某活动中需要甲、乙、丙、丁4名同学排成一排．若甲、乙两名同学不相邻，则不同的排法种数为_________．（用数字作答）【答案】12【解析】先求出甲、乙、丙、丁4名同学排成一排的全排列：4424A=；再求出甲、乙两名同学相邻的排列：2 412A=然后，4244241212A A-=-=故答案为：126．（2020·上海）2位女生3位男生排成一排，则2位女生不相邻的排法共有______种. 【答案】72【解析】根据题意，分2步进行分析：①、将3位男生排成一排，有336A=种情况，②、3名男生排好后有4个空位可选，在4个空位中，任选2个，安排两名女生，有2412A=种情况，则2位女生不相邻的排法有61272⨯=种；故答案为：727．（2020·安徽省太和第一中学高二月考（理））将A，B，C，D，E五个字母排成一排，若A与B相邻，且A 与C 不相邻，则不同的排法共有__种. 【答案】36【解析】依题意，可分三步，先排D ，E ，有22A 种方法，产生3个空位，将,A B 捆绑有22A 种方法，将,A B 捆绑看作一个元素，插入三个空位之一，有13A 种方法，这时AB 、D 、E 产生四个空位，最后将C 插入与A 不相邻的三个空位之一，有13A 种方法，根据分步乘法计数原理得：共有2211223336A A A A ⨯⨯⨯=种，故答案为：36.8．（2020·博兴县第三中学高二月考）某班上午有五节课，分别安排语文，数学，英语，物理，化学各一节课.要求语文与化学相邻，数学与物理不相邻，则不同排课法的种数是___________ 【答案】24【解析】根据题意，分3步进行分析：①要求语文与化学相邻，将语文与化学看成一个整体，考虑其顺序，有222A =种情况， ②将这个整体与英语全排列，有222A =种顺序，排好后，有3个空位， ③数学与物理不相邻，有3个空位可选，有236A =种情况，则不同排课法的种数是22624⨯⨯=种；故答案为：24. 【题组四 分组分配】1．（2020·全国）将6本不同的书分给甲、乙、丙3名学生，其中一人得1本，一人得2本，一人得3本，则有________种不同的分法． 【答案】360【解析】先把书分成三组，把这三组分给甲、乙、丙3名学生．先选1本，有16C 种选法；再从余下的5本中选2本，有25C 种选法；最后余下3本全选，有33C 种选法．故共有12365360C C C ⋅⋅=种选法．由于甲、乙、丙是不同的3人，还应考虑再分配，故共有3360360A =种分配方法.故答案为: 360.2．（2020·全国）将6本不同的书分给甲、乙、丙、丁4个人，每人至少1本的不同分法共有________种．(用数字作答) 【答案】1560【解析】把6本不同的书分成4组，每组至少1本的分法有2种．①有1组3本，其余3组每组1本，不同的分法共有31163213320lC C C C A = (种)；②有2组每组2本，其余2组每组1本，不同的分法共有22116421222245C C C C A A ⋅= (种)． 所以不同的分组方法共有20＋45＝65(种)．然后把分好的4组书分给4个人，所以不同的分法共有44651560A ⨯= (种)．故答案为：1560.3（2020·福建省泰宁第一中学高二月考）五一劳动节期间，5名游客到三个不同景点游览，每个景点至少有一人，至多两人，则不同的游览方法共有___________种.(用数字填写答案) 【答案】90【解析】把5人按人数2,2,1分成三组，然后再安排到三个景点浏览，总方法为2235332290C C A A ⨯=． 故答案为：90．4．（2020·全国）把5张不同的电影票分给4个人，每人至少一张，则不同的分法种数为________． 【答案】240．【解析】将这5张不同的电影票分成四组，每组至少一张，共有2111532133C C C C A 种分组办法，再分给4人的不同分法有211145321433240C C C C A A ⋅=种．故答案为：240． 5．（2020·全国）从6个人中选4个人值班，第一天1个人，第二天1个人，第三天2个人，共有多少种排法_________. 【答案】180【解析】112654C C C 180=.故答案为：180.6．（2020·重庆北碚区·西南大学附中高二期中）某学校安排5名高三教师去3个学校进行交流学习，且每位教师只去一个学校，要求每个学校至少有一名教师进行交流学习，则不同的安排方式共有______种. 【答案】150【解析】分2步分析：先将5名高三教师分成3组，由两种分组方法，若分成3、1、1的三组，有3510C =种分组方法， 若分成1、2、2的三组，有1225422215C C C A =种分组方法，则一共有101525+=种分组方法；再将分好的三组全排列，对应三个学校，有336A =种情况，则有256150⨯=种不同的安排方式； 故答案为：150．7．（2020·全国）2020年是全面建成小康社会目标实现之年，是脱贫攻坚收官之年根据中央对“精准扶贫”的要求，某市决定派5名党员和3名医护人员到三个不同的扶贫村进行调研，要求每个扶贫村至少派党员和医护人员各1名，则所有不同的分派方案种数为________________.（用数字作答）． 【答案】900【解析】由题意分两步完成：第一步：将5名党员分派到三个不同的扶贫村，第二步，将3名医护人员分派到三个不同的扶贫村.第一步：因为党员有5人，先分成3个组进行分派，分组情况有两种，第一种按人数是1，1，3分组有1135432210C C C A ⋅⋅=种不同情况，第二种按人数是2，2，1分组有2215312215C C C A ⋅⋅=种不同情况，再将分好的组分派到不同的扶贫村共有33(1015)150A +⨯=种不同分派方式；第二步：将3名医护人员分派到3个不同的扶贫村，共有336A =种不同情况.所以所有的不同分派方案有1506900⨯=种. 故答案为：900. 【题组五 几何问题】1．（2021·全国）直线x m =，y x =将圆面224x y +≤分成若干块，现有5种颜色给这若干块涂色，且任意两块不同色，则所有可能的涂色种数是（ ） A ．20 B ．60 C ．120 D ．240【答案】D【解析】当2m ≤-或2m ≥时，圆面224x y +≤被分成2块， 此时不同的涂色方法有5420⨯=种，当2m -<≤2m ≤<时，圆面224x y +≤被分成3块， 此时不同的涂色方法有54360⨯⨯=种，当m <时，圆面224x y +≤被分成4块，此时不同的涂色方法有5432120⨯⨯⨯=种， 所有可能的涂色种数是240． 故选：D2．（2021·安徽省）224x y +≤表示的平面区域内，以横坐标与纵坐标均为整数的点为顶点，可以构成的三角形个数为（ ） A ．286 B ．281 C ．256 D ．176【答案】C【解析】由题意可得224x y +≤表示的平面区域内的整点共有13个，其中三点共线的情况有10种，五点共线的情况有2种，所以从13个点中可以构成三角形的个数为33313351022861020256C C C --=--=个．故选C ．3．（2020·全国高二单元测试）以一个正方体的顶点为顶点的四面体的个数为( ) A ．70 B ．64 C ．58 D ．52【答案】C【解析】正方体的8个顶点中任取4个共有C 84=70个，不能组成四面体的4个顶点有：已有的6个面，对角面:有6个，共12个， ∴以一个正方体的顶点为顶点的四面体共有：70−12=58个.故答案为C. 【题组六 方程不等式问题】1．（2021·太原市）不定方程12x y z ++=的非负整数解的个数为（ ） A ．55 B ．60 C ．91 D ．540【答案】C【解析】不定方程12x y z ++=的非负整数解的个数⇔将12个相同小球放入三个盒子，允许有空盒的放法种数.现在在每个盒子里各加一个相同的小球，问题等价于将15个相同小球放入三个盒子，没有空盒的放法种数，则只需在15个小球中形成的空位（不包含两端）中插入两块板即可，因此，不定方程12x y z ++=的非负整数解的个数为21491C =.故选：C.2．（2021·湖北）若方程12348x x x x +++=，其中22x =，则方程的正整数解的个数为 A ．10 B ．15C ．20D ．30【答案】A【解析】方程12348x x x x +++=，其中22x =，则1346x x x ++=将其转化为有6个完全相同的小球，排成一列，利用挡板法将其分成3组， 第一组小球数目为1x 第二组小球数目为3x 第三组小球数目为4x共有2510C =种方法故方程的正整数解的个数为10 故选A【题组七 数字问题】1．已知集合{}A a b c d =，，，，从集合A 中任取2个元素组成集合B ，则集合B 中含有元素b 的概率为（ ） A ．16B ．13C ．12D ．1【答案】C【解析】A 中任取2个元素组成集合B ，则B 的情况有{}{}{}{}{}{}123456,,,,,,,,,,,B a b B a c B a d B b c B b d B c d ======，共6个，其中符合情况的集合为145,,B B B 共3个，故集合B 中含有元素b 的概率为3162P ==故选：C 2．如果一个四位数的各位数字互不相同，且各位数字之和等于10，则称此四位数为“完美四位数（如1036），则由数字0，1，2，3，4，5，6，7构成的“完美四位数”中，奇数的个数为（ ） A ．12 B ．44 C ．58 D ．76【答案】B【解析】分类讨论：尾数为1：则前三位的数字可能为027,036,045,共1222312C A ⋅⋅=,还可能为234,有336A =种；尾数为3：则前三位的数字可能为016,025,共122228C A ⋅⋅=,还可能为124,有336A =种；尾数为5：则前三位的数字可能为014,023,045,共122228C A ⋅⋅=；尾数为7：则前三位的数字可能为012,共12224C A ⋅=.综上所述,共有126868444+++++=种.故选：B3．从数字0，1，2，3，4，5，6中任取3个，这3个数的乘积为偶数时的不同取法共有______种（用数字作答）.【答案】34【解析】从数字0，1，2，3，4，5，6中任取3个，共有3735C =，乘积为奇数只有1,3,5一种情况故这3个数的乘积为偶数时的不同取法共有34种.故答案为：34【点睛】本题考查了组合的应用，利用排除法可以快速得到答案，是解题的关键.4．已知{}1,2,3,4,5,,,M m M n M m n =∈∈≠，则方程221x y m n+=表示焦点在x 轴上的椭圆的概率是_______ . 【答案】12【解析】因为{}1,2,3,4,5,,,M m M n M m n =∈∈≠，所以(),m n 的可能情况有：2520P =种， 又因为方程221x y m n+=表示焦点在x 轴上的椭圆，所以m n >，所以满足要求的有：2510C =种， 所以概率为：101202P ==.故答案为：12. 5．（2021·宁波市）有写好数字2，2，3，3，5，5，7，7的8张卡片，任取4张，则可以组成不同的四位数的个数为_________.【答案】204【解析】由题意得取出的4张卡片上的数字含有相同数字对的个数可能为0，1，2.当含有0对相同数字时，组成的不同的四位数的个数为4424A =个；当含有1对相同数字时，组成的不同的四位数的个数为221434144C C A =个；当含有2对相同数字时，组成的不同的四位数的个数为224436C C =个.综上，可以组成不同的四位数的个数为2414436204++=个.故答案为：204.6．（2020·江西省信丰中学）从0,1,2,3,4,5,6,7,8,9中任取七个不同的数，则这七个数的中位数是6的概率为________．【答案】1 6【解析】十个数中任取七个不同的数共有C种情况，七个数的中位数为6，那么6只有处在中间位置，有C种情况，于是所求概率P＝＝．。

高三数学排列组合综合应用试题答案及解析1.用数字1,2,3,4可以排成没有重复数字的四位偶数，共有____________个.【答案】12【解析】由题意，没有重复数字的偶数，则末位是2或4，当末位是时，前三位将，，三个数字任意排列，则有种排法，末位为时一样有种，两类共有：种，故共有没有重复数字的偶数个.【考点】排列组合.2.在高三(1)班进行的演讲比赛中，共有5位选手参加，其中3位女生，2位男生．如果2位男生不能连续出场，且女生甲不能排在第一个，那么出场顺序的排法种数为()A．24B．36C．48D．60【答案】D【解析】先排3个女生，三个女生之间有4个空，从四个空中选两个排男生，共有＝72(种)，若女生甲排在第一个，则三个女生之间有3个空，从3个空中选两个排男生，有＝12(种)，∴满足条件的出场顺序有72－12＝60(种)排法，选D．3. 20个不加区别的小球放入1号，2号，3号的三个盒子中，要求每个盒内的球数不小于它的编号数，则不同的放法种数为________．【答案】120【解析】先在编号为2,3的盒内分别放入1个，2个球，还剩17个小球，三个盒内每个至少再放入1个，将17个球排成一排，有16个空隙，插入2块挡板分为三堆放入三个盒中即可，共有＝120(种)方法．4.将5名学生分到A，B，C三个宿舍，每个宿舍至少1人至多2人，其中学生甲不到A宿舍的不同分法有()A．18种B．36种C．48种D．60种【答案】D【解析】由题意知A，B，C三个宿舍中有两个宿舍分到2人，另一个宿舍分到1人．若甲被分到B宿舍：(1)A中2人，B中1人，C中2人，有＝6种分法；(2)A中1人，B中2人，C中2人，有＝12种分法；(3)A中2人，B中2人，C中1人，有＝12种分法，即甲被分到B宿舍的分法有30种，同样甲被分到C宿舍的分法也有30种，所以甲不到A宿舍一共有60种分法，故选D．5.某城市的街道如图，某人要从A地前往B地，则路程最短的走法有()A．8种B．10种C．12种D．32种【答案】B【解析】从A到B若路程最短，需要走三段横线段和两段竖线段，可转化为三个a和两个b的不同排法，第一步：先排a有种排法，第二步：再排b有1种排法，共有10种排法，选B项．6. 5位同学站成一排准备照相的时候，有两位老师碰巧路过，同学们强烈要求与老师合影留念，如果5位同学顺序一定，那么两位老师与同学们站成一排照相的站法总数为()A．6B．20C．30D．42【答案】D【解析】因为五位学生已经排好，第一位老师站进去有6种选择，当第一位老师站好后，第二位老师站进去有7种选择，所以两位老师与学生站成一排的站法共有6×7＝42种．7.有6名男医生、5名女医生，从中选出2名男医生、1名女医生组成一个医疗小组，则不同的选法共有( )A．60种B．70种C．75种D．150种【答案】C【解析】从6名男医生中选出2名有种不同选法，从5名女男医生中选出2名有种不同选法，根据分步计数乘法原理可得，组成的医疗小组共有15×5=75种不同选法.【考点】计数原理和排列组合.8. [2014·南京模拟]用数字2,3组成四位数，且数字2,3至少都出现一次，这样的四位数共有________个．(用数字作答)【答案】14【解析】分类讨论：若2出现一次，则四位数有C14个；若2出现二次，则四位数有C24个；若2出现3次，则四位数有C34个，所以共有C14＋＋＝14个．9.[2014·郑州模拟]将6名教师分到3所中学任教，一所1名，一所2名，一所3名，则有________种不同的分法．【答案】360【解析】将6名教师分组，分三步完成：第1步，在6名教师中任取1名作为一组，有种取法；第2步，在余下的5名教师中任取2名作为一组，有种取法；第3步，余下的3名教师作为一组，有种取法．根据分步乘法计数原理，共有＝60种取法．再将这3组教师分配到3所中学，有＝6种分法，故共有60×6＝360种不同的分法．10. [2013·浙江高考]将A，B，C，D，E，F六个字母排成一排，且A，B均在C的同侧，则不同的排法共有________种(用数字作答)．【答案】480【解析】如图六个位置.若C放在第一个位置，则满足条件的排法共有种情况；若C放在第2个位置，则从3,4,5,6共4个位置中选2个位置排A，B，再在余下的3个位置排D，E，F，共·种排法；若C放在第3个位置，则可在1,2两个位置排A，B，其余位置排D，E，F，则共有·种排法或在4,5,6共3个位置中选2个位置排A，B，再在其余3个位置排D，E，F，共有·种排法；若C在第4个位置，则有＋种排法；若C在第5个位置，则有种排法；若C在第6个位置，则有种排法．综上，共有2(＋＋＋)＝480(种)排法．11.[2013·怀化模拟]将标号为1,2,3,4,5,6的6张卡片放入3个不同的信封中，若每个信封放2张，其中标号为1,2的卡片放入同一信封，则不同的放法共有()A．12种B．18种C．36种D．54种【答案】B【解析】先将1,2捆绑后放入信封中，有种方法，再将剩余的4张卡片放入另外两个信封中，有种方法，所以共有＝18(种)方法．12.从6名教师中选4名开发A、B、C、D四门课程，要求每门课程有一名教师开发，每名教师只开发一门课程，且这6名中甲、乙两人不开发A课程，则不同的选择方案共有（）A．300种 B．240种 C．144种 D．96种【答案】B【解析】依题意可得从除甲、乙外的四位老师中任取一位开发A课程共有种，再从剩下的5位老师中分别选3位开发其他项目共有.所以完成该件事共有种情况.【考点】1.排列组合问题.2.有特殊条件要先考虑.13.某写字楼将排成一排的6个车位出租给4个公司，其中有两个公司各有两辆汽车，如果这两个公司要求本公司的两个车位相邻，那么不同的分配方法共有________种．（用数字作答）【答案】24【解析】此问题相当于将4个公司全排列，因为，则此问题的不同分配方法共有24种。

四年级奥数讲座综合练习目录第一讲：乘法原理第二讲：加法原理第三讲：排列第四讲：组合第五讲：排列、组合第六讲：排列组合的综合应用第七讲：有趣的数阵第八讲：数学游戏第九讲：简单的幻方及其他数阵图第十讲：数字综合题选讲第十一讲：数字谜第十二讲：数学竞赛试题选讲第一讲：乘法原理基础班1、有五顶不同的帽子，两件不同的上衣，三条不同的裤子。

从中取出一顶帽子、一件上衣、一条裤子配成一套装束。

问：有多少种不同的装束？2、四角号码字典，用4个数码表示一个汉字。

小王自编一个"密码本"，用3个数码（可取重复数字）表示一个汉字，例如，用"011"代表汉字"车"。

问：小王的"密码本"上最多能表示多少个不同的汉字？3、"IMO"是国际数学奥林匹克的缩写，把这3个字母写成三种不同颜色。

现在有五种不同颜色的笔，按上述要求能写出多少种不同颜色搭配的"IMO"？4、在右图的方格纸中放两枚棋子，要求两枚棋子不在同一行也不在同一列。

问：共有多少种不同的放法？5、要从四年级六个班中评选出学习和体育先进集体各一个（不能同时评一个班），共有多少种不同的评选结果？6、甲组有6人，乙组有8人，丙组有9人。

从三个组中各选一人参加会议，共有多少种不同选法？7、如下图，在三条平行线上分别有一个点，四个点，三个点（且不在同一条直线上的三个点不共线）．在每条直线上各取一个点，可以画出一个三角形．问：一共可以画出多少个这样的三角形？8、在自然数中，用两位数做被减数，用一位数做减数．共可以组成多少个不同的减法算式？9、一个篮球队，五名队员A、B、C、D、E，由于某种原因，C不能做中锋，而其余四人可以分配到五个位置的任何一个上．问：共有多少种不同的站位方法？10、由数字1、2、3、4、5、6、7、8可组成多少个①三位数？②三位偶数？③没有重复数字的三位偶数？④百位为8的没有重复数字的三位数？⑤百位为8的没有重复数字的三位偶数？11、某市的电话号码是六位数的，首位不能是0，其余各位数上可以是0～9中的任何一个，并且不同位上的数字可以重复．那么，这个城市最多可容纳多少部电话机？解答1.30种。

第六讲：排列组合的综合应用基础班1.有3封不同的信，投入4个邮筒，一共有多少种不同的投法？2.甲、乙两人打乒乓球，谁先连胜头两局，则谁赢.如果没有人连胜头两局，则谁先胜三局谁赢，打到决出输赢为止，问有多少种可能情况？3.在6名女同学，5名男同学中，选4名女同学，3名男同学，男女相间站成一排，问共有多少种排法？4.用0、1、2、3、4、5、6这七个数字可组成多少个比300000大的无重复数字的六位偶数？5.有两个小盒子，第一个盒子中有标有数字1，2，3，…，10的十张卡片，第二个盒子中有标有11，12，13，…，20的十张卡片.若从两个盒子中各拿出一张卡片相加，一共可列出多少种不同的加法式子？6.小文和小静两位同学帮花店扎花，要从三只篮子中各取一只花扎在一起，已知每只篮子里都有3种不同的花，问她们可以扎成多少种不同式样的花束？7.某学校组织学生开展登山活动.在山的北坡有两条路直通山项；在山的南坡也有两条路，一条直通山顶，另一条通向山腰小亭，从小亭有两条路通向山顶；山的西坡有两条路通向山间寺庙，由寺庙有两条路通向山顶.要登上山顶共有多少种不同的道路？解答1.若投一封信看作一个步骤，则完成投信的任务可分三步，每封信4个邮筒都可投，即每个步骤都有4种方法.故由乘法原理：共有不同的投法4×4×4=64种.2.甲（或乙）胜就写一个甲（或乙）字，画树形图：由图可见共有14种可能.甲甲、甲乙甲甲、甲乙甲乙甲、甲乙甲乙乙、甲乙乙甲甲、甲乙乙甲乙、甲乙乙乙、乙甲甲甲、乙甲甲乙甲、乙甲甲乙乙、乙甲乙甲甲、乙甲乙甲乙、乙甲乙乙、乙乙.3.现有4名女同学，3名男同学，男女相间站成一排，则站在两端的都是女同学.将位置从右到左编号，第1、3、5、7号位是女同学，第2、4、6号位是男同学.于是完成适合题意的排列可分两步：第一步：从6名女同学中任选4名排在第1、3、5、7号位.有P46种排法.第二步：从5名男同学中任选3名排在第2、4、6号位，有P35种排法.因此，由乘法原理排出不同队形数为P46·P35=6×5×4×3×5×4×3=21600.4.图示：分两类：第一类：十万位上是3或5之一的六位偶数有P12·P14·P45个.第二类：十万位上是4或6之一的六位偶数有P12·P13·P45个.∴P12P14P45+P12P13P45=1680.5. 200种第一个盒子中的每一张卡片都可以与第二个盒子中的十张卡片组成 20种加法式子（包括被加数与加数交换位置，例如将 1＋11与11＋1看成为两个加法式子），而第一个盒子中共有十张卡片，则由乘法原理，共10×20＝200种不同的加法式子。

排列组合的综合应用专题讲座及同步训练（有详细解答）一、明确复习目标1.加深对排列、组合意义理解;2.掌握有关排列、组合综合题的一些常用解法;3.学会分类讨论的思想,提高分析问题和解决问题的能力.二．建构知识网络解排列组合问题，首先要用好两个计数原理和排列组合的定义,即首先弄清是分类还是分步,是排列还是组合,透过问题的表面现象,看出问题的数学本质.然后,要掌握一些常见类型的排列组合问题的解法：1.优限法:优先解决带限制条件的元素或位置，或说是“先解决特殊元素或特殊位置”.2.分类分步法:对于较复杂的排列组合问题，常需要分类讨论或分步计算,一定要做到分类明确,层次清楚,不重不漏.如：5人站成一排，甲不在排头，乙不在排尾，共有141423444433A A A A A A +- =156种排法。

3.排除法.从总体中排除不符合条件的方法数，这是一种间接解题的方法4.捆绑法:某些元素必相邻的排列.可以先将相邻的元素“捆成一个”元素,与其它元素进行排列，然后再再给那“一捆元素”内部排列.5.插空法:某些元素不相邻的排列.可以先排其它元素然,再让不相邻的元素插空;6.插板法：n 个 相同元素,分成m(m ≤n)组,每组至步一个的分组问题——把n 个元素排成一的排,从n-1个空中选m-1个空,各插一个隔板,有11--m n C .例如:n 个相同的小球分给m 个人,每人至少一个小球的分法有11--m n C 种分法.如果没有“每人至少一个”的限制,则需设想“每人先献出一个小球”,再对n+m 个小球用“插板法”,有1n m n m C +-+种.7.分组、分配法：分组问题(分成几堆,无序).有等分、不等分、部分等分之别。

一般地平均分成n 堆（组），必须除以n !, 如果有m 堆（组）元素个数相等，必须除以m ！ 例如：6本不同的书分成三组，分别是1本、2本、3本，共有123653C C C =60种分法； 6本不同的书分成三组，每组2本，共有522642C C C ÷3！=15种分法；6本不同的书分成三组，分别是1本、1本、4本，共有114654C C C ÷2！=15种分法； 分配问题(有序分组):逐个分给.例如:7本不同的书,分给甲、乙、丙三个人,依次得3、2、2本，有322742C C C =210种分法。

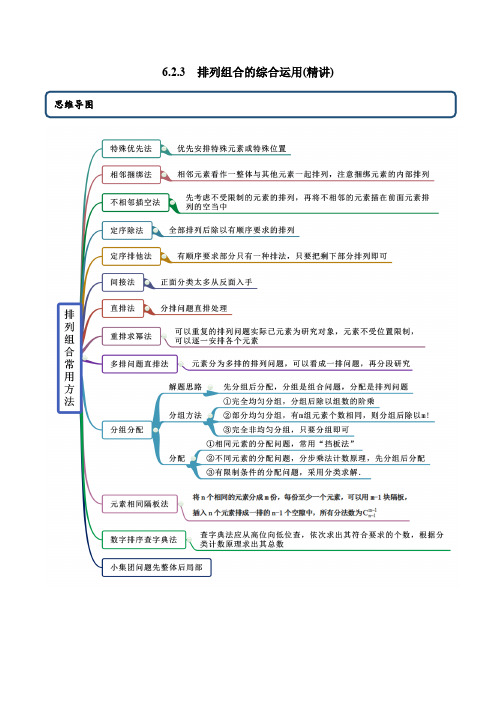
6.2.3 排列组合的综合运用(精讲)考法一全排列【例1】(全国专题练习)在新冠肺炎疫情防控期间，某记者要去武汉4个方舱医院采访，则不同的采访顺序有( )A．4种B．12种C．18种D．24种【答案】D【解析】由题意可得不同的采访顺序有4424A 种，故选：D.【举一反三】1．(全国专题练习)2020年初，我国向相关国家派出了由医疗专家组成的医疗小组．现有四个医疗小组和4个需要援助的国家，每个医疗小组只去一个国家，且4个医疗小组去的国家各不相同，则不同的分配方法有( )A．64种B．48种C．24种D．12种【答案】C【解析】4个医疗小组全排列后按顺序到四个国家即可，共有4424A=种方法．故选：C．2．(吉林吉林市·高二期末)将5本不同的数学用书放在同一层书架上，则不同的放法有( ) A．50 B．60 C．120 D．90【答案】C【解析】由题意，将5本不同的数学用书放在同一层书架上，即将5本不同数学书全排列，故有55120A=种，故选：C．3．(灵丘县豪洋中学高二期末)3本不同的课外读物分给3位同学，每人一本，则不同的分配方法有( ) A．3种B．6种C．12种D．5种【答案】B【解析】3本不同的课外读物分给3位同学，每人一本，全排列：333216A=⨯⨯=.故选：B考法二相邻问题【例2】(河北张家口市)某班优秀学习小组有甲､乙､丙､丁､戊共5人，他们排成一排照相，则甲､乙二人相邻的排法种数为( )A．24 B．36 C．48 D．60【答案】C【解析】先安排甲､乙相邻，有22A种排法，再把甲、乙看作一个元素，与其余三个人全排列，故有排法种数为424248A A⨯=.故选：C【举一反三】1．(全国专题练习)在某场新冠肺炎疫情视频会议中，甲､乙､丙､丁､戊五位疫情防控专家轮流发言，其中甲必须排在前两位，丙､丁必须排在一起，则这五位专家的不同发言顺序共有( )A．8种B．12种C．20种D．24种【答案】C【解析】当甲排在第一位时，共有323212A A=种发言顺序，当甲排在第二位时，共有1222228C A A=种发言顺序，所以一共有12820+=种不同的发言顺序.故选：C.2．(湖北随州市·高二期末)5个人排成一排照相，甲乙要相邻，则有多少种排列的方法( )A．24种B．36种C．48种D．72种【解析】5个人排成一排照相，甲乙要相邻，则有424248A A =种排列的方法.故选：C.3．(重庆高二期末)6月，也称毕业月，高三的同学们都要与相处了三年的同窗进行合影留念.现有4名男生、2名女生照相合影，若女生必须相邻，则有( )种排法. A ．24 B ．120 C ．240 D ．140【答案】C【解析】将2名女生捆绑在一起，当作1个元素，与另4名男生一起作全排列，有55120A =种排法，而2个女生可以交换位置，所以共有52521202240A A ⋅=⨯=排法，故选：C.4.(深圳市龙岗区龙城高级中学)把座位号为1、2、3、4、5、6的六张电影票全部分给甲、乙、丙、丁四个人，每人至少一张，且分给同一人的多张票必须连号，那么不同的分法种数为( ) A ．96 B ．240C ．280D ．480【答案】B【解析】因为每人至少一张，且分给同一人的多张票必须连号，又分给甲、乙、丙、丁四个人， 则在座位号1、2、3、4、5、6的五个空位插3个板子，有3510C=种，然后再分给甲、乙、丙、丁四个人，有4424A =种，所以不同的分法种数为1024240⨯=,故选：B考法三 不相邻问题【例3】(河北石家庄市·石家庄二中高二期中)省实验中学为预防秋季流感爆发，计划安排学生在校内进行常规体检，共有3个检查项目，需要安排在3间空教室进行检查，学校现有一排6间的空教室供选择使用，但是为了避免学生拥挤，要求作为检查项目的教室不能相邻，则共有( )种安排方式. A ．12 B ．24 C ．36 D ．48【答案】B【解析】6间空教室，有3个空教室不使用，故可把作为检查项目的教室插入3个不使用的教室之间，故所有不同的安排方式的总数为3424A =.故选：B.【举一反三】1．(北京高二期末)3位老师和4名学生站成一排，要求任意两位老师都不相邻，则不同的排法种数为( ) A ．77A B ．4343A A +C ．4343A AD ．4345A A【解析】根据题意，分2步进行：①将4名学生站成一排，有44A 种排法；②4人排好后，有5个空位可选，在其中任选3个，安排三名教师，有35A 种情况；则有4345A A 种排法； 故选：D .2．(北海市教育教学研究室高二期末)若5个人排成一列纵队，则其中甲、乙、丙三人两两不相邻的排法有( ) A ．12种 B ．14种 C ．5种 D ．4种【答案】A【解析】分两步完成：第一步，5个人中除去甲、乙、丙三人余2人排列有22A 种排法；第二步，从3个可插空档给甲、乙、丙3人排队有33A 种插法.由分步乘法计数原理可知，一共有2323A A 种排法.故答案选A 3．(四川省新津中学)五名学生和五名老师站成一排照相，五名老师不能相邻的排法有( ) A ．55552A A B ．5565A AC ．55562A AD ．5555A A【答案】B【解析】由题意五名老师不能相邻用插空法，排法数为5565A A ．故选：B ．4．(重庆市第七中学校高二月考)现“学习强国”平台设有“阅读文章”、“视听学习”等多个栏目.在某时段时，更新了2篇文章和4个视频，一位学习者准备学习这2篇文章和其中2个视频，则这2篇文章学习顺序不相邻的学法有( )种. A ．24 B ．36 C ．72 D ．144【答案】C【解析】根据题意，分2步进行分析：①，在4个视频中任选2个进行学习，有246C =种情况， ②，将选出的2个视频与2篇文章依次进行学习，共有4424A =种情况，其中2篇文章学习顺序相邻的情况有232312A A =种情况，故2篇文章学习顺序不相邻的情况有12种，则这2篇文章学习顺序不相邻的学法有61272⨯=种；故选：C考法四 分组分配【例4】(全国)疫情期间，上海某医院安排5名专家到3个不同的区级医院支援，每名专家只去一个区级医院，每个区级医院至少安排一名专家，则不同的安排方法共有( )A ．60种B ．90种C ．150种D ．240种【答案】C【解析】5名专家到3个不同的区级医院，分为1，2，2和1,1,3两种情况；分为1，2，2时安排有1223542322C C C A A ;分为1，1，3时安排有1133543322C C C A A 所以一共有12211333542543332222150C C C C C C A A A A +=故选：C 【举一反三】1．(广东深圳市·深圳外国语学校)有四位朋友于七夕那天乘坐高铁G 77从武汉出发(G 77只会在长沙、广州、深圳停)，分别在每个停的站点至少下一个人，则不同的下车方案有( ) A ．24种 B ．36种 C ．81种 D ．256种【答案】B【解析】依据题意每个停的站点至少下一个人，先按2+1+1分成三组，有24C 种分法，再分配到三个站点，有33A 种分法，所以一共有234336C A =种不同的下车方案.故选：B.2．(河北)特岗教师是中央实施的一项对中西部地区农村义务教育的特殊政策.某教育行政部门为本地两所农村小学招聘了6名特岗教师，其中体育教师2名，数学教师4名.按每所学校1名体育教师，2名数学教师进行分配，则不同的分配方案有( ) A ．24 B ．14 C ．12 D ．8【答案】C【解析】先把4名数学教师平分为2组，有2242223=C C A 种方法， 再把2名体育教师分别放入这两组，有222A =种方法，最后把这两组教师分配到两所农村小学，共有223212A ⨯⨯=种方法.故选：C.3．(江西高二期末)江西省旅游产业发展大会于2020年6月11日～13日在赣州举行，某旅游公司为推出新的旅游项目，特派出五名工作人员前往赣州三个景点进行团队游的可行性调研.若每名工作人员只去一个景点且每个景点至少有一名工作人员前往，则不同的人员分配方案种数为( ) A ．60 B ．90C ．150D ．240【答案】C【解析】根据题意，分2步进行分析： ①将五名工作人员分成3组，若分为3、1、1的三组，有3510C =种分法， 若分为2、2、1的三组，2215312215C C C A =种分法，则有101525+=种分组分法；②将分好的三组全排列，对应三个景点，有336A =种情况，则有256150⨯=种分配方法；故选：C ．4．(四川达州市·高二期末)公元2020年年初，19COVID -肆虐着中国武汉，为了抗击19COVID -，中国上下众志成城，纷纷驰援武汉.达州市决定派出6个医疗小组驰援武汉市甲、乙、丙三个地区，每个地区分配2个医疗小组，其中A 医疗小组必须去甲地，则不同的安排方法种数为( ) A ．30 B ．60 C ．90 D ．180【答案】A【解析】根据题意，分2步进行：①将6个医疗小组平均分成3组，每组2支医疗队，有22264233=15C C C A 种分组方法； ②将甲所在的小组安排到甲地，其他两个小组安排到乙、丙两地，有222A =种情况，则有15230⨯=种不同的安排方法. 故选：A.5．(沈阳市·辽宁省实验中学分校高二期末)据《孙子算经》中记载，中国古代诸侯的等级从低到高分为：男、子、伯、侯、公，共五级，若给获得巨大贡献的7人进行封爵，要求每个等级至少有一人，至多有两人，则伯爵恰有两人的概率为( ) A ．310B ．25C ．825D ．35【答案】B【解析】7人进行封爵，每个等级至少一人，至多两人，则共有2211225575327555322322C C C C C C A A A A A ⋅=种分法； 其中伯爵恰有两人的分法有2211142247532247543232C C C C C A C C A A A ⋅=种分法，∴伯爵恰有两人的概率2247542257552225C C A p C C A A ==.故选：B .考向五 几何问题【例5】(全国)如图，MON ∠的边OM 上有四点1A 、2A 、3A 、4A ，ON 上有三点1B 、2B 、3B ，则以O 、1A 、2A 、3A 、4A 、1B 、2B 、3B 中三点为顶点的三角形的个数为( )A ．30B ．42C ．54D ．56【答案】B【解析】利用间接法，先在8个点中任取3个点，再减去三点共线的情况，因此，符合条件的三角形的个数为33384542C C C --=.故选：B.【举一反三】1．(湖南高三开学考试)以长方体的顶点为顶点的三棱锥共有( )个 A ．70 B ．64 C ．60 D ．58【答案】D【解析】三棱锥有4个顶点，从长方体8个顶点中任取4个点共有488765C 704321⨯⨯⨯==⨯⨯⨯种取法，排除其中四点共面的有：长方体的面6个，对角面6个，可得不同的三棱锥有701258-=个.故选：D. 2．(昆明呈贡新区中学)在圆上有6个不同的点，将这6个点两两连接成弦，这些弦将圆分割成的区域数最多为( ) A ．32 B ．15C ．16D ．31【答案】D【解析】两个点可以连一条弦，将圆分为两部分，加一个点，多两条弦，将圆多分出来两部分，所以每加一条弦可以按这种方式多出一个区域，再加一个点，变成了一对相交弦和四条其他的弦，共分为8个区域，所以除去前一种方式增加的区域数，一对相交弦还会多产生一个区域，故当点数多于4个时，最多可分得总的区域数为241C C n n ++，此题6n =，所以最多可分为31个区域.故选：D .3．(北京丰台区·高二期末)平面内有8个点，以其中每2个点为端点的线段的条数为( ) A ．21 B ．28 C ．42 D ．56【答案】B【解析】线段由2个端点组成，因此只需要从8个点中选取2个即可构成一条线段，所以线段条数为2828C =，故选：B.4．(上海浦东新区·华师大二附中高二期中)以长方体1111ABCD A B C D -的任意三个顶点为顶点作三角形，从中随机取出2个三角形，则这2个三角形不共面的情兄有( )种A ．1480B ．1468C ．1516D ．1492【答案】B【解析】因为平行六面体1111ABCD A B C D -的8个顶点任意三个均不共线， 故从8个顶点中任取三个均可构成一个三角形共有38=56C 个三角形，从中任选两个，共有2561540C =种情况，因为平行六面体有六个面,六个对角面， 从8个顶点中4点共面共有12种情况， 每个面的四个顶点共确定6个不同的三角形，故任取出2个三角形，则这2个三角形不共面共有1540-12×6=1468种，故选：B.考向六 方程不等式问题【例6】(全国)方程10x y z ++=的正整数解的个数__________. 【答案】36【解析】问题中的x y z ､､看作是三个盒子，问题则转化为把10个球放在三个不同的盒子里，有多少种方法．将10个球排一排后，中间插入两块隔板将它们分成三堆球，使每一堆至少一个球．隔板不能相邻，也不能放在两端，只能放在中间的9个空内．∴共有2936C =种．故答案为：36【举一反三】1．(山西太原市)三元一次方程x +y +z =13的非负整数解的个数有_____. 【答案】105【解析】由,,x y z N ∈,则13,,,x y z x y z N ++=∈设1,1,1a x b y c z =+=+=+，则,,a b c N +∈且16a b c ++=，则三元一次方程x +y +z =13的非负整数解的个数等价于16a b c ++=,,,a b c N +∈的解的个数,等价于将16个相同的小球分成3组，每组至少1个小球的不同分法，又将16个相同的小球分成3组，每组至少1个的不同分法，只需在16个球之间的15个空中选2个空用隔板隔开即可，则共有21515141052C ⨯==种分法，即三元一次方程x +y +z =13的非负整数解的个数有105个， 故答案为：105.2．(四川雅安市·雅安中学高二月考)方程123412x x x x +++=的正整数解共有( )组 A ．165 B ．120C ．38D ．35【答案】A【解析】如图，将12个完全相同的球排成一列，在它们之间形成的11个空隙中任选三个插入三块隔板，把球分成四组，每一种分法所得球的数目依次是1x 、2x 、3x 、4x ，显然满足123412x x x x +++=，故()1234,,,x x x x 是方程123412x x x x +++=的一组解，反之，方程123412x x x x +++=的每一组解都对应着一种在12个球中插入隔板的方式，故方程123412x x x x +++=的正整数解的数目为：31111109165321C ⨯⨯==⨯⨯，故选：A.考向七 数字问题【例7】(南通西藏民族中学)从1，2，3，4，5，6中任取三个不同的数相加，则不同的结果共有( )A ．6种B ．9种C ．10种D ．15种【答案】C 【解析】在这六个数字中任取三个求和，则和的最小值为1236++=，和的最大值为45615++=， 所以当从1，2，3，4，5，6中任取三个数相加时，则不同结果有10种．故选：C.【举一反三】1．(全国)在1，2，3，4，5，6，7这组数据中，随机取出五个不同的数，则数字5是取出的五个不同数的中位数的所有取法种数为( )A ．6B ．12C ．18D ．24【答案】A【解析】根据题意，数字5是取出的五个不同数的中位数，则取出的数字中必须有5、6、7，在1，2，3，4中有2个数字，则不同的取法有246C =种，故选：A ． 2．(广东汕尾市·高二月考)从1，3，5，7，9中任取3个数宇，与0，2，4组成没有重复数字的六位数，其中偶数共有( )A ．312个B ．1560个C ．2160个D ．3120个【答案】D【解析】从1，3，5，7，9中任取3个数宇，与0，2，4组成没有重复数字的六位偶数，可分为以下两种情况：①、0放在末位，从1，3，5，7，9中任取3个数宇，再与2，4全排列即可，共有35551200C A ⋅=个； ②、0不放在末位，从1，3，5，7，9中任取3个数宇，再从2，4中选择一个作为末位数，从剩下的非首位中选择一个放置0，再将余下的数字全排列即可，共有311452441920C C C A ⋅⋅⋅=个；则满足要求的偶数共有120019203120+=个.故选：D.3．(浙江高三其他模拟)从1,2,3,4,5,6,7,8,9这9个数中取三个，所取三个数之积为偶数且能被3整除，则不同的选取方法有( )A ．55种B ．61种C ．64种D ．70种【答案】A【解析】对三个数中有没有6进行分类：①含有6时，只需从剩下的8个数中任意选两个即可，即28C 28=种；②不含6时，则需要3与9．当3与9同时存在时，需要从剩余的3个偶数中选一个，即133C =种；当3与9有1个存在时，偶数可以选1个或2个，即()11122333C C C C 24⋅+=种． 综上所述，不同的选取方法有55种，故选：A ．。