勾股定理的应用 (2)
- 格式:doc
- 大小:69.50 KB
- 文档页数:5



第10课时勾股定理的应用(2)(附答案)【基础巩固】1.小强量得家里彩电荧屏的长为58 cm,宽为46 cm,则这台电视机的尺寸是 ( ) A.9英寸(23 cm) B.21英寸(54 cm)C.29英寸(74 cm) D.34英寸(87 cm)2.如图,每个小正方形的边长为1,则△ABC的三边a,b,c的大小关系是 ( )A.a<c<b B.a<b<e C.c<a<b D.c<b<a3.如图,△ABC是等腰直角三角形,∠A=90°,BD是角平分线,DE⊥BC,BC=10 cm,则△DEC的周长是 ( )A.8 cm B.10 cm C.12 cm D.14 cm4.旗杆上的绳子垂到地面还多出1 m,如果把绳子的下端拉开距旗杆底部5m后,绷紧的绳子的末端刚好接触地面,则旗杆的高度为_______m.5.如图,大正方形网格是由16个边长为1的小正方形组成,求图中阴影部分的面积.6.在波平如镜的湖面上,有一朵美丽的红莲,它高出水面1m,一阵大风吹过,红莲被吹至一边,花朵齐及水面,如果知道红莲移动的水平距离为2m,问这里水深多少?78.如图,在△ABC中,∠A=45°,AC AB1.求边BC的长.9.如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形(涂上阴影).(1)在图①中,画一个三角形,使它的三边长都是有理数;(2)在图②、图③中,分别画两个不全等的直角三角形,使它的三边长都是无理数.【拓展提优】10,如图,已知△ABC是边长为1的等腰直角三角形,以Rt△ABC的斜边AC为直角边,画第二个等腰直角三角形ACD,再以直角三角形ACD的斜边AD为直角边,画第三个等腰直角三角形ADE,…,依此类推,第n个等腰直角三角形的斜边长是_______.11.在Rt△ABC中,∠BAC=90°.AB=AC=2,以AC为一边,在△ABC外部作等腰直角三角形ACD,则线段BD的长为_______.12.如图,数学活动课上,老师在黑板上画直线平行于射线AN(如图),让同学们在直线l 和射线AN上各找一点B和C,使得以A、B、C为顶点的三角形是等腰直角三角形,这样的三角形最多能画_______个.13.如图,在四边形ABCD中,AB=AC=AD,E是CB的中点,AE=EC,∠BAC=3∠DBC,BD=6AB=_______14.已知直角三角形的周长是2斜边上的中线为1,则此直角三角形的面积是( )A.1 B.2 C.12D.1415.如图,在长方形纸片ABCD中,AD=4 cm,AB=10 cm,按如图方式折叠,使点B与点D 重合,折痕为EF,求DE的长.16.如图,等边三角形ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是AC 边上一点,若AE=2,求EM +CM的最小值.17.如图是两个全等的直角三角形,量得它们的斜边长为10 cm,较小锐角为30°,将这两个三角形摆成如图①所示的形状,使点B、C、F、D在同一条直线上,且点C与点F重合,将图①中的△ABC绕点C顺时针方向旋转到图②的位置,使点E落在边AB上,AC交DE于点G,则线段CG的长为_______cm(保留根号).18.如图,在△ABC中,CD是高,CE为∠ACB的平分线.若AC=15,BC=20,CD=12,则CE的长等于_______.参考答案【基础巩固】1.C 2.C 3.B 4.12 5.10 6.1.5m 7.略 8.2 9.略【拓展提优】10.n 11.4或 12.5 13.12 14.C 15.5.8 16.17. 18。

学习目标:1.能用勾股定理直角三角形全等的“斜边、直角边”判定定理。
2.能应用勾股定理在数轴上画出表示无理数的点。
3.体会勾股定理在数学中的地位和作用。
学习重点:用勾股定理作出长度为无理数的线段。
教学活动流程活动1:复习孕新,引入课题1.回顾勾股定理,并以针对性练习为画作铺垫;(2)用“数学海螺”图创设情境并导入新课,明确学习目标。
活动2:运用勾股定理证明(HL)用三角板作辅助演示活动3:课件动画演示作图演示的两种作法以及“数学海螺”的作法.活动4:动手实践,会“数形互变”以前面的练习题为作图思路导向,以课件演示类比模仿,教师演示规范作图,学生会作图也会求点.活动5:当堂检测教材第27页习题活动6:拓展应用,服务生活1.用无刻度的直尺在网格上按要求画含无理数线段的三角形;(2)求蚂蚁沿圆柱表面爬行的最短路径。
活动7:小结梳理数轴图——网格图——展开图;实际问题——数学问题——建模活动8:布置作业教学过程活动1:复习孕新,引入课题1.问题(1)勾股定理的内容是什么?怎样求斜边长c或直角边长a、b?(2)求以线段a、b为直角边的直角三角形的斜边长。
a=1 b=1 (c=)a=1 b= (c=)a=2 b=3 (c=)设计意图:在复习的基础上为新课画无理数线段作铺垫,实现知识正迁移。
(3)如果直角三角形ABC的两边长分别为3和4,求第三边长。
设计意图:第三边应考虑为直角边或斜边,渗透分类讨论思想。
2.课件展示“数学海螺”图片并明确学习目标设计意图:创设情境并明确本节课学习任务。
活动2:运用勾股定理证明(HL)用三角板作演示,并要求画图并写出已知、求证并证明,利用勾股定理求得第三边长,再利用(SSS)或(SAS)可证得。
活动3:课件动画演示作图1.对比的两种作法,明确当直角边为正整数时作图方便,并引导学生如何规范作图。
2.“数学海螺”的作法活动4:动手实践,会“数形互变”1.在数轴上画出表示的点,的点呢?2.求点A在数轴上表示的点(1-)设计意图:以练习为画的思路导向,以活动3为类比模仿会作图也会求点,实现数形互变,以“数”化“形”,以“形”变“数”,渗透数形结合思想。

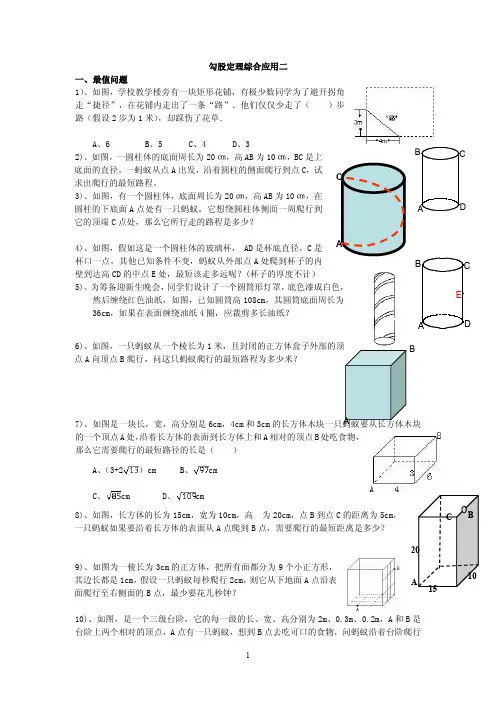

2.7勾股定理的应用(二) --- [ 教案] 班级 姓名 学号教学目标:1能运用勾股定理及直角三角形的判定条件解决实际问题.2会用勾股定理及直角三角形的判定条件解决实际问题,逐步培养“数形结合”和“转化”数学能力。
发展学生的分析问题能力和表达能力。
3在提升分析问题能力和完整表达解题过程能力的同时,感受“数形结合”和“转化”的数学思想,体会数学的应用价值和渗透数学思想给解题带来的便利。
积极参加数学学习活动,增强自主、合作意识,培养热爱科学的高尚品质。
重 难 点:勾股定理及直角三角形的判定条件的应用教学过程(一)创设情景,引入新课;这些图形都有什么共同特征?几组勾股数.3,4,5; 5,12,13; 7,24,25; 8,15,17; 9,40,41;…… (二)实践探索,揭示新知1;.图1中的x 等于多少?图2中的z y x ,,分别是多少? (三)尝试应用,反馈矫正在数轴上画出表示5的点在数轴上表示76,,76--,的点怎样画出? 图2中的图形的周长和面积分别是多少? (四)实践探索,揭示新知2;图1x 11z y 11x图2例1、如图4,等边三角形ABC 的边长是6,求△ABC 的面积。
(五)尝试应用,反馈矫正2如图5,在△ABC 中,AB=AC=17,BC=16,求△ABC 的面积。
如图6,在△ABC 中,AD ⊥BC ,AB=15,AD=12,AC=13,求△ABC 的周长和面积。
(六)实践探索,揭示新知3;如图7,在△ABC 中,AB=25,BC=7,AC=24,问△ABC 是什么三角形? (七)尝试应用,反馈矫正1如图9,在△ABC 中, AB=15,AD=12,BD=9,AC=13,求△ABC 的周长和面积。
勾股定理与它的逆定理在应用上有什么区别? 材料5:如图10,以△ABC 的三边为直径向外作半圆,且S1+S3=S2,试判断△ABC 的形状?(目的:对总结的结论的应用)(八)归纳小结,巩固提高 (九)布置作业D CBA图6图9D CBA。

主备:蔡辉审核:管华敏编号:80305班级姓名备课组长签名【学习目标】1.能运用勾股定理及直角三角形的判定条件解决实际问题。
2.在运用勾股定理解决实际问题的过程中,感受数学的“转化”思想(把解斜三角形问题转化为解直角三角形的问题),进一步发展有条理思考和有条理表达的能力,体会数学的应用价值。
【课前预习】△若△ABC的三边a、b、c满足条件a2+b2+c2+338=10a+24b+26c,试判断△ABC的形状。
【学习过程】例1.如图,在△ABC中,AB=26,BC=20,BC边上的中线AD=24,求AC.例2.在△ABC中, AB=15,AD=12,BD=9,AC=13,求△ABC的周长和面积。
△例3.如图,一个高20m,周长10m的圆柱形水塔,现制造一个螺旋形登梯,为了减小坡度,要求登梯绕塔环绕一周半到达顶端,问登梯至少多长?(建议:拿一张白纸动手操作,你一定会发现其中的奥妙)【当堂训练】1. 已知:如图①,在Rt △ABC 中,两直角边AC 、BC 的长分别为6和8,现将直角边AC 沿AD 折叠,使它落在斜边AB 上,且与AE 重合,则CD 等于 ( )A.2B.3C.4D.52.将上题中的Rt △ABC 折叠,使点B 与A 重合,折痕为DE (如图②),则CD 的长为 ( )A.1.50B.1.75C.1.95D.以上都不对3.一条河的宽度处处相等,小强想从河的南岸横游到北岸去,由于水流影响,小强上岸地点偏离目标地点200m ,他在水中实际游了520m ,那么该河的宽度为 ( )A.440 mB.460 mC.480 mD. 500 m4.已知一个直角三角形的两直角边长分别为5和12,则其周长为______________.5.旗杆上的绳子垂到地面还多出1m ,如果把绳子的下端拉开距旗杆底部5m 后,绷紧的绳子的末端刚好接触地面,则旗杆的高度为___________m.6.一架5m 长的梯子靠在一面墙上,梯子的底部离建筑物3m ,若梯子底部滑开1m ,则梯子顶部下滑的距离是___________.7.如图,已知:在Rt △ABC 中,∠ACB=90º,AC=12,BC=5,AM=AC ,BN=BC 。
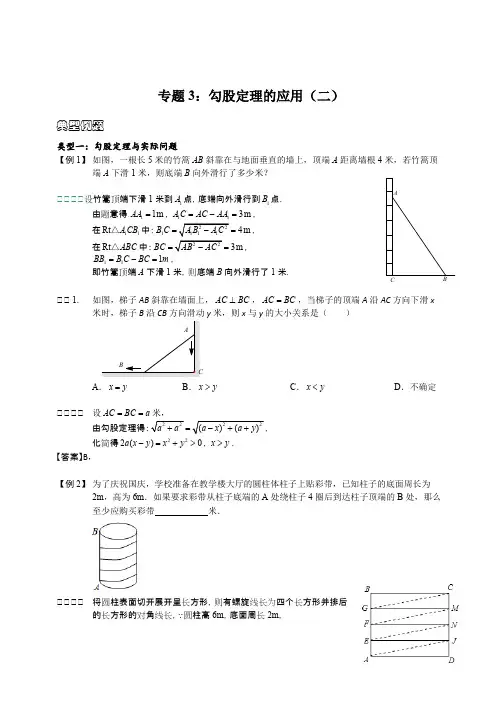


第03讲勾股定理的应用(3种题型)【知识梳理】一.勾股定理的应用(1)在不规则的几何图形中,通常添加辅助线得到直角三角形.(2)在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.(3)常见的类型:①勾股定理在几何中的应用:利用勾股定理求几何图形的面积和有关线段的长度.②由勾股定理演变的结论:分别以一个直角三角形的三边为边长向外作正多边形,以斜边为边长的多边形的面积等于以直角边为边长的多边形的面积和.③勾股定理在实际问题中的应用:运用勾股定理的数学模型解决现实世界的实际问题.④勾股定理在数轴上表示无理数的应用:利用勾股定理把一个无理数表示成直角边是两个正整数的直角三角形的斜边.二.平面展开-最短路径问题(1)平面展开﹣最短路径问题,先根据题意把立体图形展开成平面图形后,再确定两点之间的最短路径.一般情况是两点之间,线段最短.在平面图形上构造直角三角形解决问题.(2)关于数形结合的思想,勾股定理及其逆定理它们本身就是数和形的结合,所以我们在解决有关结合问题时的关键就是能从实际问题中抽象出数学模型.【考点剖析】题型一.勾股定理的实际应用例1.如图,一棵树从3m处折断了,树顶端离树底端距离4m,那么这棵树原来的高度是() A.8m B.5m C.9m D.7m【变式】如图在实践活动课上,小华打算测量学校旗杆的高度,她发现旗杆顶端的绳子垂到地面后还多出1m,当她把绳子斜拉直,且使绳子的底端刚好接触地面时,测得绳子底端距离旗杆底部5m,由此可计算出学校旗杆的高度是()A.8m B.10m C.12m D.15m例2.如图,一个直径为20cm的杯子,在它的正中间竖直放一根小木棍,木棍露出杯子外2cm,当木棍倒向杯壁时(木棍底端不动),木棍顶端正好触到杯口,求木棍长度.【变式】小明想知道学校旗杆的高,他发现旗杆上的绳子垂到地面还多了1m,当他把绳子的下端拉开5m后,发现下端刚好接触地面,求旗杆的高.题型二.平面展开-最短路径问题例3.如图,长方体的底面边长是1cm和3cm,高是6cm,如果用一根细线从点A开始经过4个侧面缠绕一圈到达B,那么用细线最短需要()A.12cm B.10cm C.13cm D.11cm例4.一个上底和下底都是等边三角形的盒子,等边三角形的高为70cm,盒子的高为240cm,M为AB的中点,在M处有一只飞蛾要飞到E处,它的最短行程多少?【变式】如图①,有一个圆柱,它的高等于12cm,底面半径等于3cm,在圆柱的底面A点有一只蚂蚁,它想吃到上底面上与A点相对的B点的食物,需要爬行的最短路程是多少?(π取3)题型三:勾股定理中的折叠问题例5.如图,矩形纸片ABCD中,4AB=,3AD=,折叠纸片使AD边与对角线BD重合,折痕为DG,则AG的长为()A.1B.43C.32D.2【变式】如图,将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F点处,已知3CE cm=,8AB cm=,求图中阴影部分的面积.【过关检测】一.选择题1.如图,在水池的正中央有一根芦苇,池底长10尺,它高出水面1尺,如果把这根芦苇拉向水池一边,它的顶端恰好到达池边的水面则这根芦苇的长度是()A.10尺B.11尺C.12尺D.13尺2.如图,已知圆柱底面的周长为12cm,圆柱高为8cm,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小为()A.10cm B.20cm C.cm D.100cm3.如图,小巷左右两侧是竖直的墙壁,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米.若梯子底端位置保持不动,将梯子斜靠在右墙时,顶端距离地面1.5米,则小巷的宽度为()A.0.8米B.2米C.2.2米D.2.7米4.如图,台阶阶梯每一层高20cm,宽30cm,长50cm,一只蚂蚁从A点爬到B点,最短路程是()A.10B.50C.120D.1305.如图,圆柱的高为8cm,底面半径为2cm,在圆柱下底面的A点处有一只蚂蚁,它想吃到上底面B处的食物,已知四边形ADBC的边AD、BC恰好是上、下底面的直径,问:蚂蚁吃到食物爬行的最短距离是cm.(π取3)6.《九章算术》中的“引葭赴岸”问题:今有池方一丈,葭(一种芦苇类植物)生其中央,出水一尺.引葭赴岸,适与岸齐,水深几何?其大意是:有一个边长为10尺的正方形池塘,一棵芦苇生长在它的正中央,高出水面1尺.如果把该芦苇拉向岸边,那么芦苇的顶部恰好碰到岸边(如图所示),则水深________尺.7.《九章算术》是我国古代一部著名的数学专著,其中记载了一个“折竹抵地”问题:今有竹高一丈,未折抵地,去本三尺,问折者高几何?其意思是:有一根与地面垂直且高一丈的竹子(1丈10尺),现被大风折断成两截,尖端落在地面上,竹尖与竹根的距离为三尺,问折断处离地面的距离为.8.《九章算术》是我国古代最重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去根四尺,问折者高几何?”翻译成数学问题是:如图所示,△ABC中,∠ACB=90°,AC+AB =10,BC=4,求AC的长.9.如图,一架25米长的梯子AB斜靠在一竖直的墙AO上,梯子底端B离墙AO有7米.(1)求梯子靠墙的顶端A距地面有多少米?(2)小燕说“如果梯子的顶端A沿墙下滑了4米,那么梯子的底端B在水平方向就滑动了4米.”她的说法正确吗?若不正确,请说明理由.10.已知某开发区有一块四边形的空地ABCD,如图所示,现计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,问要多少投入?11.我国古代的数学名著《九章算术》中记载“今有竹高一丈,末折抵地,去本三尺.问:折者高几何?”译文:一根竹子,原高一丈,虫伤有病,一阵风将竹子折断,其竹梢恰好着地,着地处离原竹子根部3尺远.问:尺)原处还有多高的竹子?(1丈1012.如图,一个梯子AB,顶端A靠在墙AC上,这是梯子的顶端距地面的垂直高度为24米,若梯子的顶端下滑4米,底端将水平滑动了8米,求滑动前梯子底端与墙的距离CB是多少?13.(2022春•蜀山区期中)在一款名为超级玛丽的游戏中,玛丽到达一个高为10米的高台A,利用旗杆顶部的绳索,划过90°到达与高台A水平距离为17米,高为3米的矮台B,(1)求高台A比矮台B高多少米?(2)求旗杆的高度OM;(3)玛丽在荡绳索过程中离地面的最低点的高度MN.14.如图,四边形ABCD是舞蹈训练场地,要在场地上铺上草坪网.经过测量得知:∠B=90°,AB=24m,BC =7m,CD=15m,AD=20m.(1)判断∠D是不是直角,并说明理由;(2)求四边形ABCD需要铺的草坪网的面积.15.如图,A,B两村在河L的同侧,A,B到河L的距离分别为1.5km和2km,AB=1.3km,现要在河边建一供水厂,同时向A,B 1.8万元,问水厂与A村的水平距离为多远时,能使铺设费用最省,并求出总费用约多少万元.。
2021年九年级数学中考复习分类专题:勾股定理实际应用(二)一.选择题1.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离BC 为0.7米,梯子顶端到地面的距离AC为2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,梯子顶端到地面的距离A'D为1.5米,则小巷的宽为()A.2.5米B.2.6米C.2.7米D.2.8米2.《九章算术》是我国古代第一部数学专著,它的出现标志中国古代数学形成了完整的体系.“折竹抵地”问题源自《九章算术》中:“今有竹高一丈,末折抵地,去本四尺,问折者高几何?”翻译成数学问题是:如图所示,△ABC中,∠ACB=90°,AC+AB=10尺,BC=4尺,求AC的长.AC的长为()A.3尺B.4.2尺C.5尺D.4尺3.将一根24cm的筷子,置于底面直径为15cm,高8cm的装满水的无盖圆柱形水杯中,设筷子浸没在杯子里面的长度为hcm,则h的取值范围是()A.h≤15cm B.h≥8cm C.8cm≤h≤17cm D.7cm≤h≤16cm 4.在我国古代数学著作《九章算术》的第九章《勾股》中记载了这样的一个问题:“今天有开门去阔一尺,不合二寸,问门广几何?”意思是:如图,推开两扇门(AD和BC),门边缘D,C两点到门槛AB的距离是1尺,两扇门的间隙CD为2寸,则门宽AB长是()寸.(1尺=10寸)A.101 B.100 C.52 D.965.《九章算术》是我国古代的数学名著,书中的“折竹抵地”问题:今有竹高一丈,末折抵地,去本三尺.问折者高几何?意思是:一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部3尺远,问折断处离地面的高度是多少?设折断后离地面的高度为x尺,则可列方程为()A.x2﹣3=(10﹣x)2B.x2﹣32=(10﹣x)2C.x2+3=(10﹣x)2D.x2+32=(10﹣x)26.如图,一个梯子AB斜靠在一竖直的墙AO上,测得AO=8米.若梯子的顶端沿墙面向下滑动2米,这时梯子的底端在水平的地面也恰好向外移动2米,则梯子AB的长度为()A.10米B.6米C.7米D.8米7.如图为小平与小聪微信对话记录,根据两人的对话记录,若下列有一种走法能从科技馆出发走到小平家,则可行的是()A.向北直走200米,再向东直走1200米B.向北直走200米,再向西直走1200米C.向北直走500米,再向东直走700米D.向北直走700米,再向西直走500米8.《九章算术》是我国古代一部著名的数学专著,其中记载了一个“折竹抵地”问题:今有竹高一丈,末折抵地,去本三尺,问折者高几何?其意思是:有一根与地面垂直且高一丈的竹子(1丈=10尺),现被大风折断成两截,尖端落在地面上,竹尖与竹根的距离为三尺.问折断处高地面的距离为()A.5.45尺B.4.55尺C.5.8尺D.4.2尺9.校园内有两棵树,相距8米,一棵树高为13米,另一棵树高7米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞()A.10米B.11米C.12米D.13米10.如图,△ABE、△BCF、△CDG、△DAH是四个全等的直角三角形,其中,AE=5,AB=13,则EG的长是()A.7B.6C.7 D.7二.填空题11.如图,有一块四边形草地ABCD,∠B=90°,AB=4m,BC=3m,CD=12m,DA=13m.则该四边形草地的面积是.12.小明想知道学校旗杆有多高,他发现旗杆上的绳子垂到地面还余1m,当他把绳子下端拉开5m后,发现下端刚好接触地面,则绳长为m.13.有一根7cm木棒,能放在长,宽,高分别为5cm,4cm,3cm的木箱中.(判断对错)14.《九章算术》第九卷《勾股》章第十五题:“今有勾五步,股十二步,问勾中容方几何?答曰三步十七分步之九.术曰:并勾股为法,勾股相乘实,实如法而一,得方一步.”如图1中直角三角形ABC中,∠B=90°,AB=5,BC=12,则内接正方形DEFB边长为x 的求法是:以勾5步、股12步之和为分母(并勾股为法),以勾5步、股12步之积为分子(勾股相乘为实)求得.即x=.我国数学家刘徽用“出入相补”原理予以证明,将图1中补成如图2的矩形,在该图形中发现一个与正方形DEFB面积相等的图形,从而建立方程求解,这个方程是.15.有一块面积为160m2的等腰三角形草地,测得它的一边长为20m.现要给这块三角形的周围围上栅栏,则栅栏的长度为.16.如图,一架长25m的云梯,斜靠在墙上,云梯底端在点A处离墙7米,如果云梯的底部在水平方向左滑动8米到点B处,那么云梯的顶端向下滑了m.17.如图所示,一根长为7cm的吸管放在一个圆柱形杯中,测得杯的内部底面直径为3cm,高为4cm,则吸管露出在杯外面的最短长度为cm.三.解答题18.如图,在笔直的铁路上A,B两点相距20km,C,D为两村庄,DA=8km,CB=14km,DA ⊥AB于A,CB⊥AB于B.现要在AB上建一个中转站E,使得C,D两村到E站的距离相等,求AE的长.19.我市某中学有一块四边形的空地ABCD(如图所示),为了绿化环境,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,DA=4m,CD=13m,BC=12m.(1)求出空地ABCD的面积.(2)若每种植1平方米草皮需要200元,问总共需投入多少元?20.如图,小明将升旗的绳子拉到旗杆底端,并在绳子上打了一个结,然后将绳子拉到离旗杆底端9米处,发现此时绳子底端距离打结处约3米,请算出旗杆的高度.21.如图,距沿海某城市A正南220千米的B处,有一台风中心,其最大风力为12级,每远离台风中心20千米,风力就减弱1级,该中心正以每小时15千米的速度沿北偏东30°的BC方向移动,且风力不变,若城市A所受风力达到或超过4级,则称为受台风影响.(1)A城市是否会受台风影响?为什么?(2)若会,将持续多长时间?(3)该城市受台风影响的最大风力为几级?22.“武黄城际铁路”是武汉市城市圈内一条连通武汉市和黄石市的快速城际铁路,如图1,以往从黄石A坐客车到武昌客运站B,现在可以在A坐城际列车到武汉青山站C,再从青山站C坐市内公共汽车到武昌客运站B.设AB=80km,BC=20km,∠ABC=120°.请你解决以下问题:(1)求A、C之间的距离;(参考数据≈4.6);(2)若客车的平均速度是60km/h,市内的公共汽车的平均速度为40km/h,城际列车的平均速度为180km/h,为了最短时间到达武昌客运站,应该选择哪种乘车方案?请说明理由.(不计候车时间)(3)“为了安全,请勿超速”.如图2,武黄城际列车通车后,在某直线路段MN限速180千米/小时,为了检测列车是否超速,铁路有关部门在铁路MN旁设立了观测点S,从观测点S测得列车从点P到达点Q行驶了1.5秒钟,已知∠SPN=45°,∠SQN=60°,SQ=200米,此列车超速了吗?请说明理由.(参考数据:≈1.41,≈1.73)参考答案一.选择题1.解:在Rt△ABC中,AB===2.5(米),∴A′B=2.5米,在Rt△A′BD中,BD===2(米),∴BC+BD=2+0.7=2.7(米),故选:C.2.解:设竹子折断处离地面x尺,则斜边为(10﹣x)尺,根据勾股定理得:x2+42=(10﹣x)2.解得:x=4.2,∴折断处离地面的高度为4.2尺,故选:B.3.解:如图,当筷子的底端在D点时,筷子露在杯子外面的长度最长,∴h=24﹣8=16(cm);当筷子的底端在A点时,筷子露在杯子外面的长度最短,在Rt△ABD中,AD=15cm,BD=8cm,∴AB==17(cm),所以h的取值范围是:8cm≤h≤17cm.故选:C.4.解:过点D作DE⊥AB,垂足为E,设单门的宽度AO是x寸,则AE=x﹣1,DE=10寸,根据勾股定理,得:AD2=DE2+AE2,则x2=102+(x﹣1)2,解得:x=50.5,故AB=101寸,故选:A.5.解:设竹子折断处离地面x尺,则斜边为(10﹣x)尺,根据勾股定理得:x2+32=(10﹣x)2.故选:D.6.解:由题意得:AC=BD=2米,∵AO=8米,∴CO=6米,设BO=x米,则DO=(x+2)米,由题意得:62+(x+2)2=82+x2,解得:x=6,AB==10(米),故选:A.7.解:从科技馆出发走到小平家应:向北直走200米,再向东直走1200米.故选:A.8.解:设折断后的竹子高AC为x尺,则AB长为(10﹣x)尺,根据勾股定理得:AC2+BC2=AB2,即:x2+32=(10﹣x)2,解得:x=4.55,故选:B.9.解:如图所示,AB,CD为树,且AB=13米,CD=7米,BD为两树距离8米,过C作CE⊥AB于E,则CE=BD=8米,AE=AB﹣CD=6米,在直角三角形AEC中,AC==10米,答:小鸟至少要飞10米.故选:A.10.解:由勾股定理得,BE===12,∵△ABE、△BCF、△CDG、△DAH是四个全等的直角三角形,∴∠AEB=∠BFC=∠CGD=90°,BF=CG=DH=AE=5,∴∠FEB=∠EFC=∠FGD=90°,EF=EH=12﹣5=7,∴四边形EFGH为正方形,∴EG==7,故选:A.二.填空题(共7小题)11.解:连结AC,在△ABC中,∵∠B=90°,AB=4m,BC=3m,∴AC==5(m),S=×3×4=6(m2),△ABC在△ACD中,∵AD=13m,AC=5m,CD=12m,∴CD2+AC2=AD2,∴△ACD是直角三角形,∴S △ACD =×5×12=30(m 2).∴四边形ABCD 的面积=S △ABC +S △ACD =6+30=36(m 2).故答案为:36m 2.12.解:设旗杆高xm ,则绳子长为(x +1)m ,∵旗杆垂直于地面,∴旗杆,绳子与地面构成直角三角形,由题意列式为x 2+52=(x +1)2, 解得x =12.∴绳子长为13m .故答案是:13.13.解:此长方体木箱的对角线长为=5>7,∴木棒能放进去.故答案为:对.14.解:设正方形DEFB 的边长为x , 由题意可得,四边形ABCH ,ADEG ,GEIH ,EFCI 都是矩形,∴S △ABC =S △AHC ,S △ADE =S △AGE ,S △EFC =S △EIC ,∴S △ABC ﹣S △ADE ﹣S △EFC =S △AHC ﹣S △AGE ﹣S △EIC ,∴S 正方形DEFB =S 矩形GEIH ,∴x 2=(12﹣x )(5﹣x ).故答案为:x 2=(12﹣x )(5﹣x ).15.解:(1)当20是等腰三角形的底边时,根据面积求得底边上的高AD是16,再根据等腰三角形的三线合一,知:底边上的高也是底边上的中线,即底边的一半BD=10,根据勾股定理即可求得其腰长AB==2,此时三角形的周长是20+4;(2)当20是腰时,由于高可以在三角形的内部,也可在三角形的外部,又应分两种情况.根据面积求得腰上的高是16;①当高在三角形的外部时,在RT△ADC中,AD==12,从而可得BD=32,进一步根据勾股定理求得其底边是BC===16,此时三角形的周长是40+16;②当高在三角形的内部时,根据勾股定理求得AD==12,BD=AB﹣AD=8,在RT△CDB中,BC===8,此时三角形的周长是40+8;故答案为:20+4或40+8或40+16.16.解:(1)由题意可得:AC=25m,AO=7m,则OC==24(m),当云梯的底部在水平方向左滑动8米到点B处,则OB=7+8=15(m),故OD==20(m),则CD=(24﹣20)m=4m.答:云梯的顶端向下滑了4米,故答案为:4.17.解:设在杯里部分长为xcm,则有:x2=32+42,解得:x=5,所以露在外面最短的长度为7cm﹣5cm=2cm,故吸管露出杯口外的最短长度是2cm,故答案为:2.三.解答题(共5小题)18.解:设AE=x,则BE=20﹣x,由勾股定理得:在Rt△ADE中,DE2=AD2+AE2=82+x2,在Rt△BCE中,CE2=BC2+BE2=142+(20﹣x)2,由题意可知:DE=CE,所以:82+x2=142+(20﹣x)2,解得:x=13.3所以,E应建在距A点13.3km.19.解:(1)连接BD,在Rt △ABD 中,BD 2=AB 2+AD 2=32+42=52,在△CBD 中,CD 2=132,BC 2=122,而122+52=132,即BC 2+BD 2=CD 2,所以∠DBC =90°,则S 四边形ABCD =S △ABD +S △DBC =3×4÷2+5×12÷2=36m 2;(2)所需费用为36×200=7200(元).20.解:设旗杆的高度为x 米,根据勾股定理,得x 2+92=(x +3)2,解得:x =12;答:旗杆的高度为12米21.解:(1)该城市会受到这次台风的影响.理由是:如图,过A 作AD ⊥BC 于D .在Rt △ABD 中,∵∠ABD =30°,AB =220, ∴,∵城市受到的风力达到或超过四级,则称受台风影响,∴受台风影响范围的半径为20×(12﹣4)=160.∵110<160,∴该城市会受到这次台风的影响.(2)如图以A 为圆心,160为半径作⊙A 交BC 于E 、F .则AE =AF =160.∴台风影响该市持续的路程为:EF =2DE =2=60.∴台风影响该市的持续时间t =60÷15=4(小时). (3)∵AD 距台风中心最近,∴该城市受到这次台风最大风力为:12﹣(110÷20)=6.5(级).22.解:(1)过点C作AB的垂线,交AB的延长线于E点,∵∠ABC=120°,BC=20,∴BE=10,CE=10,在△ACE中,∵AC2=8100+300,∴AC=20=20×4.6=92km;==1(小时);(2)乘客车需时间t1=+=1(小时);乘列车需时间t2∴选择城际列车.(3)作SH⊥MN于H,如图,∵∠SPN=45°,∠SQN=60°,SQ=200米,∴HS=PH=100,QH=100,∴PQ=100(﹣1)≈73,则速度为m/s<180千米/小时,故为超速.。
14.2章勾股定理的应用(2)
教学目标:
1.在特殊三角形中要会找出直角三角形或构建直角三角形。
2.当三角形的三边是整式时,要会判断大小,从而判断三角形的形状。
思维激活:
以△ABC 三边a,b,c 为边向外
作正方形,以三边为直径作半圆,
若S 1+S 2=S 3成立,则△ABC 是直角
三角形吗?
问题研讨:
问题1:已知:等边△ ABC 的边长是6cm
(1)求高AD 的长.
(2)求S △ ABC.
解:(1)∵ △ ABC 是等边三角形,AD 是高,
在Rt △ ABD 中,AB=6,BD=3,根据勾股定理,
∵ AD 2=AB 2-BD 2
∴
=
练一练:
1.等腰△ABC 的腰长为10cm ,底边长为16cm ,则底边上的高为 ,面积为__________.
2.等腰直角△ABC 中,∠C=90°,AC=2cm ,那么它的斜边上的高为 .
问题2:
32
1==∴BC BD
知识拓展:
问题3:等腰三角形底边上的高为8,周长为32,求这个三角形的面积。
解:作∆ABC的高AD,设BD为X,则AB为(16-X),由勾股定理得:
∴ S∆ABC=
试一试:
等腰直角三角形ABC中,∠C=90°,
AC=BC=1.
求:斜边的一半.
课堂小结:
和同学们交流一下这节课你学到了什么?
课堂作业:
课本60页,习题第1、5题
课后反思:。
第10课时勾股定理的应用(2)预学目标l.初步了解在研究等腰三角形、梯形等问题时,通常通过作底边上的高等辅助线转化为直角三角形,利用勾股定理解决.2.尝试探索解决立体图形中两点间最短路线的问题,体会将立体图形展开转化为平面图形的数学思想方法.3.熟悉利用勾股定理解决拼接、折叠问题的方法:设未知数构造方程求解.知识梳理1.勾股定理在研究等腰三角形问题中的应用如图1,△ABC为等边三角形,AD⊥BC,且ADBD=______(三线合一).设BD=x,则DC=_______,AB=BC=______.在Rt△ABD中,由勾股定理,得BD2+AD2=AB2,即______2+______2=______2,解得x=______,则BC=2BD=______,所以S△ABC=12·BC·AD=12×______×______=______.2.勾股定理在研究折叠问题中的应用如图2,有一张直角三角形纸片,两直角边分别为AC=6 cm、BC=8 cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,由题意,得△ACD≌_______,则AE=_______=_______cm,DE=_______.在Rt△ABC中,由勾股定理,得AB=_______cm,则BE=______cm.设DE=x,则DC=_______,BD=_______.在Rt△BDE中,由勾股定理,得_______2+_______2=_______2,解得x=_______,所以DE=_______,BD=______.例题精讲例1 如图①是一个长方体盒子,长AB=4,宽BC=2,高CG=1.(1) 一只蚂蚁从盒子下底面的点A沿盒子表面爬到点G,那么它所行走的最短路线的长是______.(2)这个长方体盒子内能容下的最长木棒的长度为______.提示:第(1)题需展开成平面图形,分三类讨论蚂蚁行走的路线,第(2)题即求AG的长度.锯答:(1)蚂蚁从点A爬到点G可能经过长方体的前面和右面,也可能经过长方体的前面和上面,还可能经过长方体的下面和右面,展开成平面图形如图②.由勾股定理计算出AG55;12(2)如图③,在Rt △ABC 中,由勾股定理,得AC 2=AB 2+BC 2.在Rt △ACG 中,由勾股定理,得AG 2=AC 2+CG 2=AB 2+BC 2+CG 2=42+22+12=21,则AG点评:把题中的长方体变成正方体或圆柱时,找直角三角形运用勾股定理的思想方法不变,在计算的过程中,可尝试总结计算的公式,如长方体内最长线段的长度为例2 如图,在△ABC 中,若AB>AC ,AE 为BC 边上的中线,AF 为BC 边上的高,试说明AB 2-AC 2=2BC ·EF .提示:利用勾股定理将AB 2和AC 2分别表示为另两条线段的平方和.解答:∵AF ⊥BC ,∴在Rt △AFB 中,由勾股定理,得AB 2=AF 2+BF 2.在Rt △AFC 中,由勾股定理,得AC 2=AF 2+FC 2,∴AB 2-AC 2=BF 2-FC 2=(BF +FC)(BF -FC)=BC ·(BF -FC).∵BF =BE +EF ,FC =EC -EF ,BE =EC ,∴BF -FC =2EF .∴AB 2-AC 2=B C ·2EF =2BC ·EF .点评:此题是勾股定理和乘法公式的综合,当题目中出现线段的平方时,要有主动运用勾股定理的意识,题目中若没有垂直条件,则应尝试作垂线构造直角三角形.热身练习1.一个直角三角形的斜边长比一直角边长长2,另一直角边长为6,则斜边长为 ( )A .6B .8C .10D .122.在△ABC 中,AB =15,AC =13,高AD =12,则△ABC 的周长为 ( )A .42B .32C .42或32D .37或333.如图,AB =BC =DC =DE =1,AB ⊥BC ,CD ⊥AC ,DE ⊥AD ,则AE 的长为_______.4.如图,在高5米、长13米的楼梯上铺地毯,地毯的长度至少为______米.5.在棱长为1的正方体木箱中放入一根细长的直钢管,则钢管的最大长度是______.6.如图,长方体的长为15,宽为10,高为20,点B到点C的距离为5,如果一只蚂蚁要沿着长方体的表面从点A爬到点B,那么它需要爬行的最短距离是( )A.5 B.25C.15 D.357.如图①是第七届国际数学教育大会(简称ICME-7)的会徽,它是由如图②所示的一连串直角三角形演化而成的,其中OA1=A1A2=A2A3=…=A7A8=1.如果把图②中的直角三角形继续作下去,那么OA1,OA2,…,OA25这些线段中,有______条线段的长度为正整数.8.如图,折叠长方形的一边AD,使点D落在BC边的点F处,AD=10 cm,AB=8 cm.求:(1)FC的长.(2)EF的长.参考答案1.C 2.C 3.2 4.17 56.B 7.5 8.(1) FC=4 cm (2) EF =5 cm3。
八年级数学(上)第二章勾股定理与平方根第11课时勾股定理的应用(二)(附答案)1.直角三角形中,以直角边为边长的两个正方形的面积为36 cm2和64 cm2,则以斜边为边长的正方形的面积为__________cm2.2.如图,在△ABC中,C D⊥AB于点D,且AD=BC=5,BD=3,则AC边的长为_________.3.如图,长方形网格中有△ABC,若小方格边长为1,求△ABC的面积是多少?4.等腰三角形的腰长为10,底边长为12,求其底边上的高.5.如图,在直角梯形ABCD中,AD∥BC,∠A=90°,∠C=45°,BC=2AD,CD 求梯形的面积.6.一个直角三角形的两直角边长分别为3和4,下列说法正确的是( ) A.斜边长为25 B.三角形的周长为25C.斜边长为5 D.三角形面积为207.在R t△ABC中,∠C=90°,AB=2,则AB2+BC2+CA2的值为( ) A.2 B.4 C.8 D.168.底边长为16,底边上的高为6的等腰三角形的腰长为( )A.8 B.9 C.10 D 139.如图,A C⊥CE于点C,AD=BE=13,BC=5,DE=7.试求AC的长.10.已知一直角三角形的三边长都是正整数,其中斜边长为13,并且周长为30.求这个直角三角形的面积.11.如图,长方体底面的长和宽分别为4和3,长方体的高为12.求长方体对角线的长.12.如图,小明先向东走1 m,然后向南走4 m,再向西走2 m,再向南走4 m,最后再向东走7 m,如图所示,求出发点到终点的距离.13.如图,每个小方格的边长为1,求图中以格点为端点的四边形AB C D的面积.14.第七届国际数学教育大会会徽的主题图案是由一连串如图所示的直角三角形演化而成的.设第一个Rt△OA1A2是等腰直角三角形,且OA1=A1A2=A2A3=A3A4=…=A n-1A n=1(n 为正整数).请你先把图中其他7条线段的长计算出来.观察计算结果,猜想OA n-1和OA n的长.15.如图,A市接到台风警报时,台风中心位于A市正南方125 km的B处,正以15 km/h的速度沿BC方向移动.(1)已知A市到BC的距离AD=35 km,求台风中心从B处移到D处所需的时间.(2)如果在距台风中心40 km的圆形区域内都将受台风影响,那么A市受影响的时间是多长?(精确到1 min)参考答案1.100 2 3.13 4.8 5.150 6.C 7.C 8.C 9.在Rt △BCE 中,BE 2=CE 2+BC 2,132=CE 2+52,CE=12.∴DC=5.∵BC=5,∴BC=DC .又∵AD=BE , ∴Rt △ACD ≌Rt △ECB .∴AC=EC .∴AC=12 10.30 11.13 12.10 m 13.12.514.计算略 猜想:1n OA -=n OA = 15.(1)在Rt △ABD 中,∠ADB=90°,∴120BD =(km).∴120÷15=8 h (2)以A 为圆心,40 km 为半径作圆,交BD 于点E ,交BD 延长线于点F .在Rt △ADE 中,∠ADB=90°,∴19.365DE ==(km).∴EF=38.73 km .∴38.73÷15≈2.582 h ,2.582×60≈155 min .∴A 市受影响时间约为155 min。
勾股定理的应用
一、知识框架
1、勾股定理的猜想
2、勾股定理的验证
3、勾股定理的应用
二、目标点击
1、经历探索勾股定理的过程,培养推理能和,体会数形结合起来思想。
2、能够利用定理解决一些简单的实际问题
3、培养学生良好的探究习惯,经历猜想——验证——应用的探究过程
三、重难点预见
学习重点:经历探索勾股定理的过程。
学习难点:会用勾股定理解决一些简单的实际问题。
四、学法指导
1、让学生根据教材和教师提供的预习学案先独立探究,然后在小组内交流自已在预习过程中遇到的疑难,完成对学案内容的探究。
2、学具准备:边长为整数的直角三角形纸片(每组2个),带有刻度的直尺。
五、自主探究
情境导入:
2002年在北京召开国际数学大会,在那个大会上,到处可以看到一个简洁优美的图案在流动,那个远看像旋转的风车的图案就是大会的会标,在这个会标中到底蕴含着什么样的数学奥秘呢?今天就让我们走进这人神秘的图形,一起探究数学王国中的奥妙。
学法指导:
通过学生亲自动手测量直角三角形纸片三边的长度,猜想直角三角形三边长度的平方之间的关系,从而培养学生动手操作能力和猜想能力。
(一)猜一猜
测量你们小组的两块直角三角形纸板三边长度,并将各边的长度填入下表:
三角尺直角边a 直角边b 斜边
c 关系
1
2
根据测得的数据:你能发现直角三角形纸板三边的长度的平方之间是否存在着一定的关系?你能作出怎样的猜想?把你的发现说给组内的同学听一听。
(二)想一想
1、观察图2正文形P中含有几个小方格,即P的面积为多少个单位面积?正方形Q与正方形R的面积为多少个单位面积呢?正方形P、Q、R的面积有什么关系?这说明等腰直角三角形三边的平方具有什么关系呢?
解后感悟:
通过数方格,可以发现等腰直角三角形直角边的平方和等于斜边的平方。
方法提升:计算平面图形面积经常用到的方法有:数方格、割补法、凑整法等。
2、观察图
3、并填下表:
正方形A的面积=_______平方单位。
正方形B的面积=_______平方单位。
正方形C的面积=_______平方单位。
你是如何得出正方形C的面积的?把你的想法在小组内交流。
解题关键:求出正方形C的面积是探究三个正方形C的面积是探究三个正方形面积之间关系的关键。
预见性问题:学生探究正文形C的面积时比较困难,方法比较单一。
利用分割法求正方形C 的面积时,忘记中间的一个小正方形而造成失误。
预见性措施:让学生通过小组交流,然后在班内汇报。
教师重点引导学生对不同方法,不同思路进行比较,最后得出最优的方案。
(三)议一议
三个正方形A、B、C的面积之间存在什么关系?那么,你能发现直角三角形三边长度的平方之间存在什么关系吗?与同伴交流。
学法指导:能过前面的探究,让学生在班内汇报自己的观点,班内其他同学补充完善,最后验证前面猜想的正确性。
(四)记一记
对于任意的直角三角形,如果它的两条直角边分别为a,b,斜边为c,则a^2+b^2=C^2.
勾股定理:直角三角形两直角边的平方和等于斜边的平方。
(五)想一想
运用勾股定理的前提条件是什么?钝角三角形和锐三角形三边的平方是否也具有这样的关系?
规律总结:
运用勾股定理的前提是应该直角三角形,知道直角三角形的任意两边都可以求出第三边。
六、基础在线
(1)如图,字母B所代表的正方形的面积是()
A、12
B、13
C、144
D、194
设计意图:
设计本题主要是考察学生对勾股定理探究过程的理解。
新课程标准明确提出:“在教学中,我们不仅要关注结论,更要关注过程。
”因此,通过考察本题,达到对勾股定理探究过程的考察目的。
拓展延伸:
如果说把勾股定理“直角三角形斜边的平方等于两直角边的平方之和”中的平方,理解为以直角三角形三边为边长的正方形的面积。
那么从面积的角度来说,勾股定理还可以推广。
比如:把由直角三角形三边所构作的三个正方形,推广为三边为直径的半圆,结论仍然成立。
即以斜边直径的半圆,其面积等于分别以两条直角边为直径所作的半圆的面积之各。
如果将上图斜边上的半圆沿斜边翻一个身,不难证明:“两个阴影部分的面积之和正好等于直角三角形的面积。
”
这两个阴影部分在数学史上称为“希波克拉底月牙形。
”
一个高1.5米,宽3.6米的大门,需要在相对的顶点间用一根木条加固,求这根木条的长。
关键点剖析:
解答这道题关键是将实际问题转化为数学问题,弄清题目告诉的条件是直角三角形的两条直角边,所求问题是直角三角形的斜边。
从实际问题中构建出数学模型。
(3)已知直角三角形两边的长分别是3cm和5cm,则第三边的长是_____________。
易错点剖析:
学生在解答时,大部分同学把5cm误认为是直角三角形的斜边,从而中人是求出第三条边4cm,忽略了5cm 可以是三角形的直角边这一种情况。
问题设计:
在这道题目中,5cm一定是直角三角形的一条斜边吗?5cm可以是斜边吗?本题有几种情况?
七、能力升级
(1)将长为13cm的梯子AC斜靠在墙上,BC长为5cm,求梯子上端A到墙的底端B的距离AB。
变式训练:
若将梯子的顶端A沿墙向下滑动1cm,则梯子的底端C是否也向外滑动1cm,你能否通过计算证明你的猜想?
(2)已知:如图,四边形ABCD中,AD∥BC,AD⊥DC,AB⊥AC,∠B=45°,CD=2cm .求BC 的长。
思路点击:本题要求BC的长度,应先在RT△ADC中利用勾股定理求出AC的长度,再在RT△ABC中利用勾股定理求出BC的长度。
关键点剖析:通过利用两次勾股定理求出BC的长度。
八、经典分析:
如图:为了求出位于湖两岸的两点A、B之间的距离,一个观测者在点C设桩,使三角形ABC恰为直角三角形。
通过测量,得到AC长160cm,BC长为128cm。
问从点A穿过湖到点B有多远?
思路分析:
要求点A穿过湖到点B有多远,重点是弄清线段AC在直角三角形中是斜边还是直角边。
本题实际是已知直角三形的一条直角边和一条斜边,求它的另一条直角边的长度。
拓展延伸:
日常生活中,求两点之间的距离问题,通常用到的知识点有:直角三角形的勾股定理、全等三角形、相似三角形、锐角三角函数等知识。
解后反思:
利用勾股定理解决实际问题时,关键是将实际问题转化为数学问题,弄清题目的已知条件和所求问题,构建出数学模型。
九、快乐达标
A组题目
在△ABC中,∠C=90°,(1)若a=5,b=12,则C=_________。
(2)若a=15,c=25,则b= ________。
B组题目
如图,要修建一个育苗棚,棚高1.8cm,棚宽a=2.4,棚的长为d=12cm,现要在棚顶上覆盖塑料薄膜,试求需要多少平方塑料薄膜。
C组题目
铁路上A、B两点相距25KM,C、D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建设一个土特产品收购站E,使得C、D两村到E站的距离相等,则E站应建在距A多少km处?
达标说明:
(1)将全班同学按数学成绩分为A、B、C三个小组,其中,A组为全班最后三会之一;B组同学为全班中间三分之一;C组同学为全班最优秀的三分之一。
(2)全班最后三分之一达标任务:A组题目:全班中间三分之一达标任务:B组题目:全班最优秀的三分之一达标任务:C组题目。
(3)达标方法
学生独立完成,教师收取达标测评纸条进行批阅,了解学生的达标状况,及时做好因材施教和不过关同学。