计数原理与排列组合经典题型
- 格式:doc
- 大小:1.27 MB
- 文档页数:6


计数原理与排列组合题型解题方法总结计数原理一、知识精讲1、分类计数原理:2、分步计数原理:特别注意:两个原理的共同点:把一个原始事件分解成若干个分事件来完成。
不同点:如果完成一件事情共有n类办法,这n类办法彼此之间相互独立的,无论哪一类办法中的哪一种方法都能单独完成这件事情,求完成这件事情的方法种数,就用分类计数原理。
分类时应不重不漏(即任一种方法必须属于某一类且只属于这一类)如果完成一件事情需要分成n个步骤,各个步骤都是不可缺少的,需要依次完成所有的步骤,才能完成这件事,而完成每一个步骤各有若干种不同的方法,求完成这件事情的方法种数就用分步计数原理。
各步骤有先后,相互依存,缺一不可。
3、排列(1)排列定义,排列数(2)排列数公式:(3)全排列列:4.组合(1)组合的定义,排列与组合的区别;(2)组合数公式:(3)组合数的性质二、.典例解析题型1:计数原理例1.完成下列选择题与填空题(1)有三个不同的信箱,今有四封不同的信欲投其中,则不同的投法有种。
(2)四名学生争夺三项冠军,获得冠军的可能的种数是( )(3)有四位学生参加三项不同的竞赛,①每位学生必须参加一项竞赛,则有不同的参赛方法有 ;②每项竞赛只许有一位学生参加,则有不同的参赛方法有 ;③每位学生最多参加一项竞赛,每项竞赛只许有一位学生参加,则不同的参赛方法有。
例2(1)如图为一电路图,从A到B共有条不同的线路可通电。
例3: 把一个圆分成3块扇形,现在用5种不同的颜色给3块扇形涂色,要求相邻扇形的颜色互不相同,问有多少钟不同的涂法?若分割成4块扇形呢?例4、某城在中心广场造一个花圃,花圃分为6个部分(如图).现要栽种4种不同颜色的花,每部分栽种一种且相邻部分不能栽种同样颜色的花,不同的栽种方法有 ________ 种.(以数字作答)例5、四面体的顶点和各棱的中点共10个,在其中取4个不共面的点,问共有多少种不同的取法?例6、(1)电视台在”欢乐今宵”节目中拿出两个信箱,其中存放着先后两次竞猜中成绩优秀的观众来信,甲信箱中有30封,乙信箱中有20封.现有主持人抽奖确定幸运观众,若先确定一名幸运之星,再从两信箱中各确定一名幸运伙伴,有多少种不同的结果?(2)三边均为整数,且最大边长为11的三角形的个数是题型2:排列、组合问题处理策略一.元素个数较少的排列组合问题枚举法:1、设有编号为1,2,3,4,5的五个球和编号为1,2,3,4,5的盒子现将这5个球投入5个盒子要求每个盒子放一个球,并且恰好有两个球的号码与盒子号码相同,问有多少种不同的方法?2、学号为1、2、3、4的学生坐到编号为1、2、3、4的四张凳子上,要求学生的学号与其所坐的凳子编号不同,问有多少种不同的坐法?二、特殊元素和特殊位置优先策略3、.由0,1,2,3,4,5可以组成多少个没有重复数字五位奇数.4、五个人排成一排,其中甲不在排头,乙不在排尾,不同的排法有 ( )A.120种 B.96种 C.78种 D.72种三、相邻捆绑、不相邻插空5、(1)7人站成一排照相,若要求甲、乙、丙不相邻,则有多少种不同的排法?(2)7人站成一排照相,甲、乙、丙三人相邻,有多少种不同排法?6、马路上有8只路灯,为节约用电又不影响正常的照明,可把其中的三只灯关掉,但不能同时关掉相邻的两只或三只,也不能关掉两端的灯,那么满足条件的关灯方法共有多少种?7、某人射击8枪,命中4枪,4枪命中恰好有3枪连在一起的情形的不同种数为8、一个晚会的节目有4个舞蹈,2个相声,3个独唱,舞蹈节目不能连续出场,则节目的出场顺序有多少种?四、不尽相异元素、定序问题倍缩法9、(1)7人排队,其中甲乙丙3人顺序一定共有多少不同的排法(2)10人身高各不相等,排成前后排,每排5人,要求从左至右身高逐渐增加,共有多少排法?(3)由4个A和3个B可以组成多少个7位字符信息?五、分排问题“直排法”10、7个人坐两排座位,第一排3个人,第二排坐4个人,则不同的坐法有多少种?11、8人排成前后两排,每排4人,其中甲乙在前排,丁在后排,共有多少排法六、重排问题方幂策略(住店、投邮、影射)12、把6名实习生分配到7个车间实习,共有多少种不同的分法13、某8层大楼从一楼电梯上来8名乘客人,他们到各自的一层下电梯,则他们下电梯的方法有多少种?七.构造模型的策略14、10个相同的球装5个盒中,每盒至少一个有多少装法?15、方程a+b+c+d=12有多少组正整数解?八、排列组合混合问题先选后排策略16、有5个不同的小球,装入4个不同的盒内,每盒至少装一个球,共有多少不同的装法.17、一个班有6名战士,其中正副班长各1人,现从中选4人完成四种不同的任务,每人完成一种任务,且正副班长有且只有1人参加,则不同的选法有________ 种九、.正难则反总体淘汰策略18、我们班里有43位同学,从中任抽5人,正、副班长、团支部书记至少有一人在内的抽法有多少种?十、无编号平均分组问题除法策略19、6本不同的书平均分成3堆,每堆2本共有多少分法?20、10名学生分成3组,其中一组4人, 另两组3人但正副班长不能分在同一组,有多少种不同的分组方法21、某校高二年级共有六个班级,现从外地转入4名学生,要安排到该年级的两个班级且每班安排2名,则不同的安排方案种数为十一化归策略22、 25人排成5×5方队,现从中选3人,要求3人不在同一行也不在同一列,不同的选法有多少种?23、某城市的街区由4 5条街道组成,从西南A走到东北B的最短路径有多少种?三、练习题组:1、7种不同的花种在排成一列的花盆里,若两种葵花不种在中间,也不种在两端的花盆里,问有多少不同的种法?2、把6名实习生分配到7个车间实习,共有多少种不同的分法3.(1)在这五个数字组成的没有重复数字的三位数中,各位数字之和为奇数的共有( )(A)36个 (B)24个 (C)18个 (D)6个(2)从4名男生和3名女生中选出3人,分别从事三项不同的工作,若这3人中至少有1名女生,则选派方案共有( )(A)108种 (B)186种 (C)216种 (D)270种(3)在数字1,2,3与符号+,-五个元素的所有全排列中,任意两个数字都不相邻的全排列个数是( )B. 12C. 18D. 24(4)高三(一)班学要安排毕业晚会的4各音乐节目,2个舞蹈节目和1个曲艺节目的演出顺序,要求两个舞蹈节目不连排,则不同排法的种数是( )(A)1800 (B)3600 (C)4320 (D)50404.(1)用数字0,1,2,3,4组成没有重复数字的五位数,则其中数字1,2相邻的偶数有个(用数字作答);(2)电视台连续播放6个广告,其中含4个不同的商业广告和2个不同的公益广告,要求首尾必须播放公益广告,则共有种不同的播放方式(结果用数值表示).5.(1)将5名实习教师分配到高一年级的3个班实习,每班至少1名,最多2名,则不同的分配方案有( )(A)30种 (B)90种 (C)180种 (D)270种(2)将4个颜色互不相同的球全部放入编号为1和2的两个盒子里,使得放入每个盒子里的球的个数不小于该盒子的编号,则不同的放球方法有( )种种种种6.(1)某校从8名教师中选派4名教师同时去4个边远地区支教(每地1人),其中甲和乙不同去,则不同的选派方案共有种;(2)5名志愿者分到3所学校支教,每个学校至少去一名志愿者,则不同的分派方法共有(A)150种 (B)180种 (C)200种 (D)280种7、.已知直线ax+by+c=0中的a,b,c是取自集合{-3,-2,-1,0,1,2,3}中的3个不同的元素,并且该直线的倾斜角为锐角,求符合这些条件的直线的条数8、甲、乙、丙、丁四个公司承包8项工程,甲公司承包3项工程,乙公司承包1项,丙、丁各承包2项,问共有种承包方式?9、停车场划出一排12个停车位置,今有8辆车需要停放,要求空位置连在一起,不同的停车方法有多少种?10、x+y+z+w=100求这个方程组的正整数解的组数11、.设有编号1,2,3,4,5的五个球和编号1,2,3,4,5的五个盒子,现将5个球投入这五个盒子内,要求每个盒子放一个球,并且恰好有两个球的编号与盒子的编号相同,.有多少投法12、.正方体的8个顶点可连成多少对异面直线13、3个人坐在一排8个椅子上,若每个人左右两边都有空位,则坐法的种类有多少种?14.(2008陕西,16)某地奥运火炬接力传递路线共分6段,传递活动分别由6名火炬手完成。

考向37计数原理与排列组合小题最全归纳经典题型一:两个计数原理的综合应用经典题型二:直接法经典题型三:间接法经典题型四:捆绑法经典题型五:插空法经典题型六:定序问题(先选后排)经典题型七:列举法经典题型八:多面手问题经典题型九:错位排列经典题型十:涂色问题经典题型十一:分组问题经典题型十二:分配问题经典题型十三:隔板法经典题型十四:数字排列经典题型十五:几何问题经典题型十六:分解法模型与最短路径问题经典题型十七:排队问题经典题型十八:构造法模型和递推模型经典题型十九:环排问题(2022·全国·高考真题)有甲、乙、丙、丁、戊5名同学站成一排参加文艺汇演,若甲不站在两端,丙和丁相邻,则不同排列方式共有()A.12种B.24种C.36种D.48种(2021·全国·高考真题(理))将5名北京冬奥会志愿者分配到花样滑冰、短道速滑、冰球和冰壶4个项目进行培训,每名志愿者只分配到1个项目,每个项目至少分配1名志愿者,则不同的分配方案共有()A .60种B .120种C .240种D .480种知识点1、分类加法计数原理完成一件事,有n 类办法,在第1类办法中有1m 种不同的办法,在第2类办法中有2m 种不同的方法,…,在第n 类办法中有n m 种不同的方法,那么完成这件事共有:12n N m m m =+++种不同的方法.事事A 事事事事1事事1事事2事事m 1事事事事n 事事1事事2事事m n m 1事m n 事 事事事事A 事事m 1+m 2+m 3+···+m n 事事事事事事知识点2、分步乘法计数原理完成一件事,需要分成n 个步骤,做第1步有1m 种不同的方法,做第2步有2m 种不同的方法,…,做第n 步有n m 种不同的方法,那么完成这件事共有:12n N m m m =⋅⋅⋅种不同的方法. 事事B事事1事事i ···事事2事事n m 1事m n 事事事事事B 事事m 1×m 2×m 3×···×m n 事事事事事事m 2事m i 事 注意:两个原理及其区别 分类加法计数原理和“分类”有关,如果完成某件事情有n 类办法,这n 类办法之间是互斥的,那么求完成这件事情的方法总数时,就用分类加法计数原理. 分步乘法计数原理和“分步”有关,是针对“分步完成”的问题.如果完成某件事情有n 个步骤,而且这几个步骤缺一不可,且互不影响(独立),当且仅当依次完成这n 个步骤后,这件事情才算完成,那么求完成这件事情的方法总数时,就用分步乘法计数原理. 当然,在解决实际问题时,并不一定是单一应用分类计数原理或分步计数原理,有时可能同时用到两个计数原理.即分类时,每类的方法可能运用分步完成;而分步后,每步的方法数可能会采取分类的思想求方法数.对于同一问题,我们可以从不同的角度去处理,从而得到不同的解法(但方法数相同),这也是检验排列组合问题的很好方法.知识点3、两个计数原理的综合应用如果完成一件事的各种方法是相互独立的,那么计算完成这件事的方法数时,使用分类计数原理.如果完成一件事的各个步骤是相互联系的,即各个步骤都必须完成,这件事才告完成,那么计算完成这件事的方法数时,使用分步计数原理.知识点4、排列与排列数(1)定义:从n 个不同元素中取出()m m n ≤个元素排成一列,叫做从n 个不同元素中取出m 个元素的一个排列.从n 个不同元素中取出()m m n ≤个元素的所有排列的个数,叫做从n 个不同元素中取出m 个元素的排列数,用符号m n A 表示.(2)排列数的公式:()()()()!121!m n n A n n n n m n m =---+=-. 特例:当m n =时,()()!12321m n A n n n n ==--⋅⋅;规定:0!1=.(3)排列数的性质:①11m m n n A nA --=;②111m m m n n n n A A A n m n m+-==--;③111m m m n n n A mA A ---=+. (4)解排列应用题的基本思路:通过审题,找出问题中的元素是什么,是否与顺序有关,有无特殊限制条件(特殊位置,特殊元素).注意:排列数公式的两种不同表达形式本质是一样的,但作用略有不同,()()A 11mn n n n m =-⋅⋅⋅-+常用于具体数字计算;而在进行含字母算式化简或证明时,多用!A ()!mn n n m =-. 知识点5、组合与组合数(1)定义:从n 个不同元素中取出()m m n ≤个元素并成一组,叫做从n 个不同元素中取出m 个元素的一个组合.从n 个不同元素中取出()m m n ≤个元素的所有组合的个数,叫做从n 个不同元素中取出m 个元素的组合数,用符号m n C 表示.(2)组合数公式及其推导求从n 个不同元素中取出m 个元素的排列数m n A ,可以按以下两步来考虑:第一步,先求出从这n 个不同元素中取出m 个元素的组合数m n C ;第二步,求每一个组合中m 个元素的全排列数m n A ;根据分步计数原理,得到m m m n n m A C A =⋅; 因此()()()121!m mn n m m n n n n m A C A m ---+==.这里n ,m N +∈,且m n ≤,这个公式叫做组合数公式.因为()!!m n n A n m =-,所以组合数公式还可表示为:()!!!m n n C m n m =-.特例:01n n n C C ==. 注意:组合数公式的推导方法是一种重要的解题方法!在以后学习排列组合的混合问题时,一般都是按先取后排(先组合后排列)的顺序解决问题.公式(1)(2)(1)C !mn n n n n m m --⋅⋅⋅-+=常用于具体数字计算,!C !()!m n n m n m =-常用于含字母算式的化简或证明.(3)组合数的主要性质:①m n m n n C C -=;②11m m m n n n C C C -++=.(4)组合应用题的常见题型:①“含有”或“不含有”某些元素的组合题型②“至少”或“最多”含有几个元素的题型知识点6、排列和组合的区别组合:取出的元素地位平等,没有不同去向和分工.排列:取出的元素地位不同,去向、分工或职位不同.注意:排列、组合都是研究事物在某种给定的模式下所有可能的配置数目问题,它们之间的主要区别在于是否要考虑选出元素的先后顺序,不需要考虑顺序的是组合问题,需要考虑顺序的是排列问题.排列是在组合的基础上对入选的元素进行排队,因此,分析解决排列组合综合问题的基本思维是“先组合,后排列”.知识点7、解决排列组合综合问题的一般过程1、认真审题,确定要做什么事;2、确定怎样做才能完成这件事,即采取分步还是分类或是分步与分类同时进行,弄清楚分多少类及多少步;3、确定每一步或每一类是排列(有序)问题还是组合(无序)问题,元素总数是多少及取出多少个元素;4、解决排列组合综合性问题,往往类与步交叉,因此必须掌握一些常用的解题策略.1、如图,在圆中,将圆分n 等份得到n 个区域1M ,2M ,3M ,,(2)n M n ,现取(2)k k 种颜色对这n 个区域涂色,要求每相邻的两个区域涂不同的两种颜色,则涂色的方案有(1)(1)(1)n n k k --+-种.2、错位排列公式1(1)(1)!!in n i D n n =-=+⋅∑ 3、数字排列问题的解题原则、常用方法及注意事项(1)解题原则:排列问题的本质是“元素”占“位子”问题,有限制条件的排列问题的限制条件主要表现在某元素不排在某个位子上,或某个位子不排某些元素,解决该类排列问题的方法主要是按“优先”原则,即优先排特殊元素或优先满足特殊位子,若一个位子安排的元素影响到另一个位子的元素个数时,应分类讨论.4、定位、定元的排列问题,一般都是对某个或某些元素加以限制,被限制的元素通常称为特殊元素,被限制的位置称为特殊位置.这一类问题通常以三种途径考虑:(1)以元素为主考虑,这时,一般先解决特殊元素的排法问题,即先满足特殊元素,再安排其他元素;(2)以位置为主考虑,这时,一般先解决特殊位置的排法问题,即先满足特殊位置,再考虑其他位置;(3)用间接法解题,先不考虑限制条件,计算出排列总数,再减去不符合要求的排列数.5、解决相邻问题的方法是“捆绑法”,其模型为将n 个不同元素排成一排,其中某k 个元素排在相邻位置上,求不同排法种数的方法是:先将这k 个元素“捆绑在一起”,看成一个整体,当作一个元素同其他元素一起排列,共有11n k n k A -+-+种排法;然后再将“捆绑”在一起的元素“内部”进行排列,共有k k A 种排法.根据分步乘法计数原理可知,符合条件的排法共有11n k n k kk A A -+-+⋅种. 6、解决不相邻问题的方法为“插空法”,其模型为将n 个不同元素排成一排,其中某k 个元素互不相邻(1k n k ≤-+),求不同排法种数的方法是:先将(n k -)个元素排成一排,共有n k n k A --种排法;然后把k 个元素插入1n k -+个空隙中,共有1k n k A -+种排法.根据分步乘法计数原理可知,符合条件的排法共有n k n k A --·1k n k A -+种.经典题型一:两个计数原理的综合应用......M n...M n -1M 1M 2M 31.(2022·江苏·南京市第一中学高三阶段练习)为了进一步提高广大市民的生态文明建设意识,某市规定每年4月25日为“创建文明城生态志愿行”为主题的生态活动日,现有5名同学参加志愿活动,需要携带勾子、铁锹、夹子三种劳动工具,要求每人都要携带一个工具,并且要求:带一个勾子,铁锹至少带2把,夹子至少带一个,则不同的安排方案共有()A.50种B.60种C.70种D.80种2.(2022·重庆·高三阶段练习)用1,2,3…,9这九个数字组成的无重复数字的四位偶数中,各位数字之和为奇数的共有()A.600个B.540个C.480个D.420个3.(2022·全国·高三专题练习)用0,1,2,3,4可以组成没有重复数字的四位偶数的个数为()A.36B.48C.60D.72 4.(2022·全国·模拟预测)将6盆不同的花卉摆放成一排,其中A、B两盆花卉均摆放在C 花卉的同一侧,则不同的摆放种数为()A.360B.480C.600D.720 5.(2022·全国·高三专题练习)用数字0,1,2,3,4,5组成没有重复数字的四位数,其中个位、十位和百位上的数字之和为偶数的四位数共有___________.个(用数字作答). 6.(2022·全国·高三专题练习)有四张卡片,正面和背面依次分别印有数字“1,0,2,4”和“3,5,0,7”,一小朋友把这四张卡片排成四位整数,则他能排出的四位整数的个数为_________.经典题型二:直接法7.甲、乙、丙、丁、戊共5名同学进行劳动技术比赛,决出第1名到第5名的名次.甲和乙去询问成绩,回答者对甲说:“很遗憾,你和乙都没有得到冠军.”对乙说:“你当然不会是最差的.”从这两个回答分析,5人的名次排列方式共有()种A.54B.72C.96D.120A B C D E F共6名同学进行8.某校开展研学活动时进行劳动技能比赛,通过初选,选出,,,,,决赛,决出第1名到第6名的名次(没有并列名次),A和B去询问成绩,回答者对A说“很遗㙳,你和B都末拿到冠军;对B说“你当然不是最差的”.试从这个回答中分析这6人的名次排列顺序可能出现的结果有()A.720种B.600种C.480种D.384种9.甲、乙、丙、丁四人站成一列,要求甲站在最前面,则不同的排法有()A.24种B.6种C.4种D.12种10.某学校要从5名男教师和3名女教师中随机选出3人去支教,则抽取的3人中,女教师最多为1人的选法种数为().A.10B.30C.40D.46经典题型三:间接法11.将7个人从左到右排成一排,若甲、乙、丙3人中至多有2人相邻,且甲不站在最右端,则不同的站法有().A.1860种B.3696种C.3600种D.3648种12.某学校计划从包含甲、乙、丙三位教师在内的10人中选出5人组队去西部支教,若甲、乙、丙三位教师至少一人被选中,则组队支教的不同方式共有()A.21种B.231种C.238种D.252种13.中园古代中的“礼、乐、射、御、书、数”合称“六艺”.“礼”主要指德育;“乐”主要指美育;“射”和“御”就是体育和劳动;“书”指各种历史文化知识;“数”指数学.某校国学社团开展“六艺”讲座活动,每周安排一次讲座,共讲六次.讲座次序要求“射”不在第一次,“数”和“乐”两次不相邻,则“六艺”讲座不同的次序共有()A.408种B.240种C.1092种.D.120种14.红五月,某校团委决定举办庆祝中国共产党成立100周年“百年荣光,伟大梦想”联欢会,经过初赛,共有6个节目进入决赛,其中2个歌舞类节目,2个小品类节目,1个朗诵类节目,1个戏曲类节目.演出时要求同类节目不能相邻,则演出顺序的排法总数是()A.96B.326C.336D.360经典题型四:捆绑法15.(2022·浙江邵外高三阶段练习)甲乙丙丁戊5名同学站成一排参加文艺汇演,若甲不站在两端,丙和丁相邻的不同排列方式有______种.16.(2022·江西·高三开学考试(理))中国的“五岳”是指在中国境内的五座名山:东岳泰山、西岳华山、南岳衡山、北岳恒山、中岳嵩山、坐落于东、西、南、北、中五个方位.郭靖同学决定利用今年寒假时间,游览以下五座名山:嵩山、泰山、华山、黄山、庐山,若他首先游览黄山,且属于“五岳”的名山游览顺序必须相邻,则郭靖同学游览这五座名山的顺序共有_____种(用数字作答).17.(2022·湖北·高三开学考试)五位同学站成一排合影,张三站在最右边,李四、王五相邻,则不同的站法种数为______.18.(2022·全国·高三专题练习)现有4位学生和2位教师站成一排照相,两位教师站在一起的排法有___________种.19.(2022·全国·高三专题练习(理))成语“五音不全”中的五音指古乐的五声音阶:宫、商、角、徵、羽,是中国古乐基本音阶.把这五个音阶排成一列,形成一个音序.满足“徵”“羽”两音阶相邻且在“宫”音阶之前的不同音序的种数为___________.(用数字作答)经典题型五:插空法20.(2022·湖北·高三开学考试)将语文、数学、英语、物理、化学、生物六本书排成一排,其中语文、数学相邻,且物理、化学不相邻,则不同的排法共有种___________.(用数字作答)21.(2022·全国·高三专题练习)英文单词"sentence”由8个字母构成,将这8个字母组合排列,且两个n 不相邻一共可以得到英文单词的个数为_________.(可以认为每个组合都是一个有意义的单词)22.(2022·全国·高三专题练习)某科室有4名人员,两男两女,参加会议时一排有5个位置,从左到右排,则两女员工不相邻(中间隔空位也叫不相邻),且左侧的男员工前面一定有女员工的排法有_______种(结果用数字表示).23.(2022·全国·高三专题练习)“五经”是儒家典籍《周易》、《尚书》、《诗经》、《礼记》、《春秋》的合称.为弘扬中国传统文化,某校在周末兴趣活动中开展了“五经”知识讲座,每经排1节,连排5节,则《诗经》、《春秋》分开排的情况有________种.24.(2022·山东·肥城市教学研究中心模拟预测)某等候区有9个座位(连成一排),甲、乙、丙、丁四人随机就座,因受新冠疫情影响,要求他们每两人之间至少有一个空位,则不同的坐法有_______种 .25.(2022·全国·高三专题练习)某学校为贯彻“科学防疫”理念,实行“佩戴口罩,间隔而坐”制度.若该学校的教室一排有8个座位,安排4名同学就坐,则不同的安排方法共有______种.(用数字作答)经典题型六:定序问题(先选后排)26.满足*(1,2,3,4)i x i ∈=N ,且123410x x x x <<<<的有序数组()1234,,,x x x x 共有( )个. A .49C B .49P C .410C D .410P27.,,,,A B C D E 五人并排站成一排,如果B 必须站在A 的右边,(,A B 可以不相邻)那么不同的排法有( )A .120种B .90种C .60种D .24种28.DNA 是形成所有生物体中染色体的一种双股螺旋线分子,由称为碱基的化学成分组成它看上去就像是两条长长的平行螺旋状链,两条链上的碱基之间由氢键相结合.在DNA 中只有4种类型的碱基,分别用A 、C 、G 和T 表示,DNA 中的碱基能够以任意顺序出现两条链之间能形成氢键的碱基或者是A -T ,或者是C -G ,不会出现其他的联系因此,如果我们知道了两条链中一条链上碱基的顺序,那么我们也就知道了另一条链上碱基的顺序.如图所示为一条DNA 单链模型示意图,现在某同学想在碱基T 和碱基C 之间插入3个碱基A ,2个碱基C 和1个碱基T ,则不同的插入方式的种数为( )A .20B .40C .60D .12029.某次演出有5个节目,若甲、乙、丙3个节目间的先后顺序已确定,则不同的排法有( ) A .120种 B .80种 C .20种 D .48种30.某次数学获奖的6名高矮互不相同的同学站成两排照相,后排每个人都高于站在他前面的同学,则共有多少种站法( )A .36B .90C .360D .72031.花灯,又名“彩灯”“灯笼”,是中国传统农业时代的文化产物,兼具生活功能与艺术特色.如图,现有悬挂着的8盏不同的花灯需要取下,每次取1盏,则不同取法总数为 ( )A .2520B .5040C .7560D .10080经典题型七:列举法32.三人互相传球,由甲开始发球,并作为第一次传球,经过5次传球后,球仍回到甲手中,则不同的传球方式共有( )A .6种B .8种C .10种D .16种33.三人踢毽子,互相传递,每人每次只能踢一下.由甲开始踢,经过4次传递后,毽子又被踢回甲,则不同的传递方式共有( )A .4种B .5种C .6种D .12种34.设1x ,2x ,{}31,0,1,2x ∈-,那么满足32212308x x x ≤++≤的所有有序数组()123,,x x x 的组数为( )A .45B .46C .47D .48 35.从集合{}1,2,3,4,,15中任意选择三个不同的数,使得这三个数组成等差数列,这样的等差数列有( )个A .98B .56C .84D .4936.工人在安装一个正六边形零件时,需要固定如图所示的六个位置的螺栓.若按一定顺序将每个螺栓固定紧,但不能连续....固定相邻的2个螺栓.则不同的固定螺栓方式的种数是________.经典题型八:多面手问题37.我校去年11月份,高二年级有10人参加了赴日本交流访问团,其中3人只会唱歌,2人只会跳舞,其余5人既能唱歌又能跳舞.现要从中选6人上台表演,3人唱歌,3人跳舞,有种不同的选法.A.675B.575C.512D.54538.某国际旅行社现有11名对外翻译人员,其中有5人只会英语,4人只会法语,2人既会英语又会法语,现从这11人中选出4人当英语翻译,4人当法语翻译,则共有()种不同的选法A.225B.185C.145D.11039.“赛龙舟”是端午节的习俗之一,也是端午节最重要的节日民俗活动之一,在我国南方普遍存在端午节临近,某单位龙舟队欲参加今年端午节龙舟赛,参加训练的8名队员中有3人只会划左桨,3人只会划右桨,2人既会划左桨又会划右桨.现要选派划左桨的3人、划右桨的3人共6人去参加比赛,则不同的选派方法共有()A.26种B.30种C.37种D.42种经典题型九:错位排列40.编号为1、2、3、4、5的5个人分别去坐编号为1、2、3、4、5的五个座位,其中有且只有两个人的编号与座位号一致的坐法有()A.10种B.20种C.30种D.60种41.将编号为1、2、3、4、5、6的小球放入编号为1、2、3、4、5、6的六个盒子中,每盒放一球,若有且只有两个盒子的编号与放入的小球的编号相同,则不同的放法种数为()A.90B.135C.270D.36042.若5个人各写一张卡片(每张卡片的形状、大小均相同),现将这5张卡片放入一个不透明的箱子里,并搅拌均匀,再让这5人在箱子里各摸一张,恰有1人摸到自己写的卡片的方法数有()A.20B.90C.15D.45经典题型十:涂色问题43.(2022·全国·高三专题练习)学习涂色能锻炼手眼协调能力,更能提高审美能力.现有四种不同的颜色:湖蓝色、米白色、橄榄绿、薄荷绿,欲给小房子中的四个区域涂色,要求相邻区域不涂同一颜色,且橄榄绿与薄荷绿也不涂在相邻的区域内,则共有______种不同的涂色方法.44.(2022·全国·高三专题练习)如图,一个地区分为5个行政区域,现给地图着色,要求相邻区域不得使用同一种颜色,共有5种颜色可供选择,则不同的着色方法共有________种(以数字作答).45.(2022·全国·高三专题练习)如图,用4种不同的颜色给图中的8个区域涂色,每种颜色至少使用一次,每个区域仅涂一种颜色,且相邻区域所涂颜色互不相同,则区域A,B,C,D和1A,1B,1C,1D分别各涂2种不同颜色的涂色方法共有_________种;区域A,B,C,D和1A,1B,1C,1D分别各涂4种不同颜色的涂色方法共有_________种.46.(2022·全国·高三专题练习)“赵爽弦图”是我国古代数学的瑰宝,如图所示,它是由四个全等的直角三角形和一个正方形构成.现用4种不同的颜色(4种颜色全部使用)给这5个区域涂色,要求相邻的区域不能涂同一种颜色,每个区域只涂一种颜色,则不同的涂色方案有______种.47.(2022·全国·高三专题练习(理))用红、黄、蓝、绿4种颜色给如图所示的五连圆涂色,要求相邻两个圆所涂颜色不能相同,且红色至少要涂两个圆,则不同的涂色方案种数为______.48.(2022·全国·高三专题练习)用红、黄、蓝、绿、橙五种不同颜色给如图所示的5块区域A、B、C、D、E涂色,要求同一区域用同一种颜色,有公共边的区域使用不同颜色,则共有涂色方法____.的顶点染色,定义由同一条棱49.(2022·全国·高三专题练习)如图给三棱柱ABC DEF连接的两个顶点叫相邻顶点,规定相邻顶点不得使用同一种颜色,现有4种颜色可供选择,则不同的染色方法有_________________.经典题型十一:分组问题50.为了贯彻落实中央新疆工作座谈会和全国对口支援新疆工作会议精神,促进边疆少数民族地区教育事业发展,我市教育系统选派了三位男教师和两位女教师支援新疆,这五名教师被分派到三个不同地方对口支援,每位教师只去一个地方,每个地方至少去一人,其中两位女教师分派到同一个地方,则不同的分派方法有()A.18种B.36种C.68种D.84种51.2021年春节期间电影《你好,李焕英》因“搞笑幽默不庸俗,真心实意不煽情”深受热棒,某电影院指派5名工作人员进行电影调查问卷,每个工作人员从编号为1,2,3,4的4个影厅选一个,可以多个工作人员进入同一个影厅,若所有5名工作人员的影厅编号之和恰为10,则不同的指派方法种数为()A.91B.101C.111D.12152.已知有6本不同的书.(1)分成三堆,每堆2本,有多少种不同的分堆方法?(2)分成三堆,一堆1本,一堆2本,一堆3本,有多少种不同的分堆方法?经典题型十二:分配问题53.(2022·全国·高三专题练习)某校高二年级共有6个班级,现有4名交流生要安排到该年级的2个班级,且每班安排2名,则不同的安排方案种数为__.54.(2022·全国·高三专题练习)甲乙丙丁四位同学分别去甘肃、内蒙古、北京三个地方调研新冠疫情发展情况,每个地方至少一个人去,且甲乙两人不能去同一个地方,则不同分法的种数有__种55.(2022·湖北·荆州中学高三阶段练习)某小区共有3个核酸检测点同时进行检测,有6名志愿者被分配到这3个检测点参加服务,6人中有4名“熟手”和2名“生手”,1名“生手”至少需要1名“熟手”进行检测工作的传授,每个检测点至少需要1名“熟手”,且2名“生手”不能分配到同一个检测点,则不同的分配方案种数是______.56.(2022·上海市向明中学高三开学考试)某医院从7名男医生(含一名主任医师),6名女医生(含一名主任医师)中选派4名男医生和3名女医生支援抗疫工作,若要求选派的医生中有主任医师,则不同的选派方案数为_________________.57.(2022·上海市南洋模范中学高三开学考试)将编号为1,2,3,4的四个小球放到三个不同的盒子里,每个盒子至少放一个小球且编号为1,2的两个小球不能放到同一个盒子里,则不同放法的种数有___________.(用数字作答).、、三58.(2022·上海·华师大二附中高三开学考试)有2男2女共4名学生被分派去A B C 个公司实习,每个公司至少1人,且A公司只收女生,则不同的分派方法数为___________. 59.(2022·陕西·宝鸡市陈仓高级中学高三开学考试(理))我国棉田面积在40万公顷以上有7个省份,分别为新疆、河南、江苏、湖北、山东、河北、安徽.现有5名党员同志准备分别前往新疆、湖北、山东这三个地方考察,每个地方至少安排1名同志,则不同的安排方案种数是______种.经典题型十三:隔板法60.(2022·广东中山·模拟预测)某市举行高三数学竞赛,有6个参赛名额分给甲乙丙三所学校,每所学校至少分得一个名额,共有______种不同的分配方法.(用数字作答)61.(2022·重庆巴蜀中学高三阶段练习)某地举办庆祝建党100周年“奋进新时代,学习再出发”的党史知识竞赛.已知有15个参赛名额分配给甲、乙、丙、丁四支参赛队伍,其中一支队伍分配有7个名额,余下三支队伍都有参赛名额,则这四支队伍的名额分配方案有__________种.62.(2022·全国·高三专题练习)方程11x y z ++=的非负整数解共有___________组. 63.(2022·全国·模拟预测)六元一次方程12610x x x +++=的正整数解有________组.64.(2022·新疆巴音郭楞蒙古自治州第二中学模拟预测(理))关于x ,y ,z 的方程7x y z ++=(其中x ,y ,z +∈N )的解共有_____组.65.(2022·全国·高三专题练习)方程10x y z ++=的正整数解的个数__________. 66.(2022·新疆乌鲁木齐·一模(理))已知数列{}n a 共有26项,且11a =,2620a =,11(1,2,,25)k k a a k +-==,则满足条件的不同数列{}n a 有__________ 个.经典题型十四:数字排列67.(2022·浙江·杭州高级中学模拟预测)从0,1,2,3,4这五个数字中任取3个组成无重复数字的三位数,当三个数字中有2,3时,2要排在3的前面(不一定相邻),这样的三位数有( )A .39个B .40个C .36个D .38个68.(2022·重庆南开中学模拟预测)公元五世纪,数学家祖冲之估计圆周率π的范围是:3.1415926 3.1415927π<<,为纪念祖冲之在圆周率方面的成就,把3.1415926称为“祖率”,这是中国数学的伟大成就.小明是个数学迷,他在设置手机的数字密码时,打算将圆周率的前6位数字3,1,4,1,5,9进行某种排列得到密码.如果排列时要求数字9不在最后一位,那么小明可以设置的不同密码有( )个.A .600B .300C .360D .18069.(2022·四川省内江市第六中学模拟预测(理))由0~9这10个数组成的三位数中,各位数字按严格递增(如“145”)或严格递减(如“321”)顺序排列的数的个数是( )A .120B .168C .204D .21670.(2022·海南·海口一中高三阶段练习)已知a 1,a 2,a 3∈{2,4,6},记N (a 1,a 2,a 3)为a 1,a 2,a 3中不同数字的个数,如∶N (2,2,2)=1,N (2,4,2)=2,N (2,4,6)=3,则所有的(a 1,a 2,a 3)的排列的N (a 1,a 2,a 3)平均值为( )A .199B .3C .299D .471.(2022·陕西省洛南中学高三阶段练习(理))由0,1,2,3,4这5个数组成无重复数字的五位数且为偶数,共有多少种排法( )A .24B .48C .60D .6272.(2022·辽宁·模拟预测)用数字3,6,9组成四位数,各数位上的数字允许重复,且。

计数原理题型总结
计数原理是组合数学的一个基本原理,用于计算具有特定属性的对象的个数。
常见的计数原理题型包括排列、组合和二项式系数等。
1. 排列问题:
- n个元素的全排列个数为n!,其中n表示元素的个数。
- 从n个元素中取出m(m≤n)个元素的排列个数为A(n,m)
= n!/(n-m)!,称为从n个元素中取出m个元素的排列数。
2. 组合问题:
- 从n个元素中取出m(m≤n)个元素的组合个数为C(n,m)
= n!/((n-m)!·m!),称为从n个元素中取出m个元素的组合数。
- 组合数C(n,m)满足下列性质:
(1)C(n,0) = C(n,n) = 1;
(2)C(n,m) = C(n,n-m);
(3)C(n,m) = C(n-1,m) + C(n-1, m-1);
3. 二项式系数:
- 二项式系数的计算公式为:C(n,m) = C(n-1,m) + C(n-1, m-1)。
- 二项式系数有许多重要的性质,如:
(1)二项式定理:(a+b)^n = C(n,0)a^n·b^0 + C(n,1)a^(n-1)·b^1 + ... + C(n,n)a^0·b^n;
(2)二项式系数的对称性:C(n,m) = C(n,n-m);
(3)二项式系数的递推关系:C(n,m) = C(n-1,m) + C(n-
1,m-1);
(4)二项式系数的性质:C(n,m) = C(n-1,m-1) + C(n-2,m-1)
+ ... + C(m,m-1)。
通过理解和熟练运用计数原理,可以帮助解决各种实际问题,如排列组合选择问题、概率计算问题等。

计数原理[基础训练A 组]一、选择题1.将3个不同的小球放入4个盒子中,则不同放法种数有( )A .81B .64C .12D .142.从4台甲型和5台乙型电视机中任意取出3台,其中至少有甲型与乙型电视机各1台,则不同的取法共有( )A .140种 B.84种 C.70种 D.35种3.5个人排成一排,其中甲、乙两人至少有一人在两端的排法种数有( )A .33AB .334AC .523533A A A -D .2311323233A A A A A +4.,,,,a b c d e 共5个人,从中选1名组长1名副组长,但a 不能当副组长,不同的选法总数是( )A.20 B .16 C .10 D .65.现有男、女学生共8人,从男生中选2人,从女生中选1人分别参加数学、物理、化学三科竞赛,共有90种不同方案,那么男、女生人数分别是( )A .男生2人,女生6人B .男生3人,女生5人C .男生5人,女生3人D .男生6人,女生2人.6.在82x ⎛- ⎝的展开式中的常数项是( ) A.7 B .7- C .28 D .28-7.5(12)(2)x x -+的展开式中3x 的项的系数是( ) A.120 B .120- C .100 D .100-8.22nx ⎫⎪⎭展开式中只有第六项二项式系数最大,则展开式中的常数项是( ) A .180 B .90 C .45 D .360二、填空题1.从甲、乙,……,等6人中选出4名代表,那么(1)甲一定当选,共有 种选法.(2)甲一定不入选,共有 种选法.(3)甲、乙二人至少有一人当选,共有 种选法.2.4名男生,4名女生排成一排,女生不排两端,则有 种不同排法.3.由0,1,3,5,7,9这六个数字组成_____个没有重复数字的六位奇数.4.在10(x 的展开式中,6x 的系数是 .5.在220(1)x -展开式中,如果第4r 项和第2r +项的二项式系数相等,则r = ,4r T = .6.在1,2,3,...,9的九个数字里,任取四个数字排成一个首末两个数字是奇数的四位数,这样的四位数有_________________个?7.用1,4,5,x 四个不同数字组成四位数,所有这些四位数中的数字的总和为288,则x .8.从1,3,5,7,9中任取三个数字,从0,2,4,6,8中任取两个数字,组成没有重复数字的五位数,共有________________个?三、解答题1.判断下列问题是排列问题还是组合问题?并计算出结果.(1)高三年级学生会有11人:①每两人互通一封信,共通了多少封信?②每两人互握了一次手,共握了多少次手?(2)高二年级数学课外小组10人:①从中选一名正组长和一名副组长,共有多少种不同的选法?②从中选2名参加省数学竞赛,有多少种不同的选法?(3)有2,3,5,7,11,13,17,19八个质数:①从中任取两个数求它们的商可以有多少种不同的商?②从中任取两个求它的积,可以得到多少个不同的积?2.7个排成一排,在下列情况下,各有多少种不同排法?(1)甲排头,(2)甲不排头,也不排尾,(3)甲、乙、丙三人必须在一起,(4)甲、乙之间有且只有两人,(5)甲、乙、丙三人两两不相邻,(6)甲在乙的左边(不一定相邻),(7)甲、乙、丙三人按从高到矮,自左向右的顺序,(8)甲不排头,乙不排当中。

计数原理、排列组合题型与方法☆基本思路:大的方向分类,类中可能有步或类例1:架子上有不同的2个红球,不同的3个白球,不同的4个黑球。
若从中取2个不同色的球,则取法种数为________。
解:先分类、再分步,共有取法2×3+2×4+3×4=26种.故填26.☆基本思路:大的方向分步,步中可能有类或步例1:如图所示,使电路接通,开关不同的开闭方式有( )A.11种B.20种C.21种D.12种解:分两步,第一部分接通,则可能有一个接通或者两个都接通,有3种可能;第二部分接通,则可能恰有一个接通或恰有两个接通或者都接通,有7种可能.从而总共有37=21种方式。
☆基本思路:排除法间接求解例1:(2013·济南模拟)电路如图所示,在A,B间有四个开关,若发现A,B之间电路不通,则这四个开关打开或闭合的方式有( )A。
3种B。
8种C。
13种D。
16种解:各个开关打开或闭合有2种情形,故四个开关共有24种可能,其中能使电路通的情形有:1,4都闭合且2和3中至少有一个闭合,共有3种可能,故开关打开或闭合的不同情形共有24-3=13(种).故选C.☆剔除重复元素例1:(2013·四川)从1,3,5,7,9这五个数中,每次取出两个不同的数分别记为a,b,共可得到lg a-lg b的不同值的个数是()A。
9 B.10 C。
18 D.20解:lg a-lg b=lg错误!,而错误!=错误!,错误!=错误!,故所求为A错误!-2=18个,故选C.☆投信问题例1:将5封信投入3个邮筒,不同的投法共有( )A。
53种 B。
35种 C.3种 D。
15种解:第1封信,可以投入第1个邮筒,可以投入第2个邮筒,也可以投入第3个邮筒,共有3种投法;同理,后面的4封信也都各有3种投法。
所以,5封信投入3个邮筒,不同的投法共有35种。
故选B.例2:有六名同学报名参加三个智力竞赛项目,在下列情况下各有多少种不同的报名方法?(不一定六名同学都能参加)(1)每人恰好参加一项,每项人数不限;(2)每项限报一人,且每人至多参加一项;(3)每项限报一人,但每人参加的项目不限.解(1)每人都可以从这三个比赛项目中选报一项,各有3种不同选法,由分步乘法计数原理,知共有选法36=729(种).(2)每项限报一人,且每人至多参加一项,因此可由项目选人,第一个项目有6种选法,第二个项目有5种选法,第三个项目只有4种选法,由分步乘法计数原理,得共有报名方法6×5×4=120(种).(3)由于每人参加的项目不限,因此每一个项目都可以从这六人中选出一人参赛,由分步乘法计数原理,得共有不同的报名方法63=216(种).☆数字排列问题例1:用数字0,1,2,3,4,5组成没有重复数字的四位数.(1)可组成多少个不同的四位数?(2)可组成多少个不同的四位偶数?解:(1)直接法:A错误!A错误!=300;间接法:A错误!-A错误!=300。
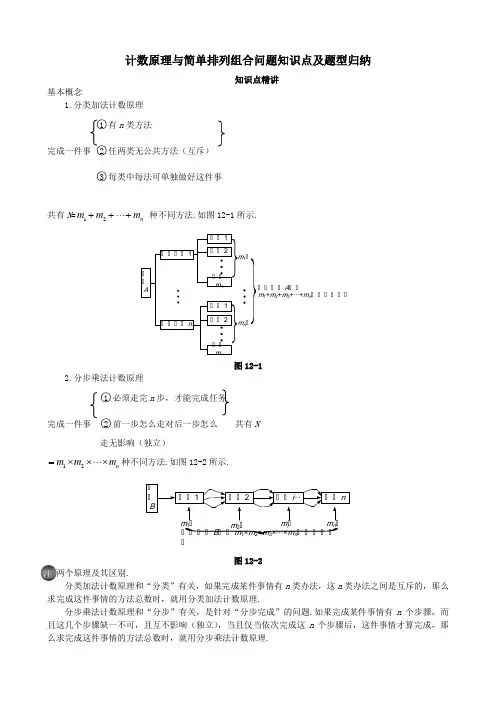


专题01两个计数原理类型一、加法原理例1.(2023·全国·高三专题练习)某奥运村有A,B,C三个运动员生活区,其中A区住有30人,B区住有15人,C区住有10人.已知三个区在一条直线上,位置如图所示.奥运村公交车拟在此间设一个停靠点,为使所有运动员步行到停靠点路程总和最小,那么停靠点位置应在()A.A区B.B区C.C区D.A,B两区之间【答案】A⨯+⨯=【解析】若停靠点为A区时,所有运动员步行到停靠点的路程和为:15100103004500米;⨯+⨯=米;若停靠点为B区时,所有运动员步行到停靠点的路程和为:30100102005000⨯+⨯=米;若停靠点为C区时,所有运动员步行到停靠点的路程和为:303001520012000若停靠点为A区和B区之间时,设距离A区为x米,所有运动员步行到停靠点的路程和为:()(),+⨯-+⨯+-=+x x x x30151001010020054500x=取最小值,故停靠点为A区.当0故选:A例2.(2023·全国·高三专题练习)现有5幅不同的油画,2幅不同的国画,7幅不同的水彩画,从这些画中选一幅布置房间,则不同的选法共有()A.7种B.9种C.14种D.70种【答案】C【解析】分为三类:从国画中选,有2种不同的选法;从油画中选,有5种不同的选法;从水彩画中选,有7种不同的选法,根据分类加法计数原理,共有5+2+7=14(种)不同的选法;故选:C例3.(2023·全国·高三专题练习)2010年世界杯足球赛预计共有24个球队参加比赛,第一轮分成6个组进行单循环赛(在同一组的每两个队都要比赛),决出每个组的一、二名,然后又在剩下的12个队中按积分取4个队(不比赛),共计16个队进行淘汰赛来确定冠亚军,则一共需比赛()场次.A.53B.52C.51D.50【答案】C【解析】第一轮分成6个组进行单循环赛共需要246C 36=场比赛,淘汰赛有如下情况:16进8需要8场比赛,8进4需要4场比赛,4进2需要2场比赛,确定冠亚军需要1场比赛,共需要36842151++++=场比赛故选:C .例4.(2023·全国·高三专题练习)在北京冬奥会短道速滑混合团体2000米接力决赛中,中国队成功夺冠,为中国体育代表团夺得本届冬奥会首金.短道速滑男女接力赛要求每队四名运动员,两男两女,假设男女队员间隔接力,且每位队员只上场一次,则不同的上场次序的种数为()A .8B .16C .18D .24【答案】A【解析】把问题分类:(1)以男运动员排第一位,上场次序的种数为:1122C C 4=;(2)以女运动员排第一位,上场次序的种数为:1122C C 4=;总的上场次序种数合计为:448+=故选:A例5.(2023·高二单元测试)某学校为落实“双减政策,在每天放学后开设拓展课程供学生自愿选择,开学第一周的安排如下表.小明同学要在这一周内选择编程、书法、足球三门课,不同的选课方案共有()周一周二周三周四周五演讲、绘画、舞蹈、足球编程、绘画、舞蹈、足球编程、书法、舞蹈、足球书法、演讲、舞蹈、足球书法、演讲、舞蹈、足球注:每位同学每天最多选一门课,每门课一周内最多选一次.A .15种B .10种C .8种D .5种【答案】A【解析】若周二选编程,则选课方案有1133C C 9=(种);若周三选编程,则选课方案有1123C C 6=(种).综上,不同的选课方案共有9615+=(种).故选:A.类型二、乘法原理例6.(2023·高二课时练习)一次时装表演,有7顶不同款式的帽子,12件不同款式的上衣和8条不同款式的裤子.一位模特要从这些帽子、上衣和裤子中各选1款穿戴,则有______种不同的选法.【答案】672【解析】模特完成穿戴需要分三步:第一步,选择帽子,共有7种选择;第二步,选择上衣,共有12种选择;第三步,选择裤子,共有8种选择;根据乘法原理,共有7128672⨯⨯=种.故答案为:672例7.(2023·高二课时练习)4个学生各写一张贺卡放在一起,然后每人从中各取一张,要求不能取自己写的那张贺卡,但有1个学生取错了,则不同的取法共有______种.【答案】8【解析】有1个学生取错了,有14C4=种可能,另外三人假设为甲、乙、丙,按要求取贺卡,甲先去拿一个贺卡,有2种取法,假设甲拿的是乙写的贺卡,接下来让乙去拿,乙此时只能⨯=种.拿丙的贺卡,而丙最后拿甲的贺卡,则不同的取法共428故答案为:8.例8.(2023·高二课时练习)有四位学生参加三项竞赛,要求每位学生必须参加其中一项竞赛,有______种参赛情况.【答案】81=种.【解析】根据乘法分步原理,每位学生都有三种选择方案,故有4381故答案为:81例9.(2023·高二课时练习)有四位学生参加三项竞赛,要求每项竞赛只需其中一位学生参加,有______种参赛情况.【答案】64=种参赛情况.【解析】根据题意,每一项竞赛都有4位同学可以选择,故有3464故答案为:64例10.(2023·高二课时练习)甲、乙、丙、丁四个人各写一张贺卡,放在一起,再各取一张不是自己所写的贺卡,共有______种不同的取法.【答案】9【解析】第一步甲取1张不是自己所写的那张贺卡,有3种取法;第二步由甲取出的那张贺卡的供卡人取,也有3种不同取法;第三步由剩余两人中任1个人取,此时只有1种取法;⨯⨯⨯=种.第四步最后1个人取,只有1种取法.根据分步计数原理可得33119故答案为:9例11.(2023·高二课时练习)某酒店的大楼有18层,每层12个房间,如果每个房间都安装一个电话分机,那么用1、2、3、4、5、6这六个数字所组成的三位数作为各分机的号码,是否够用?【解析】由题知,房间数为1812216⨯=,⨯⨯=,这六个数字组成的号码个数为666216所以号码刚好够用.例12.按序给出a,b两类元素,a类中的元素排序为甲、乙、丙、丁、戊、己、庚、辛、壬、癸,b类中的元素排序为子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥.在a,b两类中各取1个元素组成1个排列,求a类中选取的元素排在首位,b类中选取的元素排在末位的排列的个数.a类的10个元素叫作天干,b类的12个元素叫作地支.两者按固定顺序相配,形成古代纪年历法,求天干各地支相配可形成的纪年历法可以表示多少年.【解析】从a类中选取一个元素排在首位的选法有10种,从b类中选取一个元素排在末位的选法有12种,由分步乘法计数原理可得所有排列的个数为120种.例13.某班有男生30名、女生24名,从中任选男生和女生各1名代表班级参加比赛,共有多少种不同的选法?【答案】720.【解析】第一步,从30名男生中选出1人,有30种不同选法;第二步,从24名女生中选出1人,有24种不同选法.⨯=.根据分步乘法计数原理,共有不同选法的种数有3024720所以共有720种不同的选法.类型三、基本计数原理的综合应用例14.(2023秋·河北·高二河北省文安县第一中学校考期末)如图,要让电路从A处到B处接通,不同的路径条数为()A.5B.7C.8D.12【答案】C⨯+⨯=.【解析】要让电路从A处到B处接通,不同的路径条数为21238故选:C.例15.(2023·高二单元测试)一杂技团有8名会表演魔术或口技的演员,其中有6人会表演口技,有5人会表演魔术,现从这8人中选出2人上台表演,1人表演口技,1人表演魔术,则不同的安排方法有______种.【答案】27【解析】由题可知有2人只会表演魔术,3人只会表演口技,3人既会表演魔术又会表演口技,针对只会表演魔术的人讨论,先从只会表演魔术的人表演魔术有2种选择,再从其他的6⨯=种选择;人选1人表演口技有6种选择,故共有2612不选只会表演魔术的人,从既会表演魔术又会表演口技的3人中选1人表演魔术,有3种选择,再从只会表演口技的3人和既会表演魔术又会表演口技的剩余2人选1人表演口技,有5种选择,⨯=种选择;故共有3515+=种.所以不同的安排方法有121527故答案为:27.例16.(2023·全国·高三专题练习)如图,一条电路从A处到B处接通时,可以有_____________条不同的线路(每条线路仅含一条通路).【答案】9【解析】依题意按上、中、下三条线路可分为三类,上线路中有2种,中线路中只有1种,下线路中有236⨯=(种).++=(种).根据分类计数原理,共有2169故答案为:9.例17.(2023春·四川绵阳·高三绵阳中学校考阶段练习)小小的火柴棒可以拼成几何图形,也可以拼成数字.如下图所示,我们可以用火柴棒拼出1至9这9个数字比如:“1”需要2根火柴棒,“7”需要3根火柴棒.若用8根火柴棒以适当的方式全部放入右面的表格中(没有放入火柴棒的空位表示数字“0”),那么最多可以表示无重复数字的三位数有______个【答案】20【解析】由题意可得,用2根火柴棒表示数字1,3根火柴棒表示数字7,4根火柴棒表示数字4,5根火柴棒表示数字2,3或5,6根火柴棒表示数字6或9,7根火柴棒表示数字8,数字不重复,因此8根火柴棒只能分成两类:2和6,3和5,组成两个数字,还有数字只能为0,这样组成的无重复数字的三位数个数为:112112222232C C A+C C A=20.故答案为:20例18.(2023·全国·高三专题练习)某学校每天安排4项课后服务供学生自愿选择参加.学校规定:(1)每位学生每天最多选择1项;(2)每位学生每项一周最多选择1次.学校提供的安排表如下:时间周一周二周三周四周五课后服务音乐、阅读、体育、编程口语、阅读、编程、美术手工、阅读、科技、体育口语、阅读、体育、编程音乐、口语、美术、科技若某学生在一周内共选择了阅读、体育、编程3项,则不同的选择方案共有______种.(用数值表示)【答案】14【解析】由题知:周一、二、三、四均可选阅读,体育在周一、三、四,编程在周一、二、四.①若周一选编程,则体育在周三或周四,故为2种,阅读在剩下的两天中选为2种,共有224⨯=种方案.②若周二选编程,则体育在周一,周三或周四,故为3种,阅读在剩下的两天中选为2种,共有326⨯=种方案.③若周四选编程,则体育在周一或周三,故为2种,阅读在剩下的两天中选为2种,共有224⨯=种方案.综上,共有46414++=种方案.故答案为:14例19.(2023·高二课时练习)书架上放有3本不同的数学书,5本不同的语文书,6本不同的英语书.(1)从这些书中任取一本,有多少种不同的取法?(2)从这些书中取数学书、语文书、英语书各一本,有多少种不同的取法?(3)从这些书中取不同科目的书共两本,有多少种不同的取法?【解析】(1)由于书架上有35614++=本书,则从中任取一本,共有14种不同的取法.(2)由题意分步完成,第一步:取任取一本数学书,有3种取法;第二步:取任取一本语文书,有5种取法;第三步:取任取一本英语书,有6种取法;由分步乘法计数原理得共有35690⨯⨯=种不同的取法.(3)取两本不同科目的数,可以分三种情况:①一本数学书和一本语文书,有3515⨯=种情况;②一本数学书和一本英语书,有1863=⨯种情况;③一本语文书和一本英语书,有5630⨯=种情况;根据分类加法计数原理,共有15183063++=种情况.例20.(2023·高二单元测试)在某次国际高峰论坛上,组委会要从6个国内媒体团和3个国外媒体团中选出3个媒体团进行提问,要求这3个媒体团中既有国内媒体团又有国外媒体团,且国内媒体团不能连续提问,则不同的提问方式的种数是多少?【解析】由题,根据选取方式可分为2种情况:2个国内媒体团和1个国外媒体团,选取方式有2163C C 种,提问方式有22A 种,共212632C C A 90=种;1个国内媒体团和2个国外媒体团,选取方式有1263C C 种,提问方式有33A 种,共123633C C A 108=种.综上,共90108198+=种。

专题十 计数原理10.1 计数原理、排列与组合考点 计数原理、排列、组合1.(2020新高考Ⅰ,3,5分)6名同学到甲、乙、丙三个场馆做志愿者,每名同学只去1个场馆,甲场馆安排1名,乙场馆安排2名,丙场馆安排3名,则不同的安排方法共有( )A.120种B.90种C.60种D.30种 答案 C 解题思路:第一步:安排甲场馆的志愿者,则甲场馆的安排方法有C 61=6种,第二步:安排乙场馆的志愿者,则乙场馆的安排方法有C 52=10种,第三步:安排丙场馆的志愿者,则丙场馆的安排方法有C 33=1种.所以共有6×10×1=60种不同的安排方法.故选C (易错:注意分配到每个场馆的志愿者是不分顺序的,所以不用全排列).2.(2022新高考Ⅱ,5,5分,应用性)甲、乙、丙、丁、戊5名同学站成一排参加文艺汇演,若甲不站在两端,丙和丁相邻,则不同的排列方式共有( )A.12种B.24种C.36种D.48种 答案 B 丙和丁相邻共有A 22·A 44种站法,甲站在两端且丙和丁相邻共有C 21·A 22·A 33种站法,所以甲不站在两端且丙和丁相邻共有A 22·A 44−C 21·A 22·A 33=24种站法,故选B .3.(2021全国乙理,6,5分)将5名北京冬奥会志愿者分配到花样滑冰、短道速滑、冰球和冰壶4个项目进行培训,每名志愿者只分配到1个项目,每个项目至少分配1名志愿者,则不同的分配方案共有( )A.60种B.120种C.240种D.480种 答案 C 先将5人分为4组,其中一组有2人,另外三组各1人,共有C 52=10种分法,然后将4个项目全排列,共有A 44=24种排法,根据分步乘法计数原理得到不同的分配方案共有C 52·A 44=240种,故选C .易错警示 本题容易出现将5人分为4组,共有分法C 52·C 31·C 21=60种的错误结果.4.(2016四川理,4,5分)用数字1,2,3,4,5组成没有重复数字的五位数,其中奇数的个数为( )A.24B.48C.60D.72答案 D 奇数的个数为C 31A 44=72.5.(2015四川理,6,5分)用数字0,1,2,3,4,5组成没有重复数字的五位数,其中比40 000大的偶数共有( )A.144个B.120个C.96个D.72个答案B数字0,1,2,3,4,5中仅有0,2,4三个偶数,比40 000大的偶数为以4开头与以5开头的数.其中以4开头的偶数又分以0结尾与以2结尾,有2A43=48个;同理,以5开头的有3A43=72个.于是共有48+72=120个,故选B.评析本题考查了分类与分步计数原理、排列数的知识.考查学生分析问题、解决问题的能力.6.(2014大纲全国理,5,5分)有6名男医生、5名女医生,从中选出2名男医生、1名女医生组成一个医疗小组.则不同的选法共有()A.60种B.70种C.75种D.150种答案C从6名男医生中选出2名有C62种选法,从5名女医生中选出1名有C51种选法,由分步乘法计数原理得不同的选法共有C62·C51=75种.故选C.7.(2014辽宁理,6,5分)6把椅子摆成一排,3人随机就座,任何两人不相邻的坐法种数为()A.144B.120C.72D.24答案D先把三把椅子隔开摆好,它们之间和两端有4个位置,再把三人带椅子插放在四个位置,共有A43=24种放法,故选D.8.(2014四川理,6,5分)六个人从左至右排成一行,最左端只能排甲或乙,最右端不能排甲,则不同的排法共有()A.192种B.216种C.240种D.288种答案B若最左端排甲,其他位置共有A55=120种排法;若最左端排乙,最右端共有4种排法,其余4个位置有A44=24种排法,所以共有120+4×24=216种排法.9.(2014重庆理,9,5分)某次联欢会要安排3个歌舞类节目、2个小品类节目和1个相声类节目的演出顺序,则同类节目不相邻的排法种数是()A.72B.120C.144D.168答案B先不考虑小品类节目是否相邻,保证歌舞类节目不相邻的排法共有A33·A43=144种,再剔除小品类节目相邻的情况,共有A33·A22·A22=24种,于是符合题意的排法共有144-24=120种.10.(2013山东理,10,5分)用0,1,…,9十个数字,可以组成有重复数字的三位数的个数为()A.243B.252C.261D.279答案B由分步乘法计数原理知:用0,1,…,9十个数字组成三位数(可有重复数字)的个数为9×10×10=900,组成没有重复数字的三位数的个数为9×9×8=648,则组成有重复数字的三位数的个数为900-648=252,故选B.评析本题考查分步乘法计数原理,考查学生的推理运算能力.11.(2012课标理,2,5分)将2名教师,4名学生分成2个小组,分别安排到甲、乙两地参加社会实践活动,每个小组由1名教师和2名学生组成,不同的安排方案共有()A.12种B.10种C.9种D.8种答案A2名教师各在1个小组,给其中1名教师选2名学生,有C42种选法,另2名学生分配给另1名教师,然后将2个小组安排到甲、乙两地,有A22种方案,故不同的安排方案共有C42A22=12种,选A.评析本题考查了排列组合的实际应用,考查了先分组再分配的方法.12.(2012辽宁理,5,5分)一排9个座位坐了3个三口之家.若每家人坐在一起,则不同的坐法种数为()A.3×3!B.3×(3!)3C.(3!)4D.9!答案C第1步:3个家庭的全排列,方法数为3!;第2步:家庭内部3个人全排列,方法数为3!,共3个家庭,方法数为(3!)3,∴总数为(3!)×(3!)3=(3!)4,故选C.评析本题主要考查计数原理的基础知识,考查学生分析、解决问题的能力.13.(2012安徽理,10,5分)6位同学在毕业聚会活动中进行纪念品的交换,任意两位同学之间最多交换一次,进行交换的两位同学互赠一份纪念品.已知6位同学之间共进行了13次交换,则收到4份纪念品的同学人数为()A.1或3B.1或4C.2或3D.2或4答案D由题意及C62=15知只需少交换2次.记6位同学为A1、A2、A3、A4、A5、A6,不妨讨论①A1少交换2次,如A1未与A2、A3交换,则收到4份纪念品的同学仅为A2、A3 2人;②A1、A2各少交换1次,如A1与A3未交换,A2与A4未交换,则收到4份纪念品的同学有4人,为A1、A2、A3、A4.故选D.14.(2016课标Ⅱ,5,5分)如图,小明从街道的E处出发,先到F处与小红会合,再一起到位于G处的老年公寓参加志愿者活动,则小明到老年公寓可以选择的最短路径条数为()A.24B.18C.12D.9答案B分两步,第一步,从E→F,有6条可以选择的最短路径;第二步,从F→G,有3条可以选择的最短路径.由分步乘法计数原理可知有6×3=18条可以选择的最短路径.故选B.思路分析小明到老年公寓,需分两步进行,先从E到F,再从F到G,分别求各步的最短路径条数,再利用分步乘法计数原理即可得结果.15.(2016课标Ⅲ,12,5分)定义“规范01数列”{a n}如下:{a n}共有2m项,其中m项为0,m项为1,且对任意k≤2m,a1,a2,…,a k中0的个数不少于1的个数,若m=4,则不同的“规范01数列”共有()A.18个B.16个C.14个D.12个答案C当m=4时,数列{a n}共有8项,其中4项为0,4项为1,要满足对任意k≤8,a1,a2,…,a k中0的个数不少于1的个数,则必有a1=0,a8=1,a2可为0,也可为1.(1)当a2=0时,分以下3种情况:①若a3=0,则a4,a5,a6,a7中任意一个为0均可,则有C41=4种情况;②若a3=1,a4=0,则a5,a6,a7中任意一个为0均可,有C31=3种情况;③若a3=1,a4=1,则a5必为0,a6,a7中任一个为0均可,有C21=2种情况;(2)当a2=1时,必有a3=0,分以下2种情况:①若a4=0,则a5,a6,a7中任一个为0均可,有C31=3种情况;②若a4=1,则a5必为0,a6,a7中任一个为0均可,有C21=2种情况.综上所述,不同的“规范01数列”共有4+3+2+3+2=14个,故选C.思路分析根据题意可知a1=0,a8=1,进而对a2,a3,a4取不同值进行分类讨论(分类要做到不重不漏),从而利用分类加法计数原理求出不同的“规范01数列”的个数.16.(2018浙江,16,4分)从1,3,5,7,9中任取2个数字,从0,2,4,6中任取2个数字,一共可以组成个没有重复数字的四位数.(用数字作答)答案 1 260解析本小题考查排列、组合及其运用,考查分类讨论思想.含有数字0的没有重复数字的四位数共有C52C31A31A33=540个,不含有数字0的没有重复数字的四位数共有C52C32A44=720个,故一共可以组成540+720=1 260个没有重复数字的四位数.易错警示数字排成数时,容易出错的地方:(1)数字是否可以重复;(2)数字0不能排首位.17.(2015广东理,12,5分)某高三毕业班有40人,同学之间两两彼此给对方仅写一条毕业留言,那么全班共写了条毕业留言.(用数字作答)答案 1 560解析∵同学之间两两彼此给对方仅写一条毕业留言,且全班共有40人,∴全班共写了40×39=1 560条毕业留言.18.(2013北京理,12,5分)将序号分别为1,2,3,4,5的5张参观券全部分给4人,每人至少1张.如果分给同一人的2张参观券连号,那么不同的分法种数是.答案96解析5张参观券分成4份,1份2张,另外3份各1张,且2张参观券连号,则有4种分法,把这4份参观券分给4人,则不同的分法种数是4A44=96.19.(2013大纲全国理,14,5分)6个人排成一行,其中甲、乙两人不相邻的不同排法共有种.(用数字作答)答案480解析先将除甲、乙两人以外的4人排成一行,有A44=24种排法,再将甲、乙插入有A52=20种,所以6人排成一行,甲、乙不相邻的排法共有24×20=480种.20.(2013浙江理,14,4分)将A,B,C,D,E,F六个字母排成一排,且A,B均在C的同侧,则不同的排法共有种(用数字作答).答案480解析从左往右看,若C排在第1位,共有排法A55=120种;若C排在第2位,共有排法A42·A33=72种;若C排在第3位,则A、B可排C的左侧或右侧,共有排法A22·A33+A32·A33=48种;若C排在第4,5,6位时,其排法数与排在第3,2,1位相同,故共有排法2×(120+72+48)=480种.21.(2011北京理,12,5分)用数字2,3组成四位数,且数字2,3至少都出现一次,这样的四位数共有个.(用数字作答)答案14解析解法一:数字2只出现一次的四位数有C41=4个;数字2出现两次的四位数有C42C22=6个;数字2出现三次的四位数有C43=4个.故总共有4+6+4=14个.解法二:由数字2,3组成的四位数共有24=16个,其中没有数字2的四位数只有1个,没有数字3的四位数也只有1个,故符合条件的四位数共有16-2=14个.评析本题考查排列组合的基础知识,考查分类讨论思想,解题关键是准确分类,并注意相同元素的排列数等于不同元素的组合数.属于中等难度题.。

(2)排列数公式:: 第一章计数原理基本计数原理和排列组合一、概念回顾:(―)两个原理.1.加法原理每一类中的每一种方法都可以独立地完成此任务;两类不同办法中的具体方法,互不相同(即分类不事);完成此任务的任何一种方法,都属于某一类(即分类不漏)2.乘法原理任何一步的一种方浩都不熊宠廖巧任务,必须且只须连续定廖咨p步才能完成此任务;各步计数相互独立;只要有一步中所采取的方法不同,则对应的完成此事的方法也不同• • • •3.丁%有事客以零的排列.从m个不同元素中,每次取出〃个元素,元素可以重复出现,按照一定的顺序排成一排,那么第一、第二......第〃位上选取元素的方法都是77Z个,所以从个不同元素中,每次取出〃个元素可重复排列数-m n例如:〃件物品放入〃?‘个抽屉中,不限放法,共有多少种不同放法?(解:种)(―)排列组合1、排列(1)排列数的计算:从〃个不同元素中取出m(m < n)个元素排成一列,称为从〃个不同元素中取出个元素的一个排列.从〃个不同元素中取出m个元素的一个排列数,用符号表示.(2)排列数公式:A'" = n(n+ = ----------------- :—(m < n,n,m e N)注意.〃•〃!=(〃 +1)!—〃!规定0! = 1J、.注:含有可更尽素的排列问题对含有相同元素求排列个数的方法是:设重集S有A个不同元素%,但,...,%其中限重复数为叫、色、••叫,且〃 =% + % +..nk,则S的排列个数等于n - ------ - --- .例如:己知数字3、2、2,求其排列个数〃=(1 + 2)!=3又例如:数字5、5、5、求其排列个数?其排列个数心艮=1.1!2! 3!2、组合(1)组合数的计算:从/r个不同的元素中任取m(m < n)个元素并成一组,叫做从〃个不同元素中取出知个元素的一个组合.从〃个不同元素中取出m个元素的一个排列数,用符号C:表示。
一、小球放盒子问题(分组问题)(1)6个不同的小球放到6个不同的盒子里。
解析:分步乘法计数原理,每个小球都有六种放法答案:66。
(2)6个不同的小球放到6个不同的盒子里,要求每个盒子只能放一个小球。
解析:思路一:分步乘法计数原理,第一个小球有6种放法第二个小球有5种放法……第六个小球有1种放法即6*5*4*3*2*1;思路二:将小球按顺序摆放后,与不同的盒子相对应即可,即A6 6。
答案:720。
(3)6个不同的小球平均放到3个相同的盒子里。
解析:平均分组的问题因为盒子相同,相当于把小球等分成三堆,设想6个小球编号为ABCDEF,首先从6个球中选出2个,为C2 6;然后从剩下的4个球中选出2个,为C2 4;最后剩下2个球,为C2 2;但是:C2 6取出AB球、C2 4取出CD球、剩EF球;C2 6取出AB球、C2 4取出EF球、剩CD球;C2 6取出CD球、C2 4取出AB球、剩EF球;C2 6取出CD球、C2 4取出EF球、剩AB球;C2 6取出EF球、C2 4取出AB球、剩CD球;C2 6取出EF球、C2 4取出CD球、剩AB球;得到的结果是一样的,故按照C2 6C2 4C2 2组合完成后还应除去A3 3,答案:C2 6C2 4C2 2/A3 3(4)6个不同的小球平均放到3个不同的盒子里。
解析:平均分组后再分配的问题平均分组得到的结果为C2 6C2 4C2 2/A3 3,分完组后三堆小球还要放到不同的盒子里,即再进行一个A3 3的排列答案:C2 6C2 4C2 2(5)6个不同的小球按1、2、3的数量,分别放到3个相同的盒子里。
解析:非平均分组的问题因为盒子相同,相当于把小球分成数量不等的三堆,首先从6个球中选出1个,为C1 6;然后从剩下的5个球中选出2个,为C2 5;最后剩下3个球,为C3 3;注意:因为这个问题是非平均分组,故不存在(3)中出现的重复的情况,因此C1 6C2 5C3 3即为最后结果,不需要再除以A3 3答案:C1 6C2 5C3 3(6)6个不同的小球按1、2、3的数量,分别放到3个不同的盒子里。
计数原理与排列组合题型解题方法总结计数原理一、知识精讲1、分类计数原理:2、分步计数原理:特别注意:两个原理的共同点:把一个原始事件分解成若干个分事件来完成。
不同点:如果完成一件事情共有n类办法,这n类办法彼此之间相互独立的,无论哪一类办法中的哪一种方法都能单独完成这件事情,求完成这件事情的方法种数,就用分类计数原理。
分类时应不重不漏(即任一种方法必须属于某一类且只属于这一类)如果完成一件事情需要分成n个步骤,各个步骤都是不可缺少的,需要依次完成所有的步骤,才能完成这件事,而完成每一个步骤各有若干种不同的方法,求完成这件事情的方法种数就用分步计数原理。
各步骤有先后,相互依存,缺一不可。
3、排列(1)排列定义,排列数(2)排列数公式:(3)全排列列:4.组合(1)组合的定义,排列与组合的区别;(2)组合数公式:(3)组合数的性质二、.典例解析题型1:计数原理例1.完成下列选择题与填空题(1)有三个不同的信箱,今有四封不同的信欲投其中,则不同的投法有种。
A.81B.64C.24D.4(2)四名学生争夺三项冠军,获得冠军的可能的种数是( )A.81B.64C.24D.4(3)有四位学生参加三项不同的竞赛,①每位学生必须参加一项竞赛,则有不同的参赛方法有;②每项竞赛只许有一位学生参加,则有不同的参赛方法有;③每位学生最多参加一项竞赛,每项竞赛只许有一位学生参加,则不同的参赛方法有 。
例2(1)如图为一电路图,从A 到B 共有 条不同的线路可通电。
例3: 把一个圆分成3块扇形,现在用5种不同的颜色给3块扇形涂色,要求相邻扇形的颜色互不相同,问有多少钟不同的涂法?若分割成4块扇形呢?例4、某城在中心广场造一个花圃,花圃分为6个部分(如图).现要栽种4种不同颜色的花,每部分栽种一种且相邻部分不能栽种同样颜色的花,不同的栽种方法有 ________ 种.(以数字作答)例5、 四面体的顶点和各棱的中点共10个,在其中取4个不共面的点,问共有多少种不同的取法?例6、(1)电视台在”欢乐今宵”节目中拿出两个信箱,其中存放着先后两次竞猜中成绩优秀的观众来信,甲信箱中有30封,乙信箱中有20封.现有主持人抽奖确定幸运观众,若先确定一名幸运之星,再从两信箱中各确定一名幸运伙伴,有多少种不同的结果?(2)三边均为整数,且最大边长为11的三角形的个数是DA题型2:排列、组合问题处理策略一.元素个数较少的排列组合问题枚举法:1、设有编号为1,2,3,4,5的五个球和编号为1,2,3,4,5的盒子现将这5个球投入5个盒子要求每个盒子放一个球,并且恰好有两个球的号码与盒子号码相同,问有多少种不同的方法?2、学号为1、2、3、4的学生坐到编号为1、2、3、4的四张凳子上,要求学生的学号与其所坐的凳子编号不同,问有多少种不同的坐法?二、特殊元素和特殊位置优先策略3、.由0,1,2,3,4,5可以组成多少个没有重复数字五位奇数.4、五个人排成一排,其中甲不在排头,乙不在排尾,不同的排法有( )A.120种B.96种C.78种D.72种三、相邻捆绑、不相邻插空5、(1)7人站成一排照相,若要求甲、乙、丙不相邻,则有多少种不同的排法?(2)7人站成一排照相,甲、乙、丙三人相邻,有多少种不同排法?6、马路上有8只路灯,为节约用电又不影响正常的照明,可把其中的三只灯关掉,但不能同时关掉相邻的两只或三只,也不能关掉两端的灯,那么满足条件的关灯方法共有多少种?7、某人射击8枪,命中4枪,4枪命中恰好有3枪连在一起的情形的不同种数为8、一个晚会的节目有4个舞蹈,2个相声,3个独唱,舞蹈节目不能连续出场,则节目的出场顺序有多少种?四、不尽相异元素、定序问题倍缩法9、(1)7人排队,其中甲乙丙3人顺序一定共有多少不同的排法(2)10人身高各不相等,排成前后排,每排5人,要求从左至右身高逐渐增加,共有多少排法?(3)由4个A和3个B可以组成多少个7位字符信息?五、分排问题“直排法”10、7个人坐两排座位,第一排3个人,第二排坐4个人,则不同的坐法有多少种?11、8人排成前后两排,每排4人,其中甲乙在前排,丁在后排,共有多少排法六、重排问题方幂策略(住店、投邮、影射)12、把6名实习生分配到7个车间实习,共有多少种不同的分法13、某8层大楼从一楼电梯上来8名乘客人,他们到各自的一层下电梯,则他们下电梯的方法有多少种?七.构造模型的策略14、10个相同的球装5个盒中,每盒至少一个有多少装法?15、方程a+b+c+d=12有多少组正整数解?八、排列组合混合问题先选后排策略16、有5个不同的小球,装入4个不同的盒内,每盒至少装一个球,共有多少不同的装法.17、一个班有6名战士,其中正副班长各1人,现从中选4人完成四种不同的任务,每人完成一种任务,且正副班长有且只有1人参加,则不同的选法有________ 种九、.正难则反总体淘汰策略18、我们班里有43位同学,从中任抽5人,正、副班长、团支部书记至少有一人在内的抽法有多少种?十、无编号平均分组问题除法策略19、6本不同的书平均分成3堆,每堆2本共有多少分法?20、10名学生分成3组,其中一组4人, 另两组3人但正副班长不能分在同一组,有多少种不同的分组方法21、某校高二年级共有六个班级,现从外地转入4名学生,要安排到该年级的两个班级且每班安排2名,则不同的安排方案种数为十一化归策略22、25人排成5×5方队,现从中选3人,要求3人不在同一行也不在同一列,不同的选法有多少种?23、某城市的街区由4 5条街道组成,从西南A走到东北B的最短路径有多少种?三、练习题组:1、7种不同的花种在排成一列的花盆里,若两种葵花不种在中间,也不种在两端的花盆里,问有多少不同的种法?2、把6名实习生分配到7个车间实习,共有多少种不同的分法3.(1)在这五个数字组成的没有重复数字的三位数中,各位数字之和为奇数的共有( )(A)36个(B)24个(C)18个(D)6个(2)从4名男生和3名女生中选出3人,分别从事三项不同的工作,若这3人中至少有1名女生,则选派方案共有( )(A)108种(B)186种(C)216种(D)270种(3)在数字1,2,3与符号+,-五个元素的所有全排列中,任意两个数字都不相邻的全排列个数是( )A.6B. 12C. 18D. 24(4)高三(一)班学要安排毕业晚会的4各音乐节目,2个舞蹈节目和1个曲艺节目的演出顺序,要求两个舞蹈节目不连排,则不同排法的种数是( )(A)1800 (B)3600 (C)4320 (D)50404.(1)用数字0,1,2,3,4组成没有重复数字的五位数,则其中数字1,2相邻的偶数有个(用数字作答);(2)电视台连续播放6个广告,其中含4个不同的商业广告和2个不同的公益广告,要求首尾必须播放公益广告,则共有种不同的播放方式(结果用数值表示).5.(1)将5名实习教师分配到高一年级的3个班实习,每班至少1名,最多2名,则不同的分配方案有( )(A)30种(B)90种(C)180种(D)270种(2)将4个颜色互不相同的球全部放入编号为1和2的两个盒子里,使得放入每个盒子里的球的个数不小于该盒子的编号,则不同的放球方法有( )A.10种B.20种C.36种D.52种6.(1)某校从8名教师中选派4名教师同时去4个边远地区支教(每地1人),其中甲和乙不同去,则不同的选派方案共有种;(2)5名志愿者分到3所学校支教,每个学校至少去一名志愿者,则不同的分派方法共有(A)150种(B)180种(C)200种(D)280种7、.已知直线ax+by+c=0中的a,b,c是取自集合{-3,-2,-1,0,1,2,3}中的3个不同的元素,并且该直线的倾斜角为锐角,求符合这些条件的直线的条数8、甲、乙、丙、丁四个公司承包8项工程,甲公司承包3项工程,乙公司承包1项,丙、丁各承包2项,问共有种承包方式?9、停车场划出一排12个停车位置,今有8辆车需要停放,要求空位置连在一起,不同的停车方法有多少种?10、x+y+z+w=100求这个方程组的正整数解的组数11、.设有编号1,2,3,4,5的五个球和编号1,2,3,4,5的五个盒子,现将5个球投入这五个盒子内,要求每个盒子放一个球,并且恰好有两个球的编号与盒子的编号相同,.有多少投法12、.正方体的8个顶点可连成多少对异面直线13、3个人坐在一排8个椅子上,若每个人左右两边都有空位,则坐法的种类有多少种?14.(2008陕西,16)某地奥运火炬接力传递路线共分6段,传递活动分别由6名火炬手完成。
(完整版)计数原理及排列组合典型问题-(含答案)计数原理及排列组合典型问题一、计数原理:某城市在中心广场建造一个花圃,花圃分为6个部分(如右图)现要栽种4种不同颜色的花,每部分栽种一种且相邻部分不能栽种同样颜色的花,不同的栽种方法有______种.(以数字作答)【答案】 120二、排列问题:1、限定顺序问题:(1) 7位同学站成一排.甲必须站在乙的左边? 【答案】7722=2520A A(2) 7位同学站成一排.甲、乙和丙三个同学由左到右排列? 【答案】8403377=A A (3)7位同学站成一排.甲和乙在丙的同侧?【答案】33602、相邻问题:7位同学站成一排,甲、乙、丙三个同学必须站在一起,另外四个人也必须站在一起排法共有多少种?【答案】将甲、乙、丙三个同学“捆绑”在一起看成一个元素,另外四个人“捆绑”在一起看成一个元素,时一共有2个元素,∴一共有排法种数:(种)3、不相邻问题:7位同学站成一排,甲、乙和丙三个同学都不能相邻的排法共有多少种?【答案】先将其余四个同学排好有种方法,此时他们留下五个“空”,再将甲、乙和丙三个同学分别插入这五个“空”有种方法,所以一共有=1440种.4、限制位置问题:7位同学站成一排,甲、乙两同学必须相邻,而且丙不能站在排头和排尾的排法有多少种?【答案】将甲、乙两同学“捆绑”在一起看成一个元素,此时一共有6个元素,若丙站在排头或排尾有2种方法,所以,丙不能站在排头和排尾的排法342342288A A A =44A 35A 44A 35A 55A 654321有三、组合问题:1、等分问题:(1)今有10件不同奖品, 从中选6件分成三份,每份2件, 有多少种分法?【答案】62221064233=3150C C C C A(2)今有10件不同奖品, 从中选6件分给甲乙丙三人,每人2件, 有几种分法?【答案】622210642=18900C C C C2、不等分问题:(1)今有10件不同奖品, 从中选6件分给三份,其中1份一件,1份二件,1份三件, 有多少种分法?【答案】612310653=12600C C C C(2)今有10件不同奖品, 从中选6件分给甲乙丙三人,其中1人一件,1人二件,1人三件, 有多少种分法?【答案】61233106533=75600C C C C A3、元素相同问题:从6个学校中选出30名学生参加数学竞赛,每校至少有1人,这样有几种选法?【答案】529=118755C 960)2(225566 =?-A A A。
计数原理与排列组合题型解题方法总结
计数原理
一、知识精讲
1、分类计数原理:
2、分步计数原理:
特别注意:两个原理的共同点:把一个原始事件分解成若干个分事件来完成。
不同点:如果完成一件事情共有n类办法,这n类办法彼此之间相互独立的,无论哪一类办法中的哪一种方法都能单独完成这件事情,求完成这件事情的方法种数,就用分类计数原理。
分类时应不重不漏(即任一种方法必须属于某一类且只属于这一类)
如果完成一件事情需要分成n个步骤,各个步骤都是不可缺少的,需要依次完成所有的步骤,才能完成这件事,而完成每一个步骤各有若干种不同的方法,求完成这件事情的方法种数就用分步计数原理。
各步骤有先后,相互依存,缺一不可。
3、排列
(1)排列定义,排列数
(2)排列数公式:
(3)全排列列:
4.组合
(1)组合的定义,排列与组合的区别;
(2)组合数公式:
(3)组合数的性质
二、.典例解析
题型1:计数原理
例1.完成下列选择题与填空题
(1)有三个不同的信箱,今有四封不同的信欲投其中,则不同的投法有种。
A.81
B.64
C.24
D.4
(2)四名学生争夺三项冠军,获得冠军的可能的种数是( )
A.81
B.64
C.24
D.4
(3)有四位学生参加三项不同的竞赛,
①每位学生必须参加一项竞赛,则有不同的参赛方法有;
②每项竞赛只许有一位学生参加,则有不同的参赛方法有;
③每位学生最多参加一项竞赛,每项竞赛只许有一位学生参加,则不同的参赛方法有 。
例2(1)如图为一电路图,从A 到B 共有 条不同的线路可通电。
例3: 把一个圆分成3块扇形,现在用5种不同的颜色给3块扇形涂色,要求相邻扇形的颜色互不相同,问有多少钟不同的涂法?若分割成4块扇形呢?
例4、某城在中心广场造一个花圃,花圃分为6个部分(如图).现要栽种4种不同颜色的花,每部分栽种一种且相邻部分不能栽种同样颜色的花,不同的栽种方法有 ________ 种.(以数字作答)
例5、 四面体的顶点和各棱的中点共10个,在其中取4个不共面的点,问共有多少种不同的取法?
例6、(1)电视台在”欢乐今宵”节目中拿出两个信箱,其中存放着先后两次竞猜中成绩优秀的观众来信,甲信箱中有30封,乙信箱中有20封.现有主持人抽奖确定幸运观众,若先确定一名幸运之星,再从两信箱中各确定一名幸运伙伴,有多少种不同的结果?
(2)三边均为整数,且最大边长为11的三角形的个数是
D
A
题型2:排列、组合问题处理策略
一.元素个数较少的排列组合问题枚举法:
1、设有编号为1,2,3,4,5的五个球和编号为1,2,3,4,5的盒子现将这5个球投入5个盒子要求每个盒子放一个球,并且恰好有两个球的号码与盒子号码相同,问有多少种不同的方法?
2、学号为1、2、
3、4的学生坐到编号为1、2、3、4的四张凳子上,要求学生的学号与其所坐的凳子编号不同,问有多少种不同的坐法?
二、特殊元素和特殊位置优先策略
3、.由0,1,2,3,4,5可以组成多少个没有重复数字五位奇数.
4、五个人排成一排,其中甲不在排头,乙不在排尾,不同的排法有( )
A.120种B.96种C.78种D.72种
三、相邻捆绑、不相邻插空
5、(1)7人站成一排照相,若要求甲、乙、丙不相邻,则有多少种不同的排法?
(2)7人站成一排照相,甲、乙、丙三人相邻,有多少种不同排法?
6、马路上有8只路灯,为节约用电又不影响正常的照明,可把其中的三只灯关掉,但不能同时关掉相邻的两只或三只,也不能关掉两端的灯,那么满足条件的关灯方法共有多少种?
7、某人射击8枪,命中4枪,4枪命中恰好有3枪连在一起的情形的不同种数为
8、一个晚会的节目有4个舞蹈,2个相声,3个独唱,舞蹈节目不能连续出场,则节目的出
场顺序有多少种?
四、不尽相异元素、定序问题倍缩法
9、(1)7人排队,其中甲乙丙3人顺序一定共有多少不同的排法
(2)10人身高各不相等,排成前后排,每排5人,要求从左至右身高逐渐增加,共有多少排法?
(3)由4个A和3个B可以组成多少个7位字符信息?
五、分排问题“直排法”
10、7个人坐两排座位,第一排3个人,第二排坐4个人,则不同的坐法有多少种?
11、8人排成前后两排,每排4人,其中甲乙在前排,丁在后排,共有多少排法
六、重排问题方幂策略(住店、投邮、影射)
12、把6名实习生分配到7个车间实习,共有多少种不同的分法
13、某8层大楼从一楼电梯上来8名乘客人,他们到各自的一层下电梯,则他们下电梯的方法有多少种?
七.构造模型的策略
14、10个相同的球装5个盒中,每盒至少一个有多少装法?
15、方程a+b+c+d=12有多少组正整数解?
八、排列组合混合问题先选后排策略
16、有5个不同的小球,装入4个不同的盒内,每盒至少装一个球,共有多少不同的装法.
17、一个班有6名战士,其中正副班长各1人,现从中选4人完成四种不同的任务,每人完成一种任务,且正副班长有且只有1人参加,则不同的选法有________ 种
九、.正难则反总体淘汰策略
18、我们班里有43位同学,从中任抽5人,正、副班长、团支部书记至少有一人在内的抽法有多少种?
十、无编号平均分组问题除法策略
19、6本不同的书平均分成3堆,每堆2本共有多少分法?
20、10名学生分成3组,其中一组4人, 另两组3人但正副班长不能分在同一组,有多少种不同的分组方法
21、某校高二年级共有六个班级,现从外地转入4名学生,要安排到该年级的两个班级且每班安排2名,则不同的安排方案种数为
十一化归策略
22、25人排成5×5方队,现从中选3人,要求3人不在同一行也不在同一列,不同的选法有多少种?
23、某城市的街区由4 5条街道组成,从西南A走到东北B的最短路径有多少种?
三、练习题组:
1、7种不同的花种在排成一列的花盆里,若两种葵花不种在中间,也不种在两端的花盆里,问有多少不同的种法?
2、把6名实习生分配到7个车间实习,共有多少种不同的分法
3.(1)在这五个数字组成的没有重复数字的三位数中,各位数字之和为奇数的共有( )
(A)36个(B)24个(C)18个(D)6个
(2)从4名男生和3名女生中选出3人,分别从事三项不同的工作,若这3人中至少有1名女生,则选派方案共有( )
(A)108种(B)186种(C)216种(D)270种
(3)在数字1,2,3与符号+,-五个元素的所有全排列中,任意两个数字都不相邻的全排列个数是( )
A.6
B. 12
C. 18
D. 24
(4)高三(一)班学要安排毕业晚会的4各音乐节目,2个舞蹈节目和1个曲艺节目的演出顺序,要求两个舞蹈节目不连排,则不同排法的种数是( )
(A)1800 (B)3600 (C)4320 (D)5040
4.(1)用数字0,1,2,3,4组成没有重复数字的五位数,则其中数字1,2相邻的偶数有个(用数字作答);
(2)电视台连续播放6个广告,其中含4个不同的商业广告和2个不同的公益广告,要求首尾必须播放公益广告,则共有种不同的播放方式(结果用数值表示).
5.(1)将5名实习教师分配到高一年级的3个班实习,每班至少1名,最多2名,则不同的分配
方案有( )
(A)30种(B)90种(C)180种(D)270种
(2)将4个颜色互不相同的球全部放入编号为1和2的两个盒子里,使得放入每个盒子里的球的个数不小于该盒子的编号,则不同的放球方法有( )
A.10种
B.20种
C.36种
D.52种
6.(1)某校从8名教师中选派4名教师同时去4个边远地区支教(每地1人),其中甲和乙不同去,则不同的选派方案共有种;
(2)5名志愿者分到3所学校支教,每个学校至少去一名志愿者,则不同的分派方法共有
(A)150种(B)180种(C)200种(D)280种
7、.已知直线ax+by+c=0中的a,b,c是取自集合{-3,-2,-1,0,1,2,3}中的3个不同的元素,并且该直线的倾斜角为锐角,求符合这些条件的直线的条数
8、甲、乙、丙、丁四个公司承包8项工程,甲公司承包3项工程,乙公司承包1项,丙、丁各承包2项,问共有种承包方式?
9、停车场划出一排12个停车位置,今有8辆车需要停放,要求空位置连在一起,不同的停车方法有多少种?
10、x+y+z+w=100求这个方程组的正整数解的组数
11、.设有编号1,2,3,4,5的五个球和编号1,2,3,4,5的五个盒子,现将5个球投入这五个盒子内,要求每个盒子放一个球,并且恰好有两个球的编号与盒子的编号相同,.有多少投法
12、.正方体的8个顶点可连成多少对异面直线
13、3个人坐在一排8个椅子上,若每个人左右两边都有空位,则坐法的种类有多少种?14.(2008陕西,16)某地奥运火炬接力传递路线共分6段,传递活动分别由6名火炬手完成。
如果第一棒火炬手只能从甲、乙、丙三人中产生,最后一棒火炬手只能从甲、乙两人中产生,则不同的传递方案共有种(用数字作答)。
15.(2009年海南宁夏15)7名志愿者中安排6人在周六、周日两天参加社区公益活动,若每天安排3人,则不同的安排方案共有种(用数字作答).
16、(2008宁夏、海南,9)甲、乙、丙3位志愿者安排在周一至周五的5天中参加某项志
愿者活动,要求每人参加一天且每天至多安排一人,并要求甲安排在另外两位前面。
不同的安排方法共有()
A.20种B.30种
C.40种D.60种。