5.4主视图、左视图、俯视图

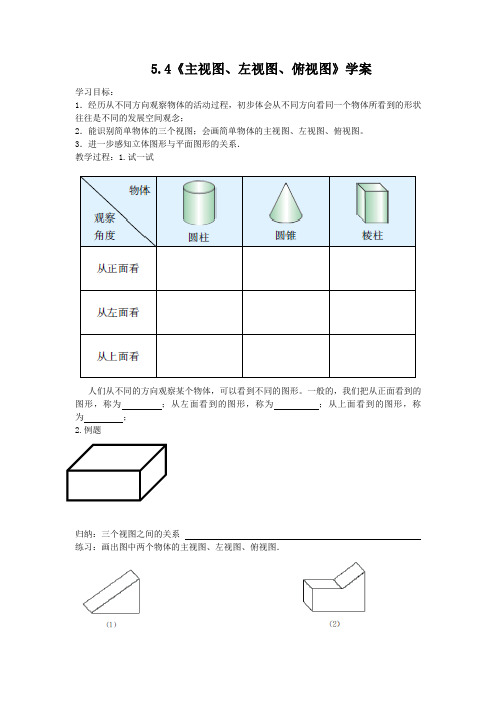
5.4《主视图、左视图、俯视图》学案
学习目标：
1．经历从不同方向观察物体的活动过程，初步体会从不同方向看同一个物体所看到的形状往往是不同的发展空间观念；
2．能识别简单物体的三个视图；会画简单物体的主视图、左视图、俯视图。

3．进一步感知立体图形与平面图形的关系．
教学过程：1.试一试
人们从不同的方向观察某个物体，可以看到不同的图形。

一般的，我们把从正面看到的图形，称为；从左面看到的图形，称为；从上面看到的图形，称为；
2.例题
归纳：三个视图之间的关系
练习：画出图中两个物体的主视图、左视图、俯视图．
3.课后练习
（3）画出下面几何体的主视图、左视图、与俯视图
（4）下面是由几个小立方块所搭几何体的俯视图，小正方形中的数字表示在该位置小立方块的个数。

请画出这个几何体的主视图和左视图
（5）用小立方块搭一个几何体，使得它的主视图和俯视图如图所示。

这样的几何体只有一种吗？它最少需要多少个小立方块？最多需要多少个小立方块？
主视图
俯视图。

第5章　走进图形世界5.4　主视图、左视图、俯视图基础过关全练知识点1　物体的三视图1.(2022江苏徐州期末)下图是由几个大小相同的小正方体搭成的几何体,若去掉1号小正方体,则下列说法正确的是( )A.左视图和俯视图不变B.主视图和左视图不变C.主视图和俯视图不变D.主视图、左视图和俯视图都不变2.(2023江苏南京期末)下图是由几个相同的小正方体搭成的一个几何体,从上方看到的图是( )A B C D知识点2　画立体图形的三视图3.(2022江苏镇江期末)图①是由一些棱长为1 cm的小正方体组成的简单几何体.(1)请直接写出该几何体的表面积(含底部): .(2)从正面看到的平面图形如图②所示,请在图③④中分别画出从左向右、从上向下看到的平面图形.4.(2023江苏无锡期末)下图是由一些棱长为1 cm的小立方块组成的几何体.(1)请画出从正面、左面、上面看到的这个几何体的形状.(2)求该几何体的表面积.(3)如果把它拼成一个无空隙的正方体,那么至少还需要同样的小立方块 块.(4)如果保持从正面和上面看到的形状不变,最多可以再添加 个小立方块.知识点3　由三视图想象物体的形状5.由若干个相同的小正方体搭成的一个几何体的主视图和俯视图如图所示,则搭成这个几何体的小正方体最多有 个.6.(2023江苏苏州期末)如图①所示的组合体的下面是一个长方体,上面是一个圆柱.(1)图②和图③是它的两个视图,在横线上分别填写两个视图的名称(填“主”“左”或“俯”);(2)根据两个视图中的尺寸,计算这个组合体的体积.(结果保留π)能力提升全练7.(2021宁夏中考,2,★☆☆)如图所示的三棱柱的主视图是( )8.(2022江苏南通中考,5,★☆☆)下图是由5个相同的正方体搭成的立体图形,则它的主视图为( )A BC D9.(2021四川攀枝花中考,4,★☆☆)下图是一个几何体的三视图,则这个几何体是( )A.圆锥B.圆柱C.三棱柱D.三棱锥10.(2022辽宁阜新中考,2,★☆☆)下列四个几何体中,俯视图和左视图相同的是( )A B C D11.(2022江苏南京六合期末,11,★★☆)某几何体的三视图如图所示,它由大小相同的小正方体木块堆成,每个小正方体木块的棱长都是1 cm,则该几何体的表面积是 cm2.12.(2021云南中考,11,★★☆)下列图形是某几何体的三视图.已知主视图和左视图是两个全等的长方形.若主视图的相邻两边长分别为2和3,俯视图是直径等于2的圆,则这个几何体的体积为 .13.【新中考】(2022青海中考,13,★★☆)由若干个相同的小正方体构成的几何体的三视图如图所示,那么构成这个几何体的小正方体的个数是 .14.(2022江苏无锡锡山期末,20,★★☆)用小立方体搭一个几何体,使它的主视图和俯视图如图所示,俯视图中小正方形里的字母表示在该位置小立方体的个数,请解答下列问题:(1)求a,b,c的值;(2)这个几何体最少由几个小立方体搭成,最多由几个小立方体搭成?(3)当d=2,e=1,f=2时,画出这个几何体的左视图.素养探究全练15.【空间观念】中央电视台曾有一个非常受欢迎的娱乐节目《墙来啦!》,选手需按墙上的空洞形状摆出相同姿势,才能穿墙而过,否则会被墙推入水池.类似地,有一个几何体恰好无缝隙地以三个不同的“姿势”穿过“墙”上的三个空洞(如图),则该几何体为( )A B C D16.【空间观念】(2023江苏扬州期中)用小正方体搭成一个几何体,使得从正面、上面看该几何体得到的图形如图所示.这样的几何体只有一种吗?(1)它最多需要多少个小正方体?(2)它最少需要多少个小正方体?请分别画出这两种情况下从左面看该几何体得到的图形.答案全解全析基础过关全练1.A　去掉1号小正方体,俯视图不变,左视图不变,主视图改变.2.D　3.解析　(1)这个几何体的表面积为[(6+4+6)×2+2]×12=34(cm2),故答案为34 cm2.(2)这个几何体的左视图、俯视图如下:4.解析　(1)如图所示:(2)(1×1)×(6×2+6×2+6×2+2)=1×38=38(cm2).故该几何体的表面积是38 cm2.(3)3×3×3-10=27-10=17(块).答:至少还需要同样的小立方块17块.(4)保持从正面和上面看到的形状不变,最多可以再添加3个小立方块.5.6解析　由主视图和俯视图易得最底层有4个小正方体,第二层最多有2个小正方体,所以搭成这个几何体的小正方体最多有4+2=6个.6.解析　(1)如图所示:(2)2×5×8+π×(2÷2)2×6=80+π×1×6=80+6π.答:这个组合体的体积是80+6π.能力提升全练7.C　主视图即从正面看到的图形,从正面看三棱柱,中间有一条看得见的棱,因此主视图中间有一条实线,故选C.8.A　主视图是从正面看到的图形,所看到的图形与选项A中的图形相同,故选A.9.A　俯视图为圆形的几何体有球、圆柱、圆锥等,结合主视图和左视图为三角形可得此几何体为圆锥.10.D　俯视图、左视图分别是从物体上面、左面看到的图形.选项D 中的俯视图与左视图都是正方形,故本选项符合题意.11.18解析　该几何体中小正方体木块有4个,其表面积是[3×2+3×2+3×2]×12=18(cm2).12.3π解析　由题意可知此几何体为圆柱,底面圆的半径是1,高是3,所以这个几何体的体积为π×12×3=3π.13.5解析　根据三视图,想象出每个位置正方体的数目:所以,构成这个几何体的小正方体的个数是1+2+1+1=5.14.解析　(1)由主视图可得,俯视图中最右边的小正方形处有3个小立方体,中间一列的两个正方形处各有1个小立方体,∴a=3,b=1,c=1. (2)若d,e,f处有一处有2个小立方体,其余两处各有1个小立方体,则该几何体最少由9个小立方体搭成;若d,e,f处各有2个小立方体,则该几何体最多由11个小立方体搭成.(3)当d=2,e=1,f=2时,这个几何体的左视图如图所示:素养探究全练15.A　A.主视图为正方形,左视图为三角形,俯视图为圆,故A选项符合题意;B.主视图,左视图,俯视图分别为三角形,三角形,带圆心的圆,故B选项不符合题意;C.主视图,左视图,俯视图分别为正方形,正方形,正方形,故C选项不符合题意;D.主视图,左视图,俯视图分别为三角形,三角形,有对角线的长方形,故D选项不符合题意.故选A.16.解析　这样的几何体不止一种.(1)最多需要6+6+2=14个.(2)最少需要4+4+2=10个.最多时的左视图如图(1).最少时的左视图如图(2)(答案不唯一).图(1) 图(2)。

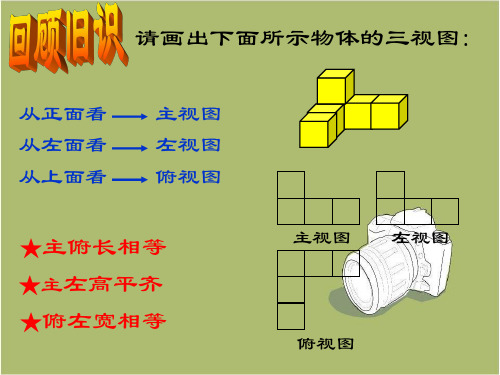
课题：从三个方向看第 1 课时教学期望（目标）：1. 在观察的过程中，初步体会从不同方向看同一个物体所看到的形状往往是不同的，发展空间观念。

2. 能识别简单物体的三个视图，会画一些简单物体的三个视图，进一步丰富对现实空间及图形的认识，发展学生的形象思维。

3.引导学生主动参与教学活动，通过观察、探究、讨论和交流等教学活动，让学生经历数学知识形成与应用的过程，激发对空间与图形学习的好奇心，增强与他人合作交流的意识。

二、探索活动1.猜一猜：请同学们根据所给的平面图形，猜一猜它可能是什么几何体?正面左面上面2.想一想：桌面上放着一个圆柱和一个长方三、学习新知我们从不同的方向观察同一个事物，可能会看到不同的结果，其中我们重点研究以上三个方向看到的图，即：主视图：从正面看到的图形左视图：从左面看到的图形俯视图：从上面看到的图形将俯视图画在主视图的然后引导学生总结归纳三个视图之间的学生回忆前面所活动的内容，主视图与俯视图不变的是什么？主视图与左视图不变左视图与俯视图不变是什么？2.如右图所示的物体，你知道下面的三幅图分别是从哪个方向看到的吗？你能说出这三幅视图的）请你用五个小立方体搭出图示的几何体。

）你能用五个小立方体，按上题的方法搭出与上题不同的几何体吗？请试着画出它的【附】作业设计：做一做⑴请你用五个小立方体搭出图示的几何体。

⑵你能用五个小立方体，按上题的方法搭出与上题不同的几何体吗？请试着画出它的三个视图，并在组内交流。

⑶在上面的实物图中，再添加一个小正方体，使得它的主视图和左视图不变。

操作后，画出可能的俯视图，与同学交流你画出的图形。

课后练习1．观察长方体，判断它的三视图是 （ ）A ．三个大小不一样的长方形，但其中有两个可能大小一样。

B ．三个正方形。

C ．三个一样大的长方形。

2．指出下图中左面三个平面图形分别是右面这个物体三视图中的哪个视图。

（1） 图 （2） 图 （3） 图3．观察左图，并在右边的三视图中标出几何体中的相应字母的位置。

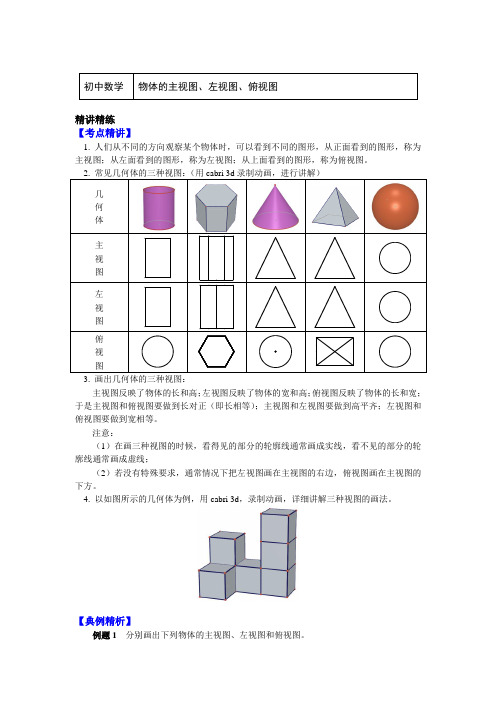
初中数学物体的主视图、左视图、俯视图精讲精练【考点精讲】1. 人们从不同的方向观察某个物体时，可以看到不同的图形，从正面看到的图形，称为主视图；从左面看到的图形，称为左视图；从上面看到的图形，称为俯视图。

2. 常见几何体的三种视图：（用cabri 3d录制动画，进行讲解）几何体主视图左视图俯视图3. 画出几何体的三种视图：主视图反映了物体的长和高；左视图反映了物体的宽和高；俯视图反映了物体的长和宽；于是主视图和俯视图要做到长对正（即长相等）；主视图和左视图要做到高平齐；左视图和俯视图要做到宽相等。

注意：（1）在画三种视图的时候，看得见的部分的轮廓线通常画成实线，看不见的部分的轮廓线通常画成虚线；（2）若没有特殊要求，通常情况下把左视图画在主视图的右边，俯视图画在主视图的下方。

4. 以如图所示的几何体为例，用cabri 3d，录制动画，详细讲解三种视图的画法。

【典例精析】例题1 分别画出下列物体的主视图、左视图和俯视图。

图1 图2 图3 思路导航：按照定义，分别从正面、左面和上面去观察几何体，然后画出看到的平面图形即可。

为了更加直观、形象，也为了培养学生的空间想象能力，录制动画，进行讲解。

答案：图1 所示几何体的主视图、左视图和俯视图如下图所示：俯视图左视图主视图图2 所示几何体的主视图、左视图和俯视图如下图所示： 主视图俯视图左视图图3 所示几何体的主视图、左视图和俯视图如下图所示： 左视图俯视图主视图点评：几何体的主视图、左视图和俯视图的画法及步骤：①确定主视图的位置，并且想象从几何体的正面进行观察，画出主视图；②在主视图的下方画俯视图，并且想象从几何体的正上方进行观察，注意与主视图“长对正”；③在主视图的正右方画左视图，并且想象从几何体的左边进行观察，注意与主视图“高平齐”，与俯视图要做到“宽相等”。

例题2 用若干个棱长为1m 的正方体堆成如图所示的物体（并且将其固定在地面上），现在要用油漆喷涂所有的暴露面，则需要喷涂油漆的总面积是多少？思路导航：分别画出主视图、左视图和俯视图，求出其面积，借助于主视图、左视图和俯视图的面积来求暴露面的面积。

苏科版数学七年级上册5.4《主视图、左视图、俯视图》教学设计1一. 教材分析《苏科版数学七年级上册5.4《主视图、左视图、俯视图》》这一节内容，主要让学生掌握三视图的概念，了解主视图、左视图、俯视图之间的关系，并能够熟练地进行图形的转换。

教材通过实例的展示，引导学生观察、思考，从而发现并掌握三视图的绘制方法。

二. 学情分析七年级的学生已经具备了一定的空间想象能力和图形认知能力，他们对平面图形有一定的了解。

但是，对于三维图形和三视图的概念，可能还比较陌生。

因此，在教学过程中，教师需要通过生动的实例和直观的演示，帮助学生建立起三视图的空间形象，使他们能够更好地理解和掌握这一部分内容。

三. 教学目标1.了解主视图、左视图、俯视图的概念，知道它们之间的关系。

2.能够根据物体的三视图，还原出物体的形状。

3.能够运用三视图的知识，解决一些实际问题。

四. 教学重难点1.重点：主视图、左视图、俯视图的概念及它们之间的关系。

2.难点：如何根据三视图还原出物体的形状，以及如何运用三视图解决实际问题。

五. 教学方法1.情境教学法：通过实例的展示，让学生在实际情境中感受三视图的概念，提高他们的空间想象力。

2.合作学习法：引导学生分组讨论，共同探讨三视图的绘制方法，提高他们的合作能力。

3.实践操作法：让学生动手操作，实际绘制一些简单物体的三视图，增强他们的实践能力。

六. 教学准备1.准备一些常见物体的三视图图片，如圆柱、正方体等。

2.准备一些绘图工具，如直尺、圆规等。

3.准备一些练习题，用于巩固所学知识。

七. 教学过程1.导入（5分钟）教师通过展示一些常见物体的三视图图片，引导学生观察、思考，让学生初步了解三视图的概念。

2.呈现（10分钟）教师通过讲解和演示，详细介绍主视图、左视图、俯视图的概念，以及它们之间的关系。

同时，让学生动手绘制一些简单物体的三视图，加深他们对三视图的理解。

3.操练（10分钟）教师提出一些练习题，让学生分组讨论，共同完成。

苏科版数学七年级上册5.4《主视图、左视图、俯视图》教学设计2一. 教材分析《苏科版数学七年级上册5.4《主视图、左视图、俯视图》》这一节主要让学生了解主视图、左视图、俯视图的概念，以及它们之间的关系。

通过观察长方体和正方体的三视图，让学生能够识别和理解三视图所反映的物体的形状。

教材通过丰富的图片和实例，让学生在实际操作中掌握三视图的知识，培养学生的空间想象能力和抽象思维能力。

二. 学情分析七年级的学生已经具备了一定的几何知识，对立体图形有一定的了解。

但是，对于主视图、左视图、俯视图的概念以及它们之间的关系，可能还比较模糊。

因此，在教学过程中，需要通过大量的实例和操作，让学生深入理解三视图的知识。

三. 教学目标1.知识与技能：让学生掌握主视图、左视图、俯视图的概念，能够识别和理解三视图所反映的物体的形状。

2.过程与方法：通过观察、操作、思考，培养学生的空间想象能力和抽象思维能力。

3.情感态度与价值观：激发学生对数学的兴趣，培养学生的团队合作意识和探究精神。

四. 教学重难点1.重点：主视图、左视图、俯视图的概念及其关系。

2.难点：如何通过三视图识别和理解物体的形状。

五. 教学方法1.情境教学法：通过丰富的图片和实例，让学生在实际操作中掌握三视图的知识。

2.小组合作学习：引导学生进行观察、讨论，培养学生的团队合作意识和探究精神。

3.启发式教学：教师提问，引导学生思考，激发学生的学习兴趣。

六. 教学准备1.准备长方体和正方体的模型，以及它们的三视图图片。

2.准备投影仪或大屏幕，用于展示图片和实例。

3.准备练习题，用于巩固所学知识。

七. 教学过程1.导入（5分钟）利用图片和实例，引导学生观察长方体和正方体的三视图，让学生初步了解主视图、左视图、俯视图的概念。

2.呈现（10分钟）展示长方体和正方体的三视图，让学生直观地感受三视图之间的关系。

教师引导学生观察、思考，总结出主视图、左视图、俯视图的特点和规律。

精讲精练【考点精讲】主视图反映了从物体正面看到的图形；左视图反映从物体左面看到的图形；俯视图反映了从物体上面看到的图形；；从俯视图可以确定物体的底面轮廓，从主视图和左视图可以确定物体的侧面轮廓。

由实物画出三种视图，然而每个视图都是确定的，但是由一个或是两个视图来想象物体，想象出的物体是不唯一的，也就是说仅有一个或者两个视图是无法确定几何体的，必须由三个视图才能唯一确定一个物体。

例如：（仅有一个视图的情况）主视图是长方形的几何体有可能是三棱柱、四棱柱、圆柱等；俯视图是圆的几何体有可能是圆锥、圆柱、球，等等；（仅有两个视图的情况）主视图和左视图都是长方形的有可能是四棱柱、圆柱；主视图和左视图都是三角形的有可能是四棱锥、圆锥。

【典例精析】例题1 如图所示，是一个几何体的三视图，说出这种几何体的名称。

主视图左视图俯视图思路导航：俯视图中有一条线段，将这条线段与左视图中的三角形的上方的顶点联系起来，它应该是两个面的交线，这两个面与三角形的两条边有联系，结合主视图和左视图，可以判断这个几何体是一个三棱柱，其形状如下图所示：答案：三棱柱点评：根据三视图想象物体的形状，要仔细观察、认真分析三个视图之间的联系，以一些特殊的点和线为突破口，千万不能孤立地去看其中一个或两个图形，一定要将三个图形结合起来，将分析和想象结合起来。

例题2 用小正方体搭一个几何体，它的俯视图如图所示，图中的数字表示该位置上的小正方体的个数，请画出这个几何体的主视图和左视图。

思路导航：从俯视图以及所标注的数字可知，这个几何体一共有小正方体7个，从正面看，主视图应该有3列，第一列有2个小正方形，第二列有1个小正方形，第三列有2个小正方形。

答案：主视图左视图点评：解决这类问题可以利用小正方体通过实际摆放、堆砌出几何体，然后进行观察、画图，有了一定的空间想象能力以后，可以直接根据俯视图以及所标注的数字，想象出小正方体的总数、列数、层数，再想象从三个不同的方向进行观察，然后画出相应的视图。