2.河北2015中考黑白卷狂押到底·扫扫刊(数学)6.20

2015年河北省中考数学试题及答案word版本文为2021年人工智能生成，由于助手能力的限制，无法提供具体年份的试题及答案。

感谢理解。

2015年河北省中考数学试题及答案一、选择题1. 已知正方形ABCD的边长为3cm，点E在边BC上，使得BE:EC = 1:2，连接AE，若AE的长度为x cm，则x = （）。

A. 1B. 2C. 3D. 4答案：B2. 如果一个正方体表面的每个小正方形的面积是S平方厘米，那么这个正方体的体积是（）。

A. SB. S平方厘米C. S立方厘米D. S的平方根倍立方厘米答案：C3.若两个交织的三角形相等，则它们的内切圆相等，这个命题的逆命题是（）。

A. 若两个三角形的内切圆相等，则它们相等。

B. 若两个三角形相等，则它们的内切圆相等。

C. 若两个三角形不相等，则它们的内切圆不相等。

D. 若两个三角形的内切圆不相等，则它们不相等。

答案：A二、解答题1. 设甲、乙两车分别以每小时60公里、每小时90公里的速度开向相对方向，甲车发车后1小时，甲、乙两车之间的距离为180公里，此时甲车超乙车30分钟。

求二车相遇时，乙车行驶的时间和已经超过乙车的路程。

解：设二车相遇时，乙车行驶的时间为t小时，已经超过乙车的路程为S公里。

因为甲、乙车之间距离为180公里，所以甲车行驶了1小时后，乙车已经行驶了90公里，剩下距离甲车还有180-90=90公里。

设甲车行驶了t小时后，乙车行驶了S公里，甲车行驶了t+1小时后，乙车行驶了S+90公里。

根据题意，甲车超乙车30分钟，即甲车行驶了t+1小时，乙车行驶了t小时。

根据速度公式，甲车行驶了t+1小时，乙车行驶了t小时，可以得到以下方程：60(t+1) = 90t + S化简得：60t + 60 = 90t + S即：S = 60 - 30t由题意得，乙车行驶的时间和已经超过乙车的路程为t小时，S公里。

此时有：S = 60 - 30t。

二车相遇时，甲车行驶了t+1小时，乙车行驶了t小时，所以二车相遇时，甲车行驶的距离为：60(t+1) = 90t + S。

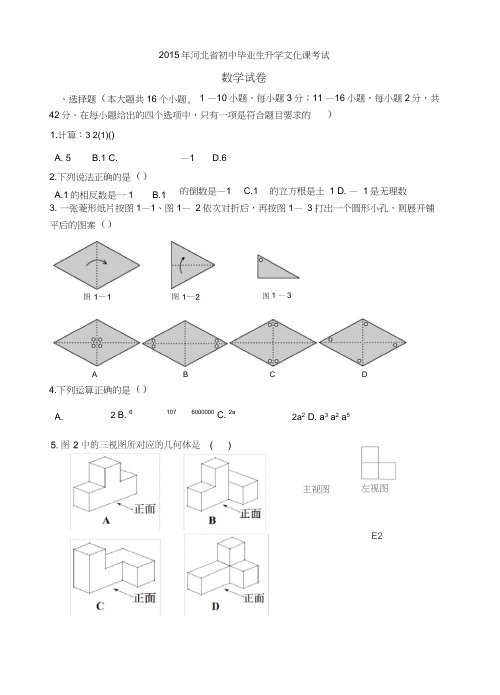
4.下列运算正确的是（）2015年河北省初中毕业生升学文化课考试数学试卷、选择题（本大题共16个小题, 1 —10小题，每小题3分；11 —16小题，每小题2分，共42分。

在每小题给出的四个选项中，只有一项是符合题目要求的）1.计算：3 2(1)()A. 5B.1C.2.下列说法正确的是（）A.1的相反数是一1B.1 —1 D.6的倒数是—1 C.1 的立方根是土 1 D. —1是无理数3. 一张菱形纸片按图1—1、图1—2依次对折后，再按图1—3打出一个圆形小孔，则展开铺平后的图案（）图1 —3A B C DA. 2B. 6 107 6000000C. 2a2a2D. a3 a2 a5主视图左视图E26.如图3,ACBE 是。

0的直径，弦AD 与BE 交于点F,下列三角形中，外心不是点0的是（） C ⑶2.62.82.9B()\c)EFDooP RQRBQc*RD)y 万册A B图5图4图34伊向上，符合条件的示意图是（）10. 一台印刷机每年印刷的书本数量 y （万册）与它的使用时间x （年）成反比例关系，当x=2时, A. △ ABE B. △ ACF△ ABD D. △ ADE9.已知：岛P 位于岛Q 的正西方，由岛 Q 分别测得船R 位于南偏东30°和南偏西45°方 y=20,则y 与x 的函数图像大致是（7.在数轴上标注了四段范围，如图 A.段① B.段②C.段③4，则表示，8的点落在D.段④8.如图 5, AB// EF ，CDL EF,/BAC=50，则/ACD=( A.120 °B.130C.140 °D.15017.若 a 2015°，贝U aA.a<1B.a>1C.a < 1D.a > 113.将一质地均匀的正方体骰子掷一次，观察向上一面的点数，与点数15.如图7,点A ，B 为定点，定直线I // AB P 是I 上一动点，点 M N 分别为PA PB 的中点，对于下列各值：①线段MN 勺长；②厶PAB 的周长；③厶PMN 勺面积；④直线MN AB 之间的距离；⑤/ APB 的大小.其中会随点P 的移动而变化的是（） A.②③ B.②⑤ C.①③④ D.④⑤16.图8是甲、乙两张不同的矩形纸片，将它们分别沿着虚 线剪开后，各自要拼一个与原来面积相等的正方形，则 （）A.甲、乙都可以B.甲、乙都不可以C.甲不可以，乙可以D. 甲可以，乙不可以 5x DA.要消去y ,可以将①5 5y 3y10①，下列做法正确的是（）B. 要消去x ，可以将①3②（ 5)C.要消去y ,可以将①5 12.若关于x 的方程x 2 2xD. 要消去x ，可以将①（5）a 0不存在实数根，则a 的取值范围是（ 相差2的概率是( )A . 1 B.1C. 1 D1235 6 14. 如图 6, 直线i :y f x3与直线y 限, 则a可i 能在（)A . 1 .a2 1 B. 2 a 0 C .3 a2 D.10 a 4a （ a 为常数）的交点在第四象 J L'、T-z甲、填空题（本大题共4个小题，每小题3分，共12分，把答案写在题中横线上）17.若 a 2015°，贝U a2 218. 若a 2b 0,则a 2b的值为 a ab19. 平面上，将边长相等的正三角形、正方形、正五边形、正六边形的一 边重合并叠在一起，如图9,则/ 3+Z 1-Z 2= __________ °20. 如图10,/ BOC=9，点A 在OB 上，且OA=1按下列要求画图： 以A 为圆心，1为半径向右画弧交OC 于点A ，得第1条线段AA ;再以A 为圆心，1为半径向右画弧交OB 于点A ，得第2条线段AA ; 再以A 为圆心，1为半径向右画弧交OC 于点A,得第3条线段AA ;…… 这样画下去，直到得第n 条线段，之后就不能再画出符合要求的线段了，则n= ________三、解答题(本大题共6个小题，共66分。

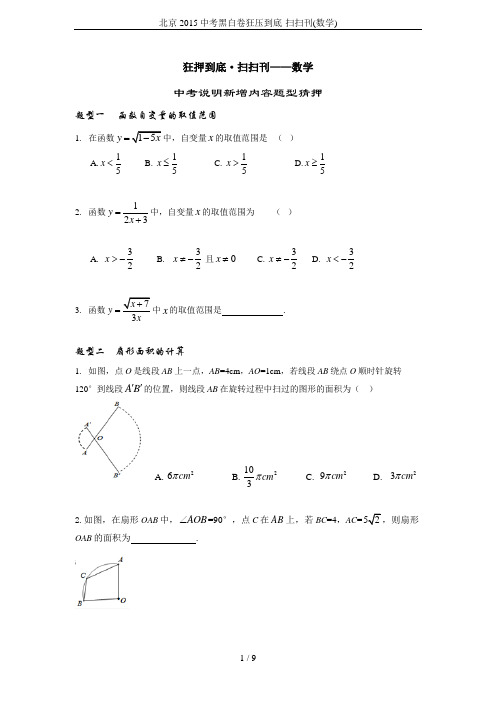
狂押到底·扫扫刊——数学 中考说明新增内容题型猜押 题型一 函数自变量的取值范围1. 在函数15y x =-中，自变量x 的取值范围是 （ ）A.15x <B. 15x ≤C. 15x >D.15x ≥2. 函数123y x =+中，自变量x 的取值范围为 （ ）A. 32x >-B. 32x ≠- 且0x ≠C. 32x ≠-D. 32x <-3. 函数73x y x+=中x 的取值范围是 .题型二 扇形面积的计算1. 如图，点O 是线段AB 上一点，AB =4cm ，AO =1cm ，若线段AB 绕点O 顺时针旋转120°到线段A B ''的位置，则线段AB 在旋转过程中扫过的图形的面积为（ ）A. 26cm πB.2103cm π C. 29cm π D. 23cm π 2.如图，在扇形OAB 中，AOB ∠=90°，点C 在AB 上，若BC =4，AC =52，则扇形OAB 的面积为 .题型三 一次函数解析式的确定1. 已知函数y kx b =+的图象如图，则k 和b 分别是 （ ）A. 1,1k b ==-B. 1,1k b =-=-C. 1,1k b =-=D. 1,1k b ==2. 若一次函数y x b =-+的图象经过点（3, 2），则一次函数的解析式为（ ）A. 1y x =+B. 5y x =-+C. 5y x =--D. 1y x =-+3. 若1y -与x 成正比例，且当2x =-时，4y =，那么y 与x 之间的函数关系式为 .题型四 平面直角坐标系中点的对称1. 若P (,3)x -与点Q (4,)y 关于y 轴对称，则x y += （ ）A. 7B. -7C. 1D. -12. 若22(5)0a b -+-=，则点P (a ,b )关于x 轴对称的点的坐标为 .3. 如图，△ABC 的三个顶点在单位正方形网格的交点上，如果△A B C '''与△ABC 关于原点对称，那么点C 的对应点C '的坐标为 .重难点题型猜押命题点一动点问题的函数图象1.如图①，在矩形ABCD中，动点P从点A出发，在边上沿A→B→C→D方向运动至点D处停止.设点P运动的路程为x，△PAD的面积为y，如果y关于x的函数图象如图②所示，则当9x 时，点P应运动到（）A. A处B. B处C.C处D.D处2.如图，扇形OAB的半径OA=6，圆心角∠AOB=90°，C是AB上不同于A、B的动点，过点C作CD⊥OA于点D，作CE⊥OB于点E，连接DE，点H在线段DE上，且EH=23DE.设EC的长为x，△CEH的面积为y，选项选项中表示y与x的函数关系式的图象可能是（）3.如图，点P是某封闭图形边上的一个作匀速运动的动点，其由点B出发沿按顺时针方向沿封闭图形运动一周，设运动时间为t，△PBC的面积为S，其S与x的大致图象如图所示，那么点P所走的图形是（）命题点二规律探索题1. 如图，在平面直角坐标系中，有若干个整数点，其顺序按图中“→”方向排列，如（1 ,0），（2,0），（2,1），（3,2），（3,1），（3,0）…根据这个规律探索可得，第100个点的坐标为 .2.如图，在数轴上，从原点A开始，以AB=1为边长化等边三角形，记为第一个等边三角形，以BC=2为边长画等边三角形，记为第二个等边三角形，以CD=4为边长画等边三角形，记为第三个等边三角形；以DE=8为边长画等边三角形，记为第四个等边三角形；…按此规律，继续画等边三角形，那么第五个等边三角形的面积是.名校内部模拟题命题点一函数图象的分析1.（2015北京市海淀区一模数学试题第4题）小明在书上看到了一个实验：如右图，一个盛了水的圆柱形容器内，有一个顶端拴了一根细绳的实心铁球，将铁球从水面下沿竖直方向慢慢地匀速向上拉动.小明将此实验进行了改进，他把实心铁球换成了材质相同的别的物体，记录实验时间t以及容器内水面的高度h，并画出表示h与t的函数关系的大致图象.如左下图所示.小明选择的物体可能是（）A B C D2.（北京是燕山区一模第10题）李阿姨每天早晨从家慢跑到小区公园，锻炼一阵后，再慢跑回家，表示李阿姨离开家的距离y（单位：米）与时间t（单位：分）的函数关系的图象大致如左图所示，则李阿姨跑步的路线可能是（用P点表示李阿姨家的位置）（）命题点二概率的计算1.（2015北京市海淀区一模数学试题第4题）某游戏的规则为：选手蒙眼在一张如图所示的正方形黑白格子纸（九个小正方形面积相等）上描一个点，若所描的点落在黑色区域，获得笔记本一个；若落在白色区域，获得钢笔一支．选手获得笔记本的概率为（）A．12 B．45C．49D．592. （2015北京东城区2014—2015学年模拟题第5题）在六张卡片上分别写有1π,, 1.5,3,0,23,从中任意抽取一张,卡片上的数为无理数的概率是（）A. 16B.13C.12D.23命题点三二次函数的综合题1．（北京市清华附中第二学期模拟第27题）在平面直角坐标系xOy 中，抛物线254y mx nx m =-+-关于y 轴对称，且经过点（1-，34-） （1）求m ，n 的值；（2）直线l 经过点（0，2-）且与y 轴垂直，点P 是抛物线上一动点，记P 到直线l 的距离为d ，试探索d 与线段OP 长度的数量关系，并证明；（3）若A （1，1），点P 是抛物线上一动点，请结合函数图像，直接写出OP +AP 的最小值，以及取得最小值时点P 的坐标。

5.30——6.10一、热点信息猜押题热点一：请从所给的三个词语中，选出一个最符合语境的填写在横线上。

（1）按照传统习俗，7日是“东方之星”号客船遇难人员的“头七”祭日。

上午9时，沉船救援现场所有人员面向遇难船舶肃立默哀3分钟，现场船舶同时鸣笛3分钟，表达对逝者的（哀号哀悼哀鸣）。

（2）高考的这两天时间里或许有欢喜、忧伤，或是遗憾，但恰恰是这些（五彩斑斓五味杂陈五光十色），才让高考充满了色彩，难以忘怀。

热点二：阅读下列材料，回答问题。

（6分）今年是世界反法西斯战争暨中国抗日战争胜利70周年。

赵一曼、张自忠、戴安澜等革命先烈在70多年前的抗日战场上，为民族存亡而奋不顾身，留下了一封封感人肺腑的家书。

九年级（1）班决定开展以“重读抗战家书”为主题的系列活动，请完成下列任务。

材料一：宁儿，母亲对于你没有尽到教育的责任，实在是遗憾的事情。

母亲因为坚决地做了反满抗日的斗争，今天已经到了牺牲的前夕了。

母亲和你在生前是永远没有再见的机会了。

希望你，宁儿啊！赶快成人，来安慰你地下的母亲！我最亲爱的孩子啊！母亲不用千言万语来教育你，就用实行来教育你。

在你长大成人之后，希望不要忘记你的母亲是为国而牺牲的！（赵一曼，东北人民革命军第3军1师2团政治委员，1936年牺牲于东北。

）材料二：“仰之吾弟如晤：现已决定于今晚往襄河东岸进发，不顾一切，向北进之敌死拼。

无论作好作坏，一定求良心得到安慰。

由现在起，以后或暂别、永离，不得而知。

专此布达。

更相信，只要我等能本此牺牲决心，我们国家及我五千年历史之民族，决不至亡于区区三岛倭奴之手。

为国家民族死之决心，海不清，石不烂，决不半点改变。

”（张自忠，中华民国陆军二级上将，第三十三集团军总司令兼第五战区右翼兵团总司令，1940年牺牲于枣宜会战。

）材料三：“亲爱的荷馨，余此次奉命固守同古，因上面大计未定，与后方联络过远，敌人行动又快，现在孤军奋斗，决以全部牺牲以报国家养育，为国战死，事极光荣。

6.11——6.20名校内部模拟题一、任务型阅读Passage 1(2015石家庄28中一模)China is a country with many colorful days and festivals. The Dragon Head Raising Day (Longtaitou) is one of them.This special day is on the second day of the second month in the Chinese lunar calendar (阴历). It stands for the start of spring and farming. This year, the day falls on March 2.The dragon is important in Chinese culture. We Chinese people call ourselves the “descendants (传人) of dragon”. Therefore, people celebrate the Dragon Head Raising Day with many customs about dragons.On the day in ancient times, people put ashes in the kitchen. This was to “lead the dragon into the house”. People ____________ that with the help of the dragon, they could have a good harvest (收成) in autumn.Also, people eat special foods on that day. The foods are usually named after dragons. For example, people eat “dragon whisker (细须)” noodles and dumpling called “dragon teeth”.Today, many customs have faded away (消退). But one that has remained is the cutting of hair It was said that a haircut during the first lunar month may bring bad luck to the uncles offamily-mainly mother’s brothers. So many people have their hair cut on the Dragon Head Raising Day.76题完成句子；77题简略回答问题；78题将文中横线处空缺的一个单词填写在下面的答题线上；79题找出并写下全文的主题句；80题将文中画线句子译成汉语。

狂押到底·扫扫刊——数学特殊题型猜押题型一几何图形的折叠与动点问题1.如图，在矩形ABCD中，AB=2，AD=5，点P在线段BC上运动，现将纸片折叠，使点A 与点P重合，得折痕EF（点E、F为折痕与矩形边的交点），设BP=x，当点E落在线段AB 上，点F落在线段AD上时，x的取值范围是.第1题图第2题图2.已知三角形纸片（△ABC）中，AB=AC=5，BC=8，点E、F分别为线段AB、BC上的动点，将三角形沿折痕EF折叠，使得点B落在边AC上，记为点B΄，若以点B΄、F、C为顶点的三角形与△ABC，则CF的长为.题型二特殊四边形的探究题1.如图，已知∆ABC，过点B作DB∥AC，且DB=12AC，E是AC的中点，连接DE.（1）求证：BC=DE；（2）填空：①连接AD、BE，当△ABC满足条件，四边形DBEA是矩形，②在①的条件下，当∠C=______.四边形DBEA是正方形．第1题图2.如图，在平行四边形ABCD 中，对角线BD =8cm ，AC =4cm ，点E 从点B 出发沿BD 方向以1cm/s 的速度向点D 运动，同时点F 从点D 出发沿DB 方向以同样的速度向点B 运动，设点E 、F 运动的时间为t （s ），其中0＜t ＜8.（1）求证：△BEC ≌△DF A ；（2）填空：①以点A 、C 、E 、F 为顶点的四边形一定是 形；②当t 的值为 时，以点A 、C 、E 、F 为顶点的四边形为矩形.第2题图题型三 类比、拓展探究题1.类比、转化、从特殊到一般等思想方法，在数学学习和研究中经常用到，如下是一个案例，请补充完整.原题：如图①，在正方形ABCD 中，对角线AC 、BD 相交于点O ，点E 是BC 边上一点，AE 与BD 交于点G ，过点E 作EF ⊥AE 交AC 于点F . 若2=CE BE ，求EGEF 的值.第1题图（1）尝试探究在图中①，过点E 作EM ⊥BD 于点M ，作EN ⊥AC 于点N ，则EM 和EN 的数量关系是 ，EGEF 的值是 . （2）类比延伸 如图②，在原题的条件下，若n CE BE =（n ＞0），则EG EF 的值是 （用含n 的代数式表示），试写出解答过程.（3）拓展迁移如图③，在矩形ABCD 中，过点B 作BH ⊥AC 于点O ，交AD 于点H ，点E 是BC 边上一点，AE 与BH 相交于点G ，过点E 作EF ⊥AE 交AC 于点F ，若a CE BE =，b AB BC =（a ＞0，b ＞0），则EGEF 的值是 （用含a 、b 的代数式表示）.2.已知∆ABC 为等边三角形，点D 为直线BC 上的一动点（点D 不与B 、C 重合），以AD 为边作菱形ADEF （A 、D 、E 、F 按逆时针排列），使∠DAF =60°，连接CF .(1)如图①，当点D 在边BC 上时，求证：①BD =CF ；②AC =CF +CD ；(2)如图②，当点D 在边BC 的延长线上且其他条件不变时，结论AC =CF +CD 是否成立？若不成立，请写出AC 、CF 、CD 之间存在的数量关系，并说明理由；(3)如图③，当点D 在边CB 的延长线上且其他条件不变时，补全图形，并直接写出AC 、CF 、CD 之间存在的数量关系.第2题图创新题猜押命题点 函数关系式如图，AB =4，射线BM 和AB 互相垂直，点D 是AB 上的一个动点，点E 在射线BM 上，12BE DE =，作EF ⊥DE 并截取EF =DE ，连结AF 并延长交射线BM 于点C.设BE =x ，BC =y ，则y 关于x 的函数解析式是 （ ）A.3+4x y x =--（44） B.121x y x =-- B.C.3+1x y x =--（44） D.124x y x =--命题点 几何动点问题如图，Rt △ABC 中，∠ACB =90°，∠ABC =60°，BC =2cm ，点D 为BC的中点，若动点E 以1cm /s 的速度从A 点出发，沿着A →B 的方向运动，设E 点的运动时间为t 秒（0≤t ＜4），连接DE ，当△BDE 是直角三角时，t 的值为 .名校内部模拟题命题点 二次函数图像与性质（2015信阳中学模拟8题3分）如图是二次函数y =ax 2+bx +c 图象的一部分，其对称轴为x =-3，且过点（-3，0）.下列说法：①abc ＜0；②2a -b =0；③4a +2b +c ＜0；④若（-5，y 1），（25，y 2）是抛物线上两点，则y 1＞y 2，其中说法正确的有 （ ）A.4个B.3个C.2个D.1个命题点 概率计算（2015平顶山一模13题3分）一个口袋中有四个完全相同的小球，把他们分别标号为1、2、3、4，随机地摸出一个小球，然后放回，在随机地摸出一个小球，则两次摸出的小球标号的和等于4的概率是 .狂押到底·扫扫刊——数学答案特殊题型猜押题型一 几何图形的折叠与动点问题1.5－21≤x ≤22.1340 题型二 特殊四边形的探究题1.【思路分析】（1）由已知判定四边形DBEA 是平行四边形即可求证；（2）①从矩形的判定着手，对角线相等的四边形是矩形解题；②由①和四边形DBEA 是正方形判断△BEC 是等腰直角三角形即可求解.（1）证明：∵E 是AC 的中点，∴EC =12AC ， 又∵DB =12AC ， ∴DB =EC ，又∵DB ∥AC ，∴四边形DBCE 是平行四边形，∴BC =DE ；（2）①AB =BC ；②45°.【解法提示】①△ABC 添加BA =BC ，同（1）可证四边形DBEA 是平行四边形，又∵BA =BC ，BC = DE ，∴AB =DE ，∴四边形DBEA 是矩形；②∵四边形DBEA 是正方形，∴BE =AE ，∠BEC =90°，∴△BEC 是直角三角形，又∵E 是AC 的中点，∴AE =EC ，∴BE =EC ，又∵△BEC 是直角三角形，∴△BEC 是等腰直角三角形，∴∠C =45°．2.（1）证明：∵四边形ABCD 是平行四边形，∴AD =BC ，AD ∥BC ，∴∠EBC =∠FDA .在△BEC 和△DF A 中⎪⎩⎪⎨⎧=∠=∠=DA BC FDA EBC DF BE ，∴△BEC ≌△DF A .（2）解：平行四边形；2或6.【解法提示】①平行四边形,理由如下：连接CF ，AE ，由（1）得：∠BEC =∠DF A ，EC =AF ，∴∠FEC =∠AFE ，即EC ∥AF∴以点A 、C 、E 、F 为顶点的四边形一定是平行四边形.②2或6，理由如下：∵四边形AECF 为矩形，∴AC =EF ，∵BD =8cm ，AC =4cm ，∴EF =4，BE =2cm 或6cm .∵速度为1cm/s ，∴t=2或6. 题型三 类比、拓展探究题1.（1）解：EM =2EN ，12. 【解法提示】∵四边形ABCD 是平行四边形，AC 、BD 是对角线，∴∠MBE =∠NCE =45°，又∵EM ⊥BM ，EN ⊥CN ，∴∠EMB =∠ENC =90°，∴△EMB ∽△ENC ， ∴2EM EB EN EC==即EM =2EN. 由正方形性质得BD ⊥AC 于点O ，则四边形OMEN 为矩形，∴∠MEN =90°，又∵AE ⊥EF ，∴∠GEM +∠GEN =90°，∠FEN +∠GEN =90°，∴∠MEG =∠FEN ，又∵∠EMG =∠ENF =90°，∴△EMG ∽△ENF ，1.2EF EN EG EM ∴== （2）解：1n . 【解法提示】如解图①，过点E 分别作EM ⊥BD 于点M ，EN ⊥AC 于点N .∴∠BME =∠CNE =90°，∵四边形ABCD 是正方形，AC 、BD 是对角线，∴∠OBC =∠OCB =45°，∴△BME ∽△CNE ， ∴.EM EB n EN EC== ∴∠MEG +∠NEG =90°，∠NEF +∠NEG =90°，∴∠MEG =∠FEN ，又∵∠EMG =∠ENF =90°，∴△EMG ∽△ENF ，,EM EG n EN EF∴== 1.EF EG n∴=第1题解图①（3）解：1.ab解法提示：如解图②，分别作EM ⊥BO 交BO 于点M ，EN ⊥AC 交AC 于点N .∴∠ENC =∠BME =90°，又∵BH ⊥AC 于点O ，则EN ∥BM ，∴∠NEC =∠MBE ，∴△BME ∽△ENC ， ∴.BM BE a EN EC== 又∵EN ⊥AC ， ∴△CEN ∽△CAB ，即,EN CN AB BC =∴1EN AB CN BC b==， 又∵△BME ∽△ENC ，则1BM EN ME CN b ==，即BM =ME b ， ∴.MEME b a ab EN EN==，即 ∵AE ⊥EF ， AC ⊥BH ，∴∠AOG =∠AEF =90°，又∵∠GAO =∠F AE ，∴Rt △AGO ∽Rt △AFE ，∴∠AGO =∠NFE ，又∵∠MGE =∠AGO ，∴∠MGE =∠NFE ，∵EM ⊥BO ，FN ⊥AC ，∴∠EMG =∠ENF =90°，∴△EMG ∽△ENF ，1,.EG EM EF ab EF EN EG ab===∴即第1题解图②2.解：（１）证明：如解图①，∵四边形ADEF 是菱形，∴AF ＝AD ，∵△ABC 是等边三角形，∴AB ＝AC ＝BC ，∠BAC ＝60°＝∠DAF ，∴∠BAC －∠DAC ＝∠DAF －∠DAC ，即∠BAD ＝∠CAF ，在△BAD 和△CAF 中AB AC BAD CAF AD AF =⎧⎪∠=∠⎨⎪=⎩，∴△BAD ≌△CAF ，∴CF ＝BD ，即证BD ＝CF ；∴AC ＝BC ＝BD ＋CD ＝CF ＋CD ，即证AC ＝CF ＋CD ；（2）如解图②，AC ＝CF ＋CD 不成立，AC 、CF 、CD 之间存在的数量关系是AC ＝CF －CD ，理由是：由（1）知：AB ＝AC ＝BC ，AD ＝AF ，∠BAC ＝∠DAF ＝60°，∴∠BAC ＋∠DAC ＝∠DAF ＋∠DAC ，即∠BAD ＝∠CAF ，∵在△BAD 和△CAF 中AC AB BAD CAF AD AF =⎧⎪∠=∠⎨⎪=⎩，∴△BAD ≌△CAF ，∴BD ＝CF ，∴CF －CD ＝BD －CD ＝BC ＝AC ；即AC ＝CF －CD ．（3）AC ＝CD －CF ．【解法提示】如解图③，∵∠BAC ＝∠DAF ＝60°，∴∠DAB ＝∠CAF ，∵在△BAD 和△CAF 中,AB AC DAB FAC AD AF =⎧⎪∠=∠⎨⎪=⎩∴△BAD ≌△CAF （SAS ），∴CF ＝BD ，∴CD －CF ＝CD －BD ＝BC ＝AC ，即AC ＝CD －CF ．第2题解图创新题猜押命题点 函数关系式A命题点 几何动点问题2或3.5名校内部模拟题命题点 二次函数图像与性质B命题点 概率计算163狂押到底·扫扫刊——数学特殊题型猜押题型一几何图形的折叠与动点问题1.如图，已知矩形ABCD，点M、N分别为AB、CD的中点，连接MN，点E为线段BC上的动点，将△ABE沿AE折叠使得点B落在MN上，点B的对应点为B'，若AB=3，则折痕AE的长为.第1题图2.如图，在△ABC中，∠B=90°，AB=6，BC=8，点D在线段AC上，点F是线段AB上的动点，将△ABC沿DE折叠，使点C落在AB上的F处，并且FD∥BC，则CD的长为.第2题图题型二与特殊四边形判定有关的证明及计算如图，已知∆ABC，在边BC的同侧分别作三个正方形．它们分别是正方形ABDI，BCFE，ACHG，连接AD、DE、EG，试探究：（1）求证四边形ADEG是平行四边形；（2）填空：①当∠BAC= 时，四边形ADEG是矩形；②在①的条件下，AC与AB满足条件时，四边形ADEG是正方形.题型三 类比、拓展探究题已知点P 是矩形ABCD 边AB 上的任意一点（与点A 、B 不重合）.（1）操作发现如图①，现将△PBC 沿PC 翻折得到△PEC ；再在AD 上取一点F ，将△P AF 沿PF 翻折得到△PGF ，并使得线段PE 、PG 重合，试问FG 与CE 的位置关系为 ；（2）猜想论证在（1）中，如图②，连接FC ，取FC 的中点H ，连接GH 、EH ，请你猜想线段GH 和线段EH 的大小关系，并说明你的理由；（3）拓展延伸如图③，分别在AD 、BC 上取点F 、C ′，使得∠APF ＝∠BPC ′，将△P AF 沿PF 翻折得到△PFG ，并将△PBC ′ 沿PC' 翻折得到△PEC ′，连接FC ′，取FC ′的中点H ，连接GH 、EH ，试问（２）中的结论还成立吗？请说明理由创新题猜押1.抛物线与x 轴交于A(1x ，0)、 B(2x ，0)两点，且1x ＜2x ，与y 轴交于点C (0，－4)，其中1x ，2x 是方程01242=--x x 的两个根，则抛物线的解析式 .2.如图，已知AB 为⊙O 的直径，过⊙O 上的点C 的切线交AB 的延长线于点E ，AD ⊥EC 于点D 且交⊙O 于点F ，连接BC ，CF ，AC ．（1）求证：BC =CF ；（2）若AD =3，DE =4，求BE 的长；第2题图名校内部模拟题命题点 实数的相关概念（2015郑州一模1题3分）下列各组数中，互为相反数的两个数是 （ ）A.-3和+2B.5和51 C.-6和6 D.2131和 命题点 阴影部分图形的面积计算（2015平顶山二模15题3分）如图，将边长为12的正方形ABCD 沿其对角线AC 剪开，再把△ABC 沿着AD 方向平移，得到△A'B'C'，当两个三角形重叠的面积为32时，则它移动的距离AA' 等于 .命题点 实际应用题（2015平顶山二模21题10分）节能灯在城市已基本普及，今年我省面向县级农村地区推广，为响应号召，某商场计划购进甲，乙两种节能灯共1200只，这两种节能灯的进价、售价如下表： 类别进价（元/只） 售价（元/只） 甲型25 30 乙型 45 60（1）如何进货，进货款恰好为46000元？（2）若何进货，商场销售完节能灯时获利最多且不超过进货价的30％，此时利润为多少元？狂押到底·扫扫刊——数学答案特殊题型猜押题型一 几何图形的折叠与动点问题1. 22.940 题型二 与特殊四边形判定有关的证明及计算【思路分析】（1）根据全等三角形的判定定理SAS 证得△BDE ≌△BAC ，所以全等三角形的对应边DE =AG ．然后利用正方形对角线的性质、周角的定义推知∠EDA +∠DAG =180°，易证ED ∥GA ；最后由“一组对边平行且相等”的判定定理证得结论；（2）根据“矩形的内角都是直角”易证∠DAG =90°．然后由周角的定义求得∠BAC =135°；（3）由“正方形的内角都是直角，四条边都相等”易证∠DAG =90°，且AG =AD ．由正方形ABDI 和正方形ACHG 的性质证得，AC =2AB ．证明：图中四边形ADEG 是平行四边形．理由如下：∵四边形ABDI 、四边形BCFE 、四边形ACHG 都是正方形，∴AC =AG ，AB =BD ，BC =BE ，∠GAC =∠EBC =∠DBA =90°．∴∠ABC =∠EBD （同为∠EBA 的余角）．在△BDE 和△BAC 中⎪⎩⎪⎨⎧=∠=∠=BC BE ABCDBE BA BD∴△BDE ≌△BAC （SAS ），∴DE =AC =AG ，∠BAC =∠BDE ．∵AD 是正方形ABDI 的对角线，∴∠BDA =∠BAD =45°．∵∠EDA =∠BDE -∠BDA =∠BDE -45°，∴∠DAG =360°-∠GAC -∠BAC -∠BAD =360°-90°-∠BAC -45°=225°-∠BAC ， ∴∠EDA +∠DAG =∠BDE -45°+225°-∠BAC =180°，∴DE ∥AG ，∴四边形ADEG 是平行四边形（一组对边平行且相等）．（2）①135°；②AC =2AB .【解法提示】①当四边形ADEG 是矩形时，∠DAG =90°，则∠BAC =360°-∠BAD -∠DAG -∠GAC =360°-45°-90°-90°=135°，即当∠BAC =135°时，平行四边形ADEG 是矩形；②当四边形ADEG 是正方形时，∠DAG =90°，且AG =AD ．由（2）知，当∠DAG =90°时，∠BAC =135°． ∵四边形ABDI 是正方形，∴AD =2AB ．又∵四边形ACHG 是正方形，∴AC =AG ，∴AC =2AB ，∴AC =2AB 时，四边形ADEG 是正方形．题型三 类比、拓展探究题解：（１）FG ∥CE ；【解法提示】在矩形ABCD 中，∠A ＝∠B ＝90°，由题意得∠G ＝∠A ＝90°，∠PEC ＝∠B ＝90°.∴∠GEC ＝90°，∴∠G ＝∠GEC ，∴FG ∥CE ．（２）GH ＝EH ．如解图①，延长GH 交CE 于点M ，由（１）得FG ∥CE ，∴∠GFH ＝∠MCH ．∵H 为CF 的中点，∴FH ＝CH ．又∵∠GHF ＝∠MHC∴△GFH ≌△MHC （ASA ），∴GH ＝HM ＝21GM ， ∵∠GEC ＝90°，∴EH =21GM ， ∴GH ＝EH .解图① 解图②（３）（２）中的结论还成立．如解图②，取PF 的中点M ，PC ′的中点N ，连接GM ，EN ，HM ，HN ，∵∠FGP ＝90°，M 为PF 的中点，∴GM =21PF ，PM =21PF ，HM ∥PC'， ∴GM ＝PM ，∴∠GPF ＝∠MGP ，∴∠GMF ＝∠GPF ＋∠MGP ＝２∠GPF ．∵H 为FC ′的中点，M 为PF 的中点，∴HM =21PC'. 同理HN =21PF ，EN =21PC'，HN ∥PF ，∠ENC'=2∠EPC'， ∴GM ＝HN ，HM ＝EN ．∵∠GPF ＝∠FP A ，∠EPC ′＝∠BPC ′．∴∠BPC ′＝∠APF ，∴∠GPF ＝∠EPC ′，∴∠GMF ＝∠ENC ′．∵HM ∥PC ′，HN ∥PF ，∴四边形HMPN 为平行四边形，∴∠HMF ＝∠HNC ′，∴∠GMH ＝∠HNE ．∵GM ＝HN ，HM ＝EN ，∴△GMH ≌△HNE ，∴GH ＝HE ．创新题猜押 1.434312--=x x y 2.（1）证明：如解图，连接OC ，∵ED 切⊙O 于点C ，∴CO ⊥ED ，∵AD ⊥EC ，∴CO ∥AD ，∴∠OCA =∠CAD ，∵∠OCA =∠OAC ，∴∠OAC =∠CAD ，∴BC CF =，∴BC =CF ；第2题解图（2）在Rt △ADE 中，AD =3，DE =4，则根据勾股定理得AE =5，∵CO ∥AD ，∴△EOC ∽△EAD ， ∴ADOC EA EO =， 设⊙O 的半径为r ，则OE =5-r ， ∴553r r -=，解得815=r ， ∴EB =5-2r =45. 名校内部模拟题命题点实数的相关概念C命题点阴影部分图形的面积计算4或8命题点实际应用题解：（1）设商场购进甲型节能灯x只，则购进乙型节能灯（1200–x）只，由题意，得25x+45（1200﹣x）=46000，解得：x=400，∴购进乙型节能灯1200﹣400=800只．答：购进甲型节能灯400只、购进乙型节能灯800只，进货款恰好为46000元；（2）设商场购进甲型节能灯a只，则购进乙型节能灯（1200–a）只，商场的获利为y元，由题意，得y=（30–25）a+（60–45）（1200–a），y=–10a+18000．∵商场销售完节能灯时获利最多且不超过进货价的30%，∴–10a+18000≤[25a+45（1200–a）]×30%，∴a≥450．∵y=–10a+18000，∴k=–10＜0，∴y随a的增大而减小，∴a=450时，y最大=13500元．∴商场购进甲型节能灯450只，购进乙型节能灯750只时的最大利润为13500元．。

2015年河北省初中毕业生升学文化课考试数 学(满分120分,考试时间120分钟)卷Ⅰ(选择题,共42分)一、选择题(本大题有16个小题,共42分.1~10小题各3分,11~16小题各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.计算:3-2×(-1)=( ) A.5 B.1 C.-1 D.6 2.下列说法正确的是 ( )A.1的相反数是-1B.1的倒数是-1C.1的立方根是±1D.-1是无理数3.一张菱形纸片按图(1)、图(2)依次对折后,再按图(3)打出一个圆形小孔,则展开铺平后的图案是( )图(1) 图(2) 图(3)A B C D4.下列运算正确的是 ( )A.(12)-1=-12B.6×107=6 000 000C.(2a )2=2a 2D.a 3·a 2=a 55.图中的三视图所对应的几何体是( )6.如图,AC ,BE 是☉O 的直径,弦AD 与BE 交于点F ,下列三角形中,外心不是点O 的是 ( )A.△ABEB.△ACFC.△ABDD.△ADE7.在数轴上标注了四段范围,如图,则表示√8的点落在 ( )A.段①B.段②C.段③D.段④8.如图,AB ∥EF ,CD ⊥EF ,∠BAC=50°,则∠ACD= ( )A.120°B.130°C.140°D.150°9.已知:岛P 位于岛Q 的正西方,由岛P ,Q 分别测得船R 位于南偏东30°和南偏西45°方向上,符合条件的示意图是( )10.一台印刷机每年可印刷的书本数量y (万册)与它的使用时间x (年)成反比例关系,当x=2时,y=20.则y 与x 的函数图象大致是( )11.利用加减消元法解方程组{2x +5y =-10,①5x −3y =6,②下列做法正确的是( )A.要消去y ,可以将①×5+②×2B.要消去x ,可以将①×3+②×(-5)C.要消去y ,可以将①×5+②×3D.要消去x ,可以将①×(-5)+②×212.若关于x 的方程x 2+2x+a=0不存在．．．实数根,则a 的取值范围是 ( ) A.a<1 B.a>1 C.a ≤1 D.a ≥113.将一质地均匀的正方体骰子掷一次,观察向上一面的点数,与点数3相差2的概率是 ( ) A.12B.13C.15D.16 14.如图,直线l :y=-23x-3与直线y=a (a 为常数)的交点在第四象限,则a 可能在( )A.1<a<2B.-2<a<0C.-3≤a ≤-2D.-10<a<-415.如图,点A ,B 为定点,定直线l ∥AB ,P 是l 上一动点,点M ,N 分别为PA ,PB 的中点,对于下列各值:①线段MN 的长; ②△PAB 的周长; ③△PMN 的面积; ④直线MN ,AB 之间的距离; ⑤∠APB 的大小.其中会随点P 的移动而变化的是 ( )A.②③B.②⑤C.①③④D.④⑤16.如图是甲、乙两张不同的矩形纸片,将它们分别沿着虚线剪开后,各自要拼一个与原来面积相等的正方形,则 ( )A.甲、乙都可以B.甲、乙都不可以C.甲不可以,乙可以D.甲可以,乙不可以卷Ⅱ(非选择题,共78分)二、填空题(本大题共4个小题,每小题3分,共12分) 17.若|a|=2 0150,则a= .18.若a=2b ≠0,则a 2-b 2a 2-ab 的值为 .19.平面上,将边长相等的正三角形、正方形、正五边形、正六边形的一边重合并叠在一起,如图,则∠3+∠1-∠2=°.20.如图,∠BOC=9°,点A在OB上,且OA=1.按下列要求画图:以A为圆心,1为半径向右画弧交OC于点A1,得第1条线段AA1;再以A1为圆心,1为半径向右画弧交OB于点A2,得第2条线段A1A2;再以A2为圆心,1为半径向右画弧交OC于点A3,得第3条线段A2A3;……这样画下去,直到得第n条线段,之后就不能再画出符合要求的线段了,则n=.三、解答题(本大题共6个小题,共66分.解答应写出文字说明、证明过程或演算步骤)21.(本小题满分10分)老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个二次三项式,形式如下:(1)求所捂的二次三项式;(2)若x=√6+1,求所捂二次三项式的值.22.(本小题满分10分)嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图所示的四边形ABCD,并写出了如下不完整的已知和求证.(1)在方框中填空,以补全已知和求证;(2)按嘉淇的想法写出证明;证明:(3)用文字叙述所证命题的逆命题为 .23.(本小题满分10分)水平放置的容器内原有210毫米高的水,如图,将若干个球逐一放入该容器中,每放入一个大球水面就上升4毫米,每放入一个小球水面就上升3毫米,假定放入容器中的所有球完全浸没水中且水不溢出.设水面高为y毫米.(1)只放入大球,且个数为x大,求y与x大的函数关系式(不必写出x大的范围);(2)仅放入6个大球后,开始放入小球,且小球个数为x小.①求y与x小的函数关系式(不必写出x小的范围);②限定水面高不超过260毫米,最多能放入几个小球?24.(本小题满分11分)某厂生产A,B两种产品,其价格随市场变化而做相应调整,营销人员根据前三次价格变化的情况,绘制了如下统计表及不完整的折线图:A,B产品价格变化统计表第一次第二次第三次A产品价格/(元/件)6 5.2 6.5B产品价格/(元/件) 3.543并求得了A产品三次价格的平均数和方差:x A=5.9;s A2=1[(6-5.9)2+(5.2-5.9)2+(6.5-5.9)2]=43.(1)补全图中B产品价格变化的折线图,B产品第三次的价格比上一次的价格降低了%;(2)求B产品三次价格的方差,并比较哪种产品的价格波动小;(3)该厂决定第四次调价,A产品的价格仍为6.5元/件,B产品的价格比3元/件上调m%(m>0),使得A产品这四次价格的中位数比B产品四次价格中位数的2倍少1,求m的值.25.(本小题满分11分)如图,已知点O(0,0),A(-5,0),B(2,1),抛物线l:y=-(x-h)2+1(h为常数)与y轴的交点为C.(1)l经过点B,求它的解析式,并写出此时l的对称轴及顶点坐标;(2)设点C的纵坐标为y C,求y C的最大值,此时l上有两点(x1,y1),(x2,y2),其中x1>x2≥0,比较y1与y2的大小;(3)当线段OA被l只分为两部分,且这两部分的比是1∶4时,求h的值.26.(本小题满分14分)平面上,矩形ABCD与直径为QP的半圆K如图(1)摆放,分别延长DA和QP交于点O,且∠DOQ=60°,OQ=OD=3,OP=2,OA=AB=1.让线段OD及矩形ABCD位置固定,将线段OQ连带着半圆K一起绕着点O按逆时针方向开始旋转,设旋转角为α(0°≤α≤60°).图(1)发现(1)当α=0°,即初始位置时,点P直线AB上(填“在”或“不在”).求当α是多少时,OQ经过点B?(2)在OQ旋转过程中,简要说明α是多少时,点P,A间的距离最小?并指出这个最小值.(3)如图(2),当点P恰好落在BC边上时,求α及S阴影.图(2)拓展如图(3),当线段OQ与CB边交于点M,与BA边交于点N时,设BM=x(x>0),用含x的代数式表示BN的长,并求x的取值范围.图(3)探究当半圆K与矩形ABCD的边相切时,求sin α的值.备用图。

6.1—6.10名校内部模拟题一、完形填空(保定市一模)Passage 1In England people can go to see a doctor nearby when they are ill. When the doctors ___1___ them, they usually ask about their ___2____ and soon give them a prescription (处方)for some medicine.When people feel ___3____, they usually go to see their doctors. But when they only have a cold, they ___4____. They usually go to the medicine shop and buy some medicine. Only when they are ___5____ ill, the doctors go to their___6___.In an emergency (紧急), people can call for an ambulance (急救车)，It can___7___ them to the hospital very soon. When they are in hospital, their friends or families can go to see them at a___8____ time ,but they can't stay for the whole day.Usually people have to ___9___ the doctors' prescriptions. And the price is the same for any kind of medicine. But when children, students, old or young people___10___ jobs go to see their doctors, they don't have to spend any money for their prescriptions.1. A. see B. visit C. find D. watch2. A. pain B. sadness C. problems D. difficulties3. A. sick B. sorry C. worried D. nervous4. A. do B. don't C. are D. aren't5. A. truly B. really C. heavily D. terribly6. A. shops B. houses C. offices D. schools7. A. carry B. drive C. take D. move8. A. busy B. free C. proper D. certain9. A. pay for B. ask for C. care for D. look for10. A. with B. without C. like D. unlike【主旨大意】本文是一篇说明文。

狂押到底·扫扫刊名校内部模拟题一、阅读理解Passage 1(2015河北石家庄市42中一模)When you leave your home to go on your vacation, you may worry about your pet at home. Don’t worry. There is a good place for you and your pet. A pet hotel has been built near the Disney World Resort in Florida.The new pet hotel is named Best Friends Pet Care Resort (度假村) and it is mainly open to dogs and cats. It has an area of 4645 square meters. About 270 dogs and 30 cats can be kept there at the same time. Besides dogs and cats, it can also provide services for birds, pigs and rabbits. However, it can’t take care of snakes and turtles.Best Friend Pet Care Resort is a very expensive hotel. There are several kinds of dog rooms, such as rooms with air conditioners and VIP rooms. There is even a “private dog park”. Owners can have a high-quality vacation with their dogs there. The cats are kept in the “Kitty City”. The “ Kitty City” is very comfortable and clean. Workers there clean it once a day.Apart from having good equipment, Best Friends Pet Care Resort also has other plans to meet the psychological(精神上的) needs of pets. Workers play music to the pets, walk with them, play with them and even read stories to them before they go to bed.“We aim to make pets have a fun vacation here, just like owners at Disney World,” said the manager of the resort.1. How many kinds of animals can be kept in Best Friends Pet Care Resort?A. Three.B. Five.C. Six.D. Seven.2. About Best Friends Pet Care Resort, which of the following is NOT true?A. It has an area of 4645 square meters.B. About 270 dogs and 30 cats can be kept there at the same time.C. Owners don’t need to pay much for keeping pets there.D. There is even a “ private dog park” in the resort.3. How often do the work ers clean the “Kitty City”?A. Once a day.B. Twice a day.C. Once a week.D. Twice a week.4. Workers from the Pet Care Resort read the stories to pets in order to _____________.A. provide pets with good equipmentB. meet the psychological needs of petsC. teach pets to learn more knowledgeD. make the pets’ owners satisfied with their service5. What’s the best title for the passage?A. Pet Care Resort in FloridaB. Popular Pets All over the WorldC. How to Take Care of Your petsD. Relationship Between Owners and Pets【主旨大意】本文是一篇说明文。

2015年河北省中考数学试卷分析一、试题总体特点2015年河北省中考数学试卷在承接2013年河北省中考数学卷变革以来的基本思路的同时在命题形式和命题方向上有了比较大的改变。

从考查形式上看2015年河北省中考数学试卷依然是选择题、填空题、解答题三大板块，分值和2014年一样是42、12、66的分布，题量也和2014年一样是16、4、6的分布，不同的是2015年河北省中考数学试卷选择题部分1-10题每题3分，11-16题每题2分。

在选择题后6道题的综合性明显高于前10道题的前提下这种分值的改动是有待商榷的，选择题前后题目分值和试题难易度、试题所花时间难成正比。

解答题的分值由2014年的10、10、11、11、11、13变为今年的10、10、10、11、11、14，分值变动不大。

从考查难度上看2015年河北省中考数学试卷一方面基本杜绝了“送分题”，基础题目也需要适当运算思考才能得出结果；另一方面试题整体难度比2014年简单，除选择题16题，填空题20题，解答题25题第3问，26题最后一问其他题目难度适中，易于上手。

河北省中考数学试卷的难度从2013年到2015年三年来持续走低。

二、典型试题评析1、选择题1-16题为选择题，选择题知识覆盖面广，多为大框架内的小切口命题，整体难度较低。

第1题是固定的有理数基础，不同的是此次考查有理数运算，利用减法或负负得正都可以解。

第2题是传统第1题的考点，考查相反数、倒数，直接锁定A项。

第3题考查折叠展开图，合理想象。

第4题考查实数运算和整式运算，套用公式。

第5题利用主视图和左视图判断。

第6题利用外心性质判断，2015年中考说明题型示例填空题第14题考查到三角形外心。

第7题考查二次根式估算，2014年河北省中考数学卷选择题第5题考查了这个内容。

第8题考查平行线的性质，过点C做EF的平行线是关键。

第9题单独考查方向角是比较独特的，利用方向角定义选择。

第10题考查反比例函数图像和性质，利用反比例函数k=x y转化求解。

2015年河北省初中毕业生升学文化课考试数学试卷本试卷分卷I和卷II两部分；卷I为选择题，卷II为非选择题. 本试卷总分120分，考试时间120分钟.卷I （选择题，共42分）注意事项：1.答卷I前，考生务必将自己的姓名、准考证号、科目填涂在答题卡上.考试结束，监考人员将试卷和答题卡一井收回.2.每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑.答在试卷上无效.—、选择题（本大題共16个小題，1〜10小题，每小题3分；11〜16小题，每小题2分，共42分.在每小题给出的四个选项中.只有一项是符合题目要求的）1. 计算：3-2x（-l） =A. 5C・-12. 下列说法正确的是A・1的相反数是一1C・1的立方根是±13. 一张菱形纸片按图1-1.图1・2依次对折后，再按图1・3打出一个圆B. 1D. 6B.】的倒数是-】D. -1是无理数形小孔，则展开铺平后的图案是D.段④8・如图 5. AB//EF, CDJLEF. ZB4C=50h 贝ljZJCD=B. 130° D. 150°4. F 列运算正确的是丄<2 B ・ 6xlO 7 =60X)000C. (2a)2 = 2a 26.如图3, AC. BE 是00的直径，弦4D 与BE 交于点F,下列三角形中，外心不是点O 的是A. ZBEB. ^ACFC. MBDD. ^ADE7.在数轴上标注了四段范IS,如图4,则表示迓的点落在26 V\2.72.8"图4A.段①B.段②C.段③ A. 120° C. 140°5.出 左視图B图3图59. 己知：岛F位于岛0的正西方，由岛几0分别测得船R位于南偏东30•和南偏西45•方向10. 一台印刷机每年可印刷的书本数量丿（万册）与它的使屋时（53x（年）成反比例关系,11. 利用加减消元法解方程组+ = -10,咚，下列做法正确的是[5x-3y = 6 ②A. 要消去y,可以将①x5 +②x2B. 要消去x,可以将①x3 +②x（-5）C. 要消去〃可以将①x5 +②x3D. 耍消去炊可以将①x（-5） +②x212.若关于x 的方程x 2+2x + a = 0不存在实数根，则a 的取值范围是• • •A. a<\B. a>\13.将一质地均匀的正方体骰子掷一次，观察向上一面的点数，与点数3相差2的概率是A.丄B.- 2 3C. \D.丄 5 6 B. 914.如图6,直线/： y = -^x-3与宜线y^a （a 为常数）的交点 在第四象限.则a 可能在A. \<a<2 B ・一2GV0 D- -10VaV-4 ・15・如图7,点儿0为定点.定直线/〃/i 乩P 是/上一动点. 点M N 分别为必.的中点. 对于下列各值 ①线段MV 的长: ②2AB 的周长; ③△PMV 的面积; ④直线MM ABZ 间的距离;图7⑤厶PB 的大小• 其中会随点P 的移动而变化的是 A.②③ C.①®® D.④⑤ 16.图8是甲.乙两张不同的矩形纸片, 着虚线剪开后，各自要拼一个与原来面积相等的正 方形.则A.甲.乙都可以B.甲、乙都不可以C.曰不可以.乙可以D.甲可以.乙不可以将它们分别沿 ►U-1 ->乙 图82015年河北省初中毕业生升学文化课考试数学试卷卷II （非选择题，共78分）注意事项：1・答卷II 前，将密封线左侧的项目填写清楚.2.答卷I 】时，将答案用黑色字迹的钢笔、签字笔或圆珠笔直接写在试卷上.题号二三2122232425261得分二、填空题（本大题共4个小题.每小题3分，共12分.把答案 写在题中横线上）17. 若|a| = 2015°,则18.•若4 = %工0,则与芒的值为 a _ab19. 平面上，将边长相等的正三角形、正方形、正五边形.正六边形的一边审合并會在一起，如图9,则Z3 + Z1-Z2 = ____________20. 如图10, Z5OC=9°,点4在OB 匕且OA^\.按下列要求画图:以/为圆心，1为半径向右画弧交OC 于点皿.得第1条线段AAxx 再以川为圆心，1为半径向右画弧交03于点力2,得第2条线段A,A 2i 再以力2为圆心，1为半径向右画弧交OC 于点冷，得第3条线段局禺；这样画下去，直到得第n 条线段，之后就不能再画出符合要求的线段了，则 ___________得分评卷人总分22.(本小题满分10分)三、解答题（本大题共6个小题■共66分.解答应写出文字说明、证明过程或演算步骤）: （1）求所捋的二次三项式;（2）若x = V6+l,求所捂二次三项式的值.21.（本小题满分10分）得分评卷人嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的.她先用尺规作出了如图11的四边形ABCD.并写出了如下不完整的己知和求证.(1) 在方框中填空.以补全已知和求证:(2) 按嘉淇的想法写岀证明；证明：(3) ______________________________________________________________________ 用文字叙述所证命题的逆命题为_______________________________________________________22.(本小题满分10分)水平放置的容器内原有210亳米髙的水，如图12・将若干个球逐一放入该容器中，每 放入一个大球水面就上升4亳米，每放入一个小球水面就上升3毫米，假定放入容器中的所有球完全浸没水中且水不溢出.设水面高为y 毫米.（1） 只放入大球，且个数为x 大，求y 与心的函数关系式仟必写出x 大的范围）; （2） 仅放入6个大球后，开始放入小球，且小球个数为©、•① 求y 与x 小的函数关系式（不必写出林的范围）； ② 限定水面高不超过260毫米，最多能放入几个小球？图12得分评卷人23.（本小题满分10分）24.（本小題满分11分）得分评卷人某厂生产A, B 两种产品.其单价随市场变化而做相应调整.营销人员根据前三次单价 变化的情况.绘制了如下统计表及不完整的折线图^X A =5.9； |[(6-5・9F + (5.2-5.9)2+ (6.5-5.9)2] =昔（1）补全图13中B 产品单价变化的折线图.B 产品第三次的单价比上一次的单价降低了 ________ %;（2） 求B 产品三次单价的方差，并比较哪种产品的单价波动小：（3） 该厂决定第四次调价，A 产品的单价仍为6.5元/件，B 产品的单价比3元/件上调使得A 产品这四次单价的中位数是B 产品四次单价中位数 的2倍少1,求加的值.第一次 第二次 第三次A 产品单价 （元/件） 6 5.2 6.5 B 产品険价 （元/件） 3.543A. B 产品单价变化统计表并求得了 A 产品三次单价的平均数和方差:田1325.（本小题满分11分）如图14,已知点0(0, 0),/(-5, 0),B(2, 1),抛物线/：J«-(X-A)2+1 (A为常数)与p轴的交点为C.（1）/经过点8,求它的解析式，并写出此时/的对称轴及顶点坐标；（2）设点C的纵坐标为％,求％的最大值，此时/上有两点（心，沖，（勺，儿），其中x,>x2^0,比较儿与儿的大小；（3）当线段Q4被/只分为两部分，且这两部分的比是1 ：4时，求的值.• • •平面上，矩形ABCD 与直径为QP 的半圆K 如图15・1 摆放，分别延长D4和0P 交于点0,且ZDO0=6O°, OQ=OD=3, 0P=2, 0A =AB = l ・让线段 OD 及矩形 ABCD 位置固定，将线段O0连带着半圆K 一起绕着点0按逆时 针方向开始旋转，设旋转角为a（0oMa=60。

2015年河北省中考数学试卷参考答案与试题解析一.选择题（1-10小题每小题3分，11-16小题每小题3分，共42分每小题的四个选项中只有一个是正确的）3．（3分）（2015•河北）一张菱形纸片按如图1、图2依次对折后，再按如图3打出一个圆形小孔，则展开铺平后的图案是（）B=25．（3分）（2015•河北）如图所示的三视图所对应的几何体是（）B6．（3分）（2015•河北）如图，AC，BE是⊙O的直径，弦AD与BE交于点F，下列三角形中，外心不是点O的是（）7．（3分）（2015•河北）在数轴上标注了四段范围，如图，则表示的点落在（）8．（3分）（2015•河北）如图，AB∥EF，CD⊥EF，∠BAC=50°，则∠ACD=（）9．（3分）（2015•河北）已知：岛P位于岛Q的正西方，由岛P，Q分别测得船R位于南偏东30°和南偏西45°方向上，符合条件的示意图是（）10．（3分）（2015•河北）一台印刷机每年可印刷的书本数量y （万册）与它的使用时间x （年）． B ． C ． D （y=，11．（2分）（2015•河北）利用加减消元法解方程组，下列做法正确的是，213．（2分）（2015•河北）将一质地均匀的正方体骰子掷一次，观察向上一面的点数，与点B的概率是：=14．（2分）（2015•河北）如图，直线l：y=﹣x﹣3与直线y=a（a为常数）的交点在第四象限，则a可能在（）﹣﹣﹣x15．（2分）（2015•河北）如图，点A，B为定点，定直线l∥AB，P是l上一动点，点M，N分别为PA，PB的中点，对下列各值：①线段MN的长；②△PAB的周长；③△PMN的面积；④直线MN，AB之间的距离；⑤∠APB的大小．其中会随点P的移动而变化的是（）MN=ABMN=16．（2分）（2015•河北）如图是甲、乙两张不同的矩形纸片，将它们分别沿着虚线剪开后，各自要拼一个与原来面积相等的正方形，则（）的正方形，图乙可以拼一个边长为二.填空题（4个小题，每小题3分，共12分）17．（3分）（2015•河北）若|a|=20150，则a=±1．18．（3分）（2015•河北）若a=2b≠0，则的值为．==故答案为：19．（3分）（2015•河北）平面上，将边长相等的正三角形、正方形、正五边形、正六边形的一边重合并叠在一起，如图，则∠3+∠1﹣∠2=24°．20．（3分）（2015•河北）如图，∠BOC=9°，点A在OB上，且OA=1，按下列要求画图：以A为圆心，1为半径向右画弧交OC于点A1，得第1条线段AA1；再以A1为圆心，1为半径向右画弧交OB于点A2，得第2条线段A1A2；再以A2为圆心，1为半径向右画弧交OC于点A3，得第3条线段A2A3；…这样画下去，直到得第n条线段，之后就不能再画出符合要求的线段了，则n=9．三.解答题（共6个小题，共66分）21．（10分）（2015•河北）老师在黑板上书写了一个正确的演算过程随后用手掌捂住了如图所示的一个二次三项式，形式如图：（1）求所捂的二次三项式；（2）若x=+1，求所捂二次三项式的值．﹣﹣22．（10分）（2015•河北）嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的，她先用尺规作出了如图1的四边形ABCD，并写出了如下不完整的已知和求证．已知：如图1，在四边形ABCD中，BC=AD，AB=CD求证：四边形ABCD是平行四边形．（1）在方框中填空，以补全已知和求证；（2）按嘉淇的想法写出证明；（3）用文字叙述所证命题的逆命题为平行四边形两组对边分别相等．，23．（10分）（2015•河北）水平放置的容器内原有210毫米高的水，如图，将若干个球逐一放入该容器中，每放入一个大球水面就上升4毫米，每放入一个小球水面就上升3毫米，假定放入容器中的所有球完全浸没水中且水不溢出．设水面高为y毫米．（1）只放入大球，且个数为x大，求y与x大的函数关系式（不必写出x大的范围）；（2）仅放入6个大球后，开始放入小球，且小球个数为x小①求y与x小的函数关系式（不必写出x小范围）；②限定水面高不超过260毫米，最多能放入几个小球？，24．（11分）（2015•河北）某厂生产A，B两种产品，其单价随市场变化而做相应调整．营销人员根据前三次单价变化的情况，绘制了如表统计表及不完整的折线图．2=[（6﹣5.9）2+（5.2﹣5.9）2+（6.5﹣5.9）2]==5.9，s（1）补全如图中B产品单价变化的折线图．B产品第三次的单价比上一次的单价降低了25%（2）求B产品三次单价的方差，并比较哪种产品的单价波动小；（3）该厂决定第四次调价，A产品的单价仍为6.5元/件，B产品的单价比3元/件上调m%（m＞0），使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1，求m的值．产品第三次的单价比上一次的单价降低了=（=产品，这四次单价的中位数为；，×1=25．（11分）（2015•河北）如图，已知点O（0，0），A（﹣5，0），B（2，1），抛物线l：y=﹣（x﹣h）2+1（h为常数）与y轴的交点为C．（1）l经过点B，求它的解析式，并写出此时l的对称轴及顶点坐标；（2）设点C的纵坐标为y c，求y c的最大值，此时l上有两点（x1，y1），（x2，y2），其中x1＞x2≥0，比较y1与y2的大小；（3）当线段OA被l只分为两部分，且这两部分的比是1：4时，求h的值．26．（14分）（2015•河北）平面上，矩形ABCD与直径为QP的半圆K如图1摆放，分别延长DA和QP交于点O，且∠DOQ=60°，OQ=0D=3，OP=2，OA=AB=1．让线段OD及矩形ABCD位置固定，将线段OQ连带着半圆K一起绕着点O按逆时针方向开始旋转，设旋转角为α（0°≤α≤60°）．发现：（1）当α=0°，即初始位置时，点P在直线AB上．（填“在”或“不在”）求当α是多少时，OQ经过点B．（2）在OQ旋转过程中，简要说明α是多少时，点P，A间的距离最小？并指出这个最小值；（3）如图2，当点P恰好落在BC边上时，求a及S阴影拓展：如图3，当线段OQ与CB边交于点M，与BA边交于点N时，设BM=x（x＞0），用含x的代数式表示BN的长，并求x的取值范围．探究：当半圆K与矩形ABCD的边相切时，求sinα的值．，如图﹣﹣﹣OS==2=2﹣KO，在=，•RE=+，即，BQ=AF=AO=2﹣OS=，﹣，KO﹣====sin60的值为：或。

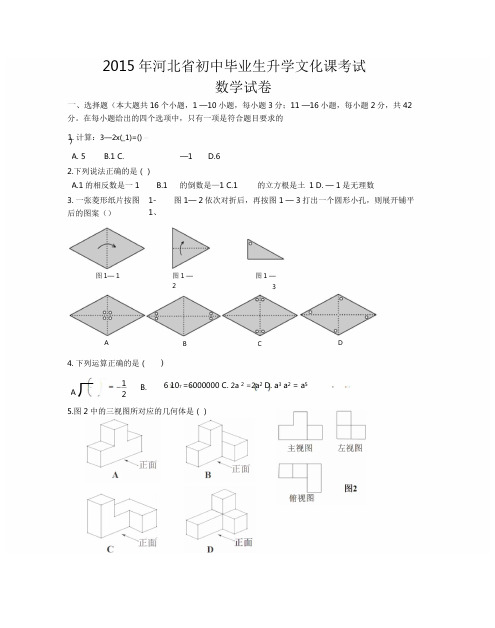
2015年河北省初中毕业生升学文化课考试A DC B 正面正面数学试卷4.下列运算正确的是（1B.2A厂 6 107 =6000000 C. 2a 2 =2a 2 D. a 3 a 2 = a 55.图2中的三视图所对应的几何体是（）正面、选择题（本大题共16个小题，1 —10小题，每小题3分；11 —16小题，每小题2分，共42 分。

在每小题给出的四个选项中，只有一项是符合题目要求的 ）1.计算：3—2x(_1)=()2.下列说法正确的是（） 后的图案（）图1— 1 图1 —2图1 —3A. 5B.1C.—1D.6A.1的相反数是一1B.1 的倒数是—1C.1 的立方根是土 1D. — 1是无理数3. 一张菱形纸片按图 主视图左视图俯视图1-1、图1— 2依次对折后，再按图1 — 3打出一个圆形小孔，则展开铺平6.如图3, AG BE是OO的直径，弦AD与BE交丁点F,下列三角形中，外心不是点。

的是（）A. △ ABEB. △ AGF G. △ ABD D. △ ADE询r奶、*）・-图47.在数轴上标注了四段范围，如图4,则表示寸8的点落在()A.段①B.段②G.段③ D.段④8.如图5, AB// EF, C8EF, Z BAC=50，则Z ACD=( )A.120 0B.130 0C.140 °D.150 °9.已知：岛P位丁岛Q的正西方，由岛P, Q分别测得船R位丁南偏东30°和南偏西450方向上, 符合条件的示意图是（）10.一台印刷机每年印刷的书本数量y（万册）与它的使用时间x（年）成反比例关系，当x=2时, y=20，则y与x的函数图像大致是（）A.要消去y,可以将①x 5+②x 2B.要消去x,可以将①x 3+②次（-5）C.要消去y,可以将①x5 +②x3D.要消去x,可以将①x （-5） +②乂 2 12.若关丁 x 的方程x 2+2x+a = 0不行在实数根，则a 的取值范围是（） A.a<1 B.a>1 C.a < 1 D.a > 113.将一质地均匀的正方体骰子掷一次，观察向上一面的点数，与点数3相差2的概率是（）C. —3£a£—2D. —10：：a ：—415.如图7,点A, B 为定点，定直线l // AB, P 是l 上一动点，点「_»M N 分别为PA PB 的中点，对丁下列各值：R F 疽①线段MN 勺长；②△ PAB 的周长；冷?*y ， PMN 勺面积；④直线MN AB 之间的距离；』以土茅 图7⑤/ APB 的大小.其中会随点P 的移动而变化的是（）A.②③B.②⑤C.①③④D.④⑤16. 图8是甲、乙两张不同的矩形纸片，将它们分别沿着虚 线剪开后，各自要拼一个与原来面积相等的正方形，则（）A.甲、乙都可以B. 甲、乙都不可以C.甲不可以，乙可以D. 甲可以，乙不可以、填空题（本大题共4个小题，每小题3分，共12分，把答案写在题中横线上）A.B.3 C . 5D.14.如图6,直线l ：y=—^x-3与直线y = a （a 为常数）的交点在第四象 3 限，则a 可能在（）A. 1 . a 2B. -2 a :: 0)17.若回=2015°，贝U a=2 218.若a=2bo0 , WJ ；2—；b的值为19.平面上，将边长相等的正三角形、正方形、正五边形、正六边形的一合并叠在一起，如图9,则Z 3+Z 1-Z 2=020.如图10, Z BOC=9，点A在OB上，且OA=1按下列要求画图：以A为圆心，1为半径向右画弧交OC于点A,得第1条线段AA;再以A为圆心，1为半径向右画弧交OB于点色，得第2条线段A1A2；再以小为圆心，1为半径向右画弧交O%点A，得第3条线段AA;……这样画下去，直到得第n条线段，之后就不能再画出符合要求的线段了，则n=三、解答题（本大题共6个小题，共66分。