2005年“中环杯”小学生思维能力训练活动六年级初赛试题

思维能力测评中环杯六年级初赛The latest revision on November 22, 20202017年度“思维100”能力评测活动六年级选拔赛1．计算1231236426421+=3213213693696⨯. 2．计算7510++=111818232333⨯⨯⨯. 3.将2148化为有限小数，为. 4.如图，在等腰ABC 中，,2,AB AC B A =∠=∠则A ∠=.5.算式5555(51)(101)(151)(201)+⨯+⨯+⨯+的运算结果的个位数字是.6.下图中共有个三角形.7.从1、2、3、4、5、6、7、8、9中选出四个数，要求第二小的数为4，不同的选法有种。

8.有浓度为20％的糖水30克，再往其中加入10克糖，搅拌均匀后得到的糖水浓度是.9.一项工程，甲单独做要10天完成，乙单独做要15天完成，现在甲、乙合作，需要天完成。

10.甲、乙两地相距360千米。

一辆汽车先从甲地行驶到乙地，每小时行40千米；再由乙地返回到甲地，每小时行60千米。

这辆汽车往返两地的平均速度是 千米/时。

11.20172015的运算结果的末三位数字为。

12.如图，在ABC 中，点D E F 、、分别AB BC CA 、、为上的点，2,2,BD AD CE BE AF FC ===。

若ADF 的面积为5,则CEF 的面积为。

AB C13.abc 为三位数，且12a b c ⨯⨯=。

这样的三位数有个。

14.如图，下面这个“花生”是由四段圆弧构成的，则四段圆弧的圆心连城正方形ABCD ，若正方形的边长为3，2AE AH CF CG ====,则这个“花生”的周长为（保留π）15.下面的除法竖式中已经填了几个数字，那么填写后完整的商是。

16.计算：5148474612233445495011112350----⋅⋅⋅⨯⨯⨯⨯=+++⋅⋅⋅+。

17.一个正整数有24个正因数，期中8个正因数为奇书，剩下16个正因数为偶数，满足条件的正整数最小为。

第六届“中环杯”小学生思维能力训练活动四年级初赛活动内容一、 填空题: (每题6分，共60分)1.()11171719201740193717÷+÷+÷+÷+÷=。

【解题过程】()()11172017371717194019=÷+÷+÷+÷+÷原式()()11203717174019=++÷++÷6817571=÷+÷ 43=+ 7=2.200592005920059999999999999⨯+个“”个“”个“”的得数的末尾有（ ）个零。

【解题过程】2005920059999999991⎛⎫=⨯+ ⎪ ⎪⎝⎭ 个“”个“”原式200592005999910000=⨯个“”个“”20059200599990000=个“”个“”3.123456789601602603604605606+-++-++-+++-++-= （ ）。

【解题过程】()()()()()456789601602603604605606++-++-++-++- 原式=1+2-3 036960060=++++++()20206032=+ 60903=4.已知有一个数学符号∆使下列等式成立；248531335119725∆=∆=∆=∆=，，，，那么73∆=（ ）。

【解题过程】由2248523133251192725⨯+=⨯+=⨯+=⨯+=，，，，可得含有∆的式子表 示：前面一个2⨯+后面一个数，所以7372317∆=⨯+=。

5.果园里有桃树、梨树、苹果树共552棵。

桃树的棵数比梨树棵数的2倍多12棵；苹果树的棵数比梨树棵数少20棵。

那么苹果树有（ ）棵，梨树有（ ）棵，桃树有（ ）棵。

【解题过程】 为了清晰地反应数量的倍数关系，我们画出线段图如下：上图可以看出桃树比梨树的2倍多12棵，苹果树比梨树少20棵，都是同梨树相比较，以梨树的棵数为标准作为1份数容易解答。

第六届“中环杯”小学生思维能力训练活动五年级初赛活动内容一、填空题：（每题6分，共60分）1. 10.911.812.713.614.515.416.317.218.119+++++++++=（）。

2.666666.6666333.3333333⨯=（）。

3.()()⨯⨯÷⨯⨯=（）。

0.720.750.0760.190.14437.54.已知a、b为自然数，2∆=，a=a a a a a a a a a，234567893039a b a b=+（）。

5.箱子里有黄、白两种乒乓球，黄球比白球的3倍多2只，每次从箱子中取出7只白球，14只黄球，如果经过若干次后，箱子中还剩40只黄球、1只白球，那么箱中原来黄球比白球多（）只。

6.下图是一个等腰三角形，它的腰长是20cm，面积是2144cm。

在底边上任取一点，向两腰作垂线得a和b，a b+=（）厘米。

7.红星小学五年级有200人参加体育比赛。

已知男生的一半与女生的0.4倍的人数参加田径比赛，其余108名同学参加其他项目的比赛。

那么，五年级中参加体育比赛的男生有（）人，女生有（）人。

8.某人骑自行车在路上前行，每隔12分钟有一辆电车从后面超过他，每隔4分钟有一辆电车迎面向他驶来。

此人与电车的速度均保持不变，且不计电车停车的时间和上、下车乘客所用的时间。

那么每隔（）分钟，从起点站发出一辆电车。

9.有红、黄、蓝、白、黑五种形状大小完全一样的小球若干，每人必须从中选3只小球。

要使有两人得到球的颜色完全一样，至少有（）人参加选球。

10.甲、乙、丙三人浇花，甲浇了68盆，乙浇了62盆，丙浇了56盆.已知共有花90盆，则三人都浇了的花有（）盆。

二、动手动脑筋：（每题8分，共40分）1.请画出一个面积是2平方厘米的正方形。

2.请画出6个边长是2厘米的正三角形，再分别将这6个三角形分成形状，大小完全一样的3个、4个、6个、8个、9个、12个图形。

请用图形表示出来。

第六届“中环杯”中小学生思维能力训练活动初预（六）年级初赛活动内容一、填空题（每题6分，共60分）1．()1111......13355720052007++++=⨯⨯⨯⨯2．()117(10.754)21211110(1.125)(2.2510)1211-⨯=+÷÷ 3．一列数112、212、312、412 (23912),这239个数不是整数的所有分数的和是（ ） 4.某运动队共有男女运动员共126人，选出的男运动员的13和16名女运动员参加比赛，剩下的男女运动员的人数刚好相等。

这个运动队中男运动员有（ ）人，女运动员有（ ）人。

5.甲、乙两人共同完成一项工程要用12天。

甲工作了2天，乙工作了3天，他们完成这件工程的15。

那么单独完成这项工程，甲要（ ）天，乙要（ ）天。

6.A 、B 、C 三个风景点，从A 出发经过B 点到C 点要走18千米，从A 点经过C 点到B 点要走16千米，从B 点出发经过A 点到C 点要走24千米，则AB 间的距离是（ ）千米，BC 间的距离是（ ）千米。

7.有8%和5%两种杀虫药水，要支撑6%的杀虫药水300克，要8%的药水（ ）克，5%的药水（ ）克。

8.有三家厂研制成为一种科技产品，生成产品要一批资金。

甲与乙投资之比为2：3，乙与丙的投资之比为4：5，甲方决定投资60万元，那么丙应该投资（ ）万元。

9.甲、乙、丙三人，甲的年龄是乙的2倍还大3岁，乙的年龄是丙的2倍少2岁，三人年龄之和是109岁，那么甲是（ ）岁，乙是（ ）岁，丙是（ ）岁。

10某两位数能被它的各位数字之和整除，得商为7.如果这个两位数的十位与各位数交换，所得新两位数减去12后，能被原两位数的十位数与各位数的差整除，得商9.原两位数是（ ）二、动手动脑题：（每题8分，共40分）1. 将下图分成三块，并拼成一个正方形。

2. 下图长方形长4.5cm 、宽3.6cm 请从一个顶点画两条直线，把这个长方形的面积分成相等的两块。

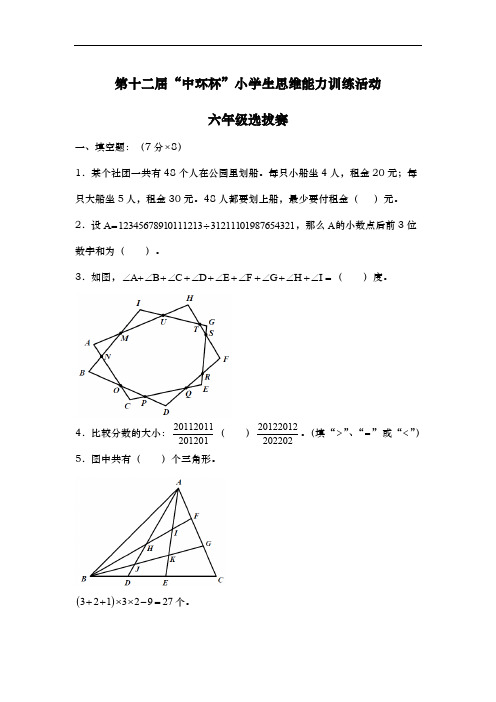
第十二届“中环杯”小学生思维能力训练活动六年级选拔赛一、填空题：（7分⨯8）1．某个社团一共有48个人在公园里划船。

每只小船坐4人，租金20元；每只大船坐5人，租金30元。

48人都要划上船，最少要付租金（ ）元。

2．设1234567891011121331211101987654321A =÷，那么A 的小数点后前3位数字和为（ ）。

3．如图，A B C D E F G H I ∠+∠+∠+∠+∠+∠+∠+∠+∠=（ ）度。

4．比较分数的大小：20112011201201（ ）20122012202202。

（填“>”、“=”或“<”） 5．图中共有（ ）个三角形。

()32132927++⨯⨯-=个。

6．一个袋子里放着很多大小完全相同的红球、黄球、白球和黑球（每种球的量足够多）。

现在大家轮流从袋中摸球，都不能用眼睛看，每人一次性摸出3个球。

那么最少有（）个人摸球，才能保证有两个人摸出的球完全一样。

7．计算：1710.754212111101.1252.25101211⎛⎫-⨯⎪⎝⎭=⎛⎫⎛⎫+÷÷⎪ ⎪⎝⎭⎝⎭（）8．如图所示，边长为16米的正方形池塘的周围是草地，池塘边A、B、C、D 处各有一棵树，且4AB BC CD===米。

现用长5米的绳子将一头羊拴在任意的一棵树上，则羊在草地上活动区域的最大面积是（）平方米。

（圆周率用π表示）二、动手动脑题：（11分⨯8）1．甲、乙两人在边长为100米的正方形水池相邻的两角上，同时按逆时针方向出发（甲在乙的前面），沿水池步行，甲的速度为每分钟44米，乙的速度为每分钟34米。

问甲、乙两人各自出发后，经过多长时间才能走到同一条边上？（结果精确到0.01）。

2．如图，共有1、2、3、4、5、6、7、8号八个房间，每相邻两个方面都有小门“O”代替，例如，由1号房间可以到2号或3号房间，由5号房间可以到6号、7号或8号房间，且有两个进口A和B，只有一个出口C。

第十一届“中环杯”小学生思维能力 六年级一、 填空题：1 计算：=⨯+⨯++⨯+⨯+⨯1082972532422312 （ ）2．学校组织一些老师和学生出去旅游，共55个人。

已知老师有23人，男性（男老师和男学生）有25人。

那么男学生比女老师多（ ）。

3．我们知道，在10进制下，能被2整除的自然数的特征是个位为0,2,4,6,8.如果在A 进制下，能被4整除的自然数的特征是个位为0,4,8。

那么A 的最小值是（）。

4. 一个身高169厘米的人正在挖一个洞，她挖了一会停下来说“我已经挖了洞深的72。

当我挖完时，我的头将在洞的地平面以下，并且到地平面的距离将是现在头高出地平面距离的3倍”，则她将挖的洞深（）米。

5．有四颗相同的骰子放在一排（如图所示），四颗骰子底数的点数之和是（）。

6. 贝贝游世博，第一站是德国馆。

从下午2点多开始排队，到5点多钟才进馆。

他一看表，发现开始和结束的两个时刻分针和时针恰好对换了位置。

那么他排队等候了（）小时。

7． △ABC 中，点D 在AB 上，AD=31AB,点E 在BC 上，BE=41BC ，点F 在CA 上，CF=51CA 。

已知阴影△DEF 的面积是25，则△ABC 的面积为（）。

AB C DE F8． 用0到9这十个数字可组成（）个能被5整除的无重复数字的三位数。

二、动手动脑题1． 已知A )201113121()2010131211(+++⨯++++= ， B )201013121()2011131211(+++⨯++++= 。

试比较A 和B 的大小关系，并求较大数减较小数的差。

2． 如图，两个正方形摆放在一起，CDF 是以C 为圆心，CD 为半径的四分之一圆。

已知大正方形边长为4。

那么阴影部分面积是多少（圆周率取3.14）AB C DF E3． 某电站按户向用户收取电费，具体规定是：如果每月用电不超过30度，就按每度7角钱收费；如果超过30度，超出的部分按每度2元收费。

第七届“中环杯”小学生思维能力训练活动四年级复赛活动内容一、填空题：（请把正确答案填在括号内，每题5分，共50分）1.()14191431914331914333191433331943++++÷=（ ）。

【解答】2.()999999555555222222999999⨯-⨯=（ ）。

【解答】3.已知：3232a b a b a b a b ∆=+∇=-，，又知，7993x ∆∇=，那么为x （ ）。

【解答】4.如果把1、2、3、4、5、6、7、8这八个数字组成两个四位自然数，再将这两个四位自然数相减，那么得出最小的自然数差是（ ）。

【解答】 要保证这两个四位数的千位相差1，百位数相差要最大。

十位数应该比百位数相差小，比个位数相差大。

根据这个要求就可以得出来两个四位数分别是5123和4876.他们的差最小为247.5.幼儿园中有红、黄、蓝、白四种颜色的积木玩具各若干件，每个小朋友可以从中任取一件或两件，那么至少有（ ）个小朋友去取，才能保证有3个小朋友取的积木是完全一样的。

【解答】 从最不利的情况考虑，各有两个小朋友取出红黄蓝白四种颜色的积木各一个，各有两个小朋友取出红黄蓝白四种颜色的积木各二个。

这时这要再来一个人无论他怎么取，都会保证有三个小朋友的积木是完全一样的。

所以至少有2424117⨯+⨯+=6.四()1班同学买了一批牙膏送给敬老院的老人，如每位老人送4支，则多8支；如每位送5支，则缺65支；那么敬老院里有（ ）位老人，这批牙膏共有（ ）支。

【解答】 每人送四支之后还剩8支，如若每人再送一支（即每人送5支），就是把剩的8支每人一支，缺了65支。

说明有73个老人。

牙膏有7348300⨯+=7.有一串这样的数字：2、0、0、6、0、6、2、0、0、6、0、6、2、0、0、6、0、6L L 共2006个数。

其中共有（ ）个0，（ ）个2，（ ）个6。

【解答】 2、0、0、6、0、6为一组，这一组中有3个0，1个2，2个6，这样的数有()141914319143319143331914333319431592569543370365++++÷=÷=()999999555555222222999999999999333333333332666667⨯-⨯=⨯=7937292936369318x x x x x x ∆∇=⨯+⨯∇⨯⨯-⨯--==（）= 21+2（3）= 21+621+6334组，还有两个数就是2，0.所以有335个2，有334311003⨯+=个0，有33421669⨯+=个6.8.15个互不相同的自然数（不包括0）相加，和是2004。

第十五届“中环杯”小学生思维能力训练活动五年级选拔赛填空题：1、已知2468135713572468mn++++++-=++++++，其中m, n 是两个互质的正整数，则10m n +=____【考点】分数计算 【答案】110 分析：20169==162020-原式 ，10m n +=10×9+20=1102、D 老师家里有五个烟囱，这五个烟囱正好从矮到高排成一排，相邻两个烟囱之间的高度差为2厘米，其中最高的烟囱又正好等于最矮的两个烟囱的高度之和，则五个烟囱的高度之和是________厘米 【考点】等差数列，方程 【答案】50分析：设这五个烟囱分别为x-4，x-2，x ，x+2，x+4，则x+4=x-2+x-4，x=10，和为5x=503、已知()()33222014a b c d ⨯+-=，其中a 、b 、c 、d 是四个正整数，请你写出满足条件的一个乘法算式：___________ 【考点】数的拆分，分解质因数 【答案】答案不唯一分析：2014=1×2014=2×1007=19×106=38×53其中一解为2014=()()22335932+⨯-4、一个长方体的长、宽分别为20厘米、15厘米，其体积的数值与表面积的数值相等，则它的高为______厘米（答案写为假分数） 【考点】立体几何，方程 【答案】6023分析：设高为h ，则20×15×h=（20×15+20h+15h ）×2，则h=60235、一次中环杯比赛，满分为100分，参赛学生中，最高分为83分，最低分为30分（所有的分数都是整数），一共有8000个学生参加，那么至少有_____个学生的分数相同 【考点】抽屉原理 【答案】149分析：83-30+1=54，800054=1488÷⋅⋅⋅，148+1=149个6、对35个蛋黄月饼进行打包，一共有两种打包规格：大包袋里每包有9个月饼，小包装里每包有4个月饼。

小学六年级思维能力竞赛初赛试题(60分钟)班别： 姓名： 得分:一．填空题(2分×10=20分)1、甲、乙、丙三个数的平均数是6，它们的比是12 ：23 ：56，甲数是（ ），乙数是（ ），丙数是（ ）。

2、甲乙两齿轮的齿数之比为3：7，它们同时工作并互相咬合，甲齿轮每分钟转420转，乙齿轮每分钟转（ ）转。

3、甲、乙两数的差是9，甲数的16和乙数的25%相等，甲数是（ ）。

4、一个正方形的边长增加110，面积增加（ ）%，周长增加（ ）% 。

5、甲乙丙三人的彩球的比为9：4：2，甲给了丙30个彩球，乙也给了丙一些彩球后，甲乙丙的比为2：1：1，乙给了丙（ ）个彩球。

6、一件衣服，先提价15%，后降价15%，现价是原价的（ ）% 。

7、有一个分数，如果分子分母都加1，则分数变为12，如果分子分母都减1，这个分数就变成25，这个分数是（ ）。

二、计算，能简算的要简算。

（4分×6=24分）9.8×114 ＋9.2÷45 －1.25 3413 ×24＋6613 ×24－4723 ÷12413 ＋115 ＋135 ＋163 ＋199 ＋1143 12 ＋56 ＋1112 ＋1920 ＋……＋98999900（1＋12 ）×（1－12 ）×（1＋13 ）×（1－13 ）×……×（1－ 199 ）×（1＋199）1×2＋2×3＋3×4＋4×5＋……99×100―12―22―32―……－992三、解决问题：（8分×7=56分）1、甲、乙两堆煤原来吨数的比是5：3，如果从甲堆运90吨放入乙堆，这时两堆吨数相等。

甲、乙原来各有煤多少吨2、学校买来16个篮球和12个足球，共付出760元，已知篮球与足球的单价比为5：6。

学校买来篮球和足球各付出多少元？3、张、王、李三家共用一个洗手间，卫生由三家人轮流平均打扫。

第十四届“中环杯”六年级初赛考题1.计算：=++++++++256112816413211618141211______。

【分析与解】计算，等比数列计算。

原式=25625512561225612561256112816413211618141211=-=-+++++++++2.下列分数：357152********、、、、、中有限小数有_____个。

【分析与解】分数化小数。

如果一个最简分数的分母分解质因数后，只含质因数2 、5 ，那么这个分数能化成有限小数；如果一个最简分数的分母分解质因数后，除了质因数2 、5 还含有其它质因数，那么这个分数能化成循环小数。

513571527421634131==、、、、、 其中能化成有限小数的有51357216341==、、，共3个。

3.如图，所有的角度都已标注在图中，∠α=______。

【分析与解】几何，角度。

根据邻补角的定义可得∠β=180°-30°=150°，∠γ=180°-110°=70°,∠δ=180°-85°=95°；根据四边形内角为360°可得∠α=360°-150°-70°-95°=45°。

4.一个圆A 的周长与面积的数值相等，另一个圆B 的半径是圆A 半径的4倍，则圆B 的面积为_____平方厘米（本题中所有的单位都是厘米，答案保留π）。

【分析与解】几何，圆。

C A =S A ，即2πr A =πr A 2； r A =2厘米； r B =4r A =8厘米；S B =即πr B 2=64π平方厘米。

5.图中白色的格子有M 个，染色的格子有N 个，则200M+N=______。

【分析与解】计数。

白色的格子有4×4=16个，即M=16； 染色的格子有5×5=25个，即N=25； 200M+N=200×16+25=3225。

小学六年级数学思维能力竞赛题小学六年级数学思维能力竞赛题全卷共4页，满分100分，时间80分钟）一、填空题(每空2分，共40分)1.冰化成水，体积会减少，水结成冰，体积会增加。

2.一个不为1的自然数与它的倒数的和是17/4，这个自然数是（）。

3.哥哥有100元钱，弟弟有80元钱，哥哥给弟弟20元钱后，哥哥和弟弟钱数的比是4:5.4.XXX原来5小时加工240个零件。

技术革新后，加工这些零件只需要4小时，时间缩短了1/5，工作效率提高了（）。

5.下图中阴影部分的面积占整个图形面积的1/3.6.上图中，已知小正方形的面积是15平方厘米，圆的面积是（15π/4）平方厘米。

7.某车间三个组共有工人169名，已知第一组和第二组人数的比是3:4，第二组与第三组人数的比是2:3，第二组有(84)人。

8.一艘轮船从甲地开往乙地，每小时行25千米，15小时到达。

返回时速度提高了20%，返回时用了（12.5）小时。

9.两个数相除的商是21，余数是3，如果把被除数、除数、商和余数相加，它们的和是225、被除数是（444），除数是(21)。

10.把一根长2米、底面半径是4厘米的圆柱形木棒截成四段，表面积比原来增加了（16π）平方厘米。

11.用4件上衣和3条裤子有（12）种搭配方法。

12.自来水水管的内直径是2厘米，水管内的水的流速是每秒8厘米，一位同学去洗手，走时忘记关水龙头，5分钟浪费（4）升水。

13.商场销售某品牌衬衣，如果按售价七折销售亏本8元，打八折销售则赚10元，这种衬衣的成本价是（70）元。

14.明明用小棒搭房子（如图），照这样搭下去，搭20间房要（84）根小棒。

15.沿一个湖泊的一周共栽了78棵苹果树，每2棵苹果树之间栽1棵梨树，那么一个栽了（26）棵树。

16.用同样长的铁丝分别围成长方形、正方形和圆，围成的（圆形）面积最大。

17.XXX按照一定规律写数：1，+2，-3,4，+5，-6,7，+8，-9，……，他一共写了50个数，这50个数中共有（25）个正数。

第十三届“中环杯”中小学生思维能力训练活动六年级决赛一、填空题(每小题5分,共50分):1.计算:25×43+1.4×1.3+145×13=()。

2.定义n !=n ×(n -1)×…×2×1,比如6!=6×5×4×3×2×1,则15!-13!的最大素因数是()。

3.在9,8,7,6,5,4,3,2,1,0这10个数字之间加入+,-,×,÷以及括号,使得最后的结果是2013,请写出一个你所得到的式子9876543210=2013。

4.一个篮子里有红、橙、黄、绿四种颜色的球。

甲、乙、丙三人开始数这些球,并把他们数到的结果记在了下表中。

很不幸的是,每人都数错了两种颜色球的数量,数对了另两种颜色球的数量。

已知一个人数错了红、橙两色的球,另一个人数错了橙、黄两色的球,第三个人数错了黄、绿两色的球的数量。

那么,篮子中一共有()个球。

5.一个老师正在统计班级的数学平均分。

已知卷子满分是100分,老师每统计到一个同学,就重新计算一次当前的平均分。

当他统计到小明的分数时,平均分上升了1分;当他统计到小红的分数时,平均分又上升了1分;已知小明的分数是91分,那么小红的分数是()分。

6.已知n 位(n 为正整数)自然数N =a 1a 2…a n ,满足2a 1a 2…a n 1:1a 1a 2…a n 2=21:12,则N=()。

7.若x 满足x +41×3×5+x +63×5×7+x +85×7×9+…+x +20122009×2011×2013=10052011,则x =()。

8.如图,在圆O 中,AB 为直径,C 为圆内一点。

作AD//BC 与CO 的延长线交于D 点。

延长OD 至E点,使得DE=2CO 。

第十三届“中环杯”中小学生思维能力训练活动六年级决赛一、填空题(每小题5分,共50分):1.计算:25×43+1.4×1.3+145×13=()。

2.定义n !=n ×(n -1)×…×2×1,比如6!=6×5×4×3×2×1,则15!-13!的最大素因数是()。

3.在9,8,7,6,5,4,3,2,1,0这10个数字之间加入+,-,×,÷以及括号,使得最后的结果是2013,请写出一个你所得到的式子9876543210=2013。

4.一个篮子里有红、橙、黄、绿四种颜色的球。

甲、乙、丙三人开始数这些球,并把他们数到的结果记在了下表中。

很不幸的是,每人都数错了两种颜色球的数量,数对了另两种颜色球的数量。

已知一个人数错了红、橙两色的球,另一个人数错了橙、黄两色的球,第三个人数错了黄、绿两色的球的数量。

那么,篮子中一共有()个球。

5.一个老师正在统计班级的数学平均分。

已知卷子满分是100分,老师每统计到一个同学,就重新计算一次当前的平均分。

当他统计到小明的分数时,平均分上升了1分;当他统计到小红的分数时,平均分又上升了1分;已知小明的分数是91分,那么小红的分数是()分。

6.已知n 位(n 为正整数)自然数N =a 1a 2…a n ,满足2a 1a 2…a n 1:1a 1a 2…a n 2=21:12,则N=()。

7.若x 满足x +41×3×5+x +63×5×7+x +85×7×9+…+x +20122009×2011×2013=10052011,则x =()。

8.如图,在圆O 中,AB 为直径,C 为圆内一点。

作AD//BC 与CO 的延长线交于D 点。

延长OD 至E点,使得DE=2CO 。