2020年秋入学检测八年级数学答题卡

数学 第1页（共6页） 数学 第2页（共6页） 数学 第3页（共6页）请在各题目的答题区域内作答，超出黑色矩形边框限定区域的答案无效！ 2024-2025学年八年级数学上学期期中测试 卷·答题卡请在各题目的答题区域内作答，超出黑色矩形边框限定区域的答案无效！ 请在各题目的答题区域内作答，超出黑色矩形边框限定区域的答案无效！ 请在各题目的答题区域内作答，超出黑色矩形边框限定区域的答案无效！ 18．（6分） 19．（8分） 20．（8分） 21．（10分）姓 名：__________________________ 准考证号： 贴条形码区 考生禁填： 缺考标记 违纪标记 以上标记由监考人员用2B 铅笔填涂 选择题填涂样例： 正确填涂 错误填涂[×] [√] [／] 1．答题前，考生先将自己的姓名，准考证号填写清楚，并认真核准条形码上的姓名、准考证号，在规定位置贴好条形码。

2．选择题必须用2B 铅笔填涂；填空题和解答题必须用0.5 mm 黑色签字笔答题，不得用铅笔或圆珠笔答题；字体工整、笔迹清晰。

3．请按题号顺序在各题目的答题区域内作答，超出区域书写的答案无效；在草稿纸、试题卷上答题无效。

4．保持卡面清洁，不要折叠、不要弄破。

注意事项 一、单项选择题（本题共10小题，每小题3分，共30分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

） 1 [A] [B] [C] [D] 2 [A] [B] [C] [D] 3 [A] [B] [C] [D] 4 [A] [B] [C] [D] 5 [A] [B] [C] [D] 6 [A] [B] [C] [D] 7 [A] [B] [C] [D] 8 [A] [B] [C] [D] 9 [A] [B] [C] [D] 10[A] [B] [C] [D] 二、填空题（本题共6小题，每小题3分，共18分．） 11．____________________ 12．____________________ 13．____________________ 14．____________________ 15．____________________ 16．____________________ 三、解答题（本题共8小题，共72分．第17-18题每题6分，第19-20题每题8分，第21-22题每题10分，第23-24题每题12分，解答应写出文字说明、证明过程或演算步骤．） 17．（6分）数学 第4页（共6页） 数学 第5页（共6页） 数学 第6页（共6页） 请在各题目的答题区域内作答，超出黑色矩形边框限定区域的答案无效！请在各题目的答题区域内作答，超出黑色矩形边框限定区域的答案无效！ 22．（10分） 请在各题目的答题区域内作答，超出黑色矩形边框限定区域的答案无效！ 请在各题目的答题区域内作答，超出黑色矩形边框限定区域的答案无效！ 23．（12分） 24．（12分） 请在各题目的答题区域内作答，超出黑色矩形边框限定区域的答案无效！ 请在各题目的答题区域内作答，超出黑色矩形边框限定区域的答案无效！。

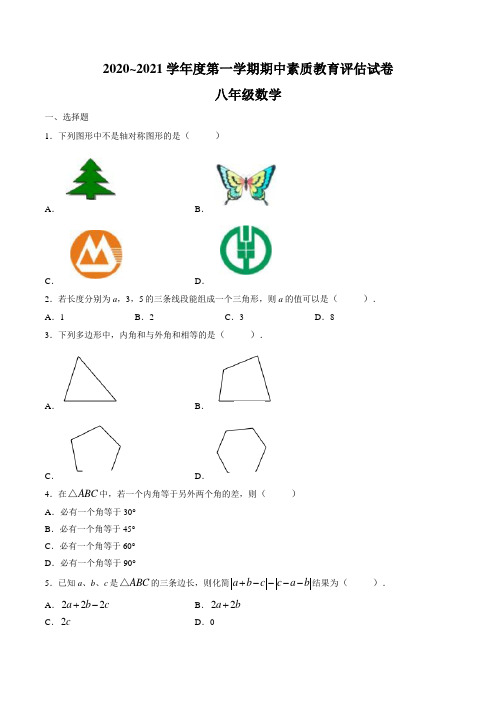
2020~2021学年度第一学期期中素质教育评估试卷八年级数学一、选择题1．下列图形中不是轴对称图形的是（ ）A ．B ．C ．D ．2．若长度分别为a ，3，5的三条线段能组成一个三角形，则a 的值可以是（）． A ．1 B ．2 C ．3 D ．83．下列多边形中，内角和与外角和相等的是（ ）．A ．B ．C ．D ．4．在ABC △中，若一个内角等于另外两个角的差，则（ ）A ．必有一个角等于30°B ．必有一个角等于45°C ．必有一个角等于60°D ．必有一个角等于90°5．已知a 、b 、c 是ABC △的三条边长，则化简a b c c a b +----结果为（）． A ．222a b c +- B ．22a b +C ．2cD ．06．如图，已知MB ND =，MBA NDC ∠=∠，下列不能判定．．．．ABM CDN △△≌的条件是（ ）．A ．M N ∠=∠B ．AB CD =C ．AM CN =D ．AM CN7．如图，在ABC △中，BE 是ABC ∠的平分线，CE 是ACM ∠的平分线，BE 与CE 相交于点E ，若60A ∠=︒，则BEC ∠是（ ）．A ．15°B ．30°C ．45°D ．60°8．如图，2AB =，6BC AE ==，7CE CF ==，8BF =，则四边形ABDE 与CDF △面积的比值是（ ）A ．1B ．34C ．23D ．129．如图所示，在ABC △中，5AB AC ==，F 是BC 边上任意一一点，过F 作FD AB ⊥于D ， FE AC ⊥于E ，若10ABC S =△，则FE FD +=（ ）．A ．2B ．4C ．6D ．810．如图，在ABC △中，AD BC ⊥于D ，且AD BC =，以AB 为底边作等腰直角三角形ABE ，连接ED 、EC ，延长CE 交AD 于点F ，下列结论：①ADE BCE △△≌；②BD DF AD +=；③CE DE ⊥；④BDE ACE S S =△△，其中正确的有（ ）．A ．①②B ．①③C ．①②③D ．①②③④二、填空题11．如图，ABC △与A B C '''△关于直线l 对称，且105A ∠=︒，30C '∠=︒，则B ∠=______．12．把一副直角三角尺按如图所示的方式摆放在一起，其中90E ∠=︒，90C ∠=︒，45A ∠=︒，30A ∠=︒，则12∠+∠=______．3．如图，在ABC △中，点E 在边AC 上，DE 是AB 的垂直平分线，若ABC △的周长为19，BCE △的周长为12，则线段AB 的长为______．14．设三角形的三个内角分别为α、β、γ，且a βγ≥≥，2αγ=，则β的最大值与最小值的和是______． 三、15．尺规作图（不写作法，但要保留作图痕迹）（1）作ABC △中B ∠的平分线；（2）作ABC △边BC 上的高．16．如图所示，在平面直角坐标系中，ABC △的三个顶点的坐标分别为()3,2A -，()1,3B -，()2,1C ．（1）在图中作出与ABC △关于x 轴对称的111A B C △；（2）点1A 的坐标是______，ABC S =△______．四、17．已知：如图所示，C 是线段AB 的中点，且A B ∠=∠，ACE BCD ∠=∠．求证：AD BE =．18．已知两个多边形的边数之比为1:2，且这两个多边形的内角之和为1440°，试求出这两个多边形的边数． 五、19．如图所示，六边形ABCDEF 中，CD AF ，CDE BAF ∠=∠，AB BC ⊥，120C ∠=︒，80E ∠=︒，求F ∠的度数．20．如图，在ABC △中AD 是BC 边上的中线，过C 作AB 的平行线交AD 的延长线于E 点．（1）求证：AB EC =；（2）若6AB =，2AC =，试求中线AD 的取值范围．六、21．如图，树AB 与树CD 之间相距13m ，小华从点B 沿BC 走向点C ，行走一段时间后他到达点E ，此时他仰望两棵大树的顶点A 和D ，且两条视线的夹角正好为90°，EA ED =．已知大树AB 的高为5m ，小华行走的速度为1m/s ，求小华行走到点E 的时间．七、22．已知BF 平分ABC △的外角ABE ∠，D 为射线BF 上一动点．（1）如图所示，若DA DC =，求证：ABC ADC ∠=∠；（2）在D 点运动的过程中，试比较BA BC +与DC DA +的大小，并说明你的理由．23．已知：如图所示，锐角ABC △中，BE 、CF 是高，在BE 的延长线上截取BQ AC =，在CF 上截取CP AB =，再分别过点P 作PM BC ⊥于M 点，过点Q 作QN BC ⊥于N 点（1）求证：Q ACB ∠=∠；（2）求证：PM QN BC +=．参考答案一、选择题1．C2．C3．B4．D5．D6．C7．B8．A9．B10．D二、填空题11．45°12．210°13．714．117°三、15.解：（1）作图正确（2）作图正确16．解：（1）作图正确（2）()13,2A --， 3.5ABC S =△四、17．证明：C 是线段AB 的中点，AC BC ∴=.ACE BCD ∠=∠，ACD BCE ∴∠=∠．在ADC △和BEC △中，AC BCACD BCE ⎪=⎨⎪∠=∠⎩， ()ADC BEC ASA ∴︒△△≌AD BE ∴=．18．解：设其中一个多边形的边数为n ，则另一个多边形的边数为2n ． 根据题意得，()()2180221801440n n -⨯+-⨯=．解得4n =.所以28n =．故这两个多边形的边数分别为4，8． 五、19．解：连接AD ．在四边形ABCD 中，360BAD ADC B C ∠+∠+∠+∠=︒．AB BC ⊥，90B ∴∠=︒．又120C ∠=︒，150BAD ADC ∴∠+∠=︒．CD AF ，CDA DAF ∴∠=∠．150BAF BAD DAF BAD CDA ∴∠=∠+∠=∠+∠=︒.150CDE BAF ∴∠=∠=︒．在六边形ABCDEF 中，720BAF B C CDE E F ∠+∠+∠+∠+∠+∠=︒， 又80E ∠=︒，90B ∠=︒，120C ∠=︒，150CDE BAF ∠=∠=︒ 130F ∴∠=︒．20．（1）证明：AD 是BC 边上的中线，BD CD ∴=．AB CE ，BAD E ∴∠=∠． 又BDA CDE ∠=∠，()ABD ECD AAS ∴△△≌．CE AB ∴=．（2）由（1）可知AD DE =在ACE △中，CE AC AE CE AC -<<+，又6AB CE ==，2AC =，即428AD <<，24AD ∴<<．六、21．解：90AED ∠=︒，90AEB DEC ∴∠+∠=︒．90ABE ∠=︒，90A AEB ∴∠+∠=︒．A DEC ∴∠=∠在ABE △和DCE △中A DEC AE DE ⎪∠=∠⎨⎪=⎩，()ABE ECD ASA ∴△△≌5EC AB ∴==m ．13BC =m ，8BE ∴=m ．∴小华走的时间是818÷=（s ）．七、22．证：（1）过D 作DM BE ⊥于M ，DN AB ⊥于N BF 平分ABE ∠．DM DN ∴=．DA DC ∴=，()Rt CDM Rt AND HL ∴△△≌．DAB DCB ∴∠=∠． AB 与CD 相交，ABC ADC ∴∠=∠．（2）BA BC DA DC +<+．理由如下：在（1）可得，BM BN =．AB BC CM AN ∴+=+AN AD <，CM CD <，AB BC AD CD ∴+<+．八、23.（1）证明：BE 是ABC △的高，90ACB EBC ∴∠+∠=︒． QN BC ⊥，90Q EBC ∴∠+∠=︒．Q ACB ∴∠=∠（2）如图，过A 作AH BC ⊥于H 点．QN BC ⊥，AH BC ⊥，90QNB CHA ∴∠=∠=︒． 又Q ACB ∠=∠，BQ AC =，()QNB CHA AAS ∴△△≌．QN CH ∴=．同理，BAH PCM ∠=∠，90AHB CMP ∠=∠=︒， 又CP AB =，()PCM BAH AAS ∴△△≌．PM BH ∴=．PM QN BH CH BC ∴+=+=．2020-2021学年第一学期期末八年级数学试题一、选择题(本题共10小题，每小题3分，共计30分)1. 下列各式运算正确的是（ ）A ．235a a a +=B ．235a a a ⋅=C ．()326ab ab = D ．1025a a a ÷= 2. 在平面直角坐标系中，有点 1(2)A -，,点A 关于y 轴的对称点是( )A.()21-，-B.(21)-，C.()2, 1D. (1)2-，3.下列说法正确的是( )A.任何一个图形都有对称轴B.两个全等三角形一定关于某直线对称C.若ABC ∆与DEF ∆成轴对称，则ABC DEF ∆≌D.点A ，点B 在直线L 两旁，且AB 与直线L 交于点O ,若AO BO =,则点A 与点B 关于直线L 对称4. 下列分解因式正确的是（ ）A ．()321x x x x -=-B ．()()2339a a a +-=-C.()()2933a a a -=+- D ．()()22x y x y x y +=+-5.()22 ( ) x a x ax a -++的计算结果是（ ）A ．3232x ax a +-B ．33x a -C.3232x a x a +- D ．222322x ax a a ++-6. 若6, 3a b ab +==, 则2233a b ab +的值是( )A ．9B ．27 C.19 D ．547. 如图，阴影部分的面积是( )A ．72xyB ．92xy C.4xy D ．2xy 8. 等腰三角形一腰上的高与另一腰的夹角为60︒，则这个等腰三角形的顶角为（ ）A ．30B ．150 C.30或 150 D ．129. 已知点()1,P a 与(),2Q b 关于x 轴成轴对称，又有点(),2Q b 与点(),M m n 关于y 轴成轴对称，则m n -的值为( )A ．3B ．3- C. 1 D ．1-10. 已知30AOB ∠=︒,点P 在AOB ∠的内部，点1P 和点P 关于OA 对称，点2P 和点P 关于OB 对称，则12P O P 、、三点构成的三角形是( )A.直角三角形B.钝角三角形C.等腰直角三角形D.等边三角形二、填空题(本题共8小题，每小题3分，共计24分)11.等边三角形是轴对称图形，它有______ 条对称轴.12.()3511m a a a ⋅=,则m 的值为 ． 13.计算()22133x y xy ⎛⎫-⋅= ⎪⎝⎭． 14. 等腰ABC 中，10 30AB AC A ==∠=︒，, 则腰AB 上的高等于 ．15. 如图是小明制作的风筝，为了平衡制成了轴对称图形，已知OC 是对称轴，35,30A BCO ∠=︒∠=︒，那么AOB ∠=_ ．16. 若22210a b b -+-+=，则a = ，b = ．17. 已知如图，3 BC ABC =∠，和ACB ∠的平分线相交于点//, //O OE AB OF AC ，, 则三角形OEF 的周长为 ．18.利用利用一个a a ⨯的正方形，1个b b ⨯的正方形和2个a b ⨯的长方形可拼成一个正方形(如图),从而可得到因式分解的公式 ．三、解答题 (本题共7小题，共46分)19. 计算：（1）()()23342a b ab ÷ （2）()32222322x y x y xy xy --+÷20. 因式分解：（1）22327a b - （2）()282x x --21. 已知:如图，已知ABC ,(1)分别画出与ABC 关于x 轴、对称的图形111A B C ;(2)写出111A B C 各顶点坐标:(3)求ABC 的面积.22. 如图， ABD AEC ∆、都是等边三角形，求证:BE DC =.23. 先化简，再求值:()()()2[2]x y x y x y x -++-÷，其中3, 1x y ==24. 已知:如图ABC 中， 30, , 4AB AC C AB AD AD cm =∠=︒⊥=，, 求BC 的长.25.下面是某同学对多项式()()2242464x x x x -+-++进行因式分解的过程， 解:设24x x y -=原式()() 2 6 4y y =+++ (第一步)2 816y y =++ (第二步)()24y =+ (第三步) ()2244x x =-+ (第四步) 回答下列问题:(1)该同学第二步到第三步运用了因式分解的 .A.提取公因式B.平方差公式C.两数和的完全平方公式D.两数差的完全平方公式(2)该同学因式分解的结果是否彻底? (填“彻底”或“不彻底”) 若不彻底，请直接写出因式分解的最后结果(3)请你模仿以上方法尝试对多项式()()222221x x x x --++进行因式分解.参考答案一、选择题1-5:BACCB 6-10:DACBD二、填空题11.3 12. 2 13. 33x y - 14. 515. 130 16.21、（对一个空给2分,两个空都对给3分） 17.3 18.()2222a ab b a b ++=+ 三、解答题(19) (每题3分)解：(1)32a b (积的乘方对的给2分) (2) 2312x y xy --+ (20) (每题3分)(1)23223273(9)3(3)(3)a b a b a b a b -=-=+-; (2)2228(2)816(4)x x x x x --=-+=-. (做对第一步的给2分)(21) (8分) (1)作图2分(2)()()()1110,2? 4,1 2,4A B C (一空一分)(3分)111341423225222ABC S ∆=⨯-⨯⨯-⨯⨯-⨯⨯= (3分) (22) (6分)证明: ABD AEC ∆、都是等边三角形, ,60AD AB AC AE DAB CAE ∴==∠=∠=︒，(2分)DAC BAE ∴∠=∠DAC BAE ∴≌(2 分)BE DC ∴=(2分)(23) (6分)x y - (去括号合并对了给2分) 2 (前面计算对了，答案错了扣1分)(24) (6分)30AB AC C =∠=︒，30,120B C BAC ∴∠=∠=︒∠=︒(2分) ,30AB AD DAC ⊥∴∠=︒ 30,DAC C AD DC ∴∠=∠=︒∴=(2分) 8BC BD CD AD DC cm =+=+= (2 分)(25).(8分)(1) C ; (2分)(2)分解不彻底: (1分) ()42x -(2分)(3) 设22x x y -= (1分) 原式() 2 1y y =++ 221y y =++ ()21y =+ ()2221x x =-+ ()41x =-(2分)。

2019-2020学年第一学期八年级期末测试-数学答题卡
八年级数学答题卡第1页（共4页）
此方框为缺考学生标记，由监考员用2B 铅笔填涂
考试编号填涂区
一、选择题（共10题，共30分） 1 6 2 7 3 8 4 9 5
10
三、解答题（共7题，共50分） 21．（6分）
学校 条 形 码
粘 贴 处
班级 姓名
注意事项：
1．选择题作答必须用2B 铅笔，修改时用橡皮擦干净。

2．笔答题作答必须用黑色签字笔填写，答题不得超过答题
边框区域。

3．保持答题卡卡面清洁，不要折叠，不要弄破。

4．在考生信息框中填写班级、姓名及考号。

5．正确填涂： 6．错误填涂：
二、填空题（共10题，共20分） 11． 12． 13． 14． 15． 16． 17． 18． 19．
20．
23．（每小题3分，共6分）
（1）（2）
24．（6分）
（1）
（2）
（1）①
②
（2）
（3）
26．（8分）
（1）
（2）
（3）
八年级数学答题卡第3页（共4页）
27．（10分）
（2）
（3）。

2020年八年级（上）开学数学试卷一、选择题1.下列计算中，正确的是()A. x3÷x=x2B. a6÷a2=a3C. x⋅x3=x3D. x3+x3=x62.下列世界博览会会徽图案中是轴对称图形的是()A. B.C. D.3.2014年全年国内生产总值按可比价格计算，比上年增长9.5%，达到136500亿元．136500亿元用科学记数法表示为()A. 1.365×1012元B. 13.65×1012元C. 1.365×1013元D. 0.1365×1014元4.如图，下列条件中，不能判断直线l1//l2的是()A. ∠1=∠3B. ∠2=∠3C. ∠4=∠5D. ∠2+∠4=180°5.等腰三角形的周长为13cm，其中一边长为3cm，则该等腰三角形的底边为()A. 7cmB. 3cmC. 7cm或3cmD. 8cm6.假如小蚂蚁在如图所示的地砖上自由爬行，它最终没有停在黑色方砖上的概率为()A. 13B. 49C. 12D. 597.已知△ABC的三个内角满足：∠A=2∠B=2∠C，则△ABC的形状是()A. 直角三角形B. 钝角三角形C. 锐角三角形D. 不能确定8.若x2+mx+9是一个完全平方式，那么m的值是()A. 9B. ±18C. 6D. ±69.某装满水的水池按一定的速度放掉水池的一半水后．停止放水并立即按一定的速度注水，水池注满后，停止注水，又立即按一定的速度放完水池的水．若水池的存水为v(立方米)，放水或注水的时间为t(分钟)，则v与t只能是()A. B.C. D.10.下面的说法正确的个数为()①若∠α=∠β，则∠α和∠β是一对对顶角；②若∠α与∠β互为补角，则∠α+∠β=180°；③一个角的补角比这个角的余角大90°；④同旁内角相等，两直线平行．A. 1B. 2C. 3D. 4二、填空题11.已知a+1a =√3，则a2+1a2=______．12.小明从镜子里看到对面电子钟示数的影像如图，这时的时刻应是______．13.一个角等于它的补角的12，则这个角的余角是______．14.一组数据1，2，3，4，5中任取三个数，能组成三角形的概率为______．15.如图，在△ABC中，AB的垂直平分线交AC于点M，交AB于点D.若CM=3cm，BC=4cm，AM=5cm，则△MBC的周长=______cm．16.声音在空气中传播的速度y(米/秒)(简称音速)与气温x(℃)之间的关系如下：气温(x℃)05101520音速y(米/秒)331334337340343某人看到发令枪的烟0.2秒后，听到了枪声，则由此可知，这个人距发令地点______米．17.已知当x=1时，2ax2+bx的值为3，则当x=2时，ax2+bx的值为______．18.△ABC的三边分别是a，b，c，试化简|a−b−c|+|b−c+a|−|c−b−a|=____；19.如图，将三角形纸片ABC沿DE折叠，当点A落在四边形BDEC的外部时，∠1=72°，∠2=26°，则∠A=______°.20.某单位急需用车，但又不想买车，他们准备和一个私营车主或一个国营出租车公司签订月租车合同，设汽车每月行驶x千米，应付给私营车主的月费用是y1元，应付给国营出租车公司的月费用是y 2元，y 1，y 2分别与x 之间的关系如图所示，观察图象回答下列问题：(1)每月行驶的路程等于______时，租两家车的费用相同；(2)求租国营公司的车合算时，每月行驶的路程x 的范围为______．21. 已知4x 2−3x +1=a(x −1)2+b(x −1)+c 对任意数x 成立，则4a +2b +c =______． 三、解答题22. (1)先化简，再求值：[(a +4b)(a −b)−(a −2b)(a +2b)]÷(−13a)，其中a =53，b =−23；(2)如图，AD 为等腰直角三角形ABC 的底角平分线，∠C =90°，试探索AC +CD 与AB 的数量关系，并说明理由．23. 计算：(1)√49−√214(2)√81√17−1(3)(x +2)2=289(4)|−3|+(π−3)0−√(−2)2+√(−2)33−√1253(5)已知27(x +1)3+64=0，求x 的值．24. 计算：(1)(14x 2y 3)2÷(34x 3y 3)2⋅(−4xy)(2)(−15)−1−(−32)+(12)−2−(π−3)0(3)(3a +1)(2a −3)−6(a −1)(a +2) (4)(2x +y −3)(2x −y −3)25. 某校将举办“心怀感恩⋅孝敬父母”的活动，为此，校学生会就全校1 000名同学暑假期间平均每天做家务活的时间，随机抽取部分同学进行调查，并绘制成如下条形统计图．(1)本次调查抽取的人数为______，估计全校同学在暑假期间平均每天做家务活的时间在40分钟以上(含40分钟)的人数为______；(2)校学生会拟在表现突出的甲、乙、丙、丁四名同学中，随机抽取两名同学向全校汇报．请用树状图或列表法表示出所有可能的结果，并求恰好抽到甲、乙两名同学的概率．26. 为了解某种车的耗油量，我们对这种车做了试验，并把试验的数据记录下来，制成下表：(2)汽车行驶5h 后，油箱中的剩余油量是多少？(3)若汽车油箱中剩余油量为14L ，则汽车行使了多少小时？(4)贮满50L汽油的汽车，最多行驶几小时？27.在直角三角形ABC中，BC=6，AC=8，点D在线段AC上从C向A运动．若设CD=x，△ABD的面积为y．(1)请写出y与x的关系式；(2)当x为何值时，y有最大值，最大值是多少？此时点D在什么位置？(3)当△ABD的面积是△ABC的面积的1时，点D在什么位置？328.如图，在△ABC中，∠ACB=90°，CE⊥AB于E，F在CE上，FD//CB，且AD=AC．(1)若∠ACE=30°，求∠B；(2)求证：CF=FD．29.将一张透明的平行四边形胶片沿对角线剪开，得到图①中的两张三角形胶片△ABC和△DEF.将这两张三角形胶片的顶点B与顶点E重合，把△DEF绕点B顺时针方向旋转，这时AC与DF相交于点O．(1)当△DEF旋转至如图②位置，点B(E)，C，D在同一直线上时，∠AFD与∠DCA的数量关系是______；(2)当△DEF继续旋转至如图③位置时，(1)中的结论还成立吗？请说明理由；(3)在图③中，连接BO，AD，探索BO与AD之间有怎样的位置关系，并证明．30.(1)已知Rt△ABC中，∠C=90°，若a=12，b=5，则c=______；(2)已知Rt△ABC中，∠C=90°，若c=10cm，b=6cm，则a=______；(3)已知Rt△ABC中，∠C=90°，若a：b=3：4，c=20，则a2=______，b2=______．31.已知Rt△ABC中，∠C=90°，若a+b=14cm，c=10cm，求Rt△ABC的面积．32.如图，牧童在A处放牛，其家在B处，A，B到河岸的距离分别为AC、BD，且AC=BD=3m，CD=8m．(1)牧童从A处把牛牵到河边饮水后再回家，试问在何处饮水，所走路程最短？在图中作出该处并标为点M，并说明理由；(2)试用勾股定理有关知识求出最短路程是多少？答案和解析1.【答案】A【解析】解：A、x3÷x=x2，故A选项正确；B、a6÷a2=a4，故B选项错误；C、x⋅x3=x4，故C选项错误；D、x3+x3=2x3，故D选项错误．故选：A．根据合并同类项的法则，同底数幂的乘法与除法的知识求解即可求得答案．此题考查了合并同类项的法则，同底数幂的乘法与除法等知识，解题要注意细心．2.【答案】D【解析】解：A、不是轴对称图形，本选项错误；B、不是轴对称图形，本选项错误；C、不是轴对称图形，本选项错误；D、是轴对称图形，本选项正确．故选：D．根据轴对称图形的概念求解即可．本题考查了轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．3.【答案】C【解析】解：136500亿元=1.365×1013，故选：C．科学记数法的表示形式为a×10n的形式，其中1≤|a|<10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值>1时，n是正数；当原数的绝对值<1时，n是负数．此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|<10，n为整数，表示时关键要正确确定a的值以及n的值．4.【答案】B【解析】解：A、根据内错角相等，两直线平行可判断直线l1//l2，故此选项不合题意；B、∠2=∠3，不能判断直线l1//l2，故此选项符合题意；C、根据同位角相等，两直线平行可判断直线l1//l2，故此选项不合题意；D、根据同旁内角互补，两直线平行可判断直线l1//l2，故此选项不合题意；故选：B．根据平行线的判定定理：同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行分别进行分析即可．此题主要考查了平行线的判定，关键是掌握平行线的判定定理．5.【答案】B【解析】解：当腰是3cm时，则另两边是3cm，7cm.而3+3<7，不满足三边关系定理，因而应舍去．当底边是3cm时，另两边长是5cm，5cm.则该等腰三角形的底边为3cm．故选：B．已知的边可能是腰，也可能是底边，应分两种情况进行讨论．本题从边的方面考查三角形，涉及分类讨论的思想方法．6.【答案】C，故其概率等于【解析】解：观察这个图可知：白色区域与黑色区域面积相等，各占121．2故选：C．根据几何概率的求法：最终没有停在黑色方砖上的概率即停在白色方砖上的概率就是白色区域面积与总面积的比值．本题考查几何概率的求法：首先根据题意将代数关系用面积表示出来，一般用阴影区域表示所求事件(A)；然后计算阴影区域的面积在总面积中占的比例，这个比例即事件(A)发生的概率．7.【答案】A【解析】解：设∠A、∠B、∠C分别为2k、k、k，则k+k+2k=180°，解得k=45°，所以，最大的角∠A=90°，所以，这个三角形是直角三角形．故选：A．根据比例设∠A、∠B、∠C分别为2k、k、k，然后根据三角形内角和定理列式进行计算求出k值，再求出最大的角∠A即可得解．本题考查了三角形的内角和定理，三角形内角和是180°.利用“设k法”求解更加简便．8.【答案】D【解析】解：∵x2+mx+9是一个完全平方式，∴x2+mx+9=(x±3)2，∴m=±6，故选：D．这里首末两项是x和3这两个数的平方，那么中间一项为加上或减去x和3积的2倍．此题主要考查了完全平方公式的应用；两数的平方和，再加上或减去它们积的2倍，就构成了一个完全平方式．注意积的2倍的符号，避免漏解．9.【答案】A【解析】解：根据题意：装满水的水池按一定的速度放掉水池的一半水后．停止放水，排除B；并立即按一定的速度注水，排除C；水池注满后，停止注水，又立即按一定的速度放完水池的水，排除D．分析可得：存水v的变化为A．故选：A．理解进水，出水的几个阶段，把握几个关键语句：“放掉水池的一半水”，“立即按一定的速度注水”，“放完水池的水”．本题要求正确理解函数图象与实际问题的关系．10.【答案】B【解析】【分析】此题综合运用了对顶角、补角余角的定义和平行线的判定方法．根据相关的定义或定理，逐个进行判断，可知有2个是正确的，故选B．【解答】解：①错误，不符合对顶角的定义．②正确，满足补角的定义．③正确，一个角的补角减去这个角的余角等于(180°−α)−(90°−α)=90°．④错误，同旁内角互补，两直线平行．故选：B．11.【答案】1【解析】解：∵a+1a=√3，∴a2+1a2=(a+1a)2−2=3−2=1，故答案为：1原式利用完全平方公式变形，将已知等式代入计算即可求出值．此题考查了完全平方公式，熟练掌握完全平方公式是解本题的关键．12.【答案】10：51【解析】解：∵实际时间和镜子中的时间关于竖直的线成轴对称，∴故答案为：10：51．实际时间和镜子中的时间关于竖直的线成轴对称，画出相关图形可得实际时间．考查镜面对称的知识；得到相应的对称轴是解决本题的关键；难点是作出相应的对称图形；注意2关于竖直的一条直线的轴对称图形是5．13.【答案】30°【解析】解：设这个角是x°，则余角是(90−x)度，补角是(180−x)度，根据题意得：x=12(180−x)解得x=60．则余角是(90−x)度=30°；故答案为：30°．相加等于90°的两角称作互为余角，也作两角互余．和是180°的两角互为补角，本题实际说明了一个相等关系，因而可以转化为方程来解决．此题考查余角和补角问题，题目反映了相等关系问题，就可以利用方程来解决．14.【答案】310【解析】解：由5个数中任意取3个数，共有10种可能结果，每种结果出现的机会相同，满足两边之和大于第三边构成三角形的有3个结果，分别是2，3，4；2，4，5；3，4，5；所以能组成三角形的概率为3；10．故答案为：310由5个数中任意取3个数，共有10种可能结果，每种结果出现的机会相同，满足两边之和大于第三边构成三角形的有3个结果．因而就可以求出概率．此题主要考查了概率计算以及三角形三边关系，用到的知识点为：概率等于所求情况数与总情况数之比；组成三角形的两条小边之和大于最大的边．15.【答案】12【解析】解：∵MD是AB的垂直平分线，AM=5，∴AM=BM=5，∵CM=3cm，BC=4cm，∴△MBC的周长为BM+MC+BC=12cm．故答案为：12．由题意可知AM=MB=5，即可推出△MBC的周长．本题主要考查线段垂直平分线的性质，关键在于根据题意求得BM=5．16.【答案】增大68.6【解析】解：从表格可以看到y随x的增大而增大；20℃时，音速为343米/秒，343×0.2=68.6米，这个人距离发令点68.6米；故答案为增大，68.6；从表格可以看到y随x的增大而增大；20℃时，音速为343米/秒，距离为343×0.2= 68.6米；本题考查变量之间的关系，函数的表示方法；能够通过表格观察出变量的变化关系，利用表格的数据计算距离是解题的关键．17.【答案】6【解析】解：将x=1代入2ax2+bx=3得2a+b=3，将x=2代入ax2+bx得4a+2b=2(2a+b)，∵2a+b=3，∴原式=2×3=6．故答案为：6．将x=1代入2ax2+bx=3得2a+b=3，然后将x=2代入ax2+bx得4a+2b=2(2a+b)，之后整体代入即可．本题考查了代数式求值，利用整体思想是解题的关键．18.【答案】−a+b+c【解析】解：因为△ABC的三边分别是a，b，c，所以a−b−c<0，b−c+a>0，c−b−a<0，所以|a−b−c|+|b−c+a|−|c−b−a|=−a+b+c+b−c+a+c−b−a=−a+b+c．故答案为：−a+b+c．根据三角形三边满足的条件是，两边和大于第三边，两边的差小于第三边，根据此来确定绝对值内的式子的正负，从而化简计算即可．此题主要考查了三角形的三边关系，以及绝对值的计算，此题的关键是先根据三角形三边的关系来判定绝对值内式子的正负．19.【答案】23【解析】解：如图，延长BD、CE相交于A′，根据翻折的性质，∠3=12(180°−∠1)=12(180°−72°)=54°，∠4=12(180°+∠2)=12(180°+26°)=103°，在△ADE中，∠A=180°−∠3−∠4=180°−54°−103°=23°．故答案为：23．延长BD、CE相交于A′，根据翻折变换的性质求出∠3，∠4，再根据三角形的内角和等于180°列式进行计算即可得解．本题考查了三角形的内角和定理，翻折的性质，熟练掌握翻折的性质求出△ADE的另两个内角的度数是解题的关键．20.【答案】1500千米x>1500【解析】解：(1)由图可得，每月行驶的路程等于1500千米时，租两家车的费用相同，故答案为：1500千米；(2)由图可得，租国营公司的车合算时，每月行驶的路程x的范围为x>1500，故答案为：x>1500．(1)根据题意和函数图象中的数据可以解答本题；(2)根据函数图象中的数据可以解答本题．本题考查一次函数的应用，解答本题的关键是明确题意，利用数形结合的思想解答．21.【答案】28【解析】解：∵a(x−1)2+b(x−1)+c=a(x2−2x+1)+bx−b+c=ax2−2ax+a+bx−b+c=ax2−(2a−b)x+a−b+c=4x2−3x+1∴a=4、−(2a−b)=−3、a−b+c=1，解得：a=4、b=5、c=2，∴4a+2b+c=4×4+2×5+2=16+10+2=28故答案为：28．将a(x−1)2+b(x−1)+c展开后合并同类项与4x2−3x+1各项的系数相同，进而求得a、b、c的值，代入4a+2b+c求出即可．本题考查了有理数的混合运算，解题的关键是将多项式展开后合并同类项，两个二次三项式相等，就是他们的各项的系数相等．22.【答案】解：(1)[(a+4b)(a−b)−(a−2b)(a+2b)]÷(−13a)=[a2−ab+4ab−4b2−a2+4b2]÷(−1 3 a)=3ab×(−3 a )=−9b∵b=−23，∴−9b=−9×(−23)=6，即原式=6．(2)如图所示：线段AC、CD与AB的数量关系AC+CD=AB.理由如下：过点D作DE⊥AB于点E．∵AD是∠CAB的底角平分线，DC⊥AC，DE⊥AB，∴DC=DE，又∵在Rt△BDE中，∠B=45°，∴∠BDE=45°，∴DE=BE，∴DC=BE；在△ACD和△AED中，{∠C=∠AED=90°∠CAD=∠EADAD=AD，∴△ACD≌△AED(AAS)，∴AC=AE，又∵AB=AE+BE，∴AB=AC+DC．【解析】(1)由整式的混合运算法则，经化简式子得−9b，再将b=−−23代入求值．(2)由角平分线的性质得DC=DE，再证明△BDE是等腰直角三角形得DE=BE，等量代换线段DC与BE相等；判定△ACD和△AED全等后由全其性质得AC=AE，最后易得线段AB=AC+DC．本题考察了(1)实数的混合运算，并化简求值，重点掌握实数的运算顺序，易错点是括号前是负号，去括号时括号里面各项都要改变符号；(2)角平分线的性质，三角形全等的判定和性质，及等腰三角形的性质，重点是掌握证明线段等量关系一般情况将线段转换到同一条直线上进行计算．23.【答案】解：(1)原式=23−32=−56；(2)原式=17−1=9(√17+1)16；(3)开方得：x+2=17或x+2=−17，解得：x=15或x=−19；(4)原式=3+1−2−2−5=−5；(5)方程整理得：(x+1)3=−6427，开立方得：x+1=−43，解得：x=−73．【解析】(1)原式利用平方根定义计算即可求出值；(2)原式利用平方根定义，分母有理化性质计算即可求出值；(3)方程利用平方根开方即可求出解；(4)原式利用零指数幂，绝对值的代数意义，平方根、立方根定义计算即可求出值；(5)方程整理后，利用立方根定义求出x的值即可．此题考查了实数的运算，熟练掌握运算法则是解本题的关键．24.【答案】解：(1)原式=116x4y6÷916x6y6⋅(−4xy)=−49x−1y=−4y9x；(2)原式=−5+9+4−1=7；(3)原式=6a2−9a+2a−3−6a2−12a+6a+12=−13a+9；(4)原式=(2x−3)2−y2=4x2−12x+9−y2．【解析】(1)先算乘方，再算乘除即可；(2)先算乘方，再算加减即可；(3)先算乘法，再合并同类项即可；(4)先根据平方差公式进行计算，再根据完全平方公式求出即可．本题考查了整式大的混合运算、零指数幂、负整数指数幂和实数的混合运算，能正确运用运算法则进行化简和计算是解此题的关键．25.【答案】解：(1)50320(2)列表如下：共有12种情况，恰好抽到甲、乙两名同学的是2种，所以P(恰好抽到甲、乙两名同学)=212=16．【解析】解：(1)8+10+16+12+4=50人，1000×12+450=320人；(2)见答案【分析】(1)把各时间段的学生人数相加即可；用全校同学的人数乘以40分钟以上(含40分钟)的人数所占的比重，计算即可得解；(2)列出图表，然后根据概率公式计算即可得解．本题考查读频数分布直方图的能力和利用统计图获取信息的能力，列表法与树状图，利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题．26.【答案】解：(1)Q =50−6t ；(2)当t =5时Q =50−6×5=20(L)，即油箱中的剩余油量是20L ；(3)当Q =14时，50−6t =14，t =6，即汽车行使了6h ；(4)当Q =0时，50−6t =0，t =253小时，即最多行驶253小时．【解析】本题主要考查了一次函数的应用，由表格中数据求函数解析式，可以根据等量关系求解即可．(1)根据表格数据易得Q =50−6t ；(2)把t =5代入上式计算求出Q 即为油箱中的剩余油量；(3)把Q =14代入(1)中关系式解方程求出t 的值，就是汽车行驶的时间；(4)把Q =0代入(1)中关系式解方程求出t 的值，就是汽车行驶的时间．贮满50L 汽油的汽车，最多行驶的时间就是油箱中剩余油量为0时的t 的值． 27.【答案】解：(1)∵CD =x ，AC =8，∴AD =8−x ，则y =12×AD ×BC =12×(8−x)×6=−3x +24；(2)y =−3x +24，−3<0，∴y 随x 的增大而减小，∵0≤x <8，∴当x =0时，y 有最大值，最大值是24，此时点D 在与点C 重合；(3)由题意得，−3x +24=13×12×6×8，解得，x =163，∴当△ABD 的面积是△ABC 的面积的13时，CD =163．【解析】(1)根据三角形的面积公式求出y 与x 的关系式；(2)根据一次函数的性质解答；(3)根据三角形的面积公式列出方程，解方程得到答案．本题考查的是三角形的面积计算，一次函数的性质，掌握三角形的面积公式是解题的关键．28.【答案】解：(1)∵∠ACB =90°，CE ⊥AB 于E ，∴∠B +∠CAB =90°，∠CAB +∠ACE =90°∴∠B =∠ACE =30°(2)连接CD ，∵AC =AD∴∠ACD =∠ADC ，∵FD//CB∴∠B =∠FDA∴∠FDA =∠ACE ，∴∠ADC −∠ADF =∠ACD −∠ACE∴∠FDC =∠FCD∴FC =FD【解析】(1)由余角的性质可得∠B =∠ACE =30°；(2)连接CD ，由等腰三角形的性质可得∠ACD =∠ADC ，由平行线的性质可得∠FDA =∠ACE ，即可证CF =FD ．本题考查了直角三角形的性质，等腰三角形的性质和判定，熟练运用直角三角形的性质是本题的关键．29.【答案】∠AFD =∠DCA【解析】解：(1)∠AFD =∠DCA ．证明：∵AB =DE ，BC =EF ，∠ABC =∠DEF ，∴△ABC≌△DEF ，∴∠ACB =∠DFE ，∴∠AFD =∠DCA ；(2)∠AFD =∠DCA(或成立)，理由如下：方法一：由△ABC≌△DEF ，得：AB =DE ，BC =EF(或BF =EC)，∠ABC =∠DEF ，∠BAC =∠EDF ，∴∠ABC −∠FBC =∠DEF −∠CBF ，∴∠ABF =∠DEC ，在△ABF 和△DEC 中，{AB=DE∠ABF=∠DEC BF=EC，∴△ABF≌△DEC(SAS)，∠BAF=∠EDC，∴∠BAC−∠BAF=∠EDF−∠EDC，∠FAC=∠CDF，∵∠AOD=∠FAC+∠AFD=∠CDF+∠DCA，∴∠AFD=∠DCA；方法二：连接AD，同方法一△ABF≌△DEC，∴AF=DC，∵△ABC≌△DEF，∴FD=CA，在△AFD和△DCA中，{AF=DC FD=CA AD=DA，∴△AFD≌△DCA，∴∠AFD=∠DCA；(3)如图，BO⊥AD．方法一：由△ABC≌△DEF，点B与点E重合，得∠BAC=∠BDF，BA=BD，∴点B在AD的垂直平分线上，且∠BAD=∠BDA，∵∠OAD=∠BAD−∠BAC，∠ODA=∠BDA−∠BDF，∴∠OAD=∠ODA，∴OA=OD，点O在AD的垂直平分线上，∴直线BO是AD的垂直平分线，即BO⊥AD；方法二：延长BO交AD于点G，同方法一，OA=OD，在△ABO和△DBO中，{AB=DB BO=BO OA=OD，∴△ABO≌△DBO，∴∠ABO=∠DBO，在△ABG和△DBG中，{AB=DB∠ABG=∠DBG BG=BG，∴△ABG≌△DBG，∴∠AGB=∠DGB=90°，∴BO⊥AD．(1)要证∠AFD=∠DCA，只需证△ABC≌△DEF即可；(2)结论成立，先证△ABC≌△DEF，再证△ABF≌△DEC，得∠BAF=∠EDC，推出∠AFD=∠DCA；(3)BO⊥AD，由△ABC≌△DEF得BA=BD，点B在AD的垂直平分线上，且∠BAD=∠BDA，继而证得∠OAD=∠ODA，OA=OD，点O在AD的垂直平分线上，即BO⊥AD．本题综合考查全等三角形、等腰三角形和旋转的有关知识．注意对三角形全等知识的综合应用．30.【答案】13 8cm144 256【解析】解：(1)在Rt△ABC中，∵∠C=90°，a=12，b=5，∴c=√122+52=13；故答案为13．(2)在Rt△ABC中，∵∠C=90°，c=10cm，b=6cm，∴a=√102−62=8(cm)；故答案为8cm．(3)在Rt△ABC中，∵∠C=90°，a：b=3：4，c=20，设a=3k，b=4k，则c=5k，∴5k=20，∴k=4，∴a=12，b=16，∴a2=144，b2=256，故答案为144，256．(1)(2)直接利用勾股定理计算即可；(3)设a=3k，b=4k，则c=5k，构建方程求出k，可得a，b的值即可解决问题；本题考查勾股定理的应用，解题的关键是熟练掌握基本知识，利用方程是思想解决问题，属于中考常考题型．31.【答案】解：∵∠C=90°，∴a2+b2=c2=100，∴(a+b)2−2ab=100，∴196−2ab=100，∴ab=48，ab=24．∴S△ABC=12【解析】利用勾股定理可得：a2+b2=c2=100，即(a+b)2−2ab=100，可得ab=48，由此即可解决问题．本题考查勾股定理，三角形的面积，完全平方公式等知识，解题的关键是熟练运用公式解决问题，属于中考常考题型．32.【答案】解：(1)如图，点M即为所求，∵MA=MA′，∴MA+MB=MA′+MB=A′B，∵两点之间线段最短，∴此时MA+MB即为最小值；(2)∵AC=BD=3m，且AC//BD，AC⊥CD，∴四边形ACBD是矩形，∴AB=CD=8m，∠A′AB=90°，∵AA′=6m，∴A′B=√AA′2+AB2=√62+82=10(m)，∴最短路程是10m．【解析】(1)作点A关于直线CD的对称点A′，连接A′B，与CD的交点即为所求点M，根据轴对称的性质及两点之间线段最短解答即可；(2)先证四边形ACDB是矩形得AB=CD=8m，∠A′AB=90°，由轴对称的性质知AA′=6m，再根据勾股定理求解可得．本题主要考查作图−应用与设计作图，解题的关键是掌握轴对称的性质和两点之间线段最短及勾股定理的应用．。