奥林匹克ABC题库·杂题(二)训练C卷

杂题〔一〕练习A卷班级______ 姓名______ 得分______1．在图形中,如果从某点出发的线的数目是偶数的,我们把这样的点称为偶顶点；如果线的数目是奇数的,我们把这样的点称为奇顶点.看下面的图形,它共有〔〕个奇顶点,〔〕个偶顶点.想一想,这个图形能不能一笔画成,请你画一画.2．请将以下图形一笔画成.如果不行,你能说明理由吗？3．以下图是某层楼房间的平面图,每个房间都有门道通往过道,每相邻两个房间之间各有一扇门道.你能不能不重复地走一次穿过每扇门？如果不能,关闭哪扇门后,就能走一次不重复地穿过所有的门.4．编一本 683页的书,问：〔1〕排印这本书的页码共用了多少个数字？〔2〕其中数字“1〞在页码中共出现了几次？5．排一本辞典的页码共用了4889个数字.这本辞典共有多少页？6．把所有小于1993的四位数按从小到大的顺序排列起来,排在当中的四位数是几？7．用1、2、3、4四个数字排列起来,组成一个四位数,其中每个数字都用一次.象这样组成的所有不重复的四位数,它们的总和是多少,8．一本故事书,每2页文字之间有3页插图；如果这本书有99页,且第一页是文字,那么这本书共有多少页插图？9．有五根铁链条,每条有三个环〔如图〕.翻开一个环要用5分钟,焊接好一个环要用7分钟.如果要把这五根铁链连成一根长铁链,最少要用多少分钟？10．三盘桔子共有45只,如果从第一盘中拿出4只放到第二盘,再从第二盘中拿出7只放到第三盘,那么三个盘子中的桔子只数就完全相等.原来每盘桔子各有多少只？11．有一个池塘中的睡莲,每天长大一倍,经过20天可以把池塘全部遮满.那么,睡莲要遮住半个池塘需要经过多少天？12．有两只空瓶,一只可盛7千克水,另一只可盛5千克水.现在要利用这两只空瓶取得6千克水,应该怎样取？13．某校进行乒乓球单打比赛,参赛选手共56人,如果采用淘汰赛,最后产生冠军.那么一共要进行多少场比赛？14．第一小组有6个男同学,4个女同学,男同学的平均身高比女同学的平均身高高4厘米.小明在计算第一小组同学的平均身高时用男同学和女同学的平均身高的和去除以2求得.试问：小明这样求出的全组平均身高比正确的平均身高数高还是低？相差多少厘米？15．有43位同学,每人身上所带的钱数从8角到5元各不相同,且都是整角数,大家用自己所带的钱全部去买画片,画片有3角一张和5角一张两种,每个人都尽量多买5角一张的画片,那么他们所买的3角一张的画片总数是多少张？。

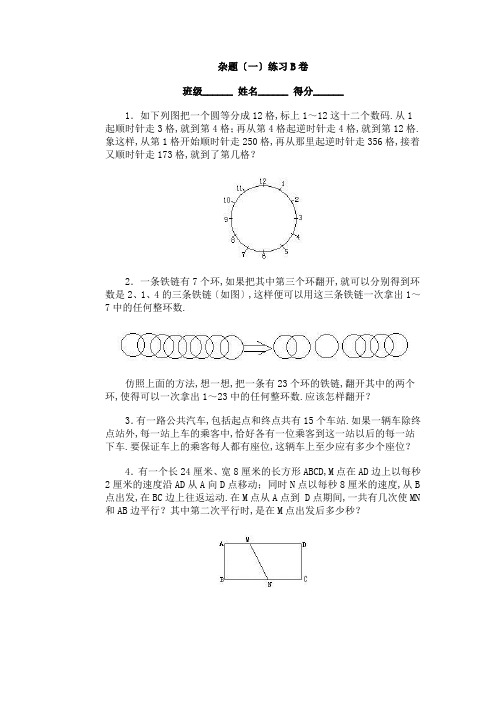
杂题〔一〕练习B卷班级______ 姓名______ 得分______1．如下列图把一个圆等分成12格,标上1～12这十二个数码.从1起顺时针走3格,就到第4格；再从第4格起逆时针走4格,就到第12格.象这样,从第1格开始顺时针走250格,再从那里起逆时针走356格,接着又顺时针走173格,就到了第几格？2．一条铁链有7个环,如果把其中第三个环翻开,就可以分别得到环数是2、1、4的三条铁链〔如图〕,这样便可以用这三条铁链一次拿出1～7中的任何整环数.仿照上面的方法,想一想,把一条有23个环的铁链,翻开其中的两个环,使得可以一次拿出1～23中的任何整环数.应该怎样翻开？3．有一路公共汽车,包括起点和终点共有15个车站.如果一辆车除终点站外,每一站上车的乘客中,恰好各有一位乘客到这一站以后的每一站下车.要保证车上的乘客每人都有座位,这辆车上至少应有多少个座位？4．有一个长24厘米、宽8厘米的长方形ABCD,M点在AD边上以每秒2厘米的速度沿AD从A向D点移动；同时N点以每秒8厘米的速度,从B 点出发,在BC边上往返运动.在M点从A点到 D点期间,一共有几次使MN 和AB边平行？其中第二次平行时,是在M点出发后多少秒？5．甲乙两人在圆形跑道上从同一点A出发,按相反方向运动,他们的速度分别是每秒2米和每秒6米.如果他们同时出发并当他们在A点第一次再相遇时为止,从出发到结束他们共相遇了几次？6．时针和分针在12点正重合,以后当他们第一次再重合时大约是什么时刻？7．工程师每天在同一时刻到达某站,然后乘上工厂定时来接的汽车按时到工厂.有一天工程师提前55分钟到某站,因汽车未到就步行向工厂走去,在路上遇见来接他的汽车后乘车比平时提前10分钟到达工厂.汽车每小时行50千米,工程师步行每小时行多少千米？8．小明放学后沿某路公共汽车路线以每小时4千米的速度回家,途中每隔9分钟有一辆公共汽车超过他；每隔6分钟遇见迎面开来的一辆公共汽车.如果公共汽车按相等的时间间隔发车,并以相同速度行驶,那么公共汽车每隔几分钟发一辆车？9．从1开始依次把自然数一一写下去得：1 2 3 4 5 6 7 8 9 10 11 12 13……从左向右数,数到第12个数字起将开始第一次出现三个连排的1.数到第几个数字起将开始出现五个连排的1.10．一个盆子内装了假设干只蟋蟀和蜘蛛,共有46只脚.蟋蟀比蜘蛛多,求盆内蟋蟀和蜘蛛各有几只？11．下列图是铅笔的截面图,中间有1支铅笔,外面要围住它,需用6支铅笔围成一周,用同样的铅笔再可在它的外面围上第二周、第三周.第三周共用几支铅笔围成？12．编号为1至10的十个果盘中,每盘都盛有水果,共盛放100个.其中第一盘里有16个,并且编号相邻的三个果盘中水果数的和都相等,求第8盘中水果最多可能有几个.。

高中物理奥林匹克竞赛试题
一、单项选择题：
1. 下列运动中，满足符合力学第二定律“力等于质量乘以加速度”的是（）
A. 抛体运动
B. 弹簧的压缩
C. 自由落体
D. 水平下抛体
2. 以下哪一种要素是正确的：（）
A. T型锁里的L型插杆的长度
B. 计算机的处理速度
C. 钢棒的弹性模量
D. 小车的最大速度
3. 绝热过程中，容积V，温度T关系为（）
A. V不变，T不变
B. V不变，T升高
C. V增大，T不变
D. V增大，T升高
4. 下列物理学术语中，错误的是（）
A. 功率：功/时
B. 电流：电位变化/时
C. 劲度：力/时
D. 速度：距离/时
二、多项选择题：
1. 关于光电效应，以下说法哪些正确（）
A. 光电效应可以产生电流
B. 光电效应是物体受到光照射后发生电磁波变化
C. 光电效应可用于探测物体的运动
D. 光电效应是原子核发射粒子时产生的现象
2. 有关烧结温度的制定，以下说法哪些正确（）
A. 烧结温度是晶体结构稳定的最低温度
B. 烧结温度较高，则晶粒较大
C. 烧结温度较高，则相的凝固程度较高
D. 烧结温度较低，则晶粒较大
3. 关于电磁波的性质，以下哪些说法正确（）
A. 电磁波的双稳态传播速度与光的传播速度相同
B. 电磁波可以反射和折射
C. 电磁波可以向物体传输能量
D. 电磁波不能靠固体传播。

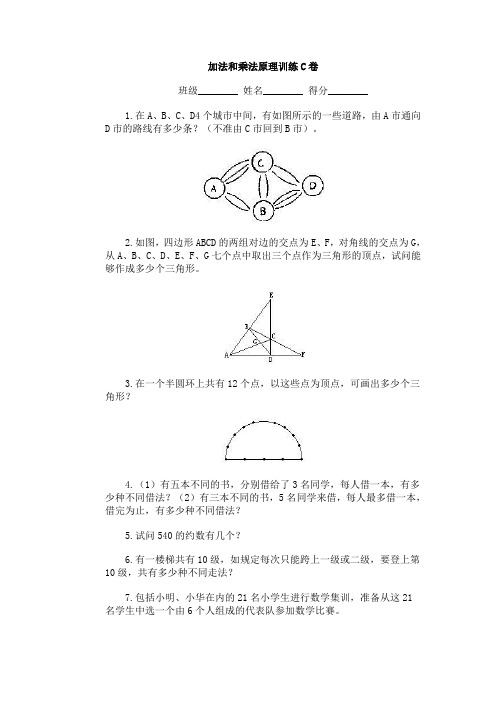
加法和乘法原理训练C卷班级________ 姓名________ 得分________1.在A、B、C、D4个城市中间，有如图所示的一些道路，由A市通向D市的路线有多少条？（不准由C市回到B市）。

2.如图，四边形ABCD的两组对边的交点为E、F，对角线的交点为G，从A、B、C、D、E、F、G七个点中取出三个点作为三角形的顶点，试问能够作成多少个三角形。

3.在一个半圆环上共有12个点，以这些点为顶点，可画出多少个三角形？4.（1）有五本不同的书，分别借给了3名同学，每人借一本，有多少种不同借法？（2）有三本不同的书，5名同学来借，每人最多借一本，借完为止，有多少种不同借法？5.试问540的约数有几个？6.有一楼梯共有10级，如规定每次只能跨上一级或二级，要登上第10级，共有多少种不同走法？7.包括小明、小华在内的21名小学生进行数学集训，准备从这21名学生中选一个由6个人组成的代表队参加数学比赛。

（1）小明、小华都是代表队员，共有多少种选法？（2）小明、小华都不是代表队员，共有多少种选法？（3）小明、小华至少有一个是代表队员，共有多少种选法？8.有10个外型相同的排球，其中正品6只，次品4只，从中任取3只，问3只中至多有2只次品的取法有多少种。

9.下图中的正方形被分割成9个相同的小正方形，它们一共有16个顶点，不在同一条直线上的三个点可以构成一个三角形，在这些三角形中与阴影三角形面积相同的有多少个？10.有男生7人，女生6人，从中选出4名中队委员，要求适合下列条件，各有多少种选法？（1）男、女学生各2名；（2）至少选1名女生。

11.父、母和4个孩子共6人，围着圆桌而坐，解答下列问题：（1）6人的坐法；（2）父母互相挨着的坐法；（3）父、母要面对面的坐法；（4）最小的孩子坐在父母中间，即父、母和最小的孩子互相挨着的坐法。

12.用数码0、1、2、3、4可以组成多少个（1）三位数；（2）没有重复数字的三位数；（3）没有重复数字的偶数；（4）小于1000的自然数。

精编小学数学奥林匹克ABC试卷02数字谜题精编小林匹克学数学奥编卷数字编编ABC02三、字编编数编编卷A班编姓名得分______ _____ _____填空编1.下列编式中每不同的编字表示个,中不同的字～求出编编使得编式成立。

数它并2.09在?入适的字～使下列算的编式成立内填当数运3.4.用,九字编成编式～把左面编式中的“个数改成相编的字。

使编式成立。

数19*”把下列编式中的“改成相编的字～使编式成立。

数5.*”下列各式左端是一位的四编算～编入数运填、、、及括等符～使得等式成立。

号号6.+-×?(1) 9 8 7 6 5 4 3 2 1=1 (2) 9 8 7 6 5 4 3 2 1=10(3) 9 8 7 6 5 4 3 2 1=100 (4) 9 8 7 6 5 4 3 2 1=1000 (5) 9 8 7 6 54 3 2 1=1993 (6) 9 8 7 65 4 3 2 1=1994 移编一根火柴～使下列等式能编成立。

7.已知一四位个数的倍是～求编四位。

个数8.abcd9dcba有一多位～的末位字是个数它数～如果把编个移到最左编～得到的新是原的数数9.444倍～求原。

数一三位～位字是个数个数～如果把位字移作百位字～原百位字移作十位个数数数10.3数字原十位字移作位字～那编所成的新比原少数个数数数～求原。

数;171编编卷B班编姓名得分_______ _______ _______ 将,七字分编入下列编式的?～使编式成立。

个数填内1.17下面的等式中?和?分编表示不同的自然～如果等式成立～那编?两个数。

2.=( );?=( )(?+?)+(?-?)+(?×?)+(???)=100把下列编式中的“改成相编的字～使编式成立。

数3.*”用个列出一加法算式～使的和等于个它。

4.(1)5228 用个列出一加法算式～使的和等于个它(2)881000 已知,??5.+?++?=16???+++?=13??++?+?=11?、?、?表示不同的自然～如果三等式都成立～编,?数个?。

杂题（二）训练C卷班级______ 姓名______ 得分______1．有一群鸡和兔，腿的总数比头的总数的2倍多60，兔子有（）只。

2．计算：1×2×3×4×5×6×7-（1+2×1×2+3×1×2×3+……+6×1×2×3×4×5×6）=（）3．租用仓库共堆放货物2吨，每月租金6千元，这些货原来估计要销售2个月，由于降低价格，结果1个月就销售完了，因而节省了租金。

结算下来，反而多赚1千元，每千克货物降低价格（）元。

4．直线1上最多能找到（）个点，使它与A、B一起组成等腰三角形的三个顶点。

5．某科学家设计了一只时钟，这只时钟每昼夜10小时，每小时100分钟（如图所示），当这只钟显示5点钟时，实际上是中午12点；当这只钟显示6点75分时，实际上是下午（）点（）分。

6．长江沿岸有A、B两码头，已知客船从A到 B航行每天行500千米，从B到A航行每天行400千米，如果客船在A、B两码头间往返航行5次共用18天，那么两码头间的距离是（）千米。

8．把1，2，3，4，5，6，7，8，9这九个数分别填在下面的九个方框中，可使以下等式成立：□□×□□=□□×□□=36349．下图是由竖直线和水平线组成的图形，（长度单位是米），过A 点画一条直线把这个图形分成面积相等的两部分，这条直线和边界相交于一点K，从A沿边界走到K点，较短的路程是（）米。

10．有一个长方形棋盘，每个小方格的边长都是1，长有200格、宽有120格（如图），纵横线交叉的点称为格点，连结A、B两点的线段共经过（）个格点（包括A、B两点）。

11. 有20个等式：1+2=34+5+6=7+89+10+11+12=13+14+15………………第20个等式的左右两边的和都是（）。

精编小学数学奥林匹克ABC试卷应用题(1)二、应用题(一)训练A卷班级______姓名______得分______(1)小阳期终考试时语文和数学的平均分数是96分，数学比语文多8分。

语文是( )分，数学是( )分。

(2)甲、乙两个仓库共存大米42吨，如果从甲仓库调3吨大米到乙仓库，那么两个仓库所存的大米就正好同样多。

原来甲仓库存大米( )吨，乙仓库存大米( )吨。

(3)爸爸和爷爷1994年的年龄加在一起是127岁，十年前爷爷比爸爸大37岁，爷爷是( )年出生的。

(4)有一个停车场上，现有24辆车，其中汽车是4个轮子，摩托车是3个轮子，这些车共有86个轮子。

其中摩托车有( )辆。

(5)参加少年宫科技小组的同学，今年比去年的3倍少35人，去年比今年少41人，今年参加科技小组的同学有( )人。

(6)父亲今年47岁，儿子今年19岁，( )年前父亲的年龄是儿子的5倍。

(7)一个植树小组植树，如果每人栽5棵，还剩14棵；如果每人栽7棵，就缺4棵。

这个植树小组有( )人，一共要栽( )棵树。

2．甲、乙、丙三数之和是1160，甲是乙的一半，乙是丙的2倍。

三个数各是多少？3．某招待所开会，每个房间住3人，则36人没床位；每个房间住4人，则还有13人没床位，如果每个房间住5人，那么情况又怎么样？4．小明读一本书，第一天读83页，第二天读74页，第三天读71页，第四天读64页，第五天读的页数比这五天中平均读的页数要多3.2页。

小明第五天读了多少页？5．在桥上测量桥高，把绳子对折后垂到水面时绳子还剩下8米；把绳子三折后，垂到水面时绳子还剩下2米，求桥高和绳长各是多少米。

6．44名学生去划船，一共乘坐10只船，其中每只大船坐6人，每只小船坐4人。

大船和小船各有多少只？7．实验小学四年级举行数学竞赛，一共出了10道题，答对一题得1 0分，答错一题倒扣5分。

张华把10道题全部做完，结果得了70分。

他答对了几道题？8．买4支铅笔和5块橡皮，共付6元；买同样的6支铅笔和2块橡皮，共付4.60元。

杂题（二）训练 A卷1．计算：275×35+88×360+53×275+365×88=（）2．计算：44444×55555÷11111＝（）3．计算：999999×999999+1999999=（）4．全班42人排成一列横队。

从左面数起，小华是第24个，从右面数起，小明是第24个，小华和小明之间有（）人。

5．如果被乘数增加15，乘数不变、积就增加180。

如果被乘数不变，乘数增加4，那么积就增加120，原来两个数相乘的积是（）。

6．有一个数自身相加、相减，相乘、相除，所得的结果的总和是81，这个数是（）。

7．把432个同样大小的正方形拼成一个长方形，一共有（）种不同的拼法。

8．把一个竹竿垂直插到一个蓄水池的池底，浸湿的部分是1.2米，掉过头把另一端垂直插到池底，这样没有浸湿的部分比全长的一半还少0.4米。

这根竹竿没有浸湿的部分长（）米。

9．小明在做减法时，把被减数十位上的8错看成3，把被减数个位上的5错看成6，这样算出来的差是108，正确的得数是（）。

10．有4个互不相等的自然数，最大数与最小数的差等于4，最小数与最大数的积是一个奇数，而这四个数的和是最小的两位奇数。

这四个数的积是多少？11．如果把一根长36厘米的铁丝围成长和宽都是整厘米数的长方形，一共有多少种围法？12．从1～9这九个数字中，每次取两个不同的数字组成一个两位数，而十位与个位上数字的和都必须比10大，这样的两位数一共有几个？13．有一块正方形木板，在它的第一边截去2分米，在相邻的第二边截去1分米，这样剩下部分的面积就比原来的少25平方分米，剩下的面积是多少平方分米？14．数一数下图中一共有（）个长方形（包括正方形）。

15．小明的妈妈买来一袋苹果和梨，已知苹果的只数是梨的2倍。

他们每天吃去5只苹果、4只梨。

几天以后，梨已吃完，还剩下15只苹果。

妈妈买来苹果多少只？16．三头牛和八只羊，一天共吃青草48千克；五头牛和十五只羊一天共吃青草85千克。

应用题〔二〕练习A卷班级_____姓名_____得分______1.填空题(1)一列快车和一列慢车,同时从甲、乙两站出发,相向而行,经过6小时相遇,相遇后快车继续行驶3小时后到达乙站.慢车每小时行45千米,甲、乙两站相距( )千米.(2)两辆卡车为农场送化肥,第一辆车以每小时30千米的速度由县城开往农场,第二辆车晚开了2小时,结果两车同时到达.县城到农场的距离是180千米,第二辆车每小时行( )千米.(3)一支队伍长450米,以每秒2米的速度前进,一个人以每秒3米的速度从队尾赶到队伍的最前面,然后再返回队尾,一共用了( )分钟.(4)一列火车长150米,每秒行19米.全车通过420米的大桥,需要( )分钟.(5)船在河中航行时,顺水速度是每小时12千米,逆水速度是每小时6千米.船速每小时( )千米,水速每小时( )千米.(6)有一根长2米的木料,如锯成每段长为4分米的短木料,需要24分钟；如果把它锯成每段长5分米的短木料,需要( )分钟.2．一列快车从甲城开往乙城,每小时行65千米,一列客车同时从乙城开往甲城,每小时行60千米,两列火车在距中点20千米处相遇,相遇时两车各行了多少千米？3．A、B两地相距38千米,甲、乙两人分别从两地同时出发,相向而行,甲每小时行8千米,乙每小时行11千米,甲到达B地后立即返回A地,乙到达A地后立即返回B地,几小时后两人在途中相遇？相遇时距A地多远？4．如图,A、B是圆的直径的两端,小张在A点,小王在B点同时出发,相向行走,他们在距A点80米处的C点第一次相遇,接着又在距B点60米处的D点第二次相遇.求这个圆的周长.15．一列火车通过一座 1000米的大桥要 65秒,如果用同样的速度通过一座 730米的隧道那么要50秒.求这列火车前进的速度和火车的长度.6．一只轮船在静水中的速度是每小时21千米,船从甲城开出逆水航行了8小时,到达相距144千米的乙城.这只轮船从乙城返回甲城需多少小时？7．相邻两根电线杆之间的距离是45米,从少年宫起到育英小学门口有36根电线杆,再往前585米是书店,求从少年宫到书店一共有多少根电线杆.8．解放军某部出动80辆汽车参加工地劳动,在途中要经过一个长120米的隧道.如果每辆汽车的长为10米,相邻两辆汽车相隔20米,那么,车队以每分钟500米的速度通过隧道,需要多少分钟？9．参加小学生运动会团体操的运发动排成一个正方形队列,如果要使这个正方形队列减少一行和一列,那么要减少33人.参加团体操表演的运发动有多少人？10．甲、乙两人从相距1100米的两地相向而行,甲每分钟走65米,乙每分钟走75米,甲出发4分钟后,乙才开始出发.乙带了一只狗和乙同时出发,狗以每分钟150米的速度向甲奔去,遇到甲后立即回头向乙奔去,遇到乙后又回头向甲奔去,直到甲、乙两人相遇时狗才停止.这只狗共奔跑了多少路程？。

夏季奥林匹克试题及答案一、选择题（每题2分，共10分）1. 夏季奥林匹克运动会的创始人是：A. 顾拜旦B. 皮埃尔·德·顾拜旦C. 奥托·哈恩D. 阿尔弗雷德·诺贝尔答案：B2. 夏季奥林匹克运动会的会旗由几个环组成？A. 4个B. 5个C. 6个D. 7个答案：B3. 第一届夏季奥林匹克运动会是在哪一年举行的？A. 1894B. 1896C. 1900D. 1912答案：B4. 夏季奥林匹克运动会的火炬接力始于：A. 1928年B. 1936年C. 1948年D. 1952年答案：B5. 下列哪项运动不是夏季奥林匹克运动会的正式比赛项目？A. 田径B. 游泳C. 滑雪D. 篮球答案：C二、填空题（每题2分，共10分）1. 夏季奥林匹克运动会每____年举办一次。

答案：42. 夏季奥林匹克运动会的口号是“更快、更高、更强”。

答案：更团结3. 夏季奥林匹克运动会的吉祥物通常代表____。

答案：东道国的文化4. 夏季奥林匹克运动会的火炬接力象征着____。

答案：和平与友谊5. 夏季奥林匹克运动会的会旗上，五个环代表的是____。

答案：五大洲三、简答题（每题5分，共20分）1. 简述夏季奥林匹克运动会的起源。

答案：夏季奥林匹克运动会起源于古希腊的奥林匹克运动会，现代奥运会由法国人皮埃尔·德·顾拜旦于1894年提出复兴，并在1896年成功举办了第一届现代奥运会。

2. 夏季奥林匹克运动会的会旗上的五个环分别代表哪些大洲？答案：夏季奥林匹克运动会的会旗上的五个环分别代表欧洲、亚洲、非洲、大洋洲和美洲。

3. 夏季奥林匹克运动会的火炬接力有何象征意义？答案：夏季奥林匹克运动会的火炬接力象征着奥林匹克精神的传递，它从希腊奥林匹亚点燃，经过各个参赛国，最终到达主办城市，象征着和平、友谊和团结。

4. 夏季奥林匹克运动会的吉祥物是如何被选定的？答案：夏季奥林匹克运动会的吉祥物由主办国设计，通常反映了东道国的文化特色和奥林匹克精神，通过公开征集和评选的方式选定。

奥林匹克ABC题库·奇偶性训练C卷奇偶性训练C卷班级_______ 姓名_______ 得分_______1.一质数连乘4次再加上3是质数,求这个数连乘5次再加上3是多少?2.一个四位数是常数,它的首位数字小于其余各位数字,而第二位数字是个位数字的3倍,第三位数字比首末两位数字和2倍多1,求这个四位数.3.师傅与徒弟加工同一种零件,各人把产品放在自己的箩筐里,师傅的产量是徒弟的2倍,师傅的产品放在4只箩筐里,徒弟的产品放在2只箩筐里,每只箩筐都标明了产品的只数:78.94.86.87.82.80,根据上述条件你能找出哪2只箩筐的产品是徒弟制造的?4.教室里共有男女生若干人,男生的上衣有5个扣子,女生的上衣有4个扣子,如果学生总数是个奇数,扣子总数是偶数,问男生人数是奇数还是偶数?5.桌子上放着7只杯子,有3只杯口朝上,4只杯口朝下,每个人任意将杯子翻动5次,问若干人翻动后,能否将7只杯子全变成杯口朝下?如能,至少需要几个人来翻动?6.某年级150名同学准备选一名同学在教师节庆祝会上给老师献花.选举的方法是:让150名同学排成一排,由第一名开始报数,报奇数的同学落选退出队列,报偶数的同学站在原位不动,然后再从头报数,如此继续下去,最后剩下的一名当选.小胖非常想去,他在第一次排队时应该站在队列的什么位置才能被选中?7.某展览馆是由5_5小正方形组成的25间展览室,相邻的两室之间有一门相通,只有一间展览室为进出口房间,一人打算从进出口开始,不重复也不遗漏地依次看完每一展室,然后出来,问此人能否做到?8.某市举办小学生数学竞赛,共30道试题,评分标准是基础分15分,答对一题给5分,不答一题给1分,答错一题倒扣1分,如果199人参赛,问参赛的同学的总得分是奇数还是偶数?9.下面是一个乘法算式,式中〝偶〞字表示偶数(0.2.4.6.8),〝奇〞字表示奇数(1.3.5.7.9),请写出这个算式.10.走廊里有10盏电灯,从1到10编号,开始时电灯全部关闭,有10个学生依次通过走廊,第一个学生把所有的开关的拖绳拉一下,第二个学生把2的倍数号灯的拖绳都拉一下,第三个学生把3的倍数号灯的拖绳都拉一下,……最后第十个学生把10的倍数号灯的拖绳都拉一下.(拖绳每拉动一次不亮的灯变亮,亮的灯变不亮)试判定:当这10个学生都拉动过拖绳后,走廊里哪些编号的灯是亮着的?。

分析与推理训练C卷班级______ 姓名______ 得分______1．小军爷爷诞生的年份数是他逝世时年龄的29倍，小军爷爷在1955年主持过一次学术会议，问小军爷爷那时的年龄多大？2．有三顶红帽、两顶白帽，现将其中三顶给排成一列的三人每人戴一顶，每人只能看见自己前面人的帽，现让三人从后到前依次回答自己头上戴的帽什么颜色，后面的人回答不明白，中间的人也回答不明白，依照这两个人的回答，你能不能明白最前面的人戴的帽是什么颜色？3．A、B、C三个足球队进行了循环赛，下表给出了竞赛的部份结果，请你依照已有的数填满下表，并指出各场竞赛的结果。

4．张教师、李教师、刘教师三人在北京、上海、广州中学教不同的课程：数学、语文、外语。

又明白：（1）张教师不在北京工作；（2）李教师不在上海工作；（3）在北京的不教外语；（4）在上海工作的教数学；（5）李教师不教语文。

问：三位教师各在哪个城市？各教什么课程？5．某校举行作文竞赛，甲、乙、丙、丁、戍五位同窗得了前五名，发奖前，教师让他们猜一猜各人的名次排列情形。

甲说：乙第三名，丙第五名；乙说：戍第四名，丁第五名；丙说：甲第一名，戍第四名；丁说：丙第一名，乙第二名；戍说：甲第三名，丁第四名；教师说：每一个名次都有人猜对。

那么名次该如何排列呢？6．四纸卡片上别离写着努、力、学、习四个字（一张上写一个字），掏出其中三张覆盖在桌面上，甲、乙、丙别离猜每张卡片上是什么字，具体如下表：结果每一张上的字至少有一人料中，所猜三次中，有一人一次也没料中，有两人别离料中了两次和三次。

问这三张卡片上各是什么字？7．A、B、C、D、E、F六人别离是中国、日本、美国、英国、法国、德国人。

此刻已知：（1）A和中国人是医生；（2）E和法国人是教师；（3）C和日本人是警察；（4）B和F曾当过兵，日本人从未当过兵；（5）英国人比A年龄大，德国人比C年龄大；（6）B同中国人下周要到中国去旅行，而C同英国人下周要到瑞士去度假。

夏季奥林匹克试题答案一、选择题1. 奥林匹克运动会的发源地是：A. 希腊B. 法国C. 英国D. 中国答案：A2. 夏季奥林匹克运动会自1896年起，每隔几年举办一次？A. 两年B. 四年C. 六年D. 八年答案：B3. 第一届现代奥林匹克运动会于1896年在哪个城市举办？A. 伦敦B. 巴黎C. 雅典D. 罗马答案：C4. 奥林匹克五环标志中，哪个颜色的环位于最中间？A. 蓝色B. 黑色C. 红色D. 绿色答案：A5. 奥林匹克运动会的格言是？A. 更快、更高、更强B. 友谊第一、比赛第二C. 公平竞争D. 团结、友谊、进步答案：A二、填空题1. 奥林匹克运动会的创始人是________，他是法国人。

答案：皮埃尔·德·顾拜旦2. 夏季奥林匹克运动会历史上，举办次数最多的城市是________。

答案：伦敦3. 奥林匹克运动会的宗旨是通过体育活动促进全世界的________和________。

答案：和平友谊4. 奥林匹克运动会的火炬传递始于________年的柏林奥运会。

答案：19365. 夏季奥林匹克运动会中，第一个设立女子比赛项目是在________年。

答案：1900三、简答题1. 请简述奥林匹克运动会的历史意义。

答：奥林匹克运动会不仅是全球最大的体育盛事，更是文化交流和国际友谊的重要平台。

它起源于古希腊的奥林匹克运动会，现代奥林匹克运动会的复兴旨在通过体育竞技促进世界各国之间的相互理解和尊重。

奥林匹克运动会的举办，不仅推动了体育运动的发展，也促进了世界各国人民之间的和平与友谊。

2. 描述奥林匹克运动会的火炬传递仪式及其象征意义。

答：奥林匹克火炬传递是奥运会开幕前的一项重要活动，象征着和平、友谊和希望的传递。

火炬由奥林匹亚的圣火点燃，然后通过成千上万的火炬手传递，穿越不同的国家和地区，最终到达主办城市的奥运会主会场。

火炬传递不仅是对古代奥林匹克传统的致敬，也是对现代奥林匹克精神的传播。