圆心距和相交两圆公共弦的关系
- 格式:doc
- 大小:17.33 KB
- 文档页数:1

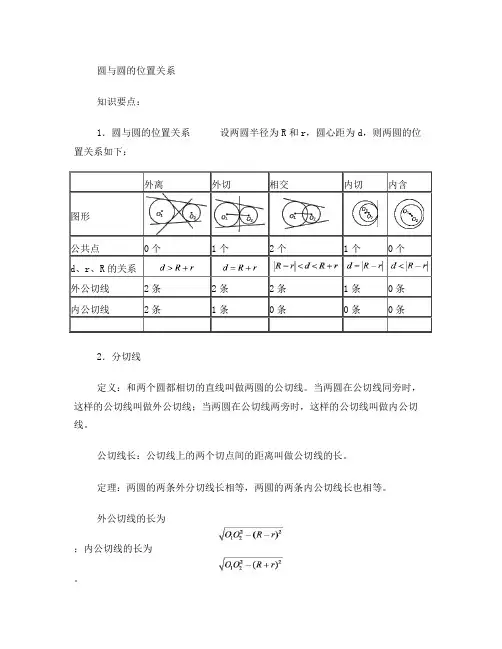
圆与圆的位置关系知识要点:1.圆与圆的位置关系设两圆半径为R和r,圆心距为d,则两圆的位置关系如下:2.分切线定义:和两个圆都相切的直线叫做两圆的公切线。
当两圆在公切线同旁时,这样的公切线叫做外公切线;当两圆在公切线两旁时,这样的公切线叫做内公切线。
公切线长:公切线上的两个切点间的距离叫做公切线的长。
定理:两圆的两条外分切线长相等,两圆的两条内公切线长也相等。
外公切线的长为;内公切线的长为。
3.相交两圆的性质定理:相交两圆的连心线垂直平分两圆的公共弦。
4.相切两圆的性质定理:相切两圆的连心线经过切点。
1.圆和圆的位置关系(设两圆半径分别为R和r,同心距为d)(1)两圆外离d>R+r;(2)两圆外切d=R+r;(3)两圆相交R-r<d<R+r;(4)两圆内切d=R-r;(5)两圆内含d<R-r。
(同心圆(6)是一种内含的特例)2.有关性质:(1)连心线:通过两圆圆心的直线。
如果两个圆相切,那么切点一定在连心线上。
(2)公共弦:相交两圆的连心线垂直平分两圆的公共弦。
(3)公切线:和两个圆都相切的直线,叫做两圆的公切线。
两个圆在公切线同旁两个圆在公切线两旁3.已知两圆半径分别为R、r,同心距为d,填定下表:名称公共点数圆心距半径关系公切线条数内外外离d=R+r相交d=R-r内含一星级题:1.如果两圆有且只有两条公切线,那么这两圆的位置关系是()A.外离 B.外切 C.相交 D.内含2.如果两圆半径分别为3㎝和5㎝,圆心距为2㎝,则两个圆的位置关系为()。
A.外离 B.外切 C.相交 D.内切3.已知⊙O1和⊙O2内切,它们的半径分别为2㎝和3㎝,则两圆圆心距O1O2= ㎝。
4.半径分别为3㎝和4㎝的两圆外切,那么这两圆的圆心距为㎝。
5.已知半径为R的两个等圆的圆心距为d,那么当两圆外切时,d与R满足的关系式是。
6.已知两圆半径分别为5㎝和2㎝,它们的圆心距为7㎝,则两圆位置关系为。
7.已知:两圆⊙O1与⊙O2的圆心距O1O2=5㎝,两圆的半径分别为㎝和㎝,则这两圆的位置关系是。

4.2.2 圆与圆的位置关系4.2.3 直线与圆的方程的应用目标定位 1.掌握圆与圆的位置关系及判定方法.2.能利用直线与圆的位置关系解决简单的实际问题.3.理解坐标法解决几何问题的一般步骤.自主预习1.圆与圆位置关系的判定(1)几何法:若两圆的半径分别为r1、r2,两圆的圆心距为d,则两圆的位置关系的判断方法如下:位置关系外离外切相交内切内含图示d与r1、r2的关系d>r1+r2d=r1+r2|r1-r2|<d<r1+r2d=|r1-r2| d<|r1-r2|(2)代数法:通过两圆方程组成方程组的公共解的个数进行判断.⎭⎪⎬⎪⎫圆C 1方程圆C 2方程――→消元一元二次方程⎩⎪⎨⎪⎧Δ>0⇒相交Δ=0⇒内切或外切Δ<0⇒外离或内含2.用坐标方法解决平面几何问题的“三步曲”:即 时 自 测1.判断题(1)两圆无公共点,则两圆外离.( ×)(2)两圆有且只有一个公共点,则两圆内切和外切.(√)(3)设两圆的圆心距为l ,两圆半径长分别为r 1,r 2,则当|r 1-r 2|<l <r 1+r 2时,两圆相交.(√)(4)两圆外切时,有三条公切线:两条外公切线,一条内公切线.(√) 提示 (1)两圆无公共点,则两圆外离和内含.2.圆O 1:x 2+y 2-2x =0和圆O 2:x 2+y 2-4y =0的位置关系为( ) A.相离B.相交C.外切D.内切解析 圆O 1的圆心坐标为(1,0),半径长r 1=1;圆O 2的圆心坐标为(0,2),半径长r 2=2;1=r 2-r 1<|O 1O 2|=5<r 1+r 2=3,即两圆相交. 答案 B3.圆x 2+y 2+4x -4y +7=0与圆x 2+y 2-4x +10y +13=0的公切线的条数是( ) A.1B.2C.3D.4解析 两圆的圆心坐标和半径分别为(-2,2),(2,-5),1,4,圆心距d =(-2-2)2+(2+5)2>8,1+4=5<8,∴两圆相离,公切线有4条. 答案 D4.两圆x 2+y 2=r 2与(x -3)2+(y +1)2=r 2(r >0)外切,则r 的值是________.解析 由题意可知(3-0)2+(-1-0)2=2r ,∴r =102. 答案102类型一 与两圆相切有关的问题【例1】 求与圆x 2+y 2-2x =0外切且与直线x +3y =0相切于点M (3,-3)的圆的方程. 解 设所求圆的方程为(x -a )2+(y -b )2=r 2(r >0), 则(a -1)2+b 2=r +1,①b +3a -3=3,② |a +3b |2=r .③ 联立①②③解得a =4,b =0,r =2,或a =0,b =-43,r =6,即所求圆的方程为(x -4)2+y 2=4或x 2+(y +43)2=36. 规律方法 两圆相切时常用的性质有:(1)设两圆的圆心分别为O 1、O 2,半径分别为r 1、r 2,则两圆相切⎩⎪⎨⎪⎧内切⇔|O 1O 2|=|r 1-r 2|外切⇔|O 1O 2|=r 1+r 2(2)两圆相切时,两圆圆心的连线过切点(两圆若相交时,两圆圆心的连线垂直平分公共弦). 【训练1】 求与圆(x -2)2+(y +1)2=4相切于点A (4,-1)且半径为1的圆的方程. 解 设所求圆的圆心为P (a ,b ),则 (a -4)2+(b +1)2=1.①(1)若两圆外切,则有(a -2)2+(b +1)2=1+2=3,②联立①②,解得a =5,b =-1,所以,所求圆的方程为(x -5)2+(y +1)2=1; (2)若两圆内切,则有(a -2)2+(b +1)2=|2-1|=1,③联立①③,解得a =3,b =-1,所以,所求圆的方程为(x -3)2+(y +1)2=1. 综上所述,所求圆的方程为(x -5)2+(y +1)2=1或(x -3)2+(y +1)2=1. 类型二 与两圆相交有关的问题(互动探究)【例2】 已知两圆x 2+y 2-2x +10y -24=0和x 2+y 2+2x +2y -8=0.(1)判断两圆的位置关系; (2)求公共弦所在的直线方程; (3)求公共弦的长度. [思路探究]探究点一 当两圆相交时,其公共弦所在直线的方程是什么? 提示 两圆的方程相减即可得公共弦所在直线的方程. 探究点二 如何求公共弦长?提示 (1)代数法:将两圆的方程联立,求出两交点的坐标,利用两点间的距离公式求弦长. (2)几何法:求出公共弦所在的直线方程,半径、弦心距、半弦长构成直角三角形的三边长,利用勾股定理求弦长.解 (1)将两圆方程配方化为标准方程,C 1:(x -1)2+(y +5)2=50, C 2:(x +1)2+(y +1)2=10,则圆C 1的圆心为(1,-5),半径r 1=52, 圆C 2的圆心为(-1,-1),半径r 2=10.又∵|C 1C 2|=25,r 1+r 2=52+10,r 1-r 2=52-10, ∴r 1-r 2<|C 1C 2|<r 1+r 2,∴两圆相交.(2)将两圆方程相减,得公共弦所在直线方程为x -2y +4=0. (3)法一 由(2)知圆C 1的圆心(1,-5)到直线x -2y +4=0的距离d =|1-2×(-5)+4|1+(-2)2=35, ∴公共弦长l =2r 21-d 2=250-45=2 5.法二 设两圆相交于点A ,B ,则A ,B 两点满足方程组⎩⎪⎨⎪⎧x -2y +4=0,x 2+y 2+2x +2y -8=0, 解得⎩⎪⎨⎪⎧x =-4,y =0,或⎩⎪⎨⎪⎧x =0,y =2.即A (-4,0),B (0,2).所以|AB |=(-4-0)2+(0-2)2=25, 即公共弦长为2 5.规律方法 1.两圆相交时,公共弦所在的直线方程若圆C 1:x 2+y 2+D 1x +E 1y +F 1=0与圆C 2:x 2+y 2+D 2x +E 2y +F 2=0相交,则两圆公共弦所在直线的方程为(D 1-D 2)x +(E 1-E 2)y +F 1-F 2=0.2.公共弦长的求法(1)代数法:将两圆的方程联立,解出交点坐标,利用两点间的距离公式求出弦长. (2)几何法:求出公共弦所在直线的方程,利用圆的半径、半弦长、弦心距构成的直角三角形,根据勾股定理求解.【训练2】 已知圆C 1:x 2+y 2+2x -6y +1=0,圆C 2:x 2+y 2-4x +2y -11=0,求两圆的公共弦所在的直线方程及公共弦长.解 设两圆交点为A (x 1,y 1),B (x 2,y 2),则A ,B 两点坐标是方程组⎩⎪⎨⎪⎧x 2+y 2+2x -6y +1=0, ①x 2+y 2-4x +2y -11=0 ②的解, ①-②得:3x -4y +6=0. ∵A ,B 两点坐标都满足此方程,∴3x -4y +6=0即为两圆公共弦所在的直线方程. 易知圆C 1的圆心(-1,3),半径r 1=3. 又C 1到直线AB 的距离为d =|-1×3-4×3+6|32+(-4)2=95. ∴|AB |=2r 21-d 2=232-⎝ ⎛⎭⎪⎫952=245.即两圆的公共弦长为245.类型三 直线与圆的方程的应用【例3】 一艘轮船沿直线返回港口的途中,接到气象台的台风预报,台风中心位于轮船正西70 km 处,受影响的范围是半径为30 km 的圆形区域,已知港口位于台风中心正北40 km 处,如果这艘轮船不改变航线,那么它是否会受到台风的影响?解 以台风中心为坐标原点,以东西方向为x 轴建立直角坐标系(如图),其中取10 km 为单位长度,则受台风影响的圆形区域所对应的圆的方程为x 2+y 2=9, 港口所对应的点的坐标为(0,4),轮船的初始位置所对应的点的坐标为(7,0), 则轮船航线所在直线l 的方程为x 7+y4=1, 即4x +7y -28=0.圆心(0,0)到航线4x+7y-28=0的距离d=|28|42+72=2865,而半径r=3,∴d>r,∴直线与圆相离,所以轮船不会受到台风的影响.规律方法解决直线与圆的方程的实际应用题时应注意以下几个方面:【训练3】台风中心从A地以20千米/时的速度向东北方向移动,离台风中心30千米内的地区为危险区,城市B在A的正东40千米处,B城市处于危险区内的时间为( )A.0.5小时B.1小时C.1.5小时D.2小时解析以台风中心A为坐标原点建立平面直角坐标系,如图,则台风中心在直线y=x上移动,又B(40,0)到y=x的距离为d=202,由|BE|=|BF|=30知|EF|=20,即台风中心从E到F时,B城市处于危险区内,时间为t=20千米20千米/时=1小时.故选B.答案 B[课堂小结]1.判断圆与圆位置关系的方式通常有代数法和几何法两种,其中几何法较简便易行、便于操作.2.直线与圆的方程在生产、生活实践以及数学中有着广泛的应用,要善于利用其解决一些实际问题,关键是把实际问题转化为数学问题;要有意识用坐标法解决几何问题,用坐标法解决平面几何问题的思维过程:1.圆x 2+y 2=1与圆x 2+y 2+2x +2y +1=0的交点坐标为( ) A.(1,0)和(0,1) B.(1,0)和(0,-1) C.(-1,0)和(0,-1)D.(-1,0)和(0,1)解析 由⎩⎪⎨⎪⎧x 2+y 2=1,x 2+y 2+2x +2y +1=0;解得⎩⎪⎨⎪⎧x =0,y =-1或⎩⎪⎨⎪⎧x =-1,y =0. 答案 C2.圆x 2+y 2-2x -5=0和圆x 2+y 2+2x -4y -4=0的交点为A 、B ,则线段AB 的垂直平分线方程为( ) A.x +y -1=0 B.2x -y +1=0 C.x -2y +1=0D.x -y +1=0解析 直线AB 的方程为:4x -4y +1=0,因此它的垂直平分线斜率为-1,过圆心(1,0),方程为y =-(x -1),即两圆连心线. 答案 A3.已知两圆x 2+y 2=10和(x -1)2+(y -3)2=20相交于A 、B 两点,则直线AB 的方程是________.解析 ⎩⎪⎨⎪⎧x 2+y 2=10,x 2+y 2-2x -6y =10⇒2x +6y =0,即x +3y =0. 答案 x +3y =04.已知圆C 1:x 2+y 2-2mx +4y +m 2-5=0,圆C 2:x 2+y 2+2x -2my +m 2-3=0,当m 的取值满足什么条件时,圆C 1与圆C 2相切?解 对于圆C 1与圆C 2的方程,化为标准方程得C 1:(x -m )2+(y +2)2=9,C 2:(x +1)2+(y -m )2=4,所以两圆的圆心分别为C 1(m ,-2),C 2(-1,m ),半径分别为r 1=3,r 2=2,且|C 1C 2|=(m +1)2+(m +2)2.当圆C 1与圆C 2相外切时,则|C 1C 2|=r 1+r 2,即(m +1)2+(m +2)2=3+2,解得m =-5或m =2.当圆C 1与圆C 2相内切时,则|C 1C 2|=|r 1-r 2|,即(m +1)2+(m +2)2=|3-2|,解得m =-1或m =-2.综上可知,当m =-5或m =2或m =-1或m =-2时,两圆相切.基 础 过 关1.圆(x +2)2+y 2=4与圆(x -2)2+(y -1)2=9的位置关系为( ) A.内切B.相交C.外切D.相离解析 两圆圆心分别为(-2,0),(2,1),半径分别为2和3,圆心距d =42+1=17.∵3-2<d <3+2,∴两圆相交. 答案 B2.若圆C 1:x 2+y 2=1与圆C 2:x 2+y 2-6x -8y +m =0外切,则m 等于( ) A.21B.19C.9D.-11解析 圆C 2的标准方程为(x -3)2+(y -4)2=25-m . 又圆C 1:x 2+y 2=1,∴|C 1C 2|=5.又∵两圆外切,∴5=1+25-m ,解得m =9. 答案 C3.一辆卡车宽1.6米,要经过一个半径为3.6米的半圆形隧道,则这辆卡车的平顶车蓬蓬顶距地面的高度不得超过( ) A.1.4米B.3.5米C.3.6米D.2米解析 建立如图所示的平面直角坐标系.如图设蓬顶距地面高度为h ,则A (0.8,h -3.6)半圆所在圆的方程为:x 2+(y +3.6)2=3.62把A (0.8,h -3.6)代入得0.82+h 2=3.62.∴h =40.77≈3.5(米).答案 B4.两圆x 2+y 2-x +y -2=0和x 2+y 2=5的公共弦长为________.解析 由⎩⎪⎨⎪⎧x 2+y 2-x +y -2=0,x 2+y 2=5,①②②-①得两圆的公共弦所在的直线方程为x -y -3=0, ∴圆x 2+y 2=5的圆心到该直线的距离为d =|-3|1+(-1)2=32,设公共弦长为l ,∴l =25-⎝ ⎛⎭⎪⎫322= 2. 答案25.已知圆C 1:x 2+y 2=4和圆C 2:x 2+y 2+4x -4y +4=0关于直线l 对称,则直线l 的方程为________.解析 圆C 2可化为(x +2)2+(y -2)2=4,则圆C 1,C 2的圆心为C 1(0,0),C 2(-2,2),所以C 1C 2的中点为(-1,1),kC 1C 2=2-0-2-0=-1,所以所求直线的斜率为1,所以直线l 的方程为y -1=x +1,即x -y +2=0. 答案 x -y +2=06.求与圆O :x 2+y 2=1外切,切点为P ⎝ ⎛⎭⎪⎫-12,-22,半径为2的圆的方程.解 设所求圆的圆心为C (a ,b ),则所求圆的方程为 (x -a )2+(y -b )2=4.∵两圆外切,切点为P ⎝ ⎛⎭⎪⎫-12,-22,∴|OC |=1+2=3,|CP |=2.∴⎩⎨⎧a 2+b 2=9,⎝ ⎛⎭⎪⎫a +122+⎝ ⎛⎭⎪⎫b +322=4,解得⎩⎪⎨⎪⎧a =-32,b =-332. ∴圆心C 的坐标为⎝ ⎛⎭⎪⎫-32,-332,故所求圆的方程为⎝ ⎛⎭⎪⎫x +322+⎝ ⎛⎭⎪⎫y +3322=4.7.已知圆C 1:x 2+y 2-10x -10y =0和圆C 2:x 2+y 2+6x -2y -40=0.求: (1)它们的公共弦所在直线的方程; (2)公共弦长.解 (1)由⎩⎪⎨⎪⎧x 2+y 2-10x -10y =0,x 2+y 2+6x -2y -40=0,两方程相减,得公共弦所在直线方程为2x +y -5=0. (2)圆x 2+y 2-10x -10y =0的圆心C 1的坐标为(5,5),半径r =52,又点C 1到相交弦的距离d =|2×5+5-5|22+12=2 5. ∴公共弦长为2(52)2-(25)2=230.能 力 提 升8.设两圆C 1,C 2都和两坐标轴相切,且都过点(4,1),则两圆心的距离|C 1C 2|等于( ) A.4B.4 2C.8D.8 2解析 ∵两圆与两坐标轴都相切,且都经过点(4,1), ∴两圆圆心均在第一象限且横、纵坐标相等. 设两圆的圆心分别为(a ,a ),(b ,b ),则有(4-a )2+(1-a )2=a 2,(4-b )2+(1-b )2=b 2, 即a ,b 为方程(4-x )2+(1-x )2=x 2的两个根, 整理得x 2-10x +17=0,∴a +b =10,ab =17. ∴(a -b )2=(a +b )2-4ab =100-4×17=32, ∴|C 1C 2|=(a -b )2+(a -b )2=32×2=8. 答案 C9.以圆C 1:x 2+y 2+4x +1=0与圆C 2:x 2+y 2+2x +2y +1=0相交的公共弦为直径的圆的方程为( )A.(x -1)2+(y -1)2=1 B.(x +1)2+(y +1)2=1C.⎝ ⎛⎭⎪⎫x +352+⎝ ⎛⎭⎪⎫y +652=45D.⎝ ⎛⎭⎪⎫x -352+⎝ ⎛⎭⎪⎫y -652=45解析 两圆方程相减得公共弦所在直线的方程为x -y =0,因此所求圆的圆心的横、纵坐标相等,排除C ,D 选项,画图(图略)可知所求圆的圆心在第三象限,排除A.故选B. 答案 B10.与直线x +y -2=0和曲线x 2+y 2-12x -12y +54=0都相切的半径最小的圆的标准方程是________.解析 曲线化为(x -6)2+(y -6)2=18,其圆心C 1(6,6)到直线x +y -2=0的距离为d =|6+6-2|2=5 2.过点C 1且垂直于x +y -2=0的直线为y -6=x -6,即y =x ,所以所求的最小圆的圆心C 2在直线y =x 上,如图所示,圆心C 2到直线x +y -2=0的距离为52-322=2,则圆C 2的半径长为 2.设C 2的坐标为(x 0,x 0),则|x 0+x 0-2|2=2, 解得x 0=2(x 0=0舍去),所以圆心坐标为(2,2),所以所求圆的标准方程为(x -2)2+(y -2)2=2.答案 (x -2)2+(y -2)2=211.已知隧道的截面是半径为4 m 的半圆,车辆只能在道路中心线一侧行驶,一辆宽为2.7 m ,高为3 m 的货车能不能驶入这个隧道?假设货车的最大宽度为a m ,那么要正常驶入该隧道,货车的限高为多少?解 以某一截面半圆的圆心为坐标原点,半圆的直径AB 所在直线为x 轴,建立如图所示的平面直角坐标系,那么半圆的方程为x 2+y 2=16(y ≥0).将x =2.7代入,得y =16-2.72=8.71<3,所以,在离中心线2.7 m 处,隧道的高度低于货车的高度.因此,货车不能驶入这个隧道.将x =a 代入x 2+y 2=16(y ≥0)得y =16-a 2.所以,货车要正常驶入这个隧道,最大高度(即限高)为16-a 2m.探 究 创 新12.已知圆C 1:x 2+y 2-4x -2y -5=0与圆C 2:x 2+y 2-6x -y -9=0.(1)求证:两圆相交;(2)求两圆公共弦所在的直线方程;(3)在平面上找一点P ,过点P 引两圆的切线并使它们的长都等于6 2.(1)证明 圆C 1:(x -2)2+(y -1)2=10, 圆C 2:(x -3)2+⎝ ⎛⎭⎪⎫y -122=734. ∵|C 1C 2|=(2-3)2+⎝ ⎛⎭⎪⎫1-122=52.且732-10<52<732+10, ∴圆C 1与圆C 2相交.(2)解 联立两圆方程,得⎩⎪⎨⎪⎧x 2+y 2-4x -2y -5=0,x 2+y 2-6x -y -9=0, ∴两圆公共弦所在的直线方程为2x -y +4=0.(3)解 设P (x ,y ),由题意,得⎩⎨⎧2x -y +4=0,x 2+y 2-6x -y -9=(62)2,解方程组,得点P 的坐标为(3,10)或⎝ ⎛⎭⎪⎫-233,-265.。

弦长公式在相交两圆中的运用-CAL-FENGHAI.-(YICAI)-Company One1弦长公式在相交两圆中的运用重庆市永川区第六中学校 潘祥万(402182)问题:求两圆04026,010102222=-+++=--+y x y x y x y x 的公共弦的长。
(高二数学(上),人教版,P 88 24题)对于此题,我们很多时候都是把这两个方程联立组成方程组,求出其交点坐标,再根据两点间的距离公式求解,这是一种常规解法。
下面,我想就相交两圆公共弦长公式的推导及运用谈点个人看法。
一、弦长公式的推导在初中,我们就知道两圆相交时弦长的求法。
对于高中数学中的相交两圆弦长如何求,大部分学生感到不知所措,甚至解题的方向也把握不准,基于此,我在教学中,我在引领学生回忆初中知识的同时,让学生把所学的知识在头脑中重组、建构,形成一定的网络,更好地为教学服务。
推导:对于圆的一般方程:022=++++F Ey Dx y x (其中0422>-+F E D )和圆的标准方程:222)()(R b y a x =-+-。
这是我们应该熟悉的两个方程,要求学生必须能够互化。
如果两圆222)()(r b y a x =-+-和222)()(R b y a x ='-+'-相交,求公共弦长。
在这里必须引导学生对问题进行分析,看它圆心在弦的同旁,还是两旁。
(一)、两圆心在公共弦的两旁时,公共弦长AB 的求法如图1:设相交两圆的圆心分别为O ),(b a ,),(b a O ''',半径分别为R r ,,圆心距(O O ')为d ,则在Rt △ACO 与Rt △AC O '中有222222,AC O A C O OC AO AC -'='-=,又O O '=OC+C O '=d ,∴C O '=d -OC,∴222222)(,AC R OC d OC r AC -=--=,∴22222)(AC R AC r d -=--,其中22)()(b b a a d -'+-'=图1化简得:AB=2AC=[][]d r R d d r R 2222)()(---+ )(r R ≥ ① (二)、两圆心在公共弦的同旁时,公共弦长AB 的求法如右图,设相交两圆的圆心分别为O ),(b a ,),(b a O ''',半径分别为)(,r R R r ≥,圆心距(O O ')为d (22)()(b b a a d -'+-'=),则在Rt △ACO 与Rt △AC O '中,同理得: [][]d r d R R r d AB 2222)()(---+= ② 说明:内切、外切时上两式也成立,只不过AB=0。



两圆位置关系的判定方法圆和圆的位置关系有五种:外离、外切、相交、内切、内含.如何判断两圆的位置关系呢?可试用以下三种方法:1、利用定义,即用两圆公共点(交点)的个数来判定两圆的位置关系.公共点的个数0 1 2两圆位置关系外离或内含外切或内切相交因为这个方法较易理解,所以不再举例.2、利用圆心距与两圆半径之间的关系来判断两圆的位置关系:d为圆心距,R与r 分别是两圆的半径,则有以下关系:两圆外切<=> d=R+r;两圆外离<=>d>R+r;两圆内含<=>d<R-r(R>r).两圆相交:<=>R-r<d<R+r两圆内切 <=>d=R-r(R>r)举两个例子帮助同学们理解一下:例题1:设⊙O1和⊙O2的半径分别为R、r,圆心距为d,当R=6cm,r=3cm,d=5cm时,⊙O1和⊙O2的位置关系是怎样的?当R=5cm,r=2cm,d=3cm时,⊙O1和⊙O2的位置关系是怎样的?例题2:已知两圆的半径分别为R和r(R>r),圆心距为 d ,若关于x的方程x2-2rx+(R-d)2=0有两个相等的实数根,那么两圆的位置关系为()A、外切B、内切C、外离D、外切或内切3、根据公切线的条数来确定两圆的位置关系公切线条数 4 3 2 1 0两圆位置关系外离外切相交内切内含例题1:如果两圆的公切线有且只有一条,那么这两个圆的位置关系是()A、相交B、外离C、内切D、外切一、填空:1、如果两个半径不相等的圆有两个公共点,那么这两个圆的位置关系是___,且这两个圆的公切线有___条.2、若两圆的公切线的条数是4条,则两圆的位置关系是____.3、若两圆的半径分别为4cm和2cm,一条外公切线长为4cm,则两圆的位置关系是___.4、在平面直角坐标系中,分别以点A(0,3)与B(4,0)为圆心,以8与3为半径作⊙A和⊙B,则这两个圆的位置关系为____.二、选择:5、若两圆没有公共点,则两圆的位置关系是()A、外离B、内含C、外切D、外离或内含6、已知⊙O1和⊙O2的半径分别为4cm和3cm,圆心距O1O2=5cm,则⊙O1和⊙O2的公切线的条数为()A、1条B、2条C、3条D、4条7、若两圆的直径分别是18+t,18-t(0<t<18),两圆的圆心距d=t,则两圆的位置关系为()A、外切B、内切C、外离D、相交垂径定理及其推论垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧。

第18讲圆与圆的位置关系4种常见考法归类1.能根据给定圆的方程,判断圆与圆的位置关系.2.能用直线和圆的方程解决一些简单的问题,体会用代数方法处理几何问题的思想.知识点1圆与圆的位置关系1.种类:圆与圆的位置关系有五种,分别为外离、外切、相交、内切、内含.2.判定方法(1)几何法:若两圆的半径分别为r1,r2,两圆连心线的长为d,则两圆的位置关系的判断方法如下:|r-r|<d<C1:x2+y2+D1x+E1y+F1=0(D21+E21-4F1>0),C2:x2+y2+D2x+E2y+F2=0(D22+E22-4F2>0),2+y2+D1x+E1y+F1=0,2+y2+D2x+E2y+F2=0,则方程组解的个数与两圆的位置关系如下:方程组解的个数2组1组0组两圆的公共点个数2个1个0个两圆的位置关系相交内切或外切外离或内含注:(1)圆和圆相离,两圆无公共点,它包括外离和内含;(2)圆和圆相交,两圆有两个公共点;(3)圆和圆相切,两圆有且只有一个公共点,它包括内切和外切.(4)圆与圆的位置关系不能简单仿照直线与圆的位置关系的判断方法将两个方程联立起来消元后用判别式判断,因为当方程组有一组解时,两圆只有一个交点,两圆可能外切,也可能内切;当方程组无解时,两圆没有交点,两圆可能外离,也可能内含.知识点2圆与圆位置关系的应用设圆C 1:x 2+y 2+D 1x +E 1y +F 1=0,①圆C 2:x 2+y 2+D 2x +E 2y +F 2=0,②若两圆相交,则有一条公共弦,由①-②,得(D 1-D 2)x +(E 1-E 2)y +F 1-F 2=0.③方程③表示圆C 1与C 2的公共弦所在直线的方程.(1)当两圆相交时,两圆方程相减,所得的直线方程即两圆公共弦所在的直线方程,这一结论的前提是两圆相交,如果不确定两圆是否相交,两圆方程相减得到的方程不一定是两圆的公共弦所在的直线方程.(2)两圆公共弦的垂直平分线过两圆的圆心.(3)求公共弦长时,几何法比代数法简单易求.1、公切线的条数与两个圆都相切的直线叫做两圆的公切线,圆的公切线包括外公切线和内公切线两种.核心技巧:利用圆心到切线的距离d r =求解知识点4圆系方程(1)以(,)a b 为圆心的同心圆圆系方程:22()()(0)x a y b λλ-+-=>;(2)与圆220x y Dx Ey F ++++=同心圆的圆系方程为220x y Dx Ey λ++++=;(3)过直线0Ax By C ++=与圆220x y Dx Ey F ++++=交点的圆系方程为22()0()x y Dx Ey F Ax By C R λλ+++++++=∈4过两圆1C 221110x y D x E y F ++++=,圆2C :222220x y D x E y F ++++=交点的圆系方程为2222111222()0x y D x E y F x y D x E y F λ+++++++++=(1λ≠-,此时圆系不含圆2C :222220x y D x E y F ++++=)特别地,当1λ=-时,上述方程为一次方程.两圆相交时,表示公共弦方程;两圆相切时,表示公切线方程.1、判断两圆的位置关系的两种方法(1)几何法:将两圆的圆心距d 与两圆的半径之差的绝对值,半径之和进行比较,进而判断出两圆的位置关系,这是在解析几何中主要使用的方法.(2)代数法:将两圆的方程组成方程组,通过解方程组,根据方程组解的个数进而判断两圆位置关系.2、圆系方程一般地过圆C 1:x 2+y 2+D 1x +E 1y +F 1=0与圆C 2:x 2+y 2+D 2x +E 2y +F 2=0交点的圆的方程可设为:x 2+y 2+D 1x +E 1y +F 1+λ(x 2+y 2+D 2x +E 2y +F 2)=0(λ≠-1),然后再由其他条件求出λ,即可得圆的方程.3、两圆相交时,公共弦所在的直线方程若圆C 1:x 2+y 2+D 1x +E 1y +F 1=0与圆C 2:x 2+y 2+D 2x +E 2y +F 2=0相交,则两圆公共弦所在直线的方程为(D 1-D 2)x +(E 1-E 2)y +F 1-F 2=0.4、公共弦长的求法(1)代数法:将两圆的方程联立,解出交点坐标,利用两点间的距离公式求出弦长.(2)几何法:求出公共弦所在直线的方程,利用圆的半径、半弦长、弦心距构成的直角三角形,根据勾股定理求解.5、求两圆的相交弦的垂直平分线的方程即为经过两圆的圆心的直线方程考点一:圆与圆位置关系的判断(一)判断圆与圆的位置关系例1.(2023秋·福建宁德·高二统考期中)圆()22(2)21x y -+-=与圆()()221225x y +++=的位置关系是()A .相切B .相交C .内含D .外离【答案】B【分析】根据给定条件,求出两圆的圆心和半径,并计算两圆的圆心距即可判断作答.【详解】圆()22(2)21x y -+-=的圆心1(2,2)C ,半径11r =,圆()()221225x y +++=的圆心2(1,2)C --,半径25r =,于是122121||5(,)C C r r r r ==∈-+,所以两圆相交.故选:B变式1.(2023春·江西萍乡·高二校联考阶段练习)圆O :221x y +=与圆C :22650x y y +++=的位置关系是()A .相交B .相离C .外切D .内切【答案】C【分析】利用两圆外切的定义判断即可.【详解】圆O 是以(0,0)O 为圆心,半径11r =的圆,圆C :22650x y y +++=改写成标准方程为()2234x y ++=,则圆C 是以(0,3)C -为圆心,半径22r =的圆,则3OC =,12r r +=3,所以两圆外切,故选:C .变式2.(2023·全国·高三专题练习)已知圆1C 的圆心在直线210x y +-=上,点()3,0与()1,2-都在圆1C 上,圆()()222:311C x y -++=,则1C 与2C 的位置关系是___________.【答案】相交【分析】利用待定系数法求得圆1C 的标准方程,求出圆心距12C C ,与两圆的半径和、差比较即可得出结论.【详解】设圆1C 的标准方程为()()2221x a y b r -+-=,因为圆心1C 在直线210x y +-=上,且该圆经过()3,0与()1,2-两点,列方程组22212221210(3)(0)(1)(2)a b a b r a b r +-=⎧⎪-+-=⎨⎪-+--=⎩,解得1102a b r =⎧⎪=⎨⎪=⎩,即圆1C 的标准方程为()2214x y -+=,圆心()11,0C ,半径12r =,又圆()()222:311C x y -++=,圆心()23,1C -,半径21r =,∴12C C =123r r +=,121r r-=,而13<<,∴1C 与2C 的位置关系是相交.故答案为:相交.变式3.【多选】(2023秋·江苏南通·高二统考期末)已知圆22:(3)(4)4C x y -+-=,则()A .点(5,5)在圆C内B .直线3)y x =-与圆C 相切C .圆229x y +=与圆C 相切D .圆2249x y +=与圆C 相切【答案】BCD【分析】根据点和圆的位置关系判断A 选项,根据圆心与直线距离判断B 选项,根据圆心间距离和半径和差比较判断圆圆位置关系判断C,D 选项.【详解】点(5,5)代入圆22:(3)(4)4C x y -+-=可得22(53)(54)414-+-=+>,点(5,5)在圆C 外,A 选项错误;圆22:(3)(4)4C x y -+-=,圆()3,4,2C r=,直线3)y x =-,圆心到直线距离2d =,B 选项正确;圆229x y +=,圆心()110,0,3C r=,11523CC r r ===+=+,圆229x y +=与圆C 相外切,C 选项正确;圆2249x y +=,圆心()220,0,7C r =,22572CC r r ==-=-,圆2249x y +=与圆C 相内切,D 选项正确.故选:BCD.变式4.(2023春·安徽阜阳·高三安徽省临泉第一中学校考专题练习)平面直角坐标系中,()2,0A -,()2,0B ,动点P满足PA =,则使PAB 为等腰三角形的点P 个数为()A .0B .2C .3D .4【答案】D【分析】设(),P x y,根据PA =可得动点P 的轨迹方程为圆22:(4)12M x y -+=,再结合PAB 为等腰三角形分析即可求解.【详解】设(),P x y ,由PA =,=整理得22(4)12x y -+=,记为圆.M又PA PB =>,PAB 为等腰三角形,则有4PA AB ==或4PB AB ==.因为圆22:(2)16A x y ++=与圆M 相交,故满足4PA AB ==点P 有2个;因为圆22:(2)16B x y -+=与圆M 相交,故满足4PB AB ==点P 有2个,故使PAB 为等腰三角形的点P 共有4个.故选:D.变式5.【多选】(2023·湖南娄底·统考模拟预测)已知圆M :22650x y y +-+=,圆N :22280x y y ++-=,直线l :340x y m -+=,则下列说法正确的是()A .圆N 的圆心为()0,1B .圆M 与圆N 相交C .当圆M 与直线l 相切时,则2m =D .当7m =时,圆M 与直线l 相交所得的弦长为【答案】BD【分析】写出圆,M N 的标准方程确定圆心坐标和半径,判断||MN 与两圆半径的关系判断A 、B ;再由点线距离及相交弦长公式判断C 、D.【详解】由题设,22:(3)4M x y +-=,则(0,3)M 且半径2r =,22:(1)9N x y ++=,则(0,1)N -且半径3R =,A 错;所以4R r MN R r -<=<+,即两圆相交,B 对;M 到直线l 的距离|012||12|55m m d -+-==,若圆M 与直线l 相切,则|12|25m -=,所以22m =或2m =,C 错;当7m =时1d r =<,即圆M 与直线l 相交,相交弦长为=D 对.故选:BD变式6.(2022·全国·高二专题练习)已知点P 在圆O :224x y +=上,点()30A -,,()0,4B ,满足AP BP ⊥的点P 的个数为()A .3B .2C .1D .0【答案】B【分析】设(,)P x y ,轨迹AP BP ⊥可得点P 的轨迹方程,即可判断该轨迹与圆的交点个数.【详解】设点(,)P x y ,则224x y +=,且(3,)(,4)AP x y BP x y =+=- ,,由AP BP ⊥,得22(3)(4)340AP BP x x y y x y x y ⋅=++-=++-=,即22325()(2)24x y ++-=,故点P 的轨迹为一个圆心为3(,2)2-、半径为52的圆,则两圆的圆心距为52,半径和为59222+=,半径差为51222-=,有159222<<,所以两圆相交,满足这样的点P 有2个.故选:B.(二)由圆的位置关系求参数例2.(2023秋·浙江丽水·高二统考期末)若圆221:4C x y +=与圆2222:20C x y mx m m +-+-=外切,则实数m =()A .-1B .1C .1或4D .4【答案】D【分析】由两圆的位置关系计算即可.【详解】由条件化简得()222:,0C x m y m m -+=∴>,即两圆圆心为()()120,0,,0C C m ,设其半径分别为12,r r ,122,r r ==121224C C m r r m ==+=+⇒=.故选:D变式1.(2023秋·高二课时练习)若两圆22(1)4x y ++=和圆22()1x a y -+=相交,则a 的取值范围是()A .02a <<B .02a <<或42a -<<-C .42a -<<-D .24a <<或20a -<<【答案】B【分析】圆()2214x y ++=与圆()221x a y -+=相交,则圆心距大于两圆的半径之差的绝对值且小于半径之和,解不等式.【详解】 圆()2214x y ++=与圆()221x a y -+=相交,∴两圆的圆心距大于两圆的半径之差的绝对值且小于半径之和,即2121-<<+,所以113a <+<.解得02a <<或42a -<<-.故选:B变式2.(2023秋·高二课时练习)当a 为何值时,两圆2222450x y ax y a +-++-=和2222230x y x ay a ++-+-=.(1)外切;(2)相交;(3)外离.【答案】(1)5a =-或2a =(2)52a -<<-或1a 2-<<(3)5a <-或2a >【分析】(1)化两圆的方程为标准方程,求得圆心坐标与半径,再求出两圆的圆心距d ,由1212||d C C r r ==+列式,即可求解.(2)由1212||r r d r r <+<-列不等式组,即可求出a 的范围.(3)由1212||d C C r r =>+列不等式,即可求出a 的范围.【详解】(1)设圆2221:2450C x y ax y a +-++-=,半径为1r ,得221:()(2)9C x a y -++=,圆心1(,2)C a -,13r =.2222:2230C x y x ay a ++-+-=,半径为2r ,得222:(1)()4C x y a ++-=,圆心1(1,)C a -,22r =.圆心距12||d C C ===因为两圆12,C C 外切,则1212||5d C C r r ==+=5=,解得5a =-或2a =.(2)因为两圆12,C C 相交,则121212||||r r C C r r -<<+,即121||5C C <<,所以15<,解得52a -<<-或1a 2-<<.(3)因为两圆12,C C 外离,则1212||d C C r r =>+,即12||5C C >,5>,解得5a <-或2a >.变式3.(2022秋·高二课时练习)若圆222x y r +=与圆222440x y x y ++-+=有公共点,则r 满足的条件是()A .1rB .1r >+C .1r ≤D .1r <【答案】C【分析】根据两圆之间的位置关系,由圆心距和半径之间的关系即可求解.【详解】由222440x y x y ++-+=得()()22121x y ++-=,∵两圆有公共点,∴11r r -≤+,1r -#1,即11r -≤,∴1r ≤,故选:C.变式4.(2023秋·浙江嘉兴·高二统考期末)已知圆1C :()()()222120x y r r -++=>与圆2C :()()224216x y -+-=有公共点,则r 的取值范围为()A .(]0,1B .[]1,5C .[]1,9D .[]5,9【答案】C【分析】根据题意得到1244r C C r -≤≤+,再解不等式即可.【详解】由题知:()11,2C -,1r r =,()24,2C ,24r =,125C C =.因为1C 和2C 有公共点,所以1244r C C r -≤≤+,解得19r ≤≤.故选:C变式5.(2023春·安徽·高二校联考期末)已知圆()()()222:3425C x y r r *-+-=+∈N ,()1,0M -,()1,0N ,若以线段MN 为直径的圆与圆C 有公共点,则r 的值可能为______.(写出一个即可)【答案】1(2,3均可)答案不唯一【分析】根据题意,由已知利用圆与圆的位置关系即可求解.【详解】由题意得,圆221x y +=与圆()()222:3425C x y r -+-=+有公共点,11≤≤,∴46≥≤,且0r >,解得0r <1r =,2,3均可.故答案为:1(2,3均可)变式6.(2022·湖南常德·常德市一中校考二模)已知圆22:(4)(3)4C x y -++=和两点(,0),(,0)(0)->A a B a a ,若圆C 上存在点P ,使得90APB ∠=︒,则a 的最小值为()A .6B .5C .4D .3【答案】C【分析】根据条件,将问题转化成圆222x y a +=与圆C 有公共交点,再利用圆与圆的位置关系即可求出结果.【详解】由90APB ∠=︒,得点P 在圆222x y a +=上,故点P 在圆222x y a +=上,又点P 在圆C 上,所以,两圆有交点,因为圆222x y a +=的圆心为原点O ,半径为a ,圆C 的圆心为(4,3)-,半径为1,所以|1|1a OC a -≤≤+,又5OC ==,所以|1|51a a -≤≤+,解得46a ≤≤,所以a 的最小值为4.故选:C.变式7.(2023秋·高一单元测试)已知圆221:()(2)9O x m y -++=与圆222:()(2)1O x n y +++=内切,则22m n +的最小值为_______【答案】2【分析】计算两圆的圆心距,令圆心距等于两圆半径之差,结合基本不等式求解最小值即可.【详解】圆1O 的圆心为(,2)m -,半径为13r =,圆2O 的圆心为(,2)n --,半径为21r =,∴两圆的圆心距||d m n =+,两圆内切,||2m n ∴+=,可得()2222222442m n mn m n mn m n ++=⇒-+=≤+,所以222m n +≥.当且仅当1m n ==时,取得最小值,22m n +的最小值为2.故答案为:2.变式8.(2023·浙江·校联考模拟预测)已知圆C 的方程为221x y +=,若直线()3y k x =-上至少存在一点,使得以该点为圆心,1为半径的圆与圆C 相外切,则k 的取值范围为__________.【答案】,55⎡-⎢⎣⎦【分析】根据题意,由圆C 的圆心到直线()3y k x =-的距离不大于两半径之和求解.【详解】解:因为直线()3y k x =-上至少存在一点,使得以该点为圆心,1为半径的圆与圆C 相外切,所以圆C 的圆心到直线()3y k x =-的距离不大于两半径之和,即2d =≤,化简得254k ≤,解得k ≤≤故答案为:⎡⎢⎣⎦考点二:与圆相交有关的问题(一)求两圆的交点坐标例3.(2022·高二课前预习)圆221x y +=与圆222210x y x y ++++=的交点坐标为()A .(1,0)和()0,1B .(1,0)和()0,1-C .(1,0)-和()0,1-D .()1,0-和()0,1【答案】C【分析】联立两圆的方程,解方程组,即可求得答案.【详解】由222212210x y x y x y ⎧+=⎨++++=⎩,可得10x y ++=,即=1y x --,代入221x y +=,解得=1x -或0x =,故得10x y =-⎧⎨=⎩或01x y =⎧⎨=-⎩,所以两圆的交点坐标为(1,0)-和()0,1-,故选:C变式1.(2022·高二课时练习)求圆22230x y x +--=与圆224230x y x y +-++=的交点的坐标.【答案】(1,2)-、(3,0)【分析】联立两圆方程可得3y x =-,将其代入其中一个圆的方程中求出点坐标.【详解】由题设,22224232300x y x y x y x +-⎧+--=++=⎪⎨⎪⎩,相减可得3y x =-,所以222(3)232860x x x x x +---=-+=,解得1x =或3x =,当1x =时,132y =-=-;当3x =时,330y =-=;所以交点坐标为(1,2)-、(3,0).变式2.(2022秋·贵州遵义·高二遵义一中校考阶段练习)圆1C :22640x y x y ++-=和圆2C :2260x y y +-=交于A ,B 两点,则线段AB 的垂直平分线的方程是______.【答案】390x y -+=【分析】由两圆的方程得两圆心坐标,两圆心所在直线的方程即为所求直线方程,【详解】圆1C 方程为22(3)(2)13x y ++-=,圆2C 方程为22(3)9x y +-=,则圆心分别为1(3,2)C -,2(0,3)C ,两圆相交于,A B 两点,则线段AB 的垂直平分线即为直线12C C ,123210(3)3C C k -==--,则直线12C C 的方程为133y x =+,即390x y -+=,故答案为:390x y -+=变式3.(2023秋·辽宁丹东·高二统考期末)已知圆22:16O x y +=与圆22:86160C x y x y ++++=交于A ,B 两点,则四边形OACB 的面积为()A .12B .6C .24D .245【答案】A【分析】由两圆标准方程得圆心坐标和半径,由()4,0A -和()4,3C --可知OA AC ⊥,则四边形OACB 的面积1222OAC S S OA AC ==⨯⋅⋅ ,计算即可.【详解】圆22:16O x y +=,圆心坐标为()0,0O ,半径14r =,圆22:86160C x y x y ++++=化成标准方程为()()22439x y +++=,圆心坐标为()4,3C --,半径23r =,圆O 与圆C 都过点()4,0-,则()4,0A -,如图所示,又()4,3C --,∴OA AC ⊥,由对称性可知,OB BC ⊥,4OA OB ==,3AC BC ==,则四边形OACB 的面积12243122OAC S S OA AC ==⨯⋅⋅=⨯= .故选:A(二)圆系方程的应用例4.(2023·全国·高三专题练习)经过点()1,1P 以及圆2240x y +-=与2244120x y x y +-+-=交点的圆的方程为______.【答案】2220x y x y ++--=【分析】求出两圆的交点坐标,设出所求圆的一般方程,将三点坐标代入,解出参数,可得答案.【详解】联立22224044120x y x y x y ⎧+-=⎨+-+-=⎩,整理得2y x =+,代入2240x y +-=,得220x x +=,解得0x =或2x =-,则圆2240x y +-=与2244120x y x y +-+-=交点坐标为(0,2),(2,0)-,设经过点()1,1P 以及(0,2),(2,0)-的圆的方程为220x y Dx Ey F ++++=,则20420420D E F E F D F +++=⎧⎪++=⎨⎪-+=⎩,解得112D E F =⎧⎪=-⎨⎪=-⎩,故经过点()1,1P 以及圆2240x y +-=与2244120x y x y +-+-=交点的圆的方程为2220x y x y ++--=,故答案为:2220x y x y ++--=变式1.(2022秋·高二单元测试)求过两圆221:240C x y y +--=和圆222:420C x y x y +-+=的交点,且圆心在直线:2410l x y +-=上的圆的方程.【答案】22310x y x y +-+-=【分析】根据过两圆交点的圆系方程设出所求圆的方程,并求出圆心坐标,把圆心坐标代入直线l 的方程,从而求出圆的方程.【详解】设圆的方程为()222242(1)240x y x y x y y λλ+-+++--=≠-,则()()()221412240x x y y λλλλ+-+++--=,即2242240111x y x y λλλλλ-+-+-=+++,所以圆心坐标为21,11λλλ-⎛⎫⎪++⎝⎭,把圆心坐标21,11λλλ-⎛⎫⎪++⎝⎭代入2410x y +-=得24102111λλλ-++⨯+⨯-=,解得13λ=,所以所求圆的方程为22310x y x y +-+-=.(三)求两圆公共弦方程例5.(2022秋·黑龙江大庆·高二大庆实验中学校考期末)圆221:130O x y +-=与圆222:650O x y x +-+=的公共弦所在直线方程为___________.【答案】30x -=【分析】判断两圆相交,将两圆方程相减即可求得答案.【详解】圆221:130O x y +-=的圆心为(0,0),半径为1r =圆222:650O x y x +-+=的圆心为(3,0),半径为22r =,则121212||3r r O O r r -<=<+,则两圆相交,故将两圆方程相减可得:6180x -=,即30x -=,即圆221:130O x y +-=与圆222:650O x y x +-+=的公共弦所在直线方程为30x -=,故答案为:30x -=变式1.(2022秋·高二课时练习)已知圆2212610C x y x y ++-+=:与圆22242110C x y x y +-+-=:,求两圆的公共弦所在的直线方程()A .3460x y ++=B .3460x y +-=C .3460x y --=D .3460x y -+=【答案】D【分析】由两圆方程相减即可得公共弦的方程.【详解】将两个圆的方程相减,得3x -4y +6=0.故选:D.变式2.(2023春·全国·高二卫辉一中校联考阶段练习)已知圆1C :222(1)x y r ++=过圆2C :22(4)(1)4x y -+-=的圆心,则两圆相交弦的方程为______.【答案】5190x y +-=【分析】求出2r ,得到圆1C ,两圆相减得到相交弦方程.【详解】圆2C :22(4)(1)4x y -+-=的圆心坐标为()4,1,因为圆1C 过圆2C 的圆心,所以222(41)1r ++=,所以226r =,所以1C :22(1)26x y ++=,两圆的方程相减可得相交弦方程为5190x y +-=.故答案为:5190x y +-=.变式3.(2022秋·高二课时练习)已知过圆224x y +=外一点()3,4P 做圆的两条切线,切点为,A B 两点,求,A B 所在的直线方程为()A .3440x y +-=B .3440x y ++=C .3440x y --=D .3440x y -+=【答案】A【分析】根据切线的特征可知,A B 所在的直线为圆224x y +=和以OP 的中点3,22M ⎛⎫⎪⎝⎭为圆心,以OP 为直径的圆的公共弦所在的直线方程,【详解】根据题意得,A B 所在的直线为圆224x y +=和以OP 的中点3,22M ⎛⎫⎪⎝⎭为圆心,以OP 为直径的圆的公共弦所在的直线方程,因为5OP =,所以圆()2222325234024M x y x y x y :+骣琪--=Þ+--=琪桫,两圆相减得,A B 所在的直线方程为3440x y +-=.故选:A.(四)求两圆公共弦长例6.(2022·高二课时练习)已知圆221:(1)5C x y +-=,圆222:420C x y x y +-+=.(1)求圆1C 与圆2C 的公共弦长;(2)求过两圆的交点且圆心在直线241x y +=上的圆的方程.【答案】(1)(2)22317222x y ⎛⎫⎛⎫-++=⎪ ⎪⎝⎭⎝⎭【分析】(1)将两圆方程作差可求出公共弦的方程,然后求出圆心1C 到公共弦的距离,再利用弦心距,半径和弦的关系可求得答案,(2)解法一:设过两圆的交点的圆为()()222242240,1x y x y x y y λλ+-+++--=≠-,求出圆心坐标代入241x y +=中可求出λ,从而可求出圆的方程,解法二:将公共弦方程代入圆方程中求出两圆的交点坐标,设所求圆的圆心坐标为(),a b ,然后列方程组可求出,a b ,再求出圆的半径,从而可求出圆的方程.【详解】(1)将两圆的方程作差即可得出两圆的公共弦所在的直线方程,即()()222242240x y x y x y y +-+-+--=,化简得10x y --=,所以圆1C 的圆心()0,1到直线10x y --=的距离为d =则22215232AB r d ⎛⎫=-=-= ⎪⎝⎭,解得AB =,所以公共弦长为(2)解法一:设过两圆的交点的圆为()()222242240,1x y x y x y y λλ+-+++--=≠-,则2242240,1111x y x y λλλλλλ-+-+-=≠-+++;由圆心21,11λλλ-⎛⎫- ⎪++⎝⎭在直线241x y +=上,则()414111λλλ--=++,解得13λ=,所求圆的方程为22310x y x y +-+-=,即22317222x y ⎛⎫⎛⎫-++= ⎪ ⎪⎝⎭⎝⎭.解法二:由(1)得1y x =-,代入圆222:420C x y x y +-+=,化简可得22410x x --=,解得22x =;当22x =时,2y =;当22x =时,2y =-;设所求圆的圆心坐标为(),a b ,则2222222222241a b a b a b ⎧⎛⎫⎛⎫⎛⎫⎛⎫⎪-+=-++ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎨⎝⎭⎝⎭⎝⎭⎝⎭⎪+=⎩,解得3212a b ⎧=⎪⎪⎨⎪=-⎪⎩;所以222317222r ⎛⎛=+--= ⎝⎭⎝⎭;所以过两圆的交点且圆心在直线241x y +=上的圆的方程为22317222x y ⎛⎫⎛⎫-++=⎪ ⎪⎝⎭⎝⎭变式1.(2023·河南·统考二模)若圆221:1C x y +=与圆222:()()1C x a y b -+-=的公共弦AB 的长为1,则直线AB 的方程为()A .210ax by +-=B .230ax by +-=C .2210ax by +-=D .2230ax by +-=【答案】D【分析】将两圆方程相减得到直线AB 的方程为22220a b ax by +--=,然后再根据公共弦AB 的长为1即可求解.【详解】将两圆方程相减可得直线AB 的方程为22220a b ax by +--=,即22220ax by a b +--=,因为圆1C 的圆心为(0,0),半径为1,且公共弦AB 的长为1,则1(0,0)C 到直线22220ax by a b +--=的距离为2,223a b +=,所以直线AB 的方程为2230ax by +-=,故选:D.变式2.(2021秋·广东深圳·高二深圳中学校考期中)已知圆C 的圆心为()2,2-,且与直线0x y ++相切.(1)求圆C 的方程;(2)求圆C 与圆224x y +=的公共弦的长.【答案】(1)22(2)(2)20x y -++=(2)【分析】(1)由题意求得圆的半径,即可求得答案;(2)将两圆方程相减,求出两圆的公共弦方程,根据弦长、弦心距以及圆的半径之间的关系即可求得答案.【详解】(1)由题意得圆C 的半径为r =故圆C 的方程为22(2)(2)20x y -++=;(2)圆224x y +=和22(2)(2)20x y -++=的圆心距为而22<<+,即两圆相交,将224x y +=和22(2)(2)20x y -++=相减得20x y -+=,圆224x y +=的圆心到20x y -+=的距离为d ==故两圆的公共弦长为=变式3.(2021秋·高二课时练习)若圆O :x 2+y 2=5与圆O 1:(x -m )2+y 2=20(m ∈R )相交于A ,B 两点,且两圆在点A 处的切线互相垂直,则直线AB 的方程为________;线段AB 的长为________.【答案】x =±14【分析】连接OO 1,记AB 与OO 1的交点为C ,利用勾股定理和等面积法,求出AC ,进而求出AB ,根据1OO ,求出m ,进而联立求出直线AB 的方程.【详解】连接OO 1,记AB 与OO 1的交点为C ,如图所示,在Rt △OO 1A 中,|OA ||O 1A |=∴|OO 1|=5,∴|AC |2,∴|AB |=4.由|OO 1|=5,得5m =±,所以,联立可得2222(5)520x y x y +-±-=-,解得直线AB 的方程为x =±1.故答案为:①1x =±;②4.变式4.(2023·安徽滁州·安徽省定远中学校考模拟预测)已知圆221:1O x y +=与圆()2222201:O x y x y F F +-++=<2O 的半径r =()A .1BC 1D【答案】D【分析】两圆方程相减可得公共弦所在直线方程,后由垂径定理结合圆2O 圆心与半径表达式可得答案.【详解】221x y+=与()2222201:O x y x y F F +-++=<两式相减得2210:l x y F ---=,即公共弦所在直线方程.圆2O 方程可化为()()22211:O x y -++2F =-,可得圆心()21,1O -,2O 半径r =则圆心2O 到l 的距离为d ==半弦长为2,则有2222r F +==-⎝⎭,解得3F =-或1F =(舍),此时r =.故选:D .变式5.(2021秋·高二课时练习)圆2221:22210C x y ax ay a ++++-=与圆2222:22220C x y bx by b ++++-=的公共弦长的最大值是()A .12B .1C .32D .2【答案】D【分析】将两圆转化成标准方程,根据标准方程得出两圆圆心均在直线y x =上,再利用几何关系即可求出结果.【详解】由222x y 2ax 2ay 2a 10++++-=,得()()22x a y a 1+++=,圆心1(,)C a a --,半径11r =;由2222:22220C x y bx by b ++++-=,得()()22x b y b 2+++=,圆心2(,)C b b --,半径2r =所以两圆圆心均在直线y x =上,半径分别为1,如图,当两圆相交且相交弦经过小圆圆心,也即大圆圆心在小圆上时,两圆公共弦长最大,最大值为小圆的直径,即最大值为2.故选:D.考点三:两圆的公切线问题(一)圆的公切线条数例7.(2022秋·贵州遵义·高二习水县第五中学校联考期末)圆221:(2)(4)25C x y +++=与圆222:(1)9C x y ++=的公切线的条数为()A .1B .2C .3D .4【答案】B【分析】先判断圆与圆的位置关系,从而可确定两圆的公切线条数.【详解】圆221:(2)(4)25C x y +++=的圆心坐标为(2,4)--,半径为5;圆222:(1)9C x y ++=的圆心坐标为(1,0)-,半径为3,所以两圆的圆心距为d因为5353-<+,所以两圆相交,所以两圆的公切线有2条.故选:B.变式1.【多选】(2023秋·高一单元测试)已知圆221:9C x y +=与圆222:(3)(4)16C x y -+-=,下列说法正确的是()A .1C 与2C 的公切线恰有4条B .1C 与2C 相交弦的方程为3490x y +-=C .1C 与2C 相交弦的弦长为125D .若,P Q 分别是圆12,C C 上的动点,则max ||12PQ =【答案】BD【分析】由根据两圆之间的位置关系确定公切线个数;如果两圆相交,进行两圆方程的做差可以得到相交弦的直线方程;通过垂径定理可以求弦长;两圆上的点的最长距离为圆心距和两半径之和,逐项分析判断即可.【详解】由已知得圆1C 的圆心()10,0C ,半径13r =,圆2C 的圆心()23,4C ,半径24r =,1221125,C C r r d r r ==-<<+,故两圆相交,所以1C 与2C 的公切线恰有2条,故A 错误;做差可得1C 与2C 相交弦的方程为3490,x y +-=1C 到相交弦的距离为95,故相交弦的弦长为245=,故C 错误;若,P Q 分别是圆12,C C 上的动点,则max 1212||12PQ C C r r =++=,故D 正确.故选:BD变式2.(2023·黑龙江大庆·统考三模)已知直线l 是圆:C ()()22211x y -+-=的切线,并且点()3,4B 到直线l的距离是2,这样的直线l 有()A .1条B .2条C .3条D .4条【答案】D【分析】由已知可推得,直线l 是圆C 与圆B 的公切线.根据两圆的圆心、半径,推得两圆的位置关系,即可得出答案.【详解】由已知可得,圆心()2,1C ,半径11r =.由点()3,4B 到直线l 的距离是2,所以直线l 是以()3,4B 为圆心,22r =为半径的圆的切线,又直线l 是圆:C ()()22211x y -+-=的切线,所以,直线l 是圆C 与圆B 的公切线.因为123BC r r ==>=+,所以,两圆外离,所以两圆的公切线有4条,即满足条件的直线l 有4条.故选:D.变式3.(2023·河北衡水·衡水市第二中学校考三模)若圆221:1Cx y +=和2221:2502C x y ay a a ⎛⎫+---=> ⎪⎝⎭有且仅有一条公切线,则=a______;此公切线的方程为______【答案】120y ++=【分析】根据两圆内切由圆心距与半径关系列出方程求a ,联立圆的方程求出切点,根据圆的切线性质得出斜率即可求解.【详解】如图,由题意得1C 与2C 相内切,又22221:()()452C x y a a a a ⎛⎫+-=+> ⎪⎝⎭,所以121C C ==,所以21a +=1a =,所以)2C,12C C k==联立(()2222119x y x y ⎧+=⎪⎨+-=⎪⎩,解得1,2x y ⎧=⎪⎪⎨⎪=-⎪⎩所以切点的坐标为122⎛⎫-- ⎪ ⎪⎝⎭,故所求公切线的方程为12y +=2x +⎭20y ++=.故答案为:120y ++=变式4.(2022秋·高二课时练习)已知两圆2211C x y +=:,()()()2222120C x y r r -+-=>:,当圆1C 与圆2C 有且仅有两条公切线时,则r 的取值范围________.22r <<【分析】根据两圆相交即可利用圆心距与半径的关系求解.【详解】若圆C 1与圆C 2有且仅有两条公切线时,则两圆相交,圆心C 1()0,0,半径R =2,圆C 2()1,2,半径r ,则12C C ==若两圆相交,则满足12<<r R C C R r -+,即22r r -<+,22r <+,22r <+变式5.(2023秋·陕西西安·高二长安一中校考期末)已知两圆2226940x y ax a +++-=和222290x y by b ++--=恰有三条公切线,若R a ∈,R b ∈,且0ab ≠,则2211a b +的最小值为()A .1625B .3225C .169D .329【答案】A【分析】确定两圆圆心和半径,根据公切线得到两圆外切,得到22925a b +=,变换得到()22222219111125b a b a b a ⎛⎫+= ⎪⎭++⎝,展开利用均值不等式计算得到答案.【详解】2226940x y ax a +++-=,即()2234x a y +=+,圆心()13,0O a -,12R =;222290x y by b ++--=,即()229x y b +-=,圆心()20,O b ,半径23R =;两圆恰有三条公切线,即两圆外切,故12125O O R R =+=,即22925a b +=,()222222222211111111610102525252599a b a b a b b a a b ⎛⎫⎛⎫⎛⎫+=+=++≥+= ⎪ ⎪ ⎪ ⎪⎝⎝⎭⎝⎭+⎭.当且仅当22229b a a b=,即22512a =,2254b =时等号成立.故选:A(二)圆的公切线方程例8.(2023·湖北黄冈·浠水县第一中学校考模拟预测)写出与圆()()224316x y -++=和圆221x y +=都相切的一条直线的方程___________.【答案】1y =(答案不唯一,247250x y ++=或4350x y --=均可以)【分析】先判断两圆位置关系,再分情况依次求解可得.【详解】圆221x y +=的圆心为()0,0O ,半径为1;圆()()224316x y -++=的圆心为()4,3C -,半径为4,圆心距为5OC =,所以两圆外切,如图,有三条切线123l l l ,,,易得切线1l 的方程为1y =;因为3l OC ⊥,且34OC k =-,所以343l k =,设34:3l y x b =+,即4330x y b -+=,则()0,0O 到3l 的距离315b =,解得53b =(舍去)或53-,所以343:50x y l --=;可知1l 和2l 关于3:4OC y x =-对称,联立341y x y ⎧=-⎪⎨⎪=⎩,解得4,13⎛⎫- ⎪⎝⎭在2l 上,在1l 上取点()0,1,设其关于OC 的对称点为()00,x y ,则0000132421314y x y x +⎧=-⨯⎪⎪⎨-⎛⎫⎪⨯-=- ⎪⎪⎝⎭⎩,解得002425725x y ⎧=-⎪⎪⎨⎪=-⎪⎩,则27124252447253l k --==--+,所以直线2244:173l y x ⎛⎫-=-+ ⎪⎝⎭,即247250x y ++=,综上,切线方程为1y =或247250x y ++=或4350x y --=.故答案为:1y =(答案不唯一,247250x y ++=或4350x y --=均可以)变式1.(2023·江西南昌·校联考模拟预测)已知圆()22:11C x y -+=与圆(22:1E x y +=,写出圆C和圆E 的一条公切线的方程______.【答案】10x +=20y +-=20y +=.【分析】设切线方程为y kx b =+,根据圆心到直线的距离均为1求解方程.【详解】设圆的公切线为y kx b =+,11==|||k b b ⇒+=,k =2k b-代入求解得:2k b ⎧=⎪⎨=⎪⎩或b k ⎧=⎪⎪⎨⎪=⎪⎩所以切线为:2,y =+或2y =+或10x +=故答案为:10x -+=20y +-=20y +=.变式2.(2023·湖南岳阳·统考三模)写出与圆221:1O x y +=和222:(3)1O x y -+=都相切的一条直线方程____________.【答案】3)52y x =±-或1y =±中任何一个答案均可【分析】先判断两圆的位置关系,可知公切线斜率存在,方程可设为y kx b =+,根据圆心到直线的距离等于半径列出方程组,解之即可得出答案.【详解】圆221x y +=的圆心为()10,0C ,半径为11r =,圆222:(3)1O x y -+=的圆心为()23,0C ,半径为21r =,则12123C C r r =>+,所以两圆外离,由两圆的圆心都在x 轴上,则公切线的斜率一定存在,设公切线方程为y kx b =+,即0kx y b -+=,则有11==,解得k b ⎧=⎪⎪⎨⎪=⎪⎩k b ⎧=⎪⎪⎨⎪=⎪⎩或01k b =⎧⎨=⎩或01k b =⎧⎨=-⎩所以公切线方程为3)2y x =-或1y =±.故答案为:1y =.(答案不唯一,写其它三条均可)变式3.【多选】(2022秋·高二单元测试)已知圆()()221:211C x y -+-=,圆()()222:211C x y +++=,则下列是圆1C 与圆2C 的公切线的直线方程为()A .0y =B .430x y -=C.20x y -=D.20x y +=【答案】ABC【分析】在同一坐标系内画出两圆图象,由两圆相离可知共有4条切线,再利用对称性设出直线方程,由点到直线距离公式即可求得切线方程.【详解】根据题意可知,两圆心()()122,1,2,1C C --关于原点对称,在同一坐标系内画出两圆图象,如下图所示:显然,圆心距1211C C =+,即两圆外离,共有4条切线;又两圆心到x 轴的距离都等于其半径,所以x 轴是其中一条公切线,即A 正确;利用对称性可知,其中一条切线1l 过原点,设其方程为y kx =,又()12,1C 到切线1l 的距离为11=,解得0k =或43k =;当0k =时,切线即为x 轴,当43k =时,切线方程为43y x =,即430x y -=,B 正确;由对称性可知,切线23,l l 与直线12C C 平行,易知12111222C C k +==+,所以直线12C C 的方程为12y x =,可设23,l l 的方程分别为12y x c =+,()1,02y x c c =->1=,解得2c =,即切线23,l l的方程分别为122y x =+,122y x =-;整理可得两切线方程为20x y -=和20x y -=,故C 正确,D 错误;故选:ABC(二)圆的公切线长例9.【多选】(2023春·山东青岛·高二统考开学考试)已知圆221:1C x y +=,圆222:2210C x x y y -+-+=,则()A .圆1C 与圆2C 相切B .圆1C 与圆2CC .圆1C 与圆2C 公共弦所在直线的方程为1x y +=D .圆1C 与圆2C 公共部分的面积为π12-【答案】BCD【分析】求出两圆圆心坐标与半径,求出圆心距,即可判断A ,B ,两圆方程作差即可得到公共弦方程,从而判断C ,求出两圆圆心到公共弦的距离,从而取出公共部分的面积,从而判断D.【详解】解:因为圆221:1C x y +=,圆222:2210C x y x y +--+=,所以圆1C 的圆心为1(0,0)C ,半径11r =,圆2C 的圆心为2(1,1)C ,半径21r =,所以121212r r C C r r -<=+,故圆1C 与圆2C 相交,即A 错误;因为两圆半径相等,则两圆公切线的长度为12C C =B 正确将两圆方程作差得10x y +-=,所以两圆公共弦所在直线l 的方程为10x y +-=,故C 正确;因为1C 的圆心为1(0,0)C ,半径11r =,所以1(0,0)C 到直线10x y +-=的距离为1d所以公共弦长为又圆心2(1,1)C 到直线10x y +-=的距离为2d ==所以圆1C 与圆2C 公共部分的面积为11π2π14222⎛⎫-=- ⎪ ⎪⎝⎭,故D 正确.故选:BCD变式1.【多选】(2022秋·广东惠州·高二惠州市惠阳高级中学实验学校校考期中)圆221:2660C x y x y ++-+=与圆222:2210C x y x y +--+=相交于A ,B 两点,则()A .AB 的直线方程为4450x y -+=B .公共弦AB 的长为8C .圆1C 与圆2C D .线段AB 的中垂线方程为20x y +-=【答案】ACD【分析】对于A ,两圆方程相减可求出直线AB 的方程,对于B ,利用弦心距、弦和半径的关系可求公共弦AB 的长,对于C ,求出12C C ,对于D ,线段AB 的中垂线就是直线12C C ,求出直线12C C 的方程即可.【详解】由222660x y x y ++-+=,得22(1)(3)4x y ++-=,则1(1,3)C -,半径12r =,由222210x y x y +--+=,得22(1)(1)1x y -+-=,则2(1,1)C ,半径21r =,对于A ,公共弦AB 所在的直线方程为2222266(221)0x y x y x y x y ++-+-+--+=,即4450x y -+=,所以A 正确,对于B ,2(1,1)C 到直线AB 的距离d =,所以公共弦AB 的长为4AB ==,所以B 错误,对于C ,因为12C C ==,12r =,21r =,。


4.2.2圆与圆的位置关系知识点两圆位置关系的判定思考1圆与圆的位置关系有几种?如何利用几何方法判断圆与圆的位置关系?答案圆与圆的位置关系有五种,分别为:相离、外切、相交、内切、内含.几何方法判断圆与圆的位置关系设两圆的圆心距为d,两圆的半径分别为r1,r2(r1≠r2),则(1)当d>r1+r2时,圆C1与圆C2相离;(2)当d=r1+r2时,圆C1与圆C2外切;(3)当|r1-r2|<d<r1+r2时,圆C1与圆C2相交;(4)当d=|r1-r2|时,圆C1与圆C2内切;(5)当d<|r1-r2|时,圆C1与圆C2内含.思考2已知两圆C1:x2+y2+D1x+E1y+F1=0和C2:x2+y2+D2x+E2y+F2=0,如何通过代数的方法判断两圆的位置关系?答案联立两圆的方程,消去y后得到一个关于x的一元二次方程,当判别式Δ>0时,两圆相交,当Δ=0时,两圆外切或内切,当Δ<0时,两圆外离或内含.梳理(1)用几何法判定圆与圆的位置关系已知两圆C1:(x-x1)2+(y-y1)2=r21,C2:(x-x2)2+(y-y2)2=r22,则圆心距d=|C1C2|=(x1-x2)2+(y1-y2)2.两圆C1,C2有以下位置关系:位置关系相离内含相交内切外切圆心距与半d>r1+r2d<|r1-r2||r1-r2|<d<r1+r2d=|r1-r2|d=r1+r2径的关系图示(2)用代数法判定圆与圆的位置关系已知两圆:C1:x2+y2+D1x+E1y+F1=0,C2:x2+y2+D2x+E2y+F2=0,将方程联立⎩⎪⎨⎪⎧x 2+y 2+D 1x +E 1y +F 1=0,x 2+y 2+D 2x +E 2y +F 2=0,消去y (或x )得到关于x (或y )的一元二次方程, 则①判别式Δ>0时,C 1与C 2相交; ②判别式Δ=0时,C 1与C 2外切或内切; ③判别式Δ<0时,C 1与C 2相离或内含.类型一 两圆的位置关系命题角度1 两圆位置关系的判断例1 已知圆M :x 2+y 2-2ay =0(a >0)截直线x +y =0所得线段的长度是22,则圆M 与圆N :(x -1)2+(y -1)2=1的位置关系是( ) A .内切 B .相交 C .外切 D .相离答案 B解析 由⎩⎪⎨⎪⎧x 2+y 2-2ay =0,x +y =0,得两交点分别为(0,0),(-a ,a ).∵圆M 截直线所得线段的长度为22, ∴a 2+(-a )2=22, 又a >0,∴a =2.∴圆M 的方程为x 2+y 2-4y =0,即x 2+(y -2)2=4,圆心为M (0,2),半径为r 1=2.又圆N :(x -1)2+(y -1)2=1,圆心为N (1,1),半径为r 2=1, ∴|MN |=(0-1)2+(2-1)2= 2. ∵r 1-r 2=1,r 1+r 2=3,1<|MN |<3, ∴两圆相交.反思与感悟 判断圆与圆的位置关系的一般步骤(1)将两圆的方程化为标准方程(若圆方程已是标准形式,此步骤不需要). (2)分别求出两圆的圆心坐标和半径长r 1,r 2. (3)求两圆的圆心距d .(4)比较d 与|r 1-r 2|,r 1+r 2的大小关系. (5)根据大小关系确定位置关系.跟踪训练1 已知圆C 1:x 2+y 2-2x +4y +4=0和圆C 2:4x 2+4y 2-16x +8y +19=0,则这两个圆的公切线的条数为( ) A .1或3 B .4 C .0 D .2 答案 D解析 由圆C 1:(x -1)2+(y +2)2=1,圆C 2:(x -2)2+(y +1)2=14,得C 1(1,-2),C 2(2,-1), ∴|C 1C 2|=(2-1)2+(-1+2)2= 2. 又r 1=1,r 2=12,则r 1-r 2<|C 1C 2|<r 1+r 2, ∴圆C 1与圆C 2相交. 故这两个圆的公切线共2条.命题角度2 已知两圆的位置关系求参数例2 当a 为何值时,两圆C 1:x 2+y 2-2ax +4y +a 2-5=0和C 2:x 2+y 2+2x -2ay +a 2-3=0:(1)外切;(2)相交;(3)相离. 解 将两圆方程写成标准方程,则C 1:(x -a )2+(y +2)2=9,C 2:(x +1)2+(y -a )2=4.∴两圆的圆心和半径分别为C 1(a ,-2),r 1=3,C 2(-1,a ),r 2=2. 设两圆的圆心距为d ,则d 2=(a +1)2+(-2-a )2=2a 2+6a +5. (1)当d =5,即2a 2+6a +5=25时,两圆外切, 此时a =-5或a =2.(2)当1<d <5,即1<2a 2+6a +5<25时,两圆相交,此时-5<a <-2或-1<a <2. (3)当d >5,即2a 2+6a +5>25时,两圆相离, 此时a >2或a <-5.反思与感悟 (1)判断两圆的位置关系或利用两圆的位置关系求参数的取值范围有以下几个步骤:①将圆的方程化成标准形式,写出圆心和半径. ②计算两圆圆心的距离d .③通过d ,r 1+r 2,|r 1-r 2|的关系来判断两圆的位置关系或求参数的范围,必要时可借助于图形,数形结合.(2)应用几何法判定两圆的位置关系或求参数的范围是非常简单清晰的,要理清圆心距与两圆半径的关系.跟踪训练2 若圆C 1:x 2+y 2=16与圆C 2:(x -a )2+y 2=1相切,则a 的值为( )A .±3B .±5C .3或5D .±3或±5答案 D解析 圆C 1与圆C 2的圆心距为d =a 2+(0-0)2=|a |. 当两圆外切时,有|a |=4+1=5,∴a =±5; 当两圆内切时,有|a |=4-1=3,∴a =±3. 类型二 两圆的公共弦问题例3 已知两圆x 2+y 2-2x +10y -24=0和x 2+y 2+2x +2y -8=0. (1)判断两圆的位置关系; (2)求公共弦所在的直线方程; (3)求公共弦的长度.解 (1)将两圆方程配方化为标准方程,则 C 1:(x -1)2+(y +5)2=50, C 2:(x +1)2+(y +1)2=10,∴圆C 1的圆心坐标为(1,-5),半径为r 1=52, 圆C 2的圆心坐标为(-1,-1),半径为r 2=10. 又∵|C 1C 2|=25,r 1+r 2=52+10, |r 1-r 2|=|52-10|, ∴|r 1-r 2|<|C 1C 2|<r 1+r 2, ∴两圆相交. (2)将两圆方程相减,得公共弦所在的直线方程为x -2y +4=0.(3)方法一 由(2)知圆C 1的圆心(1,-5)到直线x -2y +4=0的距离为d =|1-2×(-5)+4|1+(-2)2=35,∴公共弦长为l =2r 21-d 2=250-45=2 5.方法二 设两圆相交于点A ,B ,则A ,B 两点满足方程组⎩⎪⎨⎪⎧x -2y +4=0,x 2+y 2+2x +2y -8=0, 解得⎩⎪⎨⎪⎧x =-4,y =0或⎩⎪⎨⎪⎧x =0,y =2,∴|AB |=(-4-0)2+(0-2)2=2 5. 即公共弦长为2 5.反思与感悟 (1)当两圆相交时,公共弦所在的直线方程的求法若圆C 1:x 2+y 2+D 1x +E 1y +F 1=0与圆C 2:x 2+y 2+D 2x +E 2y +F 2=0相交,则两圆公共弦所在的直线方程为(D 1-D 2)x +(E 1-E 2)y +F 1-F 2=0. (2)公共弦长的求法①代数法:将两圆的方程联立,解出交点坐标,利用两点间的距离公式求出弦长.②几何法:求出公共弦所在直线的方程,利用圆的半径、半弦长、弦心距构成的直角三角形,根据勾股定理求解.跟踪训练3 (1)两圆相交于两点A (1,3)和B (m ,-1),两圆圆心都在直线x -y +c =0上,则m +c 的值为________. 答案 3解析 由题意知直线AB 与直线x -y +c =0垂直, ∴k AB ×1=-1, 即3-(-1)1-m=-1,得m =5, ∴AB 的中点坐标为(3,1).又AB 的中点在直线x -y +c =0上, ∴3-1+c =0,∴c =-2, ∴m +c =5-2=3.(2)求圆C 1:x 2+y 2=1与圆C 2:x 2+y 2-2x -2y +1=0的公共弦所在的直线被圆C 3:(x -1)2+(y -1)2=254截得的弦长.解 由题意将两圆的方程相减,可得圆C 1和圆C 2公共弦所在的直线l 的方程为 x +y -1=0.又圆C 3的圆心坐标为(1,1),其到直线l 的距离为d =|1+1-1|12+12=22,由条件知,r 2-d 2=254-12=234,所以弦长为2×232=23. 类型三 圆系方程及应用例4 求圆心在直线x -y -4=0上,且过两圆x 2+y 2-4x -6=0和x 2+y 2-4y -6=0的交点的圆的方程.解 方法一 设经过两圆交点的圆系方程为 x 2+y 2-4x -6+λ(x 2+y 2-4y -6)=0(λ≠-1),即x 2+y 2-41+λx -4λ1+λy -6=0,所以圆心坐标为(21+λ,2λ1+λ).又圆心在直线x -y -4=0上,所以21+λ-2λ1+λ-4=0,即λ=-13.所以所求圆的方程为x 2+y 2-6x +2y -6=0.方法二 由⎩⎪⎨⎪⎧x 2+y 2-4x -6=0,x 2+y 2-4y -6=0,得两圆公共弦所在直线的方程为y =x .由⎩⎪⎨⎪⎧ y =x ,x 2+y 2-4y -6=0,解得⎩⎪⎨⎪⎧x 1=-1,y 1=-1,⎩⎪⎨⎪⎧x 2=3,y 2=3. 所以两圆x 2+y 2-4x -6=0和x 2+y 2-4y -6=0的交点坐标分别为A (-1,-1),B (3,3), 线段AB 的垂直平分线所在的直线方程为y -1=-(x -1).由⎩⎪⎨⎪⎧ y -1=-(x -1),x -y -4=0,得⎩⎪⎨⎪⎧x =3,y =-1,即所求圆的圆心为(3,-1), 半径为(3-3)2+[3-(-1)]2=4. 所以所求圆的方程为(x -3)2+(y +1)2=16.反思与感悟 当经过两圆的交点时,圆的方程可设为(x 2+y 2+D 1x +E 1y +F 1)+λ(x 2+y 2+D 2x +E 2y +F 2)=0,然后用待定系数法求出λ即可.跟踪训练4 求过两圆C 1:x 2+y 2-4x +2y +1=0与C 2:x 2+y 2-6x =0的交点且过点(2,-2)的圆的方程.解 设过两圆C 1:x 2+y 2-4x +2y +1=0与C 2:x 2+y 2-6x =0的交点的圆系方程为x 2+y 2-4x +2y +1+λ(x 2+y 2-6x )=0, 即(1+λ)x 2+(1+λ)y 2-(4+6λ)x +2y +1=0.把(2,-2)代入,得4(1+λ)+4(1+λ)-2(4+6λ)-4+1=0,解得λ=-34.∴圆的方程为x 2+y 2+2x +8y +4=0.1.两圆x 2+y 2-1=0和x 2+y 2-4x +2y -4=0的位置关系是( ) A .内切 B .相交 C .外切 D .相离 答案 B解析 圆x 2+y 2-1=0的圆心为C 1(0,0),半径为r 1=1,圆x 2+y 2-4x +2y -4=0的圆心为C 2(2,-1),半径为r 2=3,两圆的圆心距为d =|C 1C 2|=(2-0)2+(-1-0)2=5,又r 2-r 1=2,r 1+r 2=4,所以r 2-r 1<d <r 1+r 2,故两圆相交.2.圆C 1:x 2+y 2=1与圆C 2:x 2+(y -3)2=1的内公切线有且仅有( ) A .1条 B .2条 C .3条 D .4条 答案 B解析 因为两圆的圆心距为3,半径之和为2,故两圆相离,所以内公切线的条数为2. 3.圆x 2+y 2-4x +6y =0和圆x 2+y 2-6x =0交于A ,B 两点,则AB 的垂直平分线的方程是( )A .x +y +3=0B .2x -y -5=0C .3x -y -9=0D .4x -3y +7=0答案 C解析 AB 的垂直平分线过两圆的圆心,把圆心(2,-3)代入,即可排除A 、B 、D. 4.已知以C (4,-3)为圆心的圆与圆O :x 2+y 2=1相切,则圆C 的方程是________. 答案 (x -4)2+(y +3)2=16或(x -4)2+(y +3)2=36 解析 设圆C 的半径为r ,圆心距为d =(4-0)2+(-3-0)2=5, 当圆C 与圆O 外切时,r +1=5,r =4, 当圆C 与圆O 内切时,r -1=5,r =6, ∴圆的方程为(x -4)2+(y +3)2=16 或(x -4)2+(y +3)3=36.5.若圆x 2+y 2=4与圆x 2+y 2+2ay -6=0(a >0)的公共弦长为23,则a =________. 答案 1解析 将两圆的方程相减,得相交弦所在的直线方程为y =1a ,圆心(0,0)到直线的距离为d =1a =22-(3)2=1,所以a =1.1.判断两圆的位置关系的方法(1)由两圆的方程组成的方程组有几个实数解确定,这种方法计算量比较大,一般不用. (2)依据圆心距与两圆半径的和或两半径的差的绝对值的大小关系.2.当两圆相交时,把两圆的方程作差消去x 2和y 2就得到两圆的公共弦所在的直线方程. 3.求弦长时,常利用圆心到弦所在的直线的距离求弦心距,再结合勾股定理求弦长.课时作业一、选择题1.圆(x-3)2+(y+2)2=1与圆x2+y2-14x-2y+14=0的位置关系是()A.外切B.内切C.相交D.相离答案 B解析圆x2+y2-14x-2y+14=0变形为(x-7)2+(y-1)2=36,圆心坐标为(7,1),半径为r1=6,圆(x-3)2+(y+2)2=1的圆心坐标为(3,-2),半径为r2=1,所以圆心距d=(7-3)2+[1-(-2)]2=5=6-1=r1-r2,所以两圆内切.2.已知圆C1:x2+y2+2x+8y-8=0与圆C2:x2+y2-4x-4y-2=0相交,则圆C1与圆C2的公共弦所在直线的方程为()A.x+2y+1=0 B.x+2y-1=0C.x-2y+1=0 D.x-2y-1=0答案 B解析两个圆的方程相减,得x+2y-1=0.故选B.3.若圆C1:(x+2)2+(y-m)2=9与圆C2:(x-m)2+(y+1)2=4外切,则m的值为() A.2 B.-5C.2或-5 D.不确定答案 C解析两圆的圆心坐标分别为(-2,m),(m,-1),两圆的半径分别为3,2,由题意得(m+2)2+(-1-m)2=3+2,解得m=2或-5.4.设r>0,圆(x-1)2+(y+3)2=r2与圆x2+y2=16的位置关系不可能是()A.相切B.相交C.内切或内含D.外切或相离答案 D解析两圆的圆心距为d=(1-0)2+(-3-0)2=10,两圆的半径之和为r+4,因为10<r+4,所以两圆不可能外切或相离,故选D.5.若圆x2+y2=r2与圆x2+y2+2x-4y+4=0有公共点,则r满足的条件是()A.r<5+1 B.r>5+1C.|r-5|≤1 D.|r-5|<1答案 C解析由x2+y2+2x-4y+4=0,得(x+1)2+(y-2)2=1,两圆圆心之间的距离为(-1)2+22= 5.∵两圆有公共点,∴|r-1|≤5≤r+1,∴5-1≤r≤5+1,即-1≤r-5≤1,∴|r-5|≤1.6.半径为6的圆与x轴相切,且与圆x2+(y-3)2=1内切,则此圆的方程是()A.(x-4)2+(y-6)2=6B.(x+4)2+(y-6)2=6或(x-4)2+(y-6)2=6C.(x-4)2+(y-6)2=36D.(x+4)2+(y-6)2=36或(x-4)2+(y-6)2=36答案 D解析由题意可设圆的方程为(x-a)2+(y-6)2=36,由题意,得a2+9=5,所以a2=16,所以a=±4.7.设两圆C1,C2都和两坐标轴相切,且都过点(4,1),则两圆心的距离|C1C2|等于() A.4 B.4 2 C.8 D.8 2答案 C解析∵两圆与两坐标轴都相切,且都经过点(4,1),∴两圆圆心均在第一象限且每个圆心的横、纵坐标相等.设两圆的圆心坐标分别为(a,a),(b,b),则有(4-a)2+(1-a)2=a2,(4-b)2+(1-b)2=b2,即a,b为方程(4-x)2+(1-x)2=x2的两个根,整理得x2-10x+17=0,∴a+b=10,ab=17.∴(a-b)2=(a+b)2-4ab=100-4×17=32,∴|C1C2|=(a-b)2+(a-b)2=32×2=8.二、填空题8.若圆x2+y2-2ax+a2=2和x2+y2-2by+b2=1相离,则a,b满足的条件是_____.答案a2+b2>3+2 2解析 由题意可得两圆的圆心坐标和半径长分别为(a,0),2和(0,b ),1.因为两圆相离,所以a 2+b 2>2+1, 即a 2+b 2>3+2 2.9.圆C 1:x 2+y 2-2x -8=0与圆C 2:x 2+y 2+2x -4y -4=0的公共弦长为________. 答案 27解析 由圆C 1与圆C 2的公共弦所在的直线l 的方程为x -y +1=0,得点C 1(1,0)到直线l 的距离为d =|1-0+1|12+12=2,圆C 1的半径为r 1=3,所以圆C 1与圆C 2的公共弦长为2r 21-d 2=232-(2)2=27.10.集合A ={(x ,y )|x 2+y 2=4},B ={(x ,y )|(x -3)2+(y -4)2=r 2},其中r >0 ,若A ∩B 中有且仅有一个元素,则r 的值是__________. 答案 3或7解析 ∵A ∩B 中有且仅有一个元素, ∴圆x 2+y 2=4与圆(x -3)2+(y -4)2=r 2相切. 当两圆内切时,由32+42=|2-r |,解得r =7; 当两圆外切时,由32+42=2+r ,解得r =3. ∴r =3或7.11.经过直线x +y +1=0与圆x 2+y 2=2的交点,且过点(1,2)的圆的方程为________. 答案 x 2+y 2-34x -34y -114=0解析 由已知可设所求圆的方程为x 2+y 2-2+λ(x +y +1)=0,将(1,2)代入,可得λ=-34,故所求圆的方程为x 2+y 2-34x -34y -114=0.三、解答题12.已知圆O 1:x 2+(y +1)2=4,圆O 2的圆心O 2(2,1). (1)若圆O 2与圆O 1外切,求圆O 2的方程;(2)若圆O 2与圆O 1交于A ,B 两点,且|AB |=22,求圆O 2的方程. 解 (1)设圆O 2半径为r 2, 因为两圆外切,所以|O 1O 2|=r 2+2. 又|O 1O 2|=22+[1-(-1)2]=22, 所以r 2=|O 1O 2|-2=2(2-1),故圆O 2的方程为(x -2)2+(y -1)2=12-8 2. (2)设圆O 2的方程为(x -2)2+(y -1)2=r 22, 因为圆O 1的方程为x 2+(y +1)2=4,将两圆的方程相减,即得两圆公共弦AB 所在的直线方程为4x +4y +r 22-8=0,作O 1H ⊥AB ,H 为垂足,则|AH |=12|AB |=2, 所以|O 1H |=r 21-|AH |2=4-2= 2.由圆心O 1(0,-1)到直线4x +4y +r 22-8=0的距离为|r 22-12|42=2, 得r 22=4或r 22=20, 故圆O 2的方程为(x -2)2+(y -1)2=4或(x -2)2+(y -1)2=20.四、探究与拓展13.已知圆C 1:x 2+y 2+4x +1=0和圆C 2:x 2+y 2+2x +2y +1=0,则以圆C 1与圆C 2的公共弦为直径的圆的方程为________.答案 (x +1)2+(y +1)2=1解析 由两圆的方程相减,得公共弦所在直线的方程为x -y =0.∵圆C 1:(x +2)2+y 2=3,圆C 2:(x +1)2+(y +1)2=1,圆心C 1(-2,0),C 2(-1,-1),∴两圆连心线所在直线的方程为y -0-1-0=x +2-1+2, 即x +y +2=0.由⎩⎪⎨⎪⎧x -y =0,x +y +2=0,得所求圆的圆心为(-1,-1). 又圆心C 1(-2,0)到公共弦所在直线x -y =0的距离d =|-2-0|2=2, ∴所求圆的半径r =(3)2-(2)2=1,∴所求圆的方程为(x +1)2+(y +1)2=1.14.求与圆C :x 2+y 2-2x =0外切且与直线l :x +3y =0相切于点M (3,-3)的圆的方程. 解 圆C 的方程可化为(x -1)2+y 2=1,圆心为C (1,0),半径为1.设所求圆的方程为(x -a )2+(y -b )2=r 2(r >0),由题意可知⎩⎪⎨⎪⎧ (a -1)2+b 2=r +1,b +3a -3×(-33)=-1,|a +3b |2=r ,解得⎩⎪⎨⎪⎧ a =4,b =0,r =2. 故所求圆的方程为(x -4)2+y 2=4.。
两圆的公共弦和圆心连线关系哎呀,今天咱们来聊聊两圆的那些事儿吧!有没有发现,其实两个圆儿也挺像我们人类的生活的。
你想想,它们俩有时候有交集,有时候又各走各的,有时候还有公共的弦哎!你得知道,两个圆如果想有公共的弦,它们的圆心之间得有一定的关系。
就像我们俩要打成一片,得有点默契,对不对?如果两个圆的圆心距离很远,那它们俩就不大可能有公共的弦了,毕竟离得太远,连话都说不到一块儿去。
可是,如果两个圆的圆心距离太近,也不行哦!就像太亲密的朋友,有时候也会导致矛盾,弄得没法看对眼。
所以,这个距离得刚刚好,不冷不热,刚刚能有那么一点交集,但又能各自为政。
再来说说那些公共的弦。
公共弦其实就是两个圆上都有的一段线段,就像你我共同认识的朋友,连接了我们俩。
这种弦,有时候像是我们之间的共同点,能让我们一起玩耍、一起工作,有了它们,我们的圈子也就更大了。
不过,有趣的是,公共弦的长度和两圆的位置关系可不简单。
它们不是一成不变的,有时候长长短短,甚至会变得无影无踪。
就像我们生活中的那些联系,有时候挺牢固,有时候转眼就没了,也不知道咋回事。
有些时候,两个圆就是纯粹地相互靠近,彼此看看,偶尔打个招呼,但是并不打成一片。
这时候,它们的圆心距离虽然近,但公共的弦却很少,就像那些认识的人,聊过天,但深交不起。
反过来,有时候两个圆可能就特别投缘,圆心距离适中,然后公共弦又多又粗,像是从小就是铁哥们儿一样。
这种情况下,它们俩的交集就会特别多,相互影响也大,就像是生活中那些密不可分的好朋友。
两个圆的关系,就像是我们和身边的人一样复杂多变。
有时候要离远一点,有时候要靠近一点,有时候又要共同拥有一些东西来联系彼此。
就看它们的圆心距离和公共弦怎么安排啦!咱们要是能像两个圆儿一样,不论远近,总能找到那些公共的点,那生活可就丰富多彩了。
有了这些共同的弦,哎呀,就像是给生活多了一把钥匙,打开了更多的可能性。
圆心距和相交两圆公共弦的关系
当两个圆相交时,它们的圆心之间的距离被称为圆心距。
假设两个圆的圆心距为d,半径分别为r1和r2。
那么,它们的公共弦的长度可以通过勾股定理计算:
公共弦长度^2 = d^2 - (r1 - r2)^2
从这个公式可以看出,当两个圆的半径相等时,它们的公共弦长度最大。
这是因为在这种情况下,两个圆的公共弦是它们的直径,它们的圆心距也等于它们的半径之和。
另外,当公共弦长度最大时,它们的圆心距也最小。
这是因为公共弦长度的增加会导致圆心距的减小。
总之,我们可以得出这样的结论:当两个圆的公共弦长度最大时,它们的圆心距最小。
这个结论在解决一些几何问题时非常有用,在实际应用中也具有重要意义。
- 1 -。