2、插值法部分练习题

二次插值计算例题二次插值是一种常用的数值计算方法，用于通过已知数据点的坐标，推导出两个数据点之间的某个点的值。

在二次插值中，我们假设数据具有二次多项式的形式，并通过插值公式求解未知点的值。

以下是一个用于说明二次插值的计算例题：例题：已知数据点的坐标为（1，1）、（2，3）、（3，7），求x=2.5时的y值。

解析：1. 首先，我们需要确定插值多项式的形式。

由于已知的数据点个数为3个，因此我们可以假设插值多项式为二次多项式的形式：P(x) = a*x^2 + b*x + c2. 接下来，我们需要确定多项式的系数a、b和c。

为了确定这些系数，我们可以使用已知数据点的坐标。

3. 首先，我们将已知的数据点代入多项式中，得到以下方程： P(1) = a*1^2 + b*1 + c = 1P(2) = a*2^2 + b*2 + c = 3P(3) = a*3^2 + b*3 + c = 7将方程整理为矩阵形式，得到以下方程组：⎡ 1 1 1 ⎤⎡ a ⎤⎡ 1 ⎤⎢ 4 2 1 ⎥ * ⎢ b ⎥ = ⎢ 3 ⎥⎣ 9 3 1 ⎦⎣ c ⎦⎣ 7 ⎦4. 解方程组，可以得到系数a、b和c的值。

首先，将方程组进行高斯消元法的操作：⎡ 1 1 1 ⎤⎡ a ⎤⎡ 1 ⎤⎡ 1 1 1 ⎤⎢ 4 2 1 ⎥ * ⎢ b ⎥ = ⎢ 3 ⎥ => ⎢ 0 -2 -3 ⎥⎣ 9 3 1 ⎦⎣ c ⎦⎣ 7 ⎦⎣ 0 0 -2 ⎦进行回代运算：-2c = -2 => c = 1-2b - 3c = 3 => -2b - 3 = 3 => b = -2a +b +c = 1 => a - 2 + 1 = 1 => a = 2因此，系数a、b和c的值为2、-2和1。

5. 最后，将得到的系数代入插值多项式中，求解x=2.5时的y 值：P(2.5) = 2*2.5^2 + (-2)*2.5 + 1 = 11.25 - 5 + 1 = 7.25因此，在已知数据点（1，1）、（2，3）、（3，7）的情况下，当x=2.5时，y的值为7.25。

1 / 21数值分析实验二：插值法1 多项式插值的震荡现象1.1 问题描述考虑一个固定的区间上用插值逼近一个函数。

显然拉格朗日插值中使用的节点越多，插值多项式的次数就越高。

我们自然关心插值多项式的次数增加时， 是否也更加靠近被逼近的函数。

龙格（Runge ）给出一个例子是极著名并富有启发性的。

设区间[-1,1]上函数21()125f x x=+ (1)考虑区间[-1,1]的一个等距划分，分点为n i nix i ,,2,1,0,21 =+-= 则拉格朗日插值多项式为201()()125nn ii iL x l x x ==+∑(2)其中的(),0,1,2,,i l x i n =是n 次拉格朗日插值基函数。

实验要求：(1) 选择不断增大的分点数目n=2, 3 …. ，画出原函数f(x)及插值多项式函数()n L x 在[-1，1]上的图像，比较并分析实验结果。

(2) 选择其他的函数，例如定义在区间[-5，5]上的函数x x g xxx h arctan )(,1)(4=+=重复上述的实验看其结果如何。

(3) 区间[a,b]上切比雪夫点的定义为 (21)cos ,1,2,,1222(1)k b a b ak x k n n π⎛⎫+--=+=+ ⎪+⎝⎭(3)以121,,n x x x +为插值节点构造上述各函数的拉格朗日插值多项式，比较其结果,试分析2 / 21原因。

1.2 算法设计使用Matlab 函数进行实验, 在理解了插值法的基础上，根据拉格朗日插值多项式编写Matlab 脚本，其中把拉格朗日插值部分单独编写为f_lagrange.m 函数，方便调用。

1.3 实验结果1.3.1 f(x)在[-1,1]上的拉格朗日插值函数依次取n=2、3、4、5、6、7、10、15、20，画出原函数和拉格朗日插值函数的图像，如图1所示。

Matlab 脚本文件为Experiment2_1_1fx.m 。

可以看出，当n 较小时，拉格朗日多项式插值的函数图像随着次数n 的增加而更加接近于f(x)，即插值效果越来越好。

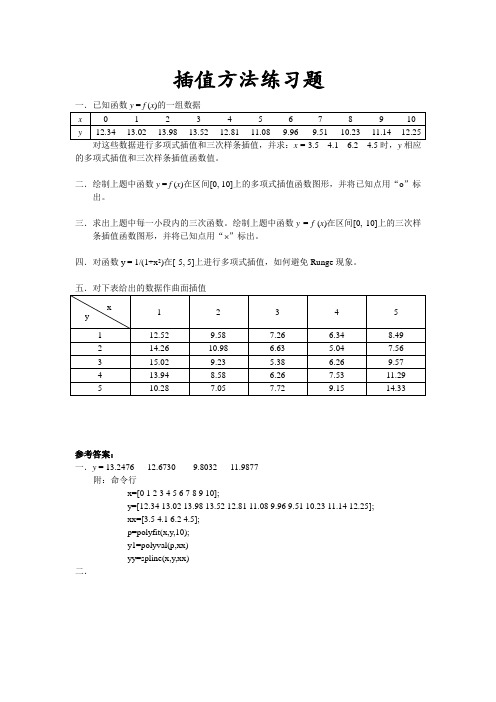
插值方法练习题一．已知函数y = f (x)的一组数据对这些数据进行多项式插值和三次样条插值，并求：x = 3.5 4.1 6.2 4.5时，y相应的多项式插值和三次样条插值函数值。

二．绘制上题中函数y = f (x)在区间[0, 10]上的多项式插值函数图形，并将已知点用“o”标出。

三．求出上题中每一小段内的三次函数。

绘制上题中函数y = f(x)在区间[0, 10]上的三次样条插值函数图形，并将已知点用“ ”标出。

四．对函数y = 1/(1+x2)在[-5, 5]上进行多项式插值，如何避免Runge现象。

五．对下表给出的数据作曲面插值参考答案：一．y = 13.2476 12.6730 9.8032 11.9877附：命令行x=[0 1 2 3 4 5 6 7 8 9 10];y=[12.34 13.02 13.98 13.52 12.81 11.08 9.96 9.51 10.23 11.14 12.25];xx=[3.5 4.1 6.2 4.5];p=polyfit(x,y,10);y1=polyval(p,xx)yy=spline(x,y,xx)二．附：命令行x=[0 1 2 3 4 5 6 7 8 9 10];y=[12.34 13.02 13.98 13.52 12.81 11.08 9.96 9.51 10.23 11.14 12.25];xx=0:0.0001:10;p=polyfit(x,y,10);y1=polyval(p,xx);plot(xx,y1,‘-‘,x,y,’o’)三．p1 = -0.4440 1.4719 -0.3479 12.3400p2 = -0.4440 1.4719 -0.3479 12.3400p3 = 0.5198 -4.3109 11.2177 4.6295p4 = -0.4654 4.5561 -15.3834 31.2307p5 = 0.5717 -7.8892 34.3977 -35.1441p6 = -0.1915 3.5588 -22.8420 60.2554p7 = 0.2542 -4.4634 25.2912 -36.0109p8 = -0.3253 7.7064 -59.8974 162.7624p9 = 0.0671 -1.7107 15.4393 -38.1354p10 = 0.0671 -1.7107 15.4393 -38.1354附：命令行x=[0 1 2 3 4 5 6 7 8 9 10];y=[12.34 13.02 13.98 13.52 12.81 11.08 9.96 9.51 10.23 11.14 12.25];xx=0:0.0001:10;yy=spline(x,y,xx);for k=1:10;p=polyfit(xx(3*k-2:3*k+1),yy(3*k-2:3*k+1),3)endplot(xx,yy,‘-‘,x,y,’x’)四．切比雪夫点插值x i =5cos((i-1)π /10)，i=1, 2, ⋯, 11，附：命令行x=-5:0.001:5;y=1./(1+x.^2);n=11;k=1:n;x0=5cos((k-1)/(n-1).*pi);y0=1./(1+x0.^2);p=polyfit(x0,y0,n-1);yy=polyval(p,x);plot(x,y,'-',x0,y0,'o',x,yy,'--')五．x0=1:5;y0=1:5;[xx,yy]=meshgrid(x0,y0); m=length(x0);n=length(y0);z=[12.52 9.58 7.26 6.34 8.49; 14.26 10.98 6.63 5.04 7.56;15.02 9.23 5.38 6.26 9.57;13.94 8.58 6.26 7.53 11.29;10.28 7.05 7.72 9.15 14.33];xp=1:0.01:5;yp=1:0.01:5;[xxp,yyp]=meshgrid(xp,yp);zp=interp2(xx,yy,z,xxp,yyp,'spline');mesh(xp,yp,zp)。

数值分析复习试题第一章 绪论 一. 填空题 1.*x 为精确值x 的近似值;()**x f y =为一元函数()x f y =1的近似值；()**,*y x f y =为二元函数()y x f y ,2=的近似值，请写出下面的公式：**e x x =-:***r x xe x -=()()()*'1**y f x x εε≈⋅ ()()()()'***1**r r x f x y x f x εε≈⋅()()()()()**,**,*2**f x y f x y y x y x yεεε∂∂≈⋅+⋅∂∂()()()()()****,***,**222r f x y e x f x y e y y x y y y ε∂∂≈⋅+⋅∂∂ 2、 计算方法实际计算时，对数据只能取有限位表示，这时所产生的误差叫 舍入误差.3、 分别用2.718281，2.718282作数e 的近似值，则其有效数字分别有 6位和 7 1.73≈（三位有效数字）-211.73 10 2≤⨯。

4、 设121.216, 3.654x x ==均具有3位有效数字,则12x x 的相对误差限为 0.0055 .5、 设121.216, 3.654x x ==均具有3位有效数字，则12x x +的误差限为 0。

01 。

6、 已知近似值 2.4560A x=是由真值T x 经四舍五入得到,则相对误差限为 0。

0000204 。

7、 递推公式,⎧⎪⎨⎪⎩0n n-1y =y =10y -1,n =1,2,如果取01.41y ≈作计算，则计算到10y 时，误差为8110 2⨯;这个计算公式数值稳定不稳定 不稳定 。

8、 精确值 14159265.3*=π，则近似值141.3*1=π和1415.3*2=π分别有 3 位和 4 位有效数字。

9、 若*2.71828x e x =≈=,则x 有 6 位有效数字，其绝对误差限为1/2＊10—5。

第一章 绪论姓名 学号 班级习题主要考察点：有效数字的计算、计算方法的比较选择、误差和误差限的计算。

1 若误差限为5105.0-⨯,那么近似数0.003400有几位有效数字？（有效数字的计算） 解：2*103400.0-⨯=x ，325*10211021---⨯=⨯≤-x x 故具有3位有效数字。

2 14159.3=π具有4位有效数字的近似值是多少？（有效数字的计算） 解：10314159.0⨯= π，欲使其近似值*π具有4位有效数字，必需41*1021-⨯≤-ππ，3*310211021--⨯+≤≤⨯-πππ，即14209.314109.3*≤≤π即取（3.14109 , 3.14209）之间的任意数，都具有4位有效数字。

3 已知2031.1=a ，978.0=b 是经过四舍五入后得到的近似值，问b a +，b a ⨯有几位有效数字？（有效数字的计算）解：3*1021-⨯≤-aa ，2*1021-⨯≤-b b ，而1811.2=+b a ，1766.1=⨯b a 2123****102110211021)()(---⨯≤⨯+⨯≤-+-≤+-+b b a a b a b a故b a +至少具有2位有效数字。

2123*****10210065.01022031.1102978.0)()(---⨯≤=⨯+⨯≤-+-≤-b b a a a b b a ab 故b a ⨯至少具有2位有效数字。

4 设0>x ，x 的相对误差为δ，求x ln 的误差和相对误差？（误差的计算） 解：已知δ=-**xx x ，则误差为 δ=-=-***ln ln xx x x x则相对误差为******ln ln 1ln ln ln xxx x xxx x δ=-=-5测得某圆柱体高度h 的值为cm h 20*=，底面半径r 的值为cm r 5*=，已知cm h h 2.0||*≤-，cm r r 1.0||*≤-，求圆柱体体积h r v2π=的绝对误差限与相对误差限。

数值分析韩旭里答案【篇一：数值分析上机题目】>1631110xxxx 材料科学与工程学院一．第2章插值法l2.7 给定数据表2-15.用newton插值公式计算3次插值多项式n3(x).表2-15x f(x)1 1.251.52.500 1.002 5.50a. matlab代码如下，two.m,%第二章，p45,练习题2第七题 clear(); x=[1,1.5,0,2];y(:,1)=[1.25,2.50,1.00,5.50];%已知点集合x和y syms t w; w(1)=1; %计算基函数序列w和差商表y，以及函数序列的权数diag(y),计算的牛顿三次多项式表述为t的函数 for j=2:length(x) fori=j:length(x)y(i,j)=(y(i,j-1)-y(i-1,j-1))/(x(i)-x(i-j+1)); i=i+1; endw(j)=prod(t-x(1:j-1)); j=j+1; enddisp(三次牛顿插值多项式为); disp(collect(w*diag(y)));plot(x,y(:,1),*); hold on;fplot(collect(w*diag(y)),[-0.5,2.5]);legend({已知点集,三次牛顿插值多项式函数},location,northwest,fontsize,14); xlabel(x,fontsize,16);ylabel(y,fontsize,16); hold off;b. 计算结果如下：二．第3章函数逼近与数据拟合a. matlab代码，three.m，%第三章函数逼近与数据拟合，p68练习题，第2题 clear(); syms x;%所使用的非线性基函数序列，用符号表示 y=abs(x);%被逼近函数f=[1,x^2,x^4];%求解法方程的系数矩阵a*gn=b，其中a和b均为行向量gn=ones(length(f),length(f)); for i=1:length(f) for j=1:length(f) gn(i,j)=int(f(i)*f(j),-1,1);j=j+1; endb(i)=int(f(i)*y,-1,1); i=i+1; enda=b/gn;%最佳平方逼近的系数行向量 disp(逼近函数表达式);disp(vpa(f*a));disp(最佳函数逼近得平方误差); disp(vpa(int(y^2,-1,1)-a*b));fplot(y,[-1,1]); hold on; fplot(a*f,[-1,1]);legend({被逼近函数,逼近函数},location,north,orientation,horizontal,fontsize,16,fontweight,b old);xlabel(x,fontsize,20,fontweight,bold);ylabel(y,fontsize,20,fontweight,bold); hold off;b. 运行结果如下：三.第4章数值积分与数值微分例4.9用romberg求积法计算定积分 01sin?(??)??a. matlab代码，four.m%romberg求积公式，外推原理 clear(); clear(); format long; a=0; b=1;t(1,1)=(b-a)/2*(f(a)+f(b));t(2,1)=1/2*t(1,1)+(b-a)/2*f((a+b)/2); t(1,2)=(4*t(2,1)-t(1,1))/(4-1);col=2;while abs(t(1,col)-t(1,col-1))0.5*10^-6%t(1,col)对应的计算的是多少步的值,col→coln关系col=col+1;%此时求得是第n+1次均分后的结果，使用的是第n次的结果，注意在矩阵 %计算的第n斜列是第n-1次均分的结果 for j=1:colif j==1h=(b-a)/2^(col-2);%使用n+1之前的第n次结果【篇二：数值分析a教学】>一、课程基本信息二、课程目的和任务“数值分析”是理工科院校计算数学、力学、物理、计算机软件等专业的学生必须掌握的一门重要的基础课程。

第一章 绪论姓名 学号 班级习题主要考察点：有效数字的计算、计算方法的比较选择、误差和误差限的计算。

1 若误差限为5105.0-⨯,那么近似数0.003400有几位有效数字？（有效数字的计算） 解：2*103400.0-⨯=x ，325*10211021---⨯=⨯≤-x x 故具有3位有效数字。

2 14159.3=π具有4位有效数字的近似值是多少？（有效数字的计算） 解：10314159.0⨯= π，欲使其近似值*π具有4位有效数字，必需41*1021-⨯≤-ππ，3*310211021--⨯+≤≤⨯-πππ，即14209.314109.3*≤≤π3 已知2031.1=a ，978.0=b 是经过四舍五入后得到的近似值，问b a +，b a ⨯有几位有效数字？（有效数字的计算）解：3*1021-⨯≤-aa ，2*1021-⨯≤-b b ，而1811.2=+b a ，1766.1=⨯b a 2123****102110211021)()(---⨯≤⨯+⨯≤-+-≤+-+b b a a b a b a故b a +至少具有2位有效数字。

2123*****10210065.01022031.1102978.0)()(---⨯≤=⨯+⨯≤-+-≤-b b a a a b b a ab 故b a ⨯至少具有2位有效数字。

4 设0>x ，x 的相对误差为δ，求x ln 的误差和相对误差？（误差的计算） 解：已知δ=-**xx x ，则误差为 δ=-=-***ln ln xx x x x则相对误差为******ln ln 1ln ln ln xxx x xxx x δ=-=-5测得某圆柱体高度h 的值为cm h 20*=，底面半径r 的值为cm r 5*=，已知cm h h 2.0||*≤-，cm r r 1.0||*≤-，求圆柱体体积h r v2π=的绝对误差限与相对误差限。

（误差限的计算） 解：*2******2),(),(h h r r r h r r h v r h v -+-≤-ππ绝对误差限为πππ252.051.02052)5,20(),(2=⨯⋅+⨯⋅⋅⋅≤-v r h v相对误差限为%420120525)5,20()5,20(),(2==⋅⋅≤-ππv v r h v 6 设x 的相对误差为%a ,求nx y =的相对误差。

一、填空题：1． 满足()a a f x x =，()b b f x x =，()c c f x x =的拉格朗日插值余项为 。

答：()()()()()3!a b c f R x x x x x x x ξ'''=---2．已知函数()f x 的函数值()()()()()0,2,3,5,6f f f f f ，以及均差如下 ()()()()()00,0,24,0,2,35,0,2,3,51,0,2,3,5,60f f f f f ===== 那么由这些数据构造的牛顿插值多项式的最高次幂的系数是 答： 1二、选择题1. 通过点()()0011,,,x y x y 的拉格朗日插值基函数()()01,l x l x 满足（ ） A ．()00l x ＝0，()110l x = B ． ()00l x ＝0，()111l x = C ．()00l x ＝1，()110l x = D ． ()00l x ＝1，()111l x = 答：D2．. 已知等距节点的插值型求积公式()()352kkk f x dx A f x =≈∑⎰，那么3kk A==∑（ ）A ．1 B. 2 C. 3 D. 4 答：C3．过点(x 0,y 0), (x 1,y 1)，…，(x 5,y 5)的插值多项式P(x)是( )次的多项式。

(A). 6 (B).5 (C).4 (D).3． 答：B 三、证明题1. 设 f (x) = (x-1) (x-2) .证明对任意的x 有： f [1, 2, x)]= 1证明:f [1, 2] = [f (1) – f (2)]/ (1 – 2) = [0 – 0]/ (-1) = 0, 对任意的x 有F[2, x] = [f (2) – f (x)]/ (2 – x) = [0 – (x-1) (x-2)]/ (2 – x) = (x-1),所以 f [1, 2, x] = [f (1, 2) - f (2, x)]/ (1 – x) = [0 - (x-1)]/ (1 – x) = 12.设在上具有二阶连续导数，且，求证：解：由，则在的线性插值多项式为：，于是由，可得：3． 试利用差分性质证明：证明：记：可以证明：， 又： 故：. 四、计算题： 1.．已知数值表试用二次插值计算()0.57681f 的近似值，计算过程保留五位小数。

1、已知 f （x ）=ln x 的数值表如下，分别用线性及二次 Lagrange 插值法计算f (0.54) 的近似值，并估计误差。

解：（1）线性插值法：因为()ln f x x = 时递增函数，所以取0.5和0.6为插值节点。

则线性插值多项式为：0011()()()()f x F x f l x f l x ==+0.540.60.540.5(0.54)(0.54)(0.5)(0.6)0.50.60.60.50.6930.6(0.510)0.40.6198f F f f --≈=+-- =-⨯+-⨯=-截断误差：101011()''()()(),(,)2R x f x x x x x x ξξ=--∈ 121(0.54)0.0012R ξ=11(0.5,0.6)110.0012(0.54)0.00120.360.25,0.0032(0.54)0.0048R R ξ∈∴⨯<<⨯<<即 （2）二次lagrange 插值法：A ：若取0.4，0.5和0.6为插值点，0120.916,0.693,0.510f f f =-=-=-012(0.540.5)(0.540.6)0.12(0.40.5)(0.40.6)(0.540.4)(0.540.6)0.84(0.50.4)(0.50.6)(0.540.4)(0.540.5)0.28(0.60.4)(0.60.5)l l l --==-----==----==--001122(0.54)(0.54)(0.54)(0.54)(0.54)0.615f F f l f l f l ≈=++=-截断误差：20121()'''()()()()3!R x f x x x x x x ξ=---则231(0.54)0.000112R ξ=333233[0.4,0.6],()111,0.60.4110.000112(0.54)0.0001120.40.6f x R ξξ∈∴<<-⨯<<-⨯递增；即20.00175(0.54)0.000519R -<<-B ：若取0.5，0.6和0.7为插值点，0120.693,0.510,0.357f f f =-=-=-012(0.540.6)(0.540.7)0.48(0.50.6)(0.50.7)(0.540.5)(0.540.7)0.64(0.60.5)(0.60.7)(0.540.5)(0.540.6)0.12(0.70.5)(0.70.6)l l l --==----==----==---001122(0.54)(0.54)(0.54)(0.54)(0.54)0.6162f F f l f l f l ≈=++=-截断误差：20121()'''()()()()3!R x f x x x x x x ξ=--- 则231(0.54)0.000128R ξ=333233[0.5,0.7],()111,0.70.5110.000128(0.54)0.0001280.70.5f x R ξξ∈∴<<⨯<<⨯递增；即20.000373(0.54)0.001024R <<2、已知f(x)=e -x 的一组数据见下表，用抛物插值法计算e -2.1的近似值。

二次插值法例题二次插值法是一种常用的数值计算方法，用于在给定的几个点之间计算线性插值函数。

下面是一个简单的二次插值法例题: 假设我们有四个点 $(x_1, y_1), (x_2, y_2), (x_3, y_3), (x_4, y_4)$ ,我们需要计算一个线性插值函数 $y$ ,使得 $y$ 在 $(x_1, y_1), (x_2, y_2), (x_3, y_3), (x_4, y_4)$ 四个点之间保持连续。

首先，我们可以使用二次插值法在四个点之间计算一个二次多项式 $y_2(x)$。

具体来说，我们可以使用以下公式:$$y_2(x) = a_0 + a_1x + a_2x^2$$其中，$a_0, a_1, a_2$ 是由四个点 $(x_1, y_1), (x_2, y_2), (x_3, y_3), (x_4, y_4)$ 计算出来的系数。

接下来，我们可以使用二次多项式 $y_2(x)$ 来计算插值函数$y$ 在 $(x_1, y_1), (x_2, y_2), (x_3, y_3), (x_4, y_4)$ 四个点之间的值。

具体来说，我们可以使用以下公式:$$y(x) = y_2(x_{target}) cdot (x - x_{target}) + y_2(x_0)$$ 其中，$x_0$ 是 $(x_1, y_1), (x_2, y_2), (x_3, y_3), (x_4, y_4)$ 四个点中的一个，$x_{target}$ 是我们需要计算插值函数的点。

例如，如果我们的目标是计算 $(x_3, y_3)$ 点的插值函数，那么我们可以使用以下公式:$$y(x) = y_2(x_{target}) cdot (x - x_{target}) + y_2(x_0)$$ 其中，$x_0$ 可以是 $(x_1, y_1), (x_2, y_2), (x_3, y_3),(x_4, y_4)$ 四个点中的一个，$x_{target}$ 则是我们需要计算插值函数的点，例如 $x_{target} = x_3$ 就是不错的选择。

专题四资金时间价值一、资金时间价值的概念定义：资金时间价值是指一定量资金在不同时点上的价值量差额。

【提示】理解资金时间价值要把握两个要点：（1）不同时点；（2）价值量差额。

二、终值和现值的计算1.终值又称将来值，是现在一定量的资金折算到未来某一时点所对应的价值，俗称“本利和”，通常记作F。

2.现值，是指未来某一时点上的一定量资金折算到现在所对应的价值，俗称“本金”，通常记作“P”。

现值和终值是一定量资金在前后两个不同时点上对应的价值，其差额即为资金的时间价值。

生活中计算利息时所称本金、本利和的概念，相当于资金时间价值理论中的现值和终值，利率（用i表示）可视为资金时间价值的一种具体表现：现值和终值对应的时点之间可以划分为n期（n≥1），相当于计息期。

【注意】终值与现值概念的相对性。

【思考】现值与终值之间的差额是什么？两者之间的差额是利息.三、利息的两种计算方式1.单利计息方式：只对本金计算利息。

以本金为基数计算利息，所生利息不再加入本金滚动计算下期利息（各期的利息是相同的）。

2.复利计息方式：既对本金计算利息，也对前期的利息计算利息。

将所生利息加入本金，逐年滚动计算利息的方法。

（各期的利息是不同的）。

【提示】除非特别指明，否则在计算利息的时候使用的都是复利计息。

四、复利终值与现值1.复利终值复利终值的计算公式为：F=P（1＋i）n在上式中，（1＋i）n称为“复利终值系数”，用符号（F/P，i，n）表示。

这样，上式就可以写为：F=P（F/P，i，n）【提示】在平时做题时，复利终值系数可以查表得到。

考试时，一般会直接给出。

但需要注意的是，考试中系数是以符号的形式给出的。

因此，对于有关系数的表示符号需要掌握。

【例题1·计算题】某人将100元存入银行，复利年利率2%，求5年后的终值。

【答案】5年后的终值=100×（1+2%）5 =100×（F/P，2%，5）=100×1.104=110.4（元）。

一、填空题：1． 满足()a a f x x =，()b b f x x =，()c c f x x =的拉格朗日插值余项为 。

答：()()()()()3!a b c f R x x x x x x x ξ'''=---2．已知函数()f x 的函数值()()()()()0,2,3,5,6f f f f f ，以及均差如下 ()()()()()00,0,24,0,2,35,0,2,3,51,0,2,3,5,60f f f f f ===== 那么由这些数据构造的牛顿插值多项式的最高次幂的系数是 答： 1二、选择题1. 通过点()()0011,,,x y x y 的拉格朗日插值基函数()()01,l x l x 满足（ ）(A ．()00l x ＝0，()110l x =B ． ()00l x ＝0，()111l x =C ．()00l x ＝1，()110l x =D ． ()00l x ＝1，()111l x = 答：D2．. 已知等距节点的插值型求积公式()()352kkk f x dx A f x =≈∑⎰，那么3kk A==∑（ ）A ．1 B. 2 C. 3 D. 4 答：C3．过点(x 0,y 0), (x 1,y 1)，…，(x 5,y 5)的插值多项式P(x)是( )次的多项式。

(A). 6 (B).5 (C).4 (D).3． 答：B 三、证明题 &1. 设 f (x) = (x-1) (x-2) .证明对任意的x 有： f [1, 2, x)]= 1证明:f [1, 2] = [f (1) – f (2)]/ (1 – 2) = [0 – 0]/ (-1) = 0, 对任意的x 有F[2, x] = [f (2) – f (x)]/ (2 – x) = [0 – (x-1) (x-2)]/ (2 – x) = (x-1), 所以 f [1, 2, x] = [f (1, 2) - f (2, x)]/ (1 – x) = [0 - (x-1)]/ (1 – x) .= 12.设在上具有二阶连续导数，且，求证：解：由，则在的线性插值多项式为：，于是由，可得：3． 试利用差分性质证明：）证明：记：可以证明：，又：故：. 四、计算题： 1.．已知数值表x（()f x试用二次插值计算()0.57681f 的近似值，计算过程保留五位小数。

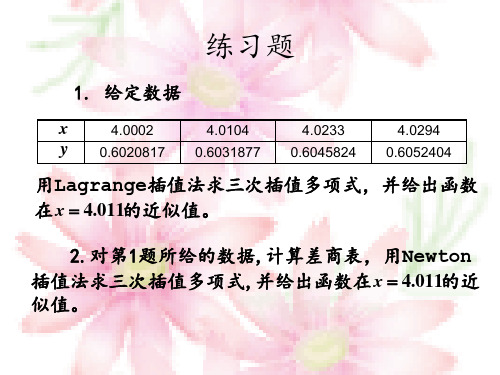
三点二次插值法例1. 用三点二次插值法求解： 3min ()21t t t ϕ=-+，精度210ε-=。

解：首先找出满足123()()()t t t ϕϕϕ><且123t t t <<的1t ，2t ，3t ； 易知，10t =，20t =，30t =； 第一次迭代：1()1t ϕ=，2()0t ϕ=，3()22t ϕ=， 代入公式，得：0.625μ=，由于()()20.0060t ϕμϕ=-<=， 并且20.375t με-=>，则继续迭代； 这时迭代点：123t t t μ<<<且12()()()t t ϕϕμϕ><， 则令：110t t ==，20.625t μ==，321t t == 第二次迭代：()11t ϕ=，()20.006t ϕ=-，()30t ϕ=， 代入公式，得：0.808μ=， 由于2()0.089()0.006t ϕμϕ=-<=-， 并且 20.183t με-=>，则继续迭代； 这时迭代点：123t t t μ<<<且23()()()t t ϕϕμϕ><， 则令：120.625t t ==，20.808t μ==，331t t == 第三次迭代：()10.006t ϕ=-，()20.089t ϕ=-，()30t ϕ=， 代入公式，得：0.815μ=，由于2()0.089()0.006t ϕμϕ=-==-， 并且 20.007t με-=<，则停止迭代， 输出近似最优解为0.815μ=或0.808μ=。

例2 用三点二次插值法求： 30min ()32t t t t ϕ≥=-+的近似最优解（精确极小点*1t =），设已确定其初始搜索区间为[]0,3，取初始插值点02t =，终止误差0.05ε=。

解：10t =，22t =，33t =，第一次迭代：()12t ϕ=，()24t ϕ=，()320t ϕ=， 代入公式，得：0.9μ=，由于2()0.029()4t ϕμϕ=-<=，并且 2 1.1t με-=>，则继续迭代； 这时迭代点：123t t t μ<<<且12()()()t t ϕϕμϕ><， 则令：110t t ==，20.9t μ==，322t t == 第二次迭代：()12t ϕ=，()20.029t ϕ=，()34t ϕ=， 代入公式，得：0.82759μ=， 由于2()0.08405()0.029t ϕμϕ=>=， 并且 20.07241t με-=>，则继续迭代； 这时迭代点：123t t t μ<<<且23()()()t t ϕμϕϕ><，则令：10.82759t μ==，220.9t t ==，332t t == 第三次迭代：()10.08405t ϕ=，()20.029t ϕ=，()34t ϕ=， 代入公式，得：0.96577μ=， 由于2()0.00347()0.029t ϕμϕ=-<=， 并且 20.06577t με-=>，则继续迭代； 这时迭代点：123t t t μ<<<且23()()()t t ϕϕμϕ><， 则令：120.9t t ==，20.96577t μ==，332t t == 第三次迭代：()10.029t ϕ=，()20.00347t ϕ=，()34t ϕ=， 代入公式，得：0.98308μ=， 由于2()0.00086()0.00347t ϕμϕ=<=， 并且 20.01731t με-=<，则停止迭代， 输出近似最优解为0.98308μ=。