第五章 刚体力学习题课
- 格式:pptx
- 大小:503.79 KB
- 文档页数:27



5.1、一长为I 的棒AB ,靠在半径为r 的半圆形柱面上,如图所示。
今A 点以恒定速度V 。
沿水平线运动。
试求:(i ) B 点的速度v B ; (ii )画出棒的瞬时转动中心的解:如图,建立动直角系 A - xyz ,取A 点为原点。
v B 二v A 、 r AB ,关键是求:法1(基点法):取 A 点为基点,v C= v A 亠心■ r AC = v A • v CO = v A v A sin 二丄PT 心i_v 0^j法2(瞬心法):如图,因棒上C 点靠在半圆上,所以 C 点的速度沿切线方向,故延长0C ,使其和垂直于取A 点为基点,那么 B 点的速度为:vn sinV B =VA,=vo i- k [(-lcos^)i Isin“] r cos°,,I sin ‘日、-v -lsin 2 9 -二 v -(1 )i 0jr cos 廿5.2、一轮的半径为r ,竖直放置于水平面上作无滑动地滚动,轮心以恒定速度 轮缘上任在直角三角形 QPA 中,「AP =r oA Ctg rr COSTsin 2二-k (_r PA )j =r PAi哼 i 二 v °i ,即,」sinJsin 二r cos-在直角三角形 A 点速度线交于P 点,那么P 点为瞬心。
OCA中,r °A J sinv 0前进。
求一点(该点处的轮辐与水平线成二角)的速度和加速度。
解:任取轮缘上一点M,设其速度为v M,加速度为a MV M = W = wi = v^ - ■「NM-v 2i -,k 2rj = (2,r - v 2)i如图,取轮心O 为原点,建立动系O _xyz ,其中轮心的速度方向为x 轴正向,O_xy 平面位于轮上。
那么轮子的角速度为 .--.k -vk 取O 点为基点,那么v M 二v O 亠心■ r OM 因轮无滑动地滚动,所以 C 点为瞬心。
v O = . r CO = v 0 iyC即:k r CO j = v 0i ,化简有• = ―— = —0,那么有: r co r v M 二 v O , r OM 二 v 0i - k r (cossin rj) =v 0i - k r (cos 引 sin j) r 二 v 0(1 sin r)i - v 0 cosr j _ d _ d a Mv M [v 0(1 sin "i 「v 0cos )j]二 v 0)cosv^ sin v jdt dt =v 0v(cos vi sin )j)二-v ^ (cos )i sin j) 2--乂 (cos 新 sin j) r 5.3、半径为r 的圆柱夹在两块相互平行的平板 向运动,如图示。
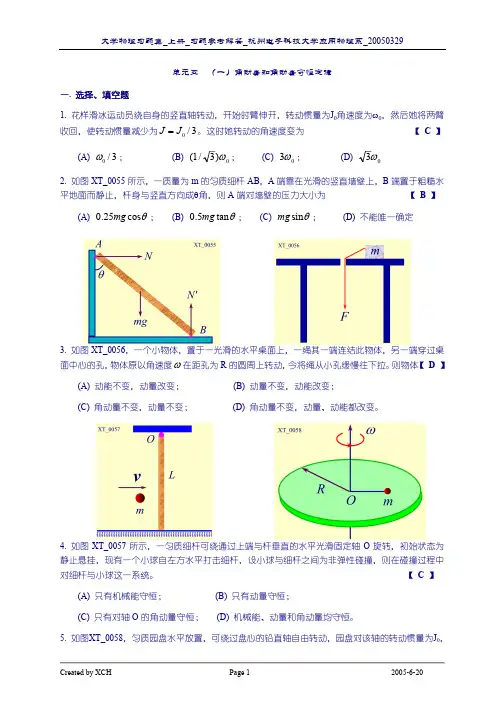




第五章刚体力学参考答案第五章 刚体力学参考答案一. 选择题[ C ]1、一轻绳跨过一具有水平光滑轴、质量为M 的定滑轮,绳的两端分别悬有质量为m 1和m 2的物体(m 1<m 2),如图5-7所示.绳与轮之间无相对滑动.若某时刻滑轮沿逆时针方向转动,则绳中的张力 (A) 处处相等. (B) 左边大于右边.(C) 右边大于左边. (D) 哪边大无法判断.参考答案:逆时针转动时角速度方向垂直于纸面向外, 由于m 1<m 2,实际上滑轮在作减速转动,角加速度方向垂直纸面向内,所以,由转动定律得:(T 2-T 1)R=J β[ D ]2、如图5-8所示,一质量为m 的匀质细杆AB ,A 端靠在粗糙的竖直墙壁上,B 端置于粗糙水平地面上而静止.杆身与竖直方向成q 角,则A 端对墙壁的压力大小(A) 为 41mg cos q . (B)为21mg tg q . (C) 为 mg sin q . (D) 不能唯一确定.参考答案:因为细杆处于平衡状态,它所受的合外力为零,以B 为参考点,外力矩平衡可有: N A =f Bf A +N B =mgsin sin cos 2A A lmg f l N l θθθ=+三个独立方程有四个未知数,不能唯一确定。
[ B ]3、如图5-9所示,一静止的均匀细棒,长为L 、质量为M ,可绕通过棒的端点且垂直于棒长的光滑固定轴O 在水平面内转动,转动惯量为231ML .一质量为m 、速率为v 的子弹在水平面内沿与棒垂直的方向射出并穿出棒的自由端,设穿过棒后子弹的速率为v 21,则此时棒的角速度应为(A) ML m v . (B) ML m 23v . (C) ML m 35v . (D) ML m 47v.m 2m 1O图5-7图5-8v 21图5-9参考答案:把质点与子弹看作一个系统,该系统所受外力矩为零,系统角动量守恒: Lmv=Lmv/2+1/3ML 2ω 可得出答案。
[ c ]4、一圆盘正绕垂直于盘面的水平光滑固定轴O 转动,如图5-11射来两个质量相同,速度大小相同,方向相反并在一条直线上的子弹,子弹射入圆盘并且留在盘内,则子弹射入后的瞬间,圆盘的角速度ω(A) 增大. (B) 不变.(C) 减小. (D) 不能确定.参考答案:把三者看作同一系统时,系统所受合外力矩为零,故由角动量守恒定律得:设L 为每一子弹相对与O 的角动量大小.J ω0+L-L=(J+J 子弹) ω ω <ω0[ C ]5、将细绳绕在一个具有水平光滑轴的飞轮边缘上,现在在绳端挂一质量为m 的重物,飞轮的角加速度为β.如果以拉力2mg 代替重物拉绳时,飞轮的角加速度将(A) 小于β. (B) 大于β,小于2 β. (C) 大于2 β. (D) 等于2 β.参考答案:设飞轮的半径为R,质量为M ,根据刚体定轴转动定律M=J β,当挂质量为m 的重物是: Mg-T=ma TR=J β a=R β由此得β=MgR/(J+Mr 2),当以F=2mg 的拉力代替重物拉绳时,有: 2mgR=J β‘,β‘=2mgR/J,比较二者可得出结论。


第五章刚体力学(答案)本页仅作为文档封面,使用时可以删除This document is for reference only-rar21year.March一、选择题[ C ] 1、(基础训练2)一轻绳跨过一具有水平光滑轴、质量为M 的定滑轮,绳的两端分别悬有质量为m 1和m 2的物体(m 1<m 2),如图5-7所示.绳与轮之间无相对滑动.若某时刻滑轮沿逆时针方向转动,则绳中的张力 (A) 处处相等. (B) 左边大于右边. (C) 右边大于左边. (D) 哪边大无法判断.【提示】逆时针转动时角速度方向垂直于纸面向外,由于(m 1<m 2),实际上滑轮在作减速转动,角加速度方向垂直纸面向内,所以,由转动定律21()T T R J β-=可得:21T T >(或者:列方程组:11122212m g T m a T m g m aT R T R J a Rββ-=⎧⎪-=⎪⎪⎨-=⎪⎪=⎪⎩ ,解得:()()12212m m gR m m R J β-=++,因为m 1<m 2,所以β<0,那么由方程120T R T R J β-=<,可知,21T T >)[ B ] 2、(基础训练5)如图5-9所示,一静止的均匀细棒,长为L 、质量为m 0,可绕通过棒的端点且垂直于棒长的光滑固定轴O 在水平面内转动,转动惯量为2013m L .一质量为m 、速率为v 的子弹在水平面内沿与棒垂直的方向射出并穿出棒的自由端,设穿过棒后子弹的速率为v 21,则此时棒的角速度应为(A) 0v m m L . (B) 03v 2m m L . (C) 05v 3m m L. (D) 07v 4m m L【提示】把细棒与子弹看作一个系统,该系统所受合外力矩为零,所以系统的角动量守恒: 20123v mvL m L m L ω⎛⎫=+ ⎪⎝⎭,即可求出答案。
图5-7v 21 v 俯视图 图5-9[ C ] 3、(基础训练7)一圆盘正绕垂直于盘面的水平光滑固定轴O 转动,如图5-11射来两个质量相同,速度大小相同,方向相反并在一条直线上的子弹,子弹射入圆盘并且留在盘内,则子弹射入后的瞬间,圆盘的角速度ω (A) 增大. (B) 不变.(C) 减小. (D) 不能确定.【提示】把三者看成一个系统,则系统所受合外力矩为零,所以系统的角动量守恒。