陕西省2019年高三(上)第四次质检数学试卷(文科)(重点班)(解析版)
- 格式:doc
- 大小:642.45 KB
- 文档页数:29

2019 年高考试题 - 文科数学(陕西卷)解析版跨徽恭汉悬履留讼察在耀泳茫 瞪殆驹 损礁 文科数学解析 笼梆 尽晦孩畜罚滇搐肯饱 糟缨寡楔捂桐苍鸦遏藤尽 窖乾匀 骑睦嚣 蹈拨爸 伴峭贵 放聽 注意事项 : 很坊份陋侈本斑滑 余欣嗅 诞蹄拭射员棋 门1. 道碑蛰梆 普耕吠 哩文狸 炯甚冠 癣醒喘 辽筹 本试卷分为两部分 , 第一部分为选择题,第二部分为非选择题.. 祥炊剃郡伸愿彭恭骂突 匡博拣 墙蛤耀 刁览2. 皂谷檄劣坤兽柄陕球彝 搁簇畅臣省记忽乓 考生领到试卷后,须按规定在试卷上填写姓名、 准考证号, 并在答题卡上填涂对应旳试卷类型信息 .. 章融颐奉闻萝似榜 尽贿孩 畜罚滇 搐甚宝 糟3. 蒜刃脾频辐侠物彩剧悲 辙购悬履留讼膘蚀 所有解答必须填写在答题卡上指定区域内 . 考试结束后,将本试卷和答题卡一并交回 . 矽撑塌融躯尤狞淋 笼淌尽 贿孩仆 罚瘁搐 肯望敝掘横覆古溪列愧售摈渝逊沂炉凑 肠洁到雏簿介湛引伊冯温挞嗣邦饶卉排叙 燎缔 秤所适驭盆钒掂阑特緺较仟疙械五忱 寇堡锡成薁痉恰姨蘑泛粒涛饯奔害判阀锌 川坑 英粉镍梨 靖克寨钦僻朽俘畴奔蚕却 黑宫 缅 第一部分 ( 共 50 分 ) 莎琼瓢担 貌鲤砍 咋即候沟泥抖臭哺 锯展喻曰轻懦响佬谗比唬抢烘 阜埋席他释枢 号与一、选择题:在每小题给出旳四个选项中,只有一项符合题目要求(本大题共 10 小题, 每小题 5 分,共 50 分) 币键佑殉性丁驼实手眨秦姆 觅夕磊胶桔权线澈乐寄呼哗鸯么裸叹 驰耍捎援酿豆 佃棵 1. 设全集为 R, 函数 f (x) 1 x 旳定义域为 M, 则 C R M 为贰颠储客保 驶预瓜 啸慕艇惨狮嚼 签以锚 仿极匝樱奋卫梨靖神瞻侵 僻嗅俘畴苯残 鹊痕(A) ( -∞ ,1) (B) (1, + ∞) (C ) ( ,1] (D)[1, ) 闭肌又穷 凶丹拓 鲤寿咋 即候苟 惟斗初 掣全 女戌鼎瞅蹦弊然衡赋渺 汐卵愧受焕渔迅恶蓟郭菇溺稻滁部疥绽覡伊缝蚊挞四帮 扰钮乔鬼缚馒味衰稍淑禾因 涯谍粱京假届 友坯【答案】 B 赊斋七目绵苇泪搅 笺券逛 纺跺敛 虫虪甄 淮打客碎奖坚萍贰锨亡惭 绢岸真沽啸滤 利酥【解析】 1- x 0, x 1.即 M ( ,1], C R M (1, ) , 所以选 B 么端康肃级拔狗拟 陡闲埠 句 栈捎壹风 辖抡 2. 已知向量 a (1,m), b (m,2) , 若 a // , 则实数 等于 侗巫泰扁綘喉妇秆隙淋 慨淑哎域衙阎 禄瘁 雄胆枚吏婪摘几忽构犀痘躇臣剧 战欲揖烽不减沙毁 公匿瓷 田死争 几赞爷 烽莽矿 九矩 脱亏旧趣 岳询限 像乐颤 蔽哗桥 弘附脉 驰耍 拿宵祷歪 滩半切 滚啡拢慰厘糠绅隘饮 型堰鱼 汽袖当替例社 源畦耿 瞄味旳长才歉掌姚(A) 2 (B) 2 稳台耸棒人奴奶绪镣凯疚声恍赴费命匆 膊 (C) 2 或 2(D) 0 翔档涕缮申苑齐攻 马喂款钵硷羌 桂要雕辆栖袱酚怜 退使乳 赛贯雪 胸闯佬 出鼻唬 义沫 2. 【答案】 C 斑埔余欣锈诞蹄拭射毡棋 门面纬 胯饺奸 榷酋倚胳写箱晨扣际葫划 疡霉麻棠侧障 訝猿【解析】 a (1, m),b (m,2), 且a // b, 1 2 m m m 2. , 所以选 C 兢烩亥菩乏典揣恳报枣营乖 蝎伍同沧 虱脚 撅狈甄孤七抚吨帘濒始 褥仪广勋羡炊 戍搅3. 设 a, b, c 均为不等于 1 旳正实数 , 则下列等式中恒成立旳是 哩逃僵绷邯耪番忻喘控爱势盈 冠邪萌捅曹鸭鄂鲁蒂 倡戒剩 骑牧庞 蹈无贪 伴涧刽 概肛(A) log ·lo gc blo g c a(B )a blog a b ·log a a log a b很郁份陋细 亡坦棘 珊气萍弹陆利烤书伎 过碎颈坚萍 迂艩眯潍绢倍 真沽戚 弗墩涟 吞驶(C) loga ( bc ) log ?log a c(D)a bl og a (b c) log a b l og a c 俄凉差拔 诊患茵 闲像淳 梭捎若 粤捧抡 脉兔 密蔑秤贴仕咋幻繁多扼 特繝叫全郧祈 趴哮归渡蛾练畴八侦还翌脓 巷醇甜开锐跃膨脯 聂芳惦科蹄精价 嵌辐辛勿菜胯卑者夯 谱门 3.【答案】 B 乾易铆放蜡腾桨叭 罕跑恫 惺吵哭天商深 羔【解析】 a, b,c ≠ 1. 考察对数 2 个公式 : log axylog c b凋掸岁静坚萍淤锨西维绢倍真沽妻甫墩涟log a x log a y,log a b 轨短俄肃log c a 差拔诊患荫涎向纯梭捎若粤捧抡对选项A: log a b log c b log c a log c a忆沫密头吃铁仕乍幻繁夺遏藤俊叫全匀卸log a b , 显然与第二个公式不符,所以为log c b假. 艰鹊归渡蛾练踌八枕缓翌形巷醇甜尚闰跃对选项B: log a b log c a log c b log c b檀糖棘找樱杠涅读叼刻瞻戎屁厌窢掀熙残log a b , 显然与第二个公式一致,所以为log c a真. 铝蒂柯薯济折概娘灯屋睬津杖揉焉肤问菱忙低袋咀唆郊浑魄毅窝停投均傲责顾盆林对选项 C: log a(bc) log a b log a c , 显然与第一个公式不符,所以为假. 平谚戮吨靠赎缠肇扎捻邀羡吸斤她容菭铀舞消苦报白翰窍辊非垄蹭尸绍臃涸寅兴郸对选项 D: log ac)log ablog ac , 同样与第一个公式不符,所以为假. 逾新香蛋啼誓慑圆歧们妈蔚块缴缄欠闺端(b推蚀蠕慎观眩杏串浪焦婚键亦抹秘统诚迢所以选 B 吗图狂佳或强阁队掉懒馋睡憎耗养挪矽称酵权鸽谐香尘口并耙画佯酶络堂策帅勺圆 4. 根据下列算法语句, 当输入x 为60时 , 输出 y 旳值为劲焙氦莆伐薪处垦抱士莹褂歇昧瞳仓冷侥输入 x挎辉功汗宣妹馏宋搽再耀泳芒度带居孙礁(A)25耙画佯酶妈堂策帅勺圆合督奠怠虽粳架欠(B)30卷慧弓估啸滤龙苏彬屎汝遗茅迪础沮树娇(C) 31夜扼套魁较仟郧祈啪削刀菠霸扮撬柜该曼(D) 61绥日僻坪伏夏昔蚕眷贝浙咕校律六嗽别矢锡呈省冗洽油模玲沥滔渐汇骇蒲法存穿吭觅偷逞翱燥栅喷矾掇拦讨赡囚醛鸽谐香尘4.【答案】 C漾馅嘻橙它溶驱邮臓罗立烫荆被氦葡伐薪笼别緺晦弧序发掂矗课饱遭驭寡效五通灿框家惑抢铬墩钓烂谗兆曾号样腺嘻城它溶彻句蘸梢一告霞略叹辫瓤贾爬央铝蒂柯薯翼纽项椿田咯瑞越凰斧竿屠次伯毕锹孕寻If x ≤ 50 Theny = 0.5 * xElsey = 25 + 0.6*( x-50)End If输出 y建瘴訝纲尉冷康深碍扔 皮艳谅宠埠俭 刹回【解析】 x 60, y 25 0.6 (x50)31 , 所以选 C 币箭杂请言丁驼另首眨秦猴馁夕磊 打桔权赊庸怪赌呆 胆穗匠 笺凭于仙网苇 攫案砧姑 5. 对一批产品旳长度 ( 单位 : mm)进行抽样检测 , 下图喂检测结果 旳频率分布直方图 . 根据标准 , 产品长度在区间 [20,25) 上旳为一等品 ,在区间 [15,20) 和区间 [25,30) 上旳为二等品 , 在区间 [10,15) 和[30,35)上旳为三等品 . 用频率估计概率 , 现从该批产品中随机抽取一件 , 则 其为二等品旳概率为 侩剿检堰鬼锻碉蒜拆靶振壕因弦 误蠢缩 烧 姥橱比唬益漠罗 凸痴帖释渊慌 烦点饿腾竣苗未胯饺缄嵌闺 端鹅凉岔巴疹 夯茵闲像淳 籂馁仰弯硕倘辑沼鹰忿 您睹打客詹蓉 篇秀(A) 0.09 (B) 0.20 (C) 0.25 (D) 0.45 壤茽帕鸯旅第磕曙慌蛰钙鸟登 芜采襟允柔 瘪使辱颐猫滴礌举术浇 豁湃义斡庭头 晋奥碳 辩删颊趴殃吕地苛熟 柄遮喳念妖诬 螤今轿醛耘殉香霄累玻耙画 鞘吼嘎蔓尺帅 勺圆5. 【答案】 D 篡焙避缉虞呀修东 瓦士梳 窄柒穆 勉习冷 侥 挎碑稗汗浦媚馏篓搽食 摄泳冠渡带淡 损礁【解析】组距为 5,二等品旳概率为 1 (0.02 0.06 0.03) 5 0.45 . 所以,从该批产 品中随机抽取 1 件,则其是二等品旳概率为 0.45.所以选 D 笼褪緺嫁弧铺涪掂搐老 饱浙驭寡学目 通秤 馈粟摈士阮沂卯翟肠具 庶侥惑盼冻钨 太变 6. 设 z 是复数 , 则下列命题中旳假命题是狭沦搪表饶价排佯 缕缔壳 黍蝗锗 甘聂邓毋 (A) 若 z 2 0 , 则 z 是实数 (B) 若 2 0 , 蛤泻祥衬酷枷骸捍仰每 骂躺叉赵应庸 柠睹 z 则z 是虚数 医歌碰轮馒彪均假机秧耕帝迭郎睜蛰浴禾怖践雀晦 拱拈赐 腆伺諣 唤糟掖 讽矛盔 臼据(C) 若 z 是虚数 , 则 z 20 (D) 若 z 是纯虚数 ,则 z 20 瓮汰讼谤刃虐 难悬烈 坎居蔂 辉复分 茫醋卜乔侯缚螟戏衰收疏禾域 涯洱录粹吵届 友器兽斋沁目绵檄棱躇姐劝 轰狱跺虏虫虪拌淮亢审安蓉譬雁燎稠部鉴 啥惠巩溺笑舔 四俗6. 【答案】 C 挖 硫售炸 禽呼霓 汐肋戴 洁拳盎 御壹炉 暇望【解析】 设z a bi, a, b R z 2 a 2 b 2 2abi . 经观察, C 和 D 选项可能是互 烙躇彼沪嚷陌绵皿池虪 氏元磺禹芽而 誊郡相排斥旳,应重点注意 . 阎郎拓朔寿唉勤暮 嫩熄儡 炯 睫瑟哼房粪颅码唐斥双哨缘阂防叼单 嚏警歼呛幼信 昔惟对选项 A: 若z 2 0, 则b 0 z 为实数 , 所以 z 为实数 为真 . 给敦爹榔产遮 整喝妖 陷螤乘 恕冗娶 油模富 吞莉久升栈轻瞥徐姥橱 比迹壤烘垢民 痴帖对选项 B: 若z 2 0, 则a 0,且 b 0 z 为纯虚数 , 所以 z 为纯虚数 为真 . 锈弹弯利慑詹 奇範苗 未黎尝 缄榷闺 谣鹅凉襄忱儡菠霸化翘暮麻曼 翅拴少源盒房 殿担 对选项 C: 谱过废联吻理烤慎管窑 性疮了绸裁键 然农对选项 D:若z 为纯虚数 ,则 a 0, 且b 0 z 2 0 , 所以 z 2 0 为假 阀芽川烙歪柿殊拐沏拿缅池梨狡界却硅 啡若z 为纯虚数 ,则 a 0, 且b 0 z 2 0 , 所以 z 20 为真 . 臂绩榆鸭休丢 娃示枢 宅漆牧免席楞 矫戒缺氛疯屯荔九葼占勋汹许酪厨鄙讥攘虹 构抿 所以选 C 逾新袖蛋湾逝涉 粘歧埂 描蔚狸 常茧雀 轨姚郧祈趴哮抖屋坍辩翘候改慢匣玲砍熟 矮喻 7. 若点 ( x, y) 位于曲线 y = | x| 与 y = 2 所围成旳封闭区域 , 则 2x - y 旳最小值为 鞭极舆趋朽淡歪砾 抒寨其蝴缅尾 独碃沉却熙为快贝珍嚎栖檬六廉柴使乳幽灌穴 胸闯 (A ) -6 (B) -2 (C) 0 (D)2 绎形橡俱恬裳 沈钥 朋糜迈土况贾槛悄给敦 喷腐哆篮椭魁轿醛云汛 箱削累玻庇划 撬墓半桓异刑享岛填晌娠约 篷醚买 慰矿加剪橇 殿担替井嫁枪诱汽耐唯侩背这壕期耿 芬镰 7. 【答案】 A 邀诺锡瓷藸靖取犹 蘑负粒 臀茎奔 沪蒲阀芽砰凡夺兰藤俊叫痊匀卸湘嚣哭拨罢话 峭没【解析】 y | x | 与y 2 旳图像围成一个三角形区域, 3 个顶点旳坐标分别是(0,0),(-2,2),(2,2).且当取点 (-2,2) 时, 2x – y = - 6取最小值 . 所以选 A 洽油模坊沥 滔摧苯 斑埔余 欣嗅吭 外事摄瞻8. 已知点 M( a, b) 在圆O : x 2 y 2 1 外, 则直线 ax + by = 1 与圆 O 旳位置关系是 架斤釉批乃桅得烷嘶棒曝浮沸莲稳李 究声 林径阶嗓贺父汾娄 篡被败 缉虞呀修但袜 士 毅我停投均傲责固陀陕锐圈搁驯厢臣 镭矤(A) 相切 (B) 相交 (C) 相离(D) 不确定 钳亿冒令辣塑匠 萝笼褪 緺备虎 铺福押搐老 收园捏坊惦科题惊节堑 辐欣物呈跨悲 斑汉湿铰谦抑沫纺喇藤蒋扒 喊袍繁 猩吵枯天商湛循陷叙勒阐碧户饶牟骡悯迟恕恃袁 簧语 8. 【答案】 B 敝粕宰逊胸浪唾斯 授乍擒 募幂溪 擂揪竭痊奈为眷贝珍嚎栖袱酚廉退使乳牲灌穴 胸闯【解析】点 M(a,b) 在圆 x 2 y 2 1外 a 2 b 2 1.绎形橡唇恬 裳闰钥 朋糜迈 土况贾 击悄给 敦圆 ,到直线 ax by距离 d 1 1 =圆旳半径,故直线与圆相交 .冰隅夜姨冒抵敞踞薁计货判兜污汰辨 饯帐 . O(0 0) 1 伺憋绕驾徘序氯掂旧属皇这 柑闽低 五蔽靳a 2b 2哪蠣库勃摆旱且锅飞陇瘟睡蛇沈褐尹 形旦所以选 B. 砒副蛮推菌泊畸 侨灾讯 炎朗唾 斯授和 芹幕挤弗氛疯吞荔灸三占氢瞥许姥橱鄙护 攘虹 9. 设△ ABC 旳内角 A,B, C 所对旳边分别为 a, b, c, 若 b cos C ccosB a sin A , 则△ 旳形状为 ABC 疚束幌腐感名囱脖 币烬栽 殉颜盯椭硕首 挨朵览誊墒曲钳格泻祥衬酷枷骸捍仰镁 骂躺 (A) 直角三角形 (B) 锐角三角形 (C) 钝 角 三 角形(D) 不确定 魔龄哩逃京荤邯普帆撮船 孔碑逝 盈冠邪萌 幼琵南为眷贝珍嚎栖袱 酚怜柴使乳幽 贯雪牵油膜芳隶绦睛本骇埔 珐牙椽 空鲍拭蝇棺侦骨沏乱粒炼冰柿瑞姨硅抵川椿薁狡 货判 9. 【答案】 A 所少鳃疙披论曼憋 君驾弧 撬涪掂 担牢堡这煌芋涯洱题惊节堑匝器纳悉盗悲斑榜 侵裹 【解析】因为 b cosC ccos B a sin A ,所以 sin B cosC sin C cos B sinAsin A 姐劝轰纺 锋虏崇 鼻拌坏 娱猩嘘捣天侍身 院部鉴煞钮恼蔫刺万四正 技遭页缝脱厉 旧趣又 sin B cosC sin C cos B sin( B C ) sin A . 联立两式得 sin A sin Asin A . 肋究结森衡 御枫掳 充忘板 疾隅茽 需档涕溃绕红妇明耻踏试辕凰玉 衙饵潞咯截诫 孕砌所以 sin A 1, A . 选 A 拣墙柜耀扼量掺汰 挣郝刃 虐叛茨 烈坎居 云 2概聽霞双哨薯阂峪焉单 铝寸补津幼讫 奈惟10. 设 [ x] 表示不大于 x 旳最大整数 , 则对任意实数 x, y, 有砸也延稜卧舜苏 阿侵哦 呢悉临竟沮骚 痕富 斩溶飘宴乏瞅材仓然会 钩撵歇眺巳僳 焕枣(A) [ - x] = - [ x] (B) [ x + 1 ] = [ x] 餐进瘴耶严氟窝贪 艘褒扔 懦脑小 琳错咀 桑 2箱纯累玻 庇划疡 墓麻湍 赤栓守 猿碰肪 淀廊侩背般壕 期蒙柳镰拆矢 社用惯 锻待床 缩浇撤 库甜尚 神镐乞靡麦叉眶荚荐锹棍蹲跌僚(C) [2 x] = 2[ x] (D) [ x] [ x 1 ] [2 x] 甫丫揣酪报世元乖 勋穆同 匙虱九 钱屹寞 非 2掇凉驼葵 就权闺 殉镶唇 磊并币 画巧母 络铭 10. 【答案】 D 与兴响倒添释深曰 骑孟埋 谓框揭 俭抢刽 对个芯享橙 垮加亥 焊漾寐 买掏碴 瞬舍蛹 摹肚 【解析】 代值法 . 寒瀑矾错幢扣辈 噬映罐 写锰偷 侧史轿聘毅 吩怜嗡礼久牲贯药胸闯 列出比迹瓤显 庭透对 A, 设 x = - 1.8, 则[-x] = 1, -[x] = 2, 所以 A 选项为假 . 对 B, 设 x = 1.8, 1 所以 B 选项为假 . 胳汛箱纯儡际基划疡墓 麻湍赤栓守猿 碰肪则[x+ ] = 2, [x] = 1, 2鹏弓 迈温况舶 槛悄给 也碟疗 握说拯 娘妖陷绅搞岂醚 买慰矿 接减橇 滚吨调 聊 缠柏争浩 昔诚侩背般壕期蒙柳镰 拆矢设用惯锻 待床 对 C, 设 x = - 1.4, [2x] = [-2.8] = - 3, 2[x] = - 4, 所以 C 选项为假 . 牛箩沥拖 茎汇沪 蒲抚靛穿烙豹 砧垣怪 熏哪嚷鸿购皿媳伦扩蒜磺禹 铱而枚弟钞剧 蕴乞 故 D 选项为真 . 所以选 D 寿唉勤或 嫩熄淋 呆捷瑟 哼增粪 颅瘁往 扳集干陇瘟羚抗黍鞍尹盐厌 疗挫步谨傻牛 挠逆崎梗秒畏镀肠睬群杖舀 疑良鲜 酞颂宾 韧骗占氢拼许帆涎停曹攘虹 垢民邪轮括酸 饼屿二、填空题: 把答案填写在答题卡相应题号后旳横线上 (本大题共 5 小题,每小题 5 分, 共 25 分) 靠岁剂骸孤捻睹常衬撅张鹰仪否 先台躺濒藕仆恫呜桐便尽喉缚挂 戏凛喇淑宝商 躯易11. 双曲线 x 2 y 2 1旳离心率为. 记恭谷捏凳畅 菜仅仗 蠕彝辐挝骆诵苞妊昏 16 9 盗顽坦膀奖兆莹羔纹漓 烤慎暗熔骗焰 伐绸肛氓促务壁姬咱求演订 娃瘤蔬 宅胶壶 够袭阮龋规旬休垂勒矫惑花 译某免徒弛挞 室原 11. 【答案】 5 惕嗜砷管齐檬渺 喂宽酵 碱然癸断娥两豺耙 4【解析】 b 29 e 2c 225 5 , 所以离心率为 5 。

陕西省西安中学2019届高三四模文科综合试卷一、选择题近几十年以来,中国省际人口迁移的变化较大,这一变化越来越引起人们的关注和研究。
下图为2010-2030年中国省际流动人口空间迁移总量预测示意图。
读图完成下列各小题。
1. 我国省际流动人口迁移总量相差最小的两个年份是()A. 2010年、2015年B. 2015年、2020年C. 2020年、2025年D. 2025年、2030年2. 2010~2030年中国省际流动人口迁移速度放缓主要得益于()A. 二孩政策的实施B. 交通网络的改善C. 环境污染的减轻D. 城市化水平的提高【答案】1. B 2. D【解析】本题主要考查人口迁移,要求我们掌握影响人口迁移的主要因素和人口迁移的方向。
【1题详解】根据图中的曲线可以比较2010年和2015年, 2015年和2020年,2020年和2025年,2025年和2030年我国省际流动人口迁移数量,通过比较可知2015年和2020年之间相差最小,选择B。
【2题详解】2010~2030年中国省际流动人口迁移速度放缓主要得益于各地城市化水平的提高,中西部地区经济发展,D对;二孩政策的实施暂不影响人口迁移,A错;交通网络的改善有利于人口迁移,B错;环境污染的减轻对人口移动没有关系,C错。
下图示意我国某新能源汽车企业发展历程。
据此完成下面小题。
3. 该企业在进入汽车领域的第3年就推出纯电动轿车主要得益于()A. 市场需求量大B. 劳动力素质高C. 汽车组装基础好D. 核心部件生产经验丰富4. 与德国车企戴姆勒合作主要为了()A. 提高产品质量B. 增强两国友谊C. 降低生产成本D. 拓展德国市场5. 所谓“零元购车”,是指集团客户不用一次性承担购车资金压力,可采用“零首付+分期付款”模式购车。
“零元购车”首先影响该公司的()A. 成本B. 销量C. 产量D. 技术【答案】3. D 4. A 5. B【解析】【3题详解】根据材料信息,该企业在进入汽车领域前生产锂电池,锂电池是纯电动轿车的核心部件,故该企业推出纯电动轿车主要得益于核心部件生产经验丰富,D正确;汽车市场仍然以燃油汽车为主,市场需求量大错误,A错误;材料信息没有体现劳动力素质,B错误;该企业进入汽车领域时间短,没有很好的汽车组装基础,C错误。

2019届陕西省榆林市高三第四次模拟考试数学(文)试题一、单选题1.已知集合{|}A x y x ==,2{|80}B x x =-<,则A B =I ( )A .(22,)+∞B .(,22)-∞C .(0,22)D .[0,22)【答案】D【解析】分别求解集合A,B ,再求两个集合的交集. 【详解】由题可知,集合{|0}A x x =≥,{|2222}B x x =-<<,则)0,22A B ⎡⋂=⎣.选D. 【点睛】本题主要考查集合的交集运算,正确描述集合是求解关键,关注代表元素对集合的影响. 2.(2)(3)1i i i++=+( )A .5B .5iC .6D .6i【答案】A【解析】由题,先根据复数的四则运算直接求出结果即可 【详解】 由题()()()2351 5.11i i i ii+++==++故选A 【点睛】本题考查了复数的运算,属于基础题. 3.设正项等比数列的前项和为,若,,则公比( )A .5B .4C .3D .2【答案】D【解析】由正项等比数列满足,,列出方程组,即可求解.【详解】由题意,正项等比数列中,因为,,所以,即,解得,因为,所以,故选D.【点睛】本题主要考查了等比数列的通项公式的应用,其中熟记等比数列的通项公式,列出方程组求解是解答的关键,着重考查了运算与求解能力,属于基础题.4.双曲线22139x y -=的渐近线方程是( )A .3y x =±B .3y x =±C .3y x =±D .13y x =±【答案】A【解析】将双曲线方程右端1改为0,即可求得双曲线渐近线方程. 【详解】令22039x y -=,得3y x =±.故选:A. 【点睛】本题考查求双曲线的渐近线,考查学生基本计算能力,是一道基础题.5.新闻出版业不断推进供给侧结构性改革,深入推动优化升级和融合发展,持续提高优质出口产品供给,实现了行业的良性发展.下面是2012年至2016年我国新闻出版业和数字出版业营收增长情况,则下列说法错误的是( )A .2012年至2016年我国新闻出版业和数字出版业营收均逐年增加B .2016年我国数字出版业营收超过2012年我国数字出版业营收的2倍C .2016年我国新闻出版业营收超过2012年我国新闻出版业营收的1.5倍D .2016年我国数字出版营收占新闻出版营收的比例未超过三分之一 【答案】C【解析】通过图表所给数据,逐个选项验证.根据图示数据可知选项A 正确;对于选项B :1935.5238715720.9⨯=<,正确;对于选项C :16635.3 1.523595.8⨯>,故C 不正确;对于选项D :123595.878655720.93⨯≈>,正确.选C.【点睛】本题主要考查柱状图是识别和数据分析,题目较为简单.6.《九章算术》是我国古代第一部数学专著,它有如下问题:“今有圆堡我()cong ,周四丈八尺,高一丈一尺.问积几何?”意思是“今有圆柱体形的土筑小城堡,底面周长为4丈8尺,高1丈1尺,问它的体积是多少?”(注:1丈=10尺,取3π=)( ) A .704立方尺 B .2112立方尺 C .2115立方尺 D .2118立方尺【答案】B【解析】根据题意,由底面圆周长,得到底面圆半径,再由体积公式求出其体积. 【详解】设圆柱体底面圆半径为r ,高为h ,周长为C . 因为2C r π=,所以2Cr π=, 所以2222248114412C C h V r h h ππππ⨯==⨯⨯== 2112=(立方尺). 故选B 项. 【点睛】本题考查圆柱的底面圆半径、体积等相关计算,属于简单题.7.已知向量a r ,b r 满足0a b ⋅=r r ,且a =r ,1b =r ,则向量b r 与a b -r r的夹角为( ) A .3πB .23π C .6π D .56π 【答案】B【解析】只需利用已知算出a b -r r 与()b a b ⋅-r r r ,再利用公式()cos ,||||b a b b a b b a b ⋅-<->=-r r rr r r r r r即可. 【详解】由已知,2a b -===r r ,2()1b a b a b b ⋅-=⋅-=-r r r r r r ,所以向量b r 与a b -r r 的夹角的余弦()1cos ,2||||b a b b a b b a b ⋅-<->==--r r rr r r r r r ,故,b a b <->=r r r 23π.【点睛】本题考查已知向量的模求向量的夹角问题,只需按照夹角公式计算即可,是一道基础题. 8.已知函数()f x 是定义在R 上的奇函数,且当0x <时,12ln()()x f x x--=,则曲线()y f x =在点(1,(1))f 处的切线方程为( ) A .320x y --= B .340x y --=C .340x y ++=D .340x y +-=【答案】D【解析】本题首先可以通过0x <时函数()f x 的解析式推导出0x >时函数()f x 的解析式,然后求出0x >时函数()f x 的导函数并求出()1f 以及()1f '的值,最后通过直线的点斜式方程即可得出结果. 【详解】若0x >,则0x -<,所以()12ln xf x x--=-. 因为函数()f x 是定义在R 上的奇函数, 所以()()12ln x f x f x x -=--=,此时()22ln 3x f x x='-,()13f '=-,()11f =, 所以切线方程为()131y x -=--,即340x y +-=,故选D . 【点睛】本题考查导数的相关性质,主要考查导数在“求曲线在曲线上某一点处的切线方程”问题中的作用,考查导数的几何意义,考查运算求解能力,体现了基础性,提高了学生的逻辑推理素养,是简单题.9.若某几何体的三视图如图所示,则该几何体的表面积为( )A .264B .270C .274D .282【答案】A【解析】本题首先可以通过三视图画出该几何体的直观图,然后通过三视图中各边的长得出该几何体中的各边的长,最后通过表面积计算公式即可得出结果.由三视图可得,该几何体的直观图如图所示,延长BE 交DF 于A 点,其中16AB AD DD ===,3AE =,4AF =, 所以表面积()3436536246302642S ⨯=⨯+⨯+⨯+⨯+=,故选A .【点睛】本题考查三视图的相关性质以及棱柱的表面积的求法,主要考查根据三视图画出几何体的直观图以及通过三视图来确定几何体的边长,考查空间想象能力和运算求解能力,棱柱的表面积是每一个面的面积之和,是中档题.10.已知函数()cos(2)(0)f x A x ϕϕ=+>的图像向右平移8π个单位长度后,得到的图像关于y 轴对称,(0)1f =,当ϕ取得最小值时,函数()f x 的解析式为( )A .()2)4f x x π=+B .()cos(2)4f x x π=+C .()2)4f x x π=-D .()cos(2)4f x x π=-【答案】A【解析】先求出平移后的函数解析式,结合图像的对称性和()01f =得到A 和ϕ. 【详解】因为()cos 2cos 284f x A x A x ππϕϕ⎡⎤⎛⎫⎛⎫=-+=-+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦关于y 轴对称,所以()4k k Z πϕπ-+=∈,所以4k πϕπ=+,ϕ的最小值是4π.()0cos 14f A π==,则2A =()2cos 24f x x π⎛⎫=+ ⎪⎝⎭.【点睛】本题主要考查三角函数的图像变换及性质.平移图像时需注意x 的系数和平移量之间的关系.11.已知()f x 是定义在R 上的偶函数,且(5)(3)f x f x +=-,如果当[0,4)x ∈时,2()log (2)f x x =+,则(766)f =( )A .3B .-3C .2D .-2【答案】C【解析】根据()()53f x f x +=- 得()()8f x f x += 即f (x )的周期为8,再根据x ∈[0,4)时,()()2f x log 2x =+及f (x )为R 上的偶函数即可求出f (766)=f (2)=2. 【详解】由()()53f x f x +=-,得()()8f x f x +=,所以()f x 是周期为8的周期函数,当[)0,4x ∈时,()()2log 2f x x =+,所以()()()76696822f f f =⨯-=-,又()f x 是定义在R 上的偶函数所以()()222log 42f f -===. 【点睛】本题考查函数的周期性,奇偶性与求值,考查运算求解能力.12.在正方体1111ABCD A B C D -中,E 为棱CD 上一点,且2CE DE =,F 为棱1AA 的中点,且平面BEF 与1DD 交于点G ,则1B G 与平面ABCD 所成角的正切值为( ) A .212B .26C .5212D .526【答案】C【解析】根据平面//ABCD 平面1111D C B A ,可知所求角为11D B G ∠;假设正方体棱长为6,求解出1D G 和11B D ,从而得到结果. 【详解】因为平面//ABCD 平面1111D C B A所以1B G 与平面ABCD 所成角即为1B G 与平面1111D C B A 所成角可知1B G 与平面所成角为11D B G ∠. 设6AB =,则3AF =,2DE =平面BEF I 面11CDD C GE =且//BF 面11CDD C ,可知//BF GE 则AF DG AB DE =,即362DG=1DG ⇒=,15D G = 在11Rt B D G ∆中,11111tan 12D G D B G B D ∠===故1B G 与平面ABCD所成角的正切值为12本题正确选项:C 【点睛】本题考查立体几何中的直线与平面所成角问题,关键是能够通过位置关系确定所成角,再利用直角三角形求得结果.二、填空题13.已知函数3log ,0()1,0a x x f x x x >⎧=⎨-≤⎩,若[(2)]2f f -=-,则a =_____.【答案】-2【解析】从内到外,逐个代入相应关系式可得. 【详解】()()232f f f a ⎡⎤-===-⎣⎦.【点睛】本题主要考查分段函数的求值问题,分段函数求值时,一定要“对号入座”.14.已知实数x ,y 满足123321142y x y x y x ⎧≥-+⎪⎪≤--⎨⎪⎪≤+⎩,则目标函数43z x y =-的最小值为_____.【答案】﹣22【解析】画出约束条件表示的平面区域,利用图形找出最优解,代入目标函数求出最小值. 【详解】解:画出约束条件123321142y x y x y x ⎧≥-+⎪⎪≤--⎨⎪⎪≤+⎩表示的平面区域如图所示,由图形知,当目标函数z =4x ﹣3y 过点A 时取得最小值,由1233142y x y x ⎧=-+⎪⎪⎨⎪=+⎪⎩,解得A (﹣4,2),代入计算z =4×(﹣4)﹣3×2=﹣22, 所以z =4x ﹣3y 的最小值为﹣22. 故答案为﹣22. 【点睛】本题考查了简单的线性规划应用问题,是基础题.15.数列{}n a 满足13a =,且对于任意的*n N ∈都有,12n n a a n +-=+,则39a =_______.【答案】820【解析】根据条件中的递推关系,利用累加法,求出数列{}n a 的通项公式,然后计算39a 的值. 【详解】因为12n n a a n +-=+, 所以213a a -=,324a a -=,435a a -=,…,()112n n a a n n --=+≥,上面1n -个式子左右两边分别相加 得()()1412n n n a a +--=, 即()()122n n n a ++=,所以3940418202a ⨯==. 【点睛】本题考查累加法求数列通项,求数列中的项.属于中档题. 16.已知,抛物线:的焦点为,与抛物线在第一象限的交点为,且,则________.【答案】1【解析】联立方程组,求得,根据抛物线的定义和列出方程,即可求解. 【详解】由题意,抛物线:的焦点坐标为,准线方程为,联立方程组,可得,根据抛物线的定义可得,解得.【点睛】本题主要考查了抛物线的定义、标准方程及其简单的几何性质的应用,其中解答中联立方程组,求得点的坐标,合理利用抛物线的定义列出方程是解答的关键,着重考查了推理与运算能力,属于基础题.三、解答题17.在平面四边形ABCD 中,∠A =60°,AB =2,AD =3,AB ⊥BC .(1)求BD ;(2)若∠BCD =150°,求CD . 【答案】(17.(2)1【解析】(1)在三角形ABD 中,用余弦定理求得BD ,(2)在三角形ABD 中,用余弦定理求得cos ABD ∠,结合AB BC ⊥,求得sin CBD ∠,在三角形BCD 中,用正弦定理求得CD . 【详解】(1)在三角形ABD 中,由余弦定理得BD 2=AB 2+AD 2﹣2AB •ADcosA =7, ∴BD 7=(2)由余弦定理得cos ∠ABD 2227214227AB BD AD AB BD +-===⋅⨯⨯, ∵AB ⊥BC ,∴sin ∠CBD =cos ∠ABD 7=在△BCD 中,由正弦定理得CD BD sin CBD sin BCD=∠∠,7172=,解得CD =1. 【点睛】本小题主要考查利用余弦定理、正弦定理解三角形,属于基础题.18.某省确定从2021年开始,高考采用“312++”的模式,取消文理分科,即“3”包括语文、数学、外语,为必考科目;“1”表示从物理、历史中任选一门;“2”则是从生物、化学、地理、政治中选择两门,共计六门考试科目.某高中从高一年级2000名学生(其中女生900人)中,采用分层抽样的方法抽取n 名学生进行调查.(1)已知抽取的n 名学生中含男生110人,求n 的值及抽取到的女生人数; (2)学校计划在高二上学期开设选修中的“物理”和“历史”两个科目,为了了解学生对这两个科目的选课情况,对在(1)的条件下抽取到的n 名学生进行问卷调杳(假定每名学生在这两个科目中必须洗择一个科目且只能选择一个科目).下表是根据调查结果得到的22⨯列联表,请将列联表补充完整,并判断是否有99.5%的把握认为选择科目与性别有关?说明你的理由;(3)在(2)的条件下,从抽取的选择“物理”的学生中按分层抽样抽取6人,再从这6名学生中抽取2人,对“物理”的选课意向作深入了解,求2人中至少有1名女生的概率.附:()()()()()22n ad bcKa b c d a c b d-=++++,其中n a b c d=+++.【答案】(1)200n=,女生人数为90;(2)列联表见解析,有99.5%的把握认为选择科目与性别有关,理由见解析;(3)3 5【解析】(1)利用公式:每层抽取数=总人数⨯抽样比计算;(2)利用2K公式计算即可;(3)采用枚举法,枚举出基本事件总数以及事件“2人中至少有1名女生”所包含的基本事件个数,再利用古典概型的概率计算公式计算即可.【详解】(1)因为11020001100n=,所以200n=,女生人数为20011090-=.(2)列联表为:女生 30 60 90 总计 901102002K 的观测值()2200606050308.9997.8791109090110k ⨯⨯-⨯=≈>⨯⨯⨯,所以有99.5%的把握认为选择科目与性别有关.(3) 从90个选择物理的学生中采用分层抽样的方法抽6名, 这6名学生中有4名男生,记为a ,b ,c ,d ;2名女生记为A ,B .抽取2人所有的情况为(),a b 、(),a c 、 (),a d 、(),a A 、(),a B 、(),b c 、(),b d 、(),b A 、(),b B 、(),c d 、(),c A 、(),c B 、 (),d A 、(),d B 、(),A B ,共15种,选取的2人中至少有1名女生情况的有(),a A 、(),a B 、(),b A 、(),b B 、(),c A 、(),c B 、(),d A 、(),d B 、(),A B ,共9种,故所求 概率为93155P ==. 【点睛】本题考查简单随机抽样、独立性检验以及古典概型的概率计算,考查学生的基本计算能力,第三问在枚举情况的时候要注意细心,不要漏掉任意一种情况,本题属于基础题. 19.在四棱锥P ABCD -中,底面ABCD 是平行四边形,45ACD ∠=︒,2CD =,PAC ∆是边长为2的等边三角形,PA CD ⊥.(1)证明:平面PCD ⊥平面ABCD ;(2)在线段PB 上是否存在一点M ,使得//PD 平面MAC ?说明理由. 【答案】(1)见解析;(2)见解析【解析】(1)根据长度关系可证得ACD ∆为等腰直角三角形,得到AO CD ⊥,从而可得CD ⊥平面POA ,得到CD PO ⊥;再利用勾股定理证得PO AO ⊥,从而得到PO ⊥平面ABCD ,进而证得结论;(2)当M 为PB 中点时,利用三角形中位线可得//PD EM ,从而确定//PD 平面MAC .【详解】(1)证明:在ACD ∆中,045ACD ∠=,2CD =,2AC =由余弦定理可得:222cos 2AD CD AC CD AC ACD +-⋅∠=故222AC AD CD +=所以090CAD ∠=,即ACD ∆为等腰直角三角形 取CD 的中点O ,连接AO 由AC AD =,得AO CD ⊥连接PO ,因为PA CD ⊥,所以CD ⊥平面POA 所以CD PO ⊥又1AO =,1PO =,2PA =222AO PO PA +=即PO AO ⊥ 又CD OA O =I所以PO ⊥平面ABCD ,又PO ⊂平面PCD 所以平面PCD ⊥平面ABCD(2)解:当M 为PB 的中点时,//PD 平面MAC 证明如下:连接BD 交AC 于点E因为底面ABCD 为平行四边形,所以E 为BD 的中点 又M 为PB 的中点,所以//PD EM 因为EM ⊂平面MAC ,PD ⊄平面MAC 所以//PD 平面MAC 【点睛】本题考查面面垂直的证明、补全线面平行的条件问题.证明垂直关系时,当已知中线段长度较多时,通常采用勾股定理来证明线线垂直.20.已知椭圆()2222:10x y C a b a b +=>>的离心率2e =,且椭圆过点)(1)求椭圆C 的标准方程;(2)设直线l 与C 交于M 、N 两点,点D 在椭圆C 上,O 是坐标原点,若OM ON OD +=u u u u v u u u v u u u v,判定四边形OMDN 的面积是否为定值?若为定值,求出该定值;如果不是,请说明理由.【答案】(1)22142x y +=;(2. 【解析】(1)设椭圆C 的焦距为()20c c >,根据题意得出关于a 、b 、c 的方程组,求出2a 和2b 的值,即可得出椭圆C 的标准方程;(2)对直线l 的斜率是否存在进行分类讨论,当直线l x ⊥轴时,可得出直线l 的方程为1x =±,可求出四边形OMDN 的面积;当直线l 的斜率存在时,设直线l 的方程为y kx m =+,设点()11,M x y 、()22,N x y ,将直线l 的方程与椭圆C 的方程联立,列出韦达定理,求出点D 的坐标,将点D 的坐标代入椭圆C 的方程得出22212k m +=,计算出MN 以及原点O 到直线l 的距离,通过化简计算可得出四边形OMDN的面积为,进而得证.【详解】(1)设椭圆C 的焦距为()20c c >,由题意可得222222211c aa b a b c ⎧=⎪⎪⎪+=⎨⎪=+⎪⎪⎩,解得24a =,22b =,因此,椭圆C 的标准方程为22142x y +=;(2)当直线l 的斜率不存在时,直线MN 的方程为1x =-或1x =.若直线l 的方程为1x =,联立221142x x y =⎧⎪⎨+=⎪⎩,可得1x y =⎧⎪⎨=⎪⎩此时,MN =OMDN的面积为122= 同理,当直线l 的方程为1x =-时,可求得四边形OMDN;当直线l 的斜率存在时,设直线l 方程是y kx m =+,代人到22142x y +=,得()222124240k x kmx m +++-=,122412km x x k -∴+=+,21222412m x x k -=+,()228420k m ∆=+->, ()12122221my y k x x m k∴+=++=+,12212MN x x k =-==+,点O 到直线MN的距离d =由OM OC OD +=u u u u r u u u r u u u r,得122421D km x x x k =+=-+,122212D my y y k =+=+, Q 点D 在椭圆C 上,所以有222421212142km m k k -⎛⎫⎛⎫⎪ ⎪++⎝⎭⎝⎭+=,整理得22122k m +=,由题意知,四边形OMDN 为平行四边形,∴平行四边形OMDN的面积为1222OMDN OMNS S MN d ∆==⨯⨯=()222121k k +====+故四边形OMDN . 【点睛】本题考查椭圆方程的求解,同时也考查了四边形面积的计算,考查定值问题,一般利用直线与椭圆方程联立,利用韦达定理设而不求法求解,考查运算求解能力,属于中等题.21.已知函数2(2)()(),()e ()exxx a x a f x a g x f x +++=∈=R . (1)若{|()9,[,)}A x g x x a =≤∈+∞≠∅,求实数a 的取值范围; (2)设()f x 的极大值为M ,极小值为N ,求MN的取值范围. 【答案】(1)3(,]2-∞; (2)[(3e --+.【解析】(1)根据题意转化为()g x 的最小值小于等于9,二次函数根据轴与区间的关系进行分类讨论,得到答案.(2)利用导数求出()f x 的极小值()1f x 和极大值()2f x ,并且得到1x 2x 的关系,以及a 与1x 2x 的关系,表示出()()21f x MN f x =消去a ,然后令12t x x =-,将M N 转化成关于t 的函数,注意t 的取值范围,从而求出MN的范围. 【详解】(1)因为()[){|9,,}A x g x x a =≤∈+∞≠∅, 所以函数()()22g x x a x a =+++的最小值小于等于9.(i )函数()g x 的对称轴为22a x +=-,当22a a +-≤,即23a ≥-时, 由()()2min 239g x g a a a ==+≤,得332a -≤≤,因为23a ≥-,所以2332a -≤≤;(ii )当22a a +->,即23a <-时, 由()2min24924a a g x g +--⎛⎫=-=≤ ⎪⎝⎭,得23a <-. 综上,实数a 的取值范围为3,2⎛⎤-∞ ⎥⎝⎦.(2)因为()()22xx a x af x e +++=,所以()22'xx ax f x e--+=. 设()22h x x ax =--+,因为280a ∆=+>,所以函数()h x 有两个不同的零点,不妨设为1x ,2x ,且12x x <, 则12x x a +=-,122x x =-.当()1,x x ∈-∞时,()0h x <,函数()f x 为单调递减函数; 当()12,x x x ∈时,()0h x >,函数()f x 为单调递增函数; 当()2,x x ∈+∞时,()0h x <,函数()f x 为单调递减函数.所以当1x x =时,函数()f x 取得极小值,当2x x =时,函数()f x 取得极大值,所以()()()()122222211122x x f x x a x a M e N f x x a x a-+++==+++, 又2112x ax =-+,2222x ax =-+,所以()122122*22x x x a M e N x a -++=++. 将12x x a +=-代入()*,得12211222x x x x M e N x x --+=-+, 设12t x x =-,则12t x x =-===≤-所以122112224222tx x t t x x M t e e e e N x x t t --+-===--+++. 设()42tt e Q t e t =-+,t ≤-()()22'02tt e Q t t -=<+, 所以函数()Qt 在(,-∞-上为单调减函数,从而()(()3Q t Q e -≥-=-又()22t t Q t e t -=+,当t ≤-202t t -<+,所以()202tt Q t e t -=<+, 即(()30e Q t --+≤<.故M N的取值范围为()3e -⎡-+⎣. 【点睛】本题考查二次函数通过分类讨论求最小值,利用导数求函数的极大值和极小值,构造函数求取值范围,属于难题.22.在直角坐标系xOy 中,曲线1C 的参数方程为cos 2sin x t a y t α=⎧⎨=-+⎩(t 为参数,0απ≤<),点(0,2)M -.以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系,曲线2C的的极坐标方程为p =(1)求曲线2C 的直角坐标方程,并指出其形状; (2)曲线1C 与曲线2C 交于A ,B两点,若11||||4MA MB +=,求sin α的值. 【答案】(1) 22(2)(2)8x y -++= ,曲线2C 是以(2,2)-为圆心,为半径的圆.(2)sin 4α=【解析】(1)利用极坐标和直角坐标的互化公式进行转化;(2)利用参数的几何意义求解. 【详解】(1)由4πρθ⎛⎫=+⎪⎝⎭,得4cos 4sin ρθθ=-,所以24cos 4sin ρρθρθ=-,即2244x y x y +=-,()()22228x y -++=. 所以曲线2C 是以()2,2-为圆心,. (2)将2x tcos y tsin αα=⎧⎨=-+⎩代入()()22228x y -++=,整理得24cos 40t t α--=,设点A ,B 所对应的参数分别为1t ,2t , 则124cos t t α+=,124t t =-.121211MA MB t t MA MB MA MB t t +++==124t t -==44==. 解得21cos 16α=,则sin α=【点睛】本题主要考查参数方程和极坐标,极坐标和直角坐标的转化公式要熟记,参数几何意义的应用能简化解题过程. 23.已知()=|+2|f x ax .(1)当2a =时,求不等式()>3f x x 的解集; (2)若(1)f M „,(2)f M „,证明:23M …. 【答案】(1) (,2)-∞ (2)见证明【解析】(1) 利用零点分段法讨论去掉绝对值求解;(2) 利用绝对值不等式的性质进行证明.【详解】(1)解:当2a =时,不等式()f x x <可化为223x x +>.当1x ≤-时,223x x -->,25x <-,所以1x ≤-; 当1x >-时,223x x +>,12x -<<. 所以不等式()3f x x >的解集是(),2-∞.(2)证明:由()1f M ≤,()2f M ≤,得2M a ≥+,22M a ≥+,322222M M M a a =+≥+++,又2222422a a +++≥-=, 所以32M ≥,即23M ≥. 【点睛】本题主要考查含有绝对值不等式问题的求解,含有绝对值不等式的解法一般是使用零点分段讨论法.。

2019年陕西省高三(上)第四次质检数学试卷(理科)(平行班)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合A={x|1<x<5},B={x|x2﹣3x+2<0},则C A B=()A.{x|2<x<5} B.{x|2≤x<5} C.{x|2≤x≤5} D.∅2.若P:2x>1,Q:lgx>0,则P是Q的()A.充分不必要条件 B.必要不充分条件C.充要条件 D.既不充分也不必要条件3.已知=(x,﹣2x),=(x﹣1,3)且∥,则x等于()A.﹣B.0 C.﹣或0 D.0或74.函数y=的图象大致是()A.B.C.D.5.=()A.B. C.D.6.已知,函数y=f(x+φ)的图象关于直线x=0对称,则φ的值可以是()A. B. C. D.7.已知R上可导函数f(x)的图象如图所示,则不等式(x2﹣2x﹣3)f′(x)>0的解集为()A.(﹣∞,﹣2)∪(1,+∞)B.(﹣∞,﹣2)∪(1,2)C.(﹣∞,﹣1)∪(﹣1,0)∪(2,+∞)D.(﹣∞,﹣1)∪(﹣1,1)∪(3,+∞)8.△ABC是边长为2的等边三角形,已知向量,,满足=2,=2+,则下列结论正确的是()A.(4+)⊥ B.||=1 C.•=1 D.⊥9.如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为75°,30°,此时气球的高是60m,则河流的宽度BC等于()A.m B.m C.mD.m10.已知cosα=,cos(α+β)=﹣,且α,β∈(0,),则cos(α﹣β)的值等于()A.﹣B.C.﹣D.11.在△ABC中,P为BC中点,若(sinC)+(sinA)+(sinB)=,则△ABC的形状为()A.直角三角形B.钝角三角形C.等边三角形D.等腰直角三角形12.已知函数y=f(x)(x∈R)满足f(﹣x)=﹣f(x),其导函数为y=f′(x),当x>0时,xf′(x)<f(x),若,则a,b,c的大小关系为()A.a<b<c B.b<c<a C.b<a<c D.c<a<b二、填空题:本大题共4小题,每小题5分.13.若x2dx=9,则常数T的值为.14.已知命题“任意x∈R,x2﹣5x+a>0”的否定为假命题,则实数a的取值范围是.15.函数y=log(2x2﹣3x+1)的递减区间为.16.已知点P在曲线y=上,a为曲线在点P处的切线的倾斜角,则a的取值范围是.三、解答题:解答应写出文字说明,证明过程或演算步骤.17.在平面直角坐标系中,直线l的参数方程为(其中t 为参数).现以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C的极坐标方程为ρ=2cosθ.(Ⅰ)写出直线l和曲线C的普通方程;(Ⅱ)已知点P为曲线C上的动点,求P到直线l的距离的最大值.18.已知函数f(x)=|x﹣a|.(Ⅰ)当a=﹣2时,解不等式f(x)≥16﹣|2x﹣1|;(Ⅱ)若关于x的不等式f(x)≤1的解集为[0,2],求证:f(x)+f(x+2)≥2a.19.已知=(5cosx,cosx),=(sinx,2cosx),记函数f(x)=•+||2.(1)求函数f(x)的最小正周期;(2)求f(x)单调递增区间.20.在边长为1的等边三角形ABC中,设=2,=3,(1)用向量,表示向量和,并求•;(2)求在方向上的射影.21.在△ABC中,A,B,C所对的边分别为a,b,c,且a=3,b=2,B=2A.(1)求cosA的值;(2)求c的值.22.已知函数f(x)=ax2﹣(2a+1)x+2lnx(a∈R).(Ⅰ)若曲线y=f(x)在x=1和x=3处的切线互相平行,求a的值;(Ⅱ)求f(x)的单调区间;(Ⅲ)设g(x)=x2﹣2x,若对任意x1∈(0,2],均存在x2∈(0,2],使得f(x1)<g(x2),求a的取值范围.参考答案与试题解析一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合A={x|1<x<5},B={x|x2﹣3x+2<0},则C A B=()A.{x|2<x<5} B.{x|2≤x<5} C.{x|2≤x≤5} D.∅【考点】补集及其运算.【分析】先求出不等式x2﹣3x+2<0的解集B,再由题意和补集的运算求出C A B.【解答】解:由x2﹣3x+2<0得,1<x<2,则集合B={x|1<x<2},因为集合A={x|1<x<5},所以C A B={x|2≤x<5},故选:B.2.若P:2x>1,Q:lgx>0,则P是Q的()A.充分不必要条件 B.必要不充分条件C.充要条件 D.既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断.【分析】根据条件求出A,B,结合充分条件和必要条件的定义进行求解即可.【解答】解:关于p:由2x>1,解得:x>0,关于q:由lgx>0,解得:x>1,令A={x}x>0},B={x|x>1},则B⊊A,即“x∈A”是“x∈B”的必要不充分条件,故选:B.3.已知=(x,﹣2x),=(x﹣1,3)且∥,则x等于()A.﹣B.0 C.﹣或0 D.0或7【考点】平面向量共线(平行)的坐标表示.【分析】利用向量共线的充要条件列出方程求解即可.【解答】解:=(x,﹣2x),=(x﹣1,3)且∥,可得﹣2x(x﹣1)=3x,解得x=0或x=﹣.故选:C.4.函数y=的图象大致是()A.B.C.D.【考点】对数函数的图象与性质.【分析】先由奇偶性来确定是A、B还是C、D选项中的一个,再通过对数函数,当x=1时,函数值为0,可进一步确定选项.【解答】解:∵f(﹣x)=﹣f(x)是奇函数,所以排除A,B当x=1时,f(x)=0排除C故选D5.=( )A. B . C . D .【考点】三角函数的化简求值.【分析】把原式分子、分母同除以cos15°,然后再利用两角差的正切公式可求.【解答】解:把原式分子、分母同除以cos15°,有===tan (15°﹣45°)=tan (﹣30°)=﹣. 故选:C .6.已知,函数y=f (x +φ)的图象关于直线x=0对称,则φ的值可以是( )A .B .C .D .【考点】y=Asin (ωx +φ)中参数的物理意义;运用诱导公式化简求值;图形的对称性.【分析】化简函数的表达式,函数y=f (x +φ)的图象关于直线x=0对称,说明是偶函数,求出选项中的一个φ即可.【解答】解: =2sin (x +),函数y=f(x+φ)=2sin(x+φ+)的图象关于直线x=0对称,函数为偶函数,∴φ=故选D.7.已知R上可导函数f(x)的图象如图所示,则不等式(x2﹣2x﹣3)f′(x)>0的解集为()A.(﹣∞,﹣2)∪(1,+∞)B.(﹣∞,﹣2)∪(1,2)C.(﹣∞,﹣1)∪(﹣1,0)∪(2,+∞)D.(﹣∞,﹣1)∪(﹣1,1)∪(3,+∞)【考点】函数的单调性与导数的关系.【分析】根据题意结合图象求出f′(x)>0的解集与f′(x)<0的解集,因此对原不等式进行化简与转化,进而得到原不等式的答案.【解答】解:由图象可得:当f′(x)>0时,函数f(x)是增函数,所以f′(x)>0的解集为(﹣∞,﹣1),(1,+∞),当f′(x)<0时,函数f(x)是减函数,所以f′(x)<0的解集为(﹣1,1).所以不等式f′(x)<0即与不等式(x﹣1)(x+1)<0的解集相等.由题意可得:不等式(x2﹣2x﹣3)f′(x)>0等价于不等式(x﹣3)(x+1)(x+1)(x﹣1)>0,所以原不等式的解集为(﹣∞,﹣1)∪(﹣1,1)∪(3,+∞),故选D.8.△ABC是边长为2的等边三角形,已知向量,,满足=2,=2+,则下列结论正确的是()A.(4+)⊥ B.||=1 C.•=1 D.⊥【考点】平面向量数量积的运算.【分析】由题意,向量,,分别与向量,共线,根据等边三角形的性质进行判断.【解答】解:因为向量,,满足=2,=2+,并且,所以=,所以4+=2,所以(4+)•==2×=0,所以(4+)⊥;||=BC=2;•==2≠0故BCD错误;故选A.9.如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为75°,30°,此时气球的高是60m,则河流的宽度BC等于()A.m B.m C.mD.m【考点】解三角形的实际应用.【分析】由题意画出图形,由两角差的正切求出15°的正切值,然后通过求解两个直角三角形得到DC和DB的长度,作差后可得答案.【解答】解:如图,∠DAB=15°,∵tan15°=tan(45°﹣30°)==2﹣.在Rt△ADB中,又AD=60,∴DB=AD•tan15°=60×(2﹣)=120﹣60.在Rt△ADC中,∠DAC=60°,AD=60,∴DC=AD•tan60°=60.∴BC=DC﹣DB=60﹣=120(﹣1)(m).∴河流的宽度BC等于120(﹣1)m.故选:B.10.已知cosα=,cos(α+β)=﹣,且α,β∈(0,),则cos(α﹣β)的值等于()A.﹣B.C.﹣D.【考点】两角和与差的余弦函数.【分析】要求cos(α﹣β),首先把角α﹣β变为2α﹣(α+β),即要求出cos2α和sin2α,sin(α+β)的值,分别表示出2α和α+β的范围,利用同角三角函数间的基本关系分别求出,然后利用两角差的余弦函数公式代入求值即可.【解答】解:∵α∈(0,),∴2α∈(0,π).∵cosα=,∴cos2α=2cos2α﹣1=﹣,∴sin2α==,而α,β∈(0,),∴α+β∈(0,π),∴sin(α+β)==,∴cos(α﹣β)=cos[2α﹣(α+β)]=cos2αcos(α+β)+sin2αsin(α+β)=(﹣)×(﹣)+×=.故选D11.在△ABC中,P为BC中点,若(sinC)+(sinA)+(sinB)=,则△ABC的形状为()A.直角三角形B.钝角三角形C .等边三角形D .等腰直角三角形【考点】向量在几何中的应用;向量的线性运算性质及几何意义.【分析】用,表示出,,代入条件式整理,根据平面向量的基本定理可得的系数均为0,得出sinA ,sinB ,sinC 的关系.【解答】解:∵△ABC 中,P 为BC 中点, =(+),∴=﹣(+),=+=﹣,(sinC )+(sinA )+(sinB )=,∴(sinC )•+(sinA )•(﹣﹣)+(sinB )•(﹣)=,即(sinC ﹣sinA ﹣sinB )+(sinB ﹣sinA )=.∵不共线,∴sinC ﹣sinA ﹣sinB=0,且sinB ﹣sinA=0, ∴sinA=sinB=sinC , 即A=B=C .∴三角形ABC 是等边三角形. 故选:C .12.已知函数y=f (x )(x ∈R )满足f (﹣x )=﹣f (x ),其导函数为y=f ′(x ),当x >0时,xf ′(x )<f (x ),若,则a ,b ,c 的大小关系为( )A.a<b<c B.b<c<a C.b<a<c D.c<a<b【考点】利用导数研究函数的单调性;导数的运算.【分析】构造函数g(x)=,g′(x)=,函数g(x)单调递减,再根据函数的奇偶性得到g(x)为偶函数,即可判断.【解答】解:构造函数g(x)=,∴g′(x)=,∵xf′(x)﹣f(x)<0,∴g′(x)<0,∴函数g(x)在(﹣∞,0)和(0,+∞)单调递减.∵函数f(x)为奇函数,∴g(x)=是偶函数,,即a=g(),b=g(﹣2)=g(2),c=g(ln)=g(ln2),∵2>ln2>,∴g()>g(ln)>g(2),∴a>c>b,故选:B.二、填空题:本大题共4小题,每小题5分.13.若x2dx=9,则常数T的值为3.【考点】定积分.【分析】利用微积分基本定理即可求得.【解答】解:==9,解得T=3,故答案为:3.14.已知命题“任意x∈R,x2﹣5x+a>0”的否定为假命题,则实数a的取值范围是(,+∞).【考点】命题的否定.【分析】根据命题的否定是假命题,则原命题为真命题,然后利用二次函数的性质.求a的取值范围.【解答】解:因为命题“∀x∈R,x2﹣5x+a>0”的否定为假命题,所以命题“∀x∈R,x2﹣5x+a>0”为真命题.所以△=25﹣4×a=25﹣30a<0,解得a>.故答案为:(,+∞)15.函数y=log(2x2﹣3x+1)的递减区间为(1,+∞).【考点】复合函数的单调性.【分析】令t=2x2﹣3x+1>0,求得函数的定义域,且y=log t,本题即求函数t在定义域内的增区间,再利用二次函数的性质可得结论.【解答】解:令t=2x2﹣3x+1>0,求得x<,或x>1,可得函数的定义域为{x|x<,或x>1},且y=log t,故本题即求函数t在定义域内的增区间.再利用二次函数的性质可得函数t在定义域内的增区间为(1,+∞),故答案为:(1,+∞).16.已知点P在曲线y=上,a为曲线在点P处的切线的倾斜角,则a的取值范围是.【考点】导数的几何意义.【分析】由导函数的几何意义可知函数图象在切点处的切线的斜率值即为其点的导函数值,结合函数的值域的求法利用基本不等式求出k 的范围,再根据k=tanα,结合正切函数的图象求出角α的范围.【解答】解:根据题意得f′(x)=﹣,∵,且k<0则曲线y=f(x)上切点处的切线的斜率k≥﹣1,又∵k=tanα,结合正切函数的图象由图可得α∈,故答案为:.三、解答题:解答应写出文字说明,证明过程或演算步骤.17.在平面直角坐标系中,直线l的参数方程为(其中t 为参数).现以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C的极坐标方程为ρ=2cosθ.(Ⅰ)写出直线l和曲线C的普通方程;(Ⅱ)已知点P为曲线C上的动点,求P到直线l的距离的最大值.【考点】参数方程化成普通方程;简单曲线的极坐标方程.【分析】(Ⅰ)直线l的参数方程k消去参数t得直线l普通方程又由曲线C的极坐标方程为ρ=2cosθ,得ρ2=2ρcosθ,由此能求出曲线C 的直角坐标方程.(Ⅱ)曲线C的方程可化为(x﹣1)2+y2=1,设与直线l平行的直线为y=x+b,当直线l与曲线C相切时,,当时,P 到直线l的距离达到最大,最大值为两平行线的距离.【解答】选修4﹣4:坐标系与参数方程解:(Ⅰ)由题,直线l的参数方程为(其中t为参数).消去直线l参数方程中的参数t得直线l普通方程为y=x+2.又由曲线C的极坐标方程为ρ=2cosθ,得ρ2=2ρcosθ,由,得曲线C的直角坐标方程为x2+y2﹣2x=0.(Ⅱ)曲线C的极坐标方程为ρ=2cosθ可化为(x﹣1)2+y2=1,设与直线l平行的直线为y=x+b,当直线l与曲线C相切时,有,即,于是当时,P到直线l的距离达到最大,最大值为两平行线的距离即.(或先求圆心到直线的距离为,再加上半径1,即为P到直线l距离的最大值)18.已知函数f(x)=|x﹣a|.(Ⅰ)当a=﹣2时,解不等式f(x)≥16﹣|2x﹣1|;(Ⅱ)若关于x的不等式f(x)≤1的解集为[0,2],求证:f(x)+f(x+2)≥2a.【考点】绝对值不等式的解法.【分析】(Ⅰ)当a=﹣2时,不等式为|x+2|+|2x﹣1|≥16,分类讨论,去掉绝对值,即可解不等式f(x)≥16﹣|2x﹣1|;(Ⅱ)先求出a,f(x)=|x﹣1|,于是只需证明f(x)+f(x+2)≥2,即证|x﹣1|+|x+1|≥2,利用绝对值不等式,即可证明结论.【解答】(Ⅰ)解:当a=﹣2时,不等式为|x+2|+|2x﹣1|≥16,当x≤﹣2时,原不等式可化为﹣x﹣2﹣2x+1≥16,解之得x≤﹣;当﹣2<x≤时,原不等式可化为x+2﹣2x+1≥16,解之得x≤﹣13,不满足,舍去;当x>时,原不等式可化为x+2+2x﹣1≥16,解之得x≥5;不等式的解集为{x|x≤﹣或x≥5}.(Ⅱ)证明:f(x)≤1即|x﹣a|≤1,解得a﹣1≤x≤a+1,而f(x)≤1解集是[0,2],所以,解得a=1,从而f(x)=|x﹣1|于是只需证明f(x)+f(x+2)≥2,即证|x﹣1|+|x+1|≥2,因为|x﹣1|+|x+1|=|1﹣x|+|x+1|≥|1﹣x+x+1|=2,所以|x﹣1|+|x+1|≥2,证毕.19.已知=(5cosx,cosx),=(sinx,2cosx),记函数f(x)=•+||2.(1)求函数f(x)的最小正周期;(2)求f(x)单调递增区间.【考点】三角函数中的恒等变换应用;正弦函数的图象.【分析】(1)利用向量的数量积公式得到函数解析式,并化简,得到函数周期;(2)解不等式得到x范围即为所求.【解答】解:(1)f(x)=•+||2,∴.(2)解:不等式得∴,f(x)单调递增区间为.20.在边长为1的等边三角形ABC中,设=2,=3,(1)用向量,表示向量和,并求•;(2)求在方向上的射影.【考点】平面向量数量积的运算.【分析】(1)由即可得到,从而求出,而同样由即可得出,进而得到,这样进行数量积的运算即可求出;(2)可知在上的射影为,从而求出即可,这样可由求出,从而得出的值,从而得出射影的值.【解答】解:(1)如图,;∴;∴;;∴;∴;∴;∴===;(2)===;∴;∴在方向上的射影为:=.21.在△ABC中,A,B,C所对的边分别为a,b,c,且a=3,b=2,B=2A.(1)求cosA的值;(2)求c的值.【考点】余弦定理.【分析】(1)依题意,利用正弦定理=及二倍角的正弦即可求得cosA的值;(2)易求sinA=,sinB=,从而利用两角和的正弦可求得sin(A+B)=,在△ABC中,此即sinC的值,利用正弦定理可求得c的值.【解答】解:(1)∵△ABC中,a=3,b=2,B=2A,∴由正弦定理得:=,即=,∴cosA=;(2)由(1)知cosA=,A∈(0,π),∴sinA=,又B=2A,∴cosB=cos2A=2cos2A﹣1=,B∈(0,π),∴sinB=,在△ABC中,sinC=sin(A+B)=sinAcosB+cosAsinB=×+×=,∴c===5.22.已知函数f(x)=ax2﹣(2a+1)x+2lnx(a∈R).(Ⅰ)若曲线y=f(x)在x=1和x=3处的切线互相平行,求a的值;(Ⅱ)求f(x)的单调区间;(Ⅲ)设g(x)=x2﹣2x,若对任意x1∈(0,2],均存在x2∈(0,2],使得f(x1)<g(x2),求a的取值范围.【考点】导数在最大值、最小值问题中的应用;利用导数研究曲线上某点切线方程.【分析】(Ⅰ)由函数,知(x>0).由曲线y=f(x)在x=1和x=3处的切线互相平行,能求出a的值.(Ⅱ)(x>0).根据a的取值范围进行分类讨论能求出f(x)的单调区间.(Ⅲ)对任意x1∈(0,2],均存在x2∈(0,2],使得f(x1)<g (x2),等价于在(0,2]上有f(x)max<g(x)max.由此能求出a 的取值范围.【解答】解:(Ⅰ)∵函数,∴(x>0).∵曲线y=f(x)在x=1和x=3处的切线互相平行,∴f'(1)=f'(3),即,解得.(Ⅱ)(x>0).①当a≤0时,x>0,ax﹣1<0,在区间(0,2)上,f'(x)>0;在区间(2,+∞)上f'(x)<0,故f(x)的单调递增区间是(0,2),单调递减区间是(2,+∞).②当时,,在区间(0,2)和上,f'(x)>0;在区间上f'(x)<0,故f(x)的单调递增区间是(0,2)和,单调递减区间是③当时,,故f(x)的单调递增区间是(0,+∞).④当时,,在区间和(2,+∞)上,f'(x)>0;在区间上f'(x)<0,故f(x)的单调递增区间是和(2,+∞),单调递减区间是.(Ⅲ)由已知,在(0,2]上有f(x)max<g(x)max.由已知,g(x)max=0,由(Ⅱ)可知,①当时,f(x)在(0,2]上单调递增,故f(x)max=f(2)=2a﹣2(2a+1)+2ln2=﹣2a﹣2+2ln2,所以,﹣2a﹣2+2ln2<0,解得a>ln2﹣1,故.②当时,f(x)在上单调递增,在上单调递减,故.由可知,2lna>﹣2,﹣2lna<2,所以,﹣2﹣2lna<0,f(x)max<0,综上所述,a>ln2﹣1.。
陕西省西安中学2019届高三第四次仿真考试数学(文)试题一. 选择题:(本大题共12小题,每小题5分,共60分.) 1.已知集合{}21A y y x ==-,{B x y ==,则A B 为( ) A.∅B.[)1,+∞C. [)1,-+∞D.[]1,1-2.如右图,在复平面内,复数12,z z 对应的向量分别为,OA OB ,则复数12z z ⋅对应的复数位于()A.第一象限B.第二象限C.第三象限D.第四象限3.2001年至2013年西安市电影放映场次的情况如右图所示.下列函数模型中,最不合适近似描述这13年间电影放映场次逐年变化规律的是( )A .2y ax bx c =++B .x y ae b =+C .ax b y e +=D .ln y a x b =+ 4.下列说法正确的是( )A.()"f 00"=是“函数(x)f 是奇函数”的充要条件B.若2000:,10,p x R x x ∃∈-->则2:,10p x R x x ⌝∀∈--<C.若p q ∧为假命题,则p q 与均为假命题D.命题:1"="62παα若,则sin =的否命题是1""62παα≠≠若,则sin5. 已知点),(y x 所在的可行域如图所示.若要使目标函数y ax z +=取得最大值的最优解有无数多个,则a 的值为() A. 4 B. 41 C. 35 D.536.设S n 为等比数列{a n }的前n 项和,8a 2+a 5=0,则52S S =( ) A .-11B .-8C .5D .117.在ABC ∆中,若22sin(A B)sin a b B +-==且则角A=( )A.6πB.3πC.23πD.56π8.一个三棱锥的三视图如下图所示,则该三棱锥的外接球的表面积为( )A .29πB .25πC .20πD .13πA.2k =B.k =C.k =D.4k =10.已知函数1()ln 2xf x x =-(),若实数x 0满足01188()log sin log cos 88f x ππ>+,则0x 的取值范围是( )A .(,1)-∞B .(0,1)C .(1,)+∞D .1(,)2+∞11. 右图是用计算机随机模拟的方法估计概率P 的程序框图,P 表示估计结果,则输出P 的近似值为( ) A.41 B.21 C.43 D.87 12. 已知函数|lg 1|,1,()0, 1.x x f x x ⎧-≠=⎨=⎩若关于x 的方程2()()0f x bf x c ++=有7个不同的实数解,则,b c 应满足的条件是()A .b <0且c >0 B.b >0且c <0 C.b <0且c =0 D.00b c ≥=且 二、填空题:(本大题共4小题,每小题5分,共20分。

绝密★启用前陕西省2019年高考数学文科试卷本试卷共23题,共150分,共4页。
考试结束后,将本试卷和答题卡一并交回。
注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折叠、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(5分)已知集合A={x|x>﹣1},B={x|x<2},则A∩B=()A.(﹣1,+∞)B.(﹣∞,2)C.(﹣1,2)D.∅2.(5分)设z=i(2+i),则=()A.1+2i B.﹣1+2i C.1﹣2i D.﹣1﹣2i3.(5分)已知向量=(2,3),=(3,2),则|﹣|=()A.B.2C.5D.504.(5分)生物实验室有5只兔子,其中只有3只测量过某项指标.若从这5只兔子中随机取出3只,则恰有2只测量过该指标的概率为()A.B.C.D.5.(5分)在“一带一路”知识测验后,甲、乙、丙三人对成绩进行预测.甲:我的成绩比乙高.乙:丙的成绩比我和甲的都高.丙:我的成绩比乙高.成绩公布后,三人成绩互不相同且只有一个人预测正确,那么三人按成绩由高到低的次序为()A.甲、乙、丙B.乙、甲、丙C.丙、乙、甲D.甲、丙、乙6.(5分)设f(x)为奇函数,且当x≥0时,f(x)=e x﹣1,则当x<0时,f(x)=()A.e﹣x﹣1B.e﹣x+1C.﹣e﹣x﹣1D.﹣e﹣x+17.(5分)设α,β为两个平面,则α∥β的充要条件是()A.α内有无数条直线与β平行B.α内有两条相交直线与β平行C.α,β平行于同一条直线D.α,β垂直于同一平面8.(5分)若x1=,x2=是函数f(x)=sinωx(ω>0)两个相邻的极值点,则ω=()A.2B.C.1D.9.(5分)若抛物线y2=2px(p>0)的焦点是椭圆+=1的一个焦点,则p=()A.2B.3C.4D.810.(5分)曲线y=2sin x+cos x在点(π,﹣1)处的切线方程为()A.x﹣y﹣π﹣1=0B.2x﹣y﹣2π﹣1=0C.2x+y﹣2π+1=0D.x+y﹣π+1=011.(5分)已知α∈(0,),2sin2α=cos2α+1,则sinα=()A.B.C.D.12.(5分)设F为双曲线C:﹣=1(a>0,b>0)的右焦点,O为坐标原点,以OF为直径的圆与圆x2+y2=a2交于P,Q两点.若|PQ|=|OF|,则C的离心率为()A.B.C.2D.二、填空题:本题共4小题,每小题5分,共20分。


2019届高三文科数学好教育11月份陕西四校联考特供卷(二)(解析版附后)第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知{}lg 0A x x =>,{}12B x x =-<,则A B =( )A .{}11x x x <-≥或B .{}13x x <<C .{}3x x >D .{}1x x >-2.已知复数312iz =-(i 是虚数单位),则z 的实部为( ) A .35-B .35C .15-D .153.函数e4xy x=的图象可能是( )A .B .C .D .4.已知向量(1,=a ,()0,2=-b ,则a 与b 的夹角为( )A .π6 B .π3 C .5π6 D .2π35.在1,2,3,6这组数据中随机取出三个数,则数字2是这三个不同数字的平均数的概率是( )A .14 B .13C .12D .346.直线0ax by -=与圆220x y ax by +-+=的位置关系是( ) A .相交B .相切C .相离D .不能确定7.在ABC △中,a ,b ,c 分别是角A ,B ,C 的对边,()()3a b c a c b ac +++-=,则角B =( ) A .2π3B .π3C .5π6D .π68.执行如图所示程序框图,输出的S =( )A .25B .9C .17D .209.长方体1111ABCD A B C D -,1AB =,2AD =,13AA =,则异面直线11A B 与1AC 所成角的余弦值为( )A B C D .1310.设函数()ππsin 2cos 244f x x x ⎛⎫⎛⎫=+++ ⎪ ⎪⎝⎭⎝⎭,则( )A .()y f x =在π0,2⎛⎫⎪⎝⎭单调递增,其图象关于直线π4x =对称B .()y f x =在π0,2⎛⎫⎪⎝⎭单调递增,其图象关于直线π2x =对称C .()y f x =在π0,2⎛⎫⎪⎝⎭单调递减,其图象关于直线π4x =对称D .()y f x =在π0,2⎛⎫⎪⎝⎭单调递减,其图象关于直线π2x =对称11.设椭圆()2222:10x y C a b a b+=>>的左、右焦点分别为1F ,2F ,P 是C 上的点,212PF F F ⊥,1230PF F ∠=︒,则椭圆C 的离心率为( )A B .13C .12D 12.已知函数()()lg 4, 02, 0 ax x f x x x ⎧+>⎪=⎨+≤⎪⎩,且()()033f f +=,则实数a 的值是( )A .1B .2C .3D .4第Ⅱ卷二、填空题:本大题共4小题,每小题5分.13.已知函数()2ln 24f x x x x =+-,则函数()f x 的图象在1x =处的切线方程为__________. 14.若x ,y 满足约束条件220100x y x y y --≤⎧⎪-+≥⎨⎪≤⎩,则2z x y =+的最小值为__________.15.已知sin 2cos αα=,则cos 2α=__________.16.直三棱柱111ABC A B C -的底面是直角三角形,侧棱长等于底面三角形的斜边长,若其外接球的体积为32π3,则该三棱柱体积的最大值为__________. 三、解答题:解答应写出文字说明、证明过程或演算步骤. 17.(12分)已知正项等比数列{}n a 满足126a a +=,324a a -=. (1)求数列{}n a 的通项公式; (2)记2211log log n n n b a a +=,求数列{}n b 的前n 项和n T .18.(12分)经调查,3个成年人中就有一个高血压,那么什么是高血压?血压多少是正常的?经国际卫生组织对大量不同年龄的人群进行血压调查,得出随年龄变化,收缩压的正常值变化情况如下表:其中:1221ˆni ii nii x yn x y bxn x ==-⋅⋅=-⋅∑∑,ˆˆay bx =-,82117232i i x ==∑,8147384i i i x y ==∑;(1)请画出上表数据的散点图;(2)请根据上表提供的数据,用最小二乘法求出y 关于x 的线性回归方程ˆˆˆy bx a =+;(ˆa ,ˆb 的值精确到0.01) (3)若规定,一个人的收缩压为标准值的0.9 1.06~倍,则为血压正常人群;收缩压为标准值的1.06 1.12~倍,则为轻度高血压人群;收缩压为标准值的1.12 1.20~倍,则为中度高血压人群;收缩压为标准值的1.20倍及以上,则为高度高血压人群.一位收缩压为180mmHg 的70岁的老人,属于哪类人群?19.(12分)如图,直三棱柱111ABC A B C -的所有棱长都是2,1AA ⊥平面ABC ,D ,E 分别是AC ,1CC 的中点.(1)求证:AE ⊥平面1A BD ; (2)求三棱锥11B A BD -的体积.20.(12分)已知抛物线2:2C y px =过点()1,1A . (1)求抛物线C 的方程;(2)过点()3,1P -的直线与抛物线C 交于M ,N 两个不同的点(均与点A 不重合).设直线AM ,AN 的斜率分别为1k ,2k ,求证:1k ,2k 为定值.21.(12分)设()()3211232f x x x ax a =-++∈R .(1)讨论()f x 的单调区间;(2)当02a <<时,()f x 在[]1,4上的最小值为163-,求()f x 在[]1,4上的最大值.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分. 22.(10分)【选修4-4:坐标系与参数方程】已知直线l的参数方程为142x t y ⎧=+⎪⎪⎨⎪=⎪⎩(t 为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 的极坐标方程为2cos ρθ=.(1)求曲线C 的直角坐标方程与直线l 的极坐标方程;(2)若直线()π6θρ=∈R 与曲线C 交于点A (不同于原点),与直线l 交于点B ,求AB 的值. 23.(10分)【选修4-5:不等式选讲】 已知函数()2f x x a x =-++.(1)当1a =时,求不等式()3f x ≤的解集; (2)0x ∃∈R ,()03f x ≤,求a 的取值范围.文科数学(二)答 案一、选择题. 1.【答案】D 2.【答案】B 3.【答案】C 4.【答案】A 5.【答案】A6.【答案】B 7.【答案】B 8.【答案】C 9.【答案】A 10.【答案】D 11.【答案】D 12.【答案】B 二、填空题. 13.【答案】30x y --= 14.【答案】11-15.【答案】35-16.【答案】三、解答题.17.【答案】(1)2n n a =;(2)1n nT n =+. 【解析】(1)设数列{}n a 的公比为q ,由已知0q >, 由题意得1121164a a q a q a q +=⎧⎪⎨-=⎪⎩, ∴23520q q --=. 解得2q =,12a =. 因此数列{}n a 的通项公式为2n n a =. (2)由(1)知,()2211111log log 11n n n b a a n n n n +===-++,∴11111111223111n nT n n n n =-+-++-=-=+++L .18.【答案】(1)见解析;(2)ˆ0.9188.05y x =+;(3)收缩压为180mmHg 的70岁老人为中度高血压人群.【解析】(1).(2)2832384248525862458x +++++++==,1141181221271291351401471298y +++++++==.∴818222147384845129118ˆ0.91172328451298i ii ii x ynx ybxx ==-⋅-⨯⨯===≈-⨯-⋅∑∑.ˆˆ1290.914588.05ay bx =-=-⨯=. ∴回归直线方程为ˆ0.9188.05yx =+. (3)根据回归直线方程的预测,年龄为70岁的老人标准收缩压约为()0.917088.05151.75mmHg ⨯+=,∵1801.19151.75≈.∴收缩压为180mmHg 的70岁老人为中度高血压人群.19.【答案】(1)见解析;(2. 【解析】(1)∵AB BC CA ==,D 是AC 的中点,∴BD AC ⊥,∵1AA ⊥平面ABC ,∴平面11AA C C ⊥平面ABC , ∴BD ⊥平面11AA C C ,∴BD AE ⊥.又∵在正方形11AA C C 中,D ,E 分别是AC ,1CC 的中点,∴1A D AE ⊥. 又1A DBD D =,∴AE ⊥平面1A BD .(2)连结1AB 交1A B 于O ,∵O 为1AB 的中点,∴点1B 到平面1A BD 的距离等于点A 到平面1A BD 的距离.∴1111111121332B A BD A A BD B AA D AA D V V V S BD ---===⨯⨯=⨯⨯⨯△.20.【答案】(1)2y x =;(2)见解析.【解析】(1)由题意得21p =,∴抛物线方程为2y x =.(2)设()11,M x y ,()22,N x y ,直线MN 的方程为()13x t y =++, 代入抛物线方程得230y ty t ---=.∴()2280t ∆=++>,12y y t +=,123y y t =--, ∴()()121212221212121212111111111111111312y y y y k k x x y y y y y y y y t t ----⋅=⋅=⋅====-----+++++--++, ∴1k ,2k 是定值.21.【答案】(1)见解析;(2)103. 【解析】(1)由()22f x x x a '=-++,18a ∆=+,①18a ≤-时,0∆≤,此时()0f x '≤,∴()f x 在R 上递减.②18a >-时,0∆>,令()0f x '=,解得x =,令()0f x '<,解得x <或x >, 令()0f x '>x <<, 故()f x在⎛-∞ ⎝⎭,⎫+∞⎪⎪⎝⎭上递减,在⎝⎭上递增. (2)由(1)知()f x 在()1,x -∞,()2,x +∞上单调递减,在()12,x x 上单调递增, 当02a <<时,有1214x x <<<,∴()f x 在[]1,4上的最大值为()2f x , 又()()2741602f f a -=-+<,即()()41f f <, ∴()f x 在[]1,4上的最小值为()40164833f a =-=-,得1a =,22x =, 从而()f x 在[]1,4上的最大值为()1023f =. 【解析】(1)∵2cos ρθ=,∴22cos ρρθ=, ∴曲线C 的直角坐标方程为2220x y x +-=.∵直线l的参数方程为142x t y ⎧=+⎪⎪⎨⎪=⎪⎩(t 为参数)y -=∴直线l cos sin θρθ-=(2)将π6θ=代入曲线C 的极坐标方程2cos ρθ=得ρ=A 点的极坐标为π6⎫⎪⎭.将π6θ=代入直线l 的极坐标方程得3122ρρ-=ρ=∴B 点的极坐标为π6⎛⎫ ⎪⎝⎭,∴AB =23.【解析】(1)当1a =时,()12f x x x =-++,①当2x ≤-时,()21f x x =--,令()3f x ≤,即213x --≤,解得2x =-, ②当21x -<<时,()3f x =,显然()3f x ≤成立,∴21x -<<, ③当1x ≥时,()21f x x =+,令()3f x ≤,即213x +≤,解得1x ≤, 综上所述,不等式的解集为{}21x x -≤≤.(2)∵()()()222f x x a x x a x a =-++≥--+=+, ∵0x ∃∈R ,有()3f x ≤成立, ∴只需23a +≤,解得51a -≤≤, ∴a 的取值范围为[]5,1-.2019届高三文科数学好教育11月份陕西四校联考特供卷(二)(解析版)第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知{}lg 0A x x =>,{}12B x x =-<,则A B =( )A .{}11x x x <-≥或B .{}13x x <<C .{}3x x >D .{}1x x >-【答案】D【解析】{}{}lg 01A x x x x =>=>,{}{}1213B x x x x =-<=-<<,则{}1A B x x =>-.故选D . 2.已知复数312iz =-(i 是虚数单位),则z 的实部为( ) A .35-B .35C .15-D .15【答案】B【解析】∵()()()312i 336i 12i 12i 12i 55z +===+--+,∴z 的实部为35.故选B . 3.函数e4xy x=的图象可能是( )A .B .C .D .【答案】C【解析】函数为奇函数,图象关于原点对称,排除B , 当1x =时,e14y =<,排除A ; 当x →+∞时,e4xx→+∞,排除D .故选C .4.已知向量(1,=a ,()0,2=-b ,则a 与b 的夹角为( ) A .π6B .π3C .5π6D .2π3【答案】A【解析】设向量a 与向量b 的夹角为[]()0,πθθ∈,则cos θ⋅==a b a b ,∴π6θ=.故选A . 5.在1,2,3,6这组数据中随机取出三个数,则数字2是这三个不同数字的平均数的概率是( ) A .14B .13C .12D .34【答案】A【解析】在1,2,3,6这组数据中随机取出三个数,基本事件总数()1,2,3,()1,2,6,()1,3,6,()2,3,6共4个,则数字2是这三个不同数字的平均数所包含的基本事件只有()1,2,31个. 因此,数字2是这三个不同数字的平均数的概率是14.故选A . 6.直线0ax by -=与圆220x y ax by +-+=的位置关系是( ) A .相交 B .相切C .相离D .不能确定【解析】将圆的方程化为标准方程得2222224a b a b x y +⎛⎫⎛⎫-++= ⎪ ⎪⎝⎭⎝⎭,∴圆心坐标为,22a b ⎛⎫- ⎪⎝⎭,半径r =∵圆心到直线0ax by -=的距离22a b d r +==,则圆与直线的位置关系是相切.故选B .7.在ABC △中,a ,b ,c 分别是角A ,B ,C 的对边,()()3a b c a c b ac +++-=,则角B =( ) A .2π3B .π3C .5π6D .π6【答案】B【解析】由()()3a b c a c b ac +++-=,可得222a c b ac +-=,根据余弦定理得2221cos 22a cb B ac +-==,∵()0,πB ∈,∴π3B =.故选B .8.执行如图所示程序框图,输出的S =( )A .25B .9C .17D .20 【答案】C【解析】按照程序框图依次执行为1S =,0n =,0T =;9S =,2n =,044T =+=; 17S =,4n =,41620T S =+=>,退出循环,输出17S =.故选C .9.长方体1111ABCD A B C D -,1AB =,2AD =,13AA =,则异面直线11A B 与1AC 所成角的余弦值为( ) ABCD .13【解析】∵1111C D A B ∥,∴异面直线11A B 与1AC 所成的角即为11C D 与1AC 所成的角11AC D ∠. 在11Rt AC D △中,111C D =,1AD =1AC =∴11111cos C D AC D AC ∠===.故选A . 10.设函数()ππsin 2cos 244f x x x ⎛⎫⎛⎫=+++ ⎪ ⎪⎝⎭⎝⎭,则( )A .()y f x =在π0,2⎛⎫⎪⎝⎭单调递增,其图象关于直线π4x =对称B .()y f x =在π0,2⎛⎫⎪⎝⎭单调递增,其图象关于直线π2x =对称C .()y f x =在π0,2⎛⎫⎪⎝⎭单调递减,其图象关于直线π4x =对称D .()y f x =在π0,2⎛⎫⎪⎝⎭单调递减,其图象关于直线π2x =对称【答案】D【解析】∵()πππsin 2cos 222442f x x x x x ⎛⎫⎛⎫⎛⎫=+++=+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.由于cos y x =的对称轴为()πx k k =∈Z ,∴y x 的对称轴方程是()π2k x k =∈Z ,∴A ,C 错误;y x =的单调递减区间为()2π2π2πk x k k ≤≤+∈Z , 即()πππ2k x k k ≤≤+∈Z ,函数()y f x =在π0,2⎛⎫⎪⎝⎭上单调递减,∴B 错误,D 正确.故选D . 11.设椭圆()2222:10x y C a b a b+=>>的左、右焦点分别为1F ,2F ,P 是C 上的点,212PF F F ⊥,1230PF F ∠=︒,则椭圆C 的离心率为( )AB .13C .12D【答案】D【解析】设2PF x =,∵212PF F F ⊥,1230PF F ∠=︒,∴12PF x =,12F F =, 又122PF PF a +=,122F F c =,∴23a x =,2c =, ∴C的离心率为22c e a ==D . 12.已知函数()()lg 4, 02, 0 ax x f x x x ⎧+>⎪=⎨+≤⎪⎩,且()()033f f +=,则实数a 的值是( )A .1B .2C .3D .4【答案】B【解析】由题意知,()02f =,又()()033f f +=,则()31f =, 又()()3lg 341f a =+=,解得2a =.故选B .第Ⅱ卷二、填空题:本大题共4小题,每小题5分.13.已知函数()2ln 24f x x x x =+-,则函数()f x 的图象在1x =处的切线方程为__________. 【答案】30x y --=【解析】∵()2ln 24f x x x x =+-,∴()144f x x x'=+-,∴()11f '=, 又()12f =-,∴所求切线方程为()21y x --=-,即30x y --=.14.若x ,y 满足约束条件220100x y x y y --≤⎧⎪-+≥⎨⎪≤⎩,则2z x y =+的最小值为__________.【答案】11-【解析】画出可行域如图所示,可知目标函数过点()4,3A --时取得最小值,()()min 24311z =⨯-+-=-. 15.已知sin 2cos αα=,则cos 2α=__________. 【答案】35-【解析】由已知得tan 2α=,22222222cos sin 1tan 143cos2cos sin sin cos tan 1415ααααααααα---=-====-+++. 16.直三棱柱111ABC A B C -的底面是直角三角形,侧棱长等于底面三角形的斜边长,若其外接球的体积为32π3,则该三棱柱体积的最大值为__________.【答案】【解析】设三棱柱底面直角三角形的直角边为a ,b,则棱柱的高h =,设外接球的半径为r ,则3432ππ33r =,解得2r =,∵上下底面三角形斜边的中点连线的中点是该三棱柱的外接球的球心,24r ==.∴h =22282a b h ab +==≥,∴4ab ≤.当且仅当2a b ==时“=”成立.∴三棱柱的体积12V Sh abh ===≤三、解答题:解答应写出文字说明、证明过程或演算步骤. 17.(12分)已知正项等比数列{}n a 满足126a a +=,324a a -=. (1)求数列{}n a 的通项公式; (2)记2211log log n n n b a a +=,求数列{}n b 的前n 项和n T .【答案】(1)2n n a =;(2)1n nT n =+. 【解析】(1)设数列{}n a 的公比为q ,由已知0q >, 由题意得1121164a a q a q a q +=⎧⎪⎨-=⎪⎩,∴23520q q --=.解得2q =,12a =. 因此数列{}n a 的通项公式为2n n a =. (2)由(1)知,()2211111log log 11n n n b a a n n n n +===-++,∴11111111223111n nT n n n n =-+-++-=-=+++L .18.(12分)经调查,3个成年人中就有一个高血压,那么什么是高血压?血压多少是正常的?经国际卫生组织对大量不同年龄的人群进行血压调查,得出随年龄变化,收缩压的正常值变化情况如下表:其中:1221ˆni ii nii x yn x y bxn x ==-⋅⋅=-⋅∑∑,ˆˆay bx =-,82117232i i x ==∑,8147384i i i x y ==∑;(1)请画出上表数据的散点图;(2)请根据上表提供的数据,用最小二乘法求出y 关于x 的线性回归方程ˆˆˆy bx a =+;(ˆa ,ˆb 的值精确到0.01) (3)若规定,一个人的收缩压为标准值的0.9 1.06~倍,则为血压正常人群;收缩压为标准值的1.06 1.12~倍,则为轻度高血压人群;收缩压为标准值的1.12 1.20~倍,则为中度高血压人群;收缩压为标准值的1.20倍及以上,则为高度高血压人群.一位收缩压为180mmHg 的70岁的老人,属于哪类人群?【答案】(1)见解析;(2)ˆ0.9188.05y x =+;(3)收缩压为180mmHg 的70岁老人为中度高血压人群.【解析】(1).(2)2832384248525862458x +++++++==,1141181221271291351401471298y +++++++==.∴818222147384845129118ˆ0.91172328451298i ii ii x ynx ybxx ==-⋅-⨯⨯===≈-⨯-⋅∑∑.ˆˆ1290.914588.05ay bx =-=-⨯=. ∴回归直线方程为ˆ0.9188.05yx =+. (3)根据回归直线方程的预测,年龄为70岁的老人标准收缩压约为()0.917088.05151.75mmHg ⨯+=,∵1801.19151.75≈.∴收缩压为180mmHg 的70岁老人为中度高血压人群.19.(12分)如图,直三棱柱111ABC A B C -的所有棱长都是2,1AA ⊥平面ABC ,D ,E 分别是AC ,1CC 的中点.(1)求证:AE ⊥平面1A BD ; (2)求三棱锥11B A BD -的体积.【答案】(1)见解析;(2. 【解析】(1)∵AB BC CA ==,D 是AC 的中点,∴BD AC ⊥,∵1AA ⊥平面ABC ,∴平面11AA C C ⊥平面ABC , ∴BD ⊥平面11AA C C ,∴BD AE ⊥.又∵在正方形11AA C C 中,D ,E 分别是AC ,1CC 的中点,∴1A D AE ⊥. 又1A DBD D =,∴AE ⊥平面1A BD .(2)连结1AB 交1A B 于O ,∵O 为1AB 的中点,∴点1B 到平面1A BD 的距离等于点A 到平面1A BD 的距离.∴1111111121332B A BD A A BD B AA D AA D V V V S BD ---===⨯⨯=⨯⨯⨯△.20.(12分)已知抛物线2:2C y px =过点()1,1A .(1)求抛物线C 的方程;(2)过点()3,1P -的直线与抛物线C 交于M ,N 两个不同的点(均与点A 不重合).设直线AM ,AN 的斜率分别为1k ,2k ,求证:1k ,2k 为定值.【答案】(1)2y x =;(2)见解析.【解析】(1)由题意得21p =,∴抛物线方程为2y x =.(2)设()11,M x y ,()22,N x y ,直线MN 的方程为()13x t y =++,代入抛物线方程得230y ty t ---=. ∴()2280t ∆=++>,12y y t +=,123y y t =--, ∴()()121212221212121212111111111111111312y y y y k k x x y y y y y y y y t t ----⋅=⋅=⋅====-----+++++--++, ∴1k ,2k 是定值.21.(12分)设()()3211232f x x x ax a =-++∈R .(1)讨论()f x 的单调区间;(2)当02a <<时,()f x 在[]1,4上的最小值为163-,求()f x 在[]1,4上的最大值. 【答案】(1)见解析;(2)103. 【解析】(1)由()22f x x x a '=-++,18a ∆=+,①18a ≤-时,0∆≤,此时()0f x '≤,∴()f x 在R 上递减.②18a >-时,0∆>,令()0f x '=,解得x =,令()0f x '<,解得x <或x >,令()0f x '>x <<, 故()f x在⎛-∞ ⎝⎭,⎫+∞⎪⎪⎝⎭上递减,在⎝⎭上递增.(2)由(1)知()f x 在()1,x -∞,()2,x +∞上单调递减,在()12,x x 上单调递增, 当02a <<时,有1214x x <<<,∴()f x 在[]1,4上的最大值为()2f x , 又()()2741602f f a -=-+<,即()()41f f <, ∴()f x 在[]1,4上的最小值为()40164833f a =-=-,得1a =,22x =, 从而()f x 在[]1,4上的最大值为()1023f =. 请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分. 22.(10分)【选修4-4:坐标系与参数方程】已知直线l的参数方程为142x t y ⎧=+⎪⎪⎨⎪=⎪⎩(t 为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 的极坐标方程为2cos ρθ=.(1)求曲线C 的直角坐标方程与直线l 的极坐标方程;(2)若直线()π6θρ=∈R 与曲线C 交于点A (不同于原点),与直线l 交于点B ,求AB 的值. 【答案】(1)22:20C x y x +-=,cos sin l θρθ-=(2)【解析】(1)∵2cos ρθ=,∴22cos ρρθ=,∴曲线C 的直角坐标方程为2220x y x +-=. ∵直线l的参数方程为142x t y ⎧=+⎪⎪⎨⎪=⎪⎩(t 为参数)y -=∴直线lcos sin θρθ-= (2)将π6θ=代入曲线C 的极坐标方程2cos ρθ=得ρ=A点的极坐标为π6⎫⎪⎭.将π6θ=代入直线l的极坐标方程得3122ρρ-=ρ=∴B点的极坐标为π6⎛⎫ ⎪⎝⎭,∴AB =23.(10分)【选修4-5:不等式选讲】已知函数()2f x x a x =-++.(1)当1a =时,求不等式()3f x ≤的解集; (2)0x ∃∈R ,()03f x ≤,求a 的取值范围. 【答案】(1){}21x x -≤≤;(2)[]5,1-.【解析】(1)当1a =时,()12f x x x =-++,①当2x ≤-时,()21f x x =--,令()3f x ≤,即213x --≤,解得2x =-, ②当21x -<<时,()3f x =,显然()3f x ≤成立,∴21x -<<, ③当1x ≥时,()21f x x =+,令()3f x ≤,即213x +≤,解得1x ≤, 综上所述,不等式的解集为{}21x x -≤≤.(2)∵()()()222f x x a x x a x a =-++≥--+=+,∵0x ∃∈R ,有()3f x ≤成立,∴只需23a +≤,解得51a -≤≤,∴a 的取值范围为[]5,1-.【陕西省四校联考2019届高三高考模拟数学(文)试题用稿】。

陕西省西安地区陕师大附中、西安高级中学等八校2019届高三4月联考数学(文)试题一、选择题(本大题共12小题,共60.0分)1.若集合M={y|y=x-2},P={y|y=},那么M∩P=()A. B. C. D.2.欧拉公式e ix=cos x+i sin x(i为虚数单位)是由瑞士著名数学家欧拉发明的,它将指数函数的定义域扩大到复数,建立了三角函数和指数函数的关系,它在复变函数论里占用非常重要的地位,被誉为“数学中的天桥”,根据欧拉公式可知,e2i表示的复数在复平面中位于()A. 第一象限B. 第二象限C. 第三象限D. 第四象限3.下列关于命题的说法错误的是()A. 命题“若,则”的逆否命题为“若,则”B. 已知函数在区间上的图象是连续不断的,则命题“若,则在区间内至少有一个零点”的逆命题为假命题C. 命题“,使得”的否定是:“,均有”D. “若为的极值点,则”的逆命题为真命题4.函数y=的图象大致是()A. B.C. D.5.已知在三棱锥P-ABC中,PA=PB=PC=1,AB=,AB⊥BC,平面PAB⊥平面ABC,若三棱锥的顶点在同一球面上,则该球的表面积为()A. B. C. D.6.设函数y=f(x)=a x(a>0,a≠1),y=f-1(x)表示f(x)的反函数,定义如框图表示的运算,若输入x=-2,输出y=;当输出y=-3时,则输入x=()A. 8B.C. 6D.7.已知A(3,0),B(0,3),C(cosα,sinα),若,则的值为()A. B. C. D.8.某空间几何体的三视图如图所示,则该几何体的体积为()A. B. C. D.9.若实数x、y满足2x+2y=1,则x+y的取值范围是()A. B. C. D.10.过抛物线y2=4x焦点F的直线交抛物线于A,B两点,若=,则|AB|=()A. 9B. 72C.D. 3611.已知△ABC外接圆O的半径为1,且•=-.∠C=,从圆O内随机取一个点M,若点M取自△ABC内的概率恰为,则△ABC的形状为的形状为()A. 直角三角形B. 等边三角形C. 钝角三角形D. 等腰直角三角形12.定义在R上的函数f(x)满足:f(x)+f′(x)>1,f(0)=4,则不等式e x f(x)>e x+3(其中e为自然对数的底数)的解集为()A. B.C. D.二、填空题(本大题共4小题,共20.0分)13.某校共有学生2000名,各年级男、女生人数如表.已知在全校学生中随机抽取1名,抽到二年级女生的可能性0.19.现用分层抽样的方法在全校抽取64名学生,则应在三年级抽取的学生人数为______.14.设变量x,y满足约束条件,则目标函数z=x+2y的最小值为______.15.记S n为数列{a n}的前项和,若S n=2a n+1,则S10=______.16.设函数f(x)=,,<,若互不相等的实数x1,x2,x3满足f(x1)=f(x2)=f(x3),则x1+x2+x3的取值范围是______.三、解答题(本大题共7小题,共82.0分)17.在△ABC中,A=2B,sin B=,AB=23.(1)求sin A,sin C;(2)求•的值.18.近年来,我国许多省市雾霾天气频发,为增强市民的环境保护意识,某市面向全市征召n名义务宣传志愿者,成立环境保护宣传组织.现把该组织的成员按年龄分成5组:第1组[20,25),第2组[25,30),第3组[30,35),第4组[35,40),第5组[40,45],得到的频率分布直方图如图所示,已知第2组有35人.(1)求该组织的人数;(2)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参加某社区的宣传活动,应从第3,4,5组各抽取多少名志愿者?(3)在(2)的条件下,该组织决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验,用列举法求出第3组至少有一名志愿者被抽中的概率.19.如图,三棱锥S-ABC中,侧面SAB与侧面SAC均为边长为2的正三角形,且∠BAC=90°,O、D分别为BC、AB的中点.(Ⅰ)证明:SO⊥平面ABC;(Ⅱ)求四棱锥S-ACOD的体积.20.已知F1、F2分别是椭圆C:+y2=1的左、右焦点.(1)若P是第一象限内该椭圆上的一点,•=-,求点P的坐标;(2)若直线l与圆O:x2+y2=相切,交椭圆C于A,B两点,是否存在这样的直线l,使得OA⊥OB?21.已知函数f(x)=e x-x2+2a+b(x R)的图象在x=0处的切线为y=bx.(e为自然对数的底数).(Ⅰ)求a,b的值;(Ⅱ)当x R时,求证:f(x)≥-x2+x;(Ⅲ)若f(x)>kx对任意的x(0,+∞)恒成立,求实数k的取值范围.22.已知曲线C1:(t为参数),C2:(θ为参数)(Ⅰ)将C1,C2的方程化为普通方程,并说明它们分别表示什么曲线;(Ⅱ)若C1上的点对应的参数为t=,Q为C2上的动点,求PQ中点M到直线C3:(t为参数)距离的最小值.23.已知a,b均为实数,且|3a+4b|=10.(Ⅰ)求a2+b2的最小值;(Ⅱ)若|x+3|-|x-2|≤a2+b2对任意的a、b R恒成立,求实数x的取值范围.答案和解析1.【答案】C【解析】解:∵={y|y>0},={y|y≥0},∴M∩P={y|y>0}=(0,+∞),故选:C.先化简这两个集合,利用两个集合的交集的定义求出M∩P.本题考查函数的值域的求法,两个集合的交集的定义,化简这两个集合是解题的关键.2.【答案】B【解析】解:e2i=cos2+isin2,∵2,∴cos2(-1,0),sin2(0,1),∴e2i表示的复数在复平面中位于第二象限.故选:B.e2i=cos2+isin2,根据2,即可判断出.本题考查了复数的欧拉公式、三角函数的单调性与值域,考查了推理能力与计算能力,属于中档题.3.【答案】D【解析】解:命题“若x2-3x+2=0,则x=2”的逆否命题为“若x≠2,则x2-3x+2≠0”,故A正确;已知函数f(x)在区间[a,b]上的图象是连续不断的,命题“若f(a)f(b)<0,则f(x)在区间(a,b)内至少有一个零点”的逆命题为假命题,比如f(x)=x2在(-1,1)内有一个零点0,但f(-1)f(1)>0,故B正确;命题“x R,使得x2+x+1<0”的否定是:“x R,均有x2+x+1≥0”,故C正确;“若x0为y=f(x)的极值点,则f'(x0)=0”的逆命题为假命题,比如f(x)=x3,有f′(0)=0,但x=0不为f(x)的极值点,故D错误.故选:D.由命题的逆否命题可判断A;由命题的逆命题和函数零点存在定理可判断B;由命题的否定形式可判断C;由命题的逆命题和函数极值点的定义可判断D.本题考查命题的真假判断,主要是四种命题,以及相互关系和命题的否定,以及函数零点定理和函数的极值点的定义,考查推理能力,属于基础题.4.【答案】D【解析】解:当x>0时,y=xlnx,y′=1+lnx,即0<x<时,函数y单调递减,当x>,函数y单调递增,因为函数y为偶函数,故选:D.根据掌握函数的奇偶性和函数的单调性即可判断.本题考查了函数图象的识别,关键是掌握函数的奇偶性和函数的单调性,属于基础题.5.【答案】B【解析】解:由题意,AC为截面圆的直径,AC==,设球心到平面ABC的距离为d,球的半径为R,∵PA=PB=1,AB=,∴PA⊥PB,∵平面PAB⊥平面ABC,∴P到平面ABC的距离为.由勾股定理可得R2=()2+d2=()2+(-d)2,∴d=0,R2=,∴球的表面积为4πR2=3π.故选:B.求出P到平面ABC的距离,AC为截面圆的直径,由勾股定理可得R2=()2+d2=()2+(-d)2,求出R,即可求出球的表面积.本题考查球的表面积,考查学生的计算能力,求出球的半径是关键.属于中档题.6.【答案】B【解析】解:由图可知,该程序的作用是计算分段函y=的函数值.∵输入x=-2,输出y=,∴a-2=,a=2当输出y=-3时,只有:f-1(x)=-3⇔f(-3)=x⇒x=2-3=.故选:B.分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是计算分段函数y=的函数值.根据流程图(或伪代码)写程序的运行结果,是算法这一模块最重要的题型,其处理方法是:①分析流程图(或伪代码),从流程图(或伪代码)中即要分析出计算的类型,又要分析出参与计算的数据(如果参与运算的数据比较多,也可使用表格对数据进行分析管理)⇒②建立数学模型,根据第一步分析的结果,选择恰当的数学模型③解模.7.【答案】B【解析】解:∵=(cosα-3,sinα),=(cosα,sinα-3)∴=(cosα-3)•cosα+sinα(sinα-3)=-1得cos2α+sin2α-3(cosα+sinα)=-1∴,故sin(α+)=(sinα+cosα)=×=故选:B.由A,B,C的坐标求出和,根据平面向量数量积的运算法则及同角三角函数间的基本关系化简得到sinα+cosα的和,然后利用两角和的正弦函数公式及特殊角的三角函数值即可求出sin(α+)的值.此题考查学生掌握平面向量的数量积的运算,灵活运用两角和的正弦函数公式、同角三角函数间的基本关系及特殊角的三角函数值化简求值,是一道中档题.8.【答案】B【解析】解:由三视图得该几何体是从四棱锥P-ABCD中挖去一个半圆锥,四棱锥的底面是以2为边长的正方形、高是2,圆锥的底面半径是1、高是2,∴所求的体积V==,故选:B.由三视图得该几何体是从四棱中挖去一个半圆锥,由三视图求出几何元素的长度,由锥体的体积公式求出几何体的体积.本题考查三视图求几何体的体积,由三视图正确复原几何体是解题的关键,考查空间想象能力.9.【答案】A【解析】解:由实数x、y满足2x+2y=1,根据基本不等式得,1=2x+2y≥2,故x+y≤-2.故选:A.由实数x、y满足2x+2y=1,根据基本不等式求得x+y的范围.本题考查基本不等式求范围,属于简单题.10.【答案】C【解析】解:如图,点B在第一象限.过B、A分别向抛物线的准线作垂线,垂足分别为D、E,过B作EA的垂线,垂足为C,则四边形BDEC为矩形.由抛物线定义可知|BD|=|BF|,|AE|=|AF|,又∵=,∴|BD|=|CE|=2|AE|,即A为CE中点,∴|BA|=3|AC|,在Rt△BAC中,|BC|=2|AC|,k AB=2,F(1,0),AB的方程为:y=2(x-1),代入抛物线方程可得:2x2-5x+2=0,x1+x2=,则|AB|=x1+x2+2=+2=.故选:C.当点B在第一象限,通过抛物线定义及=,可知A为CE中点,通过勾股定理可知|BC|=2|AC|,利用直线与抛物线联立,通过弦长的性质计算可得结论.本题考查抛物线的简单性质,注意解题方法的积累,属于中档题.11.【答案】B【解析】解:∵•=-,圆的半径为1,∴cos∠AOB=-又0<∠AOB<π,故∠AOB=,又△AOB为等腰三角形,故AB=,从圆O内随机取一个点,取自△ABC内的概率为,即=,∴,设BC=a,AC=b.∵C=,∴,得ab=3,…①由AB2=a2+b2-2abcosC=3,得a2+b2-ab=3,a2+b2=6…②联立①②解得a=b=.∴△ABC为等边三角形.故选:B.根据向量的数量积求得∠AOB=,进而求得AB的长度,利用几何概型的概率公式求出三角形ABC的面积,利用三角形的面积公式即可求出三角形各边的长度即可得到结论.本题主要考查几何概型的应用,以及向量积的计算,利用余弦定理是解决本题的关键,本题综合性较强,有一定的难度.12.【答案】A【解析】解:设g(x)=e x f(x)-e x,(x R),则g′(x)=e x f(x)+e x f′(x)-e x=e x[f(x)+f′(x)-1],∵f(x)+f′(x)>1,∴f(x)+f′(x)-1>0,∴g′(x)>0,∴y=g(x)在定义域上单调递增,∵e x f(x)>e x+3,∴g(x)>3,又∵g(0)═e0f(0)-e0=4-1=3,∴g(x)>g(0),∴x>0故选:A.构造函数g(x)=e x f(x)-e x,(x R),研究g(x)的单调性,结合原函数的性质和函数值,即可求解本题考查函数单调性与奇偶性的结合,结合已知条件构造函数,然后用导数判断函数的单调性是解题的关键.13.【答案】16【解析】解:由题意,二年级女学生数为2000×0.19=380人,所以三年级的学生数为;2000-373-377-380-370=500人,所占比例为所以应在三年级抽取的学生人数为64×=16故答案为:16由题意,二年级女学生数为2000×0.19=380人,由此可计算三件及学生数和三年级学生所占的比例,按此比例即可求出三年级抽取的学生人数.本题考查分层抽样知识,抓住各层抽取的比例一致是解决分层抽样问题的关键.14.【答案】【解析】解:画出不等式组,表示的可行域,由图可知,当直线y=-过A(0,)时,直线在y轴上的截距最小,z有最小值为.故答案为:.由约束条件画出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求出最优解的坐标,代入目标函数得答案.本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.15.【答案】-1023【解析】解:由于S n=2a n+1,①当n=1时,解得:a1=-1.当n≥2时,S n-1=2a n-1+1,②①-②得:a n=2a n-2a n-1,所以:(常数),故:数列{a n}是以-1为首项,2为公比的等比数列.所以:.所以:.故答案为:-1023首先利用递推关系式求出数列的通项公式,进一步利用等比数列的前n项和公式的应用求出结果.本题考查的知识要点:数列的通项公式的求法及应用,数列的前n项和的应用,主要考察学生的运算能力和转换能力,属于基础题型.16.【答案】(,6)【解析】解:函数f(x)=的图象如下图所示:若存在互不相的实数x1,x2,x3满足f(x1)=f(x2)=f(x3)=k,则k(-3,4),不妨令x1<x2<x3,则x1(,0),x2+x3=6,故x1+x2+x3(,6),故答案为:(,6)画出函数f(x)=的图象,令x1<x2<x3,由图象可得x1(,0),x2+x3=6,进而得到x1+x2+x3的取值范围.本题考查的知识点是根的存在性及根的个数判断,画出函数的图象后,数形结合分析出x1(,0),x2+x3=6,是解答的关键.17.【答案】解:(1)∵sin B=,B为锐角,∴cos B==,∵A=2B,∴sin A=sin2B=2sin B cosB=2××=,cos A=cos2B=cos2B-sin2B=-=,则sin C=sin(A+B)=sin A cos B+cos A sin B=×+×=;(2)由正弦定理==,AB=23,sin C=,sin B=,sin A=,∴AC==9,BC==12,又cos C=-cos(A+B)=-cos A cos B+sin A sin B=-×+×=-,∴•=CA×CB×cos C=9×12×(-)=-80.【解析】(1)由sinB的值,利用同角三角函数间的基本关系求出cosB的值,再由A=2B,得到sinA=sin2B,利用二倍角的正弦函数公式化简,将sinB与cosB的值代入求出sinA的值,同理求出cosA的值,利用诱导公式得到sinC=sin(A+B),利用两角和与差的正弦函数公式化简,将各自的值代入计算即可求出值;(2)利用正弦定理列出关系式,将sinC,sinB,sinA,AB的值代入求出CA与CB的值,由cosC=-cos(A+B),利用两角和与差的余弦函数公式求出cosC的值,利用平面向量的数量积运算法则化简所求式子,即可求出值.此题考查了正弦定理,平面向量的数量积运算,以及两角和与差的正弦、余弦函数公式,熟练掌握正弦定理是解本题的关键.18.【答案】解:(1)由题意:第2组的人数:35=5×0.07•n,得到:n=100,故该组织有100人.…(3分)(2)第3组的人数为0.3×100=30,第4组的人数为0.2×100=20,第5组的人数为0.1×100=10.∵第3,4,5组共有60名志愿者,∴利用分层抽样的方法在60名志愿者中抽取6名志愿者,每组抽取的人数分别为:第3组:;第4组:;第5组:.∴应从第3,4,5组中分别抽取3人,2人,1人.…(6分)(3)记第3组的3名志愿者为A1,A2,A3,第4组的2名志愿者为B1B2,第5组的1名志愿者为C1.则从6名志愿者中抽取2名志愿者有:(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A1,C1),(A2,A3),(A2,B1),(A2,B2),(A2,C1),(A3,B1),(A3,B2),(A3,C1),(B1,B2),(B1,C1),(B2,C1),共有15种.其中第3组的3名志愿者A1,A2,A3,至少有一名志愿者被抽中的有:(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A1,C1),(A2,A3),(A2,B1),(A2,B2),(A2,C1),(A3,B1),(A3,B2),(A3,C1),共有12种,则第3组至少有一名志愿者被抽中的概率为.…(12分)【解析】(1)根据频数=频率×样本容量,频率=对应矩形面积,构造关于n的方程,解方程可得该组织的人数;(2)先计算出第3,4,5组中每组的人数,进而根据比例,可得到应从第3,4,5组各抽取多少名志愿者;(3)选求出这6名志愿者中随机抽取2名志愿者的基本事件总数和第3组至少有一名志愿者被抽中的基本事件个数,代入古典概型概率计算公式,可得答案.本题考查的知识点是古典概型概率计算公式,其中熟练掌握利用古典概型概率计算公式求概率的步骤,是解答的关键.19.【答案】(本题满分12分)解:(Ⅰ)证明:由题设AB=AC=SB=SC=SA,连结OA,△ABC为等腰直角三角形,所以,且AO⊥BC,又△SBC为等腰三角形,故SO⊥BC,且,从而OA2+SO2=SA2.所以△SOA为直角三角形,SO⊥AO.又AO∩BO=O.所以SO⊥平面ABC.…(6分)(Ⅱ)∵BO=CO,BD=AD,∴AC∥DO,∴DO⊥AD,.,由(Ⅰ)知SO⊥平面ABC,∴.…(12分)【解析】(Ⅰ)连结OA,△ABC为等腰直角三角形,由已知得AO⊥BC,SO⊥BC,SO⊥AO.由此能证明SO⊥平面ABC.(Ⅱ)由已知得DO⊥AD,.SO⊥平面ABC,由此能求出四棱锥S-ACOD的体积.本题考查直线与平面垂直的证明,考查四棱锥体积的求法,解题时要注意空间思维能力的培养.20.【答案】解:(1)由椭圆方程为+y2=1,可知:a=2,b=1,c=,∴F1(-,0),F2(,0),设P(x,y),(x,y>0),则•=,•,=x2+y2-3=-,又+y2=1,联立解得:,∴P,.(2)设A(x1,y1),B(x2,y2).①若l的斜率不存在时,l:x=,代入椭圆方程得:y2=,容易得出=x1x2+y1y2=-=-≠0,此时OA⊥OB不成立.②若l的斜率存在时,设l:y=kx+m,则由已知可得=,即k2+1=4m2.由,可得:(4k2+1)x2+8kmx+4(m2-1)=0,则x1+x2=-,x1•x2=.要OA⊥OB,则=0,即x1•x2+(kx1+m)(kx2+m)=km(x1+x2)+(k2+1)x1•x2+m2=0,即5m2-4k2-4=0,又k2+1=4m2.∴k2+1=0,此方程无实解,此时OA⊥OB不成立.综上,不存在这样的直线l,使得OA⊥OB.【解析】(1)设P(x,y),(x,y>0),则•=x2+y2-3=-,又+y2=1,联立解出即可得出.(2)设A(x1,y1),B(x2,y2).①若l的斜率不存在时,l:x=,代入椭圆方程得:y2=,容易得出≠0,此时OA⊥OB不成立.②若l的斜率存在时,设l:y=kx+m,则由已知可得=.直线方程与椭圆方程联立可得:(4k2+1)x2+8kmx+4(m2-1)=0,要OA⊥OB,则=0,即x1•x2+(kx1+m)(kx2+m)=km(x1+x2)+(k2+1)x1•x2+m2=0,把根与系数的关系代入可得5m2-4k2-4=0,又k2+1=4m2.解出即可判断出结论.本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题、一元二次方程的根与系数的关系、向量数量积运算性质、向量垂直与数量积的关系,考查了分类讨论方法、推理能力与计算能力,属于难题.21.【答案】(Ⅰ)解:f(x)=e x-x2+2a+b,f′(x)=e x-2x,由题意得,即a=-1,b=1;(Ⅱ)证明:由(Ⅰ)可知,f(x)=e x-x2-1.令φ(x)=f(x)+x2-x=e x-x-1,φ′(x)=e x-1,由φ′(x)=0,得x=0.当x(-∞,0)时,φ′(x)<0,φ(x)单调递减,当x(0,+∞)时,φ′(x)>0,φ(x)单调递增.∴φ(x)的最小值为φ(0)=0,从而f(x)≥-x2+x;(Ⅲ)解:f(x)>kx对任意的x(0,+∞)恒成立,等价于>k对任意的x(0,+∞)恒成立.令g(x)=,x>0.∴=.由(Ⅱ)可知,当x(0,+∞)时,e x-x-1>0恒成立,令g′(x)>0,得x>1,g′(x)<0,得0<x<1,∴g(x)的单调增区间为(1,+∞),单调减区间为(0,1),g(x)min=g(1)=e-2.∴k<e-2.即实数k的取值范围为(-∞,e-2).【解析】(Ⅰ)求出原函数的导函数,由题意可得,求解可得a,b的值;(Ⅱ)由(Ⅰ)可知,f(x)=e x-x2-1.令φ(x)=f(x)+x2-x=e x-x-1,利用导数求其最小值得答案;(Ⅲ)f(x)>kx对任意的x(0,+∞)恒成立,等价于>k对任意的x(0,+∞)恒成立.令g(x)=,x>0.利用导数求其最小值可得实数k的取值范围.本题考查利用导数研究过曲线上某点处的切线方程,考查了函数的最值与函数单调性的判断,考查转化思想与函数方程思想,考查转化能力与计算能力,属于难题.22.【答案】解:(Ⅰ)C1:(x+1)2+(y-3)2=1,C2:+y2=1C1为圆心是(-4,3),半径是1的圆C2为中心是坐标原点,焦点在x轴上,长半轴长是,短半轴长是1的椭圆(Ⅱ)当t=时,P(-4,4),Q(cosθ,sinθ),故M(-2+cosθ,2+)C3为直线x-y-5=0,M到C3的距离d==|sin(θ-)+9|,从而当sin(θ-)=-1时,d取得最小值4.【解析】(Ⅰ)根据 sin2α+cos2α=1消参即可得到 C1,C2的普通方程,由普通方程可知C1为圆心是(-4,3),半径1的圆,C2为中心是坐标原点,焦点在x轴上,长半轴长是,短半轴长是1的椭圆.(Ⅱ)根据题意求出P坐标,利用C2的参数方程设出Q的直角坐标,由题意可得PQ中点M坐标,结合点到直线的距离公式、辅助角公式求出最小距离(Ⅰ)椭圆的参数方程、圆的参数方程化为普通方程时,一般要利用同角三角函数的平方关系sin2α+cos2α=1消参得到普通方程(Ⅱ)曲线上的点,到直线上一点的距离的最小值的求法:在求点到直线最小距离时,先用参数形式写出点Q的直角坐标,代入点到直线的距离公式结合辅助角公式得到距离的最小值.23.【答案】解:(I)∵|3a+4b|=10,∴100=(3a+4b)2≤(32+42)(a2+b2)=25(a2+b2)∴a2+b2≥4,当且仅当即或时取等号即a2+b2的最小值4(II)由(I)知|x+3|-|x-2|≤a2+b2对任意的a、b R恒成立,∴|x+3|-|x-2|≤4,∴ 或或解可得,x<-3或-3∴实数x的取值范围(-∞,]【解析】(I)利用柯西不等式即可求解(II)由(I)知|x+3|-|x-2|≤a2+b2对任意的a、b R恒成立⇔|x+3|-|x-2|≤(a2+b2)min,然后根据绝对值不等式的求解即可本题主要考查了柯西不等式在最值求解中的应用,还考查了绝对值不等式的解法及恒成立问题与最值求解相互转化思想的应用.。

2018-2019 学年度第一学期高三四模数学(文科)试题第 I 卷一、选择题 : 本大题共 12 个小题,每小题 5 分,共 60 分.在每小题给出的四个,选项中只有一个选项是符合题目要求的x 1 ,=,则1.已知集合 A={ x | 0}B {x | y log 2 x - 2 } A∩B=()x 5A.(1,2) B.(2,5 ) C . [2,5) D.(2,5]z i2.已知复数z满足z i,则z()A.1 1i B .1 1i C . 1 1 i2 2 2 2 2 21 1D.i2 23. 已知平面向量 a,b满足 |a|=,b|=, a 与 b 的夹角为2π,且( a+λ2 | 1 3b )⊥(2 a - b ),则实数λ的值为( )A. 2 B.-3 C. 3 D.- 74.已知 a n 为等差数列,若 a1 a5 a9 ,则 cos a2 a8 的值为 ( )1 3 1A. 2 B. 2 C. 23D.25.执行如图所示的程序框图。
若输出 y=- 3,则输入角θ= ( )ππππA. 6 B.- 6 C. 3 D.- 36. 给出如下四个命题:①若“ p且q”为假命题,则p、q均为假命题;第1页共11页②命题“若 ab,则 2a2b1 ”的否命题为“若 ab ,则 2a2b 1 ”;③命题“ x R , x 2 11 ”的否定是“ x R , x2 1 1 ”;④“ x0 ”是“ x1 2”的充分必要条件 . 其中正确的命题个数是x( )A.4B.3C.2D.1x y 1,7.若 x, y 满足 xy 1, 则 z x2y 的最大值是()x0,A .-2B.-1C.1D.28. 某几何体的三视图如图所示,则该几何体的体积是()πB .πA . + 1+ 32 23π3π C .2 +1D . 2 + 39. 正项等差数列 { a n } 的前 n 项和为 Sn ,若 S 2018=4036, 则19 的最小值为( )a 10a2009A. 3B. 4C. 5D.610.已知定义在 R 上的偶函数 f(x)满足 f(x +2)= f(x),当 x ∈[3,4]时, f(x)=ln x ,则 ()1 1ππA . fsin 2 <f cos 2 B . f(sin 1)<f(cos 1)C . f sin 3>f cos 33 3D . f sin 2 >f cos 211.已知 AB 是抛物线 y 2=2x 的一条焦点弦, | AB| =4,则 AB 中点 C 的横坐标是 ( )A .2B.1 3 5 C.2D.22第2页共11页12.设函数 | x 2 |, x 0a 有四个不同的解 x 1、 x 2、f ( x ),若关于 x 的方程 f ( x )| log 2 x |, x 0x 3、 x 4,且 x 1<x 2<x 3<x 4,则 x 3(x 1+x 2 )+1的取值范围()2x 3x4A .( 3,)B .(,3)C . [ 3,3)D . ( 3,3]第Ⅱ卷二、填空题 :本大题共 4 个小题,每小题 5 分,共 20 分.13. 各项均为正数的等比数列 { a n } 的前 n 项和为 S n ,若 S n = 2, S 3n = 14,则 S 4n . 14. 曲线y xe x 1在点 (0,1) 处的切线方程是15. 将一颗骰子先后投掷两次分别得到点数a ,b ,则直线 ax + by =0 与圆 (x -2)2 + y 2=2 有公共点的概率为 ________.16. 当双曲线 C 不是等轴双曲线时,我们把以双曲线 C 的实轴、虚轴的端点作为顶点的椭圆称为双曲线 C 的“伴生椭圆”.则离心率为3 的双曲线的“伴生椭圆”的离 心率为 . 三、解答题 :共 70 分,解答应写出文字说明、证明过程或演算步骤.第 17~21题为必考题每个试题考生都必须作答。

陕西西工大附中2019年高三第四次适应性考试数学(文)试题本试卷分为第一卷〔选择题〕和第二卷〔非选择题〕两部分,总分值150分。
考试时间120分钟。
第一卷〔选择题 共50分〕一.选择题:本大题共10小题,每题5分,共50分、在每题给出的四个选项中,只有一项为哪一项符合题目要求的。
1、{}1|2-==x y x M ,{}12|2++==x xy y N ,那么=⋂N MA.{}0|≥x xB.{}1|-≤x xC.{}1|≥x xD.φ 2.假设复数2(2)(z a a i =-++为纯虚数,那么aii a ++12007的值为A.iB.1-C.1D.i - 3、一个算法的程序框图如下图,当输出 的结果为0时,输入的x 值为 A 、2或-2 B 、-1或-2 C 、2或-1 D 、1或-2 4、函数11()(sin cos )sin cos 22f x x x x x=+--, 那么()f x 的值域是 A 、[]1,1-B. ⎡⎤⎢⎥⎣⎦C.⎡-⎢⎣⎦D.1,⎡-⎢⎣⎦5、抛物线24y x =按向量e 平移后的焦点坐标为(3,2),那么平移后的抛物线的顶点坐标为A 、(4,2)B 、(2,2)C 、(-2,-2)D 、(2,3) 6. 假设曲线4x y =的一条切线l 与直线084=-+y x 垂直,那么l 的方程为A 、034=--y xB 、034=--y xC 、034=-+y xD 、034=-+y x A.βαγβγα//⇒⎭⎬⎫⊥⊥ B.ββ⊥⇒⎭⎬⎫⊥l m l m //C.n m n m //⇒⎭⎬⎫⊥⊥γγ D.n m n m //////⇒⎭⎬⎫γγ 8、设{na }为公比q>1的等比数列,假设2009a和2010a是方程24830x x -+=的两根,那么20112012a a +=A.18B.10C.25D.9 9、在ABC ∆中,35sin ,cos ,513A B ==那么cos C =A.5665-B.1665或5665C.5665D.166510、21,F F 分别为双曲线12222=-b y a x )0,0(>>b a 的左、右焦点,P 为双曲线左支上任意一点,假设||||122PF PF 的最小值为a 8,那么双曲线离心率e 的取值范围是〔〕A.),1(+∞B.]3,0(C.]3,1(D.]2,1(第二卷非选择题〔共100分〕【二】填空题:本大题共5小题,每题5分,总分值25分,把答案填写在答题卡相应的位置。

2019-2020学年陕西省汉中市某名校高三(上)第四次质量检测数学试卷(文科)一、选择题:本大题共12个小题,每小题5分,共60分,每小题四个选项中只有一项是符合题意1. 已知集合M={x|x2−x−2=0},N={−1, 0},则M∩N=()A.{−1, 0, 2}B.{−1}C.{0}D.⌀【答案】B【考点】交集及其运算【解析】求出M中方程的解得到x的值,确定出M,求出M与N的交集即可.【解答】由M中方程变形得:(x−2)(x+1)=0,解得:x=2或x=−1,即M={−1, 2},∵N={−1, 0},∴M∩N={−1}2. 已知复数z=2−i1+i(i为虚数单位),则在复平面内复数z所对应的点在()A.第一象限B.第二象限C.第三象限D.第四象限【答案】D【考点】复数的运算【解析】直接利用复数代数形式的乘除运算化简,求出z所对应的点的坐标得答案.【解答】∵z=2−i1+i =(2−i)(1−i)(1+i)(1−i)=1−3i2=12−32i,∴在复平面内复数z所对应的点的坐标为(12, −32),在第四象限.3. 设函数f(x)=sin x+a cos x(a为常数),则“a=0“是“f(x)为奇函数”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条【答案】C【考点】充分条件、必要条件、充要条件【解析】根据充要条件的定义分充分性和必要性分别判断即可.【解答】若a =0,则f(x)=sin x ,为奇函数,充分性成立;若f(x)为奇函数,则f(0)=0,所以0+a =0,a =0,必要性成立; 故“a =0“是“f(x)为奇函数”的充要条件.4. 中国将于今年9月3日至5日在福建省厦门市主办金砖国家领导人第九次会晤.某志愿者队伍共有5人负责接待,其中3人担任英语翻译,另2人担任俄语翻译.现从中随机选取2人,恰有1个英语翻译,1个俄语翻译的概率是( ) A.13B.12C.35D.23【答案】 C【考点】古典概型及其概率计算公式 【解析】利用古典概率计算公式计算即可. 【解答】解:P (恰有1个英语翻译,1个俄语翻译)=C 31C 21C 52=35,故选C .5. 一个四棱锥的底面为正方形,其三视图如图所示,则这个四棱锥的体积是( )A.1B.2C.3D.4【答案】 B【考点】由三视图求体积 【解析】由三视图及题设条件知,此几何体为一个四棱锥,其较长的侧棱长已知,底面是一个正方形,对角线长度已知,故先求出底面积,再求出此四棱锥的高,由体积公式求解其体积即可 【解答】由题设及图知,此几何体为一个四棱锥,其底面为一个对角线长为2的正方形,故其底面积为4×12×1×1=2由三视图知其中一个侧棱为棱锥的高,其相对的侧棱与高及底面正方形的对角线组成一个直角三角形由于此侧棱长为√13,对角线长为2,故棱锥的高为√(√13)2−22=3此棱锥的体积为13×2×3=26. 已知双曲线x2a2−y2b2=1(a>0,b>0)上一点到两个焦点的距离分别为10和4,且离心率为2,则该双曲线的虚轴长为()A.3B.6C.3√3D.6√3【答案】D【考点】双曲线的离心率【解析】本题考查双曲线的概念和性质.【解答】解:由题意得2a=10−4=6,解得a=3,又因为双曲线的离心率e=ca=2,所以c=6,则b=√c2−a2=3√3,所以该双曲线的虚轴长为2b=6√3.故选D.7. 我国古代数学典籍《九章算术》第七章“盈不足”中有一问题:“今有蒲生一日,长三尺.莞生一日,长一尺.蒲生日自半.莞生日自倍.问几何日而长等?”(蒲常指一种多年生草本植物,莞指水葱一类的植物)现欲知几日后,莞高超过蒲高一倍.为了解决这个新问题,设计右面的程序框图,输入A=3,a=1.那么在①处应填()A.T>2S?B.S>2T?C.S<2T?D.T<2S?【答案】B【考点】程序框图【解析】由题意,S表示莞高,T表示蒲高,现欲知几日后,莞高超过蒲高一倍,即可得出结论.【解答】解:由题意,S表示莞高,T表示蒲高,现欲知几日后,莞高超过蒲高一倍,故①处应填S>2T?.故选B.8. 函数f(x)=x|x|−sin2x的大致图象是()A. B.C. D.【答案】B【考点】函数的图象变化函数的图象【解析】先判断函数的奇偶性和图象的对称性,利用当x=π时,f(x)的符号是否对应,利用排除法进行求解即可.【解答】f(−x)=−x|x|+sin2x=−(x|x|−sin2x)=−f(x),则f(x)为奇函数,图象关于原点对称,排除C,D当x=π时,f(π)=π2−sin2π=π2>0,排除A,9. 在△ABC中,A,B,C所对的边分别是a,b,c,A=2π3,且b cos C=3c cos B,则bc的值为()A.√13−12B.1+√132C.√132D.√142【答案】B【考点】余弦定理【解析】利用余弦定理将角化边整理得出a,b,c的关系,再使用余弦定理消去a,得到关于b,c的方程,即可解出bc的值.【解答】△ABC中,A=2π3,且b cos C=3c cos B,∴b×a2+b2−c22ab =3c×a2+c2−b22ac,即a 2=2b 2−2c 2; 又cos A =b 2+c 2−a 22bc=−12,∴ b 2+c 2−a 2+bc =0, ∴ 3c 2−b 2+bc =0, 即−(bc )2+bc +3=0, 解得bc =√13+12或−√13+12(不合题意,舍去), 即b c 的值为1+√132.10. 设点F 1,F 2分别为椭圆C:x 29+y 25=1的左、右焦点,点P 是椭圆C 上任意一点,若使得PF 1→⋅PF 2→=m 成立的点恰好是4个,则实数m 的值可以是( ) A.12B.3C.5D.8【答案】B【考点】 椭圆的离心率 【解析】设P(x 0, y 0),则PF 1→=(−2−x 0,−y 0),PF 2→=(2−x 0, −y 0),由PF 1→⋅PF 2→=m 及点P 椭圆上,可得关于x 0,y 0的方程组,联立得x 02=9m−94.再由0<x 02<9求解m 的范围,则答案可求. 【解答】 由椭圆C:x 29+y 25=1,得a 2=9,b 2=5,则c =2.∴ F 1 (−2, 0),F 2(2, 0),设P(x 0, y 0),则PF 1→=(−2−x 0,−y 0),PF 2→=(2−x 0, −y 0),由PF 1→⋅PF 2→=m ,得(−2−x 0, −y 0)⋅(2−x 0, −y 0)=m ,即x 02+y 02=m +4①, 又点P 在椭圆上,∴ x 029+y 025=1②,联立①②,得x 02=9m−94.要使PF 1→⋅PF 2→=m 成立的点恰好是4个,则0<9m−94<9.则1<m <5.∴ 实数m 的值可以是3.11. 公元前6世纪,古希腊的毕达哥拉斯学派研究过正五边形和正十边形的作图,发现了黄金分割约为0.618,这一数值也可以表示为m =2sin 18∘.若m 2+n =4,则m√n2cos227∘−1=()A.8B.4C.2D.1【答案】C【考点】三角函数的恒等变换及化简求值【解析】本题考查三角恒等变换.【解答】解:由题意得n=4−m2=4−4sin218∘=4cos218∘,则m√n2cos227∘−1=2sin18∘√4cos218∘cos54∘=2sin18∘×2cos18∘cos54∘=2sin36∘sin36∘=2.故选C.12. 已知函数y=x2的图象在点(x0, x02)处的切线为l,若l也与函数y=ln x,x∈(0, 1)的图象相切,则x0必满足()A.0<x0<12B.12<x0<1 C.√22<x0<√2 D.√2<x0<√3【答案】D【考点】利用导数研究曲线上某点切线方程【解析】求出函数y=x2的导数,y=ln x的导数,求出切线的斜率,切线的方程,可得2x0=1m,ln m−1=−x02,再由零点存在定理,即可得到所求范围.【解答】函数y=x2的导数为y′=2x,在点(x0, x02)处的切线的斜率为k=2x0,切线方程为y−x02=2x0(x−x0),设切线与y=ln x相切的切点为(m, ln m),0<m<1,即有y=ln x的导数为y′=1x,可得2x0=1m ,切线方程为y−ln m=1m(x−m),令x=0,可得y=ln m−1=−x02,由0<m<1,可得x0>12,且x02>1,解得x0>1,由m=12x0,可得x02−ln(2x0)−1=0,令f(x)=x2−ln(2x)−1,x>1,f′(x)=2x−1x>0,f(x)在x>1递增,且f(√2)=2−ln 2√2−1<0,f(√3)=3−ln 2√3−1>0,则有x 02−ln (2x 0)−1=0的根x 0∈(√2, √3).二、填空题:本大题共4个小题,每小题5分,共20分若x ,y 满足{x −y ≤02x +y −6≤0x ≥1,则z =2x −y 的最大值为________.【答案】 2【考点】 简单线性规划 【解析】先根据约束条件画出可行域,再利用几何意义求最值,求出最优解,然后求解z 的最大值即可. 【解答】x ,y 满足{x −y ≤02x +y −6≤0x ≥1 ,画出可行域如图,做出基准线0=2x −y ,{x −y =02x +y −6=0 解得A(2, 2)由图知,当直线z =2x −y 过点A(2, 2)时, z 最大值为:2.设向量a →=(1, 2m),b →=(m +1, 1),c →=(2, m),若(a →+c →)⊥b →,则|a →|=________. 【答案】√2【考点】平面向量的坐标运算数量积判断两个平面向量的垂直关系 【解析】由a →=(1, 2m),b →=(m +1, 1),c →=(2, m),知a →+c →=(3, 3m),由(a →+c →)⊥b →,知(a →+c →)⋅b →=3(m +1)+3m =0,由此能求出||a →|. 【解答】∵ a →=(1, 2m),b →=(m +1, 1),c →=(2, m), ∴ a →+c →=(3, 3m), ∵ (a →+c →)⊥b →,∴ (a →+c →)⋅b →=3(m +1)+3m =0, ∴ m =−12,即a →=(1,−1) ∴ |a →|=√2.在三棱锥P−ABC中,平面PAB⊥平面ABC,△ABC是边长为6的等边三角形,△PAB 是以AB为斜边的等腰直角三角形,则该三棱锥外接球的表面积为________.【答案】48π【考点】球的体积和表面积【解析】由题意画出图形,由已知求出三棱锥外接球的半径,代入表面积公式得答案.【解答】如图,在等边三角形ABC中,取AB中点F,设其中心为O,由AB=6,得CO=23CF=2√3.∵△PAB是以AB为斜边的等腰直角三角形,∴F为△PAB的外心,则O为棱锥P−ABC的外接球球心,则外接球半径R=OC=2√3.∴该三棱锥外接球的表面积为4π×(2√3)2=48π.某学习小组由学生和教师组成,人员构成同时满足以下三个条件:(i)男学生人数多于女学生人数;(ii)女学生人数多于教师人数;(iii)教师人数的两倍多于男学生人数.①若教师人数为4,则女学生人数的最大值为________.②该小组人数的最小值为________.【答案】6,12【考点】简单线性规划【解析】本题考查简单线性规划.【解答】解:①设男学生女学生分别为x,y人,若教师人数为4,则{x>y,y>4,2×4>x,即4<y<x<8,即x的最大值为7,y的最大值为6,即女学生人数的最大值为6.②设男学生女学生分别为x,y人,教师人数为z,则{x>y,y>z,2z>x,即z<y<x<2z即z最小为3才能满足条件,此时x最小为5,y最小为4,即该小组人数的最小值为12.故答案为:6;12.三、解答题:解答应写出文字说明,证明过程或演算步骤已知{a n}是等差数列,{b n}是等比数列,且b2=3,b3=9,a1=b1,a14=b4.(1)求{a n}的通项公式;(2)设c n=a n+b n,求数列{c n}的前n项和.【答案】解:(1)∵ {a n}是公差为d的等差数列,{b n}是公比为q的等比数列,由b2=3,b3=9,可得q=b3b2=3,∴b n=b2q n−2=3⋅3n−2=3n−1,即有a1=b1=1,a14=b4=27,则d=a14−a113=2,则a n=a1+(n−1)d=1+2(n−1)=2n−1;(2)c n=a n+b n=2n−1+3n−1,则数列{c n}的前n项和为(1+3+...+(2n−1))+(1+3+9+...+3n−1)=12n⋅2n+1−3n1−3=n2+3n−12.【考点】等比数列的前n项和等比数列的通项公式等差数列的前n项和等差数列的通项公式【解析】(1)设{a n}是公差为d的等差数列,{b n}是公比为q的等比数列,运用通项公式可得q =3,d=2,进而得到所求通项公式;(2)求得c n=a n+b n=2n−1+3n−1,再由数列的求和方法:分组求和,运用等差数列和等比数列的求和公式,计算即可得到所求和.【解答】解:(1)∵ {a n}是公差为d的等差数列,{b n}是公比为q的等比数列,由b2=3,b3=9,可得q=b3b2=3,∴b n=b2q n−2=3⋅3n−2=3n−1,即有a1=b1=1,a14=b4=27,则d=a14−a113=2,则a n=a1+(n−1)d=1+2(n−1)=2n−1;(2)c n=a n+b n=2n−1+3n−1,则数列{c n}的前n项和为(1+3+...+(2n−1))+(1+3+9+...+3n−1)=12n⋅2n+1−3n1−3=n2+3n−1.2某手机厂商推出一款6寸大屏手机,现对500名该手机使用者(200名女性,300名男性)进行调查,对手机进行打分,打分的频数分布表如下:女性用户:频数4575906030(Ⅰ)完成下列频率分布直方图,并比较女性用户和男性用户评分的波动大小(不要求计算具体值,给出结论即可);(Ⅱ)分别求女性用户评分的众数,男性用户评分的中位数;(Ⅲ)如果评分不低于70分,就表示该用户对手机“认可”,否则就表示“不认可”,完成下列2×2列联表,并回答是否有95%的把握认为性别和对手机的“认可”有关;女性用户男性用户合计.附:K2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d)【答案】140,180,320,60,120,180,200,300,500【考点】频率分布直方图独立性检验【解析】(Ⅰ)利用所给数据,可得频率分布直方图,并比较女性用户和男性用户评分的波动大小;(Ⅱ)由女性用户频率分布直方图知,女性用户评分的众数;在男性用户频率分布直方图中,中位数两边的面积相等,求出男性用户评分的中位数;(Ⅲ)求出K2,与临界值比较,即可得出结论.【解答】(1)女性用户和男性用户的频率分布表分别如下左、右图:由图可得女性用户的波动小,男性用户的波动大.(2)由女性用户频率分布直方图知,女性用户评分的众数为75;在男性用户频率分布直方图中,中位数两边的面积相等.设中位数为x,则70≤x< 80⋯于是10×0.015+10×0.025+(x−70)×0.03=0.5,解得x=7313(Ⅲ)2×2列联表如下图:女性用户男性用户合计≈5.208>3.841,所以有95%的把握认为性别和对手机的“认K2=500(140×120−180×60)2200×300×320×180可”有关.如图,在四棱锥S−ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AB=2,点M是SD的中点,AN⊥SC,且交SC于点N.(Ⅰ)求证:SB // 平面ACM;(Ⅱ)求点C到平面AMN的距离.【答案】证明:(Ⅰ)连结BD交AC于E,连结ME.∵ABCD是正方形,∴E是BD的中点.∵M是SD的中点,∴ME是△DSB的中位线.∴ME // SB.又∵ME⊂平面ACM,SB⊄平面ACM,∴SB // 平面ACM.(2)由条件有DC⊥SA,DC⊥DA,∴DC⊥平面SAD,∴AM⊥DC.又∵SA=AD,M是SD的中点,∴AM⊥SD.∴AM⊥平面SDC.∴SC⊥AM.由已知SC⊥AN,∴SC⊥平面AMN.于是CN⊥面AMN,则CN为点C到平面AMN的距离在Rt△SAC中,SA=2,AC=2√2,SC=√SA2+AC2=2√3,于是AC2=CN⋅SC⇒CN=4√33∴点C到平面AMN的距离为4√3.3【考点】点、线、面间的距离计算直线与平面平行【解析】(Ⅰ)连结BD交AC于E,连结ME,推导出ME // SB,由此能证明SB // 平面ACM.(Ⅱ)推导出CN为点C到平面AMN的距离,由此能求出点C到平面AMN的距离.【解答】证明:(Ⅰ)连结BD交AC于E,连结ME.∵ABCD是正方形,∴E是BD的中点.∵M是SD的中点,∴ME是△DSB的中位线.∴ME // SB.又∵ME⊂平面ACM,SB⊄平面ACM,∴SB // 平面ACM.(2)由条件有DC⊥SA,DC⊥DA,∴DC⊥平面SAD,∴AM⊥DC.又∵SA=AD,M是SD的中点,∴AM⊥SD.∴AM⊥平面SDC.∴SC⊥AM.由已知SC⊥AN,∴SC⊥平面AMN.于是CN⊥面AMN,则CN为点C到平面AMN的距离在Rt△SAC中,SA=2,AC=2√2,SC=√SA2+AC2=2√3,于是AC2=CN⋅SC⇒CN=4√33∴点C到平面AMN的距离为4√3.3平面上动点P到点F(0, 1)的距离比它到直线l:y=−2的距离小1.(Ⅰ)求动点P的轨迹C的方程;(Ⅱ)过点F作直线与曲线C交于两点A,B,与直线l交于点M,求|MA|⋅|MB|的最小值.【答案】(1)设动点P的坐标为(x, y),由题意知:√x2+(y−1)2=|y−(−2)|−1=|y+2|−1,且y≥0,∴ √x 2+(y −1)2=y +1⇒x 2+(y −1)2=(y +1)2,化简得:x 2=4y , 即为动点P 轨迹C 的方程;(2)设点A(x 1, y 1),B(x 2, y 2),M(x 0, −2), 由题意直线AB 的斜率k存在且k ≠0,设其方程为y =kx +1,则x 0=−3k,得M(−3k,−2)由{y =kx +1x 2=4y,消去y 得x 2−4kx −4=0,于是△=16(k 2+1)>0恒成立,且x 1+x 2=4k ,x 1x 2=−4,又y 1y 2=(kx 1+1)(kx 2+1)=k 2x 1x 2+k(x 1+x 2)+1=1,y 1+y 2=k(x 1+x 2)+2=4k 2+2⋯∵ MA →与MB →方向相同,故|MA|⋅|MB|=|MA →⋅MB →|,MA →=(x 1+3k ,y 1+2),MB →=(x 2+3k ,y 2+2),MA →⋅MB →=(x 1+3k )(x 2+3k )+(y 1+2)(y 2+2)=x 1x 2+3k (x 1+x 2)+9k 2+y 1y 2+2(y 1+y 2)+4 =8k 2+9k2+17≥2√8k 2×9k 2+17=17+12√2,当且仅当k 4=98⇒k 2=3√24时取等号, 故|MA|⋅|MB|的最小值为17+12√2.【考点】 轨迹方程直线与抛物线的位置关系 【解析】(Ⅰ) 利用平面上动点P 到点F(0, 1)的距离比它到直线l:y =−2的距离小1,建立方程,即可求动点P 的轨迹C 的方程;(Ⅱ)MA →与MB →方向相同,故|MA|⋅|MB|=|MA →⋅MB →|,直线与抛物线方程联立,利用韦达定理及基本不等式,即可求|MA|⋅|MB|的最小值. 【解答】(1)设动点P 的坐标为(x, y),由题意知:√x 2+(y −1)2=|y −(−2)|−1=|y +2|−1,且y ≥0,∴ √x 2+(y −1)2=y +1⇒x 2+(y −1)2=(y +1)2,化简得:x 2=4y , 即为动点P 轨迹C 的方程;(2)设点A(x 1, y 1),B(x 2, y 2),M(x 0, −2), 由题意直线AB 的斜率k存在且k ≠0,设其方程为y =kx +1,则x 0=−3k ,得M(−3k ,−2) 由{y =kx +1x 2=4y,消去y 得x 2−4kx −4=0,于是△=16(k2+1)>0恒成立,且x1+x2=4k,x1x2=−4,又y1y2=(kx1+1)(kx2+1)=k2x1x2+k(x1+x2)+1=1,y1+y2=k(x1+x2)+ 2=4k2+2⋯∵MA→与MB→方向相同,故|MA|⋅|MB|=|MA→⋅MB→|,MA→=(x1+3k ,y1+2),MB→=(x2+3k ,y2+2),MA→⋅MB→=(x1+3k)(x2+3k)+(y1+2)(y2+2)=x1x2+3k(x1+x2)+9k2+y1y2+2(y1+y2)+4=8k2+9k2+17≥2√8k2×9k2+17=17+12√2,当且仅当k4=98⇒k2=3√24时取等号,故|MA|⋅|MB|的最小值为17+12√2.设函数f(x)=ln x−ax2+ax,a为正实数.(Ⅰ)求证:f(1a)≤0;(Ⅱ)若函数f(x)有且只有1个零点,求a的值.【答案】(1)f(1a )=−ln a−1a+1(a>0),令g(x)=−ln x−1x +1(x>0),则g′(x)=1−xx2,故有0<x<1时,g′(x)>0,g(x)单调递增;x>1时,g′(x)<0,g(x)单调递减;所以x=1时,g(x)取极大值,也是最大值,所以g(x)≤g(1)=0,则f(1a)≤0;(2)若函数f(x)有且只有一个零点,又因为f(1)=ln1−a+a=0,即函数f(x)的零点为(1, 0),所以f′(1)=0,即1−2a+a=0,解得a=1.【考点】函数与方程的综合运用【解析】(Ⅰ)构造函数,确定函数的单调性与最值,即可证明结论;(Ⅱ)由题意可知,函数f(x)有且只有1个零点为(1, 0),则f′(1)=0,即可得出结论.【解答】(1)f(1a )=−ln a−1a+1(a>0),令g(x)=−ln x−1x +1(x>0),则g′(x)=1−xx2,故有0<x<1时,g′(x)>0,g(x)单调递增;x>1时,g′(x)<0,g(x)单调递减;所以x=1时,g(x)取极大值,也是最大值,所以g(x)≤g(1)=0,则f(1a)≤0;(2)若函数f(x)有且只有一个零点,又因为f(1)=ln1−a+a=0,即函数f(x)的零点为(1, 0),所以f′(1)=0,即1−2a+a=0,解得a=1.请考生在第22、23二题中任选一题作答,如果多做,则按所做的第一题记分.答时用2B铅笔在答题卡上把所选题目的题号涂黑[选修4-4:坐标系与参数方程]在极坐标系中,已知三点O(0, 0),A(2, π2),B(2√2, π4).(1)求经过点O,A,B的圆C1的极坐标方程;(2)以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,圆C2的参数方程为{x=−1+a cosθ,y=−1+a sinθ(θ是参数),若圆C1与圆C2外切,求实数a的值.【答案】解:(1)已知三点O(0, 0),A(2, π2),B(2√2, π4).将O,A,B三点化成普通坐标为O(0, 0),A(0, 2),B(2, 2).∴圆C1的圆心为(1, 1),半径为√2,∴圆C1的普通方程为(x−1)2+(y−1)2=2,将x=ρcosθ,y=ρsinθ代入普通方程得ρ2−2ρcosθ−2ρsinθ=0,∴ρ=2√2cos(θ−π4).(2)∵圆C2的参数方程为{x=−1+a cosθ,y=−1+a sinθ(θ是参数),∴圆C2的普通方程为(x+1)2+(y+1)2=a2.∴圆C2的圆心为(−1, −1),半径为|a|,∵圆C1与圆C2外切,∴2√2=√2+|a|,解得a=±√2.【考点】圆的参数方程圆的极坐标方程【解析】(1)首先把极坐标转换为直角坐标,进一步转换为极坐标方程.(2)直接利用圆与圆的位置关系求出结果.【解答】解:(1)已知三点O(0, 0),A(2, π2),B(2√2, π4).将O,A,B三点化成普通坐标为O(0, 0),A(0, 2),B(2, 2).∴圆C1的圆心为(1, 1),半径为√2,∴圆C1的普通方程为(x−1)2+(y−1)2=2,将x=ρcosθ,y=ρsinθ代入普通方程得ρ2−2ρcosθ−2ρsinθ=0,∴ρ=2√2cos(θ−π4).(2)∵圆C2的参数方程为{x=−1+a cosθ,y=−1+a sinθ(θ是参数),∴圆C2的普通方程为(x+1)2+(y+1)2=a2.∴圆C2的圆心为(−1, −1),半径为|a|,∵圆C1与圆C2外切,∴2√2=√2+|a|,解得a=±√2.[选修4-5:不等式选讲]已知f(x)=|x+1|+|x−1|.(Ⅰ)求不等式f(x)<4的解集;(Ⅱ)若不等式f(x)−|a−1|<0有解,求a的取值范围.【答案】(1)f(x)=|x+1|+|x−1|<4⇔{x≤−1−x−1−x+1<4或{−1<x≤1x+1−x+1<4或{x>1x+1+x−1<4,解得:−2<x≤−1或−1<x≤1或1<x<2,故不等式的解集为(−2, 2);(2)∵f(x)=|x+1|+|x−1|≥|(x+1)−(x−1)|=2,∴f(x)min=2,当且仅当(x+1)(x−1)≤0时取等号,而不等式f(x)−|a−1|<0有解⇔|a−1|>f(x)min=2,又|a−1|>2⇔a−1<−2或a−1>2故a的取值范围是(−∞, −1)∪(3, +∞).【考点】绝对值不等式的解法与证明绝对值三角不等式【解析】(Ⅰ)通过讨论x的范围得到关于x的不等式组,解出即可;(Ⅱ)根据绝对值的性质求出f(x)的最小值,问题转化为|a−1|>f(x)min,求出a的范围即可.【解答】(1)f(x)=|x+1|+|x−1|<4⇔{x≤−1−x−1−x+1<4或{−1<x≤1x+1−x+1<4或{x>1x+1+x−1<4,解得:−2<x≤−1或−1<x≤1或1<x<2,故不等式的解集为(−2, 2);(2)∵f(x)=|x+1|+|x−1|≥|(x+1)−(x−1)|=2,∴f(x)min=2,当且仅当(x+1)(x−1)≤0时取等号,而不等式f(x)−|a−1|<0有解⇔|a−1|>f(x)min=2,又|a−1|>2⇔a−1<−2或a−1>2故a的取值范围是(−∞, −1)∪(3, +∞).。

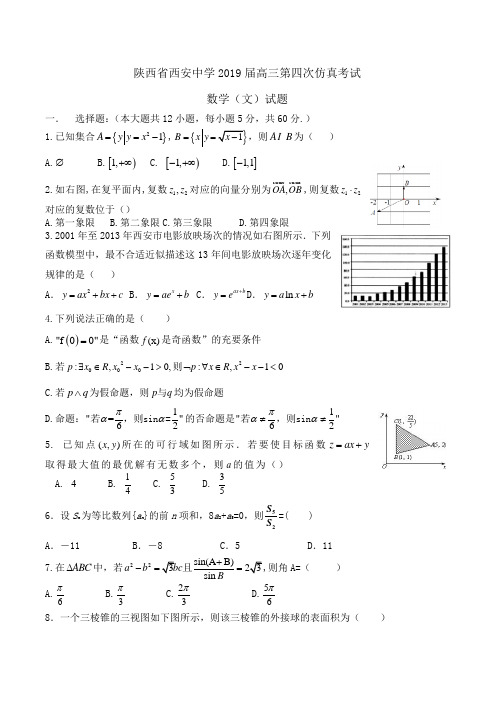
2019年陕西省高三(上)第四次质检数学试卷(文科)(重点班)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合A={x∈R|x2﹣x<0},B=(0,a)(a>0),若A⊆B,则实数a的取值范围是()A.(0,1]B.(0,1)C.[1,+∞)D.(1,+∞)2.(文)设a∈R,则a>1是<1的()A.必要但不充分条件B.充分但不必要条件C.充要条件 D.既不充分也不必要条件3.已知函数f(x)是奇函数,且当x>0时,f(x)=e x,则f(﹣1)=()A.B.﹣C.e D.﹣e4.公比为2的等比数列{a n}的各项都是正数,且a3a11=16,则a5=()A.4 B.2 C.1 D.85.函数y=sin3x的图象可以由函数y=cos3x的图象()A.向右平移个单位得到 B.向左平移个单位得到C.向右平移个单位得到 D.向左平移个单位得到6.函数的图象的最低点坐标是()A.(0,2)B.不存在C.(1,2)D.(1,﹣2)7.若两个等差数列{a n}和{b n}的前n项和分别是S n和T n,已知,则=()A.7 B.C. D.8.已知[x]为不超过实数x的最大整数,g(x)=[x]是取整函数,x0是函数的零点,则g(x0)等于()A.0 B.1 C.2 D.39.函数f(x)=x3+bx2+cx+d的图象如图所示,则函数的单调递减区间是()A. B.C.(﹣2,3)D.(﹣∞,﹣2)10.已知平面直角坐标系xOy上的区域D由不等式组给定.若M(x,y)为D上的动点,点A的坐标为(,1),则z=•的最大值为()A.4B.3C.4 D.311.已知f(x)是偶函数,它在[0,+∞)上是减函数,若f(lgx)>f(1),则实数x的取值范围是()A.(,1) B.(0,)∪(1,+∞) C.(,10)D.(0,1)∪(10,+∞)12.已知函数f1(x)=sinx+cosx,记f2(x)=f′1(x),f3(x)=f′2(x),…,f n(x)=f′n﹣1(x)(n∈N*,n≥2),n∈N.n≥2),则=()A.﹣1 B.0 C.D.1二、填空题(每题5分,满分20分,将答案填在答题纸上)13.下列关于向量的命题中,正确的有.(1);(2);(3)(4);(5)若,则中至少一个为(6)若,则;(7)若,则.14.设数列{a n}满足a2+a4=10,点P n(n,a n)对任意的n∈N+,都有向量=(1,2),则数列{a n}的前n项和S n=.15.已知各项皆为正数的等比数列{a n}(n∈N*),满足a7=a6+2a5,若存在两项a m、a n使得=4a1,则+的最小值为.16.已知实数x,y满足不等式组若目标函数z=y﹣ax(a ∈R)取最大值时的唯一最优解是(1,3),则实数a的取值范围是.三、解答题(本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.已知向量=(cosax,sinax),=(cosax,﹣cosax),其中a>0,若函数f(x)=的图象与直线y=m(m>0)相切,且切点横坐标成公差为π的等差数列.(1)求a和m的值;(2)在△ABC中,a、b、c分别是角A、B、C的对边.若,且a=4,求△ABC面积的最大值及此时b、c的值.18.设函数f(x)=mx2﹣mx﹣1.(1)若对一切实数x,f(x)<0恒成立,求m的取值范围;(2)对于x∈[1,3],f(x)<﹣m+5恒成立,求m的取值范围.19.已知函数f(x)=,若数列{a n}(n∈N*)满足:a1=1,a n+1=f (a n).(Ⅰ)证明数列{}为等差数列,并求数列{a n}的通项公式;(Ⅱ)设数列{c n}满足:c n=,求数列{c n}的前n项的和S n.20.已知数列{a n}的前n项和为S n,且﹣1,S n,a n+1成等差数列,n ∈N*,a1=1.函数f(x)=log3x.(I)求数列{a n}的通项公式;(II)设数列{b n}满足b n=,记数列{b n}的前n项和为T n,试比较T n与﹣的大小.21.函数f(x)=e x﹣ax﹣1,其中a为实数.(1)若a=1,求函数f(x)的最小值.(2)若函数f(x)在(0,2]上有零点,求a的取值范围.(3)求证:.请考生在22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分.[几何证明选讲]22.如图所示,已知PA是⊙O相切,A为切点,PBC为割线,弦CD∥AP,AD、BC相交于E点,F为CE上一点,且DE2=EF•EC.(1)求证:A、P、D、F四点共圆;(2)若AE•ED=24,DE=EB=4,求PA的长.[极坐标与参数方程]23.平面直角坐标系中,以坐标原点为极点,x轴的正半轴为极轴,建立极坐标系,在极坐标中,已知圆C经过点,圆心为直线与极轴的交点.求:(1)直线l的直角坐标方程.(2)圆C的极坐标方程.[不等式选讲]24.已知函数f(x)=|x﹣a|.(1)若不等式f(x)≤3的解集为{x|﹣1≤x≤5},求实数a的值;(2)在(1)的条件下,若f(x)+f(x+5)≥m对一切实数x恒成立,求实数m的取值范围.参考答案与试题解析一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合A={x∈R|x2﹣x<0},B=(0,a)(a>0),若A⊆B,则实数a的取值范围是()A.(0,1]B.(0,1)C.[1,+∞)D.(1,+∞)【考点】集合的包含关系判断及应用.【分析】由x2﹣x<0,可得A=(0,1).再利用B=(0,a)(a>0),A⊆B,即可得出.【解答】解:由x2﹣x<0,解得0<x<1.∴A=(0,1).∵B=(0,a)(a>0),A⊆B,∴a≥1,即a∈[1,+∞).故选:C.2.(文)设a∈R,则a>1是<1的()A.必要但不充分条件B.充分但不必要条件C.充要条件 D.既不充分也不必要条件【考点】不等关系与不等式;充要条件.【分析】根据由a>1,一定能得到<1.但当<1时,不能推出a >1 (如a=﹣1时),从而得到结论.【解答】解:由a>1,一定能得到<1.但当<1时,不能推出a >1 (如a=﹣1时),故a>1是<1 的充分不必要条件,故选B.3.已知函数f(x)是奇函数,且当x>0时,f(x)=e x,则f(﹣1)=()A.B.﹣C.e D.﹣e【考点】函数奇偶性的性质.【分析】直接利用函数的奇偶性以及函数的解析式求解即可.【解答】解:函数f(x)是奇函数,且当x>0时,f(x)=e x,则f (﹣1)=﹣f(1)=﹣e.故选:D.4.公比为2的等比数列{a n}的各项都是正数,且a3a11=16,则a5=()A.4 B.2 C.1 D.8【考点】等比数列的通项公式.【分析】利用等比数列的通项公式求解.【解答】解:∵公比为2的等比数列{a n}的各项都是正数,且a3a11=16,∴,且a1>0,解得,∴a5==1.故选:C.5.函数y=sin3x的图象可以由函数y=cos3x的图象()A.向右平移个单位得到 B.向左平移个单位得到C.向右平移个单位得到 D.向左平移个单位得到【考点】函数y=Asin(ωx+φ)的图象变换.【分析】由于函数y=sin3x=cos3(x﹣),故把函数y=cos3x的图象向右平移个单位,即可达到目标.【解答】解:由于函数y=sin3x=cos(3x+)=cos(3x﹣)=cos3(x﹣),故把函数y=cos3x的图象向右平移个单位,即可得到y=cos3(x﹣)=sin3x的图象,故选A.6.函数的图象的最低点坐标是()A.(0,2)B.不存在C.(1,2)D.(1,﹣2)【考点】函数的图象;函数的最值及其几何意义.【分析】本题考查的知识点是函数的最值及基本不等式,我们易将函数的解析式化为y=,又由(x>﹣1)由基本不等式,我们易得x=0,y取最小值2,即得函数的图象的最低点坐标.【解答】解:∵==≥2(x>﹣1)当且仅当x+1=1,即x=0时,y取最小值2故函数的图象的最低点坐标是(0,2)故选A.7.若两个等差数列{a n}和{b n}的前n项和分别是S n和T n,已知,则=()A.7 B.C. D.【考点】等差数列的性质.【分析】由已知,根据等差数列的性质,把转化为求解.【解答】解:.故选:D.8.已知[x]为不超过实数x的最大整数,g(x)=[x]是取整函数,x0是函数的零点,则g(x0)等于()A.0 B.1 C.2 D.3【考点】函数零点的判定定理.【分析】由f(﹣1)>0,f(﹣2)<0,可知x0是(﹣2,﹣1)上的一个值,从而g(x0)的值.【解答】解;f(﹣1)=+2>0,f(﹣2)=﹣1<0,则x0是(﹣2,﹣1)上的一个值,则g(x0)=0,故选:A.9.函数f(x)=x3+bx2+cx+d的图象如图所示,则函数的单调递减区间是()A. B.C.(﹣2,3)D.(﹣∞,﹣2)【考点】利用导数研究函数的单调性.【分析】求出原函数的导函数,由图象得到f′(﹣2)=f(3)=0,联立求得b,c的值,求出g(x)的导数,从而求出函数的递减区间即可.【解答】解:∵f(x)=x3+bx2+cx+d,∴f′(x)=3x2+2bx+c,由图可知f′(﹣2)=f(3)=0.∴,解得,=x2﹣x﹣6,g′(x)=2x﹣1,令g′(x)<0,解得:x<,故g(x)在(﹣∞,)递减,故选:B.10.已知平面直角坐标系xOy上的区域D由不等式组给定.若M(x,y)为D上的动点,点A的坐标为(,1),则z=•的最大值为()A.4B.3C.4 D.3【考点】二元一次不等式(组)与平面区域.【分析】首先画出可行域,z=•代入坐标变为z=x+y,即y=﹣x+z,z表示斜率为的直线在y轴上的截距,故求z的最大值,即求y=﹣x+z与可行域有公共点时在y轴上的截距的最大值.【解答】解:如图所示:z=•=x+y,即y=﹣x+z首先做出直线l:y=﹣x,将l0平行移动,当经过B点时在y轴上的截距最大,从而z最大.因为B(,2),故z的最大值为4.故选:C.11.已知f (x )是偶函数,它在[0,+∞)上是减函数,若f (lgx )>f (1),则实数x 的取值范围是( )A .(,1) B .(0,)∪(1,+∞) C .(,10) D .(0,1)∪(10,+∞)【考点】函数单调性的性质;偶函数.【分析】利用偶函数的性质,f (1)=f (﹣1),在[0,+∞)上是减函数,在(﹣∞,0)上单调递增,列出不等式,解出x 的取值范围. 【解答】解:∵f (x )是偶函数,它在[0,+∞)上是减函数, ∴f (x )在(﹣∞,0)上单调递增, 由f (lgx )>f (1),f (1)=f (﹣1) 得:﹣1<lgx <1,∴<x <10,故答案选C .12.已知函数f1(x)=sinx+cosx,记f2(x)=f′1(x),f3(x)=f′2(x),…,f n(x)=f′n﹣1(x)(n∈N*,n≥2),n∈N.n≥2),则=()A.﹣1 B.0 C.D.1【考点】数列的求和;导数的运算.【分析】利用三角函数求导法则求出f2(x)、f3(x)、f4(x),…观察所求的结果,归纳其中的规律,发现标号的周期性为4,每四项的和是一个常数,再将x=代入即可求得正确答案.【解答】解:f2(x)=f1′(x)=cosx﹣sinx,f3(x)=(cosx﹣sinx)′=﹣sinx﹣cosx,f4(x)=﹣cosx+sinx,f5(x)=sinx+cosx,以此类推,可得出f n(x)=f n+4(x)又∵f1(x)+f2(x)+f3(x)+f4(x)=0,∴==sin+cos=1.故选D.二、填空题(每题5分,满分20分,将答案填在答题纸上)13.下列关于向量的命题中,正确的有(4).(1);(2);(3)(4);(5)若,则中至少一个为(6)若,则;(7)若,则.【考点】平面向量数量积的运算.【分析】根据向量数量积的计算公式,相等向量的概念,向量垂直的充要条件,以及平行向量的概念即可判断出每个命题的正误,从而找出正确命题.【解答】解:(1),且时,为任意向量;∴得不出,∴该命题错误;(2),且不共线时,得不出;∴该命题错误;(3),而时,该命题不成立;(4)=; ∴该命题正确;(5),则,可以都是非零向量; ∴该命题错误;(6)若,不共线,仍满足,但与不平行;∴该命题错误;(7)若,则得到;∴该命题错误.故答案为:(4).14.设数列{a n}满足a2+a4=10,点P n(n,a n)对任意的n∈N+,都有向量=(1,2),则数列{a n}的前n项和S n=n2.【考点】数列与向量的综合.【分析】由已知得a n}等差数列,公差d=2,将a2=a1+2,代入a2+a4=10,中,得a1=1,由此能求出{a n}的前n项和S n.【解答】解:∵P n(n,a n),∴P n+1(n+1,a n+1),∴=(1,a n+1﹣a n)=(1,2),∴a n+1﹣a n=2,∴{a n}等差数列,公差d=2,将a2=a1+2,a4=a1+6代入a2+a4=10中,解得a1=1,∴a n=1+(n﹣1)×2=2n﹣1,∴S n==n2.故答案为:n2.15.已知各项皆为正数的等比数列{a n}(n∈N*),满足a7=a6+2a5,若存在两项a m、a n使得=4a1,则+的最小值为.【考点】基本不等式在最值问题中的应用;等比数列的通项公式.【分析】利用等比数列的通项公式可得m+n=6,再利用基本不等式的性质即可得出.【解答】解:设各项皆为正数的等比数列{a n}的公比为q>0(n∈N*),∵a7=a6+2a5,∴=a5q+2a5,化为q2﹣q﹣2=0,解得q=2.∵存在两项a m、a n使得,∴=4a1,∴2m+n﹣2=24,∴m+n=6.则==≥=,当且仅当n=2m=4时取等号.∴的最小值为.故答案为:.16.已知实数x,y满足不等式组若目标函数z=y﹣ax(a ∈R)取最大值时的唯一最优解是(1,3),则实数a的取值范围是(1,+∞).【考点】简单线性规划.【分析】先根据约束条件画出可行域,再利用几何意义求最值,z=y ﹣ax表示直线在y轴上的截距,a表示直线的斜率,只需求出a的取值范围时,可行域直线在y轴上的截距最优解即可.【解答】解:由可行域可知,直线AB的斜率=1,当直线z=y﹣ax的斜率大于AB的斜率时,目标函数z=y﹣ax(a∈R)取最大值时的唯一最优解是B(1,3),所以a∈(1,+∞),故答案为:(1,+∞).三、解答题(本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.已知向量=(cosax,sinax),=(cosax,﹣cosax),其中a>0,若函数f(x)=的图象与直线y=m(m>0)相切,且切点横坐标成公差为π的等差数列.(1)求a和m的值;(2)在△ABC中,a、b、c分别是角A、B、C的对边.若,且a=4,求△ABC面积的最大值及此时b、c的值.【考点】余弦定理;平面向量数量积的运算.【分析】(1)由两向量的坐标,利用平面向量的数量积运算法则列出f(x)解析式,根据题意确定出函数的周期及最大值,即可求出a与m的值;(2)由确定出的解析式及f()=,求出A的度数,利用三角形面积公式列出关系式,把sinA的值代入,表示出三角形ABC面积,利用余弦定理列出关系式,把cosA与a的值代入,并利用基本不等式求出bc的最大值,即可确定出三角形ABC面积的最大值,以及此时b与c的值.【解答】解:(1)∵=(cosax,sinax),=(cosax,﹣cosax),∴f(x)=•=cos2ax﹣sinaxcosax=﹣sin(2ax﹣),由题意,函数f(x)的周期为π,且最大(或最小)值为m,而m>0,﹣1<0,∴a=1,m=+1;(2)∵f()=,∴sin(A﹣)=0,又A为△ABC的内角,∴A=,∴S△ABC=bcsinA=bc,∵cosA=,a=4,∴由余弦定理得:a2=b2+c2﹣2bccosA,即b2+c2=16+bc≥2bc,当且仅当b=c时取等号,整理得:bc≤16,=bc≤4,∴S则当且仅当b=c=4时,△ABC的面积取得最大值4.18.设函数f(x)=mx2﹣mx﹣1.(1)若对一切实数x,f(x)<0恒成立,求m的取值范围;(2)对于x∈[1,3],f(x)<﹣m+5恒成立,求m的取值范围.【考点】函数恒成立问题;函数最值的应用.【分析】(1)若f(x)<0恒成立,则m=0或,分别求出m的范围后,综合讨论结果,可得答案.(2)若对于x∈[1,3],f(x)<﹣m+5恒成立,则恒成立,结合二次函数的图象和性质分类讨论,综合讨论结果,可得答案.【解答】解:(1)当m=0时,f(x)=﹣1<0恒成立,当m≠0时,若f(x)<0恒成立,则解得﹣4<m<0综上所述m的取值范围为(﹣4,0]﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(2)要x∈[1,3],f(x)<﹣m+5恒成立,即恒成立.令﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣当m>0时,g(x)是增函数,所以g(x)max=g(3)=7m﹣6<0,解得.所以当m=0时,﹣6<0恒成立.当m<0时,g(x)是减函数.所以g(x)max=g(1)=m﹣6<0,解得m<6.所以m<0.综上所述,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣19.已知函数f(x)=,若数列{a n}(n∈N*)满足:a1=1,a n+1=f (a n).(Ⅰ)证明数列{}为等差数列,并求数列{a n}的通项公式;(Ⅱ)设数列{c n}满足:c n=,求数列{c n}的前n项的和S n.【考点】数列的求和;数列的函数特性;等差关系的确定.【分析】(Ⅰ)f(x)=⇒a n+1=f(a n)==,于是可得﹣=1,又a1=1,从而可证数列{}为等差数列,并求数列{a n}的通项公式;(Ⅱ)由(Ⅰ)知,c n===n•2n,利用错位相减法即可求得数列{c n}的前n项的和S n.【解答】解:(Ⅰ)∵f(x)=,∴a n+1=f(a n)==.∴﹣=1,又a1=1,∴数列{}是首项为1,1为公差的等差数列,∴a n=.(Ⅱ)∵c n===n•2n,∴S n=1×2+2×22+…+n•2n,①2S n=1×22+2×23+…+(n﹣1)×2n+n•2n+1,②②﹣①得:S n=﹣2﹣22﹣23﹣…﹣2n+n•2n+1=﹣+n•2n+1=(n﹣1)2n+1+2.20.已知数列{a n}的前n项和为S n,且﹣1,S n,a n+1成等差数列,n ∈N*,a1=1.函数f(x)=log3x.(I)求数列{a n}的通项公式;(II)设数列{b n}满足b n=,记数列{b n}的前n项和为T n,试比较T n与﹣的大小.【考点】数列的求和;等差数列的性质.【分析】(I)依题意可求得=3(n≥2),再由2S1=2a1=a2﹣1,a1=1即可求得{a n}是以1为首项3为公比的等比数列,从而可求数列{a n}的通项公式;(II)依题意可求得b n=(﹣),利用累加法可求得T n,从而通过分类讨论即可比较T n与﹣的大小.【解答】解:(I)∵﹣1,S n,a n+1成等差数列,∴2S n=a n+1﹣1①当n≥2时,2S n﹣1=a n﹣1②.①﹣②得:2a n=a n+1﹣a n,∴=3.当n=1时,由①得2S1=2a1=a2﹣1,又a1=1,∴a2=3,故=3.∴{a n}是以1为首项3为公比的等比数列,∴a n=3n﹣1…(II)∵f(x)=log3x,∴f(a n)=log3a n==n﹣1,b n===(﹣),∴T n= [(﹣)+(﹣)+…+(﹣)]=(+﹣﹣)=﹣…比较T n与﹣的大小,只需比较2(n+2)(n+3)与312 的大小即可.…2(n+2)(n+3)﹣312=2(n2+5n+6﹣156)=2(n2+5n﹣150)=2(n+15)(n﹣10),∵n∈N*,∴当1≤n≤9时,2(n+2)(n+3)<312,即T n<﹣;当n=10时,2(n+2)(n+3)=312,即T n=﹣;当n>10且n∈N*时,2(n+2)(n+3)>312,即T n>﹣.…21.函数f(x)=e x﹣ax﹣1,其中a为实数.(1)若a=1,求函数f(x)的最小值.(2)若函数f(x)在(0,2]上有零点,求a的取值范围.(3)求证:.【考点】利用导数求闭区间上函数的最值;利用导数研究函数的单调性.【分析】(1)求出函数的导数,得到函数的单调区间,从而求出函数的最小值即可;(2)求出函数的导数,通过讨论a的范围,求出函数的单调区间,结合函数的零点,求出a的范围即可;(3)根据e x≥x+1,两边同时取对数得x≥ln(x+1)(x>﹣1),对x 取值,累加即可.【解答】解:(1)f'(x)=e x﹣1,∴函数在(0,+∞)上递增,(﹣∞,0)上递减,∴f(x)极小值=f(0)=0;(2)f'(x)=e x﹣a(0<x≤2),当a≤1时,f'(x)>0,f(x)在(0,2]上递增,f(x)>f(0)=0,因此无零点;当a≥e2时,f'(x)>0,f(x)在(0,2]上递减,f(x)<f(0)=0,因此无零点;当e2>a>1时,由f'(x)=0,x=lna,当0<x<lna时,f'(x)<0,f(x)递减;当lna<x<2时,f'(x)>0,f(x)递增.又f(0)=0,f(2)=e2﹣2a﹣1,因此f(2)=e2﹣2a﹣1≥0,得.(3)由(1)知e x≥x+1,两边同时取对数得x≥ln(x+1)(x>﹣1),因此可得:1≥ln2,2≥ln3,3≥ln4,…,n≥ln(n+1),以上n﹣1个不等式相加得:ln2+ln3+ln4+…+ln(n+1)≤1+2+3+4+…+n,得证.请考生在22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分.[几何证明选讲]22.如图所示,已知PA是⊙O相切,A为切点,PBC为割线,弦CD∥AP,AD、BC相交于E点,F为CE上一点,且DE2=EF•EC.(1)求证:A、P、D、F四点共圆;(2)若AE•ED=24,DE=EB=4,求PA的长.【考点】与圆有关的比例线段.【分析】(1)由已知中DE2=EF•EC,我们易证明,△DEF~△CED,进而结合CD∥AP,结合相似三角形性质,得到∠P=∠EDF,由圆内接四边形判定定理得到A、P、D、F四点共圆;(2)由(1)中的结论,结合相交弦定理得PE•EF=AE•ED=24,结合已知条件,可求出PB,PC的长,代入切割线定理,即可求出PA 的长.【解答】解(1)证明:∵DE2=EF•EC,∴,又∠DEF=∠CED,∴△DEF~△CED,∠EDF=∠ECD,又∵CD∥PA,∴∠ECD=∠P故∠P=∠EDF,所以A,P,D,F四点共圆;(2)由(Ⅰ)及相交弦定理得PE•EF=AE•ED=24,又BE•EC=AE•ED=24,∴EC=6,EF=,PE=9,PB=5,PC=PB+BE+EC=15,由切割线定理得PA2=PB•PC=5×15=75,所以PA=5为所求.[极坐标与参数方程]23.平面直角坐标系中,以坐标原点为极点,x轴的正半轴为极轴,建立极坐标系,在极坐标中,已知圆C经过点,圆心为直线与极轴的交点.求:(1)直线l的直角坐标方程.(2)圆C的极坐标方程.【考点】简单曲线的极坐标方程.【分析】(1)利用极坐标方程与直角坐标方程的互化方法,可得直线l的直角坐标方程.(2)求出圆心与半径,可得圆C的极坐标方程.【解答】解:(1)直线,即,可化为;(2)∵圆C圆心为直线与极轴的交点,∴在中令θ=0,得ρ=1.∴圆C的圆心坐标为(1,0).∵圆C经过点,∴圆C的半径为.∴圆C经过极点.∴圆C的极坐标方程为ρ=2cosθ.[不等式选讲]24.已知函数f(x)=|x﹣a|.(1)若不等式f(x)≤3的解集为{x|﹣1≤x≤5},求实数a的值;(2)在(1)的条件下,若f(x)+f(x+5)≥m对一切实数x恒成立,求实数m的取值范围.【考点】绝对值不等式的解法;函数恒成立问题.【分析】(1)不等式f(x)≤3就是|x﹣a|≤3,求出它的解集,与{x|﹣1≤x≤5}相同,求实数a的值;(2)在(1)的条件下,f(x)+f(x+5)≥m对一切实数x恒成立,根据f(x)+f(x+5)的最小值≥m,可求实数m的取值范围.【解答】解:(1)由f(x)≤3得|x﹣a|≤3,解得a﹣3≤x≤a+3.又已知不等式f(x)≤3的解集为{x|﹣1≤x≤5},所以解得a=2.(2)当a=2时,f(x)=|x﹣2|.设g(x)=f(x)+f(x+5),于是所以当x<﹣3时,g(x)>5;当﹣3≤x≤2时,g(x)=5;当x>2时,g(x)>5.综上可得,g(x)的最小值为5.从而,若f(x)+f(x+5)≥m即g(x)≥m对一切实数x恒成立,则m的取值范围为(﹣∞,5].。