8-电阻电路的一般分析方法

第三章电阻电路的一般分析电路的一般分析是指方程分析法，它是以电路元件的约束特性(VCR)和电路的拓扑约束特性(KCL,KVL)为依据，建立以支路电流或回路电流，或结点电压为变量的回路方程组，从中解出所要求的电流、电压、功率等。

方程分析法的特点是：（1）具有普遍适用性，即无论线性和非线性电路都适用；（2）具有系统性，表现在不改变电路结构，应用KCL，KVL,元件的VCR建立电路变量方程，方程的建立有一套固定不变的步骤和格式，便于编程和用计算机计算。

本章的重点是会用观察电路的方法，熟练运用支路法、回路法和结点电压法的“方程通式”写出支路电流方程、回路方程和结点电压方程，并加以求解。

3-1 在一下两种情况下，画出图示电路的图，并说明其节点数和支路数(1)每个元件作为一条支路处理；(2)电压源(独立或受控）和电阻的串联组合，电流源和电阻的并联组合作为一条支路处理。

解:(1)每个元件作为一条支路处理时，图(a)和(b)所示电路的图分别为题解3-1图(a1)和(b1)。

图(a1)中节点数6b==n，支路数11图(b1)中节点数7=bn，支路数12=(2)电压源和电阻的串联组合，电流源和电阻的并联组合作为一条支路处理时，图(a)和图(b)所示电路的图分别为题解图(a2)和(b2)。

图(a2)中节点数4b=n，支路数8=图(b2)中节点数15b=n，支路数9=3-2指出题3-1中两种情况下，KCL,KVL独立方程数各为多少？解：题3－1中的图(a)电路，在两种情况下，独立的KCL方程数分别为(1)51==4n1--1=6-1-=n (2)3独立的KVL方程数分别为(1)61=84+--n+=1b1=111b (2)5+6+--n=图(b)电路在两种情况下，独立的KCL方程数为(1)61=5-=1n-7n (2)41=1-=-独立的KVL方程数分别为(1)6+1=95b1-n+=-=1271b (2)51=-n++-3-3对题图(a)和(b)所示G，各画出4个不同的树，树支数各为多少？解：一个连通图G 的树T 是这样定义的：(1) T 包含G 的全部结点和部分支路；(2) T 本身是连通的且又不包含回路。

第3章电阻电路的一般分析3.1 复习笔记一、电路图论的基本概念1．图（G）图（G）是具有给定连接关系的结点和支路的集合，其中每条支路的两端都连到相应的结点上，允许孤立结点的存在，没有结点的支路不能称为图。

路径：从G的一个结点出发，依次通过图的支路和结点（每一支路和结点只通过一次），到达另一个结点（或回到原出发点），这种子图称为路径。

连通图：当G的任意两结点都是连通的，称G为连通图。

有向图：赋予支路方向的图称为有向图。

2．树（T）满足下列三个条件的子图，称为G的一棵树：①连通的；②包含G的全部结点；③本身没有回路。

树支与连支：属于树的支路称为树支；不属于树的支路称为连支。

基本回路：对于G的任意一个树，有且只有一条连支回路，这种回路称为单连支回路或基本回路。

树支数：对于有n个结点，b条支路的连通图，树支数＝n－1。

推论：连枝数＝b－n＋1；基本回路数＝连支数＝b－n＋1。

二、KCL和KVL的独立方程数KCL的独立方程数：对一个具有n个结点的电路而言，其中任意的（n－1）个结点的KCL方程是独立的。

KVL的独立方程数：对一个具有n个结点和b条支路的电路而言，其KVL的独立方程数为（b－n＋1）。

三、电路的分析方法1．支路电流法（1）支路电流法是以b个支路电流为变量列写b个方程，并直接求解。

其方程的一般形式为（2）支路电流法解题步骤①标出各支路电流的方向；②依据KCL列写（n－1）个独立的结点方程；③选取（b－n＋1）个独立回路，标出回路绕行方向，列写KVL方程。

注：①独立结点选择方法：n个结点中去掉一个，其余结点都是独立的；②独立回路选择方法：先确定一个树，再确定单连支回路（基本回路），仅含唯一的连支，其余为树支。

2．网孔电流法（1）网孔是最简单的回路，即不含任何支路的回路。

网孔数＝独立回路数＝b－n＋1。

网孔电流法是以网孔电流为未知量，根据KVL对全部网孔列出方程求解。

（2）网孔电流法解题步骤①局部调整电路，当电路中含有电流源和电阻的并联组合时，可转化为电压源和电阻的串联组合；②选取网孔电流，指定网孔电流的参考方向；③依据KVL列写网孔电流方程，自阻总为正，互阻视流过的网孔电流方向而定，两电路同向取“＋”，异向取“－”。

第二章 电阻电路分析的基本方法本章以直流电路为研究对象，讨论电路的几种普遍的分析、计算方法。

包括等效变换、支路电流法、结点电位法、叠加原理和戴维南定理等。

这些方法可统称为网络方程法；它是以电路元件的伏安关系和基尔霍夫定律为基础的，选择适当的未知变量，建立一组独立的网络方程，并求解方程组；最后得出所需要的支路电流或支路电压或其他变量。

这些电阻电路的分析计算方法只要稍加扩展，即可用于交流电路的分析计算，所以本章是分析、计算电路的基础。

§2-1 等效电阻和等效二端网络通常，工程中所接触的电路形状复杂如网，故电路又称为网络。

(a)(b)图2-1 二端网络如果电路只有一个输入端口或输出端口，则这个电路称为单口网络或二端网络。

若二端网络内部含有电源，则称为有源二端网络。

若内部不含电源，则称为无源二端网络。

如图2－1（a ）所示为一个有源二端网络，a 、b 为此网络的输出端点。

图2－1（b ）所示为一个无源二端网络。

无源二端网络是由电阻元件组成的。

在它内部，电阻的连接可能很复杂，但对外部电路来说，可以用一个等效电阻来代替它。

这个电阻就称为这一无源二端网络的等效电阻。

这里，“等效”是对外部电路来说。

如图2－1（b ）中虚线框内的四个电阻，可以用一个等效电阻来代替它们，只要端口上的U 、I 不变，则对虚线以外的电路来说是等效的，因为它不影响虚线以外的任何电路。

但对虚线框内部，也就是说对无源二端网络内部并不等效。

电路原是四个电阻组成，现只有一个电阻，电路的结构、参数完全不同，不可能等效。

所以说，等效是一个相对的概念。

一、电阻的串联与分压（一）串联电阻的等效化简所谓串联就是两个或多个元件首尾相联接流过同一电流。

如图2－2（a ）所示为两个电阻R 1、R 2串联，可以用等效电阻R 代替它们，如图2－2（b ）所示，只要R 满足如下关系即可：R = R 1+R 2 （2－1）若由n 个电阻串联，则其等效电阻为R = R 1 + R 2 + … + R n =∑=ni iR1（2－2）上式表明，串联电阻的等效电阻值总是大于其中任一个电阻阻值的。

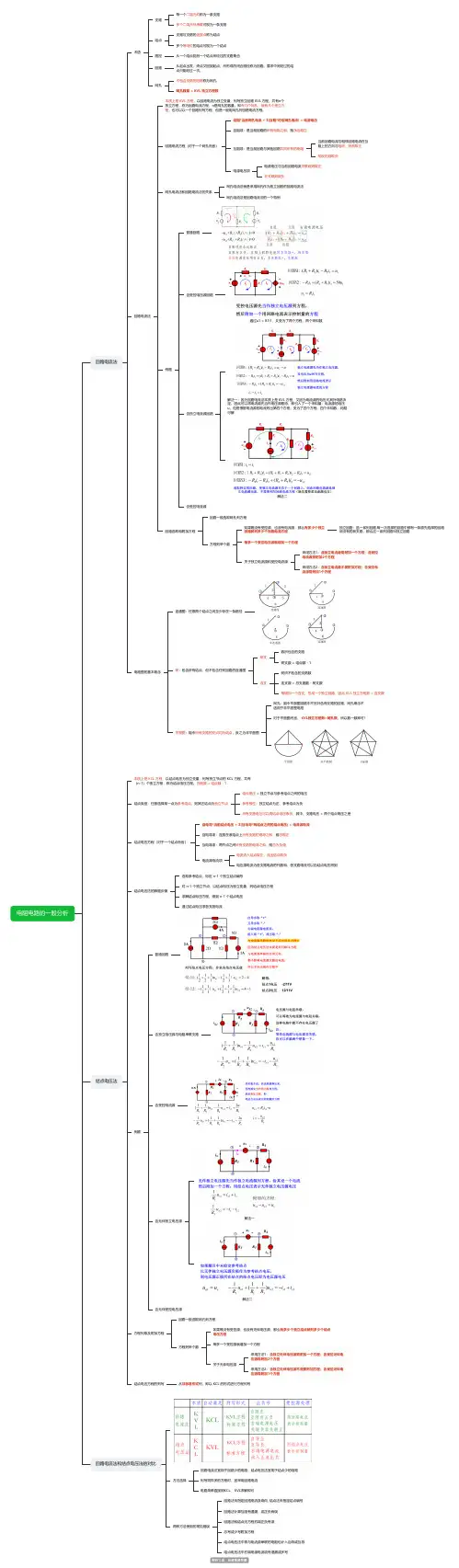
电阻电路的一般分析回路电流法术语支路每一个二端元件称为一条支路多个二端元件串联可视为一条支路结点支路与支路的连接点称为结点多个等电位的结点可视为一个结点路径从一个结点到另一个结点所经过的支路集合回路从起点出发，终点又回到起点，所形成的闭合路径称为回路。

要求中间经过的结点只能经过一次。

网孔不包含支路的回路称为网孔网孔数量 = KVL 独立方程数回路电流法本质上是 KVL 方程，以回路电流为独立变量，列写独立回路 KVL 方程，共有n个独立方程，称为回路电流方程，n是网孔的数量。

即有几个网孔，就有几个独立方程，也可以以一个回路列写方程，但是一般用网孔列回路电流方程。

回路电流方程（对于一个网孔而言）自阻*当前网孔电流 + Σ(互阻*对应网孔电流) = 电源电压自阻项：是当前回路的所有电阻之和，前永远取正互阻项：是当前回路与其他回路共同所有的电阻当前回路电流与相邻回路电流在互阻上的方向与相同，则前取正相反则前取负电源电压项电源电压与当前回路电流关联前则取正非关联则取负网孔电流法和回路电流法的关系网孔电流法就是采用网孔作为独立回路的回路电流法网孔电流法是回路电流法的一个特例例题普通回路含受控电压源回路通过u1 = R1i1，又变为了两个方程、两个未知数含独立电流源回路解法一：因为回路电流法本质上是 KVL 方程，又因为电流源的电压尤其外电路决定，因此可以将电流源先当作电压源看待，即引入了一个未知量：电流源的电压u。

但是根据电流源的电流列出第四个方程，变为了四个方程、四个未知数，问题可解解法二含受控电流源回路选取和附加方程回路一般选取网孔列方程方程列举个数如果既没有受控源，也没有电流源，那么有多少个独立回路就列多少个回路电流方程独立回路：选一系列回路,每一次选择的回路中都有一条原先选择的回路所没有的新支路，那么这一系列回路叫独立回路每多一个受控电压源就增加一个方程关于独立电流源和受控电流源采用方法1：含独立电流源需附加一个方程；含受控电流源需附加2个方程采用方法2：含独立电流源不需附加方程；含受控电流源需附加1个方程电路图的基本概念连通图：任意两个结点之间至少存在一条路径树：包含所有结点，但不包含任何回路的连通图树支数所包含的支路树支数 = 结点数 - 1连支树所不包含的支路数连支数 = 总支路数 - 树支数每增加一个连支，形成一个独立回路，因此 KVL 独立方程数 = 连支数平面图：能令所有支路的交点均为结点，反之为非平面图网孔：能令平面图回路中不另外含有支路的回路，网孔概念不适用于非平面图电路对于平面图而言，KVL独立方程数=网孔数，所以数一数即可！结点电压法本质上是 KCL 方程，以结点电压为独立变量，列写独立节点的 KCL 方程，共有（n-1）个独立方程，称为结点电压方程。

电阻电路的节点电压分析电阻电路中，电流和电压是基本的物理量。

电路中的节点电压是指电路中某个节点与参考节点之间的电压差。

节点电压分析是电路分析的常用手段之一，其通过对电路中各个节点的电压进行计算，从而得到电路的详细信息和性能参数。

1. 概述电阻电路由多个电阻器通过导线连接而成，我们需要通过节点电压分析来了解电路中各个重要节点的电压情况。

节点电压分析基于基尔霍夫定律，根据电流守恒和电压守恒原则，通过建立一系列方程组的方法求解电路中的节点电压。

2. 基尔霍夫定律基尔霍夫定律是电路分析的基础，包括基尔霍夫电流定律和基尔霍夫电压定律。

基尔霍夫电流定律表明，在电路中的任意节点处，流入该节点的电流等于流出该节点的电流之和。

基尔霍夫电压定律指出，在电路中的任意回路中，电压源和电阻器所组成的回路中的电压之和等于零。

3. 节点电压分析步骤（1）选择一个参考节点。

通常情况下，选择一个电压为零或者常用电源负极的节点作为参考节点。

（2）对电路中的每个节点，用未知量表示其电压。

（3）根据基尔霍夫电流定律，对每个节点编写电流守恒方程。

（4）根据基尔霍夫电压定律，对每个回路编写电压守恒方程。

（5）解方程组，得到每个节点的电压值。

4. 例题下面我们通过一个简单的电阻电路例题来演示节点电压分析的步骤。

假设电路中有三个电阻器，分别为R1、R2和R3。

我们要求解节点A、B和C的电压。

（1）选择参考节点为地（电压为零）。

（2）假设节点A的电压为V_A，节点B的电压为V_B，节点C的电压为V_C。

（3）根据基尔霍夫电流定律，编写电流守恒方程：在节点A：(V_A - V_B) / R1 + (V_A - V_C) / R2 = 0在节点B：(V_B - V_A) / R1 + (V_B - V_C) / R3 = 0在节点C：(V_C - V_A) / R2 + (V_C - V_B) / R3 = 0（4）根据基尔霍夫电压定律，选择一个回路编写电压守恒方程：选择回路ABC：V_A - V_B + V_B - V_C + V_C - V_A = 0（5）解方程组，得到每个节点的电压值。

电路分析的一般方法是电路分析的一般方法按照以下步骤进行：1. 确定电路的拓扑结构：首先，需要将电路图画出来，并确定电路的基本元件，如电源、电阻、电感、电容等。

然后，根据元件之间的连接关系，画出电路的连接方式，即电路的拓扑结构。

2. 应用基本电路定律：根据基本电路定律，如欧姆定律、基尔霍夫定律等，对电路中的电流、电压进行分析。

欧姆定律可以用来计算电路中的电流、电压和电阻之间的关系。

基尔霍夫定律可以用来分析电路中节点和回路之间的关系。

3. 运用戴维南-诺依曼定理：根据戴维南-诺依曼定理，可以将复杂的电路分解为简单的电路，并分别进行分析。

这个定理可以帮助我们简化电路，并通过分析简化后的电路来推导出整个电路的特性。

4. 采用网络定理：在电路分析中，可以应用网络定理，如电压分压定理和电流分流定理等。

这些定理可以帮助我们求解电路中的各个参数值，如电流、电压和功率等。

5. 使用等效电路方法：等效电路方法是一种简化电路分析的方法，通过将复杂的电路转化为等效电路来进行分析。

等效电路是指用少量的元件来代替复杂电路，但能够保持电路的特性不变。

6. 运用概率统计方法：在一些特殊的电路问题中，可以使用概率统计方法进行分析。

概率统计方法可以帮助我们分析电路的可靠性、失效率等指标。

7. 结合计算工具：在电路分析中，可以使用计算工具，如电路仿真软件、数值计算软件等。

这些工具可以帮助我们简化计算过程、提高分析精度，并可以模拟实际电路的工作情况。

总结起来，电路分析的一般方法包括确定拓扑结构、应用基本电路定律、运用戴维南-诺依曼定理、采用网络定理、使用等效电路方法、运用概率统计方法以及结合计算工具。

这些方法可以帮助我们对电路进行全面的分析，求解电路中的参数值，并理解电路的工作原理。

最终，通过电路分析，我们可以更好地设计、优化电路，并预测电路在实际应用中的性能。

第三章电阻电路的一般分析本章内容：1．电路的图及KCL和KVL独立方程数 2．支路分析法3．网孔分析法4．回路电流法5．结点分析法本章重点：主要学习电阻电路的方程建立及一般分析方法（支路分析法、网孔分析法、节点分析法、回路分析法。

其中，支路分析法是最基本的方法）。

本章难点：独立回路数的确定, 回路分析法及节点分析法.§3-1 电路的图本节介绍有关图论的初步知识，学习应用图的方法选择电路方程的独立变量一、电路的图（G）数学上的图：是边（支路）和顶点（结点）的集合，每一条边都连到相应的顶点上，边是抽象的线段，当移去边时，顶点保留，当移去顶点时，应将顶点所连的支路移走。

1．电路的图（连通图G）：是将支路画成的抽象线段形成的节点和支路的集合，结点相对于数学图的顶点，支路相当于数学图中的边。

支路是实体。

KVL和KCL 与元件的性质无关，故可用图讨论其方程。

2．无向图：画出的没有方向的图为无向图3．有向图：画出的有方向的图为有向图4．连通图：任意两个结点之间至少有一条支路或路径时的图为连通图。

二、电路的图的画法（有几种，其中简便的画法）1．一般将电阻和电压源串联的组合，电阻和电流源并联的组合看成一条支路, 将流过同一个电流的每一个分支看成一条支路。

如（b）2．指定电流和电压的参考方向，一般选关联参考方向。

如图（c）(a) (b) (c)§3-2 KCL和KVL的独立方程数一、KCL的独立方程数（n个结点电路，KCL的独立方程是n-1个）将电路的有向图，结点和支路加以编号，如下图，对结点①②③④列写KCL 方程有由于每条支路与两个结点相联，其电流从一个节点流出，从另一个结点流入，一正，一负（从表达式可见），将上面4个方程相加，等式两边为0，说明4个方程不是独立的；将上面3个方程相加，等式两边不为0，说明3个方程是独立的。

可见，n个结点电路，n-1个结点的KCL方程是独立的一、KVL的独立方程数（b条支路，n个结点，KVL为b-(n-1)个）KVL的独立方程数等于独立回路数独立回路数等于基本回路数，回路与支路的方向无关，以无向图讨论。

第三章电阻电路的一般分析一、教学基本要求电路的一般分析是指方程分析法，是以电路元件的约束特性（VCR）和电路的拓补约束特性（KCL、KVL）为依据，建立以支路电流或回路电流或结点电压为变量的电路方程组，解出所求的电压、电流和功率。

方程分析法的特点是：（1）具有普遍适用性，即无论线性和非线性电路都适用；（2）具有系统性，表现在不改变电路结构，应用KCL，KVL，元件的VCR建立电路变量方程，方程的建立有一套固定不变的步骤和格式，便于编程和用计算机计算。

本章学习的内容有：电路的图，KCL和KVL的独立方程数，支路电流法，网孔电流法，回路电流法，结点电压法。

本章内容以基尔霍夫定律为基础。

介绍的支路电流法、回路电流法和节点电压法适用于所有线性电路问题的分析，在后面章节中都要用到。

内容重点：会用观察电路的方法，熟练应用支路电流法，回路电流法，结点电压法的“方程通式”写出支路电流方程，回路电流方程，结点电压方程，并求解。

预习知识：线性代数方程的求解难点：1. 独立回路的确定2. 正确理解每一种方法的依据3. 含独立电流源和受控电流源的电路的回路电流方程的列写4. 含独立电压源和受控电压源的电路的结点电压方程的列写二、学时安排总学时：6三、教学内容§3－1 电路的图1. 网络图论图论是拓扑学的一个分支，是富有趣味和应用极为广泛的一门学科。

图论的概念由瑞士数学家欧拉最早提出，欧拉在1736年发表的论文《依据几何位置的解题方法》中应用图的方法讨论了各尼斯堡七桥难题，见图3.1a和b所示。

图3.1 a 哥尼斯堡七桥 b 对应的图19～20世纪，图论主要研究一些游戏问题和古老的难题，如哈密顿图及四色问题。

1847年，基尔霍夫首先用图论来分析电网络，如今在电工领域，图论被用于网络分析和综合、通讯网络与开关网络的设计、集成电路布局及故障诊断、计算机结构设计及编译技术等等。

2. 电路的图电路的图是用以表示电路几何结构的图形，图中的支路和结点与电路的支路和结点一一对应，如图3.2所示，所以电路的图是点线的集合。

电阻电路的纹波分析方法在电力系统中，电阻电路是最简单的一种电路。

电阻电路广泛应用于各个领域，它是研究电路中电流、电压和功率关系的基础。

纹波是指电路中电流或电压的周期性变化，对于电路性能的评估和故障检测非常重要。

本文将介绍电阻电路的纹波分析方法。

一、纹波的定义和特性在电压和电流中，纹波是指周期性的波动或震荡。

电源产生的交流电压和电流通常不是完美的正弦波，而是存在一定的纹波部分。

纹波可以用波峰-波谷幅度或者峰-峰值来表示，单位通常是百分比或毫伏。

二、方法一：示波器测量示波器是一种常用的测量仪器，用于观测和测量电压和电流信号的波形。

在电阻电路中，我们可以通过示波器测量电压波形或电流波形，然后进行纹波分析。

使用示波器进行纹波分析的步骤如下：1. 连接示波器的探头到待测电阻电路的输入端。

2. 调整示波器的设置，选择合适的量程和触发模式。

3. 打开示波器并记录波形。

4. 通过示波器的测量功能，获取纹波的幅度和频率。

示波器测量方法简单直观，可以准确地获得电路中的纹波信息。

但是它需要使用专业的仪器，所以对于一般用户来说可能不太方便。

三、方法二：多用途表测量多用途表可以用于测量电阻、电流和电压等多种电气参数。

在电阻电路中，我们可以利用多用途表测量电流和电压的平均值和峰-峰值，以进行纹波分析。

使用多用途表进行纹波分析的步骤如下：1. 将多用途表选择到恰当的电流或电压测量模式。

2. 连接多用途表的探头到待测电阻电路的输入端。

3. 打开多用途表并记录平均值和峰-峰值。

多用途表测量方法简单方便，适合一般用户使用。

但是它只能提供纹波的平均值和峰-峰值，对于更详细的纹波信息可能不够准确。

四、方法三：计算除了使用专业仪器进行测量，我们还可以利用计算方法来分析电阻电路的纹波。

在纹波分析中，最常用的计算方法是均方根（RMS）值的计算。

均方根值是一种代表波动程度的有效值，相对于纹波而言更能真实地表示电压或电流的大小。

计算均方根值的公式如下：Vrms = Vp / √2其中，Vp表示电压或电流的峰-峰值。

2023年石河子大学硕士研究生入学考试大纲（科目：电路分析基础）一、考查目标电路分析基础是电子与电气类工科专业的一门专业基础课，要求考生比较系统地理解电路分析的基本概念和基本理论，牢固掌握并灵活运用电路的基本分析方法，具有较强的运算能力，综合运用所学理论方法、分析和解决问题的能力。

二、考试形式与试卷结构（一）试卷成绩及考试时间本试卷满分为150分，考试时间为180分钟。

（二）答题方式答题方式为闭卷、笔试（三）试卷题型结构及分值单项选择题（10小题，每小题3分，共计30分）计算题（8小题，每小题12分，共计96分）分析题（2小题，共计24分）三、考查内容1.电路模型和电路定律：（1）电路模型，电流、电压及其参考方向，电功率和能量（2）独立电压源、独立电流源及受控电源（3）基尔霍夫定律2.电阻电路的等效变换（1）电路等效的概念；电阻分压电路和分流电路（2）电阻的串联和并联，电压源、电流源的串联和并联，实际电源的两种模型及其等效变换（3）输入电阻的计算3.电阻电路的一般分析（1）支路电流法，网孔电流法，回路电流法，结点电压法4.电路定理（1）叠加定理，替代定理，戴维宁定理（2）最大功率传输定理5.动态电路的时域分析（1）电容、电感的电压电流关系，电容、电感的储能（2）动态电路及其初始条件，一阶电路的零输入响应、零状态响应和全响应，三要素法的应用（3）二阶电路，RLC 串联电路的零输入响应6.正弦稳态分析（1）正弦量的基本概念和相量表示（2）基尔霍夫定律的相量形式，电阻、电感、电容元件电压电流关系的相量形式（3）正弦稳态电路的分析，正弦稳态电路的功率，最大功率传输7.含有耦合电感的电路（1）互感，含有耦合电感电路的计算（2）理想变压器的电压电流关系及阻抗变换性质8.电路的频率响应（1）网络函数，RC 电路的频率特性（2）RLC 串联谐振电路分析，谐振角频率，品质因素，通频带（3）滤波器的基本特性和类型9.三相电路（1）三相电源和三相负载的接法，线电压与相电压以及线电流与相电流的关系（2）对称三相电路的分析（3）三相电路功率的计算四、参考书目《电路》（第五版），邱关源，高教出版社。