数值线性代数第三次上机作业

本次作业是本门课程本学期的第3次作业，注释如下：一、单项选择题(只有一个选项正确，共8道小题)1. 设A为n阶方阵，且A2+A−5E=0,则(A+2E)−1=( )。

(A) A−E(B) A+E(C) 1 3 ( A−E )(D) 1 3 ( A+E )正确答案：C解答参考：A 2 +A−5E=0 ⇒A 2 +A−2E=3E⇒( A+2E )(A−E)=3E ⇒( A+2E ) −1 = 1 3 (A−E)2. 若n维向量α 1 ，α 2 ，⋯, α n 线性相关，β为任一n维向量，则( )。

(A) α 1 , α 2 ,⋯, α n ,β线性相关；(B) α 1 , α 2 ,⋯, α n ,β线性无关；(C) β一定能由α 1 , α 2 ,⋯, α n 线性表示；(D) α 1 , α 2 ,⋯, α n ,β的相关性无法确定。

正确答案：A解答参考：3. 设线性方程组{ 3 x 1 + x 2 =1, 3 x 1 +3 x 2 +3 x 3 =0 ,5 x 1 −3 x 2 −2 x 3 =1 }则此方程组。

(A) 有唯一解(B) 有无穷多解(C) 无解(D) 有基础解系正确答案：A解答参考：4. 设n维向量组α1,α2,⋯,αs,若任一维向量都可由这个向量组线性表出,必须有。

(A) s= n(B) s< n(C) s> n(D) s≥ n正确答案：D解答参考：5. 设α 1 , α 2 , α 3 ,β,γ 都是4维列向量，且4阶行列式| α 1 , α 2 , α 3 ,β |=a ，| γ, α 1 , α 2 , α 3 |=b ，则4阶行列式| α 1 , α 2 , α 3 ,β+γ |=(A) a+b(B) −a−b(C) a−b(D) b−a正确答案：C解答参考：6. 设B,C 为4阶矩阵，A=BC , R(B)=4 , R(C)=2 ，且α 1 , α 2 , α 3 是线性方程组Ax=0 的解，则它们是(A) 基础解系(B) 线性相关的(C) 线性无关的(D) A,B,C都不对正确答案：B解答参考：7. 设n维列向量α= ( 1 2 ,0,⋯,0, 1 2 ) T ，矩阵A=I−α α T ，B=I+2α α T ，则AB=(A) 0(B) −I(C) I(D) I+α α T正确答案：C解答参考：8. 设矩阵A m×n 的秩r(A)=m< ，下述结论中正确的是>(A) A的任意m个列向量必线性无关(B) A的任意一个m阶子式不等于零(C) 齐次方程组Ax=0只有零解(D) 齐次方程组Ax=0只有零解正确答案：D解答参考：二、判断题(判断正误，共5道小题)9.设A ,B 是同阶方阵，则AB=BA 。

数值分析第三次上机作业算法设计1、求解非线性方程组采用牛顿法解非线性方程组,将题目中给出的(,)i i x y 当作已知量代入题目给定的非线性方程组，求出与(,)i i x y 相对应的数组t[i][j]，u[i][j]2、分片二次代数插值对所求出的数组t[i][j]，u[i][j]，通过分片二次代数插值运算，得到与数组t[11][21]，u[11][21]对应的数组z[11][21]，得到二元函数z=(,)i i f x y ，二次插值采用教材给出的分片二次代数插值。

3、曲面插值利用x[11]，y[21]，z[11][21]建立二维函数表，进行曲面插值计算，逐步提高k 值，计算其精度，看其是否满足要求，条件满足则循环结束，并得到曲面拟合的系数矩阵C[r][s]，算法采用教材给出的曲面拟合算法，求出所需矩阵给出，然后按公式进行计算。

4、比较),(j i y x p 逼近(,)i i f x y 的效果观察和),(j i y x p 逼近(,)i i f x y 的效果时，只需要利用新的点列(,)i i x y 重复计算二次代数插值，得到与新的插值节点(,)i i x y 对应的(,)i i f x y ，再与对应的(,)i i p x y 比较即可，求解(,)i i p x y 事可以直接使用（3）中的C[r][s]和k 值。

源程序(在CodeBlock C/C++集成开发环境下编译通过)程序输出1.数表(xi,yj)和f(xi,yj)x=0 y=0.5 f(x,y)=4.46504018481E-001 x=0 y=0.55 f(x,y)=3.24683262928E-001 x=0 y=0.6 f(x,y)=2.10159686683E-001 x=0 y=0.65 f(x,y)=1.03043608316E-001 x=0 y=0.7 f(x,y)=3.40189556268E-003 x=0 y=0.75 f(x,y)=-8.87358136380E-002 x=0 y=0.8 f(x,y)=-1.73371632750E-001 x=0 y=0.85 f(x,y)=-2.50534611467E-001 x=0 y=0.9 f(x,y)=-3.20276506388E-001 x=0 y=0.95 f(x,y)=-3.82668066110E-001 x=0 y=1 f(x,y)=-4.37795766738E-001x=0 y=1.05 f(x,y)=-4.85758941444E-001 x=0 y=1.1 f(x,y)=-5.26667254884E-001 x=0 y=1.15 f(x,y)=-5.60638479797E-001 x=0 y=1.2 f(x,y)=-5.87796538768E-001 x=0 y=1.25 f(x,y)=-6.0826*******E-001 x=0 y=1.3 f(x,y)=-6.22189452876E-001x=0 y=1.35 f(x,y)=-6.29688378186E-001x=0 y=1.4 f(x,y)=-6.30899760003E-001x=0 y=1.45 f(x,y)=-6.25956152545E-001x=0 y=1.5 f(x,y)=-6.14988546609E-001x=0.08 y=0.5 f(x,y)=6.38015226511E-001 x=0.08 y=0.55 f(x,y)=5.0661*******E-001 x=0.08 y=0.6 f(x,y)=3.82176369277E-001 x=0.08 y=0.65 f(x,y)=2.64863491154E-001 x=0.08 y=0.7 f(x,y)=1.54780200285E-001 x=0.08 y=0.75 f(x,y)=5.199********E-002 x=0.08 y=0.8 f(x,y)=-4.34680402049E-002 x=0.08 y=0.85 f(x,y)=-1.31601056789E-001 x=0.08 y=0.9 f(x,y)=-2.12431088309E-001 x=0.08 y=0.95 f(x,y)=-2.86004551058E-001 x=0.08 y=1 f(x,y)=-3.52386078979E-001x=0.08 y=1.05 f(x,y)=-4.11655456522E-001 x=0.08 y=1.1 f(x,y)=-4.63904911519E-001 x=0.08 y=1.15 f(x,y)=-5.09236724701E-001 x=0.08 y=1.2 f(x,y)=-5.47761117962E-001 x=0.08 y=1.25 f(x,y)=-5.79594388339E-001 x=0.08 y=1.3 f(x,y)=-6.04857258890E-001 x=0.08 y=1.35 f(x,y)=-6.23673421332E-001 x=0.08 y=1.4 f(x,y)=-6.36168248413E-001 x=0.08 y=1.45 f(x,y)=-6.42467656690E-001 x=0.08 y=1.5 f(x,y)=-6.42697102700E-001 x=0.16 y=0.5 f(x,y)=8.40081395767E-001 x=0.16 y=0.55 f(x,y)=6.99764165673E-001 x=0.16 y=0.6 f(x,y)=5.66061442352E-001 x=0.16 y=0.65 f(x,y)=4.39171608118E-001 x=0.16 y=0.7 f(x,y)=3.19242138041E-001 x=0.16 y=0.75 f(x,y)=2.06376192387E-001 x=0.16 y=0.8 f(x,y)=1.00638523891E-001 x=0.16 y=0.85 f(x,y)=2.06074006784E-003 x=0.16 y=0.9 f(x,y)=-8.93540247670E-002 x=0.16 y=0.95 f(x,y)=-1.73626968865E-001 x=0.16 y=1 f(x,y)=-2.50799956160E-001x=0.16 y=1.05 f(x,y)=-3.20932269445E-001 x=0.16 y=1.1 f(x,y)=-3.84097735005E-001 x=0.16 y=1.15 f(x,y)=-4.40382175418E-001 x=0.16 y=1.2 f(x,y)=-4.89881152313E-001 x=0.16 y=1.25 f(x,y)=-5.32697965534E-001 x=0.16 y=1.3 f(x,y)=-5.68941879292E-001 x=0.16 y=1.35 f(x,y)=-5.98726549515E-001 x=0.16 y=1.4 f(x,y)=-6.22168629750E-001x=0.16 y=1.45 f(x,y)=-6.39386535697E-001 x=0.16 y=1.5 f(x,y)=-6.50499350788E-001 x=0.24 y=0.5 f(x,y)=1.0515*******E+000 x=0.24 y=0.55 f(x,y)=9.029********E-001 x=0.24 y=0.6 f(x,y)=7.60580266860E-001 x=0.24 y=0.65 f(x,y)=6.24715198146E-001 x=0.24 y=0.7 f(x,y)=4.95519756001E-001 x=0.24 y=0.75 f(x,y)=3.73134042775E-001 x=0.24 y=0.8 f(x,y)=2.57656748872E-001 x=0.24 y=0.85 f(x,y)=1.49150559410E-001 x=0.24 y=0.9 f(x,y)=4.76469867734E-002 x=0.24 y=0.95 f(x,y)=-4.68493232015E-002 x=0.24 y=1 f(x,y)=-1.34356760385E-001x=0.24 y=1.05 f(x,y)=-2.14913344927E-001 x=0.24 y=1.1 f(x,y)=-2.88573700635E-001 x=0.24 y=1.15 f(x,y)=-3.55406364786E-001 x=0.24 y=1.2 f(x,y)=-4.15491396489E-001 x=0.24 y=1.25 f(x,y)=-4.68918249969E-001 x=0.24 y=1.3 f(x,y)=-5.157********E-001 x=0.24 y=1.35 f(x,y)=-5.56191075200E-001 x=0.24 y=1.4 f(x,y)=-5.90246930563E-001 x=0.24 y=1.45 f(x,y)=-6.180********E-001 x=0.24 y=1.5 f(x,y)=-6.39746839258E-001 x=0.32 y=0.5 f(x,y)=1.27124675148E+000 x=0.32 y=0.55 f(x,y)=1.11500201815E+000 x=0.32 y=0.6 f(x,y)=9.64607727216E-001 x=0.32 y=0.65 f(x,y)=8.20347369475E-001 x=0.32 y=0.7 f(x,y)=6.82447678179E-001 x=0.32 y=0.75 f(x,y)=5.51085208597E-001 x=0.32 y=0.8 f(x,y)=4.26392385902E-001 x=0.32 y=0.85 f(x,y)=3.08462995633E-001 x=0.32 y=0.9 f(x,y)=1.97357129692E-001 x=0.32 y=0.95 f(x,y)=9.31056208594E-002 x=0.32 y=1 f(x,y)=-4.28599223403E-003x=0.32 y=1.05 f(x,y)=-9.48339252969E-002 x=0.32 y=1.1 f(x,y)=-1.78572990364E-001 x=0.32 y=1.15 f(x,y)=-2.55553779055E-001 x=0.32 y=1.2 f(x,y)=-3.25840150158E-001 x=0.32 y=1.25 f(x,y)=-3.89506988363E-001 x=0.32 y=1.3 f(x,y)=-4.46638204599E-001 x=0.32 y=1.35 f(x,y)=-4.97324951768E-001 x=0.32 y=1.4 f(x,y)=-5.41664032699E-001 x=0.32 y=1.45 f(x,y)=-5.79756479795E-001 x=0.32 y=1.5 f(x,y)=-6.11706288148E-001x=0.4 y=0.55 f(x,y)=1.33499863207E+000 x=0.4 y=0.6 f(x,y)=1.177********E+000x=0.4 y=0.65 f(x,y)=1.025********E+000 x=0.4 y=0.7 f(x,y)=8.78960023174E-001x=0.4 y=0.75 f(x,y)=7.39145108704E-001 x=0.4 y=0.8 f(x,y)=6.0574*******E-001x=0.4 y=0.85 f(x,y)=4.78883861067E-001 x=0.4 y=0.9 f(x,y)=3.58650625882E-001x=0.4 y=0.95 f(x,y)=2.45102236196E-001 x=0.4 y=1 f(x,y)=1.38268350928E-001x=0.4 y=1.05 f(x,y)=3.81548654070E-002 x=0.4 y=1.1 f(x,y)=-5.52528211681E-002 x=0.4 y=1.15 f(x,y)=-1.41986880814E-001 x=0.4 y=1.2 f(x,y)=-2.22094439096E-001 x=0.4 y=1.25 f(x,y)=-2.95635232460E-001 x=0.4 y=1.3 f(x,y)=-3.62679511503E-001 x=0.4 y=1.35 f(x,y)=-4.23306164224E-001 x=0.4 y=1.4 f(x,y)=-4.77601036132E-001 x=0.4 y=1.45 f(x,y)=-5.25655426667E-001 x=0.4 y=1.5 f(x,y)=-5.67564743655E-001 x=0.48 y=0.5 f(x,y)=1.73189274038E+000 x=0.48 y=0.55 f(x,y)=1.56203457721E+000 x=0.48 y=0.6 f(x,y)=1.39721691821E+000 x=0.48 y=0.65 f(x,y)=1.23780100674E+000 x=0.48 y=0.7 f(x,y)=1.0840*******E+000 x=0.48 y=0.75 f(x,y)=9.36322772315E-001 x=0.48 y=0.8 f(x,y)=7.94704449054E-001 x=0.48 y=0.85 f(x,y)=6.59387198028E-001 x=0.48 y=0.9 f(x,y)=5.30487586840E-001 x=0.48 y=0.95 f(x,y)=4.08088685454E-001 x=0.48 y=1 f(x,y)=2.92244201230E-001x=0.48 y=1.05 f(x,y)=1.82982206854E-001 x=0.48 y=1.1 f(x,y)=8.03084940354E-002 x=0.48 y=1.15 f(x,y)=-1.57904130516E-002 x=0.48 y=1.2 f(x,y)=-1.0534*******E-001 x=0.48 y=1.25 f(x,y)=-1.88398090610E-001 x=0.48 y=1.3 f(x,y)=-2.65007149319E-001 x=0.48 y=1.35 f(x,y)=-3.35237838904E-001 x=0.48 y=1.4 f(x,y)=-3.99164503887E-001 x=0.48 y=1.45 f(x,y)=-4.56868143302E-001 x=0.48 y=1.5 f(x,y)=-5.08434993278E-001 x=0.56 y=0.5 f(x,y)=1.97122178640E+000 x=0.56 y=0.55 f(x,y)=1.79532959950E+000x=0.56 y=0.65 f(x,y)=1.45783058271E+000 x=0.56 y=0.7 f(x,y)=1.29695464975E+000 x=0.56 y=0.75 f(x,y)=1.14171810545E+000 x=0.56 y=0.8 f(x,y)=9.92349533324E-001 x=0.56 y=0.85 f(x,y)=8.49032663329E-001 x=0.56 y=0.9 f(x,y)=7.11911352264E-001 x=0.56 y=0.95 f(x,y)=5.81094158922E-001 x=0.56 y=1 f(x,y)=4.56658513233E-001x=0.56 y=1.05 f(x,y)=3.38654496139E-001 x=0.56 y=1.1 f(x,y)=2.27108255770E-001 x=0.56 y=1.15 f(x,y)=1.22025089193E-001 x=0.56 y=1.2 f(x,y)=2.33922196376E-002 x=0.56 y=1.25 f(x,y)=-6.88187019710E-002 x=0.56 y=1.3 f(x,y)=-1.54649344213E-001 x=0.56 y=1.35 f(x,y)=-2.34152666459E-001 x=0.56 y=1.4 f(x,y)=-3.0739*******E-001 x=0.56 y=1.45 f(x,y)=-3.74434862348E-001 x=0.56 y=1.5 f(x,y)=-4.35360556536E-001 x=0.64 y=0.5 f(x,y)=2.21566786369E+000 x=0.64 y=0.55 f(x,y)=2.03420113361E+000 x=0.64 y=0.6 f(x,y)=1.85695514362E+000 x=0.64 y=0.65 f(x,y)=1.68435816416E+000 x=0.64 y=0.7 f(x,y)=1.51677635240E+000 x=0.64 y=0.75 f(x,y)=1.35451904115E+000 x=0.64 y=0.8 f(x,y)=1.19784408667E+000 x=0.64 y=0.85 f(x,y)=1.04696304942E+000 x=0.64 y=0.9 f(x,y)=9.020********E-001 x=0.64 y=0.95 f(x,y)=7.63226477663E-001 x=0.64 y=1 f(x,y)=6.30604821954E-001x=0.64 y=1.05 f(x,y)=5.04252814597E-001 x=0.64 y=1.1 f(x,y)=3.84216715546E-001 x=0.64 y=1.15 f(x,y)=2.70520476641E-001 x=0.64 y=1.2 f(x,y)=1.63168572400E-001 x=0.64 y=1.25 f(x,y)=6.21485581168E-002 x=0.64 y=1.3 f(x,y)=-3.25666193968E-002 x=0.64 y=1.35 f(x,y)=-1.21016534844E-001 x=0.64 y=1.4 f(x,y)=-2.03251399623E-001 x=0.64 y=1.45 f(x,y)=-2.79330359558E-001 x=0.64 y=1.5 f(x,y)=-3.49319957540E-001 x=0.72 y=0.5 f(x,y)=2.46468422266E+000 x=0.72 y=0.55 f(x,y)=2.27805897940E+000 x=0.72 y=0.6 f(x,y)=2.0952*******E+000 x=0.72 y=0.65 f(x,y)=1.91671812800E+000x=0.72 y=0.75 f(x,y)=1.57399842733E+000 x=0.72 y=0.8 f(x,y)=1.41043483523E+000 x=0.72 y=0.85 f(x,y)=1.25240175061E+000 x=0.72 y=0.9 f(x,y)=1.10009440963E+000 x=0.72 y=0.95 f(x,y)=9.53669851261E-001 x=0.72 y=1 f(x,y)=8.132********E-001x=0.72 y=1.05 f(x,y)=6.78930742966E-001 x=0.72 y=1.1 f(x,y)=5.50774848504E-001 x=0.72 y=1.15 f(x,y)=4.28825676973E-001 x=0.72 y=1.2 f(x,y)=3.131********E-001 x=0.72 y=1.25 f(x,y)=2.03615514033E-001 x=0.72 y=1.3 f(x,y)=1.00345478241E-001 x=0.72 y=1.35 f(x,y)=3.26856518657E-003 x=0.72 y=1.4 f(x,y)=-8.76530659133E-002 x=0.72 y=1.45 f(x,y)=-1.72467247819E-001 x=0.72 y=1.5 f(x,y)=-2.51230220752E-001 x=0.8 y=0.5 f(x,y)=2.71781110947E+000x=0.8 y=0.55 f(x,y)=2.52639950126E+000 x=0.8 y=0.6 f(x,y)=2.33841138686E+000x=0.8 y=0.65 f(x,y)=2.15432937728E+000 x=0.8 y=0.7 f(x,y)=1.97457455665E+000x=0.8 y=0.75 f(x,y)=1.79951057910E+000 x=0.8 y=0.8 f(x,y)=1.62944822055E+000x=0.8 y=0.85 f(x,y)=1.46465004375E+000 x=0.8 y=0.9 f(x,y)=1.30533496765E+000x=0.8 y=0.95 f(x,y)=1.151********E+000 x=0.8 y=1 f(x,y)=1.00383741991E+000x=0.8 y=1.05 f(x,y)=8.61912337228E-001 x=0.8 y=1.1 f(x,y)=7.25992371111E-001x=0.8 y=1.15 f(x,y)=5.96137711520E-001 x=0.8 y=1.2 f(x,y)=4.72386627914E-001x=0.8 y=1.25 f(x,y)=3.54758095898E-001 x=0.8 y=1.3 f(x,y)=2.43254184181E-001x=0.8 y=1.35 f(x,y)=1.37862222525E-001 x=0.8 y=1.4 f(x,y)=3.85567703264E-002x=0.8 y=1.45 f(x,y)=-5.46985959345E-002 x=0.8 y=1.5 f(x,y)=-1.41949659709E-001 2.选择过程的k和sigma值k=0 sigma=1.44288077184E+002k=1 sigma=3.22090897364E+000k=2 sigma=4.65996003327E-003k=3 sigma=1.72117537914E-004k=4 sigma=3.30953429925E-006k=5 sigma=2.54137838641E-0083.达到精度时的k值和sigma的值k=5 sigma=2.54137838641E-008C[5][0]=2.021********E+000C[5][1]=-3.66842675949E+000C[5][2]=7.09248533937E-001C[5][3]=8.48605489559E-001C[5][4]=-4.158********E-001C[5][5]=6.74320038241E-002C[5][0]=3.19190900764E+000C[5][1]=-7.41110369687E-001C[5][2]=-2.69712461395E+000C[5][3]=1.63118341965E+000C[5][4]=-4.84719981485E-001C[5][5]=6.06142831635E-002C[5][0]=2.56889815804E-001C[5][1]=1.57991865457E+000C[5][2]=-4.63408110240E-001C[5][3]=-8.134********E-002C[5][4]=1.020********E-001C[5][5]=-2.10152340394E-002C[5][0]=-2.69260339427E-001C[5][1]=-7.30247654151E-001C[5][2]=1.07614506737E+000C[5][3]=-8.0701*******E-001C[5][4]=3.028********E-001C[5][5]=-4.59726340229E-002C[5][0]=2.17459756299E-001C[5][1]=-1.78372378542E-001C[5][2]=-7.24058095248E-002C[5][3]=2.43330475719E-001C[5][4]=-1.41334739775E-001C[5][5]=2.65102413037E-002C[5][0]=-5.59032661772E-002C[5][1]=1.43199241737E-001C[5][2]=-1.36270366628E-001C[5][3]=4.0719*******E-002C[5][4]=3.77503355870E-003C[5][5]=-2.66770140049E-0034.数表(xi,yj)、f(xi,yj)、p(xi,yj)以及它们的差值x[0]=0 y[0]=0.5p(x,y)=1.94730355285E-001 f(x,y)=1.94720407918E-001 deta=9.94736690521E-006x[0]=0 y[1]=0.7p(x,y)=-1.83041842880E-001 f(x,y)=-1.83037079189E-001 deta=-4.76369108796E-006x[0]=0 y[2]=0.9p(x,y)=-4.45500048680E-001 f(x,y)=-4.45497646915E-001 deta=-2.40176486183E-006x[0]=0 y[3]=1.1p(x,y)=-5.97558867846E-001 f(x,y)=-5.97566707641E-001 deta=7.83979486330E-006x[0]=0 y[4]=1.3p(x,y)=-6.46446127384E-001 f(x,y)=-6.46459593901E-001 deta=1.34665171766E-005x[1]=0.1 y[0]=0.5p(x,y)=4.0598*******E-001 f(x,y)=4.0597*******E-001 deta=1.03485281598E-005x[1]=0.1 y[1]=0.7p(x,y)=-2.25211197537E-002 f(x,y)=-2.25159583746E-002 deta=-5.16137912467E-006x[1]=0.1 y[2]=0.9p(x,y)=-3.38224028576E-001 f(x,y)=-3.38220816040E-001 deta=-3.21253640911E-006x[1]=0.1 y[3]=1.1p(x,y)=-5.44430460440E-001 f(x,y)=-5.44437831522E-001 deta=7.37108182258E-006x[1]=0.1 y[4]=1.3p(x,y)=-6.47348025306E-001 f(x,y)=-6.47361338568E-001 deta=1.33132616271E-005x[2]=0.2 y[0]=0.5p(x,y)=6.34787451208E-001 f(x,y)=6.34777195151E-001 deta=1.025********E-005x[2]=0.2 y[1]=0.7p(x,y)=1.58796292931E-001 f(x,y)=1.58801168839E-001 deta=-4.87590857656E-006x[2]=0.2 y[2]=0.9p(x,y)=-2.0736*******E-001 f(x,y)=-2.0736*******E-001 deta=-2.89120630045E-006x[2]=0.2 y[3]=1.1p(x,y)=-4.65349931137E-001 f(x,y)=-4.65357906898E-001 deta=7.97576078648E-006x[2]=0.2 y[4]=1.3p(x,y)=-6.20257150733E-001 f(x,y)=-6.20270953075E-001 deta=1.38023420141E-005x[3]=0.3 y[0]=0.5p(x,y)=8.78969863913E-001 f(x,y)=8.78960023174E-001 deta=9.84073838783E-006x[3]=0.3 y[1]=0.7p(x,y)=3.58646040897E-001 f(x,y)=3.58650625882E-001 deta=-4.58498525391E-006x[3]=0.3 y[2]=0.9p(x,y)=-5.52554407260E-002 f(x,y)=-5.52528211681E-002 deta=-2.61955789865E-006x[3]=0.3 y[3]=1.1p(x,y)=-3.62671068876E-001 f(x,y)=-3.62679511503E-001 deta=8.44262724292E-006x[3]=0.3 y[4]=1.3p(x,y)=-5.67550591485E-001 f(x,y)=-5.67564743655E-001 deta=1.41521698724E-005x[4]=0.4 y[0]=0.5p(x,y)=1.136********E+000 f(x,y)=1.136********E+000 deta=9.44199507047E-006x[4]=0.4 y[1]=0.7p(x,y)=5.74975840930E-001 f(x,y)=5.74980340948E-001 deta=-4.50001736119E-006x[4]=0.4 y[2]=0.9p(x,y)=1.159********E-001 f(x,y)=1.159********E-001 deta=-3.0579*******E-006x[4]=0.4 y[3]=1.1p(x,y)=-2.38560423010E-001 f(x,y)=-2.38568304012E-001 deta=7.88100251645E-006x[4]=0.4 y[4]=1.3p(x,y)=-4.91420905751E-001 f(x,y)=-4.91434393656E-001 deta=1.34879048772E-005x[5]=0.5 y[0]=0.5p(x,y)=1.40605068621E+000 f(x,y)=1.40604179891E+000 deta=8.88730304549E-006x[5]=0.5 y[1]=0.7p(x,y)=8.0593*******E-001 f(x,y)=8.0594*******E-001 deta=-4.19333468360E-006x[5]=0.5 y[2]=0.9p(x,y)=3.04425830753E-001 f(x,y)=3.04429221045E-001 deta=-3.39029184432E-006x[5]=0.5 y[3]=1.1p(x,y)=-9.50089472511E-002 f(x,y)=-9.50161300996E-002 deta=7.182********E-006x[5]=0.5 y[4]=1.3p(x,y)=-3.93889839003E-001 f(x,y)=-3.93902307746E-001deta=1.24687429454E-005x[6]=0.6 y[0]=0.5p(x,y)=1.68579121671E+000 f(x,y)=1.68578351531E+000deta=7.70140288742E-006x[6]=0.6 y[1]=0.7p(x,y)=1.04987773874E+000 f(x,y)=1.04988115306E+000deta=-3.41432028650E-006x[6]=0.6 y[2]=0.9p(x,y)=5.08291044733E-001 f(x,y)=5.08293783940E-001deta=-2.73920670368E-006x[6]=0.6 y[3]=1.1p(x,y)=6.61563563891E-002 f(x,y)=6.61487967065E-002deta=7.55968266807E-006x[6]=0.6 y[4]=1.3p(x,y)=-2.76822040919E-001 f(x,y)=-2.76834341778E-001deta=1.23008586507E-005x[7]=0.7 y[0]=0.5p(x,y)=1.97458126094E+000 f(x,y)=1.97457455665E+000deta=6.70428833205E-006x[7]=0.7 y[1]=0.7p(x,y)=1.30533200403E+000 f(x,y)=1.30533496765E+000deta=-2.96362120045E-006x[7]=0.7 y[2]=0.9p(x,y)=7.25989311831E-001 f(x,y)=7.25992371111E-001deta=-3.0592*******E-006x[7]=0.7 y[3]=1.1p(x,y)=2.43260793658E-001 f(x,y)=2.43254184181E-001deta=6.60947631989E-006x[7]=0.7 y[4]=1.3p(x,y)=-1.41938782303E-001 f(x,y)=-1.41949659709E-001deta=1.0877*******E-005遇到的问题及解决办法1.在编写程序的时候要有足够的耐心和细心，否则一时疏忽输错了一个字符，都会造成输出结果错误，我是因为在输入数表时，输错了一个符号，导致程序总是输出错误，在检查了很久之后才找出问题所在。

- 1 -第三章上机习题用你所熟悉的的计算机语言编制利用QR 分解求解线性方程组和线性最小二乘问题的通用子程序，并用你编制的子程序完成下面的计算任务：（1）求解第一章上机习题中的三个线性方程组，并将所得的计算结果与前面的结果相比较，说明各方法的优劣； （2）求一个二次多项式+bt+cy=at 2，使得在残向量的2范数下最小的意义下拟合表3.2中的数据；（3）在房产估价的线性模型111122110x a x a x a x y ++++=中，1121,,,a a a 分别表示税、浴室数目、占地面积、车库数目、房屋数目、居室数目、房龄、建筑类型、户型及壁炉数目，y 代表房屋价格。

现根据表3.3和表3.4给出的28组数据，求出模型中参数的最小二乘结果。

（表3.3和表3.4见课本P99-100）解 分析：（1）计算一个Householder 变换H ： 由于TTvv I wwI H β-=-=2，则计算一个Householder 变换H 等价于计算相应的v 、β。

其中)/(2,||||12v v e x x v T=-=β。

在实际计算中，为避免出现两个相近的数出现的情形，当01>x 时，令212221||||)(-x x x x v n +++=；为便于储存，将v 规格化为1/v v v =，相应的，β变为)/(221v v v T=β为防止溢出现象，用∞||||/x x 代替 （2）QR 分解：利用Householder 变换逐步将n m A n m ≥⨯,转化为上三角矩阵A H HH n n 11-=Λ，则有⎥⎦⎤⎢⎣⎡=0R Q A ，其中n H H H Q 21=，:),:1(n R Λ=。

在实际计算中，从n j :1=，若m j <，依次计算)),:((j m j A x =对应的)1()1()~(+-⨯+-k m k m j H即对应的j v ，j β，将)1:2(+-j m v j 储存到),:1(j m j A +，j β储存到)(j d ，迭代结束后再次计算Q ，有⎥⎥⎦⎤⎢⎢⎣⎡=-~001j j j H I H，n H H H Q 21=（m n =时1-21n H H H Q =）（3）求解线性方程组b Ax =或最小二乘问题的步骤为 i 计算A 的QR 分解；ii 计算b Q c T 11=，其中):1(:,1n Q Q = iii 利用回代法求解上三角方程组1c Rx =（4）对第一章第一个线性方程组，由于R 的结果最后一行为零，故使用前代法时不计最后一行，而用运行结果计算84x 。

第三章上机作业
一、上机要求
已知Hilbert矩阵H的元素为: =1/(i+j-1), 完成如下实验:
(1)编程计算H的行范数函数;
(2)编写计算H的行范数条件数函数(可以调用求逆函数,Mathematica为Inverse[H],Matlab为
inv(H), 其它语言自己去查找相应的逆矩阵程序使用);
(3)对n=1,2,…,20, 计算H的行范数条件数, 画出n同条件数的对数之间的关系图;
(4)令x=(1,1,…,1), 计算b=Hx, 对n=1,2,…,20, 求解=b,并计算x-的无穷范数和b-H.
(5)通过以上的数值实验, 你理解到了什么.
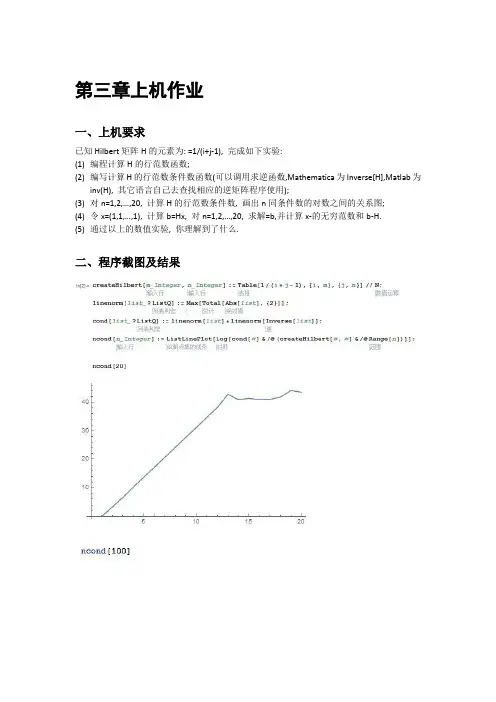
二、程序截图及结果
三、心得体会
通过实验对向量范数和矩阵范数有了更深的理解。

学习了通过编程实现对Hillbert矩阵行范数函数和行范数条件数的计算。

数值代数与计算方法上机作业作业一：Matlab的基本操作P311.根据习题12和习题13构造算法和MATLAB程序，以便精确计算所有情况下的二次方程的根，包括b?b2?4ac的情况。

2.参照例1.25，对下列3个差分方程计算出前10个数值近似值。

在每种情况下引入一个笑?1?得出是误差。

如果没有初始误差，则没个差分方程将生成序列?n? 。

构造类似表1.4、2??n?1表1.5以及图1.8至图1.10的输出。

?1rn?1，其中n=1,2,… 23(b) p0?1,p1?0.497,pn?pn?2, 其中n=2,3,…25(c) q0?1,q1?0.497,qn?qn?1?qn?2, 其中n=2,3,…2(a) r0?0.994；rn?作业二：非线性方程f(x)?0的解法P401. 使用程序2.1求解下面每个函数的不动点（尽可能多）近似值，答案精确到小数点后12为。

同时，构造每个函数和直线y=x来显示所有不动点。

（a）（b）（c）（d）g(x)?x5?3x3?2x2?2g(x)?cos(sin(x)) g(x)?x2?in(x?0.15) g(x)?xx?cos(x)P493. 修改程序2.2和程序2.3，使得输出分别类似于表2.1和表2.2的矩阵（即矩阵的第一行应当为[0a0 c0 b0 f(c0) ] ）。

P69 4，用习题11中的立方根算法修改程序2.5，并用其近似下列每个立方根到小数点后10位。

（a） p0?2，求7的近似值。

（b） p0?6，求200的近似值。

（c）p0??2，求(?7)的近似值。

作业三：线性方程组AX?B的求解方法131313P93 1. P97 2.P109 2.P120 1.P130 4.作业四：插值与多项式逼近P154Matlab的矩阵特性使其能够快速计算一个函数在其多个点处的值。

例如，如果X=[-1 0 1],则sin(X)将得到[sin(-1),sin(0),sin(1)]。

数值分析第三次作业解答思考题：1：（a ）对给定的连续函数，构造等距节点上的Lagrange 插值多项式，节点数目越多，得到的插值多项式越接近被逼近的函数。

×;(b) 对给定的连续函数，构造其三次样条函数插值，则节点数目越多，得到的样条函数越接近被逼近的函数。

√(c) 高次的Lagrange 插值多项式很常用。

×(d) 样条函数插值具有比较好的数值稳定性。

√3． 以0.1,0.15,0.2为插值节点，计算()f x = Lagrange 插值多项式 2()P x ， 比较2(0)P 和(0)f ，问定理4.1的结果是否适用本问题？ 解： 构造插值多项式：0122022(0.15)(0.2)()0.050.1(0.1)(0.2)()0.050.05(0.1)(0.15)()0.10.05()()()()(0)0;(0)0.1403x x l x x x l x x x l x P x x x x f P --=⨯--=⨯--=⨯=++==在（0，2）区间，5''''''23()(0.2)118.585458f x x f -=≤=从而，对任意的 '''3()(0,0.2),(0)0.05933!f ξξω∈≤ 不存在'''32()(0,0.2),(0)(0)(0)0.14033!f f P ξξω∈=-=。

演示程序：x=0:0.01:0.2; y=x.^(1/2);plot(x,y,'r')pause,hold onx0=[0.1,0.15 ,0.2]; y0=x0.^(1/2); x=0:0.01:0.2; y1=lagrangen(x0,y0,x); plot(x,y1,'b')5：（a ）求()f x x =在节点123452,0.5,0, 1.5,2x x x x x =-=-=== 的三次样条插值（150M M ==）。

中科院研究⽣院信息⼯程学院课件数值分析数值分析第三次作业及答案6数值分析第三次作业及答案明当h T 0时，它收敛于原初值问题的准确解 y证：梯形公式为 y n ⼗ yn+—[f(X n ，y n )+f(X n^1，y n 』] h由 f (X,y) = —y= y n+ =y n +2( — y n — yn G=L n = 3 Y y n」訓 /乂⼚％l 2+h <12 +h ⼃丫2. (P202(6))写出⽤四阶经典的龙格⼀库塔⽅法求解下列初值问题的计算公式:y n + =y n + — (k 1 +2k 2 +2k 3 +k 4)=0.2214x n +1.2214y n +0.0214 6飞=3y n ⼼+x n )2)” k 2 =3(y n +0.1k 1〃(1+Xn +0.1) )L s =3(yn +0.1k2”(1+Xn +0.1)k 4 =3(yn +0.2k 3”(1+Xn +0.2) 0 2yn + =y n +〒(k 1 +2k 2 +2k 3 +k 4).1. ( P201 (4))⽤梯形⽅法解初值问题〔爲证明其近似解为y n 偌〕:并证⽤ . f 2-h 1 因 yoT " yn F ⼃.⽤上述梯形公式以步长h 经n 步计算到y n ,故有nh ：=x.X◎ T 茹Jf 2—h \n7 l 2+h ⼃1) ]y =x + y, 0 e x ￡1; ly(0) =1;2)l y \3%+x)，O *1； [y(0)=1.解：令h =0.2k 1 = f (X n , y n )= h k2=f (Xn+；；,yn+-k1)=Xn+- + 2 2 2 h k s = f (X n +；, y n +-k 2)=X n +- +y n +-k 2 =1.11(X n + y n )+0.11 2 2 2 2X n +y nh 1)4h h ??yn +；；k i =1.1(Xn +y n )+0.1 2 2 h . . h .................................. .2 ⼋ 2 J 'k 4 = f(X n +h,y n +hk 3)=X n + h + y n +hk 3 =1.222(X n +y n )+0.2223. (P202(7))证明对任意参数t，下列龙格库塔—公式是⼆阶的:r hy n 卄yn+^g+G)；* K i = f (X n, yj；K2 = f (X n +th, y n +thK i);[K3 =f(Xn+(1—t)h,yn+(1—t)hK i).证：由⼀元函数的泰勒展开有2 '''"y(X nG =y(X n) +hy'(X n)⼸[f x(X n,y(X n)) +f y(X n,y(X n))f(X n,y(X n))]中严h'2 3!⼜由⼆元函数的泰勒展开有y n41 =y n +；2(⼼+K3)=y n +；2[(f(X n,y n) + ￡%区『)也+f y(X n, y n)thf (X n, Y n)⼗。

高等数值分析第三章作业参考答案1.考虑线性方程组Ax=b,其中A是对称正定矩阵.用Galerkin原理求解方程K=L=Span(v),这里v是一个固定的向量.e0=x∗−x0,e1=x∗−x1证明(e1,Ae1)=(e0,Ae0)−(r,v)2/(Av,v),(∗)其中r=b−Ax0.v应当取哪个向量在某种意义上是最佳的?证明.令x1=x0+αv,那么r1=r−αAv,e1=e0−αv.由Galerkin原理,有(r1,v)=0,因此α=(r,v)/(Av,v).注意到r1=Ae1,r=Ae,有(Ae1,v)=0.于是(e1,Ae1)=(e0−αv,Ae1)=(e0,Ae1)=(e0,Ae0)−α(e0,Av)=(e0,Ae0)−α(r,v)即(∗)式成立.由(∗)式知当v=e0时, e1 A=0最小,即近似解与精确解的误差在A范数意义下最小,算法一步收敛(但是实际中这个v不能精确找到);在最速下降意义下v=r时最佳.2.求证：考虑线性方程组Ax=b,其中A是对称正定矩阵.取K=L=Span(r,Ar).用Galerkin方法求解,其中r是上一步的残余向量.(a)用r和满足(r,Ap)=0的p向量构成K中的一组基.给出计算p的公式.解.设p=r+αAr,(r,Ap)=0等价于(Ar,p)=0.解得α=−(Ar,r)/(Ar,Ar).(b)写出从x0到x1的计算公式.解.设x1=x0+β1r+β2p,那么r1=r−β1Ar−β2Ap,再由Galerkin原理,有(r1,r)=(r1,p)=0,解得β1=(r,r)/(Ar,r),β2=(r,p)/(Ap,p).(c)该算法收敛吗?解.该算法可描述为：(1)选初始x0∈R n,计算初始残差r0=b−Ax0,ε>0为停机准则；(2)对k=0,1,2,...直到 r k <εαk=−(r k,Ar k) (Ar k,Ar k);p k=r k+αAr k;βk=(r k,r k) (Ar k,r k);γk=(r k,p k) (Ap k,p k);r k+1=r k−βk Ar k−γk Ap k;x k+1=x k+βk r k+γk p k.此算法本质上是由CG迭代一步就重启得到的,所以是收敛的,下面给出证法.设用此算法得到的x k+1=x k+¯p1(A)r k,那么e k+1 A=minp1∈P1e k+p1(A)r k A≤ e k+¯p1(A)r k A= e k−¯p1(A)Ae k A≤max1≤i≤n|˜p(λi)| e k A其中0<λ1≤...≤λn为A的特征值,˜p(t)=1−t¯p1(t)是过(0,1)点的二次多项式.当˜p满足˜p(λ1)=˜p(λn)=−˜p(λ1+λn2)时可使max1≤i≤n|˜p(λi)|达到最小.经计算可得min ˜p max1≤i≤n|˜p(λi)|≤(λ1−λn)2(λ1−λn)2+8λ1λn<1故若令κ=λ1/λn,则e k+1 A≤(κ−1)2κ2+6κ+1e k A,方法收敛.3.考虑方程组D1−F−E−D2x1x2=b1b2,其中D1,D2是m×m的非奇异矩阵.取L1=K1=Span{e1,e2,···,e m},L2= K2=Span{e m+1,e m+2,···,e n}.依次用(L1,K1),(L2,K2)按讲义46和47页公式Az∗=r0r0−Az m⊥LW T AV y m=W T r0x m=x0+V(W T AV)−1W T r0各进行一步计算.写出一个程序不断按这个方法计算下去,并验证算法收敛性.用L i=AK i重复上述各步骤.解.对任意给定x0=x(0)1x(0)2,令r=b−Ax0,V1=[e1,e2,...,e m],V2=[e m,e m+1,...,e n].对L i=K i情形,依次用(L1,K1),(L2,K2)各进行一步计算：(L1,K1)(L2,K2)z(1) 1=V1y1z(2)1=V2y2r0−Az(1)1⊥L1r0−Az(2)1⊥L2(V T1AV1)y1=V T1r0,D1y1=V T1r0(V T2AV2)y2=V T2r0,−D2y2=V T2r0x(1)1=x(1)+V1D−11V T1r0x(2)1=x(2)−V2D−12V T2r0得如下算法：(1)选初始x0∈R n,计算初始残差r0=b−Ax0,ε>0为停机准则；(2)对k=1,2,...直到 r k <ε求解D1y1=r k−1(1:m);求解−D2y2=r k−1(m+1:n);x k=x k−1+V1y1+V2y2;r k=r k−1−AV1y1−AV2y2.收敛性:r k=r k−1−AD−11−D−12rk−1=0−F D−12ED−11rk−1Br k−1算法收敛⇔ρ(B)<1⇔ρ(ED−11F D−12)<1.对L i=AK i情形,依次用(L1,K1),(L2,K2)各进行一步计算:(L1,K1)(L2,K2)z(1) 1=V1y1∈K1z(2)1=V2y2∈K2r0−Az(1)1⊥L1=AK1r0−Az(2)1⊥L2=AK2(V T1A T AV1)y1=V T1A T r0(V T2A T AV2)y2=V T2A T r0(D T1D1+E T E)y1=V T1A T r0(D T2D2+F T F)y2=V T2A T r0x(1) 1=x(1)+(D T1D1+E T E)−1V T1A T r0x(2)1=x(2)+(D T2D2+F T F)−1V T2A T r0得如下算法：(1)选初始x0∈R n,计算初始残差r0=b−Ax0,ε>0为停机准则；(2)对k=1,2,...直到 r k <ε求解(D T1D1+E T E)y1=(A T r k−1)(1:m);求解(D T2D2+F T F)y2=(A T r k−1)(m+1:n);x k=x k−1+V1y1+V2y2;r k=r k−1−AV1y1−AV2y2.收敛性:r k=r k−1−A(D T1D1+E T E)−1(D T2D2+F T F)−1A T rk−1(I−B)r k−1算法收敛⇔ρ(I−B)<1⇔0<λ(B)<2.4.令A=3−2−13−2...............−2−13,b=1...2用Galerkin原理求解Ax=b.取x0=0,V m=W m=(e1,e2,···,e m).对不同的m,观察 b−Ax m 和 x m−x∗ 的变化,其中x∗为方程的精确解.解.对于 b−Ax m 和 x m−x∗ ,都是前n−1步下降趋势微乎其微,到第n步突然收敛。

第四章 第三次作业1.设A 是n 阶方阵，且0=A ，但A 中某元素kl a 的代数余子式0≠kl A ，则齐次线性方程组0=X A 基础解系中线性无关解向量的个数为 1。

解 因0≠klA，故A 中有不为零的n-1阶子式，又因0=A 及()1-=n A R ，故解空间维数为1。

2．设n 阶方阵A 的各行元素之和均为零，且()1-=n A R，则齐次线性方程组0=X A 的通解为：()1,1,,1,Tkk R ∈解 解空间维数为1，又A 的各行元素的和为1及()1,,1,1 是0=X A 的一个非零解。

3．设A 为n m ⨯矩阵，则有（D ）4．已知21,ββ是非齐次线性方程组b X A =的两个不同解，21,αα 是对应齐次线性方程组0 =X A 的基础解系，21,k k 是任意常数，则b X A=的通解为（B ）5．设非齐次线性方程组⎪⎪⎩⎪⎪⎨⎧=++-=+-+=++--=--+7739183332154321432143214321x x x x x x x x x x x x x x x x ，（1）求对应齐次线性方程组的一个基础解系；（2）求该非齐次线性方程组的通解。

解 因()⎪⎪⎪⎪⎪⎭⎫⎝⎛------==77391111833312111151b A B ⎪⎪⎪⎪⎪⎭⎫⎝⎛------484140442704427011151~⎪⎪⎪⎪⎪⎭⎫⎝⎛----00000000004427011151~313131077724401~7770000000⎛⎫⎪ ⎪ ⎪---⎪ ⎪ ⎪ ⎪⎝⎭对应齐次线性方程同解方程组为134234313772277x x x x x x ⎧=--⎪⎪⎨⎪=+⎪⎩取3470,07x x ⎛⎫⎛⎫⎛⎫= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，得13313,24x x --⎛⎫⎛⎫⎛⎫= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 即得对应的齐次线性方程组基础解系为：()13,2,7,0T ξ=- ，()213,4,0,7Tξ=-该非齐次线性方程组同解方程组为13423431313777224777x x x x x x ⎧=--+⎪⎪⎨⎪=+-⎪⎩取042==x x 得2,131==x x 因而得该非齐次方程组的一个特解为()T0,2,0,1*=η ，故该非齐次方程组通解为：121212343131240,,702070x x c c c c R x x --⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪=++∈ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭6．已知四元非齐次线性方程组的系数矩阵的秩为3，,1β 32,ββ是该齐次线性方程组的3个解向量，且=+21ββT)2,0,1,1(，T)3,1,0,1(32=+ββ，求该非齐次线性方程组的通解。

线性方程组部分填空题
1．设齐次线性方程组A x=0的系数阵A的秩为r，当r= n 时，则A x=0 只有零解；当A x=0有无穷多解时，其基础解系含有解向量的个数为n-1 .
2．设η1，η2为方程组A x=b的两个解，则 η1－η2或η2－η1是其导出方程组的解。

3．设α0是线性方程组A x=b的一个固定解，设z是导出方程组的某个解，则线性方程组A x=b的任意一个解β可表示为β=α0+z .
4．若n元线性方程组A x=b有解，R（A）=r，则当r=n时，有惟一
解；当,r＜n时，有无穷多解。

5．A是m×n矩阵，齐次线性方程组A x=0有非零解的充要条件是
（A）＜n .
6．n元齐次线性方程组Ax=0仅有零解的充分必要条件是 |A|不等于0
7 线性方程组Ax=b有解的充要条件是 r(Ab)=r(A)。

8．设是线性方程组A x=b的一个特解，是其导出组的基础解系，则线性方程组A x=b的全部解可以表示为=
1．求线性方程组
的通解.
通解为：x=k1
2．求齐次线性方程组
的一个基础解系.
基础解系为v1=
3．求非齐次线性方程组的通解
同解方程组为
，通解为
4 求方程组的通解
化为同解方程组
通解为
5．已知线性方程组
（1）求增广矩阵（Ab）的秩r（Ab）与系数矩阵A的秩r（A）；
（2）判断线性方程组解的情况，若有解，则求解。

（1）r（Ab）=r（A）=4
（2）有唯一解。

x1=-1;x2=-1;x3=0;x4=1。

《线性代数》上机作业（一）一、 上机目的 1、 培养学生运用线性代数的知识解决实际问题的意识、兴趣和能力 2、 掌握常用计算方法和处理问题的方法. 二、 上机内容 1、 求向量组的最大无关组； 2、 解线性方程组； 3、 解决实际问题举例. 三、 上机作业1、设 A=[2 1 2 4; 1 2 0 2; 4 5 2 0; 0 1 1 7];求矩阵A 列向量组的一个最大无关组. 2、用Matlab 解线性方程组|2\ + 4X 2 -= -4參]-+5工？十3屯=10 匕-+ 3x 2 +2x3 - 51、解：在Matlab 中输入:> a=[2 1 2 4; 1 b=rref(a) 解得：b = 1 0 0 0 1 0 0 0 13x-i 41x 262 X 3414x-| 50x 2 3X 3 100 11x 1 38X 2 25X 3501 7];2 0 2; 4 5 2 0; 0 10 0 0 1 所以a1 ，a2,a3,a4 是一个极大无关组2、(1) 解：在Matlab 中输入>> a=[2 4 -6; 1 5 3;1 3 2]; >> b=[-4 10 5]';>> x=a\bx =-321 所以线性方程组的解为x1=-3,x2=2,x3=1 (2) 解：在Matlab 中输入>> a=[3 41 -62;4 50 3;11 38 25]; >> b=[-41 100 50]'; >> x=a\b x = -8.82212.58901.9465>>所以线性方程组的解为x1=-8.8221,x2= 2.5890,x3= 1.9465四、上机心得体会。

1、程序：x=-1:0.2:1;f=1./(1+25*x.^2);y=polyval(f,x); %计算原函数每个x 值所对应的函数值 p=polyfit(x,y,3) %对（x ，y ）进行三次拟合并输出三次多项式系数 z=polyval(p,x); %计算拟合后的多项式对应x 点的函数值 plot(x,y,'r',x,z,'b') %画图输出：p =1.8222 1.2090 -0.3619 -0.1140则三次曲线拟合的方程为：1140.03619.02090.18222.1)(233--+=x x x x p2、3次和4次多项式拟合：程序：x=[0.0 0.1 0.2 0.3 0.5 0.8 1.0];y=[1.0 0.41 0.50 0.61 0.91 2.02 2.46];%3次拟合%p3=polyfit(x,y,3)xi=0:0.1:1.0;yi=polyval(p3,xi);subplot(1,2,1);plot(x,y,'*',xi,yi,'r');xlabel('x');ylabel('y');%4次拟合%p4=polyfit(x,y,4)xi=0:0.1:1.0;yi=polyval(p4,xi);subplot(1,2,2);plot(x,y,'*',xi,yi,'r');xlabel('x');ylabel('y');输出：p3 =-6.6221 12.8147 -4.6591 0.9266p4 =2.8853 -12.3348 16.2747 -5.2987 0.9427则3次拟合多项式为：9266.06591.48147.126221.6)(233+-+-=x x x x p 4次拟合多项式为：9427.02987.52747.163348.128853.2)(2344+-+-=x x x x x p另一函数拟合：定义函数：function [C,L]=lagran(x,y)%x 为n 个节点的横坐标所组成的向量，y 为纵坐标所组成的向 %C 为所求的牛顿插值多项式的系数构成w=length(x);n=w-1;L=zeros(w,w);for k=1:n+1V=1;for j=1:n+1if k~=jV=conv(V,poly(x(j)))/(x(k)-x(j));% conv 求积，poly(x)将该多项式的系数赋给向量endendL(k,:)=V;endC=y*L输入命令：x=[0.0 0.1 0.2 0.3 0.5 0.8 1.0];y=[1.0 0.41 0.50 0.61 0.91 2.02 2.46];cc=polyfit(x,y,4);xx=x(1):0.1:x(length(x));yy=polyval(cc,xx);plot(xx,yy,'r');hold on ;plot(x,y,'x');xlabel('x');ylabel('y');x=[0.0 0.1 0.2 0.3 0.5 0.8 1.0];y=[0.94 0.58 0.47 0.52 1.00 2.00 2.46];%y 中的值是根据上面两种拟合曲线而得到的估计数据，不是真实数据[C,L]=lagran(x,y);xx=0:0.01:1.0;yy=polyval(C,xx);hold onplot(xx,yy,'b',x,y,'.');输出：C =40.6746 -110.2183 110.3671 -57.3264 23.4994 -5.4764 0.9400。

河海大学线性代数第3次作业答案朱永忠1、下列各式：①(x-2y)(2y+x)；②(x-2y)(-x-2y)；③(-x-2y)(x+2y)；④(x-2y)(-x+2y).其中能用平方差公式计算的是（）[单选题] *A. ①②(正确答案)B. ①③C. ②③D. ②④2、5．已知集合A={x|x=3k＋1，k∈Z}，则下列表示不正确的是( ) [单选题] *A．－2∈AB．2 022?AC．3k2＋1?A(正确答案)D．－35∈A3、6．下列各图中，数轴画法正确的是（）[单选题] *A．B．C．D．(正确答案)4、7．一条东西走向的道路上，小明向西走米，记作“米”，如果他向东走了米，则可记作（）[单选题] *A-2米B-7米C-3米D+7米(正确答案)5、49、如图，在△ABC中，∠A＝30°，∠ABC＝50°，若△EDC≌△ABC，且A，C，D在同一条直线上，则∠BCE＝（）[单选题] *A．20°(正确答案)B．30°C．40°D．50°6、从3点到6点，分针旋转了多少度？[单选题] *90°960°-1080°(正确答案)-90°7、6.有15张大小、形状及背面完全相同的卡片，卡片正面分别画有正三角形、正方形、圆，从这15张卡片中任意抽取一张正面的图形既是轴对称图形，又是中心对称图形的概率是1/3?，则正面画有正三角形的卡片张数为（）[单选题] *Ａ.3Ｂ.5Ｃ.10(正确答案)Ｄ.158、下列各式计算正确的是（）[单选题] *A. 2a2＋3a2＝5a?B. (－2ab)3＝－6ab3C. (3a＋b)(3a－b)＝9a2－b2(正确答案)D. a3·(－2a)＝－2a39、椭圆的离心率一定（）[单选题] *A、等于1B、等于2(正确答案)C、大于1D、等于010、32．已知m＝（）﹣2，n＝（﹣2）3，p＝﹣（﹣）0，则m，n，p的大小关系（）[单选题] *A．m＜p＜nB．n＜m＜pC．p＜n＜mD．n＜p＜m(正确答案)11、18．下列各对数中，互为相反数的是（）[单选题] *A．﹣（+1）和+（﹣1）B．﹣（﹣1）和+（﹣1）(正确答案)C．﹣（+1）和﹣1D．+（﹣1）和﹣112、? 转化成角度为（）[单选题] *A. 150°B. 120°(正确答案)C. 270°D. 90°13、25．从五边形的一个顶点出发，可以画出m条对角线，它们将五边形分成n个三角形．则m、n的值分别为（）[单选题] *A．1，2B．2，3(正确答案)C．3，4D．4，414、6．过多边形的一个顶点能引出7条对角线，则这个多边形是（）边形．[单选题]* A．七B．八C．九D．十(正确答案)15、若sinα＜0,则α角是在（）[单选题] *A、第一、二象限B、第三、四象限(正确答案)C、第一、三象限D、第二、四象限16、27.下列各函数中，奇函数的是（）[单选题] *A. y=x^(-4)B. y=x^(-3)(正确答案)C .y=x^4D. y=x^(2/3)17、12．已知点P(m，n)，且mn＞0，m+n＜0，则点P在() [单选题] *A．第一象限B．第二象限C．第三象限(正确答案)D．第四象限18、20．如图，OC是∠AOB的平分线，OD是∠BOC的平分线，那么下列各式中正确的是（）[单选题] *21．A．∠COD＝∠AOBB．∠AOD＝∠AOBC．∠BOD＝∠AODD．∠BOC＝∠AOD(正确答案)19、24．已知点M在线段AB上，点N是线段MB的中点，若AN＝6，则AM+AB的值为（）[单选题] *A．10B．8C．12(正确答案)D．以上答案都不对20、16．若过多边形的每一个顶点只有6条对角线，则这个多边形是（）[单选题] *A．六边形B．八边形C．九边形(正确答案)D．十边形21、-950°是（）[单选题] *A. 第一象限角B. 第二象限角(正确答案)C. 第三象限角D. 第四象限角22、19、如果点M是第三象限内的整数点，那么点M的坐标是（）[单选题] *（-2，-1）（-2，-2）（-3，-1）(正确答案)（-3，-2）23、2．线段是由线段平移得到的，点的对应点为，则点的对应点的坐标为（）[单选题] *A．(2,9)B(5,3)C(1,2)(正确答案)D(-9,-4)24、下列语句中，描述集合的是（）[单选题] *A、比1大很多的实数全体B、比2大很多的实数全体C、不超过5的整数全体(正确答案)D、数轴上位于原点附近的点的全体25、390°是第（）象限角？[单选题] *第一象限(正确答案)第二象限第三象限第四象限26、已知a+b=3,则代数式(a+b)(a-b)+6b的值是(? ????) [单选题] *A. -3B. 3C. -9D. 9(正确答案)27、在0°~360°范围中，与-940°终边相同的角是（）[单选题] * 140°(正确答案)500°-220°320°28、下列计算正确的是( ) [单选题] *A. (－a)·(－a)2·(－a)3＝－a?B. (－a)·(－a)3·(－a)?＝－a?C. (－a)·(－a)2·(－a)?＝a?D. (－a)·(－a)?·a＝－a?(正确答案)29、下列各角中与45°角终边相同的角是（）[单选题] *A. 405°(正确答案)B. 415°C. -45°D. -305°30、f（x）=-2x+5在x=1处的函数值为（）[单选题] *A、-3B、-4C、5D、3(正确答案)。

4.求f(x)=sin x 在[0,π/2]上的最佳一次逼近多项式。

解：设P 1(x)=a 0+a 1x 是f(x) 的最佳一次逼近多项式，则P 1(x)在[0,π/2]上有三个交错点， 满足0<=x 1<x 2<x 3<=π/2。

由于 [f(x)- P 1(x)]’’=(cos x-a 1)’= -sin x 在[0,π/2]上小于0，定号， 故(cos x-a 1)’在[0,π/2]上单调递减，且仅有一个驻点。

故f(x)- P 1(x)在[0,π/2]上只有一个偏差点x 2，满足[f(x)- P 1(x)]’|x=x2 =cos x 2-a 1=0 (1)。

另外两个偏差点x 1=0 ，x 3=π/2 .于是sin 0-a 0 =sin π/2-a 0-π/2a 1 (2)， sin x 2 –a 0-a 1x 2= -( sin 0-a 0) (3) 由（1）（2）（3）式得：a 1=2/π x 2=arccos 2/π=0.88 a 0=-1.18 所以P 1= -1.18+2/π x 。

6.求f(x)=2x 4+3x 3-x 2+1在[-1,1]上的三次最佳一致逼近多项式。

解：设f(x)的三次最佳一致逼近多项式为P 3(x)，由切比雪夫多项式的极性可得 1/2[f(x)- P 3(x)]=1/8T 4(x)=1/8(8x 4-8x 2+1)所以P 3(x)=f(x)-1/4(8x 4-8x 2+1)= 2x 4+3x 3-x 2+1-2x 4+2x 2-1/4 =3x 3+x 2+3/49.求函数f(x)在指定区间上关于Φ(x)=span{1,x}的最佳平方逼近多项式。

(3)f(x)=cosπx, x ∈[0,1]；(4)f(x)=ln x, x ∈[1,2].解：(3)在[0,1]上，经计算得 d 0= ⎰1)(f dx x =0 ，d 1=⎰1)(x dx x f = -2/π2得到法方程组为a 0+1/2a 1=0 ，1/2a 0+1/3a 1= -2/π2 由上面两式解得 a 0=12/π2 ，a 1= -24/π2所以f(x)=cosπx 在[0,1]上的最佳平方逼近多项式为 S 1*=12/π2 -24/π2 x 。