结构力学--第4章静定结构位移计算
- 格式:ppt
- 大小:1.25 MB
- 文档页数:17









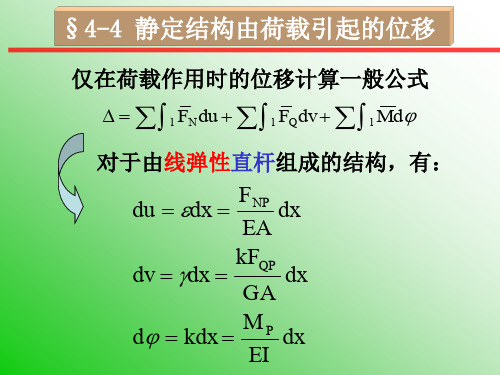
第四章 静定结构位移计算一、是非题1、虚位移原理等价于变形谐调条件,可用于求体系的位移。
2、按虚力原理所建立的虚功方程等价于几何方程。
3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下,静定结构不产生内力,但会有位移且位移只与杆件相对刚度有关。
4、用图乘法可求得各种结构在荷载作用下的位移。
5、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。
6、已知M p 、M k 图,用图乘法求位移的结果为:()/()ωω1122y y EI +。
Mk M p21y 1y 2**ωω7、图示桁架各杆EA 相同,结点A 和结点B 的竖向位移均为零。
A8、图示桁架各杆EA =常数,由于荷载P 是反对称性质的,故结点B 的竖向位移等于零。
aa9、图示简支梁,当P 11=,P 20=时,1点的挠度为0.01653l EI /,2点挠度为0.0773l EI /。
当P 10=,P 21=时,则1点的挠度为0.0213l EI /。
( )l10、图示为刚架的虚设力系,按此力系及位移计算公式即可求出杆AC 的转角。
C1P11、图示梁AB 在所示荷载作用下的M图面积为ql 3。
lAl /212、图示桁架结点C水平位移不等于零。
13、图示桁架中,结点C 与结点D 的竖向位移相等。
二、选择题1、求图示梁铰C 左侧截面的转角时,其虚拟状态应取:A.;;B.D.M C.=1=1=12、图示结构A 截面转角(设顺时针为正)为:A.22Pa EI / ;B.-Pa EI 2/ ;C.542Pa EI /() ;D.-542Pa EI /() 。
aa3、图示刚架l a >>0 , B 点的水平位移是:A .不定,方向取决于a 的大小;B .向左;C .等于零;D .向右。
4、图示静定多跨粱,当EI 2增大时,D 点挠度:A .不定,取决于EI EI 12;B .减小;C .不变;D .增大。
5、图示刚架中杆长l ,EI 相同,A 点的水平位移为:A.()2302M l EI /→;B.()M l EI 023/→;C.()2302M l EI /←;D.()023M l EI /←。

结构力学——静定结构位移计算在工程和建筑领域中,结构力学作为一门重要的学科,主要研究了结构的受力、变形、破坏机理等问题。
其中,静定结构位移计算是结构力学中的一个重要内容。
静定结构所谓静定结构,是指能够通过静力学方程求解出所有节点的受力、反力和变形的结构。
这种结构是不需要知道材料的物理性质和荷载的实际情况的。
在静定结构中,结构的支座固定方式和荷载情况是已知的,因此能够通过解决一组静力学方程,求解出结构中节点的受力和变形。
静定结构位移计算静定结构位移计算是静定结构的重要计算方法之一。
在结构分析中,位移是一种常见的形变量,它反映了物体在载荷作用下发生的形变情况。
在静定结构中,位移是结构的重要参数之一。
它可以通过求解一组线性方程组得到。
具体来说,就是通过应变—位移—节点力关系,将结构各节点位移用系数矩阵和加载节点力表示出来,再通过求解一个线性方程组,就可以得到各节点的位移值。
静定结构位移计算的步骤静定结构位移计算中的步骤包括:1.列出节点位移方程节点位移与内力之间有一定的关系,可以通过位移方程和内力方程来表示。
这些方程可以根据物理实际条件进行建立。
2.确定支座反力支座反力是从位移计算中得到的结果之一。
支座反力是指结构上所有支点所承受的力,在位移计算时是必须考虑的。
3.形成节点位移方程组形成节点位移方程组时,需要考虑杆件的个数、受力条件、材料特性、支座情况等因素。
4.解出节点位移通过解一个线性方程组,我们可以根据已知的节点力和位移方程,求出每个节点的位移值。
静定结构位移计算的应用静定结构位移计算在现代工程设计中具有广泛的应用。
它能够在保证结构稳定的前提下,可以对结构进行优化设计,提高结构的安全性、稳定性、经济性等方面的性能。
除此之外,静定结构位移计算还可以应用于建筑设计、桥梁设计、机械设计、工业生产等领域中。
它可以提供结构设计的数据支持,为结构工程的实施提供参考。
静定结构位移计算是结构力学中的一个重要方向,其计算方法基于静力学方程进行,其特点是简单、可靠和实用。