最新复杂系统决策模型与层次分析法

第六章层次分析法决策是人们选择或进行判断的一种思维活动，在人们的实践活动中，常常要对某些系统的重要性作出恰当的评价，以便列出它们的轻重缓急，从而集中解决重要的问题。

有些决策是简单易断的，而有些决策则是复杂困难的，因此常常先把复杂问题分解成因素，然后把这些因素按支配关系分组形成有序的递阶层次结构，并衡量各方面的影响，最后综合人的判断，以决定决策诸因素相对重要性的先后优劣次序，这就是层次分析法的基本思路。

层次分析法的(Analytic Hierarchy Process 简记为AHP)是美国著名的运筹学家T.L.Saaty 教授于70年代初首先提出的一种定性与定量分析相结合的多准则决策方法。

该方法是社会、经济系统决策的有效工具，目前在工程计划、资源分配、方案排序、政策制定、冲突问题、性能评价等方面都有广泛的应用。

6.1 层次分析法的基本原理层次分析法的核心问题是排序，包括递阶层次结构原理、测度原理和排序原理。

下面分别予以介绍。

1.递阶层次结构原理。

一个复杂的结构问题可分解为它的组成部分或因素，即目标、准则、方案等。

每一个因素称为元素。

按照属性的不同把这些元素分组形成互不相交的层次，上一层次的元素对相邻的下一层次的全部或部分元素起支配作用，形成按层次自上而下的逐层支配关系。

具有这种性质的层次称为递阶层次。

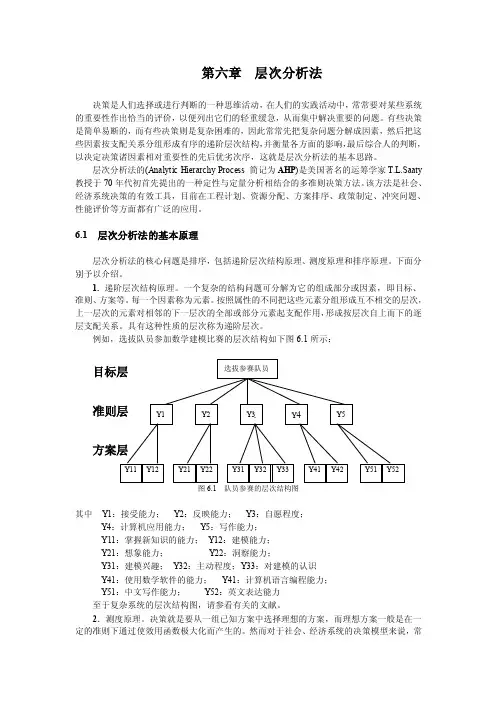
例如，选拔队员参加数学建模比赛的层次结构如下图6.1所示：图6.1 队员参赛的层次结构图其中Y1：接受能力；Y2：反映能力；Y3：自愿程度；Y4：计算机应用能力；Y5：写作能力；Y11：掌握新知识的能力；Y12：建模能力；Y21：想象能力；Y22：洞察能力；Y31：建模兴趣；Y32：主动程度；Y33：对建模的认识Y41：使用数学软件的能力；Y41：计算机语言编程能力；Y51：中文写作能力；Y52：英文表达能力至于复杂系统的层次结构图，请参看有关的文献。

2．测度原理。

决策就是要从一组已知方案中选择理想的方案，而理想方案一般是在一定的准则下通过使效用函数极大化而产生的。

综合评价决策模型方法_数学建模决策模型方法是一个重要的工具，用于解决复杂的决策问题。

综合评价决策模型方法是一个基于多个指标或因素对决策方案进行评价的方法。

该方法在数学建模中常用于分析多个决策方案的优劣，帮助决策者做出最优决策。

首先，层次分析法是一种定性与定量相结合的分析方法，用来解决多个指标之间的相对重要性问题。

它通过建立层次结构，将问题分解为若干个层次，并对各层次进行权值的确定，从而得到最终的评价结果。

层次分析法主要包括建立层次结构模型、构造判断矩阵、计算权重和一致性检验等步骤。

其优点是结构明确、能够定量地评价各指标之间的重要性，但也存在权重确定的主观性较强的问题。

其次，灰色关联度法是一种基于灰色理论的模型，用于评价多个指标之间的关联程度。

它通过建立灰色关联度模型，将多个指标的值转化为灰色数列，进行关联度计算，从而得到各指标的权重。

灰色关联度法主要包括灰色关联度计算和权重确定两个步骤。

其优点是能够考虑指标之间的关联关系，但也存在对指标值的灵敏度较高的问题。

再次，熵权法是一种基于信息熵的权重确定方法，用于评价多个指标的重要性。

它通过计算各指标的熵值和权重，得到最终的评价结果。

熵权法主要包括计算指标熵值、计算指标熵权和综合计算这三个步骤。

其优点是能够客观地确定指标的权重，但也存在对指标值范围要求较高的问题。

最后，矩阵法是一种定量化的综合评价方法，用于评价多个决策方案的优劣。

它通过构造评价指标矩阵，对各决策方案的各指标进行评分，并计算出加权总分，从而对决策方案进行排序。

矩阵法主要包括构造评价指标矩阵、对矩阵进行归一化和计算加权总分这三个步骤。

其优点是方法简单、易于理解和使用，但也存在在权重确定上存在一定主观性的问题。

总的来说，综合评价决策模型方法在数学建模中起着重要的作用。

不同的方法有不同的优缺点，适用于不同的决策问题。

决策者在选择合适的方法时，需要根据实际情况和需求综合考虑。

基于AHP(层次分析法)的企业战略决策研究【摘要】本文针对企业战略决策中常用的AHP(层次分析法)进行了研究。

在介绍了研究背景和研究意义。

接着，对AHP的原理与方法进行了详细解释，并探讨了AHP在企业战略决策中的应用。

通过案例分析，展示了AHP在实际企业中的应用效果。

分析了AHP在企业战略决策中可能存在的局限性，并提出了改进的方法。

在结论部分总结了研究成果，同时展望了未来研究方向。

通过本研究，可以为企业决策者提供更多的参考依据，提高企业战略决策的科学性和效率。

【关键词】AHP, 层次分析法, 企业战略决策, 研究背景, 研究意义, 方法原理, 应用案例, 实际应用, 局限性, 改进, 结论总结, 未来研究方向.1. 引言1.1 研究背景企业战略决策作为企业发展中至关重要的一环，对企业整体发展具有重大影响。

当前，随着市场竞争日益激烈和环境变化速度加快，企业战略决策的复杂性和风险性也在不断增加。

为了有效应对这一挑战，越来越多的企业开始借助AHP(层次分析法)来辅助进行战略决策。

通过对AHP在企业战略决策中的应用实例进行研究和总结，可以为企业提供更加科学的决策支持，提高战略决策的准确性和成功率。

研究AHP在企业战略决策中的应用具有重要的理论和实践意义。

本文旨在探讨AHP在企业战略决策中的具体应用方法，分析其优势和局限性，并提出改进措施，以期为企业战略决策提供更好的决策支持。

1.2 研究意义在实际应用中，AHP可以帮助企业对各种战略选项进行量化评估和比较，帮助企业确定最优的战略方案。

通过AHP，企业可以将主观的意见和客观的数据结合起来，避免决策者主观偏见和情绪的影响，提高决策的客观性和准确性。

研究AHP在企业战略决策中的应用具有重要的理论意义和实践价值。

通过深入研究AHP在企业战略决策中的有效性和局限性，可以为企业决策者提供更多的决策支持和工具，帮助他们更好地制定和实施战略，提高企业的竞争力和持续发展能力。

用层次分析法计算权重一、本文概述层次分析法（Analytic Hierarchy Process，简称AHP）是一种定性与定量分析相结合的多准则决策方法，由美国运筹学家T.L.Saaty教授于20世纪70年代提出。

该方法通过构建一个层次结构模型，将复杂问题分解为多个组成因素，并按照因素间的相互关联影响以及隶属关系将因素按不同层次聚集组合，形成一个多层次的分析结构模型。

通过两两比较的方式确定层次中诸因素的相对重要性，然后综合决策者的判断，确定决策方案相对重要性的总的排序。

层次分析法在权重计算中具有广泛的应用，包括项目管理、资源分配、风险评估、产品选择等各个领域。

本文将详细介绍层次分析法的原理、步骤及其在权重计算中的应用，帮助读者更好地理解和应用这一方法。

二、层次分析法基本原理层次分析法（Analytic Hierarchy Process，简称AHP）是一种定性与定量相结合的决策分析方法，由美国运筹学家T.L.Saaty在20世纪70年代初期提出。

这种方法将复杂的问题分解为各个组成因素，并将这些因素按照支配关系分组形成递阶层次结构。

通过两两比较的方式确定层次中诸因素的相对重要性，然后综合决策者的判断，确定决策方案相对重要性的总的排序。

层次分析法适用于存在多目标、多准则、多方案的系统评价、决策、预测等问题，尤其适用于那些难以完全用定量方法解决的复杂问题。

分解原理：将复杂的问题分解为若干个相对简单的子问题，这些子问题称为元素或因素。

每个元素都对应一个具体的评价准则或决策目标。

比较原理：通过两两比较的方式确定元素之间的相对重要性。

比较的结果以数值形式表示，通常使用1-9标度法，其中1表示两个元素同等重要，9表示一个元素比另一个元素极端重要，中间值表示不同等级的重要性。

合成原理：根据元素之间的相对重要性，通过合成运算得到元素的整体重要性排序。

合成运算通常采用加权求和的方法，权重由元素之间的相对重要性决定。

[收稿日期]2020-11-19　[修回日期]2021-06-17[基金项目]安徽省教育厅质量工程支持疫情防控期间重大线上教学改革研究项目(2020zdxsjg221);蚌埠医学院校级本科教学质量工程项目(2019jyxm91)[作者单位]1.蚌埠医学院第一附属医院骨科,安徽蚌埠233004;2.蚌埠医学院临床医学院,安徽蚌埠233030[作者简介]张　衡(1987-),男,博士,副教授.[通信作者]陈卫东,教授,主任医师.E⁃mail:cwd2012@[文章编号]1000⁃2200(2023)11⁃1607⁃06㊃医学教育㊃基于CIPP 模型和层次分析法的临床线上教学质量评价体系的构建张　衡1,2,李克放2,王红玉2,胡玥玥2,刘媛媛2,刘　扬1,陈　辉2,陈卫东2[摘要]目的:应用CIPP 模型和层次分析法构建临床线上教学质量评价体系㊂方法:通过文献复习㊁Delphi 法,从CIPP 模型的背景评价㊁输入评价㊁过程评价和结果评价四个方面建立临床线上教学质量评价指标,并运用层次分析法计算各指标权重,构建临床线上教学质量评价体系㊂结果:建立了包含4个一级指标㊁19个二级指标㊁45个三级指标的临床线上教学质量评价体系㊂结论:基于CIPP 模型和层次分析法的临床线上教学评价体系可基本反映临床线上教学与管理情况,对评价临床线上教学质量和探索㊁完善临床线上教学模式具有一定的参考价值㊂[关键词]临床线上教学;CIPP 模型;层次分析法;教学模式[中图法分类号]R 192 [文献标志码]A DOI :10.13898/ki.issn.1000⁃2200.2023.11.029Construction of evaluation system of clinical online teaching quality basedon CIPP model and analytic hierarchy processZHANG Heng 1,2,LI Ke⁃fang 2,WANG Hong⁃yu 2,HU Yue⁃yue 2,LIU Yuan⁃yuan 2,LIU Yang 1,CHEN Hui 2,CHEN Wei⁃dong 2(1.Department of Orthopedics ,The First Affiliated Hospital of Bengbu Medical College ,Bengbu Anhui 233004;2.School of Clinical Medicine ,Bengbu Medical College ,Bengbu Anhui 233030,China )[Abstract ]Objective :To construct an evaluation system of clinical online teaching quality using CIPP model and analytic hierarchy process.Methods :The evaluation indexes of clinical online teaching quality were established from the four aspects of context,input,process and product evaluation of CIPP model by literature review and Delphi method.The weight of each index was calculated by analytic hierarchy process to construct the evaluation system of clinical online teaching quality.Results :An evaluation system of clinical online teaching quality with 4first⁃level indicators,19second⁃level indicators and 45third⁃level indicators was constructed.Conclusions :The evaluation system of clinical online teaching quality based on CIPP model and analytic hierarchy process can basically reflect the situation of clinical online teaching and management,which has a certain reference value for evaluating the clinical online teaching quality,exploring and improving the clinical online teaching model.[Key words ]clinical online teaching;CIPP model;analytic hierarchy process;teaching model 受新型冠状病毒感染(corona virus disease2019,COVID⁃19)疫情的影响,教育部要求各高校开展线上教学㊂随着线上教学逐步开展和趋于正轨,线上教学的关注点从最初的恢复教学活动和秩序逐渐转移到提高教学水平质量[1]㊂然而,目前的线上教学实践存在一些弊端:教师激励和监管机制不足㊁课程质量良莠不齐㊁学生 逃课”现象时有发生㊁师生之间交流减少等㊂临床医学专业的教师多为在疫情防控和临床诊疗中肩负一线工作的医生,同时面临繁重的科研任务,投入到临床教学工作的时间和精力相对较少,且临床教学强调理论与实践结合,临床医学线上教学质量难以保证㊂因此,建立一个科学㊁完整的临床线上教学质量评价体系,客观评价教师教学活动,监督学生学习过程,提高教学质量是目前亟待解决的问题㊂本研究通过文献复习㊁Delphi 法,运用CIPP 模型建立临床线上教学质量评价指标,运用层次分析法计算各级指标权重,构建临床线上教学质量评价体系㊂1　资料与方法1.1　总体设计　首先通过查阅资料建立临床线上教学质量评价指标,然后应用层次分析法计算各级指标权重,构建临床线上教学质量评价体系,流程图见图1㊂1.2　资料来源　通过中国知网㊁万方㊁维普㊁Pubmed㊁Medline 等中英文数据库,搜集国内外关于CIPP模型用于临床教学㊁线上教学质量评价的论文,提取质量评价指标后应用Delphi法向专家咨询㊂1.3　研究方法　1.3.1　CIPP模型　CIPP模型也称决策导向型评价模型㊂美国著名教育评价专家Stufflebeam1965年在分析总结 教育评价之父”泰勒提出的行为目标模式的基础上提出了决策导向型评价模式[2]㊂CIPP 评价模式包括背景㊁输入㊁过程评价和结果评价,各种评价英文的首字母构成CIPP㊂背景评价是评估研究对象周围的环境㊁分析存在的问题㊁确定研究的需要和明确研究的目标㊂输入评价是在确定研究目标后,评估实现目标所需要的条件㊁资源和所设计方案的可行性和优缺点㊂过程评价是对方案实施过程中的执行效率㊁不利因素等进行及时地评估,不断地反馈和修正㊂结果评价是对所达到的目标进行衡量与解释,探讨付出与产出的关系,为扩展或终止研究提供依据[3]1.3.2　Delphi法　Delphi法[4]是将所研究的问题函询该领域的专家,收集所有专家意见并进行总结,再匿名反馈给专家,经过多次重复直至获得统一的意见㊂应用Delphi法向专家咨询㊂该方法向每个成员征求意见或看法,在实施的时候,采取背对背方式,并且利用多次征求的方式进行,最后将不同意见综合在一起㊂本研究在蚌埠医学院第一附属医院中选取临床㊁教学和管理专家20名,专家工作年限均在10年及以上,具有中级以上职称和线上临床教学管理经验,并同意支持配合完成咨询工作,专家基本信息见表1㊂将提取质量评价指标进行专家咨询,并对结果进行整理㊁归纳和总结,初步建立临床线上教学临床在线教学质量评价各级指标㊂1.3.3　层次分析法　层次分析法是一种把定性分析和定量分析相结合的层次权重决策分析方法㊂它是把复杂问题中的各个因素划分为目标㊁准则㊁方案等层次,利用数学方法对每一层次的因素的重要性权重进行计算和排序,根据计算结果选择相应的决策㊂建立层次结构模型是指把分析的问题分解成三至四层㊂第一层是目标层,即要解决的具体问题;第二层是准则层,即衡量目标层问题的具体实现方法;子准则层是对准则层的细化;最底层的方案层是决策时从中选出一个最佳方案㊂是否需要子准则层,需要根据具体的问题而定㊂示意图见图2㊂本研究通过层次分析法构建临床线上教学质量评价指标层次结构模型,计算各级指标权重,提高临床线上教学质量评价指标体系的科学性和权威性㊂表1　被函问专家一般情况项目n构成比/%性别　男945.00　女1155.00年龄/岁　<401785.00　40~<50210.00　≥501 5.00职称　中级及以下840.00　副高1050.00　正高210.00工作岗位　部门负责人210.00　教师1575.00　教务管理人员315.00工作年限/年　11~151785.00　16~201 5.00　>20210.001.3.4　专家的积极系数和权威系数　积极系数是指专家参与调查的积极程度,一般用回收的有效问卷数与发放问卷的总数比值表示㊂权威系数(Cr)是指专家的代表性,反映调查结果的可靠性和权威性,主要用判断程度(Ca)和熟悉程度(Cs)计算㊂Ca是指专家对每个问题的判断依据,通常包括理论依据㊁实践经验㊁国内外资料㊁直觉四类㊂Cs表示专家对每个问题的熟悉程度,分为5个等级㊂Ca㊁Cs 在本研究中的赋值详见表2㊂Cr≥0.7一般认为研究结果是可靠的㊂权威程度计算公式:Cr=(Cs+ Ca)/2㊂表2　判断依据及熟悉程度分类判断依据赋值/分熟悉程度赋值/分理论依据1不熟悉0.2实践经验0.8不太熟悉0.4国内外资料直觉0.60.2一般熟悉0.60.8很熟悉11.3.5　变异系数和协调系数(W)　变异系数为标准差和平均值之比㊂一般认为,变异系数<0.2,说明可信度较高㊂本研究中可进行多轮咨询,直至发现赋值的变异系数<0.2㊂Kendall′s W系数,是一个等级相关系数,可用于计算多个等级变量的关联程度㊂对各级指标的评价由专家自由评分,分值限定在0~1分,专家给出的分值越高说明专家对该项指标的认可程度越高,反之越低㊂一般情况下,0≤W ≤1㊂W值越大,说明专家的协调度和对指标的认可度越高㊂同一评价者无相同等级评定时,W的计算公式:W=12S K2(N3-N)其中,N指被评价的对象数,本研究中指各级指标数;K为评分者人数或评分所依据的标准数,本研究中指20位专家;S为每个被评价对象所评等级之和与所有这些和的平均数的离差平方和㊂1.3.6　权重　权重是指每个指标在总体中所占有的比重或地位等㊂指标中的权重具有下列特点:同一级指标的权重之和为1;同级指标被分解为各个子系统时,每个子系统中各指标权重之和为1㊂本研究用层次分析法计算各级指标权重,同时我们引入了变异系数来判断计算出来的权重结果合理性分析㊂若变异系数波动幅度较小,说明计算出的权重可靠程度更高㊂层次分析法计算方法如下:(1)构建判断矩阵㊂收集数据后构建判断矩阵,判断矩阵的标度M ij可以是1~9及其倒数㊂当2个因素相比,1表示2个因素同样重要,3表示一个元素比另一个元素稍微重要,5表示一个元素比另一个元素明显重要,7表示一个元素比另一个元素强烈重要,9表示一个元素比另一个元素极端重要,2㊁4㊁6㊁8表示上述两相邻判断的中间值,倒数表示相应2个因素交换次序比较的重要性㊂(2)利用matlab法进行层次排序和一致性检验㊂当n阶矩阵A=(a ij)n×n 的最大特征值λ≈n时,可以确定判断矩阵具有一致性,则它对应的特征向量W=(w1,w2, ,w n)能够反映各个因素的比重㊂其中,CI=(λmax-n)/ (n-1),是一致性指标;RI是平均随机一致性指标,对应1~9阶的矩阵,RI∈(0,0,0.58,0.90,1.12, 1.24,1.32,1.41,1.45);CR=CI㊁RI是一致性比率,当CR<0.1,可以认为判断矩阵具有满意的一致性㊂如果判断矩阵不具有满意的一致性,则需要调整判断矩阵以使CR<0.1㊂(3)根据综合权重分析结果建立指标体系㊂经过反复调整判断矩阵,以及专家的咨询确认,最后确定判断矩阵㊂利用上面的matlab程序判断矩阵进行层次排序和一致性检验㊂从结果分析,CR均<0.1,表明通过了一致性检验,该层次结构模型和各个指标的权重合理,可以作为临床线上教学质量评价的指标体系㊂1.4　统计学方法　对各级各项指标进行集中和离散程度分析,集中程度主要采用(x±s),离散程度主要通过对专家意见的变异系数和协调系数进行分析[5]㊂2　结果2.1　积极系数和权威系数　发放问卷20份全部收回且均有效,积极系数为100%;专家提出意见的比率为90%(18/20)㊂本研究中Cs=0.752,Ca= 0.865,Cr=0.809㊂2.2　变异系数和协调系数　本研究构建的临床线上教学质量评价指标体系共有一级评价指标4个,包括19个二级评价指标和45个三级指标㊂专家对三级指标的评分见表3㊂本轮咨询最终一级指标的肯德尔协调系数为0.580(χ2=130.01,P<0.01),说明专家意见协调较好,指标评估的结果可信度较高㊂2.3　权重　一级指标的权重分别是:0.23㊁0.24㊁0.27㊁0.26,说明一级指标均有重要作用,二级指标重要性开始出现分化(见表4)㊂表3　专家对三级指标的评分三级指标专家打分　平均值 标准差 变异系数　办学目标0.9250.145　0.114办学规划0.8100.1920.137专业课程资源0.8550.1670.195课外学习资源0.8300.1870.125线上教学经费0.7900.1860.136线上师资力量0.9200.1150.125政府支持力度0.9100.1520.167政策完善程度0.8400.1790.113学生学习设备0.8950.1570.176教师教学设备0.8800.1610.183教学时间安排0.9050.1390.154教学人员组织0.8850.1530.173网络质量评价0.8350.1530.183网络学习平台0.8900.1370.154发表学术论文数0.7600.1820.139获科技成果奖数0.6700.1530.128教学实施能力0.8600.1790.108教学研究能力0.7500.1760.135教学创新能力0.7650.1730.126高职授课情况0.8150.1810.123教学模式0.7700.1720.123教学方法0.8500.1570.185教学手段0.8200.1670.104考核方式0.8450.1730.105考核内容0.8950.1540.172考核结论0.8400.1700.202教师课堂表现0.8250.1770.115网课教学秩序0.8550.1610.188学生在线情况0.8900.1610.188学生学习状态0.7800.1770.126学习质量监管0.7650.1930.152线上课程安排0.8200.1770.115教师各院系部的满意度0.9050.1190.132教师对院校管理的满意度0.8350.1660.199组织机构0.7900.1970.149专家参与重大决策0.8000.1720.115学生思维与信息搜寻0.8000.1750.118学生线上学习自主性0.7850.1810.131学生专业成绩考核0.8000.1490.186学生实践能力0.7300.1560.114同行工作评价0.8550.1670.195学生工作评价0.8250.1620.196教师自我评估0.8900.1480.167专业建设0.8650.1630.189教材建设0.7750.1710.1213　讨论3.1　构建临床线上教学评价体系的重要性　2020年,英国联合信息系统委员会发布的报告‘评价未来:面向2025的五个原则和目标“指出,随着数字教育时代的到来,未来的教育评价应遵循真实性㊁无障碍获取㊁适当地自动化㊁持续性及安全性五大原则,需要提高教师的数字化技能,增强教师用新的方法评估教育的信心并允许教师有更多的时间去实践,从而推动数字教育的发展[6]㊂临床医学教学质量直接影响到医学生的临床思维㊁技能水平和医疗服务质量㊂在疫情背景下开展的临床线上教学,这种新的教学模式的出现使得教学质量评价无章可循,无法可依㊂因此,构建临床线上教学质量评估体系,有助于对教学方法设计㊁教学活动实施㊁教学结果反馈等方面进行全面监管和评估[7]㊂CIPP评价模式是在综合分析行为目标模式㊁目标游离评价模式等的基础上,建立起来的具有全面性㊁过程性㊁发展性等特点的教育评价模式㊂行为目标模式过于关注预期的目标,目标游离评价模式过于注重实际效果㊂CIPP模式则融合多种评价方式于一体,不仅仅局限于结果评价,可以较全面地反映线上教学的实际情况㊂它具有决策导向功能,可以为统计者提供决策信息[8]㊂本研究建立了一个含4个一级指标㊁19个二级指标㊁45个三级指标的临床线上教学评价体系,为线上教学评价提供丰富的指标和参考标准等㊂3.2　基于Delphi法的评价指标体系的构建　Delphi法应用的具体流程包括成立专门研究小组,制作咨询表,挑选专家并进行多轮函问,统计数据并进行计算,初步建立评价体系㊂本项目共询问了20位专家,集中了众多优秀教师的观点,增强了研究结果的可信度和说服力㊂本研究将提取的质量评价指标制作成问卷发放给专家,采用匿名搜集信息法,减少了专家之间的横向联系,得出数据相对真实可靠㊂从咨询表的统计结果来看[8],咨询表的回收率为100%,说明专家参与该项目的积极性较高,并且大部分专家积极地对指标提出了意见和看法㊂专家的权威系数为0.809,提示本研究的专家权威程度相对较高,给出的意见比较可靠,有相当大的参考价值㊂变异系数多数<0.2,说明专家协调程度很高㊂肯德尔协调系数为0.580,>0.5,说明专家的协调度较高㊂同时,该方法也存在一定局限性,如存在主观判断性㊁忽视小部分人的看法而可能使结果与实际不符等㊂首轮调查问卷中纳入的评价指标内容(如教学实施评价)部分来源于已发表文献[9],存在时间局限性,不知是否会对结果产生影响,所以本点评表内容仍需在后续实践中考核并进一步优化㊂表4　各级指标权重及变异系数一级指标权重变异系数二级指标 权重变异系数三级指标 权重变异系数教学背景0.230.173办学定位7.660.257办学目标47.720.225办学规划52.280.158线上资源39.780.128专业课程资源69.790.137课外学习资源30.210.195教学投入37.250.116线上教学经费40.520.187线上师资力量59.480.156政策环境15.310.149政府支持力度49.250.101政策完善程度50.750.098教学组织0.240.168教学设备28.790.156学生学习设备52.180.115教师教学设备47.820.131教学安排13.850.137教学时间安排46.540.128教学人员组织53.460.117网络空间12.850.194网络质量评价31.190.157网络学习平台69.810.126学术能力11.210.136发表学术论文数49.220.115获科技成果奖数51.880.107教学能力33.300.075教学实施能力30.890.124教学研究能力20.780.208教学创新能力24.820.103高职授课情况23.510.176教学实施0.270.076课程实施11.550.181教学模式28.410.197教学方法39.250.091教学手段32.340.156课程考核标准8.960.193考核方式17.860.217考核内容50.230.103考核结论31.910.139教师教学25.530.106教师课堂表现59.470.079网课教学秩序40.530.082学生学习35.040.065学生在线情况47.740.092学生学习状态52.260.056学校管理 5.330.194学习质量监管59.460.087线上课程安排40.540.193教学服务水平 4.320.187教师各院系部的满意度49.290.189教师对院校管理的满意度50.710.171专家治学9.270.199组织机构65.320.146专家参与重大决策34.680.175教学效果0.260.073学生能力60.580.067学生思维与信息搜寻48.670.078学生线上学习自主性37.930.069学生专业成绩考核10.240.193学生实践能力 3.160.057教师评估29.350.146同行工作评价27.210.068学生工作评价40.570.052教师自我评估32.220.135建设效果10.070.165专业建设54.740.194教材建设45,260.1913.3　基于matlab的层次分析法和权重分析　本研究应用matlab软件进行层次分析法相关因素的权重计算㊂应用matlab法计算权重具有简便易用㊁处理强大㊁程序可视化㊁提高研究效率等优点[10]㊂权重反映专家对评价指标的认可度和该指标存在的合理性㊂从权重计算结果来看,本研究中一级指标权重相差较小,而二级㊁三级指标权重相差较大㊂若评价指标权重越高,说明该指标在教学评价体系中的重要性越高,用于评价线上教学情况更合理且更具代表性㊂从整体水平上分析,各指标变异系数大都集中在0.052~0.250,一级指标权重大小几乎相当(分别是0.23㊁0.24㊁0.27㊁0.26),说明专家对指标评价的一致性较高且认为这四个指标的重要程度大致相同㊂从局部分析,如在教学背景评价方面,可以发现线上资源和教学投入评价权重占比相对较高,而办学定位㊁政策环境方面评价占比相对较低㊂这说明线上教学评价应更侧重于从专业课程资源,课外学习资源等方面进行评价㊂最后,对于权重较高的指标,说明越应从这些方面进行线上教学评价㊂综上,基于CIPP模型和层次分析法的临床线上教学质量评价体系可基本反映临床线上教学与管理情况,对评价临床线上教学质量和探索㊁完善临床线上教学模式有一定的参考价值㊂CIPP评价模式对于评价临床线上教学质量具有重要意义,有极大的探索和推广价值㊂它和层次分析法有机结合㊁互相补充,构建了一个较完备的质量评价体系㊂本研究也可说明线上教学作为一种新教学模式,既有广受欢迎之处又有亟待完善之处,需要进一步改进和优化㊂本研究尚处于初步阶段,存在评价指标不够全面㊁研究样本量小㊁代表性不够强等问题,其科学性及可行性也有待进一步验证㊂在进一步研究中,可以采取扩大试验范围㊁不断丰富和完善评价指标㊁及时科学反馈评价信息㊁有效运用评价反馈结果等[11]方式,增强评价体系的合理性和科学性㊂[参考文献][1]　JSIC.The future of assessment for Five Principles,Five Targets for2025[EB/OL].https://www.jisc.ac/reports/the⁃future ofassessment,2020⁃03⁃20.[2]　胡晨霞,李耿,陈贤春,等.中医院校双语教学CIPP模式评价体系构建探讨[J].中国高等医学教育,2015,(3):28. [3]　董颖,郑友取,李俊,等.高校创业教育CIPP评价模型体系构建及实证研究[J].中国软科学,2017,A1:314.[4]　TABRIZI JS,FARAHBAKHSH M,SHAHGOLI J,et al.Designingexcellence and quality model for training centers of primary healthcare:A Delphi method study[J].Iran J Public Health,2015,44(10):1367.[5]　苗亚杰,王君俏,梁燕,等.基于CIPP评价模式构建护理学高仿真模拟教学评价框架[J].护理学杂志,2016,31(7):58. [6]　薛成龙,李文.国外三所大学线上教学的经验与启示[J].中国高教研究,2020(4):12.[7]　李克寒,刘瑶,谢惠旭,等.新冠肺炎疫情下线上教学模式的探讨[J].中国医学教育技术,2020,34(3):264. [8]　张芮.我国STEM教育项目评价指标体系研究[D].北京:北京邮电大学教育技术研究所,2019.[9]　柳芳,陶丝雨,谢俊大,等.基于德尔菲法构建中药饮片处方点评内容[J].中国医院药学杂志,2020,40(12):1. [10]　黄惠.MATLAB在高职线性代数教学中的应用研究[J].中阿科技论坛,2020,(9):164.[11]　胡晓辉,韩芳,董大奎,等.基于CIPP模式的高职专业教学质量评价指标体系构建研究[J].中国职业技术教育,2015,(3):27.(本文编辑　赵素容)(上接第1606页)[参考文献][1]　曹朝晖,李俐娟,王五洲,等.基于PBL教学法在医学留学生‘生物化学“教学实践中的应用探索[J].广东化工,2021,48(13):236.[2]　张伟,王林涛,戚小强,等.基于微课的翻转课堂教学模式在嘌呤核苷酸的分解代谢中的教学设计与反思[J].生命的化学,2021,41(7):1403.[3]　杨静,吴刚,庞一强,等.在医学生物化学教学中应用LBL+PBL+CBL三轨教学模式的体会[J].包头医学院学报,2013,29(5):98.[4]　罗晶婧,胡梅,蔺婷,等.思维导图在中医药‘生物化学“教学中的应用[J].中国继续医学教育,2018,10(33):24. [5]　赵婷,蔡凤英,张承玉.思维导图用于高职护理专业生物化学教学的效果评价[J].继续医学教育,2020,34(6):33. [6]　东尼㊃博赞.思维导图:大脑使用说明书[M].张鼎昆,徐克茹,译.北京:外语教学与研究出版社,2005.[7]　单妍,范戎,谢薇,等.浅谈思维导图在医学生物化学教学过程中的优势[J].教育现代化,2019,6(90):42. [8]　周南香,冯国琴,刘美华,等.基于思维导图联合定量化预测模型对缺血性脑卒中合并吞咽障碍病人的护理实践[J].蚌埠医学院学报,2021,46(11):1634.[9]　南文滨,郝永伟,井长勤.思维导图用于药学专业生物化学教学效果的评价[J].基础医学教育,2020,22(1):25. [10]　李小琼,詹剑,冯赞杰,等.思维导图在生物化学理论教学中的应用[J].基础医学教育,2020,22(5):324. [11]　段正秀.思维导图在高职院校护理专业生物化学教学中的应用效果研究[J].卫生职业教育,2021,39(5):42. [12]　宋宜宁,蒋国君,董淑英,等.思维导图与概念图结合在药理学教学中的应用[J].蚌埠医学院学报,2018,43(9):1220.(本文编辑　赵素容)。

层次分析法(AHP)与网络层次分析法(ANP)的比较作者：孙铭忆来源：《中外企业家》 2014年第4期孙铭忆（济南大学，山东济南 250022）摘要：在多目标决策中，层次分析法（AHP）是使用频率较多的研究方法，网络层次分析法（ANP）是对层次分析法的拓展和延伸。

本文在论述层次分析法（AHP）与网络层次分析法（ANP）概念模型的基础上，对比了两种方法在系统模型和判断矩阵构建方面的异同点，为更好地利用这两种决策方法提供理论基础。

关键词：层次分析法；网络层次分析法；系统构建；判断矩阵；方法对比中图分类号：C931文献标志码：A文章编号：1000-8772（2014）10-0067-02著名的经济学家赫伯特·西蒙提出“管理即是决策”，因此，无论是在企业中还是在我们的日常生活中都会遇到大大小小的决策问题[1]。

从宏观层次来看，我们的国家领导人面临着政治、经济、文化和军事等方面的决策，决策的科学与否直接关系到国家的安危和兴旺，关系到整个地区的长治久安；从中观层次来讲，企业的管理者时时刻刻面临着决策问题，大到战略决策、小到生产计划决策，每一个决策都关系到企业的可持续发展；从微观层次来说，每个人也都面临着诸如学习、就业、旅行等日常决策问题，它们会影响到家庭的和谐和个人的发展。

由此可见，正确的决策是各个实体发展的基础。

就决策的方法而言，同一个问题按照不同的方法分析可以得出不同的结论，一方面是因为不同方法在数据处理时的侧重点不同，另一方面是因为选取了不适用的决策方法，得出了具有误导性的结论。

因此，选择适当的决策方法是进行恰当决策的关键所在。

简单的决策方法虽然容易实施，但会因考虑不周等原因导致非常可怕的后果，比如经验主义，拍脑袋决策等，相反，科学的决策方法则能够为我们提供合理的结果，帮助我们做出正确的决策。

对于单目标决策，依靠模型就能够精确地描述问题，其结果也能够通过统计、运筹、计算机等技术得出。

而对于多目标决策，其复杂性明显上升，我们通常会利用层次分析法及网络层次分析法等进行决策分析。

层次分析法（Analytic Hierarchy Process，简称AHP）是将与决策总是有关的元素分解成目标、准则、方案等层次，在此基础之上进行定性和定量分析的决策方法。

该方法是美国运筹学家匹茨堡大学教授萨蒂于20世纪70年代初，在为美国国防部研究"根据各个工业部门对国家福利的贡献大小而进行电力分配"课题时，应用网络系统理论和多目标综合评价方法，提出的一种层次权重决策分析方法。

层次分析法的特点是在对复杂的决策问题的本质、影响因素及其内在关系等进行深入分析的基础上，利用较少的定量信息使决策的思维过程数学化，从而为多目标、多准则或无结构特性的复杂决策问题提供简便的决策方法。

尤其适合于对决策结果难于直接准确计量的场合。

选择。

比如选择一个旅游景点时，你可以从宁波、普陀山、浙西大峡谷、雁荡山和楠溪江中选择一个作为自己的旅游目的地，在进行选择时，你所考虑的因素有旅游的费用、旅游的景色、景点的居住条件和饮食状况以及交通状况等等。

这些因素是相互制约、相互影响的。

我们将这样的复杂系统称为一个决策系统。

这些决策系统中很多因素之间的比较往往无法用定量的方式描述，此时需要将半定性、半定量的问题转化为定量计算问题。

层次分析法是解决这类问题的行之有效的方法。

层次分析法将复杂的决策系统层次化，通过逐层比较各种关联因素的重要性来为分析以及最终的决策提供定量的依据。

所谓层次分析法，是指将一个复杂的多目标决策问题作为一个系统，将目标分解为多个目标或准则，进而分解为多指标（或准则、约束）的若干层次，通过定性指标模糊量化方法算出层次单排序（权数）和总排序，以作为目标（多指标）、多方案优化决策的系统方法。

层次分析法是将决策问题按总目标、各层子目标、评价准则直至具体的备投方案的顺序分解为不同的层次结构，然后得用求解判断矩阵特征向量的办法，求得每一层次的各元素对上一层次某元素的优先权重，最后再加权和的方法递阶归并各备择方案对总目标的最终权重，此最终权重最大者即为最优方案。

层次分析法模型范文层次分析法（Analytic Hierarchy Process，简称AHP）是Thomas L. Saaty于1970年提出的一种多准则决策方法，它能够将复杂的问题分解为多个层次，便于分析和决策。

AHP通过建立层次结构模型，将决策问题分解为准则层、方案层和目标层，并通过对准则和方案进行比较和权重计算，最终得出最优方案。

AHP模型包括以下几个重要的步骤：1.建立层次结构：首先，确定决策问题的目标和准则，将其构建为一个层次结构，目标位于最顶层，准则位于中间层，方案位于底层。

层次结构类似于一颗倒置的树，从上到下逐级递减。

2.构建判断矩阵：判断矩阵是AHP模型的核心，用于比较准则和方案之间的重要性。

在判断矩阵中，行表示准则或方案，列表示准则或方案之间的相对重要性。

通过两两比较准则和方案，填写判断矩阵中的元素。

3.计算权重：利用判断矩阵，可以计算出每个准则和方案的权重，即它们在整个决策问题中的相对重要性。

计算权重的方法通常有特征值法和最大特征向量法。

4.一致性检验：在AHP模型中，一致性是一个重要的考虑因素。

一致性检验用于评估判断矩阵的可靠性，判断矩阵的一致性越高，则决策结果越可信。

一致性检验通常采用计算一致性指标CI和随机一致性指标RI，判断矩阵的一致性比率CR=CI/RI。

5.综合决策：最后，利用准则和方案的权重，可以综合计算出每个方案的综合得分。

根据得分，可以进行方案排序和最终决策。

层次分析法模型的主要优势是能够将决策问题分解为多个层次，使问题更加具体化和可操作化；通过比较和权重计算，能够客观地评估准则和方案的重要性；在一致性检验方面，能够对判断矩阵进行可靠性评估，提高决策结果的可信度。

然而，层次分析法模型也有一些局限性。

首先，判断矩阵的构建过程需要专家的主观判断，可能存在信息不准确或不完全的问题。

其次，一致性检验需要进行一致性比率的计算，但并没有明确的标准来判断什么水平的一致性是可接受的。

基于AHP(层次分析法)的企业战略决策研究层次分析法（AHP）是一种多层次的决策分析方法，被广泛应用于企业的战略决策中。

在企业的决策过程中，决策者需要考虑众多的因素，层次分析法能够通过建立层次关系模型，将整个决策过程划分为若干个层次，并分别分析每个层次的因素，最终确定最优的决策方案。

首先，决策者需要确定决策目标，将其作为最高层次的因素。

例如，企业可能需要制定一项新的市场拓展战略，这就是目标层次。

其次，决策者需要确定影响目标层次的因素，这些因素可以分为内部和外部因素。

内部因素可能包括企业的市场份额、资金情况、人力资源等，而外部因素可能包括竞争对手的市场份额、政策环境等。

这些因素构成了层次分析法的第二层次，也称为准则层次。

第三层次是对准则层次中每个因素的进一步分解。

例如，在内部因素中，资金情况可以进一步分解为现有资产、融资情况等。

这样将会形成准则层次的子层次。

接下来，对于每个子层次的因素，使用AHP方法进行比较。

这通过对每个因素进行两两比较来完成，将比较结果表示为权重系数。

比较结果可以用数学模型进行计算和分析，从而确定每个因素在整个决策模型中的权重系数。

通过这种方式，我们可以对整个决策模型进行分析和评估，从而提出一系列可能的方案和实施策略，并将它们进行比较和选择。

由于AHP方法的灵活性和有效性，它可以在众多的选择方案中帮助企业确定最优方案，在不同的决策层面提供清晰的指导。

在实际应用中，层次分析法经常用于评估不同的风险，预测购买的可能性，并为企业制定最佳战略提供支持。

总之，层次分析法是一种非常实用的企业决策方法，可以帮助决策者在复杂的决策环境中，基于准确的数据和信息制定最佳的战略和计划，并在高度不确定的市场环境中保持竞争优势。

层次分析法确定评价指标权重及计算一、本文概述层次分析法（Analytic Hierarchy Process，简称AHP）是一种多准则决策分析方法，由美国运筹学家萨蒂（T.L.Saaty）教授于20世纪70年代初期提出。

这种方法通过将复杂问题分解为若干层次和若干因素，在各因素之间进行简单的比较和计算，得出不同方案的权重，从而为决策者提供定量化的决策依据。

本文旨在详细阐述层次分析法在确定评价指标权重及计算过程中的应用，包括其基本原理、步骤、优缺点以及在实际问题中的案例分析。

通过本文的阐述，读者可以更好地理解和掌握层次分析法的核心思想和应用方法，为解决复杂的多准则决策问题提供有力的工具。

二、层次分析法的基本原理层次分析法（Analytic Hierarchy Process，简称AHP）是一种定性与定量相结合的决策分析方法，由美国运筹学家T.L.Saaty教授于20世纪70年代初提出。

这种方法通过将复杂问题分解为若干层次和若干因素，在各因素之间进行简单的比较和计算，得出不同方案的权重，从而为决策者提供科学、合理的决策依据。

建立层次结构模型：将问题分解为不同的层次，包括目标层、准则层和方案层。

目标层是决策问题的最终目标或理想结果；准则层是实现目标所需考虑的各种准则或因素；方案层是实现目标的具体方案或措施。

构造判断矩阵：通过比较同一层次中各因素对于上一层次中某一准则的重要性，构造判断矩阵。

判断矩阵的元素通常采用1-9标度法赋值，表示各因素之间的相对重要性。

计算权重向量：通过求解判断矩阵的最大特征值及其对应的特征向量，得到各因素对于上一层次准则的权重向量。

常用的求解方法有和积法和方根法。

一致性检验：为保证判断矩阵的一致性和合理性，需要进行一致性检验。

一致性检验的指标为一致性比例CR，当CR小于1时，认为判断矩阵的一致性可以接受；否则，需要重新调整判断矩阵的元素值。

通过层次分析法，我们可以将复杂的决策问题分解为若干层次和因素，通过定性与定量相结合的分析方法，得出不同方案的权重，从而为决策者提供科学、合理的决策依据。

§3.4 复杂系统决策模型与层次分析法Analitic Hierachy Process (AHP) T.L.Saaty 1970’一种定性和定量相结合的、系统化、层次化的分析方法。

一. 问题举例1. 在海尔、新飞、容声和雪花四个牌号的电冰箱中选购一种。

要考虑品牌的信誉、冰箱的功能、价格和耗电量。

2. 在泰山、杭州和承德三处选择一个旅游点。

要考虑景点的景色、居住的环境、饮食的特色、交通便利和旅游的费用。

3. 在基础研究、应用研究和数学教育中选择一个领域申报科研课题。

要考虑成果的贡献（实用价值、科学意义），可行性（难度、周期和经费）和人才培养。

二. 模型和方法1. 层次结构模型的构造步骤一：确定层次结构，将决策的目标、考虑的因素（决策准则）和决策对象按它们之间的相互关系分为最高层、中间层和最低层，绘出层次结构图。

最高层：决策的目的、要解决的问题。

最低层：决策时的备选方案。

中间层：考虑的因素、决策的准则。

对于相邻的两层，称高层为目标层，低层为因素层。

例例3.步骤二： 通过相互比较，确定下一层各因素对上一层目标的影响的权重，将定性的判断定量化，即构造因素判断矩阵。

步骤三：由矩阵的特征值确定判别的一致性；由相应的特征向量表示各因素的影响权重，计算权向量。

步骤四： 通过综合计算给出最底层（各方案）对最高层（总目标）影响的权重，权重最大的方案即为实现目标的最由选择。

2. 因素判断矩阵比较n 个因素y=(y 1,y 2,…,y n )对目标 z 的影响.采用两两成对比较，用a ij 表示因素 y i 与因素y j 对目标z 的影响程度之比。

通常用数字 1~ 9及其倒数作为程度比较的标度， 即九级标度法x i /x j 相当 较重要 重要 很重要 绝对重要a ij 1 3 5 7 92, 4, 6, 8 居于上述两个相邻判断之间。

当a ij > 1时，对目标 Z 来说 x i 比 x j 重要, 其数值大小表示重要的程度。

层次分析法综述摘要：层次分析法(AHP法) 是一种解决多目标的复杂问题的定性与定量相结合的决策分析方法。

该方法将定量分析与定性分析结合起来，用决策者的经验判断各衡量目标能否实现的标准之间的相对重要程度，并合理地给出每个决策方案的每个标准的权数，利用权数求出各方案的优劣次序，比较有效地应用于那些难以用定量方法解决的课题。

本文从层次分析法的基本概念出发，通过层次分析法的建模分析与对比，更加深入学习和了解层次分析法。

关键词：层次分析法层次结构模型判断矩阵权重1、概述1.1层次分析法的概念层次分析法（Analytic Hierarchy Process简称AHP）是将决策总是有关的元素分解成目标、准则、方案等层次，在此基础之上进行定性和定量分析的决策方法。

层次分析法（AHP）是美国运筹学家匹茨堡大学教授萨蒂(T.L.Saaty)于上世纪70年代初，为美国国防部研究“根据各个工业部门对国家福利的贡献大小而进行电力分配”课题时，应用网络系统理论和多目标综合评价方法，提出的一种层次权重决策分析方法，是对方案的多指标系统进行分析的一种层次化、结构化决策方法，它将决策者对复杂系统的决策思维过程模型化、数量化。

应用这种方法，决策者通过将复杂问题分解为若干层次和若干因素，在各因素之间进行简单的比较和计算，就可以得出不同方案的权重，为最佳方案的选择提供依据。

1.2层次分析法的特点一、层次分解性层次分析法首先找出问题所牵连的主要因素，将复杂系统的各个因素按它们的关联隶属关系，层层分解，构建有层次的结构形成阶梯层次模型，从而可以将复杂的问题分解成若干层次，在把问题变得比原来简单得多的情况下加以分析。

二、定量与定性相结合层次分析法是系统分析中对非定量事件做定量分析的一种新的决策方法。

在将复杂问题进行分解的前提下，确定思维判断的相对标度，并将人们的主观判断按照此准则做数量形式的表达、处理和分析，从而实现定性向定量的转变。

2、层次分析法的产生与发展传统的常用的研究自然科学和社会科学的定量方法有：函数分析方法：利用经典的数学工具分析观察的因果关系；统计分析方法：利用大量观测数据寻求统计规律，用随机数学方法描述（自然现象、社会现象）现象的规律。