【研究院】[北京](8)2018一模(理)分类汇编——圆锥曲线(教师版)

2018二模分类汇编——圆锥曲线1.（2018东城二模·理）已知双曲线C ：x 2a 2－y 2b 2＝1的一条渐近线的倾斜角为60º，且与椭圆x 25+y 2＝1有相等的焦距，则C 的方程为（A ）x 23－y 2＝1 （B ）x 29－y 23＝1 （C ）x 2－y 23＝1 （D ）x 23－y 29＝11.C2.（2018海淀二模·理）设曲线C 是双曲线，则“C 的方程为2214y x -=”是“C 的渐近线方程为2y x =±”的（A ）充分而不必要条件 （B ）必要而不充分条件 （C ）充分必要条件（D ）既不充分也不必要条件2.A3.（2018丰台二模·理）已知双曲线2221(0)9x y b b -=>的一条渐近线的倾斜角为π6，则b 的值为(A)3 (B)(C) (D) B4.（2018海淀二模·理）能够使得命题“曲线221(0)4x y a a-=≠上存在四个点P ，Q ，R ，S 满足四边形PQRS 是正方形”为真命题的一个实数a 的值为 .4.答案不唯一，0a <或4a >的任意实数5.（2018房山二模·理）设双曲线()222210,0-=>>x y a b a b的一条渐近线方程为20-=x y ，则该双曲线的离心率为 ．6.（2018顺义二模·理）设双曲线)0,0(1:2222>>=-b a by a x C 经过点(4,1),且与1422=-x y 具有相同渐近线,则C 的方程为________________;渐近线方程为__________________.6.x y y x 21,131222±==-. 7.（2018朝阳二模·理）双曲线22x y λ-=（0λ≠）的离心率是 ；该双曲线的两条渐近线的夹角是 .π28.（2018昌平二模·理）已知双曲线：2221(0)x y a a-=>的渐近线方程为12y x =±，则双曲线的离心率是 ．8.9.（2018海淀二模·理）（本小题共14分）已知椭圆C ：2214x y +=，F 为右焦点，圆O ：221x y +=，P 为椭圆C 上一点，且P 位于第一象限，过点P 作PT 与圆O 相切于点T ，使得点F ，T 在OP 两侧. （Ⅰ）求椭圆C 的焦距及离心率; （Ⅱ）求四边形OFPT 面积的最大值.C C8.（本小题共14分）解：（Ⅰ）在椭圆C ：2214x y +=中，2a =，1b =，所以c == ········································································· 2分 故椭圆C的焦距为2c =， ································································· 3分离心率c e a ==． ················································································· 5分 （Ⅱ）法一：设00(,)P x y （00x >，00y >），则220014x y +=，故220014x y =-． ······················ 6分 所以2222220003||||||14TPOP OT x y x =-=+-=，所以0||TP =， ········································· 8分01||||24OTP S OT TP x∆=⋅=．·············· 9分又(0,0)O ，F ，故0012OFPS OF y y ∆=⋅=． ························ 10分因此00()2OFP OTP OFPTx S S S y∆∆=+=+四边形 ······································ 11分22==． 由220014x y +=，得1≤，即001x y ⋅≤，所以OFPT S =四边形， ·················································· 13分 当且仅当2200142x y ==，即0x 02y =时等号成立. ···················· 14分 （Ⅱ）法二：设(2cos ,sin )P θθ（02πθ<<）， ················································· 6分则222222||||||4cos sin 13cos TP OP OT θθθ=-=+-=，所以||TP θ=， ·············································································· 8分1||||2OTP SOT TP θ∆=⋅=． ················································· 9分 又(0,0)O ，F，故012OFP S OF y θ∆=⋅=．···················· 10分因此(cos sin )OFP OTP OFPT S S S θθ∆∆=+=+四边形······························· 11分 )4πθ=+≤， ·················································· 13分当且仅当4πθ=时，即0x =02y =时等号成立． ······················· 14分10.（2018房山二模·理）（本小题14分）已知椭圆()222210+=>>：x y C a b a b 的离心率为12，O 为坐标原点，F 是椭圆C 的右焦点，A 为椭圆C 上一点，且⊥AF x 轴，AFO ∆的面积为34． （Ⅰ）求椭圆C 的方程；（Ⅱ）过C 上一点()()000,0≠P x y y 的直线l ：00221x x y ya b+=与直线AF 相交于点M ，与直线4x =相交于点N .证明：当点P 在C 上移动时，MFNF 恒为定值，并求此定值．10.（Ⅰ）设(,0)F c ，(,)A c d 则22221c d a b+=又12c a =||d ∴= 因AFO ∆ 的面积为341133||,224c d c b bc ∴===由2222a b c a c bc ⎧-=⎪=⎨⎪=⎩得21a b c =⎧⎪=⎨⎪=⎩所以C 的方程为22143x y += …………5分 （Ⅱ）由(1)知直线l 的方程为00143x x y y+= (y 0≠0)，即y ＝001234x x y - (y 0≠0)． 因为直线AF 的方程为x ＝1，所以直线l 与AF 的交点为M 0123(1,)4x y -， 直线l 与直线x ＝4的交点为N 0(4,33)x -，则|MF |2|NF |2＝202002220000123()4(4)331616(1)9()x y x x y x y --=-+-+ 又P (x 0，y 0)是C 上一点，则2200143x y +=.2200334x y =- 代入上式得|MF |2|NF |2＝2220002222000000(4)(4)(4)1148121632164(816)4(4)4x x x x x x x x x ---====-+-+-+- 所以|MF ||NF |=12，为定值． …………14分11.（2018朝阳二模·理）已知抛物线2:2C y x =.（1）写出抛物线C 的直线方程，并求出抛物线C 的焦点到准线的距离；（2）过点(20)，且斜率存在的直线l 与抛物线C 交于不同的两点A ，B ，且点B 关于x 轴的对称点为D ，直线AD 与x 轴交于点M . 1）求点M 的坐标；2）求OAM △与OAB △面积之和的最小值.11.【解析】（Ⅰ）由题可得22,1P P ==,所以准线方程为1,2x =- 抛物线C 的焦点到准线的距离为1.（Ⅱ）（i ）解:令1122(,),(,),A x y B x y 则22(,)D x y -且令10y >,令:2AB l x my =+222x my y x=+⎧⎨=⎩2240y my ⇒--= 所以12122,4y y m y y +=⋅=-则直线AD 方程为121112()y y y y x x x x +-=--121112()()y y y y x x m y y +-=--2111221()()2y y x y y y -=--当0y =时,21211()()2y y y x y -⋅-=-21211()()2y y y y x -⋅-+=122y y x =,2x =-所以(2,0)M - （ii ）解:1122OAMS y =⋅⋅! 121122||22OAB S y y =⋅⋅+⋅⋅!则112||OAMOAB S S y y y +=++!!1211112||42||42y y y y y y =+-=+=+≥=当且仅当1142y y =时,即1y = 12.（2018西城二模·理）（本小题满分14分）已知直线:1l y kx =+与抛物线2:4C y x =相切于点P ．。

1 / 14 北京市各地市2018年高考数学最新联考试卷分类汇编（10）圆锥曲线
一、选择题:
（7）(北京市朝阳区2018年4月高三第一次综合练习理)抛物线22y px （p ＞0）的焦点为
F ，已知点A ，B 为抛物线上的两个动点，且满足
120AFB .过弦AB 的中点M 作抛物线准线的垂线MN ，垂足为N ，则||
||MN AB 的最大值为
A.
33 B. 1 C. 233 D. 2
【答案】A （6）(北京市东城区2018年4月高三综合练习一文）已知点(2,1)A ，抛物线24y x 的焦点是
F ，若抛物线上存在一点P ，使得PA PF 最小，则P 点的坐标为
（A ）(2,1)
（B ）(1,1)（C ）1(,1)2（D ）1(,1)4【答案】D
7. (北京市海淀区2018年4月高三第二学期期中练习理)抛物线24y x 的焦点为F ，点(,)P x y 为该抛物线上的动点，又点(1,0)A ，则||||
PF PA 的最小值是A.1
2 B.2
2 C.3
2 D.
22
3【答案】 B
5. （北京市丰台区2018年高三第二学期统一练习一文）已知椭圆22212x
y a 的一个焦点与抛物
线28y x 的焦点重合，则该椭圆的离心率是
（A ）3
2（B ）233（C ）22（D ）
63【答案】D
二、填空题:。

1．已知椭圆()22:10E a b a b+=>>的右焦点为()1,0F ，过F 且与x 轴垂直的弦长为3.（1）求椭圆E 的标准方程；（2）过F 作直线l 与椭圆交于A B 、两点，问：在x 轴上是否存在点P ，使PA PB ⋅uu r uu r为定值，若存在，请求出P 点坐标，若不存在，请说明理由.解：（1）由题意知222a b c =+，1c =.又当x c =时，2b y a =±.∴223b a⋅=. 则224,3a b ==.∴椭圆E 的标准方程为22143x y +=. （2）假设存在点P 满足条件，设其坐标为(),0t ，设()11,A x y ，()22,B x y ，当l 斜率存在时，设l 方程为()1y k x =-，联立()221,143y k x x y ⎧=-⎪⇒⎨+=⎪⎩()22224384120k x k x k +-+-=，0∆>恒成立.∴2122843k x x k +=+，212241243k x x k -=+.∴()11,PA x t y =-uu r ，()22,PB x t y =-uu r.∴()()1212PA PB x t x t y y ⋅=--+uu r uu r ()()()()2121211x t x t k x x =--+-- ()()()222212121k x x k t x x k t =+-++++()()()()()22222222141284+34+3k k k t k k t k k +--+⋅++=()()2222485312=43t t k t k --+-+.当PA PB ⋅uu r uu r 为定值时，2248531243t t t ---=.∴118t =.此时223121354364t PA PB t -⋅==-=-uu r uu r .当l 斜率不存在时，11,08P ⎛⎫ ⎪⎝⎭，31,2A ⎛⎫⎪⎝⎭，31,2B ⎛⎫- ⎪⎝⎭.33,82PA ⎛⎫=- ⎪⎝⎭uu r ，33,82PB ⎛⎫=-- ⎪⎝⎭uu r ，13564PA PB ⋅=-uu r uu r . ∴存在满足条件的点P ，其坐标为11,08⎛⎫⎪⎝⎭.此时PA PB ⋅u u r u u r 的值为13564-.2.已知圆22:1O x y +=与x 轴负半轴相交于点A ，与y 轴正半轴相交于点B .（1）若过点2C ⎝⎭的直线l 被圆Ol 的方程；（2）若在以B 为圆心半径为r 的圆上存在点P，使得PA (O 为坐标原点)，求r 的取值范围；（3）设()()1122,,,M x y Q x y 是圆O 上的两个动点，点M 关于原点的对称点为1M ，点M 关于x 轴的对称点为2M ，如果直线12QM QM 、与y 轴分别交于()0,m 和()0,n ，问m n ⋅是否为定值？若是求出该定值；若不是，请说明理由. 解：（1）1︒若直线l 的斜率不存在，则l 的方程为：12x =，符合题意.2︒若直线l 的斜率存在，设l的方程为：12y k x ⎛⎫=- ⎪⎝⎭，即220kx y k --∴点O 到直线l 的距离d =l 被圆O∴221d +=⎝⎭∴k =，此时l 的方程为：10x +=∴所求直线l的方程为12x =或10x += （2）设点P 的坐标为(),x y ，由题得点A 的坐标为()1,0-，点B的坐标为()0,1 由PA ==()2212x y -+=∵点P 在圆B上，∴r r≤0r<≤∴所求r 的取值范围是0r <≤（3）∵()11,M x y ，则()()111211,,,M x y M x y ---∴直线1QM 的方程为()211121y y y y x x x x ++=++令0x =，则122112x y x y m x x -=+同理可得122112x y x y n x x +=-∴()()2212211221122122121212x y x y x y x y x y x y mn x x x x x x --+=⋅=+--()()222212212212111x x x x x x ---==- ∴m n ⋅为定值1.4．已知椭圆2222:1x y C a b +=（0ab >>）的离心率e =，过点R (1,0)-的直线l 与椭圆C 交于,P Q 两点，且2PR RQ =.（Ⅰ）当直线l 的倾斜角为060时，求三角形OPQ 的面积； （Ⅱ）当三角形OPQ 的面积最大时，求椭圆C 的方程．解:由e =得223a b =，所以222:33C x y b +=．设1122(,),(,),P x y Q x y ，则由2P R R Q=uur uuu r ，R(1,0)-，得1212213203x x y y +⎧=-⎪⎪⎨+⎪=⎪⎩由2PR RQ =uu r uu u r 知直线l 斜率存在设为k ,得直线l 的方程(1)y k x =+，代入222:33C x y b +=得22222(31)6330k x k x k b +++-=，由2PR RQ =uur uuu r 知0∆>，且2122221226313331k x x k k b x x k ⎧-+=⋅⎪⎪+⎨-⎪=⋅⎪+⎩解得21222233313331k x k k x k ⎧-+=⋅⎪⎪+⎨--⎪=⋅⎪+⎩， 12122312231OPQ k k S OR y y x x k =-=-=+V（1）k =2331OPQ k S k ==+V （2）（0k ≠时）1212231322313OPQ k k S OR y y x x k k k=-=-==≤++V21,3k k ==时三角形OPQ 的面积最大，把213k =代入得253b =．25a ∴= 于是椭圆C 的方程为223155x y +=． 5．如图，已知椭圆2222:1(0)x y E a b a b +=>>的左顶点(2,0)A -，且点3(1,)2-在椭圆上，1F 、2F 分别是椭圆的左、右焦点。

2018一模分类汇编——圆锥曲线1.（2018东城一模·理）设抛物线24y x =上一点P 到y 轴的距离是2，则P 到该抛物线焦点的距离是（A ）1 （B ）2 （C ）3 （D ） 4 1.C2.（2018石景山一模·理）如图，已知线段AB 上有一动点D （D 异于A B 、）,线段CD AB ⊥,且满足2CD AD BD λ=⋅（λ是大于0且不等于1的常数），则点C 的运动轨迹为（ ） A ．圆的一部分 B ．椭圆的一部分C ．双曲线的一部分D ．抛物线的一部分 2.B3.（2018朝阳一模·理）若三个点(2,1),(2,3),(2,1)---中恰有两个点在双曲线222:1(0)x C y a a-=>上，则双曲线C 的渐近线方程为_____________．3.2y x =±4.（2018西城一模·理）已知抛物线28y x =-的焦点与双曲线2221(0)x y a a-=>的一个焦点重合，则a =____；双曲线的渐近线方程是____．0x ±=5.（2018延庆一模·理） 设双曲线2214x y -=的焦点为12，，F F P 为该双曲线上的一点，若13PF =，则2PF = ． 5.76.（2018海淀一模·理）已知点(2,0)是双曲线:C 2221x y a-=的一个顶点，则C 的离心率为____________.6.27.（2018石景山一模·理）双曲线2212x y -=的焦距是________,渐近线方程是________.7.2y x =±8.（2018房山一模·理）抛物线24x y =的焦点坐标为 . 8.()01，9.（2018丰台一模·理）已知抛物线M 的开口向下，其焦点是双曲线2213y x -=的一个焦点，则M 的标准方程为____．9.28x y =-10.（2018延庆一模·理）（本小题满分14分）已知椭圆E ：()222210x y a b a b+=>>过点01（）,且离心率e =.（Ⅰ）求椭圆E 的方程； （Ⅱ）设动直线l 与两定直线1:0l x y -=和2:0l x y +=分别交于两点．若直线总与椭圆E 有且只有一个公共点，试探究：OPQ ∆的面积是否存在最小值？若存在，求出该最小值；若不存在，说明理由． 10.（Ⅰ）由已知得,P Q l解得222b1acb1ac1a b c=⎧⎧=⎪⎪⎪==⎨⎨⎪⎪=⎩=+⎪⎩所以椭圆的E方程为2212xy+=…………4分（Ⅱ）当直线的斜率不存在时，直线为x=x=都有122OPQS∆=⨯=. ………6分当直线的斜率存在时，设直线:(1)l y kx m k=+≠±，由2212y kx mxy=+⎧⎪⎨+=⎪⎩消去，可得222(12)4220k x kmx m+++-=228816m k∆=-++，由题可知，0∆=，有2221m k=+………8分又y kx mx y=+⎧⎨-=⎩可得(,)11m mPk k--；同理可得(,)11m mQk k-++.由原点到直线的距离为和2PQ=可得22121OPQmS d PQk∆==-………10分∵2221m k=+，∴22222111OPQm kSk k∆+==--………11分当210k-<，即11k k><-或时，2222132211OPQkSk k∆+==+>--………12分当210k->，即11k-<<时，222213211OPQkSk k∆+==-+--因为2011k<-≤，所以2331k≥-，所以23211OPQSk∆=-+≥-，当且仅当时等号成立. 综上，当时，OPQ∆的面积存在最小值为1………14分l llyOPQ d=k=k=11.（2018西城一模·理）（本小题满分14分）已知圆22:4O x y +=和椭圆22:24C x y +=，F 是椭圆C 的左焦点． （Ⅰ）求椭圆C 的离心率和点F 的坐标；（Ⅱ）点P 在椭圆C 上，过P 作x 轴的垂线，交圆O 于点Q （,P Q 不重合），l 是过点Q 的圆O 的切线．圆F 的圆心为点F ，半径长为||PF ．试判断直线l 与圆F 的位置关系，并证明你的结论．11.（本小题满分14分）解：（Ⅰ）由题意，椭圆C 的标准方程为22142x y +=． [ 1分]所以 24a =，22b =，从而 2222c a b =-=．因此 2a =，c =故椭圆C 的离心率 c e a ==． [ 3分]椭圆C 的左焦点F 的坐标为(． [ 4分]（Ⅱ）直线l 与圆F 相切．证明如下： [ 5分]设00(,)P x y ，其中022x -<<，则220024x y +=， [ 6分]依题意可设01(,)Q x y ，则22014x y +=． [ 7分]直线l 的方程为 0101()x y y x x y -=--，整理为0140x x y y+-=．[9分]所以圆F的圆心F到直线l的距离|2|2d x==+．[11分]因为22222200000011||(((4)422PF x y x x x=+=++-=++．[13分]所以22||PF d=，即||PF d=，所以直线l与圆F相切．[14分]12.（2018石景山一模·理）（本小题共13分）在平面直角坐标系xOy中，动点E到定点(1,0)的距离与它到直线1x=-的距离相等．（Ⅰ）求动点E的轨迹C的方程；（Ⅱ）设动直线:l y kx b=+与曲线C相切于点P，与直线1x=-相交于点Q．证明：以PQ为直径的圆恒过x轴上某定点．（本小题共13分）12.（Ⅰ）解：设动点E的坐标为(,)x y，由抛物线定义知，动点E的轨迹是以(1,0)为焦点，1x=-为准线的抛物线，所以动点E的轨迹C的方程为24y x=．……………5分（Ⅱ）证明：由24y kx by x=+⎧⎨=⎩，消去x得：2440ky y b-+=．因为直线l 与抛物线相切，所以16-160kb ∆==，即1b k=． ……8分 所以直线l 的方程为1y kx k=+． 令1x =-，得1y k k=-+． 所以Q 11,k k ⎛⎫--+ ⎪⎝⎭． ……………10分设切点坐标00(,)P x y ，则20044+0ky y k-=， 解得：212(,)P k k， ……………11分 设(,0)M m ，2121(1)()k MQ MP m m k k k ⎛⎫⋅=---+-+ ⎪⎝⎭221=2m m m k -+--所以当22=0-10m m m ⎧+-⎨=⎩，即10m MQ MP =⋅=时，所以MQ MP ⊥所以以PQ 为直径的圆恒过x 轴上定点(1,0)M ． ……………13分13.（2018海淀一模·理）（本小题14分）已知椭圆C ：()222210x y a b a b+=>>的离心率为2，且点()2,1T 在椭圆上.设与OT平行的直线l 与椭圆C 相交于,P Q 两点，直线,TP TQ 分别与x 轴正半轴交于,M N 两点. （Ⅰ）求椭圆C 的标准方程； （Ⅱ）判断OM ON +的值是否为定值，并证明你的结论.13.（本小题14分）（Ⅰ）由题意222224112a b a b c c e a ⎧+=⎪⎪⎪-=⎨⎪⎪==⎪⎩，解得：a =，b =c = 故椭圆C 的标准方程为22182x y += ···················································· 5分（Ⅱ）假设直线TP 或TQ 的斜率不存在，则P 点或Q 点的坐标为(2，－1)，直线l 的方程为11(2)2y x +=-，即122y x =-. 联立方程22182122x y y x ⎧+=⎪⎪⎨⎪=-⎪⎩，得2440x x -+=，此时，直线l 与椭圆C 相切，不合题意.故直线TP 和TQ 的斜率存在. 方法1：设11(,)P x y ，22(,)Q x y ，则直线111:1(2)2y TP y x x --=--， 直线221:1(2)2y TQ y x x --=-- 故112||21x OM y -=--，222||21x ON y -=--由直线1:2OT y x =，设直线1:2PQ y x t =+（0t ≠） 联立方程，2222182224012x y x tx t y x t ⎧+=⎪⎪⇒++-=⎨⎪=+⎪⎩ 当0∆>时，122x x t +=-，21224x x t ⋅=-||||OM ON +1212224()11x x y y --=-+-- 1212224()111122x x x t x t --=-++-+- 121221212(2)()4(1)411(1)()(1)42x x t x x t x x t x x t +-+--=-+-++- 22224(2)(2)4(1)411(24)(1)(2)(1)42t t t t t t t t -+----=--+-⋅-+- 4= ········································································ 14分 方法2：设11(,)P x y ，22(,)Q x y ，直线TP 和TQ 的斜率分别为1k 和2k由1:2OT y x =，设直线1:2PQ y x t =+（0t ≠） 联立方程，2222182224012x y x tx t y x t ⎧+=⎪⎪⇒++-=⎨⎪=+⎪⎩ 当0∆>时，122x x t +=-，21224x x t ⋅=-12k k +12121122y y x x --=+-- 121211112222x t x t x x +-+-=+--121212(2)()4(1)(2)(2)x x t x x t x x +-+--=--21224(2)(2)4(1)(2)(2)t t t t x x -+----=--0=故直线TP 和直线TQ 的斜率和为零 故TMN TNM ∠=∠ 故TM TN =故T 在线段MN 的中垂线上，即MN 的中点横坐标为2故||||4OM ON += ······································································ 14分14.（2018丰台一模·理）（本小题共14分）已知点3(1,)2P 在椭圆C ：22221(0)x y a b a b +=>>上，(1,0)F 是椭圆的一个焦点．（Ⅰ）求椭圆C 的方程；（Ⅱ）椭圆C 上不与P 点重合的两点D ，E 关于原点O 对称，直线PD ，PE 分别交y 轴于M ，N 两点．求证：以MN 为直径的圆被直线32y =截得的弦长是定值． 14.（本小题共14分）解：（Ⅰ）依题意，椭圆的另一个焦点为)0,1(-'F ，且1=c ． ……………………1分因为4)23(0)23(222222=+++=a ，所以2a =，b ……………………3分所以椭圆C的方程为13422=+y x ． ……………………4分 （Ⅱ）证明：由题意可知D ，E 两点与点P 不重合．因为D ，E 两点关于原点对称， 所以设(,)D m n ，(,)E m n --，)1(±≠m ． ……………………5分设以MN 为直径的圆与直线32y =交于33(,),(,)(0)22G t H t t ->两点， 所以G⊥． (6)分直线PD ：)1(12323---=-x m n y ． 当=x 时，23123+---=m n y ，所以)23123,0(+---m n M ． ……………………7分 直线PE ：)1(12323-++=-x m n y ． 当=x 时，23123+++-=m n y ，所以)23123,0(+++-m n N ． ……………………8分 所以32(,)1n G M t m -=---，32(,)1n GN t m +=--+， ……………………9分 因为G M ⊥，所以0G M G N ⋅=， ……………………10分所以2224904(1)n GM GN t m -⋅=+=-． ……………………11分因为13422=+n m ，即124322=+n m ，223394m n -=-， ……………………12分所以2304t -=，所以23=t ． ……………………13分 所以)23,23(G ，)23,23(-H ，所以GH =． 所以以MN 为直径的圆被直线23=y……………………14分15.（2018房山一模·理）（本小题14分）已知椭圆C :22221(0)x y a b a b+=>>过点()0,1-，离心率2e =.（Ⅰ）求椭圆C 的方程；（Ⅱ）过点F ()1,0作斜率为()0k k ≠的直线l ，l 与椭圆C 交于M ，N 两点，若线段MN 的垂直平分线交x 轴于点P ，求证：||||MN PF 为定值．15.（Ⅰ）根据题意22212b c e a a b c =⎧⎪⎪==⎨⎪⎪=+⎩解得：1a b ⎧=⎪⎨=⎪⎩所以椭圆C 的方程为2212x y +=…………… 5分 （Ⅱ）设直线l 的方程为(1)y k x =- 由2212(1)x y y k x ⎧+=⎪⎨⎪=-⎩ 得 2222(21)4220k x k x k +-+-=由0∆>得k R ∈且0k ≠设1122(,),(,)M x y N x y ，线段MN 中点00(,)Q x y 那么2122421k x x k +=+，21222221k x x k -=+212000222,(1)22121x x k kx y k x k k +-===-=++设(,0)P p ，根据题意PQ MN ⊥ 所以20202121221kyk k x p kp k -+==---+，得2221k p k =+所以22221 ||12121k kPFk k+=-=++|| MN==22)21kk+=+所以||||MNPF=为定值………………… 14分16.（2018东城一模·理）（本小题13分）已知椭圆22221(0)x yC a ba b+=>>：的离心率为2，且过点A(2，0)．(Ⅰ) 求椭圆C的方程；(Ⅱ) 设M，N是椭圆C上不同于点A的两点，且直线AM，AN的斜率之积等于－1 4. 试问直线MN是否过定点？若是，求出该点的坐标；若不是，请说明理由．16.（共13分）解：（I）由已知有2,a=⎧=解得2,1.ab=⎧⎨=⎩椭圆C的方程为2214xy+=. ……………………………4分（II）若直线MN斜率存在，设直线MN方程为y kx n=+.由22,1,4y kx n x y =+⎧⎪⎨+=⎪⎩消去y ，得222(14)8440k x knx n +++-=. 当0∆>，设1122(,),(,)M x y N x y ， 则122814kn x x k +=-+………..①，21224414n x x k -=+………..②. 由12121224AM AN y y k k x x ⋅=⋅=---以及11y kx n =+，22y kx n =+整理，得 221212(14)(42)()(44)0k x x nk x x n ++-+++=.将①，②代入上式，整理，得220n kn +=，解得0n =或2n k =-. 当0n =时，直线y kx n =+过(0,0)；当2n k =-时，直线y kx n =+过(2,0)（舍）. 若直线MN 斜率不存在，则直线,AM AN 斜率互为相反数. 不妨设11,22AM AN k k =-=，于是直线1:(2)2AM y x =--与椭圆交于(0,1)M ， 由对称性可知直线AN 与椭圆交于(0,1)N -.所以直线MN 也过(0,0).综上，直线MN 过定点(0,0). ……………………………13分17.（2018朝阳一模·理） (本小题满分14分) 已知椭圆2222:1(0)x y C a b a b+=>>的离心率为2，且过点(1,2．（Ⅰ）求椭圆C 的方程；（Ⅱ）过椭圆C 的左焦点的直线1l 与椭圆C 交于,A B 两点，直线2l 过坐标原点且与直线1l 的斜率互为相反数．若直线2l 与椭圆交于,E F 两点且均不与点,A B 重合，设直线AE 与x 轴所成的锐角为1θ，直线BF 与x 轴所成的锐角为2θ，判断1θ与2θ大小关系并加以证明．17. (本小题满分14分)解：（Ⅰ）由题意得22222,11 1.2c a a b c ab ⎧=⎪⎪⎪=+⎨⎪⎪+=⎪⎩解得a =1b =，1c =．故椭圆C 的方程为2212x y +=． ….….5分 （Ⅱ）12=θθ．证明如下：由题意可设直线1l 的方程为(1)y k x =+，直线2l 的方程为y kx =-，设点11(,)A x y ，22(,)B x y ，33(,)E x y ，33(,)F x y --．要证12=θθ，即证直线AE 与直线BF 的斜率之和为零，即0AE BF k k += ． 因为13231323AE BF y y y y k k x x x x -++=+-+13231323(1)(1)k x kx k x kx x x x x +++-=+-+2121231323[2()2]()()k x x x x x x x x x +++=-+． 由22(1),1,2y k x x y =+⎧⎪⎨+=⎪⎩ 得2222(12)4220k x k x k +++-=， 所以2122412k x x k -+=+，21222212k x x k -=+． 由22,1,2y kx x y =-⎧⎪⎨+=⎪⎩得22(12)2k x +=，所以232212x k =+． 所以2221212322244442()20121212k k x x x x x k k k --+++=++=+++． 2121231323[2()2]0()()AE BFk x x x x x k k x x x x ++++==-+． 所以12=θθ． ….….14分。

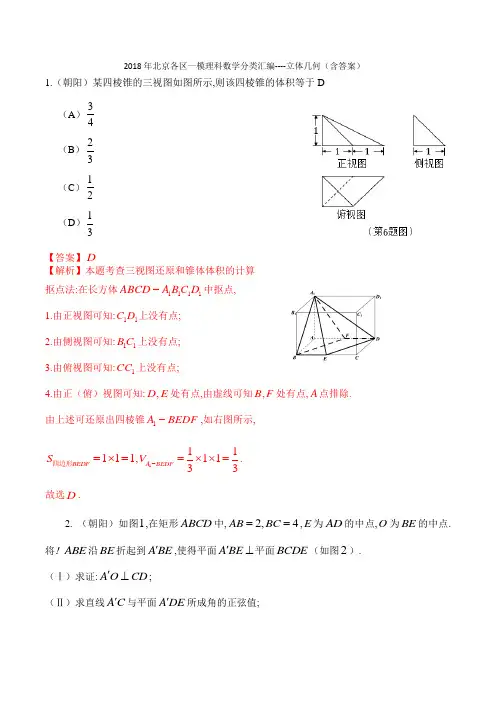
2018年北京各区一模理科数学分类汇编----立体几何（含答案）1.（朝阳）某四棱锥的三视图如图所示,则该四棱锥的体积等于D（A ）34（B ）23（C ）12（D ）13【答案】D【解析】本题考查三视图还原和锥体体积的计算 抠点法:在长方体1111ABCD A BC D -中抠点, 1.由正视图可知:11C D 上没有点; 2.由侧视图可知:11B C 上没有点; 3.由俯视图可知:1CC 上没有点;4.由正（俯）视图可知:,D E 处有点,由虚线可知,B F 处有点,A 点排除. 由上述可还原出四棱锥1A BEDF -,如右图所示,111BEDF S =⨯=四边形,1111133A BEDF V -=⨯⨯=.故选D .2. （朝阳）如图1,在矩形ABCD 中,2,4AB BC ==,E 为AD 的中点,O 为BE 的中点.将ABE !沿BE 折起到A BE ',使得平面A BE '⊥平面BCDE （如图2）.（Ⅰ）求证:A O CD '⊥;（Ⅱ）求直线A C '与平面A DE '所成角的正弦值;（Ⅲ）在线段A C '上是否存在点P ,使得//OP 平面A DE '?若存在,求出A PA C''的值;若不存在,请说明理由.【解析】（Ⅰ）如图,在矩形ABCD 中,2,4AB BC ==,E 为AD 中点,2AB AE ∴==,O 为BE 的中点,AO BE ∴⊥由题意可知,A O BE '⊥,平面A B E '⊥平面B C D E 平面A B E '平面B C D E B E =,A O '⊂平面A BE 'A O '∴⊥平面BCDECD ⊂平面BCDE ,A O CD '∴⊥（Ⅱ）取BC 中点为F ,连结OF 由矩形ABCD 性质,2,4AB BC ==,可知OF BE ⊥ 由（Ⅰ）可知,,A O BE A O OF ''⊥⊥以O 为原点,OA '为z 轴,OF 为x 轴,OE 为y 轴建立坐标系在Rt BAE !中,由2,2AB AE ==,则BE OA ==所以A E F'(0,B C DA C '=,(2,ED=,A E '=设平面A DE '的一个法向量为(,,)m xy z =则00m A E m ED ⎧'⋅=⎪⎨⋅=⎪⎩,00-=+=令1y z ==,则1x =-所以(1,1,1)m =- 设直线A C '与平面A DE '所成角为θ，2sin cos ,3A C m A C m A C mθ'⋅'=<>=='⋅ 所以直线A C '与平面A DE '所成角的正弦值为3. （Ⅲ）假设在线段A C '上存在点P,满足//OP 平面ADE '，设(01)A P A C λλ''=≤≤由A C '=,,所以,)A P '=)P -,)OP=-若//OP 平面A D E ',则0m OP ⋅=，所以0-++=,解得1[0,1]2λ=∈，所以12A P A C '='.3. （石景山）若某多面体的三视图（单位：cm ）如图所示，则此多面体的体积是（ ）AA.378cmB. 323cmC. 356cmD.312cm4.（石景山） 如图，四边形ABCD 是正方形，PA ⊥平面ABCD ，EB //PA ，4AB PA ==，2EB =，F 为PD 的中点．（Ⅰ）求证：AF PC ⊥； （Ⅱ）求证：BD //平面PEC ； （Ⅲ）求二面角DPC E --的大小．B（Ⅰ）证明：依题意，PA ⊥平面ABCD ．如图，以A 为原点，分别以AD 、AB 、AP 的方向为x 轴、y 轴、z 轴的正方向建立空间直角坐标系． ……2分依题意，可得(0,0,0)A ，(0,4,0)B ，(4,4,0)C ，(4,0,0)D ，(0,0,4)P ，(0,4,2)E ，(2,0,2)F ． 因为(2,0,2)AF =，(4,4,4)PC =-，所以80(8)0AF PC ⋅=++-=． ……5分所以AF PC ⊥（Ⅱ）证明：取PC 的中点M ，连接EM ．因为(2,2,2)M ，(2,2,0)EM =-，(4,BD =-所以2BD EM =，所以//BD EM ．分又因为EM ⊂平面PEC ，BD ⊄平面PEC ，所以//BD 平面PEC ． ……9分 （Ⅲ）解：因为AF PD ⊥，AF PC ⊥，PD PC P =，所以AF ⊥平面PCD ，故(2,0,2)AF =为平面PCD 的一个法向量．……10分 设平面PCE 的法向量为(,,)n x y z =， 因为(4,4,4)PC =-，(0,4,2)PE =-，所以0,0,n PC n PE ⎧⋅=⎪⎨⋅=⎪⎩即4440,420,x y z y z +-=⎧⎨-=⎩令1y =-，得1x =-，2z =-，故(1,1,2)n =---． ……12分所以cos ,AF n <>== ……13分 所以二面角D PC E --的大小为5π6． ……14分5.（西城） 正三棱柱的三视图如图所示，该正三棱柱的表面积是D （A） （B（C）6+ （D）6+6.（西城）．如图，在长方体1111ABCD A B C D -中，12AA AB ==，1BC =，点P 在侧面11A ABB 上．若点P 到直线1AA 和CD 的距离相等， 则1A P 的最小值是____．7. 如图1，在△ABC 中，D ，E 分别为AB ，AC 的中点，O 为DE的中点，AB AC ==4BC =．将△ADE 沿DE 折起到△1A DE 的位置，使得平面1A DE ⊥平面BCED ，如图2．（Ⅰ）求证：1AO BD ⊥；（Ⅱ）求直线1A C 和平面1A BD 所成角的正弦值；（Ⅲ）线段1A C 上是否存在点F ，使得直线DF 和BC？若存在，求出11A FA C的值；若不存在，说明理由．图1 图2解：（Ⅰ）因为 在△ABC 中，D ，E 分别为AB ，AC 的中点， 所以 //DE BC ，AD AE =．所以 11A D A E =，又O 为DE 的中点，所以 1AO DE ⊥． [ 1分]因为 平面1A DE ⊥平面BCED ，且1AO ⊂平面1A DE ，所以 1AO ⊥平面BCED ， [ 3分]所以 1AO BD ⊥． [ 4分] （Ⅱ）取BC 的中点G ，连接OG ，所以 OE OG ⊥． 由（Ⅰ）得 1A O OE ⊥，1A O OG ⊥．如图建立空间直角坐标系O xyz -． [ 5分]由题意得，1(0,0,2)A ，(2,2,0)B -，(2,2,0)C ，(0,1,0)D -． 所以 1(2,2,2)A B −−→=--，1(0,1,2)A D −−→=--，1(2,2,2)A C −−→=-． 设平面1A BD 的法向量为(,,)x y z =n ，则 110,0,A B A D −−→−−→⎧⋅=⎪⎨⎪⋅=⎩n n即 2220,20.x y z y z --=⎧⎨--=⎩令1x =，则2y =，1z =-，所以 (1,2,1)=-n ． [ 7分] 设直线1A C 和平面1A BD 所成的角为θ， 则111||sin |cos ,|||||A C A C A C θ−−→−−→−−→⋅=〈〉=n n n 所以 直线1A C 和平面1A BD． [ 9分] （Ⅲ）线段1A C 上存在点F 适合题意．设 11A F AC λ−−→−−→=，其中[0,1]λ∈． [10分] 设 111(,,)F x y z ，则有111(,,2)(2,2,2)x y z λλλ-=-， 所以 1112,2,22x y z λλλ===-，从而 (2,2,22)F λλλ-， 所以 (2,21,22)DF λλλ−−→=+-，又(0,4,0)BC −−→=， 所以|||cos ,|||||DF BC DF BC DF BC −−→−−→−−→−−→−−→−−→⋅〈〉==[12分]令， 整理得 23720λλ-+=． [13分] 解得 13λ=，舍去2λ=．所以 线段1A C 上存在点F 适合题意，且1113A F A C =． [14分]8. （延庆）某三棱锥的三视图如图所示，则该三棱锥的最长棱的长为 D（A（B（C ） 2 （D9. （延庆）如图，在几何体ABCDE 中，四边形ABCD 是矩形，AB ⊥平面BEC ，BE EC ⊥，2AB BE EC ===，点,G F 分别是线段,BE DC 的中点.（Ⅰ）求证：//GF 平面ADE ； （Ⅱ）求平面AEF 与平面BEC 所成锐二面角的余弦值；（Ⅲ）在线段CD 上是否存在一点M ，使得DE AM ⊥，若存在，求DM 的长，若不存在，请说明理由.（Ⅰ）如图，取AE 的中点H ，连接,HG HD ，又G 是BE 的中点， 所以 //GH AB ，且12GH AB =………1分 又F 是CD 中点，所以12DF CD =， 由四边形ABCD 是矩形得，AB CD =， //AB CD ， ………2分 所以GH DF =， //GH DF ，从而四边形HGFD 是平行四边形，//GF DH ， ………3分正（主）视图侧（左）视图俯 视（7题图）又D H ⊂平面ADE ，GF ⊄平面ADE 所以//GF 平面ADE ………4分 法一：（Ⅱ）如图，在平面BEC 内，过点B 作//BQ EC,因为所以A B B ⊥，,BE EC BQ BE ⊥∴⊥又因为AB ⊥平面BEC ，AB BQ ⊥ 以B 为原点，分别以的方向为x 轴，y 轴，z 轴的正方向建立空间直角坐标系，…5分 则(0,0,2)A (0,0,0)B (2,0,0)E (2,2,1).F ………6分因为AB ⊥平面BEC ，所以为平面BEC 的法向量，………7分 设为平面AEF 的法向量，又由2200220,0，得x z n AE x y z n AF ⎧-=⋅=⎧⎨⎨+-=⋅=⎩⎩取得. ………9分从而42cos ,323n BA n BA n BA⋅===⨯⋅………10分 所以平面AEF 与平面BEC 所成锐二面角的余弦值为. （Ⅲ）假设在线段CD 存在点M ，设点M 的坐标为(2,2,)a . ………11分 因为(0,0,2)A (2,0,0)E (2,2,2).D所以(0,2,2)DE =--，(2,2,2)AM a =- ………12分 因为D E AM ⊥，0DE AM ⋅=所以0a = .………13分 所以2D M = ………14分法二：（Ⅱ）以E 点为原点，EC 所在直线为x 轴，EB 所在直线为y 轴，过E 做垂直平面BEC 的直线为z 轴，建立空间直角坐标系，则(0,0,0)E ，(0,2,2)A ，(2,0,1)F(2,0,2)D ，1(0,0,1)n 为平面BEC 的法向量， ………7分设2(,,)n x y z 为平面AEF 的法向量，又()()0,2,2,2,0,1EA EF,,BE BQ BA A=(B 0,0,2)(x,y,z)n =AE (2,0,-2)AF=(2,2,-1)=，2z ==(2,-1,2)n 23由2200n EA n EF ⎧⋅=⎪⎨⋅=⎪⎩得22020y z x z +=⎧⎨+=⎩取得2(-1,-2,2)n ………9分从而12121222cos ,133n n n n n n ⋅===⨯⋅ ………10分 所以平面AEF 与平面BEC 所成锐二面角的余弦值为. （Ⅲ）假设在线段CD 存在点M ，设点M 的坐标为(2,0,)a . ………11分 因为(0,2,2)A (0,0,0)E (2,0,2)D所以(-2,0,2)DE =-，(2,-2,2)AM a =- ………12分 因为D E AM ⊥，0DE AM ⋅=所以0a = .………13分 所以2D M =………14分10.（东城） 某几何体的三视图如图所示，该几何体的表面积为____________.12+11. （东城）如图1，在边长为2的正方形ABCD 中，P 为CD 中点，分别将PAD ，PBC 沿PA ，PB 所在直线折叠，使点C 与点D 重合于点O ，如图2. 在三棱锥P OAB -中，E 为PB 的中点．（Ⅰ）求证：PO AB ⊥；（Ⅱ）求直线PB与平面POA 所成角的正弦值； （Ⅲ）求二面角P AO E --的大小.2z =23图1 图2 证明：（Ⅰ）在正方形ABCD 中，P 为CD 中点，PD AD ⊥,PC BC ⊥， 所以在三棱锥P OAB -中，PO OA ⊥，PO OB ⊥. 因为OA OB O =，所以PO ⊥平面OAB .因为AB ⊂平面OAB ,所以PO AB ⊥. ……………………4分 （Ⅱ）取AB 中点F ，连接OF ，取AO 中点M ，连接BM . 过点O 作AB 的平行线OG .因为PO ⊥平面OAB ，所以PO ⊥OF ，PO ⊥OG . 因为OA ＝OB ，F 为AB 的中点， 所以OF ⊥AB . 所以OF ⊥OG .如图所示，建立空间直角坐标系O －xyz .A ()1，3，0，B ()－1，3，0，P ()0，0，1，M (12，32，0)．因为BO ＝BA ，M 为OA 的中点，所以BM ⊥OA .因为PO ⊥平面OAB ，PO ⊂平面POA ，所以平面POA ⊥平面OAB . 因为平面POA ∩平面OAB ＝OA ，BM ⊂平面OAB ， 所以BM ⊥平面POA .因为BM uuu r ＝(32，－32，0)．所以平面POA 的法向量m ＝()3，－1，0.BP uur＝(1，－3，1)．设直线BP 与平面POA 所成角为α，则sin cos 5BP BP BPa ×=<>==uu r uu ruu r m m,m . 所以直线BP 与平面POA 所成角的正弦值为155. ………………10分 （Ⅲ）由(Ⅱ)知1122E ⎛⎫- ⎪ ⎪⎝⎭，1122OE ⎛⎫=- ⎪ ⎪⎝⎭，()OA =. 设平面OAE 的法向量为n ，则有 0,0.OA OE ⎧⋅=⎪⎨⋅=⎪⎩n n即0,0.x x z ⎧=⎪⎨-+=⎪⎩令1y =-，则xz =即=-n .所以21cos ,242⋅===⋅⨯m n m n m n .由题知二面角P －AO －E 为锐角，所以它的大小为3p. ……………………………14分 12. （房山）如图，网格纸上小正方形的边长为1，粗线画出的是某多面体的三视图，则该多面体的表面积为D（A）（B）（C）（D）13.（房山）如图，四棱锥ABCD P -中，△PAD 是以AD 为斜边的等腰直角三角形，2==CD PD ，PC =2，BC //=AD 21，AD CD ⊥. （Ⅰ）求证：⊥CD 平面PAD ；（Ⅱ）若E 为PD 中点，求CE 与面PBC 所成角的正弦值； （Ⅲ）由顶点C 沿棱锥侧面经过棱PD 到顶点A 的最短路线与PD 的交点记为F .求该最短路线的长及FDPF的值. 证明：证明：（Ⅰ） 由题，222PD PC CD =+∴ PD ⊥CDD AD PD D =⊥ ,A CDP A D CD 面⊥∴ …………5分 （Ⅱ）法1：由（Ⅰ）知OB OD OB PO OD PO ⊥⊥⊥,.,∴以点O 为坐标原点建立空间直角坐标系O-xyz,如图所示C （0,1,2）P(0,0,1), D(0,1,0) B(0,0,2) E(0,21,21))21,21,2(--=,)0,1,0(),1,0,2(=-=BC PBPAB CDE设面PBC 的法向量),,(z y x =)2,0,1(0,2,1x ,02{002{{=∴=====⇒==-⇒⋅⋅y z y x z y z x 则令 设CE 与面PBC 所成角为θ1515|,cos |sin =><=∴n CE θ…………10分（Ⅱ）法2：以点D 为坐标原点建立空间直角坐标系D-xyz,如图所示 C （0,2,0）P(-1,0,1), D(0,0,0) B(0,2,1-) E(21-,0,21) )212,21(，--=,)0,0,1(),12,0(=-=，设面PBC 的法向量),,(z y x =)2,1,0(0,2,1y ,02{002{{=∴=====⇒==-⇒⋅⋅y z y x z x z y 则令 设CE 与面PBC 所成角为θ1515|cos |sin =><=∴CE θ…………10分法3：以点A 为坐标原点建立空间直角坐标系A-xyz,如图所示C （0,2,2）P(0,1,1), D(0,2,0) B(0,1,2) E(0,23,21))21,21,2(--=CE ,)0,1,0(),1,0,2(=-=设面PBC 的法向量),,(z y x n =)2,0,1(0,2,1x ,02{002{{=∴=====⇒==-⇒⋅⋅n y z y x z y z x 则令 设CE 与面PBC 所成角为θ1515|cos |sin =><=∴CE θ…………10分（Ⅲ）为等腰直角三角形面PDC PD CD PD ∆∴⊥∴⊂PAD将侧面PCD 绕着PD 旋转，使其与侧面PAD 共面，点C 运动到C ’，连接AC ’交PD 于E ， 则AC ’为最短路线090'=∠=∠PDC APD为平行四边形四边形P ADC '//'∴=∴DC AP 的中点，为C A PD '∴E10210222,122==+=='=∴PE AP AE C A ED PE…………14分 14.（丰台） 某三棱锥的三视图如图所示，则该三棱锥的体积为 A(A)23(B)43 (C) 2 (D)8315.(丰台) 如图，在四棱锥P ABCD -中，平面PAB ⊥平面ABCD ，AB BC ⊥，AD BC ∥，3AD =，22PA BCAB===，PB =（Ⅰ）求证：BC PB ⊥；（Ⅱ）求二面角P CD A --的余弦值；（Ⅲ）若点E 在棱PA 上，且BE ∥平面PCD ，求线段BE 的长． （Ⅰ）证明：因为平面PAB ⊥平面ABCD ，且平面PAB 平面=ABCD AB ，因为BC ⊥AB ，且BC ⊂平面ABCD所以BC ⊥平面PAB ． ……………………3分 因为PB ⊂平面PAB ，所以BC ⊥PB ． ……………………4分（Ⅱ）解：在△PAB 中，因为=2PA ，=PB =1AB ，所以222=+PA AB PB ，所以PB ⊥AB ． ……………………5分 所以，建立空间直角坐标系B xyz -，如图所示． 所以(1,0,0)A -，(0,0,0)B ，(0,2,0)C ，(1,3,0)D -，P ，正视图侧视图俯视图(1,1,0)CD =-，(0,2,PC =．易知平面ABCD 的一个法向量为=(0,0,1)n ． ……………………6分 设平面PCD 的一个法向量为=(,,)x y z m ，则00CD PC ⎧⋅=⎪⎨⋅=⎪⎩m m ，即2x y y =⎧⎪⎨=⎪⎩，令=2z，则=m ． ……………………8分 设二面角P CD A --的平面角为α，可知α为锐角，则cos cos ,5α⋅=<>===⋅n m n m n m ， 即二面角P CD A --的余弦值为5． ……………………10分 （Ⅲ）解：因为点E 在棱PA ，所以AE AP λ=，[0,1]λ∈． ……………………11分因为=1AP （，所以=)AE λ（，(1)BE BA AE λ=+=-． ……………………12分 又因为//BE 平面PCD ，m 为平面PCD 的一个法向量， 所以0BE ⋅=m1)20λλ-+=，所以1=3λ． ……………………13分所以2(3BE =-，所以7==BE BE ． ……………………14分 16.（海淀） 如图所示，一个棱长为1的正方体在一个水平放置的转盘上转动，用垂直于竖直墙面的水平光线照射，该正方体在竖直墙面上的投影的面积记作S ，则S 的值不可能是D(A) 1(B)65(C)43(D)3217.（海淀）已知三棱锥P -ABC （如图1）的平面展开图（如图2）中，四边形ABCD的正方形，△ABE 和△BCF 均为正三角形．在三棱锥P -ABC 中： （Ⅰ）证明：平面P AC ⊥平面ABC ；（Ⅱ）求二面角A -PC -B 的余弦值； （Ⅲ）若点M 在棱PC 上，满足CM CP =λ，1233,⎡⎤λ∈⎢⎥⎣⎦，点N 在棱BP 上，且BM AN ⊥，求BN BP 的取值范围.解：（Ⅰ）方法1：OPCA设AC 的中点为O ，连接BO ，PO . 由题意PA PB PC ===1PO =，1AO BO CO ===因为 在PAC ∆中，PA PC =，O 为AC 的中点所以 PO AC ⊥， ······································································· 1分 因为 在POB ∆中，1PO =，1OB =，PB =所以 PO OB ⊥ ·········································································· 2分 因为 ACOB O =，,AC OB ⊂平面ABC ···································· 3分所以 PO ⊥平面ABC因为 PO ⊂平面PAC ································································· 4分 所以 平面PAC ⊥平面ABC 方法2：(图1)CAECOPCA设AC 的中点为O ，连接BO ，PO .因为 在PAC ∆中，PA PC =，O 为AC 的中点所以 PO AC ⊥， ······································································· 1分 因为 PA PB PC ==，PO PO PO ==，AO BO CO ==所以 POA ∆≌POB ∆≌POC ∆ 所以 90POA POB POC ∠=∠=∠=︒所以 PO OB ⊥ ·········································································· 2分 因为 ACOB O =，,AC OB ⊂平面ABC ····································· 3分所以 PO ⊥平面ABC因为 PO ⊂平面PAC ································································· 4分 所以 平面PAC ⊥平面ABC 方法3：OPCA BQ设AC 的中点为O ，连接PO ，因为 在PAC ∆中，PA PC =，所以 PO AC ⊥ ·········································································· 1分 设AB 的中点Q ， 连接PQ ，OQ 及OB . 因为 在OAB ∆中，OA OB =，Q 为AB 的中点 所以 OQ AB ⊥.因为 在PAB ∆中，PA PB =，Q 为AB 的中点 所以 PQ AB ⊥. 因为 PQOQ Q =，,PQ OQ ⊂平面OPQ所以 AB ⊥平面OPQ 因为 PO ⊂平面OPQ所以 PO AB ⊥ ·········································································· 2分 因为 ABAC A =，,AB AC ⊂平面ABC ····································· 3分所以 PO ⊥平面ABC因为 PO ⊂平面PAC ································································· 4分 所以 平面PAC ⊥平面ABC 法4：OPCA设AC 的中点为O ，连接BO ，PO .因为 在PAC ∆中，PA PC =，O 为AC 的中点所以 PO AC ⊥， ······································································· 1分 因为 在ABC ∆中，BA BC =，O 为AC 的中点所以 BO AC ⊥， ······································································· 2分 因为 POBO O =，PO ⊂平面PAC ，BO ⊂平面ABC ，所以∠POB 为二面角P -AC -B 的平面角。

2018届北京各区一模理科数学分类汇编----参数、极坐标、复数（含答案）1.（朝阳）直线l的参数方程为=,1+3x y tìïïíï=ïî（t 为参数），则l 的倾斜角大小为（ ） C A ．6π B ． 3π C ． 32π D ．65π 2.（石景山） 已知圆C 的参数方程为cos ,sin 2,x y θθ=⎧⎨=+⎩（θ为参数），以原点为极点，x 轴的正半轴为极轴建 立极坐标系，直线的极坐标方程为sin cos 1ρθρθ+=，则直线截圆C 所得的弦长是_____________3. （延庆）在复平面内，复数-2i 1i +的对应点位于的象限是 C （A ）第一象限（B ）第二象限 （C ）第三象限 （D ）第四象限4. （延庆）以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，设():cos sin 2l +=ρθθ，M 为l 与224x y +=的交点，则M 的极径为 ．25. (东城)复数i 1iz =-在复平面上对应的点位于 （ ）B （A ）第一象限 （B ）第二象限 （C ）第三象限 （D ）第四象限6. （东城）在极坐标系中， 圆2cos ρθ=的圆心到直线sin 1ρθ=的距离为 ．17. （房山）已知复数i 21+=z ，且复数1z ，2z 在复平面内对应的点关于实轴对称，则=21z z B （A ）1+i （B ）i 5453+ （C ）i 54-53 （D ）i 341+ 8. （房山）在极坐标系中，直线l 的方程为sin 3ρθ=，则点2,6π⎛⎫ ⎪⎝⎭到直线l 的距离为______．29. （丰台）在平面直角坐标系xOy 中，曲线C 的参数方程为1cos ,sin x y αα=+⎧⎨=⎩（α为参数）．若以射线Ox 为极轴建立极坐标系，则曲线C 的极坐标方程为 D(A) sin ρθ=(B) 2sin ρθ= (C) cos ρθ=(D) 2cos ρθ=10. （丰台）如图所示，在复平面内，网格中的每个小正方形的边长都为1，点A ，B对应的复数分别是1z ，2z ，则21z z = ____．12i -- 11. （海淀）复数2i 1i=+ _____________.1+i12.（海淀）直线2x t y t =⎧⎨=⎩（t 为参数）与曲线2cos sin x y θθ=+⎧⎨=⎩（θ为参数）的公共点个数为__________.213．（西城）已知圆的方程为2220x y y +-=．以原点为极点，x 轴正半轴为极轴建立极坐标系，该圆的极坐标方程为 B（A ）2sin ρθ=-（B ）2sin ρθ= （C ）2cos ρθ=- （D ）2cos ρθ=14．（西城）若复数(i)(34i)a ++的实部与虚部相等，则实数a =____． -7。

2009至2018年北京高考真题分类汇编之圆锥曲线精心校对版题号一二三总分得分△注意事项：1.本系列试题包含2009年-2018年北京高考真题的分类汇编。

2.本系列文档有相关的试题分类汇编，具体见封面。

3.本系列文档为北京双高教育精心校对版本4.本系列试题涵盖北京历年（2011年-2020年）高考所有学科一、填空题（本大题共10小题，共0分）1.（2013年北京高考真题数学(文)）若抛物线22y px 的焦点坐标为(1,0)，则p ，准线方程为。

2.（2011年北京高考真题数学(文)）已知双曲线2221y x b （b ＞0）的一条渐近线的方程为2y x ，则b = . 3.（2010年北京高考真题数学(文)）已知双曲线的离心率为2，焦点与椭圆的焦点相同，那么双曲线的焦点坐标为；渐近线方程为。

4.（2009年北京高考真题数学(文)）椭圆22192x y 的焦点为12,F F ，点P 在椭圆上，若1||4PF ，则2||PF ；12F PF 的大小为 . 5.（2014年北京高考真题数学(文)）设双曲线C 的两个焦点为2,0，2,0，一个顶点是1,0，则C 的方程为 . 6.（2015年北京高考真题数学(文)）已知（2，0）是双曲线x 2﹣=1（b ＞0）的一个焦点，则b= ．22221x y a b 221259x y 姓名：__________班级：__________考号：__________●-------------------------密--------------封--------------线--------------内--------------请--------------不--------------要--------------答--------------题-------------------------●。

2018二模分类汇编——圆锥曲线(教师版)1.（2018东城二模·理）已知双曲线C ：x 2a 2－y 2b 2＝1的一条渐近线的倾斜角为60º，且与椭圆x 25+y 2＝1有相等的焦距，则C 的方程为（A ）x 23－y 2＝1 （B ）x 29－y 23＝1 （C ）x 2－y 23＝1 （D ）x 23－y 29＝11.C2.（2018海淀二模·理）设曲线C 是双曲线，则“C 的方程为2214y x -=”是“C 的渐近线方程为2y x =±”的（A ）充分而不必要条件 （B ）必要而不充分条件 （C ）充分必要条件（D ）既不充分也不必要条件2.A3.（2018丰台二模·理）已知双曲线2221(0)9x y b b -=>的一条渐近线的倾斜角为π6，则b 的值为(C) 3(D) B4.（2018海淀二模·理）能够使得命题“曲线221(0)4x y a a-=≠上存在四个点P ，Q ，R ，S 满足四边形PQRS 是正方形”为真命题的一个实数a 的值为 .4.答案不唯一，0a <或4a >的任意实数5.（2018房山二模·理）设双曲线()222210,0-=>>x y a b a b的一条渐近线方程为20-=x y ，则该双曲线的离心率为 ．5.26.（2018顺义二模·理）设双曲线)0,0(1:2222>>=-b a by a x C 经过点(4,1),且与1422=-x y 具有相同渐近线,则C 的方程为________________;渐近线方程为__________________.6.x y y x 21,131222±==-. 7.（2018朝阳二模·理）双曲线22xy λ-=（0λ≠）的离心率是 ；该双曲线的两条渐近线的夹角是 .7.π28.（2018昌平二模·理）已知双曲线：2221(0)x y a a -=>的渐近线方程为12y x =±，则双曲线的离心率是 ．8.9.（2018海淀二模·理）（本小题共14分）已知椭圆C ：2214x y +=，F 为右焦点，圆O ：221x y +=，P 为椭圆C 上一点，且P 位于第一象限，过点P 作PT 与圆O 相切于点T ，使得点F ，T 在OP 两侧.（Ⅰ）求椭圆C 的焦距及离心率; （Ⅱ）求四边形OFPT 面积的最大值. 8.（本小题共14分）解：（Ⅰ）在椭圆C ：2214x y +=中，2a =，1b =，所以c= ···················· 2分 故椭圆C 的焦距为2c =， ·················· 3分 离心率c e a ==． ······················ 5分 （Ⅱ）法一：设00(,)P x y （00x >，00y >），则220014x y +=，故220014x y =-． ····· 6分所以22222203||||||14TPOP OT x y x =-=+-=所以0||TP =， ·········· 8分C C01||||2OTP S OT TP x ∆=⋅=．··· 9分又(0,0)O ，F ，故00122OFP S OF y y ∆=⋅=． ······10分因此00()2OFP OTP OFPT x S S S y ∆∆=+=+四边形 ··········11分==．由220014x y +=，得1≤，即001x y ⋅≤，所以OFPT S =四边形， ············· 13分当且仅当2200142x y ==，即0x 02y =时等号成立. ····· 14分 （Ⅱ）法二：设(2cos ,sin )P θθ（02πθ<<）， ············ 6分则222222||||||4cos sin 13cos TP OP OT θθθ=-=+-=，所以||TP θ=， ·····················8分1||||2OTP S OT TP θ∆=⋅=． ·············9分又(0,0)O ，F ，故012OFP S OF y θ∆=⋅=． ·····10分因此(cos sin )2OFP OTP OFPT S S S θθ∆∆=+=⋅+四边形 ········11分sin()242πθ=+≤， ············· 13分当且仅当4πθ=时，即0x =0y =······ 14分 10.（2018房山二模·理）（本小题14分）已知椭圆()222210+=>>：x y C a b a b 的离心率为12，O 为坐标原点，F 是椭圆C 的右焦点，A 为椭圆C上一点，且⊥AF x 轴，AFO ∆的面积为34．（Ⅰ）求椭圆C 的方程；（Ⅱ）过C 上一点()()000,0≠P x y y 的直线l ： 00221x x y ya b+=与直线AF 相交于点M ，与直线4x =相交于点N .证明：当点P 在C 上移动时，MFNF恒为定值，并求此定值． 10.（Ⅰ）设(,0)F c ，(,)A c d 则22221c d a b +=又12c a =||2d b ∴= 因AFO ∆ 的面积为341133||,2224c d c b bc ∴===由2222a b c a c bc ⎧-=⎪=⎨⎪=⎩得21a b c =⎧⎪=⎨⎪=⎩所以C 的方程为22143x y += …………5分 （Ⅱ）由(1)知直线l 的方程为00143x x y y+= (y 0≠0)，即y ＝001234x x y - (y 0≠0)．因为直线AF 的方程为x ＝1，所以直线l 与AF 的交点为M 0123(1,)4x y -， 直线l 与直线x ＝4的交点为N 0(4,33)x -，则|MF |2|NF |2＝202002220000123()4(4)331616(1)9()x y x x y x y --=-+-+ 又P (x 0，y 0)是C 上一点，则2200143x y +=.2200334x y =- 代入上式得|MF |2|NF |2＝2220002222000000(4)(4)(4)1148121632164(816)4(4)4x x x x x x x x x ---====-+-+-+- 所以|MF ||NF |=12，为定值． …………14分11.（2018朝阳二模·理）已知抛物线2:2C y x =.（1）写出抛物线C 的直线方程，并求出抛物线C 的焦点到准线的距离；（2）过点(20)，且斜率存在的直线l 与抛物线C 交于不同的两点A ，B ，且点B 关于x 轴的对称点为D ，直线AD 与x 轴交于点M .1）求点M 的坐标；2）求OAM △与OAB △面积之和的最小值. 11.【解析】（Ⅰ）由题可得22,1P P ==,所以准线方程为1,2x =-抛物线C 的焦点到准线的距离为1. （Ⅱ）（i ）解:令1122(,),(,),A x y B x y 则22(,)D x y -且令10y >,令:2AB l x my =+222x my y x=+⎧⎨=⎩2240y my ⇒--= 所以12122,4y y m y y +=⋅=-则直线AD 方程为121112()y y y y x x x x +-=--121112()()y y y y x x m y y +-=--2111221()()2y y x y y y -=--当0y =时,21211()()2y y y x y -⋅-=-21211()()2y y y y x -⋅-+=122y y x =,2x =-所以(2,0)M -（ii ）解:1122OAMS y =⋅⋅! 121122||22OAB S y y =⋅⋅+⋅⋅!则112||OAMOAB S S y y y +=++!!1211112||42||42y y y y y y =+-=+=+≥=当且仅当1142y y =时,即1y =12.（2018西城二模·理）（本小题满分14分）已知直线:1l y kx =+与抛物线2:4C y x =相切于点P ．（Ⅰ）求直线l 的方程及点P 的坐标；（Ⅱ）设Q 在抛物线C 上，A 为PQ 的中点．过A 作y 轴的垂线，分别交抛物线C 和直线l 于M ，N ．记△PMN的面积为1S ，△QAM 的面积为2S ，证明：12S S =． 12.（本小题满分14分）解：（Ⅰ）由 21,4y kx y x=+⎧⎪⎨=⎪⎩ 得 22(24)10k x k x +-+=． ① ……………… 2分依题意，有0k ≠，且22(24)40k k ∆=--=． 解得 1k =． ……………… 3分所以直线l 的方程为1y x =+． ……………… 4分 将 1k =代入①，解得 1x =，所以点P 的坐标为(1,2)． ……………… 5分 （Ⅱ）设 (,)Q m n ， 则 24n m =，所以 12(,)22m n A ++． ……………… 7分 依题意，将直线 22n y +=分别代入抛物线C 与直线l ， 得 2(2)2(,)162n n M ++，2(,)22n n N +． ……………… 8分因为 22(2)444441||16216164n n n n m n m n MN +-+-+-+=-=== ……… 10分 221(2)(88)(44)||21616m n m n n AM +++-++=-=(88)(444)1164m m n m n +-++-+==， ………………12分所以 ||||AM MN =． ………………13分又 A 为PQ 中点，所以P Q ，两点到直线AN 的距离相等， 所以 12S S =． ………………14分13.（2018东城二模·理）（本小题13分）已知抛物线C ：y 2=2px 经过点P (2，2)，A ，B 是抛物线C 上异于点O 的不同的两点，其中O 为原点． （I ）求抛物线C 的方程，并求其焦点坐标和准线方程； （II ）若OA OB ^，求△AOB 面积的最小值. 13.（共13分）解：（I ）由抛物线C ：y 2=2px 经过点P (2，2)知44p =，解得1p =.则抛物线C 的方程为22y x =.抛物线C 的焦点坐标为1(,0)2，准线方程为12x =-.………………4分 （II ）由题知，直线AB 不与y 轴垂直，设直线AB ：x ty a =+，由2,2x ty a y x=+⎧⎨=⎩消去x ，得2220y ty a --=. 设1122(,),(,)A x y B x y ，则12122,2y y t y y a +==-.因为OA OB ⊥，所以12120x x y y +=，即22121204y y y y +=， 解得120y y =（舍）或124y y =-. 所以24a -=-.解得2a =. 所以直线AB ：2x ty =+. 所以直线AB 过定点(2,0).12122AOB S y y ∆=⨯⨯-==≥4=.当且仅当122,2y y ==-或122,2y y =-=时，等号成立.所以AOB ∆面积的最小值为4. ……………………………………13分14.（2018昌平二模·理）（本小题14分）已知椭圆经过点．（I ）求椭圆E 的标准方程；（II）过右焦点F 的直线（与x 轴不重合）与椭圆交于两点，线段AB 的垂直平分线交y 轴于点(0,)M m ，求实数m 的取值范围．14.（共14分）（Ⅰ）由题意，得， 解得 1a b ⎧=⎪⎨=⎪⎩所以椭圆E 的标准方程是． -------------------5分 （II ）（1）当直线轴时，m = 0符合题意．（2）当直线与x 轴不垂直时，设直线的方程为，由22(1)220y k x x y =-⎧⎨+-=⎩，得， 由2222(4)8(12)(1)0k k k ∆=--+->，得k ∈R ．设，，则2212122242(1)1212k k x x x x k k-+=⋅=++，． 所以121222(2)12ky y k x x k-+=+-=+， ()2222:10x y E a b a b+=>>(0,1)l ,A B 2221b c e a a b c =⎧⎪⎪==⎨⎪⎪=+⎩2212x y +=x AB ⊥AB AB ()1y k x =-()()2222124210k x k x k +-+-=()11,x y A ()22,x y B所以线段AB 中点C 的坐标为．由题意可知，，故直线的方程为，令x = 0，212k y k =+，即212k m k =+当k > 0时，，得210=11242k m k kk <=≤++，当且仅当2k =时“=”成立． 同理，当 k < 0时，210=11242k m k kk>=≥-++，当且仅当2k =-时“=”成立． 综上所述，实数m的取值范围为44⎡-⎢⎣⎦．--------------------14分 15. （2018丰台二模·理）（本小题共14分）已知椭圆C ：22221(0)x y a b a b+=>>的长轴长为4，离心率为12，过右焦点F 且不与坐标轴垂直的直线l与椭圆相交于M ，N 两点，设点(,0)P m ，记直线PM ，PN 的斜率分别为1k ，2k ．（Ⅰ）求椭圆C 的方程； （Ⅱ）若120k k +=，求m 的值． 15.（本小题共14分）解：（Ⅰ）依题意得 24a =，所以 2a =． …………………1分因为 12c e a ==，所以 1c =． …………………2分 所以 23b =． …………………3分所以椭圆C 的方程为 22143x y +=． …………………4分（Ⅱ）椭圆的右焦点 (1,0)F ． …………………5分设直线 l ：(1)(0)y k x k =-≠，设 11(,)M x y ，22(,)N x y ．………6分联立方程组 ⎪⎩⎪⎨⎧-==+)1(13422x k y y x ， 2222,1212k k k k ⎛⎫- ⎪++⎝⎭0k ≠C M 222121212k k y x k k k ⎛⎫+=-- ⎪++⎝⎭消y 得 2222(34)84(3)0k x k x k +-+-=，0∆>成立． …………………8分所以 2122834k x x k +=+，21224(3)34k x x k-=+． …………………9分 因为 1212120y y k k m x m x --+=+=--， …………………10分所以122112()()0()()y m x y m x m x m x ----=--，即 1221()()0y m x y m x -+-=，…11分所以 2112()(1)()(1)0k m x x k m x x --+--=恒成立． …………………12分 因为 0k ≠，所以 1212(1)()220m x x x x m ++--=，即 222284(3)(1)2203434k k m m k k -+⋅-⋅-=++， …………………13分 化简为 2228(1)8(3)2(34)0k m k m k +---+=， 所以 4m =． …………………14分16.（2018顺义二模·理）（本小题满分14分）已知椭圆134:22=+y x G 的左焦点为F ，左顶点为A ，离心率为e ，点()0,t M ()2-<t 满足条件e AM FA =||||.（Ⅰ）求实数t 的值；（Ⅱ）设过点F 的直线l 与椭圆G 交于Q P ,两点，记MPF ∆和MQF ∆的面积分别为21,S S ，证明：||||21MQ MP S S =. 16.解：（Ⅰ）椭圆G 的标准方程为：13422=+y x ∴3,2==b a ，122=-=b a c ------------------------2分则21==a c e ，t AM FA --==2||,1||--------------------3分 ∵2121||||=--=t AM FA ，解得4-=t -------------4分（Ⅱ）方法一：①若直线l 的斜率不存在，则21S S =，||||MQ MP =，符合题意--------5分②若直线l 的斜率存在，因为左焦点()0,1-F ，则可设直线l 的方程为：()1+=x k y ，并设()()2211,,,y x Q y x P .联立方程组()⎪⎩⎪⎨⎧=++=134122y x x k y ，消去y 得：()01248432222=-+++k x k x k ---6分 ∴2221438k k x x +-=+,222143124kk x x +-=--------------------------------7分 ∵442211+++=+x y x y k k MQ MP ()()41412211+++++=x x k x x k ----------------9分 ()()()()()()444141211221+++++++=x x x x k x x k ()()()44852212121+++++=x x k x x k x kx ()()04484385431242212222=++++-∙++-∙=x x k k k k k k k ∴QMF PMF ∠=∠-------------------------------------------------------------------12分 ∵PMF MP MF S ∠=sin ||||211，QMF MQ MF S ∠=sin ||||212 ∴||||21MQ MP S S =------------------------------------------------------------------14分 方法二：依题意可设直线l 的方程为：1-=my x ，并设()()2211,,,y x Q y x P .—5分 联立方程组⎪⎩⎪⎨⎧=+-=134122y x my x ，消去x ，得()0964322=--+my y m --------6分 ∴436221+=+m m y y ,439221+-=m y y --------------------------------7分 ∵442211+++=+x y x y k k MQ MP 332211+++=my y my y ------------------------------9分()()()()3333211221+++++=my my my y my y ()()()3332212121++++=my my y y y my ()()033436343922122=+++⨯++-∙=my my m m m m ∴QMF PMF ∠=∠------------------------------------------------------------------12分 ∵PMF MP MF S ∠=sin ||||211，QMF MQ MF S ∠=sin ||||212 ∴||||21MQ MP S S =------------------------------------------------------------------14分。

专题19 圆锥曲线综合【母题原题1】【2018新课标1，理19】设椭圆的右焦点为，过的直线与交于两点，点的坐标为.（1）当与轴垂直时，求直线的方程；（2）设为坐标原点，证明：.由得.将代入得.所以，.则.从而，故MA，MB的倾斜角互补，所以.综上，.点睛：该题考查的是有关直线与椭圆的问题，涉及到的知识点有直线方程的两点式、直线与椭圆相交的综合问题、关于角的大小用斜率来衡量，在解题的过程中，第一问求直线方程的时候，需要注意方法比较简单，需要注意的就是应该是两个，关于第二问，在做题的时候需要先将特殊情况说明，一般情况下，涉及到直线与曲线相交都需要联立方程组，之后韦达定理写出两根和与两根积，借助于斜率的关系来得到角是相等的结论.【母题原题2】【2017新课标1，理20】已知椭圆C:=1(a>b>0),四点P1(1,1),P2(0,1),P3(-1,),P4(1,)中恰有三点在椭圆C上.(1)求C的方程;(2)设直线l不经过P2点且与C相交于A,B两点.若直线P2A与直线P2B的斜率的和为-1,证明:l过定点.【母题原题3】【2016新课标1，理20】设圆x2+y2+2x-15=0的圆心为A,直线l过点B(1,0)且与x轴不重合,l交圆A于C,D两点,过B作AC的平行线交AD于点E.(Ⅰ)证明|EA|+|EB|为定值,并写出点E的轨迹方程;(Ⅱ)设点E的轨迹为曲线C1,直线l交C1于M,N两点,过B且与l垂直的直线与圆A交于P,Q两点,求四边形MPNQ面积的取值范围.【解析】 (Ⅰ)因为|AD|=|AC|,EB∥AC,故∠EBD=∠ACD=∠ADC.所以|EB|=|ED|,故|EA|+|EB|=|EA|+|ED|=|AD|.又圆A(x+1)2+y2=16,从而|AD|=4,所以|EA|+|EB|=4.由题设得A(-1,0),B(1,0),|AB|=2,E的轨迹方程为:=1(y≠0).(Ⅱ)当l与x轴不垂直时,设l的方程为y=k(x-1)(k≠0),M(x1,y1),N(x2,y2),由可得当,四边形MPNQ面积的取值范围为(12,8).当,其方程为x=1,|MN|=3,|PQ|=8,四边形MPNQ的面积为12.综上,四边形MPNQ面积的取值范围为[12,8).【命题热点剖析】1.圆锥曲线的解答题新课标的要求理科一般以椭圆或抛物线为背景,而文科一般以椭圆或圆或抛物线为背景进行综合考查,由于双曲线的弱化,故以双曲线为背景的解析几何解答题不在考虑.从近几年高考来看,圆锥曲线的解答题中主要是以椭圆,抛物线为基本依托,考查椭圆,抛物线方程的求解、考查直线与曲线的位置关系,考查数形结合思想、函数与方程思想、等价转化思想、分类与整合思想等数学思想方法,这道解答题往往是试卷的压轴题之一．从近几年高考来看,计算量都不是太大,说明文理难度都在降低,特别是计算量不大,但要求的逻辑思维能力,数形结合的能力与往年差不多,体现高考重能力,轻运算．由于圆锥曲线与方程是传统的高中数学主干知识,在高考命题上已经比较成熟,考查的形式和试题的难度、类型已经较为稳定,考查方向为以椭圆,抛物线为背景,考查轨迹问题、探索性命题及最值问题,文科也有可能以圆为背景命题,也有可能继续保持题型不变,考查细节上有所变化.2.从近几年高考来看,求曲线的轨迹方程是高考的常考题型,主要以解答题的形式出现,考查轨迹方程的求法以及利用曲线的轨迹方程研究曲线的几何性质,一般用直接法、待定系数法、相关点代入法等求曲线的轨迹方程,其关键是找到与任意点有关的等量关系．轨迹问题的考查往往与函数、方程、向量、平面几何等知识相融合,着重考查分析问题、解决问题的能力,对逻辑思维能力、运算能力也有一定的要求． 【应试经验与技巧】１．判断两种标准方程的方法为比较标准形式中2x 与2y 的分母大小,若2x 的分母比2y 的分母大,则焦点在x 轴上,若2x 的分母比2y 的分母小,则焦点在y 轴上．２．注意椭圆的范围,在设椭圆)0(12222>>=+b a by a x 上点的坐标(),P x y 时,则x a ≤,这往往在求与点P 有关的最值问题中特别有用,也是容易忽略导致求最值错误的原因．３．注意椭圆上点的坐标范围,特别是把椭圆上某一点坐标视为某一函数问题求解,求函数的单调区间,最值有重要意义．4．直线和抛物线若有一个公共点,并不能说明直线和抛物线相切,还有可能直线与抛物线的对称轴平行． 5．在求得轨迹方程之后,要深入地思考一下：(1)是否还遗漏了一些点？是否还有另一个满足条件的轨迹方程存在？(2)在所求得的轨迹方程中,x ,y 的取值范围是否有什么限制？确保轨迹上的点“不多不少”． 6.作为解答题的倒数第二个,试题的难度较大,也体现在计算量上尤为明显,学生在解题时往往会思路,但计算往往不对,对此,建议如下：第一问保证准确,如轨迹方程,曲线方程,或者几何性质等,因为第二问往往以第一问为基础,故第一问要舍得花时间去验证一下；对于第二问,往往就是曲线与直线联立,建立方程组,利用判别式,韦达定理等这些都已经成立的模式,建立关系式,即使思路无法进行,也要准确的放在卷面上,一般它们都要占到部分分数；如果涉及到直线方程的探索,特别注意斜率不存在的情况,有时一些定值定点问题,可以通过这种特殊情况直接得到. 【重点知识整合】1.椭圆的第一定义：平面内到两个定点12,F F 的距离之和等于定长（12F F >）的点的轨迹.注意：椭圆中,与两个定点F 1,F 2的距离的和等于常数2a ,且此常数2a 一定要大于21F F ,当常数等于21F F 时,轨迹是线段F 1F 2,当常数小于21F F 时,无轨迹.2．直线和椭圆的位置关系 （1）位置关系判断：直线与椭圆方程联立方程组,消掉y,得到20Ax Bx C ++=的形式（这里的系数A 一定不为0）,设其判别式为∆,（1）相交：0∆>⇔直线与椭圆相交； （2）相切：0∆=⇔直线与椭圆相切； （3）相离：0∆<⇔直线与椭圆相离； (2弦长公式：（1）若直线y kx b =+与圆锥曲线相交于两点A 、B,且12,x x 分别为A 、B 的横坐标,则AB12x -,若12,y y 分别为A 、B 的纵坐标,则AB ＝21211y y k-+,若弦AB 所在直线方程设为x ky b =+,则AB＝12y -.（2）焦点弦（过焦点的弦）：焦点弦的弦长的计算,一般不用弦长公式计算,而是将焦点弦转化为两条焦半径之和后,利用第二定义求解.椭圆22221(0)x y a b a b+=>>左焦点弦12||2()AB a e x x =++,右焦点弦12||2()AB a e x x =-+.其中最短的为通径：22b a,最长为2a ；（3）椭圆的中点弦问题：遇到中点弦问题常用“韦达定理”或“点差法”求解.在椭圆12222=+by a x 中,以00(,)P x y 为中点的弦所在直线的斜率2020b x k a y =-.3.与焦点三角形相关的结论椭圆上的一点与两焦点所构成的三角,通常叫做焦点三角形.一般与焦点三角形的相关问题常利用椭圆的第一定义和正弦、余弦定理求解.设椭圆上的一点00(,)P x y 到两焦点12,F F 的距离分别为12,r r ,焦点12F PF ∆的面积为S ,设12F PF θ∠=,则在椭圆12222=+by a x 中,有以下结论：(1)θ＝)12arccos(212-r r b ,且当12r r =即P 为短轴端点时,θ最大为θm ax ＝222arccos ac b -； （2）2122||||1cos b PF PF θ=+；焦点三角形的周长为2()a c +；(3)221201sin sin tan ||21cos 2S r r b b c y θθθθ====+,当0||y b =即P 为短轴端点时,m ax S 的最大值为bc ；4.直线和抛物线的位置关系（1）位置关系判断：直线(0)y kx m m =+≠与双曲线方程22(0)y px p =>联立方程组,消掉y,得到2222()0k x mk p x m +-+=的形式,当0k =,直线和抛物线相交,且与抛物线的对称轴并行,此时与抛物线只有一个交点,当0k ≠设其判别式为∆,①相交：0∆>⇔直线与抛物线有两个交点；②相切：0∆=⇔直线与抛物线有一个交点； ③相离：0∆<⇔直线与抛物线没有交点.注意：过抛物线外一点总有三条直线和抛物线有且只有一个公共点：两条切线和一条平行于对称轴的直线. （2）焦点弦：若抛物线22(0)y px p =>的焦点弦为AB,1122(,),(,)A x y B x y ,则有12||AB x x p =++,221212,4p x x y y p ==-.（3） 在抛物线22(0)y px p =>中,以00(,)P x y 为中点的弦所在直线的斜率0p k y =. （4）若OA 、OB 是过抛物线22(0)y px p =>顶点O 的两条互相垂直的弦,则直线AB 恒经过定点(2,0)p ,反之亦成立.5.求曲线(图形)方程的方法及其具体步骤如下：注意：这五个步骤(不包括证明)可浓缩为五字“口诀”：建设现(限)代化.1．【山东、湖北部分重点中学2018年高考冲刺模拟试卷（二）】已知椭圆的离心率为，分别为椭圆的左、右焦点，点为椭圆上一点，面积的最大值为.（Ⅰ）求椭圆的方程； （Ⅱ）过点作关于轴对称的两条不同直线分别交椭圆于与，且，证明直线过定点，并求的面积的取值范围.试题解析： （Ⅰ）设，则，设，则.解得.所以椭圆的方程为.（Ⅱ）设方程为，联立，得，点睛：求定点，定值问题常见的方法有两种：(1)从特殊入手，求出定值，再证明这个值与变量无关．(2)直接推理、计算，并在计算推理的过程中消去变量，从而得到定值．2．【陕西省咸阳市2018年高考5月信息专递】已知椭圆的右焦点与抛物线的焦点重合，且椭圆的离心率为．（Ⅰ）求椭圆的方程；（Ⅱ）设是椭圆的右顶点，过点作两条直线分别与椭圆交于另一点，若直线的斜率之积为，求证：直线恒过一个定点，并求出这个定点的坐标.【解析】分析: （Ⅰ）由题意布列关于a，b的方程组，解之即可；（Ⅱ）设直线，与椭圆方程联立可得，利用根与系数的关系表示直线的斜率之积为，可得值，从而得证.详解: （Ⅰ）依题意：，解得，即椭圆；（Ⅱ）设直线，则，点睛: 定点、定值问题通常是通过设参数或取特殊值来确定“定点”是什么、“定值”是多少，或者将该问题涉及的几何式转化为代数式或三角问题，证明该式是恒定的. 定点、定值问题同证明问题类似，在求定点、定值之前已知该值的结果，因此求解时应设参数，运用推理，到最后必定参数统消，定点、定值显现.3．【山东省肥城市2018届高三适应性训练】已知点为圆的圆心，是圆上的动点，点在圆的半径上，且有点和上的点，满足，.（1）当点在圆上运动时，判断点的轨迹是什么？并求出其方程；（2）若斜率为的直线与圆相切，与（1）中所求点的轨迹交于不同的两点，，且（其中是坐标原点），求的取值范围.【解析】分析：(1)先根据垂直平分线定义得，再根据圆的半径得，最后根据椭圆定义确定轨迹，并求标准方程，(2)先设直线：，，，则，再联立直线方程与椭圆方程，利用韦达定理化简，最后解不等式得的取值范围.详解：（1）由题意是线段的垂直平分线，所以，所以点的轨迹是以点，为焦点，焦距为2，长轴长为的椭圆，∴，，，故点的轨迹方程是.点睛：直线和圆锥曲线的位置关系，一般转化为直线方程与圆锥曲线方程组成的方程组，利用韦达定理或求根公式进行转化，涉及弦长的问题中，应熟练地利用根与系数关系，设而不求法计算弦长；涉及垂直关系时也往往利用根与系数关系、设而不求法简化运算；涉及过焦点的弦的问题，可考虑用圆锥曲线的定义求解.涉及中点弦问题往往利用点差法.4．【山东省潍坊市青州市2018届高三第三次高考模拟】设椭圆的右焦点为，离心率为，过点且与轴垂直的直线被椭圆截得的线段长为 .（1）求椭圆的方程;（2）若上存在两点，椭圆上存在两个点满足：三点共线，三点共线，且，求四边形的面积的最小值.【解析】分析：（）由题意可知及，即可求得和的值，求得椭圆的标准方程；（2）讨论直线的斜率不存在，求得弦长，求得四边形的面积；当直线的斜率存在时，设直线的方程为，联立方程组，运用韦达定理和弦长公式，以及四边形的面积公式，计算即可求得最小值.∴，令，则，综上点睛：本题主要考查椭圆的标准方程与几何性质、直线与圆锥曲线的位置关系的应用问题,解答此类题目，通常利用的关系，确定椭圆（圆锥曲线）方程是基础，通过联立直线方程与椭圆（圆锥曲线）方程的方程组，应用一元二次方程根与系数的关系，得到“目标函数”的解析式，确定函数的性质进行求解，此类问题易错点是复杂式子的变形能力不足，导致错漏百出，本题能较好的考查考生的逻辑思维能力、运算求解能力、分析问题解决问题的能力等.5．【重庆市西南大学附中高2018级第四次月考】已知椭圆的两个焦点与短轴的一个顶点构成底边为，顶角为的等腰三角形．（1）求椭圆的方程；（2）设、、是椭圆上三动点，且，线段的中点为，，求的取值范围．∴椭圆（2）设，，，由∴，得：当的斜率不存在时，，由,，得，∴，当的斜率存在时，设得：，，由点在椭圆上得得：，此时总成立又，6．【辽宁省葫芦岛市2018年普通高中高三第二次模拟】已知椭圆的焦距为，离心率为，圆，是椭圆的左右顶点，是圆的任意一条直径，面积的最大值为2.（1）求椭圆及圆的方程；（2）若为圆的任意一条切线，与椭圆交于两点，求的取直范围.【解析】分析：(1)易知当线段AB在y轴时，，，结合可求，可求椭圆方程和圆的方程；（2）设直线L方程为：y=kx+m,直线为圆的切线，，直线与椭圆联立，，得，利用弦长公式点睛：本题考查椭圆方程的求法，主要考查了直线与椭圆的位置关系的应用，直线与曲线联立，根据方程的根与系数的关系解题，是处理这类问题的最为常用的方法，但圆锥曲线的特点是计算量比较大，要求考试具备较强的运算推理的能力，是难题．7．【江西省临川一中2018届高三模拟考试】已知的直角顶点在轴上，点为斜边的中点，且平行于轴.（Ⅰ）求点的轨迹方程；（Ⅱ）设点的轨迹为曲线，直线与的另一个交点为.以为直径的圆交轴于即此圆的圆心为,求的最大值.【解析】试题分析：（1）设的中点的坐标为，根据,得即；（2）（2）讨论BC的斜率，求出圆P的半径和横坐标，计算最小值，进而得到的最大值.点睛：本题主要考查直线与圆锥曲线位置关系，所使用方法为韦达定理法：因直线的方程是一次的，圆锥曲线的方程是二次的，故直线与圆锥曲线的问题常转化为方程组关系问题，最终转化为一元二次方程问题，故用韦达定理及判别式是解决圆锥曲线问题的重点方法之一，尤其是弦中点问题，弦长问题，可用韦达定理直接解决，但应注意不要忽视判别式的作用．8．【四川省双流中学2018届高三考前第二次模拟考试】在平面直角坐标系中，点、分别为双曲线的左、右焦点，双曲线的离心率为，点在双曲线上，不在轴上的动点与动点关于原点对称，且四边形的周长为.(1)求动点的轨迹的方程；(2)过点的直线交的轨迹于，两点，为上一点，且满足，其中，求的取值范围.方程为：.(2)由题意可知该直线存在斜率，设其方程为且.由得，∴，得，设，，，则，由，得，代入椭圆方程得，由得，∴，令，则，∴.点睛：本题主要考查直线与圆锥曲线位置关系，所使用方法为韦达定理法：因直线的方程是一次的，圆锥曲线的方程是二次的，故直线与圆锥曲线的问题常转化为方程组关系问题，最终转化为一元二次方程问题，故用韦达定理及判别式是解决圆锥曲线问题的重点方法之一，尤其是弦中点问题，弦长问题，可用韦达定理直接解决，但应注意不要忽视判别式的作用．9．【山东省实验中学2015级第二次模拟考试】过抛物线的焦点的直线与抛物线在第一象限的交点为，与抛物线准线的交点为，点在抛物线准线上的射影为，若的面积为 .（ 1 ）求抛物线的标准方程；（ 2 ）过焦点的直线与抛物线交于两点，抛物线在点处的切线分别为，且与相交于点，与轴交于点，求证： .联立消去得，得，，设，，，得点坐标，由，得，,所以，即.点睛：(1)直线与抛物线的位置关系和直线与椭圆、双曲线的位置关系类似，一般要用到根与系数的关系；(2)有关直线与抛物线的弦长问题，要注意直线是否过抛物线的焦点，若过抛物线的焦点，可直接使用公式|AB|＝x1＋x2＋p，若不过焦点，则必须用一般弦长公式．10．【河北省石家庄二中2018届高三三模】已知椭圆的左右顶点分别为，，右焦点的坐标为，点坐标为，且直线轴，过点作直线与椭圆交于，两点（，在第一象限且点在点的上方），直线与交于点，连接.（1）求椭圆的方程；（2）设直线的斜率为，直线的斜率为，问：的斜率乘积是否为定值，若是求出该定值，若不是，说明理由.所以点睛：圆锥曲线的定值问题会涉及到曲线上的动点及动直线，常用解题步骤为：设动点和动直线、即引入参数；结合已知条件将目标式用参变量表示，（3）通过化简消参求得定值.设而不求、整体思想和消元思想的运用可有效的简化运算.11．【河南省安阳35中2018届高三核心押题卷一】已知椭圆的上顶点为，点,是上且不在轴上的点，直线与交于另一点，若的离心率为，的最大面积等于.（Ⅰ）求的方程，（Ⅱ）若直线分别与轴交于点,试判断是否为定值.形即可求值，。

2018年北京高三模拟考试数学文科试题分类汇编----解析几何（2018年朝阳期末）10．已知双曲线C 的中心在原点，对称轴为坐标轴，它的一个焦点与抛物线28y x =的焦点重合，一条渐近线方程为0x y +=，则双曲线C 的方程是 221x y -= ．(2018年东城期末)（10）双曲线2212y x -=的渐近线方程为_____y =?____． (2018年海淀期末)（9）已知双曲线221ax y -=的一条渐近线方程为x y =，则实数a 的值为 1 .(2018年西城期末)10．已知双曲线22221x y a b-=的一个焦点是(2,0)F ，其渐近线方程为y =，该双曲线的方程是__2213y x -=__．(2018年丰台期末)7．已知抛物线24y x =的焦点为F ，点A 在y 轴上，线段AF 的中点B 在抛物线上，则AF =（ C ） A ．1 B ．32C ．3D ．6 13．能够说明“方程()()()()221313m x m y m m -+-=--的曲线不是双曲线”的一个m 的值是13m ≤≤之间的数即可 ．(2018年石景山期末5．“10m >”是“”的（ A ） A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件 D ．既不充分也不必要条件10．抛物线24y x =上一点到此抛物线焦点的距离为___3____. (2018年昌平期末)12. 已知双曲线22221(0,0)x y a b a b-=>>的左焦点为抛物线212y x =-的焦点，双曲线的渐近线方程为y =，则实数a (2018年通州期末)10．已知点(2P 为抛物线22y px =上一点，那么点P 到抛物线准线的距离是____3___.(2018年房山期末)（7）双曲线221y x m-=D ） （A ）12m >（B ）1m ≥ （C ）1m > （D ）2m > （10）若抛物线px y 22=的焦点坐标为)0,2(，则p = 4 ，准线方程为 -2 ． （2018年朝阳一模）5.已知F 为抛物线C ：24y x =的焦点，过点F 的直线l 交抛物线C 于,A B 两点，若8AB =，则线段AB 的中点M 到直线10x +=的距离为 （ B ）A ．2 B. 4 C ．8 D ．1610.双曲线2214x y -=的焦距为_____；渐近线方程为____12y x =±_____． (2018年东城一模)（10）已知抛物线22(0)y px p =>的焦点坐标为1(,0)4，则p =____12___． (2018年海淀一模)（5）若抛物线22(0)y px p =>上任意一点到焦点的距离恒大于1，则p 的取值范围是（ D ）(A) 1p < （B ） 1p > （C ） 2p < （D ） 2p >（10）已知点(2,0)是双曲线:C 2221x y a-=的一个顶点，则C 的离心率为2 .(2018年西城一模)11．已知抛物线28y x =-的焦点与双曲线2221(0)x y a a-=>的一个焦点重合，则a =；双曲线的渐近线方程是__0x =__． (2018年丰台一模)（4）已知抛物线C 的开口向下，其焦点是双曲线2213y x -=的一个焦点，则C 的标准方程为 （ B ） (A) 28y x = (B) 28x y =-(C) 2y =(D) 2x =(2018年石景山一模)10.双曲线2212x y -=的焦距是________,渐近线方程是______y =_______. (2018年房山一模)（9）抛物线24x y =的焦点到双曲线2213y x -=的渐近线的距离为 12 .(2018年顺义一模)9. 已知双曲线221x y m-=的一个焦点为(-,则该双曲线的方程为_____2217x y -=______.（2018年朝阳二模）（13）已知双曲线22221(0,0)x y a b a b-=>>与抛物线28y x =有一个公共的焦点F .设这两曲线的一个交点为P ，若5PF =，则点P 的横坐标是 3 ；该双曲线的渐近线方程为 y = ． (2018年东城二模)（10）若双曲线22221(0,0)x y a b a b-=>>的一条渐近线方程为20x y -=，则双曲线的离心率为____． (2018年海淀二模)（6）设曲线C 是双曲线，则 “C 的方程为2214y x -=”是“C 的渐近线方程为2y x =±”的（ A ） （A ）充分而不必要条件 （B ）必要而不充分条件 （C ）充分必要条件 （D ）既不充分也不必要条件（9）已知抛物线C 的焦点为(0,1)F ，则抛物线C 的标准方程为__24x y =__.(2018年西城二模)12．双曲线22:1916y x C -=的焦距是__10__；若圆222(1)(0)x y r r -+=>与双曲线C 的渐近线相切，则r =__35__．(2018年丰台二模)（3）设双曲线2221(0)x y a a-=>的一条渐近线的倾斜角为π6，则a =（ C ）(A)(B)(C)(D) (2018年昌平二模)10. 若抛物线212x y =，则焦点F 的坐标是 (0,3) .(2018年房山二模)（9）双曲线2221-=y x a 的渐近线为x y 2±=，则该双曲线的离心率为 26 ．(2018年顺义二模)12． 设双曲线()2222:10,0x y C a b a b-=>>经过点()4,1，且与2214x y -=具有相同渐近线，则C 的方程为_____221123x y -=_____，渐近线方程为_____12y x =±_____． （2018年朝阳期末） 19．（本小题满分14分）已知椭圆2222:1(0)5x y C b b b+=>的一个焦点坐标为(2,0)．（Ⅰ）求椭圆C 的方程；（Ⅱ）已知点(3,0)E ，过点(1,0)的直线l （与x 轴不重合）与椭圆C 交于,M N 两点，直线ME 与直线5x =相交于点F ，试证明：直线FN 与x 轴平行． 解：（Ⅰ）由题意可知222,5.c a b =⎧⎨=⎩所以225,1a b ==.所以椭圆C 的方程为2215x y +=. …………………………3分 （Ⅱ）①当直线l 的斜率不存在时，此时MN x ⊥轴.设(1,0)D ，直线5x =与x 轴相交于点G ，易得点(3,0)E 是点(1,0)D 和点(5,0)G 的中点，又因为||||MD DN =，所以||||FG DN =.所以直线//FN x 轴.②当直线l 的斜率存在时，设直线l 的方程为(1)(0)y k x k =-≠，1122(,),(,)M x y N x y .因为点(3,0)E ，所以直线ME 的方程为11(3)3y y x x =--. 令5x =，所以11112(53)33F y y y x x =-=--. 由22(1),55y k x x y =-⎧⎨+=⎩消去y 得2222(15)105(1)0k x k x k +-+-=. 显然0∆>恒成立.所以22121222105(1),.5151k k x x x x k k -+==++因为1211211221112(3)2(1)(3)2(1)333F y y x y k x x k x y y y x x x -------=-==--- 22221212115(1)10[35][3()5]515133k k k k x x x x k k x x --⨯+-++++==--22221516510513k k k k k x --++=⋅=+-， 所以2F y y =.所以直线//FN x 轴.综上所述，所以直线//FN x 轴. …………………………14分(2018年东城期末) （20）（本小题13分）已知椭圆:C 22221(0)x y a b a b+=>>的右焦点(1,0)F 与短轴两个端点的连线互相垂直．（Ⅰ）求椭圆C 的标准方程；（Ⅱ）设点Q 为椭圆C 上一点，过原点O 且垂直于QF 的直线与直线2y =于点P ，求△OPQ 面积S 的最小值．解：（Ⅰ）由题意，得2221,1,,b c a b c ⎧=⎪=⎨⎪=+⎩解得a =所以椭圆C 的方程为2212x y +=． ………4分（Ⅱ）设00(,)Q x y ，(,2)P m ，则220012x y +=．① 当0m =时，点(0,2)P ，Q点坐标为(或，122S ==．② 当0m ¹时，直线OP 的方程为2y x m=．即20x my -=， 直线QF 的方程为(1)2my x =--． 点00(,)Q x y 到直线OP 的距离为d，||OP =所以，000011|||2|||222mS OP d x my x y =⋅⋅=⨯-=-． 又00(1)2my x =--，所以202200000000(1)2212||||||1121x y x x S x x x x x --+=+=+=⨯--- 00001111|1|(|1|)212|1|x x x x =⨯-+=-+--0x ≥<01)x ≠， 当且仅当001|1||1|x x -=-，即00x =时等号成立，综上，当00x =时，S 取得最小值1. ………13分(2018年海淀期末) 19. （本小题14分）已知椭圆22:13+=x y C m m，直线:20+-=l x y 与椭圆C 相交于P ，Q 两点，与x 轴交于点B ，点,P Q 与点B 不重合. （Ⅰ）求椭圆C 的离心率；（Ⅱ）当2∆=OPQ S 时，求椭圆C 的方程；（Ⅲ）过原点O 作直线l 的垂线，垂足为.N 若λ=PN BQ ，求λ的值.解：（Ⅰ）m a 32=，m b =2，m c 22=， ------------------------2分32222==a c e ，故36=e . ------------------------4分（Ⅱ）设()11,y x P ，()22,y x Q⎩⎨⎧=-+=+023322y x m y x ，得到03122=-+m x x 12-4，依题意，由2(12)44(123)0m ∆=--⨯⨯->得1m >.且有121231234x x m x x +=⎧⎪⎨-=⎪⎩， ------------------------6分12|PQ x x =-== ------------------------7分原点到直线l 的距离2=d ------------------------8分所以11||222OPQ S PQ d ∆=⋅== ------------------------9分解得 73m =>1， 故椭圆方程为223177x y +=. ------------------------10分 （Ⅲ）直线l 的垂线为:ONy x =， ------------------------11分由20y xx y =⎧⎨+-=⎩解得交点)1,1(N ， ------------------------12分 因为PN BQ λ=，又123x x +=所以BQPN =λ=122212221=--=--x x x x ，故λ的值为1. ------------------------14分(2018年西城期末) 19．（本小题满分14分）已知椭圆2222:1(0)x y C a b a b+=>>过(2,0)A ，(0,1)B 两点．（Ⅰ）求椭圆C 的方程及离心率；（Ⅱ）设点Q 在椭圆C 上．试问直线40x y +-=上是否存在点P ，使得四边形PAQB 是平行四边形？若存在，求出点P 的坐标；若不存在，说明理由．解：（Ⅰ）由题意得，2a =，1b =． [ 2分]所以椭圆C 的方程为2214x y +=． [ 3分]设椭圆C 的半焦距为c ，则c == [ 4分]所以椭圆C 的离心率c e a ==． [ 5分]（Ⅱ）由已知，设(,4)P t t -，00(,)Q x y ． [ 6分]若PAQB 是平行四边形，则 PA PB PQ +=， [ 8分] 所以 00(2,4)(,3)(,4)t t t t x t y t --+--=--+，整理得 002, 3x t y t =-=-． [10分] 将上式代入 220044x y +=，得 22(2)4(3)4t t -+-=， [11分] 整理得 2528360t t -+=， 解得 185t =，或2t =． [13分] 此时 182(,)55P ，或(2,2)P ．经检验，符合四边形PAQB 是平行四边形， 所以存在 182(,)55P ，或(2,2)P 满足题意． [14分](2018年丰台期末)19．已知椭圆()2222:10x y C a b a b+=>>的左、右焦点分别是12,F F ，点(B 在椭圆C 上，12F BF ∆是等边三角形.（Ⅰ）求椭圆C 的标准方程；（Ⅱ）点A 在椭圆C 上，线段1AF 与线段2BF 交于点M ，若12MF F ∆与12AF F ∆的面积之比为2:3，求点M 的坐标.19．解：（Ⅰ）由题意(B 是椭圆C 短轴上的顶点，所以b =因为12F BF ∆是正三角形，所以122F F =，即1c =. 由2224a b c =+=，所以2a =.所以椭圆C 的标准方程是22143x y +=.（Ⅱ）设()00,M x y ，(),A A A x y ，依题意有00x >，00y >，0A x >，0A y >. 因为121223MF F AF F S S ∆∆=，所以01213A x x +=+，且023A y y =， 所以0312A x x +=，032A y y =，即00313,22x A y +⎛⎫ ⎪⎝⎭. 因为点A 在椭圆上，所以22143A A x y +=，即220031322143x y +⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭+=. 所以200152270x x -+=，解得01x =，或0715x =. 因为线段1AF 与线段2BF 交于点M ， 所以01x <，所以0715x =. 因为直线2BF的方程为)1y x =-， 将0715x =代入直线2BF的方程得到0y =. 所以点M的坐标为715⎛ ⎝⎭.(2018年石景山期末) 19．（本小题共14分）已知椭圆2222:1(0)x y C a b a b+=>>离心率等于12，(2,3)P 、(2,3)Q -是椭圆上的两点.（Ⅰ）求椭圆C 的方程；（Ⅱ）,A B 是椭圆上位于直线PQ 两侧的动点，若直线AB 的斜率为12，求四边形APBQ 面积的最大值. 解：（Ⅰ）因为12c e a ==，又222a b c =+， 所以22224,3a c b c == ……… 2分设椭圆方程为2222143x y c c+=,代入(2,3),得2224,16,12c a b === ………4分椭圆方程为2211612x y +=……… 5分 （Ⅱ）设1122(,),(,)A x yB x y………6分设AB 方程为221211612y x t x y ⎧=+⎪⎪⎨⎪+=⎪⎩，代入化简得：22120x tx t ++-= ………8分 224(12)0t t ∆=-->，44t -<<1221212x x tx x t +=-⎧⎨=-⎩，又(2,3),(2,3)P Q - APBQ APQ BPQ S S S ∆∆=+1216||2x x =⨯⨯-==………13分 当0t =时，S最大为 ………14分(2018年昌平期末) 19.（本小题满分14分）已知椭圆C ：2221(1)x y a a+=>，(,0),(0,1)A a B ，圆O ：221x y +=的圆心到直线AB.（Ⅰ）求椭圆C 的方程；（Ⅱ）若直线l 与圆O 相切，且与椭圆C 相交于,P Q 两点，求PQ 的最大值. 解：（Ⅰ）由已知得，直线AB 的方程为:1,0xy x ay a a+=+-=即：. 由1a >, 得点O 到直线AB解得a故椭圆C 的方程为 2213x y +=. ……………5分 （Ⅱ）①当直线l 的斜率不存在时，直线l 的方程为1x =±，代入2213x y +=，得y =PQ =. ②当直线l 的斜率存在时，设直线l 的方程为y kx m =+， 因为直线l 与圆O1,=即221m k =+由2213x y y kx m ⎧+=⎪⎨⎪=+⎩，消去y ，整理得222(13)63(1)0k x kmx m +++-= 所以22222223612(13)(1)12(13)24,k m k m k m k ∆=-+-=+-= 由0,∆>得0k ≠，设点1122(,),(,)P x y Q x y ，则212122263(1),1313km m x x x x k k-+=-=++，所以PQ ｜｜222(1)2213k k k++≤+ 当且仅当2212,k k +=即1k =±时，||PQ综上所述，||PQ…………… 14分(2018年通州期末) 19．（本题满分13分）已知椭圆()222210x y a b a b +=>>过点()0,1-，离心率2e =.（Ⅰ）求椭圆的方程；（Ⅱ）已知点(),0P m ，过点()1,0作斜率为()0k k ≠直线l ，与椭圆交于M ，N 两点，若x 轴平分MPN ∠ ，求m 的值．19.解：（Ⅰ）因为椭圆的焦点在x 轴上，过点()0,1-，离心率2e =， 所以1b =，c a =……………………2分所以由222a b c =+，得22.a =……………………3分所以椭圆C 的标准方程是22 1.2x y +=……………………4分 （Ⅱ）因为过椭圆的右焦点F 作斜率为k 直线l ，所以直线l 的方程是(1)y k x =-.联立方程组()221,1,2y k x x y ⎧=-⎪⎨+=⎪⎩ 消去y ，得()2222124220.k x k x k +-+-=显然0.∆>设点()11,P x y ，()22,Q x y ，所以2122412k x x k +=+，212222.12k x x k-⋅=+……………………7分 因为x 轴平分MPN ∠，所以MPO NPO ∠=∠. 所以0.MP NP k k +=……………………9分 所以12120.y y x m x m+=--所以()()12210.y x m y x m -+-= 所以()()()()1221110.k x x m k x x m --+--= 所以()()1212220.k x x k km x x km ⋅-+++=所以()2222224220.1212k k k k km km k k-⋅-++=++ 所以2420.12k kmk-+=+ 所以420.k km -+=……………………12分 因为0k ≠，所以 2.m =……………………13分(2018年房山期末) （19）（本小题14分）已知椭圆()01:2222>>=+b a b y a x C 的左顶点为()0,2-A ，且过点2⎛ ⎝⎭1，.（Ⅰ）求椭圆C 的标准方程及离心率；（Ⅱ）若直线1:-=ty x l 交椭圆C 于1122(,),(,)P x y Q x y ． （i ）求证：12234y y t =-+；（ii ）若△APQ 的面积为45，求t 的值． （19）解：（Ⅰ）由题：2=a又过点（231，），143412=+∴b1=∴b 222b a c -= 3=∴c 23==∴a c e 1422=+∴y x …………………5分（Ⅱ）（1）由题⎪⎩⎪⎨⎧=+-=14122y x ty x 整理得：032)4(2=--+ty y t 43,42221221+-=+=+∴t y y t y y 43221+-=∴t y y …………………9分（2）由题，直线l ：1-=ty x 恒过）（0,1-.设直线l 与x 轴交于点M ，则M ）（0,1- 1|AM |=∴412)42(4)(|y -y |2222122121+++=-+=t t y y y y ||||2121y y AM S APQ -⋅=∴∆=21∴412)42(222+++t t =54 4247110t t ∴+-=21,t ∴=或211-()4t =舍 1±=∴t …………………14分19.（本小题满分14分）已知椭圆2222:1(0)x y C a b a b+=>>，且过点． （Ⅰ）求椭圆C 的方程；（Ⅱ）过椭圆C 左焦点的直线1l 与椭圆C 交于,A B 两点，直线2l 过坐标原点且直线1l 与2l 的斜率互为相反数，直线2l 与椭圆交于,E F 两点且均不与点,A B 重合，设直线AE 的斜率为1k ，直线BF 的斜率为2k .证明：12k k +为定值．解：（Ⅰ）由题意得22222,111.2c a a b c ab ⎧=⎪⎪⎪=+⎨⎪⎪+=⎪⎩解得a =1b =，1c =．故椭圆C 的方程为2212x y +=． ……………… 5分（Ⅱ）证明：由题意可设直线1l 的方程为(1)y k x =+，直线2l 的方程为y kx =-，设点11(,)A x y ，22(,)B x y ，33(,)E x y ，33(,)F x y --， 则1323121323y y y y k k x x x x -++=+-+ 13231323(1)(1)k x kx k x kx x x x x +++-=+-+ 21212313232()2[]()()x x x x x k x x x x +++=-+． 由22(1),1,2y k x x y =+⎧⎪⎨+=⎪⎩ 得2222(12)4220k x k x k +++-=， 所以2122412k x x k -+=+，21222212k x x k -=+．由22,1,2y kx x y =-⎧⎪⎨+=⎪⎩得22(12)2k x +=，所以232212x k =+． 所以2221212322244442()20121212k k x x x x x k k k --+++=++=+++．所以2121231213232()2[]0()()x x x x x k k k x x x x ++++==-+． 故12k k +为定值，定值为0. ………………14分（19）（本小题共14分）已知椭圆2222:1(0)x y C a b a b +=>>的离心率为3，长轴长为（Ⅰ）求椭圆C 的方程；（Ⅱ）点M 是以长轴为直径的圆O 上一点，圆O 在点M 处的切线交直线3x =于点N ．求证：过点M 且垂直于直线ON 的直线l 过椭圆C 的右焦点．解：（Ⅰ）由题意得23a c a⎧=⎪⎨=⎪⎩解得1c =．所以2222b a c =-=．所以椭圆C 的方程为22132x y +=． ………5分（Ⅱ）由题意知，圆O 的方程为223x y +=．设(3,)N t ，00(,)M x y ， 22003x y +=． 由22||3||ON MN =+，得22220033(3)()+t x y t =+-+-， 即2222000093692t x x y ty t +=+-++-+，即2200003620x x y ty +-+-=． 因为22003x y +=， 所以00330x y t +-=．当0t =时，01x =，直线l 的方程为1x =，直线l 过椭圆C 的右焦点(1,0)F ． 当0t ≠时，直线MN 的方程为003()y y x x t-=--，即0033ty ty x x -=-+，即3(1)ty x =--，直线l 过椭圆C 的右焦点(1,0)F ． 综上所述，直线l 过椭圆C 的右焦点(1,0)F ． ………14分(2018年海淀一模) （19）（本小题14分）已知椭圆C 的两个焦点为12(1,0),(1,0)F F -，离心率为12. （Ⅰ）求椭圆C 的方程；（Ⅱ）设点A 是椭圆C 的右顶点，过点1F 的直线与椭圆C 交于,P Q 两点，直线,AP AQ 与直线4x =-分别交于M 、N 两点. 求证：点1F 在以MN 为直径的圆上.19．解：（Ⅰ）由题意，设椭圆方程为22221(0)x y a b a b +=>> ，则222112c c a a b c =⎧⎪⎪=⎨⎪⎪=+⎩ .…………………….…2分得2,a b == .…………………….…4 ，所以椭圆方程为221.43x y += .…………………….…5分（Ⅱ）证明：由（Ⅰ）可得(2,0)A .当直线PQ 不存在斜率时，可得33(1,),(1,)22P Q --- 直线AP 方程为()122y x =--，令4,x =-得(4,3)M -,同理，得(4,3)N --. 所以()()113,3,3,3F M F N =-=--,得110FM F N ⋅=. 所以190MF N ∠=︒,1F 在以MN 为直径的圆上. .…………………….…7分当直线PQ 存在斜率时，设PQ 方程为()1y k x =+ ，()11,y x P 、()22,y x Q .由()221143y k x x y =+⎧⎪⎨+=⎪⎩可得()22223484120k x k x k +++-=.显然0∆>,221212228412,3434k k x x x x k k -+=-=++, .…………………….…8分 直线AP 方程为11(2)2y y x x =--，得116(4,)2y M x --- ,同理，226(4,)2y N x ---. .…………………….…9分所以12111266(3,),(3,)22y y F M F N x x --=-=---.121112369(2)()y y F M F N x x ⋅=+--2 .…………………….…10分因为()()11221,1y k x y k x =+=+所以2121212123636(1)(1)(2)()(2)()y y k x x x x x x ++----=22 .…………………….…11分 ()()212121212222222222223612()441283436()3441216121634936369k x x x x x x x x k k k k k k k k k k k +++=-++--+++=-++++-⋅==-所以110FM F N ⋅= ..…………………….…13分 所以90MFN ∠=︒,F 在以MN 为直径的圆上. .…………………….…14分 综上，F 在以MN 为直径的圆上.(2018年西城一模) 19．（本小题满分14分）已知椭圆2222:1(0)x y C a b a b+=>>，以椭圆C的任意三个顶点为顶点的三角形的面积是（Ⅰ）求椭圆C 的方程；（Ⅱ）设A 是椭圆C 的右顶点，点B 在x 轴上．若椭圆C 上存在点P ，使得90APB ∠=，求点B 横坐标的取值范围．解：（Ⅰ）设椭圆C 的半焦距为c ．依题意，得c a =ab =222a b c =+． [ 3分] 解得 2a =，b =所以椭圆C 的方程为 22142x y +=． [ 5分]（Ⅱ）“椭圆C 上存在点P ，使得90APB ∠=”等价于“存在不是椭圆左、右顶点的点P ，使得0PA PB −−→−−→⋅=成立”． [ 6分]依题意，(2,0)A ．设(,0)B t ，(,)P m n ，则2224m n +=， [ 7分] 且 (2,)(,)0m n t m n --⋅--=，即 2(2)()0m t m n --+=． [ 9分]将 2242m n -=代入上式，得 2(2)()204m m t m ---+=． [10分] 因为 22m -<<， 所以 202mt m +-+=， 即 22m t =+． [12分] 所以 2222t -<+<， 解得 20t -<<，所以 点B 横坐标的取值范围是(2,0)-． [14分](2018年丰台一模) （19）（本小题共14分）已知椭圆C ：22221(0)x y a b a b+=>>的一个焦点为)0,3(F ，点(2,0)A -在椭圆C 上．（Ⅰ）求椭圆C 的方程与离心率；（Ⅱ）设椭圆C 上不与A 点重合的两点D ，E 关于原点O 对称，直线AD ，AE 分别交y 轴于M ，N 两点．求证：以MN 为直径的圆被x 轴截得的弦长是定值．解：（Ⅰ）依题意，c =……………………1分点(2,0)A -在椭圆C 上．所以2=a ． ……………………2分 所以2221b a c =-=． ……………………3分所以椭圆C 的方程为1422=+y x ． ……………………4分 离心率23==a c e ． ……………………5分 （Ⅱ）因为D ，E 两点关于原点对称，所以可设(,)D m n ，(,)E m n --，(2)m ≠± ……………………6分所以1422=+n m ． ……………………7分 直线AD ：(2)2ny x m =++． 当0=x 时，22+=m n y ，所以)22,0(+m nM ． ……………………8分 直线AE ：(2)2ny x m -=+-+． 当0=x 时，22+--=m n y ，所以)22,0(+--m nN ． ……………………9分 设以MN 为直径的圆与x 轴交于点0(,0)G x 和0(,0)H x -,（00x >）， 所以，02(,)2n GM x m =-+，02(,)2nGN x m -=--+， ……………………10分 所以220244n GM GN x m -⋅=+-．因为点G 在以MN 为直径的圆上，所以0GM GN ⋅=，即2202404n x m-+=-． ……………………12分 因为1422=+n m ，即2244m n -=， 所以22202244144n m x m m-===--，所以01x =． ……………………13分 所以(1,0)G ，(1,0)H -．所以2GH =．所以以MN 为直径的圆被x 轴截得的弦长是定值2． ……………………14分(2018年石景山一模) 19．（本小题共13分）已知椭圆E :22221x y a b +=(0)a b >>的离心率e =（Ⅰ）求椭圆E 的方程；（Ⅱ）若,C D 分别是椭圆E 的左、右顶点，动点M 满足MD CD ⊥，连接CM ，交椭圆E 于点P ．证明：OM OP ⋅为定值（O 为坐标原点）．（Ⅰ）解：因为2c = 所以c = ………………1分因为c e a ==b c ==． ………………3分 因为222a b c =+， 所以24a =． ………………4分所以椭圆方程为22142x y +=． ………………5分 （Ⅱ）方法一：证明：C (－2，0)，D (2，0)，设()()0112,,,M y P x y ，则OP uu u r ＝()11,x y ，OM uuu r＝()02,y ． ………………7分直线CM ：()024y y x =+，即0042y y y x =+． ………………8分代入椭圆方程2224x y +=，得222200011140822y x y x y ⎛⎫+++-= ⎪⎝⎭，所以()()22001220048281288y y x y y --=-⨯=-++． ………………10分 所以012088y y y =+． 所以OP uu u r ＝()2002200288,88y y y y ⎛⎫- ⎪-⎪++⎝⎭． ………………12分 所以OP uu u r ·OM uuu r ＝()2220002220004884324888y y y y y y -+-+==+++． 即OM uuu r ·OP uu u r为定值． ………………13分方法二：设(,),(2,)P x y M t ，由CP CM λ=uu r uuu r 可得24y t x =+，即42y t x =+. ∵点(,)P x y 在22142x y +=上∴2242(4)y x =-.∴2OM OP x ty ⋅=+u u u r u u u r 242(2)(2)22422y x x x x x x+-=+=+=++.∴OM OP ⋅uuu r uu u r为定值4.方法三：因为直线CM 不在x 轴上，故可设:2CM l x my =-.由221422x y x my ⎧+=⎪⎨⎪=-⎩得22(2)40m y my +-=， ∴222424,22P P m m y x m m -==++，即222244(,)22m mP m m -++．在直线2x my =-中令2x =，则4M y m =，即4(2,)M m． ∴2224816422m OM OP m m -⋅=+=++uuu r uu u r .∴OP OM ⋅uu u r uuu r为定值4.(2018年房山一模) （19）（本小题13分）已知椭圆C :22221(0)x y a b a b +=>>过点()0,1-，离心率2e =.（Ⅰ）求椭圆C 的方程；（Ⅱ）过点F ()1,0作斜率为()0k k ≠的直线l ，l 与椭圆C 交于M ，N 两点，若线段MN 的垂直平分线交x 轴于点P，求证：|||MN PF =． （19）（Ⅰ）根据题意22212b c e a a b c =⎧⎪⎪==⎨⎪⎪=+⎩解得：1a b ⎧=⎪⎨=⎪⎩所以椭圆C 的方程为2212x y +=…………5分 （Ⅱ）设直线l 的方程为(1)y k x =-由2212(1)x y y k x ⎧+=⎪⎨⎪=-⎩得 2222(21)4220k x k x k +-+-=由0∆>得k R ∈且0k ≠设1122(,),(,)M x y N x y ，线段MN 中点00(,)Q x y 那么2122421k x x k +=+，21222221k x x k -=+212000222,(1)22121x x k kx y k x k k +-===-=++ 设(,0)P p ，根据题意PQ MN ⊥所以20202121221ky k k x p kp k -+==---+，得2221k p k =+ 所以22221||12121k k PF k k +=-=++||MN =22)21k k +=+|||MN PF = …………14分(2018年顺义一模)20.（本小题满分14分）已知椭圆()01:2222>>=+b a b y a x E ，两点()3,01P ，⎪⎭⎫⎝⎛-23,12P 在椭圆上. （Ⅰ）求椭圆E 的方程及焦点坐标；（Ⅱ）设直线l 不经过点()3,01P 且与椭圆E 相交于N M ,两点，直线M P 1与直线N P 1的斜率分别为21,k k ，若321-=+k k .求证：直线l 恒过某定点.解：（1）∵椭圆()01:2222>>=+b a b y a x E ，过点()3,01P ，⎪⎭⎫⎝⎛-23,12P，∴b =分 ∴2191143a +⋅=，解得24,2a a ==，∴1c =-----------3分 因此椭圆E 的方程为22143x y +=，交点坐标为12(1,0),(1,0)F F - -----------5分 （2） ①当直线l 斜率不存在时，设l ：(0)x t t =≠， (,),(,)M M M t y N t y -则12M M y y k k t t-+=+=2t =， 此时直线过椭圆的右顶点，不存在两个交点，所以这种情况不成立 --------------------6分 ②当直线l 斜率存在时，设l：1122((,),(,)y kx m m M x y N x y =+由题意可知，0,k m ≠≠120,0x x ≠≠. 联立方程223412y kx mx y =+⎧⎨+=⎩，整理得：222(34)84120k x kmx m +++-=∴21212228412,(3434km m x x x x m k k-+=-=≠++ .-----------------------9分则121212y y k k x x +=+21212112()()x kx m x kx m x x +++=（2018年朝阳二模）（19）（本小题满分14分）已知椭圆W ：22214x y b +=(0)b >的一个焦点坐标为. （Ⅰ）求椭圆W 的方程和离心率；（Ⅱ）若椭圆W 与y 轴交于A ，B 两点（A 点在B 点的上方），M 是椭圆上异于A ，B 的任意一点，过点M 作MN y ⊥轴于N ，E 为线段MN 的中点，直线AE 与直线1y =-交于点C ，G 为线段BC 的中点，O 为坐标原点．求OEG ∠的大小．解：(Ⅰ)依题意，2a =，c =2221b a c =-=.则椭圆W 的方程为2214x y +=.离心率c e a ==…………4分 (Ⅱ)设M 00(,)x y ，00x ≠，则N 0(0,)y ，E 00(,)2x y ． 又A (0,1)，所以直线AE 的方程为002(1)1y y x x --=． 令1y =-，则C 0(,1)1x y --． 又B (0,1)-，G 为线段BC 的中点，所以G 00(,1)2(1)x y --．所以00(,)2x OE y =，0000(,1)22(1)x x GE y y =-+-， 000000()(1)222(1)x x x OE GE y y y ⋅=-++- 2220000044(1)x x y y y =-++-．因为点M 在椭圆W 上，则220014x y +=，所以220044x y =-． 则200014(1)x OE GE y y ⋅=-+-0011y y =--+0=．因此OE GE ⊥．故90OEG ∠=． ……………14分(2018年东城二模) （20）（本小题共14分）已知椭圆2222:1(0)x y C a b a b+=>>的右焦点为(1,0)F ，离心率为12．（Ⅰ）求椭圆C 的方程；（Ⅱ）,A B 是椭圆C 在y 轴右侧部分上的两个动点，若原点O 到直线ABABF的周长为定值．解：（Ⅰ）由题意得221,1,2a b c a ⎧=+⎪⎨=⎪⎩解得224,3.a b ⎧=⎪⎨=⎪⎩所以椭圆C 的方程为22143x y +=． …………………4分（Ⅱ）①当AB 垂直于x 轴时，AB方程为x =2A，2B -，(1,0)F ．1(42AF BF ===．因为AB =所以4AF BF AB ++=． ②当AB 不垂直于x 轴时，设AB 的方程为m kx y +=． 因为原点O 到直线AB=223(1)m k =+．由22,1,43y kx m x y =+⎧⎪⎨+=⎪⎩得222(34)84120k x kmx m +++-=，即222(34)8120k x kmx k +++=．设11(,)A x y ，22(,)B x y ，则122834km x x k -+=+，21221234k x x k =+．所以12|||AB x x =-====24||||34m k k=+． 因为A ,B 在y 轴右侧，所以0mk <，所以24||34mkAB k =-+．22211221121121(1)(1)3(1)412441(2)2.AF x y x x x x x =-+=-+-=-+=- 所以11||22AF x =-，同理21||22BF x =-． 所以121||||4()2AF BF x x +=-+221844()423434km kmk k -=-=+++． 所以2244||||||443434km kmAF BF AB k k++=+-=++． 综上，△ABF 的周长等于椭圆C 的长轴长4． ………14分(2018年海淀二模) （20）（本小题14分）已知椭圆C ：2222=+y x 的左右顶点分别为1A ，2A . （Ⅰ）求椭圆C 的长轴长与离心率；（Ⅱ）若不垂直于x 轴的直线l 与椭圆C 相交于P ，Q 两点，直线P A 1与Q A 2交于点M ，直线Q A 1与PA 2交于点N .求证：直线MN 垂直于x 轴.解：（Ⅰ）椭圆C 的方程可化为2212x y +=, …………………1分所以1,1a b c ===. …………………2分所以长轴长为2a =，离心率2c e a == …………………4分 （Ⅱ）方法1：证明：显然直线P A 1、Q A 2、Q A 1、P A 2都存在斜率，且互不相等，分别设为1234,,,.k k k k 设直线P A 1的方程为1(y k x =，Q A 2的方程为2(y k x =，……………5分联立可得2121)M k k x k k +=-. …………………6分同理可得4343)N k k x k k +=-. …………………7分下面去证明141.2k k =-设00(,)P x y ，则220022x y +=.所以22001422001222y y k k x y ====---. …………………10分 同理231.2k k =- …………………11分所以1221211211222())1122N M k k k k x x k k k k --++===----. …………………13分 所以直线MN 垂直于x 轴. …………………14分方法2：设直线l 方程为1122,(,),(,)y kx m P x y Q x y =+. …………………5分由2222y kx m x y =+⎧⎨+=⎩ 得222(12)4220k x kmx m +++-=. 当0∆>时，2121222422,1212km m x x x x k k --+==++. …………………7分直线1A P方程为y x =+，直线2A Q方程为y x =，…………………8分x x =，得x =21121221[((((y x y x x y x y x -=+ …………………9分其中，21122112((()(()(y x y x kx m x kx m x -=+-+1212()()x x m x x ++-+122121224()12()()12kmm x x km x x m x x k-=+-++=+-=+-+…………………11分12211221(()(()(y x y x kx m x kx m x ++++1212212()()kx x m x x x x =++-221222121222242()12124()12()12m km k m x x k k k x x kx x k--=++-++-=+-+=+-+ …………………12分所以2M kx m-=，即点M 的横坐标与,P Q 两点的坐标无关，只与直线l 的方程有关. …………………13分 所以2N M kx x m-==，直线MN 垂直于x 轴. …………………14分(2018年西城二模). 20．（本小题满分14分）已知椭圆C ：2222 1 (0)x y a b a b+=>>(0,1)．（Ⅰ）求椭圆C 的方程；（Ⅱ）设直线y x =与椭圆C 交于A ，B 两点，斜率为k 的直线l 与椭圆C 交于M ，N 两点，与直线y x =交于点P （点P 与点A ，B ，M ，N 不重合）． （ⅰ）当1k =-时，证明：||||||||PA PB PM PN =； （ⅱ）写出||||||||PA PB PM PN 以k 为自变量的函数式（只需写出结论）．(2018年丰台二模) （20）（本小题共14分）已知椭圆C ：22221(0)x y a b a b+=>>的长轴长为4，离心率为12，过右焦点的直线l 与椭圆相交于M ，N 两点，点P 的坐标为(4,3)，记直线PM ，PN 的斜率分别为1k ，2k ．（Ⅰ）求椭圆C 的方程； （Ⅱ）当247MN =时，求直线l 的斜率； （Ⅲ）求证：21k k +为定值．（Ⅰ）解：依题意 24a =，所以 2a =． …………………1分因为 12c e a ==，所以 1c =． …………………2分所以 23b =， …………………3分所以椭圆C 的方程为 22143x y +=． …………………4分（Ⅱ）解：椭圆得右焦点(1,0)F ．当直线l 的斜率不存在时，不妨取3(1,)2M ，3(1,)2N -，3MN =，不合题意． …………………5分当直线l 的斜率存在时，设直线l ：(1)y k x =-，11(,)M x y ，22(,)N x y ． …………………6分联立方程组 ⎪⎩⎪⎨⎧-==+)1(13422x k y y x ， 消y 得 2222(34)84(3)0k x k x k +-+-=，0∆>成立． …………………7分所以2122834kx xk+=+，21224(3)34kx xk-=+．…………………8分因为247MN==，…………………9分247=，所以2212347kk+=+，所以1k=±．…………………10分（Ⅲ）证明：当直线l的斜率不存在时，不妨取3(1,)2M，3(1,)2N-，此时123922233k k+=+=．…………………11分当直线l的斜率存在时，设直线l：(1)y k x=-，11(,)M x y，22(,)N x y．此时21211221221121)(416)4)(3()4)(3(4343xxxxxyxyxyxykk++---+--=--+--=+．分子化为21122121)(4)(324yxyxyyxx+++-+-248))(53(22121++++-=kxxkxkx．所以222222222143)3(4438416248438)53(43)3(42kkkkkkkkkkkkk+-++⨯-+++⨯+-+-⨯=+)3(8)43(4)43)(3(2)53(2)3(2222222-+-+++++--⨯=kkkkkkkkk299181822=++=kk．综上所述，12k k+为定值2．…………………14分(2018年昌平二模)19. (本小题14分)已知椭圆()2222:10x yE a ba b+=>>的经过点(0,1).（I）求椭圆E的标准方程；（II）过右焦点F的直线l（与x轴不重合）与椭圆交于,A B两点，线段AB的垂直平分线交y轴于点(0)M m，，求实数m的取值范围.解：（Ⅰ）由题意，得2221b c e a a b c =⎧⎪⎪==⎨⎪⎪=+⎩， 解得1a b ⎧=⎪⎨=⎪⎩所以椭圆E 的标准方程是2212x y +=． -------------------5分（II ）（1）当直线x AB ⊥轴时，m = 0符合题意．（2）当直线AB 与x 轴不垂直时，设直线AB 的方程为()1y k x =-，由22(1)220y k x x y =-⎧⎨+-=⎩，得()()2222124210kxk x k +-+-=，由2222(4)8(12)(1)0k k k ∆=--+->，得k ∈R ．设()11,x y A ，()22,x y B ，则2212122242(1)1212k k x x x x k k -+=⋅=++，． 所以121222(2)12k y y k x x k-+=+-=+，所以线段AB 中点C 的坐标为2222,1212k k k k ⎛⎫- ⎪++⎝⎭．由题意可知，0k ≠，故直线C M 的方程为222121212k k y x k k k ⎛⎫+=-- ⎪++⎝⎭，令x = 0，212k y k =+，即212k m k =+当k > 0时，，得210=1122k m k k k<=≤++，当且仅当k =时“=”成立． 同理，当 k < 0时，210=11242k m k kk>=≥-++，当且仅当k =时“=”成立． 综上所述，实数m的取值范围为⎡⎢⎣⎦．--------------------14分(2018年房山二模) （19）（本小题14分）椭圆()222210+=>>：x y C a b a b的离心率为12，O 为坐标原点，F 是椭圆C 的右焦点，A 为椭圆C 上一点，且⊥AF x 轴，AFO ∆的面积为34． （Ⅰ）求椭圆C 的方程；（Ⅱ）过C 上一点()()000,0≠P x y y 的直线l ：00221x x y y a b +=与直线AF 相交于点M ，与直线4x =相交于点N .证明：当点P 在C 上移动时，MFNF 恒为定值，并求此定值．（19）（Ⅰ）设(,0)F c ，(,)A c d 则22221c d a b+= 又12c a =||d ∴=，因AFO ∆ 的面积为341133||,224c d c b bc ∴===由2222ab c a c bc ⎧-=⎪=⎨⎪=⎩得21a b c =⎧⎪=⎨⎪=⎩所以C 的方程为22143x y += …………5分 （Ⅱ）由(1)知直线l 的方程为00143x x y y += (y 0≠0)，即y ＝001234x x y - (y 0≠0)． 因为直线AF 的方程为x ＝1，所以直线l 与AF 的交点为M 00123(1,)4x y -， 直线l 与直线x ＝4的交点为N 0(4,33)x -，则|MF |2|NF |2＝202002220000123()4(4)331616(1)9()x y x x y x y --=-+-+ 又P (x 0，y 0)是C 上一点，则2200143x y +=.2200334x y =- 代入上式得|MF |2|NF |2＝2220002222000000(4)(4)(4)1148121632164(816)4(4)4x x x x x x x x x ---====-+-+-+- 所以|MF ||NF |=12，为定值． …………14分(2018年顺义二模)20．（本小题满分13分） 已知椭圆22:143x y G +=的左焦点为F ，左顶点为A ，离心率为e ，点()(),02M t t <-，满足条件FA e AM =． （1）求实数t 的值．（2）设过点F 的直线与椭圆G 交于P ，Q 两点，记M PF 和MQF 的面积分别为1S ，2S ，若12=2S S ，求直线l 的方程．【解析】（1）椭圆22:143x y G +=， ∴2a =，b =1c =， 则12c e a ==， 1FA a c =-=，2AM t =--， ∵12FAe AM ==， ∴22AM t =--=，解得4t =-．（2）若直线l 的斜率不存在，则有12S S =，不符合题意； 若直线l 的斜率存在，设直线l 的方程为()1y k x =+， 由()221431x y y k x ⎧+=⎪⎨⎪=+⎩，解得()22224384120k x k x k +++-=， 则2122843k x x k -+=+，212241243k x x k -=+， ()()121211y y k x k x +=+++()122k x x k =++228243k k k k -=⨯++ 2643k k =+， ()()121211y y k x k x =+⋅+()212121k x x x x =+++22222412814343k k k k k ⎛⎫--=++ ⎪++⎝⎭ 22943k k -=+， ∵M PF 和MQF 的面积分别为1112S MF y =，2212S MF y =， ∴1112222y S y S y y ==-=， 即122y y =-， ∴122y y y +=-，()221221222y y y y y =-=-+， 则22229624343k k k k -⎛⎫=-⨯ ⎪++⎝⎭， 整理得28143k =+，解得k =，故直线l 的方程为)1y x =+或)1y x =+．。

2018北京高考 圆锥曲线 提升篇（一）1.已知椭圆()2222:10x y C a b a b +=>>()2,0A ． （Ⅰ）求椭圆C 的方程；（Ⅱ）设M ，N 是椭圆C 上不同于点A 的两点，且直线AM ，AN 的斜率之积等于14-，试问直线MN 是否过定点？若是，求出该点的坐标；若不是，请说明理由．2、已知圆22:4O x y +=和椭圆22:24C x y +=，F 是椭圆C 的左焦点．（Ⅰ）求椭圆C 的离心率和点F 的坐标；（Ⅱ）点P 在椭圆C 上，过P 作x 轴的垂线，交圆O 于点Q （,P Q 不重合），l 是过点Q 的圆O 的切线．圆F的圆心为点F ，半径长为||PF ．试判断直线l 与圆F 的位置关系，并证明你的结论．3、已知椭圆C ：()222210x y a b a b +=>>的离心率为2，且点()2,1T 在椭圆上.设与OT 平行的直线l 与椭圆C 相交于,P Q 两点，直线,TP TQ 分别与x 轴正半轴交于,M N 两点.（Ⅰ）求椭圆C 的标准方程； （Ⅱ）判断OM ON +的值是否为定值，并证明你的结论.4、已知椭圆2222:1(0)x y C a b a b +=>>，且过点． （Ⅰ）求椭圆C 的方程；（Ⅱ）过椭圆C 的左焦点的直线1l 与椭圆C 交于,A B 两点，直线2l 过坐标原点且与直线1l 的斜率互为相反数．若直线2l 与椭圆交于,E F 两点且均不与点,A B 重合，设直线AE 与x 轴所成的锐角为1θ，直线BF 与x 轴所成的锐角为2θ，判断1θ与2θ大小关系并加以证明．5、已知点3(1,)2P 在椭圆C ：22221(0)x y a b a b+=>>上，(1,0)F 是椭圆的一个焦点． （Ⅰ）求椭圆C 的方程；（Ⅱ）椭圆C 上不与P 点重合的两点D ，E 关于原点O 对称，直线PD ，PE 分别交y 轴于M ，N 两点．求证：以MN 为直径的圆被直线32y =截得的弦长是定值．6、在平面直角坐标系xOy 中，动点E 到定点(1,0)的距离与它到直线1x =-的距离相等．（Ⅰ）求动点E 的轨迹C 的方程；（Ⅱ）设动直线:l y kx b =+与曲线C 相切于点P ，与直线1x =-相交于点Q ．证明：以PQ 为直径的圆恒过x 轴上某定点．7．已知椭圆()2222:10x y C a b a b +=>>的上、下顶点分别为A ，B ，且2AB =，离心率为2，O 为坐标原点.（Ⅰ）求椭圆C 的方程；（Ⅱ）设P ，Q 是椭圆C 上的两个动点（不与A ，B 重合），且关于y 轴对称，M ，N 分别是OP ，BP 的中点，直线AM 与椭圆C 的另一个交点为D . 求证：D ，N ，Q 三点共线.8.已知抛物线:C ()022>=p px y 经过点()2,1M ，焦点为F .（Ⅰ）求抛物线C 的方程，并求其焦点F 的坐标；（Ⅱ）若过点()0,1-N 的直线l 与C 相交于Q P ,两点，点P 关于x 轴的对称点为S .求证：Q F S ,,三点共线.。

2018年全国3卷省份高考模拟理科数学分类汇编----解析几何1.（成都七中模拟）已知圆，考虑下列命题：①圆上的点到的距离的最小值为；②圆上存在点到点的距离与到直线的距离相等；③已知点，在圆上存在一点，使得以为直径的圆与直线相切，其中真命题的个数为( )CA. 0B. 1C. 2D. 3【解析】对于①，圆心到的距离减去半径的值为，即圆上点到的距离的最小值为，①错；对于②，到点与到直线的距离相等的点的轨迹是抛物线，当时，圆方程，可得圆与抛物线有两个交点，故②正确；对于③，当时，圆上存在点，使得以为直径的圆与直线相切，故③正确，正确命题个数为，故选C. 【方法点睛】本题主要通过对多个命题真假的判断，主要综合考查圆的几何性质、抛物线的定义与方程，属于难题.这种题型综合性较强，也是高考的命题热点，同学们往往因为某一处知识点掌握不好而导致“全盘皆输”，因此做这类题目更要细心、多读题，尽量挖掘出题目中的隐含条件，判断存在性结论时，也可以考虑特值法处理，另外，要注意从简单的自己已经掌握的知识点入手，然后集中精力突破较难的命题.2.（成都七中模拟）若双曲线的渐近线与圆相切，则________________.【答案】【解析】由得渐近线方程为，即圆心到渐近线的距离等于半径，，故答案为.3.（成都七中模拟）已知椭圆的左右顶点分别为、，为椭圆上不同于，的任意一点.(1)求的正切的最大值并说明理由；(2)设为椭圆的右焦点，直线与椭圆的另一交点为，的中点为，若，求直线的斜率.【答案】（1）；（2）.【解析】试题分析：（1）直线，的倾斜角分别为，，先证明，则，从而可得结果；（2）设过焦点的直线方程为，，，，联立，则，利用两点间距离公式求得，再利用韦达定理以及焦半径公式求得，解方程可得结果.试题解析：(1)设椭圆上的点，则，∴，设直线，的倾斜角分别为，，则，，，∴当且仅当时，最大值为.(2)由题可知，斜率一定存在且，设过焦点的直线方程为，，，，联立，则，∴，∴，∴，而，∵，∴，∴，∴，∴.4.(成都市模拟)已知双曲线：右支上的一点，经过点的直线与双曲线的两条渐近线分别相交于，两点.若点，分别位于第一，四象限，为坐标原点.当时，的面积为，则双曲线的实轴长为（）AA. B. C. D.【答案】A【解析】可设的面积为由题意可得，解得由，可得即为代入双曲线的方程，可得解得故选A.5.（成都市模拟）已知抛物线：的焦点为，准线与轴的交点为，是抛物线上的点，且轴.若以为直径的圆截直线所得的弦长为，则实数的值为__________．【答案】【解析】由题，直线圆心到直线的距离为由题意以为直径的圆截直线所得的弦长为，则即答案为，6.(成都市模拟)已知椭圆：的左右焦点分别为，，左顶点为，离心率为，点是椭圆上的动点，的面积的最大值为.（1）求椭圆的方程；（2）设经过点的直线与椭圆相交于不同的两点，，线段的中垂线为.若直线与直线相交于点，与直线相交于点，求的最小值.【答案】（1）.（2）.【解析】试题分析：（1）由已知，有，可得. 设点的纵坐标为.可得的最大值。

2018年全国各地高考数学模拟试题《圆锥曲线与方程》试题汇编（含答案解析）1．（2018•红河州二模）设F1，F2分别是椭圆C：的左、右焦点，M是C上一点，且MF2与x轴垂直．直线MF1与C的另一个交点为N．（1）若直线MN的斜率为，求C的离心率．（2）若直线MN在y轴上的截距为3，且|MN|=7|F1N|，求a，b．2．（2018•江苏模拟）已知中心在坐标原点的椭圆C，F1，F2分别为椭圆的左、右焦点，长轴长为6，离心率为（1）求椭圆C 的标准方程；（2）已知点P在椭圆C 上，且PF1=4，求点P到右准线的距离．3．（2018•四川模拟）已知椭圆（a＞b＞0）的左焦点F（﹣2，0）左顶点A1（﹣4，0）．（Ⅰ）求椭圆C的方程；（Ⅱ）已知P（2，3），Q（2，﹣3）是椭圆上的两点，A，B是椭圆上位于直线PQ两侧的动点．若∠APQ=∠BPQ，试问直线AB的斜率是否为定值？请说明理由．4．（2018•济宁一模）已知椭圆C：，直线l：y=kx+1（k≠0）与椭圆C相交于A，B两点，D为AB的中点．（1）若直线l与直线OD（O为坐标原点）的斜率之积为，求椭圆..的方程；（2）在（1）的条件下，y轴上是否存在定点M使得当k变化时，总有∠AMO=∠BMO（O为坐标原点）．若存在，求出定点M的坐标；若不存在，请说明理由．5．（2018•红桥区一模）已知椭圆C：+=1（a＞b＞0）的离心率为，椭圆C与y轴交于A，B两点，且|AB|=2．（Ⅰ）求椭圆C的方程；（Ⅱ）设点P是椭圆C上的一个动点，且点P在y轴的右侧．直线PA，PB与直线x=4分别交于M，N两点．若以MN为直径的圆与x轴交于两点E，F，求点P 横坐标的取值范围及|EF|的最大值．6．（2018•南通一模）如图，在平面直角坐标系xOy中，已知椭圆+=1（a ＞b＞0）的离心率为，两条准线之间的距离为4．（1）求椭圆的标准方程；（2）已知椭圆的左顶点为A，点M在圆x2+y2=上，直线AM与椭圆相交于另一点B，且△AOB的面积是△AOM的面积的2倍，求直线AB的方程．7．（2018•枣庄二模）已知抛物线C：y2=2px（0＜p＜1）上的点P（m，1）到其焦点F的距离为．（Ⅰ）求C的方程；（Ⅱ）已知直线l不过点P且与C相交于A，B两点，且直线PA与直线PB的斜率之积为1，证明：l过定点．8．（2018•沈阳三模）已知抛物线C1：x2=2py（p＞0）过点A（2，1），且它的焦点F也是椭圆C2：（a＞b＞0）的一个焦点，椭圆上的点到焦点F的最小值为2．（Ⅰ）求抛物线C1和椭圆C2的标准方程；（Ⅱ）设M，N是抛物线C1上的两个动点，且=﹣4．①求证：直线MN必过定点，并求定点Q坐标；最大时，求直线MN的方程．②直线MN交椭圆C2于R、S两点，当S△FNS9．（2018•焦作四模）已知椭圆Γ：的离心率为，椭圆的四个顶点围成的四边形的面积为4．（Ⅰ）求椭圆Γ的标准方程；（Ⅱ）直线l与椭圆Γ交于A，B两点，AB的中点M在圆x2+y2=1上，求△AOB （O为坐标原点）面积的最大值．10．（2018•宣城二模）已知椭圆（a＞b＞0）的离心率为，点在椭圆上．（Ⅰ）求椭圆C的方程；（Ⅱ）设AB是椭圆的一条弦，斜率为k（k≠0），N（t，0）是x轴上的一点，△ABN的重心为M，若直线MN的斜率存在，记为k'，问：t为何值时，k•k'为定值？11．（2018•洛阳一模）已知点M，N分别是椭圆的左右顶点，F为其右焦点，|MF|与|FN|的等比中项是，椭圆的离心率为．（1）求椭圆C的方程；（2）设不过原点O的直线l与该轨迹交于A，B两点，若直线OA，AB，OB的斜率依次成等比数列，求△OAB面积的取值范围．12．（2018•江西二模）已知椭圆E：+=1（a＞b＞0）过点，且两个焦点的坐标分别为（﹣1，0），（1，0）．（1）求E的方程；（2）若A，B，P为E上的三个不同的点，O为坐标原点，且，求证：四边形OAPB的面积为定值．13．（2018•虹口区二模）如果直线与椭圆只有一个交点，称该直线为椭圆的“切线”，已知椭圆C：，点M（m，n）是椭圆C上的任意一点，直线l过点M且是椭圆C的“切线”．（1）证明：过椭圆C上的点M（m，n）的“切线”方程是；（2）设A、B是椭圆C长轴上的两个端点，点M（m，n）不在坐标轴上，直线MA、MB分别交y轴于点P、Q，过M的椭圆C的“切线”l交y轴于点D，证明：点D是线段PQ的中点；（3）点M（m，n）不在x轴上，记椭圆C的两个焦点分别为F1和F2，判断过M的椭圆C的“切线”l与直线MF1、MF2所成夹角是否相等？并说明理由．14．（2018•揭阳一模）已知A是椭圆T：上的动点，点P（0，），点C与点A关于原点对称．（I）求△PAC面积的最大值；（II）若射线AP、CP分别与椭圆T交于点B、D，且=m，=n，证明：m+n为定值．15．（2018•聊城一模）已知圆x2+y2=4经过椭圆C：的两个焦点和两个顶点，点A（0，4），M，N是椭圆C上的两点，它们在y轴两侧，且∠MAN的平分线在y轴上，|AM|≠|AN|．（Ⅰ）求椭圆C的方程；（Ⅱ）证明：直线MN过定点．16．（2018•定远县模拟）已知椭圆C：+=1（a＞b＞0）的离心率为，其左、右焦点分别为F1，F2，点P（x0，y0）是坐标平面内一点，且|OP|=5，•=16（O为坐标原点）．（1）求椭圆C的方程；（2）过点S（0，﹣1）且斜率为k的动直线l交椭圆于A，B两点，在y轴上是否存在定点M，使以AB为直径的圆恒过该点？若存在，求出点M的坐标，若不存在，说明理由．17．（2018•南充模拟）已知椭圆C：+=1（a＞b＞0）的离心率为，点M（2，1）在椭圆C上．（1）求椭圆C的方程；（2）直线l平行于OM，且与椭圆C交于A，B两个不同的点，若∠AOB为钝角，求直线l在y轴上的截距m的取值范围．18．（2018•成都模拟）已知椭圆C：的左右焦点分别为F1，F2，左顶点为A，离心率为，点B是椭圆上的动点，△ABF1的面积的最大值为．（1）求椭圆C的方程；（2）设经过点F1的直线l与椭圆C相交于不同的两点M，N，线段MN的中垂线为l'．若直线l'与直线l相交于点P，与直线x=2相交于点Q，求的最小值．19．（2018•齐齐哈尔一模）已知椭圆C：+=1（a＞b＞0）的左、右焦点分别为F1，F2．且椭圆C过点（，﹣），离心率e=；点P在椭圆C上，延长PF1与椭圆C交于点Q，点R是PF2中点．（I）求椭圆C的方程；（II）若O是坐标原点，记△QF1O与△PF1R的面积之和为S，求S的最大值．20．（2018•唐山一模）已知椭圆Γ：（a＞b＞0）的左焦点为F，上顶点为A，长轴长为，B为直线l：x=﹣3上的动点，M（m，0）（m＜0），AM ⊥BM．当AB⊥l时，M与F重合．（1）若椭圆Γ的方程；（2）若C为椭圆Γ上一点，满足AC∥BM，∠AMC=60°，求m的值．21．（2018•南平二模）已知抛物线C：y2=2px的焦点为F，抛物线C上的点M（2，y0）到F的距离为3．（Ⅰ）求抛物线C的方程；（Ⅱ）斜率存在的直线l与抛物线相交于相异两点A（x1，y1），B（x2，y2），x1+x2=4．若AB的垂直平分线交x轴于点G，且=5，求直线l方程．22．（2018•洛阳三模）已知抛物线C：y2=2px（p＞0）的焦点为F，A为C上异于原点的任意一点，过点A的直线l交C于另一点B，交x轴的正半轴于点D，且有|FA|=|FD|，当点A的横坐标为3时，△ADF为正三角形．（Ⅰ）求C的方程；（Ⅱ）若直线l1∥l，且l1和C有且只有一个公共点E，试问直线AE是否过定点，若过定点，求出定点坐标；若不过定点，请说明理由．23．（2018•资阳模拟）已知椭圆C：的离心率，且过点．（1）求椭圆C的方程；（2）过P作两条直线l1，l2与圆相切且分别交椭圆于M，N两点．①求证：直线MN的斜率为定值；②求△MON面积的最大值（其中O为坐标原点）．24．（2018•辽宁模拟）已知M（）是椭圆C：（a＞b＞0）上的一点，F1F2是该椭圆的左右焦点，且|F1F2|=2．（1）求椭圆C的方程；（2）设点A，B是椭圆C上与坐标原点O不共线的两点，直线OA，OB，AB的斜率分别为k1，k2，k3，且k1k2=k2．试探究|OA|2+|OB|2是否为定值，若是，求出定值，若不是，说明理由．25．（2018•上饶三模）已知椭圆C1：（a＞1）的离心率，左、右焦点分别为F1、F2，直线l1过点F1且垂直于椭圆的长轴，动直线l2垂直l1于点P，线段PF2的垂直平分线交l2于点M．（1）求点M的轨迹C2的方程；（2）当直线AB与椭圆C1相切，交C2于点A，B，当∠AOB=90°时，求AB的直线方程．26．（2018•上海模拟）已知点F1、F2为双曲线C：的左、右焦点，过F2作垂直于x轴的直线，在x轴上方交双曲线C于点M，且∠MF1F2=30°．圆O的方程是x2+y2=b2．（1）求双曲线C的方程；（2）过双曲线C上任意一点P作该双曲线两条渐近线的垂线，垂足分别为P1、P2，求的值；（3）过圆O上任意一点Q（x0，y0）作圆O的切线l交双曲线C于A、B两点，AB中点为M，求证：．27．（2018•江苏一模）已知椭圆C：（a＞b＞0）经过点，，点A是椭圆的下顶点．（1）求椭圆C的标准方程；（2）过点A且互相垂直的两直线l1，l2与直线y=x分别相交于E，F两点，已知OE=OF，求直线l1的斜率．28．（2018•衡阳一模）已知椭圆的左、右焦点分别为F1、F2，离心率为，直线y=1与C的两个交点间的距离为．（Ⅰ）求椭圆C的方程；（Ⅱ）分别过F1、F2作l1、l2满足l1∥l2，设l1、l2与C的上半部分分别交于A、B 两点，求四边形ABF2F1面积的最大值．29．（2018•太原一模）已知椭圆的左顶点为A，右焦点为F2（2，0），点在椭圆C上．（1）求椭圆C的方程；（2）若直线y=kx（k≠0）与椭圆C交于E，F两点，直线AE，AF分别与y轴交于点M，N，在x轴上，是否存在点P，使得无论非零实数k怎样变化，总有∠MPN为直角？若存在，求出点P的坐标；若不存在，请说明理由．30．（2018•成都模拟）已知圆O的方程为x2+y2=4，若抛物线C过点A（﹣1，0），B（1，0），且以圆O的切线为准线，F为抛物线的焦点，点F的轨迹为曲线C′．（1）求曲线C′的方程；（2）过点B作直线L交曲线C′与P，Q两点，P，P′关于x轴对称，请问：直线P′Q 是否过x轴上的定点，如果不过请说明理由，如果过定点，请求出定点E的坐标31．（2018•秦州区校级一模）已知椭圆C：+=1（a＞b＞0）的右焦点为F2（2，0），点P（1，﹣）在椭圆C上．（Ⅰ）求椭圆C的标准方程；（Ⅱ）是否存在斜率为﹣1直线l与椭圆C相交于M，N两点，使得|F1M|=|F1N|（F1为椭圆的左焦点）？若存在，求出直线l的方程；若不存在，说明理由．32．（2018•黄山一模）已知椭圆Γ：的左、右焦点分别为F1、F2，短轴两个端点为A、B，且四边形AF1BF2是边长为2的正方形．（1）求椭圆Γ的方程；（2）若C、D分别是椭圆Γ的左、右端点，动点M满足MD⊥CD，连接CM，交椭圆于与点P．证明：为定值．33．（2018•陕西一模）已知椭圆+=1（a＞b＞0）的左右焦点分别为F1和F2，由4个点M（﹣a，b）、N（a，b）、F2和F1组成了一个高为，面积为3的等腰梯形．（1）求椭圆的方程；（2）过点F1的直线和椭圆交于两点A、B，求△F2AB面积的最大值．34．（2018•朝阳三模）如图，椭圆经过点，且点M到椭圆的两焦点的距离之和为．（1）求椭圆C的标准方程；（2）若R，S是椭圆C上的两个点，线段RS的中垂线l的斜率为且直线l与RS交于点P，O为坐标原点，求证：P，O，M三点共线．35．（2018•徐州一模）如图，在平面直角坐标系xOy中，已知椭圆+=1（a ＞0，b＞0）的离心率为，且过点（1，）．F为椭圆的右焦点，A，B为椭圆上关于原点对称的两点，连接AF，BF分别交椭圆于C，D两点．（1）求椭圆的标准方程；（2）若AF=FC，求的值；（3）设直线AB，CD的斜率分别为k1，k2，是否存在实数m，使得k2=mk1，若存在，求出m的值；若不存在，请说明理由．36．（2018•芜湖模拟）已知椭圆C：（a＞b＞0）的左右焦点分别为F1，F2，点P是椭圆C上一点，若PF1⊥PF2，|F1F2|=2，△PF1F2的面积为1．（Ⅰ）求椭圆C的方程；（Ⅱ）若A，B分别为椭圆上的两点，且OA⊥OB，求证：为定值，并求出该定值．37．（2018•马鞍山二模）在直角坐标系中，己知点A（﹣2，0），B（2，0），两动点C（0，m），D（0，n），且mn=3，直线AC与直线BD的交点为P．（1）求动点P的轨迹方程；（2）过点F（1，0）作直线l交动点P的轨迹于M，N两点，试求的取值范围．38．（2018•凉山州模拟）若A（x1，y1），B（x2，y2）是椭圆E：+y2=1上位于x轴上方两点，且x1+x2=2．（1）若y1+y2=1，求线段AB的垂直平分线的方程；（2）求直线AB在y轴上截距的最小值．39．（2018•江苏二模）如图，在平面直角坐标系xOy中，B1，B2是椭圆的短轴端点，P是椭圆上异于点B1，B2的一动点．当直线PB1的方程为y=x+3时，线段PB1的长为．（1）求椭圆的标准方程；（2）设点Q满足：QB1⊥PB1，QB2⊥PB2，求证：△PB1B2与△QB1B2的面积之比为定值．40．（2018•湖北模拟）如图，已知抛物线x2=2py（p＞0），其焦点到准线的距离为2，圆S：x2+y2﹣py=0，直线l：y=kx+与圆和抛物线自左至右顺次交于四点A、B、C、D，（1）若线段AB、BC、CD的长按此顺序构成一个等差数列，求正数k的值；（2）若直线l′过抛物线焦点且垂直于直线l，直线l′与抛物线交于点M、N，设AD、MN的中点分别为P、Q，求证：直线PQ过定点．参考答案与试题解析1．【分析】（1）设出M坐标，通过直线MN的斜率为，转化求解C的离心率．（2）通过原点O为F1F2的中点，MF2∥y轴，推出b2=6a，结合|MN|=7|F1N|，转化求解a，b．【解答】解：（1）根据及题设知，5b2=24ac将b2=a2﹣c2代入5b2=24ac解得或（舍去），故C的离心率为；………………………………………………（4分）（2）由题意得，原点O为F1F2的中点，MF2∥y轴，所以直线MF1与y轴的交点D（0，3）是线段MF1的中点，故，即b2=6a①………………………………………………（7分）由|MN|=7|F1N|得|DF1|=3|F1N|，设N（x1，y1）则，即代入C的方程，得②……………………………………………（10分）将①及代入②得解得故……………………………………………………（12分）【点评】本题考查椭圆的简单性质的应用，直线与椭圆的位置关系的应用，考查计算能力．2．【分析】（1）由已知可得a，再由离心率求得c，结合隐含条件求得b，则椭圆方程可求；（2）由题意定义结合已知求得PF2，再由椭圆的第二定义可得点P到右准线的距离．【解答】解：（1）根据题意：，解得，∴b2=a2﹣c2=4，∴椭圆C的标准方程为；（2）由椭圆的定义得：PF1+PF2=6，可得PF2=2，设点P到右准线的距离为d，根据第二定义，得，解得：．【点评】本题考查椭圆的简单性质，考查了椭圆定义的应用，是基础题．3．【分析】（Ⅰ）由题意可得，a=4，c=2由a2=b2+c2，得b2=42﹣22=12，问题得以解决．（Ⅱ）当∠APQ=∠BPQ时，PA、PB的斜率之和为0，设直线PA的斜率为k，则PB的斜率为﹣k，将PA、PB的直线方程分别代入椭圆方程，然后运用韦达定理，求出x1，x2，再由斜率公式化简即可得到定值．【解答】解：（Ⅰ）由题意可得，a=4，c=2由a2=b2+c2，得b2=42﹣22=12，所以椭圆C的方程为．（Ⅱ）当∠APQ=∠BPQ时，AP，BP的斜率之和为0，设直线PA的斜率为k，则直线PB的斜率为﹣k，设A（x1，y1）B（x2，y2），PA的方程为y﹣3=k（x﹣2）．联立消y得（3+4k2）x2+8（3k﹣k2）x+4（4k2+9﹣12k）﹣48=0所以，同理，所以，，所以k AB===，所以AB的斜率为定值．【点评】本题考查椭圆的方程及联立直线方程消去一个未知数，得到二次方程，运用韦达定理求解，考查基本的运算能力，属于中档题．4．【分析】（1）根据题意，联立直线与椭圆的方程，可得（4+a2k2）x2+2a2kx﹣3a2=0，设A（x1，y1），B（x2，y2），D（x0，y0），用k表示D的坐标，分析可得=．解可得a2的值，将其代入椭圆的方程即可得答案；（2）假设存在定点M，且设M（0，m），分析易得k AM+k BM=0，即，变形分析可得2kx1x2+x1+x2﹣m（x1+x2）=0，结合根与系数的关系分析可得，计算可得m的值，即可得答案．【解答】解：（1）由得（4+a2k2）x2+2a2kx﹣3a2=0，显然△＞0，设A（x1，y1），B（x2，y2），D（x0，y0），则，，∴，．∴=．∴a2=8．所以椭圆C的方程为．（2）假设存在定点M，且设M（0，m），由∠AMO=∠BMO得k AM+k BM=0．∴．即y1x2+y2x1﹣m（x1+x2）=0，∴2kx1x2+x1+x2﹣m（x1+x2）=0．由（1）知，，∴．∴m=4．所以存在定点M（0，4）使得∠AMO=∠BMO．【点评】本题考查直线与椭圆的位置关系，涉及椭圆的几何性质，关键是求出椭圆的标准方程．5．【分析】（Ⅰ）由题意可得，2b=2，再由椭圆的离心率公式和a，b，c的关系，解得a=2，进而得到椭圆方程；（Ⅱ）方法一、设P（x0，y0）（0＜x0≤2），A（0，﹣1），B（0，1），求出直线PA，PB的方程，与直线x=4的交点M，N，可得MN的中点，圆的方程，令y=0，求得与x轴的交点坐标，运用弦长公式，结合．即可得到所求最大值；方法二、设P（x0，y0）（0＜x0≤2），A（0，﹣1），B（0，1），求出直线PA，PB 的方程，与直线x=4的交点M，N，以MN为直径的圆与x轴相交，可得y M y N＜0，求得，再由弦长公式，可得最大值．【解答】解：（Ⅰ）由题意可得，2b=2，即b=1，，得，解得a2=4，椭圆C的标准方程为；（Ⅱ）方法一、设P（x0，y0）（0＜x0≤2），A（0，﹣1），B（0，1），所以，直线PA的方程为，同理：直线PB的方程为，直线PA与直线x=4的交点为，直线PB与直线x=4的交点为，线段MN的中点，所以圆的方程为，令y=0，则，因为，所以，所以，设交点坐标（x1，0），（x2，0），可得x1=4+，x2=4﹣，因为这个圆与x轴相交，该方程有两个不同的实数解，所以，解得．则（）所以当x0=2时，该圆被x轴截得的弦长为最大值为2．方法二：设P（x0，y0）（0＜x0≤2），A（0，﹣1），B（0，1），所以，直线PA的方程为，同理：直线PB的方程为，直线PA与直线x=4的交点为，直线PB与直线x=4的交点为，若以MN为直径的圆与x轴相交，则，即，即．因为，所以，代入得到，解得．该圆的直径为，圆心到x轴的距离为，该圆在x轴上截得的弦长为；所以该圆被x轴截得的弦长为最大值为2．【点评】本题考查椭圆的方程的求法，注意运用离心率公式和基本量的关系，考查直线和圆相交的弦长问题，注意运用圆的方程，以及直线和圆相交的条件，考查化简整理的运算能力，属于中档题．6．【分析】（1）设椭圆的焦距为2c，由题意得，=，=4，解出即可得出．（2）△AOB的面积是△AOM的面积的2倍，可得AB=2AM，即点M为AB的中点．A（﹣2，0）．设M（x0，y0），利用中点坐标公式可得：B（2x0+2，2y0）．由+=，+=1，联立解出，即可得出直线AB的方程．【解答】解：（1）设椭圆的焦距为2c，由题意得，=，=4，解得a=2，c=b=．∴椭圆的方程为：+=1．（2）△AOB的面积是△AOM的面积的2倍，∴AB=2AM，∴点M为AB的中点．∵椭圆的方程为：+=1．∴A（﹣2，0）．设M（x0，y0），则B（2x0+2，2y0）．由+=，+=1，化为：﹣18x0﹣16=0，≤x0≤．解得：x0=﹣．代入解得：y0=，∴k AB=，因此，直线AB的方程为：y=（x+2）．【点评】本题考查了椭圆与圆的标准方程及其性质、直线与椭圆相交问题、三角形面积计算公式，考查了推理能力与计算能力，属于难题．7．【分析】（Ⅰ）通过点在抛物线上，以及抛物线的定义，列出方程求解可得C的方程；（Ⅱ）证法一：设直线PA的斜率为k（显然k≠0），则直线PA的方程为y﹣1=k （x﹣1），联立直线与抛物线方程，设A（x1，y1），由韦达定理，求出A的坐标，直线PB的斜率为．得到B的坐标，通过直线的向量是否垂直，求出直线l的方程，然后求解定点坐标．证法二：由（1），得P（1，1）．若l的斜率不存在，则l与x轴垂直．设A（x1，y1），则B（x1，﹣y1），．推出l的斜率必存在．设l的斜率为k，显然k ≠0，设l：y=kx+t，利用直线方程与抛物线方程联立，设A（x1，y1），B（x2，y2），利用韦达定理，转化求解直线l：y=kx﹣1．即可说明l过定点（0，﹣1）．证法三：由（1），得P（1，1）．设l：x=ny+t，由直线l不过点P（1，1），所以n+t≠1．由消去x并整理得y2﹣ny﹣t=0．判别式△=n2+4t＞0．设A（x1，y1），B（x2，y2），则y1+y2=n①，y1y2=﹣t②，转化求解l：x=n（y+1）．说明l过定点（0，﹣1）．【解答】解：（Ⅰ）由题意，得2pm=1，即．由抛物线的定义，得．由题意，．解得，或p=2（舍去）．所以C的方程为y2=x．（Ⅱ）证法一：设直线PA的斜率为k（显然k≠0），则直线PA的方程为y﹣1=k （x﹣1），则y=kx+1﹣k．由消去y并整理得k2x2+[2k（1﹣k）﹣1]x+（1﹣k）2=0．设A（x1，y1），由韦达定理，得，即.=．所以．由题意，直线PB的斜率为．同理可得，即B（（k2﹣1）2，k﹣1）．若直线l的斜率不存在，则．解得k=1，或k=﹣1．当k=1时，直线PA与直线PB的斜率均为1，A，B两点重合，与题意不符；当k=﹣1时，直线PA与直线PB的斜率均为﹣1，A，B两点重合，与题意不符．所以，直线l的斜率必存在．直线l的方程为[x﹣（k﹣1）2]，即．所以直线l过定点（0，﹣1）．证法二：由（1），得P（1，1）．若l的斜率不存在，则l与x轴垂直．设A（x1，y1），则B（x1，﹣y1），．则==．（x1﹣1≠0，否则，x1=1，则A（1，1），或B（1，1），直线l过点P，与题设条件矛盾）由题意，，所以x1=0．这时A，B两点重合，与题意不符．所以l的斜率必存在．设l的斜率为k，显然k≠0，设l：y=kx+t，由直线l不过点P（1，1），所以k+t≠1．由消去y并整理得k2x2+（2kt﹣1）x+t2=0．由判别式△=1﹣4kt＞0，得．设A（x1，y1），B（x2，y2），则①，②，则==．由题意，．故（k2﹣1）x1x2+（kt﹣k+1）③将①②代入③式并化简整理得，即1﹣t2﹣kt﹣k=0．即（1+t）（1﹣t）﹣k（t+1）=0，即（1+t）（1﹣t﹣k）=0．又k+t≠1，即1﹣t﹣k≠0，所以1+t=0，即t=﹣1．所以l：y=kx﹣1．显然l过定点（0，﹣1）．证法三：由（1），得P（1，1）．设l：x=ny+t，由直线l不过点P（1，1），所以n+t≠1．由消去x并整理得y2﹣ny﹣t=0．由题意，判别式△=n2+4t＞0．设A（x1，y1），B（x2，y2），则y1+y2=n①，y1y2=﹣t②则==．由题意，y1y2+（y1+y2）+1=1，即y1y2+（y1+y2）=0③将①②代入③式得﹣t+n=0，即t=n．所以l：x=n（y+1）．显然l过定点（0，﹣1）．【点评】本题考查抛物线的方程的求法，直线与抛物线的位置关系的综合应用，考查直线过定点问题，考查分类讨论思想的应用．8．【分析】（I）把A代入抛物线方程求出p，根据椭圆的性质列方程组求出a，b；（II）①设MN方程为y=kx+b，根据根与系数的关系和向量的数量积公式求出b 即可得出结论；②根据弦长公式计算|SR|，求出F到直线MN的距离d，得出三角形的面积关于k的函数，根据单调性得出k的值．【解答】解：（I）把A（2，1）代入抛物线C1可得：4=2p，p=2．∴抛物线C1的方程为x2=4y．故F（0，1），又F（0，1）是椭圆C2：的焦点，且椭圆上的点到焦点F的最小值为2，∴，解得a=3，b=2，∴椭圆C2的标准方程为：=1．（II）①∵直线MN与抛物线交于M，N两点，∴直线MN斜率必存在．设直线MN的方程为y=kx+b，M（x1，y1），N（x2，y2），联立方程组，消去y可得：x2﹣4kx﹣4b=0，∴x1x2=﹣4b，∴y1y2==b2，∴=x1x2+y1y2=b2﹣4b=﹣4，即b=2．∴直线MN的方程为y=kx+2．∴直线MN过定点Q（0，2）．②联立方程组，消去y可得：（9+8k2）x2+32kx﹣40=0，设R（x3，y3），S（x4，y4），则x3+x4=﹣，x3x4=﹣，∴|RS|==，又F（0，1）代直线MN的距离d=，=|RS|×d=，∴S△FSR令=t，则t≥，==，∴S△FSR取得最大值，此时k=0．由对勾函数的性质可知当t=时，S△FSQ∴直线MN的方程为y=2．【点评】本题考查了抛物线、椭圆的性质，直线与圆锥曲线的位置关系，属于中档题．9．【分析】（Ⅰ）根据题意，由椭圆的离心率公式可得，进而可得，则椭圆的方程可以为以，由椭圆Γ的四个顶点围成的四边形的面积为4，得2ab=4，据此解可得a、b的值，将a、b的值代入椭圆的方程即可得答案；（Ⅱ）根据题意，按直线l的斜率是否存在分2种情况讨论，当直线l的斜率不存在时，令x=±1，易得△AOB的面积，当直线l的斜率存在时，设ly=kx+m，联立直线与椭圆的方程，用k表示△AOB的面积，由基本不等式的性质分析可得△AOB的面积，综合2种情况即可得答案．【解答】解：（Ⅰ）根据题意，椭圆Γ：的离心率为，则，得，，所以，由椭圆Γ的四个顶点围成的四边形的面积为4，得2ab=4，所以a=2，b=1，椭圆Γ的标准方程为．（Ⅱ）根据题意，直线l与椭圆Γ交于A，B两点，当直线l的斜率不存在时，令x=±1，得，，当直线l的斜率存在时，设l：y=kx+m，A（x1，y1），B（x2，y2），M（x0，y0），由，得（1+4k2）x2+8kmx+4m2﹣4=0，则，，所以，，将代入x2+y2=1，得，又因为=，原点到直线l的距离，所以==×==．当且仅当12k2=1+4k2，即时取等号．综上所述，△AOB面积的最大值为1．【点评】本题考查椭圆的几何性质，涉及直线与椭圆的位置关系，注意分析直线的斜率是否存在．10．【分析】（Ⅰ）由已知可得：，结合a2=b2+c2，解得，即可．（Ⅱ）设A（x1，y1），B（x2，y2），则重心，，．则，结合．可得当且仅当t=0，即N（0，0）时，k•k'为定值为．【解答】解：（Ⅰ）由已知可得：，结合a2=b2+c2，解得，∴椭圆方程为：．（Ⅱ）设A（x1，y1），B（x2，y2），则重心，，．由于AB斜率为k存在且k≠0，故，则∵则要使为定值，则当且仅当t=0，即N（0，0）时，k•k'为定值为．【点评】本题考查了椭圆的方程，性质，直线与椭圆的位置关系，属于中档题．11．【分析】（1）利用|MF|=a+c，|BN|=a﹣c，是|MF|与|FN|的等比中项．得到（a+c）（a﹣c）=3，结合椭圆的离心率求解即可．（2）直线l的斜率存在且不为0．设直线l：y=kx+m（m≠0），A（x1，y1），B（x2，y2），联立直线和椭圆，消去y可得，（3+4k2）x2+8kmx+4m2﹣12=0，利用判别式以及韦达定理，通过OA，AB，OB的斜率依次成等比数列，推出m2（4k2﹣3）=0，求出，0＜m2＜6，且m2≠3，然后求解三角形的面积的表达式，求解范围即可．【解答】解：（1）解：|MF|=a+c，|BN|=a﹣c，是|MF|与|FN|的等比中项．∴（a+c）（a﹣c）=3，∴b2=a2﹣c2=3．又，解得a=2，c=1，∴椭圆C的方程为．（2）由题意可知，直线l的斜率存在且不为0．故可设直线l：y=kx+m（m≠0），A（x1，y1），B（x2，y2），联立直线和椭圆，消去y可得，（3+4k2）x2+8kmx+4m2﹣12=0，由题意可知，△=64km﹣4（4k2+3）（4m2﹣12）=48（4k2﹣m2+3）＞0，即4k2+3＞m2，且，又直线OA，AB，OB的斜率依次成等比数列，所以，将y1，y2代入并整理得m2（4k2﹣3）=0，因为m≠0，，0＜m2＜6，且m2≠3，设d为点O到直线l的距离，则有，，所以，所以三角形面积的取值范围为．【点评】本题考查椭圆方程的求法直线与椭圆的位置关系的综合应用，三角形的面积的范围的求法，考查转化思想以及计算能力．12．【分析】（1）根据题意，由椭圆的焦点坐标可得c的值，结合椭圆的定义可得2a=+=2，即可得a的值，由椭圆的定义计算可得b的值，将a、b的值代入椭圆的方程即可得答案；（2）根据题意，按直线AB的斜率是否存在分2种情况讨论：①，直线AB的斜率不为零，②当AB的斜率为零时，分别求出四边形的面积，综合即可得结论．【解答】解：（1）根据题意，椭圆E：+=1的两个焦点的坐标分别为（﹣1，0），（1，0）．则c=1，又由椭圆经过点，则2a=+=2，即a=，b==1，则E的方程为；（2）证明：根据题意，分2种情况讨论：①，当直线AB的斜率不为零时，可设AB：x=my+t代入得：（m2+2）y2+2mty+t2﹣2=0，设A（x1，y1），B（x2，y2），则，△=8（m2+2﹣t2），设P（x，y），由，得，∵点P在椭圆E上，∴，即，∴4t2=m2+2，，原点到直线x=my+t的距离为．∴四边形OAPB的面积：．②当AB的斜率为零时，四边形OAPB的面积，∴四边形OAPB的面积为定值．【点评】本题考查椭圆的几何性质，涉及直线与椭圆的位置关系，关键是求出椭圆的标准方程．13．【分析】（1）方法一：设切线方程，代入椭圆方程，由M在椭圆方程，利用△=0，即可求得k的值，求得“切线”方程是；方法二：将直线方程代入椭圆方程，由△=0，则直线与椭圆只有一个交点，故直线与椭圆相切；（2）求得直线MA，MB的方程，令x=0，即可求得P和Q点坐标，令x=0，求得D点坐标，由y P+y Q=2y D，即可求得点D是线段PQ的中点；（3）求得交点坐标，即可求得MF1及MF2斜率，根据直线的夹角公式，求得tanθ1=tanθ1，过M的椭圆C的“切线”l与直线MF1、MF2所成夹角是否相等【解答】解：（1）方法一：当n=0时，m=±，则切线方程x=±，满足，当m≠0时，设直线y=k（x﹣m）+n，联立，整理得：（1+2k2）x2﹣4k（km﹣n）x+2（km﹣2）2﹣2=0，由△=16k2（km﹣n）2﹣4×（1+2k2）[2（km﹣2）2﹣2]=0，整理得：（2﹣m2）k2+2mnk+1﹣n2=0，由M（m，n）在椭圆上，则，2﹣m2=2n2，1﹣n2=，∴2n2k2+2mnk+=0，则（nk+）2=0，解得：k=﹣，∴切线方程y=﹣（x﹣m）+n，整理得：；综上可知：过椭圆C上的点M（m，n）的“切线”方程是；方法二：由直线，整理得：mx+2ny=2，，整理得：（2n2+m2）y2﹣4ny+2﹣m2=0，由M（m，n）在椭圆上，则，2﹣m2=2n2，2n2+m2=2，则y2﹣2ny+n2=0，则△=0，∴过椭圆C上的点M（m，n）的“切线”方程是；（2）由椭圆的左顶点A（﹣，0），右顶点B（，0），由直线MA的方程：y=（x+），令x=0，则y P=，同理y Q=，切线方程，令x=0，则y D=y P+y Q===2y D，∴点D是线段PQ的中点；（3）相等，由椭圆的焦点F1（﹣1，0），F2（1，0），过椭圆C上的点M（m，n）的“切线”方程是，则直线MF 1的斜率=，直线MF2的斜率=，则切线的斜率k=，由夹角公式tanθ1=||=，tanθ1=||=，所以所成夹角相等．【点评】本题考查椭圆的标准方程的性质，直线的切线方程的应用，直线与椭圆的位置关系，考查直线夹角公式的应用，中点坐标公式，考查转化思想，属于中档题．14．【分析】（Ⅰ）设A（x1，y1），依题意得点C（﹣x1，﹣y1），表示出△PAC面积，即可求出最大值，（Ⅱ）证法1：当直线AP的斜率存在时，设其方程为y=kx+，根据根与系数的关系可得m，n是方程9x2﹣30x+4x12+9=0的两个根，由韦达定理，m+n=；证法2：当直线AP的斜率存在时，这时点A不在y轴上，即x1≠0，设其方程为y=kx+，根据根与系数的关系，求出m，n，即可求出m+n的值．【解答】解：（Ⅰ）设A（x1，y1），依题意得点C（﹣x1，﹣y1），则S=|OP|•2|x1|=|x1|，△PAC∵点A在椭圆T：+y2=1上，∴|x1|≤2，∴S=|x1|≤1（当且仅当x1=±2时等号成立）△PAC∴△PAC面积的最大值为1；（Ⅱ）证法1：当直线AP的斜率存在时，设其方程为y=kx+，由，消去y，得（1+4k2）x2+4kx﹣3=0，设B（x2，y2），由韦达定理，得，而由=m，得（﹣x1，﹣y1）=m（x2，y2﹣），故﹣x1=mx2，x2=﹣，代入①、②，得，两式相除，得k=，代入④，整理得9m2﹣30m+4x12+9=0；对于射线CP，同样的方法可得9n2﹣30n+4x12+9=0，故m，n是方程9x2﹣30x+4x12+9=0的两个根，由韦达定理，m+n=；当直线AP的斜率不存在时，点A为椭圆T的上顶点或下顶点，当点A为（0，1）时，则B、C重合于点（0．﹣1），D、A重合，由=m，=n，得m=，n=3，这时m+n=；若点A为椭圆T的下顶点（0，﹣1），同理可得m+n=；综上可知m+n为定值，该值为．证法2：当直线AP的斜率存在时，这时点A不在y轴上，即x1≠0，设其方程为y=kx+，由，消去y，得（1+4k2）x2+4kx﹣3=0，设B（x2，y2），由韦达定理，得x1x2=﹣，又k=，代入上式得x2=，由=m，得（﹣x1，﹣y1）=m（x2，y2﹣），故﹣x1=mx2，∴m=﹣=对于射线CP，同样的方法可得n=，∴m+n==．当直线AP的斜率不存在时，点A为椭圆T的上顶点或下顶点，当点A为（0，1）时，则B、C重合于点（0．﹣1），D、A重合，当直线AP的斜率不存在时，点A为椭圆T的上顶点或下顶点，当点A为（0，1）时，则B、C重合于点（0．﹣1），D、A重合，由=m，=n，得m=，n=3，这时m+n=；若点A为椭圆T的下顶点（0，﹣1），同理可得m+n=；综上可知m+n为定值，该值为．【点评】本题考查了直线和椭圆的位置关系，向量的基本运算，考查了运算能力和转化能力，属于中档题．15．【分析】（Ⅰ）根据题意，由圆的方程分析可得椭圆的焦点和顶点坐标，即可得。

2018年高考数学试题分类汇编之圆锥曲线（解析版）一、选择题1.（浙江卷）（2）双曲线221 3=x y -的焦点坐标是A ．(0)，0)B ．(−2，0)，(2，0)C ．(0，，(0D ．(0，−2)，(0，2)解：∵双曲线方程可得双曲线的焦点在x 轴上，且a 2=3，b 2=1， 由此可得222=+=b a c ∴该双曲线的焦点坐标为（±2，0）故选：B2.（天津文）（7）已知双曲线22221(0,0)x y a b a b-=>> 的离心率为2，过右焦点且垂直于x 轴的直线与双曲线交于,A B 两点.设,A B 到双曲线的同一条渐近线的距离分别为1d 和2d ，且126,d d += 则双曲线的方程为（A ）22139x y -= （B ）22193x y -= （C ）221412x y -=（D ）221124x y -= 解：由题意可得，CD 是双曲线的一条渐近线x aby =，即0=-ay bx ，)0,(c F故选：A3.（天津理）(7)已知双曲线22221(0,0)x y a b a b-=>>的离心率为2，过右焦点且垂直于x 轴的直线与双曲线交于A ，B 两点. 设A ，B 到双曲线同一条渐近线的距离分别为1d 和2d ，且126d d +=，则双曲线的方程为A221412x y -= B221124x y -= C 22139x y -= D 22193x y -=解：由题意可得，CD 是双曲线的一条渐近线x aby =，即0=-ay bx ，)0,(c F故选：C4.（全国卷一文）（4）已知椭圆C ：22214x y a +=的一个焦点为(20)，，则C 的离心率为A ．13B ．12C D 解：椭圆的一个焦点为（2，0），可得a 2-4=4，解得22=a ，故选：C5.（全国卷一理）（8）设抛物线C ：y 2=4x 的焦点为F ，过点（–2，0）且斜率为23的直线与C 交于M ，N 两点，则FM FN ⋅=A ．5B ．6C ．7D ．8解：抛物线C ：y 2=4x 的焦点为F （1，0），过点（-2，0联立直线与抛物线C ：y 2=4x ，消去x 可得：y 2-6y+8=0， 解得y 1=2，y 2=4，不妨M （1，2），N （4，4），FM ＝(0，2)， FN ＝(3，4)．则 FM ∙FN =（0，2）•（3，4）=8． 故选：D6.（全国卷一理）（11）已知双曲线C ：2213x y -=，O 为坐标原点，F 为C 的右焦点，过F 的直线与C 的两条渐近线的交点分别为M 、N .若△OMN 为直角三角形，则|MN |= A ．32B ．3 C． D ．4故选：B7.（全国卷二文）（6）双曲线22221(0,0)x y a b a b-=>>A．y =B．y =C．y = D ．y = 解：∵双曲线的离心率为==ace则2222±=-=aa c ab 故选：A.8.（全国卷二文）（11）已知1F ，2F 是椭圆C 的两个焦点，P 是C上的一点，若12PF PF ⊥，且2160PFF ∠=︒，则C 的离心率为 A．1 B．2C D 1-解：F 1，F 2是椭圆C 的两个焦点，P 是C 上的一点，若PF 1⊥PF 2，且∠PF 2F 1=60°， 可得椭圆的焦点坐标F 2（c ，0），所以P（c 23,21故选：D9.（全国卷二理）（5）双曲线22221(0,0)x y a b a b-=>>A ．y =B ．y =C ．y x =D ．y =解：∵双曲线的离心率为==ace则2222±=-=aa c ab 故选：A ．10.（全国卷二理）（12）已知1F ，2F 是椭圆22221(0)x y C a b a b+=>>：的左，右焦点，A 是C 的左顶点，点P在过A 12PF F △为等腰三角形，12120F F P ∠=︒，则C 的离心率为 A ．23B ．12C ．13D ．14解：由题意可知：A （-a ，0），F 1（-c ，0），F 2（c ，0），直线AP 的方程为：）（a x y +=63，故选：D11.（全国卷三文）（10）已知双曲线22221(00)x y C a b a b-=>>：，(4,0)到C 的渐近线的距离为AB ．2CD ．故选：D12.（全国卷三理）（11）设12F F ，是双曲线22221x y C a b-=：（00a b >>，）的左、右焦点，O 是坐标原点．过2F 作C 的一条渐近线的垂线，垂足为P ．若1PF ，则C 的离心率为A B ．2 C D在三角形F 1PF 2中，由余弦定理可得|PF 1|2=|PF 2|2+|F 1F 2|2-2|PF 2|•|F 1F 2|COS ∠PF 2O ，故选：C二、填空题1.（北京文）（10）已知直线l 过点（1,0）且垂直于x 轴，若l 被抛物线24y ax =截得的线段长为4，则抛物线的焦点坐标为_________.解：∵直线l 过点（1，0）且垂直于x 轴，∴x=1，代入到y 2=4ax ，可得y 2=4a ，显然a ＞0，∴y=±∴抛物线的焦点坐标为（1，0）， 故答案为：（1，0）2.（北京文）（12）若双曲线2221(0)4x y a a -=>的离心率为2，则a =_________.解：双曲线的离心率为245422=+a a ，解得a=4． 故答案为：43.（北京理）（14）已知椭圆22221(0)x y M a b a b +=>>：，双曲线22221x y N m n -=：．若双曲线N 的两条渐近线与椭圆M 的四个交点及椭圆M 的两个焦点恰为一个正六边形的顶点，则椭圆M 的离心率为__________；双曲线N 的离心率为__________．解：若双曲线N 的两条渐近线与椭圆M 的四个交点及椭圆M 的两个焦点恰为一个正六边形的顶点，4.（江苏卷）（8）在平面直角坐标系xOy 中，若双曲线22221(0,0)x y a b a b -=>>的右焦点(,0)F c 到一条渐近，则其离心率的值是 ．，故答案为：25.（浙江卷）（17）已知点P (0，1)，椭圆24x +y 2=m (m >1)上两点A ，B 满足AP =2PB ，则当m =_______时，点B 横坐标的绝对值最大．解：设A （x 1，y 1），B （x 2，y 2），由P （0，1）， AP=2PB，可得-x 1=2x 2，1-y 1=2（y 2-1），即有x 1=-2x 2，y 1+2y 2=3， 又x 12+4y 12=4m ，即为x 22+y 12=m ，① x 22+4y 22=4m ，② ①-②得（y 1-2y 2）（y 1+2y 2）=-3m ，可得y 1-2y 2=-m ，即有m=5时，x 22有最大值4， 即点B 横坐标的绝对值最大． 故答案为：5．6．（全国卷三理）（16）已知点()11M -，和抛物线24C y x =：，过C 的焦点且斜率为k 的直线与C 交于A ，B 两点．若90AMB =︒∠，则k =________．解：∵抛物线C ：y 2=4x 的焦点F （1，0），∴过A ，B 两点的直线方程为y=k （x-1），联立⎩⎨⎧-==)1(42x k y xy 可得，k 2x 2-2（2+k 2）x+k 2=0，设A （x 1，y 1），B （x 2，y 2），y 1y 2=k 2（x 1-1）（x 2-1）=k 2[x 1x 2-（x 1+x 2）+1]=-4，∵M （-1，1），∴ MA =（x 1+1，y 1-1）， MB =（x 2+1，y 2-1）， ∵∠AMB=90°=0，∴MA *MB =0∴（x 1+1）（x 2+1）+（y 1-1）（y 2-1）=0，整理可得，x 1x 2+（x 1+x 2）+y 1y 2-（y 1+y 2）+2=0，∴即k 2-4k+4=0， ∴k=2． 故答案为：2三、解答题1.（北京文）（20）（本小题14分）已知椭圆2222:1(0)x y M a b a b +=>>焦距为斜率为k 的直线l 与椭圆M 有两个不同的交点A ，B .（Ⅰ）求椭圆M 的方程；（Ⅱ）若1k =，求||AB 的最大值；（Ⅲ）设(2,0)P -，直线P A 与椭圆M 的另一个交点为C ，直线PB 与椭圆M 的另一个交点为D .若C ,D和点71(,)42Q -共线，求k .解析（Ⅰ）由题意得2c =，所以c =3c e a ==，所以a =2221b a c =-=， 所以椭圆M 的标准方程为2213x y +=．（Ⅱ）设直线AB 的方程为y x m =+，由2213y x m x y =+⎧⎪⎨+=⎪⎩消去y 可得2246330x mx m ++-=， 则2223644(33)48120m m m ∆=-⨯-=->，即24m <，设11(,)A x y ，22(,)B x y ，则1232m x x +=-，212334m x x -=，则12|||AB x x =-=，易得当20m =时，max ||AB =||AB（Ⅲ）设11(,)A x y ，22(,)B x y ，33(,)C x y ，44(,)D x y ， 则221133x y += ①，222233x y += ②， 又(2,0)P -，所以可设1112PA y k k x ==+，直线PA 的方程为1(2)y k x =+， 由122(2)13y k x x y =+⎧⎪⎨+=⎪⎩消去y 可得2222111(13)121230k x k x k +++-=， 则2113211213k x x k +=-+，即2131211213k x x k =--+， 又1112y k x =+，代入①式可得13171247x x x --=+，所以13147y y x =+， 所以1111712(,)4747x y C x x --++，同理可得2222712(,)4747x y D x x --++．故3371(,)44QC x y =+- ，4471(,)44QD x y =+- ， 因为,,Q C D 三点共线，所以34437171()()()()04444x y x y +--+-=，将点,C D 的坐标代入化简可得12121y y x x -=-，即1k =．2.（北京理）（19）（本小题14分）已知抛物线C ：2y =2px 经过点P （1，2）．过点Q （0，1）的直线l 与抛物线C 有两个不同的交点A ，B ，且直线P A 交y 轴于M ，直线PB 交y 轴于N ． （Ⅰ）求直线l 的斜率的取值范围；（Ⅱ）设O 为原点，μλ==,，求证：μλ11+为定值．解析：（Ⅰ）因为抛物线y 2=2px 经过点P （1，2）， 所以4=2p ，解得p =2，所以抛物线的方程为y 2=4x ． 由题意可知直线l 的斜率存在且不为0， 设直线l 的方程为y =kx +1（k ≠0）． 由241y x y kx ⎧=⎨=+⎩得22(24)10k x k x +-+=． 依题意22(24)410k k ∆=--⨯⨯>，解得k<0或0<k<1． 又P A ，PB 与y 轴相交，故直线l 不过点（1，-2）．从而k ≠-3． 所以直线l 斜率的取值范围是（-∞，-3）∪（-3，0）∪（0，1）． （Ⅱ）设A （x 1，y 1），B （x 2，y 2）． 由（I ）知12224k x x k -+=-，1221x x k =． 直线P A 的方程为y –2=1122(1)1y y x x --=--． 令x =0，得点M 的纵坐标为1111212211M y kx y x x -+-+=+=+--． 同理得点N 的纵坐标为22121N kx y x -+=+-． 由μλ==,得=1M y λ-，1N y μ=-．所以2212121212122224112()111111=211(1)(1)11M N k x x x x x x k k y y k x k x k x x k k λμ-+---++=+=+=⋅=⋅------． 所以11λμ+为定值．3.（江苏卷）（18）（本小题满分16分）如图，在平面直角坐标系xOy 中，椭圆C过点1)2，焦点12(F F ，圆O 的直径为12F F ．（1）求椭圆C 及圆O 的方程；（2）设直线l 与圆O 相切于第一象限内的点P ．①若直线l 与椭圆C 有且只有一个公共点，求点P 的坐标； ②直线l 与椭圆C 交于,A B 两点．若OAB △，求直线l 的方程．解析：（1）因为椭圆C的焦点为12(),F F -，可设椭圆C 的方程为22221(0)x y a b a b +=>>．又点1)2在椭圆C 上，所以2222311,43,a b a b ⎧+=⎪⎨⎪-=⎩，解得224,1,a b ⎧=⎪⎨=⎪⎩因此，椭圆C 的方程为2214x y +=．因为圆O 的直径为12F F ，所以其方程为223x y +=．（2）①设直线l 与圆O 相切于0000(),,(00)P x y x y >>，则22003x y +=， 所以直线l 的方程为0000()x y x x y y =--+，即0003x y x y y =-+． 由220001,43,x y x y x y y ⎧+=⎪⎪⎨⎪=-+⎪⎩，消去y ，得222200004243640()x y x x x y +-+-=．（*）因为直线l 与椭圆C 有且只有一个公共点，所以222222000000()()(24)(44364820)4x x y y y x ∆=--+-=-=． 因为00,0x y >，所以001x y =． 因此，点P的坐标为． ②因为三角形OAB，所以1 2AB OP ⋅=，从而AB =．设1122,,()(),A x y B x y ，由（*）得001,2x =，所以2222121()()x B y y x A =-+-222000222200048(2)(1)(4)x y x y x y -=+⋅+． 因为22003x y +=， 所以22022016(2)32(1)49x AB x -==+，即42002451000x x -+=， 解得22005(202x x ==舍去），则2012y =，因此P的坐标为． 综上，直线l的方程为y =+4.（天津文）（19）（本小题满分14分） 设椭圆22221(0)x y a b a b +=>> 的右顶点为A ，上顶点为B .||AB =（I ）求椭圆的方程；（II ）设直线:(0)l y kx k =<与椭圆交于,P Q 两点，l 与直线AB 交于点M ，且点P ，M 均在第四象限.若BPM △的面积是BPQ △面积的2倍，求k 的值.解析：（I ）设椭圆的焦距为2c ，由已知得2259c a =，又由222a b c =+，可得23.a b =由||AB ==从而3,2a b ==. 所以，椭圆的方程为22194x y +=. （II ）解：设点P 的坐标为11(,)x y ，点M 的坐标为22(,)x y ，由题意，210x x >>，点Q 的坐标为11(,).x y -- 由BPM △的面积是BPQ △面积的2倍，可得||=2||PM PQ ，从而21112[()]x x x x -=--，即215x x =.易知直线AB 的方程为236x y +=，由方程组236,,x y y kx +=⎧⎨=⎩ 消去y ，可得2632x k =+.由方程组221,94,x y y kx ⎧+⎪=⎨⎪=⎩消去y，可得1x =由215x x =5(32)k =+，两边平方，整理得2182580k k ++=，解得89k =-，或12k =-. 当89k =-时，290x =-<，不合题意，舍去；当12k =-时，212x =，1125x =，符合题意. 所以，k 的值为12-. 5.（天津理）(19)(本小题满分14分) 设椭圆22221x x a b +=(a >b >0)的左焦点为F ，上顶点为B .，点A 的坐标为(,0)b ，且FB AB ⋅=.（I ）求椭圆的方程；（II ）设直线l ：(0)y kx k =>与椭圆在第一象限的交点为P ，且l 与直线AB 交于点Q .若AQAOQ PQ =∠(O 为原点) ，求k 的值. 解析（Ⅰ）：设椭圆的焦距为2c ，由已知知2259c a =，又由a 2=b 2+c 2，可得2a =3b ．由已知可得，FB a =，AB，由FB AB ⋅=ab =6，从而a =3，b =2． 所以，椭圆的方程为22194x y +=． （Ⅱ）解：设点P 的坐标为（x 1，y 1），点Q 的坐标为（x 2，y 2）．由已知有y 1>y 2>0，故12sin PQ AOQ y y ∠=-．又因为2sin y AQ OAB =∠，而∠OAB =π4，故2AQ．由AQ AOQ PQ =∠，可得5y 1=9y 2． 由方程组22194y kx x y =⎧⎪⎨+=⎪⎩，，消去x，可得1y =．易知直线AB 的方程为x +y –2=0，由方程组20y kx x y =⎧⎨+-=⎩，，消去x ，可得221k y k =+．由5y 1=9y 2，可得5（k +1）=，两边平方，整理得25650110k k -+=，解得12k =，或1128k =．所以，k 的值为111228或． 6.（浙江卷）（21）（本题满分15分）如图，已知点P 是y 轴左侧(不含y 轴)一点，抛物线C ：y 2=4x 上存在不同的两点A ，B 满足P A ，PB 的中点均在C 上．（Ⅰ）设AB 中点为M ，证明：PM 垂直于y 轴；（Ⅱ）若P 是半椭圆x 2+24y =1(x <0)上的动点，求△P AB 面积的取值范围．解析（Ⅰ）设00(,)P x y ，2111(,)4A y y ，2221(,)4B y y ． 因为PA ，PB 的中点在抛物线上，所以1y ，2y 为方程202014()422y x y y ++=⋅即22000280y y y x y -+-=的两个不同的实数根． 所以1202y y y +=．因此，PM 垂直于y 轴．（Ⅱ）由（Ⅰ）可知120212002,8,y y y y y x y +=⎧⎪⎨=-⎪⎩ 所以2221200013||()384PM y y x y x =+-=-，12||y y -= 因此，PAB △的面积32212001||||4)24PABS PM y y y x =⋅-=-△． 因为220001(0)4y x x +=<，所以2200004444[4,5]y x x x -=--+∈． 因此，PAB △面积的取值范围是7.（全国一卷文）（20）（12分）设抛物线22C y x =：，点()20A ，，()20B -，，过点A 的直线l 与C 交于M ，N 两点． （1）当l 与x 轴垂直时，求直线BM 的方程；（2）证明：ABM ABN =∠∠．解：（1）当l 与x 轴垂直时，l 的方程为x =2，可得M 的坐标为（2，2）或（2，–2）．所以直线BM 的方程为y =112x +或112y x =--． （2）当l 与x 轴垂直时，AB 为MN 的垂直平分线，所以∠ABM =∠ABN ．当l 与x 轴不垂直时，设l 的方程为(2)(0)y k x k =-≠，M （x 1，y 1），N （x 2，y 2），则x 1>0，x 2>0． 由2(2)2y k x y x=-⎧⎨=⎩，得ky 2–2y –4k =0，可知y 1+y 2=2k ，y 1y 2=–4． 直线BM ，BN 的斜率之和为1221121212122()22(2)(2)BM BN y y x y x y y y k k x x x x ++++=+=++++．① 将112y x k =+，222y x k=+及y 1+y 2，y 1y 2的表达式代入①式分子，可得 121221121224()882()0y y k y y x y x y y y k k ++-++++===． 所以k BM +k BN =0，可知BM ，BN 的倾斜角互补，所以∠ABM +∠ABN ．综上，∠ABM =∠ABN ．8.（全国一卷理）（19）（12分） 设椭圆22:12x C y +=的右焦点为F ，过F 的直线l 与C 交于,A B 两点，点M 的坐标为(2,0). （1）当l 与x 轴垂直时，求直线AM 的方程；（2）设O 为坐标原点，证明：OMA OMB ∠=∠.解：（1）由已知得(1,0)F ，l 的方程为x =1.由已知可得，点A的坐标为或(1,. 所以AM的方程为y x =+y x =. （2）当l 与x 轴重合时，0OMA OMB ∠=∠=︒.当l 与x 轴垂直时，OM 为AB 的垂直平分线，所以OMA OMB ∠=∠.当l 与x 轴不重合也不垂直时，设l 的方程为(1)(0)y k x k =-≠，1221(,),(,)A y x y x B ，则12x x <<，直线MA ，MB 的斜率之和为212122MA MB x x y y k k +=+--. 由1122,y k k x y k x k =-=-得 121212(23()42)(2)MA MB x x x x k k x x k k k -+++=--. 将(1)y k x =-代入2212x y +=得 2222(21)4220k x k x k +-+-=. 所以，21221222422,2121x x x k k k x k -+==++. 则3131322244128423()4021k k k k k k k k k x x x x --++-++==+. 从而0MA MB k k +=，故MA ，MB 的倾斜角互补，所以OMA OMB ∠=∠.综上，OMA OMB ∠=∠.9.（全国二卷文）（20）（12分）设抛物线24C y x =：的焦点为F ，过F 且斜率为(0)k k >的直线l 与C 交于A ，B 两点，||8AB =．（1）求l 的方程； （2）求过点A ，B 且与C 的准线相切的圆的方程．解：（1）由题意得F （1，0），l 的方程为y =k （x –1）（k >0）．设A （x 1，y 1），B （x 2，y 2）．由2(1)4y k x y x =-⎧⎨=⎩得2222(24)0k x k x k -++=．216160k ∆=+=，故212224k x x k ++=． 所以212244(1)(1)k AB AF BF x x k +=+=+++=． 由题设知22448k k +=，解得k =–1（舍去），k =1．因此l 的方程为y =x –1． （2）由（1）得AB 的中点坐标为（3，2），所以AB 的垂直平分线方程为2(3)y x -=--，即5y x =-+．设所求圆的圆心坐标为（x 0，y 0），则00220005(1)(1)16.2y x y x x =-+⎧⎪⎨-++=+⎪⎩，解得0032x y =⎧⎨=⎩，或00116.x y =⎧⎨=-⎩， 因此所求圆的方程为22(3)(2)16x y -+-=或22(11)(6)144x y -++=．10.（全国卷二理）（19）（12分）设抛物线24C y x =：的焦点为F ，过F 且斜率为(0)k k >的直线l 与C 交于A ，B 两点，||8AB =． （1）求l 的方程；（2）求过点A ，B 且与C 的准线相切的圆的方程．解：（1）由题意得(1,0)F ，l 的方程为(1)(0)y k x k =->.设1221(,),(,)A y x y x B ，由2(1),4y k x y x=-⎧⎨=⎩得2222(24)0k x k x k -++=. 216160k ∆=+>，故122224k x k x ++=. 所以122244||||||(1)(1)x k AB AF BF kx +=+=+++=. 由题设知22448k k +=，解得1k =-（舍去），1k =.因此l 的方程为1y x =-. （2）由（1）得AB 的中点坐标为(3,2)，所以AB 的垂直平分线方程为2(3)y x -=--，即5y x =-+. 设所求圆的圆心坐标为00(,)x y ，则00220005,(1)(1)16.2y x y x x =-+⎧⎪⎨-++=+⎪⎩解得003,2x y =⎧⎨=⎩或0011,6.x y =⎧⎨=-⎩ 因此所求圆的方程为22(3)(2)16x y -+-=或22(11)(6)144x y -++=.11.（全国卷三文）（20）（12分） 已知斜率为k 的直线l 与椭圆22143x y C +=：交于A ，B 两点．线段AB 的中点为(1,)(0)M m m >． （1）证明：12k <-； （2）设F 为C 的右焦点，P 为C 上一点，且FP FA FB ++=0 ．证明：2||||||FP FA FB =+ ．解：（1）设11()A x y ，，22()B x y ，，则2211143x y +=，2222143x y +=． 两式相减，并由1212=y y k x x --得1212043x x y y k +++⋅=．由题设知1212x x +=，122y y m +=，于是34k m=-. 由题设得302m <<，故12k <-． （2）由题意得F （1，0）．设33()P x y ，，则331122(1)(1)(1)(00)x y x y x y -+-+-=，，，，． 由（1）及题设得3123()1x x x =-+=，312()20y y y m =-+=-<．又点P 在C 上，所以34m =，从而3(1)2P -，，3||=2FP uu r ．于是1||22x FA =-uu r ．同理2||=22x FB -uu r ． 所以1214()32FA FB x x +=-+=u u r u u r ．故2||=||+||FP FA FB u u r u u r u u r ． 12.（全国卷三理）（20）（12分）已知斜率为k 的直线l 与椭圆22143x y C +=：交于A ，B 两点，线段AB 的中点为()()10M m m >，． （1）证明：12k <-； （2）设F 为C 的右焦点，P 为C 上一点,且FP FA FB ++=0 ．证明：FA ，FP ，FB 成等差数列，并求该数列的公差．解：（1）设1221(,),(,)A y x y x B ，则222212121,14343y x y x +=+=. 两式相减，并由1221y x y k x -=-得 1122043y x y k x +++⋅=. 由题设知12121,22x y x y m ++==，于是 34k m=-.① 由题设得302m <<，故12k <-. （2）由题意得(1,0)F ，设33(,)P x y ，则 331122(1,)(1,)(1,)(0,0)y x x y x y -+-+-=. 由（1）及题设得3321213()1,()20y y x x y x m =-+==-+=-<.又点P 在C 上，所以34m =，从而3(1,)2P -，3||2FP = .于是 1||22x FA ==- . 同理2||22x FB =- . 所以121||||4()32FA FB x x +=-+= . 故2||||||FP FA FB =+ ，即||,||,||FA FP FB 成等差数列.设该数列的公差为d ，则 1212||||||||||2FB FA x x d =-=-= ②将34m =代入①得1k =-. 所以l 的方程为74y x =-+，代入C 的方程，并整理得2171404x x -+=.故121212,28x x x x +==，代入②解得||d =.或。

2018北京市高三一模数学理分类汇编：圆锥曲线【2018北京市门头沟区一模文】14. 过抛物线221x y =焦点的直线与抛物线交于B A 、两点，O 是坐标原点．则=⋅ ；若该抛物线上有两点M 、N ，满足ON OM ⊥，则直线MN 必过定点 ． 【答案】43-,（0,2） 【2018北京市海淀区一模文】（4）过双曲线221916x y -=的右焦点，且平行于经过一、三象限的渐近线的直线方程是（A ）34150x y +-= （B ）34150x y --= （C ）43200x y -+= （D ）43200x y --= 【答案】D【解析】双曲线的右焦点为)0,5(，经过一、三象限的渐近线方程为x y 43=，所以平行于x y 43=的直线可以设为c x y +=43，将点)0,5(代入，解得415-=c ，所以所求方程为41543-=x y ，整理得34150x y --=，选B.【2018北京市房山区一模文】7．已知双曲线122=-my x 与抛物线x y 82=的一个交点为P ，F 为抛物线的焦点，若5=PF ，则双曲线的渐近线方程为（ ）（A ）02=±y x （B ）02=±y x（C ）03=±y x （D ）03=±y x【答案】C【2018北京市东城区一模文】(12)双曲线222x y -=的离心率为 ；若抛物线2y ax =的焦点恰好为该双曲线的右焦点，则a 的值为 .8【2018北京市朝阳区一模文】6. 已知中心在原点，焦点在x 轴上的双曲线的离心率2e =，其焦点到渐近线的距离为1，则此双曲线的方程为A ．2212x y -=B ．22123x y -= C. 2214x y -= D. 221x y -=【答案】A【2018北京市丰台区一模文】10．已知抛物线28y x =上一点P 到焦点的距离是6，则点P 的坐标是________。