2012年吉林省中考数学试题(含试题)

吉林省2012年初中毕业生学业考试数学试题数学试题共６页，包括六道大题，共26道小题.全卷满分120分.考试时间为120分钟.考试结束后，将本试题和答题卡一并交回.注意事项：1. 答题前，考生务必将自己的姓名、准考证号填写在答题卡上，并将条形码准确粘贴在条形码区域内.2. 答题时，考生务必按照考试要求在答题卡上的指定区域内作答，在草稿纸、试题上答题无效.一、单项选择题（每小题2分，共12分）1．在四个数0，2-，1-，2中，最小的数是（ ）（A ）0 （B ）2- （C ）1- （D ）22．如图，由5个完全相同的小正方体组合成一个立体图形，它的附视图是（ ）3．下列计算正确的是（ ）（A ）32a a -= （B ）22223a a a +=（C ）236a a a ∙= （D ）222()a b a b +=+4．如图，在ABC △中，8040A B ==∠，∠，D E ，分别是AB AC ，上的点，且DE BC ∥，则AED∠的度数为（ ）（A ）40（B ）60（C ）80（D ）1205．如图，菱形OABC 的顶点B 在y 轴上，顶点C 的坐标为(32)-，.若反比例函数(0)ky x x=>的图象经过点A ，则k 的值为（ ）（A ）错误！未找到引用源。

6- （B ）3- （C ）3 （D ）66．某工厂现在平均每天比原计划多生产50台机器，现在生产600台机器所需时间与原计划生产450台机器所需时间相同.设原计划平均每天生产x 台机器，则可列方程为（ ）（A ）错误！未找到引用源。

60045050x x =+ （B ）60045050x x =- （C ）60045050x x =+ （D ）60045050x x=- 二、填空题（每小题3分，共24分）7= ．8．不等式21x x ->的解集为 ．9．若方程20x x -=的两根为1212()x x x x <，，则21x x -= ．10．若甲，乙两个芭蕾舞团参加演出的女演员人数相同，平均身高相同，身高的方差分别为221.52.5s s ==乙甲，，则 芭蕾舞团参加演出的女演员身高更整齐（填空“甲”或“乙”）． 11．如图，A B C ，，是O ⊙上的三点，2535CAO BCO ==∠，∠，则AOB =∠ 度．12．如图，在Rt ABC △中，9034ACB AC BC ===∠，，.以点A 为圆心，AC 长为半径画弧，交AB 于点D ，则BD = ．13．如图，AB 是O ⊙的直径，BC 为O ⊙的切线，40ACB =∠，点P 在边BC 上，则PAB ∠的度数可能为 （写出一个符合条件的度数即可）．14．如图，在等边ABC △中，D 是边AC 上一点，连接BD .将BCD △绕点B 逆时针旋转60，得到BAE △，连接ED .若109BC BD ==，，则AED △的周长是 ．三、解答题（每小题5分，共20分）15．先化简，再求值：2()()2a b a b a +-+，其中1a b ==，16．如图，在东北大秧歌的踩高跷表演中，已知演员身高是高跷长度的2倍，高跷与腿重合部分的长度为28cm ，演员踩在高跷上时，头顶距离地面的高度为224cm.设演员的身高为x cm ，高跷的长度为y cm ，求x y ，的值.17．如图，有一游戏棋盘和一个质地均匀的正四面体骰子（各面依次标有1，2，3，4四个数字）.游戏规则是游戏者每掷一次骰子，棋子按骰子着地一面所示的数字前进相应的格数.例如：若棋子位于A 处，游戏者所掷骰子着地一面所示数字为3，则棋子由A 处前进3个方格到达B 处.请用画树形图法（或列表法）求掷骰子两次后，棋子恰好由A 处前进6个方格到达C 处的概率．18．在如图所示的三个函数图象中，有两个函数图象能近似地刻画如下a b ，两个情境：情境a ：小芳离开家不久，发现把作业本忘在家里，于是返回家里找到了作业本再去学校； 情境b ：小芳从家出发，走了一段路程后，为了赶时间，以更快的速度前进. （1）情境a b ，所对应的函数图象分别为________、________（填写序号）； （2）请你为剩下的函数图象写出一个适合的情境．四、解答题（每小题6分，共12分）19．在平面直角坐标系中，点A 关于y 轴的对称点为点B ，点A 关于原点O 的对称点为点C . （1）若点A 的坐标为（1，2），请你在给出的坐标系中画出ABC △. 设AB 与y 轴的交点为D ，则ABOABCS S =△△________；（2）若点A 的坐标为()(0)a b ab ≠，，则ABC △的形状为________．20．如图，沿AC 方向开山修一条公路，为了加快施工进度，要在小山的另一边寻找点E 同时施工.从AC 上的一点B 取127ABD =∠，沿BD 的方向前进，取37BDE =∠，测得520BD =m ，并且AC BD ，和DE 在同一平面内.（1）施工点E 离D 多远正好能使A C E ，，成一直线（结果保留整数）； （2）在（1）的条件下，若80BC =m ，求公路CE 段的长（结果保留整数）．（参考数据：sin370.60cos370.80tan370.75===，，）21．为宣传节约用水，小明随机调查了某小区部分家庭5月份的用水情况，并将收集的数据整理成如下统计图.（1）小明一共调查了多少户家庭？（2）求所调查家庭5月份用水量的众数、平均数；（3）若该小区有400户居民，请你估计这个小区5月份的用水量.22．如图，在ABC △中，AB AC D =，为边BC 上一点，以AB BD ，为邻边作ABDE Y ，连接AD EC 、. （1）求证：ADC ECD △≌△；（2）若BD CD =，求证四边形ADCE 是矩形.五、解答题（每小题8分，共16分）23．如图，在扇形OAB 中，90AOB =∠，半径6OA =.将扇形OAB 沿过点B 的直线折叠，点O 恰好落在AB 上点D 处，折痕交OA 于点C ，求整个阴影部分的周长和面积.24．如图1，A B C ，，为三个超市，在A 通往C 的道路（粗实线部分）上有一D 点，D 与B 有道路（细实线部分）相能.A 与D ，D 与C ，D 与B 之间的路程分别为25km ，10km ，5km.现计划在A 通往C 的道路上建一个配货中心H ，每天有一辆货车只为这三个超市送货.该货车每天从H 出发，单独为A 送货1次，为B 送货1次，为C 送货2次.货车每次仅能给一家超市送货，每次送货后均返回配货中心H .设H 到A 的路程为x km ，这辆货车每天行驶的路程为y km.（1）用含x 的代数式填空： 当025x ≤≤时，货车从H 到A 往返1次的路程为2x km ，货车从H 到B 往返1次的路程为________km ， 货车从H 到C 往返2次的路程为________km ， 这辆货车每天行驶的路程y =________. 当2535x <≤时，这辆货车每天行驶的路程y =________；（2）请在图2中画出y 与(025)x x ≤≤的函数图象； （3）配货中心H 建在哪段，这辆货车每天行驶的路程最短？六、解答题（每小题8分，共16分）25．如图，在ABC △中，902cm 4cm A AB AC ===∠，，.动点P 从点A 出发，沿AB 方向以1cm/s 的速度向点B 运动，动点Q 从点B 同时出发，沿BA 方向以1cm/s 的速度向点A 运动.当点P 到达点B 时，P Q ，两点同时停止运动.以AP 为一边向上作正方形APDE ，过点Q 作QF BC ∥，交AC 于点F .设点P 的运动时间为t s ，正方形APDE 和梯形BCFQ 重合部分的面积为2cm S ．（1）当t =________s 时，点P 与点Q 重合； （2）当t =________s 时，点D 在QF 上；（3）当点P 在Q B ，两点之间（不包括Q B ，两点）时，求S 与t 之间的函数关系式.26．问题情境如图，在x 轴上有两点(0)(0)(0)A m B n n m >>，，，.分别过点A ，点B 作x 轴的垂线，交抛物线2y x =于点C ，点D .直线OC 交直线BD 于点E ，直线OD 交直线AC 于点F ，点E ，点F 的纵坐标分别记为E F y y ，．特例探究填空：当12m n ==，时，________________E F y y ==，； 当35m n ==，时，________________E F y y ==，. 归纳证明对任意(0)m n n m >>，，猜想E y 与F y 的大小关系，并证明你的猜想. 拓展应用（1）若将“抛物线2y x =”改为“抛物线2(0)y ax a =>”，其它条件不变，请直接写出E y 与F y 的大小关系；（2）连接EF AE ，，当3OFE OFEB S S =△四边形时，直接写出m 与n 的关系及四边形OFEA 的形状.吉林省2012年初中毕业生学业考试数学试卷参考答案及评分标准阅卷说明：1.评卷采分最小单位为1分，每步标出的是累计分.2.考生若用本“参考答案”以外的解（证）法，可参照本“参考答案”的相应步骤给分. 一、单项选择题（每小题2分，共12分）1.B2.A3.B4.B5.D6.C 二、填空题（每小题3分，共24分）7.8. 1x > 9.1 10.甲 11. 120 12.213.大于或等于0度并且小于或等于50度的任意一个度数皆可 14.19评分说明：11题写成120°不扣分，13题不写单位不扣分. 三、解答题(每小题5分，共20分)15.解：原式2222a b a =-+··························································································· 1分 223.a b =- ································································································· 3分当1a b ==，原式2231 1.=⨯-= ······························································································· 5分 16.解：根据题意，得228224.x y x y =⎧⎨+-=⎩，····································································· 3分解得16884.x y =⎧⎨=⎩，答：x 的值为168，y 的值为84. ·················································································· 5分 评分说明：答案写成168cm 84cm x y ==，不扣分. 17.解法1：··································································································································· 3分 从树形图可以看出，所有等可能出现的结果共有16个，其中和为6的结果有3个. ∴P （恰好由A 处到达C 处）=3.16············································································· 5分 解法2：····································································································································· 3分 从表中可出，所有等可能出现的结果共有16个，其中和为6的结果有3个. ∴P （恰好由A 处到达C 处）=3.16············································································· 5分 评分说明：求和的过程和语言叙述部分不写不扣分. 18.解：（1）③，①. ········································································································ 4分 （2）例如：小芳从家出发去书店看了一会书又返回家中. ········································ 5分 小芳从家去超市购物后返回家中. 评分说明：（1）每填对一个空得2分.（2）答案不唯一，只要符合图象即可得分（所写情境需满足三条：从家出发，过程有停留，终点回到家.）四、解答题(每小题7分，共28分)19.解：（1）ABC △如图所示. ········································ 3分14（或0.25）. ·································································· 5分 （2）直角三角形. ······························································ 7分 20.解：（1）根据题意，得E ABD D ∠=∠-∠.12737=-°° 90=°. ······················· 1分在Rt BDE △中，37D ∠=°.∵cos DE D BD=， ∴cos DE BD D =· ····························································· 3分520c o s 375200.80=⨯=⨯°≈ ····················· 4分答：当DE 约为416m 时，正好能使A C E ，，成一条直线.（2）∵sin BE D BD =， ····································································································· 5分 ∴sin BE BDD =· 520s i n 375200.603=⨯=⨯°≈ ······························································ 6分∴CE BE BC =-312.080=-232.≈ ··················································································································· 7分 答：公路CE 段的长约为232m.评分说明：（1）计算过程与结果中写“≈”或“=”均不扣分. （2）求解过程中写312BE =不扣分. 21.解：（1）小明一共调查了20户家庭. ······································································· 1分 （2）所调查家庭5月份用水量的众数为4吨. ···························································· 3分 所调查家庭5月份用水量的平均数为：112133465462728120x ⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯=4.5=（吨）. ················································································································ 5分 （3）4.55001800⨯=（吨）. ······················································································ 7分 答：该小区5月份用水量约是1800吨.评分说明：（1）众数、平均数不加单位不扣分. （2）直接写出平均数，只要正确不扣分. 22.证明：（1）∵AB AC =，∴.B ACB =∠∠ ························································································· 1分 ∵四边形ABDE 是平行四边形..∴.DE AB∥ ∴.EDC B AC ED ==∠∠， ······················································································· 2分 ∴.ACB EDC =∠∠ ······································································································· 3分 又DC CD =，，∴.ADC ECD △≌△ ···································································································· 4分 （2）∵四边形ABDE 是平行四边形，∴.AE BD∥ ∵BD CD =，∴.AE CD∥ ∴四边形ADCE 为平行四边形. ···················································································· 6分 证法1：∵AB AC BD CD ==，， ∴.AD BC ⊥∴90.ADC =∠°∴四边形ADCE 为矩形. ································································································ 7分 证法2：由（1）得AC DE =，∴四边形ADCE 为矩形. ································································································ 7分五、解答题(每小题8分，共16分)23.解：由折叠性质，得.BCO BCD △≌△∴ 6.CD CO BD BO ===，∴12.AC CD BD AC CO BO AO BO ++=++=+=又 AB 的长为6390π⨯=π180，∴阴影部分的周长为123+π. ························································································ 3分 如图，连接OD . ·············································································································· 4分 ∵OB BD OD ==，∴OBD △为等边三角形.∴60.DBO =∠° ·········································································································· 5分 ∵BCO BCD △≌△，∴30.CBO CBD ==∠∠°∵tan 30OC OB =°，∴tan 306OC OB === ° ·········································· 6分∴11622BCD BCO S S OC OB ===⨯= △△ ················································ 7分 ∴2BCD OAB S S S =-△阴影扇形903602=π⨯6-9=π ····································································································· 8分 评分说明：（1）辅助线用实线不扣分.（2）“ AB 的长为”写成“ AB =”不扣分.24.解：（1）()602x - ···································································································· 1分 ()1404x - ······················································································································· 2分 4200x -+ ························································································································ 3分 100. ·································································································································· 5分（2）函数图象如图所示. ································································································ 7分。

2012年长春市初中毕业生学业考试(数学)参考答案本试卷包括七道大题，共26小题，共6页.全卷满分120分，考试时间为120分钟.考试结束后，将本试卷和答题卡一并交回.注意事项：1.答题前，考生务必将自己的姓名、准考证号填写在答题卡上，并将条形码准确粘贴在条形区域内.2.答题时，考试务必按照考试要求在答题卡上的指定区域作答，在草稿纸、试卷上答题无效.一. 选择题(每小题3分，共24分)1.在2、0、-2、-1这四个数中，最大的数是(A)(A) 2 (B) 0. (C) -2. (D) -1.2.神舟九号飞船发射成功，一条相关的微薄被转发了 3570000次，3570000这个数用科学计数法表示为(C)(A) 357xlO4. (B) 35.7xlO5(C) 3.57xlO6(D) 3.57xlO73.不等式3x-6>0的解集为(B)(A) x>2 (B) xN2. (C)x<2 (D)xW2.4.在下列正方体的表面展开图中，剪掉1个正方形(阴影部分)，剩余5个正方形组成中心对称图形的是(D)5.右图是2012年伦敦奥运会吉祥物，某校在五个班级中对认识它的人数进行了调查，结果为 (单位：人)：30, 31, 27, 26, 31.这组数据的中位数是(C)(A) 27 (B)29 (C) 30 (0)316.有一道题目：巳知一次函数y=2x+b,其中b<0,…，与这段描述相符的函数图像可能是(A)7.如图，在 RtAABC 中，ZC=90° . D 为边 CA 延长线上的一点，DE || AB, ZADE=42° ,则ZB 的大小为(C)8.如图，在平面直角坐标系中，在x轴、y轴的正半轴上分别截取OA、0B,使OA=OB;再分别以点A, B为圆心，以大于L AB长为半径作弧，两孤交于点C.若点C的坐标为(m-l,2n),则m2与n的关系为(B)(A)m+2n=l (B)m-2n=l (C)2n-m=l (D)n-2m=l二、填空题(每小题3分，共18分)9.计算：2吏)-也= V310.学校购买了一批图书，共a箱，每箱有b册，将这批图书的一半捐给社区，则捐给社区的图书为Lab册(用含a、b的代数式表示).2 —11.如图，。

2012年吉林省长春市中考数学试卷2012年吉林省长春市中考数学试卷2012年吉林省长春市中考数学试卷一、选择题（每小题3分，共24分）1．（3分）（2012•长春）在2，0，﹣2，﹣1这四个数中，最大的数是（）A．2 B．0 C．﹣2 D．﹣12．（3分）（2012•长春）神舟九号飞船发射成功，一条相关的微博被转发了3570000次，3570000这个数用科学记数法表示为（）A．357×104B．35.7×105C．3.57×106D．3.57×1073．（3分）（2012•长春）不等式3x﹣6≥0的解集为（）A． x＞2 B．x≥2 C． x＜2 D．x≤24．（3分）（2012•长春）在下列正方体的表面展开图中，剪掉1个正方形（阴影部分），剩余5个正方形组成中心对称图形的是（）A．B．C．D．5．（3分）（2012•长春）如图是2012年伦敦奥运会吉祥物，某校在五个班级中对认识它的人数进行了调查，结果为（单位：人）：30，31，27，26，31．这组数据的中位数是（）A．27 B．29 C．30 D．316．（3分）（2012•长春）有一道题目：已知一次函数y=2x+b，其中b＜0，…，与这段描述相符的函数图象可能A．B．C．D．7．（3分）（2012•长春）如图，在Rt△ABC中，∠C=90°．D为边CA延长线上一点，DE∥AB，∠ADE=42°，则∠B的大小为（）A．42°B．45°C．48°D．58°8．（3分）（2012•长春）如图，在平面直角坐标系中，在x轴、y轴的正半轴上分别截取OA、OB，使OA=OB；再分别以点A、B为圆心，以大于AB长为半径作弧，两弧交于点C．若点C的坐标为（m﹣1，2n），则m与n的关系为（）A．m+2n=1 B． m﹣2n=1 C． 2n﹣m=1 D． n﹣2m=1二、填空题（每小题3分，共18分）9．（3分）计算：=_________．10．（3分）（2012•长春）学校购买了一批图书，共a箱，每箱有b册，将这批图书的一半捐给社区，则捐给社区的图书为_________册（用含a、b的代数式表示）．11．（3分）（2012•长春）如图，⊙O与正六边形OABCDE的边OA、OE分别交于点F、G，则所对的圆周角∠FPG的大小为_________度．12．（3分）（2012•长春）如图，在△ABC中，AB=5，AC=4，点D在边AB上，∠ACD=∠B，则AD的长为_________．13．（3分）（2012•长春）如图，▱ABCD的顶点B在矩形AEFC的边EF上，点B与点E、F不重合，若△ACD 的面积为3，则图中阴影部分两个三角形的面积和为_________．14．（3分）（2012•长春）在平面直角坐标系中，点A是抛物线y=a（x﹣3）2+k与y轴的交点，点B是这条抛物线上的另一点，且AB∥x轴，则以AB为边的等边三角形ABC的周长为_________．三、解答题（每小题5分，共20分）15．（5分）（2012•长春）先化简，再求值：（a+2）（a﹣2）+2（a2+3），其中a=．16．（5分）（2012•长春）有甲、乙两个不透明的口袋，甲袋中有3个球，分别标有数字0，2，5；乙袋中有3个球，分别标有数字0，1，4．这6个球除所标数字以外没有任何其它区别，从甲、乙两袋中各随机摸出1个球，用画树状图（或列表）的方法，求摸出的两个球上数字之和是6的概率．17．（5分）（2012•长春）某班有45名同学参加紧急疏散演练，对比发现：经专家指导后，平均每秒撤离的人数是指导前的3倍，这45名同学全部撤离的时间比指导前快30秒．求指导前平均每秒撤离的人数．18．（5分）（2012•长春）如图，在同一平面内，有一组平行线l1、l2、l3，相邻两条平行线之间的距离均为4，点O在直线l1上，⊙O与直线l2的交点为A、B，AB=12，求⊙O的半径．四、解答题（每小题6分，共12分）19．（6分）（2012•长春）长春市某校准备组织七年级学生游园，供学生选择的游园地点有：东北虎园、净月潭、长影世纪城，每名学生只能选择其中一个地点．该校学生会从七年级学生中随机抽取了a名学生，对他们选择各游园地点的情况进行了调查，并根据调查结果绘制成如下条形统计图．（1）求a的值；（2）求这a名学生选择去净月潭游园的人数的百分比．（3）按上述调查结果，估计该校七年级650名学生中选择去净月潭游园的人数．20．（6分）（2012•长春）如图，有一个晾衣架放置在水平地面上，在其示意图中，支架OA、OB的长均为108cm，支架OA与水平晾衣杆OC的夹角∠AOC为59°，求支架两个着地点之间的距离AB．（结果精确到0.1cm）[参考数据：sin59°=0.86，cos59°=0.52，tan59°=1.66]五、解答题（每小题6分，共12分）21．（6分）（2012•长春）图①、图②均为4×4的正方形网络，线段AB、BC的端点均在格点上．按要求在图①、图②中以AB和BC为边各画一个四边形ABCD．要求：四边形ABCD的顶点D在格点上，且有两个角相等（一组或两组角相等均可）；所画的两个四边形不全等．22．（6分）（2012•长春）如图，在平面直角坐标系中，▱OABC的顶点A、C的坐标分别为A（2，0）、C（﹣1，2），反比例函数y=（k≠0）的图象经过点B．（1）求k的值．（2）将▱OABC沿x轴翻折，点C落在点C′处，判断点C′是否在反比例函数y=（k≠0）的图象上，请通过计算说明理由．六、解答题（每小题7分，共14分）23．（7分）（2012•长春）某加工厂为赶制一批零件，通过提高加工费标准的方式调动工人积极性．工人每天加工零件获得的加工费y（元）与加工个数x（个）之间的函数图象为折线OA﹣AB﹣BC，如图所示．（1）求工人一天加工零件不超过20个时每个零件的加工费．（2）求40≤x≤60时y与x的函数关系式．（3）小王两天一共加工了60个零件，共得到加工费220元．在这两天中，小王第一天加工的零件不足20个，求小王第一天加工零件的个数．24．（7分）（2012•长春）感知：如图①，点E在正方形ABCD的边BC上，BF⊥AE于点F，DG⊥AE于点G，可知△ADG≌△BAF．（不要求证明）拓展：如图②，点B、C分别在∠MAN的边AM、AN上，点E、F在∠MAN内部的射线AD上，∠1、∠2分别是△ABE、△CAF的外角．已知AB=AC，∠1=∠2=∠BAC，求证：△ABE≌△CAF．应用：如图③，在等腰三角形ABC中，AB=AC，AB＞BC．点D在边BC上，CD=2BD，点E、F在线段AD 上，∠1=∠2=∠BAC．若△ABC的面积为9，则△ABE与△CDF的面积之和为_________．七、解答题（每小题10分，共20分）25．（10分）（2012•长春）如图，在平面直角坐标系中，直线y=﹣2x+42交x轴于点A，交直线y=x于点B，抛物线y=ax2﹣2x+c分别交线段AB、OB于点C、D，点C和点D的横坐标分别为16和4，点P在这条抛物线上．（1）求点C、D的纵坐标．（2）求a、c的值．（3）若Q为线段OB上一点，P、Q两点的纵坐标都为5，求线段PQ的长．（4）若Q为线段OB或线段AB上一点，PQ⊥x轴，设P、Q两点间的距离为d（d＞0），点Q的横坐标为m，直接写出d随m的增大而减小时m的取值范围．[参考公式：二次函数y=ax2+bx+c（a≠0）图象的顶点坐标为（﹣，）]．26．（10分）（2012•长春）如图，在Rt△ABC中，∠ACB=90°，AC=8cm，BC=4cm．D、E分别为边AB、BC 的中点，连接DE．点P从点A出发，沿折线AD﹣DE﹣EB运动，到点B停止．点P在线段AD上以cm/s的速度运动，在折线DE﹣EB上以1cm/s的速度运动．当点P与点A不重合时，过点P作PQ⊥AC于点Q，以PQ为边作正方形PQMN，使点M在线段AQ上．设点P的运动时间为t（s）．（1）当点P在线段DE上运动时，线段DP的长为_________cm（用含t的代数式表示）．（2）当点N落在AB边上时，求t的值．（3）当正方形PQMN与△ABC重叠部分图形为五边形时，设五边形的面积为S（cm2），求S与t的函数关系式．（4）连接CD，当点N与点D重合时，有一点H从点M出发，在线段MN上以2.5cm/s的速度沿M﹣N﹣M连续做往返运动，直至点P与点E重合时，点H停止往返运动；当点P在线段EB上运动时，点H始终在线段MN的中点处，直接写出在点P的整个运动过程中，点H落在线段CD上时t的取值范围．2012年吉林省长春市中考数学试卷参考答案与试题解析一、选择题（每小题3分，共24分）1．（3分）（2012•长春）在2，0，﹣2，﹣1这四个数中，最大的数是（）A．2 B．0 C．﹣2 D．﹣1考点：有理数大小比较。

2012年长春市初中毕业生学业考试 数 学 试 卷 解 析本试卷包括七道大题，共26小题，共6页．全卷满分120分，考试时间为120分钟．考试结束后，将本试卷和答题卡一并交回． 注意事项：1. 答题前，考生务必将自己的姓名、准考证号填写在答题卡上，并将条形码准确粘贴在条形区域内． 2. 答题时，考试务必按照考试要求在答题卡上的指定区域作答，在草稿纸、试卷上答题无效． 一． 选择题（每小题3分，共24分） 1. 在2、0、-2、-1这四个数中，最大的数是（A ） 2. (B) 0. (C) -2. (D) -1.解析：A 根据正数大于0,0大于负数。

考查知识：有理数的大小比较2. 神舟九号飞船发射成功，一条相关的微薄被转发了3570000次，3570000这个数用科学计数法表示为(A)435710⨯． (B) 535.710⨯ (C) 61057.3⨯ (D) 73.5710⨯解析：C 3570000=3.57×1000000=61057.3⨯ 。

考查知识：科学计数法3.不等式3x-6≥0的解集为(A) x ＞2 (B)x ≥2. (C)x ＜2 (D)x ≤2.解析：B 3x-6≥0 x 3≥6 x ≥2。

考查知识：解不等式4. 在下列正方体的表面展开图中，剪掉1个正方形（阴影部分），剩余5个正方形组成中心对称图形的是解析：D 根据中心对称图形的概念可得。

考查知识：解不等式中心对称图形的概念5.右图是2012年伦敦奥运会吉祥物，某校在五个班级中对认识它的人数进行了调查，结果为（单位：人）：30，31，27，26，31.这组数据的中位数是(A) 27 (B)29 (C) 30 (D)31解析：C 根据中位数是把数据从小到大的顺序排列，取中间的数。

考查知识：中位数的计算6.有一道题目：已知一次函数y=2x+b,其中b＜0，…，与这段描述相符的函数图像可能是解析：A 一次函数y=2x+b,当b＜0时交y轴负半轴。

吉林省2012年初中毕业生学业考试数学试题数学试题共6页，包括六道大题，共26道小题．全卷满分120分．考试时间为120分钟．考试结束后，将本试题和答题卡一并交回．一．单项选择题（每小题2分，共12分）1.在四个数0，-2，-1，2中，最小的数是 （A ）0. （B ）-2. (C) -1 (D)2[答案]B 。

[考点]有理数大小的比较。

[解析] 根据正数大于负数，负数都小于0，两个负数之间，绝对值大的这个数反而小可得正确答案。

所以选B2. 如图，由5个完全相同的小正方形组合成一个立体图形，它的俯视图是[答案]A 。

[考点]三视图[解析]俯视图是在水平面上由上向下观察物理的图形，所以选A 。

3.下列计算正确的是(A)32a a -=； (B)22223a a a +=； (C)236a a a ⋅=； (D) 222()a b a b +=+．[答案] B .[考点] 整式的加减：合并同类项；整式的乘法：同底数幂的乘法；乘法公式：完全平方公式.[解析] 合并同类项：只把同类项的系数相加，所得的结果作为系数字母和字母的指数不变.所以22223a a a +=是正确的，故选B . 验证：32a a a -=；同底数的幂相乘，底数不变，指数相加，所以，23235a a a a +⋅==；完全平方公式：两数和的平方，等于它们的平方和加它们积的2倍，即：222()2a b a ab b +=++.所以，,,A C D 都是错的.4.如图，在ABC ∆中，80A ∠=︒，40B ∠=︒，D 、E 分别是AB 、AC 上的点，且DE BC ∥,则AED ∠的度数为(A)40° (B)60° (C) 80° (D)120°[答案] B .[考点] 平行线的性质；三角形的内角和.[解析] 由三角形的三个内角和为180︒，可得60C ∠=︒ ；又两直线平行，同位角相等，所以，由DE BC ∥，可得，AED C ∠=∠，所以60AED ∠=︒ 解：在ABC ∆中，180180804060C A B ∠=︒-∠-∠=︒-︒-︒=︒又DE BC ∥，AED C ∴∠=∠，所以60AED ∠=︒，故选B .5.如图，菱形OABC 的顶点B 在y 轴上，顶点C 的坐标为（-3，2）．若反比例函数ky x =（0x >）的图像经过点A ，则k 的值为(A) -6. (B) -3. (C) 3. (D) 6.[答案] D .[考点] 菱形的性质.直角坐标系内点的点与曲线方程的关系，求反比例函数中的待定系数.[解析] 如图，因为菱形OABC 的两条对角线互相垂直平分，又OB 在y 轴上，所以顶点C 、A 关于y 轴对称，已知C 的坐标为（-3，2），所以A 的坐标为（3，2）反比例函数k y x=（0x >）的图像经过点A ，则326k =⨯=，故选D . 6. 某工厂现在平均每天比原计划多生产50台机器，现在生产600台机器所需时间与原计划生产450台机器所需时间相同．设原计划每天生产x 台机器，则可列方程为 50450600)(+=x x A . 50450600)(-=x x B . x x C 45050600)(=+. xx D 45050600)(=- [答案] C .[考点] 分式方程运用：列分式方程.[解析] 因为原计划每天生产x 台机器，现在平均每天比原计划多生产50台，所以，现在生产600台机器所需时间是60050x +天，原计划生产450台机器所需时间是450x天，故选C . 二．填空题（每小题3分，共24分）7.=_ ____.[答案.[考点] 二次根式：最简二次根式，根式的运算.[解析] 根式的运算顺序：先把各根式化为最简根式，然后合并同类根式.解：原式==8.不等式21x x ->的解集为__________.[答案] 1x >.[考点] 不等式：解一元一次不等式.[解析] 解一元一次不等式类似解一元一次方程，即把含未知数的项移到一边，数字项移到另一边，然后系数化1，但注意如果在不等式两边同时乘或除以一个负数，要把不等号改变方向.解：移项得：21x x ->合并得： 1x >所以原不等式的解集为1x >.9.若方程20x x -=，的两个根为1212,()x x x x <，则21x x -=______.[答案]1.[考点] 一元二次方程：解一元二次方程，一元二次方程的根与系数的关系（韦达定理）.[解析] 本题给出的一元二次方程较为简单，可直接求解，再求其差；也可利用根与系数的关系求出所需.常用的关系式有：12b x x a+=-，12c x x a ⋅=，学习中还可由求根公式总结出：2112)x x x x -=< 解：[方法一]2120(1)00,1x x x x x x -=⇒-=⇒==，21101x x -=-=.[方法二] 由根与系数的关系得：211x x -== 10. 若甲，乙两个芭蕾舞团参加演出的女演员人数相同，平均身高相同，身高的方差分别为2S 甲=1.5，2S 乙=2.5，则______芭蕾舞团参加演出的女演员身高更整齐（填“甲”或“乙”）． [答案] 甲.[考点] 数据的分析：数据的波动：方差.[解析] 方差越大，数据的波动性越大；方差越小，数据的波动性越小.两组平均数相同的数据，方差小的说明身高的整齐度高，所以甲芭蕾舞团参加演出的女演员身高更整齐.11.如图，,,A B C 是O 上的三点，25CAO ∠=︒．35BCO ∠=︒，则A O B ∠= 度．[答案] 120.[考点] 等腰三角形的性质；圆：圆内同弧所对的圆周角与圆心角的关系（圆周角定理）.[解析] 利用等腰三角形两底角相等，圆内同弧所对的圆周角都等于这条弧所对的圆心角的一半，即可求解.解：如图，在AOC ∆中，AO CO =，25CAO ACO ∴∠=∠=︒，25CAO ACO ∴∠=∠=︒.253560ACB ∴∠=︒+︒=︒又ACB ∠是AC 对的圆周角，AOB ∠是AC 对的圆心角2260120AOB ACB ∴∠=∠=⨯︒=︒12. 如图，在Rt ABC ∆中，90ACB ∠=︒，3AC =，4BC =,以点A 为圆心，AC 长为半径画弧，交AB 于点D ，则BD =______.[答案] 2.[考点] 圆：圆内半径外外相等；直角三角形：勾股定理.[解析] 如图，AC 、AD 为半径，3AC AD ∴==.再由勾股定理：勾三股四弦五得5AB =，532BD AB AD ∴=-=-=.13.如图，AB 是O 的直径，BC 是O 的切线，40ACB ∠=︒，点P 在边BC 上，则PAB ∠的度数可能为 （写出一个符合条件的度数即可）．[答案] 30︒.[考点] 圆：圆的切线的性质定理：圆的切线垂直于过切点半径（或直径），直角三角形：直角三角形的两个锐角互余 .[解析] 由圆的切线垂直于过切点半径（或直径），90ABC ∴∠=︒，再由直角三角形的两个锐角互余，40ACB ∠=︒，所以 50CAB ∠=︒，故只要写出在0︒到50︒间的一个角即可.14.如图，在等边ABC ∆中，D 是边AC 上的一点，连接BD ,将BCD ∆绕点B 逆时针旋转60︒，得到BAE ∆，连接ED ，若10BC =，9BD =，则AED ∆的周长是______.[答案] 19.[考点] 图形的旋转：旋转前、后的图形全等；正三角形，三角形周长.[解析] 由BCD BAE CD AE ∆≅∆⇒=.10AE AD AC BC ∴+===.又，9BD BE ==，60DBE ∠=︒，DBE ∴∆是正三角形9DE ⇒=.ADE ∴∆的周长：91019DE EA AD DE AD ++=+=+=三．解答题（每小题5分，共20分）15.先化简，再求值：2()()2a b a b a +-+，其中1a =,b =. [答案] 1.[考点] 化简求值. .[解析] 利用平方差公式，先作整式乘法运算，合并同类项，将原式化简，然后求值. 解：222222()()223a b a b a a b a a b +-+=-+=-，1a ∴=,b =时，原式22311=⨯-=.16.如图，在东北大秧歌的踩高跷表演中，已知演员身高是高跷长度的2倍，高跷与腿重合部分的长度是28cm ，演员踩在高跷上时，头顶距离地面的高度为224cm ．设演员的身高为xcm ，高跷的长度为ycm ，求x ,y 的值．[答案] x 的值为168，y 的值为84.[考点] 实际问题与二元一次方程组 .[解析] 找出能够表示应用题全部题意的两个相等关系，列出代数式，从而列出两个方程并组成方程组求解 .解：依题意得方程组：222428x y x y =⎧⎨+=+⎩，解得：16884x y =⎧⎨=⎩ 所以，x 的值为168，y 的值为84.17.如图，有一游戏棋盘和一个质地均匀的正四面体骰子（各面依次标有1,2,3,4，四个数字）．游戏规则是游戏者每投掷一次骰子，棋子按骰子着地一面所示的数字前进相应的格数．例如；若棋子位于A 处，游戏者所投掷骰子着地一面所示数字为3，则棋子由A 处前进3个方格到达B 处．请用画树形图法（或列表法）求投掷骰子两次后，棋子恰好由A 处前进6个方格到达C 处的概率．[答案] 316. [考点] 概率初步：随机事件与概率：用列举法（列表法或画树形图法）求概率.[解析] 为不重复不遗漏地列出所有可能的结果，通常采用列表法或用画树形图法求随机事件发生的概率.在一次试验n 次所有可能的结果中，事件A 件出现m 次的概率为()m P A n= [列表法] 在这次游戏中，投掷骰子两次，棋子恰好由A 处前进6个方格到达C 处，即，由表容易看出：投掷骰子两次，所有可能的结果有16种，而棋子恰好由A 处前进6个方格到达C 处的结果为3种，所以：P （棋子恰好由A 处前进6个方格到达C 处）316=. [画树形图法] 在这次游戏中，投掷骰子两次，棋子恰好由A 处前进6个方格到达C 处，即，两次投掷骰子着地一面所示数字和为6.而所有可能的结果画树图如下：由图容易看出：投掷骰子两次，所有可能的结果有16种，而棋子恰好由A 处前进6个方格到达C 处的结果为3种，所以：P （棋子恰好由A 处前进6个方格到达C 处）316=. 18.在如图所示的三个函数图像中，有两个函数图像能近似地刻画如下a 、b 两个情境：情境a ：小芳离开家不久，发现把作业本忘在家里，于是返回家里找到了作业本再去学校； 情境b ：小芳从家出发，走了一段路程后，为了赶时间，以更快的速度前进．（1）情境a ，b 所对应的函数图像分别为 , .(填写序号)；（2）请你为剩下的函数图像写出一个适合的情境．[答案]（1）③,①；（2）小芳从家出发，到学校上学，放学回到了家.[考点] 函数的图象表示法.[解析] 从函数的图象能形象直观、清晰地呈现函数的一些性质.（1）情境a ：小芳离开家不久，发现把作业本忘在家里，于是返回家里找到了作业本再去学校，对应的函数图像为③；情境b ：小芳从家出发，走了一段路程后，为了赶时间，以更快的速度前进，对应的函数图像为①；（2）函数图像②能近似地刻画为：小芳从家出发，到学校上学，放学回到了家.此问答案不为一，只要注意到是从家里出发，出去后有停留，然后返回到家，满足了这三条就行。

2012年吉林省中考试卷物理试题一、单项选择题（每题2分，共12分）1、小明和小丽站在路边等校车，小丽说自己是运动的，她所选择的参照物是A．路灯B．路边的树木C．小明D．驶来的校车2、如图所示，能正确表示光从空气进入水中的光路是3、冬天，我们常用热水袋取暖，这主要是因为水具有A．较多的热量B．较大的密度C．较高的温度D．较大的比热容4、铅笔是我们非常熟悉的学习用品，对于一支新的普通木制铅笔，下列说法中最接近实际的是A．它的重力是1N B．它的体积是1dm3C．它的长度是18cm D．它平放时对桌面的压强是1.25×104Pa 5、在厨房中蕴含着丰富的物理知识，下列说法中正确的是A．微波炉利用电磁波来加热食品B．煮鸡蛋时水底的鸡蛋不受浮力C．菜刀表面很光滑可以增大摩擦D．使用的天然气是可再生能源6、如图所示，闭合开关后，两盏灯均不亮，电压表示数为零，产生这一现象的原因可能是A．L1短路B．L1断路C．L2短路D．L2断路二、填空题（每空1分，共18分）7、中考期间，考点周边禁止鸣笛，这是为了防止的产生。

在考场上你所听到的翻动卷子的声音是由于纸的产生的。

8、路灯总是同时亮，同时灭，它们的连接方式一定是联的；它们所消耗的电能可以用表来测量。

9、为节能减排，我省实施了“暖房子”工程。

项目之一是在楼房的外墙贴泡沫板，这样可以有效地阻碍热传递，从而减少房间里的能的损失。

在施工过程中，若出现高空坠物，其较大的重力势能转化成的能会造成事故，因此，工人进入施工现场必须戴安全帽。

10、在日常生活中，我们习惯用“粘”字表述一些现象，例如：用干毛巾擦镜子，会有很多“毛毛”粘在镜子上；用湿毛巾擦冰箱的冷冻室，湿毛巾会粘在冰箱上。

前者属于现象，后者是由于水的造成的。

11、天黑了，小明打开客厅的灯，会在窗玻璃上看到另一个“自己”，这是由于光的形成的；同时，小丽玩起了手影游戏（如图所示），墙壁上的“大雁”是由于光的形成的。

2012年吉林省中考数学试卷参考答案与试题解析一、选择题（每小题2分，共12分）1．（2012•吉林）在四个数0，﹣2，﹣1，2中，最小的数是（）A．0B．﹣2C．﹣1D．22．（2012•吉林）如图，有5个完全相同的小正方体组合成一个立方体图形，它的俯视图是（）A．B．C．D．3．（2012•吉林）下列计算正确的是（）A．3a﹣a=2B．a2+2a2=3a2C．a2•a3=a6D．（a+b）2=a2+b2 4．（2012•吉林）如图，在△ABC中，∠A=80°，∠B=40°．D、E分别是AB，AC上的点，且DE∥BC，则∠AED的度数是（）A．40°B．60°C．80°D．120°5．（2012•吉林）如图，菱形OABC的顶点B在y轴上，顶点C的坐标为（﹣3，2），若反比例函数y=（x＞0）的图象经过点A，则k的值为（）A．﹣6B．﹣3C．3D．66．（2012•吉林）某工厂现在平均每天比原计划多生产50台机器，现在生产600台机器所需的时间与原计划生产450台机器所需时间相同．设原计划每天生产x台机器，则可列方程为（）A．B．C．D．二、填空题（每小题3分，共24分）7．（2012•吉林）计算：= ．8．（2012•吉林）不等式2x﹣1＞x的解集为．9．（2012•吉林）若方程x2﹣x=0的两根为x1，x2（x1＜x2），则x2﹣x1= ．10．（2012•吉林）若甲，乙两个芭蕾舞团参加演出的女演员人数相同，平均身高相同，身高的方差分别为=1.5，=2.5，则芭蕾舞团参加演出的女演员身高更整齐（填：“甲”或“乙”）．11．（2012•吉林）如图，A，B，C是⊙O上的三点，∠CAO=25°，∠BCO=35°，则∠AOB=度．12．（2012•吉林）如图，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，以点A为圆心，AC长为半径画弧，交AB于点D，则BD= ．13．（2012•吉林）如图，AB是⊙O的直径，BC为⊙O的切线，∠ACB=40°，点P在边BC上，则∠PAB的度数可能为（写出一个符合条件的度数即可）14．（2012•吉林）如图，在等边△ABC中，D是边AC上一点，连接BD．将△BCD绕点B逆时针旋转60°得到△BAE，连接ED．若BC=10，BD=9，则△AED的周长是．三、解答题（每小题5分，共20分）15．（2012•吉林）先化简，再求值：（a+b）（a﹣b）+2a2，其中a=1，b=．16．（2012•吉林）如图，在东北大秧歌的踩高跷表演中，已知演员身高是高跷长度的2倍，高跷与腿重合部分的长度为28cm，演员踩在高跷上时，头顶距离地面的高度为224cm．设演员的身高为xcm，高跷的长度为ycm，求x，y 的值．17．（2012•吉林）如图，有一游戏棋盘和一个质地均匀的正四面体骰子（各面依次标有1，2，3，4四个数字）．游戏规则是游戏者每掷一次骰子，棋子按着地一面所示的数字前进相应的格数．例如：若棋子位于A处，游戏者所掷骰子着地一面所示数字为3，则棋子由A处前进3个方格到达B处．请用画树形图法（或列表法）求掷骰子两次后，棋子恰好由A处前进6个方格到达C处的概率．18．（2012•吉林）在如图所示的三个函数图象中，有两个函数图象能近似地刻画如下a，b两个情境：情境a：小芳离开家不久，发现把作业本忘在家里，于是返回了家里找到了作业本再去学校；情境b：小芳从家出发，走了一段路程后，为了赶时间，以更快的速度前进．（1）情境a，b所对应的函数图象分别是、（填写序号）；（2）请你为剩下的函数图象写出一个适合的情境．四、解答题（每小题7分，共28分）19．（2012•吉林）在平面直角坐标系中，点A关于y轴的对称点为点B，点A关于原点O的对称点为点C．（1）若A点的坐标为（1，2），请你在给出的坐标系中画出△ABC．设AB与y轴的交点为D，则= ；（2）若点A的坐标为（a，b）（ab≠0），则△ABC的形状为．20．（2012•吉林）如图，沿AC方向开山修一条公路，为了加快施工速度，要在小山的另一边寻找点E同时施工．从AC上的一点B取∠ABD=127°，沿BD的方向前进，取∠BDE=37°，测得BD=520m，并且AC，BD和DE在同一平面内．（1）施工点E离D多远正好能使成A，C，E一条直线（结果保留整数）；（2）在（1）的条件下，若BC=80m，求公路段CE的长（结果保留整数）．（参考数据：sin37°=0.60，cos37°=0.80，tan37°=0.75）21．（2012•吉林）为宣传节约用水，小明随机调查了某小区部分家庭5月份的用水情况，并将收集的数据整理成如下统计图．（1）小明一共调查了多少户家庭？（2）求所调查家庭5月份用水量的众数、平均数；（3）若该小区有400户居民，请你估计这个小区5月份的用水量．22．（2012•吉林）如图，在△ABC中，AB=AC，D为边BC上一点，以AB，BD为邻边作▱ABDE，连接AD，EC．（1）求证：△ADC≌△ECD；（2）若BD=CD，求证：四边形ADCE是矩形．五、解答题（每小题8分，共16分）23．（2012•吉林）如图，在扇形OAB中，∠AOB=90°，半径OA=6．将扇形OAB沿过点B的直线折叠，点O恰好落在上点D处，折痕交OA于点C，求整个阴影部分的周长和面积．24．（2012•吉林）如图1，A，B，C为三个超市，在A通往C的道路（粗实线部分）上有一D点，D与B有道路（细实线部分）相通．A与D，D与C，D与B之间的路程分别为25km，10km，5km．现计划在A通往C的道路上建一个配货中心H，每天有一辆货车只为这三个超市送货．该货车每天从H出发，单独为A送货1次，为B送货1次，为C送货2次．货车每次仅能给一家超市送货，每次送货后均返回配货中心H，设H到A的路程为xkm，这辆货车每天行驶的路程为ykm．（1）用含的代数式填空：当0≤x≤25时，货车从H到A往返1次的路程为2xkm，货车从H到B往返1次的路程为km，货车从H到C往返2次的路程为km，这辆货车每天行驶的路程y= ．当25＜x≤35时，这辆货车每天行驶的路程y= ；（2）请在图2中画出y与x（0≤x≤35）的函数图象；（3）配货中心H建在哪段，这辆货车每天行驶的路程最短？六、解答题（每小题10分，共20分）25．（2012•吉林）如图，在△ABC中，∠A=90°，AB=2cm，AC=4cm．动点P从点A出发，沿AB方向以1cm/s的速度向点B运动，动点Q从点B同时出发，沿BA方向以1cm/s的速度向点A运动．当点P到达点B时，P，Q两点同时停止运动，以AP为一边向上作正方形APDE，过点Q作QF∥BC，交AC于点F．设点P的运动时间为ts，正方形和梯形重合部分的面积为Scm2．（1）当t= s时，点P与点Q重合；（2）当t= s时，点D在QF上；（3）当点P在Q，B两点之间（不包括Q，B两点）时，求S与t之间的函数关系式．26．（2012•吉林）问题情境如图，在x轴上有两点A（m，0），B（n，0）（n＞m＞0）．分别过点A，点B作x轴的垂线，交抛物线y=x2于点C、点D．直线OC交直线BD于点E，直线OD交直线AC于点F，点E、点F的纵坐标分别记为y E，y F．特例探究填空：当m=1，n=2时，y E= 2 ，y F= 2 ；当m=3，n=5时，y E= 15 ，y F= 15 ．归纳证明对任意m，n（n＞m＞0），猜想y E与y F的大小关系，并证明你的猜想．拓展应用（1）若将“抛物线y=x2”改为“抛物线y=ax2（a＞0）”，其他条件不变，请直接写出y E与y F的大小关系；（2）连接EF，AE．当S四边形OFEA=3S△OFE时，直接写出m与n的关系及四边形OFEA的形状．2012年吉林省中考数学试卷参考答案与试题解析一、选择题（每小题2分，共12分）考点：有理数大小比较。

2012年长春中考试题数学（考试时间120分钟，满分120分）第一部分（选择题共30分）一、选择题（每题3分，共计24分）1、（2012吉林长春，1，3分）在2 ，0，－3，－1这四个数中，最大的数为（）A 2B 0.C －2D －1【答案】A2、（2012吉林长春，2，3分）神舟九号飞船发射成功，一条相关的微博被转发来3570000次。

3570000这个数用科学记数法表示为（）A 357×104B 35.7×105C . 3.57×106 D. 3.57×107 【答案】 C3、（2012吉林长春，3，3分）不等式3x–6 ≥0 的解集为（）A x＞2B x≥2C x＜2D x≤2【答案】B4、（2012吉林长春，4，3分）在下列正方体的表面展开图中，剪掉1个正方形（阴影部分），剩余5个正方形组成中心对称图形的是（）A B C D【答案】 D5、（2012吉林长春，5，3分）右图是2012年伦敦奥运会吉祥物，某校在五个年级中对认识的它的人数进行了调查，结果为（单位：人）30,31,27,26,31.这组数据的中位数是（）A 27B 29C 30D 31【答案】C6、（2012吉林长春，6，3分）有一道题目：已知一次函数y = 2x +b ,其中b<0，… ，与这段描述相符的函数图象可能是（）A B C D 【答案】 A 7、（2012吉林长春，7，3分）如图，在Rt △ABC 中，∠C =90°.D 为边CA 延长线上一点，DE ∥AB , ∠ADE =42°，则∠B 的大小为（ ） A 42° B 45° C 48° D 58°【答案】C 8、（2012吉林长春，8，3分）如图，在平面直角坐标系中，在x 轴、y 轴的正半轴上分别截取OA 、OB ，使OA =OB ;再分别以点A 、B 为圆心，以大于12AB 长为半径作弧，两弧交于点C 。

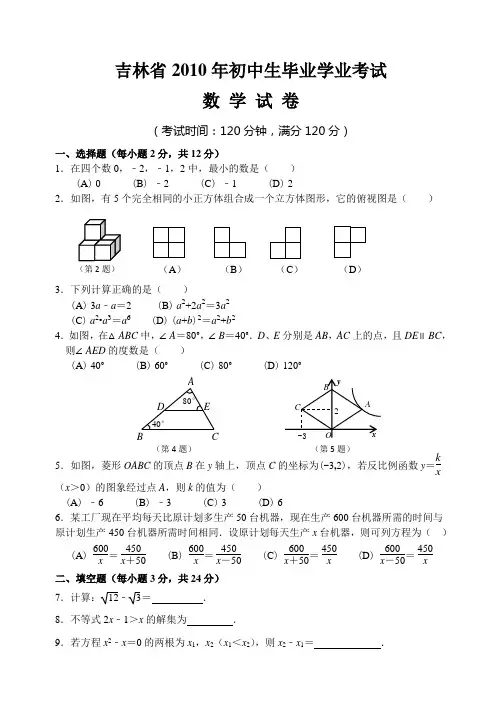
吉林省2010年初中生毕业学业考试数 学 试 卷（考试时间：120分钟，满分120分）一、选择题（每小题2分，共12分）1．在四个数0，﹣2，﹣1，2中，最小的数是（ ）(A ) 0 (B ) ﹣2 (C ) ﹣1 (D ) 22．如图，有5个完全相同的小正方体组合成一个立方体图形，它的俯视图是（ ）3．下列计算正确的是（ ）(A ) 3a ﹣a ＝2 (B ) a 2+2a 2＝3a 2(C ) a 2•a 3＝a 6 (D ) (a +b )2＝a 2+b 24．如图，在△ABC 中，∠A ＝80°，∠B ＝40°．D 、E 分别是AB ，AC 上的点，且DE ∥BC ，则∠AED 的度数是（ ）(A ) 40° (B ) 60° (C ) 80° (D ) 120°5．如图，菱形OABC 的顶点B 在y 轴上，顶点C 的坐标为(-3,2)，若反比例函数y ＝kx（x ＞0）的图象经过点A ，则k 的值为（ ）(A ) ﹣6 (B ) ﹣3 (C ) 3 (D ) 66．某工厂现在平均每天比原计划多生产50台机器，现在生产600台机器所需的时间与原计划生产450台机器所需时间相同．设原计划每天生产x 台机器，则可列方程为（ ） (A ) 600x ＝ 450x ＋50 (B ) 600x ＝ 450x －50 (C ) 600x ＋50＝ 450x (D ) 600x －50＝ 450x二、填空题（每小题3分，共24分） 7．计算：12﹣3＝ ________． 8．不等式2x ﹣1＞x 的解集为 ______ ．9．若方程x 2﹣x ＝0的两根为x 1，x 2（x 1＜x 2），则x 2﹣x 1＝ _________ ．（A ） （B ） （C ）（D ） （第2题）A B C D 80° 40° E （第4题）（第5题）10．若甲，乙两个芭蕾舞团参加演出的女演员人数相同，平均身高相同，身高的方差分别为＝1.5，＝2.5，则 ________ 芭蕾舞团参加演出的女演员身高更整齐（填：“甲”或“乙”）．11．如图，A ，B ，C 是⊙O 上的三点，∠CAO ＝25°，∠BCO ＝35°，则∠AOB ＝ 度． 12．如图，在Rt △ABC 中，∠ACB ＝90°，AC ＝3，BC ＝4，以点A 为圆心，AC 长为半径画弧，交AB 于点D ，则BD ＝ ______ ．13．如图，AB 是⊙O 的直径，BC 为⊙O 的切线，∠ACB ＝40°，点P 在边BC 上，则∠P AB 的度数可能为 _________ （写出一个符合条件的度数即可）14．如图，在等边△ABC 中，D 是边AC 上一点，连接BD ．将△BCD 绕点B 逆时针旋转60°得到△BAE ，连接ED ．若BC ＝10，BD ＝9，则△AED 的周长是 _______ ． 三、解答题（每小题5分，共20分）15．先化简，再求值：（a +b ）（a ﹣b ）+2a 2，其中a ＝1，b ＝2．16．如图，在东北大秧歌的踩高跷表演中，已知演员身高是高跷长度的2倍，高跷与腿重合部分的长度为28cm ，演员踩在高跷上时，头顶距离地面的高度为224cm ．设演员的身高为x cm ，高跷的长度为y cm ，求x ，y 的值．（第11题）AO35°BC 25°（第13题）（第14题）A EBCD（第12题）17．如图，有一游戏棋盘和一个质地均匀的正四面体骰子（各面依次标有1，2，3，4四个数字）．游戏规则是游戏者每掷一次骰子，棋子按着地一面所示的数字前进相应的格数．例如：若棋子位于A 处，游戏者所掷骰子着地一面所示数字为3，则棋子由A 处前进3个方格到达B 处．请用画树形图法（或列表法）求掷骰子两次后，棋子恰好由A 处前进6个方格到达C 处的概率．18．在如图所示的三个函数图象中，有两个函数图象能近似地刻画如下a ，b 两个情境：情境a ：小芳离开家不久，发现把作业本忘在家里，于是返回了家里找到了作业本再去学校；情境b ：小芳从家出发，走了一段路程后，为了赶时间，以更快的速度前进． （1）情境a ，b 所对应的函数图象分别是 ______ 、 ______ （填写序号）； （2）请你为剩下的函数图象写出一个适合的情境．四、解答题（每小题7分，共28分）19．在平面直角坐标系中，点A 关于y 轴的对称点为点B ，点A 关于原点O 的对称点为点C ． （1）若A 点的坐标为（1，2），请你在给出的坐标 系中画出△ABC ．设AB 与y 轴的交点为D ，则S △ADOS △ABC＝ _________ ； （2）若点A 的坐标为（a ，b ）（ab ≠0）， 则△ABC 的形状为 _________ ．20．如图，沿AC 方向开山修一条公路，为了加快施工速度，要在小山的另一边寻找点E 同时施工．从AC 上的一点B 取∠ABD ＝127°，沿BD 的方向前进，取∠BDE ＝37°，测得BD ＝520m ，并且AC ，BD 和DE 在同一平面内．（1）施工点E 离D 多远正好能使成A ，C ，E 一条直线（结果保留整数）； （2）在（1）的条件下，若BC ＝80m ，求公路CE 段的长（结果保留整数）． （参考数据：sin37°＝0.60，cos37°＝0.80，tan37°＝0.75）21．为宣传节约用水，小明随机调查了某小区部分家庭5月份的用水情况，并将收集的数据整理成如下统计图．（1）小明一共调查了多少户家庭？（2）求所调查家庭5月份用水量的众数、平均数；（3）若该小区有400户居民，请你估计这个小区5月份的用水量．/吨A B C D127°37° E22．如图，在△ABC 中，AB ＝AC ，D 为边BC 上一点，以AB ，BD 为邻边作□ABDE ，连接AD ，EC ． （1）求证：△ADC ≌△ECD ；（2）若BD ＝CD ，求证：四边形ADCE 是矩形．五、解答题（每小题8分，共16分） 23．如图，在扇形OAB 中，∠AOB ＝90°，半径OA ＝6．将扇形OAB 沿过点B 的直线折叠，点O 恰好落在⌒AB 上点D 处，折痕交OA 于点C ，求整个阴影部分的周长和面积．（第23题） A B D E C （第22题）24．如图1，A ，B ，C 为三个超市，在A 通往C 的道路（粗实线部分）上有一D 点，D 与B 有道路（细实线部分）相通．A 与D ，D 与C ，D 与B 之间的路程分别为25km ，10km ，5km ．现计划在A 通往C 的道路上建一个配货中心H ，每天有一辆货车只为这三个超市送货．该货车每天从H 出发，单独为A 送货1次，为B 送货1次，为C 送货2次．货车每次仅能给一家超市送货，每次送货后均返回配货中心H ，设H 到A 的路程为x km ，这辆货车每天行驶的路程为y km ．（1）用含的代数式填空： 当0≤x ≤25时，货车从H 到A 往返1次的路程为2x km ，货车从H 到B 往返1次的路程为 ________ km ， 货车从H 到C 往返2次的路程为 ________ km ， 这辆货车每天行驶的路程y ＝ _________ ． 当25＜x ≤35时，这辆货车每天行驶的路程y ＝ _________ ； （2）请在图2中画出y 与x （0≤x ≤35）的函数图象； （3）配货中心H 建在哪段，这辆货车每天行驶的路程最短？)图2六、解答题（每小题10分，共20分） 25．如图，在△ABC 中，∠A ＝90°，AB ＝2cm ，AC ＝4cm ．动点P 从点A 出发，沿AB 方向以1cm/s 的速度向点B 运动，动点Q 从点B 同时出发，沿BA 方向以1cm/s 的速度向点A 运动．当点P 到达点B 时，P ，Q 两点同时停止运动，以AP 为一边向上作正方形APDE ，过点Q 作QF ∥BC ，交AC 于点F ．设点P 的运动时间为ts ，正方形和梯形重合部分的面积为Scm 2．（1）当t ＝ _________ s 时，点P 与点Q 重合； （2）当t ＝ _________ s 时，点D 在QF 上；（3）当点P 在Q ，B 两点之间（不包括Q ，B 两点）时，求S 与t 之间的函数关系式．（第25题）E CBAD P QF C BA备用图26．问题情境如图，在x轴上有两点A（m，0），B（n，0）（n＞m＞0）．分别过点A，点B作x轴的垂线，交抛物线y＝x2于点C、点D．直线OC交直线BD于点E，直线OD交直线AC于点F，点E、点F的纵坐标分别记为y E，y F．特例探究填空：当m＝1，n＝2时，y E＝_________，y F＝_________；当m＝3，n＝5时，y E＝_________，y F＝_________．归纳证明对任意m，n（n＞m＞0），猜想y E与y F的大小关系，并证明你的猜想．拓展应用（1）若将“抛物线y＝x2”改为“抛物线y＝ax2（a＞0）”，其他条件不变，请直接写出y E与y F的大小关系；（2）连接EF，AE．当S四边形OFEA＝3S△OFE时，直接写出m与n的关系及四边形OFEA 的形状．备用吉林省2012年初中毕业生学业考试数学试卷参考答案一、选择题（每小题2分，共12分）1．B 2．A 3．B 4．B 5．D 6．C 二、填空题（每小题3分，共24分）78． x ＞1 9． 1 10． 甲 11． 120 12． 2 13． 45° 大于或等于0度并且小于等于50度的任意一个度数皆可 14． 19 三、解答题（每小题5分，共20分） 15．解：原式＝a 2﹣b 2+2a2＝3a 2﹣b2 当a ＝1，b ＝2 时，原式＝3×12﹣(2)2＝1．16．解：根据题意，得⎩⎨⎧x ＝2yx +y ﹣28＝224解得⎩⎨⎧x ＝168y ＝84答：x 的值为168，y 的值为84。