-初中数学竞赛教程20、图形面积的计算
- 格式:doc
- 大小:573.50 KB
- 文档页数:4

几何图形的面积计算几何图形的面积计算是数学中非常重要的一部分,它涉及到了诸多的几何知识和计算方法。
在几何学中,面积是用来描述平面图形所占的空间大小的一个指标。
不同的几何图形有不同的面积计算公式,下面将会一一介绍各个常见几何图形的面积计算方法。
一、矩形的面积计算矩形是最简单的几何图形之一,它的面积计算公式是:面积 = 长 ×宽。
例如,一个矩形的长为5cm,宽为3cm,那么它的面积 = 5cm ×3cm = 15cm²。
二、三角形的面积计算三角形也是常见的几何图形,它的面积计算公式是:面积 = 1/2 ×底边长 ×高。
例如,一个三角形的底边长为4m,高为6m,那么它的面积 = 1/2 ×4m × 6m = 12m²。
三、圆形的面积计算圆形是一种特殊的几何图形,其面积计算公式是:面积= π × 半径²。
其中,π是一个无理数,约等于3.14159。
半径是圆的半径长度。
例如,一个圆的半径为5cm,那么它的面积 = 3.14159 × 5cm × 5cm= 78.54cm²。
四、正方形的面积计算正方形是边长相等的矩形,因此它的面积计算公式与矩形相同,即:面积 = 边长 ×边长。
例如,一个正方形的边长为7cm,那么它的面积 = 7cm × 7cm =49cm²。
五、梯形的面积计算梯形也是一种常见的几何图形,它的面积计算公式是:面积 = 1/2 ×(上底 + 下底) ×高。
例如,一个梯形的上底为4cm,下底为8cm,高为5cm,那么它的面积 = 1/2 × (4cm + 8cm) × 5cm = 30cm²。
六、圆环的面积计算圆环是由两个同心圆围成的区域,它的面积计算公式是:面积= π× (外圆半径² - 内圆半径²)。

图形求解面积技巧图形求解面积是几何学中的基本内容,根据不同的图形形状,求解面积的方法也不同。
在解题过程中,我们可以利用一些技巧来更快地求解面积。
以下是一些常见的图形求解面积的技巧。
一、矩形和正方形的面积求解技巧矩形和正方形是最简单的图形,其面积求解公式是直接应用的,即面积等于长度乘以宽度。
如果给定的是边长,可以根据给定的边长求解面积。
二、三角形的面积求解技巧三角形的面积求解有多种方法。
常见的方法有:1. 正直角三角形的面积求解:对于直角三角形,可以利用两条直角边的长度来求解面积,公式为面积等于直角边乘以直角边除以2。
2. 任意三角形的面积求解:根据三角形的海伦公式,可以利用三条边长来求解面积,公式为面积等于根号下(p * (p - a) * (p - b) * (p - c)),其中 p 为半周长,p = (a +b + c) / 2。
三、圆的面积求解技巧圆的面积求解需要用到圆周率π。
常见的圆的面积求解方法有:1. 根据半径求解圆的面积:对于给定半径的圆,可以直接用公式面积等于π乘以半径的平方来求解。
2. 根据直径求解圆的面积:如果给定的是圆的直径,可以先将直径除以2得到半径的长度,然后利用公式面积等于π乘以半径的平方来求解面积。
四、梯形的面积求解技巧梯形的面积求解需要利用梯形的上底、下底和高。
常见的梯形的面积求解方法有:1. 根据上底和下底求解梯形的面积:对于给定上底、下底和高的梯形,可以利用公式面积等于上底加下底乘以高除以2来求解面积。
2. 根据对角线和高求解梯形的面积:如果给定的是梯形的对角线和高的长度,可以利用公式面积等于对角线之和乘以高除以2来求解面积。
五、平行四边形的面积求解技巧平行四边形的面积求解需要利用平行四边形的底和高。
常见的平行四边形的面积求解方法有:1. 根据底和高求解平行四边形的面积:对于给定底和高的平行四边形,可以利用公式面积等于底乘以高来求解面积。
2. 根据对角线和夹角求解平行四边形的面积:如果给定的是平行四边形的对角线和夹角,可以利用公式面积等于对角线之积乘以夹角的正弦值来求解面积。

初中数学竞赛:图形与面积一、直线图形的面积在小学数学中我们学习了几种简单图形的面积计算方法,数学竞赛中的面积问题不但具有直观性,而且变换精巧,妙趣横生,对开发智力、发展能力非常有益。
图形的面积是图形所占平面部分的大小的度量。
它有如下两条性质:1.两个可以完全重合的图形的面积相等;2.图形被分成若干部分时,各部分面积之和等于图形的面积。
对图形面积的计算,一些主要的面积公式应当熟记。
如:正方形面积=边长×边长;矩形面积=长×宽;平行四边形面积=底×高; 三角形面积=底×高÷2;梯形面积=(上底+下底)×高÷2。
此外,以下事实也非常有用,它对提高解题速度非常有益。
1.等腰三角形底边上的高线平分三角形面积;2.三角形一边上的中线平分这个三角形的面积;3.平行四边形的对角线平分它的面积;4.等底等高的两个三角形面积相等。
解决图形面积的主要方法有:1.观察图形,分析图形,找出图形中所包含的基本图形;2.对某些图形,在保持其面积不变的条件下改变其形状或位置(叫做等积变形);3.作出适当的辅助线,铺路搭桥,沟通联系;4.把图形进行割补(叫做割补法)。
例1 你会用几种不同的方法把一个三角形的面积平均分成4等份吗?解:最容易想到的是将△ABC 的底边4等分,如左下图构成4个小三角形,面积都为原来的三 角形面积的41。
另外,先将三角形△ABC 的面积2等分(如右上图),即取BC 的中点D ,连接AD ,则S △ABD=S △ADC ,然后再将这两个小三角形分别2等分,分得的4个小三角形各自的面积为原来大三角形面积的41。
还 有许多方法,如下面的三种。
请你再想出几种不同的方法。
例2 右图中每个小方格面积都是1cm2,那么六边形ABCDEF 的面积是多少平方厘米?分析:解决这类问题常用割补法,把图形分成几个简单的容易求出面积的图形,分别求出面积。
也可以求出六边形外空白处的面积,从总面积中减去空白处的面积,就是六边形的面积。
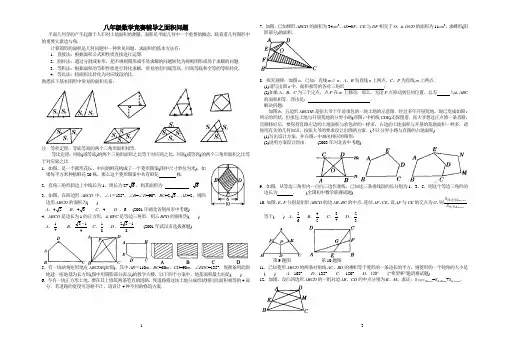
八年级数学竞赛辅导之面积问题平面几何学的产生起源于人们对土地面积的测量,面积是平面几何中一个重要的概念,联系着几何图形中的重要元素边与角.计算图形的面积是几何问题中一种常见问题,求面积的基本方法有: 1.直接法:根据面积公式和性质直接进行运算.2.割补法:通过分割或补形,把不规则图形或不易求解的问题转化为规则图形或易于求解的问题. 3.等积法:根据面积的等积性质进行转化求解,常见的有同底等高、同高等底和全等的等积转化.4.等比法:将面积比转化为对应线段的比. 熟悉以下基本图形中常见的面积关系:注 等积定理:等底等高的两个三角形面积相等.等比定理:同底(或等底)的两个三角形面积之比等于对应高之比,同高(或等高)的两个三角形面积之比等于对应底之比.1.如图,是一个圆形花坛,中间的鲜花构成了一个菱形图案(图中尺寸单位为米),如果每平方米种植鲜花20株,那么这个菱形图案中共有鲜花 株. 2.直角三角形斜边上中线长为1,周长为.3.如图,在四边形ABCD 中,∠A =135°,∠B =∠D =90°,BC =23,AD =2,则四边形ABCD 的面积为( )A .42B .43C .4D .6 (2001年湖北省荆州市中考题) 4.ABCD 是边长为1的正方形,△BPC 是等边三角形,则厶BPD 的面积为( )A .41B .413-C .81D .8132- (2001年武汉市选拔赛题)5.有一块缺角矩形地皮ABCDE (如图),其中AB =110m ,BC =80m ,CD =90m ,∠EDC =135°.现准备用此块地建一座地基为长方形(图中用阴影部分表示)的教学大楼,以下四个方案中,地基面积最大的是( ) 6.今有一块正方形土地,要在其上修筑两条笔直的道路,使道路将这块土地分成形状相同且面积相等的4部分.若道路的宽度可忽略不计,请设计4种不同的修筑方案.7.如图,已知梯形ABCD 的面积为34cm 2,AE =BF ,CE 与DF 相交于O ,△OCD 的面积为11cm 2,求蝶形(阴影部分)的面积.8.探究规律:如图a ,已知:直线m ∥ n ,A 、B 为直线n 上两点,C 、P 为直线m 上两点. (1)请写出图a 中,面积相等的各对三角形 ;(2)如果A 、B 、C 为三个定点,点P 在m 上移动,那么,无论P 点移动到任何位置,总有 与△ABC 的面积相等.理由是: . 解决问题:如图b ,五边形ABCDE 是张大爷十年前承包的一块土地的示意图.经过多年开垦荒地,现已变成如图c 所示的形状,但承包土地与开垦荒地的分界小路(即图c 中折线CDE )还保留着.张大爷想过正点修一条直路,直路修好后,要保持直路左边的土地面积与承包时的一样多,右边的土地面积与开垦的荒地面积一样多.请你用有关的几何知识,按张大爷的要求设计出修路方案.(不计分界小路与直路的占地面积) (1)写出设计方案,并在图c 中画出相应的图形; (2)说明方案设计理由. (2003年河北省中考题)9.如图,从等边三角形内一点向三边作垂线,已知这三条垂线段的长分别为1、3、5,则这个等边三角形的边长为 . (全国初中数学联赛试题)10.如图,E 、F 分别是矩形ABCD 的边AB 、BC 的中点,连结AF 、CE ,设AF 与CE 的交点为G ,则AB C D A G C D S S 矩形四边形等于( ) A .65 B .54 C .43 D .32第9题图 第10题图11.已知菱形ABCD 的两条对角线AC 、BD 的乘积等于菱形的一条边长的平方,则菱形的一个钝角的大小是( ) A .165° D .135° C . 150° D .120° (“希望杯”邀请赛试题)12.如图,设凸四边形ABCD 的一组对边AB 、CD 的中点分别为K 、M ,求证:S 四边形ABCD =S △ABM +S △DCK .13.如图,设G (也称重心)为△ABC 三条中线AD 、BE 、CF 的交点,则2===GFCGGE BG GD AG ,请读者证明.(14题图)14. 如图,在△ABC 中,已知BD 和CE 分别是两边上的中线,并且BD ⊥CE ,BD =4,CE =6,那么△ABC 的面积等于( )A .12B .14C .16D .18(全国初中数学联赛试题) 15. 如图甲,AB 、CD 是两条线段,M 是AB 的中点,S △DMC 、S △DAC 、S △DBC 分别表示△DMC 、△DAC 、△DBC的面积,当AB ∥CD 时,有S △DMC =2DBCDAC S S ∆∆+·(1)如图乙,若图甲中AB 不平行CD ,①式是否成立?请说明理由;(2)如图丙,若图甲中A 月与CD 相交于点O 时,问S △DMC 和S △DAC 和S △DBC 有何种相等关系?试证明你的结论. (2001年安徽省中考题)16.已知凸四边形ABCD 的对角线AC ,BD 相交于点O ,且△ABC ,△ACD ,△ABD 的面积分别为S 1=5,S 2=10,S 3=6.求△ABO 的面积17.如图2-129,AD ,BE ,CF 交于△ABC 内的一点P ,并将△ABC 分成六个小三角形,其中四个小三角形的面积已在图中给出.求△ABC 的面积.18.如图1,在直角坐标系中,点A是x 轴正半轴上的一个定点,点B 是双曲线y =(0x >)上的一个动点,当点B 的横坐标逐渐增大时,△OAB 的面积将会( A .逐渐增大 B .不变 C .逐渐减小 D .先增大后减小19.(2009·牡丹江)如图2,点A 、B 是双曲线3y x=上的点,分别经过A 、B 两点向x 轴、y 轴作垂线段,若1S =阴影,则12S S += . 20.(2009莆田)在x 轴的正半轴上依次截取112233445OA A A A A A A A A ====,过点12345A A A A A 、、、、分别作x 轴的垂线与反比例函数()20y x x=≠的图象相交于点12345P P P P P 、、、、,得直角三角形1112233344455OP A A P A A P A A P A A P A 2、、、、,并设其面积分别为12345S S S S S 、、、、,则5S 的值为 . 21.在直角三角形ABC 中,∠A =90°,AD ,AE 分别是高和角平分线,且△ABE ,△AED 的面积分别为S 1=30,S 2=6,求△ADC 的面积S .22.如图,△ABC 的面积为1,分别延长AB 、BC 、CA 到D 、E 、F ,使AB =BD ,BC =CE ,CA =AF ,连DE 、EF 、FD ,求△DEF 的面积。

初中求面积的常用方法
1. 直接计算法:对于简单的图形,可以直接根据公式计算面积,如长方形的面积为长乘以宽,正方形的面积为边长的平方,三角形的面积为底边乘以高再除以2等。
2. 分割法:对于复杂的图形,可以将其分割为若干个简单的图形,计算出每个简单图形的面积,然后将它们相加即可得到整个图形的面积。
例如,对于一个不规则的多边形,可以将它分割为多个三角形,计算每个三角形的面积再相加。
3. 同等面积法:若两个图形有相等的面积,可以利用较简单的图形计算出面积,然后利用两个图形的面积相等的性质,直接得到另一个图形的面积。
例如,一个不规则的四边形和一个已知面积的矩形相等,可以通过计算矩形面积知道四边形的面积。
4. 数学推导法:通过利用几何概念和数学推导,可以得到一些特殊图形的面积公式。
例如,圆的面积公式为πr²,其中r为
半径。
这种方法通常要求对相关的数学知识有一定的掌握。
以上是初中常用的求面积方法,但实际上还有很多其他的方法,具体使用哪种方法取决于图形的形状和题目要求。

图形与面积一、直线图形的面积在小学数学中我们学习了几种简单图形的面积计算方法,数学竞赛中的面积问题不但具有直观性,而且变换精巧,妙趣横生,对开发智力、发展能力非常有益。
图形的面积是图形所占平面部分的大小的度量。
它有如下两条性质:1.两个可以完全重合的图形的面积相等;2.图形被分成若干部分时,各部分面积之和等于图形的面积。
对图形面积的计算,一些主要的面积公式应当熟记。
如正方形面积=边长×边长;矩形面积=长×宽;平行四边形面积=底×高;三角形面积=底×高÷2;梯形面积=(上底+下底)×高÷2。
此外,以下事实也非常有用,它对提高解题速度非常有益。
1.等腰三角形底边上的高线平分三角形面积;2.三角形一边上的中线平分这个三角形的面积;3.平行四边形的对角线平分它的面积;4.等底等高的两个三角形面积相等。
解决图形面积的主要方法有:1.观察图形,分析图形,找出图形中所包含的基本图形;2.对某些图形,在保持其面积不变的条件下改变其形状或位置(叫做等积变形);3.作出适当的辅助线,铺路搭桥,沟通联系;4.把图形进行割补(叫做割补法)。
例1 你会用几种不同的方法把一个三角形的面积平均分成4等份吗?解:最容易想到的是将△ABC的底边4等分,如左下图构成4个小三另外,先将三角形△ABC的面积2等分(如右上图),即取BC的中点D,连接AD,则S△ABC-S△ABC,然后再将这两个小三角形分别2等分,分还有许多方法,如下面的三种。
请你再想出几种不同的方法。
例2 右图中每个小方格面积都是1cm2,那么六边形ABCDEF的面积是多少平方厘米?分析:解决这类问题常用割补法,把图形分成几个简单的容易求出面积的图形,分别求出面积。
也可以求出六边形外空白处的面积,从总面积中减去空白处的面积,就是六边形的面积。
解法1:把六边形分成6块:△ABC,△AGF,△PEF,△EKD,△CDH和正方形GHKP。
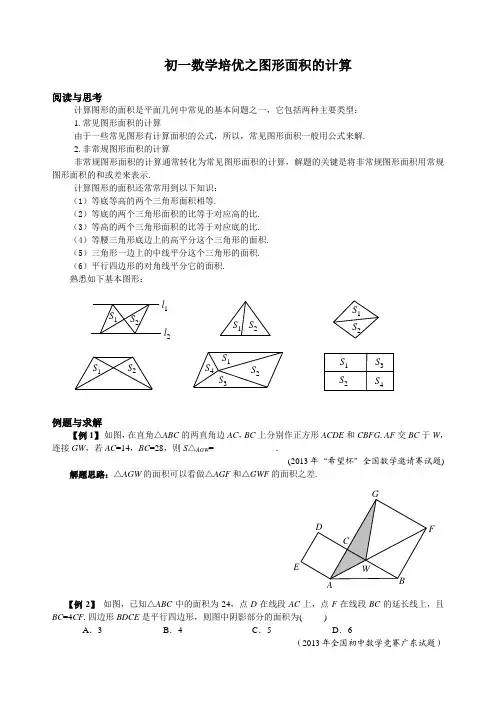
初一数学培优之图形面积的计算阅读与思考计算图形的面积是平面几何中常见的基本问题之一,它包括两种主要类型: 1.常见图形面积的计算由于一些常见图形有计算面积的公式,所以,常见图形面积一般用公式来解. 2.非常规图形面积的计算非常规图形面积的计算通常转化为常见图形面积的计算,解题的关键是将非常规图形面积用常规图形面积的和或差来表示.计算图形的面积还常常用到以下知识:(1)等底等高的两个三角形面积相等.(2)等底的两个三角形面积的比等于对应高的比. (3)等高的两个三角形面积的比等于对应底的比. (4)等腰三角形底边上的高平分这个三角形的面积. (5)三角形一边上的中线平分这个三角形的面积. (6)平行四边形的对角线平分它的面积. 熟悉如下基本图形:S 3S 4S 3S 4S 1S 2S 1S 2S 1S 2S 1S 2S 1S 2S 2S 1l 2l 1例题与求解【例1】 如图,在直角△ABC 的两直角边AC ,BC 上分别作正方形ACDE 和CBFG .AF 交BC 于W ,连接GW ,若AC =14,BC =28,则S △AGW =______________.(2013年“希望杯”全国数学邀请赛试题)解题思路:△AGW 的面积可以看做△AGF 和△GWF 的面积之差.F【例2】 如图,已知△ABC 中的面积为24,点D 在线段AC 上,点F 在线段BC 的延长线上,且BC =4CF .四边形BDCE 是平行四边形,则图中阴影部分的面积为( )A .3B .4C .5D .6(2013年全国初中数学竞赛广东试题)解题思路:设△ABC 底边BC 上的高为h .本例关键是通过适当变形找出h 和DE 之间的关系.FC B【例3】 如图,平行四边形ABCD 的面积为30cm 2,E 为AD 边延长线上的一点,EB 与DC 交于F 点,已知三角形FBC 的面积比三角形DEF 的面积大9cm 2,AD =5cm ,求DE 长.(北京市“迎春杯”竞赛试题)解题思路:由面积求相关线段,是一个逆向思维的过程,解题的关键是把条件中图形面积用DE 及其它线段表示.BACFDE【例4】 如图,四边形ABCD 被AC 与DB 分成甲、乙、丙、丁4个三角形,已知BE =80 cm ,CE =60 cm ,DE =40 cm ,AE =30 cm ,问:丙、丁两个三角形面积之和是甲、乙两个三角形面积之和的多少倍?(“华罗庚杯”竞赛决赛试题)解题思路:甲、乙、丙、丁四个三角形面积可通过线段的比而建立联系,找出这种联系是解本例的突破口.丁乙丙甲E BCDA【例5】 如图,△ABC 的面积为1,D ,E 为BC 的三等分点,F ,G 为CA 的三等分点,求四边形PECF 的面积.解题思路:连CP ,设S △PFC =x ,S △PEC =y ,建立x ,y 的二元一次方程组.Q P FG ED CBA【例6】如图,E,F分别是四边形ABCD的边AB,BC的中点,DE与AF交于点P,点Q在线段DE上,且AQ∥PC.求梯形APCQ的面积与平行四边形ABCD的面积的比值.(2013年”希望杯“数学邀请赛试题)解题思路:连接EF,DF,AC,PB,设S□ABCD=a,求得△APQ和△CPQ的面积.F DB能力训练A 级1.如图,边长为1的正方形ABCD的对角线相交于点O.过点O的直线分别交AD,BC于E,F,则阴影部分面积是______.F CB(海南省竞赛试题)2.如图,在长方形ABCD中,E是AD的中点,F是CE的中点,若△BDF的面积为6平方厘米,则长方形ABCD的面积是_____________平方厘米.EFDCBA(“希望杯”邀请赛试题)3.如图,ABCD 是边长为a 的正方形,以AB ,BC ,CD ,DA 分别为直径画半圆,则这四个半圆弧所围成的阴影部分的面积是____________.C(安徽省中考试题)4.如图,已知AB ,CD 分别为梯形ABCD 的上底、下底,阴影部分总面积为5平方厘米,△AOB 的面积是0.625平方厘米,则梯形ABCD 的面积是_________平方厘米.C(“祖冲之杯”邀请赛试题)5.如图,长方形ABCD 中,E 是AB 的中点,F 是BC 上的一点,且CF =BC 31,则长方形ABCD的面积是阴影部分面积的( )倍.A .2B . 3C . 4D .5F CBE6.如图,是一个长为a ,宽为b 的长方形,两个阴影图形都是一对长为c 的底边在长方形对边上的平行四边形,则长方形中未涂阴影部分的面积为( ).A .c b a ab )(+-B . c b a ab )(--C .))((c b c a --D .))((c b c a +-7.如图,线段AB =CD =10cm ,»BC和»DA 是弧长与半径都相等的圆弧,曲边三角形BCD 的面积是以D 为圆心、DC 为半径的圆面积的41,则阴影部分的面积是( ). A .25π B . 100 C .50π D .200CD(“五羊杯”竞赛试题)8.如图,一个大长方形被两条线段AB 、CD 中分成四个小长方形,如果其中图形Ⅰ,Ⅱ,Ⅲ的面积分别为8,6,5,那么阴影部分的面积为( ). A .29 B .27 C .310 D .815BDA9.如图,长方形ABCD 中,E ,F 分别为AD ,BC 边上的任一点,△ABG ,△DCH 的面积分别为15和20,求阴影部分的面积.CF B(五城市联赛试题)10.如图,正方形ABCD ,正方形BEFG 和正方形RKPF 的位置如图所示,点G 在线段DK 上,已知正方形BEFG 的边长为4,求△DEK 的面积.KEB AD(广西壮族自治区省南宁市中考试题)B 级1.如果图中4个圆的半径都为a ,那么阴影部分的面积为_____________.(江苏省竞赛试题)2.如图,在长方形ABCD 中,E 是BC 上的一点,F 是CD 上的一点,若三角形ABE 的面积是长方形ABCD 面积的31,三角形ADF 的面积是长方形ABCD 面积的52,三角形CEF 的面积为4cm 2,那么长方形ABCD 的面积是_________cm 2.DCFE BA(北京市“迎春杯”邀请赛试题)3.如图,边长为3厘米与5厘米的两个正方形并排放在一起,在大正方形中画一段以它的一个顶点为圆心,边长为半径的圆弧,则阴影部分的面积为___________________.(“希望杯”邀请赛试题)4.如图,若正方形APHM ,BNHP ,CQHN 的面积分别为7,4,6,则阴影部分的面积是_____.CMNDQB A(“五羊杯”竞赛试题)5.如图,把等边三角形每边三等分,使其向外长出一个边长为原来的31的小等边三角形,称为一次“生长”,在得到的多边上类似“生长”,一共“生长”三次后,得到的多边形的边数=________,面积是原三角形面积的______倍.第2次生长第1次生长原图(“五羊杯”竞赛试题)6.如图,在长方形ABCD 中,AE =BG =BF =21AD =31AB =2,E ,H ,G 在同一条直线上,则阴影部分的面积等于( ).A .8B .12C .16D .20F BGCDA7.如图,边长分别为8cm 和6cm 的两个正方形,ABCD 与BEFG 并排放在一起,连接EG 并延长交AC 于K ,则△AKE 的面积是( ).A .48cm 2B .49cm 2C .50cm 2D .51cm 2FEB A(2013年“希望杯”邀请赛试题)8.在一个由8×8个方格组成的边长为8的正方形棋盘内放一个半径为4的圆,若把圆经过的所有小方格的圆内部分的面积之和记为S 1,把圆周经过的所有小方格的圆外部分的面积之和记为S 2,则21S S 的整数部分是( ).A .0B .1C .2D .3(全国初中数学联赛试题)9.如图,△ABC 中,点D ,E ,F 分别在三边上,E 是AC 的中点,AD ,BE ,CF 交于一点G ,BD =2DC ,S △GEC =3,S △GDC =4,则△ABC 的面积是( ).A .25B .30C .35D .40GFE CBDA10.已知O (0,0),A (2,2),B (1,a ),求a 为何值时,S △ABO =5?11.如图,已知正方形ABCD 的面积为1,M 为AB 的中点,求图中阴影部分的面积.CAD(湖北省武汉市竞赛试题)12.如图,△ABC中,21===FAFBECEADBDC.求的面积△的面积△ABCGHI的值.GIHEDCBFA(“华罗庚金杯”邀请赛试题)。

八年级数学竞赛例题专题讲解:面积法阅读与思考平面几何学的产生源于人们测量土地面积的需要,面积关联着几何图形的重要元素边与角.所谓面积法是指借助面积有关的知识来解决一些直接或间接与面积问题有关的数学问题的一种方法.有许多数学问题,虽然题目中没有直接涉及面积,但由于面积联系着几何图形的重要元素,所以借助于有关面积的知识求解,常常简捷明快.用面积法解题的基本思路是:对某一平面图形面积,采用不同方法或从不同角度去计算,就可得到一个含边或角的关系式,化简这个面积关系式就可得到求解或求证的结果.下列情况可以考虑用面积法:(1)涉及三角形的高、垂线等问题;(2)涉及角平分线的问题.例题与求解【例1】如图,从等边三角形内一点向三边作垂线,已知这三条垂线段的长分别为1,3,5,则这个等边三角形的边长为______________.(全国初中数学联赛试题) 解题思路:从寻求三条垂线段与等边三角形的高的关系入手.等腰三角形底边上任一点到两腰距离之和等于一腰上的高,那么等边三角形呢?等腰梯形呢?【例2】如图,△AOB中,∠O=,OA=OB,正方形CDEF的顶点C在DA上,点D在OB上,点F在AB上,如果正方形CDEF的面积是△AOB的面积的,则OC:OD等于( )A.3:1 B.2:1C.3:2 D.5:3解题思路:由面积关系,可能想到边、角之间的关系,这时通过设元,即可把几何问题代数化来解决.【例3】如图,在□ABCD中,E为AD上一点,F为AB上一点,且BE=DF,BE与DF交于G,求证:∠BGC=∠DGC.(长春市竞赛试题)解题思路:要证∠BGC=∠DGC,即证CG为∠BGD的平分线,不妨用面积法寻找证题的突破口.【例4】如图,设P为△ABC内任意一点,直线AP,BP,CP交BC,CA,AB于点D、E、F.求证:(1);(2).(南京市竞赛试题)解题思路:过P点作平行线,产生比例线段.【例5】如图,在△ABC中,E,F,P分别在BC,CA,AB上,已知AE,BF,CP相交于一点D,且,求的值.解题思路:利用上例的结论,通过代数恒等变形求值.(黄冈市竞赛试题)【例6】如图,设点E,F,G,H分别在面积为1的四边形ABCD的边AB,BC,CD,DA上,且(是正数),求四边形EFGH的面积.(河北省竞赛试题)解题思路:连对角线,把四边形分割成三角形,将线段的比转化为三角形的面积比.线段比与面积比的相互转化,是解面积问题的常用技巧.转化的基本知识有:(1) 等高三角形面积比,等于它们的底之比;(2) 等底三角形面积比,等于它们的高之比;(3) 相似三角形面积比,等于它们相似比的平方.能力训练1.如图,正方形ABCD的边长为4cm,E是AD的中点,BM⊥EC,垂足为M,则BM=______.(福建省中考试题)2.如图,矩形ABCD中,P为AB上一点,AP=2BP,CE⊥DP于E,AD=,AB=,则CE=__________.(南宁市中考试题)第1题图第2题图第3题图3.如图,已知八边形ABCDEFGH中四个正方形的面积分别为25,48,121,114,PR=13,则该八边形的面积为____________.(江苏省竞赛试题) 4. 在△ABC中,三边长为,,,表示边上的高的长,,的意义类似,则(++)的值为____________. (上海市竞赛试题)5.如图,△ABC的边AB=2,AC=3,Ⅰ,Ⅱ,Ⅲ分别表示以AB,BC,CA为边的正方形,则图中三个阴影部分的面积之和的最大值是__________.(全国竞赛试题) 6.如图,过等边△ABC内一点P向三边作垂线,PQ=6,PR=8,PS=10,则△ABC的面积是 ( ).A. B.C.D.(湖北省黄冈市竞赛试题)第5题图第6题图第7题图7.如图,点D是△ABC的边BC上一点,若∠CAD=∠DAB=,AC=3,AB=6,则AD的长是( ).A.2 B. C.3 D.8.如图,在四边形ABCD中,M,N分别是AB,CD的中点,AN,BN,DM,CM划分四边形所成的7个区域的面积分别为,,,,,,,那么恒成立的关系式是( ).A.+=B.+=C.+= D.+=9.已知等边△ABC和点P,设点P到△ABC三边AB,AC,BC的距离分别为,,,△ABC的高为.若点P在一边BC上(如图1),此时,可得结论:++=.请直接用上述信息解决下列问题:当点P在△ABC内(如图2)、点P在△ABC外(如图3)这两种情况时,上述结论是否还成立?若成立.请给予证明;若不成立,,,与之间又有怎样的关系?请写出你的猜想,不需证明.(黑龙江省中考试题)10.如图,已知D,E,F分别是锐角△ABC的三边BC,CA,AB上的点,且AD、BE、CF相交于P点,AP=BP=CP=6,设PD=,PE=,PF=,若,求的值.(“希望杯”邀请赛试题)11.如图,在凸五边形ABCDE中,已知AB∥CE,BC∥AD,BE∥CD,DE∥AC,求证:AE∥BD.(加拿大数学奥林匹克试题)12.如图,在锐角△ABC中,D,E,F分别是AB,BC,CA边上的三等分点. P,Q,R分别是△ADF,△BDE,△CEF的三条中线的交点.(1) 求△DEF与△ABC的面积比;(2) 求△PDF与△ADF的面积比;(3) 求多边形PDQERF与△ABC的面积比.13.如图,依次延长四边形ABCD的边AB,BC,CD,DA至E,F,G,H,使,若,求的值.(上海市竞赛试题)14.如图,一直线截△ABC的边AB,AC及BC的延长线分别交于F,E,D三点,求证:.(梅涅劳斯定理)15.如图,在△ABC中,已知,求的值.(“华罗庚金杯”少年数学邀请赛试题)。

七年级数学竞赛题:图形面积的计算计算图形的面积是平面几何中常见的基本问题之一,它包括两种主要类型: 1.常见图形面积的计算 .由于一些常见图形有计算面积的公式,所以,常见图形面积一般用公式来解. 2.非常规图形面积的计算非常规图形面积的计算通常转化为常见图形面积的计算,解题的关键是将非常规图形面积用常见图形面积的和或差来表示.计算图形的面积还常常用到以下知识: 1.等底等高的两个三角形面积相等;2.等底的两个三角形面积的比等于对应高的比; 3.等高的两个三角形面积的比等于对应底的比. 熟悉如下基本图形、基本结论:例1 2002年8月,将在北京召开国际数学家大会,大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积是13,小正方形的面积是1,则每个直角三角形的两条直角边的立方和等于 .(2002年北京市竞赛题) 解题思路 从向外补形人手.例2 如图,ABC S ∆=1,若BDE S ∆=DEC S ∆=ACE S ∆,则ADE S ∆=( )(“五羊杯”竞赛题)(A)51 (B)61 (C) 71(D) 81解题思路 因条件未给出具体线段的长,故不宜用公式直接求出ADE S ∆,考虑由BDE S ∆=DEC S ∆能推出什么.例3如图,平行四边形ABCD 的面积为30 cm 2,E 为AD 边延长线上的一点,EB 与DC交于F 点,已知三角形FBC 的面积比三角形DEF 的面积大9 cm 2,AD=5cm ,求DE 长. (北京市“迎春杯”竞赛题)解题思路 由面积求相关线段,是一个逆向思维的过程,解题的关键是把条件中图形面积用DE 及其他线段表示.例4如图,四边形ABCD 被AC 与DB 分成甲、乙、丙、丁4个三角形.已知BE=80 cm ,CE=60 cm ,DE=40 cm ,AE=30 cm ,问: 丙、丁两个三角形面积之和是甲、乙两个三角形面积之和的多少倍?(“华罗康金杯”赛决赛试题)解题思路 甲、乙、丙、丁四个三角形面积可通过线段的比而建立联系,找出这种联系是解本例的突破口.例5如图,△ ABC 的面积为l ,D 、E 为 BC 的三等分点,F 、G 为CA 的三等分点,求四 边形PECF 的面积.解题思路 连CP ,设PFC S ∆=x ,PEC S ∆=y ,建立x ,y 的二元一次方程组.A1.如图,正方形的边长为a ,小圆的直径是b ,S 表示正方形面积与大圆面积的差,A 是小圆面积,设圆周率为π,则AS= .(第1题) (第2题) (第3题)2.如图,在长方形ABCD 中,E 是AD 的中点,F 是CE 的中点,若ABDF 的面积为6平方厘米,则长方形ABCD 的面积是 平方厘米.(第十一届“希望杯”邀请赛试题)3.如图,ABCD 是边长为a 的正方形,以AB 、BC 、CD 、DA 分别为直径画半圆,则这四个半圆弧所围成的阴影部分的面积是 .(安徽省中考题)4.如图,已知AB 、CD 分别为梯形ABCD 的上底、下底,阴影部分总面积为5平方厘米,△ AOB 的面积是0.625平方厘米,则梯形ABCD 的面积是 平方厘米.(“祖冲之杯”邀请赛试题)(第4题) (第5题) (第6题) 5.如图,长方形ABCD 中,E 是AB 的中点,F 是BC 上的一点,且CF=31BC ,则长方形ABCD 的面积是阴影部分面积的( )倍. (A)2 (B)3 (C)4 (D)56.如图,是一个长为a ,宽为b 的长方形,两个阴影图形都是一对长为c 的底边在长方形对边上的平行四边形,则长方形中未涂阴影部分的面积为( ) (A)ab 一(a+b)c (B)ab 一(a 一b)c (C)(a —c)(b 一c) (D)(a--c)( b+c)7.如图,线段AB=CD=10cm , 和 是弧长与半径都相等的圆弧,曲边三角形BCD 的面积是以D 为圆心,DC 为半径的圆面积的41,则阴影部分的面积是( ). (“五羊杯”竞赛题)(A)25π (B)100 (C)50π (D)2008.如图,一个大长方形被两条线段AB 、CD 分成四个小长方形,如果其中图形I 、Ⅱ、Ⅲ的面积分别为8、6、5,那么阴影部分的面积为( ). (A)29 (B)27 (C)310 (D)815(第7题) (第8题) (第9题)9.如图,长方形ABCD 中,E 、F 分别为AD 、BC 边上的任意点,△ABG、△DCH 的面积分别为15和20,求阴影部分的面积.(五城市联赛题)10.如图,一个长方形恰被分成六个正方形,其中最小的正方形面积是1平方厘米,求这个长方形的面积.B .1.如果图中4个圆的半径都为a ,那么阴影部分的面积为 .(第十七届江苏省竞赛题) 2.如图,△AB C 中,点P 在边AB 上,AP=31AB ,Q 点在边BC 上,BQ=4BC ,R 在边CA上,CR=51CA ,已知阴影△PQR 的面积是19平方厘米,那么△ABC 的面积是 平方厘米.(第1题) (第2题) (第3题)3.如图,在长方形ABCD 中,E 是BC 上的一点,F 是CD 上的一点,若三角形ABE 的面积是长方形ABCD 面积的31,三角形ADF 的面积是长方形ABCD 面积的52,三角形CEF 的面积为4cm 2,那么长方形ABCD 的面积是 cm 2.(北京市“迎春杯”邀请赛试题)4.如图,边长为3厘米与5厘米的两个正方形并排放在一起,在大正方形中画一段以它的一个顶点为圆心,边长为半径的圆弧,则阴影部分的面积为 .(第4题) (第5题)5.如图,若长方形APHM ,BNHP ,CQHN 的面积分别为7,4,6,则阴影部分的面积是 .(“五羊杯”竞赛题) 6.如图,把等边三角形每边三等分,使其向外长出一个边长为原来的31的小等边三角形,称为一次 “生长”,在得到多边形上类似“生长”,一共“生长”三次后,得到的多边形的边数= ,面积是原三角形面积的 倍.(“五羊杯”竞赛题)7.在一个由8×8个方格组成的边长为8的正方形棋盘内放一个半径为4的圆,若把圆周经过的所有小方格的圆内部分的面积之和记为1S ,把圆周经过的所有小方格的圆外部分的面积之和记为2S ,则21S S 的整数部分是( ). (全国初中数学联赛试题)(A)0 (B)1 (C)2 (D)38.如图,△ ABC 中,点D 、E 、F 分别在三边上,E 是AC 的中点,AD 、BE 、CF 交于一点G ,BD=2DC ,GEC S ∆=3,GDC S ∆=4,则△ABC 的面积是( ). (A)25 (B)30 (C)35 (D)40 BA E F B(第8题) (第9题) (第10题) 9.如图,已知长方形的面积是36平方厘米,在边AB 、AD 上分别取点E 、F ,使得AE=3EB ,DF=2AF ,DE 与CF 的交点为O ,计算△FOD 的面积是多少平方厘米?(第十一届“希望杯”邀请赛试题)10.如图,四边形ABCD 面积为S ,E ,F 为AB 的三等分点,M 、N 为DC 的三等分点,求证:EFNM S =3S .。


八年级数学竞赛例题专题-面积的计算专题23 面积的计算○阅○读○与○思○考计算图形的面积是几何问题中一种重要题型,计算图形的面积必须掌握如下与面积有关的重要知识:1常见图形的面积公式;2.等积定理:等底等高的两个三角形面积相等;3等比定理:(1) 同底(或等底)的两个三角形面积之比等于等于对应高之比;同高(或等高)的两个三角形面积之比等于等于对应底之比(2) 相似三角形的面积之比等于对应线段之比的平方熟悉下列基本图形、基本结论:例题与求解【例1】如图,△AB内三个三角形的面积分别为,8,10,四边形AEFD 的面积为,则=________ (黄冈市竞赛试题)解题思路:图中有多对小三角形共高,所以可将面积比转化为线段之比作为解题突破口【例2】如图,在△AB中,已知BD和E分别是两边上的中线,并且BD⊥E,BD=4,E=6,那么△AB的面积等于( ) (全国初中数学联赛)A.12 B.14 .16 D.18解题思路:由中点想到三角形中位线,这样△AB与四边形BDE面积存在一定的关系【例3】如图,依次延长四边形ABD的边AB,B,D,DA至E,F,G,H,使BEAB=FB=DGD=AHDA=,若S四边形EFGH=2S 四边形ABD,求的值解题思路:添加辅助线将四边形分割成三角形,充分找出图形面积比与线段比之间的关系,建立关于的方程【例4】如图,P,Q是矩形ABD的边B和D延长线上的两点,PA 与Q相交于点E,且∠PAD=∠QAD,求证:S矩形ABD=S△APQ 解题思路:图形含全等三角形、相似三角形,能得到相等的线段、等积式,将它们与相应图形联系起,促使问题的转化【例】如图,在Rt△AB中,∠A=90°,AB=8,A=6,若动点D从点B出发,沿线段BA运动到点A为止,移动速度为每秒2个单位长度过点D作DE∥B交A于点E,设动点D运动的时间为秒,AE的长为(1) 求出关于的函数关系式,并写出自变量的取值范围;(2) 当为何值时,△BDE的面积S有最大值,最大值为多少?(江西省中考试题)解题思路:对于(1)利用△ADE∽△AB可得与的关系式;对于(2)先写出S关于的函数关系式,再求最大值【例6】如图,设P为△AB内任意一点,直线AP,BP,P交B,A,AB于点D,E,F求证:(1) PDAD+PEBE+PFF=1;(2)PAAD+PBBE+PF=2解题思路:过点A,P分别作B的垂线,这样既可得到平行线,产生比例线段,又可以与面积联系起,把PAAD 转化为面积比,利用面积法证明○能○力○训○练A 级1.如图,៱ABD中,AE∶BE=1∶2,S△AEF=62,则S△DF的值为________ (济南市中考试题)2.如图,正六边形ABDEF的边长为23,P为正六边形内任一点,则点P到各边距离之和为_______3.如图,P是边长为8的正方形ABD外一点,PB=P,△PBD的面积等于48,则△PB的面积为_____________ (北京市竞赛试题)4.如图,已知△BF,△AF,△BD,△E的面积分别为30,40,3,84,则△AB的面积为________ (浙江省竞赛试题).如图,已知AD是Rt△AB斜边B上的高,DE 是Rt△AD斜边上的高,如果D∶AD=1∶2,S△DE=a,那么S△AB等于( ) (金华市中考试题)A.4a B.9a .16a D.2a6.如图,已知是៱ABD边AB的中点,交BD于点E,则图中阴影部分面积与៱ABD的面积之比为()(西省中考试题)A.16 B.14 .13 D.127.如图,在△AB中,DE∥B,DE分别交AB,A于点D,E,若S△ADE =2S△DE,则S△ADES△AB等于( )(浙江省宁波市中考试题)A.14 B.12 .23 D.498.如图,△AB是边长为6的等边三角形,被一平行于B的矩形所截,AB被截成三等分,则图中阴影部分面积面积为()2 (广东省竞赛试题)A.4 B.23 .33 D.439.如图,平面上有两个边长相等的正方形ABD和A′B′′D′,且正方形A′B′′D′的顶点A′在正方形ABD的中心,当正方形A′B′′D′绕A′ 转动时,两个正方形重合部分的面积必然是一个定值这个结论对吗?证明你的判断(“希望杯”邀请赛试题)10.如图,设凸四边形ABD的一组对边AB,D的中点分别为,求证:S四边形ABD=S△AB+S△D11.如图1,AB,D是两条线段,是AB的中点,S△D,S△DA,S△DB 分别表示△D,△DA,△DB的面积,当AB∥D时,有S△D=S△DA +S△DB2………①(1) 如图2,若图1中AB与D不平行时,①式是否成立?请说明理由(2) 如图3,若图1中AB与D相交于点时,问S△D与S△DA和S△DB 有何相等关系?试证明你的结论(安徽省中考试题)12.如图,在△AB中,∠AB=90°,∠AB=30°,将△AB绕顶点顺时针旋转,旋转角为θ(0°<θ<180°),得到△A′B′′(1) 如图1,当AB∥B′时,设A′B′与B相交于点D,证明:△A′D是等边三角形;(2) 如图2,连接A′A,B′B,设△AA′和△BB′的面积分别为S△AA′和S△BB′求证:S△AA′∶S△BB′=1∶3(3) 如图3,设A的中点为E,A′B′的中点为P,A=a,连接EP,当θ=_____时,EP长度最大,最大值是____________ (安徽省中考试题)B 级1.如图,A在线段BG上,ABD和DEFG都是正方形,面积分别为72和112,则△DE的面积等于___________2 (武汉市竞赛试题)2.如图,P为正方形ABD内一点,PA=PB=10,并且P到D边的距离也等于10,那么正方形ABD的面积是_______________ (北京市竞赛试题)3.如图,四边形ABD中,点E,F分别在B,D上,DFF=1,EBE =2,若△ADF的面积为,四边形AEF的面积为n (n>),则四边形ABD的面积为___________ (全国初中数学联赛试题)4.如图,图形ABD中,AB∥D,A和BD相交于点,若A=,BD=12,中位线长为132,△AB的面积为S1,△D的面积为S2,则S1+S2=_________ (东省竞赛试题).如图,分别延长△AB的三边AB,B,A至A′,B′,′,使得AA′=3AB,BB′=3B,′=3A,若S△AB=1,则S△A′B′′等于( )A.18 B.19 .24 D.27(东省竞赛试题)6.如图,若ABD是2×2的正方形,E是AB的中点,F是B的中点,AF与DE相交于点I,BD和AF相交于点H,那么四边形BEIH的面积是( )A.13 B..71 D.81(江苏省竞赛试题)7.如图,矩形ABD中,E是B上的一点,F是D上的点,已知S△ABE =S△ADF=13SABD,则S△AEFS△EF的值等于( ) (北京市竞赛试题) A.2 B.3 .4 D.8.(1) 探究:如图1,在៱ABD的形外分别作等腰直角三角形ABF和等腰直角三角形ADE,∠FAB=∠EAD=90°,连接A,EF 在图中找一个与△FAE全等的三角形,并加以证明(2) 应用:以៱ABD的四条边为边,在其形外分别作正方形,如图2,连接EF,GH,I,L,若៱ABD的面积为,则图中阴影部分四个三角形的面积之和为____________ (长春市中考试题)9.如图,在梯形ABD中,AD∥B,AB=AD=D=2,B=4,在等腰△PQR中,∠QPR=120°,底边QR=6,点B,,Q,R在同一条直线l上,且,Q两点重合,如果等腰△PQR以1/s的速度沿直线l 箭头所示方向匀速运动,t秒时梯形ABD与等腰△PQR重合部分的面积记为S2(1) 当t=4时,求S的值;(2) 当4≤t≤10时,求S与t的函数关系式,并求出S的最大值(广州市中考试题)10.有一根直尺的短边长为2,长边长为10,还有一块锐角为4°的直角三角纸板,它的斜边长为12,如图1将直尺的短边DE放置与直角三角纸板的斜边AB重合,且点D与点A重合将直尺沿AB方向平移,如图2,设平移的长为(0≤ ≤10),直尺与三角形纸板重叠部分(图中阴影部分)的面积S2(1) 当=0时,S=________,当时,S=________;(2) 当0<≤4时,求S关于的函数关系式;(3) 当4<<10时,求S关于的函数关系式,并求出S的最大值(徐州市中考试题)11.如图,设H是等腰三角形AB的三边上的高线的交点,在底边B 保持不变的情况下,让顶点A至底边B的距离变小(仍保持三角形为等腰三角形),这时的值变大、变小、还是不变?证明你的结论12.(1) 请你在图1中作一条直线,使它将矩形ABD分成面积相等的两部分;(2) 如图2,点是矩形ABD内一定点,请你在图2中过点作一条直线,使它将矩形ABD分成面积相等的两部分;(3) 如图3,在平面直角坐标系中,直角梯形BD是某市将要筹建的高新技术开发区用地示意图,其中D∥B,B=6,B=4,D=4 开发区综合服务管理委员会(其占地面积不计)设在点P(4,2)处为了方便驻区单位,准备过点P修一条笔直的道路(路的宽不计),并且使这条路所在的直线l将直角梯形BD分成面积相等的两部分你认为直线l 是否存在?若存在,求出直线l的表达式;若不存在,请说明理由(陕西省中考试题)。
面积法一、内容提翼.因为面积公式是用线段的代数式表示的,所以面积与线段可以互相转换。
运用面积公式及有关面积性质定理解答儿何题是常用的方法,简称面积法。
.面积公式(略)两个三角形的面积比定理.等高(底)的两个三角形的面积比,等于它们对应的底(高)的比.有一个角相等或互补的两个三角形面积的比等于夹这个角两边的乘积的比.相似三角形面积的比等于它们的相似比的平方.有公共边的两个三角形面积的比等于它们的第三顶点连线被公共边分成的两条线段的比(内分比或外分比K a A如图△ABC和AADC有公共边AC,氽M内分BD o第三顶点连线BD被公共边AC/l\/\内分或外分于点M,//X.则』空十尸汶4。
‘△ADC MD定理④是以公共边为底,面积的比等于它们的对应高的比换成对应线段的比二、例题.求证有一个30度角的菱形,边长是两条对角线的比例中项已知:菱形ABCD中,ZDAC=30°求证:ab2=acxbd证明:作高DE,VZDAE=30°.•.de=L ad=L ab S22S菱形abcd=ACXBD./.AB2=ACXBD.求证:等边三角形内任一点到各边的距离的和是一个定值已知:AABC中,AB=BC=AC,D是形内任一点,DE±BC.DF_LAC,DG±AB,E, F.G是垂足求证:DE+DF+DG是一个定值证明:连结DA,DB.DC,设边长为a,‘△abc=S mbc+S adca+S adabC lah a=-J-a(DE+DF+DG)22.•.DE+DF+DGf...等边三角形的高h,是一个定值,...DE+DF+DG是一个定值本题可推广到任意正n边形,其定值是边心距的n倍f aAD BE CF 1已知:AABC 中,——=——=——=-AB BC CA 3求:萨虬的值'△ABCBE (本题可推广到:1—,---=—,m BC n 竺=顼CA p'△DEh mn P + "1 + 〃 + p - mn - nip - np )S A abc mnP如图RtAABC 被斜边上的高CD 和直角平分线CE 分成3个三角形,已知其中两个面积的值标在图中,求第三个三角形的面积X 。
初中数学竞赛专题选讲面积法一、内容提要1. 因为面积公式是用线段的代数式表示的,所以面积与线段可以互相转换。
运用面积公式及有关面积性质定理解答几何题是常用的方法,简称面积法。
2. 面积公式(略)3. 两个三角形的面积比定理① 等高(底)的两个三角形的面积比,等于它们对应的底(高)的比 ② 有一个角相等或互补的两个三角形面积的比等于夹这个角两边的乘积的比③ 相似三角形面积的比等于它们的相似比的平方④ 有公共边的两个三角形面积的比等于它们的第三顶点连线被公共边分成的两条线段的比(内分比或外分比)。
如图△ABC 和△ADC 有公共边第三顶点连线BD 被公共边AC内分或外分于点M ,则MDBM S ADC ABC =△△S外分定理④是以公共边为底,面积的比等于它们的对应高的比换成对应线段的比二、例题例1. 求证有一个30度角的菱形,边长是两条对角线的比例中项已知:菱形ABCD 中, ∠DAC = 求证:AB 2=AC ×BD证明:作高DE ,∵∠DAE =30∴DE =21AD =21AB S 菱形ABCD =AB ×DE =21AB 2S 菱形ABCD =AC ×BD , ∴AB 2=AC ×BDDC B C A C例2. 求证:等边三角形内任一点到各边的距离的和是一个定值已知:△ABC 中,AB =BC =AC ,D 是形内任一点,DE ⊥BC ,DF ⊥AC ,DG ⊥AB ,E ,F ,G 是垂足求证:DE +DF +DG 是一个定值证明:连结DA ,DB ,DC ,设边长为a,S △ABC =S △DBC +S △DCA +S △DAB21ah a =21a (DE +DF +DG ) ∴DE +DF +DG =h a∵等边三角形的高h a 是一个定值, ∴DE +DF +DG 是一个定值本题可推广到任意正n 边形,其定值是边心距的n 倍例3. 已知:△ABC 中,31===CA CF BC BE AB AD 求:ABCDEF S △△S 的值 解:∵△ADF 和△ABC 有公共角A∴ABC ADF S △△S =AC AB AF AD ⋅⋅=AC AB AC 32AB 31⋅⋅=92, 同理92S ABC BED =△△S , ABC CFE S S △△=92, ∴ABC DEF S △△S =31 (本题可推广到:当m AB AD 1=,n BC BE 1=,=CA CF p 1时, ABCDEF S △△S =mnp np mp mn p n m mnp ---+++) 例4. 如图Rt △ABC 被斜边上的高CD 和直角平分线CE 分成3个三角形,已知其中两个面积的值标在图中,求第三个三角形的面积x 。
初中数学中的几何图形面积如何计算?在初中数学的学习中,几何图形面积的计算是一个重要的知识点。
掌握不同几何图形面积的计算方法,不仅能帮助我们解决数学问题,还能在实际生活中有着广泛的应用。
首先,咱们来聊聊最基础的长方形和正方形的面积计算。
长方形的面积等于长乘以宽,用字母表示就是 S = a×b (其中 S 表示面积,a 表示长,b 表示宽)。
比如说,一个长方形的长是 5 厘米,宽是 3 厘米,那么它的面积就是 5×3 = 15 平方厘米。
正方形呢,因为它的四条边长度都相等,所以正方形的面积等于边长乘以边长,用字母表示就是 S = a×a = a²(其中 S 表示面积,a 表示边长)。
假设一个正方形的边长是 4 厘米,那么它的面积就是 4×4 =16 平方厘米。
接下来,说说三角形的面积计算。
三角形的面积等于底乘以高除以 2,用字母表示为 S = 1/2×a×h (其中 S 表示面积,a 表示底,h 表示高)。
例如,有一个三角形,底是 6 厘米,高是 4 厘米,那它的面积就是 1/2×6×4 = 12 平方厘米。
平行四边形的面积计算方法是底乘以高,用字母表示为 S = a×h (其中 S 表示面积,a 表示底,h 表示高)。
假如有一个平行四边形,底是 8 厘米,高是 5 厘米,它的面积就是 8×5 = 40 平方厘米。
梯形的面积计算就稍微复杂一点,它等于(上底+下底)乘以高除以 2,用字母表示为 S = 1/2×(a + b)×h (其中 S 表示面积,a 表示上底,b 表示下底,h 表示高)。
比如一个梯形,上底是 3 厘米,下底是 7 厘米,高是 5 厘米,那么它的面积就是 1/2×(3 + 7)×5 = 25 平方厘米。
圆形也是常见的几何图形,它的面积计算要用到圆周率π(通常取值 314)。
初中数学几何图形面积计算的方法与练习在初中数学的学习中,几何图形面积的计算是一个重要的部分。
它不仅是考试中的常见考点,更是培养我们逻辑思维和空间想象能力的有效途径。
接下来,让我们一起深入探讨一下初中数学中几何图形面积计算的方法,并通过一些练习来巩固所学。
一、常见几何图形面积计算公式1、三角形三角形的面积计算公式为:面积=底×高÷2。
这里的底和高是相互对应的,需要注意的是,同一个三角形可以有不同的底和高,选择不同的底和高计算时,要确保底和高的对应关系正确。
2、矩形(长方形)矩形的面积等于长乘以宽。
3、正方形正方形的面积等于边长的平方。
4、平行四边形平行四边形的面积等于底乘以高。
5、梯形梯形的面积=(上底+下底)×高÷2 。
6、圆形圆的面积=π×半径的平方。
其中,π通常取 314。
二、面积计算方法1、直接运用公式法这是最基本也是最常见的方法。
当我们遇到规则的几何图形,如矩形、正方形、三角形等,且已知相关的边长、底、高等数据时,直接代入相应的公式即可求出面积。
例如:一个矩形的长为 5 厘米,宽为 3 厘米,其面积为 5×3 = 15平方厘米。
2、割补法对于一些不规则的几何图形,我们可以通过割补的方法,将其转化为我们熟悉的规则图形,然后再计算面积。
比如,一个不规则的四边形,我们可以通过添加辅助线,将其分割成两个三角形或一个三角形和一个梯形,分别计算出各部分的面积,再相加得到整个四边形的面积。
3、等积变形法利用图形的面积不变性质,通过对图形的平移、旋转、对称等变换,将图形转化为易于计算面积的形式。
例如,两个三角形等底等高,则它们的面积相等。
我们可以利用这一性质,对图形进行变形,从而更方便地计算面积。
4、整体减部分法当一个图形由几个部分组成时,我们可以先求出整体的面积,再减去不需要的部分的面积,从而得到所求图形的面积。
比如,一个大正方形中包含一个小正方形,求阴影部分的面积,就可以用大正方形的面积减去小正方形的面积。
图形的面积计算方法面积是图形的一个重要属性,它描述了图形所占有的平面区域的大小。
计算图形的面积是数学中一个基本的问题,而不同类型的图形有不同的面积计算方法。
本文将为您介绍几种常见图形的面积计算方法。
一、长方形的面积计算方法长方形是一种矩形,它的两边长度不同,但相邻两边分别相等。
长方形的面积计算方法非常简单,只需要将长方形的长度与宽度相乘即可计算得出。
设长方形的长度为l,宽度为w,则其面积S可以表示为:S = l × w。
二、正方形的面积计算方法正方形是一种特殊的长方形,它的四条边长度都相等。
正方形的面积计算方法与长方形类似,也是将正方形的边长平方即可。
设正方形的边长为a,则其面积S可以表示为:S = a × a = a²。
三、三角形的面积计算方法三角形是由三条边所围成的图形,它没有平行边。
计算三角形的面积需要使用三角形的底和高的长度。
设三角形的底为b,高为h,则其面积S可以表示为:S = 1/2 × b × h。
四、圆形的面积计算方法圆形是一个完全由曲线所围成的图形,其特点是任意两点到圆心的距离都相等。
计算圆形的面积需要使用圆的半径。
设圆的半径为r,则其面积S可以表示为:S = π × r²,其中π是一个常数,近似取值为3.14159。
五、梯形的面积计算方法梯形是一个由两条平行边和两条非平行边所围成的图形。
计算梯形的面积需要使用梯形的上底、下底及高的长度。
设梯形的上底为a,下底为b,高为h,则其面积S可以表示为:S = 1/2 × (a + b) × h。
六、其他图形的面积计算方法除了上述几种常见图形外,还有许多其他类型的图形,如圆环、扇形、多边形等。
这些图形的面积计算方法不在本文的讨论范围内,但是它们的面积计算方法一般都可以通过将图形划分为若干个已知面积的基本图形来计算。
综上所述,计算图形的面积需要根据图形的类型选择相应的面积计算方法。
2013年暑期初一数学竞赛第二十讲:图形面积的计算
【例题精选】
例1.你会用几种不同的方法把一个三角形的面积平均分成4等份吗?
变式.已知P是矩形ABCD的边AB上任意一点,试过P作两条直线,将矩形分成三个面积相等的图形。
例2.在△ABC内部或边界上任取一点P,记P到三边a,b,c的距离依次为x,y,z.求证:ax+by+cz是一个常数.
变式.不等边三角形ABC的两条高的长度分别为4和12.若第三条高也为整数,那么它的长度最大可能是().
(A)4 (B)5 (C)6 (D)7
例3.如图所示,长方形ABCD中,AB=24cm,BC=36cm,E是BC的中点,F,G分别是AB,CD 的4等分点,H为AD上任意一点。
则阴影部分面积为。
变式.如图,△ABC的面积为1,分别延长AB、BC、CA到D、E、F,
使AB=BD,BC=CE,CA=AF,连DE、EF、FD,求△DEF的面积.
B F D
E C
A
B
A F
E
D
C
D
B A F C
(3)E 例4.已知△ABC 中,31
===CA CF BC BE AB AD ,求:ABC
DEF S △△S
变式1.如图,AD=1
2
DB,AF=4FC,BE=EC,求S ΔDEF ∶S ΔABC 的值.
变式2.如图,设△ABC 的面积为1,AD=
1m AB,BE=1n BC ,CF=1
p
CA ,
则△DEF 的面积是___________.
例5.如图,三角形ABC 的面积为1,BD:DC=2:1,E 是AC 的中点,AD 与BE 相交于点P,
那么四边形PDCE 的面积为_______.
变式1.如图所示,已知 1.2,2,2.ABC S BF AF CD BD AE CE ∆====
求图中阴影部分PMN ∆的面积.
A
C
A B
C
变式2.如图,三角形ABC 各边的四等分点D 、E 、F 分别与点C 、B 、A 相连,得到一个小
三角形GHI ,那么三角形GHI 的面积与三角形ABC 的面积的比是 。
变式3.如图,已知长方形的面积是36平方厘米,在边AB 、AD
上分别取点E 、•F,•使得AE=3EB,DF=2AF,DE 与CF 的
交点为O,求△FOD 的面积.
例6.已知MN 是△ABC 的中位线,P 在MN 上,BP ,CP 交对边于求证:
1=+DC
AD
BE AE
【巩固拓展】
1.如图,一个大长方形被两条线段AB 、CD 分成四个小长方形,如 果其中图形Ⅰ、Ⅱ、Ⅲ的面积分别为8,6,5,那么阴影部分的面 积为( ). A.
92 B. 72 C. 103 D. 158
2、等腰△ABC 中,一腰上的高线长为,这个高线与底边的夹角是
,△ABC 的面积
是( )
(A
(B )
(C )2
(D B O F
D
E C
A
3.已知等腰△ABC 一腰上的中线为15,底边上的高为18,则△ABC 的面积是( ) (A )124 (B )144 (C )150 (D )以上答案都不对
4.在图的平面图形中,边AF 与CD 平行,BC 与ED 平行,各边长 为1,且∠FAB=∠BCD=,该图形的面积是( ) (A )
(B )1 (C )
(D )
(E )2
5.如图,正方形的边长为a,以各边为直径在正方形内画半圆,所围成 的图形(•阴影部分)的面积为( ). A.πa 2-a 2 B.2πa 2-a 2 C.12πa 2-a 2 D.a 2-1
4
πa 2
6.如图,△ABC 中,点D 、E 、F 分别在三边上,E 是AC 的中点,AD 、BE 、 CF 交于一点G,BD=2DC,S △GEC =3,S △GDC =4,则△ABC 的面积 是( ).
A.25
B.30
C.35
D.40 7.如图,将面积为2
a 的小正方形与面积为2
b 的大正方形放在一起
)0,0(>>b a ,则三角形ABC 的面积是 .
8.已知△ABC 中三边长分别为a ,b ,c ,对应边上的高分别为h a =4
,h b =5,hc=3. 则a ∶b ∶c= .
10.如图,平行四边形ABCD 中,AE=2EC,BF=2AF,S ΔBEF =2.则平行四边形ABCD 的面积为 .
11.这是一个正方形,图中所标的数字单位是厘米, 问:涂红色的部分的面积是多少平方厘米?
F
E
D
C
B
A 60︒60︒
D
A C B
(1)E
F
A
B C。