人教版初中数学第五章相交线与平行线知识点

- 1 -七年级数学（上）知识点 第一章、有理数知识概念 1.有理数： (1)凡能写成)0p q ,p (pq≠为整数且形式的数，都是有理数.正整数、0、负整数统称整数；正分数、负分数统称分数；整数和分数统称有理数.注意：0即不是正数，也不是负数；-a 不一定是负数，+a 也不一定是正数；π不是有理数；(2)有理数的分类: ① ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数零正分数正整数正有理数有理数 ② ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数零正整数整数有理数 2．数轴：数轴是规定了原点、正方向、单位长度的一条直线.3．相反数：(1)只有符号不同的两个数，我们说其中一个是另一个的相反数；0的相反数还是0； (2)相反数的和为0 ⇔ a+b=0 ⇔ a 、b 互为相反数. 4.绝对值：(1)正数的绝对值是其本身，0的绝对值是0，负数的绝对值是它的相反数；注意：绝对值的意义是数轴上表示某数的点离开原点的距离；(2) 绝对值可表示为：⎪⎩⎪⎨⎧<-=>=)0a (a )0a (0)0a (a a 或⎩⎨⎧<-≥=)0a (a )0a (aa ；绝对值的问题经常分类讨论；5.有理数比大小：（1）正数的绝对值越大，这个数越大；（2）正数永远比0大，负数永远比0小；（3）正数大于一切负数；（4）两个负数比大小，绝对值大的反而小；（5）数轴上的两个数，右边的数总比左边的数大；（6）大数-小数 ＞ 0，小数-大数 ＜ 0.6.互为倒数：乘积为1的两个数互为倒数；注意：0没有倒数；若 a ≠0，那么a 的倒数是a1；若ab=1⇔ a 、b 互为倒数；若ab=-1⇔ a 、b 互为负倒数. 7.有理数加法法则： （1）同号两数相加，取相同的符号，并把绝对值相加；（2）异号两数相加，取绝对值较大的符号，并用较大的绝对值减去较小的绝对值； （3）一个数与0相加，仍得这个数. 8．有理数加法的运算律：（1）加法的交换律：a+b=b+a ；（2）加法的结合律：（a+b ）+c=a+（b+c ）. 9．有理数减法法则：减去一个数，等于加上这个数的相反数；即a-b=a+（-b ）. 10 有理数乘法法则：（1）两数相乘，同号为正，异号为负，并把绝对值相乘； （2）任何数同零相乘都得零；（3）几个数相乘，有一个因式为零，积为零；各个因式都不为零，积的符号由负因式的个数决定.11 有理数乘法的运算律： （1）乘法的交换律：ab=ba ；（2）乘法的结合律：（ab ）c=a （bc ）； （3）乘法的分配律：a （b+c ）=ab+ac .12．有理数除法法则：除以一个数等于乘以这个数的倒数；注意：零不能做除数，- 2 -无意义即0a. 13．有理数乘方的法则：（1）正数的任何次幂都是正数；（2）负数的奇次幂是负数；负数的偶次幂是正数；注意：当n 为正奇数时: (-a)n =-a n 或(a -b)n =-(b-a)n , 当n 为正偶数时: (-a)n =a n 或 (a-b)n =(b-a)n . 14．乘方的定义：（1）求相同因式积的运算，叫做乘方；（2）乘方中，相同的因式叫做底数，相同因式的个数叫做指数，乘方的结果叫做幂； 15．科学记数法：把一个大于10的数记成a ³10n 的形式，其中a 是整数数位只有一位的数，这种记数法叫科学记数法.16.近似数的精确位：一个近似数，四舍五入到那一位，就说这个近似数的精确到那一位.17.有效数字：从左边第一个不为零的数字起，到精确的位数止，所有数字，都叫这个近似数的有效数字.18.混合运算法则：先乘方，后乘除，最后加减.第二章、整式的加减 知识概念1．单项式：在代数式中，若只含有乘法（包括乘方）运算。

一、相交线1、两条直线相交，有且只有一个交点。

(反之，若两条直线只有一个交点，则这两条直线相交。

)两条直线相交，产生邻补角和对顶角的概念：邻补角：两角共一边，另一边互为反向延长线。

邻补角互补。

要注意区分互为邻补角与互为补角的异同。

对顶角：两角共顶点，一角两边分别为另一角两边的反向延长线。

对顶角相等。

注：①、同角或等角的余角相等;同角或等角的补角相等;等角的对顶角相等。

反过来亦成立。

②、表述邻补角、对顶角时，要注意相对性，即“互为”，要讲清谁是谁的邻补角或对顶角。

例如：判断对错： 因为∠ABC +∠DBC = 180°，所以∠DBC是邻补角。

( )相等的两个角互为对顶角。

( )2、垂直是两直线相交的特殊情况。

注意：两直线垂直，是互相垂直，即：若线a垂直线b，则线b垂直线a 。

垂足：两条互相垂直的直线的交点叫垂足。

垂直时，一定要用直角符号表示出来。

过一点有且只有一条直线与已知直线垂直。

(注：这一点可以在已知直线上，也可以在已知直线外)3、点到直线的距离。

垂线段：过线外一点，作已知线的垂线，这点到垂足之间的线段叫垂线段。

垂线与垂线段：垂线是一条直线，而垂线段是一条线段，是垂线的一部分。

垂线段最短：连接直线外一点与直线上各点的所有线段中，垂线段最短。

(或说直角三角形中，斜边大于直角边。

)点到直线的距离：直线外一点到这条直线的垂线段的长度，叫这点到直线的距离。

注：距离指的是垂线段的长度，而不是这条垂线段的本身。

所以，如果在判断时，若没有“长度”两字，则是错误的。

4、同位角、内错角、同旁内角三线六面八角：平面内，两条直线被第三条直线所截，将平面分成了六个部分，形成八个角，其中有：4对同位角，2对内错角和2对同旁内角。

注意：要熟练地认识并找出这三种角：① 根据三种角的概念来区分 ②借助模型来区分，即：同位角——F型，内错角——Z型，同旁内角——U型。

特别注意：① 三角形的三个内角均互为同旁内角;② 同位角、内错角、同旁内角的称呼并不一定要建立在两条平行的直线被第三条直线所截的前提上才有的，这两条直线也可以不平行，也同样的有同位角、内错角、同旁内角。

初中数学相交线与平行线知识点总复习含答案一、选择题1．如图所示，b∥c，a⊥b，∠1=130°，则∠2=（）．A．30°B．40°C．50°D．60°【答案】B【解析】【分析】证明∠3=90°，利用三角形的外角的性质求出∠4即可解决问题．【详解】如图，反向延长射线a交c于点M，∵b∥c，a⊥b，∴a⊥c，∴∠3=90°，∵∠1=90°+∠4，∴130°=90°+∠4，∴∠4=40°，∴∠2=∠4=40°，故选B．【点睛】本题考查平行线的性质，垂线的性质，三角形的外角的性质等知识，解题的关键是熟练掌握基本知识2．如图，直线a∥b，直线c分别交a，b于点A，C，∠BAC的平分线交直线b于点D，若∠1=50°，则∠2的度数是()A．50°B．70°C．80°D．110°【答案】C【解析】【分析】根据平行线的性质可得∠BAD=∠1，再根据AD是∠BAC的平分线，进而可得∠BAC的度数，再根据补角定义可得答案．【详解】因为a∥b，所以∠1=∠BAD=50°，因为AD是∠BAC的平分线，所以∠BAC=2∠BAD=100°，所以∠2=180°-∠BAC=180°-100°=80°.故本题正确答案为C.【点睛】本题考查的知识点是平行线的性质，解题关键是掌握两直线平行，内错角相等．3．如图，能判定EB∥AC的条件是（）A．∠C＝∠ABE B．∠A＝∠EBD C．∠C＝∠ABC D．∠A＝∠ABE【答案】D【解析】【分析】在复杂的图形中具有相等关系的两角首先要判断它们是否是同位角或内错角，被判断平行的两直线是否由“三线八角”而产生的被截直线．【详解】A、∠C＝∠ABE不能判断出EB∥AC，故A选项不符合题意；B、∠A＝∠EBD不能判断出EB∥AC，故B选项不符合题意；C、∠C＝∠ABC只能判断出AB＝AC，不能判断出EB∥AC，故C选项不符合题意；D、∠A＝∠ABE，根据内错角相等，两直线平行，可以得出EB∥AC，故D选项符合题意．故选：D．此题考查平行线的性质，正确识别“三线八角”中的同位角、内错角、同旁内角是解题的关键，只有同位角相等、内错角相等、同旁内角互补，才能推出两被截直线平行．4．如图，已知正五边形ABCDE ，AF ∥CD ，交DB 的延长线于点F ，则∠DFA 的度数是（ ）A ．28°B ．30°C ．38°D ．36°【答案】D【解析】【分析】根据两直线平行，内错角相等，得到∠DFA=∠CDB ，根据三角形的内角和求出∠CDB 的度数从而得到∠DFA 的度数.【详解】 解：∠C=(52)1801085︒-⨯=，且CD=CB ， ∴∠CDB=∠CBD ∵由三角形的内角和∠C+∠CDB+∠CBD=180°∴∠CDB+∠CBD=180°-∠C =180°-108°=72°∴∠CDB==∠CBD=72362︒︒= 又∵AF ∥CD∴∠DFA=∠CDB=36°（两直线平行，内错角相等）故选D【点睛】本题主要考查多边形的基本概念和三角形的基本概念，正n 边形的内角读数为(2)180n n-⨯.5．如图，将一张矩形纸片折叠，若170∠=︒，则2∠的度数是（ ）A ．65︒B ．55︒C ．70︒D ．40︒【答案】B【解析】根据平行线的性质求出∠3=170∠=︒，得到∠2+∠4=110°，由折叠得到∠2=∠4即可得到∠2的度数.【详解】∵a ∥b ，∴∠3=170∠=︒，∴∠2+∠4=110°，由折叠得∠2=∠4,∴∠2=55︒，故选：B.【点睛】此题考查平行线的性质，折叠的性质.6．如图，一条公路修到湖边时，需拐弯绕湖而过，如果第一次拐弯处的∠A 是72°，第二次拐弯处的角是∠B ，第三次拐弯处的∠C 是153°，这时道路恰好和第一次拐弯之前的道路平行，则∠B 等于( )A ．81°B ．99°C ．108°D ．120°【答案】B【解析】 试题解析：过B 作BD ∥AE ，∵AE ∥CF ，∴BD ∥CF ，∴72,180A ABD DBC C ∠=∠=∠+∠=o o，∵153C ∠=o ，∴27DBC ∠=o ，则99.ABC ABD DBC ∠=∠+∠=o7．如图，将一张含有30o角的三角形纸片的两个顶点叠放在矩形的两条对边上，若∠的大小为（）∠=o，则1244α-A．14o B．16o C．90α-o D．44o【答案】A【解析】分析：依据平行线的性质，即可得到∠2=∠3=44°，再根据三角形外角性质，可得∠3=∠1+30°，进而得出结论．详解：如图，∵矩形的对边平行，∴∠2=∠3=44°，根据三角形外角性质，可得：∠3=∠1+30°，∴∠1=44°﹣30°=14°．故选A．点睛：本题主要考查了平行线的性质以及三角形外角性质的运用，解题时注意：两直线平行，同位角相等．8．下列结论中：①若a=b a b；②在同一平面内，若a⊥b，b//c，则a⊥c；③直线外一点到直线的垂线段叫点到直线的距离；33( ) A．1个B．2个C．3个D．4个【答案】B【解析】【分析】【详解】≥a b解：①若a=b0②在同一平面内，若a⊥b,b//c，则a⊥c，正确③直线外一点到直线的垂线段的长度叫点到直线的距离33正确的个数有②④两个9．下列命题是真命题的是（ ）A ．同位角相等B ．对顶角互补C ．如果两个角的两边互相平行，那么这两个角相等D ．如果点P 的横坐标和纵坐标互为相反数，那么点P 在直线y x =-的图像上．【答案】D【解析】【分析】根据平行线的性质定理对A 、C 进行判断；利用对顶角的性质对B 进行判断；根据直角坐标系下点坐标特点对D 进行判断．【详解】A ．两直线平行，同位角相等，故A 是假命题；B ．对顶角相等，故B 是假命题；C ．如果两个角的两边互相平行，那么这两个角相等或互补，故C 是假命题；D ．如果点的横坐标和纵坐标互为相反数，那么点P 在直线y x =-的图像上，故D 是真命题故选：D【点睛】本题考查了真命题与假命题，正确的命题称为真命题，错误的命题称为假命题．利用了平行线性质、对顶角性质、直角坐标系中点坐标特点等知识点．10．如图，AB CD ∥，BF 平分ABE ∠，且BF DE P ，则ABE ∠与D ∠的关系是（ ）A ．2ABE D ∠=∠B ．180ABE D ∠+∠=︒C ．90ABED ∠=∠=︒D ．3ABE D ∠=∠【答案】A【解析】【分析】 延长DE 交AB 的延长线于G ，根据两直线平行，内错角相等可得D G ∠=∠，再根据两直线平行，同位角相等可得G ABF ∠=∠，然后根据角平分线的定义解答．【详解】证明：如图，延长DE 交AB 的延长线于G ，//AB CD Q ，D G ∴∠=∠，//BF DE Q ，G ABF ∴∠=∠，D ABF ∴∠=∠，BF Q 平分ABE ∠，22ABE ABF D ∴∠=∠=∠，即2ABE D ∠=∠．故选：A ．【点睛】本题考查了平行线的性质，角平分线的定义，熟记性质并作辅助线是解题的关键．11．如图，已知AB CD ∥，ABE ∠和CDE ∠的平分线相交于F ，100BED ∠=︒，则BFD ∠的度数为（ ）A ．100°B ．130°C ．140°D ．160°【答案】B【解析】【分析】 连接BD ，因为AB ∥CD ，所以∠ABD ＋∠CDB ＝180°；又由三角形内角和为180°，所以∠ABE ＋∠E ＋∠CDE ＝180°＋180°＝360°，所以∠ABE ＋∠CDE ＝360°−100°＝260°；又因为BF 、DF 平分∠ABE 和∠CDE ，所以∠FBE ＋∠FDE ＝130°，又因为四边形的内角和为360°，进而可得答案．【详解】连接BD ，∵AB∥CD，∴∠ABD＋∠CDB＝180°，∴∠ABE＋∠E＋∠CDE＝180°＋180°＝360°，∴∠ABE＋∠CDE＝360°−100°＝260°，又∵BF、DF平分∠ABE和∠CDE，∴∠FBE＋∠FDE＝130°，∴∠BFD＝360°−100°−130°＝130°，故选B．【点睛】此题考查了平行线的性质：两直线平行，同旁内角互补．还考查了三角形内角和定理与四边形的内角和定理．解题的关键是作出BD这条辅助线．12．如图，BE平分∠DBC，点A是BD上一点，过点A作AE∥BC交BE于点E，∠DAE=56°，则∠E的度数为（）A．56°B．36°C．26°D．28°【答案】D【解析】分析：根据平行线的性质，可得∠DBC=56°，∠E=∠EBC，根据角平分线的定义，可得∠EBC=12∠DBC=28°，进而得到∠E=28°．详解：∵AE∥BC,∠DAE=56°，∴∠DBC=56°，∠E=∠EBC，∵BE平分∠DBC，∴∠EBC=12∠DBC=28°，∴∠E=28°，故选D.点睛：本题主要考查了角平分线的定义和平行线的性质，熟练掌握角平分线的定义和平行线的性质是解题的关键.13．如图，直线AB，CD相交于点O，∠2－∠1=15°，∠3=130°．则∠2的度数是()A．37.5°B．75°C．50°D．65°【答案】D【解析】【分析】先根据条件和邻补角的性质求出∠1的度数，然后即可求出∠2的度数．【详解】）∵∠3=130°，∠1+∠3=180°，∴∠1=180°-∠3=50°，∵∠2-∠1=15°，∴∠2=15°+∠1=65°；故答案为D.【点睛】本题考查角的运算，邻补角的性质，比较简单.14．给出下列说法,其中正确的是( )A．两条直线被第三条直线所截，同位角相等；B．平面内的一条直线和两条平行线中的一条相交，则它与另一条也相交；C．相等的两个角是对顶角；D．从直线外一点到这条直线的垂线段，叫做这点到直线的距离．【答案】B【解析】【分析】正确理解对顶角、同位角、相交线、平行线、点到直线的距离的概念，逐一判断．【详解】A选项：同位角只是一种位置关系，只有两条直线平行时，同位角相等，错误；B选项：强调了在平面内，正确；C选项：不符合对顶角的定义，错误；D选项：直线外一点到这条直线的垂线段的长度，叫做点到直线的距离，不是指点到直线的垂线段的本身，而是指垂线段的长度．故选：B.【点睛】对平面几何中概念的理解，一定要紧扣概念中的关键词语，要做到对它们正确理解，对不同的几何语言的表达要注意理解它们所包含的意义，要善于区分不同概念之间的联系和区别．15．把一副三角板放在同一水平桌面上，摆放成如图所示的形状，使两个直角顶点重合，两条斜边平行，则∠1的度数是（ ）A ．45°B ．60°C ．75°D ．82.5°【答案】C【解析】【分析】直接利用平行线的性质结合已知角得出答案．【详解】如图，作直线l 平行于直角三角板的斜边，可得：∠3=∠2=45°，∠4=∠5=30°，故∠1的度数是：45°+30°=75°，故选C ．【点睛】本题主要考查了平行线的性质，正确作出辅助线是解题关键．16．已知α∠的两边与β∠的两边分别平行，且α∠=20°，则∠β的度数为( ) A ．20° B ．160° C ．20°或160° D ．70°【答案】C【解析】【分析】分两种情况，画出图形，结合平行线的性质求解即可.【详解】如图1，∵a ∥b ；∴∠1=α∠=20°，∵c ∥d∴∠β=∠1=20°；如图2，∵a ∥b ；∴∠1=α∠=20°，∵c ∥d∴∠β=180°-∠1=160°；故选C.【点睛】本题考查了平行线的性质：①两直线平行同位角相等，②两直线平行内错角相等，③两直线平行同旁内角互补.在运用平行线的性质定理时，一定要找准同位角，内错角和同旁内角.本题也考查了分类讨论的数学思想.17．如图，在ABC V 中，AB AC =，30A ∠=︒，直线a b ∥，顶点C 在直线b 上，直线a 交AB 于点D ，交AC 与点E ，若1145∠=︒，则2∠的度数是（ ）A ．30°B ．35°C ．40°D ．45°【答案】C【解析】【分析】 先根据等腰三角形的性质和三角形内角和可得ACB ∠度数，由三角形外角的性质可得AED ∠的度数，再根据平行线的性质得同位角相等，即可求得2∠．【详解】∵AB AC =，且30A ∠=︒， ∴18030752ACB ∠︒-︒==︒， 在ADE ∆中，∵1145A AED ∠∠∠=+=︒，∴14514530115AED A ∠∠=︒-=︒-︒=︒，∵//a b ，∴2AED ACB ∠∠∠=+，即21157540∠=︒-︒=︒，故选：C ．【点睛】 本题考查综合等腰三角形的性质、三角形内角和定理、三角形外角的性质以及平行直线的性质等知识内容．等腰三角形的性质定理：等腰三角形两底角相等；三角形内角和定理：三角形三个内角的和等于180︒；三角形外角的性质：三角形的外角等于与它不相邻的两个内角之和；两直线平行，同位角相等．18．下列图形中线段PQ 的长度表示点P 到直线a 的距离的是（ ）A ．B ．C ．D ．【答案】C【解析】【分析】 根据点到直线的距离的定义，可得答案．【详解】由题意得PQ ⊥a ，P 到a 的距离是PQ 垂线段的长，故选C ．【点睛】本题考查了点到直线的距离，点到直线的距离是解题关键．19．在下图中，∠1,∠2是对顶角的图形是（ ）A ．B ．C ．D ．【答案】B【解析】略20．如图，四边形ABCD 中，//,,AB CD AD CD E F =、分别是AB BC 、的中点，若140,∠=︒则D ∠=（ ）A ．40︒B ．100︒C ．80︒D ．110︒【答案】B【解析】【分析】利用E、F分别是线段BC、BA的中点得到EF是△BAC的中位线，得出∠CAB的大小，再利用CD∥AB得到∠DCA的大小，最后在等腰△DCA中推导得到∠D.【详解】∵点E、F分别是线段CB、AB的中点，∴EF是△BAC的中位线∴EF∥AC∵∠1=40°，∴∠CAB=40°∵CD∥BA∴∠DCA=∠CAB=40°∵CD=DA∴∠DAC=∠DCA=40°∴在△DCA中，∠D=100°故选：B【点睛】本题考查中位线的性质和平行线的性质，解题关键是推导得出EF是△ABC的中位线.。

初中数学第五章 相交线与平行线知识点-+典型题附解析一、选择题1．如图，直线a ，b 被直线c 所截，且a//b ，若∠1=55°，则∠2等于（ ）A ．35°B ．45°C ．55°D ．125°2．如图，直角三角形ABC 的直角边AB =6，BC =8，将直角三角形ABC 沿边BC 的方向平移到三角形DEF 的位置，DE 交AC 于点G ，BE =2，三角形CEG 的面积为13.5，下列结论：①三角形ABC 平移的距离是4；②EG =4.5；③AD ∥CF ；④四边形ADFC 的面积为6．其中正确的结论是A ．①②B ．②③C ．③④D ．②④ 3．如图，在ABC 中，//EF BC ，ED 平分BEF ∠，且70∠︒=DEF ，则B 的度数为（ ）A ．70°B ．60°C ．50°D ．40°4．如图，已知AB ∥CD, EF ∥CD ，则下列结论中一定正确的是( )A ．∠BCD= ∠DCE;B ．∠ABC+∠BCE+∠CEF=360︒;C ．∠BCE+∠DCE=∠ABC+∠BCD;D ．∠ABC+∠BCE -∠CEF=180︒.5．下列说法中正确的是（ ）A．两条射线组成的图形叫做角B．小于平角的角可分为锐角和钝角两类C．射线就是直线D．两点之间的所有连线中，线段最短6．如下图，在下列条件中，能判定AB//CD的是( )A．∠1=∠3 B．∠2=∠3 C．∠1=∠4 D．∠3=∠47．下列语句是命题的是 ( )（1）两点之间，线段最短；（2）如果两个角的和是180度，那么这两个角互补；（3）请画出两条互相平行的直线；（4）一个锐角与一个钝角互补吗?A．（1）（2）B．（3）（4）C．（2）（3）D．（1）（4）8．下面是投影屏上出示的抢答题，需要回答横线上符号代表的内容，则回答正确的是（）已知：如图，∠BEC＝∠B+∠C，求证：AB∥CD证明：延长BE交__※__于点F，则∠BEC＝__⊙__+∠C又∵∠BEC＝∠B+∠C，∴∠B＝▲∴AB∥CD（__□__相等，两直线平行）A．⊙代表∠FEC B．□代表同位角C．▲代表∠EFC D．※代表AB 9．下列各命题中，属于假命题的是（）A．若0a b-＞，则a b＞B．若0a b-=，则0ab≥C．若0a b-＜，则a b＜D．若0a b-≠，则0ab≠10．如图，给出下列条件：①∠1＝∠2：②∠3＝∠4：③AB∥CE，且∠ADC＝∠B：④AB∥CE，且∠BCD＝∠BAD．其中能推出BC∥AD的条件为（）A．①②B．②④C．②③D．②③④二、填空题11．如图，//AB CD，GF与AB相交于点H，与CD 于F，FE平分HFD∠，若50EHF ∠=︒，则HFE ∠的度数为______．12．一副三角尺按如图所示叠放在一起，其中点,B D 重合，若固定三角形AOB ，将三角形ACD 绕点A 顺时针旋转一周，共有 _________次 出现三角形ACD 的一边与三角形AOB 的某一边平行．13．设a 、b 、c 为平面上三条不同直线，（1）若//,//a b b c ，则a 与c 的位置关系是_________；（2）若,a b b c ⊥⊥，则a 与c 的位置关系是_________；（3）若//a b ，b c ⊥，则a 与c 的位置关系是________．14．如图，把直角梯形ABCD 沿AD 方向平移到梯形EFGH ，28HG cm =，5MG cm =，4MC cm =，则阴影部分的面积是___15．如图，直线a ∥b ∥c ，直角∠BAC 的顶点A 在直线b 上，两边分别与直线a ，c 相交于点B ，C ，则∠1＋∠2的度数是___________．16．如果一张长方形的纸条，如图所示折叠，那么∠α等于____．17．如图，AB ∥CD ，∠B ＝75°，∠E ＝27°，则∠D 的度数为_____．18．如图，AD ∥BC ，∠D=100°，CA 平分∠BCD ，则∠DAC=________度．19．如图，CB ∥OA ，∠B ＝∠A ＝100°，E 、F 在CB 上，且满足∠FOC ＝∠AOC ，OE 平分∠BOF ，若平行移动AC ，当∠OCA 的度数为_____时，可以使∠OEB ＝∠OCA ．20．如图，直线////a b c ，直角三角板的直角顶点落在直线b 上，若135∠=︒，则2∠等于_______．三、解答题21．（感知）如图①，AB ∥CD ，点E 在直线AB 与CD 之间，连结AE 、BE ，试说明∠BAE+∠DCE=∠AEC ；（探究）当点E 在如图②的位置时，其他条件不变，试说明∠AEC+∠BAE+∠DCE=360°； （应用）点E 、F 、G 在直线AB 与CD 之间，连结AE 、EF 、FG 和CG ，其他条件不变，如图③，若∠EFG=36°，则∠BAE+∠AEF+∠FGC+∠DCG=______°.22．已知：直线l 分别交AB 、CD 与E 、F 两点，且AB ∥CD ．（1） 说明：∠1=∠2；（2） 如图2，点M 、N 在AB 、CD 之间，且在直线l 左侧，若∠EMN +∠FNM =260°， ①求：∠AEM +∠CFN 的度数；②如图3，若EP 平分∠AEM ，FP 平分∠CFN ，求∠P 的度数；（3） 如图4，∠2=80°，点G 在射线EB 上，点H 在AB 上方的直线l 上，点Q 是平面内一点，连接QG 、QH ，若∠AGQ =18°，∠FHQ =24°，直接写出∠GQH 的度数．23．问题情境：如图1，AB CD ，130PAB ∠=，120PCD ∠=．求 APC ∠ 度数． 小明的思路是：如图2，过 P 作 PE AB ，通过平行线性质，可得5060110APC ∠=+=．问题迁移：（1）如图3，AD BC ，点 P 在射线 OM 上运动，当点 P 在 A 、 B 两点之间运动时，ADP α∠=∠，BCP β∠=∠．CPD ∠ 、 α∠ 、 β∠ 之间有何数量关系?请说明理由；（2）在（1）的条件下，如果点 P 在 A 、 B 两点外侧运动时（点 P 与点 A 、 B 、 O 三点不重合），请你直接写出 CPD ∠ 、 α∠ 、 β∠ 间的数量关系．24．问题情境：如图1，AB CD ∥，130PAB ∠=︒，120PCD ∠=︒，求APC ∠的度数．小明的思路是：如图2，过P 作PE AB ，通过平行线性质，可得APC ∠=______． 问题迁移：如图3，AD BC ∥，点P 在射线OM 上运动，ADP α∠=∠，BCP β∠=∠．（1）当点P 在A 、B 两点之间运动时，CPD ∠、α∠、β∠之间有何数量关系？请说明理由．（2）如果点P 在A 、B 两点外侧运动时（点P 与点A 、B 、O 三点不重合），请你直接写出CPD ∠、α∠、β∠之间有何数量关系．25．将一副三角板中的两个直角顶点C 叠放在一起（如图①），其中30A ∠=︒，60B ∠=︒，45D E ∠=∠=︒.（1）猜想BCD ∠与ACE ∠的数量关系，并说明理由；（2）若3BCD ACE ∠=∠，求BCD ∠的度数；（3）若按住三角板ABC 不动，绕顶点C 转动三角DCE ，试探究BCD ∠等于多少度时//CE AB ，并简要说明理由.26．如图1，已知直线PQ ∥MN ，点A 在直线PQ 上，点C 、D 在直线MN 上，连接AC 、AD ，∠PAC ＝50°，∠ADC ＝30°，AE 平分∠PAD ，CE 平分∠ACD ，AE 与CE 相交于E ． （1）求∠AEC 的度数；（2）若将图1中的线段AD 沿MN 向右平移到A 1D 1如图2所示位置，此时A 1E 平分∠AA 1D 1，CE 平分∠ACD 1，A 1E 与CE 相交于E ，∠PAC ＝50°，∠A 1D 1C ＝30°，求∠A 1EC 的度数．（3）若将图1中的线段AD 沿MN 向左平移到A 1D 1如图3所示位置，其他条件与（2）相同，求此时∠A 1EC 的度数．【参考答案】***试卷处理标记，请不要删除一、选择题1．C解析：C【解析】试题分析：根据图示可得：∠1和∠2是同位角，根据两直线平行，同位角相等可得：∠2=∠1=55°.考点：平行线的性质2．B解析：B【解析】分析：(1)对应线段的长度即是平移的距离；(2)根据EC 的长和△CEG 的面积求EG ；(3)平移前后，对应点的连线平行且相等；(4)根据平行四边形的面积公式求.详解：(1)因为点B ，E 是对应点，且BE ＝2，所以△ABC 平行的距离是2，则①错误； ②根据题意得，13.5×2＝(8－2)EG ，解得EG ＝4.5，则②正确；③因为A ，D 是对应点，C ，F 是对应点，所以AD ∥CF ，则③正确；④平行四边形ADFC 的面积为AB ·CF ＝AB ·BE ＝6×2＝12，则④错误.故选B .点睛：本题考查了平移的性质，平移的性质有：①平移只改变图形的位置，不改变图形的形状和大小；②平移得到的图形与原图形中的对应线段平行(或在同一条直线上)且相等，对应角相等；对应点连线平行(或在同一条直线上)且相等.3．D解析：D【分析】由角平分线的定义求出∠BEF=140°，再根据平行线的性质“两直线平行，同旁内角互补”求出∠B 的度数即可.【详解】∵ED 平分BEF ∠，且70∠︒=DEF ，∴70DEB ∠=︒∴270140BEF ︒=∠=⨯︒∵//EF BC∴180B BEF ∠+∠=︒∴180********B BEF ∠=︒-∠=︒-︒=︒故选D【点睛】此题主要考查了平行线的性质和角平分的性质，此题难度不大，注意掌握相关性质的运用4．D解析：D【解析】分析：根据平行线的性质，找出图形中的同旁内角、内错角即可判断.详解：延长DC 到H∵AB ∥CD ，EF ∥CD∴∠ABC+∠BCH=180°∠ABC=∠BCD∠CE+∠DCE=180°∠ECH=∠FEC∴∠ABC+∠BCE+∠CEF=180°+∠FEC∠ABC+∠BCE -∠CEF=∠ABC+∠BCH+∠ECH-∠CEF=180°.故选D.点睛：此题主要考查了平行线的性质，关键是熟记平行线的性质：两直线平行，内错角相等，同旁内角互补，同位角相等.5．D解析：D【解析】根据真假命题的概念，可知：A 、有公共端点的两条射线组成的图形叫做角，选项错误；B 、小于平角的角可分为锐角、钝角，还应包含直角，选项错误．C 、射线是直线的一部分，选项错误；D 、两点之间的所有连线中，线段最短，选项正确；故选：D ．6．C解析：C【解析】根据平行线的判定，可由∠2=∠3，根据内错角相等，两直线平行，得到AD ∥BC ，由∠1=∠4，得到AB∥CD.故选C.7．A解析：A【分析】根据命题的定义对四句话进行判断．【详解】解：（1）两点之间，线段最短，它是命题；（2）如果两个角的和是90度，那么这两个角互余，它是命题；（3）请画出两条互相平行的直线，它不是命题；（4）一个锐角与一个钝角互补吗？，它不是命题．所以，是命题的为（1）（2），故选：A．【点睛】本题考查了命题与定理：判断一件事情的语句，叫做命题．许多命题都是由题设和结论两部分组成，题设是已知事项，结论是由已知事项推出的事项，一个命题可以写成如果…那么…形式．有些命题的正确性是用推理证实的，这样的真命题叫做定理．8．C解析：C【分析】延长BE交CD于点F，利用三角形外角的性质可得出∠BEC＝∠EFC+∠C，结合∠BEC＝∠B+∠C可得出∠B＝∠EFC，利用“内错角相等，两直线平行”可证出AB∥CD，找出各符号代表的含义，再对照四个选项即可得出结论．【详解】证明：延长BE交CD于点F，则∠BEC＝∠EFC+∠C．又∵∠BEC＝∠B+∠C，∴∠B＝∠EFC，∴AB∥CD（内错角相等，两直线平行）．∴※代表CD，⊙代表∠EFC，▲代表∠EFC，□代表内错角．故选：C．【点睛】本题考查了平行线的判定以及三角形外角的性质，利用各角之间的关系，找出∠B＝∠EFC 是解题的关键．9．D解析：D【分析】根据不等式的性质对各选项进行逐一判断即可．【详解】A、正确，符合不等式的性质；B、正确，符合不等式的性质．C、正确，符合不等式的性质；D、错误，例如a=2，b=0；故选D．【点睛】考查了命题与定理的知识，解题的关键是了解不等式的性质，难度不大．10．D解析：D【分析】根据平行线的判定条件，逐一判断，排除错误答案．【详解】解：①∵∠1＝∠2，∴AB∥CD，不符合题意；②∵∠3＝∠4，∴BC∥AD，符合题意；③∵AB∥CD，∴∠B+∠BCD＝180°，∵∠ADC＝∠B，∴∠ADC+∠BCD＝180°，由同旁内角互补，两直线平行可得BC∥AD，故符合题意；④∵AB∥CE，∴∠B+∠BCD＝180°，∵∠BCD＝∠BAD，∴∠B+∠BAD＝180°，由同旁内角互补，两直线平行可得BC∥AD，故符合题意；故能推出BC∥AD的条件为②③④．故选：D．【点睛】本题考查了平行线的判定，关键是掌握判定定理：同位角相等，两直线平行．内错角相等，两直线平行．同旁内角互补，两直线平行．二、填空题11．65°【分析】由AB//CD可得∠HFD=130︒，再由FE平分∠HFD可求出∠HFE．【详解】∵∴∠EHF+∠HFD=180°∵∴∠HFD=130°∵平分，∴∠HFE=∠HFD=解析：65°【分析】由AB//CD 可得∠HFD=130︒，再由FE 平分∠HFD 可求出∠HFE ．【详解】∵//AB CD∴∠EHF+∠HFD=180°∵50EHF ∠=︒∴∠HFD=130°∵FE 平分HFD ∠，∴∠HFE=12∠HFD=1130652⨯︒=︒ 故答案为：65°．【点睛】此题主要考查了平行线的性质以及角平分线的定义，熟练掌握平行线的性质以及角平分线的定义是解题的关键．12．【分析】要分类讨论，不要漏掉任何一种情况，也可实际用三角板操作找到它们之间的关系，再计算．【详解】解：分8种情况讨论：（1）如图1，AD 边与OB 边平行时，∠BAD＝45°；（2）如图2，解析：8【分析】要分类讨论，不要漏掉任何一种情况，也可实际用三角板操作找到它们之间的关系，再计算．【详解】解：分8种情况讨论：（1）如图1，AD 边与OB 边平行时，∠BAD ＝45°；（2）如图2，当AC 边与OB 平行时，∠BAD ＝90°+45°＝135°；（3）如图3，DC 边与AB 边平行时，∠BAD ＝60°+90°＝150°，（4）如图4，DC 边与OB 边平行时，∠BAD ＝135°+30°＝165°，（5）如图5，DC 边与OB 边平行时，∠BAD ＝45°﹣30°＝15°；（6）如图6，DC 边与AO 边平行时，∠BAD ＝15°+90°＝105°（7）如图7，DC 边与AB 边平行时，∠BAD ＝30°，（8）如图8，DC边与AO边平行时，∠BAD＝30°+45°＝75°；综上所述：∠BAD的所有可能的值为：15°，30°，45°，75°，105°，135°，150°，165°．故答案为：8．【点睛】本题考查了平行线的性质及判定，画出所有符合题意的示意图是解决本题的关键．13．平行平行垂直【解析】根据平行公理的推论，可由，得出a∥c；根据垂直的性质以及平行线的判定，可由，得到a∥c；根据，，得到a⊥c.故答案为平行，平行，垂直.点睛：由平解析：平行 平行 垂直【解析】根据平行公理的推论，可由//,//a b b c ，得出a ∥c ；根据垂直的性质以及平行线的判定，可由,a b b c ⊥⊥，得到a∥c；根据//a b ，b c ⊥，得到a⊥c.故答案为平行，平行，垂直.点睛：由平行于同一条直线的两条直线互相平行，可求解（1）,因为在同一平面内，垂直于同一条直线的两条直线互相平行，可求解（2），再根据平行线的性质可求解（3）． 14．130cm2．【分析】根据平移的性质可知梯形EFGH≌梯形ABCD ，那么GH=CD ，BC=FG ，观察可知梯形EFMD 是两个梯形的公共部分，那么阴影部分的面积就等于梯形MGHD ，再根据梯形的面积计解析：130cm 2．【分析】根据平移的性质可知梯形EFGH ≌梯形ABCD ，那么GH=CD ，BC=FG ，观察可知梯形EFMD 是两个梯形的公共部分，那么阴影部分的面积就等于梯形MGHD ，再根据梯形的面积计算公式计算即可．【详解】解：∵直角梯形EFGH 是由直角梯形ABCD 平移得到的，∴梯形EFGH ≌梯形ABCD ，∴GH=CD ，BC=FG ，∵梯形EFMD 是两个梯形的公共部分，∴S 梯形ABCD -S 梯形EFMD =S 梯形EFGH -S 梯形EFMD ，∴S 阴影=S 梯形MGHD =12（DM+GH ）•GM=12（28-4+28）×5=130（cm 2）． 故答案是130cm 2．【点睛】本题考查了图形的平移，解题的关键是知道平移前后的两个图形全等．15．270°【分析】根据题目条件可知∠1+∠3=∠2+∠4=180°，再结合∠BAC 是直角即可得出结果．【详解】解：如图所示，∵a∥b，∴∠1+∠3=180°，则∠3=180°-∠1，∵解析：270°【分析】根据题目条件可知∠1+∠3=∠2+∠4=180°，再结合∠BAC是直角即可得出结果．【详解】解：如图所示，∵a∥b，∴∠1+∠3=180°，则∠3=180°-∠1，∵b∥c∴∠2+∠4=180°，则∠4=180°-∠2，∵∠BAC是直角，∴∠3+∠4=180°-∠1+180°-∠2，∴90°=360°-（∠1+∠2），∴∠1+∠2=270°．故答案为：270°【点睛】本题主要考查的是平行线的性质，掌握平行线的性质是解题的关键．16．70°．【分析】依据平行线的性质，可得∠BAE=∠DCE=140°，依据折叠即可得到∠α=70°．【详解】解：如图，∵AB∥CD，∴∠BAE=∠DCE=140°，由折叠可得：，∴∠解析：70°．【分析】依据平行线的性质，可得∠BAE=∠DCE=140°，依据折叠即可得到∠α=70°．【详解】解：如图，∵AB∥CD，∴∠BAE=∠DCE=140°，由折叠可得：12DCF DCE ∠=∠，∴∠α=70°．故答案为：70°．【点睛】本题主要考查了平行线的性质，解题时注意：两直线平行，同位角相等．17．48°【分析】将BE与CD交点记为点F，由两直线平行同位角相等得出∠EFC度数，再利用三角形外角的性质可得答案．【详解】解：如图所示，将BE与CD交点记为点F，∵AB∥CD，∠B＝75°解析：48°【分析】将BE与CD交点记为点F，由两直线平行同位角相等得出∠EFC度数，再利用三角形外角的性质可得答案．【详解】解：如图所示，将BE与CD交点记为点F，∵AB∥CD，∠B＝75°，∴∠EFC＝∠B＝75°，又∵∠EFC＝∠D+∠E，且∠E＝27°，∴∠D＝∠EFC﹣∠E＝75°﹣27°＝48°，故答案为：48°．【点睛】本题考查平行线的性质和三角形外角性质，解题的关键是掌握两直线平行，同位角相等这一性质．18．40°【分析】本题主要利用两直线平行，同旁内角互补、两直线平行，内错角相等以及角平分线的定义进行做题．【详解】∵AD∥BC，∴∠BCD=180°-∠D=80°，又∵CA平分∠BCD，∴解析：40°【分析】本题主要利用两直线平行，同旁内角互补、两直线平行，内错角相等以及角平分线的定义进行做题．【详解】∵AD∥BC，∴∠BCD=180°-∠D=80°，又∵CA平分∠BCD，∴∠ACB=12∠BCD=40°，∴∠DAC=∠ACB=40°．【点睛】本题重点考查了平行线的性质及角平分线的定义，是一道较为简单的题目．19．60°【分析】设∠OCA=a,∠AOC=x,利用三角形外角，内角和定理，平行线定理即可解答. 【详解】解：设∠OCA=a,∠AOC=x,已知CB∥OA，∠B=∠A=100°，即a+x=80解析：60°【分析】设∠OCA=a,∠AOC=x,利用三角形外角，内角和定理，平行线定理即可解答.【详解】解：设∠OCA=a,∠AOC=x,已知CB∥OA，∠B=∠A=100°，即a+x=80°，又因为∠OEB=∠EOC+∠ECO=40°+x.当∠OEB=∠OCA，a=80°-x,40°+x=a,解得∠OCA=60°.【点睛】本题考查角度变换和平行线定理的综合运用，熟悉掌握是解题关键.20．【分析】如图，利用平行线的性质得出∠3=35°，然后进一步得出∠4的度数，从而再次利用平行线性质得出答案即可.【详解】如图所示，∵，，∴，∴∠4=90°−∠3=55°，∵，∴∠2解析：55︒【分析】如图，利用平行线的性质得出∠3=35°，然后进一步得出∠4的度数，从而再次利用平行线性质得出答案即可.【详解】如图所示，∵//a b ，135∠=︒，∴335∠=︒，∴∠4=90°−∠3=55°，∵////a b c ，∴∠2=∠4=55°.故答案为：55°.【点睛】本题主要考查了平行线的性质，熟练掌握相关概念是解题关键.三、解答题21．【感知】见解析；【探究】∠BAE+∠AEC+∠DCE=360°；【应用】396°.【分析】感知：如图①，过点E作EF∥AB．利用平行线的性质即可解决问题；探究：如图2中，作EG∥AB，利用平行线的性质即可解决问题；应用：作FH∥AB，利用平行线的性质即可解决问题；【详解】解：理由如下，【感知】过E点作EF//AB∵AB//CD∴EF//CD∵AB//CD∴∠BAE=∠AEF∵EF//CD∴∠CEF=∠DCE∴∠BAE+∠DCE=∠AEC.【探究】过E点作AB//EG.∵AB//CD∴EG//CD∵AB//CD∴∠BAE+∠AEG=180°∵EG//CD∴∠CEG+∠DCE=180°∴∠BAE+∠AEC+∠DCE=360°【应用】过点F作FH∥AB.∵AB ∥CD ，∴FH ∥CD ，∴∠BAE+∠AEF+∠EFH=360°，∠HFG+∠FGC+∠GCD=360°，∴∠BAE+∠AEF+∠EFH+∠HFG+∠FGC+∠GCD=720°，∴∠BAE+∠AEF+∠EFH+∠HFG+∠FGC+∠GCD+∠EFG=720°+36°，∴∠BAE+∠AEF+∠FGC+∠DCG=720°-360°+36°=396°故答案为396°.【点睛】本题考查平行线的性质，解题的关键是学会添加辅助线构造平行线解决问题，属于中考常考题型．22．（1）理由见解析；（2）①80°，②40°；（3）38°、74°、86°、122°．【分析】（1）根据平行线的性质及对顶角的性质即可得证；（2）①过拐点作AB 的平行线，根据平行线的性质推理即可得到答案；②过点P 作AB 的平行线，根据平行线的性质及角平分线的定义求得角的度数； （3）分情况讨论，画出图形，根据三角形的内角和与外角的性质分别求出答案即可．【详解】（1）//AB CD1EFD ∴∠=∠，2EFD ∠=∠12∠∠∴=； （2）①分别过点M ，N 作直线GH ，IJ 与AB 平行，则//////AB CD GH IJ ，如图：AEM EMH ∴∠=∠，CFN FNJ ∠=∠，180HMN MNJ ∠+∠=︒，()80AEM CFN EMH FNJ EMN MNF HMN MNJ ∴∠+∠=∠+∠=∠+∠-∠+∠=︒；②过点P 作AB 的平行线，根据平行线的性质可得：3AEP ∠=∠，4CFP ∠=∠， ∵EP 平分∠AEM ，FP 平分∠CFN ， ∴11344022AEP CFP AEM CFM ∠+∠=∠+∠=∠+∠=︒， 即40P ∠=︒；（3）分四种情况进行讨论：由已知条件可得80BEH ∠=︒，①如图：118082EPG BEH AGQ ∠=︒-∠-∠=︒182HPQ EPG ∴∠=∠=︒11118074GQ H EHQ HPQ ∴∠=︒-∠-∠=︒ ②如图：104 BPH FHP BEH∠=∠+∠=︒，22122BQ H BPH AGQ∴∠=∠+∠=︒；③如图：56BPH BEH FHP∠=∠-∠=︒，3338BQ H BPH AGQ∴∠=∠-∠=︒；④如图：104BPH BEH FHP ∠=∠+∠=︒ ，4486GQ H BPH AGQ ∴∠=∠-∠=︒；综上所述，∠GQH 的度数为38°、74°、86°、122°．【点睛】本题考查平行线的性质，三角形外角的性质等内容，解题的关键是掌握辅助线的作法以及分类讨论的思想．23．（1）∠CPD=∠α+∠β，理由见解析；（2）①当点P 在A 、M 两点之间时，∠CPD=∠β−∠α；②当点P 在B 、O 两点之间时，∠CPD=∠α−∠β【分析】（1）过点P 作PE ∥AD 交CD 于点E ，根据题意得出AD ∥PE ∥BC ，从而利用平行线性质可知α∠=∠DPE ，β∠=∠CPE ，据此进一步证明即可；（2）根据题意分当点P 在A 、M 两点之间时以及当点P 在B 、O 两点之间时两种情况逐一分析讨论即可.【详解】（1）∠CPD=αβ∠+∠，理由如下：如图3，过点P 作PE ∥AD 交CD 于点E ，∵AD ∥BC ，PE ∥AD ，∴AD ∥PE ∥BC ，∴α∠=∠DPE ，β∠=∠CPE ，∴∠CPD=∠DPE +∠CPE=αβ∠+∠；（2）①当点P 在A 、M 两点之间时，∠CPD=βα∠-∠，理由如下：如图4，过点P 作PE ∥AD 交CD 于点E ，∵AD ∥BC ，PE ∥AD ，∴AD ∥PE ∥BC ，∴α∠=∠EPD ，β∠=∠CPE ，∴∠CPD=∠CPE −∠EPD=βα∠-∠；②当点P 在B 、O 两点之间时，∠CPD=αβ∠-∠，理由如下：如图5，过点P 作PE ∥AD 交CD 于点E ，∵AD ∥BC ，PE ∥AD ，∴AD ∥PE ∥BC ，∴α∠=∠DPE ，β∠=∠CPE ，∴∠CPD=∠DPE −∠CPE=αβ∠-∠，综上所述，当点P 在A 、M 两点之间时，∠CPD=∠β−∠α；当点P 在B 、O 两点之间时，∠CPD=∠α−∠β.【点睛】本题主要考查了在平行线性质及判定的综合运用，熟练掌握相关概念是解题关键.24．110︒；（1）CPD αβ∠=∠+∠；理由见解析；（2）当点P 在B 、O 两点之间时，CPD αβ∠=∠-∠；当点P 在射线AM 上时，CPD βα∠=∠-∠．【分析】问题情境：理由平行于同一条直线的两条直线平行得到 PE ∥AB ∥CD ，通过平行线性质来求∠APC ．（1）过点P 作PQ AD ，得到PQ AD BC 理由平行线的性质得到ADP DPQ ∠=∠，BCP CPQ ∠=∠，即可得到CPD DPQ CPQ ADP BCP αβ∠=∠+∠=∠+∠=∠+∠（2）分情况讨论当点P 在B 、O 两点之间，以及点P 在射线AM 上时，两种情况，然后构造平行线，利用两直线平行内错角相等，通过推理即可得到答案．【详解】解：问题情境：∵AB ∥CD ，PE AB∴PE ∥AB ∥CD ， ∴∠A+∠APE=180°，∠C+∠CPE=180°，∵∠PAB=130°，∠PCD=120°，∴∠APE=50°，∠CPE=60°，∴∠APC=∠APE+∠CPE=50°+60°=110°；（1）CPD αβ∠=∠+∠过点P 作PQ AD .又因为AD BC ∥,所以PQ AD BC则ADP DPQ ∠=∠，BCP CPQ ∠=∠所以CPD DPQ CPQ ADP BCP αβ∠=∠+∠=∠+∠=∠+∠（2）情况1:如图所示，当点P 在B 、O 两点之间时过P 作PE ∥AD ，交ON 于E ，∵AD ∥BC ，∴AD ∥BC ∥PE ，∴∠DPE=∠ADP=∠α，∠CPE=∠BCP=∠β，∴∠CPD=∠DPE-∠CPE=∠α-∠β情况2：如图所示，当点P 在射线AM 上时，过P 作PE ∥AD ，交ON 于E ，∵AD ∥BC ，∴AD ∥BC ∥PE ，∴∠DPE=∠ADP=∠α，∠CPE=∠BCP=∠β，∴∠CPD=∠CPE-∠DPE=∠β-∠α【点睛】本题主要借助辅助线构造平行线，利用平行线的性质进行推理．25．（1）180BCD ACE ∠+∠=︒，理由详见解析；（2）135°；（3）BCD ∠等于150︒或30时，//CE AB .【分析】（1）依据∠BCD=∠ACB+∠ACD=90°+∠ACD ，即可得到∠BCD+∠ACE 的度数；（2）设∠ACE=α，则∠BCD=3α，依据∠BCD+∠ACE=180°，即可得到∠BCD 的度数； （3）分两种情况讨论，依据平行线的性质，即可得到当∠BCD 等于150°或30°时，CE//4B.【详解】解：（1）180BCD ACE ∠+∠=︒，理由如下：90BCD ACB ACD ACD ∠=∠+∠=︒+∠，∴90BCD ACE ACD ACE ∠+∠=︒+∠+∠9090180=︒+︒=︒；（2）如图①，设ACE α∠=，则3BCD α∠=，由（1）可得180BCD ACE ∠+∠=︒，∴3180αα+=︒，∴45α=，∴3135BCD α∠==︒；（3）分两种情况：①如图1所示，当//AB CE 时，180120BCE B ∠=︒-∠=︒， 又90DCE ∠=︒，∴36012090150BCD ∠=︒-︒-︒=︒；②如图2所示，当//AB CE 时，60BCE B ∠=∠=︒， 又90DCE ∠=︒，∴906030BCD ∠=︒-︒=︒.综上所述，BCD ∠等于150︒或30时，//CE AB .【点睛】本题考查了平行线的判定：同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行.熟练掌握定理并且能够准确识图是解题的关键.26．（1）∠AEC ＝130°；（2）∠A 1EC ＝130°；（3）∠A 1EC ＝40°．【解析】【分析】(1)由直线PQ ∥MN ，∠ADC=∠QAD=30°，可得∠PAD=150°，再求∠PAE=75°，可得∠CAE=25°；由∠PAC=∠ACN，求得∠ECA=25°，故∠AEC=180°﹣25°﹣25°；(2)先求出∠QA1D1=30°，∠PA1D1=150°，再求出∠PA1E=∠EA1D1=75°，再求出∠CAQ=130°，∠ACN=50°，根据平分线定义得∠ACE=25°，再利用四边形内角和性质可求∠CEA1；(3)根据平行线性质和角平分线定义可求得∠QA1E=∠2=15°，∠ACE=∠ECN=∠1=25°，再由∠CEA1=∠1+∠2即可求得答案.【详解】(1)如图1所示：∵直线PQ∥MN，∠ADC＝30°，∴∠ADC＝∠QAD＝30°，∴∠PAD＝150°，∵∠PAC＝50°，AE平分∠PAD，∴∠PAE＝75°，∴∠CAE＝25°，可得∠PAC＝∠ACN＝50°，∵CE平分∠ACD，∴∠ECA＝25°，∴∠AEC＝180°﹣25°﹣25°＝130°；(2)如图2所示：∵∠A1D1C＝30°，线段AD沿MN向右平移到A1D1，PQ∥MN，∴∠QA1D1＝30°，∴∠PA1D1＝150°，∵A1E平分∠AA1D1，∴∠PA1E＝∠EA1D1＝75°，∵∠PAC＝50°，PQ∥MN，∴∠CAQ＝130°，∠ACN＝50°，∵CE平分∠ACD1，∴∠ACE＝25°，∴∠CEA1＝360°﹣25°﹣130°﹣75°＝130°；(3)如图3所示：过点E作FE∥PQ，∵∠A1D1C＝30°，线段AD沿MN向左平移到A1D1，PQ∥MN，∴∠QA1D1＝30°，∵A1E平分∠AA1D1，∴∠QA1E＝∠2＝15°，∵∠PAC＝50°，PQ∥MN，∴∠ACN＝50°，∵CE平分∠ACD1，∴∠ACE＝∠ECN＝∠1＝25°，∴∠CEA1＝∠1+∠2＝15°+25°＝40°．【点睛】本题考查了平行线性质，角平分线定义，熟练运用平行线性质和角平分线定义推出角的度数是解题的关键.。

第五章相交线与平行线1.两直线相交所成的四个角中，有一条公共边，它们的另一边互为反向延长线，具有这种关系的两个角，互为_____________.2.两直线相交所成的四个角中，有一个公共顶点，并且一个角的两边分别是另一个角两边的反向延长线，具有这种关系的两个角，互为__________.对顶角的性质：______ _________.3.两直线相交所成的四个角中，如果有一个角是直角，那么就称这两条直线相互_______.垂线的性质：⑴过一点______________一条直线与已知直线垂直.⑵连接直线外一点与直线上各点的所在线段中，_______________.4.直线外一点到这条直线的垂线段的长度，叫做________________________.5.两条直线被第三条直线所截，构成八个角，在那些没有公共顶点的角中，⑴如果两个角分别在两条直线的同一方，并且都在第三条直线的同侧，具有这种关系的一对角叫做___________ ；⑵如果两个角都在两直线之间，并且分别在第三条直线的两侧，具有这种关系的一对角叫做____________ ；⑶如果两个角都在两直线之间，但它们在第三条直线的同一旁，具有这种关系的一对角叫做_______________.6.在同一平面内，不相交的两条直线互相___________.同一平面内的两条直线的位置关系只有________与_________两种.7.平行公理：经过直线外一点，有且只有一条直线与这条直线______.推论：如果两条直线都与第三条直线平行，那么_____________________.8.平行线的判定：⑴两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行.简单说成：_____________________________________.⑵两条直线被第三条直线所截，如果内错角相等，那么这两条直线平行.简单说成：___________________________.⑶两条直线被第三条直线所截，如果同旁内角互补，那么这两条直线平行.简单说成：________________________________________.9.在同一平面内，如果两条直线都垂直于同一条直线，那么这两条直线_______ .10.平行线的性质：⑴两条平行直线被第三条直线所截，同位角相等.简单说成：____________________________________.⑵两条平行直线被第三条直线所截，内错角相等.简单说成：__________________________________.⑶两条平行直线被第三条直线所截，同旁内角互补.简单说成：____________________________________ .11.判断一件事情的语句，叫做_______.命题由________和_________两部分组成.题设是已知事项，结论是______________________.命题常可以写成“如果……那么……”的形式，这时“如果”后接的部分是____________，“那么”后接的部分是_________.如果题设成立，那么结论一定成立.像这样的命题叫做___________.如果题设成立时，不能保证结论一定成立，像这样的命题叫做___________.定理都是真命题.12. 把一个图形整体沿某一方向移动，会得到一个新图形，图形的这种移动，叫做平移变换，简称_______.图形平移的方向不一定是水平的.平移的性质：⑴把一个图形整体平移得到的新图形与原图形的形状与大小完全______.⑵新图形中的每一点，都是由原图形中的某一点移动后得到的，这两个点是对应点.连接各组对应点的线段_________________.熟悉以下各题：13. 如图，,8,6,10,BC AC CB cm AC cm AB cm ⊥===那么点A 到BC 的距离是_____，点B 到AC 的距离是_______，点A 、B 两点的距离是_____，点C 到AB 的距离是________．14. 设a 、b 、c 为平面上三条不同直线，a) 若//,//a b b c ，则a 与c 的位置关系是_________；b) 若,a b b c ⊥⊥，则a 与c 的位置关系是_________；c) 若//a b ，b c ⊥，则a 与c 的位置关系是________．15. 如图，已知AB 、CD 、EF 相交于点O ，AB ⊥CD ，OG 平分∠AOE ，∠FOD ＝28°，求∠COE 、∠AOE 、∠AOG 的度数．16. 如图，AOC ∠与BOC ∠是邻补角，OD 、OE 分别是AOC ∠与BOC ∠的平分线，试判断OD 与OE 的位置关系，并说明理由．17. 如图，AB ∥DE ，试问∠B 、∠E 、∠BCE 有什么关系．解：∠B ＋∠E ＝∠BCE过点C 作CF ∥AB ，则B ∠=∠____（ ）又∵AB ∥DE ，AB ∥CF ，∴____________（ ）∴∠E ＝∠____（ ）∴∠B ＋∠E ＝∠1＋∠2即∠B ＋∠E ＝∠BCE ．18. ⑴如图，已知∠1＝∠2 求证：a ∥b ．⑵直线//a b ，求证：12∠=∠．19. 阅读理解并在括号内填注理由：如图，已知AB ∥CD ，∠1＝∠2，试说明EP ∥FQ ．证明：∵AB ∥CD ，∴∠MEB ＝∠MFD （ ）又∵∠1＝∠2，∴∠MEB －∠1＝∠MFD －∠2，即 ∠MEP ＝∠______∴EP ∥_____．（ ）20. 已知DB ∥FG ∥EC ，A 是FG 上一点，∠ABD ＝60°，∠ACE ＝36°，AP 平分∠BAC ，求：⑴∠BAC 的大小；⑵∠P AG 的大小.21. 如图，已知ABC ∆ABC ∆，AD BC ⊥AD BC ⊥于D ，E E 为AB AB 上一点，EF BC ⊥EF BC ⊥于F ，//DG BA //DG BA 交CA 于G .求证12∠=∠12∠=∠.22. 已知：如图∠1=∠2，∠C =∠D ，问∠A 与∠F 相等吗？试说明理由．参考答案1.邻补角2. 对顶角，对顶角相等3.垂直 有且只有 垂线段最短4.点到直线的距离5.同位角 内错角 同旁内角6.平行 相交 平行7.平行 这两直线互相平行8.同位角相等 两直线平行； 内错角相等 两直线平行； 同旁内角互补 两直线平行.9.平行 10.两直线平行 同位角相等；两直线平行 内错角相等；两直线平行 同旁内角互补.11.命题 题设 结论 由已知事项推出的事项 题设 结论 真命题 假命题 12.平移 相同 平行且相等 13.6cm 8cm 10cm 4.8cm. 14.平行 平行 垂直 15. 28° 118° 59° 16. OD ⊥OE 理由略 17. 1（两直线平行，内错角相等）DE ∥CF （平行于同一直线的两条直线平行） 2 （两直线平行，内错角相等）. 18.⑴∵∠1＝∠2 ，又∵∠2＝∠3（对顶角相等），∴∠1＝∠3∴a ∥b （同位角相等 两直线平行） ⑵∵a ∥b ∴∠1＝∠3(两直线平行，同位角相等)又∵∠2＝∠3（对顶角相等） ∴∠1＝∠2. 19. 两直线平行，同位角相等 MFQ FQ 同位角相等两直线平行 20. 96°，12°.21.,AD BC FE BC ⊥⊥,AD BC FE BC ⊥⊥90EFB ADB ∴∠=∠=//EF AD ∴//EF AD ∴23∴∠=∠//,31DG BA ∴∠=∠//,31DG BA ∴∠=∠ 1 2.∴∠=∠1 2.∴∠=∠ 22. ∠A ＝∠F .∵∠1＝∠DGF （对顶角相等）又∠1＝∠2 ∴∠DGF ＝∠2 ∴DB ∥EC （同位角相等，两直线平行） ∴∠DBA ＝∠C （两直线平行，同位角相等） 又∵∠C ＝∠D ∴∠DBA ＝∠D ∴DF ∥AC （内错角相等，两直线平行）∴∠A ＝∠F (两直线平行,内错角相等).。

人教版初中数学七年级下相交线和平行线知识点总结本章介绍了平面内两条直线相交与平行的关系，重点探讨了两条直线相交时形成角的特征、两条直线互相垂直的特性、两条直线平行的条件和特征，以及有关图形平移变换的性质。

本文将对其中的重点知识点进行总结。

5.1 相交线1.邻补角与对顶角当两条直线相交时，所形成的四个角具有不同的关系。

其中，对顶角是具有特殊位置关系的两个角，它们的大小相等；邻补角则是互为反向延长线的两个角，它们的和为180度。

2.垂线垂线是指当两条直线相交时，其中一个角为直角的情况。

垂线具有两个性质：一是过一点只有一条直线与已知直线垂直；二是连接直线外一点与直线上各点的垂线段最短。

3.垂线的画法画垂线的方法有两种：一是过直线上一点画已知直线的垂线；二是过直线外一点画已知直线的垂线。

画法可采用“一靠二移三画”的方法。

4.点到直线的距离点到直线的距离是指直线外一点到这条直线的垂线段的长度。

记忆时应结合图形进行理解。

本章内容的重点是垂线和其性质、平行线的判定方法和性质、平移和其性质，以及这些知识点的组织运用。

在研究这些知识点时，需要注意记忆其定义和性质，掌握其画法和应用方法。

垂线是指从一个点垂直于一条直线或平面的线段，而垂线段则是垂线的长度。

它们都具有垂直的性质，可以用来计算点到直线的距离或两点间的距离。

点到直线的距离是特殊的两点（即已知点与垂足）间距离，而两点间的距离是点与点之间的长度。

线段和距离都是长度的概念，但线段是一种图形，不能等同于距离。

平行线是指在同一平面内不相交的两条直线，它们的位置关系只有两种：相交和平行。

判断两条直线的位置关系可以根据它们的公共点个数来确定，有且只有一个公共点时两直线相交，无公共点时两直线平行，两个或两个以上公共点时两直线重合。

平行公理指出，经过直线外一点，有且只有一条直线与这条直线平行。

同时，如果两条直线都与第三条直线平行，那么这两条直线也互相平行。

三线八角是指两条直线被第三条直线所截形成的八个角，包括同位角、内错角和同旁内角。

人教版初中数学知识点总结目录七年级数学（上）知识点(1)第一章有理数(1)第二章整式的加减(3)第三章一元一次方程(4)第四章图形的认识初步(5)七年级数学（下）知识点(6)第五章相交线与平行线(6)第六章平面直角坐标系(8)第七章三角形(9)第八章二元一次方程组(12)第九章不等式与不等式组(13)第十章数据的收集、整理与描述(13)八年级数学（上）知识点(14)第十一章全等三角形(14)第十二章轴对称(15)第十三章实数(16)第十四章一次函数(17)第十五章整式的乘除与分解因式(18)八年级数学（下）知识点(19)第十六章分式(19)第十七章反比例函数(20)第十八章勾股定理(21)第十九章四边形(22)第二十章数据的分析(23)九年级数学（上）知识点(24)第二十一章二次根式(24)第二十二章一元二次根式(25)第二十三章旋转(26)第二十四章圆(27)第二十五章概率(28)九年级数学（下）知识点(30)第二十六章二次函数(30)第二十七章相似(32)第二十八章锐角三角函数(33)第二十九章投影与视图(34)1 七年级数学（上）知识点人教版七年级数学上册主要包含了有理数、整式的加减、一元一次方程、图形的认识初步四个章节的内容.第一章有理数一．知识框架二．知识概念1.有理数：(1)凡能写成)0p q ,p (pq ≠为整数且形式的数，都是有理数.正整数、0、负整数统称整数；正分数、负分数统称分数；整数和分数统称有理数.注意：0即不是正数，也不是负数；-a 不一定是负数，+a 也不一定是正数；π不是有理数；(2)有理数的分类: ①⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数零正分数正整数正有理数有理数②⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数零正整数整数有理数2．数轴：数轴是规定了原点、正方向、单位长度的一条直线.3．相反数：(1)只有符号不同的两个数，我们说其中一个是另一个的相反数；0的相反数还是0；(2)相反数的和为0 ⇔ a+b=0 ⇔ a 、b 互为相反数.4.绝对值：(1)正数的绝对值是其本身，0的绝对值是0，负数的绝对值是它的相反数；注意：绝对值的意义是数轴上表示某数的点离开原点的距离；(2) 绝对值可表示为：⎪⎩⎪⎨⎧<-=>=)0a (a )0a (0)0a (a a 或⎩⎨⎧<-≥=)0a (a )0a (a a ；绝对值的问题经常分类讨论；5.有理数比大小：（1）正数的绝对值越大，这个数越大；（2）正数永远比0大，负数永远比0小；（3）正数大于一切负数；（4）两个负数比大小，绝对值大的反而小；（5）数轴上的两个数，右边的数总比左边的数大；（6）大数-小数＞0，小数-大数＜0.6.互为倒数：乘积为1的两个数互为倒数；注意：0没有倒数；若a ≠0，那么a 的倒数是a 1；若ab=1⇔ a 、b 互为倒数；若ab=-1⇔ a 、b 互为负倒数.7. 有理数加法法则：（1）同号两数相加，取相同的符号，并把绝对值相加；（2）异号两数相加，取绝对值较大的符号，并用较大的绝对值减去较小的绝对值；（3）一个数与0相加，仍得这个数.8．有理数加法的运算律：（1）加法的交换律：a+b=b+a ；（2）加法的结合律：（a+b ）+c=a+（b+c ）.9．有理数减法法则：减去一个数，等于加上这个数的相反数；即a-b=a+（-b ）. 10 有理数乘法法则：（1）两数相乘，同号为正，异号为负，并把绝对值相乘；（2）任何数同零相乘都得零；（3）几个数相乘，有一个因式为零，积为零；各个因式都不为零，积的符号由负因式的个数决定.11 有理数乘法的运算律：（1）乘法的交换律：ab=ba ；（2）乘法的结合律：（ab ）c=a （bc ）；（3）乘法的分配律：a （b+c ）=ab+ac .12．有理数除法法则：除以一个数等于乘以这个数的倒数；注意：零不能做除数，无意义即0a . 13．有理数乘方的法则：（1）正数的任何次幂都是正数；（2）负数的奇次幂是负数；负数的偶次幂是正数；注意：当n 为正奇数时: (-a)n =-a n 或(a -b)n =-(b-a)n , 当n 为正偶数时: (-a)n =a n 或(a-b)n =(b-a)n .14．乘方的定义：（1）求相同因式积的运算，叫做乘方；（2）乘方中，相同的因式叫做底数，相同因式的个数叫做指数，乘方的结果叫做幂；15．科学记数法：把一个大于10的数记成a ×10n 的形式，其中a 是整数数位只有一位的数，这种记数法叫科学记数法.16.近似数的精确位：一个近似数，四舍五入到那一位，就说这个近似数的精确到那一位.17.有效数字：从左边第一个不为零的数字起，到精确的位数止，所有数字，都叫这个近似数的有效数字.请判断下列题的对错,并解释.1.近似数25.0的精确度与近似数25一样.2.近似数4千万与近似数4000万的精确度一样.3.近似数660万,它精确到万位.有三个有效数字.4.用四舍五入法得近似数6.40和6.4是相等的.5.近似数3.7x10的二次与近似数370的精确度一样.1、错。

初中数学相交线与平行线知识点总复习附解析一、选择题1．如图所示，某同学的家在P处，他想尽快赶到附近公路边搭公交车，他选择P→C路线，用几何知识解释其道理正确的是（）A．两点确定一条直线B．垂直线段最短C．两点之间线段最短D．三角形两边之和大于第三边【答案】B【解析】【分析】根据垂线段的定义判断即可.【详解】解：Q直线外一点与直线上各点连接的所有线段中，垂线段最短,选:B.【点睛】直线外任意一点到这条直线的垂线段的长度，叫做点到这条直线的距离．直线外一点与直线上各点连接的所有线段中，垂线段最短．简称“垂线段最短”．2．如图，若AB∥CD，则∠α、∠β、∠γ之间关系是（）A．∠α+∠β+∠γ=180°B．∠α+∠β﹣∠γ=360°C．∠α﹣∠β+∠γ=180°D．∠α+∠β﹣∠γ=180°【答案】D【解析】试题解析：如图，作EF∥AB，∵AB∥CD，∴EF∥CD，∴∠α+∠AEF=180°，∵EF ∥CD ，∴∠γ=∠DEF ，而∠AEF+∠DEF=∠β，∴∠α+∠β=180°+∠γ，即∠α+∠β-∠γ=180°．故选：D ．3．如图，已知ABC ∆，若AC BC ⊥，CD AB ⊥，12∠=∠，下列结论：①//AC DE ；②3A ∠=∠；③3EDB ∠=∠；④2∠与3∠互补；⑤1B ∠=∠，其中正确的有（ ）A ．2个B ．3个C ．4个D ．5个【答案】C【解析】【分析】 根据平行线的判定得出AC ∥DE ，根据垂直定义得出∠ACB=∠CDB=∠CDA=90°，再根据三角形内角和定理求出即可．【详解】∵∠1=∠2，∴AC ∥DE ，故①正确；∵AC ⊥BC ，CD ⊥AB ，∴∠ACB=∠CDB=90°，∴∠A+∠B=90°，∠3+∠B=90°，∴∠A=∠3，故②正确；∵AC ∥DE ，AC ⊥BC ，∴DE ⊥BC ，∴∠DEC=∠CDB=90°，∴∠3+∠2=90°（∠2和∠3互余），∠2+∠EDB=90°，∴∠3=∠EDB ，故③正确，④错误；∵AC ⊥BC ，CD ⊥AB ，∴∠ACB=∠CDA=90°，∴∠A+∠B=90°，∠1+∠A=90°，∴∠1=∠B ，故⑤正确；即正确的个数是4个，故选：C ．此题考查平行线的判定和性质，三角形内角和定理，垂直定义，能综合运用知识点进行推理是解题的关键．4．如图，直线AB AC ⊥，AD BC ⊥，如果4AB cm =，3AC cm =， 2.4AD cm =，那么点C 到直线AB 的距离为（ ）A ．3cmB ．4cmC ．2.4cmD ．无法确定【答案】A【解析】【分析】 根据点到直线的距离是指垂线段的长度，根据AB ⊥AC ，得出点C 到直线AB 的距离为AC ．【详解】解：∵AB ⊥AC ，∴点C 到直线AB 的距离是指AC 的长度，即等于3cm ．故选：A ．【点睛】此题考查点到直线的距离，解题关键在于掌握点到直线的距离是指垂线段的长度，难度适中．5．如图，点,D E 分别在BAC ∠的边,AB AC 上，点F 在BAC ∠的内部，若1,250F ︒∠=∠∠=，则A ∠的度数是（ ）A ．50︒B ．40︒C ．45︒D ．130︒【答案】A【分析】利用平行线定理即可解答.【详解】解：根据∠1=∠F，可得AB//EF，故∠2=∠A=50°.故选A.【点睛】本题考查平行线定理：内错角相等，两直线平行.6．已知△ABC中，BC=6，AC=3，CP⊥AB，垂足为P，则CP的长可能是（）A．2 B．4 C．5 D．7【答案】A【解析】试题分析：如图，根据垂线段最短可知：PC＜3，∴CP的长可能是2，故选A．考点：垂线段最短．7．如图，已知AB∥DC，BF平分∠ABE，且BF∥DE，则∠ABE与∠CDE的关系是（）A．∠ABE＝2∠CDE B．∠ABE＝3∠CDEC．∠ABE＝∠CDE+90°D．∠ABE+∠CDE＝180°【答案】A【解析】延长BF与CD相交于M，根据两直线平行，同位角相等可得∠M=∠CDE，再根据两直线平行，内错角相等可得∠M=∠ABF，从而求出∠CDE=∠ABF，再根据角平分线的定义解答．【详解】解：延长BF与CD相交于M，∵BF∥DE，∴∠M=∠CDE，∵AB∥CD，∴∠M=∠ABF，∴∠CDE=∠ABF，∵BF平分∠ABE，∴∠ABE=2∠ABF，∴∠ABE=2∠CDE．故选：A．【点睛】本题考查了平行线的性质和角平分线的定义，作辅助线，是利用平行线的性质的关键，也是本题的难点．8．如图，AB∥EF，设∠C＝90°，那么x、y和z的关系是（）A．y＝x+z B．x+y﹣z＝90°C．x+y+z＝180°D．y+z﹣x＝90°【答案】B【解析】【分析】过C作CM∥AB，延长CD交EF于N，根据三角形外角性质求出∠CNE＝y﹣z，根据平行线性质得出∠1＝x，∠2＝∠CNE，代入求出即可．【详解】解：过C作CM∥AB，延长CD交EF于N，则∠CDE＝∠E+∠CNE，即∠CNE＝y﹣z∵CM∥AB，AB∥EF，∴CM∥AB∥EF，∴∠ABC＝x＝∠1，∠2＝∠CNE，∵∠BCD＝90°，∴∠1+∠2＝90°，∴x+y﹣z＝90°．故选：B．【点睛】本题考查了平行线的性质和三角形外角性质的应用，注意：平行线的性质有：①两直线平行，同位角相等，②两直线平行，内错角相等，③两直线平行，同旁内角互补．9．如图所示，有下列五种说法：①∠1和∠4是同位角；②∠3和∠5是内错角；③∠2和∠6旁内角；④∠5和∠2是同位角；⑤<1和∠3是同旁内角；其中正确的是（）A．①②③④B．①②③④C．①②③④⑤D．①②④⑤【答案】D【解析】如图，①∠1和∠4是直线AC和直线BC被直线AB截得的同位角，所以①正确；②∠3和∠5是直线BC和直线AB被直线AC截得的内错角，所以②正确；③∠2和∠6是直线AB和直线AC被直线CB截得的内错角，所以③错误；④∠5和∠2是直线AC和直线BC被直线AB截得的同位角，所以④正确；⑤∠1和∠3是直线BC和直线AB被直线AC截得的同旁内角，所以⑤正确.故答案选D.（1）准确识别同位角、内错角、同旁内角的关键，是弄清两角是由哪两条直线被哪条直线截得，这其中的关键是辨别出截线，在截线的两旁的是内错角，在截线的同旁的为同位角或同旁内角；（2）辨别截线方法：先找出两角的边所在直线，公共直线即是截线.10．如图，直线AB，CD相交于点O，∠2－∠1=15°，∠3=130°．则∠2的度数是()A．37.5°B．75°C．50°D．65°【答案】D【解析】【分析】先根据条件和邻补角的性质求出∠1的度数，然后即可求出∠2的度数．【详解】）∵∠3=130°，∠1+∠3=180°，∴∠1=180°-∠3=50°，∵∠2-∠1=15°，∴∠2=15°+∠1=65°；故答案为D.【点睛】本题考查角的运算，邻补角的性质，比较简单.11．在下图中，∠1,∠2是对顶角的图形是（）A．B．C．D．【答案】B【解析】略12．A、B、C是直线L上三点，P为直线外一点，若PA＝2cm，PB＝3cm，PC＝5cm，则P 到直线L的距离是（）A．等于2cm B．大于2cm C．不小于2cm D．不大于2cm【答案】D【分析】从直线外一点到这条直线上各点所连的线段中，垂线段最短．【详解】∵PA=2cm ，PB=3cm ，PC=5cm ，∴PA ＜PB ＜PC ．∴①当PA ⊥L 时，点P 到直线L 的距离等于2cm ；②当PA 与直线L 不垂直时，点P 到直线L 的距离小于2cm ；综上所述，则P 到直线L 的距离是不大于2cm ．故选：D ．【点睛】本题考查了垂线段最短的性质和点到直线的距离的概念．垂线的两条性质：①从直线外一点到这条直线的垂线段的长度，叫做点到直线的距离．②从直线外一点到这条直线上各点所连的线段中，垂线段最短．13．如图，△ABC 中，∠C=90°，则点B 到直线AC 的距离是 ( )A ．线段ABB ．线段AC C ．线段BCD ．无法确定【答案】C【解析】【分析】直接利用点到直线的距离定义得出答案．【详解】解：如图，三角形ABC 中，∠C=90°，则点B 到直线AC 的距离是：线段BC ．故选：C ．【点睛】本题考查点到之间的距离，正确把握相关定义是解题关键．14．如图，//AB CD ，点E 在CD 上，点F 在AB 上，如果:6:7CEF BEF ∠∠=，50ABE ∠=︒，那么AFE ∠的度数为（ ）A ．110︒B ．120︒C ．130︒D ．140︒【答案】B【解析】由//AB CD 可得∠ABE+∠CEB=180°,∠BED=50ABE ∠=︒,即∠CEB=130°,由:6:7CEF BEF ∠∠=可得=67CEF BEF ∠∠,设=67CEF BEF ∠∠=k,则∠CEF=6k,∠FEB=7k,可得∠FEB=70°，可得∠DEF=∠FEB+∠BED=120°;又由//AB CD 可得AFE ∠=∠DEF 即可解答．【详解】解：∵//AB CD∴∠ABE+∠CEB=180°，∠BED=50ABE ∠=︒∴∠CEB=130°∵:6:7CEF BEF ∠∠=∴=67CEF BEF ∠∠ 设=67CEF BEF ∠∠=k ，则∠CEF=6k,∠FEB=7k, ∴6k+7k=130°∴∠FEB=7k=70°∴∠DEF=∠FEB+∠BED=120°∵//AB CD∴AFE ∠=∠DEF=120°故答案为B ．【点睛】本题考查的是平行线的性质以及比例的应用，.熟练掌握平行线的性质是解答本题的关键．15．如图，等边ABC V 边长为a ，点O 是ABC V 的内心，120FOG ∠=︒，绕点O 旋转FOG ∠，分别交线段AB 、BC 于D 、E 两点，连接DE ，给出下列四个结论：①ODE V 形状不变；②ODE V 的面积最小不会小于四边形ODBE 的面积的四分之一；③四边形ODBE 的面积始终不变；④BDE V 周长的最小值为1.5a ．上述结论中正确的个数是（ ）A ．4B ．3C ．2D ．1【答案】A【解析】【分析】连接OB 、OC ，利用SAS 证出△ODB ≌△OEC ，从而得出△ODE 是顶角为120°的等腰三角形，即可判断①；过点O 作OH ⊥DE ，则DH=EH ，利用锐角三角函数可得OH=12OE 和OE ，然后三角形的面积公式可得S △ODE2，从而得出OE 最小时，S △ODE 最小，根据垂线段最短即可求出S △ODE 的最小值，然后证出S 四边形ODBE =S △OBC2即可判断②和③；求出BDE V 的周长=a ＋DE ，求出DE 的最小值即可判断④．【详解】解：连接OB 、OC∵ABC V 是等边三角形，点O 是ABC V 的内心，∴∠ABC=∠ACB=60°，BO=CO ，BO 、CO 平分∠ABC 和∠ACB ∴∠OBA=∠OBC=12∠ABC=30°，∠OCA=∠OCB=12∠ACB=30° ∴∠OBA=∠OCB ，∠BOC=180°－∠OBC －∠OCB=120° ∵120FOG ∠=︒∴∠=FOG ∠BOC∴∠FOG －∠BOE=∠BOC －∠BOE∴∠BOD=∠COE在△ODB 和△OEC 中BOD COE BO COOBD OCE ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ODB ≌△OEC∴OD=OE∴△ODE 是顶角为120°的等腰三角形，∴ODE V 形状不变，故①正确；过点O 作OH ⊥DE ，则DH=EH∵△ODE 是顶角为120°的等腰三角形∴∠ODE=∠OED=12（180°－120°）=30° ∴OH=OE·sin ∠OED=12OE ，EH= OE·cos ∠∴∴S △ODE =12DE·OH=4OE 2 ∴OE 最小时，S △ODE 最小，过点O 作OE′⊥BC 于E′，根据垂线段最短，OE′即为OE 的最小值∴BE ′=12BC=12a 在Rt △OBE ′中 OE′=BE′·tan ∠OBE ′=12a 33 ∴S △ODE 3223 ∵△ODB ≌△OEC∴S 四边形ODBE =S △ODB ＋S △OBE = S △OEC ＋S △OBE =S △OBC =1223 23=1423 ∴S △ODE ≤14S 四边形ODBE 即ODE V 的面积最小不会小于四边形ODBE 的面积的四分之一，故②正确； ∵S 四边形ODBE 23 ∴四边形ODBE 的面积始终不变，故③正确；∵△ODB ≌△OEC∴DB=EC∴BDE V 的周长=DB ＋BE ＋DE= EC ＋BE ＋DE=BC ＋DE=a ＋DE∴DE 最小时BDE V 的周长最小∵3OE∴OE 最小时，DE 最小而OE 的最小值为OE′=36a ∴DE 336a =12a ∴BDE V 的周长的最小值为a ＋12a =1.5a ，故④正确； 综上：4个结论都正确，故选A ．【点睛】此题考查的是等边三角形的性质、全等三角形的判定及性质、锐角三角函数、三角形的面积公式和垂线段最短的应用，掌握等边三角形的性质、全等三角形的判定及性质、锐角三角函数、三角形的面积公式和垂线段最短是解决此题的关键．16．如图，下列判断：①若12A C ∠=∠∠=∠，，则B D ∠=∠；②若12B D ∠=∠∠=∠，，则A C ∠=∠：③若,A C B D ∠=∠∠=∠，则12∠=∠．其中，正确的个数是（ ）．A ．0B ．1C ．2D ．3【答案】D【解析】【分析】 ①根据12A C ∠=∠∠=∠，证明四边形DEBF 是平行四边形即可判断；②根据12B D ∠=∠∠=∠，证明DC ∥AB 即可判断；③根据,A C B D ∠=∠∠=∠证明DC ∥AB 即可判断.【详解】解：如图，标出∠3，①∵A C ∠=∠，∴DC ∥AB （内错角相等，两直线平行），∵2,3∠∠是对顶角，∴23∠∠=，∴13∠=∠（等量替换），∴DE ∥FB （同位角相等，两直线平行），∴四边形DEBF 是平行四边形（两组对边分别平行），∴B D ∠=∠，②∵2,3∠∠是对顶角，∴23∠∠=，∴13∠=∠（等量替换），∴DE ∥FB （同位角相等，两直线平行），∴∠B+∠DEB=180°，又∵B D ∠=∠，∴∠D+∠DEB=180°，∴DC ∥AB （同旁内角互补，两直线平行），∴A C ∠=∠（两直线平行，内错角相等）；故②正确；③∵A C ∠=∠，∴DC ∥AB （内错角相等，两直线平行），∴B CFB ∠=∠（两直线平行，内错角相等）,又∵B D ∠=∠，∴D CFB ∠=∠,∴DE ∥FB （同位角相等，两直线平行），∴13∠=∠（两直线平行，同位角相等）,∵2,3∠∠是对顶角，∴23∠∠=，∴12∠=∠（等量替换），故③正确.故D 为答案.【点睛】本题主要考查了直线平行的判定（同位角相等、内错角相等、同旁内角互补，两直线平行）、直线平行的性质、等量替换的相关知识点，掌握直线平行的判定和性质是解题的关键.17．如图，直线,a b 被直线c 所截，则图中的1∠与2∠是（ ）A ．同位角B ．内错角C ．同旁内角D ．邻补角【答案】B【解析】根据1∠与2∠的位置关系，由内错角的定义即可得到答案.【详解】解：∵1∠与2∠在截线,a b 之内，并且在直线c 的两侧，∴由内错角的定义得到1∠与2∠是内错角，故B 为答案.【点睛】本题主要考查了内错角、同位角、同旁内角、邻补角的定义，理解内错角、同位角、同旁内角、邻补角是解题的关键.18．如图，已知AB ∥CD ，直线AB ，CD 被BC 所截，E 点在BC 上，若∠1＝45°，∠2＝35°，则∠3＝（ ）A ．65°B ．70°C ．75°D ．80°【答案】D【解析】【分析】 由平行线的性质可求得∠C ，在△CDE 中利用三角形外的性质可求得∠3．【详解】解：∵AB ∥CD ，∴∠C ＝∠1＝45°，∵∠3是△CDE 的一个外角，∴∠3＝∠C+∠2＝45°+35°＝80°，故选：D ．【点睛】本题主要考查平行线的性质，掌握平行线的性质和判定是解题的关键，即①两直线平行⇔同位角相等，②两直线平行⇔内错角相等，③两直线平行⇔同旁内角互补，④a ∥b ，b ∥c ⇒a ∥c ．19．下列图形中线段PQ 的长度表示点P 到直线a 的距离的是（ ）A ．B ．C ．D ．【答案】C【解析】【分析】 根据点到直线的距离的定义，可得答案．【详解】由题意得PQ ⊥a ，P 到a 的距离是PQ 垂线段的长，故选C ．【点睛】本题考查了点到直线的距离，点到直线的距离是解题关键．20．如图，AB CD ∥，BF 平分ABE ∠，且BF DE P ，则ABE ∠与D ∠的关系是（ ）A ．2ABE D ∠=∠B ．180ABE D ∠+∠=︒C ．90ABED ∠=∠=︒D ．3ABE D ∠=∠【答案】A【解析】【分析】 延长DE 交AB 的延长线于G ，根据两直线平行，内错角相等可得D G ∠=∠，再根据两直线平行，同位角相等可得G ABF ∠=∠，然后根据角平分线的定义解答．【详解】证明：如图，延长DE 交AB 的延长线于G ，//AB CD Q ，D G ∴∠=∠，//BF DE Q ，G ABF ∴∠=∠，D ABF ∴∠=∠，BF Q 平分ABE ∠，22ABE ABF D ∴∠=∠=∠，即2ABE D ∠=∠．故选：A ．【点睛】本题考查了平行线的性质，角平分线的定义，熟记性质并作辅助线是解题的关键．。

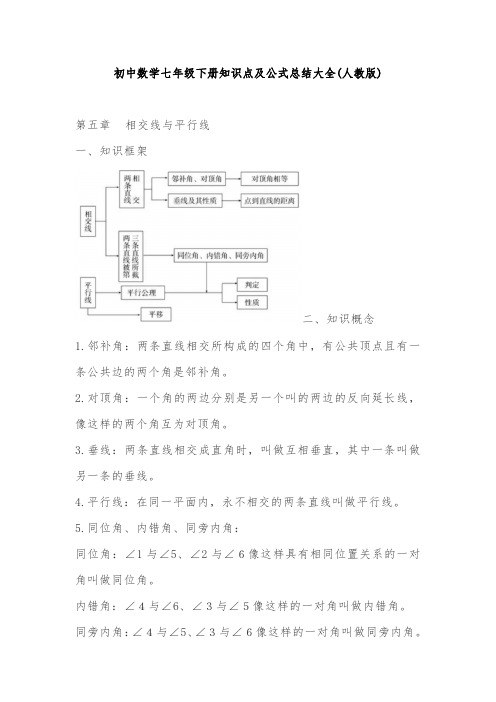
初中数学七年级下册知识点及公式总结大全(人教版)第五章相交线与平行线一、知识框架二、知识概念1.邻补角：两条直线相交所构成的四个角中，有公共顶点且有一条公共边的两个角是邻补角。

2.对顶角：一个角的两边分别是另一个叫的两边的反向延长线，像这样的两个角互为对顶角。

3.垂线：两条直线相交成直角时，叫做互相垂直，其中一条叫做另一条的垂线。

4.平行线：在同一平面内，永不相交的两条直线叫做平行线。

5.同位角、内错角、同旁内角：同位角：∠1与∠5、∠2与∠６像这样具有相同位置关系的一对角叫做同位角。

内错角：∠４与∠6、∠３与∠５像这样的一对角叫做内错角。

同旁内角：∠４与∠5、∠３与∠６像这样的一对角叫做同旁内角。

6.命题：判断一件事情的语句叫命题。

7.平移：在平面内，将一个图形沿某个方向移动一定的距离，图形的这种移动叫做平移变换，简称平移。

8.对应点：平移后得到的新图形中每一点，都是由原图形中的某一点移动后得到的，这样的两个点叫做对应点。

9.对顶角的性质：对顶角相等。

10．垂线的性质：性质1：过一点有且只有一条直线与已知直线垂直。

性质2：连接直线外一点与直线上各点的所有线段中，垂线段最短。

11.平行公理：经过直线外一点有且只有一条直线与已知直线平行。

平行公理的推论：如果两条直线都与第三条直线平行，那么这两条直线也互相平行。

12.平行线的性质：性质1：两直线平行，同位角相等。

性质2：两直线平行，内错角相等。

性质3：两直线平行，同旁内角互补。

13.平行线的判定：判定1：同位角相等，两直线平行。

判定2：内错角相等，两直线平行。

判定3：同旁内角互补，两直线平行。

第六章平面直角坐标系一．知识框架二．知识概念1.有序数对：有顺序的两个数a与b组成的数对叫做有序数对，记做（a,b）2.平面直角坐标系：在平面内，两条互相垂直且有公共原点的数轴组成平面直角坐标系。

3.横轴、纵轴、原点：水平的数轴称为x轴或横轴；竖直的数轴称为y轴或纵轴；两坐标轴的交点为平面直角坐标系的原点。

人教版初中数学七年级下 相交线与平行线知识点总结5、1相交线 1、邻补角与对顶角两直线相交所成的四个角中存在几种不同关系的角,它们的概念及性质如下表:注意点:⑴对顶角就是成对出现的,对顶角就是具有特殊位置关系的两个角;⑵如果∠α与∠β就是对顶角,那么一定有∠α=∠β;反之如果∠α=∠β,那么∠α与∠β不一定就是对顶角⑶如果∠α与∠β互为邻补角,则一定有∠α+∠β=180°;反之如果∠α+∠β=180°,则∠α与∠β不一定就是邻补角。

⑶两直线相交形成的四个角中,每一个角的邻补角有两个,而对顶角只有一个。

2、垂线⑴定义,当两条直线相交所成的四个角中,有一个角就是直角时,就说这两条直线互相垂直,其中的一条直线叫做另一条直线的垂线,它们的交点叫做垂足。

符号语言记作:如图所示:AB ⊥CD,垂足为O⑵垂线性质1:过一点有且只有一条直线与已知直线垂直 (与平行公理相比较记)⑶垂线性质2:连接直线外一点与直线上各点的所有线段中,垂线段最短。

简称:垂线段最短。

3、垂线的画法:ABCD O⑴过直线上一点画已知直线的垂线;⑵过直线外一点画已知直线的垂线。

注意:①画一条线段或射线的垂线,就就是画它们所在直线的垂线;②过一点作线段的垂线,垂足可在线段上,也可以在线段的延长线上。

画法:⑴一靠:用三角尺一条直角边靠在已知直线上,⑵二移:移动三角尺使一点落在它的另一边直角边上,⑶三画:沿着这条直角边画线,不要画成给人的印象就是线段的线。

4、点到直线的距离直线外一点到这条直线的垂线段的长度,叫做点到直线的距离 记得时候应该结合图形进行记忆。

如图,PO ⊥AB,同P 到直线AB 的距离就是PO 的长。

PO 就是垂线段。

PO 就是点P 到直线AB 所有线段中最短的一条。

现实生活中开沟引水,牵牛喝水都就是“垂线段最短”性质的应用。

5、如何理解“垂线”、“垂线段”、“两点间距离”、“点到直线的距离”这些相近而又相异的概念 分析它们的联系与区别⑴垂线与垂线段 区别:垂线就是一条直线,不可度量长度;垂线段就是一条线段,可以度量长度。

第五章 相交线与平行线5.1相交线5.1.1 相交线邻补角与对顶角 两直线相交所成的四个角中存在几种不同关系的角，它们的概念及性质如下表：图形 顶点 边的关系 大小关系 对顶角∠1与∠2有公共顶点 ∠1的两边与∠2的两边互为反向延长线 对顶角相等 即∠1=∠2 邻补角∠3与∠4 有公共顶点 ∠3与∠4有一条边公共，另一边互为反向延长线. ∠3+∠4=180°注意点：（1）对顶角是成对出现的，对顶角是具有特殊位置关系的两个角；（2）如果∠α与∠β是对顶角，那么一定有∠α=∠β；反之如果∠α=∠β，那么∠α与∠β不一定是对顶角；（3）如果∠α与∠β互为邻补角，则一定有∠α+∠β=180°；反之如果∠α+∠β=180°，则∠α与∠β不一定是邻补角；（4）两直线相交形成的四个角中，每一个角的邻补角有两个，而对顶角只有一个.例：如图，三条直线交于一点，任意找出图中的四对对顶角．错解：如图， 对顶角为：（1）∠AOC 与∠BOD ；（2）∠AOF 与∠BOD ；（3）∠COF 与∠DOE ；（4）∠AOC 与∠BOE ．错解分析：错解中把有公共顶点的角误认为是对顶角，导致（2）和（4）错误．如果对对顶角的概念没有真正理解和掌握，在比较复杂的图形识别中会产生错误．对顶角就是：一个角的两边分别是另一个角的两边的反向延长线 ．正解：（1）∠AOC 与∠BOD ；（2）∠BOE 与∠AOF ；（3）∠COF 与∠DOE ；（4）∠COE 与∠DOF ．（答案不唯一：∠ AOE 与∠BOF ，∠BOC 与∠AOD 也是对顶角）5.1.2 垂线1、定义：当两条直线相交所成的四个角中，有一个角是直角时，就说这两条直线互相垂直，其中的一条直线叫做另一条直线的垂线，它们的交点叫做垂足.符号语言记作：如图所示：AB ⊥CD ，垂足为O1 2 4 3AB C DO2、在同一平面内，过一点有且只有一条直线与已知直线垂直.3、连接直线外一点与直线上各点的所有线段中，垂线段最短.简称：垂线段最短.4、点到直线的距离直线外一点到这条直线的垂线段的长度，叫做点到直线的距离5.1.3 同位角、内错角、同旁内角两条直线被第三条直线所截形成八个角，它们构成了同位角、内错角与同旁内角.如图，直线b a ,被直线l 所截 1、∠1与∠5在截线l 的同侧，同在被截直线b a ,的上方，叫做同位角（位置相同）2、∠5与∠3在截线l 的两旁（交错），在被截直线b a ,之间（内），叫做内错角（位置在内且交错）3、∠5与∠4在截线l 的同侧，在被截直线b a ,之间（内），叫做同旁内角.例：如图，判断下列各对角的位置关系：（1）∠1与∠2；（2）∠1与∠7；（3）∠1与∠BAD ；（4）∠2与∠6；（5）∠5与∠8.解：我们将各对角从图形中抽出来（或者说略去与有关角无关的线），得到下列各图.如图所示，不难看出∠1与∠2是同旁内角；∠1与∠7是同位角；∠1与∠BAD 是同旁内角；∠2与∠6是内错角；∠5与∠8对顶角.注意：图中∠2与∠9，它们是同位角吗？不是，∵∠2与∠9的各边分别在四条不同直线上，不是两直线被第三条直线所截而成. 5.2 平行线及其判定5.2.1 平行线1、平行线的概念：在同一平面内，不相交的两条直线叫做平行线，直线a 与直线b 互相平行，记作a ∥b .1 2 3 4 5 6 78 1 6 B A D 2 3 45 7 8 9 FEC A BF 2 1 A B C 1 7 A B C D 26A DB F 1 B A F E 5 8 C2、两条直线的位置关系在同一平面内，两条直线的位置关系只有两种：⑴相交；⑵平行.因此当我们得知在同一平面内两直线不相交时，就可以肯定它们平行；反过来也一样（这里，我们把重合的两直线看成一条直线）判断同一平面内两直线的位置关系时，可以根据它们的公共点的个数来确定：①有且只有一个公共点，两直线相交；②无公共点，则两直线平行；③两个或两个以上公共点，则两直线重合（∵两点确定一条直线）3、平行公理――平行线的存在性与惟一性经过直线外一点，有且只有一条直线与这条直线平行4、平行公理的推论：如果两条直线都与第三条直线平行，那么这两条直线也互相平行如左图所示，∵b ∥a ，c ∥a∴b ∥c注意符号语言书写，前提条件是两直线都平行于第三条直线，才会结论，这两条直线都平行.例：同一平面内，不相交的两条线是平行线.错解：对 ．错解分析：平行线是同一平面内两条直线的位置关系，不相交的两条线，说的不明确．若是射线或线段有可能不相交.∴说法是错误的 ．正解：同一平面内，不相交的两条直线是平行线 ．5.2.2 平行线的判定判定方法 1 两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行简称：同位角相等，两直线平行判定方法 2 两条直线被第三条直线所截，如果内错角相等，那么这两条直线平行简称：内错角相等，两直线平行判定方法 3 两条直线被第三条直线所截，如果同旁内角互补，那么这两条直线平行简称：同旁内角互补，两直线平行几何符号语言：∵ ∠3＝∠2∴ AB ∥CD （同位角相等，两直线平行） ∵ ∠1＝∠2∴ AB ∥CD （内错角相等，两直线平行）∵ ∠4＋∠2＝180°∴ AB ∥CD （同旁内角互补，两直线平行）例：判断下列说法是否正确，如果不正确，请给予改正：（1）不相交的两条直线必定平行线.（2）在同一平面内不相重合的两条直线，如果它们不平行，那么这两条直线一定相交.（3）过一点可以且只可以画一条直线与已知直线平行解：（1）错误.平行线是在“同一平面内不相交的两条直线”.“在同一平面内”是一项重要条件，不能遗漏.（2）正确（3）错误.正确的说法是“过直线外一点”而不是“过一点”.∵如果这一点不在已知直线上，是作不出这条直线的平行线的.A B C D E F 1 2 3 4例：如图，由条件∠2＝∠B ，∠1＝∠D ，∠3＋∠F ＝180°，可以判定哪两条直线平行，并说明判定的根据是什么？解：（1）由∠2＝∠B 可判定AB ∥DE ，根据是同位角相等，两直线平行；（2）由∠1＝∠D 可判定AC ∥DF ，根据是内错角相等，两直线平行；（3）由∠3＋∠F ＝180°可判定AC ∥DF ，根据同旁内角互补，两直线平行.5.3 平行线的性质5.3.1 平行线的性质性质1：两直线平行，同位角相等；性质2：两直线平行，内错角相等；性质3：两直线平行，同旁内角互补.几何符号语言：∵AB ∥CD ∴∠1＝∠2（两直线平行，内错角相等）∵AB ∥CD∴∠3＝∠2（两直线平行，同位角相等）∵AB ∥CD ∴∠4＋∠2＝180°（两直线平行，同旁内角互补）例：已知∠1＝∠B ，求证：∠2＝∠C证明：∵∠1＝∠B （已知）∴DE ∥BC （同位角相等，两直线平行） ∴∠2＝∠C （两直线平行，同位角相等）例：如图，AB ∥DF ，DE ∥BC ，∠1＝65° 求∠2、∠3的度数解：∵DE ∥BC∴∠2＝∠1＝65°（两直线平行，内错角相等）∵AB ∥DF∴∠3＋∠2＝180°（两直线平行，同旁内角互补）∴∠3＝180°－∠2＝180°－65°＝115°A B E D F C 1 2 3 A B C D EF 1 2 3 4 AD E B C 12 A D F B E C 1 2 3例：如图，直线AB，CD分别和直线MN相交于点E，F，EG平分∠BEN，FH平分∠DFN．若AB∥CD，你能说明EG和FH也平行吗?错解：∵EG平分∠BEN，∴∠BEG =12∠BEN．同理，∵FH平分∠DFN，∴∠DFH =12∠DFN．又∵AB∥CD，∴∠BEN =∠DFN；从而∠BEG =∠DFH．∴EG∥FH．错解分析：在复杂的图形中正确地找出同位角、内错角或同旁内角，是运用平行线的判定或性质的前提．认清一对同位角、内错角或同旁内角的关键是弄清截线和被截线，截线就是它们的公共边，其余两条边就是被截线．而∠BEG和∠DFH不是直线EG，FH被某条直线所截得的同位角，∴由∠BEG=∠DFH不能判定EG∥FH．正解：∵EG平分∠BEN，∴∠BEG =∠GEN =12∠BEN，同理，∵FH平分∠DFN，∴∠DFH =∠HFN =12∠DFN，又∵AB∥CD，∴∠BEN =∠DFN，从而∠GEN =∠HFN．而∠GEN，∠HFN是直线EG，FH被直线MN所截得的同位角，∴EG∥FH．例：如图，△ABC中，已知∠1+∠2=180°，∠3=∠B，试判断DE与BC的位置关系，并说明理由．错解：∵∠1+∠2=180°，∴EF∥AB．∴∠3+∠BDE =180°．∵∠3=∠B，∴∠B+∠BDE =180°．∴DE∥BC．错解分析：由∠1＋∠2=180°，不能得到EF∥AB．虽然∠1和∠2是由直线EF和AB被直线DC所截得的角，但由于它们不是同旁内角，∴尽管∠1＋∠2=180°，也不能得到EF∥AB．正解：∵∠1=∠4，∠1＋∠2=180°，∴∠2+∠4=180°．∴EF∥DB(同旁内角互补，两直线平行)．∴∠3+∠BDE=180°(两直线平行，同旁内角互补)．∵∠3=∠B，∴∠B+∠BDE=180°．∴DE∥BC( 同旁内角互补，两直线平行)．5.3.2 命题、定理、证明1、命题的概念：判断一件事情的语句，叫做命题.2、命题的组成每个命题都是题设、结论两部分组成.题设是已知事项，结论是由已知事项推出的事项.3、如果题设成立，那么结论一定成立，这样的命题叫真命题.如果题设成立，不能保证结论一定成立，这样的命题叫做假命题.4、经过推理证实而得到的真命题叫做定理.5、在很多情况下，一个命题的正确性需要经过推理才能作出判断，这个推理过程叫做证明.5.4平移1、平移变换①把一个图形整体沿某一方向移动，会得到一个新的图形，新图形与原图形的形状和大小完全相同.②新图形的每一点，都是由原图形中的某一点移动后得到的，这两个点是对应点③连接各组对应点的线段平行且相等2、平移的特征：①经过平移之后的图形与原来的图形的对应线段平行（或在同一直线上）且相等，对应角相等，图形的形状与大小都没有发生变化.②经过平移后，对应点所连的线段平行（或在同一直线上）且相等.例：如图，△ABC经过平移之后成为△DEF，那么：（1）点A的对应点是点＿＿＿＿＿＿＿＿＿；（2）点B的对应点是点＿＿＿＿＿＿.A DB EC F（3）点＿＿＿＿＿的对应点是点F；（4）线段AB 的对应线段是线段＿＿＿＿＿＿＿；（5）线段BC的对应线段是线段＿＿＿＿＿＿＿；（6）∠A的对应角是＿＿＿＿＿＿.（7）＿＿＿＿的对应角是∠F.解：（1）D；（2）E；（3）C；（4）DE；（5）EF；（6）∠D；（7）∠ACB.。

七年级的数学知识点必看学习从来无捷径。

每一门科目都有自己的学习方法，但其实都是万变不离其中的，数学其实和语文英语一样，也是要记、要背、要讲练的。

下面是小编给大家整理的一些七年级的数学知识点的学习资料，希望对大家有所帮助。

新人教版七年级数学知识第五章相交线与平行线1、两条直线相交所成的四个角中，相邻的两个角叫做邻补角，特点是两个角共用一条边，另一条边互为反向延长线，性质是邻补角互补;相对的两个角叫做对顶角，特点是它们的两条边互为反向延长线。

性质是对顶角相等。

2、三线八角：对顶角(相等)，邻补角(互补)，同位角，内错角，同旁内角。

3、两条直线被第三条直线所截：同位角F(在两条直线的同一旁，第三条直线的同一侧)内错角Z(在两条直线内部，位于第三条直线两侧)同旁内角U(在两条直线内部，位于第三条直线同侧)4、两条直线相交所成的四个角中，如果有一个角为90度，则称这两条直线互相垂直。

其中一条直线叫做另外一条直线的垂线，他们的交点称为垂足。

5、垂直三要素：垂直关系，垂直记号，垂足6、垂直公理：过一点有且只有一条直线与已知直线垂直。

7、垂线段最短。

8、点到直线的距离：直线外一点到这条直线的垂线段的长度。

9、平行公理：经过直线外一点，有且只有一条直线与这条直线平行。

推论：如果两条直线都与第三条直线平行，那么这两条直线也互相平行。

如果b//a,c//a,那么b//c10、平行线的判定：①同位角相等，两直线平行。

②内错角相等，两直线平行。

③同旁内角互补，两直线平行。

11、推论：在同一平面内，如果两条直线都垂直于同一条直线，那么这两条直线平行。

12、平行线的性质：①两直线平行，同位角相等;②两直线平行，内错角相等;③两直线平行，同旁内角互补。

13、平面上不相重合的两条直线之间的位置关系为_______或________14、平移：①平移前后的两个图形形状大小不变，位置改变。

②对应点的线段平行且相等。

平移：在平面内，将一个图形沿某个方向移动一定的距离，图形的这种移动叫做平移平移变换，简称平移。

新初中数学相交线与平行线知识点总复习有解析一、选择题1．如图，12180∠+∠=︒，3100∠=︒，则4∠=（ ）A ．60︒B ．70︒C ．80︒D ．100︒【答案】C【解析】【分析】 首先证明a ∥b ，再根据两直线平行同位角相等可得∠3=∠6，再根据对顶角相等可得∠4．【详解】解：∵∠1+∠5=180°，∠1+∠2=180°，∴∠2=∠5，a ∥b ，∴∠3=∠6=100°，∴∠4=180°-100°=80°．故选：C ．【点睛】此题考查平行线的判定与性质，解题关键是掌握两直线平行同位角相等．2．如图，若AB ∥CD ，则∠α、∠β、∠γ之间关系是（ ）A ．∠α+∠β+∠γ=180°B ．∠α+∠β﹣∠γ=360°C ．∠α﹣∠β+∠γ=180°D ．∠α+∠β﹣∠γ=180°【答案】D试题解析：如图，作EF∥AB，∵AB∥CD，∴EF∥CD，∵EF∥AB，∴∠α+∠AEF=180°，∵EF∥CD，∴∠γ=∠DEF，而∠AEF+∠DEF=∠β，∴∠α+∠β=180°+∠γ，即∠α+∠β-∠γ=180°．故选：D．3．如图，直线a∥b，直线c分别交a，b于点A，C，∠BAC的平分线交直线b于点D，若∠1=50°，则∠2的度数是()A．50°B．70°C．80°D．110°【答案】C【解析】【分析】根据平行线的性质可得∠BAD=∠1，再根据AD是∠BAC的平分线，进而可得∠BAC的度数，再根据补角定义可得答案．【详解】因为a∥b，所以∠1=∠BAD=50°，因为AD是∠BAC的平分线，所以∠BAC=2∠BAD=100°，所以∠2=180°-∠BAC=180°-100°=80°.故本题正确答案为C.本题考查的知识点是平行线的性质，解题关键是掌握两直线平行，内错角相等．4．如图，点,D E 分别在BAC ∠的边,AB AC 上，点F 在BAC ∠的内部，若1,250F ︒∠=∠∠=，则A ∠的度数是（ ）A ．50︒B ．40︒C ．45︒D ．130︒【答案】A【解析】【分析】 利用平行线定理即可解答.【详解】解：根据∠1=∠F ，可得AB//EF ，故∠2=∠A=50°.故选A.【点睛】本题考查平行线定理：内错角相等，两直线平行.5．如图，点D 在AC 上，点F 、G 分别在AC 、BC 的延长线上，CE 平分∠ACB 交BD 于点O ，且∠EOD+∠OBF ＝180°，∠F ＝∠G ，则图中与∠ECB 相等的角有( )A ．6个B ．5个C ．4个D ．3个【答案】B【分析】由对顶角关系可得∠EOD=∠COB，则由∠COB+∠OBF=180°可知EC∥BF，再结合CE是角平分线即可判断.【详解】解：由∠EOD+∠OBF=∠COB+∠OBF=180°可知EC∥BF，结合CE是角平分线可得∠ECB=∠ACE=∠CBF，再由EC∥BF可得∠ACE=∠F=∠G，则由三角形内角和定理可得∠GDC=∠CBF.综上所得，∠ECB=∠ACE=∠CBF=∠F=∠G=∠GDC，共有5个与∠ECB相等的角，故选择B.【点睛】本题综合考查了平行线的判定及性质.6．如图所示，点E在AC的延长线上，下列条件中不能判断BD∥AE的是（）A．∠D＝∠DCE B．∠D＋∠ACD＝180° C．∠1＝∠2 D．∠3＝∠4【答案】C【解析】【分析】根据平行线的判定方法逐项进行分析即可得.【详解】A.由∠D＝∠DCE，根据内错角相等，两直线平行可得BD//AE，故不符合题意；B. 由∠D＋∠ACD＝180°，根据同旁内角互补，两直线平行可得BD//AE，故不符合题意；C.由∠1＝∠2可判定AB//CD，不能得到BD//AE，故符合题意；D.由∠3＝∠4，根据内错角相等，两直线平行可得BD//AE，故不符合题意，故选C.【点睛】本题考查了平行线的判定，熟练掌握平行线的判定方法是解题的关键.7．下列结论中：①若a=b a b；②在同一平面内，若a⊥b，b//c，则a⊥c；③直线外一点到直线的垂线段叫点到直线的距离；33( ) A．1个B．2个C．3个D．4个【答案】B【解析】【分析】【详解】解：①若a=b 0≥，则a =b②在同一平面内，若a ⊥b,b//c ，则a ⊥c ，正确③直线外一点到直线的垂线段的长度叫点到直线的距离④|3-2|=2-3，正确正确的个数有②④两个故选B8．如图，AB CD ∥，BF 平分ABE ∠，且BF DE P ，则ABE ∠与D ∠的关系是（ ）A ．2ABE D ∠=∠B ．180ABE D ∠+∠=︒C ．90ABED ∠=∠=︒D ．3ABE D ∠=∠【答案】A【解析】【分析】 延长DE 交AB 的延长线于G ，根据两直线平行，内错角相等可得D G ∠=∠，再根据两直线平行，同位角相等可得G ABF ∠=∠，然后根据角平分线的定义解答．【详解】 证明：如图，延长DE 交AB 的延长线于G ，//AB CD Q ，D G ∴∠=∠，//BF DE Q ，G ABF ∴∠=∠，D ABF ∴∠=∠，BF Q 平分ABE ∠，22ABE ABF D ∴∠=∠=∠，即2ABE D ∠=∠．故选：A ．【点睛】本题考查了平行线的性质，角平分线的定义，熟记性质并作辅助线是解题的关键．9．如图，下列条件中能判定//DE AC 的是( )A ．EDC EFC ∠=∠B ．AEF ACD ∠=∠C ．34∠=∠D ．12∠=∠【答案】C【解析】【分析】 对于A ，∠EDC=∠EFC 不是两直线被第三条直线所截得到的，据此进行判断；对于B 、D ，∠AFE=∠ACD ，∠1=∠2是EF 和BC 被AC 所截得到的同位角和内错角，据此进行判断；对于C ，∠3=∠4这两个角是AC 与DE 被EC 所截得到的内错角，据此进行判断.【详解】∠EDC=∠EFC 不是两直线被第三条直线所截得到的，因而不能判定两直线平行；∠AFE=∠ACD,∠1=∠2是EF 和BC 被AC 所截得到的同位角和内错角,因而可以判定EF ∥BC,但不能判定DE ∥AC ；∠3=∠4这两个角是AC 与DE 被EC 所截得到的内错角,可以判定DE ∥AC.故选C.【点睛】本题考查平行线的判定，掌握相关判定定理是解题的关键.10．已知直线m ∥n ，将一块含30°角的直角三角板按如图所示方式放置(∠ABC ＝30°)，并且顶点A ，C 分别落在直线m ，n 上，若∠1＝38°，则∠2的度数是( )A ．20°B ．22°C ．28°D ．38°【答案】B【解析】【分析】 过C 作CD ∥直线m ，根据平行线的性质即可求出∠2的度数．【详解】解：过C 作CD ∥直线m ，∵∠ABC ＝30°，∠BAC ＝90°，∴∠ACB ＝60°，∵直线m ∥n ，∴CD ∥直线m ∥直线n ，∴∠1＝∠ACD ，∠2＝∠BCD ，∵∠1＝38°，∴∠ACD ＝38°，∴∠2＝∠BCD ＝60°﹣38°＝22°，故选：B ．【点睛】本题考查了平行线的计算问题，掌握平行线的性质是解题的关键．11．如图，已知AB CD ∥，ABE ∠和CDE ∠的平分线相交于F ，100BED ∠=︒，则BFD ∠的度数为（ ）A ．100°B ．130°C ．140°D ．160°【答案】B【解析】【分析】 连接BD ，因为AB ∥CD ，所以∠ABD ＋∠CDB ＝180°；又由三角形内角和为180°，所以∠ABE ＋∠E ＋∠CDE ＝180°＋180°＝360°，所以∠ABE ＋∠CDE ＝360°−100°＝260°；又因为BF 、DF 平分∠ABE 和∠CDE ，所以∠FBE ＋∠FDE ＝130°，又因为四边形的内角和为360°，进而可得答案．【详解】连接BD ，∵AB ∥CD ，∴∠ABD＋∠CDB＝180°，∴∠ABE＋∠E＋∠CDE＝180°＋180°＝360°，∴∠ABE＋∠CDE＝360°−100°＝260°，又∵BF、DF平分∠ABE和∠CDE，∴∠FBE＋∠FDE＝130°，∴∠BFD＝360°−100°−130°＝130°，故选B．【点睛】此题考查了平行线的性质：两直线平行，同旁内角互补．还考查了三角形内角和定理与四边形的内角和定理．解题的关键是作出BD这条辅助线．12．如图，OB⊥CD于点O，∠1＝∠2，则∠2与∠3的关系是( )A．∠2＝∠3 B．∠2与∠3互补C．∠2与∠3互余D．不能确定【答案】C【解析】【分析】根据垂线定义可得∠1+∠3=90°，再根据等量代换可得∠2+∠3=90°．【详解】∵OB⊥CD，∴∠1+∠3=90°，∵∠1=∠2，∴∠2+∠3=90°，∴∠2与∠3互余，故选：C．【点睛】本题考查了垂线和余角，关键是掌握垂线的定义当两条直线相交所成的四个角中，有一个角是直角时，就说这两条直线互相垂直，其中一条直线叫做另一条直线的垂线．13．如图，△ABC中，∠C=90°，则点B到直线AC的距离是 ( )A．线段AB B．线段AC C．线段BC D．无法确定【答案】C【解析】【分析】直接利用点到直线的距离定义得出答案．【详解】解：如图，三角形ABC 中，∠C=90°，则点B 到直线AC 的距离是：线段BC ． 故选：C ．【点睛】本题考查点到之间的距离，正确把握相关定义是解题关键．14．如图，等边ABC V 边长为a ，点O 是ABC V 的内心，120FOG ∠=︒，绕点O 旋转FOG ∠，分别交线段AB 、BC 于D 、E 两点，连接DE ，给出下列四个结论：①ODE V 形状不变；②ODE V 的面积最小不会小于四边形ODBE 的面积的四分之一；③四边形ODBE 的面积始终不变；④BDE V 周长的最小值为1.5a ．上述结论中正确的个数是（ ）A ．4B ．3C ．2D ．1【答案】A【解析】【分析】 连接OB 、OC ，利用SAS 证出△ODB ≌△OEC ，从而得出△ODE 是顶角为120°的等腰三角形，即可判断①；过点O 作OH ⊥DE ，则DH=EH ，利用锐角三角函数可得OH=12OE 和3OE ，然后三角形的面积公式可得S △ODE =34OE 2，从而得出OE 最小时，S △ODE 最小，根据垂线段最短即可求出S △ODE 的最小值，然后证出S 四边形ODBE =S △OBC =2312即可判断②和③；求出BDE V 的周长=a ＋DE ，求出DE 的最小值即可判断④．【详解】解：连接OB 、OC∵ABC V 是等边三角形，点O 是ABC V 的内心，∴∠ABC=∠ACB=60°，BO=CO ，BO 、CO 平分∠ABC 和∠ACB∴∠OBA=∠OBC=12∠ABC=30°，∠OCA=∠OCB=12∠ACB=30°∴∠OBA=∠OCB ，∠BOC=180°－∠OBC －∠OCB=120° ∵120FOG ∠=︒∴∠=FOG ∠BOC∴∠FOG －∠BOE=∠BOC －∠BOE∴∠BOD=∠COE在△ODB 和△OEC 中BOD COE BO COOBD OCE ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ODB ≌△OEC∴OD=OE∴△ODE 是顶角为120°的等腰三角形，∴ODE V 形状不变，故①正确；过点O 作OH ⊥DE ，则DH=EH∵△ODE 是顶角为120°的等腰三角形∴∠ODE=∠OED=12（180°－120°）=30° ∴OH=OE·sin ∠OED=12OE ，EH= OE·cos ∠OED=32OE ∴DE=2EH=3OE ∴S △ODE =12DE·OH=3OE 2 ∴OE 最小时，S △ODE 最小，过点O 作OE′⊥BC 于E′，根据垂线段最短，OE′即为OE 的最小值∴BE ′=12BC=12a 在Rt △OBE ′中 OE′=BE′·tan ∠OBE ′=12a ×33=36a ∴S △ODE 的最小值为342=2348a∵△ODB ≌△OEC∴S 四边形ODBE =S △ODB ＋S △OBE = S △OEC ＋S △OBE =S △OBC =12BC·OE′=23a ∵23a =14×23a ∴S △ODE ≤14S 四边形ODBE 即ODE V 的面积最小不会小于四边形ODBE 的面积的四分之一，故②正确； ∵S 四边形ODBE =2312a ∴四边形ODBE 的面积始终不变，故③正确；∵△ODB ≌△OEC∴DB=EC∴BDE V 的周长=DB ＋BE ＋DE= EC ＋BE ＋DE=BC ＋DE=a ＋DE∴DE 最小时BDE V 的周长最小∵DE=3OE∴OE 最小时，DE 最小而OE 的最小值为OE′=3a ∴DE 的最小值为3×36a =12a ∴BDE V 的周长的最小值为a ＋12a =1.5a ，故④正确； 综上：4个结论都正确，故选A ．【点睛】此题考查的是等边三角形的性质、全等三角形的判定及性质、锐角三角函数、三角形的面积公式和垂线段最短的应用，掌握等边三角形的性质、全等三角形的判定及性质、锐角三角函数、三角形的面积公式和垂线段最短是解决此题的关键．15．如图，在△ABC 中，AB ＝AC ，∠A ＝36°，D 、E 两点分别在边AC 、BC 上，BD 平分∠ABC ，DE ∥AB ．图中的等腰三角形共有（ ）A ．3个B ．4个C ．5个D ．6个【答案】C【解析】【分析】 已知条件，根据三角形内角和等于180，角的平分线的性质求得各个角的度数，然后利用等腰三角形的判定进行判断即可．【详解】解：∵AB ＝AC ，∠A ＝36°，∴∠ABC ＝∠C ＝72°，∵BD 平分∠ABC ，∴∠ABD ＝∠DBC ＝36°，∴∠BDC ＝180°﹣36°﹣72°＝72°，∵DE ∥AB ，∴∠EDB ＝∠ABD ＝36°，∴∠EDC ＝72°﹣36°＝36°，∴∠DEC ＝180°﹣72°﹣36°＝72°，∴∠A ＝∠ABD ，∠DBE ＝∠BDE ，∠DEC ＝∠C ，∠BDC ＝∠C ，∠ABC ＝∠C ，∴△ABC 、△ABD 、△DEB 、△BDC 、△DEC 都是等腰三角形，共5个，故选C ．【点睛】本题考查了等腰三角形判定和性质、角平分线的性质、平行线的性质，由已知条件利用相关的性质求得各个角相等是解题的关键．16．如图，在ABC V 中，AB AC =，30A ∠=︒，直线a b ∥，顶点C 在直线b 上，直线a 交AB 于点D ，交AC 与点E ，若1145∠=︒，则2∠的度数是（ ）A ．30°B ．35°C ．40°D ．45°【答案】C【解析】【分析】先根据等腰三角形的性质和三角形内角和可得ACB ∠度数，由三角形外角的性质可得AED ∠的度数，再根据平行线的性质得同位角相等，即可求得2∠．【详解】∵AB AC =，且30A ∠=︒， ∴18030752ACB ∠︒-︒==︒， 在ADE ∆中，∵1145A AED ∠∠∠=+=︒，∴14514530115AED A ∠∠=︒-=︒-︒=︒，∵//a b ，∴2AED ACB ∠∠∠=+，即21157540∠=︒-︒=︒，故选：C ．【点睛】 本题考查综合等腰三角形的性质、三角形内角和定理、三角形外角的性质以及平行直线的性质等知识内容．等腰三角形的性质定理：等腰三角形两底角相等；三角形内角和定理：三角形三个内角的和等于180︒；三角形外角的性质：三角形的外角等于与它不相邻的两个内角之和；两直线平行，同位角相等．17．下列说法中错误的个数是( )(1)过一点有且只有一条直线与已知直线平行；(2)过一点有且只有一条直线与已知直线垂直；(3)不相交的两条直线叫做平行线；(4)有公共顶点且有一条公共边的两个互补的角互为邻补角．A ．1个B ．2个C ．3个D ．4个【答案】C【解析】（1）应强调过直线外一点，故错误；（2）正确；（3）不相交的两条直线叫做平行线，没有说明是否是在同一平面内，所以错误；（4）有公共顶点且有一条公共边的两个角不一定互为邻补角，角平分线的两个角也满足，但可以不是,故错误.错误的有3个，故选C.18．如图，小慧从A 处出发沿北偏东60°方向行走至B 处，又沿北偏西20°方向行走至C 处，此时需要将方向调整到与出发时一致，则方向的调整应为（ ）A．左转80°B．右转80°C．左转100°D．右转100°【答案】B【解析】【分析】如图，延长AB到D，过C作CE//AD，由题意可得∠A=60°，∠1=20°，根据平行线的性质可得∠A=∠2，∠3=∠1+∠2，进而可得答案.【详解】如图，延长AB到D，过C作CE//AD，∵此时需要将方向调整到与出发时一致，∴此时沿CE方向行走，∵从A处出发沿北偏东60°方向行走至B处，又沿北偏西20°方向行走至C处，∴∠A=60°，∠1=20°，AM∥BN，CE∥AB，∴∠A=∠2=60°，∠1+∠2=∠3∴∠3=∠1+∠2=20°+60°=80°，∴应右转80°.故选B.【点睛】本题考查了方向角有关的知识及平行线的性质，解答时要注意以北方为参照方向，进行角度调整.19．下列图形中线段PQ的长度表示点P到直线a的距离的是（）A．B．C．D．【答案】C【解析】【分析】根据点到直线的距离的定义，可得答案．【详解】由题意得PQ⊥a，P到a的距离是PQ垂线段的长，故选C．【点睛】本题考查了点到直线的距离，点到直线的距离是解题关键．20．如图所示，b∥c，a⊥b，∠1=130°，则∠2=（）．A．30°B．40°C．50°D．60°【答案】B【解析】【分析】证明∠3=90°，利用三角形的外角的性质求出∠4即可解决问题．【详解】如图，反向延长射线a交c于点M，∵b∥c，a⊥b，∴a⊥c，∴∠3=90°，∵∠1=90°+∠4，∴130°=90°+∠4，∴∠4=40°，∴∠2=∠4=40°，故选B．【点睛】本题考查平行线的性质，垂线的性质，三角形的外角的性质等知识，解题的关键是熟练掌握基本知识。