九年级数学圆的知识点总结大全

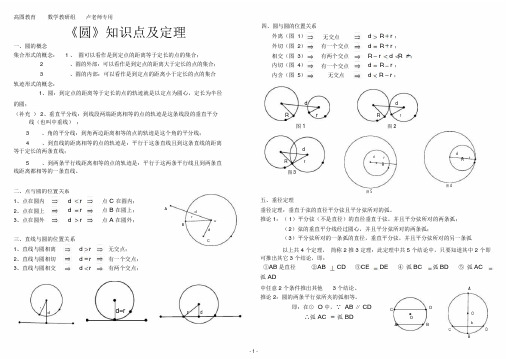
高图教育数学教研组卢老师专用《圆》知识点及定理一、圆的概念集合形式的概念： 1 、圆可以看作是到定点的距离等于定长的点的集合；2、圆的外部：可以看作是到定点的距离大于定长的点的集合；3、圆的内部：可以看作是到定点的距离小于定长的点的集合轨迹形式的概念：1、圆：到定点的距离等于定长的点的轨迹就是以定点为圆心，定长为半径的圆；（补充） 2、垂直平分线：到线段两端距离相等的点的轨迹是这条线段的垂直平分线（也叫中垂线）；四、圆与圆的位置关系外离（图 1）无交点d R r ；外切（图 2）有一个交点d R r ；相交（图 3）有两个交点R r d R r ；内切（图 4）有一个交点d R r ；内含（图 5）无交点d R r ；d dR r R r图 1图 23、角的平分线：到角两边距离相等的点的轨迹是这个角的平分线；4、到直线的距离相等的点的轨迹是：平行于这条直线且到这条直线的距离等于定长的两条直线；5、到两条平行线距离相等的点的轨迹是：平行于这两条平行线且到两条直线距离都相等的一条直线。

dR r图3d rRdR图4r二、点与圆的位置关系1、点在圆内d r点 C 在圆内；2、点在圆上d r点 B 在圆上；A d3、点在圆外d r点 A 在圆外；r OBd三、直线与圆的位置关系C1、直线与圆相离d r无交点；2、直线与圆相切d r有一个交点；3、直线与圆相交d r有两个交点；rd d=r r d图 5五、垂径定理垂径定理：垂直于弦的直径平分弦且平分弦所对的弧。

推论 1：（ 1）平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧；（2）弦的垂直平分线经过圆心，并且平分弦所对的两条弧；（3）平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧以上共 4 个定理，简称 2 推 3 定理：此定理中共 5 个结论中，只要知道其中 2 个即可推出其它 3 个结论，即：①AB是直径②AB CD③CE DE④ 弧BC弧BD⑤ 弧AC弧 AD中任意 2 个条件推出其他 3 个结论。

九年级圆知识点总结圆是几何学中最基本的图形之一，由于其特殊的性质和重要的应用，是中学数学中一个重点和难点的内容。

以下是针对九年级学习的圆知识点总结，包括圆的定义、性质、常见的定理和应用。

一、圆的定义及基本概念1. 圆的定义：圆是平面上与一个固定点距离恒定的点的集合。

2. 圆的要素：圆心、半径、弦、弧、切线等。

二、圆的性质1. 圆的周长公式：C=2πr，其中C是圆的周长，r是圆的半径。

2. 圆的面积公式：S=πr²，其中S是圆的面积，r是圆的半径。

3. 内接圆和外接圆：内接圆是一个圆，恰好与一个多边形的所有顶点相切；外接圆是一个圆，恰好与一个多边形的所有边相切。

4. 相交圆的性质：两个相交圆的交点到两个圆心的距离相等。

两个相交圆的交点确定的两条弦相互垂直的充要条件是两个弦的弧度相等。

三、常见的圆的定理1. 切线定理：切线与半径垂直。

2. 弦切角定理：弦切角等于弦对应的弧的一半。

3. 弦弧角定理：弦弧角等于弦对应的弧的一半。

4. 弦角定理：弦角等于其对应的弧缺角的一半。

5. 弧长定理：弧长等于圆心角的弧度数除以2π乘以圆的周长。

四、圆的应用1. 圆的引理：如欲使直线在给定的点上下夹定一个给定的角，只需作两条通过该点的圆，并使直线分别与两圆相切即可。

2. 圆的内切与外切：两个圆相切，其中一个圆在另一个圆内部，称为内切；两个圆相切，其中一个圆在另一个圆外部，称为外切。

3. 勾股定理的圆证法：利用圆的性质，可以简化勾股定理的证明过程。

4. 圆柱、圆锥和圆球的体积计算：圆柱的体积公式为V=πr²h，其中V是体积，r是底面半径，h是高；圆锥的体积公式为V=1/3πr²h，其中V是体积，r是底面半径，h是高；圆球的体积公式为V=4/3πr³，其中V是体积，r是半径。

以上只是关于九年级圆的知识点的简要总结，实际上圆还有许多其他的性质、定理和应用，需要通过练习和实际问题的解决来进一步加深理解和掌握。

九年级圆的知识点总结一、圆的基本定义1. 圆的定义：平面上所有与给定点（圆心）距离相等的点的集合。

2. 圆心（O）：圆心是圆的中心点，所有圆上的点到圆心的距离都等于半径。

3. 半径（r）：圆心到圆上任意一点的距离。

4. 直径（d）：通过圆心的最长弦，是半径的两倍长度。

5. 弦（c）：连接圆上任意两点的线段。

6. 弧（a）：圆上两点之间的圆周部分。

7. 优弧：大于半圆的弧。

8. 劣弧：小于半圆的弧。

9. 半圆：圆的一半，由直径所界定的弧。

10. 切线（t）：与圆只有一个公共点的直线。

二、圆的性质1. 所有半径的长度相等。

2. 直径是圆内最长的弦。

3. 圆的任意两点之间的弧，优弧总是大于劣弧。

4. 切线与半径相交于圆外的一点，形成直角。

5. 圆周角定理：圆周上任意一点引出的两条半径与圆周所形成的角，其大小是圆心角的一半。

6. 圆心角定理：同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等。

三、圆的计算公式1. 圆的周长（C）：C = πd = 2πr2. 圆的面积（A）：A = πr²3. 扇形面积：S = (θ/360) × πr²，其中θ是扇形的中心角的度数。

4. 弓形面积：S = (θ/360) × πr² - (θ/360) × rθ/2，其中θ是弓形的中心角的度数。

四、圆的应用问题1. 圆与直线的关系：相交、相切、相离。

2. 圆与圆的关系：内含、外离、相交、内切、外切。

3. 圆的切线问题：求切线长度、切点坐标等。

4. 圆的弦长问题：根据圆心距、半径、弦心距等求弦长。

5. 圆的面积问题：根据圆的半径、直径、周长等求面积。

五、圆的作图方法1. 用圆规画圆：确定圆心和半径，旋转圆规即可画出圆。

2. 作圆的切线：通过圆外一点作圆的切线，需要利用圆心到切点的垂线与切线垂直的性质。

3. 作圆的中垂线：连接圆上任意两点，作其中点的垂线，即为圆的中垂线。

九年级圆知识点归纳总结圆是数学中的一个基本几何概念，在九年级的几何学学习中占据重要的地位。

了解和掌握圆的相关知识点对于解决与圆相关的问题至关重要。

本文将对九年级圆的知识点进行归纳总结，帮助学生们更好地理解和应用这些知识。

一、圆的定义与性质1. 圆的定义：圆是一个平面上所有到圆心的距离都相等的点的轨迹。

2. 圆的要素：圆心、半径。

3. 圆的性质：- 圆上的任意一点到圆心的距离都相等。

- 圆的直径是通过圆心的一条线段，它的长度等于圆的半径的两倍。

- 圆的周长是圆周上的任意一点至邻近点的距离之和，也可以通过公式C=2πr计算（其中C表示圆的周长，r表示半径）。

- 圆的面积是圆内所有点构成的区域，可以通过公式A=πr²计算（其中A表示圆的面积）。

二、圆与直线的关系1. 切线：切线是与圆相切于一点的直线，且与半径垂直。

2. 弦：弦是圆上任意两点所确定的线段。

3. 弧：弧是圆周上两点之间的一段弧线。

4. 弧度与弧长的关系：弧度是角度的一种衡量单位，可以用弧长与半径之比来表示。

弧度制中一周对应的弧长等于圆的周长，即2πr。

三、圆的角关系1. 圆心角：由半径的两条边所夹的角称为圆心角。

2. 圆周角：由两条弧线所夹的角称为圆周角。

3. 圆心角与弧度的关系：圆心角的度数等于它所对应的弧度的长度。

四、圆的相交关系1. 相离：两个圆没有任何交点。

2. 外切：两个圆相切于一点，且其中一个圆位于另一个圆的外部。

3. 内切：两个圆相切于一点，且其中一个圆位于另一个圆的内部。

4. 相交：两个圆有两个交点。

五、圆的应用1. 利用圆求解问题：通过已知条件和圆的性质，可以解决与圆相关的实际问题，如求解圆的面积、周长等。

2. 圆的建模：在数学建模中，圆的概念具有广泛应用，可用于描述自然界中的许多现象和实际问题，如行星运动、电子轨道等。

六、圆的常见误区与解决方法1. 误区一：将弦与半径混淆。

解决方法：理解弦是由圆上的两点所确定的线段，半径是由圆心到圆上一点的线段。

九年级圆的知识点详细总结归纳一、圆的定义和关键概念圆是一个平面上的简单闭曲线，由与一个固定点的所有点到该点的距离相等的点组成。

下面是一些重要的圆的关键概念：1. 圆心 (Center)：圆心是圆的中心点，标记为O。

2. 圆周 (Circumference)：圆的周长，也称为圆周，用C表示。

3. 直径 (Diameter)：直径是通过圆心的、连接圆上两点的线段。

直径的长度是圆直径的两倍。

直径用d表示。

4. 半径 (Radius)：半径是从圆心到圆上任意一点的线段。

半径的长度是直径的一半。

半径用r表示。

5. 弧 (Arc)：圆上两点之间的一段路径叫做弧。

6. 弦 (Chord)：圆上两点之间的线段叫做弦。

7. 切线 (Tangent)：切线是切于圆的一条直线，且与圆仅有一个交点。

二、圆的性质和定理圆的性质和定理是研究圆的重要基础，下面是一些常见的圆的性质和定理：1. 直径定理：直径是最长的弦，且它把一个圆分成两个半圆。

2. 弧长定理：一个圆的弧长是根据圆的半径和弧度来计算的。

弧长等于半径乘以弧的弧度。

3. 弧心角定理：圆心角是以圆心为顶点的角，它的弧度等于弧长与半径的比值。

4. 切线定理：切线与半径的关系是垂直。

5. 切线和半径的性质：当一条直线与圆相切时，与切点相连的半径垂直于切线。

6. 切割定理：如果一个弦垂直于一个半径，那么它将被切分成两个互为正方向的弧。

7. 切割角度定理：互不相交的弧它们对应的圆心角相等，相交的弧，它们对应切线切割的角相等。

8. 重合弧定理：在同一个圆上，两个重合的弧对应的圆心角相等。

三、圆的应用圆在日常生活和实际问题中有很多应用，下面是一些常见的圆的应用：1. 圆的测量：通过测量圆的直径或半径可以计算圆的周长和面积。

2. 圆的构造：通过给定圆的半径或直径可以构造圆。

3. 圆的几何关系：圆与直线、圆与圆之间有各种几何关系，如相离、相切、相交等。

4. 圆的运动学：在物理学中，圆的运动学广泛应用于描述物体的圆周运动和周期性运动。

第二十四章 圆一、圆的有关概念及表示方法 （一）圆的定义1、描述性定义：在一个平面内，线段OA 绕它固定的一个端点O 旋转一周，另一个端点A 所形成的图形叫做圆。

其固定的端点O 叫做圆心，线段OA 叫做半径。

2、集合性定义：圆可以看成是所有到定点（圆心）的距离等于定长（半径）的点的集合。

（二）圆的表示方法：以点O 为圆心的圆，记作⨀O ，读作“圆O ”。

（三）圆具有的特性1、圆上各点到定点（圆心O ）的距离都等于定长（半径r ）。

2、到定点的距离等于定长的点都在同一个圆上。

注：（1）确定一个圆需要两个因素：圆心确定圆的位置，半径确定圆的大小。

（2）同一个圆中的所有半径都相等，所以圆上任意两点和圆心[三点不共线(直径)]构成的三角形都是等腰三角形。

（四）圆的有关概念1、弦：连接圆上任意两点的线段叫做弦，经过圆心的弦叫做直径，直径是最长的弦。

以AC 为端点的弦，记作：弦AC 。

注：圆中有无数条弦，其中直径是最长的弦，但弦不一定是直径。

2、弧2.1圆上任意两点间的部分叫做圆弧、简称弧。

以A 、B 为端点的弧记作⨀AB ，读作“圆弧AB ”或“弧AB ”。

2.2圆的任意一条直径的两个端点把圆分成两条弧，每一条弧都叫做半圆。

大于半圆的弧叫做优弧，如图中的⨀ABC 。

小于半圆的弧叫做劣弧，如图中的⨀AC。

注：（1）在一个圆中，任意一条弦都对着两条弧，任意一条弧只对着一条弦。

（2）弧包括优弧、劣弧、半圆；半圆既不是劣弧，也不是优弧。

3、同圆或等圆：能够重合的两个圆叫做等圆。

同圆或等圆的半径相等。

4、等弧：在同圆或等圆中，能够互相重合的弧叫做等弧。

等弧是全等的，不仅仅是弧的长度相等。

5、同心圆：圆心相同，半径不相等的圆叫做同心圆。

二、圆的有关性质 （一）垂直于弦的直径1、圆的轴对称性：圆是轴对称图形，任何一条直径所在的直线都是圆的对称轴。

名称 文字语言 符号语言 图示垂径 定理 垂直于弦的直径平分弦，并且平分弦所对的两条弧。

九年级初三圆知识点大汇总考点一、圆的相关概念1、圆的定义在一个个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A随之旋转所形成的图形叫做圆，固定的端点O叫做圆心，线段OA叫做半径。

2、圆的几何表示以点O为圆心的圆记作“⊙O”，读作“圆O”考点二、弦、弧等与圆有关的定义（1）弦连接圆上任意两点的线段叫做弦。

（如图中的AB）（2）直径经过圆心的弦叫做直径。

（如途中的CD）直径等于半径的2倍。

（3）半圆圆的任意一条直径的两个端点分圆成两条弧，每一条弧都叫做半圆。

（4）弧、优弧、劣弧圆上任意两点间的部分叫做圆弧，简称弧。

弧用符号“⌒”表示，以A，B为端点的弧记作“”，读作“圆弧AB”或“弧AB”。

大于半圆的弧叫做优弧（多用三个字母表示）；小于半圆的弧叫做劣弧（多用两个字母表示）考点三、垂径定理及其推论垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的弧。

推论1：（1）平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧。

（2）弦的垂直平分线经过圆心，并且平分弦所对的两条弧。

（3）平分弦所对的一条弧的直径垂直平分弦，并且平分弦所对的另一条弧。

推论2：圆的两条平行弦所夹的弧相等。

垂径定理及其推论可概括为：过圆心垂直于弦直径平分弦知二推三平分弦所对的优弧平分弦所对的劣弧考点四、圆的对称性1、圆的轴对称性，圆是轴对称图形，经过圆心的每一条直线都是它的对称轴。

2、圆的中心对称性，圆是以圆心为对称中心的中心对称图形。

考点五、弧、弦、弦心距、圆心角之间的关系定理1、圆心角，顶点在圆心的角叫做圆心角。

2、弦心距，从圆心到弦的距离叫做弦心距。

3、弧、弦、弦心距、圆心角之间的关系定理在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦想等，所对的弦的弦心距相等。

推论：在同圆或等圆中，如果两个圆的圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等，那么它们所对应的其余各组量都分别相等。

考点六、圆周角定理及其推论1、圆周角，顶点在圆上，并且两边都和圆相交的角叫做圆周角。

九年级圆的知识点总结圆是九年级数学中的一个重要内容，它具有独特的性质和广泛的应用。

下面我们来对九年级圆的知识点进行一个全面的总结。

一、圆的定义圆是平面内到定点的距离等于定长的点的集合。

这个定点称为圆心，定长称为半径。

圆的标准方程为$（x a)＾2 ＋（y b)＾2 ＝ r^2$，其中$（a, b)＄为圆心坐标，＄r$为半径。

二、圆的相关概念1、弦：连接圆上任意两点的线段叫做弦。

2、直径：经过圆心的弦叫做直径，直径是圆中最长的弦。

3、弧：圆上任意两点间的部分叫做弧。

弧分为优弧（大于半圆的弧）、劣弧（小于半圆的弧）。

4、半圆：圆的任意一条直径的两个端点把圆分成两条弧，每一条弧都叫做半圆。

5、等圆：能够重合的两个圆叫做等圆。

6、等弧：在同圆或等圆中，能够互相重合的弧叫做等弧。

三、圆的性质1、圆的对称性圆是轴对称图形，其对称轴是任意一条通过圆心的直线。

圆是中心对称图形，其对称中心是圆心。

2、垂径定理垂直于弦的直径平分弦且平分弦所对的两条弧。

推论：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧。

弦的垂直平分线经过圆心，并且平分弦所对的两条弧。

平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧。

3、圆心角、弧、弦之间的关系在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等。

推论：在同圆或等圆中，如果两条弧相等，那么它们所对的圆心角相等，所对的弦相等。

在同圆或等圆中，如果两条弦相等，那么它们所对的圆心角相等，所对的弧相等。

4、圆周角定理一条弧所对的圆周角等于它所对的圆心角的一半。

推论：同弧或等弧所对的圆周角相等。

半圆（或直径）所对的圆周角是直角，＄90^｛＼circ}＄的圆周角所对的弦是直径。

四、圆的位置关系1、点与圆的位置关系设点$P$到圆心的距离为$d$，圆的半径为$r$，则有：点$P$在圆外＄＼Leftrightarrow$ ＄d ＞ r$点$P$在圆上＄＼Leftrightarrow$ ＄d ＝ r$点$P$在圆内＄＼Leftrightarrow$ ＄d ＜ r$2、直线与圆的位置关系设圆心到直线的距离为$d$，圆的半径为$r$，则有：直线与圆相离＄＼Leftrightarrow$ ＄d ＞ r$，此时直线与圆没有公共点。

一、圆的定义和性质1.圆的定义：平面上到定点的距离等于定长的点的集合。

2.圆的要素：圆心、半径、圆周。

3.圆的性质：（1）半径相等的两个圆是同心圆；（2）同圆中，圆心角等于圆周角的1/2；（3）同弧上的两条弦所对的圆心角相等；（4）圆心角相等的弧相等；（5）相等弧所对的弦相等；（6）正多边形的内角和是定值，因此内接于一个圆的正多边形的各个内角相等；（7）直径是弦中最长的。

二、弧与圆周角1.弧的定义：圆上两点间的弧是以这两点为端点的两条互不相交的圆弧中，长的那一段。

2.弧的性质：（1）圆周角所对的弧是唯一确定的；（2）全周角所对的弧是定长的。

3.圆周角的定义：以圆心为端点的两条互不相交的射线所夹的角。

4.圆周角的度量：可以用角的度数来衡量。

三、切线与弦1.切线的定义：切线是与圆只有一个公共点的直线。

2.切线与半径的关系：切线与半径的关系是切线⊥半径。

3.弦的定义：两点之间的线段叫做弦。

4.弦的性质：（1）圆内的弦比它们所对的圆心角小，而且与一个圆心角的两个弧所对的弧一样；（2）相等的弦所对的圆心角相等。

四、相交弦定理1.弦上的点：如果一个点在弦上，则这个点到两个端点的距离相等。

2.相交弦定理：如果两个弦相交于圆内的一个点，则这两个弦上的两个点一定分别在另一个弦上的两侧。

五、余弦定理1.面积的性质：圆内、圆外的面积相等，夹在一个圆内的圆周弧的面积也相等。

2.余弦定理：在一个圆上，任意两条弧所对的圆心角的余弦值相等。

六、正多边形的面积公式1.正六边形的面积：正六边形的面积=3×（边长）²×√3÷22.正八边形的面积：正八边形的面积=2×（边长）²×√23.正十二边形的面积：正十二边形的面积=3×（边长）²×√34. 正十六边形的面积：正十六边形的面积=4×（边长）²×tan(22.5°)。

九年级圆知识点总结归纳完整版圆是初中数学中一个重要的几何概念，它有着广泛的应用。

本文将对九年级圆的相关知识点进行总结和归纳，帮助同学们更好地理解和掌握这一内容。

一、圆的定义圆是平面上的一个几何图形，由与其内部距离相等的所有点组成。

其中，距离圆心最远的点称为圆上的点，这个距离称为半径，用字母r表示。

圆上的任意两点之间的距离称为弦，圆的直径是一条穿过圆心并且与圆上的两点相接的弦，直径的长度是半径的两倍。

二、圆的性质1. 圆的周长公式：C = 2πr，其中C是圆的周长，r是圆的半径，π是一个无理数，近似值为3.14或22/7。

周长是圆上一周的长度，也可以说是圆的边界长度。

2. 圆的面积公式：A = πr²，其中A是圆的面积。

面积是圆所包围的平面区域的大小。

3. 切线的性质：切线是与圆只有一个交点的直线。

圆与切线相切时，切线与半径的夹角是直角。

4. 弦的性质：圆的直径是最长的弦，且直径平分圆。

如果两弦在圆内或圆上的交点连线通过圆心，则交线垂直于这两条弦。

三、圆的定位1. 圆的内切和外切：当一个圆与一个三角形的三条边都相切时，该圆称为三角形的内切圆；当一个圆与一个三角形的每条边的延长线相切时，该圆称为三角形的外切圆。

2. 圆的相似：两个圆的半径之比等于两个圆的周长之比，它们是相似的。

四、圆的推理与证明1. 直径在同一直线上的圆是同心圆：当两个圆的直径重合时，它们是同心圆。

2. 圆内接四边形的性质：一个四边形能够内切于一个圆的充要条件是，这个四边形的对角线互相垂直。

3. 正多边形外接圆的性质：一个正n边形可以内切与一个圆的充要条件是，这个正n边形的对角线互相垂直。

五、圆的应用1. 圆与三角形的应用：可以利用圆的性质来解决三角形的推理证明题，如证明三角形内切圆的性质、利用相似三角形证明圆的性质等。

2. 圆的平移、旋转和镜像：圆可以通过平移、旋转和镜像等变换来进行操作，这在解决几何问题时有着重要的作用。

第四章：《圆》一、知识回顾圆的周长： C=2πr或C=πd、圆的面积：S=πr²圆环面积计算方法：S=πR²-πr²或S=π（R²—r²）(R是大圆半径,r是小圆半径)二、知识要点一、圆的概念集合形式的概念: 1、圆可以看作是到定点的距离等于定长的点的集合；2、圆的外部:可以看作是到定点的距离大于定长的点的集合;3、圆的内部：可以看作是到定点的距离小于定长的点的集合轨迹形式的概念：1、圆：到定点的距离等于定长的点的轨迹就是以定点为圆心，定长为半径的圆；固定的端点O为圆心.连接圆上任意两点的线段叫做弦，经过圆心的弦叫直径.圆上任意两点之间的部分叫做圆弧，简称弧。

2、垂直平分线：到线段两端距离相等的点的轨迹是这条线段的垂直平分线；3、角的平分线：到角两边距离相等的点的轨迹是这个角的平分线;4、到直线的距离相等的点的轨迹是：平行于这条直线且到这条直线的距离等于定长的两条直线；5、到两条平行线距离相等的点的轨迹是：平行于这两条平行线且到两条直线距离都相等的一条直线。

二、点与圆的位置关系1、点在圆内⇒d r<⇒点C在圆内；2、点在圆上⇒d r=⇒点B在圆上;3、点在圆外⇒d r>⇒点A在圆外;三、直线与圆的位置关系A1、直线与圆相离⇒d r>⇒无交点；2、直线与圆相切⇒d r=⇒有一个交点；3、直线与圆相交⇒d r<⇒有两个交点;四、圆与圆的位置关系外离（图1）⇒无交点⇒d R r>+；外切（图2)⇒有一个交点⇒d R r=+；相交（图3)⇒有两个交点⇒R r d R r-<<+；内切(图4）⇒有一个交点⇒d R r=-；内含（图5）⇒无交点⇒d R r<-；五、垂径定理垂径定理:垂直于弦的直径平分弦且平分弦所对的弧。

图4图5推论1：(1）平分弦（不是直径)的直径垂直于弦,并且平分弦所对的两条弧; （2）弦的垂直平分线经过圆心，并且平分弦所对的两条弧；（3）平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧以上共4个定理，简称2推3定理：此定理中共5个结论中，只要知道其中2个即可推出其它3个结论，即：①AB 是直径 ②AB CD ⊥ ③CE DE = ④ 弧BC =弧BD ⑤ 弧AC =弧AD 中任意2个条件推出其他3个结论。

初三数学圆的知识点和公式总结数学圆的知识点和公式总结如下：1. 圆的定义：圆是由平面上所有到一个固定点的距离等于一个常数的点的集合。

2. 圆的要素：- 圆心：到圆上任意一点的距离相等的点，通常用大写字母O表示。

- 圆的半径：连接圆心和圆上任意一点的线段的长度，通常用小写字母r表示。

- 圆的直径：通过圆心的两个点之间的距离的两倍，即2r。

- 圆周：圆上所有的点构成的曲线。

- 圆内部：圆周所围成的区域。

3. 圆的相关公式：- 圆的周长：C=2πr，其中π≈3.14。

- 圆的面积：A=πr²。

- 圆的直径与周长的关系：C=πd，其中d为直径。

- 圆的直径与面积的关系：A=π(d/2)²。

4. 圆与圆的位置关系：- 相离：两个圆没有交点，且两个圆心之间的距离大于两个半径之和。

- 外切：两个圆内切于一个切点，且两个圆心之间的距离等于两个半径之和。

- 相交：两个圆有两个交点，且两个圆心之间的距离小于两个半径之和。

- 内切：一个圆在另一个圆的内部，且两个圆心之间的距离等于两个半径之差。

- 同心：两个圆的圆心重合，半径可以相等也可以不相等。

5. 圆的常用定理：- 弧长公式：弧长L=2πr(θ/360°)，其中θ为所对的圆心角的度数。

- 弦长公式：弦长l=2r*sin(θ/2)，其中θ为所对的圆心角的度数。

- 弧度制与角度制的转换：1弧度=180°/π，1°=π/180弧度。

- 正弦定理：在任意三角形ABC中，a/sinA=b/sinB=c/sinC。

- 余弦定理：在任意三角形ABC中，c²=a²+b²-2ab*cosC。

- 勾股定理：在直角三角形ABC中，a²+b²=c²。

希望以上总结对你有帮助！如有其他问题，请随时提问。

圓知識點總結知識回顧圓の周長： C=2πr 或C=πd 、圓の面積：S=πr ²圓環面積計算方法：S=πR ²-πr ²或S=π（R ²-r ²）(R 是大圓半徑，r 是小圓半徑） 知識要點 一、圓の概念集合形式の概念： 1、 圓可以看作是到定點の距離等於定長の點の集合； 2、圓の外部：可以看作是到定點の距離大於定長の點の集合； 3、圓の內部：可以看作是到定點の距離小於定長の點の集合 軌跡形式の概念：1、圓：到定點の距離等於定長の點の軌跡就是以定點為圓心，定長為半徑の圓；固定の端點O 為圓心。

連接圓上任意兩點の線段叫做弦，經過圓心の弦叫直徑。

圓上任意兩點之間の部分叫做圓弧，簡稱弧。

2、垂直平分線：到線段兩端距離相等の點の軌跡是這條線段の垂直平分線；3、角の平分線：到角兩邊距離相等の點の軌跡是這個角の平分線；4、到直線の距離相等の點の軌跡是：平行於這條直線且到這條直線の距離等於定長の兩條直線；5、到兩條平行線距離相等の點の軌跡是：平行於這兩條平行線且到兩條直線距離都相等の一條直線。

二、點與圓の位置關係1、點在圓內 ⇒ d r < ⇒ 點C 在圓內；2、點在圓上 ⇒ d r = ⇒ 點B 在圓上；3、點在圓外 ⇒ d r > ⇒ 點A 在圓外； 三、直線與圓の位置關係1、直線與圓相離 ⇒ d r > ⇒ 無交點；2、直線與圓相切 ⇒ d r = ⇒ 有一個交點；3、直線與圓相交 ⇒ d r < ⇒ 有兩個交點；四、圓與圓の位置關係外離（圖1）⇒ 無交點 ⇒ d R r >+；A外切（圖2）⇒ 有一個交點 ⇒ d R r =+； 相交（圖3）⇒ 有兩個交點 ⇒ R r d R r -<<+； 內切（圖4）⇒ 有一個交點 ⇒ d R r =-； 內含（圖5）⇒ 無交點 ⇒ d R r <-；五、垂徑定理垂徑定理：垂直於弦の直徑平分弦且平分弦所對の弧。

初中数学九年级上圆的知识点圆是初中数学九年级上的一个重要知识点，下面将从圆的定义、圆的性质、圆的相关定理以及圆的应用等方面进行论述。

一、圆的定义圆是平面上的重要几何图形之一，是由与一个定点距离相等的所有点构成的集合。

这个定点称为圆心，距离称为半径，用字母r表示。

圆通常用圆的轮廓线表示，在数学表达中用字母O表示。

二、圆的性质1. 圆的任意两点到圆心的距离相等。

这意味着圆上的每一个点到圆心的距离都相等，即圆的半径。

2. 圆的直径是圆上任意两点之间的最长距离。

直径的长度是半径的两倍。

3. 圆的弦是圆上任意两点之间的线段。

弦不一定通过圆心，可以在圆内或圆外。

4. 圆上的切线垂直于半径。

切线是与圆相切的线，与圆的切点处的半径垂直。

三、圆的相关定理1. 弧与角的关系圆上的弧对应的圆心角是两个端点在圆心所对应的角，它们的度数相等。

2. 弧长与圆周角的关系圆的弧长是圆心角所对应的弧所在圆的一部分的长度，弧长等于这个圆心角所对应的圆周角度数的比值。

3. 弦长与弦心角的关系弦上的弦长是弦心角所对应的弦所在圆的一部分的长度，弦长等于这个弦心角所对应的圆周角度数的比值的2倍。

4. 割线定理割线是两个切点之间的线段，割线上的两个切线段长度乘积等于这条割线与这两个切点之间的弦段长度乘积。

四、圆的应用1. 圆的测量圆的周长等于圆周上的任意一段弧长，即C=πd或C=2πr，其中d为直径，r为半径。

圆的面积等于圆内所包围的面积，即S=πr²。

2. 圆的位置关系两个圆之间的位置关系可以分为外切、内切、相交、相离四种情况，通过判断两个圆心的距离与两个圆的半径之间的关系可以确定两个圆的位置关系。

3. 圆的轴对称与旋转对称圆具有轴对称性和旋转对称性，利用这个特性可以解决一些与圆相关的问题。

综上所述，圆是初中数学九年级上的重要知识点，通过对圆的定义、性质、相关定理和应用进行论述，可以帮助同学们更好地理解和掌握圆的知识，提高数学学科的学习成绩。

圆是一种特殊的几何图形，是平面上所有到一些点的距离相等的点的集合。

在九年级数学中，我们学习了许多与圆相关的知识点，包括圆的性质、圆的方程、圆的切线和弦、圆与直线的位置关系等。

下面是对这些知识点的详细总结。

一、圆的性质1.圆的定义：平面上到一个固定点的距离相等的点的集合叫做圆。

2.圆的元素：圆心、半径、直径、弦、弧等。

3.圆的表示方法：圆心为O，半径为r的圆可以表示为O(r)，或者简写为O。

二、圆的方程1.标准方程：以圆心为原点O(0,0)，半径为r的圆的方程为x²+y²=r²。

2.一般方程：以圆心为(h,k)，半径为r的圆的方程为(x-h)²+(y-k)²=r²。

三、圆的切线和弦1.切线：与圆只有一个交点的直线叫做圆的切线。

切线垂直于半径。

2.弦：连接圆上两个不相邻点的线段叫做圆的弦。

圆心到弦的中点的线段垂直于弦。

四、圆与直线的位置关系1.直线与圆的位置关系有三种情况：a.直线与圆相交于两点：直线穿过圆的内部，与圆有两个交点。

b.直线与圆相切：直线与圆只有一个交点，且切点在圆上。

c.直线与圆相离：直线没有与圆的交点。

五、圆的相关定理1.切线定理：切线与半径的垂直定理。

切线与半径的垂线相互垂直。

2.弦切角定理：圆弦上的两个角对相同弧的度数相等。

3.弧上的角等于圆心角的一半：弧上的角等于它所对的圆心角的一半。

4.切线垂直半径定理：过圆的切点作切线，与过切点的半径垂直。

六、圆的计算1.弧长公式：弧长L=2πr(θ/360°)，其中r为半径，θ为圆心角度数。

2.弧度制与角度制转换：1°=π/180，1弧度=180/π。

以上是九年级数学中圆的主要知识点的总结，通过对这些知识点的学习和理解，能够更好地理解和解决与圆相关的问题。