精选七年级下数学思维拓展训练试题

七年级数学思维拓展训练（2）————有理数及其运算班级 姓名说明：本练习供学有余力的同学课外拓展选用，不作必做要求，相关解答到群文件下载。

一、精心选一选1．若a 与b 互为相反数，c 与d 互为倒数，则a b cd +-的值 ( )A ．0B ．1C ．-1D ．22.算式22222222+++可化为（ ）A.42B. 82C. 28D. 1623.若0a <,a a +的值是（ ）A. 2aB. 0C. -2aD. a 4.若41x +表示一个整数，则整数x 可取值共有（ ） A. 3个 B. 4个 C. 5个 D. 6个5.有理数a 、b 在数轴上的位置如图所示,则下列结论错误的是（ ）A.0a b +<B.0ab <C.b a ->D.0a b -<6.如图，数轴上标出若干个点，每相邻两点相距1个单位，点A 、B 、C 、D 对应的数分别是整数a 、b 、c 、d ,且210d a -=，那么数轴的原点应是（ ）A. A 点B. B 点C. C 点D. D 点二.细心填一填7.a 是最大的负整数，b 是绝对值最小的有理数，则200820092007b a +=___________ 8.有理数a 等于它的倒数，有理数b 等于它的相反数，则20142013ab +=________ 9.将3(0.2)-，31.2和31.5-按从小到大的顺序排列起来 .10.四个互不相等的整数a 、b 、c 、d 满足9abcd =，那么a b c d +++的值为_______11.若0ab >，0bc <,则ac ____0（填“>”或“<”）12.在算式1﹣|﹣2□3|中的□里，填入运算符号 ，使得算式的值最小（在符号+，﹣，×，÷中选择一个）.三．耐心算一算13.计算:（1）11413()302365÷+-- （2）111112481664+++++14. 1111212=-⨯ 1112323=-⨯ 1113434=-⨯ (1) 145=⨯ 120032004=⨯ (2) 用含n 的式子表示你发现的规律(3) 依照上述方法计算：111113355720032005++++⨯⨯⨯⨯(4) 依照上述方法计算：1111144771020022005++++⨯⨯⨯⨯15．设三个互不相等的有理数，既可表示为1，a b +，a 的形式，又可表示为0，b a ，b 的形式，求a 、b 的值.16．如果有理数a 、b 、c 满足0a b c ++>，0abc <，当a b c x a b c =++时, 试求931920x +的值．。

以下是15道思维拓展题的示例：1.有两个大小相同的圆。

一个圆的周长是另一个圆的12倍。

请问，它们的面积比是多少？2.一个正方形内有一个最大的圆，这个圆的周长和正方形的周长相等。

如果正方形的边长为6厘米，那么这个圆的面积是多少？3.假设一个正方形被切成了n个小正方形，每个小正方形的边长都是1，那么这个大正方形的边长是多少？4.一个水桶里有1加仑的水，倒进半杯咖啡，再倒进半杯牛奶，现在有多少杯水？5.有两根绳子，一根是另一根的两倍长。

如果从两根绳子上各剪去30厘米，那么短的那根绳子还剩下多少厘米？6.有两根一样长的绳子。

从第一根绳子上剪下5米，从第二根绳子上剪下15米，然后两根绳子接在一起，它们还有一样长吗？7.一根绳子绕过一个滑轮，一端系着一只玩具熊，另一端系着一只小鸟。

如果玩具熊比小鸟重10倍，那么滑轮的哪个方向会移动？8.如果你把一张纸对折4次，你会得到多少张纸？9.如果你有一个装满水的瓶子和一个空瓶子，你可以只用这两个瓶子解决什么问题？10.一只狗和一个人赛跑。

如果狗的步子大一些，那么它会赢；如果人的步子小一些，那么他会赢。

请问：如果狗一步跑3米，人一步跑4米，那么谁会赢？11.你有一块木头和一把刻刀。

你可以在木头上刻一个图案，然后把它变成一个复杂的立体形状。

请问：这个立体形状是什么？12.如果你有一个盒子和一些球，你可以把球放进盒子里或者从盒子里拿出球。

请问：这个盒子可以做什么？13.如果你有一个笔和一个纸，你可以用笔在纸上写字画画。

请问：这个纸可以做什么？14.你有一块布和一些线，你可以用这些材料缝制一个小袋子。

请问：这个小袋子可以做什么？15.如果你有一把尺子和一些铅笔，你可以用这些工具画出一条直线。

请问：这条直线可以做什么？。

七年级下册数学思维专项训练题（共10套）思维训练题（一）班级______________ 姓名_____________ 一、选择题：1．a 为任意自然数，包括a 在内的三个连续的自然数，可以表示为 （ ）A ．a －2，a －1，aB ．a －3，a －2，a －1C ．a ，a ＋1，a ＋2D ．不同于A 、B 、C 的形式二、计算题：（动动脑筋，可能会有简便的解题方法！）1．____________________56875=⨯2．____________2006200420022000...12108642=+-+-+-+-+- 3．__________________8567785667855678=+++4．()()__________888...6428002...888488868888=++++-++++5．______________125.01712517125625.05.0171251753=⨯-⨯+⨯+ 6．______________12346123451234512345=÷7．_________________31313131=-+-8．_______________99163135115131=++++ 9．_____________20042004...200432004220041=++++10．_____________90197218561742163015201412136121=++++++++三、应用与创新：1．有一高楼，每上一层需要3分钟，每下一层需要1分30秒。

小贤于下午6时15分开始从最底层不断地向上走，到了最顶层后便立即往下走，中途没有停留，他在7时36分返回最底层。

这座高楼共有多少层？2．回答下列各题：（1）用1、2、3、4、5、6、7、8可组成多少个没有重复数字的五位数？（2）在15个连续自然数中最多有多少个质数？最少有多少个质数？（3）以下是一个数列，第一项是1，第二项是4，以后每一项是前两项相乘的积。

七年级数学思维训练（共10套）（第一套）班级______________ 姓名_____________一、选择题：1．a 为任意自然数，包括a 在内的三个连续的自然数，可以表示为 （ ）A ．a －2，a －1，aB ．a －3，a －2，a －1C ．a ，a ＋1，a ＋2D ．不同于A 、B 、C 的形式二、计算题：（动动脑筋，可能会有简便的解题方法！）1．____________________56875=⨯2．____________2006200420022000...12108642=+-+-+-+-+-3．__________________8567785667855678=+++4．()()__________888...6428002...888488868888=++++-++++5．______________125.01712517125625.05.0171251753=⨯-⨯+⨯+ 6．______________12346123451234512345=÷ 7．_________________31313131=-+-8．_______________99163135115131=++++9．_____________20042004...200432004220041=++++10．_____________90197218561742163015201412136121=++++++++ 三、应用与创新：1．有一高楼，每上一层需要3分钟，每下一层需要1分30秒。

小贤于下午6时15分开始从最底层不断地向上走，到了最顶层后便立即往下走，中途没有停留，他在7时36分返回最底层。

这座高楼共有多少层？2．回答下列各题：（1）用1、2、3、4、5、6、7、8可组成多少个没有重复数字的五位数？（2）在15个连续自然数中最多有多少个质数？最少有多少个质数？（3）以下是一个数列，第一项是1，第二项是4，以后每一项是前两项相乘的积。

七年级下册数学思维题（共10套）思维训练题（一）班级______________ 姓名_____________一、选择题：1．a 为任意自然数，包括a 在内的三个连续的自然数，可以表示为 （ ）A ．a －2，a －1，aB ．a －3，a －2，a －1C ．a ，a ＋1，a ＋2D ．不同于A 、B 、C 的形式二、计算题：（动动脑筋，可能会有简便的解题方法！）1．____________________56875=⨯2．____________2006200420022000...12108642=+-+-+-+-+-3．__________________8567785667855678=+++4．()()__________888...6428002...888488868888=++++-++++5．______________125.01712517125625.05.0171251753=⨯-⨯+⨯+ 6．______________12346123451234512345=÷ 7．_________________31313131=-+-8．_______________99163135115131=++++9．_____________20042004...200432004220041=++++10．_____________90197218561742163015201412136121=++++++++三、应用与创新：1．有一高楼，每上一层需要3分钟，每下一层需要1分30秒。

小贤于下午6时15分开始从最底层不断地向上走，到了最顶层后便立即往下走，中途没有停留，他在7时36分返回最底层。

这座高楼共有多少层？2．回答下列各题：（1）用1、2、3、4、5、6、7、8可组成多少个没有重复数字的五位数？（2）在15个连续自然数中最多有多少个质数？最少有多少个质数？（3）以下是一个数列，第一项是1，第二项是4，以后每一项是前两项相乘的积。

能力拓展题
1、 已知等式1)2()1(222=--+-+z k k y k x k 与k 值无关，求x ，y ，z 的值。

2、 计算：2（3+1）（32+1）（34+1）…（332+1）+1。

3、设a ，b ，c ，d 都是整数，且,,2222d c n b a m +=+=试将mn 表示成两个整数的平方和的形式。

4、平面内有10条直线，每两条直线交于一点，这10条直线最多有几个交点？
5、①现在有6个花盆，你能把它们排排队，使得每排都有3个花盆吗？右边的小圆点表示花盆，你动手排排看吧！
②英国一位数学家于1821年出了这样一道智趣题（九树十行）：
春分艳阳暖，园中植树忙；
每行植三棵，九株栽十行；
种法有多样，请你试试看。

6、如图，∠1=∠2，∠D=90°，EF ⊥CD ，那么∠3=∠B 吗？
7、如图，在不等边三角形ABC 中，AQ=PQ ，PM ⊥AB ，
PN ⊥AC ，PM=PN 。

试说明：QP ∥AM 。

123A B C D E F A B C M N Q。

图4 七（下）数学思维拓展训练 时间：45分钟 分值：100分 一、选择题（每小题5分，共25分） 1.若n 为正整数，且x 2n =3，则(3x 3n )2－4(x 2)2n 的值为( ) （A ）207 （B ）36 （C ）45 （D ）217 2．一个长方形的长是2x 厘米，宽比长的一半少4厘米，若将长方形的长和宽都增加3厘米，则该长方形的面积增加为（ ） (A)9 （B ）2x 2+x －3 （C ）－7x －3 （D ）9x －3 3．若(x-5)·A= x 2+x+B ，则（ ） （A ）A=x+6，B=－30 （B ）A=x －6，B=30 （C ）A=x+4，B=－20 （D ）A=x －4，B=20 4.已知6141319,27,81===c b a ，则a ，b ，c 大小关系是（ ） （A ）a>c>b （B ）a>b>c （C ）a<b<c （D ）b>c>a 5.如图1，直线MN 以点O 为旋转中心，将射线OA 顺时针旋转60后，这时图中30的角的个数是 （ ） (A) 4个 (B) 3个 (C) 2个 (D) 1个二、填空题（每小题5分，共25分） 6.用如图2所示的正方形和长方形卡片若干张，需要B 类卡片_______张. 7.如图3，AB ∥CD ，M 、N 分别在AB ，CD 上，P 为两平行线间一点，那么∠1+∠2+∠3= . 8.如图4，一把矩形直尺沿直线断开并错位，点E 、D 、B 、F 在同一条直线上，若∠ADE ＝125, 则∠DBC= . 9.三个同学对问题“若方程组111222a x b y c a x b y c +=⎧⎨+=⎩的解是34x y =⎧⎨=⎩，求方程组111222325325a x b y c a x b y c +=⎧⎨+=⎩的解．”提出各自的想法．甲说：“这个题目好象条件不够，不能求解”；乙说：“它们的系数有一定的规律，可以试试”；丙说：“能不能把第二个方程组的两个方程的两边都除以5，通过换元替代的方法来解决”．参考他们的讨论，你认为这个题目的解应该是 ． 10. 数学家发明了一个魔术盒，当任意数对()b a ,进入其中时，会得到一个新的数：()()21--b a .现将数对()1,m 放入其中得到数n ，再将数对()m n ,放入其中后，如果最后得到的数是 .（结果要化简） 三、解答题（每小题10分，共50分） 11.计算：(1+2+3+…+2013)(2+3+4+…+2012)－(1+2+3+…+2012) (2+3+4+…+2013)．图1 O N M A B P Q a b 图2 3 2 C P D 1 B N A M 图312.图5是按一定规律排列的方程组集合和它解的集合的对应关系图，若方程组集合中的方程组自左至右依次记作方程组1、方程组2、方程组3、……方程组n ．（1）将方程组1的解填入图中；（2）请依据方程组和它的解变化的规律，将方程组n 和它的解直接填入集合图中；（3）若方程组⎩⎨⎧-=+1my x y x 的解是⎨⎧=10x ，求m 的值，并判断该方程组是否符合（2）中的规律13.如图6（1（2）题（1（3）利用（2214.解：设x 2－4x=y ． 原式=y 2+8y+16 ② =( y+4)2 ③=(x 2－4x+4)2 ④回答下列问题：（1）该同学②到③运用了因式分解的_______.（A ）提取公因式 （B ）平方差公式（C ）两数和的完全平方公式 （D ）两数差的完全平方公式（2）该同学因式分解的结果是否彻底________（填“彻底”或“不彻底”）；若不彻底，请直接写出因式分解的最后结果_________．（3）请模仿以上方法对多项式（x 2－2x ）（x 2－2x+2）+1进行因式分解．15．如下几个图形是五角星和它的变形．（1）图7中是一个五角星，则∠A+∠B+∠C+∠D+∠E = o ．（2）图7中的点A 向下移到BE 上时，五个角的和（即∠CAD+∠B+∠C+∠D+∠E）有无变化如图8，说明你的结论的正确性．（3）把图8中的点C 向上移到BD 上时，五个角的和（即∠CAD+∠B+∠ACE +∠D+∠E）有无1~ 11.设a(b+2013)=ab+2013b －ab －2013a=2013b －2013a=2013b －2013(b+1)= 2013b －2013 b －2013=－2013．方程组12.（1）直接消元可求出⎩⎨⎧==01y x ；（2）观察第一个方程都是x+y=1，第二个方程x 前面的系数都是1，而y 前面的系数应是－n ，常数项应是n 2，这样第二个方程应是x －ny= n 2，所以第n 个方程组为⎩⎨⎧=-=+21n ny x y x ．其解的规律是x 从1开始依次增1，y 从0开始依次减1，这样第n 个方程组的解为⎩⎨⎧-==n y n x 1；（3）把⎩⎨⎧-==9y 10x 代入方程x －my=16，得m=32．显然不符合(2)中的规律．13.（1）因为两组直线分别互相平行，所以由平行线的性质可得∠2=∠1=115o，∠3+∠2=180o，则∠3=180o－115o=65o ；（2）如果一个角的两边分别平行于另一个角的两边，那么这两个角相等或互补；（3）设其中的一个角为xo ，则另一个角为2xo ．因为xo+2xo=180o ，所以x=60o ．故这两个角分别为60o 和120o ．14.（1）C（2）不彻底，( x －2)4（3）设x 2－2x=y ．原式=y (y +2)+1= y 2+2y+1=( y+1)2=(x 2－2x+1)2=( x －1)4 ．15．（1）180o ．（2）无变化．因为∠BAC=∠C+∠E ，∠EAD=∠B+∠D ，所以∠CAD+∠B+∠C+∠D+∠E=∠BAC+∠CAD+∠EAD=180o ．（3）无变化．因为∠ACB=∠CAD+∠D ，∠ECD=∠B+∠E ，所以∠CAD+∠B+∠ACE +∠D+∠E=∠ACB+∠ACE+∠ECD=180o ．。

图4七（下）数学思维拓展训练时间：45分钟 分值：100分一、选择题（每小题5分，共25分）1.若n 为正整数，且x 2n =3，则(3x 3n )2－4(x 2)2n 的值为( )（A ）207 （B ）36 （C ）45 （D ）2172．一个长方形的长是2x 厘米，宽比长的一半少4厘米，若将长方形的长和宽都增加3厘米，则该长方形的面积增加为（ ）(A)9 （B ）2x 2+x －3 （C ）－7x －3 （D ）9x －33．若(x-5)·A= x 2+x+B ，则（ ）（A ）A=x+6，B=－30 （B ）A=x －6，B=30（C ）A=x+4，B=－20 （D ）A=x －4，B=204.已知6141319,27,81===c b a ，则a ，b ，c 大小关系是（ ）（A ）a>c>b （B ）a>b>c （C ）a<b<c （D ）b>c>a5.如图1，直线MN//PQ ，OA ⊥OB ，∠BOQ=30︒.若以点O 为旋转中心，将射线OA 顺时针旋转60︒后，这时图中30︒的角的个数是 （ ）(A) 4个 (B) 3个 (C) 2个 (D) 1个二、填空题（每小题5分，共25分）6.用如图2所示的正方形和长方形卡片若干张，拼成一个边长为a+b 的正方形，需要B 类卡片_______张.7.如图3，AB ∥CD ，M 、N 分别在AB ，CD 上，P 为两平行线间一点，那么∠1+∠2+∠3= ︒.8.如图4，一把矩形直尺沿直线断开并错位，点E 、D 、B 、F 在同一条直线上，若∠ADE ＝125︒, 则∠DBC= ︒.9.三个同学对问题“若方程组111222a x b y c a x b y c +=⎧⎨+=⎩的解是34x y =⎧⎨=⎩，求方程组111222325325a x b y c a x b y c +=⎧⎨+=⎩的解．”提出各自的想法．甲说：“这个题目好象条件不够，不能求解”；乙说：“它们的系数有一定的规律，可以试试”；丙说：“能不能把第二个方程组的两个方程的两边都除以5，通过换元替代的方法来解决”．参考他们的讨论，你认为这个题目的解应该是 ．10. 数学家发明了一个魔术盒，当任意数对()b a ,进入其中时，会得到一个新的数：图1 O N M A B P Q aa ab A 类 B 类 C 类 图2()()21--b a .现将数对()1,m 放入其中得到数n ，再将数对()m n ,放入其中后，如果最后得到的数是 .（结果要化简）三、解答题（每小题10分，共50分）11.计算：(1+2+3+…+2013)(2+3+4+…+2012)－(1+2+3+…+2012) (2+3+4+…+2013)．12.图5是按一定规律排列的方程组集合和它解的集合的对应关系图，若方程组集合中的方程组自左至右依次记作方程组1、方程组2、方程组3、……方程组n ．（1）将方程组1的解填入图中；（2）请依据方程组和它的解变化的规律，将方程组n 和它的解直接填入集合图中；（3）若方程组⎩⎨⎧-=+1my x y x 的解是⎨⎧=10x ，求m 的值，并判断该方程组是否符合（2）中的规律？13.如图6，已知两组直线分别互相平行．（1）若∠1=115º，求∠2，∠3的度数；（2）题（1）中隐含着一个规律，请你根据（1）的结果进行归纳，试用文字表述出来；（3）利用（2）中的结论解答：如果两个角的两边分别平行，其中一个角是另一个角的2倍，求这两个角的大小．方程组图514.下面是某同学对多项式（x2－4x+2）（x2－4x+6）+4进行因式分解的过程．解：设x2－4x=y．原式=(y+2) (y +6)+4 ①=y2+8y+16 ②=( y+4)2 ③=(x2－4x+4)2 ④回答下列问题：（1）该同学②到③运用了因式分解的_______.（A）提取公因式（B）平方差公式（C）两数和的完全平方公式（D）两数差的完全平方公式（2）该同学因式分解的结果是否彻底？________（填“彻底”或“不彻底”）；若不彻底，请直接写出因式分解的最后结果_________．（3）请模仿以上方法对多项式（x2－2x）（x2－2x+2）+1进行因式分解．15．如下几个图形是五角星和它的变形．（1）图7中是一个五角星，则∠A+∠B+∠C+∠D+∠E= º．（2）图7中的点A向下移到BE上时，五个角的和（即∠CAD+∠B+∠C+∠D+∠E）有无变化？如图8，说明你的结论的正确性．（3）把图8中的点C向上移到BD上时，五个角的和（即∠CAD+∠B+∠ACE +∠D+∠E）参考答案1~5.ADABA6.27.3608.559. 510x y =⎧⎨=⎩ 10. －m 2+2m 11.设1+2+3+…+2012=a ，2+3+4+…+2012=b ，则a= b+1．(1+2+3+…+2013)(2+3+4+…+2012)－(1+2+3+…+2012) (2+3+4+…+2013)= (a+2013)b －a(b+2013)=ab+2013b －ab －2013a=2013b －2013a=2013b －2013(b+1)= 2013b －2013 b －2013=－2013．12.（1）直接消元可求出⎩⎨⎧==01y x ；（2）观察第一个方程都是x+y=1，第二个方程x 前面的系数都是1，而y 前面的系数应是－n ，常数项应是n 2，这样第二个方程应是x －ny= n 2，所以第n 个方程组为⎩⎨⎧=-=+21n ny x y x ．其解的规律是x 从1开始依次增1，y 从0开始依次减1，这样第n 个方程组的解为⎩⎨⎧-==n y n x 1；（3）把⎩⎨⎧-==9y 10x 代入方程x －my=16，得m=32．显然不符合(2)中的规律．13.（1）因为两组直线分别互相平行，所以由平行线的性质可得∠2=∠1=115º，∠3+∠2=180º，则∠3=180º－115º=65º；（2）如果一个角的两边分别平行于另一个角的两边，那么这两个角相等或互补；（3）设其中的一个角为xº，则另一个角为2xº．因为xº+2xº=180º，所以x=60º．故这两个角分别为60º和120º．14.（1）C（2）不彻底，( x －2)4（3）设x 2－2x=y ．原式=y (y +2)+1= y 2+2y+1=( y+1)2=(x 2－2x+1)2=( x －1)4 ．15．（1）180º．（2）无变化．因为∠BAC=∠C+∠E ，∠EAD=∠B+∠D ，所以∠CAD+∠B+∠C+∠D+∠E=∠BAC+∠CAD+∠EAD=180º．（3）无变化．因为∠ACB=∠CAD+∠D ，∠ECD=∠B+∠E ，所以∠CAD+∠B+∠ACE +∠D+∠E=∠ACB+∠ACE+∠ECD=180º．。

七下思维创新题4
1. 某村去年种植的油菜籽亩产量达150千克，含油率为40﹪。

今年改种新选育的油菜籽后亩产量提高了30千克，含油率提高了10百分点。

今年与去年相比，油菜的种植面积减少了40亩，而村榨油厂用本村所产油菜籽的产油量提高了20﹪。

（1）求今年油菜的种植面积。

设今年油菜的种植面积是x 亩。

完成下表后再列方程解答。

亩产量（千克/亩）
种植面积
（亩）
油菜籽总产量
（千克）
150
x
（2）已知油菜种植成本为200元/亩，菜油收购价为6元/千克。

试比较这个村去今两年种植油菜的纯收入。

2. 如图1，射线OC，OD在∠AOB的内部，且∠AOB=150°，∠COD=30°，射线OM，ON分别平分∠AOD，∠BOC．
（1）若∠AOC=60°，试通过计算比较∠NOD和∠MOC的大小；
（2）如图2，若将图1中∠COD在∠AOB内部绕点O顺时针旋转．
①旋转过程中∠MON的大小始终不变．求∠MON的值；
②如图3，若旋转后OC恰好为∠MOA的角平分线，试探究∠NOD与∠MOC的数量关系.
1。

七年级下册数学思维专项训练题（共10套）思维训练题（一）班级______________ 姓名_____________ 一、选择题：1．a 为任意自然数，包括a 在内的三个连续的自然数，可以表示为 （ ）A ．a －2，a －1，aB ．a －3，a －2，a －1C ．a ，a ＋1，a ＋2D ．不同于A 、B 、C 的形式二、计算题：（动动脑筋，可能会有简便的解题方法！）1．____________________56875=⨯2．____________2006200420022000...12108642=+-+-+-+-+- 3．__________________8567785667855678=+++4．()()__________888...6428002...888488868888=++++-++++5．______________125.01712517125625.05.0171251753=⨯-⨯+⨯+ 6．______________12346123451234512345=÷7．_________________31313131=-+-8．_______________99163135115131=++++ 9．_____________20042004...200432004220041=++++10．_____________90197218561742163015201412136121=++++++++三、应用与创新：1．有一高楼，每上一层需要3分钟，每下一层需要1分30秒。

小贤于下午6时15分开始从最底层不断地向上走，到了最顶层后便立即往下走，中途没有停留，他在7时36分返回最底层。

这座高楼共有多少层？2．回答下列各题：（1）用1、2、3、4、5、6、7、8可组成多少个没有重复数字的五位数？（2）在15个连续自然数中最多有多少个质数？最少有多少个质数？（3）以下是一个数列，第一项是1，第二项是4，以后每一项是前两项相乘的积。

七年级数学思维训练题
以下是一些适合七年级学生的数学思维训练题：
1. 小明和小红同时从甲、乙两地出发相向而行，小明每分钟走60米，小红每分钟走75米，相遇时，小明比小红少走25米，求小明和小红的行程时间各是多少？甲、乙两地的路程有多少米？
2. 甲、乙两人在环形跑道上以各自的不变速度跑步，如果两人同时从同地相背而跑，乙跑4分钟后两人第一次相遇，已知甲跑一周需6分钟，那么乙跑一周需多少分钟．
3. 小王每天晚上10：00睡觉，早上7：00起床，他每天睡多少时．
4. 教室里8盏灯，全部亮着，现在关掉了6盏灯，教室里还有多少盏灯．
5. 小芳晚上9：00睡觉，早上7：00起床，她每天睡多少时．
6. 一列火车上午8：00从甲地开往乙地，晚上11：00到达乙地，火车每小时行75千米，甲乙两地相距多少千米？
7. 小芳从家到学校，每分钟走60米，15分钟就能到学校．如果每分钟走75米，可以提前几分钟到学校？
8. 小刚每天晚上10：00睡觉，早上8：00起床，他每天睡多少时．
9. 小东每天晚上11：00睡觉，早上8：00起床，他每天睡多少时．
10. 一列火车上午9：30从甲地开往乙地，下午4：30到达乙地，火车每小时行75千米，甲乙两地相距多少千米？
这些题目旨在训练学生的数学思维能力和解决实际问题的能力。

7年级数学拓展思维训练题以下是一些适合7年级学生的数学拓展思维训练题：1.一家商店进行促销，规定每购买100元商品可以返还20元现金。

小明购买了250元的商品，他最多可以拿到多少返还现金？2.一个长方形的周长是40厘米，长是宽的3倍。

求这个长方形的面积。

3.一个两位数，十位数字是个位数字的2倍，将个位数字与十位数字调换，得到一个新的两位数。

这两个两位数的和是132，求这个两位数。

4.一个三角形和一个平行四边形等底等高，已知平行四边形的面积是25平方厘米，三角形的面积是多少？5.一列火车通过一条长1260米的隧道用了63秒，用同样的速度通过一条长2010米的隧道用了93秒。

求这列火车的速度和车长。

6.一根绳子绕木桩3圈后余下2分米，如果绕4圈还差2分米。

这根绳子有多长？7.一项工程，甲单独做要10天完成，乙单独做要15天完成。

两人合做这项工程，多少天后还剩下这项工程的1/4？8.一个数去除55l0，8120，13115，16395这4个数，余数都相同。

问这个数最大可能是多少？9.有50名学生参加联欢会。

第一个到会的女生同全部男生握过手，第二个到会的女生只差一个男生没握过手，第三个到会的女生只差二个男生没握过手，……就这样，最后一个到会的女生同7个男生握过手，问这50名同学中有多少个男生？10.甲乙丙丁四人共同购买了一台液晶电视。

已知甲出的钱是其它三人总钱数的1/3，乙出的钱是其余三人总钱数的1/4，丙出的钱是其余三人总钱数的1/5，丁出了2070元，则这台电视的价格是多少元？这些问题涵盖了不同的数学领域和难度级别，旨在帮助学生提高他们的数学思维和解决问题的能力。

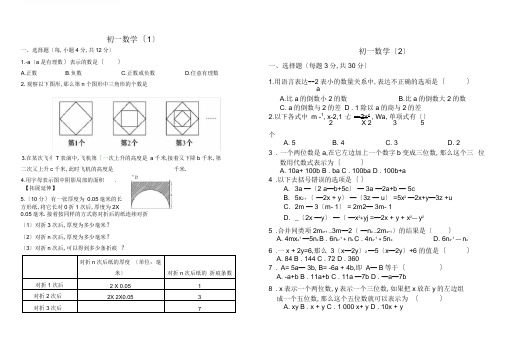
初一数学〔1〕【拓展延伸】5.〔10分〕有一张厚度为0.05毫米的长方形纸,将它长对0折1次后,厚度为2X0.05毫米.接着按同样的方式将对折后的纸连续对折〔1〕对折3次后,厚度为多少毫米？〔2〕对折n次后,厚度为多少毫米？〔3〕对折n次后,可以得到多少条折痕？对折n 次后纸的厚度〔单位：毫米〕对折n次后纸的折痕条数对折1次后 2 X 0.05 1对折2次后2X 2X0.05 3对折3次后7初一数学〔2〕一、选择题〔每题3分,共30分〕1.用语言表达--2表小的数量关系中,表达不正确的选项是〔〕aA.比a的倒数小2的数B.比a的倒数大2的数C. a的倒数与2的差D . 1除以a的商与2的差2.以下各式中m -1, x-2,1七―2x y , Wa,单项式有〔〕2 X 23 5个A. 5B. 4C. 3D. 23 . 一个两位数是a,在它左边加上一个数字b变成三位数,那么这个三位数用代数式表示为〔〕A. 10a+ 100b B . ba C . 100ba D . 100b+a4 .以下去括号错误的选项是〔〕A. 3a —〔2 a—b+5c〕— 3a —2a+b — 5cB. 5x2 + 〔—2x + y〕—〔3z — u〕 =5x2—2x+y—3z +uC. 2m — 3〔m- 1〕 = 2m2— 3m- 1D. _〔2x —y〕—〔—x2+yj =—2x + y + x2—y25 .合并同类项2m x+1 —3m—2〔—n x —2m x+1〕的结果是〔〕A. 4mx x1—5n x B . 6n x+1 + n x C . 4n x+1 + 5n x D. 6n x+1—n x6 .一x + 2y=6,那么3〔x—2y〕2 —5〔x—2y〕+6 的值是〔〕A. 84 B . 144 C . 72 D . 3607 .A= 5a— 3b, B= -6a + 4b,即A— B等于〔〕A. -a+b B . 11a+b C . 11a —7b D . —a—7b8 . x表示一个两位数,y表示一个三位数,如果把x放在y的左边组成一个五位数,那么这个五位数就可以表示为〔〕A. xy B . x + y C . 1 000 x+ y D . 10x + y一、选择题〔每,小题4分,共12分〕1.-a〔a是有理数〕表示的数是〔〕A.正数B.负数C.正数或负数D.任意有理数2.观察以下图形,那么第n个图形中三角形的个数是3.在某次飞彳T表演中,飞机第「一次上升的高度是a千米,接着又下降b千米,第千米.二次又上升c千米,此时飞机的高度是4.用字母表示图中阴影局部的面积.* b9 .当代数式x 2+4取最小值时,x 的值应是( )A. 0B.—1C.1D.410 .大家以相同的效率做某件工作,a 人做b 天可以完工,假设增 加c 人,那么完成工作提前的天数为( )ab b abbA (示一坊天 B (3一功夫 C- (b-ojc 以 D- (b-arc)初一数学(3)1. — 2xy- + x 2 3的次数是.35 37 .当mi= — 3时,代数式am+ bm+cm-5的值是7,那么当vm= 3时,它的值是.8 .下面由火柴棒拼出的一列图形中,摆第 1个图形要4根火柴 棒,摆第二个图形需要7根火柴棒,根据这样的方式继续摆下去,摆 第n 个图形时,需要 _________________ 根火柴棒.2 .当x= —J 时,代数式1—3x 2的值是.3 .如果 |m- 3|+(n —2)2= 0,那么一5xV+7x 3y 2=4 .通过找出这组图形符号中所蕴含的内在规律,在空白处的横 线上填上恰当的图形. 初一数学(4)一化简以下各式：(1)4 x 2-8x + 5-3x 2+ 6x-2； (2)5 ax-4a 2x 2—8ax 2 + 3ax —ax 2—4a 2x 2；(3)(3 x 4+ 2x —3) + (5x 4—7x+2) ; (4)5(2 x-7y ) -3(3x-10y ).假设将图①中的阴影局部拼成一个长方形,如图② .比拟图①和图②中二先化简,再求值：(1)( a 2—ab+2b 2)—2(b 2—a 2),其中 a= 一； b=5；6.假设一3x m y 2与2x 3y n 是同类项,那么mi=,n=5.如图①,边长为a 的大正方形中有一个边长为b 的小正方形, 的阴影局部的面积,你能得到的公式是(2)3 x2y—[2x2y—3(2xy —x2y) —xy],其中x=—1, y=-2.三.(10分)m是绝对值最小的有理数, 且—Z a m+'b"1与3a x b3是同类项, 试求多项式2x2—3xy + 6y2—3mni+ mxy- 9my 的值.初一数学(5)(1)如果选取1号、2号、3号卡片分别为1张、2张、3张,可拼成一个长方形(不重叠无缝隙).请画出这个长方形的草图,并运用拼图前后面积之间的关系说明这个长方形的代数意义.这个长方形的代数意义是(2)小明想用类似的方法解释多项式乘法(a+3b)(2 a + b) = 2a2+7ab+3b2,那么需用2号卡片___________ 张,3号卡片__________ 张.二.观察以下等式：第 1 个等式：a1=T17=1><(1 -1)；1X52 3 “一, 1 1 1 1弟 2 个等式：a2=T-r=3x (q-7);3 A j 2 3 5“一, 1 1 1 1弟 3 个等式：a3=7-=-x(---)；5X/ 257“一, 1 111弟 4 个等式：a4 = z--=-x (--Q)；7 A > 2 7 9请解答以下问题：(1)按以上规律列出第5个等式：35 =________ ;(2)用含n的代数式表示第n个等式：a n=: (n为正整数)；(3)求31+ 32+33+&+•••+ 31..的值.第一次对折后,纸的厚度为2X0.05毫米；可以得到折痕为1条；第二次对折后,纸的厚度为2X 2X 0.05=22X 0.05毫米；可以得到折痕为条;2X 2X 2X 0.05=2 3X 0.05毫米；可以得到折痕为2x2x2x2x (X2)n军2 x 0.05=2 n x 0.05毫米；可以到折痕为(2 n-1)条.故:⑴ 对折3次后,厚度为0.4毫米.(2)对折n次后,厚度为(2 nx 0.05)毫米.⑶ 对折n次后,可以彳#到(2n-1)条折痕.初一数学(2)初一数学(1)答案解析1 .【解析】选D.由于3可以表示任意有理数,那么-3表示的数是任意有理数.2 .4n.根据给出的3个图形可以知道：第1个图形中「三角形的个数是4,第2个图形中三角形的个数是8,第3个图形中三角形的个数是12,从而得出一般的规律,第n个图形中三角形的个数是4n.1. B考查倒数的定义.2 31 x — 2x y - 乂十=>2. B nn,彳,一黄是单项式. 2 2 33. D考查代数式的列法.4. C考查去括号的法那么.5. D合并同类项时把系数相加减,字母和字母的指数3 . (3-b+c)4 .【解析】根据题意得3=(2 2-1)第三次对折后,纸的厚度为7=(2 3-1)条；……第n次对折后,纸的厚度为5.【解析】由题意可知不变.6. B 由—x + 2y = 6可知x—2y= -6,故原式的值是144.7. C A— B= (5a—3b) —(—6a+4b)=5a— 3b+6a —4b=11a —7b.8. C考查代数式的列法.9. A当x = 0时,x2 + 4的值最小为4.10. C考查代数式的列法.初一数学(3)1. 512. 43. 2 x3y24.5. a2—b2= (a + b)( a—b)6. 3 2..当m= — 3 时,an5i+ bm3+cm-5=7,anm+bn^+ cm= 12.5.3 ―当m= +3 时,am+ bm+ cm= —12,5 3 ...am+bm+ cm- 5=- 12-5= - 17.8. (3n + 1)初一数学(4)一.(1) x2-2x + 3 原式=(4x2—3x2)+( —8x + 6x)+(5 — 2)=2x — 2x + 3;(2) -8a2x2-9ax2+8ax原式=(—4a2x2— 4a2x2) + ( — 8ax2— ax2) + (5 ax+ 3ax) = — 8a2x22 ,-9ax +8ax；(3)8 x4-5x-1 原式=3x4+ 2x —3+5x4—7x+2 =,_4 _ 4 _ _、, _ _、_4_ ,(3x +5x) +(2x-7x) + (-3+ 2)=8x -5x-1；(4) x - 5y 原式=10x —35y—9x+30y=(10x—9x)+( — 35y + 30y) =x —5y.二.解：(1)原式=a2—ab+2b2 —2b2+ 2a2=(a + 2aj + (2 b — 2b) — ab= 3a — ab.1 .一. 12 1 1 5当a=--, b=5 时,原式=3X —g - —§ X5="+- = 2;(2)原式=3x2y — 2x2y + 3(2 xy — x2y) + xy = 3x2y — 2x2y + 6xy —7. —172 2 2 2 23x y + xy= (3x y — 2x y —3x y) + (6xy + xy) = - 2x y + 7xy当x = - 1, y = — 2 时,原式——2X( — 1) X( — 2)+7X (—1) X( —2)=4+14= 18.三.解：由题意有mi= 0, mH2 = x, y+1=3,即x=2, y=2, 那么原式=2x2- 3xy —6y2 = 2X22 —3X2X2—6X22= —28.初一数学(5)一.解：(1)如图,a2 + 3ab+ 2b2= (a+b)( a+2b)；(2)3 71 111二.解:根据观察知答案分别为：(1)9^1 2x(9—五)⑵2n-1 2n+1 2X( 2n-1 -2n+1)(3) a〔 + a2 + a3+ a4+ …+ a[00= 1x(1-1)+l x(l_1)+l x(l_1)+l x(l_1)2 < 3) 2 <3 5) 2 <5 7) 2 <7 9)..1、,, 1 1 、+ …+ 2X(199-201) 2( 3 3 5 5 7 7 9 199 201) 1 12(1 一诟)1 200 100— x—=—.2 201 201。

初中数学思维拓展题1. 已知三角形ABC中，AB=AC，求证：∠B=∠C。

2. 一个长方体的长、宽、高分别是6cm、4cm、3cm，求这个长方体的对角线长度。

3. 已知一元二次方程ax^2+bx+c=0的两个根是x1和x2，求证：x1x2+x1+x2=a。

4. 一个等差数列的前10项和是210，求这个等差数列的首项和公差。

5. 计算下列各式：a) 2^3 * 3^2b) (2+3)^3c) 4^2 - 2^26. 已知函数f(x) = 2x + 3，求f(x)的图象与x轴的交点。

7. 解下列方程：a) 2x - 5 = 7b) 3(x - 2) = 128. 一个圆的半径增加了2cm，它的面积增加了多少百分比？9. 已知一个正方体的边长是4cm，求它的对角线长度。

10. 计算下列比例：a) 5:7b) 3:xc) 2x:411. 已知一个圆的直径是10cm，求这个圆的面积。

12. 已知一个等差数列的前n项和是Sn，求证：S2n-Sn=2n(a1+an)。

13. 已知函数f(x) = ax^2 + bx + c，求证：f(0) = c。

14. 解下列不等式：a) 3x - 2 > 5b) 4x + 3 ≤ 1215. 已知一个三角形的两个内角分别是30°和60°，求这个三角形的第三个内角。

16. 已知一个正方体的棱长是6cm，求它的表面积和体积。

17. 计算下列概率问题：a) 一个袋子里有5个红球和3个蓝球，随机取一个球，取到红球的概率是多少？b) 一个班级有30名学生，其中有15名女生，15名男生，随机选一名学生，选到女生的概率是多少？18. 已知函数f(x) = x^2 - 2x + 1，求f(x)的图象与x轴的交点。

19. 解下列方程组：a) 2x + 3y = 8b) 3x - 4y = 1220. 已知一个圆的周长是20cm，求这个圆的半径。

21. 计算下列平均数问题：a) 5名学生的成绩分别是80, 85, 90, 95, 100，求这5名学生的平均成绩。

一、选择题（每题5分，共25分）1. 下列各数中，有理数是（）A. √-1B. √2C. πD. 2.52. 下列各式中，正确的是（）A. 2x + 3 = 5x + 1B. 2(x + 3) = 2x + 6C. 2(x + 3) = 2x + 9D. 2(x + 3) = 2x + 123. 下列各数中，绝对值最小的是（）A. -3B. -2C. -1D. 04. 已知函数f(x) = 2x - 3，若f(x) > 0，则x的取值范围是（）A. x > 1.5B. x > 1C. x < 1D. x < 1.55. 在直角坐标系中，点A(2, 3)关于y轴的对称点B的坐标是（）A. (-2, 3)B. (2, -3)C. (-2, -3)D. (2, 3)二、填空题（每题5分，共25分）6. 已知数列{an}中，a1 = 1，an = an-1 + 2，则数列的前10项之和为______。

7. 若等腰三角形底边长为8，腰长为6，则该三角形的面积为______。

8. 已知函数f(x) = x^2 - 4x + 3，则f(2)的值为______。

9. 在直角坐标系中，点P(3, 4)关于原点的对称点Q的坐标是______。

10. 若a、b、c是等差数列，且a + b + c = 15，则a^2 + b^2 + c^2的值为______。

三、解答题（每题15分，共45分）11. （15分）已知数列{an}中，a1 = 3，an = 2an-1 + 1，求：（1）数列{an}的通项公式；（2）数列的前n项和Sn。

12. （15分）已知等腰三角形底边长为10，腰长为8，求：（1）该三角形的周长；（2）该三角形的面积。

13. （15分）已知函数f(x) = x^3 - 6x^2 + 9x - 1，求：（1）函数f(x)的零点；（2）函数f(x)的单调区间。

四、应用题（15分）14. （15分）某工厂生产一批产品，计划每天生产120件，共需10天完成。

初中数学数学思维拓展题练习及参考答案2023初中数学是培养学生数学思维的重要阶段。

在此过程中，需要适时进行一些数学思维拓展训练，让学生更好地掌握数学知识，提高数学思维能力。

为此，我们编制了一些初中数学思维拓展题及参考答案，以供学生参考。

一、综合运用1.设计一个图形，使其中既包含一个等边三角形，又包含一个等腰直角三角形。

2.某校运动会上，甲、乙两人比赛。

甲比乙多走50米，但用的时间比乙少5秒。

已知甲的速度是每秒6米，求乙的速度是多少？3.某校有一个1500元的集资活动，已经筹集到1000元，还差多少钱才能圆满完成？二、实际应用1.甲、乙两人在赛场上相距80米，它们同时起跑，甲的速度是每秒9米，乙的速度是每秒8米，那么它们第一次相遇在多少秒后？2.某超市进行特惠活动，原价15元的商品8折出售。

如果你有100元，可以买多少件该商品？3.某学生用40分钟完成一项作业，如果他有30分钟时间再做作业，那么他能提高多少完成度？若他能提高40%的完成度，还需要多长时间？三、数学证明1.如下图所示，AC ⊥ BD，且AC = BD。

证明：三角形ABC与三角形DCB全等。

2.已知a，b都是正整数，证明：若(a+b)是一个奇数，那么(a-b)一定是一个奇数。

3.如下图，AC = BC，角ACD = 60°，角DBC = 75°。

求角BDC的度数。

参考答案：一、综合运用1.如图所示，图形中ABC为等边三角形，ACD为等腰直角三角形。

2.设乙用时t秒，则甲用时t+5秒。

由v = s/t，得甲走的距离为6(t+5)，乙走的距离为vt。

因为题目中已经提示甲比乙多走了50米，所以可以列出以下方程：6(t+5) = vt + 50将v = 8带入方程中，可以解得t = 20秒。

3.筹集到的资金已经是：(1000元 / 1500元) × 100 % = 66.67 %。

还差的资金是 33.33%，即未筹100 %的资金。

初中数学思维拓展题训练及答案一、选择题1、若一次函数y=kx+1与两坐标轴围成的三角形面积为3，则k 为（C ） A 、16 B 、-16 C 、±16 D 、±132、若11m n -=3，2322m mn nm mn n+---的值是（B ） A 、1.5 B 、35 C 、-2 D 、-753、判断下列真命题有（C ）①任意两个全等三角形可拼成平行四边形②两条对角线垂直且相等的四边形是正方形③四边形ABCD ，AB=BC=CD ，∠A=90°，那么它是正方形④在同一平面内，两条线段不相交就会平行⑤有一条对角线平分一个内角的平行四边形是菱形 A 、②③ B 、①②④ C 、①⑤ D 、②③④4、如图，矩形ABCD 中,已知AB=5,AD=12,P 是AD 上的动点,PE ⊥AC ，E,PF ⊥BD 于F,则PE+PF=（B ） A 、5 B 、6013 C 、245 D 、55125、在直角坐标系中，已知两点A （-8，3）、B （-4，5）以及动点C （0，n ）、D(m,0)，则当四边形ABCD 的周长最小时，比值为 mn（B ）A 、-23B 、-32C 、-34D 、34二、填空题6、当x= 负数 时，||3x x -与3x x-互为倒数。

9、已知x 2-3x+1=0，求（x-1x ）2= 57、一个人要翻过两座山到另外一个村庄，途中的道路不是上山就是下山，已知他上山的速度为v ，下山的速度为v ′，单程的路程为s ．则这个人往返这个村庄的平均速度为 (2vv v v '+')8、将点A （4，0）绕着原点O 顺时针方向旋转30°角到对应点A '，则点A '的坐标是 (23,2)9、菱形ABCD 的一条对角线长为6，边AB 的长是方程(X-3)(X-4)=0的解，则菱形ABCD 的周长为 1610、△ABC 中，∠A=90°，AB=AC ，BD 是△ABC 的中线，△CDB 内以CD 为边的等腰直角三角形周长是 （222AB +或122AB +）11235...11231511211321④③②①11. 如图，边长为6的菱形ABCD 中，∠DAB=60°，AE=BE ，F 是AC•上一动点，EF+BF 的最小值为 (33) 12、如图，边长为3的正方形ABCD 顺时针旋转30°，得上图，交DE 于D ’,阴影部分面积是 (933-)13、如图，已知四边形ABCD 中，AC 和BD 相交于点O ， 且∠AOD ＝90°，若BC ＝2AD ，AB ＝12，CD ＝9，四边形ABCD 的周长是 (215+)14、有这样一组数：1，1，2，3，5…，现以这组数据的数作为正方形边长的长度构造如下正方形；再分别从左到右取2个、3个、4个、5个正方形拼成如下矩形记为①、②、③、④.第⑩个矩形周长是 46615、如图，在直线y=-33x+1与x 轴、y 轴交于点A 、B ，以线段AB 为直角边在第一象限内作等腰直角△ABC ，∠BAC=90°，第二象限内有一点P （a,12 ）,且△ABP 的面积与△ABC 的面积相等，则a= (342-+) 三、解答题16、如图，已知矩形ABCD ，延长CB 到E ，使CE=CA ，连结AE 并取中点F ，连结AE 并取中点F ，连结BF 、DF ，求证BF ⊥DF 。

一、选择题（每题3分，共30分）1. 下列各数中，有理数是（）A. √16B. √-16C. √-1D. √02. 若a、b是方程x^2-5x+6=0的两个根，则a+b的值是（）A. 5B. 6C. 4D. 73. 在直角坐标系中，点A（2，3）关于x轴的对称点坐标是（）A. （2，-3）B. （-2，3）C. （2，-3）D. （-2，-3）4. 下列各式中，正确的是（）A. |x|=-xB. |x|=xC. |x|≥0D. |x|≤05. 下列函数中，是反比例函数的是（）A. y=2x+3B. y=x^2C. y=2/xD. y=√x6. 若m、n是方程x^2-3x+2=0的两个根，则m^2+n^2的值是（）A. 4B. 6C. 7D. 87. 在△ABC中，∠A=60°，∠B=45°，则∠C的度数是（）A. 75°B. 90°C. 105°D. 120°8. 若a、b、c、d为等差数列，且a+c=b+d，则下列选项中一定成立的是（）A. a=dB. b=cC. a+c=2bD. a+d=2c9. 下列各数中，无理数是（）A. √4B. √9C. √-4D. √-910. 若函数y=kx+b的图象经过点（1，2），则k+b的值是（）A. 3B. 1C. 0D. -1二、填空题（每题5分，共20分）11. 若方程x^2-4x+3=0的两个根是m和n，则m+n的值是______。

12. 在△ABC中，∠A=45°，∠B=90°，则∠C的度数是______。

13. 若函数y=2x-3的图象经过点（0，y），则y的值是______。

14. 在等差数列{an}中，若a1=2，公差d=3，则第10项an的值是______。

15. 若等比数列{bn}中，b1=4，公比q=2，则第5项bn的值是______。

三、解答题（每题10分，共30分）16. 解方程：2x^2-5x+3=0。