大学物理之热学公式篇

第三章 热力学第二定律1. 卡诺定理卡诺热机效率hc h c h 11T T Q Q Q W−=+=−=η 卡诺定理：工作于高温热源T h 与低温热源T c 之间的热机，可逆热机效率最大。

卡诺定理推论：所有工作于高温热源T h 与低温热源T c 之间的可逆热机，其热机效率都相等，与热机的工作物质无关。

卡诺循环中，热温商之和等于零0cch h =+T Q T Q 任意可逆循环热温商之和也等于零，即0R=⎟⎟⎠⎞⎜⎜⎝⎛∑i iiT Q 或 0δR =⎟⎠⎞⎜⎝⎛∫T Q 2. 热力学第二定律的经典表述克劳休斯说法：不可能把热由低温物体传到高温物体, 而不引起其他变化。

开尔文说法：不可能从单一热源吸热使之完全转化为功, 而不发生其他变化。

热力学第二定律的各种说法的实质：断定一切实际过程都是不可逆的。

各种经典表述法是等价的。

3. 熵的定义TQ S revδd =或∫=ΔB ArevδTQ S熵是广度性质，其单位为。

系统状态变化时，要用可逆过程的热温商来衡量熵的变化值。

1K J −⋅4. 克劳修斯不等式T QS δd irrev ≥ 或 ∫≥ΔB A ir rev δT Q S 等号表示可逆，此时环境的温度T 等于系统的温度，为可逆过程中的热量；不等号表示不可逆，此时T 为环境的温度，为不可逆过程中的热量。

Q δQ δ5. 熵增原理0)d (irrev≥绝热S 或0)(irrev≥Δ绝热S 等号表示绝热可逆过程，不等号表示绝热不可逆过程。

在绝热条件下，不可能发生熵减少的过程。

0)d (irrev≥孤立S 或0)(irrev≥Δ孤立S 等号表示可逆过程或达到平衡态，不等号表示自发不可逆过程。

可以将与系统密切相关的环境部分包括在一起，作为一个隔离系统，则有：0irrev sur sys iso ≥Δ+Δ=ΔS S S6. 熵变计算的主要公式计算熵变的基本公式： ∫∫∫−=+=δ=−=Δ2 12 12 1rev12d d d d TpV H T V p UTQ S S S 上式适用于封闭系统，一切非体积功过程。

第四章 电 场一、常见带电体的场强、电势分布2）均匀带电球面（球面半径 ）的电场：3）无限长均匀带电直线（电荷线密度为）: E = ，方向：垂直于带电直线。

2r( rR ) 4）无限长均匀带电圆柱面（电荷线密度为）:E =2r (rR )5）无限大均匀带电平面（电荷面密度为）的电场: E =/20 ，方向：垂直于平面。

二、静电场定理 1、高斯定理：e = ÑE v dS v = q 静电场是有源场。

Sq 指高斯面内所包含电量的代数和；E 指高斯面上各处的电场强度，由高斯面内外的全 部电荷产生； Ñ E vdS v 指通过高斯面的电通量，由高斯面内的电荷决定。

2、环路定理： Ñ E v dl v =0 静电场是保守场、电场力是保守力，可引入电势能三、求场强两种方法1、利用场强势叠加原理求场强 分离电荷系统： E v = E v i ；连续电荷系统： E v = dE v i =12、利用高斯定理求场强 四、求电势的两种方法n1、利用电势叠加原理求电势 分离电荷系统：U =U i ；连续电荷系统： U = dU i =1电势零点v v 2、利用电势的定义求电势 U =电势零点Edl五、应用vv b点电荷受力： F = qE电势差： U ab =U a -U b = b EdraE =1 qU =q4r 24r1）点电荷：E =0 (rR ) q2 (rR ) 4r 2U =q (r R ) 4r q (r R ) 4Ra 点电势能：W a = qU a由 a 到 b 电场力做功等于电势能增量的负值 A ab = -W = -（W b -W a ）六、导体周围的电场1、静电平衡的充要条件： 1）、导体内的合场强为 0，导体是一个等势体。

2）、导体表面的场强处处垂直于导体表面。

E v ⊥表面。

导体表面是等势面。

2、静电平衡时导体上电荷分布： 1）实心导体： 净电荷都分布在导体外表面上。

热力学第一定律功：δW ＝δW e ＋δW f（1） 膨胀功 δW e ＝p 外dV 膨胀功为正，压缩功为负。

（2） 非膨胀功δW f ＝xdy 非膨胀功为广义力乘以广义位移。

如δW （机械功）＝fdL ，δW （电功）＝EdQ ，δW （表面功）＝rdA 。

热 Q ：体系吸热为正，放热为负。

热力学第一定律： △U ＝Q ＋W ＝Q —W e ＝Q —p 外dV （δW f ＝0） 焓 H ＝U ＋pV 理想气体的内能和焓只是温度的单值函数。

热容 C ＝δQ/dT（1） 等压热容：C p ＝δQ p /dT ＝ （∂H/∂T ）p （2） 等容热容：C v ＝δQ v /dT ＝ （∂U/∂T ）v理想气体ΔU,ΔH 的计算： 对理想气体的简单状态变化过程：定温过程：Δ U =0； Δ H =0变温过程：对理想气体， 状态变化时 dH=dU+d(PV) 若理想气体的摩尔热容没有给出，常温下有：理想气体绝热可逆过程方程式:标准态：气体的标准态：在任一温度T 、标准压力 P 下的纯理想气体状态；液体(或固体)的标准态：在任一温度T 、标准压力下的纯液体或纯固体状态。

标准态不规定温度，每个温度都有一个标准态。

摩尔反应焓：单位反应进度(ξ=1mol)的反应焓变Δr H m 。

标准摩尔生成焓：一定温度下由热力学稳定单质生成化学计量数 νB=1的物质B 的标准摩尔反应焓，称为物质B 在该温度下的标准摩尔生成焓。

用 表示 (没有规定温度，一般298.15 K 时的数据有表可查)标准摩尔燃烧焓:一定温度下， 1mol 物质 B 与氧气进行完全燃烧反应，生成规定的燃烧产物时的标准摩尔反应焓，称为B 在该温度下的标准摩尔燃烧焓。

用 表示.单位：J mol-1为可逆过程中体积功的基本计算公式，只能适用于可逆过程。

计算可逆过程的体积功时，须先求出体系的 p~V 关系式，然后代入积分。

⎰-=21d V V V p W 2112ln ln p pnRT V V nRT W -=-=适用于理想气体定温可逆过程。

大学物理热学知识点整理热运动：物质世界的一种基本运动形式，是构成宏观物体的大量微观粒子的永不停息的无规则运动。

热现象：构成宏观物质的大量微观粒子热运动的集体表现。

宏观量：表征系统状态的物理量。

微观量：描写单个分子特征的物理量。

热力学系统，简称系统：一些包含有大量微观粒子（如分子、原子)的物体或物体系。

外界或环境：系统以外的物体。

孤立系统：与外界没有任何相互作用的热力学系统。

封闭系统：与外界没有物质交换但有能量交换的系统。

开放系统：与外界既有物质交换又有能量交换的系统。

平衡态：对于一个孤立系，经过足够长的时间后，系统必将达到一个宏观性质不随时间变化的状态，这种状态称为平衡态。

热动平衡：在平衡态下，组成系统的微观粒子仍处在不停的无规则热运动之中，只是它们的统计平均效果不变，这是一种动态的平衡，又称为热动平衡。

状态参量：在平衡态下，热力学系统的宏观性质可以用一些确定的宏观参量来描述，这种描述系统状态的宏观参量称为状态参量。

态函数：由平衡态确定的其他宏观物理量可以表达为一组独立状态参量的函数，这些物理量称为“态函数”。

体积V ：气体分子所能到达的空间，即气体容器的容积。

单位立方米（ m^{3} ）,也用升（ L ）为单位。

压强p ：气体作用与容器壁单位面积上的压力，是大量分子对器壁碰撞的宏观表现。

SI单位制中单位是帕斯卡，简称帕（ Pa ）, 1\;Pa=1\;N/m^{2} 。

有时压强的单位还用大气压（ atm ）和毫米汞柱（ mmHg ）表示。

换算关系为1\;atm=1.013\times10^{5}\;Pa1\;mm\Hg=\frac{1}{760}\;atm=1.33\times10^{2}\;Pa温度：表征物体的冷热程度的物理量。

热平衡：在与外界影响隔绝的条件下，使两个热力学系统相互接触，让它们之间能发生传热，热的系统会慢慢变冷，冷的系统会慢慢变热，经过一段时间后，它们会达到一个共同的平衡状态，称这两个系统达到了热平衡。

大学物理热学知识点整理系统吸收的热量，一部分转化成系统的内能；另一部分转化为系统对外所作的功。

Q=\Delta E+A上式的各量均为代数量，其正负号规定为：系统从外界吸热时， Q 为正，向外界放热时， Q 为负；系统对外作功时，A 为正。

外界对系统作功时， A 为负；系统内能增加时，\Delta E 为正，系统的内能减少时， \Delta E 为负。

对于状态的微小变化过程，热力学第一定律的数学表达式dQ=dE+dA第一类永动机：一种不需要外界提供能量而连续不断对外作功，系统又能复原的机器。

等体过程：dV=0 ，系统作功dA=pdV=0dQ_v=dE=\frac{M}{M_{mol}}\frac{i}{2}RdT所以 Q_v=\Delta E=E_2-E_1=\frac{M}{M_{mol}}\frac{i}{2}R(T_2-T_1)在等体过程，外界传给气体的热量全部用来增加气体的内能，系统对外不作功。

等压过程： p =恒量，当气体体积从 V_1 膨胀到 V_2 时，系统对外作功为A_p=\int_{V_1}^{V_2}pdv=p(V_2-V_1)=\frac{M}{M_{mol}}R(T_2-T_1)系统吸收的热量为Q_p=\Delta E+p(V_2-V_1)=\frac{M}{M_{mol}}(\frac{i}{2}+1)R(T_2-T_1)等温过程： \Delta E=0Q_T=A_T=\int_{V_1}^{V_2}pdv=\frac{M}{M_{mol}}RT\ln\fra c{V_2}{V_1}因为 pV=常量，即 p_1V_1=p_2V_2所以 Q_T=A_T=\frac{M}{M_{mol}}RT\ln\frac{p_1}{p_2}摩尔热容 C_m: 1mol 物质温度升高（或降低） 1K 时所吸收（或放出）的热量，单位为 J/mol\cdot K 。

C_m=\frac{(dQ)_m}{dT}理想气体等体摩尔热容：C_V=\frac{dQ_V}{dT}=\frac{dE}{dT}=\frac{\frac{i}{2}RdT }{dT}=\frac{i}{2}Ri 为分子自由度； R 为普适气体常量。

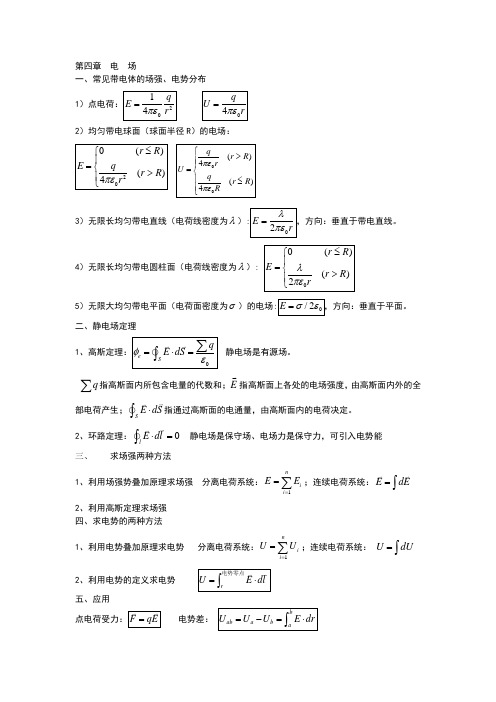
第四章 电 场一、常见带电体的场强、电势分布 1）点电荷：2014q E r πε=04q U rπε=2）均匀带电球面（球面半径R ）的电场：200()()4r R E qr R r πε≤⎧⎪=⎨>⎪⎩00()4()4qr R r U q r R R πεπε⎧>⎪⎪=⎨⎪≤⎪⎩3）无限长均匀带电直线（电荷线密度为λ）:02E rλπε=，方向：垂直于带电直线。

4）无限长均匀带电圆柱面（电荷线密度为λ）: 00()()2r R E r R rλπε≤⎧⎪=⎨>⎪⎩5）无限大均匀带电平面（电荷面密度为σ）的电场:0/2E σε=，方向：垂直于平面。

二、静电场定理 1、高斯定理：0e Sq E dS φε=⋅=∑⎰静电场是有源场。

q ∑指高斯面内所包含电量的代数和；E指高斯面上各处的电场强度，由高斯面内外的全部电荷产生；SE dS ⋅⎰指通过高斯面的电通量，由高斯面内的电荷决定。

2、环路定理：0lE dl⋅=⎰ 静电场是保守场、电场力是保守力，可引入电势能三、求场强两种方法1、利用场强势叠加原理求场强 分离电荷系统：1ni i E E ==∑；连续电荷系统：E dE =⎰2、利用高斯定理求场强 四、求电势的两种方法1、利用电势叠加原理求电势 分离电荷系统：1nii U U==∑；连续电荷系统： U dU =⎰2、利用电势的定义求电势 rU E dl =⋅⎰电势零点五、应用点电荷受力：F qE = 电势差： bab a b aU U U E dr =-=⋅⎰a由a 到b六、导体周围的电场1、静电平衡的充要条件： 1）、导体内的合场强为0，导体是一个等势体。

2）、导体表面的场强处处垂直于导体表面。

E ⊥表表面。

导体表面是等势面。

2、静电平衡时导体上电荷分布： 1）实心导体： 净电荷都分布在导体外表面上。

2）导体腔内无电荷： 电荷都分布在导体外表面，空腔内表面无电荷。

3）导体腔内有电荷+q ，导体电量为Q ：静电平衡时，腔内表面有感应电荷-q ，外表面有电荷Q ＋q 。

热力学第一定律功:δW ＝δW e ＋δW f（1）膨胀功 δW e ＝p 外dV 膨胀功为正,压缩功为负。

（2）非膨胀功δW f ＝xdy非膨胀功为广义力乘以广义位移。

如δW(机械功)＝fdL,δW(电功)＝EdQ,δW(表面功)＝rdA 。

热 Q:体系吸热为正,放热为负。

热力学第一定律: △U ＝Q —W 焓 H ＝U ＋pV 理想气体的内能与焓只就是温度的单值函数。

热容 C ＝δQ/dT（1）等压热容:C p ＝δQ p /dT ＝ (∂H/∂T)p （2）等容热容:C v ＝δQ v /dT ＝ (∂U/∂T)v 常温下单原子分子:C v,m ＝C v,m t ＝3R/2常温下双原子分子:C v,m ＝C v,m t ＋C v,m r ＝5R/2 等压热容与等容热容之差:(1)任意体系 C p —C v ＝[p ＋(∂U/∂V)T ](∂V/∂T)p (2)理想气体 C p —C v ＝nR 理想气体绝热可逆过程方程:pV γ＝常数 TV γ-1＝常数 p 1-γT γ＝常数 γ＝C p / C v 理想气体绝热功:W ＝C v (T 1—T 2)＝11－γ(p 1V 1—p 2V 2) 理想气体多方可逆过程:W ＝1nR－δ(T 1—T 2) 热机效率:η＝212T T T － 冷冻系数:β＝－Q 1/W 可逆制冷机冷冻系数:β＝121T T T －焦汤系数: μJ －T ＝H p T ⎪⎪⎭⎫⎝⎛∂∂＝－()pT C p H ∂∂ 实际气体的ΔH 与ΔU:ΔU ＝dT T U V ⎪⎭⎫ ⎝⎛∂∂＋dV V U T ⎪⎭⎫ ⎝⎛∂∂ ΔH ＝dT T H P ⎪⎭⎫⎝⎛∂∂＋dp p H T ⎪⎪⎭⎫ ⎝⎛∂∂ 化学反应的等压热效应与等容热效应的关系:Q p ＝Q V ＋ΔnRT 当反应进度 ξ＝1mol 时, Δr H m ＝Δr U m ＋∑BB γRT化学反应热效应与温度的关系:()()()dT B C T H T H 21T T m p B1m r 2m r ⎰∑∆∆，＋＝γ热力学第二定律Clausius 不等式:0TQS BAB A ≥∆∑→δ—熵函数的定义:dS ＝δQ R /T Boltzman 熵定理:S ＝kln Ω Helmbolz 自由能定义:F ＝U —TS Gibbs 自由能定义:G ＝H －TS 热力学基本公式:（1）组成恒定、不作非膨胀功的封闭体系的热力学基本方程:dU ＝TdS －pdV dH ＝TdS ＋Vdp dF ＝－SdT －pdV dG ＝－SdT ＋Vdp （2）Maxwell 关系:T V S ⎪⎭⎫⎝⎛∂∂＝VT p ⎪⎭⎫ ⎝⎛∂∂Tp S ⎪⎪⎭⎫ ⎝⎛∂∂＝－p T V ⎪⎭⎫ ⎝⎛∂∂ （3）热容与T 、S 、p 、V 的关系:C V ＝T V T S ⎪⎭⎫ ⎝⎛∂∂ C p ＝T pT S ⎪⎭⎫⎝⎛∂∂Gibbs 自由能与温度的关系:Gibbs －Helmholtz 公式 ()pT /G ⎥⎦⎤⎢⎣⎡∂∆∂T ＝－2T H ∆ 单组分体系的两相平衡: (1)Clapeyron 方程式:dT dp＝mX m X V T H ∆∆ 式中x 代表vap,fus,sub 。

大学物理化学公式总结物理化学作为一门综合性的学科，涉及到丰富而复杂的理论和实验内容。

公式作为物理化学研究的重要工具，既能简化问题的处理过程，又能揭示事物背后的规律和原理。

在这篇文章中，我们将总结一些大学物理化学中常见的公式，并探索它们背后的意义和应用。

1. 经典力学公式经典力学是物理学的基础，它研究物体在力的作用下的运动规律。

在这个领域中，公式起到了关键的作用，其中最基本的公式就是牛顿第二定律：F = ma该公式表示物体的加速度（a）与作用在物体上的力（F）的关系。

通过这个公式，我们可以推导出许多与运动相关的公式，如位移-时间关系、速度-时间关系等。

2. 热力学公式热力学研究物质的热现象和能量转化规律，是理解自然界中热现象的重要工具。

其中最基本的公式是热力学第一定律，也被称为能量守恒定律：ΔU = q + W该公式表示系统的内能（U）的变化等于系统所吸收的热量（q）与对外做功（W）的和。

这个公式揭示了能量在系统中的转化关系，并为热力学研究提供了基础。

3. 电磁学公式电磁学是物理学中的重要分支，研究电、磁场的相互作用及其规律。

其中，麦克斯韦方程组是电磁学研究的核心公式，它由四个方程组成：∇·E = ρ/ε₀∇·B = 0∇×E = -∂B/∂t∇×B = μ₀J + μ₀ε₀∂E/∂t这四个方程描述了电场（E）和磁场（B）的产生和相互作用，是现代电磁学研究的基础。

它们揭示了电磁波传播的规律，为电磁学中很多应用提供了理论依据。

4. 量子力学公式量子力学作为最前沿的物理学分支，研究微观世界的行为。

其中最著名的公式是薛定谔方程：Ĥψ =Eψ这个方程描述了量子系统的波函数（ψ）和能量（E）之间的关系。

它是揭示原子、分子结构和行为的关键公式，让我们能够理解原子和分子的性质，同时也为应用于量子计算和量子通信等领域提供了基础。

总结：在这篇文章中，我们总结了大学物理化学中的一些重要公式，并探讨了它们背后的意义和应用。

热 学 公 式令狐采学1．理想气体温标定义：0273.16limTPp TPp T K p →=⋅（定体）2．摄氏温度t 与热力学温度T 之间的关系：0//273.15t C T K =-华氏温度F t 与摄氏温度t 之间的关系：9325F t t =+3．理想气体状态方程：pV RT ν=1mol 范德瓦耳斯气体状态方程：2()()m map V b RT V +-= 其中摩尔气体常量8.31/R J mol K =⋅或28.2110/R atm L mol K -=⨯⋅⋅4．微观量与宏观量的关系：p nkT =，23kt p n ε=，32kt kT ε=5．标准状况下气体分子的数密度（洛施密特数）2530 2.6910/n m =⨯6．分子力的伦纳德-琼斯势：126()4[()()]p E r rrσσε=-，其中ε为势阱深度，σ=，特别适用于惰性气体，该分子力大致对应于昂内斯气体；分子力的弱引力刚性球模型（苏则朗模型）：6000, ()(), p r r E r r r r rφ+∞<⎧⎪=⎨-≥⎪⎩，其中0φ 为势阱深度，该分子力对应于范德瓦耳斯气体。

7．均匀重力场中等温大气分子的数密度（压强）按高度分布：00()mgz Mgz kTRTn z n en e--==，//00()mgz kT Mgz RT p z p e p e --==，大气标高：RTH Mg=。

8．麦克斯韦速率分布函数：23/222()4()2mvkT dN m f v e v Ndv kTππ-==；其简便形式：22()u f u du e du -=，其中p v u v =。

9．三个分子速率的统计平均值：最概然速率：p v ==平均速率：v ==；方均根速率：rms v ===10．分子通量14nv Γ=：单位时间内，单位面积容器壁所受到的分子碰撞次数。

12．能量均分定理：在温度为T 的平衡态下，物质分子的每一个自由度都具有相同的平均动能，其大小都等于/2kT 。

大学物理基本公式（二）引言概述:大学物理中，物理基本公式是学习和应用物理学概念和原理的基础。

本文将重点介绍大学物理中的一些基本公式（二），包括力学、电磁学和波动光学等领域的公式。

通过学习这些公式，能够更好地理解和应用物理学知识。

正文:1. 力学公式:1.1 牛顿第二定律: F = ma，描述物体在外力作用下的加速度。

1.2 动能公式: E_k = (1/2)mv^2，计算物体的动能。

1.3 势能公式: Ep = mgh，计算物体在重力场中的势能。

1.4 动量公式: p = mv，描述物体的动量。

1.5 万有引力定律: F = G(m1m2/r^2)，计算两个物体之间的引力。

2. 电磁学公式:2.1 库仑定律: F = k(q1q2/r^2)，描述两个电荷之间的作用力。

2.2 电场强度公式: E = F/q，描述电荷在电场中所受的力。

2.3 电压公式: V = IR，描述电流通过导体时的电势差。

2.4 磁场强度公式: B = µ0(I/2πr)，计算在电流通过导线时的磁场强度。

2.5 磁感应强度公式: B = µ0N/lI，计算螺线管中的磁感应强度。

3. 波动光学公式:3.1 光速公式: c = λν，描述光的传播速度。

3.2 折射定律: n1sinθ1 = n2sinθ2，描述光在两种介质中的折射现象。

3.3 成像公式: 1/f = 1/v + 1/u，计算透镜成像的距离。

3.4 焦距公式: f = R/2，计算球面镜的焦距。

3.5 干涉公式: Δd = mλ，描述两束光相干干涉时的光程差。

4. 其他公式:4.1 热力学公式: Q = mcΔT，计算物体的热量变化。

4.2 波函数公式: Ψ(x,t) = A sin(kx - ωt + φ)，描述波动的波函数。

4.3 相对论能量公式: E = mc^2，描述物体的能量与质量之间的关系。

4.4 等离子体频率公式: ω^2 = (e^2n)/(ε0m)，计算等离子体中的电磁波频率。