历年全国理科数学高考试题立体几何部分精选(含答案)

各省历年高考理科数学试题及答案汇编九立体几何（安徽、福建、广东、湖北、湖南、江西、山东七省）安徽省（试题）1、18．（12分）（2008安徽）如图，在四棱锥O﹣ABCD中，底面ABCD四边长为1的菱形，∠ABC=，OA⊥底面ABCD，OA=2，M为OA的中点，N为BC的中点．（Ⅰ）证明：直线MN∥平面OCD；（Ⅱ）求异面直线AB与MD所成角的大小；（Ⅲ）求点B到平面OCD的距离．2、18．（13分）（2009安徽）如图所示，四棱锥F﹣ABCD的底面ABCD是菱形，其对角线AC=2，BD=．AE、CF都与平面ABCD垂直，AE=1，CF=2．（1）求二面角B﹣AF﹣D的大小；（2）求四棱锥E﹣ABCD与四棱锥F﹣ABCD公共部分的体积．3、18．（12分）（2010安徽）如图，在多面体ABCDEF中，四边形ABCD是正方形，EF∥AB，EF⊥FB，AB=2EF，∠BFC=90°，BF=FC，H为BC的中点．（1）求证：FH∥平面EDB；（2）求证：AC⊥平面EDB；（3）求二面角B﹣DE﹣C的大小．4、17．（12分）（2011安徽）如图，ABEDFC为多面体，平面ABED与平面ACFD垂直，点O 在线段AD上，OA=1，OD=2，△OAB，△OAC，△ODE，△ODF都是正三角形（I）证明直线BC∥EF；（II）求棱锥F﹣OBED的体积．5、18．（12分）（2012安徽）平面图形ABB1A1C1C如图4所示，其中BB1C1C是矩形，BC=2，BB1=4，AB=AC=，A1B1=A1C1=．现将该平面图形分别沿BC和B1C1折叠，使△ABC与△A1B1C1所在平面都与平面BB1C1C垂直，再分别连接A2A，A2B，A2C，得到如图2所示的空间图形，对此空间图形解答下列问题．（Ⅰ）证明：AA1⊥BC；（Ⅱ）求AA1的长；（Ⅲ）求二面角A﹣BC﹣A1的余弦值．6、19．（13分）（2013安徽）如图，圆锥顶点为P，底面圆心为O，其母线与底面所成的角为22.5°，AB和CD是底面圆O上的两条平行的弦，轴OP与平面PCD所成的角为60°，（1）证明：平面PAB与平面PCD的交线平行于底面；（2）求cos∠COD．7、20．（13分）（2014安徽）如图，四棱柱ABCD﹣A1B1C1D1中，A1A⊥底面ABCD，四边形ABCD 为梯形，AD∥BC，且AD=2BC，过A1、C、D三点的平面记为α，BB1与α的交点为Q．（Ⅰ）证明：Q为BB1的中点；（Ⅱ）求此四棱柱被平面α所分成上下两部分的体积之比；（Ⅲ）若AA1=4，CD=2，梯形ABCD的面积为6，求平面α与底面ABCD所成二面角的大小．8、19．（13分）（2015安徽）如图所示，在多面体A1B1D1DCBA中，四边形AA1B1B，ADD1A1，ABCD均为正方形，E为B1D1的中点，过A1，D，E的平面交CD1于F．（Ⅰ）证明：EF∥B1C；（Ⅱ）求二面角E﹣A1D﹣B1的余弦值．福建省（试题）1、18．（12分）（2008福建）如图，在四棱锥P﹣ABCD中，则面PAD⊥底面ABCD，侧棱PA=PD=，底面ABCD为直角梯形，其中BC∥AD，AB⊥AD，AD=2AB=2BC=2，O为AD中点．（Ⅰ）求证：PO⊥平面ABCD；（Ⅱ）求异面直线PB与CD所成角的大小；（Ⅲ）线段AD上是否存在点Q，使得它到平面PCD的距离为？若存在，求出的值；若不存在，请说明理由．2、18．（13分）（2010福建）如图，圆柱OO1内有一个三棱柱ABC﹣A1B1C1，三棱柱的底面为圆柱底面的内接三角形，且AB是圆O的直径．（1）证明：平面A1ACC1⊥平面B1BCC1；（2）设AB=AA1，在圆柱OO1内随机选取一点，记该点取自于三棱柱ABC﹣A1B1C1内的概率为P．当点C在圆周上运动时，记平面A1ACC1与平面B1OC所成的角为θ（0°＜θ≤90°），当P取最大值时，求cosθ的值．3、20．（14分）（2011福建）如图，四棱锥P﹣ABCD中，PA⊥底面ABCD，四边形ABCD中，AB⊥AD，AB+AD=4，CD=，∠CDA=45°．（Ⅰ）求证：平面PAB⊥平面PAD；（Ⅱ）设AB=AP．（i）若直线PB与平面PCD所成的角为30°，求线段AB的长；（ii）在线段AD上是否存在一个点G，使得点G到点P，B，C，D的距离都相等？说明理由．4、18．（13分）（2012福建）如图，在长方体ABCD﹣A1B1C1D1中AA1=AD=1，E为CD中点．（Ⅰ）求证：B1E⊥AD1；（Ⅱ）在棱AA1上是否存在一点P，使得DP∥平面B1AE？若存在，求AP的长；若不存在，说明理由．（Ⅲ）若二面角A﹣B1E﹣A1的大小为30°，求AB的长．5、19．（13分）（2013福建）如图，在四棱柱ABCD﹣A1B1C1D1中，侧棱AA1⊥底面ABCD，AB∥DC，AA1=1，AB=3k，AD=4k，BC=5k，DC=6k，（k＞0）（1）求证：CD⊥平面ADD1A1（2）若直线AA1与平面AB1C所成角的正弦值为，求k的值（3）现将与四棱柱ABCD﹣A1B1C1D1形状和大小完全相同的两个四棱柱拼成一个新的四棱柱，规定：若拼成的新四棱柱形状和大小完全相同，则视为同一种拼接方案，问共有几种不同的拼接方案？在这些拼接成的新四棱柱中，记其中最小的表面积为f（k），写出f（k）的解析式．（直接写出答案，不必说明理由）6、17．（13分）（2014福建）在平面四边形ABCD中，AB=BD=CD=1，AB⊥BD，CD⊥BD，将△ABD 沿BD折起，使得平面ABD⊥平面BCD，如图．（1）求证：AB⊥CD；（2）若M为AD中点，求直线AD与平面MBC所成角的正弦值．7、17．（13分）（2015福建）如图，在几何体ABCDE中，四边形ABCD是矩形，AB⊥平面BEC，BE⊥EC，AB=BE=EC=2，G，F分别是线段BE，DC的中点．（1）求证：GF∥平面ADE；（2）求平面AEF与平面BEC所成锐二面角的余弦值．广东省（试题）1、20．（14分）（2008广东）如图所示，四棱锥P﹣ABCD的底面ABCD是半径为R的圆的内接四边形，其中BD是圆的直径，∠ABD=60°，∠BDC=45°，PD垂直底面ABCD，，E，F分别是PB，CD上的点，且，过点E作BC的平行线交PC于G．（1）求BD与平面ABP所成角θ的正弦值；（2）证明：△EFG是直角三角形；（3）当时，求△EFG的面积．2、18．（本小题满分14分）如图6，已知正方体1111ABCD A B C D -的棱长为2，点E 是正方形11BCC B 的中心，点F 、G 分别是棱111,C D AA 的中点．设点11,E G 分别是点E ，G 在平面11DCC D 内的正投影．（1）求以E 为顶点，以四边形FGAE 在平面11DCC D 内的正投影为底面边界的棱锥的体积；（2）证明：直线⊥1FG 平面1FEE ；（3）求异面直线11E G EA 与所成角的正弦值.3、18．（14分）（2010广东）如图，是半径为a 的半圆，AC 为直径，点E 为的中点，点B 和点C 为线段AD 的三等分点，平面AEC 外一点F 满足，． （1）证明：EB ⊥FD ；（2）已知点Q ，R 为线段FE ，FB 上的点，，，求平面BED 与平面RQD 所成二面角的正弦值．（13分）（2011广东）如图，在锥体P﹣ABCD中，ABCD是边长为1的菱形，且∠DAB=60°，4、18．PA=PD=，PB=2，E，F分别是BC，PC的中点（1）证明：AD⊥平面DEF（2）求二面角P﹣AD﹣B的余弦值．5、18．（13分）（2012广东）如图所示，在四棱锥P﹣ABCD中，底面ABCD为矩形，PA⊥平面ABCD，点E在线段PC上，PC⊥平面BDE．（1）证明：BD⊥平面PAC；（2）若PA=1，AD=2，求二面角B﹣PC﹣A的正切值．6、18．（14分）（2013广东）如图1，在等腰直角三角形ABC中，∠A=90°，BC=6，D，E 分别是AC，AB上的点，，O为BC的中点．将△ADE沿DE折起，得到如图2所示的四棱椎A′﹣BCDE，其中A′O=．（1）证明：A′O⊥平面BCDE；（2）求二面角A′﹣CD﹣B的平面角的余弦值．7、18．（13分）（2014广东）如图，四边形ABCD为正方形．PD⊥平面ABCD，∠DPC=30°，AF⊥PC于点F，FE∥CD，交PD于点E．（1）证明：CF⊥平面ADF；（2）求二面角D﹣AF﹣E的余弦值．8、18．（14分）（2015广东）如图，三角形△PDC所在的平面与长方形ABCD所在的平面垂直，PD=PC=4，AB=6，BC=3，点E是CD的中点，点F、G分别在线段AB、BC上，且AF=2FB，CG=2GB．（1）证明：PE⊥FG；（2）求二面角P﹣AD﹣C的正切值；（3）求直线PA与直线FG所成角的余弦值．湖北省（试题）1、18．（12分）（2009湖北）如图，四棱锥S﹣ABCD的底面是正方形，SD⊥平面ABCD，SD=2a，AD=a，点E是SD上的点，且DE=λa（0＜λ≤2）（Ⅰ）求证：对任意的λ∈（0，2），都有AC⊥BE（Ⅱ）设二面角C﹣AE﹣D的大小为θ，直线BE与平面ABCD所成的角为φ，若tanθ•tanφ=1，求λ的值．2、18．（12分）（2010湖北）如图，在四面体ABOC中，OC⊥OA，OC⊥OB，∠AOB=120°，且OA=OB=OC=1（Ⅰ）设为P为AC的中点，Q为AB上一点，使PQ⊥OA，并计算的值；（Ⅱ）求二面角O﹣AC﹣B的平面角的余弦值．3、18．（12分）（2011湖北）如图，已知正三棱柱ABC=A1B1C1的各棱长都是4，E是BC的中点，动点F在侧棱CC1上，且不与点C重合．（Ⅰ）当CF=1时，求证：EF⊥A1C；（Ⅱ）设二面角C﹣AF﹣E的大小为θ，求tanθ的最小值．4、19．（12分）（2012湖北）如图1，∠ACB=45°，BC=3，过动点A作AD⊥BC，垂足D在线段BC上且异于点B，连接AB，沿AD将△ABD折起，使∠BDC=90°（如图2所示），（1）当BD的长为多少时，三棱锥A﹣BCD的体积最大；（2）当三棱锥A﹣BCD的体积最大时，设点E，M分别为棱BC，AC的中点，试在棱CD上确定一点N，使得EN⊥BM，并求EN与平面BMN所成角的大小．5、19．（12分）（2013湖北）如图，AB是圆O的直径，点C是圆O上异于A，B的点，直线PC⊥平面ABC，E，F分别是PA，PC的中点．（Ⅰ）记平面BEF与平面ABC的交线为l，试判断直线l与平面PAC的位置关系，并加以证明；（Ⅱ）设（Ⅰ）中的直线l与圆O的另一个交点为D，且点Q满足．记直线PQ与平面ABC所成的角为θ，异面直线PQ与EF所成的角为α，二面角E﹣l﹣C的大小为β．求证：sinθ=sinαsinβ．6、19．（12分）（2014湖北）如图，在棱长为2的正方体ABCD﹣A1B1C1D1中，E，F，M，N分别是棱AB，AD，A1B1，A1D1的中点，点P，Q分别在棱DD1，BB1上移动，且DP=BQ=λ（0＜λ＜2）（Ⅰ）当λ=1时，证明：直线BC1∥平面EFPQ；（Ⅱ）是否存在λ，使面EFPQ与面PQMN所成的二面角为直二面角？若存在，求出λ的值；若不存在，说明理由．7、19．（12分）（2015湖北）《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的四面体称之为鳖臑．如图，在阳马P﹣ABCD 中，侧棱PD⊥底面ABCD，且PD=CD，过棱PC的中点E，作EF⊥PB交PB于点F，连接DE，DF，BD，BE．（1）证明：PB⊥平面DEF．试判断四面体DBEF是否为鳖臑，若是，写出其每个面的直角（只需写出结论）；若不是，说明理由；（2）若面DEF与面ABCD所成二面角的大小为，求的值．湖南省（试题）1、18．（12分）（2008湖南）把边长为2的正三角形ABC沿BC上的高AD折成直二面角，设折叠后BC的中点为P，（I）求异面直线AC，PD所成的角的余弦值；（II）求二面角C﹣AB﹣D的大小．2、17．（12分）（2008湖南）如图所示，四棱锥P﹣ABCD的底面ABCD是边长为1的菱形，∠BCD=60°，E是CD的中点，PA⊥底面ABCD，PA=2．（Ⅰ）证明：平面PBE⊥平面PAB；（Ⅱ）求平面PAD和平面PBE所成二面角（锐角）的大小．3、18．（12分）（2009湖南）如图，在正三棱柱ABC﹣A1B1C1中，AB=AA1，点D是A1B1的中点，点E在A1C1上，且DE⊥AE．（1）证明：平面ADE⊥平面ACC1A1；（2）求直线AD和平面ABC1所成角的正弦值．4、18．（12分）（2010湖南）如图所示，在正方体ABCD﹣A1B1C1D1中，E是棱DD1的中点．（Ⅰ）求直线BE与平面ABB1A1所成的角的正弦值；（Ⅱ）在棱C1D1上是否存在一点F，使B1F∥平面A1BE？证明你的结论．5、19．（12分）（2011湖南）如图，在圆锥PO中，已知PO=，⊙O的直径AB=2，C是的中点，D为AC的中点．（Ⅰ）证明：平面POD⊥平面PAC；（Ⅱ）求二面角B﹣PA﹣C的余弦值．6、18．（12分）（2012湖南）如图，在四棱锥P﹣ABCD中，PA⊥平面ABCD，AB=4，BC=3，AD=5，∠DAB=∠ABC=90°，E是CD的中点．（Ⅰ）证明：CD⊥平面PAE；（Ⅱ）若直线PB与平面PAE所成的角和PB与平面ABCD所成的角相等，求四棱锥P﹣ABCD 的体积．7、19．（12分）正四棱柱ABCD﹣A1B1C1D1的底面边长是，侧棱长是3，点E、F分别在BB1、DD1上，且AE⊥A1B，AF⊥A1D．（1）求证：A1C⊥面AEF；（2）求截面AEF与底面ABCD所成二面角θ的正切值．8、19．（12分）（2014湖南）如图，四棱柱ABCD﹣A1B1C1D1的所有棱长都相等，AC∩BD=O，A1C1∩B1D1=O1，四边形ACC1A1和四边形BDD1B1均为矩形．（Ⅰ）证明：O1O⊥底面ABCD；（Ⅱ）若∠CBA=60°，求二面角C1﹣OB1﹣D的余弦值．9、21．（2015湖南）如图，已知四棱台ABCD﹣A1B1C1D1的上、下底面分别是边长为3和6的正方形，AA1=6，且AA1⊥底面ABCD，点P、Q分别在棱DD1、BC上．（1）若P是DD1的中点，证明：AB1⊥PQ；（2）若PQ∥平面ABB1A1，二面角P﹣QD﹣A的余弦值为，求四面体ADPQ的体积．江西省（试题）1、20．（12分）（2008江西）如图，正三棱锥O﹣ABC的三条侧棱OA、OB、OC两两垂直，且长度均为2．E、F分别是AB、AC的中点，H是EF的中点，过EF作平面与侧棱OA、OB、OC或其延长线分别相交于A1、B1、C1，已知．（1）求证：B1C1⊥平面OAH；（2）求二面角O﹣A1B1﹣C1的大小．（2009江西）在四棱锥P﹣ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AD=4，（12分）2、20．AB=2．以AC的中点O为球心、AC为直径的球面交PD于点M，交PC于点N（1）求证：平面ABM⊥平面PCD；（2）求直线CD与平面ACM所成的角的大小；（3）求点N到平面ACM的距离．3、20．（12分）（2010江西）如图，△BCD与△MCD都是边长为2的正三角形，平面MCD⊥平面BCD，AB⊥平面BCD，AB=2．（1）求直线AM与平面BCD所成的角的大小；（2）求平面ACM与平面BCD所成的二面角的正弦值．4、21．（14分）（2011江西）（1）如图，对于任一给定的四面体A1A2A3A4，找出依次排列的四个相互平行的α1，α2，α3，α4，使得A i∈αi（i=1，2，3，4），且其中每相邻两个平面间的距离都相等；（2）给定依次排列的四个相互平行的平面α1，α2，α3，α4，其中每相邻两个平面间的距离都为1，若一个正四面体A1A2A3A4的四个顶点满足：A i∈αi（i=1，2，3，4），求该正四面体A1A2A3A4的体积．5、19．（12分）（2012江西）在三棱柱ABC﹣A1B1C1中，已知AB=AC=AA1=，BC=4，点A1在底面ABC的投影是线段BC的中点O．（1）证明在侧棱AA1上存在一点E，使得OE⊥平面BB1C1C，并求出AE的长；（2）求平面A1B1C与平面BB1C1C夹角的余弦值．6、20．（12分）（2013江西）如图，四棱锥P﹣ABCD中，PA⊥平面ABCD，E为BD的中点，G 为PD的中点，△DAB≌△DCB，EA=EB=AB=1，PA=，连接CE并延长交AD于F（1）求证：AD⊥平面CFG；（2）求平面BCP与平面DCP的夹角的余弦值．7、20．（12分）（2014江西）如图，四棱锥P﹣ABCD中，ABCD为矩形，平面PAD⊥平面ABCD．（1）求证：AB⊥PD；（2）若∠BPC=90°，PB=，PC=2，问AB为何值时，四棱锥P﹣ABCD的体积最大？并求此时平面BPC与平面DPC夹角的余弦值．山东省（试题）1、20．（12分）（2008山东）如图，已知四棱锥P﹣ABCD，底面ABCD为菱形，PA⊥平面ABCD，∠ABC=60°，E，F分别是BC，PC的中点．（Ⅰ）证明：AE⊥PD；（Ⅱ）若H为PD上的动点，EH与平面PAD所成最大角的正切值为，求二面角E﹣AF﹣C 的余弦值．2、18．（12分）（2009山东）如图，在直四棱柱ABCD﹣A1B1C1D1中，底面ABCD为等腰梯形，AB∥CD，AB=4，BC=CD=2，E、F是AA1、AB的中点．（Ⅰ）证明：直线EE1∥平面FCC1；（Ⅱ）求二面角B﹣FC1﹣C的余弦值．3、19．（12分）（2010山东）如图，在五棱锥P﹣ABCDE中，PA⊥平面ABCDE，AB∥CD，AC∥ED，AE∥BC，∠ABC=45°，AB=2，BC=2AE=4，三角形PAB是等腰三角形．（Ⅰ）求证：平面PCD⊥平面PAC；（Ⅱ）求直线PB与平面PCD所成角的大小；（Ⅲ）求四棱锥P﹣ACDE的体积．（12分）（2011山东）在如图所示的几何体中，四边形ABCD为平行四边形，∠ACB=90°，4、19．EA⊥平面ABCD，EF∥AB，FG∥BC，EG∥AC．AB=2EF．（Ⅰ）若M是线段AD的中点，求证：GM∥平面ABFE；（Ⅱ）若AC=BC=2AE，求二面角A﹣BF﹣C的大小．5、18．（12分）（2012山东）在如图所示的几何体中，四边形ABCD是等腰梯形，AB∥CD，∠DAB=60°，FC⊥平面ABCD，AE⊥BD，CB=CD=CF．（Ⅰ）求证：BD⊥平面AED；（Ⅱ）求二面角F﹣BD﹣C的余弦值．6、18．（12分）（2013山东）如图所示，在三棱锥P﹣ABQ中，PB⊥平面ABQ，BA=BP=BQ，D，C，E，F分别是AQ，BQ，AP，BP的中点，AQ=2BD，PD与EQ交于点G，PC与FQ交于点H，连接GH．（1）求证：AB∥GH；（2）求二面角D﹣GH﹣E的余弦值．7、17．（12分）（2014山东）如图，在四棱柱ABCD﹣A1B1C1D1中，底面ABCD是等腰梯形，∠DAB=60°，AB=2CD=2，M是线段AB的中点．（Ⅰ）求证：C1M∥平面A1ADD1；（Ⅱ）若CD1垂直于平面ABCD且CD1=，求平面C1D1M和平面ABCD所成的角（锐角）的余弦值．8、17．（12分）（2015山东）如图，在三棱台DEF﹣ABC中，AB=2DE，G，H分别为AC，BC 的中点．（Ⅰ）求证：BD∥平面FGH；（Ⅱ）若CF⊥平面ABC，AB⊥BC，CF=DE，∠BAC=45°，求平面FGH与平面ACFD所成的角（锐角）的大小．9、17．（12分）（2016山东）在如图所示的圆台中，AC是下底面圆O的直径，EF是上底面圆O′的直径，FB是圆台的一条母线．（I）已知G，H分别为EC，FB的中点，求证：GH∥平面ABC；（Ⅱ）已知EF=FB=AC=2，AB=BC，求二面角F﹣BC﹣A的余弦值．10、17．（12分）（2017山东）如图，几何体是圆柱的一部分，它是由矩形ABCD（及其内部）以AB边所在直线为旋转轴旋转120°得到的，G是的中点．（Ⅰ）设P是上的一点，且AP⊥BE，求∠CBP的大小；（Ⅱ）当AB=3，AD=2时，求二面角E﹣AG﹣C的大小．安徽省（答案）1、解：方法一（综合法）（1）取OB中点E，连接ME，NE∵ME∥AB，AB∥CD，∴ME∥CD又∵NE∥OC，∴平面MNE∥平面OCD∴MN∥平面OCD（2）∵CD∥AB，∴∠MDC为异面直线AB与MD所成的角（或其补角）作AP⊥CD于P，连接MP∵OA⊥平面ABCD，∴CD⊥MP∵，∴，，∴所以AB与MD所成角的大小为．（3）∵AB∥平面OCD，∴点A和点B到平面OCD的距离相等，连接OP，过点A作AQ⊥OP于点Q，∵AP⊥CD，OA⊥CD，∴CD⊥平面OAP，∴AQ⊥CD．又∵AQ⊥OP，∴AQ⊥平面OCD，线段AQ的长就是点A到平面OCD的距离，∵，，∴，所以点B到平面OCD的距离为．方法二（向量法）作AP⊥CD于点P，如图，分别以AB，AP，AO所在直线为x，y，z轴建立坐标系：A（0，0，0），B（1，0，0），，，O（0，0，2），M（0，0，1），（1），，设平面OCD的法向量为n=（x，y，z），则•=0，•=0即取，解得∵•=（，，﹣1）•（0，4，）=0，∴MN∥平面OCD．（2）设AB与MD所成的角为θ，∵∴，∴，AB与MD所成角的大小为．（3）设点B到平面OCD的距离为d，则d为在向量=（0，4，）上的投影的绝对值，由，得d==所以点B到平面OCD的距离为．2、解：（1）解：连接AC、BD交于菱形的中心O，过O作OG⊥AF，G为垂足，连接BG、DG．由BD⊥AC，BD⊥CF得BD⊥平面ACF，故BD⊥AF．于是AF⊥平面BGD，所以BG⊥AF，DG⊥AF，∠BGD为二面角B﹣AF﹣D的平面角．由FC⊥AC，FC=AC=2，得∠FAC=，OG=．由OB⊥OG，OB=OD=，得∠BGD=2∠BGO=．（2）解：连接EB、EC、ED，设直线AF与直线CE相交于点H，则四棱锥E﹣ABCD与四棱锥F﹣ABCD的公共部分为四棱锥H﹣ABCD．过H作HP⊥平面ABCD，P为垂足．因为EA⊥平面ABCD，FC⊥平面ABCD，所以平面ACEF⊥平面ABCD，从而P∈AC，HP⊥AC．由+=+=1，得HP=．又因为S菱形ABCD=AC•BD=，故四棱锥H﹣ABCD的体积V=S菱形ABCD•HP=．3、证明：（1）设AC于BD交于点G，则G为AC的中点，连接EG，GH，又H为BC的中点，∴GH∥AB且GH=AB，又EF∥AB且EF=AB，∴EF∥GH且EF=GH，∴四边形EFHG为平行四边形∴EG∥FH，而EG⊂平面EDB，∴FH∥平面EDB．（2）由四边形ABCD为正方形，有AB⊥BC，又EF∥AB，∴EF⊥BC而EF⊥FB，∴EF⊥平面BFC，∴EF⊥FH，∴AB⊥FH，又BF=FC，H为BC的中点，∴FH⊥BC∴FH⊥平面ABCD，∴FH⊥BC，FH⊥AC，又FH∥EG，∴AC⊥EG又AC⊥BD，EG∩BD=G，∴AC⊥平面EDB，（3）EF⊥FB，∠BFC=90°，∴BF⊥平面CDEF，在平面CDEF内过点F作FK⊥DE交DE的延长线与k，则∠FKB为二面角B﹣DE﹣C的一个平面角，设EF=1，则AB=2，FC=，DE=，又EF∥DC，∴∠KEF=∠EDC，∴sin∠EDC=sin∠KEF=，∴FK=EFsin∠KEF=，tan∠FKB==，∴∠FKB=60°，∴二面角B﹣DE﹣C为60°．4、解：（I）证明：设G是线段DA与线段EB延长线的交点，由于△OAB与△ODE都是正三角形，所以OB∥DE，OB=同理，设G′是线段DA与线段FC延长线的交点，有OG′=OD=2，又由于G与G′都在线段DA的延长线上，所以G与G′重合，在△GED和△GFD中，由和可知B，C分别是GE，GF的中点，所以BC是△GFE 的中位线，故BC∥EF（II）解：由OB=1，OE=2，∠EOB=60°，知而△OED是边长为2的正三角形，故所以过点F作FQ⊥AD，交AD于点Q．由平面ABED⊥平面ACFD，FQ就是四棱锥F﹣OBED的高，且FQ=，所以另外本题还可以用向量法解答，同学们可参考图片，自行解一下，解法略．5、（Ⅰ）证明：取BC，B1C1的中点为点O，O1，连接AO，OO1，A1O，A1O1，∵AB=AC，∴AO⊥BC∵平面ABC⊥平面BB1C1C，平面ABC∩平面BB1C1C=BC∴AO⊥平面BB1C1C同理A1O1⊥平面BB1C1C，∴AO∥A1O1，∴A、O、A1、O1共面∵OO1⊥BC，AO⊥BC，OO1∩AO=O，∴BC⊥平面OO1A1A∵AA1⊂平面OO1A1A，∴AA1⊥BC；（Ⅱ）解：延长A1O1到D，使O1D=OA，则∵O1D∥OA，∴AD∥OO1，AD=OO1，∵OO1⊥BC，平面A1B1C1⊥平面BB1C1C，平面A1B1C1∩平面BB1C1C=B1C1，∴OO1⊥面A1B1C1，∵AD∥OO1，∴AD⊥面A1B1C1，∵AD=BB1=4，A1D=A1O1+O1D=2+1=3∴AA1==5；（Ⅲ）解：∵AO⊥BC，A1O⊥BC，∴∠AOA1是二面角A﹣BC﹣A1的平面角在直角△OO1A1中，A1O=在△OAA1中，cos∠AOA1=﹣∴二面角A﹣BC﹣A1的余弦值为﹣．6、（1）证明：设平面PAB与平面PCD的交线为l，则∵AB∥CD，AB⊄平面PCD，∴AB∥平面PCD∵AB⊂面PAB，平面PAB与平面PCD的交线为l，∴AB∥l∵AB在底面上，l在底面外∴l与底面平行；（2）解：设CD的中点为F，连接OF，PF由圆的性质，∠COD=2∠COF，OF⊥CD∵OP⊥底面，CD⊂底面，∴OP⊥CD∵OP∩OF=O∴CD⊥平面OPF∵CD⊂平面PCD∴平面OPF⊥平面PCD∴直线OP在平面PCD上的射影为直线PF∴∠OPF为OP与平面PCD所成的角由题设，∠OPF=60°设OP=h，则OF=OPtan∠OPF=∵∠OCP=22.5°，∴∵tan45°==1∴tan22.5°=∴OC==在Rt△OCF中，cos∠COF===∴cos∠COD=cos（2∠COF）=2cos2∠COF﹣1=17﹣127、（Ⅰ）证明：∵四棱柱ABCD﹣A1B1C1D1中，四边形ABCD为梯形，AD∥BC，∴平面QBC∥平面A1D1DA，∴平面A1CD与面QBC、平面A1D1DA的交线平行，∴QC∥A1D∴△QBC∽△A1AD，∴=，∴Q为BB1的中点；（Ⅱ）解：连接QA，QD，设AA1=h，梯形ABCD的高为d，四棱柱被平面α所分成上、下两部分的体积为V1，V2，设BC=a，则AD=2a，∴==，V Q﹣ABCD==ahd，∴V2=，∵V棱柱=ahd，∴V1=ahd，∴四棱柱被平面α所分成上、下两部分的体积之比；（Ⅲ）解：在△ADC中，作AE⊥DC，垂足为E，连接A1E，则DE⊥平面AEA1，∴DE⊥A1E，∴∠AEA1为平面α与底面ABCD所成二面角的平面角，∵BC∥AD，AD=2BC，∴S△ADC=2S△ABC，∵梯形ABCD的面积为6，DC=2，∴S△ADC=4，AE=4，∴tan∠AEA1==1，∴∠AEA1=，∴平面α与底面ABCD所成二面角的大小为．8、（Ⅰ）证明：∵B1C=A1D且A1B1=CD，∴四边形A1B1CD为平行四边形，∴B1C∥A1D，又∵B1C⊄平面A1EFD，∴B1C∥平面A1EFD，又∵平面A1EFD∩平面B1CD1=EF，∴EF∥B1C；（Ⅱ）解：以A为坐标原点，以AB、AD、AA1所在直线分别为x、y、z轴建立空间直角坐标系A﹣xyz如图，设边长为2，∵AD1⊥平面A1B1CD，∴=（0，2，2）为平面A1B1CD的一个法向量，设平面A1EFD的一个法向量为=（x，y，z），又∵=（0，2，﹣2），=（1，1，0），∴，，取y=1，得=（﹣1，1，1），∴cos＜，＞==，∴二面角E﹣A1D﹣B1的余弦值为．福建省（答案）1、解：（Ⅰ）证明：在△PAD中，PA=PD，O为AD的中点，所以PO⊥AD又侧面PAD⊥底面ABCD，平面PAD∩平面ABCD=AD，PO⊂平面PAD所以PO⊥平面ABCD．（Ⅱ）连接BO，在直角梯形ABCD中，BC∥AD，AD=2AB=2BC=2有OD∥BC且OD=BC，所以四边形OBCD是平行四边形，所以OB∥DC由（Ⅰ）知PO⊥OB，∠PBC是锐角，所以∠PBC是异面直线PB与CD所成的角因为AD=2AB=2BC=2，在Rt△AOB中，AB=1，AO=1，所以OB=在Rt△AOP中因为AP=AO=1，所以OP=1在Rt△AOP中tan∠PBC=所以：异面直线PB与CD所成角的大小．（Ⅲ）假设存在点Q，使得它到平面PCD的距离为．设QD=x，则，由（Ⅱ）得CD=OB=，在Rt△POC中，，所以PC=CD=DP，，由V p﹣DQC=V Q﹣PCD，得x=，所以存在点Q满足题意，此时．解法二：（Ⅰ）同解法一．（Ⅱ）以O为坐标原点，的方向分别为x轴、y轴、z轴的正方向，建立空间直角坐标系O﹣xyz，依题意，易得A（0，﹣1，0），B（1，﹣1，0），C（1，0，0），D（0，1，0），P（0，0，1），所以．所以异面直线PB与CD所成的角是arccos，（Ⅲ）假设存在点Q，使得它到平面PCD的距离为，由（Ⅱ）知．设平面PCD的法向量为n=（x0，y0，z0）．则所以即x0=y0=z0，取x0=1，得平面PCD的一个法向量为=（1，1，1）．设，由，得，解y=﹣或y=（舍去），此时，所以存在点Q满足题意，此时．2、解：（Ⅰ）因为AA1⊥平面ABC，BC⊂平面ABC，所以AA1⊥BC，因为AB是圆O直径，所以BC⊥AC，又AC∩AA1=A，所以BC⊥平面A1ACC1，而BC⊂平面B1BCC1，所以平面A1ACC1⊥平面B1BCC1．（Ⅱ）设圆柱的底面半径为r，则AB=AA1=2r，故三棱柱ABC﹣A1B1C1的体积为=AC•BC•r，又因为AC2+BC2=AB2=4r2，所以=2r2，当且仅当时等号成立，从而V1≤2r3，而圆柱的体积V=πr2•2r=2πr3，故P=，当且仅当，即OC⊥AB时等号成立，所以P的最大值是．P取最大值时，OC⊥AB，于是以O为坐标原点，建立空间直角坐标系O﹣xyz，设OB为y轴的正半轴，OC为x轴正半轴，OO1为z轴的正半轴，则C（r，0，0），B（0，r，0），B1（0，r，2r），因为BC⊥平面A1ACC1，所以是平面A1ACC1的一个法向量，设平面B1OC的法向量，由，故，取z=1得平面B1OC的一个法向量为，因为0°＜θ≤90°，所以===．3、解：（I）证明：∵PA⊥平面ABCD，AB⊂平面ABCD∴PA⊥AB又∵AB⊥AD，PA∩AD=A∴AB⊥平面PAD又∵AB⊂平面PAB，∴平面PAB⊥平面PAD（II）（i）以A为坐标原点，建立空间直角坐标系A﹣xyz（如图）在平面ABCD内，作CE∥AB交于点E，则CE⊥AD 在Rt△CDE中，DE=CD•cos45°=1，CE=CD•sin45°=1设AB=AP=t，则B（t，0，0），P（0，0，t）由AB+AD=4，得AD=4﹣t，所以E（0，3﹣t，0），C（1，3﹣t，0），D（0，4﹣t，0），设平面PCD的法向量为=（x，y，z）由，，得取x=t，得平面PCD的一个法向量为又，故由直线PB与平面PCD所成的角为30°得cos（90°﹣30°）==即解得或t=4（舍去，因为AD=4﹣t＞0）所以AB=（ii）假设在线段AD上存在一个点G到P、B、C、D的距离都相等由GC=GD，得∠GCD=∠GDC=45°从而∠CGD=90°，即CG⊥AD所以GD=CD•cos45°=1设AB=λ，则AD=4﹣λ，AG=AD﹣GD=3﹣λ在Rt△ABG中，GB=这GB=GD与矛盾．所以在线段AD上不存在一个点G，使得点G到B、C、D的距离都相等．从而，在线段AD上不存在一个点G，使得点G到点P、B、C、D的距离都相等．4、解：（I）以A为原点，，，的方向为X轴，Y轴，Z轴的正方向建立空间直角坐标系，如图，设AB=a，则A（0，0，0），D（0，1，0），D1（0，1，1），E（，1，0），B1（a，0，1）故=（0，1，1），=（﹣，1，﹣1），=（a，0，1），=（，1，0），∵•=1﹣1=0∴B1E⊥AD1；（II）假设在棱AA1上存在一点P（0，0，t），使得DP∥平面B1AE．此时=（0，﹣1，t）．又设平面B1AE的法向量=（x，y，z）．∵⊥平面B1AE，∴⊥B1A，⊥AE，得，取x=1，得平面B1AE的一个法向量=（1，﹣，﹣a）．要使DP∥平面B1AE，只要⊥，即有•=0，有此得﹣at=0，解得t=，即P（0，0，），又DP⊈平面B1AE，∴存在点P，满足DP∥平面B1AE，此时AP=（III）连接A1D，B1C，由长方体ABCD﹣A1B1C1D1及AA1=AD=1，得AD1⊥A1D．∵B1C∥A1D，∴AD1⊥B1C．由（I）知，B1E⊥AD1，且B1C∩B1E=B1．∴AD1⊥平面DCB1A1，∴AD1是平面B1A1E的一个法向量，此时=（0，1，1）．设与所成的角为θ，则cosθ==∵二面角A﹣B1E﹣A1的大小为30°，∴|cosθ|=cos30°=，即||=，解得a=2，即AB的长为25、（1）证明：取DC的中点E，连接BE，∵AB∥ED，AB=ED=3k，∴四边形ABED是平行四边形，∴BE∥AD，且BE=AD=4k，∴BE2+EC2=（4k）2+（3k）2=（5k）2=BC2，∴∠BEC=90°，∴BE⊥CD，又∵BE∥AD，∴CD⊥AD．∵侧棱AA1⊥底面ABCD，∴AA1⊥CD，∵AA1∩AD=A，∴CD⊥平面ADD1A1．（2）解：以D为坐标原点，、、的方向为x，y，z轴的正方向建立空间直角坐标系，则A（4k，0，0），C（0，6k，0），B1（4k，3k，1），A1（4k，0，1）．∴，，．设平面AB1C的一个法向量为=（x，y，z），则，取y=2，则z=﹣6k，x=3．∴．设AA1与平面AB1C所成角为θ，则===，解得k=1，故所求k=1．（3）由题意可与左右平面ADD1A1，BCC1B1，上或下面ABCD，A1B1C1D1拼接得到方案新四棱柱共有此4种不同方案．写出每一方案下的表面积，通过比较即可得出f（k）=6、（1）证明：∵平面ABD⊥平面BCD，平面ABD∩平面BCD=BD，AB⊂平面ABD，AB⊥BD，∴AB⊥平面BCD，又CD⊂平面BCD，∴AB⊥CD．（2）解：建立如图所示的空间直角坐标系．∵AB=BD=CD=1，AB⊥BD，CD⊥BD，∴B（0，0，0），C（1，1，0），A（0，0，1），D（0，1，0），M．∴=（0，1，﹣1），=（1，1，0），=．设平面BCM的法向量=（x，y，z），则，令y=﹣1，则x=1，z=1．∴=（1，﹣1，1）．设直线AD与平面MBC所成角为θ．则sinθ=|cos|===．7、解法一：（1）如图，取AE的中点H，连接HG，HD，∵G是BE的中点，∴GH∥AB，且GH=AB，又∵F是CD中点，四边形ABCD是矩形，∴DF∥AB，且DF=AB，即GH∥DF，且GH=DF，∴四边形HGFD是平行四边形，∴GF∥DH，又∵DH⊂平面ADE，GF⊄平面ADE，∴GF∥平面ADE．（2）如图，在平面BEG内，过点B作BQ∥CE，∵BE⊥EC，∴BQ⊥BE，又∵AB⊥平面BEC，∴AB⊥BE，AB⊥BQ，以B为原点，分别以的方向为x轴，y轴，z轴的正方向建立空间直角坐标系，则A（0，0，2），B（0，0，0），E（2，0，0），F（2，2，1）∵AB⊥平面BEC，∴为平面BEC的法向量，设=（x，y，z）为平面AEF的法向量．又=（2，0，﹣2），=（2，2，﹣1）由垂直关系可得，取z=2可得．∴cos＜，＞==∴平面AEF与平面BEC所成锐二面角的余弦值为．解法二：（1）如图，取AB中点M，连接MG，MF，又G是BE的中点，可知GM∥AE，且GM=AE又AE⊂平面ADE，GM⊄平面ADE，∴GM∥平面ADE．在矩形ABCD中，由M，F分别是AB，CD的中点可得MF∥AD．又AD⊂平面ADE，MF⊄平面ADE，∴MF∥平面ADE．又∵GM∩MF=M，GM⊂平面GMF，MF⊂平面GMF∴平面GMF∥平面ADE，∵GF⊂平面GMF，∴GF∥平面ADE（2）同解法一．广东省（答案）1、解：（1）在Rt△BAD中，∵∠ABD=60°，∴而PD垂直底面ABCD，，，在△PAB中，PA2+AB2=PB2，即△PAB为以∠PAB为直角的直角三角形．设点D到面PAB的距离为H，由V P﹣ABD=V D﹣PAB，有PA•AB•H=AB•AD•PD，即，．（2）EG∥BC，∴，而，即，∴GF∥PD，∴GF⊥BC，∴GF⊥EG，∴△EFG是直角三角形．（3）时，，即，∴△EFG 的面积．2、解：（1）依题作点E 、G 在平面11DCC D 内的正投影1E 、1G ，则1E 、1G 分别为1CC 、1DD 的中点，连结1EE 、1EG 、ED 、1DE ，则所求为四棱锥11FG DE E -的体积，其底面11FG DE 面积为111111E D G Rt FG E Rt FG D E S S S ∆∆+=221212221=⨯⨯+⨯⨯=， 又⊥1EE 面11FG DE ，11=EE ，∴323111111=⋅=-EE S V FG DE FG DE E .（2）以D 为坐标原点，DA 、DC 、1DD 所在直线分别作x 轴，y 轴，z 轴，得)1,2,0(1E 、)1,0,0(1G ，又)1,0,2(G ，)2,1,0(F ，)1,2,1(E ，则)1,1,0(1--=FG ，)1,1,1(-=FE ，)1,1,0(1-=FE ，∴01)1(01=+-+=⋅FG ，01)1(011=+-+=⋅FE FG ，即FE FG ⊥1，11FE FG ⊥， 又F FE FE =⋂1，∴⊥1FG 平面1FEE .（3）)0,2,0(11-=G E ，)1,2,1(--=EA，则62,cos 11=>=<G E ，设异面直线11E G EA 与所成角为θ，则33321sin =-=θ3、（1）证明：连接CF ，因为是半径为a 的半圆，AC 为直径，点E 为的中点，所以EB ⊥AC ． 在RT △BCE 中，．在△BDF中，，△BDF为等腰三角形，且点C是底边BD的中点，故CF⊥BD．在△CEF中，，所以△CEF为Rt△，且CF⊥EC．因为CF⊥BD，CF⊥EC，且CE∩BD=C，所以CF⊥平面BED，而EB⊂平面BED，∴CF⊥EB．因为EB⊥AC，EB⊥CF，且AC∩CF=C，所以EB⊥平面BDF，而FD⊂平面BDF，∴EB⊥FD．（2）解：设平面BED与平面RQD的交线为DG．由，，知QR∥EB．而EB⊂平面BDE，∴QR∥平面BDE，而平面BDE∩平面RQD=DG，∴QR∥DG∥EB．由（1）知，BE⊥平面BDF，∴DG⊥平面BDF，而DR，DB⊂平面BDF，∴DG⊥DR，DG⊥DB，∴∠RDB是平面BED与平面RQD所成二面角的平面角．在Rt△BCF中，，，．在△BDR中，由知，，由余弦定理得，=由正弦定理得，，即，．故平面BED与平面RQD所成二面角的正弦值为．4、解：（1）取AD的中点G，连接PG，BG，在△ABG中，根据余弦定理可以算出BG=，发现AG2+BG2=AB2，可以得出AD⊥BG，又DE∥BG∴DE⊥AD，又PA=PD，可以得出AD⊥PG，而PG∩BG=G，∴AD⊥平面PBG，而PB⊂平面PBG，∴AD⊥PB，又PB∥EF，∴AD⊥EF．又EF∩DE=E，∴AD⊥平面DEF．（2）由（1）知，AD⊥平面PBG，所以∠PGB为二面角P﹣AD﹣B的平面角，在△PBG中，PG=，BG=，PB=2，由余弦定理得cos∠PGB=，因此二面角P﹣AD﹣B的余弦值为．5、解：（1）∵PA⊥平面ABCD∴PA⊥BD∵PC⊥平面BDE∴PC⊥BD，又PA∩PC=P∴BD⊥平面PAC（2）设AC与BD交点为O，连OE∵PC⊥平面BDE∴PC⊥平面BOE∴PC⊥BE∴∠BEO为二面角B﹣PC﹣A的平面角∵BD⊥平面PAC∴BD⊥AC∴四边形ABCD为正方形，又PA=1，AD=2，可得BD=AC=2，PC=3∴OC=在△PAC∽△OEC中，又BD⊥OE，∴∴二面角B﹣PC﹣A的平面角的正切值为36、（1）证明：连接OD，OE．因为在等腰直角三角形ABC中，∠B=∠C=45°，，CO=BO=3．在△COD中，，同理得．因为，．所以A′O2+OD2=A′D2，A′O2+OE2=A′E2．所以∠A′OD=∠A′OE=90°所以A′O⊥OD，A′O⊥OE，OD∩OE=O．所以A′O⊥平面BCDE．（2）方法一：过点O作OF⊥CD的延长线于F，连接A′F因为A′O⊥平面BCDE．根据三垂线定理，有A′F⊥CD．所以∠A′FO为二面角A′﹣CD﹣B的平面角．在Rt△COF中，．在Rt△A′OF中，．所以．所以二面角A′﹣CD﹣B的平面角的余弦值为．方法二：取DE中点H，则OH⊥OB．以O为坐标原点，OH、OB、OA′分别为x、y、z轴建立空间直角坐标系．则O（0，0，0），A′（0，0，），C（0，﹣3，0），D（1，﹣2，0）=（0，0，）是平面BCDE的一个法向量．设平面A′CD的法向量为n=（x，y，z），．所以，令x=1，则y=﹣1，．所以是平面A′CD的一个法向量设二面角A′﹣CD﹣B的平面角为θ，且所以所以二面角A′﹣CD﹣B的平面角的余弦值为7、解：（1）∵PD⊥平面ABCD，∴PD⊥AD，又CD⊥AD，PD∩CD=D，∴AD⊥平面PCD，∴AD⊥PC，又AF⊥PC，∴PC⊥平面ADF，即CF⊥平面ADF；（2）设AB=1，在RT△PDC中，CD=1，∠DPC=30°，∴PC=2，PD=，由（1）知CF⊥DF，∴DF=，AF==，∴CF==，又FE∥CD，∴，∴DE=，同理可得EF=CD=，如图所示，以D为原点，建立空间直角坐标系，则A（0，0，1），E（，0，0），F（，，0），P（，0，0），C（0，1，0）设向量=（x，y，z）为平面AEF的法向量，则有，，∴，令x=4可得z=，∴=（4，0，），由（1）知平面ADF的一个法向量为=（，1，0），设二面角D﹣AF﹣E的平面角为θ，可知θ为锐角，cosθ=|cos＜，＞|===∴二面角D﹣AF﹣E的余弦值为：8、（1）证明：在△POC中PO=PC且E为CD中点，∴PE⊥CD，又∵平面PDC⊥平面ABCD，平面PDC∩平面ABCD=CD，PE⊂平面PCD，∴PE⊥平面ABCD，又∵FG⊂平面ABCD，∴PE⊥FG；（2）解：由（1）知PE⊥平面ABCD，∴PE⊥AD，又∵CD⊥AD且PE∩CD=E，∴AD⊥平面PDC，又∵PD⊂平面PDC，∴AD⊥PD，又∵AD⊥CD，∴∠PDC为二面角P﹣AD﹣C的平面角，在Rt△PDE中，由勾股定理可得：PE===，∴tan∠PDC==；（3）解：连结AC，则AC==3，在Rt△ADP中，AP===5，∵AF=2FB，CG=2GB，∴FG∥AC，∴直线PA与直线FG所成角即为直线PA与直线FG所成角∠PAC，在△PAC中，由余弦定理得cos∠PAC===．湖北省（答案）1、解：（Ⅰ）证法1：如图1，连接BE、BD，由地面ABCD是正方形可得AC⊥BD．∵SD⊥平面ABCD，∴BD是BE在平面ABCD上的射影，∴AC⊥BE（Ⅱ）解法1：如图1，由SD⊥平面ABCD知，∠DBE=φ，∵SD⊥平面ABCD，CD⊂平面ABCD，∴SD⊥CD．又底面ABCD是正方形，∴CD⊥AD，而SD∩AD=D，CD⊥平面SAD．连接AE、CE，过点D在平面SAD内作DF⊥AE于F，连接CF，则CF⊥AE，故∠CFD是二面角C﹣AE﹣D的平面角，即∠CFD=θ．在Rt△BDE中，∵BD=2a，DE=λa∴tanφ=在Rt△ADE中，∵，DE=λa∴AE=a从而DF=在Rt△CDF中，tanθ=．由tanθ•tanφ=1，得即=2，所以λ2=2．由0＜λ≤2，解得，即为所求．（Ⅰ）证法2：以D为原点，以DA．DC．DS的方向分别作为x，y，z轴的正方向建立如图2所示的空间直角坐标系，则D（0，0，0），A（，0，0），B（a，a，0），C（0，a，0），E（0，0，λa），∴，∴，即AC⊥BE．（Ⅱ）解法2：由（I）得，，．设平面ACE的法向量为n=（x，y，z），则由，得即取，得．易知平面ABCD与平面ADE的一个法向量分别为与．∴，．∵0＜θ＜，λ＞0∴tanθ•tanφ=1⇔θ+φ=⇔sinφ=cosθ⇔⇔λ2=2．由0＜λ≤2，解得，即为所求．2、解：法一：（Ⅰ）在平面OAB内作ON⊥OA交AB于N，连接NC．又OA⊥OC，∴OA⊥平面ONC。

2020-2021高考数学真题《立体几何》专项汇编（含答案）一、空间几何体的体积、面积1．（2021·全国·高考真题）若圆锥的轴截面为等腰直角三角形，则它的底面积与侧面积之比是（ ）A ．√2:1B ．2:1C ．1:√2D ．1:2 2．（2021·全国·高考真题）已知圆锥的底面半径为√2，其侧面展开图为一个半圆，则该圆锥的母线长为（ ）A ．2B ．2√2C ．4D ．3．（2021·全国·高考真题）正四棱台的上､下底面的边长分别为2，4，侧棱长为2，则其体积为（ ）A ．20+12√3B ．28√2C ．563D 4．（2021·全国·高考真题）在正三棱柱ABC −A 1B 1C 1中，AB =AA 1=1，点P 满足BP⃗⃗⃗⃗⃗⃗ =λBC ⃗⃗⃗⃗⃗⃗ +μBB 1⃗⃗⃗⃗⃗⃗⃗⃗ ，其中λ∈[0,1]，μ∈[0,1]，则（ ）A ．当λ=1时，△AB 1P 的周长为定值B ．当μ=1时，三棱锥P −A 1BC 的体积为定值C ．当λ=12时，有且仅有一个点P ，使得A 1P ⊥BPD ．当μ=12时，有且仅有一个点P ，使得A 1B ⊥平面AB 1P5．（2020·海南·高考真题）已知正方体ABCD -A 1B 1C 1D 1的棱长为2，M 、N 分别为BB 1、AB 的中点，则三棱锥A -NMD 1的体积为____________6．（2021·全国·高考真题（文））如图，四棱锥P−ABCD的底面是矩形，PD⊥底面ABCD，M为BC的中点，且PB⊥AM．（1）证明：平面PAM⊥平面PBD；（2）若PD=DC=1，求四棱锥P−ABCD的体积．二、平行、垂直的命题判定7．（2021·全国·高考真题）已知α，β表示平面，m，n表示直线，以下命题中正确的选项是（）A．假设m⊥α，m⊥n，那么n//αB．假设m⊂α，n⊂β，α//β，那么m//nC．假设α//β，m⊂α，那么m//βD．假设m⊂α，n⊂α，m//β，n//β，那么α//β8．（2021·全国·高考真题）设m，n为两条不同的直线，α，β为两个不同的平面，则下列结论正确的是（）A．若m//n，n//α，则m//αB．若m//n，m//α，n//β，则α//βC．若α⊥β，m⊂α，n⊂β，则m⊥nD．若m⊥n，m⊥α，n⊥β，则α⊥β9．（2020·山东·高考真题）已知正方体ABCD−A1B1C1D1（如图所示），则下列结论正确的是（）A．BD1//A1A B．BD1//A1D C．BD1⊥A1C D．BD1⊥A1C110．（2021·浙江·高考真题）如图已知正方体ABCD−A1B1C1D1，M，N分别是A1D，D1B 的中点，则（）A．直线A1D与直线D1B垂直，直线MN//平面ABCDB．直线A1D与直线D1B平行，直线MN⊥平面BDD1B1C．直线A1D与直线D1B相交，直线MN//平面ABCDD．直线A1D与直线D1B异面，直线MN⊥平面BDD1B111．（2021·全国·高考真题）-（多选）如图，在正方体中，O为底面的中心，P为所在棱的中点，M，N为正方体的顶点．则满足MN⊥OP的是（）A．B．C．D．12．（2021·全国·高考真题）如下图，在四棱锥S ABCD-中，底面ABCD是正方形，平面SAD⊥平面ABCD，SA=SD=2，3AB=．（1）求SA与BC所成角的余弦值；（2）求证：AB⊥SD．三、球体-能力拓展13．（2020·天津·高考真题）若棱长为2√3的正方体的顶点都在同一球面上，则该球的表面积为（）A．12πB．24πC．36πD．144π14．（2021·天津·高考真题）两个圆锥的底面是一个球的同一截面，顶点均在球面上，若球的体积为32π3，两个圆锥的高之比为1:3，则这两个圆锥的体积之和为（）A．3πB．4πC．9πD．12π15．（2020·全国·高考真题（理））已知△ABC是面积为9√34的等边三角形，且其顶点都在球O的球面上.若球O的表面积为16π，则O到平面ABC的距离为（）A．√3B．32C．1D．√3216．（2021·全国·高考真题（理））已如A，B，C是半径为1的球O的球面上的三个点，且AC⊥BC,AC=BC=1，则三棱锥O−ABC的体积为（）A．√212B．√312C．√24D．√3417．（2020·全国·高考真题（理））已知,,A B C为球O的球面上的三个点，⊙O1为△ABC的外接圆，若⊙O1的面积为4π，AB=BC=AC=OO1，则球O的表面积为（）A．64πB．48πC．36πD．32π18．（2020·海南·高考真题）已知直四棱柱ABCD–A1B1C1D1的棱长均为2，∠BAD=60°．以D1为球心，√5为半径的球面与侧面BCC1B1的交线长为________．四、立体几何的数学应用19．（2021·全国·高考真题）北斗三号全球卫星导航系统是我国航天事业的重要成果．在卫星导航系统中，地球静止同步卫星的轨道位于地球赤道所在平面，轨道高度为36000km （轨道高度是指卫星到地球表面的距离）．将地球看作是一个球心为O，半径r为6400km 的球，其上点A的纬度是指OA与赤道平面所成角的度数．地球表面上能直接观测到一颗地球静止同步轨道卫星点的纬度最大值为α，记卫星信号覆盖地球表面的表面积为S=2πr2(1−cosα)（单位：km2），则S占地球表面积的百分比约为（）A．26%B．34%C．42%D．50%20．（2021·北京·高考真题）某一时间段内，从天空降落到地面上的雨水，未经蒸发、渗漏、流失而在水平面上积聚的深度，称为这个时段的降雨量（单位：mm）．24h降雨量的等级划分如下：在综合实践活动中，某小组自制了一个底面直径为200 mm，高为300 mm的圆锥形雨量器.若一次降雨过程中，该雨量器收集的24h的雨水高度是150 mm（如图所示)，则这24h 降雨量的等级是A．小雨B．中雨C．大雨D．暴雨21．（2020·海南·高考真题）日晷是中国古代用来测定时间的仪器，利用与晷面垂直的晷针投射到晷面的影子来测定时间．把地球看成一个球(球心记为O )，地球上一点A 的纬度是指OA 与地球赤道所在平面所成角，点A 处的水平面是指过点A 且与OA 垂直的平面.在点A 处放置一个日晷，若晷面与赤道所在平面平行，点A 处的纬度为北纬40°，则晷针与点A 处的水平面所成角为（ ）A ．20°B ．40°C ．50°D ．90°22．（2020·全国·高考真题（理））埃及胡夫金字塔是古代世界建筑奇迹之一，它的形状可视为一个正四棱锥，以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积，则其侧面三角形底边上的高与底面正方形的边长的比值为（ ）A ．√5−14BC ．√5+14D ．√5+1223．（2020·江苏·高考真题）如图，六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的．已知螺帽的底面正六边形边长为2 cm，高为2 cm，内孔半径为0.5 cm，则此六角螺帽毛坯的体积是____cm.五、立体几何与空间向量的综合应用24．（2021·全国·高考真题（理））在正方体ABCD−A1B1C1D1中，P为B1D1的中点，则直线PB与AD1所成的角为（）A．π2B．π3C．π4D．π625．（2021·全国·高考真题）如图，四棱锥P−ABCD中，底面ABCD是矩形，PA⊥平面ABCD，E为PD的中点.（1）证明：PB//平面ACE；（2）设PA=1，AD=√3，直线PB与平面ABCD所成的角为45°，求四棱锥P−ABCD 的体积.中，底面ABCD是正方形，若AD= 26．（2021·全国·高考真题）在四棱锥Q ABCD2,QD=QA=√5,QC=3．（1）证明：平面QAD⊥平面ABCD；（2）求二面角B−QD−A的平面角的余弦值．27．（2021·天津·高考真题）如图，在棱长为2的正方体ABCD−A1B1C1D1中，E为棱BC的中点，F为棱CD的中点．（I）求证：D1F//平面A1EC1；（II）求直线AC1与平面A1EC1所成角的正弦值．（III）求二面角A−A1C1−E的正弦值．28．（2021·全国·高考真题（理））已知直三棱柱ABC−A1B1C1中，侧面AA1B1B为正方形，AB=BC=2，E，F分别为AC和CC的中点，D为棱A1B1上的点．BF⊥A1B11（1）证明：BF⊥DE；（2）当B1D为何值时，面BB1C1C与面DFE所成的二面角的正弦值最小?29．（2021·北京·高考真题）如图：在正方体ABCD −A 1B 1C 1D 1中，E 为A 1D 1中点，11B C 与平面CDE 交于点F ．（1）求证：F 为11B C 的中点；（2）点M 是棱A 1B 1上一点，且二面角M −FC −E 的余弦值为√53，求A 1MA1B 1的值．30．（2020·全国·高考真题（理））如图，D为圆锥的顶点，O是圆锥底面的圆心，AE为底DO．面直径，AE=AD．△ABC是底面的内接正三角形，P为DO上一点，PO=√66（1）证明：PA⊥平面PBC；（2）求二面角B−PC−E的余弦值．2020-2021真题精编-立体几何解析版一、空间几何体的体积、面积1．（2021·全国·高考真题）若圆锥的轴截面为等腰直角三角形，则它的底面积与侧面积之比是（）A．√2:1B．2:1C．1:√2D．1:2【答案】C【分析】根据题意作图，由轴截面得出母线与底面圆半径的等量关系，再套公式求解.【详解】根据题意作图，设圆锥的底面圆半径为r，高为ℎ，母线长为l.若圆锥的轴截面为等腰直角三角形，则有2r cos45°=l，l=√2r.该圆锥的底面积与侧面积比值为πr 2πrl =2πr⋅√2r=√2.故选：C.2．（2021·全国·高考真题）已知圆锥的底面半径为√2，其侧面展开图为一个半圆，则该圆锥的母线长为（）A．2B．2√2C．4D．【答案】B【分析】设圆锥的母线长为l，根据圆锥底面圆的周长等于扇形的弧长可求得l的值，即为所求.【详解】设圆锥的母线长为l，由于圆锥底面圆的周长等于扇形的弧长，则πl=2π×√2，解得l= 2√2.故选：B.3．（2021·全国·高考真题）正四棱台的上､下底面的边长分别为2，4，侧棱长为2，则其体积为（）A ．20+12√3B ．28√2C ．563D 【答案】D 【分析】由四棱台的几何特征算出该几何体的高及上下底面面积，再由棱台的体积公式即可得解. 【详解】作出图形，连接该正四棱台上下底面的中心，如图，因为该四棱台上下底面边长分别为2，4，侧棱长为2， 所以该棱台的高ℎ=√22−(2√2−√2)2=√2， 下底面面积S 1=16，上底面面积S 2=4，所以该棱台的体积V =13ℎ(S 1+S 2+√S 1S 2)=13×√2×(16+4+√64)=283√2.故选：D.4．（2021·全国·高考真题）在正三棱柱ABC −A 1B 1C 1中，AB =AA 1=1，点P 满足BP ⃗⃗⃗⃗⃗⃗ =λBC ⃗⃗⃗⃗⃗⃗ +μBB 1⃗⃗⃗⃗⃗⃗⃗⃗ ，其中λ∈[0,1]，μ∈[0,1]，则（ ） A ．当λ=1时，△AB 1P 的周长为定值 B ．当μ=1时，三棱锥P −A 1BC 的体积为定值 C ．当λ=12时，有且仅有一个点P ，使得A 1P ⊥BP D ．当μ=12时，有且仅有一个点P ，使得A 1B ⊥平面AB 1P 【答案】BD 【分析】对于A ，由于等价向量关系，联系到一个三角形内，进而确定点的坐标；对于B ，将P 点的运动轨迹考虑到一个三角形内，确定路线，进而考虑体积是否为定值； 对于C ，考虑借助向量的平移将P 点轨迹确定，进而考虑建立合适的直角坐标系来求解P 点的个数；对于D ，考虑借助向量的平移将P 点轨迹确定，进而考虑建立合适的直角坐标系来求解P 点的个数．【详解】易知，点P 在矩形BCC 1B 1内部（含边界）．对于A ，当λ=1时，BP ⃗⃗⃗⃗⃗ =BC ⃗⃗⃗⃗⃗ +μBB 1⃗⃗⃗⃗⃗⃗⃗ =BC ⃗⃗⃗⃗⃗ +μCC 1⃗⃗⃗⃗⃗⃗⃗ ，即此时P ∈线段1CC ，△AB 1P 周长不是定值，故A 错误；对于B ，当μ=1时，BP ⃗⃗⃗⃗⃗ =λBC ⃗⃗⃗⃗⃗ +BB 1⃗⃗⃗⃗⃗⃗⃗ =BB 1⃗⃗⃗⃗⃗⃗⃗ +λB 1C 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ ，故此时P 点轨迹为线段11B C ，而B 1C 1//BC ，B 1C 1//平面A 1BC ，则有P 到平面A 1BC 的距离为定值，所以其体积为定值，故B 正确．对于C ，当λ=12时，BP ⃗⃗⃗⃗⃗ =12BC ⃗⃗⃗⃗⃗ +μBB 1⃗⃗⃗⃗⃗⃗⃗ ，取BC ，11B C 中点分别为Q ，H ，则BP ⃗⃗⃗⃗⃗ =BQ ⃗⃗⃗⃗⃗ +μQH ⃗⃗⃗⃗⃗⃗ ，所以P 点轨迹为线段QH ，不妨建系解决，建立空间直角坐标系如图，A 1(√32,0,1)，P (0,0,μ)，B (0,12,0)，则A 1P ⃗⃗⃗⃗⃗⃗⃗ =(−√32,0,μ−1)，BP ⃗⃗⃗⃗⃗ =(0,−12,μ)，()110A P BP μμ⋅=-=，所以μ=0或μ=1．故H,Q 均满足，故C 错误；对于D ，当μ=12时，BP ⃗⃗⃗⃗⃗ =λBC ⃗⃗⃗⃗⃗ +12BB 1⃗⃗⃗⃗⃗⃗⃗ ，取1BB ，1CC 中点为M,N ．BP ⃗⃗⃗⃗⃗ =BM ⃗⃗⃗⃗⃗⃗ +λMN ⃗⃗⃗⃗⃗⃗⃗ ，所以P 点轨迹为线段MN ．设P (0,y 0,12)，因为A (√32，0,0)，所以AP ⃗⃗⃗⃗⃗ =(−√32,y 0,12)，A 1B ⃗⃗⃗⃗⃗⃗⃗ =(−√32,12,−1)，所以34+12y 0−12=0⇒y 0=−12，此时P 与N 重合，故D 正确．故选：BD ． 【点睛】本题主要考查向量的等价替换，关键之处在于所求点的坐标放在三角形内．5．（2020·海南·高考真题）已知正方体ABCD -A 1B 1C 1D 1的棱长为2，M 、N 分别为BB 1、AB 的中点，则三棱锥A -NMD 1的体积为____________ 【答案】13【分析】利用V A−NMD1=V D1−AMN计算即可.【详解】因为正方体ABCD-A1B1C1D1的棱长为2，M、N分别为BB1、AB的中点所以V A−NMD1=V D1−AMN=13×12×1×1×2=13故答案为：1 3【点睛】在求解三棱锥的体积时，要注意观察图形的特点，看把哪个当成顶点好计算一些. 6．（2021·全国·高考真题（文））如图，四棱锥P−ABCD的底面是矩形，PD⊥底面ABCD，M为BC的中点，且PB⊥AM．（1）证明：平面PAM⊥平面PBD；（2）若PD=DC=1，求四棱锥P−ABCD的体积．【答案】（1）证明见解析；（2）√23．【分析】（1）由PD⊥底面ABCD可得PD⊥AM，又PB⊥AM，由线面垂直的判定定理可得AM⊥平面PBD，再根据面面垂直的判定定理即可证出平面PAM⊥平面PBD；（2）由（1）可知，AM⊥BD，由平面知识可知，△DAB~△ABM，由相似比可求出AD，再根据四棱锥P−ABCD的体积公式即可求出．【详解】（1）因为PD ⊥底面ABCD ，AM ⊂平面ABCD ， 所以PD ⊥AM ，又PB ⊥AM ，PB ∩PD =P ， 所以AM ⊥平面PBD ， 而AM ⊂平面PAM ， 所以平面PAM ⊥平面PBD ．（2）由（1）可知，AM ⊥平面PBD ，所以AM ⊥BD ， 从而△DAB~△ABM ，设BM =x ，AD =2x ，则BMAB =ABAD ，即2x 2=1，解得x AD =√2． 因为PD ⊥底面ABCD ，故四棱锥P −ABCD 的体积为V =13×(1×√2)×1=√23．【点睛】本题第一问解题关键是找到平面PAM 或平面PBD 的垂线，结合题目条件PB ⊥AM ，所以垂线可以从PB,AM 中产生，稍加分析即可判断出AM ⊥平面PBD ，从而证出；第二问关键是底面矩形面积的计算，利用第一问的结论结合平面几何知识可得出△DAB~△ABM ，从而求出矩形的另一个边长，从而求得该四棱锥的体积． 二、平行、垂直的命题判定7．（2021·全国·高考真题）已知α，β表示平面，m ，n 表示直线，以下命题中正确的选项是（ ）A ．假设m ⊥α，m ⊥n ，那么n //αB ．假设m ⊂α，n ⊂β，α//β，那么m //nC ．假设α//β，m ⊂α，那么m //βD ．假设m ⊂α，n ⊂α，m //β，n //β，那么α//β 【答案】C 【分析】根据线面垂直的性质定理，可判断A ；根据面面平行的性质定理，可判断B 、C ；根据面面平行的判定定理，可判定D 【详解】选项A ：假设m ⊥α，m ⊥n ，那么n //α或n 在α内，故选项A 错误；选项B ：假设m ⊂α，n ⊂β，α//β，那么m //n 或m 与n 异面，故选项B 错误； 选项D ：假设m ⊂α，n ⊂α，m //β，n //β，且m 、n 相交才能判定α//β，故选项C 错误；选项C ：依照两平面平行的性质可知C 正确．故选：C8．（2021·全国·高考真题）设m，n为两条不同的直线，α，β为两个不同的平面，则下列结论正确的是（）A．若m//n，n//α，则m//αB．若m//n，m//α，n//β，则α//βC．若α⊥β，m⊂α，n⊂β，则m⊥nD．若m⊥n，m⊥α，n⊥β，则α⊥β【答案】D【分析】根据线面的位置关系可判断A；举反例判断B、C；由面面垂直的判定定理可判断D，进而可得正确选项.【详解】对于A：若m//n，n//α，则m//α或m⊂α，故选项A不正确；B C为m，直线BC为对于B：如图平面ADD1A1为平面α，平面A1B1C1D1为平面β，直线11n，满足m//n，m//α，n//β，但α与β相交，故选项B不正确；对于C：如图在正方体ABCD−A1B1C1D1中，平面ADD1A1为平面α，平面A1B1C1D1为平面B C为n，满足α⊥β，m⊂α，n⊂β，则m//n，故选项C不正β，直线AD为m，直线11确；对于D：若m⊥n，m⊥α，可得n⊂α或n//α，若n⊂α，因为n⊥β，由面面垂直的判定定理可得α⊥β；若n//α，可过n作平面与α相交，则交线在平面α内，且交线与n平行，由n⊥β可得交线与β垂直，由面面垂直的判定定理可得α⊥β，故选项D正确；故选：D.9．（2020·山东·高考真题）已知正方体ABCD−A1B1C1D1（如图所示），则下列结论正确的是（）A．BD1//A1A B．BD1//A1D C．BD1⊥A1C D．BD1⊥A1C1【答案】D【分析】根据异面直线的定义，垂直关系的转化，判断选项.【详解】BB与BD1相交，所以BD1与AA1异面，故A错误；A.AA1//BB1，1B.BD1与平面ADD1A1相交，且D1∉A1D，所以BD1与A1D异面，故B错误；C.四边形A BCD是矩形，不是菱形，所以对角线BD1与A1C不垂直，故C错误；11D.连结B1D1，B1D1⊥A1C1，BB1⊥A1C1，B1D1∩BB1=B1，所以A1C1⊥平面BB1D1，所以A1C1⊥BD1，故D正确.故选：D10．（2021·浙江·高考真题）如图已知正方体ABCD−A1B1C1D1，M，N分别是A1D，D1B 的中点，则（）A．直线A1D与直线D1B垂直，直线MN//平面ABCDB．直线A1D与直线D1B平行，直线MN⊥平面BDD1B1C．直线A1D与直线D1B相交，直线MN//平面ABCDD．直线A1D与直线D1B异面，直线MN⊥平面BDD1B1【答案】A【分析】由正方体间的垂直、平行关系，可证MN//AB,A1D⊥平面ABD1，即可得出结论.【详解】连AD1，在正方体ABCD−A1B1C1D1中，M是A1D的中点，所以M为AD1中点，又N是D1B的中点，所以MN//AB，MN⊄平面ABCD,AB⊂平面ABCD，所以MN//平面ABCD.因为AB不垂直BD，所以MN不垂直BD则MN不垂直平面BDD1B1，所以选项B,D不正确；在正方体ABCD−A1B1C1D1中，AD1⊥A1D，AB⊥平面AA1D1D，所以AB⊥A1D，AD1∩AB=A，所以A1D⊥平面ABD1，D1B⊂平面ABD1，所以A1D⊥D1B，且直线A1D,D1B是异面直线，所以选项C错误，选项A正确.故选：A.【点睛】关键点点睛：熟练掌握正方体中的垂直、平行关系是解题的关键，如两条棱平行或垂直，同一个面对角线互相垂直，正方体的对角线与面的对角线是相交但不垂直或异面垂直关系. 11．（2021·全国·高考真题）如图，在正方体中，O为底面的中心，P为所在棱的中点，M，N为正方体的顶点．则满足MN⊥OP的是（）A．B．C．D．【答案】BC【分析】根据线面垂直的判定定理可得BC的正误，平移直线MN构造所考虑的线线角后可判断AD 的正误.【详解】设正方体的棱长为2，对于A，如图（1）所示，连接AC，则MN//AC，故POC（或其补角）为异面直线OP,MN所成的角，在直角三角形OPC，OC=√2，CP=1，故tan∠POC=√2=√22，故MN⊥OP不成立，故A错误.对于B，如图（2）所示，取NT的中点为Q，连接PQ，OQ，则OQ⊥NT，PQ⊥MN，由正方体SBCM−NADT可得SN⊥平面ANDT，而OQ⊂平面ANDT，故SN⊥OQ，而SN∩MN=N，故OQ⊥平面SNTM，又MN⊂平面SNTM，OQ⊥MN，而OQ∩PQ=Q，所以MN⊥平面OPQ，而PO⊂平面OPQ，故MN⊥OP，故B正确.对于C，如图（3），连接BD，则BD//MN，由B的判断可得OP⊥BD，故OP⊥MN，故C正确.对于D，如图（4），取AD的中点Q，AB的中点K，连接AC,PQ,OQ,PK,OK，则AC//MN，PQ MN，因为DP=PC，故PQ//AC，故//所以∠QPO或其补角为异面直线PO,MN所成的角，AC=√2，OQ=√AO2+AQ2=√1+2=√3，因为正方体的棱长为2，故PQ=12PO=√PK2+OK2=√4+1=√5，QO2<PQ2+OP2，故∠QPO不是直角，故PO,MN不垂直，故D错误.故选：BC.12．（2021·全国·高考真题）如下图，在四棱锥S ABCD-中，底面ABCD是正方形，平面SAD⊥平面ABCD，SA=SD=2，3AB=．（1）求SA 与BC 所成角的余弦值； （2）求证：AB ⊥SD ．【答案】（1）34；（2）证明见解析． 【分析】(1)由题意可得∠SAD 即为SA 与 BC 所成的角，根据余弦定理计算即可； (2)结合面面垂直的性质和线面垂直的性质即可证明. 【详解】【考查内容】异面直线所成的角，直线与平面垂直的判定和性质【解】（1）因为AD //BC ，因此∠SAD 即为SA 与BC 所成的角，在△SAD 中，SA =SD =2， 又在正方形ABCD 中3AD AB ==，因此cos ∠SAD =SA 2+AD 2−SD 22SA⋅AD=22+32−222×2×3=34，因此SA 与BC 所成角的余弦值是34．（2）因为平面SAD ⊥平面ABCD ，平面SAD ∩平面ABCD =AD ，在正方形ABCD 中，AB ⊥AD ，因此AB ⊥平面SAD ，又因为SD ⊂平面SAD ，因此AB ⊥SD ． 三、球体-能力拓展13．（2020·天津·高考真题）若棱长为2√3的正方体的顶点都在同一球面上，则该球的表面积为（ ） A ．12π B ．24π C ．36π D ．144π【答案】C 【分析】求出正方体的体对角线的一半，即为球的半径，利用球的表面积公式，即可得解. 【详解】这个球是正方体的外接球，其半径等于正方体的体对角线的一半， 即R =√(2√3)2+(2√3)2+(2√3)22=3，所以，这个球的表面积为S =4πR 2=4π×32=36π. 故选：C. 【点睛】本题考查正方体的外接球的表面积的求法，求出外接球的半径是本题的解题关键，属于基础题.求多面体的外接球的面积和体积问题，常用方法有：（1）三条棱两两互相垂直时，可恢复为长方体，利用长方体的体对角线为外接球的直径，求出球的半径；（2）直棱柱的外接球可利用棱柱的上下底面平行，借助球的对称性，球心为上下底面外接圆的圆心连线的中点，再根据勾股定理求球的半径；（3）如果设计几何体有两个面相交，可过两个面的外心分别作两个面的垂线，垂线的交点为几何体的球心.14．（2021·天津·高考真题）两个圆锥的底面是一个球的同一截面，顶点均在球面上，若球的体积为32π3，两个圆锥的高之比为1:3，则这两个圆锥的体积之和为（）A．3πB．4πC．9πD．12π【答案】B【分析】作出图形，计算球体的半径，可计算得出两圆锥的高，利用三角形相似计算出圆锥的底面圆半径，再利用锥体体积公式可求得结果.【详解】如下图所示，设两个圆锥的底面圆圆心为点D，设圆锥AD和圆锥BD的高之比为3:1，即AD=3BD，设球的半径为R，则4πR33=32π3，可得R=2，所以，AB=AD+BD=4BD=4，所以，BD=1，AD=3，∵CD⊥AB，则∠CAD+∠ACD=∠BCD+∠ACD=90∘，所以，CAD BCD∠=∠，又因为∠ADC=∠BDC，所以，△ACD∽△CBD，所以，AD CDCD BD=，∴CD=√AD⋅BD=√3，因此，这两个圆锥的体积之和为13π×CD2⋅(AD+BD)=13π×3×4=4π.故选：B.15．（2020·全国·高考真题（理））已知△ABC是面积为9√34的等边三角形，且其顶点都在球O的球面上.若球O的表面积为16π，则O到平面ABC的距离为（）A．√3B．32C．1D．√32【答案】C【分析】根据球O的表面积和△ABC的面积可求得球O的半径R和△ABC外接圆半径r，由球的性质可知所求距离d=√R2−r2.【详解】设球O的半径为R，则4πR2=16π，解得：R=2.设△ABC外接圆半径为r，边长为a，∵△ABC是面积为9√34的等边三角形，∴12a2×√32=9√34，解得：a=3，∴r=23×√a2−a24=23×√9−94=√3，∴球心O到平面ABC的距离d=√R2−r2=√4−3=1.故选：C.【点睛】本题考查球的相关问题的求解，涉及到球的表面积公式和三角形面积公式的应用；解题关键是明确球的性质，即球心和三角形外接圆圆心的连线必垂直于三角形所在平面. 16．（2021·全国·高考真题（理））已如A，B，C是半径为1的球O的球面上的三个点，且AC⊥BC,AC=BC=1，则三棱锥O−ABC的体积为（）A．√212B．√312C．√24D．√34【答案】A【分析】由题可得△ABC为等腰直角三角形，得出△ABC外接圆的半径，则可求得O到平面ABC的距离，进而求得体积.【详解】∵AC⊥BC,AC=BC=1，∴△ABC为等腰直角三角形，∴AB=√2，则△ABC外接圆的半径为√22，又球的半径为1，设O到平面ABC的距离为d，则d=所以V O−ABC=13S△ABC⋅d=13×12×1×1×√22=√212.故选：A.【点睛】关键点睛：本题考查球内几何体问题，解题的关键是正确利用截面圆半径、球半径、球心到截面距离的勾股关系求解.17．（2020·全国·高考真题（理））已知,,A B C为球O的球面上的三个点，⊙O1为△ABC的外接圆，若⊙O1的面积为4π，AB=BC=AC=OO1，则球O的表面积为（）A．64πB．48πC．36πD．32π【答案】A【分析】由已知可得等边△ABC的外接圆半径，进而求出其边长，得出OO1的值，根据球的截面性质，求出球的半径，即可得出结论.【详解】设圆O1半径为r，球的半径为R，依题意，得πr2=4π,∴r=2，∵△ABC为等边三角形，由正弦定理可得AB=2r sin60°=2√3，∴OO1=AB=2√3，根据球的截面性质OO1⊥平面ABC，∴OO1⊥O1A,R=OA=√OO12+O1A2=√OO12+r2=4，∴球O的表面积S=4πR2=64π.故选：A【点睛】本题考查球的表面积，应用球的截面性质是解题的关键，考查计算求解能力，属于基础题. 18．（2020·海南·高考真题）已知直四棱柱ABCD–A1B1C1D1的棱长均为2，∠BAD =60°．以D 1为球心，√5为半径的球面与侧面BCC 1B 1的交线长为________． 【答案】√22π.【分析】根据已知条件易得D 1E =√3，D 1E ⊥侧面B 1C 1CB ，可得侧面B 1C 1CB 与球面的交线上的点到E 的距离为√2，可得侧面B 1C 1CB 与球面的交线是扇形EFG 的弧FG ⏜，再根据弧长公式可求得结果. 【详解】 如图：取11B C 的中点为E ，1BB 的中点为F ，1CC 的中点为G ，因为∠BAD =60°，直四棱柱ABCD −A 1B 1C 1D 1的棱长均为2，所以△D 1B 1C 1为等边三角形，所以D 1E =√3，D 1E ⊥B 1C 1，又四棱柱ABCD −A 1B 1C 1D 1为直四棱柱，所以BB 1⊥平面A 1B 1C 1D 1，所以111BB B C ， 因为BB 1∩B 1C 1=B 1，所以D 1E ⊥侧面B 1C 1CB ， 设P 为侧面B 1C 1CB 与球面的交线上的点，则D 1E ⊥EP ，因为球的半径为√5，D 1E =√3，所以|EP|=√|D 1P|2−|D 1E|2=√5−3=√2， 所以侧面B 1C 1CB 与球面的交线上的点到E 的距离为√2，因为|EF|=|EG|=√2，所以侧面B 1C 1CB 与球面的交线是扇形EFG 的弧FG ⏜， 因为∠B 1EF =∠C 1EG =π4，所以∠FEG =π2， 所以根据弧长公式可得FG⏜=π2×√2=√22π. 故答案为：√22π.【点睛】本题考查了直棱柱的结构特征，考查了直线与平面垂直的判定，考查了立体几何中的轨迹问题，考查了扇形中的弧长公式，属于中档题.四、立体几何的数学应用19．（2021·全国·高考真题）北斗三号全球卫星导航系统是我国航天事业的重要成果．在卫星导航系统中，地球静止同步卫星的轨道位于地球赤道所在平面，轨道高度为36000km （轨道高度是指卫星到地球表面的距离）．将地球看作是一个球心为O，半径r为6400km 的球，其上点A的纬度是指OA与赤道平面所成角的度数．地球表面上能直接观测到一颗地球静止同步轨道卫星点的纬度最大值为α，记卫星信号覆盖地球表面的表面积为S=2πr2(1−cosα)（单位：km2），则S占地球表面积的百分比约为（）A．26%B．34%C．42%D．50%【答案】C【分析】由题意结合所给的表面积公式和球的表面积公式整理计算即可求得最终结果.【详解】由题意可得，S占地球表面积的百分比约为：2πr2(1−cosα)4πr2=1−cosα2=1−64006400+360002≈0.42=42%.故选：C.20．（2021·北京·高考真题）某一时间段内，从天空降落到地面上的雨水，未经蒸发、渗漏、流失而在水平面上积聚的深度，称为这个时段的降雨量（单位：mm）．24h降雨量的等级划分如下：在综合实践活动中，某小组自制了一个底面直径为200 mm，高为300 mm的圆锥形雨量器.若一次降雨过程中，该雨量器收集的24h的雨水高度是150 mm（如图所示)，则这24h 降雨量的等级是A．小雨B．中雨C．大雨D．暴雨【答案】B【分析】计算出圆锥体积，除以圆面的面积即可得降雨量，即可得解.【详解】由题意，一个半径为2002=100(mm)的圆面内的降雨充满一个底面半径为2002×150300=50(mm)，高为150(mm)的圆锥，所以积水厚度d=13π×502×150π×1002=12.5(mm)，属于中雨.故选：B.21．（2020·海南·高考真题）日晷是中国古代用来测定时间的仪器，利用与晷面垂直的晷针投射到晷面的影子来测定时间．把地球看成一个球(球心记为O)，地球上一点A的纬度是指OA与地球赤道所在平面所成角，点A处的水平面是指过点A且与OA垂直的平面.在点A处放置一个日晷，若晷面与赤道所在平面平行，点A处的纬度为北纬40°，则晷针与点A处的水平面所成角为（）A．20°B．40°C．50°D．90°【答案】B【分析】画出过球心和晷针所确定的平面截地球和晷面的截面图，根据面面平行的性质定理和线面垂直的定义判定有关截线的关系，根据点A处的纬度，计算出晷针与点A处的水平面所成角.【详解】画出截面图如下图所示，其中CD是赤道所在平面的截线；l是点A处的水平面的截线，依题意可知OA⊥l；AB是晷针所在直线.m是晷面的截线，依题意依题意,晷面和赤道平面平行，晷针与晷面垂直，根据平面平行的性质定理可得可知m//CD、根据线面垂直的定义可得AB⊥m..由于∠AOC=40°,m//CD，所以∠OAG=∠AOC=40°，由于∠OAG+∠GAE=∠BAE+∠GAE=90°，所以∠BAE=∠OAG=40°，也即晷针与点A处的水平面所成角为∠BAE=40°.故选：B【点睛】本小题主要考查中国古代数学文化，考查球体有关计算，涉及平面平行，线面垂直的性质，属于中档题.22．（2020·全国·高考真题（理））埃及胡夫金字塔是古代世界建筑奇迹之一，它的形状可视为一个正四棱锥，以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积，则其侧面三角形底边上的高与底面正方形的边长的比值为（ ）A ．√5−14B C ．√5+14D ．√5+12【答案】C 【分析】设CD =a,PE =b ，利用PO 2=12CD ⋅PE 得到关于a,b 的方程，解方程即可得到答案. 【详解】如图，设CD =a,PE =b ，则PO =√PE 2−OE 2=√b 2−a 42，由题意PO 2=12ab ，即b 2−a 24=12ab ，化简得4(b a )2−2⋅ba −1=0，解得ba=1+√54（负值舍去）.故选：C.【点晴】本题主要考查正四棱锥的概念及其有关计算，考查学生的数学计算能力，是一道容易题. 23．（2020·江苏·高考真题）如图，六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的．已知螺帽的底面正六边形边长为2 cm ，高为2 cm ，内孔半径为0.5 cm ，则此六角螺帽毛坯的体积是____cm.【答案】2π【分析】先求正六棱柱体积，再求圆柱体积，相减得结果. 【详解】正六棱柱体积为6×√34×22×2=12√3圆柱体积为π(12)2⋅2=π2所求几何体体积为2π故答案为： 2π【点睛】本题考查正六棱柱体积、圆柱体积，考查基本分析求解能力，属基础题.五、立体几何与空间向量的综合应用24．（2021·全国·高考真题（理））在正方体ABCD −A 1B 1C 1D 1中，P 为B 1D 1的中点，则直线PB 与AD 1所成的角为（ ） A ．π2 B ．π3 C ．π4 D ．π6【答案】D 【分析】平移直线AD 1至1BC ，将直线PB 与AD 1所成的角转化为PB 与1BC 所成的角，解三角形即可. 【详解】如图，连接BC 1,PC 1,PB ，因为AD 1∥1BC ， 所以∠PBC 1或其补角为直线PB 与AD 1所成的角，因为BB 1⊥平面A 1B 1C 1D 1，所以BB 1⊥PC 1，又PC 1⊥B 1D 1，1111BB B D B ⋂=， 所以PC 1⊥平面PBB 1，所以PC 1⊥PB ，设正方体棱长为2，则BC 1=2√2,PC 1=12D 1B 1=√2， sin ∠PBC 1=PC 1BC 1=12，所以∠PBC 1=π6.故选：D25．（2021·湖南·高考真题）如图，四棱锥P −ABCD 中，底面ABCD 是矩形，PA ⊥平面ABCD ，E 为PD 的中点.（1）证明：PB//平面ACE ；（2）设PA =1，AD =√3，直线PB 与平面ABCD 所成的角为45°，求四棱锥P −ABCD 的体积.【答案】（1）证明见解析；（2）√33.【分析】(1) 连接BD交AC于点O，连接OE，由三角形的中位线定理可知PB//OE，结合线面平行的判定定理可证明PB//平面AEC.(2)由题意可知∠PBA=45∘，再运用锥体体积公式可求得四棱锥的体积.【详解】（1）连接BD交AC于点O，连接OE. 在△PBD中，因为PE=DE,BO=DO，所以PB//OE，因为OE⊂平面ACE，PB⊄平面ACE，则PB//平面AEC.（2）因为PA⊥平面ABCD，所以∠PBA就是直线PB与平面ABCD所成的角，所以∠PBA=45∘，又PA=1，AD=√3，所以PA=1=AB，所以四棱锥P−ABCD的体积V P−ABCD=13×PA×AB×AD=13×1×1×√3=√33，所以四棱锥P−ABCD的体积为√33.26．（2021·全国·高考真题）在四棱锥Q ABCD中，底面ABCD是正方形，若AD=2,QD=QA=√5,QC=3．（1）证明：平面QAD⊥平面ABCD；（2）求二面角B−QD−A的平面角的余弦值．【答案】（1）证明见解析；（2）23.【分析】（1）取AD的中点为O，连接QO,CO，可证QO⊥平面ABCD，从而得到面QAD⊥面ABCD.。

高考数学理数立体几何大题训练(含答案)1.（2020·新课标Ⅲ·理）在长方体中，点P、Q分别在棱AB、CD上，且AP=CQ.（1）证明：点PQ平分长方体的体对角线；（2）若PQ在平面BCFE内，求二面角的正弦值．2.（2020·新课标Ⅱ·理）如图，已知三棱柱ABC-A1B1C1的底面是正三角形，侧面BB1C1C是矩形，M、N分别为BC、B1C1的中点，P为AM上一点，过B1C1和P的平面交AB于E，交AC于F.（1）证明：AA1∥MN，且平面A1AMN⊥EB1C1F；（2）设O为△A1B1C1的中心，若AO∥平面EB1C1F，且AO=AB，求直线B1E与平面A1AMN 所成角的正弦值.3.（2020·新课标Ⅰ·理）如图，D为圆锥的顶点，O是圆锥底面的圆心，底面是内接正三角形ABC，P为上一点，AP为底面直径，DP⊥底面．（1）证明：DP平分∠ADC；（2）求二面角平面APD与平面ABC的余弦值．4.（2020·新高考Ⅰ）如图，四棱锥P-ABCD的底面为正方形，PD⊥底面ABCD．设平面PAD与平面PBC的交线为l．（1）证明：l⊥平面PDC；（2）已知PD=AD=1，Q为l上的点，求PB与平面QCD所成角的正弦值的最大值．5.（2020·天津）如图，在三棱柱ABC-A1B1C1中，点P、Q分别在棱AB、A1B1上，且AP=A1Q，平面PQC1为棱BC1的中垂面，M为棱AC的中点．（Ⅰ）求证：PM∥B1Q，且PM=B1Q；（Ⅱ）求二面角平面PQC1与直线PM所成角的正弦值；（Ⅲ）求直线B1Q与平面PQC1所成角的正弦值．6.（2020·江苏）在三棱锥ABCD中，已知CB=CD=1，AC=2，BD=2，O为BD的中点，AO⊥平面BCD，AO=2，E为AC上一点，DE⊥平面BCD，DE=1.（1）求直线AB与DE所成角的余弦值；（2）若点F在BC上，满足BF=BC，设二面角F-DE-C的大小为θ，求sinθ的值．7.（2020·北京）如图，正方体ABCD-EFGH中，E为AD的中点，P为BF上一点．（Ⅰ）求证：PE∥CG；（Ⅱ）求直线PE与平面CGH所成角的正弦值．8.（2020·浙江）如图，三棱台DEF-ABC中，面ADFC⊥面ABC，∠ACB=∠ACD=45°，XXX．（Ⅰ）证明：EF⊥DB；（Ⅱ）求DF与面DBC所成角的正弦值．9.（2020·扬州模拟）如图，在等边三角形ABC的三棱锥ABCD中，D为底面的中点，E为线段AD上一动点，记DE=λAD.（1）当λ=1时，求证：DE与平面ABC垂直；（2）当λ=2时，求直线BE与平面ACD所成角的正弦值．求证：直线AD与平面BCD垂直；2）若平面ABD与平面ACD所成二面角为，求二面角ABC与平面BCD所成二面角的正弦值。

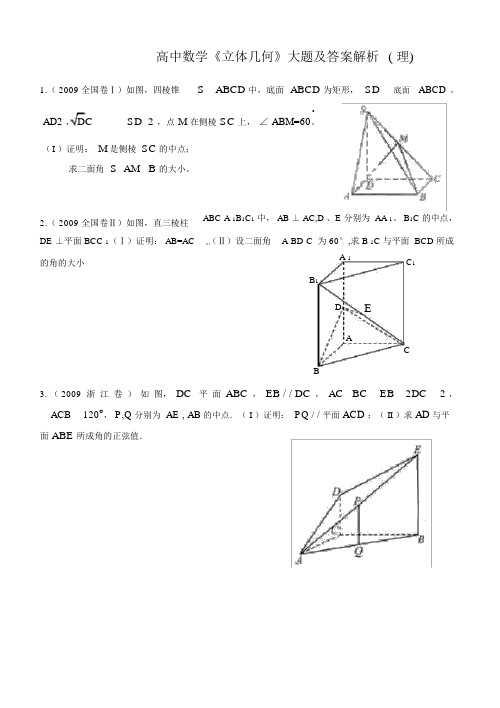
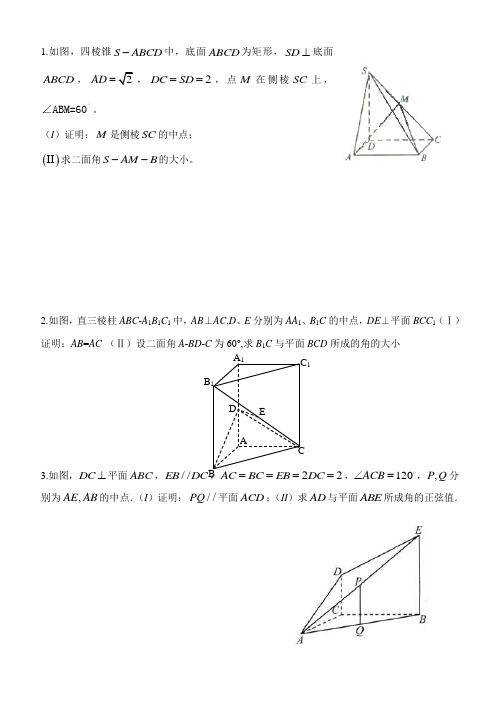
高中数学《立体几何》大题及答案解析( 理)1.（ 2009 全国卷Ⅰ）如图，四棱锥S ABCD 中，底面 ABCD 为矩形， SD底面ABCD，AD2 ，DCo SD 2 ，点 M 在侧棱 SC 上，∠ABM=60。

（I ）证明：M是侧棱SC的中点；求二面角 S AM B 的大小。

2.（ 2009 全国卷Ⅱ）如图，直三棱柱DE ⊥平面 BCC 1（Ⅰ）证明： AB=AC 的角的大小ABC-A 1B1C1中， AB ⊥ AC,D 、E 分别为 AA 1、 B1C 的中点，（Ⅱ）设二面角A-BD-C 为 60°,求 B 1C 与平面 BCD 所成A 1 C1B1D EACB3. （ 2009浙江卷）如图，DC平面ABC，EB / / DC，AC BC EB 2DC 2 ，ACB 120o， P,Q 分别为 AE , AB 的中点．（I）证明： PQ / / 平面ACD；（II）求AD与平面 ABE 所成角的正弦值．4.（ 2009 北京卷）如图，四棱锥P ABCD 的底面是正方形，PD 底面 ABCD ，点E在棱PB上.（Ⅰ）求证：平面AEC 平面 PDB ；（Ⅱ）当 PD2AB 且E为PB的中点时，求 AE 与平面 PDB 所成的角的大小.5.（ 2009 江西卷）如图，在四棱锥P ABCD 中，底面 ABCD 是矩形， PA平面ABCD，PA AD 4 ， AB 2 ．以 BD 的中点 O 为球心、 BD 为直径的球面交PD 于点 M ．（1）求证：平面ABM⊥平面PCD；（2）求直线PC与平面ABM所成的角；（3）求点O到平面ABM的距离．PMA DOBC6（. 2009 四川卷）如图，正方形ABCD所在平面与平面四边形ABEF所在平面互相垂直，△ ABE 是等腰直角三角形，AB AE , FA FE , AEF 45 （I）求证： EF 平面 BCE ；（ II ）设线段 CD 、 AE 的中点分别为 P 、 M ，求证： PM ∥平面BCE （ III ）求二面角 F BD A 的大小。

高三数学立体几何高考题1.（2012年7）如图，网格纸上小正方形的边长为1，粗线画出 的是某几何体的三视图，则此几何体的体积为 （A ）6 （B ）9 （C ）12 （D ）182.（2012年8）平面α截球O 的球面所得圆的半径为1，球心O 到平面α的距离为2，则此球的体积为（A ）6π （B ）43π （C ）46π （D ）63π3.(2013年11)某几何体的三视图如图所示， 则该几何体的体积为( )．A ．16＋8πB ．8＋8πC ．16＋16πD ．8＋16π4.(2013年15)已知H 是球O 的直径AB 上一点，AH ∶HB ＝1∶2，AB ⊥平面α，H 为垂足，α截球O 所得截面的面积为π，则球O 的表面积为______．5.(2014年8)如图，网格纸的各小格都是正方形，粗实线画出的 事一个几何体的三视图，则这个几何体是（ ） A.三棱锥 B.三棱柱 C.四棱锥 D.四棱柱6.(2014年10)正四棱锥的顶点都在同一球面上．若该棱锥的高为4， 底面边长为2，则该球的表面积为( )A.81π4 B ．16π C ．9π D.27π47.(2015年6)《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有委米依垣内角，下周八尺，高五尺，问”积及为米几何？”其意思为：“在屋内墙角处堆放米（如图，米堆为一个圆锥的四分之一），米堆底部的弧长为8尺，米堆的高为5尺，米堆的体积和堆放的米各位多少？”已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放的米有（ ） （A ）14斛 （B ）22斛 （C ）36斛 （D ）66斛8.(2015年11)圆柱被一个平面截去一部分后与半球（半径为r ）组成一个几何体，该几何体的三视图中的正视图和俯视图如图所示，若该几何体的表面积为1620π+，则r =( ) （A ）1 （B ）2 （C ）4 （D ）89（2016年7）如图，某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是28π3，则它的表面积是（A ）17π （B ）18π （C ）20π （D ）28π10（2016年11）平面α过正方体ABCD —A 1B 1C 1D 1的顶点A ，11//CB D α平面,ABCD m α=I 平面，11ABB A n α=I 平面，则m ，n 所成角的正弦值为（A ）32 （B ）22 （C ）33 （D ）1311．(2017年6)如图，在下列四个正方体中，A ，B 为正方体的两个顶点，M ，N ，Q 为所在棱的中点，则在这四个正方体中，直接AB 与平面MNQ 不平行的是12．（2017年16）已知三棱锥S-ABC 的所有顶点都在球O 的球面上，SC 是球O 的直径。

1.在一个几何体的三视图中，正视图和俯视图如右图所示，则相应的俯视图可以为2.已知矩形ABCD的顶点都在半径为4的球O的球面上，且6,==,则棱锥AB BC-的体积为。

O ABCD3.如图，四棱锥P—ABCD中，底面ABCD为平行四边形，∠DAB=60°,AB=2AD,PD⊥底面ABCD.(Ⅰ)证明：PA⊥BD；(Ⅱ)若PD=AD，求二面角A-PB-C的余弦值。

1.D2.3. 解：（Ⅰ）因为60,2DAB AB AD ∠=︒=，由余弦定理得BD =从而BD 2+AD 2= AB 2，故BD ⊥AD 又PD ⊥底面ABCD ，可得BD ⊥PD 所以BD ⊥平面PAD. 故 PA ⊥BD（Ⅱ）如图，以D 为坐标原点，AD 的长为单位长，射线DA 为x 轴的正半轴建立空间直角坐标系D-xyz ，则()1,0,0A，()0B，()C -，()0,0,1P 。

(1),(1,0,0)AB PB BC =-=-=-uu u v uu v uu u v设平面PAB 的法向量为n=（x ，y ，z ），则0,0,{n AB n PB ⋅=⋅=u u u r u u u r00z =-=因此可取n=设平面PBC 的法向量为m ，则m 0,m 0,{PB BC ⋅=⋅=u u u ru u u r可取m=（0，-1， cos ,m n == 故二面角A-PB-C 的余弦值为1. 正方体ABCD-1111A B C D 中，B 1B 与平面AC 1D 所成角的余弦值为C 232. 已知圆O 的半径为1，PA 、PB 为该圆的两条切线，A 、B 为俩切点，那么PA PB ∙的最小值为(A) 4- (B)3-+ (C) 4-+3-+3. 已知在半径为2的球面上有A 、B 、C 、D 四点，若AB=CD=2,则四面体ABCD 的体积的最大值为(C)4. 如图，四棱锥S-ABCD 中，SD ⊥底面ABCD ，AB//DC ，AD ⊥DC ，AB=AD=1，DC=SD=2，E 为棱SB 上的一点，平面EDC ⊥平面SBC .（Ⅰ）证明：SE=2EB ；（Ⅱ）求二面角A-DE-C 的大小 .1. D2. D3. B4. 解法一：(Ⅰ)连接BD,取DC 的中点G ，连接BG,由此知 1,DG GC BG ===即ABC ∆为直角三角形，故BC BD ⊥. 又ABCD,BC SD SD ⊥⊥平面故,所以，BC ⊥⊥平面BDS,BC DE .作BK ⊥EC,EDC SBC K ⊥为垂足，因平面平面，故,BK EDC BK DE DE ⊥⊥平面，与平面SBC 内的两条相交直线BK 、BC 都垂直 DE ⊥平面SBC ，DE ⊥EC,DE ⊥SBSB =SD DB DE SB ==-EB SE SB EB ====所以，SE=2EB(Ⅱ) 由1,2,,SA AB SE EB AB SA ===⊥知1,AD=1AE ==又.故ADE ∆为等腰三角形.取ED 中点F,连接AF ,则,AF DE AF ⊥==. 连接FG ，则//,FG EC FG DE ⊥.所以，AFG ∠是二面角A DE C --的平面角.连接AG,A G=,3FG ==, 2221cos 22AF FG AG AFG AF FG +-∠==-,所以，二面角A DE C --的大小为120°. 解法二：以D 为坐标原点，射线DA 为x 轴的正半轴，建立如图所示的直角坐标系D xyz -， 设A(1,0,0)，则B(1,1,0),C(0,2,0),S(0,0,2)（Ⅰ）(0,2,-2),(-1,1,0)SC BC ==设平面SBC 的法向量为n=(a, b, c) 由,n SC n BC ⊥⊥，得0,0n SC n BC == 故2b-2c=0,-a+b=0令a=1，则b=c,c=1,n=(1,1,1) 又设SE EB λ= (0)λ>，则2(,,)111E λλλλλ+++ 2(,,),(0,2,0)111DE DC λλλλλ==+++设平面CDE 的法向量m=(x,y,z) 由,m DE m DC ⊥⊥,得0m DE ⊥=，0m DC ⊥= 故20,20111x y zy λλλλλ++==+++. 令2x =，则(2,0,)m λ=-.由平面DEC ⊥平面SBC 得m ⊥n,0,20,2m n λλ=-== 故SE=2EB（Ⅱ）由（Ⅰ）知222(,,)333E ，取DE 的中点F ，则111211(,,),(,,)333333F FA =--，故0FA DE =，由此得FA DE ⊥ 又242(,,)333EC =--，故0EC DE =，由此得EC DE ⊥， 向量FA 与EC 的夹角等于二面角A DE C --的平面角 于是 1cos(,)2||||FA EC FA EC FA EC ==-所以，二面角A DE C --的大小为120（三）1. 已知三棱柱111ABC A B C -的侧棱与底面边长都相等，1A 在底面ABC 上的射影为BC 的中点，则异面直线AB 与1CC 所成的角的余弦值为（ ）（A （B （C (D) 342. 已知二面角l αβ--为60o，动点P 、Q 分别在面α、β内，P 到β，Q 到α的距离为则P 、Q 两点之间距离的最小值为（ ）(A) (B)2 (C) 3. 直三棱柱111ABC A B C -的各顶点都在同一球面上，若12AB AC AA ===, 120BAC ∠=︒，则此球的表面积等于 。

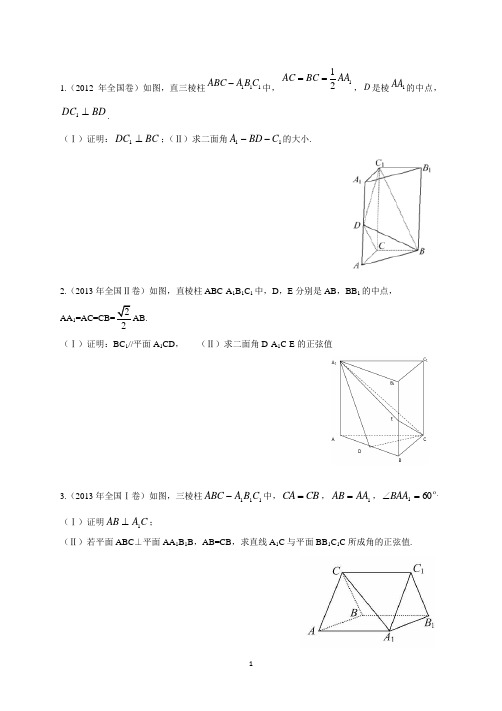
1 1.（2012年全国卷）如图，直三棱柱111ABC A B C -中，112AC BC AA ==，D 是棱1AA 的中点，BD DC ⊥1.（Ⅰ）证明：BC DC ⊥1；（Ⅱ）求二面角11C BD A --的大小.2.（2013年全国Ⅱ卷）如图，直棱柱ABC-A 1B 1C 1中，D ，E 分别是AB ，BB 1的中点，AA 1AB. （Ⅰ）证明：BC 1//平面A 1CD ， （Ⅱ）求二面角D-A 1C-E 的正弦值3.（2013年全国Ⅰ卷）如图，三棱柱111C B A ABC -中，CB CA =，1AA AB =， 601=∠BAA . （Ⅰ）证明C A AB 1⊥；（Ⅱ）若平面ABC ⊥平面AA 1B 1B ，AB=CB ，求直线A 1C 与平面BB 1C 1C 所成角的正弦值.24.（2014年全国Ⅱ卷）如图，四棱锥P-ABCD 中，底面ABCD 为矩形，PA ⊥平面ABCD ，E 为PD 的中点.(Ⅰ)证明:PB ∥平面AEC ；(Ⅱ)设二面角D-AE-C 为60°，AP=1，求三棱锥E-ACD 的体积.5.（2015年全国Ⅱ卷）如图，长方体ABCD-A 1B 1C 1D 1中，AB=16，BC=10，AA 1=8，点E ，F 分别在A 1B 1，D 1C 1上，A 1E=D 1F=4，过点E ，F 的平面α与此长方体的面相交，交线围成一个正方形. (Ⅰ)在图中画出这个正方形(不必说出画法和理由)；(Ⅱ)求直线AF 与平面α所成角的正弦值.6.（2016年全国Ⅱ卷）如图，菱形ABCD 的对角线AC 与BD 交于点O ，5,6AB AC ==，点,E F 分别在,AD CD 上，54AE CF ==，EF 交BD 于点H ．将DEF ∆沿EF 折到'D EF ∆位置，OD '=（Ⅰ）证明：D H '⊥平面ABCD ； （Ⅱ）求二面角B D A C '--的正弦值．。

高考数学-立体几何（含22年真题讲解）1．【2022年全国甲卷】如图，网格纸上绘制的是一个多面体的三视图，网格小正方形的边长为1，则该多面体的体积为（）A．8B．12C．16D．20【答案】B【解析】【分析】由三视图还原几何体，再由棱柱的体积公式即可得解.【详解】由三视图还原几何体，如图，×2×2=12.则该直四棱柱的体积V=2+42故选：B.2．【2022年全国甲卷】在长方体ABCD−A1B1C1D1中，已知B1D与平面ABCD和平面AA1B1B 所成的角均为30°，则（）A．AB=2AD B．AB与平面AB1C1D所成的角为30°C．AC=CB1D．B1D与平面BB1C1C所成的角为45°【解析】 【分析】根据线面角的定义以及长方体的结构特征即可求出． 【详解】 如图所示：不妨设AB =a,AD =b,AA 1=c ，依题以及长方体的结构特征可知，B 1D 与平面ABCD 所成角为∠B 1DB ，B 1D 与平面AA 1B 1B 所成角为∠DB 1A ，所以sin30∘=cB 1D=bB 1D ，即b =c ，B 1D =2c =√a 2+b 2+c 2，解得a =√2c ．对于A ，AB =a ，AD =b ，AB =√2AD ，A 错误；对于B ，过B 作BE ⊥AB 1于E ，易知BE ⊥平面AB 1C 1D ，所以AB 与平面AB 1C 1D 所成角为∠BAE ，因为tan∠BAE =c a=√22，所以∠BAE ≠30∘，B 错误；对于C ，AC =√a 2+b 2=√3c ，CB 1=√b 2+c 2=√2c ，AC ≠CB 1，C 错误； 对于D ，B 1D 与平面BB 1C 1C 所成角为∠DB 1C ，sin∠DB 1C =CDB 1D=a2c =√22，而0<∠DB 1C <90∘，所以∠DB 1C =45∘．D 正确． 故选：D ．3．【2022年全国甲卷】甲、乙两个圆锥的母线长相等，侧面展开图的圆心角之和为2π，侧面积分别为S 甲和S 乙，体积分别为V 甲和V 乙．若S 甲S 乙=2，则V 甲V 乙=（ ）A ．√5B ．2√2C ．√10D ．5√104【答案】C 【解析】设母线长为l ，甲圆锥底面半径为r 1，乙圆锥底面圆半径为r 2，根据圆锥的侧面积公式可得r 1=2r 2，再结合圆心角之和可将r 1,r 2分别用l 表示，再利用勾股定理分别求出两圆锥的高，再根据圆锥的体积公式即可得解. 【详解】解：设母线长为l ，甲圆锥底面半径为r 1，乙圆锥底面圆半径为r 2，则S 甲S 乙=πr 1l πr 2l =r1r 2=2， 所以r 1=2r 2， 又2πr 1l+2πr 2l=2π，则r 1+r 2l=1，所以r 1=23l,r 2=13l ，所以甲圆锥的高ℎ1=√l 2−49l 2=√53l ，乙圆锥的高ℎ2=√l 2−19l 2=2√23l ， 所以V 甲V 乙=13πr 12ℎ113πr 22ℎ2=49l 2×√53l 19l ×2√23l =√10.故选：C.4．【2022年全国乙卷】在正方体ABCD −A 1B 1C 1D 1中，E ，F 分别为AB,BC 的中点，则（ ） A ．平面B 1EF ⊥平面BDD 1 B ．平面B 1EF ⊥平面A 1BD C ．平面B 1EF//平面A 1AC D ．平面B 1EF//平面A 1C 1D【答案】A 【解析】 【分析】证明EF ⊥平面BDD 1，即可判断A ；如图，以点D 为原点，建立空间直角坐标系，设AB =2，分别求出平面B 1EF ，A 1BD ，A 1C 1D 的法向量，根据法向量的位置关系，即可判断BCD . 【详解】解：在正方体ABCD −A 1B 1C 1D 1中， AC ⊥BD 且DD 1⊥平面ABCD ， 又EF ⊂平面ABCD ，所以EF ⊥DD 1，因为E,F 分别为AB,BC 的中点， 所以EF ∥AC ，所以EF ⊥BD ， 又BD ∩DD 1=D ， 所以EF ⊥平面BDD 1， 又EF ⊂平面B 1EF ，所以平面B 1EF ⊥平面BDD 1，故A 正确；如图，以点D 为原点，建立空间直角坐标系，设AB =2，则B 1(2,2,2),E (2,1,0),F (1,2,0),B (2,2,0),A 1(2,0,2),A (2,0,0),C (0,2,0)， C 1(0,2,2)，则EF ⃑⃑⃑⃑⃑ =(−1,1,0),EB 1⃑⃑⃑⃑⃑⃑⃑ =(0,1,2)，DB ⃑⃑⃑⃑⃑⃑ =(2,2,0),DA 1⃑⃑⃑⃑⃑⃑⃑⃑ =(2,0,2)，AA 1⃑⃑⃑⃑⃑⃑⃑ =(0,0,2),AC ⃑⃑⃑⃑⃑ =(−2,2,0),A 1C 1⃑⃑⃑⃑⃑⃑⃑⃑⃑ =(−2,2,0),设平面B 1EF 的法向量为m ⃑⃑ =(x 1,y 1,z 1)， 则有{m ⃑⃑ ⋅EF ⃑⃑⃑⃑⃑ =−x 1+y 1=0m ⃑⃑ ⋅EB 1⃑⃑⃑⃑⃑⃑⃑ =y 1+2z 1=0 ，可取m ⃑⃑ =(2,2,−1)，同理可得平面A 1BD 的法向量为n 1⃑⃑⃑⃑ =(1,−1,−1)， 平面A 1AC 的法向量为n 2⃑⃑⃑⃑ =(1,1,0)， 平面A 1C 1D 的法向量为n 3⃑⃑⃑⃑ =(1,1,−1)， 则m ⃑⃑ ⋅n 1⃑⃑⃑⃑ =2−2+1=1≠0，所以平面B 1EF 与平面A 1BD 不垂直，故B 错误； 因为m ⃑⃑ 与n 2⃑⃑⃑⃑ 不平行，所以平面B 1EF 与平面A 1AC 不平行，故C 错误； 因为m ⃑⃑ 与n 3⃑⃑⃑⃑ 不平行，所以平面B 1EF 与平面A 1C 1D 不平行，故D 错误， 故选：A.5．【2022年全国乙卷】已知球O的半径为1，四棱锥的顶点为O，底面的四个顶点均在球O 的球面上，则当该四棱锥的体积最大时，其高为（）A．13B．12C．√33D．√22【答案】C【解析】【分析】先证明当四棱锥的顶点O到底面ABCD所在小圆距离一定时，底面ABCD面积最大值为2r2，进而得到四棱锥体积表达式，再利用均值定理去求四棱锥体积的最大值，从而得到当该四棱锥的体积最大时其高的值.【详解】设该四棱锥底面为四边形ABCD，四边形ABCD所在小圆半径为r，设四边形ABCD对角线夹角为α，则S ABCD=12⋅AC⋅BD⋅sinα≤12⋅AC⋅BD≤12⋅2r⋅2r=2r2（当且仅当四边形ABCD为正方形时等号成立）即当四棱锥的顶点O到底面ABCD所在小圆距离一定时，底面ABCD面积最大值为2r2又r2+ℎ2=1则VO−ABCD =13⋅2r2⋅ℎ=√23√r2⋅r2⋅2ℎ2≤√23√(r2+r2+2ℎ23)3=4√327当且仅当r2=2ℎ2即ℎ=√33时等号成立，故选：C6．【2022年新高考1卷】南水北调工程缓解了北方一些地区水资源短缺问题，其中一部分水蓄入某水库.已知该水库水位为海拔148．5m 时，相应水面的面积为140．0km 2；水位为海拔157．5m 时，相应水面的面积为180．0km 2，将该水库在这两个水位间的形状看作一个棱台，则该水库水位从海拔148．5m 上升到157．5m 时，增加的水量约为（√7≈2.65）（ ） A ．1.0×109m 3 B ．1.2×109m 3 C ．1.4×109m 3 D ．1.6×109m 3【答案】C 【解析】 【分析】根据题意只要求出棱台的高，即可利用棱台的体积公式求出． 【详解】依题意可知棱台的高为MN =157.5−148.5=9(m)，所以增加的水量即为棱台的体积V ． 棱台上底面积S =140.0km 2=140×106m 2，下底面积S ′=180.0km 2=180×106m 2， ∴V =13ℎ(S +S ′+√SS ′)=13×9×(140×106+180×106+√140×180×1012) =3×(320+60√7)×106≈(96+18×2.65)×107=1.437×109≈1.4×109(m 3)．故选：C ．7．【2022年新高考1卷】已知正四棱锥的侧棱长为l ，其各顶点都在同一球面上.若该球的体积为36π，且3≤l ≤3√3，则该正四棱锥体积的取值范围是（ ） A ．[18,814]B ．[274,814]C ．[274,643]D ．[18,27]【答案】C 【解析】 【分析】设正四棱锥的高为ℎ，由球的截面性质列方程求出正四棱锥的底面边长与高的关系，由此确定正四棱锥体积的取值范围. 【详解】∵ 球的体积为36π，所以球的半径R =3, 设正四棱锥的底面边长为2a ，高为ℎ， 则l 2=2a 2+ℎ2，32=2a 2+(3−ℎ)2, 所以6ℎ=l 2，2a 2=l 2−ℎ2所以正四棱锥的体积V =13Sℎ=13×4a 2×ℎ=23×(l 2−l 436)×l 26=19(l 4−l 636)， 所以V ′=19(4l 3−l 56)=19l 3(24−l 26)，当3≤l ≤2√6时，V ′>0，当2√6<l ≤3√3时，V ′<0， 所以当l =2√6时，正四棱锥的体积V 取最大值，最大值为643， 又l =3时，V =274，l =3√3时，V =814,所以正四棱锥的体积V 的最小值为274， 所以该正四棱锥体积的取值范围是[274，643]. 故选：C.8．【2022年新高考2卷】已知正三棱台的高为1，上、下底面边长分别为3√3和4√3，其顶点都在同一球面上，则该球的表面积为（ ） A ．100π B ．128π C ．144π D ．192π【答案】A 【解析】 【分析】根据题意可求出正三棱台上下底面所在圆面的半径r 1,r 2，再根据球心距，圆面半径，以及球的半径之间的关系，即可解出球的半径，从而得出球的表面积． 【详解】设正三棱台上下底面所在圆面的半径r 1,r 2，所以2r 1=3√3sin60∘,2r 2=4√3sin60∘，即r 1=3,r 2=4，设球心到上下底面的距离分别为d 1,d 2，球的半径为R ，所以d 1=√R 2−9，d 2=√R 2−16，故|d 1−d 2|=1或d 1+d 2=1，即|√R 2−9−√R 2−16|=1或√R 2−9+√R 2−16=1，解得R2=25符合题意，所以球的表面积为S=4πR2=100π．故选：A．9．【2022年北京】已知正三棱锥P−ABC的六条棱长均为6，S是△ABC及其内部的点构成的集合．设集合T={Q∈S|PQ≤5}，则T表示的区域的面积为（）A．3π4B．πC．2πD．3π【答案】B【解析】【分析】求出以P为球心，5为半径的球与底面ABC的截面圆的半径后可求区域的面积.【详解】设顶点P在底面上的投影为O，连接BO，则O为三角形ABC的中心，且BO=23×6×√32=2√3，故PO=√36−12=2√6.因为PQ=5，故OQ=1，故S的轨迹为以O为圆心，1为半径的圆，而三角形ABC内切圆的圆心为O，半径为2×√34×363×6=√3>1，故S的轨迹圆在三角形ABC内部，故其面积为π故选：B10．【2022年浙江】某几何体的三视图如图所示（单位：cm），则该几何体的体积（单位：cm3）是（）A．22πB．8πC．223πD．163π【答案】C【解析】【分析】根据三视图还原几何体可知，原几何体是一个半球，一个圆柱，一个圆台组合成的几何体，即可根据球，圆柱，圆台的体积公式求出．【详解】由三视图可知，该几何体是一个半球，一个圆柱，一个圆台组合成的几何体，球的半径，圆柱的底面半径，圆台的上底面半径都为1cm，圆台的下底面半径为2cm，所以该几何体的体积V=12×43π×13+π×12×2+13×2×(π×22+π×12+√π×22×π×12)=22π3cm3．故选：C．11．【2022年浙江】如图，已知正三棱柱ABC−A1B1C1,AC=AA1，E，F分别是棱BC,A1C1上的点．记EF与AA1所成的角为α，EF与平面ABC所成的角为β，二面角F−BC−A的平面角为γ，则（）A．α≤β≤γB．β≤α≤γC．β≤γ≤αD．α≤γ≤β【答案】A【解析】【分析】先用几何法表示出α，β，γ，再根据边长关系即可比较大小．【详解】如图所示，过点F作FP⊥AC于P，过P作PM⊥BC于M，连接PE，则α=∠EFP，β=∠FEP，γ=FMP，tanα=PEFP =PEAB≤1，tanβ=FPPE=ABPE≥1，tanγ=FPPM≥FPPE=tanβ，所以α≤β≤γ，故选：A．12．【2022年新高考1卷】（多选）已知正方体ABCD−A1B1C1D1，则（）A．直线BC1与DA1所成的角为90°B．直线BC1与CA1所成的角为90°C．直线BC1与平面BB1D1D所成的角为45°D．直线BC1与平面ABCD所成的角为45°【答案】ABD【解析】【分析】数形结合，依次对所给选项进行判断即可. 【详解】如图，连接B 1C 、BC 1，因为DA 1//B 1C ，所以直线BC 1与B 1C 所成的角即为直线BC 1与DA 1所成的角，因为四边形BB 1C 1C 为正方形，则B 1C ⊥ BC 1，故直线BC 1与DA 1所成的角为90°，A 正确；连接A 1C ，因为A 1B 1⊥平面BB 1C 1C ，BC 1⊂平面BB 1C 1C ，则A 1B 1⊥BC 1， 因为B 1C ⊥ BC 1，A 1B 1∩B 1C =B 1，所以BC 1⊥平面A 1B 1C ， 又A 1C ⊂平面A 1B 1C ，所以BC 1⊥CA 1，故B 正确； 连接A 1C 1，设A 1C 1∩B 1D 1=O ，连接BO ，因为BB 1⊥平面A 1B 1C 1D 1，C 1O ⊂平面A 1B 1C 1D 1，则C 1O ⊥B 1B ， 因为C 1O ⊥B 1D 1，B 1D 1∩B 1B =B 1，所以C 1O ⊥平面BB 1D 1D ， 所以∠C 1BO 为直线BC 1与平面BB 1D 1D 所成的角，设正方体棱长为1，则C 1O =√22，BC 1=√2，sin∠C 1BO =C 1O BC 1=12，所以，直线BC 1与平面BB 1D 1D 所成的角为30∘，故C 错误；因为C 1C ⊥平面ABCD ，所以∠C 1BC 为直线BC 1与平面ABCD 所成的角，易得∠C 1BC =45∘，故D 正确. 故选：ABD13．【2022年新高考2卷】（多选）如图，四边形ABCD 为正方形，ED ⊥平面ABCD ，FB ∥ED,AB =ED =2FB ，记三棱锥E −ACD ，F −ABC ，F −ACE 的体积分别为V 1,V 2,V 3，则（ ）A．V3=2V2B．V3=V1C．V3=V1+V2D．2V3=3V1【答案】CD【解析】【分析】直接由体积公式计算V1,V2，连接BD交AC于点M，连接EM,FM，由V3=V A−EFM+V C−EFM计算出V3，依次判断选项即可.【详解】设AB=ED=2FB=2a，因为ED⊥平面ABCD，FB∥ED，则V1=13⋅ED⋅S△ACD=13⋅2a⋅12⋅(2a)2=43a3，V2=13⋅FB⋅S△ABC=13⋅a⋅12⋅(2a)2=23a3，连接BD交AC于点M，连接EM,FM，易得BD⊥AC，又ED⊥平面ABCD，AC⊂平面ABCD，则ED⊥AC，又ED∩BD=D，ED,BD⊂平面BDEF，则AC⊥平面BDEF，又BM=DM=12BD=√2a，过F作FG⊥DE于G，易得四边形BDGF为矩形，则FG=BD=2√2a,EG=a，则EM=√(2a)2+(√2a)2=√6a,FM=√a2+(√2a)2=√3a，EF=√a2+(2√2a)2=3a，EM2+FM2=EF2，则EM⊥FM，S△EFM=12EM⋅FM=3√22a2，AC=2√2a，则V3=V A−EFM+V C−EFM=13AC⋅S△EFM=2a3，则2V3=3V1，V3=3V2，V3=V1+V2，故A、B错误；C、D正确.故选：CD.14．【2022年全国甲卷】小明同学参加综合实践活动，设计了一个封闭的包装盒，包装盒如图所示：底面ABCD是边长为8（单位：cm）的正方形，△EAB,△FBC,△GCD,△HDA均为正三角形，且它们所在的平面都与平面ABCD垂直．(1)证明：EF//平面ABCD；(2)求该包装盒的容积（不计包装盒材料的厚度）．【答案】(1)证明见解析；(2)6403√3．【解析】【分析】（1）分别取AB,BC的中点M,N，连接MN，由平面知识可知EM⊥AB,FN⊥BC，EM=FN，依题从而可证EM⊥平面ABCD，FN⊥平面ABCD，根据线面垂直的性质定理可知EM//FN，即可知四边形EMNF为平行四边形，于是EF//MN，最后根据线面平行的判定定理即可证出；（2）再分别取AD,DC中点K,L，由（1）知，该几何体的体积等于长方体KMNL−EFGH的体积加上四棱锥B−MNFE体积的4倍，即可解出．(1)如图所示：，分别取AB,BC 的中点M,N ，连接MN ，因为△EAB,△FBC 为全等的正三角形，所以EM ⊥AB,FN ⊥BC ，EM =FN ，又平面EAB ⊥平面ABCD ，平面EAB ∩平面ABCD =AB ，EM ⊂平面EAB ，所以EM ⊥平面ABCD ，同理可得FN ⊥平面ABCD ，根据线面垂直的性质定理可知EM//FN ，而EM =FN ，所以四边形EMNF 为平行四边形，所以EF//MN ，又EF ⊄平面ABCD ，MN ⊂平面ABCD ，所以EF//平面ABCD ． (2)如图所示：，分别取AD,DC 中点K,L ，由（1）知，EF//MN 且EF =MN ，同理有，HE//KM,HE =KM ，HG//KL,HG =KL ，GF//LN,GF =LN ，由平面知识可知，BD ⊥MN ，MN ⊥MK ，KM =MN =NL =LK ，所以该几何体的体积等于长方体KMNL −EFGH 的体积加上四棱锥B −MNFE 体积的4倍．因为MN =NL =LK =KM =4√2，EM =8sin60∘=4√3，点B 到平面MNFE 的距离即为点B 到直线MN 的距离d ，d =2√2，所以该几何体的体积V =(4√2)2×4√3+4×13×4√2×4√3×2√2=128√3+2563√3=6403√3．15．【2022年全国甲卷】在四棱锥P−ABCD中，PD⊥底面ABCD,CD∥AB,AD=DC=CB=1 ,AB=2,DP=√3．(1)证明：BD⊥PA；(2)求PD与平面PAB所成的角的正弦值．【答案】(1)证明见解析；(2)√55.【解析】【分析】（1）作DE⊥AB于E，CF⊥AB于F，利用勾股定理证明AD⊥BD，根据线面垂直的性质可得PD⊥BD，从而可得BD⊥平面PAD，再根据线面垂直的性质即可得证；（2）以点D为原点建立空间直角坐标系，利用向量法即可得出答案.(1)证明：在四边形ABCD中，作DE⊥AB于E，CF⊥AB于F，因为CD//AB,AD=CD=CB=1,AB=2，所以四边形ABCD为等腰梯形，所以AE=BF=12，故DE=√32，BD=√DE2+BE2=√3，所以AD2+BD2=AB2，所以AD⊥BD，因为PD⊥平面ABCD，BD⊂平面ABCD，所以PD⊥BD，又PD∩AD=D，所以BD ⊥平面PAD ， 又因PA ⊂平面PAD ， 所以BD ⊥PA ；(2)解：如图，以点D 为原点建立空间直角坐标系， BD =√3，则A(1,0,0),B(0,√3,0),P(0,0,√3)，则AP⃑⃑⃑⃑⃑ =(−1,0,√3),BP ⃑⃑⃑⃑⃑ =(0,−√3,√3),DP ⃑⃑⃑⃑⃑ =(0,0,√3)， 设平面PAB 的法向量n⃑ =(x,y,z)， 则有{n →⋅AP →=−x +√3z =0n →⋅BP →=−√3y +√3z =0，可取n ⃑ =(√3,1,1)， 则cos〈n ⃑ ,DP ⃑⃑⃑⃑⃑ 〉=n ⃑ ⋅DP ⃑⃑⃑⃑⃑⃑|n ⃑ ||DP ⃑⃑⃑⃑⃑⃑ |=√55， 所以PD 与平面PAB 所成角的正弦值为√55.16．【2022年全国乙卷】如图，四面体ABCD 中，AD ⊥CD,AD =CD,∠ADB =∠BDC ，E 为AC 的中点．(1)证明：平面BED⊥平面ACD；(2)设AB=BD=2,∠ACB=60°，点F在BD上，当△AFC的面积最小时，求三棱锥F−ABC 的体积．【答案】(1)证明详见解析(2)√34【解析】【分析】（1）通过证明AC⊥平面BED来证得平面BED⊥平面ACD.（2）首先判断出三角形AFC的面积最小时F点的位置，然后求得F到平面ABC的距离，从而求得三棱锥F−ABC的体积.(1)由于AD=CD，E是AC的中点，所以AC⊥DE.由于{AD=CDBD=BD∠ADB=∠CDB，所以△ADB≅△CDB，所以AB=CB，故AC⊥BD，由于DE∩BD=D，DE,BD⊂平面BED，所以AC⊥平面BED，由于AC⊂平面ACD，所以平面BED⊥平面ACD.(2)依题意AB=BD=BC=2，∠ACB=60°，三角形ABC是等边三角形，所以AC=2,AE=CE=1,BE=√3，由于AD=CD,AD⊥CD，所以三角形ACD是等腰直角三角形，所以DE=1. DE2+BE2=BD2，所以DE⊥BE，由于AC∩BE=E，AC,BE⊂平面ABC，所以DE⊥平面ABC.由于△ADB ≅△CDB ，所以∠FBA =∠FBC ， 由于{BF =BF∠FBA =∠FBC AB =CB ，所以△FBA ≅△FBC ，所以AF =CF ，所以EF ⊥AC ，由于S △AFC =12⋅AC ⋅EF ，所以当EF 最短时，三角形AFC 的面积最小值. 过E 作EF ⊥BD ，垂足为F ，在Rt △BED 中，12⋅BE ⋅DE =12⋅BD ⋅EF ，解得EF =√32，所以DF =√12−(√32)2=12,BF =2−DF =32，所以BF BD =34.过F 作FH ⊥BE ，垂足为H ，则FH //DE ，所以FH ⊥平面ABC ，且FHDE =BFBD =34， 所以FH =34,所以V F−ABC =13⋅S △ABC ⋅FH =13×12×2×√3×34=√34.17．【2022年全国乙卷】如图，四面体ABCD 中，AD ⊥CD,AD =CD,∠ADB =∠BDC ，E 为AC 的中点．(1)证明：平面BED ⊥平面ACD ；(2)设AB =BD =2,∠ACB =60°，点F 在BD 上，当△AFC 的面积最小时，求CF 与平面ABD 所成的角的正弦值．【答案】(1)证明过程见解析(2)CF 与平面ABD 所成的角的正弦值为4√37【解析】 【分析】（1）根据已知关系证明△ABD ≌△CBD ，得到AB =CB ，结合等腰三角形三线合一得到垂直关系，结合面面垂直的判定定理即可证明；（2）根据勾股定理逆用得到BE ⊥DE ，从而建立空间直角坐标系，结合线面角的运算法则进行计算即可. (1)因为AD =CD ，E 为AC 的中点，所以AC ⊥DE ；在△ABD 和△CBD 中，因为AD =CD,∠ADB =∠CDB,DB =DB ，所以△ABD ≌△CBD ，所以AB =CB ，又因为E 为AC 的中点，所以AC ⊥BE ； 又因为DE,BE ⊂平面BED ，DE ∩BE =E ，所以AC ⊥平面BED ， 因为AC ⊂平面ACD ，所以平面BED ⊥平面ACD . (2)连接EF ，由（1）知，AC ⊥平面BED ，因为EF ⊂平面BED ， 所以AC ⊥EF ，所以S △AFC =12AC ⋅EF ， 当EF ⊥BD 时，EF 最小，即△AFC 的面积最小. 因为△ABD ≌△CBD ，所以CB =AB =2， 又因为∠ACB =60°，所以△ABC 是等边三角形， 因为E 为AC 的中点，所以AE =EC =1，BE =√3， 因为AD ⊥CD ，所以DE =12AC =1,在△DEB 中，DE 2+BE 2=BD 2，所以BE ⊥DE .以E 为坐标原点建立如图所示的空间直角坐标系E −xyz ，则A (1,0,0),B(0,√3,0),D (0,0,1)，所以AD ⃑⃑⃑⃑⃑ =(−1,0,1),AB ⃑⃑⃑⃑⃑ =(−1,√3,0)， 设平面ABD 的一个法向量为n⃑ =(x,y,z )， 则{n ⃑ ⋅AD ⃑⃑⃑⃑⃑ =−x +z =0n ⃑ ⋅AB⃑⃑⃑⃑⃑ =−x +√3y =0，取y =√3，则n ⃑ =(3,√3,3)，又因为C (−1,0,0),F (0,√34,34)，所以CF⃑⃑⃑⃑⃑ =(1,√34,34)， 所以cos⟨n ⃑ ,CF ⃑⃑⃑⃑⃑ ⟩=n ⃑ ⋅CF⃑⃑⃑⃑⃑|n ⃑ ||CF⃑⃑⃑⃑⃑ |=√21×√74=4√37，设CF 与平面ABD 所成的角的正弦值为θ(0≤θ≤π2)， 所以sinθ=|cos⟨n ⃑ ,CF⃑⃑⃑⃑⃑ ⟩|=4√37， 所以CF 与平面ABD 所成的角的正弦值为4√37.18．【2022年新高考1卷】如图，直三棱柱ABC −A 1B 1C 1的体积为4，△A 1BC 的面积为2√2．(1)求A 到平面A 1BC 的距离；(2)设D 为A 1C 的中点，AA 1=AB ，平面A 1BC ⊥平面ABB 1A 1，求二面角A −BD −C 的正弦值． 【答案】(1)√2 (2)√32【解析】 【分析】（1）由等体积法运算即可得解；（2）由面面垂直的性质及判定可得BC ⊥平面ABB 1A 1，建立空间直角坐标系，利用空间向量法即可得解. (1)在直三棱柱ABC −A 1B 1C 1中，设点A 到平面A 1BC 的距离为h ， 则V A−A 1BC =13S △A 1BC ⋅ℎ=2√23ℎ=V A 1−ABC =13S △ABC ⋅A 1A =13V ABC−A 1B 1C 1=43，解得ℎ=√2，所以点A 到平面A 1BC 的距离为√2； (2)取A 1B 的中点E ,连接AE ,如图，因为AA 1=AB ，所以AE ⊥A 1B , 又平面A 1BC ⊥平面ABB 1A 1，平面A 1BC ∩平面ABB 1A 1=A 1B ， 且AE ⊂平面ABB 1A 1，所以AE ⊥平面A 1BC ， 在直三棱柱ABC −A 1B 1C 1中，BB 1⊥平面ABC ，由BC ⊂平面A 1BC ，BC ⊂平面ABC 可得AE ⊥BC ，BB 1⊥BC ， 又AE,BB 1⊂平面ABB 1A 1且相交，所以BC ⊥平面ABB 1A 1，所以BC,BA,BB 1两两垂直，以B 为原点，建立空间直角坐标系，如图，由（1）得AE =√2，所以AA 1=AB =2，A 1B =2√2，所以BC =2， 则A(0,2,0),A 1(0,2,2),B(0,0,0),C(2,0,0),所以A 1C 的中点D(1,1,1)， 则BD⃑⃑⃑⃑⃑⃑ =(1,1,1)，BA ⃑⃑⃑⃑⃑ =(0,2,0),BC ⃑⃑⃑⃑⃑ =(2,0,0), 设平面ABD 的一个法向量m ⃑⃑ =(x,y,z)，则{m ⃑⃑ ⋅BD ⃑⃑⃑⃑⃑⃑ =x +y +z =0m ⃑⃑ ⋅BA ⃑⃑⃑⃑⃑ =2y =0，可取m⃑⃑ =(1,0,−1)，设平面BDC 的一个法向量n ⃑ =(a,b,c)，则{m ⃑⃑ ⋅BD ⃑⃑⃑⃑⃑⃑ =a +b +c =0m ⃑⃑ ⋅BC ⃑⃑⃑⃑⃑ =2a =0， 可取n⃑ =(0,1,−1)， 则cos〈m ⃑⃑ ,n ⃑ 〉=m⃑⃑⃑ ⋅n ⃑ |m ⃑⃑⃑ |⋅|n ⃑ |=√2×√2=12， 所以二面角A −BD −C 的正弦值为√1−(12)2=√32.19．【2022年新高考2卷】如图，PO 是三棱锥P −ABC 的高，PA =PB ，AB ⊥AC ，E 是PB 的中点．(1)证明：OE//平面PAC ；(2)若∠ABO =∠CBO =30°，PO =3，PA =5，求二面角C −AE −B 的正弦值． 【答案】(1)证明见解析 (2)1113 【解析】 【分析】（1）连接BO 并延长交AC 于点D ，连接OA 、PD ，根据三角形全等得到OA =OB ，再根据直角三角形的性质得到AO =DO ，即可得到O 为BD 的中点从而得到OE //PD ，即可得证； （2）过点A 作Az //OP ，如图建立平面直角坐标系，利用空间向量法求出二面角的余弦值，再根据同角三角函数的基本关系计算可得； (1)证明：连接BO 并延长交AC 于点D ，连接OA 、PD ，因为PO 是三棱锥P −ABC 的高，所以PO ⊥平面ABC ，AO,BO ⊂平面ABC ， 所以PO ⊥AO 、PO ⊥BO ，又PA =PB ，所以△POA ≅△POB ，即OA =OB ，所以∠OAB =∠OBA ，又AB ⊥AC ，即∠BAC =90°，所以∠OAB +∠OAD =90°，∠OBA +∠ODA =90°， 所以∠ODA =∠OAD所以AO =DO ，即AO =DO =OB ，所以O 为BD 的中点，又E 为PB 的中点，所以OE //PD ，又OE ⊄平面PAC ，PD ⊂平面PAC ， 所以OE //平面PAC(2)解：过点A 作Az //OP ，如图建立平面直角坐标系， 因为PO =3，AP =5，所以OA =√AP 2−PO 2=4，又∠OBA =∠OBC =30°，所以BD =2OA =8，则AD =4，AB =4√3，所以AC =12，所以O(2√3,2,0)，B(4√3,0,0)，P(2√3,2,3)，C (0,12,0)，所以E (3√3,1,32)， 则AE ⃑⃑⃑⃑⃑ =(3√3,1,32)，AB ⃑⃑⃑⃑⃑ =(4√3,0,0)，AC ⃑⃑⃑⃑⃑ =(0,12,0)， 设平面AEB 的法向量为n ⃑ =(x,y,z )，则{n ⃑ ⋅AE ⃑⃑⃑⃑⃑ =3√3x +y +32z =0n ⃑ ⋅AB ⃑⃑⃑⃑⃑ =4√3x =0 ，令z =2，则y =−3，x =0，所以n ⃑ =(0,−3,2)；设平面AEC 的法向量为m⃑⃑ =(a,b,c )，则{m ⃑⃑ ⋅AE ⃑⃑⃑⃑⃑ =3√3a +b +32c =0m ⃑⃑ ⋅AC ⃑⃑⃑⃑⃑ =12b =0 ，令a =√3，则c =−6，b =0，所以m ⃑⃑ =(√3,0,−6)；所以cos⟨n⃑ ,m⃑⃑ ⟩=n⃑ ⋅m⃑⃑⃑|n⃑ ||m⃑⃑⃑ |=√13×√39=−4√313设二面角C−AE−B为θ，由图可知二面角C−AE−B为钝二面角，所以cosθ=−4√313，所以sinθ=√1−cos2θ=1113故二面角C−AE−B的正弦值为1113；20．【2022年北京】如图，在三棱柱ABC−A1B1C1中，侧面BCC1B1为正方形，平面BCC1B1⊥平面ABB1A1，AB=BC=2，M，N分别为A1B1，AC的中点．(1)求证：MN∥平面BCC1B1；(2)再从条件①、条件②这两个条件中选择一个作为已知，求直线AB与平面BMN所成角的正弦值．条件①：AB⊥MN；条件②：BM=MN．注：如果选择条件①和条件②分别解答，按第一个解答计分．【答案】(1)见解析(2)见解析【解析】【分析】（1）取AB的中点为K，连接MK,NK，可证平面MKN//平面CBB1C1，从而可证MN//平面CB B1C1.（2）选①②均可证明BB1⊥平面ABC，从而可建立如图所示的空间直角坐标系，利用空间向量可求线面角的正弦值.(1)取AB的中点为K，连接MK,NK，由三棱柱ABC −A 1B 1C 1可得四边形ABB 1A 1为平行四边形， 而B 1M =MA 1,BK =KA ，则MK //BB 1，而MK ⊄平面CBB 1C 1，BB 1⊂平面CBB 1C 1，故MK //平面CBB 1C 1， 而CN =NA,BK =KA ，则NK //BC ，同理可得NK //平面CBB 1C 1， 而NK ∩MK =K,NK,MK ⊂平面MKN ，故平面MKN //平面CBB 1C 1，而MN ⊂平面MKN ，故MN //平面CBB 1C 1， (2)因为侧面CBB 1C 1为正方形，故CB ⊥BB 1， 而CB ⊂平面CBB 1C 1，平面CBB 1C 1⊥平面ABB 1A 1， 平面CBB 1C 1∩平面ABB 1A 1=BB 1，故CB ⊥平面ABB 1A 1， 因为NK //BC ，故NK ⊥平面ABB 1A 1， 因为AB ⊂平面ABB 1A 1，故NK ⊥AB ，若选①，则AB ⊥MN ，而NK ⊥AB ，NK ∩MN =N ， 故AB ⊥平面MNK ，而MK ⊂平面MNK ，故AB ⊥MK ，所以AB ⊥BB 1，而CB ⊥BB 1，CB ∩AB =B ，故BB 1⊥平面ABC ，故可建立如所示的空间直角坐标系，则B(0,0,0),A(0,2,0),N(1,1,0),M(0,1,2)， 故BA ⃑⃑⃑⃑⃑ =(0,2,0),BN ⃑⃑⃑⃑⃑⃑ =(1,1,0),BM ⃑⃑⃑⃑⃑⃑ =(0,1,2)， 设平面BNM 的法向量为n⃑ =(x,y,z)， 则{n ⃑ ⋅BN ⃑⃑⃑⃑⃑⃑ =0n ⃑ ⋅BM ⃑⃑⃑⃑⃑⃑ =0，从而{x +y =0y +2z =0，取z =−1，则n⃑ =(−2,2,−1)， 设直线AB 与平面BNM 所成的角为θ，则 sinθ=|cos〈n ⃑ ,AB ⃑⃑⃑⃑⃑ 〉|=42×3=23. 若选②，因为NK //BC ，故NK ⊥平面ABB 1A 1，而KM ⊂平面MKN ， 故NK ⊥KM ，而B 1M =BK =1,NK =1，故B 1M =NK ， 而B 1B =MK =2，MB =MN ，故△BB 1M ≅△MKN ， 所以∠BB 1M =∠MKN =90°，故A 1B 1⊥BB 1， 而CB ⊥BB 1，CB ∩AB =B ，故BB 1⊥平面ABC ，故可建立如所示的空间直角坐标系，则B(0,0,0),A(0,2,0),N(1,1,0),M(0,1,2)， 故BA⃑⃑⃑⃑⃑ =(0,2,0),BN ⃑⃑⃑⃑⃑⃑ =(1,1,0),BM ⃑⃑⃑⃑⃑⃑ =(0,1,2)， 设平面BNM 的法向量为n⃑ =(x,y,z)，则{n ⃑ ⋅BN ⃑⃑⃑⃑⃑⃑ =0n ⃑ ⋅BM ⃑⃑⃑⃑⃑⃑ =0，从而{x +y =0y +2z =0，取z =−1，则n ⃑ =(−2,2,−1)， 设直线AB 与平面BNM 所成的角为θ，则 sinθ=|cos〈n ⃑ ,AB⃑⃑⃑⃑⃑ 〉|=42×3=23.21．【2022年浙江】如图，已知ABCD 和CDEF 都是直角梯形，AB//DC ，DC//EF ，AB =5，DC =3，EF =1，∠BAD =∠CDE =60°，二面角F −DC −B 的平面角为60°．设M ，N 分别为AE,BC 的中点．(1)证明：FN ⊥AD ；(2)求直线BM 与平面ADE 所成角的正弦值． 【答案】(1)证明见解析； (2)5√714．【解析】 【分析】（1）过点E 、D 分别做直线DC 、AB 的垂线EG 、DH 并分别交于点G 、H ，由平面知识易得FC =BC ，再根据二面角的定义可知，∠BCF =60∘，由此可知，FN ⊥BC ，FN ⊥CD ，从而可证得FN ⊥平面ABCD ，即得FN ⊥AD ；（2）由（1）可知FN ⊥平面ABCD ，过点N 做AB 平行线NK ，所以可以以点N 为原点，NK ，NB 、NF 所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系N −xyz ，求出平面ADE 的一个法向量，以及BM ⃑⃑⃑⃑⃑⃑ ，即可利用线面角的向量公式解出． (1)过点E 、D 分别做直线DC 、AB 的垂线EG 、DH 并分别交于点交于点G 、H ．∵四边形ABCD 和EFCD 都是直角梯形，AB//DC,CD//EF,AB =5,DC =3,EF =1，∠BAD =∠CDE =60°，由平面几何知识易知，DG =AH =2,∠EFC =∠DCF =∠DCB =∠ABC =90°，则四边形EFCG 和四边形DCBH 是矩形，∴在Rt △EGD 和Rt △DHA ，EG =DH =2√3， ∵DC ⊥CF,DC ⊥CB ，且CF ∩CB =C ，∴DC ⊥平面BCF,∠BCF 是二面角F −DC −B 的平面角，则∠BCF =60∘， ∴△BCF 是正三角形，由DC ⊂平面ABCD ，得平面ABCD ⊥平面BCF ，∵N 是BC 的中点，∴ FN ⊥BC ，又DC ⊥平面BCF ，FN ⊂平面BCF ，可得FN ⊥CD ，而BC ∩CD =C ，∴FN ⊥平面ABCD ，而AD ⊂平面ABCD ∴FN ⊥AD ． (2)因为FN ⊥平面ABCD ，过点N 做AB 平行线NK ，所以以点N 为原点， NK ，NB 、NF 所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系N −xyz ，设A(5,√3,0),B(0,√3,0),D(3,−√3,0),E(1,0,3)，则M (3,√32,32)，∴BM ⃑⃑⃑⃑⃑⃑ =(3,−√32,32),AD ⃑⃑⃑⃑⃑ =(−2,−2√3,0),DE⃑⃑⃑⃑⃑ =(−2,√3,3) 设平面ADE 的法向量为n⃑ =(x,y,z) 由{n ⃑ ⋅AD ⃑⃑⃑⃑⃑ =0n ⃑ ⋅DE ⃑⃑⃑⃑⃑ =0 ，得{−2x −2√3y =0−2x +√3y +3z =0 ，取n ⃑ =(√3,−1,√3)，设直线BM 与平面ADE 所成角为θ， ∴sinθ=|cos〈n⃑ ,BM ⃑⃑⃑⃑⃑⃑ 〉|=|n⃑ ⋅BM ⃑⃑⃑⃑⃑⃑⃑ ||n⃑ |⋅BM ⃑⃑⃑⃑⃑⃑⃑ |=|3√3+√32+3√32|√3+1+3⋅√9+34+94=√3√7⋅2√3=5√714．1．（2022·全国·模拟预测）已知正方体中1111ABCD A B C D -，E ，G 分别为11A D ，11C D 的中点，则直线1A G ，CE 所成角的余弦值为（ ）A B C D 【答案】C 【解析】 【分析】根据异面直线所成角的定义，取AB 的中点F ，则∠ECF （或其补角）为直线1A G 与CE 所成角，再解三角形即可得解． 【详解】如图所示：，取AB 的中点F ，连接EF ，CF ，易知1A G CF ∥，则∠ECF （或其补角）为直线1A G 与CE 所成角．不妨设2AB =，则CF =EF =3EC =，由余弦定理得cosECF ∠==，即直线1A G 与CE 故选：C ．2．（2022·全国·模拟预测（理））如图，在三棱台111ABC A B C -中，1AA ⊥平面ABC ，90ABC ∠=︒，111111AA A B B C ===，2AB =，则AC 与平面11BCC B 所成的角为（ ）A ．30B ．45︒C ．60︒D ．90︒【答案】A 【解析】 【分析】将棱台补全为棱锥，利用等体积法求A 到面11BCC B 的距离，结合线面角的定义求AC 与平面11BCC B 所成角的大小. 【详解】将棱台补全为如下棱锥D ABC -，由90ABC ∠=︒，111111AA A B B C ===，2AB =，易知：2DA BC ==，AC = 由1AA ⊥平面ABC ，,AB AC ⊥平面ABC ，则1AA AB ⊥，1AA AC ⊥，所以BD =CD =222BC BD CD +=，所以122BCD S =⨯⨯=△A 到面11BCC B 的距离为h ，又D ABC A BCD V V --=，则111222323h ⨯⨯⨯⨯=⨯h = 综上，AC 与平面11BCC B 所成角[0,]2πθ∈，则1sin 2h AC θ==，即6πθ=. 故选：A3．（2022·浙江湖州·模拟预测）如图，已知四边形ABCD ，BCD △是以BD 为斜边的等腰直角三角形，ABD △为等边三角形，2BD =，将ABD △沿对角线BD 翻折到PBD △在翻折的过程中，下列结论中不正确．．．的是（ ）A ．BD PC ⊥B ．DP 与BC 可能垂直C ．直线DP 与平面BCD 所成角的最大值是45︒ D ．四面体PBCD 【答案】C 【解析】 【分析】对于A ，取BD 的中点M ，即可得到BD ⊥面PMC ，A 选项可判断对于B ，采用反证法，假设DP BC ⊥，则BC ⊥面PCD ，再根据题目所给的长度即可判断；对于C ，当面PBD ⊥面BCD 时，此时直线DP 与平面BCD 所成角有最大值，判断即可；对于D ，当面PBD ⊥面BCD 时，此时四面体PBCD 的体积有最大值，计算最大体积判断即可 【详解】如图所示，取BD 的中点M ，连接,PM CMBCD △是以BD 为斜边的等腰直角三角形,BD CM ∴⊥ABD △为等边三角形,BD PM ∴⊥BD ∴⊥面PMC ,BD PC ∴⊥ ,故A 正确 对于B ，假设DP BC ⊥，又BC CD ⊥BC ∴⊥面PCD ，BC PC ∴⊥，又2,PB BC ==1PC ⎤⎦，故DP 与BC 可能垂直，故B 正确当面PBD ⊥面BCD 时，此时PM ⊥面BCD ，PDB ∠即为直线DP 与平面BCD 所成角 此时60PDB ︒∠=，故C 错误当面PBD ⊥面BCD 时，此时四面体PBCD 的体积最大，此时的体积为：111(332BCDV S PM ==⨯=，故D 正确 故选：C4．（2022·河南安阳·模拟预测（理））已知球O 的体积为125π6，高为1的圆锥内接于球O ，经过圆锥顶点的平面α截球O 和圆锥所得的截面面积分别为12,S S ，若125π8S =，则2S =（ ）A ．2BCD ．【答案】C 【解析】 【分析】根据给定条件，求出球O 半径，平面α截球O 所得截面小圆半径，圆锥底面圆半径，再求出平面α截圆锥所得的截面等腰三角形底边长及高即可计算作答. 【详解】球O 半径为R ，由34π125π36R =得52R =，平面α截球O 所得截面小圆半径1r ，由21128π5πS r ==得1r =因此，球心O 到平面α的距离1d r ===，而球心O 在圆锥的轴上，则圆锥的轴与平面α所成的角为45，因圆锥的高为1，则球心O 到圆锥底面圆的距离为132d =，于是得圆锥底面圆半径2r =，令平面α截圆锥所得截面为等腰PAB △，线段AB 为圆锥底面圆1O 的弦，点C 为弦AB 中点，依题意，145CPO ∠=，111CO PO ==，PC =AB ==所以212AB S PC =⋅=. 故选：C 【点睛】关键点睛：解决与球有关的内切或外接问题时，关键是确定球心的位置，再利用球的截面小圆性质求解.5．（2022·浙江·模拟预测）如图，矩形BDEF 所在平面与正方形ABCD 所在平面互相垂直，2,1BD DE ==，点P 在线段EF 上，给出下列命题：①存在点P ，使得直线//DP 平面ACF ②存在点P ，使得直线DP ⊥平面ACF③直线DP 与平面ABCD 所成角的正弦值的取值范围是⎤⎥⎣⎦④三棱锥A CDE -的外接球被平面ACF 所截取的截面面积是98π 其中所有真命题的序号是（ ） A ．①③ B ．①④C ．②④D ．①③④ 【答案】D 【解析】 【分析】取EF 中点推理判断①；假定DP ⊥平面ACF ，分析判断②；确定直线DP 与平面ABCD 所成角，求出临界值判断③；求出ACF 外接圆面积判断④作答.令AC BD O =，连接,FO DF ，令EF 中点为G ，连DG ，如图，依题意，O 是,BD AC 的中点，对于①，在矩形BDEF 中，//DO FG ，DO FG =，四边形DOFG 是平行四边形，直线//DG OF ，OF ⊂平面ACF ，DG ⊄平面ACF ，则//DG 平面ACF ，当P 是线段EF 中点G 时，直线//DP 平面ACF ，①正确；对于②，假定直线DP ⊥平面ACF ，由①知，DP OF ⊥，DP DG ⊥，当点P 在线段EF 上任意位置（除点G 外），PDG ∠均为锐角，即DP 不垂直于DG ，也不垂直于OF ，因此，不存在点P ，使得直线DP ⊥平面ACF ，②不正确；对于③，平面BDEF ⊥平面ABCD ，DP 在平面ABCD 内射影在直线BD 上，直线DP 与平面ABCD 所成角为PDB ∠，当点P 由点E 运动到点F 的过程中，PDB ∠逐渐减小，当P 与E 重合时，PDB ∠最大，为90EDB ∠=，max (sin )1PDB ∠=，当P 与F 重合时，PDB ∠最小，为FDB ∠，min (sin )BF PDB DF ∠==所以直线DP 与平面ABCD 所成角的正弦值的取值范围是⎤⎥⎣⎦，③正确；对于④，在ACF 中，2AC =，|AF CF ==FO sin OF FAC AF ∠==由正弦定理得ACF 外接圆直径2sin FC r FAC ==∠半径r =圆面积为298S r ππ==，三棱锥A CDE -的外接球被平面ACF 所截取的截面是ACF 外接圆， 因此三棱锥A CDE -的外接球被平面ACF 所截取的截面面积是98π，④正确, 所以所有真命题的序号是①③④. 故选：D6．（2022·四川省泸县第二中学模拟预测（文））已知1O 是正方体1111ABCD A B C D -的中心O 关于平面1111D C B A 的对称点，则下列说法中正确的是（ ）A ．11O C 与1A C 是异面直线B ．11OC ∥平面11A BCD C ．11O C AD ⊥ D ．11O C ⊥平面11BDD B【答案】B 【解析】 【分析】根据正方体的性质、空间直线与平面的位置关系，即可对选项做出判断. 【详解】连接1A C 、1AC ，交于点O ，连接11A C 、11B D ，交于点P . 连接AC 、BD 、1A B 、1D C 、1O O .由题可知，1O 在平面11A C CA 上，所以11O C 与1A C 共面，故A 错误；在四边形11OO C C 中，11//O O C C 且11O O C C =，所以四边形11OO C C 为平行四边形. 11//O C OC ∴.OC ⊂平面11A BCD ，11O C ⊄平面11A BCD ，11O C ∴∥平面11A BCD ，故B 正确；由正方体的性质可得1111AC B D ⊥，因为1111O B O D =，所以111O P B D ⊥，又111O P AC P =，11B D ∴⊥平面111O AC ， 1111B D O C ∴⊥，又11//B D BD ， 11BD O C ∴⊥，而AD 与BD 所成角为45︒，所以显然11O C 与AD 不垂直，故C 错误；显然11O C 与11O B 不垂直，而11O B ⊂平面11BDD B ，所以11O C 与平面11BDD B 不垂直，故D 错误. 故选：B.7．（2022·北京·北大附中三模）已知平面,,αβγ，直线m 和n ，则下列命题中正确的是（ ） A ．若,m m αβ⊥⊥，则αβ∥ B ．若,αγβγ⊥⊥，则αβ∥ C ．若,m n m α⊥⊥，则n α∥ D ．若,m n αα∥∥，则m n ∥ 【答案】A 【解析】 【分析】对于A 选项，垂直于同一条直线的两个平面互相平行；对于B 选项，垂直于同一个平面的两个平面有可能相交，也有可能互相平行； 对于C 选项，由线面垂直的性质即可判断；对于D 选项，平行于同一个平面的两条直线有可能相交、平行或异面. 【详解】选项A 正确，因为垂直于同一直线的两个平面互相平行； 选项B 错误，平面α和β也可以相交； 选项C 错误，直线n 可能在平面α内； 选项D 错误，直线m 和n 还可能相交或者异面. 故选：A.8．（2022·云南师大附中模拟预测（理））已知正方形ABCD 的边长为ABC 沿对角线AC 折起，使得二面角B AC D --的大小为90°.若三棱锥B ACD -的四个顶点都在球O 的球面上，G 为AC 边的中点，E ，F 分别为线段BG ，DC 上的动点（不包括端点），且BE ，当三棱锥E ACF -的体积最大时，过点F 作球O 的截面，则截面面积的最小值为（ ）A ．B ．2πC ．32πD ．89π【答案】D 【解析】 【分析】根据面面垂直的判定定理得BG ⊥平面ACD ，继而表示出三棱锥E ACF -的体积，求出x =V 取得最大值，在∠GCF 中，由余弦定理，得GF =当GF 垂直于截面时，截面圆的面积最小，继而得解. 【详解】因为正方形ABCD 的边长为4AC =.如图，由于平面ABC ⊥平面ACD ，平面ABC 平面ACD AC =，又G 为AC 边的中点，则有BG AC ⊥，所以BG ⊥平面ACD ．设CF x =(0x <<，则BE =，所以三棱锥E ACF -的体积13ACF V S EG ==△2111122sin 4(22))323223AC CF ACF EG x x x ⨯∠=⨯⨯-=-，当x =时，V 取得最大值．由于GA GB GC GD ===，则球O 的球心即为G ，且球O 的半径2R =．又在△GCF中，由余弦定理，得cos GF GC CF ACF =∠=。

全国各地市历年高考立体几何题汇编(含参考答案)(一)2018年高考立体几何题1.(北京理16)如图，在三棱柱ABC-me,中，CC~平面/此；D, E, F, G分别为必，AC,4G，B片的中点，AB=B(=yfs , A(=AA l=2.(I )求证：/以平面BEF-,(II )求二面角B-CAC、的余弦值；(III)证明：直线尸G与平面奶相交.2.(浙江-19)如图，已知多面体ABCAEG，AA, B、B,均垂直于平面,此；，"4，砂1，AB=B(=B Y B=2.(I )证明：刀3上平面(II)求直线WG与平面/蹈所成的角的正弦值.3.(课标III理T9)如图，边长为2的正方形ABCD所在的平面与半圆弧CD所在平面垂直, 肱是CQ上异于。

，。

的点.(1)证明：平面AMD1.平面BMC；(2)当三棱锥M -AB C体积最大时，求面MAB与面MCD所成二面角的正弦值.4.（课标II理-20）。

为AC的中如图，在三棱锥P-A8C 中，AB = BC = 2g, PA = PB = PC = AC = 4 ,(1)证明：POL平面ABC；(2)若点肱在棱BC上，且二面角为30。

，求PC与平面月皈所成角的正弦值.5.（课标I理-18）如图，四边形A3CZ)为正方形，分别为AD,B C的中点，以DF为折痕把△DPC折起, 使点C到达点F的位置，且PF LBF .(1)证明：平面PEF L平面ABFD；(2)求QP与平面A8FD所成角的正弦值.(二)2017年高考立体几何题1.(课标IIIS-19)如图，四面体，夙力中，△ABC是正三角形，△，⑦是直角三角形，/ABAZCBD, AB^BD.(1)证明：平面ACDL平面D(2)过的平面交彻于点&若平面北T把四面体⑦分成体积相等的两部分，求二面角D-AE-C的余弦值.2.（课标II理-19）如图，四棱锥巴ABCD中，侧面0〃为等边三角形且垂直于底面/次，AB = BC = -AD,ZBAD = ZABC = 90°, B是切的中 2点.(1)证明：直线CE〃平面0B；(2)点〃在棱PC上，且直线伽与底面/次所成角为45。

新课标卷高考真题1、（2016 年全国I 高考）如图，在以A，B，C，D，E，F 为顶点的五面体中，面ABEF为正方形，AF=2FD，AFD 90 ，且二面角D- AF- E与二面角C- BE- F 都是60 ．（I）证明：平面ABEF 平面EFDC；（II）求二面角E- BC- A 的余弦值．2、（2016 年全国II 高考）如图，菱形ABCD 的对角线AC 与BD 交于点O ，AB 5, AC 6，点E, F分别在AD ,CD 上，5AE CF ，EF 交BD 于点H ．将4DEF 沿EF 折到'D EF 位置，OD 10 ．（Ⅰ）证明： D H 平面ABCD ；（Ⅱ）求二面角 B D A C 的正弦值．3【2015高考新课标1，理18】如图，四边形ABCD 为菱形，∠ABC=120°，E，F 是平面ABCD 同一侧的两点，BE⊥平面ABCD，DF⊥平面ABCD，BE=2DF，AE⊥EC.（Ⅰ）证明：平面AEC⊥平面AFC；（Ⅱ）求直线AE 与直线CF 所成角的余弦值.4、[2014 ·新课标全国卷Ⅱ] 如图1-3，四棱锥P-ABCD 中，底面ABCD 为矩形，PA⊥平面ABCD，E 为PD 的中点．(1)证明：PB∥平面AEC；(2)设二面角D-AE-C 为60°，AP＝1，AD＝3，求三棱锥E-ACD 的体积．图1-35、[2014·新课标全国卷Ⅰ] 如图1-5，三棱柱ABC -A1B1C1 中，侧面BB1C1C 为菱形，AB⊥B1C.图1-5(1)证明：AC＝AB1；(2)若AC⊥AB1，∠CBB1＝60°，AB＝BC，求二面角A -A1B1 - C1 的余弦值．6、（2017?新课标Ⅱ）如图，四棱锥P﹣ABCD 中，侧面PAD 为等边三角形且垂直于底面ABCD ，AB=BC= AD ，∠BAD= ∠ABC=90°，E 是PD 的中点．（Ⅰ）证明：直线CE∥平面PAB；（Ⅱ）点M 在棱PC 上，且直线BM 与底面ABCD 所成角为45°，求二面角M ﹣AB ﹣D 的余弦值．7、（2017?新课标Ⅲ）如图，四面体ABCD 中，△ABC 是正三角形，△ACD 是直角三角形，∠ABD= ∠CBD ，AB=BD ．（Ⅰ）证明：平面ACD ⊥平面ABC ；（Ⅱ）过AC 的平面交BD 于点E，若平面AEC 把四面体ABCD 分成体积相等的两部分，求二面角D﹣AE ﹣C 的余弦值．8、（2017?新课标Ⅰ卷）如图，在四棱锥P﹣ABCD 中，AB ∥CD，且∠BAP=∠CDP=90°．（12分）(1)证明：平面PAB⊥平面PAD；(2)若PA=PD=AB=DC ，∠APD=90°，求二面角A﹣PB﹣C 的余弦值．1【解析】⑴∵ABEF 为正方形∴AF EF ∵AFD 90 ∴AF DF∵DF EF =F ∴AF 面EFDC AF 面ABEF∴平面ABEF 平面EFDC⑵由⑴知DFE CEF 60∵AB∥EF AB 平面EFDCEF 平面EFDC ∴AB∥平面ABCDAB 平面ABCD∵面ABCD 面EFDC CD∴AB∥CD ,∴CD ∥EF∴四边形EFDC 为等腰梯形以E为原点，如图建立坐标系，FD aE 0，0 ，0 B 0 ，2a，0a 3C ，0 ， a A 2a，a2，02 2EB 0 ，2a，0 ，a 3BC ，2a， a ，AB 2a ，0 ，02 2设面BEC 法向量为m x，y，z .m EB m BC 0，即2a y 01a 3x 2ay a z 01 1 12 2x1 3 ，y1 0 ，z1 1 m 3 ，0 ， 1 设面ABC 法向量为n x ，y ，z2 2 2n BC n AB =0.即a 3x 2ay az 02 2 22 22ax 02x2 0，y2 3，z2 4n 0， 3 ，4设二面角 E BC A的大小为.cos m nm n4 2 19193 1 3 16∴二面角 E BC A的余弦值为2 1992【解析】⑴证明：∵ 5AE CF ，∴4 AE CF AD CD，∴EF∥AC ．∵四边形ABCD为菱形，∴AC BD ，∴EF BD ，∴EF DH ，∴EF D H ．∵AC 6，∴AO 3；又AB 5，AO OB ，∴OB 4 ，∴OH AE OD 1AO ，∴DH D H 3 ，∴ 2 2 2OD OH D H ，'∴D'H OH ．又∵OH I EF H ，∴D 'H 面ABCD．⑵建立如图坐标系H xyz．B 5，0，0 ，C 1，3，0 ，D ' 0，0，3 ，A 1，3，0 ，u u u r A Buuur uuru，，，AD ' 1，3，3 ，AC 0，6 ，0 ，4 3 0设面ABD ' 法向量u rn x，y，z1，由n AB1n AD1得4x 3y 0x 3y 3z 0，取xyz354 ，∴u rn1 3，4，5．同理可得面AD 'C 的法向量u u rn2 3，0 ，1 ，∴cos u r u u rn n1 2 9 5 7 5u r u u r，∴5 2 10 25n n1 2sin2 9525．3，【答案】（Ⅰ）见解析（Ⅱ）3 3又∵AE⊥EC，∴EG= 3 ，EG⊥AC，在Rt△EBG 中，可得BE= 2 ，故DF=2 2.在Rt△FDG 中，可得FG=6 2.在直角梯形BDFE 中，由BD =2，BE= 2 ，DF=22可得EF=3 22，∴ 2 2 2EG FG EF ，∴EG⊥FG，∵AC∩FG=G，∴EG⊥平面AFC，∵EG 面AEC，∴平面AFC⊥平面AEC. ⋯⋯6分（Ⅱ）如图，以G 为坐标原点，分别以GB, GC 的方向为x轴，y 轴正方向，|GB| 为单位长度，建立空间直角坐标系G-xyz，由（Ⅰ）可得A（0，－3，0），E(1,0,2 )，F（－1,0，22），C（0， 3 ，0），∴AE =（1，3， 2 ），CF =（-1，- 3，22）. ⋯10分故cos , 3AE CFAE CF| AE || CF | 3.所以直线A E 与CF 所成的角的余弦值为 33 . ⋯⋯12分4，解：(1)证明：连接B D 交AC 于点O，连接E O. 因为ABCD 为矩形，所以O 为BD 的中点．又E 为PD 的中点，所以EO∥PB.因为EO? 平面AEC，PB?平面AEC，所以PB∥平面AEC.(2)因为PA⊥平面ABCD，ABCD 为矩形，所以AB，AD，AP 两两垂直．→如图，以A 为坐标原点，AB，AD，AP 的方向为x 轴、y轴、z轴的正方向，→|为单位长，建立空间直角坐标系A-xyz，则D (0，3，0)，E 0， 3|AP，2 12，A→E＝0，3 1，2 2.→设B( m，0，0)( m>0)，则C( m，3，0)，AC＝(m，3，0)．设n1＝(x，y，z)为平面ACE 的法向量，→n1·AC＝0，则即→n1·AE＝0，m x＋3y＝0，3 12 y＋2z＝0，可取n1＝3，－1， 3 . m又n2＝(1，0，0)为平面DAE 的法向量，1由题设易知|cos〈n1，n2〉|＝，即23 1 32＝，解得m＝3＋4m 22.＝1 1 3 1××3×＝×3 2 2 238 .125 解：(1)证明：连接B C1，交B1C 于点O，连接A O，因为侧面BB1C1C 为菱形，所以B1C⊥BC1，且O 为B1C 及BC1 的中点．又AB⊥B1C，所以B1C⊥平面ABO.由于AO? 平面ABO，故B1C⊥AO.又B1O＝CO，故AC＝AB1.(2)因为AC⊥AB1，且O 为B1C 的中点，所以AO＝CO.又因为AB＝BC，所以△BOA≌△BOC.故OA⊥OB，从而OA，OB，OB1两两垂直．以O 为坐标原点，OB 的方向为x 轴正方向，|O B|为单位长，建立如图所示的空间直角坐标系O- xyz.因为∠CBB1 ＝60°，所以△CBB1 为等边三角形，又AB＝BC ，则A 0，0，33，B(1，0，0)，B1 0，3，0 ，C 0，－33，0 .3→AB1＝0，3，－333→，A1B1＝AB＝1，0，－33，→B1C1＝BC＝－1，－3，0 . 3设n＝(x，y，z)是平面AA1B1 的法向量，则n·AB1＝0，即→n·A1B1＝0，333 y－3 z＝0，x－33 z＝0.所以可取n＝(1，3，3)．设m是平面A1B1C1 的法向量，→m·A1B1＝0，则同理可取m＝(1，－3，3)．→m·B1C1＝0，则c os〈n，m〉＝n·m 1＝7.|n||m|13.6、【答案】（Ⅰ）证明：取PA 的中点F，连接E F，BF，因为 E 是PD 的中点，13所以EF AD ，AB=BC= AD ，∠BAD= ∠ABC=90°，∴BC∥AD ，∴BCEF 是平行四边形，可得CE∥BF，BF? 平面PAB，CF?平面PAB，∴直线C E∥平面PAB；P﹣A BCD 中，（Ⅱ）解：四棱锥侧面PAD 为等边三角形且垂直于底面ABCD ，AB=BC= AD ，∠BAD= ∠ABC=90°，E 是PD 的中点．A D=2 ，则A B=BC=1 ，OP= ，取AD 的中点O，M 在底面ABCD 上的射影N 在OC 上，设∴∠PCO=6°0，直线B M 与底面ABCD 所成角为45°，可得：BN=MN ，CN= MN ，BC=1，可得：1+ BN 2=BN 2 ，BN= ，MN= ，作NQ⊥AB 于Q，连接M Q ，A B﹣D的平面角，MQ=所以∠MQN 就是二面角M﹣= ，A B﹣D的余弦值为：= ．二面角M﹣7、【答案】（Ⅰ）证明：如图所示，取AC 的中点O，连接B O，OD．∵△ABC 是等边三角形，∴OB⊥AC ．△ABD 与△CBD 中，AB=BD=BC ，∠ABD= ∠CBD，∴△ABD ≌△CBD ，∴AD=CD ．∵△ACD 是直角三角形，∴AC 是斜边，∴∠ADC=9°0．∴DO= AC ．∴DO 2+BO 2=AB 2=BD 2 ．∴∠BOD=9°0 ．∴OB⊥OD．又DO∩AC=O ，∴OB⊥平面ACD ．又OB? 平面ABC ，∴平面ACD ⊥平面ABC ．（Ⅱ）解：设点D，B 到平面ACE 的距离分别为h D ，h E ．则= ．∵平面AEC 把四面体ABCD 分成体积相等的两部分，∴= = =1．∴点 E 是BD 的中点．建立如图所示的空间直角坐标系．不妨设AB=2 ．则O（0，0，0），A（1，0，0），C（﹣1，0，0），D（0，0，1），B（0，，0），E ．=（﹣1，0，1），= ，=（﹣2，0，0）．设平面ADE 的法向量为=（x，y，z），则，即，取= ．同理可得：平面ACE 的法向量为=（0，1，）．∴cos = = =﹣．∴二面角D﹣AE ﹣C 的余弦值为．8、【答案】（1）证明：∵∠BAP= ∠CDP=90°，∴PA⊥AB ，PD⊥CD，∵AB ∥CD，∴AB⊥PD，又∵PA∩PD=P，且PA? 平面PAD，PD? 平面PAD，∴AB ⊥平面PAD，又AB ? 平面PAB，∴平面PAB⊥平面PAD；（2）解：∵AB ∥CD，AB=CD ，∴四边形ABCD 为平行四边形，由（1）知AB⊥平面PAD，∴AB ⊥AD ，则四边形ABCD 为矩形，在△APD 中，由PA=PD，∠APD=90°，可得△PAD 为等腰直角三角形，设PA=AB=2a ，则AD= ．取AD 中点O，BC 中点E，连接PO、OE，以O 为坐标原点，分别以OA 、OE、OP 所在直线为x、y、z 轴建立空间直角坐标系，则：D（），B（），P（0，0，），C（）．，，．设平面PBC 的一个法向量为，由，得，取y=1，得．∵AB ⊥平面PAD，AD ? 平面PAD，∴AB ⊥AD ，又PD⊥PA，PA∩AB=A ，∴PD⊥平面PAB，则为平面PAB 的一个法向量，．∴cos＜＞= = ．由图可知，二面角 A ﹣PB﹣C 为钝角，∴二面角 A ﹣PB﹣C 的余弦值为．。

设面BEC 法向量为m x , y , z .IT uur2am EB 0 即IT uura3m BC 0X 2ay i■—a z 022X i3, y 0, z1新课标卷近三年高考题1、(2016年全国I 高考)如图，在以A , B , C, D , E, F 为顶点的五面体中，面 ABEF 为正方形，AF=2FD, AFD 90°，且二面角 D - AF - E 与二面角 C - BE- F都是60° . (I) 证明：平面 ABEF 平面EFDC (II) 求二面角E - BG A 的余弦值. 【解析】 ⑴ •/ ABEF 为正方形 ••• AF EF •/ AFD 90 • AF DF •/ DF I EF=F• AF 面 EFDC•平面 ABEF 平面 EFDC⑵由⑴知 DFECEF 60•/ AB II EFAF 面 ABEFAB 平面EFDC EF 平面EFDC• AB II 平面 ABCDAB 平面ABCD•/面 ABCD I 面 EFDC CD•- AB II CD •- CD II EFJ•四边形EFDC 为等腰梯形以E 为原点，如图建立坐标系，设FD aB 0 , 2a , 0A 2a , 2a , 0uur muiEB 0, 2a , 0 , BC2a，子uu u AB2a , 0 , 0m 3, o, i设面ABC法向量为n x2, y2, z2面角E BC A的余弦值为2空192、(2016年全国II高考)如图，菱形ABCD的对角线AC与BD交于点O ,5AB 5, AC 6，点E,F 分别在AD,CD 上, AE CF ，EF 交BD 于点H .将4 DEF 沿EF 折到D'EF 位置，OD .10 .(I)证明：D H 平面ABCD ;(U)求二面角B D A C的正弦值.• •• EF II AC .• EF BD，• EF DH ，• EF D H .•/ AC 6，• AO 3;又AB 5，AO OB，• OB 4，uuu —X22ax22ay2-2az22 X2 0, y2 3, Z2 4BC A的大小为4.厂.3 162.1919【解析】⑴证明：••• AE CFAE CF ADCD，•••四边形ABCD为菱形, • AC BD，nrnBC=°即AB 0设二面角Ecosur rm n54AE二OH OD 1 ,••• DH D H 3 ,AO2 2 2• |OD 2 |OH| |D'H| , • D'H OH .又T OH I EF H , • D'H 面ABCD .⑵建立如图坐标系H xyz .B 5 , 0 , 0 ,C 1 , 3 , 0 , D' 0 ,uuu uuurAB 4 , 3, 0 , AD'uuu,AC 设面ABD'法向量niu舟n1由iuuuiABUUUTAD0得4X0 x3y3y3zir同理可得面AD'C的法向量uun0, 1 …cosir inni n2up2届--sin -------------257 525 ,TX# BC f TN^\B C = 1.又TD .•眈，故平行且等于川Mj 四边形AS/XT 为平行四边形，于罡胚V 口「 因为AT^L 平面PAB f XfN x 平面PAB f 所以A&M 平面Mg.（ID 取的中点 E, ^AE ?由 AB = AC^AE-^C ?从 ^AE-AD, & AE 二上曲 _ BE ； = J AS ：-（~y =庚.以川为坐标原点，川应的方向为x 轴正万冋，建立如團所示的空间直角坐标系A-xyz ｝由题知;2x 4z 0，即-5 ，可取 x y 2z 02n (0,2,1)，| n AN |8、、5 于是 | cos n, AN ||n || AN |25尸（024〕「C 辰皿》（芈丄2）,PW 三（027儿毂三*T ，益■（芈4■ 丄刁. （x, y, z ）为平面PMN 的法向量,则n PMn PN3、（2016年全国III 高考）如图，四棱锥P ABC 中，PA 地面ABCD , AD P BC , ABAM试题解析；（I 〉由已知得型厶斗Q 二」収恥的中点匚连接川仁由“为巩?中点知4、【2015高考新课标2,理19】如图，长方体 ABCD AB I GU 中,AB=16, BC=10, AA , 8，点 E , F 分别在AB , C ,D , 上, A ,E D ,F 4 •过点E , F 的平面 与此长方体的面相交，交 线围成一个正方形.(I)在图中画出这个正方形(不必说出画法和理由)； (U)求直线AF 与平面 所成角的正弦值.【答案】(I)详见解析；(U) 4 5 .15【解析】(I )宏线围成的正方彪EZTGF 如圈*(II)作垂足冷 4 则= 因为EZTGF 丸正方形】所以EH=EF = BC = 10・于是曲= =6,所乩也=10・以D 为坐标原鼠丙的方向沖工轴的正方向,建立如图所示的空间直角坐标系D —2 则皿阿 H(1CUO” EQCU 罔,— _ _ G 一盘=QF(0.4.£), F£ = (10.0.0),肛= (0—6一股.设是平面的法向矍，则二— 刀 I 小【考点定位】1、直线和平面平行的性质；2、直线和平面所成的角.座.所以直5平航所唤正弦值为爭【名师点睛】根据线面平行和面面平行的性质画平面与长方体的面的交线；由交线的位置可确定公共点的位置，坐标法是求解空间角问题时常用的方法，但因其计算量大的特点很容易出错，故坐标系的选择是很重要的，便于用坐标表示相r uuu关点，先求出面的法向量，利用sin cos n,AF 求直线AF与平面所成角的正弦值.5、【2015高考新课标1,理18】如图，四边形ABCD为菱形，/ ABC=120°, E，F是平面ABCD同一侧的两点，BE丄平面ABCD，DF 丄平面ABCD，BE=2DF，AE丄EC.(I)证明：平面AEC丄平面AFC;【答案】(I)见解析⑴33【解析】试題分析I( I ［连接03设珀二06连接EG FG詁在菱形中，不妨设匚41易证EG丄通过计胃可证亘G丄芒，申瞬线面垂直判定定理可知前丄平面丄y 由而面垂宜判宦定理知平而仝c丄平面2_^C ； (ID 取G 为坐标原虽，分别\iXGB.GC 的方向为工轴'「轴正方向，至 为单位民既 崔立空阊直角坐标系 g,利用向重法可求出异面直线总与 疔所成角的余弦值试題解析匚(I 〉连援设站IOG,连接三G, 56, 口 在觌萌中，不蛎设C-S=l,由厶L *O 匕冃 可得上G*=GC= .由呢丄平面尙0 .i3=3C 可知，出又••• AE 丄 EC ,： EG= 3 , EG 丄 AC ,厉在 Rt A EBG 中，可得 BE= 2，故 DF= .2在Rt A FDG 中，可得FG= 6 .2J 2o /2 在直角梯形BDFE 中，由BD=2, BE= 2 , DF= 可得EF= 3,22•'• EG 2 FG 2 EF 2，二 EG 丄 FG ,••• ACAFG=G , • EG 丄平面 AFC , ••• EG 面AEC ,：平面 AFC 丄平面AEC.……6分F(n)如图，以G 为坐标原点，分别以GB,GC 的方向为x 轴，y 轴正方向，|GB| 为单位长度，建立空间直角坐标系G-xyz ,由(I)可得A (0,—崩,0), E(1,0,J 2), F (— 1,0, 22 ), C (0, +3 , 0) , • AE = (1, P 3，、: 2 ) , CF = (-1 ,2-■73, —2) (10)分【考点定位】空间垂直判定与性质；异面直线所成角的计算；空间想象能力，推理论证能力【名师点睛】对空间面面垂直问题的证明有两种思路，思路1:几何法，先由线线垂直证明线面垂直，再由线面垂直证明面面垂直；思路2:利用向量法，通过计算两个平面的法向量，证明其法向量垂直，从而证明面面垂直；对异面直线所成角问题，也有两种思路，思路1:几何法，步骤为一找二作三证四解，一找就是先在图形中找有没有异面直线所成角，若没有，则通常做平行线或中位线作出异面直线所成角，再证明该角是异面直线所成角，利用解三角形解出该角6 [2014新课标全国卷U ]如图1-3，四棱锥P-ABCD中，底面ABCD为矩形，FA丄平面ABCD，E为PD的中点.(1) 证明：PB//平面AEC；(2) 设二面角D-AE-C为60°，AP= 1, AD = 3,求三棱锥E-ACD的体积.解：(1)证明：连接BD交AC于点0,连接EO.因为ABCD为矩形，所以O为BD的中点. 又E为PD的中点，所以EO / PB.因为EO?平面AEC，PB?平面AEC，所以PB//平面AEC.(2)因为PA丄平面ABCD，ABCD为矩形，所以AB，AD，AP两两垂直.如图，以A为坐标原点，AB，AD，AP的方向为x轴、y轴、z轴的正方向，|AP|为单位长，建立空间直角坐标系A-xyz，则D(0，3, 0)，E 0, 土，琏uuur uuuuu uuu AE?CF故cos AE,CF uuur ' uuu|AE||CF| 3所以直线AE与CF所成的角的余弦值为3 .12分设 B(m , 0, 0)(m>0)，则 C(m , 3, 0), AC= (m , 3, 0).设n i = (x ,y,z)为平面ACE 的法向量，可取 ni = m ,— 1,.3.又n 2= (1, 0, 0)为平面DAE 的法向量,1由题设易知|cos 〈n i , n 2〉| = 2, 即卩1因为E 为PD 的中点，所以三棱锥E-ACD 的高为㊁•三棱锥E-ACD 的体积V7、［2014新课标全国卷I ］如图1-5,三棱柱ABC -A 1B 1C 1中，侧面BB 1C 1C 为菱形，AB 丄B 1C.(1) 证明：AC = AB 1；(2) 若 AC 丄 AB 1, / CBB 1 = 60°, AB = BC ,求二面角 A -A 1B 1 -C 1 的余弦值. 解：(1)证明：连接BC 1，交B 1C 于点O ,连接AO ,因为侧面BB 1C 1C 为菱 形，所以B 1C 丄BC 1,且O 为B 1C 及BC 1的中点.又AB 丄B 1C ，所以BQ 丄平面ABO.由于AO?平面ABO , 故 B 1C 丄AO.又 B 1O = CO , 故 AC = AB 1.(2)因为AC 丄AB 1，且O 为B 1C 的中点，所以 AO = CO.又因为 AB = BC ,所以△ BOA 也 △ BOC.故 OA 丄OB ,从而 OA , OB , OB 1两两垂直.以O 为坐标原点，OB 的方向为x 轴正方向，|OB|为单位长，建立如图所示mx + 3y = 0, •心 0, mx + ,3y = 0,n i • AC = 0,n i • AE = 0,,图1-5的空间直角坐标系0- xyz.因为/ CBB iA 0, 0, f ,0), B i 0, f, 0 , Co ,BC ,则又AB i 3,0.B(1,3， 0,—3 ,J3A iB i = AB = 1, 0,—-3 ,BC i = BC = — 1,-f, 0 -z)是平面AA i B i 的法向量，则多-詐0， 即 X -亍=0-AB i = 0,设 n = (x , y ,n AB i = 0, n A ?B i = 0,所以可取 n = (1,〔3, •. 3).设m 是平面A i B i C i 的法向量， m A i B i = 0, 则 一m B I CI ^ 0,同理可取m = (1,— 3,3).m >所以结合图形知二面角A -A i B i1C i 的余弦值为7-。

1.在一个几何体的三视图中，正视图和俯视图如右图所示，则相应的俯视图可以为2.已知矩形ABCD的顶点都在半径为4的球O的球面上，且6,23==,则棱锥AB BC-的体积为。

O ABCD3.如图，四棱锥P—ABCD中，底面ABCD为平行四边形，∠DAB=60°,AB=2AD,PD⊥底面ABCD.(Ⅰ)证明：PA⊥BD；(Ⅱ)若PD=AD，求二面角A-PB-C的余弦值。

1.D2.833. 解：（Ⅰ）因为60,2DAB AB AD ∠=︒=， 由余弦定理得3BD AD =从而BD 2+AD 2= AB 2，故BD ⊥AD 又PD ⊥底面ABCD ，可得BD ⊥PD 所以BD ⊥平面PAD. 故 PA ⊥BD（Ⅱ）如图，以D 为坐标原点，AD 的长为单位长，射线DA 为x 轴的正半轴建立空间直角坐标系D-xyz ，则()1,0,0A ，()03,0B ，，()1,3,0C -，()0,0,1P 。

(1,3,0),(0,3,1),(1,0,0)AB PB BC =-=-=- 设平面PAB 的法向量为n=（x ，y ，z ），则0,0,{n AB n PB ⋅=⋅=即 3030x y y z -+=-=因此可取n=(3,1,3)设平面PBC 的法向量为m ，则m 0,m 0,{PB BC ⋅=⋅=可取m=（0，-1，3-） 27cos ,727m n ==- 故二面角A-PB-C 的余弦值为 27-1. 正方体ABCD-1111A B C D 中，B 1B 与平面AC 1D 所成角的余弦值为A23 B 33 C 23D 632. 已知圆O 的半径为1，PA 、PB 为该圆的两条切线，A 、B 为俩切点，那么PA PB •的最小值为(A) 42-+ (B)32-+ (C) 422-+ (D)322-+3. 已知在半径为2的球面上有A 、B 、C 、D 四点，若AB=CD=2,则四面体ABCD 的体积的最大值为(A)23 (B)43 (C) 23 (D) 83 4. 如图，四棱锥S-ABCD 中，SD ⊥底面ABCD ，AB//DC ，AD ⊥DC ，AB=AD=1，DC=SD=2，E 为棱SB 上的一点，平面EDC ⊥平面SBC .（Ⅰ）证明：SE=2EB ；（Ⅱ）求二面角A-DE-C 的大小 .1. D2. D3. B4. 解法一：(Ⅰ)连接BD,取DC 的中点G ，连接BG,由此知 1,DG GC BG ===即ABC ∆为直角三角形，故BC BD ⊥. 又ABCD,BC SD SD ⊥⊥平面故,所以，BC ⊥⊥平面BDS,BC DE .作BK ⊥EC,EDC SBC K ⊥为垂足，因平面平面，故,BK EDC BK DE DE ⊥⊥平面，与平面SBC 内的两条相交直线BK 、BC 都垂直 DE ⊥平面SBC ，DE ⊥EC,DE ⊥SB226SB SD DB =+=3SD DB DE SB == 22626-,-EB DB DE SE SB EB ==== 所以，SE=2EB (Ⅱ) 由225,1,2,,SA SD AD AB SE EB AB SA =+===⊥知22121,AD=133AE SA AB ⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭又.故ADE ∆为等腰三角形.取ED 中点F,连接AF ,则226,AF DE AF AD DF ⊥=-=. 连接FG ，则//,FG EC FG DE ⊥.所以，AFG ∠是二面角A DE C --的平面角. 连接AG,A G=2,2263FG DG DF =-=, 2221cos 22AF FG AG AFG AF FG +-∠==-,所以，二面角A DE C --的大小为120°. 解法二：以D 为坐标原点，射线DA 为x 轴的正半轴，建立如图所示的直角坐标系D xyz -， 设A(1,0,0)，则B(1,1,0),C(0,2,0),S(0,0,2) （Ⅰ）(0,2,-2),(-1,1,0)SC BC ==设平面SBC 的法向量为n=(a, b, c) 由,n SC n BC ⊥⊥，得0,0n SC n BC == 故2b-2c=0,-a+b=0令a=1，则b=c,c=1,n=(1,1,1) 又设SE EB λ= (0)λ>，则2(,,)111E λλλλλ+++ 2(,,),(0,2,0)111DE DC λλλλλ==+++设平面CDE 的法向量m=(x,y,z) 由,m DE m DC ⊥⊥,得0m DE ⊥=，0m DC ⊥= 故20,20111x y zy λλλλλ++==+++. 令2x =，则(2,0,)m λ=-.由平面DEC ⊥平面SBC 得m ⊥n,0,20,2m n λλ=-== 故SE=2EB（Ⅱ）由（Ⅰ）知222(,,)333E ，取DE 的中点F ，则111211(,,),(,,)333333F FA =--，故0FA DE =，由此得FA DE ⊥又242(,,)333EC =--，故0EC DE =，由此得EC DE ⊥， 向量FA 与EC 的夹角等于二面角A DE C --的平面角 于是 1cos(,)2||||FA EC FA EC FA EC ==-所以，二面角A DE C --的大小为120（三）1. 已知三棱柱111ABC A B C -的侧棱与底面边长都相等，1A 在底面ABC 上的射影为BC 的中点，则异面直线AB 与1CC 所成的角的余弦值为（ ）（A 3（B 5（C 7 (D) 342. 已知二面角l αβ--为60，动点P 、Q 分别在面α、β内，P 3，Q 到α的距离为3则P 、Q 两点之间距离的最小值为（ ） (A) (B)2 (C) 33. 直三棱柱111ABC A B C -的各顶点都在同一球面上，若12AB AC AA ===, 120BAC ∠=︒，则此球的表面积等于 。

新课标卷近三年高考题1、（2016年全国I 高考）如图，在以A ，B ，C ，D ，E ，F 为顶点的五面体中，面ABEF 为正方形，AF =2FD ，90AFD ∠=，且二面角D -AF -E 与二面角C -BE -F 都是60．（I ）证明：平面ABEF ⊥平面EFDC ； （II ）求二面角E -BC -A 的余弦值． 【解析】⑴ ∵ABEF 为正方形 ∴AF EF ⊥∵90AFD ∠=︒ ∴AF DF ⊥∵=DF EF F ∴AF ⊥面EFDC AF ⊥面ABEF ∴平面ABEF ⊥平面EFDC ⑵ 由⑴知60DFE CEF ∠=∠=︒ ∵AB EF ∥AB ⊄平面EFDC EF ⊂平面EFDC ∴AB ∥平面ABCD AB ⊂平面ABCD ∵面ABCD 面EFDC CD = ∴AB CD ∥,∴CD EF ∥∴四边形EFDC 为等腰梯形以E 为原点，如图建立坐标系，设FD a =()()000020E B a ，，，， ()3022022a C a A a a ⎛⎫⎪ ⎪⎝⎭，，，，()020EB a =，，，3222a BC a a ⎛⎫=- ⎪ ⎪⎝⎭，，，()200AB a =-，， 设面BEC 法向量为()m x y z =，，.0m EB m BC ⎧⋅=⎪⎨⋅=⎪⎩，即11112032022a y a x ay a z ⋅=⎧⎪⎨⋅-+⋅=⎪⎩ 111301x y z ===-，，()301m =-，，设面ABC 法向量为()222n x y z =，，=00n BC n AB ⎧⋅⎪⎨⋅=⎪⎩.即22223202220a x ay az ax ⎧-+=⎪⎨⎪=⎩ 222034x y z ===，， ()034n =，，设二面角E BC A --的大小为θ.4219cos 1931316m n m nθ⋅-===-+⋅+⋅ ∴二面角E BC A --的余弦值为21919-2、（2016年全国II 高考）如图，菱形ABCD 的对角线AC 与BD 交于点O ，5,6AB AC ==，点,E F 分别在,AD CD 上，54AE CF ==，EF 交BD 于点H ．将DEF ∆沿EF 折到'D EF ∆位置，10OD '=．（Ⅰ）证明：D H '⊥平面ABCD ； （Ⅱ）求二面角B D A C '--的正弦值．【解析】⑴证明：∵54AE CF ==，∴AE CFAD CD=， ∴EF AC ∥．∵四边形ABCD 为菱形，∴AC BD ⊥， ∴EF BD ⊥，∴EF DH ⊥，∴EF D H '⊥． ∵6AC =，∴3AO =；又5AB =，AO OB ⊥，∴4OB =，∴1AEOH OD AO=⋅=，∴3DH D H '==， ∴222'OD OH D H '=+，∴'D H OH ⊥． 又∵OH EF H =I ，∴'D H ⊥面ABCD ． ⑵建立如图坐标系H xyz -．()500B ，，，()130C ，，，()'003D ，，，()130A -，，，()430AB =uu u r ，，，()'133AD =-uuur ，，，()060AC =uuu r，，， 设面'ABD 法向量()1n x y z =，，u r，由110n AB n AD ⎧⋅=⎪⎨'⋅=⎪⎩得430330x y x y z +=⎧⎨-++=⎩，取345x y z =⎧⎪=-⎨⎪=⎩，∴()1345n =-u r，，．同理可得面'AD C 的法向量()2301n =u u r，，，∴12129575cos 255210n n n n θ⋅+===⋅u r u u ru r u u r ， ∴295sin 25θ=．3、（2016年全国III 高考）如图，四棱锥P ABC -中，PA ⊥地面ABCD ，AD BC ，3AB AD AC ===，4PA BC ==，M 为线段AD 上一点，2AM MD =，N 为PC 的中点．（I ）证明MN平面PAB ；（II ）求直线AN 与平面PMN 所成角的正弦值.设),,(z y x n =为平面PMN 的法向量，则⎪⎩⎪⎨⎧=⋅=⋅00PN n PM n ，即⎪⎩⎪⎨⎧=-+=-0225042z y x z x ，可取)1,2,0(=n ，于是2558|||||||,cos |=⋅=><AN n AN n AN n .4、【2015高考新课标2，理19】如图，长方体1111ABCD A B C D -中,=16AB ，=10BC ，18AA =，点E ，F 分别在11A B ，11C D 上，114A E D F ==．过点E ，F 的平面α与此长方体的面相交，交线围成一个正方形．（Ⅰ）在图中画出这个正方形（不必说出画法和理由）； （Ⅱ）求直线AF 与平面α所成角的正弦值． 【答案】（Ⅰ）详见解析；（Ⅱ）4515．【考点定位】1、直线和平面平行的性质；2、直线和平面所成的角．DD 1C 1A 1 EFA BCB 1A 1AB 1BD 1DC 1CFE HGM【名师点睛】根据线面平行和面面平行的性质画平面α与长方体的面的交线；由交线的位置可确定公共点的位置，坐标法是求解空间角问题时常用的方法，但因其计算量大的特点很容易出错，故坐标系的选择是很重要的，便于用坐标表示相关点，先求出面α的法向量，利用sin cos ,n AF θ=<>求直线AF 与平面α所成角的正弦值．5、【2015高考新课标1，理18】如图，四边形ABCD 为菱形，∠ABC =120°，E ，F 是平面ABCD 同一侧的两点，BE ⊥平面ABCD ，DF ⊥平面ABCD ，BE =2DF ，AE ⊥EC . （Ⅰ）证明：平面AEC ⊥平面AFC ；（Ⅱ）求直线AE 与直线CF 所成角的余弦值.【答案】（Ⅰ）见解析（Ⅱ）33又∵AE⊥EC，∴EG=3，EG⊥AC，在Rt△EBG中，可得BE=2，故DF=22.在Rt△FDG中，可得FG=62.在直角梯形BDFE中，由BD=2，BE=2，DF=22可得EF=322，∴222EG FG EF+=，∴EG⊥FG，∵AC∩FG=G，∴EG⊥平面AFC，∵EG⊂面AEC，∴平面AFC⊥平面AEC. ……6分（Ⅱ）如图，以G为坐标原点，分别以,GB GC的方向为x轴，y轴正方向，||GB 为单位长度，建立空间直角坐标系G-xyz，由（Ⅰ）可得A（0，－3，0），E(1,0,2)，F（－1,0，22），C（0，3，0），∴AE=（1，3，2），CF=（-1，-3，22）.…10分故3cos ,3||||AE CF AE CF AE CF ∙<>==-. 所以直线AE 与CF 所成的角的余弦值为33. ……12分 【考点定位】空间垂直判定与性质；异面直线所成角的计算；空间想象能力，推理论证能力【名师点睛】对空间面面垂直问题的证明有两种思路，思路1：几何法，先由线线垂直证明线面垂直，再由线面垂直证明面面垂直；思路2：利用向量法，通过计算两个平面的法向量，证明其法向量垂直，从而证明面面垂直；对异面直线所成角问题，也有两种思路，思路1：几何法，步骤为一找二作三证四解，一找就是先在图形中找有没有异面直线所成角，若没有，则通常做平行线或中位线作出异面直线所成角，再证明该角是异面直线所成角，利用解三角形解出该角. 6、[2014·新课标全国卷Ⅱ] 如图1-3，四棱锥P -ABCD 中，底面ABCD 为矩形，PA ⊥平面ABCD ，E 为PD 的中点．(1)证明：PB ∥平面AEC ； (2)设二面角D -AE -C 为60°，AP ＝1，AD ＝3，求三棱锥E -ACD 的体积．图1-3解：(1)证明：连接BD 交AC 于点O ，连接EO . 因为ABCD 为矩形，所以O 为BD 的中点． 又E 为PD 的中点，所以EO ∥PB . 因为EO ⊂平面AEC ，PB ⊄平面AEC ， 所以PB ∥平面AEC .(2)因为PA ⊥平面ABCD ，ABCD 为矩形， 所以AB ，AD ，AP 两两垂直． 如图，以A 为坐标原点，AB →，AD ，AP 的方向为x 轴、y 轴、z 轴的正方向，|AP →|为单位长，建立空间直角坐标系A -xyz ，则D ()0，3，0，E ⎝⎛⎭⎪⎫0，32，12，AE →＝⎝ ⎛⎭⎪⎫0，32，12.设B (m ，0，0)(m >0)，则C (m ，3，0)，AC →＝(m ，3，0)． 设n 1＝(x ，y ，z )为平面ACE 的法向量，则⎩⎪⎨⎪⎧n 1·AC →＝0，n 1·AE →＝0，即⎩⎨⎧mx ＋3y ＝0，32y ＋12z ＝0， 可取n 1＝⎝ ⎛⎭⎪⎫3m ，－1，3.又n 2＝(1，0，0)为平面DAE 的法向量，由题设易知|cos 〈n 1，n 2〉|＝12，即33＋4m 2＝12，解得m ＝32. 因为E 为PD 的中点，所以三棱锥E -ACD 的高为12.三棱锥E -ACD 的体积V ＝13×12×3×32×12＝38. 7、[2014·新课标全国卷Ⅰ] 如图1-5，三棱柱ABC -A 1B 1C 1中，侧面BB 1C 1C 为菱形，AB ⊥B 1C .图1-5(1)证明：AC ＝AB 1；(2)若AC ⊥AB 1，∠CBB 1＝60°，AB ＝BC ，求二面角A -A 1B 1 ­C 1的余弦值．解：(1)证明：连接BC 1，交B 1C 于点O ，连接AO ，因为侧面BB 1C 1C 为菱形，所以B 1C ⊥BC 1，且O 为B 1C 及BC 1的中点．又AB ⊥B 1C ，所以B 1C ⊥平面ABO . 由于AO ⊂平面ABO ，故B 1C ⊥AO . 又B 1O ＝CO ，故AC ＝AB 1.(2)因为AC ⊥AB 1，且O 为B 1C 的中点，所以AO ＝CO .又因为AB ＝BC ，所以△BOA ≌ △BOC .故OA ⊥OB ，从而OA ，OB ，OB 1两两垂直．以O 为坐标原点，OB 的方向为x 轴正方向，|OB |为单位长，建立如图所示的空间直角坐标系O ­ xyz .因为∠CBB 1＝60°，所以△CBB 1为等边三角形，又AB ＝BC ，则A ⎝⎛⎭⎪⎫0，0，33，B (1，0，0)，B 1⎝⎛⎭⎪⎫0，33，0，C ⎝ ⎛⎭⎪⎫0，－33，0. AB 1→＝⎝ ⎛⎭⎪⎫0，33，－33，A 1B 1→＝AB ＝⎝ ⎛⎭⎪⎫1，0，－33， B 1C →1＝BC ＝⎝ ⎛⎭⎪⎫－1，－33，0.设n ＝(x ，y ，z )是平面AA 1B 1的法向量，则 ⎩⎪⎨⎪⎧n ·AB 1＝0，n ·A 1B 1→＝0，即⎩⎪⎨⎪⎧33y －33z ＝0，x －33z ＝0.所以可取n ＝(1，3，3)．设m 是平面A 1B 1C 1的法向量， 则⎩⎪⎨⎪⎧m ·A 1B 1→＝0，m ·B 1C 1→＝0，同理可取m ＝(1，－3，3)．则cos 〈n ，m 〉＝n ·m |n ||m |＝17.所以结合图形知二面角A -A 1B 1 ­ C 1的余弦值为17.11。