上海初三数学提高题

18. 如图，点A 在直线x y 43=上，如果把抛物线2x y =沿方向平移5个单位，那么平移后的抛物线的表达式为 ▲ ．参考答案： 3)4(2+-=x y .【2020崇明一模】18．如图，在Rt ABC △中，90C =︒∠，10AB =，8AC =，点D 是AC 的中点，点E在边AB 上，将ADE △沿DE 翻折，使得点A 落在点A '处，当A E AB '⊥时，那么A A '的长为 ▲ ．参考答案：【2020奉贤一模】18．如图4，已知矩形ABCD （AB>AD ），将矩形ABCD 绕点B 顺时针旋转90°，点A 、D 分别落在点E 、F 处，联结DF ，如果点G 是DF 的中点， 那么∠BEG 的正切值是 ▲ ．参考答案：1图4D C BA18．如图，在等腰梯形ABCD 中，AD ∥BC ，sin C =45，AB=9，AD =6，点E 、F 分别在边AB 、BC 上，联结EF ，将△BEF 沿着EF 翻折，使BF 的对应线段B’F 经过顶点A ，B’F 交对角线BD 于点P ，当B’F ⊥AB 时，AP 的长为 ▲ ．参考答案：247【2020黄浦一模】18．如图8，在△ABC 中，AB =AC ，点D 、E 在边BC 上，∠DAE =∠B =30°，且32AD AE=，那么DE BC的值是 ▲ ．118C图7A BD图818.在△ABC 中，︒=∠90ACB ，10=AB ，53cos =A （如图4），把△ABC 绕着点C 按照顺时针的方向旋转，将A 、B 的对应点分别记为点A '、B '.如果B A ''恰好经过点A ，那么点A 与点'A 的距离为 ▲ .参考答案：536.【2020静安一模】18. 如图3，有一菱形纸片ABCD ，∠A ＝60°，将该菱形纸片折叠，使点A 恰好与CD的中点E 重合，折痕为FG ，点F 、G 分别在边AB 、AD 上，联结EF ，那么cos ∠EFB 的值为 ▲ ．参考答案：71图3ABCD18．如图，在等腰△ABC 中，AB = AC = 4，BC = 6，点D 在底边BC 上，且∠DAC =∠ACD ，将△ACD 沿着AD 所在直线翻折，使得点C 落到点E 处，联结BE ，那么BE 的长为 ▲ ． 参考答案：1【2020浦东一模】18．在Rt △ABC 中，∠C =90°，AC =2，BC =4，点D 、E 分别是边BC 、AB 的中点，将△BDE 绕着点B 旋转，点D 、E 旋转后的对应点分别为点D ’、E ’，当直线D ’E ’ 经过点A 时，线段CD ’的长为 ▲ ．参考答案：【2020普陀一模】18．如图8，在Rt △ABC 中，90C ∠=︒，5AC =,，点P 为边BC 上一点，3PC =，将△ABC 绕点P 旋转得到△A B C '''（点A 、B 、C 分别与点A '、B '、C '对应），使B C ''//AB ，边A C ''与边AB 交于点G ，那么A G '的长等于▲ ．参考答案：2013ACDB 图8ABC18．已知，在矩形纸片ABCD 中，AB =5cm ，点E 、F 分别是边AB 、CD 的中点，折叠矩形纸片ABCD ，折痕BM 交AD 边于点M ，在折叠的过程中，如果点A 恰好落在线段EF 上，那么边AD 的长至少是 ▲ cm ．【2020松江一模】18．如图，矩形ABCD 中，AD =1,AB =k .将矩形ABCD 绕着点B 顺时针旋转90°得到矩形A ′BC ′D ′.联结A D ′,分别交边CD ,A ′B 于E 、F .如果'AE F =,那么k = ▲ .1【2020徐汇一模】18．如图，在矩形ABCD 中，3=AB ，4=AD ，将矩形ABCD 绕着点B 顺时针旋转后得到矩形D C B A '''，点A 的对应点A '在对角线AC 上，点C 、D 分别与点C '、D '对应，D A ''与边BC 交于点E ，那么BE 的长是__▲___．参考答案：825(第18题F ED C B AC′A′ D′【2020长宁金山一模】18. 如图，在ABC Rt ∆中，︒=∠90ABC ，2=AB ，4=BC ，点P 在边BC 上，联结AP ，将ABP ∆绕着点A 旋转，使得点P 与边AC 的中点M 重合， 点B 的对应点是点B '，则B B '的长等于 ▲ ．第18题图ABC。

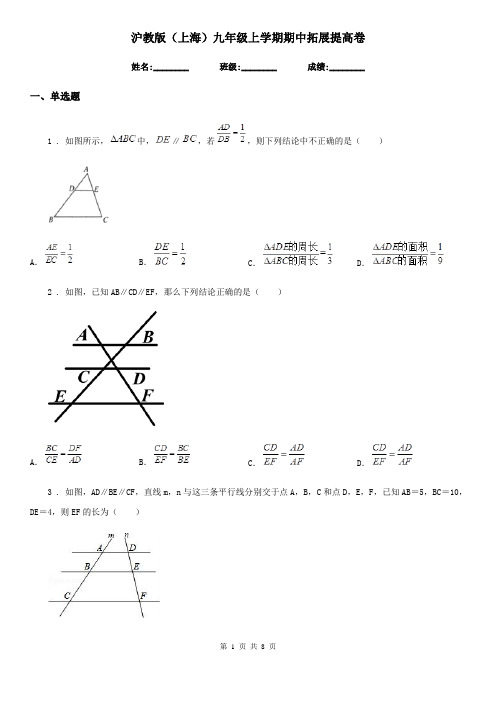
沪教版（上海）九年级上学期期中拓展提高卷姓名:________ 班级:________ 成绩:________一、单选题1 . 如图所示，中，∥，若，则下列结论中不正确的是（）A．B．C．D．2 . 如图，已知AB∥CD∥EF，那么下列结论正确的是（）A．B．C．D．3 . 如图，AD∥BE∥CF，直线m，n与这三条平行线分别交于点A，B，C和点D，E，F，已知AB＝5，BC＝10，DE＝4，则EF的长为（）A．12B．9C．8D．44 . 如果＝，那么下列各式中错误的是（）A．2a＝3b B．3a＝2bC．＝D．b＝a5 . 如图，∠APD=90°，AP=PB=BC=CD，则下列结论成立的是（）A．△PAB∽△PCA B．△ABC∽△DBA C．△PAB∽△PDA D．△ABC∽△DCA6 . 如图，在正方形网格中，△ABC和△DEF相似，则关于位似中心与相似比叙述正确的是（）A．位似中心是点B，相似比是2：1B．位似中心是点D，相似比是2：1C．位似中心在点G，H之间，相似比为2：1D．位似中心在点G，H之间，相似比为1：2二、填空题7 . 在矩形ABCD中，AB＝3，BC＝4，M是对角线BD上的动点，过点M作ME⊥BC于点E，连接AM，当△ADM是等腰三角形时，ME的长为_____.8 . 如图，△ABC中，AB＝5，AC＝6，将△ABC翻折，使得点A落到边BC上的点A′处，折痕分别交边AB、AC 于点E，点F，如果A′F∥AB，那么BE＝_____．9 . 已知点P、Q为线段AB的黄金分割点，且AB=2，则PQ=_____．（结果保留根号）10 . 观察下列图形，若第1个图形中阴影部分的面积为1，第2个图形中阴影部分的面积为，第3个图形中阴影部分的面积为，第4个图形中阴影部分的面积为，…则第n个图形中阴影部分的面积为_____.（用字母n表示）11 . 已知，则________.12 . 如图，已知等边的边长为4，，且.连结，并延长交于点，则线段的长度为__________.13 . 为了测量一条河的宽度，测量人员在对岸岸边P处观察到一根柱子，再在他们所在的这一侧岸上选点A 和B使得B、A、P在一条直线上，且与河岸垂直，然后确定点C、D，使BC⊥BP，AD⊥BP，由观测可以确定CP与AD交于点D，如图所示，他们测得AB＝45米，BC＝90米，AD＝60米，请你帮他们来计算河的宽度PA是___米．14 . 如图，△ABC中，AD：DC＝1：4，AE＝EF，则BF：FC＝_____．15 . 如图，⊙O的半径OC⊥AB，垂足为E，若∠B＝48°，则∠A的度数为_____．16 . 如图，已知Rt△ABC的直角边AC=8，斜边AB=10，一个以点P为圆心，半径为1的圆在△ABC内部沿顺时针方向滚动，且运动过程中⊙P一直保持与△ABC的边相切，当点P第一次回到它的初始位置时所经过路径的长度是______．17 . 如图，在梯形ABCD中，AD∥BC，EF是梯形ABCD的中位线，AH∥CD分别交EF、BC于点G、H，若＝，＝，则用、表示＝_____．18 . 如果，相似比，若它们的面积比为________．三、解答题19 . 在平面直角坐标系中，O为原点，四边形OABC的顶点A在轴的正半轴上，OA=4，OC=2，点P，点Q分别是边BC，边AB上的点，连结AC，PQ，点B1是点B关于PQ的对称点．（1）若四边形OABC为矩形，如图1，①求点B的坐标；②若BQ：BP=1：2，且点B1落在OA上，求点B1的坐标；（2）若四边形OABC为平行四边形，如图2，且OC⊥AC，过点B1作B1F∥轴，与对角线AC、边OC分别交于点E、点A．若B1E： B1F=1：3，点B1的横坐标为，求点B1的纵坐标，并直接写出的取值范围．20 . 如图，在平面直角坐标系中，函数y＝（k≠0，x＞0）的图象经过点A（3，4），直线AC与x轴交于点C（6，0），过点C作x轴的垂线BC交函数y＝（k≠0，x＞0）的图象于点A．（1）求k的值及点B的坐标（2）在平面内存在点D，使得以A、B、C、D为顶点的四边形是平行四边形，直接写出符合条件的所有点D的坐标．21 . 已知矩形，为边上一点，，点从点出发，以每秒个单位的速度沿着边向终点运动，连接，设点运动的时间为秒，则当的值为__________时，是以为腰的等腰三角形．22 . 如图，点C是等边△ABD的边AD上的一点，且∠ACB＝75°，⊙O是△ABC的外接圆，连结AO并延长交BD于E、交⊙O于A．（1）求证：∠BAF＝∠CBD；（2）过点C作CG∥AE交BD于点G，求证：CG是⊙O的切线；（3）在（2）的条件下，当AF＝2时，求的值．23 . 如图，网格中每一个小正方形的边长为1个单位长度．可以利用平面直角坐标系的知识回答以下问题：(1)请在所给的网格内画出以线段AB、BC为边的平行四边形ABCD；(2)填空：平行四边形ABCD的面积等于____．24 . 已知．（1）求的值；（2）若，求、、．25 . 如图，已知：E是∠AOB的平分线上一点，EC⊥OB，ED⊥OA，C、D是垂足，连接CD，且交OE于点F. （1）求证：DF=CF.（2）若∠AOB=60º，请你探究OE，EF之间有什么数量关系？并证明你的结论。

初三数学提高试题及答案一、选择题（每题3分，共30分）1. 若a、b、c是三角形的三边，且a²+b²=c²，则三角形的形状是（）。

A. 锐角三角形B. 直角三角形C. 钝角三角形D. 不等边三角形答案：B2. 下列哪个选项是二次函数y=ax²+bx+c（a≠0）的图像与x轴有两个交点的充分不必要条件？（）A. b²-4ac＞0B. b²-4ac=0C. b²-4ac＜0D. b²-4ac≥0答案：A3. 已知方程x²-2x+1=0的根是（）。

A. 1B. -1C. 1或-1D. 无实数根答案：A4. 已知函数y=kx+b（k≠0），若点（2，1）在函数的图像上，则下列哪个选项一定正确？（）A. k+b=1B. 2k+b=1C. k-b=2D. 2k-b=1答案：B5. 已知a、b、c是三角形的三边，下列哪个选项是三角形的周长为6的充分不必要条件？（）A. a+b+c=6B. a+b＞cC. a+c＞bD. b+c＞a答案：A6. 已知函数y=-2x+3与y=6-x的图像相交于点（m，n），则m+n的值为（）。

A. 3B. 5C. 7D. 9答案：B7. 已知a、b、c是三角形的三边，下列哪个选项是三角形的周长为6的充分不必要条件？（）A. a+b+c=6B. a+b＞cC. a+c＞bD. b+c＞a答案：A8. 已知方程x²-2x+1=0的根是（）。

A. 1B. -1C. 1或-1D. 无实数根答案：A9. 已知函数y=kx+b（k≠0），若点（2，1）在函数的图像上，则下列哪个选项一定正确？（）A. k+b=1B. 2k+b=1C. k-b=2D. 2k-b=1答案：B10. 已知a、b、c是三角形的三边，下列哪个选项是三角形的周长为6的充分不必要条件？（）A. a+b+c=6B. a+b＞cC. a+c＞bD. b+c＞a答案：A二、填空题（每题4分，共20分）11. 已知a、b、c是三角形的三边，且a²+b²=c²，则三角形的形状是直角三角形。

上海市2019届一模提升题汇编第24题（二次函数综合）含2019上海中考试题中考【2019届一模徐汇】24．（本题满分12分，第（1）小题4分，第（2）小题4分，第（3）小题4分）如图，在平面直角坐标系xoy 中，顶点为M 的抛物线C 1:2(0)y ax bx a =+<经过点A 和x 轴上的点B ，AO =OB =2，120AOB ∠=．（1）求该抛物线的表达式； （2）联结AM ，求AOMS；（3）将抛物线C 1向上平移得到抛物线C 2，抛物线C 2与x 轴分别交于点E 、F （点E 在点F 的左侧），如果△MBF 与△AOM 相似，求所有符合条件的抛物线C 2的表达式．【24．解：（1）过A 作AH ⊥x 轴，垂足为H ，∵OB=2，∴B （2,0）………………………………（1分） ∵120AOB ∠=︒∴60,30AOH HAO ∠=︒∠=︒．∵OA=2，∴112OH OA ==．∵222Rt AHO OH AH OA +=在中，，∴22213AH =-=．∴(1,3)A --……………………………………（1分）（第24题图）∵抛物线21:C y ax bx A B=+经过点、，∴可得：42033a a b a b b ⎧=-⎪+=⎧⎪⎪⎨⎨-=⎪⎩⎪=⎪⎩………………………………………………（1分）∴这条抛物线的表达式为233y x x =-+…………………………………………（1分）（2）过M 作MG ⊥x 轴，垂足为G，∵2y x x =+∴顶点M是⎛ ⎝⎭，得3MG = ……………………………………………………（1分）∵(1,A -，M⎛ ⎝⎭． ∴得：直线AM为33y x =- …………………………………………………（1分）∴直线AM 与x 轴的交点N 为1,02⎛⎫⎪⎝⎭……………………………………………………（1分）∴1122AOM S ON MG ON AH ∆=⋅+⋅111122322=⨯⨯+⨯=…………………………………………………………………………（1分）（3）∵）33，1（M 、)0,2(B ，∴3MG Rt BGM MBG BG ∆∠=在中，tan =，∴MBG ∠︒=30．∴MBF 150∠=︒．由抛物线的轴对称性得：MO=MB ，∴MBO MOB=150∠=∠︒． ∵OB=120A ∠︒，∴OM=150A ∠︒ ∴OM=MBF A ∠∠．∴BM BFOA OM 或BF BM OA OM 相似时，有：AOM 与MBF 当==∆∆ 即332BF 2332或BF 3322332==，∴32BF 或2BF ==． ∴）0，38）或（0，4（F ………………………………………………（2分）设向上平移后的抛物线k x x y ++-=33233:为C 22，当）0，4（F 时，338=k ，∴抛物线33833233:为C 22++-=x x y …（1分）当）0，38（F 时，27316=k ，抛物线22:3327C y x x =-++……．（1分）】【2019届一模浦东】24. （本题满分12分，其中每小题各4分）已知：如图9，在平面直角坐标系xOy 中，直线12y x b=-+与x 轴相交于点A ，与y 轴相交于点B. 抛物线（1）求抛物线的表达式; （2）求证: △BOD ∽△AOB;（3）如果点P 在线段AB 上，且∠BCP=∠DBO求点P 的坐标.【24、（1）211482y x x =-++；（2）证明略；（3）1612,55⎛⎫ ⎪⎝⎭】【2019届一模杨浦】24．（本题满分12分，每小题各4分） 在平面直角坐标系xOy 中，抛物线2(0)yax bx c a与y 轴交于点C （0,2），它的顶点为D （1,m ），且1tan 3COD.（1）求m 的值及抛物线的表达式；（2）将此抛物线向上平移后与x 轴正半轴交于点A ，与y 轴交于点B ，且OA=OB.若点A 是由原抛物线上的点E 平移所得，求点E 的坐标；（3）在（2）的条件下，点P 是抛物线对称轴上的一点（位于x 轴上方），且∠APB=45°.求P 点的坐标.Oxy1 2 3 4 1 23 4 5-1 -2 -3-1 -2 -3 （第24题图）【24．解：（1）作DH ⊥y 轴，垂足为H ，∵D （1,m ）（0m），∴DH= m ，HO=1.∵1tan 3COD，∴13OH DH ，∴m=3. ····················································· （1分）∴抛物线2y ax bx c 的顶点为D （1,3）. 又∵抛物线2yax bxc 与y 轴交于点C （0,2）， ∴3,1,22.ab c ba c （2分）∴1,2,2.a b c∴抛物线的表达式为222y x x.······ （1分）（2）∵将此抛物线向上平移， ∴设平移后的抛物线表达式为222(0)y x x k k，. ···························· （1分）则它与y 轴交点B （0,2+k ）.∵平移后的抛物线与x 轴正半轴交于点A ，且OA=OB ，∴A 点的坐标为（2+k,0）. .（1分） ∴20(2)2(2)2k k k .∴122,1k k .∵0k，∴1k.∴A （3,0），抛物线222y x x向上平移了1个单位. . ······························ （1分）∵点A 由点E 向上平移了1个单位所得，∴E （3,-1）. . ··································· （1分） （3）由（2）得A （3,0），B （0, 3），∴32AB.∵点P 是抛物线对称轴上的一点（位于x 轴上方），且∠APB=45°,原顶点D （1,3）, ∴设P （1,y ），设对称轴与AB 的交点为M ，与x 轴的交点为H ，则H （1,0）. ∵A （3,0），B （0, 3），∴∠OAB=45°, ∴∠AMH=45°. ∴M （1,2）. ∴2BM.∵∠BMP=∠AMH, ∴∠BMP=45°. ∵∠APB=45°, ∴∠BMP=∠APB.∵∠B=∠B ，∴△BMP ∽△BPA. ·································································· （2分）B APy OM H∴BP BABMBP .∴23226BPBA BM∴221(3)6BPy .∴123535y y ，（舍）.. ···························· （1分）∴(1,35)P . . ····················································································· （1分）】【2019届一模普陀】 24．（本题满分12分） 如图10，在平面直角坐标系中，抛物线23y ax bx =+-(0)a ≠与x 轴交于点A ()1,0-和点B ，且3OB OA =，与y 轴交于点C ，此抛物线顶点为点D ．（1）求抛物线的表达式及点D 的坐标；（2）如果点E 是y 轴上的一点（点E 与点C 不重合），当BE DE ⊥时，求点E 的坐标； （3）如果点F 是抛物线上的一点，且，求点F 的坐标．135FBD ∠=xOy图10【24．解：（1）∵抛物线与x 轴交于点A ()1,0-和点，且3OB OA =，∴点的坐标是()3,0． ··········································································· （1分）解法一：由抛物线23y ax bx =+-经过点()1,0-和()3,0． 得03,093 3.a b a b =--⎧⎨=+-⎩ 解得1,2.a b =⎧⎨=-⎩ ······························································ （1分）∴抛物线的表达式是223y x x =--． ······················································ （1分）点D 的坐标是()1,4-． ············································································· （1分）解法二：由抛物线23y ax bx =+-经过点()1,0-和()3,0． 可设抛物线的表达式为(1)(3)y a x x =+-， 由抛物线与y 轴的交点C 的坐标是()0,3-，得3(01)(03)a -=+-，解得1a =． ······························································ （1分）∴抛物线的表达式是223y x x =--． ························································ （1分）点D 的坐标是()1,4-． ············································································· （1分）（2）过点D 作DH OC ⊥，H 为垂足． ∴90DHO ∠=．∴90DEH EDH ∠+∠=． ∵BE DE ⊥，∴90DEH BEO ∠+∠=． ∴BEO EDH ∠=∠．又∵BOE EHD ∠=∠，∴△BOE ∽△EHD ． ········································· （1分）∴BO OEEH HD =．∵点D 的坐标是()1,4-，∴1DH =，4OH =．B B∵点的坐标是()3,0，∴3OB =．∴341OEOE =-． ·············································································· （1分）∴1OE =或3OE =． ················································································ （1分） ∵点E 与点C 不重合，∴1OE =． ∴点E 的坐标是()0,1-． ··········································································· （1分）（3）过点F 作FG x ⊥轴，G 为垂足．作45DBM ∠=，由第（2）题可得，点M 与点E 重合． ∵1OE =，1DH =，∴OE DH =． 可得△BOE ≌△EHD ． ∴BE ED =． ∵90BED ∠=，∴45DBE ∠=． ∵135FBD ∠=，∴90FBE ∠=． ················································································ （1分） ∴OBE GFB ∠=∠．∴在Rt △BOE 中，90BOE ∠=，∴cot 3OBE ∠=∴cot 3GFB ∠=． ·········· （1分） ∴3FG BG =．设点F 点的坐标为()2,23m mm --．∴223FG m m =--,3BG m =-．∴2233(3)m m m --=-． ··································································· （1分）解得3m =，4m =-． ∵3m =不合题意舍去，∴4m =-． 点F 的坐标是()4,21-． ·········································································· （1分）】【2019届一模奉贤】24．（本题满分12分，每小题满分6分）B如图10，在平面直角坐标系中，直线AB 与抛物线2yax bx 交于点A(6，0)和点B(1，－5)．（1）求这条抛物线的表达式和直线AB 的表达式；（2）如果点C 在直线AB 上，且∠BOC 的正切值是32，求点C 的坐标．【24．解：（1）由题意得，抛物线2yax bx 经过点A(6，0)和点B(1，－5)，代入得3660,5.a b a b 解得1,6.ab∴抛物线的表达式是26y x x =-. ······ （4分）由题意得，设直线AB 的表达式为ykxb ，它经过点A(6，0)和点B(1，－5)，代入得60,5.k bk b解得1,6.k b∴直线AB 的表达式是6y x =-. ········ （2分）（2）过点O 作OH AB ，垂足为点H ．设直线AB 与y 轴交点为点D ，则点D 坐标为()0,6-.∴45ODA OAD，cos45DH OH OD ==•︒= ∵2BD，∴22BH.在Rt △OBH 中，90OHB ，3tan 2OHOBHBH． ······························· （2分）∵∠BOC 的正切值是32，∴BOCCBO . ··············································· （1分） ①当点C 在点B 上方时，BOCCBO .∴COCB ． 设点C(,6)x x -，2222(6)(1)(65)x x xxOy图10ABxyo解得174x，1776644x .--------------------------------------------------------------------（2分）所以点D坐标为177,44⎛⎫-⎪⎝⎭. ②当点C 在点B 下方，BOC CBO 时，OC//AB. 点C 不在直线AB 上. ········ （1分）综上所述，如果∠BOC 的正切值是32，点C 的坐标是177,44⎛⎫-⎪⎝⎭．】【2019届一模松江】24.（本题满分12分，第（1）小题3分，第（2）小题4分，第（3）小题5分）如图，抛物线cbx x y ++-=221经过点A （﹣2，0），点B （0，4）.（1）求这条抛物线的表达式；（2）P 是抛物线对称轴上的点，联结AB 、PB ，如果∠PBO=∠BAO ，求点P 的坐标； （3）将抛物线沿y 轴向下平移m 个单位，所得新抛物线与y 轴交于点D ，过点D 作DE∥x 轴交新抛物线于点E ，射线EO 交新抛物线于点F ，如果EO=2OF ，求m 的值.【24．解：（1）∵抛物线经过点A （﹣2，0），点B （0，4）∴⎩⎨⎧==+--4022c c b …………（1分）， 解得14b c =⎧⎨=⎩………………………（1分） ∴抛物线解析式为2142y x x =-++ …………………………………………（1分）(第24题图)y xOBA（2）()2912142122+--=++-=xxxy…………………………………（1分）∴对称轴为直线x=1，过点P作PG ⊥y轴，垂足为G ∵∠PBO=∠BAO，∴tan∠PBO=tan∠BAO，∴PG BOBG AO=……………………………………………（1分）∴121BG=，∴12BG=…………………………………（1分）∴72OG=，∴P（1，27）………………………………（1分）（3）设新抛物线的表达式为2142y x x m=-++-…（1分）则()0,4D m-,()2,4E m-，DE=2……………………（1分）过点F作FH⊥y轴，垂足为H，∵DE∥FH，EO=2OF∴2=1DE EO DOFH OF OH==，∴FH=1……………………………………………（1分）点D在y轴的正半轴上，则51,2F m⎛⎫--⎪⎝⎭，∴52OH m=-∴42512DO mOH m-==-，∴m=3……………………………………………………（1分）点D在y轴的负半轴上，则91,2F m⎛⎫-⎪⎝⎭，∴92OH m=-∴42912DO mOH m-==-，∴m=5……………………………………………………（1分）∴综上所述m的值为3或5.】(第24题图)yx OBAEDF H【2019届一模嘉定】24．（本题满分12分，每小题4分）在平面直角坐标系xOy （如图7）中，抛物线22++=bx ax y 经过点)0,4(A 、)2,2(B ，与y 轴的交点为C ．（1）试求这个抛物线的表达式；（2）如果这个抛物线的顶点为M ，求△AMC 的面积； （3）如果这个抛物线的对称轴与直线BC 交于点D ，点E 在线段AB 上，且︒=∠45DOE ，求点E 的坐标．【24. 解：（1）∵抛物线22++=bx ax y 点经过)0,4(A 、)2,2(B ∴⎩⎨⎧=++=++222402416b a b a ……………………1分 ∴⎪⎪⎩⎪⎪⎨⎧=-=2141b a …………2分 ∴抛物线的表达式是221412++-=x x y …………1分 （2）由（1）得：抛物线221412++-=x x y 的顶点M 的坐标为)49,1(……1分图7O 11-1 -1∴点C 的坐标为)0,2(， ……………………1分 过点M 作y MH ⊥轴，垂足为点H ∴AOCMHC AOHM AMC S S S S ∆∆∆--= …………1分∴42211412149)41(21⨯⨯-⨯⨯-⨯+⨯=∆AMC S∴23=∆AMC S …………1分（3）联结OB过点B 作x BG ⊥轴，垂足为点G∵点B 的坐标为)2,2(，点A 的坐标为)0,4(∴2=BG ，2=GA ∴△BGA 是等腰直角三角形∴︒=∠45BAO 同理：︒=∠45BOA∵点C 的坐标为)0,2(∴2=BC ，2=OC 由题意得，△OCB 是等腰直角三角形 ∴︒=∠45DBO ,22=BO ∴DBO BAO ∠=∠∵︒=∠45DOE ∴︒=∠+∠45BOE DOB ∵︒=∠+∠45EOA BOE ∴DOB EOA ∠=∠ ∴△AOE ∽△BOD∴BO AOBD AE =…………1分 ∵抛物线221412++-=x x y 的对称轴是直线1=x ，∴点D 的坐标为)2,1(∴1=BD …………1分∴2241=AE ∴2=AE …………1分过点E 作x EF ⊥轴，垂足为点F 易得，△AFE 是等腰直角三角形 ∴1==AF EF∴点E 的坐标为)1,3( …………1分】 【2019届一模青浦】24．（本题满分12分， 其中第（1）小题3分，第（2）小题5分，第（3）小题4分）在平面直角坐标系xOy 中，将抛物线2y x =-平移后经过点A （-1，0）、B （4，0），且平移后的抛物线与y 轴交于点C （如图）． （1）求平移后的抛物线的表达式；（2）如果点D 在线段CB 上，且CAD 的正弦值；（3）点E 在y 轴上且位于点C 的上方，点P 在直线BC 上，点Q 在平移后的抛物线上，如果四边形ECPQ 是菱形，求点Q 的坐标．【24．解：（1）设平移后的抛物线的解析式为2+=-+y x bx c ． ······················· （1分）将A （-1，0）、B （4，0），代入得（第24题图）（备用图）101640.，--+=⎧⎨-++=⎩b c b c ··············································································· （1分） 解得：34.，=⎧⎨=⎩b c所以，2+34=-+y x x ． ·········································································· （1分）（2）∵2+34=-+y x x ，∴点C 的坐标为（0，4） ····································· （1分）．设直线BC 的解析式为y= kx+4，将B （4，0），代入得kx+4=0，解得k=-1，∴y= -x+4． ········································································································ 设点D 的坐标为（m ，4- m ）．∵，∴22=2m ，解得=1m 或=1-m （舍去），∴点D 的坐标为（1，3）． ········································································· （1分） 过点D 作DM ⊥AC ，过点B 作BN ⊥AC ，垂足分别为点M 、N ．∵1122⋅=⋅AC BN AB OC54=⨯BN，∴17=BN ． ········ （1分） ∵DM ∥BN ，∴=DM CD BN CB，∴=DM BN，∴17=DM ． ···················· （1分）∴sin =17221∠==DM CAD AD ． ············································· （1分）（3）设点Q 的坐标为（n ，2+34-+n n ）．如果四边形ECPQ 是菱形，则0>n ，PQ ∥y 轴，PQ=PC ，点P 的坐标为（n ，4-+n ）．∵22+3444=-++-=-PQ n n n n n，=PC ， ····································· （2分）∴24-n n，解得=4n 或=0n （舍）． ·········································· （1分） ∴点Q的坐标为（4，2）． ···················································· （1分）】【2019届一模静安】24．（本题满分12分，其中第（1）小题4分，第（2）小题3分，第（3）小题5分）在平面直角坐标系xOy 中（如图10），已知抛物线2(0)y ax bx c a =++≠的图像经过点(40)B ，、(53)D ，，设它与x 轴的另一个交点为A （点A 在点B 的左侧），且ABD ∆的面积是3．（1）求该抛物线的表达式； （2）求ADB ∠的正切值；（3）若抛物线与y 轴交于点C ，直线CD 交x 轴于点E ，点P 在射线AD 上，当APE ∆与 ABD ∆相似时，求点P 的坐标．【24．解：（1）过点D 作DH ⊥x 轴，交x 轴于点H ．∵132ABD S AB DH ∆=⋅=，又∵(5,3)D∴2AB =．····························································································· （1分） ∵(4,0)B ，点A 在点B 的左侧，∴(2,0)A ． ····························································································· （1分）把(2,0)A ，(4,0)B ，(5,3)D 分别代入2y ax bx c =++， 得04201643255a b ca b c a b c =++⎧⎪=++⎨⎪=++⎩解得168a b c =⎧⎪=-⎨⎪=⎩． ···························································· （1分）∴抛物线解析式是268y x x =-+． ······························································ （1分）（2）过点B 作BG AD ⊥，交AD 于点G ． ··················································· （1分）BD O图10xy﹒ ﹒由(2,0)A ，(5,0)H ，(5,3)D ，得ADH ∆是等腰直角三角形，且45HAD ∠=∵3AH DH ==，∴AD = ································································ （1分） ∴在等腰直角AGB ∆中，由2AB =，得AG BG ==，∴DG AD AG =-=∴在Rt DGB ∆中，1tan 2BG ADB DG ∠==． ·················································· （1分）（3）∵抛物线268y x x =-+与y 轴交于点(0,8)C ，又(5,3)D ，∴直线CD 的解析式为8y x =-+，∴(8,0)E ． ···························································································· （1分） 当点P 在线段AD 上时，APE ∆∽ABD ∆，点,,A P E 分别与点,,A B D 对应，则AP AE AB AD =，即AB AE AP AD ⨯===．………………………………………（1分）··························································································································· 过点P 作PQ ⊥∴2AQ PQ ==，即(4,2)P ． ····································································· （1分） ②当点P 在线段AD 延长线上时，APE ADB ∠=∠， ·················································· ∴EP //DB过点P 作PR x ⊥轴于点R ， ··················································································13AH AD AB AR AP AE ===，∴9AR PR ==， ······················································································ （1分） 即(11,9)P ． ···························································································· （1分） ∴APE ∆与ABD ∆相似时，点P 的坐标为 (4,2)或 (11,9)．】 【2019届一模宝山】24．（本题满分12分，第(1)小题满分6分，第(2)小题满分6分） 如图9，已知：二次函数的图像交x 轴正半轴于点A ，顶点为P,一次函数2y x bx=+。

初三数学提升试题及答案一、选择题（每题3分，共30分）1. 下列哪个选项是方程x^2 - 4x + 4 = 0的解？A. x = 0B. x = 2C. x = -2D. x = 42. 已知a、b、c是等差数列，且a + c = 10，b = 4，那么a和c的值分别是？A. a = 2, c = 8B. a = 3, c = 7C. a = 4, c = 6D. a = 5, c = 53. 一个圆的半径是5厘米，那么这个圆的面积是多少平方厘米？A. 25πC. 75πD. 100π4. 函数y = 2x + 3的图象不经过哪个象限？A. 第一象限B. 第二象限C. 第三象限D. 第四象限5. 下列哪个选项是不等式2x - 3 < 5的解集？A. x < 4B. x > 4C. x < 2D. x > 26. 如果一个数的平方根是2，那么这个数是多少？A. 4C. 2D. -27. 一个等腰三角形的底边长为6厘米，高为4厘米，那么这个三角形的周长是多少？A. 16厘米B. 18厘米C. 20厘米D. 22厘米8. 一个二次函数y = ax^2 + bx + c的顶点坐标是(1, -2)，且经过点(0, 3)，那么a的值是多少？A. 1B. -1C. 2D. -29. 一个正方体的体积是8立方厘米，那么这个正方体的棱长是多少？A. 2厘米B. 4厘米C. 8厘米D. 16厘米10. 一个角的余角是30°，那么这个角的度数是多少？A. 60°B. 90°C. 120°D. 150°二、填空题（每题4分，共20分）11. 计算：(3x^2 - 2x + 1) - (x^2 - 4x + 3) = ________。

12. 一个直角三角形的两条直角边长分别为3和4，那么这个三角形的斜边长是______。

13. 已知一个函数的解析式为y = 3x - 2，当x = 2时，y的值是______。

沪教版（上海）九年级上学期期末拓展提高卷姓名:________ 班级:________ 成绩:________一、单选题1 . 一架5米长的梯子斜靠在墙上，测得它与地面的夹角为，则梯子底端到墙角的距离为（）A．米B．米C．米D．米2 . 如图，已知△ABC中，两条中线AE、CF交于点G，设，，则向量关于、的分解式表示正确的为（）A．B．C．D．3 . 已知，在中，，则边的长度为（）A．B．C．D．4 . 如图，在平面直角坐标系中有一个3×3的正方形网格，其左下角格点A的坐标为（1，1），右上角格点B 的坐标为（4，4），若分布在直线两侧的格点数相同，则k的取值可以是（）A．B．2C．D．5 . 将抛物线向右平移一个单位，向上平移2个单位得到抛物线A．B．C．D．6 . 下列说法正确的是（）A．矩形都是相似图形B．各角对应相等的两个五边形相似C．等边三角形都是相似三角形D．各边对应成比例的两个六边形相似二、填空题7 . 如图，已知在平行四边形中，，，．（1）用、表示、；（直接写出答案）（2）求作分别在、方向上的分向量．（不要求写作法，但要指出图中表示结论的向量）8 . 如果两个相似三角形对应边之比是，那么它们的对应中线之比是___________．9 . 计算：______.10 . 抛物线的顶点坐标为______.11 . 请将下图中的相似图形的序号写出来：_______________________________12 . 已知二次函数y=ax2+bx+c的图象如图所示，它与x轴的两个交点分别为（-1，0），（3，0）．对于下列命题：①b-2a=0；②abc＜0；③a-2b+4c＜0；④8a+c＞0．其中正确的有____________。

13 . 如图，O是等边△ABC外接圆的圆心，连结OA、OB、OC，以点A为圆心，以⊙O的直径为半径画弧分别交AB、AC的延长线于点D、E．若OA=2，则图中阴影部分图形的面积和为______(结果保留根号和π)．14 . 已知是任一向量，，，用表示，其结果是______．15 . 若两个三角形的相似比为3：4，则这两个三角形的面积比为________．16 . 甲、乙两施工队共同完成某居民小区绿化改造工程，乙队先单独做2天后，再由甲、乙两队合作，一共用10天就完成了全部工程．已知乙队单独完成此项工程所需天数与甲队单独完成此项工程所需天数之比是4:5，求甲、乙两个施工队单独完成此项工程各需多少天．若设甲队单独完成此项工程需天，则根据题意可列方程为_________________．17 . 阅读下面材料：在数学课上，老师提出如下问题：已知：如图1△ABC，尺规作图：求作∠APC＝∠ABC.甲、乙两位同学的主要作法如下：甲同学的主要作法，如图甲：①作∠CAD＝∠ACB，且点D与点B在AC的异侧；②在射线AD上截取AP＝CB，连结CP.所以∠APC＝∠ABC.乙同学的主要作法，如图乙：①作线段BC的垂直平分线a；②作线段AB的垂直平分线b，与直线a交于点O；③以点O为圆心，OA为半径作⊙O；④在上取一点P（点P不与点A，B，C重合），连结AP，CP.所以∠ACP＝∠ABC.老师说：“两位同学的作法都是正确的.”请你选择一位同学的作法，并说明这位同学作图的依据.我选择的是_________的作法，这样作图的依据是_________.18 . 已知二次函数y=3(x-a)2的图象上，当x>2时，y随x的增大而增大，则a的取值范围是___.三、解答题19 . 某海域有A，B两个岛屿，B岛屿在A岛屿北偏西30°方向上，距A岛120海里，有一艘船从A岛出发，沿东北方向行驶一段距离后，到达位于B岛屿南偏东75°方向的C处，求出该船与B岛之间的距离CB的长（结果保留根号）．20 . 如图，在平面直角坐标系中，A是抛物线上的一个动点，且点A在第一象限内．AE⊥y轴于点E，点B坐标为（0，2），直线AB交轴于点C，点D与点C关于y轴对称，直线DE与AB相交于点F，连结BD．设线段AE的长为m，△BED的面积为S．（1）当时，求S的值．（2）求S关于的函数解析式．（3）①若S＝时，求的值；②当m＞2时，设，猜想k与m的数量关系并证明．21 . 已知□ABCD，点E是 BC边的中点，请回答下列问题：（1）在图中求作与的和向量：= ；（2）在图中求作与的差向量： = ；（3）如果把图中线段都画成有向线段，那么在这些有向线段所表示的向量中，所有与互为相反向量的向量是；(4) = .22 . 如图1，抛物线y＝ax2+bx﹣3与x轴交于A（1，0）、B两点，与y轴交于点C，抛物线的对称轴为直线x ＝2，交抛物线于点D，交x轴于点A．（1）请直接写出：抛物线的函数解析式及点B、点D的坐标；（2）抛物线对称轴上的一动点P从点D出发，以每秒1个单位的速度向上运动，连接OP，BP，设运动时间为t秒（t＞0）．在点P的运动过程中，请求出：当t为何值时，∠OPB＝90°？（3）如图2，点Q在抛物线上运动（点Q不与点A、B重合），当△QBC的面积与△ABC的面积相等时，请求出点Q 的坐标．23 . 计算：（1）；（2）.24 . 如图，△ABC中，AD、AE 分别是边BC上的中线和高，AE＝4，S△ABD＝10，求BC，CD 的长.25 . 如图,已知二次函数的图象与轴交于A、B两点，与轴交于点P，顶点为C（1，-2）.（1)求此函数的关系式；（2)作点C关于轴的对称点D，顺次连接A、C、B、D.若在抛物线上存在点E，使直线PE将四边形ABCD分成面积相等的两个四边形，求点E的坐标；（3）在（2）的条件下，抛物线上是否存在一点F，使得△PEF是以P为直角顶点的直角三角形？若存在，求出点F的坐标及△PEF的面积；若不存在，请说明理由.参考答案一、单选题1、2、3、4、5、6、二、填空题1、2、3、4、5、6、7、8、9、10、11、12、三、解答题1、2、3、4、5、6、7、。

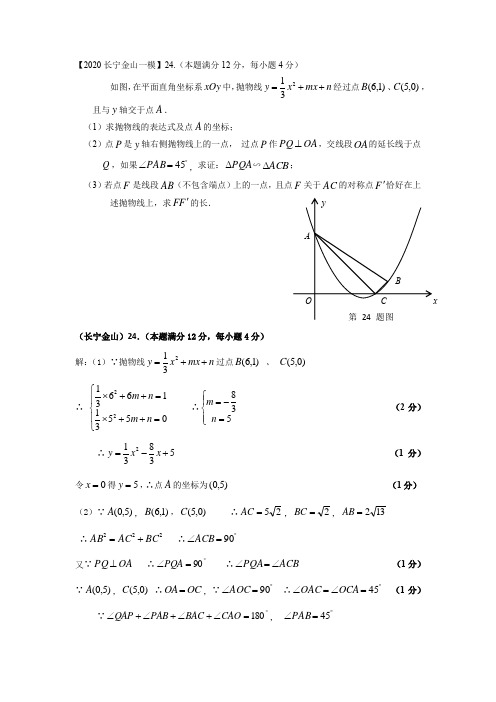
【2020长宁金山一模】24.（本题满分12分，每小题4分）如图，在平面直角坐标系xOy 中，抛物线n mx x y ++=231经过点)1,6(B 、)0,5(C ，且与y 轴交于点A ．（1）求抛物线的表达式及点A 的坐标；（2）点P 是y 轴右侧抛物线上的一点， 过点P 作OA PQ ⊥，交线段OA 的延长线于点Q ，如果︒=∠45PAB ，求证：PQA Δ∽ACB Δ；（3）若点F 是线段AB （不包含端点）上的一点，且点F 关于AC 的对称点F '恰好在上述抛物线上，求F F '的长．（长宁金山）24．（本题满分12分，每小题4分） 解：（1）∵抛物线n mx x y ++=231过点)1,6(B 、 )0,5(C ∴ ⎪⎩⎪⎨⎧=++⨯=++⨯055311663122n m n m ∴⎪⎩⎪⎨⎧=-=538n m （2分） ∴538312+-=x x y （1分） 令0=x 得5=y ，∴点A 的坐标为)5,0( （1分） （2）∵)5,0(A ，)1,6(B ，)0,5(C ∴25=AC ，2=BC ，132=AB∴222BC AC AB += ∴︒=∠90ACB又∵OA PQ ⊥ ∴︒=∠90PQA ∴ACB PQA ∠=∠ （1分） ∵)5,0(A ，)0,5(C ∴OC OA =，∵︒=∠90AOC ∴︒=∠=∠45OCA OAC （1分） ∵︒=∠+∠+∠+∠180CAO BAC PAB QAP ， ︒=∠45PAB第24题图yxCABO∴︒=∠+∠90BAC QAP ∵︒=∠+∠90BAC ABC ∴ABC QAP ∠=∠ （1分） ∴PQA Δ∽ACB Δ （1分） （3）设点B '是点B 关于直线AC 的对称点，则2=='BC C B ，︒=∠='∠90ACB B AC过点B 作x B ⊥'G 轴，垂足为点G ∵︒=∠+'∠90OCA CO B ， ︒=∠45OC A ，∴︒='∠45CO B ∴1=='GC G B ∴），（1-4B ' （1分）∵点F '同时在线段B A '与抛物线上 ，∴设)53831,(F 2+-'x x x 分别过点F '，B '作轴y H F ⊥'，轴y H ⊥''B ，垂足分别为H 、H '，则H B H//F '''∴H A AH H B H F B A F A '='''='' 即6313842xx x -= ∴27=x （1分） 又∵AC F F ⊥'，AC B B ⊥' ∴B //B F F '' ∴B B F F B A F A ''='' ∴ 87427=='''=''H B H F B B F F （1分）∵222==BC BB ∴8722='F F ∴247='F F （1分）【2020杨浦一模】已知在平面直角坐标系 xOy 中，抛物线 y = mx 2 - 2mx + 4(m ≠ 0) 与 x 轴交于点 A 、B （点 A 在点 B 的左侧）， 且 AB =6.（1） 求这条抛物线的对称轴及表达式；（2） 在 y 轴上取点 E （0,2），点 F 为第一象限内抛物线上一点，联结 BF 、EF ，如果 S 四边形OEFB= 10 ，求点 F 的坐标；（3） 在第（2）小题的条件下，点 F 在抛物线对称轴右侧，点 P 在 x 轴上且在点 B 左侧，如果直线 PF 与 y 轴的夹角等于∠EBF ，求点 P 的坐标.（杨浦）24．解：（1）抛物线对称轴212mxm... ................................................ （1分）∵AB =6，∴抛物线与x 轴的交点A 为(20)，，B (40)，.. ............................................... （1分） ∴4440m m （或16840m m）.. .............................................................. （1分）∴12m.∴抛物线的表达式为2142y x x . ................................................... （1分）（2）设点F 21(4)2x x x，. ..................................................................................... （1分）∵点E 02-（，），点B 4（，0），∴OE = 2，OB = 4. ∵=+10OEF OBF OEFB S S S ∆∆=四边形， ∴211124(4)10222x x x ⨯⨯+⨯⨯-++=.. .................. （1分）∴12x =或，∴点F 912（，）、24（，）.. .............................................................................. （2分）（3）∵=+10OBE BEF OEFB S S S ∆∆=四边形，又1142422OBE S OB OE ∆=⋅=⨯⨯=，∴6BEF S ∆=.过F 作FH BE ⊥，垂足为点H .∵162BEF S BE FH ∆=⋅=，又222425BE =+=，∴655FH =. ............................. （1分）又22(24)(40)25BF =-+-=，∴855BH =. ∴在Rt BFH ∆中，tan ∠EBF=65358455FH BH ==.................................................................. （1分） 设直线PF 与y 轴的交点为M ，则∠PMO=∠EBF ，过F 作FG x ⊥轴，垂足为点G.∵FG//y 轴，∴∠PMO=∠PFG . ∴tan ∠PFG=tan ∠EBF . .................................................. （1分）∴tan ∠PFG=34PG FG =.又FG =4，∴PG =3.∴点P 的坐标10（-，）. ........................................................................................................ （1分）【2020徐汇一模】 24．（本题满分12分）如图，将抛物线4342+-=x y 平移后，新抛物线经过原抛物线的顶点C ，新抛物线与x 轴正半轴交于点B ，联结BC ，4tan =B ，设新抛物线与x 轴的另一交点是A ，新抛物线的顶点是D ．（1）求点D 的坐标；（2）设点E 在新抛物线上，联结AC 、DC ，如果CE 平分DCA ∠，求点E 的坐标；（3）在（2）的条件下，将抛物线4342+-=x y 沿x 轴左右平移，点C 的对应点为F ，当DEF ∆和ABC ∆相似时，请直接写出平移后所得抛物线的表达式．（第24题图）AD CB O x y（徐汇）24．解：（1）由题意，设新抛物线的表达式为4342++-=bx x y ． ∵抛物线4342+-=x y 的顶点为C ，∴)4,0(C ，4=OC ； 在BOC Rt ∆中，︒=∠90BOC ， ∴4tan ==OBOCB ，得1=OB ；∴)0,1(B ； 由题意，得0434=++-b ，解得38-=b ； ∴新抛物线的表达式为438342+--=x x y ；∴)316,1(-D ． （2）由题意，可得)0,3(-A ；过点D 作OC DM ⊥，垂足为M ．∴)316,0(M ； ∴4,3,34,1====CO AO CM DM ；∴43==CO AO CM DM ； 又︒=∠=∠90AOC DMC ，∴DMC ∆∽AOC ∆， ∴ACO DCM ∠=∠；∵CE 平分DCA ∠，∴ACE DCE ∠=∠；∴︒=∠+∠180)(2DCE DCM ；∴AOC MCE ∠=︒=∠90； ∴AO CE //；∴点E 与点C 关于直线1-=x 对称；∴)4,2(-E ． （3）有两种情况满足要求，平移后所得抛物线的表达式为：4)32(342++-=x y 或4)121(342+--=x y【2020松江一模】24．（本题满分12分,第（1）小题3分，第（2）小题4分，第（3）小题5分）如图，已知抛物线y ＝﹣x 2+bx +c 经过点A (3,0)，点B （0,3）.点M （m ，0）在线段OA 上（与点A ，O 不重合），过点M 作x 轴的垂线与线段AB 交于点P ，与抛物线交于点Q ，联结BQ ．（1）求抛物线表达式；（2）联结OP ，当∠BOP =∠PBQ 时，求PQ 的长度； （3）当△PBQ 为等腰三角形时，求m 的值.24.解：（1）∵抛物线y ＝﹣x 2+bx +c 经过点A (3,0)，点B （0,3）.∴3,930.c b c =⎧⎨-++=⎩………………………………（1分） ∴b =2，c =3………（1分）∴抛物线表达式为y ＝﹣x 2+2x +3………（1分） （2）∵PM ⊥x 轴 ∴PM ∥y 轴 ∴∠OBP =∠BPQ ∵∠BOP =∠PBQ∴△OBP ∽△BPQ ………………（1分）∴OB BPBP PQ =∴2BP OB PQ =⋅………（1分） ∴22(2)3(2+3+3)m m m m =-+- 即222-39m m m =+ 解得95m =(m =0舍去)………（1分） 5425PQ =………（1分） (3)当QP =QP 时（第24题备用图）yxOBA（第24题图）y xOBAPMQ（第24题图）y xOBAPMQ点Q (2,3)此时m =2………（1分） 当BQ =BP 时，点Q （1,4）此时m =1………（2分） 当PB =PQ 时2233m m m =-++-+3m =2分）【2020青浦一模】24．（本题满分12分， 其中第（1）小题4分，第（2）小题5分，第（3）小题3分）如图，在平面直角坐标系xOy 中，抛物线2y x bx c =++与x 轴交于A 、B 两点，与y 轴交于点C ，对称轴为直线x =2，点A 的坐标为（1，0）． （1）求该抛物线的表达式及顶点坐标；（2）点P 为抛物线上一点（不与点A 重合），联结PC ．当∠PCB=∠ACB 时，求点P 的坐标；（3）在（2）的条件下，将抛物线沿平行于y 轴的方向向下平移，平移后的抛物线的顶点为点D ，点P 的对应点为点Q ，当OD ⊥DQ 时，求抛物线平移的距离．24．解：（1）∵A 的坐标为（1，0），对称轴为直线x =2，∴点B 的坐标为（3，0）（1分）将A （1，0）、B （3，0）代入2+=+y x bx c ，得10930.，++=⎧⎨++=⎩b c b c 解得：43.，=-⎧⎨=⎩b c ··················································· （2分） 所以，243=-+y x x ．当x =2时，2242+3=1=-⨯-y∴顶点坐标为（2，-1）··········································································· （1分）．（2）过点P 作PN ⊥x 轴，垂足为点N ．过点C 作CM ⊥PN ，交NP 的延长线于点M ．∵∠CON =90°，∴四边形CONM 为矩形． ∴∠CMN =90°，CO = MN ．∵243=-+y x x ，∴点C 的坐标为（0，3） ·············································· （1分）． ∵B （3，0），∴OB =OC ．∵∠COB =90°，∴∠OCB =∠BCM = 45°， ·············· （1分）． 又∵∠ACB =∠PCB ，∴∠OCB -∠ACB =∠BCM -∠PCB ，即∠OCA =∠PCM ． （1分）． ∴tan ∠OCA= tan ∠PCM ．∴13=PMMC． 设PM =a ，则MC =3a ，PN =3-a ． ∴P （3a ，3-a ）．························································································· （1分）将P （3a ，3-a ）代入243=-+y x x ，得()231233-+=-a a a ．解得111=9a ，2=0a （舍）．∴P （113，169）． ·············································· （1分） （3）设抛物线平移的距离为m ．得()221=---y x m ，∴D 的坐标为（2，1--m ）． ··············································································· （1分） 过点D 作直线EF ∥x 轴，交y 轴于点E ，交PQ 的延长线于点F ． ∵∠OED =∠QFD =∠ODQ =90°，∴∠EOD+∠ODE = 90°，∠ODE+∠QDF = 90°， ∴∠EOD =∠QDF ，························································································· （1分）∴tan ∠EOD = tan ∠QDF ．∴=DE QF OE DF ．∴1612911123-++=+-m mm ．解得15=m ．所以，抛物线平移的距离为15． ··················································· （1分）【2020普陀一模】 24．（本题满分12分）在平面直角坐标系中（如图12），已知抛物线28()3y ax a x c =+++(0)a ≠经过点A ()3,2--，与y 轴交于点B ()0,2-，抛物线的顶点为点C ，对称轴与x 轴交于点D ．（1）求抛物线的表达式及点C 的坐标；（2）点E 是x 轴正半轴上的一点，如果AED BCD ∠=∠，求点E 的坐标；（3）在（2）的条件下，点P 是位于y 轴左侧抛物线上的一点，如果△PAE 是以AE 为直角边的直角三角形，求点P 的坐标．xOy（普陀）24．解：（1）由抛物线28()3y ax a x c =+++经过点A ()3,2--和点B ()0,2-，得2,893() 2.3c a a c =-⎧⎪⎨-++=-⎪⎩ 解得4,32.a c ⎧=⎪⎨⎪=-⎩ ············································· （2分） ∴抛物线的表达式是24423y x x =+-． ············································ （1分） 点C 的坐标是3(,5)2--． ································································· （1分）（2）联结AB 交CD 于点F ，过点A 作AH OD ⊥，H 为垂足．∴A ()3,2--，B ()0,2-，∴3AB =． 由对称性可得 32BF =． ··································································· （1分） ∴5CD =，∴3CF =．在Rt △BCF 中，1tan 2BF BCF CF ∠==． ··············································· （1分） 在Rt △AEH 中，tan AHAEH EH∠=，∴AED BCD ∠=∠， ∴12AH EH =．∴4EH =． ··································································· （1分） ∴3OH =，∴1OE =．∴点E 的坐标是()1,0． ····································································· （1分） （3）∴△PAE 是以AE 为直角边的直角三角形， ∴90PAE ∠=︒或90PEA ∠=︒．图12O11设点P 点的坐标为24(,42)3m m m +-．①当90PAE ∠=︒时，点P 只能在AE 的下方． 过点P 作PG AH ⊥，G 为垂足．∴3PG m =+，2443AG m m =--．∴GAE AHE AEH ∠=∠+∠，GAE PAE PAG ∠=∠+∠，∴PAG AEH ∠=∠．∴tan tan PAG AEH ∠=∠．∴PG AHAG EH =．∴2314243m m m +=--． ·················································· （1分） 解得3m =-，32m =-．∴3m =-不合题意舍去，∴32m =-．∴点P 的坐标是3(,5)2--． ······························································ （1分）②当90PEA ∠=︒时． 同理可得点P 的坐标是912913129(,)42--+． ································· （2分）【2020浦东一模】24．（本题满分12分，其中每小题各4分）如图，在平面直角坐标系xOy 中，抛物线2y x bx c =-++与x 轴的两个交点分别为 A （−1,0）、B （3,0），与y 轴相交于点C ． （1）求抛物线的表达式；（2）联结AC 、BC ，求∠ACB 的正切值；（3）点P 在抛物线上且∠P AB =∠ACB ，求点P 的坐标．（浦东）24．解：（1）把A （−1,0）、B （3,0）分别代入2y x bx c =-++得{10,930b c b c --+=-++=．…………………………………………………………（2分）解得b =2，c =3． …………………………………………………………（1分） ∴抛物线的表达式是223y x x =-++． ………………………………（1分） （2）过点A 作AH ⊥BC ，垂足为点H ．∵抛物线223y x x =-++与y 轴相交于点C ,∴C （0, 3）．……………（1分） ∵B （3,0）、A （−1,0）、C （0, 3），∴OC =OB =3， AB =4． 在Rt △BOC 中，BC =32，∠ABC =45°．在Rt △HAB 中，∵sin AHABH AB ∠=，AB =4，∴22AH BH ==． ……………………（1分）∵32BC =，∴2CH = ． ……………………………………………（1分）∴tan 2AHACB CH ∠==． ……………………………………………（1分）（3）过点P 作PM ⊥x 轴，垂足为点M ．设P （x ，-x 2+2x +3），则PM =223x x -++，AM ＝x ＋１．∵∠PAB=∠ACB ，tan 2ACB ∠=，∴tan 2PAB ∠=． ……………（1分） （i ）P 在x 轴上方时，-x 2+2x +3=2(x +1) .解得：x 1=1，x 2= -1（舍）. …………………………………………（1分） （ii ）P 在x 轴下方时，-（-x 2+2x +3）=2(x +1) .解得：x 1=5，x 2= -1（舍）. …………………………………………（1分） ∴P 的坐标为（1，４）或（5，-12）. ………………………………（1分）【2020闵行一模】24．（本题共3题，每小题4分，满分12分）已知：在平面直角坐标系xOy 中，对称轴为直线x = -2的抛物线经过点C （0，2），与x 轴交于A （-3，0）、B 两点（点A 在点B 的左侧）． （1）求这条抛物线的表达式； （2）联结BC ，求∠BCO 的余切值；（3）如果过点C 的直线，交x 轴于点E ，交抛物线于点P ，且∠CEO =∠BCO ，求点P 的坐标．yx12 3 4 5–1 –2–3 –4 –51 2 3 4 5–1 –2 –3 –4 –5 O（闵行）24．解：（1）设抛物线的表达式为2(0)y ax bx c a =++≠．由题意得：229302ba abc c ⎧-=-⎪⎪-+=⎨⎪=⎪⎩………………………………………………（1分）解得：23a =，83b =．……………………………………………………（2分）∴这条抛物线的表达式为228233y x x =++．……………………………（1分）注：用对称性求解析式酌情给分．（2）令y = 0，那么2282033x x ++=，解得13x =-，21x =-．………………………………………………………（1分） ∵点A 的坐标是（-3，0）∴点B 的坐标是（-1，0）．…………………（1分） ∵C （0，2）∴1OB =，2OC =．…………………………………………（1分） 在Rt △ OBC 中，∠BOC =90º，∴cot 2OCBCO OB∠==．………………………………………………………（1分） （3）设点E 的坐标是（x ，0），得OE =x ．∵CEO BCO ∠=∠， ∴cot cot CEO BCO ∠=∠．在Rt△ EOC 中，∴cot 22xOE CEO OC ∠===．∴x =4，∴点E 坐标是（4，0）或 （-4，0）．………………………（1分） ∵点C 坐标是（0，2），∴11:2=222CE l y x y x =+-+或．……………………………………………（1分）∴212228233y x y x x ⎧=+⎪⎪⎨⎪=++⎪⎩ ，或212228233y x y x x ⎧=-+⎪⎪⎨⎪=++⎪⎩解得13438x y ⎧=-⎪⎪⎨⎪=⎪⎩和02x y =⎧⎨=⎩（舍去），或194358x y ⎧=-⎪⎪⎨⎪=⎪⎩和02x y =⎧⎨=⎩（舍去）；∴点P 坐标是（134-，38）或（194-，358）．………………………（2分）【2020静安一模】24．（本题满分12分，其中第（1）小题4分，第（2）小题4分，第（3）小题4分）在平面直角坐标系xOy 中（如图8），已知二次函数c bx ax y ++=2（其中a 、b 、c 是常数，且a ≠0）的图像经过点A （0，-3）、B （1，0）、C （3，0），联结AB 、AC ． （1）求这个二次函数的解析式；（2）点D 是线段AC 上的一点，联结BD ，如果2:3:=∆∆BCD ABD S S ，求tan△DBC 的值；（3）如果点E 在该二次函数图像的对称轴上，当AC 平分∠BAE 时，求点E 的坐标．（静安）24．解：（1）将A （0，-3）、B （1，0）、C （3，0）代入）（02≠++=a c bx ax y 得， ⎪⎩⎪⎨⎧++=--+=-+=cb a b a 003,4390,30…………………………………………………………………………………（3分）解得⎪⎩⎪⎨⎧-==-=.3,4,1c b a ∴此抛物线的表达式是342-+-=x x y ．…………………………………（1分）（2）过点D 作DH ⊥BC 于H ，在△ABC 中，设AC 边上的高为h ，则23:)21(:)21(：：==⋅⋅=∆∆DC AD h DC h AD S S BCD ABD （1分）又∵DH //y 轴，∴52===OA DH AC DC OC CH ．∴56352=⨯==DH CH ．………………………（1分）∴54562=-=-=CH BC BH ．…………………………………………………………………（1分）∴tan△DBC=23=BH DH ．……………………………………………………………………………（1分）图8 Oyx（3）方法一：∵1)2(3422+--=-+-=x x x y ，所以对称轴为直线x =2，设直线x =2与x 轴交于点G ．（1分）过点A 作AF 垂直于直线x =2，垂足为F ．∵OA =OC =3，∠AOC =90°，∴△OAC=△OCA=45°．∵AF //x 轴，∴△FAC=△OCA=45°． ∵AC 平分∠BAE ，∴△BAC=△EAC∵△BAO=△OAC -△BAC ，△EAF=△FAC -△EAC ，∴△BAO=△EAF ………………………（1分） ∵∠AOB =∠AFE =90°，∴△OAB ∽△FEA ，∴31==AF EF OA OB ． ∵AF =2，∴32=EF ．…………………………………………………………………………………（1分） ∴EG =GF -EF =AO -EF =3-32=37． ∴E （2，37-）．……………………………………………（1分） 方法二：延长AE 至x 轴，与x 轴交于点F ， ∵OA =OC =3，∴△OAC=△OCA=45°，∵△OAB=△OAC -△BAC=45°-△BAC ，△OFA=△OCA -△FAC=45°-△FAC ，∵△BAC =△FAC ，∴△OAB=△OFA ．………………………………………………………………（1分）∴△OAB ∽△OFA ，∴31==OF OA OA OB ．∴OF =9，即F （9，0）…………………………………（1分）设直线AF 的解析式为y =kx +b （k ≠0），可得⎩⎨⎧=-+=,3,90b b k 解得⎪⎩⎪⎨⎧-==,3,31b k ∴直线AF的解析式为331-=x y ……………………………（1分）将x =2代入直线AF 的解析式得37-=y ，∴E （2，37-）……………………………………（1分）【2020嘉定一模】 24．（本题满分12分，每小题4分）在平面直角坐标系xOy 中，将点)(1a b a P -，定义为点)(b a P ，的“关联点”. 已知：点)(y x A ，在函数2x y =的图像上（如图9所示），点A 的“关联点”是点1A . （1）请在图9的基础上画出函数22-=x y 的图像，简要说明画图方法；（2）如果点1A 在函数22-=x y 的图像上，求点1A 的坐标； （3）将点),(2na b a P -称为点)(b a P ，的“待定关联点”（其中，0≠n ）.如果点)(y x A ，的“待定关联点”2A 在函数n x y -=2的图像上，试用含n 的代数式表示点2A 的坐标.（嘉定）24．（本题满分12分，每小题4分）解：（1）图像基本正确（开口方向、对称轴、顶点、大致光滑） ·· 2分将图9中的抛物线2x y =向下平移2个单位长，可得抛物线22-=x y ················· 2分备注：如果使用“列表、描点、连线”的方式叙述，需要呈现列表使用的表格. （2）由题意，得点),(y x A 的“关联点”为),(1x y x A - ·············································· 1分 由点),(y x A 在抛物线2x y =上，可得),(2x x A ，),(21x x x A -··································· 1分 又∵),(1x y x A -在抛物线22-=x y 上，∴222-=-x x x ·········································· 1分 解得2=x .将2=x 代入),(21x x x A -，得)2,2(1A ·················································· 1分 （3）点),(y x A 的“待定关联点”为),(22nx x x A -， ····················································· 1分 ∵),(22nx x x A -在抛物线n x y -=2的图像上，∴n x nx x -=-22. ························ 1分 ∴0=-nx n ,0)1(=-x n .又∵0≠n ，∴1=x . ······················································· 1分当1=x 时，n nx x -=-12，故可得)11(2n A -，. ······················································ 1分【2020黄浦一模】 24．（本题满分12分）在平面直角坐标系xOy 中，平移一条抛物线，如果平移后的新抛物线经过原抛物线顶点，且新抛物线的对称轴是y 轴，那么新抛物线称为原抛物线的“影子抛物线”． （1）已知原抛物线表达式是225y x x =-+，求它的“影子抛物线”的表达式；（2）已知原抛物线经过点（1，0），且它的“影子抛物线”的表达式是25y x =-+，求原抛图9物线的表达式；（3）小明研究后提出：“如果两条不重合的抛物线交y 轴于同一点，且它们有相同的“影子抛物线”，那么这两条抛物线的顶点一定关于y 轴对称．”你认为这个结论成立吗？请说明（黄埔）24．（本题满分12分） （1）由题意，可知原抛物线顶点是(1,4)．………………………………………………（1分）设影子抛物线表达式是2y x n =+，………………………………………………（1分） 将(1,4)代入2y x n =+，解得3n =．………………………………………………（1分） 所以“影子抛物线”的表达式是23y x =+．………………………………………（1分）（2）设原抛物线表达式是2()y x m k =-++，则原抛物线顶点是(,)m k -．将(,)m k -代入25y x =-+，得2()5m k --+=① ………………………………（1分） 将（1，0）代入2()y x m k =-++，20(1)m k =-++②…………………………（1分）由①、②解得 1114m k =⎧⎨=⎩，2221m k =-⎧⎨=⎩． 所以，原抛物线表达式是2(1)4y x =-++或2(2)1y x =--+．…………………（2分）（3）结论成立．……………………………………………………………………（1分） 设影子抛物线表达式是2y ax n =+．原抛物线于y 轴交点坐标为(0,)c则两条原抛物线可表示为211y ax b x c =++与抛物线222y ax b x c =++（其中a 、1b 、2b 、c 是常数，且0a ≠，12b b ≠）由题意，可知两个抛物线的顶点分别是21114(,)24b ac b P a a --、22224(,)24b ac b P a a-- 将1P 、2P 分别代入2y ax n =+，得221122224()244()24b ac b a n a a b ac b a n a a ⎧--+=⎪⎪⎨-⎪-+=⎪⎩…………………………………………………………（1分） 消去n 得2212b b =．………………………………………………………………………（1分）xOy∵12b b ≠，∴12b b =-∴22214(,)24b ac b P a a -，22224(,)24b ac b P a a--， ………………………………………（1分）∴1P 、2P 关于y 轴对称．【2020虹口一模】 24．（本题满分12分，第（1）小题满分4分，第（2）小题满分8分）如图12，在平面直角坐标系xOy 中，抛物线2y x bx c =-++与x 轴交于A （-1，0）、B两点，与y 轴交于点C （0，3），点P 在抛物线的对称轴上，且纵坐标为23． （1）求抛物线的表达式以及点P 的坐标；（2） 当三角形中一个内角α是另一个内角β的两倍时，我们称α为此三角形的“特征角”．①点D 在射线AP 上，如果∠DAB 为△ABD 的特征角，求点D 的坐标；②点E 为第一象限内抛物线上一点，点F 在x 轴上，CE ⊥EF ，如果∠CEF 为△ECF 的特征角，求点E 的坐标．（虹口）24．解：（1） ∵过A (－1， 0)，C (0，3)∴0=1;3.b c c --+⎧⎨=⎩ 解得：=2;3.b c ⎧⎨=⎩……………………………………………（2分）∴………………………………………………………………（1分）对称轴为直线x =1∵点P 在对称轴上，且纵坐标为，∴点P 的坐标为（1，）……………………………………………………（1分）（2）设直线x=1交x 轴于点Q∵A (－1，0)，P （1，）∴AQ =2 PQ = ∴tan 3PAQ ∠=∴△PAQ =60° 即∠DAB=60°……………………………………………………（1分） ∵点D 在射线AP 上，且∠DAB 为△ABD 的特征角， ∴∠ABD =30°或∠ADB =30°，…………………………………………………（1分） ∴点D 的坐标为（0，）或（3，43 ）…………………………………（2分） （3）过点E 作EG ⊥x 轴于点G ，过点C 作CH ⊥GE 的延长线于点H .∵CE ⊥EF 且△CEF 为△ECF 的特征角，c bx x y ++-=2322++-=x x y 323232323O A y 图12x B C∴∠ECF =△CFE =45°……………………………………………………………（1分） ∴CE =EF在Rt △CHE 中，∠HCE+∠CEH =90° ∵∠CEH +∠FEG =90°∴∠HCE =∠FEG ∵∠H =∠EGF =90°∴△CHE ≌△EGF∴CH =EG …………………………………………………………………………（1分） ∵点E 为第一象限内抛物线上一点 ∴设E （a ，223a a -++）∴223a a a =-++ ……………………………………………………………（1分）解得a =（舍负）∴E …………………（1分）【2020奉贤一模】24．（本题满分12分，每小题满分4分）如图10，在平面直角坐标系中，抛物线2y x bx c 经过点A (2，-3)和点B (5，0)，顶点为C ．（1）求这条抛物线的表达式和顶点C 的坐标； （2）点A 关于抛物线对称轴的对应点为点D ， 联结OD 、BD ，求∠ODB 的正切值； （3）将抛物线2yx bx c 向上平移t （t >0）个单位，使顶点C 落在点E 处，点B 落在点F 处，如果 BE=BF ，求t 的值．（奉贤）24．解：（1）由题意得，抛物线2y x bx c 经过点A (2，-3)和点B (5，0)，代入得423,2550.b cbc解得 6,5.b c··························································· （2分）∴抛物线的表达式是265y x x =-+. ····································································· （1分） 它的顶点C 的坐标是（3，-4）. ················································································· （1分）（2）∵点A （2，-3）关于抛物线对称轴的对应点为点D ， ∴点D 的坐标是(4，-3) . ····························································································· （1分） ∴OD =OB =5，∴ODB OBD ∠=∠ . ············································································ （1分） 过点D 作DH OB ，垂足为点H ，在Rt △DHB 中，90DHB ，DH =3，BH =1，∴tan 3DHOBD BH∠==． ······························································································· （1分） ∴tan 3ODB ∠=，即∠ODB 的正切值是3． ······························································· （1分）（3）由题意得，当 BE=BF 时，点E 在x 轴下方， 由平移可知，CE =BF =t ，∴BE t =. ············································································ （1分） 设对称轴与x 轴的交点为Q ，则CQ =4，BQ =2. ························································· （1分）在Rt △BEQ 中，90BEQ ，222EQ BQ BE ，∴222(4)2t t ，解得52t. ················································································ （2分） 即当BE=BF ， t 的值是52．【2020崇明一模】 24．（本题满分12分，第(1)小题4分，第(2)小题4分，第(3)小题4分）如图，抛物线与x 轴相交于点(3,0)A -、点(1,0)B ，与y 轴交于点(0,3)C ，点D 是抛物xOy。

【2020长宁金山一模】23.（本题满分12分，第（1）小题5分，第（2）小题7分）如图，在ABC ∆中，点D 、E 分别在边AB 、BC 上，AE 与CD 交于点F ．若AE 平分BAC ∠，AE AC AF AB ⋅=⋅． （1）求证：AEC AFD ∠=∠；（2）若CD EG //，交边AC 的延长线于点G ，求证：BD FC CG CD ⋅=⋅．（长宁金山）23．（本题满分12分，第（1）小题5分，第（2）小题7分） 证明：（1）∵AE AC AF AB ⋅=⋅ ∴AFAEAC AB = （1分） ∵AE 平分BAC ∠ ∴CAF BAE ∠=∠ （1分） ∴ABE ∆∽ACF ∆ （1分） ∴ACF B ∠=∠ （1分） 又∵BAE B AEC CAF ACF AFD ∠+∠=∠∠+∠=∠,∴AEC AFD ∠=∠ （1分） (2)∵AEC AFD ∠=∠，CFE AFD ∠=∠ ∴AEC CFE ∠=∠ （1分）∴CE FC = （1分） ∵CD EG // ∴CEG DCB ∠=∠ G ACF ∠=∠又∵B ACF ∠=∠ ∴G B ∠=∠ （2分） ∴BCD ∆∽GEC ∆ （1分） ∴CGBDCE CD = （1分） ∴CGBDFC CD = 即BD FC CG CD ⋅=⋅． （1分）第23题图 GAC B ED F【2020杨浦一模】23．（本题满分12分，每小题各6分）如图，已知在ABC △中，AD 是ABC △的中线，DAC B ∠=∠，点E 在边AD 上，CE CD =.（1）求证：AC BDAB AD=； （2）求证：22AC AE AD =⋅.（杨浦）23．证明：（1）∵CD =CE ，∴∠CED =∠CDA . ··········································· （1分） ∴∠AEC =∠BDA . ······················································································ （1分） 又∵∠DAC =∠B ，∴△ACE ∽△BAD. ························································· （1分）∴AC CEAB AD=. ···························································································· （1分） ∵AD 是ABC △的中线，∴BD CD =. ····················································· （1分）∵CD =CE ，∴BD CE =.∴AC BDAB AD=. ······················································· （1分） （2）∵∠DAC =∠B ，又∠ACD =∠BCA ，∴△ACD ∽△BCA. ····································· （1分）∴AC CD BC AC=，∴2AC CD CB =?. ································································· （1分） ∵AD 是ABC △的中线，∴2BC CD =，∴222AC CD =. ························ （1分）∵△ACE ∽△BAD ，∴CE AEAD BD=. ·································································· （1分） 又∵CD =CE=BD ，∴2CD AD AE =?. ······························································ （1分） ∴22AC AD AE =?. ····················································································· （1分）第23题图 AB CD E【2020徐汇一模】 23．（本题满分12分）如图，在ACB ∆中，点D 、E 、F 、G 分别在边AB 、AC 、BC 上，AD AB 3=，AE CE 2=，CG FG BF ==，DG 与EF 交于点H ．（1）求证： AB HG AC FH ⋅=⋅；（2）联结DF 、EG ，求证：GEF FDG A ∠+∠=∠．（徐汇）23．证明：（1）∵AD AB 3=，AE CE 2=，CG FG BF ==，∴31,31,31,31====BC CG BC BF AC AE AB AD ； ∴BCBFAC AE BC CG AB AD ==,； ∴AC DG //，AB EF //；∴C HGF ∠=∠，B HFG ∠=∠； ∴HFG ∆∽ABC ∆； ∴ABFHAC HG =；即AB HG AC FH ⋅=⋅． （2）∵AB EF //，AC DG //，∴1==FB GF HD GH ，1==GFCGFH HE ； ∴FHHEHD GH =；∴DF EG //； ∴HGE FDG ∠=∠；又HEG HGE FHG ∠+∠=∠，∴HEG FDG FHG ∠+∠=∠； ∵HFG ∆∽ABC ∆，∴A FHG ∠=∠； ∴GEF FDG A ∠+∠=∠．A BC D E F G H （第23题图）【2020松江一模】23．（本题满分12分,第（1）小题5分，第（2）小题7分）已知：如图，点D 、F 在△ABC 边AC 上，点E 在边BC 上，且DE ∥AB ，2CD CF CA =⋅. （1）求证：EF ∥BD ；（2）如果AC CF BC CE ⋅=⋅，求证：2BD DE BA =⋅.23．证明： （1）∵DE ∥AB ∴CD CECA CB=………（1分） ∵2CD CF CA =⋅∴CD CFCA CD =………（1分） ∴CE CF CB CD=………（2分） ∴EF ∥BD ………（1分） (2)∵AC CF BC CE ⋅=⋅ ∴CA CECB CF= ∵∠C =∠C∴△CAB ∽△CEF ………（1分） ∴∠CAB =∠CEF ………（1分） ∵EF ∥BD∴∠CBD =∠CEF ………（1分）∴∠CBD =∠CAB ………（1分）F C BADE (第23题图)F CBAD E (第23题图)FCBAD E (第23题图)∵DE ∥AB ，∴∠BDE =∠DBA ………（1分） ∴△BDE ∽△ABD ………（1分） ∴BD ABDE BD=∴2BD DE BA =⋅………（1分）【2020青浦一模】23．（本题满分12分，第（1）小题6分，第（2）小题6分）已知：如图，在△ABC 中，点D 在边BC 上，AE ∥BC ，BE 与AD 、AC 分别相交于点F 、G ， 2AF FG FE =⋅． （1）求证：△CAD ∽△CBG ；（2）联结DG ，求证：DG AE AB AG ⋅=⋅．23．证明：（1）∵2AF FG FE =⋅，∴=AF FEFG AF．··················································· （1分） 又∵∠AFG =∠EFA ，∴△FAG ∽△FEA ． ················································· （1分） ∴∠FAG =∠E ． ························································································· （1分） ∵AE ∥BC ，∴∠E =∠EBC ． ····································································· （1分） ∴∠EBC =∠FAG ． ···················································································· （1分） 又∵∠ACD =∠BCG ，∴△CAD ∽△CBG ． ············································· （1分） （2）∵△CAD ∽△CBG ，∴=CA CDCB CG． ······················································· （1分） 又∵∠DCG =∠ACB ，∴△CDG ∽△CAB ． ············································· （1分）∴=DG CGAB CB． ······················································································· （1分） ∵AE ∥BC ，∴=AE AGCB GC． ··································································· （1分） ∴=AG GC AE CB ，∴=DG AGAB AE， ··························································· （1分） ∴⋅=⋅DG AE AB AG ． ········································································ （1分）EFGDCBA【2020普陀一模】 本题满分12分）23、已知：如图11，四边形ABCD 的对角线AC 、BD 相交于点O ，AOD BOC S S =△△． （1）求证：OACOOB DO =； （2）设△OAB 的面积为S ，k ABCD=，求证：2(1)ABCD S k S =+四边形．（普陀）23．证明：（1）过点A 作AH ⊥BD ，垂足为点H . ·················································· （1分）∵S △AOD =AH DO ⋅⋅21, S △AOB =AH OB ⋅⋅21, ∴OB DOAH OB AHDO S S AOBAOD=⋅⋅⋅⋅=∆∆2121. ··························································· （2分） 同理，BOC AOB S COS OA∆∆=． ········································································ （1分） ∵AOD BOC S S =△△， ∵DO COOB OA=． ·············································································· （1分）CDBAO图11（2）∵OACOOB DO =，AOB COD ∠=∠， ∵△OCD ∵△OAB ． ····································································· （1分） ∵CD DO COk AB BO AO===． ································································· （1分） 22k AB CD S S OAB OCD =⎪⎭⎫ ⎝⎛=∆∆． ································································· （1分） ∵△OAB 的面积为S ，∴S k S OCD ⋅=∆2. ··········································· （1分） 又∵k OBDOS S OAB AOD ==∆∆，∵S k S AOD ⋅=∆． ··········································· （1分） 同理，S k S BOC ⋅=∆. ···································································· （1分） ∴AOB BOC COD DOA ABCD S S S S S =+++△△△△四边形S k S k S k S ⋅+⋅+⋅+=2 S k k ⋅++=)12(2S k 2)1(+=． ······························································· （1分）【2020浦东一模】23．（本题满分12分，其中每小题各6分）如图，已知△ABC 和△ADE ，点D 在BC 边上，DA =DC ，∠ADE =∠B ，边DE 与AC 相交于点F ．（1）求证：AB AD DF BC ⋅=⋅；（2）如果AE ∥BC ，求证：BD DF DC FE =．（浦东）23. 证明：（1）∵DA =DC ，∴∠DCA=∠DAC ．……………………………………（1分）∵∠B=∠ADE ，∴△ABC ∽△FDA ． ……………………………………（3分）∴AB BC FD DA =． ……………………………………………………………（1分） ∴AB DA FD BC ⋅=⋅．………………………………………………………（1分）（2）∵AE // BC ，∴DF DCEF EA =，∠BDA=∠DAE ． ……………………（2分） ∵∠B=∠ADE ，∴△ABD ∽△EDA ．………………………………………（1分） ∴ADBD AE AD =． ……………………………………………………………（1分） ∵DA =DC ，∴AEDCDC BD =．…………………………………………………（1分） ∴FEDF DC BD =． ……………………………………………………………（1分）（第23题图）【2020闵行一模】23．（本题共2小题，每小题6分，满分12分）如图，在△ABC 中，BD 是AC 边上的高，点E 在边AB 上，联结CE 交BD 于点O ，且AD OC AB OD ⋅=⋅，AF 是∠BAC 的平分线，交BC 于点F ，交DE 于点G ．求证：（1）CE ⊥AB ；（2）AF DE AG BC ⋅=⋅．（闵行）23．证明：（1）∵AD OC AB OD ⋅=⋅，∴AD ABOD OC=．………………………………（1分） ∵BD 是AC 边上的高，∴∠BDC = 90°，△ADB 和△ODC 是直角三角形．…………………（1分） ∴Rt △ADB ∽Rt △ODC ．………………………………………………（1分） ∴∠ABD =∠OCD ．……………………………………………………（1分） 又∵∠EOB =∠DOC ，∠DOC +∠OCD +∠ODC =180°，∠EOB +∠ABD+∠OEB =180°．∴∠OEB = 90°．…………………………………………………………（1分） ∴CE ⊥AB ．………………………………………………………………（1分） （2）在△ADB 和△AEC 中，∵∠BAD =∠CAE ，∠ABD =∠OCD ，∴△ADB ∽△AEC ．………………………………………………………（2分） ∴AD AB AE AC =， 即AD AEAB AC=．…………………………………………（1分） 在△DAE 和△BAC 中 ∵∠DAE =∠BAC ，AD AEAB AC=． ∴△DAE ∽△BAC ．………………………………………………………（2分） ∵AF 是∠BAC 的平分线，A BDC（第23题图）EFG O∴AG DEAF BC=， 即AF DE AG BC ⋅=⋅．………………………………（1分）【2020静安一模】23．（本题满分12分，其中第（1）小题6分，第（2）小题6分）如图7，在梯形ABCD 中，AD //BC ，AC 与BD 相交于点O ，点E 在线段OB 上，AE 的延长线与BC 相交于点F ，OD 2 = OB ·OE ．（1）求证：四边形AFCD 是平行四边形； （2）如果BC =BD ，AE ·AF =AD ·BF ，求证：△ABE ∽△ACD ．（静安）23．证明：（1）∵OD 2 =OE · OB ，∴OBODOD OE =． ……………………………………………………（1分） ∵AD //BC ，∴OBODOC OA =．……………………………………………………………………（2分） ∴ODOE OC OA =．………………………………………………………（1分） ∴ AF//CD ．………………………………………………………………（1分） ∴四边形AFCD 是平行四边形．……………………………………………（1分）（2）∵AF//CD ，∴∠AED =∠BDC ，BCBFBD BE =．…………………（1分） ∵BC =BD ，∴BE =BF ，∠BDC =∠BCD …………………………………………………………（1分）∴∠AED =∠BCD ．∵∠AEB =180°-∠AED ，∠ADC =180°-∠BCD ，∴∠AEB =∠ADC ．…………………………（1分）∵AE ·AF =AD ·BF ，∴AF ADBF AE =．…………………………………………………………（1分）∵四边形AFCD 是平行四边形，∴AF =CD ．…………………………………………………（1分）图7 A B D C E F O∴DCADBE AE =．………………………………………………………………（1分） ∴△ABE ∽△ADC ．【2020嘉定一模】 23．（本题满分12分，第（1）小题4分，第2小题8分）已知：如图8，在ABC △中，点D 、E 分别在边AB 、AC 上，DE ∥BC ，C ABE ∠=∠. （1）求证：BC DE BE ⋅=2； （2）当BE 平分ABC ∠时，求证：.（嘉定）23.（本题满分12分，第（1）小题4分，第（2）小题8分） 证明：（1）∵DE ∥BC ，∴CBE BED ∠=∠. ········································································ 1分又∵C ABE ∠=∠，∴△BDE ∽△CBE . ······································································ 1分 ∴BCBEBE DE =.·········································································································· 1分 ∴BC DE BE ⋅=2. ·································································································· 1分 （2）∵DE ∥BC ，∴C AED ∠=∠.又C ABE ∠=∠，∴ABE AED ∠=∠. ······················· 1分 又∵BAE EAD ∠=∠，∴△ADE ∽△ABE . ······························································· 1分∴AEADAB AE =. ······································································································· 1分 ∵DE ∥BC ，∴CEAE BD AD =，即CE BDAE AD =. ························································ 1分 ∴CEBDAB AE =. ······································································································· 1分 ∵BE 平分ABC ∠，∴CBE ABE ∠=∠，又∵C ABE ∠=∠，∴C CBE ∠=∠. ······· 1分∴CE BE =. ··········································································································· 1分∴ABAE BE BD =.··········································································································1分ABAEBE BD =B.图8CAED图11 E DCA【2020黄埔一模】 23．（本题满分12分）已知：如图11，在平行四边形ABCD 中，过点C 分别作AD 、AB 的垂线，交边AD 、AB 延长线于点E 、F ．（1）求证：AD DE AB BF ⋅=⋅；（2）联结AC ，如果CF ACDE CD=，求证：22AC AF BC BF =．（黄埔）23．（本题满分12分） （1）∵四边形ABCD 是平行四边形， ∴CD ∥AB ，AD ∥BC ，∴∠CDE =∠DAB ，∠CBF =∠DAB ．∴∠CDE =∠CBF ．……………………………………………………………………（2分） ∵CE ⊥AE ，CF ⊥AF ，∴∠CED =∠CFB =90°．………………………………………………………………（1分） ∴△CDE ∽△CBF ．…………………………………………………………………（1分）∴BC CDBF DE=．…………………………………………………………………………（1分）∵四边形ABCD 是平行四边形，∴BC =AD ，CD =AB ．∴AD ABBF DE=． ∴AD DE AB BF ⋅=⋅．…………………………………………………………（1分） （2）∵CF ACDE CD=，∠CED =∠CFB =90°， ∴ △ACF ∽△CDE ．………………………………………………………（2分） 又 ∵ △CDE ∽△CBF ，∴ △ACF ∽△CBF ．………………………………………………………（1分）∴22ACF CBF S AC S BC =V V ．………………………………………………………………………（1分）∵△ACF 与△CBF 等高，∴ACF CBF S AFS BF=V V ．………………………………………………………………………（1分）∴22AC AFBC BF=．………………………………………………………………………（1分）【2020虹口一模】 23．（本题满分12分，第（1）小题满分6分，第（2）小题满分6分）如图11，在Rt △ABC 中，∠ACB =90°，点D 是边BC 的中点，联结AD ，过点C 作 CE ⊥AD 于点E ，联结BE ．（1）求证：2BD DE AD =⋅；（2）如果∠ABC =∠DCE ，求证：BD CE BE DE ⋅=⋅．（虹口）23．证明：（1）∵CE ⊥AD ，∠ACB =90°∴∠ACB =∠CED =90°∵∠EDC =∠CDA∴△EDC ∽△CDA …………………………………………………………………（3分） ∴DE CDCD AD= ∴CD 2=DE ·AD ………………………………………………………………………（2分）∵点D 是边BC 的中点 ∴CD =BD∴BD 2=DE ·AD ………………………………………………………………………（1分） （2）由（1）得DE BDBD AD=且∠EDB =∠BDA ∴△BDE ∽△ADB ……………………………………………………………………（2分） ∴∠ABC =∠BED ……………………………………………………………………（1分） ∵∠ABC =∠DCE ， ∴∠BED =∠DCE ∵∠EBD =∠CBE∴△EBD ∽△CBE ……………………………………………………………………（2分） ∴BD ED BE CE= 即BD CE BE DE ⋅=⋅………………………………………………（1分）D图11 AEC B【2020奉贤一模】23．（本题满分12分，每小题满分6分）已知：如图9，在平行四边形ABCD 中，点 E 在边AD 上，点F 在边CB 的延长线上，联结CE 、EF ，CF DE CE ⋅=2．（1）求证：∠D =∠CEF ；（2）联结AC ，交EF 与点G ，如果AC 平分∠ECF ， 求证：CG CB AE AC ⋅=⋅．（奉贤）23．证明：（1）∵CF DE CE ⋅=2，∴CE CFDE CE=． ··································· （1分） ∵四边形ABCD 是平行四边形，∴//AD BC ， ∴DEC ECF ∠=∠． ········ （1分）∴△EDC ∽△CEF ． ····································································································· （2分） ∴∠D =∠CEF ． ········································································································· （2分） （2）∵AC 平分∠ECF ，∴ECG ACB ∠=∠． ∵//AD BC ， ∴DAC ACB ∠=∠．∴ECG DAC ∠=∠． ······························································································ （1分） 又∵∠D =∠CEF ，∴△EGC ∽△BAC ． ····································································· （2分）∴CG CEAC CB=． ········································································································· （1分） 又AE CE =， ········································································································· （1分） ∴CG AE AC CB =，∴CG CB AE AC ⋅=⋅． ··································································· （1分）ABCDEF图9。

一、选择题1．抛物线y ＝ax 2+bx +c （a ≠0）的图象大致如图所示，下列说法：①2a +b ＝0；②当﹣1＜x ＜3时，y ＜0；③若（x 1，y 1）（x 2，y 2）在函数图象上，当x 1＜x 2时，y 1＜y 2；④9a +3b +c ＝0，其中正确的是（ ）A ．①②④B ．①④C ．①②③D ．③④ 2．在同一直角坐标系中，一次函数y=ax+c 和二次函数y=ax 2+c 的图象大致为（ ） A ． B ． C ． D ．3．二次函数()20y ax bx c a =++≠的图象如图所示，对称轴是直线1x =-．下列结论：①240b ac ->，②0abc <，③420a b c -+>．其中正确的是（ ）A ．①②B ．①③C ．②③D ．①②③ 4．如图是抛物线y ＝ax 2+bx+c （a≠0）的部分图象，其顶点坐标为（1，n ），且与x 轴的一个交点在点（3，0）和（4，0）之间．则下列结论：①a ﹣b+c ＞0；②3a+b ＝0；③b 2＝4a （c ﹣n ）；④一元二次方程ax 2+bx+c ＝n ﹣1有两个不相等的实数根．其中正确结论的个数是（ ）A ．1个B ．2个C ．3个D ．4个 5．若飞机着陆后滑行的距离()s m 与滑行的时间()t s 之间的关系式为s=60t-1.5t 2，则函数图象大致为（ ） A ． B ．C ．D ．6．一次函数y ＝ax +c 与二次函数y ＝ax 2+bx +c 在同一个平面坐标系中图象可能是（ ） A ． B ．C ．D ．7．已知二次函数2(0)y ax bx c a =++≠的图象如图，有下列5个结论：①0abc <；②420a b c ++>；③b a c <+；④230c b -<；⑤2(1)a b an bn n +>+≠，其中正确的个数有（ ）A ．1个B ．2个C ．3个D ．4个 8．已第二次函数()2240y ax ax a =-+->图象上三点()11,A y -、()21,B y 、()32,C y ，则1y ，2y ，3y 的大小关系为（ ）A ．132y y y <<B ．312y y y <<C ．123y y y <<D ．213y y y << 9．如图1，是某次排球比赛中运动员垫球时的动作，垫球后排球的运动路线可近似地看作抛物线，在图2所示的平面直角坐标系中，运动员垫球时（图2中点A ）离球网的水平距离为5米，排球与地面的垂直距离为0.5米，排球在球网上端0.26米处（图2中点B ）越过球网（女子排球赛中球网上端距地面的高度为2.24米），落地时（图2中点C ）距球网的水平距离为2.5米，则排球运动路线的函数表达式为（ ）．A ．2148575152y x x =--+ B ．2148575152y x x =-++ C ．2148575152y x x =-+ D ．2148575152y x x =++ 10．已知抛物线229(0)y x mx m =-->的顶点M 关于坐标原点O 的对称点为M '，若点M '在这条抛物线上，则点M 的坐标为（ ）A ．(1,5)-B ．(2,8)-C ．(3,18)-D ．(4,20)- 11．已知二次函数()()2y x p x q =---，若m ，n 是关于x 的方程()()20x p x q ---=的两个根，则实数m ，n ，p ，q 的大小关系可能是（ ） A ．m ＜p ＜q ＜nB ．m ＜p ＜n ＜qC ．p ＜m ＜n ＜qD ．p ＜m ＜q ＜n12．如图是抛物线y 1＝ax 2+bx +c （a ≠0）图象的一部分，抛物线的顶点坐标是A （1，3），与x 轴的一个交点B （4，0），直线y 2＝mx +n （m ≠0）与抛物线交于A 、B 两点．下列结论：①2a +b ＝0；②abc ＞0；③方程ax 2+bx +c ＝3有两个相等的实数根；④抛物线与x 轴的另一个交点是（﹣1，0）；⑤当1＜x ＜4时，有y 2＜y 1；⑥a +b ≥m （am +b ）（m 实数）其中正确的是（ ）A ．①②③⑥B ．①③④C ．①③⑤⑥D ．②④⑤ 13．若二次的数2y ax bx c =++的x 与y 的部分对应值如下表： x 7- 6- 5- 4- 3- 2- y 27- 13-3- 3 5 3 则当1x =时，y 的值为（ ） A ．5 B ．3- C ．13- D ．27-14．若关于x 的不等式组232x a x a ≥+⎧⎨<-⎩有解，则函数21(3)4y x x a =--+-图象与x 轴的交点个数为（ ）A ．0个B ．1个C ．2个D ．1或2个 15．已知二次函数2y ax bx c =++，当2x =时，该函数取最大值9．设该函数图象与 x 轴的一个交点的横坐标为1x ，若15x >则a 的取值范围是（ ）A ．3a 1-<<-B ．2a 1-<<C ．1a 0-<<D ．2a 4<<二、填空题16．如图，抛物线2y ax c =+与直线y mx n =+交于()1,A p -，()3,B q 两点，则不等式2ax mx c n -+<的解集是_____________．17．将抛物线2y x 向上平移1个单位，再向左平移2个单位后，得到的抛物线的顶点坐标是__________．18．抛物线2y x x =+向下平移2个单位长度，再向左平移3个单位长度，得到的抛物线表达式为____．19．如图，在平面直角坐标系中，菱形ABCD 的顶点A 的坐标为（5，0），顶点B 在y 轴正半轴上，顶点D 在x 轴负半轴上．若抛物线y ＝－x 2－13x +c 经过点B 、C ，则菱形ABCD 的面积为________．20．如图，在喷水池的中心A 处竖直安装一个水管AB ，水管的顶端B 处有一个喷水孔，喷出的抛物线形水柱在与池中心A 的水平距离为1m 处达到最高点C ，高度为3m ，水柱落地点D 离池中心A 处3m ，则水管AB 的长为_____m ．21．二次函数223y x =的图象如图所示，点0A 位于坐标原点，点1A ，2A ，3A ，…，2013A 在y 轴的正半轴上，点1B ，2B ，3B ，…，2013B 在二次函数223y x =位于第一象限的图象上，若011A B A △，122A B A △，233A B A △，…，201220132013A B A △都为等边三角形，则201220132013A B A △的边长=________．22．如图，抛物线224y x x =-+与x 轴交于点O ，A ，把抛物线在x 轴及其上方的部分记为1C ，将1C 以y 轴为对称轴作轴对称得到2C ，2C 与x 轴交于点B ，若直线y = m 与1C ，2C 共有4个不同的交点，则m 的取值范围是_______________．23．如图是二次函数2(0)y ax bx c a =++≠图象的一部分，有下列4个结论：①0abc >；②240b ac ->；③关于x 的方程20ax bx c ++=的两个根是12x =-，23x =；④关于x 的不等式20ax bx c ++>的解集是2x >-．其中正确的结论是___________．24．如图，在平面直角坐标系中，点A ，B 是一次函数y x =图像上两点，它们的横坐标分别为1，4，点E 是抛物线248y x x =-+图像上的一点，则ABE △的面积最小值是______．25．某种洒杯的轴截面是一条抛物线段，在酒杯中加酒，当酒水深为lcm 时，液面宽为2cm ，将酒杯装满酒后，再倾斜至与水平面成30°，此时酒杯中余下酒深度为2cm ，这个酒杯的杯口直径为______cm ．26．将抛物线y ＝2（x ﹣1）2+3绕着点A （2，0）旋转180°，则旋转后的抛物线的解析式为_____．三、解答题27．如图用长为30m 的篱笆围成一个一边靠墙的矩形养鸡场ABCD ，已知墙长14m ，设边AB 的长为xm ，矩形ABCD 的面积为ym 2．（1）求y 与x 之间的函数关系式，并求出函数y 的最大值．（2）当y ＝108时，求x 的值．28．如图，已知抛物线y ＝ax 2+bx +c （a ≠0）经过A （﹣1，0），B （3，0），C （0，﹣3）三点，直线l 是抛物线的对称轴．（1）求抛物线的函数解析式；（2）在抛物线的对称轴上是否存在一点M ，使得△ACM 的周长最短？若存在，求点M 的坐标；若不存在，请说明理由．29．（1）若抛物线23y x x a =++与x 轴只有一个交点，求实数a 的值；（2）已知点()3,0在抛物线()233y x k x k =-++-上，求此抛物线的对称轴．30．某片果园有果树60棵，现准备多种一些果树提高果园产量，但是如果多种树，那么树与树之间的距离和每棵树所受光照就会减少，单棵树的产量随之降低．若该果园每棵果树产果y(千克)与增种果树x(棵)之间的函数关系如图所示．（1）求每棵果树产果y(千克)与增种果树x(棵)之间的函数关系式；（2）设果园的总产量为w(千克)，求w与x之间的函数表达式；（3）试说明（2）中总产量w(千克)随增种果树x(棵)的变化而变化的情况，并指出增种果树x为多少棵时获得最大产量，最大产量w是多少？。

一、选择题1．(0分)[ID：11121]如图，以O为圆心，任意长为半径画弧，与射线OM交于点A，再以A为圆心，AO长为半径画弧，两弧交于点B，画射线OB．则cos∠AOB的值等于（）A．√33B．12C．√22D．√322．(0分)[ID：11108]若35xx y=+，则xy等于（）A．32B．38C．23D．853．(0分)[ID：11107]如图，平面直角坐标系中，点A是x轴上任意一点，BC平行于x轴，分别交y=3x（x＞0）、y=kx（x＜0）的图象于B、C两点，若△ABC的面积为2，则k值为（）A．﹣1B．1C．12-D．124．(0分)[ID：11095]在函数y＝21ax+（a为常数）的图象上有三个点（﹣1，y1），（﹣1 4，y2），（12，y3），则函数值y1、y2、y3的大小关系是（）A．y2＜y1＜y3B．y3＜y2＜y1C．y1＜y2＜y3D．y3＜y1＜y25．(0分)[ID：11091]已知两个相似三角形的面积比为 4：9，则周长的比为 ( ) A．2：3B．4：9C．3：2D236．(0分)[ID：11089]如图，△ABC 中，AD 是中线，BC=8，∠B=∠DAC，则线段AC 的长为（）A ．43B ．42C ．6D ．47．(0分)[ID ：11086]如图，△OAB ∽△OCD ，OA ：OC ＝3：2，∠A ＝α，∠C ＝β，△OAB 与△OCD 的面积分别是S 1和S 2，△OAB 与△OCD 的周长分别是C 1和C 2，则下列等式一定成立的是( )A ．32OB CD=B ．32αβ= C ．1232S S = D ．1232C C =8．(0分)[ID ：11077]如图，正方形ABCD 中，M 为BC 上一点，ME ⊥AM ，ME 交CD 于点F ，交AD 的延长线于点E ，若AB ＝4，BM ＝2，则△DEF 的面积为（ ）A ．9B ．8C ．15D ．14.59．(0分)[ID ：11073]已知2x =3y ，则下列比例式成立的是（ ）A ．x2=3yB ．x+y y=43C ．x3=y 2D ．x+y x=3510．(0分)[ID ：11058]如图，在矩形ABCD 中，DE AC ⊥于E ，设ADE α∠=，且3cos 5α=，5AB =，则AD 的长为（ ）A ．3B ．163C ．203D ．16511．(0分)[ID ：11056]如图，在以O 为原点的直角坐标系中，矩形OABC 的两边OC 、OA 分别在x 轴、y 轴的正半轴上，反比例函数ky x=(x ＞0)与AB 相交于点D ，与BC 相交于点E ，若BD=3AD ，且△ODE 的面积是9,则k 的值是( )A．92B．74C．245D．1212．(0分)[ID：11048]如图所示，在平面直角坐标系中，已知点A（2，4），过点A作AB⊥x轴于点B．将△AOB以坐标原点O为位似中心缩小为原图形的12，得到△COD，则CD的长度是（）A．2 B．1 C．4 D．2513．(0分)[ID：11042]如图所示，在△ABC 中，AB＝6，AC＝4，P 是AC 的中点，过 P 点的直线交AB 于点Q，若以 A、P、Q 为顶点的三角形和以A、B、C为顶点的三角形相似，则AQ 的长为 ( )A．3B．3或43C．3或34D．4314．(0分)[ID：11059]如图，在△ABC中，AC＝8，∠ABC＝60°，∠C＝45°，AD⊥BC，垂足为D，∠ABC的平分线交AD于点E，则AE的长为A．423B．2C．823D．215．(0分)[ID：11037]制作一块3m×2m长方形广告牌的成本是120元，在每平方米制作成本相同的情况下，若将此广告牌的四边都扩大为原来的3倍，那么扩大后长方形广告牌的成本是（）A．360元B．720元C．1080元D．2160元二、填空题16．(0分)[ID：11231]如果把两条邻边中较短边与较长边的比值为512-的矩形称作黄金矩形.那么，现将长度为20cm的铁丝折成一个黄金矩形，这个黄金矩形较短的边长是_____cm.17．(0分)[ID：11189]一天，小青想利用影子测量校园内一根旗杆的高度，在同一时刻内，小青的影长为2米，旗杆的影长为20米，若小青的身高为1.60米，则旗杆的高度为__________米.18．(0分)[ID：11157]如图，一条河的两岸有一段是平行的，在河的南岸边每隔5米有一棵树，在北岸边每隔50米有一根电线杆．小丽站在离南岸边15米的P点处看北岸，发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住，并且在这两棵树之间还有三棵树，则河宽为________米．19．(0分)[ID：11150]如图，在同一时刻两根木杆在太阳光下的影子如图所示，其中木杆2AB m=，它的影子 1.6BC m=，木杆PQ的影子有一部分落在了墙上， 1.2PM m=，0.8MN m=，则木杆PQ的长度为______m．20．(0分)[ID：11142]一个几何体由若干大小相同的小立方块搭成，如图所示的分别是从它的正面、左面看到的图形，则搭成该几何体最多需要__个小立方块.21．(0分)[ID：11139]如图，在平行四边形ABCD中，AB＝12，AD＝8，∠ABC的平分线交CD于点F，交AD的延长线于点E，CG⊥BE，垂足为G，若EF＝2，则线段CG的长为_____．22．(0分)[ID：11213]如图，当太阳光与地面成55°角时，直立于地面的玲玲测得自己的影长为1.25m，则玲玲的身高约为________m．（精确到0. 01m）（参考数据：sin55°≈0.8192，cos55°≈0.5736，tan55°≈1.428）.23．(0分)[ID：11197]若ab＝34，则a bb+＝__________.24．(0分)[ID：11195]如图所示的网格是正方形网格，点P到射线OA的距离为m，点P 到射线OB的距离为n，则m __________ n．（填“>”，“=”或“<”）25．(0分)[ID：11222]如果a c eb d f===k（b+d+f≠0），且a+c+e=3（b+d+f），那么k=_____．三、解答题26．(0分)[ID：11325]如图，铁路MN和公路PQ在点O处交汇，∠QON＝30°，在点A 处有一栋居民楼，AO＝320m，如果火车行驶时，周围200m以内会受到噪音的影响，那么火车在铁路MN上沿ON方向行驶时．（1）居民楼是否会受到噪音的影响？请说明理由；（2）如果行驶的速度为72km/h，居民楼受噪音影响的时间为多少秒？27．(0分)[ID：11316]由一些大小相同，棱长为1的小正方体搭成的几何体的俯视图如图所示，数字表示该位置的正方体个数．（1）请画出它的主视图和左视图；（2）给这个几何体喷上颜色（底面不喷色），需要喷色的面积为 ； （3）在不改变主视图和俯视图的情况下，最多可添加 块小正方体．28．(0分)[ID ：11309]如图1，为放置在水平桌面l 上的台灯，底座的高AB 为5cm .长度均为20cm 的连杆BC ，CD 与AB 始终在同一水平面上.（1）旋转连杆BC ，CD ，使BCD ∠成平角，150ABC ∠=︒，如图2，求连杆端点D 离桌面l 的高度DE .（2）将（1）中的连杆CD 绕点C 逆时针旋转，使165BCD ∠=︒，如图3，问此时连杆端点D 离桌面l 的高度是增加了还是减少？增加或减少了多少？（精确到0.1cm ，参考数2 1.41≈3 1.73≈）29．(0分)[ID ：11279]如图，已知反比例函数11k y x=（k 1＞0）与一次函数2221(0)y k x k =+≠相交于A 、B 两点，AC ⊥x 轴于点C . 若△OAC 的面积为1，且tan ∠AOC ＝2 .（1）求出反比例函数与一次函数的解析式；（2）请直接写出B 点的坐标，并指出当x 为何值时，反比例函数y 1的值大于一次函数y 2的值.30．(0分)[ID：11319]如图，一艘轮船位于灯塔P的北偏东60°方向，与灯塔P的距离为80海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东45°方向的B 处，求此时轮船所在的B处与灯塔P的距离．（参考数据：6≈2.449，结果保留整数）【参考答案】2016-2017年度第*次考试试卷参考答案**科目模拟测试一、选择题1．B2．A3．A4．A5．A6．B7．D8．A9．C10．C11．C12．A13．B14．C15．C二、填空题16．【解析】【分析】设这个黄金矩形较长的边长是xcm根据题意得：解方程可得【详解】设这个黄金矩形较长的边长是xcm根据题意得：解得：x=则这个黄金矩形较短的边长是cm故答案为：【点睛】考核知识点：黄金分17．16【解析】【分析】易得△AOB∽△ECD利用相似三角形对应边的比相等可得旗杆OA 的长度【详解】解：∵OA⊥DACE⊥DA∴∠CED=∠OAB=90°∵CD∥OE∴∠CDA=∠OBA∴△AOB∽△E18．5【解析】根据题意画出图形构造出△PCD∽△PAB利用相似三角形的性质解题解：过P作PF⊥AB交CD于E交AB于F如图所示设河宽为x米∵AB∥CD∴∠PDC=∠PBF∠PCD=∠PAB∴△PDC∽△19．3【解析】【分析】先根据同一时刻物高与影长成正比求出QD的影长再根据此影长列出比例式即可【详解】解：过N点作ND⊥PQ于D又∵AB=2BC=16PM=12NM=08∴PQ=QD+DP=QD+NM=120．14【解析】试题解析：根据主视图和左视图可得：搭这样的几何体最多需要6+3+5=14个小正方体；故答案为：14点睛：主视图是从物体的正面看得到的视图左视图是从物体的左面看得到的视图；注意主视图主要告21．2【解析】【分析】首先证明CF=BC=12利用相似三角形的性质求出BF再利用勾股定理即可解决问题【详解】解：∵四边形ABCD是平行四边形∴AB＝CD＝12AE∥BCAB∥CD∴∠CFB＝∠FBA∵B22．79【解析】【分析】身高影长和光线构成直角三角形根据tan55°=身高：影长即可解答【详解】解：玲玲的身高=影长×tan55°=125×1428≈179（m）故答案为179【点睛】本题考查了解直角三23．【解析】【分析】由比例的性质即可解答此题【详解】∵∴a=b∴=故答案为【点睛】此题考查了比例的基本性质熟练掌握这个性质是解答此题的关键24．>【解析】【分析】由图像可知在射线上有一个特殊点点到射线的距离点到射线的距离于是可知利用锐角三角函数即可判断出【详解】由题意可知：找到特殊点如图所示：设点到射线的距离点到射线的距离由图可知【点睛】本25．3【解析】∵=k∴a=bkc=dke=fk∴a+c+e=bk+dk+fk=k(a+b+c)∵a+c+e=3(b+d+f)∴k=3故答案为：3三、解答题26．27．28．29．30．2016-2017年度第*次考试试卷参考解析【参考解析】**科目模拟测试一、选择题1．B解析：B【解析】【分析】根据作图可以证明△AOB是等边三角形，则∠AOB=60°，据此即可求解．【详解】连接AB，由图可知：OA=0B，AO=AB∴OA=AB=OB，即三角形OAB为等边三角形，∴∠AOB=60°，∴cos∠AOB=cos60°=12．故选B．【点睛】本题主要考查了特殊角的三角函数值，正确理解△ABC是等边三角形是解题的关键．2．A解析：A【解析】【分析】先根据比例的基本性质进行变形，得到2x=3y，再根据比例的基本性质转化成比例式即可得.【详解】根据比例的基本性质得：5x=3（x+y），即2x=3y，即得32xy，故选A．【点睛】本题考查了比例的基本性质，熟练掌握比例的基本性质是解本题的关键.3．A解析：A【解析】【分析】连接OC、OB，如图，由于BC∥x轴，根据三角形面积公式得到S△ACB=S△OCB，再利用反比例函数系数k的几何意义得到12×|3|+12•|k|=2，然后解关于k的绝对值方程可得到满足条件的k的值．【详解】连接OC、OB，如图，∵BC∥x轴，∴S△ACB=S△OCB，而S△OCB=12×|3|+12•|k|，∴12×|3|+12•|k|=2，而k＜0，∴k=﹣1，故选A．【点睛】本题考查了反比例函数系数k的几何意义：在反比例函数y=kx图象中任取一点，过这一个点向x轴和y轴分别作垂线，与坐标轴围成的矩形的面积是定值|k|．在反比例函数的图象上任意一点向坐标轴作垂线，这一点和垂足以及坐标原点所构成的三角形的面积是12|k|，且保持不变．4．A解析：A【解析】【分析】先根据反比例函数的解析式判断出反比例函数的图象所在的象限及增减性，再根据各点横坐标的值判断出y1，y2，y3的大小关系即可．【详解】∵反比例函数的比例系数为a2+1＞0，∴图象的两个分支在一、三象限，且在每个象限y随x的增大而减小．∵﹣114-＜＜0，∴点（﹣1，y1），（14-，y2）在第三象限，∴y2＜y1＜0．∵12＞0，∴点（12，y3）在第一象限，∴y3＞0，∴y2＜y1＜y3．故选A．【点睛】本题考查了反比例函数图象上点的坐标特点，即反比例函数图象上各点的坐标一定适合此函数的解析式．5．A解析：A【解析】【分析】由于相似三角形的面积比等于相似比的平方，已知了两个相似三角形的面积比，即可求出它们的相似比；再根据相似三角形的周长比等于相似比即可得解．【详解】∵两个相似三角形的面积之比为4：9，∴两个相似三角形的相似比为2：3，∴这两个相似三角形的周长之比为2：3．故选：A【点睛】本题考查的是相似三角形的性质：相似三角形的周长比等于相似比，面积比等于相似比的平方．6．B解析：B【解析】【分析】由已知条件可得ABC DAC ~,可得出AC BC DC AC =,可求出AC 的长． 【详解】解：由题意得：∠B =∠DAC ，∠ACB =∠ACD,所以ABC DAC ~，根据“相似三角形对应边成比例”，得AC BC DC AC=，又AD 是中线，BC =8，得DC=4,代入可得AC= 故选B.【点睛】本题主要考查相似三角形的判定与性质．灵活运用相似的性质可得出解答． 7．D解析：D【解析】A 选项，在△OAB ∽△OCD 中，OB 和CD 不是对应边，因此它们的比值不一定等于相似比，所以A 选项不一定成立；B 选项，在△OAB ∽△OCD 中，∠A 和∠C 是对应角，因此αβ=，所以B 选项不成立； C 选项，因为相似三角形的面积比等于相似比的平方，所以C 选项不成立；D 选项，因为相似三角形的周长比等于相似比，所以D 选项一定成立.故选D.8．A解析：A【解析】【分析】由勾股定理可求AM 的长，通过证明△ABM ∽△EMA ，可求AE=10，可得DE=6，由平行线分线段成比例可求DF 的长，即可求解．【详解】解：∵AB＝4，BM＝2，∴AM===，∵四边形ABCD是正方形，∴AD∥BC，∠B＝∠C＝90°，∴∠EAM＝∠AMB，且∠B＝∠AME＝90°，∴△ABM∽△EMA，∴BM AM AM AE=AE=∴AE＝10，∴DE＝AE﹣AD＝6，∵AD∥BC，即DE∥MC，∴△DEF∽△CMF，∴DE DF MC CF=，∴642DFCF=-＝3，∵DF+CF＝4，∴DF＝3，∴S△DEF＝12DE×DF＝9，故选：A．【点睛】本题考查了相似三角形的判定与性质，正方形的性质，勾股定理；熟练掌握相似三角形的性质，并能进行推理计算是解决问题的关键.9．C解析：C【解析】【分析】把各个选项依据比例的基本性质，两内项之积等于两外项之积，已知的比例式可以转化为等积式2x=3y，即可判断．【详解】A．变成等积式是：xy=6，故错误；B．变成等积式是：3x+3y=4y，即3x=y，故错误；C．变成等积式是：2x=3y，故正确；D．变成等积式是：5x+5y=3x，即2x+5y=0，故错误．故选C．【点睛】本题考查了判断两个比例式是否能够互化的方法，即转化为等积式，判断是否相同即可．10．C解析：C【解析】【分析】根据矩形的性质可知：求AD 的长就是求BC 的长，易得∠BAC =∠ADE ，于是可利用三角函数的知识先求出AC ，然后在直角△ABC 中根据勾股定理即可求出BC ，进而可得答案.【详解】解：∵四边形ABCD 是矩形，∴∠B =∠BAC =90°，BC=AD ，∴∠BAC +∠DAE =90°， ∵DE AC ⊥，∴∠ADE +∠DAE =90°，∴∠BAC =ADE α∠=，在直角△ABC 中，∵3cos 5α=，5AB =，∴25cos 3AB AC α==，∴AD=BC 203==. 故选：C.【点睛】本题考查了矩形的性质、勾股定理和解直角三角形的知识，属于常考题型，熟练掌握矩形的性质和解直角三角形的知识是解题关键.11．C解析：C【解析】【分析】设B 点的坐标为（a ，b ），由BD=3AD ，得D （4a ，b ），根据反比例函数定义求出关键点坐标，根据S △ODE =S 矩形OCBA -S △AOD -S △OCE -S △BDE = 9求出k.【详解】 ∵四边形OCBA 是矩形，∴AB=OC ，OA=BC ，设B 点的坐标为（a ，b ），∵BD=3AD ，∴D （4a ，b ）， ∵点D ，E 在反比例函数的图象上， ∴4ab =k ， ∴E （a ， k a）， ∵S △ODE =S 矩形OCBA -S △AOD -S △OCE -S △BDE =ab-12•4ab -12•4ab -12•34a •（b-k a ）=9，∴k=245， 故选：C 【点睛】 考核知识点：反比例函数系数k 的几何意义. 结合图形，分析图形面积关系是关键.12．A解析：A【解析】【分析】直接利用位似图形的性质结合A 点坐标可直接得出点C 的坐标，即可得出答案．【详解】∵点A （2，4），过点A 作AB ⊥x 轴于点B ，将△AOB 以坐标原点O 为位似中心缩小为原图形的12，得到△COD ， ∴C （1，2），则CD 的长度是2，故选A ． 【点睛】本题主要考查了位似变换以及坐标与图形的性质，正确把握位似图形的性质是解题关键．13．B解析：B【解析】AP AQ AB AC =,264AQ =，AQ=43，AP AQ AC AB =,246AQ =，AQ =3.故选B.点睛：相似常见图形（1）称为“平行线型”的相似三角形（如图,有“A 型”与“X 型”图）（2）如图：其中∠1=∠2，则△ADE ∽△ABC 称为“斜交型”的相似三角形，有“反A 共角型”、“反A 共角共边型”、 “蝶型”，如下图：14．C解析：C【解析】【分析】由已知可知△ADC 是等腰直角三角形，根据斜边AC=8可得2，在Rt △ABD 中，由∠B=60°，可得BD=tan 60AD ︒46，再由BE 平分∠ABC ，可得∠EBD=30°，从而可求得DE 长，再根据AE=AD-DE 即可【详解】∵AD ⊥BC ，∴△ADC 是直角三角形，∵∠C=45°，∴∠DAC=45°，∴AD=DC ，∵AC=8，∴2，在Rt △ABD 中，∠B=60°，∴BD=tan 60AD ︒423=463， ∵BE 平分∠ABC ，∴∠EBD=30°，∴463=23， ∴AE=AD-DE=428242= 故选C.【点睛】本题考查了解直角三角形的应用，熟练掌握直角三角形中边角之间的关系是解题的关键.15．C解析：C【解析】【分析】根据题意求出长方形广告牌每平方米的成本，根据相似多边形的性质求出扩大后长方形广告牌的面积，计算即可．【详解】3m×2m=6m 2，∴长方形广告牌的成本是120÷6=20元/m 2， 将此广告牌的四边都扩大为原来的3倍，则面积扩大为原来的9倍，∴扩大后长方形广告牌的面积=9×6=54m 2， ∴扩大后长方形广告牌的成本是54×20=1080元， 故选C ．【点睛】本题考查的是相似多边形的性质，掌握相似多边形的面积比等于相似比的平方是解题的关键．二、填空题16．【解析】【分析】设这个黄金矩形较长的边长是xcm 根据题意得：解方程可得【详解】设这个黄金矩形较长的边长是xcm 根据题意得：解得：x=则这个黄金矩形较短的边长是cm 故答案为：【点睛】考核知识点：黄金分解析：(15-【解析】【分析】设这个黄金矩形较长的边长是xcm ，根据题意得：220x x ⎛⎫+= ⎪⎝⎭，解方程可得. 【详解】设这个黄金矩形较长的边长是xcm ，根据题意得：220x x ⎛⎫+= ⎪⎝⎭，解得：x= 5，则这个黄金矩形较短的边长是15)(152⨯=-cm ．故答案为：(15-【点睛】考核知识点：黄金分割点的应用.理解黄金分割的意义是关键.17．16【解析】【分析】易得△AOB∽△ECD利用相似三角形对应边的比相等可得旗杆OA的长度【详解】解：∵OA⊥DACE⊥DA∴∠CED=∠OAB=90°∵CD∥OE∴∠CDA=∠OBA∴△AOB∽△E解析：16【解析】【分析】易得△AOB∽△ECD，利用相似三角形对应边的比相等可得旗杆OA的长度．【详解】解：∵OA⊥DA，CE⊥DA，∴∠CED=∠OAB=90°，∵CD∥OE，∴∠CDA=∠OBA，∴△AOB∽△ECD，∴CE OA16OA,DE AB220==，解得OA=16．故答案为16．18．5【解析】根据题意画出图形构造出△PCD∽△PAB利用相似三角形的性质解题解：过P作PF⊥AB交CD于E交AB于F如图所示设河宽为x米∵AB∥CD∴∠PDC=∠PBF∠PCD=∠PAB∴△PDC∽△解析：5【解析】根据题意画出图形，构造出△PCD∽△PAB，利用相似三角形的性质解题．解：过P作PF⊥AB，交CD于E，交AB于F，如图所示设河宽为x米．∵AB∥CD，∴∠PDC=∠PBF，∠PCD=∠PAB，∴△PDC∽△PBA，∴AB PF CD PE =， ∴AB 15x CD 15+=， 依题意CD=20米，AB=50米， ∴1520 5015x =+， 解得：x=22.5（米）．答：河的宽度为22.5米．19．3【解析】【分析】先根据同一时刻物高与影长成正比求出QD 的影长再根据此影长列出比例式即可【详解】解：过N 点作ND ⊥PQ 于D 又∵AB=2BC=16PM=12NM=08∴PQ=QD+DP=QD+NM=1解析：3【解析】【分析】先根据同一时刻物高与影长成正比求出QD 的影长，再根据此影长列出比例式即可．【详解】解：过N 点作ND ⊥PQ 于D ，BC DN AB QD∴= 又∵AB=2，BC=1.6，PM=1.2，NM=0.8， 1.5AB DN QD BC ⋅∴== ∴PQ=QD+DP=QD+NM=1.5+0.8=2.3（m ）．故答案为：2.3．【点睛】在运用相似三角形的知识解决实际问题时，要能够从实际问题中抽象出简单的数学模型，然后列出相关数据的比例关系式，从而求出结论．20．14【解析】试题解析：根据主视图和左视图可得：搭这样的几何体最多需要6+3+5=14个小正方体；故答案为：14点睛：主视图是从物体的正面看得到的视图左视图是从物体的左面看得到的视图；注意主视图主要告解析：14【解析】试题解析：根据主视图和左视图可得：搭这样的几何体最多需要6+3+5=14个小正方体；故答案为：14．点睛：主视图是从物体的正面看得到的视图，左视图是从物体的左面看得到的视图；注意主视图主要告知组成的几何体的层数和列数．21．2【解析】【分析】首先证明CF=BC=12利用相似三角形的性质求出BF再利用勾股定理即可解决问题【详解】解：∵四边形ABCD是平行四边形∴AB＝CD＝12AE∥BCAB∥CD∴∠CFB＝∠FBA∵B解析：【解析】【分析】首先证明CF=BC=12，利用相似三角形的性质求出BF，再利用勾股定理即可解决问题．【详解】解：∵四边形ABCD是平行四边形，∴AB＝CD＝12，AE∥BC，AB∥CD，∴∠CFB＝∠FBA，∵BE平分∠ABC，∴∠ABF＝∠CBF，∴∠CFB＝∠CBF，∴CB＝CF＝8，∴DF＝12﹣8＝4，∵DE∥CB，∴△DEF∽△CBF，∴EFBF＝DFCF，∴2BF＝48，∴BF＝4，∵CF＝CB，CG⊥BF，∴BG＝FG＝2，在Rt△BCG中，CG＝故答案为【点睛】本题考查平行四边形的性质，相似三角形的判定和性质，勾股定理等知识，解题的关键是正确寻找相似三角形解决问题，属于中考常考题型．22．79【解析】【分析】身高影长和光线构成直角三角形根据tan55°=身高：影长即可解答【详解】解：玲玲的身高=影长×tan55°=125×1428≈179（m）故答案为179【点睛】本题考查了解直角三解析：79【解析】【分析】身高、影长和光线构成直角三角形，根据tan55°=身高：影长即可解答． 【详解】解：玲玲的身高=影长×tan55°=1.25×1.428≈1.79（m ）．故答案为1.79．【点睛】本题考查了解直角三角形的应用、正切的概念、计算器的使用．23．【解析】【分析】由比例的性质即可解答此题【详解】∵∴a=b∴=故答案为【点睛】此题考查了比例的基本性质熟练掌握这个性质是解答此题的关键 解析：74【解析】【分析】由比例的性质即可解答此题.【详解】 ∵34a b =， ∴a=34b ， ∴a b b +=3744b b b b b+= ， 故答案为74【点睛】 此题考查了比例的基本性质，熟练掌握这个性质是解答此题的关键.24．>【解析】【分析】由图像可知在射线上有一个特殊点点到射线的距离点到射线的距离于是可知利用锐角三角函数即可判断出【详解】由题意可知：找到特殊点如图所示：设点到射线的距离点到射线的距离由图可知【点睛】本 解析：>【解析】【分析】由图像可知在射线OP 上有一个特殊点Q ,点Q 到射线OA的距离QD =Q 到射线OB 的距离1QC =，于是可知AOP BOP ∠>∠ ,利用锐角三角函数sin sin AOP BOP ∠>∠ ,即可判断出m n >【详解】由题意可知：找到特殊点Q ，如图所示：设点Q 到射线OA 的距离QD ，点Q 到射线OB 的距离QC 由图可知2QD =1QC =∴ 2sin QD AOP OP ∠==1sin QC BOP OP OP ∠== ∴sin sin AOP BOP ∠>∠, ∴m n OP OP> ∴m n >【点睛】本题考查了点到线的距离，熟知在直角三角形中利用三角函数来解角和边的关系是解题关键.25．3【解析】∵=k ∴a=bkc=dke=fk ∴a+c+e=bk+dk+fk=k(a+b+c)∵a+c+e=3(b+d+f)∴k=3故答案为：3解析：3【解析】 ∵a c e b d f===k ，∴a=bk，c=dk ，e=fk ，∴a+c+e=bk+dk+fk=k(a+b+c)， ∵a+c+e=3(b+d+f)，∴k=3，故答案为：3.三、解答题26．（1）居民楼会受到噪音的影响；（2）影响时间应是12秒．【解析】【分析】（1）作AC ⊥ON 于C ，利用含30度的直角三角形三边的关系得到AC ＝12AO ＝160，则点A 到MN 的距离小200，从而可判断学校会受到影响；（2）以A 为圆心，100为半径画弧交MN 于B 、D ，如图，则AB ＝AD ＝200，利用等腰三角形的性质得BC ＝CD ，接下来利用勾股定理计算出BC ＝120，所以BD ＝2BC ＝240，然后利用速度公式计算出学校受到的影响的时间．【详解】（1）如图：过点A作AC⊥ON，∵∠QON＝30°，OA＝320米，∴AC＝160米，∵AC＜200，∴居民楼会受到噪音的影响；（2）以A为圆心，200m为半径作⊙A，交MN于B、D两点，即当火车到B点时直到驶离D点，对居民楼产生噪音影响，∵AB＝200米，AC＝160米，∴由勾股定理得：BC＝120米，由垂径定理得BD＝2BC＝240米，∵72千米/小时＝20米/秒，∴影响时间应是：240÷20＝12秒．【点睛】此题是解直角三角形的应用，主要考查的是垂径定理的应用及勾股定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．27．(1)见解析；（2）32.（3）1.【解析】试题分析：（1）根据图示可知主视图有3列，每列小正方形的个数依次为3、1、3，左视图有两列，每列小正方形的个数依次为3、2，据此即可画出；（2）根据三视图画出几何体，根据几何体即可得；（3）要不改变主视图和俯视图的情况下，根据题意画出添加小正方体后的图形（如图2）即可.试题解析：（1）它的主视图和左视图，如图所示，（2）如图1，给这个几何体喷上颜色(底面不喷色)，根据图形可知需要喷色的面有32个，所以喷色的面积为32；（3）如图2，在不改变主视图和俯视图的情况下，最多可添加1个小正方体，28．（1）39.6DE cm ≈；（2）下降了，约3.2cm .【解析】【分析】（1）如图2中，作BO ⊥DE 于O ．解直角三角形求出OD 即可解决问题．（2）作DF ⊥l 于F ，CP ⊥DF 于P ，BG ⊥DF 于G ，CH ⊥BG 于H ．则四边形PCHG 是矩形，求出DF ，再求出DF-DE 即可解决问题．【详解】（1）过点B 作BO DE ⊥，垂足为O ，如图2，则四边形ABOE 是矩形，1509060OBD =-=∠， ∴sin 6040sin 60203DO BO =⋅=⨯=，∴203539.6DE DO OE DO AB cm =+=+=+≈.（2）下降了.如图3，过点D 作DF l ⊥于点F ，过点C 作CP DF ⊥于点P ，过点B 作BG DF ⊥于点G ，过点C 作CH BG ⊥于点H ，则四边形PCHG 为矩形，∵60CBH ︒∠=，∴30BCH ︒∠=，又∵165BCD ︒∠=，∴45DCP ︒∠=，∴sin 60CH BC ︒==*sin 45DP CD ==，∴DF DP PG GF DP CH AB =++=++5=.∴下降高度：55DE DF -=-=3.2cm ≈.【点睛】本题考查解直角三角形的应用，解题的关键是学会添加常用辅助线，构造直角三角形解决问题．29．（1）12y x =；21y x =+；（2）B 点的坐标为（－2，－1）；当0＜x ＜1和x ＜－2时，y 1＞y 2.【解析】【分析】（1）根据tan ∠AOC ＝AC OC＝2，△OAC 的面积为1，确定点A 的坐标，把点A 的坐标分别代入两个解析式即可求解；（2）根据两个解析式求得交点B 的坐标，观察图象，得到当x 为何值时，反比例函数y 1的值大于一次函数y 2的值．【详解】解：（1）在Rt △OAC 中，设OC ＝m ．∵tan ∠AOC ＝AC OC ＝2，∴AC ＝2×OC ＝2m ． ∵S △OAC ＝12×OC×AC ＝12×m×2m ＝1，∴m 2＝1．∴m ＝1（负值舍去）． ∴A 点的坐标为（1，2）．把A 点的坐标代入11k y x=中，得k 1＝2． ∴反比例函数的表达式为12y x =． 把A 点的坐标代入221y k x =+中，得k 2＋1＝2，∴k 2＝1．∴一次函数的表达式21y x =+．（2）B 点的坐标为（－2，－1）．当0＜x ＜1和x ＜－2时，y 1＞y 2．【点睛】本题考查反比例及一次函数的的应用；待定系数法求解析式；图象的交点等，掌握反比例及一次函数的性质是本题的解题关键．30．此时轮船所在的B处与灯塔P的距离是98海里．【解析】【分析】过点P作PC⊥AB，则在Rt△APC中易得PC的长，再在直角△BPC中求出PB的长即可．【详解】作PC⊥AB于C点，∴∠APC=30°，∠BPC=45°，AP=80（海里），在Rt△APC中，cos∠APC=PC PA，∴PC=PA•cos∠3（海里），在Rt△PCB中，cos∠BPC=PC PB，∴PB=403cos cos45PCBPC=∠︒6≈98（海里），答：此时轮船所在的B处与灯塔P的距离是98海里．【点睛】本题考查了解直角三角形的应用举例，正确添加辅助线构建直角三角形是解题的关键.。

一、选择题1．(0分)[ID ：11126]已知一次函数y 1=x －1和反比例函数y 2=2x 的图象在平面直角坐标系中交于A 、B 两点，当y 1＞y 2时，x 的取值范围是( )A ．x ＞2B ．－1＜x ＜0C ．x ＞2，－1＜x ＜0D ．x ＜2，x ＞0 2．(0分)[ID ：11111]如图所示，在△ABC 中， cos B ＝22，sin C ＝35，BC ＝7，则△ABC 的面积是( )A ．212B ．12C ．14D ．213．(0分)[ID ：11104]如图，在△ABC 中，DE ∥BC ，12AD DB =，DE=4，则BC 的长是（ ）A ．8B ．10C ．11D ．124．(0分)[ID ：11100]若37a b =，则b a a -等于（ ） A ．34 B ．43 C ．73 D ．375．(0分)[ID ：11089]如图，△ABC 中，AD 是中线，BC =8，∠B =∠DAC ，则线段 AC 的长为（ ）A ．43B ．42C ．6D ．46．(0分)[ID ：11087]观察下列每组图形，相似图形是（ ）A ．B ．C ．D ．7．(0分)[ID ：11067]如图，在△ABC 中，cos B ＝22，sin C ＝35，AC ＝5，则△ABC 的面积是( )A ． 212B ．12C ．14D ．218．(0分)[ID ：11061]如图，AB 是⊙O 的直径，弦CD 交AB 于点P ，AP=2，BP=6，∠APC=30°，则CD 的长为（ ）A ．15B ．25C ．215D ．89．(0分)[ID ：11058]如图，在矩形ABCD 中，DE AC ⊥于E ，设ADE α∠=，且3cos 5α=，5AB =，则AD 的长为（ ）A ．3B ．163C ．203D ．16510．(0分)[ID ：11054]如图,在平行四边形ABCD 中，点E 在边CD 上, AC 与BE 相交于点F ,且DE:CE =1:2,则△CEF 与△ABF 的周长之比为（ ）A ．1 : 2B ．1 : 3C ．2 : 3D ．4 : 911．(0分)[ID ：11039]在反比例函数4y x=的图象中，阴影部分的面积不等于4的是（ ）A．B． C．D．12．(0分)[ID：11076]在小孔成像问题中，如图所示，若为O到AB的距离是18 cm，O 到CD的距离是6 cm，则像CD的长是物体AB长的（）A．13B．12C．2倍D．3倍13．(0分)[ID：11075]如图，一张矩形纸片ABCD的长BC＝xcm，宽AB＝ycm，以宽AB为边剪去一个最大的正方形ABEF，若剩下的矩形ECDF与原矩形ABCD相似，则xy的值为（）A．512-B．512+C．2D．212+14．(0分)[ID：11071]如图，∠APD=90°，AP=PB=BC=CD，则下列结论成立的是（）A．△PAB∽△PCA B．△ABC∽△DBA C．△PAB∽△PDA D．△ABC∽△DCA 15．(0分)[ID：11038]下列变形中：①由方程125x-=2去分母，得x﹣12=10；②由方程29x=92两边同除以29，得x=1；③由方程6x﹣4=x+4移项，得7x=0；④由方程2﹣5362x x-+=两边同乘以6，得12﹣x﹣5=3（x+3）．错误变形的个数是（）个．A ．4B ．3C ．2D ．1二、填空题16．(0分)[ID ：11202]如图，P （m ，m ）是反比例函数9y x =在第一象限内的图象上一点，以P 为顶点作等边△PAB ，使AB 落在x 轴上，则△POB 的面积为_____．17．(0分)[ID ：11199]已知反比例函数21k y x+=的图像经过点(2,1)-，那么k 的值是__． 18．(0分)[ID ：11174]一个4米高的电线杆的影长是6米，它临近的一个建筑物的影长是36米．则这个建筑的高度是_____m ．19．(0分)[ID ：11164]已知A （﹣4，y 1），B （﹣1，y 2）是反比例函数y =﹣4x图象上的两个点，则y 1与y 2的大小关系为__________．20．(0分)[ID ：11154]在▱ABCD 中，E 是AD 上一点，且点E 将AD 分为2：3的两部分，连接BE 、AC 相交于F ，则AEF CBF S S ∆∆：是_______．21．(0分)[ID ：11148]如图，在平面直角坐标系中，已知点A 、B 的坐标分别为（8，0）、（0，23），C 是AB 的中点，过点C 作y 轴的垂线，垂足为D ，动点P 从点D 出发，沿DC 向点C 匀速运动，过点P 作x 轴的垂线，垂足为E ，连接BP 、EC ．当BP 所在直线与EC 所在直线垂直时，点P 的坐标为____22．(0分)[ID ：11142]一个几何体由若干大小相同的小立方块搭成，如图所示的分别是从它的正面、左面看到的图形，则搭成该几何体最多需要__个小立方块.23．(0分)[ID ：11138]如图，等腰直角三角形ABC 中， AB=4 cm.点是BC 边上的动点，以AD 为直角边作等腰直角三角形ADE.在点D 从点B 移动至点C 的过程中，点E 移动的路线长为________cm.24．(0分)[ID ：11226]如图，l 1∥l 2∥l 3，直线a 、b 与l 1、l 2、l 3分别相交于点A 、B 、C 和点D 、E 、F ．若AB =3，DE =2，BC =6，则EF =______．25．(0分)[ID ：11195]如图所示的网格是正方形网格，点P 到射线OA 的距离为m ，点P 到射线OB 的距离为n ，则m __________ n ．（填“>”，“=”或“<”）三、解答题26．(0分)[ID ：11307]计算：（1）20(3)3cos 30π︒-+（2）214tan 45|5|2-︒⎛⎫-+- ⎪⎝⎭（3）已知α为锐角，()2sin 152α︒-=，计算2cos 3tan 12αα-+-的值． 27．(0分)[ID ：11300]如图，四边形ABCD 中，AC 平分∠DAB ，∠ADC=∠ACB=90°，E 为AB 的中点，（1）求证：AC 2=AB•AD ；（2）求证：CE ∥AD ；（3）若AD=4，AB=6，求的值．28．(0分)[ID ：11294]如图，△ABC 内接于⊙O ，AB=AC ，∠BAC=36°，过点A 作AD ∥BC ，与∠ABC 的平分线交于点D ，BD 与AC 交于点E ，与⊙O 交于点F ．（1）求∠DAF 的度数；（2）求证：AE 2=EF•ED ；29．(0分)[ID ：11263]自开展“全民健身运动”以来，喜欢户外步行健身的人越来越多，为方便群众步行健身，某地政府决定对一段如图1所示的坡路进行改造．如图2所示，改造前的斜坡200AB =米，坡度为1:3；将斜坡AB 的高度AE 降低20AC =米后，斜坡AB 改造为斜坡CD ，其坡度为1:4．求斜坡CD 的长．（结果保留根号）30．(0分)[ID ：11244]如图，在路灯下，小明的身高如图中线段AB 所示，他在地面上的影子如图中线段AC 所示，小亮的身高如图中线段FG 所示，路灯灯泡在线段DE 上． （1）请你确定灯泡所在的位置，并画出小亮在灯光下形成的影子．（2）如果小明的身高AB ＝1.6m ，他的影子长AC ＝1.4m ，且他到路灯的距离AD ＝2.1m ，求灯泡的高．【参考答案】2016-2017年度第*次考试试卷参考答案**科目模拟测试一、选择题1．C2．A3．D4．B5．B6．D7．A8．C9．C10．C11．B12．A13．B14．B15．B二、填空题16．【解析】【详解】如图过点P作PH⊥OB于点H∵点P（mm）是反比例函数y=在第一象限内的图象上的一个点∴9=m2且m＞0解得m=3∴PH=OH=3∵△PAB是等边三角形∴∠PAH=60°∴根据锐角三17．【解析】【分析】将点的坐标代入可以得到-1=然后解方程便可以得到k的值【详解】∵反比例函数y＝的图象经过点（2-1）∴-1=∴k＝−；故答案为k＝−【点睛】本题主要考查函数图像上的点满足其解析式可以18．24米【解析】【分析】先设建筑物的高为h米再根据同一时刻物高与影长成正比列出关系式求出h的值即可【详解】设建筑物的高为h米由题意可得：则4：6=h：36解得：h=24（米）故答案为24米【点睛】本题19．y1＜y2【解析】分析：根据反比例函数的性质和题目中的函数解析式可以判断y1与y2的大小从而可以解答本题详解：∵反比例函数y=--4＜0∴在每个象限内y随x的增大而增大∵A（-4y1）B（-1y2）20．或【解析】【分析】分两种情况根据相似三角形的性质计算即可【详解】解：①当时∵四边形ABCD是平行四边形②当时同理可得故答案为：或【点睛】考查的是相似三角形的判定和性质平行四边形的性质掌握相似三角形的21．(1)【解析】【分析】先根据题意求得CD和PE的长再判定△EPC∽△PDB列出相关的比例式求得DP的长最后根据PEDP的长得到点P的坐标【详解】由题意可知OB=2AO=8∵CD⊥BOC是AB的中点∴22．14【解析】试题解析：根据主视图和左视图可得：搭这样的几何体最多需要6+3+5=14个小正方体；故答案为：14点睛：主视图是从物体的正面看得到的视图左视图是从物体的左面看得到的视图；注意主视图主要告23．【解析】试题解析：连接CE如图：∵△ABC和△ADE为等腰直角三角形∴AC=ABAE=AD∠BAC=45°∠DAE=45°即∠1+∠2=45°∠2+∠3=45°∴∠1=∠3∵∴△ACE∽△ABD∴∠24．4【解析】【分析】利用平行线分线段成比例定理列出比例式求出EF结合图形计算即可【详解】∵∥∥∴又DE=2∴EF=4故答案为：4【点睛】本题考查的是平行线分线段成比例定理灵活运用定理找准对应关系是解题25．>【解析】【分析】由图像可知在射线上有一个特殊点点到射线的距离点到射线的距离于是可知利用锐角三角函数即可判断出【详解】由题意可知：找到特殊点如图所示：设点到射线的距离点到射线的距离由图可知【点睛】本三、解答题26．27．28．29．30．2016-2017年度第*次考试试卷 参考解析【参考解析】**科目模拟测试一、选择题1．C解析：C【解析】【分析】因为一次函数和反比例函数交于A 、B 两点，可知x-1=2x，解得x=-1或x=2，进而可得A 、B 两点的坐标，据此，再结合函数解析式画图，据图可知当x>2时，以及当-1<x<0时，y 1>y 2．【详解】解方程x −1=2x，得 x =−1或x =2，那么A 点坐标是(−1,−2),B 点坐标是(2,1)，如右图，当x >2时, 12y y >,以及当−1<x <0时, 12y y >.故选C.【点睛】本题考查了反比例函数与一次函数交点问题，解题的关键是能根据解析式画出函数的图象，并能根据图象解決问题2．A解析：A 【解析】【分析】【详解】试题分析：过点A作AD⊥BC，∵△ABC中，cosB=22，sinC=35，AC=5，∴cosB=22=BDAB，∴∠B=45°，∵sinC=35=ADAC=5AD，∴AD=3，∴CD=4，∴BD=3，则△ABC的面积是：12×AD×BC=12×3×（3+4）=212．故选A．考点：1．解直角三角形；2．压轴题．3．D解析：D【解析】【分析】根据ADDB=12，可得ADAB=13，再根据DE∥BC，可得DEBC=ADAB；接下来根据DE=4，结合上步分析即可求出BC的长.【详解】∵ADDB=12，∴ADAB=13，∵在△ABC中，DE∥BC，∴DEBC=ADAB=13.∵DE=4，∴BC=3DE=12.故答案选D.【点睛】本题考查了平行线分线段成比例的知识，解题的关键是熟练的掌握平行线分线段成比例定理.4．B解析：B【解析】由比例的基本性质可知a=37b ，因此b a a -=347337b b b -=. 故选B.5．B解析：B【解析】【分析】由已知条件可得ABC DAC ~,可得出AC BC DC AC =,可求出AC 的长． 【详解】解：由题意得：∠B =∠DAC ，∠ACB =∠ACD,所以ABC DAC ~，根据“相似三角形对应边成比例”，得AC BC DC AC=，又AD 是中线，BC =8，得DC=4,代入可得AC= 故选B.【点睛】本题主要考查相似三角形的判定与性质．灵活运用相似的性质可得出解答． 6．D解析：D【解析】【分析】根据相似图形的定义，形状相同，可得出答案．【详解】解：A 、两图形形状不同，故不是相似图形；B 、两图形形状不同，故不是相似图形；C 、两图形形状不同，故不是相似图形；D 、两图形形状相同，故是相似图形；故选：D ．【点睛】本题主要考查相似图形的定义，掌握相似图形形状相同是解题的关键．7．A解析：A【解析】【分析】根据已知作出三角形的高线AD ，进而得出AD ，BD ，CD ，的长，即可得出三角形的面积．【详解】解：过点A作AD⊥BC，∵△ABC中，cosB=22，sinC=35，AC=5，∴cosB=22=BDAB，∴∠B=45°，∵sinC=35=ADAC=5AD，∴AD=3，∴CD=2253=4，∴BD=3，则△ABC的面积是：12×AD×BC=12×3×（3+4）=212．故选：A．【点睛】此题主要考查了解直角三角形的知识，作出AD⊥BC，进而得出相关线段的长度是解决问题的关键．8．C解析：C【解析】【分析】作OH⊥CD于H，连结OC，如图，根据垂径定理由OH⊥CD得到HC=HD，再利用AP=2，BP=6可计算出半径OA=4，则OP=OA－AP=2，接着在Rt△OPH中根据含30°的直角三角形的性质计算出OH=12OP=1，然后在Rt△OHC中利用勾股定理计算出CH=15，所以CD=2CH=215．【详解】作OH⊥CD于H，连结OC，如图，∵OH⊥CD，∴HC=HD ，∵AP=2，BP=6，∴AB=8，∴OA=4，∴OP=OA ﹣AP=2，在Rt △OPH 中，∵∠OPH=30°，∴∠POH=30°，∴OH=12OP=1， 在Rt △OHC 中，∵OC=4，OH=1，∴∴故选C ．【点睛】本题主要考查圆中的计算问题，熟练掌握垂径定理、含30°的直角三角形的性质以及勾股定理等知识点，掌握数形结合的思想是解答的关键9．C解析：C【解析】【分析】根据矩形的性质可知：求AD 的长就是求BC 的长，易得∠BAC =∠ADE ，于是可利用三角函数的知识先求出AC ，然后在直角△ABC 中根据勾股定理即可求出BC ，进而可得答案.【详解】解：∵四边形ABCD 是矩形，∴∠B =∠BAC =90°，BC=AD ，∴∠BAC +∠DAE =90°， ∵DE AC ⊥，∴∠ADE +∠DAE =90°，∴∠BAC =ADE α∠=，在直角△ABC 中，∵3cos 5α=，5AB =，∴25cos 3AB AC α==，∴AD=BC 203==. 故选：C.【点睛】本题考查了矩形的性质、勾股定理和解直角三角形的知识，属于常考题型，熟练掌握矩形的性质和解直角三角形的知识是解题关键.10．C解析：C【解析】【分析】根据已知可得到相似三角形，从而可得到其相似比，再根据相似三角形的周长比等于相似比就可得到答案．【详解】∵四边形ABCD是平行四边形，∴DC∥AB，CD=AB．∴△DFE∽△BFA，∵DE：EC=1：2，∴EC：DC=CE：AB=2：3，∴C△CEF：C△ABF=2：3．故选C．11．B解析：B【解析】【分析】根据反比例函数kyx=中k的几何意义，过双曲线上任意一点引x轴、y轴垂线，所得矩形面积为|k|解答即可．【详解】解：A、图形面积为|k|=4；B、阴影是梯形，面积为6；C、D面积均为两个三角形面积之和，为2×（12|k|）=4．故选B．【点睛】主要考查了反比例函数kyx=中k的几何意义，即过双曲线上任意一点引x轴、y轴垂线，所得矩形面积为|k|，是经常考查的一个知识点；这里体现了数形结合的思想，做此类题一定要正确理解k的几何意义．图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=12|k|．12．A解析：A【解析】【分析】作OE⊥AB于E，OF⊥CD于F，根据题意得到△AOB∽△COD，根据相似三角形的对应高的比等于相似比计算即可．【详解】作OE⊥AB于E，OF⊥CD于F，由题意得,AB∥CD，∴△AOB∽△COD，∴CDAB=OFOE=13，∴像CD的长是物体AB长的1 3 .故答案选：A.【点睛】本题考查了相似三角形的应用，解题的关键是熟练的掌握相似三角形的应用. 13．B解析：B【解析】【分析】根据相似多边形对应边的比相等，可得到一个方程，解方程即可求得．【详解】∵四边形ABCD是矩形，∴AD＝BC＝xcm，∵四边形ABEF是正方形，∴EF＝AB＝ycm，∴DF＝EC＝（x﹣y）cm，∵矩形FDCE与原矩形ADCB相似，∴DF：AB＝CD：AD，即：x y y y x -=∴x y故选B．【点睛】本题考查了相似多边形的性质、矩形的性质、翻折变换的性质；根据相似多边形对应边的比相等得出方程是解决本题的关键．14．B解析：B【解析】【分析】根据相似三角形的判定，采用排除法，逐条分析判断．【详解】∵∠APD=90°，而∠P AB≠∠PCA，∠PBA≠∠P AC，∴无法判定△P AB与△PCA相似，故A错误；同理，无法判定△P AB与△PDA，△ABC与△DCA相似，故C、D错误；∵∠APD=90°，AP=PB=BC=CD，∴AB=√2P A，AC=√5P A，AD=√10P A，BD=2P A，∴ABDB =√2PA2PA=√2BC2BA=√2PA=√2AC2DA=√5PA√10PA=√22，∴ABDB=BCBA=ACDC，∴△ABC∽△DBA，故B正确．故选B．【点睛】本题考查了相似三角形的判定．识别两三角形相似，除了要掌握定义外，还要注意正确找出两三角形的对应边、对应角，可根据图形提供的数据计算对应角的度数、对应边的比．本题中把若干线段的长度用同一线段来表示是求线段是否成比例时常用的方法．15．B解析：B【解析】【分析】根据方程的不同特点，从计算过程是否正确、方法应用是否得当等方面加以分析．【详解】①方程125x-=2去分母，两边同时乘以5，得x﹣12=10，故①正确．②方程29x=92，两边同除以29，得x=814；要注意除以一个数等于乘以这个数的倒数，故②错误．③方程6x﹣4=x+4移项，得5x=8；要注意移项要变号，故③错误．④方程2﹣5362x x-+=两边同乘以6，得12﹣（x﹣5）=3（x+3）；要注意去分母后，要把是多项式的分子作为一个整体加上括号，故④错误．故②③④变形错误．故选B．【点睛】在解方程时，要注意以下问题：（1）去分母时，方程两端同乘各分母的最小公倍数时，不要漏乘没有分母的项，同时要把分子（如果是一个多项式）作为一个整体加上括号；（2）移项时要变号．二、填空题16．【解析】【详解】如图过点P作PH⊥OB于点H∵点P（mm）是反比例函数y=在第一象限内的图象上的一个点∴9=m2且m＞0解得m=3∴PH=OH=3∵△PAB是等边三角形∴∠PAH=60°∴根据锐角三．【解析】【详解】如图，过点P作PH⊥OB于点H，∵点P（m，m）是反比例函数y=9x在第一象限内的图象上的一个点，∴9=m2，且m＞0，解得，m=3.∴PH=OH=3.∵△P AB是等边三角形，∴∠P AH=60°.∴根据锐角三角函数，得3∴OB3∴S△POB=12OB•PH933+.17．【解析】【分析】将点的坐标代入可以得到-1=然后解方程便可以得到k的值【详解】∵反比例函数y＝的图象经过点（2-1）∴-1=∴k＝−；故答案为k＝−【点睛】本题主要考查函数图像上的点满足其解析式可以解析：32 k=-【解析】【分析】将点的坐标代入，可以得到-1=212k+，然后解方程，便可以得到k的值．【详解】∵反比例函数y＝21kx+的图象经过点（2，-1），∴-1=21 2 k+∴k＝− 32；故答案为k＝−32．【点睛】本题主要考查函数图像上的点满足其解析式，可以结合代入法进行解答18．24米【解析】【分析】先设建筑物的高为h 米再根据同一时刻物高与影长成正比列出关系式求出h 的值即可【详解】设建筑物的高为h 米由题意可得：则4：6=h ：36解得：h=24（米）故答案为24米【点睛】本题解析：24米．【解析】【分析】先设建筑物的高为h 米，再根据同一时刻物高与影长成正比列出关系式求出h 的值即可．【详解】设建筑物的高为h 米，由题意可得：则4：6=h ：36，解得：h=24（米）．故答案为24米．【点睛】本题考查的是相似三角形的应用，熟知同一时刻物高与影长成正比是解答此题的关键．19．y1＜y2【解析】分析：根据反比例函数的性质和题目中的函数解析式可以判断y1与y2的大小从而可以解答本题详解：∵反比例函数y=--4＜0∴在每个象限内y 随x 的增大而增大∵A（-4y1）B （-1y2）解析：y 1＜y 2【解析】分析：根据反比例函数的性质和题目中的函数解析式可以判断y 1与y 2的大小，从而可以解答本题．详解：∵反比例函数y=-4x，-4＜0， ∴在每个象限内，y 随x 的增大而增大， ∵A （-4，y 1），B （-1，y 2）是反比例函数y=-4x 图象上的两个点，-4＜-1， ∴y 1＜y 2，故答案为：y 1＜y 2．点睛：本题考查反比例函数图象上点的坐标特征，解答本题的关键是明确反比例函数的性质，利用函数的思想解答．20．或【解析】【分析】分两种情况根据相似三角形的性质计算即可【详解】解：①当时∵四边形ABCD 是平行四边形②当时同理可得故答案为：或【点睛】考查的是相似三角形的判定和性质平行四边形的性质掌握相似三角形的 解析：425：或925：【解析】【分析】分2332AE ED AE ED ：＝：、：＝：两种情况，根据相似三角形的性质计算即可．【详解】解：①当23AE ED ：＝：时，∵四边形ABCD 是平行四边形，//25AD BC AE BC ∴，：＝：，AEF CBF ∴∆∆∽，224255AEF CBF S S ∆∆∴：＝（）＝：； ②当32AE ED ：＝：时，同理可得，239255AEF CBF S S ∆∆：＝（）＝：， 故答案为：425：或925：．【点睛】考查的是相似三角形的判定和性质、平行四边形的性质，掌握相似三角形的面积比等于相似比的平方是解题的关键．21．(1)【解析】【分析】先根据题意求得CD 和PE 的长再判定△EPC∽△PDB 列出相关的比例式求得DP 的长最后根据PEDP 的长得到点P 的坐标【详解】由题意可知OB=2AO=8∵CD⊥BOC 是AB 的中点∴解析：(1,3)【解析】【分析】先根据题意求得CD 和PE 的长，再判定△EPC ∽△PDB ，列出相关的比例式，求得DP 的长，最后根据PE 、DP 的长得到点P 的坐标．【详解】由题意可知，OB=23，AO=8，∵CD ⊥BO ，C 是AB 的中点，∴BD=DO=12BO==PE ，CD=12AO=4. 设DP=a ，则CP=4﹣a ，当BP 所在直线与EC 所在直线第一次垂直时，∠FCP=∠DBP ， 又∵EP ⊥CP ，PD ⊥BD ，∴∠EPC=∠PDB=90°，∴△EPC ∽△PDB.DP DB PE PC ∴= 343a =-，∴a1=1，a2=3（舍去）.∴DP=1，∵PE=3，∴P（1，3）.考点：1相似三角形性质与判定；2平面直角坐标系.22．14【解析】试题解析：根据主视图和左视图可得：搭这样的几何体最多需要6+3+5=14个小正方体；故答案为：14点睛：主视图是从物体的正面看得到的视图左视图是从物体的左面看得到的视图；注意主视图主要告解析：14【解析】试题解析：根据主视图和左视图可得：搭这样的几何体最多需要6+3+5=14个小正方体；故答案为：14．点睛：主视图是从物体的正面看得到的视图，左视图是从物体的左面看得到的视图；注意主视图主要告知组成的几何体的层数和列数．23．【解析】试题解析：连接CE如图：∵△ABC和△ADE为等腰直角三角形∴AC=ABAE=AD∠BAC=45°∠DAE=45°即∠1+∠2=45°∠2+∠3=45°∴∠1=∠3∵∴△ACE∽△ABD∴∠解析：42【解析】试题解析：连接CE，如图：∵△ABC和△ADE为等腰直角三角形，∴2AB，2AD，∠BAC=45°，∠DAE=45°，即∠1+∠2=45°，∠2+∠3=45°，∴∠1=∠3，∵AC AE AB AD== ∴△ACE ∽△ABD ， ∴∠ACE=∠ABC=90°，∴点D 从点B 移动至点C 的过程中，总有CE ⊥AC ，即点E 运动的轨迹为过点C 与AC 垂直的线段，，当点D 运动到点C 时，，∴点E 移动的路线长为cm ．24．4【解析】【分析】利用平行线分线段成比例定理列出比例式求出EF 结合图形计算即可【详解】∵∥∥∴又DE=2∴EF=4故答案为：4【点睛】本题考查的是平行线分线段成比例定理灵活运用定理找准对应关系是解题解析：4【解析】【分析】利用平行线分线段成比例定理列出比例式，求出EF ，结合图形计算即可．【详解】∵1l ∥2l ∥3l ， ∴36DE AB EF BC == 又DE=2，∴EF=4，故答案为：4．【点睛】本题考查的是平行线分线段成比例定理，灵活运用定理、找准对应关系是解题的关键．25．>【解析】【分析】由图像可知在射线上有一个特殊点点到射线的距离点到射线的距离于是可知利用锐角三角函数即可判断出【详解】由题意可知：找到特殊点如图所示：设点到射线的距离点到射线的距离由图可知【点睛】本 解析：>【解析】【分析】由图像可知在射线OP 上有一个特殊点Q ,点Q 到射线OA 的距离QD =Q 到射线OB 的距离1QC =，于是可知AOP BOP ∠>∠ ,利用锐角三角函数sin sin AOP BOP ∠>∠ ,即可判断出m n >【详解】由题意可知：找到特殊点Q ，如图所示：设点Q 到射线OA 的距离QD ，点Q 到射线OB 的距离QC 由图可知2QD =1QC =∴ 2sin QD AOP OP ∠==1sin QC BOP OP OP ∠== ∴sin sin AOP BOP ∠>∠, ∴m n OP OP> ∴m n >【点睛】本题考查了点到线的距离，熟知在直角三角形中利用三角函数来解角和边的关系是解题关键.三、解答题26．（1）72．（2）7；（3）﹣3 【解析】【分析】 （1）先计算乘方和三角函数值，再计算加减法即可；（2先计算乘方和三角函数值、绝对值，再计算加减法即可；（3）先由特殊角的三角函数值计算出α，再代入求值即可.【详解】解：（1）原式＝3﹣332 ＝2+32 ＝72． （2）原式＝4﹣2×1+5 ＝4﹣2+5＝7．（3）∵α为锐角，()sin 152α︒-=， ∴α﹣15°＝45°．∴α＝60°．∴2cos 3tan αα-+＝﹣2×12﹣＝﹣﹣＝﹣．【点睛】 本题考查了含特殊角的三角函数值的四则运算，掌握特殊角的三角函数值是解题的关键. 27．（1）见解析（2）见解析（3）AC 7AF 4=． 【解析】【分析】 （1）由AC 平分∠DAB ，∠ADC=∠ACB=90°，可证得△ADC ∽△ACB ，然后由相似三角形的对应边成比例，证得AC 2=AB•AD ．（2）由E 为AB 的中点，根据在直角三角形中，斜边上的中线等于斜边的一半，即可证得CE=12AB=AE ，从而可证得∠DAC=∠ECA ，得到CE ∥AD ． （3）易证得△AFD ∽△CFE ，然后由相似三角形的对应边成比例，求得AF CF 的值，从而得到AC AF的值． 【详解】 解：（1）证明：∵AC 平分∠DAB∴∠DAC=∠CAB ．∵∠ADC=∠ACB=90°∴△ADC ∽△ACB ． ∴AD AC AC AB= 即AC 2=AB•AD ．（2）证明：∵E 为AB 的中点∴CE=12AB=AE∵∠DAC=∠CAB ∴∠DAC=∠ECA ∴CE∥AD．（3）∵CE∥AD ∴△AFD∽△CFE∴AD AF CE CF=．∵CE=12AB∴CE=12×6=3．∵AD=4∴4AF 3CF =∴AC7 AF4=．28．（1）36°；（2）证明见解析【解析】【分析】（1）求出∠ABC、∠ABD、∠CBD的度数，求出∠D度数，根据三角形内角和定理求出∠BAF和∠BAD度数，即可求出答案；（2）求出△AEF∽△DEA，根据相似三角形的性质得出即可.【详解】（1）∵AD∥BC，∴∠D=∠CBD，∵AB=AC，∠BAC=36°，∴∠ABC=∠ACB=12×（180°﹣∠BAC）=72°，∴∠AFB=∠ACB=72°，∵BD平分∠ABC，∴∠ABD=∠CBD=12∠ABC=12×72°=36°，∴∠D=∠CBD=36°，∴∠BAD=180°﹣∠D﹣∠ABD=180°﹣36°﹣36°=108°，∠BAF=180°﹣∠ABF﹣∠AFB=180°﹣36°﹣72°=72°，∴∠DAF=∠DAB﹣∠FAB=108°﹣72°=36°；（2）∵∠CBD=36°，∠FAC=∠CBD，∵∠AED=∠AEF ，∴△AEF ∽△DEA ， ∴AE ED EF AE=， ∴AE 2=EF×ED. 【点睛】 本题考查了圆周角定理，三角形内角和定理，等腰三角形的性质等知识点，能综合运用定理进行推理是解此题的关键．29．斜坡CD 的长是【解析】【分析】根据题意和锐角三角函数可以求得AE 的长，进而得到CE 的长，再根据锐角三角函数可以得到ED 的长，最后用勾股定理即可求得CD 的长．【详解】∵90AEB =︒∠，200AB =，坡度为∴tan3ABE ∠==， ∴30ABE ∠=︒， ∴11002AE AB ==， ∵20AC =，∴80CE =，∵90CED ∠=︒，斜坡CD 的坡度为1:4， ∴14CE DE =， 即8014ED =， 解得，320ED =，∴CD =米，答：斜坡CD 的长是【点睛】本题考查解直角三角形的应用﹣坡度坡角问题，解答本题的关键是明确题意，利用锐角三角函数和数形结合的思想解答．30．(1)画图见解析；(2)DE=4.【解析】【分析】（1）连接CB延长CB交DE于O，点O即为所求．连接OG，延长OG交DF于H．线段FH即为所求．（2）根据AB CAOD CD=，可得1.6 1.41.42.1DO=+，即可推出DO=4m．【详解】（1）解：如图，点O为灯泡所在的位置，线段FH为小亮在灯光下形成的影子．（2）解：由已知可得，AB CA OD CD=，∴1.6 1.41.42.1 DO=+，∴OD=4m，∴灯泡的高为4m．【点睛】本题考查中心投影、解题的关键是正确画出图形，记住物长与影长的比的定值，属于基础题，中考常考题型．。

一、选择题1．方程22(1)110m x m x -++-=是关于x 的一元二次方程，则m 的取值范围是（ ） A ．m≠±l B ．m≥-l 且m≠1 C ．m≥-lD ．m ＞-1且m≠12．用直接开平方的方法解方程22(31)(25)x x +=-，做法正确的是（ ） A ．3125x x +=- B ．31(25)x x +=-- C ．31(25)x x +=±-D ．3125x x +=±-3．27742322x -±+⨯⨯=⨯是下列哪个一元二次方程的根（ ）A ．22730x x ++=B ．22730x x --=C ．22730x x +-=D ．22730x x -+=4．方程2240x x --=经过配方后，其结果正确的是（ ） A ．()215x -=B ．()217x -=C ．()214x -=D ．()215x +=5．已知4是关于x 的方程()2120x m x m -++=的一个实数根，并且这个方程的两个实数根恰好是等腰△ABC 的两条边的边长，则△ABC 的周长为（ ） A ．7B ．7或10C ．10或11D ．116．若关于x 的一元二次方程2(2)210m x x --+=有实数根，则m 的取值范围是（ ） A ．3m <B ．3mC ．3m <且2m ≠D ．3m 且2m ≠7．一个大正方形内放入两个同样大小的小正方形纸片，按如图1放置，两个小正方形纸片的重叠部分面积为4；按如图2放置（其中一小张正方形居大正方形的正中），大正方形中没有被小正方形覆盖的部分（阴影部分）的面积为44，则把两张小正方形按如图3放置时，两个小正方形重叠部分的面积为（ ）A ．10B ．12C ．14D ．168．方程22x x =的解是（ ）A ．0x =B ．2x =C ．10x =，22x =D ．10x =，22x =9．将4张长为a 、宽为b （a ＞b ）的长方形纸片按如图的方式拼成一个边长为（a ＋b ）的正方形，图中空白部分的面积之和为S 1，阴影部分的面积之和为S 2．若S 1＝53S 2，则a ，b 满足（ ）A ．2a ＝5bB ．2a ＝3bC ．a ＝3bD ．3a ＝2b10．若m 是方程220x x c --=的一个根，设2(1)p m =-，2q c =+，则p 与q 的大小关系为（ ） A ．p ＜qB ．p ＝qC ．p ＞qD ．与c 的取值有关11．小刚在解关于x 的方程20(a 0)++=≠ax bx c 时，只抄对了1a =，4b =，解出其中一个根是1x =-．他核对时发现所抄的c 比原方程的c 值小2．则原方程的根的情况是（ ）A ．不存在实数根B ．有两个不相等的实数根C ．有一个根是xD ．有两个相等的实数根 12．方程(2)2x x x -=-的解是（ ）A ．2B ．2-，1C ．1-D ．2，1- 13．若关于x 的一元二次方程ax 2＋2x －12＝0（a ＜0）有两个不相等的实数根，则a 的取值范围是（ ） A ．a ＜－2B ．a ＞－2C ．－2＜a ＜0D ．－2≤a ＜014．为促进消费，重庆市政府开展发放政府补贴消费的“消费券活动”，某超市的月销售额逐步增加；据统计4月份的销售额为200万元，接下来5月，6月的月增长率相同，6月份的销售额为500万元，若设5月、6月每月的增长率为x ，则可列方程为（ ） A ．()2001500x += B ．()2002001500x ++= C ．()22001500+=x D ．()20012500+=x15．已知a 、b 、m 、n 为互不相等的实数，且(a +m )( a +n )＝2，(b +m )( b +n )＝2，则ab ﹣mn的值为（ ） A ．4B ．1C ．﹣2D ．﹣1二、填空题16．若关于x 的一元二次方程210(0)ax bx a +-=≠有一根为2020x =，则一元二次方程2(1)(1)1a x b x +++=必有一根为________．17．对于实数m ，n ，定义一种运算“*”为：*m n mn n =+．如果关于x 的方程()**1x a x 4=-有两个相等的实数根，则a =_______．18．一元二次方程-+=(5)(2)0x x 的解是______________．19．设a ，b 是方程220190x x +-=的两个实数根，则11a b+=_____． 20．已知一元二次方程2x 2+3x ﹣1＝0的两个根是x 1，x 2，则x 1•x 2＝_____． 21．已知方程22610x x -+=的两根为12,x x ，则2212x x +=_______．22．三角形两边长分别为3和5，第三边满足方程x 2-6x+8=0，则这个三角形的形状是__________．23．已知等腰三角形的边长是方程213360x x -+=的两个根，则这个等腰三角形的周长是______．24．“新冠肺炎”防治取得战略性成果．若有一个人患了“新冠肺炎”，经过两轮传染后共有16个人患了“新冠肺炎”，则每轮传染中平均一个人传染了______人．25．2019女排世界杯于9月14月至29日在日本举行，赛制为单循环比赛(即每两个队之间比赛一场)一共比赛66场，中国女排以全胜成绩卫冕世界杯冠军为国庆70周年献上大礼，则中国队在本届世界杯比赛中连胜__场26．已知关于x 的方程28m 0x x ++=有一根为2-，则方程的另一根为______三、解答题27．解方程： （1）()2316x -=（2）22410x x --=（用公式法解） 28．解下列方程： （1）2410x x --=； （2）(4)123x x x -=-．29．某地区2018年投入教育经费2000万元，2020年投入教育经费2420万元 （1）求2018年至2020年该地区投入教育经费的年平均增长率；（2）按照义务教育法规定，教育经费的投入不低于国民生产总值的百分之四，结合该地区国民生产总值的增长情况，该地区到2022年需投入教育经费2900万元，如果按（1）中教育经费投入的增长率，到2022年该地区投入的教育经费是否能达到2900万元?请说明理由．30．物美商场于今年年初以每件25元的进价购进一批商品．当商品售价为40元时，一月份销售256件．二、三月该商品十分畅销，销售量持续走高．在售价不变的基础上，三月底的销售量达到400件，设二、三这两个月月平均增长率不变． （1）求二、三这两个月的月平均增长率；（2）从四月份起，商场决定采用降价促销的方式回馈顺客，经调查发现，销售单价与月平均销售的关系如下表：。

一、选择题1．方程22(1)10m x -+-=是关于x 的一元二次方程，则m 的取值范围是（ ） A ．m≠±lB ．m≥-l 且m≠1C ．m≥-lD ．m ＞-1且m≠1D 解析：D【分析】根据一元二次方程的定义及二次根式有意义的条件求解可得．【详解】∵方程22(1)10m x -+-=是关于x 的一元二次方程，∴210m -≠，解得1m ≠±，10m +≥，解得：1m ≥-，∴1m >-且1m ≠，故选：D ．【点睛】本题考查了一元二次方程的概念，判断一个方程是否是一元二次方程，首先要看是否是整式方程，然后看化简后是否是只含有一个未知数且未知数的最高次数是2．2．用配方法解方程x 2﹣4x ﹣7＝0，可变形为（ ）A ．（x+2）2＝3B ．（x+2）2＝11C ．（x ﹣2）2＝3D ．（x ﹣2）2＝11D 解析：D【分析】方程常数项移到右边，两边加上4变形得到结果即可．【详解】解：x 2﹣4x ﹣7＝0，移项得：247x x -=配方得：24474x x -+=+ ，即2()211x -=故答案为：D ．【点睛】本题考查了解一元二次方程-配方法，熟练掌握完全平方公式是解题的关键．3．某口罩厂六月份的口罩产量为100万只，由于市场需求量减少，八月份的产量减少到81万只，则该厂七八月份的口罩产量的月平均减少率为 （ ）A ．10%B ．29%C ．81%D ．14.5%A解析：A【分析】 设该厂七八月份的口罩产量的月平均减少率为x ，根据该厂六月份及八月份的口罩产量，即可得出关于x 的一元二次方程，解之取其正值即可得出结论．【详解】解：设该厂七八月份的口罩产量月平均减少率为x ，根据题意得，()2100181x -=，解得10.110%x ==，2 1.9x =（不合题意，舍去）．故选A ．【点睛】本题考查了一元二次方程的应用，找准等量关系，正确列出一元二次方程是解题的关键． 4．某超市今年1月份的营业额为50万元，已知2月至3月营业额的月增长率是1月至2月营业额的月增长率的2倍，3月份的营业额是66万元，设该超市1月至2月营业额的月增长率为x ，根据题意，可列出方程（ ）A ．()50166x +=B ．()250166x +=C ．()2501266x +=D ．()()5011266x x ++=D 解析：D【分析】根据2月份的营业额=1月份的营业额×（1+x ），3月份的营业额=2月份的营业额×（1+2x ），把相关数值代入即可得到相应方程．【详解】解：∵1月份的营业额为50万元，2月份的营业额比1月份增加x ，∴2月份的营业额=50×（1+x ），∴3月份的营业额=50×（1+x ）×（1+2x ），∴可列方程为：50（1+x ）（1+2x ）=66．故选：D ．【点睛】本题考查了由实际问题抽象出一元二次方程中求平均变化率的方法．若设变化前的量为a ，变化后的量为b ，平均变化率为x ，则经过两次变化后的数量关系为a （1±x ）2=b ．注意先求得2月份的营业额．5．已知4是关于x 的方程()2120x m x m -++=的一个实数根，并且这个方程的两个实数根恰好是等腰△ABC 的两条边的边长，则△ABC 的周长为（ ）A ．7B ．7或10C ．10或11D ．11C解析：C【分析】把x=4代入已知方程求得m 的值；然后通过解方程求得该方程的两根，即等腰△ABC 的两条边长，由三角形三边关系和三角形的周长公式进行解答即可．【详解】解：把x=4代入方程得16-4（m+1）+2m=0，解得m=6，则原方程为x 2-7x+12=0，解得x 1=3，x 2=4，因为这个方程的两个根恰好是等腰△ABC 的两条边长，①当△ABC 的腰为4，底边为3时，则△ABC 的周长为4+4+3=11；②当△ABC 的腰为3，底边为4时，则△ABC 的周长为3+3+4=10．综上所述，该△ABC 的周长为10或11．故选C ．【点睛】本题考查了一元二次方程的解：能使一元二次方程左右两边相等的未知数的值是一元二次方程的解．又因为只含有一个未知数的方程的解也叫做这个方程的根，所以，一元二次方程的解也称为一元二次方程的根．也考查了三角形三边的关系．6．某小区2018年屋顶绿化面积为22000m ，计划2020年屋顶绿化面积要达到22880m ．设该小区2018年至2020年屋顶绿化面积的年平均增长率为x ，则可列方程为（ ）A ．2000(12)2880x +=B ．2000(1)2880x ⨯+=C ．220002000(1)2000(1)2880x x ++++=D ．22000(1)2880x +=D解析：D【分析】一般用增长后的量=增长前的量×（1+增长率），如果设绿化面积的年平均增长率为x ，根据题意即可列出方程．【详解】解：设平均增长率为x ，根据题意可列出方程为：2000（1+x ）2=2880．故选：D ．【点睛】此题考查了由实际问题抽象出一元二次方程，即一元二次方程解答有关平均增长率问题．对于平均增长率问题，在理解的基础上，可归结为a （1+x ）2=b （a ＜b ）；平均降低率问题，在理解的基础上，可归结为a （1-x ）2=b （a ＞b ）．7．已知a ，b ，c 分别是三角形的三边长，则关于x 的方程()()220a b x cx a b ++++=根的情况是（ ）A ．有两个不相等的实数根B ．有两个相等的实数根C ．有且只有一个实数根D ．没有实数根D 解析：D【分析】由于这个方程是一个一元二次方程，所以利用根的判别式可以判断其根的情况．而()()2(2)4c a b a b =-++，根据三角形的三边关系即可判断．【详解】∵a ，b ，c 分别是三角形的三边，∴a+b ＞c ．∴c+a+b ＞0，c-a-b ＜0，∴()()2(2)4c a b a b =-++2244()c a b =-+()()40c a b c a b =++--<，∴方程没有实数根．故选：D ．【点睛】本题主要考查了三角形三边关系、一元二次方程的根的判别式等知识点．重点是对2244()c a b -+进行因式分解．8．方程23x x =的解为（ ）A ．3x =B ．3x =-C ．10x =，23x =D ．10x =，23x =-C解析：C【分析】方程变形后分解因式，利用两数相乘积为0，两因式中至少有一个为0转化为两个一元一次方程来求解．【详解】解：方程变形得：x 2-3x=0，分解因式得：x （x-3）=0，可得x=0或x-3=0，解得：x 1=3，x 2=0．故选：C ．【点睛】此题考查了解一元二次方程-因式分解法，熟练掌握因式分解的方法是解本题的关键． 9．下列方程中，有两个不相等的实数根的是（ ）A ．x 2＝0B ．x ﹣3＝0C ．x 2﹣5＝0D ．x 2+2＝0C 解析：C【分析】利用直接开平方法分别求解可得．【详解】解：A ．由x 2＝0得x 1＝x 2＝0，不符合题意；B ．由x ﹣3＝0得x ＝3，不符合题意；C ．由x 2﹣5＝0得x 1=x 2=，符合题意； D ．x 2+2＝0无实数根，不符合题意；故选：C ．【点睛】本题主要考查解一元二次方程的能力，熟练掌握解一元二次方程的几种常用方法：直接开平方法、因式分解法、公式法、配方法，结合方程的特点选择合适、简便的方法是解题的关键．10．实数,m n 分别满足方程2199910m m ++=和219990n n ++=，且1mn ≠，求代数式41mn m n++的值（ ） A ．5-B ．5C ．10319-D ．10319A 解析：A【分析】 由219990n n ++=可得211199910n n⋅+⋅+=，进而可得1,m n 是方程2199910x x ++=的两个根，然后根据一元二次方程的根与系数的关系可求解．【详解】 解：由219990n n ++=可得211199910n n ⋅+⋅+=， ∴1,m n是方程2199910x x ++=的两个根， ∴19911,1919m m n n +=-⋅=， ∴4119914451919mn m m m n n n ++=+⋅+=-+⨯=-； 故选A ．【点睛】本题主要考查一元二次方程根与系数的关系，熟练掌握一元二次方程根与系数的关系是解题的关键．二、填空题11．填空：（1）214x x ++________2(7)x =+；（2）29x x -+_______=（x-____）249【分析】运用配方法的运算方法填写即可【详解】解：（1）x2+14x+49=（x+7）2故答案为：49；（2）x2-9x+=（x-）2故答案为：【点睛】此题主要考查了配方法的应用熟练掌握完全平方公解析：49814 92【分析】运用配方法的运算方法填写即可．【详解】解：（1）x 2+14x+49=（x+7）2故答案为：49；（2）x 2-9x+814=（x-92）2， 故答案为：814，92． 【点睛】 此题主要考查了配方法的应用，熟练掌握完全平方公式是关键．12．某校八年级举行足球比赛，每个班级都要和其他班级比赛一次，结果一共进行了6场比赛，则八年级共有_____个班级．3【分析】设共有个班级参加比赛根据共有45场比赛列出方程求出方程的解即可得到结果【详解】解：设共有个班级参加比赛根据题意得：整理得：即解得：或（舍去）则共有3个班级球队参加比赛故答案为：3【点睛】此解析：3．【分析】设共有x 个班级参加比赛，根据共有45场比赛列出方程，求出方程的解即可得到结果．【详解】解：设共有x 个班级参加比赛， 根据题意得：(1)62x x -=， 整理得：260x x --=，即(3)(2)0x x -+=， 解得：3x =或2x =-（舍去）．则共有3个班级球队参加比赛．故答案为：3．【点睛】此题考查了一元二次方程的应用，解题的关键是找出等量关系“需安排6场比赛”． 13．已知 12,x x 是一元二次方程()23112x -=的两个解，则12x x +=_______．2【分析】先将方程整理为x2-2x-3=0再根据根与系数的关系可得出x1+x2即可【详解】解：一元二次方程整理为∵x1x2是一元二次方程x2-2x-3=0的两个根∴x1+x2=2故答案为：2【点睛】解析：2【分析】先将方程整理为x 2-2x-3=0，再根据根与系数的关系可得出x 1+x 2即可．【详解】解：一元二次方程()23112x -=整理为2230x x --=，∵x 1、x 2是一元二次方程x 2-2x-3=0的两个根，∴x 1+x 2=2．故答案为：2．【点睛】本题考查了根与系数的关系，牢记两根之和等于b a-是解题的关键． 14．用因式分解法解关于x 的方程 260x px --=，将左边分解因式后有一个因式为3x -，则的p 值为_______1【分析】方法一：根据题意因式分解得到再展开去括号根据恒等式即可求出p 的值；方法二：将代入方程可得一个关于p 的一元一次方程解方程即可得【详解】方法一：由题意得解得则；方法二：由题意得是关于x 的方程的解析：1【分析】方法一：根据题意因式分解得到26(3)()x px x x a --=-+，再展开去括号，根据恒等式即可求出p 的值；方法二：将3x =代入方程可得一个关于p 的一元一次方程，解方程即可得．【详解】方法一：由题意得，226(3)()(3)3x px x x a x a x a --=-+=+--， 3p a ∴-=-，36a -=-，解得2a =，则1p =；方法二：由题意得，3x =是关于x 的方程260x px --=的一个解，则将3x =代入得：23360p --=，解得1p =，故答案为：1．【点睛】本题考查了多项式因式分解的方法、利用因式分解法解一元二次方程，熟练掌握多项式的运算法则和方程的解法是解题关键．15．一元二次方程()10x x -=的根是________________________．【分析】利用因式分解法把原方程转化为x=0或x-1=0然后解两个一次方程即可；【详解】∵∴x=0或x-1=0解得故答案为：【点睛】本题考查了一元二次方程的解法先把方程的右边化为0再把左边通过因式分解解析：120,1x x ==【分析】利用因式分解法把原方程转化为x=0或x-1=0，然后解两个一次方程即可；【详解】∵()10x x -= ，∴ x=0或x-1=0，解得1x =0，21x = ，故答案为：1x =0，21x =【点睛】本题考查了一元二次方程的解法，先把方程的右边化为0，再把左边通过因式分解化为两个一次因式的积的形式，求解即可；16．方程2350x x -=的一次项系数是______．-5【分析】根据一元二次方程的一般形式解答【详解】解：方程的一次项是其系数是故答案是：【点睛】本题考查一元二次方程的一般式解题的关键是掌握一次项系数的定义解析：-5【分析】根据一元二次方程的一般形式解答．【详解】解：方程2350x x -=的一次项是5x -，其系数是5-．故答案是：5-．【点睛】本题考查一元二次方程的一般式，解题的关键是掌握一次项系数的定义．17．已知()0n n ≠是一元二次方程240x mx n ++=的一个根，则m n +的值为______．【分析】根据一元二次方程的解的定义把代入得到继而可得的值【详解】∵是关于x 的一元二次方程的一个根∴即∵∴即故答案为：【点睛】本题考查了一元二次方程的解的定义因式分解的应用注意：能使一元二次方程左右两解析：4-【分析】根据一元二次方程的解的定义把x n =代入240x mx n ++=得到240n mn n ++=，继而可得m n +的值．【详解】∵n 是关于x 的一元二次方程240x mx n ++=的一个根，∴240n mn n ++=，即()40n n m ++=，∵0n ≠，∴4n m ++，即4m n +=-，故答案为：4-．【点睛】本题考查了一元二次方程的解的定义、因式分解的应用．注意：能使一元二次方程左右两边相等的未知数的值是一元二次方程的解．18．已知（x 2+y 2）（x 2+y 2﹣5）=6，则x 2+y 2=_____．6【分析】设x2+y2=m 把原方程转化为含m 的一元二次方程先用因式分解法求解再确定x2+y2的值【详解】设x2+y2=m 原方程可变形为：m(m ﹣5)=6即m2﹣5m ﹣6=0∴(m ﹣6)(m+1)=0解析：6【分析】设x 2+y 2=m ，把原方程转化为含m 的一元二次方程，先用因式分解法求解，再确定x 2+y 2的值．【详解】设x 2+y 2=m ，原方程可变形为：m (m ﹣5)=6，即m 2﹣5m ﹣6=0．∴(m ﹣6)(m +1)=0，解得m 1=6，m 2=﹣1．∵m =x 2+y 2≥0，∴x 2+y 2=6．故答案为：6．【点睛】本题考查了一元二次方程的解法，掌握换元法和因式分解法解一元二次方程是解决本题的关键．19．当m ______时，关于x 的一元二次方程2350mx x -+=有两个不相等的实数根．m ＜且m≠0【分析】根据一元二次方程的定义及判别式的意义得出m≠0且△=（-3）2-4m×5=9-20m ＞0解不等式组确定m 的取值范围【详解】解：∵关于x 的一元二次方程mx2-3x+5=0有两个不相解析：m ＜920且m≠0． 【分析】根据一元二次方程的定义及判别式的意义得出m≠0，且△=（-3）2-4m×5=9-20m ＞0，解不等式组，确定m 的取值范围．【详解】解：∵关于x 的一元二次方程mx 2-3x+5=0有两个不相等的实数根，∴m≠0，且△=（-3）2-4m×5=9-20m ＞0，解得m ＜920且m≠0， 故当m ＜920且m≠0时，关于x 的一元二次方程mx 2-3x+5=0有两个不相等的实数根． 故答案是：m ＜920且m≠0． 【点睛】本题考查了根的判别式，一元二次方程ax 2+bx+c=0（a≠0）的根与△=b 2-4ac 有如下关系： （1）△＞0⇔方程有两个不相等的实数根；（2）△=0⇔方程有两个相等的实数根；（3）△＜0⇔方程没有实数根．20．若关于x 的一元二次方程()21210k x x -+-=有两个不相等的实数根，则k 的取值范围是______．且【分析】根据题意结合一元二次方程的定义和根的判别式可得关于k 的不等式然后解不等式即可求解【详解】解：∵关于的一元二次方程有两个不相等的实数根∴∴的取值范围是且故答案为：且【点睛】本题考查了一元二次解析：0k >且1k ≠【分析】根据题意，结合一元二次方程的定义和根的判别式可得关于k 的不等式，然后解不等式即可求解．【详解】解：∵关于x 的一元二次方程()21210k x x -+-=有两个不相等的实数根， ∴21024(1)(1)0k k -≠⎧⎨∆=--⨯->⎩，10k k ≠⎧⎨>⎩， ∴k 的取值范围是0k >且1k ≠，故答案为：0k >且1k ≠．【点睛】本题考查了一元二次方程的定义、根的判别式、解一元一次不等式，熟练掌握一元二次方程的根的判别式与根的关系是解答的关键．三、解答题21．商店销售某种商品，每件成本为30元．经市场调研，售价为40元时，可销售200件；售价每增加2元，销售量将减少20件．如果这种商品全部销售完，该商店可盈利2250元，那么该商品每件售价多少元？解析：每件售价为45元【分析】设该商品的单价为x 元，根据题意得到方程，解方程即可求解．【详解】解：设该商品的单价为x 元．根据题意，得()()3020010402250---=⎡⎤⎣⎦x x ．解这个方程，得1245x x ==．答：每件售价为45元．【点睛】本题考查一元一次方程的应用，解题的关键是根据利润得到相应的等量关系是解题的关键．22．解方程：（1）26160x x +-=．（2）22430x x --=．解析：（1）18x =-，22x =；（2）122x +=，222x =．【分析】（1）运用因式分解法求解即可；（2）运用公式法求解即可．【详解】解：（1）26160x x +-=()()820x x +-=解得18x =-，22x =．（2）22430x x --=，∵2a =，4b =-，3c =-，∴224(4)42(3)162440b ac -=--⨯⨯-=+=，x ===∴1x =，2x =． 【点睛】本题考查了解一元二次方程，在解答中注意计算的正确性．23．某商场销售一批名牌衬衫，平均每天可售出20件，每件盈利45元，为了扩大销售、增加盈利，尽快减少库存，商场决定采取适当的降价措施，经调查发现，如果每件衬衫每降价1元，商场平均每天可多售出4件．（1）若每件衬衫降价5元，则每件商品盈利________元，每天可售出________件，商场每天盈利________元；（2）若每件衬衫降价x 元，则每件商品盈利________元，每天可售出________件（用含x 的代数式表示）；（3）若商场平均每天盈利2100元，每件衬衫应降价多少元？解析：（1）40，40，1600；（2）45x -，204x +；（3）每件衬衫应降价30元【分析】（1）每件衬衫降价5元，每件盈利=原来的盈利-5元；所售件数=20+多售出的件数；商场每天盈利=（原来的盈利-5元）×（20+多售出的件数）；（2）每件衬衫降价x 元，每件盈利=原来的盈利-x 元；所售件数=20+多售出的件数； （3）商场平均每天盈利数=每件的盈利×售出件数；每件的盈利=原来每件的盈利-降价数．设每件衬衫应降价x 元，然后根据前面的关系式即可列出方程，解方程即可求出结果．【详解】解：（1）若每件衬衫降价5元，则每件商品盈利：45-5=40（元），每天可售出：20+4×5=40（件），商场每天盈利：40×40=1600（元），故答案为：40，40，1600；（2）若每件衬衫降价x 元，则每件商品盈利：45-x （元），每天可售出：20+4x （件）故答案为：45x -，204x +；（3）每件衬衫应降价x 元，根据题意得：(45)(20)2100x x --=2403000x x -+=解得：110x =，230x =当10x =时，20460x +=；当30x =时，204140x +=；∵要减少库存，∴应增加销售量，∴30x =∴每件衬衫应降价30元．【点睛】此题主要考查了一元二次方程的应用的销售问题，关键是正确理解题意，找出题目中等量关系，列出方方程.24．计算题（1）解方程：2690x x ++= （2）解不等式组：3152(2)7x x x ->⎧⎨+<+⎩解析：（1）123x x ==-； （2）23x <<【分析】（1）利用因式分解法求解即可．（2）分别求出两个不等式的解集，最后找出公共部分即可．【详解】解：（1）2690x x ++=因式分解得：()230x +=解得：123x x ==-． （2）()31512272x x x ->⎧⎨+<+⎩ 解不等式1得：2x >解不等式2得：3x <∴不等式组的解集是23x <<．【点睛】本题考察解一元二次方程和一元一次不等式组，解题的关键是：（1）用因式分解法求解一元二次方程（2）不等式组解集的确定，原则是“同大取大，同小取小，大小小大中间找，大大小小找不到”．25．请回答下列各题：（1）先化简，再求值：2319369x x x x x x x +--⎛⎫-÷ ⎪--+⎝⎭，其中x = （2）已知关于x 的方程2320x x m +-=没有实数根，求实数m 的取值范围．解析：（1）1-2）13m <-． 【分析】（1）根据分式的加减乘除混合运算法则计算即可，求值时注意分母有理化.（2）根据方程没有实数根，可知∆<0，进而求得m 得取值范围.【详解】（1）由题意得：原式23193(3)x x x x x x +--⎛⎫=-÷ ⎪--⎝⎭ 2(3)(3)(1)(3)(3)9x x x x x x x x ⎡⎤+----=⨯⎢⎥--⎣⎦ 2229(3)(3)9x x x x x x x --+-=⨯-- 29(3)(3)9x x x x x --=⨯-- 29(3)(3)9x x x x x --=⨯--3x x-=．3x =，∴原式1===． （2）该方程没有实数根，2242430b ac m ∴∆=-=+⨯⨯<，故4120m +<，解得13m <-． 【点睛】本题考查分式的混合运算以及一元二次方程根的判别，熟练掌握分式运算法则以及根的判别公式是解题关键.26．解方程：（1）2237x x +=；（2）x(2x+5)=2x+5．解析：（1）112x =，23x =；（2）11x =，252x =- 【分析】（1）先把方程化为一般式，然后利用因式分解法解方程；（2）利用因式分解法求解．【详解】解：（1）2x 2-7x+3=0，（2x-1）（x-3）=0，2x-1=0或x-3=0，所以x 1=12，x 2=3； （3）移项得，x （2x+5）-（2x+5）=0，因式分解得，（2x+5）（x-1）=0，∴x-1=0，2x+5=0，∴11x =，252x =-； 【点睛】本题考查了解一元二次方程的能力，熟练掌握解一元二次方程的几种常用方法：直接开平方法、因式分解法、公式法、配方法，结合方程的特点选择合适、简便的方法是解题的关键．27．解答下列各题．（1）解方程：2(1)90x --=．（2）已知1x =，求225x x -+的值．解析：（1）14x =，22x =-；（2）6．【分析】（1）方程整理后，直接开平方即可求解；（2）代数式225x x -+配方整理成()214x -+后，把x 的值代入计算即可．【详解】（1）由原方程得2(1)9x -=， ∴13x -=±，解得：14x =，22x =-；（2）∵2225(1)4x x x -+=-+，将1x =代入得：原式)2114=-+ 24=+6=．【点睛】本题考查了解一元二次方程－直接开平方法以及求代数式的值，熟练掌握完全平方公式是解本题的关键．28．解方程（1）2420x x -+=（2）()255210x x ++=（3）2560x x -+=（4）()3133x x x +=+解析：（1）1222x x ==2）121x x ==-；（3）1232x x ==，；（4）1211x x =-=， 【分析】（1）直接利用配方法解方程得出答案即可；（2）方程整理后，利用利用配方法解方程得出答案即可；（3）利用分解因式法解方程即可；（4）方程整理后，利用提取公因式法分解因式进而解方程即可．【详解】（1）2420x x -+=，移项得：242x x -=-，配方得：24424x x -+=-+，即2(2)2x -=，开方得：2x -=，解得：1222x x ==（2）()255210x x ++=， 整理得：2210x x ++=，即2(1)0x +=，∴121x x ==-；（3）2560x x -+=，因式分解得：()()320x x --=，∴30x -=，20x -=，∴1232x x ==，；（4）()3133x x x +=+，整理得：()()110x x x +-+=，因式分解得：()()110x x +-=，∴10x +=，10x -=， ∴1211x x =-=，． 【点睛】本题主要考查了解一元二次方程，熟练掌握解一元二次方程的几种常用方法：直接开平方法、因式分解法、公式法、配方法，结合方程的特点选择合适、简便的方法是解题的关键．。