人工智能作业答案(中国矿大)
- 格式:doc
- 大小:1.10 MB
- 文档页数:8

人工智能试题及答案眉山市公需科目培训2020年度人工智能与健康试题及答案(四)答案(四) 一、单选题一、单选题一、单选题 1.2014 1.2014年,年,()投资并开始部署由人工智能驱动的交易平台。
目前,其纽约总部已经有600个交易岗位被200个电脑工程师取代,只剩下两个交易员。
(2.0分)分) A. A.高盛高盛 B. B.淡马锡淡马锡 C. C.商汤科技商汤科技 D. D.摩根士丹利 我的答案:我的答案:我的答案:A A √答对√答对 2. 2.()含有丰富的淀粉、膳食纤维以及多种维生素和矿物质。
(2.0分) A.蔬菜蔬菜 B. B.水果水果C.C.薯类薯类薯类D. D.菌藻类菌藻类 我的答案:我的答案:我的答案:C C √答对√答对 3. 3.成年人一天的合理睡眠时间是()小时。
(2.0分)分) A.5 A.5~6 B.6~7 C.7C.7~~8 D.9~10 我的答案:我的答案:我的答案:C C √答对√答对 4. 4.下列关于人工智能对实体经济的影响说法不正确的是()。
(2.0分)分) A. A.人工智能能够提升实体经济能级人工智能能够提升实体经济能级 B. B.人工智能能够加快经济转型济转型 C. C.人工智能能够加快创新驱动发展人工智能能够加快创新驱动发展 D. D.人工智能能够促进数字经济繁荣能够促进数字经济繁荣 我的答案:我的答案:我的答案:B B √答对√答对 5. 5.()被称为“人工智能之父”。
(2.0分) A.约翰·冯·诺依曼诺依曼 B. B.约翰·麦卡锡约翰·麦卡锡 C. C.唐纳德·赫布唐纳德·赫布 D. D.亚瑟·塞缪尔亚瑟·塞缪尔 我的我的答案:B √答对√答对 6.1956 6.1956年之前,人工智能的发展处于()。
(2.0分)分) A. A.萌芽期萌芽期 B. B.第一次繁荣期第一次繁荣期 C. C.第一次低谷期第一次低谷期D.D.复苏期复苏期复苏期 我的答案:我的答案:我的答案:A A √答对√答对 7. 7.新生儿的正常脉搏为每分钟()次。
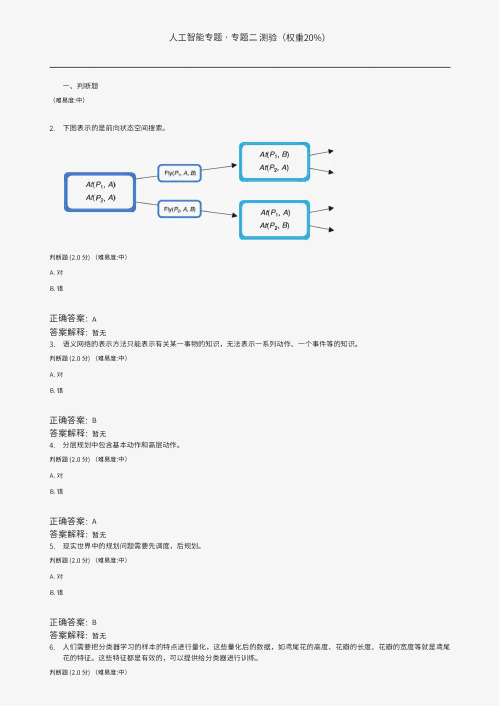
人工智能专题.专题二测验(权重20%)一、判断题(难易度:中)2. 下图表示的是前向状态空间搜索。
A�P1, A)A� 乌,A)判断题(2.0分)(难易度:中)A. 对B. 错正确答案:A答案解释:暂无At(P1, 印At(P2, A)At(P1, A)At(P2, 印3. 语义网络的表示方法只能表示有关某—事物的知识,无法表示—系列动作、—个事件等的知识。
判断题(2.0分)(难易度:中)A. 对B. 错正确答案:B答案解释:暂无4. 分层规划中包含基本动作和高层动作。
判断题(2.0分)(难易度:中)A. 对B. 错正确答案:A答案解释:暂无5. 现实世界中的规划问题需要先调度,后规划。
判断题(2.0分)(难易度:中)A. 对B. 错正确答案:B答案解释:暂无6. 人们需要把分类器学习的样本的特点进行量化,这些噩化后的数据,如鸯尾花的高度、花瓣的长度、花瓣的宽度等就是莺尾花的特征。
这些特征都是有效的,可以提供给分类器进行训练。
判断题(2.0分)(难易度:中)寸昔又令..A B 正确答案:B 答案解释:暂无7. 启发式规划的两种方法是减少更多的边或者状态抽象。
判断题(2.0分)(难易度:中)A . 对B. 错正确答案:B 答案解释:暂无8. 深度学习是计算机利用其计算能力处理大量数据,获得看似人类同等智能的工具。
判断题(2.0分)(难男度:中)A . 对B. 错正确答案:A 答案解释:暂无9. 人工智能利用遗传算法在求解优化问题时,会把问题的解用"O"和"1"表示。
0,1就是就是“遗传基因", 01组成的字符串,称为—个染色体或个体。
判断题(2.0分)(难易度:中)A . 对B. 错正确答案:A 答案解释:暂无10. 谓词逻辑是应用千计算机的逻辑形式,其逻辑规则、符号系统与命题逻辑是一样的。
判断题(2.0分)(难易度:中)A. 对B. 错正确答案:B 答案解释:暂无11. P (A I B)代表事件A发生的条件下事件B发生的概率。

人工智能基础(习题卷66)第1部分:单项选择题,共50题,每题只有一个正确答案,多选或少选均不得分。
1.[单选题]K折法是下列哪个函数?A)RepeatedKFoldB)KFoldC)LeaveOneOut答案:B解析:2.[单选题]阿里云RPA支持图像录制控件,针对于锚点,说法正确的是?A)锚点是图像的中心不可以移动B)移动锚点可是图片放大或缩小C)锚点是指定鼠标操作位置D)锚点移动了就要重新录制答案:C解析:3.[单选题]选择哪一个解作为输出,将由学习算法的归纳偏好决定,常见的做法是引( )。
A)线性回归B)线性判别分析C)正则化项D)偏置项答案:C解析:4.[单选题]表达式 3 or 5 的值为_____。
A)TRUEB)3C)5D)2答案:B解析:5.[单选题]( )有跟环境进行交互,从反馈当中进行不断的学习的过程。
A)监督学习B)非监督学习C)强化学习D)线性回归答案:A解析:6.[单选题]CNN中用来完成分类的是()A)卷积层7.[单选题]一般的神经网络模型通常假定网络结构是事先固定的,与此不同,结构自适应网络则将网络结构也当作学习的目标之一,()网络是重要代表。
A)级联相关B)能量相关C)网格相关D)以上都不对答案:A解析:8.[单选题]国网公司提出“两库一平台”架构中,样本库对于哪些类型样本数据进行分类管理及统计,并提供图像标注、语音标注以及文本标注功能?A)图像类B)音频类C)文本类D)以上都是答案:D解析:9.[单选题]不属于模型集成方法的是( )。
A)直接集成法B)增强法C)堆叠法D)递归法答案:D解析:模型集成方法包括直接集成法、自助法、随机森林、增强法和堆叠法等。
10.[单选题]( )业务应用,发挥智能配变终端边缘计算优势和就地管控能力,统筹协调换相开关.智能电容器.SVG等设备,实现对电网的三相不平衡.无功.谐波等电能质量问题快速响应及治理。
A)故障快速处置B)状态在线评价C)设备预先检修D)台区能源自治答案:D解析:11.[单选题]关于函数中的return说法正确的是?A)函数一定要包含 return 语句B)renturn 不能返回一个小数C)函数中不用 return 也可以D)函数中只能有一个 return 语句答案:C解析:12.[单选题]无人车的( )技术发展,给老年人和残疾人带来福音。

人工智能基础(习题卷1)第1部分:单项选择题,共53题,每题只有一个正确答案,多选或少选均不得分。
1.[单选题]声明1:可以通过将所有权重初始化为0来训练网络。
声明2:可以通过将偏差初始化为0来很好地训练网络以上哪些陈述是真实的?A、1对2错A)1错2对B)1和2都对C)1和2都错答案:B解析:2.[单选题]下列哪个函数可以组合估计器?A)RepeatedKFoldB)KFoldC)LeaveOneOutD)make_pipeline答案:D解析:3.[单选题]输入图像已被转换为大小为28×28的矩阵和大小为7×7的步幅为1的核心/滤波器。
卷积矩阵的大小是多少?A)22X22B)21X21C)28X28D)7X7答案:A解析:4.[单选题]人工神经网络的相关研究最早可以追溯到上世纪40年代,由心理学家麦卡洛克和数学逻辑学家皮茨提出的( )。
A)M-P神经元模型B)B-P神经元模型C)M-N神经元模型D)N-P神经元模型答案:A解析:5.[单选题]要在某一台机器上为某种语言构造一个编译程序,必须掌握哪些内容()A)汇编语言、高级语言、编译方法B)程序设计方法、测试方法、编译方法C)源语言、目标语言、编译方法D)高级语言、程序设计方法、机器语言答案:C解析:C)奇异点阈值D)点云分辨率答案:A解析:7.[单选题]Hadoop生态系统中,HBase是一种()。
A)分布式文件系统B)数据仓库C)实时分布式数据库D)分布式计算系统答案:C解析:HBase是一个面向列的实时分布式数据库。
8.[单选题]人工神经元网络与深度学习的关系是A)人工神经元网络是深度学习的前身B)深度学习是人工神经元网络的一个分支C)深度学习是人工神经元网络的一个发展D)深度学习与人工神经元网络无关答案:C解析:深度学习是实现机器学习的一种技术,现在所说的深度学习大部分都是指神经网络9.[单选题]在编制自动化需求时,实践证明采用()时最有效的方式A)流程图B)视频说明C)电子表格D)流程图加视频说明答案:D解析:10.[单选题]关于用4V来表示大数据的主要特征,描述错误的是A)大数据的时间分布往往不均匀,近几年生成数据的占比最高B)“如何从海量数据中洞见(洞察)出有价值的数据”是数据科学的重要课题之一C)数据类型的多样性往往导致数据的异构性,进而加大数据处理的复杂性,对数据处理能力提出了更高要求D)数据价值与数据量之间存在线性关系答案:D解析:11.[单选题]常用的的灰度内插法不包括()。

人工智能概论_北京联合大学中国大学mooc课后章节答案期末考试题库2023年1.李明的父亲是教师,用谓词逻辑可以表示为Teacher(father(Liming))这里father(Liming)是()。
答案:函数2.在语音识别中,按照从微观到宏观的顺序排列正确的是()。
答案:帧-状态-音素-单词3.有研究统计,可用于AI技术处理的医疗数据中,有超过80%的数据来自于()。
答案:医学影像4.从人工智能研究流派来看,西蒙和纽厄尔提出的“逻辑理论家”(LT)方法,应当属于()。
答案:符号主义5.假设我们需要训练一个卷积神经网络,来完成0~9和英文字母(不区分大小写)的图像分类。
该卷积神经网络最后一层是分类层,则最后一层输出向量的维数大小可能是()。
答案:366.A* 算法是一种有信息搜索算法,在罗马尼亚度假问题中引入的辅助信息是()。
答案:任意一个城市到目标城市之间的直线距离7.DBpedia、Yago 等系统从()上获取大规模数据并自动构建知识图谱。
答案:Wikipedia8.知识图谱的初衷是为了提高()。
答案:搜索引擎的性能9.以下描述的是专家系统的是()。
答案:一般由事实库、规则库、推理机构成10.专家系统中知识库知识获取的来源是()。
答案:专家11.()是知识图谱中最基本的元素。
答案:实体12.2012 年的 ILSVRC 竞赛,获得冠军的队伍是由()领导的团队。
答案:Geoffrey Hinton13.机器学习系统中通常将数据集划分为训练集和测试集,其中被用来学习得到模型中参数值的是()。
答案:训练集14.使用 ID3 算法构建决策树时,选择属性的度量依据是()。
答案:信息增益15.在机器学习中,如果数据较少,同时采用的模型较复杂,得到的模型在给定的训练集上误差非常小,接近于0,但是在训练集之外的数据上预测效果很差,这种现象称为()。
答案:过拟合16.一般来说,在机器学习中,用计算机处理一幅彩色的图像,维度是()。

人工智能作业答案(中国矿大)1把以下合适公式化简为合取范式的子句集:(1⌝ (∀x(∃y(∃z{P(x ⇒ (∀x[Q(x, y ⇒ R(z]}(2( ∀x( ∃y{{P(x ∧ [Q(x ∨ R(y]} ⇒ (∀y[P(f(y ⇒ Q(g(x]}(3 (∀x( ∃y{P(x ∧ [Q(x∨ R(y]}⇒ (∀y{[P(f(y⇒ Q(g(y]⇒ (∀xR(x} (1∙⌝(∀x( ∃y( ∃z{P(x ⇒ (∀x[Q(x,y ⇒ R(z]}∙⌝(∀x( ∃y( ∃z{ ⌝P(x ∨ ( ∀x[⌝Q(x,y ∨ R(z]}∙ (∃x( ∀y( ∀z{ P(x ∧ (∃ x[Q(x,y ∧⌝R(z]}∙ P(A ∧ [Q(f(y,z, y ∧⌝R(z]∙ {P(A, Q(f(y,z,y, ∧⌝R(w}(2∙ (∀x(∃y{{P(x ∧ [Q(x ∨ R(y]} ⇒ (∀y[P(f(y ⇒ Q(g(x]}∙ (∀x(∃y{⌝{P(x ∧ [Q(x ∨ R(y]} ∨(∀y[⌝P(f(y ∨ Q(g(x]}∙ (∀x(∃y{⌝P(x ∨ [⌝Q(x ∧⌝R(y] ∨(∀w[⌝P(f(w ∨ Q(g(x]}∙ (∀x{⌝P(x ∨ [⌝Q(x ∧⌝R(h(x] ∨(∀w[⌝P(f(w ∨ Q(g(x]}∙ [⌝P(x ∨⌝Q(x ∨⌝P(f(w ∨ Q(g(x] ∧[⌝P(x ∨⌝R(h(x ∨⌝P(f(w ∨ Q(g(x]∙ {⌝P(x1 ∨⌝Q(x1 ∨⌝P(f(w1 ∨ Q(g(x1,⌝P(x2 ∨⌝R(h(w2 ∨⌝P(f(w2 ∨ Q(g(x2} (3 ∙ (∀x(∃y{P(x ∧ [Q(x ∨ R(y]} ⇒(∀y{[P(f(y ⇒ Q(g(y]⇒(∀xR(x}∙⌝(∀x(∃y{P(x ∧ [Q(x ∨ R(y]} ∨( ∀y{⌝[⌝P(f(y ∨ Q(g(y] ∨ (∀xR(x} ∙ (∃x(∀y{ ⌝P(x ∨ [⌝Q(x ∧⌝R(y]} ∨(∀w{⌝[⌝P(f(w ∨ Q(g(w] ∨ (∀vR(v} ∙ {⌝P(A ∨[⌝Q(A ∧⌝R(y]} ∨{[P(f(w ∧⌝Q(g(w] ∨ R(v}∙⌝P(A ∨ {[⌝Q(A ∨ P(f(w] ∧ [⌝Q(A ∨⌝Q(g(w] ∧[⌝R(y ∨ P(f(w] ∧ [⌝R(y ∨⌝Q(g(w]} ∨ R(v ∙ {⌝P(A ∨⌝Q(A ∨ P(f(w1 ∨R(v1,⌝P(A ∨⌝Q(A ∨ Q(g(w2 ∨ R(v2,⌝P(A ∨⌝R(y3 ∨ P(f(w3 ∨ R(v3,⌝P(A ∨⌝R(y4 ∨ Q(g(w4 ∨ R v4}2假设已知下列事实:1小李(Li喜欢容易的(Easy课程(Course。

1把以下合适公式化简为合取范式的子句集:(1)⌝ (∀x)(∃y)(∃z){P(x) ⇒ (∀x)[Q(x, y) ⇒ R(z)]}(2)( ∀x)( ∃y){{P(x) ∧ [Q(x) ∨ R(y)]} ⇒ (∀y)[P(f(y)) ⇒ Q(g(x))]}(3) (∀x)( ∃y){P(x) ∧ [Q(x)∨ R(y)]}⇒ (∀y){[P(f(y))⇒ Q(g(y))]⇒ (∀x)R(x)} (1) •⌝(∀x)( ∃y)( ∃z){P(x) ⇒ (∀x)[Q(x,y) ⇒ R(z)]}•⌝(∀x)( ∃y)( ∃z){ ⌝P(x) ∨ ( ∀x)[⌝Q(x,y) ∨ R(z)]}• (∃x)( ∀y)( ∀z){ P(x) ∧ (∃ x)[Q(x,y) ∧⌝R(z)]}• P(A) ∧ [Q(f(y,z), y) ∧⌝R(z)]• {P(A), Q(f(y,z),y), ∧⌝R(w)}(2)• (∀x)(∃y){{P(x) ∧ [Q(x) ∨ R(y)]} ⇒ (∀y)[P(f(y)) ⇒ Q(g(x))]} • (∀x)(∃y){⌝{P(x) ∧ [Q(x) ∨ R(y)]} ∨(∀y)[⌝P(f(y)) ∨ Q(g(x))]}• (∀x)(∃y){⌝P(x) ∨ [⌝Q(x) ∧⌝R(y)] ∨(∀w)[⌝P(f(w)) ∨ Q(g(x))]}• (∀x){⌝P(x) ∨ [⌝Q(x) ∧⌝R(h(x))] ∨(∀w)[⌝P(f(w)) ∨ Q(g(x))]}• [⌝P(x) ∨⌝Q(x) ∨⌝P(f(w)) ∨ Q(g(x))] ∧[⌝P(x) ∨⌝R(h(x)) ∨⌝P(f(w)) ∨ Q(g(x))] • {⌝P(x1) ∨⌝Q(x1) ∨⌝P(f(w1) ∨ Q(g(x1)),⌝P(x2) ∨⌝R(h(w2)) ∨⌝P(f(w2)) ∨ Q(g(x2))} (3) • (∀x)(∃y){P(x) ∧ [Q(x) ∨ R(y)]} ⇒(∀y){[P(f(y)) ⇒ Q(g(y))]⇒(∀x)R(x)}•⌝(∀x)(∃y){P(x) ∧ [Q(x) ∨ R(y)]} ∨( ∀y){⌝[⌝P(f(y)) ∨ Q(g(y))] ∨ (∀x)R(x)}• (∃x)(∀y){ ⌝P(x) ∨ [⌝Q(x) ∧⌝R(y)]} ∨(∀w){⌝[⌝P(f(w)) ∨ Q(g(w))] ∨ (∀v)R(v)}• {⌝P(A) ∨[⌝Q(A) ∧⌝R(y)]} ∨{[P(f(w)) ∧⌝Q(g(w))] ∨ R(v)}•⌝P(A) ∨ {[⌝Q(A) ∨ P(f(w))] ∧ [⌝Q(A) ∨⌝Q(g(w))] ∧[⌝R(y) ∨ P(f(w))] ∧ [⌝R(y) ∨⌝Q(g(w))]} ∨ R(v) • {⌝P(A) ∨⌝Q(A) ∨ P(f(w1)) ∨ R(v1),⌝P(A) ∨⌝Q(A) ∨ Q(g(w2)) ∨ R(v2),⌝P(A) ∨⌝R(y3) ∨ P(f(w3)) ∨ R(v3),⌝P(A) ∨⌝R(y4) ∨ Q(g(w4)) ∨ R v4)}2假设已知下列事实:1)小李(Li)喜欢容易的(Easy)课程(Course)。

可编辑修改精选全文完整版人工智能导论第四版第二章王万良课后答案1、(杭州市)弟弟对地球充满了好奇,关于地球和地球的运动,说法不正确的是([单选题] *A.托勒密坚持“地心说”,他认为地球处于宇宙中心B.“日心说”最早的提出者是哥白尼,他认为地球在运动,并且24小时自转一周(正确答案)C.贝塞尔用量日仪的观测结果,证明了地球在围绕着太阳公转2、以下()的船首形状可以让船在水中行驶得更快。
[单选题] *A.尖型(正确答案)B.方形C.圆形3、谚语说“一猪生九崽,连母十个样”,主要指的是( )现象。
[单选题] *A.遗传B.变异(正确答案)C.遗传和变异4、.“人间四月芳菲尽,山寺桃花始盛开。
”高山上的桃花迟开的主要原因是缺水。
[判断题] *对错(正确答案)5、为了让辣椒、西瓜等提早上市,农民在冬季就用温水浸泡种子和用塑料薄膜大棚催芽,主要改变的是()。
[单选题] *A.水分B.温度(正确答案)C.光照6、世界是由物质构成的,物质在不断地发生变化。
( ) [单选题]对(正确答案)错7、船的载重量与以下哪种因素无关()。
[单选题] *A.船的材料B货物放置的位置C.货物的重量(正确答案)8、在下列废品中如果没有分类回收,对环境会造成危害最大的是( )。
[单选题] *A.废纸B.废玻璃C.纽扣电池(正确答案)9、运动员身体肌肉强壮,他们的子女肌肉不一定强壮。
[判断题] *对(正确答案)错10、冥王星属于( )。
[单选题] *A.行星B.小行星C.矮行星(正确答案)11、在组成花岗岩的矿物中,硬度最硬的是( )。
[单选题] *A.云母B.石英(正确答案)C.金刚石12、下列说法正确的是( ) 。
[单选题] *A.种子只有在土壤里才能发芽B.种子发芽一定要有阳光C.种子发芽必须要有水(正确答案)13、下列说法正确的是()。
[单选题] *A.绿豆种子发芽需要高温B.只要有合适的温度,绿豆种子就可以发芽C.绿豆种子发芽必须要合适的温度、水分和充足的空气(正确答案)14、圭表主要是利用()的周期性变化规律来计时的。


2021年中国矿业大学数据科学与大数据技术专业《计算机组成原理》科目期末试卷B(有答案)一、选择题1、下述说法中正确的是()。
I.半导体RAM信息可读可写,且断电后仍能保持记忆Ⅱ.动态RAM是易失性RAM,而静态RAM中的存储信息是不易失的Ⅲ.半导体RAM是易失性RAM,但只要电源不断电,所存信息是不丢失的IV.半导体RAM是非易失性的RAMA.I、ⅢB.只有ⅢC.Ⅱ、IVD.全错2、某机器的主存储器共32KB,由16片16K×l位(内部采用128×128存储阵列)的DRAM芯片字和位同时扩展构成。
若采用集中式刷新方式,且刷新周期为2ms,那么所有存储单元刷新一遍需要()个存储周期。
A.128B.256C.1024D.163843、下列关于进制的说法中正确的是()。
I.任何二进制整数都可用十进制表示Ⅱ.任何二进制小数都可用十进制表示Ⅲ.任何十进制整数都可用二进制表示IⅣ.任何十进制小数都可用二进制表示A.I、ⅢB. I、Ⅱ、ⅢC.I、Ⅱ、Ⅲ、ⅣD.Ⅱ、IV4、在补码加减交替除法中,参加操作的数和商符分别是()。
A.绝对值的补码在形成商值的过程中自动形成B.补码在形成商值的过程中自动形成C.补码由两数符号位“异或”形成D.绝对值的补码由两数符号位“异或”形成5、一个浮点数N可以用下式表示:N=mr me,其中,e=rc g;m:尾数的值,包括尾数采用的码制和数制:e:阶码的值,一般采用移码或补码,整数;Tm:尾数的基;re:阶码的基;p:尾数长度,这里的p不是指尾数的:进制位数,当ra=16时,每4个二进制位表示一位尾数;q:阶码长度,由于阶码的基通常为2,因此,在一般情况下,q就是阶码部分的二进制位数。
研究浮点数表示方式的主要目的是用尽量短的字长(主要是阶码字长q和尾数字长的和)实现尽可能大的表述范围和尽可能高的表数精度。
根据这一目的,上述6个参数中只有3个参数是浮点数表示方式要研究的对象,它们是()。
单选题:1.()提出人工智能发展过程需要面对“可知”“可控”“可用”“可靠”四个问题。
(2.0分)A.斯蒂芬.霍金B.斯蒂芬.霍金C.潘云鹤D.马化腾我的答案:D√答对2.成年男性的正常脉搏为每分钟()次。
(2.0分)A.60~80B.70~90C.80~100D.90~120我的答案:A√答对3.实现智能制造的重要条件是()。
(2.0分)A.互联网的革新B.创新商业模式C.生产工具的革命性演进D.大数据的应用我的答案:C√答对4.DeepMind公司开发的()程序专门用于平面设计,可以通过选取素材制作精美的海报。
(2.0分)A.AlphaGoB.AlphaZeroC.AlphaGdD.Alpha-Beta我的答案:C√答对5.2018年10月31日,中共中央政治局就人工智能发展现状和趋势举行()集体学习。
(2.0分)A.第一次B.第五次C.第九次D.第十次我的答案:C√答对6.()是没有人驾驶、靠遥控或自动控制在水下航行的器具。
(2.0分)A.无人机B.战场机器人C.无人潜航器D.无人作战飞船我的答案:C√答对7.对于同一个人来说,下列测量位置中,测出体温最低的是()。
(2.0分)A.口腔B.腋下C.肛门D.测量结果都一样我的答案:B√答对8.目前,人工智能发展存在的问题不包括()。
(2.0分)A.泡沫化B.重复化C.与应用结合不够紧密D.缺乏热情我的答案:D√答对9.对于中国人来说,膳食应当以()为主。
(2.0分)A.肉类B.谷类C.蔬菜D.豆类我的答案:B√答对10.适量献血是安全、无害的。
对于健康的成年人来说,这个标准是每次献血()。
(2.0分)A.100~200毫升B.200~300毫升C.200~400毫升D.400~500毫升我的答案:C√答对11.西蒙和纽厄尔给“物理符号系统”下了定义,提出了“物理符号系统假说”,成为人工智能中影响最大的()的创始人和代表人物。
(2.0分)A.符号主义学派B.联结主义学派C.行为主义学派D.逻辑主义学派我的答案:A√答对12.“四害”中,会传播疟疾的是()。

第一章已达成成绩:分1【单项选择题】2016 年 3 月,人工智能程序 ()在韩国首尔以4:1 的比分战胜的人类围棋冠军李世石。
A、AlphaGoB、DeepMindC、DeepblueD、AlphaGo Zero我的答案: A 得分:分2【单项选择题】首个在新闻报导的翻译质量和正确率上能够比肩人工翻译的翻译系统是()。
A、苹果B、谷歌C、微软D、科大讯飞我的答案: C 得分:分3【多项选择题】属于家中的人工智能产品的有()。
A、智能音箱B、扫地机器人C、声控灯D、个人语音助手我的答案: ABD 得分:分4【多项选择题】目前外科手术领域的医用机器人的长处有()。
A、定位偏差小B、手术创口小C、不需要人类医生进行操作D、能够及时监控患者的状况E、能够帮助医生诊疗病情我的答案: AB 得分:分5【判断题】在神经网络方法以前,机器翻译主假如鉴于统计模型的翻译。
()我的答案:√得分:分6【判断题】人工智能拥有学会下棋的学习能力,是实现通用人工智能算法的基础。
()我的答案:√得分:分7【判断题】目前还没有成功进行无人自动驾驶的事例。
()我的答案:×得分:分8【判断题】智能家居应当能自动感知四周的环境,不需要人的控制。
()我的答案:√得分:分9【判断题】智能音箱实质上是音箱、智能语音交互系统、互联网、内容叠加的产物。
()我的答案:√得分:分10【判断题】鉴于句法的机器翻译是目前较为流行的翻译方法,基本达到了预期的理想。
()我的答案:×第二章已达成成绩:分1【单项选择题】被誉为计算机科学与人工智能之父的是()。
A、图灵B、费根鲍姆C、纽维尔D、西蒙我的答案: A 得分:分2【单项选择题】第一个成功应用的专家系统是()。
A、ELIZAB、DendralC、XconD、Deepblue我的答案: B 得分:分3【单项选择题】依据科学流行定义,人工智能就是和人类()相像的计算机程序。
A、思虑方式B、表达方式C、行为方式D、外观相貌我的答案: C 得分:分4【多项选择题】人工智能的基础包含()。


1把以下合适公式化简为合取范式的子句集:(1)⌝ (∀x)(∃y)(∃z){P(x) ⇒ (∀x)[Q(x, y) ⇒ R(z)]}(2)( ∀x)( ∃y){{P(x) ∧ [Q(x) ∨ R(y)]} ⇒ (∀y)[P(f(y)) ⇒ Q(g(x))]}(3) (∀x)( ∃y){P(x) ∧ [Q(x)∨ R(y)]}⇒ (∀y){[P(f(y))⇒ Q(g(y))]⇒ (∀x)R(x)} (1) •⌝(∀x)( ∃y)( ∃z){P(x) ⇒ (∀x)[Q(x,y) ⇒ R(z)]}•⌝(∀x)( ∃y)( ∃z){ ⌝P(x) ∨ ( ∀x)[⌝Q(x,y) ∨ R(z)]}• (∃x)( ∀y)( ∀z){ P(x) ∧ (∃ x)[Q(x,y) ∧⌝R(z)]}• P(A) ∧ [Q(f(y,z), y) ∧⌝R(z)]• {P(A), Q(f(y,z),y), ∧⌝R(w)}(2)• (∀x)(∃y){{P(x) ∧ [Q(x) ∨ R(y)]} ⇒ (∀y)[P(f(y)) ⇒ Q(g(x))]} • (∀x)(∃y){⌝{P(x) ∧ [Q(x) ∨ R(y)]} ∨(∀y)[⌝P(f(y)) ∨ Q(g(x))]}• (∀x)(∃y){⌝P(x) ∨ [⌝Q(x) ∧⌝R(y)] ∨(∀w)[⌝P(f(w)) ∨ Q(g(x))]}• (∀x){⌝P(x) ∨ [⌝Q(x) ∧⌝R(h(x))] ∨(∀w)[⌝P(f(w)) ∨ Q(g(x))]}• [⌝P(x) ∨⌝Q(x) ∨⌝P(f(w)) ∨ Q(g(x))] ∧[⌝P(x) ∨⌝R(h(x)) ∨⌝P(f(w)) ∨ Q(g(x))]• {⌝P(x1) ∨⌝Q(x1) ∨⌝P(f(w1) ∨ Q(g(x1)),⌝P(x2) ∨⌝R(h(w2)) ∨⌝P(f(w2)) ∨ Q(g(x2))} (3) • (∀x)(∃y){P(x) ∧ [Q(x) ∨ R(y)]} ⇒(∀y){[P(f(y)) ⇒ Q(g(y))]⇒(∀x)R(x)}•⌝(∀x)(∃y){P(x) ∧ [Q(x) ∨ R(y)]} ∨( ∀y){⌝[⌝P(f(y)) ∨ Q(g(y))] ∨ (∀x)R(x)} • (∃x)(∀y){ ⌝P(x) ∨ [⌝Q(x) ∧⌝R(y)]} ∨(∀w){⌝[⌝P(f(w)) ∨ Q(g(w))] ∨ (∀v)R(v)} • {⌝P(A) ∨[⌝Q(A) ∧⌝R(y)]} ∨{[P(f(w)) ∧⌝Q(g(w))] ∨ R(v)}•⌝P(A) ∨ {[⌝Q(A) ∨ P(f(w))] ∧ [⌝Q(A) ∨⌝Q(g(w))] ∧[⌝R(y) ∨ P(f(w))] ∧ [⌝R(y) ∨⌝Q(g(w))]} ∨ R(v) • {⌝P(A) ∨⌝Q(A) ∨ P(f(w1)) ∨ R(v1),⌝P(A) ∨⌝Q(A) ∨ Q(g(w2)) ∨ R(v2),⌝P(A) ∨⌝R(y3) ∨ P(f(w3)) ∨ R(v3),⌝P(A) ∨⌝R(y4) ∨ Q(g(w4)) ∨ R v4)}2假设已知下列事实:1)小李(Li)喜欢容易的(Easy)课程(Course)。
2)小李不喜欢难的(Difficult)课程。
3)工程类(Eng)课程都是难的。
4)物理类(Phy)课程都是容易的。
5)小吴(Wu)喜欢所有小李不喜欢的课程。
6)Phy200是物理类课程。
7)Eng300是工程类课程。
请用归结反演法回答下列问题:1)小李喜欢什么课程?2)证明小吴喜欢Eng300课程将已知事实形式化表示为合适公式:(1)(∀x)[Course(x) ∧ Easy(x) ⇒ Like(Li,x)];(2) (∀x)[Course(x) ∧⌝Easy(x) ⇒⌝Like(Li,x)];(3) (∀x)[Course(x) ∧ Eng(x) ⇒⌝Easy(x)];(4) (∀x)[Course(x) ∧ Phg(x) ⇒ Easy(x)];(5) (∀x)[Course(x) ∧⌝Like(x) ⇒ Like(Wu,x)];(6) Course(Phy200) ∧ Phy(Phy200);(7) Course(Eng300) ∧ Eng(Eng300);·问题表示为以下合适公式(目标公式):(1)( ∃x)[Coure(x) ∧ Like(Li,x)];(2)Like(Wu),Eng300);·将所有事实和对应于问题的目标公式取反加以化简,并标准化为合取范式子句集:(1) ⌝Course(x1) ∨⌝Easy(x1) ∨ Like(Li,x1);(2) ⌝Course(x2) ∨ Easy(x2) ∨⌝Like(Li,x2);(3) ⌝Course(x3) ∨⌝Eny(x) ∨⌝Easy(x3);(4) ⌝Course(x4) ∨⌝Phy(x4) ∨ Easy(x4);(5) ⌝Course(x5) ∨ Like(Li,x5) ∨ Like(Wu,x5);(6) Course(Phy200);(7) Phy(Phy200);(8) Course(Eng300);(9)Eng(Eng300);(10)目标公式(1)的取反: (1) ⌝Course(x6) ∨⌝Like(Li,x6);(11)目标公式(2)的取反: (1) ⌝Like(Wu,Eng300);·解决问题(1)令(10)的取反为:Ask(x6)=Course(x6) ∧ Like(Li,x6)提取的问题回答为: Course(Phy200) Like(Li,Phy200) 即小李喜欢Phy200课程.·解决问题(2)3.对于规则P ⇒ Q ,已知p(Q)=0.04,LS=100,LN=0.4,利用主观Bayes 方法求出P(Q/P)和p(Q/⌝P):O(θ/P)=LS *O(θ)=100*0.04/(1-0.04)=4.2P(θ/P)=O(θ/P))/(1+O(θ/P))=4.2/5.2=0.81O(θ/¬P)=LN *O(θ)=0.4*0.04/(1-0.04)=0.017P(θ/¬P)=O(θ/¬P)/(1+O(θ/¬P))=0.017/1.017=0.0174.在上题中,若P 自身的确定性依赖P ’,且有p(P)=0.05,规则P ’ ⇒ P 的LS=120,LN=0.3,用观Bayes 方法求出P(θ/P')。
(1).求P(P/P')O(P/P')=LS *O(P)=120*0.05/(1-0.05)=6.4P(P/P')=O(P/P')/(1+O(P/P'))=6.4/7.4=0.87(2).求P(θ/P')因为P(P/P')=0.87> p(P),根据P(θ/P')=0.04+(0.81-0.04)*(0.87-0.05)/(1-0.05)=0.04+0.66=0.705. 在MYCIN 中,设有如下规则: ⎪⎪⎪⎩⎪⎪⎪⎨⎧≤'≤-'•--+<'≤'•⌝-+⌝='1)/()())()/(()(1)()/()()()/(0)/()()/()()/()/(P P p P p P p P P p P p Q p P Q p Q p P p P P p P P p P p P Q p Q p P Q p P Q pR1: IF E1 THEN H (0.8)R2: IF E2 THEN H (0.6)R3: IF E3 THEN H (-0.5)R4: IF E4 AND (E5 OR E6) THEN E1 (0.7)R5: IF E7 AND E8 THEN E3 (0.9)在系统运行中已从用户处得CF(E2)=0.8, CF(E4)=0.5, CF(E5)=0.6, CF(E6)=0.7, CF(E7)=0.6, CF(E8)=0.9, 求H 的综合可信度CF(H)。
解 (1)求证据E4,E5,E6逻辑组合的可信度)}}(),(max{),(min{))((654654E CF E CF E CF E OR E AND E CF =5.0}}7.0,6.0max{,5.0min{==(2)根据规则R4,求CF(E1)))}((,0max{7.0)(6541E OR E AND E CF E CF ⨯=)}}(),(min{,0max{7.0654E OR E CF E CF ⨯=)}}}(),(max{),(min{,0max{7.0654E CF E CF E CF ⨯=}}}7.0,6.0max{,5.0min{,0max{7.0⨯=}5.0,0max{7.0⨯=35.05.07.0=⨯=(3)求证据E7,E8逻辑组合的可信度6.0}9.0,6.0min{)}(),(min{)(8787===E CF E CF E AND E CF(4)根据规则R5, 求CF(E3)54.06.09.0)}(,0max{9.0)(873=⨯=⨯=E AND E CF E CF(5)根据规则R1, 求CF1(H)28.035.08.0)}(,0max{8.0)(11=⨯=⨯=E CF H CF(6)根据规则R2, 求CF2(H)48.08.06.0)}(,0max{6.0)(22=⨯=⨯=E CF H CF(7)根据规则R3, 求CF3(H)27.054.05.0)}(,0max{5.0)(33-=⨯-=⨯-=E CF H CF(8)组合由独立证据导出的假设H 的可信度CF1(H),CF2(H)和CF3(H),得到H 的综合可信度:)()()()()(21212,1H CF H CF H CF H CF H CF ⋅-+=63.048.028.048.028.0=⨯-+=49.0}27.0,63.0min{127.063.0|})(||,)(min{|1)()()(32,13123,2,1=--=-+=H CF H CF H CF H CF H CF 6.设学生考试成绩的论域为{A ,B ,C ,D ,E},小王成绩得A 、得B 、得A 或B 的基本概率分别分配到0.2、0.1、0.3,Bel({C, D, E})为0.2;请给出Bel({A, B})、Pl({A, B})和f({A, B})。
答:Bel({A, B}) = m({A}) + m({B}) + m({A, B}) = 0.2 + 0.1 + 0.3 = 0.6 Pl({A, B})= 1 - Bel({C, D, E}) = 1 - 0.2 = 0.8f({A, B}) = Bel({A, B}) + |{A, B}| / |U| · [Pl({A, B}) -Bel({A, B})] = 0.6 + 2/5 ·(0.8 - 0.6) =0.6 + 0.08 = 0.68。